全国初中数学竞赛试题及参考答案 .doc
全国初中数学竞赛试题及答案

全国初中数学竞赛试题及答案
全国初中数学竞赛试题及答案
1. 角函数的计算和证明问题
在解三角函数问题之前,除了熟知初三教材中的有关知识外,还应该掌握:
(1)三角函数的单调性当a为锐角时,sina与tga的值随a的值增大而增大;cosa与ctga随a的值增大而减小;当a为钝角时,利用诱导公式转化为锐角三角函数讨论.
注意到sin45=cos45= ,由(1)可知,当时0sina;当45
(2)三角函数的有界性|sina|1,|cosa|1,tga、ctga可取任意实数值(这一点可直接利用三角函数定义导出).
例1(1986年全国初中数学竞赛备用题)在△ABC中,如果等式sinA+cosA= 成立,那么角A是( )
(A)锐角 (B)钝角 (C)直角
分析对A分类,结合sinA和cosA的单调性用枚举法讨论.
解当A=90时,sinA和cosA=1;
当45 ,cosA0,
sinA+cosA 当A=45时,sinA+cosA= 当00,cosA sinA+cosA ∵ 1, 都大于 .
淘汰(A)、(C),选(B).
例2(1982年上海初中数学竞赛题)ctg6730的值是( )
(A) -1 (B)2- (C) -1
(D) (E) 分析构造一个有一锐角恰为6730的Rt△,再用余切定义求之.
解如图36-1,作等腰Rt△ABC,设B=90,AB=BC=1.延长BA到D使AD=AC,连DC,则AD=AC= ,D=22.5,DCB=67.5.这时,
ctg6730=ctgDCB= 选(A).。
全国初中数学竞赛试题

全国初中数学竞赛试题【试题一】:代数基础1. 已知 \( a, b, c \) 是一个三角形的三边长,且满足 \( a^2 + b^2 = c^2 \),求证 \( a + b \geq c \)。
【试题二】:几何问题2. 给定一个圆,圆心为 \( O \),半径为 \( r \)。
在圆上任取两点\( A \) 和 \( B \),连接 \( OA \) 和 \( OB \)。
求证 \( \angle AOB \) 的度数小于 \( 180^\circ \)。
【试题三】:数列与级数3. 一个等差数列的首项是 \( a_1 = 3 \),公差 \( d = 2 \)。
求这个数列的第 \( n \) 项 \( a_n \) 的表达式,并计算前 \( n \) 项的和 \( S_n \)。
【试题四】:函数与方程4. 已知函数 \( f(x) = x^2 - 4x + 4 \),求该函数的最小值。
【试题五】:概率统计5. 一个袋子里有 \( 5 \) 个红球和 \( 3 \) 个蓝球。
随机抽取两个球,求两个球颜色相同的概率。
【试题六】:组合数学6. 有 \( 8 \) 个不同的球,需要将它们放入 \( 3 \) 个不同的盒子中,每个盒子至少有一个球。
求不同的放法有多少种。
【试题七】:逻辑推理7. 在一个逻辑推理题中,有三个人分别说了以下的话:- 甲说:“乙是说谎者。
”- 乙说:“丙是说谎者。
”- 丙说:“甲和乙都是说谎者。
”如果三个人中只有一个人说谎,那么谁说的是真话?【试题八】:创新问题8. 一个正方体的体积是 \( 8 \) 立方厘米,求这个正方体的表面积。
【试题九】:应用题9. 一个水池可以以恒定的速率 \( r \) 进水,同时也以另一个恒定的速率 \( s \) 出水。
如果水池开始时是空的,求水池被填满的时间\( t \)。
【试题十】:综合题10. 一个圆的半径是 \( 5 \) 厘米,圆内接一个等边三角形。
全国初中数学竞赛试题及解答

ABCD全国初中数学竞赛试卷及解析一、选择题(本题共6小题,每小题5分,满分30分.每小题均给出了代号为A ,B ,C ,D 的四个结论,其中只有一个是正确的。
请将正确答案的代号填在题后的括号里)1、设a ,b ,c 的平均数为M ,a ,b 的平均数为N ,N ,c 的平均数为P ,若c b a ,则M 与P 的大小关系是( )A 、P MB 、P MC 、P MD 、不确定 答案:B 解析:∵3c b a M ,2b a N ,222c b a c N P ,122cb a P M ∵c b a ∴0122122c c c c b a P M ,即0 P M ,即P M 2、某人骑车沿直线旅行,先前进了a 千米,休息了一段时间,又原路返回b 千米(a b ),再前进c 千米,则此人离起点的距离S 与时间t 的关系示意图是( )答案:C解析:因为图(A )中没有反映休息所消耗的时间;图(B )虽表明折返后S 的变化,但没有表示消耗的时间;图(D )中没有反映沿原始返回的一段路程,唯图(C )正确地表述了题意。
3、甲是乙现在的年龄时,乙10岁;乙是甲现在的年龄时,甲25岁,那么( ) A 、甲比乙大5岁 B 、甲比乙大10岁 C 、乙比甲大10岁 D 、乙比甲大5岁 答案:A解析:由题意知3×(甲-乙)151025 ∴甲-乙=5。
4、一个一次函数图象与直线49545x y 平行,与x 轴、y 轴的交点分别为A 、B ,并且过点(-1,-25),则在线段AB 上(包括端点A 、B ),横、纵坐标都是整数的点有( )A 、4个B 、5个C 、6个D 、7个 答案:B解析:在直线AB 上,横、纵坐标都是整数的点的坐标是N x 41 ,N y 525 ,(N 是整数).在线段AB 上这样的点应满足041 N ,且0525 N ,∴541N ,即1 N ,2,3,4,55、设a ,b ,c 分别是ABC 的三边的长,且cb a ba b a,则它的内角A 、B 的关系是( )A 、AB 2 B 、A B 2C 、A B 2D 、不确定 答案:B解析:由c b a b a b a得c a bb a ,延长CB 至D ,使AB BD ,于是c a CD 在ABC 与DAC 中,C C ,且DC ACAC BC∴ABC ∽DAC ,D BAC ∵D BAD∴BAC D BAD D ABC 226、已知ABC 的三边长分别为a ,b ,c ,面积为S ,111C B A 的三边长分别为1a ,1b ,1c ,面积为1S ,且1a a ,1b b ,1c c ,则S 与1S 的大小关系一定是( )A 、1S SB 、1S SC 、1S SD 、不确定 答案:D解析:分别构造ABC 与111C B A 如下:①作ABC ∽111C B A ,显然1211a a S S ,即1S S ;②设101b a ,20c ,则1 c h ,10 S ,10111 c b a ,则10100431S ,即1S S ;③设101 b a ,20 c ,则1 c h ,10 S ,2911 b a ,101 c ,则2 c h ,101 S ,即1S S ;因此,S 与1S 的大小关系不确定。
全国初三初中数学竞赛测试带答案解析

全国初三初中数学竞赛测试班级:___________ 姓名:___________ 分数:___________一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)842.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.1003.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.4.若不等式ax2+7x-1>2x+5对-1≤a≤1恒成立,则x的取值范围是( ).A.2≤x≤3B.2<x<3C.-1≤x≤1D.-1<x<15.在Rt△ABC中,∠B=60°,∠C=90°,AB=1,分别以AB、BC、CA为边长向△ABC外作等边△ABR、等边△BCP、等边△CAQ,联结QR交AB于点T.则△PRT的面积等于( ).(A) (B) (C) (D)6.在3×5的棋盘上,一枚棋子每次可以沿水平或者垂直方向移动一小格,但不可以沿任何斜对角线移动.从某些待定的格子开始,要求棋子经过全部的小正方格恰好一次,但不必回到原来出发的小方格上.在这15个小方格中,有( )个可以是这枚棋子出发的小方格.A.6B.8C.9D.10二、填空题1.正方形ABCD的边长为5,E为边BC上一点,使得BE=3,P是对角线BD上的一点,使得PE+PC的值最小.则PB= .2.设a、b、c为整数,且对一切实数x,(x-a)(x-8)+1="(x-b)(x-c)" 恒成立.则a+b+c的值为 .3.如图,在以O为圆心的两个同心圆图2中,MN为大圆的直径,交小圆于点P、Q,大圆的弦MC交小圆于点A、B.若OM=2,OP= 1,MA=AB=BC,则△MBQ的面积为 .4.从1, 2,…, 2 006中,至少要取出个奇数,才能保证其中必定存在两个数,它们的和为2 008.三、解答题1.(20分)实数x、y、z、w满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w的最大值和最小值.2.(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.3.(25分)在中,有多少个不同的整数(其中,[x]表示不大于x的最大整数)?全国初三初中数学竞赛测试答案及解析一、选择题1.如图,已知在Rt△ABC中,AB=35,一个边长为12的正方形CDEF内接于△ABC.则△ABC的周长为( ).(A)35 (B)40 (C)81 (D)84【答案】D【解析】分析:首先设BC=a,AC=b,由勾股定理与正方形的性质,可得:a2+b2=352,Rt△AFE∽Rt△ACB,再由相似三角形的对应边成比例,可得12(a+b)=ab,解方程组即可求得.解答:解:如图,设BC=a,AC=b,则a2+b2=352=1225.①又Rt△AFE∽Rt△ACB,所以=,即=,故12(a+b)=ab.②由①②得(a+b)2=a2+b2+2ab=1225+24(a+b),解得a+b=49(另一个解-25舍去),所以a+b+c=49+35=84.故答案为D.2.设n=9+99+…+99…9(99个9).则n的十进制表示中,数码1有( )个.A.50B.90C.99D.100【答案】C【解析】由于9=10-1,99=100-1,…,所以n="9+99+999+…+" =10+102+103+…1099-99×1.然后据此等式求出n的值后,即能得出n的十进制表示中,数码1有多少个.解:n=9+99+999+…+=10+102+103+…1099-99×1,=1111111…10(99个1)-99,=11111…1011(99个1).所以在十进制表示中,数码1有99个.故答案为:99.根据式中数据的特点将式中的数据变为10的n次方相加的形式是完成本题的关键.3.已知f(x)=x2+6ax-a,y=f(x)的图像与x轴有两个不同的交点(x1,0),(x2,0),且=8a-3.则a的值是( ).A.1B.2C.0或D.【答案】D【解析】本题考查二次函数与一元二次方程关系的综合应用问题。
2024全国初中数学竞赛试题

1、已知直角三角形的两条直角边长度分别为3和4,则斜边上的高为:A. 2.4B. 1.2C. 5D. 不能确定(答案)A2、若a、b、c为三角形的三边长,且满足a² + b² + c² + 50 = 10a + 6b + 8c,则此三角形为:A. 直角三角形B. 等腰三角形C. 等边三角形D. 不能确定(答案)A3、解方程组 { x + 2y = 5, 3x - 4y = -2 } 时,若先消去y,则得到的方程是:A. 5x = 14B. 5x = 10C. 7x = 16D. 7x = 22(答案)B4、在平行四边形ABCD中,若∠A : ∠B = 2 : 3,则∠C的度数为:A. 60°B. 90°C. 120°D. 不能确定(答案)C5、已知 |x| = 5,y = 3,则x - y等于:A. 8或-2B. 2或-8C. -2或8D. -8或2(答案)D6、若关于x的一元二次方程x² - (k - 1)x - k = 0有两个相等的实数根,则k的值为:A. -3B. 3C. -1D. 1(答案)D7、在圆O中,弦AB的长度等于半径OA,则∠AOB的度数为:A. 30°B. 60°C. 120°D. 30°或150°(答案)B8、若a > b > 0,c < d < 0,则一定有:A. a² > b²B. c² > d²C. a/d > b/cD. a/d < b/c(答案)A9、已知一次函数y = kx + b的图像经过点(2, 3)和(-1, -3),则它的图像不经过:A. 第一象限B. 第二象限C. 第三象限D. 第四象限(答案)C10、在△ABC中,若∠A = 60°,∠B = 45°,则∠C的度数为:A. 45°B. 60°C. 75°D. 90°(答案)C。
全国初中数学联赛试题(含参考答案)

全国初中数学联合竞赛试题参考答案第一试一、选择题(本题满分42分,每小题7分) 1、设17-=a ,则=--+12612323a a a ( A )A 、24B 、 25C 、1074+D 、1274+ 2、在ABC ∆中,最大角A ∠是最小角C ∠的两倍,且7=AB ,8=AC ,则=BC ( C ) A 、27 B 、10 C 、105 D 、37 3、用[]x 表示不大于x 的最大整数,则方程[]0322=--x x 的解的个数为( C ) A 、1 B 、2 C 、3 D 、 44、设正方形ABCD 的中心为点O ,在以五个点A 、B 、C 、D 、O 为顶点所构成的所有三角形中任意取出两个,它们的面积相等的概率为 ( B )A 、143 B 、73 C 、21 D 、74 5、如图,在矩形ABCD 中,3=AB ,2=BC ,以BC 为直径在矩形内作半圆,自点A 作半圆的切线AE ,则=∠CBE sin ( D )A 、36 B 、32C 、31D 、10106、设n 是大于1909的正整数,使得nn --20091909为完全平方数的n 的个数是 ( B )A 、3B 、 4C 、 5D 、6 二、填空题(本题满分28分,每小题7分)1、已知t 是实数,若a ,b 是关于x 的一元二次方程0122=-+-t x x 的两个非负实根,则()()1122--b a的最小值是____________.答案:3-2、设D 是ABC ∆的边AB 上的一点,作BC DE //交AC 于点E ,作AC DF //交BC 于点F ,已知ADE ∆、DBF ∆的面积分别为m 和n ,则四边形DECF 的面积为______.答案:mn 23、如果实数a ,b 满足条件122=+b a ,2212|21|a b a b a -=+++-,则____=+b a . 答案:1-4、已知a ,b 是正整数,且满足⎪⎪⎭⎫ ⎝⎛+b a 15152是整数,则这样的有序数对(a ,b )共有_对。
全国初中数学竞赛试题及答案

全国初中数学竞赛试题及答案全国初中数学竞赛试题及答案一、选择题1、在一张纸上,我们画了一个圆和一条直径,直径与圆相交于A、B 两点。
如果我们在这张纸上连续地画了8个点,使得这些点都在圆上,那么这8个点的最密集分布是()。
A. 像一个“十”字形,两边各4个点 B. 像一个“十”字形,两边各3个点 C. 像一个“米”字形,上面各4个点 D. 像一个“米”字形,上面各3个点答案:C 解析:根据圆的对称性,我们可以得知,直径两侧的点到圆心的距离相等,因此在一个“十”字形中,中间的交点是最密集的。
而在“米”字形中,上面的4个点距离交点的距离相等且最短,因此是最密集的。
2、在一个等边三角形ABC中,D、E、F分别是AB、BC、CA的中点。
现在以D为圆心,DE为半径画圆弧,交AB于G。
则△DFE的面积是阴影部分面积的()。
A. 2倍 B. 3倍 C. 4倍 D. 6倍答案:C 解析:由题意可知,DE是△ABC的中位线,因此DE=1/2AB。
而△DFE是直角三角形,斜边DE是直径,因此∠DFE=90°。
所以,△DFE的高是DE的一半,即1/4AB。
因此,△DFE的面积是1/2×1/2AB×1/4AB=1/8AB²。
而阴影部分的面积是△ABC面积的一半,即1/2×1/2AB×√3/2AB=√3/4AB²。
所以,△DFE的面积是阴影部分面积的4倍。
3、在一个等腰直角三角形ABC中,∠C=90°,AC=BC=1。
现在以这个三角形的顶点为圆心,1为半径画圆弧,则这三个圆弧的长度之和为()。
A. 3π/2 B. π C. 2π D. 5π/2 答案:C 解析:根据题意,我们可以得到三个圆弧的半径都是1。
其中第一个圆弧的长度为1/4×2π×1=π/2,第二个圆弧的长度也为π/2,第三个圆弧的长度为1/4×2π×√2=π√2/2。
初中数学竞赛试题(含答案)
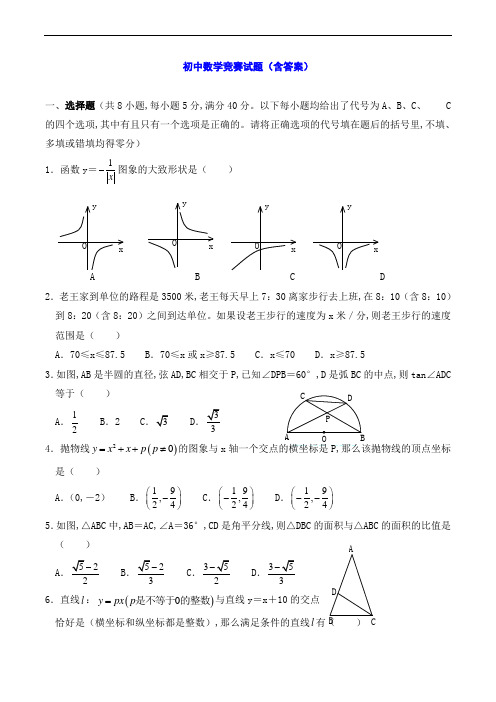
DC B A初中数学竞赛试题(含答案)一、选择题(共8小题,每小题5分,满分40分。
以下每小题均给出了代号为A 、B 、C 、 C 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填在题后的括号里,不填、多填或错填均得零分) 1.函数y =1x-图象的大致形状是( )A B C D2.老王家到单位的路程是3500米,老王每天早上7:30离家步行去上班,在8:10(含8:10)到8:20(含8:20)之间到达单位。
如果设老王步行的速度为x 米/分,则老王步行的速度范围是( )A .70≤x ≤87.5B .70≤x 或x ≥87.5C .x ≤70D .x ≥87.53.如图,AB 是半圆的直径,弦AD,BC 相交于P,已知∠DPB =60°,D 是弧BC 的中点,则tan ∠ADC 等于( ) A .12B.2 CD4.抛物线()20y x x p p =++≠的图象与x 轴一个交点的横坐标是P,那么该抛物线的顶点坐标是( )A .(0,-2)B .19,24⎛⎫- ⎪⎝⎭C .19,24⎛⎫- ⎪⎝⎭D .19,24⎛⎫-- ⎪⎝⎭5.如图,△ABC 中,AB =AC,∠A =36°,CD 是角平分线,则△DBC 的面积与△ABC 的面积的比值是( )ABCD 6.直线l :()0y px p =是不等于的整数与直线y =x +10的交点恰好是(横坐标和纵坐标都是整数),那么满足条件的直线l 有() yxOyxOyxOyxOA .6条B .7条C .8条D .无数条7.把三个连续的正整数a,b,c 按任意次序(次序不同视为不同组)填入20x x ++= 的三个方框中,作为一元二次方程的二次项系数、一次项系数和常数项,使所得方程至少有一个整数根的a,b,c ( )A .不存在B .有一组C .有两组D .多于两组 8.六个面上分别标有1,1,2,3,3,5六个数字的均匀立方体的表面如图所示,掷这个立方体一次,记朝上一面的数为平面直角坐标系中某个点的横坐标,朝下一面的数主该点的纵坐标。
最新全国初中数学竞赛试题及答案

全国初中数学竞赛试题及参考答案一.选择题(5×7'=35')1.对正整数n ,记n !=1×2×...×n,则1!+2!+3!+...+10!的末位数是( ).A .0B .1C .3D .5【分析】5≥n 时,n !的个位数均为0,只考虑前4个数的个位数之和即可,1+2+6+4=13,故式子的个位数是3. 本题选C .2.已知关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧<-+->-+x t x x x 235352恰好有5个整数解,则t 的取值范围是( ). 2116.-<<-t A 2116.-<≤-t B 2116.-≤<-t C 2116.-≤≤-t D 【分析】2023235352<<-⇒⎪⎪⎩⎪⎪⎨⎧<-+->-+x t x t x x x ,则5个整数解是15,16,17,18,19=x .注意到15=x 时,只有4个整数解.所以2116152314-≤<-⇒<-≤t t ,本题选C 3.已知关于x 的方程xx x a x x x x 22222--=-+-恰好有一个实根,则实数a 的值有( )个. A .1 B .2 C .3 D .4【分析】422222222+-=⇒--=-+-x x a xx x a x x x x ,下面先考虑增根: ⅰ)令0=x ,则4=a ,当4=a 时,0,1,022212===-x x x x (舍);ⅱ)令2=x ,则8=a ,当8=a 时,2,1,0422212=-==--x x x x (舍);再考虑等根:ⅲ)对04222=-+-a x x ,270)4(84=→=--=∆a a ,当21,272,1==x a . 故27,8,4=a ,21,1,1-=x 共3个.本题选C .4.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC=4CF ,DCFE 是平行四边形,则图中阴影部分的面积为( ).A .3B .4C .5D .6【分析】设ABC ∆底边BC 上的高为h ,则DE CF CF BC h 121244848====,)(2121212121h h DE h DE h DE S S BDE ADE +⋅⋅=⋅⋅+⋅⋅=+∆∆本题选D .6122121=⋅⋅=⋅⋅=DE DE h DE5.在分别标有号码2,3,4,...,10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是( ).41.A 92.B 185.C 367.D 【分析】9236811291214==+++=C C C P 本题选B .二.填空题(5×7'=35')6.设33=a ,b 是a 2的小数部分,则3)2+b (的值为 . 【分析】考虑到33=a ,则33333332292,29,327982,93=+-==<<===b b a 则9)9()2333==+b (7.一个质地均匀的正方体的六个面上分别标有数1、2、3、4、5、6.掷这个正方体三次,则其朝上的面的数的和为3的倍数的概率是 .【分析】对第一次向上面为1时,后面两次所得数字与1的和是3的倍数有111,114,123,126,132,135,141,144,153,156,162,165共12种;对于首次掷得向上的面是2,3,4,5,6的,后面两次与首次的和为3的倍数是轮换对称的,故和为3的倍数共有612⨯,而总次数是666⨯⨯次,则其概率为31666612=⨯⨯⨯=P .8.已知正整数a 、b 、c 满足a +b 2-2c -2=0,3a 2-8b +c=0,则abc 的最大值为 .【分析】先消去c ,再配方估算.24166)8()121(621662222+=-++⇒=-++b a b b a a 观察易知上式中3≤a ,故3,2,1=a ,经试算,2,1=a 时,b 均不是整数;当3=a 时,11,5=b ,于是有)61,11,3(),13,5,3(),,(=c b a ,故201361113m ax =⨯⨯=abc .9. 实数a 、b 、c 、d 满足:一元二次方程x 2+cx +d=0的两根为a 、b ,一元二次方程x 2+ax +b=0的两根为c 、d ,则所有满足条件的数组(a 、b 、c 、d )为 .【分析】由根与系数关系知b cd d ab d b a d c c b a ===⇒=++=++,,0,然后可得 (a 、b 、c 、d )=(1,-2,1,-2)本题在化简过程中,总感觉还有,此处仅给出一组,好像不严谨,期待官方答案.10.小明某天在文具店做志愿者卖笔,铅笔每支售4元,园珠笔每支售7元,开始时他有铅笔和圆珠笔共350支,当天虽然没有全部卖完,但是他的销售收入恰好是2013元,则他至少卖出了 支圆珠笔.【分析】设4元的卖x 支,7元的卖y 支,则350,201374<+=+y x y x4125031820124201374++-=⇒++-=⇒=+y y x y y x y x 令1441-=⇒=+k y k y ,则k k k x 7505)14(2503-=+--=,又350≤+y x ,即523151350147505≥−−→−≥⇒≤-+-∈k k k k N k ,207152414=-⨯≥-=k y 即他至少卖了207支圆珠笔.三.解答题(4×20'=80')11.如图,抛物线y =ax 2+bx -3,顶点为E ,该抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,且OB=OC=3OA .直线131+-=x y 与y 轴交于点D ,求∠DBC -∠CBE .【分析】易知4)1(3222--=--=x x x y ,)4,1()3,0()0,3(),0,1(---D C B A ,,,作EF ⊥C O 于F ,连CE ,易知△OBC 、△CEF 都是等腰直角三角形,则△CBE 是直角三角形.分别在Rt△OBD 、Rt △BCE 中运用正切定义,即有31232tan 31tan =====BC CE ,OB OD βα,则βα= 从而可得∠DBC -∠CBE=45º.12.如图,已知AB 为圆O 的直径,C 为圆周上一点,D为线段OB 内一点(不是端点),满足CD ⊥AB ,DE ⊥CO ,E 为垂足,若CE =10,且AD 与DB 的长均为正整数,求线段AD 的长.【分析】设圆O 半径为r ,则由相似或三角函数或射影定理可知,)10(1022-=⇒⋅=r DE OE CE DE ,又r r DE CE CD 10)10(10102222=-+=+=由相交弦定理(考虑垂径时)或连AC 、BC 用相似或三角函数,易知r CD BD AD 102==⋅①,而r BD AD 2=+②令y BD x AD ==,,①/②即155210-=⇒==+y x y r r y x xy ,显然有x y <<0,则10<<x y ,即1051150<<⇒<-<y y ,y 为正整数,故9,8,7,6=y ,又x 也为正整数,经逐一试算,仅当30,6==x y 这一组是正整数,故30=AD .13.设a 、b 、c 是素数,记c b a z b a c y a c b x -+=-+=-+=,,,当2,2=-=y x y z 时,a 、b 、c 能否构成三角形的三边长?证明你的结论. 【分析】281102222a z a z z y z a z y c b a z b a c y +±-=⇒=-+−−−→−==+⇒⎩⎨⎧-+=-+=a 、b 、c 是素数,则z c b a =-+为整数,则1281+=+k a ,k 为正整数.化简整理后,有a k k 2)1(=+⎩⎨⎧=+==+==⇒=+==+=⇒3121,2(121121,1a k k )a a k k 非质数 2,332811-=−−→−=+±-=z a a z ⅰ)112,2529,9,3=⇒=-=⇒=-==b b z x x x y z ,c b a b =<=+=+=1720173,17不能围成三角形;ⅱ)是合数9,16,4,2====b x y z综上所述,以a 、b 、c 不能围成三角形.14.如果将正整数M 放在正整数m 左侧,所得到的新数可被7整除,那么称M 为m 的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数) .求正整数n 的最小值,使得存在互不相同的正整数a 1,a 2,...,a n ,满足对任意一个正整数m ,在a 1,a 2,...,a n 中都至少有一个为m 的“魔术数”.【分析】考虑到魔术数均为7的倍数,又a 1,a 2,...,a n 互不相等,不妨设n a a a <<<...21,余数必为1、2、3、4、5、6,0,设t k a i i +=7,(6,5,4,3,2,1,0;,...,3,2,1==t n i ),至少有一个为m 的“魔术数”.因为m a k i +⋅10(k 是m 的位数),是7的倍数,当6≤i 时,而k i a 10⋅除以7的余数都是0,1,2,3,4,5,6中的6个;当7=i 时,而ki a 10⋅除以7的余数都是0,1,2,3,4,5,6这7个数字循环出现,当7=i 时,依抽屉原理,k i a 10⋅与m 二者余数的和至少有一个是7,此时m a k i +⋅10被7整除,即n =7.。
数学竞赛初中试题及答案

数学竞赛初中试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 2答案:B2. 计算下列表达式的值:(3x^2 - 2x + 1) + (x^2 + 4x - 3) = ?A. 4x^2 + 2x - 2B. 4x^2 + 2x + 2C. 5x^2 + 2x - 2D. 5x^2 + 2x + 2答案:D3. 一个圆的半径是5厘米,那么它的周长是多少?A. 10π厘米B. 20π厘米C. 25π厘米D. 30π厘米答案:C4. 如果一个数的平方是36,那么这个数是?A. 6B. ±6C. 36D. ±36答案:B5. 以下哪个分数是最简分数?A. 6/8B. 9/12C. 5/10D. 7/14答案:B6. 一个等差数列的第一项是2,公差是3,那么第5项是多少?A. 17B. 14C. 11D. 8答案:A7. 下列哪个图形的面积是最大的?A. 边长为4的正方形B. 半径为2的圆C. 长为5,宽为3的矩形D. 底为6,高为2的三角形答案:B8. 一个正方体的体积是27立方厘米,那么它的表面积是多少?A. 54平方厘米B. 63平方厘米C. 81平方厘米D. 108平方厘米答案:A9. 一个数的立方根是2,那么这个数是?A. 6B. 8C. 2D. 4答案:D10. 下列哪个方程的解是x=2?A. x^2 - 4x + 4 = 0B. x^2 - 3x + 2 = 0C. x^2 - 5x + 6 = 0D. x^2 - 6x + 9 = 0答案:A二、填空题(每题4分,共20分)11. 一个数的相反数是-5,那么这个数是________。
答案:512. 一个等腰三角形的底边长是6厘米,两腰长分别是8厘米,那么这个三角形的周长是________厘米。
答案:2213. 如果一个数除以3余1,除以5余2,那么这个数最小是________。
初中数学全国竞赛试题及答案

初中数学全国竞赛试题及答案一、选择题(每题2分,共10分)1. 下列哪个数是最小的正整数?A. 0B. 1C. -1D. 22. 如果一个数的平方等于16,那么这个数是:A. 4B. ±4C. 16D. ±163. 一个直角三角形的两条直角边分别为3和4,那么斜边的长度是:A. 5B. 6C. 7D. 84. 将一个圆分成四个相等的扇形,每个扇形的圆心角是多少度?A. 45°B. 60°C. 90°D. 120°5. 一个数的立方等于-8,这个数是:A. -2B. 2C. -8D. 8二、填空题(每题2分,共10分)6. 一个数的平方根等于它本身,这个数是______。
7. 如果一个数的绝对值等于5,那么这个数可以是______。
8. 一个数的倒数是1/4,那么这个数是______。
9. 一个数的平方是25,这个数可以是______。
10. 一个数的立方根是2,那么这个数是______。
三、解答题(每题10分,共30分)11. 已知一个长方体的长、宽、高分别是a、b、c,求长方体的体积。
12. 一个圆的半径是r,求圆的面积。
13. 已知一个等腰三角形的两个腰长为a,底边长为b,求三角形的面积。
四、证明题(每题15分,共30分)14. 证明:直角三角形的斜边的平方等于两直角边的平方和。
15. 证明:如果一个角的余弦值等于1/2,那么这个角是60°。
五、应用题(每题20分,共20分)16. 某工厂生产一种零件,每个零件的成本是5元,售价是10元。
如果工厂想要获得10000元的利润,需要生产和销售多少个这种零件?初中数学全国竞赛试题答案一、选择题1. B2. B3. A4. C5. A二、填空题6. 0或17. ±58. 49. ±510. 8三、解答题11. 长方体的体积 = 长× 宽× 高= a × b × c。
初二数学竞赛试题及参考答案

初二数学竞赛试题及参考答案一、选择题(每题3分,共15分)1. 下列哪个数是无理数?A. 3.14159B. πC. 0.33333D. √22. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是多少?A. 5B. 6C. 7D. 83. 一个数的平方根是它本身,这个数是:A. 0B. 1C. -1D. 44. 以下哪个表达式等于0?A. 2 + 3B. 2 - 2C. 2 × 3D. 2 ÷ 25. 如果一个圆的半径为5,那么它的面积是多少?A. 25πB. 50πC. 100πD. 125π二、填空题(每题2分,共10分)6. 一个数的立方根是它本身,这个数可以是______。
7. 一个数的绝对值是它本身,这个数可以是______。
8. 一个数的相反数是它本身,这个数是______。
9. 一个数的倒数是它本身,这个数是______。
10. 如果一个数的平方是16,那么这个数可以是______。
三、简答题(每题5分,共20分)11. 解释什么是勾股定理,并给出一个例子。
12. 解释什么是有理数和无理数,并给出一个例子。
13. 解释什么是因式分解,并给出一个例子。
14. 解释什么是二次方程,并给出一个例子。
四、解答题(每题10分,共30分)15. 一个长方体的长、宽、高分别是10厘米、8厘米和6厘米,求它的体积。
16. 一个等腰三角形的底边长为8厘米,两腰边长为5厘米,求它的面积。
17. 一个二次方程 \( ax^2 + bx + c = 0 \) 的系数 a、b、c 分别为 2、-7 和 3,求它的根。
五、附加题(每题5分,共5分)18. 一个数列的前三项是 1, 1, 2,从第四项开始,每一项都是前三项的和。
求这个数列的前10项。
参考答案一、选择题1. D2. A3. A4. B5. B二、填空题6. 0, 1, -1, 17. 非负数8. 09. ±110. ±4三、简答题11. 勾股定理是指在一个直角三角形中,直角边的平方和等于斜边的平方。
全国初中数学竞赛试题及答案

全国初中数学竞赛试题及答案This manuscript was revised on November 28, 2020中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题(共5小题,每小题6分,共30分.)1(甲).如果实数a ,b ,c 在数轴上的位置如图所示,那么代数式22||()||a a b c a b c -++-++可以化简为( ).(A )2c a - (B )22a b - (C )a - (D )a 1(乙).如果22a =-+11123a+++的值为( ).(A )2- (B 2(C )2 (D )22(甲).如果正比例函数y = ax (a ≠ 0)与反比例函数y =x b(b ≠0 )的图象有两个交点,其中一个交点的坐标为(-3,-2),那么另一个交点的坐标为( ).(A )(2,3) (B )(3,-2) (C )(-2,3) (D )(3,2)2(乙). 在平面直角坐标系xOy 中,满足不等式x 2+y 2≤2x +2y 的整数点坐标(x ,y )的个数为( ).(A )10 (B )9 (C )7 (D )53(甲).如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数与中位数之差的绝对值是( ). (A )1 (B )214a - (C )12(D )143(乙).如图,四边形ABCD 中,AC ,BD 是对角线,△ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5,则CD 的长为( ). (A )23 (B )4 (C )52 (D )OAB CED4(甲).小倩和小玲每人都有若干面值为整数元的人民币.小倩对小玲说:“你若给我2元,我的钱数将是你的n 倍”;小玲对小倩说:“你若给我n 元,我的钱数将是你的2倍”,其中n 为正整数,则n 的可能值的个数是( ). (A )1 (B )2 (C )3 (D )44(乙).如果关于x 的方程 20x px q p q --=(,是正整数)的正根小于3, 那么这样的方程的个数是( ).(A ) 5 (B ) 6 (C ) 7 (D ) 85(甲).一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,则0123p p p p ,,,中最大的是( ). (A )0p (B )1p (C )2p (D )3p5(乙).黑板上写有111123100, , ,, 共100个数字.每次操作先从黑板上的数中选取2个数a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,则经过99次操作后,黑板上剩下的数是( ).(A )2012 (B )101 (C )100 (D )99 二、填空题(共5小题,每小题6分,共30分) 6(甲).按如图的程序进行操作,规定:程序运行从“输入一个值x ”到“结果是否>487”为一次操作. 如果操作进行四次才停止,那么x 的取值范围是 . 6(乙).如果a ,b ,c 是正数,且满足9a b c ++=,111109a b b c c a ++=+++,那么a b cb c c a a b+++++的值为 .7(甲).如图,正方形ABCD 的边长为215,E ,F 分别是AB ,BC 的中点,AF 与DE ,DB 分别交于点M ,N ,则△DMN 的面积是 . 7(乙).如图所示,点A 在半径为20的圆O 上,以OA为一条对角线作矩形OBAC ,设直线BC 交圆O 于D 、E 两点,xyO ECABD若12OC =,则线段CE 、BD 的长度差是 。
全国初中数学竞赛试题及答案

中国教育学会中学数学教学专业委员会全国初中数学竞赛试题一、选择题〔共5小题,每题6分,共30分.〕1〔甲〕.如果实数a ,b ,c 22||()||a a b c a b c ++-+可以化简为〔 〕.〔A 〕2c a - 〔B 〕22a b - 〔C 〕a - 〔D 〕a 1〔乙〕.如果22a =- 〕.〔A 〕2- 〔B 2 〔C 〕2 〔D 〕22〔甲〕.如果正比例函数y = ax 〔a ≠ 0〕及反比例函数y =xb 〔b ≠0 〕的图象有两个交点,其中一个交点的坐标为〔-3,-2〕,那么另一个交点的坐标为〔 〕. 〔A 〕〔2,3〕 〔B 〕〔3,-2〕 〔C 〕〔-2,3〕 〔D 〕〔3,2〕2〔乙〕. 在平面直角坐标系xOy 中,满足不等式x 2+y 2≤2x +2y 的整数点坐标〔x ,y 〕的个数为〔 〕. 〔A 〕10 〔B 〕9 〔C 〕7 〔D 〕53〔甲〕.如果a b ,为给定的实数,且1a b <<,那么1121a a b a b ++++,, ,这四个数据的平均数及中位数之差的绝对值是〔 〕. 〔A 〕1 〔B 〕 〔C 〕12 〔D 〕143〔乙〕.如图,四边形ABCD 中,AC ,BD 是对角线, △ABC 是等边三角形.30ADC ∠=︒,AD = 3,BD = 5, 那么CD 的长为〔 〕. 〔A 〕23 〔B 〕4 〔C 〕52 〔D 〕4〔甲〕.小倩和小玲每人都有假设干面值为整数元的人民币.小倩对小玲说:“你假设给我2元,我的钱数将是你的n 倍〞;小玲对小倩说:“你假设给我n 元,我的钱数将是你的2倍〞,其中n 为正整数,那么n 的可能值的个数是〔 〕.OAB CED〔A 〕1 〔B 〕2 〔C 〕3 〔D 〕44〔乙〕.如果关于x 的方程 20x px q p q --=(,是正整数〕的正根小于3, 那么这样的方程的个数是〔 〕.〔A 〕 5 〔B 〕 6 〔C 〕 7 〔D 〕 85〔甲〕.一枚质地均匀的正方体骰子的六个面上的数字分别是1,2,3,4,5,6.掷两次骰子,设其朝上的面上的两个数字之和除以4的余数分别是0,1,2,3的概率为0123p p p p ,,,,那么0123p p p p ,,,中最大的是〔 〕.〔A 〕0p 〔B 〕1p 〔C 〕2p 〔D 〕3p5〔乙〕.黑板上写有共100个数字.每次操作先从黑板上的数中选取2个数a b ,,然后删去a b ,,并在黑板上写上数a b ab ++,那么经过99次操作后,黑板上剩下的数是〔 〕. 〔A 〕2021 〔B 〕101 〔C 〕100 〔D 〕99二、填空题〔共5小题,每题6分,共30分〕6〔甲〕.按如图的程序进展操作,规定:程序运行从“输入一个值x 〞到“结果是否>487?〞为一次操作. 如果操作进展四次才停顿,那么x 的取值范围是 .6〔乙〕.如果a ,b ,c 是正数,且满足9a b c ++=,111109a b b c c a ++=+++,那么的值为 . 7〔甲〕.如图,正方形ABCD 的边长为215, E ,F 分别是AB ,BC 的中点,AF 及DE ,DB分别交于点M ,N ,那么△DMN 的面积是 . 7〔乙〕.如下图,点A 在半径为20的圆O 上,以OA 为一条对角线作矩形OBAC ,设直线BC 交圆O 于D 、E 两点,假设12OC =,那么线段CE 、BD 的长度差是 。
全国初中数学联合竞赛试题含答案

( ) 2.满足等式 2 − m m2 −m−2 = 1 的所有实数 m 的和为(A)
(A)3 (B)4 (C)5 (D)6
3.已知 AB 是圆 O 的直径,C 为圆 O 上一点, CAB = 15 , ABC 的平分线交圆 O 于点 D,若 CD = 3 ,则 AB=(A) (A)2 (B) 6 (C) 2 2 (D)3
等式 (at + m)(bt + m) = 17m 即 abt2 + m(a + b)t + m2 = 17m,
( ) ( ) 即 ab 3 − 2 2 + m(a + b) 2 −1 + m2 = 17m ,
整理得 m(a + b) − 2ab 2 + 3ab − m(a + b) + m2 −17m = 0
3.已知 AB 是圆 O 的直径,C 为圆 O 上一点, CAB = 15 , ABC 的平分线交圆 O 于点 D,若 CD = 3 ,则 AB=( ) (A)2 (B) 6 (C) 2 2 (D)3
4.不定方程 3x2 + 7xy − 2x − 5y −17 = 0 的全部正整数角(x,y)的组数为( )
于是可得
a + b = 2(17 −
ab
=
17m
−
m2
m .
)
,
因此,a,b 是关于 x 的一元二次方程 x2 + 2(m −17)x +17m − m2 = 0 ……○1 的两个整数根,
( ) 方程○1 的判别式 = 4(m −17)2 − 4 17m − m2 = 4(17 − m)(17 − 2m) 0.
初中数学竞赛试题及答案

初中数学竞赛试题及答案一、选择题(每题3分,共30分)1. 下列哪个数不是质数?A. 2B. 3C. 4D. 52. 如果一个数的平方等于其本身,那么这个数可能是:A. 0B. 1C. -1D. 23. 一个直角三角形的两条直角边分别为3和4,斜边的长度是:A. 5B. 6C. 7D. 84. 一个数的绝对值是其本身,这个数可能是:A. 正数B. 0C. 负数D. 正数或05. 以下哪个表达式的结果不是整数?A. 3 + 2C. 4 × 2D. 6 ÷ 26. 如果一个数的立方等于其本身,那么这个数可能是:A. 0B. 1C. -1D. 27. 一个圆的半径是5,它的面积是:A. 25πB. 50πC. 100πD. 125π8. 如果一个数的倒数是其本身,那么这个数可能是:A. 1B. -1C. 2D. 09. 一个数的平方根是其本身,这个数可能是:A. 0B. 1C. -1D. 210. 一个数的立方根是其本身,这个数可能是:A. 0B. 1D. 8答案:1. C2. A, B3. A4. D5. C6. A, B, C7. C8. A, B9. A, B10. A, B, C二、填空题(每题4分,共20分)11. 一个数的平方是16,这个数可能是________。
12. 如果一个数的绝对值是5,那么这个数可能是________。
13. 一个三角形的内角和是________度。
14. 一个数的立方是-27,这个数可能是________。
15. 一个数的平方根是2,那么这个数是________。
答案:11. ±412. ±513. 18014. -315. 4三、解答题(每题10分,共50分)16. 证明勾股定理。
17. 解方程:2x + 5 = 15。
18. 一个长方体的长、宽、高分别是3厘米、4厘米和5厘米,求其体积。
19. 一个圆的周长是12π,求其半径。
全国初中数学竞赛试题及答案大全

全国初中数学竞赛试题及答案大全试题一:代数基础题目:若\( a \), \( b \), \( c \)为实数,且满足\( a + b + c = 3 \),\( ab + ac + bc = 1 \),求\( a^2 + b^2 + c^2 \)的值。
解答:根据已知条件,我们可以使用配方法来求解。
首先,我们知道\( (a + b + c)^2 = a^2 + b^2 + c^2 + 2(ab + ac + bc) \)。
将已知条件代入,得到\( 3^2 = a^2 + b^2 + c^2 + 2 \times 1 \)。
简化后,我们得到\( a^2 + b^2 + c^2 = 9 - 2 = 7 \)。
试题二:几何问题题目:在直角三角形ABC中,∠A=90°,AB=6,AC=8,求斜边BC的长度。
解答:根据勾股定理,直角三角形的斜边BC的平方等于两直角边的平方和,即\( BC^2 = AB^2 + AC^2 \)。
代入已知数值,得到\( BC^2 = 6^2 + 8^2 = 36 + 64 = 100 \)。
因此,\( BC = \sqrt{100} = 10 \)。
试题三:数列问题题目:一个等差数列的首项是2,公差是3,求第10项的值。
解答:等差数列的第n项可以通过公式\( a_n = a_1 + (n - 1)d \)来计算,其中\( a_1 \)是首项,d是公差,n是项数。
将已知条件代入公式,得到\( a_{10} = 2 + (10 - 1) \times 3 = 2 + 9 \times 3 = 29 \)。
试题四:概率问题题目:一个袋子里有5个红球和3个蓝球,随机取出2个球,求取出的两个球颜色相同的概率。
解答:首先计算总的可能情况,即从8个球中取2个球的组合数,用组合公式C(8,2)计算。
然后计算取出两个红球或两个蓝球的情况。
两个红球的情况有C(5,2)种,两个蓝球的情况有C(3,2)种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国初中数学竞赛试题及参考答案(湖北省3月17日复试)一.选择题(5×7'=35')1.对正整数n ,记n !=1×2×...×n,则1!+2!+3!+...+10!的末位数是( ).A .0B .1C .3D .5【分析】5≥n 时,n !的个位数均为0,只考虑前4个数的个位数之和即可,1+2+6+4=13,故式子的个位数是3. 本题选C .2.已知关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧<-+->-+x t x x x 235352恰好有5个整数解,则t 的取值范围是( ).2116.-<<-t A 2116.-<≤-t B 2116.-≤<-t C 2116.-≤≤-t D 【分析】2023235352<<-⇒⎪⎪⎩⎪⎪⎨⎧<-+->-+x t x t x x x ,则5个整数解是15,16,17,18,19=x .注意到15=x 时,只有4个整数解.所以2116152314-≤<-⇒<-≤t t ,本题选C3.已知关于x 的方程xx x a x x x x 22222--=-+-恰好有一个实根,则实数a 的值有( )个.A .1B .2C .3D .4 【分析】422222222+-=⇒--=-+-x x a xx x a x x x x ,下面先考虑增根: ⅰ)令0=x ,则4=a ,当4=a 时,0,1,022212===-x x x x (舍); ⅱ)令2=x ,则8=a ,当8=a 时,2,1,0422212=-==--x x x x (舍); 再考虑等根:ⅲ)对04222=-+-a x x ,270)4(84=→=--=∆a a ,当21,272,1==x a .故27,8,4=a ,21,1,1-=x 共3个.本题选C .4.如图,已知△ABC 的面积为24,点D 在线段AC 上,点F 在线段BC 的延长线上,且BC=4CF ,DCFE 是平行四边形,则图中阴影部分的面积为( ).A .3B .4C .5D .6 【分析】设ABC ∆底边BC 上的高为h ,则DE CF CF BC h 121244848====,)(2121212121h h DE h DE h DE S S BDE ADE +⋅⋅=⋅⋅+⋅⋅=+∆∆本题选D .6122121=⋅⋅=⋅⋅=DE DE h DE5.在分别标有号码2,3,4,...,10的9个球中,随机取出两个球,记下它们的标号,则较大标号被较小标号整除的概率是( ).41.A 92.B 185.C 367.D 【分析】9236811291214==+++=C C C P 本题选B .二.填空题(5×7'=35')6.设33=a ,b 是a 2的小数部分,则3)2+b (的值为 .【分析】考虑到33=a ,则33333332292,29,327982,93=+-==<<===b b a 则9)9()2333==+b (7.一个质地均匀的正方体的六个面上分别标有数1、2、3、4、5、6.掷这个正方体三次,则其朝上的面的数的和为3的倍数的概率是 .【分析】对第一次向上面为1时,后面两次所得数字与1的和是3的倍数有111,114,123,126,132,135,141,144,153,156,162,165共12种;对于首次掷得向上的面是2,3,4,5,6的,后面两次与首次的和为3的倍数是轮换对称的,故和为3的倍数共有612⨯,而总次数是666⨯⨯次,则其概率为31666612=⨯⨯⨯=P .8.已知正整数a 、b 、c 满足a +b 2-2c -2=0,3a 2-8b +c=0,则abc 的最大值为 . 【分析】先消去c ,再配方估算.24166)8()121(621662222+=-++⇒=-++b a b b a a观察易知上式中3≤a ,故3,2,1=a ,经试算,2,1=a 时,b 均不是整数;当3=a 时,11,5=b ,于是有)61,11,3(),13,5,3(),,(=c b a ,故201361113max =⨯⨯=abc .9. 实数a 、b 、c 、d 满足:一元二次方程x 2+cx +d=0的两根为a 、b ,一元二次方程x 2+ax +b=0的两根为c 、d ,则所有满足条件的数组(a 、b 、c 、d )为 .【分析】由根与系数关系知b cd d ab d b a d c c b a ===⇒=++=++,,0,然后可得 (a 、b 、c 、d )=(1,-2,1,-2)本题在化简过程中,总感觉还有,此处仅给出一组,好像不严谨,期待官方答案.10.小明某天在文具店做志愿者卖笔,铅笔每支售4元,园珠笔每支售7元,开始时他有铅笔和圆珠笔共350支,当天虽然没有全部卖完,但是他的销售收入恰好是2013元,则他至少卖出了 支圆珠笔. 【分析】设4元的卖x 支,7元的卖y 支,则350,201374<+=+y x y x4125031820124201374++-=⇒++-=⇒=+y y x y y x y x令1441-=⇒=+k y k y ,则k k k x 7505)14(2503-=+--=,又350≤+y x ,即523151350147505≥−−→−≥⇒≤-+-∈k k k k Nk ,207152414=-⨯≥-=k y即他至少卖了207支圆珠笔.三.解答题(4×20'=80')11.如图,抛物线y =ax 2+bx -3,顶点为E ,该抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,且OB=OC=3OA .直线131+-=x y 与y 轴交于点D ,求∠DBC -∠CBE .【分析】易知4)1(3222--=--=x x x y ,)4,1()3,0()0,3(),0,1(---D C B A ,,,作EF ⊥CO 于F ,连CE ,易知△OBC 、△CEF 都是等腰直角三角形,则△CBE 是直角三角形.分别在Rt △O BD 、Rt △BCE 中运用正切定义,即有31232tan 31tan =====BC CE ,OB OD βα,则βα= 从而可得∠DBC -∠CBE=45º.12.如图,已知AB 为圆O 的直径,C 为圆周上一点,D 为线段OB 内一点(不是端点),满足CD ⊥AB ,DE ⊥CO ,E 为垂足,若CE =10,且AD 与DB 的长均为正整数,求线段AD 的长.【分析】设圆O 半径为r ,则由相似或三角函数或射影定理可知,)10(1022-=⇒⋅=r DE OE CE DE ,又r r DE CE CD 10)10(10102222=-+=+=由相交弦定理(考虑垂径时)或连AC 、BC 用相似或三角函数,易知r CD BD AD 102==⋅①,而r BD AD 2=+②令y BD x AD ==,,①/②即155210-=⇒==+yx y r r y x xy ,显然有x y <<0,则10<<xy ,即1051150<<⇒<-<y y,y 为正整数,故9,8,7,6=y ,又x 也为正整数,经逐一试算,仅当30,6==x y 这一组是正整数,故30=AD .13.设a 、b 、c 是素数,记c b a z b a c y a c b x -+=-+=-+=,,,当2,2=-=y x y z 时,a 、b 、c能否构成三角形的三边长?证明你的结论.【分析】281102222a z a z z yz a z y cb a z b ac y +±-=⇒=-+−−−→−==+⇒⎩⎨⎧-+=-+= a 、b 、c 是素数,则z c b a =-+为整数,则1281+=+k a ,k 为正整数.化简整理后,有a k k 2)1(=+⎩⎨⎧=+==+==⇒=+==+=⇒3121,2(121121,1a k k )a a k k 非质数 2,332811-=−−→−=+±-=z a a zⅰ)112,2529,9,3=⇒=-=⇒=-==b b z x x x y z ,c b a b =<=+=+=1720173,17不能围成三角形;ⅱ)是合数9,16,4,2====b x y z 综上所述,以a 、b 、c 不能围成三角形.14.如果将正整数M 放在正整数m 左侧,所得到的新数可被7整除,那么称M 为m 的“魔术数”(例如,把86放在415的左侧,得到的数86415能被7整除,所以称86为415的魔术数) .求正整数n 的最小值,使得存在互不相同的正整数a 1,a 2,...,a n ,满足对任意一个正整数m ,在a 1,a 2,...,a n 中都至少有一个为m 的“魔术数”.【分析】考虑到魔术数均为7的倍数,又a 1,a 2,...,a n 互不相等,不妨设n a a a <<<...21,余数必为1、2、3、4、5、6,0,设t k a i i +=7,(6,5,4,3,2,1,0;,...,3,2,1==t n i ),至少有一个为m 的“魔术数”.因为m a k i +⋅10(k 是m 的位数),是7的倍数,当6≤i 时,而ki a 10⋅除以7的余数都是0,1,2,3,4,5,6中的6个;当7=i 时,而ki a 10⋅除以7的余数都是0,1,2,3,4,5,6这7个数字循环出现,当7=i 时,依抽屉原理,k i a 10⋅与m 二者余数的和至少有一个是7,此时m a ki +⋅10被7整除,即n =7.。
