九年级数学上册第23章图形的相似知识归纳华东师大版.doc
华东师大版九年级数学上册《23章 图形的相似 23.3 相似三角形 相似三角形的性质》精品课件_9

对应角 。对应边 。对
应高的比等
。
对应中线的比等于 。
对应角平分线的比等于 。
周长比等于 。
面积比等于
。
巩固练习
提升练习
观察可能导致发现,观察将揭示某 种规则、模式或定律。
——波利亚
第24章 图形的相似
23.3.3 相似三角形的性质
驶向胜利 的彼岸
23.3.3 相似三角形的性质 复习导入
1.相似三角形的判定方法有哪些? 2.相似三角形有哪些性质?
3.三角形中的主要线段有哪些? 4.什么是相似三角形的相似比?
探索新知
两个三角形相似,除了对应边成比例、对应角相等之外,还可以 得到许多有用的结论,如图:△ABC和△A'B'C'是两个相似三角形, 相似比为k,其中AD、A'D'分别为BC、B'C'边上的高,那么AD、 A'D'之间有什么关系。
△ABC和△A'B'C'是两个相 似三角形,相似比为k,其中AD、 A'D'分别为角BAC、角B'A'C'边 上中线, ,那么AD、A'D'之间有 什么关系?
△ABC和△A‘B’C‘是两个相似 三角形,相似比为k,那么它们 的周长比与相似比之间有什么 关系?
△ABC和△A‘B’C‘是两个相似 三角形,相似比为k,那么它们 的面积比与相似比之间有什么 关系?
相似三角形的对应高的比等于相似比.
三、小组合作探究 1、两相似三角形对应边上的 角平分线之比、中线之比和 相似比有什么关系? 2、两相似三角形的周长比、 面积比和相似比有什么关系?
△ABC和△A'B'C'是两个相 似三角形,相似比为k,其中AD、 A'D'分别为角BAC、角B'A'C'边 上的角平分线,那么AD、A'D' 之间有什么关系?
九年级数学上册第23章图形的相似章末复习上课pptx课件新版华东师大版

例2 已知:如图所示, PN∥BC,AD⊥BC 交 PN 于点 E,交 BC 于点 D.
(1)当AP : PB = 1 : 2,S△ABC = 18cm2 时,S△APN =_______;
(2)若S△APN:S四边形PBCN = 1:2,求AE:AD 的值 ;
(3)若 BC = 15cm,AD = 10cm,且PN = ED = x,求 x 的值.
4. 点 A(-2,3)先向上平移 2 个单位,再向 左平移 2 个单位,得到 B 点的坐标为(_-4_,__5_)_____, B 点关于 x 轴对称点的坐标为(_-_4_,__-5_)_____.
5.如图,在6×8网格中,每个小正方形边长均 为1,点 O 和△ABC 的顶点均为小正方形的顶点.
知识结构
相似多边形的对应边成比例,对应 角相等;对应边成比例、对应角相 等的两个多边形是相似多边形
相似三角形的性 质和判定方法
相似 图形
相似多边形 位似图形
相似三角形
三角形中位线 三角形重心
坐标表示物 体的位置
图形的变换与坐标
1.相似三角形的性质
要点巩固
①对应边成比例.
②对应角相等.
③对应线段的比等于相似比,面积比等于相似
随堂演练
1.若如图所示的两个四边形相似,则 α 的度数 是( A )
A.97° B.87° C.77° D.90°
2.如图,在正方形网格中,有△ABC、△DEF、 △GHP,则下列说法正确的是( D )
A. △ABC ∽ △DEF B. △DEF ∽ △PGH C. △ABC ∽ △GHP D. △ABC ∽ △PGH
(2)图形变换与坐标
图形变换 关于
x轴 对称
九年级数学上册第23章图形的相似23.3相似三角形2相似三角形的判定第2课时授课课件新版华东师大版

最新中小学教案、试题、试卷、课 件
6
最新中小学教案、试题、试卷、课 件
7
最新中小学教案、试题、试卷、课 件
8
最新中小学教案、试题、试卷、课 件
9
最新中小学教案、试题、试卷、课 件
4
在一张方格纸上任意画一个三角形,再画一个三角形,使它的各边 长都是原来三角形各边长的k倍,度量这两个三角形的对应角,它们 相等吗?这两个三角形相似吗?交流一下,看看是否有同样的结论.
结论:如果两个三角形的三组对应边的比相等,那么这两个三 角形相似.
最新中小学教案、试题、试卷、课 件 5
华师版·九年级数学·上册
最新中小学教案、试题、试试卷、课 件
2
由于没有两个角对应相等,同学们可以动手量一量,量 什么东西后可以判断它们是否相似?
最新中小学教案、试题、试卷、课 件
3
结论:如果两个三角形的两组对应边的比相等,并且相应 的夹角相等,那么这两个三角形相似.
华东师大版中学数学九年级上第23章图形的相似23

第23章图形的相似23.5位似图形教学目标教学反思1.理解位似图形、位似中心的概念,理解位似变换是特殊的相似变换.2.会画位似图形,能根据相似比的大小把一个图形放大或缩小.3.理解位似图形上任意一组对应点到位似中心的距离之比等于位似比.教学重难点重点:理解位似图形、位似中心的概念.难点:位似多边形的判断,从位似中心的不同方向绘制位似多边形.教学过程复习巩固1.什么叫相似多边形呢?两个边数相同的多边形,如果各边对应成比例,各角对应相等,那么这两个多边形叫做相似多边形.2.什么叫相似比?相似多边形对应边的比叫做相似比.导入新课【问题1】活动1(学生交流,教师点评)【思考】1.前面我们已经学习了图形的哪些变换?平移:平移的方向,平移的距离.轴对称:对称轴.旋转:(中心对称)旋转中心,旋转方向,旋转角度.2.下列图形中,每个图中的四边形ABCD和四边形A′B′C′D′都是相似图形.分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?对应边有何位置关系?(2)教师:这就是本节要学习的内容. 教师引出课题:23.5 位似图形探究新知探究点一 位似图形 【问题2】活动2(学生交流,教师点评)如图,下面两个多边形相似,将两个图形的对应顶点相连,观察发现连结的直线相交于点O .,,,,OA OB OC OD OE OA OB OC OD OE'''''有什么关系?【答案】OA OB OC OD OE OA OB OC OD OE'''''====【总结】教学反思.OA A A B B C C O OA OB OC k O OB OC''''=''===两个图形的对应点与、与、与的连线都交于一点,并且,这两个图形叫做位似图形,点叫做位似中心即两个相似多边形,如果它们对应顶点的连线相交于一点,并且这点与对应顶点所连线段成比例,我们就把这样的两个图形叫做位似图形,这个交点叫做位似中心.探究点二 位似图形的性质 活动3(学生交流,教师点评)从图(1)中我们可以看到,△OAB ∽△OA ′B ′, 则OA OB AB OA OB A B=='''',AB ∥A ′B ′. 图(2)呢?你得到了什么?(1) (2)【总结】位似图形的性质:(1)位似图形上任意一对对应点到位似中心的距离之比等于位似比. (2)位似图形上对应点的连线或延长线交于一点.(3)位似图形中的对应线段平行(或在一条直线上).(4)位似图形是特殊的相似图形,因此位似图形具有相似图形的一切性质. 典例讲解(师生互动)例1 如图所示,四边形ABCD 和四边形A ′ B ′ C ′ D ′位似,相似比k 1 = 2,四边形A ′ B ′ C ′D ′和四边形A″ B″ C″D″位似,相似比k 2=1. 则四边形A″ B″ C″ D″和四边形ABCD 是位似图形吗?如果是,请说明理由并求出相似比.【解】∵ 四边形ABCD 和四边形A ′ B ′ C ′ D ′位似, ∴ 四边形ABCD ∽四边形A ′ B ′ C ′ D ′ .∵ 四边形A ′ B ′ C ′ D ′和四边形A″ B″ C″ D″位似, ∴ 四边形A ′ B ′ C ′ D ′∽四边形A″ B″ C″ D″ . ∴ 四边形A″ B″ C″ D″∽四边形ABCD.又∵ 四边形A ″B ″C ″D ″和四边形ABCD 的对应顶点的连线经过同一点O , ∴ 四边形A″ B″ C″ D″和四边形ABCD 是位似图形.∵ 四边形ABCD 和四边形A ′ B ′ C ′ D ′位似,相似比k 1=2,教学反思四边形A′ B′ C′ D′和四边形A″ B″ C″ D″位似,相似比k2=1,∴四边形A″ B″ C″ D″和四边形ABCD 的相似比为1 2 .探究点三位似图形的画法【问题3】活动4(学生交流,教师点评)例2如图,已知△ABC,以点O为位似中心画△DEF,使其与△ABC位似,且位似比为2.【解】作法:画射线OA、OB、OC;在射线OA、OB、OC上分别取点D、E、F,使OD =2OA,OE=2OB,OF=2OC;顺次连结D、E、F,这样就得到与△ABC位似,相似比为2的△DEF.想一想:你还有其他的画法吗?思考:如果点O在两个三角形之间呢?能不能画出这时的图形?作法:画射线OA、OB、OC;沿着射线OA、OB、OC反方向上分别取点D、E、F,OD =2OA,OE =2OB,OF =2OC;顺次连结D、E、F,这样就得到与△ABC位似,相似比为2的△DEF.【归纳】画位似图形的一般步骤:(1)确定位似中心;(2)分别连结位似中心和能代表原图的关键点并延长;(3)根据相似比,确定能代表所画的位似图形的关键点;(4)按照原图的形状,顺次连结上述各点,得到放大或缩小后的图形.【即学即练】教学反思如图,已知四边形ABCD,把四边形ABCD 缩小到原来的12.(画出一种情形)【解】作法:(1)在四边形ABCD外任选一点O(如图);(2)分别在射线OA、OB、OC、OD上取点A′、B′、C′、D′,使得OAOA'=OBOB'=OCOC'=ODOD'=12;(3)顺次连结点A′、B′、C′、D′,则四边形A′B′C′D′就是所要画的图形.【题后总结】利用位似,可以将一个图形放大或缩小.课堂练习1.下列关于位似图形的表述错误的是()A.相似图形一定是位似图形,位似图形一定是相似图形B.位似图形一定有位似中心C.如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么这两个图形是位似图形D.位似图形上任意一对对应点与位似中心的距离之比等于相似比2.如图所示的两个三角形是位似图形,它们的位似中心是()A.点PB.点OC.点MD.点N3.如图所示,将平行四边形AEFG变换成平行四边形ABCD,其中E,G分别是AB,AD的中点,下列叙述不正确的是()教学反思A.这种变换是相似变换B.对应边扩大到原来的2倍C.各对应角度数不变D.面积扩大到原来的2倍 4.下列4个图中的两个相似三角形是位似三角形的是( )(1)(2)(3)(4)A.图(3)、图(4)B.图(2)、图(3)、图(4)C.图(2)、图(3)D.图(1)、图(2)5.如图所示,线段AB 两个端点的坐标分别为A (6,6),B (8,2),以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的12后得到线段CD ,则端点C 的坐标为( )A.(3,3)B.(4,3)C.(3,1)D.(4,1)6.如图,△ABC 和△111A B C 是以点O 为位似中心的位似三角形,若C 1为OC 的中点,AB =4,则11A B 的长为()A.1B.2C.4D.8教学反思7.如图,五边形ABCDE 是由五边形FGHMN 经过相似变换得到的,点O 是位似中心,F 、G 、H 、M 、N 分别是OA 、OB 、OC 、OD 、OE 的中点,求五边形ABCDE 与五边形FGHMN 的面积比.8.已知边长为1的正方形ABCD ,以它的两条对角线的交点为位似中心,画一个边长为2且与它位似的正方形.参考答案1.A 【解析】相似图形不一定是位似图形.2.A 【解析】利用位似图形的概念找出每组对应点所在直线的交点,显然交点为点P .3.D 【解析】面积比等于相似比的平方,所以面积应扩大到原来的4倍.4.B 【解析】利用“每组对应点的连线所在的直线都经过同一点(位似中心)”检验.5.A 【解析】分别过点A ,C 作两坐标轴的垂线,利用相似三角形的性质可求解.6.B 【解析】∵ C 1为OC 的中点,∴ 112OC =OC .∵ △ABC 和△111A B C 是以点O 为位似中心的位似三角形, ∴ A 1B 1∥AB ,1OC OC =1OBOB, ∴ △OA 1B 1∽△ OAB ,11OB OC OB OC ==11A BAB, ∴11142A B =, ∴11A B =2,故选B.7.【解】∵ 五边形ABCDE 是由五边形FGHMN 经过相似变换得到的, ∴ 五边形ABCDE ∽五边形FGHMN . ∵ F 为OA 的中点,∴ OF =12AO ,∴ OA ∶OF =2∶1,∴ 五边形ABCDE 与五边形FGHMN 的面积比为4∶1.教学反思8.【解】如图,画射线OA 、OB 、OC 、OD ;在射线OA 、OB 、OC 、OD 上分别取点G 、H 、E 、F ,使OE =2OA ,OF =2OB ,OG =2OC ,OH =2OD ;顺次连结E 、F 、G 、H ,与便到与正方形ABCD 位似,位似比为1∶2的正方形EFGH.课堂小结(学生总结,老师点评)→⎧⎪⎪⎪⎨⎪⎪⎪⎩→定义两个相似多边形,如果它们对应顶点 所在的直线相交于一点,并且这点与 对应顶点所连线段成比例.我们就把这 样的两个图形叫做位似图形,这个交点 叫做位似中心.①两个图形相似.位似图形②对应点的连线相交于一点,对应边互相性质平行或在同一直线上.③任意一对对应点到位似中心的距离之比等于相似比.画法作位似图形:关键是确定位似中心、 ⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩ 相似比和关键点的对应点.布置作业教材第81页练习题,第82页习题23.5第1,2题.板书设计课题 23.5 位似图形【问题1】 探究点一 位似图形的定义【问题2】 例1 位似图形的性质【问题3】 例2 位似图形的画法教学反思。
华师版九年级上册数学第23章 图形的相似 相似图形(2)

知识点 1 相似多边形的定义
知1-导
问题(一)
图23.2.1是大小不同的两张地图,当然,它们是相似 的图形.设在大地图中有A、B、C三地,在小地图 中相应的三地记为A′、B′、C′,试用刻度尺量一量两 张地图中A(A′)与B(B′)两地之间的图上距离和B(B′)与 C(C′)两地之间的图上距离,用量角器量一量∠ABC 和∠A′B′C′的大小.
解:∵两个四边形相似, ∴,18 x 12 18 ∴x=27.
根据对应角相等,可得
α=360°-(77°+83°+116°)
=84°.
知2-讲
总结
知2-讲
利用相似多边形的性质求边长或角度,关键扣住“对 应”二字,找准对应边和对应角是解决问题 的关键.需要注意的是对应边是比相等,而对应角 是直接相等.
1下列四组图形中,不是相似图形的是( )
知2-练
知2-练
2若一个三角形三边之比为3∶5∶7,与它相似的三 角形的最长边的长为21,则最短边的长为( ) A.15B.10 C.9D.3
知2-讲
思考 两个三角形一定是相似图形吗?两个等腰三角形 呢?两个等边三角形呢?
1.相似多边形的定义可作为判断两个多边形是否相 似的判定,即在多边形中,只有“边数相同” “角分别相等”“边成比例”这三个条件同时成立 时,才能说明这两个多边形是相似多边形. 2.相似比的值与两个多边形的前后顺序有关. 3.相似比为1的两个相似多边形是全等多边形.
第23章图形的相似
23.2相似图形
1 课堂讲解 相似多边形的定义
相似多边形的性质
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
日常生活中,我们会碰到很多形状相同、大小不一定 相同的图形,例如下面两张照片,右边的照片是由左 边的照片放大得来的.尽管它们大小不同,但形状相 同.
九年级数学上册 23.2 相似图形典型例题素材 (新版)华
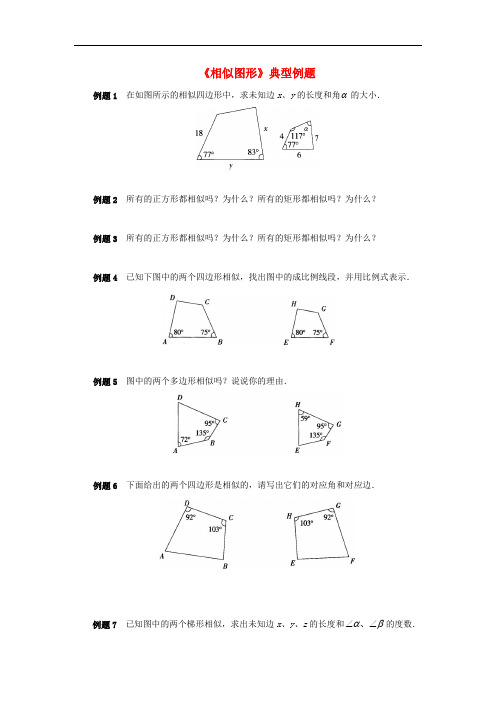
《相似图形》典型例题例题1 在如图所示的相似四边形中,求未知边x 、y 的长度和角α的大小.例题2 所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?例题3 所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?例题4 已知下图中的两个四边形相似,找出图中的成比例线段,并用比例式表示.例题5 图中的两个多边形相似吗?说说你的理由.例题6 下面给出的两个四边形是相似的,请写出它们的对应角和对应边.例题7 已知图中的两个梯形相似,求出未知边x 、y 、z 的长度和βα∠∠、的度数.例题8在如图所示的相似四边形中,求未知边x、y的长度和角 的大小.参考答案例题1 解答 ∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==, ∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.例题2 解答:所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.例题3 解答:所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.例题4 解答 HEDA GH CD FG BC EF AB === 例题5 解答 不相似.︒=︒-︒-︒-︒=∠587295135360D ,而︒=︒-︒-︒-︒=∠715995135360E ,不可能有“对应角相等”.例题6 解答 F A ∠→∠ E B ∠→∠ H C ∠→∠ G D ∠→∠FE AB → EH BC → HG CD → GF DA →例题7 分析 解题中要充分利用相似多边形的特征和梯形的性质.解答 由于对应边成比例,所以232.38.45.442====z y x . 所以3,6,3===z y x .由于对应角相等,所以 ︒=∠-︒=∠=∠118180A D α,︒='∠-︒='∠=∠70180C B β.例题8 解答 ∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==,∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.。
华东师大版九上数学第23章 图形的相似

华东师大版九上数学第23章 图形的相似1. 比例线段的有关概念==在比例式::中,、叫外项,、叫内项,、叫前项,a c(a b c d )a d b c a c b db 、d 叫后项,d 叫第四比例项,如果b =c ,那么b 叫做a 、d 的比例中项. 2. 比例性质①基本性质:a b cdad bc =⇔= ②更比性质(交换比例的内项或外项): ()()()()⎧=⎪⎪⎪=⎪=⇒⎨⎪=⎪⎪⎪=⎩交换内项交换外项同时交换内外项同时交换比的前项和后项a bc d d c a cb a d b b dc a b da c②合比性质:±±a b c d a b b c d d =⇒= ③等比性质:……≠……a b c d m n b d n a c m b d n ab===+++⇒++++++=()03. 黄金分割在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC >BC ),如果ACBCAB AC =,即AC 2=AB ×BC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比.其中AB AC 215-=≈0.618AB . 4. 平行线分线段成比例定理①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3.则,,,…AB BC DE EF AB AC DE DF BC AC EFDF===②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边. 5. 相似三角形的判定①两角对应相等,两个三角形相似;②两边对应成比例且夹角相等,两三角形相似;③三边对应成比例,两三角形相似. 6. 相似三角形的性质①相似三角形的对应角相等,对应边成比例;②相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;③相似三角形周长的比等于相似比;面积的比等于相似比的平方. 7. 六种相似基本模型:C ABDCABDE E D BACDE ∥BC∠B =∠AED∠B =∠ACDABCDO B ACO DC BAX 型 母子型AC ∥BD∠B =∠C AD 是Rt △ABC 斜边上的高8. 射影定理由_____________,得______________,即_______________; 由_____________,得______________,即_______________; 由_____________,得______________,即_______________.9. 中位线1) 三角形的中位线:连结三角形两边中点的线段. 三角形的中位线平行于第三边并且等于第三边的一半.三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的线段的长是对应中线长的31.2) 梯形的中位线:连结梯形两腰中点的线段.梯形的中位线平行于两底边,并且等于两底边和的一半. 10. 位似①如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比.②位似图形上任意一对对应点到位似中心的距离之比等于位似比.ADBC。
华东师大版九年级数学上册《23章 图形的相似 23.3 相似三角形 相似三角形的性质》精品课件_10

对应边上的中线的比等于相似比; 图 24.3.11 你可以从中探索
对应角上的角平分线的比到等什于么相呢似?比。
1.如果两个三角形相似,相似比为3∶5,那么对 应角的角平分线的比等于多少?
1、什么叫做相似三角形? 对应边成比例,对应角相等的三角
形是相似三角形。
2、有几种方法判定两个三角形是相似 三角形?
回顾与思考
某技术工人准备按照比例尺3:4的图纸制
作三角形零件,如图,图纸上的△ABC表示
该零件的横断面△A′B′C′,CD和C′D′分别
是它们的高.
1) AB
A 'B '
BC B 'C '
巩固练习
如图所示,在矩形DEFG内接于△ABC,点D、E在BC上 点F,G分别在AC,AB上,且DE=2EF,BC=21mm,
△ABC的高AH=14mm,求矩形DEFG的面积。
Байду номын сангаас
A
G
F
B
C
D HE
变式练习:
1、如图是一个照相机成像的示意图。如果底片AB宽35mm, 焦距是70mm,拍摄5m外的景物A′B ′有多宽?如果焦距是 50mm呢?
3∶5
2_0._._相__4似_,三对角应形角对的应角边平的分比线为的0.比4为,_那0__.么__相4_似,比周为长 的比为__0_.___4,面积的比为_0__.__1_.6
3、若两个三角形面积之比为16:9,则它们的对高
之比为_4__:_3_,对应中线之比为_4__:__3
华东师大版初中九年级上册数学精品授课课件 第23章 图形的相似 相似三角形的判定 第1课时

E
又∵ EF∥AB,
∴∠EFC =∠B ,
∴∠ADE =∠EFC,
∴△ADE∽△EFC (两角分别B相等 Fຫໍສະໝຸດ C的两个三角形相似).
随堂演练
1. △ABC 中,∠ACB = 90°,CD⊥AB 于 D, 找出图中所有的相似三角形.
C
A
B
D
△ABC ∽△ACD∽△CBD
2.△ABC中,D 是 AB 的边上一点,过点 D 作一直线与 AC 相交于 E,要使 △ADE 与 △ABC 相似,你怎样画这条直线?说明理由. 和你的同伴 交流作法是否一样.
探索
① 任意画两个三角形,使其三对角分别对应相 等.用刻度尺量一量两个三角形的对应边,看看这 两个三角形的边是否对应成比例?你能得出什么 结论?
B
B'
A
C A'
C'
B B'
A
C A'
C'
我们可以发现它们的边对应成比例, 于
是这两个三角形相似.
②
根据三角形内角和等于180°,如果两个三 角形有两对角分别对应相等,那么第三对角也 一定对应相等.
教学反思
本课时从学生所熟悉的特殊三角板入手,通 过学生动手操作探究相似三角形的判定定理 1, 从中感受学习几何的乐趣,从而激发学生学习兴 趣,培养学生的几何推理能力.
A
D
C
B
A E
E
D
C
B
有两种不同的画法:
①过 D 点作 DE∥BC,DE 交 AC 于点 E; ②以 AD 为一边在△ABC 内部作∠ADE =∠C, 另一边 DE 交 AC 于点 E.
课堂小结
相似三角形的判定定理1 两角分别相等 的两个三角形相似.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第23章 图形的相似
1. 比例线段的有关概念
==在比例式::中,、叫外项,、叫内项,、叫前项,
a c
(a b c d )a d b c a c b d
b 、d 叫后项,d 叫第四比例项,如果b =
c ,那么b 叫做a 、
d 的比例中项. 2. 比例性质
①基本性质:
a b c
d
ad bc =⇔= ②更比性质(交换比例的内项或外项):
()()()()⎧=⎪⎪
⎪=⎪=⇒⎨
⎪=⎪⎪⎪=⎩交换内项交换外项同时交换内外项同时交换比的前项和后项a b
c d d c a c
b a d b b d
c a b d
a c
②合比性质:
±±a b c d a b b c d d =⇒= ③等比性质:……≠……a b c d m n b d n a c m b d n a
b
===+++⇒++++++=()0
3. 黄金分割
在线段AB 上,点C 把线段AB 分成两条线段AC 和BC (AC >BC ),如果
AC
BC
AB AC =
,即AC 2=AB ×BC ,那么称线段AB 被点C 黄金分割,点C 叫做线段AB 的黄金分割点,AC 与
AB 的比叫做黄金比.其中AB AC 2
1
5-=
≈0.618AB . 4. 平行线分线段成比例定理
①定理:三条平行线截两条直线,所得的对应线段成比例,如图:
l 1∥l 2∥l 3.则
,,,…AB BC DE EF AB AC DE DF BC AC EF
DF
=== ②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例.
③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边. 5. 相似三角形的判定
①两角对应相等,两个三角形相似;②两边对应成比例且夹角相等,两三角形相似; ③三边对应成比例,两三角形相似. 6. 相似三角形的性质
①相似三角形的对应角相等,对应边成比例;
②相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比;
③相似三角形周长的比等于相似比;面积的比等于相似比的平方. 7. 六种相似基本模型:
C
A
B
D C
A
B
D
E E D B
A
C
DE ∥BC
∠B ∠AED
∠B ∠ACD
A
D
B
C
D
O
B
A
C
O D
C
B
A
X 型
母子型
AC ∥BD
∠B ∠C
AD 是Rt △ABC 斜边上的高
8. 射影定理
由_____________,得______________,即_______________; 由_____________,得______________,即_______________; 由_____________,得______________,即_______________.
9. 中位线
1) 三角形的中位线:连结三角形两边中点的线段. 三角形的中位线平行于第三边并且等于第三边的一半. 三角形三条边上的中线交于一点,这个点就是三角形的重心,重心与一边中点的线段的
长是对应中线长的
3
1
. 2) 梯形的中位线:连结梯形两腰中点的线段.
梯形的中位线平行于两底边,并且等于两底边和的一半. 10. 位似
①如果两个图形不仅是相似图形,而且每组对应点所在的直线都经过同一个点,那么这
样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比. ②位似图形上任意一对对应点到位似中心的距离之比等于位似比.
A
D B C。
