六年级寒假班第8讲:一次方程(组)和一次不等式(组)章节复习-教师版
沪教版六年级下册数学——一次方程(组)和一次不等式(组)章节复习
5 / 17
【练习 15】 若不等式 ax b 的解集是 x 【难度】★ 【答案】 【解析】
b ,那么 a 的取值范围是________. a
【练习 16】 若 a 2 1 x 2 a 1 x 2a 3 y 3b 0 是关于 x、y 的二元一次方程, 则 a b ______. 【难度】★★ 【答案】 【解析】
【难度】★★ 【答案】 【解析】
10 / 17
【练习 36】 解不等式: 5 4x 1 7 (1) x; 9 3 6 【难度】★★ 【答案】 【解析】
5 3 1 (2) x 1 x 1 4 . 3 4 6
【练习 37】 解不等式组:
5 x 1 3 x 4 (1) 1 ; 2 x x 3 3 1 2 x 2 x 4 3 3 (2) . 2 x 1 10 x 1 5 x 5 6 4 3
7 / 17
x 2 【练习 25】 若关于 x 的不等式组 x 1 无解,则 a 的取值范围是______. x a
【难度】★★ 【答案】 【解析】
mx 3ny 1 5 x ny n 2 【练习 26】 已知关于 x、y 的方程组 与 有相同的解, 3 x y 6 2 x y 4
【练习 23】 当 x______时,代数式 【难度】★★ 【答案】 【解析】
2x 3 x4 与 的差不小于 1. 4 3
【练习 24】 已知关于 x 的不等式 2a 1 x 1 2a 的解集是 x 1 ,则 a 的范围是 _______________. 【难度】★★ 【答案】 【解析】
x4 x3 2; 0.2 0.5
第六章-一次方程(组)和一次不等式(组)-六年级(下)-知识点汇总-沪教版

第六章-一次方程(组)和一次不等式(组)-六年级(下)-知识点汇总-沪教版第六章一次方程(组)及一次不等式(组)6.1 列方程1、用字母x、y、等表示所要求的未知的数量,这些字母称为未知数。
含有未知数的等式叫做方程。
在方程中,所含的未知数又称为元2、为了求得未知数,在未知数和已知数之间建立一种等量关系式,就是列方程6.2 方程的解如果未知数所取的某个值能使方程左右两边的值相等,那么这个未知数的值叫做方程的解6.3 一元一次方程及其解法1、只含有一个未知数且未知数的次数是一次的方程叫做一元一次方程2、等式性质:1)等式两边同时加上(或减去)同一个数或一个含有字母的式子,说得结果仍是等式2)等式两边同时乘以同一个数(或除以同一个不为零的数),所得结果仍是等式3、去括号的法则是:括号前带“+”号,去掉括号时括号内各项都不变符号。
括号前带“—”号,去掉括号时括号内各项都改变符号。
4、解一元一次方程的一般步骤是:1)去分母;2)去括号;3)移项;4)化成ax=b(a≠0)的形式5)两边同除以未知数的系数,得到方程的解x=b/a6.4 一元一次方程的应用列方程解应用题的一般步骤是:1)设未知数(元);2)列方程;3)解方程;4)检验并作答。
6.5 不等式及其性质1、用不等号“<”“>”“≤”“≥”表示的关系式,叫做“不等式”。
2、不等式性质:1)不等式的两边同时加上(或减去)同一个数或同一个含有字母的式子,不等号的方向不变,即:如果a>b,那么a+m>b+m如果a<b,那么a+m<b+m2)不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变,即:如果a>b,且m>0,那么am>bm(或a/m>b/m)如果a<b,且m>0,那么am<bm(或a/m<b/m=3)不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变,即:如果a>b,且m<0,那么am<bm(或a/m>b/m)如果a<b,且m<0,那么am>bm(或a/m<b/m)6.6 一元一次不等式的解法1、在含有未知数的不等式中,能使不等式成立的未知数的值,叫做不等式的解2、一般情况下,一元一次方程的解只有一个,一元一次不等式的解可以有无数个。
《不等式与不等式组》单元复习教案
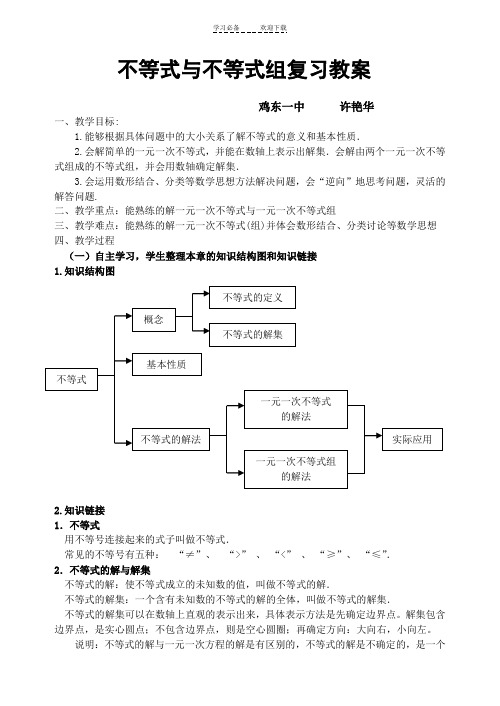
不等式与不等式组复习教案鸡东一中许艳华一、教学目标:1.能够根据具体问题中的大小关系了解不等式的意义和基本性质.2.会解简单的一元一次不等式,并能在数轴上表示出解集.会解由两个一元一次不等式组成的不等式组,并会用数轴确定解集.3.会运用数形结合、分类等数学思想方法解决问题,会“逆向”地思考问题,灵活的解答问题.二、教学重点:能熟练的解一元一次不等式与一元一次不等式组三、教学难点:能熟练的解一元一次不等式(组)并体会数形结合、分类讨论等数学思想四、教学过程(一)自主学习,学生整理本章的知识结构图和知识链接1.知识结构图2.知识链接1.不等式用不等号连接起来的式子叫做不等式.常见的不等号有五种:“≠”、“>” 、“<” 、“≥”、“≤”.2.不等式的解与解集不等式的解:使不等式成立的未知数的值,叫做不等式的解.不等式的解集:一个含有未知数的不等式的解的全体,叫做不等式的解集.不等式的解集可以在数轴上直观的表示出来,具体表示方法是先确定边界点。
解集包含边界点,是实心圆点;不包含边界点,则是空心圆圈;再确定方向:大向右,小向左。
说明:不等式的解与一元一次方程的解是有区别的,不等式的解是不确定的,是一个范围,而一元一次方程的解则是一个具体的数值. 3.不等式的基本性质(1)不等式的两边都加上(或减去)同一个数或同一个整式.不等号的方向不变.如果a b >,那么__a c b c ±±(2)不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.如果,0a b c >>,那么__ac bc (或___a b c c) (3)不等式的两边都乘以(或除以)同一个负数,不等号的方向改变.如果a b >,0c <那么__ac bc (或___a b c c) 说明:任意两个实数a 、b 的大小关系:①a -b>O ⇔a>b ;②a -b=O ⇔a=b ;③a-b<O ⇔a<b .4.一元一次不等式只含有一个未知数,且未知数的次数是1.系数不等于0的不等式叫做一元一次不等式.注:一元一次不等式的一般形式是ax+b>O 或ax+b<O(a ≠O ,a ,b 为已知数). 5.解一元一次不等式的一般步骤解一元一次不等式的一般步骤:(1)去分母;(2)去括号;(3)移项; (4)合并同类项;(5)化系数为1.说明:解一元一次不等式和解一元一次方程类似.不同的是:一元一次不等式两边同乘以(或除以)同一个负数时,不等号的方向必须改变,这是解不等式时最容易出错的地方. 6.一元一次不等式组含有相同未知数的几个一元一次不等式所组成的不等式组,叫做一元一次不等式组. 说明:判断一个不等式组是一元一次不等式组需满足两个条件:①组成不等式组的每一个不等式必须是一元一次不等式,且未知数相同;②不等式组中不等式的个数至少是2个,也就是说,可以是2个、3个、4个或更多. 7.一元一次不等式组的解集一元一次不等式组中,几个不等式解集的公共部分.叫做这个一元一次不等式组的解集.一元一次不等式组的解集通常利用数轴来确定.9.解一元一次不等式组的步骤(1)分别求出不等式组中各个不等式的解集;(2)利用数轴求出这些解集的公共部分,即这个不等式组的解集. 尝试练习1.判断下列式子哪些是不等式?为什么?(1)3> 2 (2)a 2+1> 0 (3)3x 2+2x (4)x < 2x+1 (5)x=2x-5(6)x 2+4x < 3x+1 (7)a+b ≠c 2.用不等式表示:(1) a 是负数;(2) a 是非负数; (3) x 的6倍减去3大于10; (4)y 的 与6的差小于1; (5)y 的 与6的差不小于1 3.单项选择:(1)由 x >y 得 ax >ay 的条件是( ) A.a >0 B.a <0 C.a ≥0 D.a ≤0 (2)由 x >y 得 ax ≤ay 的条件是( ) A.a >0 B.a <0 C.a ≥0 D.a ≤0 (3)由 a >b 得 am2>bm2 的条件是( )A.m >0B.m <0C.m ≠0D.m 是任意有理数 (4)若 a >1,则下列各式中错误的是( )A.4a >4B.a+5>6C. <D.a-1<0 4.设a >b ,用“<”或“>”填空:(1)a-3 b-3 (2) (3) -4a -4b (二)展示交流.,545312).(1表示出来并把它的解集在数轴上解不等式内江市例-≥-x x例2:高速公路施工需要爆破,根据现场实际情况,操作人员点燃导火线后,要在炸药爆破前跑到400米外的安全区域,已知导火索燃烧速度是1.2厘米/秒,人跑步的速度是5米/秒,问导火索至少需要多长?例3.根据下列条件,分别求出a的值或取值范围:1)已知不等式的解集是x<5;2)已知x=5是不等式的解(三)检测反馈1,填空(1)若2a<-b,则-2a___b.(2)不等式x-3>-4的解集是________.(3)若a+2=4,则不等式2x+a<3的解集是_______.(4)当x=________时,代数式3x+4的值为正数.(5)代数式3m+2的值小于-2,则m的取值范围为______.(6)若2x=3+k的解集是负数,那么k的取值范围是______.(7)若a+|a|=0,那么a_____;若a-|a|<0,那么a_______;若a+|a|>0,那么a______.(8)若|3a-5|=5-3a,则a______.2.解·一元一次不等式,并在数轴上表示它的解集强化记忆1.在判断不等式成立与否或由不等式变形求某些字母的范围时,要认真观察不等式的形式与不等号方向。
(学生~基础)《不等式与一次不等式组》全章复习与巩固 知识讲解

《不等式与一次不等式组》全章复习与巩固(基础)知识讲解【学习目标】1.理解不等式的有关概念,掌握不等式的三条基本性质;2.理解不等式的解(解集)的意义,掌握在数轴上表示不等式的解集的方法;3.会利用不等式的三个基本性质,熟练解一元一次不等式或不等式组;4.会根据题中的不等关系建立不等式(组),解决实际应用问题;5.通过对比方程与不等式、等式性质与不等式性质等一系列教学活动,理解类比的方法是学习数学的一种重要途径.【知识网络】【要点梳理】要点一、不等式1.不等式:用符号“<”(或“≤”),“>”(或“≥”),≠连接的式子叫做不等式.要点诠释:(1)不等式的解:能使不等式成立的未知数的值叫做不等式的解.(2)不等式的解集:对于一个含有未知数的不等式,它的所有解组成这个不等式的解集.解集的表示方法一般有两种:一种是用最简的不等式表示,例如x a>,x a≤等;另一种是用数轴表示,如下图所示:(3)解不等式:求不等式的解集的过程叫做解不等式.2. 不等式的性质:不等式的基本性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变.用式子表示:如果a>b,那么a±c>b±c不等式的基本性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.用式子表示:如果a>b,c>0,那么ac>bc(或a bc c >).不等式的基本性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变.用式子表示:如果a>b,c<0,那么ac<bc(或a bc c <).要点二、一元一次不等式1.定义:不等式的左右两边都是整式,经过化简后只含有一个未知数,并且未知数的最高次数是1,这样的不等式叫做一元一次不等式,要点诠释:ax+b>0或ax+b<0(a≠0)叫做一元一次不等式的标准形式.2.解法:解一元一次不等式步骤:去分母、去括号、移项、合并同类项、系数化为1.要点诠释:不等式解集的表示:在数轴上表示不等式的解集,要注意的是“三定”:一是定边界点,二是定方向,三是定空实.3.应用:列不等式解应用题的基本步骤与列方程解应用题的步骤相类似,即:(1)审:认真审题,分清已知量、未知量;(2)设:设出适当的未知数;(3)找:找出题中的不等关系,要抓住题中的关键字,如“大于”“小于”“不大于”“至少”“不超过”“超过”等关键词的含义;(4)列:根据题中的不等关系,列出不等式;(5)解:解出所列的不等式的解集;(6)答:检验是否符合题意,写出答案.要点诠释:列一元一次不等式解应用题时,经常用到“合算”、“至少”、“不足”、“不超过”、“不大于”、“不小于”等表示不等关系的关键词语,弄清它们的含义是列不等式解决问题的关键. 要点三、一元一次不等式组关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.要点诠释:(1)不等式组的解集:不等式组中各个不等式的解集的公共部分叫做这个不等式组的解集. (2)解不等式组:求不等式组解集的过程,叫做解不等式组.(3)一元一次不等式组的解法:分别解出各不等式,把解集表示在数轴上,取所有解集的公共部分,利用数轴可以直观地表示不等式组的解集.(4)一元一次不等式组的应用:①根据题意构建不等式组,解这个不等式组;②由不等式组的解集及实际意义确定问题的答案.【典型例题】类型一、不等式1.用适当的符号语言表达下列关系.。
沪教版数学六年级下册第六章《一次方程(组)和一次不等式(组)》教学设计

沪教版数学六年级下册第六章《一次方程(组)和一次不等式(组)》教学设计一. 教材分析《一次方程(组)和一次不等式(组)》是沪教版数学六年级下册第六章的内容。
本章主要介绍一次方程(组)和一次不等式(组)的概念、解法及其应用。
通过本章的学习,学生能够理解一次方程(组)和一次不等式(组)的定义,掌握解法,并能运用其解决实际问题。
二. 学情分析六年级的学生已经具备了一定的代数基础,对解方程和不等式有一定的了解。
但在解决实际问题时,还需要进一步培养学生的抽象思维能力和解决问题的能力。
此外,学生可能对一次方程(组)和一次不等式(组)的解法掌握不够熟练,需要通过大量的练习来巩固。
三. 教学目标1.知识与技能:理解一次方程(组)和一次不等式(组)的概念,掌握解法,并能运用其解决实际问题。
2.过程与方法:通过自主学习、合作交流,培养学生的抽象思维能力和解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识。
四. 教学重难点1.重点:一次方程(组)和一次不等式(组)的概念、解法及其应用。
2.难点:一次方程(组)和一次不等式(组)的解法,以及如何运用其解决实际问题。
五. 教学方法1.自主学习:鼓励学生自主探究,发现问题,解决问题。
2.合作交流:引导学生与他人合作,共同探讨问题,分享解题经验。
3.案例分析:通过分析实际问题,培养学生运用数学知识解决实际问题的能力。
4.巩固练习:通过大量练习,巩固所学知识。
六. 教学准备1.教学课件:制作课件,展示一次方程(组)和一次不等式(组)的概念、解法及应用。
2.练习题:准备适量的一次方程(组)和一次不等式(组)的练习题,用于巩固所学知识。
3.小组讨论:安排学生分组,进行合作交流。
七. 教学过程1.导入(5分钟)利用实例引入一次方程(组)和一次不等式(组)的概念,激发学生的学习兴趣。
2.呈现(15分钟)展示一次方程(组)和一次不等式(组)的定义、解法及应用,让学生初步了解其基本概念和解题方法。
方程(组)与不等式(组)知识点

中考复习三 方程(组)与不等式(组)【一次方程及方程】一、等式与方程的有关概念1.等式及其性质 ⑴ 等式:用等号“=”来表示 关系的式子叫等式. ⑵ 性质:① 如果b a =,那么=±c a ;② 如果b a =,那么=ac ;如果b a =()0≠c ,那么=ca. 2. 方程、一元一次方程的概念⑴ 方程:含有未知数的 叫做方程;使方程左右两边值相等的 ,叫做方程 的解;求方程解的 叫做解方程. 方程的解与解方程不同.⑵ 一元一次方程:在整式方程中,只含有 个未知数,并且未知数的次数是 ,系 数不等于0的方程叫做一元一次方程;它的一般形式为 ()0≠a . 3. 解一元一次方程的步骤:①去 ;②去 ;③移 ;④合并 ;⑤系数化为1. 二、二元一次方程(组)及解法1.二元一次方程:含有 未知数(元)并且未知数的次数是 的整式方程.2. 二元一次方程组:由2个或2个以上的 组成的方程组叫二元一次方程组.3.二元一次方程的解: 适合一个二元一次方程的 未知数的值叫做这个二元一次方程的一个解,一个二元一次方程有 个解.4.二元一次方程组的解: 使二元一次方程组的 ,叫做二元一次方程组的解. 5. 解二元一次方程的方法步骤: 二元一次方程组方程.消元是解二元一次方程组的基本思路,方法有 消元和 消元法两种. 6.易错知识辨析:(1)解方程的基本思想就是应用等式的基本性质进行转化,要注意:①方程两边不能乘 以(或除以)含有未知数的整式,否则所得方程与原方程不同解;②去分母时,不要漏 乘没有分母的项;③解方程时一定要注意“移项”要变号.(2)二元一次方程有无数个解,它的解是一组未知数的值;(3)二元一次方程组的解是两个二元一次方程的公共解,是一对确定的数值; (4)利用加减法消元时,一定注意要各项系数的符号.1.(2009年,3分)如图9加入水后,一根露出水面的长度是它的13,另一根露出水面的长度是它的15.两根铁棒长度之和为55 cm ,此时木桶中水的深度是 cm .2.(2010年,2分)小悦买书需用48元钱,付款时恰好用了1元和5元的纸币共12张.设所用的1元纸币为x 张,根据题意,下面所列方程正确的是 A .48)12(5=-+x x B .48)12(5=-+x x C .48)5(12=-+x x D .48)12(5=-+x x 【一元二次方程及其应用】1.一元二次方程:在整式方程中,只含 个未知数,并且未知数的最高次数是 的方程叫做一元二次方程.一元二次方程的一般形式是 .其中叫做二次项, 叫做一次项, 叫做常数项; 叫做二次项的系数, 叫做一次项的系数.2. 一元二次方程的常用解法:(1)直接开平方法:形如)0(2≥=a a x 或)0()(2≥=-a a b x 的一元二次方程,就可用 直接开平方的方法.(2)配方法:用配方法解一元二次方程()02≠=++a o c bx ax 的一般步骤是:①化二 次项系数为1,即方程两边同时除以二次项系数;②移项,使方程左边为二次项和一次项, 右边为常数项,③配方,即方程两边都加上一次项系数一半的平方,④化原方程为2()x m n +=的形式,⑤如果是非负数,即0n ≥,就可以用直接开平方求出方程的解.如果n <0,则原方程无解.(3)公式法:一元二次方程20(0)ax bx c a ++=≠的求根公式是21,240)x b ac =-≥.(4)因式分解法:因式分解法的一般步骤是:①将方程的右边化为 ;②将方程的左边化成两个一次因式的乘积;③令每个因式都等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解. 3. 一元二次方程根的判别式:关于x 的一元二次方程()002≠=++a c bx ax 的根的判别式为 .(1)ac b 42->0⇔一元二次方程()002≠=++a c bx ax 有两个 实数根,即=2,1x .(2)ac b 42-=0⇔一元二次方程有 相等的实数根,即==21x x .(3)ac b 42-<0⇔一元二次方程()002≠=++a c bx ax 实数根.4. 一元二次方程根与系数的关系若关于x 的一元二次方程20(0)ax bx c a ++=≠有两根分别为1x ,2x ,那么=+21x x ,=⋅21x x .5.列一元二次方程解应用题的一般步骤:审、找、设、列、解、答六步。
一次函数、一次方程和一元一次不等式(基础)知识讲解

一次函数、一次方程和一元一次不等式(基础)责编:杜少波【学习目标】1.能用函数的观点认识一次函数、一次方程与一元一次不等式之间的联系,能直观地用图形(在平面直角坐标系中)来表示方程的解及不等式的解,建立数形结合的思想及转化的思想.2.能运用一次函数的性质解决简单的不等式问题及实际问题.【要点梳理】要点一、一次函数与一元一次方程一次函数y kx b =+(k ≠0,b 为常数).当函数y =0时,就得到了一元一次方程0kx b +=,此时自变量x 的值就是方程kx b +=0的解.所以解一元一次方程就可以转化为:当某一个一次函数的值为0时,求相应的自变量的值.从图象上看,这相当于已知直线y kx b =+(k ≠0,b 为常数),确定它与x 轴交点的横坐标的值.要点二、一次函数与一元一次不等式由于任何一个一元一次不等式都可以转化为ax b +>0或ax b +<0或ax b +≥0或ax b +≤0(a 、b 为常数,a ≠0)的形式,所以解一元一次不等式可以看作:当一次函数y ax b =+的值大于0(或小于0或大于等于0或小于等于0)时求相应的自变量的取值范围.要点诠释:求关于x 的一元一次不等式ax b +>0(a ≠0)的解集,从“数”的角度看,就是x 为何值时,函数y ax b =+的值大于0?从“形”的角度看,确定直线y ax b =+在x 轴(即直线y =0)上方部分的所有点的横坐标的范围.要点三、一元一次方程与一元一次不等式我们已经学过,利用不等式的性质可以解得一个一元一次不等式的解集,这个不等式的解集的端点值就是我们把不等式中的不等号变为等号时对应方程的解.要点四、如何确定两个不等式的大小关系ax b cx d +>+(a ≠c ,且0ac ≠)的解集⇔y ax b =+的函数值大于y cx d =+的函数值时的自变量x 取值范围⇔直线y ax b =+在直线y cx d =+的上方对应的点的横坐标范围.【典型例题】类型一、一次函数与一元一次方程1、若直线y kx b =+与x 轴交于(5,0)点,那么关于x 的方程0kx b +=的解为______.【答案】5x =【解析】kx b +=0的解是直线y kx b =+与x 轴交点横坐标.【总结升华】当函数0y =时,就得到了一元一次方程kx b +=0,此时自变量x 的值就是方程kx b +=0的解.举一反三:【变式1】如图,已知直线y ax b =-,则关于x 的方程1ax b -=的解x =_________.【答案】4;提示:根据图形知,当y =1时,x =4,即1a x b -=时,x =4.∴方程1ax b -=的解x =4.【变式2】如图,直线y kx b =+分别交x 轴和y 轴于点A 、B ,则关于x 的方程kx b +=0的解为_______.【答案】2x =-;提示:方程kx b +=0的解其实就是当0y =时一次函数y kx b =+与x 轴的交点横坐标.由图知:直线y kx b =+与x 轴交于点(-2,0),即当x =-2时,y kx b =+=0.类型二、一次函数与一元一次不等式2、(2015•乐山模拟)如图,直线y=kx+b 交坐标轴于A (﹣3,0)、B (0,1)两点,则不等式﹣kx ﹣b <0的解集为( )A .x >﹣3B .x <﹣3C .x >3D .x <3【思路点拨】求﹣kx ﹣b <0的解集,即为kx+b >0,就是求函数值大于0时,x 的取值范围.【答案】A ;【解析】解:∵要求﹣kx ﹣b <0的解集,即为求kx+b >0的解集,∴从图象上可以看出等y >0时,x >﹣3.故选:A .【总结升华】本题考查了一次函数与不等式的关系及数形结合思想的应用.解决此类问题关键是仔细观察图形,注意几个关键点(交点、原点等),做到数形结合.举一反三:【高清课堂:393614 一次函数与一元一次不等式,例2】【变式】如图,直线y kx b =+与坐标轴的两个交点分别为A (2,0)和B (0,-3),则不等式kx b ++3≥0的解集是( )A .x ≥0B .x ≤0C .x ≥2D .x ≤2【答案】A ;提示:从图象上知,直线y kx b =+的函数值y 随x 的增大而增大,与y 轴的交点为B (0,-3),即当x =0时,y =-3,所以当x ≥0时,函数值kx b +≥-3.3、直线b x k y l +=11:与直线x k y l 22:=在同一平面直角坐标系中的图象如图所示,则关于x 的不等式x k b x k 21>+的解为( ).A .1->xB .1-<xC .2-<xD .无法确定【答案】B ;【解析】从图象上看x k b x k 21>+的解,就是找到1l 在2l 的上方的部分图象,看这部分图象自变量的取值范围.当1-<x 时,x k b x k 21>+,故选B.【总结升华】本题考察了用数形结合的方法求解不等式的大小关系,解题的关键是找出表示两条直线的交点的横坐标,再根据在上方的图象表示的函数值大,下方的图象表示的函数值小来解题.举一反三:【变式】直线1l :1y k x b =+与直线2l :2y k x c =+在同一平面直角坐标系中的图象如图所示,则关于x 的不等式1k x b +<2k x c +的解集为( )A .x >1B .x <1C .x >-2D .x <-2【答案】B ;提示:1y k x b =+与直线2l :2y k x c =+在同一平面直角坐标系中的交点是(1,-2),根据图象得到x <1时不等式1k x b +<2k x c +成立.4、画出函数21y x =+的图象,并利用图象求:(1)方程2x +1=0的解;(2)不等式2x +1≥0的解集;(3)当y ≤3时,x 的取值范围;(4)当-3≤y ≤3时,x 的取值范围.【思路点拨】可用两点法先画出函数21y x =+的图象,方程2x +1=0的解从“数”看就是自变量x 取何值时,函数值是0,从“形”看方程2x +1=0的解就相当于确定直线21y x =+与x 轴的交点,故图象与x 轴交点的横坐标就是方程2x +1=0的解.同理:图象在x 轴上方所有点的横坐标的集合就构成不等式2x +1>0的解集.【答案与解析】解:列表:在坐标系内描点(0,1)和1,02⎛⎫-⎪⎝⎭,并过这两点画直线,即得函数21y x =+的图象.如图所示.(1)由图象可知:直线21y x =+与x 轴交点1,02⎛⎫-⎪⎝⎭, ∴ 方程2x +1=0的解为12x =-; (2)由图象可知:直线21y x =+被x 轴在1,02⎛⎫-⎪⎝⎭点分成两部分,在点1,02⎛⎫- ⎪⎝⎭右侧,图象在x 轴的上方.故不等式2x +1≥0的解集为12x ≥-; (3)过点(0,3)作平行于x 轴的直线交直线21y x =+于点M ,过M 点作x 轴的垂线,垂足为N .则N 点坐标为(1,0);从图象上观察,在点(1,0)的左侧,函数值y ≤3,则当y ≤3时,自变量x 的取值范围是x ≤1;(4)过(0,-3)作x 轴的平行线交直线21y x =+于点P ,过P 作x 轴的垂线,垂足为H ,则点H 的坐标为(-2,0).观察图象,在(-2,0)的右侧,在(1,0)的左侧,函数值-3≤y ≤3.∴ 当-3≤y ≤3时,自变量的取值范围是-2≤x ≤1.【总结升华】仔细体会一次函数与一元一次方程及一元一次不等式之间的内在联系:(1)一元一次方程0kx b y +=(0y 是已知数)的解就是直线y kx b =+上0y y =这点的横坐标;(2)一元一次不等式1y ≤kx b +≤2y (1y ,2y 是已知数,且1y <2y )的解集就是直线y kx b =+上满足1y ≤y ≤2y 那条线段所对应的自变量的取值范围;(3)一元一次不等式kx b +≤0y (或kx b +≥0y )(0y 是已知数)的解集就是直线y kx b =+上满足y ≤0y (或y ≥0y )那条射线所对应的自变量的取值范围.举一反三:【变式】(2015秋•蒙城县校级月考)画出函数y=2x+6的图象,利用图象:(1)求方程2x+6=0的解;(2)求不等式2x+6>0的解;(3)若﹣2≤y≤2,求x 的取值范围.【答案】解:图象为:(1)观察图象知:该函数图象经过点(﹣3,0),故方程2x+6=0的解为x=﹣3;(2)观察图象知:当x >﹣3时,y >0,故不等式2x+6>0的解为x >﹣3;(3)当﹣2≤y≤2时,﹣4≤x≤﹣2.类型三、用一次函数的性质解决不等式的实际问题5、(1)如图,是函数y kx b =+的图象,它与x 轴的交点坐标是(-3,0),则方程kx b +=0的解是_________;不等式kx b +>0的解集是__________.(2)如图:OC ,AB 分别表示甲、乙两人在一次赛跑中.各自的路程S (米)和时间t (秒)的函数图象,根据图象写出一个正确的结论___________.【答案】(1)3x =-;3x <-;(2)根据图象的性质可以得到,两个两个函数的交点意义是当x =9秒时,两个人跑的路程相等,即两个人相遇;或者从图象上看出乙的速度比甲的速度快.【解析】(1)从图象上得到函数的增减性及与x 轴的交点的横坐标,即能求得方程kx b +=0的解和不等式kx b +>0的解集.(2)根据图象的性质可以得到,两个两个函数的交点意义是当x =9秒时,两个人跑的路程相等,即两个人相遇;或者从图象上看出乙的速度比甲的速度快.【总结升华】认真体会一次函数与一元一次方程及一元一次不等式之间的内在联系.理解数形结合思想的应用.。
初中数学:一次方程(组)和一次不等式(组)章节知识清单

三元一次方程组二元一次方程组一元一次方程消元消元初中数学:一次方程(组)和一次不等式(组)章节知识清单一、一元一次方程1、一元一次方程的概念:只含有一个未知数且未知数的次数是一次的方程叫做一元一次方程.2、解方程:求方程的解的过程叫做解方程.3、解一元一次方程的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)化成ax b =(0a ≠)的形式;(5)两边同除以未知数的系数,得到方程的解b x a =.二、二元一次方程1、二元一次方程:含有两个未知数的一次方程叫做二元一次方程.2、二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.3、二元一次方程的解集:二元一次方程的解有无数个,二元一次方程的解的全体叫做这个二元一次方程的解集.三、二元一次方程组1、二元一次方程组:如果方程组中含有两个未知数,且含未知数的次数都是一次,那么这样的方程叫做二元一次方程组.2、二元一次方程组的解:在二元一次方程组中,使每个方程都适合的解,叫做二元一次方程组的解.3、代入消元法:通过“代入”消去一个未知数,将方程组转化为一元一次方程,这种解法叫做代入消元法,简称代入法.4、加减消元法:通过两个方程相加(或相减)消去一个未知数,将方程组转化为一元一次方程,这种解法叫做加减消元法.四、三元一次方程组1、三元一次方程组:如果方程组中含有三个未知数,且含有未知数的项的次数都是一次,这样的方程组叫做三元一次方程组.2、解三元一次方程组的思想:五、不等式1、不等式的概念:用不等号“>”、“<”、“≤”或“≥”表示的关系式,叫做不等式.2、不等式的性质1:不等式的两边同时加上(或减去)同一个数或用一个含字母的式子,不等号的方向不变.即:如果a>b,那么a+m>b+m;如果a<b,那么a+m<b+m.3、不等式的性质2:不等式的两边同时乘以(或除以)同一个正数,不等号的方向不变.即:已知m>0,如果a>b,那么am>bm(或a bm m>);如果a<b,那么am<bm(或a bm m<).4、不等式的性质3:不等式的两边同时乘以(或除以)同一个负数,不等号的方向改变.即:已知m<0,如果a>b,那么am<bm(或a bm m<);如果a<b,那么am>bm(或a bm m>).六、一元一次不等式只含有一个未知数,且未知数的次数是一次且系数不为零的不等式,称为一元一次不等式.解一元一次不等式的一般步骤:(1)去分母;(2)去括号;(3)移项;(4)化成ax b>(或ax b<等)的形式(其中0a≠);(5)两边同时除以未知数的系数,得到不等式的解集.七、一元一次不等式组1.一元一次不等式组:有几个含有同一个未知数的一次不等式组成的不等式组,叫做一元一次不等式组.2、不等式组的解集:不等式组中所有不等式的解集的公共部分叫做这个不等式组的解集.3、解不等式组:求不等式组解集的过程叫做解不等式组.4、解一元一次不等式组的一般步骤:(1)求出不等式组中各个不等式的解集;(2)在数轴上表示各个不等式的解集;(3)确定各个不等式解集的公共部分,就得到这个不等式组的解集.1.方程的解和解方程⎧⎨⎩方程的解:使方程的左右两边的叫方程的解;解方程:求方程的解的过程知数的值;相等未2.一元一次方程(0)0(0)(0).ax b a ax b a b ax b a x a ⎧⎪=≠⎧⎪⎨⎪⎪+=≠⎩⎨⎪⎪⎪=≠=⎪⎩定义:只含有,并且未知数的次数是的;最简形式:表示形式标准形式:解一元一次方程步骤:去分母;去括号;移项; 化成一个未知数一次方程;① ②③④⑤3.等式的性质⎧⎨⎩等式两边同时加上(减去)或,所得结果仍是等式;等式两同一个数同一个代数式同一个不等于零边同时乘以同一个数(或除以的数),所得结果仍是等式;①②4.一元一次方程的应用:==+=1+=+====.=1a b ⎧⎪⎪⎪⨯⨯⨯⨯⎪⎨⨯⎪⎪⨯⨯⨯⎪⨯⎪⎩步骤分配ax bx 利率本金利率期数折扣:审题;设元;列方程;解方程;检验;作答.问题:两个量之比为,则设这两个量为和;问题:利息;本利和本金利息本金(利率期数)问题:售价成本价;新售价原售价折扣.问题:路程速度时间;相遇路程时间;追及路程追及时间问题:工作时间(工作总量)利润行程速度和速度差工程工作效率①②③④⑤⑥5.不等式的概念><≥≤≠⎧⎪>≥≠⎧⎨⎨⎪<≤⎩⎩不等关系大于大于或等于不(1)概念:用不等号“”、“”、“”、“”、“”表示的式子;; 表示“”或“”小于不等于小于小于; 表;(2)常见不等号:; 表示“”或”不大于“或等于6.不等式的基本性质1;002;.3;.a b a b a b a b am bm m m a b a b a m m bm m m m mm ⎧⎪>⇒>⎪⎪>⇒±±>>><<⎨⎪⎪>⇒⎪⎩<(1)不等式的基本性质:(2)不等式的基本性质:且(3)不等式的基本性质:且7.一元一次不等式的解法(0);ax b a ⎧⎪⎪⎪⎨⎪⎪⎪⎩>≠(1)不等式的解:能使不等式成立的;(2)不等式的解集:一个含有未知数的不等式的,组成这个不等式的解集;(3)解不等式:求不等式解集的过程;(4)解一元一次不等式未知数的值所有解去分母去括号移项未知数的系的步骤:;;;化成两边同除以数.① ②③④⑤8.一元一次不等式组(1)(2),;;;(3)x a x x a x a x a x a a b x b x b x b x b x a b b ><<>⎧⎧⎧⎧>⎨⎨⎨⎨><>><⎩⎩<<<⎩⎩同一个未知数几个一元一次不等式公定义:关于的合在一起组成一个元一次不等式组;解集:各个不等式的解集的叫这个一元一次不等式组的解集; 设的解集的解集的解集的解集;解法:一般步骤求各不等式的;在表示各不等式解集; 共部分无解解 确集轴上定数 ①②③⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩各不等式解集的.公共部分9.二元一次方程:含有两个未知数,并且所含未知数的项的次数都是1的方程;具备两个条件:1 1.⎧⎨⎩①含有未知数;②所含的次数两个未知数的的项未知数都是,而不是的次数都是10.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫二元一次方程的解;二元一次方程的解集:二元一次方程的解有无数个,它们的解的全体叫二元一次方程的解集.11.二元一次方程组:如果方程组中含有两个未知数,且含未知数的项的次数都是一次;注意:.⎧⎪⎨⎪⎩①方程的个数可以;②组成方程组的方程的,也可以是一元的;③保证超过两个不一定都是二元方程组有两个未知数中二元一次方程组的解:使二元一次方程组中的两个方程左、右两边的值都相等的两个未知数的值.二元一次方程组的解法⎫⎧⎪⎨⎬⎪⎩⎭代入代入一元一次加减相消元法:通过“”消去一个未知数,将方程组转化为方程.消元法:通过将两个方程()消去一个未知数加减12.三元一次方程组.⎧⎪⎨−−−−→−−−−→⎪⎩加减或代入加减或代入消元消元三个未知定义:如果方程组中含有,且的次数都是.解法:三元一次方程组二元一次方程组一元一次方数含未知数的项程一次。
【6年级数学】六年级寒假班第8讲:一次方程(组)和一次不等式(组)章节复习-教师版
六年级寒假班数学(教师版)最新教案六年级寒假班数学(教师版)最新教案一次方程(组)和一次不等式(组)是初中数学六年级下学期第2章的内容.本章学习了一元一次方程、二元一次方程(组)、三元一次方程组以及一元一次不等式(组)的概念及其解法,学习时应注意方程与不等式及其解法之间的联系与区别,体会消元与化归的数学方法和数学思想,加强用方程解决实际问题的意识.单元练习:一次方程(组)和一次不等式(组)内容分析知识结构一次方程(组)一次不等式(组)三元一次方程组一元一次方程二元一次方程(组) 一元一次不等式(组)三元一次方程组一元一次方程二元一次方程组 消元消元多元一元化归思想实际问题检验解方程方程获得问题的解构建方程解决 问 题 方程意识【练习1】 下列各式中,方程有( )个(1)633-+=-;(2)35x +=;(3)22ππ⨯=;(4)38a =;(5)7y =;(6)32p q -;(7)719nm +=;(8)1a a =+. A .3B .4C .5D .6【难度】★【答案】C【解析】含有未知数的等式叫做方程;(2)、(4)、(5)、(7)、(8)都是方程. 【总结】本题考查了方程的定义.【练习2】 下列各式中,一元一次方程有( )个(1)30x =; (2)437x y -=; (3)21303x -=;(4)()397y y --=; (5)23x -; (6)4x ≠. A .1B .2C .3D .4【难度】★【答案】B【解析】含有一个未知数,并且未知数的最高次数式一次的方程为一元一次方程; 故(1)、(4)都是.【总结】本题考查了一元一次方程的定义.【练习3】 下列各式中,二元一次方程有( )个(1)2311x y -=;(2)23xy =-;(3)35m y+=;(4)25p q ->;(5)221x x +=;(6)21953m n -=.A .1B .2C .3D .4【难度】★【答案】B【解析】含有两个未知数,并且未知数的最高次数式一次的方程为二元一次方程; 故(1)、(6)都是.【总结】本题考查了二元一次方程的定义.【练习4】 下列各式中,二元一次方程组有( )个选择题(1)()()23111x y xy x y +=-⎧⎪⎨=+-⎪⎩;(2)31230x y x y +=⎧⎨-=⎩;(3)235x x y =⎧⎨+=-⎩;(4)3227x y x y -=+=+.A .1B .2C .3D .4【难度】★【答案】D【解析】含有两个相同未知数的两个一次方程所组成的方程组叫做二元一次方程组; (1)中虽然有二次项,但是左右两边会抵消;故全都是二元一次方程组. 【总结】本题考查了二元一次方程组的定义.【练习5】 二元一次方程组324526x y x y -=⎧⎨-=⎩的解是( )A .11x y =⎧⎨=-⎩B .112x y =-⎧⎪⎨=⎪⎩C .112x y =-⎧⎪⎨=-⎪⎩D .112x y =⎧⎪⎨=-⎪⎩【难度】★【答案】D【解析】解:⎩⎨⎧=-=-,②,①625423y x y x ,由①-②得:22-=-x ,解得:1=x ,代入①:42-13=⨯y ,解得:21-=y ,所以方程组的解为:112x y =⎧⎪⎨=-⎪⎩.【总结】本题考查了二元一次方程组的解法.【练习6】 如果0m n <<,那么下列各式中正确的是( )A .0.30.3m n <B .22m n <C .11m n <D .m n m n -<+【难度】★【答案】A【解析】由不等式的性质可知A 正确. 【总结】本题考查了不等式的性质的运用.【练习7】 下列判断中正确的是( )A .如果0x <,那么15x x <B .不等式35x ->-的解集是53x <C .如果113x <-,那么3x >-D .不等式组11x x >⎧⎨<⎩的解集为1x =【难度】★【答案】B【解析】由不等式的性质(1)、(2)、(3)可以判断;必须熟练掌握. 【总结】本题考查了不等式及不等式组的解集的确定.【练习8】 若方程()2210a x bx c +++=是表示字母x 的一元一次方程,则( )A .12a =,0b ≠,c 为任意数 B .12a ≠,0b ≠,0c = C .12a =-,0b ≠,0c ≠D .12a =-,0b ≠,c 为任意数【难度】★★【答案】D【解析】由题意得:此方程为一元一次方程,故012=+a ,解得:21-=a ,0≠b ,c 为任意数即可.【总结】本题考查了一元一次方程的概念.【练习9】 下列式子中一定正确的是( )A .23a a <B .a b a -<C .2a a >D .322x x-< 【难度】★★【答案】D【解析】D 中左右两边同时乘以2,则x x <-3,再同时减掉x ,则03<-成立. 【总结】本题考查了不等式的性质应用.【练习10】 下列说法中错误的是( )A .方程ax b =的解是bx a=(0a ≠)B .如果ax b ->,则bx a<-(0a ≠)C .若2k =时,方程()22k x k -=无解D .8-是不等式32x ->一个解【难度】★★【答案】B【解析】B 中a 的正负不确定,当0>a 时,0<-a ,则a b x -<;当0<a 时,0>-a ,则abx ->. 【总结】 本题考查了不等式的性质及方程的解的应用.【练习11】 下列各对数值,是方程342x y +=的解的为( )A .012x y =⎧⎪⎨=-⎪⎩B .22x y =-⎧⎨=⎩C . 114x y =⎧⎪⎨=-⎪⎩D . 21x y =-⎧⎨=⎩【难度】★★【答案】B【解析】二元一次方程的解有无数组,代入验证即可. 【总结】本题考查了二元一次方程的解.【练习12】 某运输队运煤,第一天运了总量的27,第二天运煤恰好是第一天的23,还剩14 吨,设一共运煤x 吨,则可列出方程( )A .22214773x x x +⨯=-B .221473x x x ++=C .222114737x x x ⎛⎫+-=- ⎪⎝⎭D .22214773x x x +÷+=【难度】★★【答案】A【解析】找出等量关系列方程:第一天运煤+第二天运煤=共运煤-剩下的. 【总结】本题考查了列方程解应用题的思想.【练习13】 学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3 : 2,求两种球各有多少个?若设篮球有x 个,排球有y 个,则根据题意得到的方程组是( ) A .2332x y x y =-⎧⎨=⎩B .2332x y x y =+⎧⎨=⎩C .2323x y x y =-⎧⎨=⎩D .2323x y x y =+⎧⎨=⎩【难度】★★【答案】C【解析】找准题目中的两个等量关系:①32-=y x ,②2:3:=y x ,故y x 32=. 【总结】本题考查了由实际问题抽象出二元一次方程组.【练习14】 已知不等式组00x a x b -<⎧⎨-<⎩的解集为x a <,则不等式组00x a x b +>⎧⎨+>⎩的解集为( )A .x a <-B .x a >-C .x b >-D .x b <-【难度】★★【答案】B【解析】解: 不等式组⎩⎨⎧<-<-00b x a x 的解集为a x <, ∴b a <, ∴b a ->-,不等式组⎩⎨⎧>+>+00b x a x 的解为⎩⎨⎧->->b x ax , ∴不等式组的解集为a x ->.【总结】本题考查了不等式组解得确定:同大取大、同小取小.【练习15】 323x y+=的正整数解的个数为( )个A .1B .2C .3D .4【难度】★★【答案】B【解析】方程两边同时乘以6去分母:1823=+y x ,则x y 239-=,其中x 从1开始取整数 即可验证.【总结】本题考查了对二元一次方程的整数解的理解.【练习16】 观察下列方程组,无解的是( )A .61x y x y -=⎧⎨+=-⎩B .52210x y x y -=-⎧⎨-=⎩C .5229x y x y -=⎧⎨+=⎩D .423x y x y +=⎧⎨-=⎩【难度】★★【答案】B【解析】B 中方程组可化为⎩⎨⎧=--=-55y x y x ,此方程组无解.【总结】本题考查了判断二元一次方程组是否有解.【练习17】 已知不等式组5x x m >⎧⎨>⎩的解集为5x >,则m 的取值范围是( )A .5m >B .5m ≥C .5m <D .5m ≤【难度】★★【答案】D【解析】根据不等式组有解可知,必须是同大取大,所以5≤m . 【总结】本题考查了不等式的解集的确定.【练习18】 已知方程组35223x y k x y k +=+⎧⎨+=⎩,其中x 是y 的2倍,则k 的值是( )A .72-B .72C .0D .以上都不对【难度】★★【答案】B【解析】由题意得:⎩⎨⎧=++=+,②,①k y x k y x 32253,①-②:22=+y x ,又y x 2=,所以方程组的解集为⎪⎩⎪⎨⎧==211y x ,则2732=+=y x k .。
第8讲用数轴表示不等式的解集及一元一次不等式组(教师版)

第8讲用数轴表示不等式的解集及一元一次不等式组知识精要一、不等式的解集1、不等式解的全体叫做不等式的解集。
(注:一般情况下一元一次方程的解只有一个,一元一次不等式的解可以有无数个。
)2、不等式的解集可以再数轴上直观的表示出来。
如:在数轴上表示大于3的数的点应该数3所对应点的左边还是右边?(右边)因此我们可以在数轴上把x>3直观地表示出来.画图时要注意方向(向右)和端点(不包括数3,在对应点画空心圆圈).如图所示:同样,如果某个不等式的解集为x≤-2,那么它表示x取那些数?此时在作x≤-2的数轴表示时,要包括-2的对应点,因而在该点处应画实心圆点.如图所示:引导学生总结出在数轴上表示不等式解集的要点:小于向左画,大于向右画;无等号画空心圆圈,有等号画实心圆点。
2、一元一次不等式组1、有几个含有同一个未知数的一次不等式组成的不等式组,叫做一元一次不等式组。
2、不等式组中所有不等式的解集的公共部分叫做这个不等式组的解集。
3、求不等式组的解集的过程叫做解不等式组。
4、解一元一次不等式组的一般步骤是:(1)求出不等式组中各个不等式的解集;(2)在数轴上表示各个不等式的解集;(3)确定各个不等式解集的公共部分,就得到这个不等式组的解集。
【典型例题】例1. 解不等式3(1)5182x x x +-+>-【思路点拨】不等式中含有分母,应先根据不等式的基本性质2去掉分母,再作其他变形.去分母时,不要忘记给分子加括号.【答案与解析】解:去分母,得8x+3(x+1)>8-4(x -5), 去括号,得8x+3x+3>8-4x+20, 移项,得8x+3x+4x >8+20-3,合并同类项,得15x >25,系数化为1.得.53x >∴不等式的解集为.53x >【总结升华】解一元一次不等式与解一元一次方程的步骤异同见下表:ax =bax >bax <b解:当a ≠0时,;b x a=当a =0,b ≠0时,无解;当a =0,b =0时,x为任意有理数.解:当a >0时,;b x a>当a <0时,;b x a<当a =0,b ≥0时,无解;当a =0,b <0时,x 为任意有理数.解:当a >0时,;b x a<当a <0时,;b xa>当a =0,b ≤0时,无解;当a =0,b >0时,x 为任意有理数.【变式】(湖南益阳)解不等式,并把解集在数轴上表示出来.5113x x -->解:去分母得5x -1-3x >3,移项、合并同类项,得2x >4, 系数化为1,得x >2,解集在数轴上的表示如图所示.例2.某市居民用电的电价实行阶梯收费,收费标准如下表:一户居民每月用电量x (单位:度)电费价格(单位:元/度)0<x≤200a 200<x≤400b x >4000.92(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a ,b 的值.(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?【思路点拨】(1)根据题意即可得到方程组,然后解此方程组即可求得答案;(2)根据题意列不等式,解不等式.【答案与解析】解:(1)根据题意得:,解得:.(2)设李叔家六月份最多可用电x 度,根据题意得:200×0.61+200×0.66+0.92(x﹣400)≤300,解得:x≤450.答:李叔家六月份最多可用电450度.【总结升华】考查了一元一次方程组与一元一次不等式的应用.注意根据题意得到等量关系是关键.例3. 解不等式组: ,并求出正整数解。
一次方程(组)复习教案

一次方程(组)复习教案教学目标:1. 掌握一次方程的概念和解法。
2. 学会解一次方程组的方法和技巧。
3. 能够应用一次方程(组)解决实际问题。
教学内容:1. 一次方程的定义和解法。
2. 一次方程组的定义和解法。
3. 一次方程(组)的解的判定。
4. 一次方程(组)的应用。
教学步骤:一、导入:1. 复习一次方程的概念和解法。
2. 引入一次方程组的定义和解法。
二、新课内容:1. 讲解一次方程的解法,包括解的定义、解的判定、解的求法。
2. 讲解一次方程组的解法,包括解的定义、解的判定、解的求法。
三、实例解析:1. 提供几个一次方程的实例,让学生独立求解,并判断解的正确性。
2. 提供几个一次方程组的实例,让学生独立求解,并判断解的正确性。
四、练习:1. 让学生做一些一次方程的练习题,巩固解法。
2. 让学生做一些一次方程组的练习题,巩固解法。
五、应用拓展:1. 提供一些实际问题,让学生应用一次方程(组)解决。
2. 讨论一次方程(组)在实际问题中的应用和意义。
教学评价:1. 课后作业:布置一些一次方程(组)的练习题,检验学生掌握情况。
2. 课堂问答:提问学生一次方程(组)的概念和解法,检验学生理解情况。
教学资源:1. 教案、PPT、练习题。
2. 教材、辅导书。
教学时间:1. 课时:45分钟。
2. 备课时间:1小时。
一次方程(组)复习教案教学目标:1. 掌握一次方程的概念和解法。
2. 学会解一次方程组的方法和技巧。
3. 能够应用一次方程(组)解决实际问题。
教学内容:1. 一次方程的定义和解法。
2. 一次方程组的定义和解法。
3. 一次方程(组)的解的判定。
4. 一次方程(组)的应用。
教学步骤:六、巩固练习:1. 提供几个一次方程的实例,让学生独立求解,并判断解的正确性。
2. 提供几个一次方程组的实例,让学生独立求解,并判断解的正确性。
七、拓展提升:1. 提供一些一次方程(组)的综合性实例,让学生独立求解。
2. 引导学生探讨一次方程(组)在不同情境下的应用。
专题复习2—一次方程(组)和不等式(组)

C. ; D. ;
4、下列方程变形正确的是( )
A. 由 ,得 ; B.由 ,得 ;
C.由 ,得 ; D.由 ,得 ;
5、长方形的周长为14厘米,长比宽的3倍少1厘米,设宽为 ,依题意列方程,下列正确的是( )
A. ; B. ;
C. ; D. ;
6、已知方程 ,用含 的式子表示 正确的是( )
注意:①方程组的解必须用“{”表示;
②二元一次方程组的解是组成方程组的两个二元一次方程的公共解;
③方程组的解一定是两个二元一次方程的解,而两个二元一次方程的解不一定是方程组的解。
(2)检验:
将这组数值分别代入方程组中的每个方程,当这组数值满足所有方程时,就说这组数值是方程组的解,否则,就不是。
6、用代入消元法解二元一次方程组
(4) (5) (6)
3、一元一次不等式的解法
主要依据:不等式的基本性质
注意:①在不等式的两边乘以(或除以)同一个负数,不等号方向一定要改变。
②不等式两边不能都乘以0,否则不等式就变为等式了。
4、如何用数轴表示不等式的解集
数形结合:(1)确定“界点”,确定“方向”
(2)若解集包含“界点”,则用实心圆点;若解集不包含“界点”,则用空心圆圈。对于方向,相对于“界点”而言,大于向右,小于向左。
3、项的次数:在一项中,所有未知数的指数和称为这一项的次数。
4、常数项:不含未知数的项,称为常数项。
3、列方程的方法
1、列方程:为了求得未知数,在未知数和已知数之间建立一种等量关系,就是列方程。
2、列方程步骤:第一、先根据题设条件设未知数;第二、找未知数和已知数之间的等量关系
4、方程的解:使方程的左右两边相等的未知数的值叫做方程的解
六年级《一次方程(组)复习》教案

一次方程(组)复习
教学目标:通过问题串的解决,复习一次方程(组)的相关概念,进一步熟练掌握解一次方程和一次方程组的方法,加深理解解题的思想方法;能正确分析实际问题中的数量关系,列出正确的方程(组);在学习过程中领悟解方程(组)中化归、消元的数学思想方法,体会实际生活与数学的联系。
教学重点:一次方程(组)的相关概念的复习、列方程(组)解应用问题的复习
教学难点:实际问题中的数量关系的正确理解
教案设计说明:
目前基本结束了新课的学习,进入期末复习的阶段。
方程的内容是本学期学习的重点,
学生要掌握的主要内容有:一次方程(组)的相关概念、一次方程(组)的解法、列一次方程(组)解应用题。
学生存在困难和出错情况最多的是:一次方程(组)的计算、不会分析应用问题的数量关系。
所以本节课主要针对这两方面复习。
方程在初等数学中占有较大的比重,一次方程(组)的概念和解法也是后续学习二元一次方程、分式方程等内容的基础。
所以在复习中要重视学生对相关概念的理解,能判别一元一次方程、二元一次方程、二元一次方程组合三元一次方程组。
在掌握一元一次方程的解法的基础上,掌握运用化归的思想解二元一次方程组和三元一次方程组。
列方程解应用题不但在培训学生分析问题和解决问题的能力方面起到相当大的作用,而且还是解决实际问题的有利工具。
通过学习,进一步培养学生有意识、有目的地用方程或方程组解决实际问题的能力,突出用方程模型解决实际问题的优越性。
一次方程(组)复习教案

一次方程(组)复习教案第一章:一次方程的定义与解法1.1 方程的定义:解释方程的概念,方程是一个含有未知数的等式。
强调方程中的等号表示两边的值相等。
1.2 一次方程的定义:介绍一次方程的概念,一次方程是最高次数为1的方程。
举例说明一次方程的一般形式:ax + b = 0。
1.3 解一次方程的步骤:讲解解一次方程的步骤,包括:1. 将方程写成标准形式ax + b = 0。
2. 移项,将未知数移到方程的一边,常数移到另一边。
3. 化简方程,消去系数。
4. 求解未知数的值。
1.4 解一次方程的练习:提供一些练习题,让学生根据解一次方程的步骤求解。
引导学生运用加减法、乘除法等运算来化简方程。
第二章:二元一次方程的定义与解法2.1 二元一次方程的定义:介绍二元一次方程的概念,二元一次方程是含有两个未知数的一次方程。
举例说明二元一次方程的一般形式:ax + = c。
2.2 解二元一次方程的步骤:讲解解二元一次方程的步骤,包括:1. 将方程组写成标准形式,即两个方程分别写成ax + = c 的形式。
2. 利用代入法或消元法求解未知数的值。
3. 检验解的可行性,确保解满足原方程组的所有方程。
2.3 解二元一次方程组的练习:提供一些练习题,让学生根据解二元一次方程的步骤求解。
引导学生运用代入法、消元法等方法来求解方程组。
第三章:一次方程与一次不等式的关系3.1 一次方程与一次不等式的定义:介绍一次方程与一次不等式的概念,一次方程是等式,而一次不等式是不等号连接的两个表达式。
举例说明一次不等式的一般形式:ax + b > c 或ax + b ≤c。
3.2 一次方程与一次不等式的关系:解释一次方程的解集是一次不等式的解集的特殊情况。
讲解如何从一次方程的解集中找出满足一次不等式的解。
3.3 解一次不等式的步骤:讲解解一次不等式的步骤,包括:1. 将不等式写成标准形式,即ax + b ≤c 或ax + b > c。
沪教版数学六年级下册第六章《一次方程(组)和一次不等式(组)》复习课教学设计

沪教版数学六年级下册第六章《一次方程(组)和一次不等式(组)》复习课教学设计一. 教材分析沪教版数学六年级下册第六章《一次方程(组)和一次不等式(组)》复习课,主要是对本章内容的一次全面梳理和巩固。
本章内容主要包括一次方程(组)和一次不等式(组)的定义、解法及其应用。
通过复习,使学生能够熟练掌握一次方程(组)和一次不等式(组)的解法,能够灵活运用到实际问题中。
二. 学情分析六年级的学生已经掌握了初步的代数知识,对于一次方程(组)和一次不等式(组)的概念和解法有一定的了解。
但在实际应用中,部分学生可能会遇到一些困难,如对概念理解不深,解法运用不熟练等。
因此,在复习课中,需要针对这些情况,进行有针对性的教学。
三. 教学目标1.使学生掌握一次方程(组)和一次不等式(组)的概念、解法及其应用。
2.提高学生解决实际问题的能力,培养学生的逻辑思维和运算能力。
3.培养学生独立思考、合作交流的学习习惯,提高学生的数学素养。
四. 教学重难点1.重难点:一次方程(组)和一次不等式(组)的解法及其应用。
2.难点:对一次方程(组)和一次不等式(组)概念的理解,解法的灵活运用。
五. 教学方法1.采用问题驱动法,引导学生主动探索、思考。
2.使用案例分析法,让学生在实际问题中运用一次方程(组)和一次不等式(组)的解法。
3.采用小组合作交流法,培养学生的团队协作能力。
六. 教学准备1.准备相关的教学案例和问题,用于引导学生思考和练习。
2.准备PPT,用于辅助教学。
七. 教学过程1.导入(5分钟)通过一个实际问题,引入一次方程(组)和一次不等式(组)的概念,激发学生的学习兴趣。
2.呈现(10分钟)呈现一次方程(组)和一次不等式(组)的定义、解法及其应用,让学生对所学知识有一个全面的回顾。
3.操练(10分钟)针对一次方程(组)和一次不等式(组)的解法,设计一些练习题,让学生独立完成,巩固所学知识。
4.巩固(10分钟)针对学生在操练中遇到的问题,进行讲解和辅导,使学生能够熟练掌握一次方程(组)和一次不等式(组)的解法。
【六年级寒假班讲义】第8讲:一次方程(组)和一次不等式(组)章节复习(学生版)
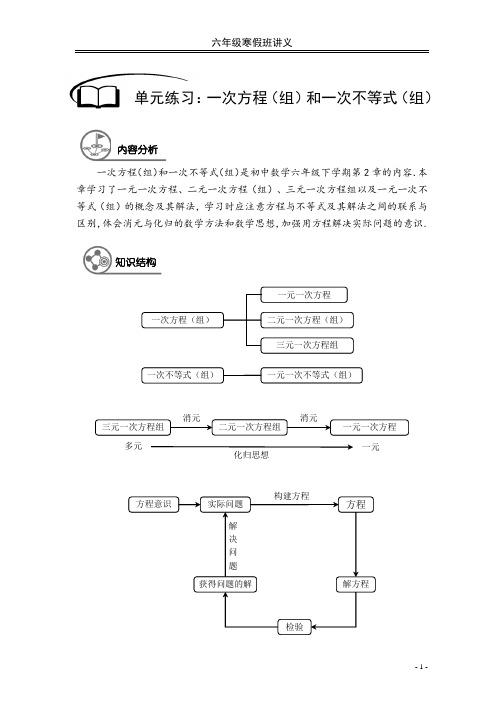
- 1 -一次方程(组)和一次不等式(组)是初中数学六年级下学期第2章的内容.本章学习了一元一次方程、二元一次方程(组)、三元一次方程组以及一元一次不等式(组)的概念及其解法,学习时应注意方程与不等式及其解法之间的联系与区别,体会消元与化归的数学方法和数学思想,加强用方程解决实际问题的意识.单元练习:一次方程(组)和一次不等式(组)内容分析知识结构一次方程(组)一次不等式(组)三元一次方程组一元一次方程二元一次方程(组) 一元一次不等式(组) 三元一次方程组一元一次方程二元一次方程组 消元消元多元一元化归思想实际问题检验解方程方程获得问题的解构建方程解决 问 题 方程意识- 2 -【练习1】 下列各式中,方程有( )个(1)633-+=-;(2)35x +=;(3)22ππ⨯=;(4)38a =;(5)7y =;(6)32p q -;(7)719nm +=;(8)1a a =+. A .3B .4C .5D .6【练习2】 下列各式中,一元一次方程有( )个(1)30x =;(2)437x y -=;(3)21303x -=;(4)()397y y --=;(5)23x -;(6)4x ≠. A .1B .2C .3D .4【练习3】 下列各式中,二元一次方程有( )个(1)2311x y -=;(2)23xy =-;(3)35m y+=;(4)25p q ->;(5)221x x +=;(6)21953m n -=.A .1B .2C .3D .4【练习4】 下列各式中,二元一次方程组有( )个(1)()()23111x y xy x y +=-⎧⎪⎨=+-⎪⎩;(2)31230x y x y +=⎧⎨-=⎩;(3)235x x y =⎧⎨+=-⎩;(4)3227x y x y -=+=+.A .1B .2C .3D .4【练习5】 二元一次方程组324526x y x y -=⎧⎨-=⎩的解是( )A .11x y =⎧⎨=-⎩B .112x y =-⎧⎪⎨=⎪⎩C .112x y =-⎧⎪⎨=-⎪⎩D .112x y =⎧⎪⎨=-⎪⎩【练习6】 如果0m n <<,那么下列各式中正确的是( )A .0.30.3m n <B .22m n <C .11m n <D .m n m n -<+选择题- 3 -【练习7】 下列判断中正确的是( )A .如果0x <,那么15x x <B .不等式35x ->-的解集是53x <C .如果113x <-,那么3x >-D .不等式组11x x >⎧⎨<⎩的解集为1x =【练习8】 若方程()2210a x bx c +++=是表示字母x 的一元一次方程,则( )A .12a =,0b ≠,c 为任意数 B .12a ≠,0b ≠,0c = C .12a =-,0b ≠,0c ≠D .12a =-,0b ≠,c 为任意数【练习9】 下列式子中一定正确的是( )A .23a a< B .a b a -< C .2a a >D .322x x-< 【练习10】 下列说法中错误的是( )A .方程ax b =的解是bx a=(0a ≠)B .如果ax b ->,则bx a<-(0a ≠)C .若2k =时,方程()22k x k -=无解D .8-是不等式32x ->一个解【练习11】 下列各对数值,是方程342x y +=的解的为( )A .012x y =⎧⎪⎨=-⎪⎩B .22x y =-⎧⎨=⎩C . 114x y =⎧⎪⎨=-⎪⎩D . 21x y =-⎧⎨=⎩【练习12】 某运输队运煤,第一天运了总量的27,第二天运煤恰好是第一天的23,还剩14 吨,设一共运煤x 吨,则可列出方程( )A .22214773x x x +⨯=-B .221473x x x ++=C .222114737x x x ⎛⎫+-=- ⎪⎝⎭D .22214773x x x +÷+=【练习13】 学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3 : 2,求两种球各有多少个?若设篮球有x 个,排球有y 个,则根据题意得到的方程组是( ) A .2332x y x y =-⎧⎨=⎩B .2332x y x y =+⎧⎨=⎩C .2323x y x y =-⎧⎨=⎩D .2323x y x y =+⎧⎨=⎩【练习14】 已知不等式组00x a x b -<⎧⎨-<⎩的解集为x a <,则不等式组00x a x b +>⎧⎨+>⎩的解集为( )A .x a <-B .x a >-C .x b >-D .x b <-- 4 - 【练习15】 323x y+=的正整数解的个数为( )个A .1B .2C .3D .4【练习16】 观察下列方程组,无解的是( )A .61x y x y -=⎧⎨+=-⎩B .52210x y x y -=-⎧⎨-=⎩C .5229x y x y -=⎧⎨+=⎩D .423x y x y +=⎧⎨-=⎩【练习17】 已知不等式组5x x m >⎧⎨>⎩的解集为5x >,则m 的取值范围是( )A .5m >B .5m ≥C .5m <D .5m ≤【练习18】 已知方程组35223x y k x y k+=+⎧⎨+=⎩,其中x 是y 的2倍,则k 的值是( )A .72-B .72C .0D .以上都不对【练习19】 如果关于x 的不等式32x a ->的所有正整数解之和为6,则a 的取值范围为( ) A .5a ≥-B .3a <-C .53a -<<-D .53a -≤<-【练习20】 如果关于x 的不等式组30310x m x m -->⎧⎨-+<⎩无解,那么m 的取值范围是( )A .2m <B .2m ≤C .2m >D .2m ≥【练习21】 若3350m x ---=是一元一次方程,则m =______.【练习22】 把方程5239x y -+=化成用含x 的式子表示y 的形式,得______________.【练习23】 用不等式表示:2x y+减去()21x --所得的差是非负数________________. 填空题- 5 -【练习24】 用不等号填空,并说明不等式变形过程.(1)若x y >,则4x -______4y -; (2)若235x +≤-,则3x ______7-; (3)若1233x x -≥-,则x ______2; (4)若x y >,则6x -______6y -; (5)若x y >,则2x -______2y -; (6)若x y >,0m >,则mx ______my ; (7)若m n ≥,20k +<,则mk ______nk .【练习25】 解集32x -≤<中的整数解为__________________.【练习26】 不等式组340731x x +>⎧⎨-≥-⎩的解集为____________________.【练习27】 判断:(1)如果a b >,那么3232a b ->-;( ) (2)如果a b <,那么22a b <;( ) (3)如果22a b >,那么a b >;( ) (4)如果a b >,那么a b >;( ) (5)如果1a >,那么a 比1a大;( ) (6)如果5a >,那么55a a -=-;( ) (7)如果144m <-,那么1m <-;( )(8)如果x y >,那么()()2211m x m y -->--.( ) 【练习28】 若0a b +<,且0ab >,则a ______0,b ______0.- 6 - 【练习29】 满足不等式()10484x x ++≤的最大整数解是_______.【练习30】 当x ______时,52x -的值是正的,此时最小的整数x =_______.【练习31】 如果43x y =⎧⎨=-⎩是方程436x ay -=的一个解,则a =______.【练习32】 如果3235351m n m n x y +--++=-是二元一次方程,那么m =______,n =_______.【练习33】 若357x -+=,则x =______.- 7 -【练习34】 若:5:3x y =,且x 与y 的和是10,则x =______,y =______.【练习35】 已知1y =是方程()1223m y y --=的解,那么关于x 的方程 ()()3225m x m x --=-的解是______.【练习36】 若关于x 、y 方程组352278x y ax y a -=⎧⎨+=-⎩的解互为相反数,则a =______.【练习37】 如果()222303x y x ⎛⎫+++-= ⎪⎝⎭,那么2016y =______.- 8 - 【练习38】 甲、乙两班共有88名学生,若从乙班调25人到甲班,则甲班人数是乙班人数的3倍,设甲班x 人,乙班y 人,可列出方程组_______________________,并解得甲班有______人,乙班有______人.【练习39】 有一个两位数,个位数字和十位数字之和是9,且这个两位数不大于63,求这个两位数.可设这个两位数的个位数字为x ,根据题意,可列不等式 ________________________,最后这个两位数为_______________________.【练习40】 若关于x 的不等式()22a x a +>+的解集是1x <,则a 的取值范围是______.- 9 -【练习41】 解方程:(1)1071253x x x +=--;(2)()()160%2180%22x x +-+=;(3)111257918643x ⎧⎫⎡+⎤⎛⎫+-+=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭; (4)1.88 1.5350.401.220.3x x x -----=.【练习42】 解不等式:(1)()23213x x +-≤;(2)()30%151%x x +<+;(3)()()11221225x x x ⎡⎤-+≤-⎢⎥⎣⎦; (4)()()0.20.30.40.50.10.21110.030.066x x --->+.解答题【练习43】解不等式组:(1)()()3241353324x xx x⎧-->-⎪⎨+≤+⎪⎩;(2)()210381274332xxxxx⎧---≤-⎪⎪⎨⎪-<+⎪⎩;(3)13222364553522x xx xx x⎧+>+⎪⎪+>+⎨⎪⎪-<-⎩;(4)()1226323112184xxx xx x⎧+>⎪⎪⎪+≥+⎨⎪+-⎪-<-⎪⎩.【练习44】解方程组:(1)521347a ba b+=-⎧⎨+=⎩;(2)5.3 4.7804.75.320x yx y+=⎧⎨+=⎩;- 10 -- 11 -(3)34135353x y z x y z x y z +-=⎧⎪-+=⎨⎪+-=⎩;(4)2636315764949x y z x y z x y z ++=⎧⎪++=⎨⎪-+=⎩.【练习45】 关于x 的方程()143321223x x x a x x +----=-的解是最小的质数的倒数,求a 的值.【练习46】 解方程:2015122320152016x x x +++=⨯⨯⨯.【练习47】若关于x、y的方程组2323ax byx y-=⎧⎨-=-⎩和3424y xax by-=⎧⎨+=-⎩有相同的解,求a、b的值.【练习48】甲、乙两人同时求7mx ny-=的整数解,甲求出一组解为34xy=⎧⎨=⎩,而乙把7mx ny-=中的7看成1,求出一组解为12xy=⎧⎨=⎩,求m、n的值.【练习49】已知关于x、y的方程组321431x y px y p+=+⎧⎨+=-⎩满足x > y,求p的取值范围.【练习50】解方程组:252821126x yy zz uu x+=⎧⎪+=⎪⎨+=⎪⎪+=⎩.- 12 -。
第08讲_一轮复习_一次方程(组)(教师版)A4-精品文档资料整理

高斯教育学科教师辅导讲义学员姓名:年级:辅导科目:学科教师:五块石1 上课时间授课主题第08讲_一轮复习_一次方程(组)一次方程(组)一.一元一次方程的概念只含有一个未知数,并且未知数的最高次数是1的整式方程叫做一元一次方程.一元一次方程的一般形式:0(0)ax b a+=≠,a为一次项系数,b为常数项.1.判断是一元一次方程的标准:①整式方程②一元方程③一次方程二.一元一次方程的解一元一次方程的解:使方程左、右两边相等的未知数的值叫做方程的解.三.二元一次方程组含有两个未知数,并且两个未知数项的次数都是1的方程叫做二元一次方程.判定一个方程是二元一次方程必须同时满足三个条件:(1)方程两边的代数式都是整式——分母中不能含有字母;知识图谱错题回顾知识精讲(2)有两个未知数——“二元”;(3)含有未知数的项的最高次数为1——“一次”.关于x 、y 的二元一次方程的一般形式:ax by c +=(0a ≠且0b ≠).方法点拨列方程组解应用题的步骤与列一元一次方程解应用题的步骤类似,具体是:1.审题:透彻理解题意,弄清问题中的已知量和未知量,找出问题给出和涉及的相等关系.2.设元(未知数):根据题意,可以直接设未知数,也可以间接设未知数.3.列代数式和方程组:用含所设未知数的代数式表示其他未知数,根据题中给出的等量关系列出方程组,一般情况下,未知数个数与方程个数是相同的.4.解方程(组).5.检验:检验方程的根是否符合题意.6.作答:检验后作出符合题目要求的答案.列方程(组)解应用题的实质是先把实际问题转化为数学问题(设元、列方程(组)),再将数学问题解决从而解决实际问题.在这个过程中,列方程起着承前启后的作用.一.考点:解一次方程(组),含参数的一次方程(组),一次方程(组)的实际应用.二.重难点:解含参数的一次方程(组)三. 易错点:1. 一般的,二元一次方程都有无数组解,但如果确定了一个未知数的值,那么另一个未知数的值也就随之确定了.2. 无论是二元一次方程还是二元一次方程组,已知它们的解,代入之后都满足对应的方程.题模一:解一次方程(组)例1.1.1下列方程中是关于x 的一元一次方程的是( )A .10x x +=B .20ax bx c ++=C .223252x x x --=D .()()121x x -+= 【答案】D【解析】由一元一次方程的定义:含有一个未知数,且未知数的最高次数是1的整式方程可知D 选项正确.三点剖析题模精讲例1.1.2解方程:1521824x x x ⎛⎫++=+ ⎪⎝⎭. 【答案】3x =【解析】方程去括号得:328x x +=+,移项合并得:26x =,解得:3x =.例1.1.3若方程()211m x m x -+=是关于x 的一元一次方程,则m 的取值是__________.【答案】1m =【解析】由题意可得,二次项系数10m -=,即1m =m 0m ≥,所以m 的取值是1m =.例1.1.4已知关于,x y 的议程组31331x y a x y a +=+⎧⎨+=-⎩的解满足0x y +<,则a 的取值范围是( ) A .1a >- B .1a <- C .1a <D .1a >【答案】B【解析】该题考查的是二元一次方程组的解.31331x y a x y a +=+⎧⎨+=-⎩①② +①②得4422x y a +=+,∴1122x y a +=+, ∴0x y +<, ∴11022a +<, ∴1a <-. 故答案是B .题模二:含参数的一次方程(组) 例1.2.1解关于x 的方程:()0x n x m m mn m n n---=≠. 【答案】①当m n ≠时,方程的解为2n x n m=-;②当m n =时,由于0n ≠,所以方程无解 【解析】原方程可整理为()2n m x n -=,①当m n ≠时,方程的解为2n x n m=- ②当m n =时,由于0n ≠,所以方程无解例1.2.2已知关于x 的方程23mx x =+有正整数解...,求整数..m 的值 【答案】3m =或5m =【解析】该题考查的是含参的一元一次方程.由题可知()23m x -=,①若20m -=即2m =,此时方程化为03=,无解;②若20m -≠即2m ≠,此是系数化1可得:32x m =-,由于x 为正整数,且m 为正数, ∴21m -=或23m -=,即3m =或5m =.例1.2.3甲、乙二人同解关于x 、y 的二元一次方程组278ax by cx y +=⎧⎨-=⎩,甲得正确解为32x y =⎧⎨=-⎩;乙将c 看错,得其解为22x y =-⎧⎨=⎩,求a 、b 、c 的值. 【答案】4a =、5b =、2c =-【解析】转化为关于a 、b 、c 的三元一次方程组3223148222a b c a b -=⎧⎪+=⎨⎪-+=⎩,解得452a b c =⎧⎪=⎨⎪=-⎩题模三:一次方程(组)的实际应用例1.3.1某工程队承包了某标段全长1755米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进0.6米,经过5天施工,两组共掘进了45米.(1)求甲、乙两个班组平均每天各掘进多少米?(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.2米,乙组平均每天能比原来多掘进0.3米.按此施工进度,能够比原来少用多少天完成任务?【答案】(1)甲班组平均每天掘进4.8米,乙班组平均每天掘进4.2米(2)少用10天【解析】(1)设甲、乙班组平均每天掘进x 米,y 米,得0.65()45x y x y -=⎧⎨+=⎩, 解得 4.84.2x y =⎧⎨=⎩. ∴甲班组平均每天掘进4.8米,乙班组平均每天掘进4.2米.(2)设按原来的施工进度和改进施工技术后的进度分别还需a 天,b 天完成任务,则a=(1755-45)÷(4.8+4.2)=190(天)b=(1755-45)÷(4.8+0.2+4.2+0.3)=180(天)∴a -b=10(天)∴少用10天完成任务.例1.3.2为了援助失学儿童,初三学生李明从2012年1月份开始,每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内,准备每6个月一次将储蓄盒内存款一并汇出(汇款手续费不计).已知2月份存款后清点储蓄盒内有存款80元,5月份存款后清点储蓄盒内有存款125元.(1)在李明2012年1月份存款前,储蓄盒内已有存款多少元?(2)为了实现到2015年6月份存款后存款总数超过1000元的目标,李明计划从2013年1月份开始,每月存款都比2012年每月存款多t 元(t 为整数),求t 的最小值.【答案】(1)50(2)11【解析】(1)设李明每月存款x 元,储蓄盒内原有存款y 元,依题意得,2805125x y x y +=⎧⎨+=⎩, 解得1550x y =⎧⎨=⎩, 答:李明2012年1月份存款前,储蓄盒内已有存款50元;(2)由(1)得,李明2012年共有存款12×15+50=230元,2013年1月份后每月存入(15+t )元,2013年1月到2015年6月共有30个月,依題意得,230+30(15+t )>1000,解得t >1023, 因为t 为整数,所以t 的最小值为11.答:t 的最小值为11.例1.3.3列方程解应用题油桶制造厂的某车间主要负责生产制造油桶用的的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套. 生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?【答案】24;18【解析】该题考查的是解方程的应用.设生产圆形铁片的工人为x 人,则生产长方形铁片的工人为42x -人,……1分可列方程()12028042x x =⨯-.…………2分解得:24x =……3分则4218x-=.…………4分答:生产圆形铁片的有24人,生产长方形铁片的有18人……5分例1.3.4某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能地少?【答案】(1)每名熟练工和新工人每月分别可以安装4、2辆电动汽车(2)有4种新工人的招聘方案.①n=8,a=1,即新工人8人,熟练工1人;②n=6,a=2,即新工人6人,熟练工2人;③n=4,a=3,即新工人4人,熟练工3人;④n=2,a=4,即新工人2人,熟练工4人.(3)新工人4人,熟练工3人【解析】(1)设每名熟练工和新工人每月分别可以安装x、y辆电动汽车.根据题意,得28 2314x yx y⎧+=⎨+=⎩,解得42xy⎧=⎨=⎩.答:每名熟练工和新工人每月分别可以安装4、2辆电动汽车.(2)设工厂有a名熟练工.根据题意,得12(4a+2n)=240,2a+n=10,n=10-2a,又a,n都是正整数,0<n<10,所以n=8,6,4,2.即工厂有4种新工人的招聘方案.①n=8,a=1,即新工人8人,熟练工1人;②n=6,a=2,即新工人6人,熟练工2人;③n=4,a=3,即新工人4人,熟练工3人;④n=2,a=4,即新工人2人,熟练工4人.(3)结合(2)知:要使新工人的数量多于熟练工,则n=8,a=1;或n=6,a=2;或n=4,a=3.根据题意,得W=2000a+1200n=2000a+1200(10-2a )=12000-400a .要使工厂每月支出的工资总额W (元)尽可能地少,则a 应最大.显然当n=4,a=3时,工厂每月支出的工资总额W (元)尽可能地少.随练1.15121136x x +--= 【答案】38x =【解析】去分母:()()251216x x +--=;去括号:102216x x +-+=;移项: 102621x x -=--合并同类项:83x =;系数化为1:38x =. ∴原方程的解是38x =. 随练1.2若()2116m x m y -+-=是关于x 、y 的二元一次方程,则m 的值是()A .1B .0C .0或1D .任意实数 【答案】B【解析】该题考查的是二元一次方程.()2116m x m y -+-=是关于x 、y 的二元一次方程,则211m -=,10m -≠,解得0m =.故本题选B .随练1.3 已知关于x 、y 的方程组2331x y ax by -=⎧⎨+=-⎩和3211233x y ax by +=⎧⎨+=⎩的解相同,求a 、b 的值.【答案】25a b =-⎧⎨=⎩【解析】可先解方程组2333211x y x y -=⎧⎨+=⎩,解得31x y =⎧⎨=⎩.因此可得关于a 、b 的二元一次方程组31633a b a b +=-⎧⎨+=⎩,解得25a b =-⎧⎨=⎩.随练1.4解关于x 的方程:()()1234m x n x m -=+. 随堂练习【答案】①当34m ≠时,方程的解为()22343m n x m +=-; ②当34m =,32n =-时,方程的解为任意实数; ③当34m =,32n ≠-时,方程无解 【解析】原方程可整理为()()43223m x m n -=+,①当34m ≠时,方程的解为()22343m n x m +=-; ②当34m =,32n =-时,方程的解为任意实数; ③当34m =,32n ≠-时,方程无解. 随练1.5解方程:(1)1342x x -=- (2)247236x x ---=- (3)()231mx x +=- 【答案】(1)143x =(2)133x =(3)()133x m m =≠-+;3m =-时,无解 【解析】该题考查的是解方程. (1)1342x x -=-移项:1432x x +=+,合并同类项:372x =,解得143x =, 经检验143x =是方程的解, ∴原方程的解是143x =(2)247236x x ---=-两边同乘以6:()()122427x x --⨯=--,去括号:12487x x -+=-+,移项:41287x x -+=--+,合并同类项:313x -=-, 系数化为1:133x =, 经检验,133x =是方程的解,∴原方程的解为133x =. (3)()231mx x +=-去括号:233mx x +=-,移项:332mx x +=-,合并同类项:()31m x +=,系数化为1:()133x m m =≠-+; 经检验,当3m ≠-时,13x m =+是方程的解, ∴当3m ≠-时,原方程的解为13x m =+; 当3m =-时,原方程无解.随练1.6m 取何整数值时,关于x 、y 的方程组2441x my x y +=⎧⎨+=⎩的解x 和y 都是整数? 【答案】9,7,10,6m =.【解析】把m 作为已知数,解方程组得81828x m y m ⎧=-⎪⎪-⎨⎪=⎪-⎩. ∵x 是整数,∴8m -取8的约数1±,2±,4±,8±.∵y 是整数,∴8m -取2的约数±1,±2.取它们的公共部分,81,2m -=±±,解得9,7,10,6m =.经检验9,7,10,6m =时,方程组的解都是整数.随练1.7我市举办的“义博会”是国内第三大展会,从1995年以来已成功举办了15届.(1)1995年“义博会”成交金额为 1.01亿元,1999年“义博会”成交金额为35.2亿元,求1999年的成交金额比1995年的增加了几倍?(结果精确到整数)(2)2000年“义博会”的成交金额与2009年的成交金额的总和是153.99亿元,且2009年的成交金额是2000年的3倍少0.25亿元,问2009年“义博会”的成交金额是否突破了百亿元大关?【答案】(1)34倍(2)是【解析】找到相应的关系式是解决问题的关键;注意增加的倍数是求到增加的金额占原来的金额的多少.(1)(35.2-1.01)÷1.01≈34答:1999年的成交金额比1995年约增加了34倍;(2)设2000年成交金额为x 亿元,则2009年成交金额为(3x -0.25)亿元.由题意得:x+3x -0.25=153.99,解得:x=38.56,∴3x -0.25=115.43>100,∴2009年“义博会”的成交金额突破了百亿元大关.作业1解方程:21352 34x x--=+.【答案】13x=-【解析】该题考查的是解一元一次方程.去分母,乘以12,得:()()42133524x x-=-+去括号,得:8491524x x-=-+移项、合并同类项,得:13x-=系数化为1,得:13x=-作业2设a,b,c都是非负数,且满足a+b+c=3,3a+b﹣c=5,则5a+4b+2c的最大值是__________.【答案】13【解析】由335a b ca b c++=⎧⎨+-=⎩解得122a cb c=+⎧⎨=-⎩,所以5a+4b+2c=5+5c+8﹣8c+2c=13﹣c,∴c是非负数,∴c≥0∴5a+4b+2c=5+5c+8﹣8c+2c=13﹣c的最大值为13.作业3如果关于x,y的二元一次方程组316215x ayx by-=⎧⎨+=⎩的解是71xy=⎧⎨=⎩,那么关于x,y的二元一次方自我总结课后作业程组()()()()316215x y a x y x y b x y +--=⎧⎪⎨++-=⎪⎩的解是__________.【答案】43x y =⎧⎨=⎩【解析】由于两个二元二次方程组都是316215m an m bn -=⎧⎨+=⎩的形式,所以解相同.∴71x y x y +=⎧⎨-=⎩,∴43x y =⎧⎨=⎩. 作业4已知关于x 的方程()()2153a x a x b -=-+有无数多解,求a 、b 的值.【答案】53a =,109b =- 【解析】移项、合并,得()3532a x b a -=+,由于原方程有无数多解,所以350320a b a -=⎧⎨+=⎩,解得53109a b ⎧=⎪⎪⎨⎪=-⎪⎩. 作业5已知方程1ax x b +=-,问a 、b 分别满足什么条件时:(1)方程有唯一解?(2)方程无解?(3)方程有无穷多个解?【答案】(1)1a ≠(2)1a =,1b ≠-(3)1a =,1b =-【解析】原方程可整理为()11a x b -=--,方程有唯一解,则10a -≠,即1a ≠;方程无解,则10a -=且10b --≠,即1a =且1b ≠-;方程有无数解,则10a -=且10b --=,即1a =且1b =-.作业6已知方程组3247x y mx ny -=⎧⎨+=⎩与231953mx ny y x -=⎧⎨-=⎩有相同的解,求m 、n 的值. 【答案】41m n =⎧⎨=-⎩【解析】由题意得32453x y y x -=⎧⎨-=⎩,解得21x y =⎧⎨=⎩将21x y =⎧⎨=⎩代入72319mx ny mx ny +=⎧⎨-=⎩,得274319m n m n +=⎧⎨-=⎩,解得41m n =⎧⎨=-⎩作业7我们规定:若x 的一元一次方程ax b =的解为b a -,则称该方程为定解方程,例如:932x =的解为93322-=,则该方程932x =就是定解方程. 请根据上边规定解答下列问题:(1)若x 的一元一次方程2x m =是定解方程,则m = ;(2)若x 的一元一次方程2x ab a =+是定解方程,它的解为a ,求a ,b 的值;(3)若x 的一元一次方程2x mn m =+和2x mn n -=+都是定解方程,求代数式()(){}()2212114322m n mn m m mn n n ⎡⎤⎡⎤-+---+--+-⎣⎦⎣⎦的值. 【答案】(1)4m =(2)2a =,1b =(3)149- 【解析】(1)由题意可知2x m =-,由一元一次方程可知2m x =, 因此22m m -=,解得4m =. (2)由题意可知2x ab a =+-,由一元一次方程可知2ab a x +=, 又因为方程的解为a ,因此2ab a a +=,2ab a a +-= 解得2a =,1b =.(3)由题意可知4mn m +=,43mn n +=-, 两式相减,得163m n -=.代入,求得原式149=-. 作业8已知关于x 的方程6362m x +=的解是方程2101313124x m x x ++-=-的解的11倍,求m 的值和两个方程的解. 【答案】76m =-,方程的解分别为193,1933【解析】关于x 的方程6362m x +=的解为42x m =-,关于x 的方程2101313124x m x x ++-=-的解为41111m x +=.由题意可得411421111m m +-=⨯,解得76m -=,代回42x m =-和41111m x +=后可以得到方程的解为1919,333x x ==. 作业9若k 为整数,则使方程()199920012000k x x -=-的解也是整数的k 的值有( )A .4个B .8个C .12个D .16个【答案】D 【解析】解方程,得200113232911x k k ⨯⨯⨯==++,要使x 为整数,1k +可取1±,3±,23±,29±,()323±⨯()329±⨯,()32329±⨯⨯,即k 的值有16个,答案为D .作业10要使关于x 、y 的方程组21x ky k x y +=⎧⎨-=⎩的解都是整数,k 应取哪些整数值?【答案】5,31,1k =---【解析】解关于x 、y 的方程组21x ky k x y +=⎧⎨-=⎩,得3212k x k k y k ⎧=⎪⎪+⎨-⎪=⎪+⎩. 由于()326363222k k k k k +-==-+++,13122k k k -=-++. ∵x 是整数,∴21,2,3,6k +=±±±±.∵y 是整数,∴21,3k +=±±.∴5,31,1k =--- 作业11解关于x 的方程(1)1+=32x -;(2)()38382x x x --+=+; (3)132134x x x --=+-;(4)0.50.02 3.60.20.03x x +-=; (5)ax b =.【答案】(1)8x =-(2)8x =(3)2x =-(4)30465x =; (5)当0a ≠时,b x a=;当0a =且0b =时,x 为任意数;当0a =且0b ≠时,无解. 【解析】本题考查的是一元一次方程.(1)132x +=-,两边同时乘以2,得8x =-; (2)()38382x x x --+=+,移项,合并同类项,得8x =;(3)132134x x x --=+-,方程两边同时乘以3,4的最简公分母12,得2x =-; (4)0.50.02 3.60.20.03x x +-=,化简为50218535x x +-=,方程两边同时乘以15,得65304x =,即30465x =; (5)ax b =,当0a ≠时,b x a=; 当0a =且0b =时,x 为任意数;当0a =且0b ≠时,无解.作业12现有A ,B 两种商品,买2件A 商品和1件B 商品用了90元,买3件A 商品和2件B 商品用了160元.(1)求A ,B 两种商品每件各是多少元?(2)如果小亮准备购买A ,B 两种商品共10件,总费用不超过350元,但不低于300元,问有几种购买方案,哪种方案费用最低?【答案】(1)20,50(2)见解析【解析】(1)设A 商品每件x 元,B 商品每件y 元,依题意,得29032160x y x y +=⎧⎨+=⎩,解得2050x y =⎧⎨=⎩. 答:A 商品每件20元,B 商品每件50元.(2)设小亮准备购买A 商品a 件,则购买B 商品(10-a )件2050(10)3002050(10)350a a a a +-≥⎧⎨+-≤⎩ 解得5≤a≤623根据题意,a 的值应为整数,所以a=5或a=6.方案一:当a=5时,购买费用为20×5+50×(10-5)=350元;方案二:当a=6时,购买费用为20×6+50×(10-6)=320元;∴350>320∴购买A 商品6件,B 商品4件的费用最低.答:有两种购买方案,方案一:购买A 商品5件,B 商品5件;方案二:购买A 商品6件,B 商品4件,其中方案二费用最低.作业13为了贯彻落实国务院关于促进家电下乡的指示精神,有关部门自2007年12月底起进行了家电下乡试点,对彩电、冰箱(含冰柜)、手机三大类产品给予产品销售价格13%的财政资金直补.企业数据显示,截至2008年12月底,试点产品已销售350万台(部),销售额达50亿元,与上年同期相比,试点产品家电销售量增长了40%.(1)求2007年同期试点产品类家电销售量为多少万台(部)?(2)如果销售家电的平均价格为:彩电每台1500元,冰箱每台2000元,手机每部800元,已知销售的冰箱(含冰柜)数量是彩电数量的32倍,求彩电、冰箱、手机三大类产品分别销售多少万台(部),并计算获得的政府补贴分别为多少万元?【答案】(1)250万台(部)(2)彩电、冰箱、手机三大类产品分别销售88万台、132万台、130万部,获得的政府补贴分别为17160万元、34320万元、13520万元【解析】 (1)设2007年销量为a 万台,则a (1+40%)=350,解之得:a=250; 答:2007年同期试点产品类家电销售量为250万台(部);(2)设销售彩电x 万台,则销售冰箱32x 万台,销售手机(350-52x )万台.由题意得:1500x+2000×32x+800(350-52x)=500000.解得:x=88.∴32x=132,350-52x=130.所以,彩电、冰箱(含冰柜)、手机三大类产品分别销售88万台、132万台、130万部.∴88×1500×13%=17160(万元),132×2000×13%=34320(万元),130×800×13%=13520(万元).获得的政府补贴分别是17160万元、34320万元、13520万元.答:彩电、冰箱、手机三大类产品分别销售88万台、132万台、130万部,获得的政府补贴分别为17160万元、34320万元、13520万元.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一次方程(组)和一次不等式(组)是初中数学六年级下学期第2章的内容.本章学习了一元一次方程、二元一次方程(组)、三元一次方程组以及一元一次不等式(组)的概念及其解法,学习时应注意方程与不等式及其解法之间的联系与区别,体会消元与化归的数学方法和数学思想,加强用方程解决实际问题的意识.单元练习:一次方程(组)和一次不等式(组)内容分析知识结构一次方程(组)一次不等式(组)三元一次方程组一元一次方程二元一次方程(组) 一元一次不等式(组) 多元一元化归思想【练习1】 下列各式中,方程有( )个(1)633-+=-;(2)35x +=;(3)22ππ⨯=;(4)38a =;(5)7y =;(6)32p q -;(7)719nm +=;(8)1a a =+. A .3B .4C .5D .6【难度】★【答案】C【解析】含有未知数的等式叫做方程;(2)、(4)、(5)、(7)、(8)都是方程. 【总结】本题考查了方程的定义.【练习2】 下列各式中,一元一次方程有( )个(1)30x =; (2)437x y -=; (3)21303x -=;(4)()397y y --=; (5)23x -; (6)4x ≠. A .1B .2C .3D .4【难度】★【答案】B【解析】含有一个未知数,并且未知数的最高次数式一次的方程为一元一次方程; 故(1)、(4)都是.【总结】本题考查了一元一次方程的定义.【练习3】 下列各式中,二元一次方程有( )个(1)2311x y -=;(2)23xy =-;(3)35m y+=;(4)25p q ->;(5)221x x +=;(6)21953m n -=.A .1B .2C .3D .4【难度】★【答案】B【解析】含有两个未知数,并且未知数的最高次数式一次的方程为二元一次方程; 故(1)、(6)都是.【总结】本题考查了二元一次方程的定义.【练习4】 下列各式中,二元一次方程组有( )个选择题(1)()()23111x y xy x y +=-⎧⎪⎨=+-⎪⎩;(2)31230x y x y +=⎧⎨-=⎩;(3)235x x y =⎧⎨+=-⎩;(4)3227x y x y -=+=+.A .1B .2C .3D .4【难度】★【答案】D【解析】含有两个相同未知数的两个一次方程所组成的方程组叫做二元一次方程组; (1)中虽然有二次项,但是左右两边会抵消;故全都是二元一次方程组. 【总结】本题考查了二元一次方程组的定义.【练习5】 二元一次方程组324526x y x y -=⎧⎨-=⎩的解是( )A .11x y =⎧⎨=-⎩B .112x y =-⎧⎪⎨=⎪⎩C .112x y =-⎧⎪⎨=-⎪⎩D .112x y =⎧⎪⎨=-⎪⎩【难度】★【答案】D【解析】解:⎩⎨⎧=-=-,②,①625423y x y x ,由①-②得:22-=-x ,解得:1=x ,代入①:42-13=⨯y ,解得:21-=y ,所以方程组的解为:112x y =⎧⎪⎨=-⎪⎩.【总结】本题考查了二元一次方程组的解法.【练习6】 如果0m n <<,那么下列各式中正确的是( )A .0.30.3m n <B .22m n <C .11m n <D .m n m n -<+【难度】★【答案】A【解析】由不等式的性质可知A 正确. 【总结】本题考查了不等式的性质的运用.【练习7】 下列判断中正确的是( )A .如果0x <,那么15x x <B .不等式35x ->-的解集是53x <C .如果113x <-,那么3x >-D .不等式组11x x >⎧⎨<⎩的解集为1x =【难度】★【答案】B【解析】由不等式的性质(1)、(2)、(3)可以判断;必须熟练掌握. 【总结】本题考查了不等式及不等式组的解集的确定.【练习8】 若方程()2210a x bx c +++=是表示字母x 的一元一次方程,则( )A .12a =,0b ≠,c 为任意数 B .12a ≠,0b ≠,0c = C .12a =-,0b ≠,0c ≠D .12a =-,0b ≠,c 为任意数【难度】★★【答案】D【解析】由题意得:此方程为一元一次方程,故012=+a ,解得:21-=a ,0≠b ,c 为任意数即可.【总结】本题考查了一元一次方程的概念.【练习9】 下列式子中一定正确的是( )A .23a a <B .a b a -<C .2a a >D .322x x-< 【难度】★★【答案】D【解析】D 中左右两边同时乘以2,则x x <-3,再同时减掉x ,则03<-成立. 【总结】本题考查了不等式的性质应用.【练习10】 下列说法中错误的是( )A .方程ax b =的解是bx a=(0a ≠)B .如果ax b ->,则bx a<-(0a ≠)C .若2k =时,方程()22k x k -=无解D .8-是不等式32x ->一个解【难度】★★【答案】B【解析】B 中a 的正负不确定,当0>a 时,0<-a ,则a b x -<;当0<a 时,0>-a ,则abx ->. 【总结】 本题考查了不等式的性质及方程的解的应用.【练习11】 下列各对数值,是方程342x y +=的解的为( )A .012x y =⎧⎪⎨=-⎪⎩B .22x y =-⎧⎨=⎩C . 114x y =⎧⎪⎨=-⎪⎩D . 21x y =-⎧⎨=⎩【难度】★★【答案】B【解析】二元一次方程的解有无数组,代入验证即可. 【总结】本题考查了二元一次方程的解.【练习12】 某运输队运煤,第一天运了总量的27,第二天运煤恰好是第一天的23,还剩14 吨,设一共运煤x 吨,则可列出方程( )A .22214773x x x +⨯=-B .221473x x x ++=C .222114737x x x ⎛⎫+-=- ⎪⎝⎭D .22214773x x x +÷+=【难度】★★【答案】A【解析】找出等量关系列方程:第一天运煤+第二天运煤=共运煤-剩下的. 【总结】本题考查了列方程解应用题的思想.【练习13】 学校的篮球数比排球数的2倍少3个,篮球数与排球数的比是3 : 2,求两种球各有多少个?若设篮球有x 个,排球有y 个,则根据题意得到的方程组是( ) A .2332x y x y =-⎧⎨=⎩B .2332x y x y =+⎧⎨=⎩C .2323x y x y =-⎧⎨=⎩D .2323x y x y =+⎧⎨=⎩【难度】★★【答案】C【解析】找准题目中的两个等量关系:①32-=y x ,②2:3:=y x ,故y x 32=. 【总结】本题考查了由实际问题抽象出二元一次方程组.【练习14】 已知不等式组00x a x b -<⎧⎨-<⎩的解集为x a <,则不等式组00x a x b +>⎧⎨+>⎩的解集为( )A .x a <-B .x a >-C .x b >-D .x b <-【难度】★★【答案】B【解析】解: 不等式组⎩⎨⎧<-<-00b x a x 的解集为a x <, ∴b a <, ∴b a ->-,不等式组⎩⎨⎧>+>+00b x a x 的解为⎩⎨⎧->->b x ax , ∴不等式组的解集为a x ->.【总结】本题考查了不等式组解得确定:同大取大、同小取小.【练习15】 323x y+=的正整数解的个数为( )个A .1B .2C .3D .4【难度】★★【答案】B【解析】方程两边同时乘以6去分母:1823=+y x ,则x y 239-=,其中x 从1开始取整数 即可验证.【总结】本题考查了对二元一次方程的整数解的理解.【练习16】 观察下列方程组,无解的是( )A .61x y x y -=⎧⎨+=-⎩B .52210x y x y -=-⎧⎨-=⎩C .5229x y x y -=⎧⎨+=⎩D .423x y x y +=⎧⎨-=⎩【难度】★★【答案】B【解析】B 中方程组可化为⎩⎨⎧=--=-55y x y x ,此方程组无解.【总结】本题考查了判断二元一次方程组是否有解.【练习17】 已知不等式组5x x m >⎧⎨>⎩的解集为5x >,则m 的取值范围是( )A .5m >B .5m ≥C .5m <D .5m ≤【难度】★★【答案】D【解析】根据不等式组有解可知,必须是同大取大,所以5≤m . 【总结】本题考查了不等式的解集的确定.【练习18】 已知方程组35223x y k x y k +=+⎧⎨+=⎩,其中x 是y 的2倍,则k 的值是( )A .72-B .72C .0D .以上都不对【难度】★★【答案】B【解析】由题意得:⎩⎨⎧=++=+,②,①k y x k y x 32253,①-②:22=+y x ,又y x 2=,所以方程组的解集为⎪⎩⎪⎨⎧==211y x ,则2732=+=y x k .【总结】本题考查了二元一次方程组的解.【练习19】 如果关于x 的不等式32x a ->的所有正整数解之和为6,则a 的取值范围为( ) A .5a ≥-B .3a <-C .53a -<<-D .53a -≤<-【难度】★★★【答案】D【解析】解:由题意得:原不等式的解集为23ax -<,因为所有整数解之和为6,有6321=++, 所以4233≤-<a,解得:35-<≤-a . 【总结】本题考查了不等式的整数解及解一元一次不等式的综合运用.【练习20】 如果关于x 的不等式组30310x m x m -->⎧⎨-+<⎩无解,那么m 的取值范围是( )A .2m <B .2m ≤C .2m >D .2m ≥【难度】★★★【答案】B【解析】解:由题意得:⎩⎨⎧<+->--,②,①01303m x m x ,由①得:m x +>3,由②得:13-<m x ,因为不等式组无解,则:133-≥+m m ,解得:2≤m .【总结】本题考查了利用不等式组的解确定字母的取值范围,综合性较强.【练习21】 若3350m x ---=是一元一次方程,则m =______. 【难度】★【答案】4.【解析】解:由题意得方程为一元一次方程,所以13=-m ,则4=m . 【总结】本题考查了一元一次方程的概念.【练习22】 把方程5239x y -+=化成用含x 的式子表示y 的形式,得______________. 【难度】★【答案】256xy --=.【解析】解:由题意得:625=-y x ,则x y 562-=-,所以256xy --=.【总结】本题考查了用字母表示数.【练习23】 用不等式表示:2x y+减去()21x --所得的差是非负数________________. 填空题【难度】★【答案】()[]0122≥---+x yx . 【解析】读懂题意,抓住关键词,弄清运算的先后顺序和不等关系,才能把文字语言的不等 关系转化为用数字符号表示的不等式.【总结】本题考查了根据已知数量关系列不等式的方法.【练习24】 用不等号填空,并说明不等式变形过程.(1)若x y >,则4x -______4y -; (2)若235x +≤-,则3x ______7-; (3)若1233x x -≥-,则x ______2; (4)若x y >,则6x -______6y -; (5)若x y >,则2x -______2y -; (6)若x y >,0m >,则mx ______my ; (7)若m n ≥,20k +<,则mk ______nk .【难度】★【答案】(1)>;(2)≤;(3)≥;(4)<;(5)<;(6)>;(7)≤. 【解析】利用不等式的三个性质可得结论.【总结】本题考查了不等式的性质的运用.【练习25】 解集32x -≤<中的整数解为__________________. 【难度】★【答案】3-、2-、1-、0、1.【解析】搞清整数定义,寻找整数解. 【总结】本题考查了不等式的整数解的确定.【练习26】 不等式组340731x x +>⎧⎨-≥-⎩的解集为____________________.【难度】★【答案】3834≤<-x . 【解析】解:⎩⎨⎧-≥->+,②,①137043x x ,由①得:34->x ,由②得:38≤x ,所以原不等式组的解集为:3834≤<-x .【总结】本题考查了不等式组的解集的确定.【练习27】 判断:(1)如果a b >,那么3232a b ->-;( ) (2)如果a b <,那么22a b <;( ) (3)如果22a b >,那么a b >;( ) (4)如果a b >,那么a b >;( )(5)如果1a >,那么a 比1a大;( ) (6)如果5a >,那么55a a -=-;( ) (7)如果144m <-,那么1m <-;( )(8)如果x y >,那么()()2211m x m y -->--.( ) 【难度】★★【答案】(1)×;(2)×;(3)×;(4)×;(5)√;(6)×;(7)×;(8)×. 【解析】根据不等式的性质解答.【总结】本题考查了不等式的性质的运用.【练习28】 若0a b +<,且0ab >,则a ______0,b ______0. 【难度】★★【答案】<,<.【解析】解:由题意得:0>ab ,则b a 、同号,又0<+b a ,所以b a 、同负. 【总结】本题考查了不等式性质的应用.【练习29】 满足不等式()10484x x ++≤的最大整数解是_______. 【难度】★★【答案】4【解析】解:由题意得:原不等式可化为:114084x +≤,解得:4≤x , 所以最大整数解为4.【总结】本题考查了一元一次不等式组的整数解的确定及对最大整数解的理解.【练习30】 当x ______时,52x -的值是正的,此时最小的整数x =_______. 【难度】★★【答案】5>;6.【解析】解:由题意得:025>-x ,解得:5>x ,则最小的整数是6.【总结】本题考查了不等式的解集及满足条件的最小的整数.【练习31】 如果43x y =⎧⎨=-⎩是方程436x ay -=的一个解,则a =______.【难度】★★【答案】910-. 【解析】解:把34-==y x 、代入方程()63344=-⨯⨯-⨯a ,解得:910-=a . 【总结】本题考查了二元一次方程的解及解一元一次方程.【练习32】 如果3235351m n m n x y +--++=-是二元一次方程,那么m =______,n =_______. 【难度】★★【答案】58;512. 【解析】由题意得:312351m n m n +-=⎧⎨-+=⎩①②,由2⨯①得:228m n +=③;则:②③-得:512=n ,代入①中:58=m ,所以⎪⎩⎪⎨⎧==51258n m . 【总结】本题考查了二元一次方程的概念及解二元一次方程组.【练习33】 若357x -+=,则x =______. 【难度】★★【答案】1或5.【解析】解:由题意得:23=-x ,则23=-x 或23-=-x ,解得:5=x 或1=x . 【总结】本题考查了绝对值的意义及方程的解,注意对绝对值的准确理解.【练习34】 若:5:3x y =,且x 与y 的和是10,则x =______,y =______. 【难度】★★【答案】425;415. 【解析】解:由题意得:⎩⎨⎧=+=,②,①1053y x y x ,解得:⎪⎩⎪⎨⎧==415425y x . 【总结】本题考查了二元一次方程组的解.【练习35】 已知1y =是方程()1223m y y --=的解,那么关于x 的方程 ()()3225m x m x --=-的解是______.【难度】★★【答案】0=x .【解析】解:由题意得:把1=y 代入方程中,则:()21312=--m ,解得:1=m , 再将1=m 代入关于x 的方程,则()()521231-=--⨯x x ,解得:0=x . 【总结】本题考查了方程解的应用及解一元一次方程.【练习36】 若关于x 、y 方程组352278x y ax y a -=⎧⎨+=-⎩的解互为相反数,则a =______.【难度】★★【答案】932. 【解析】解:由题意得:0=+y x ,则x y -=,代入方程组有⎩⎨⎧-=-=8528a x a x ,解得:932=a .【总结】本题考查了相反数的应用及解二元一次方程组.【练习37】 如果()222303x y x ⎛⎫+++-= ⎪⎝⎭,那么2016y=______. 【难度】★★【答案】1.【解析】解:由题意得:⎪⎩⎪⎨⎧=⎪⎭⎫ ⎝⎛-+=+032032x y x ,解得:⎪⎩⎪⎨⎧-=-=123y x ,所以()1120162016=-=y . 【总结】本题考查了非负数的意义及解方程.【练习38】 甲、乙两班共有88名学生,若从乙班调25人到甲班,则甲班人数是乙班人数的3倍,设甲班x 人,乙班y 人,可列出方程组_______________________,并解得甲班有______人,乙班有______人. 【难度】★★★【答案】见解析.【解析】解:由题意得:()⎩⎨⎧-=+=+2532588y x y x ,解得:⎩⎨⎧==4741y x ,所以甲班有41人,乙班有47人.【总结】本题考查了二元一次方程组在实际生活中的应用,找等量关系列方程解决.【练习39】 有一个两位数,个位数字和十位数字之和是9,且这个两位数不大于63,求这个两位数.可设这个两位数的个位数字为x ,根据题意,可列不等式 ________________________,最后这个两位数为_______________________. 【难度】★★★【答案】见解析.【解析】解:由题意得个位数字是x ,则十位数字是()x -9,有()⎩⎨⎧≤-≤≤-69163910x x ,解得:83≤≤x ,当3=x 时,这个两位数为63;当4=x 时,这个两位数为54; 当5=x 时,这个两位数为45;当6=x 时,这个两位数为36; 当7=x 时,这个两位数为27;当8=x 时,这个两位数为18.【总结】本题考查了利用一元一次不等式组解应用题及分类讨论思想的运用.【练习40】 若关于x 的不等式()22a x a +>+的解集是1x <,则a 的取值范围是______. 【难度】★★★【答案】2-<a .【解析】解:原不等式两边同时除以()2+a ,得1<x ,所以根据不等式性质3:02<+a , 解得:2-<a .【总结】本题考查了不等式的性质及应用.【练习41】 解方程:(1)1071253x x x +=--;(2)()()160%2180%22x x +-+=;(3)111257918643x ⎧⎫⎡+⎤⎛⎫+-+=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭; (4)1.88 1.5350.401.220.3x x x -----=. 【难度】★★【答案】见解析.【解析】解:(1)x x x 3512710--=+, (2)()()212%8012%60=+-+x x , 7531210--=+-x x x , ()()621825x x +-+=, 12-=x ; 1268165x x +--=, 415x =,154x =;(3)197532416181=⎭⎬⎫⎩⎨⎧+⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛++x , (4)03.04.05235.12.18-8.1=----x x x ,175324161-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛++x , 03450235.1128018=-----x x x ,153241=⎪⎭⎫⎝⎛++x , ()()0450435.168018=-----x x x ,132-=+x , 25262-=-x , 5-=x ; 26225=x . 【总结】本题考查了一元一次方程的解法,注意解题时的方法选择,以及计算时要细心.解答题【练习42】 解不等式:(1)()23213x x +-≤;(2)()30%151%x x +<+;(3)()()11221225x x x ⎡⎤-+≤-⎢⎥⎣⎦; (4)()()0.20.30.40.50.10.21110.030.066x x --->+. 【难度】★★【答案】见解析【解析】解:(1)()13322≤+-x x , (2)()x x +<+%511%30, ()3326≤+-x x , ()x x 10051130+<+, 94≤x , 2170<-x ,解得:49≤x ; 解得:103->x ;所以原不等式的解集为49≤x ; 所以原不等式的解集为103->x ; (3)()()15222121-≤⎥⎦⎤⎢⎣⎡+-x x x , (4)()()61106.02.01.05.0103.04.03.02.0+->--x x ,112212255x x ⎛⎫-≤- ⎪⎝⎭, 6761051386+->--x x ,11224255x x -≤-, ()71056862+->--x x , 312010x -≤, 66>-x ,解得:23x ≥- 解得:1-<x .所以原不等式的解集为23x ≥-; 所以原不等式的解集为1-<x .【总结】本题考查了不等式的解法,注意解题时细心计算.【练习43】 解不等式组:(1)()()3241353324x x x x ⎧-->-⎪⎨+≤+⎪⎩;(2)()210381274332x x x x x ⎧---≤-⎪⎪⎨⎪-<+⎪⎩;(3)132********522x x x x x x ⎧+>+⎪⎪+>+⎨⎪⎪-<-⎩;(4)()1226323112184x x x x x x ⎧+>⎪⎪⎪+≥+⎨⎪+-⎪-<-⎪⎩.【难度】★★【答案】见解析.【解析】解:(1)()()⎩⎨⎧+≤+->--,②,①4233513423x x x x ,由①得:32->x ,解得:23->x ,由②得:9-≥x ,所以不等式组的解集为23->x ; (2)()⎪⎩⎪⎨⎧+<---≤--,②,①323417102283xx x x x ,由①得:()()1410483714--≤--x x x ,解得:10≥x ,由②得:712<x ,所以原不等式组无解; (3)⎪⎪⎩⎪⎪⎨⎧-<-+>++>+,③,②,①52325546323212x x x x x x ,由①得:1->x ,由②得:1<x ,由③得:5>x ,所以原不等式组无解; (4)()1226323112184xx x x x x ⎧+>⎪⎪⎪+≥+⎨⎪+-⎪-<-⎪⎩,①,②,③,由①得:2->x ,由②得:4≤x ,由③得:3>x , 所以不等式组的解集为43≤<x .【总结】本题考查了不等式组的解法,解题时注意方法的选择,细心计算.【练习44】 解方程组:(1)521347a b a b +=-⎧⎨+=⎩;(2) 5.3 4.7804.7 5.320x y x y +=⎧⎨+=⎩;(3)34135353x y z x y z x y z +-=⎧⎪-+=⎨⎪+-=⎩;(4)2636315764949x y z x y z x y z ++=⎧⎪++=⎨⎪-+=⎩.【难度】★★【答案】见解析.【解析】解:(1)⎩⎨⎧=+-=+,②,①743125b a b a ,②①-⨯2得:97-=a ,则79-=a ,把79-=a 代入①中:12795-=+⎪⎭⎫ ⎝⎛-⨯b ,解得:719=b ,所以原方程组的解为:⎪⎩⎪⎨⎧=-=71979b a .(2)⎩⎨⎧=+=+,②,①203.57.4807.43.5y x y x ,由②①+得:1001010=+y x ,则,③y x -=10,把③代入①中:()807.4103.5=+-y y ,解得:45-=y ,把45-=y 代入③中, 解得:55=x ,所以原方程组的解为⎩⎨⎧-==4555y x .(3)由②①+:,④188=-z x ;③②+:,⑤43=+z x ;由④、⑤解得:⎩⎨⎧-==22z x ,把22-==z x 、代入③中:322=++y , 解得:1-=y , 所以原方程组的解为⎪⎩⎪⎨⎧-=-==212z y x .(4)由③①-⨯2得:,④3221=+z y ;由32⨯-⨯①②得:1256y z +=-⑤; 由25⨯-⨯⑤④得:31=y ,将31=y 代入④得:2-=z ;将31=y ,2-=z , 代入①得:5=x ;所以原方程组的解为⎪⎩⎪⎨⎧-===2315z y x .【总结】本题考查了方程组的解法,注意方法的选择,解完后注意检验所求的解是否正确.【练习45】 关于x 的方程()143321223x xx a x x +----=-的解是最小的质数的倒数,求a 的值.【难度】★★【答案】1625=a . 【解析】解:由题意得:最小质数为2,则原方程的解为21,则 3213422*********211⎪⎭⎫ ⎝⎛⨯---⨯=+--a36441101+--=-a 64410+-=a 解得:1625=a .【总结】本题考查了方程的解的运用及一元一次方程的解法.【练习46】 解方程:2015122320152016x x x+++=⨯⨯⨯.【难度】★★★【答案】2016=x .【解析】解:对原方程进行变形:20152016120151 (3)121211=⎪⎭⎫ ⎝⎛-++-+-x ,化简得:2015201611=⎪⎭⎫ ⎝⎛-x ,即:201520162015=x , 解得:2016=x .【总结】本题考查了数学简算中的裂项相消思想的运用,综合性较强.【练习47】 若关于x 、y 的方程组2323ax by x y -=⎧⎨-=-⎩和3424y x ax by -=⎧⎨+=-⎩有相同的解,求a 、b 的值.【难度】★★★【答案】21-==b a 、.【解析】解:由题意得:⎩⎨⎧=--=-4332x y y x ,解得:⎩⎨⎧=-=11y x ,将y x 、的值代入⎩⎨⎧-=+=-4232by ax by ax 中,则:⎩⎨⎧-=+-=--4232b a b a ,解得:⎩⎨⎧-==21b a .【总结】本题考查了二元一次方程组的解的运用.【练习48】 甲、乙两人同时求7mx ny -=的整数解,甲求出一组解为34x y =⎧⎨=⎩,而乙把7mx ny -=中的7看成1,求出一组解为12x y =⎧⎨=⎩,求m 、n 的值. 【难度】★★★【答案】25==n m 、.【解析】解:把43==y x 、代入7=-ny mx 中,得,①743=-n m把21==y x 、代入1=-ny mx 中,得,②12=-n m ; 由①、②,得:⎩⎨⎧==25n m .【总结】本题考查了二元一次方程解的定义及解二元一次方程组.【练习49】 已知关于x 、y 的方程组321431x y p x y p +=+⎧⎨+=-⎩满足x > y ,求p 的取值范围.【难度】★★★【答案】6->p .【解析】解:⎩⎨⎧-=++=+,②,①134123p y x p y x ,由23⨯-⨯②①得:5+=p x ,由34⨯-⨯②①得:7+=-p y ,所以7--=p y ,因为y x >,所以75-->+p p ,解得:6->p , 所以p 的取值范围为6->p .【总结】本题考查了二元一次方程组的解法及解不等式的综合运用.【练习50】 解方程组:252821126x y y z z u u x +=⎧⎪+=⎪⎨+=⎪⎪+=⎩.【难度】★★★【答案】见解析.【解析】解:由题意得:⎪⎪⎩⎪⎪⎨⎧-=-=-=-=,④,③,②,①x u u z z y y x 262112825,所以()()()x u u z z y x 26833833211411411282525--=-=-+-=+-=--=-= x 1615+-=,即:x x 1615+-=,则1=x ,将1=x 代入④中得:4=u ;将4=u 代入③中得:3=z ;将3=z 代入②中得:2=y , 所以原方程组的解为⎪⎪⎩⎪⎪⎨⎧====4321u z y x .【总结】本题考查三元一次方程组的求解,注意利用加减消元法将元减少为二元一次方程组, 然后再进行计算.。
