平行四边形知识点与经典例题-2
初二数学八下平行四边形所有知识点总结和常考题型练习题

初二数学八下平行四边形所有知识点总结和常考题型练习题平行四边形知识点一、四边形相关1、四边形的内角和定理及外角和定理四边形的内角和定理:四边形的内角和等于360°。
四边形的外角和定理:四边形的外角和等于360°。
推论:多边形的内角和定理:n边形的内角和等于(n-2)×180°;多边形的外角和定理:任意多边形的外角和等于360°。
2、多边形的对角线条数的计算公式设多边形的边数为n,则多边形的对角线条数为n(n-3)/2.二、平行四边形1.定义:两组对边分别平行的四边形是平行四边形。
平行四边形的定义既是平行四边形的一条性质,又是一个判定方法。
2.平行四边形的性质:平行四边形的有关性质和判定都是从边、角、对角线三个方面的特征进行简述的。
1)角:平行四边形的对角相等,邻角互补;2)边:平行四边形两组对边分别平行且相等;3)对角线:平行四边形的对角线互相平分;4)面积:①S=底×高=ah;②平行四边形的对角线将四边形分成4个面积相等的三角形。
3.平行四边形的判别方法①定义:两组对边分别平行的四边形是平行四边形②方法1:两组对边分别相等的四边形是平行四边形③方法2:一组对边平行且相等的四边形是平行四边形④方法3:两组对角分别相等的四边形是平行四边形⑤方法4:对角线互相平分的四边形是平行四边形三、矩形1.矩形定义:有一个角是直角的平行四边形是矩形。
2.矩形性质①边:对边平行且相等;②角:对角相等、邻角互补,矩形的四个角都是直角;③对角线:对角线互相平分且相等;④对称性:轴对称图形(对边中点连线所在直线,2条)。
3.矩形的判定:满足下列条件之一的四边形是矩形①有一个角是直角的平行四边形;②对角线相等的平行四边形;③四个角都相等识别矩形的常用方法①先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的任意一个角为直角。
②先说明四边形ABCD为平行四边形,再说明平行四边形ABCD的对角线相等。
(完整版)平行四边形基本知识点总结

(完整版)平行四边形基本知识点总结平行四边形基本知识点总结
平行四边形是一种特殊的四边形,它具有一些独特的性质和特点。
以下是平行四边形的基本知识点总结:
定义
平行四边形是指具有两组对边分别平行的四边形。
性质
1. 对边平行性质:平行四边形的两组对边分别平行。
2. 对角线性质:平行四边形的对角线互相平分,并且长度相等。
3. 内角和性质:平行四边形的内角的和为180度。
4. 外角性质:平行四边形的外角的和为360度。
5. 对边长度性质:平行四边形的对边长度相等。
6. 同底角性质:与平行四边形的一条边相邻,另一条边平行的两个内角相等。
7. 同旁内角性质:与平行四边形的两条边相邻,另一条边平行的两个内角互补。
判定方法
1. 对边平行判定:如果一个四边形中有两组对边分别平行,则它是一个平行四边形。
2. 对角线平分判定:如果一个四边形的对角线互相平分,并且长度相等,则它是一个平行四边形。
特殊类型
1. 矩形:具有四个内角都为90度的平行四边形。
2. 正方形:具有四个内角都为90度,且四条边长度相等的平
行四边形。
相关公式
1. 平行四边形的面积公式:面积 = 底边长度 ×高度。
2. 平行四边形的周长公式:周长= 2 ×(底边长度+ 侧边长度)。
以上是关于平行四边形的基本知识点总结。
通过了解这些性质
和定理,可以更好地理解和解决相关的数学问题。
平行四边形的性质与判定经典例题练习

平行四边形的性质与判定经典例题练习一、平行四边形的性质1. 定义:平行四边形是一种具有两对对边平行的四边形。
定义:平行四边形是一种具有两对对边平行的四边形。
2. 性质1:平行四边形的对边相等。
性质1:平行四边形的对边相等。
3. 性质2:平行四边形的对角线相等。
性质2:平行四边形的对角线相等。
4. 性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
5. 性质4:平行四边形的两组对边分别互相平行并且相互等长。
性质4:平行四边形的两组对边分别互相平行并且相互等长。
二、平行四边形的判定1. 判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
2. 判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
三、经典例题练1. 例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
2. 例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
3. 例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
- (a)根据对边平行和相等的判定方法,若AB = CD且AD与BC互相垂直,则四边形ABCD是平行四边形。
平行四边形专题详解

平行四边形专题详解18.1 平行四边形知识框架{基础知识点{ 平行四边形的定义平行四边形的性质平行四边形的判定定理三角形中位线定理典型题型{利用平行线的性质求角度平行线间距离的运用平行四边形的证明难点题型{平行四边形间距离的应用平行四边形有关的计算平行四边形的有关证明一、基础知识点知识点1 平行四边形的定义1)平行四边形的定义:两组对边分别平行的四边形。
平行四边形用“▱”表示,平行四边形ABCD 表示为“▱ABCD ”,读作“平行四边形ABCD ”注:只要满足对边平行的四边形都是平行四边形。
矩形、菱形、正方形都是特殊的平行四边形 2)平行四边形的高:一条边上任取一点作另一边的垂线,该垂线的长度称作平行四边形在该边上的高。
3)两条平行线之间的距离:一条直线上任一点到另一直线的距离。
平行线间距离处处相等。
例1.如图,AB ∥EG ,EF ∥BC ,AC ∥FG ,A ,B ,C 分别在EF ,EG 上,则图中有 个平行四边形,可分别记作 。
例2.如图,▱ABCD 中,DE ⊥AB ,BF ⊥CD ,垂足分别为E ,F .求证:BE=DF 。
例3.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,点E,G为垂足,则下列说法错误的是()A.AB=CDB.CE=FGC.直线a,b之间的距离是线段AB的长D.直线a,b之间的距离是线段CE的长知识点2 平行四边形的性质平行四边形的性质,主要讨论:边、角、对角线,有时还会涉及对称性。
如下图,四边形ABCD是平行四边形:1)性质1(边):①对边相等;②,即:AB=CD,AD=BC;AB∥CD,AD∥BC2)性质2(角):对角相等,即:∠BAD=∠BCD,∠ABC=∠ADC3)性质3(对角线):对角线相互平分,即:AO=OC,BO=OD注:①平行四边形仅对角线相互平分,对角线不相等,即AC≠BD(矩形的对角线才相等);②平行四边形对角相等,但对角线不平分角,即∠DAO≠∠BAO(菱形对角线才平分角)4)性质4(对称性):平行四边形不是轴对称图形,是中心对称图形。
平行四边形知识点归纳和题型归类

平行四边形知识点归纳和题型归类平行四边形知识点归纳和题型归类要点梳理】要点一、平行四边形1.定义:有两组对边分别平行的四边形叫做平行四边形。
2.性质:(1)对边相等;(2)同位角相等;(3)相邻角互补;(4)是中心对称图形。
3.面积:S = 底 ×高。
4.判定:边:(1)有两组对边分别平行的四边形是平行四边形;(2)对边相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形。
角:(4)有一组对边平行,且同位角相等的四边形是平行四边形。
对角线:有一组对边相等,且互相平分的四边形是平行四边形。
要点诠释:平行线的性质:(1)平行线间的距离相等;(2)等底等高的平行四边形面积相等。
要点二、矩形1.定义:有四个角都是直角的平行四边形叫做矩形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形。
3.面积:S = 长 ×宽。
4.判定:有四个角都是直角的平行四边形是矩形。
要点诠释:由矩形得直角三角形的性质:(1)直角三角形斜边上的中线等于斜边的一半;(2)直角三角形中,30度角所对应的直角边等于斜边的一半。
要点三、菱形1.定义:有四个边都相等的平行四边形叫做菱形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形。
3.面积:S = 对角线之积的一半。
4.判定:有一组对边平行且相等的四边形是菱形。
要点四、正方形1.定义:四条边都相等,四个角都是直角的平行四边形叫做正方形。
2.性质:(1)对边相等;(2)相邻角互补;(3)对角线相等;(4)是中心对称图形,也是轴对称图形;(5)两条对角线把正方形分成四个全等的等腰直角三角形。
3.面积:S = 边长的平方,也可以用对角线的平方的一半求解。
4.判定:(1)有一组对边平行且相等的菱形是正方形;(2)有四个角都是直角的矩形是正方形;(3)对角线互相垂直平分且相等的四边形是正方形;(4)四条边都相等,四个角都是直角的四边形是正方形。
平行四边形判定经典题型

平行四边形判定经典题型摘要:一、平行四边形的定义和性质二、平行四边形的判定方法1.两组对边分别平行2.两组对边分别相等3.一组对边平行且相等4.两组对角分别相等5.对角线互相平分三、经典题型解析1.题目一2.题目二3.题目三4.题目四5.题目五正文:平行四边形是初中数学中一个重要的基本图形,它具有许多独特的性质,其中最重要的性质之一就是可以通过一些特定的条件来判定一个四边形是否为平行四边形。
这些判定方法包括两组对边分别平行、两组对边分别相等、一组对边平行且相等、两组对角分别相等以及对角线互相平分。
首先,如果一个四边形的两组对边分别平行,那么这个四边形就是平行四边形。
这是最直接的判定方法。
其次,如果两组对边分别相等,那么这个四边形也是平行四边形。
这种情况下,四边形的一组对边可能相等,也可能不等。
再者,如果一组对边平行且相等,那么这个四边形也是平行四边形。
这种情况下,另一组对边可能平行,也可能相等。
此外,如果两组对角分别相等,那么这个四边形也是平行四边形。
最后,如果对角线互相平分,那么这个四边形也是平行四边形。
在实际做题过程中,我们需要根据题目给出的条件,灵活运用这些判定方法。
下面,我们通过五个经典题型来具体解析这些判定方法的应用。
题目一:如果一个四边形的两组对边分别平行,那么这个四边形是什么?解析:根据上述判定方法,这个四边形是平行四边形。
题目二:如果一个四边形的两组对边分别相等,那么这个四边形是什么?解析:根据上述判定方法,这个四边形是平行四边形。
题目三:如果一个四边形的一组对边平行且相等,那么这个四边形是什么?解析:根据上述判定方法,这个四边形是平行四边形。
题目四:如果一个四边形的两组对角分别相等,那么这个四边形是什么?解析:根据上述判定方法,这个四边形是平行四边形。
题目五:如果一个四边形的对角线互相平分,那么这个四边形是什么?解析:根据上述判定方法,这个四边形是平行四边形。
平行四边形10道经典例题

平行四边形经典例题一、已知平行四边形的性质求角度例题:在平行四边形ABCD 中,∠A 的度数比∠B 的度数小40°,求∠A 和∠B 的度数。
解析:因为平行四边形的邻角互补,即∠A + ∠B = 180°。
又已知∠A 比∠B 小40°,即∠B - ∠A = 40°。
联立这两个方程可得:∠A = 70°,∠B = 110°。
二、利用平行四边形的性质求边长例题:平行四边形ABCD 的周长为40,AB = 6,求BC 的长。
解析:平行四边形的对边相等,所以AB = CD = 6,BC = AD。
周长为40,则2(AB + BC) = 40,即2×(6 + BC) = 40,解得BC = 14。
三、判断四边形是否为平行四边形例题:已知四边形ABCD 中,AB∠CD,AB = CD,判断四边形ABCD 是否为平行四边形。
解析:一组对边平行且相等的四边形是平行四边形,所以四边形ABCD 是平行四边形。
四、根据平行四边形的性质求线段长度例题:在平行四边形ABCD 中,AC、BD 是对角线,AC = 10,BD = 8,且AC 与BD 的夹角为60°,求AB 的长度。
解析:过 A 作AE∠BD 于E。
设O 为AC 与BD 的交点,则AO = 5,BO = 4。
在直角三角形AOE 中,因为∠AOE = 60°,所以OE = AO×cos60° = 5×1/2 = 2.5,AE = AO×sin60° = 5×√3/2。
在直角三角形ABE 中,根据勾股定理可得AB = √(AE² + BE²) = √[(5×√3/2)²+(4 + 2.5)²]。
五、利用平行四边形的性质证明线段相等例题:在平行四边形ABCD 中,E、F 分别是AB、CD 的中点,连接DE、BF。
(word完整版)苏教版四年级下学期第七单元三角形平行四边形和梯形(2)

第七单元 三角形、平行四边形和梯形姓名------- 一、 平行四边形知识点两组对边互相平行的四边形叫平行四边形,它的对边平行且相等,对角相等。
从一个顶点向对边可以作两种不同的高。
底和高一定要对应。
一个平行四边形有无数条高。
正方形、长方形属于特殊的平行四边形。
两个完全一样的三角形,能拼成平行四边形。
二,常考题型1、下面的四边形中,( )不是平行四边2、平行四边形的( )相等。
① 四个角 ② 四条边 ③ 对边3、当一个四边形的两组对边分别平行,四条边都相等,四个角都相等时,这个四边形是( )①平行四边形 ②正方形 ③菱形 ④长方形 4、下面四句话中,错误的是( )A 、平行四边形的四条边一定相等 ;B 、平行四边形的对边平行且相等;C 、长方形是特殊的平行四边形;D 、平行四边形对角一定相等。
5、两个完全一样的三角形一定可以拼成一个( )。
A 、平行四边形 B 、梯形 C 、长方形 6、下面图形中,不是轴对称图形的是( )。
A 、长方形B 、圆形C 、平行四边形D 、等腰梯形 7、平行四边形的( )组对边分别平行。
8、以平行四边形的一条边为底,能做出( )条高,这些高的长度都( )。
判断:1、长方形是特殊的平行四边形,正方形又是特殊的长方形。
()2、从平行四边形的一个顶点可以向对边作无数条高。
()3、长方形和正方形都是特殊的平行四边形。
()4、沿着平行四边形的任意一条高剪开,可以拼成一个长方形。
()5、有四个角是直角的图形一定是长方形。
()6、周长相等的两个平行四边形,他们的形状一定完全一样()解决问题:1、平行四边形的周长是38厘米,其中一条边长是12厘米。
平行四边形另外三条边分别是多少厘米?2、一个平行四边形的一条边长12厘米,它的邻边比它少2厘米。
这个平行四边形的周长是多少厘米?3、平行四边形的周长是56厘米,其中一条边长是10厘米。
平行四边形另外三条边分别是多少厘米?4、一个平行四边形的周长是38厘米,其中一条边是9厘米,另外三条边长分别是多少厘米?三、平行四边形容易变形(不稳定性)。
人教八下平行四边形专题知识点 常考(典型)题型 重难点题型(含详细答案)

平行四边形专题知识点+常考题型+重难点题型(含详细答案)一、目录一、目录 (1)二、基础知识点 (2)1.平行四边形的定义 (2)2.平行四边形的性质 (3)3.平行四边形的判定定理 (7)4.三角形中位线定理 (10)三、重难点题型 (14)1.平行四边形的共性 (14)2.平行四边形间距离的应用 (16)3.与平行四边形有关的计算 (17)4.与平行四边形有关的证明 (19)二、基础知识点1.平行四边形的定义平行四边形:两组对边分别平行的四边形。
平行四边形ABCD记作“□ABCD”注:只要满足对边平行的四边形都是平行四边形。
矩形、菱形、正方形都是特殊的平行四边形例1.如图,□ABCD中,DE⊥AB,BF⊥CD,垂足分别为E,F.求证:BE=DF.答案:∵四边形ABCD为平行四边形∴AD∥CB,AD=CB∵DE⊥AB,BF⊥CD∴∠DEA=∠CFB∴△ADE≌△CFB∴AE=CF∵DC=AB∴BE=DF例2.在平面直角坐标系中,有A(0,1),B(-1,0),C(1,0)三点,若点D与A,B,C构成平行四边形,求D的坐标。
(3解)答案:如下图,有三种情况,坐标分别为:(0,-1);(2,1);(-2,1)2.平行四边形的性质性质1(边):平行四边形的对边相等(AB=CD,AC=BD)证明:∵∠CAD=∠ADB ∠DAB=∠ADC AD=AD ∴△ACD≌△DBA(ASA)∴AB=CD AC=BD性质2(角):平行四边形对角相等,邻角互补(∠A=∠D,∠C=∠B;∠A+∠C=∠B+∠D=180°)证明:∵△ACD≌△DBA(ASA)又∵∠CAB=∠CAD+∠DAB ∠CDB=∠CDA+∠ADB∴∠CAB=∠CDB∵AB∥CD∴∠B+∠BDC=180°性质3(对角线):平行四边形对角线互相平分(AO=OC;BO=OD)证明:∵AD=BC ∠OAD=∠OCB ∠ODA=∠OBC∴△AOD≌△COB(ASA)∴AO=OC OB=OD注1:平行四边形对角线互相平分,但两对角线不一定相等解析:假设平行四边形对角线相等∴∠OAD=∠ADO=∠OBC=∠OCB∠OAB=∠OBA=∠OCD=∠CDO又∵∠DAB+∠CBA=180°∴∠DAB=∠ABC=∠BCD=∠CDA=90°∴仅在平行四边形的四个角为直角时(即矩形),对角线相等注2:对角线不一定平分角解析:假设平行四边形对角线平分角,则∠ADB=∠BDC ∠ACD=∠ACB ∵∠DCB=∠BAD∴∠ACD=∠CAD又∵OD=OD∴△AOD≌△COD(AAS)∴AD=DC=BC=AB∴仅当平行四边形四条边相等时(即菱形),对角线平分角性质4:平行四边形是中心对称图形,对称中心为对角线交点。
初二数学:平行四边形知识点总结及压轴题练习(附答案解析)

A C BD 初二平行四边形所有知识点总结和常考题知识点:1、平行四边形定义:有两组对边分别平行的四边形叫做平行四边形。
2、平行四边形的性质:⑴平行四边形的对边相等;⑵平行四边形的对角相等:⑶平行四边形的对角线互相平分。
3平行四边形的判定:⑴.两组对边分别相等的四边形是平行四边形; ⑵对角线互相平分的四边形是平行四边形;⑶两组对角分别相等的四边形是平行四边形; ⑷一组对边平行且相等的四边形是平行四边形。
4、矩形的定义:有一个角是直角的平行四边形。
5、矩形的性质:⑴矩形的四个角都是直角;⑵矩形的对角线相等。
6、矩形判定定理:⑴ 有三个角是直角的四边形是矩形;⑵对角线相等的平行四边形是矩形。
7、中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。
直角三角形斜边上的中线等于斜边的一半。
(连接三角形两边中点的线段叫做三角形的中位线。
)8、菱形的定义 :有一组邻边相等的平行四边形。
9、菱形的性质:⑴菱形的四条边都相等;⑵菱形的两条对角线互相垂直,并且每一条对角线平分一组对角。
S 菱形=1/2×ab (a 、b 为两条对角线长)10、菱形的判定定理:⑴四条边相等的四边形是菱形。
⑵对角线互相垂直的平行四边形是菱形。
11、正方形定义:一个角是直角的菱形或邻边相等的矩形。
12正方形判定定理:⑴ 邻边相等的矩形是正方形。
⑵有一个角是直角的菱形是正方形。
(矩形+菱形=正方形)常考题:一.选择题(共14小题)1.矩形具有而菱形不具有的性质是( )A .两组对边分别平行B .对角线相等C .对角线互相平分D .两组对角分别相等2.平行四边形ABCD 中,AC 、BD 是两条对角线,如果添加一个条件,即可推出平行四边形ABCD 是矩形,那么这个条件是( )A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD3.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形4.顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形5.在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)6.如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.117.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.168.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°9.如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.1010.如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.1711.如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.812.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.1913.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF ⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣414.如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°二.填空题(共13小题)15.已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为cm2.16.如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD的周长等于.17.如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO 的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=厘米.18.如图,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD 和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为.19.如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是.20.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于度.21.如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是.22.如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF⊥CD于F,∠B=60°,则菱形的面积为.23.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是.24.如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C (0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为.25.如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标.26.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.27.如图,四边形ABCD中,∠A=90°,AB=3,AD=3,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为.三.解答题(共13小题)28.如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.求证:四边形BECF是平行四边形.29.已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,(1)求证:四边形ADCE为矩形;(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.30.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.31.如图,矩形ABCD中,AC与BD交于点O,BE⊥AC,CF⊥BD,垂足分别为E,F.求证:BE=CF.32.如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)线段BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.33.如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形;(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.34.如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?35.如图,在△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.(1)求证:EO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.36.如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:(1)△AEH≌△CGF;(2)四边形EFGH是菱形.37.如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.(1)求证:△ABD≌△EBD;(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.38.如图①,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.(1)求证:△BCP≌△DCP;(2)求证:∠DPE=∠ABC;(3)把正方形ABCD改为菱形,其它条件不变(如图②),若∠ABC=58°,则∠DPE=度.39.在数学活动课中,小辉将边长为和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF.(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长.40.数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BC的中点.∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F,求证:AE=EF.经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.初二平行四边形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一.选择题(共14小题)1.(2013•宜宾)矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线相等C.对角线互相平分 D.两组对角分别相等【分析】根据矩形与菱形的性质对各选项分析判断后利用排除法求解.【解答】解:A、矩形与菱形的两组对边都分别平行,故本选项错误;B、矩形的对角线相等,菱形的对角线不相等,故本选项正确;C、矩形与菱形的对角线都互相平分,故本选项错误;D、矩形与菱形的两组对角都分别相等,故本选项错误.故选B.【点评】本题考查了矩形的性质,菱形的性质,熟记两图形的性质是解题的关键.2.(2014•河池)平行四边形ABCD中,AC、BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是()A.AB=BC B.AC=BD C.AC⊥BD D.AB⊥BD【分析】根据对角线相等的平行四边形是矩形判断.【解答】解:A、是邻边相等,可得到平行四边形ABCD是菱形,故不正确;B、是对角线相等,可推出平行四边形ABCD是矩形,故正确;C、是对角线互相垂直,可得到平行四边形ABCD是菱形,故不正确;D、无法判断.故选B.【点评】本题主要考查的是矩形的判定定理.但需要注意的是本题的知识点是关于各个图形的性质以及判定.3.(2008•扬州)如图,已知四边形ABCD是平行四边形,下列结论中不正确的是()A.当AB=BC时,它是菱形B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD时,它是正方形【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;C、有一个角是直角的平行四边形是矩形,故C选项正确;D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;综上所述,符合题意是D选项;故选:D.【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.4.(2011•张家界)顺次连接任意四边形四边中点所得的四边形一定是()A.平行四边形B.矩形C.菱形D.正方形【分析】顺次连接任意四边形四边中点所得的四边形,一组对边平行并且等于原来四边形某一对角线的一半,说明新四边形的对边平行且相等.所以是平行四边形.【解答】解:连接BD,已知任意四边形ABCD,E、F、G、H分别是各边中点.∵在△ABD中,E、H是AB、AD中点,∴EH∥BD,EH=BD.∵在△BCD中,G、F是DC、BC中点,∴GF∥BD,GF=BD,∴EH=GF,EH∥GF,∴四边形EFGH为平行四边形.故选:A.【点评】本题三角形的中位线的性质考查了平行四边形的判定:三角形的中位线平行于第三边,且等于第三边的一半.5.(2006•南京)在平面直角坐标系中,平行四边形ABCD的顶点A,B,D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()A.(3,7) B.(5,3) C.(7,3) D.(8,2)【分析】因为D点坐标为(2,3),由平行四边形的性质,可知C点的纵坐标一定是3,又由D点相对于A点横坐标移动了2,故可得C点横坐标为2+5=7,即顶点C的坐标(7,3).【解答】解:已知A,B,D三点的坐标分别是(0,0),(5,0),(2,3),∵AB在x轴上,∴点C与点D的纵坐标相等,都为3,又∵D点相对于A点横坐标移动了2﹣0=2,∴C点横坐标为2+5=7,∴即顶点C的坐标(7,3).故选:C.【点评】本题主要是对平行四边形的性质与点的坐标的表示及平行线的性质和互为余(补)角的等知识的直接考查.同时考查了数形结合思想,题目的条件既有数又有形,解决问题的方法也要既依托数也依托形,体现了数形的紧密结合,但本题对学生能力的要求并不高.6.(2014•河南)如图,▱ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=4,AC=6,则BD的长是()A.8 B.9 C.10 D.11【分析】利用平行四边形的性质和勾股定理易求BO的长,进而可求出BD的长.【解答】解:∵▱ABCD的对角线AC与BD相交于点O,∴BO=DO,AO=CO,∵AB⊥AC,AB=4,AC=6,∴BO==5,∴BD=2BO=10,故选:C.【点评】本题考查了平行四边形的性质以及勾股定理的运用,是中考常见题型,比较简单.7.(2013•南充)如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12D.16【分析】在矩形ABCD中根据AD∥BC得出∠DEF=∠EFB=60°,由于把矩形ABCD 沿EF翻折点B恰好落在AD边的B′处,所以∠EFB=∠DEF=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中可知∠DEF=∠EFB=∠EB′F=60°故△EFB′是等边三角形,由此可得出∠A′B′E=90°﹣60°=30°,根据直角三角形的性质得出A′B′=AB=2,然后根据矩形的面积公式列式计算即可得解.【解答】解:在矩形ABCD中,∵AD∥BC,∴∠DEF=∠EFB=60°,∵把矩形ABCD沿EF翻折点B恰好落在AD边的B′处,∴∠DEF=∠EFB=60°,∠B=∠A′B′F=90°,∠A=∠A′=90°,AE=A′E=2,AB=A′B′,在△EFB′中,∵∠DEF=∠EFB=∠EB′F=60°∴△EFB′是等边三角形,Rt△A′EB′中,∵∠A′B′E=90°﹣60°=30°,∴B′E=2A′E,而A′E=2,∴B′E=4,∴A′B′=2,即AB=2,∵AE=2,DE=6,∴AD=AE+DE=2+6=8,∴矩形ABCD的面积=AB•AD=2×8=16.故选D.【点评】本题考查了矩形的性质,翻折变换的性质,两直线平行,同旁内角互补,两直线平行,内错角相等的性质,解直角三角形,作辅助线构造直角三角形并熟记性质是解题的关键.8.(2013•扬州)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.50°B.60°C.70°D.80°【分析】连接BF,根据菱形的对角线平分一组对角求出∠BAC,∠BCF=∠DCF,四条边都相等可得BC=DC,再根据菱形的邻角互补求出∠ABC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠ABF=∠BAC,从而求出∠CBF,再利用“边角边”证明△BCF和△DCF全等,根据全等三角形对应角相等可得∠CDF=∠CBF.【解答】解:如图,连接BF,在菱形ABCD中,∠BAC=∠BAD=×80°=40°,∠BCF=∠DCF,BC=DC,∠ABC=180°﹣∠BAD=180°﹣80°=100°,∵EF是线段AB的垂直平分线,∴AF=BF,∠ABF=∠BAC=40°,∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS),∴∠CDF=∠CBF=60°.故选:B.【点评】本题考查了菱形的性质,全等三角形的判定与性质,线段垂直平分线上的点到线段两端点的距离相等的性质,综合性强,但难度不大,熟记各性质是解题的关键.9.(2015•河南)如图,在▱ABCD中,用直尺和圆规作∠BAD的平分线AG交BC 于点E.若BF=6,AB=5,则AE的长为()A.4 B.6 C.8 D.10【分析】由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.【解答】解:连结EF,AE与BF交于点O,如图,∵AB=AF,AO平分∠BAD,∴AO⊥BF,BO=FO=BF=3,∵四边形ABCD为平行四边形,∴AF∥BE,∴∠1=∠3,∴∠2=∠3,∴AB=EB,而BO⊥AE,∴AO=OE,在Rt△AOB中,AO===4,∴AE=2AO=8.故选C.【点评】本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.也考查了等腰三角形的判定与性质和基本作图.10.(2013•凉山州)如图,菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为()A.14 B.15 C.16 D.17【分析】根据菱形得出AB=BC,得出等边三角形ABC,求出AC,长,根据正方形的性质得出AF=EF=EC=AC=4,求出即可.【解答】解:∵四边形ABCD是菱形,∴AB=BC,∵∠B=60°,∴△ABC是等边三角形,∴AC=AB=4,∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16,故选C.【点评】本题考查了菱形性质,正方形性质,等边三角形的性质和判定的应用,关键是求出AC的长.11.(2013•泰安)如图,在平行四边形ABCD中,AB=4,∠BAD的平分线与BC 的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的边长为()A.2 B.4 C.4 D.8【分析】由AE为角平分线,得到一对角相等,再由ABCD为平行四边形,得到AD与BE平行,利用两直线平行内错角相等得到一对角相等,等量代换及等角对等边得到AD=DF,由F为DC中点,AB=CD,求出AD与DF的长,得出三角形ADF 为等腰三角形,根据三线合一得到G为AF中点,在直角三角形ADG中,由AD 与DG的长,利用勾股定理求出AG的长,进而求出AF的长,再由三角形ADF 与三角形ECF全等,得出AF=EF,即可求出AE的长.【解答】解:∵AE为∠DAB的平分线,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F为DC的中点,∴DF=CF,∴AD=DF=DC=AB=2,在Rt△ADG中,根据勾股定理得:AG=,则AF=2AG=2,∵平行四边形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,,∴△ADF≌△ECF(AAS),∴AF=EF,则AE=2AF=4.故选:B【点评】此题考查了平行四边形的性质,全等三角形的判定与性质,勾股定理,等腰三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.12.(2013•菏泽)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为()A.16 B.17 C.18 D.19【分析】由图可得,S1的边长为3,由AC=BC,BC=CE=CD,可得AC=2CD,CD=2,EC=;然后,分别算出S1、S2的面积,即可解答.【解答】解:如图,设正方形S2的边长为x,根据等腰直角三角形的性质知,AC=x,x=CD,∴AC=2CD,CD==2,∴EC2=22+22,即EC=;∴S2的面积为EC2==8;∵S1的边长为3,S1的面积为3×3=9,∴S1+S2=8+9=17.故选:B.【点评】本题考查了正方形的性质和等腰直角三角形的性质,考查了学生的读图能力.13.(2013•连云港)如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为()A.1 B.C.4﹣2D.3﹣4【分析】根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE 的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的倍计算即可得解.【解答】解:在正方形ABCD中,∠ABD=∠ADB=45°,∵∠BAE=22.5°,∴∠DAE=90°﹣∠BAE=90°﹣22.5°=67.5°,在△ADE中,∠AED=180°﹣45°﹣67.5°=67.5°,∴∠DAE=∠AED,∴AD=DE=4,∵正方形的边长为4,∴BD=4,∴BE=BD﹣DE=4﹣4,∵EF⊥AB,∠ABD=45°,∴△BEF是等腰直角三角形,∴EF=BE=×(4﹣4)=4﹣2.故选:C.【点评】本题考查了正方形的性质,主要利用了正方形的对角线平分一组对角,等角对等边的性质,正方形的对角线与边长的关系,等腰直角三角形的判定与性质,根据角的度数的相等求出相等的角,再求出DE=AD是解题的关键,也是本题的难点.14.(2014•福州)如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE 相交于点F,则∠BFC为()A.45°B.55°C.60°D.75°【分析】根据正方形的性质及全等三角形的性质求出∠ABE=15°,∠BAC=45°,再求∠BFC.【解答】解:∵四边形ABCD是正方形,∴AB=AD,又∵△ADE是等边三角形,∴AE=AD=DE,∠DAE=60°,∴AB=AE,∴∠ABE=∠AEB,∠BAE=90°+60°=150°,∴∠ABE=(180°﹣150°)÷2=15°,又∵∠BAC=45°,∴∠BFC=45°+15°=60°.故选:C.【点评】本题主要是考查正方形的性质和等边三角形的性质,本题的关键是求出∠ABE=15°.二.填空题(共13小题)15.(2008•恩施州)已知菱形的两对角线长分别为6cm和8cm,则菱形的面积为24cm2.【分析】根据菱形的面积等于两对角线乘积的一半求得其面积即可.【解答】解:由已知得,菱形的面积等于两对角线乘积的一半即:6×8÷2=24cm2.故答案为:24.【点评】此题主要考查菱形的面积等于两条对角线的积的一半.16.(2015•梅州)如图,在▱ABCD中,BE平分∠ABC,BC=6,DE=2,则▱ABCD 的周长等于20.【分析】根据四边形ABCD为平行四边形可得AE∥BC,根据平行线的性质和角平分线的性质可得出∠ABE=∠AEB,继而可得AB=AE,然后根据已知可求得结果.【解答】解:∵四边形ABCD为平行四边形,∴AE∥BC,AD=BC,AB=CD,∴∠AEB=∠EBC,∵BE平分∠ABC,∴∠ABE=∠EBC,∴∠ABE=∠AEB,∴AB=AE,∴AE+DE=AD=BC=6,∴AE+2=6,∴AE=4,∴AB=CD=4,∴▱ABCD的周长=4+4+6+6=20,故答案为:20.【点评】本题考查了平行四边形的性质,解答本题的关键是根据平行线的性质和角平分线的性质得出∠ABE=∠AEB.17.(2013•厦门)如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=3厘米.【分析】根据AC+BD=24厘米,可得出出OA+OB=12cm,继而求出AB,判断EF 是△OAB的中位线即可得出EF的长度.【解答】解:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,又∵AC+BD=24厘米,∴OA+OB=12cm,∵△OAB的周长是18厘米,∴AB=6cm,∵点E,F分别是线段AO,BO的中点,∴EF是△OAB的中位线,∴EF=AB=3cm.故答案为:3.【点评】本题考查了三角形的中位线定理,解答本题需要用到:平行四边形的对角线互相平分,三角形中位线的判定定理及性质.18.(2007•临夏州)如图,矩形ABCD的对角线AC和BD相交于点O,过点O 的直线分别交AD和BC于点E、F,AB=2,BC=3,则图中阴影部分的面积为3.【分析】根据矩形是中心对称图形寻找思路:△AOE≌△COF,图中阴影部分的面积就是△BCD的面积.【解答】解:∵四边形ABCD是矩形,∴OA=OC,∠AEO=∠CFO;又∵∠AOE=∠COF,在△AOE和△COF中,,∴△AOE≌△COF,∴S△AOE =S△COF,∴图中阴影部分的面积就是△BCD的面积.S△BCD=BC×CD=×2×3=3.故答案为:3.【点评】此题主要考查了矩形的性质以及全等三角形的判定和性质,能够根据三角形全等,从而将阴影部分的面积转化为矩形面积的一半,是解决问题的关键.19.(2014•宿迁)如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B 的坐标分别为(﹣3,0),(2,0),点D在y轴上,则点C的坐标是(5,4).【分析】利用菱形的性质以及勾股定理得出DO的长,进而求出C点坐标.【解答】解:∵菱形ABCD的顶点A,B的坐标分别为(﹣3,0),(2,0),点D 在y轴上,∴AB=5,∴DO=4,∴点C的坐标是:(5,4).故答案为:(5,4).【点评】此题主要考查了菱形的性质以及坐标与图形的性质,得出DO的长是解题关键.20.(2015•黄冈)如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.若∠CBF=20°,则∠AED等于65度.【分析】根据正方形的性质得出∠BAE=∠DAE,再利用SAS证明△ABE与△ADE 全等,再利用三角形的内角和解答即可.【解答】解:∵正方形ABCD,∴AB=AD,∠BAE=∠DAE,在△ABE与△ADE中,,∴△ABE≌△ADE(SAS),∴∠AEB=∠AED,∠ABE=∠ADE,∵∠CBF=20°,∴∠ABE=70°,∴∠AED=∠AEB=180°﹣45°﹣70°=65°,故答案为:65【点评】此题考查正方形的性质,关键是根据正方形的性质得出∠BAE=∠DAE,再利用全等三角形的判定和性质解答.21.(2013•十堰)如图,▱ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=,则AB的长是1.【分析】根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,根据直角三角形性质求出CE长,即可求出AB的长.【解答】解:∵四边形ABCD是平行四边形,∴AB∥DC,AB=CD,∵AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE=CD,即D为CE中点,∵EF⊥BC,∴∠EFC=90°,∵AB∥CD,∴∠DCF=∠ABC=60°,∴∠CEF=30°,∵EF=,∴CE==2,∴AB=1,故答案为:1.【点评】本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.22.(2013•黔西南州)如图所示,菱形ABCD的边长为4,且AE⊥BC于E,AF ⊥CD于F,∠B=60°,则菱形的面积为.【分析】根据已知条件解直角三角形ABE可求出AE的长,再由菱形的面积等于底×高计算即可.【解答】解:∵菱形ABCD的边长为4,∴AB=BC=4,∵AE⊥BC于E,∠B=60°,∴sinB==,∴AE=2,∴菱形的面积=4×2=8,故答案为8.【点评】本题考查了菱形的性质:四边相等以及特殊角的三角函数值和菱形面积公式的运用.23.(2013•鞍山)如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是11.【分析】利用勾股定理列式求出BC的长,再根据三角形的中位线平行于第三边并且等于第三边的一半求出EH=FG=AD,EF=GH=BC,然后代入数据进行计算即可得解.【解答】解:∵BD⊥CD,BD=4,CD=3,∴BC===5,∵E、F、G、H分别是AB、AC、CD、BD的中点,∴EH=FG=AD,EF=GH=BC,∴四边形EFGH的周长=EH+GH+FG+EF=AD+BC,又∵AD=6,∴四边形EFGH的周长=6+5=11.故答案为:11.【点评】本题考查了三角形的中位线定理,勾股定理的应用,熟记三角形的中位线平行于第三边并且等于第三边的一半是解题的关键.24.(2015•攀枝花)如图,在平面直角坐标系中,O为坐标原点,矩形OABC中,A(10,0),C(0,4),D为OA的中点,P为BC边上一点.若△POD为等腰三角形,则所有满足条件的点P的坐标为(2.5,4),或(3,4),或(2,4),或(8,4).【分析】由矩形的性质得出∠OCB=90°,OC=4,BC=OA=10,求出OD=AD=5,分情况讨论:①当PO=PD时;②当OP=OD时;③当DP=DO时;根据线段垂直平分线的性质或勾股定理即可求出点P的坐标.【解答】解:∵四边形OABC是矩形,∴∠OCB=90°,OC=4,BC=OA=10,∵D为OA的中点,∴OD=AD=5,①当PO=PD时,点P在OD得垂直平分线上,∴点P的坐标为:(2.5,4);②当OP=OD时,如图1所示:则OP=OD=5,PC==3,∴点P的坐标为:(3,4);③当DP=DO时,作PE⊥OA于E,则∠PED=90°,DE==3;分两种情况:当E在D的左侧时,如图2所示:OE=5﹣3=2,∴点P的坐标为:(2,4);当E在D的右侧时,如图3所示:OE=5+3=8,∴点P的坐标为:(8,4);综上所述:点P的坐标为:(2.5,4),或(3,4),或(2,4),或(8,4);故答案为:(2.5,4),或(3,4),或(2,4),或(8,4).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;本题有一定难度,需要进行分类讨论才能得出结果.25.(2013•阜新)如图,已知△ABC的三个顶点的坐标分别为A(﹣2,0),B(﹣1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D 的坐标(3,2),(﹣5,2),(1,﹣2).【分析】首先根据题意画出图形,分别以BC,AB,AC为对角线作平行四边形,即可求得答案.【解答】解:如图:以A,B,C为顶点的平行四边形的第四个顶点D的坐标分别为:(3,2),(﹣5,2),(1,﹣2).故答案为:(3,2),(﹣5,2),(1,﹣2).【点评】此题考查了平行四边形的性质.注意坐标与图形的关系.26.(2014•丹东)如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,则t的值为.【分析】延长AB至M,使BM=AE,连接FM,证出△DAE≌EMF,得到△BMF 是等边三角形,再利用菱形的边长为4求出时间t的值.。
(完整版)平行四边形知识点及典型例题,推荐文档
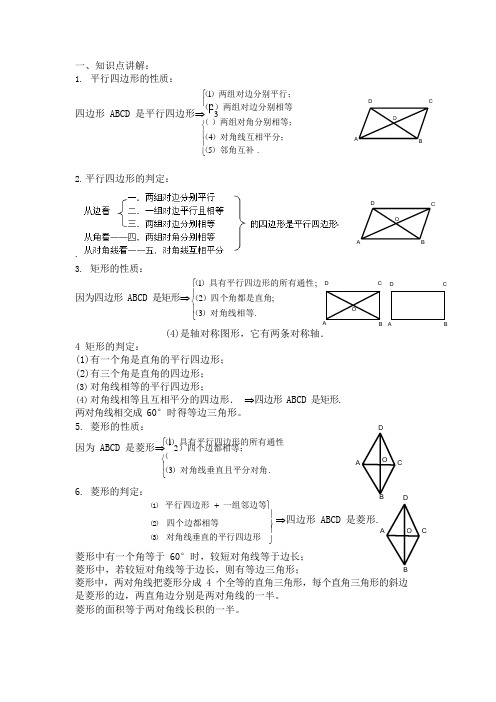
OOO ⎪ ⎨ ⎩ ⎩⎬ 一、知识点讲解:1. 平行四边形的性质:(⎧ 1)两组对边分别平行;⎪ DC(2)两组对边分别相等四边形 ABCD 是平行四边形⇒ ⎪ 3(⎨ )两组对角分别相等; (⎪ 4)对角线互相平分; AB(⎩ 5)邻角互补 .2. 平行四边形的判定:DC.3.矩形的性质: A B(⎧ 1)具有平行四边形的所有通性; DC DC因为四边形 ABCD 是矩形⇒ (⎪ 2)四个角都是直角; (⎪ 3)对角线相等.AB AB(4)是轴对称图形,它有两条对称轴.4 矩形的判定:(1)有一个角是直角的平行四边形; (2)有三个角是直角的四边形; (3) 对角线相等的平行四边形;(4) 对角线相等且互相平分的四边形. ⇒四边形 ABCD 是矩形. 两对角线相交成 60°时得等边三角形。
5. 菱形的性质:D(⎧ 1)具有平行四边形的所有通性 因为 ABCD 是菱形⇒ ⎪ 2)四个边都相等;6. 菱形的判定:(⎨(⎪ 3)对角线垂直且平分对角. ACBD(1) 平行四边形 + 一组邻边等⎫ (2) 四个边都相等(3) 对角线垂直的平行四边形 ⎪⇒四边形 ABCD 是菱形. ⎪A C⎭菱形中有一个角等于 60°时,较短对角线等于边长;菱形中,若较短对角线等于边长,则有等边三角形;B 菱形中,两对角线把菱形分成 4 个全等的直角三角形,每个直角三角形的斜边是菱形的边,两直角边分别是两对角线的一半。
菱形的面积等于两对角线长积的一半。
OOEFOAEO F C⎩ (⎨ ⇒ 7.正方形的性质:D(⎧ 1)具有平行四边形的所有通性;C DC四边形 ABCD 是正方形⇒ ⎪2)四个边都相等,四个角都是直角 (⎪ 3)对角线相等垂直且平分对角.A B A B8. 正方形的判定:(1) 平行四边形 + 一组邻边等+ 一个直角⎫ ⎪(2) 菱形 +一个直角 (3) 菱形 +对角线相等 (4) 矩形 + 一组邻边等 (5) 矩形 + 对角线互相垂直⎪ ⎪⎬ 四边形 ABCD 是正方形. ⎪ ⎪ ⎭9. 1.三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三遍的一半。
八年级初二数学 平行四边形知识点及练习题及解析

八年级初二数学 平行四边形知识点及练习题及解析一、解答题1.如图,在正方形ABCD 中,点G 在对角线BD 上(不与点B ,D 重合),GE ⊥DC 于点E ,GF ⊥BC 于点F ,连结AG .(1)写出线段AG ,GE ,GF 长度之间的数量关系,并说明理由;(2)若正方形ABCD 的边长为1,∠AGF=105°,求线段BG 的长.2.如图,在矩形ABCD 中,点E 是AD 上的一点(不与点A ,D 重合),ABE ∆沿BE 折叠,得BEF ,点A 的对称点为点F .(1)当AB AD =时,点F 会落在CE 上吗?请说明理由.(2)设()01AB m m AD=<<,且点F 恰好落在CE 上. ①求证:CF DE =.②若AE n AD=,用等式表示m n ,的关系. 3.在四边形ABCD 中,90A B C D ∠∠∠∠====,10AB CD ==,8BC AD ==.()1P 为边BC 上一点,将ABP 沿直线AP 翻折至AEP 的位置(点B 落在点E 处) ①如图1,当点E 落在CD 边上时,利用尺规作图,在图1中作出满足条件的图形(不写作法,保留作图痕迹,用2B 铅笔加粗加黑).并直接写出此时DE =______;②如图2,若点P 为BC 边的中点,连接CE ,则CE 与AP 有何位置关系?请说明理由; ()2点Q 为射线DC 上的一个动点,将ADQ 沿AQ 翻折,点D 恰好落在直线BQ 上的点'D 处,则DQ =______; 4.如图1,在正方形ABCD 和正方形BEFG 中,点,,A B E 在同一条直线上,P 是线段DF 的中点,连接,PG PC .(1)求证:,PG PC PG PC ⊥=.简析:由Р是线段DF 的中点,//DC CF ,不妨延长GP 交DC 于点M ,从而构造出一对全等的三角形,即_______≅________.由全等三角形的性质,易证CMG 是_______三角形,进而得出结论;(2)如图2,将原问题中的正方形ABCD 和正方形BEFG 换成菱形ABCD 和菱形BEFG ,且60ABC BEF ∠=∠=︒,探究PG 与PC 的位置关系及PG PC的值,写出你的猜想并加以证明;(3)当6,2AB BE ==时,菱形ABCD 和菱形BEFG 的顶点都按逆时针排列,且60ABC BEF ∠=∠=︒.若点A B E 、、在一条直线上,如图2,则CP =________;若点A B G 、、在一条直线上,如图3,则CP =________.5.如图,在矩形ABCD 中,E 是AD 的中点,将ABE ∆沿BE 折叠,点A 的对应点为点G .图1 图2(1)填空:如图1,当点G 恰好在BC 边上时,四边形ABGE 的形状是________; (2)如图2,当点G 在矩形ABCD 内部时,延长BG 交DC 边于点F .①求证:BF AB DF =+. ②若3AD AB =,试探索线段DF 与FC 的数量关系.6.如图①,已知正方形ABCD 的边长为3,点Q 是AD 边上的一个动点,点A 关于直线BQ 的对称点是点P ,连接QP 、DP 、CP 、BP ,设AQ =x .(1)BP +DP 的最小值是_______,此时x 的值是_______;(2)如图②,若QP 的延长线交CD 边于点M ,并且∠CPD =90°.①求证:点M 是CD 的中点;②求x 的值.(3)若点Q 是射线AD 上的一个动点,请直接写出当△CDP 为等腰三角形时x 的值.7.矩形ABCD 中,AB =3,BC =4.点E ,F 在对角线AC 上,点M ,N 分别在边AD ,BC 上. (1)如图1,若AE =CF =1,M ,N 分别是AD ,BC 的中点.求证:四边形EMFN 为矩形. (2)如图2,若AE =CF =0.5,02AM CN x x ==<<(),且四边形EMFN 为矩形,求x 的值.8.如图,在正方形ABCD 中,点E 是BC 边所在直线上一动点(不与点B 、C 重合),过点B 作BF ⊥DE ,交射线DE 于点F ,连接CF .(1)如图,当点E 在线段BC 上时,∠BDF=α.①按要求补全图形;②∠EBF =______________(用含α的式子表示);③判断线段 BF ,CF ,DF 之间的数量关系,并证明.(2)当点E 在直线BC 上时,直接写出线段BF ,CF ,DF 之间的数量关系,不需证明.9.如图,已知平面直角坐标系中,1,0A 、()0,2C ,现将线段CA 绕A 点顺时针旋转90︒得到点B ,连接AB .(1)求出直线BC 的解析式;(2)若动点M 从点C 出发,沿线段CB 10,过M 作//MN AB 交y 轴于N ,连接AN .设运动时间为t 分钟,当四边形ABMN 为平行四边形时,求t 的值.(3)P 为直线BC 上一点,在坐标平面内是否存在一点Q ,使得以O 、B 、P 、Q 为顶点的四边形为菱形,若存在,求出此时Q 的坐标;若不存在,请说明理由.10.如图,在长方形ABCD 中,AB =CD =6cm ,BC =10cm ,点P 从点B 出发,以2cm /秒的速度沿BC 向点C 运动,设点P 的运动时间为t 秒:(1)PC = cm .(用t 的代数式表示)(2)当t 为何值时,△ABP ≌△DCP ?(3)当点P 从点B 开始运动,同时,点Q 从点C 出发,以vcm /秒的速度沿CD 向点D 运动,是否存在这样v 的值,使得△ABP 与△PQC 全等?若存在,请求出v 的值;若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)AG2=GE2+GF2,理由见解析;(2)3266【分析】(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,3,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(3x)2,解得x=624,推出BN=624,再根据BG=BN÷cos30°即可解决问题.【详解】解:(1)结论:AG2=GE2+GF2.理由:连接CG.∵四边形ABCD是正方形,∴A、C关于对角线BD对称,∵点G在BD上,∴GA=GC,∵GE⊥DC于点E,GF⊥BC于点F,∴∠GEC=∠ECF=∠CFG=90°,∴四边形EGFC是矩形,∴CF=GE,在Rt△GFC中,∵CG2=GF2+CF2,∴AG2=GF2+GE2.(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,∴∠AMN=30°,∴AM=BM=2x,3x,在Rt △ABN 中,∵AB 2=AN 2+BN 2,∴1=x 2+(2x+3x )2,解得x=62-, ∴BN=62+, ∴BG=BN÷cos30°=3266+.【点睛】本题考查正方形的性质,矩形的判定和性质,勾股定理,直角三角形30度的性质.2.(1)不会,理由见解析;(2)①见解析;②²²20m n n =+-【分析】(1)根据BEF BEA ≅得到BF BA =,根据三角形的三边关系得到BC BF BA >=,与已知矛盾;(2)①根据90BFC BFE ∠=∠=︒、DEC FCB ∠=∠和BF=CD ,利用AAS 证得BCF CED ≅,根据全等三角形的性质即可证明;②设1AD =,则可表示出AE 和AB ,然后根据等角对等边证得CE=CB ,然后在Rt CDE ∆中应用勾股定理即可求解.【详解】(1) 由折叠知BEF BEA ≅ ,所以90BF BA BFE A =∠=∠=︒, .若点F 在CE 上,则90BFC ∠=︒,BC BF BA >=,与AB AD =矛盾,所以点F 不会落在CE 上.(2)①因为()01AB m m AD=<<,则AB AD < , 因为点F 落在CE 上,所以90BFC BFE ∠=∠=︒ ,所以BF BA CD == .因为//AD BC ,所以DEC FCB ∠=∠ ,所以BCF CED ≅ ,所以CF DE =.②若AE n AD=,则AE nAD =. 设1AD =,则AE n AB m ==,.因为//AD BC ,所以BEA EBC ∠=∠ .因为BEF BEA ∠=∠ ,所以EBC BEC ∠=∠ ,所以1CE CB AD === .在Rt CDE ∆中,11DE n CE CD m ===一,, ,所以22211()n m -+= ,所以²²20m n n =+-.故答案为(1)不会,理由见解析;(2)①见解析;②²²20m n n =+-.【点睛】本题考查了三角形全等的性质和判定,和等边对等角,此题属于矩形的折叠问题类综合题,熟练掌握三角形全等的性质,和做出示意图是本题的关键.3.(1)①6;②结论://P EC A ;(2)为4和16.【分析】 ()1①如图1中,以A 为圆心AB 为半径画弧交CD 于E ,作EAB ∠的平分线交BC 于点P ,点P 即为所求.理由勾股定理可得DE .②如图2中,结论:EC//PA.只要证明PA BE ⊥,EC BE ⊥即可解决问题. ()2分两种情形分别求解即可解决问题.【详解】解:()1①如图1中,以A 为圆心AB 为半径画弧交CD 于E ,作EAB ∠的平分线交BC 于点P ,点P 即为所求.在Rt ADE 中,90D ∠=,10AE AB ==,8AD =, 22221086DE AE AD ∴=-=-=,故答案为6.②如图2中,结论://P EC A .理由:由翻折不变性可知:AE AB =,PE PB =,PA ∴垂直平分线段BE ,即PA BE ⊥,PB PC PE ==,90BEC ∠∴=,EC BE ∴⊥, //EC PA ∴. ()2①如图31-中,当点Q 在线段CD 上时,设DQ QD'x ==.在Rt AD'B 中,AD'AD 8==,AB 10=,AD'B 90∠=,22BD'AB AD'6∴=-=, 在Rt BQC 中,222CQ BC BQ +=, 222(10x)8(x 6)∴-+=+,x 4∴=,DQ 4∴=.②如图32-中,当点Q 在线段DC 的延长线上时,DQ //AB ,DQA QAB ∠∠∴=,DQA AQB ∠∠=,QAB AQB ∠∠∴=,AB BQ 10∴==,在Rt BCQ 中,CQ BQ 6==,DQ DC CQ 16∴=+=,综上所述,满足条件的DQ 的值为4或16.故答案为4和16.【点睛】本题属于几何变换综合题,考查了矩形的性质,翻折变换,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.4.(1)ΔDPM,ΔFPG ;等腰直角;(2)线段PG 与PC 的位置关系是PG ⊥PC ;PG PC =3;(3)213【分析】(1)延长GP 交DC 于点M ,由Р是线段DF 的中点,//DC CF ,可得∠MDP=∠GFP ,DP=FP ,利用ASA 可证明△DPM ≌△FPG ;可得DM=GF ,MP=GP ,根据正方形的性质可得CM=CG ,即可证明△CMG 是等腰直角三角形,即可得答案;(2)如图,延长GP 交DC 于点H ,利用ASA 可证明△GFP ≌△HDP ,可得GP =HP ,GF =HD ,进而根据菱形的性质可证明△CHG 是等腰三角形,根据等腰三角形“三线合一”的性质可得PG ⊥PC ,∠HCP=∠GCP ,由∠ABC=60°可得∠HCG=120°,进而可得∠CGP=30°,根据含30°角的直角三角形的性质及勾股定理即可得答案;(3)利用线段的和差关系可求出图2中CG 的长,由(2)可知∠CGP=30°,根据含30°角的直角三角形的性质即可求出CP 的长;在图3中,延长GP 到N ,使GP=PN ,连接DN 、CN、CG,过N作NK⊥CD,交CD延长线于K,利用SAS可证明△FGP≌△DNP,可得GF=DN,∠GFP=∠NDP,根据角的和差关系可得∠CDN=120°,根据平角的定义可得∠GBC=120°,利用菱形的性质及等量代换可得DN=GB,利用SAS可证明△NDC≌△GBC,可得CN=CG,∠DCN=∠BCG,根据等腰三角形的性质可得PC⊥GN,根据角的和差关系可得∠NCG=120°,进而可得出∠CNP=30°,可得PC=12CG,根据平角的定义可得∠KDN=60°,即可得出∠KND=30°,根据含30°角的直角三角形的性质可得得出KD的长,利用勾股定理可求出KN的长,再利用勾股定理可求出CN的长,根据含30°角的直角三角形的性质即可得出PC的长.【详解】(1)如图,延长GP交DC于点M,∵Р是线段DF的中点,四边形ABCD、BEFG是正方形,点,,A B E在同一条直线上,∴//DC CF,DP=FP,CD=BC,FG=BG,在△DPM和△FPG中,MDP GFP DP FPDPM FPG ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△DPM≌△FPG,∴DM=FG,KP=GP,∴CD-DM=BC-BC,即CM=CG,∴△CMG是等腰直角三角形,∴PG⊥PC,PG=PC.故答案为:ΔDPM,ΔFPG;等腰直角(2)猜想:线段PG与PC的位置关系是PG⊥PC;PGPC3.如图,延长GP交DC于点H,∵P是线段DF的中点,∴FP=DP,∵四边形ABCD和四边形BEFG是菱形,∴CD//AB,CF//BE,CD=CB,GF=GB,∵点A B E、、在一条直线上,∴DC∥GF,∴∠GFP=∠HDP,在△GFP和△HDP中,GFP HDP FP DPGPF HPD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△GFP≌△HDP,∴GP=HP,GF=HD,∴CD-DH=CB-GB,即CG=CH,∴△CHG是等腰三角形.∴PG⊥PC,(三线合一),∠HCP=∠GCP,∵∠ABC=∠BEF=60°,∴∠HCG=120°,∴∠CGP=12(180°-120°)=30°,∴CG=2PC,∴PG=2222(2)3CG PC PC PC PC-=-=,∴PGPC=3.(3)如图2,∵AB=6,BE=2,∴CG=AB-BE=4,由(2)可知∠CGP=30°,PG⊥PC,∴PC=12CG=2,如图3,延长GP到N,使GP=PN,连接DN、CN、CG,过N作NK⊥CD,交CD延长线于K,在△DNP和△FGP中,DP FPNPD GPFPN PG=⎧⎪∠=∠⎨⎪=⎩,∴△DNP≌△FGP,∴DN=GF=BG=BE=2,∠NDP=∠GFP,∵四边形ABCD和四边形BEFG是菱形,∴CD//AB,EF//BC,∵点A、B、G在一条直线上,∴DC∥EF,∴∠CDP=∠EFP,∵∠ABC=∠BEF=60°,∴∠EFG=∠CBG=120°,∴∠NDP+CDP=∠GFP+∠EFP=∠EFG=120°,即∠NDC=120°,∴∠KDN=60°,∠KND=30°,∴KD=12DN=1,NK=223DN KD-=,∴CK=CD+KD=7,∴CN=22CK NK+=213,在△CDN和△CBG中,CD BCCDN CBGND BG=⎧⎪∠=∠⎨⎪=⎩,∴CN=CG,∠DCN=∠BCG,∴PC⊥GN,∠DCN+∠NCB=∠BCG+∠NCB=∠DCB=120°,即∠NCG=120°,∴∠CNP=12(180°-∠NCG)=30°,∴PC=12CN=13.故答案为:213【点睛】本题考查正方形的性质、菱形的性质、等腰直角三角形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质及勾股定理,正确作出辅助线、熟记30°角所对的直角边等于斜边的一半的性质及全等三角形的判定定理是解题关键.5.(1)四边形ABGE的形状是正方形;(2)①详见解析;②DF=3CF【分析】(1)由四边形ABCD是矩形,可得90A ABC︒∠=∠=,由折叠得:90BGE A︒∠=∠=,根据三个内角是直角可判断四边形ABGE为矩形,由折叠得:AB=BG,根据一组邻边相等的矩形是正方形可判断矩形ABGE为正方形;(2)①如图,连结EF,在矩形ABCD中,AB=DC,AD=BC,∠A=∠C=∠D=90°,由△ABE沿BE折叠后得到△GBE,可得BG=AB,EG=AE=ED,∠A=∠BGE=90°,故∠EGF=∠D=90°,由HL 可判断Rt △EGF ≌Rt △EDF ,得到DF=FG ,问题得证;②设AB=DC=a ,则AD=BC=3a ,另设CF=x ,则DF=DC-CF=a-x ,由①得BF=AB+DF =2a-x ,在Rt △BCF 中,由勾股定理得:BF 2=BC 2+CF 2,代入数据运算可得:x=14a ,即CF=14a ,DF=a-x=34a ,进而可得DF 与CF 关系. 【详解】 (1)四边形ABGE 的形状是正方形.理由是:∵四边形ABCD 是矩形,∴90A ABC ︒∠=∠=,由折叠得:90BGE A ︒∠=∠=,∴四边形ABGE 为矩形,由折叠得:AB=BG ,∴矩形ABGE 为正方形;故答案为:正方形.(2)①如图,连结EF ,在矩形ABCD 中,AB=DC ,AD=BC ,∠A=∠C=∠D=90°,∵E 是AD 的中点,∴AE=DE ,∵△ABE 沿BE 折叠后得到△GBE ,∴BG=AB ,EG=AE=ED ,∠A=∠BGE=90°,∴∠EGF=∠D=90°,Rt △EGF 和Rt △EDF 中,EG ED EF EF=⎧⎨=⎩, ∴Rt △EGF ≌Rt △EDF (HL ),∴DF=FG ,∴BF=BG+GF=AB+DF ;②不妨假设AB=DC=a ,则3,另设CF=x ,则DF=DC-CF=a-x ,由①得BF=AB+DF=a+a-x=2a-x ,在Rt △BCF 中,由勾股定理得:BF 2=BC 2+CF 2,即(2a-x)2=(3a)2+x 2, 整理得:x=14a , ∴CF=14a ,DF=a-x=34a , ∴DF=3CF .【点睛】本题主要考查了折叠的性质,正方形的判定,三角形全等的判定,勾股定理等内容,根据图形作出辅助线找出线段的等量关系列出方程是解题的关键.6.(1)32;323-;(2)①见详解;②x=1;(3)△CDP 为等腰三角形时x 的值为:633-或3或633+.【分析】(1)BP+DP 为点B 到D 两段折线的和.由两点间线段最短可知,连接DB ,若P 点落在BD 上,此时和最短,且为32.考虑动点运动,这种情形是存在的,由AQ=x ,则QD=3-x ,PQ=x .又PDQ=45°,所以QD =2PQ ,即3-x=2x .求解可得答案;(2)由已知条件对称分析,AB=BP=BC ,则∠BCP=∠BPC ,由∠BPM=∠BCM=90°,可得∠MPC=∠MCP .那么若有MP=MD ,则结论可证.再分析新条件∠CPD=90°,易得①结论.②求x 的值,通常都是考虑勾股定理,选择直角三角形QDM ,发现QM ,DM ,QD 都可用x 来表示,进而易得方程,求解即可.(3)若△CDP 为等腰三角形,则边CD 比为改等腰三角形的一腰或者底边.又P 点为A 点关于QB 的对称点,则AB=PB ,以点B 为圆心,以AB 的长为半径画弧,则P 点只能在弧AB 上.若CD 为腰,以点C 为圆心,以CD 的长为半径画弧,两弧交点即为使得△CDP 为等腰三角形(CD 为腰)的P 点.若CD 为底边,则作CD 的垂直平分线,其与弧AC 的交点即为使得△CDP 为等腰三角形(CD 为底)的P 点.则如图所示共有三个P 点,那么也共有3个Q 点.作辅助线,利用直角三角形性质求之即可.【详解】解:(1)连接DB ,若P 点落在BD 上,此时BP+DP 最短,如图:由题意,∵正方形ABCD 的边长为3,∴223332BD =+=∴BP +DP 的最小值是32由折叠的性质,PQ AQ x ==,则3QD x =-,∵∠PDQ=45°,∠QPD=90°,∴△QPD 是等腰直角三角形, ∴22QD QP x ==,∴32x x -=,解得:323x =-;故答案为:32;323-;(2)如图所示:①证明:在正方形ABCD 中,有AB=BC ,∠A=∠BCD=90°.∵P 点为A 点关于BQ 的对称点,∴AB=PB ,∠A=∠QPB=90°,∴PB=BC ,∠BPM=∠BCM ,∴∠BPC=∠BCP ,∴∠MPC=∠MPB-∠CPB=∠MCB-∠PCB=∠MCP ,∴MP=MC .在Rt △PDC 中,∵∠PDM=90°-∠PCM , ∠DPM=90°-∠MPC ,∴∠PDM=∠DPM ,∴MP=MD ,∴CM=MP=MD ,即M 为CD 的中点.②解:∵AQ=x ,AD=3,∴QD=3-x ,PQ=x ,CD=3.在Rt △DPC 中,∵M 为CD 的中点,∴DM=QM=CM=32, ∴QM=PQ+PM=x+32,∴(x+32)2=(3−x)2+(32)2,解得:x=1.(3)如图,以点B为圆心,以AB的长为半径画弧,以点C为圆心,以CD的长为半径画弧,两弧分别交于P1,P3.此时△CDP1,△CDP3都为以CD为腰的等腰三角形.作CD的垂直平分线交弧AC于点P2,此时△CDP2以CD为底的等腰三角形.;①讨论P1,如图作辅助线,连接BP1、CP1,作QP1⊥BP1交AD于Q,过点P1,作EF⊥AD 于E,交BC于F.∵△BCP1为等边三角形,正方形ABCD边长为3,∴P1F 33,P1E=333.在四边形ABP1Q中,∵∠ABP1=30°,∴∠AQP1=150°,∴△QEP1为含30°的直角三角形,∴31=9 332.∵AE=32,∴x=AQ=AE-QE=39(33)633 22--=-.②讨论P2,如图作辅助线,连接BP2,AP2,过点P2作QG⊥BP2,交AD于Q,连接BQ,过点P2作EF⊥CD于E,交AB于F.∵EF垂直平分CD,∴EF垂直平分AB,∴AP2=BP2.∵AB=BP2,∴△ABP2为等边三角形.在四边形ABP2Q中,∵∠BAD=∠BP2Q=90°,∠ABP2=60°,∴∠AQG=120°∴∠EP2G=∠DQG=180°-120°=60°,∴P2E=33 3∴EG=9 332,∴DG=DE+GE=3933333 22+=,∴QD=33,∴3③对P3,如图作辅助线,连接BP1,CP1,BP3,CP3,过点P3作BP3⊥QP3,交AD的延长线于Q,连接BQ,过点P1,作EF⊥AD于E,此时P3在EF上,不妨记P3与F重合.∵△BCP 1为等边三角形,△BCP 3为等边三角形,BC=3,∴P 1P 3=33P 1E =3332-, ∴EF =333+. 在四边形ABP 3Q 中∵∠ABF=∠ABC+∠CBP 3=150°,∴∠EQF=30°,∴39332. ∵AE=32, ∴x=AQ=AE+QE=32+9333362=. 综合上述,△CDP 为等腰三角形时x 的值为:633-3633+.【点睛】本题第一问非常基础,难度较低.第二问因为动点的原因,思路不易找到,这里就需要做题时充分分析已知条件,尤其是新给出的条件.其中求边长是勾股定理的重要应用,是很重要的考点.第三问是一个难度非常高的题目,可以利用尺规作图的思想将满足要求的点P 找全.另外求解各个Q 点也是考察三角函数及勾股定理的综合应用,有着极高的难度.7.(1)见详解;(2)72x = 【分析】(1)连接MN ,由勾股定理求出AC=5,证出四边形ABNM 是矩形,得MN=AB=3,证△AME ≌△CNF (SAS ),得出EM=FN ,∠AEM=∠CFN ,证EM ∥FN ,得四边形EMFN 是平行四边形,求出MN=EF ,即可得出结论;(2)连接MN ,作MH ⊥BC 于H ,则MH=AB=3,BH=AM=x ,得HN=BC-BH-CN=4-2x ,由矩形的性质得出MN=EF=AC-AE-CF=4,在Rt △MHN 中,由勾股定理得出方程,解方程即可.【详解】(1)证明:连接MN ,如图1所示:∵四边形ABCD 是矩形,∴AD ∥BC ,AD=BC ,∠B=90°,∴∠EAM=∠FCN ,2222345AB BC +=+=,∵M ,N 分别是AD ,BC 的中点,∴AM=DM=BN=CN ,AM ∥BN ,∴四边形ABNM 是平行四边形,又∵∠B=90°,∴四边形ABNM 是矩形,∴MN=AB=3,在△AME 和△CNF 中,AM CN EAM FCN AE CF =⎧⎪∠=∠⎨⎪=⎩,∴△AME ≌△CNF (SAS ),∴EM=FN ,∠AEM=∠CFN ,∴∠MEF=∠NFE ,∴EM ∥FN ,∴四边形EMFN 是平行四边形,又∵AE=CF=1,∴EF=AC-AE-CF=3,∴MN=EF ,∴四边形EMFN 为矩形.(2)解:连接MN ,作MH ⊥BC 于H ,如图2所示:则四边形ABHM 是矩形,∴MH=AB=3,BH=AM=x ,∴HN=BC-BH-CN=4-2x ,∵四边形EMFN 为矩形,AE=CF=0.5,∴MN=EF=AC-AE-CF=4,在Rt △MHN 中,由勾股定理得:32+(4-2x )2=42,解得:x=72±, ∵0<x <2,∴x=722-. 【点睛】本题考查了矩形的判定与性质、平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定、勾股定理等知识;熟练掌握矩形的判定与性质和勾股定理是解题的关键.8.(1)①详见解析;②45°-α;③2DF BF CF =+,详见解析;(2)2DF BF CF =,或2BF DF CF =,或2BF DF CF +=【分析】(1)①由题意补全图形即可;②由正方形的性质得出1452DBE ABC ∠=∠=,由三角形的外角性质得出45BEF DBE BDF α∠=∠+∠=+,由直角三角形的性质得出9045EBF BEF α∠=-∠=-即可;③在DF 上截取DM=BF ,连接CM ,证明△CDM ≌△CBF ,得出CM=CF , ∠DCM=∠BCF ,得出2CF 即可得出结论;(2)分三种情况:①当点E 在线段BC 上时,2CF ,理由同(1)③; ②当点E 在线段BC 的延长线上时,2CF ,在BF_上截取BM=DF ,连接CM .同(1)③得△CBM ≌△CDF 得出CM=CF ,∠BCM=∠DCF ,证明△CMF 是等腰直角三角形,得出2CF ,即可得出结论;③当点E 在线段CB 的延长线上时,2CF ,在DF 上截取DM=BF ,连接CM ,同(1) ③得:ACDM ≌△CBF 得出CM=CF ,∠DCM=∠BCF ,证明△CMF 是等腰直角三角形,得出MF=2CF ,即可得出结论.【详解】解:(1)①如图,②∵四边形ABCD 是正方形,∴∠ABC=90°,1452DBE ABC ∠=∠=, ∴45BEF DBE BDF α∠=∠+∠=+,∵BF ⊥DE,∴∠BFE=90°,∴9045EBF BEF α∠=-∠=-,故答案为:45°-α;③线段BF ,CF ,DF 之间的数量关系是2DF BF CF =+.证明如下:在DF 上截取DM =BF ,连接CM .如图2所示,∵ 正方形ABCD ,∴ BC =CD ,∠BDC =∠DBC =45°,∠BCD =90°∴∠CDM =∠CBF =45°-α,∴△CDM ≌△CBF (SAS ).∴ DM =BF , CM =CF ,∠DCM =∠BCF .∴ ∠MCF =∠BCF+∠MCE=∠DCM+∠MCE=∠BCD =90°,∴ MF 2CF .∴2.DF DM MF BF CF =+=+(2)分三种情况:①当点E 在线段BC 上时,2CF ,理由同(1)③; ②当点E 在线段BC 的延长线上时,2CF ,理由如下:在BF 上截取BM=DF ,连接CM ,如图3所示,同(1) ③,得:△CBM ≌△CDF (SAS),∴CM=CF , ∠BCM=∠DCF .∴∠MCF=∠DCF+∠MCD=∠BCM+∠MCD= ∠ BCD=90°,∴△CMF 是等腰直角三角形,∴MF=2CF , ∴BF=BM+MF=DF+2CF ;③当点E 在线段CB 的延长线上时,BF+DF=2CF ;理由如下:在DF 上截取DM=BF ,连接CM ,如图4所示,同(1)③得:△CDM ≌△CBF ,∴CM=CF ,∠DCM=∠BCF ,∴∠MCF=∠DCF+ ∠MCD= ∠DCF+∠BCF=∠BCD=90°,∴△CMF 是等腰直角三 角形,∴MF=2CF ,即DM+DF=2CF ,∴BF+DF=2CF ;综上所述,当点E 在直线BC 上时,线段BF ,CF ,DF 之间的数导关系为:2DF BF CF =+,或2BF DF CF =+,或2BF DF CF +=.【点睛】此题是四边形的一道综合题,考查正方形的性质,等腰直角三角形的判定及性质,全等三角形的判定及性质,注意解题中分情况讨论避免漏解.9.(1)123y x=-+;(2)t=23s时,四边形ABMN是平行四边形;(3)存在,点Q坐标为:618,55⎛⎫⎪⎝⎭或(3,1)-或(3,1)-或155,88⎛⎫-⎪⎝⎭.【分析】(1)如图1中,作BH⊥x轴于H.证明△COA≌△AHB(AAS),可得BH=OA=1,AH=OC=2,求出点B坐标,再利用待定系数法即可解决问题.(2)利用平行四边形的性质求出点N的坐标,再求出AN,BM,CM即可解决问题.(3)如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,分别求解即可解决问题.【详解】(1)如图1中,作BH⊥x轴于H.∵A(1,0)、C(0,2),∴OA=1,OC=2,∵∠COA=∠CAB=∠AHB=90°,∴∠ACO+∠OAC=90°,∠CAO+∠BAH=90°,∴∠ACO=∠BAH,∵AC=AB,∴△COA≌△AHB(AAS),∴BH=OA=1,AH=OC=2,∴OH=3,∴B (3,1),设直线BC 的解析式为y=kx+b ,则有231b k b =⎧⎨+=⎩, 解得:132k b ⎧=-⎪⎨⎪=⎩,∴123y x =-+; (2)如图2中,∵四边形ABMN 是平行四边形,∴AN ∥BM ,∴直线AN 的解析式为:1133y x =-+, ∴10,3N ⎛⎫ ⎪⎝⎭, ∴103BM AN ==, ∵B (3,1),C (0,2),∴10,∴210CM BC BM =-=∴2102103t ==, ∴t=23s 时,四边形ABMN 是平行四边形; (3)如图3中,如图3中,当OB为菱形的边时,可得菱形OBQP,菱形OBP1Q1.菱形OBP3Q3,连接OQ交BC于E,∵OE⊥BC,∴直线OE的解析式为y=3x,由3123y xy x=⎧⎪⎨=-+⎪⎩,解得:3595xy⎧=⎪⎪⎨⎪=⎪⎩,∴E(35,95),∵OE=OQ,∴Q(65,185),∵OQ1∥BC,∴直线OQ1的解析式为y=-13 x,∵OQ110,设Q1(m,-1m3),∴m2+19m2=10,∴m=±3,可得Q1(3,-1),Q3(-3,1),当OB为菱形的对角线时,可得菱形OP2BQ2,点Q2在线段OB的垂直平分线上,易知线段OB的垂直平分线的解析式为y=-3x+5,由3513y xy x=-+⎧⎪⎨=-⎪⎩,解得:15858xy⎧=⎪⎪⎨⎪=-⎪⎩,∴Q2(158,58-).综上所述,满足条件的点Q坐标为:618 ,55⎛⎫⎪⎝⎭或(3,1)-或(3,1)-或155,88⎛⎫-⎪⎝⎭.【点睛】本题属于一次函数综合题,考查了平行四边形的判定和性质,菱形的判定和性质,一次函数的性质等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.10.(1)(10﹣2t);(2)t=2.5;(3)2.4或2【分析】(1)根据P点的运动速度可得BP的长,再利用BC﹣BP即可得到CP的长;(2)当t=2.5时,△ABP≌△DCP,根据三角形全等的条件可得当BP=CP时,再加上AB =DC,∠B=∠C可证明△ABP≌△DCP;(3)此题主要分两种情况①当BA=CQ,PB=PC时,再由∠B=∠C,可得△ABP≌△QCP;②当BP=CQ,AB=PC时,再由∠B=∠C,可得△ABP≌△PCQ,然后分别计算出t的值,进而得到v的值.【详解】解:(1)点P从点B出发,以2cm/秒的速度沿BC向点C运动,点P的运动时间为t秒时,BP=2t,则PC=(10﹣2t)cm;故答案为:(10﹣2t);(2)当t=2.5时,△ABP≌△DCP,∵当t=2.5时,BP=2.5×2=5,∴PC=10﹣5=5,∵在△ABP和△DCP中,90AB DCB CBP CP=⎧⎪∠=∠=︒⎨⎪=⎩,∴△ABP≌△DCP(SAS);(3)①如图1,当BA=CQ,PB=PC时,再由∠B=∠C,可得△ABP≌△QCP,∵PB=PC,∴BP=PC=12BC=5,2t=5,解得:t=2.5,BA=CQ=6,v×2.5=6,解得:v=2.4(秒).②如图2,当BP=CQ,AB=PC时,再由∠B=∠C,可得△ABP≌△PCQ,∵AB=6,∴PC=6,∴BP=10﹣6=4,2t=4,解得:t=2,CQ=BP=4,2v=4,解得:v=2;综上所述:当v=2.4秒或2秒时△ABP与△PQC全等.【点睛】此题主要考查了全等三角形的判定,关键是掌握全等三角形全等的条件,找准对应边.。
专题25平行四边形的判定定理-重难点题型

专题4.3 平行四边形的判定定理-重难点题型【知识点1 平行四边形的判定】(1)两组对边分别平行的四边形是平行四边形.(2)两组对边分别相等的四边形是平行四边形.(3)一组对边平行且相等的四边形是平行四边形.(4)两组对角分别相等的四边形是平行四边形.(5)对角线互相平分的四边形是平行四边形.【题型1 平行四边形的判定条件】【例1】(2021春•玄武区期中)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是()A.∠ABC=∠ADC,AD∥BC B.∠ABD=∠BDC,∠BAD=∠DCBC.∠ABD=∠BDC,OA=OC D.∠ABC=∠ADC,AB=CD【变式1-1】(2021春•驿城区期末)在四边形ABCD中,对角线AC、BD相交于点O,在下列条件中,①AB∥CD,AD∥BC,②AB=CD,AD=BC;③AB∥CD,AD=BC,④OA=OC,OB=OD,⑤AB∥CD,∠BAD=∠BCD,能够判定四边形ABCD是平行四边形的个数有()A.2个B.3个C.4个D.5个【变式1-2】(2021春•凤翔县期末)在四边形ABCD中,对角线AC,BD相交于点O.给出下列四组条件:①AB ∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.其中一定能判定这个四边形是平行四边形的条件有()A.①②③B.②③④C.①②④D.①③④【变式1-3】(2021春•宜兴市月考)四边形ABCD中,对角线AC、BD相交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AB∥CD,AD=BC;④AO=CO,BO=DO.其中一定能判定这个四边形是平行四边形的条件有()A.4组B.3组C.2组D.1组【题型2 平行四边形的判定与坐标】【例2】(2021春•江油市期末)如图,△OAB的顶点O、A、B的坐标分别是(0,0)(3,0),(1,1),下列点M中,O、A、B、M为顶点的四边形不是平行四边形的是()A .(1,﹣1)B .(2,﹣1)C .(﹣2,1)D .(4,1)【变式2-1】(2021春•石狮市期末)在平面直角坐标系中,已知点A (0,0)、B (2,2)、C (3,0),若以点A 、B 、C 、D 为顶点的四边形是平行四边形,则点D 的坐标不可能为( )A .(﹣1,2)B .(5,2)C .(1,﹣2)D .(2,﹣2)【变式2-2】(2020春•彭州市期末)如图,Rt △OAB 的两直角边OA 、OB 分别在x 轴和y 轴上,A (﹣2,0),B (0,4),将△OAB 绕O 点顺时针旋转90°得到△OCD ,直线AC 、BD 交于点E .点M 为直线BD 上的动点,点N 为x 轴上的点,若以A ,C ,M ,N 四点为顶点的四边形是平行四边形,则符合条件的点M 的坐标为 .【变式2-3】(2021春•开封期末)如图,在平面直角坐标系中,点A 的坐标为(1,0),点B 的坐标为(4,0),点C 在y 的正半轴上,且OB =2OC ,在直角坐标平面内确定点D ,使得以点D 、A 、B 、C 为顶点的四边形是平行四边形,请写出点D 的坐标为 .【题型3 平行四边形的判定与动点】【例3】(2021春•阳谷县期末)如图,在四边形ABCD 中,AD ∥BC ,且AD <BC ,BC =6cm ,动点P ,Q 分别从点D ,B 同时出发,点P 以1cm /s 的速度向点A 运动,点Q 以2cm /s 的速度向点C 运动,几秒后四边形CDPQ 是平行四边形( )A .1B .2C .3D .4 【变式3-1】(2021秋•芝罘区期末)如图,四边形ABCD 中,AD ∥BC ,AD =8cm ,BC =12cm ,M 是BC 上一点,且BM =9cm ,点E 从点A 出发以1cm /s 的速度向点D 运动,点F 从点C 出发,以3cm /s 的速度向点B 运动,当其中一点到达终点,另一点也随之停止,设运动时间为t (s ),则当以A 、M 、E 、F 为顶点的四边形是平行四边形时,t 的值是( )A .34B .3C .3或32D .32或34 【变式3-2】(2021春•抚州期末)在平面直角坐标系中,已知点A (4,0),点B (﹣3,2),点C (0,2),点P 从点B 出发,以2个单位每秒的速度沿射线BC 运动,点Q 从点A 出发,开始以1个单位每秒的速度向原点O 运动,到达原点后立刻以原来3倍的速度沿射线OA 运动,若P ,Q 两点同时出发,设运动时间为t 秒,则当t=时,以点A,Q,C,P为顶点的四边形为平行四边形.【变式3-3】(2021春•惠来县期末)如图,在△ABC中,AB=AC=20cm,BD⊥AC于点D,且BD=16cm.点M 从点A出发,沿AC方向匀速运动,速度为4cm/s;同时点P由B点出发,沿BA方向匀速运动,速度为1cm/s,过点P的直线PQ∥AC,交BC于点Q,连接PM,设运动时间为t(s)(0<t<5),解答下列问题:(1)线段AD=cm;(2)求证:PB=PQ;(3)当t为何值时,以P、Q、D、M为顶点的四边形是平行四边形?【题型4 平行四边形的判定与证明】【例4】(2021•郓城县模拟)如图,F、C是线段AD上的两点,AB∥DE,BC∥EF,AF=DC,连结AE、BD,求证:四边形ABDE是平行四边形.【变式4-1】(2021春•西安期末)如图,在△AFC中,∠F AC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD,求证:四边形ABCD是平行四边形.【变式4-2】如图,四边形ABCD的对角线AC、BD相交于点O,过点O画直线EF分别交AD、BC于点E、F,已知OE=OF,且AO+AE=CO+CF,求证:四边形ABCD为平行四边形.【变式4-3】(2020春•长宁区期末)已知:如图,△ABC和△ADE都是等边三角形,点D在BC边上,EF∥BC 交AC于点F,联结BE.求证:四边形BEFC为平行四边形.【题型5 二次证明平行四边形】【例5】如图,在平行四边形ABCD中,AE=CF,M、N分别为ED、FB的中点,试说明四边形ENFM为平行四边形.【变式5-1】如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.【变式5-2】如图,E、F是△ABC的边AB、BC边的中点,在AC上取G、H两点,使AG=GH=HC,连接EG、FH并延长交于点D求证:四边形ABCD是平行四边形.【变式5-3】如图,E、F是四边形ABCD的对角线BD上两点,DF=BE,AE∥CF,AE=CF.求证:四边形ABCD 是平行四边形.【题型6 平行四边形的判定与性质综合】【例6】(2021春•西湖区校级月考)如图,已知△ABC为等边三角形,动点P在△ABC内,以PB,PC为边向外作等边三角形△PBD,△PCE.(1)若PB=8,PC=6,BC=10,①求证:四边形PEAD是平行四边形;②求出四边形PEAD的面积;(2)随着点P在△ABC所在平面上运动时,当△PBC满足什么条件时,平行四边形PEAD一定存在?(直接写出答案)【变式6-1】(2021秋•南岗区校级月考)如图,在△AFC中,∠F AC=45°,FE⊥AC于点E,在EF上取一点B,连接AB、BC,使得AB=FC,过点A作AD⊥AF,且AD=BC,连接CD.(1)如图1,求证:四边形ABCD是平行四边形;(2)如图2,若AB平分∠F AC,延长FE交CD于点H,请直接写出与∠ABE相等的角.【变式6-2】(2021春•安国市期末)如图,平面直角坐标系中,四边形ABCD是平行四边形,A(﹣3,0),B(3,0),C(0,4),连接OD,点E是线段OD的中点.(1)求点E和点D的坐标;(2)平面内是否存在一点N,使以C、D、E、N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.【变式6-3】(2021春•修水县期末)如图,在▱ABCD中,对角线AC,BD相交于点O,OA=5cm,E,F为直线BD上的两个动点(点E,F始终在▱ABCD的外面),连接AE,CE,CF,AF.(1)若DE=12OD,BF=12OB,①求证:四边形AFCE为平行四边形;②若CA平分∠BCD,∠AEC=60°,求四边形AFCE的周长.(2)若DE=13OD,BF=13OB,四边形AFCE还是平行四边形吗?请写出结论并说明理由.若DE=1n OD,BF=1n OB呢?请直接写出结论.。
(完整版)平行四边形相关知识梳理与常考题型

(完整版)平行四边形相关知识梳理与常考题型平行四边形相关知识梳理与常考题型总结知识梳理(1 )定义:两组对边分别平行的四边形是平行四边形;(2)表示:平行四边形用符号“ □”来表示。
2. 平行四边形性质:(1)边:两组对边分别平行且相等;(2) 角:对角相等、邻角互补;(3) 对角线:对角线互相平分。
3?平行四边形的判别方法:① 两组对边分别平行的四边形是平行四边形② 对角线互相平分的四边形是平行四边形③ 一组对边平行且相等的四边形是平行四边形④ 两组对边分别相等的四边形是平行四边形⑤ 两组对角分别相等的四边形是平行四边形4、三角形中位线一一构造平行四边形(1) 定义:连结三角形两边中点的线段叫做三角形的中位线.(2) 三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半.三角形中位线定理的作用:①位置关系:可以证明两条直线平行.②数量关系:可以证明线段的倍分关系.1.平行四边形的定义 CE 、F、G 、H 分别是四边形 ABCD 各边中点. EFGH 是平行四边形的三边为边向同一侧作等边△ ABD 、△ BCE 、△ ACF ,连接 DE 、EF.求是平行四边形?3、已知如图,在四边形 ABCD 中,E 、F 分别为AB 、CD 的中点.求证:EF *(AC BD )4、已知:如图,四边形 ABCD 是平行四边形,且 EAD BAF 。
(1)说明 CEF 是等腰三角形。
(2) CEF 的哪两边之和等于平行四边形 ABCD 的周长,为什么?E经典题型1已知如图, 求证:四边形2、分别以△ ABC 证:四边形AFED5. (黄冈市中考题)如图所示,平行四边形ABCD 中, G H 是对角线BD 上两点,且 DG= BH, DM BE.求证:四边形 EHFG 是平行四边形?6 已知:如图,在平行四边形ABCD 中,AE=2EC,E, F 在直线BC 上,且EE =B C =CF .求证:AF 丄DE.7.(江西省中考题)已知:如图,平行四边形ABCD 中,AE 丄BC, CF 丄BD,垂足分别为 E 、 F , G H 分别是AD BC 的中点,GH 交BD 于点0.求证:GH 与 EF 互相平分.能力提咼ABCD 中, AB = 2BC E 为 AB 中点,DF 丄 BC,垂足 F.8.(河南省中考题)已知:如图,平行四边形延长线于点 M N,交AB BC 于点P 、Q.求证:MQ= NP. ABCD 中,对角线 AC 的平行线MN 分别交DA DC 1.已知:如图,平行四边形求证:/ AED=Z EFB. A2. 如图,在平行四边形ABCD中, BC=2AB,M为AD的中点,CEL AB,垂足为E,求证:/ DME=2 AEM.作业1.如下图所示,ABCD是平行四边形,以AD BC为边在形外作等边三角形ADE和CBF, 连结BD EF,且它们相交于0,求证:EO=FO D0=B0.2.如图所示,/ EDA是平行四边形ABCD的外角,DF平分/ EDA 与BA延长线交于F, FD 延长线与BC延长线交于G.求证:BF=BG.3. 如图所示,平行四边形ABCD中,作AF L BC于F,交BD于E,若DE=2AB求证:/ ABD=2 / EBC.取G为DE中点,连接AG.在RT△ ADE中,AG为斜边上的中线。
第18章 《平行四边形》知识点及考点典例

第十八章《平行四边形》知识点及考点典例一、平行四边形1、平行四边形的概念两组对边分别__________的四边形叫做平行四边形。
2、平行四边形的性质(1)平行四边形的邻角_______,对角_______。
(2)平行四边形的对边_______且________。
推论:夹在两条平行线间的平行线段_______。
(3)平行四边形的对角线_________。
(4)若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积。
3、平行四边形的判定(1)定义:两组对边分别________的四边形是平行四边形(2)定理1:两组对角分别_________的四边形是平行四边形(3)定理2:两组对边分别_________的四边形是平行四边形(4)定理3:对角线___________的四边形是平行四边形(5)定理4:一组对边_________的四边形是平行四边形二、矩形1、矩形的概念有一个角是_______的平行四边形叫做矩形。
2、矩形的性质(1)具有平行四边形的一切性质(边、角、对角线);(2)矩形的四个角都是_______;(3)矩形的对角线_______;(4)矩形是______对称图形。
3、矩形的判定(1)定义:有一个角是________的平行四边形是矩形。
(2)定理1:有___________是直角的四边形是矩形。
(3)定理2:对角线相等的_______________是矩形。
4、矩形的面积S矩形=长×宽=ab三、菱形1、菱形的概念有一组___________的平行四边形叫做菱形2、菱形的性质(1)具有平行四边形的一切性质(边、角、对角线);(2)菱形的________边相等(3)菱形的对角线________,并且每一条对角线平分一组对角(4)菱形是________对称图形3、菱形的判定(1)定义:有一组___________的平行四边形是菱形(2)定理1:___________都相等的四边形是菱形(3)定理2:对角线___________的平行四边形是菱形4、菱形的面积S菱形=底边长×高=两条对角线乘积的一半四、正方形1、正方形的概念有一组邻边相等并且有一个角是直角的______________叫做正方形。
八年级数学《平行四边形的特征》重点知识及经典例题

八年级数学《平行四边形的特征》重点知识及经典例题学习目标1.掌握平行四边形的定义及平行四边形的特征.2.能够灵活运用平行四边形的特征进行有关的计算.3.了解解决平行四边形问题的基本思想、是转化为三角形来处理.4.掌握平行线的性质即平行线之间的距离相等.学法指导在理解的基础上识记平行四边形的概念及其性质,并根据相应的条件选用相应的性质利用平行四边形是中心对称图形来解决一些实际问题更容易.基础知识讲解1.平行四边形的定义两组对边分别平行的四边形叫做平行四边形,用符合“□”表示,四个顶点分别为A.B.C.D.则这个平行四边形记作□ABCD.2.平行四边形的特征(1)平行四边形的两组对边分别平行.(2)平行四边形的对边相等,对角相等.(3)平行四边形的对角线互相平分.(4)平行四边形是中心对称图形.注意:特征(2)(3)利用平行四边形是中心对称图形的性质可推出.3.平行线的性质平行线的距离为其中一条直线上任一点到另一条直线的距离叫做两条平行线之间的距离.由平行线距离的定义可知,每作两条距离与两平行线组成—个平行四边形,为此有无数个平行四边形,根据平行四边形的特征可得,平行线之间的距离处处相等.重点难点重点:平行四边形的定义和特征难点:1.运用中心对称图形的特征来理解平行四边形的特征.2.作适当的辅助线把平行四边形分解成三角形来解决一些问题.3.平行线之间的距离处处相等,实质是平行四边形对边相等.易错误区分析1.利用平行四边形的定义判定一个四边形是平行四边形易犯如下错误.例如:已知如图12-1-1所示,在□ABCD中,AE=CF.求证:四边形EBFD是平行四边形错证:∵四边形ABCD是平行四边形.∴AB=DC,AD=BC∴在△ABE和△CDF中AB=DC ∠A=∠C AE=CF∴△ABE≌△CDF(SAS)∴BE=DF ∴四边形EBFD为平行四边形分析:BE=DF不能得出四边形EBFD是平行四边形,而由BE∥DF,再由已知□ABCD才能得出.正确证:连结BD∵四边形ABCD为平行四边形∴AD BC 又∴AE=CF ∴ED=BF∴∠1=∠2 ∴△BED≌△BFD∴∠3=∠4 ∴BE∥DF又∵ED∥BF ∴四边形BEDF为平行四边形2.运用平行四边形的性质和平行线距离处处相等,易犯下面的错误.例如:求证平行四边形对角线上的交点到一组对边的距离相等.已知:如图12-1-2,□ABCD的对角线AC、BD相交于点O,OE⊥AB OF⊥CD,垂足分别为E,F.求证:OE=OF错证:∵四边形ABCD为平行四边形∴OA=OC AB∥CD∴∠3=∠4 ∵∠2=∠1 ∴△OAE≌△OCF ∴OE=0F分析:错在用∠1=∠2,即把∠1与∠2当成对顶角了,因为OE,OF是从O点分别向AB、CD作两条垂线,而OE与OF是否是同一条直线还需证明,故不能直接利用∠1=∠2 正确证明:∵四边形ABCD为平形四边形∴OA=OC AB∥CD∴∠3=∠4 ∵OE⊥AB OF⊥CD∴∠AE0=∠CF0=90°∴△OAE≌△OCF ∴OE=OF典型例题例1.已知如图12-1-4所示,□ABCD中,AB的延长线上取一点E,使BE=AB,在CE 上取一点M使CM=CD,连结DM并延长交AE的延长线于点F.求证BD=BF分析:由于BD,BF是△BDF的两边,所以要证BD=BF,可由证△BDF中∠BDF=∠F入手,易知∠F=∠CDM=∠CMD=∠EMF,故只要证BD∥CE,由此由证法一又注意到BF=BE+EF,易知BE=AB=CD=CM,EF=EM,故BF=CE,从而只要证BD=CE,由此有证法二.证法(一):∵四边形ABCD为平行四边形∴AB CD又∵E点在AB延长线上,且BE=AB ∴AB CD∴四边形BECD是平行四形∴BD∥CE ∴∠BDF=∠EMF∵∠EMF=∠CMD ∴∠BDF=∠CMD又∵CM=CD ∴∠CMD=∠CDM ∴∠BDF=∠CDM∵AF∥CD ∴∠CDM=∠F ∴BDF=∠F即BD=BF证法(二):∵四边形ABCD为平行四边形∴AB CD又∵E点在AB延长线上且BE=AB ∴BE CD∴四边形BECD是平行四边形∴BD=CE,BE=CD又∵∠EMF=∠CMD,CD=CM ∴∠CMD=∠CDM∴∠EMF=∠CDM ∵BE∥CD ∴∠F=∠EMF ∴EF=EM∴BF=BE+EF=CD+EM=CM+EM=CE=BD即BF=BD例2.如图12-1-5所示:L1∥L2、AB∥CD、CE⊥L2、FG⊥L2、E、G分别为垂足,则下列说法中错误的是()A.AB=CDB.CE=FGC.A,B两点的距离就是线段AB的长D.L1与L2间的距离就是线段CD的长分析:根据平行线之间的距离处处相等,推出夹在两平行线之间的平行线段也相等.(由图象的平移也可得到)答:选D.例3.如图12-1-6所示:已知六边形ABCDEF的6个内角均为120°,CD=2cm,BC=8cm,AB=8cm,AF=5cm,试求此六边形的周长.分析:分别求出六条边的长度,再求六边形的周长显然不可能,从图中可以发现AF分别绕A点,F点旋转60°后分别与BA,EF在同一直线上.同理DC分别绕D,C旋转60°后,分别与ED,BC在同一直线上,如图所示,得到一个平行四边形EMBN,△MFA与△DCN都为等边三角形,所以六边形的周长应等于平行四边形的周长减去AF+DC.解:由已知可得∠M=∠N=60°,又∠B=∠E=120°所以EN∥MB,EM∥NB,所以四边形MBNE为平行四边形又因为△AMF,△CDN为等边三角形所以MA=AF=MF=5cm,CD=CN=DN=2cmMB=EN=8+5=13cm,ME=BN=8+2=10cm故ED=13-2=11cm,EF=ME-MF=10-5=5cm得六边形的周长为8+8+2+11+5+5=39cm例4.把边长为3cm,5cm和7cm的两个三角形拼成一个四边形,一共能拼成几种不同的四边形?其中有几种是平形四边形?分析:由于要拼成四边形,故两个三角形一定有两条边重合在一起,这条重合的边即为四边形的对角线.因此找出问题的突破口,分三种情况讨论不难得出正确的答案.(1)以3cm长的边为对角线,有两种拼法,得到两个四边形中有一个是平行四边形.如图所示:(2)以7cm长的边为对角线,也有两种拼法,得到两个四边形,其中有一个平行四边形.如图所示:(3)以5cm长的边为对角线,也有两种拼法,得到两个四边形,其中也有一个是平行四边形,如图所示:答:总共拼成6种不同的四边形,其中有3种是平行四边形.创新思维例1.一块平行四边形菜地,若它的面积是144,测得相邻两边上的高分别为8和9,请你用平行四边行形的特征和有关的知识计算出它的周长.分析:如图12-1-7所示:要求周长必须求出BC,CD的长.从面积入手得.BC·AE=144 CD·AF=144 因而可求出周长.解:因为BC·AE=144,AE=8,所以BC=18因为DC·AF=144,AF=9,所以DC=16所以平行四边形菜地的周长=2(BC+DC)=2(18+16)=68例2.如图12-1-8,△ABC中AB=AC,点P在BC上任一点,PE∥AC,PF∥AB分别交AB,AC于E、F,试问线段PE,PF,AB之间有什么关系?试证明你的结论.分析:对于由给定条件寻求结论的这类探索性问题,其解题思路一般是从给的条件出发探索、归纳、猜想出结论,然后对猜想的结论进行证明.答:由线段PE,PF,AB之线段长度,不难得出三线段之间的关系为PE+PF=AB证明:∵PE∥AC ∴∠EPB=∠C又∵AB=AC ∴∠B=∠C∴∠EPB=∠B ∴PE=EB①∵PE∥AC PF∥AB ∴四边形AEPF是平行四边形∴PF=AE②由①+②得PE+PF=EB+AE,即PE+PF=AB例3.如右图:田村有一口呈四边形的池塘,在它的四个角A、B、C、D处均有一棵大核桃树,田村准备开挖池塘养鱼,想使池塘面积扩大一倍,又想保持核桃树不动,并要求扩建后的池塘为平行四边形,请问田村能否实现这一设想,若能,请你画出图形,若不能,请说明理由.(画图要留下痕迹,不写作法)分析:由平行四边形的特征可知,四棵树应在平行四边形的边上,面积要扩大一倍,则把△BOA、△BOC、△COD、△AOD的面积扩一倍即可,分别过点B,点D作AC的平行线;过点A,点C分别BD的平行线,不难证明四边形A′B′C′D′就是符合条件的平行四边形的池塘.答:能,画法如图.中考练兵1.已知如图12-1-9,平行四边形ABCD中E,F分别是BC,AD边上的点,且BE=DF,AC与EF交于点O.求证:OE=OF证明:∵四边形ABCD是平行四边形∴AD BC ∴∠1=∠2∵BE=DF ∴BC-BE=AD-DF即EC=AF在△AOF和△COE中∴△AOF≌△COE(AAS)∴OF=OE2.如图12-1-10,□ABCD中,对角线AC和BD交于O,若AC=8,BD=6,则AB长的取什范围是()A.1<AB<7 B.2<AB<4C.6<AB<8 D.3<AB<4解:由平行四边形的性质对角线互相平分得OA=4 OB=3,由三角形三边关系得OA-OB<AB<OA+OB即1<AB<7答:故选A3.如图12-1-12,将□ABCD沿AC折叠点B落在B′处,AB′交DC于点M,求证:折叠后重合的部分(即△MAC)是等腰三角形.证明:∵△BAC≌B′AC ∴AB′=AB,B′C=BC又∵AD=BC CD=AB ∴AD=B′C CD=AB′∴△ADC≌△CB′A(SSS) ∴∠ACD=∠CAB′∴MA=MC 即△MAC是等腰三角形4.如图12-1-13,E、F是平行四边形ABCD对角线上的两点,且AE=CF,求证:△ABF ≌△CDE证明:∵四边形ABCD为平行四边形∴AB∥CD,∠CAB=∠DCA∵AE二CF ∴AE+EF=CF+EF即AF=CE ∴△ABF≌△CDE。
平行四边形知识点及练习题及解析

平行四边形知识点及练习题及解析一、解答题1.如图,在ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别为OB 、OD 的中点,延长AE 至G ,使EG AE =,连接CG .(1)求证:AOE COF ∆≅∆;(2)四边形EGCF 是平行四边形吗?请说明理由;(3)若四边形EGCF 是矩形,则线段AB 、AC 的数量关系是______.2.如图,点E 为▱ABCD 的边AD 上的一点,连接EB 并延长,使BF =BE ,连接EC 并延长,使CG =CE ,连接FG .H 为FG 的中点,连接DH ,AF . (1)若∠BAE =70°,∠DCE =20°,求∠DEC 的度数; (2)求证:四边形AFHD 为平行四边形;(3)连接EH ,交BC 于点O ,若OC =OH ,求证:EF ⊥EG .3.如图1,AC 是平行四边形ABCD 的对角线,E 、H 分别为边BA 和边BC 延长线上的点,连接EH 交AD 、CD 于点F 、G ,且//EH AC . (1)求证:AEF CGH ∆≅∆(2)若ACD ∆是等腰直角三角形,90ACD ∠=,F 是AD 的中点,8AD =,求BE 的长:(3)在(2)的条件下,连接BD ,如图2,求证:22222()AC BD AB BC +=+4.如图,正方形ABCO 的边OA 、OC 在坐标轴上,点B 坐标为(6,6),将正方形ABCO 绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED 的延长线交线段OA于点H,连结CH、CG.(1)求证:CG平分∠DCB;(2)在正方形ABCO绕点C逆时针旋转的过程中,求线段HG、OH、BG之间的数量关系;(3)连结BD、DA、AE、EB,在旋转的过程中,四边形AEBD是否能在点G满足一定的条件下成为矩形?若能,试求出直线DE的解析式;若不能,请说明理由.5.如图,在平面直角坐标系中,已知▱OABC的顶点A(10,0)、C(2,4),点D是OA 的中点,点P在BC上由点B向点C运动.(1)求点B的坐标;(2)若点P运动速度为每秒2个单位长度,点P运动的时间为t秒,当四边形PCDA是平行四边形时,求t的值;(3)当△ODP是等腰三角形时,直接写出点P的坐标.6.已知:在矩形ABCD中,点F为AD中点,点E为AB边上一点,连接CE、EF、CF,EF平分∠AEC.(1)如图1,求证:CF⊥EF;(2)如图2,延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若,点H为FG上一点,连接CH,若∠CHG=∠BCE, 求证:CH=FK;(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.7.在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm。
平行四边形(知识点、经典例题、常考题型练习)

平行四边形(一)【知识梳理】1、平行四边形:平行四边形的定义决定了它有以下几个基本性质:(1)平行四边形对角相等;(2)平行四边形对边相等;(3)平行四边形对角线互相平分。
除了定义以外,平行四边形还有以下几种判定方法:(1)两组对角分别相等的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)对角线互相平分的四边形是平行四边形;(4)一组对边平行且相等的四边形是平行四边形。
2、特殊平行四边形:一、矩形(1)有一角是直角的平行四边形是矩形(2)矩形的四个角都是直角;(3)矩形的对角线相等。
(4)矩形判定定理1:有三个角是直角的四边形是矩形(5)矩形判定定理2:对角线相等的平行四边形是矩形二、菱形(1)把一组邻边相等的平行四边形叫做菱形.(2)定理1:菱形的四条边都相等(3)菱形的对角线互相垂直,并且每条对角线平分一组对角.(4)菱形的面积等于菱形的对角线相乘除以2(5)菱形判定定理1:四边都相等的四边形是菱形(6)菱形判定定理2:对角线互相垂直的平行四边形是菱形。
三、正方形(1)有一组邻边相等,并且有一个角是直角的平行四边形叫做正方形(2)性质:①四个角都是直角,四条边相等②对角线相等,并且互相垂直平分,每条对角线平分一组对角(3)判定:①一组邻边相等的矩形是正方形②有一个角是直角的菱形是正方形平行四边形矩形 菱形正方 形 等腰梯形 直角梯形梯形四边形知识结构如下图(1)弄清定义及四边形之间关系图1:(2)四边形之间关系图2:2、几种特殊的四边形的性质和判定:3、一些定理和推论:三角形中位线定理:三角形的中位线平行于第三边,且等于第三边的一半。
推论:夹在两平行线间的平行线段相等。
推论:直角三角形斜边上的中线等于斜边的一半;推论:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
【例题精讲】填空题:四边形正方形【巩固】1、下列说法中错误..的是( ) A .四个角相等的四边形是矩形 B .四条边相等的四边形是正方形 C .对角线相等的菱形是正方形 D .对角线互相垂直的矩形是正方形2、如果一个四边形的两条对角线互相平分,互相垂直且相等,那么这个四边形是 ( ) A .矩形 B .菱形 C .正方形 D .菱形、矩形或正方形3、下面结论中,正确的是( )A .对角线相等的四边形是矩形B .对角线互相平分的四边形是平行四边形C .对角线互相垂直的四边形是菱形D .对角线互相垂直且相等的四边形是正方形4、如图,在ABC △中,点D 、E 、F 分别在边AB 、BC 、CA 上,且DE CA ∥,DF BA ∥.下列四种说法:①四边形AEDF 是平行四边形;②如果90BAC ∠=,那么四边形AEDF 是矩形; ③如果AD 平分BAC ∠,那么四边形AEDF 是菱形;④如果AD BC ⊥且AB AC =,那么四边形AEDF 是菱形. 其中,正确的有 .(只填写序号)【例1】如图,在平行四边形ABCD 中,点E ,F 分别是AD ,BC 的中点. 求证:四边形BFDE 是平行四边形.【巩固】已知,如图9,E 、F 是四边形ABCD 的对角线AC 上的两点,AF =CE ,DF =BE ,DF ∥BE . 四边形ABCD 是平行四边形吗?请说明理由.【例2】如图,梯形ABCD 中,AB ∥CD ,AC 平分∠BAD ,CE ∥AD 交AB 于点E .F ED CBAA FCDEAEDCFB求证:四边形AECD 是菱形.【例3】如图,在等边△ABC 中,点D 是BC 边的中点,以AD 为边作等边△ADE . (1)求∠CAE 的度数;(2)取AB 边的中点F ,连结CF 、CE ,试证明四边形AFCE 是矩形.【巩固】如图,O 为矩形ABCD 对角线的交点,DE ∥AC ,CE ∥BD . (1)试判断四边形OCED 的形状,并说明理由; (2)若AB =6,BC =8,求四边形OCED 的面积.【例4】如图所示,在△ABC 中,分别以AB 、AC 、BC 为边在BC 的同侧作等边△ABD 、等边△ACE 、等边△BCF .(1)求证:四边形DAEF 是平行四边形;三角形ABD,三角形ACE,三角形BCF 都是等边三角形 首先我们来证明DAEF 为平行四边形 角DBF=60度-角FBA=角ABC 而DB=AB, BF=BC三角形DBF 全等于三角形ABC 所以:DF=AC=AE 同理可证:DA=FE所以:DAEF 为平行四边形ABCDEF CA DFE(1)如图,如果角DAE=90度,则DAEF为矩形则必须:角BAC=360度-2*60度-90度=150度(而如果,另一种情况,BC为短边,F将落在DAECB的包围之中,角DAE=2*60度+角BAC>90度,DAEF不可能为矩形,而BC为短边,角BAC<90度)(2)如果:DA=AE,则:DAEF为菱形则必须:AB=AC(3)如果:角BAC=60度则:角DAE=3*60度=180度D,A,E共线,所以:以D、A、E、F为顶点的四边形不存在据此,(2)的结论应稍加改变为:当AB=AC,且角BAC不等于60度时,四边形DAEF是菱形(2)探究下列问题:(只填满足的条件,不需证明)①当△ABC满足_________________________条件时,四边形DAEF是矩形;②当△ABC满足_________________________条件时,四边形DAEF是菱形;③当△ABC满足_________________________条件时,以D、A、E、F为顶点的四边形不存在.平行四边形(二)【知识梳理】由平行四边形的结构知,平行四边形可以分解为一些全等的三角形,并且包含着平行线的有关性质,因此,平行四边形是全等三角形知识和平行线性质的有机结合,平行四边形包括矩形、菱形、正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形一、 基础知识平行四边形二、1、三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三遍的一半。
2、由矩形的性质得到直角三角形的一个性质:直角三角形斜边上的中线等于斜边的一半。
三、例题例1、如图1,平行四边形ABCD 中,AE⊥BD,CF⊥BD,垂足分别为E 、F. 求证:∠BAE =∠DCF.例2、如图2,矩形ABCD 中,AC 与BD 交于O 点,BE⊥AC 于E ,CF⊥BD 于F.求证:BE = CF.例3、已知:如图3,在梯形ABCD 中,AD∥BC,AB = DC ,点E 、F 分别在AB 、CD 上,且BE = 2EA ,CF = 2FD. 求证:∠BEC =∠CFB.例4、如图6,E 、F 分别是 平行四边形ABCD 的AD 、BC 边上的点,且AE = CF.(1)求证:△ABE≌△CDF;(2)若 M 、N 分别是BE 、DF 的中点,连结MF 、EN ,试判断四边形MFNE 是怎样的四边形,并证明你的结论.(图1)BA DBCE F (图M NOABCDE F(图2)例5、如图7 ABCD的对角线AC的垂直平分线与边AD,BC分别相交于点E,F.,求证:四边形AFCE是菱形.例6、如图8,四边形ABCD是平行四边形,O是它的中心,E、F是对角线AC上的点.(1)如果,则△DEC≌△BFA(请你填上一个能使结论成立的一个条件);(2)证明你的结论.例7、如图9,已知在梯形ABCD中,AD∥BC,AB = DC,对角线AC和BD相交于点O,E是BC边上一个动点(点E不与B、C两点重合),EF∥BD交AC于点F,EG∥AC交BD于点C.(1)求证:四边形EFOG的周长等于2OB;(2)请你将上述题目的条件“梯形ABCD中,AD∥BC,AB = DC”改为另一种四边形,其他条件不变,使得结论,“四边形EFOG的周长等于2OB”仍成立,并将改编后的题目画出图形,写出已知、求证、不必证明.例8、有一块梯形形状的土地,现要平均分给两个农户种植(即将梯形的面积两等分),试设计两种方案(平分方案画在备用图13(1)、(2)上),并给予合理的解释.备用图(1)备用图(2)图13BCRPDCBAEF 第12题图四、练习 一、选择题1.下列命题正确的是( )(A)、一组对边相等,另一组对边平行的四边形一定是平行四边形 (B)、对角线相等的四边形一定是矩形(C)、两条对角线互相垂直的四边形一定是菱形 (D)、在两条对角线相等且互相垂直平分的四边形一定是正方形 2. 已知平行四边形ABCD 的周长32, 5AB=3BC,则AC 的取值范围为( ) A. 6<AC<10; B. 6<AC<16; C. 10<AC<16; D. 4<AC<16 3.两个全等的三角形(不等边)可拼成不同的平形四边形的个数是( ) (A )1 (B )2 (C )3 (D )44.延长平形四边形ABCD 的一边AB 到E ,使BE =BD ,连结DE 交BC 于F ,若∠DAB =120°,∠CFE =135°,AB =1,则AC 的长为( )(A )1 (B ) (C )32(D ) 5.若菱形ABCD 中,AE 垂直平分BC 于E ,AE =1cm ,则BD 的长是( ) (A )1cm (B )2cm (C )3cm (D )4cm6.若顺次连结一个四边形各边中点所得的图形是矩形,那么这个四边形的对角线( ) (A )互相垂直 (B )相等 (C )互相平分 (D )互相垂直且相等7. 如图,等腰△ABC 中,D 是BC 边上的一点,DE ∥AC ,DF ∥AB ,AB=5那么四边形AFDE 的周长是( )(A )5 (B )10 (C )15 (D )20(第7题) (第8题) (第9题) (第10题)8.如图,将边长为8cm 的正方形纸片ABCD 折叠,使点D 落在BC 边中点E 处,点A 落在点F 处,折痕为MN ,则线段CN 的长是( ). (A )3cm (B )4cm (C )5cm (D )6cm9. 如图,在直角梯形ABCD 中,AD∥BC,∠B=90°,AC 将梯形分成两个三角形,其中△ACD 是周长为18 cm 的等边三角形,则该梯形的中位线的长是( ). (A)9 cm (B)12cm (c)29cm (D)18 cm 10.如图,在周长为20cm 的□ABCD中,AB≠AD,AC 、BD 相交于点O ,OE ⊥BD 交AD 于E ,则△ABE的周长为( ) (A)4cm (B)6cm (C)8cm (D)10cm11. 如图2,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边的中点E 处,折痕为AF .若CD =6,则AF 等于 ( )(A )34 (B )33 (C )24(D )8 12.如图,已知四边形ABCD 中,R 、P 分别是BC 、CD 上的点,E 、F 分别是 AP 、RP 的中点,当点P 在CD 上从C 向D 移动而点R 不动时,那么下列结论 成立的是 ( )A 、线段EF 的长逐渐增大B 、线段EF 的长逐渐减小C 、线段EF 的长不变D 、线段EF 的长与点P13. 在梯形ABCD 中,ADcm AC 5B. 7cmC.D. 6cm14. 国家级历史文化名城——金华,风光秀丽,花木葱茏.某广场上一个形状是 平行四边形的花坛(如图),分别种有红、黄、蓝、绿、橙、紫6种颜色的花. 如果有AB EF DC ∥∥,BC GH AD ∥∥,那么下列说法中错误的是( )AB CDOEABCDEF图 2黄蓝紫 橙 红绿A G EDHC B第14题ABCDEFO第10题图DABCPMN(1)(2)图9A B CD E FO 图A .红花、绿花种植面积一定相等B .紫花、橙花种植面积一定相等C .红花、蓝花种植面积一定相等D .蓝花、黄花种植面积一定相等 二、填空题1.如果四边形四个内角之比1:2:3:4,则这四边形为____形。
2.若正方形的对角线长为2cm ,则正方形的面积为___。
3.若矩形一个内角的平分线,把另一边分为4cm,5cm 两部分,则这个矩形周长是___4.已知:平行四边形ABCD 的周长是30cm ,对角线AC ,BD 相交于点O ,△AOB的周长比△BOC的周长长5cm ,则这个平行四边形的各边长为_____。
5. 已知:平行四边形ABCD 中, AE ⊥BC 交CB 的延长线于点E ,AF ⊥CD 交CD 的延长线于点F ,AB +BC +CD +DA =32cm ,BC =35AB ,∠EAF =2∠C ,则BE 长为___,则∠C ___.6. 在平面直角坐标系中,点A 、B 、C 的坐标分别是A(-2,5),B(-3,-1),C(1,-1),在第一象限内找一点D ,使四边形ABCD 是平行四边形,那么点D 的坐标是 .7.已知:如图8,正方形ABCD 中,对角线AC 和BD 相交于点O ,E 、F 分别是边AB 、BC 上的点,若AE =4cm ,DF =3cm ,且OE ⊥OF ,则EF 的长为 。
8. 如图9(1)是一个等腰梯形,由6个这样的等腰梯形恰好可以拼出如图10(2)所示的一个菱形.对于图10(1)中的等腰梯形,请写出它的内角的度数或腰与底边长度之间关系的一个正确结论:.9.如图,在四边形ABCD 中,P 是对角线BD 的中点,E F ,分别是AB CD ,的中点,18AD BC PEF =∠=,,则PFE ∠的度数是 .10.如图,菱形ABCD 的两条对角线分别长6和8,点P 是对角线AC 上的一个动点,点M 、N 分别是边AB 、BC 的中点,则PM +PN 的最小值是_____________.11. 如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,要使四边形EFGH是菱形,四边形ABCD 还应满足的一个条件是 。
(12题) (13题) (14题)12、 如图所示,O 为矩形ABCD 的对角线交点,DF 平分∠ADC 交AC 于E ,BC 于F ,∠BDF=15°,则∠COF=______. 13. 如图,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,23AB BC ==,,则图中阴影部分的面积为 .14、如图,矩形1111ABCD的面积为4,顺次连结各边中点得到四边形2222AB CD,再顺次连结四边形2222AB CD四边中点得到四边形3333ABCD,依此类推,求四边形n n n n ABCD的面积是 。
15、如图⑴已知O 是□ABCD 的对角线交点,AC =24,BD =38,AD =14,那么△OBC 的周长等于_____。
CFDBEAP(第9题)O FEDCBAABD CO ⑴A BCO⑵A B D⑶CFE ⑷16、在平行四边形ABCD中,∠C=∠B+∠D,则∠A=___,∠D=___。
17、一个平行四边形的周长为70cm,两边的差是10cm,则平行四边形各边长为____cm。
18、已知菱形的一条对角线长为12cm,面积为30cm2,则这个菱形的另一条对角线长为__________cm。
19、菱形ABCD中,∠A=60o,对角线BD长为7cm,则此菱形周长_____cm。
202,那么它的面积______。
21、如图2矩形ABCD的两条对角线相交于O,∠AOB=60o,AB=8,则矩形对角线的长___。
22、如图3,等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AB=6,AD=5则△CDE周长___。
21、正方形的对称轴有___条22、如图4,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是______23、要从一张长为40cm,宽为20cm的矩形纸片中,剪出长为18cm,宽为12cm的矩形纸片,最多能剪出______张。
三、解答题1.如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=2,CD=3,求AB的长。
2.如图,在等腰梯形ABCD中,AD∥BC,AB=CD=2,∠BAD=120°,对角线AC平分∠BCD,求等腰梯形ABCD的周长。
3.将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形证明你的结论4.已知:如图,在梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD相交于点E,∠ADB=60°,BD=10,BE∶ED=4∶1,求梯形ABCD的腰长.5. 如图,菱形ABCD,E,F分别是BC,CD上的点,∠B=∠EAF=60°,∠BAE=18°求∠CEF的度数。
