2015-2019历次高考三视图(试题+答案)A4版
2019年全国高考历史试题及其参考答案14页word

2019年全国高考历史试题及其参考答案本试卷分第I卷(选择题)和第II卷(非选择题)两部分。
满分150分。
考试时间120分钟。
第I卷(选择题,共72分)注意事项:答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
每小题选出答案后,用铅笔把答案卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试题卷上。
一选择题(本大题共28小题,第小题1.5分,共42分。
在每小题列出的四个选项中,只有一项是符合题目要求的)1、我国的氏族社会始于A元谋人 B. 北京人 C. 山顶洞人 D.河姆渡人2、今桂林与长沙之间,历史上的水路交通最早开通于A战国 B 秦朝 C西汉 D隋朝3、史书记载:“水激轮转,人筒兜水,次第下倾于岸上…以灌稻田,日夜不息,绝胜人力。
”这种提水灌溉工具最早出现于A东汉 B曹巍 C唐朝 D北宋4、元朝最大的对外贸易港口是图中的A (1)B (2)C (3)D (4)5、《天朝田亩制度》和《资政新篇》中关于社会经济的主张A互相矛盾 B大同小异 C完全一致 D互为补充6、甲午战争后,列强竟相对清政府代款,是为了(1)取高额回扣利息(2) 长期把持中国海关(3)进一步控制中国命脉(4) 扩大在华政治势力A、(1) (2) B (1) (2) (3) C (1) (2) (4) D (1) (2) (3) (4)7、康有为向光绪帝呈递的《应诏统筹全局折》实际上是维新派的施政纲领,因为它A提出了各方面具体的变法建议 B主张实行君主立宪政治体制C系统论证了维新变法的理论 D明确指出变法是救亡图存的唯一的出路8、门户开放”政策的提出,是美国侵略中国新阶段的标志。
这主要是因为该政策A得到了列强的认可 B可使美国在华获得的权益居列强之首C表明美国承认列强的在华特权 D有利于美国加快侵华步骤9、武昌起义后,列强由准备武装干涉转为“严守中立”,导致这一变化的决定因素是A列强之间利益冲突,争执不下 B受到“门户开放”政策的约束C革命形势的发展超出列强的预料 D袁世凯出任内阁总理大臣足以应付局面10、列关于二次革、护国运动和护法运动的表述,不正确的是A都是国民党直接领导的 B都是为了维护辛亥革命C都反对北洋军阀的反动统治 D最终都未取得成功11、前期新文化运动的主要功绩在于A确立了“民主”和“科学”的主导地位B批判了资产阶级改良主义思潮C揭开了传播马克思主义的新篇章D沉重打击了封建正统思想的权威12、抗日战争进入相持阶段的原因是A日本侵略军战线太长 B抗日根据地有力牵制敌军C中国人民抗日力量尚未充分发展 D英美主张接受“近卫声明”13、中共中央提出“坚持抗战、反对投降,坚持团结、反对分裂,坚持进步、反对倒退”三大口号,主要是针对A近卫关于“建立东亚新秩序”的声明 B汪精际集团公开叛国投敌成立伪政权C国民党五届五中全会前后的政策转变 D国民党/顽固派制造皖南事变破抗战14、中国共产党在新民主主义革命不同时期提出的土地政策的共同点是(1) 体现中国共产党的民主革命纲领 (2) 消灭封建剥削制度(3)农民基本利益(4) 促进社会经济发展A (1) (2)B (1) (2) (3)C (1) (3) (4)D (1) (2) (3) (4)15、中国共产党七届三中全会提出的急取国家财政经济状况基本好转的条件中,不包括A没收官僚资本 B完成土地改革C合理调整工商业 D节减国家机构经费16、造成1959—1961年我国国民经济严重困难的多种因素中,主要的是A空前严重的自然灾害 B国际反共势力的破坏C“大跃进”、人民公社化和“反右倾”的后果 D苏联撕毁两国经济技术合作协议17、1975年邓小平主持全面整顿的实质是A把国民经济搞上去 B系统地纠正“文化大革命”的错误C实现社会秩序的稳定 D以实现“四个现代化”为全党工作大局18、国共产党第十四次全国代表大会提出的经济体制改革的目标是A建立社会主义市场经济体制,进一步解放和发展生产力B逐步扩大企业自主权,加强国营大中型企业的市场竞争能力C巩固和完善农村家庭联产承包责任制,大力发展乡镇企业D以公有制为主体多种所有制经济成分长期共同发展19、17世纪的英国革命是资产阶级性质的革命。
2015年高考试题历史试题和参考答案

2015年高考试题(历史)选择题共12题,每题4分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
24.《吕氏春秋·上农》在描述农耕之利时不无夸张地说,一个农夫耕种肥沃的土地可以养活九口人,耕种一般的土地也能养活五口人。
战国时期农业收益的增加()A.促进了个体小农经济的形成B.抑制了手工业和商业的发展C.导致畜力与铁制农具的使用D.阻碍了大土地所有制的成长25.两汉时期,皇帝的舅舅、外祖父按例封侯,若皇帝幼小,执政大臣也主要从他们之中选择。
这被当时人视为“安宗庙,重社稷”的“汉家之制”。
汉代出现外戚干政的背景是()A.皇帝依靠外戚抑制相权B.“家天下”观念根深蒂固C.母族亲属关系受到重视D.刘氏同姓诸侯王势力强大26.宋代东南沿海地区出现了一些民间崇拜,如后来被视为海上保护神的妈祖、被视为妇幼保护神的临水夫人等。
这些崇拜得到朝廷认可,后世影响不断扩大。
这反映出()A.朝廷不断鼓励海洋开发B.女性地位逐渐得到提高C.东南沿海经济社会影响力上升D.统治思想与民众观念趋向一致27.表1 河南、江苏两地科举考试状元人数表表1呈现的变化反映了()A.理学的影响力不断扩大B.经济发展促进文化兴盛C.中原地区经济急剧衰退D.政治重心南移趋势明显28.1852年,一位在华英国人在报告中称,英国商人运往伦敦的中国生丝是以“无用的”曼彻斯特上等棉布包装的。
而在此之前,用于包装的主要是中国产的土布。
包装布的这种变化反映了当时()A.中国的土布质量粗糙B.英国棉布价格更具优势C.中国生丝在英国畅销D.英国棉布在中国滞销29.《申报》“时评”栏目曾评述说:“今之时局,略似春秋战国时之分裂。
中央政府之对于各省,犹东周之对于诸侯也。
南北相攻,皖直交斗,滇蜀不靖,犹诸侯相侵伐也。
”这一时局出现在()A.太平天国运动时期B.义和团运动时期C.辛亥革命时期D.北洋军阀统治时期30.1933年到1937年上半年,国民政府军事委员会先后统筹完成了江宁、镇江、虎门、马尾、连云港等要塞区的建设,又大规模构筑了京沪、沪杭、豫北、晋北、绥东等侧重于城市和交通线防御的工事。
高三数学空间几何体的三视图与直观图试题
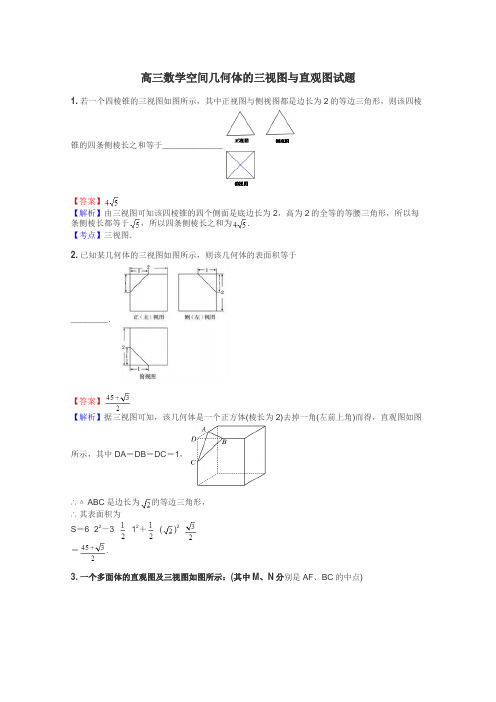
高三数学空间几何体的三视图与直观图试题1.若一个四棱锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于_____________【答案】【解析】由三视图可知该四棱锥的四个侧面是底边长为2,高为2的全等的等腰三角形,所以每条侧棱长都等于,所以四条侧棱长之和为.【考点】三视图.2.已知某几何体的三视图如图所示,则该几何体的表面积等于________.【答案】【解析】据三视图可知,该几何体是一个正方体(棱长为2)去掉一角(左前上角)而得,直观图如图所示,其中DA=DB=DC=1,∴△ABC是边长为的等边三角形,∴其表面积为S=6×22-3××12+×()2×=.3.一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.【答案】(1)见解析(2)【解析】解:由三视图可知,AB=BC=BF=2,DE=CF=2,∠CBF=.(1)证明:取BF的中点G,连接MG、NG,由M、N分别为AF、BC的中点可得,NG∥CF,MG∥EF,∴平面MNG∥平面CDEF,又MN⊂平面MNG,∴MN∥平面CDEF.(2)取DE的中点H.∵AD=AE,∴AH⊥DE,在直三棱柱ADE-BCF中,平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE.∴AH⊥平面CDEF.∴多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=.S矩形=DE·EF=4,CDEF∴棱锥A-CDEF的体积为V=·S·AH=×4×=.矩形CDEF4.一个几何体的主视图和俯视图如图所示,主视图是边长为的正三角形,俯视图是边长为的正六边形,则该几何体左视图的面积是【答案】【解析】左视图的面积为.【考点】三视图.5.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.6.三棱柱的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)⑴当x=4时,求几何体的侧面积和体积⑵当x取何值时,直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。
(完整版)高中数学3三视图课后习题(带答案)

(完整版)高中数学3三视图课后习题(带答案)332 正视图侧视图俯视图图1 三视图课后习题1.(陕西理5)某几何体的三视图如图所示,则它的体积是A .283π-B .83π-C .82π-D .23π2.(全国新课标理6)。
在一个几何体的三视图中,正视图与俯视图如右图所示,则相应的侧视图可以为3.(湖南理3)设图1是某几何体的三视图,则该几何体的体积为A .9122π+B .9182π+C .942π+D .3618π+4.(广东理7)如图1-3,某几何体的正视图(主视图)是平行四边形,侧视图(左视图)和俯视图都是矩形,则该几何体的体积为A .63 B .93C .123D .1835.(北京理7)某四面体的三视图如图所示,该四面体四个面的面积中,最大的是A .8B .62C .10D .826.(安徽理6)一个空间几何体的三视图如图所示,则该几何体的表面积为(A )48 (B )32+817 (C )48+817 (D )807.(辽宁理15)一个正三棱柱的侧棱长和底面边长相等,体积为32,它的三视图中的俯视图如右图所示,左视图是一个矩形,则这个矩形的面积是.8.(天津理10)一个几何体的三视图如右图所示(单位:m ),则该几何体的体积为__________3m9.(2010湖南文数)13.图2中的三个直角三角形是一个体积为20cm 2的几何体的三视图,则h= cm10.(2010浙江理数)(12)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是___________3cm .11.(2010辽宁文数)(16)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为 .12.(2010辽宁理数)(15)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.13.(2010天津文数)(12)一个几何体的三视图如图所示,则这个几何体的体积为。
2015-2019全国卷高考数学分类汇编——三视图
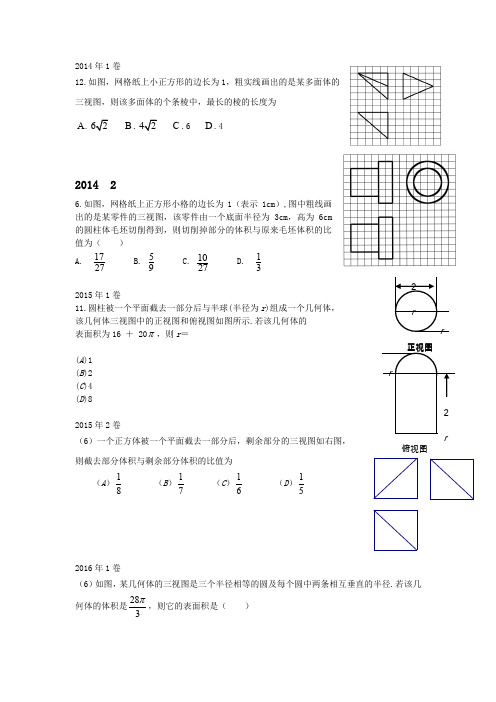
2014年1卷12.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的个条棱中,最长的棱的长度为A. B.C .6 D .42014 26.如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )A. 1727B. 59C. 1027D. 132015年1卷11.圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体, 该几何体三视图中的正视图和俯视图如图所示.若该几何体的 表面积为16 + 20π,则r = (A )1 (B )2 (C )4 (D )82015年2卷(6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图, 则截去部分体积与剩余部分体积的比值为(A )81 (B )71 (C )61 (D )512016年1卷(6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是283π,则它的表面积是( )2016-2(6)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A)20π(B)24π(C)28π(D)32π2016-3(9)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,学.科.网则该多面体的表面积为()(A)18+(B)54+(C)90(D)812017-17.某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为A .10B .12C .14D .162017-24.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π2018-17.某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为A .172B .52C .3D .22018-33.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是。
全国卷三视图与立体几何专题(含答案)

全国卷三视图与立体几何专题(含答案)三视图与立体几何部分1.(2014年全国新课标卷Ⅰ第8题)如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( ) A.三棱锥 B.三棱柱 C.四棱锥 D.四棱柱2.(2014年全国新课标卷Ⅰ第19题)(本题满分12分)如图,三棱柱111C B A ABC -中,侧面C C BB 11为菱形,CB 1的中点为O ,且C C BB AO 11平面⊥.(Ⅰ)证明:AB C B ⊥1(Ⅱ)若AC ⊥AB 1,∠CBB 1=60°,BC=1,求三棱柱ABC-A 1B 1C 1的高.3.(2014年全国新课标卷Ⅱ第6题)如图,网格纸上正方形小格的边长为1(表示1cm ),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm ,高为6cm 的圆柱体毛坯切削得到,则切削的部分的体积与原来毛坯体积的比值为( )A.2717B. 95C. 2710D. 314.(2014年全国新课标卷Ⅱ第7题)正三棱柱111C B A ABC -的底面边长为2,侧棱长为3,D 为BC 中点,则三棱锥11DC B A -的体积为( )A.3B.23C.1D.235.(2014年全国新课标卷Ⅱ第18题)(本小题满分12分)如图,四棱锥ABCD P -中,底面ABCD 为矩形,⊥PA 平面ABCD ,E 是PD 的中点. (1)证明:PB //平面AEC ;(2)设1=AP 3=AD ,三棱锥ABD P -的体积43=V ,求A到平面PBC 的距离.6.(2013年全国新课标第9题)一个四面体的顶点在空间直角坐标系xyz O -中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx 平面为投影面,则得到的正视图可以为 ( )7.(2013年全国新课标第15题)、已知正四棱锥ABCD O -的体积为223,底面边长为3,则以O 为球心,OA 为半径的球的表面积为 .8.(2013年全国新课标第18题)如图,直三棱柱111C B A ABC -中,ED ,分别是1BB AB ,的中点.(I)证明:CDA BC 11//平面;(Ⅱ)设2221====AB CB AC AA ,,求三棱锥DE A C 1-的体积.9.(2014年全国新课标Ⅰ第11题)、某几何体的三视图如图所示,则该几何体的体积为( )A. π816+B.π88+C.π616+D.π168+10.(2013年全国新课标Ⅰ第15题)已知H 是球O 的直径AB 上的一点,AH:HB=1:2,α平面⊥AB ,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为11.(2013年全国新课标Ⅰ第19题)如图,三棱柱111C B A ABC -中,.6011ο=∠==BAAAA AB CB CA ,,( I ) 证明:C A AB 1⊥;(Ⅱ)若621===C A CB AB ,,求三棱柱的111C B A ABC -体积.12.(2014年全国新课标Ⅱ第7题) 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( )A.6B.9C.12D.18 13.(2012年全国新课标第8题)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为( ) A.π6 B. π34C. π64 D.π3614.(2012年全国新课标第19题)如图,在三棱柱111C B A ABC -中,侧棱垂直于底面,12190AA BC AC ACB ===∠,ο,D 是棱1AA 的中点.(I)证明:BDCBDG平面平面⊥1;(Ⅱ)平面1BDC 分此棱柱为两部分,求这两部分体积的比.15.(2011年全国新课标第8题)在一个几何体的三视图中,正视图和俯视图如右图所示, 则相应的俯视图可以为16.(2011年全国新课标第16题)已知两个圆锥有公共底面,且两圆锥的顶点和底面的圆周都在同一球面上.若圆锥底面面积是这个球3,则这两个圆锥中,体积较小者的面面积的16高与体积较大者的高的比值为 .17.(2011年全国新课标第18题)如图,四棱锥ABCDP-中,底面ABCD为平行四边形,DAB底面,,⊥=∠ο,=AD.260ABCDPDAB(I)证明:BDPA⊥;(Ⅱ)设1=D-的高.=ADPA,求棱锥PBC18.(2010年全国新课标第7题)设长方体的长、宽、高分别为2a、a、a,其顶点都在一个球面上,则该球的表面积为A.23aπB.26aπC.212aπD. 224aπ19.(2010年全国新课标第15题)一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱20.(2010年全国新课标第18题)如图,已知四棱锥ABCDP-的底面为等腰梯形,BDACCDAB⊥,//,垂足为H,PH是四棱锥的高.(Ⅰ)证明:PBDPAC平面平面⊥;(Ⅱ)若ο606=∠=∠=ADBAPBAB,,求四棱锥ABCDP-的体积.1.B 【命题立意】本题考查三视图等基础知识,意在考查考生空间想象能力,难度中度. 【解题思路】原几何体为如图所示的三棱柱,故选B.2.解:(Ⅰ)连接1BC ,则O 为C B 1与1BC 的交点.因为侧面CC BB 11为菱形,所以11BC C B ⊥.又CC BB AO 11平面⊥,所以AOC B ⊥1,故ABOC B 平面⊥1.由于ABOAB 平面⊂,故ABC B ⊥1(6分)(Ⅱ)作BC OD ⊥,垂足为D ,连接AD .作AD OH ⊥,垂足为H . 由于AO BC ⊥,OD BC ⊥,故BC 平面AOD ,所以BC OH ⊥.又AD OH ⊥,所以OH 平面ABC.因为ο601=∠CBB ,所以1CBB ∆为等边三角形,又1=BC ,可得43=OD .由于1AB AC ⊥ ,所以21211==C B OA . 由OA OD AD OH ⋅=⋅,且4722=+=OA OD AD ,得1421=OH又O 为C B 1的中点,所以点1B 到平面ABC 的距离为721,故三棱柱111C B A ABC -的距离为721.(12分)3.C 【命题立意】本题考查了三视图,空间几何体的体积计算,意在考查三视图与直观图的转换所体现的空间想象能力,难度中等.【解题思路】几何体的直观图为“螺栓”.切削部分的体积为424322⋅⋅-⋅⋅ππ,所以比值为2710634243222=⋅⋅⋅⋅-⋅⋅πππ,故选C.4.C 【命题立意】本题考查空间几何体的体积计算,侧重考察利用割补法求体积,难度中等. 【解题思路】取11C B 的中点E ,截面ADE 的面积为233321=⨯=S ,所以所求的体积为1223313111=⨯⨯=⋅=CB S V ,故选C. 5.解:(I )证明:设BD 与AC 的交点为O ,连结EO .因为ABCD 为矩形,所以O 为BD的中点,又E为PD 的中点,所以PB EO //. EO ⊂平面AEC ,PB ⊄平面AEC ,所以PB ∥平面AEC .(Ⅱ)V 1366PA AB AD AB =⋅⋅=.由34V =,可得32AB =.作AH PB ⊥交PB 于H .由题设知BC ⊥平面PAB ,所以BC AH ⊥,故AH ⊥平面PBC.又PA AB AH PB⋅=313=. 所以A 到平面PBC 3136.A 【命题立意】本题考查空间直角坐标系下几何体的建构及其对应的三视图的作图问题,难度中等.【解题思路】如图所示,点)000()110()011()101(11,,,,,,,,,,,D C B A ,此四点恰为正方体ABCDD C B A -1111的四个顶点,此四点构成了一个棱长为2的正四面体,该正四面体的投影面zOx 上的正视图为正方形DA D A 11,故应选A.7.π24【命题立意】本题考查正四棱锥的体积计算及球的表面积计算,体现了空间想象能力的应用,难度中等.【解题思路】如图所示,由()2233313122=⋅⨯=⋅=-ON ON AB V ABCD O ,可得223=ON ,在ONARt ∆中,由222OA NA ON=+,可得626223222=⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛=OA ,∴以OA为半径的球的表面积πππ246442=⨯=⋅=OAS .8.解:(Ⅰ)证明:连接1AC 交C A 1予点F ,则F 为1AC 的中点.又D 是AB 的中点,连接DF ,则DFBC//1.因为CDA BCCD A DF 111平面,平面⊄⊂,所以CDA BC11//平面.(Ⅱ)因为111C B A ABC -是直三棱柱,所以CDAA ⊥1.由已知AB CD AB D CB AC ⊥=中点,所以为,. 又111A ABB CD A AB AA 平面,于是⊥=I.由ο902221=∠====ACB AB CB AC AA得,,336211====E A DE D A CD ,,,, DA DE E A DE D A 121221⊥=+,即.所以123621311=⨯⨯⨯⨯=-DEA C V.9.A 【命题立意】本题考查了三视图及其对应的几何体的体积计算问题,体现了空间想象能力的实际应用,难度较大.【解题思路】由三视图可得,该几何体是由一个底面圆半径为2,高为4的圆柱体的一般与一个底面正方形边长为2,高为4的正四棱柱组成的组合体,∴其体积ππ81642422122+=⨯+⨯⨯=V ,故应选A.【易错点拨】由三视图回溯几何体的原型是一个难点,也是一个易错点,解决此类问题应当从俯视图入手,结合另两个视图综合想象原直观图的组合关系.10.π29【命题立意】本题考查了球及球的表面积计算问题,难度较大.【解题思路】如图所示,设球O 的直径为R 2,则由2:1:=HB AH ,可得R AH 32=,在OCH Rt ∆中222289R OH OC CH =-=的表面积球,,可得由O R R CH ∴===⋅8998222ππππππ2989442===R S11.解:(Ⅰ),的中点取O AB B A OA OC 11,,连接..AB OC CB CA ⊥=,所以因为由于,,ο6011=∠=BAA AA AB 故B AA 1∆为等边三角形,所以ABOA⊥1.因为OOA OC =1I ,所以C OA AB 1平面⊥.又C OA C A 11平面⊂,故CA AB 1⊥(6分)(Ⅱ)由题设知B AA ABC 1与∆都是边长为2的等边三角形,所以31==OA OC ,又61=C A ,则21221OA OC CA +=,故OCOA ⊥1,因为OAB OC =I,所以ABCOA平面⊥1,1OA 为三棱柱111C B A ABC -的高.又ABC ∆的面积3=∆ABCS,故三棱柱111C B A ABC -的体积31=⨯=∆OA SV ABC.(12分)12.B 【命题立意】本题考查三视图及空间几何体的体积求解,考生是否具有一定空间想象能力将图形还原(包含数量关系及位置关系)是命题立意所在,难度较小.【解题思路】据三视图可知三棱锥底面是腰长为23的等腰直角三角形,棱锥的高为3,故体积为923232131=⨯⨯⨯=V ,故选B.13.B 【命题立意】本题考查球的性质应用及球的体积公式,难度较小.【解题思路】由于球心与截面圆心的连线垂直于截面α,故球的半径()3212222=+=+=d r R ,因此体积()ππ343342==V ,故选B.14.解:(I)证明:由题设知,,,C AC CC AC BC CC BC =⊥⊥I 11所以11A ACC BC 平面⊥.又BCDC A ACC DC⊥⊂1111,所以平面.由题设知,ο4511=∠=∠ADC DC A 所以BDCDC CDC 平面,即⊥=∠1190ο.又.1BDC DC C BC DC 平面,所以⊥=I又BDCBDC BDC DC 平面,故平面平面⊥⊂111..(6分)(Ⅱ)设棱锥1DACC B -的体积为11=AC V ,.又题意得2111221311=⨯⨯+⨯=V。
2015年全国高考-三视图专练及详细答案
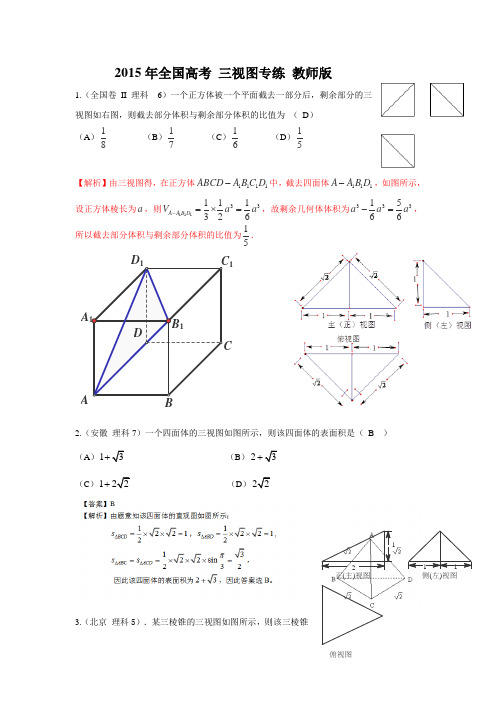
2015年全国高考 三视图专练 教师版
1.(全国卷II 理科 6)一个正方体被一个平面截去一部分后,剩余部分的三视图如右图,则截去部分体积与剩余部分体积的比值为 ( D )
(A )81 (B )71 (C )61 (D )51
【解析】由三视图得,在正方体1111ABCD A B C D -中,截去四面体111A A B D -,如图所示,设正方体棱长为a ,则11133111326A A B D V a a -=
⨯=,故剩余几何体体积为3331566a a a -=,所以截去部分体积与剩余部分体积的比值为51.
2.(安徽 理科7)一个四面体的三视图如图所示,则该四面体的表面积是( B )
(A )13+ (B )23+
(C )122+ (D )22
3.(北京 理科5).某三棱锥的三视图如图所示,则该三棱锥
C B
A D D 1C 1
B 1A 1正(主)视图11俯视图
侧(左)视图
2
1
的表面积是(C )
A .25+
B .45+
C .225+
D .5
【解析】由三视图得其几何体为右图,
4.(陕西理科5) 一个几何体的三视图如图所示,则该几何体的表面积为
A .3π
B .4π
C .24π+
D .34π+
5.(重庆理科5)某几何体的三视图如图所示,则该几何体的体积为()
A 、
13π+ B 、23
π+ C 、123π+ D 、223π+。
高三数学空间几何体的三视图与直观图试题答案及解析
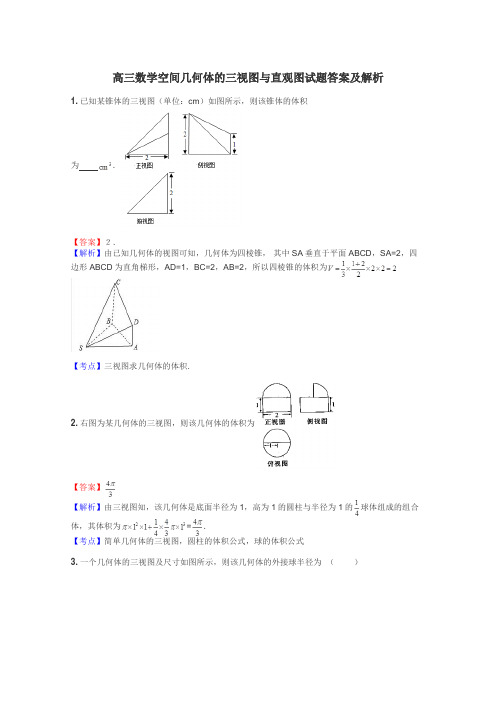
高三数学空间几何体的三视图与直观图试题答案及解析1.已知某锥体的三视图(单位:cm)如图所示,则该锥体的体积为.【答案】2.【解析】由已知几何体的视图可知,几何体为四棱锥,其中SA垂直于平面ABCD,SA=2,四边形ABCD为直角梯形,AD=1,BC=2,AB=2,所以四棱锥的体积为【考点】三视图求几何体的体积.2.右图为某几何体的三视图,则该几何体的体积为【答案】【解析】由三视图知,该几何体是底面半径为1,高为1的圆柱与半径为1的球体组成的组合体,其体积为=.【考点】简单几何体的三视图,圆柱的体积公式,球的体积公式3.一个几何体的三视图及尺寸如图所示,则该几何体的外接球半径为()A.B.C.D.【答案】C【解析】由三视图可知:该几何体是一个如图所示的三棱锥P-ABC,它是一个正四棱锥P-ABCD 的一半,其中底面是一个两直角边都为6的直角三角形,高PE=4.设其外接球的球心为O,O点必在高线PE上,外接球半径为R,则在直角三角形BOE中,BO2=OE2+BE2=(PE-EO)2+BE2,即R2=(4-R)2+(3)2,解得:R=,故选C.【考点】三视图,球与多面体的切接问题,空间想象能力4.如图是一个几何体的三视图,则该几何体的表面积是____________【答案】28+12【解析】这是一个侧放的直三棱柱,底面是等腰直角三角形,侧棱长为6故表面积为2×(×2×2)+(2+2+2)×6=28+12.【考点】三视图,几何体的表面积.5.在长方体中割去两个小长方体后的几何体的三视图如图,则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图,几何体的体积..6.某空间几何体的正视图是三角形,则该几何体不可能是()圆柱圆锥四面体三棱柱【答案】A【解析】由于圆柱的三视图不可能是三角形所以选A.【考点】三视图.7.某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是________.【答案】2(π+)【解析】由三视图可知此几何体的表面积分为两部分:底面积即俯视图的面积为2;侧面积为一个完整的圆锥的侧面积,且圆锥的母线长为2,底面半径为1,所以侧面积为2π.两部分加起来即为几何体的表面积,为2(π+).8.一个锥体的主(正)视图和左(侧)视图如图所示,下面选项中,不可能是该锥体的俯视图的是()【答案】C【解析】俯视图是选项C的锥体的正视图不可能是直角三角形.另外直观图如图1的三棱锥(OP⊥面OEF,OE⊥EF,OP=OE=EF=1)的俯视图是选项A,直观图如图2的三棱锥(其中OP,OE,OF两两垂直,且长度都是1)的俯视图是选项B,直观图如图3的四棱锥(其中OP⊥平面OEGF,底面是边长为1的正方形,OP=1)的俯视图是选项D.9.如图所示,正方形O′A′B′C′的边长为1,它是水平放置的一个平面图形的直观图,则原图形的周长是()A.6B.8C.2+3D.2+2【答案】B【解析】如图,OB=2,OA=1,则AB=3.∴周长为8.10.某几何体的三视图如图所示,且该几何体的体积是2,则正(主)视图的面积等于()A.2B.C.D.3【答案】A【解析】由三视图可知该几何体是一个四棱锥,其底面积就是俯视图的面积S=(1+2)×2=3,其高就是正(主)视图以及侧(左)视图的高x,因此有×3×x=2,解得x=2,于是正(主)视图的面积S=×2×2=2.11.如图,三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥底面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,则该三棱柱的侧视图的面积为( )A. C.4 D.【答案】A【解析】侧视图也为矩形,底宽为原底等边三角形的高,侧视图的高为侧棱长,所以侧视图的面积为,故选B.【考点】三视图12.一个几何体的三视图如图所示,则该几何体内切球的体积为 .【答案】【解析】依题意可得该几何体是一个正三棱柱,底面边长为2,高为.由球的对称性可得内切球的半径为.由已知计算得底面内切圆的半径也为.所以内切球的体积为.【考点】1.三视图.2.几何体内切球的对称性.3.球的体积公式.4.空间想象力.13.已知一个正三棱柱的所有棱长均等于2,它的俯视图是一个边长为2的正三角形,那么它的左视图面积的最小值是________.【答案】【解析】如图,正三棱柱中,分别是的中点,则当面与侧面平行时,左视图面积最小,且面积为.【考点】三视图.14.某几何体的三视图如图3所示,则其体积为________.【答案】【解析】原几何体可视为圆锥的一半,其底面半径为1,高为2,∴其体积为×π×12×2×=.15.已知正△ABC的边长为2,那么用斜二测画法得到的△ABC的直观图△A′B′C′的面积为()A.B.C.D.【答案】D【解析】∵正△ABC的边长为2,故正△ABC的面积S==设△ABC的直观图△A′B′C′的面积为S′则S′=S=•=故选D16.一个体积为12的正三棱柱的三视图如图所示,则这个三棱柱的侧视图的面积为()A.B.C.D.【答案】A【解析】依题意可得三棱柱的底面是边长为4正三角形.又由体积为.所以可得三棱柱的高为3.所以侧面积为.故选A.【考点】1.三视图的知识.2.棱柱的体积公式.3.空间想象力.17.某几何体的三视图如题(6)所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成的菱形,则这个几何体的体积为()A.1B.C.D.【答案】C【解析】这是由两个三棱锥拼成的几何体,其体积为.选C.【考点】三视图及几何体的体积.18.一个四面体的顶点在空间直角坐系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到的正视图可以为()A.B.C.D.【答案】A【解析】设O(0,0,0),A(1,0,1),B(1,1,0),C(0,1,1),将以O,A,B,C为顶点的四面体补成一正方体后,因为OA⊥BC,所以补成的几何体以zOx平面为投影面的正视图为A.19.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几体的体积为()A.6B.9C.12D.18【答案】B【解析】由三视图可知,此几何体为如图所示的三棱锥,其底面△ABC为等腰三角形且AB=BC,AC=6,AC边上的高为3,SB⊥底面ABC,且SB=3,因此此几体的体积为V=××6×3×3=920.如图所示,一个空间几何体的正视图和侧视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为 .【答案】【解析】由三视图知,该几何体是一个圆柱,其表面积为.【考点】三视图及几何体的表面积.21.在三棱锥中,,平面ABC,.若其主视图,俯视图如图所示,则其左视图的面积为【答案】【解析】左视图是一个直角三角形,其直角边分别是2与.所以面积为.【考点】1.三视图知识.2.三角形面积的计算.22.一个几何体的三视图如图所示,则这个几何体的体积是_________.【答案】【解析】由三视图还原几何体,该几何体为底面半径为,高为的圆柱,去掉底面半径为,高为的圆锥的剩余部分,则其体积为.【考点】1、三视图;2、几何体的体积.23.棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是( ).A.B.4C.D.3【答案】B【解析】如图,红色虚线表示截面,可见这个截面将正方体分为完全相同的两个几何体,则所求几何体的体积即是原正方体的体积的一半,.【考点】1.三视图;2.正方体的体积24.如图,一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积为()A.1B.2C.3D.4【答案】B【解析】由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为的正方形,故其底面积为,由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形,由于此侧棱长为,对角线长为,故棱锥的高为,此棱锥的体积为,故选B.【考点】由三视图求面积、体积.25.已知某几何体的三视图如右图所示,其中,正视图,侧视图均是由三角形与半圆构成,俯视图由圆与内接三角形构成,根据图中的数据可得此几何体的体积为()A.B.C.D.【答案】C【解析】由已知的三视图可知原几何体是上方是三棱锥,下方是半球,∴,故选C.【考点】1.三视图;2.几何体的体积.26.如图是一个组合几何体的三视图,则该几何体的体积是.【答案】36+128π【解析】由三视图还原可知该几何体是一个组合体,下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.27.某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为()A.B.C.D.【答案】D【解析】由三视图可知,该几何体是三分之一个圆锥,其体积为.【考点】三视图及几何体的体积.28.某几何体的三视图(图中单位:cm)如图所示,则此几何体的体积是()A.36 cm3B.48 cm3C.60 cm3D.72 cm3【答案】B【解析】由三视图可知几何体上方是一长方体,下方是一放倒的直四棱柱,且四棱柱底面是等腰梯形,上底长为2 cm,下底长为6 cm,高为2 cm,故几何体的体积是2×2×4+×(2+6)×2×4=48(cm3),故选B.29.如图是某三棱柱被削去一个底面后的直观图、侧(左)视图与俯视图.已知CF=2AD,侧视图是边长为2的等边三角形,俯视图是直角梯形,有关数据如图所示.求该几何体的体积.【答案】3【解析】解:取CF中点P,过P作PQ∥CB交BE于Q,连接PD,QD,则AD∥CP,且AD=CP.所以四边形ACPD为平行四边形,所以AC∥PD.所以平面PDQ∥平面ABC.该几何体可分割成三棱柱PDQ-CAB和四棱锥D-PQEF,所以V=V-CAB+V D-PQEFPDQ=×22sin 60°×2+××=3.30.一个几何体的三视图如图所示,则该几何体的表面积是()A.6+8B.12+7C.12+8D.18+2【答案】C【解析】该空间几何体是一个三棱柱.底面为等腰三角形且底面三角形的高是1,底边长是2 ,两个底面三角形的面积之和是2,侧面积是(2+2+2)×3=12+6,故其表面积是12+8.31. 已知四棱锥P-ABCD 的三视图如右图所示,则四棱锥P-ABCD 的四个侧面中的最大面积是( ).A .6B .8C .2D .3【答案】A【解析】四棱锥如图所示:PM =3,S △PDC =×4×=2,S △PBC =S △PAD =×2×3=3,S △PAB =×4×3=6,所以四棱锥P-ABCD 的四个侧面中的最大面积是6.32. 若某几何体的三视图如图所示,则这个几何体的直观图可以是( ).【答案】B【解析】分别从三视图中去验证、排除.由正视图可知,A 不正确;由俯视图可知,C ,D 不正确,所以选B.33. 一个几何体的三视图如图所示,已知这个几何体的体积为,则h________.【答案】【解析】依题意可得四棱锥的体积为.所以可得.解得.故填.本小题的是常见的立几中的三视图的题型,这类题型关键是要能还原几何体的直观图形.所以培养空间的思想很重要.【考点】1.三视图的识别.2.空间几何体的直观图.34.图中的网格纸是边长为的小正方形,在其上用粗线画出了一四棱锥的三视图,则该四棱锥的体积为()A.B.C.D.【答案】C【解析】由三视图知,该几何体是一个四棱锥,且其底面为一个矩形,底面积,高为,故该几何体的体积,故选C.【考点】1.三视图;2.锥体的体积35.已知某几何体的三视图如图,其中主视图中半圆直径为2,则该几何体的体积____________【答案】24-【解析】由三视图可知,该几何体是有长方体里面挖了一个半圆柱体,可知,长方体的长为4,宽为3,高为2,那么圆柱体的高位3,底面的半径为1,则可知该几何体的体积为,故答案为.【考点】由三视图求面积、体积.36.把边长为的正方形沿对角线折起,连结,得到三棱锥,其正视图、俯视图均为全等的等腰直角三角形(如图所示),则其侧视图的面积为()A.B.C.D.【答案】B【解析】在三棱锥中,在平面上的射影为的中点,∵正方形边长为,∴,∴侧视图的面积为.【考点】1.三视图;2.三角形的面积.37.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的()A.外接球的半径为B.体积为C.表面积为D.外接球的表面积为【答案】D.【解析】由题意设外接球半径为,则,A错误;外接球的表面积为,D正确;此几何体的体积为,故B错误;此几何体的表面积为,C错误.【考点】三视图及球的表面积公式.38.一个几何体的三视图如图所示,则该几何体的体积为( )A.4B.8C.D.【答案】B【解析】有三视图可以看出,该几何体是一个三棱锥,它的体积为.【考点】三视图,几何体的体积.39.如图,直三棱柱的侧棱长和底面边长均为2,正视图和俯视图如图所示,则其侧视图的面积为()A.B.C.4D.2【答案】A【解析】由题意易知,直三棱柱的底面是边长为2的正三角形.其侧视图为矩形,矩形的高为2,宽为底面正三角形的高.易知边长为2的正三角形的高为.所以面积为.【考点】三视图40.如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是( )A.B.21C.D.24【答案】A【解析】还原几何体,得棱长为2的正方体和高为1的正四棱锥构成的简单组合体,如图所示,=,选A.【考点】1、几何体的表面积;2、三视图.41.某几何体的三视图如图所示,则它的表面积为()A.B.C.D.【答案】A【解析】易知该三视图的直观图是倒立的半个三棱锥,其表面积由底面半圆,侧面三角形和侧面扇形,所以,故选A.【考点】1.立体几何三视图;2.表面积和体积的求法.42.一几何体的三视图如图所示,则该几何体的体积为()A.200+9πB.200+18πC.140+9πD.140+18π【答案】A【解析】通过观察三视图,易知该几何体是由半个圆柱和长方体组成的,则半个圆柱体积;长方体的体积为,所以该几何体的最终体积,故选A.【考点】1.三视图的应用;2.简单几何体体积的求解.43.一个几何体的三视图如图所示,其中主视图和左视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为( )A.B.C.D.【解析】把原来的几何体补成以为长、宽、高的长方体,原几何体四棱锥与长方体是同一个外接球,,,.【考点】1.补体法;2.几何体与外接球之间的元素换算.44.一个几何体的三视图如图所示,其中府视图为正三角形,则侧视图的面积为()A.8B.C.D.4【答案】B【解析】由三视图可知:该几何体是一个正三棱柱,高为4,底面是一个边长为2的正三角形.因此,侧视图是一个长为4,宽为的矩形,.【考点】三视图与几何体的关系、几何体的侧面积的求法能力.45.某几何体的三视图如图所示,则它的侧面积为()A.B.C.24D.【答案】A【解析】由三视图得,这是一个正四棱台,由条件,侧面积.【考点】1.三视图;2.正棱台侧面积的求法.46.一个几何体的三视图如图所示,其中正视图与侧视图都是底边长为6、腰长为5的等腰三角形,则这个几何体的全面积为()A.B.C.D.【解析】由三视图知,该几何体是一个圆锥,且圆锥的底面直径为,母线长为,用表示圆锥的底面半径,表示圆锥的母线长,则,,故该圆锥的全面积为.【考点】三视图、圆锥的表面积47.一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为的圆,且这个几何体是球体的一部分,则这个几何体的表面积为( )A.3πB.4πC.6πD.8π【答案】B【解析】此空间几何体是球体切去四分之一的体积,表面积是四分之三的球表面积加上切面面积,切面面积是两个半圆面面积.故这个几何体的表面积是.【考点】1、几何体的三视图; 2、球的表面积公式.48.右图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为和,腰长为的等腰梯形,则该几何体的表面积是.【答案】【解析】从三视图可以看出:几何体是一个圆台,上底面是一个直径为4的圆,下底面是一个直径为2的圆,侧棱长为4.上底面积,下底面积,侧面是一个扇环形,面积为,所以表面积为.【考点】空间几何体的三视图、表面积的计算.49.某零件的正(主)视图与侧(左)视图均是如图所示的图形(实线组成半径为的半圆,虚线是等腰三角形的两腰),俯视图是一个半径为的圆(包括圆心),则该零件的体积是 ( )A.B.C.D.【解析】由题意易知该几何体为一半球内部挖去一圆锥所成,故体积为.故选C.【考点】1.体积; 2.三视图.50.某四棱台的三视图如图所示,则该四棱台的体积是 ( )A.B.C.D.【答案】B【解析】由三视图可知,该四棱台的上下底面边长分别为和的正方形,高为,故,故选B.【考点】三视图与四棱台的体积51.若一个底面是正三角形的三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为()A.B.C.D.【答案】B【解析】由已知底面是正三角形的三棱柱的正视图,我们可得该三棱柱的底面棱长为2,高为1,则底面外接圆半径,球心到底面的球心距,则球半径,则该球的表面积,故选B.【考点】由三视图求面积、体积.点评:本题考查的知识点是由三视图求表面积,其中根据截面圆半径、球心距、球半径满足勾股定理计算球的半径,是解答本题的关键.52.如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图像是()A. B. C. D.【答案】B【解析】由三视图可知该几何体是圆锥,顶点在下,底面圆在上,在匀速注水过程中水面高度随着时间的增大而增大,且刚开始时截面积较小,所以高度变化较快,随着水面的升高,截面圆面积增大,高度变化速度减缓,因此函数的瞬时变化率逐渐减小,导数减小,图像为B项【考点】函数导数的定义点评:本题通过高度的瞬时变化率的变化情况得到函数的导数的大小,从而通过做出的切线斜率的变化得出正确图像53.已知一个三棱锥的主视图与俯视图如图所示,则该三棱锥的侧视图面积为()A.B.C.D.【答案】B【解析】根据题意,由于三棱锥的俯视图为直角三角形,正视图为直角三角形,且斜边长为2,直角边长为,那么结合图像可知其侧视图为底面边长为1,高为的三角形,因此其面积为,故选B.【考点】三棱锥点评:解决的关键是根据三棱锥的三视图来得到底面积和高进而求解侧视图,属于基础题。
高考三视图(含解析)理试题汇总

专题21 三视图1.某几何体的三视图如图所示,则其表面积为()A.2πB.3πC.4πD.5π【答案】B点睛:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.2.已知三棱锥的正视图与俯视图如图所示,俯视图是边长为2的正三角形,则该三棱锥的侧视图可能为( )A .B .C .D .【答案】B【解析】由正视图和俯视图还原几何体如图所示,由正视图和俯视图对应线段可得2AB BD AD ===,当BC ABD ⊥平面时, BC=2, ABD ∆的边AB ,只有B 选项符合,当BC 不垂直平面ABD 时,没有符合条件的选项,故选B .点睛:1.解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图. 2.三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,可以根据三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据 3.某个长方体被一个平面所截,得到几何体的三视图如图所示,则这个几何体的体积为( )A . 4B .C . 203D . 8 【答案】D4.如图,正三棱柱111ABC A B C 的主视图是边长为4的正方形,则此正三棱柱的左视图的面积为( )A . 16B .C .D . 【答案】D点睛:三视图问题的常见类型及解题策略(1)由几何体的直观图求三视图.注意正视图、侧视图和俯视图的观察方向,注意看到的部分用实线表示,不能看到的部分用虚线表示.(2)由几何体的部分视图画出剩余的部分视图.先根据已知的一部分三视图,还原、推测直观图的可能形式,然后再找其剩下部分三视图的可能形式.当然作为选择题,也可将选项逐项代入,再看看给出的部分三视图是否符合.(3)由几何体的三视图还原几何体的形状.要熟悉柱、锥、台、球的三视图,明确三视图的形成原理,结合空间想象将三视图还原为实物图.5.某几何体的三视图如图所示,则该几何体的体积为 ( )(A) 168π+ (B) 88π+ (C) 1616π+ (D) 816π+ 【答案】A【解析】将三视图还原为原来的几何体,再利用体积公式求解.原几何体为组合体;上面是长方体,下面是圆柱的一半(如图所示), 其体积为21422241682V ππ=⨯⨯+⨯⨯=+.故选A; 6.如图5,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的几条棱中,最长的棱的长度为( )(A) (B) (C) 6 (D)4 【答案】C 【解析】如图所示点睛:对于小方格中的三视图,可以放到长方体,或者正方体里面去找到原图,这样比较好找;7.某几何体的三视图如图所示,则该几何体的表面积为( )A . 24π-B . 24π+C . 20π-D . 20π+ 【答案】A8.已知某空间几何体的三视图如图所示,则该几何体的表面积是( )A.B.C.D.【答案】A【解析】由三视图知:几何体为四棱锥,且四棱锥的一条侧棱与底面垂直,如图,平面,,,,,经计算,,,,∴,∴,,,,∴,故选A.9.一个几何体由多面体和旋转体的整体或一部分组合而成,其三视图如图所示,则该几何体的体积是()A .1π+B .2π+C .21π+D .35π++【答案】A 【解析】考点:由三视图求体积.10.如图是一个由两个半圆锥与一个长方体组合而成的几何体的三视图,则该几何体的体积为( )A .263π+B .83π+C .243π+ D .43π+【答案】C 【解析】试题分析:相当于一个圆锥和一个长方体,故体积为122221433ππ⋅+⋅⋅=+.考点:三视图.11.一个几何体的三视图如图所示,则该几何体的体积为()A.143B.5 C.163D.6【答案】A【解析】考点:三视图.12.一个几何体的三视图如图所示,则该几何体的体积为____.【答案】1 3【解析】本题考查三视图、四棱锥的体积计算等知识,难度中等.由三视图可知该几何体是底面为长和高均为1的平行四边形,高为1的四棱锥,故其体积为1111133V=⨯⨯⨯=.。
2019年全国统一高考历史试卷以及答案解析(全国1卷)

绝密★启用前2019年高考普通高等学校招生全国统一考试(全国1卷)历史注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题4分,共48分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(4分)据学者考订,商朝产生了17代30位王,多为兄终弟及;而西周产生了11代12位王。
这反映出()A.禅让制度的长期影响B.王位继承方式的变化C.君主寿命的时代差异D.血缘纽带关系的弱化2.(4分)汉武帝时,朝廷制作出许多一尺见方的白鹿皮,称为“皮币”,定价为40万钱一张。
诸侯王参加献礼时,必须购皮币用来置放礼物,而当时一个“千户侯”一年的租税收入约为20万钱。
朝廷这种做法()A.加强了货币管理B.确立了思想上的统一C.削弱了诸侯实力D.实现了对地方的控制3.(4分)唐代之前,荆楚民间存在一种祈求丰收的“牵钩之戏”,至唐代称作“拔河”,广为流传。
唐玄宗《观拔河俗戏》诗云:“壮徒恒贾勇,拔拒抵长河。
欲练英雄志,须明胜负多……预期年岁稔,先此乐时和。
”据此可知,在唐代()A.江南文化成为主流B.耕战结合观念深入人心C.阳刚与力量受到推崇D.诗歌以描写宫廷生活为主4.(4分)明中后期,大运河流经的东昌府是山东最重要的棉花产区,所产棉花多由江淮商人坐地收揽,沿运河运至江南,而后返销棉布。
这一现象产生的主要因素是()A.交通方式的变革B.土地制度的调整C.货币制度的改变D.地区经济的差异5.(4分)表川沙县部分名人简历表黄彬国学生,干练有才,上海招商局创办时,章程皆其手订。
朱纯祖监生,幼时孤苦伶仃,学习米业,中年创设朱丽记花米行。
姚光第南邑生员,感于地方贫瘠日甚,就其家设机器轧棉厂。
2015——2019年全国一卷高考历史试题分类解析汇编(中国古代史)

2015——2019 年全国一卷高考历史试题分类解析汇编专题1:中国古代史题型一:选择题1.(全国一卷2019年4分)据学者考订,商朝产生了17代30位王,多为兄终弟及;而西周产生了11代12位王。
这反映出A.禅让制度的长期影响B.王位继承方式的变化C.君主寿命的时代差异D.血缘纽带关系的弱化【答案】B【考点】西周宗法制【解析】本题涉及到我国古代王位世袭制和宗法制的知识点。
从夏朝开始,世袭制取代禅让制,故A 排除;材料“多为兄终弟及” ,说明商朝时期这一传承方式占据重要地位。
但是结合所学知识,西周实行宗法制,核心是嫡长子继承制,说明继承方式的改变,故选B;君主寿命长短属于偶然性时间,不能作为主要依据,故C 排除;不管是兄终弟及还是宗法制,都体现了血缘关系,而且宗法制还体现了血缘纽带的强化,故D 排除。
2.(全国一卷2019年4分)汉武帝时,朝廷制作出许多一尺见方的白鹿皮,称为“皮币”,定价为40 万钱一张。
诸侯王参加献礼时,必须购皮币用来置放礼物,而当时一个“千户侯”一年的租税收入约为20 万钱。
朝廷这种做法A.加强了货币管理B.确立了思想上的统一C.削弱了诸侯实力D.实现了对地方的控制【答案】C【考点】古代中央集权【解析】汉初实行郡国并行制,各诸侯国诸侯有较大的实权,不利于中央集权的加强。
据材料可知,“皮币”的购买具有强制性,和专卖性,有利于增加中央的财政收入,而且强制诸侯购买,也可以削弱诸侯的经济实力,故选C;材料跟货币没关系,排除A;罢黜百家,独尊儒术确立了思想上的统一,故B 排除;应该是加强了对地方的控制而不是实现了,故D 排除。
3.(全国一卷2019年4分)唐代之前,荆楚民间存在一种祈求丰收的“牵钩之戏”,至唐代称作“拔河”,广为流传。
唐玄宗《观拔河俗戏》诗云:“壮徒恒贾勇,拔拒抵长河。
欲练英雄志,须明胜负多⋯⋯预期年岁稔,先此乐时和。
”据此可知,在唐代A.江南文化成为主流B.耕战结合观念深入人心C.阳刚与力量受到推崇D.诗歌以描写宫廷生活为主【答案】C【考点】古代社会风俗(唐代)【解析】材料“壮徒恒贾勇,拔拒抵长河。
三视图历年高考真题
2010年高考题一、选择题1(2010陕西文) 8.若某空间几何体的三视图如图所示,则该几何体的体积是 [B](A )2 (B )1(C )23(D )13如图,该立体图形为直三棱柱所以其体积为122121=⨯⨯⨯ 2.(2010安徽文)(9)一个几何体的三视图如图,该几何体的表面积是(A )372 (B )360 (C )292 (D )280【解析】该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之和2(10810282)2(6882)360S =⨯+⨯+⨯+⨯+⨯=.3.(2010重庆文)(9)到两互相垂直的异面直线的距离相等的点 (A )只有1个 (B )恰有3个 (C )恰有4个 (D )有无穷多个【解析】放在正方体中研究,显然,线段1OO 、EF 、FG 、GH 、HE 的中点到两垂直异面直线AB 、CD 的距离都相等, 所以排除A 、B 、C ,选D 亦可在四条侧棱上找到四个点到两垂直异面直线AB 、CD 的距离相等4.(2010浙江文)(8)若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是(A)3523cm3(B)3203cm(C)2243cm3(D)1603cm3【解析】选B5.(2010广东理)6.如图1,△ ABC为三角形,AA'//BB'//CC', CC'⊥平面ABC 且3AA'=32BB'=CC' =AB,则多面体△ABC -A B C'''的正视图(也称主视图)是【答案】D6.(2010福建文)3.若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积等于 ( )A3B.2C.23D.6三棱柱是以底面边长为2,高为1的正三棱柱,选D.7.(2010广东文)8.(2010全国卷1文)(12)已知在半径为2的球面上有A 、B 、C 、D 四点,若AB=CD=2,则四面体ABCD 的体积的最大值为 (A)33 (B)433 (C) 333【解析】过CD 作平面PCD ,使AB ⊥平面PCD,交AB 与P,设点P 到CD 的距离为h ,则有ABCD 11222323V h h =⨯⨯⨯⨯=四面体,当直径通过AB 与CD 的中点时,22max 22123h =-故max 43V =二、填空题1.(2010上海文)6.已知四棱椎P ABCD -的底面是边长为6 的正方形,侧棱PA ⊥底面ABCD ,且8PA =,则该四棱椎的体积是 。
五年高考:2015-2019年高考全国卷II历史试卷及答案

文科综合(历史部分)
注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答题前,考生务必在将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。写在试卷上无效。
材料二
公元前399年,苏格拉底被雅典陪审法庭以亵渎神明和蛊惑青年的罪名判处死刑。他与他的弟子们都认为判决不公,当弟子们安排苏格拉底逃走时,他却认为,虽然逃走是一种正义,但审判过程符合雅典法律程序,遵守合法的判决也是正义的要求,而且是更大的正义。因为如果他不服从判决,就等于践踏法律,倘若人人都以自己认为的正义为借口而任意践踏法律,社会秩序将混乱不堪,城邦将无法存在,最终他选择在弟子面前饮下毒药,从容赴死。(摘编自[古希腊]柏拉图《苏格拉底的申辩》等)
46.(15分)
(1)在国家政治生活中,多数国民须自觉居于主人地位,具有主动精神;自觉参与建设政府、制定并维护宪法。(6分)
(2)从思想文化层面反思清末民初民主政治失败的原因;认识民众觉悟才是实现民主政治的关键,要唤醒国民的政治自觉;发展了民主思想;推动了新文化运动的开展,起到了思想解放作用。(9分)
(摘编自俄菲利波夫《俄罗斯现代史》)
(1)根据材料并结合所学知识,概括苏联制定和实施原子武器研制计划的背景。(5分)
(2)根据材料并结合所学知识,说明苏联原子武器研制成功的条件和在当时历史条件下的积极作用。(10分)
48.(15分)中外历史人物评说
材料
19世纪70年代,德国统一后,资本主义经济迅速发展,一系列社会问题也随之出现。工业生产中的伤亡事故频繁,工人生活与健康状况不断恶化。与此同时,工人阶级的力量迅速壮大,工人运动日益高涨。1878年,俾斯麦政府强迫帝国议会通过了《非常法》,对深受工人拥护的社会民主党进行严厉镇压。在《非常法》实行的12年里,许多社会民主党党员被监禁和驱逐,大量拥护社会民主党的工人被解雇,大批报刊、出版物及工人组织被查禁或取缔。
2015-2019 三视图高考真题(含解析)

专题19 三视图以及表面积体积2019年1.(2019全国II 文16)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)2.(2019全国II 文17)如图,长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,AB =3,求四棱锥11E BB C C -的体积.3.(2019全国III 文16)学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O −EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9 g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.4.(2019江苏9)如图,长方体1111ABCD A B C D 的体积是120,E 为1CC 的中点,则三棱锥E -BCD 的体积是 .5.(2019天津文12)已知四棱锥的底面是边长为2的正方形,侧棱长均为5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为__________.6.(2019北京文12)某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.7.(2019浙江4)祖暅是我国南北朝时代的伟大科学家.他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体体积公式V 柱体=Sh ,其中S 是柱体的底面积,h 是柱体的高.若某柱体的三视图如图所示,则该柱体的体积是A .158B .162C .182D .322015-2018年一、选择题1.(2018全国卷Ⅰ)已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 A .122πB .12πC .82πD .10π2.(2018全国卷Ⅰ)某圆柱的高为2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为BAA .217B .25C .3D .23.(2018全国卷Ⅰ)在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为 A .8B .2C .82D .834.(2018全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是5.(2018全国卷Ⅲ)设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为3,则三棱锥D ABC 体积的最大值为 A .123B .183C .3D .36.(2018浙江)某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是俯视图正视图2211A .2B .4C .6D .87.(2018北京)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为俯视图侧(左)视图正(主)视图1221A .1B .2C .3D .48.(2017新课标Ⅲ)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.πB.34πC.2πD.4π9.(2017北京)某三棱锥的三视图如图所示,则该三棱锥的体积为A.60 B.30 C.20 D.1010.(2017浙江)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:3cm)是俯视图11311A.12π+B.32π+C.312π+D.332π+11.(2017新课标Ⅱ)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A .90πB .63πC .42πD .36π12.(2016年山东)一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为A .1233π+ B .123π+ C .123π+ D .21π+ 13.(2016年全国I )如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径,若该几何体的体积是28π3,则它的表面积是A .17πB .18πC .20πD .28π 14.(2016年全国II )如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A .20πB .24πC .28πD .32π15.(2016年全国III )如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为A.18+ B.54+ C .90 D .81 二、填空题16.(2018天津)如图,已知正方体1111ABCD A B C D -的棱长为1,则四棱锥111A BB D D -的体积为__.D 1C 1B 1A 1D CBA17.(2018江苏)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .18.(2017新课标Ⅰ)已知三棱锥S ABC -的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB ,SA AC =,SB BC =,三棱锥S ABC -的体积为9,则球O 的表面积为________.19.(2017新课标Ⅱ)长方体的长、宽、高分别为3,2,1,其顶点都在球O 的球面上,则球O 的表面积为 .20.(2017天津)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 . 21.(2017山东)由一个长方体和两个14圆柱体构成的几何体的三视图如图,则该几何体的体积为 .俯视图侧视图(左视图)正视图(主视图)22.(2017江苏)如图,在圆柱12O O 内有一个球O ,该球与圆柱的上、下底面及母线均相切。
三视图与解答题.docx

(2015年四川高考题)18.三棱锥A-BCD及其侧视图、俯视图如图所示.设肱,N分别为线段40, AB的中点,P为线段BC±的点,且MN1NP .(I)证明:P是线段8。
的中点;(II)求二面角A-NP-M的余弦值.立意:本题主要考查简单空间图形的二视图、空间线面垂直的判定与性质、空间面面夹角的计算等基础知识,考查空间想象能力、推理论证能力、运算求解能力.解答:(I)如图,取BD中点。
,连接A。
,CO.山侧视图及俯视图知,AABD,△BCD为正二角形,因此AO±BD, OC±BD.因为AO, OCu平面AOC内,且AOC|OC=。
,NN. \所以3D上平面AOC./I又因为ACu平面AQC,所以BD±AC.取3。
的中点H,连接NH, PH.又M, N分别为线段AD, A3的中点,所以NH//AO, MN//BD.因为所以NHLBD.因为MNLNP,所以NPLBD.因为NH, NFu平面NHP,且NHC\ NP= N ,所以BOL平面NHP.又因为HFu平面NHF,所以BD±HP.X 0C1BD, HFu平面BCD, OCu 平面BCD,所以HP//OC.因为H为BO中点,故P为BC中点.(II)解法一:如图,作NQ1AC于Q,连接构2.由(I)知,NP//AC,所以NQ±NP.因为MN1NP,所以为二面角A-NP-M的一个平面角.由(I)知,MBD,△BCD为边长为2的正三角形,所以AO = OC =也.由俯视图可知,AO_L平面BCD.因为OCu平面BCD,所以AOLOC,因此在等腰RtAAOC中,AC = $ . 作BR1AC于R,二2 一芒)2=业在AABC 中,AB=BC,所以BR =2 2因为在平面ABC内,NQLAC, BRLAC,所以NQ//BR.又因为N为AB的中点,所以Q为AR的中点,m“八BR V10因jt 匕NQ — -=——-.同理’可得仔隼MN BD 所以在等腰AMN 。
备战2014高考数学真题集锦:《三视图》

(正视图)(俯视图)【三年真题重温】1.【2011⋅新课标全国】在一个几何体的三视图中,正视图和俯视图如右图所示,则相应的侧视图可以为( ). 【答案】D【解析】本题主要考查简单几何体的三视图及空间想象能力. 由几何体得正视图与俯视图知,其对应的几何体如图所示是半个圆锥 与棱锥的组合体,故其侧视图选D .2.【2010⋅新课标全国理】正视图为一个三角形的几何体可以是______(写出三种) 【答案】三棱锥、三棱柱、圆锥【解析】正视图为一个三角形的几何体可以是三棱锥、三棱柱、圆锥、四棱锥等等.命题意图:本题主要考查三视图以及常见的空间几何体的三视图,考查空间想象能力. 3.【2010⋅新课标全国文】一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的_______(填入所有可能的几何体前的编号)①三棱锥 ②四棱锥 ③三棱柱 ④四棱柱 ⑤圆锥 ⑥圆柱 【答案】①②③⑤4. 【2012⋅新课标全国】 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为( ) (A )6 (B)9 (C)12 (D)18【命题意图猜想】1.2011年的题目给出三视图中的正视图和俯视图,考查几何体的侧视图;2010年试题比较开放,考查几何体的正视图.2012年的题目给出了三视图,求解几何体的体积,难度中档。
【连续两年没有和几何体的体积和表面积联系到一起.试题题目变的较为简单.猜想2012年高考题对本热点的考查有两种可能,一是与几何体的体积或表面积相联系,若与组合体相联系,题目难度会增大;二是可能在解答题中出现,根据三视图得到几何体,一般难度较低.】根据这三年高考试题对三视图的考查的难度逐渐加强的趋势,且和几何体的体积等有效的联系到一起,不仅考查学生的还原几何体的能力,还要求学生能够求解几何体的相关的量.预测2013年高考题很能出现三视图和组合体相结合的题目,难度再次增大.也可能保留试题难度,从三视图的难度上进行设置,使得题目有一定的区分度.2.从近几年的高考试题来看,几何体的三视图是高考的热点,题型多为选择题、填空题,难A .B .C .D .度中、低档.主要考查几何体的三视图,以及由三视图构成的几何体,在考查三视图的同时,又考查了学生的空间想象能力及运算与推理能力.预测2013年高考仍将以空间几何体的三视图为主要考查点,重点考查学生读图、识图能力以及空间想象能力.【最新考纲解读】1.能画出简单空间图形的三视图,能识别三视图所表示的立体模型,会用斜二测画法画出它们的直观图.2.会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.【回归课本整合】三视图的画法要求:(1)在画三视图时,重叠的线只画一条,挡住的线要画成虚线,尺寸线用细实线标出.(2)三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体画出的轮廓线.画三视图的基本要求是:主俯一样长,俯左一样宽,主左一样高.由三视图想象几何体特征时要根据“长对正、宽相等、高平齐”的原则作出判断.【方法技巧提炼】1.画三视图时,应牢记其要求的“长对正、高平齐、宽相等”,注意虚、实线的区别,同时应熟悉一些常见几何体的三视图.解决由三视图想象几何体,进而进行有关计算的题目,关键是准确把握三视图和几何体之间的关系.2.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征,熟练掌握三视图的投影方向及正视图原理,才能迅速破解三视图问题,由三视图画出其直观图.3.求解几何体的体积时,注意利用结论“正视图(侧视图)的高与该几何体的高是相等”进行求解可避免还原几何体的这一步.【考场经验分享】对于简单几何体的组合体的三视图,首先要确定正视、侧视、俯视的方向,其次要注意组合体由哪些几何体组成,弄清它们的组成方式,特别应注意它们的交线的位置.解题时一定耐心加细心,观察准确线与线的位置关系,区分好实线和虚线的不同.此类题目若只是单纯考查三视图,一般难度较低,需保证的全分;若与体积、表面积或组合体相结合,有时难度较大,需要较强的空间想象能力和准确的画图能力,此时若空间想象能力不够的同学,不要花费过多的时间.【新题预测演练】1.【2013河北省名校名师俱乐部高三3月模拟考试】如图是一个几何体的三视图,则这个几何体的体积是()- 2 -A .26B .27C .572D .28 2.【北京市房山区2013届高三上学期期末考试】若正三棱柱的三视图如图所示,该三棱柱的表面积是A. 3B.932C. 63+D. 623+ 3.【安徽省黄山市2013届高中毕业班第一次质量检测】 如图,右边几何体的正视图和侧视图可能正确..的是【答案】A【解析】根据三视图的定义,可知正视图为一个正方形以及内部的一个三角形;侧视图和正正视图 侧视图D.正视图 侧视图B.正视图 侧视图A. 正视图 侧视图 C.- 4 -D 2522233CBAPNM视图一样,故答案为A.4.【2013届贵州天柱民中、锦屏中学、黎平一中、黄平民中四校联考】如图是某几何体的三视图,其中正视图为正方形,俯视图是腰长为2的等腰直角三角形,则该几何体的体积是A .3B .25C .6D .8222俯视图侧视图正视图433图12【答案】 C【解析】三棱锥如图所示,3PM =,145252PDCS ∆=⨯=,12332PBC PAD S S ∆∆==⨯⨯=,14362PAB S ∆=⨯⨯= 6.【北京市昌平区2013届高三上学期期末理】已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的全面积为A. 104342++ B .102342++ C. 142342++ D. 144342++ 【答案】B【解析】根据三视图复原的几何体是底面为直角梯形,一条侧棱垂直直角梯形的直角顶点的四棱锥其中ABCD 是直角梯形,AB ⊥AD , AB=AD=2,BC=4,即PA ⊥平面ABCD ,PA=2。
