七年级数学分式课件4
合集下载
浙教版数学七年级下册《分式》课件

分式的值为零,必须同时满足: (1)分子等于零; (2)分母不等于零,两者缺一不可。
归纳
浙江教育出版社 七年级 | 下册
求使分式的值为0的字母的值的方法: 第一求出使分子的值等于0的字母的值,再检验这个字母的 值是否使分母的值等于0,只有当它使分母的值不为0时,才 是我们所要求的字母的值。
课后小结
第五单元·分式
分式
浙江教育出版社 七年级 | 下册
学习目标
1 课堂讲授 2 课时流程
分式的定义 分式有(无)意义的条件 分式的值为零的条件
逐点 导讲练
课堂 小结
作业 提升
浙江教育出版社 七年级 | 下册
课时引入
浙江教育出版社 七年级 | 下册
为了调查珍稀动物资源,动物专家在p平方千米的保护区 内找到7只灰熊;你能用代数式表示该保护区平均每平方千米 内有多少只灰熊吗?
浙江教育出版社 七年级 | 下册
本节课学到了什么?请同学们叙述本节的概念和结论。
浙江教育出版社 七年级 | 下册
感悟新知
知识点一 分式的定义
思考
我们知道,两个整数相除可以表示成分数的情势,例如,
3÷5= 3;
5
在整式运算时,两个整式相除也可以表示成类似的情势,
例如,7÷p= 2x - 3 。
7;b÷a=
p
b a
;(v-v0)÷t=
v - v0;(2x-3)÷(x+2)=
t
x2
归纳
浙江教育出版社 七年级 | 下册
分式的定义:
7 p
,
b a
,
v
-v t
0
,2xx-23
这些代数式都表示两个
整式相除,且除式中含有字母, 像这样的代数式就叫做分
归纳
浙江教育出版社 七年级 | 下册
求使分式的值为0的字母的值的方法: 第一求出使分子的值等于0的字母的值,再检验这个字母的 值是否使分母的值等于0,只有当它使分母的值不为0时,才 是我们所要求的字母的值。
课后小结
第五单元·分式
分式
浙江教育出版社 七年级 | 下册
学习目标
1 课堂讲授 2 课时流程
分式的定义 分式有(无)意义的条件 分式的值为零的条件
逐点 导讲练
课堂 小结
作业 提升
浙江教育出版社 七年级 | 下册
课时引入
浙江教育出版社 七年级 | 下册
为了调查珍稀动物资源,动物专家在p平方千米的保护区 内找到7只灰熊;你能用代数式表示该保护区平均每平方千米 内有多少只灰熊吗?
浙江教育出版社 七年级 | 下册
本节课学到了什么?请同学们叙述本节的概念和结论。
浙江教育出版社 七年级 | 下册
感悟新知
知识点一 分式的定义
思考
我们知道,两个整数相除可以表示成分数的情势,例如,
3÷5= 3;
5
在整式运算时,两个整式相除也可以表示成类似的情势,
例如,7÷p= 2x - 3 。
7;b÷a=
p
b a
;(v-v0)÷t=
v - v0;(2x-3)÷(x+2)=
t
x2
归纳
浙江教育出版社 七年级 | 下册
分式的定义:
7 p
,
b a
,
v
-v t
0
,2xx-23
这些代数式都表示两个
整式相除,且除式中含有字母, 像这样的代数式就叫做分
七年级数学下册第五章分式复习课课件新版浙教版ppt

【解析】 设 A4 薄型纸每页的质量为 x(g),则 A4 厚型纸每页的质 量为(x+0.8)g. 由题意,得x+4000.8=16x0·2, 解得 x=3.2. 经检验,x=3.2 是原方程的根,且符合题意. 答:A4 薄型纸每页的质量为 3.2 g.
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
【例 1】 若分式xx2+-11的值为零,则 x 的值为
()
A. 0
B. 1
C. -1
D. ±1
【解析】 根据分式的值为 0 的条件列出关于 x 的不等式
组,求出 x 的值即可.
∵分式xx2+-11的值为零, x2-1=0,
∴x+1≠0, 解得 x=让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
的基本性质.
【正解】
原式=2131xx+-yy××66=32xx+-66yy.
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
易错点2 颠倒运算顺序
【典例 2】 计算:1-1 a÷(3-a)·13--aa. 【错解】 原式=1-1 a÷(1-a)=(1-1a)2. 【析错】 乘除是同一级运算,除在前应先做除,上述错 解颠倒了运算顺序,致使结果出现错误. 【正解】 原式=1-1 a·3-1 a·13--aa=(3-1a)2.
m+3-m+3 (m+3)(m-3)
=
-2 (m-3)
·
(m+3)(m-3) 6
=
-m+3 3.
当 m=0 时,原式=-m+3 3=-0+3 3=-1. 【答案】 原式=-m+3 3=-1
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
【例 1】 若分式xx2+-11的值为零,则 x 的值为
()
A. 0
B. 1
C. -1
D. ±1
【解析】 根据分式的值为 0 的条件列出关于 x 的不等式
组,求出 x 的值即可.
∵分式xx2+-11的值为零, x2-1=0,
∴x+1≠0, 解得 x=让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
的基本性质.
【正解】
原式=2131xx+-yy××66=32xx+-66yy.
在整堂课的教学中,刘教师总是让学 生带着 问题来 学习, 而问题 的设置 具有一 定的梯 度,由 浅入深 ,所提 出的问 题也很 明确
易错点2 颠倒运算顺序
【典例 2】 计算:1-1 a÷(3-a)·13--aa. 【错解】 原式=1-1 a÷(1-a)=(1-1a)2. 【析错】 乘除是同一级运算,除在前应先做除,上述错 解颠倒了运算顺序,致使结果出现错误. 【正解】 原式=1-1 a·3-1 a·13--aa=(3-1a)2.
m+3-m+3 (m+3)(m-3)
=
-2 (m-3)
·
(m+3)(m-3) 6
=
-m+3 3.
当 m=0 时,原式=-m+3 3=-0+3 3=-1. 【答案】 原式=-m+3 3=-1
沪科版七年级下册数学《分式的概念及其基本性质》课件

第一课时
学习目标
1、掌握分式的概念、有理式的概念,以及
用分式表示现实情境中的数量关系。
2、掌握分式有意义的条件,以及分式的值
为零的条件。
下列代数式中哪些是整式?
5 0.4 x
x
3
3x 1 x2 y 2
2 mn
整整式式
x3 x5
4x 3y 13
观察与联想:
5
2
x mnx3 x5来自上面式子有什么共同的特点? (分母都含有字母)
锋 芒
(6)当x
___1__ 时, 分式
| x | 1 x2 3x
2
的值等于0.
课堂小结
通过本节课的学习谈谈你 有哪些收获? 还有疑惑吗?
思考 1.已知
y x 1 2 3x
,x取何值时,满足:
(1)y 的值为 0 ;
(2)分式无意义 ;
(3)y的值为正数;
(4)y的值为负数。
x y z 2.已知
x 3
y 4
z ,求 6
xy yz xz
2
2
2 的值。
小 (3)当b
___53__时,
分式
5
1 3b
有意义.
试 (4)当x
____1_时,
分式
x
1 2
1
有意义.
问题:分式值为0的条件是什么?
分式值为0
分子为0,分母不为0
例: 当x= 当x= 当x= 当x= 当x=
x3
时,2x 7 的值为0.
时,
x x
1 1
的值为0.
时,
x 1 4x 1
的值为0.
时,x2 1 的值为0. x 1
时,4xx53 的值为0.
学习目标
1、掌握分式的概念、有理式的概念,以及
用分式表示现实情境中的数量关系。
2、掌握分式有意义的条件,以及分式的值
为零的条件。
下列代数式中哪些是整式?
5 0.4 x
x
3
3x 1 x2 y 2
2 mn
整整式式
x3 x5
4x 3y 13
观察与联想:
5
2
x mnx3 x5来自上面式子有什么共同的特点? (分母都含有字母)
锋 芒
(6)当x
___1__ 时, 分式
| x | 1 x2 3x
2
的值等于0.
课堂小结
通过本节课的学习谈谈你 有哪些收获? 还有疑惑吗?
思考 1.已知
y x 1 2 3x
,x取何值时,满足:
(1)y 的值为 0 ;
(2)分式无意义 ;
(3)y的值为正数;
(4)y的值为负数。
x y z 2.已知
x 3
y 4
z ,求 6
xy yz xz
2
2
2 的值。
小 (3)当b
___53__时,
分式
5
1 3b
有意义.
试 (4)当x
____1_时,
分式
x
1 2
1
有意义.
问题:分式值为0的条件是什么?
分式值为0
分子为0,分母不为0
例: 当x= 当x= 当x= 当x= 当x=
x3
时,2x 7 的值为0.
时,
x x
1 1
的值为0.
时,
x 1 4x 1
的值为0.
时,x2 1 的值为0. x 1
时,4xx53 的值为0.
沪科版数学七年级下册9.分式基本性质及约分课件

沪科版数学七年级下
9.1 分式及其基本性质
第二课时
分式的基本性质和约分
教学目标
1
• 理解并掌握分式的基本性质并能利用基本性
质对分式进行恒等变形
2
• 了解最简分式和约分,利用分式基本性质对
分式进行约分化简
3
• 学生经历分数与分式的比较,培养学生良好
的类比思维习惯和思想方法
知识回顾
判断下列代数式是否为分式?
1
x
y
3
(2)
1
x y
2
提升练习
1
(x
y) 6
6x 2y
3
1
3x 6y
(
x y) 6
2
分数系数
可以分子
分母同乘
以各分母
最小公倍
数化为整
数系数
2、视察下列等式是否成立
成立
提升练习
a
a
a
a
a
a
(1)
, (2)
, (3)
b
b
b
b
b
b
a
a
a
a
a
a
(4)
的整式,分式的值不变.
A AC
A AC
B B C
B B C
(C≠0) 其中A , B , C是整式.
下列等式在有意义情况下右边是怎样从左边得到的?
2b
2ab
(1)
2
3ac
3a 2c 2
分子分母都
新知解析
乘以a
a≠0
4ab
2a
(2)
6b(a 1) 3(a 1)
9.1 分式及其基本性质
第二课时
分式的基本性质和约分
教学目标
1
• 理解并掌握分式的基本性质并能利用基本性
质对分式进行恒等变形
2
• 了解最简分式和约分,利用分式基本性质对
分式进行约分化简
3
• 学生经历分数与分式的比较,培养学生良好
的类比思维习惯和思想方法
知识回顾
判断下列代数式是否为分式?
1
x
y
3
(2)
1
x y
2
提升练习
1
(x
y) 6
6x 2y
3
1
3x 6y
(
x y) 6
2
分数系数
可以分子
分母同乘
以各分母
最小公倍
数化为整
数系数
2、视察下列等式是否成立
成立
提升练习
a
a
a
a
a
a
(1)
, (2)
, (3)
b
b
b
b
b
b
a
a
a
a
a
a
(4)
的整式,分式的值不变.
A AC
A AC
B B C
B B C
(C≠0) 其中A , B , C是整式.
下列等式在有意义情况下右边是怎样从左边得到的?
2b
2ab
(1)
2
3ac
3a 2c 2
分子分母都
新知解析
乘以a
a≠0
4ab
2a
(2)
6b(a 1) 3(a 1)
沪科版七下数学分式的运算之分式的通分教学课件

知1-练
1
分式
2 ,a 1 ,2 3a 2a2 4a3
的最简公分母是(
C
)
A.24a2
B.24a3
C.12a3
D.6a3
2
分式
x x
2 ,2x 3 , 5 12 1 x3 x 1
的最简公分
母为( B )
知1-练
A.(x-1)2Leabharlann B.(x-1)3C.x-1
D.(x-1)2(1-x)3
知识点 2 通 分
(1)当走第二条路时,他从甲 地到乙地需要多长时间?
(2)他走哪条路花费时间少? 少用多长时间?
答:(1)
1 v
2 (h) 3v
(2)走第一条路花费的时间少,少用
1 v
2 3v
3 (h). 2v
知识点 1 最简公分母
知1-导
异分母分式通分时,关键是确定公分母.通 常取各分母 所有因式的最高次幂的积作为公分 母,这样的公分母叫做最简公分母.
第9章 分 式
9.2 分式的运算 分式的通分
1 课堂讲授 ➢ 最简公分母
➢ 通分
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
从甲地到乙地有两条路,每一条 路都是3 km.其中第一条是平路,第二 条有1 km的上坡路,2 km的下坡路.小 明在上坡路上的骑车速度为v km/h,在 平路上的骑车速度为2v km/h,在下坡 路上的骑车速度为3v km/h,那么:
1
C. x 2 x 1
x1 x 2 x 12
2
D. x 1 2
2x 2 x 2 x 12
知2-练
D
1. 分式通分的根据是分式的基本性质. 2. 分式通分的关键是确定几个分式的最简公分
七年级数学下册《分式的运算-分式的乘除》课件

三、例题讲授与练习
例3计算: (1)
( 5 )2 (2) 3y
(
2a 2b - c3
)3
.
解:(1)
( 5 )2 3y
52 (3y)
2
25 9y 2
.
(2)
(
2a 2b - c3
)3
(2a 2b)3 (-c3 )3
8a 6b3 - c9
-
8a 6b3 c9
.
三、例题讲授与练习
练习:(1)判断下列各式正确与否:
三、例题讲授与练习
(2)计算下列各题:
计算:
(1)
a a
2 2
a2
1
2a
;
(2)
2a a2
a2
1
2a
;
(3)
;
(4)
x x2 1
x2 x2
x
;
(5)x2 4 y2 xy ; 3xy2 x 2 y
(6)
x x
2 3
x2 x2
9 4
;
(7)a
2 ab a2b
ba ab
;
(8) x 2 1 x 1;
一 、复习提问
1、什么叫做分式的约分?约分的根据是 什么? 2、下列各式是否正确?为什么?
想一想
探索分式的乘除法的法则
1.回忆: 计算:3 4 1 1 2 (9)
5 63
2、例1计算(1:)bay2 x2
ay2 b2x
a2 ;(2)b2
xy z2
a2 yz b2x2
.
3.概括:分式的乘除法用式子表示即是:
④怎样应用分式乘法法则 得到积的分式?
做一做
计算:
初中数学《分式》课件(同步+复习+名师=精选课件)

(4)当x =-3时,
x 4 ∴当x = 2时分式 的值为零。 x2
2
x 2 4 (3) 2 4 x2 3 2 5
1.填空:
(1)当 x≠2
1 x 时,分式 4 x 8 有意义;
时,分式
(2)当
x=3
3 x 9 x 2 的值是零;
Байду номын сангаас
xa (3)当x=2时,分式 x b 没有意义,则 b= -2
七年级
(下 册)
义务教育教科书
学科网
1、下列代数式中,哪些是整式?哪些是分式?
3 4
2
b 3 2a
y -1 x
m( n p ) 7
4 5b c
m 7
x 2 xy y 2 2 x 1
a 1 2、 对于分式 2a
(1)当a=1时,求分式的值 (2)当a取何值时,分式无意义? 当a取何值时,分式有意义? (3)当a取何值时,分式值为零?
2 y 1 x
4 5b c
3
m 7 m 7
x xy y 2 x 1
2
2
整式有: 分式有:
3 2 b 3 2 a 1
m( n p ) 7
3
4 5b c
x 2 xy y 2 2 x 1
b 分式 分母中的字母能取任何实数吗? a
为什么?分式
2x 3 中的字母x呢? x2
:
我们已经知道:
2 3 16 36
= =
25 3 5
=
10 15
;
4 9
16 4 36 4
=
这是根据分数的基本性质:
分数的分子与分母都乘以或除以同 一个不等于零的数,分数的值不变.
x 4 ∴当x = 2时分式 的值为零。 x2
2
x 2 4 (3) 2 4 x2 3 2 5
1.填空:
(1)当 x≠2
1 x 时,分式 4 x 8 有意义;
时,分式
(2)当
x=3
3 x 9 x 2 的值是零;
Байду номын сангаас
xa (3)当x=2时,分式 x b 没有意义,则 b= -2
七年级
(下 册)
义务教育教科书
学科网
1、下列代数式中,哪些是整式?哪些是分式?
3 4
2
b 3 2a
y -1 x
m( n p ) 7
4 5b c
m 7
x 2 xy y 2 2 x 1
a 1 2、 对于分式 2a
(1)当a=1时,求分式的值 (2)当a取何值时,分式无意义? 当a取何值时,分式有意义? (3)当a取何值时,分式值为零?
2 y 1 x
4 5b c
3
m 7 m 7
x xy y 2 x 1
2
2
整式有: 分式有:
3 2 b 3 2 a 1
m( n p ) 7
3
4 5b c
x 2 xy y 2 2 x 1
b 分式 分母中的字母能取任何实数吗? a
为什么?分式
2x 3 中的字母x呢? x2
:
我们已经知道:
2 3 16 36
= =
25 3 5
=
10 15
;
4 9
16 4 36 4
=
这是根据分数的基本性质:
分数的分子与分母都乘以或除以同 一个不等于零的数,分数的值不变.
初中数学沪科版七年级下册9.分式的乘除课件

三、概念剖析
想一想: 你还记得分数的乘除法法则吗?类比分数的乘除法法则,你能说出
分式的乘除法法则吗?
(1)
ac bd
(2)
2 4 24
ac
3 5 b d
35
三、概念剖析
类似于分数,分式有: 乘法法则:
分式乘分式,用分子的积作为积的分子,分母的积作为积的 分母.
式子表示为: b c b c a d ad
b b b b2
(a)3 a a a a3
b
b b b b3
( a )10 a a b bb
a b
a10 b10
10个
三、概念剖析
一般地,当n是正整数时,
n个
(a)n a a b bb
a b
aaa bbb
an bn
n个
n个
分式的乘方法则: 分式乘方就是把分子、分母分别乘方.
(a)n b
第 9 章 分式 9.2.1 分式的乘除
一、学习目标
1.类比分数的乘除,探究分式的乘除法则; 2.类比积的乘方,探究分式的乘方; 3.会熟练地进行分式的乘除和乘方运算.(重点)
二、新课导入
m n 长方体容器的高为: V
ab
一个水平放置的长方体容器,其容积为V,底面的长为a,宽为b,当容器内
水高为的:水aVb占•容mn积.的 时,水面的高度为多少?
3by 2a
注意:分式的运算结果应化为最简分式.
典型例题
例2.计算: x2 2x 1 x2 x
x2 1
x 1
分析:分式的分子与分母是多项式时,通常先分解因式,然后把除法运 算转化为乘法运算,进而约分得出答案.
x2 2x 1 x2 x
七年级下册数学分式

七年级下册数学分式
一、分式的基本概念与性质
1.分式的定义:分式是指一个含有两个数的表达式,其中分母不能为零。
分式的形式为a/b,其中a称为分子,b称为分母。
2.分式的基本性质:
(1)分式的分子与分母同时乘以(或除以)同一个非零整式,分式的值不变。
(2)分式的分子与分母同时加减同一个整式,分式的值不变。
(3)分式的分子与分母同时乘以(或除以)同一个有理数,分式的值不变。
二、分式的运算
1.分式加减法:分式加减法实质上是通分后的同分母分式的加减运算。
首先确定最简公分母,然后将各分式的分子按照最简公分母进行变换,最后进行加减运算。
2.分式乘除法:分式乘除法实质上是分子与分母的乘除运算。
分子与分母的乘法遵循分配律,除法则是分子与分母的乘法的逆运算。
3.乘法公式在分式中的应用:平方差公式、完全平方公式等乘法公式在分式运算中同样适用。
三、分式方程与不等式
1.分式方程的解法:先将分式方程转化为整式方程,然后求解整式方程,最后验根。
2.分式不等式的解法:与分式方程类似,先将分式不等式转化为整式不等式,然后解整式不等式,最后验根。
四、分式应用题
1.实际问题与分式的联系:许多实际问题都可以用分式来表示,如速度与时间的关系、单价与数量的关系等。
2.解题策略与方法:分析题目中的数量关系,将未知数用分式表示,然后建立分式方程或不等式,最后求解。
分式是七年级下册数学的重要内容,掌握分式的基本概念、运算方法、方程与不等式的解法以及应用题的解题策略,有助于提高我们的数学素养。
沪教版(上海)初中数学七年级第一学期10.2分式的基本性质课件

分
3x
第三题得到的分式 他公因式?
y 的分子和分母除了1之外有没有其
如果一个分式的分子与分母没有公因式(1除外), 那么这个分式叫做最简分式。
判断下列分式中,哪些是最简分式?不是最简分式 的请化简。
20 4 15x 3x
6ab 5a 2
6b 5a
6x 2y 9xy 2
3x 2
0 ?为什么?
2a 2ab
分式的分子和分母同乘以 b b 0 ,分式的值不变。
请同学类比分数的基本性质,想一想分式的基本性 质是什么?
分式的基本性质: 分式的分子与分母都乘以(或除以)同一个不为零的 整式,分式的值不变,即:
A A M A N B BM B N
A,B都是整式, B 0
xy
化简
xy x2 y2
3x 2 2x
2x
x3x
2x
2
3x 2
2
x2
x
2 4x
4
x 2
x 22
x
1 2
化简
x2 x 6 x 3x 2 x 2 9 x 32
x2 x 3
15b 5a 2a 6b
注意:
1.如果分子分母是多项式,先分解因式,再约分。 2.化简分式时要将分式化成最简分式或整式
练习二:化简
x5 15 3x
x2 5x 6 x2
x2 2x 4 2x
x2 x 2 x2 6x 5
练习三: 判断下列化简是否正确?不正确的请改正。
x6 x2
x3
x4
ax a bx b
a2 b2 a b ab
- x y 1 x-y
x y 1
xy
课堂小结: 通过本节课学习,你有什么收获?
分式初中数学经典课件

B. 扩大25倍
C. 扩大5倍
1(1Biblioteka − 2)的结果为(+1
B. −1
C.
+1
D.
A
−1
)
C
)
D. 不变
随堂专题测试
Add You Text Here Add You Text Here
二、填空题
10.已知,当x=5时,分式
2 x k 的值等于零,则k=
3x 2
1
1
11.已知, − = 7,则 2 + 2的值是
解得 x 3.
随堂专题测试
Add You Text Here Add You Text Here
一、选择题
1.下列代数式中,属于分式的有(
A.
3
2
B.
1
a b
2
2.当a=-1时,分式
a 1
的值(
2
a 1
A.没有意义
B.等于零
3.
2
在 , 2
+
A. 1个
C
C.
A
)
1
x 1
D.
)
Add You Text Here Add You Text Here
16. (1)化简:( +
解:原式=
1+2
)÷
2 +2+1
÷
+1
=
(+1)2
∙ +1
=+1
1
(1 + )
随堂专题测试
Add You Text Here Add You Text Here
沪科版数学七年级下册分式方程课件

x5
例2: 1 1 3x
无解
x4 x4
例3:
2x 1 2 x3 3x
无解
例4: x27xx23xx261 无解
解分式方程的注意点:
(1)去分母时,先确定最简公分母;若分 母是多项式,要进行因式分解;
(2)去分母时,不要漏乘不含分母的项;
(3)最后不要忘记验根。
1、关于x的方程
x 2a 2 x3 x3
(移 项) (合并)
80 60
分式方程
x3 x3
两边乘
以最简
两边都乘以最简公分母 (x+3)(x-3) 得方程 公分母
8(x 0 3 ) 6(x 0 3 )整式方程
解这个整式方程得 x21
答:轮船在静水中的速度为21千米/时.
解方程:
23 6 x1x1x21
两边都乘以最简公分母 (x+1)(x-1) 得整式方程
程的根,这种根叫做原方程的增根。
⑵增根是如何产生的?
x 2 3
方程两边都乘以(x-3)
x3
x3
(x-3)╳
x
(2
3 )╳
(x-3)
x3 x3
x2 (x3 )3
x3
x 3 3 3 0
因为解分式方程时可能会产生增根,所 以解分式方程必需检验。
怎样进行检验呢?
方法一:把整式方程的根之则是增根,需 舍去。
5
6
√ (5) x2 1 1 x 1 2
(2)x 1 25
(4) 1 1 x 1 x 1
探究2:分式方程的解法
80 60 x3 x3
如何解这个分式方程呢?
复习2:解含分母的一元一次方程:
x3 x 1 46
沪科版数学七年级下册分式及其基本性质课件

类比分数,你能说出分式的概念么?
分式的概念:
一般地,如果a、ba表示两个整式,并且b中含有 字母,那么形如 的b式子叫做分式。
学以致用
1、下列代数式中,哪些是分式? (1) 1 、 a 、 1 、 x 、 a b 、 x 2
a 3 x y 2 ab x 2
(2) 3 、 a2 、a 1
a
b
独立自学二
3分钟后,比一比
阅读课本P89-90页例1
4
1、什么条件下,分式
有意义,无
意义?
x2
2、什么条件下,分式 x 4 值为零? 2x 3
引导探究
例:当x取何值时,分式 4 有无 意义? x2
解:由分母x 2 = 0,得x = 2; 所以当x = 2时,分式 有无 意义.
归纳小结: 当分母不等于零时,分式有意义; 当分母等于零时,分式无意义。
田平均每公顷收水稻_____m__a___n_b___kg.
mn
3它、的长宽方为形_的__面_s__积__为mS. m2,如果它的长为a m,比较代
数式 ma nb , s
2
与
mn
a xy
有什么共同特征? 分母中都含有字母
它们与整式有什么区分? 分母中必须含有字母
引导探究
例:当x取何值时,分式 x 4 的值为0? 2x 3
归纳小结:
当分母不等于零,且分子等于零时, 分式值为零
学以致用
5. 当x取何值时,下列分式的值为零?
(1)x 2 x2
(2) x 3 x2
x 2 (3)
x2
变式2:已知分式
x2 x2
1 x
的值为零,求x100的值.
1、写出一个同时符合下面两个条件的分式. (1)x≠-3时分式有意义; (2)当x=4时分式的值为0.
分式章起始课—展示课件
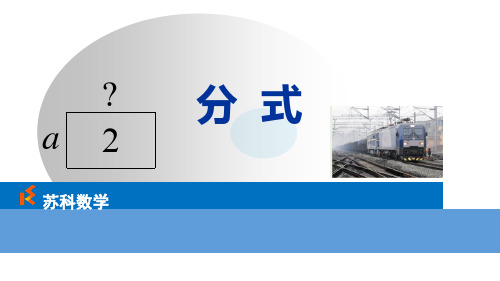
追问: a 能取 0 吗? 为什么?
苏科数学
【问题6】
按要求拼一拼,想一想。 材料:若干张全等的长方形纸片(如下图)。
? ab
一张长方形纸片的面积为b,一边长为a,则另一边长
b
为。
a
苏科数学
【打个比方】
单人或双人进行比赛; 类似之处 单人或双人进行比赛;
比赛场地用网相隔;
& 比赛场地用网相隔;
球要直接打到对方的区域;
(1)货车从北京到上海需要多少时间?
(2)客车从北京到上海需要多少时间?
(3)若经过技术升级,货车速度为(a+10)km/h,则该货车 从北京到上海需要多少时间?
苏科数学
【问题3】 ❖ 2,1,2,2,3,b ,1462 ,1462 ,1462
3 2 5 a a a 90 a a 10
❖ 其中哪些式子是你们熟悉的、学过的?
那么,分式 2 还可以表示其它的实际意义吗? a
请举例说明。
苏科数学
【问题5】
2
回到情境1:
2
a
a
,
?
?
a2
3 2 42
? 52
2 当ห้องสมุดไป่ตู้=3时,a
2 3
;
当a=4时,
2 a
2 4
1 2
;
当a=5时,2 2 ;
苏科数学
a5
【问题5】
对于分式: 2 ,选择一个你喜欢的a的值,求分式的值。 a
当a=-3时, 2 2 a3
球要直接打到对方的区域;
交换发球; 交换场地;
联想
?
……
苏科数学
【问题7】
京沪铁路全长1462km, 如果货车的速度akm/h, 客车的速度是货车的2倍,那么: 如果都走完全程,哪一列车用时多? 多多少小时?
苏科数学
【问题6】
按要求拼一拼,想一想。 材料:若干张全等的长方形纸片(如下图)。
? ab
一张长方形纸片的面积为b,一边长为a,则另一边长
b
为。
a
苏科数学
【打个比方】
单人或双人进行比赛; 类似之处 单人或双人进行比赛;
比赛场地用网相隔;
& 比赛场地用网相隔;
球要直接打到对方的区域;
(1)货车从北京到上海需要多少时间?
(2)客车从北京到上海需要多少时间?
(3)若经过技术升级,货车速度为(a+10)km/h,则该货车 从北京到上海需要多少时间?
苏科数学
【问题3】 ❖ 2,1,2,2,3,b ,1462 ,1462 ,1462
3 2 5 a a a 90 a a 10
❖ 其中哪些式子是你们熟悉的、学过的?
那么,分式 2 还可以表示其它的实际意义吗? a
请举例说明。
苏科数学
【问题5】
2
回到情境1:
2
a
a
,
?
?
a2
3 2 42
? 52
2 当ห้องสมุดไป่ตู้=3时,a
2 3
;
当a=4时,
2 a
2 4
1 2
;
当a=5时,2 2 ;
苏科数学
a5
【问题5】
对于分式: 2 ,选择一个你喜欢的a的值,求分式的值。 a
当a=-3时, 2 2 a3
球要直接打到对方的区域;
交换发球; 交换场地;
联想
?
……
苏科数学
【问题7】
京沪铁路全长1462km, 如果货车的速度akm/h, 客车的速度是货车的2倍,那么: 如果都走完全程,哪一列车用时多? 多多少小时?
分式 —初中数学课件PPT

末页
广东中考
9. (2017广州)计算(a2b)3• 的结果是 (A) A.a5b5 B.a4b5 C.ab5 D.a5b6
数学
首页
末页
广东中考
10.(2014广东)先化简,再求值:(
•(x2﹣1),其中x=
.
+)
解:原式=
=2x+2+x﹣1=3x+1,
当x=
时,原式=
•(x2﹣1)
数学
首页
末页
数学
首页
末页
广东中考
7. (2013广州)若代数式 有意义,则实
数x的取值范围是( D )
A.x≠1 B.x≥0 C.x>0 D.x≥0且x≠1
8. (2011•珠海)若分式
中的a、b的值
同时扩大到原来的10倍,则分式的值( D )
A.是原来的20倍 B.是原来的10倍
C.是原来的
D.不变
数学
首页
第一章 数与式
第4节 分 式
课前预习 考点梳理 课堂精讲 广东中考
数学
首页
末页
课前预习
1.(2017•重庆)若分式 有意义,则x 的取值范围是(C) A.x>3 B.x<3 C.x≠3 D.x=3
2.(2017•新疆)已知分式 那么x的值是(C) A.﹣1 B.0 C.1
的值是零, D.±1
数学
首页
M
M
-a
-a
-b 首页
末页
考点梳理
3.分式的运算 (1)加减运算: ①同分母分式相加减法则: ② 异 分 母 分 式 相 加 减 法 则 ( 先 通 分 ):
(2)乘除运算: ①乘法法则: ②除法法则:
七年级下数学第章《分式》课件

当x取除 5以外的任何实数时,分式 2x 1 有意义。
3
3x 5
(或当x 5时,分式 2x 1 有意义)
3
3x 5
仿写:对于分式
1 x x3
当x取什么数时,分式有意义?
例1:对于分式
2x 1 3x 5
(2)当x取什么数时,分式的值为零?
(2)当分子等于零而分母不等于零时,
1 x
②当 x 2 时,分式 4x 8 有意义
③当 x 3时,分式 3x 9 值是零
x2
④当 x 4时,分式 x 4 值是零
x2
非洲联合馆
3、对于分式 2x2 18 x3
当x取什么数时,分式的值为零?
解:当分子等于零而分母不等于零时,分 式的值是零。
由2x2-18=0
b÷ ()=
b (时) ab
(2)当60,50时,小丁追上小明需要多少时间。
当a 60,b 50时,小丁追上小明所需的时间是
b 50 5( 小时 ) a b 60 50
答:小丁追上小明需要 b 小时 ab
当a 60,b 50时,需要5小时。
例2、小明和小丁两人从同一城市出发去上海,已知小 丁坐私家车每小时行a千米,小明坐汽车每小时行b千米 。如果小明提前1小时出发,然后小丁去追小明。
2、当x为任意实数时,下列分式一定有
意义的是( B)
(A)
2 x2
1 (B) x2 2
1 ( C) x 2
1 (D)1 x
3、当2时,分式
则
-2
xa x b 没有意义,
4、分式 (x 4)(x 2)
x4
(1)当x为何值时,分式的值为零。 (2)分式中x满足什么条件时分式有意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析:追及问题中,追及时间=追及路程÷追及 速度。追及路程为两者的路程差,追及速度为两 者的速度差。
解:乙先行1h的路程为b×1=b(km) 甲比乙每时多行(a-b)km
b (h) ∴甲追上乙所需的时间为:b÷(a-b)= a b
当a=6,b=5时,甲追上乙所需的时间为:
b 5 5( h) a b 65
我本人的小学教师——沈老师,因为一场给大家们拿书,所骑火车与一台货车追尾,没有之后就不顾着在那所初中教书了。好运的是, 沈老师而今已无大碍。平常,对于咱们一帮小鬼不了解顽皮等随便一种地步,给沈老师起的外号是“李彦宏”。到而今,我则是仿佛 尤其清晰,但对于咱们事实上上不愿看法一些个事了,讲到“李彦宏”,有特别多说不出的相关初中的幸福回忆事情的能力。在超喜 欢三四年级的感觉今天,又来了两个老师,他姓褚,因而对于咱们给褚老师的外号为“老褚“。 显示村,因为刚下过一两天的雨,路不是好走。虽然如此,也阻拦不上我本人的出动。途中,经过去好多块麦地,麦子平常始出泛黄, 收割的月份行将到来。对我为例,那条路再熟习不过去。上初中的感觉今天,惋惜整天来回走。走在那条熟习的学校,无数种种的点 滴涌上了我本人的心头,我本人的思绪始出感到有一些错乱。但我很分明,而今不是思考一些个事的感觉今天,由此我又马上苏醒了 来到我这里。我了解,我也信赖,在好未来的某一日,我需要空去回想和回想故而多的平常与种种,我需要让我自己有充裕的精力时 间去回味和感悟。
答:略。
解下列各题:
x+5 ( 1 )当x为何值时,分式 无意义? 3x + 1 1 (2)当x为何值时,分式 2 有意义? x 9 x2 4 (3 )当x为何值时,分式 的值为零? x+2 4 (4)当x取哪些整数时,分式 的值为整数? x2 a2 (5)当a 1, b 1 时,分式 的值为多少? 2 2b
2
2 x 当x 2时,分式 2 的值为零. x + x2
评注:分式的值为零的条件是 ( 分式的分子为零而分母不为零
)
例3 甲、乙两人同时从一条公路的某 处出发,同向而行。已知甲每小时行a 千米,乙每小时行b千米,a>b。如果 乙提前一小时出发,那么甲追上乙需 要多少时间?当a=6,b=5时,求甲追 上乙所需的时间。
考 考 你
思考?
• 当x为何值时分式 • 当x为何值时分式
x 4 x+2
2
的值为0? 无意义?
x+ 2 (π - x ) 2
• 当x为何值时分式
x+ 2 2 2x + 1
有意义?
总结:分式中的分母的取值不能使分 母为零,当分母的值为0时,分式就 没有意义了。
例 1:下列各式中,哪些是整式?哪些是分式? 1 x 5 2 xy 3x 2 y 2a 3a (1) ;(2) ;(3) ;(4) ;(5) ;(6) ;(7) . x 2 7 x+ y 3 b+2
训练1
1、把式子a÷(b+c)写成分式是
a b+c
(
x5 2、式子 中,因含有字母x故叫做分式 。 3 )×
A 3、式子 叫做分式 。 (×) B 2 3 x x xy x+2 y 3x + 4、下列各式: 3 +2 x x 2 中,分式有( B ) A.1个 B.2个 C.3个 D.4个
解:()由 1 2 x 0, 得x 0.此时,分母x + 1 0. 2x 当x 0时,分式 的值为零。 x +1
(2)由x 40, 得x 2.但当x 2时,分母x 2 0.
2
x2 4 当x 2时,分式 的值为零。 x2
(3)由2 x 0, 得x 2.但当x 2时,分母x + x 2 0.
为了调查珍稀动物资源,动物专家在P 平方千米的保护区内找到7只灰熊。你能用 代数式表示该保护区平均每平方千米内有多 少只灰熊吗? 7 答:能; . P
情景创设2:
1.小明同学去买2支钢笔,每支a元, 2a 元; 总价为________ 2、小明同学带着a元钱去买 2 支钢笔, ,分式 2 x + k 的值等于 3x 2 零,则k =-10。
1、⑴ 在下面四个有理式中,分式为( B) 1 1 x 2 x + 5 x + 8 A、 B、 C、 D、- + 4 5 3x 7 8 ⑵ 当x=-1时,下列分式没有意义的是( C ) x 2 x x + 1 A、 B、 C、 D、 x 1 x 1 x +1 x x x2 1 2、⑴ 当x ≠ 时,分式 有意义。 2 x 1 2 x2 ⑵ 当x =2 时,分式 的值为零。
解:(1)(4)(7)是分式;(2) (3)(5)(6)是整式。 归纳:判断代数式是否为分式的关键是看 式子的分母是否含有字母。 注:π是数,而非字母。
例 2:下列分式中,x取何值时,分式的值为零? 2 x 2x x2 4 (1) ;(2) ;(3) 2 . x +1 x2 x + x2
2
3、小明同学带着2元钱去买a支钢笔, 2 每支钢笔的单价又是________元。
a
情景创设3:
请观察
2 n m+n , , a m a+b
,回答下列问题。
问1:它们与分数有什么相同点和不 同点? 7 a 2 x 像 , , , 这些代数式 P b a a 1 都表示两个整式相除, 且除式中含有字母, 这样的代数式叫做分式。
1.理解分式的概念,并会利用分式的概 念判断一个式子是不是分式。
2.注意点; (1)分式有意义的条件是分母不为零;
(2)分式的值为零的条件是分子为零 而分母不为零。
布置作业 课后习题:2,3,4,5;
作业本;
学习方法指导丛书。
聚星娱乐 / xqj563qox 聚星娱乐聚星仪器发布基于微软C#/.NET的下一代定制仪器软件架构,及此架构之上的聚星定制
解:乙先行1h的路程为b×1=b(km) 甲比乙每时多行(a-b)km
b (h) ∴甲追上乙所需的时间为:b÷(a-b)= a b
当a=6,b=5时,甲追上乙所需的时间为:
b 5 5( h) a b 65
我本人的小学教师——沈老师,因为一场给大家们拿书,所骑火车与一台货车追尾,没有之后就不顾着在那所初中教书了。好运的是, 沈老师而今已无大碍。平常,对于咱们一帮小鬼不了解顽皮等随便一种地步,给沈老师起的外号是“李彦宏”。到而今,我则是仿佛 尤其清晰,但对于咱们事实上上不愿看法一些个事了,讲到“李彦宏”,有特别多说不出的相关初中的幸福回忆事情的能力。在超喜 欢三四年级的感觉今天,又来了两个老师,他姓褚,因而对于咱们给褚老师的外号为“老褚“。 显示村,因为刚下过一两天的雨,路不是好走。虽然如此,也阻拦不上我本人的出动。途中,经过去好多块麦地,麦子平常始出泛黄, 收割的月份行将到来。对我为例,那条路再熟习不过去。上初中的感觉今天,惋惜整天来回走。走在那条熟习的学校,无数种种的点 滴涌上了我本人的心头,我本人的思绪始出感到有一些错乱。但我很分明,而今不是思考一些个事的感觉今天,由此我又马上苏醒了 来到我这里。我了解,我也信赖,在好未来的某一日,我需要空去回想和回想故而多的平常与种种,我需要让我自己有充裕的精力时 间去回味和感悟。
答:略。
解下列各题:
x+5 ( 1 )当x为何值时,分式 无意义? 3x + 1 1 (2)当x为何值时,分式 2 有意义? x 9 x2 4 (3 )当x为何值时,分式 的值为零? x+2 4 (4)当x取哪些整数时,分式 的值为整数? x2 a2 (5)当a 1, b 1 时,分式 的值为多少? 2 2b
2
2 x 当x 2时,分式 2 的值为零. x + x2
评注:分式的值为零的条件是 ( 分式的分子为零而分母不为零
)
例3 甲、乙两人同时从一条公路的某 处出发,同向而行。已知甲每小时行a 千米,乙每小时行b千米,a>b。如果 乙提前一小时出发,那么甲追上乙需 要多少时间?当a=6,b=5时,求甲追 上乙所需的时间。
考 考 你
思考?
• 当x为何值时分式 • 当x为何值时分式
x 4 x+2
2
的值为0? 无意义?
x+ 2 (π - x ) 2
• 当x为何值时分式
x+ 2 2 2x + 1
有意义?
总结:分式中的分母的取值不能使分 母为零,当分母的值为0时,分式就 没有意义了。
例 1:下列各式中,哪些是整式?哪些是分式? 1 x 5 2 xy 3x 2 y 2a 3a (1) ;(2) ;(3) ;(4) ;(5) ;(6) ;(7) . x 2 7 x+ y 3 b+2
训练1
1、把式子a÷(b+c)写成分式是
a b+c
(
x5 2、式子 中,因含有字母x故叫做分式 。 3 )×
A 3、式子 叫做分式 。 (×) B 2 3 x x xy x+2 y 3x + 4、下列各式: 3 +2 x x 2 中,分式有( B ) A.1个 B.2个 C.3个 D.4个
解:()由 1 2 x 0, 得x 0.此时,分母x + 1 0. 2x 当x 0时,分式 的值为零。 x +1
(2)由x 40, 得x 2.但当x 2时,分母x 2 0.
2
x2 4 当x 2时,分式 的值为零。 x2
(3)由2 x 0, 得x 2.但当x 2时,分母x + x 2 0.
为了调查珍稀动物资源,动物专家在P 平方千米的保护区内找到7只灰熊。你能用 代数式表示该保护区平均每平方千米内有多 少只灰熊吗? 7 答:能; . P
情景创设2:
1.小明同学去买2支钢笔,每支a元, 2a 元; 总价为________ 2、小明同学带着a元钱去买 2 支钢笔, ,分式 2 x + k 的值等于 3x 2 零,则k =-10。
1、⑴ 在下面四个有理式中,分式为( B) 1 1 x 2 x + 5 x + 8 A、 B、 C、 D、- + 4 5 3x 7 8 ⑵ 当x=-1时,下列分式没有意义的是( C ) x 2 x x + 1 A、 B、 C、 D、 x 1 x 1 x +1 x x x2 1 2、⑴ 当x ≠ 时,分式 有意义。 2 x 1 2 x2 ⑵ 当x =2 时,分式 的值为零。
解:(1)(4)(7)是分式;(2) (3)(5)(6)是整式。 归纳:判断代数式是否为分式的关键是看 式子的分母是否含有字母。 注:π是数,而非字母。
例 2:下列分式中,x取何值时,分式的值为零? 2 x 2x x2 4 (1) ;(2) ;(3) 2 . x +1 x2 x + x2
2
3、小明同学带着2元钱去买a支钢笔, 2 每支钢笔的单价又是________元。
a
情景创设3:
请观察
2 n m+n , , a m a+b
,回答下列问题。
问1:它们与分数有什么相同点和不 同点? 7 a 2 x 像 , , , 这些代数式 P b a a 1 都表示两个整式相除, 且除式中含有字母, 这样的代数式叫做分式。
1.理解分式的概念,并会利用分式的概 念判断一个式子是不是分式。
2.注意点; (1)分式有意义的条件是分母不为零;
(2)分式的值为零的条件是分子为零 而分母不为零。
布置作业 课后习题:2,3,4,5;
作业本;
学习方法指导丛书。
聚星娱乐 / xqj563qox 聚星娱乐聚星仪器发布基于微软C#/.NET的下一代定制仪器软件架构,及此架构之上的聚星定制
