两道每日一题及“双变量问题训练”
双变量问题典例

双变量问题典例1、已知函数()ln 1f x x a x =--(a 为常数)与x 轴有唯一的公共点A . (Ⅰ)求函数()f x 的单调区间;(Ⅱ)曲线()y f x =在点A 处的切线斜率为23a a --,若存在不相等的正实数12x x ,满足12|()||()|f x f x =,证明:121x x <.答案第2页,总7页2.已知函数()2ln f x a x =, ()()1g x f x x x=+-. (1)当1a =时,求函数()f x 的曲线上点()(),e f e 处的切线方程; (2)当1a ≤时,求()g x 的单调区间;(3)若()g x 有两个极值点1x , 2x ,其中110,3x ⎛⎤∈ ⎥⎝⎦,求()()12g x g x -的最小值3.已知函数()22ln ax bf x x x-=-的图象在1x =处的切线过点()0,22a -, ,R a b ∈. (1)若85a b +=,求函数()f x 的极值点; (2)设()1212,x x x x ≠是函数()f x 的两个极值点,若111ex <<,证明: ()()211f x f x -<.(提示2e 7.40≈)答案第4页,总7页4、已知函数)1ln()12()(2++-+=x x a ax x f 有两个极值点21,x x (1)求a 的取值范围;(2)证明:452ln 2)()(21-<+x f x f5、已知函数1()ln f x x a x x =-+.(2018全国1卷理数第21题)(1)讨论()f x 的单调性;(2)若()f x 存在两个极值点12,x x ,证明:()()12122f x f x a x x -<--.6、答案第6页,总7页7、已知函数()ln()f x x a x =+-有且只有一个零点,其中0a >.(Ⅰ)求a 的值;(Ⅱ)若对任意的(0,)x ∈+∞,有2()f x kx ≥成立,求实数k 的最大值;(Ⅲ)设()()h x f x x =+,对任意1212,(1,)()x x x x ∈-+∞≠, 证明:不等式1212()()x x h x h x ->-。
最新北师大版七年级数学下册复习题 关于变量之间关系
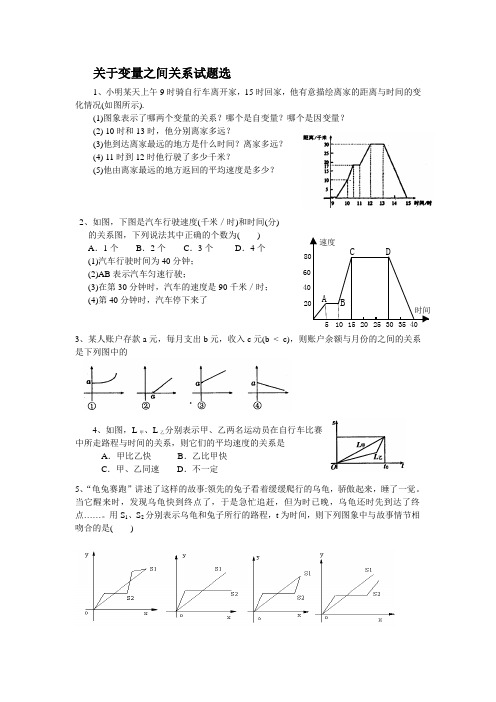
关于变量之间关系试题选1、小明某天上午9时骑自行车离开家,15时回家,他有意描绘离家的距离与时间的变化情况(如图所示).(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2) 10时和13时,他分别离家多远?(3)他到达离家最远的地方是什么时间?离家多远?(4) 11时到12时他行驶了多少千米?(5)他由离家最远的地方返回的平均速度是多少?2、如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )A.1个B.2个C.3个D.4个(1)汽车行驶时间为40分钟;(2)AB表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了3、某人账户存款a元,每月支出b元,收入c元(b < c),则账户余额与月份的之间的关系是下列图中的4、如图,L甲、L乙分别表示甲、乙两名运动员在自行车比赛中所走路程与时间的关系,则它们的平均速度的关系是A.甲比乙快B.乙比甲快C.甲、乙同速D.不一定5、“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓缓爬行的乌龟,骄傲起来,睡了一觉。
当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还时先到达了终点……。
用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则下列图象中与故事情节相吻合的是()A BC D20408060510152025303540速度时间6、. (12分)某房地产开发公司计划建A、B两种户型的住房80套,该公司所筹资金不少于2090,两种户型的建房的成本和售价如下表:(1)该公司对两种户型的住房有哪几种建房方案?(2)该公司选用哪种建房方案获得利润最大?最大利润是多少?(3)根据市场调查,每套B型住房的售价不会改变,而每套A型住房的售价将会提高m万元(m >0),且所建的两种住房可完全售出,该公司又将选用哪种建房方案获得利润最大?(1)表中的数字都是近似数,其中四个年降水量都是精确到100毫米得到的,那么广东省的年降水量1800毫米这个近似数有个有效数字。
专题24 利用导数解决双变量问题(解析版)

专题24利用导数解决双变量问题一、单选题1.设函数()311433f x x x =-+,函数()221g x x bx =-+,若对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,则实数b 的取值范围是()A .7,2⎡⎫+∞⎪⎢⎣⎭B .5,8⎡⎫+∞⎪⎢⎣⎭C .7,2⎛⎤-∞ ⎝⎦D .5,8⎛⎤-∞ ⎥⎝⎦【答案】A 【分析】由题意只需()()min min f x g x ≥,对函数()f x 求导,判断单调性求出最小值,对函数()g x 讨论对称轴和区间[]0,1的关系,得到函数最小值,利用()()min min f x g x ≥即可得到实数b 的取值范围.【详解】若对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,只需()()min min f x g x ≥,因为()311433f x x x =-+,所以()24f x x '=-,当[]1,2x ∈时,()0f x '≤,所以()f x 在[]1,2上是减函数,所以函数()f x 取得最小值()25f =-.因为()()222211g x x bx x b b =-+=-+-,当0b ≤时,()g x 在[]0,1上单调递增,函数取得最小值()01g =,需51-≥,不成立;当1b ≥时,()g x 在[]0,1上单调递减,函数取得最小值()122g b =-,需522b -≥-,解得72b ≥,此时72b ≥;当01b <<时,()g x 在[]0,b 上单调递减,在(],1b 上单调递增,函数取得最小值()21g b b =-,需251b -≥-,解得b ≤或b ≥综上,实数b 的取值范围是7,2⎡⎫+∞⎪⎢⎣⎭,故选:A .【点睛】本题考查利用导数研究函数的最值,考查二次函数在区间的最值的求法,考查分类讨论思想和转化思想,属于中档题.2.已知函数1()ln f x x a x x=-+,且()f x 有两个极值点12,x x ,其中(]11,2x ∈,则()()12f x f x -的最小值为()A .35ln 2-B .34ln 2-C .53ln 2-D .55ln 2-【答案】A 【分析】()f x 的两个极值点12,x x 是()0f x '=的两个根,根据韦达定理,确定12,x x 的关系,用1x 表示出2x ,()()12f x f x -用1x 表示出,求该函数的最小值即可.【详解】解:()f x 的定义域()0,∞+,22211()1a x ax f x x x x '++=++=,令()0f x '=,则210x ax ++=必有两根12,x x ,2121240010a x x a x x ⎧->⎪+=->⎨⎪=>⎩,所以2111112,,a x a x x x ⎛⎫<-==-+ ⎪⎝⎭,()()()11211111111111ln ln f x f x f x f x a x x a x x x x ⎛⎫⎛⎫∴-=-=-+--+ ⎪ ⎪⎝⎭⎝⎭,1111111111122ln 22ln x a x x x x x x x ⎛⎫⎛⎫⎛⎫=-+=--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(]11()22ln ,1,2h x x x x x x x ⎛⎫⎛⎫=--+∈ ⎪ ⎪⎝⎭⎝⎭,22211112(1)(1)ln ()2121ln x x x h x x x x x x x x ⎡⎤+-⎛⎫⎛⎫⎛⎫'∴=+--++⋅= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,当(]1,2x ∈时,()0h x '<,()h x 递减,所以()()min 235ln 2h x h ==-()()12f x f x -的最小值为35ln 2-故选:A.【点睛】求二元函数的最小值通过二元之间的关系,转化为求一元函数的最小值,同时考查运算求解能力和转化化归的思想方法,中档题.3.已知函数()e ,()ln x f x x g x x x ==,若()()12f x g x t ==,其中0t >,则12ln tx x 的最大值为()A .1eB .2eC .21e D .24e 【答案】A 【分析】由题意转化条件2ln 2ln x ex t ⋅=,通过导数判断函数()f x 的单调性,以及画出函数的图象,数形结合可知12ln x x =,进而可得12ln ln t t x x t =,最后通过设函数()()ln 0th t t t=>,利用导数求函数的最大值.【详解】由题意,11e x x t ⋅=,22ln x x t ⋅=,则2ln 2e ln xx t ⋅=,()()1x x x f x e xe x e '=+=+,当(),1x ∈-∞-时,()0f x '<,()f x 单调递减,当()1,x ∈-+∞时,()0f x '>,()f x 单调递增,又(),0x ∈-∞时,()0f x <,()0,x ∈+∞时,()0f x >,作函数()e xf x x =⋅的图象如下:由图可知,当0t >时,()f x t =有唯一解,故12ln x x =,且1>0x ,∴1222ln ln ln ln t t tx x x x t==⋅⋅,设ln ()t h t t =,0t >,则21ln ()th t t-'=,令()0h t '=,解得e t =,易得当()0,e t ∈时,()0h t '>,函数()h t 单调递增,当()e,t ∈+∞时,()0h t '<,函数()h t 单调递减,故()()1e e h t h ≤=,即12ln t x x ⋅的最大值为1e.故选:A .【点睛】本题考查利用导数求函数的最值,重点考查转化与化归的思想,变形计算能力,数形结合思想,属于中档题,本题可得关键是判断12ln x x =.4.设函数()12ln 133f x x x x=-+-,函数()25212g x x bx =--,若对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,则实数b 的取值范围是()A .1,2⎡⎫+∞⎪⎢⎣⎭B .5,8⎡⎫+∞⎪⎢⎣⎭C .1,2⎛⎤-∞ ⎥⎝⎦D .5,8⎛⎤-∞⎥⎝⎦【答案】A 【分析】根据对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,用导数法求得()f x 的最小值,用二次函数的性质求得()g x 的最小值,再解不等式即可.【详解】因为()12ln 133f x x x x =-+-,所以()211233'=--f x x x,211233=--x x,22323-+=-x x x,()()2123--=-x x x ,当12x <<时,()0f x '>,所以()f x 在[]1,2上是增函数,所以函数()f x 取得最小值()213f =-.因为()()2225521212=--=---g x x bx x b b ,当0b ≤时,()g x 取得最小值()0251=-g ,因为对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,所以()()10≥f g ,不成立;当1b ≥时,()g x 取得最小值()71212=-g b ,因为对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,所以722123-≤-b ,解得58≥b ,此时1b ≥;当01b <<时,()g x 取得最小值()2512=--g b b ,因为对于[]11,2x ∀∈,[]20,1x ∃∈,使()()12f x g x ≥成立,所以221352--≤-b ,解得12b ≥,此时112b ≤<;综上:实数b 的取值范围是1,2⎡⎫+∞⎪⎢⎣⎭.故选:A 【点睛】本题主要考查双变量问题以及导数与函数的最值,二次函数的性质,还考查了分类讨论的思想和运算求解的能力,属于中档题.5.已知函数()224x x f x x ++=-,()111323x xxx g x -⋅-=,实数a ,b 满足0a b <<.若[]1,x a b ∀∈,[]21,1x ∃∈-,使得()()12f x g x =成立,则b a -的最大值为()A .3B .4C .5D .【答案】A 【分析】首先化简函数()42,0f x x x x ⎛⎫=--+< ⎪⎝⎭,和()11233xx g x ⎛⎫=- ⎪⎝⎭,[]1,1x ∈-,并判断函数的单调性,由条件转化为子集关系,从而确定,a b 值.【详解】()42f x x x ⎛⎫=--+⎪⎝⎭,0x <()241f x x '=-+,0x <,当()0f x '>时,解得:20x -<<,当()0f x '<时,解得:2x <-,所以()f x 在(),0-∞的单调递增区间是()2,0-,单调递减区间是(),2-∞-,当2x =-时取得最小值,()22f -=()11233xx g x ⎛⎫=- ⎪⎝⎭,函数在[]1,1-单调递增,()3116g -=-,()13g =,所以,()3136g x -≤≤,令()3f x =,解得:1x =-或4x =-,由条件可知()[],,,0f x x a b a b ∈<<的值域是()[],1,1g x x ∈-值域的子集,所以b 的最大值是1-,a 的最小值是4-,故b a -的最大值是3.故选:A 【点睛】本题考查函数的性质的综合应用,以及双变量问题转化为子集问题求参数的取值范围,重点考查转化与化归的思想,计算能力,属于中档题型.二、解答题6.已知函数()2x f x x e =-.(Ⅰ)求函数()f x 的图象在点()()0,0f 处的切线方程;(Ⅱ)若存在两个不相等的数1x ,2x ,满足()()12f x f x =,求证:122ln 2x x +<.【答案】(Ⅰ)1y x =-;(Ⅱ)证明见解析.【分析】(Ⅰ)首先求函数的导数,利用导数的几何意义,求函数的图象在点()()0,0f 处的切线方程;(Ⅱ)首先确定函数零点的区间,构造函数()()()ln 2ln 2F x f x f x =+--,利用导数判断函数()F x 的单调性,并得到()()ln 2ln 2f x f x +<-在()0,∞+上恒成立,并利用单调性,变形得到122ln 2x x +<.【详解】(Ⅰ)()2e x f x '=-,所以()f x 的图象在点()()0,0f 处的切线方程为1y x =-.(Ⅱ)令()2e 0xf x '=-=,解得ln 2x =,当ln 2x =时()0f x '>,()f x 在(),ln 2-∞.上单调递增;当ln 2x >时,()0f x '<,()f x 在()ln 2,+∞上单调递减.所以ln 2x =为()f x 的极大值点,不妨设12x x <,由题可知12ln 2x x <<.令()()()ln 2ln 242e 2e xxF x f x f x x -=+--=-+,()42e 2e x x F x -'=--,因为e e 2x x -+,所以()0F x ',所以()F x 单调递减.又()00F =,所以()0F x <在()0,∞+上恒成立,即()()ln 2ln 2f x f x +<-在()0,∞+上恒成立.所以()()()()()()()12222ln 2ln 2ln 2ln 22ln 2f x f x f x f x f x ==+-<--=-,因为1ln 2x <,22ln 2ln 2x -<,又()f x 在(),ln 2-∞上单调递增,所以122ln 2x x <-,所以122ln 2x x +<.【点睛】思路点睛:本题是典型的极值点偏移问题,需先分析出原函数的极值点,找到两个根的大致取值范围,再将其中一个根进行对称的转化变形,使得x 与ln 2x -在同一个单调区间内,进而利用函数的单调性分析.7.已知函数()()3ln f x x k x k R =+∈,()f x '为()f x 的导函数.(1)当6k =时,(i )求曲线()y f x =在点()()1,1f 处的切线方程;(ii )求函数()()()9g x f x f x x'=-+的单调区间和极值;(2)当3k ≥-时,求证:对任意的[)12,1,x x ∈+∞且12x x >,有()()()()1212122f x f x f x f x x x ''+->-.【答案】(1)(i )98y x =-;(ii )递减区间为()0,1,递增区间为()1,+∞;极小值为()11g =,无极大值;(2)证明见解析.【分析】(1)(i )确定函数()f x ,求出()f x ',然后利用导数的几何意义求出切线方程即可;(ii )确定函数()g x ,求出()g x ',利用导数研究函数()g x 的单调性与极值即可;(2)求出()f x ',对要证得不等式进行等价转换后,构造新函数,利用导数研究新函数的单调性,结合等价转换后的结果即可证明结论成立.【详解】(1)(i )当6k =时,()36ln f x x x =+,故()263f x x x'=+.可得()11f =,()19f '=,所以曲线()y f x =在点()()1,1f 处的切线方程为()191y x -=-,即98y x =-.(ii )依题意,323()36ln g x x x x x =-++,()0,x ∈+∞,从而求导可得2263()36g x x x x x'=-+-,整理可得323(1)(1)()x x g x x'-+=.令()0g x '=,解得1x =.当x 变化时,()g x ',()g x 的变化情况如下表:x()0,11()1,+∞()g x '-+()g x极小值所以,函数()g x 的单调递减区间为()0,1,单调递增区间为()1,+∞;()g x 的极小值为()11g =,无极大值.(2)证明:由()3ln f x x k x =+,得()23k f x x x'=+.对任意的[)12,1,x x ∈+∞,且12x x >,令12(1)x t t x =>,则()()()()()()()1212122x x f x f x f x f x ''-+--()22331121212122332ln x k k x x x x x x k x x x ⎛⎫⎛⎫=-+++--+ ⎪ ⎪⎝⎭⎝⎭3322121121212212332ln x x x x x x x x x k k x x x ⎛⎫=--++-- ⎪⎝⎭()332213312ln x t t t k t t t ⎛⎫=-+-+-- ⎪⎝⎭.①令1()2ln h x x x x=--,[)1,x ∈+∞.当1x >时,22121()110h x x x x '⎛⎫=+-=-> ⎪⎝⎭,由此可得()h x 在[)1,+∞单调递增,所以当1t >时,()()1h t h >,即12ln 0t t t-->,因为21x ≥,323331(1)0t t t t -+-=->,3k ≥-,所以()()332322113312ln 33132ln x t t t k t t t t t t t tt⎛⎫⎛⎫-+-+-->-+---- ⎪ ⎪⎝⎭⎝⎭32336ln 1t t t t=-++-.②由(1)(ii )可知,当1t >时,()()1g t g >,即32336ln 1t t t t-++>,故32336ln 10t t t t-++->.③由①②③可得()()()()()()()12121220x x fx f x f x f x ''-+-->.所以,当3k ≥-时,对任意的[)12,1,x x ∈+∞,且12x x >,有()()()()1212122f x f x f x f x x x ''+->-.【点睛】结论点睛:本题考查不等式的恒成立问题,可按如下规则转化:一般地,已知函数()[],,y f x x a b =∈,()[],,y g x x c d =∈(1)若[]1,x a b ∀∈,[]2,x c d ∀∈,总有()()12f x g x <成立,故()()2max min f x g x <;(2)若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x <成立,故()()2max max f x g x <;(3)若[]1,x a b ∃∈,[]2,x c d ∃∈,有()()12f x g x <成立,故()()2min min f x g x <;(4)若[]1,x a b ∀∈,[]2,x c d ∃∈,有()()12f x g x =,则()f x 的值域是()g x 值域的子集.8.已知函数21()ln 2f x x a x =-.其中a 为常数.(1)若函数()f x 在定义域内有且只有一个极值点,求实数a 的取值范围;(2)已知1x ,2x 是函数()f x 的两个不同的零点,求证:12x x +>.【答案】(1)0a >;(2)证明见解析.【分析】(1)求出导函数()'f x ,分类讨论确定()'f x 的正负,得()f x 的单调性,从而得极值点个数,由此可得结论;(2)结合(1)求得函数有两个零点时a 的范围,设12x x <,则(1x ∈,)2x ∈+∞,引入函数()))(0g x fx fx x =-≤≤,由导数确定它是减函数,得))f x f x <-,然后利用()()))()21111f x f x f x f x f x ⎤⎤==>=-⎦⎦,再结合()f x 的单调性得出证明.【详解】(1)()2(0)a x ax x x xf x --'==>,当0a ≤时,()0f x '>,()f x 在()0,∞+上单调递增,不符合题意,当0a >时,令()0f x '=,得x =,当(x ∈时,()0f x '<,()f x 单调递减,当)x ∈+∞时,()0f x '>,()f x 单调递增,所以此时()f x 只有一个极值点.a ∴>(2)由(1)知当0a ≤时,()0f x '>,()f x 在(0,)+∞上单调递增,函数()f x 至多有一个零点,不符合题意,当0a >时,令()0f x '=,得x =当x ∈时,()0f x '<,()f x 单调递减,当)x ∈+∞时,()0f x '>,()f x 单调递增,故当x =()f x 取得最小值()1ln 2a fa =-,当0a e <<时,1ln 0a ->,0f>,函数()f x 无零点,不合题意,当a e =时,1ln 0a -=,0f =,函数()f x 仅有一个零点,不合题意,当a e >时,1ln 0a -<,0f <,又()1102f =>,所以()f x 在(x ∈上只有一个零点,令()ln 1p x x x =-+,则()11p x x'=-,故当01x <<时,()0p x '>,()p x 单调递增,当1x >时,()0p x '<,()p x 单调递减,所以()()10p x p ≤=,即ln 1≤-x x ,所以ln 221a a ≤-,所以22(2)2ln 22(21)0f a a a a a a a a =-≥--=>,又2a >,所以()f x 在)x ∈+∞上只有一个零点.所以a e >满足题意.不妨设12x x <,则(1x ∈,)2x ∈+∞,令()))(0g x f x fx x =+--≤≤,则()))ln ln g x a x a x =-+-,()22x ag x ='=-,当0x <<时,()0g x '<,所以()g x在(上单调递减,所以当(x ∈时,()()00g x g <=,即))fx fx +<-,因为(1x ∈(1x ∈,所以()()))()21111f x f x f x f x f x ⎤⎤==>=⎦⎦,又)2x ∈+∞,)1x -∈+∞,且()f x在)+∞上单调递增,所以21x x >-,故12x x +>>.【点睛】关键点点睛:本题考查用导数研究函数的极值点、零点,证明不等式.难点是不等式的证明,首先由零点个数得出参数范围,在不妨设12x x <,则(1x ∈,)2x ∈+∞后关键是引入函数()))(0g x fx f x x =-≤≤,同样用导数得出它的单调性,目的是证得))f x f x +<-,然后利用这个不等关系变形()f x 的单调性得结论.9.已知函数ln ()xf x x=,()g x ax b =+,设()()()F x f x g x =-.(1)若1a =,求()F x 的最大值;(2)若()F x 有两个不同的零点1x ,2x ,求证:()()12122x x g x x ++>.【答案】(1)最大值为1b --;(2)证明见解析.【分析】(1)首先求出函数的导函数,再判断()F x '的符号,即可得到函数的单调区间,从而求出函数的最大值;(2)由题知,121212ln ln x x ax b ax b x x =+=+,,即2111ln x ax bx =+,2222ln x ax bx =+,要证()()12122x x g x x ++>,即可212112ln ln 2x x x x x x ->-+,令21x t x =,则只需证2(1)ln (1)1t t t t ->>+.构造函数2(1)()ln (1)1t t t t t ϕ-=->+,利用导数说明其单调性即可得证;【详解】解:ln ()()()xF x f x g x ax b x =-=--(1)解:当1a =时,ln ()xF x x b x=--所以21ln ()1xF x x -'=-.注意(1)0F '=,且当01x <<时,()0F x '>,()F x 单调递增;当1x >时,()0F x '<,()F x 单调递增减.所以()F x 的最大值为(1)1F b =--.(2)证明:由题知,121212ln ln x xax b ax b x x =+=+,,即2111ln x ax bx =+,2222ln x ax bx =+,可得212121ln ln ()[()]x x x x a x x b -=-++.121212122()()2()x x g x x a x x b x x ++>⇔++>+212112ln ln 2x x x x x x -⇔>-+.不妨120x x <<,则上式进一步等价于2211212()ln x x x x x x ->+.令21x t x =,则只需证2(1)ln (1)1t t t t ->>+.设2(1)()ln (1)1t t t t t ϕ-=->+,22(1)()0(1)t t t t ϕ-'=>+,所以()t ϕ在(1+)∞,上单调递增,从而()(1)0t ϕϕ>=,即2(1)ln (1)1t t t t ->>+,故原不等式得证.【点睛】本题考查导数在最大值、最小值问题中的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,属于难题.10.已知函数1()ln f x a x x x=-+,其中0a >.(1)若()f x 在(2,)+∞上存在极值点,求a 的取值范围;(2)设()10,1x ∈,2(1,)x ∈+∞,若()()21f x f x -存在最大值,记为()M a ,则当1a e e≤+时,()M a 是否存在最大值?若存在,求出其最大值;若不存在,请说明理由【答案】(1)5(2a ∈,)+∞;(2)M (a )存在最大值,且最大值为4e.【分析】(1)求出函数()f x 的导数,将题意转换为1a x x =+在(2,)x ∈+∞上有解,由1y x x=+在(2,)x ∈+∞上递增,得15(2x x +∈,)+∞,求出a 的范围即可;(2)求出函数()f x 的导数,得到21[()()]()()max f x f x f n f m -=-,求出M (a )11()()()()n f n f m alnm n m n m=-=+-+-,根据函数的单调性求出M (a )的最大值即可.【详解】解:(1)2221(1)()1a x ax f x x x x--+'=--=,(0,)x ∈+∞,由题意得,210x ax -+=在(2,)x ∈+∞上有根(不为重根),即1a x x =+在(2,)x ∈+∞上有解,由1y x x=+在(2,)x ∈+∞上递增,得15(2x x +∈,)+∞,检验,52a >时,()f x 在(2,)x ∈+∞上存在极值点,5(2a ∴∈,)+∞;(2)210x ax -+=中2=a 4∆-,若02a <,即2=a 40∆-≤22(1)()x ax f x x --+∴'=在(0,)+∞上满足()0f x ',()f x ∴在(0,)+∞上递减,12x x < ()()12f x f x ∴>21()()0f x f x ∴-<,21()()f x f x ∴-不存在最大值,则2a >;∴方程210x ax -+=有2个不相等的正实数根,令其为m ,n ,且不妨设01m n <<<,则01m n a mn +=>⎧⎨=⎩,()f x 在(0,)m 递减,在(,)m n 递增,在(,)n +∞递减,对任意1(0,1)x ∈,有1()()f x f m ,对任意2(1,)x ∈+∞,有2()()f x f n ,21[()()]()()max f x f x f n f m ∴-=-,M ∴(a )11()()()()n f n f m alnm n m n m=-=+-+-,将1a m n n n =+=+,1m n=代入上式,消去a ,m 得:M (a )112[()()]n lnn n n n =++-,12a e e <+,∴11n e n e++,1n >,由1y x x=+在(1,)x ∈+∞递增,得(1n ∈,]e ,设11()2()2()h x x lnx x x x =++-,(1x ∈,]e ,21()2(1h x lnx x'=-,(1x ∈,]e ,()0h x ∴'>,即()h x 在(1,]e 递增,[()]max h x h ∴=(e )4e =,M ∴(a )存在最大值为4e.【点睛】本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道综合题.11.已知函数()ln(1)ax f x e x =+,2()ln g x x a x=+-,其中a R ∈.(1)若函数()y f x =的图象与直线y x =在第一象限有交点,求a 的取值范围.(2)当2a <时,若()y g x =有两个零点1x ,2x ,求证:12432x x e <+<-.【答案】(1)1(0,)2;(2)证明见解析.【分析】(1)根据题意设()()(1)ln ax g x f x x e x x =-=+-,问题转化为方程()0g x =,在(0,)+∞有解,求导,分类讨论①若0a ,②若102a <<,③若12a 时,分析单调性,进而得出结论.(2)运用分析法和构造函数法,结合函数的单调性,不等式的性质,即可得证.【详解】解:(1)设()()(1)ln ax g x f x x e x x =-=+-,则由题设知,方程()0g x =,在(0,)+∞有解,而1()()1[ln(1)]1()11axax g x f x e a x e F x x '='-=++-=-+.设()()1ax h x e F x =-,则22221()[()()][(1)](n 1)l ax ax ax a h x e aF x F x e a x x +-'=+'=+++.①若0a ,由0x >可知01ax e <,且11()ln(1)111F x a x x x =++<++,从而()()10ax g x e F x '=-<,即()g x 在(0,)+∞上单调递减,从而()(0)0g x g <=恒成立,因而方程()0g x =在(0,)+∞上无解.②若102a <<,则221(0)0(1)a h x -'=<+,又x →+∞时,()h x '→+∞,因此()0h x '=,在(0,)+∞上必存在实根,设最小的正实根为0x ,由函数的连续性可知,0(0,)x x ∈上恒有()0h x '<,即()h x 在0(0,)x 上单调递减,也即()0g x '<,在0(0,)x 上单调递减,从而在0(0,)x 上恒有()(0)0g x g '<'=,因而()g x 在0(0,)x 上单调递减,故在0(0,)x 上恒有()(0)0g x g <=,即0()0g x <,注意到ax e ax >,因此()(1)ln(1)ln [ln(1)1]ax g x e x x ax x x x a x =+->+-=+-,令1ax e=时,则有()0>g x ,由零点的存在性定理可知函数()y g x =在0(x ,1)a e 上有零点,符合题意.③若12a时,则由0x >可知,()0h x '>恒成立,从而()h x 在(0,)+∞上单调递增,也即()g x '在(0,)+∞上单调递增,从而()(0)0g x g >=恒成立,故方程()0g x =在(0,)+∞上无解.综上可知,a 的取值范围是1(0,2.(2)因为()f x 有两个零点,所以f (2)0<,即21012ln a a ln +-<⇒>+,设1202x x <<<,则要证121244x x x x +>⇔-<,因为1244x <-<,22x >,又因为()f x 在(2,)+∞上单调递增,所以只要证明121(4)()()0f x f x f x -<==,设()()(4)g x f x f x =--(02)x <<,则222222428(2)()()(4)0(4)(4)x x x g x f x f x x x x x ----'='-'-=+=-<--,所以()g x 在(0,2)上单调递减,()g x g >(2)0=,所以124x x +>,因为()f x 有两个零点,1x ,2x ,所以12()()0f x f x ==,方程()0f x =即2ln 0ax x x --=构造函数()2ln h x ax x x =--,则12()()0h x h x ==,()1ln h x a x '=--,1()0a h x x e -'=⇒=,记12(1ln 2)a p e a -=>>+,则()h x 在(0,)p 上单调递增,在(,)p +∞上单调递减,所以()0h p >,且12x p x <<,设2()()ln ln x p R x x p x p-=--+,22214()()0()()p x p R x x x p x x p -'=-=>++,所以()R x 递增,当x p >时,()()0R x R p >=,当0x p <<时,()()0R x R p <=,所以11111112(2ln )x x p ax x lnx x p x p--=<++,即22111111(2)()22l l n n ax x p x px x p x p p -+<-++,211(2ln )(22ln )20p a x ap p p p x p +-+--++>,1(a p e -=,1)lnp a =-,所以21111(23)20a a x e x e --+-+>,同理21122(23)20a a x ex e --+-+<,所以2112111111(23)2(23)2a a a a x e x e x e x e ----+-+<+-+,所以12121()[(23)]0a x x x x e --++-<,所以12123a x x e -+<-+,由2a <得:1122332a x x e e -+<-+<-,综上:12432x x e <+<-.【点睛】本题考查导数的综合应用,不等式的证明,关键是运用分类讨论,构造函数的思想去解决问题,属于难题.12.已知函数()2211ln 24f x x ax x x ax ⎛⎫=--+ ⎪⎝⎭.(1)若()f x 在()0,+¥单调递增,求a 的值;(2)当1344a e <<时,设函数()()f x g x x=的最小值为()h a ,求函数()h a 的值域.【答案】(1)1;(2)0,4e ⎛⎫ ⎪⎝⎭.【分析】(1)由()f x 在()0,+¥单调递增,利用导数知()0f x ¢³在()0,+¥上恒成立即可求参数a 的值;(2)由()()f x g x x =有()11ln 24g x x a x x a ⎛⎫=--+ ⎪⎝⎭,利用二阶导数可知()g x '在()0,+¥上单调递增,进而可知()01,x e ∃∈,使得()00g x '=,则有()g x 的单调性得最小值()()000011ln 24g x x a x x a h a ⎛⎫=--+= ⎪⎝⎭,结合1344a e <<并构造函数可求0x 取值范围,进而利用导数研究()000031ln ln 42h a x x x x ⎛⎫=- ⎪⎝⎭的单调性即可求范围;【详解】(1)()()ln f x x a x '=-,又()f x 在()0,+¥单调递增,∴()0f x ¢³,即()ln 0x a x -≥在()0,+¥上恒成立,(i )当1x >时,ln 0x >,则需0x a -≥,故min a x ≤,即1a ≤;(ii )当1x =时,ln 0x =,则a R ∈;(iii )当01x <<时,ln 0x <,则需0x a -≤,故max a x ≥,即1a ≥;综上所述:1a =;(2)()()11ln 24f x g x x a x x a x ⎛⎫==--+ ⎪⎝⎭,()11ln 24a g x x x '=-+,()212a g x x x ''=+,∵1344a e <<,有()0g x ''>,∴()g x '在()0,+¥上单调递增,又()1104g a '=-+<,()304a g e e '=-+>,∴()01,x e ∃∈,使得()00g x '=,当()00,x x ∈时,()0g x ¢<,函数()g x 单调递减,当()0,x x ∈+∞时,()0g x ¢>,函数()g x 单调递增,故()g x 的最小值为()()000011ln 24g x x a x x a h a ⎛⎫=--+=⎪⎝⎭,由()00g x '=得00011ln 24a x x x =+,因此()000031ln ln 42h a x x x x ⎛⎫=- ⎪⎝⎭,令()11ln 24t x x x x =+,()1,x e ∈,则()13ln 024t x x '=+>,∴()t x 在()1,e 上单调递增,又1344a e <<,()114t =,()34t e e =,∴0x 取值范围为()1,e ,令()31ln ln 42x x x x x ϕ⎛⎫=-⎪⎝⎭(1x e <<),则()()()21131ln ln 2ln 3ln 102444x x x x x ϕ'=--+=-+->,∴函数()ϕx 在()1,e 上单调递增,又()10ϕ=,()4ee ϕ=,∴()04e x ϕ<<,即函数()h a 的值域为0,4e ⎛⎫ ⎪⎝⎭.【点睛】本题考查了利用导数研究函数的单调性求参数,由原函数得到最值,构造中间函数并根据其导数讨论单调性,求最值的取值范围;中间函数需要根据步骤中的研究对象及目的确定;13.已知函数2()22ln ()f x x ax x a R =-+∈.(1)讨论函数()f x 的单调性;(2)若()f x 存在两个极值点()1221,x x x x >,求证:()()()2121(2)f x f x a x x -<--.【答案】(1)答案不唯一,具体见解析;(2)证明见解析.【分析】(1)求出导函数,根据二次函数的∆与0的关系来分类讨论函数的单调性,并注意一元二次方程根的正负与定义域的关系;(2)由()1212,x x x x <是两个极值点得到对应的韦达定理形式,然后利用条件将()()21f x f x -转变为关于12x x ,函数,再运用12x x ,的关系将不等式转化为证22212ln 0x x x -->,构造函数1()2ln (1)g x x x x x=-->,分析函数()g x 的单调性,得出最值,不等式可得证.【详解】(1)解:函数()f x 的定义域为(0,)+∞,()2'212()22x ax f x x a x x-+=-+=,则24a ∆=-.①当0a ≤时,对(0,),()0x f x '∀∈+∞>,所以函数()f x 在(0,)+∞上单调递增;②当02a <≤时,0∆≤,所以对(0,),()0x f x '∀∈+∞≥,所以函数()f x 在(0,)+∞上单调递增;③当2a >时,令()0f x '>,得02a x <<或42a x >,所以函数()f x在0,2a ⎛- ⎪⎝⎭,⎫+∞⎪⎪⎝⎭上单调递增;令'()0f x <,得4422a a x +<<,所以()f x 在4422a a ⎛+ ⎪⎝⎭上单调递减.(2)证明:由(1)知2a >且1212,1,x x a x x +=⎧⎨=⎩,所以1201x x <<<.又由()()()()222122211122ln 22ln f x f x x ax x x ax x -=-+--+()()()()()()22222222221212121212111122ln22ln 2ln x x x x x a x x x x x x x x x x x x x =---+=--+-+=--+.又因为()()()()()()()()222121212121212121(2)222a x x x x a x x x x x x x x x x x x --=---=--+-=---.所以要证()()()2121(2)f x f x a x x -<--,只需证()22112ln2x x x x <-.因为121=x x ,所以只需证22221ln x x x <-,即证22212ln 0x x x -->.令1()2ln (1)g x x x x x =-->,则2'2121()110g x x x x ⎛⎫=+-=-> ⎪⎝⎭,所以函数()g x 在(1,)+∞上单调递增,所以对1,()(1)0x g x g ∀>>=.所以22212ln 0x x x -->.所以若()f x 存在两个极值点()1221,x x x x >,则()()()2121(2)f x f x a x x -<--.【点睛】本题考查函数与导数的综合应用,属于较难题.导数中通过双极值点求解最值或证明不等式时,可通过双极值点对应的等式将待求的式子或待证明的式子转变为关于同一变量(注意变量的范围)的式子,然后通过构造新函数,分析新函数的单调性后从而达到求解最值或证明不等式的目的.14.已知函数2()(2)()x f x xe a x x a R =-+∈.(1)当1a =时,求函数()f x 的单调区间;(2)当1a e >时,函数()f x 有三个不同的零点1x ,2x ,3x ,求证:1232x x x lna ++<.【答案】(1)增区间为(,1)-∞-,(2,)ln +∞;减区间为(1,2)ln -;(2)证明见解析.【分析】(1)求出原函数的导函数,得到函数零点,由导函数零点对定义域分段,再由导函数在不同区间段内的符号得到原函数的单调区间;(2)由(0)0f =,可得0x =是函数的一个零点,不妨设30x =,把问题转化为证122x x lna +<,即证122x x a e+>.由()0f x =,得(2)0x e a x -+=,结合1x ,2x 是方程(2)0x e a x -+=的两个实根,得到1212x x e e a x x -=-,代入122x x a e +>,只需证1212212x x x x e e e x x +->-,不妨设12x x >.转化为证1212212()10x x x x ex x e----->.设122x x t -=,则等价于2210(0)t t e te t -->>.设2()21(0)t t g t e te t =-->,利用导数证明()0g t >即可.【详解】(1)解:()(22)(1)(2)x x x f x e xe x x e '=+-+=+-,令()0f x '=,得11x =-,22x ln =.当1x <-或n 2>x l 时,()0f x '>;当12x ln -<<时,()0f x '<.()f x ∴增区间为(,1)-∞-,(2,)ln +∞;减区间为(1,2)ln -;(2)证明:(0)0f = ,0x ∴=是函数的一个零点,不妨设30x =,则要证122x x lna +<,只需证122x x a e +>.由()0f x =,得(2)0x e a x -+=,1x ,2x 是方程(2)0x e a x -+=的两个实根,∴11(2)x e a x =+,①22(2)x e a x =+,②,①-②得:1212x x e e a x x -=-,代入122x x a e+>,只需证1212212x x x x e e e x x +->-,不妨设12x x >.120x x -> ,∴只需证1212212()x x x x e e x x e+->-.20x e >,∴只需证1212212()10x x x x e x x e ----->.设122x x t -=,则等价于2210(0)t t e te t -->>.设2()21(0)t t g t e te t =-->,只需证()0g t >,又()2(1)t t g t e e t =--',设()1(0)t t e t t ϕ=-->,则()10t t e ϕ'=->,()t ϕ∴在(0,)+∞上单调递增,则()(0)0t ϕϕ>=.()0g t ∴'>,从而()g t 在(0,)+∞上是增函数,()(0)0g t g ∴>=.综上所述,1232x x x lna ++<.【点睛】本题考查利用导数研究函数的单调性,考查利用导数求函数的极值,考查数学转化思想方法,属难题.15.已知函数()223x xe f x e -+=,其中e 为自然对数的底数.(1)证明:()f x 在(),0-∞上单调递减,()0,∞+上单调递增;(2)设0a >,函数()212cos cos 3g x x a x a =+--,如果总存在[]1,x a a ∈-,对任意2x R ∈,()()12f x g x 都成立,求实数a 的取值范围.【答案】(1)证明见解析;(2)ln 2a ≥.【分析】(1)直接对函数求导,判断导函数在对应区间上的符号即可证明;(2)总存在1[x a ∈-,](0)a a >,对任意2x R ∈都有12()()f x g x ,即函数()y f x =在[a -,]a 上的最大值不小于()y g x =,x ∈R 的最大值;借助单调性换元法,结合二次函数的性质分别求最值列不等式求解即可【详解】(1)证明:()()23x xe ef x -='-令()0f x '>,解得0x >,∴()f x 在()0,∞+上单调递增令()0f x '<,解得0x <,∴()f x 在(),0-∞上单调递减(2)总存在1[x a ∈-,](0)a a >,对任意2x R ∈都有12()()f x g x ,即函数()y f x =在[a -,]a 上的最大值不小于()y g x =,x ∈R 的最大值()()()()max 23a af x f a f a e e -=-==+令[]()cos 1,1t x t =∈-,∴()2123g t t at a =+--,对称轴02a t =-<∴()()max 513g t g ==∴()2533a a e e -+≥,52a a e e -+≥,令(),0ae m m =>,∴152m m +≥,∴2m ≥∴2a e ≥,∴ln 2a ≥【点睛】本题考查利用导数研究函数的单调性,考查三角函数的有界性,二次函数的最值以及恒成立问题的转化,考查转化思想以及计算能力,属于中档题.16.已知函数()()21ln 212h x x b x =+-,()21ln 2f x x a x =-.其中a ,b 为常数.(1)若函数()h x 在定义域内有且只有一个极值点,求实数b 的取值范围;(2)已知1x ,2x 是函数()f x 的两个不同的零点,求证:12x x +>.【答案】(1)(),0-∞;(2)证明见解析.【分析】(1)首先求函数的导数,根据题意转化为222y x x b =-+在1,2⎛⎫+∞⎪⎝⎭内有且仅有一个变号零点,根据二次函数的单调性,列式求解b 的取值范围;(2)求出当函数()f x 有两个零点时,求出a e >,再构造函数()))(0g x fx f x x =-≤≤,利用导数判断函数的单调性,得到))f x f x +<-,再通过构造得到()()21f x f x >-,利用函数的单调性证明结论.【详解】(1)()2222121212'b x x b x x x x h x -+⎛⎫=+=> ⎪--⎝⎭,因为函数()h x 在定义域有且仅有一个极值点,所以222y x x b =-+在1,2⎛⎫+∞⎪⎝⎭内有且仅有一个变号零点,由二次函数的图象和性质知21122022b ⎛⎫⨯-+< ⎪⎝⎭,解得0b <,即实数b 的取值范围为(),0-∞.(2)()2'(0)a x ax x x xf x -=-=>,当0a ≤时,()'0f x >,()f x 在()0,∞+上单调递增,函数()f x 至多有一个零点,不符合题意,当0a >时,令()'0f x =,得x =当(x ∈时,()'0f x <,()f x 单调递减,当)x ∈+∞时,()'0f x >,()f x 单调递增,故当x =()f x 取得最小值()1ln 2afa =-,当0a e <<时,1ln 0a ->,0f>,函数()f x 无零点,不合题意,当a e =时,1ln 0a -=,0f =,函数()f x 仅有一个零点,不合题意,当a e >时,1ln 0a -<,0f <,又()1102f =>,所以()f x 在(x ∈上只有一个零点,令()ln 1p x x x =-+,则()1'1p x x=-,故当01x <<时,()'0p x >,()p x 单调递增,当1x >时,()'0p x <,()p x 单调递减,所以()()10p x p ≤=,即ln 1≤-x x ,所以ln 221a a ≤-,所以22(2)2ln 22(21)0f a a a a a a a a =-≥--=>,又2a >,所以()f x 在)x ∈+∞上只有一个零点.所以a e >满足题意.不妨设12x x <,则(1x ∈,)2x ∈+∞,令()))(0g x f x f x x =+--≤≤,则()))ln ln g x a x a x =-+-,()22'g x x a==-,当0x <<时,()'0g x <,所以()g x 在(上单调递减,所以当(x ∈时,()()00g x g <=,即))fx fx +<-,因为(1x ∈(1x ∈,所以()()))()21111f x f x f x f x f x ⎤⎤==-->+-=-⎦⎦,又)2x ∈+∞,)1x -∈+∞,且()f x 在)+∞上单调递增,所以21x x >,故12x x +>>【点睛】本题考查利用导数证明函数的单调性,极值,最值,零点,函数与方程,不等式的综合应用,重点考查逻辑推理,转化与变形,计算能力,属于难题.17.已知函数()()()1xxf x ae ea x a R -=--+∈,()f x 既存在极大值,又存在极小值.(1)求实数a 的取值范围;(2)当01a <<时,1x ,2x 分别为()f x 的极大值点和极小值点.且()()120f x kf x +>,求实数k 的取值范围.【答案】(1)()()0,11,+∞ ;(2)1k ≤-.【分析】(1)求出函数的导数,结合函数的单调性确定a 的范围即可;(2)求出函数的极值点,问题转化为11(1)1a lna k a -<++ ,设11()(1))1x g x lnx k x -=-++ ,根据函数的单调性确定k 的范围即可.【详解】解:(1)由()()1xxf x ae e a x -=--+得()()'1x x f x ae e a -=+-+,即()()()1'1xxx f ee x ea -=--,由题意,若()f x 存在极大值和极小值,则()'0f x =必有两个不相等的实数根,由10x e -=得0x =,所以10x ae -=必有一个非零实数根,∴0a ≠,1xe a =,∴10a>且11a ≠,∴01a <<或1a >.综上,实数a 的取值范围为()()0,11,+∞ .(2)当01a <<时,由(1)可知()f x 的极大值点为10x =,极小值点为2ln x a =-,此时()11f x a =-,()()211ln f x a a a =-++,依题意得()()111ln 0a k a a a -+-++>对任意01a <<恒成立,由于此时()()210f x f x <<,所以k 0<;所以()()()1ln 11k a a a k +>--,即11ln 11a a k a -⎛⎫<-⎪+⎝⎭,设()11ln 11x x k x g x -⎛⎫=--⎪+⎝⎭,()0,1x ∈,则()()()()2221121112111'x x k x k x x x g x ⎛⎫+-- ⎪⎛⎫⎝⎭=--= ⎪⎝⎭++()22211x x k x x ++=+,令()2210*x x k ++=,判别式244k∆=-.①当1k ≤-时,0∆≤,所以()'0g x ≥,()g x 在()0,1单调递增,所以()()10g x g <=,即11ln 11a a k a -⎛⎫<-⎪+⎝⎭,符合题意;②当10k -<<时,>0∆,设()*的两根为3x ,4x ,且34x x <,则3420x x k+=->,341x x =,因此3401x x <<<,则当31x x <<时,()'0g x <,()g x 在()3,1x 单调递减,所以当31x a <<时,()()10g a g >=,即11ln 11a a k a -⎛⎫>- ⎪+⎝⎭,所以()()120f x kf x +<,矛盾,不合题意;综上,k 的取值范围是1k ≤-.【点睛】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法,考查了推理能力与计算能力,属于难题.18.已知函数()()22ln xg x x t t R e =-+∈有两个零点1x ,2x .(1)求实数t 的取值范围;(2)求证:212114x x e+>.【答案】(1)ln 21t >-;(2)证明见解析.【分析】(1)写出函数()g x 定义域并求导,从而得到函数的单调性,根据单调性得到函数的最大值,要使()g x 有两个零点,只需最大值202e g ⎛⎫> ⎪⎝⎭即可.(2)函数()g x 有两个零点1x ,2x ,可得1122222ln 02ln 0x x t e x x t e ⎧-+=⎪⎪⎨⎪-+=⎪⎩,两式相减得21221ln ln 2x x e x x -=-,欲证212114x x e +>,即证()2112212ln ln 11x x x x x x -+>-,设21(1)x t t x =>,构造函数1()2ln (1)f t t t t t=-->,通过函数()f t 的单调性即可得到证明.【详解】(1)函数()()22ln x g x x t t R e =-+∈定义域为()0,∞+,()222122=x e x xe g x e -=-'.令()0g x '=得22ex =,可得()g x 在20,2e ⎛⎫ ⎪⎝⎭上单调递增,在2,2e ⎛⎫+∞ ⎪⎝⎭上单调递减,又0x →时,()g x →-∞,x →+∞时,()g x →-∞,故欲使()g x 有两个零点,只需22ln 11ln 2022e e g t t ⎛⎫=-+=-+> ⎪⎝⎭,即ln 21t >-.(2)证明:不妨设12x x <,则由(1)可知21202e x x <<<,且1122222ln 02ln 0x x t e x x t e ⎧-+=⎪⎪⎨⎪-+=⎪⎩,两式相减可得21221ln ln 2x x e x x -=-.欲证212114x x e +>,即证()2112212ln ln 11x x x x x x -+>-,设21(1)x t t x =>,则即证12ln (1)t t t t->>,构造函数1()2ln (1)f t t t t t=-->,则()22212(1)10t t t tf t -=+-=>',所以()f t 在()1,+∞上单调递增,故()()10f t f >=,所以12ln (1)t t t t->>,原不等式得证.【点睛】本题考查利用导数研究函数的零点,单调性以及最值问题,考查利用变量集中的思想解决不等式的证明,考查构造函数的思想,属于中档题.19.已知函数()1ln f x x x=-,()g x ax b =+.(1)若函数()()()h x f x g x =-在()0,+¥上单调递增,求实数a 的取值范围;(2)当0b =时,若()f x 与()g x 的图象有两个交点()11,A x y ,()22,B x y ,试比较12x x 与22e 的大小.(取e 为2.8,取ln 2为0.7为1.4)【答案】(1)(],0-∞;(2)2122x x e >.【分析】(1)根据条件得到()0h x '≥对()0,x ∈+∞恒成立,由此得到关于a 的不等式,采用分离常数的方法求解出a 的取值范围;(2)根据交点坐标列出对应的方程组,用关于12,x x 的式子表示出a ,由此得到关于12,x x 的等式,通过设变量21x t x =得到关于t 的函数,利用导数分析出关于t 的函数的最值,再借助基本不等式以及构造函数()G x 并利用()G x 的单调性分析出12x x 与22e 的关系.【详解】。
高三数学专题 破译函数中双变量问题

高三数学专题破译函数中双变量问题破译函数中双变量问题单选题1.已知函数 $f(x)=e^{4x-1},g(x)=\frac{1}{2}+\ln(2x)$,若$f(m)=g(n)$ 成立,则 $n-m$ 的最小值为()A。
3B。
3.5C。
4D。
4.5答案:C解析:本题主要考查利用导数研究函数的单调性进而求最值,属于难题。
求最值问题往往先将所求问题转化为函数问题,然后根据配方法、换元法、不等式法、三角函数法、图像法、函数单调性法求解。
利用函数的单调性求最值,首先确定函数的定义域,然后准确地找出其单调区间,最后再根据其单调性求函数的最值即可。
填空题2.已知 $f(x)=(x+1)e^{2-x+1}$,则 $f(x)$ 的定义域是__________。
答案:$(-\infty,+\infty)$。
3.已知 $f(x)=(x+1)e^{2-x+1},g(x)=(x+1)+a$,若 $\existsx_1,x_2\in\mathbb{R}$,使得 $f(x_2)\geq g(x_1)$ 成立,则实数 $a$ 的取值范围是__________。
答案:$(-\infty,27/e^{27})$。
解析:$\exists x_1,x_2\in\mathbb{R}$,使得 $f(x_2)\geq g(x_1)$ 成立,即为 $f(x)\max\geq g(x)\min$。
又$f'(x)=(x+1)e^{-x+2}$,由 $f'(x)=0$ 得 $x=-1$ 或 $x=2$,且当$x0$,$f(x)$ 单调递增;当 $x>2$ 时,$f'(x)<0$,$f(x)$ 单调递减,所以 $f(x)\max=f(2)=27/e^{27}$,又 $g(x)\min=a$,则$a\leq 27/e^{27}$,故实数 $a$ 的取值范围是 $(-\infty,27/e^{27}]$。
4.若不等式 $x-2y\leq c(x-y)$ 对任意满足 $x>y$ 的实数$x,y$ 恒成立,则实数 $c$ 的最大值为__________。
专题10 利用导数研究双变量问题(全题型压轴题)试题含解析

专题10利用导数研究双变量问题(全题型压轴题)目录①12()()f x g x =型......................................................1②12()()f x g x ≥型(或12()()f x g x ≤型) (2)③构造函数法 (5)①12()()f x g x =型②12()()f x g x ≥型(或12()()f x g x ≤型)6.(2023春·河南信阳·高一校考期中)已知函数()()2log 221x f x a x ⎡⎤=-+-⎣⎦,函数()22x x g x t -=-⋅.(1)若()g x 是偶函数,求实数t 的值,并用单调性的定义判断()g x 在[)0,∞+上的单调性;(2)在(1)的条件下,若对于[)10,x ∀∈+∞,2x R ∀∈,都有()()1222log 2f x g x a +≤+成立,求实数a 的取值范围.③构造函数法专题10利用导数研究双变量问题(全题型压轴题)目录①12()()f x g x =型......................................................1②12()()f x g x ≥型(或12()()f x g x ≤型) (8)③构造函数法 (15)①12()()f x g x =型对于D 选项,由上述分析可知,()21,x ∈+∞,则()[)2e,f x ∈+∞,1R x ∈,()1g x a ≥,要使“对1x ∀∈R ,()21,x ∃∈+∞,使得()1g x f =则需e a ≥,所以D 选项正确.故选:BD.4.(2023·全国·高二专题练习)已知函数()f x②12()()f x g x ≥型(或12()()f x g x ≤型)③构造函数法。
函数中双变量问题专题

函数中双变量问题一、单选题1.已知函数()ln(f x x =满足对于任意11[,2]2x ∈,存在21[,2]2x ∈,使得22112ln (2)()x f x x a f x ++≤成立,则实数a 的取值范围为( ) A .ln 2[8,)2-+∞ B .ln 25[8,2ln 2]24--- C .ln 2(,8]2-∞-D .5(,2ln 2]4-∞-- 2. 设函数()()32,,,0f x ax bx cx a b c R a =++∈≠,若不等式()()5xf x af x '-≤对x R ∀∈恒成立,则b 2ca-的取值范围为( ) A .5,3⎡⎫+∞⎪⎢⎣⎭B .1,3⎡⎫+∞⎪⎢⎣⎭C .5,3⎡⎫-+∞⎪⎢⎣⎭D .1,3⎡⎫-+∞⎪⎢⎣⎭3. 已知函数ln 1,1()1(2),13x x f x x x -≥⎧⎪=⎨+<⎪⎩,若αβ<且()()f f αβ=,则βα-的取值范围是( )A .[]83ln3,6-B .)283ln3,1e ⎡--⎣ C .[]94ln3,6-D .)294ln 3,1e ⎡--⎣4. 已知函数()x f x e ax =-有两个零点1x ,2x ,则下列判断:①a e <;②122x x +<;③121x x >;④有极小值点0x ,且1202x x x +<.则正确判断的个数是( ) A .4个B .3个C .2个D .1个5. 已知实数a ,b 满足225ln 0a a b --=,c R ∈的最小值为( )A .12 B.2C.2 D .92 6. 已知直线()1y a x =+与曲线()xf x e b =+相切,则ab 的最小值为( ) A .14e -B .12e -C .1e -D .2e-7. α,,22ππβ⎡⎤∈-⎢⎥⎣⎦,且sin sin 0ααββ->,则下列结论正确的是( ) A .αβ> B .0αβ+> C .αβ< D .22αβ> 8. 已知函数()1()ln 1,,2xf x ex x ⎡⎫=-∈+∞⎪⎢⎣⎭,若存在[]2,1a ∈-,使得21223f a a e m ⎛⎫-≤+-- ⎪⎝⎭成立,则实数m 的取值范围为( ) A .2,13⎡⎤⎢⎥⎣⎦B .[)1,+∞C .2,3⎡⎫+∞⎪⎢⎣⎭D .31,2⎡⎤⎢⎥⎣⎦9. 已知曲线()()0xf x ae a =>与曲线()()20g x x m m =->有公共点,且在该点处的切线相同,则当m 变化时,实数a 的取值范围是( ) A .240,e ⎛⎫ ⎪⎝⎭B .61,e ⎛⎫ ⎪⎝⎭C .40,e ⎛⎫ ⎪⎝⎭D .281,e ⎛⎫ ⎪⎝⎭二、填空题10. 已知函数()2ln x f x a x x a =+-,对任意的[]12,0,1x x ∈,不等式()()121f x f x a -≤-恒成立,则实数a 的取值范围是___.11. 已知函数2()2ln 3f x x ax =-+,若存在实数,[1,5]m n ∈满足2n m -≥时,()()f m f n =成立,则实数a 的最大值为_____ 12. 设函数()321x x f x -=+,()2xg x xe =,若()11,x ∃∈-+∞,使得()21,x ∀∈-+∞,不等式()()2214emg x m f x >恒成立,则实数m 的取值范围是______.13. 若a 为实数,对任意[1,1]k ∈-,当(0,4]x ∈时,不等式26ln 9x x x a kx +-+≤恒成立,则a 的最大值是_________. 三、解答题14. 设,a b ∈R ,已知函数()2ln f x a x x bx =++存在极大值.(1)若2a =,求b 的取值范围;(2)求a 的最大值,使得对于b 的一切可能值,()f x 的极大值恒小于0.15. 已知函数(R ).(1)当14a =时,求函数()y f x =的单调区间; (2)若对任意实数(1,2)b ∈,当(1,]x b ∈-时,函数()f x 的最大值为()f b ,求a 的取值范围.16. 已知函数()13ln 144f x x x x=-+- (1)求函数()f x 的单调区间;(2)设()224g x x bx =-+-,若对任意()[]120,2,1,2x x ∈∈,不等式()()12f x g x ≥恒成立,求实数b的取值范围.17. 已知函数()2ln 2f x x ax bx =---,a R ∈.(1)当2b =时,试讨论()f x 的单调性;(2)若对任意的3,b e ⎛⎫∈-∞- ⎪⎝⎭,方程()0f x =恒有2个不等的实根,求a 的取值范围.答 案一、单选题1.(2020·湖南省长郡中学高三)已知函数()ln(f x x =满足对于任意11[,2]2x ∈,存在21[,2]2x ∈,使得22112ln (2)()x f x x a f x ++≤成立,则实数a 的取值范围为( ) A .ln 2[8,)2-+∞ B .ln 25[8,2ln 2]24--- C .ln 2(,8]2-∞- D .5(,2ln 2]4-∞--【答案】C【解析】由函数()ln(f x x =在定义域单调递增,对于任意11[,2]2x ∈,存在21[,2]2x ∈,使得22112ln (2)()x f x x a f x ++≤成立, 即任意11[,2]2x ∈,存在21[,2]2x ∈,使得22112ln 2x x x a x ++≤成立, 即满足()2211max2maxln 2x x x a x ⎛⎫++≤ ⎪⎝⎭,令2111()2g x x x a =++,对称轴方程为11x =-,在11[,2]2x ∈可得1max ()(2)=8g x g a =+ 令222ln ()x h x x =,求导可得22221ln ()x h x x -'=,2()0h x '=,可得2x e =,在()20,x e ∈,2()0h x '>,2()h x 单调递增, 所以在21[,2]2x ∈,2max ln 2()(2)2h x h ==,即ln 282a +≤, 解得ln 282a ≤-,故选C . 2.(2020·江西省南城一中高三期末)设函数()()32,,,0f x ax bx cx a b c R a =++∈≠,若不等式()()5xf x af x '-≤对x R ∀∈恒成立,则b 2ca-的取值范围为( )A.5,3⎡⎫+∞⎪⎢⎣⎭B.1,3⎡⎫+∞⎪⎢⎣⎭C.5,3⎡⎫-+∞⎪⎢⎣⎭D.1,3⎡⎫-+∞⎪⎢⎣⎭【答案】C【解析】()32f x ax bx cx=++Q,()232f x ax bx c'∴=++,由不等式()()5xf x af x'-≤对x R∀∈恒成立,可得()()()2323250a a xb ab xc ac x-+-+--≤对x R∀∈恒成立,所以,230a a-=且0a≠,解得3a=,则不等式2250bx cx++≥对x R∀∈恒成立,所以24200bc b>⎧⎨∆=-≤⎩,则25cb≥,所以,()222125252210553315153c c cb c b c c ca------=≥==≥-.因此,b2ca-的取值范围为5,3⎡⎫-+∞⎪⎢⎣⎭.故选:C.3.(2020·新疆维吾尔自治区高三)已知函数ln1,1()1(2),13x xf xx x-≥⎧⎪=⎨+<⎪⎩,若αβ<且()()f fαβ=,则βα-的取值范围是()A.[]83ln3,6-B.)283ln3,1e⎡--⎣C.[]94ln3,6-D.)294ln3,1e⎡--⎣【答案】B【解析】因为ln1,1()1(2),13x xf xx x-≥⎧⎪=⎨+<⎪⎩,故其函数图像如下所示:令11lnx-=,解得2x e=;令11lnx-=-,解得1x=.数形结合可知,若要满足()()f f αβ=,且αβ<, 则()21,eβ∈,且()1213ln αβ+=-,解得35ln αβ=-. 故βα-35ln ββ=-+,()21,e β∈.令()()235,1,g x x lnx x e =-+∈,则()31g x x'=-,令()0g x '=,解得3x =, 故()g x 在区间()1,3单调递减,在区间()23,e 单调递增,则()()()2216,3833,1g g ln g ee==-=-,故())2833,1g x ln e ⎡∈--⎣.即可得βα-)2833,1ln e ⎡∈--⎣.故选:B.4.(2020·江西省临川第二中学高三期中)已知函数()xf x e ax =-有两个零点1x ,2x ,则下列判断:①a e <;②122x x +<;③121x x >;④有极小值点0x ,且1202x x x +<.则正确判断的个数是( ) A .4个 B .3个 C .2个 D .1个【答案】D【解析】对于①,∵()xf x e ax =-,∴()x f x e a '=-,令()0xf x e a '=->,当0a ≤时,()0xf x e a '=->在x ∈R 上恒成立, ∴()f x 在R 上单调递增.当0a >时,由()0f x '>,解得ln x a >;由()0f x '<,解得ln x a <; ∴()f x 在(,ln )a -∞单调递减,在(ln ,)a +∞单调递增. ∵函数()xf x e ax =-有两个零点1x ,2x ,∴0a >,(ln )0f a <,即ln ln 0a e a a -<,即ln 0a a a -<, 解得:a e >;所以①不正确;对于②,因为函数()xf x e ax =-有两个零点1x ,2x ,所以1x ,2x 是方程0x e ax -=的两根,因此11ln x ax =,22ln x ax =,所以()()()212121212ln 2ln ln 2ln x x a x x a x x x x +==+>+,取22e a =,2(2)20f e a =-=,∴22x =,(0)10=>f ,∴101x <<,∴122x x +>,所以②不正确;对于③,(0)10=>f ,∴101x <<,121x x >不一定,∴所以③不正确; 对于④,f (x )在(,ln )a -∞单调递减,在(ln ,)a +∞单调递增, ∴有极小值点0ln x a =,且12022ln x x x a +<=,所以④正确. 综上,正确的命题序号是④.故选:D5.(2020·湖南省高三期末)已知实数a ,b 满足225ln 0a a b --=,c R ∈,则22()()a c b c -++的最小值为( ) A .12B .22C .322D .92【答案】C【解析】由题意,得,代换,代换,则满足:,即,以代换,可得点,满足,因此求()()22a cbc -++的最小值即为求曲线上的点到直线的距离的最小值,设直线与曲线相切于点,则,解得,所以切点为,所以点到直线的距离,则()()22a cbc -++的最小值为,综上所述,选C.6.(2020·全国高三专题练习)已知直线()1y a x =+与曲线()xf x e b =+相切,则ab 的最小值为( )A .14e-B .12e-C .1e-D .2e-【答案】B【解析】设切点为00(,)xx e b +,因为()x f x e b =+,所以()xf x e '=,所以00()x f x e a '==,所以0ln x a =,又切点00(,)xx e b +在直线(1)y a x =+上,所以00(1)xe b a x +=+, 所以0a b ax a +=+,所以0ln b ax a a ==,所以2ln ab a a =, 令2()ln (0)g a a a a =>, 则21()2ln 2ln (2ln 1)g a a a a a a a a a a'=+⋅=+=+, 令()0g a '<,得120a e -<<, 令()0g a '>,得12a e ->, 所以()g a 在12(0,)e -上递减,在12(,)e -+∞上递增,所以12a e-=时,()g a 取得最小值11122221()()ln 2g e e ee---==-. 即ab 的最小值为12e-.故选:B 7.(2020·黑龙江省双鸭山一中高三期末)α,,22ππβ⎡⎤∈-⎢⎥⎣⎦,且sin sin 0ααββ->,则下列结论正确的是( ) A .αβ> B .0αβ+>C .αβ<D .22αβ>【答案】D【解析】构造()sin f x x x =形式,则()sin cos f x x x x +'=,0,2x π⎡⎤∈⎢⎥⎣⎦时导函数()0f x '≥,()f x 单调递增;,02x π⎡⎫∈-⎪⎢⎣⎭时导函数()0f x '<,()f x 单调递减.又Q ()f x 为偶函数,根据单调性和对称性可知选D.故本小题选D.8.(2020·广西壮族自治区高三月考)已知函数()1()ln 1,,2xf x ex x ⎡⎫=-∈+∞⎪⎢⎣⎭,若存在[]2,1a ∈-,使得21223f a a e m ⎛⎫-≤+-- ⎪⎝⎭成立,则实数m 的取值范围为( )A .2,13⎡⎤⎢⎥⎣⎦B .[)1,+∞ C .2,3⎡⎫+∞⎪⎢⎣⎭D .31,2⎡⎤⎢⎥⎣⎦【答案】A【解析】1'()ln 1xf x e x x ⎛⎫=+- ⎪⎝⎭,令1()ln 1g x x x=+-,则22111'()x g x x x x -=-=, 故当112x <<时,)'(0g x <,()g x 单调递减,当1x >时,'()0,()g x g x >单调递增,()(1)0g x g ∴≥=,从而当1,2x ⎡⎫∈+∞⎪⎢⎣⎭时,'()0f x ≥,()f x 在区间1,2⎡⎫+∞⎪⎢⎣⎭上单调递增. 设()()222314h a a a e a e =+--=+--,则()h a 在[]2,1--上单调递减,在[]1,1-上单调递增,()max ()1h a h e ==-, 存在[]2,1a ∈-,使21223f a a e m ⎛⎫-≤+-- ⎪⎝⎭成立,等价于()121f e f m ⎛⎫-≤-= ⎪⎝⎭.1211122m m ⎧-≤⎪⎪∴⎨⎪-≥⎪⎩,解得213m ≤≤.故选:A .9.(2020·重庆南开中学高三月考)已知曲线()()0xf x aea =>与曲线()()20g x x m m =->有公共点,且在该点处的切线相同,则当m 变化时,实数a 的取值范围是( ) A .240,e ⎛⎫ ⎪⎝⎭B .61,e ⎛⎫ ⎪⎝⎭C .40,e ⎛⎫ ⎪⎝⎭D .281,e ⎛⎫⎪⎝⎭【答案】A【解析】由()(0)xf x ae a =>,2()g x x m =-,得()xf x ae '=,()2g x x '=,设()(0)xf x ae a =>与曲线2()g x x m =-的公共点为(,)s t ,则()sf s ae '=,()2g s s '=,∴两曲线在切点处的切线方程分别为()s s y ae ae x s -=-与22()y s m s x s -+=-,即sssy ae x ae sae =+-与22y sx s m =--.则22ss s s ae ae sae s m ⎧=⎨-=--⎩,整理得222s m s s s a e ⎧=-⎪⎨=⎪⎩①②. 由①且0m >,得0s <或2s >,当0s <时,两曲线无公共切线,则2s >. 由②得,2(2)s sa s e=>. 令2()(2)s s h s s e =>,则2(1)()0s s h s e-'=<,函数()h s 在(2,)+∞上为单调减函数, ()(2)h s h ∴<24e=,又当s →+∞时,()0h s →,∴实数a 的取值范围是24(0,)e.故选:A.二、填空题10.(2020·江苏省高三专题练习)已知函数()2ln xf x a x x a =+-,对任意的[]12,0,1x x ∈,不等式()()121f x f x a -≤-恒成立,则实数a 的取值范围是___.【答案】[),e +∞【解析】由题意可得max min ()()1f x f x a -≤-,且1a >,由于()ln 2ln (1)ln 2x x f x a a x a a a x =+-=-+',所以当0x >时,()0f x '>,函数()f x 在[0,1]上单调递增,则max min ()(1)1ln ,()(0)1f x f a a f x f ==+-==,所以max min ()()ln f x f x a a -=-,故1ln ln 1a a a a -≥-⇒≥,即a e ≥,应填答案[),e +∞.11.(2020·湖南省明达中学高三)已知函数2()2ln 3f x x ax =-+,若存在实数,[1,5]m n ∈满足2n m -≥时,()()f m f n =成立,则实数a 的最大值为_____【答案】ln 34【解析】由22()()2ln 32ln 3f m f n n an m am =⇒-+=-+,所以222(ln ln )n m a n m-=-, 令n m t =+,(2t ≥),则ln(1)(2)t m a t m t +=+,([1,5]m ∈,2t ≥), 显然ln(1)()(2)t m g m t m t +=+,在[1,)m ∈+∞单调递减,∴ln(1)(1)(2)t a g t t +≤=+(2t ≥)令ln(1)()(1)(2)t h t g t t +==+,(2t ≥),22222(1)ln(1)()[(2)](1)t t t t h t t t t +-++'=++,∵2t ≥,∴2ln(1)1t +>,则2222(1)ln(1)t t t t +-++,∴令ln(1)()(1)(2)t h t g t t +==+在[2,)+∞单调递减,∴ln 3(2)4a h ≤=,∴实数a 的最大值为ln 34.故答案为:ln 3412.(2020·河南省高三月考)设函数()321x x f x -=+,()2xg x xe =,若()11,x ∃∈-+∞,使得()21,x ∀∈-+∞,不等式()()2214emg x m f x >恒成立,则实数m 的取值范围是______. 【答案】()1,+∞ 【解析】()()2155211x x f x x -++==-+++Q ,当()1,x ∈-+∞时,有()2f x >-. 因为()2xg x xe =,所以()()222212xx x g x e xe x e '=+=+,当112x -<<-时,()0g x '<,函数()y g x =在11,2⎛⎫-- ⎪⎝⎭上单调递减,当12x >-时,()0g x '>,函数()y g x =在1,2⎛⎫-+∞ ⎪⎝⎭上单调递增,()1122g x g e ⎛⎫∴≥-=- ⎪⎝⎭,所以当1x >-时,()1,2g x e ⎡⎫∈-+∞⎪⎢⎣⎭.若0m >,则()214422emg x em m e ⎛⎫≥⋅-=- ⎪⎝⎭,()2212m f x m >-. 根据题意可知222m m ->-,解得1m >;若0m ≤,则()(]24,2emg x m ∈-∞-,()2212m f x m >-,不符合条件.综上所述,实数m 的取值范围是()1,+∞.故答案为:()1,+∞.13.(2020·浙江省高三期中)若a 为实数,对任意[1,1]k ∈-,当(0,4]x ∈时,不等式26ln 9x x x a kx +-+≤恒成立,则a 的最大值是_________. 【答案】7【解析】因为对任意[1,1]k ∈-,当(0,4]x ∈时,不等式26ln 9x x x a kx +-+≤恒成立,所以对任意[1,1]k ∈-,当(0,4]x ∈时,不等式26ln 9x x x ak x+-+≤恒成立即222min 6ln 96ln 916l 8n x x x a x x x a k a x x x x x+-++-+≤⇒≤-⇒≤+--所以当(0,4]x ∈时,不等式2n 86l a x x x --+≤恒成立 令2()6l ,48n ,(0]f x x x x x =--+∈ 则min ()a f x ≤2286(22)(3)()x x x x f x x x-+----'==当()0f x '>时,(22)(3)01304x x x x --<⎧⇒<<⎨<≤⎩当()0f x '<时,(22)(3)004x x x -->⎧⇒⎨<≤⎩01x <<或34x <≤ 所以函数()f x 在区间(0,1)和(3,4]上单调递减,在区间(1,3)上单调递增(1)0187,(4)6ln 41632166ln 4f f =-+==--+=-因为3166ln 4796ln 43(3ln16)3ln 016e --=-=-=>所以min ()7f x =所以7a ≤,a 的最大值为:7 故答案为:7 三、解答题14.(2020·贵州省贵阳一中高三月考)设,a b ∈R ,已知函数()2ln f x a x x bx =++存在极大值.(1)若2a =,求b 的取值范围;(2)求a 的最大值,使得对于b 的一切可能值,()f x 的极大值恒小于0. 【答案】(1)4b <-,(2)32e【解析】(1)当2a =,()()2220x bx f x x x++'=>,由()f x 存在极大值,可知方程2220x bx ++=有两个不等的正根,则2160,0,210,b b⎧∆=->⎪⎪->⎨⎪>⎪⎩∴4b <-.(2)()()220x bx af x x x++'=>,由()f x 存在极大值,可知方程220x bx a ++=有两个不等的正根, 设为12,x x 且12x x <,∴122a x x =,∴0a >,102ax <<. 由()120f x x x x '<⇒<<,∴()f x 的极大值为()21111ln f x a x x bx =++,∵2112bx x a =--,∴()2111ln f x a x x a =--,构造函数()2ln g x a x x a =--,当02a x <<时,()2220a a x g x x x x -'=-=>,所以()g x 在0,2a ⎛⎫ ⎪ ⎪⎝⎭上递增, 由102ax <<,则()1ln 3222a a a g x g ⎛⎫⎛⎫<=- ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以当302a e <≤时,()()()1102a f x f x g x g ⎛⎫==<≤ ⎪⎪⎝⎭极大值. 而当32a e >时,取332222a b e e -⎛⎫=-+ ⎪⎝⎭,即321x e =,3222a x e -=,此时()33202af x f e e ⎛⎫==-> ⎪⎝⎭极大值,不符合题意.综上所述,a 的最大值为32e .15.(2020·湖南省长沙一中高三月考)已知函数(R ).(1)当14a =时,求函数()y f x =的单调区间;(2)若对任意实数(1,2)b ∈,当(1,]x b ∈-时,函数()f x 的最大值为()f b ,求a 的取值范围.【答案】(Ⅰ)函数()f x 的单调递增区间为(1,0)-和(1,)+∞,单调递减区间为(0,1);(Ⅱ)[1ln 2,)-+∞ 【解析】(1)当14a =时,21()ln(1)4f x x x x =++-,则11(1)()1(1)122(1)x x f x x x x x -=+-=>-++', 令()0f x '>,得10x -<<或1x >;令()0f x '<,得01x <<, ∴函数()f x 的单调递增区间为(1,0)-和(1,)+∞,单调递减区间为(0,1). (2)由题意[2(12)]()(1)(1)x ax a f x x x -->-+'=,(1)当0a ≤时,函数()f x 在(1,0)-上单调递增,在(0,)+∞上单调递减,此时,不存在实 数(1,2)b ∈,使得当(1,]x b ∈-时,函数()f x 的最大值为()f b . (2)当0a >时,令()0f x '=,有10x =,2112x a=-, ①当12a =时,函数()f x 在(1,)-+∞上单调递增,显然符合题意. ②当1102a ->即102a <<时,函数()f x 在(1,0)-和1(1,)2a -+∞上单调递增, 在1(0,1)2a-上单调递减,()f x 在0x =处取得极大值,且(0)0f =, 要使对任意实数(1,2)b ∈,当(1,]x b ∈-时,函数()f x 的最大值为()f b , 只需(1)0f ≥,解得1ln 2a ≥-,又102a <<, 所以此时实数a 的取值范围是11ln 22a -≤<. ③当1102a -<即12a >时,函数()f x 在1(1,1)2a --和(0,)+∞上单调递增, 在1(1,0)2a-上单调递减,要存在实数(1,2)b ∈,使得当(1,]x b ∈-时, 函数()f x 的最大值为()f b ,需1(1)(1)2f f a-≤, 代入化简得1ln 2ln 2104a a ++-≥,① 令11()ln 2ln 21()42g a a a a =++->,因为11()(1)04g a a a =-'>恒成立, 故恒有11()()ln 2022g a g >=->,所以12a >时,①式恒成立,综上,实数a 的取值范围是[1ln 2,)-+∞.16.(2020·广西壮族自治区高二期末)已知函数()13ln 144f x x x x=-+- (1)求函数()f x 的单调区间;(2)设()224g x x bx =-+-,若对任意()[]120,2,1,2x x ∈∈,不等式()()12f x g x ≥恒成立,求实数b的取值范围.【答案】(1)函数()f x 在()1,3上单调递增;在()0,1和()3,+∞上单调递减; (2)⎛-∞ ⎝⎦.【解析】(1)()13ln 44f x x x x =-+的定义域是()0,+∞,()22211343444x x f x x x x-='-=-- 由0x >及()0f x '>得13x <<,由0x >及()0f x '<得01x <<或3x >; 所以函数()f x 在()1,3上单调递增;在()0,1和()3,+∞上单调递减.(2)若对任意()[]120,2,1,2x x ∈∈,不等式()()12f x g x ≥恒成立,问题等价于()()min max f x g x ≥ 由(1)可知,在()0,2上,1x =是函数极小值点,这个极小值是唯一的极值点 故也是最小值点,所以()()min 112f x f ==-,()[]224,1,2g x x bx x =-+-∈ 当1b <时,()()max 125g x g b ==-;当12b ≤≤,()()2max 4g x g b b ==- 当2b >时,()()248g x g b ==-问题等价于1{1252b b <-≥-或212{142b b ≤≤-≥-或2{1482b b >-≥- 解得1b <或12b ≤≤或b =∅即b ≤b的取值范围是⎛-∞ ⎝⎦. 17.(2020·浙江省学军中学高三期中)已知函数()2ln 2f x x ax bx =---,a R ∈.(1)当2b =时,试讨论()f x 的单调性;(2)若对任意的3,b e ⎛⎫∈-∞- ⎪⎝⎭,方程()0f x =恒有2个不等的实根,求a 的取值范围.【答案】(1)0a >,()f x 在⎛ ⎝⎭单调递增,⎫+∞⎪⎪⎝⎭单调递减; 0a =,()f x 在10,2⎛⎫ ⎪⎝⎭单调递增,1,2⎛⎫+∞ ⎪⎝⎭单调递减;102a -<<,()f x 在⎛ ⎝⎭单调递增,⎝⎭单调递减,24a ⎛⎫-+∞ ⎪ ⎪⎝⎭单调递增; 12a ≤-,()f x 在()0,∞+单调递增.(2)220a e <≤【解析】(1)()2122x ax f x x--'=,0x > (i )0a >,令()0f x '=,得到21220x ax --=,解得24x a -=,24x a-=(舍)所以当x ⎛∈ ⎝⎭时,()0f x '>,()f x 单调递增,当24x a ⎛⎫-+∈+∞ ⎪⎪⎝⎭时,()0f x '<,()f x 单调递减,所以()f x 在20,4a ⎛⎫-+ ⎪ ⎪⎝⎭单调递增,24a ⎛⎫-+∞ ⎪ ⎪⎝⎭单调递减; (ii )0a =,令()0f x '=,得到12x = 当10,2x ⎛⎫∈ ⎪⎝⎭时,()0f x '>,()f x 单调递增, 当1,2x ⎛⎫∈+∞⎪⎝⎭时,()0f x '<,()f x 单调递减,所以()f x 在10,2⎛⎫ ⎪⎝⎭单调递增,1,2⎛⎫+∞ ⎪⎝⎭单调递减; (iii )102a -<<,令()0f x '=,得到24x a -=,24x a-=当x ⎛⎫∈+∞ ⎪ ⎪⎝⎭⎝⎭U 时,()0f x '>,()f x 单调递增,当2244x a a ⎛-+-∈ ⎝⎭时,()0f x '<,()f x 单调递减,()f x 在⎛ ⎝⎭单调递增,⎝⎭单调递减,⎫+∞⎪⎪⎝⎭单调递增; (iiii )12a ≤-,()0f x '>在()0,∞+恒成立,所以()f x 在()0,∞+单调递增; 综上所述,0a >,()f x 在⎛ ⎝⎭单调递增,⎫+∞⎪⎪⎝⎭单调递减; 0a =,()f x 在10,2⎛⎫ ⎪⎝⎭单调递增,1,2⎛⎫+∞ ⎪⎝⎭单调递减;102a -<<,()f x 在⎛ ⎝⎭单调递增,⎝⎭单调递减,24a ⎛⎫-+∞ ⎪ ⎪⎝⎭单调递增; 12a ≤-,()f x 在()0,∞+单调递增.(2)因为对任意的3,b e ⎛⎫∈-∞- ⎪⎝⎭,方程()0f x =恒有2个不等的实根所以将问题等价于ln 2x ax b x-=+有两解 令()ln 2x g x x -=,0x >有()23ln xg x x -'=,0x >()30g e ∴=;()g x 在()30,e 递增,()3,e +∞递减;0x →,()g x →-∞;x →+∞,()0g x →;∴有图象知要使()ln 2x g x x-=的图像和y ax b =+的图像有两个交点, 0a >,过30,e ⎛⎫- ⎪⎝⎭作切线时,斜率a 最大.设切点为()00,x y ,有002003ln 2ln 5x x y x x x --=+, 002ln 53x x e-∴=-,0x e ∴= 此时斜率a 取到最大22e 220a e ∴<≤.。
专题07 函数中的双变量问题(学生版) -2025年高考数学压轴大题必杀技系列导数

专题7 函数中的双变量问题函数与导数一直是高考中的热点与难点, 近几年高考试卷及各地模拟试卷中常出现在函数背景下借组导数处理含有两个变量的等式与不等式问题,这类问题由于变量多,不少同学不知如何下手,其实如能以函数思想为指导,把双变量问题转化为一个或两个一元函数问题,再利用导数就可有效地加以解决.(一) 与函数单调性有关的双变量问题此类问题一般是给出含有()()1212,,,x x f x f x 的不等式,若能通过变形,把不等式两边转化为同源函数,可利用函数单调性定义构造单调函数,再利用导数求解.常见结论:(1)若对任意12,x x D Î,当12x x ¹时恒有()()12120f x f x x x ->-,则()y f x =在D 上单调递增;(2)若对任意12,x x D Î,当12x x ¹时恒有()()1212f x f x k x x ->-,则()y f x kx =-在D 上单调递增;(3)若对任意12,x x D Î,当12x x ¹时恒有()()121212f x f x kx x x x ->-,则()k y f x x =+在D 上单调递增;(4)若对任意12,x x D Î,当12x x ¹时恒有()()121212f x f x x x x x ->+-,则()2y f x x =-在D 上单调递增.【例1】(2024届四川省仁寿第一中学校高三上学期调研)已知函数212ln ()xf x x +=.(1)求()f x 的单调区间;(2)存在12,(1,)x x Î+¥且12x x ¹,使()()1212ln ln f x f x k x x -³-成立,求k 的取值范围.【解析】(1)由题意得()34ln xf x x -¢=,令()0f x ¢=得1x =,(01),x Î时,()0f x ¢>,()f x 在(0,1)上单调递增;,(1)x Î+¥时,()0f x ¢<,()f x 在(1,)+¥上单调递减;综上,()f x 单调递增区间为(0,1),单调递减区间为(1,)+¥.(2)由题意存在12,(1,)x x Î+¥且12x x ¹,不妨设121x x >>,由(1)知,(1)x Î+¥时,()f x 单调递减.()()1212ln ln f x f x k x x -³-等价于()()()2112ln ln f x f x k x x -³-,即()()2211ln ln f x k x f x k x +³+,即存在12,(1,)x x Î+¥且12x x >,使()()2211ln ln f x k x f x k x +³+成立.令()()ln h x f x k x =+,则()h x 在(1,)+¥上存在减区间.即234ln ()0kx x h x x-¢=<在(1,)+¥上有解集,即24ln x k x <在(1,)+¥上有解,即2max 4ln x k x æö<ç÷èø,(1,)x Î+¥;令()24ln x t x x =,(1,)x Î+¥,()()3412ln x t x x -¢=,(x Î时,()0t x ¢>,()t x在(上单调递增,)x ¥Î+时,()0t x ¢<,()t x在)+¥单调递减,∴max 2()e t x t ==,∴2ek <. (二) 与极值点有关的双变量问题与极值点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x ¢=的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数,此外若题中含有参数也可考虑把所给式子转化为关于参数的表达式.【例2】(2024届黑龙江省双鸭山市高三下学期第五次模拟)已知函数2()ln (1)(R)f x x a x a x=+-+Î.(1)当1a =-时,讨论()f x 的单调性;(2)若()1212,x x x x <是()f x 的两个极值点,证明:()()21f x f x -<【解析】(1)当1a =-时,2()ln 1,()f x x x f x x=+++的定义域为(0,)+¥,所以2222122(2)(1)()1x x x x f x x x x x¢+-+-=-+==,令()0f x ¢=,解得1x =,当(0,1)x Î时,()0f x ¢<,当(1,)x Î+¥时,()0f x ¢>,故()f x 在(0,1)上单调递减,在(1,)+¥上单调递增.(2)222122()ax x f x a x x x ¢-+-=--=,由题意可知,()1212,x x x x <是方程220ax x -+-=的两根,则102180a a ì>ïíïD =->î,解得108a <<,所以121x x a +=,122x x a =,要证()()21f x f x -<====即证()()22112122ln 1ln 1x a x x a x x x éù+-+-+-+êúëû只需证()()122211122lnx x x a x x x x x -+--<需证()()212211122ln2x x x a x x x x x -<-=++令21(1)x t t x =>,则需证2(1)ln 1t t t -<++,设()ln 1)g t t t =>,则2111111442222111(1)11222()02t t t t t t t g t t t tt---¢æö-ç÷----+èø=-==-<,所以函数()g t 在(1,)+¥上单调递减,所以()(1)0g t g <=,因此ln t <由1t >得,2(1)01t t ->+,所以2(1)ln 1t t t -<+,故()()21f x f x -<,【例3】(2023届云南省曲靖市高三下学期第二次联考)已知函数()()21ln 402f x x a x x a =+->.(1)当3a =时,试讨论函数()f x 的单调性;(2)设函数()f x 有两个极值点()1212,x x x x <,证明:()()12ln 10f x f x a +>-.【解析】(1)当3a =时,()213ln 42f x x x x =+-定义域为()0,x Î+¥,()()()2133434x x x x f x x x x x---+=+-==¢,令()0f x ¢=解得1x =或3,且当01x <<或3x >时,()0f x ¢>,当13x <<时,()0f x ¢<,所以当01x <<或3x >时,()f x 单调递增,当13x <<时,()f x 单调递减,综上()f x 在区间()0,1,()3,+¥上单调递增,()f x 在区间()1,3单调递减.(2)由已知()21ln 42f x x a x x =+-,可得()244a x x af x x x x-+=+-=¢,函数()f x 有两个极值点()1212,x x x x <,即240x x a -+=在()0,¥+上有两个不等实根,令()24h x x x a =-+,只需()()00240h a h a ì=>ïí=-<ïî,故04a <<,又124x x +=,12x x a =,所以()()221211122211ln 4ln 422f x f x x a x x x a x x æöæö+=+-++-ç÷ç÷èøèø()()()2212121214ln ln ln 82x x a x x x x a a a =-+++++=--,要证()()12ln 10f x f x a +>-,即证ln 8ln 10a a a a -->-,只需证()1ln 20a a a -+-<,令()()1ln 2m a a a a =-+-,()0,4a Î,则()11ln 1ln a m a a a a a-=-++=-¢,令()()n a m a ¢=,则()2110n a a a¢=--<恒成立,所以()m a ¢在()0,4a Î上单调递减,又()110m ¢=>,()12ln202m =-<¢,由零点存在性定理得,()01,2a $Î使得()00m a ¢=,即001ln a a =,所以()00,a a Î时,()0m a ¢>,()m a 单调递增,()0,4a a Î时,()0m a ¢<,()m a 单调递减,则()()()()0000000max 00111ln 2123m a m a a a a a a a a a ==-+-=-+-=+-,又由对勾函数知0013y a a =+-在()01,2a Î上单调递增,所以00111323022a a +-<+-=-<,所以()0m a <,即()()12ln 10f x f x a +>-得证.(三) 与零点有关的双变量问题与函数零点12,x x 有关的双变量问题,一般是根据12,x x 是方程()0f x =的两个根,确定12,x x 的关系,再通过消元转化为只含有1x 或2x 的关系式,再构造函数解题,有时也可以把所给条件转化为12,x x 的齐次式,然后转化为关于21x x 的函数,有时也可转化为关于12x x -的函数,若函数中含有参数,可考虑把参数消去,或转化为以参数为自变量的函数.【例4】(2024届四川省南充高中高三下学期月考)已知函数())ln 2f x x a =-ÎR .(1)讨论函数()f x 的单调性,并求()f x 的极值;(2)若函数()f x 有两个不同的零点12,x x (12x x <),证明:1e a<<.【解析】(1)函数()f x 的定义域为(0,)+¥,由题意,()1f x x ==¢,当0a £时,()0f x ¢>,函数()f x 在(0,)+¥单调递增,无极值.当0a >时,令()0f x ¢=,得21x a =∴()f x 在210,a æöç÷èø单调递增,在21,a ¥æö+ç÷èø单调递减,所以函数()f x 在21x a =时取极大值,极大值为212ln 2f a a æö=--ç÷èø,无极小值.x210,a æöç÷èø21a 21,a ¥æö+ç÷èø()f x ¢+-()f x 递增极大值递减(212t t ==,且12x x <,则有1122ln ln t at t at =ìí=î,两式相减可得,1212ln ln t t a t t-=-1a <.12121ln ln t t a t t-<=-12ln 0t t Û>,令u =121ln02ln 0(01)t u u u t u >Û-+><<,设()12ln g u u u u =-+,则()222212110u u g u u u u -+-=--=<¢,所以()g u 在()0,1上单调递减,所以()()10g u g >=1a<.1122ln ln t at t at =ìí=î,两式子相加得,()1212ln t t a t t =+e >,即证212e t t >,由上式只需证()122a t t +>,即证()1121212112221ln ln 2ln 201t t t t t t t t t t t t --×+>Û-<-+,令12t v t =,11212211ln 20ln 20(01)11t t t v v v t t v t --æö-<Û-<<<ç÷+èø+,设()()1ln 2011v h v v v v -æö=-<<ç÷+èø,则()22(1)0(1)v h v v v +¢-=>,所以()h v 在()0,1上单调递增,所以()()10h v h <=e >.综上:1e a<<. (四) 独立双变量,各自构造一元函数此类问题一般是给出两个独立变量,通过变形,构造两个函数,再利用导数知识求解.【例5】(2024届陕西省宝鸡实验高中高三一模)已知函数2()ln (,,1)x f x a x x a b a b R a =+--Î>,e 是自然对数的底数.(1)当e,4a b ==时,求整数k 的值,使得函数()f x 在区间(,1)k k +上存在零点;(2)若存在12,[1,1],x x Î-使得12|()()|e 1f x f x -³-,试求a 的取值范围.【解析】(1)2()e 4x f x x x =+--,()e 21x f x x ¢\=+-,(0)0f ¢\=当0x >时,e 1x >,()0f x ¢\>,故()f x 是(0,)+¥上的增函数,同理()f x 是(,0)-¥上的减函数,2(0)30,(1)e 40,(2)e 20f f f =-<=-<=->,且2x >时,()0f x >,故当0x >时,函数()f x 的零点在()1,2内,1k \=满足条件.同理,当0x <时,函数()f x 的零点在()2,1--内,2k \=-满足条件,综上1,2k =-.(2)问题Û当[1,1]x Î-时,max min max min |()()|()()e 1f x f x f x f x -=-³-,()ln 2ln 2(1)ln x x f x a a x a x a a ¢=+-=+-,①当0x >时,由1a >,可知10,ln 0,()0x a a f x ¢->>\>;②当0x <时,由1a >,可知10,ln 0,()0x a a f x ¢-<>\<;③当0x =时,()0f x ¢=,()f x \在[1,0]-上递减,[0,1]上递增,\当[1,1]x Î-时,min max ()(0),()max{(1),(1)}f x f f x f f ==-,而1(1)(1)2ln f f a a a--=--,设1()2ln (0),g t t t t t =-->22121()1(1)0g t t t t¢=+-=-³Q (仅当1t =时取等号),()g t \在(0,)+¥上单调递增,而(1)0g =,\当1t >时,()0g t >即1a >时,12ln 0a a a-->,(1)(1),(1)(0)e 1f f f f \>-\-³-即ln e 1e ln e a a -³-=-,构造()ln (1)h a a a a =->,易知()0¢>h a ,()h a \在(1,)+¥递增,e a \³,即a 的取值范围是[e,)+¥.(五) 构造一元函数求解双变量问题当两个以上的变元或是两个量的确定关系在解题过程中反复出现.通过变量的四则运算后,把整体处理为一个变量,从而达到消元的目的.【例6】(2024届山东省菏泽市高考冲刺押题卷)已知函数2()ln 1(02)f x tx x x t =-+<£.(1)求函数()f x 的单调区间(2)若0a b >>,证明:2244a b a b <-.【解析】(1)()ln 2,0f x t x t x x ¢=+->,令()()ln 2g x f x t x t x ¢==+-,所以()2,0tg x x x¢=->,由()0g x ¢>可得02t x <<,由()0g x ¢<可得2t x >,所以()f x ¢在(0,)2t 上单调递增,在(,)2t+¥上单调递减,所以max ()(ln ln 222t t tf x f t t t t ¢¢==+-=.又因为02t <£,所以ln02t£,即()0f x ¢£,且()f x ¢至多在一个点处取到0.所以()f x 在(0,)+¥上单调递减,故()f x 的单调递减区间为()0,+¥,没有单调递增区间.(2)证明2244a b a b <-,只需证:22222222222222+)))()11((ln 24(a b a b a b a b a b a b --<-++-,即证:2222222222222ln a b a b a b a b a b a b ++-<---+,令2222,0a b x a b a b +=>>-,所以1x >,只需证:12ln x x x<-,即证:22ln 10x x x -+<,由(1)知,当2t =时,2()2ln 1f x x x x =-+在(0,)+¥上单调递减,1x >()(1)0f x f <=,即22ln 10x x x -+<,所以2244a b a b<-.(六) 独立双变量,把其中一个变量看作常数若问题中两个变量没有明确的数量等式关系,有时可以把其中一个当常数,另外一个当自变量【例7】已知函数,(1)若函数在处的切线也是函数图像的一条切线,求实数a 的值;(2)若函数的图像恒在直线的下方,求实数a 的取值范围;(3)若,且,证明:>【解析】 (1),在处切线斜率,,所以切线,又,设与相切时的切点为,则斜率,则切线的方程又可表示为,由,解之得.(2)由题可得对于恒成立,即对于恒成立,令,则,由得,x20,e a æöç÷èø2e a2e a æö+¥ç÷èø,()h x ¢+0-()h x ↗极大值↘则当时,,由,得:,即实数的取值范围是.(3)由题知,由得,当时,,单调递减,因为,所以,即,所以,①同理,②①+②得,()ln (0)af x x a x=×>()e xg x =0x =()f x ()f x 10x y -+=12,(,)e 2a a x x Î12x x ¹412()x x +212a x x ()e xg x ¢=()g x 0x =()01k g ¢==()01g =:1l y x =+()ln1af x x =¢-l ()f x 000,ln a x x x æöç÷èø()00ln 1a k f x x ¢==-l ()000000ln 1ln ln 1a a ay x x x x x x x x æöæö=--+=-+ç÷ç÷èøèø00ln 111ax x ì-=ïíï=î2e a =()10f x x --<0x >ln 10ax x x--<0x >()ln 1a h x x x x =--()ln 2ah x x =¢-()0h x ¢=2ea x =0x >()22max 1e ea a h x h æö==-ç÷èø210e a -<20e a <<a ()20,e ()ln 1af x x=¢-()0f x ¢=e a x =e a x a <<()0f x ¢<()()ln 0af x x a x=>112x x x a +<<()()112f x f x x >+()112112ln ln a ax x x x x x >++121112lnln x x a a x x x x +>+122212ln ln x x a ax x x x +>+1212121212lnln ln x x x x a a ax x x x x x æöç÷èø>+++++因为,由得,即,所以,即,所以.(七) 双变量,通过放缩消元转化为单变量问题此类问题一般是把其中一个变量的式子放缩成常数,从而把双变量问题转化为单变量问题【例8】(2024届河北省衡水市高三下学期联合测评)过点(),P a b 可以作曲线e x y x =+的两条切线,切点为,A B .(1)证明:()1ea b a ->-;(2)设线段AB 中点坐标为()00,x y ,证明:00a y b x +>+.【解析】(1)证明:设切点(),e tA t t +,1e xy ¢=+,所以e 1e t tPAt bk t a+-=+=-,即关于t 的方程()1e 0tt a b a --+-=有两个不相等的实数根.设()()1e t f t t a b a =--+-,则()()e 0tf t t a =-=¢,t a =.当t a <时,()0f t ¢<,则()f t 在(),a ¥-上单调递减;当t a >时,()0f t ¢>,则()f t 在(),a ¥+上单调递增,所以()f t 在t a =处取值得最小值,即()e af a b a =--.当t ®+¥时,()f t ¥®+,当t ®-¥时,()f t b a ®-,若满足方程有两个不相等的实数根,则0e 0ab a b a ->ìí--<î,于是0e a b a <-<,即()ln b a a -<,得()()()ln b a b a b a a --<-,设()ln g x x x =,()ln 10g x x +¢==,得1ex =,在10,e æöç÷èø上,()0g x ¢<,则()g x 单调递减,在1,e ¥æö+ç÷èø上,()0g x ¢>,则()g x 单调递增,所以()ln g x x x =,在1e x =处取得最小值,即11e e g æö=-ç÷èø,所以()1e a b a ->-.(2)证明:设()()1122,,,A x y B x y ,则()()12012011e e 22x x y y y x =+=++,即()()12001211e e 22x x y x y y -=+=+,121221121224x x x x x x x x x x +++=++³12x x a +<121a x x +>12ln 0ax x >+1212ln ln 4ln a a a x x x x +>+421212a a x x x x æö>ç÷+èø()421212x x a x x +>在点()()1122,,,A x y B x y 处的切线方程都过(),P a b ,于是,由()()1111e 1e x xb x a x --=+-,得()1110e x b a x a --++=,由()()2222e 1e x xb x a x --=+-,得()2210e x b a x a --++=两式相减整理得:()121212e e e x x x x x x b a +--=-,()()()()1212121200e 1e ee e 2x x x x x x x x b a y x +----=-+-()()121212122212e e e 2e 2e e x x x x x x x x x x ++éù-=--êú-ëû()()1212121212e 12e e 2e e x x x x x x x x x x +--éù=--+êú-ëû,不妨设1212,0x x m x x >=->,所以()1212e 02e e x x x x +>-,则()12e e m mh m m =-+,()12e 220e m mh m ¢=--£-=,所以()h m 在()0,¥+上单调递减,于是()()00h m h <=,于是()()000b a y x ---<,即00a y b x +>+.【例1】(2024届陕西省西安市一中高三考前模拟)已知函数()2e 2xx f x a =++.(1)若4a =-,求()f x 的极值;(2)若0a >,不相等的实数,m n 满足()()228f m f n m n +=++,求证:0m n +<.【解析】(1)依题意,()2e 42x f x x =-+,则()2e 4xf x =¢-,令()0f x ¢=,解得ln 2x =,故当(),ln 2x ¥Î-时,()0f x ¢<,当()ln 2,x ¥Î+时,()0f x ¢>,故函数()f x 在(),ln 2¥-上单调递减,在()ln 2,¥+上单调递增,故函数()f x 的极小值为()ln 244ln 2264ln 2f =-+=-,无极大值;(2)令()()222e 2x g x f x x ax x =-=+-+,则()2e 2xg x x a =¢-+,令()e xt x x =-,则()e 1x t x ¢=-,当0x <时,()0t x ¢<,当0x >时,()0t x ¢>,所以函数()t x 在(),0¥-上单调递减,在()0,¥+上单调递增,所以()()e 010x t x x t =-³=>,又0a >,所以()()2e 0xg x x a =-+>¢,所以()g x 在R 上单调递增,()()228f m f n m n +=++,即()()8g m g n +=,因为()04g =,所以,0m n ¹,要证0m n +<,即证n m <-,只需证()()g n g m <-,即()()8g m g m -<-,即()()8g m g m +->,令函数()()()22e 2e 24x x h x g x g x x -=+-=+-+,则()2e 2e 4x x h x x -=--¢,令()()x h x j =¢,则()2e 2e 40xx x j -=-¢+³,所以()h x ¢为R 上的增函数,当0x <时,()()00h x h ¢¢<=,当0x >时,()()00h x h ¢¢>=,所以()h x 在(),0¥-上单调递减,在()0,¥+上单调递增,所以对任意0m ¹,都有()()()()08h m g m g m h =+->=,从而原命题得证.【例2】(2024届河北省衡水市部分示范性高中高三下学期三模)已知()e xf x x =-.(1)求()f x 的单调区间和最值;(2)定理:若函数()f x 在(,)a b 上可导,在[]a b ,上连续,则存在(,)a b x Î,使得()()()f b f a f ξb a-¢=-.该定理称为“拉格朗日中值定理”,请利用该定理解决下面问题:若0m n <<,求证:()2e e 111m n m n m n m æö-<+-ç÷èø.【解析】(1)()e 1x f x ¢=-,令()0f x ¢=,解得0x =,当(,0)x Î-¥时,()0,()¢<f x f x 单调递减;当,()0x Î+¥时,()0,()¢>f x f x 单调递增. 当0x =时,()f x 取得最小值1,无最大值;(2)要证2e e 11(1)m n m n m n m æö-<+-ç÷èø,只需证2e e (1)()m n m n m m n -<+-,因为0m n <<,故只需证2e e (1)m nm n m m n->+-. 令()e (0)x g x x x =>,显然()g x 在(,)m n 上可导,在[]m n ,上连续,故由拉格朗日中值定理知存在(,)m n x Î,使得e e()m nm n g m nx ¢-=-,而()(1)e 0,()x g x x g x ¢¢=+>在(0,)+¥上单调递增,因为m n x <<,故()()g g m x ¢¢>,即()(1)e m g m x ¢>+,故只需证2(1)e (1)m m m +³+即可,因为0m >,故只需证e 1m m ³+.由(1)知e 1x x ³+恒成立,因此原命题得证.【例3】(2024届天津市部分区高三二模)已知,R a b Î,函数()sin ln f x x a x b x =++.(1)当0,1a b ==-时,求()f x 的单调区间;(2)当1,02a b =-¹时,设()f x 的导函数为()f x ¢,若()0f x ¢>恒成立,求证:存在0x ,使得()01f x <-;(3)设01,0a b <<<,若存在()12,0,x x Î+¥,使得()()()1212f x f x x x =¹>.【解析】(1)由函数()sin ln f x x a x b x =++,可得其定义域为()0,¥+,当0,1a b ==-时,可得()ln f x x x =-,则()111x f x x x¢-=-=,当()0,1x Î时,可得()0f x ¢<,()f x 单调递减;当()1,x ¥Î+时,可得()0f x ¢>,()f x 单调递增,\函数()f x 的单调递增区间为()1,¥+,单调递减区间为()0,1.(2)当1,02a b =-¹时,可得()1sin ln 2f x x x b x =-+,则()11cos 2bf x x x =-+¢,Q ()0f x ¢>恒成立,即11cos 02b x x -+>恒成立,令()11cos ,02bh x x x x=-+>,若0b <,则0b x <,存在2b x =-,使得111cos 21cos 022222b b b h æöæöæö-=---=---<ç÷ç÷ç÷èøèøèø,即()0f x ¢<,不符合题意,>0b \,取30e bx -=,则001x <<,可得()3301esin e 312bb f x --=--<-,即存在0x ,使得()01f x <-.(3)由函数()sin ln f x x a x b x =++,可得()1cos bf x a x x ¢=++,设12x x <,由()()12f x f x =,可得111222sin ln sin ln x a x b x x a x b x ++=++,则()()()22121211sin sin ln ln lnx x x a x x b x x b x -+-=--=-,又由sin y x x =-,可得'1cos 0y x =-³,\函数sin y x x =-为单调递增函数,\2211sin sin x x x x ->-,即2121sin sin x x x x -<-,\()()2211ln1x b a x x x -<+-,设()1ln 21x h x x x -=-´+,可得()()()()222114011x h x x x x x -=-=+¢³+,\当1x >时,()()10h x h >=,即ln 2x >\2>即ln 4x =>\21ln 44x x >=代入可得:()()()()21411b a x x a ×-<+-=+,则()241b a -×<++,\>【例4】(2024届四川省百师联盟高三联考三)已知函数()214ln 2f x x x a x =-+.(1)当1a =时,求曲线()f x 在点()()1,1f 处的切线方程;(2)设函数()y f x =有两个不同的极值点1x ,2x .证明:()()2121135ln 244f x f x a a +--≥.【解析】(1)当1a =时()214ln 2x f x x x =-+,()14f x x x ¢=-+,()171422f =-=-,()14121f ¢=-+=-,则切线方程为()7212y x +=--,化简得4230x y ++=.(2)证明:由题()244a x x af x x x x=¢-+=-+,函数()f x 有两个极值点1x ,2x ,即240x x a -+=在()0,¥+上有两个不等实根,令()24h x x x a =-+,只需故()()00240h a h a ì=>ïí=-<ïî,故04a <<.又124x x +=,12x x a =,所以()()221211122211ln 4ln 422f x f x x a x x x a x x æöæö+=+-++-ç÷ç÷èøèø()()()2212121214ln ln ln 82x x a x x x x a a a =-+++++=--.若证()()2121135ln 244f x f x a a +--≥,即证21135ln 8ln 244a a a a a ----≥,即2113ln ln 0244a a a a a --++≥.令()2113ln ln 244x x x x x x j =--++,()0,4x Î,()11ln 2x x xx j æö¢=+-ç÷èø,则()x j ¢在()0,4上递增,且有()01j ¢=,当()0,1x Î时,()0x j ¢<,所以()x j 在()0,1上递减;当()1,4x Î时,()0x j ¢>,所以()x j 在()1,4上递增;所以()()113ln11ln101244x j j =--++=≥,()0,4x Î.即()()2121135ln 244f x f x a a +--≥得证.【例5】(2024陕西省西安八校高三下学期联考)已知函数的图象在处的切线过原点.(1)求的值;(2)设,若对总,使成立,求整数的最大值.【解析】(1)易知的定义域为,又,的图象在处的切线方程为,将代入,得;(2).当时,取得最小值,.由(1)知,.,得的定义域为.则,易知单调递增,又.即在上有唯一解,故.()()()e ln 1R ,xf x m x x m f x =-+-Î()()1,1f m ()()()2,2g x f x x h x x x a =-=-+()10,x ¥"Î+2x $ÎR ()1g x >()2h x a ()f x ()()0,,1e f ¥+=()()e 1,1e 1x mf x f m x¢¢=-+=-+()f x \()()1,1f ()()e e 11y m x -=-+-0,0x y ==1m =()222(1)1h x x x a x a =-+=-+-\1x =()h x ()()min []11h x h a ==-1m =()e ln 1x f x x x \=-+-()()e ln 1,x g x x g x =--()0,¥+()1e xg x x =¢-()1e 0xy x x=->()120,1e 102g g æö¢¢=-ç÷èø()0g x ¢=1,12æöç÷èø0x 000011e ,e x x x x ==于是当时,在上单调递减;当时,在上单调递增.在处取得极小值也是最小值.则,对总,使成立,只需,得.故整数的最大值为.1.(2024届广东省汕头市第二次模拟)设M 是由满足下列条件的函数()f x 构成的集合:①方程()0fx x-=有实根;②()f x 在定义域区间D 上可导,且()f x ¢满足()01f x ¢<<.(1)判断()ln 322x xg x =-+,()1,x Î+¥是否是集合M 中的元素,并说明理由;(2)设函数()f x 为集合M 中的任意一个元素,证明:对其定义域区间D 中的任意a 、b ,都有()()a b a b -£-f f .2.(2024届山东省滨州市高三下学期二模)定义:函数()f x 满足对于任意不同的12,[,]x x a b Î,都有()()1212f x f x k x x -<-,则称()f x 为[],a b 上的“k 类函数”.(1)若2()13x f x =+,判断()f x 是否为[]1,3上的“2类函数”;(2)若2()(1)e ln 2xx f x a x x x =---为[1,e]上的“3类函数”,求实数a 的取值范围;(3)若()f x 为[1,2]上的“2类函数”,且(1)(2)f f =,证明:1x ",2[1,2]x Î,()()121f x f x -<.3.(2024届辽宁省沈阳市第一二〇中学高三最后一卷)设函数()21ln 2f x x x x ax =--的两个极值点分别为()1212,x x x x <.(1)求实数a 的取值范围;(2)若不等式()12a x x l <+恒成立,求正数l 的取值范围(其中e 271828=L .为自然对数的底数).00x x <<()()0,g x g x ¢<()00,x 0x x >()()0,g x g x ¢>()0,x ¥+()g x \0x x =()000min 015e ln 112,2xg x x x x æö=--=+-Îç÷èø\()10,x ¥"Î+2x $ÎR ()()12g x h x >11a ³-2a £a 24.(2024届湖南省高三“一起考”大联考下学期模拟)已知函数()2f x ax =,()lng x x =,函数()f x ,()g x 有两条不同的公切线(与()f x ,()g x 均相切的直线)1l ,2l .(1)求实数a 的取值范围;(2)记1l ,2l 在y 轴上的截距分别为1d ,2d ,证明:121d d +<-.5.(2024届天津市民族中学高三下学期4月模拟)已知函数()()22ln 0f x x x a x a =-+>.(1)当2a =时,试求函数图象在点()()1,1f 处的切线方程;(2)若函数()f x 有两个极值点1x 、()212x x x <;(ⅰ)求a 的取值范围;(ⅱ)不等式()12f x mx ³恒成立,试求实数m 的取值范围.6.(2024届陕西省部分学校(菁师联盟)高三下学期5月份高考适应性考试)已知函数()2ln f x x x x =-.(1)求曲线()y f x =在2e x =处的切线方程;(2)若()()12f x f x =,且12x x <.求证:212e x x +<.7.(2024届广东省广州市二模)已知函数()()21e x f x a x x -=++.(1)讨论()f x 的零点个数;(2)若()f x 存在两个极值点,记0x 为()f x 的极大值点,1x 为()f x 的零点,证明:0122x x ->.8.(2024届重庆市名校联盟高三下学期全真模拟)T 性质是一类重要的函数性质,具有T 性质的函数被称为T 函数,它可以从不同角度定义与研究.人们探究发现,当()y f x =的图像是一条连续不断的曲线时,下列两个关于T 函数的定义是等价关系.定义一:若()y f x =为区间(),a b 上的可导函数,且()y f x ¢=为区间(),a b 上的增函数,则称()y f x =为区间(),a b 上的T 函数.定义二:若对()12,,x x a b "Î,()0,1l "Î,都有()()()()121211f x x f x f x l l l l éù+-£+-ëû恒成立,则称()y f x =为区间(),a b 上的T 函数.请根据上述材料,解决下列问题:(1)已知函数()πtan 02f x x x æö=Îç÷èø,,.①判断()y f x =是否为π0,2x æöÎç÷èø上的T 函数,并说明理由;②若π0,2a b æöÎç÷èø,且π22a b +=,求()()2f f a b +的最小值(2)设11111m n m n >>+=,,,当00a b >>,时,证明:11m na b ab m n+³.9.(2024届河南省九师联盟高三下学期5月联考)已知函数1()ln (0)f x a x a x=+¹.(1)若()f x a >对,()0x Î+¥恒成立,求a 的取值范围;(2)当3a =时,若关于x 的方程211()42f x x x b x =-++有三个不相等的实数根1x ,2x ,3x ,且1x <23x x <,求b 的取值范围,并证明:314x x -<.10.(2024届湖北省宜荆荆随恩高三5月联考)设函数,(1)讨论的单调性.(2)若函数存在极值,对任意的,存在正实数,使得(ⅰ)证明不等式.(ⅱ)判断并证明与的大小.11.(2024届江西省上饶市六校高三5月第二次联合考试)已知函数.(1)若,求的极值;(2)若,求的最大值.12.(2024届山西省临汾市高三下学期考前适应性训练)已知函数.(1)求在处的切线方程;(2)若曲线与直线有且仅有一个交点,求的取值范围;(3)若曲线在处的切线与曲线交于另外一点,求证:.13.(2024届江苏省扬州市仪征市四校高三下学期4月联合学情检测)已知函数.()()24ln 42f x x ax a x =-+-a ÎR()f x ()f x 120x x <<0x ()()()()21021f x f x f x x x ¢-=-212121ln ln 2x x x x x x ->-+122x x +0x ()()ln ,,0f x x a x b a b a =--ιR 1a b ==()f x ()0f x ³ab ()()21ln 12=++f x x x ()f x 0x =()y f x =y ax =a ()y f x =()()(),0m f m m >()y f x =()(),n f n 21mm n m -<<-+()()()ln 0f x mx x m =->(1)若恒成立,求的取值范围;(2)若有两个不同的零点,证明.14.(2024届河北省保定市高三下学期第二次模拟)已知函数为其导函数.(1)若恒成立,求的取值范围;(2)若存在两个不同的正数,使得,证明:.15.(2024届云南省高中毕业生第二次复习统一检测)已知常数,函数.(1)若,求的取值范围;(2)若、是的零点,且,证明:.()0f x £m ()f x 12,x x 122x x +>()ln ,()f x ax x x f x ¢=-()1f x £a 12,x x ()()12f x f x=0f ¢>0a >221()2ln 2f x x ax a x =--20,()4x f x a ">>-a 1x 2x ()f x 12x x ¹124x x a +>。
变量之间关系专项练习(含答案)

变量之间的关系专项练习一.选择题(共25小题)1.下列各图能表示y是x的函数是()A.B.C.D.2.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据(如下表):下列说法错误的是()A.在这个变化中,自变量是温度,因变量是声速B.温度越高,声速越快C.当空气温度为20C︒时,声音5s可以传播1740mD.当温度每升高10C︒,声速增加6/m s3.早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是()A.B.C.D.4.在下列各图象中,y不是x函数的是()A .B .C .D .5.在圆的周长2C R π=中,常量与变量分别是( ) A .2是常量,C 、π、R 是变量 B .2π是常量,C 、R 是变量C .C 、2是常量,R 是变量D .2是常量,C 、R 是变量6.弹簧挂上物体后会伸长,测得一弹簧的长度()y cm 与所挂的物体的质量()x kg 间有下面的关系:下列说法不正确的是( )A .x 与y 都是变量,且x 是自变量,y 是因变量B .所挂物体质量为4kg 时,弹簧长度为12cmC .弹簧不挂重物时的长度为0cmD .物体质量每增加1kg ,弹簧长度y 增加0.5cm7.下列各曲线表示的y 与x 的关系中,y 不是x 的函数的是( )A .B .C .D .8.以固定的速度0v (米/秒)向上抛一个小球,小球的高度h (米)与小球的运动的时间t (秒)之间的关系式是20 4.9h v t t =-,在这个关系式中,常量、变量分别为( ) A .4.9是常量,t 、h 是变量 B .0v 是常量,t 、h 是变量 C .0v 、 4.9-是常量,t 、h 是变量D .4.9是常量,0v 、t 、h 是变量9.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是()A.金额B.数量C.单价D.金额和数量10.小李家距学校3千米,中午12点他从家出发到学校,途中路过文具店买了些学习用品,12点50分到校.下列图象中能大致表示他离家的距离S(千米)与离家的时间t(分钟)之间的函数关系的是()A.B.C.D.11.均匀地向如图所示的容器中注满水,下列图象中,能反映在注水过程中水面高度h随时间t变化的函数关系的图象大致是()A.B.C.D.D次六安至汉口动车在金寨境内匀速通过一条隧道(隧道长大于火车长),12.如图,3081火车进入隧道的时间x与火车在隧道内的长度y之间的关系用图象描述大致是()A.B.C.D.13.某人要在规定的时间内加工100个零件,则工作效率η与时间t 之间的关系中,下列说法正确的是( ) A .数100和η,t 都是变量 B .数100和η都是常量 C .η和t 是变量D .数100和t 都是常量14.实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加,后10秒冲刺,中间速度保持不变,则跳绳速度v (个/秒)与时间t (秒)之间的函数图象大致为( )A .B .C .D .15.一个蓄水池有315m 的水,以每分钟30.5m 的速度向池中注水,蓄水池中的水量3()Q m 与注水时间t (分)间的函数表达式为( ) A .0.5Q t =B .15Q t =C .150.5Q t =+D .150.5Q t =-16.某批发市场对外批发某品脾的玩具,其价格与件数关系如图所示,请你根据图中描述判断:下列说法中错误的是( )A .当件数不超过30件时,每件价格为60元B .当件数在30到60之间时,每件价格随件数增加而减少C .当件数为50件时,每件价格为55元D .当件数不少于60件时,每件价格都是45元17.如图,下图是汽车行驶速度(千米/时)和时间(分)的关系图,下列说法其中正确的个数为( )(1)汽车行驶时间为40分钟;(2)AB 表示汽车匀速行驶;(3)在第30分钟时,汽车的速度是90千米/时;(4)第40分钟时,汽车停下来了.A.1个B.2个C.3个D.4个18.如图,是某蓄水池的横断面示意图,蓄水池分为深水区和浅水区,如果向这个蓄水池以固定的速度注水,下面能表示水的深度h与时间t的关系的图象大致是()A.B.C.D.19.匀速地向一个容器内注水,在注满水的过程中,水面的高度h与时间t之间的函数关系如图所示,则该容器可能是()A.B.C.D.20.弹簧挂重物会伸长,测得弹簧长度()x kg间有下面y cm最长为20cm,与所挂物体重量()的关系.下列说法不正确的是()A.x与y都是变量,x是自变量,y是因变量B.所挂物体为6kg,弹簧长度为11cmC.物体每增加1kg,弹簧长度就增加0.5cmD.挂30kg物体时一定比原长增加15cm21.某天,某同学早上8点坐车从余姚图书馆出发去宁波大学,汽车离开余姚图书馆的距离S(千米)与所用时间t(分)之间的函数关系如图所示.已知汽车在途中停车加油一次,则下列描述不正确的是()A.汽车在途中加油用了10分钟B.若//OA BC,则加满油以后的速度为80千米/小时C.若汽车加油后的速度是90千米/小时,则25a=D.该同学8:55到达宁波大学22.下列曲线反映了变量y随变量x之间的关系,其中y是x的函数的是() A.B.C.D.23.已知函数6(2)2(2)x xyx x-+⎧=⎨>⎩,则当函数值8y=时,自变量x的值是()A.2-或4B.4C.2-D.2±或4±24.正方形的边长为4,若边长增加x,那么面积增加y,则y关于x的函数表达式为() A.216y x=+B.2(4)y x=+C.28y x x=+D.2164y x=-25.下列关系中,y不是x的函数关系的是()A.长方形的长一定时,其面积y与宽xB.高速公路上匀速行驶的汽车,其行驶的路程y与行驶的时间xC.||y x=D.||y x=二.填空题(共3小题)26.甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程()S km 随时间t (分)变化的函数图象.以下说法: ①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时; ③乙走了8km 后遇到甲; ④乙出发6分钟后追上甲. 其中正确的有 (填所有正确的序号)27.圆周长C 与圆的半径r 之间的关系为2C r π=,其中变量是 ,常量是 . 28.某市出租车的收费标准是:3千米以内(包括3千米)收费5元,超过3千米,每增加1千米加收1.2元,则路程(3)x x 时,车费y (元)与路程x (千米)之间的关系式为: . 三.解答题(共10小题)29.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图. 根据图中提供的信息回答下列问题: (1)小明家到学校的路程是 米. (2)小明在书店停留了 分钟.(3)本次上学途中,小明一共行驶了 米.一共用了 分钟.(4)在整个上学的途中 (哪个时间段)小明骑车速度最快,最快的速度是 米/分.30.小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图. 根据图中提供的信息回答下列问题: (1)小明家到学校的路程是多少米?(2)在整个上学的途中哪个时间段小明骑车速度最快,最快的速度是多少米/分? (3)小明在书店停留了多少分钟?(4)本次上学途中,小明一共行驶了多少米?一共用了多少分钟?31.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.(1)填空:折线OABC表示赛跑过程中的路程与时间的关系,线段OD表示赛跑过程中的路程与时间的关系.赛跑的全程是米.(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)乌龟用了多少分钟追上了正在睡觉的兔子?(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?32.李大爷按每千克2.1元批发了一批黄瓜到镇上出售,为了方便,他带了一些零钱备用.他先按市场售出一些后,又降低出售.售出黄瓜千克数x与他手中持有的钱数y元(含备用零钱)的关系如图所示,结合图象回答下列问题:(1)李大爷自带的零钱是多少?(2)降价前他每千克黄瓜出售的价格是多少?(3)卖了几天,黄瓜卖相不好了,随后他按每千克下降1.6元将剩余的黄瓜售完,这时他手中的钱(含备用的钱)是530元,问他一共批发了多少千克的黄瓜?(4)请问李大爷亏了还是赚了?若亏(赚)了,亏(赚)多少钱?33.中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分,由于业务多,小明的爸爸打电话已超出了包月费. 下表是超出部分国内拨打的收费标准(1)这个表反映了哪两个变量之间的关系?哪个是自变量?(2)如果用x 表示超出时间,y 表示超出部分的电话费,那么y 与x 的表达式是什么? (3)如果打电话超出25分钟,需付多少电话费?(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?34.已知动点P 以每秒2cm 的速度沿如图甲所示的边框按从B C D E F A -----的路径移动,相应的ABP ∆的面积S 与关于时间t 的图象如图乙所示,若6AB cm =,求: (1)BC 长为多少cm ? (2)图乙中a 为多少2cm ? (3)图甲的面积为多少2cm ? (4)图乙中b 为多少s ?35.国家规定个人发表文章、 出版图书所得稿费的纳税计算方法是:①稿费不高于 800 元的不纳税;②稿费高于 800 元, 而低于 4000 元的应缴纳超过 800 元的那部分稿费的14%的税; ③稿费为 4000 元或高于 4000 元的应缴纳全部稿费的11%的税 . 试根据上述纳税的计算方法作答:(1) 若王老师获得的稿费为 2400 元, 则应纳税 元, 若王老师获得的稿费为 4000 元, 则应纳税 元;(2) 若王老师获稿费后纳税 420 元, 求这笔稿费是多少元?36.一列快车、一列慢车同时从相距300km 的两地出发,相向而行.如图,分别表示两车到目的地的距离()s km 与行驶时间()t h 的关系.(1)快车的速度为 /km h ,慢车的速度为 /km h ; (2)经过多久两车第一次相遇?(3)当快车到达目的地时,慢车距离目的地多远?37.如图,正方形ABCD 的边长为6cm ,动点P 从A 点出发,在正方形的边上由A B C D →→→运动,设运动的时间为()t s ,APD ∆的面积为2()S cm ,S 与t 的函数图象如图所示(1)求点P在BC上运动的时间范围;(2)当t为何值时,APD的面积为210cm.38.为响应教育局组织的三热爱教育活动,某学校要给每位学生印制一份宣传资料,甲印刷厂提出:每份收0.1元印刷费,另收100元制版费;乙印刷厂提出:每份收0.2元印刷费,不收制版费.(1)分别写出两厂的收费y甲(元)、y乙(元)与印制数量x(本)之间的关系式;(2)当印制多少份资料时,两个印刷厂费用一样多?(3)如果该校有800人,那么应选哪家印刷厂划算?变量之间的关系专项练习一.选择题(共25小题)1.【解答】解:A 、对于x 的每一个取值,y 有时有两个确定的值与之对应,所以y 不是x 的函数,故A 选项错误;B 、对于x 的每一个取值,y 有时有两个确定的值与之对应,所以y 不是x 的函数,故B 选项错误;C 、对于x 的每一个取值,y 有时有两个确定的值与之对应,所以y 不是x 的函数,故C 选项错误;D 、对于x 的每一个取值,y 都有唯一确定的值与之对应关系,所以y 是x 的函数,故D 选项正确.故选:D .2.【解答】解:在这个变化中,自变量是温度,因变量是声速,∴选项A 正确;根据数据表,可得温度越高,声速越快,∴选项B 正确;34251710()m ⨯=,∴当空气温度为20C ︒时,声音5s 可以传播1710m ,∴选项C 错误;3243186(/)m s -=,3303246(/)m s -=,3363306(/)m s -=,3423366(/)m s -=,3483426(/)m s -=,∴当温度每升高10C ︒,声速增加6/m s ,∴选项D 正确.故选:C .3.【解答】解:由题意可得,小明从家出发到妈妈发现小明的作业本落在家里这段时间,y 随x 的增大而增大, 小明的妈妈开始给你小明送作业到追上小明这段时间,y 随x 的增大而减小, 小明妈妈追上小明到各自继续行走这段时间,y 随x 的增大不变,小明和妈妈分别去学校、回家的这段时间,y 随x 的增大而增大,故选:B .4.【解答】解:函数的一个变量不能对应两个函数值,故选:C .5.【解答】解:在圆的周长公式2C r π=中,C 与r 是改变的,π是不变的; ∴变量是C ,r ,常量是2π.故选:B .6.【解答】解:A .x 与y 都是变量,且x 是自变量,y 是因变量,故A 正确; B .所挂物体质量为4kg 时,弹簧长度为12cm ,故B 正确;C .弹簧不挂重物时的长度为10cm ,故C 错误;D .物体质量每增加1kg ,弹簧长度y 增加0.5cm ,故D 正确.故选:C .7.【解答】解:根据函数的意义可知:对于自变量x 的任何值,y 都有唯一的值与之相对应,所以只有选项C 不满足条件.故选:C .8.【解答】解:20 4.9h v t t =-中的0v (米/秒)是固定的速度, 4.9-是定值,故0v 和 4.9-是常量,t 、h 是变量,故选:C .9.【解答】解:常量是固定不变的量,变量是变化的量,单价是不变的量,而金额是随着数量的变化而变化,故选:C .10.【解答】解:小李距家3千米,∴离家的距离随着时间的增大而增大,途中在文具店买了一些学习用品,∴中间有一段离家的距离不再增加,综合以上C 符合,故选:C .11.【解答】解:最下面的容器较细,第二个容器最粗,那么第二个阶段的函数图象水面高度h 随时间t 的增大而增长缓慢,用时较长,最上面容器最大,那么用时最长.故选:A .12.【解答】解:根据题意可知火车进入隧道的时间x 与火车在隧道内的长度y 之间的关系具体可描述为:当火车开始进入时y 逐渐变大,火车完全进入后一段时间内y 不变,当火车开始出来时y 逐渐变小,故反映到图象上应选A .故选:A .13.【解答】解:某人要在规定的时间内加工100个零件,则工作效率η与时间t 之间的关系中:η和t 是变量,零件的个数100是常量.故选:C .14.【解答】解:随着时间的变化,前20秒匀加速进行,所以此时跳绳速度y 随时间x 的增加而增加,再根据20秒至50秒保持跳绳速度不变,所以此时跳绳速度y 随时间x 的增加而不变,再根据后10秒继续匀加速进行,所以此时跳绳速度y 随时间x 的增加而增加,故选:C .15.【解答】解:一个蓄水池有315m 的水,以每分钟30.5m 的速度向池中注水, ∴蓄水池中的水量3()Q m 与注水时间t (分)间的函数表达式是:150.5Q t =+,故选:C .16.【解答】解:由图象可得,当件数不超过30件时,每件价格为60元,故选项A 正确,当件数在30到60之间时,每件价格随件数增加而减少,故选项B 正确,当件数为50件时,每件价格为:604560(5030)506030--⨯-=-(元),故选项C 错误, 当件数不少于60件时,每件价格都是45元,故选项D 正确,故选:C .17.【解答】解:读图可得,在40x =时,速度为0,故(1)(4)正确;AB 段,y 的值相等,故速度不变,故(2)正确;30x =时,80y =,即在第30分钟时,汽车的速度是80千米/时;故(3)错误; 故选:C .18.【解答】解:根据题意和图形的形状,可知水的最大深度h 与时间t 之间的关系分为两段,先快后慢.故选:C .19.【解答】解:相比较而言,前一个阶段,用时较少,高度增加较快,那么下面的物体应较细.由图可得上面立方体的体积应大于下面立方体的体积.故选:D .20.【解答】解:A 、正确.x 与y 都是变量,x 是自变量,y 是因变量;B 、正确.所挂物体为6kg ,弹簧长度为11cm ;C 、正确.物体每增加1kg ,弹簧长度就增加0.5cm ;D 、错误,弹簧长度最长为20cm ;故选:D .21.【解答】解:A 、图中加油时间为25至35分钟,共10分钟,故本选项正确;B 、因为//OA BC ,所以602520a a -=,解得1003a =,所以加满油以后的速度1003802560==千米/小时,故本选项正确.C 、由题意:60902060a -=,解得30a =,本选项错误. D 、该同学8:55到达宁波大学,正确.故选:C .22.【解答】解:对于x 的每一个取值,y 都有唯一确定的值,A 、对于x 的每一个取值,y 都有两个值,故A 错误;B 、对于x 的每一个取值,y 都有两个值,故B 错误;C 、对于x 的每一个取值,y 都有两个值,故C 错误;D 、对于x 的每一个取值,y 都有唯一确定的值,故D 正确;故选:D .23.【解答】解:把8y =代入函数6(2)2(2)x x y x x -+⎧=⎨>⎩, 先代入上边的方程得2x =-,2x ,故2x =-;再代入下边的方程4x =,2x >,故4x =,综上,x 的值为4或2-.故选:A .24.【解答】解:新正方形边长是4x +,原正方形边长是4,∴新正方形面积是2(4)x +,原正方形面积是16,∴增加的面积2(4)16y x =+-即28y x x =+故选:C .25.【解答】解:A 、对于x 的每一个取值,y 都有唯一确定的值,故A 正确; B 、对于x 的每一个取值,y 都有唯一确定的值,故B 正确;C 、对于x 的每一个取值,y 都有唯一确定的值,故C 正确;D 、对于x 的每一个取值,y 没有唯一确定的值,故D 错误;故选:D .二.填空题(共3小题)26.【解答】解:①乙在28分时到达,甲在40分时到达,所以乙比甲提前了12分钟到达;故①正确;②根据甲到达目的地时的路程和时间知:甲的平均速度40101560=÷=千米/时;故②正确; ④设乙出发x 分钟后追上甲,则有:1010(18)281840x x ⨯=⨯+-,解得6x =,故④正确; ③由④知:乙第一次遇到甲时,所走的距离为:10662818km ⨯=-,故③错误; 所以正确的结论有三个:①②④,故答案为:①②④.27.【解答】解:在圆的周长公式2C r π=中,C 与r 是改变的,π是不变的; ∴变量是C ,r ,常量是2π.故答案为:C ,r ;2π.28.【解答】解:根据题意得出:当03x <时,5y =当3x >时,5(3) 1.2y x =+-⨯5 1.2 3.6x =+-1.2 1.4x =+,故答案为: 1.2 1.4y x =+.三.解答题(共10小题)29.【解答】解:(1)y 轴表示路程,起点是家,终点是学校,∴小明家到学校的路程是1500米.(2)由图象可知:小明在书店停留了4分钟.(3)150060022700+⨯=(米)即:本次上学途中,小明一共行驶了 2700米.一共用了 14分钟.(4)折回之前的速度12006200=÷=(米/分)折回书店时的速度(1200600)2300=-÷=(米/分),从书店到学校的速度(1500600)2450=-÷=(米/分)经过比较可知:小明在从书店到学校的时候速度最快即:在整个上学的途中 从12分钟到14分钟小明骑车速度最快,最快的速度是 450 米/分30.【解答】解:(1)根据图象,学校的纵坐标为1500,小明家的纵坐标为0, 故小明家到学校的路程是1500米;(2)根据图象,1214x 时,直线最陡,故小明在1214-分钟最快,速度为15006004501412-=-米/分. (3)根据题意,小明在书店停留的时间为从8分到12分,故小明在书店停留了4分钟.(4)读图可得:小明共行驶了12006009002700++=米,共用了14分钟.31.【解答】解:(1)乌龟是一直跑的而兔子中间有休息的时刻;∴折线OABC 表示赛跑过程中兔子的路程与时间的关系;线段OD 表示赛跑过程中乌龟的路程与时间的关系;由图象可知:赛跑的路程为1500米;故答案为:兔子、乌龟、1500;(2)结合图象得出:兔子在起初每分钟跑700米.15003050÷=(米)乌龟每分钟爬50米.(3)7005014÷=(分钟)乌龟用了14分钟追上了正在睡觉的兔子.(4)48千米48000=米4800060800∴÷=(米/分)(1500700)8001-÷=(分钟)300.51228.5+-⨯=(分钟)兔子中间停下睡觉用了28.5分钟.32.【解答】解:(1)由图可得农民自带的零钱为50元.(2)(41050)100-÷360100=÷3.6=(元).答:降价前他每千克黄瓜出售的价格是3.6元;(3)(530410)(3.6 1.6)-÷-1202=÷60=(千克), 10060160+=(千克). 答:他一共批发了160千克的黄瓜;(4)530160 2.150144-⨯-=(元).答:李大爷一共赚了144元钱.33.【解答】解:(1)国内拨打时间与电话费之间的关系,打电话时间是自变量、电话费是因变量;(2)由题意可得:0.36y x =;(3)当25x =时,0.36259y =⨯=(元),即如果打电话超出25分钟,需付1869195+=(元)的电话费;(4)当54y =时,541500.36x ==(分钟). 答:小明的爸爸打电话超出150分钟.34.【解答】解:(1)由图象可得,点P 从点B 到点C 运动的时间是4s ,运动的速度是每秒2cm ,故BC 的长度是:428cm ⨯=,即BC 长是8cm ;(2)8BC cm =,6AB cm =,2862422BC AB S cm ⨯∴===, 即图乙中a 的值为224cm ;(3)由图可知, 428BC cm =⨯=,(64)24CD cm =-⨯=,(96)26DE cm =-⨯=,6AB cm =, 14AF BC DE cm ∴=+=,∴图甲的面积是:261446842460AB AF CD DE cm ⋅-⋅=⨯-⨯=-=;(4)由题意可得,846(64)(68)1722BC CD DE EF FA b s +++++++-++===, 即b 的值是17s . 35.【解答】解: (1) 若王老师获得的稿费为 2400 元, 则应纳税 224 元, 若王老师获得的稿费为 4000 元, 则应纳税 440 元;(2) 因为王老师纳税 420 元, 所以由 (1) 可知王老师的这笔稿费高于 800 元, 而低于 4000 元,设王老师的这笔稿费为x 元, 根据题意得:14%(800)420x -=3800x =元 .答: 王老师的这笔稿费为 3800 元 .36.【解答】解:(1)快车的速度为2030045/3km h ÷=,慢车的速度为3001030/km h ÷=, 故答案为:45,30;(2)30044530h =+ 答:经过4h 两车第一次相遇; (3)20(10)301003km -⨯=, 答:当快车到达目的地时,慢车距离目的地多100km .37.【解答】解:(1)根据图象得:点P 在BC 上运动的时间范围为612t ;(2)点P 在AB 上时,APD ∆的面积1632S t t =⨯⨯=; 点P 在BC 时,APD ∆的面积166182=⨯⨯=; 点P 在CD 上时,62(12)302PD t t =--=-,APD ∆的面积116(302)90622S AD PD t t =⋅=⨯⨯-=-; ∴当06t 时,3S t =,APD ∆的面积为210cm ,即10S =时,310t =,103t =, 当1215t 时,90610t -=,403t =, ∴当t 为103s 或403s 时,APD ∆的面积为210cm . 38.【解答】解:(1)0.1100y x =+甲,0.2y x =乙;(2)由题意得:y y =乙甲,0.11000.2x x ∴+=解之得:1000x =答:当印刷1000份时,两个印刷厂费用一样多.(3)当800x =时,0.1800100180y =⨯+=甲;0.2800160y =⨯=乙; 180160>∴选择乙印刷厂划算.。
第13讲 双变量问题(解析版)

第13讲 双变量问题参考答案与试题解析一.选择题(共5小题)1.(2021•海淀区校级月考)若2233x y x y ---<-,则( ) A .(1)0ln y x -+>B .(1)0ln y x -+<C .||0ln xy >D .||0ln xy <【解答】解:若2233x y x y ---<-,即112233x yx y-<-, 由于函数1()23x xf x =-是R 上的增函数,且()()f x f y <,x y ∴<,11y x ∴-+>,(1)1ln y x -+>,故A 正确、B 错误,由于不能得出||xy 与1的大小关系,故不能确定C 、D 是否正确, 故选:A .2.(2021•全国月考)已知实数x ,y 满足22log log y x x e y e --+<+,则下列结论一定正确的是( ) A .x y >B .||0ln x y -<C .|1|0ln x y -+>D .|1|0ln y x -+>【解答】解:实数x ,y 满足22log log y x x e y e --+<+,则22log log x y x e y e ---<-, 再根据2()log x f x x e -=-为(0,)+∞上的增函数,x y ∴<, 11y x ∴-+>,|1|0ln y x ∴-+>,故选:D .3.(2021•鼓楼区校级二模)已知α,(0,)βπ∈,αβ≠,若cos 2cos e e αβαβ-=-,则下列结论一定成立的是( ) A .sin sin αβ<B .cos cos αβ<C .sin sin αβ>D .cos cos αβ>【解答】解:构造函数()cos x f x e x =-,(0,)x π∈,则()sin 0x f x e x '=+>,∴函数()f x 在(0,)π上单调递增,又cos 2cos e e αβαβ-=-,即cos cos cos e e αβαββ-=--,亦即()()cos f f αββ=-, ①当,(0,)2παβ∈时,cos 0β>,则()()f f βα>,βα∴>;②当,(,)2παβπ∈时,cos 0β<,则()()f f βα<,αβ∴>;又函数sin y x =在(0,)2π单调递增,在(,)2ππ单调递减,故由①②可知,选项A 一定成立. 故选:A .4.(2021春•顺义区期末)已知函数()x f x e =,2()g x x ax =-+(其中)a R ∈.对于不相等的实数1x ,2x ,设1212()()f x f x m x x -=-,1212()()g x g x n x x -=-,给出下列三个结论:①对于任意不相等的实数1x ,2x ,都有0m >;②对于任意的a 及任意不相等的实数1x ,2x ,都有0n <; ③对于任意的a ,存在不相等的实数1x ,2x ,使得m n =. 其中,所有正确结论的序号是( ) A .①B .①③C .②③D .①②③【解答】解:对于①,由于1e >,由指数函数的单调性可得()f x 在R 上递增,即有0m >,则①正确;对于②,由二次函数的单调性可得()g x 在(,)2a -∞-递减,在(2a-,)+∞递增,则0n >不恒成立,则②错误;对于③,由m n =,可得1212()()()()f x f x g x g x -=-,即为1122()()()()g x f x g x f x -=-, 考查函数2()x h x x ax e =-+-,()2x h x x a e '=-+-,当a →-∞,()h x '小于0,()h x 单调递减,则③错误;故选:A .5.(2021•龙凤区校级月考)已知0a <,不等式1?0a x x e alnx ++对于任意(1,)x ∈+∞恒成立,则a 的取值范围是( ) A .[e -,1]-B .[e -,0)C .(,1)-∞-D .(-∞,]e -【解答】解:不等式1?0a x x e alnx ++对于任意(1,)x ∈+∞恒成立, 则()()()a a x xa a a ln x aalnx x xe alnx xe x ln x ln x e x-----⋅-⇔=⋅=⋅⋯⋯①对于任意1x >恒成立, 令()x f x xe =,则()(())a f x f ln x -在1x >时恒成立,因为()(1)0x f x e x '=+>在(1,)-+∞恒成立,故()f x 在(1,)-+∞上单调递增,而()0a ln x ->, 故①式即为()a x ln x alnx -=-在(1,)+∞上恒成立,即xa lnx-⋯⋯②在(1,)+∞上恒成立, 令()xg x lnx=,1x >,令21()0()lnx g x lnx -'==得x e =,当(1x ∈,)()0e g x '<;当(,)x e ∈+∞时,()0g x '>,故()g x 在(1,)e 上单调递减,在(,)e +∞上单调递增,故()min g x g =(e )e =,要使②式成立,只需a e -,即0e a -<. 故选:B .二.多选题(共1小题)6.(2021•武进区校级期中)已知正实数x ,y 满足21211log log ()()22x y x y +<-,则下列结论正确的是( ) A .11x y< B .33x y < C .(1)0ln y x -+> D .122x y -<【解答】解:正实数x ,y 满足21211log log ()()22x y x y +<-,22log 2log 2x y x y --∴-<-.令2()log 2x f x x -=-,则2()log 2y f y y -=-,则()()f x f y <. 函数()f x 在(0,)+∞上单调递增,故由()()f x f y <可得0x y <<,∴11x y>,故A 错误; 33x y ∴<,故B 正确;11y x ∴-+>,(1)10ln y x ln ∴-+>=,故C 正确;根据0221x y -<=,故D 不一定正确, 故选:BC .三.解答题(共45小题)7.(2021•扬州月考)已知函数3()()x f x x ke k R =+∈,()f x '为()f x 的导函数. (1)当1k =时,求函数3()()2()2g x xf x f x x x '=--++的单调区间; (2)当0k 时,求证:对任意的1x ,2x R ∈,且12x x >,有121212()()()()2f x f x f x f x x x -'+'<-. 【解答】解:(1)当1k =时,3()x f x x e =+,2()3x f x x e '=+,则3()()2()222x x g x xf x f x x x xe e x ='--++=-++, 求导,()21(1)1x x x x g x e xe e x e '=+-+=-+, 令()(1)1x x x e ϕ=-+,()x x xe ϕ'=,所以当(,0)x ∈-∞时,()0x ϕ'<,()x 单调递减, 当(0,)x ∈+∞时,()0x ϕ'>,()x ϕ单调递增, 所以,当0x =时,()(0)0min x ϕϕ==, 则()0x ϕ,即()0g x ',故()g x 的单调递增区间为(,)-∞+∞.(2)证明:因为3()x f x x ke =+,则2()3x f x x ke '=+.要证:121212()()()()2f x f x f x f x x x -'+'<-,即证12123322121212332x x x x x ke x ke x ke x ke x x +--+++<-, 又12x x >,所以12123322121212123()()220x x x x x x e e x x k e e k x x x x --+++-⨯-⨯>--, 即证1212122121212()[()2]0x x x x x x e e e e x x k x x x x e e +--+⨯--⨯>-+,(*) 令12t x x =-,则0t >, 所以12121212121211(1)2(1)(2)2()2()221111x x x x t t t t x x x x t t t e e e e t e e t e t x x x x t e e e e e e -----+---++--⨯=--⨯=-⨯==+++++,又(1)可知,()(2)2x g x x e x =-++,在(,)-∞+∞上单调递增,有(0)0g =. 所以,当0x >,()0g x >,即当0t >,(2)20t t e t -++>, 所以,121212()20x x x x e e x x e e ---⨯>+,则(*)成立,故原不等式成立.8.(2021•浙江月考)已知0a >且1a ≠,函数()(0)a x f x x a x =->. (Ⅰ)当2a =时,设()f x 的导函数()f x ',求()f x '的单调区间; (Ⅱ)若函数()y f x =恰有两个互异的零点m ,(0)n m n >>. (ⅰ)求实数a 的取值范围; (ⅱ)求证:2mn e >.【解答】解:(Ⅰ)当2a =时,2()2x f x x =-,()222x f x x ln '=-,2()2(2)2f x ln ''=-x , 令()0f x ''=,即22(2)2ln -0x =,解得222(2)x log ln =, 因为2()2(2)2f x ln ''=-x 单调递减, 当222(2)x log ln 时,()0f x '',所以()f x '在222[,)(2)log ln +∞单调递减, 当2220(2)x log ln <<时,()0f x ''>,所以222()(0,)(2)f x log ln '单调递增; (Ⅱ)(ⅰ)由()0a x f x x a =-=,则x a a x =,xlna alnx =,所以lnx lnax a=, 设函数()lnxg x x=,则21()lnx g x x -'=,()0g x '=,解得x e =, 在(0,)e 内()0g x '>,()g x 单调递增;在(,)e +∞上()0g x '<,()g x 单调递减;所以,1()()max g x g e e==, 又g (1)0=,当x 趋近于+∞时,()g x 趋近于0, 函数()y f x =恰有两个互异的零点m ,n 充分必要是10lna a e<<, 这即是0g <(a )g <(e ),所以a 的取值范围是(1,)(e e ⋃,)+∞; (ⅱ)证明:所以lnm lnnm n=,即()()g m g n =, 又(ⅰ)可知,()g x 在(0,)e 上单调递增,在(,)e +∞上单调递减,且g (1)0=,则1n e m <<<, 要证2mn e >,即证2e m e n >>,即证2()()e g m g n <,即证2()()e g n g n <,即证:2(2)lnn n lnn n e -<,由1n e <<,即01lnn <<,即证2222e lnn n n lnn <-, 令222()2(1)G x e lnx x x lnx x e =-+<<, 则22()()()42()2(1)2(1)e e e x e x G x x xlnx x x x lnx x lnx x x x+-'=-++=-+-=+-,则222()[2(1)]e x G x x lnx x -'=+-,设222()2(1)e x h x lnx x -=+-,因为1x e <<,22233222()()0e x e h x x x x -'=-+=<,所以,()h x h >(e )0=,即()()0G x xh x '=>, ()0G x '>恒成立,所以()G x 在(1,)e 单调递增,所以()G x G <(e )0=,在(1,)x e ∈恒成立, 所以2mn e >.9.(2021•南平月考)已知函数.(1)求f (x )的单调区间与极值.(2)设m ,n 为两个不相等的正数,且mlnn ﹣nlnm =m ﹣n ,证明:mn >e 4. 【解答】解:(1)∵f ′(x )==,当x ∈(﹣∞,2)时,f ′(x )>0,f (x )单调递增, 当x ∈(2,+∞)时,f ′(x )<0,f (x )单调递减,∴当x =2时,f (x )取得极大值,综上,f (x )的单调递增区间为(﹣∞,2),递减区间为(2,+∞),极大值为,无极小值;(2)证明:由(1)知,x →﹣∞时,f (x )→﹣∞,x →+∞时,f (x )→0+, ∴f (x )∈(﹣∞,],由mlnn ﹣nlnm =m ﹣n 得=,又f (lnm )==,同理,f (lnn )=,∴lnm 与lnn 是f (x )=t (0<t <)的两个正根,其中0<lnm <2,lnn >2,4﹣lnn ∈(0,2), 要证明mn >e 4,只需证明:lnm +lnn >4,即证lnm >4﹣lnn , 又f (x )在(0,2)单调递增,∴只需证f (lnm )=f (lnn )>f (4﹣lnn ), 令h (x )=f (x )﹣f (4﹣x )(x >2), 则h ′(x )=f ′(x )+f ′(4﹣x )=+=(2﹣x )(﹣)>0,∴h (x )=f (x )﹣f (4﹣x )>h (2)=f (2)﹣f (2)=0, ∴f (x )>f (4﹣x ),即结论成立.10.(2021•广州月考)已知函数2()(1)x f x e a x =--. (1)讨论函数()f x 的单调性;(2)若0a >,设()f x '为()f x 的导函数,若函数()f x 有两个不同的零点1x ,2x ,求证:12()02x x f +'<. 【解答】(1)解:2()2x f x e a '=-,当0a 时,()0f x '>,函数()f x 在R 上单调递增;当0a >时,令()0f x '>,得122a x ln >,令()0f x '<,得122a x ln <,所以()f x 在1(,)22a ln -∞上单调递减,在1(22aln ,)+∞上单调递增.(2)证明:由题意得122122(1)0(1)0x x e a x e a x ⎧--=⎪⎨--=⎪⎩,两式相减得212221x x e e a x x -=-,不妨设12x x <,由2()2x f x e a'=-,得21121212212212212121()2[2()]2x x x x x x x x x x x x e e e f e x x e e x x x x ++--+-'=-=-+---,令21t x x =-,()2t t h t t e e -=-+,因为当0t >时,()22()0t t t t h t e e e e --'=--=-+<, 所以()h t 在(0,)+∞上单调递减, 所以当0t >时,()(0)0h t h <=,又12210x x e x x +>-,故12()02x xf +'<. 11.(2021•和平区校级开学)已知函数()f x lnx =.(Ⅰ)若()f x 在1x x =,212()x x x ≠; (Ⅱ)在(Ⅰ)的条件下,证明:12()()882f x f x ln +>-;(Ⅲ)若342a ln -,证明:对于任意0k >,直线y kx a =+与曲线()y f x =有唯一公共点.【解答】解:(Ⅰ)1()f x x '=-1211x x =-1211x x =-=;4122x x >则4122x x 得12256x x>,则1212()()f x f x lnx x +=设12256t x x =>,()g t lnt =,()0g t '=>,()g t 在(256,)+∞上单调递增,所以()(256)882g t g ln >=-, 所以12()()882f xf x ln +>-;(Ⅲ)记()()(0)h x f x kx a kx lnx a x =--=-->,()h x '=,令t =,记2()22q t kt t =-+,则△116k =-, ①当116k 时,()0q t ,有()0hx ',()h x kx >,21x k <;当0lnx a +<,所以取021{x min k =,}a e -时,有()0h x,又221()(1(1)0a a e h e ln k k-+=+<,所以()0h x =有唯一零点.②当116k<<时,△0>,令()0h x'=,解得21x=,22x=,则当20x <<和2x>时,()h x单调递减,当22x<<,()h x单调递增,记2m=,2n=,则()()1h x h m km lnm a lnm a=--=-+-极小值,记()_1m lnm aϕ--,注意216m=<,所以016m<<,()0mϕ'=<,z则()(16)342m ln aϕϕ>=--,所以()0h x>极小值,又()()0h n h m>>,221()(1(1)0aaeh e lnk k-+=+<,且21an ek-<+,结合单调性,可知()0h x=有唯一零点.综上可知,若342a ln-,对于任意0k>,直线y kx a=+与曲线()y f x=有唯一公共点.12.(2021春•浙江月考)已知函数()af x lnxx=+(1)若函数()f x有极值,求实数a的取值范围;(2)当1a=时,若()f x在1x x=,212()x x x≠处导数相等,证明:12()()122f x f x ln+>+;(3)若函数()f x在(0,)+∞上有两个零点1x,212()x x x≠,证明:122x xe+>.【解答】解:(1)函数()af x lnxx=+,2()x af xx-∴'=,0x>,若函数()f x有极值,则()0f x'=有正实数解,所以实数a的取值范围是0a>;(2)证明:1a=时,21()xf xx-'=,由()f x在1x x=,212()x x x≠处导数相等,得12()()f x f x'=',∴12221211x xx x--=,即1212x x x x+=;又1x、2x>,且12x x≠,所以1212x x x x=+>,得124x x>;所以1212121211()()141122f x f x lnx lnx lnx x ln ln x x +=+++=+>+=+; (3)证明:令()0af x lnx x=+=,则a xlnx -=, 设()g x xlnx =,则()1g x lnx '=+;则函数()g x xlnx =在1(0,)e 内单调递减,在1(e ,)+∞上单调递增,且11()g e e=-;令t x e -=,其中0t >,则()t t ttg x e lne e --==-; 212tt e t >++,∴2111122tt t t t e t t <=++++;当t →+∞时,0t t e +→,0tt e-∴-→; 所以当1(a e-∈-,0)时有两个零点;不妨设1210x x e <<<,若22x e,则结论成立; 若22x e <,即21(x e ∈,2)e时, 令222()()()()()h x g x g x xlnx x ln x e e e =--=---,1(0,)x e∈;则2()()2h x lnx ln x e'=+-+,从而12()11()022()x e h x x x x x e e --''=+=>--, ()h x ∴'在1(0,)e 上单调递增,且1()()0h x h e '<'=;()h x ∴在1(0,)e上单调递减,1()()0h x h e ∴>=,即2()()g x g x e >-在1(0,)e上恒成立;2112()()()g x g x g x e∴=>-;又21(x e ∈,2)e ,121(x e e -∈,2)e,且()g x 在1(e ,2)e 上单调递增,212x x e ∴>-,即证122x x e+>. 13.设函数21()(1)2f x x ax a lnx =-+-,1a >. (1)曲线()y f x =在点(2,f (2))处的切线与x 轴平行,求实数a 的值; (2)讨论函数()f x 的单调性;(3)证明:若5a <,则对任意1x ,2(0,)x ∈+∞,12x x ≠,有1212()()1f x f x x x ->--.【解答】解:(1)函数21()(1)2f x x ax a lnx =-+-的导数为 1()a f x x a x-'=-+, ()y f x =在点(2,f (2))处的切线斜率为k f ='(2)1202a a -=-+=, 解得3a =;(2)()f x 的定义域为(0,)+∞.1()a f x x a x-'=-+, ()i 若11a -=即2a =,则2(1)()x f x x-'=, 故()f x 在(0,)+∞单调增. ()ii 若11a -<,而1a >,故12a <<,则当(1,1)x a ∈-时,()0f x '<; 当(0,1)x a ∈-及(1,)x ∈+∞时,()0f x '> 故()f x 在(1,1)a -单调减, 在(0,1)a -,(1,)+∞单调增. ()iii 若11a ->,即2a >,同理可得()f x 在(1,1)a -单调减, 在(0,1),(1,)a -+∞单调增. (3)考虑函数21()()(1)2g x f x x x ax a lnx x =+=-+-+则211()12111)a a f x x a x a x x--'=-++-+=-, 由于15a <<,故()0g x '>, 即()g x 在(0,)+∞单调增加,从而当120x x >>时有12()()0g x g x ->, 即1212()()0f x f x x x -+->,故1212()()1f x f x x x ->--成立.14.(2012春•顺庆区校级月考)已知函数21()ax f x x b+=+是奇函数,且f (1)2=.(1)求()f x 的解析式;(2)判断函数()f x 的单调性,并证明你的结论; (3)若1x ,2(1,)x ∈+∞,且12x x ≠.求证12121()[()()]22x x f f x f x +<+. 【解答】解:(1)f 21()ax x x b +=+为奇函数,且f (1)121a b+==+ 1(1)1a f fb +∴-==--(1)2=-,解得:1a =,0b =. 21()x f x x+∴=. (2)函数()f x 在区间(1,)+∞上是增函数,在区间(0,1)上是减函数,在(1,0)-上单调递减,在(,1)-∞-上单调递增证明:函数的定义域为{|0}x x ≠ 在区间(0,)+∞上任取1x ,2x ,令120x x << 121212121212()(1)11()()x x x x f x f x x x x x x x --∴-=+--= 1201x x <<<120x x ∴-<,1210x x ->,120x x >,①当121x x <<时,1210x x ->, 12()()0f x f x ∴-<即12()()f x f x <故函数()f x 在区间(1,)+∞上是增函数. ②121x x <时,1210x x -< 12()()0f x f x ∴->即12()()f x f x >故函数()f x 在区间(0,1)上是减函数根据奇函数的对称性可知,函数在(1,0)-上单调递减,在(,1)-∞-上单调递增 (3)1x ,2(1,)x ∈+∞,且12x x ≠.∴1212121212121112()[()()]22222x x x x x x x x f f x f x x x ++++-+=+--+2212121212121212124()()20222x x x x x x x x x x x x x x x x +-+--=-==<+ ∴12121()[()()]22x x f f x f x +<+ 15.(2021•湖北月考)已知函数23()3xe f x ax =+的定义域为R .(1)当a 取得最小值时,记函数()f x 在x a =处的切线方程为()y g x =.若()()f x g x 恒成立且a Z ∈,求a 的最大值;(2)若()f x 有两个极值点1x 和2x ,求证:1212()()13332244f x f x e e ea x x a+-+<<++. 【解答】解:(1)由题意可知,函数定义域为R ,所以0a ,即a 的最小值为0,所以(0)1f =, 又2223(23)()(3)xax ax e f x ax -+'=+,所以(0)1f '=,所以()1g x x =+,因为()()f x g x 恒成立,即2(1)(3)3x x ax e -++恒成立, 当10x +即1x -时,2(1)(3)03x x ax e -++<,显然成立, 当10x +>即1x >-时,令1x =,得12(3)3a e -+, 解得3333332222ae -<⨯-=<, 又因为333 2.73 1.05122e ->⨯-=>,由a Z ∈且0a ,可得a 的最大值为1.下证1a =时符合题意,即证2(1)(3)3x x ax e -++, 令2()(1)(3)3x m x x x e -=++-,则2()()(1)x m x x x e -'=--, 当0x <时,()0m x '>,当0x >时,()0m x ',所以函数()m x 在(,0)-∞上单调递增,在(0,)+∞上单调递减, 所以()(0)0max m x m ==,所以2(1)(3)3x x ax e -++. 故a 的最大值为1;(2)证明:由2223(23)()(3)xax ax e f x ax -+'=+,故1x 和2x 是方程2230ax ax -+=的实根,所以122x x +=,123x x a=, 所以12122112121222121212()()()()331()()()223344x x x x x x f x f x f x f x e e e e x e x e x x ax ax a x x ++==+=+=++++, 令()(1)1x h x e e x =---,则()(1)x h x e e '=--,当()0h x '<时,(x ∈-∞,(1))ln e -;当()0h x '>时,((1)x ln e ∈-,)+∞, 所以函数()h x 在(-∞,(1))ln e -上单调递减,在((1)ln e -,)+∞上单调递增, 所以3()((1))(1)(1)02min h x h ln e e e ln e =-=---->,即11(1)(1)2e e ln e ->--+, 所以1(1)2x e e x >-+, 所以12121212()()11331[2(1)()]4222f x f x e e x x x x x x a +->-++=++.令11()22x t x e ex e =--,则1()2x t x e e '=-,当()0t x '<时,2e x ln <;当()0t x '>时,2ex ln >;所以()t x 在(,)2eln -∞上单调递减;在(2e ln ,)+∞上单调递增,所以()()022222min e e e e et x t ln ln ==--<,所以1122x e ex e<+,则12122112121222121122()()()()331()()()223344x x x x x x f x f x f x f x e e e e x e x e x x ax ax a x x ++==+=+=++++1212113[()]4244e eex x e x x a<++=+, 故1212()()13332244f x f x e e ea x x a+-+<<++. 16.(2009•卢湾区二模)已知函数1()|21|x f x -=-,()x R ∈.(1)证明:函数()f x 在区间(1,)+∞上为增函数,并指出函数()f x 在区间(,1)-∞上的单调性; (2)若函数()f x 的图象与直线y t =有两个不同的交点(,)A m t ,(,)B n t ,其中m n <,求m n +的取值范围.【解答】解:(1)证明:任取1(1,)x ∈+∞,2(1,)x ∈+∞,且12x x <,12121212111111121()()|21||21|(21)(21)22(22)2x x x x x x x x f x f x -------=---=---=-=-,12x x <,∴1222x x <,∴12220x x -<,12()()f x f x ∴<.所以()f x 在区间(1,)+∞上为增函数.(5分) 函数()f x 在区间(,1)-∞上为减函数.(6分)(2)因为函数()f x 在区间(1,)+∞上为增函数,相应的函数值为(0,)+∞,在区间(,1)-∞上为减函数,相应的函数值为(0,1),由题意函数()f x 的图象与直线y t =有两个不同的交点,故有(0,1)t ∈,(8分)易知(,)A m t ,(,)B n t 分别位于直线1x =的两侧,由m n <,得1m n <<,故1210m --<,1210n -->,又A ,B 两点的坐标满足方程1|21|x t -=-,故得112m t -=-,121n t -=-,即2log (22)m t =-,2log (22)n t =+,(12分) 故2222log (22)log (22)log (44)m n t t t +=-++=-, 当01t <<时,20444t <-<,22log (44)2t -∞<-<. 因此,m n +的取值范围为(,2)-∞.(17分)17.(2021•商丘二模)已知直线y x b =+与函数()f x lnx =的图象交于两个不同的点A ,B ,其横坐标分别为1x ,2x ,且12x x < (Ⅰ)求b 的取值范围;(Ⅱ)当22x 时,证明2122x x <. 【解答】解:(Ⅰ)由题意可得0x lnx b -+=有两个不同的实根, 设()g x x lnx b =-+,0x >,1()1g x x'=-, 当01x <<时,()0g x '<,()g x 递减; 当1x >时,()0g x '>,()g x 递增. 可得()g x 在1x =处取得最小值1b +,当1b <-时,b lnx x =-在(0,1)和(1,)+∞各有一个不同的实根, 则b 的范围是(,1)-∞-;(Ⅱ)证明:由(Ⅰ)可得101x <<,21x >,12()()0g x g x ==, 111222222222()()()()g x g x lnx b ln b x x x -=-+--+ 2222222222222()()32x lnx b ln b x lnx ln x x x =-+--+=--+, 令22()32h t t lnt ln t=--+,则23334(2)(1)()1t t h t t t t -+'=-+=, 当2t 时,()0h t ',()h t 递增, 即有()h t h (2)32202ln =->, 当22x 时,1222()()0g x g x ->,即1222()()g x g x >, 又()g x 在(0,1)递减,101x <<,22201x <<, 即有1222x x <,可得2122x x <.18.(2021•西湖区校级模拟)设函数2()(1)f x x aln x =++有两个极值点1x ,2x ,且12x x <. (1)求a 的取值范围,并讨论()f x 的单调性. (2)证明:2122()4ln f x ->. 【解答】解:(1)由题意知,函数()f x 的定义域是1x >-,222()1x x af x x ++'=+,且()0f x '=有两个不同的实数根1x ,2x ,故2220x x a ++=的判别式△480a =->,即12a <,且1x =2x =,①又11x >-,故0a >,因此a 的取值范围是1(0,)2,当x 变化时()f x 与()f x '的变化情况如下表:1212)上是减函数. (2)由题意和①知,2102x -<<,222(1)a x x =-+,于是222222()2(1)(1)f x x x x ln x =-++,设函数2()2(1)(1)g t t t t ln t =-++,则()2(12)(1)g t t ln t '=-++, 当12t =-时,()0g t '=,当1(2t ∈-,0)时,()0g t '>,故()g t 在1[2-,0)上是增函数.于是,当1(2t ∈-,0),1122()()24ln g t g ->-=,因此22122()()4ln f x g x -=>. 19.(2010•辽宁)已知函数2()(1)1f x a lnx ax =+++. (1)讨论函数()f x 的单调性;(2)设1a <-.如果对任意1x ,2(0,)x ∈+∞,1212|()()|4||f x f x x x --,求a 的取值范围.【解答】解:(Ⅰ)()f x 的定义域为(0,2121).()2a ax a f x ax x x+++'+∞=+=. 当0a 时,()0f x '>,故()f x 在(0,)+∞单调递增;当1a -时,()0f x '<,故()f x 在(0,)+∞单调递减;当10a -<<时,令()0f x '=,解得x则当x ∈时,()0f x '>;)x ∈+∞时,()0f x '<.故()f x 在单调递增,在)+∞单调递减. (Ⅱ)不妨假设12x x ,而1a <-,由(Ⅰ)知在(0,)+∞单调递减, 从而1x ∀,2(0,)x ∈+∞,1212|()()|4||f x f x x x -- 等价于1x ∀,2(0,)x ∈+∞,2211()4()4f x x f x x ++① 令()()4g x f x x =+,则1()24a g x ax x+'=++ ①等价于()g x 在(0,)+∞单调递减,即1240a ax x+++. 从而22222241(21)42(21)2212121x x x x a x x x ------==-+++故a 的取值范围为(-∞,2]-.(12分)20.(2015•南通校级模拟)已知函数2()(1)1f x a lnx ax =+++. (1)讨论函数()f x 的单调性;(2)设1a <-,若对任意1x 、2x 恒有1212|()()|4||f x f x x x --,求a 的取值范围.【解答】解:(1)2121()2a ax a f x ax x x+++'=+=,((0,))x ∈+∞. 当0a 时,()0f x '>,因此函数()f x 在(0,)x ∈+∞单调递增. 当1a -时,()0f x '<,因此函数()f x 在(0,)x ∈+∞单调递减.当10a -<<时,令()0f x '=,解得x当x ∈时,()0f x '>,函数()f x 在x ∈单调递增.当)x ∈+∞时,()0f x '<,函数()f x 在)x ∈+∞单调递减. (2)不妨设120x x <,对任意1x 、2x 恒有1212|()()|4||f x f x x x -- 1221()()4()f x f x x x ⇔--, 1122()4()4f x x f x x ⇔++,(*)令()()4g x f x x =+,则1()()424a g x f x ax x+'='+=++,(*)等价于()g x 在(0,)+∞上单调递减,即1240a ax x+++, 从而22241(21)222121x x a x x ---=--++, a ∴的取值范围是(-∞,2]-.21.已知函数()n f x nx x =-,x R ∈.其中n N ∈.2n . (1)讨论()f x 的单调性;(2)设曲线()y f x =与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()y g x =,求证:对于任意的正实数x ,都有()()f x g x ;(3)设5n =,若关于x 的方程()(f x a a =为实数)有两个正实根1x ,2x ,求证:21||24ax x -<-. 【解答】解:(1)由()n f x nx x =-,可得11()(1)n n f x n nx n x --'=-=-,其中n N ∈,且2n . 下面分两种情况讨论:①当n 为奇数时,令()0f x '=,解得1x =,或1x =-, 当x 变化时,()f x ',()f x 的变化情况如下表:②当n 为偶数时,当()0f x '>,即1x <时,函数()f x 单调递增; 当()0f x '<,即1x >时,函数()f x 单调递减; 所以,()f x 在(,1)-∞单调递增,在(1,)+∞上单调递减; (2)证明:设点P 的坐标为0(x ,0),则110n x n-=,20()f x n n '=-,曲线()y f x =在点P 处的切线方程为00()()y f x x x ='-, 即00()()()g x f x x x ='-,令()()()F x f x g x =-,即00()()()()F x f x f x x x =-'-, 则0()()()F x f x f x '='-'.由于1()n f x nx n -'=-+在(0,)+∞上单调递减,故()F x '在(0,)+∞上单调递减, 又因为0()0F x '=,所以当0(0,)x x ∈时,()0F x '>,当0(x x ∈,)+∞时,()0F x '<, 所以()F x 在0(0,)x ∈内单调递增,在0(x ,)+∞上单调递减, 所以对应任意的正实数x ,都有0()()0F x F x =,即对于任意的正实数x ,都有()()f x g x . (3)证明:不妨设12x x ,由(2)知20()()()g x n n x x =--,设方程()g x a =的根为2x ', 可得202ax x n n '=+-,由(Ⅱ)知222()()()g x f x a g x '==,可得22x x '. 类似地,设曲线()y f x =在原点处的切线方程为()y h x =,可得()h x nx =, 当(0,)x ∈+∞,()()0n f x h x x -=-<, 即对于任意的(0,)x ∈+∞,()()f x h x <, 设方程()h x a =的根为1x ',可得1a x n'=, 因为()h x nx =在(,)-∞+∞上单调递增, 且111()()()h x a f x h x '==<,因此11x x '<, 由此可得:212101ax x x x x n''-<-=+-, 因为2n ,所以11112(11)111n n n C n n ---=++=+-=,故:1102n nx -=.则21||21ax x n -<+-, 所以当5n =时,即有21||24a x x -<-. 22.(2015•天津)已知函数()n f x nx x =-,x R ∈,其中n N ⋅∈,且2n . (Ⅰ)讨论()f x 的单调性;(Ⅱ)设曲线()y f x =与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()y g x =,求证:对于任意的正实数x ,都有()()f x g x ;(Ⅲ)若关于x 的方程()(f x a a =为实数)有两个正实数根1x ,2x ,求证:21||21ax x n-<+-. 【解答】(本题满分为14分)解:(Ⅰ)由()n f x nx x =-,可得11()(1)n n f x n nx n x --'=-=-,其中n N ⋅∈,且2n . 下面分两种情况讨论:(1)当n 为奇数时,令()0f x '=,解得1x =,或1x =-,当x 变化时,()f x ',()f x 的变化情况如下表:所以,()f x 在(,1)-∞-,(1,)+∞上单调递减,在(1,1)-单调递增. (2)当n 为偶数时,当()0f x '>,即1x <时,函数()f x 单调递增; 当()0f x '<,即1x >时,函数()f x 单调递减; 所以,()f x 在(,1)-∞单调递增,在(1,)+∞上单调递减; (Ⅱ)证明:设点P 的坐标为0(x ,0),则110n x n-=,20()f x n n '=-,曲线()y f x =在点P 处的切线方程为00()()y f x x x ='-,即00()()()g x f x x x ='-, 令()()()F x f x g x =-,即00()()()()F x f x f x x x =-'-,则0()()()F x f x f x '='-'. 由于1()n f x nx n -'=-+在(0,)+∞上单调递减,故()F x '在(0,)+∞上单调递减, 又因为0()0F x '=,所以当0(0,)x x ∈时,()0F x '>,当0(x x ∈,)+∞时,()0F x '<, 所以()F x 在0(0,)x ∈内单调递增,在0(x ,)+∞上单调递减, 所以对应任意的正实数x ,都有0()()0F x F x =, 即对于任意的正实数x ,都有()()f x g x . (Ⅲ)证明:不妨设12x x , 由(Ⅱ)知20()()()g x n n x x =--, 设方程()g x a =的根为2x ',可得202ax x n n '=+-, 由(Ⅱ)知222()()()g x f x a g x ==',可得22x x '. 类似地,设曲线()y f x =在原点处的切线方程为()y h x =, 可得()h x nx =,当(0,)x ∈+∞,()()0n f x h x x -=-<, 即对于任意的(0,)x ∈+∞,()()f x h x <, 设方程()h x a =的根为1x ',可得1a x n'=, 因为()h x nx =在(,)-∞+∞上单调递增,且111()()()h x a f x h x '==<, 因此11x x '<,由此可得:212101ax x x x x n-<'-'=+-, 因为2n ,所以11112(11)111n n n C n n ---=++=+-=,故:1102n nx -=.所以:21||21ax x n-<+-. 23.(2021•呼和浩特二模)已知函数2()(2)f x lnx ax a x =-+-.①讨论()f x 的单调性; ②设0a >,证明:当10x a <<时,11()()f x f x a a+>-; ③函数()y f x =的图象与x 轴相交于A 、B 两点,线段AB 中点的横坐标为0x ,证明0()0f x '<.【解答】解:①函数()f x 的定义域为(0,)+∞, 1(21)(1)()2(2)x ax f x ax a x x+-'=-+-=-, ()i 当0a >时,则由()0f x '=,得1x a=, 当1(0,)x a ∈时,()0f x '>,当1(x a ∈,)+∞时,()0f x '<,()f x ∴在1(0,)a 单调递增,在1(a,)+∞上单调递减;()ii 当0a 时,()0f x >恒成立, ()f x ∴在(0,)+∞单调递增; ②设函数11()()()g x f x f x a a=+--,则22111111()[()()(2)()][()()(2)()](1)(1)2g x ln x a x a x ln x a x a x ln ax ln ax axa a a a a a=+-++-+----+--=+---,32222()2111a a a x g x a ax ax a x '=+-=+--, 当1(0,)x a∈时,()0g x '>,而(0)0g =,()(0)0g x g ∴>=,故当10x a <<时,11()()f x f x a a+>-; ③由①可得,当0a 时,函数()y f x =的图象与x 轴至多有一个交点, 故0a >,从而()f x 的最大值为1()f a ,且1()0f a>,不妨设1(A x ,0),2(B x ,0),120x x <<,则1210x x a<<<, 由②得,1112211()()()()0f x f x f x f x a a a -=+->==,又()f x 在1(a,)+∞上单调递减,∴122x x a -<,于是12012x x x a+=>, 由①知,(f '0)0x <.24.(2021•定远县期末)已知函数21()(0)2f x x x alnx a =-+>. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,求证:12322()()4ln f x f x --+>. 【解答】解:(1)2()1(0)a x x af x x a x x-+'=-+=>,①若21,0,()04ax x a f x '-+,所以()f x 在(0,)+∞上单调递增;②若104a <<,解20x x a -+>,得0x <<,或x >解20x x a -+<x <,此时()f x 在上单调递减.在上单调递增,在)+∞上单调递增. 综上,当14a 时,()f x 在(0,)+∞上单调递增,当104a <<时,()f x 在上单调递减,在上单调递增,在)+∞上单调递增.(2)由(1)知104a <<时,()f x 存在两个极值点1x ,2x , 且1x ,2x 是方程20x x a -+=的两根,所以121x x +=,12x x a ⋅=, 所以222121112221212121211111()()()()()122222f x f x x x alnx x x alnx x x x x x x aln x x a alna alna a +=-++-+=+--++=--+=--,令11()(0),()024g x xlnx x x g x lnx '=--<<=<,所以()g x 在1(0,)4上单调递减,所以1322()()44ln g x g -->=,所以12322()()4ln f x f x --+>25.(2021•临沂期中)已知函数21()(0)2f x x x alnx a =-+>. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,212()x x x <,且不等式12()0f x mx +恒成立,求实数m 的取值范围. 【解答】解:(1)21()(0)2f x x x alnx a =-+>, 2()1a x x af x x x x-+∴'=-+=,(0)x >, 令()0f x '=,得20x x a -+=, ①当△0,即14a时,()0f x ', ()f x ∴在(0,)+∞上是增函数.②当△0>时,即104a<<时,由20x x a -+=,得1,2x =当x ∈,x ,)+∞时,()0f x '>, 当x ∈时,()0f x '<,()f x ∴在,)+∞上单调递增,在上单调递减.(2)由(1)知,若()f x 在(0,)+∞上有两个极值点1x ,2x ,则104a <<, 由()0f x '=,得20x x a -+=,设1x ,2x 为20x x a -+=的两根,121x x ∴+=,1x 2x a =, 12x x <,1102x ∴<<,2112x <<, 由12()0f x mx +,得12()f x m x -,222111111211111112222111(1)()222x x alnx x x x x lnx x x x x lnx f x x x x x -+-+-+-=== 111111(1)22(1)x x lnx x =-++-,11(0)2x << 令11()(1)22(1)h x x xlnx x =-++-,1(0)2x <<,222111111()1[1]22(1)22(1)2(1)h x lnx lnx lnx x x x ∴'=--++=-+=-+---,102x <<,1112x ∴-<-<-,∴21(1)14x <-<, ∴2141(1)x -<-<--,∴2110(1)x -<-,又0lnx <,()0h x ∴'<,()h x ∴在1(0,)2上单调递减,所以有131()()2242h x h ln >=--,即()31242f x ln x >--,∴31242m ln ---, 即31242mln + 26.(2021春•新乡期末)已知函数21()(1)(41)2f x x a lnx x =++-+.(1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,且1212()()()4f x f x f x x a '+-,求a 的取值范围. 【解答】解:(1)21()(1)(41)2f x x a lnx x =++-+,24()4a x ax af x x a x x-+'∴=-+=,0x >, 当104a时,△21640a a =-,()0f x '>, ()f x ∴在(0,)+∞上单调递增,当0a <时,令()0f x '=,即240x ax a -+=,解得120x a =,220x a =+>,当(0,2x a ∈+时,()0f x '<,()f x 单调递减,当(2)x a ∈++∞时,()0f x '>,()f x 单调递增,∴函数()f x 在区间(0,2a +单调递减,在(2)a ++∞单调递增,当14a >时,令()0f x '=,即240x ax a -+=,解得得120x a =->,220x a =+,当(0,2x a ∈时,()0f x '>,()f x 单调递增,当(2x a a ∈时,()0f x '<,()f x 单调递减,当(2)x a ∈+∞时,()0f x '>,()f x 单调递增,故函数()f x 在区间(0,2a,(2)a ++∞单调递增,在区间(2a a +单调递减,综上所述,当104a 时,()f x 在(0,)+∞上单调递增, 当14a >时,()f x在区间(0,2a +单调递减,在(2)a +∞单调递增, 当0a <时,()f x 在区间(0,2a,(2)a ++∞单调递增,在区间(2a a +单调递减.(2)由(1)可得,当14a >时,函数()f x 存在两个极值点1x ,2x ,且124x x a +=,12x x a =, 1212()()()4f x f x f x x a '+-,∴22111222121211(1)(41)(1)(41)822ax a lnx x x a lnx x x x a x x ++-++++-+-+, 228162181a a alna a a a a ∴-+-++-+,即2880a a alna --,14a >, 880a lna ∴--,令g (a )88a lna =--,14a >,g '(a )180a=->, g ∴(a )在1(,)4+∞为单调递增函数,又g (1)0=,∴当1(,1]4a ∈时,g (a )0,故实数a 的取值范围为1(,1]4.27.(2021•湖北月考)已知函数221()2(0)2f x ax x a lnx a =-+≠(1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,证明:121212()()11f x f x x x x x -<+-【解答】解:(1)22222()1a ax x a f x ax x x-+'=-+=, 设22()2p x ax x a =-+.(0)x >,△318a =-,。
变量之间的关系典型练习题1

变量之间的关系典型练习题题型一、用关系式表示变量之间的关系1、某种储蓄的月利率是0.2%,存入100元本金后,则本息和y (元)与所存月数x 之间的关系式为__________(不考虑利息税).2、某移动通信公司开设了两种通信业务,“全球通”:使用时首先缴50元月租费,然后每通话1分钟,自付话费0.4元;“动感地带”:不缴月租费,每通话1分钟,付话费0.6元(本题的通话均指市内通话),若一个月通话x 分钟,两种方式的费用分别为1y 元和2y 元. (1)写出1y 、2y 与x 之间的关系式;(2)一个月内通话多少分钟,两种移动通讯费用相同?(3)某人估计一个月内通话300分钟,应选择哪种移动通信合算些?题型二、用图象表示变量之间的关系3、小明在暑期社会实距活动中,以每千克0.8元的价格从批发市场购进若干千克瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图7所示.请你根据图象提供的信息完成以下问题:(1)求降价前销售金额y (元)与售出西瓜x (千克)之间的关系式; (2)小明从批发市场共购进多少千克西瓜? (3)小明这次卖瓜赚子多少钱?图74 小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如右图所示).(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?(2)10时和13时,他分别离家多远?(3)他到达离家最远的地方是什么时间?离家多远?(4)11时到12时他行驶了多少千米?(5)他可能在哪段时间内休息,并吃午餐?(6)他由离家最远的地方返回时的平均速度是多少?5 小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡速度仍然保持不变,那么他从学校回到家需要的时间是多少6、某空军加油飞机接到命令,立即给另一架正在飞行的运输飞机进行空中加油,在加油过程中,设运输飞机的油箱余油量为Q 1吨,加油飞机的加油油箱余油量为Q 2吨,加油时间为t 分钟,Q 1、Q 2与t 之间的函数图像如图所示,结合图像回答下列问题:(1)加油飞机的加油油箱中装载了多少吨油?将这些油全部加给运输飞机需多少分钟?(2)运输飞机加完油后,以原速继续飞行,需10小时到达目的地,油料是否够用?说明理由。
初一数学上册变量练习题

初一数学上册变量练习题
题目一
利用变量解决下面的问题:小明有一些苹果,小红有一些苹果,小青有一些苹果。
假设小明有$m$个苹果,小红有$n$个苹果,小
青有$p$个苹果。
那么他们三个一共有多少个苹果?
解答:
他们三个一共有$m+n+p$个苹果。
题目二
某商场举行了一次打折活动,打折后的价格为原价的70%。
现
在有一个商品的原价为$x$元,那么打折后的价格是多少元?
解答:
打折后的价格为$x \times 0.7$元。
题目三
某公司的员工工资计算方法是每月固定的基本工资加上做加班的小时数乘以每小时的加班费。
现在小张的基本工资为$y$元,他这个月加班了$t$小时,每小时的加班费为$w$元。
那么他这个月的工资是多少元?
解答:
他这个月的工资为$y + t \times w$元。
题目四
小明和小红进行一场马拉松比赛。
设小明的用时为$x$小时,小红的用时为$y$小时。
已知小红的用时比小明多2小时。
那么小红的用时是多少小时?
解答:
小红的用时为$x + 2$小时。
题目五
某汽车行驶的距离和时间之间存在以下的关系:距离等于速度乘以时间。
现在某辆汽车以速度$v$每小时行驶了$t$小时,那么这辆汽车行驶的距离是多少?
解答:
这辆汽车行驶的距离为$v \times t$。
---
以上是初一数学上册变量练习题的内容,希望能够帮助你加深对变量的理解。
函数中双变量问题专题

2 )成立,则实数 a 的取值范围为( )A . ⎢ , +∞ ⎪B . ⎢ , +∞ ⎪C . ⎢- , +∞ ⎪D . ⎢- , +∞ ⎪⎡ 53. 已知函数 f ( x ) = ⎨ 1 ,若 α < β 且 f (α ) = f (β ) ,则 β - α 的取值范围是()B . ⎡⎣8 - 3ln3, e 2 - 1C . [9 - 4ln3,6 ])A . - 1⎡ π π ⎤7. α , β ∈ ⎢ - 2 2⎥⎦函数中双变量问题一、单选题1 11. 已知函数 f ( x) = ln( x +x 2 + 1) 满足对于任意 x 1∈ [ 2 , 2] ,存在 x 2 ∈ [ 2 , 2] ,使得f ( x 2 + 2 x + a) ≤ f (11 ln x x2A . [ ln 2 ln 2 5- 8, +∞) B . [ - 8, - - 2ln 2]2 2 4C . (-∞, ln 2 5 - 8]D . (-∞, - - 2ln 2]2 42. 设函数 f (x ) = ax 3 + bx 2 + cx (a, b , c ∈ R, a ≠ 0),若不等式 xf ' (x )- af (x ) ≤ 5 对 ∀x ∈ R 恒成立,则b - 2ca的取值范围为( )⎫ ⎡ 1 ⎫ ⎡ 5 ⎫ ⎡ 1 ⎫ ⎣ 3⎭⎣ 3 ⎭ ⎣ 3 ⎭⎣ 3 ⎭⎧ln x - 1, x ≥ 1⎪⎪⎩ 3 ( x + 2), x < 1A . [8 - 3ln3,6 ])D . ⎡⎣9 - 4ln 3, e 2 - 14. 已知函数 f ( x) = e x - ax 有两个零点 x 1 , x 2 ,则下列判断:① a < e ;② x 1 + x 2 < 2 ;③ x 1x 2 > 1 ;④有极小值点 x 0,且 x 1 + x 2 < 2 x 0 .则正确判断的个数是()A .4 个B .3 个C .2 个D .1 个5. 已知实数 a ,b 满足 2a 2 - 5lna - b = 0 , c ∈ R ,则 (a - c)2 + (b + c)2 的最小值为 ()A .122 3 2B .C .D .2 29 26. 已知直线 y = a (x + 1)与曲线 f (x ) = e x + b 相切,则 ab 的最小值为()1 12 B . -C . -D . -4e2eee⎣, ,且 α sin α - β sin β > 0 ,则下列结论正确的是( )f ( x) = e x (ln x - 1), x ∈ ⎢ , +∞ ⎪ ,若存在 a ∈[-2,1],使得 f 2 - ⎪ ≤ a 2 + 2a - 3 - e 成 A . ⎢ ,1⎥⎡2⎤C . ⎢ , +∞ ⎪⎡ 2⎭D . ⎢1,⎥4 ⎫ ⎛ 6 ⎫ ⎛ 4 ⎫ ⎛ 8 ⎫ e 2⎭B . 1, ⎪⎝ e ⎭ C . 0, ⎪e ⎭D . 1,⎝ e 2 ⎭⎛A . α > βB . α + β > 0C . α < βD . α 2 > β 28. 已知函数⎡ 1 ⎫ ⎣ 2 ⎭ ⎛ 1 ⎫ ⎝ m ⎭立,则实数 m 的取值范围为()⎣ 3 ⎦B .[1,+∞)⎫ ⎡ 3 ⎤ ⎣ 3 ⎣ 2 ⎦9. 已知曲线 f (x ) = ae x (a > 0) 与曲线 g (x ) = x 2 - m (m > 0)有公共点,且在该点处的切线相同,则当 m变化时,实数 a 的取值范围是()A . 0, ⎝二、填空题10. 已知函数 f (x ) = a x + x 2 - x ln a ,对任意的 x 1, x 2 ∈ [0,1],不等式 f (x 1 ) - f (x 2 ) ≤ a - 1 恒成立,则实数 a 的取值范围是___.11. 已知函数 f ( x ) = 2ln x - ax 2 + 3 ,若存在实数 m , n ∈[1,5] 满足 n - m ≥ 2 时, f (m ) = f (n ) 成立,则实数 a的最大值为_____12. 设函数 f (x ) = 3 - 2 x x + 1, g (x ) = xe 2x ,若 ∃x ∈ (-1, +∞) ,使得 ∀x ∈ (-1,+∞),不等式1 24emg (x ) > m 2 f (x )恒成立,则实数 m 的取值范围是______.2113. 若 a 为实数,对任意 k ∈ [-1,1],当 x ∈ (0, 4] 时,不等式 6ln x + x 2 - 9 x + a ≤ kx 恒成立,则 a 的最大值是_________.三、解答题14. 设 a, b ∈ R ,已知函数 f (x ) = a ln x + x 2 + bx 存在极大值.(1)若 a = 2 ,求 b 的取值范围;(2)求 a 的最大值,使得对于 b 的一切可能值, f (x )的极大值恒小于 0 .15. 已知函数( R ).16. 已知函数 f (x ) = ln x - 1b ∈ -∞ , - ⎪ ,方程 f (x ) = 0 恒有 2 个不等的实根,求 a 的取值范围.(1)当 a = 1 4时,求函数 y = f ( x ) 的单调区间;(2)若对任意实数 b ∈ (1,2) ,当 x ∈ (-1,b ] 时,函数 f ( x ) 的最大值为 f (b ) ,求 a 的取值范围.3x +- 1 44 x(1)求函数 f (x )的单调区间;的取值范围.17. 已知函数 f (x ) = ln x - ax 2 - bx - 2 , a ∈ R .(1)当 b = 2 时,试讨论 f (x )的单调性;(2)若对任意的 ⎛ 3 ⎫ ⎝ e ⎭答 案1.(2020·湖南省长郡中学高三)已知函数f ( x ) = ln( x +1, 2] ,存在 x ∈ [ , 2] ,使得 f ( x 12 + 2 x 1 + a) ≤ f (22 ) 成立,则实数 a 的取值范围为( )x ∈ [ , 2] ,存在 x ∈ [ , 2] ,使得 f ( x 12 + 2 x 1 + a) ≤ f ( 2 22 ) 成立, x 2 + 2 x + a ≤ 即任意 x ∈ [ , 2] ,存在 x ∈ [ , 2] ,使得 1 2 21 2 x ( 即满足 xmax ≤ 2 ⎪ , x ⎭max ⎝ 在 x ∈ [ , 2] 可得 g ( x 1 )max = g (2)=8 + a22 令 h ( x ) = 2,求导可得 h '( x ) = x x 22一、单选题22 1 ln x x 2A . [ ln 2 2- 8, +∞)B . [ ln 2 5- 8, - - 2ln 2]2 4C . (-∞,ln 2 2- 8] 5D . (-∞, - - 2ln 2]4【答案】C【解析】由函数 f ( x ) = ln( x +x 2 + 1) 在定义域单调递增,对于任意1 2 1 1 ln x x 21 11 ln x2 成立,22 1+ 2 x + a )1⎛ ln x ⎫2令 g ( x 1 ) = x 1 + 2 x 1 + a ,对称轴方程为 x 1 = -1 ,1 12 ln x 22 1 - ln x 2 , 2h '( x ) = 0 ,可得 x = e ,2 2在 x 2 ∈ (0, e ), h '( x 2 ) > 0 , h( x 2 ) 单调递增,1所以在 x ∈ [ , 2] , h ( x )2 2 max= h (2) = ln 2 ln 2 ,即 8 + a ≤ , 2 2解得 a ≤ ln 2 2- 8 ,故选 C .2.(2020·江西省南城一中高三期末)设函数 f (x ) = ax 3 + bx 2 + cx (a, b , c ∈ R, a ≠ 0),若不等式xf ' (x )- af (x ) ≤ 5 对 ∀x ∈ R 恒成立,则 b - 2c a的取值范围为( )⎭ D . ⎢- , +∞ ⎪A . ⎢ , +∞ ⎪⎭B . ⎢ , +∞ ⎪⎭ C . ⎢- , +∞ ⎪ ( )c 2 - 10c (c - 5)2 - 25 5 所以, b - 2c b - 2c 5 因此, b - 2c ⎡ 5 的取值范围为 ⎢- , +∞ ⎪ .故选:C.3. 2020·新疆维吾尔自治区高三)已知函数 f ( x ) = ⎨ 1 ,若 α < β 且 f (α ) = f (β ) ,则 β - α B . ⎡⎣8 - 3ln3, e 2 - 1 C . [9 - 4ln3,6])【解析】因为 f ( x ) = ⎨ 1 ,故其函数图像如下所示:⎪⎩ 3⎡ 5 ⎫ ⎡ 1 ⎫⎡ 5 ⎫⎡ 1 ⎫⎣ 3⎣ 3 ⎣ 3 ⎣ 3 ⎭【答案】C【解析】Q f (x ) = ax 3 + bx 2 + cx ,∴ f ' (x ) = 3ax 2 + 2bx + c ,由不等式 xf ' (x )- af (x ) ≤ 5 对 ∀x ∈ R 恒成立,可得 3a - a 2 x 3 + (2b - ab ) x 2 + (c - ac ) x - 5 ≤ 0 对 ∀x ∈ R 恒成立,所以, 3a - a 2 = 0 且 a ≠ 0 ,解得 a = 3 ,⎧b > 0 c 2则不等式 bx 2 + 2cx + 5 ≥ 0 对 ∀x ∈ R 恒成立,所以 ⎨ ,则 b ≥ ,⎩∆ = 4c 2 - 20b ≤ 0 51c 2- 2c = ≥ = = ≥- .a 3 3 15 15 3⎫a ⎣ 3 ⎭⎧ln x - 1, x ≥ 1⎪(⎪⎩ 3 ( x + 2), x < 1的取值范围是()A . [8 - 3ln3,6])D . ⎡⎣9 - 4ln 3, e 2 - 1【答案】B⎧ln x - 1, x ≥ 1 ⎪( x + 2), x < 1令 lnx -1 = 1,解得 x = e 2;令 lnx -1 = -1 ,解得 x = 1 .( )故 g (x )在区间 (1,3 )单调递减,在区间 3, e 2 单调递增,( )故 g (x )∈ ⎡⎣8 - 3ln3, e 2 - 1 .即可得 β - α ∈ ⎡⎣8 - 3ln3, e 2 - 1.故选:B.)数形结合可知,若要满足 f (α ) = f (β ) ,且 α < β ,则 β ∈ (1,e 2),且 1 (α + 2 ) = ln β - 1,解得 α = 3ln β - 5 .3故 β - α = β - 3ln β + 5 , β ∈ (1,e 2).令 g (x ) = x - 3lnx + 5, x ∈ 1,e 2 ,则 g ' (x ) = 1 - 3x,令 g ' (x ) = 0 ,解得 x = 3 ,( )则 g (1) = 6, g (3) = 8 - 3ln3, g e 2 = e 2 - 1 ,)4.(2020·江西省临川第二中学高三期中)已知函数 f ( x) = e x - ax 有两个零点 x 1 , x 2 ,则下列判断:①a < e ;② x + x < 2 ;③ x x > 1 ;④有极小值点 x ,且 x + x < 2 x .则正确判断的个数是()121 20 1 2 0A .4 个B .3 个C .2 个D .1 个【答案】D【解析】对于①,∵ f ( x ) = e x - ax ,∴ f '( x ) = e x - a ,令 f '( x ) = e x - a > 0 ,当 a ≤ 0 时, f '( x ) = e x - a > 0 在 x ∈ R 上恒成立,∴ f ( x ) 在 R 上单调递增.当 a > 0 时,由 f '( x ) > 0 ,解得 x > ln a ;由 f '( x ) < 0 ,解得 x < ln a ;∴ f ( x ) 在 (-∞,ln a) 单调递减,在 (ln a, +∞) 单调递增.∵函数 f ( x) = e x - ax 有两个零点 x 1 , x 2 ,∴ a > 0 , f (ln a) < 0 ,即 e ln a - a ln a < 0 ,即 a - a ln a < 0 , 解得: a > e ;所以①不正确;对于②,因为函数 f ( x) = e x - ax 有两个零点 x 1 , x 2 ,所以 x 1 , x 2 是方程 e x - ax = 0 的两根,因此 x 1 = ln ax 1 , x 2 = ln ax 2 ,取a=,f(2)=e2-2a=0,∴x=2,f(0)=1>0,∴0<x1<1,22B.22C.A.-1所以x+x=ln (a2x x)=2ln a+ln(x x)>2+ln(x x),12121212e22∴x1+x2>2,所以②不正确;对于③,f(0)=1>0,∴0<x1<1,x1x2>1不一定,∴所以③不正确;对于④,f(x)在(-∞,ln a)单调递减,在(ln a,+∞)单调递增,∴有极小值点x0=ln a,且x1+x2<2x0=2ln a,所以④正确.综上,正确的命题序号是④.故选:D5.(2020·湖南省高三期末)已知实数a,b满足2a2-5lna-b=0,c∈R,则(a-c)2+(b+c)2的最小值为()A.1【答案】C 322D.92【解析】由题意,得,代换,代换,则满足:,即,以代换,可得点,满足,因此求(a-c)2+(b+c)2的最小值即为求曲线上的点到直线相切于点的距离的最小值,设直线,则与曲线,解得,所以切点为,所以点到直线的距离,则(a-c)2+(b+c)2的最小值为,综上所述,选C.6.(2020·全国高三专题练习)已知直线y=a(x+1)与曲线f(x)=e x+b相切,则ab的最小值为()4e B.-12e C.-1e D.-2e【答案】B【解析】设切点为(x,e x0+b),因为f(x)=e x+b,所以f'(x)=e x,所以f'(x0)=e x0=a,所以x=ln a,所以 g (a) 在 (0, e - 2 ) 上递减,在 (e - 2 , +∞) 上递增, 所以 a = e- 12时,g (a) 取得最小值 g (e 2 ) = (e 2 )2 ln e 2 = -122, ⎥ ,且 α sin α - β sin β > 0 ,则下列结论正7.(2020·黑龙江省双鸭山一中高三期末) α , β ∈ ⎢ - f (x ) = xsinx 形式,则 f ' (x ) = sinx + xcosx , x ∈ ⎢0, ⎥ 时导函数 f ' (x ) ≥ 0 , f (x )单调x ∈ ⎢-⎡ π ,0 ⎪ 时导函数 f ' (x ) < 0 , f (x )单调递减.又Q f (x )为偶函数,根据单调性和对称性可f ( x) = e x (ln x - 1), x ∈ ⎢ , +∞ ⎪ ,若存在 a ∈[-2,1],使 ⎪ ≤ a 2 + 2a - 3 - e 成立,则实数 m 的取值范围为( )⎛又切点 ( x , e x 0 + b ) 在直线 y = a( x + 1) 上,所以 e x 0 + b = a( x + 1) ,所以 a + b = ax 0 + a ,所以 b = ax 0 = a ln a ,所以 ab = a 2 ln a ,令 g (a) = a 2 ln a(a > 0) ,则 g '(a) = 2a ln a + a 2 ⋅ 1 a= 2a ln a + a = a(2ln a + 1) ,令 g '(a) < 0 ,得 0 < a < e - 1 ,令 g '(a) > 0 ,得 a > e - 1 ,1 1- 1 - 1 - 1 2e.即 ab 的最小值为 -12e.故选:B⎡ π π ⎤ ⎣ 2 2 ⎦确的是()A . α > β【答案】D【解析】构造B . α + β > 0C . α < βD . α 2 > β 2⎡ π ⎤ ⎣ 2 ⎦递增;⎣ 2 ⎫ ⎭知选 D.故本小题选 D.8.(2020·广西壮族自治区高三月考)已知函数⎡ 1 ⎫ ⎣ 2 ⎭得 f 2 - ⎝ 1 ⎫ m ⎭A . ⎢ ,1⎥C . ⎢ , +∞ ⎪⎡ 2⎭D . ⎢1,⎥【解析】 f '(x) = e x ln x + - 1⎪ ,令 g ( x) = ln x + - 1 ,则 g '(x) = - x ∈ ⎢ , +∞ ⎪ 时, f '(x) ≥ 0 , f ( x) 在区间 ⎢ , +∞ ⎪ 上单调递增.存在 a ∈[-2,1],使 f 2 - ⎪ ≤ a 2 + 2a - 3 - e 成立,等价于 f 2 -⎪ ≤ -e = f (1).⎪⎪ ⎪2 - 1 ≥ 1 ⎩ 4 ⎫ ⎛ 6 ⎫ ⎛ 4 ⎫ ⎛ 8 ⎫ e 2⎭B . 1, ⎪⎝ e ⎭ C . 0, ⎪e ⎭D . 1,⎝ e 2 ⎭⎛⎡ 2 ⎤ ⎣ 3 ⎦B .【答案】A[1,+∞)⎫ ⎡ 3 ⎤ ⎣ 3 ⎣ 2 ⎦⎛⎝1 ⎫ 1 1 1 x - 1=x ⎭ x x x 2 x 2 ,故当 1 2 < x < 1时,g '(x) < 0 , g ( x ) 单调递减,当 x > 1 时, g '(x) > 0, g ( x ) 单调递增,∴ g ( x ) ≥ g (1) = 0 ,从而当 ⎡ 1 ⎫ ⎡ 1 ⎫ ⎣ 2 ⎭ ⎣ 2 ⎭设 h (a ) = a 2 + 2a - 3 - e = (a + 1)2 - 4 - e ,则 h (a ) 在 [-2, -1]上单调递减,在 [-1,1]上单调递增, h(a)max= h (1) = -e ,⎛ ⎝1 ⎫ m ⎭ ⎛ 1 ⎫ ⎝ m ⎭⎧ 12 - ≤ 1 m 2∴⎨ ,解得 ≤ m ≤ 1 .故选: A . 3⎪ m 29.(2020·重庆南开中学高三月考)已知曲线 f (x ) = ae x (a > 0) 与曲线 g (x ) = x 2 - m (m > 0)有公共点,且在该点处的切线相同,则当 m 变化时,实数 a 的取值范围是()A . 0, ⎝【答案】A【解析】由 f ( x ) = ae x (a > 0) , g ( x ) = x 2 - m ,得 f '( x ) = ae x , g '( x ) = 2 x ,设 f ( x ) = ae x (a > 0) 与曲线 g ( x ) = x 2 - m 的公共点为 (s, t ) ,则 f '(s) = ae s , g '(s) = 2s ,∴ 两曲线在切点处的切线方程分别为 y - ae s = ae s ( x - s) 与 y - s 2 + m = 2s( x - s) ,即 y = ae s x + ae s - sae s 与 y = 2sx - s 2 - m .⎧m = s 2 - 2s ①⎩ae s - sae s = -s 2 - m ⎪ a = (s > 2) ,则 h '(s) = < 0 ,函数 h (s) 在 (2, +∞) 上为单调减函数, s + 3 = 2ln m - am m ,( m ∈[1,5] , t ≥ 2 ), m ,在 m ∈ [1,+∞) 单调递减,⎧2s = ae s ⎪ 则 ⎨ ,整理得 ⎨ 2s⎩ e s② .由①且 m > 0 ,得 s < 0 或 s > 2 ,当 s < 0 时,两曲线无公共切线,则 s > 2 .由②得, a = 2s e s(s > 2) .令 h (s) =2s 2(1- s)e e s∴ h (s) < h (2) = 4e 2 ,又当 s →+∞ 时, h (s) → 0 ,∴ 实数 a 的取值范围是 (0, 4 e 2) .故选:A.二、填空题10.(2020·江苏省高三专题练习)已知函数 f (x ) = a x + x 2 - x ln a ,对任意的 x , x ∈ [0,1],不等式1 2f (x ) - f (x 12) ≤ a - 1 恒成立,则实数 a 的取值范围是___.【答案】 [ e , +∞)【解析】由题意可得 f max ( x) - f min ( x) ≤ a - 1,且 a > 1 ,由于f '( x ) = a x ln a + 2 x - ln a = (a x - 1)ln a + 2 x ,所以当 x > 0 时, f '( x ) > 0 ,函数 f ( x ) 在 [0,1] 上单调递增,则 f max ( x) = f (1) = a + 1 - ln a, f min ( x) = f (0) = 1 ,所以 f max ( x) - f min ( x) = a - ln a ,故a -1 ≥ a - ln a ⇒ ln a ≥ 1 ,即 a ≥ e ,应填答案 [e , +∞) .11.(2020·湖南省明达中学高三)已知函数 f ( x ) = 2ln x - ax 2 + 3 ,若存在实数 m , n ∈[1,5] 满足 n - m ≥ 2 时,f (m ) = f (n ) 成立,则实数 a 的最大值为_____【答案】 ln34【解析】由 f (m ) = f (n) ⇒ 2ln n - an 2 2 + 3 ,所以 a = 2(ln n - ln m )n 2 - m 2,令 n = m + t ,( t ≥ 2 ),则 a =tln(1+ )t(2m + t)显然 g (m ) = t ln(1+ )t(2m + t)令 h (t) = g (1) = ,( t ≥ 2 ), h '(t ) = ,,∴实数 a 的最大值为 .故答案为:时, g ' (x ) < 0 ,函数 y = g (x )在 -1,- ⎪ 上单调递减, 时, g ' (x ) > 0 ,函数 y = g (x )在 - , +∞ ⎪ 上单调递增, g (x )∈ ⎢- , +∞ ⎪ .∴ g (x ) ≥ g - ⎪ = - ⎝ 2 ⎭ ⎣ 2e ⎭2e ⎪ = -2m , m 2 f (x 1 ) > -2m 2 .若 m > 0 ,则 4emg (x ) ≥ 4em ⋅ - ⎝ 2e ⎭1∴ a ≤ g (1) = ln(1+ t)( t ≥ 2 )t(2 + t)ln(1+ t) t 2 + 2t - 2(t + 1)2 ln(t + 1)t(2 + t) [t (t + 2)]2 (t + 1)∵ t ≥ 2 ,∴ 2ln( t + 1) > 1 ,则 t 2 + 2t - 2(t + 1)2 ln(t + 1) ,∴令 h (t) = g (1) =ln(1+ t) t(2 + t)在 [2, +∞) 单调递减,∴ a ≤ h (2) = ln 3 ln 3 ln 34 4 412.(2020·河南省高三月考)设函数 f (x ) = 3 - 2 x x + 1, g (x ) = xe 2 x ,若 ∃x ∈ (-1, +∞) ,使得1∀x ∈ (-1,+∞),不等式 4emg (x ) > m 2 f (x )恒成立,则实数 m 的取值范围是______.221【答案】 (1,+∞ )【解析】Q f (x ) = -2 (x + 1)+ 5 5= -2 +x + 1 x + 1,当 x ∈ (-1,+∞ ) 时,有 f (x ) > -2 .因为 g (x ) = xe 2x ,所以 g ' (x ) = e 2x + 2xe 2x = (1 + 2x )e 2x ,当 -1 < x < -1 ⎛ 1 ⎫2 ⎝ 2 ⎭当 x >- 1 ⎛ 1 2 ⎝ 2 ⎫ ⎭⎛ 1 ⎫ ⎡ 1 ⎫ ,所以当 x > -1 时,⎛ 1 ⎫ 2根据题意可知 -2m > -2m 2 ,解得 m > 1 ;若 m ≤ 0 ,则 4emg (x )∈ (-∞, -2m ] , m 2 f (x ) > -2m 2 ,不符合条件.2 1综上所述,实数 m 的取值范围是 (1,+∞ ) .故答案为: (1,+∞ ) .13.(2020·浙江省高三期中)若 a 为实数,对任意 k ∈ [-1,1],当 x ∈ (0, 4] 时,不等式6ln x + x 2 - 9 x + a ≤ kx 恒成立,则 a 的最大值是_________.【答案】7k ∈ [-1,1],当 x ∈ (0, 4] 时,不等式 ≤ k 恒成立min ⇒ ≤ -1 ⇒ a ≤ -6l n x - x2 + 8x'( x ) > 0 时, ⎨0 < x ≤ 4【解析】因为对任意 k ∈ [-1,1],当 x ∈ (0, 4] 时,不等式 6ln x + x 2 - 9 x + a ≤ kx 恒成立,所以对任意6ln x + x 2 - 9 x + a x6ln x + x 2 - 9 x + a 6ln x + x 2 - 9 x + a即 ≤ k xx所以当 x ∈ (0, 4] 时,不等式 a ≤ -6ln x - x 2 + 8x 恒成立令 f ( x ) = -6l n x - x 2 + 8x, x ∈ (0, 4]则 a ≤ f ( x)min-2 x 2 + 8x - 6 -(2 x - 2)( x - 3)f '( x ) = =x x当 f当 f ⎧(2 x - 2)( x - 3) < 0⎩⎧(2 x - 2)( x - 3) > 0'( x ) < 0 时, ⎨⎩ 0 < x ≤ 4⇒ 1 < x < 3⇒ 0 < x < 1 或 3 < x ≤ 4所以函数 f ( x ) 在区间 (0,1) 和 (3,4] 上单调递减,在区间 (1,3)上单调递增f (1) = 0 - 1 + 8 = 7, f (4) = -6ln 4 -16 + 32 = 16 - 6ln 4e 3 因为16 - 6ln 4 - 7 = 9 - 6ln 4 = 3(3 - ln16) = 3ln > 016所以 f ( x)min = 7所以 a ≤ 7 , a 的最大值为: 7故答案为: 7三、解答题14.(2020·贵州省贵阳一中高三月考)设 a, b ∈ R ,已知函数 f (x ) = a ln x + x 2 + bx 存在极大值.(1)若 a = 2 ,求 b 的取值范围;(2)求 a 的最大值,使得对于 b 的一切可能值, f (x )的极大值恒小于 0 .【答案】(1) b < -4 ,(2) 2e 3【解析】(1)当 a2 , f x x 0 ,由 f x 存在极大值,(2) f x x 0 ,由 f x 存在极大值,1.当 0 x时, g x 2x 0 ,所以 g x 在 0, a a 3 3 e ,即 x e , x 2 e 2 , 2 22x 2 bx 2xb 2 16 0,可知方程 2x 2bbx 2 0 有两个不等的正根,则 0, ∴ b 4 .21 0,2x 2 bx ax可知方程 2x 2 bx a0 有两个不等的正根,设为 x ,x 且 x121x ,∴ x x2 1 2a a,∴ a 0 , 0 x2 2由 f x0 x1x x ,2∴ f x 的极大值为 f x1a lnx1x 2 bx ,∵ bx1 1 12x 2 1a ,∴ f x1a lnx1x 2 a ,构造函数 g x a lnx x 2 a ,1a a a 2x 22 x x a 2上递增,由 0x1a 2,则 g x1a a ag ln 3 .2 2 2所以当 0 a2e 3 时, f x极大值f x1g x1ga 20 .3 而当 a2e 3时,取 b2 e 22 13 2此时 f x极大值3 af e2 e30 ,不符合题意.2综上所述, a 的最大值为 2e 3 .15.(2020·湖南省长沙一中高三月考)已知函数( R ).(1)当 a1 4时,求函数 y f(x)的单调区间;- 1 > 0 即 0 < a < 时,函数 f ( x ) 在 (-1,0) 和 ( - 1,+∞) 上单调递增, - 1 < 0 即 a > 时,函数 f ( x ) 在 (-1, - 1) 和 (0, +∞) 上单调递增,(2)若对任意实数 b ∈ (1,2) ,当 x ∈ (-1,b ] 时,函数 f ( x ) 的最大值为 f (b ) ,求 a 的取值范围.【答案】(Ⅰ)函数 f ( x ) 的单调递增区间为 (-1,0) 和 (1, +∞) ,单调递减区间为 (0,1) ;(Ⅱ) [1- ln 2, +∞)【解析】(1)当 a =1 1时, f ( x ) = ln( x + 1) + x 2 - x , 4 4则 f '( x ) =1 1 x( x - 1)+ x - 1 = ( x > -1) , x + 1 2 2( x + 1)令 f '( x ) > 0 ,得 -1 < x < 0 或 x > 1 ;令 f '( x ) < 0 ,得 0 < x < 1 ,∴函数 f ( x ) 的单调递增区间为 (-1,0) 和 (1, +∞) ,单调递减区间为 (0,1) .(2)由题意 f '( x ) = x[2ax - (1- 2a)]( x > -1) ,( x + 1)(1)当 a ≤ 0 时,函数 f ( x ) 在 (-1,0) 上单调递增,在 (0, +∞) 上单调递减,此时,不存在实数 b ∈ (1,2) ,使得当 x ∈ (-1,b ] 时,函数 f ( x ) 的最大值为 f (b ) .(2)当 a > 0 时,令 f '( x) = 0 ,有 x 1 = 0 , x 2 = 1 2a- 1 ,①当 a = 1 2时,函数 f ( x ) 在 (-1, +∞) 上单调递增,显然符合题意.②当1 1 12a 2 2a在 (0,1 2a- 1) 上单调递减, f ( x ) 在 x = 0 处取得极大值,且 f (0) = 0 ,要使对任意实数 b ∈ (1,2) ,当 x ∈ (-1,b ] 时,函数 f ( x ) 的最大值为 f (b ) ,只需 f (1) ≥ 0 ,解得 a ≥ 1 - ln 2 ,又 0 < a < 1 2,所以此时实数 a 的取值范围是1 - ln 2 ≤ a < 1 2.③当1 1 12a 2 2a在 ( 1 2a- 1,0) 上单调递减,要存在实数 b ∈ (1,2) ,使得当 x ∈ (-1,b ] 时,函数 f ( x ) 的最大值为 f (b ) ,需 f ( 1 2a- 1) ≤ f (1),代入化简得 ln 2a + 1 4a+ ln 2 - 1 ≥ 0 ,①令 g (a) = ln 2a + 1 1 1 1+ ln 2 - 1 (a > ) ,因为 g '(a) = (1- ) > 0 恒成立,4a 2 a 4a1 1 1故恒有 g (a) > g ( ) = ln 2 - > 0 ,所以 a > 时,①式恒成立,2 2 2综上,实数 a 的取值范围是 [1- ln 2, +∞) .【解析】(1) f x lnxx 的定义域是 0, , f x( )2 ,16.(2020·广西壮族自治区高二期末)已知函数 f xlnx(1)求函数 f x 的单调区间;1 3x 1 4 4x(2)设 g xx 2 2bx 4 ,若对任意 x10,2 ,x21,2 ,不等式 f x1g x 恒成立,求实数b2的取值范围.【答案】(1)函数 f x 在 1,3 上单调递增;在 (0,1)和 3,上单调递减; (2) ,142 .1 3 1 1 3 4x x2 34 4xx 4 4x 2 4x 2由 x 0 及 f x0 得1 x 3 ,由 x 0 及 f x 0 得 0 x 1 或 x 3 ;所以函数 f x 在 1,3 上单调递增;在 0,1 和 3,上单调递减.(2)若对任意 x10,2 ,x21,2 ,不等式 f x1g x 恒成立,问题等价于 f x2ming xmax由(1)可知,在 0,2 上, x 1 是函数极小值点,这个极小值是唯一的极值点故也是最小值点,所以 f x min f 11 2, g xx 2 2bx 4,x 1,2当 b 1时, g xmaxg 1 2b 5 ;当1 b 2 , g x maxg b b 2 4当 b2 时, g xg 24b 8b 11 b2 b 2 问题等价于{ 1或 { 1 或 { 12b 5 b 4 4b 822 2解得 b 1或1 b14 或 b214 14 即 b,所以实数 b 的取值范围是.2217.(2020·浙江省学军中学高三期中)已知函数 f xlnx ax 2 bx 2 , aR .(1)当 b2 时,试讨论 f x 的单调性;b ∈ -∞ , - ⎪ ,方程 f (x ) = 0 恒有 2 个不等的实根,求 a 的取值范围. f (x )在 0, ⎪ 单调递增,a = 0 , f (x )在 0, ⎪ 单调递增, , +∞ ⎪ 单调递减;- < a < 0 , f (x )在 0, ⎪⎪ 单调递增, ⎪⎪ 单调递减, 2 4a 4a 4a a ≤ - , f (x )在 (0, +∞ )单调递增. 【解析】(1) f ' (x ) = , x > 0解得 x = -2 + 4 + 8a ⎪⎪ 时, f ' (x ) > 0 , f (x )单调递增, 4a⎛ x ∈ ⎛ -2 + 4 + 8a, +∞ ⎪⎪ 时, f ' (x ) < 0 , f (x )单调递减,4af (x )在 0, ⎪ 单调递增, x ∈ 0, ⎪ 时, f ' (x ) > 0 , f (x )单调递增, x ∈ , +∞ ⎪ 时, f ' (x ) < 0 , f (x )单调递减,(2)若对任意的 ⎛ 3 ⎫ ⎝ e ⎭【答案】(1) a > 0 ,⎛ ⎝ -2 + 4 + 8a ⎫ ⎛ -2 + 4 + 8a ⎫ 4a 4a , +∞ ⎪ 单调递减;⎭ ⎝ ⎭⎛ 1 ⎫ ⎛ 1 ⎫⎝ 2 ⎭ ⎝ 2 ⎭1 ⎛ -2 + 4 + 8a ⎫ ⎛ -2 + 4 + 8a -2 - 4 + 8a ⎫, ⎝ ⎭ ⎝ ⎭⎛ -2 - 4 + 8a ⎫ 4a , +∞ ⎪ 单调递增;⎝ ⎭1 2(2) 0 < a ≤2e 21 -2 x - 2ax 2x(i ) a > 0 ,令 f ' (x ) = 0 ,得到1 - 2 x - 2ax 2 = 0 ,-2 - 4 + 8a, x = (舍)4a 4a所以当 x ∈ 0, ⎝-2 + 4 + 8a ⎫⎭ 当⎫ ⎝ ⎭所以⎛ -2 + 4 + 8a ⎫ ⎛ -2 + 4 + 8a ⎫ 4a 4a , +∞ ⎪ 单调递减;⎝ ⎭ ⎝ ⎭(ii ) a = 0 ,令 f ' (x ) = 0 ,得到 x =12当当⎛ 1 ⎫ ⎝ 2 ⎭⎛ 1 ⎫ ⎝ 2 ⎭f (x )在 0, ⎪单调递增, , +∞ ⎪ 单调递减; , +∞ ⎪⎪ 时, f ' (x ) > 0 , f (x )单调递增, ⎪⎪ U ⎪⎪ 时, f ' (x ) < 0 , f (x )单调递减, 当 x ∈ 4a 4a(x )在 ⎛ 0, -2 + ⎪⎪ 单调递减, ⎪ 单调递增, , 4a 4af (x )在 0, ⎪ 单调递增, a = 0 , f (x )在 0, ⎪ 单调递增, , +∞ ⎪ 单调递减;- < a < 0 , f (x )在 0, ⎪⎪ 单调递增, ⎪⎪ 单调递减, 2 4a 4a 4a a ≤ - , f (x )在 (0, +∞ )单调递增. b ∈ -∞ , - ⎪ ,方程 f (x ) = 0 恒有 2 个不等的实根 令 g (x ) = , x > 0 有 g ' (x ) = , x > 0所以 ⎛ 1 ⎫ ⎛ 1 ⎫ ⎝ 2 ⎭ ⎝ 2 ⎭(iii ) - 1 2< a < 0 ,令 f ' (x ) = 0 ,得到 x = -2 + 4 + 8a -2 - 4 + 8a, x =4a 4a当 ⎛ -2 + 4 + 8a ⎫ ⎛ -2 - 4 + 8a ⎫ x ∈ 0,4a 4a⎝ ⎭ ⎝ ⎭⎛ -2 + 4 + 8a -2 - 4 + 8a ⎫ ,⎝⎭f 4 + 8a ⎫ ⎛ -2 + 4 + 8a -2 - 4 + 8a ⎫ ⎛ -2 - 4 + 8a ⎫ 4a 4a , +∞ ⎪ 单 ⎝ ⎭ ⎝ ⎭ ⎝ ⎭调递增;(iiii ) a ≤ -综上所述,1 2, f ' (x ) > 0 在 (0,+∞ )恒成立,所以 f (x )在 (0, +∞ )单调递增;a > 0 ,⎛ -2 + 4 + 8a ⎫ ⎛ -2 + 4 + 8a ⎫ 4a 4a , +∞ ⎪ 单调递减;⎝ ⎭ ⎝ ⎭⎛ 1 ⎫ ⎛ 1 ⎫⎝ 2 ⎭ ⎝ 2 ⎭1 ⎛ -2 + 4 + 8a ⎫ ⎛ -2 + 4 + 8a -2 - 4 + 8a ⎫, ⎝ ⎭ ⎝ ⎭⎛ -2 - 4 + 8a ⎫4a , +∞ ⎪ 单调递增; ⎝ ⎭1 2(2)因为对任意的 ⎛ 3 ⎫ ⎝ e ⎭所以将问题等价于ln x - 2 x= ax + b 有两解ln x - 2 3 - ln xx x 2a>0,过 0,-⎪作切线时,斜率a最大.(x,y),有y=3-ln x0x+2ln x0-5,此时斜率a取到最大2∴g (e3)=0;g(x)在(0,e3)递增,(e3,+∞)递减;x→0,g(x)→-∞;x→+∞,g(x)→0;∴有图象知要使g(x)=ln x-2的图像和y=ax+b的图像有两个交点,x⎛3⎫⎝e⎭设切点为00x2x00∴2ln x-5x=-3e,∴x=e2∴0<a≤.e2e2。
高考数学二轮复习考点知识专题提升练习13 双变量问题

高考数学二轮复习考点知识专题提升练习第13讲双变量问题一.选择题(共5小题)1.(2021•海淀区校级月考)若2233x y x y ---<-,则() A .(1)0ln y x -+>B .(1)0ln y x -+<C .||0ln xy >D .||0ln xy <2.(2021•全国月考)已知实数x ,y 满足22log log y x x e y e --+<+,则下列结论一定正确的是()A .x y >B .||0ln x y -<C .|1|0ln x y -+>D .|1|0ln y x -+>3.(2021•鼓楼区校级二模)已知α,(0,)βπ∈,αβ≠,若cos 2cos e e αβαβ-=-,则下列结论一定成立的是()A .sin sin αβ<B .cos cos αβ<C .sin sin αβ>D .cos cos αβ>4.(2021春•顺义区期末)已知函数()x f x e =,2()g x x ax =-+(其中)a R ∈.对于不相等的实数1x ,2x ,设1212()()f x f x m x x -=-,1212()()g x g x n x x -=-,给出下列三个结论:①对于任意不相等的实数1x ,2x ,都有0m >;②对于任意的a 及任意不相等的实数1x ,2x ,都有0n <; ③对于任意的a ,存在不相等的实数1x ,2x ,使得m n =. 其中,所有正确结论的序号是() A .①B .①③C .②③D .①②③5.(2021•龙凤区校级月考)已知0a <,不等式1?0a x x e alnx ++对于任意(1,)x ∈+∞恒成立,则a 的取值范围是()A .[e -,1]-B .[e -,0)C .(,1)-∞-D .(-∞,]e - 二.多选题(共1小题)6.(2021•武进区校级期中)已知正实数x ,y 满足21211log log ()()22x y x y +<-,则下列结论正确的是() A .11xy <B .33x y <C .(1)0ln y x -+>D .122x y -< 三.解答题(共45小题)7.(2021•扬州月考)已知函数3()()x f x x ke k R =+∈,()f x '为()f x 的导函数. (1)当1k =时,求函数3()()2()2g x xf x f x x x '=--++的单调区间; (2)当0k 时,求证:对任意的1x ,2x R ∈,且12x x >,有121212()()()()2f x f x f x f x x x -'+'<-. 8.(2021•浙江月考)已知0a >且1a ≠,函数()(0)a x f x x a x =->. (Ⅰ)当2a =时,设()f x 的导函数()f x ',求()f x '的单调区间; (Ⅱ)若函数()y f x =恰有两个互异的零点m ,(0)n m n >>. (ⅰ)求实数a 的取值范围; (ⅱ)求证:2mn e >. 9.(2021•南平月考)已知函数.(1)求f (x )的单调区间与极值.(2)设m ,n 为两个不相等的正数,且mlnn ﹣nlnm =m ﹣n ,证明:mn >e 4. 10.(2021•广州月考)已知函数2()(1)x f x e a x =--.(1)讨论函数()f x 的单调性;(2)若0a >,设()f x '为()f x 的导函数,若函数()f x 有两个不同的零点1x ,2x ,求证:12()02x x f +'<. 11.(2021•和平区校级开学)已知函数()f x lnx =.(Ⅰ)若()f x 在1x x =,212()x x x ≠=; (Ⅱ)在(Ⅰ)的条件下,证明:12()()882f x f x ln +>-;(Ⅲ)若342a ln -,证明:对于任意0k >,直线y kx a =+与曲线()y f x =有唯一公共点. 12.(2021春•浙江月考)已知函数()a f x lnx x=+ (1)若函数()f x 有极值,求实数a 的取值范围;(2)当1a =时,若()f x 在1x x =,212()x x x ≠处导数相等,证明:12()()122f x f x ln +>+; (3)若函数()f x 在(0,)+∞上有两个零点1x ,212()x x x ≠,证明:122x x e+>. 13.设函数21()(1)2f x x ax a lnx =-+-,1a >.(1)曲线()y f x =在点(2,f (2))处的切线与x 轴平行,求实数a 的值; (2)讨论函数()f x 的单调性;(3)证明:若5a <,则对任意1x ,2(0,)x ∈+∞,12x x ≠,有1212()()1f x f x x x ->--.14.(2012春•顺庆区校级月考)已知函数21()ax f x x b+=+是奇函数,且f (1)2=.(1)求()f x 的解析式;(2)判断函数()f x 的单调性,并证明你的结论; (3)若1x ,2(1,)x ∈+∞,且12x x ≠.求证12121()[()()]22x x f f x f x +<+.15.(2021•湖北月考)已知函数23()3xe f x ax =+的定义域为R .(1)当a 取得最小值时,记函数()f x 在x a =处的切线方程为()y g x =.若()()f x g x 恒成立且a Z ∈,求a 的最大值;(2)若()f x 有两个极值点1x 和2x ,求证:1212()()13332244f x f x e e ea x x a+-+<<++. 16.(2009•卢湾区二模)已知函数1()|21|x f x -=-,()x R ∈.(1)证明:函数()f x 在区间(1,)+∞上为增函数,并指出函数()f x 在区间(,1)-∞上的单调性; (2)若函数()f x 的图象与直线y t =有两个不同的交点(,)A m t ,(,)B n t ,其中m n <,求m n +的取值范围.17.(2021•商丘二模)已知直线y x b =+与函数()f x lnx =的图象交于两个不同的点A ,B ,其横坐标分别为1x ,2x ,且12x x < (Ⅰ)求b 的取值范围;(Ⅱ)当22x 时,证明2122x x <. 18.(2021•西湖区校级模拟)设函数2()(1)f x x aln x =++有两个极值点1x ,2x ,且12x x <. (1)求a 的取值范围,并讨论()f x 的单调性. (2)证明:2122()4ln f x ->. 19.(2010•辽宁)已知函数2()(1)1f x a lnx ax =+++. (1)讨论函数()f x 的单调性;(2)设1a <-.如果对任意1x ,2(0,)x ∈+∞,1212|()()|4||f x f x x x --,求a 的取值范围. 20.(2015•南通校级模拟)已知函数2()(1)1f x a lnx ax =+++. (1)讨论函数()f x 的单调性;(2)设1a <-,若对任意1x 、2x 恒有1212|()()|4||f x f x x x --,求a 的取值范围. 21.已知函数()n f x nx x =-,x R ∈.其中n N ∈.2n . (1)讨论()f x 的单调性;(2)设曲线()y f x =与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()y g x =,求证:对于任意的正实数x ,都有()()f x g x ;(3)设5n =,若关于x 的方程()(f x a a =为实数)有两个正实根1x ,2x ,求证:21||24a x x -<-. 22.(2015•天津)已知函数()n f x nx x =-,x R ∈,其中n N ⋅∈,且2n . (Ⅰ)讨论()f x 的单调性;(Ⅱ)设曲线()y f x =与x 轴正半轴的交点为P ,曲线在点P 处的切线方程为()y g x =,求证:对于任意的正实数x ,都有()()f x g x ;(Ⅲ)若关于x 的方程()(f x a a =为实数)有两个正实数根1x ,2x ,求证:21||21ax x n-<+-. 23.(2021•呼和浩特二模)已知函数2()(2)f x lnx ax a x =-+-. ①讨论()f x 的单调性;②设0a >,证明:当10x a<<时,11()()f x f x aa+>-;③函数()y f x =的图象与x 轴相交于A 、B 两点,线段AB 中点的横坐标为0x ,证明0()0f x '<. 24.(2021•定远县期末)已知函数21()(0)2f x x x alnx a =-+>. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,求证:12322()()4ln f x f x --+>. 25.(2021•临沂期中)已知函数21()(0)2f x x x alnx a =-+>.(1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,212()x x x <,且不等式12()0f x mx +恒成立,求实数m 的取值范围.26.(2021春•新乡期末)已知函数21()(1)(41)2f x x a lnx x =++-+. (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,且1212()()()4f x f x f x x a '+-,求a 的取值范围. 27.(2021•湖北月考)已知函数221()2(0)2f x ax x a lnx a =-+≠ (1)讨论()f x 的单调性;(2)若()f x 存在两个极值点1x ,2x ,证明:121212()()11f x f x x x x x -<+-28.(2021•登封市校级月考)已知函数2()(2)(1)x f x x e a x =-+-有两个零点. (1)求a 的取值范围;(2)已知()g x 图象与()y f x =图象关于1x =对称,证明:当1x <时,()()f x g x <. (3)设1x ,2x 是两个零点,证明:122x x +<.29.(2010•湖南)已知函数2()(,)f x x bx c b c R =++∈,对任意的x R ∈,恒有()()f x f x '. (Ⅰ)证明:当0x 时,2()()f x x c +;(Ⅱ)若对满足题设条件的任意b ,c ,不等式f (c )f -(b )22()M c b -恒成立,求M 的最小值.30.(2009•海南)已知函数32()(3)x f x x x ax b e -=+++. (1)如3a b ==-,求()f x 的单调区间;(2)若()f x 在(,)α-∞,(2,)β单调增加,在(,2)α,(,)β+∞单调减少,证明:6βα->.31.(2021春•深圳月考)已知函数()x f x e =,x R ∈,()g x lnx =,(0,)x ∈+∞. (Ⅰ)若直线2y kx =+与()g x 的图象相切,求实数k 的值;(Ⅱ)设0x >,讨论曲线()y f x =与曲线2(0)y mx m =>公共点的个数. (Ⅲ)设a b <,比较()()2f a f b +与()()f b f a b a--的大小,并说明理由. 32.(2006•四川)已知函数22()(0)f x x alnx x x=++>,()f x 的导函数是()f x '.对任意两个不相等的正数1x 、2x ,证明: (Ⅰ)当0a 时,1212()()()22f x f x x xf ++>; (Ⅱ)当4a 时,1212|()()|||f x f x x x '-'>-.33.(2013•揭阳二模)已知0a >,函数2()f x ax lnx =-. (1)求()f x 的单调区间;(2)当18a =时,证明:方程2()()3f x f =在区间(2,)+∞上有唯一解;(3)若存在均属于区间[1,3]的α,β且1βα-,使()()f f αβ=,证明:32253ln ln ln a-. 34.(2021•金安区校级月考)已知函数21()22f x x x alnx =-+. (1)若函数()f x 存在两个极值点1x ,212()x x x <,求a 的取值范围; (2)在(1)的条件下,若不等式12()f x mx 恒成立,求m 的取值范围. 35.(2021•信阳月考)已知函数21()422f x x alnx x =---,其中a 为正实数. (Ⅰ)若函数()y f x =在1x =处的切线斜率为2,求a 的值; (Ⅱ)讨论函数()y f x =的单调性;(Ⅲ)若函数()y f x =有两个极值点1x ,2x ,求证:12()()6f x f x lna +<-.36.(2021•和平区校级月考)已知函数21()()2f x x ax lnx a R =-+-∈. (1)当1a =时,求曲线()y f x =在点(1,f (1))处的切线方程; (2)求()f x 的单调区间;(3)若函数()f x 有两个极值点1x ,212()x x x <,求证:124()2()132f x f x ln -+. 37.(2021•茂名月考)已知函数2()f x lnx x ax =+-.(1)当3a =时,求曲线()y f x =在点(1P ,f (1))处的切线方程;(2)若1x ,212()x x x <是函数()f x 的两个极值点,证明:2412264()()816a a f x f x ln a -->+.38.(2021•沈阳月考)已知函数()x f x e ax =-有两个零点1x ,2x ,且12x x <. (1)求证:a e >; (2)求证:122x x +>.39.(2021•海淀区校级月考)已知0a >,函数()x f x xe ax =-. (Ⅰ)当1a =时,求曲线()y f x =在点(1,f (1))处的切线方程; (Ⅱ)求()f x 的极值点个数;(Ⅲ)若存在a ,使得()f x b a >-对任意x R ∈成立,求实数b 的取值范围.40.(2021•重庆月考)已知函数()x f x axe x lnx -=+-有三个不同的极值点1x ,2x ,3x ,且123x x x <<.(1)求实数a 的取值范围; (2)若12323253x x x ln +++,求31x x 的最大值. 41.(2021•浙江月考)已知a R ∈,函数2()()f x x a lnx =++. (Ⅰ)讨论函数()f x 的单调性;(Ⅱ)若()f x 有两个极值点1x ,2x 且12x x <,试把12()x f x ⋅表示成2x 的函数,并证明此函数存在极值点3x ,4x ,且34)x x ∈∈+∞. 42.(2021•广州月考)已知函数()(,)x f x e ax x b a b R =-+-∈. (1)讨论()f x 的单调性;(2)当3a =时,函数()f x 存在两个零点1x ,212()x x x <,求证:124x x e e +>.43.(2021•长治月考)已知函数21()4412f x x ax lnx =-++,a R ∈. (1)讨论()f x 的单调性;(2)设()f x 有两个极值点1x ,212()x x x >,求证:1212()()2(1)()f x f x a x x -<---. 44.(2021•河北月考)已知221()2x f x e a x =-,0a >. (1)若()0f x ,求a 的取值范围;(2)若12()()f x f x =,且12x x ≠,证明:122x x e e a +>.45.(2021•涪城区校级开学)已知函数213()2(0)22f x lnx ax x a =+-+>. (1)讨论()f x 在的单调性;(2)若函数()f x 存在两个极值点1x ,2x ,证明:12()()0f x f x +<. 46.(2021•光明区月考)已知函数221()2x f x ae x ax =--,a R ∈. (1)当1a =时,求函数2()()g x f x x =+的单调区间; (2)当4401a e <<-,时,函数()f x 有两个极值点1x ,212()x x x <,证明:212x x ->. 47.(2021春•洛阳期中)已知函数21()(1)2f x alnx x a x =---,()a R ∈ (1)讨论函数()f x 的单调性;(2)若“1x ∀,2(0,)x ∈+∞,1212()()1f x f x a x x -<--”为真命题,求实数a 的取值范围.48.(2021•河南月考)已知函数2()f x xlnx ax =+,0a .(Ⅰ)若曲线()y f x =在x e =处的切线在y 轴上的截距为e -,求a 的值; (Ⅱ)证明:对于任意两个正数1x ,212()x x x ≠,12122()()()2x x f f x f x +<+. 49.(2021•朝阳区校级月考)已知函数()(1)f x xlnx a x =-++,a R ∈. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若关于x 的不等式()2f x a 在[2,)+∞上恒成立.求a 的取值范围; (Ⅲ)若实数b 满足21a b <-+且1b >,证明:2()12f x lnb <-. 50.(2021春•浙江期中)已知函数22()(0)f x x ax a lnx a =+-≠. (Ⅰ)讨论函数()f x 的单调性; (Ⅱ)若函数()f x 有两个零点1x ,2x . (ⅰ)求a 的范围;(ⅱ)若0a >,求证:12x x a +>.51.(2021春•丽水期中)已知函数()2f x xlnx =,2()1g x x ax =+-,a R ∈. (Ⅰ)若对任意[1x ∈,)+∞,不等式()()f x g x 恒成立,求a 的取值范围; (Ⅱ)若函数()|()|2h x f x a =-有3个不同的零点1x ,2x ,3123()x x x x <<. (ⅰ)求证:122x x e+>;(ⅱ)求证:32x x ->.。
第3章3.1.1两个变量的线性关系训练

1.在10件产品中,有8件正品,2件次品,从中任取3件产品,其中必然事件为( )A .3件都是正品B .至少有1件次品C .3件都是次品D .至少有1件正品解析:选D.因为10件产品中只有2件次品,而取出3件产品,所以至少有1件正品.2.下列事件中,随机事件有( )①明天是阴天;②异种电荷相互吸引;③十二五计划中期城镇人口超过农村人口.A .3个B .2个C .1个D .0个解析:选B.①③为随机事件.3.从一批准备出厂的电视机中随机抽取10台进行质量检查,其中有1台是次品.若用C 表示抽到次品这一事件,则对C 这一事件发生的说法正确的是( )A .概率为110B .频率为110C .概率接近110D .每抽10台电视机,必有1台次品解析:选B.10台电视机中有1台次品,连续从这10台中抽取,每次抽取一台,10次试验中必会抽到这台次品一次,故C 发生的频率为110. 4.《优化方案》对本公司发行的三百多种教辅用书实行跟踪式问卷调查,连续五年的调查结果如表所示:则本公司问卷返回的概率为________.解析:949÷1006≈0.94334,1430÷1500≈0.95333,1913÷2010≈0.95174,2890÷3050≈0.94754, 4940÷5200=0.95.都稳定于0.95,故所求概率为0.95.答案:0.951.下列说法不正确的是( )A .不可能事件的概率为0,必然事件的概率是1B .某人射击10次,击中靶心8次,则他击中靶心的频率是0.8C .“直线y =k (x +1)过定点(-1,0)”是必然事件D .势均力敌的两支足球队,甲队主场作战,则甲队必胜无疑解析:选D.A 、B 、C 均正确.甲、乙两支足球队势均力敌,不论在何处比赛,甲队都可能输掉比赛,故D 不正确.2.某人将一枚硬币连续抛掷了10次,正面朝上的情形出现了6次,若用A 表示正面朝上这一事件,则A 的( )A .概率为23B .频率为35C .频率为6D .概率接近0.6解析:选B.事件A ={正面朝上}的概率为12,因为试验的次数较少,所以事件A 的频率35与概率值相差太大,并不接近.3.下列说法中正确的是( )A .任何事件的概率总是在(0,1)之间B .频率是客观存在的,与试验次数无关C .随着试验次数的增加,频率一般会越来越接近概率D .概率是随机的,在试验前不能确定解析:选C.任何事件的概率总是在[0,1]之间,其中必然事件的概率是1,不可能事件的概率是0,“任何事件”包含“必然事件”和“不可能事件”,故A 错误;只有通过试验,才会得到频率的值,故频率不是客观存在的,一般来说,当试验的次数不同时,频率是不同的,它与试验次数有关,故B 错误;当试验次数增多时,频率呈现出一定的规律性,频率值越来越接近于某个常数,这个常数就是概率,故C 正确;虽然在试验前不知道概率的确切值,但概率是一个确定的值,它不是随机的,通过多次试验,不难发现它是频率的稳定值,故D 错误.4.下列说法正确的是( )A .一个人打靶,打了10发子弹,有7发子弹中靶,因此这个人中靶的概率为710B .一个同学做掷硬币试验,掷了6次,一定有3次“正面朝上”C .某地发行福利彩票,其回报率为47%,有个人花了100元钱买彩票,一定会有47元的回报D .大量试验后,可以用频率近似估计概率解析:选D.A 的结果是频率;B 错的原因是误解了概率是12的含义;C 错的原因是忽略了整体与部分的区别.5.给出关于满足A B 的非空集合A 、B 的四个命题:①若任取x ∈A ,则x ∈B 是必然事件;②若任取x ∉A ,则x ∈B 是不可能事件;③若任取x ∈B ,则x ∈A 是随机事件;④若任取x ∉B ,则x ∉A 是必然事件.其中正确的命题有( )A .1个B .2个C .3个D .4个解析:选C.∵A B ,∴A 中的任一个元素都是B 中的元素,而B 中至少有一个元素不在A 中,因此①正确,②错误,③正确,④正确.6.从2004名学生中选取50名组成参观团,若采用下面的方法选取,先用简单随机抽样法从2004人中剔除4人,剩下的2000人按系统抽样的方法进行,则每人入选的概率( )A .不全相等B .均不相等C .都相等且为251002D .都相等且为140解析:选C.每人入选的概率相等,P =502004=251002,故选C. 7.一袋中有红球3只,白球5只,还有黄球若干只.某人随意摸100次,其摸到红球的频数为30次,那么袋中的黄球约有________只.解析:设x 为袋中黄球的只数,则由35+3+x =30100,解得x =2. 答案:28.某人抛掷一枚硬币100次,结果正面朝上有53次,设正面朝上为事件A ,则事件A 出现的频数为________,事件A 出现的频率为________.解析:由题意,试验次数n =100,事件A 出现的次数n A =53,即为频数,故事件A 出现的频率f n (A )=n A n =53100=0.53.答案:530.539(1)(2)该市男婴出生的概率约为________.解析:(1)2007年男婴出生的频率为1145321840≈0.524.同理可求得2008年、2009年和2010年男婴出生的频率分别为0.521,0.512,0.513.(2)该市男婴出生的概率约为0.52.答案:(1)0.524,0.521,0.512,0.513(2)0.5210.指出下列试验的结果:(1)从装有红、白、黑三种颜色的小球各1个的袋子中任取2个小球;(2)从1,3,6,10四个数中任取两个数(不重复)作差.解:(1)结果:红球,白球;红球,黑球;白球,黑球.(2)结果:1-3=-2,3-1=2,1-6=-5,3-6=-3,1-10=-9,3-10=-7,6-1=5,10-1=9,6-3=3,10-3=7,6-10=-4,10-6=4.11从这100(1)事件A:螺母的直径介于(6.93,6.95];(2)事件B:螺母的直径介于(6.91,6.95];(3)事件C:螺母的直径大于6.96.解:(1)螺母的直径介于(6.93,6.95]范围内的频数n A=26+15=41,所以事件A的频率为41100=0.41.(2)螺母的直径介于(6.91,6.95]范围内的频数n B=17+17+26+15=75,所以事件B的频率为75100=0.75.(3)螺母的直径大于6.96的频数n C=2+2=4,所以事件C的频率为4100=0.04. 12(1)计算表中进球的频率;(2)这位运动员投篮一次,进球的概率约是多少?解:(1)由公式可计算出每场比赛该运动员罚球进球的频率依次为68=34,810=45,912=34,79,710,1216=34. (2)由(1)知,每场比赛进球的频率虽然不同,但频率总是在34的附近摆动,可知该运动员进球的概率约为34.。
导数专题:双变量导数压轴题训练

导数专题:双变量导数压轴题一.选择题(共10小题)1.设函数()(ln ),x f x xe a x x =-+若()0f x ≥恒成立,则实数a 的取值范国是 ( )A .[0,]e B .[0,1] C .(,]e -∞D .[,)e +∞2.函数2()2(1)x f x e a x =--有且只有一个零点,则实数a 的取值范围是 ( )A .(,1)4eB.(1, C .3(0,)2e D .3(,)2e -∞3.定义在R 上的函数()f x 的导函数为()f x ',且2(1)(0)(),2x f f f x e x x e '=+-若存在实数x 使不等式2()3f x m am ≤--对于a ∈[0,2]恒成立,则实数m 的取值范围为 ( )A .(,2][2,)-∞-⋃+∞ B.(,1[1)-∞⋃+∞ C.(,1[2,)-∞⋃+∞D.(,2][1)-∞-⋃++∞4.已知函数232,(1(2.))33xf x xg x e x x x c -==-+-+若对12(0)[]13x x ∀∈+∞∃∈,,,, 12)(()f x g x 使=成立,则c 的取值范围是 ( )A .244(,)3e B .244[,]3e C .4(,]3-∞D .24[,)e +∞5.已知函数32()f x x x ax a =-+-存在极值点x 0,且10(())f x f x =,其中10102x x x x +=≠,( )A .3B .2C .1D .06.设点P 为函数21()22f x x ax =+与2()3(0)g x a lnx b a =+>的图象的公共点,以P 为切点可作直线与两曲线都相切,则实数b 的最大值为 ( )A .2323eB .2332eC .3223eD .3232e7.设函数32()232x ax f x bx c =+++的两个极值点分别为12x x ,,若12(01)(12)x x ∈∈,,,,且存在,a b 使得2t a b +>成立,则实数t 的取值范围为 ( )A .(5,4)--B .(4,2)--C .(4,)-+∞D .(5,)-+∞8.已知函数3211()32xf x xe ax ax =--有三个极值点,则a 的取值范围是 ( )A .(0,)eB .1(0,)eC .(,)e +∞D .1(,)e+∞9.已知函数ln(1),0(),,0xx x f x xe x +≥⎧=⎨-<⎩函数1(x)(())g f f x e =-零点的个数为 ( ) A .3B .4C .1D .210.已知函数1()(ln )x e f x k x x x=-+有两个极值点,则实数k 的取值范围是 ( ) A .(,0]-∞ B .(1,)(,)e e ⋃+∞C .(0,)(,)e e ⋃+∞D .(,)e +∞解答题训练第Ⅱ卷(非选择题)二.解答题(共10小题) 11.已知函数21()2ln ,2f x x x a x =-+其中a >0. (1)讨论()f x 的单调性;(2)若()f x 有两个极值点12x x ,,证明:12)3((2)f x f x -<+<-.12.已知函数2()2ln ()f x x ax x a R =-+∈. (1)讨论()f x 的单调性;(2)若()f x 有两个极值点1212()x x x x <,,当a ≥21(())f x f x -的最大值.13.已知()ln f x x x =,(1)设()(),g x f x x =-求()g x 的增区间,并证明:当121x x <<时,2121))((1f x f x x x -->(2)如果对任意的120x x <<,均存在正数0x 使得11022(())()f x f x x x f x -'=-成立,求证:01x x >.14.已知函数2() 1.g x x ax =-+(1)求()0g x <的解集; (2)已知函数1()ln f x x a x x=-+,当122()a x x y g x =>时,、是的两个零点, 证明:1212))((2f x f x a x x -<--.(可能用到的参考结论:函数12ln y x x x=+-在区间(0)+∞,上单调递减)15.已知a ∈R ,函数2()2(4)ln f x x ax a x =++-有两个不同的极值点12x x 、. (1)求a 的取值范围;(2)证明:12))1(4(6ln 22f x f x +<-.16.已知函数())(xxf x e e ax a -=+有两个极值点12x x 、. (1)求a 的取值范围; (2)求证:12122x x x x <+.一.选择题(共10小题)1.设函数()(ln ),x f x xe a x x =-+若()0f x ≥恒成立,则实数a 的取值范国是 ( ) A .[0,]eB .[0,1]C .(,]e -∞D .[,)e +∞ 【解答】解:1()(1)(1)(1)(),xxa f x x e a x e xx'=+-+=+-0a <时,()f x '在(0,)+∞上单调递增,x →0+时,()f x →-∞;()x f x →+∞→+∞,.0a =时,()0x f x xe =≥恒成立,因此0a =满足条件.0a >时,令()(1)()0x af x x e x'=+-=,解得00000,ln ln ,0.x a e x x a x x +==>则0x 是函数()f x 的极小值点,此时0x x =,函数()f x 取得最小值,00000()(ln )ln 0,x f x x e a x x a a a =-+=-≥化为:ln 1a ≤,解得0a e <≤.综上可得:[0,]a e ∈a ∈[0,e ]. 故选:A .2.函数2()2(1)x f x e a x =--有且只有一个零点,则实数a 的取值范围是 ( )A .(,1)4eB.(1, C .3(0,)2e D .3(,)2e -∞【解答】解:f (x )=2e x ﹣a (x ﹣1)2=0, x =1时不成立, x ≠1时,化为:a ==g (x )(x ≠1).g ′(x )=.可得:x <1时,g ′(x )>0,函数g (x )单调递增; 1<x <3时,g ′(x )<0时,函数g (x )单调递减; x >3时,g ′(x )>0,函数g (x )单调递增. 画出图象. g (3)=.可得:当且仅当时,函数y =a 与函数y =g (x )由且仅有一个交点.即函数f (x )=2e x ﹣a (x ﹣1)2有且只有一个零点,则实数a 的取值范围是(0,).故选:C .3.定义在R 上的函数()f x 的导函数为()f x ',且2(1)(0)(),2x f f f x e x x e '=+-若存在实数x 使不等式2()3f x m am ≤--对于a ∈[0,2]恒成立,则实数m 的取值范围为 ( )A .(,2][2,)-∞-⋃+∞B .(,1[1)-∞⋃+∞C .(,1[2,)-∞⋃+∞D .(,2][1)-∞-⋃++∞【解答】解:,令x =0,可得:f (0)=,f ′(x )=e x +f (0)x ﹣1,令x =1可得:f (0)﹣1=0.解得:f (0)=1,f ′(1)=e . ∴f (x )=e x +x 2﹣x .∴f ′(x )=e x +x ﹣1在R 上单调递增,又f ′(0)=0. ∴x =0时,函数f (x )取得极小值即最小值,f (0)=1. 存在实数x 使不等式f (x )≤m 2﹣am ﹣3对于a ∈[0,2]恒成立, ∴1=f (x )min =m 2﹣am ﹣3对于a ∈[0,2]恒成立, ∴﹣ma +m 2﹣4≥0.∴,解得:m ≥1+,或m ≤﹣2.则实数m 的取值范围为(﹣∞,﹣2]∪[1+,+∞).故选:D .4.已知函数232,(1(2.))33xf x xg x e x x x c -==-+-+若对12(0)[]13x x ∀∈+∞∃∈,,,, 12)(()f x g x 使=成立,则c 的取值范围是 ( )A .244(,)3e B .244[,]3e C .4(,]3-∞D .24[,)e +∞【解答】解:f (x )=x 2•e ﹣x ,x ∈(0,+∞), f ′(x )=,令f ′(x )=0,解得:x =2,故f (x )在(0,2)递增,在(2,+∞)递减, 故f (x )max =f (2)=,而x →0时,f (x )→0,x →+∞时,f (x )→+∞, 故f (x )∈(0,],g (x )=﹣x 3+2x 2﹣3x +c , g ′(x )=﹣(x ﹣3)(x ﹣1), 令g ′(x )>0,解得:1<x <3, 故g (x )在[1,3]递增, 而g (x )min =g (1)=﹣+c , g (x )max =g (3)=c , 故g (x )∈[﹣+c ,c ],若对∀x 1∈(0,+∞),∃x 2∈[1,3],使f (x 1)=g (x 2)成立, 则(0,]⊆[﹣+c ,c ],故,解得:≤c ≤,故选:B .5.已知函数32()f x x x ax a =-+-存在极值点x 0,且10(())f x f x =,其中10102x x x x +=≠,( )A .3B .2C .1D .0【解答】解:f ′(x )=3x 2﹣2x +a .∵函数f (x )=x 3﹣x 2+ax ﹣a 存在极值点x 0,∴﹣2x 0+a =0,即a =﹣+2x 0.∵f (x 1)=f (x 0),其中x 1≠x 0, ∴﹣+ax 1﹣a =﹣+ax 0﹣a ,化为:+x 1x 0+﹣(x 1+x 0)+a =0,把a =﹣+2x 0代入上述方程可得:+x 1x 0+﹣(x 1+x 0)﹣+2x 0=0,化为:+x 1x 0﹣2+x 0﹣x 1=0,因式分解:(x 1﹣x 0)(x 1+2x 0﹣1)=0,x 1﹣x 0≠0. ∴x 1+2x 0=1. 故选:C .6.设点P 为函数21()22f x x ax =+与2()3(0)g x a lnx b a =+>的图象的公共点,以P 为切点可作直线与两曲线都相切,则实数b 的最大值为 ( )A .2323eB .2332eC .3223eD .3232e【解答】解:设点P (x 0,y 0),由于点P 为两函数曲线的切点, 则+2ax 0=3a 2lnx 0+b ;又点P 的切线相同,则f ′(x 0)=g ′(x 0), 即x 0+2a =,即(x 0+3a )(x 0﹣a )=0; 又a >0,x 0>0,所以x 0=a , 于是b =a 2﹣3a 2lna ,其中a >0; 设h (x )=x 2﹣3x 2lnx ,其中x >0, 则h ′(x )=2x (1﹣3lnx ),其中x >0;所以h (x )在(0,)内单调递增,在(,+∞)内单调递减;所以实数b 的最大值为h ()=.故选:B .7.设函数32()232x ax f x bx c =+++的两个极值点分别为12x x ,,若12(01)(12)x x ∈∈,,,,且存在,a b 使得2t a b +>成立,则实数t 的取值范围为 ( )A .(5,4)--B .(4,2)--C .(4,)-+∞D .(5,)-+∞【解答】解:∵f (x )的两个极值点x 1∈(0,1),x 2∈(1,2), 且f ′(x )=x 2+ax +2b 开口向上,故,故,问题转化为线性规划问题, 故﹣5<2a +b <﹣2,根据题意存在a ,b 使得t >2a +b , 则t >﹣5,故选:D .8.已知函数3211()32xf x xe ax ax =--有三个极值点,则a 的取值范围是 ( ) A .(0,)eB .1(0,)eC .(,)e +∞D .1(,)e +∞【解答】解:函数的导数f ′(x )=e x +Me x ﹣ax 2﹣ax ,若函数有三个极值点,等价为f′(x)=e x+Me x﹣ax2﹣ax=0有三个不同的实根,即(1+x)e x﹣ax(x+1)=0,即(x+1)(e x﹣ax)=0,则x=﹣1,则e x﹣ax=0,有两个不等于﹣1的根,则a=,设h(x)=,则h′(x)==,则由h′(x)>0得x>1,由h′(x)<0得x<1且x≠0,则当x=1时,h(x)取得极小值h(1)=e,当x<0时,h(x)<0,作出函数h(x)=,的图象如图,要使a=有两个不同的根,则满足a>e,即实数a的取值范围是(e,+∞),故选:C.9.已知函数ln(1),0(),,0xx x f x xe x +≥⎧=⎨-<⎩函数1(x)(())g f f x e =-零点的个数为 ( ) A .3B .4C .1D .2【解答】解:由g (x )=f (f (x ))﹣=0得f (f (x ))=, 设t =f (x ),则f (t )=,当x <0时,f (x )=﹣Me x ,则f (x )>0, 函数的导数f ′(x )=﹣(e x +Me x )=﹣(1+x )e x , 由f ′(x )>0得1+x <0,得x <﹣1,由f ′(x )<0得1+x >0,得﹣1<x <0,则当x =﹣1时,函数取得极大值f (﹣1)=, 则当t <0时,由f (t )=,得t =﹣1,作出函数f (x )的图象如图:由图象知f (x )=t =﹣1时,方程f (x )=﹣1无解, 当x ≥0时,由Ln (x +1)=得x +1=e ,则x =e ﹣1,则当t ≥0时,由f (t )=得t =e ﹣1>,此时f (x )=e ﹣1只有一个交点, 即函数g (x )的零点个数只有1个, 故选:C .10.已知函数1()(ln )x e f x k x x x=-+有两个极值点,则实数k 的取值范围是 ( ) A .(,0]-∞ B .(1,)(,)e e ⋃+∞C .(0,)(,)e e ⋃+∞D .(,)e +∞【解答】解:因为f (x )=﹣k (+lax )有两个极值点,所以f ′(x )=+﹣==0有两个不同正实根,(e x ﹣k )(x ﹣1)=0有两个不同正实根,∴e x ﹣k =0有一个不等于1的正根, ∴x =ink >0且ink ≠1, ∴k >1,k ≠e 故选:B .二.解答题(共10小题) 11.已知函数21()2ln ,2f x x x a x =-+其中a >0. (1)讨论()f x 的单调性;(2)若()f x 有两个极值点12x x ,,证明:12)3((2)f x f x -<+<-.【解答】解:(1)由题得,其中x >0,考察g (x )=x 2﹣2x +a ,x >0,其中对称轴为x =1,△=4﹣4a . ①若a ≥1,则△≤0,此时g (x )≥0,则f '(x )≥0,所以f (x )在(0,+∞)上单调递增; ②若0<a <1,则△>0, 此时x 2﹣2x +a =0在R 上有两个根,,且0<x 1<1<x 2,所以当x ∈(0,x 1)时,g (x )>0,则f '(x )>0,f (x )单调递增; 当x ∈(x 1,x 2)时,g (x )<0,则f '(x )<0,f (x )单调递减; 当x ∈(x 2,+∞)时,g (x )>0,则f '(x )>0,f (x )单调递增, 综上,当a ≥1时,f (x )在(0,+∞)上单调递增; 当0<a <1时,f (x )在上单调递增,在上单调递减,在上单调递增.(2)证明:由(1)知,当0<a <1时,f (x )有两个极值点x 1,x 2,且x 1+x 2=2,x 1x 2=a , 所以===.令h (x )=lynx ﹣x ﹣2,0<x <1, 则只需证明﹣3<h (x )<﹣2, 由于h '(x )=lax <0,故h (x )在(0,1)上单调递减, 所以h (x )>h (1)=﹣3.又当0<x <1时,lax ﹣1<﹣1,x (lax ﹣1)<0, 故h (x )=lynx ﹣x ﹣2=x (lax ﹣1)﹣2<﹣2, 所以对任意的0<x <1,﹣3<h (x )<﹣2. 综上,可得﹣3<f (x 1)+f (x 2)<﹣2, 故命题得证.12.已知函数2()2ln ()f x x ax x a R =-+∈. (1)讨论()f x 的单调性;(2)若()f x 有两个极值点1212()x x x x <,,当a ≥21(())f x f x -的最大值. 【解答】解:(1)∵f (x )=x 2﹣ax +2lnx ,x >0, ∴f ′(x )=2x ﹣a +=,∴x +≥2=2,当且仅当x =1时取等号,∴a ≤4时,f ′(x )≥0恒成立,故f (x )在(0,+∞)上单调递增, 当a >4时,此时△=a 2﹣16>0,令f ′(x )=0,解得x 1=,x 2=,当0<x <x 1 或x >x 2时,f ′(x )>0,函数f (x )单调递增, 当x 1<x <x 2时,f ′(x )<0,函数f (x )单调递减, 综上所述:当a ≤4时,f (x )在(0,+∞)上单调递增, 当a >4时,f (x )在(0,),(,+∞)上单调递增,在(,)上单调递减;(2)由(1)可得2x 2﹣ax +2=0的两个根为x 1,x 2,∴x 1+x 2=,x 1x 2=1, ∴=x 2+,a ≥2+,∴x 2+≥+,∴x 2≥,其中0<x 1<1<x 2,∴f (x 2)﹣f (x 1)=x 22﹣ax 2+2lnx 2﹣x 12+ax 1﹣2lnx 1=x 22﹣ax 2﹣x 12+ax 1+2ln=(x 2﹣x 1)(x 2+x 1)﹣a (x 2﹣x 1)+2ln =﹣(x 2﹣x 1)+2ln=2lnx 22﹣(x 2+)(x 2﹣)=2lnx 22﹣x 22+,令x =x 22,x ≥e ,∴h (x )=2lnx ﹣x +,x ≥e ,∴h ′(x )=﹣1﹣==﹣<0恒成立,∴h (x )在[e ,+∞)上单调递减,∴h (x )max =h (e )=2lne ﹣e +=2﹣e + 故f (x 2)﹣f (x 1)的最大值为2﹣e +. 13.已知()ln f x x x =,(1)设()(),g x f x x =-求()g x 的增区间,并证明:当121x x <<时,2121))((1f x f x x x -->(2)如果对任意的120x x <<,均存在正数0x 使得11022(())()f x f x x x f x -'=-成立,求证:01x x >.【解答】证明:(1)由g (x )=f (x )﹣x =lynx ﹣x ,(x >1) 得g '(x )=lax >0,∴g (x )在(1,+∞)上是增函数,故g (x 2)>g (x 1), 即f (x 2)﹣x 2>f (x 1)﹣x 1 ∴f (x 2)﹣f (x 1)>x 2﹣x 1即(2)∵f '(x 0)=lnx 0+1, ∴=====lnx 1+=,∴,令则,设h (t )=Ont ﹣(t ﹣1),∴h (t )在(0,1)上是增函数,h (t )<h (1)=0 即,∴lnx 0>lnx 1,故x 0>x 1. 14.已知函数2() 1.g x x ax =-+(1)求()0g x <的解集; (2)已知函数1()ln f x x a x x=-+,当122()a x x y g x =>时,、是的两个零点, 证明:1212))((2f x f x a x x -<--.(可能用到的参考结论:函数12lny x xx=+-在区间(0)+∞,上单调递减)【解答】解:(1)x2﹣ax+1<0,△=a2﹣4.△≤0时,解得﹣2≤a≤2,g(x)<0的解集为∅;△>0,解得a>2或a<﹣2时,由x2﹣ax+1=0,解得x=.∴x2﹣ax+1<0,解得<x<.∴g(x)<0的解集为{x|<x<}.(2)证明:当a>2时,x1、x2是y=g(x)的两个零点,∴x1+x2=a,x1x2=1.不妨设0<x1<1<x2.函数,要证明:.⇔<a﹣2,化为:Ln>x1﹣x2,把x1=代入可得:即证明:﹣x2+2lnx2<0.x2>1.∵函数在区间(0,+∞)上单调递减,∴﹣x2+2lnx2<﹣1+2ln1=0.因此:﹣x2+2lnx2<0.即:.15.已知a ∈R ,函数2()2(4)ln f x x ax a x =++-有两个不同的极值点12x x 、. (1)求a 的取值范围;(2)证明:12))1(4(6ln 22f x f x +<-.【解答】解:(1)a ∈R ,函数f (x )=x 2+2ax +(4﹣a )1nx 定义域:{x |>0}., ∴f ′(x )=2x +2a +(4﹣a )=,函数f (x )有两个不同的极值点x 1,x 2.对于f ′(x )中的2x 2+2ax +(4﹣a )应满足①②③三个条件:∴x 对=﹣>0,①△=4a 2﹣4×2×(4﹣a )>0,② 4﹣a >0,③由①②③可得a 的取值范围:{a |a <﹣4}, (2)证明:∵f ′(x )=2x +2a +(4﹣a )=,得:x 1+x 2=﹣a ,x 1.x 2=,f (x 1)+f (x 2)=(x 1+x 2)2﹣2x 1x 2+2a (x 1+x 2)+(4﹣a )1nx 1x 2=﹣a 2+a ﹣4+(4﹣a )1n ,令t =>4,则f (x 1)+f (x 2)=2t 1nt ﹣4t 2+14t ﹣16,将其令为h (t )即:h (t )=f (x 1)+f (x 2) 则有:h ′(t )=21nt ﹣8t +16, h ″(t )=﹣8,∵h ″(t )=﹣8<0,∴h ′(t )=21nt ﹣8t +16在定义域是单调递减的函数, ∴h ′(t )<h ′(4)<0,∴h (t )在定义域也是单调递减的函数, ∴h (t )<h (4)=16ln 2﹣24. 即:f (x 1)+f (x 2)<16ln 2﹣24得证.16.已知函数())(xxf x e e ax a -=+有两个极值点12x x 、.(1)求a 的取值范围; (2)求证:12122x x x x <+.【解答】解:(1)因为函数f (x )=e x (e x ﹣ax +a )有两个极值点x 1,x 2, 所以f ′(x )=e x (e x ﹣ax +a )+e x (e x ﹣a )=e x (2e x ﹣ax ), 令f ′(x )=0,则:2e x =ax , 当a =0时,不成立; 当a ≠0时,=,令g (x )=,所以g ′(x )=,当x <1时,g ′(x )>0,当x >1时,g ′(x )<0,所以g (x )在(﹣∞,1)上单调递增,在(1,+∞)上单调递减,又因为g (1)=,当x →﹣∞时,g (x )→﹣∞,当x →+∞时,g (x )→0, 因此,当,0<<时,f (x )有2个极值点, 即a 的取值范围为:(2e ,+∞);(2)由(1)不妨设0<x 1<1<x 2 且 ,所以,所以x 2﹣x 1=lnx 2﹣lnx 1,要证明2x 1x 2<x 1+x 2,只要证明2x 1x 2( lnx 2﹣lnx 1)<,即证明2ln <﹣,设=t ,t >1,即要证明2lnt ﹣t +<0在t ∈(1,+∞)上恒成立,记h (t )=2lnt ﹣t +,t >1,h ′(t )=﹣1﹣==<0,所以h (t )在区间(1,+∞)上单调递减,所以h (t )<h (1)=0,即2lnt ﹣t +<0,即2x 1x 2<x 1+x 2.。
四年级双变量应用题及答案

四年级双变量应用题及答案一、选择题1、可以清楚地表示数量的增减变化的统计图是()A、折线统计图B、条形统计图C、扇形统计图2、1、2、3、5都是30的()A、质因数B、公因数C、约数3、在11、57、2、95、62五个数中,合数的个数有()A、5个B、3个C、1个D、4个4、5/8的分子加上10,要使分数的大小不变,分母应加上()A、10B、8C、16D、205、下列各数中,与6是互质数的合数是()A、9B、11C、C、356、互质的两个数的公因数()。
A、只有1个B、有2个C、有3个D、有无限个。
二、填空题7、3/8= _________÷24=30________=()/56=_________(填小数)8、同时是2、3、5的倍数的最小三位数是__________。
9、16和24的最大公因数是________;6和10的最小公倍数是_________。
10、甲数=2×3×3,乙数=5×3×2,甲乙两数的最大公因数是_________,它们的最小公倍数是_________。
11、自然数中最小的奇数是_________;最小的偶数是_________;最小的自然数是_________;最小的合数是_________;最小的质数是_________;除零外所有的自然数单位是_________。
12、一个数的最小倍数是12,这个数是________;一个数的最大因数是33,这个数是_________。
13、在自然数中,最小的奇数是_________,最小的偶数是_________,最小的素数是_________,最小的合数是_________。
14、5/6的分子扩大5倍,要使分数值不变,分母应();5/6的分子加上15,要使分数的大小不变,分母应()。
三、判断题15、小芳每天睡眠9小时,她一天的睡眠时间占全天的( )。
16、圆的周长与它的直径的比值是π_________(判断对错)。
导数中双变量问题 培优练习(含解析)

导数中双变量问题 培优练习1.设函数1()ln f x x m xx =--.(Ⅰ)若函数f (x )在定义域上为增函数,求实数m 的取值范围; (Ⅱ)在(Ⅰ)的条件下,若函数1()ln h x x x e=--,12,[1,]x x e ∃∈使得12()()f x h x ≥成立,求实数m 的取值范围.【解析】:函数的定义域为(0,)+∞.21()1m f x x x =+-'.(Ⅰ)∵()f x 在其定义域内为增函数,即()0f x '≥在(0,)+∞上恒成立, ∴2110m x x +-≥恒成立,故有1m x x≤+. ∵1122x x x x+≥⨯=(当且仅当1x =时取等号). 故m 的取值范围为(,2]-∞.(Ⅱ)由12,[1,]x x e ∃∈使得12()()f x h x ≥成立, 可知[1,]x e ∈时,max min ()()f x h x ≥.,所以当[1,]x e ∈时,()0h x '≥,()h x 在[1,]e 上单调递增,所以()h x 在[1,]e 上的最小值为11(1)1ln11h e e=--=-. 由(Ⅰ)知,2m ≤且221()x mx f x x-+'=,22()4114m m ∆=--⨯⨯=-, 当[2,2]m ∈-时,0∆≤,故()0f x '≥恒成立,()f x ∴在[1,]e 上单调递增,故()f x 在[1,]e 上的最大值为1()f e e m e=--. 即111e m e e--≥-,1m e ∴≤-. 又[2,2]m ∈-,所以[2,1]m e ∈--.②当2m <-时,0∆>,()0f x '=的两根为2142m m x -=,2242m m x +-=.此时10x <,20x <,故()f x 在[1,]e 上单调递增,由①知,1m e ≤-,又2m <-,故2m <-综上所述,m 的取值范围为[2,1](,2)(,1]e e --⋃-∞-=-∞-. 12分2.已知函数1()(1)ln 2f x a x ax x =++-+.(1)讨论f (x )的单调性;(2)若f (x )有两个极值点1x ,2x 12()x x <,且至少存在两个零点,求1212()()f x f x x x ++的取值范围.【详解】解:(1)由题,()f x 的定义域为(0,)+∞,()22221111(1)(1)()ax a x a x ax f x a x x x x-++-+--=--=-'=, 当0a =时,()21x f x x-'=,则当1x >时,()0f x '>,当01x <<时,()0f x '<,所以()f x 在()0,1上单调递减,在()1,+∞上单调递增;当0a ≠时,令()0f x '=,得1x =或1x a=, 当0a <时,10a<,所以()f x 在(0,1)上单调递减,在(1,)+∞上单调递增; 当01a <<时,即11a >时,所以()f x 在(0,1)上单调递减,在1(1,)a上单调递增,在1(,)a +∞上单调递减;当1a =时,()0f x '≤在(0,)+∞上恒成立,所以()f x 在(0,)+∞上单调递减;当1a >时,101a <<,所以()f x 在1(0,)a上单调递减,在1(,1)a 上单调递增,在(1,)+∞上单调递减(2)由(1)知,因为()f x 有两个极值点1x ,2x 12()x x <,所以01a <<或1a >,因为(1)30f a =->,所以01a <<不合题意;因为1a >时,()f x 在1(0,)a 上单调递减,在1(,1)a上单调递增,在(1,)+∞上单调递减,所以1()0(1)0f a f ⎧≤⎪⎨⎪≥⎩即(1)(1ln )030a a a +-≤⎧⎨-≥⎩, 解得3e a ≤≤,此时1212()()3(1)(1ln )4ln 111f x f x a a a aa ax x a a+-++-==-+++, 记4()ln (3)1ag a a a e a a =-≤≤+,则224(1)(1ln )()(1)a a g a a -+=+'+, 因为3e a ≤≤,所以()0g a '<,所以()g a 在区间[,3]e 上单调递减, 所以(3)()()g g a g e ≤≤,解得433ln 3()1eg a e e -≤≤-+, 所以,1212()()f x f x x x ++的取值范围为4[33ln 3,]1ee e --+3.已知函数()222ln f x x kx x=-+(k R +∈).(1)当k =f (x )单调性;(2)若()()11221()()4x H f x f x H x =-≥,(1x ,2x 为()'f x 的两个零点,且12x x <)求k 的取值范围. 【详解】解:(1)当k =时,()2'2f x x x =-=令()'0f x >,解得0x <<或x >, 令()'0f x <x <<, 所以()f x在(0,<和)+∞上单调递增,在上单调递减; (2)()22222'22x kx f x x k x x-+=-+=,由题意知方程22220x kx -+=在(0,)+∞上有两个不等的实根1x ,2x (12x x <), 所以2121240010k x x k x x ⎧∆=->⎪+=>⎨⎪=>⎩,解得2k >,()()1122()x H f x f x x =-()()()2212121222ln ln x x k x x x x =---+- ()()()()221212121222ln ln x x x x x x x x =--+-+-()2221122ln ln x x x x =-+- 222111222ln x x x x x x -=+2111222ln x x x x x x =-+, 令12(0,1)x t x =∈,则()12ln H t t t t=-+, ()212'1H t t t =--+2221t t t -+=-()2210t t-=-<, 所以()H t 在(0,1)上单调递减,又()1()4H t H ≥,所以104t <≤,而221212()x x k x x +=12212x x x x =++12524t t =++≥,当且仅当14t =等号成立 即52k ≥,综上:实数k 的取值范围为5[,)2+∞.4.已知函数21()ln (1)2f x x a x a x e =--≤≤,()1xg x e x =--,其中a R ∈,e 为自然对数的底数. (1)求函数f (x )的最小值;(2)若对于任意的1[0,1]x ∈,都存在唯一的2[1,]x e ∈,使得()()12g x f x =,求实数a 的取值范围. 【详解】(1)由题:21()ln (1)2f x x a x a x e =--≤≤, 222(),(1),1,a x a f x x x e x e x x-'⎡⎤=-=≤≤∈⎣⎦, 当1a ≤时,()0f x '≥恒成立,所以函数()f x 在[]1,x e ∈单调递增,最小值为()112f a =-, 当2a e ≥时,()0f x '≤恒成立,所以函数()f x 在[]1,x e ∈单调递减,最小值为()222e f e a =-,当1a e <<时,由()0f x '>得x e ⎤∈⎦,由()0f x '<得x ⎡∈⎣, ()f x在x ⎡∈⎣递减,在x e ⎤∈⎦递增,所以函数的最小值为1ln 22afa a =-- 综上所述:当1a ≤时,()f x 最小值为12a -,当2a e ≥时,最小值为222e a -,当1a e <<时,最小值为1ln 22aa a --;(2)函数()1x g x e x =--,[0,1]x ∈,()10xg x e '=-≥当且仅当x =0时,导数值为0,所以()1xg x e x =--在[0,1]x ∈单调递增,值域为[0,2]e -, 结合(1)可得:当1a ≤时,函数()f x 在[]1,x e ∈单调递增,()112f a =-,()222e f e a =-,只需2222102e a e a ⎧-≥-⎪⎪⎨⎪-≤⎪⎩,解得:112a ≤≤,当2a e ≥时,函数()f x []1,x e ∈单调递减,()()1102f x f a ≤=-<,不合题意,舍去,当1a e <<时,()f x在x ⎡∈⎣递减,在x e ⎤∈⎦递增,()1102f a =-<,1ln 022af a a =--<, 所以只需()2222e f e a e =-≥-,解得21142e ea <≤-+综上所述211242e ea ≤≤-+5.已知函数()()1ln f x x a ax =+∈R 在1x =处的切线与直线210x y -+=平行.(1)求实数a 的值,并判断函数f (x )的单调性;(2)若函数()f x m =有两个零点1x ,2x ,且12x x <,求证:121x x +>. 【详解】(1)函数()f x 的定义域:()0,+∞,()11112f a =-=',解得2a =, ()1ln 2f x x x ∴=+,()22112122x f x x x x -∴=-=' 令()0f x '<,解得102x <<,故()f x 在10,2⎛⎫⎪⎝⎭上是单调递减; 令()0f x '>,解得12x >,故()f x 在1,2⎛⎫+∞ ⎪⎝⎭上是单调递增.(2)由12,x x 为函数()f x m =的两个零点,得121211ln ,ln 22x m x m x x +=+= 两式相减,可得121211ln ln 022x x x x -+-= 即112212ln 2x x x x x x -=,1212122ln x xx x x x -=, 因此1211212ln x x x x x -=,2121212lnx x x x x -=令12x t x =,由12x x <,得01t <<. 则121111+=2ln 2ln 2ln t t t t x x t t t---+=, 构造函数()()12ln 01h t t t t t=--<<,则()()22211210t h t t t t -=+-=>'所以函数()h t 在()0,1上单调递增,故()()1h t h <,即12ln 0t t t--<,可知112ln t t t->.故命题121x x +>得证.6.设函数2()(1)x f x xe a x =++,其中a ∈R .(1)讨论函数f (x )的单调性;(2)当1a >时,试证明:函数f (x )有且仅有两个零点()1212,x x x x <,且122x x +<-.【详解】(1)函数()f x 定义域为R ,()()(1)2xf x x e a '=++,0a ≥时,20x e a +>恒成立,故()0f x '>的解集为(1,)-+∞. 所以()f x 在(,1)-∞-上单调递减,在(1,)-+∞上单调递增. 0a <时,()0f x '=有两个实根:-1,ln(2)a -.当102a e-<<时,ln(2)1a -<-,令()0f x '>,解得(,ln(2))(1,)x a ∈-∞-⋃-+∞. 故()f x 在(ln(2),1)a --上单调递减,在(,ln(2))a -∞-,(1,)-+∞上单调递增;当12ea <-时,ln(2)1a ->-,令()0f x '>,解得(,1)(ln(2),)x a ∈-∞-⋃-+∞. 故()f x 在(1,ln(2))a --上单调递减,在(,1)-∞-,(ln(2),)a -+∞上单调递增;当12ea =-时,()0f x '≥恒成立,()f x 为R 上的增函数. (2)由(1)知,当1a >时,()f x 在(,1)-∞-上单调递减,在(1,)-+∞上单调递增.故min 1()(1)0f x f e=-=-<. 又(0)0f a =>,2222(2)10f a e e-=-+>->.由零点存在性定理知,函数()f x 仅有两个零点121,,(2,1)x x x ∈--,2(1,0)x ∈-.令()()(2)F x f x f x =---,有(1)0F -=.()2()()(2)(1)x x F x f x f x x e e --'''=---=+-.(1,)x ∈-+∞时,()0F x '>,函数()F x 单调递增,所以()2(1)0F x F >-=.即()()2220f x f x --->,又()()12f x f x =,所以()()122f x f x >--.122(,1),x x --∈-∞-,函数()f x 在(,1)-∞-上单调递减,所以122x x <--.所以122x x +<-.7.已知函数()()21ln 2f x x x ax a =++∈R .(1)讨论f (x )的单调性;(2)若12,x x 为f (x )的两个极值点,证明:()()21212+44282f x f x a a x x f +++⎛⎫-> ⎪⎝⎭. 【详解】(1)()f x 的定义域为()0,∞+,()()210x ax f x x x'++=>,对于函数21y x ax =++,①当240a ∆=-≤时,即22a -≤≤时,210x ax ++≥在0x >恒成立.()210x ax f x x++∴=≥'在()0,∞+恒成立,()f x ∴在()0,∞+为增函数;②当>0∆,即2a <-或2a >时,当2a <-时,由()0f x '>,得2a x -<或2a x -+>,0<<()f x ∴在⎛⎫ ⎪ ⎪⎝⎭为增函数,⎛⎫⎪ ⎪⎝⎭减函数,2a ⎛⎫-++∞⎪ ⎪⎝⎭为增函数, 当2a >时,由()210x ax f x x++=>'在()0,∞+恒成立,()f x ∴在()0,∞+为增函数.综上,当2a <-时,()f x在0,2a ⎛⎫- ⎪ ⎪⎝⎭为增函数,22a a ⎛⎫---+⎪ ⎪⎝⎭减函数,2a ⎛⎫-++∞⎪ ⎪⎝⎭为增函数; 当2a ≥-时,()f x 在()0,∞+为增函数.(2)由(1)知2a <-,且1212,1x x a x x +=-=, 故()()121222f x f x x x f ++⎛⎫- ⎪⎝⎭()()21222111222121211ln ln 222ln 2222x x x x ax x x ax x x x x a +⎛⎫+++++ ⎪++⎛⎫⎛⎫⎝⎭=--- ⎪ ⎪⎝⎭⎝⎭21ln +228a a ⎛⎫=--- ⎪⎝⎭故只需证明ln 1022a a⎛⎫----> ⎪⎝⎭,令2at =-,故1t >, 原不等式等价于ln 1t t 对1t >成立,令1()ln (1),'()0tg t t t g t t,所以()ln (1)g t t t 单调递减,有()ln (1)(1)0g t t t g 得证.8.已知函数()()20f x lnx ax x a =--+≥.(1)讨论函数f (x )的极值点的个数;(2)若函数f (x )有两个极值点1x ,2x ,证明:()()12322f x f x ln +>-. 【详解】解:()1函数()()20f x lnx ax x a =--+≥,()()2212121210ax x ax x f x ax x x x x-+-+-∴=--+>=-'=, 0x > 0a ≥,∴当0a =时,()1x f x x'-=,0x >, 当()0,1x ∈时,()0f x '<,()f x 单调递减;当()1,x ∈+∞时,()0f x '>,()f x 单调递增;∴当1x =时,()f x 有极小值;当18a ≥时,0∆≤,故()0f x '≤, ()f x ∴在()0,+∞上单调递减,故此时()f x 无极值;当108a <<时,0>,方程()0f x '=有两个不等的正根1x ,2x .可得114x a -=,214x a+=.则当x ⎛∈ ⎝⎭及x ⎫∈+∞⎪⎪⎝⎭时, ()0f x '<,()f x 单调递减;当x ∈⎝⎭时,()0f x '> ;()f x 单调递增; ()f x ∴在1x x =处有极小值,在2x x =处有极大值.综上所述:当0a =时,()f x 有1个极值点;当18a ≥时,()f x 没有极值点; 当108a <<时,()f x 有2个极值点.()2由()1可知当且仅当10,8a ⎛⎫∈ ⎪⎝⎭时()f x 有极小值点1x 和极大值点2x ,且1x ,2x 是方程的两个正根, 则1212x x a +=,1212x x a=. ()()()(()()2121212121211[)2ln 212144f x f x x x a x x x x lnx lnx a lna ln a a⎤∴+=+-+--+=++=+++⎦; 令()1214g a lna ln a =+++, 108a <<;()24104a g x a -'=<,()g a ∴在10,8⎛⎫⎪⎝⎭上单调递减,故()13228g a g ln ⎛⎫>=- ⎪⎝⎭,()()12322f x f x ln ∴+>-.9.已知函数21()1f x ax x nx =--(1)若f (x )在点()(1)1f ,处的切线与直线21y x =+平行,求f (x )在点()(1)1f ,的切线方程; (2)若函数f (x )在定义城内有两个极值点1x ,2x ,求证:()()122ln23f x f x +<-. 【详解】解:(1)2()ln ,f x ax x x =-+1()21f x ax x'∴=-+ '(1)2k f a ∴==因为()f x 在点(1,(1))f 处的切线与直线21y x =+平行,22a ∴=,即1a =(1)0,f ∴=故切点坐标为()1,0 ∴切线方程为22y x =-(2)2121()21,ax x f x ax x x-+'=-+=∴由题知方程2210ax x -+=在()0+∞,上有两个不等实根12,x x .1212180,10,210,2a x x a x x a ⎧⎪∆=->⎪⎪∴+=>⎨⎪⎪=>⎪⎩10.8a ∴<<又2212121212()()()ln ln f x f x ax ax x x x x +=+-+++ 22121212 ()()ln()a x x x x x x =+-++212121212=[()2]()ln()a x x x x x x x x +--++11=ln1,24a a-- 令1,2t a =()ln 1,(4,),2t g t t t =--∈+∞ 则112()0,22tg t t t-'=-=< ()g t ∴在(4,)+∞上单调递减. ()(4)ln 432ln 2 3.g t g ∴<=-=-即12()()2ln 2 3.f x f x +<-10.已知函数()212ln 2x f x ax x =+-,其中a R ∈.(1)讨论函数f (x )的单调性;(2)若3a ≥,记函数f (x )的两个极值点为1x ,2x (其中21x x >),求()()21f x f x -的最大值.【详解】(1)()()2'220x ax x a x x xf x -+=+-=>.令()22g x x ax =-+,则28a ∆=-.①当0a ≤或0∆≤,即a ≤时,得()'0f x ≥恒成立, ∴()f x 在()0,∞+上单调递增.②当00a >⎧⎨∆>⎩,即a >由()'0f x >,得0x <<或x >由()'0f x <,得22a a x -+<<.∴函数()f x 在⎛ ⎝⎭和⎫+∞⎪⎪⎝⎭上单调递增,在⎝⎭上单调递减.综上所述,当a ≤()f x 在()0,∞+上单调递增;当a >()f x 在0,2a ⎛ ⎪⎝⎭和,2a ⎛⎫++∞ ⎪ ⎪⎝⎭上单调递增,在22a a ⎛+⎪⎝⎭上单调递减.(2)由(1)得,当a >()f x 有两极值点1x ,2x (其中21x x >). 则1x ,2x 为()220x a g x x =-+=的两根,∴12x x a +=,122x x =.()()()()222212121112ln2x f x f x x x a x x x -=+--- 222222122111122ln 2ln 2x x x x x x x x x x --=-=-2211122lnx x x x x x =-+. 令()211x t t x =>, 则()()()2112ln f x f x h t t t t-==-+.由3a ≥,得()22121219222x x a t x x t +==++≥,即22520t t -+≥,解得2t ≥.∵()()22222121211'0t t t t t t th t ---+-=--==<, ∴()h t 在[)2,+∞上单调递减, ∴()()max 322ln 22h t h ==-. 即()()21f x f x -的最大值为32ln 22-.11.已知函数()()()ln f x x x ax a =-∈R .(Ⅰ)若1a =,求函数f (x )的图象在点()()1,1f 处的切线方程;(Ⅱ)若函数f (x )有两个极值点1x 、2x ,且12x x <,求证:()10<f x 且()212f x >-. 【详解】解:(Ⅰ)1a =时,()()ln f x x x x =-,()11f =-, 因为()ln 12f x x x '=+-,()11f '=-,所以()f x 的图象在点()()1,1f 处的切线方程为()11y x +=--即0x y +=; (Ⅱ)由已知可得,()ln 12f x x ax '=+-,0x >,由0fx可得,1ln 2xa x+=, 令()1ln xg x x +=,则()2ln x g x x -'=,易得()g x 在0,1上单调递增,在1,上单调递减,且()11g =,10g e ⎛⎫= ⎪⎝⎭,故当1x >时,()0gx >,x →+∞时,()0g x →,函数()f x 有两个极值点;1x 、2x ,且12x x <,即0fx有两个零点1x 、2x ,且12x x <,则021a <<,所以102a <<, ∴121x x ,当()1,1x x ∈时,1ln 2xa x+>,0f x,()f x 单调递增,所以()()110f x f a <=-<,当()21,x x ∈时,1ln 2xa x+>,0f x,()f x 单调递增,∴()()2112f x f a >=->-,综上,()10f x <且()212f x -.12.已知函数(),xf x e ax a R =+∈,其中e 为自然对数的底数. (Ⅰ)讨论f (x )单调性;(Ⅱ)当3a =-时,设函数()()()g x f x m m R =-∈存在两个零点1212,()x x x x <,求证:126x x e e +>.【详解】解:(1)()xf x e a '=+,当0a ≥时,()0f x '>,()f x 在(,)-∞+∞上单调递增;当0a <时,令()0f x '=得ln()x a =-,()f x 在(,ln())a -∞-上单调递减,在(ln())a -+∞上单调递增;(Ⅱ)解法一:由题意知()3xg x e x m =--,由()()1200g x g x ⎧=⎪⎨=⎪⎩得121233xx e x me x m⎧-=⎨-=⎩,两式相减得()12123xx e ex x -=-,因为12x x <,故()121230x x e e x x -=-<,要证126x x e e +>,只需证()()()12121236xx x x x x e ee e -+<-,两边同除以23x e 得()()()121212121x x x x x x ee ---+<-,令120u x x =-<,故只需证(2)20uu e u -++<即可.令()(2)2u G u u e u =-++,()(1)1uG u u e '=-+,令()(1)1,()u uh u u e h u ue '=-+=,当(,0)u ∈-∞时,()0h u '<,故()h u 在(,0)-∞上单调递减,故()(0)0h u h >=,故()G u 在(,0)-∞上单调递增,故()(0)0G u G <=,故原命题得证.【解法二】由题意知()3xg x e x m =--,由()()1200g x g x ⎧=⎪⎨=⎪⎩得121233x x e x m e x m⎧-=⎨-=⎩,令121212,,0x x e t e t t t ==<<,即11223ln 3ln t t mt t m=+⎧⎨=+⎩,两式相减得11223ln 0t t t t -=<,要证126x x e e +>,即只需证126t t +>,即证1122123ln 6t t t t t t ->+,即()1212122ln 0t t t t t t --<+,即12112221ln 01t t t t t t ⎛⎫- ⎪⎝⎭-<+, 令12(0,1)t u t =∈,只需证2(1)ln 01u u u --<+即可. 令2(1)()ln 1u G u u u -=-+,22214(1)()(1)(1)u G u u u u u -'=-=++,当(0,1)u ∈时,()0G u '>,故()G u 在(0,1)上单调递增,故()(1)0G u G <=,因此原不等式成立.13.设函数()2ln f x x ax x=-+.(1)若当1x =时,f (x )取得极值,求a 的值,并求f (x )的单调区间. (2)若f (x )存在两个极值点12,x x ,求a 的取值范围,并证明:()()212142f x f x ax x a >---.【详解】(1)()()21212,0x ax f x x a x x x-+'=-+=>1x =时,()f x 取得极值.()0,31f a ∴'==.()()()2211231 x x x x f x x x---+'∴==解()0f x '>得102x <<或1x >解()0f x '<得112x <<()f x ∴的单调增区间为10,,(1,)2⎛⎫+∞ ⎪⎝⎭,单调减区间为1,12⎛⎫⎪⎝⎭.(2)()()221,0x ax f x x x-+'=>()f x 存在两个极值点∴方程()0f x '=即2210x ax -+=在(0,)+∞上有两个不等实根.212180,02a x x ∆=->=>,1202a x x +=>a ∴>()()22212221112121ln ln f x f x x ax x x ax x x x x x -+-+--=--2121212121ln ln ln ln 2x x x x a x x a x x x x --=+-+=-+--∴所证不等式()()212142f x f x ax x a >---等价于2121ln ln 4x x x x a ->- 即212121ln ln 2x x x x x x ->-+ 不妨设210x x >>,即证2212111ln21x x x x x x ->+ 令211x t x =>,()()21ln 1t h t t t -=-+ ()()()()222114011t h t t t t t -'=-=>++,()h t ∴在(1,)+∞上递增. ()()10h t h ∴>=2212111ln 21x x x x x x -∴>+成立.()()212142f x f x ax x a ∴>---成立.14.已知函数()2ln f x x x ax =-,a R ∈.(1)若函数f (x )存在单调增区间,求实数a 的取值范围;(2)若1x ,2x 为函数f (x )的两个不同极值点,证明:2112x x e ->.【详解】(1)由题函数存在增区间,即需()'1ln 20f x x ax =+->有解,即1ln 2xa x+>有解, 令()1ln x g x x +=,()2ln 'xg x x=-,且当()0,1x ∈时,()'0g x >, 当()1,x ∈+∞时,()'0g x <,如图得到函数()g x 的大致图象,故当()max 21a g x <=,∴12a <时,函数()f x 存在增区间;(2)法1:1x ,2x 为函数()f x 的两个不同极值点知1x ,2x 为()'0f x =的两根, 即111ln 20x ax +-=,221ln 20x ax +-=, ∴111ln 2x ax +=,221ln 2x ax +=① ∴1212ln ln 2x x a x x -=-②,要证2112x x e ->,即证122ln ln 1x x +>-,由①代入,即证:()12221211ax ax -+->-,()12222a x x +>, 将②代入即证:()121212ln ln 22x x x x x x -+>-③且由(1)知121,,x x e⎛⎫∈+∞ ⎪⎝⎭,若120x x >>,则③等价于()1122112122212ln 221x x x x x x x x x x ⎛⎫- ⎪-⎝⎭>=++,令12x t x =,1t >, 即证()()()21ln 0121t t t t t ϕ-=->>+成立,而()()()()()()222222161642100212121't t t t t t t t t t t t ϕ+--+=-==>>+++, ∴()()21ln 21t t t t ϕ-=-+在()0,t ∈+∞单调递增,∴当()1,t ∈+∞时,∴()()()21ln 1021t t t t ϕϕ-=->=+,所以得证;若210x x >>,则③等价于()1122112122212ln 221x x x x x x x x x x ⎛⎫- ⎪-⎝⎭<=++,令12x t x =,01t <<, ()()21ln 021t t t t ϕ-=-<+,显然()()10t ϕϕ<=成立.法2:要证122ln ln 10x x ++>,又由(1)知121,,x x e ⎛⎫∈+∞ ⎪⎝⎭,102a <<,当11x >时,要证上式成立,即证12ln 0x ax +>,易知显然成立; 当111x e<<时,11ln 0x +>,故只需12ln ln 0x x +>,即证121x x >,也即证12110x x >>>,由于()0,1x ∈时()g x 单调递增,故即证()121g g x x ⎛⎫< ⎪⎝⎭,而()()12g x g x =, 只需证()221g g x x ⎛⎫<⎪⎝⎭,21>x 成立,令()()1p x g x g x ⎛⎫=- ⎪⎝⎭, 只需证()()10p x g x g x ⎛⎫=->⎪⎝⎭在1x >时成立, 而()()()()222ln 111'''01x x p x g x g x x x x -⎛⎫=+⋅=>> ⎪⎝⎭,故()p x 在1x >单调递增, 所以()()10p x p >=,故原不等式得证.15.已知函数()31(),3f x x bx c b c R =-+∈(1)若函数f (x )在点()()1,1f 处的切线方程为21y x =+,求b 、c 的值; (2)若1b =,函数f (x )在区间(0,2)内有唯一零点,求c 的取值范围; (3)若对任意的[]12,1,1x x ∈-,均有()()1243f x f x -≤,求b 的取值范围. 【解析】:(1)()2f x x b '=-,所以()112f b ='-=,得1b =-又(1)213f =+=,所以133b c -+=,得53c = (2)因为1b =所以()313f x x x c =-+,2()1f x x =-'当()0,1x ∈时,()0f x '<,当()1,2x ∈时,()0f x '>所以()f x 在0,1上单调递减,在1,2上单调递增 又()()2023f c f c =<=+,可知()f x 在区间()0,2内有唯一零点等价于 ()10f =或()()00{20f f ≤>得23c =或203c -<≤(3)若对任意的[]12,1,1x x ∈-,均有()()1243f x f x -≤,等价于()f x 在[]1,1-上的最大值与最小值之差43M ≤(ⅰ)当0b ≤时,在[]1,1-上()0f x '≥,()f x 在[]1,1-上单调递增由()()2411233M f f b =--=-≤,得13b ≥- 所以103b -≤≤ (ⅱ)当0b >时,由()0f x '=得x b =±由()(f x f b =-得x b =x b =所以((2f b f b =-,同理(2f b f b -=1)1b >,即1b >时,()()2411233M f f b =--=->,与题设矛盾 2)当12b b ≤≤114b ≤≤时,(332442333M f b f b b b b b=--=-+=≤恒成立3)当1b <,即104b <<时,()()2411233M f f b =--=-≤恒成立 综上所述,b 的取值范围为1,13⎡⎤-⎢⎥⎣⎦.16.已知函数1()ln f x x a xx =--(a R ∈且0a >)(1)若f (x )在定义域内单调递增,求实数a 的取值范围;(2)若f (x )有两个不同的极值点12,x x ,记过点()()11,A x f x ,()()22,B x f x 的直线的斜率为k ,求证:2k a >-.【详解】解:()f x 定义域22211(0,)()1a x ax f x x x x'-++∞=+--=, 由()f x 在定义域内单调递增,等价于对任意(0,)x ∈+∞,都有()0f x '≥,即1a x x ≤+恒成立,而1122x x x x+≥⋅=, 故2a ≤,又0a >,所以(0,2]a ∈.(2)定义域22211(0,)()1a x ax f x x x x'-++∞=+--=,设2()1g x x ax =-+,其判别式24a ∆=-,当02a <≤时,由(1)得由()f x 在定义域内单调递增,无极值点,当2a >时,>0∆,()0g x =0x <<时,()0f x '>x <<()0f x '<;当x >时,()0f x '>.故()f x在0,,22a a ⎛⎫⎛⎫++∞ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭单调递增,在⎝⎭单调递减.即是函数的极值点,不妨设12a x =,22a x +=则120x x <<且121=x x .()()()()()()()12121212121212ln ln 2ln ln x x f x f x x x ax x x x a x x x x --=-+--=---,所以1212ln ln 2x x k ax x -=--,而()()1212121212ln ln ln ln (2)1x x x x x x k a a a x x x x ⎡⎤---⎡⎤---=-=⎢⎥⎢⎥--⎣⎦⎣⎦, 而120x x <<且121=x x 得211201x x x <<=,故101x <<,所以()()12121111ln ln 2ln x x x x x x x ---=--,101x <<. 设1()2ln h t t t t =--,(01t <<),而22212(1)()10t h t t t t -'=+-=>,所以()g t 在0,1()上单调递增,所以()(1)0h t h <=,而120,0x x a -<>,故2k a >-.17.已知函数()(1)ln ()f x ax x x a =--∈R .(1)设()(-1)( -1)-()g x x a x f x =,求函数()g x 的极值;(2)当0a <时,函数()f x 有两个极值点()1212,x x x x <,证明:()294f x >. 【详解】(1)解:()(1)(1)(1)ln ln (1)g x x ax ax x x x x =----+=--,则11()1x g x x x-'=-=. 令()0g x '=,得1x =.所以当x 变化时,(),()g x g x '的变化情况如下表:因此()g x 有极大值()10g =,无极小值.(2)证明:2121()2ax ax f x ax a x x'--=--=.由题意得,1212x x +=. 因为12x x <,所以214x >.由()20f x '=,得222210ax ax --=, 则222102a x x =<-,解得2102x <<. 所以21142x <<. 由(1)得22ln 1x x ≤-,所以()()()()()()22222222222222211141ln 11111222x x f x ax x x ax x x x x x x x -⎛⎫=-----=--=++- ⎪-⎝⎭- 令212t x =-,则1|0,4t ⎛⎫∈ ⎪⎝⎭. 分析可得14y t t =+在区间10,4⎛⎫ ⎪⎝⎭上单调递减. 当14t =时.11514444y =+=⨯ 所以()215911444f x t t ++>+=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两道每日一题1.已知12,F F 是椭圆22:14x C y +=的左,右焦点,直线l 与椭圆相切。
(1)分别过12,F F 作切线l 的垂线,垂足分别为M N ,,求12F M F N⋅的值(2)设直线l 与x 轴,y 轴分别交于两点,A B ,求AB 的最小值。
2.已知椭圆22:194x yC+=,过点()03P,作直线l与椭圆顺次交于,A B两点(A在,P B之间)。
(1)求PAPB的取值范围;(2)是否存在这样的直线l,使得以弦AB为直径的圆经过坐标原点?若存在,求l的方程,若不存在,说明理由。
利用导数解决“双变量”问题例1.(全国卷III) 已知函数()2472x f x x-=-,[]01x ∈,.(Ⅰ)求()f x 的单调区间和值域;(Ⅱ)设1a ≥,函数()[]323201g x x a x a x =--∈,,,若对于任意[]101x ∈,,总存在[]001x ∈,,使得()()01g x f x =成立,求a 的取值范围.在主干条件“函数()2472x f x x-=-,[]01x ∈,,32()32g x x a x a =--,[0,1]x ∈,1a ≥”不变的前提下,对问题(Ⅱ)进行如下变式:变式1 若存在1x ,2[0,1]x ∈,使得12()()f x g x =成立,求实数a 的范围;变式2 若存在1x ,2[0,1]x ∈,使得12()()f x g x >成立,求实数a 的范围;变式3 若对任意1[0,1]x ∈,总存在2[0,1]x ∈,使得12()()f x g x >成立,求实数a 的范围;变式4 若对任意1[0,1]x ∈,总存在2[0,1]x ∈,使得12()()f x g x <成立,求实数a 的范围;变式5 若对任意1x ,2[0,1]x ∈,使得12()()f x g x >成立,求实数a 的范围;变式6 若存在1x ,2[0,1]x ∈,使得12|()()|1f x g x -<成立,求实数a 的范围.2.已知函数211()ln()22f x ax x ax =++-(a 为常数,0a >). (I )若12x =是函数()f x 的一个极值点,求a 的值; (II )求证:当02a <≤时,()f x 在1[,)2+∞上是增函数;(III )若对任意..的(1,2),a ∈ 总存在..01[,1]2x ∈,使不等式20()(1)f x m a >-成立,求实数m 的取值范围.3.已知函数2()(22)ln m f x m x mx x+=-++-(1m ≥-). (I )讨论()f x 的单调性;(II )设225 (1),()113 (1).22x x x x g x x ⎧--≥⎪=⎨-<⎪⎩ 当2m =时,若对任意1(0,2)x ∈,存在2[,1]x k k ∈+(k N ∈),使12()()f x g x <,求实数k 的最小值.4.已知函数2()(33)x f x x x e =-+⋅,其定义域为[2,]t -(2t >-),设(2)f m -=,()f t n =. (1)试确定t 的取值范围,使得函数()f x 在[2,]t -上为单调函数;(2)试判断m ,n 的大小并说明理由;(3)求证:对于任意的2t >-,总存在0(2,)x t ∈-,满足020()2(1)3x f x t e '=-,并确定这样的0x 的个数.5.设函数1()ln xf x x ax-=+在[1,)+∞上是增函数. (1)求正实数a 的取值范围; (2)设0b >,1a >,求证:1ln a b a ba b b b++<<+.6.(2010山东理数) 已知函数1()ln 1af x x ax x-=-+-()a R ∈. (Ⅰ)当12a ≤时,讨论()f x 的单调性; (Ⅱ)设2()24g x x bx =-+.当14a =时,若对任意1(0,2)x ∈,存在[]21,2x ∈,使12()()f x g x ≥,求实数b 取值范围.解:(Ⅰ)因为1()ln 1af x x ax x-=-+-, 所以 222111()a ax x af x a x x x--+-'=-+=,(0,)x ∈+∞. 令 2()1,(0,)h x a x x a x =-+-∈+∞, (1)当0a =时,()1h x x =-+,(0,)x ∈+∞.∴ 当(0,1)x ∈时,()0h x >,此时()0f x '<,函数()f x 单调递减; 当(1,)x ∈+∞时,()0h x <,此时()0f x '>,函数单调递增.(2)当0a ≠时,由()0f x '=,即210ax x a -+-=,解得11x =,211x a=-. ① 当12a =时,12x x =,()0h x ≥恒成立,此时()0f x '≤,函数()f x 在(0,)+∞上单调递减;② 当102a <<时,1110a->> ∴ (0,1)x ∈时,()0h x >,此时()0f x '<,函数()f x 单调递减;1(1,1)x a∈-时,()0h x <,此时()0f x '>,函数()f x 单调递增; 1(1,)x a∈-+∞时,()0h x >,此时()0f x '<,函数()f x 单调递减. ③ 当0a <时,110a-<,∴ (0,1)x ∈时,()0h x >,()0f x '<,函数()f x 单调递减;(1,)x ∈+∞时,()0h x <,()0f x '>,函数()f x 单调递增.综上所述: 当0a ≤时,函数()f x 在(0,1)上单调递减,函数()f x 在(1,)+∞上单调递增;当12a =时,函数()f x 在(0,)+∞上单调递减; 当102a <<时,函数()f x 在(0,1)上单调递减;函数()f x 在1(1,1)a -上单调递增;函数()f x 在1(1,)a-+∞上单调递减.(Ⅱ)因为11(0,)22a =∈,由(Ⅰ)知,121,3(0,2)x x ==∉,当(0,1)x ∈时,()0f x '<,函数()f x 单调递减; 当(1,2)x ∈时,()0f x '>,函数()f x 单调递增. 所以()f x 在(0, 2)上的最小值为1(1)2f =-. 由于“对任意1(0,2)x ∈,存在2[1,2]x ∈,使12()()f xg x ≥”等价于又22()()4g x x b b =-+-,[1,2]x ∈,所以:① 当1b <时,因为min [()](1)520g x g b ==->,此时与(*)矛盾; ② 当[1,2]b ∈时,因为2min [()]40g x b =-≥,同样与(*)矛盾; ③ 当(2,)b ∈+∞时,因为min [()](2)84g x g b ==-.解不等式1842b -≤-,可得178b ≥. 综上,b 的取值范围是17[,)8+∞.8.(2010辽宁理数)已知函数1ln )1()(2+++=ax x a x f . (Ⅰ)讨论函数)(x f 的单调性;(II )设1-<a ,如果对任意),0(,21+∞∈x x ,||4)()(|2121x x x f x f -≥-,求a 的取值范围.解:(Ⅰ)()f x 的定义域为(0,)+∞,2121()2a ax a f x ax x x+++'=+=. 当0a ≥时,()0f x '>,故()f x 在(0,)+∞单调递增; 当1a ≤-时,()0f x '<,故()f x 在(0,)+∞单调递减;当10a -<<时,令()0f x '=,解得x =则当x ∈时,'()f x >0;)x ∈+∞时,'()f x <0.故()f x 在单调递增,在)+∞单调递减. (Ⅱ)不妨假设12x x ≥,而1a <-,由(Ⅰ)知在(0,)+∞单调递减,从而12,(0,)x x ∀∈+∞,1212|()()|4||f x f x x x -≥-, 等价于 12,(0,)x x ∀∈+∞,2211()4()4f x x f x x +≥+ ① 令()()4g x f x x =+,则1'()24a g x ax x +=++. ①等价于()g x 在(0,+∞)单调减少,即 1240a ax x+++≤. 从而22222241(21)42(21)2212121x x x x a x x x ------≤==-+++. 故a 的取值范围为(,2]-∞-.9.设a R ∈且0a ≠,e 为自然对数的底数,函数()1x f x e x =--,2()2xa g x x e =. (1)求证:当1a ≥时,()()f x g x ≤对一切非负实数x 恒成立;(2)对于(0,1)内的任意常数a ,是否存在与a 有关的正常数0x ,使得00()()f x g x >成 立?如果存在,求出一个符合条件的0x ;否则,请说明理由.10.设3x =是函数23()()x f x x ax b e -=++(x R ∈)的一个极值点. (1)求a 与b 的关系式(用a 表示b ),并求()f x 的单调区间;(2)设0a >,225()()4xg x a e =+,若存在1ξ,2[0,4]ξ∈使得12|()()|1f g ξξ-<成立,求a 的取值范围.。
