管理经济学计算题(个人整理,供参考)
管理经济学计算题试题
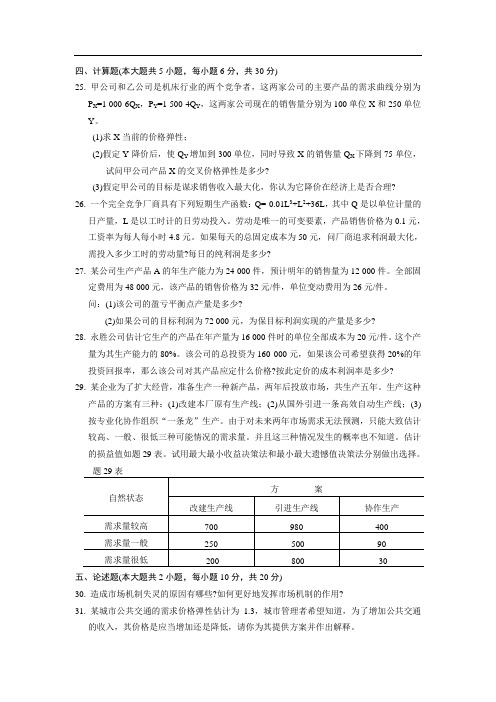
25. 甲公司和乙公司是机床行业的两个竞争者,这两家公司的主要产品的需求曲线分别为P X=1 000-6Q X,P Y=1 500-4Q Y,这两家公司现在的销售量分别为100单位X和250单位Y。
(1)求X当前的价格弹性;(2)假定Y降价后,使Q Y增加到300单位,同时导致X的销售量Q X下降到75单位,试问甲公司产品X的交叉价格弹性是多少?(3)假定甲公司的目标是谋求销售收入最大化,你认为它降价在经济上是否合理?26. 一个完全竞争厂商具有下列短期生产函数:Q=-0.01L3+L2+36L,其中Q是以单位计量的日产量,L是以工时计的日劳动投入。
劳动是唯一的可变要素,产品销售价格为0.1元,工资率为每人每小时4.8元。
如果每天的总固定成本为50元,问厂商追求利润最大化,需投入多少工时的劳动量?每日的纯利润是多少?27. 某公司生产产品A的年生产能力为24 000件,预计明年的销售量为12 000件。
全部固定费用为48 000元,该产品的销售价格为32元/件,单位变动费用为26元/件。
问:(1)该公司的盈亏平衡点产量是多少?(2)如果公司的目标利润为72 000元,为保目标利润实现的产量是多少?28. 永胜公司估计它生产的产品在年产量为16 000件时的单位全部成本为20元/件。
这个产量为其生产能力的80%。
该公司的总投资为160 000元,如果该公司希望获得20%的年投资回报率,那么该公司对其产品应定什么价格?按此定价的成本利润率是多少?29. 某企业为了扩大经营,准备生产一种新产品,两年后投放市场,共生产五年。
生产这种产品的方案有三种:(1)改建本厂原有生产线;(2)从国外引进一条高效自动生产线;(3)按专业化协作组织“一条龙”生产。
由于对未来两年市场需求无法预测,只能大致估计较高、一般、很低三种可能情况的需求量。
并且这三种情况发生的概率也不知道。
估计的损益值如题29表。
试用最大最小收益决策法和最小最大遗憾值决策法分别做出选择。
管理经济学计算题(完整)

1、Tang牌果珍是一种鲜橙口味速溶饮品的商标,属于卡夫特食品公司。
著名的广告代理商扬雅(Young and Rubicam)就广告预算对Tang牌果珍销售的影响做了研究并得出在两个不同地区两者之间的关系如下:S1= 10+5A1-1.5A12S2= 12+4A2-0.5A22其中S1和S2分别代表地区1和地区2Tang牌果珍的销售额(单位:100万美元/年),A1和A2分别代表地区1和地区2的广告费用。
假如目前卡夫特食品公司在地区1投入的广告费为50万美元/年,在地区2为100万美元/年。
请分析:从提高销售收入的角度来看,这一广告预算的分配是否合理?应如何调整?5-3 A12=4-1 A22A1+ A2=1.5A1=0.625 A2=0.8752、例题:扑克牌需求的价格弹性假定扑克牌的市场需求方程为:Q=6000000-1000000P,如果价格从每付2元增加到3元,问弧价格弹性是多少?当P=2时,Q=6000000-1000000*2=4000000,即为Q1当P=3时,Q=6000000-1000000*3=3000000,即为Q2EP=-1000000/1*5/7000000=-0.713、假设手提电脑的需求方程为:Q= -700P+ 200 I – 500S + 0.01A,假设人均可支配收入I为13000美元,软件的平均价格S为400美元,广告支出A为5000万美元。
求:P为3000美元时的需求价格弹性。
EP=(dQ/dP)*(P/Q)(1)dQ/dP=-700Q= -700P+ 200 I -500S + 0.01A”,由于是Q对P求导,所以把200 I、500S、0.01A全部当作常数,常数的导数为0,所以dQ/dP=d(-700P)/dP+0-0=0=-700把I=13000,S=400,A=50000000,P=3000代入上述公式,得出,q=-2100000+2600000-200000+500000=800000则P/Q=0.00375(3)EP=(dQ/dP)*(P/Q)=-700*0.00375=-2.6254、得克萨斯州像美国其他州一样,出售个性化车牌。
CQU-MBA管理经济学计算题(完整版)

管理经济学复习计算题边际收益、边际成本:P8利润最大化条件:利润函数的一阶导数为0,由此得出MR=MC :P8 计划数需求函数:P11 需求规律:P12 供给函数:P14 供给规律:P14计算题1题详解(课本内容P20)某市场供给函数为:Qs =-50+3P ,需求函数为:Qd =100-2P (1)求市场均衡(2)若由于某种原因,市场需求函数扩大为:Qd =250-2P ,求 A 、新的市场均衡B 、若政府维持(1)价格不变,并以40的单价从其他市场购买产品后以原均衡价格投放市场,需耗资若干?C 、若政府对供给方进行补贴以维持价格不变,每单位产品需补贴若干?政府共需耗资若干?(3)在原供求曲线上,政府对企业每单位产品征税1元,求新的市场均衡及税赋分担 (4)在原供求曲线上,政府对消费者每单位产品征税1元,求新的市场均衡及税赋分担题解:(1)1002503305033040d Sd S Q Q P P P Q Q =-=-+===-+⨯=市场供求均衡(元)(2)①新的市场供求均衡25025036050360130d SE d S Q Q P P P Q Q =-=-+===-+⨯=(元)②在新的需求条件下,30元的价格对应的需求量是250230=190D Q '=-⨯根据供给方程此时市场范围内生产者能够提供的产品数量仍然是40 政府为维持30的价格不变从别的市场购入商品需要消耗的资金是()()()()1904040301500D S G b C Q Q P P '=-⨯-=-⨯-=③对生产者进行补贴。
生产D Q '的产品,生产者希望的市场价格是50319080S D Q Q P P ''=-+='= 政府补贴:()()19080309500D G C Q P P ''=⨯-=⨯-=(3)征税后的平衡(课本P20)=50311002503130.650330.6138.8S d S d S Q P Q Q P P P Q Q '-+-'=-=-+-'='==-+-=()()(元)()消费者税赋:30.6300.6P P '-=-=生产者税赋:()30(30.61)0.4P P T '--=--= (4)(课本P20)=100211002(1)50329.650329.638.8D d Sd S Q P Q Q P P P Q Q '-+'=-+=-+'='==-+⨯=()(元)消费者税赋:29.61300.6P T P '+-=+-= 生产者税赋:3029.60.4P P '-=-=2题详解(课本内容P23)在国际市场上签字笔每支9元,处于高度竞争 。
管理经济学试题及答案

管理经济学试题及答案一、选择题(每题2分,共20分)1. 管理经济学中,边际成本与平均成本的关系是:A. 总是相等B. 当边际成本低于平均成本时,平均成本下降C. 当边际成本低于平均成本时,平均成本上升D. 没有固定关系2. 完全竞争市场的特点不包括:A. 产品同质性B. 买卖双方众多C. 买卖双方对市场信息完全了解D. 市场存在明显的进入和退出壁垒3. 以下哪项不是规模经济的来源?A. 专业化B. 批量购买C. 固定成本分摊D. 市场垄断4. 企业进行价格歧视的前提条件是:A. 产品差异化B. 市场分割C. 成本固定D. 消费者收入相同5. 以下哪个选项是管理经济学中的“公共品”特点?A. 非排他性B. 非竞争性C. 私人生产A和B6. 垄断竞争市场与完全竞争市场的主要区别在于:A. 产品价格B. 产品差异化C. 市场进入壁垒D. 企业数量7. 企业在进行成本效益分析时,需要考虑的是:A. 直接成本B. 间接成本C. 机会成本D. 所有上述选项8. 以下哪个是管理经济学中的外部性?A. 企业内部的成本B. 企业外部的成本或效益C. 企业内部的效益D. 企业外部的成本9. 企业在决定是否进入一个新市场时,需要评估的是:A. 市场需求B. 竞争程度C. 潜在利润D. 所有上述因素10. 以下哪个是管理经济学中的“道德风险”?A. 消费者购买劣质产品B. 消费者购买产品后不满意C. 保险购买者由于保险的存在而减少预防措施D. 保险公司故意夸大损失以获取更多赔偿二、简答题(每题10分,共30分)1. 简述管理经济学中的“边际分析”方法及其在企业决策中的应用。
2. 描述完全竞争市场与垄断市场的主要区别,并举例说明。
3. 解释什么是“囚徒困境”,并说明它在商业策略中的应用。
三、计算题(每题25分,共50分)1. 假设某企业生产一种产品,其总成本函数为TC(q) = 100 + 20q +3q^2,其中q代表产量。
管理经济学计算题

一、计算题已知某产品的市场需求函数为Q=a-Bp,a,b为正常数。
(1)求市场价格的市场需求价格弹性;(2)当a=3,b=1.5时的市场价格和市场需求量。
解:(1)由Q=a-bP,得Dq/Dp=-b,于是Ed=-Dq/DpP/ Q=-(-b)P/Q=Bp/A-Bp当P=P1时,Q1=A-BP1,于是Ed(p1)=bP1/a-bP1(2)当a=3,b=1.5,和Ed=1.5时,有Ed=bP1/a-bP1=1.5P/3-1.5P=1.5解得P=1.2此时市场需求为Q=a-bP=3-1.5*1.2=1.22、已知某人的生产函数U=xy, 他打算购买x和y两种商品,当其每月收入为120元,Px=2元,Py=4元时,试问:(1)为获得最大效用,他应该如何选择x和y的组合?(2)货币的边际效用和总效用各是多少?(3)假设x的价格提高44%,y的价格不变,他必须增加多少收入才能保持原有的效用水平?⑴因为MUx=y,MUy=x,由MUx/MUy=y/x=Px/Py, PxX+PyY=120则有Y/x=2/3 2x=3y=120解得X=30 , y=20⑵货币的边际效用Mum=MUx/Px=y/Px=10货币的总效用TUm=MUmM=1200⑶由MUx/MUy=y/x=Px/Py xy=60,解得x=25, y=24所以M1=2.88=3y=144M1-M=241.设某市场上只有两个消费者,其需求曲线为:Q1=100﹣2P (P≤50);Q1=0 (P>50);Q2=160﹣4P (P≤40);Q2=0 (P>40)试求市场需求曲线.解:对P分区间计算。
当P≤40时,Q1=100-2P;Q2=160-4P∴Q=Q1+Q2=260-6P当40<P≤50时,Q1=100-2PQ2=0 ∴Q=Q1+Q2=100-2P当P>50时,Q1=0 Q2=0 ∴Q=Q1+Q2=01.设需求曲线的方程为Q=10-2P,求其点弹性为多少?怎样调整价格,可以使总收益增加?解:根据点弹性的定义Edp = —(dQ/Q)/ (dP/P)= —(dQ/dP)·(P/Q) = —(-2)·(P/Q)=2·(P/Q)价格的调整与总收益的变化之间的关系与弹性的大小有关。
《管理经济学》统考计算题训练

《管理经济学》计算题(部分)西北大学经济管理学院杨小卿(答案见手写本)1.已知某种商品的需求函数为Q d=30-3P,供给函数为Q S=-26+5P。
试求:(1)该商品的均衡价格与均衡产量;(2)P=2时的需求价格点弹性;(3)价格在2与4之间的需求价格弧弹性;(4)当P为多少时,E d=1?2.某商品的价格由40元上升至50元,需求量由7500单位下降至4500单位,问该商品的需求价格弹性是多少?提价后总收益是增加了还是减少了?增加或减少了多少?其原因是什么?3.2007年1月远东航空公司的飞机票价下降5%,使得大洋航空公司的乘客数量从去年同期10000人下降到8000人,求大洋航空公司对远东航空公司的需求交叉弹性。
4.假设汽车的需求与人均国民收入之间的的关系可用函数Q d=100+0.2Y 来表示,这里Q d为需求量,单位为万辆,Y是人均国民收入,单位是美元。
问:(1)人均国民收入在4000美元时的收入点弹性系数;(2)汽车生产的增长速度能不能快于人均国民收入的增长速度?为什么?5.某公司是一家生产X产品的企业,该公司分析得到公司产品的需求曲线为:Q=300-60P+0.1I+80PL,其中,Q为产品的需求量,P为产品价格,I为人均收入,PL为相关产品Y的价格。
问:当P=2,I=2000,PL=0.8时,(1)产品X的需求量的是多少?(2)产品X的价格弹性是多少?(3)产品X的点收入弹性是多少?X是正常品还是低档品?(4)产品X与产品Y的交叉价格弹性是多少?6.2007年1月,A制衣公司的衬衫以每件200元的价格每月销售9000件,2005年2月竞争者将价格从220元降到180元,这个月,A公司只销售了8000件衬衫。
(1)计算A公司衬衫与竞争者衬衫的需求弧交叉弹性(假设A公司衬衫价格不变);(2)如果A公司衬衫的需求价格弹性为-2. 0,又设其竞争者衬衫的价格保持在180元,要使A公司的销售恢复到9000件,价格要降低多少?7.需求是P=200-4Q,供给是P=2+2Q。
管理经济学试题及答案

管理经济学试题及答案一、选择题(每题2分,共20分)1. 管理经济学的主要研究对象是什么?A. 个人消费行为B. 企业生产行为C. 政府宏观调控D. 社会福利分配2. 在完全竞争市场中,价格是如何决定的?A. 由市场供求关系决定B. 由生产成本决定C. 由企业单方面决定D. 由政府规定3. 边际成本与平均成本的关系是什么?A. 边际成本总是高于平均成本B. 边际成本总是低于平均成本C. 边际成本与平均成本没有固定关系D. 当边际成本低于平均成本时,平均成本下降4. 以下哪项不是企业的主要经济目标?A. 最大化利润B. 增加市场份额C. 提高员工满意度D. 社会责任5. 什么是价格弹性?A. 价格变化对需求量的影响B. 价格变化对供给量的影响C. 价格变化对生产成本的影响D. 价格变化对企业利润的影响二、简答题(每题10分,共30分)6. 简述规模经济的概念及其对企业的意义。
7. 解释什么是垄断市场,并举例说明。
8. 描述完全竞争市场的特征。
三、计算题(每题25分,共50分)9. 某企业生产一种产品,其总成本函数为TC(q) = 0.5q^2 - 10q + 100。
请计算该企业在生产100单位产品时的平均成本和边际成本。
10. 假设某产品的市场需求函数为Qd = 120 - 2P,供给函数为Qs = 4P - 60。
求市场均衡价格和数量。
四、论述题(共30分)11. 论述管理经济学在现代企业管理中的应用及其重要性。
答案一、选择题1. B2. A3. D4. C5. A二、简答题6. 规模经济是指随着生产规模的扩大,单位产品的平均成本下降的现象。
对企业而言,规模经济可以降低生产成本,提高市场竞争力,但同时也要注意规模经济的过度扩张可能导致管理效率下降。
7. 垄断市场是指市场上只有一个卖方,能够控制市场价格和产量。
例如,某些地区的自来水供应公司。
8. 完全竞争市场的特征包括:市场上有大量买家和卖家,产品同质,自由进入和退出市场,完全信息,以及没有交易成本。
管理经济学典型计算题

1.某居民有间空房,假设出租每月可得租金250元,假设留着自己经营小商品那么每月收入为400元,其中各项本钱开支共约200元,问:〔1〕该居民经营商品的显本钱和隐本钱各为多少?〔2〕出租房的时机本钱是多少?〔3〕他将作何选择获利最大?解:〔1〕该居民经营商品的显本钱为200元,隐本钱为250元。
〔一题一题答〕〔2〕作为出租房,会计本钱=0 时机本钱=250元〔3〕自己经营小商品经济利润=400-〔250+200〕=-50元因经济利润小于0,所以出租房收取租金是获利最大的方式。
〔P为价格,单位为元;Q D、Q S分别为需求量和供应量,单位为万千克〕。
DS问:〔1〕砂糖的均衡价格是多少?〔2〕砂糖的均衡交易量是多少?〔3〕假设政府规定砂糖的最高价格为7元/万千克,砂糖的供求关系会是何种状况?〔4〕如果政府对砂糖每万千克征税1元,征税后的均衡价格是多少?解:〔1〕供求均衡时,即Q D =Qs〔要有步骤过程〕,SDQ D=〔12-P〕÷,Q S= P÷那么〔12-P〕÷0.3=P÷解得P=7.5(元)〔2〕Q D =Qs=(12-P) ÷0.3=15(万千克)〔3〕需求量:Q D =(12-P) ÷0.3=16.7〔万千克〕供应量:Qs=P÷0.5=14〔万千克〕可见P=7时,Q D> Qs所以,假设政府规定砂糖的最高价格为7元/万千克,就会出现供不应求的局面。
〔4〕设税后价格为P’,征税后新的供应曲线就应为:〔注意左移后的供应曲线公式,加减不要搞错,注意验证〕Qs=(P’-1) ÷均衡条件为Q D =Qs(12-P’) ÷0.3=(P’-1) ÷P’=7.875 (元/万千克)故税后的均衡价格为7.875元。
3.:某种商品的需求函数为Q=800-20P+P2,其中Q为需求量,P为价格。
试求:〔1〕P=5时的需求价格弹性;〔2〕P=10时的需求价格弹性;〔3〕根据上述计算结果说明该商品在P=5、P=10时的弹性特点。
管理经济学计算题试题

七夕,古今诗人惯咏星月与悲情。
吾生虽晚,世态炎凉却已看透矣。
情也成空,且作“挥手袖底风”罢。
是夜,窗外风雨如晦,吾独坐陋室,听一曲《尘缘》,合成诗韵一首,觉放诸古今,亦独有风韵也。
乃书于纸上。
毕而卧。
凄然入梦。
乙酉年七月初七。
-----啸之记。
四、计算题(本大题共5小题,每小题6分,共30分)25. 甲公司和乙公司是机床行业的两个竞争者,这两家公司的主要产品的需求曲线分别为P X=1 000-6Q X,P Y=1 500-4Q Y,这两家公司现在的销售量分别为100单位X和250单位Y。
(1)求X当前的价格弹性;(2)假定Y降价后,使Q Y增加到300单位,同时导致X的销售量Q X下降到75单位,试问甲公司产品X的交叉价格弹性是多少?(3)假定甲公司的目标是谋求销售收入最大化,你认为它降价在经济上是否合理?26. 一个完全竞争厂商具有下列短期生产函数:Q=-0.01L3+L2+36L,其中Q是以单位计量的日产量,L是以工时计的日劳动投入。
劳动是唯一的可变要素,产品销售价格为0.1元,工资率为每人每小时4.8元。
如果每天的总固定成本为50元,问厂商追求利润最大化,需投入多少工时的劳动量?每日的纯利润是多少?27. 某公司生产产品A的年生产能力为24 000件,预计明年的销售量为12 000件。
全部固定费用为48 000元,该产品的销售价格为32元/件,单位变动费用为26元/件。
问:(1)该公司的盈亏平衡点产量是多少?(2)如果公司的目标利润为72 000元,为保目标利润实现的产量是多少?28. 永胜公司估计它生产的产品在年产量为16 000件时的单位全部成本为20元/件。
这个产量为其生产能力的80%。
该公司的总投资为160 000元,如果该公司希望获得20%的年投资回报率,那么该公司对其产品应定什么价格?按此定价的成本利润率是多少?29. 某企业为了扩大经营,准备生产一种新产品,两年后投放市场,共生产五年。
管理经济学计算题

1.假定某企业的生产函数为0.3750.625Q L K =,其中劳动(L)的价格为3元,资本(K)的价格为5元。
生产10个单位的产品,应投入L 和K 各为多少时才能使成本最低?解:当产量一定时,要使成本最小化,所满足的条件为:L KL KMP MP P P =0.6250.6250.3750.3750.6250.6250.3750.3750.3750.6250.37530.6255L K dQMP L K dL dQ MP L K dLL K L K L K----====∴=∴= 把L=K 代入0.3750.625Q LK =中,且Q=10时,有L=K =102.一个完全竞争厂商在短期内经营,且劳动力是唯一可变投入要素,其生产函数为:Q=-L 3+10L 2+88L ,其中Q 是周产量,L 是工人人数,固定成本为150元。
问当周工资为324元、产品价格为每吨3.24元时,为了实现利润最大化,厂商将雇佣多少工人?此时厂商的利润是多少?解:因为该完全竞争厂商再生产过程中,劳动是唯一可变的投入要素,所以当厂商实现利润最大化时满足:L L MRP MC W == 即:L Q MP P W ⨯=232088L dQMP L L dL==-++ 又因为 3.24,324Q P W == 所以:22320881003201202,63L L L L L L -++=∴-+===因为当厂商利润达到最大时,厂商的生产应选择第二阶段,所以L=23不符题意,舍去。
83.28TR TC QP WL F π=-=--=3.完全竞争的成本固定不变行业包含许多厂商,每个厂商的长期总成本函数为:LTC=0.1q 3-1.2q 2+11.1q (q 为每个厂商的年产量)。
试计算厂商长期平均成本为最小的产量和销售价格。
解:厂商长期平均成本:20.3 2.411.1LAC q q =-+当厂商长期成本最小时有:0dLACdq=0.6 2.40q ∴-= 4q ∴=当厂商达到长期均衡时,有2min 0.34 2.44 1.1 6.3P LAC ==⨯-⨯+=4.大昌公司产品X 的需求函数为:Q=36-10PX+20PY+0.04I ,其中PX 为产品本身的价格,PY 为相关产品的价格,I 为居民收入。
管理经济学计算题及参考答案(已分类整理)复习过程

一、计算题某种商品的需求曲线为QD=260-60P,供给曲线为QS=100+40P。
其中,QD与QS分别表示需求量和供给量(万斤),P表示价格(元/斤)。
假定政府对于每单位产品征收0.5元税收。
①求税收后的均衡产量Q与消费者支付的价格PD以及生产者获得的价格PS。
②计算政府的税收收入与社会的福利净损失。
解:(1)在征税前,根据QD=QS,得均衡价格P=1.6, Q=164令T=0.5,新的均衡价格为P',新的供给量为QS',新的需求量为QD'.则有:QS'=100+40( P'-T) QD'=260-60 P'得新的均衡价格为P'= 1.8新的均衡价格为Q'=152所以税收后的均衡产量为152万斤,消费者支付价格1.8元,生产者获得价格1.3元.(2)政府的税收收入=T×Q'=76万元,社会福利损失=(1/2)×0.5×(164-152)=3万元.2.设砂糖的市场需求函数为:P=12-0.3QD;砂糖的市场供给函数为P=0.5QS。
(P为价格,单位为元;QD、QS分别为需求量和供给量,单位为万千克)。
问:(1)砂糖的均衡价格是多少?(2)砂糖的均衡交易量是多少?(3)若政府规定砂糖的最高价格为7元/万千克,砂糖的供求关系会是何种状况?(4)如果政府对砂糖每万千克征税1元,征税后的均衡价格是多少?7.875元/万千克7解:(1)供求均衡时,即QD =QsP=12-0.3Q D,P=0.5Q SQ D=(12-P)÷0.3,Q S= P÷0.5 那么(12-P)÷0.3=P÷0.5 解得P=7.5(元)(2)Q D =Qs=(12-P) ÷0.3=15(万千克)(3)需求量:Q D =(12-P) ÷0.3=16.7(万千克)供给量:Qs=P÷0.5=14(万千克)可见P=7时,Q D> Qs所以,若政府规定砂糖的最高价格为7元/万千克,就会出现供不应求的局面。
管理经济学练习中全部的20个计算题
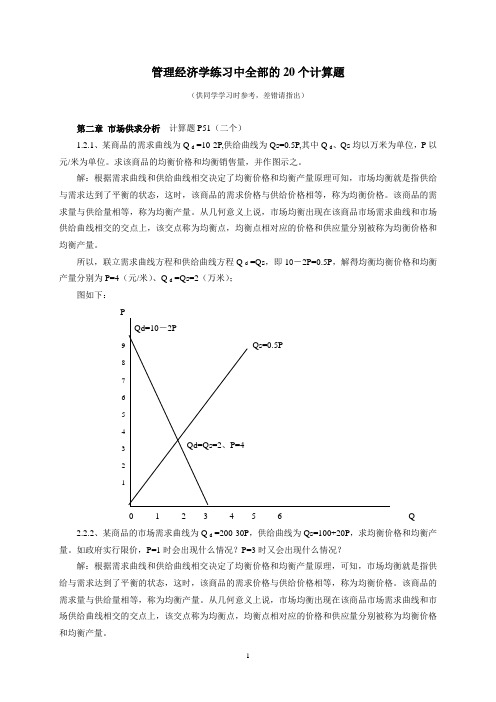
管理经济学练习中全部的20个计算题(供同学学习时参考,差错请指出)第二章市场供求分析计算题P51(二个)1.2.1、某商品的需求曲线为Q d =10-2P,供给曲线为Qs=0.5P,其中Q d、Qs均以万米为单位,P以元/米为单位。
求该商品的均衡价格和均衡销售量,并作图示之。
解:根据需求曲线和供给曲线相交决定了均衡价格和均衡产量原理可知,市场均衡就是指供给与需求达到了平衡的状态,这时,该商品的需求价格与供给价格相等,称为均衡价格。
该商品的需求量与供给量相等,称为均衡产量。
从几何意义上说,市场均衡出现在该商品市场需求曲线和市场供给曲线相交的交点上,该交点称为均衡点,均衡点相对应的价格和供应量分别被称为均衡价格和均衡产量。
所以,联立需求曲线方程和供给曲线方程Q d =Qs,即10-2P=0.5P,解得均衡均衡价格和均衡产量分别为P=4(元/米)、Q d =Qs=2(万米);图如下:0 1 2 3 4 5 6 Q2.2.2、某商品的市场需求曲线为Q d =200-30P,供给曲线为Qs=100+20P,求均衡价格和均衡产量。
如政府实行限价,P=1时会出现什么情况?P=3时又会出现什么情况?解:根据需求曲线和供给曲线相交决定了均衡价格和均衡产量原理,可知,市场均衡就是指供给与需求达到了平衡的状态,这时,该商品的需求价格与供给价格相等,称为均衡价格。
该商品的需求量与供给量相等,称为均衡产量。
从几何意义上说,市场均衡出现在该商品市场需求曲线和市场供给曲线相交的交点上,该交点称为均衡点,均衡点相对应的价格和供应量分别被称为均衡价格和均衡产量。
所以,联立需求曲线方程和供给曲线方程Q d =Qs,即200-30P=100+20P,解得均衡均衡价格和均衡产量分别为P=2、Q d =Qs=140;若:P=1时,则Q d =200-30P=200-30×1=170,Qs=100+20P=Qs=100+20×1=120,Q d>Qs,出现商品供不应求现象。
管理经济学计算题

1:已知某商品的市场需求函数为QD=30-P,市场供给函数为QS=3P-10。
如果政府对该商品每件征收1元税,则征税后的市场均衡价格为多少?解:设QS’=3P-x,则:当QS ’=0时,P’=x/3。
∵QS=0时,P=10/3。
∴P’=10/3+1=13/3 =x/3∴x=13则:QS’=3P-13=3(P-1)-10令QD=QS’:30-P=3(P-1)-10∴P=10.75(元)2:需求曲线弧弹性计算需求曲线上a、b两点,价格、需求量分别为(5,400)和(4,800)(1)价格由5下降为4时,(2)价格由4上升为5时,分别计算弧弹性。
(1)Ed=-[(400-800)/(5-4)]×(5/400)=5(2)Ed=-[(800-400)/(4-5)]×(4/800)=23:电视机Ed=2,P1=500元/台,Q1=100台,如价格下调10%?试分析以下收益状况。
如价格下调10%,则数量增加20%,P2=500 –500*10%=450元/台,Q2=100+100*20%=120台TR2=P2×Q2=450×120=54000元TR1=50000TR2 –TR1=54000 –50000=4000元TR2 >TR1,表明价格下跌,总收益增加。
如果价格上调10%?已知:电视机Ed=2,P1=500元/台,Q1=100台。
如价格上调10%,数量则减少20%。
●P3=500 +500×10%=550元/台,●Q3=100 -100×20%=80台●TR3=P3×Q3=550×80=44000元●TR3 –TR1=44000 –50000= -6000元TR3<TR1,表明价格上调,总收益减少4:已知:面粉Ed=0.5,P1=0.2元/斤,Q1=100斤。
❖如价格上调10%,数量则减少5%,❖P3=0.2 +0.2*10%=0.22元/斤,❖Q3=100 -100*5%=95斤TR3=P3×Q3=0.22×95=20.9元TR3 –TR1=20.9 –20= 0.9元TR3>TR1,表明面粉价格上调,总收益增加。
管理经济学计算题范例

计算题1.假定某企业的生产函数为Q=10LK,其中劳动L的价格为5元,资本K的价格为10元。
如果企业计划生产2000件产量,应投入L和K各多少才能使成本最低?此时成本是多少?解:1、先求两种投入要素的边际产量MPL=dQ/dL=d(10LK)/dL=10K MPK=dQ/dK=d(10LK)/dK=10L已知PL=5,PK=102、要使成本最低须满足MPL /PL=MPK/PK 即10K/5=10L/10 可得L=2K3、根据生产函数Q=10LK,当Q=2000时,可得2000=10LK,2000=20K*K,K2=100 K=10 则L=204、此时成本为K*10+L*5=10*10+20*5=200(元)答:应投入20单位L和10单位K,才能使成本最低,此时成本为200元。
2.大明公司是生产胡桃的一家小公司(该行业属于完全竞争市场),胡桃的市场价格为每单位640元,公司的成本函数为TC=240Q-20Q2+Q3,正常利润已包括在成本函数之中,要求:(1)利润最大化时的产量及此时的利润是多少?(2)若投入要素价格长期不变,那么,当行业处于长期均衡时,企业的产量及单位产量的成本为多少?此时的市场价格为多少?解:(1)因为是完全竞争市场,所以,P=MR=MC=640元MC=TC'=240-40Q+3Q2 ∴240-40Q+3Q2 =640 Q=20∏=TR-TC=P*Q-(240Q-20Q2+Q3)=640*20-(240*20-20*400+8000)=8000元(2)∵AC=TC/Q=240-20Q+Q2 ,MC=TC'=240-40Q+3Q2长期均衡时,P=MC=AC ∴240-20Q+Q2=240-40Q+3Q2 Q=10AC=240-20Q+Q2 =240-20*10+100=140元,∴P=140元3.某企业产品单价为100元,单位变动成本为60元,固定总成本12万元,试求:(1)盈亏分界点产量是多少?(2)如果企业要实现目标利润6万元,则产销量应为多少?解:(1)Q0=F/(P-CV)=120000/(100-60)=120000/40=3000(2)Q=F+∏/(P-CV)=(120000+60000)/(100-60)=180000/40=4500件4.某垄断性公司,其产品可在两个完全分割的市场上销售,且产品的成本函数和两个市场需求函数分别为:TC=100+60Q Q1=32-0.4P1 Q2=18-0.1P2要求:(1)计算两个市场上的最优差别价格、销量和最大利润.(2)如果采取统一定价,则最优产品价格、销量和利润又为多少?解:(1)MC=TC'=60 P1=80-2.5Q1 P2=180-10Q2TR1=P1*Q1=80Q1-2.5Q12 TR2=P2*Q2=180Q2-10Q22MR1=TR1'=80-5Q1 MR2=TR2'=180-20Q2利润最大化时,MC=MR1=MR2=60 ∴Q1=4 ,Q2=6 P1=70 P2=120 ∏=T(R1+R2)-TC=(P1*Q1+P2*Q2)-[100+60*(Q1+Q2)]=(280+720)-[100+600]=1000-700=300 (2)若采取统一定价时,P=P1=P2Q=Q1+Q2=50 - 0.5P ∴P=100 -2Q ∴TR=P*Q=100Q-2Q2MR=TR' =100-4Q MC=TC'=60根据企业最优产品价格条件,MC=MR ∴100 - 4Q=60 Q=10∴P=80=P1=P2∏=P*Q-TC=80*10-(100+60*10)=800-700=100元5.某企业生产两种联产品,两种产品的比例是固定的,假设它们的需求曲线分别是:P1=10-0.001Q1 P2=8-0.001Q2若边际成本为1元,则:①为使利润最大,两种产品的价格、产量应各定多少?②若企业追求的是销售收入最大化,两种产品的价格、产量应各定为多少?解:(1)TR1=P1*Q1=10Q1-0.001Q12TR2=P2*Q2=8Q2-0.001Q22∴MR1=10-0.002Q1 MR2=8-0.002Q2为使利润最大,则MR1=MC=1 ,MR2=MC=1∴10-0.002Q1=1 Q1=4500 P1=5.5元8-0.002Q2=1 Q2=3500 P2=4.5元(2)TR1=P1*Q1=P1*(10000-1000P1)=10000P1-1000P12TR2=P2*Q2=P2*(8000-1000P2)=8000P2-1000P22若企业追求销售收入最大化,则dTR1/dP1=0 ,dTR2/dP2=0∴10000-2000P1=0 P1=5 Q1=50008000-2000P2=0 P2=4 Q2=40006.公司甲和已是某行业的两个竞争者,目前两家公司的销售量分别100单位和250单位,其产品的需求曲线分别如下:甲公司:P甲=1000-5Q甲乙公司:P乙=1600-4Q乙①求这两家公司当前的点价格弹性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、管理经济学计算题市场均衡1.某种商品的需求曲线为QD=260-60P,供给曲线为QS=100+40P。
其中,QD与QS 分别表示需求量和供给量(万斤),P表示价格(元/斤)。
假定政府对于每单位产品征收0.5元税收。
①求税收后的均衡产量Q与消费者支付的价格PD以及生产者获得的价格PS。
②计算政府的税收收入与社会的福利净损失。
解:(1)在征税前,根据QD=QS,得均衡价格P=1.6, Q=164令T=0.5,新的均衡价格为P',新的供给量为QS',新的需求量为QD'.则有:QS'=100+40( P'-T) , QD'=260-60 P'得新的均衡价格为P'= 1.8新的均衡价格为Q'=152所以税收后的均衡产量为152万斤,消费者支付价格1.8元,生产者获得价格1.3元.(2)政府的税收收入=T×Q'=76万元,社会福利损失=(1/2)×0.5×(164-152)=3万元.2.设砂糖的市场需求函数为:P=12-0.3QD;砂糖的市场供给函数为P=0.5QS。
(P为价格,单位为元;QD、QS分别为需求量和供给量,单位为万千克)。
问:(1)砂糖的均衡价格是多少?(2)砂糖的均衡交易量是多少?(3)若政府规定砂糖的最高价格为7元/万千克,砂糖的供求关系会是何种状况?(4)如果政府对砂糖每万千克征税1元,征税后的均衡价格是多少?解:(1)供求均衡时,即QD =QsP=12-0.3QD,P=0.5QSQD=(12-P)÷0.3,QS= P÷0.5 那么(12-P)÷0.3=P÷0.5 解得P=7.5(元)(2)QD =Qs=(12-P) ÷0.3=15(万千克)(3)需求量:QD =(12-P) ÷0.3=16.7(万千克)供给量:Qs=P÷0.5=14(万千克)可见P=7时,QD> Qs所以,若政府规定砂糖的最高价格为7元/万千克,就会出现供不应求的局面。
(4)征税前QS=2P, QD=(12-P)/0.3征税后QS'= 2( P'-T), QD'= (12- P') /0.3(12- P') /0.3 =2 (P'-1)P'=7.875 (元)即征税后的均衡价格为7.875元。
效用1、已知某人的生产函数U=xy, 他打算购买x和y两种商品,当其每月收入为120元,Px=2元,Py=3元时,试问:(1)为获得最大效用,他应该如何选择x和y的组合?(2)假设x的价格提高44%,y的价格不变,他必须增加多少收入才能保持原有的效用水平?⑴因为MUx=y, MUy=x,由MUx/MUy=y/x=Px/Py, PxX+PyY=120则有y/x=2/3 2x=3y=120解得x=30 , y=20(2)由MUx/MUy=y/x=Px/Py ,xy=600可得2.88x=3y, (1)xy=600, (2)联立(1)、(2)解得x=25, y=24所以M1=2.88x+3y=144M1-M=144-120=24(元)即他必须增加24元收入才能保持原有的效用水平。
2.若消费者张某的收入为270元,他在商品X和Y的无差异曲线上的斜率为dY/dX=-20/Y的点上实现均衡。
已知商品X和商品Y的价格分别为PX=2,PY=5,那么此时张某将消费X和Y各多少?消费者的均衡的均衡条件dY/dX=MRS=-PX/PY(MRS=无差异曲线的斜率=预算线的斜率;MRS=-MU X/MU Y=-P X/P Y)所以-20/Y=-2/5 Y=50根据收入I=XPX+YPY,可以得出270=X*2+50*53.某人每周花 360元买x 和y,Px=3,Py=2,效用函数为:U=2x 2y,求在均衡状态下,他如何购买效用最大?解:max:U=2x 2yS.T 360=3x+2y构造拉格朗日函数得:W=2x2y+λ(360-3x-2y)dW/Dx=MUx-3λ=4xy-3λ=0dW/Dy=MUy-2λ=2x 2-2λ=0求得:4y=3x,又360=3x+2y,得x=80,y=60PS :就本题而言,因本人未参与考研,拉格朗日函数已然忘却,发现用一般方法亦可计算如下: 根据消费者最优消费选择条件y x x y xyx P P MU MU 2y x y x 43232424=⇒===,即 (1) 3X+2y=360 (2)联立(1)、(2)解得x=80,y=604.所有收入用于购买x,y 的一个消费者的效用函数为u=xy ,收入为100,y 的价格为10,当x 的价格由2上升至8时,其补偿收入(为维持效用水平不变所需的最小收入)是多少?解:最初的预算约束式为2x+10y=100效用极大化条件MUx/Muy=Px/Py=2/10由此得y/x=1/5x=25,y=5,u=125价格变化后,为维持u=125效用水平,在所有组合(x,y)中所需收入为m=8x+10y=8x+10·125/x 最小化条件(在xy=125的约束条件下)dm/dx=8-1250x-2=0解得x=12.5,y=10,m=2005.设某消费者的效用函数为U (x,y )=2lnx+(1-α)lny ;消费者的收入为M; x,y 两商品的价格分别为PX ,PY ;求对于X 、Y 两商品的需求。
解: 方法一:构造拉格朗日函数L=2lnX+(1-α)lnY+λ(M-PXX-PYY)对X 、Y 分别求一阶偏导得2Y/(1-α)X=PX/PY 代入PXX+PYY=M得:X=2M/(3-α) PX Y=(1-α)M/(3-α) PY方法二:思路见本部分第3题。
弹性问题之点弹性1 .某种化妆品的需求弹性系数为3,如果其价格下降25%,则需求量会增加多少?假设当价格为2元时,需求量为2000瓶,降价后需求量应该为多少?总收益有何变化?已知Ed=-3, ΔP/P=-25%,P1=2,Q1=2000ΔQ/Q, Q2 ,TR2 。
(1)根据计算弹性系数的一般公式: Ed=ΔQ/Q /ΔP/P将已知数据代入公式,则有:ΔQ/Q=Ed*ΔP/P=-3*-25%=%75 ,即需求量会增加75%。
(2)降价后的需求量Q2为: Q2=Q1(1+75%)=2000+2000×75%=3500(瓶)(3)降价前的总收益:TR1=P1*Q1=2×2000=4000(元)。
降价后的总收益:TR2=P2*Q2=P1(1-25%)*Q2=2(1-25%)×3500=5250(元)。
从而: TR2-TR1= 5250-4000=1250(元)即商品降价后总收益增加了1250元。
2.设需求曲线的方程为Q=10-2P,求其点弹性为多少?怎样调整价格,可以使总收益增加?解:根据点弹性的定义Edp =—(dQ/Q )/ (dP/P)= —(dQ/dP )· (P/Q) = —(-2)·(P/Q ) =2·(P/Q )价格的调整与总收益的变化之间的关系与弹性的大小有关。
若Edp <1,则表示需求缺乏弹性。
此时若提高价格,则需求量降低不太显著,从而总收益会增加;若Edp >1,则表示需求富于弹性。
此时若降低价格,则需求量会增加很多,从而总收益会增加; 若Edp =1,则表示单位需求弹性。
此时调整价格,对总收益没有影响。
3.已知某商品的需求方和供给方程分别为: QD=14-3P ;QS=2+6P 试求该商品的均衡价格,以及均衡时的需求价格和供给价格弹性解:均衡时,供给量等于需求量,即:QD=QS 也就是14-3P=2+6P解得P=4/3,QS=QD=10需求价格弹性为EDP= -(dQD/dP)·(P/QD)=3·(P/QD),所以,均衡时的需求价格弹性为EDP=3*[(4/3)/10]=2/5同理,供给价格弹性为ESP=(dQS/dP)·(P/QS)=6·(P/QS),所以,均衡时的供给弹性为ESP=6*[(4/3)/10]=4/54.某商品的需求价格弹性系数为0.15,现价格为1.2元,试问该商品的价格上涨多少元,才能使其消费量减少10%?已知Ed = 0.15,P=1.2,△Q/Q=10% ,根据计算弹性系数的一般公式:Ed = △Q/Q÷△P/P将已知数据代人上式:0.15=10%÷△P/1.2△P = 0.8 (元),该商品的价格上涨0.8元才能使其消费量减少10%。
弹性问题之交叉弹性、弧弹性1.出租车与私人汽车之间的需求交叉弹性为0.2,如果出租车服务价格上升20%,私人汽车的需求量会如何变化?已知Ecx=0.2,△Py/Py=20%。
根据交叉弹性系数的计算公式:Ecx=△Qx/Qx/△Py/Py。
将已知数据代入公式,则有:△Qx/Qx/20%=0.2,△Qx/Qx=4%,即私人汽车的需求量会增加4%。
2.公司甲和已是某行业的两个竞争者,目前两家公司的销售量分别100单位和250单位,其产品的需求曲线分别如下:甲公司:P甲=1000-5Q甲乙公司:P乙=1600-4Q乙1求这两家公司当前的点价格弹性。
2若乙公司降价,使销售量增加到300单位,导致甲公司的销售量下降到75单位,问甲公司产品的交叉价格弹性是多少?③若乙公司谋求销售收入最大化,你认为它降价在经济上是否合理?根据题意:(1) Q甲=200-(1/5)P甲, Q乙=400-(1/4)P乙当Q甲=100, Q乙=250时,P甲=500,P乙=600所以E甲=(dQ甲/ dP甲)×(P甲/ Q甲)=(-1/5)×(500/100)=-1E乙=(dQ乙/ dP乙)×(P乙/ Q乙)=(-1/4)×(600/250)=-0.6(2) ΔQ甲/Q甲(75-100)/100E甲=———————=——————————————————————=0.75 ΔP乙/P乙 [(1600-4×300)-(1600-4×250)]/( 1600-4×250)(3) TR乙= P乙×Q乙=1600Q乙-4Q²乙TR最大时,MTR=0,则1600-8Q乙=0,得Q乙=200因此,应提价,使Q乙从250下降到200。
3.甲公司生产皮鞋,现价每双60美元,2005年的销售量每月大约10000双。
2005年1月其竞争者乙公司把皮鞋价格从每双65美元降到55美元。
甲公司2月份销售量跌到8000双。
(1)甲公司和乙公司皮鞋的交叉弹性是多少(甲公司价格不变)?(2)若甲公司皮鞋的价格弧弹性是-2.0,乙公司把皮鞋价格保持在55美元,甲公司想把销售量恢复到每月10000双的水平,问每双要降低到多少?解:(1)已知Q甲1=10000(双),Q甲2=8000(双)P乙1=65(元), P乙2=55(元)E甲乙=(8000-10000)/(55-65)×(55+65)/(8000+10000)=1.33(2)假设甲公司鞋的价格降到P甲2,那么E甲2=(10000-8000)/(P甲2-60)×(P甲2+60)/(10000+8000) =-2.0解得P甲2=53.7(元)所以甲公司想把销售量恢复到每月10000双的水平,问每双要降低到53.7元生产过程1.已知某企业的单一可变投入(X)与产出(Q)的关系如下:Q=1000X+1000X2-2X3当X分别为200、300、400单位时,其边际产量和平均产量各为多少?它们分别属于那一个生产阶段?该函数的三个生产阶段分界点的产出量分别为多少?先求出边际产量函数和平均产量函数MP=dQ/dX=1000+2000X-6X2AP=Q/X=1000+1000X-2X2当X=200单位时:MP=1000+2000*(200)-6(200)2=1000+400000-240000=161000(单位)AP=1000+1000*(200)-2(200)2=1000+200000-80000=121000(单位)根据上述计算,既然MP>AP,说明AP仍处于上升阶段,所以,它处于阶段Ⅰ。
