电路分析第4章4 互易定理
电路分析基础--互易定理
0
图a 图b
Ik
I kj
Δ jk Δ
uj
Ij
I jj
Δ jj Δ
uj
Ij
I jk
Δ kj Δ
uk
Ik
I kk
Δ kk Δ
uk
图a
Ik
I kj
Δ jk Δ
uj
图b
Ij
I jk
Δ kj Δ
uk
Ij
I jj
Δ jj Δ
uj
Ik
I kk
Δ kk Δ
uk
无受控源,系数矩阵对称
Δ jk Δ kj
+ 10V –
2 I1
8
I3
3 I2
2
4
10 I1 8 (2 // 2 3) // 4 1A I2 = 0.5 I1=0.5A I3 = 0.5 I2=0.25A I= I1-I3 = 0.75A
应用互易定理时应注意:
(1) 适用于线性网络只有一个电源时,电源支路和另一支路 间电压、电流的关系。
j行 k行
图a 图b
j列
k列
R11I1 R1 j I j R1k Ik R1l Il 0
0
R j1I1 R jj I j R jk Ik R jl Il u j
0
Rk1I1 RkjI j Rkk Ik RklIl 0
uk
Rl1I1 Rlj I j Rlk Ik Rll Il 0
c
线性
–
电阻 网络
ikj
ijk
电阻 网络
uk
N
N
+
d
b
d
(a)
(b)
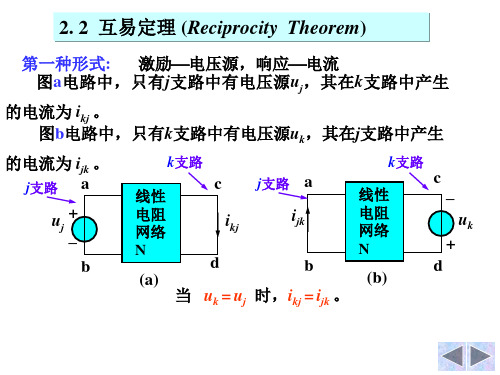
当 uk = uj 时,ikj = ijk 。
四、互易定理
四、互易定理对于线性单一激励的不含受控源的线性电阻电路(即仅有一个独立源作用的电阻电路)还有一个很重要的性质互易性,反映互易性的原理称作互易原理。
此原理有三种形式。
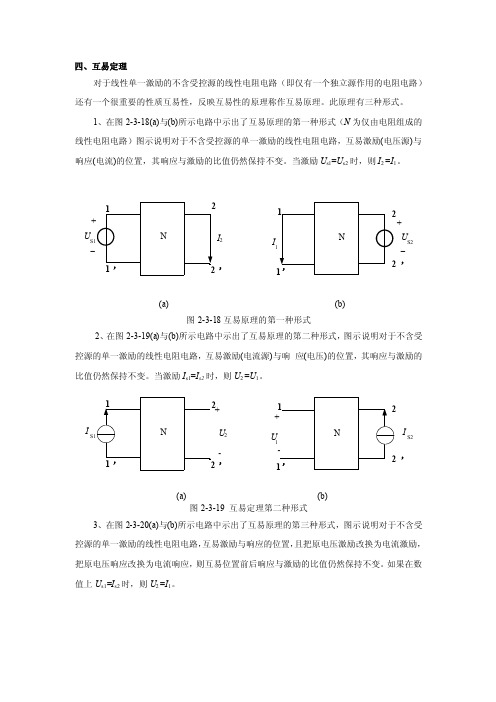
1、在图2-3-18(a)与(b)所示电路中示出了互易原理的第一种形式(N 为仅由电阻组成的线性电阻电路)图示说明对于不含受控源的单一激励的线性电阻电路,互易激励(电压源)与响应(电流)的位置,其响应与激励的比值仍然保持不变。
当激励U s1=U s2时,则I 2 =I 1。
_U ’I 2 S2 (a) (b)图2-3-18互易原理的第一种形式2、在图2-3-19(a)与(b)所示电路中示出了互易原理的第二种形式,图示说明对于不含受控源的单一激励的线性电阻电路,互易激励(电流源)与响 应(电压)的位置,其响应与激励的比值仍然保持不变。
当激励I s1=I s2时,则U 2 =U 1。
I ’U 2S2+- (a) (b)图2-3-19 互易定理第二种形式3、在图2-3-20(a)与(b)所示电路中示出了互易原理的第三种形式,图示说明对于不含受控源的单一激励的线性电阻电路,互易激励与响应的位置,且把原电压激励改换为电流激励,把原电压响应改换为电流响应,则互易位置前后响应与激励的比值仍然保持不变。
如果在数值上U s1=I s2时,则U 2 =I 1。
_U S1+ ’U 2 S2 -(a) (b)图2-3-20【例15】:电路如图2-3-21(a)所示,试求电流I 。
(a) (b)图2-3-21例15电路图【解】:原电路为一不平衡桥式电路,但为仅有一个独立源单独作用的线性电阻电路,可使用互易定理进行分析。
互易后的电路如右图所示。
此时应注意互易前后对应支路上的电压电流的参考方向必须同时关联或非关联。
在图2-3-21(b)中可以求得:A I 224241212281=+⨯++⨯+=根据分流公式:A I I 3221112=+=A II 3442413=+=由KCL 可得:A I I I 3223=-=∴原电路中所求电流AI 32=d 8V。
互易定理的条件

互易定理的条件互易定理是物理学中的一个重要定理,描述了线性系统的输入和输出之间的关系。
根据互易定理,系统的输入与输出之间的关系在时间域和频率域之间存在一种对应关系。
在下面的文章中,我会详细解释互易定理的条件,并提供相关的背景知识。
互易定理是傅里叶分析的一个关键概念,它指出了在频率域中,信号的傅里叶变换(频谱)与该信号的共轭复数的傅里叶变换之间存在一种对称关系。
具体而言,如果一个信号在时间域中的函数为f(t),它的傅里叶变换为F(ω),那么互易定理可以用下面的公式来表示:F(ω) = ∫[f(t) * e^(-jωt)] dt其中,F(ω)是信号f(t)在频率域中的傅里叶变换,e^(-jωt)是复指数函数,表示频率为ω的正弦波。
公式中的积分表示对信号f(t)在所有时间点上的加权求和。
为了满足互易定理,信号f(t)必须满足一些条件。
以下是互易定理的主要条件:1. 信号必须是连续的。
互易定理适用于连续信号而不是离散信号。
连续信号是在连续时间范围内定义的信号,而离散信号则是在离散时间点上定义的信号。
2. 信号必须是带限的。
带限信号是指其频谱在一定频率范围内有限。
这意味着信号在频率域中没有无限宽的频带,而是在某个频率范围内存在。
如果信号的频谱是无限宽的,那么它将无法满足互易定理。
3. 信号必须满足一定的可积条件。
具体而言,信号的幅度必须在整个时间域上是有界的,即信号的绝对值不能无限增大。
这是为了确保信号的傅里叶变换存在。
4. 信号必须具有有限的能量。
信号的能量定义为信号幅度的平方在整个时间域上的积分。
信号的能量必须是有限的,以便信号的傅里叶变换存在。
需要注意的是,互易定理通常用于描述线性时不变系统,这些系统对输入信号的响应与输入信号的傅里叶变换之间存在相似的关系。
互易定理在信号处理、通信系统、电路分析等领域中有广泛的应用。
总之,互易定理是描述线性系统中输入和输出之间关系的一个重要定理。
它要求信号是连续、带限的,并满足可积和有限能量的条件。
电路理论_(4)

例:电路如图(a), 电路响应
i2 i2 iS 0 i2 uS 0 i2(1) i2(2)
u1 u1 iS 0 u1 uS 0 u1(1) u1(2)
电路等效为下图
i (1)
2
uS R1 R2
i(2)
2
R1iS R1 R2
u (1) 1
R1uS R1 R2
u(2) 1
R1R2iS R1 R2
18
二、 诺顿定理
诺顿定理:任何一个线性含源二端网络,对外电路来讲,可 以用一个电流源和电导的并联组合等效变换。其电流源的电 流 iS = isc 为网络端口的短路电流;电导Geq=(1/ Req )为网络 内部电源均为0时的端口的输入电导。
含源一端 口网络
戴维宁等效电路 诺顿等效电路
两种等效电路共有3个参数: uoc , isc ,Req 其关系为: uoc = isc Req 戴维宁等效电路和诺顿等效电路统称为一端口的等效发电机。
33
4-6 对偶原理
注意以下关系式:u Ri, i Gu 对于CCVS: u2 ri1, 对于VCCS: i2 gu1
对偶元素:电压与电流;电阻与电导;CCVS与VCCS;r与g
n
R Rk k 1
i u R
uk
Rk R
u
两个电路互为对偶
n
G Gk k 1
u i G
ik
Gk G
i
显然,在上式中将对偶元素互 换,则对应关系式彼此转换
+
6
例:4-2 求图示电路中的电压 u3 。
+
7
例:4-3 求图示电路中的电压 u3 。
+
8
线性电路的齐性定理:当所有激励(独立电压源和独立电流源) 都同时增大或减小K倍时,响应(电压或电流)也将同样增大或 减小。 例:4-4 求图示电路中的各支路电流。
第四章 电路定理 互易定理

–
d
2A
(c)
a Req
b
线性 电阻 网络 NR
c
a I 5 5 + 5V – 戴维宁等 效电路
(d)
d
b
Req u1 2 10 2 5
(2) 结合a图,知c 图的等效电阻:
I 5 55 0.5A
解2
应用特勒根定理:
ˆ ˆ u1i1 u2 i2 u1 i1 u 2 i2
求(a)图电流I ,(b)图电压U。 2 4 + I 12V – (a) 1 + I 6
12V
+ 6A
U
4 2 (b)
-
-
6A 1 + 6 U –
解
I
利用互易定理
12 1 6 // 6 1 2 1.5A
U 3 2 6V
例2 解
I'
求电流I 。
利用互易定理
ˆ ˆ 10i1 5 ( 2) 5i1 ( 2) u 2 0
ˆ i1 I 0.5 A
如要电路具有互易性,则: U ab U cd
( 1) 3 ( 3 )
2
一般有受控源的电 路不具有互易性。
例3
测得a图中U1=10V,U2=5V,求b图中的电流I 。
a 2A
b 解1
+ 线性 电阻 u1 网络 –
NR
c
+ – d u2
a
5
I
(a)
b
线性 电阻 网络 NR
c + – 2A
(b)
d
a – b
(1) 利用互易定理知c 图的
电路分析基础第04章电路定理

Pmax
uo2c 4 Req
•最大功率匹配条件
RL Req
最大功率 匹配条件
Pmax
uo2c 4 Req
匹配:RL=Req时,P达到最大值, 称负载电阻与一端口的输入电阻匹配
扩音机为例
Ri
变
压
R=8Ω
ui
器
信号源的内阻Ri为 1kΩ, 扬声器上不可能得到最大功率。 为了使阻抗匹配,在信号源和扬声器之间连上一个变 压器。
第四章 电路定理
§4.1 叠加定理** §4.2 替代定理 §4.3 戴维宁定理** §4.4 特勒根定理 §4.5 互易定理 §4.6 对偶原理
§4.1 叠加定理
一、内容
在线性电阻电路中,任一支路电流(或支路电 压)都是电路中各个独立电源单独作用时在该 支路产生的电流(或电压)之叠加。
i i(1) i(2)+ uu(1)u(2)+
pmax
uo2c 4Req
0.2mW
注
(1) 最大功率传输定理用于一端口电路给定,
(2)
负载电阻可调的情况;
(2) 一端口等效电阻消耗的功率一般并不等于
(3) 大
端口内部消耗的功率,因此当负载获取最
(4)
功率时,电路的传输效率并不一定是50%;
(3) 计算最大功率问题结合应用戴维宁定理
(4) 或诺顿定理最方便.
4、恢复原电路
a
R0
+ Uabo
-
I b
I = U abo 9 R 0 10
例. 求U0 。
解
6
+ 9V 3
–
– 6I + a
+
I
电路分析第4章

2A 6
解: (1)求开路电压
UOC= 4×2-18 = -10V
负载开路等效电路
28
4 18V +
I 2A 6
4
(2)求等效电阻Req Req= 4
电源置零后的等效电路
(3)画出等效电路
I = -1A
也可以用电源等效变 换法求得。
4 10V +
I 6
29
等效电路
复习:用电源等效变换法求电路的I。
25
4.含有受控源的电路
例4-7(P94) i1
+
解: 求uoc 1
+
对节点1应用KCL
i1 i2 ic 0
5K
i2
20K
ic uoc
-
对网孔1应用KVL
1.75i1 i2 0
1
-
40V
求Req
1′
5i1 20i2 40 i2 1.75mA uoc 20i2 35V
+
-
8V 4
+ 4
4V 1
1A
I
3A
1
2
1
2
戴维宁定理
诺顿定理
20
1. 几个名词
(1) 端口( port ) i
A
a 端口指电路引出的一对端钮,其中从一 个端钮(如a)流入的电流一定等于从另一 b 端钮(如b)流出的电流。
i (2) 一端口网络 (network) (也称二端网络) 网络与外部电路只有一对端钮(或一个端口)联接。 (3) 含源(active)与无源(passive)一端口网络 网络内部含有独立电源的一端口网络称为含源一端口网络。 网络内部不含有独立电源的一端口网络称为无源一端口网络。
电路分析基础互易定理PPT课件

测量值:
10107 101107
9.99999
Rx
RM3
IN
误差: 109.999990.0001% 10
如果 Rx 5M ,则测量值为 3.333M
要想使测量结果比较准确,必须使万用表等效电阻远大于
被测电阻。
返回
X
电所流示us+为,i1 根iu+121 据,线无互当性源 易把定激u+22理励i,u2 s 有和:i响ˆ1iˆ1应=u+ˆ11
i2
i2
- - N0
-
-
互换位置时,如图(b)
线性 无源 N0
2 iˆ2
++
uˆ 2
us
-
-
1' (a)
2'
1' (b) 2'
互易定理
形式2:如图(a)所示电路,N 0内部不含有任何独立源
对偶关系
自然界中很多物理系统虽然属于不同的领域,但却 有相似的性能,能够用同一类的数学模型来描述,
这样的系统就具有对偶(dual)关系。 u Ri i Gu
电路中的一些对偶元素
电压 电阻 短路 串联
KCL
电流 电导 开路 并联 KVL
网孔电流 电压源
磁链 电感
节点电压 电流源
电荷 电容
对偶关系
d
所以
ik
im'
2 3
A
X
注意事项:
1.互易的支路在互易前后电压、电流的参考方向不 能发生变化。
2.利用互易定理只能求出互易支路的电量,互易后 其他支路的电压、电流发生变化。
3.当线性电路中含有多个独立源时,需要应用叠加 定理,分别对每个独立源单独处理。
电路分析第四章 电路定理

Uoc = U1 + U2
= -104/(4+6)+10 6/(4+6)
= -4+6=2V I a
Ri
+
(2) 求等效电阻Ri
Rx
a
Ri b
Uoc – b (3) Rx =1.2时,I= Uoc /(Ri + Rx) =0.333A I= Rx =5.2时, Uoc /(Ri + Rx) =0.2A Rx = Ri =4.8时,其上获最大功率。
计算; 2 加压求流法或加流求压法。
3 开路电压,短路电流法。
2 3 方法更有一般性。
(3) 外电路发生改变时,含源一端口网络的等效电路不变(伏安特性等效)。 (4) 当一端口内部含有受控源时,控制电路与受控源必须包 含在被化简的同一部分电路中。
21
第4章 电路定理
例1.
4 a Rx 6 + I b 10V
2.5A
10V 2 5V
?1A
?
这里替代后,两并联理想电压源 5V 5 1.5A 电流不确定,该支路不能被替代
14
第4章 电路定理
例.
3 + 1 Rx – U Ix + 0.5 0.5 若要使 I x 试求Rx。
1 8
I,
10V
–
I
0.5
解: 用替代:
1
1
I 0.5
8
I
1
0.5
又证:
ik
A
+ uk –
支 路 k
A
ik
+
–
uk
A
+ uk – uk
支 路 k
uk
电路分析-互易定理

-
7 1
(2) 由互易定理可知i1可由图(b)所示电路求得,
试求解。
解:
i1
R
12 R//R//R//1 8
R//R//R R//R//R 18
69.8 μA
i1
1 4
18
12 R//R//R//R
69.8 μA
例 4
例4-7-1 如图所示电路 求电路中I5
-
7
-
1
2
解:
R22'4 42 22.96AI1I2
I 2'
I 2''
2 11
I1
I 2' '
当R
2,4
2 11
5
I
2''
I 2' '
54 11
当R
4,I 2
2 11
80 27
54 11
4.37
5I 5I2' 0 3.5I I - I1 - I2' 0
2 I2' 11 I1
例 例题4 求图(a)所示电路的等效电阻Rab。
并非电源与负载的
明 互换位置,所以互易前后电路结构形式不能发生变化;
在应用互易定理时,电路中不能有第二个激励源,激励可 以是电压源或电流源,响应是指电流或电压;
互易前后电压电流的参考方向关系要一致,即要关联都关 联,要非关联都非关联。
+
—
例 4
例4-7-1 (1) 电路如图(a)所示,试求电流i1,R=100k;
Pmax
U
2 OC
4RS
52 45
1.25W
要点:求最大功率时通常要应用戴维南定理对问题进行
电路第4章

B i5 R5 i4 2Ω 20Ω R6 20Ω
第4章 41
_
设
'
C
K us us
'
i5 i5 1 A , 则
' '
u BC ( R 5 R 6 ) i 5 22 V
120 33 . 02
'
3 . 63
i4
'
'
u BC R4
'
'
1 . 1 A i3 i 4 i5 2 . 1 A
-
2i
b
分析: (1)由于原电路接有负载,因此首先断开负载;
(2)由于原电路中含有受控源,只能用外加电压源法 或短路电流法。
第4章 43
解:(1) 求开路电压 1A 1 i + -
u n1 5
2
3 a 2Ω 2i
5Ω 5V
6Ω
+ uoc
- b
1 5
u n1 ( 1 2
1 5
1 2 1 2
电阻和电压源的串联与电导和电流源的并联可以进行等效变换, 它们可以相互进行等效变换。维宁定理和诺顿定理统称为等效 发电机定理。
例4.3:求下图的诺顿等效电路。 解:<1> 求短路电流isc <2> 求等效电导Geq
i
2u1
3
i sc 10
3
A
1
isc
2
u1
a uoc
实验模拟
1A
b
+ 29.13Ω 48.89V -
解: (1)求开路电压uoc (2) 求等效电阻
10Ω 20Ω 1KΩ
电路分析第四章

A
u
2 3
2 3i
8 9
v
-
0.5A
+
14 3
V
2 3
V
+
+
1V -
a
i
a
+
-
1V + 10 i1 2 N1 4 0.5A
a i1 1/3A b 图(c) 2 4 1/6A
图(d)
(3) 为求i1,将N2用1/3A电流源替代(图(c) 、(d))
4.1 叠加定理 (Superposition Theorem)
一、线性电路的齐次性和叠加性 线性电路:由线性元件和独立源构成的电路。 1.齐次性(homogeneity)(又称比例性,proportionality) 齐次性:若输入x(t) → 响应y(t) ,则输入K x(t) → Ky(t)
+ x(t) -
电 路
+ y(t) -来自+ Kx(t) -
+
电路
Ky(t) -
2.叠加性(superposition)
若输入x1(t) → y1(t)(单独作用) ,
x2(t) → y2(t) … xn(t) → yn(t) 则x1(t) 、x2(t) … xn(t) 同时作用时 响应y (t)= y1(t)+ y2(t)+ … +yn(t) + x1(t) -
3.替代后外电路及参数不能改变(只在一点等效)。
4. 3 互易定理 (Reciprocity Theorem)
例:
a
Us + 对(a): 对(b):
电路理论 第4章

B
B
24
A
第 4 章
+ 20V _ 5Ω
+ _ 15V R3 5 Ω 3Ω
R4 4Ω B
I
有源二端网络等效为电 流源模型 ——诺顿定理 有源二端网络等效为电 压源模型—— 戴维南定理
有 源 二 端 网 络
R4 4Ω
I
等 效 电 源
R4 4Ω
第四章
第 4 章
电路分析方法之三
--电路定理法
叠加原理 等效电源定理 特勒根定理 互易定理
教学重点:替代定理
难点:线性电路的线性关系 戴维南定理 特勒根定理 运用多个定理的综合解题
1
§4-2 替代定理或置换定理
第 4 章
替代定理(又称置换定理): 在具有唯一解的线性网络中,若某条支路的电压UK (或电流IK)为已知,则这条支路可以用一个电压值为 UK的独立电压源(或用一个电流值为IK的独立电流源) 来替代,若替代后电路仍具有唯一解,则该网络所有支 路的电压和电流均保持不变。 说明: 1. 替代定理适用于线性、非线性电路、定常和时变电路。 2. 替代定理的应用必须满足的条件: 1) 原电路和替代后的电路必须有唯一解。 2) 被替代的K支路必须是独立的、和电路其它 部分应无耦 合及受控关系。
I1 2Ω I2 10A I 3 1Ω I4 4Ω 5Ω + 10V _
原电路 根据叠加定理
I1’’ 2Ω I2’’ I3’’ 1Ω I4’’ 4Ω 5Ω + 10V _
11
I 1 = I 1 ′ − I 1 ″, I 2 = I 2 ′ − I 2 ″ I3 = I3′ + I3 ″, I4 = I4 ′ + I4 ″
US"= 10I1 " + U1" =10×1.6 + 9.6 =25.6V US= US' +US"=-6+25.6=19.6V
3-4 互易定理

3.4 互易定理1. 互易定理的内容互易定理:对于一个线性电阻网络而言,如果只有一个激励和一个响应,那么当激励与响应互换位置后,激励与响应的比值保持不变。
这里的激励指电压源或电流源,响应指电压或电流。
互易定理的示意图如图1所示。
u 1i 2u 2i 1212u u i i =图1 互易定理示意图根据互易定理和图1,1212(u u i i =激励)(互换位置后的激励)(响应)(互换位置后的响应) (1)由式(1)可以看出,如果激励(电压源电压)相同,则互换位置后的响应(电流)也相同。
这是互易定理的一种特殊情况。
由互易定理的内容可以看出,互易定理是很难自己想象出来的。
由于互易定理很难想象,要证明互易定理自然也是一件非常困难的事情。
不过,为了令人信服,下面我们来证明一下互易定理。
2. 互易定理的证明在证明互易定理之前,需要先证明两个定理和一个定理推论,即特勒根定理1、特勒根定理2和特勒根定理2推论。
特勒根定理1的内容是,任意一个电路,如果每一条支路的电流参考方向都是从电压参考方向的正极流入,则所有支路的电压电流乘积加起来一定等于零。
电压电流乘积就是功率,可见特勒根定理1的物理含义就是任何一个电路总的功率为零,也就是发出功率等于吸收功率,即功率守恒。
下面我们来证明特勒根定理1。
假设任意一个电路总计有b 条支路,n 个结点,第p 、q 个结点之间的电压记为pq u ,电流记为pq i ,则1111111111111()02222bn n n n n n nnk kpq pq p q pq p pq q pq k p q p q p q q p u i u i u u i u i u i ===========−=−=∑∑∑∑∑∑∑∑∑ (2)由式(2)即证明了特勒根定理1。
式(2)乍一看很难理解,下面对其中的细节进行解释。
式(2)中第一个等号是将支路电压电流乘积之和转化为结点与结点之间电压与电流乘积之和。
电路第4章

4-1 叠加定理 示电路求电压U和电流I 一、引例 图示电路求电压U和电流I。
R1
Us
R2
Is
=
U s / R1 + I s U= 1 1 ( + ) R1 R2
+
R2 R2R 1 U= Us + Is =U′ +U′ ′ R + R2 R + R2 1 1
⊥
U s R 2 + R1 R 2 I s = R1 + R 2
三、应用举例: 应用举例:
求图示电路中的U 求图示电路中的 S和R。 。 解: I=2A U=28v US
US=43.6v 利用替代定理, 有 利用替代定理
U1 = 28−20×0.6−6
=10v I1=0.4A + IR=0.6-0.4=0.2A ∴ R=50Ω. Ω 28V I1 + U1 9 IR
R0 =
不除源
3、含受控源单口有源网络不一定同时存在两种等效电源; 、含受控源单口有源网络不一定同时存在两种等效电源; 4、含源单口网络与外电路应无耦合; 受控源及控制量均在线 、含源单口网络与外电路应无耦合;
性含源网络内部
5、含源单口网络应为线性网络; 、含源单口网络应为线性网络; 6、等效参数计算。 、等效参数计算。
ϕ
⊥
1、10V电压源单独作用时: 、 电压源单独作用时: 电压源单独作用时
10 − 2I ′ I′ = 2 +1
ϕ
I ′ = 2A
3 I′′ = − A 5
2、3A电流源单独作用时,有 、 电流源单独作用时, 电流源单独作用时 ′ 3+ 2I′ /1 ϕ ϕ=
电路分析第4章4 互易定理

特勒根定理设有电路,A B ,满足:(1)两者的拓扑图完全相同,均有n 个节点b 条支路;(2)对应的支路和节点均采用相同的编号,其中B 电路的电流、电压加“^”号;(3)各支路电流、电压参考方向均取为一致,则有: 功率守恒定理:01bU I k k k =∑=ˆˆ01bU I k kk =∑= 似功率守恒定理:ˆ01bU I k k k =∑= 1ˆ0b k k k U I ==∑适用于各种电路:直流、交流;线性、非线性;被称为基尔霍夫第三定律。
§2-2互易定理在线性电路中,若只有一个独立电源作用,网络只含有线性电阻(不含受控源),则在一定的激励与响应的定义下,二者的位置互易后,响应与激励的比值不变。
互易定理的证明需要特勒根定理(或二端网络等效的概念)。
根据激励和响应是电压还是电流,互易定理有三种形式:1、互易定理的第一种形式S uS u ˆ+-电路在方框内仅含线性电阻,不含任何独立电源和受控源。
电压源s u 接在端子1-1',支路2-2'短路,其电流为2i 。
如果把激励和响应位置互换,此时ˆs u接于2-2',而响应则是接于1-1',短路电流1ˆi 。
21ˆˆs s i i u u=,若 ˆs s u u =,则21ˆi i =。
对一个仅含线性电阻的电路,在单一电压源激励而响应为电流时,激励和响应互换位置,不改变同一激励产生的响应。
2、互易定理的第二种形式2'21'121ˆˆs s u u i i= 若ˆs s i i=,则21ˆu u =。
3 互易定理的第三种形式21ˆˆs s i u i u= 若数值上ˆs s i u =,则数值上21ˆi u =。
例 用互易定理求下图中电流i 。
解:根据互易定理,图(a)和(b)中电流i 相同。
从图(b)中易于求得:024361236261236i A ==⨯⨯++++00123161236i i i A =-=++例 互易双口的输入电流为2A 时,输入端电压为10V ,输出端电压为5V 。
电路分析之互易定理

9
§2-10互易定理
例4、图中网络N仅由线性电阻组成。根据图(a)和图(b) 的已知条件,求图(c)中电流i1和i2。
3A 4Ω
1A
20V N 5Ω
4Ω
2A
20V N
(a)
(b)
i1 4Ω
5Ω i2
20V N
20V
(c)
2009-10-13
10
§2-10互易定理
例:(续)
§2-10互易定理
解:用叠加、互易、戴维南定理
⑴
N u1S1i11’
1'
2
u22’ i22’
2'
N 1
^i11'
^u11’
1'
^i22’u^2S2
2'
有 i22' = iˆ11' uS1 uˆ S 2
若uˆ S 2 = uS1 则iˆ11' = i22'
使用式: u11'iˆ11' + u22'iˆ22' = uˆ11'i11' + uˆ 22'i22'
需使用互易定理基本关系式有:
(uS - R1 i1) (-i1’) + u2i2’ = (uS’ - R1’ i1’) (-i1)+ u2’i2
并且:i2’ = u2’/R2’ 得:u2’ = 1.6 V
8
例3:电路如图所示,求电流 I
§2-10互易定理
4Ω
2Ω
a
b
2Ω
应用
c
1Ω 8V 2Ω
I 互易定理
§2-10互易定理
§2-10互易定理
电路分析原理第四章 线性网络的几个定理及等效网络

第四章 线性网络的几个定理及等效网络
第一节 叠加定理 第二节 互易定理 第三节 替代定理 第四节 戴维宁定理 第五节 诺 顿 定 理 第六节 最大功率传输定理 第七节 Y形网络与△形网络的等效变换 ∗第八节 理想电源的转移
第一节 叠加定理
一、叠加定理的陈述 二、叠加定理的证明 三、应用叠加定理要注意的几个问题 四、叠加定理的应用
图4-8 互易现象三, / = / (注意参考方向)
a) 1-1′
2-2′开路 b) 2-2′
1-1′短接
4.互易现象四
1) 在图4-9a中, 1-1′间由电流源IS1激励, 2-2′间的短路电流为I2 2) 在图4-9b中, 2-2′间由电压源S2激励, 1-1′间的开路电压为1
4.互易现象四
/ = / (注意参考方向)
2-2′短接 b) 2-2′
1-1′开路
三、互易定理的形象化讲法
1)互易定理陈述一指出,线性网络中唯一的一个电压源,与任 一支路中零内阻的电流表交换位置时,电流表的读数不变。 2)互易定理陈述二给出,线性网络中的唯一的一个电流源,与 跨接在任意两端、内阻为无穷大的电压表交换位置时,电压表 的读数不变。
图4-9 互易现象四, / = / (注意参考方向)
a) 1-1′
2-2′短接 b) 2-2′
1-1′开路
二、互易定理
1.陈述一(互易定理一) 2.陈述二(互易定理二) 3.陈述三 4.陈述四(互易定理四)
1.陈述一(互易定理一)
图4-10 a) 1-1′
/ = / (注意参考方向)
2-2′短接 b) 2-2′
一、叠加定理的陈述
图4-1 叠加定理示图
a)
电路互易定理

电路互易定理
嘿,你知道电路互易定理吗?这可真是个神奇又有趣的东西啊!它就像是电路世界里的一把神奇钥匙,能打开好多奇妙的大门呢!
电路互易定理说的是,在一个只含线性电阻的电路中,在单一激励的情况下,当激励和响应互换位置时,响应与激励的比值保持不变。
这听上去是不是有点玄乎?但其实很好理解啦!就好比你和朋友换了个位置,但你们之间的关系还是那么铁!
想象一下,电路就像一个复杂的迷宫,而互易定理就是帮我们找到正确路径的指南。
它让我们能够更轻松地分析和理解电路的行为。
没有它,我们可能就会在电路的迷宫里晕头转向,不知所措。
你看,在实际应用中,电路互易定理可太重要了!比如在通信系统中,它能帮助我们优化信号的传输和接收;在电子设备的设计中,它能让我们的设备更加高效和可靠。
这难道不令人惊叹吗?
而且哦,电路互易定理可不是孤立存在的,它和其他的电路定理一起,共同构建了电路理论的大厦。
它们相互配合,相互支持,就像一个团队一样,为我们的电子世界提供坚实的基础。
难道你不觉得这很了不起吗?它就像是一个默默无闻的英雄,在背后默默地为我们的科技发展贡献着力量。
我们每天使用的手机、电脑、电视等等,都离不开电路互易定理的功劳。
所以啊,我们真的应该好好感谢电路互易定理,感谢它为我们的生活带来的便利和精彩。
它让我们的世界变得更加丰富多彩,让我们能够享受到高科技带来的种种好处。
总之,电路互易定理就是这么神奇,这么重要!它是电路世界里不可或缺的一部分,是我们探索电子奥秘的有力工具。
让我们一起为它点赞吧!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特勒根定理
设有电路,A B ,满足:(1)两者的拓扑图完全相同,均有n 个节点b 条支路;(2)对应的支路和节点均采用相同的编号,其中B 电路的电流、电压加“^”号;(3)各支路电流、电压参考方向均取为一致,则有: 功率守恒定理:
01
b
U I k k k =∑=
ˆˆ01b
U I k k
k =∑= 似功率守恒定理:
ˆ01
b
U I k k k =∑= 1
ˆ0b k k k U I ==∑
适用于各种电路:直流、交流;线性、非线性;
被称为基尔霍夫第三定律。
§2-2互易定理
在线性电路中,若只有一个独立电源作用,网络只含有线性电阻(不含受控源),则在一定的激励与响应的定义下,二者的位置互易后,响应与激励的比值不变。
互易定理的证明需要特勒根定理(或二端网络等效的概念)。
根据激励和响应是电压还是电流,互易定理有三种形式:
1、互易定理的第一种形式
S u
S u ˆ+-
电路在方框内仅含线性电阻,不
含任何独立电源和受控源。
电压源s u 接在端子1-1',支路2-2'短路,其电流为2i 。
如果把激励和响应位置互
换,此时ˆs u
接于2-2',而响应则是接于1-1',短路电流1ˆi 。
21ˆˆs s i i u u
=,若 ˆs s u u =,则21ˆi i =。
对一个仅含线性电阻的电路,在单一电压源激励而响应为电流时,激励和响应互换位置,不改变同一激励产生的响应。
2、互易定理的第二种形式
2'
2
1'
1
21ˆˆs s u u i i
= 若ˆs s i i
=,则21ˆu u =。
3 互易定理的第三种形式
2
1ˆˆs s i u i u
= 若数值上ˆs s i u =,则数值上21ˆi u =。
例 用互易定理求下图中电流i 。
解:根据互易定理,图(a)和(b)中电流i 相同。
从图(b)中易于求得:
024
361236261236
i A ==⨯⨯++
++
00123161236
i i i A =-=++
例 互易双口的输入电流为2A 时,输入端电压为10V ,输出端电压为5V 。
把电流源移到输出端,同时在输入端跨接5Ω电阻,求5Ω电阻的电流。
例 互易双口的输入电压为10V 时,输入端电流为5A ,输出端短路电流为1A 。
把电压源移到输出端,同时在输入端跨接2Ω电阻,求2Ω电阻
的电压。
例P99,例题。
