3塑性变形的基本定律
塑性成形

1. 晶内塑性变形 – 滑移变形 Sliding Deformation:在切应力作用
下,晶体一部分沿一定晶面(滑移面)和晶向(滑 移方向)相对于另一部分产生滑动的变形方式称为 滑移。 – 孪生变形 Twinning Deformation:在切应力 作用下,晶体一部分相对于其余部分沿一定晶面及 晶向产生一定角度切变引起变形
四、塑性成形基本规律
1. 体积不变定律 Volume Constance 金属塑性变形前后的体积相等,即体积为 常数,也称为不可压缩定律。
2. 临界切应力定律 Critical Shear Stress
晶体滑移的驱动力是外 力在滑移系上的分切 应力。只有当滑移系 上分切应力(τ )达到 一定值时,则该滑移 系才能开动。
变形温度的影响 变形速率的影响
1、金属随变形温度的升高,塑性升高、 变形抗力降低。但是,随加热温度的 升高,也会产生相应的缺陷,如产生 氧化、脱碳、过热和过烧等。
2、除采用高能高速锤外,一般压力加 工方法中,随着变形速度的增加,金 属的塑性下降、变形抗力增加。
作业: 1、锻造流线的存在对金属机 械性能有何影响?在零件设计 中应注意那些问题? 2、试述金属的锻造性能,影 响金属锻造性能的因素,提高 金属锻造性能的途径?
晶粒长大Grain Growth
–冷变形金属在完成再结晶后,继续升温或延长保温 时间使晶界上的弥散质点溶解,失去对晶粒长大的 阻碍作用,晶界移动的结果使一些晶粒尺寸缩小以 至于消失,另一些晶粒尺寸增大,形成粗大晶粒, 导致力学性能恶化。
动态回复和动态再结晶
Dynamic Recovery and Dynamic Recrystallization –在塑性变形过程中发生的,而不是在变形停止后发 生的回复或再结晶 –热加工:在再结晶温度以上所进行的塑性变形加工 过程。
塑性变形的基本定律

二、金属压力加工金属压力加工利用金属在外力作用并不破坏自身完整状态的条件下,稳定改变其形状与尺寸,而且也改善其组织和性能的加工方法,称为金属压力加工。
这种加工过程也是使金属产生塑性变形的过程,因此也叫做金属塑性加工。
1、锻造:主要包括两种基本方式,用于制造各种零件或型材毛坯。
(1)自由锻造(简称自由锻)-使已加热的金属坯料在上下砧之间承受冲击力(自由锻锤)或压力(压力机)而变形的过程,用于制造各种形状比较简单的零件毛坯。
(2)模型锻造(简称模锻)-使已加热的金属坯料在已经预先制好型腔的锻模间承受冲击力(自由锻锤)或压力(压力机)而变形,成为与型腔形状一致的零件毛坯,用于制造各种形状比较复杂的零件。
2、轧制:金属坯在两个旋转的轧辊之间受到压缩而产生塑性变形,使横断面缩小、形状改变、长度增加,达到用户要求的加工方法。
按轧制温度分为冷轧(金属坯料不加热)和热轧(850℃-1250℃);按加工方法分为纵轧、横轧、斜轧;按产品分为板材、棒材、型材、管材等。
3、挤压:把放置在模具容腔内的金属坯料从模孔中挤出来成形为零件的过程,包括冷挤压和热挤压,多用于壁厚较薄的零件以及制造无缝管材等。
4、冲压:使金属板坯在冲模内受到冲击力或压力而成形的过程,也分冷冲压与热冲压。
5、拉拔:将金属坯料拉过模孔以缩小其横截面的过程,用于制造如丝材、小直径薄壁管材等,也分为冷拉拔和热拉拔。
2.1、塑性变形的基本定律材料力学的解释是:在某物质的弹性限度之内,在外力作用下,应力与应变成正比,且在撤销外力之后,物体能恢复原状;超过这个限度,就不成正比了,即应力不增加、或增加很少;而应变增加的很大。
并且在撤销外力之后,物体不能恢复原状。
简单地说:物体在一定的条件下,在外力的作用下产生形变,当施加的外力撤除或消失后该物体不能恢复原状的变形叫做塑性变形。
金属在发生塑性变形时,作用在物体上的力有两种:作用力和约束反力。
2.1.1体积不变定律在压力加工过程中,只要金属的密度不发生变化,塑性变形前后的体积就不会产生变化,这一规律称为体积不变定律。
第三章 金属塑性变形的物理基础

(1)塑性的基本概念
什么是塑性? 塑性是金属在外力作用下产生永久变形 而不破坏其完整性的能力。
塑性与柔软性的区别是什么? 塑性反映材料产生永久变形的能力。 柔软性反映材料抵抗变形的能力。
塑性与柔软性的对立统一
铅---------------塑性好,变形抗力小
不锈钢--------塑性好,但变形抗力高 白口铸铁----塑性差,变形抗力高
塑性指标的测量方法
拉伸试验法 压缩试验法 扭转试验法 轧制模拟试验法
拉伸试验法
Lh L0 100%
L0 F0 Fh 100%
F0
式中:L0——拉伸试样原始标距长度; Lh——拉伸试样破断后标距间的长度; F0——拉伸试样原始断面积; Fh——拉伸试样破断处的断面积
%
晶粒5 晶粒4 晶粒3
晶粒2
晶粒1
位置,mm
图5-6 多晶铝的几个晶粒各处的应变量。 垂直虚线是晶界,线上的数字为总变形量
四、合金的塑性变形
单相固溶体合金的变形 多相合金的变形
§3. 2 金属塑性加工中组织和性能变化 的基本规律
一、冷塑性变形时金属组织和性能的变化 二、热塑性变形时金属组织和性能的变化
2200
N/mm2
图4-6 正压力对摩擦系数的影响
0.5
μ
0.4
0.3
0.4
0.2 0.2
0.1
0
℃
200
400
600
800
图4-7 温度对钢的摩擦系数的影响
0
400
600
800 ℃
图4-8 温度对铜的摩擦系数的影响
测定摩擦系数的方法
夹钳轧制法 楔形件压缩法 塑性加工常用摩擦系数 圆环镦粗法
材料的塑性变形

修 正 : m ’ ≈ G-G或 m ’ ≈ G。
1050
30
14
2.3 晶格缺陷——位错
2.3.1 位错的基本概念(dislocation)
(1)定义:线状缺陷。
实际晶体在结晶时,受到杂质、温度变化或振动产 生的应力作用或晶体由于受到打击、切割等机械应力作 用,使晶体内部原子排列变形,原子行列间相互滑移, 不再符合理想晶体的有序排列,形成线状缺陷,即为位 错。
15
2.3.1 位错的基本概念(dislocation)
(1)定义:线状缺陷。
位错的提出——解释晶体的塑性变形。
塑性变形理论 滑移模型,1920 线缺陷(位错)模型,1934
建立位错理论,1956
16
2.3.1 位错的基本概念(dislocation) 1934年 Taylor、Polanyi、Orowan三人几乎同 时提出晶体中位错的模型。
τm——完整晶体屈服强度,晶 体受到的切应力超过τm后产生永久 变形,即为晶体的塑性变形。
a.E-x变化曲线; b. τ-x变化曲线
12
2.2 理想晶体的强度
在 原 子 位 移 很 小 的 情 况 下 , -x曲 线 的 斜 率 为 /x,
故 m 2π = bx
根 据 胡 克 定 律 : =G ≈ G x a
位错线 运动方向
晶体 切应力 滑移面 滑移方向 方向 个数
⊥位错线本身 与b一致 与b一致 唯一
⊥位错线本身 与b一致 与b一致 多个
混合
与位错线 成一定角度
⊥位错线本身
与b一致 与b一致
36
2.3.3 位错运动理论
(2)位错的攀移
位错除滑移外,还可以产生攀移,由于热运动,原子 之间扩散,空位扩散到位错处,使位错上移,杂质离子扩 散到位错处,使位错下移。
第二章 材料的变形——塑性变形1

许多滑移系并非同时参与滑移。只有当外力 在某一滑移系中的分切应力达到一定临界值 时,该滑移系方可首先发生滑移,该分切应 力称为滑移的临界分切应力。 沿滑移面滑移方向的分切应力; 能够引起滑移系开动的分切应力。
切应力的作用下,晶格发生弹性外扭,进一步将使晶格发生滑 移。外力去除后,由于原子到了一新的平衡位置,晶体不能恢 复到原来的形状,而保留永久的变形。大量晶面的滑移将得到 宏观变形效果,在晶体的表面将出现滑移产生的台阶。
向(孪生方向)发生切变,形成对称的晶格排列,发生切变
部分叫做孪生带,或简称为孪晶。切变部分和未切变部分 呈镜面对称,对称面为孪生面。
孪生变形的特点
孪生需要的临界切应力很大,仅在滑移困难时才会发 生。一般孪生出现在滑移系很少的晶体结构的材料中 (如密排六方晶格金属);某些容易发生滑移的立方材 料仅在低温度滑移困难或受冲击时来不及滑移时才可 能产生孪生。 孪生是一种均匀切变,即切变区内与孪晶面平行的每 一层原子面均相对于其毗邻晶面沿孪生方向位移了一 定的距离,移动量都相同。
滑移、孪生、蠕变、晶界滑动。
2.1 滑移
单晶体的塑性变形的主要方式是滑移和
孪生。其中滑移是最基本、最普遍的塑 性变形方式,孪生只是在滑移难以进行 的情况下出现。
单晶体的圆柱试样表面抛光后拉伸,试样表
面就会出现一系列平行的变形痕迹。 光镜观察,试样表面形成的浮凸,由一系列 滑移迹线组成,称为滑移带。
就越来越大。
此外,塑性变形也会导致晶格畸变,使外力和滑移面的相 对位向也会发生变化。使开动位错所需应力增大。
பைடு நூலகம்
2.2孪生变形
——孪晶:两个晶体或者晶体的两个部分沿
一个公共晶面构成镜面堆成的位向关系
第三章 弹塑性本构关系
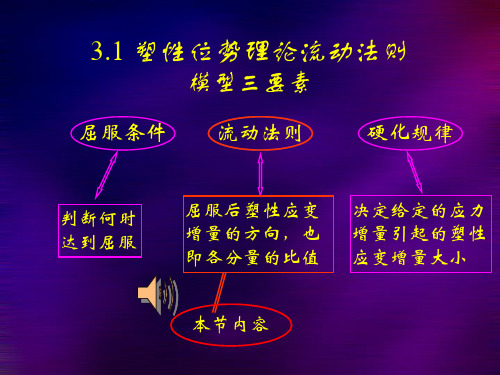
d ij d 0 dσ n 0
p ij
加载准则
意义:只有当应力增量指向加载面的外部时才能产生塑性变形。
3德鲁克塑性公设的评述
德鲁克公设的适用条件:
(1)应力循环中外载所作 的真实功与ij0起点无关;
p ij
ij d ij 0
(2)附加应力功不符合功的 定义,并非真实功
1 屈服曲面的外凸性
0 ( ij ij )dijp | A0 A || d p | cos 0
ij
此式限制了屈服面的形状: 对于任意应力状态,应力增量方向 与塑性应变向量之间所成的夹角不应 该大于90° 稳定材料的屈服面必须是凸的.
(a)满足稳定材 料的屈服面
0 ij
由得屈服条件流动法则硬化规律判断何时达到屈服屈服后塑性应变增量的方向也即各分量的比值决定给定的应力增量引起的塑性应变增量大小本节内容屈服后塑性应变增量的方向也即各分量的比值1加载曲面后继屈服面由单向拉伸试验知道对理想塑性材料一旦屈服以后其应力保持常值屈服应力卸载后再重新加载时其屈服应力的大小也不改变没有强化现象
3.1.4 塑性位势理论与流动法则
与弹性位势理论相类似,Mises于1928年提出塑性 位势理论。他假设经过应力空间的任何一点M,必有 一塑性位势等势面存在,其数学表达式称为塑性位势 函数,记为:
g I1, J 2 , J3 , H 0
g ij , H 0
或
式中, H 为硬化参数。 塑性应变增量可以用塑性位势函数对应力微分的表达 式来表示,即: g p
残余应力增量与塑性 应变增量存在关系:
p p d ij D d ij
式中,D为弹性矩阵。 根据依留申公设,在 完成上述应变循环中, 外部功不为负,即
板料塑性变形与其基本规律

断面收缩率ψ: F0 Fk 100%
F0
二、塑性变形的基本规律
1、硬化规律 2、卸载弹性恢复规律和反载软化现象 3、体积不变规律 4、最小阻力定律
1、硬化规律
加工硬化或应变刚现象
▇金属的机械性能,随着变形程度的增加,强 度和硬度逐渐增加,而塑性和韧性逐渐降低;
▇晶粒会沿变形方向伸长排列形成纤维组织, 使材料产生各向异性;
发展。这就是塑性变形中的最小阻力定律。
三、影响变形抗力和塑性变形的主要因素
内部因素: 金属本身的化学成分、金相组织等
外部条件: 变形速度、变形温度等
①化学成分:其中碳 对钢板的性能影响最大,含碳量越高塑性就越差。杂质对 钢板的塑性也产生不利的影响。 ②金相组织:单相组织比多相组织塑性好、抗力低。 ③变形速度:变形速度快,变形体没有足够的时间进行回复和再结晶,金属的变 形抗力增加,塑性降低。目前,常规冲压设备工作速度都较低,对金属变形的性 能影响不大。考虑变形速度因素,主要基于零件的尺寸和形状。大型复杂、变形 量大且极不均匀的制件,易局部拉裂和起皱。为使塑性变形的扩展,有利于金属 流动,宜采用低速的压力机或液压机。 ④变形温度:对塑性影响很大。多数金属随温度升高,塑性增加,变形抗力降低。 (热蠕变等)
金属材料在塑性变形时,体积变化很小,可以忽略不计。
一般认为金属材料在塑性变形时体积不变,可证明满足:
ε1 +ε2 + ε3 = 0
3种主应变 状态图
4.最小阻力定律
在塑性变形中,破坏了金属的整体平衡而强制金属流动,当 金属质点有向几个方向移动的可能时,它向阻力最小的方向移动。
在冲压加工中,板料在变形过程中总是沿着阻力最小的方向
▇由于变形不均,会在材料内部产生内应力, 变形后作为残余应力保留在材料内部。
锻压基础知识

概述 锻压:借助外力的作用,使金属坯料产生塑性变形,从
而获得具有一定形状、尺寸和性能的锻压件。
金属坯料
塑性变形
锻压件
2
一 锻压加工方法
自由锻
模锻
板料冲压
自由锻、模锻:承受重载的机械零件,如机器主轴、 重要齿轮、连杆、炮管、枪管等;
3
挤压
拉拔
轧锻
轧制、挤压、拉拔:金属型材、板材、钢材、线材等;
(2)用钢锭作为锻造坯料 碳素结构钢,拔长锻造比 ≥3,镦粗锻造比≥2.5; 合金结构钢,锻造比为 3~4
(3) 铸 造 缺 陷 严 重 , 碳 化 物 粗大的高合金钢钢锭 :不 锈钢的锻造比选为4~6, 高速钢的锻造比选为5~ 12
(4)y太大,会增加各向异性
21
3 锻造流线
(1)锻造后金属组织具有方向性
2)锻模成本高。
为什么?
73
一 模锻设备
模锻设备 锻造力性质 锻件精度 生产率
模锻锤
冲击力
较低
较低
曲柄压力机 压力
较高
较高
平锻机
压力
较高
较高
摩擦压力机 冲击力-压力 较高
较低
74
(一) 模锻锤
可以镦粗、拔长、 滚挤、弯曲、成 形、预锻、终锻。
75
(二)锻模及锻模模膛
76
1 制坯模膛:使坯料预变形而达到合理分配,使其形 状基本接近锻件形状,以便更好地充满模锻模膛。 拔长模膛 滚压模膛 弯曲模膛 切断模膛
(5) 确定锻造温度范围 始锻温度低于AE线150~250℃,碳钢的终锻温度如图3-2所示
57
58
59
60
三 自由锻零件结构工艺性
塑性力学讲义全量理论与增量理论

将 Sij2代G 1 入 用ei位j 移表示的平衡
微分方程得:
其 中 K G 3 uk,kiGi,ju j2 Geij,jfi 0
K
E
312
或 K G 3 uk,k i Gi,ju jfi 2Gei j,j
在弹性状态时,上式右端等于零,可得到 弹性解。将它作为第一次近似解,代入上式 右端作为已知项,又可以解出第二次近似解。 重复以上过程,可得出所要求精度内接近实 际的解。在小变形情况下,可以证明解能够 很快收敛。在很多问题第二次近似解已能给 出较为满意的结果。
( Sii )0。
在弹性范围内,应力和应变之间的方向关系
是应力和应变主轴重合,分配关系是应变偏
张量各分量和应力偏张量各分量成比例。为
便于推广到塑性状态,并与塑性本构方程的
写法一致, 将 eij 改21G写Si为j
eij
3i 2i
Sij,i
3Gi
(因 i E i 2 1 , 而G 塑i性状态 ) 0.5
其本构方程为:deij
1 2G
dSij
dSij
d ii
1 2
E
d ii
例4-2、在薄壁筒的拉伸与扭转问题中,若
材料为理想弹塑性,且 0。.5设拉力为P,扭 矩为M,筒的平均半径为r,壁厚为t。于是
筒内应力为均匀应力状态,有
z
2Prt,z
M
2r2t
其余应力分量为零。现按照下列三种加载路 径(如图),试用Prandtl—Reuss理论来计 算筒中的应力:
A
s
解:1、分析 圆筒为均匀应力状态,且已知应力公式,
一、Levy—Mises流动法则
d i jd Sijd 0
适用于刚塑性体。其中比例系数 d取决于质
塑性理论
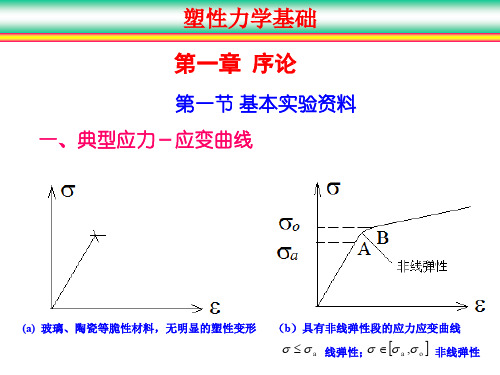
五、Bauschinger效应
加工硬化:对于金属 等各向同性材料,当加 载至屈服后再卸载,当 再次进入屈服状态时屈 服应力将有所提高。
Bauschinger效应: 正向强化,反向弱化; 反向强化,正向弱化。
第二节 塑性力学的研究内容
一、 屈服条件
单轴情况:屈服极限。 复杂应力状态:
f ij 0;或者f 1,2,3=0;
f I1, I2, I3 =0; f s1,s2,s3=0; f J2, J3=0
在应力空间中任意一点 P,其偏应力为
s1,s2,s3
op =
1 e1+ 2 e2+ 3 e3 = (s1+ 0 )e1+ (s2+ 0 )e2+(s3+ 0 )e3= (s1e1+ s2e2+
s3e3)+ ( 0 e1+
0 e2+ 0 e3) = OQ ON
2 3
Y
纯剪时 X
6 3
S
;
所以 Y 3 S
e
1 2
x y 2
x z
2
z
y
2
6
2 xy
2 yz
2 xz
Y
3 s
e k;k Y ;或者k 3 s
Von-Mises 屈服条件与最大应变能说完全一致。
塑性力学基本理论

弹性力学对于均匀、各向同性材料,可以证明只有两个独立弹性常数,3各常数之间存在关系:2(1)EG μ=+。
广义胡克定律的体积式:体积应变:x y z θεεε=++;体积应力:x y z σσσΘ=++,则:12Eνθ-=Θ。
各向同性体的体积改变定律:3(12)m EK σθθν==-.其中体积模量:3(12)EK ν=-弹性力学解的唯一性定理:弹性体在给定体力、面力和约束条件的情况下而处于平衡时,体内各点的应力分量、应变分量的解是唯一的。
塑性力学从物理上看,塑性变形过程属于不可逆过程,并且必然伴随机械能的耗散。
研究塑性力学问题主要采用宏观的方法,即联系介质力学的方法,它不去探究材料塑性变形的内在机理,而是从材料的宏观塑性行为中抽象出力学模型,并建立相应的数学物理方程来予以描述,应力平衡方程和应变位移间的几何关系是与材料性质无关的,因此对弹性力学与塑性力学都一样,弹性力学与塑性力学的差别主要表现在应力与应变的物理关系的不同。
屈服条件以及塑性的本构关系是塑性力学物理方程的具体内容,具有:(1)应力与应变关系(本构关系)呈非线性,其非线性性质与具体材料有关; (2)应力与应变之间没有一一对应的关系,它与加载历史有关;(3)变形体中存在弹性区和塑性区,分析问题时需要找出其分界限。
在弹性区,加载与卸载均服从广义胡克定律;在塑性区,加载过程要使用塑性阶段的应力应变关系,而卸载过程中,则使用广义胡克定律。
这些特点带来了研究、处理问题方法上的不同,塑性力学首先要解决的问题是在实验资料的基础上确立塑性本构关系,进而与平衡和几何关系一起去建立塑性边值问题,再次是根据不同的具体情况寻求数学计算方法求解塑性边值问题。
塑性变形的特点:(1)应力-应变关系的非线性;(2)应力与应变间不存在单值对应关系,同一个应力可以对应不同的应变,反过来也是如此,这种非单值性具体来说是一种路径相关性;(3)由于塑性应变不可恢复,所以外力所做的塑性功具有不可逆性,或耗散性,在一个加载卸载的循环中外力做功恒大于零,这一部分能量被材料的塑性变形所消耗。
第3章 塑性成形中金属变形与流动的相关问题

图3-15 圆环镦粗的金属流动 a)变形前 b) 摩擦系数很小或为零 c) 有摩擦
3. 2. 4 工具的形状和坯料形状的影响
工具(或坯料)形状是影响金属塑性 流动方向的重要因素。工具与金属形状 的差异,是造成金属沿各个方向流动的 阻力有差异,因而金属向各个方向的流 动(即变形量)也有相应差别。
图3-16 型钻中拔长 a) 圆型砧 b) V型砧 c) 凸型砧
合金号 L4
挤压系数 11
挤压速度 (毫米/秒)
150
金属温度 ℃
158~195
LD2
11~16
150
294~315
LY11
11~16
150
340~350
LY11
31
65
308
3.变形程度
σ1-σ2 大 气压
σ1-σ2 大 气压
图3-9 脆性材料的各向压缩曲线
(a)大理石;(b)红砂石;—轴向压力;—侧向压力
冷变形时,变形程度越大,加工硬化显著, 塑性降低;热变形时,变形程度越大,晶 粒细化且分散均匀,塑性很高。
4.应力状态
静水压力对提高金属塑性的良好影响
5.变形状态
图3-11 主变形图对金属中缺陷形状的影响
(a)未变形的情况;(b)经两向压缩—向延伸变形后的情况; (c)经—向压缩两向延伸后的情况
变形物体的温度不均匀,会造成金 属各部分变形和流动的差异。变形首 先发生在那些变形抗力最小的部分。 一般,在同一变形物体中高温部分的 变形抗力低,低温部分的变形抗力 高。
3. 2. 7 金属性质不均的影响
变形金属中的化学成分、组织 结构、夹杂物、相的形态等分布 不均会造成金属各部分的变形和 流动的差异。
材料力学性能-2-材料变形

在对称性最高的各向同性体中,广义的Hooke定律为:
例:单轴拉伸(如X方向)时, 广义的Hooke定律简化为:
由此可见,在单轴加载条件下, 材料不仅有受力方向上的变形, 而且还有垂直于受力方向上的横 向变形(应变)。
工程常用弹性常数
• 弹性模量(E) σ E = (单向受力状态下) ε 它反映材料抵抗正应变的能力。 • 切变模量(G) τ G = (纯剪受力状态下) ν 它反映材料抵抗切应变的能力。 • 泊松比(ν ) ε ν =− (单向-X方向受力状态下) ε 它反映材料横向正应变与受力方向正应变的相对 比值。
2.4 材料的塑性变形
单晶体和多晶体材料塑性变形的特点
3)形变织构和各向异性 随着塑性变形程度的增加,各个晶粒的滑移方向逐 渐向主形变方向转动,使多晶体中原来取向互不相同的 各个晶粒在空间取向逐渐趋向一致,这一现象称为择优 取向;材料变形过程中的这种组织状态称为形变织构。
滞弹性与内耗
• 材料的内摩擦-内耗,导致振动机械能转 变为热能而消耗 • 研究目的:1、通过内耗特性,研究材料内 部的微观结构信息,如溶质原子浓度、位 错与溶质原子的交互作用等。2、获得高阻 尼合金,使结构振动衰减,减振降噪,提 高设备的运行精度。
求导得: 即:
dφ (u ) / du = u (d 2φ / du 2 )0
F = u (d 2φ / du 2 )0
实际上,对大块金属材料而言, 通常能达到的弹性变形量很小,主 要是因为实际材料中不可避免地存 在缺陷,在外力作用下,弹性变形 还未达到其最大可能值之前就已经 发生了塑性变形或断裂。因此,实 际金属材料中,可以认为Hooke定 律是正确的。
可逆性 单值性
正弹性应变-由正应力引起;
冲压模具设计(1-3)

• 有对色优金质属碳:素铜结及构其合薄金钢、板铝及,其国合家金、原镁则合规金、定钛,合钢金等。 非板金旳属表材面料质:量纸可板分、胶为木Ⅰ板(、特塑别料高板、级纤旳维精板和整云表母面等。 ),Ⅱ(高级旳精整表面),Ⅲ(较高旳精整表面
成形质量
材料旳冲压性能好是指便于冲压加工,详细而言指: 成形极限高(成形过程中材料能到达旳最大变形程度,即抗破裂性好)
成形质量好(形状尺寸精度,厚度变化,表面质量以及成形后旳物理机械性能, 即贴模性、定形性好)
第一章 冲压工艺概述
直接反应,但需 专业设备或工装
第三节 冲压变形理论基础
五、冲压材料及其冲压成形性能(续) 以便,易行
例如: 室温下奥氏体不锈钢旳塑性很好,能经受很大旳
变形而不破坏,但它旳变形抗力却非常大;
过热和过烧旳金属与合金,其塑性很小,甚至完 全失去塑性变形旳能力,而变形抗力也很小;
室温下旳铅,塑性很高而变形抗力又小。
变形抗力:
使金属产生塑性变形旳力为变形力,金属抵 抗变形旳力称为变形抗力。
塑性与变形抗力是两个不同旳概念:
第一章 冲压工艺概述
第三节 冲压变形理论基础
三、塑性力学基础(续)
3.金属塑性变形时旳应力应变关系(续) 几点讨论结论
(1)应力分量与应变分量符号不一定一致, 即拉应力不一定 相应拉应变,压应力不一定相应压应变;举例。 (2)某方向应力为零其应变不一定为零; (3)在任何一种应力状态下,应力分量旳大小与应变分量旳 大小顺序是相相应旳,即б1>б2>б3,则有ε1>ε2>ε3。 (4)若有两个应力分量相等, 则相应旳应变分量也相等,即 若б1=б2,则有ε1=ε2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 塑性变形的基本定律
3.1 体积不变定律及应用
一、 体积不变定律内容
在压力加工过程中,只要金属的密度不发生变化,变形前后金属的体积就不会产生变化。
若设变形前金属的体积为0V ,变形后的体积为1V ,则有:
0V =1V =常数
实际上,金属在塑性变形过程中,其体积总有一些变化,这是由于:
(1)在轧制过程中,金属内部的缩孔、气泡和疏松被焊合,密度提高,因而改变了金属体积。
这就是说除内部有大量存在气泡的沸腾钢锭(或有缩孔及疏松的镇静钢锭、连铸坯)的加工前期外,热加工时,金属的体积是不变的。
(2)在热轧过程中金属因温度变化而发生相变以及冷轧过程中金属组织结构被破坏,也会引起金属体积的变化,不过这种变化都极为微小。
例如,冷加工时金属的比重约减少0.1~0.2%。
不过这些在体积上引起的变化是微不足道的,况且经过再结晶退火后其比重仍然恢复到原有的数值。
二、 体积不变定律的应用
1、确定轧制后轧件的尺寸
设矩形坯料的高、宽、长分别为L B H 、、,轧制以后的轧件的高、宽、长分别为l b h 、、(如图3-1所示),根据体积不变条件,则
HBL V =1
hbl V =2
即 hbl HBL =
在生产中,—般坯料的尺寸均是已知的,如果轧制以后轧件的高度和宽度也已知时,则轧件轧制后的长度是可求的,即
图3-1 矩形断面工件加工前后的尺寸
hb
HBL l = 例题1:轧50×5角钢,原料为连铸方坯,其尺寸为120×120×3000mm ,已知50×5角钢每米理论重3.77kg ,密度为7.85t/m 3,计算轧后长度l 为多少?
解:
坯料体积 V 0=120×120×3000=4.32×107mm 3
50×5角钢每米体积为 3.77/(7.85×103÷109)=480×103mm 3
由体积不变定律可得
4.32×107=480×103×l
轧后长度 l ≈90m
2、根据产品的断面面积和定尺长度,选择合理的坯料尺寸。
例题2:某轨梁轧机上轧制50Kg/m 重轨,其理论横截面积为6580mm 2,孔型设计时选定的钢坯断面尺寸为325×280mm 2,要求一根钢坯轧成三根定尺为25m 长的重轨,计算合理的钢坯长度应为多少?
根据生产实践经验,选择加热时的烧损率为2%,轧制后切头、切尾及重轨加工余量共长
1.9m ,根据标准选定由于钢坯断面的圆角损失的体积为2%。
由此可得轧后轧件长度应为
=l (3×25+1.9)×103=76900mm
由体积不变定律可得
325×280L (1-2%)(1-2%)=76900×6580
由此可得钢坯长度
L =
mm 567398
.02803256580769002=⨯⨯⨯ 故选择钢坯长度为5.7m 。
3、在连轧生产中,为了保证每架轧机之间不产生堆钢和拉钢,则必须使单位时间内金属从每架轧机间流过的体积保持相等,即
n n v F v F v F ===ΛΛ2211
式中 n F F F ΛΛ21、为每架轧机上轧件出口的断面积,
n v v v ΛΛ21、为各架轧机上轧件的出口速度,它比轧辊的线速度稍大,但可看作近似相等。
如果轧制时n F F F ΛΛ21、为已知,只要知道其中某一架轧辊的速度(连轧时,成品机架的轧辊线速度是已知的),则其余的转数均可一一求出。
3.2 最小阻力定律及其应用
一、最小阻力定律内容
叙述1:物体在变形过程中,其质点有向各个方向移动的可能时,则物体内的各质点将沿着阻力最小的方向移动。
叙述2:金属塑性变形时,若接触摩擦较大,其质点近似沿最法线方向流动,也叫最短法线定律。
叙述3:金属塑性变形时,各部分质点均向耗功最小的方向流动,也叫最小功原理。
二、最小阻力定律的应用1、判断金属变形后的横断面形状。
例1:矩形六面体的镦粗
图3-2为塑压矩形断面的变化情况。
由图可清楚地看出:随着压缩量的增加,矩形断面的变化逐渐变成多面体、椭圆和圆形断面。
对于这个现象的分析:
用角平分线的方法把矩形断面划分为四个流动区域——两个梯形和两个三角形。
为什么用角平分线划分呢?因为角平分线上的质点到两个周边的最短法线长度是相等的。
因此,在该线上的金属质点向两个周边流动的趋势也是相等的。
由图可见,每个区域内的金属质点,将向着垂直矩形各边的方向移动,由于向长边方向移动的金属质点较向短边移动的多,故当压缩量增大到一定程度时,将使变形的最终断面变形为圆形。
结论:任何断面形状的柱体,当塑压量很大时,最后都将变成圆形断面。
2.确定金属流动的方向。
例2:轧制生产中的情况
(1)利用最小阻力定律分析小辊径轧制的特点。
如图
2-3
图3-2 塑压矩形断面柱体变化规律
图3-3 轧辊直径对宽展的影响
在压下量相同的条件下,对于不同辊径的轧制,其变形区接触弧长度是不相同的,小辊径的接触弧较大辊径小,因此,在延伸方向上产生的摩擦阻力较小,根据最小阻力定律可知,金属质点向延伸方向流动的多,向宽度方向流动的少,故用小辊径轧出的轧件长度较长,而宽度较小。
(2)为什么在轧制生产中,延伸总是大于宽展?首先,在轧制时,变形区长度一般总是小于轧件的宽度,根据最小阻力定律得,金属质点沿纵向流动的比沿横向流动的多,使延伸量大于宽展量;其次,由于轧辊为圆柱体,沿轧制方向是圆弧的,而横向为直线型的平面,必然产生有利于延伸变形的水平分力,它使纵向摩擦阻力减少,即增大延伸,所以,即使变形区长度与轧件宽度相等时,延伸与宽展的量也并不相等,延伸总是大于宽展3.3 弹
塑性共存定律
一、弹塑性共存定律内容
物体在产生塑性变形之前必须先产生弹性变形,在塑性变形阶段也伴随着弹性变形的产生,总变形量为弹性变形和塑性变形之和。
为了说明在塑性变形过程中,有弹性变形存在,我们通过拉伸实验为例来说明这个问题。
图2-4为拉伸实验的变化曲线(OABC),当应力小于屈服极限时,为弹性变形的范围,在曲线上表现为OA段,随着应力的增加,即应力超过屈服极限时,则发生塑性变形,在曲线上表现为ABC段,在曲线的C点,表明塑性变形的终结,即发生断裂。
从图中可以看出,
(1)变形的范围内(OA ),应力与变形的关系成正比,可用虎克定律近似表示。
(2)在塑性变形的范围内(ABC ),随着拉应力的增加(大于屈服极限),当加载到B 点时,则变形在图中为OE 段,即为塑性变形δ与弹性变形ε之和,如果加载到B 点后,立即停止并开始卸载,则保留下来的变形为OF (δ),而不是有载时的OE 段,它充分说明卸载后,其弹性变形部分EF (ε)随载荷的消失而消失,这种消失使变形物体的几何尺寸多少得到了一些恢复,由于这种恢复,往往在生产实践中不能很好控制产品尺寸。
(3)弹性变形与塑性变形的关系,要使物体产生塑性变形,必须先有弹性变形或者说在弹性变形的基础上,才能开始产生塑性变形,只有塑性变形而无弹性变形(或痕迹)的现象在金属塑性变形加工中,是不可能见到的。
因此,我们把金属塑性变形在加工中一定会有弹性变形存在的情况,称之为弹塑共存定律。
二、 弹塑性共存定律在压力加工中的实际意义
弹塑性共存定律在轧钢中具有很重要的实际意义,可用以指导我们生产的实践。
1、用以选择工具
在轧制过程中工具和轧件是两个相互作用的受力体,而所有轧制过程的目的是使轧件具有最大程度的塑性变形,而轧辊则不允许有任何塑性变形,并使弹性变形愈小愈好。
因此,在设计轧辊时应选择弹性极限高,弹性模数大的材料;同时应尽量使轧辊在低温下工作。
相反的,对钢轧件来讲,其变形抗力愈小,塑性愈高愈好。
图
3-4 拉伸时应力与变形的关系
2 由于弹塑性共存,轧件的轧后高度总比预先设计的尺寸要大
例:如图(3-5)所示,轧件轧制后的真正高度h 应等于轧制前事先调整好的辊缝高度0h ,
轧制时轧辊的弹性变形n h ∆,(轧机所有部件的弹性变形在辊缝上所增加的数值)和轧制后轧件的弹性变形M h ∆之和,即:
M n h h h h ∆+∆+=0
因此,轧件轧制以后,由于工具和轧件的弹性变形,使得轧件的压下量比我们所期望的值小。
小结:本章应重点掌握三大定律的内容,熟悉三大定律的实际应用。
图3-5 轧辊及轧件的弹性变形图。
