竖曲线计算程序供参考

合集下载

4800竖曲线计算放样程序

4800竖曲线计算放样程序SJBGJS(主程序)Lb1 1:｛KB X｝:Prog“YSJG”:N=-V－W:N>0＝＞N=-1:≠＞S=0.14L÷（0.07+0.035I）：Y=（0.07+0.035I）÷LC=Abs（K-Q）:K>Q＝＞C<T＝＞D=（K-Q+T）2÷（2RLb1 2:C<T＝＞D=（K-Q-T）2÷（2RLb1 3:K<Q＝＞P=V÷100: ≠＞P=W÷＝＞Prog“123”NormProg“BBBB”:Goto 1123K<J-L＝＞Prog“11”: ≠＞K<J＝＞Prog“22”: ≠＞K≤○＝＞Prog “33”: ≠＞K≤○+L＝＞Prog“22”: ≠＞Prog“11”33G=G+0.01I（MB）11G=G-Abs B×0.0222M=1＝＞Prog“44”: ≠＞Prog“55”44K≤J-L+S＝＞Prog“E”: ≠＞K<J＝＞Prog“C”: ≠＞K<○+L-S＝＞Prog“C”: ≠＞Prog“F”55K≤J-L+S＝＞Prog“A”: ≠＞K<J＝＞Prog“C”: ≠＞K<J＝＞Prog “C”: ≠＞K<○+L-S＝＞Prog“C”: ≠＞Prog“B”EB≤0＝＞G=G+0.02B: ≠＞G=G+B((K-J+L)×Y-0.07)÷FB≤0＝＞G=G+0.02B: ≠＞G=G+B((○+L-K)×Y-0.07)÷CK<J＝＞G=G((K-J+L)×Y-0.07)÷3.5×MB: ≠＞G=G+((○+L-K)×Y-0.07)÷3.5×AB>0＝＞G=G-0.02B: ≠＞G=G-B((K-J+L)×Y-0.07)÷BB>0＝＞G=G-0.02B: ≠＞G=G-B((○+L-K)×Y-0.07)÷BBBBLb1 0:｛Z｝H=G-Z:H>0＝＞Prog“BBB”: ≠＞Prog“SBB”Fix 3:C=C+0.0001:“LL=”:Pause 0BBF“P11”U“P22”H≥-10＝＞C=Abs B+1.9-（H+0.03）F: ≠＞C=Abs B+1.9+9.97F+1-（H+10.03）H<8＝＞C=Abs B+1.5H+0.3: ≠＞H≤16＝＞C=Abs B+13.433+（H-8）×1.5+0.3: ≠＞Abs B+26.865+（H-16）×ACB>0＝＞G=G-○×B: ≠＞G=G-B((K-J+L)×Y-0)÷BCB>0＝＞G=G-○×B: ≠＞G=G-B((○+L-K)×Y-0)÷SBBF“P11”U“P22”H≥-10＝＞C=Abs B+1.9-（H+0.03）F: ≠＞H≥-20＝＞C=Abs B+1.9+9.97F+1-（H+10.03）U：≠＞H≥-30＝＞C=Abs B+1.9+9.97F+9.97U+2-（H+20.03）U: ≠＞H≥-40＝＞………SJGK≤30231.33＝＞Q=30350:A=311.580:R=15000:T=105.061:V=-0.967: W=+2.368:J=30049.62:○=30141.33:L=90:M=+1:I=7:Goto 1: ≠＞K ≤30594.22＝＞Q=30350:A=311.580:R=15000:T=105.061:V=-0.967:W =+2.368:J=30311.33:○=30391.27:L=80:M=+1:I=7:Goto 1: ≠＞K≤31123.63＝＞Q=30350:A=311.580:R=15000:T=105.061:V=-0.967:W=+ 2.368:J=30674.22:○=30768.06:L=80:M=+1:I=7:Goto 1: ≠＞K≤31 123.63＝＞………Lb1 1Q----为该段竖曲线的变坡点桩号A----变坡点高程R----竖曲线半径R----竖曲线切线长E----竖曲线外距P1---变坡点前一个纵坡坡率P2---变坡点后一个纵坡坡率N----竖曲线纵要素因子，凸为-1，凹为+1 K0---直线直线段边桩放样辅助程序BBBBBB（主程序）Defm 3Lb1 0:｛G ,Z｝H=G-Z:H>0＝＞Prog“BBBBB”: ≠＞Prog“BBBB”Goto 0BBBBBH<12＝＞L=9+1.5H: ≠＞H≤20＝＞L=9+8×1.5+1.5+（H-8）×1.75: H ≤20＝＞L=9+8×1.5+1.5+8×1.75+3+（H-16）×2:BBBBC“P1”:D“P2”:S“P3”H>-12＝＞L=11.25-（H+0.045）C: ≠＞H>-20＝＞L=11.25+9.955 C+1.5-（H+10+0.045）D: ≠＞L=11.25+9.955 C+9.955 D+3-（H+20+0.045）说明：G---路肩设计高Z---实测高L---理论宽度H---填挖值。

竖曲线计算公式及计算方法

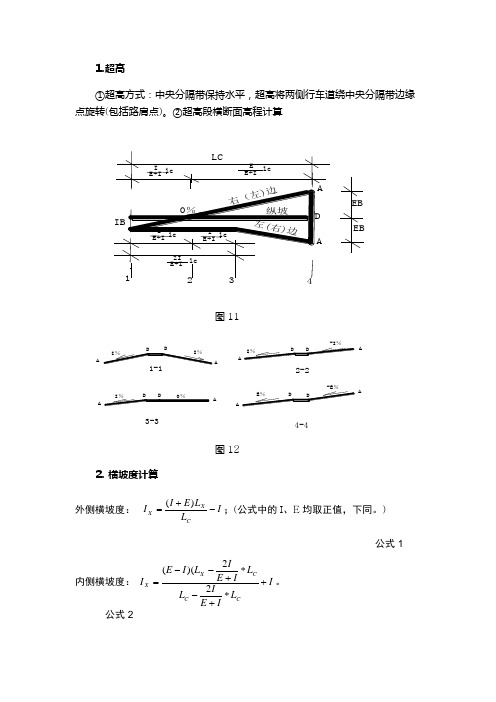
⒈超高①超高方式：中央分隔带保持水平，超高将两侧行车道绕中央分隔带边缘点旋转(包括路肩点)。

②超高段横断面高程计算图11AA AAAAAA2-23-34-4-I％图12⒉横坡度计算外侧横坡度：ILLEIICXX-+=)(；(公式中的I、E均取正值，下同。

)公式 1内侧横坡度：ILIEILLIEILIEICCCXX+*+-*+--=22)((。

公式 2EBEB式中：2 I/(E+I)* L C—在L C段内横坡等于I％的长度,m。

X在区间0～2 I/(E+I)*LC时，横坡度为I；在区间2 I/(E+I)* L C～L C段内时，横坡度为I～E。

I—横坡度设计值，E—超高设计值，L C—缓和曲线长，m。

⒊竖曲线计算公式：W=I1-I2；当w＞0时，为凸曲线；当w＜0时，为凹曲线。

L=R*W；E=T2/2R；H=l2/2r；T=TA=TB=L/2=R*W/2。

式中：H—切线上任一点至竖曲线上的垂直距离；M．l—曲线上相应于H的P点至切点A或B点的距离，M．R—二次抛物线的参数。

(原点处的曲率半径)通常称竖曲率半径，M．I1、I2—切线的斜率，即纵坡度，％．纵坡度(％)，从左向右上坡取“+”，下坡取“-”值．当α很小时，tanα1≈α1=I1, tan α2≈α2=I2。

T—切线长(M)，ZH路线平面图L—竖曲线的曲线长(M)。

竖曲线计算实例

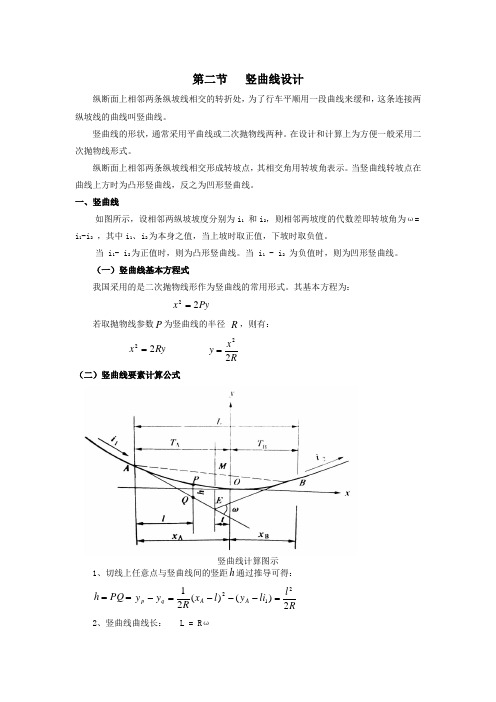
第二节竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i 1 和i 2，则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ，其中i 1、i 2为本身之值，当上坡时取正值，下坡时取负值。

当 i 1- i 2为正值时，则为凸形竖曲线。

当 i 1 - i 2 为负值时，则为凹形竖曲线。

（一）竖曲线基本方程式我国采用的是二次抛物线形作为竖曲线的常用形式。

其基本方程为：Py x 22=若取抛物线参数P 为竖曲线的半径 R ，则有：Ry x 22= Rx y 22=（二）竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得：==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长： L = R ω3、竖曲线切线长： T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距： E =RT 22⑤竖曲线上任意点至相应切线的距离：Rx y 22=式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；R —为竖曲线的半径，m 。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1.凸形竖曲线极限最小半径确定考虑因素（1）缓和冲击汽车行驶在竖曲线上时，产生径向离心力，使汽车在凸形竖曲线上重量减小，所以确定竖曲线半径时，对离心力要加以控制。

（2）经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时，即使竖曲线半径较大，竖曲线长度也有可能较短，此时汽车在竖曲线段倏忽而过，冲击增大，乘客不适；从视觉上考虑也会感到线形突然转折。

竖曲线标高计算程序

竖曲线标高计算程序（加了数据库）主程序名：SQXBGLbi1：｛H｝：H：Prog＂SJK＂：F=C-D：T=Abs(RF÷2：R=R AbsF÷FH≤B-T=＞K=0：≠=＞H≥B+T=＞K=0：C=D：≠=＞K=H-B+T⊿⊿G=A-（B-H）C-K2÷2R▲Goto1 ――――――――――――――――――――――――――――――――――子程序：SJK H≤第二竖曲线起点桩号（5569.108）=＞A=第一竖曲线交点高程（820.968）：B=第一竖曲线交点桩号（4980）：C=第一竖曲线前坡度（.03）：D=第一竖曲线后坡度（-.02902）：R=第一竖曲线半径（13000）⊿H≤第三竖曲线起点桩号（7174.4）=＞A=第二竖曲线交点高程（798.331）：B=第二竖曲线交点桩号（5760）：C=第二竖曲线前坡度（-.02902）：D=第二竖曲线后坡度（.0187）：R=第二竖曲线半径（8000）⊿H≤第四竖曲线起点桩号（7898.584）=＞A=第三竖曲线交点高程（828.438）：B=第三竖曲线交点桩号（7370）：C=第三竖曲线前坡度（.0187）：D=第三竖曲线后坡度（.035）：R=第三竖曲线半径（24000）⊿………………………继续添加要素――――――――――――――――――――――――――――――――――说明：1、A：交点高程2、B：交点桩号3、C：前坡度（上坡为正，下坡为负）4、D：坡度（上坡为正，下坡为负）5、R：竖曲线半径6、H：待求点桩号7、数据库中（）内的数字用于网友试算，现根据（）内的数据提供几个设计高程：H=5400 G=808.7796H=5450 G=807.3286H=6000 G=802.819H=6112 G=804.9134H=6980 G=821.145今天终于讲到了Excel函数的最后一部分——文本和数据函数。

再往后我们会陆续给大家介绍一些函数应用实例，每一则都会有详细的分析与指导，让您把理论上升为实际，敬请关注。

竖曲线高程计算方法(一)

竖曲线高程计算方法(一)竖曲线高程计算在道路、桥梁、隧道等工程中，竖曲线是公路线形设计中的重要元素，而竖曲线高程计算则是道路设计过程中必不可少的一项工作。

本文将详细介绍竖曲线高程计算的各种方法。

直接法直接法是最简单的竖曲线高程计算方法，公式如下：H=R+L2 2R其中，H为竖曲线起点和终点高程差，R为竖曲线半径，L为竖曲线长度。

坡度法坡度法是一种常用的竖曲线高程计算方法，公式如下：H=∑(l i+l i+1)2d i24R ini=1其中，n为竖曲线段数，l i和l i+1分别为第i段和第i+1段的长度，d i为第i段的坡度，R i为第i段的半径。

求解法求解法是一种基于数值解的竖曲线高程计算方法，公式如下：H i=H i−1+l2(k i+k i−1)+l3240(k i−k i−1)2其中，H i为第i个点的高程，H i−1为第i−1个点的高程，l为第i个点和第i−1个点之间的水平距离，k i和k i−1分别为第i个点和第i−1个点的曲率。

分段求解法分段求解法是一种将竖曲线按照不同的半径等级分段求解的高程计算方法，公式如下：s iH i=H i−1+∫k(ρ(s))dss i−1其中，H i为第i个点的高程，H i−1为第i−1个点的高程，s i−1和s i分别为第i−1个点和第i个点之间的弧长，k(ρ(s))为曲率半径为ρ(s)时的曲率。

以上就是竖曲线高程计算的各种方法，根据不同的情况和要求，可以选择不同的方法进行计算。

混合法混合法是将直接法、坡度法、求解法和分段求解法结合起来的一种综合性高程计算方法，可以根据需要选择不同的计算方法进行竖曲线高程的计算。

混合法的具体过程如下：1.根据竖曲线长度和曲率要求选择直接法或坡度法计算竖曲线起点和终点的高程差。

2.确定分段长度和半径等级，使用分段求解法计算竖曲线半径变化较为平缓的区间的高程，并将计算结果与直接法或坡度法的计算结果进行校核。

3.使用求解法计算竖曲线半径变化较为显著的区间的高程，将计算结果与分段求解法和直接法或坡度法的计算结果进行校核。

公路竖曲线高程计算程序

fx-4800P计算器公路竖曲线高程计算程序（程序名：GAO CHENG-HP）Lb1 0︰｛CDAB｝︰C“K1=”︰D“H1=”︰A“PV-K0=”︰B “PV-H0=”↙Lb1 1 ︰｛REF ｝︰R“R=”︰E“K2=”︰F“H2=”↙Lb1 2︰U =（B－D）÷（A－C）︰V =（F－B）÷（E－A）︰U ＞V =＞N = 0︰T = R ( U－V ) ÷2︰≠＞N = 1︰T = R ( V－U ) ÷2 ︰⊿G = A －T ︰Q = A ＋T ︰W = T 2÷（2 R）↙Lb1 3︰｛K｝︰K “I.T.E.ZY-K.YZ-K=0,1”︰K =0 =＞Goto 4 ︰⊿U “I 1”= U ▲V “I 2”= V ▲T = T ▲W “E”= W ▲G “ZY-K”= G ▲Q “YZ-K”= Q▲↙Lb1 4︰｛M｝︰M“PK=”︰M ≤A =＞Goto 5︰⊿Goto 6 ↙Lb1 5︰M ≤G =＞H = B－U ( A－M ) ︰Goto 7 ︰≠＞Prog “H1 ”︰N = 1 =＞H = B＋X－Y ︰Goto 7︰≠＞N = 0 =＞H = B－X －Y ︰Goto 7↙Lb1 6︰M ≥Q =＞H = B＋V ( M－A ) ︰Goto 7 ︰≠＞Prog “H2 ”︰N = 1 =＞H = B＋X＋Y ︰Goto 7︰≠＞N = 0 =＞H = B－X ＋Y ↙Lb1 7︰H “HP”= H ▲｛L｝︰L“BZ-T=0,L”︰L = 0 =＞Goto 8 ︰⊿｛S｝︰S “IL=”︰H “HL”= H ＋S L ▲↙Lb1 8︰｛Z ｝︰Z “NEXT-PV=0,1”︰Z = 0 =＞Goto 4 ︰⊿C= A ︰D= B ︰A =E ︰B= F ︰Goto 1↙子程序:H1:X = ( M－G ) 2÷( 2 R ) ︰Y = U ( A－M ) ↙H2:X = ( Q－M ) 2÷( 2 R ) ︰Y = V ( M－A ) ↙二00二年元月二十三日公路竖曲线高程计算程序（程序名：GAO CHENG-HP）使用说明1、按“ON”-“FILE”-“GAO CHEHG-HP”-“EXE”2、输入竖曲线后方直线段任一点桩号、高程（K1=？，H1=？），变坡点桩号、高程（PV-K0=？，PV-H0=？）-“EXE”3、输入竖曲线半径（R=？）, 竖曲线前方直线段任一点桩号、高程（K2=？，H2=？） -“EXE”4、是否显示重要参数（后坡度%I1、前坡度%I2、以及竖曲线切线长T、外距E、曲线起点桩号ZY-K、曲线终点桩号YZ-K？，显示：输入1；不显示：输入0。

竖曲线计算程序供参考

竖曲线计算程序本程序只需按程序提示输入三个变坡点的桩号和高程，再输入竖曲线半径，即可随心所欲的计算任意点的纵断高程。

可以大大减少使用者在现场的工作量。

一、程序清单1、CASIO Fχ5800 计算程序“BP1”？A: “BP1H”？G: “BPD”？B: “BPDH”？I :LbI 0: “BP2”?→C: “BP2H”?→J: “R”?→R: B-A→D: C-B→F: I-G→K: J-I→M: K ÷D→N: M÷F→O :N-O→P: “T”:Abs (RP÷2) →T▲“E”:T²÷﹙2R) ▲B-T→W :B+T→X:G+N(W-A)→Y﹕I+OT→Z︰LbI 1“KM”?→Q: Q>X=>Goto 2: While Q﹤W﹕Q-A→S︰G+SN→V▲Goto 1: WhileEnd: While Q≦B And Q>W﹕Q-W→S︰If P﹥0∶Then Y+SN- S²÷(2R)→V▲Else Y+SN+S²÷(2R)→V▲IfEnd∶Goto 1: WhileEnd: While Q≦X And Q>B﹕X-Q→S︰If P﹥0∶Then Z-SO- S²÷(2R)→V▲Else Z-SO+S²÷(2R)→V▲IfEnd∶Goto 1: WhileEnd: LbI 2: B→A: C→B: I→G J→I :Goto 02、CASIO Fχ4500 4800计算程序LbI 0: {CJR}:A“BP1”:G “BP1H” :B “BPD” :I “BPDH” : C“BP2”: J“BP2H”:D=B-A: F=C-B: K=I-G:M= J-I: N=K/D: O=M/F :P=N-OT=Abs (RP÷2) ▲E=T²÷﹙2R) ▲W=B-T:X=B+T:Y=G+N(W-A)﹕Z=I+OTLbI 1:{Q}:Q“KM”:Q>X=>Goto 2⊿Q﹤W=>S=Q-A︰V=G+SN▲⊿Q≦B=> Q>W=>S=Q-W: P﹥0=>V= Y+SN-S²/(2R)▲≠> V=Y+SN+ S²/(2R)▲⊿⊿⊿Q≦X => Q>B=>S=X-Q︰P>0 =>V=Z-SO-S²/(2R)▲≠>V= Z-SO+ S²/(2R)▲⊿⊿⊿Goto 1LbI 2: A=B:B=C: G=I:I=J :Goto 03、程序提示符号含义及程序使用说明BP1 BP1H-------前一变坡点里程桩号及高程；BPD BPDH-------竖曲线变坡点里程桩号及高程；BP2 BP2H-------后一变坡点里程桩号及高程；R----竖曲线半径T-----切线长；E-----外矢距；ZXG-----计算中线高程首先按程序提示输入7个参数，计算前一变坡点至竖曲线终点的纵段高程。

竖曲线计算程序

列3
列4
竖距h1
切线高程设计高程
2.617 2326.375 2323.758
ห้องสมุดไป่ตู้
3.741 2324.875 2321.134
5.064 2323.375 2318.311
6.587 2321.875 2315.288
8.310 2320.375 2312.065
桩号
155 175 195 215 235
38.32 0.367
2331.542 52.680
2334.049 129.320 2329.769
列1
横距x1 102.32 122.32 142.32 162.32 182.32
体部分,绿色字体的是结果
列3
列4
列5
自动计算结果
列3
列4
列5
为凹形曲线
列2
第一步修改红色字体部分,绿色字体的
参数（点击参数名查询规范）
列2
桩号
91
高程H0
2331.175
竖曲线半径R 前纵坡i1 后纵坡i2
2000 -7.50% -3.67%
第二步：自动计算结果
参数竖曲线要素
i2 i1 竖曲线长度L=R|ω|
计算结果
3.83% 76.64
切线长度T=L/2 外距E=T^2/2R 设计高程计算变坡点处设计高程竖曲线始点桩号=变坡点桩号-T 竖曲线起点高程=变坡点标高-T•i1 竖曲线终点桩号=变坡点桩号+T 竖曲线终点高程=变坡点标高+T•i2 整20M桩设计高程（有要求就做）

5800竖曲线高程计算程序

竖曲线高程计算主程序（5800）Lbl A：？K：Prog：“竖曲线元素库子程序”：A-T→E：A+T→F ←If K=A：Then Goto 5：IfEnd ←If K≤E：Then Goto 3：IfEnd ←If K≥F：Then Goto 4：IfEnd ←If K＜A：Then Goto 1：IfEnd ←If K＞A：Then Goto 2：IfEnd ←Lbl 1：K-E→X：X2÷(2R)→Y：B+I(K-A)→G：Goto 6 ←Lbl 2：F-K→X：X2÷(2R)→Y：B+J(K-A)→G：Goto 6 ←Lbl 3：B+I(K-A)→H ▲Goto A ←Lbl 4：B+J(K-A)→H ▲Goto A ←Lbl 5：B+CM→H ▲Goto A ←Lbl 6：G+CY→H ▲Goto A ←竖曲线要素库子程序（5800）If K≤竖曲线终点桩号：Then 凹（凸）竖曲线交点桩号→A：第一坡度→I：第二坡度→J：外矢距(E值)→M：交点高程→B：切线长→T：竖曲线半径→R：（凹）1、（凸）-1→C：（曲线段）Goto B：IfEnd ←If K≤直线终点桩号：Then 直线起点桩号→A：直线段坡度→I：直线段坡度→J：0（零）→M：直线段起点高程→B：0（零）→T：1045→R：0（零）→C：（直线段）Goto B：IfEnd ←If ……………………如有多段竖曲线加入，以此类推Lbl B：Return（程序用语“结束”）说明：1、本程序为设计高程计算程序，输入里程K就得出设计高程。

主程序可计算整条线高程乃至多条线路高程。

2、如有多段竖曲线可直接加入到“竖曲线子程序”中，如有多条线路可编多个“竖曲线子程序”，只要在主程序中改“竖曲线子程序”名。

3、直线段外矢距为零、切线长为零、半径为无穷大，以10的45次方代替、C值为零。

4、←符号表示换行。

全线竖曲线精确计算程序(For TI)V1.0

竖曲线精确计算程序（For TI）V1.0主程序：sqxDefine a.sqx()=PrgmRequest "左线=1,右线=2",zyLbl a1Request "计算桩号Z=",zsqxsjk()w:=tan-1 (iq)-tan-1 (ih)e:=((r)/(cos(((w)/(2)))))-rt:=√((r+e)^(2)-r^(2))j:=abs(t*cos(tan-1(iq)))o:=abs(r*sin(tan-1 (iq)))i:=bpz-jk:=bpz+abs(t*cos(tan-1 (ih)))If z≤i Thenh:=bph-(bpz-z)*iqDisp "高程H=",hGoto a1EndIfIf z>k Thenh:=bph+(z-bpz)*ihDisp "高程H=",hGoto a1EndIfIf z<k ThenIf iq>ih Thenf:=1If iq<0 Thenp:=1Elsep:=−1EndIfEndIfIf iq<ih Thenf:=−1If iq>0 Thenp:=1Elsep:=−1EndIfEndIfh:=bph-f*(√((r+e)^(2)-(o+p*j)^(2))-√(r^(2)-(o+p*(z-i))^(2)))Disp "高程H=",hGoto a1EndIfEndPrgm子程序：sqxsjkDefine sqxsjk()=PrgmIf zy=1 ThenGoto b1ElseIf zy=2 ThenGoto b2EndIfLbl b1If z<zbpz[1] or z>zbpz[4] Then text "桩号超出"StopEndIfIf zbpz[1]≤z<11290 Theniq:=zi[2]ih:=zi[3]r:=zr[2]bpz:=zbpz[2]bph:=zbph[2]EndIfIf 11290≤z≤11667.107 Then iq:=zi[3]ih:=zi[4]r:=zr[3]bpz:=zbpz[3]bph:=zbph[3]EndIfReturnLbl b2If z<ybpz[1] or z>ybpz[8] Then text "桩号超出"StopEndIfIf 7950≤z<11316.142 Then iq:=yi[2]ih:=yi[3]r:=yr[2]bpz:=ybpz[2]bph:=ybph[2]EndIfIf 11316.142≤z<11647.011 Then iq:=yi[3]ih:=yi[4]r:=yr[3]bpz:=ybpz[3]bph:=ybph[3]EndIfIf 11647.011≤z<11957.99 Then iq:=yi[4]ih:=yi[5]r:=yr[4]bpz:=ybpz[4]bph:=ybph[4]EndIfIf 11957.99≤z<12206.77 Then iq:=yi[5]ih:=yi[6]r:=yr[5]bpz:=ybpz[5]bph:=ybph[5]EndIfIf 12206.77≤z<12435.774 Then iq:=yi[6]ih:=yi[7]r:=yr[6]bpz:=ybpz[6]bph:=ybph[6]EndIfIf 12435.774≤z≤12646.243 Then iq:=yi[7]ih:=yi[8]r:=yr[7]bpz:=ybpz[7]bph:=ybph[7]EndIfReturnEndPrgm右线竖曲线参数文件左线竖曲线参数文件。

竖曲线的计算

竖曲线的计算
1、竖曲线分类
凸曲线：按路线前进方向，前坡比＞后坡比，高程改正值取负号。

凹曲线：按路线前进方向，前坡比＜后坡比，高程改正值取正号。

2、计算测设要素
两相邻纵坡的坡度分别为i1和i2.竖曲线半径为R
则曲线长：L=α×R
由于竖曲线转角α很小，故可以为：α=i1-i2
于是： L=R(i1-i2)
切线长： T=R×tan（α/2）
=0.5×R×（i1-i2）
外距： E=T2/2R
3、竖曲线上任意一点的高程计算
竖曲线任意一点至切线的纵距（高程改正值）
y=X2/2R
式中：y——为高程改正值。

在凹曲线中取正值，在凸曲线中取负值。

X——竖曲线任意点至竖曲线起点或者终点的水平距离。

R——竖曲线半径。

竖曲线上任意点的坡道高程
H`=H0+X×i
式中：H`——竖曲线上任意点的坡道高程。

H0——竖曲线起点或者中终点高程
X——竖曲线任意点至竖曲线起点或者终点的水平距离。

i——纵坡坡度。

竖曲线上任意点高程
H=H`+y
式中：H——竖曲线上任意点高程。

H`——竖曲线上任意点的坡道高程。

y——竖曲线上任意点的高程改正值。

竖曲线运算步骤及公式讲解

竖曲线上高程计算
已知：①第一坡度：i 1(上坡为“＋”，下坡为“－”)
②第二坡度：i 2(上坡为“＋”，下坡为“－”)
③变坡点桩号：S Z
④变坡点高程：H Z
⑤竖曲线的切线长度：T
⑥待求点桩号：S
计算过程：
1、切线上任意点与竖曲线间的竖距h 通过推导可得：
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长： L = R ω
3.竖曲线切线长： T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距： E =R
T 22
5. 竖曲线上任意点至相应切线的距离：R
x y 22= 式中：x —为竖曲任意点至竖曲线起点（终点）的距离, m ；
R —为竖曲线的半径，m 。

竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高，其计算步骤如下：
（1）计算竖曲线的基本要素：竖曲线长：L ；切线长：T ；外距：E 。

（2）计算竖曲线起终点的桩号：竖曲线起点的桩号 = 变坡点的桩号－T
（3）计算竖曲线上任意点切线标高及改正值：
切线标高 = 变坡点的标高±（x T -）⨯i ；改正值：y=R
x 22 （4）计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高－ y。

竖曲线计算范例【共3页】

竖曲线计算范例----------专业最好文档，专业为你服务，急你所急，供你所需------------- 文档下载最佳的地方第8讲课题：第三节竖曲线第四节公路平、纵线形组合设计教学内容：理解竖曲线最小半径的确定；能正确设置竖曲线；掌握竖曲线的要素计算、竖曲线与路基设计标高的计算；能正确进行平、纵线形的组合设计。

重点：1、竖曲线最小半径与最小长度的确定；2、竖曲线的设置；3、平、纵线形的组合设计。

难点：竖曲线与路基设计标高的计算；平、纵线形的组合设计。

第三节竖曲线设计纵断面上相邻两条纵坡线相交的转折处，为了行车平顺用一段曲线来缓和，这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状，通常采用平曲线或二次抛物线两种。

在设计和计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点，其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线，反之为凹形竖曲线。

一、竖曲线如图所示，设相邻两纵坡坡度分别为i1 和i2，则相邻两坡度的代数差即转坡角为ω= i1-i2 ，其中i1、i2为本身之值，当上坡时取正值，下坡时取负值。

当 i1- i2为正值时，则为凸形竖曲线。

当 i16所列，在竖曲线设计时，不但保证竖曲线半径要求，还必须满足竖曲线最小长度规定。

公路竖曲线最小半径和竖曲线最小长度表3—6 设计速度(Km/h)1201008060403020 凸形竖曲线半径(m)极限最小值11000650030001400450250100 一般最小值170001000045002000700400200 凹形竖曲线半径(m)极限最小值4000300020001000450250100 一般最小值6000450030001500700400200 竖曲线最小长度(m)100857050352520三、竖曲线的设计和计算 (一)竖曲线设计竖曲线设计，首先应确定合适的半径。

在不过分增加工程量的情况下，宜选择较大的竖曲线半径；只有当地形限制或其它特殊困难时，才选用极限最小半径。

竖曲线计算实例

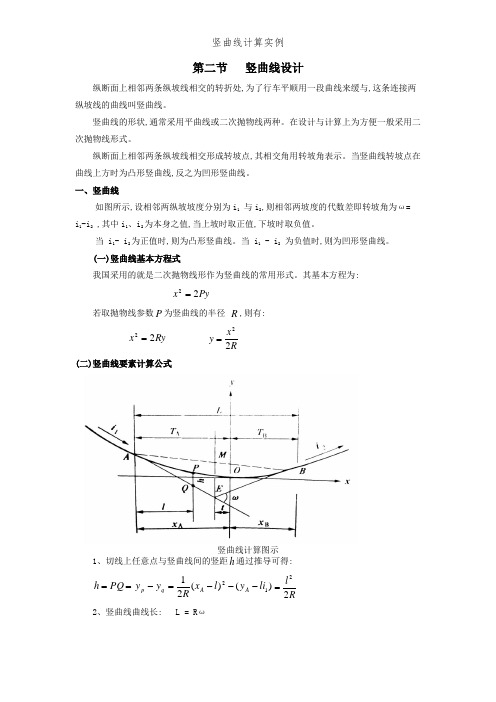
第二节竖曲线设计纵断面上相邻两条纵坡线相交的转折处,为了行车平顺用一段曲线来缓与,这条连接两纵坡线的曲线叫竖曲线。

竖曲线的形状,通常采用平曲线或二次抛物线两种。

在设计与计算上为方便一般采用二次抛物线形式。

纵断面上相邻两条纵坡线相交形成转坡点,其相交角用转坡角表示。

当竖曲线转坡点在曲线上方时为凸形竖曲线,反之为凹形竖曲线。

一、竖曲线如图所示,设相邻两纵坡坡度分别为i 1 与i 2,则相邻两坡度的代数差即转坡角为ω= i 1-i 2 ,其中i 1、i 2为本身之值,当上坡时取正值,下坡时取负值。

当 i 1- i 2为正值时,则为凸形竖曲线。

当 i 1 - i 2 为负值时,则为凹形竖曲线。

(一)竖曲线基本方程式我国采用的就是二次抛物线形作为竖曲线的常用形式。

其基本方程为:Py x 22=若取抛物线参数P 为竖曲线的半径 R ,则有:Ry x 22= Rx y 22=(二)竖曲线要素计算公式竖曲线计算图示1、切线上任意点与竖曲线间的竖距h 通过推导可得:==PQ h )()(2112li y l x R y y A A q p ---=-Rl 22=2、竖曲线曲线长: L = R ω3、竖曲线切线长: T= T A =T B ≈ L/2 =2ωR 4、竖曲线的外距: E =RT 22⑤竖曲线上任意点至相应切线的距离:Rx y 22=式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m;R —为竖曲线的半径,m 。

二、竖曲线的最小半径(一)竖曲线最小半径的确定1、凸形竖曲线极限最小半径确定考虑因素 (1)缓与冲击汽车行驶在竖曲线上时,产生径向离心力,使汽车在凸形竖曲线上重量减小,所以确定竖曲线半径时,对离心力要加以控制。

(2)经行时间不宜过短当竖曲线两端直线坡段的坡度差很小时,即使竖曲线半径较大,竖曲线长度也有可能较短,此时汽车在竖曲线段倏忽而过,冲击增大,乘客不适;从视觉上考虑也会感到线形突然转折。