梁的振动实验报告
悬臂梁的振动模态实验报告

实验 等截面悬臂梁模态测试实验一、 实验目的1. 熟悉模态分析原理;2. 掌握悬臂梁的测试过程。
二、 实验原理1. 模态分析基本原理理论上,连续弹性体梁有无限多个自由度,因此需要无限多个连续模型才能描述,但是在实际操作中可以将连续弹性体梁分为n 个集中质量来研究。
简化之后的模型中有n 个集中质量,一般就有n 个自由度,系统的运动方程是n 个二阶互相耦合(联立)的常微分方程。
这就是说梁可以用一种“模态模型”来描述其动态响应。
模态分析的实质,是一种坐标转换。
其目的在于把原在物理坐标系统中描述的响应向量,放到所谓“模态坐标系统”中来描述。
这一坐标系统的每一个基向量恰是振动系统的一个特征向量。
也就是说在这个坐标下,振动方程是一组互无耦合的方程,分别描述振动系统的各阶振动形式,每个坐标均可单独求解,得到系统的某阶结构参数。
多次锤击各点,通过仪器记录传感器与力锤的信号,计算得到第i个激励点与定响应点(例如点2)之间的传递函数H i (ω),从而得到频率响应函数矩阵中的一行频响函数的任一行包含所有模态参数,而该行的r 阶模态的频响函数 的比值,即为r 阶模态的振型。
2. 激励方法为进行模态分析,首先要测得激振力及相应的响应信号,进行传递函数分析。
传递函数分析实质上就是机械导纳,i 和j 两点之间的传递函数表示在[]∑==Nr iN ri ri r H H H 121...[]Nr r r Nr rr r irk c j m ϕϕϕωωϕ (2112)∑=++-=[]{}[]Tr ir Nr r iN i i Y H H H ϕϕ∑==121...j点作用单位力时,在i点所引起的响应。
要得到i和j点之间的传递导纳,只要在j点加一个频率为ω的正弦的力信号激振,而在i点测量其引起的响应,就可得到计算传递函数曲线上的一个点。
如果ω是连续变化的,分别测得其相应的响应,就可以得到传递函数曲线。
根据模态分析的原理,我们要测得传递函数矩阵中的任一行或任一列,由此可采用不同的测试方法。
力学桥梁振动实验报告

一、实验目的1. 理解桥梁振动的基本原理和影响因素。
2. 通过实验,验证桥梁振动的理论公式,如固有频率、振型等。
3. 掌握桥梁振动实验的基本操作和数据处理方法。
4. 分析桥梁在不同载荷和结构参数下的振动特性。
二、实验原理桥梁振动是指桥梁在外力作用下发生的周期性运动。
根据振动形式,桥梁振动可分为自由振动和强迫振动。
本实验主要研究桥梁的自由振动。
桥梁的自由振动可以由以下公式描述:\[ m\frac{d^2x}{dt^2} + c\frac{dx}{dt} + kx = 0 \]其中,\( m \) 为桥梁的质量,\( x \) 为桥梁的位移,\( t \) 为时间,\( c \) 为阻尼系数,\( k \) 为桥梁的刚度。
桥梁的固有频率 \( \omega_n \) 可以通过以下公式计算:\[ \omega_n = \sqrt{\frac{k}{m}} \]三、实验设备和仪器1. 桥梁振动实验台2. 力传感器3. 数据采集器4. 激振器5. 激光测距仪6. 振动传感器7. 计算机四、实验步骤1. 搭建实验装置:将桥梁振动实验台安装好,连接好力传感器、数据采集器、激振器、激光测距仪和振动传感器。
2. 调整实验参数:根据实验要求,调整桥梁的初始状态,如初始位移、初始速度等。
3. 激发振动:使用激振器激发桥梁振动,同时记录力传感器和振动传感器的数据。
4. 采集数据:使用数据采集器实时采集力传感器和振动传感器的数据,并存储到计算机中。
5. 数据处理:对采集到的数据进行处理,如滤波、计算固有频率、振型等。
五、实验结果与分析1. 固有频率的测定:通过实验数据,计算桥梁的固有频率,并与理论计算值进行比较。
2. 振型的测定:通过实验数据,绘制桥梁的振型图,分析桥梁在不同频率下的振动模式。
3. 影响因素分析:分析桥梁在不同载荷和结构参数下的振动特性,如桥面质量、阻尼系数、刚度等。
六、结论1. 通过实验,验证了桥梁振动的理论公式,并计算出桥梁的固有频率和振型。
振动测量实验报告

振动测量实验报告振动测量实验报告引言振动是物体在空间中周期性的运动,广泛存在于自然界和工程实践中。
对振动的测量和分析对于了解物体的结构和性能具有重要意义。
本实验旨在通过振动测量实验,探究振动现象的特性和相关参数的测量方法。
实验目的1. 了解振动的基本概念和特性;2. 掌握振动参数的测量方法;3. 学习振动测量仪器的使用和操作;4. 分析振动测量结果,得出相应结论。
实验仪器和材料1. 振动测量仪器:包括加速度传感器、振动传感器、振动分析仪等;2. 实验样品:可选取弹簧振子、悬臂梁等。
实验步骤1. 准备工作:检查仪器是否正常工作,确保传感器与分析仪器连接良好;2. 安装样品:根据实验要求,选择合适的样品并固定在测量平台上;3. 连接传感器:将加速度传感器或振动传感器与样品连接,并确保传感器位置合适;4. 开始测量:启动振动分析仪器,进行振动测量;5. 记录数据:根据实验要求,记录振动参数的数值,包括振幅、频率、相位等;6. 分析结果:根据测量数据,进行振动特性的分析和对比;7. 结论和讨论:根据实验结果,得出相应结论,并进行讨论。
实验结果与讨论通过实验测量和分析,我们得到了一系列振动参数的数值。
以弹簧振子为例,我们观察到随着振动频率的增加,振幅逐渐减小,这符合振动能量逐渐耗散的特性。
同时,我们还发现在某些频率下,振幅会出现明显的共振现象,这是由于外界激励与振动系统的固有频率相吻合所致。
通过对不同样品的振动测量和对比分析,我们还可以得出不同结构和材料的振动特性差异。
例如,悬臂梁相比弹簧振子更容易发生共振现象,这是由于其固有频率较低,容易与外界激励相吻合。
这些实验结果有助于我们理解和优化工程结构的振动性能。
实验误差分析在实验过程中,可能存在一些误差,例如传感器的位置不准确、测量仪器的精度限制等。
这些误差可能对测量结果产生一定影响。
为了减小误差,我们应该在实验前进行充分的准备工作,确保仪器和样品的状态良好,并在测量过程中注意操作细节。
梁的振动实验报告

梁的振动实验报告实验目的改变梁的边界条件,对比分析不同边界条件,梁的振动特性(频率、振型等)。
对比理论计算结果与实际测量结果。
正确理解边界条件对振动特性的影响。
实验内容对悬臂梁、简支梁进行振动特性对比,利用锤击法测量系统模态及阻尼比等。
实验原理1、固有频率的测定悬臂梁作为连续体的固有振动,其固有频率为:()1,2,.......r r l r ωλ==其中,其一、二、三、四阶时, 1.87514.69417.854810.9955.....r l λ=、、、 简支梁的固有频率为:()1,2,.......r r l r ωλ==其中其一、二、三、四阶时, 4.73007.853210.995614.1372.....r l λ=、、、 其中E 为材料的弹性模量,I 为梁截面的最小惯性矩,ρ为材料密度,A 为梁截面积,l 为梁的长度。
试件梁的结构尺寸:长L=610mm, 宽b=49mm, 厚度h=8.84mm. 材料参数: 45#钢,弹性模量E =210 (GPa), 密度ρ=7800 (Kg/m 3)横截面积:A =4.33*10-4 (m 2),截面惯性矩:J =312bh =2.82*10-9(m 4)则梁的各阶固有频率即可计算出。
2、实验简图图1 悬臂梁实验简图图2简支梁实验简图实验仪器本次实验主要采用力锤、加速度传感器、YE6251数据采集仪、计算机等。
图3和图4分别为悬臂梁和简支梁的实验装置图。
图5为YE6251数据采集仪。
图3 悬臂梁实验装置图图4 简支梁实验简图图5 YE6251数据采集分析系统实验步骤1:"在教学装置选择"中,选择结构类型为"悬臂梁",如果选择等份数为17,将需要测量17个测点。
2:本试验可采用多点激励,单点响应的方式,如果是划分为17等份,请将拾振点放在第5点。
3:请将力锤的锤头换成尼龙头,并将力通道的低通滤波器设置为1KHz,将拾振的加速度通道的低通滤波器设置为2KHz。
两端悬挂梁各阶固有频率和主振形的测定试验

两端悬挂梁各阶固有频率及主振形的测定试验一、实验目的1、用共振法确定两端悬挂梁横向振动时的前五阶固有频率;2、熟悉和了解两端悬挂梁振动的规律和特点;3、观察和测试两端悬挂梁振动的各阶主振型,分析各阶固有频率及其主振型的实测值与理论计算值的误差。
二、仪器和设备两端悬挂支座;脉冲锤1个;圆形截面钢梁标准件一个;加速度传感器一个;LMS振动噪声测试系统。
三、实验基本原理实验基本同悬臂梁实验四、实验结果记录前五阶固有频率表阶数固有频率(Hz)1 8.47352 54.69353 152.16244 295.96015 490.4713实验测得前5阶振型图如下:1阶振型图2阶振型图3阶振型图4阶振型图5阶振型图五、ANSYS有限元模拟仿真结果5.1前五阶固有频率仿真数据5.2前五阶振型仿真图1阶振型仿真图2阶振型仿真图3阶振型仿真图4阶振型仿真图5阶振型仿真图六、结果误差分析悬臂梁理论计算固有频率理论值、有限元仿真值与实测值表 梁几何尺寸 梁长 L=1m梁直径D=12mm 固有频率(Hz ) 1f2f 3f4f5f实验值 8.4735 54.6935 152.1624 295.9601 490.4713 有限元仿真值 053.884148.43290.69479.87结论:由以上表可以看梁一阶频率的实验值和仿真值完全不同,并且仿真值为0,其余四阶的数值比较接近,推测出现此结果的原因是:(1)有限元仿真中梁为无约束梁,其六个自由度均未约束,因此会出现前六个仿真值均接近0的情况,即悬挂梁不存在一阶振型。
(2)由于悬挂梁的六个自由度都未约束,实际震动中会将能量分散到整个空间,因此难以测得悬挂梁的一阶固有频率。
梁模态分析实验报告

一、实验目的1. 通过实验了解梁的模态特性,包括固有频率和振型;2. 掌握梁模态分析的基本方法,包括激振、信号采集、数据处理等;3. 熟悉实验设备的操作和调试,提高实验技能。
二、实验原理梁的模态分析是研究结构振动特性的重要手段。
本实验采用共振法进行梁的模态分析,即通过激振使梁产生振动,通过信号采集和数据处理得到梁的固有频率和振型。
三、实验设备与材料1. 实验设备:激振器、加速度传感器、信号采集系统、数据采集卡、计算机等;2. 实验材料:一根等截面简支梁。
四、实验步骤1. 将梁固定在实验台上,确保梁的支承条件符合简支梁的要求;2. 将加速度传感器粘贴在梁上,用于采集梁的振动信号;3. 连接信号采集系统和数据采集卡,确保信号采集系统与计算机正常连接;4. 开启激振器,进行激振实验;5. 采集梁的振动信号,并对信号进行预处理,如滤波、去噪等;6. 利用信号处理软件对采集到的信号进行频谱分析,得到梁的固有频率和振型。
五、实验结果与分析1. 实验数据(1)梁的几何参数:长度L=1000mm,宽度b=50mm,高度h=100mm;(2)材料参数:弹性模量E=2.06×10^5 MPa,密度ρ=7850 kg/m^3;(3)实验得到的固有频率和振型。
2. 实验结果分析(1)固有频率:根据实验数据,得到梁的前三阶固有频率分别为f1=50Hz、f2=120Hz、f3=180Hz;(2)振型:通过频谱分析,得到梁的前三阶振型如图1所示。
图1 梁的前三阶振型从实验结果可以看出,梁的固有频率和振型与理论计算值基本吻合,说明本实验所采用的模态分析方法具有较高的精度。
六、实验总结1. 通过本次实验,掌握了梁的模态分析基本方法,提高了实验技能;2. 熟悉了实验设备的操作和调试,为今后进行类似实验奠定了基础;3. 实验结果表明,本实验所采用的模态分析方法具有较高的精度,为工程实际提供了参考。
七、实验建议1. 在实验过程中,注意激振器的激振频率应与梁的固有频率接近,以提高实验精度;2. 信号采集时,应确保传感器粘贴牢固,避免信号干扰;3. 在数据处理过程中,注意滤波、去噪等预处理步骤,以提高数据质量;4. 实验过程中,应仔细观察梁的振动现象,以便及时发现问题并进行调整。
实验五简支梁固有频率测试实验1

实验五 简支梁固有频率测试实验一、 实验目的:1、 掌握固有频率测试的工程意义及测试方法。
2、 掌握用共振法、李萨育图形法测量振动系统的固有频率的方法及步骤。
3、 加深了解常用简单振动测试仪器的使用方法。
二、实验设备和工具1.机械振动综合实验装置(安装简支梁) 1套2.激振器及功率放大器 1套3.加速度传感器 1台4.电荷放大器 1台5.数据采集仪 1台6.信号分析软件 1套三、实验内容1.用共振法测量简支梁固有频率共振法测量振动系统的固有频率是比较常用的方法之一。
共振是指当激振频率达到某一特定值时,振动量的振动幅值达到极大值的现象。
由弹性体振动理论可知,计算简支梁固有频率理论解为:APEJ L f 20115.49 式中,L 为简支梁长度(cm );E 为材料弹性系数(kg/cm 2);A 为梁横截面积(cm 2);P 为材料比重(kg/cm 3);J 为梁截面弯曲惯性矩(cm 4)。
用共振法测量简支梁固有频率的仪器连接如图1所示图1测量双简支梁固有频率框图2.用李萨育图形法测量简支梁固有频率李萨育图形是由运动方向相互垂直的两个简谐振动的合成运动轨迹。
李萨育图形可以通过示波器或数据采集软件的X-Y轨迹图观察到。
在图的X、Y 轴上同时输入简谐振动两个信号,这两个信号不同的相位差合成不同的李萨育图形如图2所示。
振动的位移、速度及加速度的幅值其各自达到极大值时频率是不同的,只有在无阻尼的情况下,它们频率才相等,并且等于振动系统的固有频率。
但在弱阻尼的情况下,三种共振频率接近系统的固有频率。
只有速度共振频率真正和固有频率相等,所以用速度共振的相位差判别共振。
判别依据是系统发生速度共振时,激振力和速度响应之间的相位差为90°,依据位移、速度、加速度响应判断速度共振的李萨育图形如图3~5所示。
θ=00 θ=450 θ=900 θ=1350 θ=1800图2 不同相位差信号合成的李萨育图形n ωω< n ωω= n ωω>图3用位移响应判断速度共振n ωω< n ωω= n ωω>图4用速度响应判断速度共振n ωω< n ωω= n ωω>图5用加速度响应判断速度共振四、实验原理固有频率是振动系统的一项重要参数。
振动实验报告讲解

振动实验报告讲解振动与控制系列实验姓名:李⽅⽴学号:201520000111电⼦科技⼤学机械电⼦⼯程学院实验1 简⽀梁强迫振动幅频特性和阻尼的测量⼀、实验⽬的1、学会测量单⾃由度系统强迫振动的幅频特性曲线。
2、学会根据幅频特性曲线确定系统的固有频率f 0和阻尼⽐。
⼆、实验装置框图图3.1表⽰实验装置的框图图3-1 实验装置框图KCX图3-2 单⾃由度系统⼒学模型三、实验原理单⾃由度系统的⼒学模型如图3-2所⽰。
在正弦激振⼒的作⽤下系统作简谐强迫振动,设激振⼒F 的幅值B 、圆频率ωo(频率f=ω/2π),系统的运动微分⽅程式为:扫频信号源动态分析仪计算机系统及分析软件打印机或绘图仪简⽀梁振动传感器激振器⼒传感器质量块M或 M F x dt dxdt x d M F x dt dx n dtx d FKx dt dx C dtx d M /2/222222222=++=++=++ωξωω(3-1)式中:ω—系统固有圆频率ω =K/Mn ---衰减系数 2n=C/M ξ---相对阻尼系数ξ=n/ωF ——激振⼒ )2sin(sin 0ft B t B F πω== ⽅程①的特解,即强迫振动为:)2sin()sin(0?π?ω-=-=f A A x (3-2)式中:A ——强迫振动振幅--初相位20222024)(/ωωωn M B A +-=(3-3)式(3-3)叫做系统的幅频特性。
将式(3-3)所表⽰的振动幅值与激振频率的关系⽤图形表⽰,称为幅频特性曲线(如图3-3所⽰):3-2 单⾃由度系统⼒学模型 3-3 单⾃由度系统振动的幅频特性曲线图3-3中,Amax 为系统共振时的振幅;f 0为系统固有频率,1f 、2f 为半功率点频率。
振幅为Amax 时的频率叫共振频率f 0。
在有阻尼的情况下,共振频率为:221ξ-=f f a (3-4) 当阻尼较⼩时,0f f a =故以固有频率0f 作为共振频率a f 。
梁的振动分析和动力测试实验研究的开题报告

梁的振动分析和动力测试实验研究的开题报告题目:梁的振动分析和动力测试实验研究一、研究背景与意义梁是结构工程中常用的一种承载构件,其振动特性的研究对于结构的设计与优化具有重要意义。
同时,随着科学技术的发展,传统的数值模拟方法已经无法满足工程实际需求,需要结合实验手段来探究梁的振动特性。
因此,本研究旨在通过理论分析与动力测试实验相结合,深入研究正弦波和实际载荷下梁的振动特性,并探索梁的优化设计方法,为结构工程的发展提供技术支持和理论指导。
二、研究内容与方案(一)研究内容1. 对正弦波激励下的梁进行振动分析,建立梁的振动理论模型。
2. 设计梁的动力测试实验方案,选取合适的测试仪器和测量方法。
3. 将实测数据与理论计算结果进行比较分析,验证梁的振动理论模型的可靠性。
4. 对梁的振动特性进行分析,探究梁的共振频率、振动模态及其影响因素。
5. 研究梁在实际载荷下的振动特性,并探析梁的优化设计方法。
(二)研究方案1. 确定研究对象及材料,选择合适的梁材料以及尺寸,并预先进行理论计算。
2. 设计正弦波激励下梁的振动实验方案,包括研究参数的选择及测量方法的确定。
3. 进行实验测量,获得实际的振动数据,并进行初步处理分析。
4. 建立梁的振动模型,通过理论计算获得梁的振动特性参数。
5. 对实验数据与理论计算结果进行验证和比较分析,确定梁的振动理论模型的可靠性和适用范围。
6. 研究梁在实际载荷下的振动特性,探索针对不同载荷的梁的优化设计方法。
三、研究意义与预期成果本研究旨在探究梁的振动特性,通过理论分析和实验测试相结合,建立梁的振动理论模型,并探索梁在实际载荷下的振动特性及其影响因素,为梁的优化设计提供理论支持和指导。
预期的成果包括:1. 建立梁的振动理论模型,为梁的振动特性分析提供理论基础。
2. 确定梁的共振频率、振动模态及其影响因素,为梁的优化设计提供参考。
3. 探索梁在实际载荷下的振动特性及其优化设计方法,为结构工程的发展提供技术支持和理论指导。
梁的振动实验报告

梁的振动实验报告摘要:本实验主要研究了梁的振动现象,通过对梁的不同振动模式进行测量和分析,验证了梁的振动特性与理论模型的吻合程度。
实验结果表明,梁的自由振动频率与其长度、材质和截面形状有关,可以通过实验测量得到的频率与理论计算结果相符。
Ⅰ.实验目的1.研究梁的振动现象,了解梁的振动特性。
2.通过实验测量梁的自由振动频率,并与理论计算结果进行比较,验证梁的振动模型。
Ⅱ.实验原理1.梁的自由振动:当梁在无外力作用下发生振动时,称为自由振动。
自由振动的频率与梁的长度、材质和截面形状有关。
2.理论分析:利用梁的挠度方程和边界条件,可以得到梁的振动模式及其频率。
Ⅲ.实验仪器和材料1.实验仪器:梁振动实验装置、电子计时器。
2.实验材料:金属梁、木梁、塑料梁。
Ⅳ.实验步骤1.准备工作:将不同材料的梁装在振动实验装置上,并调整装置的参数。
2.实验测量:将梁拉到一定偏置位置,释放后记录振动的周期,并测量梁的长度。
3.实验重复:重复以上步骤,分别对不同梁进行测量。
Ⅴ.实验数据处理与分析1.实验数据整理:将测得的振动周期和梁的长度整理成表格。
2.实验数据分析:根据实验数据,计算不同梁的自由振动频率,并与理论计算结果进行比较。
Ⅵ.结果与讨论1.实验结果:通过实验测量得到了不同梁的自由振动频率。
2.数据分析:将实验测量的频率与理论计算结果进行对比,分析其吻合程度。
3.结果讨论:根据实验结果和分析,讨论梁的振动特性、材料对振动频率的影响等。
Ⅶ.实验结论1.梁的自由振动频率与其长度、材质和截面形状有关。
2.实验测量得到的梁的自由振动频率与理论计算结果吻合较好,实验验证了梁的振动模型。
Ⅷ.实验心得通过本次实验,我对梁的振动特性有了更深入的了解,学会了利用实验方法进行梁的振动测量和分析。
实验结果的验证也增加了我对理论知识的信心。
但是,在实验过程中还存在一些误差和改进的地方,需要进一步加强实验技巧和方法。
普通混凝土梁实验报告

普通混凝土梁实验报告1. 实验目的本实验旨在通过对普通混凝土梁的试验研究,了解混凝土梁的受力性能和破坏特点,并掌握常见的梁的受力计算方法。
2. 实验原理混凝土梁是一种常见的结构构件,其受力性能和破坏特点对于工程设计和施工具有重要的指导意义。
混凝土梁在受力过程中主要承受弯曲力和剪力,因此梁的设计实际上是通过计算其抗弯能力和抗剪能力来确定尺寸和配筋。
混凝土梁的抗弯能力主要由混凝土的抗压强度和钢筋的抗拉强度共同决定。
普通混凝土梁通常采用双筋梁设计方法,将钢筋设置在梁的上、下两面,以承受混凝土在受弯过程中产生的拉应力。
为了确保梁的抗剪能力,还需设置横向钢筋。
本实验通过对普通混凝土梁的弯曲破坏和剪切破坏进行试验,探究混凝土梁的受力性能,验证结构力学理论计算方法的正确性。
3. 实验设备和材料3.1 实验设备- 弯曲试验机- 剪切试验机3.2 实验材料- 普通硅酸盐水泥- 砂子- 碎石- 水- 钢筋4. 实验步骤4.1 实验材料准备根据设计要求,按照一定比例准备混凝土的组分材料,包括水泥、砂子和碎石。
将这些材料按照一定比例混合并加水,搅拌均匀,制备出混凝土。
4.2 模具准备按照设计要求,制作适当尺寸的混凝土梁模具。
在模具内涂抹一层防粘剂,以便后续混凝土的顺利取出。
4.3 混凝土浇筑和养护将制备好的混凝土倒入模具中,并使用振动器进行振实。
待混凝土凝固后,将模具放置于恒温恒湿的养护室中,以保证混凝土逐渐达到预期的强度。
4.4 弯曲试验在混凝土梁的两个支点处,用试验机夹住梁体进行弯曲试验。
通过加载到梁上的力和变形的测量,得到梁的荷载-位移曲线。
根据曲线的变化可以分析梁的破坏特点。
4.5 剪切试验使用试验机进行混凝土梁的剪切试验。
通过加载到梁上的剪切力和剪切变形的测量,得到梁的剪切荷载-位移曲线。
根据曲线的变化可以分析梁的破坏特点。
5. 实验结果分析根据实验所得的弯曲试验和剪切试验数据,进行如下分析:5.1 弯曲试验结果分析从荷载-位移曲线可见,混凝土梁的初始阶段呈现线性变化,当加载达到一定荷载后,梁开始出现明显的非线性变形,直至破坏。
实验二悬臂梁各阶固有频率及主振形的测定试验

实验二 悬臂梁各阶固有频率及主振形的测定试验一、实验目的1、用共振法确定悬臂梁横向振动时的各阶固有频率。
2、熟悉和了解悬臂梁振动的规律和特点。
3、观察和测试悬臂梁振动的各阶主振型。
分析各阶固有频率及其主振型的实测值与理论计算值的误差。
二、基本原理悬臂梁的振动属于连续弹性体的振动,它具有无限多自由度及其相应的固有频率和主振型,其振动可表示为无穷多个主振型的叠加。
对于梁体振动时,仅考虑弯曲引起的变形,而不计剪切引起的变形及其转动惯量的影响,这种力学分析模型称为欧拉-伯努利梁。
运用分离变量法,结合悬臂梁一端固定一端自由的边界条件,通过分析可求得均质、等截面悬臂梁的频率方程1 L Lch cos -=ββ (2-1) 式中:L ——悬臂梁的长度。
梁各阶固有园频率为AEIiin 2 ρβω= (2-2)对应i 阶固有频率的主振型函数为),3,2,1()sin (sin cos cos )( =-++--=i x x sh LL sh L L ch x x ch x Xi i i i i i i i iββββββββ (2-3)对于(2-1)式中的β,不能用解析法求解,用数值计算方法求得的一阶至四阶固有园频率和主振型的结果列于表2-1。
各阶固有园频率之比1f ﹕1f ﹕1f ﹕1f ﹕… = 1﹕6.269﹕17.56﹕34.41﹕… (2-4)A B x 图2-1 悬臂梁振动模型表(2-1)给出了悬臂梁自由振动时i =1~4阶固有园频率及其相应主振型函数。
除了悬臂梁固定端点边界位移始终为零外,对于二阶以上主振型而言,梁上还存在一些点在振动过程中位移始终为零的振型节点。
i 阶振型节点个数等于i -1,即振型节点个数比其振型的阶数小1。
实验测试对象为矩形截面悬臂梁(见图2-2所示)。
在实验测试时,给梁体施加一个大小适当的激扰作用力,其频率正好等于梁体的某阶固有频率,则梁体便会产生共振,这时梁体变形即为该阶固有频率所对应的主振型,其它各阶振型的影响很小可忽略不计。
振动实验报告1

振动实验报告1实验⼀振动系统固有频率的测试⼀、实验⽬的:1、学习振动系统固有频率的测试⽅法;2、学习共振动法测试振动固有频率的原理与⽅法;3、学习锤击法测试振动系统固有频率的原理与⽅法;⼆、实验原理1、简谐⼒激振1)幅值判别法在激振功率输出不变的情况下,由低到⾼调节激振器的激振频率,通过⽰波器,我们可以观察到在某⼀频率下,任⼀振动量(位移、速度、加速度)幅值迅速增加,这就是机械振动系统的某阶固有频率。
这种⽅法简单易⾏,但在阻尼较⼤的情况下,不同的测量⽅法得出的共振动频率稍有差别,不同类型的振动量对振幅变化敏感程度不⼀样,这样对于⼀种类型的传感器在某阶频率时不够敏感。
2)相位判别法相位判法是根据共振时特殊的相位值以及共振动前后相位变化规律所提出来的⼀种共振判别法。
在简谐⼒激振的情况下,⽤相位法来判定共振是⼀种较为敏感的⽅法,⽽且共振是的频率就是系统的⽆阻尼固有频率,可以排除阻尼因素的影响。
A.位移判别共振将激振动信号输⼊到采集仪的第⼀通道(即X 轴),位移传感器输出信号或通过ZJY-601A 型振动教学仪积分档输出量为位移的信号输⼊到第⼆通道(即Y 轴),此时两通道的信号分别为激振信号为:位移信号为:共振时,,X 轴信号和Y 轴信号的相位差为p / 2,根据利萨如图原理可知,屏幕上的图象将是⼀个正椭圆。
当w 略⼤于n w 或略⼩于n w 时,图象都将由正椭圆变为斜椭圆,其变化过程如下图所⽰。
因此图象图象由斜椭圆变为正椭圆的频率就是振动体的固有频率。
B.速度判别共振将激振信号输⼊到采集仪的第⼀通道(即X 轴),速度传感器输出信号或通过ZJY-601A 型振动教学仪积分档输出量为速度的信号输⼊到第⼆通道(即Y 轴),此时两通道的信号分别为:激振信号为:速度信号为:共振时,,X 轴信号和Y 轴信号的相位差为p / 2。
根据利萨如图原理可知,屏幕上的图象应是⼀条直线。
当w 略⼤于n w 或略⼩于n w 时,图象都将由直线变为斜椭圆,其变化过程如下图所⽰。
单自由度系统强迫振动(悬臂梁)
单自由度系统强迫振动(悬臂梁)一、实验目的 1、 测定带有集中荷重的悬臂梁系统,在自由端部位移激励下引起的强迫振动的振幅频率特性曲线;借助幅频特性曲线,求出系统的固有频率及阻尼常数; 2、 初步了解振动测试的一些仪器设备及测试方法。
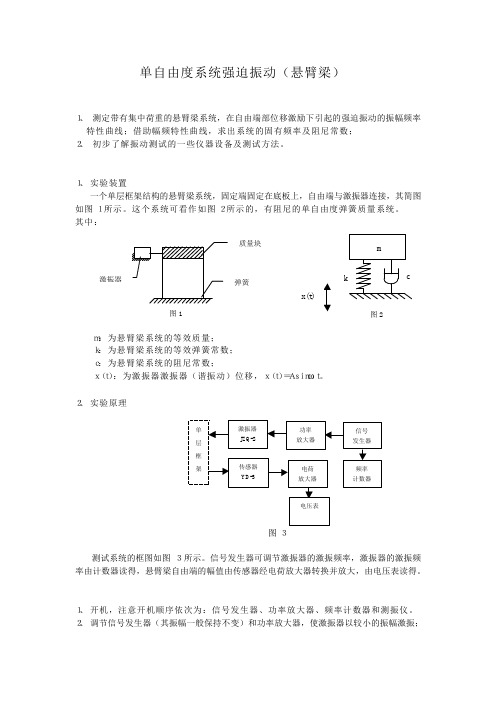
二、实验装置及原理 1、 实验装置 一个单层框架结构的悬臂梁系统,固定端固定在底板上,自由端与激振器连接,其简图如图1所示。
这个系统可看作如图2所示的,有阻尼的单自由度弹簧质量系统。
其中: m:为悬臂梁系统的等效质量; k:为悬臂梁系统的等效弹簧常数; c:为悬臂梁系统的阻尼常数; x(t):为激振器激振器(谐振动)位移,x(t)=Asinωt。
2、 实验原理 图3 测试系统的框图如图3所示。
信号发生器可调节激振器的激振频率,激振器的激振频率由计数器读得,悬臂梁自由端的幅值由传感器经电荷放大器转换并放大,由电压表读得。
三、实验步骤 1、 开机,注意开机顺序依次为:信号发生器、功率放大器、频率计数器和测振仪。
2、 调节信号发生器(其振幅一般保持不变)和功率放大器,使激振器以较小的振幅激振;激振器然后调节信号发生器的频率,从10-40Hz扫频,使振幅达到最大,即找到系统的共振频率,再轻微调节功率放大器的振幅峰F0,使共振时的位移达到所需振幅。
3、 然后从低频段各点扫描,找出各点频率下对应的位移振幅,频率间隔根据不同情况选取(最好以位移振幅选取),并把各点数据记录表中和填入方格纸中,完成幅频曲线的绘制。
4、 检查幅频曲线的正确与否,偏差较大时,重新找取相应点的数据。
根据图示幅频曲线,由如下关系式计算系统的固有频率和阻尼常数。
5、 关机,把功率放大器的振幅调至最小,然后关闭仪器的电源,关机顺序正好与开机顺序相反。
四、实验数据记录及计算结果 序号 频率 振幅 1 2 …. 按照幅频曲线,运用半功率原理得到: 10 36Frequency Response Function CurveA /A maxf (Hz)1固有频率:m n f f =, 带宽:12f f f −=∆ 相对阻尼系数:nf f2∆=ζ 五、实验要求 1、 实验前必须带好方格纸,在实验过程中,将所测数据填入方格纸中,画出曲线的草图,并让老师检查方可离开。
混凝土梁震动试验标准

混凝土梁震动试验标准一、前言混凝土梁是建筑工程中常用的结构元件,其受到地震等外力作用时会产生震动反应,对于保证结构的安全性和稳定性具有重要意义。
因此,混凝土梁震动试验是建筑工程领域的重要研究内容之一。
本文旨在提供一份全面的具体的详细的混凝土梁震动试验标准,以期能够规范试验过程,提高试验数据的准确性和可靠性。
二、试验对象混凝土梁是试验的对象,其形状和尺寸应符合相关标准要求。
试验时应选择同一品种、同一批次的混凝土材料,避免试验结果受材料质量的影响。
三、试验设备1.振动器:振动器应符合相关标准要求,其振动频率应可调节,调节范围应在试验要求内。
2.加速度计:加速度计应符合相关标准要求,其量程应能满足试验要求,测量误差应在0.5%以内。
3.数据采集系统:数据采集系统应能够采集振动信号,并将其转换成数字信号。
数据采集系统应具有良好的稳定性和可靠性。
4.电子天平:电子天平应符合相关标准要求,其分度值应能满足试验要求,测量误差应在0.1%以内。
5.其他辅助设备:如支撑架、夹具、导轨等。
四、试验方法1.试验前准备(1)对试验设备进行检查和调试,确保其正常工作。
(2)根据试验要求选择合适的振动频率和振动幅度。
(3)在混凝土梁的两端固定支撑架,并保证支撑架的水平度。
(4)根据试验要求在混凝土梁上安装加速度计,并调整其位置和方向。
2.试验过程(1)将振动器与混凝土梁相连,调节振动器的频率和幅度,开始振动实验。
(2)记录混凝土梁的振动参数,如加速度、振幅、振动频率等。
(3)在试验过程中,应对振动器、加速度计等设备进行监测,确保其正常工作。
3.试验结束(1)试验结束后,停止振动并记录振动器的停止时间。
(2)将混凝土梁从支撑架上取下,并进行重量测量。
(3)将采集到的振动信号进行处理和分析,得到混凝土梁的动态特性参数。
五、试验数据处理1.数据采集采集加速度计的振动信号,并将其转换成数字信号,保存在计算机上。
2.数据处理(1)对采集到的信号进行滤波和去噪处理,保证数据的准确性和可靠性。
振动测试实验报告

竭诚为您提供优质文档/双击可除振动测试实验报告篇一:振动实验报告l机械振动实验报告1.测量简支梁的固有频率和振型1.1实验目的用激振法测量简支梁的固有频率和固有振型。
掌握多自由度系统固有频和振型的简单测量方法。
1.2实验原理共振法测量振动系统的固有频率是比较常用的方法之一。
共振是指当激振频率达到某一特定值时,振动量的振动幅值达到极大值的现象。
本次试验主要利用调整激振频率使简支梁达到位移振动幅值的方法来测量简支梁的一阶,二阶以及三阶固有频率以及从计算机上读取其当时的振型!1.3实验内容与结果分析(1)将激振器通过顶杆连接到简支梁上(注意确保顶杆与激振器的中心线在一直线上),激振点位于简支梁中心偏左50mm处(已有安装螺孔),将信号发生器输出端分别与功率放大器和数据采集仪的输入端连接,并将功率放大器与激振器相连接。
(2)用双面胶纸(或传感器磁座)将加速度传感器A粘贴在简支梁上5#测点(实验时固定不动,用于与其他测点比较相位),将加速度传感器连接,将电荷放大器输出端与数据采集仪的输入端连接。
(3)将信号发生器和功率放大器的幅值旋钮调至最小,打开所有仪器电源。
打开控制计算机,打开做此次试验所需的测试软件,进入页面设置好各项参数。
通过调节激振频率,观察简支梁位置幅值振动情况。
可以通过放在简支梁上的装有一定量塑质小球的小型透明容器直观的观察里面小球的振动情况,小球振动越厉害,也就说明简支梁振动的位移幅值越大;还可以通过分辨简支梁在不同激振频率下的发出的振动声音,声音越大,说明振动幅值越大!(4)通过(3)中的方法,可以测量出在简支梁在某一激振频率范围内的振动幅值,则此激振频率就是我们需要测量的一阶,二阶以及三阶固有频率,在测出固有频率的同时将计算机上画出的各阶振型的图像保存,以便结果的分析。
(5)在完成所有的试验内容之后,通过记录下的实验数据分析实验的结果。
所得的实验结果如下:测得的简支梁的一阶、二阶以及三阶的固有频率为?=35.42hZ,?=131.54hZ,?3=258.01hZ。
单自由度系统强迫振动(悬臂梁)

单自由度系统强迫振动(悬臂梁)一、实验目的 1、 测定带有集中荷重的悬臂梁系统,在自由端部位移激励下引起的强迫振动的振幅频率特性曲线;借助幅频特性曲线,求出系统的固有频率及阻尼常数; 2、 初步了解振动测试的一些仪器设备及测试方法。
二、实验装置及原理 1、 实验装置 一个单层框架结构的悬臂梁系统,固定端固定在底板上,自由端与激振器连接,其简图如图1所示。
这个系统可看作如图2所示的,有阻尼的单自由度弹簧质量系统。
其中: m:为悬臂梁系统的等效质量; k:为悬臂梁系统的等效弹簧常数; c:为悬臂梁系统的阻尼常数; x(t):为激振器激振器(谐振动)位移,x(t)=Asinωt。
2、 实验原理 图3 测试系统的框图如图3所示。
信号发生器可调节激振器的激振频率,激振器的激振频率由计数器读得,悬臂梁自由端的幅值由传感器经电荷放大器转换并放大,由电压表读得。
三、实验步骤 1、 开机,注意开机顺序依次为:信号发生器、功率放大器、频率计数器和测振仪。
2、 调节信号发生器(其振幅一般保持不变)和功率放大器,使激振器以较小的振幅激振;激振器然后调节信号发生器的频率,从10-40Hz扫频,使振幅达到最大,即找到系统的共振频率,再轻微调节功率放大器的振幅峰F0,使共振时的位移达到所需振幅。
3、 然后从低频段各点扫描,找出各点频率下对应的位移振幅,频率间隔根据不同情况选取(最好以位移振幅选取),并把各点数据记录表中和填入方格纸中,完成幅频曲线的绘制。
4、 检查幅频曲线的正确与否,偏差较大时,重新找取相应点的数据。
根据图示幅频曲线,由如下关系式计算系统的固有频率和阻尼常数。
5、 关机,把功率放大器的振幅调至最小,然后关闭仪器的电源,关机顺序正好与开机顺序相反。
四、实验数据记录及计算结果 序号 频率 振幅 1 2 …. 按照幅频曲线,运用半功率原理得到: 10 36Frequency Response Function CurveA /A maxf (Hz)1固有频率:m n f f =, 带宽:12f f f −=∆ 相对阻尼系数:nf f2∆=ζ 五、实验要求 1、 实验前必须带好方格纸,在实验过程中,将所测数据填入方格纸中,画出曲线的草图,并让老师检查方可离开。
实验二 梁的振动测试

实验二梁的振动测试
一、实验目的
1.了解差动变压器的结构工作原理和特性;
2.了解差动变压器测量振动的原理和方法;
二、实验设备及器材
1.差动变压器式位移传感器一个
2.螺旋测微仪一台
3.正弦信号发生器(U0=0-5V,f=1-5kHz)一台
4.低频振荡器
5.示波器
三、实验原理
根据差动变压器的结构,差动变压器的原、副边之间的互感随铁心的移动而变化。
当铁心处于中间位置时,副边线圈的互感系数相等,因副边线圈绕向相反,所以输出电压为零。
当铁心移动时,副边两线圈的感应电动势不同,输出就不为零。
通过测量输出电压大小就可以反映铁心位移的大小。
将低频振荡器输出接入振动源的低频输入端,调节低频振荡器的幅度旋钮和频率旋钮,使振动平台的振荡较为明显,用示波器观测波形。
保持低频振荡器幅度不变,改变振动频率,发现振动频率和输出电压呈比例关系。
四、实验内容及数据处理
1.将差动变压器装在差动变压器实验模板上,螺旋测微器用两只螺母固定在支架上并将铁心插入传感器螺线管内;系统调零;满度调节;
使铁心上移或下移到满量程(1mm),调节信号发生器输出电压。
表头读数为零时作为起点,分别上旋,下旋1mm,每次移动0.2mm,分别将位移量和对应的输出电压填入表中。
2.将低频振荡器输出接入振动源的低频输入端,调节低频振荡器的幅度旋钮和频率旋钮,使振动平台的振荡较为明显,用示波器观测波形。
保持低频振荡器幅度不变,改变振动频率,用示波器观测输出,读出峰峰电压,记录实验数据。
五、思考题
1.零点残余电压如何消除?
2.如何用压电传感器,电涡流传感器进行振动测量试验。
悬臂梁的振动模态实验报告

悬臂梁的振动模态实验报告悬臂梁是一种常见的结构,广泛应用于工程中。
在实际应用中,悬臂梁的振动特性是非常重要的,因为它会对悬臂梁结构的稳定性和安全性产生影响。
因此,了解悬臂梁的振动模态是一项必要的研究任务。
本次实验旨在通过实验方法测量和分析悬臂梁的振动模态,并探究不同参数对振动模态的影响。
实验过程中使用的设备和仪器包括悬挂系统、激励源、传感器、数据采集系统等。
实验步骤如下:1.悬挂梁结构:将悬挂系统固定在实验室的支架上,确保悬臂梁能够在完全自由的情况下自由振动。
2.激励源:将激励源与悬挂梁连接,通过激励源提供外力。
3.传感器:在悬臂梁上选择合适的位置安装传感器,用于测量悬臂梁的振动信号。
4.数据采集系统:将传感器与数据采集系统相连,用于实时采集和记录振动信号。
5.实施实验:通过激励源提供激励力,使悬臂梁产生振动,并同时记录悬挂梁的振动信号。
6.数据处理:通过数据采集系统获得的数据,使用相应的信号处理技术对振动信号进行处理,得到振动模态的相关参数。
7.结果分析:根据实验结果,分析悬臂梁的振动特性和模态,并探究不同参数对振动模态的影响。
通过以上实验步骤,我们可以获得悬臂梁的振动模态,并了解不同参数对振动模态的影响。
实验结果有助于工程设计中的结构设计和改进。
在实验过程中,我们还需要注意以下几个方面的问题:1.悬挂系统的稳定性和刚度:确保悬挂系统能够提供稳定的支撑,并且具有足够的刚度,以保证悬臂梁在振动过程中不会产生偏差。
2.激励源的选取:根据实际需求和悬臂梁的特性,选择合适的激励源,以提供适当的激励力。
3.传感器的准确性:选择合适的传感器,并保证传感器的准确性和灵敏度,以获得准确的振动信号。
4.数据采集和处理的准确性:使用合适的数据采集系统和信号处理技术,以保证数据采集和处理的准确性。
总之,通过本次实验,我们可以深入了解悬臂梁的振动模态,并探究不同参数对振动模态的影响。
这对于工程设计和结构改进具有重要意义,可以提高悬臂梁结构的稳定性和安全性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梁的振动实验报告
实验目的
改变梁的边界条件,对比分析不同边界条件,梁的振动特性(频率、振型等)。
对比理论计算结果与实际测量结果。
正确理解边界条件对振动特性的影响。
实验内容
对悬臂梁、简支梁进行振动特性对比,利用锤击法测量系统模态及阻尼比等。
实验原理
1、固有频率的测定
悬臂梁作为连续体的固有振动,其固有频率为:
,
其一、二、三、四阶时,
简支梁的固有频率为:
其一、二、三、四阶时,
其中E为材料的弹性模量,I为梁截面的最小惯性矩,ρ为材料密度,A为梁截面积,l为梁的长度。
试件梁的结构尺寸:长L=610mm, 宽b=49mm, 厚度h=8.84mm.
材料参数: 45#钢,弹性模量E=210 (GPa), 密度=7800 (Kg/m3)
横截面积:A=4.33*10-4 (m2),
截面惯性矩:J==2.82*10-9(m4)
则梁的各阶固有频率即可计算出。
2、实验简图
图1 悬臂梁实验简图
图2简支梁实验简图
实验仪器
本次实验主要采用力锤、加速度传感器、YE6251数据采集仪、计算机等。
图3和图4分别为悬臂梁和简支梁的实验装置图。
图5为YE6251数据采集仪。
图3 悬臂梁实验装置图
图4 简支梁实验简图
图5 YE6251数据采集分析系统
实验步骤
1:"在教学装置选择"中,选择结构类型为"悬臂梁",如果选择等份数为17,将需要测量17个测点。
2:本试验可采用多点激励,单点响应的方式,如果是划分为17等份,请将拾振点放在第5点。
3:请将力锤的锤头换成尼龙头,并将力通道的低通滤波器设置为1KHz,将拾振的加速度通道的低通滤波器设置为2KHz。
4:用力锤对第1点激振,对应的激励为f1,响应为1,平均3次,对应的数据为第1批数据,以此类推,测量完全部测点。
5:选择"教学装置模态分析和振型动画显示",调入测量数据进行分
析。
6:"在教学装置选择"中,选择结构类型为"简支梁",如果选择等份数为17,将需要测量17个测点。
重复2—5的步骤,得到简支梁的试验数据和结果。
实验数据记录和整理
图6 悬臂梁的传递函数幅值和相位
图7 悬臂梁的固有振型、频率和阻尼比
图8 简支梁的传递函数幅值和相位
图9 简支梁的固有振型、频率和阻尼比。
