高二数学文科周测4

合集下载

高二数学周考卷(文科)

高二数学周考卷（文科）一、选择题：1.用反证法证明命题：“三角形的内角中至少有一个不大于60度”时，反设正确的是（）。

(A)假设三内角都不大于60度； (B) 假设三内角都大于60度；(C) 假设三内角至多有一个大于60度； (D) 假设三内角至多有两个大于60度。

2.由①正方形的对角线相等；②平行四边形的对角线相等；③正方形是平行四边形，根据“三段论”推理出一个结论，则这个结论是（）(A) 正方形的对角线相等 (B) 平行四边形的对角线相等(C) 正方形是平行四边形 (D)其它3.一同学在电脑中打出如下若干个圈:○●○○●○○○●○○○○●○○○○ ○●…若将此若干个圈依此规律继续下去,得到一系列的圈,那么在前120个圈中的●的个数是 ( )(A)12 (B) 13 (C)14 (D)154.观察下列数:1,3,2,6,5,15,14,x,y,z,122,…中x,y,z 的值依次是 ( )(A)42,41,123; (B) 13,39,123; (C)24,23,123; (D)28,27,123.5．复数101()1i i-+的值是（） A ．－1B ．1C ．32D ．－32 6．复数534+i的共轭复数是（） A ．34-i B ．3545+i C ．34+i D ．3545-i 7．设0||,2=+∈z z C z 则方程的根是（）A ．4个B ．2个C ．3个D ．1个8．已知复数z 1＝3+4i ，z 2＝t+i ，且12z z 是实数，则实数t ＝（）A ．43B ．34C ．-34D ．-43 二、填空题9.由数列的前四项:23,1 , 85,83,……归纳出通项公式a n =___ _。

10.数列}{n a 中，211=a ，031=-+n n a a ，则n a 的通项公式为。

11．集合N M C z i z i z Z N C z x z M 则},|,||||{},1|1||{∈-=+=∈=-=是 . 12．=-=⋅+∈z i z z z C z 则若,421, . 三、解答题13．求虚数z ，使R zz ∈+9，且33=-z .14．已知复数z 满足2||=z ，2z 的虚部为 2 ，（1）求z ；（2）设z ，2z ，2z z -在复平面对应的点分别为A ，B ，C ，求ABC ∆的面积. 15.求证：(1)2233()a b ab a b ++≥++; (2) 6+7>22+5。

高二上学期期末考试数学(文)试题及答案 (4)

学年第一学期阶段性考试高二数学（文科）试卷第Ⅰ卷一、选择题：本大题共12小题。

每小题5分，在每小题给出的四个选项中，只有一项符合题目要求． 1．已知命题2015log ,:2=∈∀x R x p ，则p ⌝为( )A ．2015log ,2=∉∀x R xB ．2015log ,2≠∈∀x R xC ．2015log ,020=∈∃x R xD ．2015log ,020≠∈∃x R x2．为了检查某超市货架上的奶粉是否含有三聚氰胺，要从编号依次为1到50的袋装奶粉中抽取5袋进行检验，用系统抽样方法确定所选取的5袋奶粉的编号可能是( )A ．5,10,15,20,25B ．2,4,8,16,32C ．5,6,7,8,9D ．6,16,26,36,46 3．如果一个家庭有两个小孩，则两个孩子是一男一女的概率为( ) A ．14 B ．13 C ．12 D ．234．双曲线1222=-y x 的渐近线方程为（） A. 02=±y x B. 02=±y x C ．02=±y x D ．02=±y x5．甲、乙两名学生五次数学测验成绩(百分制)如图所示． ①甲同学成绩的中位数大于乙同学成绩的中位数； ②甲同学的平均分与乙同学的平均分相等； ③甲同学成绩的方差大于乙同学成绩的方差．以上说法正确的是（） A ．①②B ．②③C ．①③D ．①②③6．用秦九韶算法求多项式7234)(234++++=x x x x x f 的值，则)2(f 的值为( ) A ．98 B ．105 C ．112 D ．119 7．运行如右图的程序后，输出的结果为（） A ．6053 B ．54 C ．65 D ．76 8．已知椭圆221164x y +=过点)1,2(-P 作弦且弦被P 平分，则此弦所在的直线方程为（）7 90 1 38 90 1 289甲乙ENDS PRINT WEND i i i i S S i WHILE S i 1))1(/(1601+=+*+=<==A ．032=--y xB ．012=--y xC ．042=--y xD ．042=+-y x9．已知)(x g 为函数)0(1232)(23≠--=a ax ax ax x f 的导函数，则它们的图象可能是（）A ．B ．C ．D ．10．已知倾斜角为︒45的直线l 过抛物线x y 42=的焦点，且与抛物线交于B A ,两点，则OAB ∆（其中O 为坐标原点）的面积为（） A ．2B ．22C ．23D ．811．已知(),()f x g x 都是定义在R 上的函数，且满足以下条件：①()()xf x ag x =⋅(0,a >1)a ≠且；②()0g x ≠；③)(')()()('x g x f x g x f ⋅<⋅．若(1)(1)5(1)(1)2f fg g -+=-，则实数a 的值为 ( )A ．21 B ．2 C ．45 D ．2或21 12．如图，直线m x =与抛物线y x 42=交于点A ，与圆4)1(22=+-x y 的实线部分（即在抛物线开口内的圆弧）交于点B ，F 为抛物线的焦点，则ABF ∆的周长的取值范围是( ) A ．()4,2 B ．()6,4 C ．[]4,2 D ． []6,4第Ⅱ卷二、填空题：本大题共四小题，每小题5分．13．将十进制数)10(2016化为八进制数为 . 14．已知变量x 与y 的取值如下表：x 23 5 6y 7a -8 a +9 12从散点图可以看出y 对x 呈现线性相关关系，则y 与x 的线性回归直线方程a bx y+=ˆ必经过的定点为．15．已知P 为圆4)2(:22=++y x M 上的动点，)0,2(N ，线段PN 的垂直平分线与直线PM 的交点为Q ，点Q 的轨迹方程为．16．已知函数xxe x f =)(，现有下列五种说法：①函数)(x f 为奇函数；②函数)(x f 的减区间为()-1∞，,增区间为()1+∞，；频率组距50 55 60 65 70 75 80体重（kg)O0.070.060.050.040.030.020.01③函数)(x f 的图象在0x =处的切线的斜率为1； ④函数)(x f 的最小值为1e-. 其中说法正确的序号是_______________（请写出所有正确说法的序号）．三、解答题：解答应写出文字说明，证明过程或演算步骤． 17．（本小题满分10分）设命题p ：12>-x ；命题q ：0)1()12(2≥+++-a a x a x .若p ⌝是q ⌝的必要不充分条件，求实数a 的取值范围.18．（本小题满分12分）某校对高二年段的男生进行体检，现将高二男生的体重()kg 数据进行整理后分成6组，并绘制部分频率分布直方图（如图所示）．已知第三组[)65,60的人数为200.根据一般标准，高二男生体重超过65kg 属于偏胖，低于55kg 属于偏瘦．观察图形的信息，回答下列问题：(1)求体重在[)6560，内的频率，并补全频率分布直方图；（2）用分层抽样的方法从偏胖的学生中抽取6人对日常生活习惯及体育锻炼进行调查，则各组应分别抽取多少人？（3）根据频率分布直方图，估计高二男生的体重的中位数与平均数．19. （本小题满分12分）（1）执行如图所示的程序框图，如果输入的[]3,1-∈t ，若输出的s 的取值范围记为集合A ，求集合A ；（2）命题p ：A a ∈，其中集合A 为第（1）题中的s 的取值范围；命题q ：函数a x ax x x f +++=2331)(有极值；若q p ∧为真命题，求实数a 的取值范围.20．（本小题满分12分）已知双曲线C ：)00(12222>>=-，b a by a x .（1）有一枚质地均匀的正四面体玩具，玩具的各个面上分别写着数字1，2，3，4．若先后两次投掷玩具，将朝下的面上的数字依次记为b a ,，求双曲线C 的离心率小于5的概率；（2）在区间[]61，内取两个数依次记为b a ,，求双曲线C 的离心率小于5的概率.21．（本小题满分12分）已知椭圆C:)0(12222>>=+b a by a x 的中心在坐标原点O ，对称轴在坐标轴上，椭圆的上顶点与两个焦点构成边长为2的正三角形．（1）求椭圆C 的标准方程；（2）若斜率为k 的直线l 经过点)0,4(M ，与椭圆C 相交于A ，B 两点，且21>⋅OB OA ，求k 的取值范围．22. （本小题满分12分）已知函数)(2ln )(2R a x xa x a x f ∈++-=．（1）当1=a 时,求曲线)(x f y =在点))1(,1(f 处的切线方程；（2）当0>a 时，若函数()f x 在[1,]e 上的最小值记为)(a g ，请写出)(a g 的函数表达式.高二数学（文科）试卷参考答案一、ＤＤＣＤＢＢＣＤＡＢＡＢ二、13．)8(3740 14．()9,4 15．)0(1322<=-x y x 16．③④ 三、17．解：由p ：12>-x 解得1<x 或3>x .……………………………… 3分由q ：0)1()12(2≥+++-a a x a x 得[]0)1()(≥+--a x a x ，解得a x ≤或1+≥a x .……………………………… 6分∵p ⌝是q ⌝的必要不充分条件，∴p 是q 的充分不必要条件. …………………… 8分 ∴⎩⎨⎧≤+≥311a a ，则21≤≤a .∴实数a 的取值范围是[]21，.……………………………… 10分 18．解：（1）体重在[)65,60内的频率2.05)01.002.003.007.003.0(1=⨯++++-=04.052.0==组距频率补全的频率分布直方图如图所示. ……………4分（2）设男生总人数为n ，由2.0200=n，可得1000=n 体重超过kg 65的总人数为30010005)01.002.003.0(=⨯⨯++在[)70,65的人数为1501000503.0=⨯⨯，应抽取的人数为33001506=⨯，在[)70,65的人数为1001000502.0=⨯⨯，应抽取的人数为23001006=⨯，在[)80,75的人数为501000501.0=⨯⨯，应抽取的人数为1300506=⨯. 所以在[)70,65 ，[)75,70，[]80,75三段人数分别为3，2，1.…………………… 8分（3）中位数为60kg 平均数为(52.50.0357.50.0762.50.0467.50.0372.50.0277.50.01)561.75⨯+⨯+⨯+⨯+⨯+⨯⨯=(kg)…12分19．解：（1）由程序框图可知，当11<≤-t 时，t s 2=，则[)2,2-∈s . 当31≤≤t 时，()322+--=t s组距kg)O0.0.0.0.0.0.0.∵该函数的对称轴为2=t ，∴该函数在[]21，上单调递增，在[]3,2上单调递减. ∴2,3min max ==s s ∴[]3,2∈s综上知，[]3,2-∈s ，集合[]3,2-=A ……………………………… 4分（１）函数a x ax x x f +++=2331)(有极值,且12)(2'++=ax x x f ， 0)('=x f 有两个不相等的实数根，即04)2(2>-=∆a 解得1-<a 或1>a即命题p ：1-<a 或1>a .……………………………… 8分q p ∧为真命题，则⎩⎨⎧≤≤->-<3211a a 或a ，解得3112≤<-<≤-a 或a ；∴实数a 的取值范围是[)(]2,113--⋃，.……………………………… 12分20．解：双曲线的离心率22221ab ac a c e +===．因为5e <a b ab 20422<<∴<∴．……………………………… 2分 (1) 因玩具枚质地是均匀的，各面朝下的可能性相等，所以基本事件),(b a 共有16个：（1，1），（1，2），（1，3），（1，4），（2，1），（2，2），（2，3），（2，4），（3，1），（3，2），（3，3），（3，4），（4，1），（4，2），（4，3），（4，4）．设“双曲线C 的离心率小于5”为事件A ，则事件A 所包含的基本事件为（1，1），（2，1），（2，2），（2，3），（3，1），（3，2），（3，3），（3，4），（4，1），（4，2），（4，3），（4，4）共有12个．故双曲线C 的离心率小于5的概率为431612)(==A P ．…………………………… 7分(2) ∵[][]6,1,6,1∈∈b a∴⎪⎩⎪⎨⎧<<≤≤≤≤a b b a 206161 所以以a 为横轴，以b 为纵轴建立直角坐标系，如图所示，21422155=⨯⨯-⨯=阴影S ，由几何概型可知，双曲线C 的离心率小于5的概率为2521=P ．……………………………… 12分21．解：（1）∵椭圆的上顶点与两个焦点构成边长为2的正三角形，32,22222=-=∴==∴c a b a c∴椭圆C 的标准方程为13422=+y x .……………………………… 4分 (2) 设直线l 的方程为)4(-=x k y ,设A （x 1，y 1），B （x 2，y 2）联立⎩⎨⎧=+-=1243)4(22y x x k y ，消去y 可得（0126432)43(2222=-+-+k x k x k∵直线l 与椭圆C 相交于A ，B 两点，∴0>∆由0)1264)(43(4)32(2222>-+-=∆k k k 解得412<k 设),(11y x A ,),(22y x B则34322221+=+k k x x ,3412642221+-=k k x x ……………………………… 7分211643324431264)1(16)(4)1()4()4(2222222221221221212121>++-+-+=++-+=--+=+=⋅k k k k k k k k x x k x x k x k x k x x y y x x OB OA解得196272>k ∴41196272<<k所以k 的取值范围是211433143321<<-<<-k 或k .……………………………… 12分22．解：（1）∵)(2ln )(2R a x x a x a x f ∈++-=，∴12)(22'+--=xa x a x f 当1=a 时，121)(,2ln )(2'+--=++-=xx x f x x x x f 2)1(,3)1('-===f k f曲线)(x f y =在点))1(,1(f 处的切线方程为)1(23--=-x y 即052=-+y x .……………………………… 3分（2）222222'))(2(212)(x a x a x x a ax x x a x a x f +-=--=+--=0,0>>x a ,由0)('>x f 得a x 2>，由0)('<x f 得a x 20<<)(x f ∴在(]a 2,0上为减函数，在()+∞,2a 上为增函数．……………………………… 5分①当210120≤<≤<a 即a 时，)(x f 在[]e ,1上为增函数． 12)1()(2+==∴a f a g 在(]a 2,0上为减函数，在()+∞,2a 上为增函数．…………… 7分②当22121ea e 即a <<<<时，)(x f 在[]a 2,1上为减函数，在(]e a ,2上为增函数． a a a a f a g 3)2ln()2()(+-==∴……………………………… 9分③当22ea e 即a ≥≥时，)(x f 在[]e ,1上为减函数． e ea a e f a g ++-==∴22)()(……………………………… 11分综上所述，⎪⎪⎪⎩⎪⎪⎪⎨⎧≥++-<<+-≤<+=)2(2)221(3)2ln()210(12)(22e a e e a a e a a a a a a a g ……………………………… 12分。

人教版高二上学期数学第一次月考文试题(解析版)

【详解】解：（1）由题意得，，
因为，所以解得，
所以的方程为，
（2）由题意可得直线方程为，设直线与椭圆交于，
将代入椭圆方程得，，即，
所以，
所以
【点睛】此题考查求椭圆的标准方程，考查直线与椭圆的位置关系，考查弦长公式的应用，考查计算能力，属于基础题
22.已知椭圆的焦点是F1(0，－1)，F2(0，1)，离心率e＝ .
（1）求椭圆的标准方程；
（2）设P在这个椭圆上且|PF1|－|PF2|＝1，求∠F1PF2的余弦值．
【答案】（1），（2）
【解析】
【分析】
（1）根据题意可得：，解得，从而可得椭圆的方程；
（2）由椭圆定义得：，结合题意可得：，再根据余弦定理可求得结果
【详解】解：（1）由已知设椭圆方程为，
【详解】由不等式的解集为，得无解，即对 , 恒成立，①当时，显然满足题意，②当时，有，解得：，综上，
故答案为：
【点睛】本题结合二次函数得性质，考查命题的真假，属于容易题.
三、解答题(本大题共6小题，满分70分)
17.当c<0时，若ac>bc，则a<b.请写出该命题的逆命题、否命题、逆否命题，并分别判断真假．
考点：本小题主要考查椭圆的标准方程，考查学生的推理能力.
点评：解决本小题时，不要忘记，否则就表示圆了.
15.若椭圆的离心率为，则的短轴长为___________．
【答案】
【解析】
【分析】
判断出椭圆的焦点在轴上，得出的值，根据离心率的概念可得，解出的值可得短轴长.
【详解】由椭圆得焦点在轴上，，，，
10.已知△ABC的顶点B、C在椭圆＋y2＝1上，顶点A是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC的周长是( )

高二文科数学周检测

付出总有回报一分耕耘一分收获高二文科数学周检测题1．集合A ＝{(x ，y )|y ＝a }，集合B ＝{(x ，y )|y ＝b x ＋1，b >0，b ≠1}，若集合A ∩B 只有一个子集，则实数a 的取值范围是( )A ．(－∞，1)B ．(－∞，1]C ．(1，＋∞)D ．R 2．函数y ＝(a 2－3a ＋3)a x 是指数函数，则有( )A ．a ＝1或a ＝2B ．a ＝1C ．a ＝2D ．a ＞0且a ≠1 3．若f (x )，则f (x )的定义域为( )．A ．⎝ ⎛⎭⎪⎫－120B ．⎝ ⎛⎦⎥⎤－12，0C ．⎝ ⎛⎭⎪⎫－12 D ．(0，＋∞) 4．已知实数a 、b满足等式a1123b⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭，下列五个关系式：①0<b <a ； ②a <b <0； ③0<a <b ； ④b <a <0； ⑤a ＝b .其中不可能成立的关系式有( )A ．1个B ．2个C ．3个D ．4个 5、下列说法中，正确的是( )①任取x ∈R 都有3x >2x ；②当a >1时，任取x ∈R 都有a x >a －x ；③y ＝(3)－x 是增函数；④y ＝2|x |的最小值为1；⑤在同一坐标系中，y ＝2x 与y ＝2－x 的图象对称于y 轴．A ．①②④B ．④⑤C ．②③④D ．①⑤6．若函数y ＝a x ＋b －1(a >0且a ≠1)的图象经过第二、三、四象限，则一定有( )A ．0<a <1，且b >0B ．a >1，且b >0C ．0<a <1，且b <0D ．a >1，且b <0 7．已知f (x )是定义在(－∞，＋∞)上的偶函数，且在(－∞，0]上是增函数，设a ＝f (log 47)，b ＝f ⎝ ⎛⎭⎪⎫log 123，c ＝f (0.2－0.6)，则a ，b ，c 的大小关系是( ) A ．c <a <b B ．c <b <a C ．b <c <a D ．a <b <c8．设0＜a ＜1，函数f (x )＝log a (a 2x －2a x －2)，则使f (x )<0的x 的取值范围是( )A ．(－∞，0)B ．(0，＋∞)C ．(－∞，log a 3)D ．(log a 3，＋∞)9．已知函数f (x )满足：x ≥4，则f (x )＝⎝ ⎛⎭⎪⎫12x ；当x ＜4时，f (x )＝f (x ＋1)，则f (2＋log 23)＝( )A.124B.112C.18D.3810．已知函数f (x )＝a x －1＋3(a >0且a ≠1)的图象过一个定点P ，且点P 在直线 mx ＋ny －1＝0(m >0，且n >0)上，则1m ＋4n 的最小值是( )．A ．12B ．16C ．25D ．2411、设函数f (x )定义在实数集上，f (2－x )＝f (x )，且当x ≥1时，f (x )＝ln x ，则有( )A ．f 13<f (2)<f 12B ．f 12<f (2)<f 13C ．f 12<f 13<f (2)D ．f (2)<f 12<f 1312．设函数f (x )的定义域为R ，f (x )＝⎩⎪⎨⎪⎧x ，0≤x ≤1，12x －1，－1≤x ＜0，且对任意的x ∈R 都有f (x＋1)＝f (x －1)．若在区间[－1，3]上函数g (x )＝f (x )－mx －m 恰有四个不同零点，则实数m 的取值范围是( )A ．0，12B ．0，14C ．0，12D ．0，14二、填空题：13．已知函数f (x )＝ln x －x ＋2有一个零点所在的区间为(k ，k ＋1)(k ∈N *)，则k 的值为________．14．计算：(log 25)2－4log 25＋4＋log 215＝________.15．对于任意实数a ，b ，定义运算“*”如下：a *b ＝⎩⎨⎧a (a ≤b )，b (a >b )，则函数f (x )＝log 12x－2)*log 2x 的值域为________．16．函数y ＝lg(3－4x ＋x 2)的定义域为M ，当x ∈M 时，则f (x )＝2x ＋2－3×4x 的最大值为________．三、解答题17．已知关于x 的一元二次方程x 2＋2mx ＋2m ＋1＝0.(1)若方程有两根，其中一根在区间(－1，0)内，另一根在区间(1，2)内，求m 的取值范围；(2)若方程两根均在(0，1)内，求m 的取值范围．18．定义在[－1,1]上的奇函数f(x)，已知当x∈[－1,0]时，f(x)＝14x a2x(a∈R)．(1)求f(x)在[0,1]上的最大值；(2)若f(x)是[0,1]上的增函数，求实数a的取值范围．。

厦门市2015—2016学年度第一学期高二年级质量检测数学(

厦门市2015—2016学年度第一学期高二年级质量检测数学（文科）参考答案一、选择题：（本大题共12小题，每小题5分，共60分）12.设11(,)A x y 、22(,)B x y ，由2(1)y x y k x ⎧=⎨=-⎩得222(21)0k x k x k -++=，即121x x ⋅=.又211222y x y x ⎧=⎪⎨=⎪⎩，∴21212()1y y x x ⋅=⋅=即121y y ⋅=-，∴12120x x y y ⋅+⋅=，即OA OB ⊥.设33(,)C x y 、44(,)D x y ，直线OA ：1y k x =，直线OB ：2y k x =，则121k k ⋅=-.由21y x y k x ⎧=⎨=⎩得00x y =⎧⎨=⎩或21111x k y k ⎧=⎪⎪⎨⎪=⎪⎩即21111(,)A k k ，同理22211(,)B k k .由221(2)4x y yk x ⎧-+=⎨=⎩得00x y =⎧⎨=⎩或211214141x k k y k ⎧=⎪+⎪⎨⎪=⎪+⎩即1221144(,)11k D k k ++，同理2222244(,)11k E k k ++.∴OA =，OB = OD =OE =∴221122221211111(1)(1)2(1)(1)12116161642OABODEk k OA OB S k k k k S OD OE ∆∆++++++====≥. 二、填空题：（本大题共4小题，每小题5分，共20分）13．,x R ∀∈21xx ≠+； 14．815y x =- ； 15．3λ<； 16．20．三、解答题：（本大题共6小题，共70分．解答应写出文字说明，或演算步骤）． 17．本题考查等差、等比数列的通项公式及前n 项和公式等基础知识，考查运算求解能力.考查化归与转化思想、方程思想．满分10分. 【解析】(Ⅰ)设等比数列{}n a 的首项为1a ，公比为q .364,32a a ==，解得12,1q a ==， ··································· 3分 1112n n n a a q --∴==. ······················································· 4分(Ⅱ)设等差数列{}n b 的首项为1b ，公差为d .4145b =+=，21b =，∴4224,d b b =-=即2d =，11=-b ， ·········· 6分∴23n b n =-， ··································································· 7分 ∴数列{}+n n a b 的前n 项和为11()(1)12n n n n b b a q T q +-=+-12(123)122n n n --+-=+- ···························································· 9分 2221n n n =+-- . ···································································· 10分18．本题考查正弦、余弦定理和解三角形等基础知识，考查运算能力、思维分析能力，考查化归与转化思想、方程思想、分类讨论思想．本题满分12分．【解析】(Ⅰ) 由正弦定理，结合条件：sin (sin sin c C a A b B ⋅⋅⋅＝＋(可得，2(a c b a b -⋅=⋅＋( ································· 2分22a b =＋22b b a =＋．222b a c ∴＋-， ··········································································· 4分2222a c ab b ==＋-，即 cos C =，0C π<<，6C π∴=． ········· 6分(Ⅱ)法一：由余弦定理，结合条件：32=a ，2c =, 又由(Ⅰ)知6C π=，可得 2222cos c a b ab C =+-，∴24122b =+-⋅，即2680b b -+=， ··········· 8分解得2b =或4b =，经检验，两解均有意义． ··········· 11分综上，ABC ∆周长为4+6+ ··· 12分法二：由正弦定理，结合条件：32=a ，2c =,又由(Ⅰ)知6C π=，可得1sin 2sin 2a C A c === ············································ 7分 a c > A C ∴> 3A π∴=或23π，从而2B π=或6π. ······························· 8分当2B π=时，ABC ∆为直角三角形，4b ∴=，ABC ∴∆周长为6+ 当6B π=时，ABC ∆为等腰三角形，2b c ∴==，ABC ∴∆周长为4+ 11分综上，ABC ∆周长为4+6+ ··· 12分 19．本题考查抛物线定义，直线与抛物线关系，考查运算求解能力．考查化归与转化思想、数形结合思想、分类讨论思想．本题满分12分．【解析】(Ⅰ)由题意得，M 到点（3,0）的距离与到直线3x =-的距离都等于半径，由抛物线的定义可知， C 的轨迹是抛物线，设其方程为22y px =，32p=， ∴M 的轨迹方程为212y x =． ··································· 3分 (Ⅱ)法一：显然斜率不为0，设直线l ：6x ty =+，11(,)A x y 、22(,)B x y2AP PB =，∴1122(6,)2(6,)x y x y --=-，∴122y y =-， ···················· 6分由2126y x x ty ⎧=⎨=+⎩得212720y ty --=∴12121272y y t y y +=⎧⎨⋅=-⎩， ································ 8分又122y y =-，∴ 121260.5y y t =⎧⎪=-⎨⎪=⎩或121260.5y y t =-⎧⎪=⎨⎪=-⎩ ， ······································ 10分∴ 直线l 的方程是212y x =-或212y x =-+． ·································· 12分法二：①当直线l 的斜率不存在时，直线l ：x =6，显然不成立． ················ 4分 ②当直线l 的斜率存在时，设直线l ：(6)y k x =-，11(,)A x y 、22(,)B x y ，2AP PB =， ∴1122(6,)2(6,)x y x y --=-，∴12218x x +=， ··············· 7分由212(6)y x y k x ⎧=⎨=-⎩得222212(1)360k x k x k -++=，∴21221212(1)36k x x k x x ⎧++=⎪⎨⎪⋅=⎩， ·· 9分 ∴121232x x k =⎧⎪=⎨⎪=±⎩······················································································ 11分 ∴直线l 的方程是212y x =-或212y x =-+． ·············· 12分20.本题考查等差等比数列的定义、性质，等差等比数列的综合运用，及求数列的前n 项和，考查运算求解能力．考查化归与转化思想、方程思想．本题满分12分. 【解析】（I ）13,,n n a a +成等差数列，1123,32(3),n n n n a a a a ++∴=+∴-=- ··· 2分即11323n n n n b a b a ++-==-，又131a -=，······································· 4分 ∴{}n b 是首项为1，公比为2的等比数列. ··································· 5分（II ）{}n b 是首项为1，公比为2的等比数列,∴132n n n b a -=-=，即123n n a -=+. ··················································· 7分又22log (26)log 2n n n c a n =-==, ··············································· 8分212111111()(21)(21)22121n n c c n n n n -+∴==--+-+, ······································· 9分 13352121111n n n T c c c c c c -+∴=+++111111(1)23352121n n =-+-++--+ ················································· 10分 111(1)2212n =-<+.······························································ 12分 21．本题考查解二次不等式、利用二次函数和基本不等式求最值，考查数学建模能力，信息处理能力和运算能力，考查化归转化思想、数形结合思想、函数方程思想和分类讨论思想．本题满分12分．【解析】（Ⅰ）设该企业计划在A 国投入的总成本为()Q x （亿元），则当010x ≤≤时，25()1644x x Q x =++，依题意：25()51644x x Q x =++≤, ············································· 1分即24600x x +-≤，解得106x -≤≤, ··················· 3分结合条件010x ≤≤，06x ∴≤≤.················· 4分（Ⅱ）依题意，该企业计划在A 国投入的总成本为25,010,1644()42,10.5x x x Q x x x x ⎧++≤≤⎪⎪=⎨⎪+->⎪⎩5分则平均处理成本为251,010,()1644421,10.5x x Q x x x x x x⎧++≤≤⎪⎪=⎨⎪-+>⎪⎩ ·········· 6分(i) 当010x ≤≤时，()51116444Q x x x x =++≥=5164x x =，即x =min()Q x x ⎛⎫= ⎪⎝⎭. ·············· 8分 (ii) 当10x >时， 22()42119914()520100Q x x x x x =-+=-+, ∴当1120x =即x =20时，min ()99100Q x x ⎛⎫=> ⎪⎝⎭. ············· 10分 ∴当x =min()Q x x ⎛⎫= ⎪⎝⎭. ···················· 11分答：（Ⅰ）该工艺处理量x 的取值范围是06x ≤≤.（Ⅱ）该企业处理量为亿元. ······························································································· 12分 22．本题考查曲线的轨迹方程、直线和椭圆的位置关系、弦长公式、定点定值问题等知识，考查运算求解能力，探究论证能力．考查化归与转化思想、数形结合思想、函数方程思想、分类讨论思想．本题满分12分．【解析】（I ）设M 的坐标为(,)x y ，则1A M k x =≠，2A M k x =≠，12=-(x ≠， ········································· 1分化简得点M的轨迹方程是221(2x y x +=≠． ····································· 3分（Ⅱ）①当直线l的斜率不存在时，PQ = ···································· 4分②当直线l 的斜率存在时，设11(,)P x y ，22(,)Q x y ，直线l 的方程为：(1)y k x =-，则2212(1)x y y k x ⎧+=⎪⎨⎪=-⎩得，2222(21)4220k x k x k +-+-=，∴212221224212221k x x k k x x k ⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩， · 6分222)1)2121k PQ k k +===+>++ ·· 7分综上所述，PQ． ··············· 8分（Ⅲ）假设点N 存在，由椭圆的对称性得，则点N 一定在x 轴上，不妨设点(,0)N n ，当直线l 的斜率存在时，由（Ⅱ）得212221224212221k x x k k x x k ⎧+=⎪⎪+⎨-⎪⋅=⎪+⎩， ∴22121212122(1)(1)[()1]21k y y k x k x k x x x x k ⋅=--=⋅-++=-+，11(,)NP x n y =-，22(,)NQ x n y =-，∴21212121212()()()NP NQ x n x n y y x x n x x n y y ⋅=-⋅-+⋅=⋅-+++⋅∴22222222222224(241)221212121k k k n n k n NP NQ n n k k k k --++-⋅=-+-=++++ ·· 10分对于任意的k ，0NP NQ ⋅=，∴22241020n n n ⎧-+=⎪⎨-=⎪⎩， ······························· 11分方程组无解，∴点N 不存在．综上所述，不存在符合条件的点N ． ············································· 12分。

陕西省西安市周至县重点中学2022-2023学年高二下学期4月月考文科数学试题及参考答案

高二数学（文科）一､单选题（共12题，每题5分）1.用反证法证明某命题时，对结论：“自然数a ，b ，c 中恰有一个是偶数”的正确假设为（）A.自然数a ，b ，c 中至少有两个偶数B.自然数a ，b ，c 中至少有两个偶数或都是奇数C.自然数a ，b ，c 都是奇数D.自然数a ，b ，c 都是偶数2.某单位为了落实“绿水青山就是金山银山”理念，制定节能减排的目标，先调查了用电量y （单位：千瓦·时）与气温x （单位：℃）之间的关系，随机选取了4天的用电量与当天气温，并制作了以下对照表：由表中数据得线性回归方程：2ˆˆyx a =-+，则由此估计：当某天气温为2℃时，当天用电量约为（）A.56千瓦·时B.62千瓦·时C.64千瓦·时D.68千瓦·时3.抛掷一枚均匀骰子2次，在下列事件中，与事件“第一次得到6点”不相互独立的是（）A.第二次得到6点B.第二次的点数不超过3C.第二次的点数是奇数D.两次得到的点数和是124.现在，很多人都喜欢骑“共享单车”，但也有很多市民并不认可.为了调查人们对这种交通方式的认可度，某同学从交通拥堵不严重的A 城市和交通拥堵严重的B 城市分别随机调查了20名市民，得到如下22⨯列联表：附：22(),()()()()n ad bc K n a b c d a b c d a c b d -==+++++++.P （K 2≥k ） 0.250.15 0.10 0.05 0.025 0.010 0.001 k1.3232.0722.7063.8415.0246.63510.828根据表中的数据，下列说法中正确的是（）A.没有95%以上的把握认为“是否认可与城市的拥堵情况有关”B.有99%以上的把握认为“是否认可与城市的拥堵情况有关”C.可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”D.可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”5.已知事件A ，B 相互独立，P （A ）=0.4，P （B ）=0.3，给出下列四个式子：①P （AB ）=0.12；②P （A B ）=0.18；③P （A B ）=0.28；④P （A B ）=0.42.其中正确的有（） A.4个 B.2个 C.3个 D.1个6.已知袋子内有6个球，其中3个红球，3个白球，从中不放回地依次抽取2个球，那么在已知第一次抽到红球的条件下，第二次也抽到红球的概率是（）A.0.5B.0.6C.0.4D.0.27.甲､乙两人独立地对同一目标各射击一次，其命中率分别为0.6，0.5，现已知目标被击中，则它是被甲击中的概率是（） A.0.45 B.0.6 C.0.65 D.0.75 8.证明不等式112(2)a a a a a +-<---≥所用的最适合的方法是（） A.综合法 B.分析法 C.间接证法 D.合情推理法9.执行如图所示的程序框图输出的结果是（）A.8B.6C.5D.310.一份数学单元试卷中有4个填空题，某同学答对每个题的概率都是45，那么，4个题中答对2个题的概率是（） A.16625 B.96625 C.192625 D.25662511.将正奇数按如图所示的规律排列，则第21行从左向右的第5个数为（）A.811B.809C.807D.80512.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽，周四丈八尺，高一丈一尺.问积几何？答曰：二千一百一十二尺.术曰：周自相乘，以高乘之，十二而一”.这里所说的圆堡瑽就是圆柱体，它的体积为“周自相乘，以高乘之，十二而一”.就是说：圆堡瑽（圆柱体）的体积为112V =⨯（底面圆的周长的平方⨯高），则由此可推得圆周率π的取值为（） A.3 B.3.1 C.3.14 D.3.2二､填空题（共4题，每题5分）13.复数i(12i)z =-（i 是虚数单位）的实部为__________.14.如图，EFGH 是以O 为圆心､半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内，用A 表示事件“豆子落在正方EFGH 内”，B 表示事件“豆子落在扇形OHE （阴影部分）内”，则（1）()P A =___________（2）()P B A =__________.15.“开心辞典”中有这样一个问题：给出一组数，要你根据规律填出后面的第几个数.现给出一组数：11315,,,,228432---，…，则第8个数可以是___________. 16.现有A ，B 两队参加关于“十九大”知识问答竞赛，每队3人，每人回答一个问题，答对者为本队赢一分，答错得0分.A 队中每人答对的概率均为23，B 队中3人答对的概率分别为221,,332，且各答题人答题正确与否之间互无影响，若事件M 表示A 队得2分“，事件N 表示”B 队得1分“，则P （MN ）=___________. 三､解答题（共6题）17.（10分）已知m R ∈，复数()()22231i z m m m =--+-. （1）实数m 取什么值时，复数z 为实数､纯虚数；（2）实数m 取值范围是什么时，复数z 对应的点在第三象限.18.（12分）某学校高三年级有学生1000名，经调查，其中750名同学经常参加体育锻炼（称为A 类同学），另外250名同学不经常参加体育锻炼（称为B 类同学），现用分层抽样方法（按A 类､B 类分两层）从该年级的学生中抽查100名同学.如果以身高达到165厘米作为达标的标准，对抽取的100名学生进行统计，得到以下列联表：（1）完成上表；（2）能否有犯错率不超过0.05的前提下认为体育锻炼与身高达标有关系？（2K 的观测值精确到0.001）.参考公式：()()()()()22n ad bc K a b c d a c b d -=++++，参考数据：19.（12分）（1）若,x y 都是正实数，且2x y +>，求证：12x y +<与12yx+<中至少有一个成立.（2）求证：()n N *>∈20.（12分）甲､乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，乙的中靶概率为0.9，求下列事件的概率：（1）两人都中靶；（2）恰好有一人中靶；（3）两人都脱靶； 21.（12分）求证：（1）222a b c ab ac bc ++≥++；（2）>22.（12分）某单位为了了解用电量y 度与气温C x 之间的关系，随机统计了某4天的用电量与当天气温. C 量(度)（1）求线性回归方程；（参考数据：442111120,440i ii i i x yx ====∑∑）（2）根据（1）的回归方程估计当气温为10C ︒时的用电量.附：回归直线的斜率和截距的最小二乘法估计公式分别为：1221ˆni ii nii x y nx ybxnx==-⋅=-∑∑，ˆˆay b x =-⋅.高二数学（文科）答案1.【答案】B2.【答案】A3.【答案】D4.【答案】D5.【答案】A6.【答案】C7.【答案】D8.【答案】B9.【答案】A 10.【答案】B11.【答案】B 12.【答案】A13.【答案】2 14.【答案】（1）.2π（2）.1415.【答案】13216.【答案】108117.【答案】（1）3m =（2）(1,1)m ∈-【解析】（1）由虚部为0求得使z 为实数的m 值，再由实部为0且虚部不为0求得使z 为纯虚数的m 值；（2）由实部与虚部均小于0求解. 解：（1）当210m -=，即1m =±时，复数()()22231z m m m i =--+-为实数；当2223010m m m ⎧--=⎨-≠⎩，即3m =时，复数()()22231z m m m i =--+-是纯虚数；（2）由题意，2223010m m m ⎧--<⎨-<⎩，解得11m -<<. ∴当(1,1)m ∈-时，复数z 对应的点在第三象限.本题考查复数的代数表示法及其几何意义，考查复数的基本概念，是基础题.18.【答案】（1）（2）不能在犯错误的概率不超过0.05的前提下认为体育锻炼与身高达标有关系.【解析】（1）由分层抽样的计算方法可求得积极参加锻炼与不积极参加锻炼的人数，填入表格中，根据表格中的总计及各项值求出其它值即可；（2）由公式计算出2K，与参考数据表格中3.841作比较，若小于3.841则不可以，若大于3.841则可以.（1）填写列联表如下：（2）K2的观测值为22100(40153510)75255050K⨯⨯-⨯=⨯⨯⨯≈1.333<3.841.所以不能在犯错误的概率不超过0.05的前提下认为体育锻炼与身高达标有关系.本题考查独立性检验，根据抽样方法进行计算填表，将数值代入公式求出2K，注意保留三位小数，注意观测值与概率之间的大小关系与趋势.19.【答案】（1）见解析（2）见解析【解析】试题分析：（1）本题证明结论中结构较复杂，而其否定结构简单，故可用反证法证明其否定不成立，以此来证明结论成立.（2）采用分析法从要证的结果入手去证明不等式即可.解析：（1）假设1x y +<2和1y x +<2都不成立，即1x y +≥2和1yx+≥2同时成立.∵x >0且y >0，∴1+x ≥2y ，且1+y ≥2x .两式相加得2+x +y ≥2x +2y ，∴x +y ≤2.这与已知条件x +y >2矛盾，∴1x y +<2和1yx+<2中至少有一个成立.（2）原式子等价于)*n N >∈，两边平方得到()4122221n n n n +>+++>+>22212n n n n -++>+，得证.20.【答案】（1）0.72（2）0.26（3）0.0221.【解析】分析：（1）利用基本不等式，即可证得222a b c ab bc ac ++≥++；（2）根据题意，利用分析法证明，寻找使不等式成立的充分条件即可. 详解：（1）2222222,2,2a b ab a c ac b c bc +≥+≥+≥，222a b c ab bc ac ∴++≥++；（2）要证>，只要证22>，只要证1313+>+只要证>只要证4240>，显然成立，故>点睛：本题主要考查了均值不等式的应用，考查不等式的证明方法，用分析法证明不等式，关键是寻找使不等式成立的充分条件，着重考查了推理与论证能力，属于中档试题. 22.【答案】（1）250y x =-+. （2）30度.【解析】分析：（1）求出,x y 的均值，再由公式，计算出系数的值，即可求出线性回归方程；10x =代入线性回归方程，计算出y 得值，即为当气温为10C 时的用电量.详解：（1）4421110,30,1120,440,2i ii i i x y x yx b ======∴=-∑∑把(10,30)代入回归方程得30210a =-⨯+，解得50a =.∴回归方程为250y x =-+；（2）当10x =时，30y =，估计当气温为10C 时的用电量为30度.点睛：本题主要考查了线性回归分析的实际应用问题，其中根据最小二乘法求解回归系数是解答的关键和计算的难点，着重考查了推理与运算能力，属于基础题.。

★2013年2月23日高二数学第4次周练(文科含答案)

★ 2013年2月16日晚2012—2013学年下学期第四次周练高二文科数学A 组（必做）1.（2011年高考文科)复数z=22ii-+(i 为虚数单位)在复平面内对应的点所在象限为（A ）第一象限 (B)第二象限 (C)第三象限 (D)第四象限【解析】因为22(2)34255i i iz i ---===+,故复数z 对应点在第四象限,选D. 2. （海南卷文科)复数512ii-=( ) A.2i - B.12i - C.2i -+ D.12i -+ 【解析】因为512i i-=5(12)25i i i +=-+,故选C. 3．设2,{|20},U R M x x x ==->，则U M ð=A ．[0，2]B ．()0,2C ．()(),02,-∞⋃+∞D ．(][),02,-∞⋃+∞【答案】A4.(全国)下面四个条件中，使a b >成立的充分而不必要的条件是（A ）1a b +＞（B ）1a b -＞（C ）22a b ＞（D ）33a b ＞【答案】A5．(北京) 如果,0log log 2121<<y x 那么A ．y< x<1B ．x< y<1C ．1< x<yD ．1<y<x【答案】D6.（陕西文）设0a b <<，则下列不等式中正确的是（）（A ） 2a b a b ab +<<<（B ）2a ba ab b +<<< （c ）2a b a ab b +<<< (D) 2a bab a b +<<< 【解】选B 根据不等式的性质，结合作差法，放缩法，基本不等式或特殊值法等进行比较．7．（2011陕西文）设抛物线的顶点在原点，准线方程为2x =-，则抛物线的方程是A ．28y x =-B ．24y x =-C ．28y x =D ．24y x =【答案】C8.（天津文）设变量x ，y 满足约束条件1,40,340,x x y x y ≥⎧⎪+-≤⎨⎪-+≤⎩则目标函数3z x y =-的最大值为A ．-4B ．0C ．43D ．4 【答案】D9．通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：男女总计爱好 40 20 60 不爱好 20 30 50 总计6050110由22()()()()()n ad bc K a d c d a c b d -=++++ 算得，22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表：2()p K k ≥0.050 0.010 0.001 k3.8416.63510.828参照附表，得到的正确结论是A ．有99%以上的把握认为“爱好该项运动与性别有关”B ．有99%以上的把握认为“爱好该项运动与性别无关”C ．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别有关”D ．在犯错误的概率不超过0.1%的前提下，认为 “爱好该项运动与性别无关” 【答案】A10．如图，正六边形ABCDEF 中，BA CD EF ++=（A ）0 （B ）BE（C ）AD （D ）CF 答案：D11．在△ABC 中，222sin sin sin sin sin A B C B C ≤+-，则A 的取值范围是（A ）(0,]6π（B ）[,)6ππ（C ）(0,]3π（D ）[,)3ππ答案：C解析：由222sin sin sin sin sin A B C B C ≤+-得222a b c bc ≤+-，即222122b c a bc +-≥，∴1cos 2A ≥，∵0A π<<，故03A π<≤，选C ．12．函数2cosxy =的最小正周期=T ． 13.(2011年高考江苏卷)设复数i 满足i z i 23)1(+-=+（i 是虚数单位），则z 的实部是____。

高二数学文科周五检测

高二数学文科周五检测一、选择题1、下列变量关系是相关关系的是（）①学生的学习态度与学习成绩之间的关系；②老师的执教水平与学生的学习成绩之间的关系； ③学生的身高与学生的学习成绩的关系；④家庭的经济条件与学生的学习成绩之间的关系． A ．①② B ．①③ C ．②③ D ．②④2、下列说法： ①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变； ②设有一个回归方程ˆ35y x =-，变量x 增加一个单位时，y 平均增加5个单位； ③线性回归方程ˆˆˆybx a =+必过(,)x y ； ④自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系； ⑤线性回归方程对应的直线ˆˆˆybx a =+至少经过其样本数据点1122(,),(,),,(,)n n x y x y x y 中的一个点；⑥在一个2×2列联中，由计算得213.079K =则有99%的把握确认这两个变量间有关系；其中错误的个数是（）A ．1B ．2C ．3D ．43、函数f (x )的定义域为R ，f (－1)＝2，对任意x ∈R ，f ′(x )＞2，则f (x )＞2x ＋4的解集为 ( )A ．(－1,1)B ．(－1，＋∞)C ．(－∞，－1)D ．(－∞，＋∞)4、用反证法证明命题：“若整系数一元二次方程20(0)ax bx c a ++=≠有有理根，那么,,a b c 中恰有一个是偶数时，下列假设中正确的是（）A ．假设,,a b c 都是偶数B ．假设,,a b c 都是奇数C ．假设,,a b c 至少有两个偶数D ．假设,,a b c 都是奇数或至少有两个偶数 5、已知：①正方形的对角线相等，②矩形的对角线相等，③正方形是矩形。

根据“三段论”推理出一个结论，则这个结论是（）A ．正方形的对角线相等B ．矩形的对角线相等C ．正方形是矩形D ．其它 6、已知复数122iz i+=-，则z 的共轭复数z =（）（A ）12i - （B ）2i + （C ）i - （D ）i7、i 是虚数单位，则238238i i i i ++++= （）A ．iB ．2iC ．4i -D ．44i -8、若复数312a iz i +=- （,a R i ∈是虚数单位），且z 是纯虚数，则2a i +等于( )A ． C ．．40 9、已知,x y R ∈，i 为虚数单位，且(2)1x i y i --=-+，则(1)x yi ++的值为（）A ．4B ．44i +C ．4-D ．2i 10、已知i 虚数单位，a 为实数，复数(2)(1)z a i i =-+在复平面内对应的点为M ，则“1a =”是“点M 在第四象限”的（）A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件图1…11、按照图1中的规律，第10个图形中圆点的个数为（）．A ．40B ．36C ．44D ．5212、定义在R 上的函数()f x ，如果存在函数()g x kx b =+(,k b 为常数)，使得()()f x g x ≥对一切实数x 都成立，则称()g x 为函数()f x 的一个承托函数.现有如下命题： ①对给定的函数()f x ，其承托函数可能不存在，也可能有无数个； ②()2g x x =为函数()2xf x =的一个承托函数；③定义域和值域都是R 的函数()f x 不存在承托函数. 下列选项正确的是 ( )A.①B.②C.①③D.②③二、填空题13、将正整数1,2,3,…，按照如图的规律排列，则100应在从左到右的第_________列． 14、已知为虚数单位，则= .15、关于x 的方程2(2)0x i x k i -+++=有实数根，则实数k =16、下面有四个命题：①若x 1，y 1，x 2，y 2∈R ，且x 1+y 1i ＞x 2+y 2i ，则x 1＞x 2，y 1=y 2=0；②若2x R Î，则x R Î；③ 若1122i i x y x y +=+（1212,,,x x y y ∈C ），则21x x =且21y y =；④若21x x =且21y y =，则1122i i x y x y +=+（1212,,,x x y y ∈C ）．其中正确命题的序号为 . 17、(2009山东卷文)已知函数321()33f x ax bx x =+++,其中0a ≠（1）当b a ,满足什么条件时,)(x f 取得极值?（2）已知0>a ,且)(x f 在区间(0,1]上单调递增,试用a 表示出b 的取值范围.1 2 3 6 5 4 7 8 91015 14 131211……。

盐城市2012—2013学年度高二数学文科调研测试

参考公式：样本数据 x1 ， x2 ，L ， xn 的方差 s =
2
1 [( x1 - x) 2 + ( x 2 - x) 2 + L + ( x n - x) 2 ] （ x 为样本平均数） n
一、填空题：本大题共 14 小题，每小题 5 分，共计 70 分.请把答案填写在答题卡相应位置上. 1． "x Î R ， sin x £ 1 的否定是 ▲ ．
1- x 1+ x + lg = lg1 = 0 ，\ 当 a = 1 时，函数 f ( x ) 为奇函数．…… 10 分 1+ x 1- x 必要性：由函数 f ( x ) 为奇函数，即 f ( x ) + f ( - x ) =0，
又 f ( x ) + f ( - x ) = lg
2a 2a 2a - 1 - x 2a - 1 + x \ lg( - 1) + lg( - 1) = lg( ) + lg( ) =0，化简得 (2a - 1) 2 = 1 ，Q a > 0 ， 1+ x 1- x 1+ x 1- x \ a = 1 ，\ 当函数 f ( x ) 为奇函数时， a = 1 ．…………………………………… 14 分（注：必要性的证明也可由定义域的对称性得到 a = 1 ）
1 1 1 n + +L + n > 2 3 2 -1 2
10． a ³ 4
(
)
13． 2 p 14．8 二、解答题：本大题共 6 小题,共计 90 分.
15．解: （1）当 a = 3 时， ( x - 3)( x + 1) £ 0 ，则解集 P 为 x -1 £ x £ 3} ．……………… 7 分（2）由题意，解集为 Q= x 0 £ x £ 2} ，所以 a ³ 2 ．……………………………………… 14 分 16．解：（1） f ( x ) = cos 2 x - sin 2 x + 2 3 sin x cos x = cos 2 x + 3 sin 2 x = 2 sin ç 2 x + 所以函数 f ( x ) 的最小正周期 T =

高二数学周测试卷(含答案解析)

（1）求证；
（2）求二面角的平面角的余弦值。(理科做）
求点F到平面ABE的距离。（文科做）
21.已知椭圆的，离心率为，是其焦点，点在椭圆上。
（Ⅰ）若，且的面积等于。求椭圆的方程；
（Ⅱ）直线交椭圆于另一点，分别过点作直线的垂线，交轴于点，
当取最小值时，求直线的斜率。
22.已知函数
（1）曲线在点处的切线方程为，求的值；
（2）当时，，试求的取值范围。
参考答案及评分标准
一、选择题:共12小题，每小题5分，共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
B
B
A
A
D
A
A
D
B
C
D
C
1.选B.【解析】∵ ，，∴ ，故选B.
2.选B.【解析】∵ ，对应的点为在第二象限，故选B.
……………………………………5分
（Ⅱ）
函数的图象为：
当时，，依题意，，则
∴ 的取值范围是 …………………………………………………………10分
18.（Ⅰ）∵ 由正弦定理得
∴
即，易知，且，
上式两边除以 ,得 ……………………………………6分
（Ⅱ）∵ ,∴ ，
由，又，，得
而
∴ …12分
19．（12分）
二、填空题共4小题，每小题5分，共20分.
13.填 .【解析】如图可知的最小值是．
14.填 .【解析】由题意得四面体是底面边长为的正三角形，侧棱垂直底面，且，，，则外接球球心在过底面中心垂直于底面的垂线上，且到底面的距离等于的一半，∴

赣州三中高二文科数学小周练 - 副本

赣州三中高二数学（文科）周练试题命题：方勤 2014.5班级：姓名：一、选择题1. 若复数11i a bi i +=+-，则a + b =（） A ．0 B ．1 C ．－1 D ．22. 已知函数(1),0()(1),0x x x f x x x x +<⎧=⎨-≥⎩，则函数()f x 的零点个数为（） A 、1 B 、2 C 、3 D 、43. 下列命题：①若p ，q 为两个命题，则“p 且q 为真”是“p 或q 为真”的必要不充分条件.②若p 为：02,2≤+∈∃⨯x x R ，则p ⌝为：02,2>+∈∀⨯x x R .③命题“032,2>+-∀x x x ”的否命题是“032,2<+-∃x x x ”.④命题“若,p ⌝则q ”的逆否命题是“若p ，则q ⌝”.其中正确结论的个数是 ( )A 、1B 、2C 、3D 、44. 已知函数：c bx x x f ++=2)(，其中：40,40≤≤≤≤c b ，记函数)(x f 满足条件：(2)12(2)4f f ≤⎧⎨-≤⎩为事件为A ，则事件A 发生的概率为 ( ) A ． 14 B ． 58 C ．38 D ．125. 已知⎩⎨⎧>-≤-=0,230,2)(2x x x x x f ,若ax x f ≥|)(|在]1,1[-∈x 上恒成立,则实数a 的取值范围是 ( )A.),0[]1(+∞--∞B.]0,1[-C.]1,0[D.)0,1[-6. 定义在R 上的函数()f x 满足下列三个条件：(1)1(3)()f x f x +=-；(2)对任意1236x x ≤<≤，都有12()()f x f x <；(3)(3)y f x =+的图像关于y 轴对称.则下列结论中正确的是 ( )A ．(3)(7)(4.5)f f f <<B ．(3)(4.5)(7)f f f <<C ．(7)(4.5)(3)f f f <<D ．(7)(3)(4.5)f f f <<二、填空题 7. 已知)(x f y =是定义在R 上的奇函数，当x ＜0时，x x x f 2)(2-=，则当x ≥0时，)(x f = .8. 已知幂函数()y f x =的图象过点12⎛ ⎝⎭，则2log (2)f =_______.9. 已知函数a x e x f x +-=2)(有零点，则a 的取值范围是 .10. 已知函数2()2ln f x ax x x =-+．若)(x f 有两个极值点，则a 的取值范围是 .三、解答题11.如图，矩形ABCD 中，ABE AD 平面⊥，2===BC EB AE ，G 是AC 中点，F 为CE 上的点，且ACE BF 平面⊥．（Ⅰ）求证：BCE AE 平面⊥；（Ⅱ）求三棱锥BGF C -的体积．12. 已知椭圆22:14x G y +=.过点（m ,0）作圆221x y +=的切线I 交椭圆G 于A ，B 两点. （1）求椭圆G 的焦点坐标和离心率；（2）将AB 表示为m 的函数，并求AB 的最大值.13.对于定义域为D 的函数)(x f y =，若同时满足下列条件：①)(x f 在D 内单调递增或单调递减；②存在区间[b a ,]D ⊆，使)(x f 在[b a ,]上的值域为[b a ,]；那么把)(x f y =（D x ∈）叫闭函数。

人教版高二数学(文科)选修1-2单元测试题(四)及答案

2010级高二数学（文科）选修1-2单元测试题（四）班级______________姓名______________一、选择题1．复数2i i +在复平面内对应的点位于A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2．复数()21i -的虚部为A ．－2B ．2C ．2i -D ．2i3．若复数1(1)m m i ++-是虚数，则实数m 满足A ．1m ≠B ．1m ≠-C ．1m =D ．1m =- 4．复数534+i 的共轭复数是 A ．3455i + B ．34i - C ．34i + D ．3455i -5．已知i 是虚数单位，m 、n ∈R ，且i 1i m n +=+，则ii m n m n +=- A ．1- B ．1 C ．i -D ．i6．已知集合{1,0,1}A =-，则 A ．1i A +∈ B ．21i A +∈ C ．31i A +∈ D ．41i A +∈7．设a 是实数，且211i i a +++是实数，则=a A ．21 B ．1 C ．23D ．28．下列空间几何体能较合适作为平面等边三角形的类比对象的是A ．正四棱锥B ．正方体C ．正四面体D ．球9．下列表述：①综合法是由因导果法；②综合法是顺推法；③分析法是执果索因法；④分析法是间接证法．则正确的语句个数有 A ．2 B ．3 C ．4 D ．110．用演绎法证明函数3y x =是增函数时的小前提是 A ．增函数的定义B ．函数3y x =满足增函数的定义C ．若12x x <，则12()()f x f x <D ．若12x x >，则12()()f x f x >11．定义集合A 、B 的一种运算：1212{,,}A B x x x x x A x B *==+∈∈其中，若{1,2,3}A =，{1,2}B =，则A B *中的所有元素数字之和为A ．9B ．14C ．18D ．212．将正奇数按下表排列： 1 35 7 9 11 13 15 17... ... ... ... (199)A ．第11行B ．第12行C ．第10列D ．第11列13．从222576543,3432,11=++++=++=‥‥‥中得出第n 个等式是 A ．2123...(21)n n ++++=- B ．2(1)...(21)(21)n n n n ++++-=+ C ．2(1)...(32)(21)n n n n ++++-=- D ．2(1)...(32)(21)n n n n ++++-=+14．已知数阵111213212223313233a a a a a a a a a ⎛⎫⎪⎪ ⎪⎝⎭中，每行的三个数依次成等差数列，每列的三个数也依次成等差数列，若224a =，则所有这九个数的和为 A ．16 B ．32C ．36D ．4015．如图所示的5×5正方形表格中尚有20个空格，若在每一个空格中填入一个正整数，使得每一行和每一列都成等差数列，则字母a 所代表的正整数是 A ．16 B ．17 C ．18 D ．19二、填空题 16．定义运算a b ad bc c d =-，若复数z 满足112zi z=；则复数z 为．17．已知复数z a bi =+（a 、R b ∈）,且满足ii b i a +=-+-35211，则复数z 在复平面内对应的点位于第象限．18．用火柴棒按下图的方法依次搭三角形：按图示的规律搭下去，则所用火柴棒根数n a 与所搭三角形的个数n 之间的关系式可以是；数列{}n a 的递推关系为：1n n a a +-= （n N +∈）．三、解答题19．对于等差数列{n a }有如下命题：“若{n a }为等差数列，且01=a ，s ．t 为互不相等的正整数，则有（s t a t a s )1()1-=-”．类比此命题，给出等比数列{n b }相应的一个正确命题．20．按要求完成下列各题：（Ⅰ）计算10)11(ii +-；（Ⅱ）已知：12,z z C ∈，求证：1212z z z z +=+．21．研究问题：“已知关于x 的不等式02>+-c bx ax 的解集为)2,1(，解关于x 的不等式02>+-a bx cx ”，有如下解法：解：由02>+-c bx ax ⇒0)1()1(2>+-x c x b a ，令xy 1=，则)1,21(∈y ，所以不等式02>+-a bx cx 的解集为)1,21(．参考上述解法：已知关于x 的不等式0<++++cx bx a x k 的解集为)3,2()1,2( --，求关于x 的不等式0111<--+-cx bx ax kx 的解集．22．设)(x f 是定义在实数集R 上的函数，且满足)()1()2(x f x f x f -+=+．已知15lg )2(,23lg)1(==f f ．（Ⅰ）通过计算(3)f ，(4)f ，(5)f ，……，由此猜测函数的周期T ，并据周期函数的定义给出证明；（Ⅱ）求(2012)f 的值．2010级高二数学（文科）选修1-1单元测试题（四）参考答案一、选择题1-----5 BAAAD 6-----10 BBCBB 11-----15 BCCCB二、填空题16．1i + 17．四 18．21n a n =+；2 三、解答题19．解：若{}n b 为等比数列，且11=b ，s ．t 为互不相等的正整数，则有11--=t ss t b b ．20．解：（Ⅰ）10210])1)(1()1([)11(i i i i i -+-=+-1)22(10-=-=i（Ⅱ）证明：设i y x z i y x z 222111,+=+=（1122,,,x y x y R ∈）则左i y y x x i y x i y x z z )()(2121221121+++=+++=+= i y y x x )()(2121+-+=右i y x i y x i y x i y x z z 2211221121-+-=+++=+=i y y x x )()(2121+-+=左 = 右，即2121z z z z +=+得证21．解：由于不等式0<++++c x bx a x k 的解集为)3,2()1,2( --，则方程0<++++cx bx a x k =0的根分别为-2,-1,2,3 由0111<--+-cx bx ax kx ,得0111<--+-x c x b x a k 因此，方程0111=--+-xc x b x a k 的根为: 31,21,1,21-- ∴不等式0111<--+-cx bx ax kx 的解集:)1,21()31,21( --22．解：（Ⅰ）23lg )1(=f 15lg )2(=f)2lg 3(lg 15lg )1()2()3(--=-=f f f 110lg 2lg 5lg ==+= 15lg 1)2()3()4(-=-=f f f15lg 115lg 1)3()4()5(-=--=-=f f f )15lg 1(15lg )4()5()6(---=-=f f f =－1 23lg 1015lg 15lg 1)5()6()7(==+-=-=f f f 由此猜测：6=T 证明：由⎩⎨⎧+-+=+-+=+)1()2()3()()1()2(x f x f x f x f x f x f得：)()3(x f x f -=+又)()3()6(x f x f x f =+-=+ 据定义知:6=T（Ⅱ）(2012)(63352)(2)lg15f f f =⨯+==。

2024-2025学年四川省内江市隆昌一中高二(上)开学数学试卷(文科)(含答案)

2024-2025学年四川省内江市隆昌一中高二（上）开学数学试卷（文科）一、单选题：本题共8小题，每小题5分，共40分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.设复数z 满足(1−i)z =3−i 3，则−z =( )A. 2+i B. 2−iC. 1−2iD. 1+2i 2.从小到大排列的数据1，2，3，7，8，9，10，11的第75百分位数为( )A. 172B. 9C. 192D. 103.已知向量a =(−2,m)，b =(1,1+m)，则“a ⊥b ”是“m =1”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.将函数f(x)=sin2x 的图象上所有的点向左平移π6个单位长度，得到的图象所对应的函数的解析式为( )A. y =sin (2x +π6)B. y =sin (2x +π3)C. y =sin (2x−π6)D. y =sin (2x−π3)5.甲、乙、丙3人独立参加一项挑战，已知甲、乙、丙能完成挑战的概率分别为13、13、14，则甲、乙、丙中有人完成挑战的概率为( )A. 15B. 13C. 25D. 236.圆心角为135°，面积为B 的扇形围成一个圆锥，若圆锥的全面积为A ，则A ：B 等于( )A. 11：8B. 3：8C. 8：3D. 13：87.科技是一个国家强盛之根，创新是一个民族进步之魂，科技创新铸就国之重器，极目一号(如图1)是中国科学院空天信息研究院自主研发的系留浮空器，2022年5月，“极目一号”Ⅲ型浮空艇成功完成10次升空大气科学观测，最高升空至9050米，超过珠穆朗玛峰，创造了浮空艇大气科学观测海拔最高的世界纪录，彰显了中国的实力，“极目一号”Ⅲ型浮空艇长53米，高18米，若将它近似看作一个半球，一个圆柱和一个圆台的组合体，轴截面图如图2所示，则“极目一号”Ⅲ型浮空艇的体积约为( )A. 2530πm 3B. 3016πm 3C. 3824πm 3D. 4350πm 38.如图，在三棱锥S−ABC 中，SA ⊥平面ABC ，AB =AC =2，∠BAC =120°，若三棱锥外接球的表面积为52π，则此三棱锥的体积为( )A. 1B. 3C. 2 3D. 6 3二、多选题：本题共3小题，共18分。

河南省洛阳市宜阳县第一高级中学2022-2023学年高二上学期第四次月考数学文科试题(含答案)

2022-2023学年河南省洛阳市宜阳第一高级中学高二（上）第四次月考数学试卷（文科）一､单选题（本大题共12题，每题5分，共60分）1.直线l 过点()1,2-且与直线2310x y -+=垂直，则l 的方程是（） A.3270x y ++= B.2350x y -+= C.3210x y +-= D.2380x y -+=2.设直线l 的方程为3410x y ++=，直线m 的方程为6830x y ++=，则直线l 与m 的距离为（） A.25 B.110 C.15 D.3103.()2,5P 关于直线0x y +=的对称点的坐标是（） A.()5,2 B.()2,5- C.()5,2-- D.()2,5--4.已知0a <，若直线1:210l ax y +-=与直线()2:140l x a y +++=平行，则它们之间的距离为（） 72 52 5 5725.已知，圆221:O x y m +=与圆222:420O x y y +++=外切，则m 的值为（）A.22B.642-C.22D.642+6.若直线210x y +-=是圆22()1x a y -+=的一条对称轴，则a =（） A.12 B.12- C.1 D.1- 7.若点()1,P a 到直线310ax y --=3a 的取值范围是（） A.230,230⎡--+⎣ B.6⎡-⎣C.6,6⎡-⎣D.26,26⎡-+⎣8.数学家默拉在1765年提出定理，三角形的外心，重心，垂心（外心是三角形三条边的垂直平分线的交点，重心是三角形三条中线的交点，垂心是三角形三条高的交点）依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后人称之为三角形的欧拉线，已知ABC 的顶点()()1,0,0,2,B C AB AC -=，则ABC 的欧拉线方程为（）A.2430x y --=B.2430x y ++=C.4230x y --=D.2430x y +-=9.点P 为圆22(1)2x y -+=上一动点，点P 到直线3y x =+的最短距离为（） A.22B.1 2 D.22 10.一束光线从点()2,3A 射出，经x 轴上一点C 反射后到达圆22(3)(2)2x y ++-=上一点B ，则AC BC +的最小值为（）A.32B.52C.42D.6211.古希腊几何学家阿波罗尼斯证明过这样一个命题：平面内到两定点距离之比为常数(0,1)k k k >≠的点的轨迹是圆，后人将这个圆称为阿波罗尼斯圆.若平面内两定点,A B 的距离为2，动点P 满足3PB PA=P 不在直线AB 上，则PAB 面积的最大值为（）A.1 3 C.2 D.2312.已知圆22(1)4x y -+=内一点()2,1P ，则过P 点的最短弦所在的直线方程是（） A.10x y --=B.30x y +-=C.30x y ++=D.2x =二､填空题（本大题共4题，每题5分，共20分）13.圆221:100C x y y +-=与圆222:10C x y +=的公共弦长为__________.14.已知实数,x y 满足直线l 的方程230x y ++=2221x y y +-+__________. 15.若圆224x y +=上恰有230x y m -+=的距离等于1，则m 的取值范围是__________. 16.过点()2,1与圆225x y +=相切的直线的方程为：__________.三､解答题（本大题共6题，共70分）17.（1）已知直线()1:2140l x m y +++=与直线2:320l mx y +-=平行，求实数m 的值（2）已知直线()()1:2110l a x a y ++--=与直线()()2:12320l a x a y -+++=垂直，求实数C 的值.18.直线34120x y -+=与坐标轴的交点是圆C 一条直径的两端点（1）求圆C 的方程；（2）圆C 的弦AB 2111,2⎛⎫⎪⎝⎭，求弦AB 所在直线的方程. 19.已知圆C 经过()()2,4,1,3两点，圆心C 在直线10x y -+=上，过点()0,1A 且斜率为k 的直线l 与圆C 相交于,M N 两点. （1）求圆C 的标准方程；（2）若12OM ON ⋅=（O 为坐标原点），求直线l 的斜率.20.已知三点()()()2,0,1,3,2,2A B C 在圆C 上，直线:360l x y +-=，（1）求圆C 的方程；（2）判断直线l 与圆C 的位置关系；若相交，求直线l 被圆C 截得的弦长.21.已知直线():2130l x ay a a R --+=∈与圆22:440C x y x y +--=相交于,A B 两点. （1）求直线l 过定点P 的坐标；（2）若直线l 斜率存在，且__________，求直线l 的方程.从以下三个条件中任选一个，补充在横线上，并求解.①直线l 平分圆C ；①弦AB 最短；①27AB =. 22.已知点(),x y 在圆22(2)(3)1x y -++=上. （1）求x y +的最大值；（2）求yx的最大值；（322245x y x y ++-+.答案和解析1.【答案】C 【解析】解：直线2310x y -+=的斜率为23，由垂直可得所求直线的斜率为32-， ∴所求直线的方程为()3212y x -=-+，化为一般式可得3210x y +-=故选：C . 2.【答案】B【解析】解：直线m 的方程可化为33402x y ++=，由两条平行直线间的距离公式知，2231121034-=+.故选：B . 3.【答案】C【解析】解：0,,x y y x x y +==-=-，所以对称点是()5,2--，故选：C . 4.【答案】A【解析】解：直线1:210l ax y +-=与直线()2:140l x a y +++=平行，所以()121a a +=⨯，且()2411,0a a ⨯≠-⨯+<，解得2a =-或1a =（舍），所以直线1:2210l x y -+=，直线2:2280l x y -+=，可得它们的距离22187242(2)d -==+-，故选：A . 5.【答案】B【解析】解：由两圆外切，圆()2:0,2O -，圆()1:0,0O ，且12,2r m r ，则圆心距为半径的和，所以有1222OO m ==，得642m =-B . 6.【答案】A【解析】解：圆22()1x a y -+=的圆心坐标为(),0a ，直线210x y +-=是圆22()1x a y -+=的一条对称轴，∴圆心在直线210x y +-=上，可得2010a +-=，即12a =.故选：A . 7.【答案】A【解析】解：由点到直线的距离公式及题意可得P 到直线的距离2223121(3)9a a a d a a--+==+-+，22139a a ++，整理可得：24260a a +-，解得230230a --+A . 8.【答案】D【解析】解：由于AB AC =，可得：ABC 的外心､重心､垂心都位于线段BC 的垂直平分线上，即ABC 的欧拉线即为线段BC 的垂直平分线.()()1,0,0,2B C -，BC ∴中点坐标为1,12⎛⎫- ⎪⎝⎭，直线BC 的斜率为()20201BC k -==--，设线段BC 垂直平分线的斜率为k ，则11,2BC k k k ⋅=-∴=-， ABC ∴的欧拉线的方程为：11122y x ⎛⎫-=-+ ⎪⎝⎭，整理得：2430x y +-=故选：D . 9.【答案】C【解析】解：点P 到直线3y x =+的最短距离为圆心到直线距离再减去半径. 圆22(1)2x y -+=圆心为()1,0，则圆心()1,0到直线:30l x y -+=的距离为22103221(1)d -+==+-，又圆的半径2r =所以点P 到直线:30l x y -+=的最短距离为2222=故选C .10.【答案】C【解析】解：圆22(3)(2)1x y ++-=的圆心()3,2-关于x 轴的对称点为()3,2P --，则52242AC BC AP r +-==故选：C . 11.【答案】B【解析】解：设经过点,A B 的直线为x 轴，AB 的方向为x 轴正方向，线段AB 的垂直平分线为y 轴，线段AB 的中点O 为原点，建立平面直角坐标系，则()()1,0,1,0A B -，设(),P x y ，2222(1)3,3,(1)PB x y PAx y -+==++整理得22410x y x +++=，即22(2)3x y ++=，即点P 的轨迹为以点()2,0-3的圆，如图所示：要使PAB 面积的最大值，只需点P 到(AB x 轴）的距离最大时，即为圆22(2)3x y ++=3时面积为12332⨯=B .12.【答案】B【解析】解：由题意得圆心()1,0O ，当所求弦与OP 垂直时，弦长最短，因为OP 的斜率为1，此时弦所在的直线斜率为1-，此时直线方程为3y x =-+，即30x y +-=. 故选：B . 13.【答案】6【解析】解：因为圆221:100C x y y +-=与圆222:10C x y +=，两式相减得，公共弦所在直线的方程1010y =，即1y =，因为圆心()20,0C ，半径210r =，所以圆心1C 到公共弦的距离为1d =，所以公共弦长为21016-=.故答案为6. 14.5【解析】解：直线l 的方程230x y ++=，可得23x y =--，所以22222221(23)21510105(1)55x y y y y y y y y +-+=--+-+=++++，当1y =-2221x y y +-+55. 15.【答案】()()6,22,6--⋃【解析】解：根据题意，圆224x y +=的圆心()0,0，半径为2，圆心()0,030x y m -+=的距离2m d =，若圆224x y +=上恰有230x y m -+=的距离等于1，则13d <<，即：132m <<，所以26m <<，解得：62m -<<-或26m <<，故答案为：()()6,22,6--⋃. 16.【答案】250x y +-=【解析】解：根据点()2,1在圆225x y +=上，故过点()2,1与圆225x y +=相切的直线的方程为25x y +=，即250x y +-=，故答案为：250x y +-=.由条件根据过圆222x y r +=上的一点()00,x y 的圆的切线方程为200x x y y r +=，可得结论.17.【答案】解：（1）根据题意，直线()1:2140l x m y +++=与直线2:320l mx y +-=平行，则()2310m m ⨯-+=，解得3m =-或2m =，当3m =-时，此时直线1:2240l x y -+=与直线2:3320l x y -+-=平行，当2m =时，此时直线1:2340l x y ++=与直线2:2320l x y +-=平行，故3m =-或2m =. （2）直线()()1:2110l a x a y ++--=与直线()()2:12320l a x a y -+++=互相垂直，所以()()()()211230a a a a +-+-+=，解得1a =±. 18.【答案】解：（1）由题意可得，()()0,34,0A B -AB 的中点32,2⎛⎫- ⎪⎝⎭为圆的圆心，直径5AB = 以线段AB 为直径的圆的方程22325(2)24x y ⎛⎫++-= ⎪⎝⎭；（2）圆C 的弦AB 211，设直线方程为()112y k x -=-，即102kx y k --+=， 23111k k --=+，所以0k =或34-，所以弦AB 所在直线的方程为12y =或3450x y +-=.19.【答案】解：设圆C 的方程为：222()()x a y b r -+-=，依题意得：222222(2)(4)(1)(3)1a b r a b r r ⎧-+-=⎪-+-=⎨⎪=⎩解得23,1a b r =⎧⎪=⎨⎪=⎩则圆C 的方程为：22(2)(3)1x y -+-=（2）设直线l 的方程为1y kx =+，设()()1122,,,M x y N x y ，将1y kx =+代入圆的方程并整理得：()()2214170k xk x +-++=，所以()121222417,11k x x x x k k++==++，所以()()()212121212241118121k k OM ON x x y y k x x k x x k+⋅=+=++++=+=+，即()24141k k k +=+，解得1k =，又当1k =时，Δ0>，所以1k =，即直线斜率为1.20.【答案】解：（1）设圆C 的方程为：220x y Dx Ey F ++++=，由题意得：24031002280D F D E F D E F ++=⎧⎪+++=⎨⎪+++=⎩，消去F 得：362D E D E -=⎧⎨-+=-⎩，解得：02D E =⎧⎨=-⎩，4F ∴=-，∴圆C 的方程为：22240x y y +--=.（2）由（1）知：圆C 的标准方程为：22(1)5x y +-=，圆心()0,1C ，半径5r =点()0,1C 到直线l 的距离2230161031d ⨯+-==+ 由d r <知：直线l 与圆C 相交；直线l 被圆C 截得的弦长为：2255102r d -=-=. 21.【答案】解：（1）由直线():2130l x ay a a R --+=∈得()()1230x a y ---=，由10230x y -=⎧⎨-=⎩，解得13,2x y =⎧⎪⎨=⎪⎩∴直线l 过定点31,2P ⎛⎫ ⎪⎝⎭（2）由圆22:440C x y x y +--=，得22(2)(2)8x y -+-=，圆C 的圆心()2,2C ，半径22r =若选①：直线l 平分圆C ，则直线l 过圆心,222130C a a ∴-⨯-+=，1,a ∴=∴直线l 的方程为220x y -+=.若选①：当直线l 与PC 垂直时弦长最短，由3212212PCk -==-， ∴直线l 的斜率为2-，故直线l 的方程为()3212y x -=--，即4270x y +-=，若选①：设圆心到直线l 的距离为d ，由27AB =22221,(7)8,12d AB r d d ⎛⎫∴+=∴+=∴= ⎪⎝⎭，22413114a aa --+=+，解得0a =或23a =-，∴直线l 的方程为1,3490x x y =∴+-=.22.【答案】解：（1）设x y z +=，即0x y z +-=，当直线和圆相切时，圆心()2,3C -到直线的距离23111z d --==+，即12z +21z =或21z =-，故x y +21. （2）设yk x=，则直线方程为0kx y -=，当直线和圆相切时，圆心()2,3-到直线的距离22311k d k+=+，即231280k k ++，6236233k---+，故y x 623-+；（32222245(1)(2)x y x y x y ++-+=++- 则根式的几何意义为圆上点到定点()1,2D -的距离，则22(12)(32)34CD =--+--=22245x y x y ++-+341.。

高二数学周测试卷（含答案）

2019-2020学年度文科数学周测试卷本试卷分第I卷和第II卷两部分，共150分，考试时间120分钟。

学校：___________姓名：___________班级：___________考号：分卷I一、选择题(共12小题,每小题5.0分，共60分)1.设集合M={xl(x+3)(x-2)<0},则MAN等于()A.(1.2)B.U.2JC.(2.3JD.[2.3]2.已知i为虚数单位，复数z=l+2i,z与5共辘，则zf等于()A.3B.V3C.V5D.53.(2O18・全国III)若sina=f则cos2a等于()A.5B.IC.~lD.4.为了得到函数y=3sin(2x+§,XGR的图象，只需把函数y=3sin(x+5.XER的图象上所有点的()A. 横坐标伸长到原来的2倍，纵坐标不变B.横坐标缩短到原来的?倍，纵坐标不变C. 纵坐标伸长到原来的2倍，横坐标不变D. 纵坐标缩短到原来的！倍，横坐标不变5. 设向量c=(2.0), h=(l,l).则下列结论中正确的是()A,lal=ISI B.a b=0 C.all b D.(a—b)b6.函数y=log a(x-l)+2(a>09Hl)的图象恒过点()A.(1.2)B.(2,2)C.(23)D.(4.4)7.圆"+尸=4截直线岳+y—2旧=0所得的弦长为()10.某中学有高中生3 500人，初中生1500人,为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为。

的样本，已知从高中生中抽取70人，则”为()A.100B. 150C.200D.25011.己知定义在R上的可导函数人x)的导函数为f(x),满足/VX/OO,且y(x+2)为偶函数，f(4)=l,则不等式f(x)<e的解集为()A.(一2,+cc)B. (O.+对C.(1,+oc)D.(4,+oo)12.己知直线/的参数方程为为参数.t£R)・极坐标系的极点是平而直角坐标系的原点。

高二数学周末作业(文科)

高二数学周末作业（文科）一、选择题1．(1－i)2·i ＝（） A ．2－2i B ．2+2i C ． 2 D ．－22．设复数ωω++-=1,2321则i =（）A ．ω-B ．2ωC ．ω1-D ．21ω3．复数4)11(i+的值是（）A ．4iB ．－4iC ．4D ．－44．在复平面上复数i,1,4+2i 所对应的点分别是A 、B 、C,则平行四边形ABCD 的对角线BD 的长为 ( )(A)5 (B)13 (C)15 (D) 175.在下列表格中,每格填上一个数字后,使每一行成等差数列,每一列成等比数列,则a+b+c 的值是( )1 2 0.5 1 a b c(A) 1 (B) 2 (C) 3 (D) 46.设,,a b c 大于0，则3个数：1a b +，1b c +，1c a +的值 ( )A 、都大于2B 、至少有一个不大于2C 、都小于2D 、至少有一个不小于27.已知'''1213243()cos ,()(),()(),()()f x x f x f x f x f x f x f x ====，。

'1()(),n n f x f x -=则2005()f x = （）A 、sin xB 、sin x -C 、cos xD 、 cos x - 8.函数4522++=x x y 的最小值为 ( )A 、1B 、25C 、2D 、3 二、填空题9．实数x 、y 满足（1–i ）x+(1+i)y=2,则xy 的值是 .10．已知复数z 与 (z +2)2－8i 均是纯虚数，则 z = ____________．11.平面内的1条直线把平面分成两部分，2条直线把平面分成4部分，3条相交直线但不共点的直线把平面分成7部分， n 条彼此相交而无3条直线共点的直线把平面分成_______部分。

12.若数列{a n }，(n ∈N *)是等差数列,则有数列b n =n a a a n+⋯++21(n ∈N *)也是等差数列，类比上述性质，相应地：若数列{C n }是等比数列,且C n ＞0(n ∈N *),则有d n =____________ (n ∈N *)也是等比数列。

高二数学试题(文科)WORD

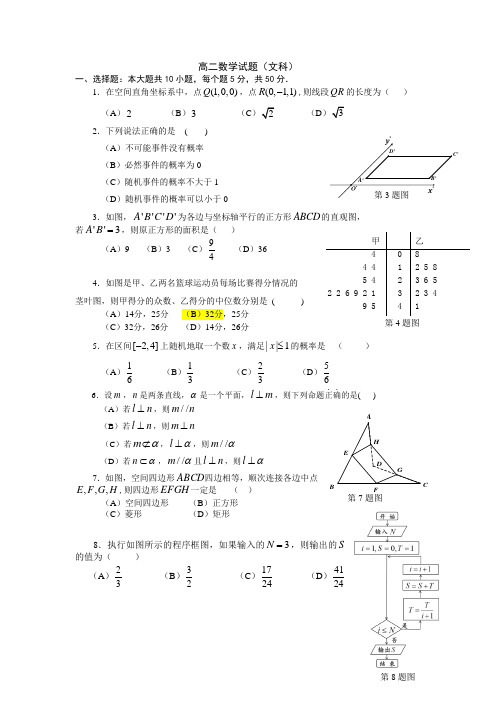
高二数学试题（文科）一、选择题：本大题共10小题，每个题5分，共50分．1．在空间直角坐标系中，点(1,0,0)Q ，点(0,1,1)R -,则线段QR 的长度为（）（A ）2（B ）3 （C ）2 （D ）32．下列说法正确的是 ( ) （A ）不可能事件没有概率（B ）必然事件的概率为0 （C ）随机事件的概率不大于1 （D ）随机事件的概率可以小于03．如图，''''A B C D 为各边与坐标轴平行的正方形ABCD 的直观图，若''3A B =，则原正方形的面积是（）（A ）9 （B ）3 （C ）94（D ）364．如图是甲、乙两名篮球运动员每场比赛得分情况的茎叶图，则甲得分的众数、乙得分的中位数分别是 ( )（A ）14分，25分（B ）32分，25分（C ）32分，26分（D ）14分，26分5．在区间[2,4]-上随机地取一个数x ，满足||1x ≤的概率是（）（A ）16 （B ）13（C ）23 （D ）566．设m ，n 是两条直线，α是一个平面，l m ⊥，则下列命题正确．．的是( ) （A ）若l n ⊥，则//m n（B ）若l n ⊥，则m n ⊥（C ）若m α⊄，l α⊥，则//m α （D ）若n α⊂，//m α且l n ⊥，则l α⊥7．如图，空间四边形ABCD 四边相等，顺次连接各边中点H G F E ,,,,则四边形EFGH 一定是（）（A ）空间四边形（B ）正方形（C ）菱形（D ）矩形8．执行如图所示的程序框图，如果输入的3N =，则输出的S 的值为（）（A ）23 （B ）32 （C ）1724 （D ）4124甲乙 4 0 84 4 1 25 85 4 2 36 52 2 6 9 2 13 2 3 49 5 4 1第4题图C'D'A'B'第3题图第8题图GHBCADEF第7题图9．一个四面体的顶点在空间直角坐标系O xyz -中的坐标分别是(0,0,0)，(3,0,3)，(0,3,3)，(3,2,0)，若以yOz 为投影面画出该三棱锥的正视图，则得到的正视图为（）（A ）（B ）（C ）（D ）10．已知区域2{(,)|04}x y y x Ω=≤≤-，函数2()()1x xa f x a a a -=--，其中 0a >且1a ≠，集合2{0|(1)(1)0}A m f m f m =>-+-≤，区域{(,)M x y =∈Ω |2,}y mx m m A =+∈，向区域Ω上随机投一点P ，点P 落在区域M 内的概率()P M =( )（A ）14ππ- （B ）22ππ- （C ）22π- （D ）14π-二、填空题：本大题共5个小题，每个题5分，共25分．11．某班有男生30名，女生20名，采用分层抽样的方法从这50名学生中抽取一个容量为5的一个样本，则应抽取的男生人数为________．12．阅读如图所示的程序，若输入的t 的值为6，则执行程序后输出的结果是________．13．某厂节能降耗技术改造后，生产某产品过程中记录的产量x (吨)与相应的生产能耗y (吨)的几组对应数据如下表：x 1 2 3 4 y22.534.5根据上表提供的数据，求得y 关于x 的线性回归方程为ˆy＝0.8x ＋ a ，那么 a 的值为________．14．三棱柱ABC A B C -111中，上、下两底面共有111111,,,,,AB BC CA A B B C C A 六条棱，从中任选两条棱，它们所在直线是异面直线的概率为_________．INPUT t IF t<＝4 THEN c ＝0.2 ELSEc ＝0.2＋0.1*(t －3) END IF PRINT c END15．如图，正方体 1111D C B A ABCD -，棱长为a ，下列命题正确的是：_________．（写出所有正确命题的编号）①P 点在BDC ∆1所在平面上运动，棱锥11D AB P -体积不变； ②直线1AC 与平面1BDC 的交点为三角形1BDC 的外心； ③若点M N L 、、分别是线段A B A D A A 11111、、上与端点不重合的三个动点，则MNL ∆必为锐角三角形；④若Q 为AA 1的中点，G 为底面A B C D 1111（包含边界）内的一个动点，且始终满足GQ A C ⊥1，则动点G 的轨迹长度为23a ．三、解答题：本大题共6小题，共75分．解答过程应写明文字说明、证明过程或推演步骤．16．（本小题满分12分）如图，棱长为1的正方体ABCD -A 1B 1C 1D 1中．（Ⅰ）求异面直线1A D 与AC 所成角的大小；（Ⅱ）求证：平面1ACB ⊥平面11BB D D ．17．（本小题满分12分）袋中共有6个除颜色以外完全相同的小球，其中有标记为A ，B 的红球2个，标记为a ，b ，c ，d 的白球4个，若从中任意选取2个球．（Ⅰ）记{,}A a （不考虑顺序）为一种选取结果，试写出所有选取结果，并指出所有结果的个数；（Ⅱ）试求所选的两个球中至少有一个红球的概率．ABCDD 1C 1B 1A 1QG第15题图BD 1C 1 B 1A 1CDA第16题图18．（本小题满分12分）如图，在四棱锥P ABCD -中，PA ⊥平面A B C D ，底面A B C D 是菱形，2P A A B ==，60BAD ∠= ，且M 为PA 中点．（Ⅰ）求证：//PC 平面MBD ；（Ⅱ）对线段PC 上任意一点G ，求证三棱锥G MBD -的体积为定值，并求出该值．19．（本小题满分12分）教育部、国家体育总局和共青团中央共同号召全国各级各类学校要广泛、深入地开展全国亿万大中学生阳光体育运动．为此，某校学生会对高二年级学生2013年6月这一个月时间内参加体育运动的情况进行统计，随机抽取了M 名学生作为样本，得到这M 名学生该月参加体育运动总时间的小时数．根据此数据作出了频数与频率的统计表和频率分布直方图（如图①）如下：分组序号 2013年6月参加体育运动总时间（小时）组中值（i a ）频数频率()i f1 [20,25)22.5 10 0.252 [25,30) 27.5 25n 3 [30,35) 32.5 mp4 [35,40)37.5 2 0.05合计——M1M BACD P G 第18题图a频率/组距2025303540参加体育运动小时数O（Ⅰ）求出表中M ，p 及图①中a 的值；（Ⅱ）现以这M 人为样本来估计总体，若该校高二学生有720人，试估计该校高二学生在2013年6月参加体育运动总时间不超过30小时的人数；（Ⅲ）该校数学兴趣小组利用算法流程（如图②），对样本数据作进一步统计分析，求输出的S 的值．20．（本小题满分13分）将如图①所示的直角梯形ABEF （图中数字表示对应线段的长度）沿直线CD 折成直二面角，连接部分线段后围成一个空间几何体，如图②所示．（Ⅰ）设M 是FB 的中点，求证：EM ⊥平面BDF ；（Ⅱ）求空间几何体ABCDFE 的表面积．第19题图图②图①第20题图图①①12111A B F E D C图② ②M C DB A FE21．（本小题满分14分）如图，在四面体A BCD -中，AD ⊥平面BCD ，BC CD ⊥，2AD =，22BD =．M是AD 的中点，P 是BM 的中点，点Q 在线段AC 上，且QC AQ 3=．（Ⅰ）求证：PQ AD ⊥；（Ⅱ）若45BDC ∠=︒，求直线CD 与平面ACB 所成角的大小；（Ⅲ）若1CD =，则在线段BD 上是否存在点E ，使得平面CPE ⊥平面CMB ？若存在，请通过计算找出点E 的位置；若不存在，请说明理由．DBACMPQ第21题图。

高二年级第一学期周考(四)文科直线与圆的方程

2012---2013学年度第一学期高二年级周考（四）数学（文）分值：100分时间：100分钟命题人：第I 卷（选择题共40分）一．选择题：本大题共10小题，每题4分，共40分，每小题只有一个正确答案.1. 圆22460x y x y +-+=的圆心坐标是（）A ．(2，3)B ．(－2，3)C ．(－2，－3)D ．(2，－3)2. 直线01=+-y x 与圆1)1(22=++y x 的位置关系是（）A ．相切B ．直线过圆心C ．直线不过圆心但与圆相交D ．相离3. 过点（1，0）且与直线x-2y-2=0平行的直线方程是（）A ．x-2y-1=0B ．x-2y+1=0C ．2x+y-2=0D ．x+2y-1=04. 两圆229x y +=和228690x y x y +-++=的位置关系是 ( )A ．相离B ．相交C ．内切D ．外切5. 已知直线3430x y +-=与直线6140x my ++=平行，则它们之间的距离是（）A ．1710 B ． 175 C ．8 D ．26．已知空间两点P 1(－1,3,5)，P 2(2,4，－3)，则|P 1P 2|等于 ( )A ．74B ．310C. 14D. 537．已知圆1C ：2(1)x ++2(1)y -=1，圆2C 与圆1C 关于直线10x y --=对称，则圆2C 的方程为（）A ．2(2)x ++2(2)y -=1B ．2(2)x -+2(2)y +=1C ．2(2)x ++2(2)y +=1D ．2(2)x -+2(2)y -=1 8. 经过圆2220x x y ++=的圆心C ，且与直线0x y +=垂直的直线方程是（）A ．10x y ++=B ．10x y +-=C ． 10x y -+=D ．10x y --=9. 两圆1C ：224470x y x y ++-+=，2C ：22410130x y x y +--+=的公切线有（）A ．2条B ．3条C ．4条D ．0条10. 若直线k 24kx y ++=与曲线2x4y -=有两个交点，则k 的取值范围是（） A ．[)∞+,1 B ． )43,1[-- C ． ]1,43(D ．]1,(--∞第II 卷（非选择题共60分）二．填空题：本大题共4小题，每题4分，共16分，把答案填在答题卡的相应位置.11. 点P (3，4，5)关于原点的对称点是________12. 不论m 为何实数，直线(1)10m x y -++=恒过定点13. 若直线m 被两平行线12:10:30l x y l x y -+=-+=与所截得的线段的长为22，则m 的倾斜角可以是①15 ②30 ③45 ④60⑤75 14. 如果直线y ＝kx ＋1与圆0422=-+++my kx y x 交于M 、N 两点，且M 、N 关于直线x ＋y ＝0对称，若),(b a P 为平面区域 ⎪⎩⎪⎨⎧≥≤-≥+-0001y my kx y kx 内任意一点，则11-+a b 的取值范围是三．解答题：本大题共4小题，共44分，前两小题每题10分，后两小题每题12分，解答应写出文字说明、证明过程或演算步骤，解答写在答题卡上指定的区域内.15. (本题满分10分)当m 为何值时，直线(2m 2＋m －3)x ＋(m 2－m )y ＝4m －1.(1) 倾斜角为45°；(2) 在x 轴上的截距为1．16．(本题满分10分)已知圆C 同时满足下列3个条件：①与y 轴相切； ②在直线x y =上截得弦长为 72； ③圆心在直线03=-y x 上．求圆C 的方程．17．(本题满分12分)已知圆C ：012822=+-+y y x ，直线l ：02=++a y ax .(1) 当a 为何值时，直线l 与圆C 相切；(2) 当直线l 与圆C 相交于A 、B 两点，且22=AB 时，求直线l 的方程.18．(本题满分12分)已知：以点C (t , 2t)(t ∈R , t ≠ 0)为圆心的圆与x 轴交于点O , A ，与y 轴交于点O , B ，其中O 为原点．（1）求证：△OAB 的面积为定值；（2）设直线y = –2x +4与圆C 交于点M , N ，若OM = ON ，求圆C 的方程．。

高二文数检测卷及答案

高二数学试题（文科）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列四个命题：其中为真命题的是（ C ） ①“若x+y=0,则x,y 互为相反数”的逆命题； ②“全等三角形的面积相等”的否命题；③“若q ≤1,则220x x q ++=有实根”的逆命题； ④“不等边三角形的三个内角相等”的逆否命题； A 、①② B 、②③ C 、①③ D 、③④ 2、设0<+b a ，且0>b ，则（ D ）A ．ab a b ->>22B ．ab a b -<<22C ．22b ab a <-<D ．22b ab a >->3．设a 、b 、c 是互不相等的正数，则下列不等式中不恒成立的是（）A ．c b c a b a -+-≤-B ．a a aa 1122+≥+C ．a a a a -+<+-+213D ．21≥-+-ba b a4．命题“存在04,2<-+∈a ax x R x 使为假命题”是命题“016≤≤-a ”的（ A ）A ．充要条件B ．必要不充分条件C ．充分不必要条件D ．既不充分也不必要条件5.与椭圆2214924yx+=有公共焦点，且离心率54e =的双曲线的方程是（ D ）(A)221916xy-= (B)221169xy-= (C)221916yx-= (D)221169yx-=6．已知斜率为2的直线l 过抛物线2y ax =的焦点F ，且与y 轴相交于点A ，若△OAF （O 为坐标原点）的面积为4，则抛物线方程为(D)A ．24y x = B ．28y x =C ．24y x =或24y x =- D ．28y x =或28y x =-7.过双曲线22221(0,0)x y a b ab-=>>的左焦点(,0)(0)F c c ->，作圆：2224ax y +=的切线，切点为E ，延长FE 交双曲线右支于点P ，若1()2OE OF OP =+，则双曲线的离心率为（ C ）O 2x1x y12 A ．102B ．105C ．10D ．28．与直线14-=x y 平行的曲线3y x x =+的切线方程是（ B ）A. 04=-y xB. 420x y -+=或024=--y xC. 024=--y xD. 04=-y x 或044=--y x9.已知函数()y f x =的导函数()f x '的图象如右图所示，则函数()y f x =的图象可能是（ D ）(A) (B) (C) (D)10．已知函数32()f x x bx cx =++的图象如图所示，则2221x x +等于(C) A ．32 B ．34 C ．38 D ．316二、填空题：本大题共5小题，每小题5分，共35分.11设a ，b ，c ，d 是1，2，3，4的任意排列,则2a+3b+4c+5d 的最小值是__30______12. 已知椭圆22149xy+=的上下两个焦点分别为12F F 、，点P 为该椭圆上一点，若1PF `2PF 为方程2250x mx ++=的两根，则m = -313设x ，y 为实数，满足3≤xy 2≤8,4≤x 2y ≤9，则x 3y4的最大值为________14已知0,0a b >>，则112ab ab++的最小值是____4_________15不等式| x-1|+|x-2|<2的解集_(-∞,2]∪[6,+∞),________OxyO xy Ox y x yOxyO16函数y=x x -+-4322的最_______17．下面四个图中有一个是函数321()1(0)3f x x ax a R a =-+∈≠且的导函数'()f x 的图象，则(1)f -等于 13-．三解答题：本大题共5小题, 共65分. 解答应写出文字说明、证明过程或演算步骤. 18（本小题满分12分）(1)解不等式1|31|2x <-<(2)已知902x <<，求2(92)y x x =-的最大值18、解：(1) 21|1033x x x ⎧⎫<<<<⎨⎬⎩⎭或-(2)法一：392(92)()273x x xy x x x -++=-⋅⋅≤=当且仅当92x x -=即3x =时取“＝”，此时有m ax 27y =法二：求导19 (12分) 函数f （x ）= 4x 3+ax 2+bx+5的图在x=1处的切线方程为12y x =-；（1）求函数f （x ）的解析式；（2）求函数f （x ）在 [—3，1]上的最值。