精选-高考数学专题十七圆锥曲线的几何性质精准培优专练理

合集下载

圆锥曲线几何性质精华

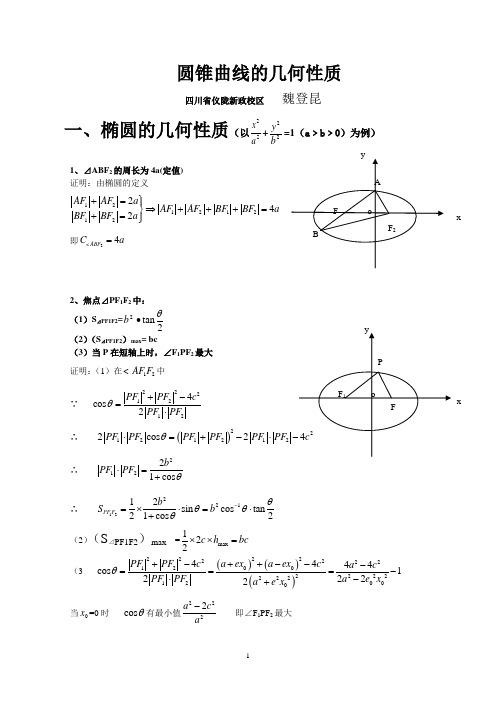
圆锥曲线的几何性质四川省仪陇新政校区魏登昆一、椭圆的几何性质（以22ax+22by =1（a ﹥b ﹥0）为例）1、⊿ABF 2的周长为4a(定值) 证明：由椭圆的定义12121212242AF AF a AF AF BF BF a BF BF a +=⎫⎪⇒+++=⎬+=⎪⎭即24ABF C a =2、焦点⊿PF 1F 2中：（1）S ⊿PF1F2=2tan2θ∙b（2）（S ⊿PF1F2）max = bc（3）当P 在短轴上时，∠F 1PF 2最大证明：（1）在12AF F 中∵ 22212124cos 2P F P F cP F P F θ+-=⋅∴ ()2121212c o s 2P F P F P F P F P F θ⋅=+-⋅∴ 21221cos bPF PF θ⋅=+∴ 1222112sin cos tan 21cos 2PF F bS b θθθθ-=⨯⋅=⋅+（2）（S ⊿PF1F2）max =m ax 122c h bc⨯⨯=（3 ()()()2222222212002222222120004444cos 12222PF PF ca ex a ex ca cPF PF a e x a e x θ+-++---===-⋅-+当0x =0时 cos θ有最小值2222a c a- 即∠F 1PF 2最大xx3、过点F 1作⊿PF 1F 2的∠P 的外角平分线的垂线，垂足为M ，则M 的轨迹是x 2+y 2=a 2证明：延长1F M 交2F P 于F ，连接OM 由已知有 1P F F P= M 为1F F 中点 ∴ 212O M F F ==()1212P F P F +=a所以M 的轨迹方程为 222x y a +=4、以椭圆的任意焦半径为直径的圆，都与圆x 2+y 2=a 2内切证明：取1PF 的中点M ，连接OM 。

令圆M 的直径1PF ，半径为∵ OM=()2111112222PF a PF a PF a r =-=-=-∴ 圆M 与圆O 内切∴ 以椭圆的任意焦半径为直径的圆，都与圆x 2+y 2=a 2内切5、任一焦点⊿PF 1F 2的内切圆圆心为I ，连结PI 延长交长轴于则 ∣IR ∣：∣IP ∣=e证明：证明：连接12,F I F I 由三角形内角角平分线性质有 ∵1212121222F R F R F R F R I R ce P IP FP FP F P F a +=====+ ∴IR P I= e6、以任一焦点弦为直径的圆与相应准线相离。

高考数学专题十七圆锥曲线的几何性质精准培优专练理

届高考数学专题十七圆锥曲线的几何性质精准培优专练理————————————————————————————————作者：————————————————————————————————日期：培优点十七圆锥曲线的几何性质1．椭圆的几何性质例1：如图，椭圆()2222+10x y a b a b =>>的上顶点、左顶点、左焦点分别为B 、A 、F ，中心为O ，其离心率为32，则:ABF BFO S S =△△（）A ．()23:3- B ．()233:3-C ．()23:2-D ．()233:2-【答案】B【解析】由ABF ABO BFO S S S =-△△△，得()():::ABF BFO ABO BFO BFO S S S S S ab bc bc =-=-△△△△△ 而32c a =，所以():233:3ABF BFO S S =-△△，故选B ．2．抛物线的几何性质例2：已知抛物线()2:20C y px p =>的焦点为F ，准线:1l x =-，点M 在抛物线C 上，点M 在直线:1l x =-上的射影为A ，且直线AF 的斜率为3-，则MAF △的面积为（） A ．3 B ．23C ．43D ．83【答案】C 【解析】设准线l 与x 轴交于点N ，所以2FN =，因为直线AF 的斜率为3-，所以60AFN ∠=︒，所以4AF =，由抛物线定义知，MA MF =，且60MAF AFN ∠=∠=︒，所以MAF △是以4为边长的正三角形，其面积为234434⨯=．故选C ．3．双曲线的几何性质例3：已知点P 是双曲线2213664x y -=的右支上一点，M ，N 分别是圆()22104x y ++=和()22101x y -+=上的点，则PM PN -的最大值为_________．【答案】15【解析】在双曲线2213664x y -=中，6a =，8b =，10c =，()110,0F ∴-，()210,0F ，12212PF PF a -==，11MP PF MF ≤+，22PN PF NF ≥-，112215PM PN PF MF PF NF ∴-≤+-+=．一、单选题1．抛物线()220y px p =>上的动点Q 到其焦点的距离的最小值为1，则p =（） A ．12B ．1C ．2D ．4【答案】C【解析】抛物线()220y px p =>上的动点Q 到其焦点的距离的最小值即到准线的最小值，很明显满足最小值的点为抛物线的顶点，据此可知：12p=，2p ∴=．本题选择C 选项． 2．设点1F ，2F 是双曲线2213y x -=的两个焦点，点P 是双曲线上一点，若1234PF PF =，则12PF F △的面积等于（） A ．53B ．315C ．45D ．210对点增分集训【答案】B【解析】据题意，1243PF PF =，且122PF PF -=，解得18PF =，26PF =．又124F F =，在12PF F △中由余弦定理，得222121212127cos 28PF PF F F F PF PF PF +-∠==．从而2121215sin 1cos 8F PF F PF ∠=-∠=，所以121156831528PF F S =⨯⨯⨯=△，故选B ． 3．经过椭圆2222x y +=的一个焦点作倾斜角为45︒的直线l ，交椭圆于M ，N 两点，设O 为坐标原点，则OM ON ⋅等于（） A ．3- B ．13±C ．13-D ．12-【答案】C【解析】椭圆方程为2212x y +=，2a =，1b =，1c =，取一个焦点()1,0F ，则直线方程为1y x =-，代入椭圆方程得2340x x -=，()0,1M -，41,33N ⎛⎫⎪⎝⎭，所以13OM ON =⋅-，故选C ．4．过抛物线()20y mx m =>的焦点作直线交抛物线于P ，Q 两点，若线段PQ 中点的横坐标为3，54PQ m =，则m =（）A ．4B ．6C ．8D ．10【答案】B【解析】设PQ 的坐标分别为()11,x y ，()22,x y ，线段PQ 中点的横坐标为3，则1232x x +=，125644m PQ x x p m =++=+=，由此解得6m =．故选B ． 5．已知双曲线()222210,0x y a b a b -=>>的右焦点为F ，点A 在双曲线的渐近线上，OAF △是边长为2的等边三角形（O 为原点），则双曲线的方程为（） A ．2213x y -=B ．2213y x -=C ．221412x y -=D ．221124x y -=【答案】B【解析】双曲线()222210,0x y a b a b -=>>的右焦点为F ，点A 在双曲线的渐近线上，OAF△是边长为2的等边三角形（O 为原点），可得2c =，3ba =，即223b a =，2223c a a -=，解得1a =，3b =，双曲线的焦点坐标在x 轴，所得双曲线的方程为2213y x -=，故选B ．6．如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道I 绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月飞行．已知椭圆轨道I 和Ⅱ的中心与F 在同一直线上，设椭圆轨道I 和Ⅱ的长半轴长分别为1a ，2a ，半焦距分别为1c ，2c ，则有（）A ．1212c c a a =B ．1122a c a c -<-C ．1212c c a a >D ．1122a c a c ->-【答案】C【解析】设圆形轨道Ⅲ的半径为R ，1122a c a c R -=-=，111111c a R Ra a a -==-，222221c a R R a a a -==-，由12a a >知1212c c a a >，故选C ． 7．已知双曲线221:14x C y -=，双曲线()22222:10x y C a b a b-=>>的左、右焦点分别为1F ，2F ，M 是双曲线2C 的一条渐近线上的点，且2OM MF ⊥，O 为坐标原点，若216OMF S =△，且双曲线1C ，2C 的离心率相同，则双曲线2C 的实轴长是（） A ．32B ．4C ．8D ．16【答案】D【解析】双曲线221:14x C y -=的离心率为52，设()2,0F c ，双曲线2C 一条渐近线方程为by x a=，可得222bc F M b a b ==+，即有22OM c b a =-=，由216OMF S =△，可得1162ab =，即32ab =，又222a b c +=，且52c a =，解得8a =，4b =，45c =，即有双曲线的实轴长为16．故选D ．8．已知F 是抛物线2:2C y x =的焦点，N 是x 轴上一点，线段FN 与抛物线C 相交于点M ，若2FM MN =，则FN =（） A ．1 B ．12C ．52D ．58【答案】D【解析】由题意得点F 的坐标为10,8⎛⎫⎪⎝⎭，设点M 的坐标()00,x y ，点N 的坐标(),0a ，所以向量：00,18FM x y ⎛⎫=- ⎪⎝⎭，()00,MN a x y =--，由向量线性关系可得：03x a =，00124y y -=-，解得：0112y =，代入抛物线方程可得：0612x =±，则64a =±，由两点之间的距离公式可得：58FN =．故选D ．9．已知椭圆()221112211:10x y C a b a b +=>>与双曲线()222222222:10,0x y C a b a b -=>>有相同的焦点1F ，2F ，点P 是曲线1C 与2C 的一个公共点，1e ，2e 分别是1C 和2C 的离心率，若12PF PF ⊥，则22124e e +的最小值为（）A ．92B ．4C ．52D ．9【答案】A【解析】由题意设焦距为2c ，椭圆长轴长为12a ，双曲线实轴为22a ，令P 在双曲线的右支上，由双曲线的定义1222PF PF a =-，① 由椭圆定义1212PF PF a +=，②又∵12PF PF ⊥，∴222124PF PF c +=，③ 22+①②，得2222121244PF PF a a +=+，④将④代入③，得222122a a c +=， ∴22222221122222121224559422222a a c c e e a a a a +=+=++≥+=，故选A ．10．已知F 为抛物线2:4C y x =的焦点，A ，B ，C 为抛物线C 上三点，当FA FB FC ++=0时，称ABC △为“和谐三角形”，则“和谐三角形”有（） A ．0个 B ．1个 C ．3个 D ．无数个【答案】D【解析】抛物线方程为24y x =，A ，B ，C 为曲线C 上三点，当FA FB FC ++=0时，F 为ABC △的重心，用如下办法构造ABC △，连接AF 并延长至D ，使12FD AF =，当D 在抛物线内部时，设()00,D x y ，若存在以D 为中点的弦BC ，设()11,B m n ，()22,C m n ，则1202m m x +=，1202n n y +=，1212BC n n k m m -=-，则21122244n m n m ⎧==⎪⎨⎪⎩，两式相减化为()1212124n n n n m m -+=-，121202BCn nkm m y-==-，所以总存在以D为中点的弦BC，所以这样的三角形有无数个，故选D．11．已知双曲线()22122:10,0x ya ba bΓ-=>>的左右焦点分别为1F，2F，椭圆222:134x yΓ+=的离心率为e，直线MN过点2F与双曲线交于M，N两点，若112cos cosF MN F F M∠=∠，且11F MeF N=，则双曲线1Γ的两条渐近线的倾斜角分别为（）A．30︒，150︒B．45︒，135︒C．60︒，120︒D．15︒，165︒【答案】C【解析】由题112cos cosF MN F F M∠=∠，112F MN F F M∴∠=∠，1122MF F F c∴==，由双曲线的定义可得|21|222MF MF a c a=-=-，∵椭圆222:134x yΓ+=的离心率为：43122e-==，∴1112F MeF N=＝，14NF c∴=，242NF c a=-，在12MF F△中，由余弦定理的()()222124224cos22222c c a c c aF F Mc c a c+---∠==⋅⋅-，在12NF F△中，由余弦定理可得：()()()2222212442164cos224222c c a c a c acF F Nc c a c c a+--+-∠==⋅⋅--，∵1212πF F M F F N∠+∠=，1212cos cos0F F M F F N∴∠+∠=，即()224222c a a c acc c c a-+-+=-，整理得，设双曲线的离心率为1e ，2113720e e ∴-+=，解得12e =或13（舍）．∴2224a b a +=，223a b ∴=，即3b a =．∴双曲线的渐近线方程为3y x =±， ∴渐近线的倾斜角为60︒，120︒．故选C ．12．已知P 为椭圆22143x y +=上一个动点，过点P 作圆()2211x y ++=的两条切线，切点分别是A ，B ，则PA PB ⋅的取值范围为（）A ．3,2⎡⎫+∞⎪⎢⎣⎭B ．356,29⎡⎤⎢⎥⎣⎦C ．56223,9⎡⎤-⎢⎥⎣⎦D ．)223,⎡-+∞⎣【答案】 C【解析】如图，由题意设2APB θ∠=，则1tan PA PB θ==，∴211cos2cos2cos2cos21cos2tan PA PB PA PB θθθθθθ+⋅==⋅=⋅-，设cos2t θ=，则()()()122132********t t PA PB t t tt t+⋅==-+-≥-⋅-=----，当且仅当211t t-=-，即12t =-时等号成立，此时cos212θ=-．又当点P 在椭圆的右顶点时，1sin 3θ=，∴27cos212sin 9θθ=-=，此时PA PB ⋅最大，且最大值71756979919+⨯=-．∴PA PB ⋅的取值范围是56223,9⎡⎤-⎢⎥⎣⎦，故选C ．二、填空题13．已知过抛物线22y x =-的焦点F ，且斜率为3的直线与抛物线交于A 、B 两点，则AF BF AB⋅=__________．【答案】12【解析】由22y x =-知1p =，由焦点弦性质112+2AF BF p==，而1111+22+AF BF AF BF p ABAF BFAF BF⋅⋅====． 14．已知椭圆2221x y a +=的左、右焦点为1F 、2F ，点1F 关于直线y x =-的对称点P 仍在椭圆上，则12PF F △的周长为__________．【答案】222+【解析】设()1,0F c -，()()2,00F c c >，1F 关于直线y x =-的对称点P 坐标为()0,c ，点P 在椭圆上，则：2201c a+=，则1c b ==，2222a b c =+=，则2a =，故12PF F △的周长为：121222222PF PF F F a c ++=+=+．15．P 为双曲线22149x y -=右支上一点，1F ，2F 分别为双曲线的左、右焦点，且120PF PF ⋅=，直线2PF 交y 轴于点A ，则1AF P △的内切圆半径为__________．【答案】2【解析】∵12PF PF ⊥，1APF △的内切圆半径为r ，∴112PF PA AF r -+=，∴2122PF a PA AF r -++=， ∴2124AF AF r =--，∵由图形的对称性知：21AF AF =，∴2r =．故答案为2．16．已知直线l 与椭圆()222210,0x y a b a b +=>>相切于第一象限的点()00,P x y ，且直线l 与x轴、y 轴分别交于点A 、B ，当AOB △(O 为坐标原点)的面积最小时，1260F PF ∠=︒(1F 、2F 是椭圆的两个焦点)，若此时在12PF F △中，12F PF ∠的平分线的长度为3a m，则实数m 的值是__________．【答案】52【解析】由题意，切线方程为00221x y x y ab+=，直线l 与x 轴分别相交于点A ，B ，20,0a A x ⎛⎫∴ ⎪⎝⎭，20,b B y ⎛⎫ ⎪⎝⎭，220012AOB a b S x y ∴=⋅△， 2200002221x y x y ab a b +=≥，0012x y ab ∴≥，AOB S ab ∴≥△，当且仅当0022x y a b ==时，AOB △（O 为坐标原点）的面积最小，设1PF x =，2PF y =，由余弦定理可得2222443c x y xy a xy =+-=-，243xy b ∴=，12213sin 6023PF F S xy b ∴=︒=△，2013223c y b ∴⨯⨯=， 203232b y b c ∴==，63c b ∴=，153a b ∴=，12F PF ∠的内角平分线长度为3a m，2131131322223x a y a b m m ∴⨯⨯⨯+⨯⨯⨯=， ()2133223a x y b m ∴⨯+=，22133153222293a ab b m m ∴⨯⨯=⨯=， 52m ∴=，故答案为52．三、解答题17．设常数2t >．在平面直角坐标系xOy 中，已知点()2,0F ，直线l ：x t =，曲线Γ：()280,0y x x t y =≤≤≥．l 与x 轴交于点A 、与Γ交于点B ．P 、Q 分别是曲线Γ与线段AB上的动点．（1）用t 表示点B 到点F 距离；（2）设3t =，2FQ =，线段OQ 的中点在直线FP ，求AQP △的面积；（3）设8t =，是否存在以FP 、FQ 为邻边的矩形FPEQ ，使得点E 在Γ上？若存在，求点P 的坐标；若不存在，说明理由．【答案】（1）2t +；（2）736；（3）存在，245,55P ⎛⎫ ⎪ ⎪⎝⎭．【解析】（1）方法一：由题意可知：设(),22B t t ，则()2282BF t t t =-+=+，∴2BFt =+；方法二：由题意可知：设(),22B t t ，由抛物线的性质可知：22pBF t t =+=+，∴2BF t =+；（2）()2,0F ，2FQ =，3t =，则1FA =，∴3AQ =，∴()3,2Q ，设OQ 的中点D ，32,22D ⎛⎫⎪ ⎪⎝⎭，3023322QFk -==--，则直线PF 方程：()32y x =--，联立()2328y x y x=--=⎧⎪⎨⎪⎩，整理得：2320120x x -+=，解得：23x =，6x =（舍去），∴AQP △的面积17733236S =⨯+=；（3）存在，设2,8y P y ⎛⎫ ⎪⎝⎭，2,8m E m ⎛⎫ ⎪⎝⎭，则2281628PF y yk y y ==--，2168FQ y k y -=，直线QF 方程为()21628y y x y -=-，∴()22164838284Q y y y y y --=-=，248384y Q y ⎛⎫- ⎪⎝⎭，，根据FP FQ FE +=，则22486,84y y E y ⎛⎫++ ⎪⎝⎭， ∴222488648y y y ⎛⎫⎛⎫+=+ ⎪ ⎪⎝⎭⎝⎭，解得：2165y =，∴存在以FP 、FQ 为邻边的矩形FPEQ ，使得点E 在Γ上，且245,55P ⎛⎫⎪ ⎪⎝⎭．18．与椭圆相交于A 、B 两点，2F 关于直线1l 的对称点E 在椭圆上．斜率为1-的直线2l 与线段AB 相交于点P ，与椭圆相交于C 、D 两点．（1）求椭圆的标准方程；（2）求四边形ACBD 面积的取值范围．【答案】（1）22184x y +=；（2）3232,93⎛⎤⎥⎝⎦．【解析】（1）由椭圆焦距为4，设()12,0F -，()22,0F ，连结1EF ，设12EF F α∠=，则tan b cα=，又222a b c =+，得sin b a α=，cos c a α=，()12122sin9012||sin sin 90F F c a ce b c a EF EF b c aa aαα︒∴======++︒-++，解得222a bc c b c =+⇒==，28a =，所以椭圆方程为22184x y +=．（2）设直线2l 方程：y x m =-+，()11,C x y 、()22,D x y ，由22184x y y x m +==-+⎧⎪⎨⎪⎩，得2234280x mx m -+-=，所以1221243283x x m m x x +=-=⎧⎪⎪⎨⎪⎪⎩，由（1）知直线1l ：y x =，代入椭圆得226,633A ⎛⎫-- ⎪⎝⎭，226,633B ⎛⎫⎪⎝⎭，得833AB =，由直线2l 与线段AB 相交于点P ，得446,633m ⎛⎫∈-⎪⎝⎭， ()()2222121212428164228212933m m CD x x x x x x m -=-=+-=-=-+，而21l k =-与11l k =，知21l l ⊥，211631229ACBD S AB CD m ∴=⨯=-+，由446,633m ⎛⎫∈-⎪⎝⎭，得232,03m ⎛⎤-∈- ⎥⎝⎦，所以2163323212,993m ⎛⎤-+∈ ⎥⎝⎦，四边形ACBD 面积的取值范围3232,93⎛⎤⎥⎝⎦．。

2020届高考数学专题十七圆锥曲线的几何性质精准培优专练理

培优点十七圆锥曲线的几何性质例1：已知点P 是椭圆22154x y +=上y 轴右侧的一点，且以点P 及焦点1F ，2F 为顶点的三角形的面积等于1，则点P 的坐标为________．【答案】2)或,2)1- 【解析】1F ，2F 是椭圆22154x y +=的左、右焦点，1c ==，则1(1,0)F -，2(1,0)F ，设(,)(0)P x y x >是椭圆上的一点，由三角形的面积公式可知1212S c y =⋅⋅=，即1y =，将1y =代入椭圆方程得21154x +=，解得x =∴点P的坐标为(,12)，(2)1-．例2：如图，已知抛物线24y x =的焦点为F ，过点F 且斜率为1的直线依次交抛物线及圆()22114x y -+=于点A ，B ，C ，D 四点，则AB CD +的值是（）二、抛物线的几何性质一、椭圆的几何性质A ．6B ．7C ．8D ．9【答案】B【解析】设()11,A x y ，()22,D x y ，代入抛物线方程消去y ，得2610x x -+=，∴126x x +=，则121212222117AB CD AF r DF r x x r x x x x +=-+-=++-=++-=++=．例3：过双曲线22115y x -=的右支上一点P ，分别向圆221:(4)4C x y ++=和圆222:(4)1C x y -+= 作切线，切点分别为M ，N ，则22PM PN -的最小值为．【答案】13【解析】圆221:(4)4C x y ++=的圆心为(4,0)-，半径为12r =；圆222:(4)1C x y -+=的圆心为(4,0)，半径为21r =，设双曲线22115y x -=的左右焦点为1(4,0)F -，2(4,0)F ，三、双曲线的几何性质连接1PF ，2PF ，1F M ，2F N ，可得2222221122|(())|||PM PN PF r PF r -=---2212(4)(1)PF PF =---22123PF PF =--1212(())3PF PF PF PF =-+-122()322313a PF PF c =+-≥⋅-=．当且仅当P 为右顶点时，取得等号，即最小值13．一、选择题1．抛物线的焦点为，点是上一点，，则（）A ．B ．C ．D ．【答案】A【解析】根据抛物线焦半径公式可得：，所以． 2．设椭圆的左焦点为，直线（）与椭圆交于，两点， 2:2(0)C y px p =>F 0(6,)A y C ||2AF p =p =4321||622pAF p =+=4p =22:14x C y +=F :l y kx =0k ≠C A B 对点增分集训则的值是（）A．B．C．D．【答案】C【解析】设椭圆的右焦点为，连接，，因为，，所以四边形是平行四边形，所以，所以．3．已知双曲线22:12xC y-=上任意一点为G，则G到双曲线C的两条渐近线距离之积为（）A．13B．23C．1D．43【答案】B【解析】渐近线方程为y=，设点(,)G x y，则1d=，2d=，∴2212|2|233x yd d-==．4．已知抛物线的准线与圆相切，则的值为（）A．B．C．18D．或【答案】D【解析】抛物线，即，准线方程为，因为抛物线的准线与圆相切，||| |AF BF+242F2AF2BFOA OB=2OF OF=2AFBF2||||BF AF=2||||||||4AF BF AF AF+=+=2y ax=22670x y y+--=a14128-14128-2y ax=21x ya=14ya=-21x ya=22(3)16x y+-=当时，，解得；当时，，解得． 5．定义平面上两条相交直线的夹角为：两条相交直线交成的不超过的正角．已知双曲线，当其离心率时，对应双曲线的渐近线的夹角的取值范围为（） A ． B ． C ． D ．【答案】D【解析】由题意可得：，∴，设双曲线的渐近线与轴的夹角为，双曲线的渐近线为，则．结合题意相交直线夹角的定义可得双曲线的渐近线的夹角的取值范围为．6．已知直线l 过点(3,2)P -且与椭圆22:12016x y C +=相交于A ，B 两点，则使得点P 为弦AB 中点的直线斜率为（）A ．35-B ．65-C ．65D ．35【答案】C【解析】设11(,)A x y ，22(,)B x y ，则221112016x y +=，222212016x y +=，两式相减12121212()()()()02016x x x x y y y y -+-++=．又由点(3,2)P -为弦AB 的中点，∴126x x +=，124y y +=-，0a >1344a +=14a =0a <1344a --=128a =-90︒2222:1(0,0)x y E a b a b-=>>e ∈[0,]6π[,]63ππ[,]43ππ[,]32ππ222221[2,4]c b e a a ==+∈22[1,3]b a∈x θb y x a =±[,]43ππθ∈[,]32ππ∴121265y y k x x -==-．7．设，是抛物线上的两个不同的点，是坐标原点，若直线与的斜率之积为，则（） A ．B ．以为直径的圆的面积大于C ．直线过抛物线的焦点D ．到直线的距离不大于【答案】D【解析】当直线的斜率不存在时，设，，由斜率之积为，可得，即， ∴的直线方程为，当直线的斜率存在时，设直线方程为，联立，可得，此时设，，则，，∴，即， ∴直线方程为，则直线过定点，则到直线的距离不大于．M N 2y x =O OM ON 12-||||OM ON +≥MN 4πMN 2y x =O MN 2MN 200(),M y y 200(,)N y y -12-20112y -=-202y =MN 2x =y kx m =+2y kx m y x=+⎧⎨=⎩20ky y m -+=11(,)M x y 22(,)N x y 12m y y k =2122mx x k=121212OM ON y y k k k x x m ⋅===-2m k =-2(2)y kx k k x =-=-MN (2,0)O MN 28．椭圆与双曲线焦点相同，为左焦点，曲线与在第一象限，第三象限的交点分别为，，且，则当这两条曲线的离心率之积最小时，双曲线有一条渐近线方程是（）A ．B ．C ．D【答案】C【解析】设双曲线的右焦点为，由题意点与点关于原点对称，因此，又，所以，由椭圆与双曲线定义可得，，所以，，根据余弦定理可得，即，化简得，2222:1(0)x y a b a b Γ+=>>2222:1(0,0)x y m n m nΩ-=>>F ΓΩA B 23AFB π∠=20x y -=20x y +=0x -=0y +=1F A B 1||||AF BF=23AFBπ∠=13FAF π∠=1||||2AF AF a +=1||||2AF AF m -=||AF a m =+1||AF a m =-2221111||||||2||||cos FF AF AF AF AF F AF =+-∠2224()()2()()cos3c a m a m a m a m π=++--+-22243cm a =+≥=所以离心率乘积为，当且仅当①时，取等号，由，所以，所以②，再将①②代入可得，所以双曲线的渐近线方程为或．二、填空题9．已知抛物线24x y =的焦点为F ，点A 在x 轴的正半轴上，过AF 的直线与抛物线在第一象限交于点B ，与抛物线的准线l 交于点C ，若2AB BF =，则FC =．【答案】10【解析】由题可知(0,1)F ，设点(,0)A a ，00(,)B x y ，则0000(,)2(,1)x a y x y -=--，解得03a x =，023y =，代入抛物线24x y =，得2893a =，解得a =故A ，可得5AF =，根据对称性得，5AC =，所以10FC FA AC =+=．10．已知椭圆（）的离心率为椭圆上的一个动点，则与定点连线距离的最大值为．【答案】【解析】椭圆（）的离心率，可得， 22c c c am am ⋅=≥223m a =2222a b mn -=+2222243c m b m n --=+223b n =2222a b m n -=+222m n =0x =0x +=2221y x a+=1a >e =P P (1,0)B -522221y x a+=1a >5e =5a =解得，椭圆方程为，设，则与定点，当时，取得最大值．三、解答题11．已知抛物线C 的方程22(0)px p y =>，焦点为F ，已知点P 在C 上，且点P 到点F 的距离比它到y轴的距离大1．（1）试求出抛物线C 的方程；（2）若抛物线C 上存在两动点,M N （,M N 在对称轴两侧），满足OM ON ⊥（O 为坐标原点），过点F 作直线交C 于,A B 两点，若AB MN ∥，线段MN 上是否存在定点E ，使得||||4||EM EN AB ⋅=恒成立?若存在，请求出E 的坐标，若不存在，请说明理由．【答案】（1）24y x =；（2）存在，(4,0)E ．【解析】（1）因为P 到点F 的距离比它到y 轴的距离大1，由题意和抛物线定义，12p=，所以抛物线C 的方程为24y x =，（2）由题意，0MN k ≠，设211(,)4y M y ，22221(,)()4y N y y y >，由OM ON ⊥，得1216y y =-，a =2215y x +=(cos )P θθP (1,0)B -=52==1cos 4θ=52①若直线MN 斜率存在，设斜率为k ，直线124:M k y y N =+，112124()4y y y x y y -=-+，整理可得124(4)y x y y =-+，直线:AB (1)y k x =-，与C 联立得2440ky y k --=，故可得21||4(1)AB k=+，若点E 存在，设点E 坐标为00(,)x y ，))0120||||y EM E y N y y ⋅=--200214(1)(16)y y k k =+-+， ||||4||EM EN AB ⋅=时，20041616y y k -+=，解得00y =或04y k=（不是定点，舍去），则点E 为(4,0)，经检验，此点满足24y x <，所以在线段MN 上，②若斜率不存在，则||4AB =，||||4416EM EN ⋅=⋅=，此时点(4,0)E 满足题意，综上所述，定点E 为(4,0)．12．设椭圆的左、右焦点分别为，，下顶点为，为坐标原点，点到直线的距离为，为等腰直角三角形．（1）求椭圆的标准方程；（2）直线与椭圆交于，两点，若直线与直线的斜率之和为，证明：直线恒过定点，并求出该定点的坐标．【答案】（1）；（2）见解析．【解析】（1）由题意可知：直线的方程为，即， 2222:1(0)x y C a b a b+=>>1F 2F A O O 2AF 212AF F ∆C l C M N AM AN 2l 2212x y +=2AF 1x y c b+=-0bx cy bc -++=，因为为等腰直角三角形，所以，又，可解得，，所以椭圆的标准方程为．（2）证明：由（1）知，当直线的斜率存在时，设直线的方程为，代入，得．所以，即，设，，则，，因为直线与直线的斜率之和为，所以，整理得，所以直线的方程为，显然直线经过定点，当直线的斜率不存在时，设直线的方程为，因为直线与直线的斜率之和为，设，则，2bc a ==12AF F ∆b c =222a b c =+a =1b =1c =C 2212x y +=(0,1)A -l l (1)y kx t t =+≠±2212x y +=222(12)4220k x ktx t +++-=2222164(12)(22)0k t k t ∆=-+->2221t k -<11(,)M x y 22(,)N x y 122412kt x x k+=-+21222212t x x k -=+AM AN 2121212121111AM AN y y kx t kx t k k x x x x +++++++=+=+()12212(1)(1)422222t x x t kt k k x x t +++⋅=+=-=-1t k =-l 1(1)1y kx t kx k k x =+=+-=-+(1)1y k x =-+(1,1)l l x m =AM AN 2(,)M m n (,)N m n -所以，解得，此时直线的方程为，显然直线也经过该定点，综上，直线恒过点．1122AM AN n n k k m m m+-++=+==1m =l 1x =1x =(1,1)l (1,1)。

方法技巧专题07 圆锥曲线的概念及其几何性质(解析版)

方法技巧专题7 圆锥曲线的概念及其几何性质解析版一、圆锥曲线的概念及其几何性质知识框架二、圆锥曲线的定义、方程【一】圆锥曲线的定义1、椭圆（1）秒杀思路：动点到两定点(距离为2c )距离之和为定值(2a )的点的轨迹；（2）秒杀公式：过抛圆的一个焦点作弦AB ,与另一个焦点F 构造FAB ∆，则FAB ∆的周长等于a 4。

（3） ①当c a 22>时，表示椭圆；②当c a 22=时，表示两定点确定的线段；③当c a 22<时，表示无轨迹。

2、双曲线（1）秒杀思路： ①双曲线上任意一点到两焦点距离之差的绝对值是常数2a ;②注意定义中两个加强条件:（I ）绝对值; （II ）22a c <； ③加绝对值表示两支(或两条),不加绝对值表示一支(或一条);（2）秒杀公式：过双曲线的一个焦点作弦AB （交到同一支上），与另一个焦点F 构造FAB ∆，则FAB ∆的周长等于AB a 24+。

（3） ①当22a c <时，表示双曲线； ②当22a c =时，表示以两定点为端点向两侧的射线；③当22a c >时，无轨迹； ④当20a =时表示两定点的中垂线。

3、抛物线（1）秒杀思路：到定点(焦点)距离等于到定直线(准线)距离。

所以，一般情况下,抛物线已知到焦点的距离需转化为到准线的距离,已知到准线的距离需转化为到焦点的距离。

（2）秒杀公式一：焦点在x 轴上的圆锥曲线,曲线上的点到同一个焦点的距离成等差数列，则横坐标成等差数列，反过来也成立。

（3）秒杀公式二：作过抛物线焦点且倾斜角为︒60或︒120的弦,两段焦半径分别为:32,2pp .1. 例题【例1】设P 是椭圆2212516x y +=上的点,若21,F F 是椭圆的两个焦点,则12PF PF +等于 ( )A.4B.5C.8D.10【解析】利用椭圆的定义得12PF PF +=102=a ,选D 。

【例2】已知椭圆C :22194x y +=,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为B A ,,线段MN 的中点在C 上,则||||AN BN += .【解析】如图,22QF BN =,12QF AN =,||||AN BN +=124)(221==+a QF QF .【例3】已知双曲线122=-y x ,点21,F F 为其两个焦点,点P 为双曲线上一点,若21PF PF ⊥,则21PF PF +的值为_______.【解析】,8,2222121=+=-r r r r 得21PF PF +=32. 【例4】设椭圆1C 的离心率为135,焦点在x 轴上且长轴长为26,若曲线2C 上的点到椭圆1C 的两个焦点的距离的差的绝对值等于8,则曲线2C 的标准方程为 ( )A.1342222=-y xB.15132222=-y xC.1432222=-y xD.112132222=-y x【解析】由双曲线定义得4=a ，5=c ，3=b ，选A 。

高考数学必做61道圆锥曲线问题——圆锥曲线性质大全.doc

高考数学必做61道圆锥曲线问题——圆锥曲线性质大全.doc
高考数学必做 61 道圆锥曲线问题——圆
锥曲线性质大全
一、神奇曲线，定义统一
01. 距离和差，轨迹椭双
02. 距离定比，三线统一
二、过焦半径，相关问题
03．切线焦径，准线作法
04. 焦点切线，射影是圆
05. 焦半径圆，切于大圆
06. 焦点弦圆，准线定位
07. 焦三角形，内心轨迹
三、焦点之弦，相关问题
08．焦点半径，倒和定值
09．正交焦弦，倒和定值
10. 焦弦中垂，焦交定长
11. 焦弦投影，连线截中
12. 焦弦长轴，三点共线
13. 对焦连线，互相垂直
14. 相交焦弦，轨迹准线
15. 相交焦弦，角分垂直
16. 定点交弦，轨迹直线
17. 焦弦直线，中轴分比。

圆锥曲线的定义、方程与性质(题型归纳)

圆锥曲线的定义、方程与性质【考情分析】1.考查特点:(1)圆锥曲线的方程与几何性质是高考的重点,多以选择题、填空题或解答题第(1)问的形式命题,难度中等;(2)直线与圆锥曲线的位置关系是命题的热点,尤其是有关弦长计算及存在性问题,运算量大,能力要求高,突出方程思想、转化化归与分类讨论思想方法的考查.2.关键能力:逻辑思维能力、运算求解能力以及创新能力.3.学科素养:逻辑推理、直观想象、数学运算.【题型一】圆锥曲线的定义及标准方程【典例分析】1（2021·山东省实验中学高三模拟）已知双曲线22525x y -=上一点P 到其左焦点F 的距离为8，则PF 的中点M 到坐标原点O 的距离为（）A ．9B ．6C ．5D ．4【答案】A【解析】由22525x y -=，得221255x y -=，则2225,5a b ==，所以230c =，所以5,a b c ===，设双曲线的右焦点为1F ，因为P 到其左焦点F 的距离为85a c <+=+P 在双曲线的左支上，所以1210PF PF a -==，所以118PF =，因为M 为PF 的中点，O 为1FF 的中点，所以1192OM PF ==，故选：A 2．已知抛物线()220y px p =>的焦点为F ，准线为l ，若点A 在l 上，点B 在抛物线上，l 与x 轴的交点为C ，ABF是正三角形，且四边形ABFC 的面积是，则p =（）A ．1B ．32C ．2D ．3【答案】C【解析】由抛物线的定义及ABF 为正三角形，可知//AB x 轴，所以60AFC ︒∠=，从而可知2AB p =，AC =，又因为四边形ABFC 的面积是，所以有22p p+=2p =.故选：C.【提分秘籍】【变式演练】1．（2021·江苏金陵中学高三模拟）以椭圆()2222:10x y C a b a b+=>>的短轴的一个端点和两焦点为顶点的三角形为等边三角形，且椭圆C 上的点到左焦点的最大距离为6，则椭圆C 的标准方程为（）A ．22143x y +=B ．22184x y +=C ．2211612x y +=D ．2216448x y +=【答案】C【解析】由题意知：短轴端点与焦点形成等边三角形，则2a c =，椭圆上的点到左焦点最大距离为6，即6a c +=，则4a =，2c =，23b =则椭圆的标准方程为：2211612x y +=.故选：C.2．【多选】（2021·福建福州市·高三二模）在ABC 中，4AB =，M 为AB 的中点，且CA CB CM -=，则下列说法中正确的是（）A ．动点C 的轨迹是双曲线B ．动点C 的轨迹关于点M 对称C ．ABC 是钝角三角形D ．ABC面积的最大值为【答案】BD【解析】以M 为原点，AB 为x 轴建立直角坐标系．设CM =r ，此时C 点在以M 为圆心，r为半径的动圆上．由CA CB r -=，知C 点在以AB 为焦点，2r a =的双曲线22221x y a b -=上且22242AB a b ⎛⎫+== ⎪⎝⎭．对点(),C x y 有222x y r +=，22221444x y r r-=-，从而2223(16)64y r r =-，当28r =时，2y最大，故yABC S ，故D 正确；2r =时，得到另一个C 点'C ，此时ABC 为直角三角形，故C 错误；∵CA CB -非定值，∴C 不以双曲线为轨迹，故A 错误；∵CM CA CB -=，∴一定有C 关于M 的对称点关于原点对称，故B 正确．故选：BD ．3.已知抛物线C ：x 2＝4y 的焦点为F ，M 是抛物线C 上一点，若FM 的延长线交x 轴的正半轴于点N ，交抛物线C 的准线l 于点T ，且FM →＝MN →，则|NT |＝________.【答案】3【解析】由x 2＝4y ，知F (0，1)，准线l ：y ＝－1.设点M (x0，y 0)，且x 0>0，y 0>0.由FM →＝MN →，知点M 是线段FN 的中点，N 是FT 中点，利用抛物线定义，|MF |＝|MM ′|＝y 0＋1，且|FF ′|＝2|NN ′|＝2.又2(y 0＋1)＝|FF ′|＋|NN ′|＝3，知y 0＝12.∴|MF |＝12＋1＝32，从而|NT |＝|FN |＝2|MF |＝3.【题型二】圆锥曲线的几何性质【典例分析】1．已知1F ，2F 分别为椭圆E ：()222210y x a b a b +=>>的两个焦点，P 是椭圆E 上的点，12PF PF ⊥，且2112sin 3sin PF F PF F ∠=∠，则椭圆E 的离心率为（）A ．102B ．4C D ．54【答案】B【解析】1F ，2F 分别为椭圆E ：()222210y x a b a b+=>>的两个焦点，P 是椭圆E 上的点，12PF PF ⊥，且2112sin 3sin PF F PF F Ð=Ð，由正弦定理可得213PF PF =，令1233PF PF n ==，则32n n a +=，22294n n c +=，可得22542a c =，所以椭圆的离心率为：104c e a===.故选：B ．2．（2021·天津南开中学高三模拟）已知双曲线()222210,0x y a b a b-=>>的中心为O ，左焦点为F ，左顶点为A ，点P 为双曲线右支上一点，直线OP 交双曲线于另一点Q ，若直线AQ 恰好平分线段PF ，则该双曲线的离心率为__________．【答案】3【解析】设PF 的中点为M ，连接OM ，O 、M 分别为PQ 、PF 的中点，则//OM FQ 且12OM FQ =，所以，12OA OM AF FQ ==，即12a c a =-，3c a =∴，因此，该双曲线的离心率为3ce a ==.故答案为：3.【提分秘籍】【变式演练】1．（2021湖南长沙长郡中学高三模拟）已知抛物线28y x =的焦点为F ，经过点P (1，1)的直线l 与该曲线交于A ､B 两点，且点P 恰好为AB 的中点，则||||+=AF BF （）A ．4B ．6C ．8D ．12【答案】B【解析】抛物线28y x =中，4p =，其焦点()2,0F ，准线方程2x =-，如图过点,,A B P 作准线的垂线，垂足为,,M N R ，由抛物线定义可知，||||AF BF AM BN +=+，而P 恰好为AB 的中点，故PR 是梯形ABNM 的中位线，故2AM BN PR +=，又P (1，1)，故132pPR =+=，所以||||236AF BF +=⨯=.故选：B.2．已知1F ，2F 分别为双曲线22221x ya b-=（0a >，0b >）的左、右焦点，过点2F 作圆222x y a +=的切线交双曲线左支于点M ，且1260F MF ∠︒＝，则该双曲线的渐近线方程为__________．【答案】313y x ⎛⎫=±+⎪ ⎪⎝⎭．【解析】设切点为A ，过1F 作21F B MF ⊥，垂足为B ，由题意可得OA a =，2OF c =，222AF c a b =-=，由OA 为12BF F △的中位线，可得12BF a =，22BF b =，又1260F MF ∠=︒，可得114sin 603BF a MF ==︒，23aMB =，22223aMF MB BF b =+=+，又21242233a a MF MF b a -=+-=，所以313b a ⎛⎫=+ ⎪ ⎪⎝⎭，所以双曲线的渐近线方程为313y x ⎛⎫=±+ ⎪ ⎪⎝⎭．故答案为：313y x ⎛⎫=±+ ⎪ ⎪⎝⎭．3.已知椭圆M ：x 2a 2＋y 2b 2＝1(a >b >0)，双曲线N ：x 2m 2－y 2n 2＝1.若双曲线N 的两条渐近线与椭圆M 的四个交点及椭圆M 的两个焦点恰为一个正六边形的顶点，则椭圆M 的离心率为________.【答案】3－1.【解析】设椭圆的右焦点为F (c ，0)，双曲线N 的渐近线与椭圆M 在第一象限内的交点为A ，由题意可知A )23,2(c c，由点A 在椭圆M 上得，c 24a 2＋3c 24b2＝1，∴b 2c 2＋3a 2c 2＝4a 2b 2，∵b 2＝a 2－c 2，∴(a 2－c 2)c 2＋3a 2c 2＝4a 2(a 2－c 2)，则4a 4－8a 2c 2＋c 4＝0，e 4－8e 2＋4＝0，∴e 2＝4＋23(舍)，e 2＝4－2 3.由0<e <1，得e ＝3－1.【题型三】直线与圆锥曲线【典例分析】1．（2021·浙江镇海中学高三模拟）已知直线1y x =-与抛物线24y x =交于A ，B 两点.若点(1,)C m -满足90ACB ∠= ，则m =（）A ．1-B ．1C ．2D ．3【答案】C【解析】直线1y x =-与抛物线24y x =联立得：2216104y x x x y x=-⎧⇒-+=⎨=⎩，设1122(,),(,)A x y B x y ，所以12126,1x x x x +==，点(1,)C m -满足90ACB ∠= ，所以有：21121121212120(1,)(1,)01()0,CA CB x y m x y m x x x x y y m y y m ⋅=⇒+-+-=⇒++++-++=121212121212,24,(1)(1)()14y y x x y y x x x x x x +=+-==--=-++=-，所以2161440,m m ++--+=解得2m =，故选：C2．已知椭圆22221x y a b +=(0a b >>)的右焦点为F ，离心率为2，过点F 的直线l 交椭圆于A ，B 两点，若AB 的中点为()1,1，则直线l 的斜率为（）A ．14-B ．34-C ．12-D ．1【答案】A【解析】设()11,A x y ，()22,B x y ，则AB 的中点坐标为1212,22x x y y ++⎛⎫⎪⎝⎭，由题意可得122x x +=，122y y +=，将A ，B 的坐标的代入椭圆的方程：22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩，作差可得22221212220x x y y a b--+=，所以221212221212y y x x b b x x a y y a-+=-⋅=--+，又因为离心率2c e a ==，222c a b =-，所以22234a b a -=，所以2214b a -=-，即直线AB 的斜率为14-，故选：A.【提分秘籍】1.求解弦长的4种方法(1)当弦的两端点坐标易求时,可直接利用两点间的距离公式求解.(2)联立直线与圆锥曲线方程,解方程组求出两个交点坐标,代入两点间的距离公式求解.(3)联立直线与圆锥曲线方程,消元得到关于x 或y 的一元二次方程,利用根与系数的关系得到(x 1-x 2)2或(y 1-y 2)2,代入两点间的距离公式求解.(4)当弦过焦点时,可结合焦半径公式求解弦长.[提醒]利用弦长公式求弦长要注意斜率k 不存在的情形,若k 不存在,可直接求交点坐标再求弦长.涉及焦点弦长时要注意圆锥曲线定义的应用.2.处理中点弦问题常用的2种方法(1)点差法:设出弦的两端点坐标后,代入圆锥曲线方程,并将两式相减,式中含有x 1+x 2,y 1+y 2,2121x x y y --三个未知量,这样就直接联系了中点和直线的斜率,借用中点公式即可求得斜率.(2)根与系数的关系:联立直线与圆锥曲线的方程得到方程组,化为一元二次方程后由根与系数的关系求解.[提醒]中点弦问题常用的两种求解方法各有弊端:根与系数的关系在解题过程中易产生漏解,需关注直线的斜率问题;点差法在确定范围方面略显不足.【变式演练】1．（2021·陕西高三模拟）已知抛物线22(0)x py p =>焦点为,F O 为坐标原点，直线l 过点F 与抛物线交于,A B 两点，与x 轴交于()2,0C p ，若17AB =，则OCF △的面积为___________.【答案】32【解析】抛物线22(0)x py p =>焦点(0,)2p F ，而直线l 过点(2,0)C p ，则直线l 的斜率为14k =-，其方程为124p y x -=-，即42x y p =-+，由2422x y px py=-+⎧⎨=⎩消去x 得228920y py p -+=，显然0∆>，设1122(,),(,)A x y B x y ，则1298py y +=，而17AB =，由抛物线定义知，1217||||()()17228p p p AB AF BF y y =+=+++==，解得8p =，即(0,4)F ，()16,0C ，而90FOC ∠= ，于是得1||||322OCF S OC OF =⋅⋅= ，所以OCF △的面积为32.故答案为：322．（2021·湖南长沙长郡中学高三模拟）已知椭圆C ：2214x y +=.（1）椭圆C 是否存在以点11,2⎛⎫- ⎪⎝⎭为中点的弦？若存在，求出弦所在的直线l 的方程，若不存在，请说明理由；（2）已知椭圆C 的左､右顶点分别为A ，B ，点P 是椭圆C 上的点，若直线AP ，BP 分别与直线3y =交于G ，H 两点，求线段GH 的长度取得最小值时直线GP 的斜率.【解析】（1）因为22(1)111422-⎛⎫+=< ⎪⎝⎭，所以点11,2⎛⎫- ⎪⎝⎭在椭圆C 的内部，则椭圆C 存在以点11,2⎛⎫- ⎪⎝⎭为中点的弦.设弦所在的直线l 与椭圆C 相交于()11,M x y ，()22,N x y ，则221122221414x y x y ⎧+=⎪⎪⎨⎪+=⎪⎩，两式相减，得22222121044x x y y -+-=，即()()()()2121212104x x x x y y y y -++-+=.又122x x +=-，121y y +=，()()2121(2)104x x y y --∴+-⨯=，整理得212112y y x x -=-.所以直线l 的方程为11(1)22y x =+-，即220x y -+=.（2）因为A ，P ，G 三点共线所以可知当线段GH 的长度取得最小值时，直线AP 的斜率k 显然存在，且0k >，()2,0A -，设直线AP 的方程为(2)y k x =+，从而点32,3G k ⎛⎫- ⎪⎝⎭.联立22(2)14y k x x y =+⎧⎪⎨+=⎪⎩，消y 整理得()222214161640k x k x k +++-=，0∆>设点()00,P x y ，则202164(2)14k x k--⋅=+.所以2022814k x k -=+，从而02414k y k =+，所以222284,1414k k P k k ⎛⎫- ⎪++⎝⎭.又点()2,0B ，则直线PB 的斜率为14k-.由1(2)43y x k y ⎧=--⎪⎨⎪=⎩，得1223x k y =-+⎧⎨=⎩，所以(122,3)H k -+.故332122124GH k k k k=-+-=+-.又0k >，则31212k k +≥=，当且仅当312k k =，即12k =时等号成立所以当12k =时，线段GH 的长度取得最小值.所以此时直线GP 的斜率为12.1．（2021山师大附中高三模拟）“1n >”是“方程221x ny +=表示焦点在x 轴上的圆锥曲线”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】当0n <时，方程221x ny +=表示焦点在x 轴上的双曲线；当0n >时，221x ny +=可化为2211y x n+=，因为椭圆的焦点在x 轴上，所以11n>即1n >，故方程221x ny +=表示焦点在x 轴上的圆锥曲线时，0n <或1n >，故“1n >”是“方程221x ny +=表示焦点在x 轴上的圆锥曲线”的充分不必要条件，故选：A.2．（2021·浙江镇海中学高三模拟）已知抛物线2y =的准线与双曲线()22210x y a a-=>相交于A ，B 两点，F 为抛物线的焦点，若FAB 为直角三角形，则实数a 的值为（）A ．19B ．29C ．13D．3【答案】D【解析】2y =的准线x =，焦点)，不妨设A点坐标2a ⎛⎫⎪ ⎪⎝⎭，FAB 为直角三角形，∠AFB ＝90°，由对称性可知，FAB 为等腰直角三角形，由直角三角形的性质得a a=，解得23a =.故选：D 3．已知双曲线()222:1016x y C a a -=>的一条渐近线方程为20x y -=，1F 、2F 分别是双曲线C 的左、右焦点，P 为双曲线C 上一点，若15PF =，则2PF =（）A ．1B ．1或9C ．3或9D ．9【答案】D【解析】由题意知42a=，所以2a =，所以c ==，所以152PF a c =<+=+，所以点P 在双曲线C 的左支上，所以214PF PF -=，所以29PF =，故选：D.4．（2021·山东省淄博市实验中学高三模拟）2016年1月14日，国防科工局宣布，嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过，正式开始实施.如图所示，假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c 1和2c 2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a 1和2a 2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：①a 1＋c 1＝a 2＋c 2；②a 1－c 1＝a 2－c 2；③c 1a 2>a 1c 2.④1212c c a a <其中正确式子的序号是（）A ．①③B ．②③C ．①④D ．②④【答案】B【解析】由图可得1212,a a c c >>，所以1122a c a c +>+，即①错误；因为1122,a c PF a c PF -=-=，所以1122a c a c -=-，即②正确，由1122a c a c -=-，得1221a c a c +=+，即22221212212122a c a c a c a c ++=++，即22221112222122a c a c a c a c -+=-+,即221221122()0b b a c a c -=->，可得2112a c a c >，即③正确，由2112a c a c >，可得1212c c a a >，即④错误；综上所述选项B 正确.故选:B.5．（2021·湖南长沙雅礼中学高三模拟）P 为双曲线2222:1x y C a b-=（0a >，0b >）上一点，1F ，2F 分别为其左、右焦点，O 为坐标原点.若OP b =，且2112sin 3sin PF F PF F ∠∠＝，则C 的离心率为（）ABC ．2D【答案】B【解析】由2112sin 3sin PF F PF F ∠∠＝，以及正弦定理可得213PF PF =，因为122PF PF a -=，所以13PF a =，2PF a =，因为2OF c =，OP b =，所以22OPF π∠=，所以2cos a OF P cÐ=，在12F F P 中，()()22212223cos cos 22a c a a F F P OF P a cc+-Ð==Ð=×.化简可得c =，所以C的离心率==ce a.故选：B 6．设1F ，2F 为椭圆1C 与双曲线2C 的公共焦点，1F ，2F 分别为左､右焦点，1C 与2C 在第一象限的交点为M .若12MF F △是以线段1MF 为底边的等腰三角形，且双曲线2C 的离心率72,2e ⎡⎤∈⎢⎥⎣⎦，则椭圆1C 离心率的取值范围是（）A ．45,99⎡⎤⎢⎥⎣⎦B ．70,16⎡⎤⎢⎥⎣⎦C ．27,516⎡⎤⎢⎥⎣⎦D ．2,17⎡⎤⎢⎥⎣⎦【答案】C【解析】设椭圆长轴长为2a ，双曲线实轴长为2a '，焦点为2c ，2122MF F F c ==，则1MF =2222a c a c '+=-，又c e a ='，所以c a e '=，即242c c a e +=，又7[2,2e ∈，所以椭圆的离心率为127,15162c e a e⎡⎤'==∈⎢⎥⎣⎦+．故选：C ．7．（2021·重庆南开中学高三模拟）已知曲线C 的方程为()22113x y m R m m+=∈+-，则（）A ．当1m =时，曲线C 为圆B ．当5m =时，曲线C 为双曲线，其渐近线方程为33y x =±C ．当1m >时，曲线C 为焦点在x 轴上的椭圆D ．存在实数m 使得曲线C【答案】AB【解析】对于A 选项：m =1时，方程为22122x y +=，即222x y +=，曲线C 是圆，A 正确；对于B 选项：m =5时，方程为22162x y -=，曲线C为双曲线，其渐近线方程为3y x =±，B 正确；对于C 选项：m >1时，不妨令m =5，由选项B 知，曲线C 为双曲线，C 不正确；对于D 选项：要曲线C 为双曲线，必有(1)(3)0m m +-<，即m <-1或m >3，m <-1时，曲线C ：2213(1)y x m m -=--+，m >3时，曲线C ：22113x y m m -=+-，时，它实半轴长与虚半轴长相等，而-(m +1)≠3-m ，m +1≠m -3，D 不正确.故选：AB11．（2021·湖南雅礼中学高三模拟）设抛物线2:4C y x =的焦点为F ，O 为坐标原点，过F 的直线与C 分别交于()1122(),,A x y B x y ，两点，则（）A ．12y y 为定值B ．AOB ∠可能为直角C ．以BF 为直径的圆与y 轴有两个交点D ．对于确定的直线AB ，在C 的准线上存在三个不同的点P ，使得ABP △为直角三角形【答案】AD【解析】设:1AB l x ty =+，与24y x =联立可得：2124404y ty y y --==-，，故A 对；因为221212116y y x x ==，所以12121OA OBy y k k x x ⋅=≠-，∴2AOB π∠≠，故B 错；设BF 的中点11111,,2222BF x y x M ++⎛⎫=⎪⎝⎭，则以BF 为直径的圆与y 轴相切，故C 错；设AB 的中点1212,22x x y y N ++⎛⎫ ⎪⎝⎭，N 到C 准线的距离为当1212x x ++，因为12122AB x x +=+故有以AB 为直径的圆与C 的准线相切，对于确定的直线AB ，当P ∠为直角，此时P 为切点；当A ∠或B Ð为直角，此时P 为过A （或B ）的AB 的垂线与准线的交点，故D 正确．故选：AD12．已知双曲线22:139x y C -=的左､右顶点分别为A ，B ，点P 是C 上的任意一点，则（）A ．双曲线C 的离心率为233B ．焦点到渐近线的距离为3C ．点P 到两条渐近线的距离之积为94D ．当P 与A ､B 不重合时，直线PA ，PB 的斜率之积为3【答案】BCD【解析】对于A ，,3a b c ===2e ==，故A 错误；对于B ，双曲线的右焦点2F 到渐近线y x ==的距离为3d ==，故B 正确；对于C ，设()00,P x y ，满足2200139x y -=，即220039x y -=，则点P到两条渐近线的距离之积为2200123944x y d d -⋅==，故C 正确；对于D ，设()00,P x y ，由C 得2239x y -=，PAPB k k ==2200220039333PA PB y x k k x x -⋅===--，故D 正确；故选：BCD13．（2021·湖北襄阳五中高三模拟）已知椭圆G：2221(06x y b b+=<<的两个焦点分别为1F 和2F ，短轴的两个端点分别为1B 和2B ，点P 在椭圆G 上，且满足1212PB PB PF PF +=+，当b 变化时，给出下列三个命题：①点P 的轨迹关于y 轴对称；②OP 的最小值为2；③存在b 使得椭圆G 上满足条件的点P 仅有两个，其中，所有正确命题的序号是__________．【答案】①②【解析】椭圆(222:106x y G b b+=<<的两个焦点分别为)1F和()2F ，短轴的两个端点分别为()10,B b -和()20,B b ，设(),P x y ，点P 在椭圆G 上，且满足1212PB PB PF PF +=+，由椭圆定义可得，1222PB PB a b +==，即有P 在椭圆222166y x b+=-上，对于①，将x 换为x -方程不变，则点P 的轨迹关于y 轴对称，故①正确.；对于②，由图象可得，当P 满足22x y =，即有226b b -=，即b =时，OP 取得最小值，可得222x y ==时，即有2OP ==取得最小值为2，故②正确；对于③，由图象可得轨迹关于,x y 轴对称，且0b <<，则椭圆G 上满足条件的点P 有4个，不存在b 使得椭圆G 上满足条件的点P 有2个，故③不正确.，故答案为①②.14．（2021·山东滕州一中高三模拟）某中学张燕同学不仅学习认真，而且酷爱体育运动，经过艰苦的训练，终于在校运会的投铅球比赛中创造佳绩．已知张燕所投铅球的轨迹是一段抛物线（人的身高不计，铅球看成一个质点），如图所示，设初速度为定值0v ，且与水平方向所成角为变量θ，已知张燕投铅球的最远距离为10m ．当她投得最远距离时，铅球轨迹抛物线的焦点到准线的距离为____m ．（空气阻力不计，重力加速度为210m /s ）【答案】5【解析】设铅球运动时间为0t ，t 时刻的水平方向位移为x ，则0cos x v t θ=．由001sin 02v gt θ-=知002sin v t g θ=20sin 2v x g θ∴=故当4x π=时，20max 10v x g==，210m /s g =∴解得：0t =，010m /sv =201 2.5m22t h g ⎛⎫∴== ⎪⎝⎭如图建立平面直角坐标系，(5, 2.5)P --，设抛物线方程为22x py=-则抛物线的焦点到准线的距离22(5)5m 22 2.5x p y -===-⨯故答案为：515．（2021·山东枣庄一中高三模拟）已知双曲线2222:1x y C a b-=（0a >，0b >）的左、右焦点分别为1F 、2F ，O为坐标原点，P 是双曲线上在第一象限内的点，直线PO 、2PF 分别交双曲线C 左、右支于另一点M 、N ，213PF PF =，且260MF N ∠=︒，则双曲线C 的离心率为________；渐近线方程为________.【答案】22y x =±【解析】由213PF PF =，122PF PF a -=，解得13PF a =，2PF a =，由题意可得四边形12PF MF 为平行四边形，又260MF N ∠=︒，可得1260F PF ∠=︒，在12PF F △中，可得()22224323cos 607c a a a a a =+-⋅⋅⋅︒=，即有2c a =，则2c e a ==，所以2b a ===，则渐近线方程为2y x =±.故答案为：72；32y x =±.16.（2021•南充模拟）已知椭圆2222:1(0)x y C a b a b +=>>的左，右焦点分别为1(2,0)F -，2(2,0)F ，点15(1,)3P --在椭圆C 上．（1）求椭圆C 的标准方程；（2）是否存在斜率为一1的直线l 与椭圆C 相交于M ，N 两点，使得11||||F M F N =？若存在，求出直线的方程；若不存在，说明理由．【解析】（1）由题意得，2c =，2211519a b +=，222a b c =+，解得：26a =，22b =，所以椭圆的标准方程：22162x y +=；（2）假设存在满足条件的直线l ，设直线l 的方程：y x t =-+，设(,)M x y ，(,)N x y ''与椭圆联立整理：2246360x tx t -+-=，△223644(36)0t t =-->，t -<<，32t x x '+=，2364t xx -'=，由于11||||F M F N =，设线段MN 的中点为E ，则1F E MN ⊥，所以111F E MN k k =-=又3(4t E ，)3t ，所以141324F E tk t ==+，解得4t =-，当4t =-时，不满足t -<<，所以不存在满足条件的直线l ．17．（2021·湖南高三模拟）已知双曲线2222:1(0,0)x y C a b a b -=>>的离心率为72，双曲线上的点到焦点的最小距离为2.（1）求双曲线C 的方程；（2）四边形MNPQ 的四个顶点均在双曲线C 上，且//MQ NP ，MQ x ⊥轴，若直线MN 和直线QP 交于点()4,0S ，四边形MNPQ 的对角线交于点D ，求点D 到双曲线C 的渐近线的距离之和.【解析】（1）由题意，22222c a c a a b c ⎧-=⎪⎪=⎨⎪+=⎪⎩，解得24a =，23b =，所以双曲线C 的方程为22143x y -=；（2）由MQ x ⊥轴，//MQ NP ，可知四边形MNPQ 为等腰梯形，且关于x 轴对称，故四边形MNPQ 的对角线的交点D 在x轴上，如图所示：设点(,0)D t ，则对角线MP 的方程为(0)x my t m =+≠，设1122(,),(,)M x y P x y ，由对称性知1122(,),(,)Q x y N x y --，联立22143x y x my t ⎧-=⎪⎨⎪=+⎩，消去x 得222(34)63120m y mty t -++-=，所以22222(6)4(34)(312)48(34)0mt m t m t ∆=---=-+>，即2234m t +>，由韦达定理得21212226312,3434mt t y y y y m m --+==--，由,,M N S 三点共线知MS NS k k =，即121244y y x x -=--，所以1221(4)(4)0y my t y my t +-++-=，整理得12122(4)()0my y t y y +-+=，所以222(312)(4)(6)034m t t mt m -+--=-，所以224(1)034m t m -=-，即24(1)0,1m t t -==，所以直线MP 过定点()1,0，即D ()1,0，因为双曲线C 20y ±=20y -=时，由点到直线距离公式得217d ==，由对称性知点D 到双曲线C 的渐近线的距离之和为2217.。

（完整版）圆锥曲线知识点+例题+练习含答案（整理）.docx

（完整版）圆锥曲线知识点+例题+练习含答案（整理）.docx圆锥曲线⼀、椭圆：（ 1）椭圆的定义：平⾯内与两个定点F1 , F2的距离的和等于常数（⼤于| F1 F2 |）的点的轨迹。

其中：两个定点叫做椭圆的焦点，焦点间的距离叫做焦距。

注意： 2a | F1F2 | 表⽰椭圆；2a | F1F2|表⽰线段F1F2； 2a| F1F 2 |没有轨迹；（2）椭圆的标准⽅程、图象及⼏何性质：中⼼在原点，焦点在x 轴上中⼼在原点，焦点在y 轴上标准⽅程图形x2y2y2x2a2b 21( a b 0)a 2b21(ab 0)yB 2yB 2P F2 PA 1 A 2x A 1xA 2OF1O F21B 1FB 1顶点对称轴焦点焦距离⼼率通径2b2aA1 (a,0), A2 (a,0)A1( b,0), A2 (b,0)B1 (0, b), B2(0, b)B1( 0,a), B2 (0, a) x 轴，y轴；短轴为2b，长轴为2aF1 (c,0), F2(c,0)F1 ( 0,c), F2 (0,c)| F1 F2 | 2c(c 0)c2 a 2 b 2(0 e 1) （离⼼率越⼤，椭圆越扁）a（过焦点且垂直于对称轴的直线夹在椭圆内的线段）3．常⽤结论：（1）椭圆x2y21(a b 0) 的两个焦点为F1, F2，过F1的直线交椭圆于A, B两a2 b 2点，则ABF 2的周长=（2）设椭圆x2y2221( a b 0)左、右两个焦点为 F1, F2，过 F1且垂直于对称轴的直线a b交椭圆于 P, Q 两点，则 P, Q 的坐标分别是| PQ |⼆、双曲线：（ 1）双曲线的定义：平⾯内与两个定点F1 , F2的距离的差的绝对值等于常数（⼩于| F1F2 | ）的点的轨迹。

其中：两个定点叫做双曲线的焦点，焦点间的距离叫做焦距。

注意： | PF1 || PF2 | 2a 与 | PF2 | | PF1 |2a （ 2a| F1F2 | ）表⽰双曲线的⼀⽀。

精品高考数学专题十七圆锥曲线的几何性质精准培优专练理

【最新】2019年高考数学专题十七圆锥曲线的几何性质精准
培优专练理
1．椭圆的几何性质
例1：如图，椭圆的上顶点、左顶点、左焦点分别为、、，中心为，其
离心率为，则（
A．B．C．
D
【答案】B
【解析】由，得
而，所以，故选B
2．抛物线的几何性质
例2：已知抛物线的焦点为，准线，点在抛物线上，点在直线上的射影为，且直线的斜率为，则的面积为（）
A．B．C．D
【答案】C
【解析】
设准线与轴交于点，所以，因为直线的斜率为，所以，所以，
由抛物线定义知，，且，所以是以4为边长的正三角形，其面积
为．故选C
3．双曲线的几何性质
例3：已知点是双曲线的右支上一点，，分别是圆和上的点，则的最大
值为_________
【答案】15
M
≤
P P
一、单选题
1．抛物线上的动点到其焦点的距离的最小值为1，则（）
A．B．1 C．2 D．
【答案】C
【解析】抛物线上的动点到其焦点的距离的最小值即到准线的最小
很明显满足最小值的点为抛物线的顶点，据此可知：，．本题选择C。

2021高三数学(理)精准培优专项训练《17圆锥曲线的几何性质》学生版

A． 1 4
B． 1 28
C． 1 8
D． 1 或 1 4 28
5．定义平面上两条相交直线的夹角为：两条相交直线交成的不超过 90 的正角．已知双曲线
E
:
x2 a2
y2 b2
1(a
0,b
0) ，当其离心率 e[
2,2] 时，对应双曲线的渐近线的夹角的取值范围为（
）
A．[0, ] 6
B． [
并求出该定点的坐标．
4
培优点十七圆锥曲线的几何性质答案
例 1：【答案】 ( 15 ,1) 或 ( 15 , 1)
2
2
【解析】
F1 ，
F2 是椭圆
x2 5
y2 4
1的左、右焦点， c
54 1，
则 F1(1, 0) ， F2 (1, 0) ，
设 P(x, y)(x 0) 是椭圆上的一点，
由三角形的面积公式可知 S 1 2c y 1 ，即 y 1， 2
设双曲线
x2
y2 15
1的左右焦点为
F1(4, 0) ，
F2 (4, 0)
，
连接 PF1 ， PF2 ， F1M ， F2N ，可得
| PM |2 | PN |2 ( PF1 2 r12 ) ( PF2 2 r22 ) ( PF1 2 4) ( PF2 2 1) PF1 2 PF2 2 3 ( PF1 PF2 )( PF1 PF2 ) 3 2a( PF1 PF2 ) 3 2 2c 3 13 ．
轴的距离大1．
（1）试求出抛物线 C 的方程；
（2）若抛物线 C 上存在两动点 M , N （ M , N 在对称轴两侧），满足 OM ON （ O 为坐标原点），过点 F

圆锥曲线的几何性质例题和知识点总结

圆锥曲线的几何性质例题和知识点总结圆锥曲线是高中数学中的重要内容，包括椭圆、双曲线和抛物线。

它们具有独特的几何性质，在数学和物理学等领域都有广泛的应用。

下面我们将通过一些例题来深入理解圆锥曲线的几何性质，并对相关知识点进行总结。

一、椭圆的几何性质椭圆的标准方程为：＄＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝1$（＄a ＞ b ＞ 0$），其中$a$为长半轴，＄b$为短半轴，＄c$为半焦距，满足$c^2 ＝ a^2 b^2$。

1、范围椭圆位于直线$x ＝＼pm a$和$y ＝＼pm b$所围成的矩形内。

2、对称性椭圆关于$x$轴、＄y$轴和原点对称。

3、顶点椭圆的顶点坐标为$（＼pm a, 0)＄和$（0, ＼pm b)＄。

4、离心率离心率$e ＝＼frac{c}｛a}＄，反映了椭圆的扁平程度，＄0 ＜ e ＜1$，＄e$越接近 0，椭圆越接近于圆；＄e$越接近 1，椭圆越扁平。

例题 1：已知椭圆方程为$＼frac{x^2}｛9} ＋＼frac{y^2}｛4} ＝ 1$，求其顶点坐标、离心率和焦点坐标。

解：由方程可知，＄a ＝ 3$，＄b ＝ 2$，则$c ＝＼sqrt{a^2 b^2}＝＼sqrt{5}＄。

顶点坐标为$（＼pm 3, 0)＄和$（0, ＼pm 2)＄。

离心率$e ＝＼frac{c}｛a} ＝＼frac{＼sqrt{5}｝｛3}＄。

焦点坐标为$（＼pm ＼sqrt{5}， 0)＄。

二、双曲线的几何性质双曲线的标准方程为：＄＼frac{x^2}｛a^2} ＼frac{y^2}｛b^2} ＝1$（＄a ＞ 0$，＄b ＞ 0$），其中$a$为实半轴，＄b$为虚半轴，＄c$为半焦距，满足$c^2 ＝ a^2 ＋ b^2$。

1、范围双曲线在$x ＼leq a$或$x ＼geq a$上取值。

2、对称性双曲线关于$x$轴、＄y$轴和原点对称。

3、顶点双曲线的顶点坐标为$（＼pm a, 0)＄。

圆锥曲线的几何性质-2021年高考数学备考优生百日闯关系列【含答案详解】

，所以
AD 和
BC
的中点重合，
所以 AB CD ，所以 AC BD 恒成立．故 A 正确．
因为 AD 和 BC 的中点重合为 P ，所以 AB CD ，
又 S△BOC
1 3
S△ AOD
，所以
BC
1 3
AD
，
所以 AB BC CD ，故 B 正确．
设直线 l 方程为 x ty m ， t (1, 0) (0,1), m 1 ，
母的目标函数，然后研究该函数的值域或最值情况，从而得到特定字母的取值范围．
（3）数形结合法：研究特定字母所对应的几何意义，然后根据相关曲线的定义、几何性质，利用数形结合的方法求解. 3.圆锥曲线中的最值问题：
一是利用几何方法，即通过利用曲线的定义、几何性质以及平面几何中的定理、性质等进行求解；二是利用代数方法，即把要求最值的几何量或代数表达式表示为某个(些)参数的函数(解析式)，然后利用函数方法、不等式方法等进行求解．常见的几何方法有：
小距离为 (实轴长)；③椭圆上的点到焦点的距离的取值范围为
，与分别表
示椭圆焦点到椭圆上点的最小与最大距离；④抛物线上的点中顶点与抛物线的准线距离最近．
常用的代数方法有：
（1）利用二次函数求最值；
（2）通过三角换元，利用正、余弦函数的有界性求最值；（3）利用基本不等式求最值；（4）利用导数法求最值；（5）利用函数单调性求最值.
坐标原点，下列选项中正确的为（）
A． AC BD 恒成立
B．若 S△BOC
1 3
S△ AOD
，则
AB
BC
CD
C． △AOD 面积的最小值为 1
D．对每一个确定的 n ，若 AB BC CD ，则 △AOD 的面积为定值

高考数学专题十七圆锥曲线的几何性质精准培优专练理

培优点十七圆锥曲线的几何性质1．椭圆的几何性质例1：如图，椭圆()2222+10x y a b a b=>>的上顶点、左顶点、左焦点分别为B 、A 、F ，中心为O :ABF BFO S S =△△（）A ．(2:3-B ．()3:3C ．(2:2-D ．()3:2【答案】B【解析】由ABF ABO BFO S S S =-△△△，得()():::A B F B F O A B O BF O BF O S S S S S a b b c b c =-=-△△△△△而c a =():3:3ABF BFO S S =△△，故选B ．2．抛物线的几何性质例2：已知抛物线()2:20C y px p =>的焦点为F ，准线:1l x =-，点M 在抛物线C 上，点M在直线:1l x =-上的射影为A ，且直线AF 的斜率为MAF △的面积为（）A B ．C ．D ．【答案】C 【解析】设准线l 与x 轴交于点N ，所以2FN =，因为直线AF 的斜率为60AFN ∠=︒，所以4AF =，由抛物线定义知，MA MF =，且60M A F A F N ∠=∠=︒，所以MAF △是以4为边长的正三24=．故选C ．3．双曲线的几何性质例3：已知点P 是双曲线2213664x y -=的右支上一点，M ，N 分别是圆()22104x y ++=和()22101x y -+=上的点，则PM PN -的最大值为_________．【答案】15【解析】在双曲线2213664x y -=中，6a =，8b =，10c =，()110,0F ∴-，()210,0F ，12212PF PF a -==，11MP PF MF ≤+，22PN PF NF ≥-，112215PM PN PF MF PF NF ∴-≤+-+=．一、单选题1．抛物线()220y px p =>上的动点Q 到其焦点的距离的最小值为1，则p =（） A ．12B ．1C ．2D ．4【答案】C【解析】抛物线()220y px p =>上的动点Q 到其焦点的距离的最小值即到准线的最小值，很明显满足最小值的点为抛物线的顶点，据此可知：12p=，2p ∴=．本题选择C 选项． 2．设点1F ，2F 是双曲线2213y x -=的两个焦点，点P 是双曲线上一点，若1234PF PF =，则12PF F △的面积等于（）A ．B ．C ．D ．对点增分集训【答案】B【解析】据题意，1243PF PF =，且122PF PF -=，解得18PF =，26PF =．又124F F =，在12PF F △中由余弦定理，得222121212127cos 28PF PF F F F PF PF PF +-∠==．从而12sin F PF ∠=121682PF F S =⨯⨯=△，故选B ． 3．经过椭圆2222x y +=的一个焦点作倾斜角为45︒的直线l ，交椭圆于M ，N 两点，设O 为坐标原点，则OM ON ⋅等于（） A ．3- B ．13±C ．13-D ．12-【答案】C【解析】椭圆方程为2212x y +=，a =1b =，1c =，取一个焦点()1,0F ，则直线方程为1y x =-，代入椭圆方程得2340x x -=，()0,1M -，41,33N ⎛⎫⎪⎝⎭，所以13OM ON =⋅-，故选C ．4．过抛物线()20y mx m =>的焦点作直线交抛物线于P ，Q 两点，若线段PQ 中点的横坐标为3，54PQ m =，则m =（）A ．4B ．6C ．8D ．10【答案】B【解析】设PQ 的坐标分别为()11,x y ，()22,x y ，线段PQ 中点的横坐标为3，则1232x x +=，125644m PQ x x p m =++=+=，由此解得6m =．故选B ． 5．已知双曲线()222210,0x y a b a b-=>>的右焦点为F ，点A 在双曲线的渐近线上，OAF △是边长为2的等边三角形（O 为原点），则双曲线的方程为（） A ．2213x y -=B ．2213y x -= C ．221412x y -=D ．221124x y -= 【答案】B【解析】双曲线()222210,0x y a b a b-=>>的右焦点为F ，点A 在双曲线的渐近线上，OAF△是边长为2的等边三角形（O 为原点），可得2c =，ba 即223b a =，2223c a a -=，解得1a =，b双曲线的焦点坐标在x 轴，所得双曲线的方程为2213y x -=，故选B ． 6．如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P 变轨进入以月球球心F 为一个焦点的椭圆轨道I 绕月飞行，之后卫星在P 点第二次变轨进入仍以F 为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P 点第三次变轨进入以F 为圆心的圆形轨道Ⅲ绕月飞行．已知椭圆轨道I 和Ⅱ的中心与F 在同一直线上，设椭圆轨道I 和Ⅱ的长半轴长分别为1a ，2a ，半焦距分别为1c ，2c ，则有（）A ．1212c c a a = B ．1122a c a c -<-C ．1212c c a a >D ．1122a c a c ->-【答案】C【解析】设圆形轨道Ⅲ的半径为R ，1122a c a c R -=-=，111111c a R Ra a a -==-，222221c a R R a a a -==-，由12a a >知1212c c a a >，故选C ． 7．已知双曲线221:14x C y -=，双曲线()22222:10x y C a b a b-=>>的左、右焦点分别为1F ，2F ，M 是双曲线2C 的一条渐近线上的点，且2OM MF ⊥，O 为坐标原点，若216OMF S =△，且双曲线1C ，2C 的离心率相同，则双曲线2C 的实轴长是（） A ．32B ．4C ．8D ．16【答案】D【解析】双曲线221:14x C y -=()2,0F c ，双曲线2C 一条渐近线方程为by x a=，可得2F M b ==，即有OM a =，由216OMF S =△，可得1162ab =，即32ab =，又222a b c +=，且c a =解得8a =，4b =，c =16．故选D ．8．已知F 是抛物线2:2C y x =的焦点，N 是x 轴上一点，线段FN 与抛物线C 相交于点M ，若2FM MN =，则FN =（） A ．1 B ．12C ．52D ．58【答案】D【解析】由题意得点F 的坐标为10,8⎛⎫⎪⎝⎭，设点M 的坐标()00,x y ，点N 的坐标(),0a ，所以向量：00,18FM x y ⎛⎫=- ⎪⎝⎭，()00,MN a x y =--，由向量线性关系可得：03x a =，00124y y -=-，解得：0112y =，代入抛物线方程可得：0x =a =，由两点之间的距离公式可得：58FN =．故选D ．9．已知椭圆()221112211:10x y C a b a b +=>>与双曲线()222222222:10,0x y C a b a b -=>>有相同的焦点1F ，2F ，点P 是曲线1C 与2C 的一个公共点，1e ，2e 分别是1C 和2C 的离心率，若12PF PF ⊥，则22124e e +的最小值为（）A ．92B ．4C ．52D ．9【答案】A【解析】由题意设焦距为2c ，椭圆长轴长为12a ，双曲线实轴为22a ，令P 在双曲线的右支上，由双曲线的定义1222PF PF a =-，① 由椭圆定义1212PF PF a +=，②又∵12PF PF ⊥，∴222124PF PF c +=，③ 22+①②，得2222121244PF PF a a +=+，④将④代入③，得222122a a c +=， ∴22222221122222121224559422222a a c c e e a a a a +=+=++≥+=，故选A ．10．已知F 为抛物线2:4C y x =的焦点，A ，B ，C 为抛物线C 上三点，当FA FB FC ++=0时，称ABC △为“和谐三角形”，则“和谐三角形”有（） A ．0个 B ．1个 C ．3个 D ．无数个【答案】D【解析】抛物线方程为24y x =，A ，B ，C 为曲线C 上三点，当FA FB FC ++=0时，F 为ABC △的重心，用如下办法构造ABC △，连接AF 并延长至D ，使12FD AF =，当D 在抛物线内部时，设()00,D x y ，若存在以D 为中点的弦BC ，设()11,B m n ，()22,C m n ，则1202m m x +=，1202n n y +=，1212BC n n k m m -=-，则21122244n m n m ⎧==⎪⎨⎪⎩，两式相减化为()1212124n n n n m m -+=-，121202BC n n k m m y -==-，所以总存在以D 为中点的弦BC ，所以这样的三角形有无数个，故选D ．11．已知双曲线()22122:10,0x y a b a bΓ-=>>的左右焦点分别为1F ，2F ，椭圆222:134x y Γ+=的离心率为e ，直线MN 过点2F 与双曲线交于M ，N 两点，若112cos cos F MN F F M ∠=∠，且11F M e F N=，则双曲线1Γ的两条渐近线的倾斜角分别为（）A ．30︒，150︒B ．45︒，135︒C ．60︒，120︒D ．15︒，165︒【答案】C 【解析】由题112cos cos F MN F F M ∠=∠，112F MN F F M ∴∠=∠，1122MF F F c ∴==，由双曲线的定义可得| 21|222MF MF a c a =-=-， ∵椭圆222:134x y Γ+=的离心率为：12e ==，∴1112F M e F N =＝，14NF c ∴=，242NF c a =-，在12MF F △中，由余弦定理的()()222124224cos 22222c c a c c aF F M c c a c+---∠==⋅⋅-，在12NF F △中，由余弦定理可得：()()()2222212442164cos 224222c c a c a c acF F N c c a c c a +--+-∠==⋅⋅--， ∵1212πF F M F F N ∠+∠=，1212cos cos 0F F M F F N ∴∠+∠=，即()2240222c a a c acc c c a -+-+=-，设双曲线的离心率为1e ，2113720e e ∴-+=，解得12e =或13（舍）．∴2224a b a +=，223a b ∴=，即b a=y =， ∴渐近线的倾斜角为60︒，120︒．故选C ．12．已知P 为椭圆22143x y +=上一个动点，过点P 作圆()2211x y ++=的两条切线，切点分别是A ，B ，则PA PB ⋅的取值范围为（） A ．3,2⎡⎫+∞⎪⎢⎣⎭B ．356,29⎡⎤⎢⎥⎣⎦C．563,9⎡⎤⎢⎥⎣⎦D．)3,⎡+∞⎣【答案】C【解析】如图，由题意设2APB θ∠=，则1tan PA PB θ==，∴211cos2cos2cos2cos21cos2tan PA PB PA PB θθθθθθ+⋅==⋅=⋅-，设cos 2t θ=，则()()12133311t t PA PB t tt +⋅==-+-≥=--，当且仅当211t t-=-，即1t =-cos21θ= 又当点P 在椭圆的右顶点时，1sin 3θ=，∴27cos212sin 9θθ=-=，此时PA PB ⋅最大，且最大值7175699919+⨯=-．∴PA PB ⋅的取值范围是563,9⎡⎤⎢⎥⎣⎦，故选C ．二、填空题13．已知过抛物线22y x =-的焦点FA 、B 两点，则AF BF AB⋅=__________．【答案】12【解析】由22y x =-知1p =，由焦点弦性质112+2AF BF p==，而1111+22+AF BF AF BF p ABAF BFAF BF⋅⋅====． 14．已知椭圆2221x y a+=的左、右焦点为1F 、2F ，点1F 关于直线y x =-的对称点P 仍在椭圆上，则12PF F △的周长为__________．【答案】2【解析】设()1,0F c -，()()2,00F c c >，1F 关于直线y x =-的对称点P 坐标为()0,c ，点P 在椭圆上，则：2201c a+=，则1c b ==，2222a b c =+=，则a = 故12PF F △的周长为：1212222PF PF F F a c ++=+=．15．P 为双曲线22149x y -=右支上一点，1F ，2F 分别为双曲线的左、右焦点，且120PF PF ⋅=，直线2PF 交y 轴于点A ，则1AF P △的内切圆半径为__________．【答案】2【解析】∵12PF PF ⊥，1APF △的内切圆半径为r ，∴112PF PA AF r -+=，∴2122PF a PA AF r -++=， ∴2124AF AF r =--，∵由图形的对称性知：21AF AF =，∴2r =．故答案为2．16．已知直线l 与椭圆()222210,0x y a b a b+=>>相切于第一象限的点()00,P x y ，且直线l 与x轴、y 轴分别交于点A 、B ，当AOB △(O 为坐标原点)的面积最小时，1260F PF ∠=︒(1F 、2F 是椭圆的两个焦点)，若此时在12PF F △中，12F PF ∠，则实数m 的值是__________．【答案】52【解析】由题意，切线方程为00221x y x y ab+=，直线l 与x 轴分别相交于点A ，B ，20,0a A x ⎛⎫∴ ⎪⎝⎭，200,b B y ⎛⎫ ⎪⎝⎭，220012AOB a b S x y ∴=⋅△，2200002221x y x y ab a b +=≥，0012xy ab∴≥，AOB S ab ∴≥△，当且仅当00x y a b ==AOB △（O 为坐标原点）的面积最小，设1PF x =，2PF y =，由余弦定理可得2222443c x y xy a xy =+-=-，243xy b ∴=，1221sin 602PF F S xy ∴=︒=△，20122cy ∴⨯⨯=，0y ∴==，c ∴=，a ∴=，12F PF ∠，211112222x y ∴⨯⨯+⨯⨯=，)212x y ∴+=，22115229a b ∴==， 52m ∴=，故答案为52．三、解答题17．设常数2t >．在平面直角坐标系xOy 中，已知点()2,0F ，直线l ：x t =，曲线Γ：()280,0y x x t y =≤≤≥．l 与x 轴交于点A 、与Γ交于点B ．P 、Q 分别是曲线Γ与线段AB 上的动点．（1）用t 表示点B 到点F 距离；（2）设3t =，2FQ =，线段OQ 的中点在直线FP ，求AQP △的面积；（3）设8t =，是否存在以FP 、FQ 为邻边的矩形FPEQ ，使得点E 在Γ上？若存在，求点P 的坐标；若不存在，说明理由．【答案】（1）2t +；（2；（3）存在，25P ⎛ ⎝⎭．【解析】（1）方法一：由题意可知：设()B t ，则2BF t =+，∴2BFt =+；方法二：由题意可知：设()B t ，由抛物线的性质可知：22pBF t t =+=+，∴2BF t =+；（2）()2,0F ，2FQ =，3t =，则1FA =，∴AQ =(Q ，设OQ 的中点D，32D ⎛ ⎝⎭，02322QFk -==-PF方程：)2y x =-，联立)228y x y x=-=⎧⎪⎨⎪⎩，整理得：2320120x x -+=，解得：23x =，6x =（舍去），∴AQP △的面积1723S ==（3）存在，设2,8y P y ⎛⎫ ⎪⎝⎭，2,8m E m ⎛⎫ ⎪⎝⎭，则2281628PF y yk y y ==--，2168FQ y k y -=，直线QF 方程为()21628y y x y -=-，∴()22164838284Q y y y y y --=-=，248384y Q y ⎛⎫- ⎪⎝⎭，，根据FP FQ FE +=，则22486,84y y E y ⎛⎫++ ⎪⎝⎭， ∴222488648y y y ⎛⎫⎛⎫+=+ ⎪⎪⎝⎭⎝⎭，解得：2165y =，∴存在以FP 、FQ 为邻边的矩形FPEQ ，使得点E 在Γ上，且25P ⎛ ⎝⎭．18．与椭圆相交于A 、B 两点，2F 关于直线1l 的对称点E 在椭圆上．斜率为1-的直线2l 与线段AB 相交于点P ，与椭圆相交于C 、D 两点．（1）求椭圆的标准方程；（2）求四边形ACBD 面积的取值范围．【答案】（1）22184x y +=；（2）3232,93⎛⎤ ⎥⎝⎦．【解析】（1）由椭圆焦距为4，设()12,0F -，()22,0F ，连结1EF ，设12EF F α∠=，则tan b cα=，又222a b c =+，得sin b a α=，cos c a α=，()12122sin9012||sin sin 90F F c a ce a EF EF b c aa aαα︒∴======++︒-++，解得222a bc c b c =+⇒==，28a =，所以椭圆方程为22184x y +=．（2）设直线2l 方程：y x m =-+，()11,C x y 、()22,D x y ，由22184x y y x m +==-+⎧⎪⎨⎪⎩，得2234280x mx m -+-=，所以1221243283x x m m x x +=-=⎧⎪⎪⎨⎪⎪⎩，由（1）知直线1l ：y x =，代入椭圆得A ⎛ ⎝，B，得AB =，由直线2l 与线段AB 相交于点P，得m ⎛∈ ⎝，12CD x =-=而21l k =-与11l k =，知21l l ⊥，12ACBD S AB CD ∴=⨯=，由m ⎛∈ ⎝，得232,03m ⎛⎤-∈- ⎥⎝⎦3232,93⎛⎤⎥⎝⎦，ACBD 面积的取值范围3232,93⎛⎤⎥⎝⎦．。

2020届高三精准培优专练十七圆锥曲线的几何性质(理) 教师版

2020届高三好教育精准培优专练例1：已知点P 是椭圆22154x y +=上y 轴右侧的一点，且以点P 及焦点1F ，2F 为顶点的三角形的面积等于1，则点P 的坐标为________．【答案】)或)1- 【解析】1F ，2F 是椭圆22154x y +=的左、右焦点，1c ==，则1(1,0)F -，2(1,0)F ，设(,)(0)P x y x >是椭圆上的一点，由三角形的面积公式可知1212S c y =⋅⋅=，即1y =，将1y =代入椭圆方程得21154x +=，解得2x =∴点P 的坐标为)，)1-．例2：如图，已知抛物线24y x =的焦点为F ，过点F 且斜率为1的直线依次交抛物线及圆()22114x y -+=于点A ，B ，C ，D 四点，则AB CD +的值是（）二、抛物线的几何性质一、椭圆的几何性质培优点十七圆锥曲线的几何性质A ．6B ．7C ．8D ．9【答案】B【解析】设()11,A x y ，()22,D x y ，代入抛物线方程消去y ，得2610x x -+=，∴126x x +=，则121212222117AB CD AF r DF r x x r x x x x +=-+-=++-=++-=++=．例3：过双曲线22115y x -=的右支上一点P ，分别向圆221:(4)4C x y ++=和圆222:(4)1C x y -+= 作切线，切点分别为M ，N ，则22PM PN -的最小值为．【答案】13【解析】圆221:(4)4C x y ++=的圆心为(4,0)-，半径为12r =；圆222:(4)1C x y -+=的圆心为(4,0)，半径为21r =，设双曲线22115y x -=的左右焦点为1(4,0)F -，2(4,0)F ，连接1PF ，2PF ，1F M ，2F N ，可得2222221122|(())|||PM PN PF r PF r -=---2212(4)(1)PF PF =---22123PF PF =--1212(())3PF PF PF PF =-+-122()322313a PF PF c =+-≥⋅-=．当且仅当P 为右顶点时，取得等号，即最小值13．三、双曲线的几何性质一、选择题1．抛物线的焦点为，点是上一点，，则（）A ．B ．C ．D ．【答案】A【解析】根据抛物线焦半径公式可得：，所以． 2．设椭圆的左焦点为，直线（）与椭圆交于，两点，则的值是（） A ． B ．C ．D ．【答案】C【解析】设椭圆的右焦点为，连接，，因为，，所以四边形是平行四边形，所以，所以．3．已知双曲线22:12x C y -=上任意一点为G ，则G 到双曲线C 的两条渐近线距离之积为（） A ．13B ．23C ．1D ．43【答案】B2:2(0)C y px p =>F 0(6,)A y C ||2AF p =p =4321||622pAF p =+=4p =22:14x C y +=F :l y kx =0k ≠C A B ||| |AF BF +242F 2AF 2BF OA OB =2OF OF =2AFBF 2||||BF AF =2||||||||4AF BF AF AF +=+=对点增分集训【解析】渐近线方程为y x =，设点(,)G x y，则1d =，2d =，∴2212|2|233x y d d -==． 4．已知抛物线的准线与圆相切，则的值为（） A ．B ．C ．18D ．或【答案】D【解析】抛物线，即，准线方程为，因为抛物线的准线与圆相切，当时，，解得；当时，，解得． 5．定义平面上两条相交直线的夹角为：两条相交直线交成的不超过的正角．已知双曲线，当其离心率时，对应双曲线的渐近线的夹角的取值范围为（） A ． B ． C ． D ．【答案】D【解析】由题意可得：，∴，设双曲线的渐近线与轴的夹角为，双曲线的渐近线为，则．结合题意相交直线夹角的定义可得双曲线的渐近线的夹角的取值范围为．6．已知直线l 过点(3,2)P -且与椭圆22:12016x y C +=相交于A ，B 两点，则使得点P 为弦AB 中点的直线斜率为（） A ．35- B ．65-C ．65D ．35【答案】C2y ax =22670x y y +--=a 14128-14128-2y ax =21x y a =14y a=-21x y a=22(3)16x y +-=0a >1344a +=14a =0a <1344a --=128a =-90︒2222:1(0,0)x y E a b a b-=>>e ∈[0,]6π[,]63ππ[,]43ππ[,]32ππ222221[2,4]c b e a a ==+∈22[1,3]b a∈x θb y x a =±[,]43ππθ∈[,]32ππ【解析】设11(,)A x y ，22(,)B x y ，则221112016x y +=，222212016x y +=，两式相减12121212()()()()02016x x x x y y y y -+-++=．又由点(3,2)P -为弦AB 的中点，∴126x x +=，124y y +=-， ∴121265y y k x x -==-．7．设，是抛物线上的两个不同的点，是坐标原点，若直线与的斜率之积为，则（） A ．B ．以为直径的圆的面积大于C ．直线过抛物线的焦点D ．到直线的距离不大于【答案】D【解析】当直线的斜率不存在时，设，，由斜率之积为，可得，即， ∴的直线方程为，当直线的斜率存在时，设直线方程为，联立，可得，此时设，，则，，∴，即， ∴直线方程为，则直线过定点，则到直线的距离不大于．M N 2y x =O OM ON 12-||||OM ON +≥MN 4πMN 2y x =O MN 2MN 200(),M y y 200(,)N y y -12-20112y -=-202y =MN 2x =y kx m =+2y kx my x =+⎧⎨=⎩20ky y m -+=11(,)M x y 22(,)N x y 12m y y k =2122mx x k=121212OM ON y y k k k x x m ⋅===-2m k =-2(2)y kx k k x =-=-MN (2,0)O MN 28．椭圆与双曲线焦点相同，为左焦点，曲线与在第一象限，第三象限的交点分别为，，且，则当这两条曲线的离心率之积最小时，双曲线有一条渐近线方程是（）A ．B ．C ．D【答案】C【解析】设双曲线的右焦点为，由题意点与点关于原点对称，因此，又，所以，由椭圆与双曲线定义可得，，所以，，根据余弦定理可得，即，化简得，所以离心率乘积为，当且仅当①时，取等号，由，所以，所以②，再将①②代入可得，所以双曲线的渐近线方程为或．2222:1(0)x y a b a b Γ+=>>2222:1(0,0)x y m n m nΩ-=>>F ΓΩA B 23AFB π∠=20x y -=20x y +=0x=0y +=1F A B 1||||AF BF =23AFB π∠=13FAF π∠=1||||2AF AF a +=1||||2AF AF m -=||AF a m =+1||AF a m =-2221111||||||2||||cos FF AF AF AF AF F AF =+-∠2224()()2()()cos 3c a m a m a m am π=++--+-22243cm a =+≥=22c c c a m am ⋅=≥223m a =2222a b m n -=+2222243c m b m n --=+223b n =2222a b m n -=+222m n =0x =0x +=二、填空题9．已知抛物线24x y =的焦点为F ，点A 在x 轴的正半轴上，过AF 的直线与抛物线在第一象限交于点B ，与抛物线的准线l 交于点C ，若2AB BF =u u u r u u u r ，则FC =u u u r．【答案】10【解析】由题可知(0,1)F ，设点(,0)A a ，00(,)B x y ，则0000(,)2(,1)x a y x y -=--，解得03a x =，023y =，代入抛物线24x y =，得2893a =，解得a =故A ，可得5AF =u u u r ，根据对称性得，5AC =u u u r，所以10FC FA AC =+=．10．已知椭圆（）的离心率为椭圆上的一个动点，则与定点连线距离的最大值为．【答案】【解析】椭圆（）的离心率，可得，解得，椭圆方程为，设，则与定点，当时，取得最大值．三、解答题11．已知抛物线C 的方程22(0)px p y =>，焦点为F ，已知点P在C 上，且点P 到点F 的距离比它到y 轴的距离大1．（1）试求出抛物线C 的方程；（2）若抛物线C 上存在两动点,M N （,M N 在对称轴两侧），满足OM ON ⊥（O 为坐标原点），过点F2221y x a+=1a >e =P P (1,0)B -522221y x a+=1a >5e =5a =a =2215y x +=(cos )P θθP (1,0)B -=52==1cos 4θ=52作直线交C 于,A B 两点，若AB MN ∥，线段MN 上是否存在定点E ，使得||||4||EM EN AB ⋅=恒成立?若存在，请求出E 的坐标，若不存在，请说明理由．【答案】（1）24y x =；（2）存在，(4,0)E ．【解析】（1）因为P 到点F 的距离比它到y 轴的距离大1，由题意和抛物线定义，12p=，所以抛物线C 的方程为24y x =，（2）由题意，0MN k ≠，设211(,)4y M y ，22221(,)()4y N y y y >，由OM ON ⊥，得1216y y =-，①若直线MN 斜率存在，设斜率为k ，直线124:M k y y N =+，112124()4y y y x y y -=-+，整理可得124(4)y x y y =-+，直线:AB (1)y k x =-，与C 联立得2440ky y k --=，故可得21||4(1)AB k=+，若点E 存在，设点E 坐标为00(,)x y ，))0120||||y EM E y N y y ⋅=--200214(1)(16)y y k k =+-+， ||||4||EM EN AB ⋅=时，20041616y y k -+=，解得00y =或04y k=（不是定点，舍去），则点E 为(4,0)，经检验，此点满足24y x <，所以在线段MN 上，②若斜率不存在，则||4AB =，||||4416EM EN ⋅=⋅=，此时点(4,0)E 满足题意，综上所述，定点E 为(4,0)．12．设椭圆的左、右焦点分别为，，下顶点为，为坐标原点，点到直线的距离为，为等腰直角三角形．（1）求椭圆的标准方程；2222:1(0)x y C a b a b+=>>1F 2F A O O 2AF 212AF F ∆C（2）直线与椭圆交于，两点，若直线与直线的斜率之和为，证明：直线恒过定点，并求出该定点的坐标．【答案】（1）；（2）见解析．【解析】（1）由题意可知：直线的方程为，即，，因为为等腰直角三角形，所以，又，可解得，，所以椭圆的标准方程为．（2）证明：由（1）知，当直线的斜率存在时，设直线的方程为，代入，得．所以，即，设，，则，，因为直线与直线的斜率之和为，所以，整理得，所以直线的方程为，显然直线经过定点，当直线的斜率不存在时，设直线的方程为，因为直线与直线的斜率之和为，设，则，所以，解得， l C M N AM AN 2l 2212x y +=2AF 1x y c b+=-0bx cy bc -++=bc a ==12AF F ∆b c =222a b c =+a =1b =1c =C 2212x y +=(0,1)A -l l (1)y kx t t =+≠±2212x y +=222(12)4220k x ktx t +++-=2222164(12)(22)0k t k t ∆=-+->2221t k -<11(,)M x y 22(,)N x y 122412ktx x k+=-+21222212t x x k -=+AM AN 2121212121111AM AN y y kx t kx t k k x x x x +++++++=+=+()12212(1)(1)422222t x x t ktk k x x t +++⋅=+=-=-1t k =-l 1(1)1y kx t kx k k x =+=+-=-+(1)1y k x =-+(1,1)l l x m =AM AN 2(,)M m n (,)N m n -1122AM AN n n k k m m m+-++=+==1m =此时直线的方程为，显然直线也经过该定点，综上，直线恒过点．l 1x =1x =(1,1)l (1,1)。

(整理)圆锥曲线定义几何性质.

专题：圆锥曲线一、圆锥曲线的定义的考查1、已知△ABC 的顶点B 、C 在椭圆x 23＋y 2＝1上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC边上，则△ABC 的周长是 ( )（A ）2 3 （B ）6 （C ）4 3 （D ）122、已知双曲线9322=-y x ,则双曲线右支上的点P 到右焦点的距离与点P 到右准线的距离之比等于（）A.2 B.332 C. 2 D.4 3、已知定点A 、B 且|AB|=4，动点P 满足|PA|－|PB|=3，则|PA|的最小值是（）A ．21 B ．23 C ．27 D ．54、已知⎪⎭⎫ ⎝⎛-0,21A ，B 是圆F ：42122=+⎪⎭⎫ ⎝⎛-y x (F 为圆心)上一动点，线段AB 的垂直平分线交BF 于P ，则动点P 的轨迹方程为。

二、圆锥曲线的几何性质的考查：1、抛物线2mx y =的焦点坐标为。

2、在给定椭圆中，过焦点且垂直于长轴的弦长为2，焦点到相应准线的距离为1，则该椭圆的离心率为 ( )(A)2 (B)22 (C) 21(D)42 3、点P(-3,1)在椭圆22221(0)x y a b a b+=>>的左准线上.过点P 且方向为a =(2,-5)的光线,经直线y =-2反射后通过椭圆的左焦点,则这个椭圆的离心率为( ) ( A )33 ( B ) 31 ( C ) 22 ( D ) 21 4、已知双曲线2212yx-=的焦点为F 1、F 2，点M 在双曲线上且120,MF MF ⋅=则点M 到x 轴的距离为（C ）（A ）43 （B ）53（C（D5、已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，若过点F 且倾斜角为60o的直线与双曲线的右支有且只有一个交点，则此双曲线离心率的取值范围是（）（A ）(1,2] （B ）(1,2) （C ）[2,)+∞ （D ）(2,)+∞6、如图，把椭圆221x y +=的长轴AB 分成8等份，过每个分点作x 轴的垂线交椭圆的上半部分于1234567,,,,,,P P P P P P P 七个点，F 是椭圆的一个焦点，则1234567PF P F P F P F P F P F P F ++++++=________________;7、若动点(x ,y )在曲线14222=+by x (b >0)上变化，则x 2+2y 的最大值为(A ) (A) ⎪⎩⎪⎨⎧≥<<+)4(2)40(442b b b b ；(B) ⎪⎩⎪⎨⎧≥<<+)2(2)20(442b bb b ；(C) 442+b ； (D) 2b 。

【山东省】2017年高考数学(理科)-圆锥曲线的定义、方程、几何性质-专题练习-答案

＋
y12 b2
y22
＝0,
即

x1

x2 x1
4b2

x2
＋
y1

y2
b2
y1

y2
＝0,
即

32 17

x1 4

x2

＋4 17
(
y1－y2
)＝0,
从而kPQ＝
y1 y2 x1 x2
＝2,
6
分
直线l的方程为y－ 2 17
＝2
x

16 17

＝2ay(a≠0),椭圆常设 mx2＋ny2＝1(m＞0,n＞0),双曲线常设为 mx2－ny2＝1(mn＞0). 【变式训练一】
1 （1）A 抛物线 y＝8x2,即 x2＝8y 的焦点为 F(0,2),
a 即 c＝2,双曲线的渐近线方程为 y＝±bx,
bc 可得 F 到渐近线的距离为 d＝ a2＋b2＝b＝ 3,
b2 1＋a2＝
53 1＋4＝2.]
1 pp 2px02－2 2 ∵kMF′＝kFF′,∴ x0 ＝－2.①
1
13
又∵y′＝px,∴y′|x＝x0＝px0＝ 3 .②
43 由①②得 p＝ 3 .] 回访三弦长问题
6．B [抛物线 y2＝8x 的焦点为(2,0),∴椭圆中 c＝2,
c1 又a＝2,∴a＝4,b2＝a2－c2＝12,
x2 y2 从而椭圆方程为16＋12＝1．
∵抛物线 y2＝8x 的准线为 x＝－2,
∴xA＝xB＝－2, 将 xA＝－2 代入椭圆方程可得|yA|＝3, 由图象可知|AB|＝2|yA|＝6．故选 B．]

高考数学《圆锥曲线的方程与性质》专题

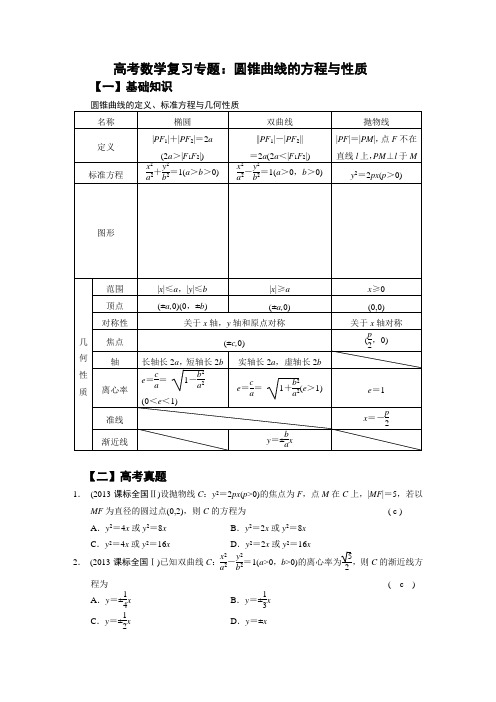
高考数学复习专题：圆锥曲线的方程与性质【一】基础知识【二】高考真题1． (2013·课标全国Ⅱ)设抛物线C ：y 2＝2px (p >0)的焦点为F ，点M 在C 上，|MF |＝5，若以MF 为直径的圆过点(0,2)，则C 的方程为( c )A ．y 2＝4x 或y 2＝8xB ．y 2＝2x 或y 2＝8xC ．y 2＝4x 或y 2＝16xD ．y 2＝2x 或y 2＝16x2． (2013·课标全国Ⅰ)已知双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为52，则C 的渐近线方程为( c )A ．y ＝±14xB ．y ＝±13xC ．y ＝±12xD ．y ＝±x3． (2013·山东)抛物线C 1：y ＝12p x 2(p >0)的焦点与双曲线C 2：x 23－y 2＝1的右焦点的连线交C 1于第一象限的点M .若C 1在点M 处的切线平行于C 2的一条渐近线，则p 等于(d )4． (2013·福建)椭圆Г：x 2a 2＋y2b2＝1(a >b >0)的左，右焦点分别为F 1，F 2，焦距为2c .若直线y ＝3(x ＋c )与椭圆Г的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则该椭圆的离心率等于3－15． (2013·浙江)设F 为抛物线C ：y 2＝4x 的焦点，过点P (－1,0)的直线l 交抛物线C 于A 、B 两点，点Q 为线段AB 的中点，若|FQ |＝2，则直线l 的斜率等于 ±1．【三】题型和方法题型一圆锥曲线的定义与标准方程例1(1)在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点F 1，F 2在x 轴上，离心率为22.过F 1的直线l 交C 于A ，B 两点，且△ABF 2的周长为16，那么椭圆C 的方程为 __________．(2)已知P 为椭圆x 24＋y 2＝1和双曲线x 2－y 22＝1的一个交点，F 1，F 2为椭圆的两个焦点，那么∠F 1PF 2的余弦值为________．变式训练1 (1)已知双曲线x 2a 2－y 2b2＝1 (a >0，b >0)的两个焦点F 1，F 2，M 为双曲线上一点，且满足∠F 1MF 2＝90°，点M 到x 轴的距离为72.若△F 1MF 2的面积为14，则双曲线的渐近线方程为__________．答案 y ＝±7x(2)设斜率为2的直线l 过抛物线y 2＝ax (a ≠0)的焦点F ，且和y 轴交于点A ，若△OAF (O 为坐标原点)的面积为4，则抛物线方程为________．答案 y 2＝±8x题型二圆锥曲线的性质例2 (1)等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2＝16x 的准线交于A ，B 两点，|AB |＝43，则C 的实轴长为( )B ．2 2C ．4D ．8(2)设圆锥曲线C 的两个焦点分别为F 1，F 2，若曲线C 上存在点P 满足|PF 1|∶|F 1F 2|∶|PF 2|＝4∶3∶2，则曲线C 的离心率等于 ( )或32或2 或2 或32变式训练2 (1)已知O 为坐标原点，双曲线x 2a 2－y 2b2＝1(a >0，b >0)的右焦点为F ，以OF 为直径作圆与双曲线的渐近线交于异于原点的两点A ，B ，若(AO →＋AF →)·OF →＝0，则双曲线的离心率e 为( )A ．2B ．3答案 C(2)已知双曲线x 2a 2－y 2b 2＝1 (a >0，b >0)的左顶点与抛物线y 2＝2px (p >0)的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为(－2，－1)，则双曲线的焦距为( )A ．2 3B ．2 5C ．4 3D ．4 5答案 B题型三直线与圆锥曲线的位置关系例3已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A (x 1，y 1)， B (x 2，y 2)(x 1<x 2)两点，且|AB |＝9. (1)求该抛物线的方程．(2)O 为坐标原点，C 为抛物线上一点，若OC →＝OA →＋λOB →，求λ的值．变式训练3 已知平面内一动点P 到点F (1,0)的距离与点P 到y 轴的距离的差等于1.(1)求动点P 的轨迹C 的方程；(2)过点F 作两条斜率存在且互相垂直的直线l 1，l 2，设l 1与轨迹C 相交于点A ，B ，l 2与轨迹C 相交于点D ，E ，求AD →·EB →的最小值．【例4(14分)在平面直角坐标系xOy 中，已知椭圆C 1：x 2a 2＋y 2b2＝1(a >b >0)的左焦点为F 1(－1,0)，且点P (0,1)在C 1上．(1)求椭圆C 1的方程；(2)设直线l 同时与椭圆C 1和抛物线C 2：y 2＝4x 相切，求直线l 的方程．【四】能力训练1． (2013·四川)抛物线y 2＝4x的焦点到双曲线x 2－y 23＝1的渐近线的距离是 ( )C ．1 2． (2013·湖北)已知0＜θ<π4 ，则双曲线C 1：x 2cos 2θ－y 2sin 2θ＝1与C 2：y 2sin 2θ－x 2sin 2θtan 2θ＝1的( )A ．实轴长相等B ．虚轴长相等C ．焦距相等D ．离心率相等3．已知方程x 22－k ＋y 22k －1＝1表示焦点在y 轴上的椭圆，则实数k 的取值范围是 ( )B ．(1，＋∞)C ．(1,2)D ．⎝⎛⎭⎫12，14． (2013·江西)抛物线x 2＝2py (p >0)的焦点为F ，其准线与双曲线x 23－y 23＝1相交于A 、B 两点，若△ABF 为等边三角形，则p ＝________.5． (2013·湖南)设F 1，F 2是双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的两个焦点，P 是C 上一点，若|PF 1|＋|PF 2|＝6a 且△PF 1F 2的最小内角为30°，则双曲线C 的离心率为______．6． (2013·辽宁)已知椭圆C ：x 2a 2＋y 2b2＝1(a ＞b ＞0)的左焦点为F ，椭圆C 与过原点的直线相交于A ，B 两点，连接AF ，BF .若|AB |＝10，|AF |＝6，cos ∠ABF ＝45，则C 的离心率e ＝________.专题模拟训练一、选择题1． (2013·广东)已知中心在原点的双曲线C 的右焦点为F (3,0)，离心率等于32，则C 的方程是( )－y 25＝1－y 25＝1 －y 25＝1－y 25＝12．已知抛物线关于x 轴对称，它的顶点在坐标原点O ，并且经过点M (2，y 0)．若点M 到该抛物线焦点的距离为3，则|OM |等于( )A ．2 2B ．2 3C ．4D ．2 5 3．已知双曲线C ：x 2a 2－y2b2＝1 (a >0，b >0)的左，右焦点分别为F 1，F 2，过F 2作双曲线C 的一条渐近线的垂线，垂足为H ，若F 2H 的中点M 在双曲线C 上，则双曲线C 的离心率为( )C ．2D ．3 4．设F 1、F 2分别是双曲线x 2－y 29＝1的左、右焦点，若点P 在双曲线上，且PF 1→·PF 2→＝0，则|PF 1→＋PF 2→|等于 ( )B ．210D ．2 55．已知抛物线y 2＝2px (p >0)的焦点为F ，P 、Q 是抛物线上的两个点，若△PQF 是边长为2的正三角形，则p 的值是( )A ．2±3B ．2＋ 3±1－16． (2013·浙江)如图，F 1，F 2是椭圆C 1：x 24＋y 2＝1与双曲线C 2的公共焦点，A ，B 分别是C 1，C 2在第二、四象限的公共点．若四边形AF 1BF 2为矩形，则C 2的离心率是( )7．已知双曲线x2a2－y2b2＝1(a>0，b>0)的两条渐近线均和圆C：x2＋y2－6x＋5＝0相切，且双曲线的右焦点为圆C的圆心，则该双曲线的方程为()－y24＝1 －y25＝1－y26＝1 －y23＝18．(2012·安徽)过抛物线y2＝4x的焦点F的直线交该抛物线于A，B两点，O为坐标原点．若|AF|＝3，则△AOB的面积为()D．2 2二、填空题9．已知F1、F2为椭圆x225＋y29＝1的两个焦点，过F1的直线交椭圆于A、B两点．若|F2A|＋|F2B|＝12，则|AB|＝________.10．已知双曲线C1：x2a2－y2b2＝1(a>0，b>0)与双曲线C2：x24－y216＝1有相同的渐近线，且C1的右焦点为F(5，0)，则a＝________，b＝________.11．设F1、F2分别是椭圆x225＋y216＝1的左、右焦点，P为椭圆上任一点，点M的坐标为(6,4)，则|PM|＋|PF1|的最大值为________．12．过双曲线x2a2－y2b2＝1 (a>0，b>0)的左焦点F作圆x2＋y2＝a24的切线，切点为E，延长FE交双曲线的右支于点P，若E为PF的中点，则双曲线的离心率为________．三、解答题13．(2012·安徽)如图，F1、F2分别是椭圆C：x2a2＋y2b2＝1(a>b>0)的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C 的另一个交点，∠F1AF2＝60°.(1)求椭圆C的离心率；(2)已知△AF 1B 的面积为403，求a ，b 的值．14．(2013·课标全国Ⅱ)平面直角坐标系xOy 中，过椭圆M ：x 2a 2＋y 2b2＝1(a >b >0)右焦点的直线x ＋y －3＝0交M 于A ，B 两点，P 为AB 的中点，且OP 的斜率为12.(1)求M 的方程；(2)C ，D 为M 上的两点，若四边形ACBD 的对角线CD ⊥AB ，求四边形ACBD 面积的最大值．。

精选-高考数学专题十七圆锥曲线的几何性质精准培优专练理

圆锥曲线几何性质精华

高考数学专题十七圆锥曲线的几何性质精准培优专练理

2020届高考数学专题十七圆锥曲线的几何性质精准培优专练理

方法技巧专题07 圆锥曲线的概念及其几何性质(解析版)

高考数学必做61道圆锥曲线问题——圆锥曲线性质大全.doc

圆锥曲线的定义、方程与性质(题型归纳)

（完整版）圆锥曲线知识点+例题+练习含答案（整理）.docx

精品高考数学专题十七圆锥曲线的几何性质精准培优专练理

2021高三数学(理)精准培优专项训练《17圆锥曲线的几何性质》学生版

圆锥曲线的几何性质例题和知识点总结

圆锥曲线的几何性质-2021年高考数学备考优生百日闯关系列【含答案详解】

高考数学专题十七圆锥曲线的几何性质精准培优专练理

2020届高三精准培优专练十七 圆锥曲线的几何性质(理) 教师版

(整理)圆锥曲线定义几何性质.

【山东省】2017年高考数学(理科)-圆锥曲线的定义、方程、几何性质-专题练习-答案

高考数学《圆锥曲线的方程与性质》专题

2020届高三精准培优专练十七圆锥曲线的几何性质(理) 教师版