第四章 流体通过颗粒层的流动-第二节-颗粒床层特性
颗粒床层的特性

2.2颗粒群的特性
频率函数 (粒级质量分率~dp) 2.2颗粒群的特性
xi fi d i 1 d i
特点:某粒级范围的颗粒质量分率 =该范围曲线下的面积 曲线下的面积和=1
2.2颗粒群的特性
分布函数F与频率函数f的关系
dF f d(d )
p
F (d ) fd (d )
dp p 0 p
L u
实际床层简化模型
(a)
u (b)
u L de
流体在固定床内流动的简化模型
u le
固体颗粒 床层体积
de
4 流通截面积
润湿周边
4V 4 细管的全部内表面积 a BV a1 4 细管的流动空间
a B a1
(2)流体压降的数学模型
le u2 流体流过圆管的阻力损失数学描述:h f d 2 e
球形颗粒
非球形颗粒
2.1单颗粒的特性参数
② 颗粒的比表面积
颗粒表面积 (:V相同时,a↓, 则颗粒越接近球形。
a球 S 6 V dp
球形颗粒比表面积: (2)非球形颗粒 ①体积等效 ②表面积等效
dev d es
3
6V
S
定义体积当量直径和形状系数
流体通过颗粒层的流动
一、学习要求:
本章主要介绍了过滤分离非均相物系的方法。
通过本章学习,应重点掌握: 1.流体相对于颗粒床层的流动规律 2.过滤过程的基本原理,影响因素分析及强化措施, 恒压过滤的计算,过滤常数的测定方法,过滤机 生产能力的计算,典型设备的结构特性。
1概述
• 流体通过颗粒层的流动: • ①从含有粉尘或液滴的气体中分离出粉尘 或液滴 • ②从含有固体颗粒的悬浮液中分离出固体 颗粒; • ③流体通过由大量固体颗粒堆集而成的颗 粒或床层的流动(如过滤、离子交换器、催 化反应器等)。
第四章 流体通过颗粒层的流动-第二节-颗粒床层特性_图文_百.

西北大学化工原理课件频率函数的重要特性①在一定范围内的颗粒占全部试样的质量分率等于该颗粒范围内频率函数曲线下的面积;②频率函数曲线下的全部面积为1。
3. 颗粒群的平均直径xi 1 1 mi 1 = ∑( 或dm = =∑ xi dm d pi m d pi ∑ d pi 式中:m—总质量 mi—相邻两号筛之间的颗粒质量,其直径为dpi;对非球形颗粒以(ψdei代替式中的dpi
西北大学化工原理课件三、床层特性 1. 床层空隙率床层体积−颗粒所占体积ε= 床层体积空隙率通过实验测得,一般乱堆床层的空隙率:ε=0.47~0.7 2. 床层的各向同性非球形颗粒乱堆时,各颗粒的定向应是随机的,即认为床层是各向同性的。
其特点是:
西北大学化工原理课件某截面上的空隙面积ε= 床层截面积但壁效应存在,当D/dp较大时壁效应可忽略。
3. 床层的比表面积aB 单位床层体积所具有的颗粒表
面积称为床层的比表面积,以aB表示。
ns nva V p a V (1 − ε a aB = = = = = (1 − ε a V V V V。
流体通过颗粒层的流动

de为床层空隙的当量直径
de=4流通截面/润湿周边
= (4流通截面Le)/(润湿周边Le )
=4 流动空间/细管的全部内表面
=4V/(aB v)= 4/(a (1- ))
Le为固定床层颗粒的当量高度,Le 与L有关。
流体通过固定床的压降等于流体通过一组当量直 径为de,长度为Le的细管压降。
(3)建立数学模型 引入模型参数
对简化的物理模型建立数学模型,引入模型参数。
由范宁方程
hf
p
Le
de
u12 2
而u=u1或u1 =u/, de= 4/(a (1- ))代入上式, 得
p Le 1 a u2 ' 1 a u2
瓷环等塔用填料。
分析康采尼或欧根方程,影响床层流动压降的 变量有三类:
① 操作变量u ② 流体物性ρ,μ ③ 床层特性ε,α 其中影响最大的是ε。
数学模型法是处理工程问题的基本研究方法之 一,其核心是合理的简化,本质的近似。
4.4过滤
过滤是指以某种多孔物质作为介质,在外力的作用 下,使流体通过介质的孔道而固体颗粒被截留下来, 从而实现固体颗粒与流体分离目的的操作。
L 8L 3
3
(4-1)
式中
'
Le
8L
模型参数,流动摩擦系数。
(4)模型的检验和模型参数的确定
上述的简化处理只是一种假设,其有效性必须 通过实验检验,其中的模型参数亦经由实验结 果确定。‘与床层雷诺数Re’相关。
定义床层雷诺数
Re' deu1 u
流体通过颗粒层的流动

形状不规则的颗粒:
比表面积的定义同上,颗粒的形状及大小分别表示为: (1)颗粒的形状系数(Shape factor):用形状系数表示颗粒的形
状,最常用的形状系数是球形度ψ,它的定义式为
与非球形颗粒体积相等 的球的表面积
非球形颗粒的表面积
标准筛:有不同的系列,其中泰勒(Tyler)
标准筛是较为常用的标准筛之一,其筛孔 的大小以每英寸长度筛网上所具有的筛孔 数目表示,称为目,每个筛的筛网金属丝 的直径也有规定,因此一定目数的筛孔尺 寸一定。例如200目的筛子即指长度为1英 寸的筛网上有200个筛孔。所以筛号越大, 筛孔越小。此标准系列中各相邻筛号(按 从大到小的次序)的筛孔大小按筛孔的净 宽度计以 20.5的倍数递增,即筛孔面积按2 的倍数递增。 筛号(目数):每英寸边长的筛孔数目 筛过量:通过筛孔的颗粒量 筛余量:截留于筛面上的颗粒量
一般颗粒床层的空隙率为0.47~0.7。 测量床层的空隙率的方法:充水法和称量法。
(2)床层的比表面积 单位体积床层中颗粒的表面积称为床层的比表面积。若忽略因颗粒 相互接触而减小的裸露面积,则床层的比表面积αB与颗粒的比表面 积α的关系为: αB= α(1- ε)
影响床层的比表面积的主要因素:颗粒尺寸。一般,颗粒尺寸越小, 床层的比表面积越大。
(2)颗粒群的平均特性参数
颗粒群的平均粒径有不同的表示法,但对于流体 与颗粒之间的相对运动过程,主要涉及流体与颗粒表 面间的相互作用,即颗粒的比表面积起重要作用,因 此通常用等比表面积当量直径来表示颗粒的平均直径, 则混合颗粒的平均比表面积dm。
dm
1 xi
d pi
xi——第i层筛网上颗粒的质量分率 dpi=(di-1+di)/2
化工原理第四章流体通过颗粒层的流动

4.4 过滤原理及设备 4.4.1 过滤原理
过滤将固—液两相的悬浮液分离 成滤饼和滤液。 两种过滤方法 滤饼过滤(表面过滤) 颗粒截留在过虑介质表面。适用于较高浓度的悬浮液 架桥现象——对表面过滤,真正起过滤作用的是滤饼本身,
过滤介质仅给架桥现象提供条件 深层过滤 颗粒靠静电力、表面力吸附于过滤。 介质内部。 适用于低浓度、细颗粒的分离
(2)q与τ的关系;
(3)K与τ的关系;
由 q K c, K
2(q qe ) q c 得K 2c2 2qec
(4)ΔP 与τ的关系。 K
必须注意:使用恒速速率 方程时,应使K与τ严格 对应。
q
τ
τ
ΔP
qe≠0
τ
qe=0,s=0 τ
ΔP
qe=0
τ
qe≠0,s≠0 30 τ
恒压过滤方程 P c,
C.床层特性的影响 (1)空隙率ε: 空隙率ε对压降ΔP 的影响非常大,反映在 ε的可变性大,可靠性差; ε较小的误差,将引起压降明显的误差 (2)比表面积α ΔP ∝α2,对同形状颗粒,dp↓, α越大↑,hf(ΔP )↑。 例:其他条件不变空隙率ε由0.5降为0.4,单位床层压降 增加2.8倍。
4
则
4 u
Re' a(1 ) 4
u
a1
当Re’<2时,λ=k’/Re’,
k’=5.0
代入得: P k / a2 1 2 u
L
3
上式称为康采尼方程(注意适用条件:层流);
欧根在更宽的Re’范围内,得出: ' 4.17 0.29
代入基本式:
Re'
P
L
4.17
a2
1
由康采尼公式得

学习目的 与要求
通过本章学习,掌握颗粒床层的特性、固定 床层的压降、过滤等过程的原理、计算方法、 典型设备的结构特性,能够根据生产工艺的要求, 合理选择设备。
1
第四章、流体通过颗粒层 的流动
4.1 概述
2
概述
第一章主要阐述了均相流体在管道中流动的基本规律,讨论 了流体在密闭管道中流动时压力的变化和能量的损失,着重 研究固体壁面对于流体的作用。 在化工生产中,还经常遇到非均相混合物的分离及流动 问题,其中最常见的有:
4
概述
非均相混和物分离的应用:
(1)收集分散物质 (2)净化分散介质 (3)环境保护
5
第四章、流体通过颗粒层 的流动
4.1 概述 4.2 颗粒床层的特性
6
一、单颗粒的特性
1. 球形颗粒:球形颗粒的几何特征可用单一参数
——直径dp确定。
体积 表面积 比表面积
3 v dp 6
2 S d p
2 d s 6 p a v 3 dp d
6
p
7
一、单颗粒的特性
2.非球形颗粒 非球形颗粒以某种当量的球形颗粒来代替,在 考察的领域内使非球形颗粒的特性与球形颗粒等 效,非球形颗粒的直径称为当量直径。 不同形状、不同尺寸的颗粒,当量球体的直径 de是不同的。 问题:根据什么准则来保证非球形颗粒的特性 与当量球体在流动方面的等效性? 非球形颗粒的当量直径如何确定?
1、从含有固体颗粒的悬浮液中分离出固体颗粒; 2、流体通过由大量固体颗粒堆集而成的颗粒层或床层的流 动(如过滤、离子交换器、固定床吸附器等)。 这些过程均涉及到流体相对于固体颗粒及颗粒床层流动 时的基本规律以及与之有关的非均相混合物的机械分离问题。
流体通过颗粒层的流动

反应器 催化剂颗粒层等概念
以上化工操作中均为流体通过颗粒层的流动,与流体
在管道中的流动相比较:阻力增大,速度分布均一,
流动特点:层流,绕流(因速度慢也称爬流)。
爬流:爬流速度很小,流动很 缓慢,颗粒迎流面与背流面的 流线对称。
颗粒层中流体流动特点:
(1)床截面的流体速度分布均匀,床层两端产生很大压降△P 原因:大量颗粒随机堆积,颗粒对流体的流动造成很大 的阻力
真正的过滤介质:架桥作用 。
滤浆
滤饼 过滤介质
滤液
滤饼过滤
(2)深层过滤——本质不同于表面过滤,是依靠吸附作用。
深层过滤 深层过滤主要用于含固量很少的悬浮液 化工生产广泛使用的是滤饼过滤。
3、过滤介质 织物介质: 滤布滤网(截留颗粒dp:5~6μm) 多孔性固体介质:素瓷、多孔塑料(dp: 1~3μm) 堆积介质: 固体颗粒如砂、木炭、非编织纤维如玻璃纤维 ——用于含固量少的悬浮液
2、颗粒床层的数学模型
ΔP
hf
Le de
u12 2
;Le
L,Le L
常数
ΔP 1
L
u
de、u1
流体在固定床内流动的简化模型
Le Δ P 1
Δ P Le u12 de 2
表观流速(空床流速)u与实际流速 u1 的关系 :
uA
u1 A1
u
u1
A1 A
u1
化简得到单位床层高度压降: Δ P ( 1 )a u2
影 响
2 、空隙率随装填情况而变,
L
同种物料同样方式装填,空隙率未必能重复
第四节 过滤原理及设备
一、过滤 固液分离的常用方法是通过过滤获得清净的液体或
作为产品的固体颗粒 1、过滤原理 利用重力或人为造成的压差使悬浮液通过某种多孔性 过滤介质分离悬浮液。 2、两种过滤方式 (1)滤饼过滤——依靠通道尺度小于颗粒直径,滤饼是
化工原理第四章 1-2

③床层比表面
aB
=
S V床
=
S(1 Vp
e
)
=
a(1 - e )
3.流体通过固定床的压降
几何边界复杂,无法解析解,要靠实验 数学模型法主要步骤:
3.1 简化模型(数模思想) 过程特征: ①爬流,表面剪切力为主,
形体力(压差力)为次 ②空隙中实际速度与空隙大小有关
简化原则: 模型与原型①表面积要相等
e3
e
)2
µu
=
K
a2 (1 -
e3
e
)2
µu
DP L
=
a2 (1 -
5 e3
e
)2
µu
适用范围:Re’<2
床层雷诺数
4e
u
宽范围:
a(1 - e ) e
Re'= deu1r = ru 4µ a(1 - e )µ
细管
hf
=
DP
r
= l Le
de
u12 2
DP L
=
l
Le L
ru12
2de
=
l
Le a(1 -
第四章 流体通过颗粒层的流动
(1)
化工定床—由许多固体颗粒堆积成的静止颗粒层
1.2 固定床阻力的影响因素
①流体物性:ρ,µ ②操作因素: u ③设备因素: 颗粒直径,
颗粒大小分布, 空隙大小
2 颗粒床层的特性
2.1 单颗粒的特性
球形颗粒,只需一个参数dp
颗粒特性:体积
L
u=0.9m/s时 DP = 2300Pa / m 。
L
求:CO以u=0.5m/s通过时的 DP 。
L
流体通过颗粒层的流动

4. 流体通过颗粒层的流动4.1 概述由众多固体颗粒堆积而成的静止的颗粒床层称为固定床。
许多化工操作都与流体通过固定床的流动有关,其中最常见的有:(1)固定床反应器(组成固定床的是粒状或片状催化剂)(2)悬浮液的过滤(组成固定床的是悬浮液中的固定颗粒堆积而成的滤饼看作是固定床)4.2颗粒床层的特性(1)床层空隙率ε固定床层中颗粒堆积的疏密程度可用空隙率来表示,其定义如下:ε=空隙体积床层体积=V v -床层体积颗粒所占体积床层体积V =1-v Vε的大小反映了床层颗粒的紧密程度,ε对流体流动的阻力有极大的影响。
ε↑,f h ↑∑。
ε<1 (2)床层自由截面积分率A 。
A 0 =流动截面积床层截面积=P A 床层截面积A-颗粒所占的平均截面积A 床层截面积=1-P A A现在我们来分析一下空降率ε与床层自由截面积分率0A 之间有何关系。
假设床层颗粒是均匀堆积(即认为床层是各向同性的)。
想象用力从床层四周往中间均匀压紧,把颗粒都压到中间直径为1D 长为L 的圆柱中(圆柱内设有空隙)。
ε=1-v V0A =1-P A A =1-21244D LD L ππ=1-21244D D ππ =1-21D D ⎛⎫ ⎪⎝⎭ =1-21D D ⎛⎫ ⎪⎝⎭所以对颗粒均匀堆积的床层(各向同性床层),在数值上ε=A 。
(3)床层比表面B aB a =V颗粒表面积S 床层体积 , 颗粒比表面a =S V 颗粒表面积颗粒体积 取V =13m 床层考虑,B a =1S ,a =S v =1S ε- 所以 B a =a (1-ε) 此式是近似的,在忽略床层中固颗粒相互接触而彼此覆盖使裸露的颗粒表面积减少时成立。
4.3流体通过固定床的压降固定床中颗粒间存在着网络状的空隙形成许多可供流体通过的细小通道。
这些通道是曲折而且互相交联,其截面大小和形状又是很不规则的。
流体通过如此复杂的通道时的阻力(压降)自然难以进行理论计算,必须依靠实验来解决问题。
第四章 流体通过颗粒层的流动

l u2 hf d 2
Le u12 P hf de 2
Le u12 ΔP 通过单位床层高度压降: L de L 2 u u1 空床流速: u u1 代入上式 P ( e ) (1 )a u 2 L 8L 3
dq d
累计滤 液量V
开始滤饼层薄速率大
时间τ
时间τ
二、过滤设备 1、叶滤机: 加压过滤
2、板框压滤机:大型板框压滤机;滤框 3、回转真空过滤机,2
4、非球形颗粒的参数表达
球形颗粒V、S 和 a 均可以颗粒直径 dP 确定, 非球形颗粒必须定义两个参数
dev
一般定义dev作为当量直径,简写为de 形状系数
V
6
de3
2 e
d es
d ev
与球形颗粒 比较相差 1
S
d
d e2 2 S d es
a 6 6 dea dev dea de
S 6 a V dp
6 6 mi dm d pi m
dm
1 xi d pi
mi xi (相邻两筛号间颗粒质量 mi 占总质量 m 的比例) m
三、床层特性 1、床层的空隙率
V颗粒 V床 V颗粒 1 V床 V床
dp
3
均匀球形颗粒按最松排列时空隙率0.48,最紧密排列空隙率0.26
b)在最大粒径dpmax处,分布函数为
1。 0
dpi
粒径dp
( 2 ) 频率函数曲线(分布密度函数)
频 率 函 数f
f
i
相邻两号筛孔直径di~di-1之间颗粒占全
部试样的质量百分率 xi,以矩形面积 表示,则:
第4章流体通过颗粒层的流动
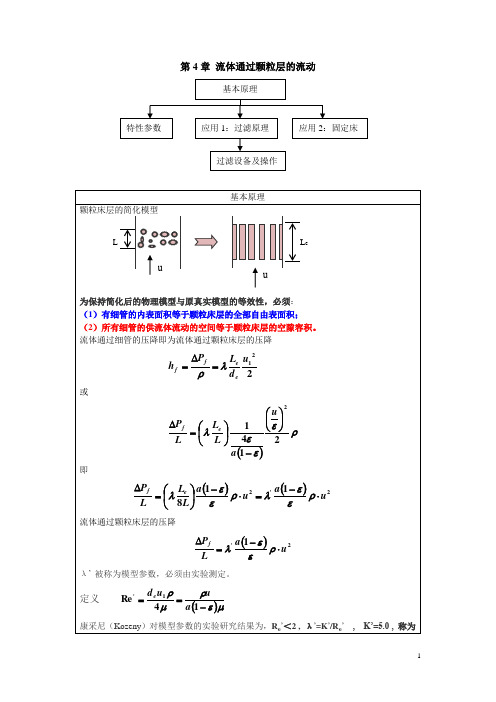
康采尼(Kozeny)对模型参数的实验研究结果为,Re’<2 ,λ’=K’/Re’, K’=5.0 ,称为Kozeny常数。
将模型参数的表达式代入到床层压降的表达式中
欧根(Ergun)在较宽的 范围内, ,获得了关系式
代入到床层压降的表达式中
特性参数
1、颗粒的比表面积
2、颗粒床层的空隙率
3、颗粒床层的比表面积 ,
第4章流体通过颗粒层的流动
基本原理
颗粒床层的简化模型
为保持简化后的物理模型与原真实模型的等效性,必须:
(1)有细管的内表面积等于颗粒床层的全部自由表面积;
(1)
(2)所有细管的供流体流动的空间等于颗粒床层的空隙容积。
流体通过细管的压降即为流体通过颗粒床层的压降
或
即
流体通过颗粒床层的压降
λ’被称为模型参数,必须由实验测定。
单位过滤面积上的滤液体积量
滤饼厚度 、悬浮液中颗粒体积分率 、滤饼空隙率 与单位过滤面积上的滤液体积量 的关系式为
单位过滤面积上过滤速率的表达式则为
定义: , 称为滤饼的比阻。则过滤速率表达式为
或者
考虑过滤介质的阻力后,过滤速率为
令
则
或
定义过滤常数:
自开始即进行恒压过滤,则K为常数,并且 时, ,过滤时间 与累计滤液体积量 (单位面积上累计滤液体积量 )的关系
或
过滤设备及操作
1、板框式压滤机
在保持洗涤水粘度与滤液粘度相同,洗涤操作时的压差与过滤操作时的压差相同时,总面积上的洗涤速率与过滤终了时过滤的速率之间的关系
横穿流洗法, ;置换洗法,
洗涤时间 与过滤时间 的关系
一个生产周期的时间 ,
最佳时间分配:
流体通过颗粒层的流动-1-2015-11

4.1.1 工业背景固定床是由许多固体颗粒堆积成的静止颗粒层。
①流体物性:ρ,μ②操作因素:u③设备因素:颗粒直径,22eS eVd d =ψψ≤1 与球形差异度4.2.3 床层特性①床层空隙率ε受充填方式的影响均匀颗粒0.26—0.48与dp 分布有关乱堆床层0.47—0.7床床床空V V V V V p −==ε床V V p )1(ε−=ε对反映床层紧密程度,对流体流动的阻力有极大影响非球形乱堆的ε大于球形颗粒,非均匀颗粒ε小于均与颗粒。
,1f h εε↓↑<∑。
几何边界复杂,无法解析解,要靠实验需要用数学模型法来考虑②空隙中实际速度与空隙大小有关。
4.4 过滤过程 4.4.1基本原理 最简单的过滤操作: 布氏漏斗 悬浮液中固体颗粒被 过滤介质截留,清液在 压差下通过多孔过滤介 质,使固液分离。
过滤介质缝隙并不需要比颗粒小---架桥现象5%以上颗粒大 于过滤介质孔径 “穿滤”⎧深层过滤 两种过滤方式 ⎨ ⎩滤饼过滤 推动力:重力、压力、离心力滤浆 滤饼 过滤介质 滤液深层过滤滤饼过滤过滤介质: 多孔性介质、耐腐蚀、耐热并具有 足够的机械强度。
工业用过滤介质主要有:滤浆 滤饼织物介质,如棉、麻、丝、毛、合过滤介质 成纤维、金属丝等编织 滤液 成的滤布; 多孔性固体介质,如素瓷板或管、 烧结金属等。
滤饼过滤滤饼的压缩性:空隙结构易变形的滤饼为可压缩滤饼。
助滤剂: 是不可压缩的粉状或纤维状固体, 如硅藻土、纤维粉末、活性炭、石棉。
使用时,可预涂,也可以混入待滤 的滤浆中一起过滤。
滤浆 滤饼过滤介质 滤液方式1.预涂滤饼过滤方式2.混入悬浮液4.4.2 过滤过程的数学描述 4.4.2.1 物料衡算 过滤过程的数学描述 物料衡算滤浆 滤饼 过滤介质 滤液滤饼过滤定 义w :质量分数(kg固/kg悬) φ :体积分数(m3固/m3悬) ε:滤饼空隙率 V悬 :悬浮液总量 L: 滤饼厚度 A:过滤面积 LA:滤饼体积(包括ε)悬浮液含固量表示方法: 质量分数w, kg固体/kg悬浮液 3 3 φ , m /m 体积分数 固体 悬浮液滤浆 滤饼 过滤介质 滤液滤饼过滤取1m3悬浮液w=φρ p φρ p + (1 − φ ) ρw :质量分数(kg固/kg悬) 3固/m3悬) :体积分数( m φ注意:①滤液、滤饼、清液方向要清楚 ②基准要选好 滤饼空隙率ε与含清液质量分率w’关系 取1kg滤饼 取1m3滤饼 ερ w' / ρ w' = ε= ερ + (1 − ε ) ρ p w' / ρ + ( 1 − w' ) / ρ p物料恒算基本关系式• • • • • 悬浮液中固体质量=滤饼中颗粒质量 悬浮液中清液量=滤液量+滤饼中清液量 悬浮液的总量=颗粒量+全部清液 =滤饼的量+滤液 滤饼的量=固体颗粒的量+滤饼中滤液的量颗粒在液体中不发生溶胀V ⎧V悬 = V + LA q = ,单位面积滤液量 ⎨ A φ = − ε V LA 1 ( ) ⎩ 悬φ V φ = L= q 1−ε −φ A 1−ε −φL为滤饼厚度φ=w/ρp w / ρ p + (1 − w ) / ρw :质量分数(kg固/kg悬) φ :体积分数(m3固/m3悬)。
第四章流体通过颗粒层的流动

n xn x 1 1 x1 x2 i d m d d1 d 2 d n i 1 di
14
华东交通大学化工原理课件
3.颗粒密度 (1)真密度:单位体积颗粒所具有的质量 m s V (2)堆积密度(表观密度):单位体积床 层所具有的质量,即
(3)两者关系:
m b Vb
空降率与床层自由截面积分率之间有何关系?假 设床层颗粒是均匀堆积(即认为床层是各向同性 的)。想象用力从床层四周往中间均匀压紧,把 颗粒都压到中间直径为长为L的圆柱中(圆柱内设 有空隙)。
v D 1 1 4 1 1 2 V D D L 4
D12 L
2
A D A0 1 P 1 4 1 1 2 A D D 4
由于体积相同时,球形颗粒的表面积最小,故非 球形颗粒的s <1,而且颗粒与球形差别愈大,其 s值愈小。 对非球形颗粒必须有两个参数才能确定其几何特 性,通常选用de和s来表征。
11华东交通大来自化工原理课件二、颗粒群的特性
1.粒度分布(粒径分布) (1) 定义:不同粒径范围内所含粒子的个数 或质量 (2)测定方法:标准筛法、透射电镜法等 (3)筛分结果的图示:分布函数和频率函数 分布函数:令某号筛子的筛过量占试样总量 的分率为Fi,不同筛号的Fi与筛孔尺寸绘成 的曲线称为分布函数曲线。
上式称为欧根方程,其实验范围为Re’=0.17420。 当Re’<3时,等式右方第二项可以略去;当Re’ >100时,右方第一项可以略去。
26
华东交通大学化工原理课件
从康采尼方程或欧根方程可看出,影响床层 压降的变量有三类: ①操作变量 u ②流体物性 和 ③床层特性 和 在上述因素中,影响最大的是空隙率
化工原理课件 流体通过颗粒层的流动

4.4.1过滤原理 4.4.2过滤设备
4.4.1过滤原理
(1)过滤
过滤是在外力作用下,使悬浮液中的液体通过多孔介 质的孔道,而悬浮液中的固体颗粒被截留在介质上, 从而实现固、液分离的操作。 几点说明: 1)过滤介质:将过滤操作所使用的多孔性物质称为 过滤介质,其作用是截留悬浮液中的固体颗粒。
K ——称为康采尼常数 ,其值为5.0
a (1 ) 2 u 3 L K K a(1 ) Re u
a 2 (1 ) 2 K u 3 L
——康采尼方程
4.3.1颗粒床层的简化模型
欧根在较宽的 Re/范围内研究了λ/与 Re/的关系: 4.17 0.29 Re a (1 ) 2 u 3 L (1 )2 a 2 (1 )a 2 4.17 u 0.29 u 3 3 L
1 xi (d ) pi
对非球形颗粒以(ψde)i代替式中的dpi
4-1 筛分分析计算
取颗粒试样500克作筛分分析,所用的筛号及筛孔 尺寸见表4-1中1、2列。筛分后称取各号筛面上的 颗粒筛余量列于表第3列。试作该颗粒群的分布函 数曲线与频率曲线,设颗粒为球形,试以比表面积 相等为准则计算颗粒群的平均直径。
a 2 (1 ) 2 K u 3 L
1 3 1 a L K (1 ) 2 u
校验床层雷诺数:
Re'< 2 ,上述计算有效。
4.3. 2 量纲分析法和数学模型法的比较
化工过程具有复杂性难以采用数学解析法求解,而必 须依靠实验 。 ①化学工程学科本身的基本规律和基本观点 ②正确的实验方法论
Le a(1 ) 2 ) u 3 8L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
π
6
dp
2
3
d ev =
3
6V
π
S
S = π dp
d es =
6 比表面积等效—比表面当量直径 a = dp 6 S π d es 2 = = a= d ea V π d 3 ev 6 d ev 3 d d ea = 2 = ( ev ) 2 d ev = ψ d ev d es d es
π 6 d ea = a
西北大学化工原理课件
π d ev 2 与非球形颗粒具有相同体积的球的表面积 ψ= = 2 π d es 非球形颗粒的实际表面积
称ψ为形状系数。对体积相同的实体,球形的表 面积最小。 结论 :任何非球形颗粒 ψ<1 对非球形颗粒通常定义dev (简为de) 和ψ:
V=
π
6
de
3
π de2 S= ψ
6 a= ψ de
xi fi = di −1 − di 1 d pi = (di −1 + di ) 2
xi=(某号筛面上的颗粒质量/试样总量)
西北大学化工原理课件
频率函数的重要特性 ① 在一定范围内的颗粒占全部试样的质量分率 等于该颗粒范围内频率函数曲线下的面积; ② 频率函数曲线下的全部面积为1。 3. 颗粒群的平均直径 xi 1 1 mi 1 = ∑( 或 dm = )=∑ xi dm d pi m d pi ∑ d pi 式中:m—总质量
西北大学化工原理课件
二、颗粒群的特性
1. 粒度分布的筛分分析 对大于70μm的颗粒,采用一套标准筛进行测量。 常用泰勒标准筛:每英寸边长上开的孔数为目数。 2. 分布函数和频率函数 (1)分布函数: i号筛子—筛孔尺寸dpi Fi=(筛过量/试样总量)
西北大学化工原理课件
分布函数的重要特性 ①对应于某一尺寸dpi的Fi 表示直径小于dpi的颗粒 占全部试样的质量分率; ②在该批颗粒的最大直 径dpmax处,分布函数Fi =1。 (2)频率函数:
西北大学化工原理课件
某截面上的空隙面积 ε= 床层截面积
但壁效应存在,当D/dp较大时壁效应可忽略。 3. 床层的比表面积aB 单位床层体积所具有的颗粒表面积称为床层 的比表面积,以aB表示。
ns nva V p a V (1 − ε )a aB = = = = = (1 − ε )a V V V V
西北大学化工原理课件
第二节 颗粒床层的特性
一、单颗粒的特性
1. 球形颗粒 体 积
V=
π
6
= π dp
S 6 a= = V dp
( m 2 / m3 )
式中:dp——球形颗粒的直径
西北大学化工原理课件
2. 非球形颗粒——定义当量直径 在体积等效—体积当量直径 表面积等效—面积当量直径
mi—相邻两号筛之间的颗粒质量,其直径为dpi; 对非球形颗粒以(ψde)i代替式中的dpi
西北大学化工原理课件
三、床层特性
1. 床层空隙率
床层体积 − 颗粒所占体积 ε= 床层体积
空隙率通过实验测得,一般乱堆床层的空隙率: ε=0.47~0.7 2. 床层的各向同性 非球形颗粒乱堆时,各颗粒的定向应是随机的, 即认为床层是各向同性的。其特点是:
