环流与旋度
2.4矢量场的环量及旋度分析

1 (er e ez ) r r z 1 (rFr ) 1 F Fz F (r ) r r r z
3) 在球面坐标系下: 1 1 (er e e ( ) ) r r r sin
1、散度的定义 在场空间 A(r ) 中任意点M 处作一个闭合曲面,所围的体积 为 V ,则定义场矢量 A(r ) 在M 点处的散度为:
divA( r ) lim
s
A(r ) dS v
v 0
2、散度的物理意义 1) 矢量场的散度代表矢量场的通量源的分布特性;
2) 矢量场的散度是一个标量;
F (r ) lim
s
F (r ) dS V
V
d lim V V dV
由于 F 是通量源密度, 即穿过包围单位体积的闭合面的 通量,对 F 体积分后,为穿 出闭合面S的通量
式中:S为包围V的闭合面
则在一定体积V内的总的通量为:
F (r )dV
S
( A) dS
意义:矢量场的旋度在曲面上的积分等于该 矢量场在限定该曲面的闭合曲线上的线积分。
斯托克斯定理的证明: 由旋度的定义
S 0
c
lim
c
Α dl S
ˆn rot A e
c
A d l ( A) dS
)
c1
A dl ( A) dS1 A dl ( A ) dS2
旋度
ˆ S S n
A
矢量场除了有散度源外,还有另一种源—旋度源。
P
空间中,取一有向闭合路
第七节 Stokes 公式 环流量与旋度

S
I = ∫∫ − zdzdx − ydxdy
S
z
平面方程为: 平面方程为:
Γ
S
平面 S 的法向量
n = (0,1, −1)
z=y
法方向的方向余弦为
o x
2
y
因此
I = ∫∫ (− z ⋅ cos β − y cos γ ) d S
S
= ∫∫
S
1 ( y − z) d S = 0 2
n
∑
右手法则
Γ是有向曲面 Σ 的
Γ
正向边界曲线
证明
∂Z ∂Y ∂X ∂Z ∂Y ∂X ∫∫( ∂y − ∂z )dydz + ( ∂z − ∂x )dzdx + ( ∂x − ∂y )dxdy Σ
= ∫ Xdx +Ydy + Zdz
Γ
思路
曲面积分 1 二重积分 2
曲线积分
便于记忆形式
dydz dzdx dxdy ∂ ∂ ∂ ∫∫ ∂x ∂y ∂z = ∫Γ Xdx +Ydy + Zdz Σ X Y Z
Γ
y 2 dx + z 2 dy + x 2 dz , 其 中 Γ 是 球 面
四、利用斯托克斯公式把曲面积分 ∫∫ rot A ⋅ nds 化成曲
∑
线积分,并计算积分值, 分别如下: 线积分,并计算积分值,其中 A ,∑ 及n 分别如下: A = y 2 i + xy j + xz k ,∑ 为上半个球面 的上侧, 的单位法向量. z = 1 − x 2 − y 2 的上侧, n 是∑ 的单位法向量. 五、求向量场 A = ( x − z )i + ( x 3 + yz ) j − 3 xy 2 k 沿闭曲 线Γ 为圆 周 z = 2 − x 2 + y 2 , z = 0 时针方向) (从 z 轴 正向看Γ 依逆 时针方向)的环流量 . 设 具有二阶连续偏导数, 六、 u = u( x , y , z ) 具有二阶连续偏导数,求rot ( gradu) .
从定义出发给出旋度公式的推导

从定义出发给出旋度公式的推导一班 唐浩月 131 旋度的概念由于矢量场在点M 出的环流密度与面元∆S 的法线方向n e 有关,因此,在矢量场中,一个给定点M 处延不同方向,它的环流密度值一般是不同的。
在某一个确定方向上,环流面密度可能取很大的值。
为了描述这个问题,引入了旋度的概念。
矢量场F 在点M 处的旋度是一个矢量,记为rotF,它的方向沿着使得环流密度去的最大值的面元法线方向,大小等于该环流密度最大值,即max 01lim c S rot F n F dl S →→→∆→=∆⎰ 2 公式推导若在场A (M )中的一点M 处存在这样的一个向量,其方向为A ,在点M 处环量密度最大的方向,其模等于环量密度的最大值,则称此向量为A (M )在M 的旋度,记为rot A 。
我们首先推导环量密度的计算公式。
建立直角坐标系,设((,,),(,,),(,,))A P x y z Q x y z R x y z =为区域上的3G R ⊆上的(1)C 类函数,(cos ,cos ,cos )n e αβγ=, 由环量密度的定义以及Stokes 公式的向量形式可知:11lim lim (*)nc S M S M S dT AdS A e dS dS S S →∆→∆→∆==∇∆∆⎰⎰⎰利用积分中值定理可知:(*)[(*)],()n n M S A e dS A e S M S ∆∇=∇∆∈∆⎰⎰由于(*)*n A e ∇在M 处连续,从而 11lim lim (*)n c S M S M SdT AdS A e dS dS SS →∆→∆→∆==∇∆∆⎰⎰⎰ 或 ()cos ()cos ()cos dT R Q P R Q P dS y z z x xyδδδδδδαβγδδδδδδ=-+-+- 上面两公式就是环量密度的计算公式。
从而可知:*cos n dT A e dSϕ=∇ 其中为向量与的夹角,因而当,即取于向量同向时,环量密度最大,为。
动力气象学第四章

r d(ζ + f ) ⇒ + (ζ + f )∇⋅V = 0 dt
r dζ a ⇒ + ζ a∇ ⋅V = 0 dt
与连续方程:
r dρ + ρ∇⋅V = 0 dt
——质量守恒类似,体现了绝对角 动量守恒。
水平散度= 水平散度=水平截面 积的相对变化率, 积的相对变化率,即:
r 1 dσ ∇⋅V = σ dt
β —平面近似:
f = 2Ωsin ϕ df df 2Ωcosϕ = β= = dy a ⋅ dϕ a ⇒ f = f ( y), β = β( y) d 一 系数 方程 。 了 ⇒求解 ζ = −βv是 个变 dt 但一 β ≠ 0即可 般 ,故 如下 作 近似:
f = 2Ωsin ϕ 把f在ϕ0处作Taylor展开⇒对y展开 1 d2 f df (ϕ −ϕ0 ) + (ϕ −ϕ0 )2 +⋅⋅⋅ f =fϕ + 2 0 2 dϕ ϕ2 dϕ ϕ0 = Ωsin ϕ0 + 2Ωcosϕ0 (ϕ −ϕ0 ) + o[(ϕ −ϕ0 ) ] 2
位涡是一个热力学与动力学量 组合的物理量。 组合的物理量。 位涡方程由涡度方程、 位涡方程由涡度方程、连续方 位温方程三个方程导出。 程、位温方程三个方程导出。 3.位涡守恒的条件: 绝热无摩擦
r F = ; &= γ 0 Q 0 d 1 r ⇒ ( ζ a ⋅ ∇ln θ) = 0 ⇒位 守 涡 恒 dt ρ
r ① − (ζ + f )∇⋅V r ≈ − f∇⋅V
散度项
∂v ∂u V ζ= − ∝ ≈ 10−5 s−1 << f ≈ 10−4 s−1 ∂x ∂y L
②
第1章 矢量分析(3)

v v v v v v v rotF = rot x F ex + rot y F ey + rot z F ez
v ∂Fz ∂Fy v ∂Fx ∂Fz v ∂Fy ∂Fx = ex − − − + ey + ez ∂z ∂x ∂y ∂z ∂y ∂x
第1章 矢量分析
3
1.5 矢量场的环流与旋度
1.5.1 环流 1、线元矢量 、
在矢量场中,从一点沿着某一指定的曲线 到另一点的 在矢量场中,从一点沿着某一指定的曲线C到另一点的 v 路径上,每一线元都是一个矢量,称之为“ 路径上,每一线元都是一个矢量,称之为“线元矢量 ”, dl 其方向就是曲线C在该点处的切线方向 在该点处的切线方向, 其方向就是曲线 在该点处的切线方向,大小为 dl。
磁感应线要 么穿过曲面
磁感应线 磁感应线要么同时 穿入和穿出曲面
说明: 说明: ⅰ与矢量穿过闭合面的通量一样,矢量的环流也是 与矢量穿过闭合面的通量一样, 描述矢量场性质的重要参量。 描述矢量场性质的重要参量。 ⅱ如果矢量沿闭合曲线的环量不为零,则矢量场存 如果矢量沿闭合曲线的环量不为零, 在“旋涡源”。 旋涡源” ⅲ旋涡源与通量源不同,它既不发出矢量线,也不 旋涡源与通量源不同,它既不发出矢量线, 汇集矢量线。 汇集矢量线。 这种源所产生的矢量场的矢量线是闭合的曲 线,因此称为旋涡源。 因此称为旋涡源。
1.6 无旋场与无散场
1.6.1 无旋场
v v 若一矢量场 F 中,其旋度处处为零,即 ∇ × F ≡ 0 其旋度处处为零, v v 则该场称为无旋场, 则该场称为无旋场,有 ∫ F ⋅ dl = 0
c
标量场梯度重要性质:标量场梯度的旋度恒等于零。 标量场梯度重要性质:标量场梯度的旋度恒等于零。 旋度恒等于零
环量和旋度

2πR2
方法二:
rot A A
ex ey ez
x y z y x c
2ez
由斯托克斯定理得
lA d l s ( A ) d S 2 s e z d S 2 π R 2
【例】用以下两种方法求矢量场A x ( z y ) e x y ( x z ) e y z ( y x ) e z
的边界曲线记为l。 若当S 收缩至P 点附近时存在极限
lim l A dl
S 0 S
SnS
P A
l
(b)
则此极限称为矢量场 A 在P 点沿n方向的环量(面)密度
或环量强度。该极限值与S的形状无关,但与S的方向n有
关。
2. 旋度 定义:
矢量场A在某给定点的旋度用rotA表示为
Adl
rotAAlim [ l S 0 S
在点M(1,2,3) 处沿方向 lex2ey2ez 的环量面密度。 ①直接应用环量面密度的计算公式; ②作为旋度在该方向的投影。
【解】:
①矢量 lex2ey2ez的方向余弦为
cos1,cos2,cos2
3
3
3
矢量场为 A x ( z y ) e x y ( x z ) e y z ( y x ) e z 由环量面密度公式
在点M(1,2,3) 处旋度为
rotA(1,2,3)5ex4ey3ez
l
方向的单位矢量
lo
l l
13(ex 2ey 2ez)
在点 M(1,2,3)处沿 l 方向的环量面密度为:
A lo58619 M 333 3
内容小结
主要概念:
❖ 环量 ❖ 旋度
旋涡源
若环量(旋度)等 于零,该矢量场为 无旋场或保守场
环流与旋
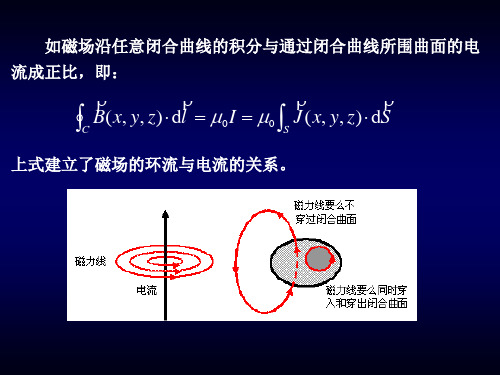
流成正比,即:
B(x, y, z)dl
C
0I
0
J (x, y, z) dS
S
上式建立了磁场的环流与电流的关系。
环流的概念
矢量场对于闭合曲线C 的环流定义为该矢量对闭合曲线C
的线积分,即
C F(x, y, z) dl
如果矢量场的任意闭合回路的环流恒为零,称该矢量场为无
无旋场可以用标量场的梯度表示为
F u
F (u) 0
例如:静电场
E 0 E
(2)无散场
仅有旋度源而无散度源的矢量场,即
F 0
性质:
F dS 0
S
无散场可以表示为另一个矢量场的旋度
F A
F ( A) 0
例如,恒定磁场
B 0 B A
(3)无旋、无散场(源在所讨论的区域之外)
计算公式: 直角坐标系 2u 2u 2u 2u x2 y2 z2
圆柱坐标系
2u
1
(
u )
1
2
2u
2
2u z2
球坐标系
2u
1 r2
r
(r2
u) r
1
r2 sin
(sin
u )
1
r2 sin2
2u
2
• 矢量拉普拉斯运算 2F
概念: 2F ( F) ( F)
直角坐标系中:2F ex2Fx ey2Fy ez2Fz
此外,格林定理反映了两种标量场之间满足的关系。因此, 如果已知其中一种场的分布,即可利用格林定理求解另一种场 的分布。
格林定理广泛地用于电磁理论。
1.8 亥姆霍兹定理
亥姆霍兹定理:
矢量
20
直角坐标系中 由梯度公式(1.3.7):
和散度公式 (1.4.9):
可得▽2u的表达式为:
u u u u 2 2 2 x y z
2 2 2 2
(1.7.1)
21 圆柱坐标系中源自由梯度公式(1.3.10):
和散度公式 (1.4.11):
可得▽2u的表达式为:
2
1 u 1 u u u ( ) 2 ( 2 ) 2 z
一、概念
(1.5.3)
即环流面密度取得最大值的面元正法线单位矢量
4
二、物理意义
矢量的旋度为矢量,是空间位置的函数; 矢量在空间某点处的旋度表征矢量场在该点处的漩涡源密 度; 矢量场在某个方向的环量密度是旋度在该方向上的投影。 如图1.5.2所示,即:
rotn F en rotF
MC模拟发展的背景、意义
作 业
1.23、1.27、 1.28、 1.31
32
2
S
dS n
(1.7.7)
由式(1.7.6)与式(1.7.7)相减,得到格林第二恒等式为:
V
( )dV
2 2
S
( )dS n n
(1.7.8)
格林定理描述了两个标量场之间满足的关系。如果已知 其中一个场的分布,就可以用格林定理求解另一个场的分 布。
23
二、 矢量场的拉普拉斯运算
F ( F ) ( F )
2
矢量场F的拉普拉斯运算定义为:
(1.7.4)
在直角坐标系中为:
2 2 2 F ex Fx ey Fy ez Fz
2
(1.7.5)
24
散度,旋度,涡度

散度,旋度,涡度假设有一个三维空间,显然空间的每一个点都能用坐标(x, y, z)唯一地标识出来。
假如给空间的每一个点都赋予一个数字,那么整个空间就充满了数字。
此时,这个充满数字的三维空间在数学上就叫做“场”。
上述的场叫做标量场,因为单纯的一个数字叫做“标量(scalar)”。
如果我们给空间的每一个点都赋予一个矢量(vector),即一个既有大小,又有方向的东西,那么整个空间就变成充满了矢量,这个空间就叫做矢量场。
矢量场中的每一点都对应于一个矢量,而矢量能够根据规则进行各种运算,例如加、减和乘等(数学上没有矢量的除法)。
显然,我们可以对整个矢量场中的每一个矢量同时进行某种运算,例如同时将它们乘以一个数,或加上一个数等。
但是我们可以对整个矢量场进行一些更复杂的运算,其中散度就是其中一种。
三维空间中的一个矢量可以沿x、y和z方向分解,现假设空间的某一点被赋予的矢量能够沿着这3个方向分解为大小为P、Q和R的三个分量,表示为(P,Q,R)。
注意,由于空间中每个点被赋予的矢量一般来说是不同的,所以P、Q和R的大小在空间的不同的点一般有不同的值,也就是说P、Q和R中每一个都是x、y和z的函数。
对三维矢量场来说,我们可以对其中一个点的矢量,假设为(P,Q,R)进行以下操作: 1、求出dP/dx,dQ/dy,dR/dz的值,其中dP/dx表示求P对x的一阶偏导数,其余雷同; 2、将这个值赋予这个点对整个矢量场的每个点均进行以上运算,就等于给整个三维空间的每个点都赋予了一个值,于是我们就得出了一个新的标量场,这个标量场就叫做原来的矢量场的散度(divergence),这种运算就叫做“对矢量场取散度”。
除了散度运算以外,我们还可以对矢量场进行其它的运算,例如旋度运算(curl)。
跟散度运算不同,旋度运算的结果不是标量场,而是另一个矢量场。
旋度运算的规则比较繁复,但是网上很多地方都有解释,这里就不讲了。
而涡度就是一个速度场的旋度,显然涡度是一个矢量场,而散度是一个标量场,这就是两者的本质区别了。
《环流量与旋度》课件

05
CHAPTER
环流量与旋度的物理意义
环流量的物理意义
01Biblioteka 0203描述流体在封闭曲线上 的流动特性
反映流体在空间中流动 的总体效果
是流体运动的一个重要 参数,对于研究和解决 流体运动问题具有重要
意义
旋度的物理意义
表示向量场中某点附近的旋转程 度
反映向量场中某点附近的旋转特 性和流动趋势
是描述向量场的一个重要参数, 对于研究和解决流体动力学问题
旋度的计算方法
微分法
定义
通过微分运算来计算旋度,利用向量场中点的变化率来定义旋度。
公式
$nabla times vec{F} = lim_{Delta rightarrow 0} frac{Delta vec{S}}{Delta V}$,其中 $Delta vec{S}$是曲面上的面积向量,$Delta V$是体积增量。
《环流量与旋度》ppt课件
目录
CONTENTS
• 环流量与旋度概述 • 环流量的计算方法 • 旋度的计算方法 • 环流量与旋度的应用 • 环流量与旋度的物理意义
01
CHAPTER
环流量与旋度概述
环流量的定义与性质
定义
环流量是矢量场中封闭曲线上矢 量所围成的面积分。
性质
环流量与路径无关,只与起点和 终点的位置有关;环流量是矢量 场的一个重要物理量,反映了矢 量场中某区域的通量分布情况。
电磁场涡旋
在研究电磁波的传播和辐射问题时 ,需要用到电场和磁场的涡旋,它 们与磁场和电场的旋度有关。
在量子力学中的应用
量子旋度
在量子力学中,旋度被用来描述微观粒子的自旋角动量,对 于理解量子力学的各种现象,如自旋、角动量等具有重要意 义。
环流和旋度的物理意义

环流和旋度的物理意义1. 引言嘿,朋友们,今天我们来聊聊环流和旋度,听起来是不是有点高大上?别担心,我会把它们变得简单明了。
环流和旋度,这俩小家伙可不是随便的名词,它们在物理学,尤其是流体力学中可是一手抓的大明星。
想象一下,空气和水在动,像跳舞一样,咱们就能看到环流的魅力。
2. 什么是环流?2.1 环流的概念那么,环流到底是什么呢?简单来说,环流就是流体在某个区域内旋转的趋势。
就像你在洗澡的时候,水在浴缸里旋转,形成一个小漩涡,这就是环流的体现。
你想想,水流在河里,风在空中,它们不都是在做这种“旋转运动”吗?环流不仅存在于水和空气中,甚至在气候系统中也有它的身影。
2.2 环流的例子比如说,台风!这个大家都知道,台风就是个大旋转的气团,刮得那叫一个猛啊。
环流在这儿可是主角,它把大量的水汽吸上来,导致狂风暴雨,真是“雨打梨花深闭门”。
而我们的天气预报,也经常提到环流现象。
你说,这环流跟我们的生活真是息息相关。
3. 旋度的含义3.1 旋度的概念接下来聊聊旋度,这词听起来就像是个高深的数学概念,实际上,它就是衡量流体旋转的强度和方向的。
就像你在舞会上看到的那些舞者,旋度告诉你他们的转身速度和方向。
想象一下,你在河流中划船,如果你划的方向与水流的旋转方向相同,那你就能感觉到旋度的力量。
3.2 旋度与生活旋度其实在我们的日常生活中也随处可见。
比如,旋风、漩涡,甚至是小朋友们在公园里转圈圈,都能看到旋度的影子。
它就像一个无形的力量,让流体在某个方向上旋转。
说到这,我就想起小时候在游乐园里玩的旋转木马,真是让人晕得不要不要的,恰恰是旋度在作怪。
4. 环流与旋度的关系4.1 二者的联系环流和旋度这俩小伙伴,虽然听上去各有各的特点,但其实它们之间有着密不可分的关系。
可以这么说,环流是一个大场面,而旋度则是舞台上的小演员。
环流决定了大方向,旋度则负责具体的旋转。
就像做菜,调料决定了味道,火候则决定了成品的样子。
4.2 共同的影响在天气预报中,环流和旋度一起影响着我们的气候。
《环流量与旋度》课件

水流环流量的实际应用包括水力发电和水资源管理。风力发电机叶片的环流量分析可以提高 风能利用效率。
三、旋度
3.1 定义和计算方法
旋度是流体流动的旋转性质。通过旋度的计算 公式,可以描述流体流动的强度和方向。
3.2 示例分析
旋度在天气学中的应用可以帮助预测气旋、龙 卷风等天气现象。在流体力学中,旋度可用于 分析湍流等复杂流动。
四、比较与总结
1
异同点分析
环流量和旋度都描述流体运动性质,但环流量强调流体的循环运动,而旋度描述 流体的旋转性质。
2
应用差异
环流量在水力学、风力学等领域有着广泛应用,而旋度在气象学、流体力学等领 域具有重要意义。
五、结论
基本物理量的重要性
环流量和旋度作为基本物理量,对于研究流体力 学和相关学科具有重要意义。
未来和旋度的计算方 法,探索更多领域中的应用。
六、参考文献
1. 张三, "环流量与旋度的原理与应用", 中国物理学报, 2020, 42(2): 123-135
2. 李四, "环流量和旋度在气象学中的应用研究", 天气科学研究, 2018, 36(4): 256-267
3. 王五, "环流量与旋度的计算方法研究进展", 流体力学进展, 2019, 54(3): 189202
《环流量与旋度》PPT课 件
环流量与旋度是物理学中重要的概念。本课件将介绍环流量和旋度的定义、 计算方法以及在不同领域的应用。
一、引言
环流量和旋度是描述流体运动性质的重要物理量。它们在天气学、流体力学等领域有着广泛的应用。
二、环流量
2.1 定义和计算方法
环流量是流体横截面上的循环运动量。根据横截面积的环流量计算公式,可以准确计算流体 环流量。
旋度就是任意方向的环量密度

旋度就是任意方向的环量密度
环旋度是描述一个物质(包括物理现象和化学现象)在各级方向上旋转角度的一个物
理量,也叫环量密度。
它是用以描述流体(气体或液体)及其他物质流动时环境中服从其
物理规律的量测指标。
环旋度可以用来研究物质流动的特性,有助于深入分析物质流动的
本质,如温度、压力分布等,从而获得有效的结果。
环旋度的定义如下:环旋度是某一物质在某一时间在某一特定方向上的环形流量密度,它以半径(r)为基础,以旋转角度(θ)为量度,可表示为Ω=r/θ 。
环旋度有三种不同的表示方式:带标量,带方向,带矢量。
其中,带标量表示的环
旋度乘以一个半径(r),单位是1 /米,表示流动态环旋度,可用于具体的流体模拟;与此同时,带方向的环旋度另外定义了r的方向,多次应用在流体力学和软件编程中;带矢
量的环旋度跟带标量的环旋度类似,用类向量表达,更多地用于定义流体映射方程和理论
计算。
环旋度研究表明,当物质进行空气或液体流动时,周围空气或液体旋转方向与空气或
液体流动之间存在一定程度上的变化,即环旋度由空气或液体流动方向所影响。
有时,较
大的环旋度密度可以导致气泡形成、小范围换向现象产生等不利的结果,需要加以控制。
因此,环旋度可以用来衡量流体物质切换方向的频率。
环旋度的广泛应用,主要表现在流体力学、软件工程和电子设计等领域;在环境动力学、气象学、流体动力学、航空技术、火箭、导弹及其他一些科学和工程领域也有较为重
要的应用。
环旋度可以跟踪运动物体旋转角度的变化,从而实现合适的动力控制,增强目
标的定位准确性和有效性。
科斯第二定理简单举例

科斯第二定理简单举例
科斯第二定理(Kelvin–Stokes theory)是一个重要的物理定律,它提
供了评估流体矢量场的实用方法。
它表明,流体矢量场等效于一个正
交于流体中各点的旋度(Curl),定义为空间尺度上曲流系数的质量扰动。
这意味着,流体边界可以用简单的旋度计算来定义,这样就可以计算
出流体定义的空间结构。
科斯第二定理的一个很好的例子是用于分析气旋的问题。
气旋由一系
列的对流循环支配,这些循环本质上是一种旋度,这是科斯第二定理
的好例子。
科斯第二定理的应用在气旋的模拟中也很重要,特别是在
预报气旋形成和发展的情况下。
此外,科斯第二定理也可以用于计算许多水文地质问题。
举个例子,
当河流按照一定流向向海洋扩展时,它们会产生环流,即沿着河流有
一系列旋度可以检测到。
科斯第二定理可以用来预测这些环流的准确
流动路径,以及从陆地到海洋的流体输送。
科斯第二定理在流体动力学中发挥着重要作用,它可以用来计算各种
流体力学和水力学问题。
换句话说,科斯第二定理提供了通过旋度计
算流体尺度物理过程的强有力的技术手段。
它也可以用来预测各种湍
流反应,例如在自洽理论中用来计算随机流体力学问题的比率。
它使
得针对普通流体进行定量研究变得更容易,这种定量研究可以探索出
流体动力学的定律以及现实的流体动力学应用,然后用定量方法给出
案例解释。
1.5 旋度

2
1 2 2 ( cos 2 ) |0 4 另外在平面xy内,闭合路径为x2+y2=1,(z=0),dl ex dx e y dy
因此有
l
A dl
( zdx xdy) xdy
l l
1 1
1
1
1 y dy ( 1 y 2 )dy
S x 0
lim
1234
A dl S x
Az Ay rot x A y z
rot A在x轴上的分量
同理可得
lim
S y 0
A dl A
S y
S z
Az rot y A z x
x
rot A在y轴上的分量
S z 0
lim
A dl A
球坐标系:
e
F ez z Fz
4.旋度计算相关公式: 1) C 0
标量场的梯度 的旋度恒为零
er 1 F 2 r sin r Fr
re rF
r sin e r sin F
2) (k A) k A 3) ( A B) A B 4) (uA) u A u A
Ax Ay Az divA A x y z
5)在散度公式中,矢量场 A 的场分量 Ax , Ay , Az 分别只对 x, y, z 求偏导数,所以矢量场的散度描述的是场分量沿着各自方 向上的变化规律。
10
三、斯托克斯定理
l A dl
S
( A) dS
3 2
A (e x e y e z ) (e x x 2 e y y 2 e z z 2 ) 0 x y z
旋度的数学意义

旋度的数学意义全文共四篇示例,供读者参考第一篇示例:旋度(Curl)是矢量场的一个概念,它在数学上具有重要意义。
在向量分析中,旋度描述了矢量场的局部旋转特性,是矢量场在某个点上的旋转量。
旋度的数学意义是研究矢量场的旋转性质以及它在某一点上的旋转速率。
旋度的定义是一个矢量运算,通常表示为\nabla \times\textbf{F},其中\nabla是梯度算子,\textbf{F}是矢量场。
旋度的计算方式可以通过叉乘来得到,即\nabla \times \textbf{F} =\begin{bmatrix}\textbf{i} & \textbf{j} & \textbf{k} \\\frac{\partial}{\partial x} & \frac{\partial}{\partial y} &\frac{\partial}{\partial z} \\F_x & F_y & F_z\end{bmatrix}。
\textbf{i},\textbf{j},\textbf{k}分别表示x,y,z方向的单位矢量。
在物理学中,旋度是描述流体力学、电磁学等领域中的旋转运动的重要工具。
在电磁学中,麦克斯韦方程组描述了电场和磁场的演化规律,而其中的法拉第电磁感应定律和安培环路定理中都出现了旋度的概念。
在流体力学中,旋度揭示了流体在某点的局部旋转性质,对于流体的运动规律有着关键的影响。
旋度的数学意义还可以通过它的几何释义来理解。
几何上,旋度表示矢量场在某点上的局部旋转性质。
当旋度不为零时,说明该点处存在旋转运动;当旋度为零时,说明该点处的矢量场是无旋场,即不存在旋转运动。
旋度的大小表示了旋转运动的强度,方向表示了旋转的方向。
旋度与梯度、散度一起构成了向量分析中的基本运算符。
梯度描述了标量场的变化率和最快增长方向,散度描述了矢量场的发散程度,而旋度描述了矢量场的旋转性质。
旋度的量纲

旋度的量纲1. 介绍在物理学中,旋度是描述矢量场旋转程度的物理量。
它是一个矢量,用于表示矢量场的环流或涡旋性质。
旋度的量纲是一个非常重要的概念,它可以帮助我们理解旋度的物理意义和在各种领域中的应用。
本文将介绍旋度的定义、性质以及与量纲相关的内容,并探讨旋度的量纲在不同物理量中的具体应用。
2. 旋度的定义与性质旋度的定义可以通过矢量微积分中的旋度运算符进行。
对于一个三维矢量场A,旋度运算符可以表示为:∇ × **A** = (∂A₃/∂y - ∂A₂/∂z) **i** + (∂A₁/∂z - ∂A₃/∂x) **j** + (∂A₂/∂x - ∂A₁/∂y) **k**其中,∇指代梯度运算符,∂/∂x、∂/∂y和∂/∂z分别表示对坐标x、y、z的偏导数,i、j和k是单位矢量。
旋度描述了矢量场在某一点处的旋转程度和旋转方向。
如果旋度为零,表示矢量场是无旋的,其环流沿任何封闭路径都等于零;如果旋度非零,表示矢量场具有旋转特性。
旋度的物理意义在于它可以描述流体力学、电磁场等领域中的涡旋行为。
例如,在流体力学中,涡旋是流体流动中产生的旋涡,旋度可以量化涡旋的强度和方向。
3. 旋度的量纲旋度的量纲可以通过对旋度运算符中各个分量进行分析来确定。
根据上述定义的旋度运算符:∇ × **A** = (∂A₃/∂y - ∂A₂/∂z) **i** + (∂A₁/∂z - ∂A₃/∂x) **j** + (∂A₂/∂x - ∂A₁/∂y) **k**我们可以得到每个分量的量纲:•(∂A₃/∂y - ∂A₂/∂z)的量纲为[A]/[L]•(∂A₁/∂z - ∂A₃/∂x)的量纲为[A]/[L]•(∂A₂/∂x - ∂A₁/∂y)的量纲为[A]/[L]其中,[A]表示矢量场A的量纲,[L]表示长度的量纲。
因此,旋度的量纲为[A]/[L]。
4. 旋度量纲的应用旋度量纲的应用广泛存在于各个物理领域中。
下面以两个具体的例子来说明旋度量纲的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r r r r r F (r ) = − ∇ u (r ) + ∇ × A(r )
如磁场沿任意闭合曲线的积分与通过闭合曲线所围曲面的电 流成正比,即: 流成正比,
∫
C
r r r r B ( x, y, z ) ⋅ dl = µ 0 I = µ 0 ∫ J ( x, y, z ) ⋅ dS
S
上式建立了磁场的环流与电流的关系。 上式建立了磁场的环流与电流的关系。
环流的概念 矢量场对于闭合曲线C 的环流定义为该矢量对闭合曲线C 矢量场对于闭合曲线 的环流定义为该矢量对闭合曲线 的线积分, 的线积分,即
无旋场部分 无散场部分
1.7 拉普拉斯运算与格林定理
1、拉普拉斯运算 、 • 标量拉普拉斯运算 ∇ 2 u 概念: 概念: ∇ ( ∇ u ) = ∇ 2 u 计算公式: 计算公式: 直角坐标系
∇2
—— 拉普拉斯算符
∂ 2u ∂ 2u ∂ 2u ∇ u= 2 + 2 + 2 ∂x ∂y ∂z
2
2
1 ∂ ∂u 1 ∂ 2u ∂ 2u 圆柱坐标系 ∇ u = (ρ )+ 2 + 2 2 ∂ρ ∂z ρ ∂ρ ρ ∂φ
圆柱面坐标系 r r e ρ ρ eφ r 1 ∂ ∂ ∇×F = ρ ∂ρ ∂φ F ρ ρ Fφ
∂F y r ∂Fx ∂Fz r ∂F y ∂Fx + ey − + ez ∂x − ∂y ∂z ∂x ∂z r ez ∂ ∂z Fz
以上两式称为标量第一格林定理。 以上两式称为标量第一格林定理。 标量第一格林定理
基于上式还可获得下列两式: 基于上式还可获得下列两式:
∫
V
(Ψ ∇ Φ − Φ ∇ Ψ )d V =
2 2
∫
S
r (Ψ ∇ Φ − Φ ∇ Ψ ) ⋅ d S
∫
V
(Ψ ∇ Φ − Φ ∇ Ψ )d V =
2 2
∫
∂Φ ∂Ψ (Ψ −Φ )d S S ∂n ∂n
1.5 矢量场的环流和旋度
1. 矢量场的环流与旋涡源 不是所有的矢量场都由通量源激发。 不是所有的矢量场都由通量源激发。存在另一类不同于通量 源的矢量源,它所激发的矢量场的力线是闭合的, 源的矢量源,它所激发的矢量场的力线是闭合的,它对于任何闭 合曲面的通量为零。 合曲面的通量为零。但在场所定义的空间中闭合路径的积分不为 零。 例如: 例如:流速场
r r ∇ F = ∇ (∇ × A ) ≡ 0
例如,恒定磁场 例如,
r r r ∇⋅B = 0 ⇒ B = ∇ × A
源在所讨论的区域之外) (3)无旋、无散场(源在所讨论的区域之外) 无旋、
r ∇×F =0 r ∇⋅F = 0
r F = −∇ u
∇ ⋅ (−∇ u ) = 0
∇ u=0
2
(4)有散、有旋场 有散、 这样的场可分解为两部分: 这样的场可分解为两部分:无旋场部分和无散场部分 r r r r r r r r r F ( r ) = Fl ( r ) + FC ( r ) = −∇ u ( r ) + ∇ × A ( r )
1.8 亥姆霍兹定理
亥姆霍兹定理: 亥姆霍兹定理: 若矢量场在无限空间中处处单值,且其导数连续有界, 若矢量场在无限空间中处处单值,且其导数连续有界,源分 布在有限区域中,则当矢量场的散度及旋度给定后, 布在有限区域中,则当矢量场的散度及旋度给定后,该矢量场可 表示为
r r r 1 ∇ ′ ⋅ F ( r ′) 式中: 式中: u ( r ) = ∫V rr − rr ′ d V ′ 4π r r r r 1 ∇ ′ × F ( r ′) A(r ) = ∫V rr − rr ′ d V ′ 4π
r r r ∇ × F = e n [rot n F ] M ax
物理意义:旋涡源密度矢量。 物理意义:旋涡源密度矢量。 性质: 性质:
r r r rot n F = n ⋅ ∇ × F
旋度的计算公式: 旋度的计算公式:
r r ∂Fz 直角坐标系 ∇ × F = e x ∂y − r r ex e y ∂ ∂ = ∂x ∂y Fx F y
n
Stokes定理是闭合曲线积 定理是闭合曲线积 分与曲面积分之间的一个变换 关系式,也在电磁理论中有广 关系式, 泛的应用。 泛的应用。
S
C
曲面的剖分 图 1.5.5 曲面的划分 曲面的剖分
4、散度和旋度的区别 、
v v ∇ ⋅ F = 0, ∇ × F = 0
v v ∇ ⋅ F ≠ 0.∇ × F = 0
r
r ro t n F = lim
∆S → 0
1 ∆S
∫
C
r r F ⋅ dl
r n
∆S
v F
M
称为矢量场在点 环流面密度。 称为矢量场在点M 处沿方向n的环流面密度。 矢量场在 特点:其值与 有关。 特点:其值与点M 处的方向n有关。
C
(2)矢量场的旋度 ) 概念:矢量场在 点处的旋度为一矢量 其数值为M点的环流面 点处的旋度为一矢量, 概念:矢量场在M点处的旋度为一矢量,其数值为 点的环流面 密度最大值, 密度最大值,其方向为取得环量密度最大值时面积元的法 线方向, 线方向,即
上两式称为标量第二格林定理。 上两式称为标量第二格林定理。 标量第二格林定理 格林定理说明了区域 V 中的场与边界 S 上的场之间的关系。 上的场之间的关系。 因此, 因此 ,利用格林定理可以将区域中场的求解问题转变为边界上 场的求解问题。 场的求解问题。 此外,格林定理反映了两种标量场之间满足的关系。因此, 此外,格林定理反映了两种标量场之间满足的关系。因此, 如果已知其中一种场的分布, 如果已知其中一种场的分布,即可利用格林定理求解另一种场 的分布。 的分布。 格林定理广泛地用于电磁理论。 格林定理广泛地用于电磁理论。
∂ 式中S 为包围V 的闭合曲面, 式中S 为包围V 的闭合曲面, Φ 为标
量场 Φ 在 S 表面的外法线 en 方向上 的偏导数。 的偏导数。
根据方向导数与梯度的关系, 根据方向导数与梯度的关系,上式又可写成
∫
V
( ∇ Ψ ⋅ ∇ Φ + Ψ ∇ Φ )d V =
2
∫
S
= 0, ∇ × F ≠ 0
v v ∇ ⋅ F ≠ 0, ∇ × F ≠ 0
1.6 无旋场与无散场
1、矢量场的源 、 散度源:是标量, 散度源:是标量,产生的矢量场在包围源的封闭面上的通量 等于(或正比于)该封闭面内所包围的源的总和, 等于(或正比于)该封闭面内所包围的源的总和, 源在一给定点的( 源在一给定点的(体)密度等于(或正比于)矢量 密度等于(或正比于) 场在该点的散度; 场在该点的散度; 旋度源:是矢量,产生的矢量场具有涡旋性质, 旋度源:是矢量,产生的矢量场具有涡旋性质,穿过一曲面 的旋度源等于(或正比于) 的旋度源等于(或正比于)沿此曲面边界的闭合回 路的环量,在给定点上,这种源的( 路的环量,在给定点上,这种源的(面)密度等于 (或正比于)矢量场在该点的旋度。 或正比于)矢量场在该点的旋度。
2、矢量场的旋度( ∇ × F ) 、矢量场的旋度( 矢量场的环流给出了矢量场与积分回路所围曲面内旋涡源的 宏观联系。为了给出空间任意点矢量场与旋涡源的关系, 宏观联系。为了给出空间任意点矢量场与旋涡源的关系,引入矢 量场的旋度。 量场的旋度。 (1)环流面密度 ) 过点M 作一微小曲面∆ ,它的边界曲线记为C, 过点 作一微小曲面∆S,它的边界曲线记为 ,曲面的法线 方向n与曲线的绕向成右手螺旋法则。 方向 与曲线的绕向成右手螺旋法则。当∆S→0时,极限 与曲线的绕向成右手螺旋法则 → 时
1 ∂ 2 ∂u 1 ∂ ∂u 1 ∂ 2u 球坐标系 ∇ 2 u = 2 ( r )+ 2 (sin θ ) + 2 2 r ∂r ∂ r r sin θ ∂ θ ∂ θ r sin θ ∂ φ 2
r • 矢量拉普拉斯运算 ∇ F r r r 2 概念: 概念: ∇ F = ∇ ( ∇ F ) − ∇ × ( ∇ × F ) r r 2 r r 2 直角坐标系中: 直角坐标系中:∇ F = e x ∇ F x + e y ∇ 2 F y + e z ∇ 2 F z r 2 即 ( ∇ F ) i = ∇ 2 Fi (i = x , y , z ) r 2 注意:对于非直角分量, ( ∇ F ) i ≠ ∇ 2 Fi 注意:对于非直角分量,
2、矢量场按源的分类 、 (1)无旋场 )
r 仅有散度源而无旋度源的矢量场, 仅有散度源而无旋度源的矢量场,∇ × F ≡ 0 r r 性质: 性质: F ⋅ d l = 0,线积分与路径无关,是保守场。 线积分与路径无关,是保守场。 ∫
C
无旋场可以用标量场的梯度表示为 无旋场可以用标量场的梯度表示为
球面坐标系
r ez ∂ ∂z Fz
r er r 1 ∂ ∇×F = 2 r s in θ ∂ r Fr
r r eθ ∂ ∂θ rFθ
r r s in θ eφ ∂ ∂φ r s in θ Fφ
旋度的有关公式: 旋度的有关公式: 矢量场的旋度 的散度恒为零
标量场的梯度 的旋度恒为零
r ∇ × C = 0 r r ∇ × (C f ) = ∇ f × C r r r ∇ × ( fF ) = f ∇ × F r+ ∇ f × F r r r ∇ × ( F ± G ) = ∇ × F ± ∇ × G r r r r r r ∇ ⋅ ( F × G ) = G ⋅ ∇ × F − F ⋅ ∇ × G r ∇ ⋅ (∇ × F ) ≡ 0 ∇ × (∇ u ) ≡ 0
