高数积分

高数微积分公式大全

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '= ⑷()cos sin x x '=- ⑸()2tan sec x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=⋅ ⑻()csc csc cot x x x '=-⋅ ⑼()x x e e '= ⑽()ln x x a a a '= ⑾()1ln x x'= ⑿()1log ln x a x a '=⒀()arcsin x '= ⒁()arccos x '= ⒂()21arctan 1x x '=+ ⒃()21arccot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑ 四、基本初等函数的n 阶导数公式（1）()()!n n x n = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x dx μμμ-= ⑶()sin cos d x xdx = ⑷()cos sin d x xdx =- ⑸()2tan sec d x xdx = ⑹()2cot csc d x xdx =- ⑺()sec sec tan d x x xdx =⋅ ⑻()csc csc cot d x x xdx =-⋅⑼()x x d e e dx = ⑽()ln x x d a a adx = ⑾()1ln d x dx x= ⑿()1logln x a d dx x a =⒀()arcsin d x =⒁()arccos d x = ⒂()21arctan 1d x dx x =+ ⒃()21arccot 1d x dx x=-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v-⎛⎫=⎪⎝⎭ 七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x dx c μμμ+=++⎰ ⑶ln dxx c x=+⎰ ⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹cos sin xdx x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221sec tan cos dx xdx x c x==+⎰⎰ ⑼221csc cot sin xdx x c x ==-+⎰⎰ ⑽21arctan 1dx x c x=++⎰ ⑾arcsin x c =+八、补充积分公式九、下列常用凑微分公式十、分部积分法公式⑴形如n ax x e dx ⎰，令n u x =，ax dv e dx =形如sin n x xdx ⎰令n u x =，sin dv xdx = 形如cos n x xdx ⎰令n u x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，n dv x dx = 形如ln n x xdx ⎰，令ln u x =，n dv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos ax u e x x =均可。

高数导数和积分大全

定理设 f ( x, y) 在矩形区域 D [a, b][c, d]
上可积，且对每个 y [c, d], 积分
b
f ( x, y)dx
a
存在，则累次积分
d
b
dy f ( x, y)dx
c
a
也存在，且
d
b
f ( x, y)d c dya f ( x, y)dx
D
特别当 f ( x, y) 在矩形区域 D [a, b][c, d] 连续时，有
则 a a
f
( x) dx
a
20
f
( x) dx
(2) 若
则 a f (x) dx 0 a
证:
a
0
a
f (x)dx f (x)dx f (x)dx
a
a
0
a
a
0 f (t) d t 0 f (x) dx
a
0[ f (x) f (x)]dx
令 x t
f (x) f (x)时
f (x) f (x)时
b
d
d
b
f ( x, y)d a dxc f ( x, y)dy c dya f ( x, y)dx
D
例 1 计算 ( x y)2 d 其中 D [0,1][1,0]
D
解
( x y)2 d
1
dx
0 ( x y)2dy
0
1
D
1 ( x y)3 0
1 x3 ( x 1)3
0 3 dx 0 ( 3 3 )dx
x
第二节定积分
一、定积分的定义
积分上限
[a , b] 称为积分区间
b
n
a

高数导数和积分大全

添加副标题
高数导数和积分
汇报人：
目录
CONTENTS
01 添加目录标题
02 高数导数和积分概述
03 高数导数的性质和应用
04 高数积分的性质和应用
05 高数导数和积分的关系
06 高数导数和积分的实际应用
添加章节标题
高数导数和积分概述
高数导数和积分的定义
高数导数：表示函数在某一点的切线斜率是函数在某一点的变化率
导数：描述函数在某一点附近的变化率是函数的局部性质。
积分：对一个函数在某个区间上的定积分或不定积分可以用来计算面积、体积等。
高数导数的性质和应用
导数的定义和性质
导数的定义：函数在某一点的导数描述了该函数在该点的切线斜率。
导数的几何意义：导数在几何上表示函数图像在该点的切线斜率。
导数的物理意义：在物理中导数可以描述物理量的变化率例如速度、加速度等。导数的运算性质：导数具有一些基本的运算性质如加法、减法、乘法和除法的导数规则。
导数与积分的综合应用示例
计算曲线下面积
求解变速直线运中的最优化问题
高数导数和积分的实际应用
导数在经济学中的应用
导数用于研究经济函数的单调性、极值和最值
导数在边际分析和弹性分析中的应用
导数在最优问题中的应用如最优生产、最优定价和最优分配等
导数在预测经济趋势和政策效果分析中的应用
积分可以表示曲线下的面积积分可以计算旋转体的体积积分可以解决实际问题如物理、工程等领域积分可以用于优化问题如最值、极值等
高数导数和积分的关系
导数与积分的关系
导数描述函数在某一点的切线斜率而积分描述函数与坐标轴围成
的面积。

高等数学积分公式大全

高等数学积分公式大全高等数学是一门非常重要的学科，在很多领域都有应用。

其中，积分学是高等数学中的一个重要章节。

积分可以理解为求解曲线图形下面的面积，不同类型的积分公式有着不同的概念和应用，下面，就为大家整理了一份高等数学积分公式大全，让大家对这个知识点有一个更全面的认识。

1. 常数积分公式$$\int kdx=kx+C$$2. 幂函数积分公式$$\int x^ndx=\frac{x^{n+1}}{n+1}+C$$3. 指数函数积分公式$$\int e^xdx=e^x+C$$4. 对数函数积分公式$$\int \frac{1}{x}dx=\ln|x|+C$$5. 三角函数积分公式$$\int \sin xdx=-\cos x+C$$$$\int \cos xdx=\sin x+C$$6. 反三角函数积分公式$$\int \frac{1}{\sqrt{1-x^2}}dx=\arcsin x+C$$$$\int \frac{1}{1+x^2}dx=\arctan x+C$$$$\int \frac{1}{\sqrt{x^2-1}}dx=\ln|x+\sqrt{x^2-1}|+C$$7. 换元法积分公式$$\int f(u)du=\int f(u(x))\frac{du}{dx}dx$$8. 分部积分公式$$\int u(x)v'(x)dx=u(x)v(x)-\int v(x)u'(x)dx$$9. 定积分公式$$\int_a^bf(x)dx=F(b)-F(a)$$10. 积分中值定理$$\int_a^bf(x)dx=f(c)(b-a)$$这便是几种高等数学积分公式的介绍，这些公式是数学中不可或缺的知识点，掌握这些公式不仅有助于学生学好数学，还对应用数学的工作有相当多的帮助。

除了这些基本的积分公式之外，高等数学还涉及到一些比较复杂的积分公式，如多重积分、线性代数积分、微积分方程等等。

1. 多重积分公式多重积分是指对多元函数的积分，通常被用于几何问题、概率论问题和物理学问题中。

高数微积分公式大全

高等数学微积分公式大全一、基本导数公式⑴()0c '= ⑵1x x μμμ-= ⑶()sin cos x x '=⑷()cos sin x x '=- ⑸()2t a ns e c x x '= ⑹()2cot csc x x '=- ⑺()sec sec tan x x x '=⋅ ⑻()c s cc s c c o tx x x '=-⋅ ⑼()xxe e '= ⑽()ln xxa aa '= ⑾()1ln x x'=⑿()1log ln xax a'= ⒀()a r c s i n x '= ⒁()a r c c o s x '=⒂()21arctan 1x x '=+ ⒃()21arc cot 1x x '=-+⒄()1x '=⒅'=二、导数的四则运算法则()u v u v '''±=± ()u v uv u v '''=+ 2u u vu v v v '''-⎛⎫= ⎪⎝⎭三、高阶导数的运算法则（1）()()()()()()()n n n u x v x u x v x ±=±⎡⎤⎣⎦ （2）()()()()n n cu x cu x =⎡⎤⎣⎦（3）()()()()n n nu ax b a uax b +=+⎡⎤⎣⎦（4）()()()()()()()0nn n k k k n k u x v x c u x v x -=⋅=⎡⎤⎣⎦∑四、基本初等函数的n 阶导数公式（1）()()!n nxn = （2）()()n ax b n ax b e a e ++=⋅ (3)()()ln n x x n a a a =(4)()()sin sin 2n n ax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (5) ()()cos cos 2n nax b a ax b n π⎛⎫+=++⋅⎡⎤ ⎪⎣⎦⎝⎭ (6)()()()11!1n n nn a n ax b ax b +⋅⎛⎫=- ⎪+⎝⎭+ (7) ()()()()()11!ln 1n n n na n axb ax b -⋅-+=-⎡⎤⎣⎦+五、微分公式与微分运算法则⑴()0d c = ⑵()1d x x d x μμμ-= ⑶()sin cos d x xdx =⑷()cos sin d x xdx =- ⑸()2t a n s e c d x x d x = ⑹()2c o t c s cd x x d x=- ⑺()sec sec tan d x x xdx =⋅ ⑻()c s c c s c c o t d x xx dx =-⋅ ⑼()x x d e e dx = ⑽()ln x xd a a adx = ⑾()1ln d x dx x=⑿()1logln xad dx x a =⒀()arcsin d x = ⒁()a r c c o s d x d x = ⒂()21arctan 1d x dx x =+ ⒃()21a r c c o t 1d x d x x=-+ 六、微分运算法则⑴()d u v du dv ±=± ⑵()d cu cdu = ⑶()d uv vdu udv =+ ⑷2u vdu udvd v v -⎛⎫= ⎪⎝⎭七、基本积分公式⑴kdx kx c =+⎰ ⑵11x x d x c μμμ+=++⎰ ⑶ln dx x c x =+⎰⑷ln xxa a dx c a=+⎰ ⑸x x e dx e c =+⎰ ⑹c o s s i n x d x x c =+⎰ ⑺sin cos xdx x c =-+⎰ ⑻221s e c t a n c o s d x x d x x c x ==+⎰⎰⑼221csc cot sin xdx x c x ==-+⎰⎰⑽21arctan 1dx x c x =++⎰ ⑾arcsin x c =+八、补充积分公式tan ln cos xdx x c =-+⎰ c o t l n s i n x d x x c =+⎰ sec ln sec tan xdx x x c =++⎰ c s c l n c s cc o t xd x x x c=-+⎰ 2211arctan x dx c a x a a=++⎰ 2211ln 2x adx c x a a x a-=+-+⎰arcsin xc a =+ln x c =++十、分部积分法公式⑴形如n ax x e dx ⎰，令nu x =，ax dv e dx =形如sin n x xdx ⎰令nu x =，sin dv xdx =形如cos n x xdx ⎰令nu x =，cos dv xdx =⑵形如arctan n x xdx ⎰，令arctan u x =，ndv x dx =形如ln n x xdx ⎰，令ln u x =，ndv x dx =⑶形如sin ax e xdx ⎰，cos ax e xdx ⎰令,sin ,cos axu e x x =均可。

高数积分公式大全

高数积分公式大全高等数学中的积分是数学分析的重要内容之一，它是求函数面积、定积分、不定积分等的方法，被广泛应用于科学和工程领域。

下面是高等数学中常用的积分公式大全，供大家参考和学习。

一、基本积分公式：1. 常数函数积分公式：∫c dx = cx + C（其中c为常数，C为积分常数）2. 幂函数积分公式：∫x^n dx = (1/(n+1)) * x^(n+1) + C（其中n不等于-1，C 为积分常数）3. 指数函数积分公式：∫e^x dx = e^x + C4. 三角函数积分公式：∫sin(x) dx = -cos(x) + C∫cos(x) dx = sin(x) + C5. 乘方函数积分公式：∫(a^x) dx = (1/log(a)) * (a^x) + C（其中a为正数且不等于1，C为积分常数）6. 对数函数积分公式：∫(1/x) dx = ln|x| + C二、常用积分公式：1. 三角函数的复合积分：∫sin(ax) dx = - (1/a) * cos(ax) + C∫cos(ax) dx = (1/a) * sin(ax) + C2. 反三角函数的积分：∫1/(√(1-x^2)) dx = arcsin(x) + C∫1/(1+x^2) dx = arctan(x) + C3. 指数函数的积分：∫e^(ax) dx = (1/a) * e^(ax) + C4. 对数函数的积分：∫(1/x) dx = ln|x| + C5. 分式函数的积分：∫(1/(x-a)) dx = ln|x-a| + C（其中a不等于0）∫(1/(x^2+a^2)) dx = (1/a) * arctan(x/a) + C（其中a不等于0）6. 三角函数的积分：∫sin^n(x) cos^m(x) dx7. 部分分式的积分：∫(p(x)/q(x)) dx8. 具体函数的特殊积分：∫e^x sin(x) dx∫e^x cos(x) dx∫(sin(x))^n (cos(x))^m dx（其中n和m为正整数）三、数列求和公式：1. 等差数列求和公式：S_n = (n/2)(a_1 + a_n)（其中S_n为前n项和，a_1为首项，a_n为末项）2. 等比数列求和公式：S_n = (a_1(1-q^n))/(1-q)（其中S_n为前n项和，a_1为首项，q为公比）以上是高等数学中一些常见的积分公式，通过掌握和灵活运用这些公式，可以帮助我们更好地解决数学中的问题。

高数积分公式大全

常用积分公式（一）含有ax b +的积分(0a ≠) 1．d x ax b +⎰＝1ln ax b C a++ 2．()d ax b x μ+⎰＝11()(1)ax b C a μμ++++（1μ≠-）3．d x x ax b +⎰＝21(ln )ax b b ax b C a+-++ 4．2d x x ax b +⎰＝22311()2()ln 2ax b b ax b b ax b C a ⎡⎤+-++++⎢⎥⎣⎦5．d ()xx ax b +⎰＝1lnax b C b x +-+ 6．2d ()xx ax b +⎰＝21ln a ax b C bx b x +-++ 7．2d ()x x ax b +⎰＝21(ln )b ax b C a ax b++++ 8．22d ()x x ax b +⎰＝231(2ln )b ax b b ax b C a ax b+-+-++ 9．2d ()xx ax b +⎰＝211ln ()ax b C b ax b b x +-++的积分10．x C +11．x ⎰＝22(3215ax b C a -+12．x x ⎰＝22232(15128105a x abx b C a-++13．x＝22(23ax b C a -14．2x＝22232(34815a x abx b C a -++15．＝(0)(0)C b C b ⎧+><16．2a b - 17．x＝b +18．x＝2a x -+ （三）含有22x a ±的积分 19．22d x x a +⎰=1arctan x C a a+ 20．22d ()n x x a +⎰=2221222123d 2(1)()2(1)()n n x n xn a x a n a x a ---+-+-+⎰21．22d xx a -⎰=1ln 2x a C a x a-++ （四）含有2(0)ax b a +>的积分22．2d x ax b +⎰＝(0)(0)C b C b ⎧+>+<23．2d x x ax b +⎰＝21ln 2ax b C a++ 24．22d x x ax b +⎰＝2d x b x a a ax b -+⎰25．2d ()x x ax b +⎰＝221ln 2x C b ax b++ 26．22d ()x x ax b +⎰＝21d a xbx b ax b--+⎰27．32d ()x x ax b +⎰＝22221ln 22ax b a C b x bx +-+28．22d ()x ax b +⎰＝221d 2()2x xb ax b b ax b+++⎰ （五）含有2ax bx c ++(0)a >的积分29．2d x ax bx c ++⎰＝22(4)(4)C b ac Cb ac +<+>30．2d x x ax bx c ++⎰＝221d ln 22b x ax bx c a a ax bx c++-++⎰(0)a >的积分 31．＝1arsh xC a+＝ln(x C + 32．C +33．xC34．x＝C +35．2x2ln(2a x C ++ 36．2x＝ln(x C +++37．1ln aC a x -+ 38．C + 39．x2ln(2a x C ++40．x ＝2243(25ln(88x x a a x C ++++41．x ⎰C42．x x ⎰＝422(2ln(88x a x a x C +++43．d x x ⎰ln a a C x ++44．2d x x ⎰＝ln(x C x-+++(0)a >的积分45．＝1arch x xC x a+=ln x C ++ 46．C +47．x C +48．x ＝C +49．2x 2ln 2a x C ++50．2x ＝ln x C +++51．1arccosaC ax+52．C +53．x 2ln 2a x C ++54．x ＝2243(25ln 88x x a a x C -++55．x ⎰C56．x x ⎰＝422(2ln 88x a x a x C -++57．d x x⎰arccos a a C x +58．2d x x ⎰＝ln x C x-+++(0)a >的积分 59．＝arcsin xC a+ 60．C +61．x ＝C62．x C +63．2x ＝2arcsin 2a x C a + 64．2x arcsinxC a-+65．1ln a C a x +66．C +67．x 2arcsin 2a x C a+68．x ＝2243(52arcsin 88x x a x a C a-+69．x ⎰＝C +70．x x ⎰＝422(2arcsin 88x a x x a C a-+71．x a C ++72．x ＝arcsin xC a-+(0)a >的积分73．2ax b C +++74．x75．x 76．＝C +77．x 2C ++78．x ＝C +79．x ＝((x b b a C --++80．x ＝((x b b a C --81．C ()a b <82．x 2()4b a C -++ （十一）含有三角函数的积分83．sin d x x ⎰＝cos x C -+ 84．cos d x x ⎰＝sin x C + 85．tan d x x ⎰＝ln cos x C -+ 86．cot d x x ⎰＝ln sin x C +87．sec d x x ⎰＝ln tan()42x C π++＝ln sec tan x x C ++ 88．csc d x x ⎰＝ln tan2xC +＝ln csc cot x x C -+ 89．2sec d x x ⎰＝tan x C + 90．2csc d x x ⎰＝cot x C -+ 91．sec tan d x x x ⎰＝sec x C + 92．csc cot d x x x ⎰＝csc x C -+93．2sin d x x ⎰＝1sin 224x x C -+94．2cos d x x ⎰＝1sin 224x x C ++95．sin d n x x ⎰＝1211sin cos sin d n n n x x x x n n----+⎰ 96．cos d n x x ⎰＝1211cos sin cos d n n n x x x x n n ---+⎰97．d sin n x x ⎰＝121cos 2d 1sin 1sin n n x n xn x n x ----⋅+--⎰ 98．d cos n x x ⎰＝121sin 2d 1cos 1cos n n x n xn x n x---⋅+--⎰ 99．cos sin d m n x x x ⎰＝11211cos sin cos sin d m n m nm x x x x x m n m n -+--+++⎰＝11211cos sin cos sin d m n m n n x x x x x m n m n+----+++⎰ 100．sin cos d ax bx x ⎰＝11cos()cos()2()2()a b x a b x C a b a b -+--++-101．sin sin d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b -++-++-102．cos cos d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b ++-++-103．d sin xa b x +⎰tanxa b C ++22()a b >104．d sin x a b x +⎰C +22()a b <105．d cos xa b x+⎰)2x C +22()a b >106．d cos x a b x +⎰C +22()a b <107．2222d cos sin x a x b x +⎰＝1arctan(tan )bx C ab a+ 108．2222d cos sin xa xb x-⎰＝1tan ln 2tan b x a C ab b x a ++- 109．sin d x ax x ⎰＝211sin cos ax x ax C a a -+ 110．2sin d x ax x ⎰＝223122cos sin cos x ax x ax ax C a a a -+++111．cos d x ax x ⎰＝211cos sin ax x ax C a a ++112．2cos d x ax x ⎰＝223122sin cos sin x ax x ax ax C a a a+-+（十二）含有反三角函数的积分（其中0a >） 113．arcsin d xx a ⎰＝arcsin x x C a+114．arcsin d xx x a ⎰＝22()arcsin 24x a x C a -+115．2arcsin d xx x a⎰＝3221arcsin (239x x x a C a +++116．arccos d x x a ⎰＝arccos x x C a117．arccos d xx x a ⎰＝22()arccos 24x a x C a --+118．2arccos d xx x a⎰＝3221arccos (239x x x a C a -++119．arctan d xx a ⎰＝22arctan ln()2x a x a x C a -++ 120．arctan d x x x a ⎰＝221()arctan 22x a a x x C a +-+121．2arctan d xx x a⎰＝33222arctan ln()366x x a a x a x C a -+++（十三）含有指数函数的积分122．d x a x ⎰＝1ln xa C a + 123．e d ax x ⎰＝1e ax C a +124．e d ax x x ⎰＝21(1)e ax ax C a -+125．e d n ax x x ⎰＝11e e d n ax n ax nx x x a a--⎰126．d x xa x ⎰＝21ln (ln )x xx a a C a a -+ 127．d n x x a x ⎰＝11d ln ln n x n xn x a x a x a a --⎰ 128．e sin d ax bx x ⎰＝221e (sin cos )ax a bx b bx C a b -++129．e cos d ax bx x ⎰＝221e (sin cos )ax b bx a bx C a b+++130．e sin d ax n bx x ⎰＝12221e sin (sin cos )ax n bx a bx nb bx a b n--+131．e cos d ax n bx x ⎰＝12221e cos (cos sin )ax n bx a bx nb bx a b n-++（十四）含有对数函数的积分 132．ln d x x ⎰＝ln x x x C -+133．d ln xx x⎰＝ln ln x C + 134．ln d n x x x ⎰＝111(ln )11n x x C n n +-+++135．(ln )d n x x ⎰＝1(ln )(ln )d n n x x n x x --⎰ 136．(ln )d m n x x x ⎰＝111(ln )(ln )d 11m n m n nx x x x x m m +--++⎰ （十五）含有双曲函数的积分 137．sh d x x ⎰＝ch x C + 138．ch d x x ⎰＝sh x C + 139．th d x x ⎰＝lnch x C + 140．2sh d x x ⎰＝1sh224xx C -++ 141．2ch d x x ⎰＝1sh224x x C ++ （十六）定积分142．cos d nx x π-π⎰＝sin d nx x π-π⎰＝0 143．cos sin d mx nx x π-π⎰＝0144．cos cos d mx nx x π-π⎰＝0,,m nm n ≠⎧⎨π=⎩145．sin sin d mx nx x π-π⎰＝0,,m nm n≠⎧⎨π=⎩146．0sin sin d mx nx x π⎰＝0cos cos d mx nx x π⎰＝0,,2m n m n ≠⎧⎪⎨π=⎪⎩147． n I ＝20sin d nx x π⎰＝20cos d n x x π⎰n I ＝21n n I n-- 1342253n n n I n n --=⋅⋅⋅⋅-L （n 为大于1的正奇数），1I ＝1 13312422n n n I n n --π=⋅⋅⋅⋅⋅-L （n 为正偶数），0I ＝2π。

高数-专题二积分计算的基本公式

专题二
第四章
积分计算的基本公式
一、基本积分表二、积分上限的函数及其导数三、牛顿 – 莱布尼茨公式
目录上页下页返回结束
一、基本积分表
(1) kdx kxC ( k 为常数)
(2) xdx11x1C (1)
(3) dxx lnx C
(4)
dx 1x2
目录上页下页返回结束
例3. 求 tan2xdx. 解: 原式 = (se2xc1)dx
se2xcdxdx ta x x n C
例4. 求
1 x x2 x (1 x2)
dx
.
解: 原式 =
x (1 x2) x(1 x2)
dx

1 1 x2
(x)
x
f(t)dt
a
是f(x)在[a,b]上的一个原. 函数
说明: 1) 定理 1 证明了连续函数的原函数是存在的. 同时为
通过原函数计算定积分开辟了道路 .
目录上页下页返回结束
2) 其他变限积分求导:
d dx
b
x
f
(t)dt
f(x)
d (x)
dx a
f
(t)dt
f[(x) ](x)
d
dx
(x)
f (t)dt
(x)
d d x a(x)f(t)dta (x)f(t)dt

f [( x ) ( ] x ) f [( x ) ( ] x )
目录上页下页返回结束
例7. 求 lim
1 et2 dt
cosx
0
F(x)在（ 0， )内为单调.增函数

高数不定积分

1 2
sin2x
+
C.
利用基本积分表与积分的性质，所能计算的不定积分是非常有限的；我们可以把复合函数的微分法反过来用于求不定积分，利用中间变量的代换，得到复合函数的积分法，称为换元积分法。
x2 1 - x2 dx ? 令 x sint
x2 1 - x2dx (sint)2 1 - sin2 t costdt
2
2
例1140．
1
dx 4
sin2 x cos2 x
1 sin2
x
dx
-4ctg
x+C。
22
)
1 x
dx ln|x|+(C1，1)
1 dx arctgx+C。 1+ x2
例1151．
1 + x + x2 dx x(1 + x 2 )
x + (1 + x 2 ) dx x(1 + x 2 )
函数f(x)的原函数的图形称为f(x)的积分曲线。
2xdx x 2 + C
y
函数f(x)的积分曲线也有无限多条。函数f(x)的不定积分表示f(x)的一簇积分曲线，而f(x)正是积分曲线的斜率。
C1 -1 O 1
y=x2+C1 y=x2
y=x2+C2 y=x2+xC3
C2
C3
例4．求过点(1, 3)，且其切线斜率为2x的曲线方程。解：设所求的曲线方程为 yf(x)，则 y f (x) 2x，即f(x)是2x 的一个原函数。
f
(x)dx
f
(x)
4) f ' (x)dx f (x) + C

高数积分总结

高数积分总结一、不定积分1、不定积分的概念也性质定义1：如果在区间I 上，可导函数F （x ）的导函数为f(x ），即对任一I x ∈，都有F`（x)=f （x)或dF(x)=f(x)dx,那么函数F(x)就称为f （x ）（或f(x)dx)在区间I 上的原函数。

定义2：在区间I 上，函数f （x ）的带有任意常数项的原函数称为f(x ）(或者f （x ）dx)在区间I 上的不定积分，记作⎰dx x f )(.性质1:设函数f （x)及g （x ）的原函数存在,则⎰⎰⎰+=+dx x g dx x f dx x g x f )()()]()([。

性质2：设函数f （x ）的原函数存在，k 为非零常数,则⎰⎰=dx x f k dx x kf )()(。

2、换元积分法 (1）第一类换元法:定理1：设f （u ）具有原函数,)(x ϕμ=可导，则有换元公式)(])([)(')]([x d f dx x x f ϕμμμϕϕ=⎰⎰=。

例：求⎰xdx 2cos 2解 ⎰⎰⎰⎰=•=•=μμd dx x x dx x xdx cos )'2(2cos 22cos 2cos 2 将x 2=μ代入，既得⎰+=C x xdx 2sin 2cos 2(2)第二类换元法:定理2:设)(t x ψ=是单调的、可导的函数，并且.0)('≠t ψ又设)(')]([t t f ψψ具有原函数，则有换元公式,])(')]([[)()(1x t dt t t f dx x f -=⎰⎰=ψψψ其中)(1x -ψ是)(t x ψ=的反函数。

例：求⎰>+)0(22a ax dx解 ∵t t 22sec tan 1=+，设⎪⎭⎫ ⎝⎛<<-=22tan ππαt t x ，那么 tdt a dx t a t a t a a a x 2222222sec ,sec tan 1tan ==+=+=+，于是⎰⎰⎰==+tdt dt t a ta a x dx sec sec sec 222 ∴C t t ax dx ++=+⎰tan sec ln 22∵aa x t 22sec +=,且0tan sec >+t t ∴1222222)ln(ln C a x x C aa x a xa x dx+++=+⎪⎪⎭⎫⎝⎛++=+⎰，a C C ln 1-=3、分部积分法定义：设函数)(x μμ=及)(x υυ=具有连续导数。

高数积分公式

常用积分公式（一）含有ax b +的积分(0a ≠) 1．d x ax b +⎰＝1ln ax b C a ++2．()d ax b x μ+⎰＝11()(1)ax b C a μμ++++（1μ≠-）3．d x x ax b +⎰＝21(ln )ax b b ax b C a +-++ 4．2d x x ax b +⎰＝22311()2()ln 2ax b b ax b b ax b C a ⎡⎤+-++++⎢⎥⎣⎦5．d ()x x ax b +⎰＝1ln ax bC b x +-+6．2d ()x x ax b +⎰＝21ln a ax b C bx b x+-++ 7．2d ()xx ax b +⎰＝21(ln )b ax b C a ax b++++ 8．22d ()x x ax b +⎰＝231(2ln )b ax b b ax b C a ax b +-+-++ 9．2d ()x x ax b +⎰＝211ln ()ax b C b ax b b x+-++的积分10．x C +11．x ⎰＝22(3215ax b C a -12．x x ⎰＝22232(15128105a x abx b C a-+13．x⎰＝22(23ax b C a -14．2x＝22232(34815a x abx b C a -+15．(0)(0)C b C b ⎧+>+<16．2a bx b -- 17．d x x ⎰＝b 18．x＝2a +（三）含有22x a ±的积分 19．22d x x a +⎰=1arctan x C a a+ 20．22d ()n xx a +⎰=2221222123d 2(1)()2(1)()n n x n x n a x a n a x a ---+-+-+⎰21．22d x x a -⎰=1ln 2x a C a x a-++ （四）含有2(0)ax b a +>的积分22．2d x ax b +⎰＝(0)(0)C b C b ⎧+>+<23．2d x x ax b +⎰＝21ln 2ax b C a++ 24．22d x x ax b+⎰＝2d x b x a a ax b -+⎰25．2d ()xx ax b +⎰＝221ln 2x C b ax b++ 26．22d ()xx ax b +⎰＝21d a x bx b ax b --+⎰27．32d ()x x ax b +⎰＝22221ln 22ax b a C b x bx+-+ 28．22d ()xax b +⎰＝221d 2()2x x b ax b b ax b +++⎰（五）含有2ax bx c ++(0)a >的积分29．2d x ax bx c ++⎰＝22(4)(4)C b ac C b ac +<+> 30．2d x x ax bx c ++⎰＝221d ln 22b x ax bx c a a ax bx c++-++⎰(0)a >的积分 31．＝1arshxC a+＝ln(x C ++ 32．C +33．xC34．x＝C +35．2x2ln(2a x C ++ 36．2x ⎰＝ln(x C +++37．1C a + 38．2C a x -+ 39．x2ln(2a x C ++40．x ＝2243(25ln(88x x a a x C +++41．x ⎰C42．xx ⎰＝422(2ln(88x a x a x C +++43．x a C +44．2d x x ⎰＝ln(x C x-+++(0)a >的积分45．＝1arch x xC x a+=ln x C ++ 46．C +47．x C48．x ＝C +49．2x 2ln 2a x C ++50．2x ⎰＝ln x C +++51．1arccos aC a x+52．2C a x +53．x 2ln 2a x C +54．x ＝2243(25ln 88x x a a x C -++55．x ⎰C56．xx ⎰＝422(2ln 88x a x a x C -++57．d x x⎰arccos a a C x -+58．x ＝ln x C +++(0)a >的积分 59．＝arcsinxC a+ 60．C +61．x ＝C +62．x C +63．2x ＝2arcsin 2a x C a + 64．2x ⎰arcsinxC a-+65．1lna C a x +66．C +67．x 2arcsin 2a x C a+68．x ＝2243(52arcsin 88x x a x a C a -+69．x ⎰＝C70．xx ⎰＝422(2arcsin 88x a x x a C a-++71．x a C72．2d x x ⎰＝arcsin xC x a--+(0)a >的积分73．2ax b C +++74．x2n 2a x b c C++++75．xn 2a x b c C-+++ 76．＝C +77．x 2C ++78．x ＝C +79．x ＝((x b b a C --+80．x ＝((x b b a C --81．C()a b <82．x 2()4b a C -()a b < （十一）含有三角函数的积分 83．sin d x x ⎰＝cos x C -+ 84．cos d x x ⎰＝sin x C + 85．tan d x x ⎰＝ln cos x C -+ 86．cot d x x ⎰＝ln sin x C + 87．sec d x x ⎰＝ln tan()42xC π++＝ln sec tan x x C ++ 88．csc d x x ⎰＝ln tan2xC +＝ln csc cot x x C -+ 89．2sec d x x ⎰＝tan x C + 90．2csc d x x ⎰＝cot x C -+ 91．sec tan d x x x ⎰＝sec x C + 92．csc cot d x x x ⎰＝csc x C -+93．2sin d x x ⎰＝1sin 224x x C -+ 94．2cos d x x ⎰＝1sin 224x x C ++95．sin d nx x ⎰＝1211sin cos sin d n n n x x x x n n----+⎰ 96．cos d nx x ⎰＝1211cos sin cos d n n n x x x x n n---+⎰ 97．d sin n x x ⎰＝121cos 2d 1sin 1sin n n x n xn x n x ----⋅+--⎰98．d cos n x x ⎰＝121sin 2d 1cos 1cos n n x n xn x n x---⋅+--⎰99．cos sin d m nx x x ⎰＝11211cos sin cos sin d m n m n m x x x x x m n m n -+--+++⎰ ＝11211cos sin cos sin d m n m n n x x x x x m n m n +----+++⎰100．sin cos d ax bx x ⎰＝11cos()cos()2()2()a b x a b x C a b a b -+--++-101．sin sin d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b -++-++-102．cos cos d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b ++-++-103．d sin xa b x +⎰tan xa b C ++22()a b >104．d sin x a b x +⎰C+22()a b <105．d cos x a b x +⎰)2xC +22()a b >106．d cos x a b x +⎰C +22()a b <107．2222d cos sin x a x b x +⎰＝1arctan(tan )bx C ab a + 108．2222d cos sin x a x b x -⎰＝1tan ln 2tan b x a C ab b x a ++-109．sin d x ax x ⎰＝211sin cos ax x ax C a a -+ 110．2sin d x ax x ⎰＝223122cos sin cos x ax x ax ax C a a a -+++111．cos d x ax x ⎰＝211cos sin ax x ax C a a ++112．2cos d x ax x ⎰＝223122sin cos sin x ax x ax ax C a a a+-+（十二）含有反三角函数的积分（其中0a >）113．arcsin d x x a ⎰＝arcsin x x C a114．arcsin d x x x a ⎰＝22()arcsin 24x a x C a -+115．2arcsin d x x x a ⎰＝3221arcsin (239x x x a C a ++116．arccos d x x a ⎰＝arccosxx C a- 117．arccos d x x x a ⎰＝22()arccos 24x a x C a --118．2arccos d x x x a ⎰＝3221arccos (239x x x a C a -+119．arctand x x a ⎰＝22arctan ln()2x a x a x C a -++ 120．arctan d x x x a ⎰＝221()arctan 22x a a x x C a +-+121．2arctan d x x x a ⎰＝33222arctan ln()366x x a a x a x C a -+++ （十三）含有指数函数的积分122．d xa x ⎰＝1ln xa C a + 123．e d axx ⎰＝1e ax C a +124．e d axx x ⎰＝21(1)e ax ax C a-+125．e d n axx x ⎰＝11e e d n ax n ax n x x x a a--⎰126．d xxa x ⎰＝21ln (ln )x x x a a C a a -+ 127．d nxx a x ⎰＝11d ln ln n x n x nx a x a x a a --⎰ 128．e sin d axbx x ⎰＝221e (sin cos )ax a bx b bx C a b -++ 129．e cos d axbx x ⎰＝221e (sin cos )ax b bx a bx C a b+++ 130．e sin d ax nbx x ⎰＝12221e sin (sin cos )ax n bx a bx nb bx a b n--+ 22222(1)e sin d ax n n n b bx x a b n --++⎰131．e cos d ax nbx x ⎰＝12221e cos (cos sin )ax n bx a bx nb bx a b n-++ 22222(1)e cos d axn n n b bx x a b n--++⎰ （十四）含有对数函数的积分 132．ln d x x ⎰＝ln x x x C -+133．d ln xx x ⎰＝ln ln x C +134．ln d nx x x ⎰＝111(ln )11n x x C n n +-+++135．(ln )d nx x ⎰＝1(ln )(ln )d n nx x n x x --⎰136．(ln )d m nx x x ⎰＝111(ln )(ln )d 11m n m n nx x x x x m m +--++⎰ （十五）含有双曲函数的积分 137．sh d x x ⎰＝ch x C + 138．ch d x x ⎰＝sh x C + 139．th d x x ⎰＝ln ch x C +140．2sh d x x ⎰＝1sh224x x C -++ 141．2ch d x x ⎰＝1sh224x x C ++（十六）定积分 142．cos d nx x π-π⎰＝sin d nx x π-π⎰＝0143．cos sin d mx nx x π-π⎰＝0144．cos cos d mx nx x π-π⎰＝0,,m nm n ≠⎧⎨π=⎩145．sin sin d mx nx x π-π⎰＝0,,m nm n≠⎧⎨π=⎩ 146．0sin sin d mx nx x π⎰＝0cos cos d mx nx x π⎰＝0,,2m n m n ≠⎧⎪⎨π=⎪⎩147． n I ＝20sin d nx x π⎰＝20cos d n x x π⎰n I ＝21n n I n-- 1342253n n n I n n --=⋅⋅⋅⋅- （n 为大于1的正奇数），1I ＝1 13312422n n n I n n --π=⋅⋅⋅⋅⋅- （n 为正偶数），0I ＝2π。

高数上4.1 不定积分概念与性质

f (x)dx dF(x) F(x) C,
从形式上看, 若能把 f ( x)dx 中的被积函数 f(x) 凑
到微分号后, 即把积分号下的 f (x)dx 转变成 dF(x) 则微分号后的函数 F ( x)就是所求的一个原函数。
因此积分运算可以看成是微分运算的逆运算。
例2 求下列不定积分
2
x 2
dx
12(1 cos x)dx 12 (1 cos x)dx
1 2
[
dx
cos
xdx]
1 2
(
x
sin
x)
C
.
例11 求满足下列条件的F ( x).
F ( x) 1 x , 13 x
F (0) 1.
解根据题设条件, 有
F( x) F( x)dx 1 x dx (1 3 x 3 x2 )dx 13 x
即 kf ( x)dx k f ( x)dx (k 0); 证[k f ( x)dx] k[ f ( x)dx] kf ( x) [ kf ( x)dx]
证毕.
五、直接积分法
从前面的例题知道, 利用不定积分的定义来计算不定积分是非常不方便的. 为解决不定积分的计算问题, 这里我们先介绍一种利用不定积分的运算性质和积分基本公式, 直接求出不定积分的方法, 即直接积分法.
第四章不定积分
一、不定积分的概念与性质二、换元积分法三、分部积分法四、有理函数的积分
第一节不定积分的概念与性质
一、原函数与不定积分的概念二、不定积分的几何意义三、基本积分表四、不定积分的性质五、直接积分法
一、原函数的概念
定义设 f ( x)是定义在空间 I上的函数, 若存在函数F ( x)对任何 x I均有

高数积分总结

高数积分总结一、不定积分1、不定积分的概念也性质定义1：如果在区间I 上，可导函数F （x ）的导函数为f(x)，即对任一I x ∈,都有F`(x)=f(x)或dF(x)=f(x)dx,那么函数F(x)就称为f(x)(或f(x)dx)在区间I 上的原函数。

定义2：在区间I 上，函数f （x ）的带有任意常数项的原函数称为f （x ）（或者f(x)dx ）在区间I 上的不定积分，记作⎰dx x f )(。

性质1：设函数f(x)及g(x)的原函数存在，则⎰⎰⎰+=+dx x g dx x f dx x g x f )()()]()([。

性质2：设函数f(x)的原函数存在，k 为非零常数，则⎰⎰=dx x f k dx x kf )()(。

2、换元积分法 (1)第一类换元法：定理1：设f(u)具有原函数，)(x ϕμ=可导，则有换元公式)(])([)(')]([x d f dx x x f ϕμμμϕϕ=⎰⎰=。

例：求⎰xdx 2cos 2 解⎰⎰⎰⎰=•=•=μμd dx x x dx x xdx cos )'2(2cos 22cos 2cos 2将x 2=μ代入，既得⎰+=C x xdx 2sin 2cos 2(2)第二类换元法：定理2：设)(t x ψ=是单调的、可导的函数，并且.0)('≠t ψ又设)(')]([t t f ψψ具有原函数，则有换元公式,])(')]([[)()(1x t dt t t f dx x f -=⎰⎰=ψψψ其中)(1x -ψ是)(t x ψ=的反函数。

例：求⎰>+)0(22a ax dx解 ∵t t 22sec tan 1=+，设⎪⎭⎫ ⎝⎛<<-=22tan ππαt t x ，那么 tdt a dx t a t a t a a a x 2222222sec ,sec tan 1tan ==+=+=+，于是⎰⎰⎰==+tdt dt t a ta a x dx sec sec sec 222 ∴C t t ax dx ++=+⎰tan sec ln 22∵aa x t 22sec +=，且0tan sec >+t t ∴1222222)ln(ln C a x x C aa x a x a x dx+++=+⎪⎪⎭⎫⎝⎛++=+⎰，a C C ln 1-=3、分部积分法定义：设函数)(x μμ=及)(x υυ=具有连续导数。

高数微积分公式大全

高数微积分公式大全1.极限和连续：- 函数f(x)在x=a处连续的充分必要条件是：$\lim_{x\toa}f(x)=f(a)$- 若$\lim_{x\to a}f(x)=A$，$\lim_{x\to a}g(x)=B$，则$\lim_{x\to a}[f(x)\pm g(x)]=A\pm B$- $\lim_{x\to a}[f(x)g(x)]=\lim_{x\to a}f(x)\cdot\lim_{x\to a}g(x)$- 若$\lim_{x\to a}f(x)=A$，$\lim_{x\to a}g(x)=B\neq0$，则$\lim_{x\to a}\frac{f(x)}{g(x)}=\frac{A}{B}$- $f(x)$在$a$点附近可导的充分必要条件是：存在常数$A$和$B$，使得$x\to a$时，$f(x)-f(a)=A(x-a)+o(x-a)$，且$A=B$-若$f(x)$在$a$点可导，则$f(x)$在$a$点连续2.微分中值定理：- 若$f(x)$在闭区间$[a,b]$上连续，在开区间$(a,b)$上可微，则在$(a,b)$内存在一点$c$，使得$f'(c)=\frac{f(b)-f(a)}{b-a}$ - 若$f(x)$在闭区间$[a,b]$上连续，且在开区间$(a,b)$上可导，且存在常数$M$，使得$，f'(x)，\leq M$，则$f(x)$在闭区间$[a,b]$上有界3.微分法：-$(C)'=0$，其中$C$为常数- $(x^n)'=nx^{n-1}$，其中$n$为实数- $(\sin x)'=\cos x$，$(\cos x)'=-\sin x$，$(\tan x)'=\sec^2 x$- $(e^x)'=e^x$，$(a^x)'=a^x\ln a$- $(\ln x)'=\frac{1}{x}$，$(\log_a x)'=\frac{1}{x\ln a}$4.积分法：- $\int k\,dx=kx+C$，其中$k$为常数，$C$为常数- $\int x^n\,dx=\frac{1}{n+1}x^{n+1}+C$，其中$n$为实数，$C$为常数- $\int \frac{1}{x}\,dx=\ln ，x，+C$，其中$C$为常数- $\int e^x\,dx=e^x+C$- $\int \sin x\,dx=-\cos x+C$，$\int \cos x\,dx=\sin x+C$，$\int \sec^2 x\,dx=\tan x+C$- $\int \frac{1}{\sqrt{1-x^2}}\,dx=\arcsin x+C$5.微分方程：- $y'+P(x)y=Q(x)$的通解为$y=e^{-\int P(x)\,dx}\left(\intQ(x)e^{\int P(x)\,dx}\,dx+C\right)$，其中$P(x)$和$Q(x)$是已知函数- $y''+P(x)y'+Q(x)y=R(x)$的通解是$y=e^{-\intP(x)\,dx}\left[A\int e^{\intP(x)\,dx}R(x)\,dx+B\right]+C_1e^{kx}+C_2e^{kx}$，其中$k$为$P(x)$的重根，$A$和$B$为任意常数，$C_1$和$C_2$为任意常数这只是微积分中的一些重要公式，还有许多其他的公式和定理可以用于不同的问题和应用中。

高数-积分学

x
2 x x x
x x
x e 2( xe e ) C .
2
e ( x 2 x 2) C
x 2
例 4 已知 f ( x ) 的一个原函数是 e
x2
, 求 xf ( x )dx .
解

f ( x )dx f ( x ), f ( x )dx e
积分学
一、不定积分
二、定积分
三、广义积分四、重积分
五、平面曲线积分六、积分应用
一、不定积分
1. 直接积分法
通过简单变形, 利用基本积分公式和运算法则求不定积分的方法 (要求记住基本积分公式）. 2. 换元积分法
第一类换元的基本思路
g ( x)dx
f [ ( x)]d [ ( x)] F [ ( x)] C
d b( x ) F ( x ) f ( t )dt f b( x )b( x ) f a( x )a( x ) dx a ( x )
4、牛顿—莱布尼茨公式
如果 F ( x ) 是连续函数 f ( x ) 在区间[a , b]上的一个原函数，则
a f ( x )dx F (b) F (a )
注：这里要求f ( x)的原函数易求，且F ( x) f ( x)
第一类换元的关键是凑微分，常用的凑微分结果有
1 1 k dx d (ax b) x dx d (ax k 1 b) a (k 1)a
e dx d (e )
x x
1 dx d (ln x) ( x 0) x
x arcsin x 1 x2
2
1
dx
1
解：
1

高数微积分公式大全

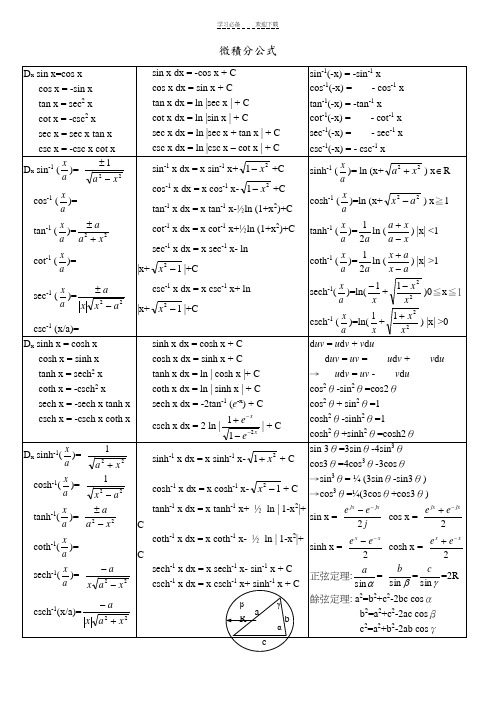
微積分公式sin x dx = -cos x + C cos x dx = sin x + C tan x dx = ln |sec x | + C cot x dx = ln |sin x | + Csec x dx = ln |sec x + tan x | + C csc x dx = ln |csc x – cot x | + C sin -1(-x) = -sin -1 xcos -1(-x) = - cos -1 x tan -1(-x) = -tan -1 x cot -1(-x) = - cot -1 x sec -1(-x) = - sec -1 x csc -1(-x) = - csc -1 xsin -1 x dx = x sin -1 x+21x -+C cos -1 x dx = x cos -1 x-21x -+C tan -1 x dx = x tan -1 x-½ln (1+x 2)+C cot -1 x dx = x cot -1 x+½ln (1+x 2)+C sec -1 x dx = x sec -1 x- ln |x+12-x |+Ccsc -1 x dx = x csc -1 x+ ln |x+12-x |+Csinh x dx = cosh x + C cosh x dx = sinh x + C tanh x dx = ln | cosh x |+ C coth x dx = ln | sinh x | + C sech x dx = -2tan -1 (e -x ) + C csch x dx = 2 ln |xx ee 211---+| + Cd uv = u d v + v d ud uv = uv = u d v + v d u→ u d v = uv - v d u cos 2θ-sin 2θ=cos2θ cos 2θ+ sin 2θ=1 cosh 2θ-sinh 2θ=1cosh 2θ+sinh 2θ=cosh2θsinh -1 x dx = x sinh -1 x-21x ++ Ccosh -1 x dx = x cosh -1 x-12-x + C tanh -1 x dx = x tanh -1 x+ ½ ln | 1-x 2|+ Ccoth -1 x dx = x coth -1 x- ½ ln | 1-x 2|+ C sech -1 x dx = x sech -1 x- sin -1 x + C csch -1 x dx = x csch -1 x+ sinh -1 x + Ca bcαβγ R希腊字母 (Greek Alphabets)倒数关系: sin θcsc θ=1; tan θcot θ=1; cos θsec θ=1 商数关系: tan θ=θθcos sin ; cot θ= θθsin cos 平方关系: cos 2θ+ sin 2θ=1; tan 2θ+ 1= sec 2θ; 1+ cot 2θ= csc 2θ順位低順位高; 顺位高d 顺位低 ;0*=∞1 * =∞∞ = 0*01 = 00 00 = )(0-∞e ; 0∞ = ∞⋅0e ; ∞1 = ∞⋅0e1 000 000 000 000 000 000 000 000 10 yotta Y1 000 000 000 000 000 000 000 1021 zetta Z1 000 000 000 000 000 000 1018 exa E1 000 000 000 000 000 1015 peta P1 000 000 000 000 1012 tera T 兆1 000 000 000 109 giga G 十亿1 000 000 106 mega M 百万1 000 103 kilo K 千100 102 hecto H 百10 101 deca D 十0.1 10-1 deci d 分，十分之一0.01 10-2 centi c 厘（或写作「厘」），百分之一0.001 10-3 milli m 毫，千分之一0.000 001 10-6 micro ? 微，百万分之一0.000 000 001 10-9 nano n 奈，十亿分之一0.000 000 000 001 10-12 pico p 皮，兆分之一0.000 000 000 000 001 10-15 femto f 飞（或作「费」），千兆分之一0.000 000 000 000 000 001 10-18 atto a 阿0.000 000 000 000 000 000 001 10-21 zepto z0.000 000 000 000 000 000 000 001 10-24 yocto y重点在三方面：一、函数与反函数的关系：(Function and Inverse Function)以前我们学过的相反运算有：加<------->减；乘<------->除；平方<----->开方；指数<----->对数；三角<----->反三角。

高数积分的定义

高数积分的定义积分是数学中一项重要的概念，它涉及到求解函数在给定范围内的面积。

在高等数学中，积分概念比较复杂，引入了高数积分一词，即在更高维度上求解函数积分的概念。

而计算高数积分就是解决在高维度上求解函数积分问题，它有多种方法，如梯形公式、辛普森积分和拉格朗日积分等。

首先，高数积分是一种高维积分，即在高维度上求解函数的积分。

关于高数积分的定义可以简述为：在n维坐标空间中，从某个给定的点到另一个给定的点，求解函数在这两点之间的数值积分。

其中n维坐标可以是二维的或者三维的，也可以是更高的维度。

其次，高数积分可以被定义为在多维空间求解数学积分的方法。

由于维度的提升，求解多维空间数学积分比在二维空间求解数学积分要复杂得多，因此一般情况下需要引入专业的数值计算软件来实现。

除此之外，多维空间数学积分也可以引入辛普森积分、梯形公式和拉格朗日积分等积分方法来求解。

梯形公式，又称为梯形公式，它是一种计算高数积分的有效方法，即在指定的函数空间中，使用梯形规则对函数进行采样，然后根据采样定理近似求解函数的积分。

由于梯形规则比较简单，通常可以忽略函数关于变量的微小变化，因此，这种方法求解高数积分较为简单，但是由于误差的放大，它的准确性也比较差。

辛普森积分，又称为自适应辛普森积分，它是一种更准确的高数积分方法，即根据多元函数的特性，通过自适应技术选择分割的点，然后重新根据函数的特性重新调整分割点，从而计算函数的积分。

由于大量分割点的使用，以及非要素技术的使用，使得这种方法可以更快准确地求解函数的积分。

最后，拉格朗日积分是求解高数积分的重要方法之一，其定义可以简述为：在函数的给定区域内，将函数进行多次分割，每个分割点处求解函数的有限积分，最后得到函数的积分。

拉格朗日积分比其他方法更加准确，也更加庞大，其基本特点是采用多次分割，每个分割点处求解函数的有限积分，再求出整体的积分。

综上所述，高数积分是指在多维空间求解函数积分的概念，其基本定义是在n维坐标空间中，从某个给定的点到另一个给定的点，求解函数在这两点之间的数值积分。

01高数——积分学

D f (x, y)d f ( , )
在闭区域D上使
第24页，共48页。
2.在直角坐标系下计算二重积分
若D为 X – 型区域
D
:
1
(
x) a
y x
b
2
(
x)
y
y 2(x)
D x
则
f (x, y) dx dy
b
dx
2 (x)
oa f (x, y) dy
y 1(x) b
x
D
a 1( x)
t arcsin x
2 2 t sin tdt 2 0
第18页，共48页。
例7 计算 1 (x 4 x2 )2 dx 1 解：1 ( x 4 x2 )2 dx 1 1 [ x2 2 x 4 x2 (4 x2 )]dx 1 1 4 dx 8 1
第19页，共48页。
1 1
3) 2
C
2 1 1
2
3
1 (x2 3)2 C 3
第6页，共48页。
第二类换元的解题思路为
(t) f [ (t)] (t)
x (t )
f (x)dx f [ (t)] (t)dt
(t) C [ 1(x)] C
使用该公式的关键为
1. x (t)单调可导，有反函数存在。
2. 积分 f [ (t)] (t)dt易求。
f ( x)dx ex2 C ,
两边同时对 x求导, 得 f ( x) 2 xex2 ,
xf ( x)dx xf ( x) f ( x)dx
2
x
2
e
x
2
ex2
C.
第10页，共48页。
二、定积分
1、定积分定义：

高数积分公式大全

常用积分公式（一）含有ax b +的积分(0a ≠) 1．d x ax b +⎰＝1ln ax b C a++ 2．()d ax b x μ+⎰＝11()(1)ax b C a μμ++++（1μ≠-）3．d x x ax b +⎰＝21(ln )ax b b ax b C a+-++ 4．2d x x ax b +⎰＝22311()2()ln 2ax b b ax b b ax b C a ⎡⎤+-++++⎢⎥⎣⎦5．d ()xx ax b +⎰＝1lnax b C b x +-+ 6．2d ()xx ax b +⎰＝21ln a ax b C bx b x +-++ 7．2d ()x x ax b +⎰＝21(ln )b ax b C a ax b++++ 8．22d ()x x ax b +⎰＝231(2ln )b ax b b ax b C a ax b+-+-++ 9．2d ()xx ax b +⎰＝211ln ()ax b C b ax b b x +-++的积分10．x C +11．x ⎰＝22(3215ax b C a -+12．x x ⎰＝22232(15128105a x abx b C a-++13．x＝22(23ax b C a -14．2x＝22232(34815a x abx b C a -++15．＝(0)(0)C b C b ⎧+><16．2a b - 17．x＝b +18．x＝2a x -+ （三）含有22x a ±的积分 19．22d x x a +⎰=1arctan x C a a+ 20．22d ()n x x a +⎰=2221222123d 2(1)()2(1)()n n x n xn a x a n a x a ---+-+-+⎰21．22d xx a -⎰=1ln 2x a C a x a-++ （四）含有2(0)ax b a +>的积分22．2d x ax b +⎰＝(0)(0)C b C b ⎧+>+<23．2d x x ax b +⎰＝21ln 2ax b C a++ 24．22d x x ax b +⎰＝2d x b x a a ax b -+⎰25．2d ()x x ax b +⎰＝221ln 2x C b ax b++ 26．22d ()x x ax b +⎰＝21d a xbx b ax b--+⎰27．32d ()x x ax b +⎰＝22221ln 22ax b a C b x bx +-+28．22d ()x ax b +⎰＝221d 2()2x xb ax b b ax b+++⎰ （五）含有2ax bx c ++(0)a >的积分29．2d x ax bx c ++⎰＝22(4)(4)C b ac Cb ac +<+>30．2d x x ax bx c ++⎰＝221d ln 22b x ax bx c a a ax bx c++-++⎰(0)a >的积分 31．＝1arsh xC a+＝ln(x C + 32．C +33．xC34．x＝C +35．2x2ln(2a x C ++ 36．2x＝ln(x C +++37．1ln aC a x -+ 38．C + 39．x2ln(2a x C ++40．x ＝2243(25ln(88x x a a x C ++++41．x ⎰C42．x x ⎰＝422(2ln(88x a x a x C +++43．d x x ⎰ln a a C x ++44．2d x x ⎰＝ln(x C x-+++(0)a >的积分45．＝1arch x xC x a+=ln x C ++ 46．C +47．x C +48．x ＝C +49．2x 2ln 2a x C ++50．2x ＝ln x C +++51．1arccosaC ax+52．C +53．x 2ln 2a x C ++54．x ＝2243(25ln 88x x a a x C -++55．x ⎰C56．x x ⎰＝422(2ln 88x a x a x C -++57．d x x⎰arccos a a C x +58．2d x x ⎰＝ln x C x-+++(0)a >的积分 59．＝arcsin xC a+ 60．C +61．x ＝C62．x C +63．2x ＝2arcsin 2a x C a + 64．2x arcsinxC a-+65．1ln a C a x +66．C +67．x 2arcsin 2a x C a+68．x ＝2243(52arcsin 88x x a x a C a-+69．x ⎰＝C +70．x x ⎰＝422(2arcsin 88x a x x a C a-+71．x a C ++72．x ＝arcsin xC a-+(0)a >的积分73．2ax b C +++74．x75．x 76．＝C +77．x 2C ++78．x ＝C +79．x ＝((x b b a C --++80．x ＝((x b b a C --81．C ()a b <82．x 2()4b a C -++ （十一）含有三角函数的积分83．sin d x x ⎰＝cos x C -+ 84．cos d x x ⎰＝sin x C + 85．tan d x x ⎰＝ln cos x C -+ 86．cot d x x ⎰＝ln sin x C +87．sec d x x ⎰＝ln tan()42x C π++＝ln sec tan x x C ++ 88．csc d x x ⎰＝ln tan2xC +＝ln csc cot x x C -+ 89．2sec d x x ⎰＝tan x C + 90．2csc d x x ⎰＝cot x C -+ 91．sec tan d x x x ⎰＝sec x C + 92．csc cot d x x x ⎰＝csc x C -+93．2sin d x x ⎰＝1sin 224x x C -+94．2cos d x x ⎰＝1sin 224x x C ++95．sin d n x x ⎰＝1211sin cos sin d n n n x x x x n n----+⎰ 96．cos d n x x ⎰＝1211cos sin cos d n n n x x x x n n ---+⎰97．d sin n x x ⎰＝121cos 2d 1sin 1sin n n x n xn x n x ----⋅+--⎰ 98．d cos n x x ⎰＝121sin 2d 1cos 1cos n n x n xn x n x---⋅+--⎰ 99．cos sin d m n x x x ⎰＝11211cos sin cos sin d m n m nm x x x x x m n m n -+--+++⎰＝11211cos sin cos sin d m n m n n x x x x x m n m n+----+++⎰ 100．sin cos d ax bx x ⎰＝11cos()cos()2()2()a b x a b x C a b a b -+--++-101．sin sin d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b -++-++-102．cos cos d ax bx x ⎰＝11sin()sin()2()2()a b x a b x C a b a b ++-++-103．d sin xa b x +⎰tanxa b C ++22()a b >104．d sin x a b x +⎰C +22()a b <105．d cos xa b x+⎰)2x C +22()a b >106．d cos x a b x +⎰C +22()a b <107．2222d cos sin x a x b x +⎰＝1arctan(tan )bx C ab a+ 108．2222d cos sin xa xb x-⎰＝1tan ln 2tan b x a C ab b x a ++- 109．sin d x ax x ⎰＝211sin cos ax x ax C a a -+ 110．2sin d x ax x ⎰＝223122cos sin cos x ax x ax ax C a a a -+++111．cos d x ax x ⎰＝211cos sin ax x ax C a a ++112．2cos d x ax x ⎰＝223122sin cos sin x ax x ax ax C a a a+-+（十二）含有反三角函数的积分（其中0a >） 113．arcsin d xx a ⎰＝arcsin x x C a+114．arcsin d xx x a ⎰＝22()arcsin 24x a x C a -+115．2arcsin d xx x a⎰＝3221arcsin (239x x x a C a +++116．arccos d x x a ⎰＝arccos x x C a117．arccos d xx x a ⎰＝22()arccos 24x a x C a --+118．2arccos d xx x a⎰＝3221arccos (239x x x a C a -++119．arctan d xx a ⎰＝22arctan ln()2x a x a x C a -++ 120．arctan d x x x a ⎰＝221()arctan 22x a a x x C a +-+121．2arctan d xx x a⎰＝33222arctan ln()366x x a a x a x C a -+++（十三）含有指数函数的积分122．d x a x ⎰＝1ln xa C a + 123．e d ax x ⎰＝1e ax C a +124．e d ax x x ⎰＝21(1)e ax ax C a -+125．e d n ax x x ⎰＝11e e d n ax n ax nx x x a a--⎰126．d x xa x ⎰＝21ln (ln )x xx a a C a a -+ 127．d n x x a x ⎰＝11d ln ln n x n xn x a x a x a a --⎰ 128．e sin d ax bx x ⎰＝221e (sin cos )ax a bx b bx C a b -++129．e cos d ax bx x ⎰＝221e (sin cos )ax b bx a bx C a b+++130．e sin d ax n bx x ⎰＝12221e sin (sin cos )ax n bx a bx nb bx a b n--+131．e cos d ax n bx x ⎰＝12221e cos (cos sin )ax n bx a bx nb bx a b n-++（十四）含有对数函数的积分 132．ln d x x ⎰＝ln x x x C -+133．d ln xx x⎰＝ln ln x C + 134．ln d n x x x ⎰＝111(ln )11n x x C n n +-+++135．(ln )d n x x ⎰＝1(ln )(ln )d n n x x n x x --⎰ 136．(ln )d m n x x x ⎰＝111(ln )(ln )d 11m n m n nx x x x x m m +--++⎰ （十五）含有双曲函数的积分 137．sh d x x ⎰＝ch x C + 138．ch d x x ⎰＝sh x C + 139．th d x x ⎰＝lnch x C + 140．2sh d x x ⎰＝1sh224xx C -++ 141．2ch d x x ⎰＝1sh224x x C ++ （十六）定积分142．cos d nx x π-π⎰＝sin d nx x π-π⎰＝0 143．cos sin d mx nx x π-π⎰＝0144．cos cos d mx nx x π-π⎰＝0,,m nm n ≠⎧⎨π=⎩145．sin sin d mx nx x π-π⎰＝0,,m nm n≠⎧⎨π=⎩146．0sin sin d mx nx x π⎰＝0cos cos d mx nx x π⎰＝0,,2m n m n ≠⎧⎪⎨π=⎪⎩147． n I ＝20sin d nx x π⎰＝20cos d n x x π⎰n I ＝21n n I n-- 1342253n n n I n n --=⋅⋅⋅⋅-L （n 为大于1的正奇数），1I ＝1 13312422n n n I n n --π=⋅⋅⋅⋅⋅-L （n 为正偶数），0I ＝2π。

高数微积分公式大全

高数导数和积分大全

高数导数和积分大全

高等数学积分公式大全

高数微积分公式大全

高数积分公式大全

高数积分公式大全

高数-专题二 积分计算的基本公式

高数不定积分

高数积分总结

高数积分公式

高数上4.1 不定积分概念与性质

高数积分总结

高数微积分公式大全

高数-积分学

高数微积分公式大全

高数积分的定义

01高数——积分学

高数积分公式大全

高数-专题二积分计算的基本公式