22第4讲__MATLAB矩阵分析及符号运算
matlab 符号运算 矩阵公式推导

matlab 符号运算矩阵公式推导
在MATLAB中进行符号运算,可以使用符号数学工具箱(Symbolic Math Toolbox)中提供的函数和工具。
要进行矩阵公式的推导,可以使用符号变量来表示矩阵和变量,并使用符号数学工具箱中的函数进行运算和化简。
下面是一个简单的矩阵公式推导的示例:
假设有一个矩阵A和一个向量x,要推导矩阵乘法(A*x)的结果,可以按照以下步骤进行:
1. 定义符号变量:
```matlab
syms A x
```
2. 用符号变量表示矩阵和向量:
```matlab
A = [a b; c d]; % 替换为实际的矩阵元素
x = [x1 x2]'; % 替换为实际的向量元素
```
3. 计算矩阵乘法(A*x)的结果:
```matlab
result = A*x;
```
4. 对结果进行化简:
```matlab
simplified_result = simplify(result);
```
5. 可以使用disp函数显示结果:
```matlab
disp(simplified_result);
```
通过这种方法,你可以进行更复杂的矩阵推导,包括求逆矩阵、行列式、特征值等。
你可以使用符号数学工具箱中提供的函数,如inv、det、eig等,进行矩阵的运算和分析。
希望以上内容对你有所帮助!。
如何使用Matlab进行矩阵运算

如何使用Matlab进行矩阵运算随着科学技术的不断发展,矩阵运算在各个领域的应用日益广泛。
Matlab作为一款功能强大的数学软件,其矩阵运算能力非常强大。
本文将介绍如何使用Matlab进行矩阵运算,希望能对读者在科学研究和工程实践中的矩阵计算有所帮助。
一、Matlab的基本矩阵运算1. 创建矩阵在Matlab中,可以使用一对方括号`[]`来创建矩阵。
例如,要创建一个3行3列的矩阵A,可以使用如下命令:A = [1 2 3; 4 5 6; 7 8 9]。
这样就创建了一个元素分别为1到9的3行3列矩阵。
2. 矩阵加法和减法Matlab中可以使用加号和减号来进行矩阵的加法和减法运算。
例如,要计算矩阵A和B的和,可以使用命令C = A + B;要计算矩阵A和B的差,可以使用命令D = A - B。
3. 矩阵乘法Matlab中使用乘号`*`来进行矩阵的乘法运算。
例如,要计算矩阵A和B的乘积,可以使用命令C = A * B。
需要注意的是,矩阵乘法是满足结合律的,即A *(B * C) = (A * B) * C。
4. 矩阵转置在Matlab中,可以使用单引号`'`来对矩阵进行转置操作。
例如,对矩阵A进行转置,可以使用命令B = A'。
需要注意的是,转置操作只能应用于二维矩阵。
5. 求逆矩阵在Matlab中,可以使用inv函数来求解矩阵的逆矩阵。
例如,要求矩阵A的逆矩阵,可以使用命令B = inv(A)。
需要注意的是,只有方阵才有逆矩阵。
6. 矩阵的特征值和特征向量Matlab中可以使用eig函数来求解矩阵的特征值和特征向量。
例如,要求矩阵A的特征值和特征向量,可以使用命令[V,D] = eig(A),其中V为特征向量矩阵,D 为特征值对角矩阵。
二、Matlab的高级矩阵运算1. 矩阵的点乘和叉乘Matlab中使用.*和.^来进行矩阵的点乘和叉乘运算。
例如,要计算矩阵A和B 的点乘,可以使用命令C = A .* B;要计算矩阵A和B的叉乘,可以使用命令D =A .^ B。
matlab 符号矩阵运算

matlab 符号矩阵运算
在MATLAB中进行符号矩阵运算,需要使用符号计算工具箱。
以下是一些常见的符号矩阵运算:
1. 转置:符号矩阵的转置可以通过符号“ ' ”或函数transpos来实现。
例如,如果A是一个符号矩阵,则A.' 是A 的转置。
2. 乘法:两个符号矩阵的乘法可以通过函数mtimes来实现。
例如,如果A和B是两个符号矩阵,则C=A*B是A和B的乘积。
3. 加法:两个符号矩阵的加法可以通过加法运算符“+”来实现。
例如,如果A和B是两个具有相同尺寸的符号矩阵,则
C=A+B是A和B的加积。
4. 逆运算:一个方阵的逆运算可以通过函数inv来实现。
例如,如果A是一个方阵,则inv(A)是A的逆矩阵。
需要注意的是,不是所有的方阵都有逆矩阵。
5. 行列式运算:一个方阵的行列式运算可以通过函数determ或det来实现。
例如,如果A是一个方阵,则det(A)或determ(A)是A的行列式。
6. 求秩运算:一个符号矩阵的求秩运算可以通过函数rank 来实现。
例如,如果A是一个符号矩阵,则rank(A)是A的秩。
7. 特征值和特征向量运算:一个符号矩阵的特征值和特征向量运算可以通过函数eig、eigensys等来实现。
例如,如果A
是一个符号矩阵,则[V,D]=eig(A)将返回特征向量V和特征值D。
以上是一些常见的符号矩阵运算,但MATLAB符号计算工具箱还提供了许多其他函数和运算符来进行符号矩阵运算。
MATLAB的符号运算V精简版

ans=[2+y,4+y,6+y]
>> subs(f,x,[1:3]) >> subs(f,{x,y},{[1:3],[5:7]})
ans=[7 10 13]
>> subs(f,{x,y},{a+b,a-b}) >> subs(f,{x,y},{x+y,x-y})
Copyright © CUGB
2024/4/3
Matlab的符号运算
符号对象建立时可以附加属性: real、positive 和 unreal
>> x=sym('x','real') >> k=sym('k','positive') >> x=sym('x','unreal')
表明 x 是实的 表明 k 是正的 去掉 x 的附加属性
Copyright © CUGB 2024/4/3
Matlab的符号运算
符号表达式的建立
>> syms x >> f1=sin(x)+cos(x)
推荐!
>> f2=sym(’sin(x)+cos(x)’)
Copyright © CUGB 2024/4/3
Matlab的符号运算
相关函数
➢ findsym: 查找符号表达式中的符号变量
findsym(f) 按字母顺序列出符号表达式 f 中的所有自由变量 findsym(f,N) 列出 f 中距离 x 最近的 N 个自由变量(i,j 除外)
Matlab的符号运算
其它运算
matlab符号运算知识点总结

matlab符号运算知识点总结符号运算在Matlab中的应用非常广泛,包括代数运算、微积分、方程求解、矩阵运算等。
下面对Matlab中符号运算的一些重要知识点进行总结:代数运算在Matlab中进行代数运算,可使用符号工具箱中的函数,如syms,sym,和符号运算的基本运算符包括加减乘除、指数、对数、幂函数等。
另外,Matlab还提供了一些用于多项式运算的特殊函数,如expand、factor、simplify、collect等。
通过这些函数,可以对代数表达式进行化简、因式分解、展开等操作。
微积分在Matlab中进行微积分运算,可使用符号工具箱中的函数,如diff,int,limit等。
这些函数可用于求导、积分、极限等微积分运算。
通过这些函数,可以对符号表达式进行微积分运算,得到导数、积分、极限等结果。
方程求解在Matlab中进行方程求解,可使用符号工具箱中的函数,如solve,dsolve等。
这些函数可用于求解方程、微分方程等问题。
通过这些函数,可以对符号表达式进行方程求解,得到方程的根、微分方程的解等结果。
矩阵运算在Matlab中进行矩阵运算,可使用符号工具箱中的函数,如inv,det,eig等。
这些函数可用于求逆矩阵、求行列式、求特征值等操作。
通过这些函数,可以对符号矩阵进行各种运算,得到矩阵的逆、行列式、特征值等结果。
符号计算的优点符号计算在Matlab中的应用有许多优点。
首先,符号计算能够保留数学表达式的符号形式,不会将其计算成数值,这对于一些需要保留符号的问题非常重要。
其次,符号计算具有精度高、灵活性强的特点,能够处理复杂的数学问题。
此外,符号计算还能够进行符号表达式的化简、因式分解、展开等操作,有助于分析数学表达式的性质。
总之,Matlab中的符号运算功能丰富,能够处理各种数学问题,包括代数运算、微积分、方程求解、矩阵运算等。
符号计算在Matlab中的应用具有许多优点,能够保留数学表达式的符号形式,处理复杂的数学问题,并进行符号表达式的化简、因式分解、展开等操作。
如何在Matlab中进行矩阵运算和线性代数计算

如何在Matlab中进行矩阵运算和线性代数计算矩阵运算和线性代数计算在科学计算中起着至关重要的作用。
Matlab是一种强大的科学计算软件,其中内置了丰富的矩阵运算和线性代数函数,使得我们能够轻松地进行各种复杂的数学计算。
本文将介绍如何在Matlab中进行矩阵运算和线性代数计算。
一、矩阵的表示与生成在Matlab中,我们可以使用一对方括号来表示矩阵。
例如,下面的代码可以生成一个3×3的矩阵A:```A = [1, 2, 3; 4, 5, 6; 7, 8, 9];```我们也可以使用内置函数来生成一些特殊矩阵,如零矩阵、单位矩阵和对角矩阵。
下面的代码分别生成一个3×3的零矩阵B、一个3×3的单位矩阵C和一个对角元素为1、2、3的对角矩阵D:```B = zeros(3);C = eye(3);D = diag([1, 2, 3]);```二、矩阵的基本运算1. 矩阵的加法和减法在Matlab中,我们可以使用运算符"+"和"-"对矩阵进行加法和减法运算。
下面的代码演示了如何对两个3×3的矩阵A和B进行加法和减法运算:```A = [1, 2, 3; 4, 5, 6; 7, 8, 9];B = [9, 8, 7; 6, 5, 4; 3, 2, 1];C = A + B; % 矩阵相加D = A - B; % 矩阵相减```2. 矩阵的乘法矩阵的乘法在Matlab中使用运算符"*"表示。
下面的代码演示了如何对两个矩阵A和B进行乘法运算:```A = [1, 2, 3; 4, 5, 6]; % 2×3 矩阵B = [7, 8; 9, 10; 11, 12]; % 3×2 矩阵C = A * B; % 矩阵相乘```需要注意的是,矩阵的乘法是满足结合律的,但不满足交换律。
也就是说,如果A是m×n的矩阵,B是n×p的矩阵,那么A*B是m×p的矩阵,而B*A是n×n 的矩阵。
Matlab矩阵、数组和符号运算PPT课件

2021/6/7
5
第3章 矩阵、数组和符号运算
➢这种方法输入符号矩阵与字符串矩阵的输入相似。但要 保证在同一列中各元素字符串有同样的长度,在较短的字 符串前后用空格符填充; ➢这种方法要求符号矩阵每一行的两端都有方括号,而字 符串矩阵仅在首尾有方括号。
>> B=['[4+x x^2 x ]';'[x^3 5*x-3 x*a]']
计算速度最快,占用计算机内存最少的算法,与 C、
FORTRAN 语言中的浮点运算算法完全相同。在机器内
的表达和计算都是一个被“ 截断”的8 位浮点近似值。
➢针对精确运算的符号算法
计算时间最长,内存占用最多,精度也最高。
➢任意精度的算法
运算时间、内存占用和计算精度均介于以上两种运算之间。
采用函数 digits 来控制十进制结果的有效位数。digits 的
第3章 矩阵、数组和符号运算
二、符号及运算
掌握内容:
(1)了解 MATLAB 6.0 的符号变量,掌握 MATLAB 符
号表达式、符号矩阵的两种创建方法。
(2)掌握 MATLAB 符号数学函数的创建。
(3)掌握符号矩阵的基本运算及MATLAB 关于不同精度
的控制方法。
(4)掌握符号微积分内容,包括求函数的极限、对符号表
同类项合并
>> syms x y >> collect(x^2*y+y*x-x^2-2*x) ans = (y-1)*x^2+(y-2)*x
分式通分
>> syms x y >> [n,d]=numden(x/y+y/x) n= x^2+y^2 d= y*x
matlab 矩阵运算程序

matlab 矩阵运算程序摘要:1.MATLAB 简介2.MATLAB 矩阵运算的基本概念3.MATLAB 矩阵运算的实例4.MATLAB 矩阵运算的优点正文:1.MATLAB 简介MATLAB(Matrix Laboratory)是一款广泛应用于科学计算、数据分析、可视化等领域的编程软件。
它以矩阵计算为核心,为用户提供了丰富的函数库和强大的矩阵运算能力。
MATLAB 可以进行各种矩阵运算,包括矩阵加法、乘法、转置、求逆等,使得矩阵计算变得更加简单、快速。
2.MATLAB 矩阵运算的基本概念在MATLAB 中,矩阵运算通常涉及到以下几个基本概念:- 矩阵:MATLAB 中的矩阵是一个二维数组,可以用来表示线性方程组、线性变换等数学概念。
- 单位矩阵:单位矩阵是一个方阵,其中主对角线上的元素都是1,其余元素都是0。
单位矩阵的作用类似于数学中的1,即任何矩阵与单位矩阵相乘,结果仍为原矩阵。
- 零矩阵:零矩阵是一个所有元素都是0 的矩阵,通常用0 表示。
- 矩阵的转置:将一个矩阵的行和列互换,得到一个新的矩阵,这个新矩阵称为原矩阵的转置。
- 矩阵的逆矩阵:对于一个可逆矩阵,存在一个矩阵,使得两者相乘等于单位矩阵。
这个矩阵称为原矩阵的逆矩阵。
3.MATLAB 矩阵运算的实例下面通过一个简单的实例,介绍如何在MATLAB 中进行矩阵运算。
假设有一个2x3 的矩阵A:```A = [1, 2, 3;4, 5, 6];```我们可以进行以下矩阵运算:- 矩阵加法:```B = 2 * A;C = A + B;```- 矩阵乘法:```D = A * B;```- 矩阵转置:```E = A";```- 矩阵求逆:```F = AB;```4.MATLAB 矩阵运算的优点MATLAB 矩阵运算具有以下优点:- 简单易用:MATLAB 提供了丰富的矩阵运算函数,用户只需调用相应的函数,即可完成复杂的矩阵运算。
matlab对矩阵运算

matlab对矩阵运算Matlab是一种强大的数学软件,它提供了丰富的矩阵运算功能。
矩阵运算是数学中重要的概念之一,它在科学计算、工程设计、数据分析等领域中广泛应用。
本文将分析和介绍Matlab中常用的矩阵运算方法和技巧。
我们需要了解矩阵的基本概念。
矩阵是一个二维的数学结构,由行和列组成。
在Matlab中,矩阵可以用方括号[ ]表示,行与行之间用分号;分隔,例如:A = [1 2 3; 4 5 6; 7 8 9]这是一个3行3列的矩阵A,它由1到9的整数填充。
在Matlab中,我们可以通过索引来访问矩阵中的元素。
例如,A(2,3)表示矩阵A 中第2行第3列的元素,即6。
在Matlab中,可以进行各种矩阵运算,包括加法、减法、乘法、转置等。
下面我们将重点介绍几种常用的矩阵运算方法。
1. 矩阵加法矩阵加法是指对两个矩阵对应元素进行相加的运算。
在Matlab中,可以使用加号+进行矩阵加法运算。
例如,给定两个3行3列的矩阵A和B:A = [1 2 3; 4 5 6; 7 8 9]B = [9 8 7; 6 5 4; 3 2 1]可以使用以下代码进行矩阵加法运算:C = A + B运行结果为:C =10 10 1010 10 1010 10 102. 矩阵减法矩阵减法是指对两个矩阵对应元素进行相减的运算。
在Matlab中,可以使用减号-进行矩阵减法运算。
例如,给定两个3行3列的矩阵A和B:A = [1 2 3; 4 5 6; 7 8 9]B = [9 8 7; 6 5 4; 3 2 1]可以使用以下代码进行矩阵减法运算:D = A - B运行结果为:D =-8 -6 -4-2 0 24 6 83. 矩阵乘法矩阵乘法是指对两个矩阵进行相乘的运算。
在Matlab中,可以使用星号*进行矩阵乘法运算。
例如,给定两个3行3列的矩阵A和B:A = [1 2 3; 4 5 6; 7 8 9]B = [9 8 7; 6 5 4; 3 2 1]可以使用以下代码进行矩阵乘法运算:E = A * B运行结果为:E =30 24 1884 69 54138 114 904. 矩阵转置矩阵转置是指将矩阵的行和列进行交换的运算。
22第4讲__MATLAB矩阵分析及符号运算

a, 2*b] [3*a, 0] A1=sym(A,2,2, '4*b') A(2,2)='4*b' A1 =[ a, 2*b] A3 = [ a, 2*b] [3*a, 4*b]
c =14
32
23
11
d=[-1;0;2];f=pi*d f = -3.1416 0 6.2832 矩阵除的运算在线性代数中没有,
有矩阵逆的运算,在matlab中有两种
矩阵除运算
12
3. 矩阵乘方—— a^n,a^p,p^a
a ^ p —— a 自乘p次幂
方阵 >1的整数
对于p的其它值,计算将涉及特征值 和特征向量,如果p是矩阵,a是标量 a^p使用特征值和特征向量自乘到p次
例:建立3*3,3*2的和矩阵A同样大小的零矩阵 Zero(3,3) Zero(3,2) Zero(size(A))
3. 矩阵的修改
直接修改 可用键找到所要修改的矩阵,用键移 动到要修改的矩阵元素上即可修改。 指 令修改 可以用A(,)= 来修改。
8
例如 a=[1 2 0;3 0 5;7 8 9] a =1 2 0 3 0 5 7 8 9 a(3,3)=0 a =1 2 0 3 0 5 7 8 0
幂;如a,p都是矩阵,a^p则无意义。
13
a=[1,2,3;4,5,6;7,8,9];a^2 ans =30 36 42 66 81 96
102 126 150
※当一个方阵有复数特征值或负实 特征值时,非整数幂是复数阵。
14
a^0.5
ans =
0.4498 + 0.7623i 0.5526 + 0.2068i 0.6555 -0.3487i 1.0185 + 0.0842i 1.2515 + 0.0228i 1.4844 - 0.0385i 1.5873 - 0.5940i 1.9503 - 0.1611i 2.3134 + 0.2717iMATLAB对矩阵A实施上翻转的函数是flipud(A)。
如何利用Matlab技术进行矩阵运算

如何利用Matlab技术进行矩阵运算矩阵运算是数学中的重要部分,可以应用于多个领域,如自然科学、工程学和经济学等。
而对于如何利用Matlab技术进行矩阵运算,是每个数学爱好者和研究者都应该掌握的技能。
本文将深入探讨如何使用Matlab进行矩阵运算,并提供一些例子和技巧供读者参考。
首先,让我们来了解一下Matlab是什么。
Matlab是一种强大的数学计算软件,被广泛应用于科学计算和工程设计中。
它不仅可以进行矩阵运算,还能进行符号计算、绘图和数据分析等任务。
Matlab具有直观友好的用户界面,使得使用者可以轻松地进行各种计算操作。
在Matlab中,可以使用一维和二维数组来表示矩阵。
一维数组称为向量,而二维数组称为矩阵。
当我们需要进行矩阵运算时,需要首先定义并初始化一个矩阵。
在Matlab中,可以通过直接输入矩阵元素的值来创建一个矩阵。
例如,我们可以使用以下命令创建一个2x2的矩阵:```MatlabA = [1 2; 3 4];```这个矩阵将被存储在变量"A"中,并且可以通过输入"A"来显示。
在进行矩阵运算前,我们需要了解一些基本的矩阵运算符。
Matlab中的加法运算使用"+"符号,减法运算使用"-"符号,乘法运算使用"*"符号。
此外,Matlab还提供了一些特殊的运算符来进行矩阵运算,如点乘运算符"."、转置运算符"'"和逆运算符"\"等。
这些运算符可以使我们更加便捷地进行矩阵计算。
接下来,让我们来探讨一些矩阵运算的实际应用。
首先,矩阵的加法和减法可以用于求解多个物理量的叠加或差值。
例如,在电路分析中,我们可以使用矩阵运算来计算电路中各个元件的电流和电压。
假设有一个电路由两个电阻和一个电源组成,我们可以使用以下命令计算电源电流I和电阻电压V:```MatlabR = [10; 20];V = 5; % 电源电压I = R \ V; % 计算电源电流V_R = R .* I; % 计算电阻电压```上述代码中,电阻值被存储在矩阵R中,电源电压被存储在变量V中。
如何利用MATLAB进行矩阵运算

如何利用MATLAB进行矩阵运算概述在科学和工程领域,矩阵运算是一项非常重要的技能。
MATLAB作为一种高级数值计算和数据可视化软件,提供了丰富的功能和工具来处理矩阵运算。
本文将介绍如何使用MATLAB进行矩阵运算,包括矩阵的创建、矩阵的运算、矩阵的转置和逆矩阵等。
1. 矩阵的创建在MATLAB中,矩阵可以通过不同的方式进行创建。
最常见的方法是使用"["和"]"符号。
例如,以下命令将创建一个3x3的零矩阵:A = [0 0 0; 0 0 0; 0 0 0]除了手动创建矩阵外,MATLAB还提供了一些内置的函数来创建特殊类型的矩阵。
例如,下面的代码将创建一个单位矩阵:I = eye(3)2. 矩阵的运算使用MATLAB进行矩阵运算非常简单。
可以使用标准的数学运算符来执行加法、减法、乘法和除法等操作。
以下是一些示例代码:A = [1 2 3; 4 5 6; 7 8 9]B = [9 8 7; 6 5 4; 3 2 1]C = A + B % 矩阵加法D = A - B % 矩阵减法E = A * B % 矩阵乘法除了标准的数学运算符,MATLAB还提供了一些特殊的函数来执行矩阵运算。
例如,使用"inv"函数可以计算矩阵的逆矩阵:A = [1 2; 3 4]B = inv(A) % 计算A的逆矩阵3. 矩阵的转置矩阵的转置是指将矩阵的行和列互换。
在MATLAB中,可以使用"'"符号来实现矩阵的转置。
以下是一个示例:A = [1 2 3; 4 5 6; 7 8 9]B = A' % 矩阵A的转置4. 矩阵的逆矩阵逆矩阵是指对于一个方阵A,存在一个方阵B,使得AB=BA=I,其中I是单位矩阵。
在MATLAB中,可以使用"inv"函数来计算矩阵的逆矩阵。
以下是一个示例:A = [1 2; 3 4]B = inv(A) % 计算A的逆矩阵然而需要注意的是,并非所有的矩阵都有逆矩阵。
matlab矩阵逻辑运算

matlab矩阵逻辑运算摘要:一、引言二、MATLAB 逻辑运算符号与用法1.与(&)运算符2.或(|)运算符3.非(~)运算符4.异或(xor)函数三、MATLAB 矩阵逻辑运算1.逻辑与(a&b)2.逻辑或(ab)3.异或(xor(a,b))四、MATLAB 矩阵运算1.矩阵加法2.矩阵乘法3.矩阵转置五、总结正文:一、引言MATLAB 是一种广泛使用的数学软件,它提供了丰富的矩阵操作和逻辑运算功能。
在MATLAB 中,逻辑运算主要用于处理二进制数据,例如0 和1。
逻辑运算的结果也是二进制数据,通常为0 或1。
本文将介绍MATLAB 中的逻辑运算符号、用法以及矩阵逻辑运算。
二、MATLAB 逻辑运算符号与用法在MATLAB 中,逻辑运算有以下几种符号和用法:1.与(&)运算符:对应位上都为1 时,结果为1,否则为0。
例如,3(二进制表示为11)与2(二进制表示为10)进行与运算,结果为1(二进制表示为10)。
2.或(|)运算符:对应位上有至少一个为1 时,结果为1,否则为0。
例如,3(二进制表示为11)或2(二进制表示为10)进行或运算,结果为3(二进制表示为11)。
3.非(~)运算符:对一个二进制数取反,即将0 变为1,将1 变为0。
例如,对二进制数11 取反得到00。
4.异或(xor)函数:相同为0,不同为1。
例如,3(二进制表示为11)和2(二进制表示为10)进行异或运算,结果为1(二进制表示为01)。
三、MATLAB 矩阵逻辑运算在MATLAB 中,矩阵逻辑运算主要用于处理二进制矩阵。
以下是一些常用的矩阵逻辑运算:1.逻辑与(a&b):对应位置上都为1 时,结果矩阵的对应位置为1,否则为0。
2.逻辑或(ab):对应位置上有至少一个为1 时,结果矩阵的对应位置为1,否则为0。
3.异或(xor(a,b)):对应位置上相同为0,不同为1。
结果矩阵的对应位置为a 和b 对应位置不相同的值。
matlab解符号矩阵

matlab解符号矩阵
在MATLAB中,可以使用符号工具箱来解符号矩阵。
以下是
一个详细的步骤:
1. 首先,确保你已经安装了MATLAB符号工具箱。
你可以
在MATLAB主界面的"Home"选项卡中的"Add-Ons"下找到并
安装它。
2. 在MATLAB命令窗口中,创建一个符号矩阵。
你可以使
用`syms`命令来定义符号变量,然后使用这些符号变量来
构建矩阵。
例如,下面的代码创建了一个3x3的符号矩阵A:
syms a b c d e f g h i
A = [a b c; d e f; g h i];
3. 使用`solve`函数来解符号矩阵。
`solve`函数可以用于
求解一组方程或不等式。
你可以将符号矩阵的每个元素视
为一个方程,并使用`solve`函数来求解这些方程。
例如,
下面的代码解符号矩阵A:
solution = solve(A);
4. 如果你想要得到解的具体数值,可以使用`double`函数
将解转换为双精度数。
例如,下面的代码将解转换为双精
度数:
solution_double = double(solution);
5. 最后,你可以使用`disp`函数来显示解。
例如,下面的代码将解打印到命令窗口:
disp(solution_double);
这样,你就可以通过以上步骤在MATLAB中解符号矩阵了。
注意,这个方法适用于小规模的符号矩阵。
对于大规模的符号矩阵,可能需要使用更高级的数值计算方法来解决。
MATLAB矩阵及其运算函数.docx
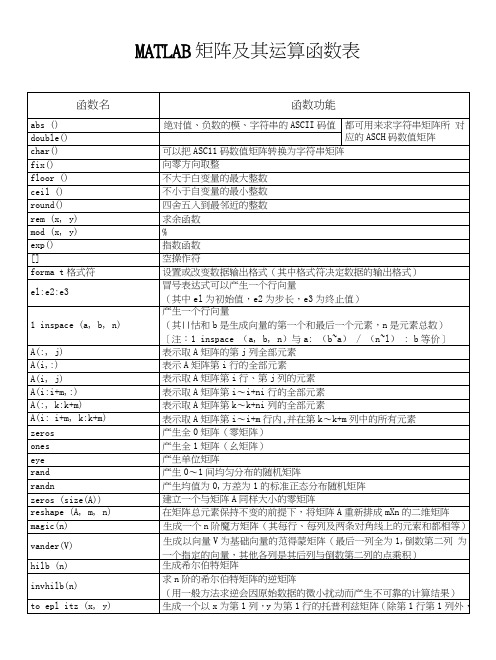
MATLAB矩阵及其运算函数表不大于白变量的最大整数不小于自变量的最小整数四舍五入到最邻近的整数求余函数%指数函数空操作符设置或改变数据输出格式(其中格式符决定数据的输出格式)冒号表达式可以产生一个行向量(其中el为初始值,e2为步长,e3为终止值)产生一个行向量(其||怙和b是生成向量的第一个和最后一个元素,[注:1 inspace (a, b, n)与a: (b~a表示取A矩阵的第j列全部元素表示A矩阵第i行的全部元素表示取A矩阵第i行、第j列的元素表示取A矩阵第i〜i+ni行的全部元素表示取A矩阵第k〜k+ni列的全部元素表示取A矩阵第i〜i+m行内,并在第k〜k+m产生全0矩阵(零矩阵)产生全1矩阵(幺矩阵)产生单位矩阵量(其中A为!nXn矩阵)提取矩阵A的第k条对角线的元素求矩阵A的上三角阵求矩阵A的第k条对角线以上的元素求矩阵A的下三角阵求矩阵A的第k条对角线以下的元素将矩阵A旋转90o的k倍对矩阵A实施左右翻转对矩阵A实施上下翻转求A矩阵的逆矩阵求A矩阵的伪逆(也称为广义逆矩阵)求方阵A所对应的行列式的值(把一个方阵看作一个行列式,并对其按行列式规则求得的值)求矩阵A的秩(矩阵线性无关的行数与列数称为矩阵的秩)求矩阵A的迹(矩阵的迹等于矩阵的对角线元素之和,也等于矩阵的特征值之和)计算向量V的2—范数计算向量V的1—范数计算向量V的g—范数计算A的1—范数下的条件数计算A的2—范数数下的条件数计算A的8—范数下的条件数为正弦,余弦,正切为反正弦,反反余弦,反正切给出一个向量所有相邻分量的差,组成一个前一个分量)。
matlab 符号矩阵运算

matlab 符号矩阵运算摘要:1.引言2.Matlab 符号矩阵介绍3.符号矩阵的创建4.符号矩阵的基本操作5.符号矩阵的运算6.符号矩阵的转置与逆7.总结正文:Matlab 是一种广泛应用于科学计算和数据分析的编程语言,其内置的符号计算功能可以方便地进行符号矩阵运算。
本文将详细介绍Matlab 中符号矩阵的运算方法。
首先,我们需要了解什么是符号矩阵。
符号矩阵是具有符号(例如+、-、*、/等)元素的矩阵。
在Matlab 中,符号矩阵用大写字母表示,如A、B 等。
接下来,我们来看一下如何创建符号矩阵。
在Matlab 中,可以使用`sym`函数创建符号矩阵。
例如:```matlabA = sym("A", [2, 3]);B = sym("B", [3, 2]);```上述代码创建了两个2x3 的符号矩阵A 和B。
创建符号矩阵后,可以进行一些基本操作,如访问元素、修改元素等。
访问符号矩阵的元素时,需要使用圆括号,如:```matlabA(1, 1) = sym("a");B(2, 3) = sym("b");```此外,还可以通过`eval`函数对符号矩阵的元素进行修改:```matlabeval(A(1, 1)) = 2;eval(B(2, 3)) = 3;```在Matlab 中,符号矩阵可以进行加、减、乘、除等运算。
这些运算可以通过`+`、`-`、`*`、`/`等符号进行。
例如:```matlabC = A + B;D = A * B;E = A / B;```需要注意的是,在进行除法运算时,除数不能为零。
符号矩阵还可以进行转置操作,转置后的矩阵具有与原矩阵相同的行数和列数,但元素的排列顺序相反。
可以使用`transpose`函数进行转置:```matlabA_transpose = transpose(A);```此外,如果符号矩阵A 是非奇异的,还可以求其逆矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如:A = sym('[a , 2*b ; 3*a , 0]') A=
[
a, 2*b]
0]
[3*a,
这就完成了一个符号矩阵的创建。 注意:符号矩阵的每一行的两端都有方括号, 这是与 matlab数值矩阵的一个重要区别。
用字符串直接创建矩阵
模仿matlab数值矩阵的创建方法
需保证同一列中各元素字符串有相
maple软件——主要功能是符号运算,
它占据符号软件的主导地位。
2. 符号变量与符号表达式
f = 'sin(x)+5x' f —— 符号变量名 sin(x)+5x—— 符号表达式 ' '—— 符号标识 符号表达式一定要用' ' 单引 号括起来 matlab才能识别。
' ' 的内容可以是符号表达式,也可以是 符号方程。 例: f1='ax^2+bx+c' —— 二次三项式 f2= 'ax^2+bx+c=0' —— 方程 f3='Dy+y^2=1' ——微分方程 ※符号表达式或符号方程可以赋给符号变 量,以后调用方便;也可以不赋给符号变 量直接参与运算
24
2. 数组乘除(,./,.\) ab —— a,b两数组必须有相同的行 和列两数组相应元素相乘。
a=[1 2 3;4 5 6;7 8 9]; b=[2 4 6;1 3 5;7 9 10]; a.*b ans = 2 8 18 4 15 30 49 72 90 a*b ans = 25 37 46 55 85 109 85 133 172
对应元素相加减(与矩阵加 减等效)高等版本去掉了点
23
点乘是数组的运算,不加点是矩阵的运算;2 点乘要 求参与运算的两个量两必须是维数相同,是对应元素 的相乘; 而不加点表示的是矩阵相乘(除的时候通过逆矩阵来 实现),要求内维相同,也就是前一个矩阵的列的维 数等于后一个矩阵的行 的维数。举个简单的例子 例如: x=[1 1;1 1]; >> x.^2 ans = 11 11 >> x^2 ans = 22 22
c =14
32
23
11
d=[-1;0;2];f=pi*d f = -3.1416 0 6.2832 矩阵除的运算在线性代数中没有,
有矩阵逆的运算,在matlab中有两种
矩阵除运算
12
3. 矩阵乘方—— a^n,a^p,p^a
a ^ p —— a 自乘p次幂
方阵 >1的整数
对于p的其它值,计算将涉及特征值 和特征向量,如果p是矩阵,a是标量 a^p使用特征值和特征向量自乘到p次
a, 2*b] [3*a, 0] A1=sym(A,2,2, '4*b') A(2,2)='4*b' A1 =[ a, 2*b] A3 = [ a, 2*b] [3*a, 4*b]
MATLAB对矩阵A实施上下翻转的函数是flipud(A)。
关系运算
关系符号
< <= > >= == ~=
意义
小于 小于或等于 大于 大于或等于 等于 不等于
22
5. 矩阵的数组运算
数组运算指元素对元素的算术运算, 与通常意义上的由符号表示的线性代数
矩阵运算不同
1.
数组加减(.+,.-) a.+b a.- b
3.符号矩阵的创建
数值矩阵A=[1,2;3,4] A=[a,b;c,d] —— 不识别
用matlab函数sym创建矩阵(
symbolic 的缩写)
命令格式:A=sym('[ ※ 需用sym指令定义 ※ 需用' '标识
]')
※ 符号矩阵内容同数值矩阵
2.矩阵的秩和迹
(1)矩阵的秩 矩阵线性无关的行数与列数称为矩阵的秩。在MATLAB中, 求矩阵秩的函数是rank(A)。 (2)矩阵的迹 矩阵的迹等于矩阵的对角线元素之和,也等于矩阵的特征 值之和。在MATLAB中,求矩阵的迹的函数是trace(A)。
3.矩阵的特征值与特征向量
在MATLAB中,计算矩阵A的特征值和特征向量的函数 是eig(A),常用的调用格式有3种:
一、符号运算的基本操作
什么是符号运算 与数值运算的区别 ※ 数值运算中必须先对变量赋值,然后才能 参与运算。 ※ 符号运算无须事先对独立变量赋值,运算
结果以标准的符号形式表达。
特点:
运算对象可以是没赋值的符号变量
可以获得任意精度的解 Symbolic Math Toolbox——符号运算工具包通过调用Maple 软件实现符号计算的。
矩阵的变维 a=[1:12];b=reshape(a,3,4) c=zeros(3,4);c(:)=a(:) 矩阵的变向 rot90:旋转; fliplr:上翻; flipud:下翻 矩阵的抽取 diag:抽取主对角线;tril: 抽取主下三角; triu:抽取主上三角 矩阵的扩展
18
例:建立3*3,3*2的和矩阵A同样大小的零矩阵 Zero(3,3) Zero(3,2) Zero(size(A))
3. 矩阵的修改
直接修改 可用键找到所要修改的矩阵,用键移 动到要修改的矩阵元素上即可修改。 指 令修改 可以用A(,)= 来修改。
8
例如 a=[1 2 0;3 0 5;7 8 9] a =1 2 0 3 0 5 7 8 9 a(3,3)=0 a =1 2 0 3 0 5 7 8 0
zeros(m,n)
ones(m,n) eye(m,n) diag(X) tril(A) triu(A) rand(m,n) randn(m,n)
特殊矩阵生成函数
生成一个m行n列的零矩阵,m=n 时可简写为 zeros(n)
生成一个m行n列的元素全为1的矩阵, m=n 时可写为 ones(n) 生成一个主对角线全为1的m行n列矩阵, m=n 时可简写为 eye(n),即为 n 维单位矩阵 若X是矩阵,则diag(X)为X的主对角线向量 若X是向量,diag(X)产生以X为主对角线的对角矩阵 提取一个矩阵的下三角部分 提取一个矩阵的上三角部分 产生 0~1 之间均匀分布的随机矩阵 m=n 时简写为 rand(n) 产生均值为0,方差为1的标准正态分布随机矩阵 m=n 时简写为 rand(n)
15
4. 矩阵的其它运算
inv —— 矩阵求逆
det —— 行列式的值
eig —— 矩阵的特征值
diag —— 对角矩阵
’ —— 矩阵转置
sqrt —— 矩阵开方
16
例 先建立5×5矩阵A,然后将A的第一行元素乘以1,第
二行乘以2,…,第五行乘以5。
diag([1 1 1])
5.矩阵的一些特殊操作
第三讲 MATLAB的符号运算
—— matlab 不仅具有数值运算 功能,还开发了在matlab环境下 实现符号计算的工具包Symbolic Math Toolbox
符号运算的功能
符号表达式、符号矩阵的创 建 符号线性代数 因式分解、展开和简化 符号代数方程求解 符号微积分 符号微分方程
>> A=[1 2 3;4 5 6;7 8 9];
>> triu(A) ans = 1 2 0 5 0 0 >> tril(A,-1) ans = 0 0 0 4 0 0 7 8 0 >> tril(A,1) ans = 1 2 0 4 5 6 7 8 9
3 6 9
>> triu(A,1) ans = 0 2 3 0 0 6 0 0 0
当一个指令或矩阵太长时,可用••• 续行
4
冒号的作用 用于生成等间隔的向量,默认间隔为1。 1:1:10,1:10 用于选出矩阵指定行、列及元素。
a=[1,2,3;4 5 6]
a([1 3])%选择矩阵a的第一个和第三个元素,先列 再行
循环语句
5
2.用matlab函数创建矩阵 一些生成特殊矩阵的函数
同的长度。
例:A =['[ a,2*b]'; '[3*a, 0]'] A= [ a, 2*b] [3*a, 0]
符号矩阵的修改
a.直接修改 可用、 键找到所要修改的矩 阵,直接修改 b.指令修改 用A1=sym(A,,,'new') 来修改。 用A1=subs(A, 'new', 'old')来修改 A1=subs(S, 'old' ,'new')
第4章 MATLAB矩阵分析与处理
4.1 特殊矩阵 4.2 矩阵的结构变换 4.3 矩阵的逆
4.4 矩阵求值
一、命令行的基本操作
创建矩阵的方法 直接输入法 规则: 矩阵元素必须用[ ]括住 矩阵元素必须用逗号或空格分隔 在[ ]内矩阵的行与行之间必须 用分号分隔 分号如果出现在指令后,屏幕上将不显示结果。
>> triu(A,-1) ans = 1 2 3 4 5 6 0 8 9
2 矩阵的转置与旋转
(1)矩阵的转置 转置运算符是单撇号(‘)。 (2)矩阵的旋转 利用函数rot90(A,k)将矩阵A旋转90º 的k倍,当k为1时可省略。
(3)矩阵的左右翻转
对矩阵实施左右翻转是将原矩阵的第一列和最后一列 调换,第二列和倒数第二列调换,…,依次类推。 MATLAB对矩阵A实施左右翻转的函数是fliplr(A)。 (4)矩阵的上下翻转
