2013数学竞赛题含答案
全国大学生数学竞赛初赛2013年第五届《非数学专业》竞赛题目及答案解析高清无水印版

所求极限为
lim
r
I
a
(r
)
0,a ,a1, 2,a
1, 1.
1
1
1
第七题:(14 分)判断级数
2
n 的敛散性,若收敛,求其和。
(n 1)(n 2)
n 1
1
1
【参考解答】:(1) 记a 1 , u
a n
, n 1, 2, 。
n
2
n n (n 1)(n 2)
因为n 充分大时
x x 2y
【参考解答】:方程两边对x 求导,得 3x2 6xy 3x2y 6y2y 0 y 2y2 x2
令y(x) 0 x 0, x 2y 。将x 0, x 2y 代入所给方程,得 x 0, y 1; x 2 , y 1.
2y2 x2 2x 2xy 2y x2 2xy 4yy 2x
n
原式
lim
n
1
sin
1
4n 2
2n
exp
lim n
n
ln
1
sin
1
4n 2
2n
exp lim n sin n
n
exp lim
e4.
n 1 4n 2 2n
1 4n 2 2n
sin x
2.证明广义积分 0
d x 不是绝对收敛的。 x
(n1) | sin x |
【参考证明】:an n
d x . 只要证明
x
an 发散.
n 0
1
(n 1)
1
2
因为an (n 1) n
| sin x | d x
sin xdx
.
(n 1) 0
18届2013年小高组华杯赛竞赛题初赛 决赛A卷 B卷 C卷 完美版

第十八届华罗庚金杯少年邀请赛初赛试题A(小学高年级组)(时间2013年3月23日10:00~11:00)一、选择题(每题10分,满分60分,以下每题的四个选项中,仅有一个是正确的,请将表示正确答案的英文字母写在每题的圆括号内。
)1.2012.25×2013.75-2010.25×2015.75=()。
A.5 B.6 C.7 D.82.2013年的钟声敲响了, 小明哥哥感慨地说: 这是我有生以来第一次将要渡过一个没有重复数字的年份。
已知小明哥哥出生的年份是19的倍数, 那么2013年小明哥哥的年龄是()岁。
A.16 B.18 C.20 D.223.一只青蛙8点从深为12米的井底向上爬, 它每向上爬3米, 因为井壁打滑, 就会下滑1米,下滑1米的时间是向上爬3米所用时间的三分之一。
8点17分时, 青蛙第二次爬至离井口3米之处, 那么青蛙从井底爬到井口时所花的时间为()分钟。
A.22 B.20 C.17 D.164.一个盒子里有黑棋子和白棋子若干粒, 若取出一粒黑子, 则余下的黑子数与白子数之比为9:7, 若放回黑子, 再取出一粒白子, 则余下的黑子数与白子数之比为7:5, 那么盒子里原有的黑子数比白子数多()个。
A.5 B.6 C.7 D.85. 右图ABCD 是平行四边形, M 是DC 的中点, E 和F 分别位于AB 和AD上, 且EF 平行于BD 。
若三角形MDF 的面积等于5平方厘米, 则三角形CEB 的面积等于( )平方厘米。
A .5B .10C .15D .206. 水池A 和B 同为长3米, 宽2米, 深1.2米的长方体。
1号阀门用来向A 池注水, 18分钟可将无水的A 池注满; 2号阀门用来从A 池向B 池放水, 24分钟可将A 池中满池水放入B 池。
若同时打开1号和2号阀门, 那么当A 池水深0.4米时, B 池有( )立方米的水。
A .0.9B .1.8C .3.6D .7.2二、填空题(每小题 10 分, 满分40分)7. 小明、小华、小刚三人分363张卡片, 他们决定按年龄比来分。
西师版三年级上册数学竞赛试题

西师版三年级上册数学竞赛试题第一篇:西师版三年级上册数学竞赛试题三年级上册数学竞赛试题一、填空 1、3005 kg=()吨()kg 5 kg50g=()g 3时48分=()分 200分=()时()分2、甲有45本书,乙有14本书,丙有28本书,甲给乙()本,给丙()本后,甲、乙、丙三人本数相等。
3、已知□+□+□=△+△△+△+△+△=★+★ □+★+△+△=210 那么△=()□=()★=()4、把3个周长都是16厘米的正方形拼成一个大长方形,拼成的长方形的周长是()厘米。
5、一个分数,分子、分母的和是16,分母比分子大2,这个分数是()。
6、一根绳子对折三次后,得到的1小段是这根绳子的(—)。
7、小亮把除数3看成了5,结果商15余2,正确结果应是()。
8、一块正方形菜地,一面靠墙,其他三面围篱芭,篱笆长是36米,这块菜地的边长是()米。
9、一个长方形的宽增加2分米后,这时长方形的周长就增加()分米。
如果长增加3分米,宽增加2分米,这时长方形的周长就增加()分米。
10、芳芳和婷婷去买同一本书,芳芳少35元,婷婷少28元,如果两人的钱合起来正好买这本书,这本书的单价是()元。
11、数学竞赛出了20道题,做对一道得5分,做错一道扣2分,小光做完了所有的题,共得72分,他做对了()道题。
12、儿子今年5岁,爸爸今年是儿子年龄的6倍。
10年后爸爸的年龄比儿子大()岁。
13、被减数、减数、差三个数相加等于56,被减数是()14、一个数除以7的商和余数相同,这个数最大是()15、在一个有余数的除法算式()÷8=3……()里,被除数最大是();被除数最小是()16、一个正方形的边长增加2厘米,它的周长增加()厘米。
17、一个长方形长10厘米,宽8厘米,从中截一个最大的正方形,剩下的长方形周长是()厘米。
18、小明星期天想帮妈妈做事情,下面是分别所需的时间:用洗衣机洗衣服(20分钟)扫地(5分钟)搬家具(10分钟)晾衣服(5分钟)他至少要花()分钟才能把这些事情全部做完。
2013年北京市初二数学竞赛试题及解答

(2)同样道理,一个月有 31 天,就不可能仅有星期一的天数比星期二的天数多.
(3)一个月 28 天,则星期一的天数和星期二的天数同样多. 也不会发生“仅有星
期一的天数比星期二的天数多”的情况.
(4)一个月 29 天,1 日是星期一,29 日也是星期一,共有 5 个星期一,4 个星期
二;所以“仅有星期一的天数比星期二的天数多”的情况只能在 29 日的月份里发生.
A
D
B
于是,∠BDE=∠CED−∠DBE=∠A−∠B=∠B=∠DBE,
所以△BDE 是等腰三角形,BE=DE.
因此,BC=BE+CE=AD+AC=8+16=24.
2013 年北京市中学生数学竞赛初二年3 级竞赛试题及解答 共 5页 第 3页
4.已知质数 p 和 q,使得 p3−q5=(p+q)2,则 8( p2013 − p q 2010 5) =
.2013 年北京市中学生数学竞赛 初二年级竞赛试题及解答
2013 年 5 月 12 日 13:00~15:00
一、选择题(满分 25 分,每小题只有一个正确答案,答对得 5 分,将答案写在下面相 应的空格中)
题号
1
2
3
4
5
答案
A
C
D
D
B
1.2013+2012−2011−2010+2009+2008−2007−2006+…+5+4−3−2+1 等于
4
4
5.如图,在直角△ABC 的两直角边 AC、BC 上分别
G
作正方形 ACDE 和 CBFG,连接 DG,线段 AB、BF、FG、
I
高中数学竞赛-历届IMO试题(1-46届)及答案

1.求证(21n+4)/(14n+3) 对每个自然数 n都是最简分数。
2.设√(x+√(2x-1))+√(x-√(2x-1))=A,试在以下3种情况下分别求出x的实数解:(a) A=√2;(b)A=1;(c)A=2。
3.a、b、c都是实数,已知 cos x的二次方程a cos2x +b cos x +c = 0,试用a,b,c作出一个关于 cos 2x的二次方程,使它的根与原来的方程一样。
当a=4,b=2,c=-1时比较 cos x和cos 2x的方程式。
4.试作一直角三角形使其斜边为已知的 c,斜边上的中线是两直角边的几何平均值。
5.在线段AB上任意选取一点M,在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF,这两个正方形的外接圆的圆心分别是P、Q,设这两个外接圆又交于M、N,(a.) 求证 AF、BC相交于N点;(b.) 求证不论点M如何选取直线MN 都通过一定点 S;(c.) 当M在A与B之间变动时,求线断 PQ的中点的轨迹。
6.两个平面P、Q交于一线p,A为p上给定一点,C为Q上给定一点,并且这两点都不在直线p上。
试作一等腰梯形ABCD(AB平行于CD),使得它有一个内切圆,并且顶点B、D分别落在平面P和Q上。
1.找出所有具有下列性质的三位数 N:N能被11整除且 N/11等于N的各位数字的平方和。
2.寻找使下式成立的实数x:4x2/(1 - √(1 + 2x))2< 2x + 93.直角三角形ABC的斜边BC的长为a,将它分成 n 等份(n为奇数),令α为从A点向中间的那一小段线段所张的锐角,从A到BC边的高长为h,求证:tan α = 4nh/(an2 - a).4.已知从A、B引出的高线长度以及从A引出的中线长,求作三角形ABC。
5.正方体ABCDA'B'C'D'(上底面ABCD,下底面A'B'C'D')。
2013全国大学生数学建模比赛B题-答案

2013高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括、电子、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):邮电大学参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2013 年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):2013高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):碎纸片的拼接复原摘要本文研究的是碎纸片的拼接复原问题。
由于人工做残片复原虽然准确度高,但有着效率低的缺点,仅由计算机处理复原,会由于各类条件的限制造成误差与错误,所以为了解决题目中给定的碎纸片复原问题,我们采用人机结合的方法建立碎纸片的计算机复原模型解决残片复原问题,并把计算机通过算法复原的结果优劣情况作为评价复原模型好坏的标准,通过人工后期的处理得到最佳结果。
面对题目中给出的BMP格式的黑白文字图片,我们使用matlab软件的图像处理功能把图像转化为矩阵形式,矩阵中的元素表示图中该位置像素的灰度值,再对元素进行二值化处理得到新的矩阵。
题目每一个附件中的碎纸片均为来自同一页的文件,所以不需考虑残片中含有未知纸的残片以及残片中不会含有公共部分。
第24届希望杯全国数学竞赛八年级试题及答案

第24届“希望杯”全国数学邀请赛初二 第二试2013年4月15日 上午8:30至10:30一、 选择题(本大题共10小题,每小题4分,菜40分。
)以下每题的四个选项中,仅有一个是正确的,请将正确答案的英文字母写在每题后面的圆括号内。
1、红丝带是关注艾滋病防治问题的国际性标志,人胶将红丝带剪成小段,并用别针将折叠好的红丝带加紧在胸前,如图1所示,红丝带重叠部分形成的图形是( ) (A )正方形 (B )矩形 C )菱形 (D )梯形2、设a 、b 、C 是不为零的实数,那么||||||a b cx a b c =+-的值有( ) (A )3种 (B )4种 (C )5种 (D )6种3、ABC ∆的边长分别是21a m =-,21b m =+,()20c m m =>,则ABC ∆是( )(A )等边三角形 (B )钝角三角形 (C )直角三角形 (D )锐角三角形4、古人用天干和地支记序,其中天干有10个;甲乙丙丁戊己庚辛壬癸,地支有12个;子丑寅卯辰巳午未申酉戌亥,将天干的10个汉字和地支的12个汉字对应排列成如下两行; 甲乙丙丁戊己庚辛壬癸甲乙丙丁戊己庚辛壬癸甲乙丙丁…… 子丑寅卯辰巳午未申酉戌亥子丑寅卯辰巳午未申酉戌亥……从左向右数,第1列是甲子,第2列是乙丑,第3列是丙寅……,我国的农历纪年就是按这个顺序得来的,如公历2007年是农历丁亥年,那么从今年往后,农历纪年为甲亥年的那一年在公历中( )(A )是2019年, (B )是2031年, (C )是2043年, (D )没有对应的年号5、实数 a 、b 、m 、n 满足a<b, -1<n<m, 若1a mb M m +=+,1a nbN n+=+,则M 与N 的大小关系是( )(A )M>N (B)M=N (C)M<N (D)无法确定的。
6、若干个正方形和等腰直角三角形拼接成如图2所示的图形,若最大的正方形的边长是7cm ,则正方形A 、B 、C 、D 的面积和是( )(A )214cm (B )242cm (C )249cm (D )264cm图27、已知关于x 的不等式组230320a x a x +>⎧⎨-≥⎩恰有3个整数解,则a 的取值范围是( )(A )23≤a ≤32 (B)43≤a ≤32 (C)43<a ≤32 (D)43≤a <328 、The number of intersection point of the graphs of function||k y x=and function (0)y kx k =≠ is( ) (A)0 (B)1 (C)2 (D)0 or 2.9、某医药研究所开发一种新药,成年人按规定的剂量限用,服药后每毫升血液中的含药量y (毫克)与时间t (小时)之间的函数关系近似满足如图3所示曲线,当每毫升血液中的含药量不少于0.25毫克时治疗有效,则服药一次治疗疾病有效的时间为() (A )16小时 (B )7158小时 (C )151516小时 (D )17小时 )10、某公司组织员工一公园划船,报名人数不足50人,在安排乘船时发现,每只船坐6人,就剩下18人无船可乘;每只船坐10人,那么其余的船坐满后内参有一只船不空也不满,参加划船的员工共有( )(A )48人 (B )45人 (C )44人 (D )42人 二、填空题(本大题共10小题,每小题4分,共40分)11、已知a b c ⋅⋅o 为ABC ∆三边的长,则化简|a b c -+12、自从扫描隧道显微镜发明后,世界上便诞生了一间新科学,这就是“纳米技术”,已知1毫米微米,1微米纳米,那么2007纳米的长度用科学记数法表示为__米。
【期望杯】第六届小学三年级数学竞赛试题(含答案)

2013湖州市第六届“期望杯”小学三年级数学竞赛试题(2013年12月15日上午9:00—10:30;满分100分)学校:班级:座位号:姓名:成绩:题号一(1~11)二(12~16)得分得分一、填空(每小题5分,共55分)1. 计算: 24―23+22-21+……+ 4-3+2-1=()2.计算: 248+249+250+251+252=()3.在减法算式中,如果被减数减少16,减数增加16,那么差就比原来()4. 如图,在3×3的正方形格子中有一个三角形,如果把包含着三角形的正方形涂上颜色,会有()种不同的涂法。
5.算式□÷□=8……8中,被除数最小等于()。
6.如图,有3只一样的杯子,装的水不一样多。
如果在每只杯子里放入一块同样的方糖,()杯子里的水最甜。
7.蛋糕店的柜台里放着五种不同包装的蛋糕,每袋分别装1块、2块、3块、4块、5块,每种包装的蛋糕有足够多。
小华要买5块蛋糕,她有()种不同的买法。
8.有33个桔子,拿掉若干个,可以使剩下的桔子能平均分给5个小朋友(每个小朋友都要分到桔子),请问,最多有()种不同的拿法。
9. 下图中的数是按规律排列的,那么A+B=()。
10. 在1~9这9个数字中选出5个,分别代表“湖、州、期、望、杯”这5个汉字,可以使下面竖式中的4个两位数之和最大,这个最大的和是()。
11. 小聪在纸条上写了一个四位数,让小明猜。
小明猜了三次,小聪分别作出了回答:小明猜“2974”,小聪答:“1个数字对,而且位置也正确。
”小明猜“5236”,小聪答:“2个数字对,但位置都不对。
”小明猜“1302”,小聪答:“数字都对,但位置都不对。
”小聪写的四位数是()。
二、解答(要求写出过程,每小题9分,共45分,无解答过程不给分)12.今天是星期日,从今天算起,第30天是星期几?13. 超市将5大袋牛奶和1小袋牛奶捆在一起出售(买5大赠1小),现在有60大袋和20小袋牛奶,问捆多少捆后,剩下的大袋牛奶和小袋牛奶的袋数相等?14.学校有足球、篮球、排球共67个,其中篮球的个数比足球的2倍多1个,排球的个数比篮球的2倍多1,足球有多少个?15.狼和羊在一起时,狼要吃掉羊,所以我们规定一种运算,用符号▲表示:“羊▲羊=羊”,表示羊和羊在一起,还是羊;“狼▲狼=狼”,表示狼和狼在一起,还是狼;“狼▲羊=狼”或“羊▲狼=狼”,表示狼和羊在一起,羊被狼吃掉,只剩下狼。
AMC8(美国数学竞赛)历年真题、答案及中英文解析

AMC8(美国数学竞赛)历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析:AMC8-2020年:真题 --- 答案---解析(英文解析+中文解析)AMC8 - 2019年:真题----答案----解析(英文解析+中文解析)AMC8 - 2018年:真题----答案----解析(英文解析+中文解析)AMC8 - 2017年:真题----答案----解析(英文解析+中文解析)AMC8 - 2016年:真题----答案----解析(英文解析+中文解析)AMC8 - 2015年:真题----答案----解析(英文解析+中文解析)AMC8 - 2014年:真题----答案----解析(英文解析+中文解析)AMC8 - 2013年:真题----答案----解析(英文解析+中文解析)AMC8 - 2012年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 2010年:真题----答案----解析(英文解析+中文解析)AMC8 - 2009年:真题----答案----解析(英文解析+中文解析)AMC8 - 2008年:真题----答案----解析(英文解析+中文解析)AMC8 - 2007年:真题----答案----解析(英文解析+中文解析)AMC8 - 2006年:真题----答案----解析(英文解析+中文解析)AMC8 - 2005年:真题----答案----解析(英文解析+中文解析)AMC8 - 2004年:真题----答案----解析(英文解析+中文解析)AMC8 - 2003年:真题----答案----解析(英文解析+中文解析)AMC8 - 2002年:真题----答案----解析(英文解析+中文解析)AMC8 - 2001年:真题----答案----解析(英文解析+中文解析)AMC8 - 2000年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1998年:真题----答案----解析(英文解析+中文解析)AMC8 - 1997年:真题----答案----解析(英文解析+中文解析)AMC8 - 1996年:真题----答案----解析(英文解析+中文解析)AMC8 - 1995年:真题----答案----解析(英文解析+中文解析)AMC8 - 1994年:真题----答案----解析(英文解析+中文解析)AMC8 - 1993年:真题----答案----解析(英文解析+中文解析)AMC8 - 1992年:真题----答案----解析(英文解析+中文解析)AMC8 - 1991年:真题----答案----解析(英文解析+中文解析)AMC8 - 1990年:真题----答案----解析(英文解析+中文解析)AMC8 - 1989年:真题----答案----解析(英文解析+中文解析)AMC8 - 1988年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1986年:真题----答案----解析(英文解析+中文解析)AMC8 - 1985年:真题----答案----解析(英文解析+中文解析)◆AMC介绍◆AMC(American Mathematics Competitions) 由美国数学协会(MAA)组织的数学竞赛,分为 AMC8 、 AMC10、 AMC12 。
【期望杯】第六届小学六年级数学竞赛试题(含答案)
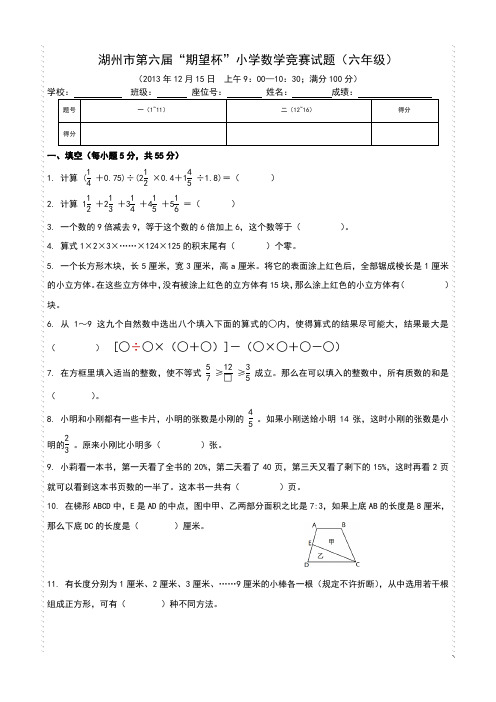
湖州市第六届“期望杯”小学数学竞赛试题(六年级)(2013年12月15日 上午9:00—10:30;满分100分) 学校: 班级: 座位号: 姓名: 成绩: 题号 一(1~11) 二(12~16) 得分 得分一、填空(每小题5分,共55分)1. 计算 ({ EQ \F(1,4) |+0.75)÷(212 |×0.4+145|÷1.8)=( ) 2. 计算 112 |+213 |+314 |+415 |+516|=( ) 3. 一个数的9倍减去9,等于这个数的6倍加上6,这个数等于( )。
4. 算式1×2×3×……×124×125的积末尾有( )个零。
5. 一个长方形木块,长5厘米,宽3厘米,高a 厘米。
将它的表面涂上红色后,全部锯成棱长是1厘米的小立方体。
在这些立方体中,没有被涂上红色的立方体有15块,那么涂上红色的小立方体有( )块。
6. 从1~9这九个自然数中选出八个填入下面的算式的○内,使得算式的结果尽可能大,结果最大是( ) [○÷○×(○+○)]-(○×○+○-○)7. 在方框里填入适当的整数,使不等式 57 |≥12□ |≥35|成立。
那么在可以填入的整数中,所有质数的和是( )。
8. 小明和小刚都有一些卡片,小明的张数是小刚的 45|。
如果小刚送给小明14张,这时小刚的张数是小明的23 |。
原来小刚比小明多( )张。
9. 小莉看一本书,第一天看了全书的20%,第二天看了40页,第三天又看了剩下的15%,这时再看2页就可以看到这本书页数的一半了。
这本书一共有( )页。
10. 在梯形ABCD 中,E 是AD 的中点,图中甲、乙两部分面积之比是7:3,如果上底AB 的长度是8厘米,那么下底DC 的长度是( )厘米。
11. 有长度分别为1厘米、2厘米、3厘米、……9厘米的小棒各一根(规定不许折断),从中选用若干根组成正方形,可有( )种不同方法。
高中数学竞赛赛题精选(带答案)

高中数学竞赛赛题精选一、选择题(共12题)1.定义在R 上的函数()y f x =的值域为[m,n ],则)1(-=x f y 的值域为( ) A .[m,n ]B .[m-1,n-1]C .[)1(),1(--n f m f ]D .无法确定解:当函数的图像左右平移时,不改变函数的值域.故应选A.2.设等差数列{n a }满足13853a a =,且n S a ,01>为其前n 项之和,则)(*∈N n S n 中最大的是( ) A. 10S B. 11S C. 20S D. 21S 解:设等差数列的公差为d,由题意知3(1a +7d)=5(1a +12d),即d=-3921a , ∴n a = 1a +( n-1)d= 1a -3921a (n-1)= 1a (3941-392n),欲使)(*∈N n S n 最大,只须n a ≥0,即n ≤20.故应选C.3.方程log 2x=3cosx 共有( )组解.A .1B .2C .3D .4解:画出函数y=log 2x 和y=3cosx 的图像,研究其交点情况可知共有3组解.应选C .4.已知关于x 的一元二次方程()02122=-+-+a x a x 的一个根比1大,另一个根比1小,则()A.11<<-a B.1-<a 或1>aC.12<<-aD.2-<a 或1>a解:令f(x)= ()2122-+-+a x a x ,其图像开口向上,由题意知f(1)<0,即 ()211122-+⨯-+a a <0,整理得022<-+a a ,解之得12<<-a ,应选C .5.已知βα,为锐角,,cos ,sin y x ==βα53)cos(-=β+α,则y 与x 的函数关系为( ) A .1)x 53( x 54x 153y 2<<+--= B .1)x (0 x 54x 153y 2<<+--=C .)53x (0 x 54x 153y 2<<---= D .1)x (0 x 54x 153y 2<<---= []xx y 54153sin )sin(cos )cos()(cos cos 2+-⋅-=⋅+++=-+==αβααβααβαβ解: 而)1,0(∈y 15415302<+-⋅-<∴x x , 得)1,53(∈x .故应选A. 6.函数sin y x =的定义域为[],a b ,值域为11,2⎡⎤-⎢⎥⎣⎦,则b a-的最大值是( )A. πB. π2C.34πD. 35π解:如右图,要使函数sin y x =在定义域[],a b 上,值域为11,2⎡⎤-⎢⎥⎣⎦,则b a -的最大值是74()663πππ--=.故应选C. 7.设锐角使关于x 的方程x 2+4x cos+cot =0有重根,则的弧度数为 ( )A .6B .12或512C .6或512D .12解:由方程有重根,故14=4cos 2-cot =0,∵ 0<<2,2sin2=1,=12或512.选B . 8.已知M={(x ,y )|x 2+2y 2=3},N={(x ,y )|y=mx+b }.若对于所有的m ∈R ,均有M ∩N ,则b 的取值范围是 ( )A .[-62,62] B .(-62,62) C .(-233,233] D .[-233,233] 解:点(0,b )在椭圆内或椭圆上,2b 2≤3,b ∈[-62,62].选A .9.不等式log 2x -1+12log 12x 3+2>0的解集为A .[2,3)B .(2,3]C .[2,4)D .(2,4] 解:令log 2x=t ≥1时,t -1>32t -2.t ∈[1,2),x ∈[2,4),选C .10.设点O 在ABC 的内部,且有+2+3=,则ABC 的面积与AOC 的面积的比为( )A .2B .32C .3D .53解:如图,设AOC=S ,则OC 1D=3S ,OB 1D=OB 1C 1=3S ,AOB=OBD=1.5S .OBC=0.5S ,ABC=3S .选C .11.设三位数n=,若以a ,b ,c 为三条边长可以构成一个等腰(含等边)三角形,则这样的三位数n 有( )A .45个B .81个C .165个D .216个 解:⑴等边三角形共9个;⑵ 等腰但不等边三角形:取两个不同数码(设为a ,b ),有36种取法,以小数为底时总能构成等腰三角形,而以大数为底时,b <a <2b .a=9或8时,b=4,3,2,1,(8种);a=7,6时,b=3,2,1(6种);a=5,4时,b=2,1(4种);a=3,2时,b=1(2种),共有20种不能取的值.共有236-20=52种方法,而每取一组数,可有3种方法构成三位数,故共有523=156个三位数即可取156+9=165种数.选C .12.顶点为P 的圆锥的轴截面是等腰直角三角形,A 是底面圆周上的点,B 是底面圆内的点,O 为底面圆圆心,AB ⊥OB ,垂足为B ,OH ⊥PB ,垂足为H ,且PA=4,C 为PA 的中点,则当三棱锥O -HPC 的体积最大时,OB 的长为 ( )A .53 B .253 C .63 D .263解:AB ⊥OB ,PB ⊥AB ,AB ⊥面POB ,面PAB ⊥面POB .OH ⊥PB ,OH ⊥面PAB ,OH ⊥HC ,OH ⊥PC ,又,PC ⊥OC ,PC ⊥面OCH .PC 是三棱锥P -OCH 的高.PC=OC=2.而OCH 的面积在OH=HC=2时取得最大值(斜边=2的直角三角形).当OH=2时,由PO=22,知∠OPB=30,OB=PO tan30=263.又解:连线如图,由C 为PA 中点,故V O -PBC =12V B -AOP ,S B 11OABCABPO H C而V O -PHC ∶V O -PBC =PH PB =PO 2PB2(PO 2=PH ·PB ).记PO=OA=22=R ,∠AOB=,则V P —AOB =16R 3sin cos =112R 3sin2,V B -PCO =124R 3sin2. PO 2PB 2=R 2R 2+R 2cos 2=11+cos 2=23+cos2.V O -PHC =sin23+cos2112R 3. ∴ 令y=sin23+cos2,y=2cos2(3+cos2)-(-2sin2)sin2(3+cos2)2=0,得cos2=-13,cos =33, ∴ OB=263,选D .二、填空题(共10题)13. 设n S 为等差数列{}n a 的前n 项和,若510S =,105S =-,则公差为 解:设等差数列{}n a 的首项为1a ,公差为d .由题设得⎩⎨⎧-=+=+,,545101010511d a d a 即 ⎩⎨⎧-=+=+,,1922211d a d a 解之得1-=d .14. 设()log ()a f x x b =+(0a >且1)a ≠的图象经过点(21),,它的反函数的图象经过点(28),,则b a +等于 4 .解:由题设知 log (2)1log (8)2a a b b +=⎧⎨+=⎩,, 化简得 2(2)(8).b a b a +=⎧⎨+=⎩,解之得 1131a b =⎧⎨=⎩,; 2224.a b =-⎧⎨=-⎩,(舍去). 故a b +等于4.15.已知函数()y f x =的图象如图,则满足22221()(lg(620))021x x f f x x x x --⋅-+≤-+的 x 的取值范围为 [21)x ∈-, .解: 因为 ()()22lg 620lg (3)11lg111x x x -+=-+≥>,所以()2lg 6200x x -+<. 于是,由图象可知,2111x x +≤-,即 201x x +≤-,解得 21x -≤<. 故x 的取值范围为 [21)x ∈-,.16.圆锥曲线0|3|102622=+--+-++y x y x y x 的离心率是 2 .解:原式变形为|3|)1()3(22+-=-++y x y x ,即=2|3|2+-y x .所以动点),(y x 到定点(31)-,的距离与它到直线03=+-y x 的距离之比为2.故此动点轨迹为双曲线,离心率为2.17.在ABC ∆中,已知3tan =B ,322sin =C ,63=AC ,则ABC ∆的面积为ABC S ∆=解:在ABC ∆中,由3tan =B 得︒=60B .由正弦定理得sin 8sin AC CAB B⋅==.因为︒>60322arcsin,所以角C 可取锐角或钝角,从而31cos ±=C .sin sin()sin cos cos sin A B C B C B C =+=+=sin 2ABC AC ABS A ∆⋅== 18. 设命题P :2a a <,命题Q : 对任何x ∈R ,都有2410x ax ++>. 命题P 与Q 中有 且仅有一个成立,则实数a 的取值范围是 021≤<-a 或 121<≤a . 解:由a a <2得10<<a .由0142>++ax x 对于任何x ∈R 成立,得04162<-=∆a ,即2121<<-a .因为命题P 、Q 有且仅有一个成立,故实数 a 的取值范围是 021≤<-a 或 121<≤a .19.22cos 75cos 15cos75cos15++⋅的值是 . 解:22cos 75cos 15cos75cos15++⋅ =cos²75°+sin²75°+sin15°·cos15° =1+°30sin 21=5420.定义在R 上的函数()f x 满足(1)2f =,且对任意的x R ∈,都有1()2f x '<,则不等式22log 3(log )2x f x +>的解集为 . 解:令g ﹙x ﹚=2f ﹙x ﹚-x ,由f '(x ) <1/2得,2f '(x ) -1<0,即'g ﹙x ﹚<0,g(x)在R 上为减函数,且g(1)=2f(1)-1=3,不等式f(log2X)>2log 2X化为2f(log2X)—log2X≥3,即g(log2X)>g(1),由g(x)的单调性得:log2X<1,解得,0<x<2. 21.圆O 的方程为221x y +=,(1,0)A ,在圆O 上取一个动点B ,设点P 满足()AP OB R λλ=∈且1AP AB ⋅=.则P 点的轨迹方程为 .解:设P(x,y), AB =λOB (λϵR)得B(k(x —1),ky),(λ=k1)。
浙江省绍兴县柯岩中学2012-2013学年七年级竞赛模拟数学试题(含答案)

初一数学竞赛试卷学校_________班级_________姓名_________一、细心选一选(本题共30分,每小题3分)1.如果四个互不相同的正整数m,n,p,q满足(6-m)(6-n)(6-p)(6-q)=4,那么m+n+p+q=()A、24B、25C、26D、282.如图,把△ABC纸片沿着DE折叠,当点A落在四边形BCED内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变.请试着找一找这个规律,你发现的规律是()A.∠A=∠1+∠2 B.2∠A=∠1+∠2C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)3.如果两个三角形的两条边和其中一条边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是()A.相等B.互余C.互补或相等D.不相等4.文具店的老板均以60元的价格卖了两个计算器,其中一个赚了20﹪,另一个亏了20﹪,则该老板()A、赚了5元B、亏了25元C、赚了25元D、亏了5元5.如图△ABC中,已知D、E、F分别是BC、AD、CE的中点,且S△ABC=4,那么阴影部分的面积等于()A.2 B.1 C.D.6.如图,是由大小一样的小正方形组成的网格,△ABC的三个顶点均落在小正方形的顶点上.在网格上能画出的三个顶点都落在小正方形的顶点上,且与△ABC成轴对称的三角形共有()A.5个B.4个C.3个D.2个7.在数轴上表示整数的点称为整数点,某数轴的单位长度是1㎝,若在这个数轴上随意画出一条长2009㎝的线段AB,被线段AB盖住的整数有( )A、2006个或2007个B、2007个或2008个C、2008个或2009个D、2009个或2010个8.给出下列命题:①三条线段组成的图形叫三角形②三角形相邻两边组成的角叫三角形的内角③三角形的角平分线是射线④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外⑤任何一个三角形都有三条高、三条中线、三条角平分线⑥三角形的三条角平分线交于一点,且这点在三角形内.正确的命题有( )A .1个B .2个C .3个D .4个9.下列四张扑克牌图案中,旋转180°后能与原来图案重合的是( )A .B .C .D .10.如图,直线l 1、l 2、l 3表示三条相互交叉的公路,现要建一个货物中转站, 要求它到三条公路的距离相等,则供选择的地址有( ) A .1处B .2处C .3处D .4处二、精心填一填(本大题共30分,每小题3分)11.计算:若(a —2)2与88|b - 1|2003 互为相反数,则a-b a+b= 。
2000-2017年(大同杯原新知杯)历年上海市初中数学竞赛试卷和参考答案

上海市大同杯(原新知杯、宇振杯)初中数学竞赛试题和参考答案目录2017年上海市初中数学竞赛(大同中学杯)试题 3 2017年上海市初中数学竞赛(大同中学杯)试题参考答案 6 2016年上海市初中数学竞赛(大同中学杯)试题11 2016年上海市初中数学竞赛(大同中学杯)试题参考答案14 2015年上海市初中数学竞赛(大同中学杯)试题18 2015年上海市初中数学竞赛(大同中学杯)试题详解22 2014年上海市初中数学竞赛(大同中学杯)试题29 2014年上海市初中数学竞赛(大同中学杯)试题参考答案31 2013年上海市初中数学竞赛(新知杯)试题35 2013年上海市初中数学竞赛(新知杯)试题参考答案38 2012年上海市初中数学竞赛(新知杯)试题43 2012年上海市初中数学竞赛(新知杯)试题详解46 2011年上海市初中数学竞赛(新知杯)试卷50 2011年上海市初中数学竞赛(新知杯)试卷详解53 2010年上海市初中数学竞赛(新知杯)试卷59 2010年上海市初中数学竞赛(新知杯)试卷详解61 2009年上海市初中数学竞赛(新知杯)试卷68 2009年上海市初中数学竞赛(新知杯)试卷参考答案71 2008年上海市初中数学竞赛(新知杯)试卷752008年上海市初中数学竞赛(新知杯)试卷参考答案79 2007年上海市初中数学竞赛(新知杯)试卷81 2007年上海市初中数学竞赛(新知杯)试卷答案详解83 2006年上海市初中数学竞赛(新知杯)试卷87 2006年上海市初中数学竞赛(新知杯)试卷答案详解90 2005年上海市初中数学竞赛(宇振杯)试卷94 2005年上海市初中数学竞赛(宇振杯)试卷参考答案97 2004年上海市初中数学竞赛(宇振杯)试卷99 2004年上海市初中数学竞赛(宇振杯)试卷参考答案101 2003年上海市初中数学竞赛(宇振杯)试卷104 2003年上海市初中数学竞赛(宇振杯)试卷参考答案106 2002年上海市初中数学竞赛(宇振杯)试卷107 2002年上海市初中数学竞赛(宇振杯)试卷参考答案108 2000年上海市初中数学竞赛(弘晟杯)试题110 2000年上海市初中数学竞赛(弘晟杯)试题参考答案1112017年上海市初中数学竞赛(大同中学杯)试卷一、 填空题(每题10分,共80分)1. 已知抛物线c bx ax y ++=2过点(0,0),(22.5,2020.5),(62.5,1812.5),则抛物线与x 轴的另一交点的横坐标为 (精确到0.001)。
2013全国大学生数学建模比赛B题-答案

2013高教社杯全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):所属学校(请填写完整的全名):重庆邮电大学参赛队员(打印并签名) :1.2.3.指导教师或指导教师组负责人(打印并签名):日期: 2013 年 9 月 13 日赛区评阅编号(由赛区组委会评阅前进行编号):2013高教社杯全国大学生数学建模竞赛编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):碎纸片的拼接复原摘要本文研究的是碎纸片的拼接复原问题。
由于人工做残片复原虽然准确度高,但有着效率低的缺点,仅由计算机处理复原,会由于各类条件的限制造成误差与错误,所以为了解决题目中给定的碎纸片复原问题,我们采用人机结合的方法建立碎纸片的计算机复原模型解决残片复原问题,并把计算机通过算法复原的结果优劣情况作为评价复原模型好坏的标准,通过人工后期的处理得到最佳结果。
面对题目中给出的BMP格式的黑白文字图片,我们使用matlab软件的图像处理功能把图像转化为矩阵形式,矩阵中的元素表示图中该位置像素的灰度值,再对元素进行二值化处理得到新的矩阵。
题目每一个附件中的碎纸片均为来自同一页的文件,所以不需考虑残片中含有未知纸张的残片以及残片中不会含有公共部分。
2013年全国数学竞赛试题详细参考答案

(第3题)一、选择题(共5小题,每小题6分,满分30分. 以下每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的. 请将正确选项的代号填入题后的括号里. 不填、多填或错填都得0分)1.已知实数x y ,满足 42424233y y x x -=+=,,则444y x+的值为( ).(A )7 (B )12+ (C )72+ (D )5 【答】(A )解:因为20x >,2y ≥0,由已知条件得21x ==2y ==, 所以444y x +=22233y x ++- 2226y x=-+=7. 另解:由已知得:2222222()()30()30x xy y ⎧-+--=⎪⎨⎪+-=⎩,显然222y x -≠,以222,y x -为根的一元二次方程为230t t +-=,所以 222222()1,()3y y x x-+=--⨯=- 故444y x +=22222222[()]2()(1)2(3)7y y x x-+-⨯-⨯=--⨯-= 2.把一枚六个面编号分别为1,2,3,4,5,6的质地均匀的正方体骰子先后投掷2次,若两个正面朝上的编号分别为m ,n ,则二次函数2y x mx n =++的图象与x 轴有两个不同交点的概率是( ).(A )512 (B )49 (C )1736(D )12【答】(C )解:基本事件总数有6×6=36,即可以得到36个二次函数. 由题意知∆=24m n ->0,即2m >4n .通过枚举知,满足条件的m n ,有17对. 故1736P =. 3.有两个同心圆,大圆周上有4个不同的点,小圆周上有2个不同的点,则这6个点可以确定的不同直线最少有( ).(A )6条 (B ) 8条 (C )10条 (D )E12条【答】(B )解:如图,大圆周上有4个不同的点A ,B ,C ,D ,两两连线可以确定6条不同的直线;小圆周上的两个点E ,F 中,至少有一个不是四边形ABCD 的对角线AC 与BD 的交点,则它与A ,B ,C ,D 的连线中,至少有两条不同于A ,B ,C ,D 的两两连线.从而这6个点可以确定的直线不少于8条.当这6个点如图所示放置时,恰好可以确定8条直线. 所以,满足条件的6个点可以确定的直线最少有8条.4.已知AB 是半径为1的圆O 的一条弦,且1AB a =<.以AB 为一边在圆O 内作正△ABC ,点D 为圆O 上不同于点A 的一点,且DB AB a ==,DC 的延长线交圆O 于点E ,则AE 的长为( ). (A(B )1 (C (D )a 【答】(B )解:如图,连接OE ,OA ,OB . 设D α∠=,则 120ECA EAC α∠=︒-=∠.又因为()1160180222ABO ABD α∠=∠=︒+︒-120α=︒-,所以ACE △≌ABO △,于是1AE OA ==. 另解:如图,作直径EF ,连结AF ,以点B 为圆心,AB 作⊙B ,因为AB =BC =BD ,则点A ,C ,D 都在⊙B 上,由11603022F EDA CBA ∠=∠=∠=⨯︒=︒所以2301AE EF sim F sim =⨯∠=⨯︒=5.将1,2,3,4,5三个数之和都能被这三个数中的第一个数整除,那么满足要求的排法有( ).(A )2种 (B )3种 (C )4种 (D )5种 【答】(D )解:设12345a a a a a ,,,,是1,2,3,4,5的一个满足要求的排列.首先,对于1234a a a a ,,,,不能有连续的两个都是偶数,否则,这两个之后都是偶数,与已知条件矛盾.又如果i a (1≤i ≤3)是偶数,1i a +是奇数,则2i a +是奇数,这说明一个偶数后面一定要(第4题)(第8题)接两个或两个以上的奇数,除非接的这个奇数是最后一个数.所以12345a a a a a ,,,,只能是:偶,奇,奇,偶,奇,有如下5种情形满足条件: 2,1,3,4,5; 2,3,5,4,1; 2,5,1,4,3; 4,3,1,2,5; 4,5,3,2,1. 二、填空题(共5小题,每小题6分,满分30分)6.对于实数u ,v ,定义一种运算“*”为:u v uv v *=+.若关于x 的方程1()4x a x **=-有两个不同的实数根,则满足条件的实数a 的取值范围是 .【答】0a >,或1a <-.解:由1()4x a x **=-,得21(1)(1)04a x a x ++++=,依题意有 210(1)(1)0a a a +≠⎧⎨∆=+-+>⎩,,解得,0a >,或1a <-.7.小王沿街匀速行走,发现每隔6分钟从背后驶过一辆18路公交车,每隔3分钟从迎面驶来一辆18路公交车.假设每辆18路公交车行驶速度相同,而且18路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是 分钟.【答】4.解:设18路公交车的速度是x 米/分,小王行走的速度是y 米/分,同向行驶的相邻两车的间距为s 米.每隔6分钟从背后开过一辆18路公交车,则 s y x =-66. ① 每隔3分钟从迎面驶来一辆18路公交车,则s y x =+33. ② 由①,②可得 x s 4=,所以4=xs. 即18路公交车总站发车间隔的时间是4分钟.8.如图,在△ABC 中,AB =7,AC =11,点M 是BC 的中点, AD 是∠BAC 的平分线,MF ∥AD ,则FC 的长为 . 【答】9.解:如图,设点N 是AC 的中点,连接MN ,则MN ∥AB . 又//MF AD ,所以 FMN BAD DAC MFN ∠=∠=∠=∠,所以 12FN MN AB ==. 因此 1122FC FN NC AB AC =+=+=9.(第8题答案)(第9题答案)另解:如图,过点C 作AD 的平行线交BA 的延长线为E ,延长MF 交 AE 于点N.则E BAD DAC ACE ∠=∠=∠=∠所以11AE AC ==. 又//FN CE ,所以四边形CENF 是等腰梯形, 即11(711)922CF EN BE ===⨯+=9.△ABC 中,AB =7,BC =8,CA =9,过△ABC 的内切圆圆心I 作DE ∥BC ,分别与AB ,AC 相交于点D ,E ,则DE 的长为 .【答】163. 解:如图,设△ABC 的三边长为a ,b ,c ,内切圆I 的半径为r , BC 边上的高为a h ,则11()22a ABC ah S abc r ==++△, 所以a r ah a b c=++. 因为△ADE ∽△ABC ,所以它们对应线段成比例,因此a a h r DEh BC-=, 所以 (1)(1)a a a h r r a DE a a a h h a b c -=⋅=-=-++()a b c a b c+=++, 故 879168793DE ⨯+==++().另解:ABC S rp ∆===(这里2a b cp ++=)所以12r ==2ABC a S h a ===△ 由△ADE ∽△ABC ,得23a a h r DE BC h -===, 即21633DE BC === 10.关于x ,y 的方程22208()x y x y +=-的所有正整数解为 .【答】481603232.x x y y ==⎧⎧⎨⎨==⎩⎩,,,解:因为208是4的倍数,偶数的平方数除以4所得的余数为0,奇数的平方数除以4所得的余数为1,所以x ,y 都是偶数.设2,2x a y b ==,则22104()a b a b +=-,同上可知,a ,b 都是偶数.设2,2a c b d ==,则2252()c d c d +=-,所以,c ,d 都是偶数.设2,2c s d t ==,则2226()s t s t +=-,于是 22(13)(13)s t -++=2213⨯, 其中s ,t 都是偶数.所以222(13)213(13)s t -=⨯-+≤2222131511⨯-<.所以13s -可能为1,3,5,7,9,进而2(13)t +为337,329,313,289,257,故只能是2(13)t +=289,从而13s -=7.于是62044s s t t ==⎧⎧⎨⎨==⎩⎩,,;,因此 481603232.x x y y ==⎧⎧⎨⎨==⎩⎩,,,另解:因为222(104)(104)210421632x y -++=⨯= 则有2(104)21632,y +≤ 又y 正整数,所以 143y ≤≤令22|104|,|104|,21632a x b y a b =-=++= 则 因为任何完全平方数的个位数为:1,4,5,6,9由2221632a b +=知22,a b 的个位数只能是1和1或6和6; 当22,a b 的个位数是1和1时,则,a b 的个位数字可以为1或9但个位数为1和9的数的平方数的十位数字为偶数,与22a b +的十位数字为3矛盾。
高中数学竞赛赛题精选(带答案)

高中数学竞赛赛题精选一、选择题(共12题)1.定义在R 上的函数()y f x =的值域为[m,n ],则)1(-=x f y 的值域为( ) A .[m,n ]B .[m-1,n-1]C .[)1(),1(--n f m f ]D .无法确定解:当函数的图像左右平移时,不改变函数的值域.故应选A.2.设等差数列{n a }满足13853a a =,且n S a ,01>为其前n 项之和,则)(*∈N n S n 中最大的是( ) A. 10S B. 11S C. 20S D. 21S 解:设等差数列的公差为d,由题意知3(1a +7d)=5(1a +12d),即d=-3921a , ∴n a = 1a +( n-1)d= 1a -3921a (n-1)= 1a (3941-392n),欲使)(*∈N n S n 最大,只须n a ≥0,即n ≤20.故应选C.3.方程log 2x=3cosx 共有( )组解.A .1B .2C .3D .4解:画出函数y=log 2x 和y=3cosx 的图像,研究其交点情况可知共有3组解.应选C .4.已知关于x 的一元二次方程()02122=-+-+a x a x 的一个根比1大,另一个根比1小,则()A.11<<-a B.1-<a 或1>aC.12<<-aD.2-<a 或1>a解:令f(x)= ()2122-+-+a x a x ,其图像开口向上,由题意知f(1)<0,即 ()211122-+⨯-+a a <0,整理得022<-+a a ,解之得12<<-a ,应选C .5.已知βα,为锐角,,cos ,sin y x ==βα53)cos(-=β+α,则y 与x 的函数关系为( ) A .1)x 53( x 54x 153y 2<<+--= B .1)x (0 x 54x 153y 2<<+--=C .)53x (0 x 54x 153y 2<<---= D .1)x (0 x 54x 153y 2<<---= []xx y 54153sin )sin(cos )cos()(cos cos 2+-⋅-=⋅+++=-+==αβααβααβαβ解: 而)1,0(∈y 15415302<+-⋅-<∴x x , 得)1,53(∈x .故应选A. 6.函数sin y x =的定义域为[],a b ,值域为11,2⎡⎤-⎢⎥⎣⎦,则b a-的最大值是( )A. πB. π2C.34πD. 35π解:如右图,要使函数sin y x =在定义域[],a b 上,值域为11,2⎡⎤-⎢⎥⎣⎦,则b a -的最大值是74()663πππ--=.故应选C. 7.设锐角使关于x 的方程x 2+4x cos+cot =0有重根,则的弧度数为 ( )A .6B .12或512C .6或512D .12解:由方程有重根,故14=4cos 2-cot =0,∵ 0<<2,2sin2=1,=12或512.选B . 8.已知M={(x ,y )|x 2+2y 2=3},N={(x ,y )|y=mx+b }.若对于所有的m ∈R ,均有M ∩N ,则b 的取值范围是 ( )A .[-62,62] B .(-62,62) C .(-233,233] D .[-233,233] 解:点(0,b )在椭圆内或椭圆上,2b 2≤3,b ∈[-62,62].选A .9.不等式log 2x -1+12log 12x 3+2>0的解集为A .[2,3)B .(2,3]C .[2,4)D .(2,4] 解:令log 2x=t ≥1时,t -1>32t -2.t ∈[1,2),x ∈[2,4),选C .10.设点O 在ABC 的内部,且有+2+3=,则ABC 的面积与AOC 的面积的比为( )A .2B .32C .3D .53解:如图,设AOC=S ,则OC 1D=3S ,OB 1D=OB 1C 1=3S ,AOB=OBD=1.5S .OBC=0.5S ,ABC=3S .选C .11.设三位数n=,若以a ,b ,c 为三条边长可以构成一个等腰(含等边)三角形,则这样的三位数n 有( )A .45个B .81个C .165个D .216个 解:⑴等边三角形共9个;⑵ 等腰但不等边三角形:取两个不同数码(设为a ,b ),有36种取法,以小数为底时总能构成等腰三角形,而以大数为底时,b <a <2b .a=9或8时,b=4,3,2,1,(8种);a=7,6时,b=3,2,1(6种);a=5,4时,b=2,1(4种);a=3,2时,b=1(2种),共有20种不能取的值.共有236-20=52种方法,而每取一组数,可有3种方法构成三位数,故共有523=156个三位数即可取156+9=165种数.选C .12.顶点为P 的圆锥的轴截面是等腰直角三角形,A 是底面圆周上的点,B 是底面圆内的点,O 为底面圆圆心,AB ⊥OB ,垂足为B ,OH ⊥PB ,垂足为H ,且PA=4,C 为PA 的中点,则当三棱锥O -HPC 的体积最大时,OB 的长为 ( )A .53 B .253 C .63 D .263解:AB ⊥OB ,PB ⊥AB ,AB ⊥面POB ,面PAB ⊥面POB .OH ⊥PB ,OH ⊥面PAB ,OH ⊥HC ,OH ⊥PC ,又,PC ⊥OC ,PC ⊥面OCH .PC 是三棱锥P -OCH 的高.PC=OC=2.而OCH 的面积在OH=HC=2时取得最大值(斜边=2的直角三角形).当OH=2时,由PO=22,知∠OPB=30,OB=PO tan30=263.又解:连线如图,由C 为PA 中点,故V O -PBC =12V B -AOP ,S B 11OABCABPO H C而V O -PHC ∶V O -PBC =PH PB =PO 2PB2(PO 2=PH ·PB ).记PO=OA=22=R ,∠AOB=,则V P —AOB =16R 3sin cos =112R 3sin2,V B -PCO =124R 3sin2. PO 2PB 2=R 2R 2+R 2cos 2=11+cos 2=23+cos2.V O -PHC =sin23+cos2112R 3. ∴ 令y=sin23+cos2,y=2cos2(3+cos2)-(-2sin2)sin2(3+cos2)2=0,得cos2=-13,cos =33, ∴ OB=263,选D .二、填空题(共10题)13. 设n S 为等差数列{}n a 的前n 项和,若510S =,105S =-,则公差为 解:设等差数列{}n a 的首项为1a ,公差为d .由题设得⎩⎨⎧-=+=+,,545101010511d a d a 即 ⎩⎨⎧-=+=+,,1922211d a d a 解之得1-=d .14. 设()log ()a f x x b =+(0a >且1)a ≠的图象经过点(21),,它的反函数的图象经过点(28),,则b a +等于 4 .解:由题设知 log (2)1log (8)2a a b b +=⎧⎨+=⎩,, 化简得 2(2)(8).b a b a +=⎧⎨+=⎩,解之得 1131a b =⎧⎨=⎩,; 2224.a b =-⎧⎨=-⎩,(舍去). 故a b +等于4.15.已知函数()y f x =的图象如图,则满足22221()(lg(620))021x x f f x x x x --⋅-+≤-+的 x 的取值范围为 [21)x ∈-, .解: 因为 ()()22lg 620lg (3)11lg111x x x -+=-+≥>,所以()2lg 6200x x -+<. 于是,由图象可知,2111x x +≤-,即 201x x +≤-,解得 21x -≤<. 故x 的取值范围为 [21)x ∈-,.16.圆锥曲线0|3|102622=+--+-++y x y x y x 的离心率是 2 .解:原式变形为|3|)1()3(22+-=-++y x y x ,即=2|3|2+-y x .所以动点),(y x 到定点(31)-,的距离与它到直线03=+-y x 的距离之比为2.故此动点轨迹为双曲线,离心率为2.17.在ABC ∆中,已知3tan =B ,322sin =C ,63=AC ,则ABC ∆的面积为ABC S ∆=解:在ABC ∆中,由3tan =B 得︒=60B .由正弦定理得sin 8sin AC CAB B⋅==.因为︒>60322arcsin,所以角C 可取锐角或钝角,从而31cos ±=C .sin sin()sin cos cos sin A B C B C B C =+=+=sin 2ABC AC ABS A ∆⋅== 18. 设命题P :2a a <,命题Q : 对任何x ∈R ,都有2410x ax ++>. 命题P 与Q 中有 且仅有一个成立,则实数a 的取值范围是 021≤<-a 或 121<≤a . 解:由a a <2得10<<a .由0142>++ax x 对于任何x ∈R 成立,得04162<-=∆a ,即2121<<-a .因为命题P 、Q 有且仅有一个成立,故实数 a 的取值范围是 021≤<-a 或 121<≤a .19.22cos 75cos 15cos75cos15++⋅的值是 . 解:22cos 75cos 15cos75cos15++⋅ =cos²75°+sin²75°+sin15°·cos15° =1+°30sin 21=5420.定义在R 上的函数()f x 满足(1)2f =,且对任意的x R ∈,都有1()2f x '<,则不等式22log 3(log )2x f x +>的解集为 . 解:令g ﹙x ﹚=2f ﹙x ﹚-x ,由f '(x ) <1/2得,2f '(x ) -1<0,即'g ﹙x ﹚<0,g(x)在R 上为减函数,且g(1)=2f(1)-1=3,不等式f(log2X)>2log 2X化为2f(log2X)—log2X≥3,即g(log2X)>g(1),由g(x)的单调性得:log2X<1,解得,0<x<2. 21.圆O 的方程为221x y +=,(1,0)A ,在圆O 上取一个动点B ,设点P 满足()AP OB R λλ=∈且1AP AB ⋅=.则P 点的轨迹方程为 .解:设P(x,y), AB =λOB (λϵR)得B(k(x —1),ky),(λ=k1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2013年全国高中数学联合竞赛一试试题
一、填空题:本大题共8小题,每小题8分,共64分
1.设集合A ={2,0,1,3},集合B =A x x ∈-|{,}22A x ∉-.则集合B 中所有元素的和为 ___________
2.在平面直角坐标系xOy 中,点A 、B 在抛物线x y 42=上,满足4-=∙,F 是抛物线的焦点.则
O FB O FA S S ∆∆∙=___________
3.在△ABC 中,已知C B A sin sin 10sin =,C B A cos cos 10cos =,则A tan 的值为____________
4.已知正三棱锥P —ABC 底面边长为1,高为2,则其内切球半径为___________
5.设a ,b 为实数,函数b ax x f +=)(满足:对任意∈x [0,1],有1|)(|≤x f .则ab 的最大值为___________
6.从1,2,…,20中任取5个不同的数,其中至少有两个是相邻数的概率为___________
7.若实数x y ,满足y x y x -=-24,则x 的取值范围是___________
8.已知数列}{n a 共有9项,其中191==a a ,且对每个∈i {1,2,…,8},均有}2
1
,1,2{1-∈+i i a a ,则这样的数列的个数为__________
二、解答题:本大题共3小题,共56分.解答应写出文字说明、证明过程或演算步骤
9. (本题满分16分)给定正数数列}{n x 满足12-≥n n S S ,n =2,3,…,这里+=1x S n …n x +.证明:存
在常数0>C ,使得n
n C x 2∙≥,n =1,2,…
10. (本题满分20分)在平面直角坐标系xOy 中,椭圆的方程为)0(122
22>>=+b a b
y a x ,1A 、2A 分别
为椭圆的左、右焦点,1F 、2F 分别为椭圆的左、右焦点,P 为椭圆上不同于1A 和2A 的任意一点.若平面
中两个点Q 、R 满足11PA QA ⊥,22PA QA ⊥,11PF RF ⊥,22PF RF ⊥,试确定线段QR 的长度与b 的大小关系,并给出证明.
11.(本题满分20分)设函数b ax x f +=2)(,求所有的正实数对),(b a ,使得对任意实数x ,y ,有
)()()()(y f x f y x f xy f ≥++.
2013年全国高中数学联合竞赛加试试题
一、(本题满分40分)如图,AB 是圆ω的一条弦,P 为弧AB 内一点,E 、F 为线段AB 上两点,满足
AE =EF =FB .连接PE 、PF 并延长,与圆ω分别相交于点C 、D .求证:EF ·CD =AC ·BD .
(解题时请将图画在答卷纸上)
二、(本题满分40分)给定正整数u ,v .数列}{n a 定义如下:v u a +=1,对整数1≥m , ⎩⎨
⎧+=+=+v
a a u
a a m m m m 122
记++=21a a S m …,2,1(=+m a m …).证明:数列}{n S 中有无穷多项是完全平方数.
B
三、(本题满分50分)一次考试共有m 道试题,n 个学生参加,其中m ,2≥n 为给定的整数.每道题的得分规则是:若该题恰有x 个学生没有答对,则每个答对该题的学生得x 分,未答对的学生得零分.每个学生的总分为其m 道题的得分总和.将所有学生总分从高到低排列为≥≥21p p …n p ≥,求n p p +1的最大可能值.
四、(本题满分50分)设n ,k 为大于1的整数,k n 2<.证明:存在k 2个不被n 整除的整数,若将它们任意分成两组,则总有若干个数的和被n 整除.。
