(理数)华师附中2014届高三热身试题
广东省华附、省实、广雅、深中四校2014届高三上学期期末联考数学理试题(最新整理)

响的程度决定给分,但不得超过该部分正确解答应得分数的一半;如果后续部分的解答有较严重的错 误,就不再给分. 三、解答右端所注分数,表示考生正确做到这一步应得的累加分数. 四、只给整数分数,选择题和填空题不给中间分数. 一、选择题:本大题共 8 小题,每小题 5 分,满分 40 分.在每小题给出的四个选项 中,只有一项符合要求.
5π
x
12
② f (x) tan x ;③ f (x) x sin x.其中图像能等分圆 C 面积的函数有
A. 3 个
B. 2 个
C. 1 个
D. 0 个
5. (x 1 )12 展开式中的常数项为 3x
A. 220
B. 220 C.1320
D. 1320
6.执行如图所示的程序框图,输出的 S 值为
_4 _正视图
_2 _2 _侧视图
围成的平面区域的面积为 S, 则 p ______ , S
.
13.
已知函数
f
(
x)
x 1, 0
2x
1 2
,
x
x 1
1
,
若
ab0,
且
_俯视图
f (a) f (b) ,则 bf (a) 的取值范围是
.
选做题(请考生在以下两小题中任选一题做答,若两小题都做,则按第 14 题记分).
(2)
设
m
(2
sin(
π
B),1),
n
(sin( π
B),
1),
求
m
n
的值.
华师一附中2014届高三毕业生5月29日适应性考试答题卡

语文答题卡13.(3分)请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!14.(8分)15.(5分)请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!17.(4分)18.(4分)19.(8分)21.(4分)20.(4分)22.(4分)请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!请在本题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!贴条形码区试卷类型A B姓名准考证号数学答题卡(理科)贴条形码区试卷类型A B姓名准考证号17.请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效!三、解答题(12分)18.(12分)19.(12分)(12分)(13分)(14分) 20.21.22.数学答题卡(文科)18.三、解答题(12分)19.(13分)贴条形码区试卷类型A B姓名准考证号(13分)(14分)24.(续25题)26.27.25.贴条形码区试卷类型A B姓名准考证号(1)(2)(3)(4)(1)(2)(3)①(5)(6)②28.30.29.(1)(2)(4)(1)(3)(4)(1)(3)(4)(5)31.(1)(2)32.(1)(2)②(3)(2)(2)(3)(3)①③33(2)图34(2)图35(2)图(2)(3)37.(1)(2)(4)38.(1)(2)(3)贴条形码区试卷类型A B姓名准考证号(4)(2)41.39.(1)(2)(3)40.(1)。
2014.10高三数学月考试卷(理科卷)

华师大二附中2014学年度第一学期高三数学10月月考试卷(理科卷)一. 填空题(本大题满分56分)本大题共有14小题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.1.设复数z 满足(2)(2)5z i i --=,则z = .2.)11141131121(lim 2222-++-+-+-∞→n n = . 3.关于x 的不等式01log )5(log 2221>+-+x x 的解集为____________. 4.等比数列{}n a 中,452,5a a ==,则数列{lg }n a 的前8项和为 .5.()()8x y x y -+的展开式中27x y 的系数为________.6.三棱锥P ABC -中,D ,E 分别为PB ,PC 的中点,记三棱锥D ABE -的体积为1V ,P ABC -的体积为2V ,则12V V =________. 7. 在极坐标系中,曲线1C 和2C 的方程分别为22cos sin ρθθ=和cos 1ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴正半轴,建立平面直角坐标系,则曲线1C 和2C 交点的直角坐标为_________.8.如果关于x 的不等式()0f x <和()0g x <的解集分别为(,)a b 和11(,)b a,那么称这两个不等式为对偶不等式.如果不等式2cos 220x θ-⋅+<与不等式224sin 210x x θ+⋅+<为对偶不等式,且(,)2πθπ∈,则cos θ=_______________. 9.已知甲盒中仅有1个球且为红球,乙盒中有m 个红球和n 个蓝球()3,3m n ≥≥,从乙盒中随机抽取()1,2i i =个球放入甲盒中. 记放入i 个球后,甲盒中含有红球的个数为()1,2i i ξ=,从甲盒中取1个球是红球的概率为()1,2i p i =.则p 1与p 2、E (ξ1)与E (ξ2)的大小关系分别为 .10.若集合{a ,b ,c ,d }={1,2,3,4},且下列四个关系:①a =1;②b ≠1;③c =2;④d ≠4中有且仅有一个是正确的,则符合条件的有序数组(a ,b ,c ,d )的个数是 .11.定义在R 上的奇函数f (x ),当x ≥0时,()[)[)12log 1,0,1()13,1,⎧+∈⎪=⎨⎪--∈+∞⎩x x f x x x ,则函数F (x )= f (x )-a (0<a <1)的所有零点之和为_____________.12.在平面直角坐标系xOy 中,已知向量a 、b ,1a b ==,0a b ⋅=,点Q 满足OQ =)a b +.曲线C ={P |OP =a cos θ+b sin θ,0≤θ<2π},区域Ω={P |0<r ≤PQ ≤R ,r <R }.若C ∩Ω为两段分离的曲线,则R 的取值范围是 .13.已知函数y =f (x )(x ∈R ),对函数y =g (x )(x ∈I ),定义g (x )关于f (x )的“对称函数”为函数y =h (x )(x ∈I ),y =h (x )满足:对任意x ∈I ,两个点(x ,h (x )),(x ,g (x ))关于点(x ,f (x ))对称.若h (x )是g (x )=4-x 2关于f (x )=3x +b 的“对称函数”,且h (x )>g (x )恒成立,则实数b 的取值范围是____________.14.对于数对序列P :(a 1,b 1),(a 2,b 2),…,(a n ,b n ),记T 1(P )=a 1+b 1,T k (P )=b k +max{T k -1(P ),a 1+a 2+…+a k }(2≤k ≤n ),其中max{T k -1(P ),a 1+a 2+…+a k }表示T k -1(P )和a 1+a 2+…+a k 两个数中最大的数.在由五个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,使T 5(P )最小的一个数对序列P 的T 5(P )的值为 .二.选择题(本大题满分20分)本大题共有4小题,每题都给出四个结论,其中有且只有一个结论是正确的,选对得 5分,否则一律得零分.15.U 为全集,A ,B 是集合,则“存在集合C 使得A ⊆C ,B ⊆∁U C ”是“A ∩B =∅”的( )A .充分非必要条件B . 必要非充分条件C . 充要条件D . 既非充分也非必要条件16.定义在R 上的函数()f x 满足:对任意,R αβ∈,总有()()()2014f f f αβαβ+-+=⎡⎤⎣⎦,则下列说法正确的是( )A .()1f x +是奇函数B .()1f x -是奇函数C .()2014f x +是奇函数D .()2014f x -是奇函数17.样本12(,,...,)n x x x 的平均数为x ,样本12(,,...,)m y y y 的平均数为y ,若样本1212(,,...,,,,...,)n m x x x y y y 的平均数为(1)z x y αα=+-,其中102α<<,则,n m 的大小关系是( )A .n m <B .n m =C .n m >D .不能确定18.如图在长方体ABCD - A 1B 1C 1D 1中,AB =11,AD =7,AA 1=12.一质点从顶点A 射向点E (4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i -1次到第i 次反射点之间的线段记为L i (i =2,3,4),L 1=AE ,则线段L 1,L 2,L 3,L 4的长度关系为( )A. L 1=L 2=L 3=L 4B. L 1=L 2>L 3=L 4C. L 1=L 2>L 3>L 4D.L 1=L 2>L 4>L 3三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对应的题号)内写出必要的步骤.19.(本题满分12分)本题共有2个小题,第1小题满分6分,第2小题满分6分.如图1-6所示,为保护河上古桥OA ,规划建一座新桥BC ,同时设立一个圆形保护区.规划要求:新桥BC 与河岸AB 垂直;保护区的边界为圆心M 在线段OA 上并与BC 相切的圆,且古桥两端O 和A 到该圆上任意一点的距离均不少于80 m .经测量,点A 位于点O 正北方向60 m 处,点C 位于点O 正东方向170 m处(OC 为河岸),tan ∠BCO =43. (1)求新桥BC 的长.(2)当OM 多长时,圆形保护区的面积最大?20.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.如图在棱长为2的正方体ABCD -A 1B 1C 1D 1中,E ,F ,M ,N 分别是棱AB ,AD ,A 1B 1,A 1D 1的中点,点P ,Q 分别在棱DD 1,BB 1上移动,且DP =BQ =λ(0<λ<2).(1)当λ=1时,证明:直线BC1∥平面EFPQ .(2)是否存在λ,使面EFPQ 与面PQMN 所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分. 如果存在非零常数c ,对于函数()y f x =定义域R 上的任意x ,都有()()f x c f x +>成立,那么称函数()y f x =为Z 函数.(1) 求证:若()y f x =()x R ∈是单调函数,则它是Z 函数;(2) 若函数32()g x x bx =+是Z 函数.求实数b 满足的条件.22.(本题满分16分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分6分.已知点P 是圆x 2+y 2=4上一动点,PD ⊥x 轴于点D ,记满足1()2OM OP OD =+的动点M 的轨迹为F .(I )求轨迹F 的方程;(Ⅱ)已知直线l :y=kx+m 与轨迹F 交于不同两点A ,B ,点G 是线段AB 中点,射线OG 交轨迹F 于点Q ,且,OQ OG λλ=∈R .①求λ、m 与k 的关系式;②求△AOB 的面积S (λ)的解析式,并计算S (λ)最大值.23.(本题满分18分).本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.对于自然数数组(,,)a b c ,如下定义该数组的极差:三个数的最大值与最小值的差.如果(,,)a b c 的极差1d ≥,可实施如下操作f :若,,a b c 中最大的数唯一,则把最大数减2,其余两个数各增加1;若,,a b c 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为1(,,)f a b c ,其级差为1d .若11d ≥,则继续对1(,,)f a b c 实施操作f ,…,实施n 次操作后的结果记为(,,)n f a b c ,其极差记为n d .例如:1(1,3,3)(3,2,2)f =,2(1,3,3)(1,3,3)f =.(Ⅰ)若(,,)(1,3,14)a b c =,求12,d d 和2014d 的值;(Ⅱ)已知(,,)a b c 的极差为d 且a b c <<,若1,2,3,n =时,恒有n d d =,求d 的所有可能取值;(Ⅲ)若,,a b c 是以4为公比的正整数等比数列中的任意三项,求证:存在n 满足0n d =.得分一、填空题(本大题满分56分)本大题共有14小题,只要求直接填写结果,每个空格填对得4分,否则一律得零分.1. ;2. ;3. ;4. ;5. ;6. ;7. ;8. ;9. ;10. ;11. ;12. ;13. ;14. ;二.选择题(本大题满分20分)本大题共有4小题,每题都给出四个结论,其中有且只有一个结论是正确的,选对得 5分,否则一律得零分.三.解答题(本大题满分74分)本大题共有5题,解答下列各题必须在答题纸的规定区域(对应的题号)内写出必要的步骤.19.(本题满分12分)第1小题满分6分,第2小题满分6分.20.(本题满分14分)本题共2个小题,第1小题满分7分,第2小题满分7分.21.(本题满分14分)本题共2小题,第1题6分,第2题8分.小题满分4分.。
广东省华南师范大学附属中学届高三综合测试第一次考理数试题含解析

广东省华南师范大学附属中学2018-2019学年高三综合测试(一)(第一次月考)理数试题一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设全集{}|2U x N x =∈≥,集合{}2|5A x N x =∈≥,则U C A =( )A .∅B .{}2C .{}5D .{}2,5【答案】B考点:1、二次不等式;2、集合的基本运算.2.“()0,10x x x ∀>->”的否定是( )A .()0,10x x x ∀>-≤B .0,01x x ∀<≤≤C .()0,10x x x ∃>-≤D .0,01x x ∃>≤≤【答案】D【解析】试题分析:原的否定为0,01x x ∃>≤≤,故选D.考点:的否定.3.设248log 3,log 6,log 9a b c ===,则下列关系中正确的是( )A .a b c >>B .c a b >>C .c b a >>D .a c b >>【答案】A【解析】 试题分析:248lg3lg 2lg32lg3log 3,log 6,log 9lg 22lg 23lg 2a b c +======⇒ 2lg3lg3lg3lg 2lg32lg 22lg 22lg 2a b ++==>=⇒3lg 23lg 3lg 33lg 34lg 36lg 26lg 26lg 2b c ++=>==⇒a b c >>,故选A.考点:1、对数的大小比较;2、对数的基本运算.4.设x R ∈,则“12x >”是“2210x x +->”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件【答案】A【解析】 试题分析:2121012x x x +->⇔<-或x>,故“12x >”是“2210x x +->”的充分不必要条件,故选A.考点:充要条件.KS5U 5.已知()()1,41,42x f x x f x x ⎧+<⎪=⎨⎛⎫≥⎪ ⎪⎝⎭⎩,则()2log 3f =( )A .112B .124C .14D .12【答案】B考点:分段函数.6.由曲线y =2y x =-+及x 轴所围成图形的面积是( ) A .103 B .4 C .76 D .6【答案】C【解析】试题分析:32122201121237(2)|(2)|(2)32326x dx x x x +-+=+-+=+-=⎰⎰,故选C. 考点:定积分公式.7.已知函数()()20.5log 3f x x ax a =-+在[)2,+∞单调递减,则a 的取值范围是( ) A .(],4-∞ B .[)4,+∞ C .[]4,4-D .(]4,4-【答案】C考点:复合函数的单调性.【方法点晴】本题主要考查复合函数的单调性,其中涉及数形结合思想和转化化归思想,考查逻辑推理能力、转化化归能力,综合性较强,属于较难题型. 首先利用转化化归思想将转化为函数23t x ax a =-+在[)2,+∞单调递增,然后结合二次函数的图象可得2223022a a a ⎧-+≥⎪⎨≤⎪⎩,从而解得44a -≤≤.数形结合思想和转化化归思想是本题的解题关键,可以化繁为简.8.函数()21log f x x =+与()12x g x -=在同一直角坐标系下的图象大致是( )A .B .C .D .【答案】C【解析】 试题分析:由(0)2g =排除B,D ,由(1)1f =排除A,故选C.考点:函数的图象.9.已知()1f x +在偶函数,且()f x 在[)1,+∞单调递减,若()20f =,则()0f x >的解集为( )A .()1,1-B .()0,1C .()1,2D .()0,2【答案】D【解析】试题分析:取特殊函数2()2f x x x =-⇒()0f x >的解集为()0,2,故选D. 考点:函数的性质.10.已知函数()sin f x x x =g ,则()1113f f f ππ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭、、的大小关系为( ) A .()1311f f f ππ⎛⎫⎛⎫->-> ⎪ ⎪⎝⎭⎝⎭ B .()1311f f f ππ⎛⎫⎛⎫->-> ⎪ ⎪⎝⎭⎝⎭C .()1113f f f ππ⎛⎫⎛⎫>->-⎪ ⎪⎝⎭⎝⎭ D .()1311f f f ππ⎛⎫⎛⎫->>- ⎪ ⎪⎝⎭⎝⎭ 【答案】A考点:1、函数的奇偶性;2、函数的单调性.【方法点晴】本题主要考查数的奇偶性、函数的单调性.,其中涉及数形结合思想和转化化归思想,考查逻辑推理能力、转化化归能力,综合性较强,属于较难题型. 首先利用转化化归思想将转化即: ()1f -=(1),(),33f f f ππ⎛⎫=-= ⎪⎝⎭,然后作图,观察图像并结合单调性可得()1311f f f ππ⎛⎫⎛⎫->-> ⎪ ⎪⎝⎭⎝⎭.善于应用数形结合思想和转化化归思想是,方能轻松解题.KS5U 11.下列中是假的是( )A .m R ∃∈,使()()2431m m f x m x -+=-g 是幂函数,且在()0,+∞上递减B .函数()()21lg 14f x x a x a ⎡⎤=++-+⎢⎥⎣⎦的值域为R ,则60a a ≤-≥或 C .关于x 的方程2210ax x ++=至少有一个负根的弃要条件是1a ≤D .函数()y f a x =+与函数()y f a x =-的图像关于直线x a =对称【答案】D【解析】试题分析:选项A 中12()m f x x -=⇒=在()0,+∞上递减成立,故为真;选项B 中函数()()21lg 14f x x a x a ⎡⎤=++-+⎢⎥⎣⎦的值域为21(1)4R t x a x a ⇒=++-+ 与x 至少有一个交点221(1)4()604a a a a ⇒∆=+--+=+≥⇒60a a ≤-≥或,故为真;①当0a =时,显然成立.②当0a ≠时,显然方程无零根.若方程有一正一负根,则440010a a a∆=->⎧⎪⇒<⎨<⎪⎩;若方程有两负根,则440100120a a aa⎧⎪∆=-≥⎪⎪>⇒<≤⎨⎪⎪-<⎪⎩.综上,若方程至少有一个负根,则1a ≤.反之,若1a ≤,则方程至少有一个负根,因此为真.排除A 、B 、C ,故选D.考点:的真假.12.已知函数()f x 是定义在R 上的以4为周期的函数,当(]1,3x ∈-时,()(]()(]1,112,1,3x f x t x x ⎧∈-⎪=⎨--∈⎪⎩g,其中0t >.若函数()15f x y x =-的零点个数是5,则t 的取值范围为( )A .2,15⎛⎫ ⎪⎝⎭B .26,55⎛⎫ ⎪⎝⎭C .61,5⎛⎫ ⎪⎝⎭D .()1,+∞【答案】B考点:1、函数的周期性;2、分段函数;3、函数的零点;4、函数的图象与性质.【方法点晴】本题主要考查函数的周期性、分段函数、函数的零点和函数的图象与性质,其中涉及数形结合思想和转化化归思想,考查逻辑推理能力、转化化归能力,综合性较强,属于较难题型. 首先利用数形结合思想和转化化归思想将转化为函数()f x 的图象与直线15y x =有5个交点,然后作图,观察图象可得2655x <<.数形结合思想和转化化归思想是本题的解题关键,可以四两拨千斤.KS5U第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.函数()2log 1y x =-的定义域为____________. 【答案】()2,+∞【解析】试题分析:由已知可得(1)2390102log 0x x x x -⎧-≥⎪->⇒>⎨⎪≠⎩,故定义域为()2,+∞.考点:函数的定义域.14.已知集合{}{}|10,1,1A x ax B =+==-,若A B A =I ,则实数a 的所有可能取值的集合为____________.【答案】{}1,0,1-考点:集合基本运算.【方法点晴】本题主要考查集合基本运算,其中涉及分类讨论思想和转化化归思想,考查逻辑推理能力、转化化归能力,综合性较强,属于中等难题. 首先将A B A =I 转化为A B ⊆,然后对0a =与0a ≠进行分类讨论,从而求得实数a 的所有可能取值的集合为{}1,0,1-.分类讨论思想和转化化归思想是本题的解题关键.15.若25a b m ==,且112a b+=,则m =__________.【解析】试题分析:2525log ,log a b m a m b m ==⇒==⇒211log 2log 5log 10210m m m m a b+=+==⇒=m ⇒=.考点:指数式与对数式的综合运算.16.过函数()32325f x x x x =-++图像上一个动点作函数的切线,则切线倾斜角的范围是 __________. 【答案】30,,24πππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭U 考点:1、函数的导数;2、切线的斜率与倾斜角.【方法点晴】本题主要考查函数的导数、切线的斜率与倾斜角,其中涉及数形结合思想和转化化归思想,综合性较强,属于较难题型. 首先函数()f x 图象上一个动点的切线斜率转化为函数的导数,并求出()'1,f x ≥-再结合直线斜率图象,逆推出切线倾斜角的范围是30,,24πππ⎡⎫⎡⎫⎪⎪⎢⎢⎣⎭⎣⎭U ,数形结合思想和转化化归思想是本题的解题关键. 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分10分)已知集合{}{}2|3327,|log 1x A x B x x =≤≤=>.(1)分别求(),R A B C B A I U ;(2)已知集合{}|1C x x a =<<,若C A ⊆,求实数a 的取值集合.【答案】(1){}|23A B x x =<≤I ,{}|3R C B A x x =≤U .(2)3a ≤.【解析】试题分析:(1)由3327x ≤≤ ⇒13x ≤≤⇒{}|13A x x =≤≤,再2log 1x >⇒2x >⇒{}|2B x x =>⇒{}{}|23;|2R A B x x C B x x =<≤=≤I ⇒{}|3R C B A x x =≤U ;(2)由(1)知{}|13A x x =≤≤,再分情况讨论 C 为空集与非空集合,从而求出3a ≤.试题解析:(1)∵3327x ≤≤,即13333x ≤≤,∴13x ≤≤,∴{}|13A x x =≤≤,...........2分 ∵2log 1x >,即22log log 2x >,∴2x >,∴{}|2B x x =>,..................3分 ∴{}{}|23;|2R A B x x C B x x =<≤=≤I ,∴{}|3R C B A x x =≤U .....................................5分(2)由(1)知{}|13A x x =≤≤,当C 为空集时,1a ≤,当C 为非集合时,可得13a <≤,综上所述3a ≤........................................10分考点:1、不等式;2、集合的基本运算.KS5U18.(本小题满分12分)已知:p 实数x 满足22430x ax a -+<,其中0;:a q >实数x 满足23x <≤.(1)若1a =,且p q ∧为真,求实数x 的取值范围;(2)若p 是q 的必要不充分条件,求实数a 的取值范围.【答案】(1)()2,3;(2)(]1,2.试题解析:(1)对:p 由22430x ax a -+<得()()30x a x a --<, 因为0a >,所以3a x a <<............................... 2分当1a =时,解得13x <<,即p 为真时,实数x 的取值范围是13x <<.又q 为真时实数x 的取值范围是23x <≤...................4分若p q ∧为真,则p 真且q 零点,所以实数x 的取值范围是()2,3................................. 6分(2)p 是q 的必要不充分条件 ,即q p ⇒,且p q ≠,设(){}(){}|,|A x p x B x q x ==,则B A ≠...................8分又(]()2,3,,3B A a a ==;所以有233a a≤⎧⎨≤⎩解得12a ≤≤,所以实数a 的取值范围是(]1,2................12分考点:简易逻辑.19.(本小题满分12分)函数()()01x x f x ka a a a -=->≠且是定义在实数集R 上的奇函数.(1)若()10f >,试求不等式()()2240f x x f x ++->的解集;(2)若()312f =且()()222x xg x a a m f x -=+-g 在[)1,+∞上的最小值为-2,求m 的值. 【答案】(1){}|14x x x ><-或;(2)2m =.试题解析:(1)∵()f x 是定义在R 上的奇函数,∴()00f =,∴10k -=,∴1k =....................2分∵()10f >,∴10a a->,又0a >且1a ≠,∴1a >....................4分 易知()f x 在R 上单调递增,原不等式化为:()()224f x x f x +>-, ∴1x >或4x <-,∴不等式的解集为{}|14x x x ><-或...................6分考点:函数的性质.20.(本小题满分12分)某山区外围有两条相互垂直的直线型公路,为进一步改善山区的交通现状,计划修建一条连接两条公路和山区边界的直线型公路.记两条相互垂直的公路为12l l 、,山区边界曲线为C .计划修建的公路为l ,如图所示,,M N 为C 的两个端点,测得点M 到12l l 、的距离分别为5千米和40千米,点N 到12l l 、的距离分别为20千米和2.5千米,以12l l 、所在直线分别为,x y 轴,建立平面直角坐标系xOy .假设曲线C 符合函数2a y x b=+(其中,a b 为常数)模型. (1)求,a b 的值;(2)设公路l 与曲线C 相切于P 点,P 的横坐标为t .①请写出公路l 长度的函数解析式()f t ,并写出其定义域;②当t 为何值时,公路l 的长度最短?求出最短长度.【答案】(1)10000a b =⎧⎨=⎩;(2)①()[]5,20f t t =∈;②当t =路l的长度最短,最短长度为【解析】试题分析:(1)由题意得,M N 分别为 ()()5,40,20,2.5⇒2a y x b =+⇒4025 2.5400a b a b⎧=⎪⎪+⎨⎪=⎪+⎩⇒ 10000a b =⎧⎨=⎩;(2)①由(1)知()21000520y x x =≤≤⇒P 21000,t t ⎛⎫ ⎪⎝⎭,求导得32000y x '=-⇒ l ;()2310002000y x t t t -=--⇒233000,0,0,2t A B t ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭⇒()[]5,20f t t =∈;②设()624410g t t t ⨯=+⇒()6516102g t t t ⨯'=-,令()0g t '=⇒t =可得:当t =()g t 有极小值,也是最小值,所以()min 300g t =,此时()min f t =(2)①由(1)知,()21000520y x x =≤≤,则点P 的坐标为21000,t t ⎛⎫ ⎪⎝⎭, 设在点P 处的切线l 交,x y 轴分别交于,A B 点,32000y x '=-, 则l 的方程为()2310002000y x t t t -=--,由此得233000,0,0,2t A B t ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭.故()[]5,20f t t ==∈...............8分②设()624410g t t t ⨯=+,则()6516102g t t t ⨯'=-,令()0g t '=,解得t =当(t ∈时,()0g t '<,()g t 是减函数;当()t ∈时,()()0,g t g t '>是增函数.从而,当t =()g t 有极小值,也是最小值,所以()min 300g t =,此时()min f t =答:当t =l 的长度最短,最短长度为...............12分 考点:导数及其应用.KS5U21.(本小题满分12分)已知定义为R 的函数()f x 满足下列条件:①对任意的实数,x y 都有:()()()1f x y f x f y +=+-;②当0x >时,()1f x >.(1)求()0f ;(2)求证:()f x 在R 上为增函数;(3)若()67,3f a =≤-,关于x 的不等式()()223f ax f x x -+-<对任意[)1,x ∈-+∞恒成立,求实数a 的取值范围.【答案】(1)()01f =;(2)证明见解析;(3)(]5,3--.(3)由已知条件有:()()()22221f ax f x x f ax x x -+-=-+-+⇒()2213f ax x x -+-+<⇒()2122f x a x ⎡⎤-++-<⎣⎦,又()()()11f n nf n =--⇒()12f =⇒()()2121f x a x f ⎡⎤-++-<⎣⎦⇒()2130x a x -++>在[)1,x ∈-+∞上恒成立,令()()213g x x a x =-++,即()min 0g x >成立即可.然后对12a +取值进行分类讨论可得:实数a 的取值范围是(]5,3--.(3)由已知条件有:()()()22221f ax f x xf ax x x -+-=-+-+, 故原不等式可化为:()2213f ax x x -+-+<,即()2122f x a x ⎡⎤-++-<⎣⎦,而当*n N ∈时,()()()()()()()()()1112212331311f n f n f f n f f n f nf n =-+-=-+-=-+-==--L ,所以()()6615f f =-,所以()12f =,故不等式可化为()()2121f x a x f ⎡⎤-++-<⎣⎦,由(2)可知()f x 在R 上为增函数,所以()2121x a x -++-<,即()2130x a x -++>在[)1,x ∈-+∞上恒成立, 令()()213g x x a x =-++,即()min 0g x >成立即可. ①当112a +<-,即3a <-时,()g x 在[)1,x ∈-+∞上单调递增, 则()()()min 11130g x g a =-=+++>解得5a >-,所以53a -<<-, ②当112a +≥-即3a ≥-时,有()()2min 111130222a a a g x g a +++⎛⎫⎛⎫==-++> ⎪ ⎪⎝⎭⎝⎭g解得11a -<<,而13-<-,所以31a -≤<,综上,实数a 的取值范围是(]5,3--......................12分考点:导数及其应用.【方法点晴】本题考查导数与函数单调性的关系、不等式的证明与恒成立问题,以及逻辑思维能力、等价转化能力、运算求解能力、分类讨论的思想与转化思想. 利用导数处理不等式问题.在解答题中主要体现为不等式的证明与不等式的恒成立问题.常规的解决方法是首先等价转化不等式,然后构造新函数,利用导数研究新函数的单调性和最值来解决,当然要注意分类讨论思想的应用.22.(本小题满分12分)已知函数()ln x m f x e x +=-.(1)设1x =是函数()f x 的极值点,求m 并讨论()f x 的单调性;(2)设0x x =是函数()f x 的极值点,且()0f x ≥恒成立,求m 的取值范围(其中常数a 满足ln 1a a =).【答案】(1)1m =-,()f x 在()0,1单调递减,在()1,+∞单调递增;(2)[)ln ,a a --+∞.试题解析:(1)()()1,0x mf x e x x+'=->,因为1x =是函数()f x 的极值点, 所以()1110m f e +'=-=,所以1m =-,所以()11x f x e x-'=-.................2分 当01x <<时,1101,1x e x-<<-<-,所以()0f x '<, 当1x >时,111,10x e x ->-<-<,所以()0f x '>, 所以()f x 在()0,1单调递减,在()1,+∞单调递增............................5分(2)()()1,0x m f x e x x +'=->,设()1x m g x e x +=-,则()210x m g x e x+'=+>, 所以()g x 在()0,+∞单调递增,即()f x '在()0,+∞单调递增.由于0x x =是函数()f x 的极值点,所以0x x =是()0f x '=在()0,+∞的唯一零点, 所以00001,ln x m e x m x x +=+=-.............................6分 由于00x x <<时,()()00f x f x ''<=;当0x x >时,()()00f x f x ''>=,所以函数()f x 在()00,x 单调递减,在()0,x +∞单调递增.....................8分 且函数()f x 在0x x =处取得最小值,所以()()000001ln x m f x f x e x x m x +≥=-=++,因为()0f x ≥恒成立,所以0010x m x ++≥.....................9分 ∴00001ln x m x x x +≥-=+,即001ln x x ≥. 又因为ln 1a a =,故可解得0x a ≤...............................11分所以00,ln ln x a x a -≥--≥-,所以00ln ln m x x a a =--≥--,即m 的取值范围是[)ln ,a a --+∞..................................12分 考点:导数及其应用.KS5U【方法点晴】本题考查导数与函数单调性的关系、不等式的证明与恒成立问题,以及逻辑思维能力、等价转化能力、运算求解能力、分类讨论的思想与转化思想. 利用导数处理不等式问题.在解答题中主要体现为不等式的证明与不等式的恒成立问题.常规的解决方法是首先等价转化不等式,然后构造新函数,利用导数研究新函数的单调性和最值来解决.。
2014届华附、省实、深中、广雅高三年级四校联考 (理数)

2014届华附、省实、深中、广雅高三年级四校联考 (理数)本试卷分选择题和非选择题两部分,共4页,满分150分,考试用时120分钟.注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的校名、姓名、考号、座位号等相关信息填写在答题卡指定区域内.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其它答案;不能答在试卷上.3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内的相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液.不按以上要求作答的答案无效.4.考生必须保持答题卡的整洁.第一部分选择题一、选择题:本大题共8小题,每小题5分,满分40分.在每小题给出的四个选项中,只有一项符合要求.1.若集合{}21,A m =,{}2,4B =,则“2m =”是“{}4A B = ”的( )A. 充要条件B. 既不充分也不必要条件C. 必要不充分条件D. 充分不必要条件 2. 若0.52a =,πlog 3b =,22πlog sin5c =,则( ) A .b c a >>B . b a c >>C .a b c >>D .c a b >>3.函数()sin()(0,0)f x A x A ωθω=+>>的部分图象如图所示,则()f x =()A π)6x -B. π)3x -C.π)3x +D. π)6x +4.已知圆22:1O x y +=及以下3个函数:①3()f x x =;②()tan f x x =③()sin .f x x x =其中图像能等分圆C 面积的函数有( )A .3个 B. 2个 C. 1 个 D. 0个 5. 12(x 展开式中的常数项为( ) A .220 B .220- C .1320 D .1320-6.执行如图所示的程序框图,输出的S 值为( ) A .2- B. 1- C. 0 D. 17. 已知数列{}n a 满足:11,7a =对于任意的n *∈N ,17(1),2n n n a a a +=-则14131314a a -=( )A .27- B. 27C. 37-D. 378.点O 是平面α内的定点,点(A 与点O 不同)的“对偶点”A '是指:点A '在射线OA 上且1OA OA '⋅=厘米2.若平面α内不同四点,,,P Q R S 在某不过点O 的直线l 上,则它们相应的“对偶点”,,,P Q R S ''''在( )A .一个过点O 的圆上B .一个不过点O 的圆上C .一条过点O 的直线上D .一条不过点O 的直线上第二部分非选择题二、填空题:本大题共6小题,每小题5分,共30分.9. 某学校高一、高二、高三年级的学生人数之比为334::,现用分层抽样的方法从该校高中三个年级的学生中抽取容量为50的样本,则应从高二年级抽取 名学生.10. 若向量(1,2),(4,)BA CA x == ,且BA 与CA的夹角为0,︒则BC = .11. 某几何体的三视图如图所示,其中正(主)视图与侧(左)视图的边界均为直角三 角形,俯视图的边界为直角梯形,则该 几何体的体积为 .12. 已知直线:l x p =过抛物线2:4C y x =的焦点,直线l 与抛物线C 围成的平面区域的面积为,S 则p =______ ,S = .13. 已知函数1,01()12,12x x x f x x +≤<⎧⎪=⎨-≥⎪⎩,若0a b >≥,且()()f a f b =,则()bf a 的取值范围是 ._ 俯视图_ 侧视图_ 正视图选做题(请考生在以下两小题中任选一题做答,若两小题都做,则按第14题记分).14.(几何证明选讲选做题) 如图,过点C 作ABC ∆的外接圆O 的切线交BA 的延长线 于点D .若CD = 2AB AC ==,则BC = .15.(坐标系与参数方程选做题) 在极坐标系O ρθ(0,02π)ρθ≥≤<中,点(2,)2A π关于直线:cos 1l ρθ=的对称点的极坐标为 . 三、解答题:本大题共6小题,共80分,解答应写出必要的文字说明、证明过程或演算步骤. 16.(本小题满分12分)在ABC ∆中,三个内角,,A B C 所对的边分别为,a ,.b c222)2b c a bc +-=,2B A =. (1) 求tan A ;(2) 设ππ(2sin(),1),(sin(),1),44m B n B =-=+-求m n ⋅的值.17.(本小题满分12分)盒子中装有四张大小形状均相同的卡片,卡片上分别标有数i,i,2,2,--其中i 是虚数单位.称“从盒中随机抽取一张,记下卡片上的数后并放回”为一次试验(设每次试验的结果互不影响). (1)求事件A “在一次试验中,得到的数为虚数”的概率()P A 与事件B “在四次试验中,至少有两次得到虚数” 的概率()P B ;(2)在两次试验中,记两次得到的数分别为,a b ,求随机变 量a b ξ=⋅的分布列与数学期望.E ξDH PGFED CB18.(本小题满分14分)如图,四边形ABCD 是正方形,EA ⊥平面ABCD , EA ∥PD,2AD PD EA ==,F ,G , H 分别 为PB ,EB ,PC 的中点. (1)求证:FG ∥平面PED ;(2)求平面FGH 与平面PBC 所成锐二面角的大小.19. (本小题满分14分)已知数列{}n a 的前n 项和为,n S 记11()2(2),.n n n n f n a S n S a n *++=-+∈N (1)若数列{}n a 是首项与公差均为1的等差数列, 求(2014)f ; (2)若121,2,a a ==且数列{}{}212,n n a a -均是公比为4的等比数列,求证:对任意正整数n ,()0.f n ≥20. (本小题满分14分)在平面直角坐标系中,已知点F及直线:0l x y +=,曲线1C 是满足下列两个条件的动点(,)P x y的轨迹:①,PF =其中d 是P 到直线l 的距离;②00.225x y x y >⎧⎪>⎨⎪+<⎩(1) 求曲线1C 的方程;(2) 若存在直线m 与曲线1C 、椭圆22222:1(0)x y C a b a b+=>>均相切于同一点,求椭圆2C 离心率e的取值范围.21. (本小题满分14分)已知函数22()en nxx x a f x --=,其中,,N R n a *∈∈e 是自然对数的底数. (1)求函数12()()()g x f x f x =-的零点;(2)若对任意,N n *∈()n f x 均有两个极值点,一个在区间(1,4)内,另一个在区间[]1,4外,求a 的取值范围;(3)已知,,,N k m k m *∈<且函数()k f x 在R 上是单调函数,探究函数()m f x 的单调性.2014届华附、省实、深中、广雅高三年级四校联考 (理数)一、选择题: 1~4 D C B B 5~8 B C D A 1.【解析】{}244 2.A B m m =⇔=⇔=±2. 【解析】0.50221,>= πππ0log 1log 3log π1,=<<=222πlog sinlog 10.5<=3.【解析】由图知()f x 在5π12x =,且最小正周期T 满足312543ππ+=T故A =32π3π,2,4ωω⨯==5π)12θ⨯+=5πsin()1,6θ+= 5πππ2π,2π,623k k k θθ+=+=-∈Z .所以π()(2).3x f x -=或由5(π)12f =π()(2).3x f x -=4.【解析】圆O 关于原点O 对称. 函数3y x =与函数tan y x =是定义域上的奇函数,其图像关于原点对称, 能等分圆O 面积;而sin y x x =是R 上的偶函数,其图像关于y 轴对称,且当01x <≤时sin 0,x x >不能等分圆O 面积5. 【解析】12(x 展开式中的通项为41212311212((1)(0,1,2,,12).kk k k k k k T C x C x k --+==-= 1k T +为常数项的充要条件是9.k =常数项91012220.T C =-=- 6.【解析】0,11,01,1T S T S T S ==⇒==⇒==-0,11,0.T S T S ⇒==-⇒=-=7. 【解析】11,7a =234716373467613,,,.277727772777a a a =⨯⨯==⨯⨯==⨯⨯= 由数学归纳法可证明:当n 为大于1的奇数时, 67n a =;当n 为正偶数时, 3.7n a =故14131314a a -=3.78.【解析】过O 作与直线l 垂直的直线,m 以O 为原点,直线m 为x 轴,单位为1厘米,建立平面直角平面坐标系. 设直线1:(0)l x a a =≠,01(,)P y a是直线l 上任意一点,它的“对偶点”为(,)P x y ',则存在0,λ>使得O P O Pλ'= ,即01,x y y a λλ==,又01xOP OP OP OP y y a ''⋅=⋅=+= ,消去λ,得220x y ax +-=.故,,,P Q R S ''''在过点O 的圆22:0x y ax +-=上.二、填空题: 9. 15 10. (3,6)-- 11. 8 12. 81,.3 13. 3,24⎡⎫⎪⎢⎣⎭14. 15. ).4π 9. 【解析】根据分层抽样的方法步骤,按照一定比例抽取,样本容量为50,那么根据题意得:A从高三一共可以抽取人数为:1510350=⨯. 10. 【解析】由BA 与CA的夹角为0,︒知8x =,(3,6).BC BA AC BA CA =+=-=--11. 【解析】由三视图可知该几何体是一个四棱锥,根据“正侧等高,正俯等长,侧俯等宽”的规则,其体积为11(24)428.32V =⨯+⨯⨯= 12. 【解析】抛物线2:4C y x =的焦点为(1,0)F ,知1p =.311202824.33S dx x ==⨯=⎰ 13. 【解析】如图,()f x 在[)0,1,[)1,+∞上均单调递增, 由0a b >≥及()f a f =11.2a b ≥>≥()()(1)b f a bf b b b ⋅==+的取值范围113(1),(11),2224⎡⎫⎡⎫++=⎪⎪⎢⎢⎣⎭⎣⎭14. 【解析】由2()CD DA DB DA DA AB =⨯=⨯+知2230DA DA +-=, 解得1, 3.DA DB ==由DCB DAC ∆∆~得AC CD BC BD =,即AC BDBC CD⨯==15. 【解析】如图,在极坐标系(0,02π)O ρθρθ≥≤<中,设(2,)2A π关于直线:cos 1l ρθ=的对称点为(,),B ρθ则2OA AB ==,且.OA AB ⊥ 从而π,4OB AOB =∠=即πππ.244ρθ==-= 三、解答题:16.解: (1)222)2,b c a bc +-=222c os .2b c a A bc +-∴== ………………2分0π,A << sin A ∴==……… 4分 s i n t a n c o s AA A ==………6分 (2)(法一)ππ(2sin(),1),(sin(),1),44m B n B =-=+-ππ2sin()sin()144m n B B ∴⋅=-+-… 7分2sin )(cos sin )122BB B B =⨯-⨯+-22cos sin 1B B =-- 22sin .B =- …… 10分 2B A = , sin sin 22sin cos 3B A A A ∴===16.9m n ⋅=- …………12分 (2)(法二)ππ(2sin(),1),(sin(),1),44m B n B =-=+-ππ2sin()sin()144m n B B ∴⋅=-+-… 7分πππ2cos ()sin()1244B B ⎡⎤=--+-⎢⎥⎣⎦ππ2cos()sin()144B B =++-πsin(2)12B =+-cos21B =-22sin .B =- (10)分2B A = , sin sin 22sin cos 3B A A A ∴===16.9m n ⋅=- …………12分 (2)(法三) 2B A = ,sin sin 22sin cos 3B A A A ∴===21cos cos 212sin .3B A A ==-=-………………………9分π4(2sin(),1)sin ),1)(,1),43m B B B ∴=-=-=- (10)分π(sin(),1)cos ),1)1).4n B B B =+-=+-=-……11分44161.369m n ∴⋅=-⨯-=-………………………12分17.解:(1)21()42P A ==, ……………………………………………………………2分004113441111511()1()1()()()()1.22221616P B P B C C ⎡⎤=-=-+=-=⎢⎥⎣⎦ ………… 5分(2),,a b ξ的可能取值如下左表所示:i - i 2- 2 i - 11 2 2 i 1 1 2 2 2- 2 2 4 4 2 2244……………………………………………………………6分由表可知:418141(1),(2),(4).164162164P =P =P =ξξξ====== ………………9分 所以随机变量X 的分布列为(如上右表) …………………………………… 10分所以1119()124.4244E =ξ⨯+⨯+⨯= ………………………………………………12分 18. (1)证明:F ,G 分别为PB ,BE 的中点,FG ∴∥PE . ……………1分又FG ⊄平面PED ,PE ⊂平面PED ,…………3分 FG ∴∥平面PED (2)解:EA ⊥ 平面ABCD ,EA PD ,PD ∴⊥平面.ABCD,AD CD ⊂ 平面,ABCD PD AD ∴⊥,PD CD ⊥. 四边形ABCD AD CD ∴⊥. 以D 为原点,分别以直线,,DA DC DP 为x 轴, y 轴,z 轴abξQ P H GF E D CBA建立如图所示的空间直角坐标系,设 1.EA = ………………………7分2AD PD EA == , D ∴()0,0,0,P ()0,0,2,A ()2,0,0,C ()0,2,0,B ()2,2,0,(2,0,1)E , (2,2,2)PB =- ,(0,2,2)PC =-. F ,G , H 分别为PB ,EB ,PC 的中点,F ∴()1,1,1,G 1(2,1,)2,H (0,1,1),1(1,0,)2GF =- ,1(2,0,).2GH =- …… ………8分(法一)设1111(,,)x y z =n 为平面FGH 的一个法向量,则1100GF GH ⎧⋅=⎪⎨⋅=⎪⎩n n ,即11111021202x z x z ⎧-+=⎪⎪⎨⎪-+=⎪⎩, 令11y =,得1(0,1,0)=n . …10分 设2222(,,)x y z =n 为平面PBC 的一个法向量,则220PB PC ⎧⋅=⎪⎨⋅=⎪⎩n n , 即222222220220x y z y z +-=⎧⎨-=⎩,令21z =,得2(0,1,1)=n . …… …………………12分所以12cos ,n n =1212⋅⋅n n n n=2. ……………………………………………13分 所以平面FGH 与平面PBC 所成锐二面角的大小为π4(或45︒). …………14分 (法二) (0,1,1)(2,0,0)0DH BC ⋅=⋅-= ,(0,1,1)(0,2,2)0DH PC ⋅=⋅-=,DH ∴是平面PBC 一个法向量. …… ……………… …………………10分 (0,2,0)(1,0,0)0DC FH ⋅=⋅-= ,1(0,2,0)(1,0,)02DC FG ⋅=⋅-= ,DC ∴是平面平面FGH 一个法向量. …… ……………… …………………12分cos ,2DH DC DH DC DH DC ⋅===⋅ …………………13分 ∴平面FGH 与平面PBC 所成锐二面角的大小为π4(或45︒).……14分(法三) 延长AE 到,Q 使得,AE EQ =连,.PQ BQ2PD EA AQ == ,EA PD ,∴四边形ADPQ 是平行四边形,.PQ AD 四边形ABCD 是正方形,,.BC AD PQ BC ∴ F ,H 分别为PB ,PC 的中点,,.FH BC FH PQ ∴FH ⊄平面PED ,PQ ⊂平面PED , FH ∴ 平面PED . ………7分,,FH FG F FH FG =⊂ 平面,ADPQ ∴平面FGH 平面.ADPQ ………9分故平面FGH 与平面PBC 所成锐二面角与二面角D PQ C --相等. … …10分,PQ CD PQ PD ⊥⊥ ,,,PD CD D PD DC =⊂ 平面,PDC PQ ∴⊥平面.PDCPC ⊂ 平面,,PDC PQ PC ∴⊥DPC ∠是二面角D PQ C --的平面角. …12分,,45.AD PD AD PD DPC =⊥∴∠=︒ … …………13分∴平面FGH 与平面PBC 所成锐二面角的大小为π4(或45︒). … …………14分19. 解:(1) 数列{}n a 是首项与公差均为1的等差数列, ……………………1分∴,N n *∀∈1(1),1,.2n n n n n a n a n S ++==+=………………………………3分 11()2(2)n n n n f n a S n S a ++=-+(1)(1)2(1)2(1)22n n n n n n n ++⎡⎤=+⨯-⨯++⎢⎥⎣⎦22(1)(1)0.n n n n =+-+= 故(2014)0.f = …………………………6分(2)由题意,n *∀∈N 12221142,n n n a ---=⨯=…………7分 1212242.n n n a --=⨯= ………8分故12.n n a -= ………9分 ,n *∀∈N 1122,21,12nnn n n a S +-===--11()2(2)n n n n f n a S n S a ++=-+1112(21)(222)2(232)2.n n n n n n n n n +++=---+=--+ ……………………10分(法一)当1n =时,(1)0f =; ……………………………11分 当2n ≥时,[]1124(11)41(1)4n n n n +-=⨯+≥+-=, ……………………………12分1()2(232)22(432)22(2)220.n n n n f n n n n n n n n n +=--+≥--+=-+≥>………13分故对任意正整数n ,()0.f n > ………………………………………………………14分(法二),n *∀∈N (1)()f n f n +-1212(235)222(232)2n n n n n n n n +++⎡⎤⎡⎤=--++---+⎣⎦⎣⎦2122(235)(232)2n n n n n ++⎡⎤=-----+⎣⎦2(6238) 2.n n n =⨯--+ ……………………………11分012(11)1n n n n C C n =+≥+=+ ,,(1)()2(6638)22(32)2220N n n n n f n f n n n n *∴∀∈+-≥+--+=-+≥+>,数列{}()f n 是递增数列. ………………………………………………………12分2(1)2(232)20,f =--+= ………13分 ,()0.N n f n *∴∀∈≥ …………14分20. 解:(1)PF ==d =…2分由①,PF =得:2222)42)2x y x y x y xy x y +-++=++-++,即 1.xy =…4分将1xy =代入②得:1150,0,2x x x x >>+<,解得: 12.2x << 所以曲线1C 的方程为:1y x = 1(2).2x << ………………………………6分(2)(解法一)由题意,直线m 与曲线1C 相切,设切点为1(,)M t t , 12.2t <<则直线m 的方程为2111()()()y x t x t x tt xt '-=⨯-=--=,即212.y x t t=-+ ……………7分 将212y x t t=-+代入椭圆2C 的方程222222b x a y a b +=,并整理得: 242222222()4(4)0.b t a x a tx a b t t +-+-=M 由题意,直线m 与椭圆2C 相切于点1(,)M t t ,则4222422222242224164()(4)4(4)0a t a b t a b t t a b t a t b t ∆=-+-=-+=,即22424.a b t t += ……9分又222211,t a b t += 即242222.b t a a b t += 联解得:22222,2.b a t t == ………10分 由12,2t <<及22a b >得1 2.t <<故2222411a b e a t -==-, ………………12分 得2150,16e <<又01,e <<故04e <<所以椭圆2C 离心率e的取值范围是(0,4……14分 (2)(法二)设直线m 与曲线111:(2)2C y x x =<<、椭圆22222:1(0)x y C a b a b +=>> 均相切于同一点1(,),M t t 则22221 1.t a b t +=…………7分 由1y x =知21y x'=-;由22221(0)x y y a b +=>知y =2222.xb x y a y -'===- 故2224221,.1b t a b t t a t-=-= …………9分 联解222222411t a b t a b t ⎧+=⎪⎨⎪=⎩,得22222,2.b a t t ==…………10分11由12,2t <<及22a b >得1 2.t <<故2222411a b e a t -==-, ……………12分 得2150,16e <<又01,e <<故0e <<所以椭圆2C 离心率e的取值范围是(0, ……14分 21. 解:(1)222122222(2)(e 1)()()()e e ex x x xx x a x x a x x a g x f x f x -------=-=-=,44a ∆=+ ① 当1a <-时,0,∆<函数()g x 有1个零点:10.x = ………………………1分 ② 当1a =-时,0,∆=函数()g x 有2个零点:120, 1.x x == ……………………2分 ③ 当0a =时,0,∆>函数()g x 有两个零点:120, 2.x x == ……………………3分④ 当1,0a a >-≠时,0,∆>函数()g x有三个零点:1230,11x x x === …4分(2)222(22)e (2)e 2(1)2().e e nx nx n nx nxx n x x a nx n x a n f x -----+++⋅-'== …………5分设2()2(1)2n g x nx n x a n =-+++⋅-,()n g x 的图像是开口向下的抛物线. 由题意对任意,N n *∈()0n g x =有两个不等实数根12,x x ,且()[]121,4,1,4.x x ∈∉则对任意,N n *∈(1)(4)0n n g g <,即6(1)(8)0n a n a n ⎡⎤⋅+⋅⋅--<⎢⎥⎣⎦, ………………7分又任意,N n *∈68n-关于n 递增,681n ->-,故min 61(8),186 2.a a n -<<--<<-=所以a 的取值范围是()1,2.- ……………………………………………9分(3)由(2)知, 存在,R x ∈22(1)2()0e k kxkx k x a k f x -+++⋅-'=<,又函数()k f x 在R 上是单调函数,故函数()k f x 在R 上是单调减函数, ……………………………………10分 从而2224(1)4(2)4(1)0,k k k ka k a k ∆=++-=++≤即21(1).a k ≤-+……11分 所以2222222214()4(1)41(1).m k m m m a m m k k -⎡⎤∆=++≤+-+=⎢⎥⎣⎦ 由,,,N k m k m *∈<知0.m ∆< …………………………………………13分即对任意,R x ∈22(1)2()0e k kxkx k x a k f x -+++⋅-'=<故函数()m f x 在R 上是减函数. ………14分。
(理综参考答案)2014届华南师大附中高三综合测试

2014届华南师大附中高三综合测试(一)理科综合参考答案生物部分LB 2.D 3a 4.C 弓 4 fB 24«AC 25^D26,(0有以核厲海界限的细胞核(2》主动运辑;协助扩规細胞质基质和线粒体厂AT 上ADP+Pi^f ■能H (3) 降低活牝能更加显著(4) 氨基酸的种类、敕目、排列顺序不同』以及狀链的空间站构(:和数量)不圜 27* (1) a ;绿 (2) 丙酮酸*内朧(3) 类菱体垛疊形成基粒]内膜向内折叠形成蜡 (4) 温度;温度影响壽的活性 (5) 如右图 28.(1)彻底氧化分解有机物,释放能量”⑵减少匸酒精;1/4.(3) 叶绿索;根削胞峽氧,无氧呼吸生咸的酒精證害细腕,导致植物根细胞死亡(4) 淹水时KM 对根有氧呼吸谨睾下降有减毀作用,其中30^1 • 1/的酬压溶裁作用数果最好. 29.■<-)方法与步軌 加酶饲料]尊盘的普通饲祐 称畫(-)结果与绪论’添加植酸酶的饲料能促进协鱼幼体的生长 (三〉问题与时论(1)成体生怏缓慢.实验效果不明显^⑵ 水温、盐度和溶#m 寻-..'(3)植酸醯濯化植巖盐分解得到的磷酸盐,鮭胡鱼主动吸收后可用于合成瞬脂等犹合物*用于构成细胞的绪构光會fl 1用强化学部分♦ 3®擇超* 7.B 乱C 9A 10.D 1LB 12,C 22.AD23,BC 3ft.3LCB SMSn+lOHNOj^SnCNOjh+NlWOj+aH^O ©snOj+ac^M^acoi <2) (DPb. SGi ; PbSg PbS ®6 ©COaOjHjO 32.(l)3Cu^8tr+2NQ 3'i -3Cu 1++2NO^+4HiO (CuMH^+NOj'-Cu^+Nth^+^O) Au Pt.。
應瘠涯中的F 尹转化为F 尹 产物为水.不产生杂质*(3廉发诙缩、冷却结晶、过忍 ⑷A1(或铝单厨.(5)12^33.⑴ FcjO +,⑺分) ⑵ SFe^+MnO^+Slf^Fe^+Mn^HjO*<3)防止玻璃曾呻的空肌和CO 在加热时郵炸"物理部分• 选择屋 1 13. C 14.C 1516 A 灯上D 1S.AC 19«AD 20,BD 2L BC♦非选择题t34.r(1)(3)对静聘;C 水平方向T / = V ;sin30* hL 竖亶方附 N 2-mg^N[ COS SO" »又】珂而由题意*扎二枫 应该满足:f m ^f 解得:is —«0J929①小车的总质倉,所挂钩码的重力:® I )在质量不变的条件下*加速度与外力成正比:.U )平術摩擦力r挂上钩码、 无滑執 匀速C 直线)运动"m> (»35,0)小球的愛力图;斟劈的受力图,■ (2)对小球;「水平方向T ^311)30^ r sin30*L 竖宜方向;?7i C0s3O B ^rcQs3O*=mg3&(1)分离前,由牛顿第二定律乂叫十叫 1 + 2由于分离前系统的加逋度是一定值.因此厶於两物块在未分离前做加速度^4m/s 2的%加速直疑运动⑵分离时,A. E 间没有拥互柞用力.但仍有相同加逸度.易徐' A 二乞叫 m 2秋日里,阳光并不刺眼,天空是一碧如洗的蓝,点缀着飘逸的流云。
华南师大附中2007—2008学年度高三综合测试(二)数学试题(理科)
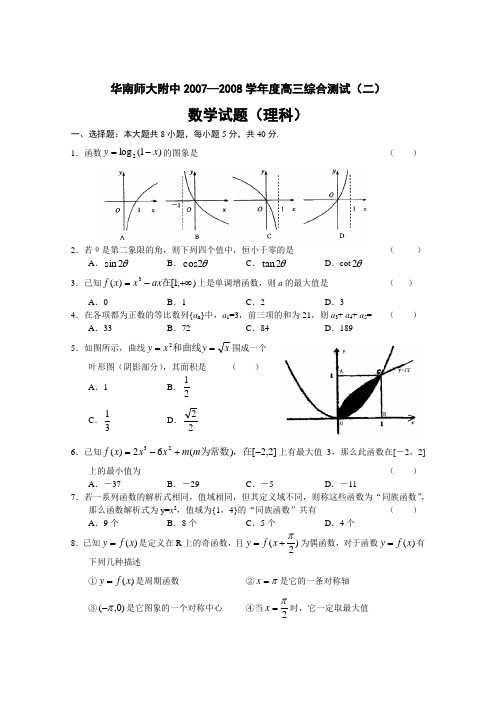
华南师大附中2007—2008学年度高三综合测试(二)数学试题(理科)一、选择题:本大题共8小题,每小题5分,共40分. 1.函数)1(log 2x y -=的图象是( )2.若θ是第二象限的角,则下列四个值中,恒小于零的是( )A .θ2sinB .θ2cosC .θ2tanD .cot θ23.已知),1[)(3+∞-=在ax x x f 上是单调增函数,则a 的最大值是( )A .0B .1C .2D .34.在各项都为正数的等比数列{a n }中,a 1=3,前三项的和为21,则a 3+ a 4+ a 5= ( )A .33B .72C .84D .1895.如图所示,曲线x y x y ==和曲线2围成一个叶形图(阴影部分),其面积是 ( )A .1B .21C .31 D .22 6.已知]2,2[)(62)(23-+-=,在为常数m m x x x f 上有最大值3,那么此函数在[-2,2]上的最小值为 ( ) A .-37 B .-29 C .-5 D .-117.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为y=x 2,值域为{1,4}的“同族函数”共有 ( ) A .9个 B .8个 C .5个 D .4个 8.已知)(x f y =是定义在R 上的奇函数,且)2(π+=x f y 为偶函数,对于函数)(x f y =有下列几种描述 ①)(x f y =是周期函数②π=x 是它的一条对称轴③)0,(π-是它图象的一个对称中心④当2π=x 时,它一定取最大值其中描述正确的是 ( )A .①②B .①③C .②④D .②③ 二、填空题:本大题共6小题,每小题5分,共30分.9.已知等差数列{a n }前17项和S 17=51,则a 7+ a 11= 10.若==⎰a dx x a,则902 ;⎰--2224dx x .11.在4和67之间插入一个n 项的等差数列后,仍是一个等差数列,且新等差数列的所有项之和等于781,则n 的值为 12.已知函数)(x f 的定义域)1,0[,则函数)(cos x f 的定义域是13.在△ABC 中,a ,b ,c 分别为∠A 、∠B 、∠C 、的对边,若a ,b ,c 成等差数列,54sin =B ,且△ABC 的面积为23,则b= 14.规定一种运算:⎩⎨⎧>≤=⊗ba b ba ab a ,,,例如:1⊗2=1,3⊗2=2,则函数xx x f cos sin )(⊗=的值域为 .三、解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分12分)已知函数⎪⎪⎩⎪⎪⎨⎧<+-->++=)0(4)0(4)(22x x x x x xx x x f(Ⅰ)求证:函数)(x f 是偶函数;(Ⅱ)判断函数)(x f 分别在区间),2[],2,0(+∞上的单调性,并加以证明.16.(本小题满分12分)已知函数)0(cos sin )(>++=b x c x b a x f 其中的图象经过点A (0,1)、B (1,2π). 当]2,0[π∈x 时,)(x f 的最大值为.122-(Ⅰ)求)(x f 的解析式;(Ⅱ)由x y sin =的图象经过怎样的变换可得到)(x f 的图象.17.(本小题满分14分)在数列.*,134,2}{11N n n a a a a n n n ∈+-==+中, (Ⅰ)证明数列}{n a n -是等比数列; (Ⅱ)求数列{n a }的前n 项和S n .18.(本小题满分14分)如图,四边 形ABCD 是一个边长为100米的正方形地皮,其中ATPS 是一半径为90米的扇形小山,其余部分都是平地,P 是弧TS 上一点,现有一位开发商想在平地上建造一个两边落在BC 与CD 上的长方形停车场PQCR ,求长方形停车场PQCR 面积的最大值. 19.(本小题满分14分) 已知b>-1,c>0,函数b x x f +=)(的图象与函数c bx x x g ++=2)(的图象相切. (Ⅰ)设);()(c c b ϕϕ,求=(Ⅱ)是否存在常数c ,使得函数),()()()(+∞-∞=在x g x f x H 内有极值点?若存在,求出c 的取值范围;若不存在,请说明理由.20.(本小题满分14分)已知函数)(x f y =,若存在000)(x x f x =,使得,则0x 称是函数)(x f y =的一个不动点,设.7232)(-+-=x x x f(Ⅰ)求函数)(x f y =的不动点;(Ⅱ)对(Ⅰ)中的二个不动点a 、b (假设a>b ),求使bx ax k b x f a x f --⋅=--)()(恒成立的常数k 的值;(Ⅲ)对由a 1=1,a n =)(1-n a f 定义的数列{a n },求其通项公式a n .华南师大附中2007—2008学年度高三综合测试(二)数学试题(理科)参考答案一、选择题1.C 解析:x y x y 22log )1(log =-=可先作关于y 轴的对称图形,可得)(log 2x y -=的图象,再向右平移一个单位,即可得)]1([log 2--=x y 的图象,即)1(log 2x y -=的图 象,故选C.2.A 解析:由题可知ππθππππθππ2424222+<<++<<+k k k k ,所以,故选A.3.D 解析:),1[03)(3)(22+∞≥-='-='在,可已知可得a x x f a x x f 上恒成立,即23x a ≤恒成立,故选D.4.C 解析:令公比为q ,由a 1=3,前三项的和为21可得q 2+q -6=0,各项都为正数,所以q=2,所以84)(3212543=++=++a a a q a a a ,故选C.5.C 解析:由图可知,阴影部分面积31)(2112=-=⎰⎰xdx dx x S . 6.A 解析:,可得,令2,00)(126)(212==='-='x x x f x x x f 故在[-2,2]上最大值为3)0(==m f ,所以最小值为37)2(-=-f ,故选A.7.A 解析:y 值对应1,x 可对应±1,y 值对应4,x 可对应±2,故定义域共有{1,2},{1,-2},{-1,2},{-1,-2},{1,-1,2},{1,-1,-2},{1,2,-2},{-1,2,-2},{-,1,-2,2}共9种情况. 8.B 可采取特例法,例x y x y sin sin -==,皆为满足条件的函数,一一验证可知选B. 二、填空题:9.答案:6 解析:∵512)(172)(1711717117=+=+=a a a a S ∴a 7+a 11=6.10.答案a=3、2π 解析:⎰⎰-=+-==222220302449|31y x dx x x dx x aa表示圆,的上半圆 面积,故为2π.11.答案:20 解析:由数列相关知识可知.7812)674)(2(=++n12.答案:)](22,2()2,22[z k k k k k ∈+⋃-ππππππ解析:由题可知 1cos 0<≤x ,故定义域为)](22,2()2,22[z k k k k k ∈+⋃-ππππππ13.答案:2 解析:由a ,b ,c 成等差数列知b c a 2=+①,由41523sin 21=⇒=ac B ac ②,由c>b>a 知角B 为锐角,53253cos 222=-+⇒=ac b c a B ③,联立①②③得b=2. 14.答案:]22,1[- 解析:b a ⊗为a 、b 的最小值. 故可得)(x f 为图象的实线曲线. 故当41)(min ππ=-==x x f x ,当时,时,.22)(max =x f 三、解答题: 15.解:(Ⅰ)由题可知函数定义域关于原点对称.当00<->x x 时,, 则xx x x x x x f x x x x f 4)(4)()()(,4)(222++=-+---=-++=, ∴).()(x f x f -=当,00>-<x x 时,则xx x x x x x f x x x x f 4)(4)()()(,4)(222+--=-+-+-=-+--=, ∴).()(x f x f -=综上所述,对于)()( 0x f x f x -=≠有,都,∴函数)(x f 是偶函数.(Ⅱ)当x>0时,144)(2++=++=xx x x x x f , 设)4()()(02121121212-⋅⋅-=->>x x x x x x x f x f x x ,则当,0)()(02;0)()(212121212<->>≥>-≥>x f x f x x x f x f x x 时,当时,∴函数]2,0()(在x f 上是减函数,函数),2[)(+∞在x f 上是增函数.(另证:当2241)(144)(0xx f x x x x x x f x -='++=++=>,时,; ∵0411********≤-⇔≥⇔≤<⇒≤<x x x x 04114042222≥-⇔≤<⇔≥⇔≥xx x x∴函数]2,0()(在x f 上是减函数,在),2[+∞上是增函数. 16.解:(Ⅰ)∵函数图象过点A (0,1)、B (2π,1) ⎩⎨⎧=+=+②①1 1b a c a ∴b=c ∴)0( )4sin(2 cos sin )(>+=++=b x b a x b x b a x f π∵当.122)(]2,0[-∈的最大值为时,x f x π∴1222-=+a b ③ 联立②③得 ⎩⎨⎧=-=21b a 1)4sin(22)(-+=πx x f(Ⅱ)①由x y sin =图象上所有点向左平移4π个单位得到)4sin()(π+=x x f 的图象②由)4sin()(π+=x x f 的图象上所有点的纵坐标变为原来的22倍,得到 )4sin(22)(π+=x x f 的图象③由)4sin(22)(π+=x x f 的图象上所有点向下平移一个单位,得到1)4sin(22)(-+=πx x f 的图象17.(1)证明:由题设1341+-=+n a a n n ,得*),(4)1(1N n n a n a n n ∈-=+-+又a 1-1=1,所以数列{a n -n}是首项为1,且公比为4的等比数列.(Ⅱ)解:由(Ⅰ)可知14-=-n n n a ,于是数列{ a n }的通项公式为.41n a n n +=-所以数列{a n }的前n 项和.2)1(314++-=n n S n n 18.分析:求停车场面积,需建立长方形的面积函数. 这里自变量的选取十分关键,通常有代数和三角两种设未知数的方法,如果设长方形PQCR 的一边长为x (不妨设PR=x ),则另一边长22)100(90100x PQ ---=,这样S PQCR =PQ ·PR=x ·(100-22)100(90x --),但该函数的最值不易求得,如果将∠BAP 作为自变量,用它可表示PQ 、PR ,再建立面积函数,则问题就容易得多,于是可求解如下;解:延长RP 交AB 于M ,设∠PAB=)900(︒<<︒αα,则AM=90.sin 90100,cos 100,sin 90,cos αααα-=-==PR PQ MP ∴)sin 90100)(cos 90100(αα--=⋅=PR PQ S PQCR .sin cos 8100)sin (cos 900010000αααα++-= 设ααsin cos +=t , ∵︒≤≤︒900α∴.21sin cos ],2,1(2-=∈t t αα .950)910(405021810090001000022+-=-⨯+-=t t t S PQCR∴当时2=t ,S PQCR 有最大值.2900014050-答:长方形停车场PQCR 面积的最大值为2900014050-平方米. 19.解:(Ⅰ)【方法一】由0)1()()(2=-+-+⇒=b c x b x x g x f ,依题设可知,△=(b+1)2-4c=0. ∵0,1>->c b .∴12)(21-===+c c b c b ϕ,即【方法二】依题设可知,12)()(=+'='b x x g x f ,即∴21bx -=为切点横坐标, 于是)21()21(b g b f -=-,化简得.4)1(2c b =+同法一得.12)(-==c c b ϕ(Ⅱ)由,)(2))(()(2232bc x c b bx x c bx x b x x H ++++=+++= 可得).(43)(22c b bx x x H +++='令,0)(4322=+++c b bx x 依题设欲使函数),()(+∞-∞在x H 内有极值点,则须满足0)14(4)3(42>+-=-=∆c c c b亦即 3232014+>-<>+-c c c c 或,解得,又34734700+>-<<∴>c c c 或,故存在常数),347()347,0(+∞+⋃-∈c ,使得函数),()(+∞-∞在x H 内有极值点. (注:若0≥∆,则应扣1分. )20.解:(Ⅰ)设函数3217-232-,)(000000=-==+=x x x x x x x f y ,,解得则的不动点为(Ⅱ)由(Ⅰ)可知2138212482172323723221,3+-⋅=--+-=+-+---+--==x x x x x x x x b a ,可知使bx ax k b x f a x f --⋅=--)()(恒成立的常数k=8.(Ⅲ)由(Ⅱ)知213821311+-=+---n n n n a a a a 可知数列213}213{11+-+-a a a a n n 是以为首项,8为公比的等比数列即以34-为首项,8为公比的等比数列. 则1834213-⋅-=+-n n na a 11118438298341834213----⋅+⋅-=⋅+⋅⋅-=n n n n n a .。
华师附中2014届高三热身试题

华师附中2014届高三热身试题语文一、本大题4小題,每小埋3分,共12分。
1.下列词语中加点的字,毎对读音都不相同的一组是A.创.冰/创.平水泵./蚌.壳剥.皮/褒.扬B.恸.哭/恫.吓陡峭./讥诮.中.肯/中.意C.玷.污/粘.连复辟./开辟.焚膏继晷./咎.由自取D.情愫./塑.料肄.业/防疫.强.弩之末/强.词守理2.下面语段中画线的词语,使用不恰当的一项是时至今日,仍难掩戾气,连恩音内心积蓄着何等极端的负面情绪,其“杀医逻辑”背后是何等严重的病态人格。
更可怕的是,他在营造一种正义幻觉,把自己打扮成除暴安良、瘅恶彰善的“英雄”。
在自以为是的错觉支配下,他接受釆访时始终安之若素,不时伴以夸张的肢体动作和怪弃的冷笑。
A.戾气B.瘅恶彰善C.自以为是D.安之若素3.下列句子中,没有语病的一项是A. 作为全国最高权力机关和最髙参政议政机构,和两会闭幕后的总理记者会一样,愈来愈成为中国新闻发布的渠道和政府最高层释放政策信息的窗口。
B. 余额宝是电子商务巨头阿里巴巴去年6月发行的一款互联网货币基金,到今年2月底,其投资者总人数已经突破8100万人次。
C. 虽然海水淡化具有洁净、环保、供给稳定等特点,未来的发展前景十分广阔,但是目前还没有被广大沿海地区所釆用。
D. 美国与欧盟持续施压俄罗斯,换来的却是一个又一个的嘲讽式举动。
俄总统普京将自己的工资转入受美制裁的银行,以此显示他对来自美欧制裁的不以为意。
4.把下列句子组成语意连贯的语段;排序最恰当的一项是①才会有效遏制住当前频频发生的非伤即亡的暴力征收拆迁事件②而且,依法执政本就是行政机关的天然职责③只有追究非法拆迁人背后的雇主责任④才能使本就是出于行政行为的行政机关担当起职责⑤他们不能为了避免与被征收拆迁人之间发生矛盾冲突就私下把职责转给开发商或拆迁公司⑥而不是让那些直接施暴者当替罪羊了事A. ③④⑥①②⑤B. ③⑥④①②⑤C. ③④①②⑤⑥D. ②⑤③⑥①④二、本大題7小题,共35分。
[华附三模]2014年高考考前热身语文试题与参考答案范文
![[华附三模]2014年高考考前热身语文试题与参考答案范文](https://img.taocdn.com/s3/m/c8ac7659a26925c52cc5bf3d.png)
2014年高考考前热身语文试题一、本大题4小题,每小题3分,共12分。
1.下列词语中加点的字,每对读音都不相同的一组是A.刨冰/刨平水泵/蚌壳剥皮/褒扬B.恸哭/恫吓陡峭/讥诮中肯/中意C.玷污/粘连复辟/开辟焚膏继晷/咎由自取D.情愫/塑料肄业/防疫强弩之末/强词夺理2.下面语段中画线的词语,使用不恰当的一项是时至今日,仍难掩戾气,连恩青内心积蓄着何等极端的负面情绪,其“杀医逻辑”背后是何等严重的病态人格。
更可怕的是,他在营造一种正义幻觉,把自己打扮成除暴安良、瘅恶彰善的“英雄”。
在自以为是的错觉支配下,他接受采访时始终安之若素,不时伴以夸张的肢体动作和怪异的冷笑。
A. 戾气B.瘅恶彰善C.自以为是D.安之若素3.下列句子中,没有语病的一项是A.作为全国最高权力机关和最高参政议政机构,和两会闭幕后的总理记者会一样,愈来愈成为中国新闻发布的渠道和政府最高层释放政策信息的窗口。
B.余额宝是电子商务巨头阿里巴巴去年6月发行的一款互联网货币基金,到今年2月底,其投资者总人数已经突破8100万人次。
C.虽然海水淡化具有洁净、环保、供给稳定等特点,未来的发展前景十分广阔,但是目前还没有被广大沿海地区所采用。
D.美国与欧盟持续施压俄罗斯,换来的却是一个又一个的嘲讽式举动。
俄总统普京将自己的工资转入受美制裁的银行,以此显示他对来自美欧制裁的不以为意。
4.把下列句子组成语意连贯的语段,排序最恰当的一项是①才会有效遏制住当前频频发生的非伤即亡的暴力征收拆迁事件②而且,依法执政本就是行政机关的天然职责③只有追究非法拆迁人背后的雇主责任④才能使本就是出于行政行为的行政机关担当起职责⑤他们不能为了避免与被征收拆迁人之间发生矛盾冲突就私下把职责转给开发商或拆迁公司⑥而不是让那些直接施暴者当替罪羊了事A.③④⑥①②⑤B.③⑥④①②⑤C.③④①②⑤⑥D.②⑤③⑥①④二、本大题7小题,共35分。
阅读下面的文言文,完成5-9题。
【Ks5u首发】上海市华师大二附中2014届高三综合练习数学9试题Word版含答案

上海市华师大二附中高三年级综合练习[9]数学一、填空题(本大题满分48分)本大题共有12题,只要求直接填写结果,每个空格填对得4分,否则一律得零分。
1、方程018379=-⋅-xx的解是 。
2、已知集合{})2lg(-==x y x A ,{}xy y B 2==,则=B A 。
3、若数列{}n a 的前n 项和210(123)n S n n n =-=,,,,则=5a 。
4、从5名候选同学中选出3名,分别保送北大小语种(每个语种各一名同学):俄罗斯语、阿拉伯语与希伯莱语,其中甲、乙二人不愿学希伯莱语,则不同的选法共有 种。
5、复数i i-++111(i 是虚数单位)是方程022=+-c x x 的一个根,则实数=c 。
6、在ABC △中,角AB C ,,所对的边分别为a b c ,,,若1a =,c =π3C =,则A = 。
7、如图,正四棱柱1111ABCD A B C D -中,12AA AB=,则异面直线1A B与1AD 所成角为 。
8、(理)若322sin )cos(cos )sin(=---αβααβα,β在第三象限,则=+)4tan(πβ 。
(文)已知α∈(2π,π),sin α=53,则tan=+)4(πα 。
9、(理)21nx x ⎛⎫- ⎪⎝⎭的展开式中,常数项为15,则n = 。
(文)若y x ,满足条件⎪⎪⎩⎪⎪⎨⎧≤+≤≤≤≤231010y x y x 下,则目标函数y x u +=2的最大值为__________。
10、已知函数xx f 2)(=的反函数为)(1x f-,若4)()(11=+--b fa f,则b a 11+的最小值AB1B1A1D1CCD为 。
11、若不等式n a n n1)1(2)1(+-+<-对于任意正整数n 恒成立,则实数a 的取值范围是 。
12、为了了解学生遵守《中华人民共和国交通安全法》的情况,调查部门在某学校进行了如下的随机调查:向被调查者提出两个问题:(1)你的学号是奇数吗?(2)在过路口的时候你是否闯过红灯?要求被调查者背对调查人抛掷一枚硬币,如果出现正面,就回答第(1)个问题;否则就回答第(2)个问题。
(理综参考答案)2014届华南师大附中高三综合测试

2014届华南师大附中高三综合测试(一)
理科综合参考答案
生物部分
化学部分
物理部分
倚窗远眺,目光目光尽处必有一座山,那影影绰绰的黛绿色的影,是春天的颜色。
周遭流岚升腾,没露出那真实的面孔。
面对那流转的薄雾,我会幻想,那里有一个世外桃源。
在天阶夜色凉如水的夏夜,我会静静地,静静地,等待一场流星雨的来临…
许下一个愿望,不乞求去实现,至少,曾经,有那么一刻,我那还未枯萎的,青春的,诗意的心,在我最美的年华里,同星空做了一次灵魂的交流…
秋日里,阳光并不刺眼,天空是一碧如洗的蓝,点缀着飘逸的流云。
偶尔,一片飞舞的落叶,会飘到我的窗前。
斑驳的印迹里,携刻着深秋的颜色。
在一个落雪的晨,这纷纷扬扬的雪,飘落着一如千年前的洁白。
窗外,是未被污染的银白色世界。
我会去迎接,这人间的圣洁。
在这流转的岁月里,有着流转的四季,还有一颗流转的心,亘古不变的心。
