中考数学抛物线难题解析(含答案)

合集下载

(已整理)中考数学必刷压轴题专题：抛物线之角度关系处理(含解析)

中考数学抛物线压轴题之角度关系处理（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC＝∠BAC？若存在，求出Q点坐标；若不存在，说明理由．2．如图，直线y＝﹣3x+3与x轴、y轴分别交于A，B两点，抛物线y＝﹣x2+bx+c与直线y＝c分别交y轴的正半轴于点C和第一象限的点P，连接PB，得△PCB≌△BOA（O为坐标原点）．若抛物线与x轴正半轴交点为点F，设M是点C，F间抛物线上的一点（包括端点），其横坐标为m．（1）直接写出点P的坐标和抛物线的解析式；（2）当m为何值时，△MAB面积S取得最小值和最大值？请说明理由；（3）求满足∠MPO＝∠POA的点M的坐标．3．如图，已知抛物线y＝ax2+bx+c的顶点D的坐标为（1，﹣），且与x轴交于A、B两点，与y轴交于C 点，A点的坐标为（4，0）．P点是抛物线上的一个动点，且横坐标为m．（l）求抛物线所对应的二次函数的表达式；（2）若动点P满足∠PAO不大于45°，求P点的横坐标m的取值范围；（3）当P点的横坐标m＜0时，过P点作y轴的垂线PQ，垂足为Q．问：是否存在P点，使∠QPO＝∠BCO？若存在，请求出P点的坐标；若不存在，请说明理由．4．如图，抛物线y＝ax2+bx﹣5（a≠0）与x轴交于点A（﹣5，0）和点B（3，0），与y轴交于点C．（1）求该抛物线的解析式；（2）若点E为x轴下方抛物线上的一动点，当S△ABE＝S△ABC时，求点E的坐标；（3）在（2）的条件下，抛物线上是否存在点P，使∠BAP＝∠CAE？若存在，求出点P的横坐标；若不存在，请说明理由．5．如图，抛物线y＝ax2+bx﹣3a经过A（﹣1，0）、C（0，﹣3）两点，与x轴交于另一点B．（1）求此抛物线的解析式；（2）已知点D（m，﹣m﹣1）在第四象限的抛物线上，求点D关于直线BC对称的点D'的坐标．（3）在（2）的条件下，连接BD，问在x轴上是否存在点P，使∠PCB＝∠CBD？若存在，请求出P点的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，抛物线y＝ax2﹣3ax﹣4a的图象经过点C（0，2），交x轴于点A、B（A点在B点左侧），顶点为D．（1）求抛物线的解析式及点A、B的坐标；（2）将△ABC沿直线BC对折，点A的对称点为A′，试求A′的坐标；（3）抛物线的对称轴上是否存在点P，使∠BPC＝∠BAC？若存在，求出点P的坐标；若不存在，请说明理由．7．如图，已知抛物线y＝ax2+bx+c与x轴交于点A、B，与直线AC：y＝﹣x﹣6交y轴于点C，点D是抛物线的顶点，且横坐标为﹣2．（1）求出抛物线的解析式．（2）判断△ACD的形状，并说明理由．（3）直线AD交y轴于点F，在线段AD上是否存在一点P，使∠ADC＝∠PCF？若存在，直接写出点P的坐标；若不存在，说明理由．8．如图，在平面直角坐标系中，抛物线y＝x2+bx+c经过点A（，0）和点B（1，），与x轴的另一个交点为C．（1）求抛物线的函数表达式；（2）点D在对称轴的右侧，x轴上方的抛物线上，且∠BDA＝∠DAC，求点D的坐标；（3）在（2）的条件下，连接BD，交抛物线对称轴于点E，连接AE．①判断四边形OAEB的形状，并说明理由；②点F是OB的中点，点M是直线BD的一个动点，且点M与点B不重合，当∠BMF＝∠MFO时，请直接写出线段BM的长．9．如图，在平面直角坐标系中，抛物线y＝ax2+bx与x轴交于点A，顶点B的坐标为（﹣2，﹣2）．（1）求a，b的值；（2）在y轴正半轴上取点C（0，4），在点A左侧抛物线上有一点P，连接PB交x轴于点D，连接CB交x 轴于点F，当CB平分∠DCO时，求点P的坐标；（3）在（2）的条件下，连接PC，在PB上有一点E，连接EC，若∠ECB＝∠PDC，求点E的坐标．10．如图，在平面直角坐标系中，一次函数y＝x﹣2的图象分别交x、y轴于点A、B，抛物线y＝x2+bx+c 经过点A、B，点P为第四象限内抛物线上的一个动点．（1）求此抛物线对应的函数表达式；（2）如图1所示，过点P作PM∥y轴，分别交直线AB、x轴于点C、D，若以点P、B、C为顶点的三角形与以点A、C、D为顶点的三角形相似，求点P的坐标；（3）如图2所示，过点P作PQ⊥AB于点Q，连接PB，当△PBQ中有某个角的度数等于∠OAB度数的2倍时，请直接写出点P的横坐标．11．如图，直线y＝x+c与x轴交于点B（4，0），与y轴交于点C，抛物线y＝x2+bx+c经过点B，C，与x轴的另一个交点为点A．（1）求抛物线的解析式；（2）点P是直线BC下方的抛物线上一动点，求四边形ACPB的面积最大时点P的坐标；（3）若点M是抛物线上一点，请直接写出使∠MBC＝∠ABC的点M的坐标．12．如图，二次函数y＝ax2﹣3ax+c的图象与x轴交于点A、B，与y轴交于点C直线y＝﹣x+4经过点B、C．（1）求抛物线的表达式；（2）过点A的直线交抛物线于点M，交直线BC于点N．①点N位于x轴上方时，是否存在这样的点M，使得AM：NM＝5：3？若存在，求出点M的坐标；若不存在，请说明理由．②连接AC，当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时，请求出点M的横坐标．13．如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c经过A、B、C三点，已知点A（﹣3，0），B（0，3），C（1，0）．（1）求此抛物线的解析式；（2）点P是直线AB上方的抛物线上一动点，（不与点A、B重合），过点P作x轴的垂线，垂足为F，交直线AB于点E，作PD⊥AB于点D．动点P在什么位置时，△PDE的周长最大，求出此时P点的坐标；（3）在直线x＝﹣2上是否存在点M，使得∠MAC＝2∠MCA，若存在，求出M点坐标．若不存在，说明理由．14．在平面直角坐标系中，直线y＝x﹣2与x轴交于点B，与y轴交于点C，二次函数y＝x2+bx+c的图象经过B，C两点，且与x轴的负半轴交于点A，动点D在直线BC下方的二次函数图象上．（1）求二次函数的表达式；（2）如图1，连接DC，DB，设△BCD的面积为S，求S的最大值；（3）如图2，过点D作DM⊥BC于点M，是否存在点D，使得△CDM中的某个角恰好等于∠ABC的2倍？若存在，直接写出点D的横坐标；若不存在，请说明理由．15．如图，抛物线y＝ax2+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．（1）求该抛物线的函数解析式．（2）如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD．OD交BC于点F，当S△COF：S△CDF＝3：2时，求点D的坐标．（3）如图2，点E的坐标为（0，），点P是抛物线上的点，连接EB，PB，PE形成的△PBE中，是否存在点P，使∠PBE或∠PEB等于2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．16．如图，在平面直角坐标系中，直线y＝x+2与x轴交于点A，与y轴交于点C，抛物线y＝﹣x2+bx+c 经过A、C两点，与x轴的另一交点为点B．（1）求抛物线的函数表达式；（2）点D为直线AC上方抛物线上一动点，①连接BC、CD，设直线BD交线段AC于点E，△CDE的面积为S1，△BCE的面积为S2，求的最大值；②过点D作DF⊥AC，垂足为点F，连接CD，是否存在点D，使得△CDF中的某个角恰好等于∠BAC的2倍？若存在，求点D的横坐标；若不存在，请说明理由．17．二次函数y＝ax2+bx+2的图象交x轴于点（﹣1，0），B（4，0）两点，交y轴于点C．动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）连接BD，当t＝时，求△DNB的面积；（3）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标；（4）当t＝时，在直线MN上存在一点Q，使得∠AQC+∠OAC＝90°，求点Q的坐标．18．如图，抛物线y＝ax2+2x+c（a＜0）与x轴交于点A和点B（点A在原点的左侧，点B在原点的右侧），与y轴交于点C，OB＝OC＝3．（1）求该抛物线的函数解析式；（2）如图1，连接BC，点D是直线BC上方抛物线上的点，连接OD，CD，OD交BC于点F，当S△COF：S△CDF＝3：2时，求点D的坐标．（3）如图2，点E的坐标为（0，），在抛物线上是否存在点P，使∠OBP＝2∠OBE？若存在，请直接写出符合条件的点P的坐标；若不存在，请说明理由．19．如图1，抛物线y＝x2﹣（m﹣1）x﹣m（m＞0）与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，且OB＝3OA．（1）求该抛物线的函数表达式；（2）动点D在线段BC下方的抛物线上．①连接AC、BC，过点D作x轴的垂线，垂足为E，交BC于点F．过点F作FG⊥AC，垂足为G．设点D的横坐标为t，线段FG的长为d，用含t的代数式表示d；②过点D作DH⊥BC，垂足为H，连接CD．是否存在点D，使得△CDH中的一个角恰好等于∠ABC的2倍？如果存在，求出点D的横坐标；如果不存在，请说明理由．1．如图，已知点A（﹣1，0），B（3，0），C（0，1）在抛物线y＝ax2+bx+c上．（1）求抛物线解析式；（2）在直线BC上方的抛物线上求一点P，使△PBC面积为1；（3）在x轴下方且在抛物线对称轴上，是否存在一点Q，使∠BQC＝∠BAC？若存在，求出Q点坐标；若不存在，说明理由．【分析】（1）设抛物线的解析式为y＝a（x+1）（x﹣3），将C（0，1）代入求得a的值即可；（2）过点P作PD⊥x，交BC与点D，先求得直线BC的解析式为y＝﹣x+1，设点P（x，﹣x2+x+1），则D（x，﹣x+1），然后可得到PD与x之间的关系式，接下来，依据△PBC的面积为1列方程求解即可；（3）首先依据点A和点C的坐标可得到∠BQC＝∠BAC＝45°，设△ABC外接圆圆心为M，则∠CMB＝90°，设⊙M的半径为x，则Rt△CMB中，依据勾股定理可求得⊙M的半径，然后依据外心的性质可得到点M为直线y＝﹣x与x＝1的交点，从而可求得点M的坐标，然后由点M的坐标以及⊙M的半径可得到点Q的坐标．【解答】解：（1）设抛物线的解析式为y＝a（x+1）（x﹣3），将C（0，1）代入得﹣3a＝1，解得：a＝﹣，∴抛物线的解析式为y＝﹣x2+x+1．（2）过点P作PD⊥x，交BC与点D．设直线BC的解析式为y＝kx+b，则，解得：k＝﹣，∴直线BC的解析式为y＝﹣x+1．设点P（x，﹣x2+x+1），则D（x，﹣x+1）∴PD＝（﹣x2+x+1）﹣（﹣x+1）＝﹣x2+x，∴S△PBC＝OB•DP＝×3×（﹣x2+x）＝﹣x2+x．又∵S△PBC＝1，∴﹣x2+x＝1，整理得：x2﹣3x+2＝0，解得：x＝1或x＝2，∴点P的坐标为（1，）或（2，1）．（3）存在．∵A（﹣1，0），C（0，1），∴OC＝OA＝1∴∠BAC＝45°．∵∠BQC＝∠BAC＝45°，∴点Q为△ABC外接圆与抛物线对称轴在x轴下方的交点．设△ABC外接圆圆心为M，则∠CMB＝90°．设⊙M的半径为x，则Rt△CMB中，由勾股定理可知CM2+BM2＝BC2，即2x2＝10，解得：x＝（负值已舍去），∵AC的垂直平分线的为直线y＝﹣x，AB的垂直平分线为直线x＝1，∴点M为直线y＝﹣x与x＝1的交点，即M（1，﹣1），∴Q的坐标为（1，﹣1﹣）．【点评】本题主要考查的是二次函数的综合应用，解答本题主要应用了待定系数法求二次函数的解析式、三角形的外心的性质，求得点M的坐标以及⊙M的半径的长度是解题的关键．2．如图，直线y＝﹣3x+3与x轴、y轴分别交于A，B两点，抛物线y＝﹣x2+bx+c与直线y＝c分别交y轴的正半轴于点C和第一象限的点P，连接PB，得△PCB≌△BOA（O为坐标原点）．若抛物线与x轴正半轴交点为点F，设M是点C，F间抛物线上的一点（包括端点），其横坐标为m．（1）直接写出点P的坐标和抛物线的解析式；（2）当m为何值时，△MAB面积S取得最小值和最大值？请说明理由；（3）求满足∠MPO＝∠POA的点M的坐标．【分析】（1）代入y＝c可求出点C、P的坐标，利用一次函数图象上点的坐标特征可求出点A、B的坐标，再由△PCB≌△BOA即可得出b、c的值，进而可得出点P的坐标及抛物线的解析式；（2）利用二次函数图象上点的坐标特征求出点F的坐标，过点M作ME∥y轴，交直线AB于点E，由点M的横坐标可得出点M、E的坐标，进而可得出ME的长度，再利用三角形的面积公式可找出S＝﹣（m﹣3）2+5，由m的取值范围结合二次函数的性质即可求出S的最大值及最小值；（3）分两种情况考虑：①当点M在线段OP上方时，由CP∥x轴利用平行线的性质可得出：当点C、M重合时，∠MPO＝∠POA，由此可找出点M的坐标；②当点M在线段OP下方时，在x正半轴取点D，连接DP，使得DO＝DP，此时∠DPO＝∠POA，设点D的坐标为（n，0），则DO＝n，DP＝，由DO＝DP 可求出n的值，进而可得出点D的坐标，由点P、D的坐标利用待定系数法即可求出直线PD的解析式，再联立直线PD及抛物线的解析式成方程组，通过解方程组求出点M的坐标．综上此题得解．【解答】解：（1）当y＝c时，有c＝﹣x2+bx+c，解得：x1＝0，x2＝b，∴点C的坐标为（0，c），点P的坐标为（b，c）．∵直线y＝﹣3x+3与x轴、y轴分别交于A、B两点，∴点A的坐标为（1，0），点B的坐标为（0，3），∴OB＝3，OA＝1，BC＝c﹣3，CP＝b．∵△PCB≌△BOA，∴BC＝OA，CP＝OB，∴b＝3，c＝4，∴点P的坐标为（3，4），抛物线的解析式为y＝﹣x2+3x+4．（2）当y＝0时，有﹣x2+3x+4＝0，解得：x1＝﹣1，x2＝4，∴点F的坐标为（4，0）．过点M作ME∥y轴，交直线AB于点E，如图1所示．∵点M的横坐标为m（0≤m≤4），∴点M的坐标为（m，﹣m2+3m+4），点E的坐标为（m，﹣3m+3），∴ME＝﹣m2+3m+4﹣（﹣3m+3）＝﹣m2+6m+1，∴S＝S梯形OEMB﹣S△OEB﹣S△AEM＝OA•ME＝﹣m2+3m+＝﹣（m﹣3）2+5．∵﹣＜0，0≤m≤4，∴当m＝0时，S取最小值，最小值为；当m＝3时，S取最大值，最大值为5．（3）①当点M在线段OP上方时，∵CP∥x轴，∴当点C、M重合时，∠MPO＝∠POA，∴点M的坐标为（0，4）；②当点M在线段OP下方时，在x正半轴取点D，连接DP，使得DO＝DP，此时∠DPO＝∠POA．设点D的坐标为（n，0），则DO＝n，DP＝，∴n2＝（n﹣3）2+16，解得：n＝，∴点D的坐标为（，0）．设直线PD的解析式为y＝kx+a（k≠0），将P（3，4）、D（，0）代入y＝kx+a，，解得：，∴直线PD的解析式为y＝﹣x+．联立直线PD及抛物线的解析式成方程组，得：，解得：，．∴点M的坐标为（，）．综上所述：满足∠MPO＝∠POA的点M的坐标为（0，4）或（，）．【点评】本题考查了待定系数法求一次函数解析式、一次（二次）函数图象上点的坐标特征、全等三角形的性质、二次函数的性质、三角形的面积以及等腰三角形的性质，解题的关键是：（1）利用全等三角形的性质求出b、c的值；（2）利用三角形的面积公式找出S＝﹣（m﹣3）2+5；（3）分点M在线段OP上方和点M在线段OP下方两种情况求出点M的坐标．3．如图，已知抛物线y＝ax2+bx+c的顶点D的坐标为（1，﹣），且与x轴交于A、B两点，与y轴交于C 点，A点的坐标为（4，0）．P点是抛物线上的一个动点，且横坐标为m．（l）求抛物线所对应的二次函数的表达式；（2）若动点P满足∠PAO不大于45°，求P点的横坐标m的取值范围；（3）当P点的横坐标m＜0时，过P点作y轴的垂线PQ，垂足为Q．问：是否存在P点，使∠QPO＝∠BCO？若存在，请求出P点的坐标；若不存在，请说明理由．【分析】（1）根据函数值相等的点关于对称轴对称，可得B点坐标，根据待定系数法，可得函数解析式；。

抛物线专题(附答案)

抛物线专题考点1 抛物线的定义题型利用定义,实现抛物线上的点到焦点的距离与到准线的距离之间的转换1.已知点P 在抛物线y 2 = 4x 上，那么点P 到点Q （2，－1）的距离与点P 到抛物线焦点距离之和的最小值为【[解析]过点P 作准线的垂线l 交准线于点R ，由抛物线的定义知，PR PQ PF PQ +=+，当P 点为抛物线与垂线l 的交点时，PR PQ +取得最小值，最小值为点Q 到准线的距离 ,因准线方程为x=-1,故最小值为32. 已知点),4,3(A F 是抛物线x y 82=的焦点,M 是抛物线上的动点,当MF MA +最小时, M 点坐标是 ( )A. )0,0(B. )62,3(C. )4,2(D. )62,3(-[解析] 设M 到准线的距离为MK ,则MK MA MF MA +=+|||，当MK MA +最小时，M 点坐标是)4,2(，选C考点2 抛物线的标准方程题型:求抛物线的标准方程3.求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程：(1)过点(-3,2) (2)焦点在直线上【解题思路】以方程的观点看待问题，并注意开口方向的讨论.[解析] (1)设所求的抛物线的方程为22y px =-或22(0)x py p =>, ∵过点(-3,2) ∴229)3(24⋅=--=p p 或 ∴2934p p ==或 ∴抛物线方程为243y x =-或292x y =,前者的准线方程是1,3x =后者的准线方程为98y =- (2)令0x =得2y =-，令0y =得4x =，∴抛物线的焦点为(4,0)或(0,-2),当焦点为(4,0)时,42p =, ∴8p =，此时抛物线方程216y x =;焦点为(0,-2)时22p = ∴4p =，此时抛物线方程28x y =-.∴所求抛物线方程为216y x =或28x y =-,对应的准线方程分别是4,2x y =-=.4.对于顶点在原点的抛物线，给出下列条件：①焦点在y 轴上；②焦点在x 轴上；③抛物线上横坐标为1的点到焦点的距离等于6；④抛物线的通径的长为5；⑤由原点向过焦点的某条直线作垂线，垂足坐标为（2，1）.能使这抛物线方程为y 2=10x 的条件是____________.（要求填写合适条件的序号）[解析] 用排除法，由抛物线方程y 2=10x 可排除①③④，从而②⑤满足条件.5. 若抛物线的顶点在原点，开口向上，F 为焦点，M 为准线与Y 轴的交点，A 为抛物线上一点,且3||,17||==AF AM ，求此抛物线的方程[解析] 设点'A 是点A 在准线上的射影，则3|'|=AA ，由勾股定理知22|'|=MA ，点A 的横坐标为)23,22(p -，代入方程py x 22=得2=p 或4，抛物线的方程y x 42=或y x 82= 考点3 抛物线的几何性质题型：有关焦半径和焦点弦的计算与论证6.设A 、B 为抛物线px y22=上的点,且 90=∠AOB (O 为原点),则直线AB 必过的定点坐标为__________.【解题思路】由特殊入手，先探求定点位置［解析］设直线OA 方程为kx y =,由⎩⎨⎧==px y kx y 22解出A 点坐标为)2,2(2k p k p ⎪⎩⎪⎨⎧=-=px y x k y 212解出B 点坐标为)2,2(2pk pk -，直线AB 方程为221)2(2k pk x k pk y ---=+,令0=y 得p x 2=，直线AB 必过的定点)0,2(p【指引】（1）由于是填空题，可取两特殊直线AB, 求交点即可；（2）B 点坐标可由A 点坐标用k1-换k 而得。

初三抛物线试题大全及解析

初三抛物线试题大全及解析一、抛物线的基本概念抛物线是一种重要的几何图形，它在中考数学试题中占有重要地位。

抛物线通常由一条直线和一个二次曲线组成，它可以用来描述一些常见的数学问题，如二次函数、几何问题等。

二、抛物线试题类型1. 已知抛物线解析式求未知量2. 抛物线的性质与应用3. 抛物线的形状与开口方向、对称轴、顶点坐标的关系4. 抛物线与方程的综合题5. 与抛物线有关的实际问题三、抛物线试题解析【例1】（基础题）已知抛物线解析式为y=x²-2x-3，请回答下列问题：（1）求该抛物线的开口方向、对称轴和顶点坐标；（2）当x在什么范围内时，y随x的增大而增大？【解析】（1）因为a=1>0，所以抛物线开口向上。

对称轴为直线x=-b/2a=-(-2)/2=1，顶点坐标为（1，-4）。

（2）因为对称轴为直线x=1，且开口向上，所以当x>1时，y随x的增大而增大。

【例2】（提高题）已知二次函数y=ax²+bx+c的图像经过A（1，0），B（0，-6），C（2，-4）三点，求这个二次函数的解析式。

【解析】由题意可设y=ax²+bx-6，把C（2，-4）代入得4a+2b-6=-4，即b-a=1。

再由点A（1，0）在抛物线上可求c值，即可得到二次函数的解析式。

【答案】解：由题意可设y=ax²+bx-6。

把C（2，-4）代入得4a+2b-6=-4，即b-a=1。

又因为图像经过A（1，0），B（0，-6），所以y=x²+x-6。

【例3】（压轴题）已知二次函数y=ax²+bx+c的图像经过A（0，5），B（1，3），C（-2，7）三点。

求这个二次函数的解析式和图像的对称轴。

【解析】这道题需要用到待定系数法。

首先根据条件确定系数可能取到的值，再代入求出解析式。

然后根据对称性求出对称轴。

【答案】设这个二次函数的解析式为y=a(x-h)²+k，将A（0，5），B（1，3），C（-2，7）三点代入得{c=5a+b+c=39a−2a+k=7解得{a=2k=5∴y=2(x−1)2+3图像的对称轴为直线x=1。

人教版中考数学解答题压轴题突破重难点突破七二次函数的实际应用类型二：抛物线型问题

解：∵a＝－510，b＝190，∴y＝－510x2＋190x＋66， ∵基准点K到起跳台的水平距离为75m， ∴y＝－510×752＋190×75＋66＝21， ∴基准点K的高度h为21 m.
9 ②若a＝－510时，运动员落地点要超过K点，则b的取值范围为bb＞＞10 ；【分层分析】运动员落地点要超过K点，即是x＝75时，y＞221 1，故－ 510×752＋75b＋66＞2211 ，即可解得答案；
(1)求抛物线的解析式；解：由题意知，点(5，3.2)是抛物线 y＝a(x－h)2 ＋k的顶点，∴y＝a(x－5)2 ＋3.2. 又∵抛物线经过点(0，0.7)， ∴ 0.7＝a(0－5)2 ＋ 3.2，解得a＝－ 0.1. ∴抛物线的解析式为 y＝－0.1(x－5)2 ＋3.2(或y＝－0.1x2 ＋x ＋0.7)．
解： b＝6，c＝1.
(2)求大棚的最高处到地面的距离；
解：∵y＝－16x2＋76x＋1＝－16x－722＋7234， ∴当x＝72时，y有最大值7234，
73 即大棚最高处到地面的距离为24 m.
37 (3)小明的爸爸欲在大棚内种植黄瓜，需搭建高为 24 m的竹竿支架若干，已知大棚内可以搭建支架的土地平均每平方米需要4根竹竿，则共需要准备多少根竹竿？
【分层分析】运动员飞行的水平距离为25m时，恰好达到最大高度76 m，即是抛物线的顶点为((225，5，76)7，6)设抛物线解析式为y＝＝a(xa－(x225)25＋，可得抛物线解析式为y＝－－1225((xx－－2255))2＋2＋7676，当x＝777556时，y＝ 3366，从而可知他的落地点能超超过K点．
解：令y＝－16x2＋76x＋1＝3274， 1 13
解得x1＝2，x2＝ 2 ， 1 11

抛物线曲线经典题目(含答案解析)

抛物线曲线经典题目(含答案解析)
问题描述
某物体被抛向空中，并沿着抛物线轨迹运动。

该抛物线由方程
y = ax^2 + bx + c 描述，其中 a、b、c 为常数。

给定 a = 2, b = -4, c = 1，求该抛物线的顶点坐标和对称轴方程。

解答分析
首先，我们需要确定抛物线的顶点坐标。

抛物线的顶点坐标可
以通过以下公式计算：
x = -b / (2a)
y = a * (x^2) + b * x + c
代入 a = 2, b = -4, c = 1，即可得到抛物线的顶点坐标。

其次，我们还需要确定抛物线的对称轴方程。

对称轴方程可以
通过以下公式计算：
x = -b / (2a)
代入 a = 2, b = -4，即可得到抛物线的对称轴方程。

计算过程与结果
根据计算公式，我们可以得到抛物线的顶点坐标和对称轴方程的具体计算过程如下：
1. 计算顶点坐标：
x = -(-4) / (2 * 2) = 1
y = 2 * (1^2) + (-4) * 1 + 1 = -1
因此，该抛物线的顶点坐标为 (1, -1)。

2. 计算对称轴方程：
x = -(-4) / (2 * 2) = 1
因此，该抛物线的对称轴方程为 x = 1。

结论
该抛物线的顶点坐标为 (1, -1)，对称轴方程为 x = 1。

以上是对题目的完整解答与分析。

通过计算，我们可以得到抛物线的顶点坐标和对称轴方程，进一步了解抛物线的特征和形态。

初三抛物线试题及答案

初三抛物线试题及答案一、选择题1. 抛物线y = ax^2 + bx + c的顶点坐标是什么？A. (-b, c)B. (-b/2a, c - b^2/4a)C. (-b/2a, c + b^2/4a)D. (-b/a, c)答案：B2. 如果抛物线y = x^2 + 2x + 1的对称轴是直线x = -1，那么a的值是多少？A. 1B. -1C. 0D. 2答案：A3. 抛物线y = 2x^2 - 4x + 3的开口方向是：A. 向上B. 向下C. 水平D. 无法确定答案：A二、填空题4. 已知抛物线y = 3x^2 - 6x + 5，求抛物线的顶点坐标。

答案：顶点坐标为(1, 2)5. 抛物线y = -x^2 + 4x - 3的焦点坐标是什么？答案：焦点坐标为(2, -2)三、解答题6. 已知抛物线y = 2x^2 - 8x + 7，求其与x轴的交点。

答案：首先将方程化为标准形式：y = 2(x - 2)^2 - 1。

抛物线与x轴的交点即为y = 0时的x值。

解方程2(x - 2)^2 - 1 = 0，得到x= 2 ± √(1/2)，即x = 2 ± √2/2。

7. 已知抛物线y = ax^2 + bx + c经过点(1, 3)和(-1, 1)，求a和b 的值。

答案：将点(1, 3)和(-1, 1)代入方程，得到两个方程：3 = a(1)^2 + b(1) + c1 = a(-1)^2 + b(-1) + c解这两个方程，得到a + b + c = 3和a - b + c = 1。

相减消去c，得到2b = 2，即b = 1。

将b的值代入任一方程，得到a + 1 + c = 3，即a + c = 2。

由于c = 3 - a - b = 3 - a - 1 = 2 - a，代入得到a + 2 - a = 2，这是一个恒等式，说明a可以是任意实数。

四、应用题8. 一个物体从地面向上抛，其高度h（米）与时间t（秒）的关系为h = -5t^2 + 20t。

2023年中考数学复习难点突破专题17 二次函数与实际问题：图形运动问题(含答案)

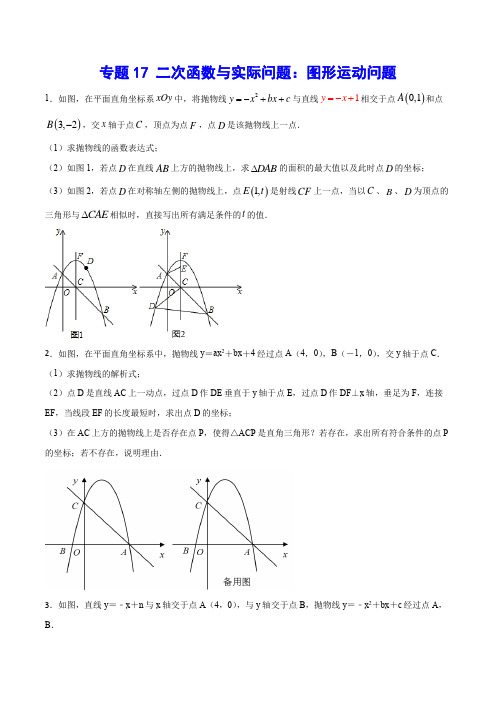
专题17 二次函数与实际问题：图形运动问题1．如图，在平面直角坐标系xOy 中，将抛物线2y x bx c =-++与直线1y x =-+相交于点()0,1A 和点()3,2B -，交x 轴于点C ，顶点为点F ，点D 是该抛物线上一点．（1）求抛物线的函数表达式；（2）如图1，若点D 在直线AB 上方的抛物线上，求DAB ∆的面积的最大值以及此时点D 的坐标；（3）如图2，若点D 在对称轴左侧的抛物线上，点()1,E t 是射线CF 上一点，当以C 、B 、D 为顶点的三角形与CAE ∆相似时，直接写出所有满足条件的t 的值．2．如图，在平面直角坐标系中，抛物线y ＝ax 2＋bx ＋4经过点A （4，0），B （－1，0），交y 轴于点C ．（1）求抛物线的解析式；（2）点D 是直线AC 上一动点，过点D 作DE 垂直于y 轴于点E ，过点D 作DF ⊥x 轴，垂足为F ，连接EF ，当线段EF 的长度最短时，求出点D 的坐标；（3）在AC 上方的抛物线上是否存在点P ，使得△ACP 是直角三角形？若存在，求出所有符合条件的点P 的坐标；若不存在，说明理由．3．如图，直线y ＝﹣x ＋n 与x 轴交于点A （4，0），与y 轴交于点B ，抛物线y ＝﹣x 2＋bx ＋c 经过点A ，B ．（1）求抛物线的解析式；（2）E （m ，0）为x 轴上一动点，过点E 作ED ⊥x 轴，交直线AB 于点D ，交抛物线于点P ，连接BP ． ①点E 在线段OA 上运动，若△BPD 直角三角形，求点E 的坐标；②点E 在x 轴的正半轴上运动，若∠PBD ＋∠CBO ＝45°．请直接写出m 的值．4．在平面直角坐标系中，抛物线22y x kx k =--（k 为常数）的顶点为N ．（1）如图，若此抛物线过点()3,1A -，求抛物线的函数表达式；（2）在（1）的条件下，抛物线与y 轴交于点B ，①求ABO ∠的度数；①连接AB ，点P 为线段AB 上不与点A ，B 重合的一个动点，过点P 作//CD x 轴交抛物线在第四象限部分于点C ，交y 轴于点D ，连接PN ，当BPN BNA △△时，线段CD 的长为___．（3）无论k 取何值，抛物线都过定点H ，点M 的坐标为()2,0，当90MHN ∠=︒时，请直接写出k 的值．5．如图，已知二次函数图象的顶点坐标为C （1，0），直线y ＝x+m 的图象与该二次函数的图象交于A 、B 两点，其中A 点坐标为（3，4），B 点在y 轴上．（1）求m 的值及这个二次函数的解析式；（2）若P是线段AB下方抛物线上一动点，当△ABP面积最大时，求P点坐标以及△ABP面积最大值；（3）若D为直线AB与这个二次函数图象对称轴的交点，Q为线段AB之间的一个动点，过Q作x轴的垂线，与这个二次函数图象交于点E，问是否存在这样的点Q，使得四边形DCEQ为平行四边形，若存在，请求出Q点的坐标；若不存在，请说明理由．6．在Rt△ABC中，AB=BC=12cm，点D从点A开始沿边AB以2cm/s的速度向点B移动，移动过程中始终保持DE∥BC，DF∥AC．（1）试写出四边形DFCE的面积S（cm2）与时间t（s）之间的函数关系式并写出自变量t的取值范围．（2）试求出当t为何值时四边形DFCE的面积为20cm2？（3）四边形DFCE的面积能为40吗？如果能，求出D到A的距离；如果不能，请说明理由．（4）四边形DFCE的面积S（cm2）有最大值吗？有最小值吗？若有，求出它的最值，并求出此时t的值．7．如图，平面直角坐标系中，矩形ABCO的边OA，OC分别在坐标轴上，OA=2，OC=1，以点A为顶点的抛物线经过点C．（1）求抛物线的函数表达式；（2）将矩形ABCO绕点A旋转，得到矩形AB'C'O'，使点C'落在x轴上，抛物线是否经过点C'？请说明理由．8．如图，抛物线243y ax ax a =-+（0a >），与y 轴交于点A ，在x 轴的正半轴上取一点B ，使2OB OA =，抛物线的对称轴与抛物线交于点C ，与x 轴交于点D ，与直线AB 交于点E ，连接BC ．（1）求点B ，C 的坐标（用含a 的代数式表示）；（2）若BCD △与BDE 相似，求a 的值；（3）连接OE ，记OBE △的外心为M ，点M 到直线AB 的距离记为h ，请探究h 的值是否会随着a 的值变化而变化？如果变化，请写出h 的取值范围：如果不变，请求出h 的值．9．已知：直线2l y x =+：与过点(0,2)-且平行于x 轴的直线交于点A ，点A 关于直线1x =- 的对称点为点B ．（1）求A B 、两点的坐标；（2）若抛物线2y x bx c =-++的顶点(,)m n 在直线l 上移动．①当抛物线2y x bx c =-++与坐标轴仅有两个公共点，求抛物线解析式；②若抛物线2y x bx c =-++与线段AB 有交点，当抛物线的顶点(,)m n 向上运动时，抛物线与y 轴的交点也向上运动，求m 的取值范围．10．如图，在平面直角坐标系中，O为坐标原点，点A在x轴的正半轴上，△AOB为等腰三角形，且OA ＝OB，B（8，6），过点B作y轴的垂线，垂足为D，点C在线段BD上，点D关于直线OC的对称点在腰OB上．（1）求AB的长；（2）求点C的坐标；（3）点P从点C出发，以每秒1个单位的速度沿折线CB﹣BA运动；同时点Q从A出发，以每秒1个单位的速度沿AO向终点O运动，当一点停止运动时，另一点也随之停止运动．设△BPQ的面积为S，运动时间为t，求S与t的函数关系式．11．如图，抛物线y=﹣12x2+32x+2，与x轴交于A、B两点，与y轴交于点C，抛物线的对称轴交x轴于点D，已知A（﹣1，0），C（0，2）．（1）求直线BC的解析式；（2）点E①线段BC上的一个动点，过点E作x轴的垂线与抛物线相交于点F，当点E运动到什么位置时，△CBF的面积最大？求出△CBF的最大面积及此时E点的坐标．（3）在抛物线的对称轴上是否存在点P，使△PCD是以CD为腰的等腰三角形？如果存在，直接写出P点的坐标；如果不存在，请说明理由；12．如图，正方形ABCD 的边长为4，点P 是BC 边上的一个动点（点P 不与点B 、C 重合），连接AP ，过点P 作PQ ⊥AP 交DC 于点Q ．设BP 的长为x ，CQ 的长为y ．（1） y 与x 之间的函数关系式，并写出自变量x 的取值范围，（2）当x 取何值时，y 的值最大？最大值是多少？13．如图，已知二次函数23y ax ax =--的图象交x 轴于点A ，B ，交y 轴于点C ，且5AB =，直线y kx b =+（0k >）与二次函数的图象交于点M ，N （点M 在点N 的右边），交y 轴于点P ，交x 轴于点Q ．（1）求二次函数的解析式；（2）若5b =-，254OPQ S =△，求CMN △的面积；（3）若3b k =-，直线AN 与y 轴相交于点H ，求CP CH 的取值范围． 14．已知抛物线26(0)y ax bx a =++≠交x 轴于点()6,0A 和点()1,0B -．（1）求抛物线的解析式和顶点C 的坐标；（2）抛物线对称轴右侧两点M ，N （点M 在点N 的左侧）到对称轴的距离分别为1.5个单位长度和4.5个单位长度，点Q 为抛物线上点M ，N 之间（含点M ，N ）的一个动点，求点Q 的纵坐标Q y 的取值范围． 15．如图，已知边长为10的正方形ABCD ，E 是BC 边上一动点（与B 、C 不重合），连结AE ，H 是BC 延长线上的一点，过点E 作AE 的垂线交DCH ∠的角平分线于点F ．（1）求证：BAE CEF ∠=；（2）若2EC =时，求CEF △的面积；（3）EC 为何值时，CEF △的面积最大，最大值是多少？16．如图，在Rt ABC 中，90ACB ∠=︒，8AC =，4BC =，动点D 从点B 出发，以每秒1个单位长度的速度沿BA 向点A 运动，到达点A 停止运动，过点D 作ED AB ⊥交射线BC 于点E ，以BD 、BE 为邻边作平行四边形BDFE ．设点D 运动时间为t 秒，平行四边形BDFE 与Rt ABC 的重叠部分面积为S ．（1）当点F 落在AC 边上时，求t 的值；（2）求S 关于t 的函数解析式，并直接写出自变量t 的取值范围．17．如图，在平面直角坐标系中，已知抛物线22(0)y ax bx a =+-≠与x 轴交于(1,0)A 、(3,0)B 两点，与y 轴交于点C ，其顶点为点D ，点E 的坐标为(0,1)-，该抛物线与BE 交于另一点F ，连接BC ．（1）求该抛物线的解析式；（2）若点(1,)H y 在BC 上，连接FH ，求FHB △的面积；（3）一动点M 从点D 出发，以每秒1个单位的速度沿平行于y 轴方向向上运动，连接OM ，BM ，设运动时间为t 秒(0)t >，在点M 的运动过程中，当t 为何值时，90OMB ∠=︒？18．如图在平面直角坐标系中，已知抛物线y ＝x 2﹣2x ＋c 与两坐标轴分别交于A ，B ，C 三点，且OC ＝OB ，点G 是抛物线的顶点．（1）求抛物线的解析式．（2）若点M 为第四象限内抛物线上一动点，点M 的横坐标为m ，四边形OCMB 的面积为S ．求S 关于m 的函数关系式，并求出S 的最大值．（3）若点P 是抛物线上的动点，点Q 是x 轴上的动点，判断有几个位置能够使得点P 、Q 、A 、G 为顶点的四边形为平行四边形，直接写出相应的点P 的坐标．19．在平面直角坐标系xOy中，点A（0，4）、B（3，0），抛物线y＝x2﹣4x+3a+2（a为实数）．（1）写出抛物线的对称轴；（2）若点（m，y1）（m+2，y2）在抛物线上，且y1＞y2，求m的取值范围．（3）若该抛物线图象在﹣1≤x≤3的部分与△AOB两直角边的交点个数为2，求a的取值范围．专题17 二次函数与实际问题：图形运动问题1．如图，在平面直角坐标系xOy 中，将抛物线2y x bx c =-++与直线1y x =-+相交于点()0,1A 和点()3,2B -，交x 轴于点C ，顶点为点F ，点D 是该抛物线上一点．（1）求抛物线的函数表达式；（2）如图1，若点D 在直线AB 上方的抛物线上，求DAB ∆的面积的最大值以及此时点D 的坐标；（3）如图2，若点D 在对称轴左侧的抛物线上，点()1,E t 是射线CF 上一点，当以C 、B 、D 为顶点的三角形与CAE ∆相似时，直接写出所有满足条件的t 的值．【答案】（1）221y x x =-++；（2）面积最大为278，此时37,24D ⎛⎫ ⎪⎝⎭；（3）1t =或2t =或1t =+或1t =．【分析】（1）将A 、B 两点坐标代入即可求解函数解析式；（2）过D 作DM//y 轴交AB 于点M ，设D 点坐标为()2,21a a a -++，则M (),1a a -+，用a 表示出DM ，然后根据割补法表示出DAB ∆的面积，利用二次函数的性质得出最大值和D 点坐标；（3）根据题意，45ACE ACO ∠=∠=︒,则BCD ∆中必有一个内角为45°，有两种情况：①若45CBD ∠=︒，得出BCD ∆是等腰直角三角形，因此ACE ∆也是等腰直角三角形，在对ACE ∆进行分类讨论；②若45CDB ∠=︒，根据圆的性质确定D 1的位置，求出D 1的坐标，在对ACE ∆与1CD B ∆相似分类讨论．【详解】（1）由题意得，将将A 、B 两点坐标代入函数解析式有：100293c b c =++⎧⎨-=-++⎩，解得21b c =⎧⎨=⎩ ∴抛物线解析式为221y x x =-++；（2）如图1，过D 作DM//y 轴交AB 于点M ，设D 点坐标为()2,21a a a -++，则M (),1a a -+， ∴()222113DM a a a a a =-++--+=-+ ()()()221133322ADB ADM BDM S S S a a a a a a ∆∆∆=+=-++-+- =23993244a a ⎛⎫--+- ⎪⎝⎭ =3327228a ⎛⎫--+ ⎪⎝⎭ ∴当32a =时，DAB ∆的面积的最大值278ADB S ∆=，此时D 点坐标为37,24⎛⎫ ⎪⎝⎭；（3）∵OA//OC ，如图2，CF//y 轴∴45ACE ACO ∠=∠=︒∴BCD ∆中必有一个内角为45°，由题意得BCD ∠不能为45°①若45CBD ∠=︒，则BD//x 轴。

中考压轴题——抛物线平行四边形(含详细答案分析)

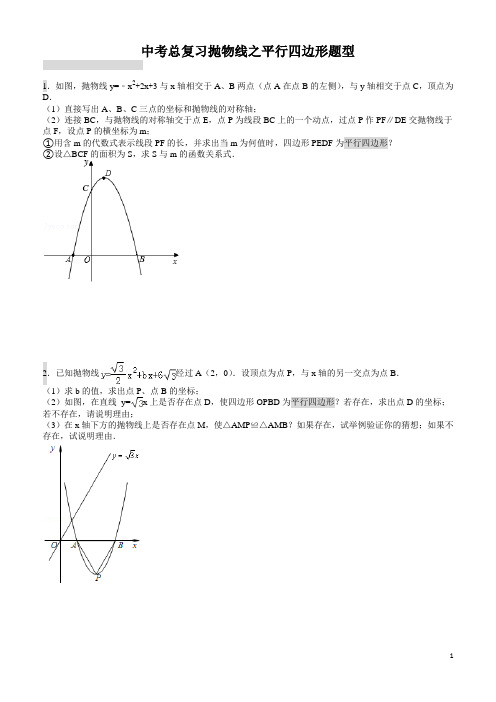
中考总复习抛物线之平行四边形题型1．如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．（1）直接写出A、B、C三点的坐标和抛物线的对称轴；（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P的横坐标为m；①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？②设△BCF的面积为S，求S与m的函数关系式．2．已知抛物线经过A（2，0）．设顶点为点P，与x轴的另一交点为点B．（1）求b的值，求出点P、点B的坐标；（2）如图，在直线y=x上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．3．如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．4．已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，（1）求抛物线的解析式．（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．5．已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．6．边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E 在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．（1）求抛物线的解析式；（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．7．如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：y=x+2经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线y=﹣x2+bx+c．（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；（3）设抛物线与y轴交于G点，当顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．8．已知抛物线：（1）求抛物线y1的顶点坐标．（2）将抛物线y1向右平移2个单位，再向上平移1个单位，得到抛物线y2，求抛物线y2的解析式．（3）如图，抛物线y2的顶点为P，x轴上有一动点M，在y1、y2这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．9．如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c经过O，D，C三点．（1）求AD的长及抛物线的解析式；（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO 以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t 为何值时，以P、Q、C为顶点的三角形与△ADE相似？（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．10．如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．11．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．（1）求该抛物线的解析式及顶点M坐标；（2）求△BCM面积与△ABC面积的比；（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．12．如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．13．如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；（1）求该抛物线的解析式；（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．14．如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B 的抛物线y=﹣x2+bx+c与直线BC交于点D（3，﹣4）．（1）求直线BD和抛物线的解析式；（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP 是平行四边形时，试求动点P的坐标．15．综合与探究：如图，在平面直角坐标系xOy中，四边形OABC是平行四边形，A、C两点的坐标分别为（4，0），（﹣2，3），抛物线W经过O、A、C三点，D是抛物线W的顶点．（1）求抛物线W的解析式及顶点D的坐标；（2）将抛物线W和▱OABC一起先向右平移4个单位后，再向下平移m（0＜m＜3）个单位，得到抛物线W′和▱O′A′B′C′，在向下平移的过程中，设▱O′A′B′C′与▱OABC的重叠部分的面积为S，试探究：当m为何值时S有最大值，并求出S的最大值；（3）在（2）的条件下，当S取最大值时，设此时抛物线W′的顶点为F，若点M是x轴上的动点，点N是抛物线W′上的动点，试判断是否存在这样的点M和点N，使得以D、F、M、N为顶点的四边形是平行四边形？若存在，请直接写出点M的坐标；若不存在，请说明理由．16．如图，抛物线与x轴交于点A（﹣5，0）和点B（3，0）．与y轴交于点C（0，5）．有一宽度为1，长度足够的矩形（阴影部分）沿x轴方向平移，与y轴平行的一组对边交抛物线于点P和Q，交直线AC于点M和N．交x轴于点E和F．（1）求抛物线的解析式；（2）当点M和N都在线段AC上时，连接MF，如果sin∠AMF=，求点Q的坐标；（3）在矩形的平移过程中，当以点P，Q，M，N为顶点的四边形是平行四边形时，求点M的坐标．17．如图，在平面直角坐标系xOy中，抛物线y=a（x+1）2﹣3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C（0，﹣），顶点为D，对称轴与x轴交于点H，过点H的直线l交抛物线于P，Q两点，点Q在y轴的右侧．（1）求a的值及点A，B的坐标；（2）当直线l将四边形ABCD分为面积比为3：7的两部分时，求直线l的函数表达式；（3）当点P位于第二象限时，设PQ的中点为M，点N在抛物线上，则以DP为对角线的四边形DMPN能否为菱形？若能，求出点N的坐标；若不能，请说明理由．1.解：（1）A（﹣1，0），B（3，0），C（0，3）．抛物线的对称轴是：直线x=1．（2）①设直线BC的函数关系式为：y=kx+b．把B（3，0），C（0，3）分别代入得：解得：．所以直线BC的函数关系式为：y=﹣x+3．当x=1时，y=﹣1+3=2，∴E（1，2）．当x=m时，y=﹣m+3，∴P（m，﹣m+3）．在y=﹣x2+2x+3中，当x=1时，y=4．∴D（1，4）当x=m时，y=﹣m2+2m+3，∴F（m，﹣m2+2m+3）∴线段DE=4﹣2=2，线段PF=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m∵PF∥DE，∴当PF=ED时，四边形PEDF为平行四边形．由﹣m2+3m=2，解得：m1=2，m2=1（不合题意，舍去）．因此，当m=2时，四边形PEDF为平行四边形．②设直线PF与x轴交于点M，由B（3，0），O（0，0），可得：OB=OM+MB=3．∵S=S△BPF+S△CPF即S=PF•BM+PF•OM=PF•（BM+OM）=PF•OB．∴S=×3（﹣m2+3m）=﹣m2+m（0≤m≤3）．方法二：（3）∵B（3，0），C（0，3），D（1，4），∴，∴，∵∠DEC=∠COB=90°，∴△DEC∽△COB，∴∠DCE=∠CBO，∴∠DCE+∠OCB=90°，∴DC⊥BC，∴△BCD的外接圆圆心M为BD中点，∴M X==2，M Y==2，∴△BCD的外接圆圆心M（2，2）．2．（2012•东营）已知抛物线经过A（2，0）．设顶点为点P，与x轴的另一交点为点B．（1）求b的值，求出点P、点B的坐标；（2）如图，在直线y=x上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；（3）在x轴下方的抛物线上是否存在点M，使△AMP≌△AMB？如果存在，试举例验证你的猜想；如果不存在，试说明理由．【解答】解：（1）由于抛物线经过A（2，0），所以，解得．所以抛物线的解析式为，①将①式配方，得，所以顶点P的坐标为（4，﹣2），令y=0，得，解得x1=2，x2=6．所以点B的坐标是（6，0）．（2）在直线y=x上存在点D，使四边形OPBD为平行四边形．理由如下：设直线PB的解析式为y=kx+b，把B（6，0），P（4，﹣2）分别代入，得，解得，所以直线PB的解析式为．又因为直线OD的解析式为，所以直线PB∥OD．设直线OP的解析式为y=mx，把P（4，﹣2）代入，得，解得．如果OP∥BD，那么四边形OPBD为平行四边形．设直线BD的解析式为，将B（6，0）代入，得0=，所以所以直线BD的解析式为，解方程组，得，同样还存在第二种情况，如图所示，D′点和D关于原点对称，因此D′的坐标为（﹣2，﹣2），所以D点的坐标为（2，2）或（﹣2，﹣2）．（3）符合条件的点M存在．验证如下：过点P作x轴的垂线，垂足为C，则PC=2，AC=2，由勾股定理，可得AP=4，PB=4，又AB=4，所以△APB是等边三角形，只要作∠PAB的平分线交抛物线于M点，连接PM，BM，由于AM=AM，∠PAM=∠BAM，AB=AP，可得△AMP≌△AMB．因此即存在这样的点M，使△AMP≌△AMB．方法二：（4）过点G作x轴垂线，垂足为H，∵⊙G为△OBD的外接圆，∴点G在线段OH的垂直平分线上，且GO=GD，∵B（6，0），∴l GH：x=3，设G点坐标为（3，m），O（0，0），D（2，2），∴（3﹣0）2+（m﹣0）2=（3﹣2）2+（m﹣2）2，∴m=，∴G点的坐标为（3，）．3．（2012•宜宾）如图，抛物线y=x2﹣2x+c的顶点A在直线l：y=x﹣5上．（1）求抛物线顶点A的坐标；（2）设抛物线与y轴交于点B，与x轴交于点C、D（C点在D点的左侧），试判断△ABD的形状；（3）在直线l上是否存在一点P，使以点P、A、B、D为顶点的四边形是平行四边形？若存在，求点P的坐标；若不存在，请说明理由．【解答】方法一：解：（1）∵顶点A的横坐标为x=﹣=1，且顶点A在y=x﹣5上，∴当x=1时，y=1﹣5=﹣4，∴A（1，﹣4）．（2）△ABD是直角三角形．将A（1，﹣4）代入y=x2﹣2x+c，可得，1﹣2+c=﹣4，∴c=﹣3，∴y=x2﹣2x﹣3，∴B（0，﹣3）当y=0时，x2﹣2x﹣3=0，x1=﹣1，x2=3∴C（﹣1，0），D（3，0），BD2=OB2+OD2=18，AB2=（4﹣3）2+12=2，AD2=（3﹣1）2+42=20，BD2+AB2=AD2，∴∠ABD=90°，即△ABD是直角三角形．（3）存在．由题意知：直线y=x﹣5交y轴于点E（0，﹣5），交x轴于点F（5，0）∴OE=OF=5，又∵OB=OD=3∴△OEF与△OBD都是等腰直角三角形∴BD∥l，即PA∥BD则构成平行四边形只能是PADB或PABD，如图，过点P作y轴的垂线，过点A作x轴的垂线交过P且平行于x轴的直线于点G．设P（x1，x1﹣5），则G（1，x1﹣5）则PG=|1﹣x1|，AG=|5﹣x1﹣4|=|1﹣x1|PA=BD=3由勾股定理得：（1﹣x1）2+（1﹣x1）2=18，x12﹣2x1﹣8=0，x1=﹣2或4∴P（﹣2，﹣7）或P（4，﹣1），存在点P（﹣2，﹣7）或P（4，﹣1）使以点A、B、D、P为顶点的四边形是平行四边形．方法二：（1）略．（2）把A（1，﹣4）代入y=x2﹣2x+c，得c=3，∴y=x2﹣2x+3=（x﹣3）（x+1），∴D（3，0），B（0，﹣3），A（1，﹣4），K BD==1，K AB==﹣1，∴K BD•K AB=﹣1，∴AB⊥BD，即△ABD为直角三角形．（3）略．（4）∵，解得：x1=1（舍），x2=2，∴G（2，﹣3），∵A（1，﹣4），B（0，﹣3），D（3，0），∴GA==，BD==3，AB==，∴S△BDG==4．4．（2015•德州）已知抛物线y=﹣mx2+4x+2m与x轴交于点A（α，0），B（β，0），且=﹣2，（1）求抛物线的解析式．（2）抛物线的对称轴为l，与y轴的交点为C，顶点为D，点C关于l的对称点为E，是否存在x轴上的点M，y轴上的点N，使四边形DNME的周长最小？若存在，请画出图形（保留作图痕迹），并求出周长的最小值；若不存在，请说明理由．（3）若点P在抛物线上，点Q在x轴上，当以点D、E、P、Q为顶点的四边形是平行四边形时，求点P的坐标．【解答】解：（1）由题意可得：α，β是方程﹣mx2+4x+2m=0的两根，由根与系数的关系可得，α+β=，αβ=﹣2，∵=﹣2，∴=﹣2，即=﹣2，解得：m=1，故抛物线解析式为：y=﹣x2+4x+2；（2）存在x轴上的点M，y轴上的点N，使得四边形DNME的周长最小，∵y=﹣x2+4x+2=﹣（x﹣2）2+6，∴抛物线的对称轴l为x=2，顶点D的坐标为：（2，6），又∵抛物线与y轴交点C的坐标为：（0，2），点E与点C关于l对称，∴E点坐标为：（4，2），作点D关于y轴的对称点D′，点E关于x轴的对称点E′，则D′的坐标为；（﹣2，6），E′坐标为：（4，﹣2），连接D′E′，交x轴于M，交y轴于N，此时，四边形DNME的周长最小为：D′E′+DE，如图1所示：延长E′E，′D交于一点F，在Rt△D′E′F中，D′F=6，E′F=8，则D′E′===10，设对称轴l与CE交于点G，在Rt△DGE中，DG=4，EG=2，∴DE===2，∴四边形DNME的周长最小值为：10+2；（3）如图2，P为抛物线上的点，过点P作PH⊥x轴，垂足为H，若以点D、E、P、Q为顶点的四边形为平行四边形，则△PHQ≌△DGE，∴PH=DG=4，∴|y|=4，∴当y=4时，﹣x2+4x+2=4，解得：x1=2+，x2=2﹣，当y=﹣4时，﹣x2+4x+2=﹣4，解得：x3=2+，x4=2﹣，故P点的坐标为；（2﹣，4），（2+，4），（2﹣，﹣4），（2+，﹣4）．5．（2015•绵阳）已知抛物线y=﹣x2﹣2x+a（a≠0）与y轴相交于A点，顶点为M，直线y=x﹣a分别与x轴、y轴相交于B，C两点，并且与直线MA相交于N点．（1）若直线BC和抛物线有两个不同交点，求a的取值范围，并用a表示交点M，A的坐标；（2）将△NAC沿着y轴翻转，若点N的对称点P恰好落在抛物线上，AP与抛物线的对称轴相交于点D，连接CD，求a的值及△PCD的面积；（3）在抛物线y=﹣x2﹣2x+a（a＞0）上是否存在点P，使得以P，A，C，N为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．【解答】解：（1）由题意得，，整理得2x2+5x﹣4a=0．∵△=25+32a＞0，解得a＞﹣．∵a≠0，∴a＞﹣且a≠0．令x=0，得y=a，∴A（0，a）．由y=﹣（x+1）2+1+a得，M（﹣1，1+a）．（2）设直线MA的解析式为y=kx+b（k≠0），∵A（0，a），M（﹣1，1+a），∴，解得，∴直线MA的解析式为y=﹣x+a，联立得，，解得，∴N（，﹣）．∵点P是点N关于y轴的对称点，∴P（﹣，﹣）．代入y=﹣x2﹣2x+a得，﹣=﹣a2+a+a，解得a=或a=0（舍去）．∴A（0，），C（0，﹣），M（﹣1，），|AC|=，∴S△PCD=S△PAC﹣S△ADC=|AC|•|x p|﹣|AC|•|x0|=••（3﹣1）=；（3）①当点P在y轴左侧时，∵四边形APCN是平行四边形，∴AC与PN互相平分，N（，﹣），∴P（﹣，）；代入y=﹣x2﹣2x+a得，=﹣a2+a+a，解得a=，∴P1（﹣，）．②当点P在y轴右侧时，∵四边形ACPN是平行四边形，∴NP∥AC且NP=AC，∵N（，﹣），A（0，a），C（0，﹣a），∴P（，﹣）．代入y=﹣x2﹣2x+a得，﹣=﹣a2﹣a+a，解得a=，∴P2（，﹣）．综上所述，当点P1（﹣，）和P2（，﹣）时，A、C、P、N能构成平行四边形．6．（2015•湖北）边长为2的正方形OABC在平面直角坐标系中的位置如图所示，点D是边OA的中点，连接CD，点E在第一象限，且DE⊥DC，DE=DC．以直线AB为对称轴的抛物线过C，E两点．（1）求抛物线的解析式；（2）点P从点C出发，沿射线CB每秒1个单位长度的速度运动，运动时间为t秒．过点P作PF⊥CD于点F，当t为何值时，以点P，F，D为顶点的三角形与△COD相似？（3）点M为直线AB上一动点，点N为抛物线上一动点，是否存在点M，N，使得以点M，N，D，E为顶点的四边形是平行四边形？若存在，请直接写出满足条件的点的坐标；若不存在，请说明理由．【解答】解：（1）方法一：过点E作EG⊥x轴于G点．∵四边形OABC是边长为2的正方形，D是OA的中点，∴OA=OC=2，OD=1，∠AOC=∠DGE=90°．∵∠CDE=90°，∴∠ODC+∠GDE=90°．∵∠ODC+∠OCD=90°，∴∠OCD=∠GDE．在△OCD和△GED中，∴△ODC≌△GED （AAS），∴EG=OD=1，DG=OC=2．∴点E的坐标为（3，1）．∵抛物线的对称轴为直线AB即直线x=2，∴可设抛物线的解析式为y=a（x﹣2）2+k，将C、E点的坐标代入解析式，得．解得，抛物线的解析式为y=（x﹣2）2+；方法二：过点E作EG⊥x轴于G点．DE⊥DC⇒∠CDO+∠EDH=90°，EG⊥x轴⇒∠DEH+∠EDH=90°，∴∠CDO=∠DEH，DC=DE，∴△ODC≌△GED⇒DG=OC=2，EG=OD=1，∴E（3，1），∴9a+3b+2=0，∵﹣=2，抛物线的解析式为y=（x﹣2）2+；（2）方法一：①若△DFP∽△COD，则∠PDF=∠DCO，∴PD∥OC，∴∠PDO=∠OCP=∠AOC=90°，∴四边形PDOC是矩形，∴PC=OD=1，∴t=1；②若△PFD∽△COD，则∠DPF=∠DCO，=．∴∠PCF=90°﹣∠DCO=90﹣∠DPF=∠PDF．∴PC=PD，∴DF=CD．∵CD2=OD2+OC2=22+12=5，∴CD=，∴DF=．∵=，∴PC=PD=×=，t=，综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；方法二：过点F作x轴的垂线，分别交BC，OA于G，H，PF⊥CD⇒∠PFG+∠DFH=90°，GH⊥OA⇒∠FDH+∠DFH=90°，∴∠PFG=∠FDH⇒△PFG∽△FDH⇒，∵PF⊥CD⇒K PF×K CD=﹣1，∴l CD：y=﹣2x+2，∴F（m，﹣2m+2），P（t，2），∴，∴m=，∴F（，﹣），∴=，∴以P，F，D为顶点的三角形与△COD相似，①，∴，∴t=，②，∴，∴t=1，综上所述：t=1或t=时，以点P，F，D为顶点的三角形与△COD相似；方法三：若以P，F，D为顶点的三角形与△COD相似，则∠OCD=∠PDF或∠ODC=∠PDF，①∠OCD=∠PDF⇒PD∥OC，∴CP=OD=1，∴t=1，②∠ODC=∠PDF，作OO′⊥CD交CD于H，∴K OO′×K CD=﹣1，∴l CD：y=﹣2x+2，∴H（m，﹣2m+2），∴﹣2×=﹣1，∴m=，∴H（，），∵H为OO′中点，∴O′（，），∴l O′D：y=，令y=2，∴x=，即P（，2），∴t=．（3）存在，四边形MDEN是平行四边形时，M1（2，1），N1（4，2）；四边形MNDE是平行四边形时，M2（2，3），N2（0，2）；四边形NDME是平行四边形时，M3（2，），N3（2，）．7．（2015•广安）如图，边长为1的正方形ABCD一边AD在x负半轴上，直线l：y=x+2经过点B（x，1）与x轴，y轴分别交于点H，F，抛物线y=﹣x2+bx+c．（1）求A，D两点的坐标及抛物线经过A，D两点时的解析式；（2）当抛物线的顶点E（m，n）在直线l上运动时，连接EA，ED，试求△EAD的面积S与m之间的函数解析式，并写出m的取值范围；（3）设抛物线与y轴交于G点，当顶点E在直线l上运动时，以A，C，E，G为顶点的四边形能否成为平行四边形？若能，求出E点坐标；若不能，请说明理由．【解答】解：（1）∵直线l：y=x+2经过点B（x，1），∴1=x+2，解得x=﹣2，∴B（﹣2，1），∴A（﹣2，0），D（﹣3，0），∵抛物线经过A，D两点，∴，解得，∴抛物线经过A，D两点时的解析式为y=﹣x2﹣5x﹣6；（2）∵点E（m，n）在直线l上，∴n=m+2，∴S=×1×[±（m+2）]=±（m+1），即S=m+1（m＞﹣4）或S=﹣m﹣1（m＜﹣4）；（3）如图，若以A，C，E，G为顶点的四边形能成为平行四边形，则AC=EG，AC∥EG，作EH∥y轴交过G点平行于x轴的直线相交于H，则EH⊥GH，△EHG≌△CDA，∴GH=AD=1，∴E的横坐标为±1，∵点E在直线l上，∴y=×（﹣1）+2=，或y=×1+2=当AC为对角线时，有E和G的横坐标之和等于A和C的横坐标之和，故可求得E（﹣5，﹣1/2）∴E（﹣1，）；（1，）或（﹣5，﹣1/2）；由于E为抛物线的顶点，G为抛物线与y轴的交点，故将其坐标代入y=﹣x2+bx+c，检验可知当E取（1，）或（﹣5，﹣1/2）时，与此时的A、C、E构成平行四边形的G点并不是y轴与抛物线的交点，与前提相矛盾；综上，满足题意的E的坐标为（﹣1，）．8．（2012秋•义乌市校级期中）已知抛物线：（1）求抛物线y1的顶点坐标．（2）将抛物线y1向右平移2个单位，再向上平移1个单位，得到抛物线y2，求抛物线y2的解析式．（3）如图，抛物线y2的顶点为P，x轴上有一动点M，在y1、y2这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形？若存在，求出N点的坐标；若不存在，请说明理由．【解答】解：（1）依题意把抛物线：y1=﹣x2+2x=﹣（x2﹣4x）=﹣[（x﹣2）2﹣4]=﹣（x﹣2）2+2，故抛物线y1的顶点坐标为：（2，2）；（2）∵抛物线y1向右平移2个单位，再向上平移1个单位，得到y2=﹣（x﹣4）2+3，整理得y2=﹣x2+4x﹣5；（3）符合条件的N点存在．如图：作PA⊥x轴于点A，NB⊥x轴于点B，∴∠PAO=∠MBN=90°，若四边形OPMN为符合条件的平行四边形，则OP∥MN，且OP=MN，∴∠POA=∠BMN，在△POA和△NMB中∴△POA≌△NMB（AAS），∴PA=BN，∵点P的坐标为（4，3），∴NB=PA=3，∵点N在抛物线y1、y2上，且P点为y1、y2的最高点∴符合条件的N点只能在x轴下方，①点N在抛物线y1上，则有：﹣x2+2x=﹣3解得：x1=2﹣，x2=2+，②点N在抛物线y2上，则有：﹣（x﹣4）2+3=﹣3解得：x3=4﹣2或x4=4+2故符合条件的N点有四个：N1（2﹣，﹣3），N2（4﹣2，﹣3），N3（2+，﹣3），N4（4+2，﹣3）．9．（2012•襄阳）如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B 落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线y=ax2+bx+c 经过O，D，C三点．（1）求AD的长及抛物线的解析式；（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO 以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t 为何值时，以P、Q、C为顶点的三角形与△ADE相似？（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．【解答】方法一：解：（1）∵四边形ABCO为矩形，∴∠OAB=∠AOC=∠B=90°，AB=CO=8，AO=BC=10．由题意，△BDC≌△EDC．∴∠B=∠DEC=90°，EC=BC=10，ED=BD．由勾股定理易得EO=6．∴AE=10﹣6=4，设AD=x，则BD=ED=8﹣x，由勾股定理，得x2+42=（8﹣x）2，解得，x=3，∴AD=3．∵抛物线y=ax2+bx+c过点D（3，10），C（8，0），O（0，0）∴，解得∴抛物线的解析式为：y=﹣x2+x．（2）∵∠DEA+∠OEC=90°，∠OCE+∠OEC=90°，∴∠DEA=∠OCE，由（1）可得AD=3，AE=4，DE=5．而CQ=t，EP=2t，∴PC=10﹣2t．当∠PQC=∠DAE=90°，△ADE∽△QPC，∴=，即=，解得t=．当∠QPC=∠DAE=90°，△ADE∽△PQC，∴=，即=，解得t=．∴当t=或时，以P、Q、C为顶点的三角形与△ADE相似．（3）假设存在符合条件的M、N点，分两种情况讨论：①EC为平行四边形的对角线，由于抛物线的对称轴经过EC中点，若四边形MENC是平行四边形，那么M点必为抛物线顶点；则：M（4，）；而平行四边形的对角线互相平分，那么线段MN必被EC中点（4，3）平分，则N（4，﹣）；②EC为平行四边形的边，则EC MN，设N（4，m），则M（4﹣8，m+6）或M（4+8，m﹣6）；将M（﹣4，m+6）代入抛物线的解析式中，得：m=﹣38，此时N（4，﹣38）、M（﹣4，﹣32）；将M（12，m﹣6）代入抛物线的解析式中，得：m=﹣26，此时N（4，﹣26）、M（12，﹣32）；综上，存在符合条件的M、N点，且它们的坐标为：①M1（﹣4，﹣32），N1（4，﹣38）；②M2（12，﹣32），N2（4，﹣26）；③M3（4，），N3（4，﹣）．方法二：（1）略．（2）∵E（0，6），C（8，0），∴l EC：y=﹣x+6，∵，EP=2t，∴P x=t，∴P（t，﹣t+6），Q（8﹣t，0），∵△PQC∽△ADE，且∠ECO=∠AED，∴PQ⊥OC或PQ⊥PC．当PQ⊥OC时，Px=Qx，即t=8﹣t，∴t1=，当PQ⊥PC时，K PQ•K PC=﹣1，∴t2=．（3）M，N，C，E为顶点的四边形是平行四边形．设N（4，t），C（8，0），E（0，6），∴，∴M1（4，6﹣t），同理M2（﹣4，t+6），M3（12，t﹣6），∴﹣t，∴t=﹣，﹣×（﹣4）2+（﹣4）=t+6，∴t=﹣38，﹣×122+×12=t﹣6，∴t=﹣26，综上，存在符合条件的M、N点，且它们的坐标为：①M1（4，），N1（4，﹣）；②M2（12，﹣32），N2（4，﹣26）；③M3（﹣4，﹣32），N3（4，﹣38）．10．（2012•恩施州）如图，已知抛物线y=﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N．其顶点为D．（1）抛物线及直线AC的函数关系式；（2）设点M（3，m），求使MN+MD的值最小时m的值；（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由；（4）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值．【解答】解：（1）由抛物线y=﹣x2+bx+c过点A（﹣1，0）及C（2，3）得，，解得，故抛物线为y=﹣x2+2x+3又设直线为y=kx+n过点A（﹣1，0）及C（2，3）得，解得故直线AC为y=x+1；（2）如图1，作N点关于直线x=3的对称点N′，则N′（6，3），由（1）得D（1，4），故直线DN′的函数关系式为y=﹣x+，当M（3，m）在直线DN′上时，MN+MD的值最小，则m=﹣×=；（3）由（1）、（2）得D（1，4），B（1，2），∵点E在直线AC上，设E（x，x+1），①如图2，当点E在线段AC上时，点F在点E上方，则F（x，x+3），∵F在抛物线上，∴x+3=﹣x2+2x+3，解得，x=0或x=1（舍去）∴E（0，1）；②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，x﹣1）由F在抛物线上∴x﹣1=﹣x2+2x+3解得x=或x=∴E（，）或（，）综上，满足条件的点E的坐标为（0，1）、（，）或（，）；（4）方法一：如图3，过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，设Q （x，x+1），则P（x，﹣x2+2x+3）∴PQ=（﹣x2+2x+3）﹣（x+1）=﹣x2+x+2又∵S△APC=S△APQ+S△CPQ=PQ•AG=（﹣x2+x+2）×3=﹣（x﹣）2+∴面积的最大值为．方法二：过点P作PQ⊥x轴交AC于点Q，交x轴于点H；过点C作CG⊥x轴于点G，如图3，设Q（x，x+1），则P（x，﹣x2+2x+3）又∵S△APC=S△APH+S直角梯形PHGC﹣S△AGC=（x+1）（﹣x2+2x+3）+（﹣x2+2x+3+3）（2﹣x）﹣×3×3=﹣x2+x+3=﹣（x﹣）2+∴△APC的面积的最大值为．11．（2014•赤峰）如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．（1）求该抛物线的解析式及顶点M坐标；（2）求△BCM面积与△ABC面积的比；（3）若P是x轴上一个动点，过P作射线PQ∥AC交抛物线于点Q，随着P点的运动，在抛物线上是否存在这样的点Q，使以A，P，Q，C为顶点的四边形为平行四边形？若存在，请求出Q点坐标；若不存在，请说明理由．【解答】方法一：解：（1）设抛物线解析式为y=a（x+1）（x﹣3），∵抛物线过点（0，﹣3），∴﹣3=a（0+1）（0﹣3），∴a=1，∴抛物线解析式为y=（x+1）（x﹣3）=x2﹣2x﹣3，∵y=x2﹣2x﹣3=（x﹣1）2﹣4，∴M（1，﹣4）．（2）如图1，连接BC、BM、CM，作MD⊥x轴于D，∵S△BCM=S梯形OCMD+S△BMD﹣S△BOC=•（3+4）•1+•2×4﹣•3•3=+﹣=3S△ABC=•AB•OC=•4•3=6，∴S△BCM：S△ABC=3：6=1：2．（3）存在，理由如下：①如图2，当Q在x轴下方时，作QE⊥x轴于E，∵四边形ACQP为平行四边形，∴PQ平行且相等AC，∴△PEQ≌△AOC，∴EQ=OC=3，∴﹣3=x2﹣2x﹣3，解得x=2或x=0（与C点重合，舍去），∴Q（2，﹣3）．②如图3，当Q在x轴上方时，作QF⊥x轴于F，∵四边形ACPQ为平行四边形，∴QP平行且相等AC，∴△PFQ≌△AOC，∴FQ=OC=3，∴3=x2﹣2x﹣3，解得x=1+或x=1﹣，∴Q（1+，3）或（1﹣，3）．综上所述，Q点为（2，﹣3）或（1+，3）或（1﹣，3）方法二：（1）略．（2）连接BC、BM、CM，作MD⊥x轴于D，交BC于H，∵B（3，0），C（0，﹣3），∴l BC：y=x﹣3，当x=1时，y=﹣2，∴H（1，﹣2）∴S△BCM=（3﹣0）（﹣2+4）=3，∵S△ABC=AB×OC=×3×4=6，∴S△BCM：S△ABC=3：6=1：2，（3）∵PQ∥AC，∴当PQ=AC时，A、P、Q、C为顶点的四边形为平行四边形，即|Q Y|=|C Y|，设Q（t，t2﹣2t﹣3），∴|t2﹣2t﹣3|=3，①t2﹣2t﹣3=3，解得：t1=1+，t2=1﹣，②t2﹣2t﹣3=﹣3，解得：t1=0（舍），t2=2，综上所述，Q点为（2，﹣3）或（1+，3）或（1﹣，3）．12．（2014•潍坊）如图，抛物线y=ax2+bx+c（a≠0）与y轴交于点C（0，4），与x轴交于点A和点B，其中点A的坐标为（﹣2，0），抛物线的对称轴x=1与抛物线交于点D，与直线BC交于点E．（1）求抛物线的解析式；（2）若点F是直线BC上方的抛物线上的一个动点，是否存在点F使四边形ABFC的面积为17，若存在，求出点F的坐标；若不存在，请说明理由；（3）平行于DE的一条动直线l与直线BC相交于点P，与抛物线相交于点Q，若以D、E、P、Q为顶点的四边形是平行四边形，求点P的坐标．【解答】方法一：解：（1）∵抛物线y=ax2+bx+c（a≠0）过点C（0，4），∴c=4 ①．∵对称轴x=﹣=1，∴b=﹣2a ②．∵抛物线过点A（﹣2，0），∴0=4a﹣2b+c ③，由①②③解得，a=﹣，b=1，c=4，∴抛物线的解析式为y=﹣x2+x+4；（2）假设存在满足条件的点F，如图所示，连结BF、CF、OF，过点F作FH⊥x轴于点H，FG⊥y轴于点G．设点F的坐标为（t，﹣t2+t+4），其中0＜t＜4，则FH=﹣t2+t+4，FG=t，∴S△OBF=OB•FH=×4×（﹣t2+t+4）=﹣t2+2t+8，S△OFC=OC•FG=×4×t=2t，∴S四边形ABFC=S△AOC+S△OBF+S△OFC=4﹣t2+2t+8+2t=﹣t2+4t+12．令﹣t2+4t+12=17，即t2﹣4t+5=0，则△=（﹣4）2﹣4×5=﹣4＜0，∴方程t2﹣4t+5=0无解，故不存在满足条件的点F；（3）设直线BC的解析式为y=kx+n（k≠0），∵B（4，0），C（0，4），∴，解得，∴直线BC的解析式为y=﹣x+4．由y=﹣x2+x+4=﹣（x﹣1）2+，∴顶点D（1，），又点E在直线BC上，则点E（1，3），于是DE=﹣3=．若以D、E、P、Q为顶点的四边形是平行四边形，因为DE∥PQ，只须DE=PQ，设点P的坐标是（m，﹣m+4），则点Q的坐标是（m，﹣m2+m+4）．①当0＜m＜4时，PQ=（﹣m2+m+4）﹣（﹣m+4）=﹣m2+2m，由﹣m2+2m=，解得：m=1或3．当m=1时，线段PQ与DE重合，m=1舍去，∴m=3，P1（3，1）．②当m＜0或m＞4时，PQ=（﹣m+4）﹣（﹣m2+m+4）=m2﹣2m，由m2﹣2m=，解得m=2±，经检验适合题意，此时P2（2+，2﹣），P3（2﹣，2+）．综上所述，满足题意的点P有三个，分别是P1（3，1），P2（2+，2﹣），P3（2﹣，2+）．方法二：（1）略．（2）∵B（4，0），C（0，4），∴l BC：y=﹣x+4，过F点作x轴垂线，交BC于H，设F（t，﹣t2+t+4），∴H（t，﹣t+4），∵S四边形ABFC=S△ABC+S△BCF=17，∴（4+2）×4+（﹣t2+t+4+t﹣4）×4=17，∴t2﹣4t+5=0，∴△=（﹣4）2﹣4×5＜0，∴方程t2﹣4t+5=0无解，故不存在满足条件的点F．（3）∵DE∥PQ，∴当DE=PQ时，以D、E、P、Q为顶点的四边形是平行四边形，∵y=﹣x2+x+4，∴D（1，），∵l BC：y=﹣x+4，∴E（1，3），∴DE=﹣3=，设点F的坐标是（m，﹣m+4），则点Q的坐标是（m，﹣m2+m+4），∴|﹣m+4+m2﹣m﹣4|=，∴m2﹣2m=或m2﹣2m=﹣，∴m=1，m=3，m=2+，m=2﹣，经检验，当m=1时，线段PQ与DE重合，故舍去．∴P1（3，1），P2（2+，2﹣），P3（2﹣，2+）．13．（2014•济宁）如图，抛物线y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，过点A作直线AC⊥x轴，交直线y=2x于点C；（1）求该抛物线的解析式；（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．【解答】方法一：解：（1）∵y=x2+bx+c与x轴交于A（5，0）、B（﹣1，0）两点，∴，解得．∴抛物线的解析式为y=x2﹣x﹣．（2）如答图所示，过点A′作A′E⊥x轴于E，AA′与OC交于点D，∵点C在直线y=2x上，∴C（5，10）∵点A和A′关于直线y=2x对称，∴OC⊥AA′，A′D=AD．∵OA=5，AC=10，∴OC===．∵S△OAC=OC•AD=OA•AC，∴AD=．∴AA′=，在Rt△A′EA和Rt△OAC中，∵∠A′AE+∠A′AC=90°，∠ACD+∠A′AC=90°，∴∠A′AE=∠ACD．又∵∠A′EA=∠OAC=90°，∴Rt△A′EA∽Rt△OAC．∴，即．∴A′E=4，AE=8．∴OE=AE﹣OA=3．∴点A′的坐标为（﹣3，4），当x=﹣3时，y=×（﹣3）2+3﹣=4．所以，点A′在该抛物线上．（3）存在．理由：设直线CA′的解析式为y=kx+b，则，解得∴直线CA′的解析式为y=x+设点P的坐标为（x，x2﹣x﹣），则点M为（x，x+）．∵PM∥AC，∴要使四边形PACM是平行四边形，只需PM=AC．又点M在点P的上方，∴（x+）﹣（x2﹣x﹣）=10．解得x1=2，x2=5（不合题意，舍去）当x=2时，y=﹣．∴当点P运动到（2，﹣）时，四边形PACM是平行四边形．方法二：（1）略．（2）设AA′与直线OC的交点为H，∵点A，点A′关于直线OC：y=2x对称，∴AA′⊥OC，K OC•K AA′=﹣1，∵K OC=2，∴K AA′=﹣，∵A（5，0），∴l AA′：y=﹣x+，l OC：y=2x，∴H（1，2），∵H为AA′的中点，∴⇒，∴A′X=﹣3，A′Y=4，∴A′（﹣3，4），当x=﹣3时，y=×（﹣3）2+3﹣=4，∴点A在抛物线上．（3）∵PM∥AC，要使四边形PACM是平行四边形，只需PM=AC，∵直线AC⊥x轴，∴C x=A x，∵A（5，0），∴C x=5，∵l OC：y=2x，∴C Y=10，∴C（5，10），∵A′（﹣3，4），∴l CA′：y=x+，∵M在线段CA′上，点M在点P的上方，∴设M（t，），∴P（t，t2﹣t﹣），∴﹣（t2﹣t﹣）=10，∴t1=2，t2=5（舍），∴P（2，﹣）．14．（2014•东营）如图，直线y=2x+2与x轴交于点A，与y轴交于点B，把△AOB沿y轴翻折，点A落到点C，过点B的抛物线y=﹣x2+bx+c与直线BC交于点D（3，﹣4）．（1）求直线BD和抛物线的解析式；（2）在第一象限内的抛物线上，是否存在一点M，作MN垂直于x轴，垂足为点N，使得以M、O、N为顶点的三角形与△BOC相似？若存在，求出点M的坐标；若不存在，请说明理由；（3）在直线BD上方的抛物线上有一动点P，过点P作PH垂直于x轴，交直线BD于点H，当四边形BOHP 是平行四边形时，试求动点P的坐标．。

初三抛物线试题大全及解析

初三抛物线试题大全及解析抛物线是数学中一个重要而有趣的概念，初中阶段也常常学习与抛物线相关的知识。

下面将为大家整理一些初三抛物线的试题，并给出解析，希望对同学们的学习有所帮助。

试题一已知抛物线y = (x-1)^2 - 3的顶点坐标为A(1, -3)，求抛物线的对称轴和焦点坐标。

解析：根据已知信息，我们知道顶点坐标为(1, -3)，根据抛物线的性质可知顶点坐标即为对称轴的坐标。

对称轴的方程即为x = 1，所以对称轴的坐标为x = 1。

抛物线的焦点坐标可以通过顶点坐标和抛物线的焦距计算得出。

由抛物线的标准方程可以得出焦距的公式：f = 1 / (4a)，其中a为抛物线的系数。

由于抛物线的系数a为1，所以焦距f = 1 / (4 * 1) = 1/4。

根据焦点与顶点的对称关系可知，顶点的y坐标减去焦距即为焦点的y坐标。

所以，焦点的坐标为：(1, -3 + 1/4) = (1, -2.75)。

综上所述，抛物线的对称轴坐标为x = 1，焦点的坐标为(1, -2.75)。

试题二已知抛物线过点A(1, -1)和点B(3, 7)，求抛物线的二次函数方程。

解析：设抛物线的二次函数方程为y = ax^2 + bx + c。

由已知条件，可以列出两个方程来求解未知数a、b和c。

分别根据点A和点B 的坐标带入方程中。

代入点A的坐标，可以得到方程：-1 = a + b + c。

代入点B的坐标，可以得到方程：7 = 9a + 3b + c。

解这个方程组，可以得到a = 2，b = 0，c = -3。

所以，抛物线的二次函数方程为y = 2x^2 - 3。

试题三已知一架飞机从距离地面1000米的高度竖直上抛，并保持竖直方向上的初速度为10m/s，求飞机的运动方程。

解析：设飞机的运动方程为y = ax^2 + bx + c。

由于飞机是竖直上抛，所以在竖直方向上的运动符合自由落体运动的规律。

自由落体运动的方程可以表示为y = -1/2gt^2 + v0t + h0，其中g为重力加速度，v0为初速度，h0为初始高度。

湖南省各地市2023-中考数学真题分类汇编-03解答题(较难题)知识点分类②

湖南省各地市2023-中考数学真题分类汇编-03解答题（较难题）知识点分类②一．二次函数综合题（共6小题）1．（2023•岳阳）已知抛物线Q1：y＝﹣x2+bx+c与x轴交于A（﹣3，0），B两点，交y轴于点C（0，3）．（1）请求出抛物线Q1的表达式．（2）如图1，在y轴上有一点D（0，﹣1），点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E，F使得四边形DAEF为正方形？若存在，请求出点E，F的坐标；若不存在，请说明理由．（3）如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK＝∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．2．（2023•衡阳）如图，已知抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0）和点B，与y 轴交于点C，连接AC，过B、C两点作直线．（1）求a的值．（2）将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点．在直线B ′C′上方的抛物线上是否存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．若存在，请求出点D的坐标；若不存在，请说明理由．（3）抛物线上是否存在点P，使∠PBC+∠ACO＝45°，若存在，请求出直线BP的解析式；若不存在，请说明理由．3．（2023•怀化）如图一所示，在平面直角坐标系中，抛物线y＝ax2+bx﹣8与x轴交于A （﹣4，0）、B（2，0）两点，与y轴交于点C．（1）求抛物线的函数表达式及顶点坐标；（2）点P为第三象限内抛物线上一点，作直线AC，连接PA、PC，求△PAC面积的最大值及此时点P的坐标；（3）设直线l1：y＝kx+k﹣交抛物线于点M、N，求证：无论k为何值，平行于x轴的直线l2：y＝﹣上总存在一点E，使得∠MEN为直角．4．（2023•湘西州）如图（1），二次函数y＝ax2﹣5x+c的图象与x轴交于A（﹣4，0），B （b，0）两点，与y轴交于点C（0，﹣4）．（1）求二次函数的解析式和b的值．（2）在二次函数位于x轴上方的图象上是否存在点M，使？若存在，请求出点M的坐标；若不存在，请说明理由．（3）如图（2），作点A关于原点O的对称点E，连接CE，作以CE为直径的圆．点E′是圆在x轴上方圆弧上的动点（点E′不与圆弧的端点E重合，但与圆弧的另一个端点可以重合），平移线段AE，使点E移动到点E′，线段AE的对应线段为A′E′，连接E′C，A′A，A′A的延长线交直线E′C于点N，求的值．5．（2023•邵阳）如图，在平面直角坐标系中，抛物线y＝ax2+x+c经过点A（﹣2，0）和点B（4，0），且与直线l：y＝﹣x﹣1交于D、E两点（点D在点E的右侧），点M为直线l上的一动点，设点M的横坐标为t．（1）求抛物线的解析式．（2）过点M作x轴的垂线，与抛物线交于点N．若0＜t＜4，求△NED面积的最大值．（3）抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．6．（2023•永州）如图1，抛物线y＝ax2+bx+c（a，b，c为常数）经过点F（0，5），顶点坐标为（2，9），点P（x1，y1）为抛物线上的动点，PH⊥x轴于H，且．（1）求抛物线的表达式；（2）如图1，直线OP：交BF于点G，求的最大值；（3）如图2，四边形OBMF为正方形，PA交y轴于点E，BC交FM的延长线于C，且BC⊥BE，PH＝FC，求点P的横坐标．二．四边形综合题（共1小题）7．（2023•湘潭）问题情境：小红同学在学习了正方形的知识后，进一步进行以下探究活动：在正方形ABCD的边BC上任意取一点G，以BG为边长向外作正方形BEFG，将正方形BEFG绕点B顺时针旋转．特例感知：（1）当BG在BC上时，连接DF，AC相交于点P，小红发现点P恰为DF的中点，如图①．针对小红发现的结论，请给出证明；（2）小红继续连接EG，并延长与DF相交，发现交点恰好也是DF中点P，如图②．根据小红发现的结论，请判断△APE的形状，并说明理由；规律探究：（3）如图③，将正方形BEFG绕点B顺时针旋转α，连接DF，点P是DF中点，连接AP，EP，AE，△APE的形状是否发生改变？请说明理由．三．圆的综合题（共1小题）8．（2023•永州）如图，以AB为直径的⊙O是△ABC的外接圆，延长BC到点D．使得∠BAC ＝∠BDA，点E在DA的延长线上，点M在线段AC上，CE交BM于N，CE交AB于G．（1）求证：ED是⊙O的切线；（2）若，BD＝5，AC＞CD，求BC的长；（3）若DE•AM＝AC•AD，求证：BM⊥CE．四．几何变换综合题（共1小题）9．（2023•岳阳）如图1，在△ABC中，AB＝AC，点M，N分别为边AB，BC的中点，连接MN．初步尝试：（1）MN与AC的数量关系是，MN与AC的位置关系是．特例研讨：（2）如图2，若∠BAC＝90°，BC＝4，先将△BMN绕点B顺时针旋转α（α为锐角），得到△BEF，当点A，E，F在同一直线上时，AE与BC相交于点D，连接CF．①求∠BCF的度数；②求CD的长．深入探究：（3）若∠BAC＜90°，将△BMN绕点B顺时针旋转α，得到△BEF，连接AE，CF．当旋转角α满足0°＜α＜360°，点C，E，F在同一直线上时，利用所提供的备用图探究∠BAE与∠ABF的数量关系，并说明理由．湖南省各地市2023-中考数学真题分类汇编-03解答题（较难题）知识点分类②参考答案与试题解析一．二次函数综合题（共6小题）1．（2023•岳阳）已知抛物线Q1：y＝﹣x2+bx+c与x轴交于A（﹣3，0），B两点，交y轴于点C（0，3）．（1）请求出抛物线Q1的表达式．（2）如图1，在y轴上有一点D（0，﹣1），点E在抛物线Q1上，点F为坐标平面内一点，是否存在点E，F使得四边形DAEF为正方形？若存在，请求出点E，F的坐标；若不存在，请说明理由．（3）如图2，将抛物线Q1向右平移2个单位，得到抛物线Q2，抛物线Q2的顶点为K，与x轴正半轴交于点H，抛物线Q1上是否存在点P，使得∠CPK＝∠CHK？若存在，请求出点P的坐标；若不存在，请说明理由．【答案】（1）y＝﹣x2﹣2x+3．（2）存在，E（﹣2，3），F（1，2）．（3）点P的坐标为（1，0）或（﹣2，3）．【解答】解：（1）∵抛物线Q1：y＝﹣x2+bx+c经过A（﹣3，0），C（0，3）两点，∴，解得：，∴抛物线Q1的表达式为y＝﹣x2﹣2x+3．（2）存在点E，F使得四边形DAEF为正方形．理由：如图1，过点E作EG⊥x轴于点G，则∠AGE＝90°＝∠AOD，∵A（﹣3，0），D（0，﹣1），∴OA＝3，OD＝1，∵四边形DAEF是正方形，∴AE＝AD＝DF，∠DAE＝∠ADF＝90°，∵∠EAG+∠DAO＝90°，∠DAO+∠ADO＝90°，∴∠EAG＝∠ADO，∴△EAG≌△ADO（AAS），∴AG＝OD＝1，EG＝OA＝3，∴E（﹣2，3），当x＝﹣2时，y＝﹣x2﹣2x+3＝﹣（﹣2）2﹣2×（﹣2）+3＝3，∴点E在抛物线上，过点F作FL⊥y轴于点L，同理，△DFL≌△ADO（AAS），∴FL＝OD＝1，DL＝OA＝3，∴OL＝DL﹣OD＝3﹣1＝2，F（1，2）．（3）抛物线Q1上存在点P，使得∠CPK＝∠CHK．∵y＝﹣x2﹣2x+3＝﹣（x+1）2+4，∴抛物线Q1的顶点坐标为（﹣1，4），∵将抛物线Q1向右平移2个单位，得到抛物线Q2，∴抛物线Q2的解析式为y＝﹣（x+1﹣2）2+4＝﹣（x﹣1）2+4，∵抛物线Q2的顶点为K，与x轴正半轴交于点H，∴K（1，4），H（3，0），过点K作KT⊥y轴于点T，连接BC，如图2，过点C作PS⊥y轴交BK于点S，交抛物线Q1于点P，连接PK，则T（0，4），∴KT＝TC＝1，∠KTC＝90°，∴△CKT是等腰直角三角形，∴∠KCT＝45°，CK＝KT＝，∵OH＝OC＝3，∠COH＝90°，∴△COH是等腰直角三角形，∴∠HCO＝45°，CH＝OC＝3，∴∠KCH＝180°﹣∠KCT﹣∠HCO＝90°，∴tan∠CHK＝＝＝，∵∠CPK＝∠CHK，∴tan∠CPK＝tan∠CHK＝，∵tan∠BCO＝＝，∴∠BCO＝∠CHK，∵BK∥OC，∴∠CBK＝∠BCO，∴∠CBK＝∠CHK，即点P与点B重合时，∠CPK＝∠CHK，∴P1（1，0）；∵SK＝1，PS＝3，∴tan∠CPK＝＝，∴∠CPK＝∠CHK，∵点P与点C关于直线x＝﹣1对称，∴P（﹣2，3）；综上所述，抛物线Q1上存在点P，使得∠CPK＝∠CHK，点P的坐标为（1，0）或（﹣2，3）．2．（2023•衡阳）如图，已知抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0）和点B，与y 轴交于点C，连接AC，过B、C两点作直线．（1）求a的值．（2）将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点．在直线B ′C′上方的抛物线上是否存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．若存在，请求出点D的坐标；若不存在，请说明理由．（3）抛物线上是否存在点P，使∠PBC+∠ACO＝45°，若存在，请求出直线BP的解析式；若不存在，请说明理由．【答案】（1）a＝﹣1．（2）存在，D（，）．（3）抛物线上存在点P，使∠PBC+∠ACO＝45°，直线BP的解析式为y＝﹣x+1或y ＝﹣3x+9．．【解答】解：（1）∵抛物线y＝ax2﹣2ax+3与x轴交于点A（﹣1，0），∴a+2a+3＝0，∴a＝﹣1．（2）存在定点D，无论m取何值时，都是点D到直线B′C′的距离最大．∵y＝﹣x2+2x+3，当x＝0时，y＝3，∴C（0，3），当y＝0时，﹣x2+2x+3＝0，解得：x1＝﹣1，x2＝3，∴B（3，0），设直线BC的解析式为y＝kx+b，则，解得：，∴直线BC的解析式为y＝﹣x+3，∵将直线BC向下平移m（m＞0）个单位长度，交抛物线于B′、C′两点，∴直线B′C′的解析式为y＝﹣x+3﹣m，设D（t，﹣t2+2t+3），过点D作DE∥y轴，交B′C′于点E，作DF⊥B′C′于点F，设直线B′C′交y轴于点G，如图，∴E（t，﹣t+3﹣m），∴DE＝﹣t2+2t+3﹣（﹣t+3﹣m）＝﹣t2+3t+m，∵OB＝OC＝3，∠BOC＝90°，∴∠BCO＝∠CBO＝45°，∵B′C′∥BC，∴∠B′GO＝∠BCO＝45°，∵DE∥y轴，∴∠DEF＝∠B′GO＝45°，∵∠DFE＝90°，∴△DEF是等腰直角三角形，∴DF＝DE＝（﹣t2+3t+m）＝﹣（t﹣）2+（+m），∵﹣＜0，∴当t＝时，DF取得最大值（+m），此时点D的坐标为（，）．（3）存在．当∠PBC在BC的下方时，在y轴正半轴上取点M（0，1），连接BM交抛物线于点P，如图，∵A（﹣1，0），B（3，0），C（0，3），M（0，1），∴OB＝OC＝3，OM＝OA＝1，∠BOM＝∠COA＝90°，∴△BOM≌△COA（SAS），∴∠MBO＝∠ACO，∵∠CBO＝45°，∴∠CBP+∠MBO＝45°，∴∠CBP+∠ACO＝45°，设直线BM的解析式为y＝k′x+b′，则，解得：，∴直线BM的解析式为y＝﹣x+1，联立，得，解得：（舍去），，∴P（﹣，）；当∠PBC在BC的上方时，作点M关于直线BC的对称点M′，如图，连接MM′，CM ′，直线BM′交抛物线于P，由对称得：MM′⊥BC，CM′＝CM＝2，∠BCM′＝∠BCM＝45°，∴∠MCM′＝90°，∴M′（2，3），则直线BM′的解析式为y＝﹣3x+9，联立，得：，解得：（舍去），，综上所述，抛物线上存在点P，使∠PBC+∠ACO＝45°，直线BP的解析式为y＝﹣x+1或y＝﹣3x+9．3．（2023•怀化）如图一所示，在平面直角坐标系中，抛物线y＝ax2+bx﹣8与x轴交于A （﹣4，0）、B（2，0）两点，与y轴交于点C．（1）求抛物线的函数表达式及顶点坐标；（2）点P为第三象限内抛物线上一点，作直线AC，连接PA、PC，求△PAC面积的最大值及此时点P的坐标；（3）设直线l1：y＝kx+k﹣交抛物线于点M、N，求证：无论k为何值，平行于x轴的直线l2：y＝﹣上总存在一点E，使得∠MEN为直角．【答案】（1）抛物线的函数表达式为y＝x2+2x﹣8，顶点坐标为（﹣1，﹣9）；（2）S△PAC的最大值为8，点P（﹣2，﹣8）；（3）证明见解答．【解答】（1）解：∵抛物线y＝ax2+bx﹣8与x轴交于A（﹣4，0）、B（2，0）两点，∴，解得：，∴抛物线的函数表达式为y＝x2+2x﹣8，∵y＝x2+2x﹣8＝（x+1）2﹣9，∴抛物线的顶点坐标为（﹣1，﹣9）；（2）解：∵抛物线y＝x2+2x﹣8与y轴交于点C，设直线AC的解析式为y＝mx+n，则，解得：，∴直线AC的解析式为y＝﹣2x﹣8，设P（t，t2+2t﹣8），过点P作PF∥y轴，交AC于点F，如图，则F（t，﹣2t﹣8），∴PF＝﹣2t﹣8﹣（t2+2t﹣8）＝﹣t2﹣4t，∴S△PAC＝S△PAF+S△PCF＝PF•（t+4）+PF•（﹣t）＝2PF＝2（﹣t2﹣4t）＝﹣2（t+2）2+8，∵﹣2＜0，∴当t＝﹣2时，S△PAC的最大值为8，此时点P（﹣2，﹣8）；（3）证明：∵直线l1：y＝kx+k﹣交抛物线于点M、N，∴x2+2x﹣8＝kx+k﹣，整理得：x2+（2﹣k）x+﹣k＝0，∴x M+x N＝k﹣2，x M x N＝﹣k，∵y M＝kx M+k﹣，y N＝kx N+k﹣，∴y M﹣y N＝k（x M﹣x N），∴MN2＝（x M﹣x N）2+（y M﹣y N）2＝（1+k2）（x M﹣x N）2＝（1+k2）[（x M+x N）2﹣4x M x N]＝（1+k2）[（k﹣2）2﹣4（﹣k）]＝（1+k2）2，∵设MN的中点为O′，∴O′（，k2﹣），过点O′作O′E⊥直线l2：y＝﹣，垂足为E，如图，∴E（，﹣），∴O′E＝k2﹣﹣（﹣）＝（1+k2），∴O′E＝MN，∴以MN为直径的⊙O′一定经过点E，∴∠MEN＝90°，∴在直线l2：y＝﹣上总存在一点E，使得∠MEN为直角．4．（2023•湘西州）如图（1），二次函数y＝ax2﹣5x+c的图象与x轴交于A（﹣4，0），B （b，0）两点，与y轴交于点C（0，﹣4）．（1）求二次函数的解析式和b的值．（2）在二次函数位于x轴上方的图象上是否存在点M，使？若存在，请求出点M的坐标；若不存在，请说明理由．（3）如图（2），作点A关于原点O的对称点E，连接CE，作以CE为直径的圆．点E′是圆在x轴上方圆弧上的动点（点E′不与圆弧的端点E重合，但与圆弧的另一个端点可以重合），平移线段AE，使点E移动到点E′，线段AE的对应线段为A′E′，连接E′C，A′A，A′A的延长线交直线E′C于点N，求的值．【答案】（1）y＝﹣x2﹣5x﹣4，b＝﹣1；（2）不存在，理由见解析；（3）1．【解答】解：（1）∵二次函数y＝ax2﹣5x+c的图象与x轴交于A（﹣4，0），B（b，0）两点，与y轴交于点C（0，﹣4），∴，解得：，∴二次函数的解析式为y＝﹣x2﹣5x﹣4，当y＝0时，得：﹣x2﹣5x﹣4＝0，解得：x1＝﹣4，x2＝﹣1，∴B（﹣1，0），∴二次函数的解析式为y＝﹣x2﹣5x﹣4，b＝﹣1；（2）不存在．理由如下：如图，设M（m，﹣m2﹣5m﹣4），∵A（﹣4，0），B（﹣1，0），C（0，﹣4），∴AB＝﹣1﹣（﹣4）＝3，OB＝1，OC＝4，∵点M在二次函数位于x轴上方的图象上，且，∴，整理得：m2+5m+8＝0，∵Δ＝52﹣4×8＝﹣7＜0，∴方程无实数根，∴不存在符合条件的点M；（3）如图，设CE′交x轴于点M，∵A（﹣4，0），C（0，﹣4），∴OA＝OC＝4，∵点E与点A关于原点O对称，∴OE＝OA＝OC＝4，∵∠AOC＝∠EOC＝90°，∴∠OAC＝∠OCA＝45°＝∠OCE＝∠OEC，∴AC＝EC，∵CE为圆的直径，∴∠CE′E＝90°，∵平移线段AE，使点E移动到点E′，线段AE的对应线段为A′E′，①当点E′与点O不重合时，∴A′E′＝AE，A′E′∥AE，∴四边形AEE′A′是平行四边形，∴A′A∥E′E，A′A＝E′E，∴∠ANE′＝∠CE′E＝90°，∠MAN＝∠MEE′，∴∠ANC＝90°，在Rt△ANM和Rt△COM中，∵∠MAN＝90°﹣∠AMN，∠MCO＝90°﹣∠CMO，∴∠MAN＝∠MCO，∵∠OAC＝∠OCE＝45°，∴∠CAN＝∠ECE′，又∵∠ANC＝∠CE′E＝90°，在△ANC和△CE′E中，，∴△ANC≌△CE′E（AAS），∴CN＝EE′，∴AA′＝CN，∴，②当点E′与点O重合时，此时点N与点O重合，∴AA′＝EE′＝OE＝4，CN＝CO＝4，∴，综上所述，的值为1．5．（2023•邵阳）如图，在平面直角坐标系中，抛物线y＝ax2+x+c经过点A（﹣2，0）和点B（4，0），且与直线l：y＝﹣x﹣1交于D、E两点（点D在点E的右侧），点M为直线l上的一动点，设点M的横坐标为t．（1）求抛物线的解析式．（2）过点M作x轴的垂线，与抛物线交于点N．若0＜t＜4，求△NED面积的最大值．（3）抛物线与y轴交于点C，点R为平面直角坐标系上一点，若以B、C、M、R为顶点的四边形是菱形，请求出所有满足条件的点R的坐标．【答案】（1）抛物线解析式为y＝﹣x2+x+4；（2）△NED面积的最大值是7；（3）R的坐标为（，）或（，）或（，）或（，）或（，）．【解答】解：（1）把A（﹣2，0），B（4，0）代入y＝ax2+x+c得：，解得：，∴抛物线解析式为y＝﹣x2+x+4；（2）联立，解得或，∴D（2+，﹣3﹣），E（2﹣，﹣3+），∵点M为直线l上的一动点，横坐标为t，∴M（t，﹣t﹣1），∴N（t，﹣t2+t+4），∴MN＝﹣t2+t+4﹣（﹣t﹣1）＝﹣t2+2t+5，∴S△NED＝MN•|x D﹣x E|＝×（﹣t2+2t+5）×2＝﹣（t﹣2）2+7，∵﹣＜0，0＜t＜4，∴当t＝2时，S△NED取最大值7，∴△NED面积的最大值是7；（3）在y＝﹣x2+x+4中，令x＝0得y＝4，∴C（0，4），设M（t，﹣t﹣1），R（m，n），又B（4，0），①当BC，MR为对角线时，BC，MR的中点重合，且BM＝CM，∴，解得，∴R（，）；②当BM，CR为对角线时，BM，CR的中点重合，且BC＝CM，∴，解得或，∴R（，）或（，）；③当BR，CM为对角线时，BR，CM的中点重合，且BC＝BM，∴，解得或，∴R（，）或（，）；综上所述，R的坐标为（，）或（，）或（，）或（，）或（，）．6．（2023•永州）如图1，抛物线y＝ax2+bx+c（a，b，c为常数）经过点F（0，5），顶点坐标为（2，9），点P（x1，y1）为抛物线上的动点，PH⊥x轴于H，且．（1）求抛物线的表达式；（2）如图1，直线OP：交BF于点G，求的最大值；（3）如图2，四边形OBMF为正方形，PA交y轴于点E，BC交FM的延长线于C，且BC⊥BE，PH＝FC，求点P的横坐标．【答案】（1）抛物线的表达式为y＝﹣x2+4x+5；（2）的最大值为；（3）点P的横坐标为．【解答】解：（1）∵抛物线y＝ax2+bx+c（a，b，c为常数）经过点F（0，5），顶点坐标为（2，9），∴，解得，∴抛物线的表达式为y＝﹣x2+4x+5；（2）过点G作GT⊥x轴于点T，如图所示，在y＝﹣x2+4x+5中，令y＝0得0＝﹣x2+4x+5，解得x＝5或x＝﹣1，∴A（﹣1，0），B（5，0），∵F（0，5），∴BO＝FO＝5，设直线BF的解析式为：y＝kx+5，∴y＝5k+5，解得k＝﹣1，∴直线BF的解析式为y＝﹣x+5，由G在直线BF上，设G（m，﹣m+5），∵G在直线OP上，直线OP为，∴﹣m+5＝m，∴，∴，由P（x1，y1）在抛物线y＝﹣x2+4x+5上，知P（x1，﹣+4x1+5），∴，∵S△BPG＝S△BPO﹣S△BOG，∴＝＝﹣1＝﹣1＝﹣1，∵＝＝，∴＝﹣1＝﹣1＝﹣1＝﹣（x1﹣）2+，∵，，∴当时，取最大值，最大值为；（3）设MF交PH于T，如图：∵OBFM为正方形，F（0，5），∴FM＝BM＝OF＝BO＝5，∠MBO＝90°，FC∥OB，∵PH⊥x，∠MBO＝90°，FC∥OB，∴MTBH为矩形，∴TH＝MB＝FM＝5，∵PH＝FC，∴PT＝MC，∵BC⊥BE，∴∠MBC+∠MBE＝90°，∵∠MBO＝90°，∴∠OBE+∠MBE＝90°，∴∠OBE＝∠MBC，∴∠CMB＝∠EOB＝90°，∴△EOB∽△CMB，∴，∵OB＝MB，∴EO＝MC，∵PH＝FC，∴PT＝MC，∴EO＝MC＝PT，设EO＝MC＝PT＝a，∴PH＝PT+TH＝5+a，E（0，a），∵A（﹣1，0），设直线AP的解析式为y＝kx+b，则，∴，∴直线AP的解析式为y＝ax+a，∵PH＝a+5，P在直线AP上，∴a+5＝ax+a，∴，即P点横坐标为，∴x1＝，y1＝a+5，∴a＝，y1＝+5∴+5＝﹣+4x1+5，∴﹣4+5＝0，∴（x1+1）（﹣5x1+5）＝0，解得x1＝1或x1＝或x1＝，∵x1≥，∴x1＝，∴点P的横坐标为．方法2：设P（m，﹣m2+4m+5），∴OH＝m，PH＝﹣m2+4m+5，∵＝tan∠EAO＝，∴＝，∴EO＝5﹣m，∵BC⊥BE，∴∠CBM＝90°﹣∠MBE＝∠EBO，∵∠CMB＝90°＝∠EOB，BM＝OB，∴△CMB≌△EOB（ASA），∴CM＝EO＝5﹣m，∴CF＝CM+FM＝5﹣m+5＝10﹣m，∵PH＝CF，∴﹣m2+4m+5＝10﹣m，解得m＝或m＝，∵m≥，∴m＝，∴点P的横坐标为．二．四边形综合题（共1小题）7．（2023•湘潭）问题情境：小红同学在学习了正方形的知识后，进一步进行以下探究活动：在正方形ABCD的边BC上任意取一点G，以BG为边长向外作正方形BEFG，将正方形BEFG绕点B顺时针旋转．特例感知：（1）当BG在BC上时，连接DF，AC相交于点P，小红发现点P恰为DF的中点，如图①．针对小红发现的结论，请给出证明；（2）小红继续连接EG，并延长与DF相交，发现交点恰好也是DF中点P，如图②．根据小红发现的结论，请判断△APE的形状，并说明理由；规律探究：（3）如图③，将正方形BEFG绕点B顺时针旋转α，连接DF，点P是DF中点，连接AP，EP，AE，△APE的形状是否发生改变？请说明理由．【答案】（1）证明过程详见解答；（2）△APE是等腰直角三角形；（3）△APE仍然是等腰直角三角形．【解答】解：（1）如图1，延长FG，交AC于H，∵四边形ABCD和四边形BEFG是正方形，∴BC＝CD，FG＝BG，CD∥AE，FG∥AE，∠CGH＝∠BGF＝90°，∴∠CHG＝45°，CD∥FG，∴∠ACB＝∠CHG，∠CDP＝∠HFP，∠DCP＝∠FHP，∴CG＝GH，∴CG+BG＝GH+FG，∴BC＝FH，∴CD＝FH，∴△CDP≌△HFP（ASA），∴点P是DF的中点；（2）如图2，△APE是等腰直角三角形，理由如下：延长EG，交AD的延长线于点M，设DF和EG交于点Q，∵四边形ABCD和四边形BEFG是正方形，∴∠BAD＝90°，∠BEG＝45°，AD＝AB，BE＝EF，AD∥BC∥EF，∠BAC＝45°，∴∠M＝45°，∠M＝∠GEF，∠MDQ＝∠EFQ，∴∠M＝∠BEG，∴AM＝AE，∴AM﹣AD＝AE﹣AB，∴DM＝BE，∴DM＝EF，∴△DQM≌△FQE（ASA），∴DQ＝FQ，∴点Q和点P重合，即：EG与DF的交点恰好也是DF中点P，∵∠BAC＝45°，∠BEG＝45°，∴∠APE＝90°，AP＝EP，∴△APE是等腰直角三角形；（3）如图3，△APE仍然是等腰直角三角形，理由如下：延长EP至Q，是PQ＝PE，连接DQ，延长DA和FE，交于点N，∵DP＝PF，∠DPQ＝∠EPF，∴△PDQ≌△PFE（SAS），∴DQ＝EF，∠PQD＝∠PEF，∴∠N+∠ADQ＝180°，∵四边形ABCD和四边形BEFG是正方形，∴∠BAN＝∠DAB＝90°，∠BEN＝∠BEF＝90°，AB＝AD，BE＝EF，∴∠N+∠ABE＝360°﹣∠BAN﹣∠BEN＝360°﹣90°﹣90°＝180°，DQ＝BE，∴∠ABE＝∠ADQ，∴△ADQ≌△ABE（SAS），∴AE＝AQ，∠DAQ＝∠BAE，∴∠BAE+∠BAQ＝∠DAQ+∠BAQ＝∠BAD＝90°，∴∠QAE＝90°，∴AP⊥EQ，AP＝PE＝，∴△APE是等腰直角三角形．三．圆的综合题（共1小题）8．（2023•永州）如图，以AB为直径的⊙O是△ABC的外接圆，延长BC到点D．使得∠BAC ＝∠BDA，点E在DA的延长线上，点M在线段AC上，CE交BM于N，CE交AB于G．（1）求证：ED是⊙O的切线；（2）若，BD＝5，AC＞CD，求BC的长；（3）若DE•AM＝AC•AD，求证：BM⊥CE．【答案】（1）证明见解答过程；（2）BC＝3；（3）证明见解答过程．【解答】（1）证明：∵AB是⊙O的直径，∴∠ACB＝90°，∴∠BAC+∠ABC＝90°，∵∠BAC＝∠BDA，∴∠BDA+∠ABC＝90°，∴∠BAD＝90°，∴ED是⊙O的切线；（2）解：∵∠BAC＝∠BDA，∠ACB＝∠DCA＝90°，∴△ACB∽△DCA，∴，∴，解得BC＝2或BC＝3，当BC＝2时，CD＝BD﹣BC＝3，当BC＝3时，CD＝BD﹣BC＝2，∵AC＞CD，即＞CD，∴BC＝3；（3）证明：∵AB是⊙O的直径，∴∠ACB＝∠DCA＝90°，∵∠BAC＝∠BDA，∴△ABC∽△DAC，∴，∴AC•AD＝CD•AB，∵DE•AM＝AC•AD，∴DE．AM＝CD•AB，∴，∵∠BAM+∠CAD＝∠CDE+∠CAD＝90°，∴∠BAM＝∠CDE，∴△AMB∽△DCE，∴∠E＝∠ABM，∵∠EGA＝∠BGN，∴∠EGA+∠E＝∠ABM+∠BGN＝90°，∴∠BNG＝90°，∴BM⊥CE．四．几何变换综合题（共1小题）9．（2023•岳阳）如图1，在△ABC中，AB＝AC，点M，N分别为边AB，BC的中点，连接MN．初步尝试：（1）MN与AC的数量关系是　MN＝AC　，MN与AC的位置关系是　MN∥AC　．特例研讨：（2）如图2，若∠BAC＝90°，BC＝4，先将△BMN绕点B顺时针旋转α（α为锐角），得到△BEF，当点A，E，F在同一直线上时，AE与BC相交于点D，连接CF．①求∠BCF的度数；②求CD的长．深入探究：（3）若∠BAC＜90°，将△BMN绕点B顺时针旋转α，得到△BEF，连接AE，CF．当旋转角α满足0°＜α＜360°，点C，E，F在同一直线上时，利用所提供的备用图探究∠BAE与∠ABF的数量关系，并说明理由．【答案】（1）；MN∥AC；（2）①∠BCF＝30°；②；（3）∠BAE＝∠ABF或∠BAE+∠ABF＝180°．【解答】解：（1）∵AB＝AC，点M，N分别为边AB，BC的中点，∴MN是△ABC的中位线，∴，MN∥AC；故答案为：MN＝AC，MN∥AC；（2）特例研讨：①如图所示，连接EM，MN，NF，∵MN是△BAC的中位线，∴MN∥AC，∴∠BMN＝∠BAC＝90°，∵将△BMN绕点B顺时针旋转α（α为锐角），得到△BEF，∴BE＝BM，BF＝BN；∠BEF＝∠BMN＝90°，∵点A，E，F在同一直线上，∴∠AEB＝∠BEF＝90°，在Rt△ABE中，M是斜边AB的中点，∴，∴BM＝ME＝BE，∴△BME是等边三角形，∴∠ABE＝60°，即旋转角α＝60°，∴∠NBF＝60°，BN＝BF，∴△BNF是等边三角形，又∵BN＝NC，BN＝NF，∴NF＝NC，∴∠NCF＝∠NFC，∴∠BNF＝∠NCF+∠NFC＝2∠NFC＝60°，∴∠FCB＝30°；（2）如图所示，连接AN，∵AB＝AC，∠BAC＝90°，∴，∠ACB＝∠ABC＝45°，∵∠ADN＝∠BDE，∠ANB＝∠BED＝90°，∴△ADN∽△BDE，∴，设DE＝x，则，在Rt△ABE中，，则，在Rt△ADN中，AD2＝DN2+AN2，∴，解得：或（舍去），∴；（3）如图所示，当点C，E，F在同一直线上时，且点E在FC上时，∵AB＝AC，∴∠ABC＝∠ACB，设∠ABC＝∠ACB＝θ，则∠BAC＝180°﹣2θ，∵MN是△ABC的中位线，∴MN∥AC，∴∠MNB＝∠MBN＝θ，∵将△BMN绕点B顺时针旋转α，得到△BEF，∴△EBF≌△MBN，∠MBE＝∠NBF＝α，∴∠EBF＝∠EFB＝θ，∴∠BEF＝180°﹣2θ，∵点C，E，F在同一直线上，∴∠BEC＝2θ，∴∠BEC+∠BAC＝180°，∴A，B，E，C在同一个圆上，∴∠EAC＝∠EBC＝α﹣θ，∴∠BAE＝∠BAC﹣∠EAC＝（180°﹣2θ）﹣（α﹣θ）＝180°﹣α﹣θ，∵∠ABF＝α+θ，∴∠BAE+∠ABF＝180°，如图所示，当F在EC上时，∵∠BEF＝∠BAC，BC＝BC，∴A，B，E，C在同一个圆上，设∠ABC＝∠ACB＝θ，则∠BAC＝∠BEF＝180°﹣2θ，将△BMN绕点B顺时针旋转α，得到△BEF，设∠NBF＝β，则∠EBM＝β，则α+β＝360°，∴∠ABF＝θ﹣β，∵∠BFE＝∠EBF＝θ，∠EFB＝∠FBC+∠FCB，∴∠ECB＝∠FCB＝∠EFB﹣∠FBC＝θ﹣β，∵，∴∠EAB＝∠ECB＝θ﹣β，∴∠BAE＝∠ABF，综上所述，∠BAE＝∠ABF或∠BAE+∠ABF＝180°．。

山东省各地市2023-中考数学真题分类汇编-03解答题(较难题)知识点分类

山东省各地市2023-中考数学真题分类汇编-03解答题（较难题）知识点分类一．一次函数的应用（共1小题）1．（2023•日照）要制作200个A，B两种规格的顶部无盖木盒，A种规格是长、宽、高都为20cm的正方体无盖木盒，B种规格是长、宽、高各为20cm，20cm，10cm的长方体无盖木盒，如图1．现有200张规格为40cm×40cm的木板材，对该种木板材有甲、乙两种切割方式，如图2．切割、拼接等板材损耗忽略不计．（1）设制作A种木盒x个，则制作B种木盒个；若使用甲种方式切割的木板材y张，则使用乙种方式切割的木板材张；（2）该200张木板材恰好能做成200个A和B两种规格的无盖木盒，请分别求出A，B 木盒的个数和使用甲，乙两种方式切割的木板材张数；（3）包括材质等成本在内，用甲种切割方式的木板材每张成本5元，用乙种切割方式的木板材每张成本8元．根据市场调研，A种木盒的销售单价定为a元，B种木盒的销售单价定为（20﹣a）元，两种木盒的销售单价均不能低于7元，不超过18元．在（2）的条件下，两种木盒的销售单价分别定为多少元时，这批木盒的销售利润最大，并求出最大利润．二．二次函数综合题（共5小题）2．（2023•淄博）如图，一条抛物线y＝ax2+bx经过△OAB的三个顶点，其中O为坐标原点，点A（3，﹣3），点B在第一象限内，对称轴是直线x＝，且△OAB的面积为18．（1）求该抛物线对应的函数表达式；（2）求点B的坐标；（3）设C为线段AB的中点，P为直线OB上的一个动点，连接AP，CP，将△ACP沿CP翻折，点A的对应点为A1．问是否存在点P，使得以A1，P，C，B为顶点的四边形是平行四边形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．3．（2023•东营）如图，抛物线过点O（0，0），E（10，0），矩形ABCD的边AB在线段OE 上（点B在点A的左侧），点C，D在抛物线上．设B（t，0），当t＝2时，BC＝4．（1）求抛物线的函数表达式；（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？（3）保持t＝2时的矩形ABCD不动，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，求抛物线平移的距离．4．（2023•枣庄）如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于点D．（1）求该抛物线的表达式；（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；（3）若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．5．（2023•日照）在平面直角坐标系xOy内，抛物线y＝﹣ax2+5ax+2（a＞0）交y轴于点C，过点C作x轴的平行线交该抛物线于点D．（1）求点C，D的坐标；（2）当时，如图1，该抛物线与x轴交于A，B两点（点A在点B的左侧），点P 为直线AD上方抛物线上一点，将直线PD沿直线AD翻折，交x轴于点M（4，0），求点P的坐标；（3）坐标平面内有两点E（，a+1），F（5，a+1），以线段EF为边向上作正方形EFGH．①若a＝1，求正方形EFGH的边与抛物线的所有交点坐标；②当正方形EFGH的边与该抛物线有且仅有两个交点，且这两个交点到x轴的距离之差为时，求a的值．6．（2023•聊城）如图①，抛物线y＝ax2+bx﹣9与x轴交于点A（﹣3，0），B（6，0），与y 轴交于点C，连接AC，BC．点P是x轴上任意一点．（1）求抛物线的表达式；（2）点Q在抛物线上，若以点A，C，P，Q为顶点，AC为一边的四边形为平行四边形时，求点Q的坐标；（3）如图②，当点P（m，0）从点A出发沿x轴向点B运动时（点P与点A，B不重合），自点P分别作PE∥BC，交AC于点E，作PD⊥BC，垂足为点D．当m为何值时，△PED面积最大，并求出最大值．三．三角形综合题（共1小题）7．（2023•临沂）如图，∠A＝90°，AB＝AC，BD⊥AB，BC＝AB+BD．（1）写出AB与BD的数量关系．（2）延长BC到E，使CE＝BC，延长DC到F，使CF＝DC，连接EF．求证：EF⊥AB．（3）在（2）的条件下，作∠ACE的平分线，交AF于点H，求证：AH＝FH．四．四边形综合题（共2小题）8．（2023•淄博）在数学综合与实践活动课上，小红以“矩形的旋转”为主题开展探究活动．（1）操作判断小红将两个完全相同的矩形纸片ABCD和CEFG拼成“L”形图案，如图①．试判断：△ACF的形状为．（2）深入探究小红在保持矩形ABCD不动的条件下，将矩形CEFG绕点C旋转，若AB＝2，AD＝4．探究一：当点F恰好落在AD的延长线上时，设CG与DF相交于点M，如图②．求△CMF 的面积．探究二：连接AE，取AE的中点H，连接DH，如图③．求线段DH长度的最大值和最小值．9．（2023•东营）（1）用数学的眼光观察如图①，在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是AB的中点，N是DC的中点．求证：∠PMN＝∠PNM．（2）用数学的思维思考如图②，延长图①中的线段AD交MN的延长线于点E，延长线段BC交MN的延长线于点F．求证：∠AEM＝∠F．（3）用数学的语言表达如图③，在△ABC中，AC＜AB，点D在AC上，AD＝BC，M是AB的中点，N是DC 的中点，连接MN并延长，与BC的延长线交于点G，连接GD．若∠ANM＝60°，试判断△CGD的形状，并进行证明．五．圆的综合题（共3小题）10．（2023•枣庄）如图，AB为⊙O的直径，点C是的中点，过点C做射线BD的垂线，垂足为E．（1）求证：CE是⊙O的切线；（2）若BE＝3，AB＝4，求BC的长；（3）在（2）的条件下，求阴影部分的面积（用含有π的式子表示）．11．（2023•日照）在探究“四点共圆的条件”的数学活动课上，小霞小组通过探究得出：在平面内，一组对角互补的四边形的四个顶点共圆．请应用此结论，解决以下问题：如图1，△ABC中，AB＝AC，∠BAC＝α（60°＜α＜180°）．点D是BC边上的一动点（点D不与B，C重合），将线段AD绕点A顺时针旋转α到线段AE，连接BE．（1）求证：A，E，B，D四点共圆；（2）如图2，当AD＝CD时，⊙O是四边形AEBD的外接圆，求证：AC是⊙O的切线；（3）已知α＝120°，BC＝6，点M是边BC的中点，此时⊙P是四边形AEBD的外接圆，直接写出圆心P与点M距离的最小值．12．（2023•济宁）如图，已知AB是⊙O的直径，CD＝CB，BE切⊙O于点B，过点C作CF⊥OE交BE于点F，EF＝2BF．（1）如图1，连接BD，求证：△ADB≌△OBE；（2）如图2，N是AD上一点，在AB上取一点M，使∠MCN＝60°，连接MN．请问：三条线段MN，BM，DN有怎样的数量关系？并证明你的结论．六．相似三角形的判定与性质（共1小题）13．（2023•泰安）如图，△ABC和△CDE均是等腰直角三角形，∠BAC＝∠DCE＝90°，点E在线段AC上，BC，DE相交于点F，连接BE，BD，作EH⊥BD，垂足为点H，交BC与点G．（1）若点H是BD的中点，求∠BED的度数；（2）求证：△EFG∽△BFD；（3）求证：＝．七．相似形综合题（共2小题）14．（2023•济南）在矩形ABCD中，AB＝2，AD＝2，点E在边BC上，将射线AE绕点A逆时针旋转90°，交CD延长线于点G，以线段AE，AG为邻边作矩形AEFG．（1）如图1，连接BD，求∠BDC的度数和的值；（2）如图2，当点F在射线BD上时，求线段BE的长；（3）如图3，当EA＝EC时，在平面内有一动点P，满足PE＝EF，连接PA，PC，求PA+PC的最小值．15．（2023•菏泽）（1）如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】（2）如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC到点H，使CH＝DE，连接DH．求证：∠ADF＝∠H．【类比迁移】（3）如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．山东省各地市2023-中考数学真题分类汇编-03解答题（较难题）知识点分类参考答案与试题解析一．一次函数的应用（共1小题）1．（2023•日照）要制作200个A，B两种规格的顶部无盖木盒，A种规格是长、宽、高都为20cm的正方体无盖木盒，B种规格是长、宽、高各为20cm，20cm，10cm的长方体无盖木盒，如图1．现有200张规格为40cm×40cm的木板材，对该种木板材有甲、乙两种切割方式，如图2．切割、拼接等板材损耗忽略不计．（1）设制作A种木盒x个，则制作B种木盒　（200﹣x）　个；若使用甲种方式切割的木板材y张，则使用乙种方式切割的木板材　（200﹣y）　张；（2）该200张木板材恰好能做成200个A和B两种规格的无盖木盒，请分别求出A，B 木盒的个数和使用甲，乙两种方式切割的木板材张数；（3）包括材质等成本在内，用甲种切割方式的木板材每张成本5元，用乙种切割方式的木板材每张成本8元．根据市场调研，A种木盒的销售单价定为a元，B种木盒的销售单价定为（20﹣a）元，两种木盒的销售单价均不能低于7元，不超过18元．在（2）的条件下，两种木盒的销售单价分别定为多少元时，这批木盒的销售利润最大，并求出最大利润．【答案】（1）（200﹣x），（200﹣y）；（2）制作A种木盒100个，B种木盒100个；使用甲种方式切割的木板150张，使用乙种方式切割的木板50张；（3）A种木盒的销售单价定为18元，B种木盒的销售单价定为11元时，这批木盒的销售利润最大，最大利润为1750元．【解答】解：（1）∵要制作200个A，B两种规格的顶部无盖木盒，制作A种木盒x个，故制作B种木盒（200﹣x）个；∵有200张规格为40cm×40cm的木板材，使用甲种方式切割的木板材y张，故使用乙种方式切割的木板材（200﹣y）张；故答案为：（200﹣x），（200﹣y）；（2）使用甲种方式切割的木板材y张，则可切割出4y个长、宽均为20cm的木板，使用乙种方式切割的木板材（200﹣y）张，则可切割出8（200﹣y）个长为10cm、宽为20cm 的木板；设制作A种木盒x个，则需要长、宽均为20cm的木板5x个，制作B种木盒（200﹣x）个，则需要长、宽均为20cm的木板（200﹣x）个，需要长为10cm、宽为20cm的木板4（200﹣x）个；故，解得：，故制作A种木盒100个，制作B种木盒100个，使用甲种方式切割的木板150张，使用乙种方式切割的木板材50张；（3）∵用甲种切割方式的木板材每张成本5元，用乙种切割方式的木板材每张成本8元，且使用甲种方式切割的木板150张，使用乙种方式切割的木板材50张，故总成本为150×5+8×50＝1150（元）；∵两种木盒的销售单价均不能低于7元，不超过18元，∴，解得：7≤a≤18，设利润为w元，则w＝100a+100（20﹣a）﹣1150，整理得：w＝850+50a，∵50＞0，∴w随a的增大而增大，故当a＝18时，有最大值，最大值为850+50×18＝1750（元），则此时B种木盒的销售单价定为20﹣×18＝11（元），即A种木盒的销售单价定为18元，B种木盒的销售单价定为11元时，这批木盒的销售利润最大，最大利润为1750元．二．二次函数综合题（共5小题）2．（2023•淄博）如图，一条抛物线y＝ax2+bx经过△OAB的三个顶点，其中O为坐标原点，点A（3，﹣3），点B在第一象限内，对称轴是直线x＝，且△OAB的面积为18．（1）求该抛物线对应的函数表达式；（2）求点B的坐标；（3）设C为线段AB的中点，P为直线OB上的一个动点，连接AP，CP，将△ACP沿CP 翻折，点A的对应点为A1．问是否存在点P，使得以A1，P，C，B为顶点的四边形是平行四边形？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．【答案】（1）y＝x2﹣3x；（2）（6，6）；（3）存在，P点坐标为（，）或（﹣，﹣）或（+6，+6）或（﹣+6，﹣+6）．【解答】解：（1）∵对称轴为直线x＝，∴﹣＝，∴b＝﹣a①，将点A（3，﹣3）代入y＝ax2+bx，∴9a+3b＝﹣3②，联立①②可得，a＝，b＝﹣3，∴函数的解析式为y＝x2﹣3x；（2）设B（m，m2﹣3m），如图1，过A点作EF⊥y轴交于E点，过B点作BF⊥EF交于F点，∴△OAB的面积＝•m（m2﹣3m+3+3）﹣3×3﹣（m﹣3）（m2﹣3m+3）＝18，解得m＝6或m＝﹣3（舍），∴B（6，6）；（3）存在点P，使得以A1，P，C，B为顶点的四边形是平行四边形，理由如下：∵A（3，﹣3），B（6，6），∴C（，），设直线OB的解析式为y＝kx，∴6k＝6，解得k＝1，∴直线OB的解析式为y＝x，设P（t，t），如图2，当BP为平行四边形的对角线时，BC∥A1P，BC＝A1P，∵AC＝BC，∴AC＝A1P，由对称性可知AC＝A1C，AP＝A1P，∴AP＝AC，∴＝，解得t＝，∴P点坐标为（，）或（﹣，﹣）；如图3，当BC为平行四边形的对角线时，BP∥A1C，BP＝A1C，由对称性可知，AC＝A1C，∴BP＝AC，∴＝，解得t＝+6或t＝﹣+6，∴P（+6，+6）或（﹣+6，﹣+6）；综上所述：P点坐标为（，）或（﹣，﹣）或（+6，+6）或（﹣+6，﹣+6）．3．（2023•东营）如图，抛物线过点O（0，0），E（10，0），矩形ABCD的边AB在线段OE 上（点B在点A的左侧），点C，D在抛物线上．设B（t，0），当t＝2时，BC＝4．（1）求抛物线的函数表达式；（2）当t为何值时，矩形ABCD的周长有最大值？最大值是多少？（3）保持t＝2时的矩形ABCD不动，向右平移抛物线，当平移后的抛物线与矩形的边有两个交点G，H，且直线GH平分矩形ABCD的面积时，求抛物线平移的距离．【答案】（1）y＝x2﹣x；（2）当t＝1时，矩形ABCD的周长有最大值，最大值为；（3）抛物线向右平移的距离是4个单位．【解答】解：（1）设抛物线解析式为y＝ax（x﹣10），∵当t＝2时，BC＝4，∴点C的坐标为（2，﹣4），∴将点C坐标代入解析式得2a（2﹣10）＝﹣4，解得：a＝，∴抛物线的函数表达式为y＝x2﹣x；（2）由抛物线的对称性得AE＝OB＝t，∴AB＝10﹣2t，当x＝t时，点C的纵坐标为t2﹣t，∴矩形ABCD的周长＝2（AB+BC）＝2[（10﹣2t）+（﹣t2+t）]＝﹣t2+t+20＝﹣（t﹣1）2+，∵﹣＜0，∴当t＝1时，矩形ABCD的周长有最大值，最大值为；（3）如图，连接AC，BD相交于点P，连接OC，取OC的中点Q，连接PQ，∵t＝2，∴B（2，0），∴A（8，0），∵BC＝4．∴C（2，﹣4），∵直线GH平分矩形ABCD的面积，∴直线GH过点P，由平移的性质可知，四边形OCHG是平行四边形，∴PQ＝CH，∵四边形ABCD是矩形，∴点P是AC的中点，∴P（5，﹣2），∴PQ＝OA，∵OA＝8，CH＝PQ＝OA＝4，∴抛物线向右平移的距离是4个单位4．（2023•枣庄）如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），C（0，3）两点，并交x轴于另一点B，点M是抛物线的顶点，直线AM与y轴交于点D．（1）求该抛物线的表达式；（2）若点H是x轴上一动点，分别连接MH，DH，求MH+DH的最小值；（3）若点P是抛物线上一动点，问在对称轴上是否存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形？若存在，请直接写出所有满足条件的点Q的坐标；若不存在，请说明理由．【答案】（1）y＝﹣x2+2x+3；（2）MH+DH的最小值为；（3）对称轴上存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形，点Q的坐标为（1，3）或（1，1）或（1，5）．【解答】解：（1）∵抛物线y＝﹣x2+bx+c经过A（﹣1，0），C（0，3）两点，∴，解得：，∴该抛物线的表达式为y＝﹣x2+2x+3；（2）∵y＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴顶点M（1，4），设直线AM的解析式为y＝kx+d，则，解得：，∴直线AM的解析式为y＝2x+2，当x＝0时，y＝2，∴D（0，2），作点D关于x轴的对称点D′（0，﹣2），连接D′M，D′H，如图，则DH＝D′H，∴MH+DH＝MH+D′H≥D′M，即MH+DH的最小值为D′M，∵D′M＝＝，∴MH+DH的最小值为；（3）对称轴上存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形．由（2）得：D（0，2），M（1，4），∵点P是抛物线上一动点，∴设P（m，﹣m2+2m+3），∵抛物线y＝﹣x2+2x+3的对称轴为直线x＝1，∴设Q（1，n），当DM、PQ为对角线时，DM、PQ的中点重合，∴，解得：，∴Q（1，3）；当DP、MQ为对角线时，DP、MQ的中点重合，∴，解得：，∴Q（1，1）；当DQ、PM为对角线时，DQ、PM的中点重合，∴，解得：，∴Q（1，5）；综上所述，对称轴上存在点Q，使得以D，M，P，Q为顶点的四边形是平行四边形，点Q的坐标为（1，3）或（1，1）或（1，5）．5．（2023•日照）在平面直角坐标系xOy内，抛物线y＝﹣ax2+5ax+2（a＞0）交y轴于点C，过点C作x轴的平行线交该抛物线于点D．（1）求点C，D的坐标；（2）当时，如图1，该抛物线与x轴交于A，B两点（点A在点B的左侧），点P 为直线AD上方抛物线上一点，将直线PD沿直线AD翻折，交x轴于点M（4，0），求点P的坐标；（3）坐标平面内有两点E（，a+1），F（5，a+1），以线段EF为边向上作正方形EFGH．①若a＝1，求正方形EFGH的边与抛物线的所有交点坐标；②当正方形EFGH的边与该抛物线有且仅有两个交点，且这两个交点到x轴的距离之差为时，求a的值．【答案】（1）C（0，2），D（5，2）；（2）；（3）①（1，6），（4，6），（5，2）；②a＝0.5．【解答】解：（1）在y＝﹣ax2+5ax+2（a＞0）中，当x＝0时，y＝2，∴C（0，2），∵抛物线解析式为y＝﹣ax2+5ax+2（a＞0），∴抛物线对称轴为直线，∵过点C作x轴的平行线交该抛物线于点D，∴C、D关于抛物线对称轴对称，∴D（5，2）；（2）当时，抛物线解析式为，当y＝0时，，解得x＝﹣1或x＝6，∴A（﹣1，0），如图，设DP上与点M关于直线AD对称的点为N（m，n），由轴对称的性质可得：AN＝AM，DN＝DM，，∴3m+n＝12，∴n＝12﹣3m∴m2+2m+1+144﹣72m+9m2＝25，∴m2﹣7m+12＝0，解得m＝3或m＝4（舍去），∴n＝12﹣3m＝3，∴N（3，3），设直线DP的解析式为y＝kx+b1，∴，解得，∴直线DP的解析式为，联立，解得或，∴P（，）；（3）①当a＝1时，抛物线解析式为y＝﹣x2+5x+2，E（1，2），F（5，2），∴EH＝EF＝FG＝4，∴H（1，6），G（5，6），当x＝1时，y＝﹣12+5×1+2＝6，∴抛物线y＝﹣x2+5x+2 恰好经过H（1，6）；∵抛物线对称轴为直线，由对称性可知抛物线经过（4，6），∴点（4，6）为抛物线与正方形的一个交点，又∵点F与点D重合，∴抛物线也经过点F（5，2）；综上所述，正方形EFGH的边与抛物线的所有交点坐标为（1，6），（4，6），（5，2）；②如图，当抛物线与GH、GF分别交于T、D时，∵当正方形EFGH的边与该抛物线有且仅有两个交点，且这两个交点到x轴的距离之差为，∴点T的纵坐标为2+2.5＝4.5，∴，∴a2+1.5a﹣1＝0，解得a＝﹣2（舍去）或a＝0.5；如图，当抛物线与GH、EF分别交于T、S，∵当正方形EFGH的边与该抛物线有且仅有两个交点，且这两个交点到x轴的距离之差为，∴，解得a＝0.4（舍去，因为此时点F在点D下方）如图，当抛物线与EH、EF分别交于T、S，∵当正方形EFGH的边与该抛物线有且仅有两个交点，且这两个交点到x轴的距离之差为，∴﹣a（）2+5a•+2＝a+1+2.5，解得或（舍去）；当时，y＝﹣ax2+5ax+2＝6.25a+2，当时，6.25a+2＞6+a﹣，∴不符合题意；综上所述，a＝0.5．6．（2023•聊城）如图①，抛物线y＝ax2+bx﹣9与x轴交于点A（﹣3，0），B（6，0），与y 轴交于点C，连接AC，BC．点P是x轴上任意一点．（1）求抛物线的表达式；（2）点Q在抛物线上，若以点A，C，P，Q为顶点，AC为一边的四边形为平行四边形时，求点Q的坐标；（3）如图②，当点P（m，0）从点A出发沿x轴向点B运动时（点P与点A，B不重合），自点P分别作PE∥BC，交AC于点E，作PD⊥BC，垂足为点D．当m为何值时，△PED面积最大，并求出最大值．【答案】（1）y＝；（2）Q（3，﹣9）或（，9）或（，9）；（3）当m＝时，△PDE的面积最大值为：．【解答】解：（1）设抛物线的表达式为：y＝a（x+3）（x﹣6），∴﹣9＝a•3×（﹣6），∴a＝，∴y＝（x+3）（x﹣6）＝；（2）如图1，抛物线的对称轴为：直线x＝＝，由对称性可得Q1（3，﹣9），当y＝9时，＝9，∴x＝，∴Q2（，9），Q3（，9），综上所述：Q（3，﹣9）或（，9）或（，9）；（3）设△PED的面积为S，由题意得：AP＝m+3，BP＝6﹣m，OB＝6，OC＝9，AB＝9．∴BC＝＝3，∵sin∠PBD＝，∴，∴PD＝，∵PE∥BC，∴△APE∽△ABC，∠EPD＝∠PDB＝90°，∴，∴，∴PE＝，∴S＝PE•PD＝（m+3）（6﹣m）＝﹣，∴当m＝时，S最大＝，∴当m＝时，△PDE的面积最大值为：．三．三角形综合题（共1小题）7．（2023•临沂）如图，∠A＝90°，AB＝AC，BD⊥AB，BC＝AB+BD．（1）写出AB与BD的数量关系．（2）延长BC到E，使CE＝BC，延长DC到F，使CF＝DC，连接EF．求证：EF⊥AB．（3）在（2）的条件下，作∠ACE的平分线，交AF于点H，求证：AH＝FH．【答案】（1）结论：AB＝（+1）BD．理由见解析部分；（2）（3）证明见解析部分．【解答】（1）解：结论：AB＝（+1）BD．理由：在BC上取一点T，使得BT＝BD，连接DT，AT．设AB＝AC＝a，则BC＝a．∵∠BAC＝90°，AB＝AC，∴∠ABC＝∠ACB＝45°，∵BD⊥AB，∴∠ABD＝90°，∴∠DBT＝45°，∵BD＝BT，∴∠BDT＝∠BTD＝67.5°，∵BC＝AB+BD＝AC+BD＝BT+AC，∴CT＝CA＝a，∴BD＝BT＝BC﹣CT＝a﹣a，∴＝＝+1，∴AB＝（+1）BD；（2）证明：如图2中，在△BCD和△ECF中，，∴△BCD≌△ECF（SAS），∴∠CBD＝∠E＝45°，BD＝EF，∴BD∥EF，∵BD⊥AB，∴EF⊥AB；（3）证明：延长CH交EF的延长线于点J．∵∠ACE＝180°﹣∠ACB＝135°，CH平分∠ACE，∴∠ACH＝∠ECH＝67.5°，∵∠ACB＝∠E＝45°，∴AC∥EJ，∴∠J＝∠ACH＝∠ECJ＝67.5°，∴CE＝EJ＝CB，∵BC＝BD+AB，EJ＝EF+FJ，∴FJ＝AB＝AC，∵∠AHC＝∠FHJ，∠ACH＝∠J，∴△ACH≌△FJH（AAS），∴AH＝FH．四．四边形综合题（共2小题）8．（2023•淄博）在数学综合与实践活动课上，小红以“矩形的旋转”为主题开展探究活动．（1）操作判断小红将两个完全相同的矩形纸片ABCD和CEFG拼成“L”形图案，如图①．试判断：△ACF的形状为　等腰直角三角形　．（2）深入探究小红在保持矩形ABCD不动的条件下，将矩形CEFG绕点C旋转，若AB＝2，AD＝4．探究一：当点F恰好落在AD的延长线上时，设CG与DF相交于点M，如图②．求△CMF 的面积．探究二：连接AE，取AE的中点H，连接DH，如图③．求线段DH长度的最大值和最小值．【答案】（1）等腰直角三角形；（2）探究一：；探究二：DH的最大值为+1，最小值为﹣1．【解答】解：（1）在Rt△ABC中，AC＝，在Rt△CFG中，CF＝，∵AB＝GF，BC＝CG，∴AC＝CF，∴△ACF是等腰三角形，∵AB＝GF，∠FGC＝∠ABC＝90°．BC＝CG，∴△ABC≌△FGC（SAS），∴∠ACG＝∠GFC，∵∠GCF+∠GFC＝90°，∴∠ACG+∠GCF＝90°，∴∠ACF＝90°，∴△ACF是等腰直角三角形，故答案为：等腰直角三角形；（2）探究一：∵CD＝GF，∠FMG＝∠DMC，∠G＝∠CDF＝90°，∴△CDM≌△FGM（AAS），∴CM＝MF，∵AC＝CF，CD⊥AF，∴AD＝DF，∵AB＝CD＝2，AD＝DF＝4，∴DM＝4﹣CM，在Rt△CDM中，CM2＝CD2+DM2，∴CM2＝22+（4﹣CM）2，解得CM＝，∴MF＝，∴△CMF的面积＝2×＝；探究二：连接DE，取DE的中点P，连接HP，取AD、BC的中点为M、N，连接MN，MH，NH，∵H是AE的中点，∴MH∥DE，且MH＝DE，∵CD＝CE，∴CP⊥DE，DP＝PE，∵MH∥DP，且MH＝DP，∴四边形MHPD是平行四边形，∴MD＝HP，MD∥HP，∵AD∥BC，MD＝CN，∴HP∥CN，HP＝CN，∴四边形HNCP是平行四边形，∴NH∥CP，∴∠MHN＝90°，∴H点在以MN为直径的圆上，设MN的中点为T，∴DT＝＝，∴DH的最大值为+1，最小值为﹣1．方法二：设AC的中点为T，连接HT，∵HT是△ACE的中位线，∴HT＝CE＝1，∴H在以T为圆心，1为半径的圆上，∵DT＝＝，∴DH的最大值为+1，最小值为﹣1．9．（2023•东营）（1）用数学的眼光观察如图①，在四边形ABCD中，AD＝BC，P是对角线BD的中点，M是AB的中点，N是DC的中点．求证：∠PMN＝∠PNM．（2）用数学的思维思考如图②，延长图①中的线段AD交MN的延长线于点E，延长线段BC交MN的延长线于点F．求证：∠AEM＝∠F．（3）用数学的语言表达如图③，在△ABC中，AC＜AB，点D在AC上，AD＝BC，M是AB的中点，N是DC 的中点，连接MN并延长，与BC的延长线交于点G，连接GD．若∠ANM＝60°，试判断△CGD的形状，并进行证明．【答案】（1）证明见解析；（2）证明见解析；（3）直角三角形，理由见解析．【解答】（1）证明：∵P是BD的中点，N是DC的中点，∴PN是△BCD的中位线，PM是△ABD的中位线，∴PN＝BC，PM＝AD，∵AD＝BC，∴PM＝PN，∴∠PMN＝∠PNM；（2）证明：由（1）知，PN是△BDC的中位线，PM是△ABD的中位线，∴PN∥BC，PM∥AD，∴∠PNM＝∠F，∠PMN＝∠AEM，∵∠PNM＝∠PMN，∴∠AEM＝∠F；（3）解：△CGD是直角三角形，理由如下：如图③，取BD的中点P，连接PM、PN，∵N是CD的中点，M是AB的中点，∴PN是△BCD的中位线，PM是△ABD的中位线，∴PN ∥BC ，PN ＝BC ，PM ∥AD ，PM ＝AD ，∵AD ＝BC∴PM ＝PN ，∴∠PNM ＝∠PMN ，∵PM ∥AD ，∴∠PMN ＝∠ANM ＝60°，∴∠PNM ＝∠PMN ＝60°，∵PN ∥BC ，∴∠CGN ＝∠PNM ＝60°，又∵∠CNG ＝∠ANM ＝60°，∴△CGN 是等边三角形．∴CN ＝GN ，又∵CN ＝DN ，∴DN ＝GN ，∴∠NDG ＝∠NGD ＝CNG ＝30°，∴∠CGD ＝∠CGN +∠NGD ＝90°，∴△CGD 是直角三角形．五．圆的综合题（共3小题）10．（2023•枣庄）如图，AB 为⊙O 的直径，点C 是的中点，过点C 做射线BD 的垂线，垂足为E ．（1）求证：CE 是⊙O 的切线；（2）若BE ＝3，AB ＝4，求BC 的长；（3）在（2）的条件下，求阴影部分的面积（用含有π的式子表示）．【答案】（1）证明见解答．（2）BC的长为2．（3）阴影部分的面积为．【解答】（1）证明：如图，连接OC，∵点C是的中点，∴，∴∠ABC＝∠EBC，∵OB＝OC，∴∠ABC＝∠OCB，∴∠EBC＝∠OCB，∴OC∥BE，∵BE⊥CE，∴半径OC⊥CE，∴CE是⊙O的切线．（2）解：如图，连接AC，∵AB为⊙O的直径，∴∠ACB＝90°，∴∠ACB＝∠CEB＝90°，∵∠ABC＝∠EBC，∴△ACB∽△CEB，∴，∴，∴．答：BC的长为2．（3）解：如图，连接OD、CD，∵AB＝4，∴OC＝OB＝2，在Rt△BCE中，，∴，∴∠CBE＝30°，∴∠COD＝60°，∴∠AOC＝60°，∵OC＝OD，∴△COD是等边三角形，∴∠CDO＝60°，∴∠CDO＝∠AOC，∴CD∥AB，∴S△COD＝S△CBD，∴．答：阴影部分的面积为．11．（2023•日照）在探究“四点共圆的条件”的数学活动课上，小霞小组通过探究得出：在平面内，一组对角互补的四边形的四个顶点共圆．请应用此结论，解决以下问题：如图1，△ABC中，AB＝AC，∠BAC＝α（60°＜α＜180°）．点D是BC边上的一动点（点D不与B，C重合），将线段AD绕点A顺时针旋转α到线段AE，连接BE．（1）求证：A，E，B，D四点共圆；（2）如图2，当AD＝CD时，⊙O是四边形AEBD的外接圆，求证：AC是⊙O的切线；（3）已知α＝120°，BC＝6，点M是边BC的中点，此时⊙P是四边形AEBD的外接圆，直接写出圆心P与点M距离的最小值．【答案】（1）证明见解析；（2）证明见解析，（3）．【解答】（1）证明：由旋转的性质可得AE＝AD，∠DAE＝α，∴∠BAC＝∠DAE，∴∠BAC﹣∠BAD＝∠DAE﹣∠BAD，即∠BAE＝∠CAD，又∵AB＝AC，∴△ABE≌△ACD（SAS），∴∠AEB＝∠ADC，∵∠ADC+∠ADB＝180°，∴∠AEB+∠ADB＝180°，∴A、B、D、E四点共圆；（2）证明：如图所示，连接OA，OD，∵AB＝AC，AD＝CD，∴∠ABC＝∠ACB＝∠DAC，∵⊙O是四边形AEBD的外接圆，∴∠AOD＝2∠ABC，∴∠AOD＝2∠ABC＝2∠DAC，∵OA＝OD，∴∠OAD＝∠ODA，∵∠OAD+∠ODA+∠AOD＝180°，∴2∠DAC+2∠OAD＝180°，∴∠DAC+∠OAD＝90°，即∠OAC＝90°，∴OA⊥AC，又∵OA是⊙O的半径，∴AC是⊙O的切线；（3）解：如图所示，作线段AB的垂直平分线，分别交AB、BC于G、F，连接AM，PM，如图：∵AB＝AC，∠BAC＝120°，∴∠ABC＝∠ACB＝30°，∵点M是边BC的中点，∴，AM⊥BC，∴，，在Rt△BGF中，，∴FM＝BM﹣BF＝3﹣2＝1，∵⊙P是四边形AEBD的外接圆，∴点P一定在AB的垂直平分线上，∴点P在直线GF上，∴当MP⊥GF时，PM有最小值，∴∠PFM＝∠BFG＝90°﹣∠ABC＝60°，在Rt△MPF中，PM＝MF•sin∠PFM＝1×sin60°＝，∴圆心P与点M距离的最小值为．12．（2023•济宁）如图，已知AB是⊙O的直径，CD＝CB，BE切⊙O于点B，过点C作CF ⊥OE交BE于点F，EF＝2BF．（1）如图1，连接BD，求证：△ADB≌△OBE；（2）如图2，N是AD上一点，在AB上取一点M，使∠MCN＝60°，连接MN．请问：三条线段MN，BM，DN有怎样的数量关系？并证明你的结论．【答案】（1）证明过程见解答；（2）MN＝BM+DN，理由见解答．【解答】（1）证明：∵CF⊥OE，OC是半径，∴CF是圆O的切线，∵BE是圆O的切线，∴BF＝CF，∵EF＝2BF，∴EF＝2CF，sin E＝＝，∴∠E＝30°，∠EOB＝60°，∵CD＝CB，∴＝，∴OC⊥BD，∵AB是直径，∴∠ADB＝90°＝∠EBO，∵∠E+∠EBD＝90°，∠ABD+∠EBD＝90°，∴∠E＝∠ABD＝30°，∴AD＝BO＝AB，∴△ABD≌△OEB（AAS）；（2）解：MN＝BM+DN，理由如下：延长ND至H使得DH＝BM，连接CH，BD，如图2所示，∵∠CBM+∠NDC＝180°，∠HDC+∠NDC＝180°，∴∠HDC＝∠MBC，∵CD＝CB，DH＝BM，∴△HDC≌△MBC（SAS），∴∠BCM＝∠DCH，CM＝CH，由（1）可得∠ABD＝30°，∵AB是直径，∴∠ADB＝90°，∴∠DCB＝180°﹣∠A＝120°，∵∠MCN＝60°，∴∠BCM+∠NCD＝120°﹣∠NCM＝120°﹣60°＝60°，∴∠DCH+∠NCD＝∠NCH＝60°，∴∠NCH＝∠NCM，∵NC＝NC，∴△CNH≌△CNM（SAS），∴NH＝MN，∴MN＝DN+DH＝DN+BM，∴MN＝BM+DN．六．相似三角形的判定与性质（共1小题）13．（2023•泰安）如图，△ABC和△CDE均是等腰直角三角形，∠BAC＝∠DCE＝90°，点E在线段AC上，BC，DE相交于点F，连接BE，BD，作EH⊥BD，垂足为点H，交BC与点G．（1）若点H是BD的中点，求∠BED的度数；（2）求证：△EFG∽△BFD；（3）求证：＝．【答案】（1）60°；（2）证明过程详见解答；（3）证明过程详见解答．【解答】（1）解：∵△ABC、△CDE是两个等腰直角三角形，∴∠ACB＝∠ABC＝45°，∠CED＝∠CDE＝45°，∴∠CFE＝180°﹣∠ACB﹣∠CED＝90°，∴EF＝DF＝DE，∵BH＝DH，EH⊥BD，∴BE＝DE，∴EF＝BE，∴cos∠BED＝，∴∠BED＝60°；（2）证明：由（1）得：∠CFE＝90°，∴CF⊥DE，∴∠BFD＝∠EFG＝∠BHE＝90°，∵∠BGH＝∠EGF，∴∠DBF＝∠FEG，∴△EFG∽△BFD；（3）证明：如图，作BQ∥AC，交EH的延长线于点Q，∴△BGQ∽△CGE，∴，∠Q＝∠CEH，∠QBE＝∠AEB，∴，设∠DBF＝DEH＝α，由（1）知：BC是DE的垂直平分线，∴BE＝BD，∴∠EBF＝∠DBF＝α，∴∠AEB＝∠ACB+∠EBF＝45°+α，∠CEH＝∠CED+∠FEG＝45°+α，∴∠AEB＝∠CEH，∴∠Q＝∠QBE，∴BE＝EQ，∴＝．七．相似形综合题（共2小题）14．（2023•济南）在矩形ABCD中，AB＝2，AD＝2，点E在边BC上，将射线AE绕点A逆时针旋转90°，交CD延长线于点G，以线段AE，AG为邻边作矩形AEFG．（1）如图1，连接BD，求∠BDC的度数和的值；（2）如图2，当点F在射线BD上时，求线段BE的长；（3）如图3，当EA＝EC时，在平面内有一动点P，满足PE＝EF，连接PA，PC，求PA+PC 的最小值．【答案】（1）∠BDC＝60°，；（2）；（3）4．【解答】解：（1）∵矩形ABCD中，AB＝2，，∴∠C＝90°，CD＝AB＝2，，∴，∴∠BDC＝60°，∵∠ABE＝∠BAD＝∠EAG＝∠ADG＝90°，∴∠EAG﹣∠EAD＝∠BAD﹣∠EAD，即∠DAG＝∠BAE，∴△ADG∽△ABE，∴；（2）如图2，过点F作FM⊥CG于点M，∵∠ABE＝∠AGF＝∠ADG＝90°，AE＝GF，∴∠BAE＝∠DAG＝∠CGF，∠ABE＝∠GMF＝90°，∴△ABE≌△GMF（AAS），∴BE＝MF，AB＝GM＝2，∴∠MDF＝∠BDC＝60°，FM⊥CG，∴，∴，设DM＝x，则，∴DG＝GM+MD＝2+x，由（1）可知：，∴，解得x＝1，∴；（3）如图3，连接AC，将△AEP绕点E顺时针旋转120°，EA与EC重合，得到△CEP'，连接PP'，矩形ABCD中，AD＝BC＝，AB＝2，∴tan∠ACB＝＝，∴∠ACB＝30°，∴AC＝2AB＝4，∵EA＝EC，∴∠EAC＝∠ACE＝30°，∠AEC＝120°，∴∠ACG＝∠GAC＝90°﹣30°＝60°，∴△AGC是等边三角形，AG＝AC＝4，∴PE＝EF＝AG＝4，∵将△AEP绕点E顺时针旋转120°，EA与EC重合，得到△CEP'，∴PA＝P'C，∠PEP'＝120°，EP＝EP'＝4，∴，∴当点P，C，P′三点共线时，PA+PC的值最小，此时为．15．（2023•菏泽）（1）如图1，在矩形ABCD中，点E，F分别在边DC，BC上，AE⊥DF，垂足为点G．求证：△ADE∽△DCF．【问题解决】（2）如图2，在正方形ABCD中，点E，F分别在边DC，BC上，AE＝DF，延长BC到点H，使CH＝DE，连接DH．求证：∠ADF＝∠H．【类比迁移】（3）如图3，在菱形ABCD中，点E，F分别在边DC，BC上，AE＝DF＝11，DE＝8，∠AED＝60°，求CF的长．【答案】（1）证明见解析；（2）证明见解析；（3）3．【解答】（1）证明：∵四边形ABCD是矩形，∴∠C＝∠ADE＝90°，∴∠CDF+∠DFC＝90°，∵AE⊥DF，∴∠DGE＝90°，∴∠CDF+∠AED＝90°，∴∠AED＝∠DFC，∴△ADE∽△DCF；（2）证明：∵四边形ABCD是正方形，∴AD＝DC，AD∥BC，∠ADE＝∠DCF＝90°，∵AE＝DF，∴Rt△ADE≌Rt△DCF（HL），∴DE＝CF，∵CH＝DE，∴CF＝CH，∵点H在BC的延长线上，∴∠DCH＝∠DCF＝90°，又∵DC＝DC，∴△DCF≌△DCH（SAS），∴∠DFC＝∠H，∵AD∥BC，∴∠ADF＝∠DFC，∴∠ADF＝∠H；（3）解：如图3，延长BC至点G，使CG＝DE＝8，连接DG，∵四边形ABCD是菱形，∴AD＝DC，AD∥BC，∴∠ADE＝∠DCG，∴△ADE≌△DCG（SAS），∴∠DGC＝∠AED＝60°，AE＝DG，∵AE＝DF，∴DG＝DF，∴△DFG是等边三角形，∴FG＝DF＝11，∵CF+CG＝FG，∴CF＝FG﹣CG＝11﹣8＝3，即CF的长为3．。

中考数学真题模拟题汇编二次函数抛物线(带答案解析)

中考数学真题模拟题汇编二次函数抛物线（带答案解析）姓名：_______________班级：_______________考号：_______________题号一、简答题二、综合题三、选择题四、填空题总分得分一、简答题（每空？分，共？分）1、如图，抛物线y=﹣经过A（4，0），C（0，4）两点，点B是抛物线与x轴的另一个交点，点E是OC 的中点，作直线AC、点M在抛物线上，过点M作MD⊥x轴，垂足为点D，交直线AC于点N，设点M的横坐标为m，MN 的长度为d．（1）直接写出直线AC的函数关系式；（2）求抛物线对应的函数关系式；（3）求d关于m的函数关系式；（4）当以点M、N、E、O为顶点的四边形为平行四边形时，直接写出m的值．2、如图，抛物线y=﹣（x﹣1）2+c与x轴交于A，B（A，B分别在y轴的左右两侧）两点，与y轴的正半轴交于点C，顶点为D，已知A（﹣1，0）．（1）求点B，C的坐标；（2）判断△CDB的形状并说明理由；（3）将△COB沿x轴向右平移t个单位长度（0＜t＜3）得到△QPE．△QPE与△CDB重叠部分（如图中阴影部分）面积为S，求S与t的函数关系式，并写出自变量t的取值范围．评卷人得分3、如图，抛物线y=﹣x2+2x+3与x轴相交于A、B两点（点A在点B的左侧），与y轴相交于点C，顶点为D．（1）直接写出A、B、C三点的坐标和抛物线的对称轴；（2）连接BC，与抛物线的对称轴交于点E，点P为线段BC上的一个动点，过点P作PF∥DE交抛物线于点F，设点P 的横坐标为m；①用含m的代数式表示线段PF的长，并求出当m为何值时，四边形PEDF为平行四边形？②设△BCF的面积为S，求S与m的函数关系式．4、如图，在平面直角坐标系中，一次函数分别与x轴、y轴相交于A、B两点，二次函数的图像经过点A．（1）试证明二次函数的图像与x轴有两个交点；（2）若二次函数图像的顶点D在直线AB上，求m，n的值；（3）设二次函数的图像与x轴的另一个交点为点C，顶点D关于x轴的对称点设为点E，以AE，AC 为邻边作平行四边形EACF，顶点F能否在该二次函数的图像上？如果在，求出这个二次函数的表达式；如果不在，请说明理由？二、综合题评卷人得分（每空？分，共？分）5、如图，二次函数y=x2+bx+c的图象与x轴交于A、B两点，且A点坐标为（﹣3，0），经过B点的直线交抛物线于点D（﹣2，﹣3）．（1）求抛物线的解析式；（2）过x轴上点E（a，0）（E点在B点的右侧）作直线EF∥BD，交抛物线于点F，求直线BD和直线EF的解析式；（3）是否存在实数a使四边形BDFE是平行四边形？如果存在，求出满足条件的a；如果不存在，请说明理由．6、如图，已知抛物线＝22－2与轴交于A，B两点（点A在点B 的左侧），与轴交于点C．（1）写出以A，B，C为顶点的三角形的面积；（2）过点E（0，6）且与轴平行的直线l1与抛物线相交于M，N两点（点M在点N的左侧），以MN为一边，抛物线上的任一点P为另一顶点作平行四边形。

函数的实际应用--抛物线型问题(专题训练)(解析版)-中考数学重难点题型专题汇总

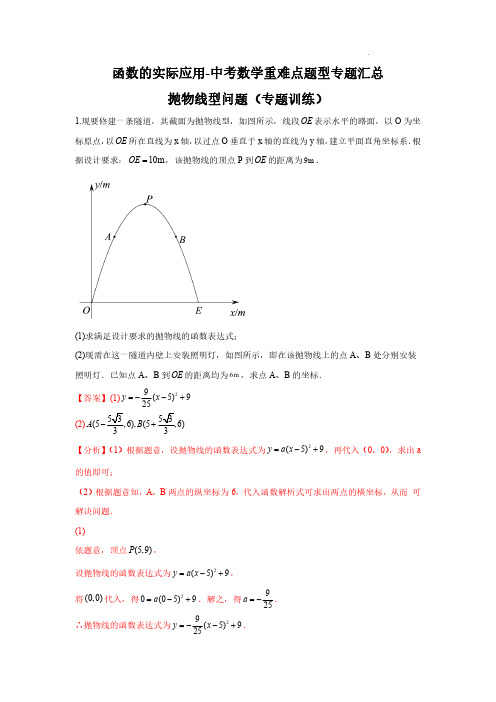
函数的实际应用-中考数学重难点题型专题汇总抛物线型问题（专题训练）1.现要修建一条隧道，其截面为抛物线型，如图所示，线段OE 表示水平的路面，以O 为坐标原点，以OE 所在直线为x 轴，以过点O 垂直于x 轴的直线为y 轴，建立平面直角坐标系．根据设计要求：10m OE =，该抛物线的顶点P 到OE 的距离为9m ．(1)求满足设计要求的抛物线的函数表达式；(2)现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A 、B 处分别安装照明灯．已知点A 、B 到OE 的距离均为6m ，求点A 、B 的坐标．【答案】(1)29(5)925y x =--+(2)(5(5A B +【分析】（1）根据题意，设抛物线的函数表达式为2(5)9y a x =-+，再代入（0，0），求出a 的值即可；（2）根据题意知，A ，B 两点的纵坐标为6，代入函数解析式可求出两点的横坐标，从而可解决问题．(1)依题意，顶点(5,9)P ，设抛物线的函数表达式为2(5)9y a x =-+，将(0,0)代入，得20(05)9a =-+．解之，得925a =-．∴抛物线的函数表达式为29(5)925y x =--+．(2)令6y =，得29(5)9625x --+=．解之，得125,5x x +=+．∴(5(5A B +．【点睛】本题考查了运用待定系数法求二次函数的解析式的运用，由函数值求自变量的值的运用，解答时求出二次函数的解析式是关键．2.甲秀楼是贵阳市一张靓丽的名片．如图①，甲秀楼的桥拱截面OBA 可视为抛物线的一部分，在某一时刻，桥拱内的水面宽8m OA =，桥拱顶点B 到水面的距离是4m ．（1）按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；（2）一只宽为1.2m 的打捞船径直向桥驶来，当船驶到桥拱下方且距O 点0.4m 时，桥下水位刚好在OA 处．有一名身高1.68m 的工人站立在打捞船正中间清理垃圾，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）；（3）如图③，桥拱所在的函数图象是抛物线()20y ax bx c a =++≠，该抛物线在x 轴下方部分与桥拱OBA 在平静水面中的倒影组成一个新函数图象．将新函数图象向右平移()0m m >个单位长度，平移后的函数图象在89x ≤≤时，y 的值随x 值的增大而减小，结合函数图象，求m 的取值范围．【答案】（1）y=14-x 2+2x （0≤x≤8）；（2）他的头顶不会触碰到桥拱，理由见详解；（3）【分析】（1）设二次函数的解析式为：y=a(x-8)x ，根据待定系数法，即可求解；（2）把：x =1，代入y=14-x 2+2x ，得到对应的y 值，进而即可得到结论；（3）根据题意得到新函数解析式，并画出函数图像，进而即可得到m 的范围．【详解】（1）根据题意得：A(8，0)，B(4，4)，设二次函数的解析式为：y=a(x-8)x ，把(4，4)代入上式，得：4=a×(4-8)×4，解得：14a =-，∴二次函数的解析式为：y=14-(x-8)x=14-x 2+2x （0≤x≤8）；（2）由题意得：x=0.4+1.2÷2=1，代入y=14-x 2+2x ，得y=14-×12+2×1=74＞1.68，答：他的头顶不会触碰到桥拱；（3）由题意得：当0≤x≤8时，新函数表达式为：y=14x 2-2x ，当x ＜0或x ＞8时，新函数表达式为：y=-14x 2+2x ，∴新函数表达式为：2212(08)41(08)4x x x y x x x ⎧-≤≤⎪⎪=⎨⎪-+⎪⎩或，∵将新函数图象向右平移()0m m >个单位长度，∴O '（m ，0），A '（m+8，0），B '（m+4，-4），如图所示，根据图像可知：当m+4≥9且m≤8时，即：5≤m≤8时，平移后的函数图象在89x ≤≤时，y 的值随x 值的增大而减小．本题主要考查二次函数的实际应用，掌握二次函数的待定系数法，二次函数的图像和性质，二次函数图像平移和轴对称变换规律，是解题的关键．3.2022年北京冬奥会即将召开，激起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x 轴，过跳台终点A 作水平线的垂线为y 轴，建立平面直角坐标系．图中的抛物线2117C :1126y x x =-++近似表示滑雪场地上的一座小山坡，某运动员从点O 正上方4米处的A 点滑出，滑出后沿一段抛物线221:8C y x bx c =-++运动．（1）当运动员运动到离A 处的水平距离为4米时，离水平线的高度为8米，求抛物线2C 的函数解析式（不要求写出自变量x 的取值范围）；（2）在（1）的条件下，当运动员运动水平线的水平距离为多少米时，运动员与小山坡的竖直距离为1米？（3）当运动员运动到坡顶正上方，且与坡顶距离超过3米时，求b 的取值范围．【答案】（1）213482y x x =-++；（2）12米；（3）3524b ≥．【分析】（1）根据题意可知：点A （0，4）点B （4，8），利用待定系数法代入抛物线221:8C y x bx c=-++即可求解；（2）高度差为1米可得21=1C C -可得方程，由此即可求解；（3）由抛物线2117C :1126y x x =-++可知坡顶坐标为61(7,)12，此时即当7x =时，运动员运动到坡顶正上方，若与坡顶距离超过3米，即2161773812y b c =-⨯++≥+，由此即可求出b的取值范围．【详解】解：（1）根据题意可知：点A （0，4），点B （4，8）代入抛物线221:8C y x bx c =-++得，2=4144=88c b c ⎧⎪⎨-⨯++⎪⎩，解得：=43=2c b ⎧⎪⎨⎪⎩，∴抛物线2C 的函数解析式213482y x x =-++；（2）∵运动员与小山坡的竖直距离为1米，∴221317(4)(1)182126x x x x -++--++=，解得：14x =-（不合题意，舍去），212x =，故当运动员运动水平线的水平距离为12米时，运动员与小山坡的竖直距离为1米；（3）∵点A （0，4），∴抛物线221:48C y x bx =-++，∵抛物线2211761C :1=7)12612y x x x =-++-+，∴坡顶坐标为61(7,12，∵当运动员运动到坡顶正上方，且与坡顶距离超过3米时，∴21617743812y b =-⨯++≥+，解得：3524b ≥．【点睛】本题属二次函数应用中的难题.解决函数应用问题的一般步骤为：（1）审题：弄清题意，分清条件和结论，理清数量关系；(2)建模：将文字语言转化为数学语言，利用数学知识建立相应的数学模型；（3）求模：求解数学模型，得到数学结论；(4)还原：将用数学方法得到的结论还原为实际问题．4.如图是一块铁皮余料，将其放置在平面直角坐标系中，底部边缘AB 在x 轴上，且8AB =dm ，外轮廓线是抛物线的一部分，对称轴为y 轴，高度8OC =dm ．现计划将此余料进行切割：(1)若切割成正方形，要求一边在底部边缘AB 上且面积最大，求此正方形的面积；(2)若切割成矩形，要求一边在底部边缘AB 上且周长最大，求此矩形的周长；(3)若切割成圆，判断能否切得半径为3dm 的圆，请说明理由．【答案】(1)296-；(2)20dm ；(3)能切得半径为3dm 的圆．【分析】（1）先把二次函数解析式求出来，设正方形的边长为2m ，表示在二次函数上点的坐标，代入即可得到关于m （2）如详解2中图所示，设矩形落在AB 上的边DE=2n ，利用函数解析式求解F 点坐标，进而表示出矩形的周长求最大值即可；（3）为了保证尽可能截取圆，应保证圆心H 坐标为（0，3），表示出圆心H 到二次函数上个点之间的距离与半径3进行比较即可．(1)由题目可知A （-4，0），B （4，0），C （0，8）设二次函数解析式为y=ax²+bx+c ，∵对称轴为y 轴，∴b=0，将A 、C 代入得，a=12-，c=8则二次函数解析式为2182y x =-+，如下图所示,正方形MNPQ 即为符合题意得正方形，设其边长为2m ，则P 点坐标可以表示为（m ，2m ）代入二次函数解析式得，21822m m -+=，解得122,2m m =-=-（舍去），∴2m=4，()()222496m =-=-则正方形的面积为296-；(2)如下如所示矩形DEFG ，设DE=2n ，则E （n ，0）将x=n 代入二次函数解析式，得2182y n =-+，则EF=2182n -+，矩形DEFG 的周长为：2（DE+EF ）=2（2n+2182n -+）=22416(2)20n n n -++=--+，当n=2时，矩形的周长最大，最大周长为20dm ；(3)如下图所示，为了保证尽可能截取圆，应保证圆心H 坐标为（0，3），则圆心H 到二次函数上个点之间的距离为3≥，∴能切得半径为3dm 的圆．【点睛】本题考查了二次函数与几何结合，熟练掌握各图形的性质，能灵活运用坐标与线段长度之间的转换是解题的关键．5.跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点K 为飞行距离计分的参照点，落地点超过K 点越远，飞行距离分越高．2022年北京冬奥会跳台滑雪标准台的起跳台的高度OA 为66m ，基准点K 到起跳台的水平距离为75m ，高度为m h （h 为定值）．设运动员从起跳点A 起跳后的高度(m)y 与水平距离(m)x 之间的函数关系为2(0)y ax bx c a =++．(1)c 的值为__________；(2)①若运动员落地点恰好到达K 点，且此时19,5010a b =-=，求基准点K 的高度h ；②若150a =-时，运动员落地点要超过K 点，则b 的取值范围为__________；(3)若运动员飞行的水平距离为25m 时，恰好达到最大高度76m ，试判断他的落地点能否超过K点，并说明理由．【答案】(1)66(2)①基准点K的高度h为21m；②b＞9 10；(3)他的落地点能超过K点，理由见解析．【分析】（1）根据起跳台的高度OA为66m，即可得c＝66；（2）①由a＝﹣150，b＝910，知y＝﹣150x2+910x+66，根据基准点K到起跳台的水平距离为75m，即得基准点K的高度h为21m；②运动员落地点要超过K点，即是x＝75时，y＞21，故﹣150×752+75b+66＞21，即可解得答案；（3）运动员飞行的水平距离为25m时，恰好达到最大高度76m，即是抛物线的顶点为（25，76），设抛物线解析式为y＝a（x﹣25）2+76，可得抛物线解析式为y＝﹣2125（x﹣25）2+76，当x＝75时，y＝36，从而可知他的落地点能超过K点．(1)解：∵起跳台的高度OA为66m，∴A（0，66），把A（0，66）代入y＝ax2+bx+c得：c＝66，故答案为：66；(2)解：①∵a＝﹣150，b＝910，∴y＝﹣150x2+910x+66，∵基准点K到起跳台的水平距离为75m，∴y＝﹣150×752+910×75+66＝21，∴基准点K的高度h为21m；②∵a＝﹣1 50，∴y＝﹣150x2+bx+66，∵运动员落地点要超过K点，∴当x＝75时，y＞21，即﹣150×752+75b+66＞21，解得b＞9 10，故答案为：b＞9 10；(3)解：他的落地点能超过K点，理由如下：∵运动员飞行的水平距离为25m时，恰好达到最大高度76m，∴抛物线的顶点为（25，76），设抛物线解析式为y＝a（x﹣25）2+76，把（0，66）代入得：66＝a（0﹣25）2+76，解得a＝﹣2 125，∴抛物线解析式为y＝﹣2125（x﹣25）2+76，当x＝75时，y＝﹣2125×（75﹣）2+76＝36，∵36＞21，∴他的落地点能超过K点．【点睛】本题考查二次函数的应用，解题的关键是读懂题意，能根据题意把实际问题转化为数学问题．6.根据以下素材，探索完成任务．如何设计拱桥景观灯的悬挂方案？素材1图1中有一座拱桥，图2是其抛物线形桥拱的示意图，某时测得水面宽20m，拱顶离水面5m．据调查，该河段水位在此基础上再涨1.8m达到最高．素材2为迎佳节，拟在图1桥洞前面的桥拱上悬挂40cm 长的灯笼，如图3.为了安全，灯笼底部距离水面不小于1m ；为了实效，相邻两盏灯笼悬挂点的水平间距均为1.6m ；为了美观，要求在符合条件处都挂上灯笼，且挂满后成轴对称分布．问题解决任务1确定桥拱形状在图2任务2探究悬挂范围在你所建立的坐标系中，仅在安全的条件下，确定悬挂点的纵坐标的最小值和横坐标的取值范围．任务3拟定设计方案给出一种符合所有悬挂条件的灯笼数量，并根据你所建立的坐标系，求出最左边一盏灯笼悬挂点的横坐标．【答案】任务一：见解析，2120y x =-；任务二：悬挂点的纵坐标的最小值是 1.8-；66x -≤≤；任务三：两种方案，见解析【分析】任务一：根据题意，以拱顶为原点，建立如图1所示的直角坐标系，待定系数法求解析式即可求解；任务二：根据题意，求得悬挂点的纵坐标5 1.810.4 1.8y ≥-+++=-，进而代入函数解析式即可求得横坐标的范围；任务三：有两种设计方案，分情况讨论，方案一：如图2（坐标系的横轴，图3同），从顶点处开始悬挂灯笼；方案二：如图3，从对称轴两侧开始悬挂灯笼，正中间两盏与对称轴的距离均为0.8m ，根据题意求得任意一种方案即可求解．【详解】任务一：以拱顶为原点，建立如图1所示的直角坐标系，则顶点为(0,0)，且经过点(10,5)-．设该抛物线函数表达式为2(0)y ax a =≠，则5100a -=，∴120a =-，∴该抛物线的函数表达式是2120y x =-．任务二：∵水位再上涨1.8m 1m ，灯笼长0.4m ，∴悬挂点的纵坐标5 1.810.4 1.8y ≥-+++=-，∴悬挂点的纵坐标的最小值是 1.8-．当 1.8y =-时，211.820x -=-，解得16x =或26x =-，∴悬挂点的横坐标的取值范围是66x -≤≤．任务三：有两种设计方案方案一：如图2（坐标系的横轴，图3同），从顶点处开始悬挂灯笼．∵66x -≤≤，相邻两灯笼悬挂点的水平间距均为1.6m ，∴若顶点一侧挂4盏灯笼，则1.646⨯>，⨯<，若顶点一侧挂3盏灯笼，则1.636∴顶点一侧最多可挂3盏灯笼．∵挂满灯笼后成轴对称分布，∴共可挂7盏灯笼．-．∴最左边一盏灯笼悬挂点的横坐标是 4.8方案二：如图3，从对称轴两侧开始悬挂灯笼，正中间两盏与对称轴的距离均为0.8m，+⨯->，∵若顶点一侧挂5盏灯笼，则0.8 1.6(51)6+⨯-<，若顶点一侧挂4盏灯笼，则0.8 1.6(41)6∴顶点一侧最多可挂4盏灯笼．∵挂满灯笼后成轴对称分布，∴共可挂8盏灯笼．-．∴最左边一盏灯笼悬挂点的横坐标是 5.6【点睛】本题考查了二次函数的应用，根据题意建立坐标系，掌握二次函数的性质是解题的关键．7.公路上正在行驶的甲车，发现前方20m处沿同一方向行驶的乙车后，开始减速，减速后甲车行驶的路程s（单位：m）、速度v（单位：m/s）与时间t（单位：s）的关系分别可以用二次函数和一次函数表示，其图象如图所示．（1）当甲车减速至9m/s时，它行驶的路程是多少？（2）若乙车以10m/s的速度匀速行驶，两车何时相距最近，最近距离是多少？【答案】（1）87.5m ；（2）6秒时两车相距最近，最近距离是2米【分析】（1）根据图像分别求出一次函数和二次函数解析式，令v=9求出t ，代入求出s 即可；（2）分析得出当v=10m/s 时，两车之间距离最小，代入计算即可．【详解】解：（1）由图可知：二次函数图像经过原点，设二次函数表达式为2s at bt =+，一次函数表达式为v kt c =+，∵一次函数经过（0，16），（8，8），则8816k c c =+⎧⎨=⎩，解得：116k c =-⎧⎨=⎩，∴一次函数表达式为16v t =-+，令v=9，则t=7，∴当t=7时，速度为9m/s ，∵二次函数经过（2，30），（4，56），则423016456a b a b +=⎧⎨+=⎩，解得：1216a b ⎧=-⎪⎨⎪=⎩，∴二次函数表达式为21162s t t =-+，令t=7，则s=491672-+⨯=87.5，∴当甲车减速至9m/s 时，它行驶的路程是87.5m ；（2）∵当t=0时，甲车的速度为16m/s ，∴当10＜v ＜16时，两车之间的距离逐渐变小，当0＜v ＜10时，两车之间的距离逐渐变大，∴当v=10m/s 时，两车之间距离最小，将v=10代入16v t =-+中，得t=6，将t=6代入21162s t t =-+中，得78s =，此时两车之间的距离为：10×6+20-78=2m ，∴6秒时两车相距最近，最近距离是2米．【点睛】本题考查了二次函数与一次函数的实际应用，理解题意，读懂函数图像，求出表达式是解题的基本前提．8.如今我国的大棚（如图1）种植技术已十分成熟．小明家的菜地上有一个长为16米的蔬菜大棚，其横截面顶部为抛物线型，大棚的一端固定在离地面高1米的墙体A 处，另一端固定在离地面高2米的墙体B 处，现对其横截面建立如图2所示的平面直角坐标系．已知大棚上某处离地面的高度y （米）与其离墙体A 的水平距离x （米）之间的关系满足216y x bx c =-++，现测得A ，B 两墙体之间的水平距离为6米．图2（1）直接写出b ，c 的值；（2）求大棚的最高处到地面的距离；（3）小明的爸爸欲在大棚内种植黄瓜，需搭建高为3724米的竹竿支架若干，已知大棚内可以根竹竿，则共需要准备多少根竹竿？【答案】（1）76b =，1c =；（2）7324米；（3）352【分析】（1）根据题意，可直接写出点A 点B 坐标，代入216y x bx c =-++，求出b 、c 即可；（2）根据（1）中函数解析式直接求顶点坐标即可；（3根据2173716624y x x =-++=，先求得大棚内可以搭建支架的土地的宽，再求得需搭建支架的面积，最后根据每平方米需要4根竹竿计算即可．【详解】解：（1）由题意知点A 坐标为(0)1，，点B 坐标为(6)2，，将A 、B 坐标代入216y x bx c =-++得：21=12666c b c ⎧⎪⎨=-⨯++⎪⎩解得：761b c ⎧=⎪⎨⎪=⎩，故76b =，1c =；（2）由221717731666224y x x x ⎛⎫=-++=--+ ⎪⎝⎭，可得当72x =时，y 有最大值7324，即大棚最高处到地面的距离为7324米；（3）由2173716624y x x =-++=，解得112x =，2132x =，又因为06x ≤≤，可知大棚内可以搭建支架的土地的宽为111622-=（米），又大棚的长为16米，故需要搭建支架部分的土地面积为1116882⨯=（平方米）共需要884352⨯=（根）竹竿．【点睛】本题主要考查根据待定系数法求函数解析式，根据函数解析式求顶点坐标，以及根据函数值确定自变量取值范围，掌握此题的关键是熟练掌握二次函数图像的性质．9.如图1是一座抛物线型拱桥侧面示意图．水面宽AB 与桥长CD 均为24m ，在距离D 点6米的E 处，测得桥面到桥拱的距离EF 为1.5m ，以桥拱顶点O 为原点，桥面为x 轴建立平面直角坐标系．（1）求桥拱项部O 离水面的距离．（2）如图2，桥面上方有3根高度均为4m 的支柱CG ，OH ，DI ，过相邻两根支柱顶端的钢缆呈形状相同的抛物线，其最低点到桥面距离为1m ．①求出其中一条钢缆抛物线的函数表达式．②为庆祝节日，在钢缆和桥拱之间竖直装饰若干条彩带，求彩带长度的最小值．【答案】（1）6m ；（2）①21'(6)112y x =++；②2m 【分析】（1）设211y a x =，由题意得(6,1.5)F -，求出抛物线图像解析式，求当x=12或x=-12时y 1的值即可；（2）①由题意得右边的抛物线顶点为(6,1)，设222(6)1y a x =-+，将点H 代入求值即可；②设彩带长度为h ，则12h y y =-，代入求值即可．【详解】解（1）设211y a x =，由题意得(6,1.5)F -，11.536a ∴-=，1124a ∴=-，21124y x ∴=-，∴当12x =时，21112624y =-⨯=-，∴桥拱顶部离水面高度为6m ．（2）①由题意得右边的抛物线顶点为(6,1)，∴设222(6)1y a x =-+，(0,4)H ，224(06)1a ∴=-+，2112a ∴=，221(6)112y x ∴=-+，(左边抛物线表达式：21'(6)112y x =++)②设彩带长度为h ，则22221111(6)1()412248h y y x x x x =-=-+--=-+，∴当4x =时，2min h =，答：彩带长度的最小值是2m ．【点睛】本题主要考查待定系数法求二次函数的解析式，以及二次函数最值得求解方法，结合题意根据数形结合的思想设出二次函数的顶点式方程是解题的关键．。

2024年九年级中考数学专题复习：二次函数实际应用(抛物线型问题)(含答案)

2024年九年级中考数学专题复习：二次函数实际应用（抛物线型问题）一、单选题 1．飞机着陆后滑行的距离s （单位：m ）关于滑行的时间t （单位：s ）的函数解析式是21.560s t t =-+．飞机着陆后到停下来滑行的距离是（）mA ．300B ．400C ．500D ．6002．如图，将一个小球从斜坡的点O 处抛出，小球的抛出路线可以用二次函数2142y x x =-刻画，斜坡可以用一次函数12y x =刻画．下列结论错误的是（）A ．小球距O 点水平距离超过4米呈下降趋势B ．当小球水平运动2米时，小球距离坡面的高度为6米C ．小球落地点距O 点水平距离为7米D ．当小球拋出高度达到8m 时，小球距O 点水平距离为4m3．小康在体育训练中掷出的实心球的运动路线呈如图所示的抛物线形，若实心球运动的抛物线的解析式为()2116399y x =--+，其中y 是实心球飞行的高度，x 是实心球飞行的水平距离，则小康此次掷球的成绩（即OA 的长度）是（）A ．8mB ．7mC ．6mD ．5m4．如图，要修建一个圆形喷水池，在池中心O 点竖直安装一根水管，在水管的顶端A 处安一个喷水头，使喷出的抛物线形水柱与水池中心O 点的水平距离为1m 处达到最高，高度为3m ，水柱落地处离池中心O 点3m ，则水管OA 的高是（）A．2m B．2.25m C．2.5m D．2.8m5．学校组织学生去同安进行研学实践活动，小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液（如图①）.于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时，洗手液从喷口B 流出，路线近似呈抛物线状，且喷口B为该抛物线的顶点．洗手液瓶子的截面图下面部分是矩形CGHD．小王同学测得：洗手液瓶子的底面直径12cmGH=，喷嘴位置点B距台面的距离为16cm，且B、D、H三点共线．小王在距离台面15.5cm处接洗于液时，手心Q到直线DH的水平距离为3cm，若小王不去接，则洗手液落在台面的位置距DH的水平距离是（）A．122cm B．123cm C．62cm D．6cm6．某公园有一个圆形喷水池，喷出的水流呈抛物线形，一条水流的高度h（单位：m）与水流运动时间t（单位：s）之间的函数解析式为2305h t t=-，那么水流从喷出至回落到地面所需要的时间是（）A．6s B．4s C．3s D．2s7．如图所示，某工厂的大门是抛物线形水泥建筑物，大门的地面宽度为8m，两侧距地面3m高处各有一壁灯，两壁灯间的水平距离为6m，则厂门的高度约为（）A．307B．387C．487D．5078．如图，一座拱桥的轮廓是抛物线型，桥高10米，拱高8米，跨度24米，相邻两支柱间的距离均为6米，则支柱MN的长度为（）A．6米B．5米C．4.5米D．4米二、填空题9．如图，已知一抛物线形大门，其地面宽度AB长10米，一位身高1.8米的同学站在门下离门角B点1米的D 处，其头顶刚好顶在抛物线形门上C处．则该大门的最高处离地面高h为米．10．如图所示，抛物线形拱桥的顶点距水面2m时，测得拱桥内水面宽为12m．当水面升高1m后，拱桥内水面的宽度减少m．11．从地面竖直向上抛出一小球，小球的高度h（米）与小球的运动时间（秒）之间的关系式是()2h t t t=-≤≤，若抛出小球1秒钟后再抛出同样的第二个小球．则第二个小球抛出秒时，两个30506小球在空中相撞．12．从地面竖直向上跑出一小球，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是()2=-≤≤，小球运动到s时，达到最大高度．h t t t3020613．如图，以40m/s的速度将小球沿与地面成30︒角的方向击出时，小球的飞行路线将是一条抛物线，如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间t（单位：s）之间具有函数关系2=-+，小520h t t球飞行过程中能达到的最大高度为m．14．如图，在喷水池的中心A处竖直安装一个水管AB，水管的顶端B处有一个喷水孔，喷出的抛物线形水柱在与池中心A的水平距离为1m处达到A最高点C，高度为3m，水柱落地点D离池中心A处3m，则水管AB的长为m．15．如图，水池中心点O处竖直安装一水管，水管喷头喷出抛物线形水柱，喷头上下移动时，抛物线形水柱随之竖直上下平移，水柱落点与点O在同一水平面．安装师傅调试发现，喷头高2.5m时，水柱落点距O点2.5m；喷头高4m时，水柱落点距O点3m．那么喷头高8m时，水柱落点距O点为m．16．某次踢球，足球的飞行高度h（米）与水平距离x（米）之间满足2=-+，则足球从离地到落地的560h x x水平距离为米．三、解答题AA的17．如图，隧道的截面由抛物线和长方形构成，长方形的长为16m，宽为6m，抛物线的最高点C离地面1距离为8m.(1)按如图所示的直角坐标系，求该抛物线的函数表达式.(2)一大型汽车装载某大型设备后，高为7m ，宽为4m ，如果该隧道内设双向行车道，那么这辆货车能否安全通过？18．掷实心球是中考体育考试的项目．如图是一男生所掷实心球的行进路线（抛物线的一部分）的高度()y m 与水平距离()x m 之间的函数图象，且掷出时起点处高度为2m ，当到起点的水平距离为4m 时，实心球行进至最高点，此时实心球与地面的距离为3m ．(1)求抛物线的函数解析式；(2)在该市的评分标准中，实心球从起点到落地点的水平距离大于等于10m 时，即可得满分，试判断该男生在此项考试中能否得满分，并说明理由（参考数据：3 1.73≈）．19．南湖大桥作为我市首个全面采用数控技术的桥体音乐喷泉项目，历经多年已经成为长春市民夜间休闲放松的网红打卡地．其中喷水头喷出的水柱轨迹呈抛物线形状，喷水头P 距水面7.5m ，水柱喷射水平距离为5m 时，达到最大高度，此时距水面10m ，水柱落在水面A 点处．将收集到数据建立如图所示的平面直角坐标系，水柱喷出的高度()m y 与水平距离()m x 之间的函数关系式是21()y a x h k =-+．(1)求抛物线的表达式．(2)现调整P 的出水角度，其喷出的水柱高度()m y 与水平距离()m x 之间的函数关系式是220.1 1.2y x x m =-++，落点恰好在A 点右边的B 点处，求AB 的长．（结果精确到0.1m ，参考数据：11110.54=）20．图①是古代的一种远程投石机，其投出去的石块运动轨迹是抛物线的一部分．据《范蠡兵法》记载：“飞石重十二斤，为机发，行二百步”，其原理蕴含了物理中的“杠杆原理”．在如图②所示的平面直角坐标系中，将投石机置于斜坡OA 的底部点O 处，石块从投石机竖直方向上的点C 处被投出，已知石块运动轨迹所在抛物线的顶点坐标是()50,25，5OC =．(1)求抛物线的表达式；(2)在斜坡上的点A 建有垂直于水平线OD 的城墙AB ，且75OD =，12AD =，9AB =，点D ，A ，B 在一条直线上．通过计算说明石块能否飞越城墙AB ．参考答案：1．D2．B3．B4．B。

《抛物线》典型例题12例(含标准答案解析]

《抛物线》典型例题12例典型例题一例1 指出抛物线的焦点坐标、准线方程．（1）y x 42= （2）)0(2≠=a ay x分析：（1）先根据抛物线方程确定抛物线是四种中哪一种，求出p ，再写出焦点坐标和准线方程．（2）先把方程化为标准方程形式，再对a 进行讨论，确定是哪一种后，求p 及焦点坐标与准线方程．解：（1）2=p ，∴焦点坐标是（0，1），准线方程是：1-=y （2）原抛物线方程为：x a y 12=，ap 12=∴ ①当0>a 时，ap 412=，抛物线开口向右， ∴焦点坐标是)0,41(a ，准线方程是：a x 41-=． ②当0<a 时，a p 412-=，抛物线开口向左， ∴焦点坐标是)0,41(a ，准线方程是：ax 41-=．综合上述，当0≠a 时，抛物线2ay x =的焦点坐标为)0,41(a ，准线方程是：ax 41-=．典型例题二例2 若直线2-=kx y 与抛物线x y 82=交于A 、B 两点，且AB 中点的横坐标为2，求此直线方程．分析：由直线与抛物线相交利用韦达定理列出k 的方程求解．另由于已知与直线斜率及弦中点坐标有关，故也可利用“作差法”求k ．解法一：设),(11y x A 、),(22y x B ，则由：⎩⎨⎧=-=xy kx y 822可得：04)84(22=++-x k x k ．∵直线与抛物线相交，0≠∴k 且0>∆，则1->k ． ∵AB 中点横坐标为：2842221=+=+∴kk x x ，解得：2=k 或1-=k （舍去）．故所求直线方程为：22-=x y ．解法二：设),(11y x A 、),(22y x B ，则有22212188x y x y ==．两式作差解：)(8))((212121x x y y y y -=+-，即2121218y y x x y y +=--． 421=+x x 444)(22212121-=-+=-+-=+∴k x x k kx kx y y ，448-=∴k k 故2=k 或1-=k （舍去）．则所求直线方程为：22-=x y ．典型例题三例3 求证：以抛物线的焦点弦为直径的圆心与抛物线的准线相切．分析：可设抛物线方程为)0(22>=p px y ．如图所示，只须证明12MM AB =，则以AB 为直径的圆，必与抛物线准线相切．证明：作l AA ⊥1于l BB A ⊥11,于1B ．M 为AB 中点，作l MM ⊥1于1M ，则由抛物线的定义可知：BF BB AF AA ==11,在直角梯形A A BB 11中：AB BF AF BB AA MM 21)(21)(21111=+=+=AB MM 211=∴，故以AB 为直径的圆，必与抛物线的准线相切．说明：类似有：以椭圆焦点弦为直径的圆与相对应的准线相离，以双曲线焦点弦为直径的圆与相应的准线相交．典型例题四例4（1）设抛物线x y 42=被直线k x y +=2截得的弦长为53，求k 值．（2）以（1）中的弦为底边，以x 轴上的点P 为顶点作三角形，当三角形的面积为9时，求P 点坐标．分析：（1）题可利用弦长公式求k ，（2）题可利用面积求高，再用点到直线距离求P 点坐标．解：（1）由⎩⎨⎧+==kx y x y 242得：0)44(422=+-+k x k x设直线与抛物线交于),(11y x A 与),(22y x B 两点．则有：4,122121k x x k x x =⋅-=+[][])21(5)1(54)(5))(21(22212212212k k k x x x x x x AB -=--=-+=-+=∴53)21(5,53=-∴=∴k AB ，即4-=k （2）9=∆S ，底边长为53，∴三角形高5565392=⨯=h ∵点P 在x 轴上，∴设P 点坐标是)0,(0x 则点P 到直线42-=x y 的距离就等于h ，即55612402220=+--x 10-=∴x 或50=x ，即所求P 点坐标是（－1，0）或（5，0）．典型例题五例5 已知定直线l 及定点A （A 不在l 上），n 为过A 且垂直于l 的直线，设N 为l 上任一点，AN 的垂直平分线交n 于B ，点B 关于AN 的对称点为P ，求证P 的轨迹为抛物线．分析：要证P 的轨迹为抛物线，有两个途径，一个证明P 点的轨迹符合抛物线的定义，二是证明P 的轨迹方程为抛物线的方程，可先用第一种方法，由A 为定点，l 为定直线，为我们提供了利用定义的信息，若能证明PN PA =且l PN ⊥即可．证明：如图所示，连结PA 、PN 、NB ．由已知条件可知：PB 垂直平分NA ，且B 关于AN 的对称点为P ．∴AN 也垂直平分PB ．则四边形PABN 为菱形．即有PN PA =．..l PN l AB ⊥∴⊥则P 点符合抛物线上点的条件：到定点A 的距离与到定直线的距离相等，所以P 点的轨迹为抛物线．典型例题六例6 若线段21P P 为抛物线)0(2:2>=p px y C 的一条焦点弦，F 为C 的焦点，求证：p F P FP 21121=+．分析：此题证的是距离问题，如果把它们用两点间的距离表示出来，其计算量是很大的．我们可以用抛物线的定义，巧妙运用韦达定理，也可以用抛物线的定义与平面几何知识，把结论证明出来．证法一：)0,2(pF ，若过F 的直线即线段21P P 所在直线斜率不存在时，则有p F P F P ==21,p p p F P FP 2111121=+=+∴．若线段21P P 所在直线斜率存在时，设为k ，则此直线为：)0)(2(≠-=k px k y ，且设),(),,(222111y x P y x P ．由⎪⎪⎩⎪⎪⎨⎧-=-=)2()2(p x k y px k y 得：04)2(22222=++-p k x k p x k 2221)2(k k p x x +=+∴ ①4221p x x =⋅ ②根据抛物线定义有：p x x P P px F P p x F P ++=∴+=+=21211211,2,2则F P F P F P F P F P F P 21212111⋅+=+4)(2)2)(2(22121212121p x x p x x p x x p x p x p x x +++++=++++= 请将①②代入并化简得：p F P FP 21121=+ 证法二：如图所示，设1P 、2P 、F 点在C 的准线l 上的射影分别是'1P 、'2P 、F '，且不妨设1122P P m n P P '=<='，又设2P点在F F '、11P P '上的射影分别是A 、B 点，由抛物线定义知，p F F m F P n F P ='==,,12又AF P 2∆∽12BP P ∆，1221P P F P BP AF =∴即nm nn m n p +=-- pn m m nn m p 2112)(=+∴=+∴ 故原命题成立．典型例题七例7 设抛物线方程为)0(22>=p px y ，过焦点F 的弦AB 的倾斜角为α，求证：焦点弦长为α2sin 2pAB =．分析：此题做法跟上题类似，也可采用韦达定理与抛物线定义解决问题．证法一：抛物线)0(22>=p px y 的焦点为)0,2(p，过焦点的弦AB 所在的直线方程为：)2(tan px y -=α由方程组⎪⎩⎪⎨⎧=-=px y p x y 2)2(tan 2α消去y 得：0tan )(tan 4tan 422222=+-αααp p x设),(),,(2211y x B y x A ，则⎪⎪⎩⎪⎪⎨⎧=⋅+=+=+4)cot 21(tan )2(tan 22122221p x x p p x x ααα 又)(tan 2121x x y y -=α[]ααααααααα242222222222122122212sin 2sin 14)cot 1(cot 4sec 44)cot 1()tan 1(4)()tan 1())(tan 1(pp p p p x x x x x x AB =⋅=+⋅=⎥⎦⎤⎢⎣⎡⋅-++=-++=-+=∴即α2sin 2pAB =证法二：如图所示，分别作1AA 、1BB 垂直于准线l ．由抛物线定义有：ααcos cos 11⋅-==+⋅==BF p BB BF p AF AA AF于是可得出：αcos 1-=p AF αcos 1+=pBFαααα22sin 2cos 12cos 1cos 1p pp p BFAF AB =-=++-=+=∴ 故原命题成立．典型例题八例8 已知圆锥曲线C 经过定点)32,3(P ，它的一个焦点为F （1，0），对应于该焦点的准线为1-=x ，过焦点F 任意作曲线C 的弦AB ，若弦AB 的长度不超过8，且直线AB 与椭圆22322=+y x 相交于不同的两点，求（1）AB 的倾斜角θ的取值范围．（2）设直线AB 与椭圆相交于C 、D 两点，求CD 中点M 的轨迹方程．分析：由已知条件可确定出圆锥曲线C 为抛物线，AB 为抛物线的焦点弦，设其斜率为k ，弦AB 与椭圆相交于不同的两点，可求出k 的取值范围，从而可得θ的取值范围，求CD 中点M 的轨迹方程时，可设出M 的坐标，利用韦达定理化简即可．解：（1）由已知得4=PF ．故P 到1-=x 的距离4=d ，从而d PF = ∴曲线C 是抛物线，其方程为x y 42=．设直线AB 的斜率为k ，若k 不存在，则直线AB 与22322=+y x 无交点． ∴k 存在．设AB 的方程为)1(-=x k y由⎩⎨⎧-==)1(42x k y x y 可得：0442=--k y ky 设A 、B 坐标分别为),(11y x 、),(22y x ，则：442121-=⋅=+y y ky y222122122212)1(44)(1))(11(k k y y y y k k y y kAB +=-++=-+=∴∵弦AB 的长度不超过8，8)1(422≤+∴k k 即12≥k 由⎩⎨⎧=+-=223)1(22y x x k y 得：0)1(24)32(2222=-+-+k x k x k∵AB 与椭圆相交于不同的两点，32<∴k 由12≥k 和32<k 可得：31<≤k 或13-≤<-k 故3tan 1≤≤θ或1tan 3-<<-θ 又πθ<≤0，∴所求θ的取值范围是：34πθπ<≤或4332πθπ≤< （2）设CD 中点),(y x M 、),(33y x C 、),(44y x D由⎩⎨⎧=+-=223)1(22y x x k y 得：0)1(24)32(2222=-+-+k x k x k 9325313231322232)1(2,324222224322132243<+≤∴<≤+-=∴+=+=+-=⋅+=+∴k k k x k k x x x k k x x k k x x则323211522<+-≤k 即3252<≤x ． 3)1(2)1(23221222222+-⋅-⋅=+=∴-=x y x y k k x x y k 化简得：032322=-+x y x∴所求轨迹方程为：)3252(032322<≤=-+x x y x典型例题九例9 定长为3的线段AB 的端点A 、B 在抛物线x y =2上移动，求AB 的中点到y 轴的距离的最小值，并求出此时AB 中点的坐标．分析：线段AB 中点到y 轴距离的最小值，就是其横坐标的最小值．这是中点坐标问题，因此只要研究A 、B 两点的横坐标之和取什么最小值即可．解：如图，设F 是x y =2的焦点，A 、B 两点到准线的垂线分别是AC 、BD ，又M 到准线的垂线为MN ，C 、D 和N 是垂足，则2321)(21)(21=≥+=+=AB BF AF BD AC MN ．设M 点的横坐标为x ，纵坐标为y ，41+=x MN ，则454123=-≥x ．等式成立的条件是AB 过点F ．当45=x 时，41221-=-=P y y ，故 22122)(212221221=-=++=+x y y y y y y ， 221±=+y y ，22±=y ．所以)22,45(±M ，此时M 到y 轴的距离的最小值为45．说明：本题从分析图形性质出发，把三角形的性质应用到解析几何中，解法较简．典型例题十例10 过抛物线px y 2=的焦点F 作倾斜角为θ的直线，交抛物线于A 、B 两点，求AB 的最小值．分析：本题可分2πθ=和2πθ≠两种情况讨论．当2πθ≠时，先写出AB 的表达式，再求范围．解：(1)若2πθ=，此时p AB 2=． (2)若2πθ≠，因有两交点，所以0≠θ． )2(tan p x y AB -=θ：，即2tan py x +=θ．代入抛物线方程，有0tan 222=--p y py θ．故θθ22222212csc 44tan 4)(p p p y y =+=-， θθθ2222212212tan csc 4tan )()(p y y x x =-=-．故θθθ422222csc 4)tan 11(csc 4p p AB =+=．所以p p AB 2sin 22>=θ．因2πθ≠，所以这里不能取“=”．综合(1)(2)，当2πθ=时，p AB 2=最小值．说明：(1)此题须对θ分2πθ=和2πθ≠两种情况进行讨论； (2)从解题过程可知，抛物线点弦长公式为θ2sin 2pl =； (3)当2πθ=时，AB 叫做抛物线的通径．通径是最短的焦点弦．典型例题十一例11 过抛物线px y 22=)0(>p 的焦点F 作弦AB ，l 为准线，过A 、B 作l 的垂线，垂足分别为'A 、'B ，则①''FB A ∠为（），②B AF '∠为（）．A ．大于等于︒90B ．小于等于︒90C ．等于︒90D 不确定分析：本题考查抛物线的定义、直线与圆的位置关系等方面的知识，关键是求角的大小以及判定直线与圆是否相切．解：①点A 在抛物线上，由抛物线定义，则21'∠=∠⇒=AF AA ，又x AA //'轴31∠=∠⇒．∴32∠=∠，同理64∠=∠，而︒=∠+∠+∠+∠1804632，∴︒=∠+∠9063，∴︒=∠90''FB A ．选C ．②过AB 中点M 作l MM ⊥'，垂中为'M ，则AB BF AF BB AA MM 21)(21)(21'''=+=+=．∴以AB 为直径的圆与直线l 相切，切点为'M ．又'F 在圆的外部，∴︒<∠90'B AF ．特别地，当x AB ⊥轴时，'M 与'F 重合，︒=∠90'B AF ．即︒≤∠90'B AF ，选B ．典型例题十二例12 已知点)2,3(M ，F 为抛物线x y 22=的焦点，点P 在该抛物线上移动，当PF PM +取最小值时，点P 的坐标为__________．分析：本题若建立目标函数来求PF PM +的最小值是困难的，若巧妙地利用抛物线定义，结合图形则问题不难解决．解：如图，由定义知PE PF =，故213=≥≥+=+MN ME PM PF PF PM ．取等号时，M 、P 、E 三点共线，∴P 点纵坐标为2，代入方程，求出其横坐标为2，所以P 点坐标为)2,2(．。

2021年中考数学复习-抛物线型问题(解析版)

类型四抛物线形问题【典例1】已知平面直角坐标系xOy （如图1），直线m x y +=的经过点)0,4(-A 和点)3,(n B .（1）求m 、n 的值；（2）如果抛物线c bx x y ++=2经过点A 、B ，该抛物线的顶点为点P ，求ABP ∠sin 的值；（3）设点Q 在直线m x y +=上，且在第一象限内，直线m x y +=与y 轴的交点为点D ，如果DOB AQO ∠=∠，求点Q 的坐标.【答案】：（1）1-=n （2）1010sin =∠ABP （3）（4,8）【解析】：（1） ∵直线m x y +=的经过点)0,4(-A∴04=+-m∴4=m∵直线m x y +=的经过点)3,(n B ∴34=+n∴1-=n（2）由可知点B 的坐标为)3,1(-∵抛物线c bx x y ++=2经过点A 、B ∴⎩⎨⎧=+-=+-310416c b c b∴6=b ， 8=c∴抛物线c bx x y ++=2的表达式为862++=x x y∴抛物线862++=x x y 的顶点坐标为)1,3(--P∴23=AB ,2=AP ,52=PB图1∴222PB BP AB =+ ∴︒=∠90PAB∴PB AP ABP =∠sin ∴1010sin =∠ABP（3）过点Q 作x QH ⊥轴，垂足为点H ，则QH ∥y 轴 ∵DOB AQO ∠=∠,QBO OBD ∠=∠∴△OBD ∽△QBO ∴OBDBQB OB = ∵直线4+=x y 与y 轴的交点为点D ∴点D 的坐标为)4,0(,4=OD又10=OB ，2=DB∴25=QB ，24=DQ∵23=AB∴28=AQ ,24=DQ ∵QH ∥y 轴 ∴AQADQH OD = ∴28244=QH ∴8=QH即点Q 的纵坐标是8又点Q 在直线4+=x y 上点Q 的坐标为)8,4(【典例2】如图在直角坐标平面内，抛物线32-+=bx ax y 与y 轴交于点A ，与x 轴分别交于点B （-1，0）、点C （3，0），点D 是抛物线的顶点. （1）求抛物线的表达式及顶点D 的坐标；（2）联结AD 、DC ，求ACD ∆的面积；（3）点P 在直线DC 上，联结OP ，若以O 、P 、C 为顶点的三角形与△ABC 相似，求点P 的坐标．备用图第2题图【答案】（1）（1，-4）（2）3（3）)518,56(1-P 或)2,2(2-P 【解析】：（1）点B （-1，0）、C （3，0）在抛物线32-+=bx ax y 上∴⎩⎨⎧=-+=--033903b a b a ，解得⎩⎨⎧-==21b a∴抛物线的表达式为322--=x x y ，顶点D 的坐标是（1，-4）（2）∵A （0，-3），C （3，0），D （1，-4） ∴23=AC ，52=CD ，2=AD∴222AD AC CD += ∴︒=∠90CAD ∴.32232121=⨯⨯=⋅⋅=∆AD AC S ACD （3）∵︒=∠=∠90AOB CAD ，2==AOACBO AD ， ∴△CAD ∽△AOB ，∴OAB ACD ∠=∠∵OA =OC ，︒=∠90AOC ∴︒=∠=∠45OCA OAC∴ACD OCA OAB OAC ∠+∠=∠+∠，即BCD BAC ∠=∠ 若以O 、P 、C 为顶点的三角形与△ABC 相似，且△ABC 为锐角三角形则POC ∆也为锐角三角形，点P 在第四象限由点C （3，0），D （1，-4）得直线CD 的表达式是62-=x y ，设)62,(-t t P （30<<t ）过P 作PH ⊥OC ，垂足为点H ，则t OH =，t PH 26-=①当ABC POC ∠=∠时,由ABC POC ∠=∠tan tan 得BO AO OH PH =，∴326=-t t ，解得56=t ， ∴)518,56(1-P ②当ACB POC ∠=∠时,由145tan tan tan =︒=∠=∠ACB POC 得1=OHPH ，∴126=-tt，解得2=t ，∴)2,2(2-P 综上得)518,56(1-P 或)2,2(2-P 【典例3】已知抛物线经过点(0,3)A 、(4,1)B 、(3,0)C ．（1）求抛物线的解析式；（2）联结AC 、BC 、AB ，求BAC ∠的正切值；（3）点P 是该抛物线上一点，且在第一象限内，过点P 作PG AP ⊥交y 轴于点G ，当点G在点A 的上方，且APG △与ABC △相似时，求点P 的坐标．【答案】：（1）解得12523a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩（2）13BC tan BAC AC ===∠ （3）点P 的坐标为(11,36)或1744(,)39【解析】：（1）设所求二次函数的解析式为2(0)y ax bx c a =++≠，将A （0,3）、B （4，）、C （3,0）代入，得 1641,930,3.a b c a b c c ++=⎧⎪++=⎨⎪=⎩解得12523a b c ⎧=⎪⎪⎪=-⎨⎪=⎪⎪⎩所以，这个二次函数的【解析】式为215322y x x =-+ （2）∵A （0,3）、B （4，）、C （3,0）∴AC =BC =AB =∴222AC BC AB +=∴90ACB =︒∠ ∴21332BC tan BAC AC ===∠ （3）过点P 作PH y ⊥轴，垂足为H设P 215(,3)22x x x -+，则H 215(0,3)22x x -+ ∵A （0,3） ∴21522AH x x =-，PH x = ∵90ACB APG ==︒∠∠∴当△APG 与△ABC 相似时，存在以下两种可能：①PAG CAB =∠∠ 则13tan PAG tan CAB ==∠∠ 即13PH AH = ∴2115322x x x =- 解得11x = ∴点P 的坐标为(11,36)②PAG ABC =∠∠ 则3tan PAG tan ABC ==∠∠即3PH AH = ∴231522x x x =- 解得173x = ∴点P 的坐标为1744(,)39【典例4】平面直角坐标系xOy 中（如图8），已知抛物线2y x bx c =++经过点A （1,0）和B （3,0），与y 轴相交于点C ，顶点为P ．（1）求这条抛物线的表达式和顶点P 的坐标；（2）点E 在抛物线的对称轴上，且EA =EC ，求点E 的坐标；（3）在（2）的条件下，记抛物线的对称轴为直线MN ，点Q 在直线MN 右侧的抛物线图4上，∠MEQ =∠NEB ，求点Q 的坐标．【答案】：（1）P 的坐标是（2，-1）（2）m=2（3）5t =，点E 的坐标为（5，8）【解析】：（1）∵二次函数2y x bx c =++的图像经过点A （1，0）和B （3，0），∴10930b c b c ++=⎧⎨++=⎩，解得：4b =-，3c =．∴这条抛物线的表达式是243y x x =-+顶点P 的坐标是（2，-1）．（2）抛物线243y x x =-+的对称轴是直线2x =，设点E 的坐标是（2，m ）．根据题意得：=，解得：m=2， ∴点E 的坐标为（2，2）．（3）解法一：设点Q 的坐标为2(,43)t t t -+，记MN 与x 轴相交于点F ．作QD ⊥MN ，垂足为D ，则2DQ t =-，2243241DE t t t t =-+-=-+ ∵∠QDE=∠BFE=90°，∠QED=∠BEF ，∴△QDE ∽△BFE ，∴DQ DEBF EF=，∴224112t t t --+=，解得11t =（不合题意，舍去），25t =．∴5t =，点E 的坐标为（5，8）．解法二：记MN 与x 轴相交于点F ．联结AE ，延长AE 交抛物线于点Q ，∵AE=BE ， EF ⊥AB ，∴∠AEF=∠NEB ，又∵∠AEF=∠MEQ ，∴∠QEM=∠NEB ，点Q 是所求的点，设点Q 的坐标为2(,43)t t t -+，作QH ⊥x 轴，垂足为H ，则QH =243t t -+，OH =t ，AH =t -1， ∵EF ⊥x 轴，∴EF ∥QH ，∴EF AFQH AH=，∴221431t t t =-+-，解得11t =（不合题意，舍去），25t =． ∴5t =，点E 的坐标为（5，8）．【典例5】在平面直角坐标系xOy 中，已知点B （8,0）和点C （9，3-）．抛物线c ax ax y +-=82（a ，c 是常数，a ≠0）经过点B 、C ，且与x 轴的另一交点为A ．对称轴上有一点M ，满足MA =MC ．（1）求这条抛物线的表达式；（2）求四边形ABCM 的面积；（3）如果坐标系内有一点D ，满足四边形ABCD且AD //BC ，求点D 的坐标．【答案】：（1）抛物线的表达式：x x y 38312+-=（2）3（3）点D 的坐标)539,513(-【解析】：（1）由题意得：抛物线对称轴aax 28-=，即4=x ．点B （8,0）关于对称轴的对称点为点A （0,0）∴0=c ，将C （9，-3）代入ax ax y 82-=，得31-=a∴抛物线的表达式：x x y 38312+-=（2）∵点M 在对称轴上，∴可设M （4，y ）又∵MA =MC ，即22MCMA =∴2222)3(54++=+y y , 解得y =-3, ∴M （4，-3） ∵MC //AB 且MC ≠AB , ∴四边形ABCM 为梯形，,AB =8,MC =5,AB 边上的高h = y M = 3 ∴2393)58(21)(21=⨯+⨯=⨯+=MH MC AB S(3) 将点B （8,0）和点C （9，﹣3）代入b kx y BC += 可得⎩⎨⎧-=+=+3908b k b k ，解得⎩⎨⎧=-=243b k 由题意得，∵AD //BC , 3-=BC k ∴3-=AD k ，xy AD 3-=又∵AD 过（0,0），DC =AB =8，设D (x ,-3x ) 2228)33()9(=+-+-x x , 解得11=x (不合题意，舍去)， 5132=x ∴5393-=-=x y ∴点D 的坐标)539,513(-．【典例6】如图，已知在平面直角坐标系xOy 中，抛物线22y ax x c =-+与x 轴交于点A 和点B （1，0），与y 轴相交于点C （0，3）．（1）求抛物线的解析式和顶点D 的坐标；（2）求证：∠DAB=∠ACB ；（3）点Q 在抛物线上，且△ADQ 是以AD 为底的等腰三角形，求Q 点的坐标．【答案】：（1）顶点坐标D （－1，4）．（2）DAB ACB ∠=∠（3）点Q的坐标是⎝⎭，⎝⎭【解析】：（1）把B （1，0）和C （0，3）代入22y ax x c =-+中，得9603a c c ++=⎧⎨=⎩，解得13a c =-⎧⎨=⎩．∴抛物线的解析式是：223y x x =--+． ∴顶点坐标D （－1，4）．（2）令0y =，则2230x x --+=，13x =-，21x =，∴A （－3，0）∴3OA OC ==，∴∠CAO =∠OCA ．在Rt BOC ∆中，1tan 3OB OCB OC ∠==．∵AC =DC =AD =， ∴2220AC DC +=，220AD =；∴222AC DC AD +=，ACD ∆是直角三角形且90ACD ∠=，∴1tan 3DC DAC AC ∠==，又∵∠DAC 和∠OCB 都是锐角，∴∠DAC =∠OCB ． ∴DAC CAO BCO OCA ∠+∠=∠+∠，即DAB ACB ∠=∠．（3）令(Q x ，)y 且满足223y x x =--+，(3A -,0)，(1D -，4）∵ADQ ∆是以AD 为底的等腰三角形，∴22QD QA =，即2222(3)(1)(4)x y x y ++=++-，（第6题图）化简得：220x y -+=．由222023x y y x x -+=⎧⎨=--+⎩，解得11341411418x y ⎧-+=⎪⎪⎨-⎪=⎪⎩，22341411418x y ⎧--=⎪⎪⎨+⎪=⎪⎩．∴点Q 的坐标是3411141,48⎛⎫-+- ⎪ ⎪⎝⎭，3411141,48⎛⎫---+ ⎪ ⎪⎝⎭．【典例7】如图7，在平面直角坐标系xOy 中，直线3y kx =+与x 轴、y 轴分别相交于点A 、B ，并与抛物线21742y x bx =-++的对称轴交于点()2,2C ，抛物线的顶点是点D ．（1）求k 和b 的值；（2）点G 是y 轴上一点，且以点B 、C 、G 为顶点的三角形与△BCD 相似，求点G 的坐标；（3）在抛物线上是否存在点E ：它关于直线AB 的对称点F 恰好在y 轴上．如果存在，直接写出点E 的坐标，如果不存在，试说明理由．【答案】：（1）b=1（2）点G 有两个，其坐标分别是()0,1和10,2⎛⎫ ⎪⎝⎭ （3）点E 的坐标是91,4⎛⎫- ⎪⎝⎭或92,2⎛⎫ ⎪⎝⎭【解析】：（1）由直线3y kx =+经过点()2,2C ，可得12k =-.由抛物线21742y x bx =-++的对称轴是直线2x =，可得1b =. （2） ∵直线132y x =-+与x 轴、y 轴分别相交于点A 、B ，∴点A 的坐标是()6,0，点B 的坐标是()0,3.图7xy 11 O∵抛物线的顶点是点D ，∴点D 的坐标是92,2⎛⎫ ⎪⎝⎭. ∵点G 是y 轴上一点，∴设点G 的坐标是()0,m . ∵△BCG 与△BCD 相似，又由题意知，GBC BCD ∠=∠， ∴△BCG 与△BCD 相似有两种可能情况： ①如果BG BC CB CD ＝52，解得1m ＝，∴点G 的坐标是()0,1. ②如果BG BC CD CB ＝，那么352m -，解得12m ＝，∴点G 的坐标是10,2⎛⎫ ⎪⎝⎭. 综上所述，符合要求的点G 有两个，其坐标分别是()0,1和10,2⎛⎫ ⎪⎝⎭．（3）点E 的坐标是91,4⎛⎫- ⎪⎝⎭或92,2⎛⎫ ⎪⎝⎭.【典例8】已知：如图8，在平面直角坐标系xOy 中，抛物线23y ax bx =++的图像与x 轴交于点A （3，0），与y 轴交于点B ，顶点C 在直线2x =上，将抛物线沿射线AC 的方向平移，当顶点C 恰好落在y 轴上的点D 处时，点B 落在点E 处．（1）求这个抛物线的解析式；（2）求平移过程中线段BC 所扫过的面积；（3）已知点F 在x 轴上，点G 在坐标平面内，且以点C 、E 、F 、G 为顶点的四边形是矩形，求点F 的坐标．．【答案】：（1）抛物线的解析式为243=-+y x x（2）12（3）有152F （,0），252F （-,0），3F ）），4F （）．【解析】：（1）∵顶点C 在直线2x =上，∴22=-=b x a ，∴4=-b a ．将A （3，0）代入23y ax bx =++，得933=0++a b ，解得1=a ，4=-b ．∴抛物线的解析式为243=-+y x x ．（2）过点C 作CM ⊥x 轴，CN ⊥y 轴，垂足分别为M 、N ．∵243=-+y x x =()221=--x ，∴C （2，1-）∵1==CM MA ，∴∠MAC =45°，∴∠ODA =45°，∴3==OD OA ．∵抛物线243=-+y x x 与y 轴交于点B ，∴B （0，3），∴6=BD ．∵抛物线在平移的过程中，线段BC 所扫过的面积为平行四边形BCDE 的面积， ∴12262122==⨯⨯⋅=⨯=BCDE BCD S S BD CN ．（3）联结CE .∵四边形BCDE 是平行四边形，∴点O 是对角线CE 与BD 的交点，即 OE OC ==（i ）当CE 为矩形的一边时，过点C 作1CF CE ⊥，交x 轴于点1F ，设点1F a （,0），在1Rt OCF 中，22211=OF OC CF +，即 22(2)5a a =-+，解得 52a =，∴点152F （,0）同理，得点252F （-,0）（ii ）当CE 为矩形的对角线时，以点O 为圆心，OC 长为半径画弧分别交x 轴于点3F 、4F ，可得 34=OF OF OC ==3F ）、4F （）综上所述：满足条件的点有152F （,0），252F （-,0），3F ）），4F （）．。

中考数学抛物线难题解析(含答案)

如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c 经过A，B两点，抛物线的顶点为D．（1）求b，c的值；（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由．在平面直角坐标系中，已知抛物线经过A（-4，0），B（0，-4），C（2，0）三点．（1）求抛物线的解析式；（2）若点M为第三象限抛物线上一动点，点M的横坐标为m，△AMB的面积为S、求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线y=-x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．(4)补充：在（3）的条件下，点P、Q、B、O为顶点的四边形能否成为梯形，若能，求出相应Q的坐标。

41直角坐标系XOY中，将直线y=kx沿y轴下移3个单位长度后恰好经点B（-3,0）及y 轴上的C点。

若抛物y=-x2+bx+c与x轴交于A点B点，（点A在点B的右侧），且过点C 。

（1）求直线BC及抛物线解析式（2）设抛物线的顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求p点坐标如图，已知抛物线y=x2+bx+c与x轴交于A，B两点（A点在B点左侧），与y轴交于点C（0，-3），对称轴是直线x=1，直线BC交抛物线对称轴交于点D.（1）求抛物线的函数表达式；（2）求直线BC的函数表达式；（3）点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P，Q两点，且点P在第三象限.①当线段PQ=3AB/4时，求tan∠CED的值；②当以点C，D，E为顶点的三角形是直角三角形时，请直接写出点P的坐标.温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答.第25题图第25题备用图直角坐标系XOY中，半径2√5的⊙C与x轴交于A（-1，0），B（3，0）且点C在X轴上方。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c 经过A，B两点，抛物线的顶点为D．（1）求b，c的值；（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由．在平面直角坐标系中，已知抛物线经过A（-4，0），B（0，-4），C（2，0）三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△AMB的面积为S、求S关于m的函数关系式，并求出S的最大值．（3）若点P是抛物线上的动点，点Q是直线y=-x上的动点，判断有几个位置能够使得点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．(4)补充：在（3）的条件下，点P、Q、B、O为顶点的四边形能否成为梯形，若能，求出相应Q的坐标。

41直角坐标系XOY中，将直线y=kx沿y轴下移3个单位长度后恰好经点B（-3,0）及y 轴上的C点。

若抛物y=-x2+bx+c与x轴交于A点B点，（点A在点B的右侧），且过点C 。

（1）求直线BC及抛物线解析式（2）设抛物线的顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求p点坐标如图，已知抛物线y=x 2+bx+c 与x 轴交于A ，B 两点（A 点在B 点左侧），与y 轴交于点C （0， -3），对称轴是直线x =1，直线BC 交抛物线对称轴交于点D .（1）求抛物线的函数表达式；（2）求直线BC 的函数表达式；（3）点E 为y 轴上一动点，CE 的垂直平分线交CE 于点F ，交抛物线于P ，Q 两点，且点P 在第三象限. ①当线段PQ =3AB/4时，求tan ∠CED 的值；②当以点C ，D ，E 为顶点的三角形是直角三角形时，请直接写出点P 的坐标. 温馨提示：考生可以根据第（3）问的题意，在图中补出图形，以便作答.第25题图第25题备用图直角坐标系XOY中，半径2√5的⊙C与x轴交于A（-1，0），B（3，0）且点C在X轴上方。

（1）求圆心C的坐标。

（Xc=1, c(1,4)）（2）已知一个二次函数的图像过A、B、C三点。

求解析式. (y=-(x+1)(x-3))（3）设点P在y轴上，点M在（2）的二次函数图像上，如果以点P、M、A、B为顶点的四边形是平行四边形，直接写出点M坐标。

26.如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB=90，AC=BC，OA=1，OC=4，抛物线y=x2+bx+c经过A，B两点，抛物线的顶点为D．（1）求b，c的值；（2）点E是直角三角形ABC斜边AB上一动点（点A、B除外），过点E作x轴的垂线交抛物线于点F，当线段EF的长度最大时，求点E的坐标；（3）在（2）的条件下：①求以点E、B、F、D为顶点的四边形的面积；②在抛物线上是否存在一点P，使△EFP是以EF为直角边的直角三角形？若存在，求出所有点P的坐标；若不存在，说明理由．41分析：（1）由∠ACB=90°，AC=BC ，OA=1，OC=4，可得A （﹣1，0）B （4，5），然后利用待定系数法即可求得b ，c 的值；（2）由直线AB 经过点A （﹣1，0），B （4，5），即可求得直线AB 的解析式，又由二次函数y=x2﹣2x ﹣3，设点E （t ，t+1），则可得点F 的坐标，则可求得EF 的最大值，求得点E 的坐标；（3）①顺次连接点E 、B 、F 、D 得四边形EBFD ，可求出点F 的坐标（错误！未找到引用源。

，错误！未找到引用源。

），点D 的坐标为（1，﹣4）由S 四边形EBFD=S △BEF+S △DEF 即可求得； ②过点E 作a ⊥EF 交抛物线于点P ，设点P （m ，m2﹣2m ﹣3），可得m2﹣2m ﹣2=5/2，即可求得点P 的坐标，又由过点F 作b ⊥EF 交抛物线于P3，设P3（n ，n2﹣2n ﹣3），可得n2﹣2n ﹣2=﹣15/4，求得点P 的坐标，则可得使△EFP 是以EF 为直角边的直角三角形的P 的坐标．解答：解：（1）由已知得：A （﹣1，0），B （4，5）， ∵二次函数y=x2+bx+c 的图象经过点A （﹣1，0），B （4，5）， ∴错误！未找到引用源。

，解得：b=﹣2，c=﹣3；（2）如图：∵直线AB 经过点A （﹣1，0），B （4，5），∴直线AB 的解析式为：y=x+1， ∵二次函数y=x2﹣2x ﹣3，∴设点E （t ，t+1），则F （t ，t2﹣2t ﹣3），∴EF=（t+1）﹣（t2﹣2t ﹣3）=﹣（t ﹣3/2）2+25/4，∴当t=错误！未找到引用源。

时，EF 的最大值为25/4，∴点E 坐标（3/2，5/2）；（3）①如图：顺次连接点E 、B 、F 、D 得四边形EBFD ．可求出点F 的坐标（3/2，-15/4），点D 的坐标为（1，﹣4）S 四边形EBFD=S △BEF+S △DEF =错误！未找到引用源。

×错误！未找到引用源。

×（4﹣错误！未找到引用源。

）+错误！未找到引用源。

×错误！未找到引用源。

×（错误！未找到引用源。

﹣1）=错误！未找到引用源。

； ②如图：ⅰ）过点E 作a ⊥EF 交抛物线于点P ，设点P （m ，m2﹣2m ﹣3）则有： m2﹣2m ﹣2=错误！未找到引用源。

，解得：m1=错误！未找到引用源。

，m2=错误！未找到引用源。

，∴P 1（错误！未找到引用源。

，错误！未找到引用源。

），P2（错误！未找到引用源。

，错误！未找到引用源。

），ⅱ）过点F 作b ⊥EF 交抛物线于P3，设P3（n ，n2﹣2n ﹣3）则有：n2﹣2n ﹣2=﹣15/4，解得：n1=1/2，n2=3/2（与点F 重合，舍去），∴P 3（错误！未找到引用源。

，错误！未找到引用源。

），综上所述：所有点P 的坐标：P1（错误！未找到引用源。

，错误！未找到引用源。

），P2（错误！未找到引用源。

，错误！未找到引用源。

），P3（错误！未找到引用源。

，错误！未找到引用源。

）能使△EFP 组成以EF 为直角边的直角三角形．点评：此题考查了待定系数法求二次函数的解析式，四边形与三角形面积问题以及直角三角形的性质等知识．此题综合性很强，解题的关键是注意方程思想与数形结合思想的应用． 23、（2010河南）在平面直角坐标系中，已知抛物线经过A （-4，0），B （0，-4），C （2，0）三点．（1）求抛物线的解析式；（2）若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S 、求S 关于m 的函数关系式，并求出S 的最大值．（3）若点P 是抛物线上的动点，点Q 是直线y=-x 上的动点，判断有几个位置能够使得点P 、Q 、B 、O 为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标．(4)补充：在（3）的条件下，点P 、Q 、B 、O 为顶点的四边形能否成为梯形，若能，求出相应Q的坐标。

-------------------------------------------------------------------------------------------------------------------------------(2011上海奉贤区P34)直角坐标系XOY中，将直线y=kx沿y轴下移3个单位长度后恰好经点B（-3,0）及y 轴上的C点。

若抛物y=-x2+bx+c与x轴交于A点B点，（点A在点B的右侧），且过点C 。

（1）求直线BC及抛物线解析式（2）设抛物线的顶点为D，点P在抛物线的对称轴上，且∠APD=∠ACB，求p点坐标BA O CD 11 x=1xyE FP QG-------------------------------------------------------------------------------------------------------------------------25. （沈阳市2011年p36）如图，已知抛物线y=x 2+bx+c 与x 轴交于A ，B 两点（A 点在B 点左侧），与y 轴交于点C （0， -3），对称轴是直线x =1，直线BC 交抛物线对称轴交于点D .（1）求抛物线的函数表达式；（2）求直线BC 的函数表达式；（3）点E 为y 轴上一动点，CE 的垂直平分线交CE 于点F ，交抛物线于P ，Q 两点，且点P 在第三象限. ①当线段PQ =3AB/4时，求tan ∠CED 的值；②当以点C ，D ，E 为顶点的三角形是直角三角形时，请直接写出点P 的坐标. -25．⑴∵抛物线的对称轴为直线x=1，∴1221b b a -=-=⨯ ∴b =－2．∵抛物线与y 轴交于点C （0，－3）， ∴c =－3，∴抛物线的函数表达式为y =x 2－2x －3．⑵∵抛物线与x 轴交于A 、B 两点，当y =0时，x 2－2x －3=0． ∴x 1=－1,x 2=3.∵A 点在B 点左侧，∴A （－1，0），B （3，0）设过点B （3，0）、C （0，－3）的直线的函数表达式为y =kx ＋m ，则033k m m =+⎧⎨-=⎩，∴13k m =⎧⎨=-⎩∴直线BC 函数表达式为y =x －3．⑶①∵AB=4，PO=34AB，∴PO=3∵PO⊥y轴∴PO∥x轴，则由抛物线的对称性可得点P的横坐标为12 -，∴P（12-，74-）∴F（0，74-），∴FC=3－OF=3－74=54．∵PO垂直平分CE于点F，∴CE=2 FC=52∵点D在直线BC上，∴当x=1时，y=－2，则D（1，－2）．过点D作DG⊥CE于点G，∴DG=1，CG=1，∴GE=CE－CG=52－1=32．在Rt△EGD中，tan∠CED=23 GDEG=．②P1（1－2，－2），P2（1－62，52）．直角坐标系XOY中，半径2√5的⊙C与x轴交于A（-1，0），B（3，0）且点C在X轴上方。

求圆心C的坐标。

（Xc=1, c(1,4)）（1）已知一个二次函数的图像过A、B、C三点。

求解析式. (y=-(x+1)(x-3))（2）设点P在y轴上，点M在（2）的二次函数图像上，如果以点P、M、A、B为顶点的四边形是平行四边形，直接写出点M坐标。

中考数学抛物线难题解析(含答案)

(已整理)中考数学必刷压轴题专题：抛物线之角度关系处理(含解析)

抛物线专题(附答案)

初三抛物线试题大全及解析

人教版中考数学解答题压轴题突破 重难点突破七 二次函数的实际应用 类型二：抛物线型问题

抛物线曲线经典题目(含答案解析)

初三抛物线试题及答案

2023年中考数学复习难点突破专题17 二次函数与实际问题：图形运动问题(含答案)

中考压轴题——抛物线平行四边形(含详细答案分析)

初三抛物线试题大全及解析

湖南省各地市2023-中考数学真题分类汇编-03解答题(较难题)知识点分类②

山东省各地市2023-中考数学真题分类汇编-03解答题(较难题)知识点分类

中考数学真题模拟题汇编 二次函数抛物线(带答案解析)

函数的实际应用--抛物线型问题(专题训练)(解析版)-中考数学重难点题型专题汇总

2024年九年级中考数学专题复习：二次函数实际应用(抛物线型问题)(含答案)

《抛物线》典型例题12例(含标准答案解析]

2021年中考数学复习-抛物线型问题(解析版)

中考数学抛物线难题解析(含答案)

人教版中考数学解答题压轴题突破重难点突破七二次函数的实际应用类型二：抛物线型问题

中考数学真题模拟题汇编二次函数抛物线(带答案解析)