高考数学一轮复习第十二章算法初步第1讲算法初步配套课时作业理(含解析)新人教A版
核按钮(新课标)2017高考数学一轮复习第十二章算法初步、推理与证明12.1算法与程序框图习题理

§12.1 算法与程序框图1.算法的概念及特点(1)算法的概念在数学中,算法通常是指按照一定______解决某一类问题的________和________的步骤.(2)算法的特点之一是具有______性,即算法中的每一步都应该是确定的,并能有效地执行,且得到确定的结果,而不应是模棱两可的;其二是具有______性,即算法步骤明确,前一步是后一步的前提,只有执行完前一步才能进行后一步,并且每一步都准确无误才能解决问题;其三是具有______性,即一个算法应该在有限步操作后停止,而不能是无限的;另外,算法还具有不唯一性和普遍性,即对某一个问题的解决不一定是唯一的,可以有不同的解法,一个好的算法应解决的是一类问题而不是一两个问题.2.程序框图(1)程序框图的概念程序框图又称流程图,是一种用______、______及______来表示算法的图形.(2)构成程序框图的图形符号、名称及其功能3.算法的基本逻辑结构(1)顺序结构顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按__________的顺序进行的.它是由若干个__________的步骤组成的,它是任何一个算法都离不开的基本结构.顺序结构可用程序框图表示为如图所示的形式.(2)条件结构在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.常见的条件结构可以用程序框图表示为如图所示的两种形式.(3)循环结构在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是_______反复执行的步骤称为________.循环结构有如下两种形式:①如图1,这个循环结构有如下特征:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.因此,这种循环结构称为____________.②如图2表示的也是常见的循环结构,它有如下特征:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.因此,这种循环结构称为____________.自查自纠1.(1)规则明确有限(2)确定有序有穷2.(1)程序框流程线文字说明(2)①终端框(起止框) ②输入、输出框③处理框(执行框) ④判断框⑤流程线⑥连接点3.(1)从上到下依次执行(3)循环结构循环体①直到型循环结构②当型循环结构下列各式中的S 值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+13+…+110000D .S =1+2+3+4+…解:由算法的有限性知,D 不正确,而A ,B ,C 都可以通过有限步骤操作,输出确定结果,故选D .给出下列算法:第一步,输入正整数n (n >1).第二步,判断n 是否等于2,若n =2,则输出n ;若n >2,则执行第三步.第三步,依次从2到n -1检验能不能整除n ,若不能整除n ,则执行第四步;若能整除n ,则执行第一步.第四步,输出n .则输出的n 的值是( )A .奇数B .偶数C .质数D .合数解:根据算法可知n =2时,输出n 的值为2;若n =3,输出n 的值为3;若n =4,2能整除4,则重新输入n 的值,…,故输出的n 的值为质数.故选C .(2014·北京)执行如图所示的程序框图,输出的S 值为( )A .1B .3C .7D .15 解:由程序框图知:S =1+21+22=7.故选C .(2014·辽宁)执行下面的程序框图,若输入x =9,则输出y =____________.解:输入x =9,则y =5,|y -x |=4>1,不满足条件;x =5,y =113,|y -x |=43>1,不满足条件;x =113,y =299,|y -x |=49<1,满足条件,输出y =299.故填299.如图所示,程序框图(算法流程图)的输出结果是__________.解:初始值s =0,n =2.第一次循环得s =12,n =4;第二次循环得s =12+14,n =6;第三次循环得s =12+14+16=1112,n =8,此时退出循环,输出的s =1112.故填1112.类型一 算法的概念下列语句是算法的个数为( )①从济南到巴黎:先从济南坐火车到北京,再坐飞机到巴黎;②统筹法中“烧水泡茶”的故事;③测量某棵树的高度,判断其是否为大树;④已知三角形的两边及夹角,利用三角形的面积公式求出该三角形的面积.A .1B .2C .3D .4解:①中勾画了从济南到巴黎的行程安排,完成了任务;②中节约时间,烧水泡茶完成了任务;③中对“树的大小”没有明确的标准,无法完成任务,不是有效的算法构造;④是纯数学问题,利用三角形的面积公式求出三角形的面积.故选C .【点拨】算法过程要做到一步一步地执行,每一步执行的操作必须确切,不能含糊不清,且在有限步后必须得到问题的结果.下列叙述能称为算法的个数为( )①植树需要运苗、挖坑、栽苗、浇水这些步骤;②顺序进行下列运算:1+1=2,2+1=3,3+1=4,…,99+1=100;③从宜昌乘火车到武汉,从武汉乘飞机到北京;④3x >x +1;⑤求所有能被3整除的正数,即3,6,9,12,….A.2 B.3 C.4 D.5解:①②③可称为算法,④⑤不是,故选B.类型二经典算法“韩信点兵”问题.韩信是汉高祖刘邦手下的大将,为了保守军事机密,他在点兵时采用下述方法:先令士兵从1~3报数,结果最后一个士兵报2;再令士兵从1~5报数,结果最后一个士兵报3;又令士兵从1~7报数,结果最后一个士兵报4.这样,韩信很快就知道了自己部队士兵的总人数.请设计一个算法,求出士兵至少有多少人.解:在本题中,士兵从1~3报数,最后一个士兵报2,说明士兵的总人数是除以3余2,其他两种情况依此类推.(算法一)步骤如下:第一步:先确定最小的满足除以7余4的数是4;第二步:依次加7就得到所有满足除以7余4的数:4,11,18,25,32,39,46,53,60,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:18;第四步:依次加上35,得18,53,88,…;第五步:在第四步得到的一列数中,找到最小的满足除以3余2的正整数:53,这就是我们要求的数.(算法二)步骤如下:第一步:先确定最小的满足除以3余2的数是2;第二步:依次加3就得到所有满足除以3余2的数:2,5,8,11,14,17,20,23,26,29,32,35,38,41,44,47,50,53,56,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:8;第四步:然后依次加15就得8,23,38,53,…,不难看出,这些数既满足除以3余2,又满足除以5余3;第五步:在第四步所得的一列数中找到满足除以7余4的最小数是53,这就是我们要求的数.【点拨】给出一个问题,设计算法时要注意:(1)认真分析问题,研究解决此问题的一般方法;(2)将解决问题的过程分解成若干步骤;(3)用简练的语言将各步骤表示出来;(4)把解题过程条理清楚地表达出来,就得到一个明确的算法.对于同一问题,可以设计不同的算法,其最终的结果是一样的,但解决问题的繁简程度不同,我们要寻找最优算法.一位商人有9枚银元,其中有一枚略轻的是假银元.请设计一种算法,用天平(不用砝码)将假银元找出来.解:算法如下:第一步:把银元分成3组,每组3枚;第二步:先将两组分别放在天平的两边,如果天平不平衡,那么假银元就在轻的那一组;如果天平左右平衡,则假银元就在未称的第3组内;第三步:取出含假银元的那一组,从中任取两枚银元放在天平的两边.如果左右不平衡,则轻的那一边就是假银元;如果天平两边平衡,则未称的那一枚就是假银元.类型三 顺序结构已知点P (x 0,y 0)和直线l :Ax +By +C =0,求点P (x 0,y 0)到直线l 的距离d ,写出其算法并画出流程图.解:算法如下:第一步:输入x 0,y 0及直线方程的系数A ,B ,C .第二步:计算z 1=Ax 0+By 0+C .第三步:计算z 2=A 2+B 2.第四步:计算d =||z 1z 2.第五步:输出d .流程图如图所示.【点拨】顺序结构是一种最简单、最基本的结构,可严格按照传统的解题思路写出算法步骤,画出程序框图.注意语句与语句之间,框与框之间是按从上到下的顺序进行的.阅读如图所示的程序框图,若输入的a ,b ,c 的值分别是21,32,75,则输出的a ,b ,c 分别是( )A .75,21,32B .21,32,75C .32,21,75D .75,32,21 解:该程序框图的执行过程是:输入21,32,75;x =21;a =75;c =32;b =21;输出75,21,32.故选A .类型四 条件结构(2015·深圳调研)执行如图所示的程序框图,如果依次输入函数:f (x )=3x ,f (x )=sin x ,f (x )=x 3,f (x )=x +1x,那么输出的函数f (x )为( )A .f (x )=3xB .f (x )=sin xC .f (x )=x 3D .f (x )=x +1x解:依题意得,输出的函数应满足:f (-x )=-f (x )(x ∈R ),即函数f (x )是定义在R 上的奇函数,且f (x +m )>f (x ),其中m >0,即函数f (x )是定义在R 上的增函数.对于A ,函数f (x )=3x 不是奇函数;对于B ,函数f (x )=sin x 不是定义在R 上的增函数;对于C ,函数f (x )=x 3既是奇函数又是定义在R 上的增函数;对于D ,函数f (x )=x +1x的定义域不是实数集.综上所述,只能输出f (x )=x 3,故选C .【点拨】条件结构的运用与数学的分类讨论有关.设计算法时,哪一步要分类讨论,哪一步就需要用条件结构.(2015·全国卷Ⅱ)如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a =( )A.0 B.2 C.4 D.14解:执行该程序,输入a,b的值依次为a=14,b=18;a=14,b=4;a=10,b=4;a=6,b=4;a=2,b=4;a=b=2,此时退出循环,输出的a=2.故选B.类型五循环结构(2014·安徽)如图所示,程序框图(算法流程图)的输出结果是( )A.34 B.55 C.78 D.89解:运行程序:x=1,y=1,z=2;x=1,y=2,z=3;x=2,y=3,z=5;x=3,y =5,z=8;x=5,y=8,z=13;x=8,y=13,z=21;x=13,y=21,z=34;x=21,y =34,z=55,跳出循环,输出结果是55.故选B.【点拨】如果算法问题里涉及的运算进行了许多次重复的操作,且先后参与运算的数之间有相同的规律,就可引入变量循环参与运算(我们称之为循环变量),应用循环结构.在循环结构中,要注意根据条件设计合理的计数变量、累加和累乘变量及其个数等,特别要使条件的表述恰当、准确.(2015·陕西)根据下边的框图,当输入x为2006时,输出的y=( )A.28 B.10 C.4 D.2解:初始条件:x=2006.第1次运行:x=2004;第2次运行:x=2002;第3次运行:x=2000;…;第1003次运行:x=0;第1004次运行:x=-2,不满足条件,跳出循环,所以输出的y=32+1=10,故选B.1.设计算法时,要根据题目进行选择,以简单、程序短、易于在计算机上执行为原则.2.画程序框图首先要进行结构选择,套用格式.若求只含有一个关系式的函数的函数值时,只用顺序结构就能够解决;若是分段函数或执行时需要先判断才能执行后继步骤的,就必须引入条件结构;如果问题涉及的运算进行了许多重复的步骤,有规律,就可引入变量,应用循环结构.当然,应用循环结构一定要用到顺序结构与条件结构.3.循环结构的循环控制通过累加变量记录循环次数,通过判断框决定循环终止与否.用循环结构来描述算法,在画出算法程序框图之前,需要确定的三件事是:(1)确定循环变量与初始条件;(2)确定循环体;(3)确定终止条件.注意直到型循环与当型循环的区别,二者判断框内的条件表述在解决同一问题时恰好相反.解决循环结构框图问题,当循环次数比较少时,可依次列出;当循环次数较多时,可先循环几次,找出规律.要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.4.在具体绘制程序框图时,要注意以下几点:(1)流程线上要标有执行顺序的箭头.(2)判断框后边的流程线应根据情况标注“是(Y)”或“否(N)”.(3)框图内的内容包括累加(积)变量初始值,计数变量初始值,累加值,前后两个变量的差值都要仔细斟酌,不能有丝毫差错.(4)判断框内条件常用“>”“≥”“<”“≤”“=”等符号,它们的含义是各不相同的,要根据所选循环结构的类型,正确地进行选择.1.结合下面的算法:第一步:输入x .第二步:判断x 是否小于0,若是,则输出x +2,否则执行第三步.第三步:输出x -1.当输入的x 的值为-1,0,1时,输出的结果分别为( )A .-1,0,1B .-1,1,0C .1,-1,0D .0,-1,1解:根据x 值与0的关系,选择执行不同的步骤,当x 的值为-1,0,1时,输出的结果分别为1,-1,0,故选C .2.如图的程序框图输出的结果是( )A .4B .3C .2D .0解:该算法首先将1,2,3三个数分别赋给x ,y ,z ;然后先让x 取y 的值,即x 变成2,再让y 取x 的值,即y 的值是2,接着让z 取y 的值,即z 的值为2,从而最后输出z 的值为2.故选C .3.(2014·湖南)执行如图所示的程序框图,如果输入的t ∈[-2,2],则输出的S 属于( )A .[-6,-2]B .[-5,-1]C .[-4,5]D .[-3,6]解:由程序框图可得S =⎩⎪⎨⎪⎧2t 2+1-3,t ∈[-2,0),t -3,t ∈[0,2],其值域为[-3,6].故选D . 4.(2015·福建)阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )A .2B .1C .0D .-1解:执行程序,得S =0,i =2;S =-1,i =3;S =-1,i =4;S =0,i =5;S =0,i =6>5,跳出循环,输出S =0.故选C .5.(2014·重庆)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >45 解:当输出k 的值为6时,s =1×910×89×78=710,结合各选项知,C 符合要求.故选C . 6.(2015·全国课标Ⅰ)执行如图所示的程序框图,如果输入的t =0.01,则输出的n =( )A .5B .6C .7D .8解法一:执行程序,S =12,m =14,n =1;S =14,m =18,n =2;S =18,m =116,n =3;S =116,m =132,n =4;S =132,m =164,n =5;S =164,m =1128,n =6;S =1128<t =0.01,m =1256,n =7,循环结束,输出n =7.解法二:记第n 次循环后S 的值为a n ()n =0,1,2,…,其中a 0=1,则a n =a n -1-⎝ ⎛⎭⎪⎫12n ,递推可得a n =a 0-⎝ ⎛⎭⎪⎫12+122+…+12n =1-12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=12n ≤t =0.01. 显然n >6,故n =7.故选C .7.(2015·安徽)执行如图所示的程序框图(算法流程图),输出的n 为________.解:各次循环中变量当a =1.416·时,跳出循环,输出的n 为4.故填4.8.(2014·湖北)设a 是一个各位数字都不是0且没有重复数字的三位数.将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a =815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b =________.解法一:当a=123时,b=321-123=198≠123;当a=198时,b=981-189=792≠198;当a=792时,b=972-279=693≠792;当a=693时,b=963-369=594≠693;当a=594时,b=954-459=495≠594;当a=495时,b=954-459=495=a,终止循环,输出b=495.解法二:设I(a)=100x+10y+z,D(a)=100z+10y+x,x<y<z,x,y,z∈N*,则D(a)-I(a)=99(z-x),因此各位数字都不是0且没有重复数字,而且是99的倍数的三位数有:198,297,396,495,594,693,792,891,经检验知只有495满足题意.故填495.9.某人带着一只狼和一只羊及一捆青菜过河,只有一条船,船仅可载重此人和狼、羊及青菜三者之一,没有人在的时候,狼会吃羊,羊会吃青菜.请设计安全过河的算法.解:第一步,人带羊过河.第二步,人自己返回.第三步,人带青菜过河.第四步,人带羊返回.第五步,人带狼过河.第六步,人自己返回.第七步,人带羊过河.10.设计一个算法,找出区间[1,1000]内的能被7整除的整数,画出程序框图.解:第一步,取k=1.第二步,判断k≤1000是否成立,若不成立,则执行第五步.第三步,若k除以7的余数为0,则输出k.第四步,将k的值增加1,返回执行第二步.第五步,结束.程序框图如图.11.设计一个算法计算11×3+13×5+15×7+…+12013×2015的值,并画出程序框图. 解:算法步骤如下:第一步,令S =0,k =1.第二步,若k <2015成立,则执行第三步,否则输出S .第三步,计算S =S +1k (k +2),k =k +2,返回第二步. 程序框图如图所示:意大利数学家斐波那契,在1202年出版的《算盘全书》一书里提出了这样一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子?试画出解决此问题的程序框图.解:根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N 个月有F 对兔子,第N -1个月有S 对兔子,第N -2个月有Q 对兔子,则有F =S +Q ,一个月后,即第N +1个月时,式中变量S 的新值应变为第N 个月兔子的对数(F 的旧值),变量Q 的新值应变为第N -1个月兔子的对数(S 的旧值),这样,用S +Q 求出变量F 的新值就是N +1个月兔子的对数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第x (x ≥3)个月的i 从3逐次增加1,一直变化到12,再循环一次得到的F ”就是所求结果.流程图如图所示.。
核按钮(新课标)高考数学一轮复习 第十二章 算法初步与框图、推理与证明训练 文

第十二章算法初步与框图、推理与证明考纲链接1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想.(2)理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.2.基本算法语句了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.3.框图(1)通过具体实例进一步认识程序框图.(2)通过实例了解工序的流程图.(3)能绘制简单实际问题的流程图,体会流程图在解决实际问题中的作用.(4)通过实例了解结构图.(5)会运用结构图梳理已学过的知识结构、整理收集到的信息资料.4.了解合情推理的含义,能进行简单的归纳推理和类比推理,体会合情推理在数学发现中的作用.5.了解演绎推理的含义,了解合情推理和演绎推理的联系和差异;掌握演绎推理的“三段论”,能运用“三段论”进行一些简单的演绎推理.6.了解直接证明的两种基本方法:综合法和分析法;了解综合法和分析法的思考过程和特点.7.了解反证法的思考过程和特点.§12.1算法、程序框图、结构图1.算法的概念及特点(1)算法的概念在数学中,算法通常是指按照一定______解决某一类问题的________和________的步骤.(2)算法的特点之一是具有______性,即算法中的每一步都应该是确定的,并能有效地执行,且得到确定的结果,而不应是模棱两可的;其二是具有______性,即算法步骤明确,前一步是后一步的前提,只有执行完前一步才能进行后一步,并且每一步都准确无误才能解决问题;其三是具有______性,即一个算法应该在有限步操作后停止,而不能是无限的;另外,算法还具有不唯一性和普遍性,即对某一个问题的解决不一定是唯一的,可以有不同的解法,一个好的算法应解决的是一类问题而不是一两个问题.2.程序框图(1)程序框图的概念程序框图又称流程图,是一种用________、________及________来表示算法的图形.结构图一般由构成系统的若干要素和表达各要素之间关系的连线(或方向箭头)构成.4.算法的基本逻辑结构(1)顺序结构顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按__________的顺序进行的.它是由若干个__________的步骤组成的,它是任何一个算法都离不开的基本结构.顺序结构可用程序框图表示为如图所示的形式.(2)条件结构在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.常见的条件结构可以用程序框图表示为如图所示的两种形式.(3)循环结构在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是________.反复执行的步骤称为________.循环结构有如下两种形式:①如图1,这个循环结构有如下特征:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.因此,这种循环结构称为____________.②如图2表示的也是常见的循环结构,它有如下特征:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.因此,这种循环结构称为____________.自查自纠: 1.(1)规则 明确 有限 (2)确定 有序 有穷2.(1)程序框 流程线 文字说明(2)①终端框(起止框) ②输入、输出框 ③处理框(执行框) ④判断框 ⑤流程线 ⑥连接点4.(1)从上到下 依次执行 (3)循环结构 循环体 ①直到型循环结构 ②当型循环结构下列各式中的S 值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+13+…+110000D .S =1+2+3+4+…解:由算法的有限性知,D 不正确,而A ,B ,C 都可以通过有限步骤操作,输出确定结果,故选D.给出下列算法:第一步,输入正整数n (n >1).第二步,判断n 是否等于2,若n =2,则输出n ;若n >2,则执行第三步.第三步,依次从2到n -1检验能不能整除n ,若不能整除n ,则执行第四步;若能整除n ,则执行第一步.第四步,输出n .则输出的n 的值是( )A .奇数B .偶数C .质数D .合数解:根据算法可知n =2时,输出n 的值为2;若n =3,输出n 的值为3;若n =4,2能整除4,则重新输入n 的值,…,故输出的n 的值为质数.故选C.(2014·北京)执行如图所示的程序框图,输出的S 值为()A .1B .3C .7D .15解:由程序框图知:S =1+21+22=7.故选C.(2014·辽宁)执行下面的程序框图,若输入x =9,则输出y =____________.解:输入x =9,则y =5,|y -x |=4>1,不满足条件;x =5,y =113,|y -x |=43>1,不满足条件;x =113,y =299,|y -x |=49<1,满足条件,输出y =299.故填299.如图所示,程序框图(算法流程图)的输出结果是__________.解:初始值s =0,n =2.第一次循环得s =12,n=4;第二次循环得s =12+14,n =6;第三次循环得s =12+14+16=1112,n =8,此时退出循环,输出的s =1112.故填1112.类型一 算法的概念下列语句是算法的个数为( ) ①从济南到巴黎:先从济南坐火车到北京,再坐飞机到巴黎;②统筹法中“烧水泡茶”的故事;③测量某棵树的高度,判断其是否为大树; ④已知三角形的两边及夹角,利用三角形的面积公式求出该三角形的面积.A .1B .2C .3D .4 解:①中勾画了从济南到巴黎的行程安排,完成了任务;②中节约时间,烧水泡茶完成了任务;③中对“树的大小”没有明确的标准,无法完成任务,不是有效的算法构造;④是纯数学问题,利用三角形的面积公式求出三角形的面积.故选C .点拨:算法过程要做到一步一步地执行,每一步执行的操作必须确切,不能含糊不清,且在有限步后必须得到问题的结果.下列叙述能称为算法的个数为( )①植树需要运苗、挖坑、栽苗、浇水这些步骤; ②顺序进行下列运算:1+1=2,2+1=3,3+1=4,…,99+1=100;③从宜昌乘火车到武汉,从武汉乘飞机到北京; ④3x >x +1;⑤求所有能被3整除的正数,即3,6,9,12,…. A .2 B .3 C .4 D .5解:①②③可称为算法,④⑤不是,故选B.类型二 经典算法“韩信点兵”问题.韩信是汉高祖刘邦手下的大将,为了保守军事机密,他在点兵时采用下述方法:先令士兵从1~3报数,结果最后一个士兵报2;再令士兵从1~5报数,结果最后一个士兵报3;又令士兵从1~7报数,结果最后一个士兵报4.这样,韩信很快就知道了自己部队士兵的总人数.请设计一个算法,求出士兵至少有多少人.解:在本题中,士兵从1~3报数,最后一个士兵报2,说明士兵的总人数是除以3余2,其他两种情况依此类推.(算法一)步骤如下:第一步:先确定最小的满足除以7余4的数是4;第二步:依次加7就得到所有满足除以7余4的数:4,11,18,25,32,39,46,53,60,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:18;第四步:依次加上35,得18,53,88,…; 第五步:在第四步得到的一列数中,找到最小的满足除以3余2的正整数:53,这就是我们要求的数.(算法二)步骤如下:第一步:先确定最小的满足除以3余2的数是2;第二步:依次加3就得到所有满足除以3余2的数:2,5,8,11,14,17,20,23,26,29,32,35,38,41,44,47,50,53,56,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:8;第四步:然后依次加15就得8,23,38,53,…,不难看出,这些数既满足除以3余2,又满足除以5余3;第五步:在第四步所得的一列数中找到满足除以7余4的最小数是53,这就是我们要求的数.点拨:给出一个问题,设计算法时要注意:(1)认真分析问题,研究解决此问题的一般方法;(2)将解决问题的过程分解成若干步骤;(3)用简练的语言将各步骤表示出来;(4)把解题过程条理清楚地表达出来,就得到一个明确的算法.对于同一问题,可以设计不同的算法,其最终的结果是一样的,但解决问题的繁简程度不同,我们要寻找最优算法.一位商人有9枚银元,其中有一枚略轻的是假银元.请设计一种算法,用天平(不用砝码)将假银元找出来.解:算法如下:第一步:把银元分成3组,每组3枚;第二步:先将两组分别放在天平的两边,如果天平不平衡,那么假银元就在轻的那一组;如果天平左右平衡,则假银元就在未称的第3组内;第三步:取出含假银元的那一组,从中任取两枚银元放在天平的两边.如果左右不平衡,则轻的那一边就是假银元;如果天平两边平衡,则未称的那一枚就是假银元.类型三 顺序结构已知点P (x 0,y 0)和直线l :Ax +By +C=0,求点P (x 0,y 0)到直线l 的距离d ,写出其算法并画出流程图.解:算法如下:第一步:输入x 0,y 0及直线方程的系数A ,B ,C .第二步:计算z 1=Ax 0+By 0+C .第三步:计算z 2=A 2+B 2.第四步:计算d =||z 1z 2.第五步:输出d . 流程图如图所示.点拨:顺序结构是一种最简单、最基本的结构,可严格按照传统的解题思路写出算法步骤,画出程序框图.注意语句与语句之间,框与框之间是按从上到下的顺序进行的.阅读如图所示的程序框图,若输入的a ,b ,c 的值分别是21,32,75,则输出的a ,b ,c 分别是( )A .75,21,32B .21,32,75C .32,21,75D .75,32,21解:该程序框图的执行过程是:输入21,32,75;x =21;a =75;c =32;b =21;输出75,21,32.故选A.类型四 条件结构(2015·深圳调研)执行如图所示的程序框图,如果依次输入函数:f (x )=3x ,f (x )=sin x ,f (x )=x 3,f (x )=x +1x,那么输出的函数f (x )为( )A .f (x )=3xB .f (x )=sin xC .f (x )=x 3D .f (x )=x +1x解:依题意得,输出的函数应满足:f (-x )=-f (x )(x ∈R ),即函数f (x )是定义在R 上的奇函数,且f (x +m )>f (x ),其中m >0,即函数f (x )是定义在R 上的增函数.对于A ,函数f (x )=3x不是奇函数;对于B ,函数f (x )=sin x 不是定义在R 上的增函数;对于C ,函数f (x )=x 3既是奇函数又是定义在R 上的增函数;对于D ,函数f (x )=x +1x的定义域不是实数集.综上所述,只能输出f (x )=x 3,故选C.点拨:条件结构的运用与数学的分类讨论有关.设计算法时,哪一步要分类讨论,哪一步就需要用条件结构.(2015·全国卷Ⅱ)如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( )A .0B .2C .4D .14解:执行该程序,输入a ,b 的值依次为a =14,b =18;a =14,b =4;a =10,b =4;a =6,b =4;a =2,b =4;a =b =2,此时退出循环,输出的a =2.故选B.类型五 循环结构(2014·安徽)如图所示,程序框图(算法流程图)的输出结果是()A .34B .55C .78D .89解:运行程序:x =1,y =1,z =2;x =1,y =2,z =3;x =2,y =3,z =5;x =3,y =5,z =8;x =5,y =8,z =13;x =8,y =13,z =21;x =13,y =21,z =34;x =21,y =34,z =55,跳出循环,输出结果是55.故选B.点拨:如果算法问题里涉及的运算进行了许多次重复的操作,且先后参与运算的数之间有相同的规律,就可引入变量循环参与运算(我们称之为循环变量),应用循环结构.在循环结构中,要注意根据条件设计合理的计数变量、累加和累乘变量及其个数等,特别要使条件的表述恰当、准确.(2015·陕西)根据下边的框图,当输入x 为2006时,输出的y =()A .28B .10C .4D .2 解:初始条件:x =2006.第1次运行:x =2004;第2次运行:x =2002;第3次运行:x =2000;…;第1003次运行:x =0;第1004次运行:x =-2,不满足条件,跳出循环,所以输出的y =32+1=10,故选B.类型六 结构图总结高中所有有关函数的内容,画出知识结构图.解:如图所示:点拨:画结构图时,首先要确定组成结构图的基本要素,然后通过连线来标明各要素之间的关系.某公司的组织结构是:总经理之下设执行经理、人事经理和财务经理.执行经理领导生产经理、工程经理、品质管理经理和物料经理.生产经理领导线长,工程经理领导工程师,工程师管理技术员,物料经理领导计划员和仓库管理员.解:如图所示:1.设计算法时,要根据题目进行选择,以简单、程序短、易于在计算机上执行为原则.2.画程序框图首先要进行结构选择,套用格式.若求只含有一个关系式的函数的函数值时,只用顺序结构就能够解决;若是分段函数或执行时需要先判断才能执行后继步骤的,就必须引入条件结构;如果问题涉及的运算进行了许多重复的步骤,有规律,就可引入变量,应用循环结构.当然,应用循环结构一定要用到顺序结构与条件结构.3.循环结构的循环控制通过累加变量记录循环次数,通过判断框决定循环终止与否.用循环结构来描述算法,在画出算法程序框图之前,需要确定的三件事是:(1)确定循环变量与初始条件;(2)确定循环体;(3)确定终止条件.注意直到型循环与当型循环的区别,二者判断框内的条件表述在解决同一问题时恰好相反.解决循环结构框图问题,当循环次数比较少时,可依次列出;当循环次数较多时,可先循环几次,找出规律.要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.4.在具体绘制程序框图时,要注意以下几点:(1)流程线上要标有执行顺序的箭头.(2)判断框后边的流程线应根据情况标注“是(Y)”或“否(N)”.(3)框图内的内容包括累加(积)变量初始值,计数变量初始值,累加值,前后两个变量的差值都要仔细斟酌,不能有丝毫差错.(4)判断框内条件常用“>”“≥”“<”“≤”“=”等符号,它们的含义是各不相同的,要根据所选循环结构的类型,正确地进行选择.5.结构图与流程图的异同相同点:绘制结构图的一般步骤与绘制流程图类似,先确定组成系统的基本要素,以及这些要素之间的关系,然后画出框图表示整个系统.不同点:流程图描述具有时间特征的动态过程,结构图刻画静态的系统结构.流程图通常会有一个“起点”,一个或多个“终点”,其基本单元之间由流程线连接;结构图则更多地表现为“树”形结构,其基本要素之间一般为概念上的从属关系或逻辑上的先后关系.1.结合下面的算法:第一步:输入x.第二步:判断x是否小于0,若是,则输出x +2,否则执行第三步.第三步:输出x-1.当输入的x的值为-1,0,1时,输出的结果分别为( )A.-1,0,1 B.-1,1,0C.1,-1,0 D.0,-1,1解:根据x值与0的关系,选择执行不同的步骤,当x的值为-1,0,1时,输出的结果分别为1,-1,0,故选C.2.如图的程序框图输出的结果是()A.4 B.3 C.2 D.0解:该算法首先将1,2,3三个数分别赋给x,y,z;然后先让x取y的值,即x变成2,再让y 取x的值,即y的值是2,接着让z取y的值,即z 的值为2,从而最后输出z的值为2.故选C.3.(2014·湖南)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于()A.[-6,-2] B.[-5,-1]C.[-4,5] D.[-3,6]解:由程序框图可得S=⎩⎪⎨⎪⎧2t2+1-3,t∈[-2,0),t-3,t∈[0,2],其值域为[-3,6].故选D.4.(2015·福建)阅读如图所示的程序框图,运行相应的程序,则输出的结果为()A.2 B.1 C.0 D.-1解:执行程序,得S=0,i=2;S=-1,i=3;S =-1,i =4;S =0,i =5;S =0,i =6>5,跳出循环,输出S =0.故选C.5.(2014·重庆)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是()A .s >12B .s >35C .s >710D .s >45解:当输出k 的值为6时,s =1×910×89×78=710,结合各选项知,C 符合要求.故选C .6.(2015·全国课标Ⅰ)执行如图所示的程序框图,如果输入的t =0.01,则输出的n =()A .5B .6C .7D .8解法一:执行程序,S =12,m =14,n =1;S =14,m =18,n =2;S =18,m =116,n =3;S =116,m =132,n =4;S =132,m =164,n =5;S =164,m =1128,n =6;S =1128<t =0.01,m =1256,n =7,循环结束,输出n =7.解法二:记第n 次循环后S 的值为a n ()n =0,1,2,…,,其中a 0=1,则a n =a n -1-⎝ ⎛⎭⎪⎫12n ,递推可得a n =a 0-⎝ ⎛⎭⎪⎫12+122+…+12n =1-12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=12n ≤t =0.01. 显然n >6,故n =7.故选C.7.(2015·安徽)执行如图所示的程序框图(算法流程图),输出的n 为________.当a =1.416时,跳出循环,输出的n 为4.故填4.8.(2014·湖北)设a 是一个各位数字都不是0且没有重复数字的三位数.将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a =815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b =________.解法一:当a =123时,b =321-123=198≠123;当a =198时,b =981-189=792≠198; 当a =792时,b =972-279=693≠792; 当a =693时,b =963-369=594≠693; 当a =594时,b =954-459=495≠594; 当a =495时,b =954-459=495=a , 终止循环,输出b =495.解法二:设I (a )=100x +10y +z ,D (a )=100z+10y +x ,x <y <z ,x ,y ,z ∈N *,则D (a )-I (a )=99(z -x ),因此各位数字都不是0且没有重复数字,而且是99的倍数的三位数有:198,297,396,495,594,693,792,891,经检验知只有495满足题意.故填495.9.某人带着一只狼和一只羊及一捆青菜过河,只有一条船,船仅可载重此人和狼、羊及青菜三者之一,没有人在的时候,狼会吃羊,羊会吃青菜.请设计安全过河的算法.解:第一步,人带羊过河. 第二步,人自己返回. 第三步,人带青菜过河. 第四步,人带羊返回. 第五步,人带狼过河. 第六步,人自己返回. 第七步,人带羊过河.10.设计一个算法,找出区间[1,1000]内的能被7整除的整数,画出程序框图.解:第一步,取k =1.第二步,判断k ≤1000是否成立,若不成立,则执行第五步.第三步,若k 除以7的余数为0,则输出k . 第四步,将k 的值增加1,返回执行第二步. 第五步,结束. 程序框图如图.11.设计一个算法计算11×3+13×5+15×7+…+12013×2015的值,并画出程序框图. 解:算法步骤如下: 第一步,令S =0,k =1.第二步,若k <2015成立,则执行第三步,否则输出S .第三步,计算S =S +1k (k +2),k =k +2,返回第二步.程序框图如图所示:意大利数学家斐波那契,在1202年出版的《算盘全书》一书里提出了这样一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子?试画出解决此问题的程序框图.解:根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N 个月有F 对兔子,第N -1个月有S 对兔子,第N -2个月有Q 对兔子,则有F =S +Q ,一个月后,即第N +1个月时,式中变量S 的新值应变为第N 个月兔子的对数(F 的旧值),变量Q 的新值应变为第N -1个月兔子的对数(S 的旧值),这样,用S +Q 求出变量F 的新值就是N +1个月兔子的对数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第x (x ≥3)个月的i 从3逐次增加1,一直变化到12,再循环一次得到的F ”就是所求结果.流程图如图所示.§12.2基本算法语句1.输入(INPUT)语句输入语句的一般格式:_______________.要求:(1)输入语句要求输入的值是具体的常量;(2)提示内容提示用户输入的是什么信息,必须加双引号,“提示内容”原原本本地在计算机屏幕上显示,提示内容与变量之间要用分号隔开;(3)一个输入语句可以给多个变量赋值,中间用“,”分隔.2.输出(PRINT)语句输出语句的一般格式:_______________.功能:实现算法输出信息(表达式).要求:(1)表达式是指算法和程序要求输出的信息;(2)提示内容提示用户要输出的是什么信息,提示内容必须加双引号,提示内容要用分号和表达式分开;(3)如同输入语句一样,输出语句可以一次完成输出多个表达式的功能,不同的表达式之间可用“,”分隔.3.赋值语句赋值语句的一般格式: .赋值语句中的“=”叫做赋值号,它和数学中的等号不完全一样.作用:赋值语句的作用是将表达式所代表的值赋给变量.要求:(1)赋值语句左边只能是变量,而不是表达式,右边表达式可以是一个常量、变量或含变量的运算式.如:2=x是错误的;(2)赋值号的左右两边不能对换.赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量.如“A=B”“B=A”的含义和运行结果是不同的,如x=5是对的,5=x是错的,A+B=C是错的,C=A+B是对的;(3)不能利用赋值语句进行代数式的演算(如化简、因式分解、解方程等).4.条件语句(1)“IF—THEN”语句格式:____________________.说明:当计算机执行“IF—THEN”语句时,首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体,否则执行END IF之后的语句.(2)“IF—THEN—ELSE”语句格式:____________________.说明:当计算机执行“IF—THEN—ELSE”语句时,首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体1,否则(ELSE)执行语句体2.5.循环语句(1)直到型循环语句直到型(UNTIL型)语句的一般格式为:______________.(2)当型循环语句当型(WHILE型)语句的一般格式为:________________.自查自纠:1.INPUT “提示内容”;变量2.PRINT “提示内容”;表达式3.变量=表达式4.(1)IF 条件THEN语句体END IF5.(1)WHILE 条件循环体WEND(2)DO循环体LOOP UNTIL 条件下列赋值语句正确的是( )A.S=S+i2B.A=-AC.x=2x+1 D.P=x解:在程序语句中乘方要用“^”表示,所以A项不正确;乘号“*”不能省略,所以C项不正确;D项中x应用SQR(x)表示,所以D项不正确;B选项是将变量A的相反数赋给变量A,则B项正确.故选B.下面程序运行后输出结果是3,则输入的x.0解:该程序语句是求函数y=|x|的函数值,∵y=3,∴x=±3.故选C.i的值是( )解:这是一个当型循环程序,当i=(1+5)+5=11>10时,退出循环,输出的i=11.故选D.(2)输入x=20,则p=____________.解:(1)x=6满足x≤10,∴p=6×0.35=2.1;(2)x=20时不满足x≤10,∴p=10×0.35+(20-10)×0.7=10.5.故填2.1;10.5.下列循环语句,循环终止时,n=____________.n=2WHILE n<=7n=n+1WEND解:该循环语句是当型循环语句,循环终止时,条件n≤7开始不成立,故填8.类型一输入、输出和赋值语句请写出下面运算输出的结果.(1)a=5b=3c=(a+b)/2d=c*cPRINT “d=”;d(2)a=1b=2c=a+bb=a+c-bPRINT “a=,b=,c=”;a,b,c(3)a=10b=20c=30a=bb=cc=aPRINT “a=,b=,c=”;a,b,c解:(1)语句“c=(a+b)/2”是将a,b之和的一半赋值给变量c,语句“d=c*c”是将c的平方赋值给d,最后输出d的值.故输出结果为d=16.(2)语句“c=a+b”是将a,b之和赋值给c,语句“b=a+c-b”是将a+c-b的值赋值给了b.故输出结果为a=1,b=2,c=3.(3)经过语句“a=b”后a,b,c的值是20,20,30,经过语句“b=c”后a,b,c的值是20,30,30,经过语句“c=a”后a,b,c的值是20,30,20.故输出结果为a=20,b=30,c=20.点拨:①将一个变量的值赋给另一个变量,前一个变量的值保持不变;②可先后给一个变量赋多个不同的值,但变量的取值总是最后被赋予的值.阅读下列两个程序,回答问题:①x=3y=4x=y②x=3y=4y=x①中程序输出的x值为__________,②中程序输出的y值为__________.解:程序①中的x=y是将y的值4赋给x,赋值后x的值变为4;②中y=x是将x的值3赋给y,赋值后y的值为3.故填4;3.类型二 条件语句已知函数y =⎩⎪⎨⎪⎧x 2-1,x ≥0,2x 2-5,x <0,画出程序框图并编写一个程序,对每输入的一个x 值,都得到相应的函数值.解:程序框图如下.点拨:条件语句:“IF THEN ”及“IFTHENELSE”的用法在“考点梳理”栏有说明,需要注意的是,若是三段或三段以上的分段函数,通常需用条件语句的嵌套结构.编写程序,使得任意输入的3个整数按从小到大的顺序输出.解:算法分析:用a ,b ,c 表示输入的3个整数,为了节约变量,把它们重新排列后,仍用a ,b ,c 表示,并使a ≤b ≤c .具体操作步骤如下.第一步:输入3个整数a ,b ,c .第二步:将a 与b 比较,并把大者赋给b ,小者赋给a .第三步:将a 与c 比较,并把大者赋给c ,小者赋给a (此时a 已是三者中最小的).第四步:将b 与c 比较,并把大者赋给c ,小者赋给b (此时a ,b ,c 已按从小到大的顺序排列好).第五步:按顺序输出a ,b ,c .上述操作步骤可以用程序框图直观地表达出来.程序框图如图.类型三 循环语句若下面程序中输入的n 值为2017,则解:本程序是计算S =1×2+2×3+…+1n (n +1).裂项得S =⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=n n +1.所以当n =2017时,S =20172018.故填20172018.点拨:计算机执行此程序时,遇到WHILE 语句,先判断条件是否成立,如果成立,则执行WHILE 和WEND 之间的循环体,然后返回到WHILE 语句再判断上述条件是否成立,直至返回到WHILE 语句判断上述条件不成立为止,这时不再执行循环体,而执行WEND 后面的语句,这是当型循环.计算12+22+32+…+1002的值,分别用WHILE 型语句和UNTIL 型语句编写程序.当型循环与直到型循环的区别(1)WHILE 型是先判断条件,后执行循环体,而UNTIL 型则是先执行循环体,后判断条件;(2)WHILE 型是当条件满足时执行循环体,不满足时结束循环,而UNTIL 型则是条件不满足时执行循环体,条件满足时结束循环;(3)UNTIL 型至少执行一次循环体,而WHILE 型执行循环体的次数可能为0.A 的值为( )A .1B .5C .15D .120 解:该程序的功能是计算A ×2×3×4×5的值,则120=A ×2×3×4×5,故A =1,即输入A 的值为1.故选A.A .1B .10C .25D .26解:由条件可知,b =5×5+1=26.故选D. 3.读程序回答问题.( )A .程序不同,结果不同B .程序不同,结果相同C .程序相同,结果不同D .程序相同,结果相同 解:甲、乙两程序显然不同,但都是求1+2+…+1000的和,所以结果相同,故选B .4.下列程序语句是求函数y =|x -4|+1的函5 C .y =5-x D .y =x +5解:y =|x -4|+1=⎩⎪⎨⎪⎧x -3,x ≥4,5-x ,x <4,故选C.5.(2014·陕西模拟)下面程序运行后,输出的值是( )解:程序的功能是利用循环计算i 2<2000(i ∈N )的最大i 值,∵442<2000,452>2000,∴输出的i 为44.故选C.,那么输出的结果为( )A .6B .720C .120D .1解:当n =6时,这个程序的实际含义是计算S =1×2×3×4×5×6,结果是720.故选B.7.运行如图所示的程序,输出的结果是.a =1b =2a =a +b PRINT a END解:a =1,b =2,则a +b =3,根据赋值语句的含义,有a =3.故填3.8.下列程序输出结果为____________.(SQR(a )4,b =-2,执行第五句后,a =4×(-2)4×4=128,故输出a 的值为128.故填128.s =10,n =9;s =19,n =8;s =27,n =7;s =34,n =6;s =40,n =5,这时s ≥40,跳出循环,输出结果为5.10.高等数学中经常用到符号函数y =sgnx ,其定义为y =⎩⎪⎨⎪⎧1,x >0,0,x =0,-1,x <0,试编写程序,根据输入的x 值,输出对应的 y 值.解:根据x 的取值,此函数为三段分段函数,则需用条件语句嵌套.程序如下.。
高考数学一轮复习 算法初步课时作业 理(含解析)新人教A版
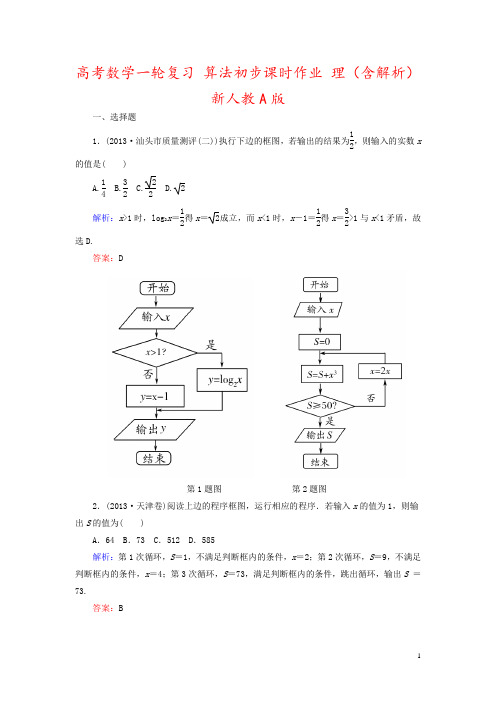
高考数学一轮复习 算法初步课时作业 理(含解析)新人教A 版一、选择题1.(2013·汕头市质量测评(二))执行下边的框图,若输出的结果为12,则输入的实数x的值是( )A.14B.32C.22D. 2 解析:x >1时,log 2x =12得x =2成立,而x <1时,x -1=12得x =32>1与x <1矛盾,故选D.答案:D第1题图 第2题图2.(2013·天津卷)阅读上边的程序框图,运行相应的程序.若输入x 的值为1,则输出S 的值为( )A .64B .73C .512D .585解析:第1次循环,S =1,不满足判断框内的条件,x =2;第2次循环,S =9,不满足判断框内的条件,x =4;第3次循环,S =73,满足判断框内的条件,跳出循环,输出S =73.答案:B3.(2013·浙江卷)某程序框图如图所示,若该程序运行后输出的值是95,则( )A .a =4B .a =5C .a =6D .a =7解析:k =1,S =1+1-12=32;k =2,S =1+1-13=53;k =3,S =1+1-14=74;k =4,S=1+1-15=95.输出结果是95,这时k =5>a ,故a =4.答案:A第3题图 第4题图4.(2013·湖北七市联考)已知全集U =Z ,Z 为整数集,如上图程序框图所示,集合A ={x |框图中输出的x 值},B ={y |框图中输出的y 值};当x =-1时,(∁U A )∩B =( )A .{-3,-1,5}B .{-3,-1,5,7}C .{-3,-1,7}D .{-3,-1,7,9}解析:由程序框图的运行程序可知,集合A ={0,1,2,3,4,5,6},B ={-3,-1,1,3,5,7,9},所以(∁U A )∩B ={-3,-1,7,9},故选D.答案:D5.(2013·辽宁大连第一次模拟)如图是用模拟方法估计椭圆x 24+y 2=1面积的程序框图,S 表示估计的结果,则图中空白处应该填入( )A .S =N 250 B .S =N 125 C .S =M 250 D .S =M125解析:区间0~2构成边长为2的正方形,其面积为4,由程序框图的运行程序可知在2 000个点中落在椭圆第一象限内的点共有M 个,而椭圆自身是关于x 轴、y 轴、原点对称的,故空白处应填入M 2 000×4×4=M125,故选D.答案:D6.(2013·辽宁卷)执行如图所示的程序框图,若输入n =10,则输出S =( ) A.511 B.111 C.3655 D.7255解析:S =122-1+142-1+162-1+182-1+1102-1=511.答案:A第6题图 第7题图7.(2013·重庆六区高三调研抽测)一个算法的程序框图如图所示,若该程序输出的结果为910,则判断框内应填入的条件是( )A .i >9B .i ≥9 C.i >10 D .i ≥8 解析:S =11×2+12×3+…+1n n +1=1-12+12-13+…+1n -1n +1=n n +1,由S =910,得n =9,故选A.答案:A8.(2013·山西适应性训练考试)执行如图所示的程序框图,输入m=1 173,n=828,则输出的实数m的值是( )A.68B.69C.138D.139解析:1 173÷828=1…345,828÷345=2…138,354÷138=2…69,138÷69=2…0,∴m=n=69,n=r=0.∴输出的实数m的值为69.答案:B9.(2013·石家庄第二次模拟)定义min{a1,a2,…,a n}是a1,a2,…,a n中的最小值,执行程序框图(如图),则输出的结果是( )A.15B.14C.13D.23解析:n=2时,a2=2,n=3时,a3=1a2=12;n=4时,a4=a2+1=3,n=5时,a5=1a4=1 3;n =6时,a 6=a 3+1=32,n =7时,a 7=1a 6=23;n =8时,a 8=a 4+1=4,T =min⎩⎨⎧⎭⎬⎫1,2,12,3,13,32,23,4=13. 答案:C第9题图 第10题图10.(2013·云南昆明高三调研)某班有24名男生和26名女生,数据a 1,a 2,…,a 50是该班50名学生在一次数学学业水平模拟考试中的成绩(成绩不为0),如图所示的程序用来同时统计全班成绩的平均数:A ,男生平均分:M ,女生平均分:-W .为了便于区别性别,输入时,男生的成绩用正数,女生的成绩用其成绩的相反数,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的( )A .T >0?,A =M +W50 B .T <0?,A =M +W50 C .T <0?,A =M -W 50D .T >0?,A =M -W50解析:依题意得,全班成绩的平均数应等于班级中所有的学生的成绩总和除以总人数,注意到当T>0时,输入的成绩表示的是某男生的成绩;当T<0时,输入的成绩表示的是某女生的成绩的相反数.因此结合题意得,选D.答案:D二、填空题11.(2013·广东卷)执行如图所示的程序框图,若输入n的值为4,则输出s的值为________.解析:第1次循环:s=1+(1-1)=1,i=1+1=2;第2次循环:s=1+(2-1)=2,i=2+1=3;第3次循环:s=2+(3-1)=4,i=3+1=4;第4次循环:s=4+(4-1)=7,i=4+1=5.循环终止,输出s的值为7.答案:7第11题图第12题图12.(2013·山东卷)执行上面的程序框图,若输入的ε的值为0.25,则输出的n的值为________.解析:逐次计算的结果是F1=3,F0=2,n=2;F1=5,F0=3,n=3,此时输出,故输出结果为3.答案:313.(1)(2013·宁德质检)运行下图所示的程序,输入3,4时,则输出________.INPUT a ,bIF a >b THENm =aELSE m =bEND IFPRINT mENDS ←0n ←0While S ≤1 023S ←S +2nn ←n +1End WhilePrint n第(1)题图 第(2)题图(2)(2013·常州市高三教学期末调研测试)根据上图所示的算法,可知输出的结果为________.解析:(1)程序的功能是比较两个数的大小且输出较大的数,所以输入3,4时输出4. (2)根据算法语句可知这是一个循环结构,S n 是一个以1为首项,2为公比的等比数列的前n 项和,即:S n =1-2n1-2=2n-1,可见n =10时,S 10=1 023,所以n =10时进行最后一次循环,故n =11.答案:(1)4 (2)11 [热点预测]14.(1)(2013·安徽省“江南十校”高三联考)下图是寻找“徽数”的程序框图.其中“S mod 10”表示自然数S 被10除所得的余数,“S /10”表示自然数S 被10除所得的商.则根据上述程序框图,输出的“徽数S ”为( )A .18B .16C .14D .12第(1)题图 第(2)题图(2)(2013·江西重点中学第一次联考)如图所示的程序框图中,令a =tan θ,b =sinθ,c =cos θ,若在集合⎩⎨⎧⎭⎬⎫θ|-π4<θ<3π4,θ≠0,π4,π2中,给θ取一个值,输出的结果是sin θ,则θ的值所在范围为( )A.⎝ ⎛⎭⎪⎫-π4,0 B.⎝ ⎛⎭⎪⎫0,π4C.⎝⎛⎭⎪⎫π2,3π4D.⎝⎛⎭⎪⎫π4,π2解析:(1)法一:S =10,则x =S MOD 10=10,y =S /10=1,3(x +y +1)=6,不符合判断条件,S =11,则x =1,y =1,3(x +y +1)=9,不符合判断条件.S =12,则x =2,y =1,3(x +y +1)=12,符合判断条件,输出S =12,选D.法二:由题意知,此程序的功能是寻找“徽数”,所谓“徽数”的定义是个位数与S 被10除所得的商的和加1后,再乘以3等于这个数本身,所以从选项验证可知D 正确.(2)由程序框图可知,本程序的功能是输入的三个数中输出最大的一个,现在tan θ,sin θ,cos θ,输出了sin θ,所以sin θ是最大的,在集合⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫θ⎪⎪⎪-π4<θ<3π4,θ≠0,π4,π2中θ的取值范围是⎝ ⎛⎭⎪⎫π2,34π.答案:(1)D (2)C。
2025版高考数学一轮复习第十二章算法初步第1讲算法初步配套课时作业理含解析新人教A版

第1讲 算法初步配套课时作业1.(2024·山东高考)执行两次如图所示的程序框图,若第一次输入的x 的值为7,其次次输入的x 的值为9,则第一次、其次次输出的a 的值分别为( )A .0,0B .1,1C .0,1D .1,0 答案 D解析 当x =7时,∵b =2,∴b 2=4<7=x . 又7不能被2整除,∴b =2+1=3.此时b 2=9>7=x ,∴退出循环,a =1,∴输出a =1. 当x =9时,∵b =2,∴b 2=4<9=x . 又9不能被2整除,∴b =2+1=3.此时b 2=9=x ,又9能被3整除,∴退出循环,a =0. ∴输出a =0.故选D.2.设x ∈[0,3],执行如图所示的程序框图,从输出的结果中随机取一个数a ,则“a ≤5”的概率为( )A.23B.56C.27D.57 答案 C解析 由程序框图可知y =⎩⎪⎨⎪⎧x +3,0≤x <2,x 2+1,2≤x ≤3,该函数的值域是[3,10],所以所求概率为5-310-3=27.3.(2024·青岛模拟)执行如图所示的程序框图,若输出的结果为48,则推断框中可以填( )A .n ≤5 B.n >5 C .n ≤4 D.n >4 答案 B解析 n =1,S =3,a =5;n =2,S =8,a =7;n =3,S =15,a =9;n =4,S =24,a =11;n =5,S =35,a =13,不满意推断框中的条件;n =6,S =48,a =15,满意推断框中的条件,退出循环,输出的S =48,所以推断框中可以填n >5.4.执行如图所示的程序框图,若输入向量a =c =(-2,2),b =(1,0),则输出S 的值是( )A .18B .20C .22D .24 答案 B解析 程序对应的运算:a =c =(-2,2),则a ·c =8,S =0+8=8,i =1,c =c +b =(-1,2);a =(-2,2),b =(1,0),c =(-1,2),则a ·c =6,S =8+6=14,i =2,c =c +b =(0,2);a =(-2,2),b =(1,0),c =(0,2),则a ·c =4,S =14+4=18,i =3,c =c +b =(1,2); a =(-2,2),b =(1,0),c =(1,2),则a ·c =2,S =18+2=20,i =4,c =c +b =(2,2); a =(-2,2),b =(1,0),c =(2,2),则a ·c =0,此时跳出循环体.故输出S 的值为20,故选B.5.(2024·郑州一检)执行如图所示的程序框图,若输出的结果是7,则推断框内m 的取值范围是( )A .(30,42]B .(30,42)C .(42,56]D .(42,56) 答案 A解析 k =1,S =2;k =2,S =2+4=6;k =3,S =6+6=12;k =4,S =12+8=20;k =5,S =20+10=30;k =6,S =30+12=42;k =7,此时不满意S =42<m ,退出循环,所以30<m ≤42,故选A.6.(2024·昆明调研)如图所示的程序框图来源于中国古代数学著作《孙子算经》,其中定义[x ]表示不超过x 的最大整数,例如[0.6]=0,[2]=2,[3.6]=3.执行该程序框图,则输出的a =( )A .9B .16C .23D .30 答案 C解析 执行程序框图,k =1,a =9,9-3·⎣⎢⎡⎦⎥⎤93=0≠2;k =2,a =16,16-3·⎣⎢⎡⎦⎥⎤163=1≠2;k =3,a =23,23-3·⎣⎢⎡⎦⎥⎤233=2,23-5·⎣⎢⎡⎦⎥⎤235=3,满意条件,退出循环.则输出的a =23.故选C.7.“中国剩余定理”是中国古代求解一次同余式组的方法,若正整数N 除以正整数m 后的余数为n ,则记为N ≡n (MOD m ),例如10≡4(MOD 6),如图所示的程序框图的算法源于“中国剩余定理”,若执行该程序框图,则输出的N =( )A .16B .14C .13D .11 答案 A解析 起先,N =10,N =10+1=11,N ≡1(MOD 3)不成立,N =11+1=12,N ≡1(MOD 3)不成立,N =12+1=13,N ≡1(MOD 3)成立,N ≡1(MOD 5)不成立,N =13+1=14,N ≡1(MOD 3)不成立,N =14+1=15,N ≡1(MOD 3)不成立,N =15+1=16,N ≡1(MOD 3)成立,N ≡1(MOD 5)成立,输出的N =16.故选A.8.执行如图所示的程序框图,假如输入的t ∈[-2,2],则输出的S ∈( )A .[-4,2]B .[-2,2]C .[-2,4]D .[-4,0] 答案 A解析 当-2≤t <0时,S =2t ∈[-4,0);当0≤t ≤2时,S =t 3-3t ,易知S =t 3-3t 在t ∈[0,1)上单调递减,在t ∈(1,2]上单调递增,且当t =0时,S =0,当t =1时,S =-2,当t =2时,S =2,所以S ∈[-2,2].综上,S ∈[-4,2],故选A.9.(2024·全国卷Ⅱ)为计算S =1-12+13-14+…+199-1100,设计了下面的程序框图,则在空白框中应填入( )A .i =i +1B .i =i +2C .i =i +3D .i =i +4 答案 B解析 由S =1-12+13-14+…+199-1100,知程序框图先对奇数项累加,偶数项累加,最终再相减.因此在空白框中应填入i =i +2,选B.10.执行如图所示的程序框图,则输出的值是( )A.155 B.158 C.161 D.164答案 C解析 执行程序框图,可得,A =1,i =1,第1次执行循环体,A =14,i =2,满意条件i ≤20,第2次执行循环体,A =17,i =3,满意条件i ≤20,第3次执行循环体,A =110,i=4,满意条件i ≤20,第4次执行循环体,A =113,i =5,满意条件i ≤20,第5次执行循环体,A =116,i =6,……视察可知,当i =20时,满意条件i ≤20,第20次执行循环体,A =14+20-1×3=161,i =21,此时,不满意条件i ≤20,退出循环,输出A 的值为161.故选C.11.(2024·江西六校联考)如图是某算法的程序框图,当输出的结果T >70时,正整数n 的最小值是________.答案 4解析由程序框图知,每次循环中K,T的值依次为1,1;2,4;3,16;4,72.又T=72>70,故正整数n的最小值为4.12.下面程序运行后输出的结果为________.N=5S=0WHILE S<15S=S+NN=N-1WENDPRINT NEND答案0解析执行第一次后,S=5,N=4;执行其次次后,S=9,N=3;执行第三次后,S=12,N=2;执行第四次后,S=14,N=1;执行第五次后,S=15,N=0;跳出循环结构,输出N的值,N=0.13.执行如图所示的程序框图,若a=0.182,b=log20.18,c=20.18,则输出的结果是________.答案20.18解析易知该程序框图的功能是输出a,b,c中的最大者.结合函数y=x2,y=log2x,y=2x的图象(图略)易知0<a<1,b<0,c>1,∴b<a<c.故输出的结果是20.18.14.《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元一世纪左右.“更相减损术”便是《九章算术》中记录的一种求最大公约数的算法,按其算理流程有如下程序框图,若输入的a,b分别为96,36,则输出的i为________.答案 4解析当a=96,b=36时,满意a>b,则a=96-36=60,i=1,由a>b,得a=60-36=24,i=2,由a<b,得b=36-24=12,i=3,由a>b,得a=24-12=12,i=4,由a=b,得输出i=4.15.假如以下程序运行后输出的结果是132,求程序中UNTIL后面的条件中a的取值范围.解程序的功能是计算S=12×11×10×…,输出结果为132,即循环体只执行了两次,即i=10时,就结束了循环,所以a满意10<a≤11.故a的取值范围为(10,11].16.(2024·陕西模拟)执行如图的程序框图,假如输入的x,y∈R,求输出的S的最大值.解 由程序框图可知,若输入的x ,y 满意约束条件⎩⎪⎨⎪⎧x ≥0,y ≥0,x +y ≤1,则输出目标函数S=2x +y 的值,否则,输出S =1.如图,作出满意条件的可行域.当x =1,y =0时,目标函数S =2x +y 取得最大值2,2>1,故输出的S 的最大值为2.。
高考数学一轮复习 第十二章算法初步、推理与证明、复

12.2 基本算法语句考纲要求理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.1.输入语句(1)输入语句的一般格式:______________________.(2)注意事项:“提示内容”与变量之间用“;”隔开,“提示内容”之间用“,”隔开,各变量之间也用“,”隔开,最后一个变量的后面不能加标点符号.2.输出语句(1)输出语句的一般格式:______________________.(2)输出语句中的“提示内容”与表达式之间必须用“;”隔开,“提示内容”之间用“,”隔开,各变量之间也用“,”隔开,最后一个表达式的后面不能加标点符号.输出语句可以输出常量、变量的值以及系统信息.3.赋值语句(1)赋值语句的一般格式:____________.(2)在研究问题的过程中可以取不同数值的量称为______,把一个值a赋给变量b的过程称为______,“____”为赋值符号.注意事项:赋值号“=”左边只能是变量名,右边是表达式,左右边不能交换;每一个赋值语句只能出现一次“=”,即只能给一个变量赋值.赋值号“=”的理解:把右边的数值赋给左边的变量或计算右边表达式的值并把计算结果赋给左边的变量.4.条件语句(1)IF—THEN—ELSE语句的一般格式:(2)IF—THEN语句的一般格式:5.循环语句(1)UNTIL语句的一般格式:(2)WHILE语句的一般格式:1.执行PRINT “2+2 008=”;2+2 008的输出结果是( ).A.2 010 B.2+2 008=2+2 008C.2+2 008=2 010 D.2 010=2 0102.下列语句是正确的赋值语句的是( ).A.5=x B.x+y=3C.x=y=-2 D.y=y*y3.(2012沈阳模拟)如图程序输出的结果是( ).A.3,4 B.4,4C.3,3 D.4,34.当a=1,b=3时,执行完下面一段过程后x的值是__________.一、输入、输出和赋值语句【例1】写出下列语句的输出结果:(1)(2)方法提炼1.输入、输出、赋值语句是任何一个算法中必不可少的语句.一个输出语句可以输出多个表达式的值.在赋值语句中,变量的值始终等于最近一次赋给它的值,先前的值将被替换.2.一个赋值语句只给一个变量赋值,但一个语句行可以写多个赋值语句.3.不能利用赋值语句进行代数式的演算(如化简、分解因式、解方程等).4.编写程序的关键在于搞清问题的算法,特别是算法的结构,然后确定采取哪一种算法语句.5.编写程序时,要注意常见运算符号的书写方式如a^b(a b);a*b(a×b);a/b(ab );SQR(x)(x);ABS(x)(|x|);a\b(a除以b的整数商,如5\2=2);a MOD b(a除以b的余数,如5 MOD 2=1)等,还要明确它们的运算规则:先乘除,后加减;乘幂优于乘除;函数优于乘幂;同级运算从左向右按顺序进行;括号内最优先,多层括号则从内到外依次进行〔注意表达式中的括号一律用小括号“( )”〕请做演练巩固提升2二、条件循环语句【例2】(2012东北三校模拟)下面程序运行的结果为( ).A.4 B.5 C.6 D.7方法提炼1.在用WHILE语句和UNTIL语句编写程序解决问题时,一定要注意它们的格式及条件的表述方法.WHI LE语句中是当条件满足时执行循环体,而UNTIL语句中是当条件不满足时执行循环体.2.在解决一些需要反复执行的运算任务,如累加求和、累乘求积等问题时,应考虑利用循环语句来实现.3.在循环语句中,也可以嵌套条件语句,甚至是循环语句,此时要注意嵌套这些语句应保证语句的完整性,否则就会造成程序无法执行.请做演练巩固提升1不理解算法语句的功能及格式易致误【典例】(2012湖南衡阳模拟)下面程序运行后输出的结果为( ).A.0 B.1 C.2 D.4解析:当j=1时,余数a=1;当j=2时,余数a=3;当j=3时,余数a=1;当j=4时,余数a=0;当j=5时,余数a=0;当j=6时,不满足条件,此时退出循环.答案:A答题指导:1.在解答本题时,易错选D而导致错误,错误原因是:对循环过程不理解,误认为j=1时,余数a=0,即j=1时,没有执行第一次循环.其错误过程如下:当j=1时,余数a=0;当j=2时,余数a=2;当j=3时,余数a=0;当j=4时,余数a=4;当j=5时,余数a=4.2.解决算法语句的有关问题时,还有以下几点易造成失误,备考时要高度关注:(1)对基本算法语句的功能及格式要求不熟悉.(2)条件语句中的嵌套结构混乱,不能用分段函数的形式直观描述.(3)对循环结构的循环过程把握不准.1.下面程序运行的结果为( ).A.4 B.5 C.6 D.72.(2012黑龙江大庆模拟)以上表示的函数表达式是__________.3.运行如图所示的程序,输出的结果是__________.4.完成下列程序,输入x的值,求函数y=|8-2x2|的值.①__________,②__________.参考答案基础梳理自测 知识梳理1.(1)INPUT “提示内容”;变量 2.(1)PRINT “提示内容”;表达式 3.(1)变量=表达式 (2)变量 赋值 = 基础自测1.C 解析:这是一个计算2+2 008的值的简单程序,输出的结果是2+2 008=2 010. 2.D 解析:赋值语句中“=”的左右两边不能互换,不能给常量赋值,左边必须是变量,右边是表达式,故A ,B 错.C 错,一个赋值语句只能给一个变量赋值.D 正确,该语句的功能是将当前的y 平方后赋给变量y .3.B 解析:程序主要为赋值.a =b ,则a =4,b =a =4.4.4 解析:x =⎩⎪⎨⎪⎧a +b ,a <b ,a -b ,a ≥b .∵a =1,b =3,满足a <b , ∴x =1+3=4. 考点探究突破【例1】解:(1)∵a =5,b =3,∴c =a +b 2=4,d =c 2=16,即输出d =16.(2)∵a =1,b =2,∴c =1+2=3,b =1+3-2=2,故输出a =1,b =2,c =3.【例2】C 解析:第一次执行后,S =100-10=90,n =10-1=9;第二次执行后,S =90-9=81,n =9-1=8;第三次执行后,S =81-8=73,n =8-1=7;第四次执行后,S =73-7=66,n =7-1=6.此时S =66≤70,结束循环,输出n =6.演练巩固提升1.C 解析:该程序依次运行的结果为S =90,n =9; S =81,n =8;S =73,n =7;S =66,n =6. 此时程序结束,故输出n 的值为6.2.y =⎩⎨⎧2x -3,x ≤2x ,x >2解析:当x ≤2时,y =2x -3;当x >2时,y =x .3.3 解析:a =1,b =2, a =a +b =1+2=3. ∴输出的结果为3.4.①x>=-2 AND x <=2 THEN ②y=8-2*x^2。
核按钮(新课标)高考数学一轮复习第十二章算法初步、推

§12.5 数学归纳法1.数学归纳法的证题步骤一般地,证明一个与正整数n 有关的命题,可按下列步骤进行: (1)(归纳奠基)证明当n 取第一个值n 0(n 0∈N *)时命题成立;(2)(归纳递推)假设____________(k ≥n 0,k ∈N *)时命题成立,证明当____________时命题也成立. 只要完成这两个步骤,就可以断定命题对从n 0开始的所有__________都成立. 2.数学归纳法的适用范围数学归纳法主要用于解决与________有关的数学命题,证明时,它的两个步骤(归纳奠基与归纳递推)缺一不可.自查自纠1.(2)n =k n =k +1 正整数n 2.正整数用数学归纳法证明1+12+13+…+12n -1<n (n ∈N *,n >1)时,第一步应验证不等式( )A .1+12<2B .1+12+13<2C .1+12+13<3D .1+12+13+14<3解:∵n ∈N *,n >1,∴n 取的第一个数为2,左端分母最大的项为122-1=13,故选B .设f (n )=1n +1+1n +2+ (12)(n ∈N *),那么f (n +1)-f (n )等于( )A.12n +1B.12n +2C.12n +1+12n +2D.12n +1-12n +2解:f (n +1)-f (n )=[1(n +1)+1+1(n +1)+2+…+12n +12n +1+12(n +1)]-⎣⎢⎡⎦⎥⎤1n +1+1n +2+…+12n =12n +1+12(n +1)-1n +1=12n +1-12n +2.故选D . (2013·黑龙江模拟)设f (x )是定义在正整数集上的函数,且f (x )满足:“当f (k )≥k +1成立时,总可推出f (k +1)≥k +2成立”.那么,下列命题总成立的是( )A .若f (1)<2成立,则f (10)<11成立B .若f (3)≥4成立,则当k ≥1时,均有f (k )≥k +1C .若f (2)<3成立,则f (1)≥2成立D .若f (4)≥5成立,则当k ≥4时,均有f (k )≥k +1成立解:根据题意,若f (4)≥5成立,则f (n 0+1)≥n 0+2(n 0≥4),即f (k )≥k +1(k ≥5).综合f (4)≥5,可知当k ≥4时,均有f (k )≥k +1成立.故选D .已知数列11×2,12×3,13×4,…,1n (n +1),通过计算得S 1=12,S 2=23,S 3=34,由此可猜测S n =____________.解法一:通过变化规律猜测S n =nn +1.解法二:S n =11×2+12×3+13×4+…+1n (n +1)=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+⎝ ⎛⎭⎪⎫13-14+…+⎝ ⎛⎭⎪⎫1n -1n +1= 1-1n +1=n n +1.故填n n +1. 用数学归纳法证明“(n +1)(n +2)·…·(n +n )=2n ·1·3·…·(2n -1)(n ∈N *)”时,从n =k 到n =k +1,等式的左边需要增乘的代数式是____________.解:当n =k 时,等式左边=(k +1)(k +2)·…·(k +k ),当n =k +1时, 等式左边=(k +2)(k +3)·…·(k +1+k +1)=(k +1)(k +2)(k +3)·…·(k +k )(k +k +1)(k +k +2)k +1=2(2k +1)(k +1)(k +2)(k +3)·…·(k +k ).观察、比较可知,从n =k 到n =k +1,等式的左边需要增乘的代数式是2(2k +1).故填2(2k +1).类型一 证明等式证明:1-12+13-14+...+12n -1-12n =1n +1+1n +2+ (12)(n ∈N *).证明:(1)当n =1时,左边=1-12=12,右边=12,等式成立.(2)假设n =k (k ∈N *)时等式成立,即1-12+13-14+…+12k -1-12k =1k +1+1k +2+…+12k , 那么,当n =k +1时, 1-12+13-14+…+12k -1-12k +12k +1-12k +2 =1k +1+1k +2+…+12k +12k +1-12k +2 =1k +2+1k +3+…+12k +12k +1+12k +2. 根据(1)和(2),可知等式对任何n ∈N *都成立.【点拨】用数学归纳法证明与正整数n 有关的一些等式时,关键在于“先看项”,弄清从n =k 到n =k +1时等式两边的构成规律,然后正确写出归纳证明的步骤,即可证明待证等式.求证:12-22+32-42+…+(2n -1)2-(2n )2=-n (2n +1)(n ∈N *).证明:①n =1时,左边=12-22=-3,右边=-3,等式成立. ②假设n =k 时,等式成立,即12-22+32-42+…+(2k -1)2-(2k )2=-k (2k +1).当n =k +1时,12-22+32-42+…+(2k -1)2-(2k )2+(2k +1)2-(2k +2)2=-k (2k +1)+(2k +1)2-(2k +2)2=-k (2k +1)-(4k +3)=-(2k 2+5k +3)=-(k +1)[2(k +1)+1],所以n =k +1时,等式也成立.由①②得,等式对任何n ∈N *都成立.类型二 证明不等式已知f (n )=1+123+133+143+…+1n 3,g (n )=32-12n 2,n ∈N *.(1)当n =1,2,3时,试比较f (n )与g (n )的大小关系; (2)猜想f (n )与g (n )的大小关系,并给出证明.解:(1)当n =1时,f (1)=1,g (1)=1,所以f (1)=g (1); 当n =2时,f (2)=98,g (2)=118,所以f (2)<g (2);当n =3时,f (3)=251216,g (3)=312216,所以f (3)<g (3).(2)由(1),猜想f (n )≤g (n ),下面用数学归纳法证明: ①当n =1,2,3时,不等式显然成立.②假设当n =k (k ≥3,k ∈N *)时不等式成立,即1+123+133+143+…+1k 3<32-12k2,那么,当n =k +1时, f (k+1)=f (k )+1(k +1)3<32-12k 2+1(k +1)3,因为12(k +1)2-⎣⎢⎡⎦⎥⎤12k 2-1(k +1)3=k +32(k +1)3-12k 2=-3k -12(k +1)3k 2<0,所以f (k +1)<32-12(k +1)2=g (k +1).由①、②可知,对一切n ∈N *,都有f (n )≤g (n )成立.【点拨】用数学归纳法证明不等式,同样要弄清增加的项,很多情况下,还要利用放缩法进行证明.已知函数f (x )=13x 3-x ,数列{a n }满足条件:a 1≥1,a n +1≥f ′(a n +1).试比较11+a 1+11+a 2+11+a 3+…+11+a n与1的大小,并说明理由. 解:∵f ′(x )=x 2-1,a n +1≥f ′(a n +1), ∴a n +1≥(a n +1)2-1.∵函数g (x )=(x +1)2-1=x 2+2x 在区间[-1,+∞)上单调递增,于是由a 1≥1,及a 2≥(a 1+1)2-1得,a 2≥22-1,进而得a 3≥(a 2+1)2-1≥24-1>23-1,由此猜想:a n ≥2n-1.下面用数学归纳法证明这个猜想: ①当n =1时,a 1≥21-1=1,结论成立;②假设当n =k (k ≥1且k ∈N *)时结论成立,即a k ≥2k -1,则当n =k +1时,由g (x )=(x +1)2-1在区间[-1,+∞)上单调递增知,a k +1≥(a k +1)2-1≥22k-1≥2k +1-1,即n =k +1时,结论也成立.由①②知,对任意n ∈N *,都有a n ≥2n-1.∴11+a 1+11+a 2+…+11+a n <12+122+…+12n =1-12n <1.1.用数学归纳法进行证明时,“归纳奠基”和“归纳递推”两个步骤缺一不可.2.证第二步的关键是合理运用归纳假设,以“n =k 时命题成立”为条件,证明“当n =k +1时命题成立”.这里,易出现的错误是:不使用“n =k 时命题成立”这一条件,而直接将n =k +1代入命题,便断言此时命题成立.注意:没有运用归纳假设的证明不是数学归纳法.3.在n =k 到n =k +1的证明过程中寻找由n =k 到n =k +1的变化规律是难点,突破的关键是分析清楚p (k )与p (k +1)的差异与联系,利用拆、添、并、放、缩等手段,从p (k +1)中分离出p (k ).4.证明不等式的方法多种多样,故在用数学归纳法证明不等式的过程中,比较法、放缩法、分析法等要灵活运用.1.用数学归纳法证明“1+a +a 2+…+a n +1=1-a n +21-a (a ≠1,n ∈N *)”,在验证n =1时,左端计算所得的结果是( )A .1B .1+aC .1+a +a 2D .1+a +a 2+a 3解:当n =1时,左边=1+a +a 2.故选C .2.设凸k 边形的内角和为f (k ),则f (k +1)-f (k )=( )A .2πB .π C.π2 D.π3解:将k +1边形A 1A 2…A k A k +1的顶点A 1与A k 相连,则原多边形被分割为k 边形A 1A 2…A k 与三角形A 1A k A k +1,其内角和f (k +1)是k 边形的内角和f (k )与△A 1A k A k +1的内角和π的和,故选B .3.用数学归纳法证明:12+22+…+n 2+…+22+12=n (2n 2+1)3,第二步证明由“k 到k +1”时,左边应加( )A .k 2B .(k +1)2C .k 2+(k +1)2+k 2D .(k +1)2+k 2解:当n =k 时,左边=12+22+…+k 2+…+22+12,当n =k +1时,左边=12+22+…+k 2+(k +1)2+k 2+…+22+12,故选D .4.用数学归纳法证明命题“当n 为正奇数时,x n +y n能被x +y 整除”中,第二步归纳假设应写成( ) A .假设n =2k +1(k ∈N *)成立,再推出n =2k +3成立 B .假设n =2k -1(k ∈N *)成立,再推出n =2k +1成立 C .假设n =k (k ∈N *)成立,再推出n =k +1成立 D .假设n =k (k ≥1)成立,再推出n =k +2成立解:第二步归纳假设n =2k -1(k ∈N *)成立,再推出n =2k -1+2=2k +1成立.故选B . 5.对于不等式n 2+n <n +1(n ∈N *),某同学的证明过程如下: (1)当n =1时,12+1<1+1,不等式成立;(2)假设当n =k (k ∈N *)时,不等式成立,即k 2+k <k +1,则n =k +1时,(k +1)2+(k +1)=k 2+3k +2<k 2+3k +2+k +2=(k +2)2=(k +1)+1,故当n =k +1时,不等式成立.根据(1)和(2),可知不等式n 2+n <n +1(n ∈N *)成立.上述证法中( ) A .过程全部正确 B .n =1验证不正确 C .归纳假设不正确D .从n =k (k ∈N *)到n =k +1的推理不正确解:证明过程没有用到归纳假设的结论,所以证明方法不正确.故选D .6.已知f (n )=(2n +7)·3n+9,存在自然数m ,使得对任意n ∈N *,都能使m 整除f (n ),则m 的最大值为( ) A .30B .26C .36D .6解:∵f (1)=36,f (2)=108=3×36,f (3)=360=10×36,所以f (1),f (2),f (3)能被36整除,推测m 的最大值为36.可以利用数学归纳法作如下简要证明:f (n +1)=[2(n +1)+7]·3n +1+9,∴f (n +1)-f (n )=2·3n +1+2·(2n +7)·3n=(4n +20)·3n,当n =1时,该式的值为72可被36整除,当n ≥2时,4n +20可被4整除,3n可被9整除,则(4n +20)·3n可被36整除,即证.故选C .7.在应用数学归纳法证明凸n 边形的对角线为12n (n -3)条时,第一步检验n =________时命题成立.解:凸多边形至少有3条边.故填3.8.(2014·广东东莞模拟)观察下列不等式: ①12<1;②12+16<2;③12+16+112<3;…,则第5个不等式为____________.解:∵2=1×2,6=2×3,12=3×4,∴第n 个不等式的左边有n 项,分子都是1,分母依次为1×2,2×3,…,n (n +1),右边为n ,即12+16+…+1n (n +1)<n .∴第5个不等式为12+16+112+120+130< 5.故填12+16+112+120+130<5.9.试证:n 为正整数时, f (n )=32n +2-8n -9能被64整除.证明:(1)当n =1时, f (1)=34-8-9=64能被64整除. (2)假设当n =k (k ∈N *)时, f (k )=32k +2-8k -9能被64整除,则当n =k +1时, f (k +1)=32(k +1)+2-8(k+1)-9=9·32k +2-8k -17=9(32k +2-8k -9)+64k +64.由归纳假设知f (k +1)也能被64整除. 综合(1)(2)知,当n 为正整数时, f (n )=32n +2-8n -9能被64整除.10.(2015·大庆模拟)数列{a n }满足S n =2n -a n (n ∈N *).(1)计算a 1,a 2,a 3,并猜想a n 的通项公式; (2)用数学归纳法证明(1)中的猜想.解:(1)当n =1时,a 1=S 1=2-a 1,∴a 1=1;当n =2时,a 1+a 2=S 2=2×2-a 2,∴a 2=32;当n =3时,a 1+a 2+a 3=S 3=2×3-a 3,∴a 3=74.由此猜想a n =2n-12n -1(n ∈N *).(2)证明:①当n =1时,a 1=1结论成立,②假设n =k (k ≥1,且k ∈N *)时结论成立,即a k =2k-12k -1,当n =k +1时,a k +1=S k +1-S k =2(k +1)-a k +1-2k +a k =2+a k -a k +1,∴2a k +1=2+a k ,∴a k +1=2+a k 2=2k +1-12k, ∴当n =k +1时结论成立,于是对于一切的自然数n ∈N *,a n =2n-12n -1成立.11.(2015·湖北八市三月联考)已知数列{x n }满足x 1=12,且x n +1=x n 2-x n (n ∈N *).(1)用数学归纳法证明:0<x n <1;(2)设a n =1x n,求数列{a n }的通项公式.解:(1)证明:①当n =1时,x 1=12∈(0,1),②假设当n =k 时,结论成立,即x k ∈(0,1), 则当n =k +1时,x k +1=x k2-x k,∵x k ∈(0,1),∴2-x k >0,即x k +1>0.又∵x k +1-1=2(x k -1)2-x k <0,∴0<x k +1<1.综合①②可知0<x n <1. (2)由x n +1=x n2-x n可得1x n +1=2-x n x n =2x n-1,即a n +1=2a n -1,∴a n +1-1=2(a n -1).令b n =a n -1,则b n +1=2b n ,又b 1=a 1-1=1x 1-1=1,∴{b n }是以1为首项,以2为公比的等比数列,即b n =2n -1.∴a n =2n -1+1.设数列a 1,a 2,…,a n ,…中的每一项都不为0. 求证:若1a 1a 2+1a 2a 3+…+1a n a n +1=na 1a n +1,n ∈N +,则{a n }为等差数列.证明:当n =2时,已知1a 1a 2+1a 2a 3=2a 1a 3,两端同乘a 1a 2a 3,得a 1+a 3=2a 2,所以a 1,a 2,a 3成等差数列.假设当n =k 时,a 1,a 2,…,a k +1成等差数列,记公差为d . 那么当n =k +1时,因为1a 1a 2+1a 2a 3+…+1a k a k +1+1a k +1a k +2=k a 1a k +1+1a k +1a k +2=k +1a 1a k +2,分子同乘a 1a k +1a k +2,得ka k +2+a 1=(k +1)a k +1,又a k +1=a 1+kd ,代入可得ka k +2+a 1=(k +1)(a 1+kd ),即a k +2=a 1+(k +1)d .所以{a n }是公差为d 的等差数列.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2015·开封市月考)算法有三种基本逻辑结构:顺序结构、条件结构、循环结构,在下列说法中正确的是( )A.一个算法中只能含有一种逻辑结构B.一个算法中可以含有以上三种逻辑结构C.一个算法中必须含有以上三种逻辑结构D.一个算法中最多可以含有以上两种逻辑结构解:算法中的逻辑结构可以是一种或多种,故选B.2.计算机执行下面的程序段后,输出的结果是( )a=1b=3a=a+bb=a-bPRINT a,bA.1,3 B.4,1C.0,0 D.6,0解:把1赋给变量a,把3赋给变量b,由语句“a=a+b”得a=4,即把4赋给变量a,由语句“b=a-b”得b=1,即把1赋给变量b,输出a,b,即输出4,1.故选B.3.(2015·武汉华师一附中期中考试)用反证法证明命题“若sinθ1-cos2θ+cosθ1-sin2θ=1,则sinθ≥0且cosθ≥0”时,下列假设的结论正确的是( )A.sinθ≥0或cosθ≥0 B.sinθ<0且cosθ<0C.sinθ<0或cosθ<0 D.sinθ>0且cosθ>0解:用反证法证明,只需要否定命题的结论,即sinθ<0或cosθ<0.故选C.4.(2015·广东清远一中期中)观察按下列顺序排列的等式:9×0+1=1,9×1+2=11,9×2+3=21,9×3+4=31,…,猜想第n(n∈N+)个等式应为( )A.9(n+1)+n=10n+9B.9(n-1)+n=10n-9C.9n+(n-1)=10n-1D.9(n-1)+(n-1)=10n-10解:结合前4个式子的共同特点可知第n个式子为9(n-1)+n=10n-9,故选B.5.(2015·云南玉溪高三统考)执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )A .870B .30C .6D .3解:A =3,N =1,输出3,N =2,N ≤4成立;A =6,输出6,N =3,N ≤4成立;A =30,输出30,N =4,N ≤4成立;A =870,输出870,N =5,N ≤4不成立,终止循环.所以这个数列的第3项是30,故选B .6.(2014·陕西五校联考)设△ABC 的三边长分别为a ,b ,c ,△ABC 的面积为S ,内切圆半径为r ,则r =2Sa +b +c;类比这个结论可知:若四面体P ABC 的四个面的面积分别为S 1,S 2,S 3,S 4,四面体P ABC 的体积为V ,内切球的半径为R ,则R =( )A.VS 1+S 2+S 3+S 4B.2VS 1+S 2+S 3+S 4C.3VS 1+S 2+S 3+S 4D.4VS 1+S 2+S 3+S 4 解:设四面体P ABC 的内切球球心为O ,那么V =V O ABC +V O PAB +V O PAC +V O PBC ,即V =13S 1R +13S 2R +13S 3R +13S 4R ,可得R =3VS 1+S 2+S 3+S 4,故选C .7.阅读下列程序,输出结果为2的是( )n =0 DO n =n +1 LOOP UNTIL n>=2 PRINT n END n =0 DO n =n +1 LOOP UNTIL n<=2 PRINT n END A . B. n =0WHILE n<=2 n =n +1 WEND PRINT n END n =0WHILE n>=2 n =n +1 WEND PRINT n END C .D.解:运行各选项程序,易知A 选项的输出结果为2.故选A .8.设f (x )是定义在正整数集上的函数,且f (x )满足:“当f (k )≥k 2成立时,总可推出f (k +1)≥(k +1)2成立”.那么,下列命题总成立的是( )A.若f(3)≥9成立,则当k≥1时,均有f(k)≥k2成立B.若f(5)≥25成立,则当k≤5时,均有f(k)≥k2成立C.若f(7)<49成立,则当k≥8时,均有f(k)>k2成立D.若f(4)=25成立,则当k≥4时,均有f(k)≥k2成立解:易判断A,B,C均不正确.对于D,f(4)=25≥42,由题设的递推关系,可知结论成立,故选D.9.观察下列各式:72=49,73=343,74=2401,…,则72016的末两位数字为( )A.01 B.43 C.07 D.49解:75=16807,76=117649,又71=07,观察可见7n(n∈N*)的末两位数字呈周期出现,且周期为4,∵2016=504×4,∴72016与74末两位数字相同,故选A.10.(2015·深圳五校联考)执行如图所示的程序框图,则输出的y=( )A.12B.1 C.-1 D.2解:由初始条件y=2,i=1得:运行第1次:y=1-12=12,i=2;运行第2次:y=1-112=-1,i=3;运行第3次:y=1-1-1=2,i=4;运行第4次:y=1-12=12,i=5.其结果呈周期性的出现,且周期是3,由于2016÷3=672,故运行第2016次:y=2,i=2016+1=2017≥2017,所以输出的结果是2,故选D.11.(2014·江西赣州四所重点中学联考)已知函数f(x)=ax3+12x2在x=-1处取得极大值,记g(x)=1f′(x).程序框图如图所示,若输出的结果S=20162017,则判断框中可以填入的关于n的判断条件是( )A .n ≤2016B .n ≤2017C .n >2016D .n >2017解:f ′(x )=3ax 2+x ,因为f (x )在x =-1处取得极大值,所以f ′(-1)=0,即3a -1=0,解得a =13,检验知合要求,故f ′(x )=x 2+x .则g (x )=1f ′(x )=1x 2+x ,g (n )=1n 2+n =1 n -1n +1,输出的结果为S =g (1)+g (2)+g (3)+…+g (n )=1-1n +1=n n +1,由S =20162017,得n =2016,故判断框内可以填入的条件是n ≤2016.故选A .12.(2015·吉林市期中考试)如图,第n 个图形由正n +2边形“扩展”而来(n =1,2,3,…),则在第n 个图形中顶点的个数为( )A .(n +1)(n +2)B .(n +2)(n +3)C .n 2D .n解:第1个图形由三角形“扩展”而来,共3×4=12个顶点;第2个图形由正方形“扩展”而来,共4×5=20个顶点;第3个图形由正五边形“扩展”而来,共5×6=30个顶点;第4个图形由正六边形“扩展”而来,共6×7=42个顶点;…;第n 个图形由正n +2边形“扩展”而来,共(n +2)(n +3)个顶点.故选B .二、填空题:本大题共4小题,每小题5分,共20分.13.(2015·山东)执行下边的程序框图,输出的T 的值为____________.解:初始条件n =1,T =1,运行第一次:T =1+⎠⎛01x d x =1+12=32,n =2;运行第二次:T =32+⎠⎛01x 2d x =32+13=116,n =3,n <3不成立,输出T 的值为116.故填116.14.(2015·哈尔滨市高三模拟)我们把平面内与直线垂直的非零向量称为直线的法向量.在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A (-3,4),且法向量为n =(1,-2)的直线(点法式)方程为1×(x +3)+(-2)×(y -4)=0,化简得x -2y +11=0.类比以上方法,在空间直角坐标系中,经过点A (1,2,3),且法向量为n =(-1,-2,1)的平面方程为____________.解:类比可得:-1×(x -1)+(-2)×(y -2)+1×(z -3)=0,即x +2y -z -2=0.故填x +2y -z -2=0. 15.有以下程序:INPUT xIF x<=-1 THEN f(x)=x +2 ELSEIF x>-1 AND x<=1 THENf(x)=x*x ELSE f(x)=-x +2 END IF END IF PRINT f(x) END根据如上程序,若函数g (x )=f (x )-m 在R 上有且只有两个零点,则实数m 的取值范围是__________. 解:由题意知,f (x )=⎩⎪⎨⎪⎧x +2,x ≤-1,x 2,-1<x ≤1,-x +2,x >1,画出f (x )的图象如图所示.∵函数g (x )=f (x )-m 有两个零点,即直线y =m 与函数y =f (x )有两个交点,∴m <0或m =1. 故填(-∞,0)∪{1}.16.(2014·福建)已知集合{a ,b ,c }={0,1,2},且下列三个关系:①a ≠2;②b =2;③c ≠0有且只有1个正确,则100a +10b +c =________.解:若①a ≠2正确,②③错误,则b ≠2,c =0,此时a =b =1,与集合的互异性矛盾;若②b =2正确,①③错误,则a =2,c =0,与集合的互异性矛盾;若③c ≠0正确,①②错误,则a =2,b ≠2,此时c =1,b =0,符合题意.综上知,a =2,b =0,c =1,100a +10b +c =201.故填201.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(10分)观察:①sin 26°+cos 236°+sin6°cos36°=34;②sin 210°+cos 240°+sin10°cos40°=34.由上面两个式子的结构规律,请提出一个一般性的猜想,并证明你的猜想.解:猜想:sin 2α+cos 2(30°+α)+sin αcos(30°+α)=34.证明:左边=1-cos2α2+1+cos (60°+2α)2+sin α(32cos α-12sin α)=1-14cos2α-34sin2α+34sin2α-14+14cos2α=1-14=34=右边,得证.18.(12分)某函数f (x )给出x 的值时,求相应函数值y 的程序框图如图所示.(1)写出函数f (x )的解析式;(2)若输入的x 取x 1和x 2(|x 1|<|x 2|)时,输出的y 值相同,试简要分析x 1与x 2的取值范围.解:(1)由程序框图知,该程序框图执行的功能是求函数f (x )=|x 2-1|的值,故f (x )的解析式为f (x )=|x 2-1|.(2)画出f (x )=|x 2-1|的草图如图.由图象的对称性知:要使f (x 1)=f (x 2)且|x 1|<|x 2|, 需-1<x 1<1,同时2≥x 2>1或-2≤x 2<-1, ∴x 1的取值范围是{x |-1<x <1},x 2的取值范围是{x |1<x ≤2或-2≤x <-1}.19.(12分)△ABC 的三个内角A ,B ,C 成等差数列,A ,B ,C 的对边分别为a ,b ,c .求证:1a +b +1b +c =3a +b +c. 证法一:采用分析法.要证1a +b +1b +c =3a +b +c ,即证a +b +c a +b +a +b +c b +c =3,也就是ca +b +ab +c=1,只需证c (b +c )+a (a +b )=(a +b )(b +c ), 需证c 2+a 2=ac +b 2,又△ABC 三内角A ,B ,C 成等差数列,故B =60°,由余弦定理,有b 2=c 2+a 2-2ac cos60°,即b 2=c 2+a 2-ac ,故c 2+a 2=ac +b 2,得证. 证法二:采用综合法.∵△ABC 三内角A ,B ,C 成等差数列, ∴B =60°.由余弦定理,有b 2=c 2+a 2-2ca cos60°, 得c 2+a 2=ac +b 2, 等式两边同时加上ab +bc 得c (b +c )+a (a +b )=(a +b )(b +c ),等式两边同除以(a +b )(b +c )得,c a +b +ab +c=1,∴⎝ ⎛⎭⎪⎫c a +b +1+⎝ ⎛⎭⎪⎫a b +c +1=3=a +b +c a +b +a +b +c b +c , 即1a +b +1b +c =3a +b +c. 20.(12分)是否存在常数a ,b ,c 使等式1·(n 2-12)+2(n 2-22)+…+n (n 2-n 2)=an 4+bn 2+c 对一切正整数n 成立?证明你的结论.解:分别将n =1,2,3代入得方程组:⎩⎪⎨⎪⎧a +b +c =0,16a +4b +c =3,81a +9b +c =18,⇒⎩⎪⎨⎪⎧a =14,b =-14,c =0.下面用数学归纳法证明:①当n =1时,由上可知等式成立;②假设当n =k (k ≥1,k ∈N *)时,等式成立,即1·(k 2-12)+2(k 2-22)+…+k (k 2-k 2)=14k 4-14k 2,则当n =k +1时,左边=1·[(k +1)2-12]+2[(k +1)2-22]+…+k [(k +1)2-k 2]+(k +1)[(k +1)2-(k +1)2]=1·(k 2-12)+2(k 2-22)+…+k (k 2-k 2)+1·(2k +1)+2(2k +1)+…+k (2k +1)=14k 4-14k 2+k (k +1)2·(2k +1)=14(k +1)4-14(k +1)2. ∴当n =k +1时,等式也成立. 由①②得等式对一切n ∈N *均成立.21.(12分)(2013·四川)某算法的程序框图如图所示,其中输入的变量x 在1,2,3,…,24这24个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y 的值为i 的概率P i (i =1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n 次后,统计记录了输出y 的值为i (i =1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.运行 次数n 输出y 的值 为1的频数输出y 的值 为2的频数输出y 的值 为3的频数30 14 6 10 … … … … 2 1001 027376697运行 次数n 输出y 的值 为1的频数输出y 的值 为2的频数输出y 的值 为3的频数30 12 11 7 … … … … 2 1001 051696353 当n =2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y 的值为i (i =1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;(3)将按程序框图正确编写的程序运行3次,求输出y 的值为2的次数ξ的分布列及数学期望.解:(1)变量x 是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能.当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y 的值为1,故P 1=12;当x 从2,4,8,10,14,16,20,22这8个数中产生时,输出y 的值为2,故P 2=13;当x 从6,12,18,24这4个数中产生时,输出y的值为3,故P 3=16.所以,输出y 的值为1的概率为12,输出y 的值为2的概率为13,输出y 的值为3的概率为16.(2)当n =2 100时,甲、乙所编程序各自输出y 的值i (i =1,2,3)的频率如下:比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大. (3)随机变量ξ可能的取值为0,1,2,3.P (ξ=0)=C 03×⎝ ⎛⎭⎪⎫130×⎝ ⎛⎭⎪⎫233=827,P (ξ=1)=C 13×⎝ ⎛⎭⎪⎫131×⎝ ⎛⎭⎪⎫232=49,P (ξ=2)=C 23×⎝ ⎛⎭⎪⎫132×⎝ ⎛⎭⎪⎫231=29,P (ξ=3)=C 33×⎝ ⎛⎭⎪⎫133×⎝ ⎛⎭⎪⎫230=127.故ξ的分布列为所以,E ξ=0×827+1×49+2×9+3×27=1,即ξ的数学期望为1.22.(12分)把正整数按从小到大、左小右大的原则依次排成如图所示的数表: 1 2 3 4 5 6 78 9 10 11 12 13 14 15 ……设a ij (i ,j ∈N *)是数表中从上往下数第i 行,从左往右数第j 个数,数表中第i 行共有2i -1个正整数,(1)若a ij =2013,求i ,j 的值;(2)设A n =a 11+a 22+a 33+…+a nn (n ∈N *),试比较A n 与n 2+n 的大小,并说明理由.解:(1)由于前10行共有1+21+22+…+29=210-1=1023个数,而2013-1023=990,所以i =11,j =990. (2)∵a 11=20,a 22=21+1,a 33=22+2,a 44=23+3,…,a nn =2n -1+(n -1),∴A n =20+(21+1)+(22+2)+(23+3)+…+[2n -1+(n -1)]=(20+21+22+23+…+2n -1)+[1+2+3+…+(n -1)]=2n +1+n 2-n -22.∴A n -(n 2+n )=2n +1-(n 2+3n +2)2.验证知,当n =1,2,3时,A n <n 2+n ;当n ≥4时,可猜测A n >n 2+n . 以下用数学归纳法证明:当n ≥4时,2n +1>n 2+3n +2.①当n=4时,25=32>42+3×4+2=30,不等式成立;②假设n=k时,2k+1>k2+3k+2成立,则当n=k+1时,2k+2=2·2k+1>2(k2+3k+2)=k2+2k+1+3k+3+k2+k>(k+1)2+3(k+1)+2.即n=k+1时,不等式也成立.综上①②知,当n≥4时,2n+1>n2+3n+2.亦即当n≥4时,A n>n2+n.第十三章选考内容1.几何证明选讲(1)理解相似三角形的定义与性质,了解平行截割定理.(2)会证明和应用以下定理:①直角三角形射影定理;②圆周角定理;③圆的切线判定定理与性质定理;④相交弦定理;⑤圆内接四边形的性质定理与判定定理;⑥切割线定理.2.坐标系与参数方程(1)了解坐标系的作用,了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.(2)了解极坐标的基本概念,会在极坐标系中用极坐标刻画点的位置,能进行极坐标和直角坐标的互化.(3)能在极坐标系中给出简单图形表示的极坐标方程.(4)了解参数方程,了解参数的意义.(5)能选择适当的参数写出直线、圆和椭圆的参数方程.3.不等式选讲(1)理解绝对值的几何意义,并了解下列不等式成立的几何意义及取等号的条件:①|a+b|≤|a|+|b|(a,b∈R);②|a-b|≤|a-c|+|c-b|(a,b∈R).(2)会利用绝对值的几何意义求解以下类型的不等式:|ax+b|≤c;|ax+b|≥c;|x-c|+|x-b|≥a.(3)通过一些简单问题了解证明不等式的基本方法:比较法、综合法、分析法.。
核按钮(新课标)高考数学一轮复习第十二章算法初步、推

§12.2 基本算法语句1.输入(INPUT)语句输入语句的一般格式:____________________.要求:(1)输入语句要求输入的值是具体的常量;(2)提示内容提示用户输入的是什么信息,必须加双引号,“提示内容”原原本本地在计算机屏幕上显示,提示内容与变量之间要用分号隔开;(3)一个输入语句可以给多个变量赋值,中间用“,”分隔.2.输出(PRINT)语句输出语句的一般格式:____________________.功能:实现算法输出信息(表达式).要求:(1)表达式是指算法和程序要求输出的信息;(2)提示内容提示用户要输出的是什么信息,提示内容必须加双引号,提示内容要用分号和表达式分开;(3)如同输入语句一样,输出语句可以一次完成输出多个表达式的功能,不同的表达式之间可用“,”分隔.3.赋值语句赋值语句的一般格式:____________________.赋值语句中的“=”叫做赋值号,它和数学中的等号不完全一样.作用:赋值语句的作用是将表达式所代表的值赋给变量.要求:(1)赋值语句左边只能是变量,而不是表达式,右边表达式可以是一个常量、变量或含变量的运算式.如:2=x是错误的.(2)赋值号的左右两边不能对换.赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量.如“A=B”“B=A”的含义和运行结果是不同的,如x=5是对的,5=x是错的,A+B=C是错的,C=A+B是对的.(3)不能利用赋值语句进行代数式的演算(如化简、因式分解、解方程等).4.条件语句(1)“IF—THEN”语句格式:____________________.说明:当计算机执行“IF—THEN”语句时,首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体,否则执行END IF之后的语句.(2)“IF—THEN—ELSE”语句格式:____________________.说明:当计算机执行“IF—THEN—ELSE”语句时,首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体1,否则(ELSE)执行语句体2.5.循环语句(1)直到型循环语句直到型(UNTIL型)语句的一般格式为:______________.(2)当型循环语句当型(WHILE型)语句的一般格式为:________________.自查自纠1.INPUT “提示内容”;变量2.PRINT “提示内容”;表达式3.变量=表达式4.(1)IF 条件THEN语句体END IF(2)IF 条件THEN语句体1ELSE语句体2END IF5. (1)DO循环体LOOP UNTIL 条件(2)WHILE 条件循环体WEND下列赋值语句正确的是( ) A.S=S+i2B.A=-AC.x=2x+1 D.P=x解:在程序语句中乘方要用“^ ”表示,所以A项不正确;乘号“*”不能省略,所以C项不正确;D项中x应用SQR(x)表示,所以D项不正确;B选项是将变量A的相反数赋给变量A,则B项正确.故选B.下面程序运行后输出结果是3,则输入的x值一定是( )INPUT xIF x>0 THENy=xELSEy=-xEND IFPRINT yENDA.3 B.-3 C.3或-3 D.0解:该程序语句是求函数y=|x|的函数值,∵y=3,∴x=±3.故选C.执行下列程序后,输出的i的值是( )i=1WHILE i<=10i=i+5WENDPRINT iENDA.5 B.6 C.10 D.11解:这是一个当型循环程序,当i=(1+5)+5=11>10时,退出循环,输出的i=11.故选D.某程序如下:INPUT “x=”;xIF x<=10 THENp=x*0.35ELSEp=10*0.35+(x-10)*0.7END IFPRINT pEND(1)输入x=6,则p=____________;(2)输入x=20,则p=____________.解:(1)x=6满足x≤10,∴p=6×0.35=2.1;(2)x=20时不满足x≤10,∴p=10×0.35+(20-10)×0.7=10.5.故填2.1;10.5.下列循环语句,循环终止时,n=________.n=2WHILE n<=7n=n+1WEND解:该循环语句是当型循环语句,循环终止时,条件n≤7开始不成立,故填8.类型一输入、输出和赋值语句请写出下面运算输出的结果.(1)a=5b=3c=(a+b)/2d=c*cPRINT “d=”;d(2)a=1b=2c=a+bb=a+c-bPRINT “a=,b=,c=”;a,b,c(3)a=10b=20c=30a=bb=cc=aPRINT “a=,b=,c=”;a,b,c解:(1)语句“c=(a+b)/2”是将a,b之和的一半赋值给变量c,语句“d=c*c”是将c的平方赋值给d,最后输出d的值.故输出结果为d=16.(2)语句“c=a+b”是将a,b之和赋值给c,语句“b=a+c-b”是将a+c-b的值赋值给了b.故输出结果为a=1,b=2,c=3.(3)经过语句“a=b”后a,b,c的值是20,20,30,经过语句“b=c”后a,b,c的值是20,30,30,经过语句“c=a”后a,b,c的值是20,30,20.故输出结果为a=20,b=30,c=20.【点拨】①将一个变量的值赋给另一个变量,前一个变量的值保持不变;②可先后给一个变量赋多个不同的值,但变量的取值总是最后被赋予的值.阅读下列两个程序,回答问题:① x=3 y=4x=y②x=3 y=4 y=x①中程序输出的x 值为__________,②中程序输出的y 值为__________.解:程序①中的x =y 是将y 的值4赋给x ,赋值后x 的值变为4;②中y =x 是将x 的值3赋给y ,赋值后y 的值为3.故填4;3.类型二 条件语句已知函数y =⎩⎪⎨⎪⎧x 2-1,x ≥0,2x 2-5,x <0,画出程序框图并编写一个程序,对每输入的一个x值,都得到相应的函数值.解:程序框图如下.程序如下.INPUT “x=”;x IF x>=0 THEN y =x^2-1 ELSEy =2*x^2-5 END IFPRINT “y=”;y END【点拨】条件语句:“IF THEN ”及“IF THEN ELSE ”的用法在“考点梳理”栏有说明,需要注意的是,若是三段或三段以上的分段函数,通常需用条件语句的嵌套结构.编写程序,使得任意输入的3个整数按从小到大的顺序输出. 解:算法分析:用a ,b ,c 表示输入的3个整数,为了节约变量,把它们重新排列后,仍用a ,b ,c 表示,并使a ≤b ≤c .具体操作步骤如下.第一步:输入3个整数a ,b ,c .第二步:将a与b比较,并把大者赋给b,小者赋给a.第三步:将a与c比较,并把大者赋给c,小者赋给a(此时a已是三者中最小的).第四步:将b与c比较,并把大者赋给c,小者赋给b(此时a,b,c已按从小到大的顺序排列好).第五步:按顺序输出a,b,c.上述操作步骤可以用程序框图直观地表达出来.程序框图如图.根据程序框图,写出计算机程序为:INPUT “a,b ,c =”;a ,b ,c IF b<a THENt =a a =b b =t END IF IF c<a THENt =a a =c c =t END IF IF c<b THENt =b b =c c =t END IF PRINT a ,b ,c END类型三 循环语句若下面程序中输入的n 值为2017,则输出的值为____________.INPUT “n=”;n S =0 i =1WHILE i<=nS =S +1/(i*(i +1)) i =i +1 WEND PRINT SEND 解:本程序是计算S =11×2+12×3+…+1n (n +1).裂项得S =⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=n n +1.所以当n =2017时,S =20172018.故填20172018. 【点拨】计算机执行此程序时,遇到WHILE 语句,先判断条件是否成立,如果成立,则执行WHILE 和WEND 之间的循环体,然后返回到WHILE 语句再判断上述条件是否成立,直至返回到WHILE 语句判断上述条件不成立为止,这时不再执行循环体,而执行WEND 后面的语句,这是当型循环.计算12+22+32+…+1002的值,分别用WHILE型语句和UNTIL型语句编写程序.解:WHILE型:UNTIL型:i=1S=0WHILE i<=100S=S+i^2i=i+1WENDPRINT SENDi=1S=0DOS=S+i^2i=i+1LOOP UNTIL i>100PRINT SEND当型循环与直到型循环的区别(1)WHILE型是先判断条件,后执行循环体,而UNTIL型则是先执行循环体,后判断条件;(2)WHILE型是当条件满足时执行循环体,不满足时结束循环,而UNTIL型则是条件不满足时执行循环体,条件满足时结束循环;(3)UNTIL型至少执行一次循环体,而WHILE型执行循环体的次数可能为0.1.给出下列程序:INPUT “A=”;AA=A*2A=A*3A=A*4A=A*5PRINT AEND若输出的A的值为120,则输入的A的值为( )A.1 B.5 C.15 D.120解:该程序的功能是计算A×2×3×4×5的值,则120=A×2×3×4×5,故A=1,即输入A的值为1.故选A.2.给出程序:a=5IF a>5 THENb=2*aELSEb=a*a+1END IFPRINT bEND该程序运行的结果为( )A.1 B.10 C.25 D.26 解:由条件可知,b=5×5+1=26.故选D. 3.读程序回答问题.甲i=1S=0WHILE i<=1000S=S+ii=i+1WENDPRINT SEND乙i=1000S=0DOS=S+ii=i-1LOOP UNTIL i<1PRINT SEND对甲、乙两程序和输出结果判断正确的是( )A.程序不同,结果不同B.程序不同,结果相同C.程序相同,结果不同D.程序相同,结果相同解:甲、乙两程序显然不同,但都是求1+2+…+1000的和,所以结果相同,故选B. 4.下列程序语句是求函数y=|x-4|+1的函数值,则①处为( )INPUT “x=”;xIF x>=4 THENy=x-3ELSE__①__END IFPRINT yENDA.y=3-x B.y=x-5C.y=5-x D.y=x+5解:y =|x -4|+1=⎩⎪⎨⎪⎧x -3,x ≥4,5-x ,x <4,故选C .5.(2014·陕西模拟)下面程序运行后,输出的值是( )i =0 DO i =i +1LOOP UNTIL i*i>=2000 i =i -1 PRINT i ENDA .42B .43C .44D .45解:程序的功能是利用循环计算i 2<2000(i ∈N )的最大i 值,∵442<2000,452>2000,∴输出的i 为44.故选C .6.读下面的程序:INPUT n i =1 S =1 WHILE i<=n S =S*i i =i +1 WEND PRINT S END上面的程序在执行时输入6,那么输出的结果为( ) A .6 B .720C .120D .1解:当n =6时,这个程序的实际含义是计算S =1×2×3×4×5×6,结果是720.故选B .7.运行如图所示的程序,输出的结果是 .a =1b =2 a =a +b PRINT a END解:a =1,b =2,则a +b =3,根据赋值语句的含义,有a =3.故填3. 8.下列程序输出结果为____________.(SQR(a )表示非负数a 的算术平方根)b =2a =a -bb =b -aa =a*b^a*SQR(a)PRINT aEND解:执行第三、四句后,a =4,b =-2,执行第五句后,a =4×(-2)4×4=128,故输出a 的值为128.故填128.9.求下面程序的运行结果.n =10s =0DOs =s +nn =n -1LOOP UNTIL s>=40PRINT nEND解:n =10,s =0直接进入循环体后,s =10,n =9;s =19,n =8;s =27,n =7;s =34,n =6;s =40,n =5,这时s ≥40,跳出循环,输出结果为5.10.高等数学中经常用到符号函数y =sgn x ,其定义为y =⎩⎪⎨⎪⎧1,x >0,0,x =0,-1,x <0,试编写程序,根据输入的x 值,输出对应的 y 值.解:根据x 的取值,此函数为三段分段函数,则需用条件语句嵌套.程序如下.INPUT xIF x>0 THENy =1ELSEIF x =0 THENy =0ELSEy =-1END IFEND IFPRINT yEND11.编写一个程序,求1!+2!+…+10!的值.解:程序如下.i=1j=1WHILE i<=10j=j*is=s+ji=i+1WENDPRINT sEND某商场第一年销售计算机5000台,如果平均每年销售量比上一年增加10%,那么从第一年起,大约几年可使总销售量达到30000台?画出解决该问题的程序框图,并编写相应程序.解:根据题意,每年销售量比上一年增加的百分率相同,设总销售量为S,n年达到30000台.则S=5000+5000(1+10%)+5000(1+10%)2+…+5000(1+10%)n-1=50000(1.1n-1).令S≥30000,可得n≥5,即大约5年可使总销售量达30000台.程序框图如图所示.程序如下.m=5000S=0i=0WHILE S<30000S=S+mm=m*(1+0.1)i=i+1WENDPRINT iEND。
高考数学一轮复习 第十二章算法初步、推理与证明、复

课时作业65 基本算法语句一、选择题1.给出程序如图所示,若该程序执行的结果是3,则输入的x值是( ).INPUT xIF x>=0 THENy=xELSEy=-xEND IFPRINT yENDA.3 B.-3C.3或-3 D.02.计算机执行下面的程序段后,输出的结果是( ).a=1b=3a=a+bb=a-bPRINT a,bA.1,3 B.4,1C.0,0 D.6,03.(2012杭州联考)将两个数a=8,b=17交换,使a=17,b=8,下面语句正确的是( ).A.a=bb=aB.c=bb=aa=cC.b=aa=bD.a=cc=bb=a4.计算机执行下面的程序后,输出的结果是( ).A=2B=3A=A*BB=A*BPRINT A,BENDA.1,3 B.4,1 C.6,18 D.6,05.对赋值语句,描述正确的是( ).①可以给变量提供初值;②赋值号左、右不能对换;③可以给一个变量重复赋值;④不能给一个变量重复赋值.A.①②③ B.①②C.②③④ D.①②④6.对该程序判断正确的是( ).S=0;WHILE i<=1 000S=S+i;i=i+1;WENDPRINT S;ENDA.求从1 000到1这1 000个自然数的和B.求从1到1 000这1 000个自然数的和C.求从1到1 000这1 000个自然数的积D.求从1 000到1这1 000个自然数的积7.下面为一个求20个数的平均数的程序,则在横线上应填的语句为( ).i=1S=0DOINPUT xS=S+xi=i+1LOOP UNTILa=S/20PRINT aENDA.i>20B.i<20C.i>=20D.i<=20二、填空题8.运行下列程序,则其输出的结果为__________.S=0n=2i=1DOS=S+1/nn=n*2i=i+1LOOP UNTIL i>=7PRINT SEND9.下列程序是求一个函数的函数值的程序,在键盘上输入一个自变量x的值,输出它的函数值.IF x<=0THENPRINT -xELSE IF x<=1 THENPRINT 0 ELSEPRINT x -1END IFEND IFEND若执行的结果为3,则输入的x 值为__________. 10.运行下面程序框内的程序,在两次运行中分别输入-4和4,则运行结果依次为__________.三、解答题 11.阅读下面的程序,试求其输出的结果是多少.S =1k =2WHILE k<=10S =S +k k =k +2WENDPRINT SEND12.设计算法求1+13+15+…+119的值,画出程序框图,并编写程序.参考答案一、选择题1.C 解析:该算法对应的函数为y =|x |,已知y =3,则x =±3.2.B 解析:由语句知a =1+3=4,b =1.3.B 解析:由赋值语句可知B 正确.4.C 解析:A =A×B =2×3=6,B =A×B=6×3=18.5.D 解析:不可以给一个变量重复赋值.6.B 解析:由S =S +i ,i =i +1,知该程序是求从1到1 000这1 000个自然数之和.7.A 解析:加完第20个数后有i =21.故选A.二、填空题8.6364 解析:第1次循环:S =12,n =4,i =2;第2次循环:S =34,n =8,i =3; 第3次循环:S =78,n =16,i =4; 第4次循环:S =1516,n =32,i =5; 第5次循环:S =3132,n =64,i =6; 第6次循环:S =6364,n =128,i =7. 满足条件结束循环,输出S 的值为6364. 9.4或-3 解析:此函数解析式为y =⎩⎪⎨⎪⎧ -x ,x ≤0,0,0<x ≤1,x -1,x >1.当y =3时,x =4或x =-3.10.-1,20 解析:当x =-4时,y =-42=-2,y +1=-1;当x =4时,y =3+42=19,y +1=20.三、解答题11.解:该程序是一当型循环结构,计数变量是k ,当k ≤10时运行循环体. 其功能是计算S =1+2+4+6+8+10的值,易知S =31,即输出的结果为31.12.解:程序框图:程序:。
高考数学一轮复习 第十二章 算法初步、推理与证明 12.1 算法初步课件 理

解:因为算法的步骤是有限的,所以②不能设计算法 求解,故选 B.
2021/12/11
第二十二页,共四十八页。
类型二 顺序结构
已知直角三角形两直角边长为 a,b,求斜边长 c
的一个算法分下列三步:
①计算 c= a2+b2;
②输入直角三角形两直角边长 a,b 的值;
②统筹法中“烧水泡茶”的故事;
③测量某棵树的高度,判断其是否为大树;
④已知三角形的两边及夹角,利用三角形的面积公式求出该三
角形的面积.
A.1
B.2
C.3
D.4
2021/12/11
第十九页,共四十八页。
解:①中勾画了从济南到巴黎的行程安排, 完成了任务;②中节约时间,烧水泡茶完成了 任务;③中对“树的大小”没有明确的标准, 无法完成任务,不是有效的算法构造;④是纯 数学问题,利用三角形的面积公式求出三角形 的面积.故选 C.
(2)赋值号的左右两边不能对换.赋值语句是将赋值号右边的表达式的值赋
给赋值号左边的变量.如“A=B”“B=A”的含义和运行结果是不同的,如 x
=5 是对的,5=x 是错的,A+B=C 是错的,C=A+B 是对的.
(3)不能利用赋值语句进行代数式的演算(如化简、因式分解、解方程等).
2021/12/11
2021/12/11
第二十六页,共四十八页。
类型三 条件结构
下面的程序框图能判断任意输入的整数 x 是奇数还是偶 数.其中判断框内的条件是( )
A.m=0?
2021/12/11
B.m=1?
C.x=0?
第二十七页,共四十八页。
D.x=1?
解:由程序框图所体现的算法可知判断一个整 数是奇数还是偶数,看这个数除以 2 的余数是 1 还 是 0.由图可知应该填 m=1?.故选 B.
核按钮(新课标)高考数学一轮复习第十二章算法初步与框图、推理与证明12.2基本算法语句课件文

解:(1)语句“c=(a+b)/2”是将 a,b 之和的一半赋值给变量 c,
语句“d=c*c”是将 c 的平方赋值给 d,最后输出 d 的值.故输出
结果为 d=16. (2)语句“c=a+b”是将 a,b 之和赋值给 c,语句“b=a+c
-b”是将 a+c-b 的值赋值给了 b.故输出结果为 a=1,b=2,c= 3.
UNTIL 型: i=1 S=0 DO
S=S+i^2 i=i+1 LOOP UNTIL PRINT S END
i>100
第二十三页,共24页。
当型循环与直到型循环的区别 (1)WHILE 型是先判断条件,后执行循环体,而 UNTIL 型则是先执行循环体,后判断条件; (2)WHILE 型是当条件满足时执行循环体,不满足时 结束循环,而 UNTIL 型则是条件不满足时执行循环体,条 件满足时结束循环; (3)UNTIL 型至少执行一次循环体,而 WHILE 型执行 循环体的次数可能为 0.
说明:当计算机执行“IF—THEN”语句时,首先对 IF 后的条件进 行判断,如果(IF)条件符合,那么(THEN)执行语句体,否则执行 END IF
之后的语句.
(2)“IF—THEN—ELSE”语句 格式:
____________________.
说明:当计算机执行“IF—THEN—ELSE”语句时,首先对 IF 后的 条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体 1,否则(ELSE) 执行语句体 2.
第二十四页,共24页。
i=i+5 WEND PRINT i END A.5 B.6 C.10 D.11
解:这是一个当型循环程序,当 i=(1+5)+5=11>10 时,退出循环,输出的 i=11.故选 D.
核按钮(新课标)高考数学一轮复习 第十二章 算法初步、

§12.1 算法与程序框图1.算法的概念及特点(1)算法的概念在数学中,算法通常是指按照一定______解决某一类问题的________和________的步骤.(2)算法的特点之一是具有______性,即算法中的每一步都应该是确定的,并能有效地执行,且得到确定的结果,而不应是模棱两可的;其二是具有______性,即算法步骤明确,前一步是后一步的前提,只有执行完前一步才能进行后一步,并且每一步都准确无误才能解决问题;其三是具有______性,即一个算法应该在有限步操作后停止,而不能是无限的;另外,算法还具有不唯一性和普遍性,即对某一个问题的解决不一定是唯一的,可以有不同的解法,一个好的算法应解决的是一类问题而不是一两个问题.2.程序框图(1)程序框图的概念程序框图又称流程图,是一种用______、______及______来表示算法的图形.(2)构成程序框图的图形符号、名称及其功能3.算法的基本逻辑结构(1)顺序结构顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按__________的顺序进行的.它是由若干个__________的步骤组成的,它是任何一个算法都离不开的基本结构.顺序结构可用程序框图表示为如图所示的形式.(2)条件结构在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.常见的条件结构可以用程序框图表示为如图所示的两种形式.(3)循环结构在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是_______反复执行的步骤称为________.循环结构有如下两种形式:①如图1,这个循环结构有如下特征:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.因此,这种循环结构称为____________.②如图2表示的也是常见的循环结构,它有如下特征:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.因此,这种循环结构称为____________.自查自纠1.(1)规则明确有限(2)确定有序有穷2.(1)程序框流程线文字说明(2)①终端框(起止框) ②输入、输出框③处理框(执行框) ④判断框⑤流程线⑥连接点3.(1)从上到下依次执行(3)循环结构循环体①直到型循环结构②当型循环结构下列各式中的S 值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+13+…+110000D .S =1+2+3+4+…解:由算法的有限性知,D 不正确,而A ,B ,C 都可以通过有限步骤操作,输出确定结果,故选D .给出下列算法:第一步,输入正整数n (n >1).第二步,判断n 是否等于2,若n =2,则输出n ;若n >2,则执行第三步.第三步,依次从2到n -1检验能不能整除n ,若不能整除n ,则执行第四步;若能整除n ,则执行第一步.第四步,输出n .则输出的n 的值是( )A .奇数B .偶数C .质数D .合数解:根据算法可知n =2时,输出n 的值为2;若n =3,输出n 的值为3;若n =4,2能整除4,则重新输入n 的值,…,故输出的n 的值为质数.故选C .(2014·北京)执行如图所示的程序框图,输出的S 值为( )A .1B .3C .7D .15 解:由程序框图知:S =1+21+22=7.故选C .(2014·辽宁)执行下面的程序框图,若输入x =9,则输出y =____________.解:输入x =9,则y =5,|y -x |=4>1,不满足条件;x =5,y =113,|y -x |=43>1,不满足条件;x =113,y =299,|y -x |=49<1,满足条件,输出y =299.故填299.如图所示,程序框图(算法流程图)的输出结果是__________.解:初始值s =0,n =2.第一次循环得s =12,n =4;第二次循环得s =12+14,n =6;第三次循环得s =12+14+16=1112,n =8,此时退出循环,输出的s =1112.故填1112.类型一 算法的概念下列语句是算法的个数为( )①从济南到巴黎:先从济南坐火车到北京,再坐飞机到巴黎;②统筹法中“烧水泡茶”的故事;③测量某棵树的高度,判断其是否为大树;④已知三角形的两边及夹角,利用三角形的面积公式求出该三角形的面积.A .1B .2C .3D .4解:①中勾画了从济南到巴黎的行程安排,完成了任务;②中节约时间,烧水泡茶完成了任务;③中对“树的大小”没有明确的标准,无法完成任务,不是有效的算法构造;④是纯数学问题,利用三角形的面积公式求出三角形的面积.故选C .【点拨】算法过程要做到一步一步地执行,每一步执行的操作必须确切,不能含糊不清,且在有限步后必须得到问题的结果.下列叙述能称为算法的个数为( )①植树需要运苗、挖坑、栽苗、浇水这些步骤;②顺序进行下列运算:1+1=2,2+1=3,3+1=4,…,99+1=100;③从宜昌乘火车到武汉,从武汉乘飞机到北京;④3x >x +1;⑤求所有能被3整除的正数,即3,6,9,12,….A.2 B.3 C.4 D.5解:①②③可称为算法,④⑤不是,故选B.类型二经典算法“韩信点兵”问题.韩信是汉高祖刘邦手下的大将,为了保守军事机密,他在点兵时采用下述方法:先令士兵从1~3报数,结果最后一个士兵报2;再令士兵从1~5报数,结果最后一个士兵报3;又令士兵从1~7报数,结果最后一个士兵报4.这样,韩信很快就知道了自己部队士兵的总人数.请设计一个算法,求出士兵至少有多少人.解:在本题中,士兵从1~3报数,最后一个士兵报2,说明士兵的总人数是除以3余2,其他两种情况依此类推.(算法一)步骤如下:第一步:先确定最小的满足除以7余4的数是4;第二步:依次加7就得到所有满足除以7余4的数:4,11,18,25,32,39,46,53,60,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:18;第四步:依次加上35,得18,53,88,…;第五步:在第四步得到的一列数中,找到最小的满足除以3余2的正整数:53,这就是我们要求的数.(算法二)步骤如下:第一步:先确定最小的满足除以3余2的数是2;第二步:依次加3就得到所有满足除以3余2的数:2,5,8,11,14,17,20,23,26,29,32,35,38,41,44,47,50,53,56,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:8;第四步:然后依次加15就得8,23,38,53,…,不难看出,这些数既满足除以3余2,又满足除以5余3;第五步:在第四步所得的一列数中找到满足除以7余4的最小数是53,这就是我们要求的数.【点拨】给出一个问题,设计算法时要注意:(1)认真分析问题,研究解决此问题的一般方法;(2)将解决问题的过程分解成若干步骤;(3)用简练的语言将各步骤表示出来;(4)把解题过程条理清楚地表达出来,就得到一个明确的算法.对于同一问题,可以设计不同的算法,其最终的结果是一样的,但解决问题的繁简程度不同,我们要寻找最优算法.一位商人有9枚银元,其中有一枚略轻的是假银元.请设计一种算法,用天平(不用砝码)将假银元找出来.解:算法如下:第一步:把银元分成3组,每组3枚;第二步:先将两组分别放在天平的两边,如果天平不平衡,那么假银元就在轻的那一组;如果天平左右平衡,则假银元就在未称的第3组内;第三步:取出含假银元的那一组,从中任取两枚银元放在天平的两边.如果左右不平衡,则轻的那一边就是假银元;如果天平两边平衡,则未称的那一枚就是假银元.类型三 顺序结构已知点P (x 0,y 0)和直线l :Ax +By +C =0,求点P (x 0,y 0)到直线l 的距离d ,写出其算法并画出流程图.解:算法如下:第一步:输入x 0,y 0及直线方程的系数A ,B ,C .第二步:计算z 1=Ax 0+By 0+C .第三步:计算z 2=A 2+B 2.第四步:计算d =||z 1z 2.第五步:输出d .流程图如图所示.【点拨】顺序结构是一种最简单、最基本的结构,可严格按照传统的解题思路写出算法步骤,画出程序框图.注意语句与语句之间,框与框之间是按从上到下的顺序进行的.阅读如图所示的程序框图,若输入的a ,b ,c 的值分别是21,32,75,则输出的a ,b ,c 分别是( )A .75,21,32B .21,32,75C .32,21,75D .75,32,21 解:该程序框图的执行过程是:输入21,32,75;x =21;a =75;c =32;b =21;输出75,21,32.故选A .类型四 条件结构(2015·深圳调研)执行如图所示的程序框图,如果依次输入函数:f (x )=3x ,f (x )=sin x ,f (x )=x 3,f (x )=x +1x,那么输出的函数f (x )为( )A .f (x )=3xB .f (x )=sin xC .f (x )=x 3D .f (x )=x +1x解:依题意得,输出的函数应满足:f (-x )=-f (x )(x ∈R ),即函数f (x )是定义在R 上的奇函数,且f (x +m )>f (x ),其中m >0,即函数f (x )是定义在R 上的增函数.对于A ,函数f (x )=3x 不是奇函数;对于B ,函数f (x )=sin x 不是定义在R 上的增函数;对于C ,函数f (x )=x 3既是奇函数又是定义在R 上的增函数;对于D ,函数f (x )=x +1x的定义域不是实数集.综上所述,只能输出f (x )=x 3,故选C .【点拨】条件结构的运用与数学的分类讨论有关.设计算法时,哪一步要分类讨论,哪一步就需要用条件结构.(2015·全国卷Ⅱ)如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为14,18,则输出的a =( )A.0 B.2 C.4 D.14解:执行该程序,输入a,b的值依次为a=14,b=18;a=14,b=4;a=10,b=4;a=6,b=4;a=2,b=4;a=b=2,此时退出循环,输出的a=2.故选B.类型五循环结构(2014·安徽)如图所示,程序框图(算法流程图)的输出结果是( )A.34 B.55 C.78 D.89解:运行程序:x=1,y=1,z=2;x=1,y=2,z=3;x=2,y=3,z=5;x=3,y =5,z=8;x=5,y=8,z=13;x=8,y=13,z=21;x=13,y=21,z=34;x=21,y =34,z=55,跳出循环,输出结果是55.故选B.【点拨】如果算法问题里涉及的运算进行了许多次重复的操作,且先后参与运算的数之间有相同的规律,就可引入变量循环参与运算(我们称之为循环变量),应用循环结构.在循环结构中,要注意根据条件设计合理的计数变量、累加和累乘变量及其个数等,特别要使条件的表述恰当、准确.(2015·陕西)根据下边的框图,当输入x为2006时,输出的y=( )A.28 B.10 C.4 D.2解:初始条件:x=2006.第1次运行:x=2004;第2次运行:x=2002;第3次运行:x=2000;…;第1003次运行:x=0;第1004次运行:x=-2,不满足条件,跳出循环,所以输出的y=32+1=10,故选B.1.设计算法时,要根据题目进行选择,以简单、程序短、易于在计算机上执行为原则.2.画程序框图首先要进行结构选择,套用格式.若求只含有一个关系式的函数的函数值时,只用顺序结构就能够解决;若是分段函数或执行时需要先判断才能执行后继步骤的,就必须引入条件结构;如果问题涉及的运算进行了许多重复的步骤,有规律,就可引入变量,应用循环结构.当然,应用循环结构一定要用到顺序结构与条件结构.3.循环结构的循环控制通过累加变量记录循环次数,通过判断框决定循环终止与否.用循环结构来描述算法,在画出算法程序框图之前,需要确定的三件事是:(1)确定循环变量与初始条件;(2)确定循环体;(3)确定终止条件.注意直到型循环与当型循环的区别,二者判断框内的条件表述在解决同一问题时恰好相反.解决循环结构框图问题,当循环次数比较少时,可依次列出;当循环次数较多时,可先循环几次,找出规律.要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.4.在具体绘制程序框图时,要注意以下几点:(1)流程线上要标有执行顺序的箭头.(2)判断框后边的流程线应根据情况标注“是(Y)”或“否(N)”.(3)框图内的内容包括累加(积)变量初始值,计数变量初始值,累加值,前后两个变量的差值都要仔细斟酌,不能有丝毫差错.(4)判断框内条件常用“>”“≥”“<”“≤”“=”等符号,它们的含义是各不相同的,要根据所选循环结构的类型,正确地进行选择.1.结合下面的算法:第一步:输入x .第二步:判断x 是否小于0,若是,则输出x +2,否则执行第三步.第三步:输出x -1.当输入的x 的值为-1,0,1时,输出的结果分别为( )A .-1,0,1B .-1,1,0C .1,-1,0D .0,-1,1解:根据x 值与0的关系,选择执行不同的步骤,当x 的值为-1,0,1时,输出的结果分别为1,-1,0,故选C .2.如图的程序框图输出的结果是( )A .4B .3C .2D .0解:该算法首先将1,2,3三个数分别赋给x ,y ,z ;然后先让x 取y 的值,即x 变成2,再让y 取x 的值,即y 的值是2,接着让z 取y 的值,即z 的值为2,从而最后输出z 的值为2.故选C .3.(2014·湖南)执行如图所示的程序框图,如果输入的t ∈[-2,2],则输出的S 属于( )A .[-6,-2]B .[-5,-1]C .[-4,5]D .[-3,6]解:由程序框图可得S =⎩⎪⎨⎪⎧2t 2+1-3,t ∈[-2,0),t -3,t ∈[0,2],其值域为[-3,6].故选D . 4.(2015·福建)阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )A .2B .1C .0D .-1解:执行程序,得S =0,i =2;S =-1,i =3;S =-1,i =4;S =0,i =5;S =0,i =6>5,跳出循环,输出S =0.故选C .5.(2014·重庆)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >45 解:当输出k 的值为6时,s =1×910×89×78=710,结合各选项知,C 符合要求.故选C . 6.(2015·全国课标Ⅰ)执行如图所示的程序框图,如果输入的t =0.01,则输出的n =( )A .5B .6C .7D .8解法一:执行程序,S =12,m =14,n =1;S =14,m =18,n =2;S =18,m =116,n =3;S =116,m =132,n =4;S =132,m =164,n =5;S =164,m =1128,n =6;S =1128<t =0.01,m =1256,n =7,循环结束,输出n =7.解法二:记第n 次循环后S 的值为a n ()n =0,1,2,…,其中a 0=1,则a n =a n -1-⎝ ⎛⎭⎪⎫12n ,递推可得a n =a 0-⎝ ⎛⎭⎪⎫12+122+…+12n =1-12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=12n ≤t =0.01. 显然n >6,故n =7.故选C .7.(2015·安徽)执行如图所示的程序框图(算法流程图),输出的n 为________.解:各次循环中变量当a =1.416·时,跳出循环,输出的n 为4.故填4.8.(2014·湖北)设a 是一个各位数字都不是0且没有重复数字的三位数.将组成a 的3个数字按从小到大排成的三位数记为I (a ),按从大到小排成的三位数记为D (a )(例如a =815,则I (a )=158,D (a )=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a ,输出的结果b =________.解法一:当a=123时,b=321-123=198≠123;当a=198时,b=981-189=792≠198;当a=792时,b=972-279=693≠792;当a=693时,b=963-369=594≠693;当a=594时,b=954-459=495≠594;当a=495时,b=954-459=495=a,终止循环,输出b=495.解法二:设I(a)=100x+10y+z,D(a)=100z+10y+x,x<y<z,x,y,z∈N*,则D(a)-I(a)=99(z-x),因此各位数字都不是0且没有重复数字,而且是99的倍数的三位数有:198,297,396,495,594,693,792,891,经检验知只有495满足题意.故填495.9.某人带着一只狼和一只羊及一捆青菜过河,只有一条船,船仅可载重此人和狼、羊及青菜三者之一,没有人在的时候,狼会吃羊,羊会吃青菜.请设计安全过河的算法.解:第一步,人带羊过河.第二步,人自己返回.第三步,人带青菜过河.第四步,人带羊返回.第五步,人带狼过河.第六步,人自己返回.第七步,人带羊过河.10.设计一个算法,找出区间[1,1000]内的能被7整除的整数,画出程序框图.解:第一步,取k=1.第二步,判断k≤1000是否成立,若不成立,则执行第五步.第三步,若k除以7的余数为0,则输出k.第四步,将k的值增加1,返回执行第二步.第五步,结束.程序框图如图.11.设计一个算法计算11×3+13×5+15×7+…+12013×2015的值,并画出程序框图. 解:算法步骤如下:第一步,令S =0,k =1.第二步,若k <2015成立,则执行第三步,否则输出S .第三步,计算S =S +1k (k +2),k =k +2,返回第二步. 程序框图如图所示:意大利数学家斐波那契,在1202年出版的《算盘全书》一书里提出了这样一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子?试画出解决此问题的程序框图.解:根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N 个月有F 对兔子,第N -1个月有S 对兔子,第N -2个月有Q 对兔子,则有F =S +Q ,一个月后,即第N +1个月时,式中变量S 的新值应变为第N 个月兔子的对数(F 的旧值),变量Q 的新值应变为第N -1个月兔子的对数(S 的旧值),这样,用S +Q 求出变量F 的新值就是N +1个月兔子的对数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第x (x ≥3)个月的i 从3逐次增加1,一直变化到12,再循环一次得到的F ”就是所求结果.流程图如图所示.。
核按钮(新课标)高考数学一轮复习 第十二章 算法初步、推理与证明 12.5 数学归纳法习题 理-人教

§12.5 数学归纳法1.数学归纳法的证题步骤一般地,证明一个与正整数n 有关的命题,可按下列步骤进行: (1)(归纳奠基)证明当n 取第一个值n 0(n 0∈N *)时命题成立;(2)(归纳递推)假设____________(k ≥n 0,k ∈N *)时命题成立,证明当____________时命题也成立. 只要完成这两个步骤,就可以断定命题对从n 0开始的所有__________都成立. 2.数学归纳法的适用范围数学归纳法主要用于解决与________有关的数学命题,证明时,它的两个步骤(归纳奠基与归纳递推)缺一不可.自查自纠1.(2)n =k n =k +1 正整数n 2.正整数用数学归纳法证明1+12+13+…+12n -1<n (n ∈N *,n >1)时,第一步应验证不等式( )A .1+12<2B .1+12+13<2C .1+12+13<3D .1+12+13+14<3解:∵n ∈N *,n >1,∴n 取的第一个数为2,左端分母最大的项为122-1=13,故选B .设f (n )=1n +1+1n +2+ (12)(n ∈N *),那么f (n +1)-f (n )等于( )A.12n +1B.12n +2C.12n +1+12n +2D.12n +1-12n +2解:f (n +1)-f (n )=[1(n +1)+1+1(n +1)+2+…+12n +12n +1+12(n +1)]-⎣⎢⎡⎦⎥⎤1n +1+1n +2+…+12n =12n +1+12(n +1)-1n +1=12n +1-12n +2.故选D . (2013·黑龙江模拟)设f (x )是定义在正整数集上的函数,且f (x )满足:“当f (k )≥k +1成立时,总可推出f (k +1)≥k +2成立”.那么,下列命题总成立的是( )A .若f (1)<2成立,则f (10)<11成立B .若f (3)≥4成立,则当k ≥1时,均有f (k )≥k +1C .若f (2)<3成立,则f (1)≥2成立D .若f (4)≥5成立,则当k ≥4时,均有f (k )≥k +1成立解:根据题意,若f (4)≥5成立,则f (n 0+1)≥n 0+2(n 0≥4),即f (k )≥k +1(k ≥5).综合f (4)≥5,可知当k ≥4时,均有f (k )≥k +1成立.故选D .已知数列11×2,12×3,13×4,…,1n (n +1),通过计算得S 1=12,S 2=23,S 3=34,由此可猜测S n =____________.解法一:通过变化规律猜测S n =nn +1.解法二:S n =11×2+12×3+13×4+…+1n (n +1)=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+⎝ ⎛⎭⎪⎫13-14+…+⎝ ⎛⎭⎪⎫1n -1n +1= 1-1n +1=n n +1.故填n n +1. 用数学归纳法证明“(n +1)(n +2)·…·(n +n )=2n ·1·3·…·(2n -1)(n ∈N *)”时,从n =k 到n =k +1,等式的左边需要增乘的代数式是____________.解:当n =k 时,等式左边=(k +1)(k +2)·…·(k +k ),当n =k +1时, 等式左边=(k +2)(k +3)·…·(k +1+k +1)=(k +1)(k +2)(k +3)·…·(k +k )(k +k +1)(k +k +2)k +1=2(2k +1)(k +1)(k +2)(k +3)·…·(k +k ).观察、比较可知,从n =k 到n =k +1,等式的左边需要增乘的代数式是2(2k +1).故填2(2k +1).类型一 证明等式证明:1-12+13-14+...+12n -1-12n =1n +1+1n +2+ (12)(n ∈N *).证明:(1)当n =1时,左边=1-12=12,右边=12,等式成立.(2)假设n =k (k ∈N *)时等式成立,即1-12+13-14+…+12k -1-12k =1k +1+1k +2+…+12k , 那么,当n =k +1时, 1-12+13-14+…+12k -1-12k +12k +1-12k +2 =1k +1+1k +2+…+12k +12k +1-12k +2 =1k +2+1k +3+…+12k +12k +1+12k +2. 根据(1)和(2),可知等式对任何n ∈N *都成立.【点拨】用数学归纳法证明与正整数n 有关的一些等式时,关键在于“先看项”,弄清从n =k 到n =k +1时等式两边的构成规律,然后正确写出归纳证明的步骤,即可证明待证等式.求证:12-22+32-42+…+(2n -1)2-(2n )2=-n (2n +1)(n ∈N *).证明:①n =1时,左边=12-22=-3,右边=-3,等式成立. ②假设n =k 时,等式成立,即12-22+32-42+…+(2k -1)2-(2k )2=-k (2k +1).当n =k +1时,12-22+32-42+…+(2k -1)2-(2k )2+(2k +1)2-(2k +2)2=-k (2k +1)+(2k +1)2-(2k +2)2=-k (2k +1)-(4k +3)=-(2k 2+5k +3)=-(k +1)[2(k +1)+1],所以n =k +1时,等式也成立.由①②得,等式对任何n ∈N *都成立.类型二 证明不等式已知f (n )=1+123+133+143+…+1n 3,g (n )=32-12n 2,n ∈N *.(1)当n =1,2,3时,试比较f (n )与g (n )的大小关系; (2)猜想f (n )与g (n )的大小关系,并给出证明.解:(1)当n =1时,f (1)=1,g (1)=1,所以f (1)=g (1); 当n =2时,f (2)=98,g (2)=118,所以f (2)<g (2);当n =3时,f (3)=251216,g (3)=312216,所以f (3)<g (3).(2)由(1),猜想f (n )≤g (n ),下面用数学归纳法证明: ①当n =1,2,3时,不等式显然成立.②假设当n =k (k ≥3,k ∈N *)时不等式成立,即1+123+133+143+…+1k 3<32-12k2,那么,当n =k +1时, f (k+1)=f (k )+1(k +1)3<32-12k 2+1(k +1)3,因为12(k +1)2-⎣⎢⎡⎦⎥⎤12k 2-1(k +1)3=k +32(k +1)3-12k 2=-3k -12(k +1)3k 2<0,所以f (k +1)<32-12(k +1)2=g (k +1).由①、②可知,对一切n ∈N *,都有f (n )≤g (n )成立.【点拨】用数学归纳法证明不等式,同样要弄清增加的项,很多情况下,还要利用放缩法进行证明.已知函数f (x )=13x 3-x ,数列{a n }满足条件:a 1≥1,a n +1≥f ′(a n +1).试比较11+a 1+11+a 2+11+a 3+…+11+a n与1的大小,并说明理由. 解:∵f ′(x )=x 2-1,a n +1≥f ′(a n +1), ∴a n +1≥(a n +1)2-1.∵函数g (x )=(x +1)2-1=x 2+2x 在区间[-1,+∞)上单调递增,于是由a 1≥1,及a 2≥(a 1+1)2-1得,a 2≥22-1,进而得a 3≥(a 2+1)2-1≥24-1>23-1,由此猜想:a n ≥2n-1.下面用数学归纳法证明这个猜想:①当n =1时,a 1≥21-1=1,结论成立;②假设当n =k (k ≥1且k ∈N *)时结论成立,即a k ≥2k -1,则当n =k +1时,由g (x )=(x +1)2-1在区间[-1,+∞)上单调递增知,a k +1≥(a k +1)2-1≥22k-1≥2k +1-1,即n =k +1时,结论也成立.由①②知,对任意n ∈N *,都有a n ≥2n-1.∴11+a 1+11+a 2+…+11+a n <12+122+…+12n =1-12n <1.1.用数学归纳法进行证明时,“归纳奠基”和“归纳递推”两个步骤缺一不可.2.证第二步的关键是合理运用归纳假设,以“n =k 时命题成立”为条件,证明“当n =k +1时命题成立”.这里,易出现的错误是:不使用“n =k 时命题成立”这一条件,而直接将n =k +1代入命题,便断言此时命题成立.注意:没有运用归纳假设的证明不是数学归纳法.3.在n =k 到n =k +1的证明过程中寻找由n =k 到n =k +1的变化规律是难点,突破的关键是分析清楚p (k )与p (k +1)的差异与联系,利用拆、添、并、放、缩等手段,从p (k +1)中分离出p (k ).4.证明不等式的方法多种多样,故在用数学归纳法证明不等式的过程中,比较法、放缩法、分析法等要灵活运用.1.用数学归纳法证明“1+a +a 2+…+a n +1=1-a n +21-a (a ≠1,n ∈N *)”,在验证n =1时,左端计算所得的结果是( )A .1B .1+aC .1+a +a 2D .1+a +a 2+a 3解:当n =1时,左边=1+a +a 2.故选C .2.设凸k 边形的内角和为f (k ),则f (k +1)-f (k )=( )A .2πB .π C.π2 D.π3解:将k +1边形A 1A 2…A k A k +1的顶点A 1与A k 相连,则原多边形被分割为k 边形A 1A 2…A k 与三角形A 1A k A k +1,其内角和f (k +1)是k 边形的内角和f (k )与△A 1A k A k +1的内角和π的和,故选B .3.用数学归纳法证明:12+22+…+n 2+…+22+12=n (2n 2+1)3,第二步证明由“k 到k +1”时,左边应加( )A .k 2B .(k +1)2C .k 2+(k +1)2+k 2D .(k +1)2+k 2解:当n =k 时,左边=12+22+…+k 2+…+22+12,当n =k +1时,左边=12+22+…+k 2+(k +1)2+k 2+…+22+12,故选D .4.用数学归纳法证明命题“当n 为正奇数时,x n +y n能被x +y 整除”中,第二步归纳假设应写成( ) A .假设n =2k +1(k ∈N *)成立,再推出n =2k +3成立 B .假设n =2k -1(k ∈N *)成立,再推出n =2k +1成立 C .假设n =k (k ∈N *)成立,再推出n =k +1成立 D .假设n =k (k ≥1)成立,再推出n =k +2成立解:第二步归纳假设n =2k -1(k ∈N *)成立,再推出n =2k -1+2=2k +1成立.故选B . 5.对于不等式n 2+n <n +1(n ∈N *),某同学的证明过程如下: (1)当n =1时,12+1<1+1,不等式成立;(2)假设当n =k (k ∈N *)时,不等式成立,即k 2+k <k +1,则n =k +1时,(k +1)2+(k +1)=k 2+3k +2<k 2+3k +2+k +2=(k +2)2=(k +1)+1,故当n =k +1时,不等式成立.根据(1)和(2),可知不等式n 2+n <n +1(n ∈N *)成立.上述证法中( ) A .过程全部正确 B .n =1验证不正确 C .归纳假设不正确D .从n =k (k ∈N *)到n =k +1的推理不正确解:证明过程没有用到归纳假设的结论,所以证明方法不正确.故选D .6.已知f (n )=(2n +7)·3n+9,存在自然数m ,使得对任意n ∈N *,都能使m 整除f (n ),则m 的最大值为( ) A .30B .26C .36D .6解:∵f (1)=36,f (2)=108=3×36,f (3)=360=10×36,所以f (1),f (2),f (3)能被36整除,推测m 的最大值为36.可以利用数学归纳法作如下简要证明:f (n +1)=[2(n +1)+7]·3n +1+9,∴f (n +1)-f (n )=2·3n +1+2·(2n +7)·3n=(4n +20)·3n,当n =1时,该式的值为72可被36整除,当n ≥2时,4n +20可被4整除,3n可被9整除,则(4n +20)·3n可被36整除,即证.故选C .7.在应用数学归纳法证明凸n 边形的对角线为12n (n -3)条时,第一步检验n =________时命题成立.解:凸多边形至少有3条边.故填3.8.(2014·广东东莞模拟)观察下列不等式: ①12<1;②12+16<2;③12+16+112<3;…,则第5个不等式为____________.解:∵2=1×2,6=2×3,12=3×4,∴第n 个不等式的左边有n 项,分子都是1,分母依次为1×2,2×3,…,n (n +1),右边为n ,即12+16+…+1n (n +1)<n . ∴第5个不等式为12+16+112+120+130< 5.故填12+16+112+120+130<5.9.试证:n 为正整数时, f (n )=32n +2-8n -9能被64整除.证明:(1)当n =1时, f (1)=34-8-9=64能被64整除. (2)假设当n =k (k ∈N *)时, f (k )=32k +2-8k -9能被64整除,则当n =k +1时, f (k +1)=32(k +1)+2-8(k+1)-9=9·32k +2-8k -17=9(32k +2-8k -9)+64k +64.由归纳假设知f (k +1)也能被64整除. 综合(1)(2)知,当n 为正整数时, f (n )=32n +2-8n -9能被64整除.10.(2015·大庆模拟)数列{a n }满足S n =2n -a n (n ∈N *). (1)计算a 1,a 2,a 3,并猜想a n 的通项公式; (2)用数学归纳法证明(1)中的猜想.解:(1)当n =1时,a 1=S 1=2-a 1,∴a 1=1;当n =2时,a 1+a 2=S 2=2×2-a 2,∴a 2=32;当n =3时,a 1+a 2+a 3=S 3=2×3-a 3,∴a 3=74.由此猜想a n =2n-12n -1(n ∈N *).(2)证明:①当n =1时,a 1=1结论成立,②假设n =k (k ≥1,且k ∈N *)时结论成立,即a k =2k-12k -1,当n =k +1时,a k +1=S k +1-S k =2(k +1)-a k +1-2k +a k =2+a k -a k +1,∴2a k +1=2+a k ,∴a k +1=2+a k 2=2k +1-12k, ∴当n =k +1时结论成立,于是对于一切的自然数n ∈N *,a n =2n-12n -1成立.11.(2015·湖北八市三月联考)已知数列{x n }满足x 1=12,且x n +1=x n 2-x n (n ∈N *).(1)用数学归纳法证明:0<x n <1;(2)设a n =1x n,求数列{a n }的通项公式.解:(1)证明:①当n =1时,x 1=12∈(0,1),②假设当n =k 时,结论成立,即x k ∈(0,1), 则当n =k +1时,x k +1=x k2-x k,∵x k ∈(0,1),∴2-x k >0,即x k +1>0.又∵x k +1-1=2(x k -1)2-x k <0,∴0<x k +1<1.综合①②可知0<x n <1. (2)由x n +1=x n2-x n可得1x n +1=2-x n x n =2x n-1,即a n +1=2a n -1,∴a n +1-1=2(a n -1).令b n =a n -1,则b n +1=2b n ,又b 1=a 1-1=1x 1-1=1,∴{b n }是以1为首项,以2为公比的等比数列,即b n =2n -1.∴a n =2n -1+1.设数列a 1,a 2,…,a n ,…中的每一项都不为0. 求证:若1a 1a 2+1a 2a 3+…+1a n a n +1=na 1a n +1,n ∈N +,则{a n }为等差数列.证明:当n =2时,已知1a 1a 2+1a 2a 3=2a 1a 3,两端同乘a 1a 2a 3,得a 1+a 3=2a 2,所以a 1,a 2,a 3成等差数列.假设当n =k 时,a 1,a 2,…,a k +1成等差数列,记公差为d . 那么当n =k +1时,因为 1a 1a 2+1a 2a 3+…+1a k a k +1+1a k +1a k +2=k a 1a k +1+1a k +1a k +2=k +1a 1a k +2,分子同乘a 1a k +1a k +2,得ka k +2+a 1=(k +1)a k +1,又a k +1=a 1+kd ,代入可得ka k +2+a 1=(k +1)(a 1+kd ),即a k +2=a 1+(k +1)d .所以{a n }是公差为d 的等差数列.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2015·开封市月考)算法有三种基本逻辑结构:顺序结构、条件结构、循环结构,在下列说法中正确的是( )A.一个算法中只能含有一种逻辑结构B.一个算法中可以含有以上三种逻辑结构C.一个算法中必须含有以上三种逻辑结构D.一个算法中最多可以含有以上两种逻辑结构解:算法中的逻辑结构可以是一种或多种,故选B.2.计算机执行下面的程序段后,输出的结果是( )a=1b=3a=a+bb=a-bPRINT a,bA.1,3 B.4,1C.0,0 D.6,0解:把1赋给变量a,把3赋给变量b,由语句“a=a+b”得a=4,即把4赋给变量a,由语句“b=a-b”得b=1,即把1赋给变量b,输出a,b,即输出4,1.故选B.3.(2015·武汉华师一附中期中考试)用反证法证明命题“若sinθ1-cos2θ+cosθ1-sin2θ=1,则sinθ≥0且cosθ≥0”时,下列假设的结论正确的是( )A.sinθ≥0或cosθ≥0 B.sinθ<0且cosθ<0C.sinθ<0或cosθ<0 D.sinθ>0且cosθ>0解:用反证法证明,只需要否定命题的结论,即sinθ<0或cosθ<0.故选C.4.(2015·广东清远一中期中)观察按下列顺序排列的等式:9×0+1=1,9×1+2=11,9×2+3=21,9×3+4=31,…,猜想第n(n∈N+)个等式应为( )A.9(n+1)+n=10n+9B.9(n-1)+n=10n-9C.9n+(n-1)=10n-1D.9(n-1)+(n-1)=10n-10解:结合前4个式子的共同特点可知第n个式子为9(n-1)+n=10n-9,故选B.5.(2015·云南玉溪高三统考)执行如图所示的程序框图,会输出一列数,则这个数列的第3项是( )A .870B .30C .6D .3解:A =3,N =1,输出3,N =2,N ≤4成立;A =6,输出6,N =3,N ≤4成立;A =30,输出30,N =4,N ≤4成立;A =870,输出870,N =5,N ≤4不成立,终止循环.所以这个数列的第3项是30,故选B .6.(2014·陕西五校联考)设△ABC 的三边长分别为a ,b ,c ,△ABC 的面积为S ,内切圆半径为r ,则r =2Sa +b +c;类比这个结论可知:若四面体P ABC 的四个面的面积分别为S 1,S 2,S 3,S 4,四面体P ABC 的体积为V ,内切球的半径为R ,则R =( )A.VS 1+S 2+S 3+S 4B.2VS 1+S 2+S 3+S 4C.3VS 1+S 2+S 3+S 4D.4VS 1+S 2+S 3+S 4 解:设四面体P ABC 的内切球球心为O ,那么V =V O ABC +V O PAB +V O PAC +V O PBC ,即V =13S 1R +13S 2R +13S 3R +13S 4R ,可得R =3VS 1+S 2+S 3+S 4,故选C .7.阅读下列程序,输出结果为2的是( )n =0 DO n =n +1 LOOP UNTIL n>=2 PRINT n END n =0 DO n =n +1 LOOP UNTIL n<=2 PRINT n END A . B. n =0WHILE n<=2 n =n +1 WEND PRINT n END n =0WHILE n>=2 n =n +1 WEND PRINT n END C .D.解:运行各选项程序,易知A 选项的输出结果为2.故选A .8.设f (x )是定义在正整数集上的函数,且f (x )满足:“当f (k )≥k 2成立时,总可推出f (k +1)≥(k +1)2成立”.那么,下列命题总成立的是( )A .若f (3)≥9成立,则当k ≥1时,均有f (k )≥k 2成立 B .若f (5)≥25成立,则当k ≤5时,均有f (k )≥k 2成立 C .若f (7)<49成立,则当k ≥8时,均有f (k )>k 2成立 D .若f (4)=25成立,则当k ≥4时,均有f (k )≥k 2成立解:易判断A ,B ,C 均不正确.对于D ,f (4)=25≥42,由题设的递推关系,可知结论成立,故选D . 9.观察下列各式:72=49,73=343,74=2401,…,则72016的末两位数字为( )A .01B .43C .07D .49解:75=16807,76=117649,又71=07,观察可见7n(n ∈N *)的末两位数字呈周期出现,且周期为4,∵2016=504×4,∴72016与74末两位数字相同,故选A .10.(2015·深圳五校联考)执行如图所示的程序框图,则输出的y =( )A.12B .1C .-1D .2解:由初始条件y =2,i =1得:运行第1次:y =1-12=12,i =2;运行第2次:y =1-112=-1,i =3;运行第3次:y =1-1-1=2,i =4;运行第4次:y =1-12=12,i =5.其结果呈周期性的出现,且周期是3,由于2016÷3=672,故运行第2016次:y =2,i =2016+1=2017≥2017, 所以输出的结果是2,故选D .11.(2014·江西赣州四所重点中学联考)已知函数f (x )=ax 3+12x 2在x =-1处取得极大值,记g (x )=1f ′(x ).程序框图如图所示,若输出的结果S =20162017,则判断框中可以填入的关于n 的判断条件是( )A .n ≤2016B .n ≤2017C .n >2016D .n >2017解:f ′(x )=3ax 2+x ,因为f (x )在x =-1处取得极大值,所以f ′(-1)=0,即3a -1=0,解得a =13,检验知合要求,故f ′(x )=x 2+x .则g (x )=1f ′(x )=1x 2+x ,g (n )=1n 2+n =1 n -1n +1,输出的结果为S =g (1)+g (2)+g (3)+…+g (n )=1-1n +1=n n +1,由S =20162017,得n =2016,故判断框内可以填入的条件是n ≤2016.故选A .12.(2015·吉林市期中考试)如图,第n 个图形由正n +2边形“扩展”而来(n =1,2,3,…),则在第n 个图形中顶点的个数为( )A .(n +1)(n +2)B .(n +2)(n +3)C .n 2D .n解:第1个图形由三角形“扩展”而来,共3×4=12个顶点;第2个图形由正方形“扩展”而来,共4×5=20个顶点;第3个图形由正五边形“扩展”而来,共5×6=30个顶点;第4个图形由正六边形“扩展”而来,共6×7=42个顶点;…;第n 个图形由正n +2边形“扩展”而来,共(n +2)(n +3)个顶点.故选B .二、填空题:本大题共4小题,每小题5分,共20分.13.(2015·山东)执行下边的程序框图,输出的T 的值为____________.解:初始条件n =1,T =1,运行第一次:T =1+⎠⎛01x d x =1+12=32,n =2;运行第二次:T =32+⎠⎛01x 2d x =32+13=116,n =3,n <3不成立,输出T 的值为116.故填116.14.(2015·哈尔滨市高三模拟)我们把平面内与直线垂直的非零向量称为直线的法向量.在平面直角坐标系中,利用求动点轨迹方程的方法,可以求出过点A (-3,4),且法向量为n =(1,-2)的直线(点法式)方程为1×(x +3)+(-2)×(y -4)=0,化简得x -2y +11=0.类比以上方法,在空间直角坐标系中,经过点A (1,2,3),且法向量为n =(-1,-2,1)的平面方程为____________.解:类比可得:-1×(x -1)+(-2)×(y -2)+1×(z -3)=0,即x +2y -z -2=0.故填x +2y -z -2=0. 15.有以下程序:INPUT xIF x<=-1 THEN f(x)=x +2 ELSEIF x>-1 AND x<=1 THENf(x)=x*x ELSE f(x)=-x +2 END IF END IF PRINT f(x) END根据如上程序,若函数g (x )=f (x )-m 在R 上有且只有两个零点,则实数m 的取值范围是__________. 解:由题意知,f (x )=⎩⎪⎨⎪⎧x +2,x ≤-1,x 2,-1<x ≤1,-x +2,x >1,画出f (x )的图象如图所示.∵函数g (x )=f (x )-m 有两个零点,即直线y =m 与函数y =f (x )有两个交点,∴m <0或m =1. 故填(-∞,0)∪{1}.16.(2014·福建)已知集合{a ,b ,c }={0,1,2},且下列三个关系:①a ≠2;②b =2;③c ≠0有且只有1个正确,则100a +10b +c =________.解:若①a ≠2正确,②③错误,则b ≠2,c =0,此时a =b =1,与集合的互异性矛盾;若②b =2正确,①③错误,则a =2,c =0,与集合的互异性矛盾;若③c ≠0正确,①②错误,则a =2,b ≠2,此时c =1,b =0,符合题意.综上知,a =2,b =0,c =1,100a +10b +c =201.故填201.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.(10分)观察:①sin 26°+cos 236°+sin6°cos36°=34;②sin 210°+cos 240°+sin10°cos40°=34.由上面两个式子的结构规律,请提出一个一般性的猜想,并证明你的猜想.解:猜想:sin 2α+cos 2(30°+α)+sin αcos(30°+α)=34.证明:左边=1-cos2α2+1+cos (60°+2α)2+sin α(32cos α-12sin α)=1-14cos2α-34sin2α+34sin2α-14+14cos2α=1-14=34=右边,得证.18.(12分)某函数f (x )给出x 的值时,求相应函数值y 的程序框图如图所示.(1)写出函数f (x )的解析式;(2)若输入的x 取x 1和x 2(|x 1|<|x 2|)时,输出的y 值相同,试简要分析x 1与x 2的取值范围.解:(1)由程序框图知,该程序框图执行的功能是求函数f (x )=|x 2-1|的值,故f (x )的解析式为f (x )=|x 2-1|.(2)画出f (x )=|x 2-1|的草图如图.由图象的对称性知:要使f (x 1)=f (x 2)且|x 1|<|x 2|, 需-1<x 1<1,同时2≥x 2>1或-2≤x 2<-1, ∴x 1的取值范围是{x |-1<x <1},x 2的取值范围是{x |1<x ≤2或-2≤x <-1}.19.(12分)△ABC 的三个内角A ,B ,C 成等差数列,A ,B ,C 的对边分别为a ,b ,c .求证:1a +b +1b +c =3a +b +c. 证法一:采用分析法.要证1a +b +1b +c =3a +b +c ,即证a +b +c a +b +a +b +c b +c=3,也就是ca +b +ab +c=1,只需证c (b +c )+a (a +b )=(a +b )(b +c ), 需证c 2+a 2=ac +b 2,又△ABC 三内角A ,B ,C 成等差数列,故B =60°, 由余弦定理,有b 2=c 2+a 2-2ac cos60°,即b 2=c 2+a 2-ac ,故c 2+a 2=ac +b 2,得证. 证法二:采用综合法.∵△ABC 三内角A ,B ,C 成等差数列, ∴B =60°.由余弦定理,有b 2=c 2+a 2-2ca cos60°, 得c 2+a 2=ac +b 2, 等式两边同时加上ab +bc 得c (b +c )+a (a +b )=(a +b )(b +c ),等式两边同除以(a +b )(b +c )得,c a +b +ab +c=1,∴⎝ ⎛⎭⎪⎫c a +b +1+⎝ ⎛⎭⎪⎫a b +c +1=3=a +b +c a +b +a +b +c b +c , 即1a +b +1b +c =3a +b +c. 20.(12分)是否存在常数a ,b ,c 使等式1·(n 2-12)+2(n 2-22)+…+n (n 2-n 2)=an 4+bn 2+c 对一切正整数n 成立?证明你的结论.解:分别将n =1,2,3代入得方程组:⎩⎪⎨⎪⎧a +b +c =0,16a +4b +c =3,81a +9b +c =18,⇒⎩⎪⎨⎪⎧a =14,b =-14,c =0.下面用数学归纳法证明:①当n =1时,由上可知等式成立;②假设当n =k (k ≥1,k ∈N *)时,等式成立,即1·(k 2-12)+2(k 2-22)+…+k (k 2-k 2)=14k 4-14k 2,则当n =k +1时,左边=1·[(k +1)2-12]+2[(k +1)2-22]+…+k [(k +1)2-k 2]+(k +1)[(k +1)2-(k +1)2]=1·(k 2-12)+2(k 2-22)+…+k (k 2-k 2)+1·(2k +1)+2(2k +1)+…+k (2k +1)=14k 4-14k 2+k (k +1)2·(2k +1)=14(k +1)4-14(k +1)2. ∴当n =k +1时,等式也成立. 由①②得等式对一切n ∈N *均成立.21.(12分)(2013·四川)某算法的程序框图如图所示,其中输入的变量x 在1,2,3,…,24这24个整数中等可能随机产生.(1)分别求出按程序框图正确编程运行时输出y 的值为i 的概率P i (i =1,2,3);(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n 次后,统计记录了输出y 的值为i (i =1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.运行 次数n 输出y 的值 为1的频数输出y 的值 为2的频数输出y 的值 为3的频数30 14 6 10 … … … … 2 1001 027376697运行 次数n 输出y 的值 为1的频数输出y 的值 为2的频数输出y 的值 为3的频数30 12 11 7 … … … … 2 1001 051696353 当n =2 100时,根据表中的数据,分别写出甲、乙所编程序各自输出y 的值为i (i =1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合算法要求的可能性较大;(3)将按程序框图正确编写的程序运行3次,求输出y 的值为2的次数ξ的分布列及数学期望.解:(1)变量x 是在1,2,3,…,24这24个整数中随机产生的一个数,共有24种可能.当x 从1,3,5,7,9,11,13,15,17,19,21,23这12个数中产生时,输出y 的值为1,故P 1=12;当x 从2,4,8,10,14,16,20,22这8个数中产生时,输出y 的值为2,故P 2=13;当x 从6,12,18,24这4个数中产生时,输出y的值为3,故P 3=16.所以,输出y 的值为1的概率为12,输出y 的值为2的概率为13,输出y 的值为3的概率为16.比较频率趋势与概率,可得乙同学所编程序符合算法要求的可能性较大. (3)随机变量ξ可能的取值为0,1,2,3.P (ξ=0)=C 03×⎝ ⎛⎭⎪⎫130×⎝ ⎛⎭⎪⎫233=827,P (ξ=1)=C 13×⎝ ⎛⎭⎪⎫131×⎝ ⎛⎭⎪⎫232=49,P (ξ=2)=C 23×⎝ ⎛⎭⎪⎫132×⎝ ⎛⎭⎪⎫231=29,P (ξ=3)=C 33×⎝ ⎛⎭⎪⎫133×⎝ ⎛⎭⎪⎫230=127.故ξ的分布列为所以,E ξ=0×827+1×49+2×9+3×27=1,即ξ的数学期望为1.22.(12分)把正整数按从小到大、左小右大的原则依次排成如图所示的数表: 1 2 3 4 5 6 78 9 10 11 12 13 14 15 ……设a ij (i ,j ∈N *)是数表中从上往下数第i 行,从左往右数第j 个数,数表中第i 行共有2i -1个正整数,(1)若a ij =2013,求i ,j 的值;(2)设A n =a 11+a 22+a 33+…+a nn (n ∈N *),试比较A n 与n 2+n 的大小,并说明理由.解:(1)由于前10行共有1+21+22+…+29=210-1=1023个数,而2013-1023=990,所以i =11,j =990. (2)∵a 11=20,a 22=21+1,a 33=22+2,a 44=23+3,…,a nn =2n -1+(n -1),∴A n =20+(21+1)+(22+2)+(23+3)+…+[2n -1+(n -1)]=(20+21+22+23+…+2n -1)+[1+2+3+…+(n -1)]=2n +1+n 2-n -22.∴A n -(n 2+n )=2n +1-(n 2+3n +2)2.验证知,当n =1,2,3时,A n <n 2+n ;当n ≥4时,可猜测A n >n 2+n . 以下用数学归纳法证明:当n ≥4时,2n +1>n 2+3n +2.①当n =4时,25=32>42+3×4+2=30,不等式成立; ②假设n =k 时,2k +1>k 2+3k +2成立,则当n =k +1时,2k +2=2·2k +1>2(k 2+3k +2)=k 2+2k +1+3k +3+k 2+k >(k +1)2+3(k +1)+2.即n =k +1时,不等式也成立. 综上①②知,当n ≥4时,2n +1>n 2+3n +2.亦即当n ≥4时,A n >n 2+n .第十三章选考内容1.几何证明选讲(1)理解相似三角形的定义与性质,了解平行截割定理.(2)会证明和应用以下定理:①直角三角形射影定理;②圆周角定理;③圆的切线判定定理与性质定理;④相交弦定理;⑤圆内接四边形的性质定理与判定定理;⑥切割线定理.2.坐标系与参数方程(1)了解坐标系的作用,了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.(2)了解极坐标的基本概念,会在极坐标系中用极坐标刻画点的位置,能进行极坐标和直角坐标的互化.(3)能在极坐标系中给出简单图形表示的极坐标方程.(4)了解参数方程,了解参数的意义.(5)能选择适当的参数写出直线、圆和椭圆的参数方程.3.不等式选讲(1)理解绝对值的几何意义,并了解下列不等式成立的几何意义及取等号的条件:①|a+b|≤|a|+|b|(a,b∈R);②|a-b|≤|a-c|+|c-b|(a,b∈R).(2)会利用绝对值的几何意义求解以下类型的不等式:|ax+b|≤c;|ax+b|≥c;|x-c|+|x-b|≥a.(3)通过一些简单问题了解证明不等式的基本方法:比较法、综合法、分析法.。
核按钮(新课标)高考数学一轮复习 第十二章 算法初步与

第十二章算法初步与框图、推理与证明考纲链接1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想.(2)理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.2.基本算法语句了解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.3.框图(1)通过具体实例进一步认识程序框图.(2)通过实例了解工序的流程图.(3)能绘制简单实际问题的流程图,体会流程图在解决实际问题中的作用.(4)通过实例了解结构图.(5)会运用结构图梳理已学过的知识结构、整理收集到的信息资料.4.了解合情推理的含义,能进行简单的归纳推理和类比推理,体会合情推理在数学发现中的作用.5.了解演绎推理的含义,了解合情推理和演绎推理的联系和差异;掌握演绎推理的“三段论”,能运用“三段论”进行一些简单的演绎推理.6.了解直接证明的两种基本方法:综合法和分析法;了解综合法和分析法的思考过程和特点.7.了解反证法的思考过程和特点.§12.1算法、程序框图、结构图1.算法的概念及特点(1)算法的概念在数学中,算法通常是指按照一定______解决某一类问题的________和________的步骤.(2)算法的特点之一是具有______性,即算法中的每一步都应该是确定的,并能有效地执行,且得到确定的结果,而不应是模棱两可的;其二是具有______性,即算法步骤明确,前一步是后一步的前提,只有执行完前一步才能进行后一步,并且每一步都准确无误才能解决问题;其三是具有______性,即一个算法应该在有限步操作后停止,而不能是无限的;另外,算法还具有不唯一性和普遍性,即对某一个问题的解决不一定是唯一的,可以有不同的解法,一个好的算法应解决的是一类问题而不是一两个问题.2.程序框图(1)程序框图的概念程序框图又称流程图,是一种用________、________及________来表示算法的图形.结构图一般由构成系统的若干要素和表达各要素之间关系的连线(或方向箭头)构成.4.算法的基本逻辑结构(1)顺序结构顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按__________的顺序进行的.它是由若干个__________的步骤组成的,它是任何一个算法都离不开的基本结构.顺序结构可用程序框图表示为如图所示的形式.(2)条件结构在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.常见的条件结构可以用程序框图表示为如图所示的两种形式.(3)循环结构在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是________.反复执行的步骤称为________.循环结构有如下两种形式:①如图1,这个循环结构有如下特征:在执行了一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.因此,这种循环结构称为____________.②如图2表示的也是常见的循环结构,它有如下特征:在每次执行循环体前,对条件进行判断,当条件满足时,执行循环体,否则终止循环.因此,这种循环结构称为____________.自查自纠:1.(1)规则明确有限(2)确定有序有穷2.(1)程序框流程线文字说明(2)①终端框(起止框) ②输入、输出框③处理框(执行框) ④判断框⑤流程线⑥连接点4.(1)从上到下依次执行(3)循环结构循环体①直到型循环结构②当型循环结构下列各式中的S 值不可以用算法求解的是( )A .S =1+2+3+4B .S =12+22+32+…+1002C .S =1+12+13+…+110000D .S =1+2+3+4+…解:由算法的有限性知,D 不正确,而A ,B ,C 都可以通过有限步骤操作,输出确定结果,故选D.给出下列算法:第一步,输入正整数n (n >1).第二步,判断n 是否等于2,若n =2,则输出n ;若n >2,则执行第三步.第三步,依次从2到n -1检验能不能整除n ,若不能整除n ,则执行第四步;若能整除n ,则执行第一步.第四步,输出n .则输出的n 的值是( )A .奇数B .偶数C .质数D .合数解:根据算法可知n =2时,输出n 的值为2;若n =3,输出n 的值为3;若n =4,2能整除4,则重新输入n 的值,…,故输出的n 的值为质数.故选C.(2014·北京)执行如图所示的程序框图,输出的S 值为( )A .1B .3C .7D .15解:由程序框图知:S =1+21+22=7.故选C.(2014·辽宁)执行下面的程序框图,若输入x =9,则输出y =____________.解:输入x =9,则y =5,|y -x |=4>1,不满足条件;x =5,y =113,|y -x |=43>1,不满足条件;x =113,y =299,|y -x |=49<1,满足条件,输出y =299.故填299. 如图所示,程序框图(算法流程图)的输出结果是__________.解:初始值s =0,n =2.第一次循环得s =12,n=4;第二次循环得s =12+14,n =6;第三次循环得s =12+14+16=1112,n =8,此时退出循环,输出的s=1112.故填1112.类型一算法的概念下列语句是算法的个数为( )①从济南到巴黎:先从济南坐火车到北京,再坐飞机到巴黎;②统筹法中“烧水泡茶”的故事;③测量某棵树的高度,判断其是否为大树;④已知三角形的两边及夹角,利用三角形的面积公式求出该三角形的面积.A.1 B.2 C.3 D.4 解:①中勾画了从济南到巴黎的行程安排,完成了任务;②中节约时间,烧水泡茶完成了任务;③中对“树的大小”没有明确的标准,无法完成任务,不是有效的算法构造;④是纯数学问题,利用三角形的面积公式求出三角形的面积.故选C.点拨:算法过程要做到一步一步地执行,每一步执行的操作必须确切,不能含糊不清,且在有限步后必须得到问题的结果.下列叙述能称为算法的个数为( )①植树需要运苗、挖坑、栽苗、浇水这些步骤;②顺序进行下列运算:1+1=2,2+1=3,3+1=4,…,99+1=100;③从宜昌乘火车到武汉,从武汉乘飞机到北京;④3x>x+1;⑤求所有能被3整除的正数,即3,6,9,12,….A.2 B.3 C.4 D.5解:①②③可称为算法,④⑤不是,故选B.类型二经典算法“韩信点兵”问题.韩信是汉高祖刘邦手下的大将,为了保守军事机密,他在点兵时采用下述方法:先令士兵从1~3报数,结果最后一个士兵报2;再令士兵从1~5报数,结果最后一个士兵报3;又令士兵从1~7报数,结果最后一个士兵报4.这样,韩信很快就知道了自己部队士兵的总人数.请设计一个算法,求出士兵至少有多少人.解:在本题中,士兵从1~3报数,最后一个士兵报2,说明士兵的总人数是除以3余2,其他两种情况依此类推.(算法一)步骤如下:第一步:先确定最小的满足除以7余4的数是4;第二步:依次加7就得到所有满足除以7余4的数:4,11,18,25,32,39,46,53,60,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:18;第四步:依次加上35,得18,53,88,…;第五步:在第四步得到的一列数中,找到最小的满足除以3余2的正整数:53,这就是我们要求的数.(算法二)步骤如下:第一步:先确定最小的满足除以3余2的数是2;第二步:依次加3就得到所有满足除以3余2的数:2,5,8,11,14,17,20,23,26,29,32,35,38,41,44,47,50,53,56,…;第三步:在第二步所得的一列数中确定最小的满足除以5余3的正整数:8;第四步:然后依次加15就得8,23,38,53,…,不难看出,这些数既满足除以3余2,又满足除以5余3;第五步:在第四步所得的一列数中找到满足除以7余4的最小数是53,这就是我们要求的数.点拨:给出一个问题,设计算法时要注意:(1)认真分析问题,研究解决此问题的一般方法;(2)将解决问题的过程分解成若干步骤;(3)用简练的语言将各步骤表示出来;(4)把解题过程条理清楚地表达出来,就得到一个明确的算法.对于同一问题,可以设计不同的算法,其最终的结果是一样的,但解决问题的繁简程度不同,我们要寻找最优算法.一位商人有9枚银元,其中有一枚略轻的是假银元.请设计一种算法,用天平(不用砝码)将假银元找出来.解:算法如下:第一步:把银元分成3组,每组3枚;第二步:先将两组分别放在天平的两边,如果天平不平衡,那么假银元就在轻的那一组;如果天平左右平衡,则假银元就在未称的第3组内;第三步:取出含假银元的那一组,从中任取两枚银元放在天平的两边.如果左右不平衡,则轻的那一边就是假银元;如果天平两边平衡,则未称的那一枚就是假银元.类型三顺序结构已知点P(x0,y0)和直线l:Ax+By+C=0,求点P(x0,y0)到直线l的距离d,写出其算法并画出流程图.解:算法如下:第一步:输入x0,y0及直线方程的系数A,B,C.第二步:计算z1=Ax0+By0+C.第三步:计算z2=A2+B2.第四步:计算d=||z1z2.第五步:输出d.流程图如图所示.点拨:顺序结构是一种最简单、最基本的结构,可严格按照传统的解题思路写出算法步骤,画出程序框图.注意语句与语句之间,框与框之间是按从上到下的顺序进行的.阅读如图所示的程序框图,若输入的a,b,c的值分别是21,32,75,则输出的a,b,c分别是( )A.75,21,32 B.21,32,75C.32,21,75 D.75,32,21解:该程序框图的执行过程是:输入21,32,75;x=21;a=75;c=32;b=21;输出75,21,32.故选A.类型四条件结构(2015·深圳调研)执行如图所示的程序框图,如果依次输入函数:f(x)=3x,f(x)=sin x,f(x)=x3,f(x)=x+1x,那么输出的函数f(x)为( )A .f (x )=3xB .f (x )=sin xC .f (x )=x 3D .f (x )=x +1x解:依题意得,输出的函数应满足:f (-x )=-f (x )(x ∈R ),即函数f (x )是定义在R 上的奇函数,且f (x +m )>f (x ),其中m >0,即函数f (x )是定义在R 上的增函数.对于A ,函数f (x )=3x不是奇函数;对于B ,函数f (x )=sin x 不是定义在R 上的增函数;对于C ,函数f (x )=x 3既是奇函数又是定义在R 上的增函数;对于D ,函数f (x )=x +1x的定义域不是实数集.综上所述,只能输出f (x )=x 3,故选C.点拨:条件结构的运用与数学的分类讨论有关.设计算法时,哪一步要分类讨论,哪一步就需要用条件结构.(2015·全国卷Ⅱ)如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a ,b 分别为14,18,则输出的a =( )A .0B .2C .4D .14 解:执行该程序,输入a ,b 的值依次为a =14,b =18;a =14,b =4;a =10,b =4;a =6,b =4;a =2,b =4;a =b =2,此时退出循环,输出的a =2.故选B.类型五 循环结构(2014·安徽)如图所示,程序框图(算法流程图)的输出结果是( )A.34 B.55 C.78 D.89解:运行程序:x=1,y=1,z=2;x=1,y =2,z=3;x=2,y=3,z=5;x=3,y=5,z=8;x=5,y=8,z=13;x=8,y=13,z=21;x=13,y=21,z=34;x=21,y=34,z=55,跳出循环,输出结果是55.故选B.点拨:如果算法问题里涉及的运算进行了许多次重复的操作,且先后参与运算的数之间有相同的规律,就可引入变量循环参与运算(我们称之为循环变量),应用循环结构.在循环结构中,要注意根据条件设计合理的计数变量、累加和累乘变量及其个数等,特别要使条件的表述恰当、准确.(2015·陕西)根据下边的框图,当输入x为2006时,输出的y=( )A.28 B.10 C.4 D.2解:初始条件:x=2006.第1次运行:x=2004;第2次运行:x=2002;第3次运行:x=2000;…;第1003次运行:x=0;第1004次运行:x=-2,不满足条件,跳出循环,所以输出的y=32+1=10,故选B.类型六结构图总结高中所有有关函数的内容,画出知识结构图.解:如图所示:点拨:画结构图时,首先要确定组成结构图的基本要素,然后通过连线来标明各要素之间的关系.某公司的组织结构是:总经理之下设执行经理、人事经理和财务经理.执行经理领导生产经理、工程经理、品质管理经理和物料经理.生产经理领导线长,工程经理领导工程师,工程师管理技术员,物料经理领导计划员和仓库管理员.解:如图所示:1.设计算法时,要根据题目进行选择,以简单、程序短、易于在计算机上执行为原则.2.画程序框图首先要进行结构选择,套用格式.若求只含有一个关系式的函数的函数值时,只用顺序结构就能够解决;若是分段函数或执行时需要先判断才能执行后继步骤的,就必须引入条件结构;如果问题涉及的运算进行了许多重复的步骤,有规律,就可引入变量,应用循环结构.当然,应用循环结构一定要用到顺序结构与条件结构.3.循环结构的循环控制通过累加变量记录循环次数,通过判断框决定循环终止与否.用循环结构来描述算法,在画出算法程序框图之前,需要确定的三件事是:(1)确定循环变量与初始条件;(2)确定循环体;(3)确定终止条件.注意直到型循环与当型循环的区别,二者判断框内的条件表述在解决同一问题时恰好相反.解决循环结构框图问题,当循环次数比较少时,可依次列出;当循环次数较多时,可先循环几次,找出规律.要特别注意最后输出的是什么,不要出现多一次或少一次循环的错误.4.在具体绘制程序框图时,要注意以下几点:(1)流程线上要标有执行顺序的箭头.(2)判断框后边的流程线应根据情况标注“是(Y)”或“否(N)”.(3)框图内的内容包括累加(积)变量初始值,计数变量初始值,累加值,前后两个变量的差值都要仔细斟酌,不能有丝毫差错.(4)判断框内条件常用“>”“≥”“<”“≤”“=”等符号,它们的含义是各不相同的,要根据所选循环结构的类型,正确地进行选择.5.结构图与流程图的异同相同点:绘制结构图的一般步骤与绘制流程图类似,先确定组成系统的基本要素,以及这些要素之间的关系,然后画出框图表示整个系统.不同点:流程图描述具有时间特征的动态过程,结构图刻画静态的系统结构.流程图通常会有一个“起点”,一个或多个“终点”,其基本单元之间由流程线连接;结构图则更多地表现为“树”形结构,其基本要素之间一般为概念上的从属关系或逻辑上的先后关系.1.结合下面的算法:第一步:输入x.第二步:判断x是否小于0,若是,则输出x +2,否则执行第三步.第三步:输出x-1.当输入的x的值为-1,0,1时,输出的结果分别为( )A.-1,0,1 B.-1,1,0C.1,-1,0 D.0,-1,1解:根据x值与0的关系,选择执行不同的步骤,当x的值为-1,0,1时,输出的结果分别为1,-1,0,故选C.2.如图的程序框图输出的结果是( )A.4 B.3 C.2 D.0解:该算法首先将1,2,3三个数分别赋给x,y,z;然后先让x取y的值,即x变成2,再让y 取x的值,即y的值是2,接着让z取y的值,即z 的值为2,从而最后输出z的值为2.故选C.3.(2014·湖南)执行如图所示的程序框图,如果输入的t∈[-2,2],则输出的S属于( )A.[-6,-2] B.[-5,-1]C.[-4,5] D.[-3,6]解:由程序框图可得S=⎩⎪⎨⎪⎧2t2+1-3,t∈[-2,0),t-3,t∈[0,2],其值域为[-3,6].故选D.4.(2015·福建)阅读如图所示的程序框图,运行相应的程序,则输出的结果为( )A .2B .1C .0D .-1解:执行程序,得S =0,i =2;S =-1,i =3;S =-1,i =4;S =0,i =5;S =0,i =6>5,跳出循环,输出S =0.故选C.5.(2014·重庆)执行如图所示的程序框图,若输出k 的值为6,则判断框内可填入的条件是( )A .s >12B .s >35C .s >710D .s >45解:当输出k 的值为6时,s =1×910×89×78=710,结合各选项知,C 符合要求.故选C .6.(2015·全国课标Ⅰ)执行如图所示的程序框图,如果输入的t =0.01,则输出的n =( )A .5B .6C .7D .8解法一:执行程序,S =12,m =14,n =1;S =14,m =18,n =2;S =18,m =116,n =3;S =116,m =132,n =4;S =132,m =164,n =5;S =164,m =1128,n =6;S =1128<t =0.01,m =1256,n =7,循环结束,输出n =7.解法二:记第n 次循环后S 的值为a n ()n =0,1,2,…,,其中a 0=1,则a n =a n -1-⎝ ⎛⎭⎪⎫12n ,递推可得a n =a 0-⎝ ⎛⎭⎪⎫12+122+…+12n =1-12⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12=12n ≤t =0.01. 显然n >6,故n =7.故选C.7.(2015·安徽)执行如图所示的程序框图(算法流程图),输出的n 为________.当a=1.416时,跳出循环,输出的n为4.故填4.8.(2014·湖北)设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=________.解法一:当a=123时,b=321-123=198≠123;当a=198时,b=981-189=792≠198;当a=792时,b=972-279=693≠792;当a=693时,b=963-369=594≠693;当a=594时,b=954-459=495≠594;当a=495时,b=954-459=495=a,终止循环,输出b=495.解法二:设I(a)=100x+10y+z,D(a)=100z +10y+x,x<y<z,x,y,z∈N*,则D(a)-I(a)=99(z-x),因此各位数字都不是0且没有重复数字,而且是99的倍数的三位数有:198,297,396,495,594,693,792,891,经检验知只有495满足题意.故填495.9.某人带着一只狼和一只羊及一捆青菜过河,只有一条船,船仅可载重此人和狼、羊及青菜三者之一,没有人在的时候,狼会吃羊,羊会吃青菜.请设计安全过河的算法.解:第一步,人带羊过河.第二步,人自己返回.第三步,人带青菜过河.第四步,人带羊返回.第五步,人带狼过河.第六步,人自己返回.第七步,人带羊过河.10.设计一个算法,找出区间[1,1000]内的能被7整除的整数,画出程序框图.解:第一步,取k=1.第二步,判断k≤1000是否成立,若不成立,则执行第五步.第三步,若k除以7的余数为0,则输出k.第四步,将k的值增加1,返回执行第二步.第五步,结束.程序框图如图.11.设计一个算法计算11×3+13×5+15×7+…+12013×2015的值,并画出程序框图.解:算法步骤如下:第一步,令S=0,k=1.第二步,若k<2015成立,则执行第三步,否则输出S.第三步,计算S=S+1k(k+2),k=k+2,返回第二步.程序框图如图所示:意大利数学家斐波那契,在1202年出版的《算盘全书》一书里提出了这样一个问题:一对兔子饲养到第二个月进入成年,第三个月生一对小兔,以后每个月生一对小兔,所生小兔能全部存活并且也是第二个月成年,第三个月生一对小兔,以后每月生一对小兔.问这样下去到年底应有多少对兔子?试画出解决此问题的程序框图.解:根据题意可知,第一个月有1对小兔,第二个月有1对成年兔子,第三个月有两对兔子,从第三个月开始,每个月的兔子对数是前面两个月兔子对数的和,设第N个月有F对兔子,第N-1个月有S对兔子,第N-2个月有Q对兔子,则有F=S +Q,一个月后,即第N+1个月时,式中变量S的新值应变为第N个月兔子的对数(F的旧值),变量Q 的新值应变为第N-1个月兔子的对数(S的旧值),这样,用S+Q求出变量F的新值就是N+1个月兔子的对数,依此类推,可以得到一个数序列,数序列的第12项就是年底应有兔子对数,我们可以先确定前两个月的兔子对数均为1,以此为基准,构造一个循环程序,让表示“第x(x≥3)个月的i从3逐次增加1,一直变化到12,再循环一次得到的F”就是所求结果.流程图如图所示.§12.2基本算法语句1.输入(INPUT)语句输入语句的一般格式:_______________.要求:(1)输入语句要求输入的值是具体的常量;(2)提示内容提示用户输入的是什么信息,必须加双引号,“提示内容”原原本本地在计算机屏幕上显示,提示内容与变量之间要用分号隔开;(3)一个输入语句可以给多个变量赋值,中间用“,”分隔.2.输出(PRINT)语句输出语句的一般格式:_______________.功能:实现算法输出信息(表达式).要求:(1)表达式是指算法和程序要求输出的信息;(2)提示内容提示用户要输出的是什么信息,提示内容必须加双引号,提示内容要用分号和表达式分开;(3)如同输入语句一样,输出语句可以一次完成输出多个表达式的功能,不同的表达式之间可用“,”分隔.3.赋值语句赋值语句的一般格式: .赋值语句中的“=”叫做赋值号,它和数学中的等号不完全一样.作用:赋值语句的作用是将表达式所代表的值赋给变量.要求:(1)赋值语句左边只能是变量,而不是表达式,右边表达式可以是一个常量、变量或含变量的运算式.如:2=x是错误的;(2)赋值号的左右两边不能对换.赋值语句是将赋值号右边的表达式的值赋给赋值号左边的变量.如“A=B”“B=A”的含义和运行结果是不同的,如x=5是对的,5=x是错的,A+B=C是错的,C=A+B是对的;(3)不能利用赋值语句进行代数式的演算(如化简、因式分解、解方程等).4.条件语句(1)“IF—THEN”语句格式:____________________.说明:当计算机执行“IF—THEN”语句时,首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体,否则执行END IF之后的语句.(2)“IF—THEN—ELSE”语句格式:____________________.说明:当计算机执行“IF—THEN—ELSE”语句时,首先对IF后的条件进行判断,如果(IF)条件符合,那么(THEN)执行语句体1,否则(ELSE)执行语句体2.5.循环语句(1)直到型循环语句直到型(UNTIL型)语句的一般格式为:______________.(2)当型循环语句当型(WHILE型)语句的一般格式为:________________.自查自纠:1.INPUT “提示内容”;变量2.PRINT “提示内容”;表达式3.变量=表达式4.(1)IF 条件THEN语句体END IF5.(1)WHILE 条件循环体WEND(2)DO循环体LOOP UNTIL 条件下列赋值语句正确的是( )A.S=S+i2B.A=-AC.x=2x+1 D.P=x解:在程序语句中乘方要用“^”表示,所以A 项不正确;乘号“*”不能省略,所以C项不正确;D项中x应用SQR(x)表示,所以D项不正确;B选项是将变量A的相反数赋给变量A,则B项正确.故选B.下面程序运行后输出结果是3,则输入的x值一定是.0解:该程序语句是求函数y=|x|的函数值,∵y=3,∴x=±3.故选C.( )解:这是一个当型循环程序,当i=(1+5)+5=11>10时,退出循环,输出的i=11.故选D.(2)输入x=20,则p=____________.解:(1)x=6满足x≤10,∴p=6×0.35=2.1;(2)x=20时不满足x≤10,∴p=10×0.35+(20-10)×0.7=10.5.故填2.1;10.5.下列循环语句,循环终止时,n=____________.n=2WHILE n<=7n=n+1WEND解:该循环语句是当型循环语句,循环终止时,条件n≤7开始不成立,故填8.类型一输入、输出和赋值语句请写出下面运算输出的结果.(1)a=5b=3c=(a+b)/2d=c*cPRINT “d=”;d(2)a=1b=2c=a+bb=a+c-bPRINT “a=,b=,c=”;a,b,c(3)a=10b=20c=30a=bb=cc=aPRINT “a=,b=,c=”;a,b,c解:(1)语句“c=(a+b)/2”是将a,b之和的一半赋值给变量c,语句“d=c*c”是将c的平方赋值给d,最后输出d的值.故输出结果为d=16.(2)语句“c=a+b”是将a,b之和赋值给c,语句“b=a+c-b”是将a+c-b的值赋值给了b.故输出结果为a=1,b=2,c=3.(3)经过语句“a=b”后a,b,c的值是20,20,30,经过语句“b=c”后a,b,c的值是20,30,30,经过语句“c=a”后a,b,c的值是20,30,20.故输出结果为a=20,b=30,c=20.点拨:①将一个变量的值赋给另一个变量,前一个变量的值保持不变;②可先后给一个变量赋多个不同的值,但变量的取值总是最后被赋予的值.阅读下列两个程序,回答问题:①x=3y=4x=y②x=3y=4y=x①中程序输出的x值为__________,②中程序输出的y值为__________.解:程序①中的x=y是将y的值4赋给x,赋值后x的值变为4;②中y=x是将x的值3赋给y,赋值后y的值为3.故填4;3.类型二条件语句已知函数y=⎩⎪⎨⎪⎧x2-1,x≥0,2x2-5,x<0,画出程序框图并编写一个程序,对每输入的一个x值,都得到相应的函数值.解:程序框图如下.点拨:条件语句:“IFTHEN”及“IFTHENELSE”的用法在“考点梳理”栏有说明,需要注意的是,若是三段或三段以上的分段函数,通常需用条件语句的嵌套结构.编写程序,使得任意输入的3个整数按从小到大的顺序输出.解:算法分析:用a,b,c表示输入的3个整数,为了节约变量,把它们重新排列后,仍用a,b,c表示,并使a≤b≤c.具体操作步骤如下.第一步:输入3个整数a,b,c.第二步:将a与b比较,并把大者赋给b,小者赋给a.第三步:将a与c比较,并把大者赋给c,小者赋给a(此时a已是三者中最小的).第四步:将b与c比较,并把大者赋给c,小者赋给b(此时a,b,c已按从小到大的顺序排列好).第五步:按顺序输出a,b,c.上述操作步骤可以用程序框图直观地表达出来.程序框图如图.根据程序框图,写出计算机程序为:类型三循环语句若下面程序中输入的n值为2017,则输出的值为解:本程序是计算S=1×2+2×3+…+1n(n+1).裂项得S =⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+…+⎝ ⎛⎭⎪⎫1n -1n +1=n n +1.所以当n =2017时,S =20172018.故填20172018.点拨:计算机执行此程序时,遇到WHILE 语句,先判断条件是否成立,如果成立,则执行WHILE 和WEND 之间的循环体,然后返回到WHILE 语句再判断上述条件是否成立,直至返回到WHILE 语句判断上述条件不成立为止,这时不再执行循环体,而执行WEND 后面的语句,这是当型循环.计算12+22+32+…+1002的值,分别用WHILE 型语句和UNTIL 型语句编写程序.当型循环与直到型循环的区别(1)WHILE 型是先判断条件,后执行循环体,而UNTIL 型则是先执行循环体,后判断条件;(2)WHILE 型是当条件满足时执行循环体,不满足时结束循环,而UNTIL 型则是条件不满足时执行循环体,条件满足时结束循环;(3)UNTIL 型至少执行一次循环体,而WHILE 型执行循环体的次数可能为0.A 的值为( )A .1B .5C .15D .120解:该程序的功能是计算A×2×3×4×5的值,则120=A×2×3×4×5,故A=1,即输入A的值为1.故选A.A.1 B.10 C.25 D.26解:由条件可知,b=5×5+1=26.故选D.3.读程序回答问题.( )A.程序不同,结果不同B.程序不同,结果相同C.程序相同,结果不同D.程序相同,结果相同解:甲、乙两程序显然不同,但都是求1+2+…+1000的和,所以结果相同,故选B.4.下列程序语句是求函数y=|x-4|+1的函5C.y=5-x D.y=x+5解:y=|x-4|+1=⎩⎪⎨⎪⎧x-3,x≥4,5-x,x<4,故选C.5.(2014·陕西模拟)下面程序运行后,输出的值是( )解:程序的功能是利用循环计算i2<2000(i∈N)的最大i值,∵442<2000,452>2000,∴输出的i为44.故选C.6,那么输出的结果为( )A.6 B.720 C.120 D.1解:当n=6时,这个程序的实际含义是计算S =1×2×3×4×5×6,结果是720.故选B.7.运行如图所示的程序,输出的结果是.a=1b=2a=a+bPRINT aEND解:a=1,b=2,则a+b=3,根据赋值语句的含义,有a=3.故填3.8.下列程序输出结果为____________.(SQR(a)表示非负数4,b =-2,执行第五句后,a =4×(-2)4×4=128,故输出a 的值为128.故填128.s =10,n =9;s =19,n =8;s =27,n =7;s =34,n =6;s =40,n =5,这时s ≥40,跳出循环,输出结果为5.10.高等数学中经常用到符号函数y =sgnx ,其定义为y =⎩⎪⎨⎪⎧1,x >0,0,x =0,-1,x <0,试编写程序,根据输入的x 值,输出对应的 y 值.解:根据x的取值,此函数为三段分段函数,则需用条件语句嵌套.程序如下.11.编写一个程序,求满足1+12+13+…+1n>10的n 的最小值.某商场第一年销售计算机5000台,如果平均每年销售量比上一年增加10%,那么从第一年起,大约几年可使总销售量达到30000台?画出解决该问题的程序框图,并编写相应程序.解:根据题意,每年销售量比上一年增加的百分率相同,设总销售量为S ,n 年达到30000台.则S =5000+5000(1+10%)+5000(1+10%)2+…+5000(1+10%)n -1=50000(1.1n-1).令S ≥30000,可得n ≥5,即大约5年可使总销售量达30000台.程序框图如图所示.程序如下.。
高三数学高考(理)第一轮复习精品课件:第12单元 算法初步与复数 新人教A

第62讲│要点探究
图 62-4
第62讲│要点探究
【点评】利用公式求解问题,先写出公式,看公式 中的条件是否满足,若不满足,先求出需要的量,看要 求的全部输入,求出未知的量,然后将公式中 涉及的量全部代入求值即可.
第62讲│要点探究
► 探究点3 条件结构
2.对复数的考查难度降低,集中考查了复数的概念及 代数形式的四则运算,复数问题实数化是解决复数问题的 最基本的思想方法.
第十二单元│命题趋势
3.以小题为主.大多以选择题、填空题的形式命题, 一般为基础题,难度不大.
预测在2011年高考中,程序框图在选择题、填空题中 重点考查基本知识和技能,如输出结果、判断条件、程序 的功能等;复数会以选择、填空的形式考查基本概念、基 本运算和复数的几何意义.
第62讲│要点探究
方法一:
方法二:
图 62-7
图 62-8
第62讲│要点探究
【点评】实际生活中很多问题都可以利用框图的方 法处理,而解决实际问题的方法本身就是对算法的一个 体现.解决此类问题时,首先要认真分析,联系解决此 类问题的数学方法,综合考虑此类问题中可能涉及的算 法,明确选择合适的算法逻辑结构来画出程序框图.利 用循环结构表示算法,第一要先确定是利用当型循环结 构,还是直到型循环结构;第二要选择准确的表示累计 的变量;第三要注意确定在哪一步开始循环.循环语句 是高考考查的热点,解题时特别注意循环的类型,如下 变式题.
第62讲│要点探究
变式题 [2009·浙江卷] 某程序框图如图 62-9 所 示,该程序运行后输出的 k 的值是( )
A.4
图 62-9
B.5 C.6
D.7
第62讲│要点探究
【思路】 此题为当型循环,判断好执行循环的次 数即可.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学一轮复习第十二章算法初步第1讲算法初步配套课时
作业理(含解析)新人教A版
配套课时作业
1.(2017·山东高考)执行两次如图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为( )
A.0,0 B.1,1 C.0,1 D.1,0
答案 D
解析当x=7时,∵b=2,∴b2=4<7=x.
又7不能被2整除,∴b=2+1=3.
此时b2=9>7=x,∴退出循环,a=1,∴输出a=1.
当x=9时,∵b=2,∴b2=4<9=x.
又9不能被2整除,∴b=2+1=3.
此时b2=9=x,又9能被3整除,∴退出循环,a=0.
∴输出a=0.故选D.
2.设x∈[0,3],执行如图所示的程序框图,从输出的结果中随机取一个数a,则“a≤5”的概率为( )
A.2
3
B.
5
6
C.
2
7
D.
5
7
答案 C
解析 由程序框图可知y =⎩
⎪⎨⎪⎧
x +3,0≤x <2,
x 2
+1,2≤x ≤3,该函数的值域是[3,10],所以所求概
率为5-310-3=2
7
.
3.(2019·青岛模拟)执行如图所示的程序框图,若输出的结果为48,则判断框中可以填( )
A .n ≤5 B.n >5 C .n ≤4 D.n >4 答案 B
解析 n =1,S =3,a =5;n =2,S =8,a =7;n =3,S =15,a =9;n =4,S =24,a =11;n =5,S =35,a =13,不满足判断框中的条件;n =6,S =48,a =15,满足判断框中的条件,退出循环,输出的S =48,所以判断框中可以填n >5.
4.执行如图所示的程序框图,若输入向量a =c =(-2,2),b =(1,0),则输出S 的值是( )
A .18
B .20
C .22
D .24 答案 B
解析 程序对应的运算:
a =c =(-2,2),则a ·c =8,S =0+8=8,i =1,c =c +
b =(-1,2);
a =(-2,2),
b =(1,0),
c =(-1,2),则a ·c =6,S =8+6=14,i =2,c =c +b =(0,2); a =(-2,2),b =(1,0),c =(0,2),则a ·c =4,S =14+4=18,i =3,c =c +b =(1,2); a =(-2,2),b =(1,0),c =(1,2),则a ·c =2,S =18+2=20,i =4,c =c +b =(2,2); a =(-2,2),b =(1,0),c =(2,2),则a ·c =0,此时跳出循环体.故输出S 的值为20,
故选B.
5.(2019·郑州一检)执行如图所示的程序框图,若输出的结果是7,则判断框内m 的取值范围是( )
A .(30,42]
B .(30,42)
C .(42,56]
D .(42,56) 答案 A
解析 k =1,S =2;k =2,S =2+4=6;k =3,S =6+6=12;k =4,S =12+8=20;k =5,S =20+10=30;k =6,S =30+12=42;k =7,此时不满足S =42<m ,退出循环,所以30<m ≤42,故选A.
6.(2019·昆明调研)如图所示的程序框图来源于中国古代数学著作《孙子算经》,其中定义[x ]表示不超过x 的最大整数,例如[0.6]=0,[2]=2,[3.6]=3.执行该程序框图,则输出的a =( )
A .9
B .16
C .23
D .30 答案 C
解析 执行程序框图,k =1,a =9,9-3·⎣⎢⎡⎦⎥⎤93=0≠2;k =2,a =16,16-3·⎣⎢⎡⎦
⎥⎤163=1≠2;
k =3,a =23,23-3·⎣⎢⎡⎦⎥⎤233=2,23-5·⎣⎢⎡⎦
⎥⎤235
=3,满足条件,退出循环.则输出的a =23.故
选C.
7.“中国剩余定理”是中国古代求解一次同余式组的方法,若正整数N 除以正整数m 后的余数为n ,则记为N ≡n (MOD m ),例如10≡4(MOD 6),如图所示的程序框图的算法源于“中国剩余定理”,若执行该程序框图,则输出的N =( )
A .16
B .14
C .13
D .11 答案 A
解析 开始,N =10,N =10+1=11,N ≡1(MOD 3)不成立,N =11+1=12,N ≡1(MOD 3)不成立,N =12+1=13,N ≡1(MOD 3)成立,N ≡1(MOD 5)不成立,N =13+1=14,N ≡1(MOD 3)不成立,N =14+1=15,N ≡1(MOD 3)不成立,N =15+1=16,N ≡1(MOD 3)成立,N ≡1(MOD 5)成立,输出的N =16.故选A.
8.执行如图所示的程序框图,如果输入的t ∈[-2,2],则输出的S ∈( )
A .[-4,2]
B .[-2,2]
C .[-2,4]
D .[-4,0] 答案 A
解析 当-2≤t <0时,S =2t ∈[-4,0);当0≤t ≤2时,S =t 3
-3t ,易知S =t 3
-3t 在t ∈[0,1)上单调递减,在t ∈(1,2]上单调递增,且当t =0时,S =0,当t =1时,S =-2,当t =2时,S =2,所以S ∈[-2,2].综上,S ∈[-4,2],故选A.
9.(2018·全国卷Ⅱ)为计算S =1-12+13-14+…+199-1
100,设计了下面的程序框图,
则在空白框中应填入( )
A .i =i +1
B .i =i +2
C .i =i +3
D .i =i +4 答案 B
解析 由S =1-12+13-14+…+199-1
100,知程序框图先对奇数项累加,偶数项累加,
最后再相减.因此在空白框中应填入i =i +2,选B.
10.执行如图所示的程序框图,则输出的值是( )
A.
155 B.158 C.161 D.1
64
答案 C
解析 执行程序框图,可得,A =1,i =1,第1次执行循环体,A =1
4
,i =2,满足条件
i ≤20,第2次执行循环体,A =17,i =3,满足条件i ≤20,第3次执行循环体,A =110
,i
=4,满足条件i ≤20,第4次执行循环体,A =1
13,i =5,满足条件i ≤20,第5次执行循
环体,A =1
16
,i =6,……观察可知,当i =20时,满足条件i ≤20,第20次执行循环体,
A =
14+20-1×3=161,i =21,此时,不满足条件i ≤20,退出循环,输出A 的值为1
61.
故选C.
11.(2019·江西六校联考)如图是某算法的程序框图,当输出的结果T >70时,正整数
n 的最小值是________.
答案 4
解析由程序框图知,每次循环中K,T的值依次为1,1;2,4;3,16;4,72.又T=72>70,故正整数n的最小值为4.
12.下面程序运行后输出的结果为________.
N=5
S=0
WHILE S<15
S=S+N
N=N-1
WEND
PRINT N
END
答案0
解析执行第一次后,S=5,N=4;执行第二次后,S=9,N=3;执行第三次后,S=12,N=2;执行第四次后,S=14,N=1;执行第五次后,S=15,N=0;跳出循环结构,输出N的值,N=0.
13.执行如图所示的程序框图,若a=0.182,b=log20.18,c=20.18,则输出的结果是________.
答案20.18
解析易知该程序框图的功能是输出a,b,c中的最大者.结合函数y=x2,y=log2x,y=2x的图象(图略)易知0<a<1,b<0,c>1,∴b<a<c.故输出的结果是20.18.
14.《九章算术》是中国古代第一部数学专著,是《算经十书》中最重要的一种,成于公元一世纪左右.“更相减损术”便是《九章算术》中记录的一种求最大公约数的算法,按其算理流程有如下程序框图,若输入的a,b分别为96,36,则输出的i为________.
答案 4
解析当a=96,b=36时,
满足a>b,则a=96-36=60,i=1,
由a>b,得a=60-36=24,i=2,
由a<b,得b=36-24=12,i=3,
由a>b,得a=24-12=12,i=4,
由a=b,得输出i=4.
15.如果以下程序运行后输出的结果是132,求程序中UNTIL后面的条件中a的取值范围.
解程序的功能是计算S=12×11×10×…,输出结果为132,即循环体只执行了两次,即i=10时,就结束了循环,所以a满足10<a≤11.故a的取值范围为(10,11].16.(2019·陕西模拟)执行如图的程序框图,如果输入的x,y∈R,求输出的S的最大值.。
