浙江省数学学业水平考试模拟试卷

合集下载

浙江温州2023-2024学年上学期学业水平检测九年级数学模拟试卷+答案

温州市2023学年第一学期学业水平检测九年级数学模拟试卷学校:___________姓名：___________班级：___________考号：___________ 一、选择题（每题3分，共30分）的半径为2．已知OA．P点5．如图，已知圆心角A．156°A ．B ．C ．D ．7．已知抛物线21y x x −−，与x 轴的一个交点为()0m ，，则代数式22023m m −+的值为（） A ．2021 B ．2022 C ．2023 D ．20248．如图，将ABD △绕顶点B 顺时针旋转36°得到CBE △，且点C 刚好落在线段AD 上，若30CBD ∠=°，则E∠的度数是（）A ．42°B ．44°C ．46°D ．48°9．如图，Rt ABC △中，90BAC ∠=°，AD BC ⊥，垂足为D ，点E ，F 分别是AB ，AC 边上的动点，DE DF ⊥，若5BC =， 3.2CD =，那么DE 与DF 的比值是（）A ．0.6B ．0.75C ．0.8D ．不确定的值10．已知抛物线()20y ax bx c a ++≠与x 轴的交点为()0A 1，和()30B ，，点()111P x y ，，()222P x y ，是抛物线上不同于A B ，的两个点，记1P AB △的面积为1S ，2P AB △的面积为2S ，则下列结论正确的是（）二、填空题（每题分，共分）11．如图，ABC 中，40A ∠=°，60C ∠=°，O 与边AB ，AC 的另一个交点分别为D ， E ．则AED ∠的大小为 °．12．下表记录了某种苹果树苗在一定条件下移植成活的情况：移植的棵数 100 200 500 1000 2000 成活的棵数 81 156 395 8001600 成活的频率 0.81 0.78 0.790.8 0.8 由此估计这种苹果树苗的移植成活的概率为．13．已知二次函数235y x =−，当14x −≤≤时，y 的最小值为．14．如图（1）是一座石拱桥，它是一个横断面为抛物线形状的拱桥，当水面在图示位置时，拱顶（拱桥洞的最高点）离水面3m ，水面宽6m ．如图（2）建立平面直角坐标系，则抛物线的关系式是．15．如图，已知D 、E 、F 分别是ABC 的边AB AC BC 、、上的点，DE BC EF AB ∥，∥，ADE EFC △、△的面积分别为1、4，四边形BFED 的面积为．16．如图，△ABC 是⊙O 的内接三角形，∠A =30°，3BC =,则⊙O 的半径为．17．如图1，筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理．筒车盛水桶的运行轨道是以轴心O 为圆心的圆，如图2，已知圆心O 在水面上方，且O 被水面截得的弦AB 长为4m ，O 的半径长为3m ，若点C 为运行轨道的最低点，则点C 到弦AB 所在直线的距离是 m ．18．如图，在Rt ABC △中，90ACB ∠=°，点D 在AB 上，点E 为BC 上的动点，将BDE △沿DE 翻折得到FDE ，EF 与AC 相交于点G ，若3AB AD =，3AC =，6BC =，0.8CG =，则CE 的值为．三、解答题（46分）19．（6分）如图，点D 是△ABC 的边AB 上一点，∠ABC ＝∠ACD ．(1)求证：△ABC ∽△ACD ；(2)当AD ＝2，AB ＝3时，求AC 的长．20．（6分）已知二次函数2y x bx c ++=-经过点30A （，）与03B （，）． (1)求b ，c 的值．(2)求该二次函数图象的顶点坐标．21．如图所示，已知AB 为O 的直径，CD 是弦，且AB CD ⊥于点E ．连接AC 、OC BC 、．(1)求证：ACO BCD ∠=∠；(2)若96AE BE CD ==，，求O 的直径．（1）请用画树状图或列表的方法，求抽出的两张卡片上的图案都是片分别记为1A 、2A ,图案为“黑脸”的卡片记为（2）若第一次抽出后不放回，请直接写出求抽出的两张卡片上的图案都是y24．（8分）如图，ABC 内接于⊙O ，过点O 作OH BC ⊥于点H ，延长OH 交⊙O 于点D ，连接AD 、BD ，AD 与BC 交于点E ，9AD =(1)求证：BAD CAD ∠=∠． (2)若OH DH =．①求BAC ∠的度数．②若⊙O 的半径为6，求DE 的长．(3)设BD x =，AB CE y ⋅=，求y 关于x 的函数表达式．参考答案：答案第1页，共1页。

2024年7月浙江省普通高中学业水平考试——数学仿真模拟试卷01(解析版)

2024年7月浙江省普通高中学业水平合格性考试数学仿真模拟试卷01（考试时间：80分钟；满分：100分）注意事项：1．答题前填写好自己的姓名、班级、考号等信息2．请将答案正确填写在答题卡上一、单项选择题（本大题共12小题，每小题3分，共36分.每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1．集合{}|12A x x =-≤≤，{}|1B x x =<，则()A B ⋃R ð＝（）A ．{}|1x x >B ．{}1|x x ≥-C ．{}|12<≤x x D ．{}|12x x ≤≤【答案】B【分析】由补集和并集的定义直接求解.【详解】集合{}|12A x x =-≤≤，{}|1B x x =<，则{}1|B x x =≥R ð，(){}1|=A B x x ≥-R ð.故选：B2．已知复数z 满足(1i)2i z -=，则z 在复平面内对应的点位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】B【分析】化简复数1i z =-+，结合复数的坐标表示，即可求解.【详解】由题意，复数z 满足(1i)2i z -=，可得()()()2i 1i 2i 1i 1i 1i 1i z ⋅+===-+--+，所以复数z 在复平面内对应的点(1,1)Z -位于第二象限.故选：B.3．函数lg(2)y x =-的定义域是（）A ．(0,2]B ．(0,2)C ．(,2)-∞D ．(2,)+∞【答案】C【分析】由对数函数的性质可得函数lg(2)y x =-的定义域．【详解】由函数lg(2)y x =-，得到20x ->解得x 2<，则函数的定义域是(),2∞-，故选：C ．4．三个数0.35a =，50.3b =，515c ⎛⎫= ⎪⎝⎭大小的顺序是（）A ．a b c >>B ．a c b >>C ．b a c >>D ．c a b>>【答案】A【解析】利用指数函数、幂函数的单调性即可求解.【详解】由5x y =为增函数，则0.30551a =>=，由5y x =为增函数，555110.35⎛⎫>> ⎪⎝⎭，所以a b c >>.故选：A5．已知向量()1,2a =r ，(),3b λ= ，若a b ⊥，则λ=（）A ．6-B ．32-C ．32D ．6【答案】A【分析】根据向量垂直的坐标表示进行求解.【详解】因为()1,2a =r ，(),3b λ= ，a b ⊥，所以60a b λ⋅=+=，解得6λ=-.故选：A.6．从甲、乙等4名同学中随机选出2名同学参加社区活动，则甲，乙两人中只有一人被选中的概率为（）A ．56B ．23C ．12D ．13【答案】B【分析】利用古典概型，列举计算事件数，即得解.【详解】将甲，乙分别记为x ，y ，另2名同学分别记为a ，b ．设“甲，乙只有一人被选中”为事件A ，则从4名同学中随机选出2名同学参加社区活动的所有可能情况有(),x y ，(),x a ，(),x b ，(),y a ，(),y b ，(),a b ，共6种，其中事件A 包含的可能情况有(),x a ，(),x b ，(),y a ，(),y b ，共4种，故42()63P A ==．故选：B7．在ABC 中，已知D 是AB 边上的中点，G 是CD 的中点，若AG AB AC λμ=+u u u r u u u r u u u r，则实数λμ+=（）A ．14B ．12C ．34D ．1【答案】C【分析】根据D 是AB 边上的中点，G 是CD 的中点，得到11,22AD AB CG CD ==u u u r u u u r u u u r u u u r ，再利用平面向量的线性运算求解.【详解】解：因为D 是AB 边上的中点，G 是CD 的中点，所以11,22AD AB CG CD ==u u u r u u u r u u u r u u u r ，所以12AG AC CG AC CD =+=+u u u r u u u r u u u r u u u r u u u r，()111242AC AD AC AB AC =+-=+u u u r u u u r u u u r u u u r u u u r ，又因为AG AB AC λμ=+u u u r u u u r u u u r，所以11,42λμ==，则34λμ+=，故选：C8．若棱长为）A ．12πB ．24πC ．36πD ．144π【答案】C【分析】求出正方体的体对角线的一半，即为球的半径，利用球的表面积公式，即可得解.【详解】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即3R ==，所以，这个球的表面积为2244336S R πππ==⨯=.故选：C.【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心.9．如图，在四面体ABCD 中，,E F 分别是AC 与BD 的中点，若24CD AB ==，EF BA ⊥，则EF 与CD 所成角的度数为（）A ．90°B ．45°C ．60°D ．30°【答案】D【分析】设G 为AD 的中点，连接,GF GE ，由三角形中位线定理可得GF AB ∥，GE CD ∥，则GEF ∠或其补角即为EF 与CD 所成的角，结合2AB =，4CD =，EF AB ⊥，在GEF △中，利用三角函数相关知识即可得到答案.【详解】设G 为AD 的中点，连接,GF GE ，则,GF GE 分别为,ABD ACD △△的中位线，所以GF AB ∥，112GF AB ==，GE CD ∥，122GE CD ==，则EF 与CD 所成角的度数等于EF 与GE 所成角的度数，即GEF ∠或其补角即为EF 与CD 所成角，又因为EF AB ⊥，GF AB ∥，所以EF GF ⊥，则GEF △为直角三角形，1GF =，2GE =，90GFE ∠=︒，在直角GEF △中，1sin 2GEF ∠=，即30GEF ∠=︒，所以EF 与CD 所成角的度数为30°.故选：D10．我国著名数学家华罗庚曾说：“数缺形时少直观，形少数时难入微，数形结合白般好，隔离分家万事休.”在数学的学习和研究中，有时可凭借函数的图象分析函数解析式的特征.已知函数()f x 的部分图象如图所示，则函数()f x 的解析式可能为（）A ．()21xf x x=-B ．()221x f x x =+C ．()221xf x x =-D ．()2211x f x x +=-【答案】C【分析】根据图象函数为奇函数，排除D ；再根据函数定义域排除B ；再根据1x >时函数值为正排除A ；即可得出结果.【详解】由题干中函数图象可知其对应的函数为奇函数，而D 中的函数为偶函数，故排除D ；由题干中函数图象可知函数的定义域不是实数集，故排除B ；对于A ，当1x >时，0y <，不满足图象；对于C ，当1x >时，0y >，满足图象.故排除A ，选C.故选：C11．已知π17tan tan 422θθ⎛⎫+=- ⎪⎝⎭，则cos 2θ=（）A ．12-B ．12C ．45-D ．45【答案】C【分析】利用两角和的正切公式可得出关于tan θ的方程，解出tan θ的值，再利用二倍角的余弦公式以及弦化切可求得cos 2θ的值.【详解】因为πtan tanπtan 1174tan tan π41tan 221tan tan 4θθθθθθ++⎛⎫+===- ⎪-⎝⎭-，整理可得2tan 6tan 90θθ-+=tan 3θ=，所以，222222cos sin 1tan 194cos 2cos sin 1tan 195θθθθθθθ---====-+++.故选：C.12．若0x >，0y >且x y xy +=，则211x y x y +--的最小值为（）A ．3B．52C．3D．3+【答案】D【分析】先把x y xy +=转化为111x y +=，再将2211x yx y x y +=+--，根据基本不等式即可求出．【详解】0x >，0y >且x y xy +=，111x y∴+=，211x y x y +-- ，()()2211xy x xy y x y -+-=--，21x y xy x y +=--+2x y =+，()112x y x y ⎛⎫=++ ⎪⎝⎭2333x yy x =++≥++当且仅当2x yy x =，即12x =+，1y =+故211x y x y +--的最小值为3+故选：D ．二、多项选择题（本大题共4小题，每小题4分，共16分.每小题列出的四个备选项中有多个是符合题目要求的，全部选对得4分，部分选对且没错选得2分，不选、错选得0分.）13．下列说法中正确的是（）A ．直线10x y ++=在y 轴上的截距是1B ．直线()20mx y m m +++=∈R 恒过定点()1,2--C ．点()0,0关于直线10x y --对称的点为()1,1-D ．过点()1,2且在x 轴､y 轴上的截距相等的直线方程为30x y +-=【答案】BC【分析】对于A 项，将直线方程化成斜截式方程即得；对于B 项，把直线方程化成关于参数m 的方程，依题得到1020x y +=⎧⎨+=⎩，解之即得；对于C 项，只需验证两点间的线段中点在直线上，且两点的直线斜率与已知直线斜率互为负倒数即可；对于D 项，需注意截距相等还包括都为0的情况.【详解】对于A 项，由10x y ++=可得：=1y x --，可得直线10x y ++=在y 轴上的截距是1-，故A 项错误；对于B 项，由20mx y m +++=可得：(1)20m x y +++=，因R m ∈，则有：1020x y +=⎧⎨+=⎩，故直线()20mx y m m +++=∈R 恒过定点()1,2--，故B 项正确；对于C 项，不妨设(0,0),(1,1)A B -,直线:10l x y --=，因直线AB 的斜率为1-与直线l 的斜率为1的乘积为1-，则得AB l ⊥,又由点A 到直线l与点B 到直线l 相等，且在直线l 的两侧，故点()0,0关于直线10x y --=对称的点为()1,1-，即C 项正确；对于D 项，因过点()1,2且在x 轴､y 轴上的截距相等的直线还有2y x =，故D 项错误.故选：BC.14．已知()π,0θ∈-，7sin cos 13θθ+=，则下列结论正确的是（）A ．ππ,2θ⎛⎫∈ ⎪⎝-⎭-B ．12cos 13θ=C ．5tan 12θ=D ．17sin cos 13θθ-=-【答案】BD【分析】先利用题给条件求得sin ,cos θθ的值，进而得到θ的范围，tan θ的值和sin cos θθ-的值.【详解】由7sin cos 13θθ+=可得，7cos sin 13θθ=-，则227sin sin 113θθ⎛⎫-+= ⎪⎝⎭，即524sin 2sin 01313θθ⎛⎫⎛⎫+-= ⎪⎪⎝⎭⎝⎭解之得12sin 13θ=或5sin 13θ=-,又()π,0θ∈-，则5sin 13θ=-，故12cos 13θ=，则选项B 判断正确；由5sin 013θ=-<，12cos 013θ=>可得θ为第四象限角，又()π,0θ∈-，则π,02θ⎛⎫∈- ⎪⎝⎭，则选项A 判断错误；sin θ5tan θcos θ12==-，则选项C 判断错误；51217sin cos 131313θθ-=--=-，则选项D 判断正确.故选：BD15．已知函数()()e ,021,0xx f x f x x ⎧≤⎪=⎨->⎪⎩，若关于x 的方程()f x a =有两解，则实数a 的值可能为（）A ．1ea =B ．1a =C ．ea =D ．3a =【答案】BD【分析】根据题意分析可得方程()f x a =的根的个数可以转化为()y f x =与y a =的交点个数，结合()y f x =的单调性与值域以及图象分析判断.【详解】①当0x ≤时，()e xf x =在(],0-∞内单调递增，且()01f =，所以()(]0,1f x ∈；②当0x >时，则()(]*2e ,1,,k x k f x x k k k -=∈-∈N ，可知()f x 在(]*1,,k k k -∈N 内单调递增，且()()21,2ekk f k f k -==，所以()*2,2,e k k f x k ⎛⎤∈∈ ⎥⎝⎦N ，且12222,e e k k kk ++<<∈N .方程()f x a =的根的个数可以转化为()y f x =与y a =的交点个数，可得：当0a ≤时，()y f x =与y a =没有交点；当20e a <≤时，()y f x =与y a =有且仅有1个交点；当122,ek k a k +<≤∈N 时，()y f x =与y a =有且仅有2个交点；当222,ek ka k +<≤∈N 时，()y f x =与y a =有且仅有1个交点；若关于x 的方程()f x a =有两解，即()y f x =与y a =有且仅有2个交点，所以实数a 的取值范围为12,2,e k k k +⎛⎤∈ ⎥⎝⎦N ，因为281,1,3,4e e ⎛⎤⎛⎤∈∈ ⎥⎥⎝⎦⎝⎦，而A 、C 不在相关区间内，所以A 、C 错误，B 、D 正确.故选：BD.16．如图，在直三棱柱111ABC A B C -中，12AA =，1AB BC ==，120ABC ︒∠=，侧面11AAC C 的对角线交点O ，点E 是侧棱1BB 上的一个动点，下列结论正确的是（）A ．直三棱柱的侧面积是4+B ．直三棱柱的外接球表面积是4πC ．三棱锥1E AAO -的体积与点E 的位置无关D ．1AE EC +的最小值为【答案】ACD【分析】首先计算AC 长，再根据直棱柱的侧面积公式，即可判断A ；首先计算ABC 外接圆的半径，再根据几何关系求外接球的半径，代入公式，即可判断B ；根据体积公式，结合线与平面平行的关系，即可判断C ；利用展开图，结合几何关系，即可判断D.【详解】A.ABC 中，AC =，所以直棱柱的侧面积为(1124++⨯=+，故A 正确；B.ABC 外接圆的半径12sin120ACr ==，所以直棱柱外接球的半径R =则直三棱柱外接球的表面积24π8πS R ==，故B 错误；C.因为11//BB AA ，且1BB ⊄平面11AAC C ，1AA ⊂平面11AAC C ，所以1//BB 平面11AAC C ，点E 在1BB 上，所以点E 到平面11AAC C 的距离相等，为等腰三角形ABC 底边的高为12，且1AAO 的面积为122⨯=则三棱锥1E AAO -的体积为定值1132=，与点E 的位置无关，故C 正确；D.将侧面展开为如图长方形，连结1AC ,交1BB 于点E ，此时1AE EC +=D 正确.故选：ACD【点睛】关键点点睛：本题D 选项解决的关键是将平面11AA B B 与11CC B B 展开到同一个面，利用两点之间距离最短即可得解.三、填空题（本大题共4小题，每空3分，共15分.）17．已知函数()21,02,0x x f x x x ⎧+≤=⎨->⎩，则()2f =；若()10f x =，则x =．【答案】4-；3-.【分析】利用分段函数的性质计算即可.【详解】由条件可知()2224f =-⨯=-；若()201103x f x x x ≤⇒=+=⇒=-，若()021050x f x x x >⇒=-=⇒=-<，不符题意.故答案为：4-；3-18．已知双曲线2222:1(0,0)x y C a b a b-=>>的离心率为2，右焦点与抛物线216y x =的焦点重合，则双曲线C 的顶点到渐近线的距离为.【解析】求出抛物线的焦点，可得双曲线的c ，运用离心率公式可得a ，再由a ，b ，c 的关系，求得b ，求出顶点到渐近线的距离，即可得到所求值．【详解】解：抛物线216y x =的焦点为(4,0)，则双曲线的4c =，双曲线的离心率等于2，即2ca=，可得2a =，b ==则双曲线的渐近线方程为y =，顶点坐标为(20)±,，可得双曲线的顶点到其渐近线的距离等于d =【点睛】本题考查双曲线的方程和性质，主要是渐近线方程和离心率公式的运用，考查运算能力，属于中档题．19．已知a 、b 、c 分别为ABC 的三个内角A 、B 、C 的对边，2a =，且()(sin sin )()sin a b A B c b C +-=-，则ABC 面积的最大值为．【分析】先求出角A 的大小，由1sin 2S bc A =，考虑余弦定理建立,b c 的方程，再由基本不等式求bc 的最大值.【详解】解析：因为()(sin sin )()sin a b A B c b C +-=-，根据正弦定理可知(a b)()(c b)a b c +-=-，即222b c a bc +-=，由余弦定理可知1cos 2A =，又(0,π)A ∈，故π3A =，又因为2a =，所以224b c bc +-=，2242b c bc bc bc bc =+-≥-=（当且仅当b c =时取等号），即4bc ≤所以11sin 422S bc A =≤⨯=ABC20．已知定义在R 上的函数()f x 在(,3)-∞-上是减函数，若()() 3g x f x =-是奇函数，且()03g =，则满足不等式()0xf x ≤的x 的取值范围是．【答案】][3(),6,-∞-⋃-+∞【分析】由已知条件，可得()g x 是奇函数，则()f x 关于(3,0)-对称，可得()f x 在(,3)-∞-与(3,)-+∞上是减函数，且()()060f f -==，(3)0f -=，画出()f x 对应的函数草图，可得不等式()0xf x ≤的x 的取值范围.【详解】解：将()f x 向右平移3个单位，可得到()3f x -，由()() 3g x f x =-是奇函数，可得()g x 关于原点对称，则()f x 关于(3,0)-对称，且()00(3)g f =-=，由()f x 在(,3)-∞-上是减函数，可得()f x 在(3,)-+∞上也是减函数，由()03g =，可得()()033g g =-=，故可得：()()060f f -==，可得()f x 对应的函数草图如图，可得()0xf x ≤的解集为：][3(),6,-∞-⋃-+∞，故答案为：][3(),6,-∞-⋃-+∞.【点睛】本题主要考查函数单调性与奇偶性的综合，注意数形结合解题，属于难题.四、解答题（本大题共3小题，共33分.解答应写出文字说明、证明过程或演算步骤.）21．为了解某项基本功大赛的初赛情况，一评价机构随机抽取40名选手的初赛成绩(满分100分)，作出如图所示的频率分布直方图：（1）根据上述频率分布直方图估计初赛的平均分；（2）假设初赛选手按1:8的比例进入复赛(即按初赛成绩由高到低进行排序，前12.5%的初赛选手进入复赛)，试估计能进入复赛选手的最低初赛分数.注：直方图中所涉及的区间是：[50,60),[60,70),[70,80),[80,90),[90,100].【答案】（1）平均分的估计值为72分；（2）最低初赛分数为85分.【分析】（1）利用每小组中间值乘以每小组频率，再求和即可；（2）先设最低分数为x ，依题意大于x 的成绩的频率为0.125，即解得x .【详解】解：（1）由频率分布直方图得样本平均分550.15650.25750.4850.15950.0572x =⨯+⨯+⨯+⨯+⨯=.因此，初赛平均分的估计值为72分；（2）根据频率分布直方图，设40名选手进入复赛的最低分数为x ，依题意成绩落入区间[90,100]的频率是0.05，成绩落入区间[80,90)的频率是0.15，按初赛成绩由高到低进行排序，前12.5%的初赛选手进入复赛，可判断x 在[80,90)内，则(90)0.0150.050.125x -⨯+=，解得85x =.因此，估计能进入复赛选手的最低初赛分数为85分.22．已知函数()()sin 0f x x x ωωω=+>的最小正周期是π.（1）求ω值；（2）求()f x 的对称中心；（3）将()f x 的图象向右平移3π个单位后，再将所得图象所有点的横坐标伸长到原来的2倍，纵坐标不变，得到函数()y g x =的图象，求()g x 的单调递增区间.【答案】（1）2；（2）,026k ππ⎛⎫- ⎪⎝⎭，Z k ∈；（3）52,266k k ππππ⎡⎤-+⎢⎥⎣⎦，Z k ∈.【分析】（1）由()2sin 3f x x πω⎛⎫=+ ⎪⎝⎭且2T ππω==，即可求ω值；（2）由（1）知()2sin 23f x x π⎛⎫=+ ⎪⎝⎭，结合正弦函数的对称中心即可求()f x 的对称中心；（3）由函数平移知()sin 23g x x π⎛⎫- ⎝=⎪⎭，结合正弦函数的单调性即可求()g x 的单调递增区间.【详解】（1）()sin 2sin 3f x x x x πωωω⎛⎫=+=+ ⎪⎝⎭，又0ω>，∵2T ππω==，∴2ω=.（2）由（1）知，()2sin 23f x x π⎛⎫= ⎪⎝⎭，令23x k ππ+=，解得26k x ππ=-.∴()f x 的对称中心是,026k ππ⎛⎫- ⎪⎝⎭，Z k ∈.（3）将()f x 的图像向右平移3π个单位后可得：2sin 23y x π⎛⎫=- ⎪⎝⎭，再将所得图像横坐标伸长到原来的2倍，纵坐标不变得到：()sin 23g x x π⎛⎫- ⎝=⎪⎭，由22232k x k πππππ-≤-≤+，解得52266k x k ππππ-≤≤+，Z k ∈.∴()g x 的单调递增区间为52,266k k ππππ⎡⎤-+⎢⎥⎣⎦，Z k ∈.【点睛】关键点点睛：（1）应用辅助角公式求三角函数解析式，结合最小正周期求参数.（2）根据正弦函数的对称中心，应用整体代入求()f x 的对称中心.（3）由函数图像平移得()g x 解析式，根据正弦函数的单调增区间，应用整体代入求()g x 的单调增区间.23．函数()221a xb f x x +=+是定义在()1,1-上的奇函数，且1225f ⎛⎫= ⎪⎝⎭．(1)求实数,a b 的值；(2)用定义证明函数()f x 在()1,1-上是增函数；(3)解关于x 的不等式()()10f x f x -+<．【答案】(1)1a =±，0b =(2)证明见解析(3)102x x ⎧⎫<<⎨⎬⎩⎭．【分析】（1）利用奇函数的性质，结合条件即可得解；（2）利用函数单调性的定义，结合作差法即可得解；（3）利用()f x 的奇偶性、单调性与定义域列式即可得解.【详解】（1）函数()221a xb f x x +=+是定义在()1,1-上的奇函数所以()00f =，则()0001b f b ===+，所以()221a x f x x =+因为1225f ⎛⎫= ⎪⎝⎭，则2112212514a f ⎛⎫== ⎪⎝⎭+，则21a =，所以1a =±，此时()21x f x x =+，定义域关于原点对称，又()()()2211xx f x f x x x --==--+-+，所以()f x 是奇函数，满足题意，故1a =±，0b =.（2）由（1）知()21x f x x =+．设12,x x 是()1,1-内的任意两个实数，且12x x <，()()()()()()221221121222221212111111x x x x x x f x f x x x x x +-+-=-=++++()()()()12122212111x x x x x x --=++，因为()()22121212110,0,10x x x x x x --<+>>+，所以()()120f x f x -<，即()()12f x f x <，所以函数()f x 在()1,1-上是增函数.（3）因为()()10f x f x -+<，所以()()1f x f x -<-，即()()1f x f x -<-，则111111xxx x-<-<⎧⎪-<-<⎨⎪-<-⎩，所以021112xxx⎧⎪<<⎪-<<⎨⎪⎪<⎩，所以12x<<，即此不等式解集为12x x⎧⎫<<⎨⎬⎩⎭．。

2023年浙江省学业水平考试仿真模拟卷(四)+答案解析(附后)

2021-2022学年浙江省学业水平考试仿真模拟卷（四）一、单选题（本大题共18小题，共54分。

在每小题列出的选项中，选出符合题目的一项）1.已知，，，，则集合A可以为( )A. B. C. D.2.( )A. B. C. D.3.i为虚数单位，在复平面内，复数对应的点位于( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限4.已知命题，，则p的否定为( )A. ，B. ，C. ，D. ，5.已知向量，满足，和的夹角为，则( )A. B. C. D. 16.已知a，，则是的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件7.已知函数是定义在上的偶函数，且当时，的图象如图所示，则的值域是( )A. B. C. D.8.为了解学生的身体状况，某校随机抽取了一批学生测量体重.经统计，这批学生的体重数据单位：千克全部介于45至70之间.将数据分成5组，并得到如图所示的频率分布直方图.图中a的值为( )A. B. C. D.9.若，，则的值为( )A. B. C. D.10.的值为( )A. B. C. 1 D. 211.的零点所在区间是( )A. B. C. D.12.随着网络技术的发展，非现金支付变得愈发流行，微信支付和支付宝支付就是两种常用的非现金支付方式.某群体中的成员只用现金支付的概率为，既用现金支付又用非现金支付的概率为，则只用非现金支付的概率为( )A. B. C. D.13.函数的图象可能是( )A. B.C. D.14.在空间中，设m，n为两条不同的直线，，为两个不同的平面，则下列说法中正确的是( )A. 若且，则B. 若，，，则C. 若且，则 D. 若m 不垂直于，且，则m 必不垂直于n15.在三角形ABC 中，，，P 为线段DE 上的动点，若，l ，，则( )A. 1B.C.D. 216.已知三棱柱的侧棱与底面边长都相等，在底面ABC 上的射影为BC 的中点，则异面直线AB 与所成的角的余弦值为( )A. B. C. D.17.如图所示，在长方形ABCD 中，，，E 为线段DC 上的一个动点，现将沿AE折起，使点点D 折起后的点在平面ABC 内的射影K 在直线AE 上，则当点E 从D 运动到C 时，点K所形成的轨迹的长度为( )A. B. C. D.18.已知函数则函数的零点个数是( )A. 2B. 3C. 4D. 5二、填空题（本大题共4小题，共15分）19.已知向量，，__________，__________.20.已知，，当时，关于x的不等式恒成立，则的最小值是__________.21.在中，，，且，则__________.22.在矩形ABCD中，，点E为线段CD中点，如图所示，将沿着AE翻折至点不在平面ABCD内，记线段中点为F，若三棱锥体积的最大值为，则线段AB长度的最大值为__________.三、解答题（本大题共3小题，共31分。

2024年浙江省嘉兴市初中学业水平考试数学模拟试题

2024年浙江省嘉兴市初中学业水平考试数学模拟试题一、单选题1．某校九年1班期末考试数学的平均成绩是82分，小明得了90分，记作8+分，若小亮的成绩记作4-分，表示小亮得了（）分 A ．16B ．76C ．78D ．742．如图是由5个相同的小正方体组成的几何体，该几何体从左面看得到的平面图形是（）A ．B ．C ．D ．3．下列运算结果正确的是（）A ．2=B ．34a a a +=C ．222()ab a b =D ．632a a a ÷=4．若关于x 的不等式组的解表示在数轴上如图所示．则这个不等式组的解集是（）A ．1x ≤B ．1x >C ．01x ≤<D ．01x <≤5．如图，90C ∠=︒，将直角三角形ABC 沿着射线BC 方向平移5cm ，得到三角形A B C '''，并且3cm B C ''=，4cm A C ''=则阴影部分的面积为（）A ． 210cmB ． 214cmC ． 228cmD ． 235cm6．为庆祝中国共产主义青年团成立100周年，某区举办了团课知识竞赛，甲、乙学各派5名学生参加，两队学生的竞赛成绩如图所示，下列关系完全正确的是（）A ．22S S x x <=甲乙甲乙， B ．22S S x x =>甲乙甲乙，C ．22S S x x >=甲乙甲乙， D ．22S S x x =<甲乙甲乙，7．“践行垃圾分类・助力双碳目标”主题班会结束后，米乐和琪琪一起收集了一些废电池，米乐说：“我比你多收集了7节废电池”琪琪说：“如果你给我8节废电池，我的废电池数量就是你的2倍．”如果他们说的都是真的，设米乐收集了x 节废电池，琪琪收集了y 节废电池，根据题意可列方程组为（）A ．()7288x y x y -=⎧⎨-=+⎩B ．782(8)x y x y -=⎧⎨-=+⎩C ．72(8)x y x y -=⎧⎨-=⎩D ．782(8)y x x y -=⎧⎨+=-⎩8．如图1的晾衣架中存在多组平行关系，将晾衣架的侧面抽象成如图2的数学问题，已知P P AB MN PQ ，若2100∠=︒，3130∠=︒，则1∠的度数为（）A ．40︒B ．50︒C ．60︒D ．70︒9．如图，等腰直角ABC V 位于第一象限，2AB AC ==，直角顶点A 在直线y x =上，A 点横坐标为1，两条直角边AB AC 、分别平行于x 轴、y 轴，若双曲线()0ky k x=≠与ABC V 有交点，则k 的取值范围（）A ．12k <<B ．13k ≤≤C ．14k ≤≤D ．14k ≤<10．如图，O e 的半径为4，AB 是O e 的弦，若30OAB ∠=︒，则AB 的长为 ( )．A ．B ．1C ．2D二、填空题11．分解因式：2222m n -=．12．已知二次函数的解析式为21y x bx =++，从数字0，1，2中随机选取一个数作为b 的值，得到的二次函数图像的顶点在坐标轴上的概率是．13．一个三角形3条边长分别为cm x 、()1cm x +、()2cm x +，它的周长不超过39cm ，则x 的取值范围是．14．如图，正方形ABCD 的对角线相交于点O ，点O 又是另一个正方形A B C O '''的一个顶点．若两个正方形的边长均为2，则图中阴影部分图形的面积为．15．一根蜡烛长30厘米，点燃后匀速燃烧，经过50分钟其长度恰为原长的一半．在燃烧的过程中，如果设蜡烛的长为y （厘米），燃烧的时间为t （分钟），那么y 关于t 的函数解析式为（不写定义域）．16．如图．将扇形AOB 翻折，使点A 与圆心O 重合，展开后折痕所在直线l 与»AB 交于点C ，连接AC ．若3OA =，则图中阴影部分的面积是．三、解答题17．（13- （2）求x 的值：2327x =18．如图，矩形ABCD 的对角线AC ，BD 相交于点O ，过点C 作BD 的平行线交AB 的延长线于点E ．(1)求证：AC CE =．(2)若120BOC ∠=︒，4CE =，求AB 的长． 19．计算（12 (220141142π-⎛⎫--+-- ⎪⎝⎭（2）找规律：观察下列一组算式的特征，并探索规律：① 11=；123=+= ；③ 1236=++=；④ 123410=+++=．根据以上算式的规律，解答下列问题：（1）()23333312345++++==；（2；（用含n 的代数式表示）（3）简便计算：3331112...20+++20．已知小明所在学校的宿舍、食堂、图书馆依次在同一条直线上，食堂离宿舍0.6km ，图书馆离宿舍1.2km ．周末，小明从宿舍出发，匀速走了10min 到食堂；在食堂停留15min 吃早餐后，匀速走了10min 到图书馆；在图书馆停留30min 借书后，匀速走了15min 返回宿舍．下面图中x 表示时间，y 表示离宿舍的距离，图象反映了这个过程中小明离宿舍的距离与时间之间的对应关系．请根据相关信息，解答下列问题： (1)①填表：②填空：小明从图书馆返回宿舍的速度为______km/min ；③当3580x ≤≤时，请直接写出小明离宿舍的距离y 关于时间x 的函数解析式．(2)当小明在图书馆停留25min 时，同宿舍的小亮也从宿舍出发匀速步行直接到图书馆，如果小亮的速度为0.08km/min ，那么他在去图书馆的途中遇到小明时离宿舍的距离是多少？（直接写出结果即可）21．如图1是某门禁自动识别系统，主要由可旋转摄像机和其下方固定的显示屏构成．图2是其示意图，已知摄像机长20cm AB =，点O 为摄像机旋转轴心，O 为AB 的中点，显示屏的上沿CD 与AB 平行，15cm CD =，AB 与CD 连接，杆OE AB ⊥，10cm OE =，2CE ED =，点C 到地面的距离为60cm ．若AB 与水平地面所成的角的度数为35︒．(参考数据：sin350.574︒≈，cos350.819︒≈，tan350.700︒≈，结果精确到0.1cm )(1)求显示屏所在部分的宽度CM ； (2)求镜头A 到地面的距离．22．芜湖市已建成并开放“芜湖书屋”55家，可谓“半城山水，满城书香”．政府着力打造高品质城市阅读空间，努力做到人人享阅读，处处能阅读，时时可阅读，切实提升了城市品位和文化氛围．市区某校九年级二班调查了同学们最喜欢的“芜湖书房”情况，上榜五大书房，分别是A 、滨江书苑，B 、悦享书吧，C 、赤铸书院，D 、葵月书房，E 、占川书局，并绘制了如下两幅不完整的统计图．(1)该班共有学生______人，请把条形统计图补充完整；(2)扇形统计图中，m =______，n =______，最喜欢滨江书苑所对应的扇形圆心角为______度；(3)小鹏和小兵均选择了葵月书房，若从选择了葵月书房的学生中随机选取2人参加该书房志愿者活动，求恰好是小鹏和小兵当选葵月书房志愿者的概率，并说明理由．23．如图，在平面直角坐标系中，已知直线142y x =-+与y 轴交于点A ，与x 轴交于点B ，点C 的坐标为()2,0-．(1)求经过A ，B ，C 三点的抛物线的表达式；(2)如果M 为抛物线的顶点，连接,AM BM ，求ABM V 的面积． 24．【教材呈现】如图是人教版八年级下册第48页部分内容：如图，点D 、E 分别是ABC V 的边AB 与AC 的中点，根据画出的图形，可以猜想：DE BC ∥且12DE BC =．对此，我们可以用演绎推理给出证明（1）请完成教材的证明；【结论应用】（2）如图1，在四边形ABCD 中，AD BC =，P 是对角线BD 的中点，M 是DC 的中点，N 是AB 的中点．请判断PMN V 的形状，并说明理由．（3）如图2，四边形ABCD 中，AD BC =，M 是DC 中点，N 是AB 中点，连接NM ，延长BC 、NM 交于点E ．若234D DCB ∠+∠=︒，求E ∠的度数．。

2024年浙江省初中学业水平考试数学模拟试题

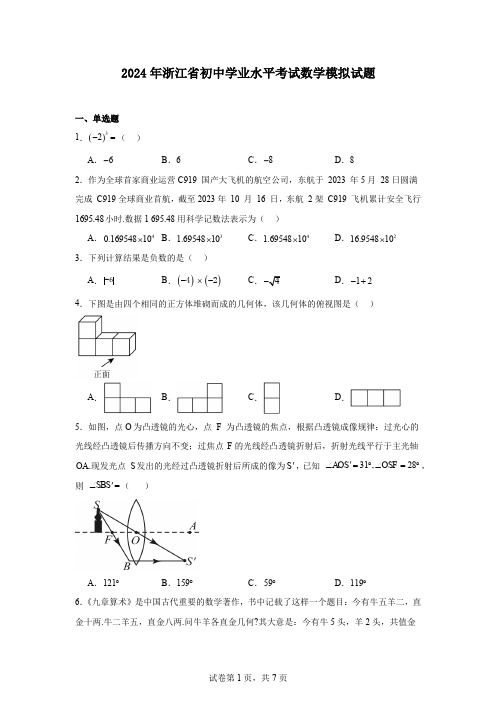
2024年浙江省初中学业水平考试数学模拟试题一、单选题 1．()32-=（） A ．6-B ．6C ．8-D ．82．作为全球首家商业运营C919 国产大飞机的航空公司，东航于 2023 年5月 28日圆满完成 C919全球商业首航，截至2023年 10 月 16 日，东航 2架 C919 飞机累计安全飞行1695.48小时.数据1 695.48用科学记数法表示为（）A ．40.16954810⨯B ．31.6954810⨯C ．41.6954810⨯D ．216.954810⨯3．下列计算结果是负数的是（）A ．6-B ．()()42-⨯-C ．D ．12-+4．下图是由四个相同的正方体堆砌而成的几何体，该几何体的俯视图是（）A ．B ．C ．D ．5．如图，点O 为凸透镜的光心，点 F 为凸透镜的焦点，根据凸透镜成像规律：过光心的光线经凸透镜后传播方向不变；过焦点 F 的光线经凸透镜折射后，折射光线平行于主光轴OA .现发光点 S 发出的光经过凸透镜折射后所成的像为S '，已知 31,28AOS OSF ∠=︒∠='︒，则 SBS '∠=（）A ．121︒B ．159︒C ．59︒D ．119︒6．《九章算术》是中国古代重要的数学著作，书中记载了这样一个题目：今有牛五羊二，直金十两.牛二羊五，直金八两.问牛羊各直金几何?其大意是：今有牛5头，羊2头，共值金10两；牛2头，羊5头，共值金8两．问牛、羊每头各值金多少?设每头牛值x 两金，每头羊值y 两金，则可列方程组为( ) A ．5282510x y x y +=⎧⎨+=⎩ B ．5210258x y x y +=⎧⎨+=⎩C ．2285210x y x y +=⎧⎨+=⎩D ．5510528x y x y +=⎧⎨+=⎩7．为检测学生体育锻炼效果，从某班随机抽取10名学生进行篮球定时定点投篮检测，投篮进球数统计如图所示．对于这10名学生的定时定点投篮进球数，下列说法中错误的是（）A ．中位数是5B ．众数是5C ．平均数是5.2D ．方差是2二、多选题8．如图，在ABCD Y 中，10AB =，6BC =. E 是边AB 的中点，过点E 作AD 的平行线，交以AB 为直径的E e 于点F ，交 CD 于点H ，连接DF 并延长，交BC 于点G ，则BG 的长为( )A ．3B ．4C ．5D ．6三、单选题9．已知二次函数²y x bx c =++与x 轴只有一个交点，且图象经过两点()1,4A p -，()21,4B q p +，则p q ，满足的关系为( )A ．24g p =B ．2qp =C ．()212q p +=D ．()214q p +=10．如图，在矩形ABCD 中，6AB =，8BC =，点E 在线段BD 上(不与点B ，点D 重合)，2AED ADE ∠=∠，则DE 的长为( )A ．7.8BC ．7.5D ．8四、填空题11．因式分解：24a -=．12．两个不透明的布袋内装有除颜色外，其余完全相同的小球.甲袋中有2 个红球，1个白球，乙袋中有1 个红球，1个白球．搅匀后，从两个袋子中各随机摸出一个球，则摸出的两个球都为白球的概率为.13．如图，已知线段 AB ，分别以点 A 、点 B 为圆心，AB 的长为半径画弧，两弧交于点 C ，连结AC BC ，，则tan ABC ∠=．14．关于x 的一元二次方程²20ax bx ++=（0a ≠，a 和b 为常数)的两个根分别为1221x x =-=，，则抛物线22y ax bx =++的对称轴为直线.15．如图，O e 与直线l 相交，圆心O 到直线l 的距离OA =在直线l 上取点B 使3AB =，将直线l 绕点B 逆时针旋转15︒后得到的直线m ，若直线m 恰好与O e 相切于点C ，则O e 的半径为．16．如图，正方形ABCD 中，点E 在边AB 上，且 114BE AB ==，点F 在边BC 上，点G 在边CD 上，90GFE ∠=︒．(1)若tan 3GEF ∠=，则GE 的长为； (2)若EFG V 与△FCG 相似，则GE 的长为．五、解答题17．化简并求值：()()262x x x x -+++，其中2x =-．18．已知平面直角坐标系中，一次函数 1y k x b =+（1,k b 为常数， 10k ≠）的图象与反比例函数 2k y x=(2k 为常数， 20k ≠)的图象都经过点()1,9A 和点(),3B a ，求,a b 的值． 19．如图，AB 为O e 的直径，C 是O e 上一点，连结AC ，以点A 为圆心，AC 的长为半径作弧交O e 于点D ，连接AD CD ，，CD 与AB 相交于点E ．(1)求证：CE DE = ；(2)若 330CE ACE =∠=︒，，求线段 BE 的长．20．某校九年级共8个班准备开展数学项目化学习，学生根据前期调研确定了“时光刻漏”“制作杆秤”“话说杭州GDP ”三个项目，每个班单独成立学习小组，其中每4人为一个小组(若最后剩余不足3人，则剩余的学生全部加入其中一个已成立的小组；否则剩余的学生单独成立一个学习小组)，每小组只选择一个项目进行研究学习，依据收集的学生选择情况，绘制了如下表格：结合上述信息回答下列问题： (1)=a ________； b =________.(2)方方根据表格估计该校九年级的人数，方方说：“根据表格信息我可以估计出该校九年级至少有320人．”方方的说法是否正确？请说明理由． 21．在劳动课上，小华同学所在小组进行了风筝框架设计比赛(1)小华设计的风筝框架平面图如图1，已知. AB AD CB CD ==，，AC 与BD 交于点O ，求证: BO DO =(2)小明提出了改进建议：制作风筝框架只需要两个支架AC 和BD (如图2)，当AC 垂直平分BD 时即可固定风筝.现在有总长度为120cm 的细木条用于制作该风筝框架，小明同学想做面积最大的风筝，请你帮他设计：当AC 为何值时，风筝的面积最大，面积最大值为多少？ 22．综合与实践【问题情境】在一次数学探究课上，老师带领大家一起研究特殊三角形的性质.圆圆小组对直角三角形进行了各种类型的折叠探究，并尝试用数学方法说明发现的结论. 类型 1．如图1，沿着DE 折叠，使点B 与点A 重合，折痕交AB 于点E ，交BC 于点D ，他们发现：点D 的位置与AC 和BC 的长有关．问题1.若3BC =，1AC =，则BD =________．【变式探究】类型2．如图2，点D 为CB 上一点，沿着AD 折叠，AC 恰好落在AB 上，点C 的对称点为'C ，折痕交BC 于点 D ．问题 2．①若 53AB AC =，则 BD CD=． ②请猜测AB AC 与 BD CD有何关系，并证明．【拓展思考】方方小组对等腰三角形进行了各种折叠探究.如图3，在等腰三角形ABC 中，BC 为底边，A ∠为钝角，点D 为边AC 上一点，将ABD △沿直线BD 翻折得到A BD 'V ．问题3．若4AD CD ==，6A C '=，求BD 的长．23．在生活中，我们会观察到这样的现象：当道路上车辆增多，车流密度增大，司机会被迫降低车速；当车流密度减小，车速又会增加.我们通常用车流密度K ，速度 v ，交通量Q 对道路的交通状况进行宏观描述.车流密度K 是指在单位长度(通常为1km )路段上，一条道路上某一瞬时的车辆数，它是表示在一条道路上车辆的密集程度.交通量Q 是指单位时间(通常为1小时)通过道路某断面的车辆数目.已知车流速度 v (单位：km/h )是车流密度K (单位：辆/km )的函数.某城市某条道路上，v 关于K 的函数图象如图所示.当车流密度030K <<时，则速度v 的值为理论最高值 80f v =；②当车流密度30270K ≤≤时，v 关于K 的函数关系为v a bK =- (a ，b 是常数)，若车流密度K 达到最大值270时，则0v =.已知v 关于K 的函数图象经过0(30)8B ，. (1)若 120K =辆/km 时，求对应v 的值.(2)点,()P K v 是图象BC 上一个动点，过点 P 作横轴的垂线交于点 E ，作纵轴的垂线交于点 D ，此时矩形PDOE 所围成的面积为交通量Q (单位：辆/小时)，求交通量Q 的最大值. 24．如图1， ABC V 是等边三角形，点 D ，点 E 分别是AB ，BC 上的动点，且满足 AD BE =，连接CD ，AE 交于点H ，以CE 为直径作O e 交CD 于点F ．(1)求证：BAE ACD ≌△△． (2)如图 2，连接,AF EF ，①若 630AH AFH CF =∠==o ，，求直径CE 的长．②若()3,DH a FH a FH CF λ=⋅>=⋅，当 CHE AHF S S =V V 时，用含λ的代数式表示a ．。

浙江省普通高中学业水平考试数学模拟试题

浙江省普通高中学业水平考试数学模拟试题一、选择题(共25小题，1－15每小题2分,16－25每小题3分,共60分.每小题给出的选项中只有一个是符合题目要求的，不选、多选、错选均不得分.)1、设集合M={0，1，2｝，则（）A.1∈M B。

2∉M C。

3∈M D.｛0｝∈M2、函数y=(）A。

［0,+∞）B。

［1,+∞)C。

(－∞，0] D。

(－∞，1］3、若关于x的不等式mx－2>0的解集是{x｜x>2｝,则实数m等于(）A.－1 B。

－2 C.1 D.24、若对任意的实数k，直线y－2=k(x+1）恒经过定点M，则M的坐标是（）A。

（1，2) B。

（1，－2）C。

（－1,2) D。

（－1，－2）5、与角－6π终边相同的角是（)A.56πB。

3πC。

116π D.23π6、若一个正方体截去一个三棱锥后所得的几何体如图所示，则该几何体的正视图是（）（第6题图）A. B。

C。

D.7、以点（0，1）为圆心，2为半径的圆的方程是（）A。

x2+(y－1）2=2 B. （x－1）2+y2=2 C。

x2+（y－1）2=4 D. （x－1）2+y2=48、在数列｛a n }中，a1=1,a n+1=3a n(n∈N＊），则a4等于(）A.9B.10C.27 D。

819、函数y=的图象可能是(）xxxA。

B. C。

D。

10、设a,b是两个平面向量，则“a＝b”是“|a｜＝｜b|”的（）A.充分而不必要条件B 。

必要而不充分条件 C.充要条件D.既不充分也不必要条件11、设双曲线C ：2221(0)3y x a a-=>的一个顶点坐标为（2，0),则双曲线C 的方程是（） A. 221163y x -=B 。

221123y x -=C 。

22183y x -= D.22143y x -= 12、设函数f （x)＝sinxcosx ，x ∈R ，则函数f(x ）的最小值是（）A.14-B 。

2022年7月浙江省普通高中学业水平考试数学仿真模拟试卷_3

2022年7月浙江省普通高中学业水平合格性考试数学仿真模拟试卷04一、单选题(本大题共18小题，每小题3分，共54分) 1．设集合P={1，2，3，4}，Q={x|﹣2≤x≤2，x ∈R}则P∩Q 等于 A ．{﹣2，﹣1，0，1，2}B ．{3，4}C ．{1，2}D ．{1} 【答案】C 【解析】【详解】试题分析：依题意，共同元素为{}1,2. 2．函数()4ln 1xf x x x-=++的定义域为（） A ．()1,4- B ．()(]1,00,4-⋃ C ．()()1,00,4- D ．(]1,4-【答案】B 【解析】【分析】根据对数的真数为正数、分母不为零以及偶次根式的被开方非负列式可得结果. 【详解】要使函数有意义，则有10400x x x +>⎧⎪-≥⎨⎪≠⎩解得14x -<≤且0x ≠.所以函数()f x 的定义域为(1,0)(0,4]-. 故选：B3．在同一坐标系中，函数12xy ⎛⎫= ⎪⎝⎭与2log y x =的图象大致是（）A ．B ．C ．D ．【答案】A【分析】利用指数函数和对数函数的图象和性质判断即可. 【详解】解：由于12xy ⎛⎫= ⎪⎝⎭中的底数1012<<，所以为减函数，所以排除BC ，由于2log y x =中的底数21>，所以为增函数，所以排除D ，故选：A.4．若α为钝角，4sin 5α，则cos α=（） A ．15-B ．15C ．35D ．35【答案】D 【解析】【分析】直接利用同角三角函数基本关系式22cos sin 1αα+=求解. 【详解】α为钝角，4sin 5α，3cos 5α∴==-.故选：D.5．若()()12212,a e me m R b e e m =-∈=--与平行则的值是（） A ．m=0 B ．m= -1C ．m=12D ．m= -2【答案】C 【解析】【详解】∵2112(2)2b e e e e =--=-又∵()()12212a e me m R b e e =-∈=--与平行 ∴121m-=-，即12m =6．图所示几何体的左视图是（）A ．B ．C ．D ．【答案】A 【解析】直接根据三视图定义得到答案. 【详解】根据图形知：几何体的左视图是A 选项. 故选：A.7．函数221()x f x x+=．A ．是奇函数且在区间2⎫+∞⎪⎪⎝⎭上单调递增B ．是奇函数且在区间2⎫+∞⎪⎪⎝⎭上单调递减 C ．是偶函数且在区间2⎫+∞⎪⎪⎝⎭上单调递增D ．是偶函数且在区间2⎫+∞⎪⎪⎝⎭上单调递减【答案】A 【解析】【详解】由222()121()()x x f x f x x x -++-==-=--可知()f x 是奇函数，排除C ，D ，且()()819212,13221f f ++====，由(2)(1)f f >可知B 错误，故选A ． 8．不等式22150x x -++≤的解集为（）A ．532x x ⎧⎫-≤≤⎨⎬⎩⎭B ．52x x ⎧≤-⎨⎩或}3x ≥C ．532x x ⎧⎫-≤≤⎨⎬⎩⎭D ．{3x x ≤-或52x ⎫≥⎬⎭【答案】B 【解析】【分析】将式子变形再因式分解，即可求出不等式的解集；【详解】解：依题意可得22150x x --≥，故()()2530x x +-≥，解得52x ≤-或3x ≥，所以不等式的解集为52x x ⎧≤-⎨⎩或}3x ≥故选：B ．9．已知函数()22,0,0x x f x x x ⎧<=⎨-≥⎩，若x ∀∈R ，()()29430f mx f x +-≤恒成立，则实数m 的取值范围为（） A ．[)21,+∞ B ．[)13,+∞C ．27,16⎡⎫+∞⎪⎢⎣⎭D ．[)15,+∞【答案】C 【详解】解：因为()22,0,0x x f x x x ⎧<=⎨-≥⎩，所以函数图象如下所示：由函数图象可知函数为定义域R 上单调递减的奇函数，当0x ≥时()2f x x =-，则()()()223399f x x x f x =-=-=，当0x <时()2f x x =，则()()()223399f x x x f x ===，所以()()39f x f x =，因为x ∀∈R ，()()29430f mx f x +-≤恒成立，即x ∀∈R ，()()()()2943934912f mx f x f x f x ≤--=-=-恒成立，所以2912mx x ≥-恒成立，即29120mx x -+≥恒成立，当0m =，显然不成立，当0m ≠时，则，解得2716m ≥，即27,16m ⎡⎫∈+∞⎪⎢⎣⎭；故选：C10．已知1cos 64πα⎛⎫+= ⎪⎝⎭，则sin 26πα⎛⎫-= ⎪⎝⎭（）A ．78- B ．78 C ．716D ．716-【答案】B 【详解】∵1cos 64πα⎛⎫+= ⎪⎝⎭，∴2sin 2sin 2cos 212cos 66266πππππαααα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-+=-+ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦2171248⎛⎫=-⨯= ⎪⎝⎭.故选：B.11．已知,R αβ∈，“tan tan αβ=”是“π,k k αβ=+∈Z ”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A 【解析】【分析】结合函数tan y x =的周期分别判断充分性与必要性是否成立. 【详解】当tan tan αβ=时，由于函数tan y x =的周期为π，所以可得π,k k αβ=+∈Z ，即充分性满足；当3,22ππαβ==时，其正切值不存在，所以π,k k αβ=+∈Z 推不出tan tan αβ=，不满足必要性，所以“tan tan αβ=”是“π,k k αβ=+∈Z ”的充分不必要条件. 故选：A12．要得到函数sin 2y x =的图象，只需将函数cos 2y x =的图象上的所有点沿x 轴A ．向右平移4π个单位长度 B ．向右平移2π个单位长度 C ．向左平移4π个单位长度D ．向左平移2π个单位长度【答案】A 【解析】【分析】根据sin 2cos(2)2x x π=-及平移变换的规则可得正确的选项.【详解】因为sin 2cos(2)2x x π=-，所以由cos2y x =图像平移到cos(2)2y x π=-，只需向右平移4π个单位．故选：A.13．已知二次函数221y x ax =-+在区间()2,3内是单调函数，则实数a 的取值范围是（） A ．(][),23,-∞⋃+∞ B ．[]2,3 C ．(][),32,-∞-⋃-+∞ D ．[]3,2--【答案】A 【解析】【分析】结合图像讨论对称轴位置可得. 【详解】由题知，当222a --≤或232a--≥，即2a ≤或3a ≥时，满足题意. 故选：A14．已知向量1a =，3a b +=，26a b -=，则23a b +=（）A B C D 【答案】D 【解析】【分析】由已知平方可得232b =，14⋅a b =，再对23a b +平方即可求出.【详解】因为1a =，3a b +=，26a b -=，平方可得21a =，2223a a b b +⋅+=，22446a a b b -⋅+=，解得232b =，14⋅a b =，故22231412349124912242a b a b a b +=++⋅=+⨯+⨯=，∴82232a b +=. 故选：D ．15．如图，在长方体1111ABCD A B C D -中，2AB BC ==，11AA =，则1BC 与平面11BB D D 所成角的余弦值为（）A 10B 26C 15D 6 【答案】C 【解析】【分析】连接11A C 交11B D 于点O ，连接BO ，证明1OC ⊥平面11BB D D ，则1C BO ∠为则1BC 与平面11BB D D 所成角，在1Rt BOC △中，求出1C BO ∠即可. 【详解】解：连接11A C 交11B D 于点O ，连接BO ，由2AB BC ==，可得1111D C B A 为正方形即111OC B D ⊥，由长方体的性质可知1BB ⊥面1111D C B A ，1OC ⊂面1111D C B A ，所以11OC BB ⊥，且1111BB B D B ⋂=， ∴1OC ⊥平面11BB D D ，则1C BO ∠为则1BC 与平面11BB D D 所成角，在1Rt BOC △中，12OC =，15,3BC OB ==， ∴11315cos 55OB OBC BC ∠===，即1BC 与平面11BB D D 所成角的余弦值为155. 故选：C.16．若0,0,1x y x y >>+=，且14m x y+>恒成立，则实数m 的取值范围是（）A ．{}3m m <B ．{}6m m <C ．{}5m m <D ．{}9m m <【答案】D 【解析】【分析】结合“1”的代换，利用基本不等式求得14x y+的最小值后可得m 的范围．【详解】因为0,0,1x y x y >>+=，所以141444()5529x y x yx y x y x y y x y x ⎛⎫+=++=++≥+⨯= ⎪⎝⎭，当且仅当4x y y x =，即12,33x y ==时等号成立，所以9m <．即m 的范围是{|9}m m <．故选：D ．17．平面向量,a b 满足4a =，a 与a b -的夹角为120，记()()1m ta t b t =+-∈R ，当m 取最小值时，a m ⋅=（） A ．23 B ．12C ．43D ．4【答案】B 【解析】【分析】设OA a =，OB b =，作出图象，根据平面向量基本定理可知,,m a b 起点相同，终点在直线AB 上，可知min 23m =且,30a m <>=，由向量数量积定义可求得结果. 【详解】设OA a =，OB b =，则a b BA -=，如图所示，a 与ab -的夹角为120，120OAB ∴∠=，60OAC ∠=；()()1m ta t b t =+-∈R 且()11t t +-=，,,m a b ∴起点相同时，终点共线，即在直线AB 上，∴当m AB ⊥时，m 最小，又4a =，min 23m ∴=,30a m <>=，42312a m ∴⋅=⨯=. 故选：B.18．设函数()f x 的定义域为R ，()1f x +为偶函数，()2f x +为奇函数，当[]1,2x ∈时，()2f x ax b =+，若()()036f f +=，则12f ⎛⎫= ⎪⎝⎭（）A ．94-B ．32-C ．72-D ．52【答案】C 【详解】因为()1f x +是偶函数，所以()()11f x f x -+=+①，因为()2f x +是奇函数，所以()()22f x f x -+=-+②．令1x =，由①得：()()024f f a b ==+，由②得：()()()31f f a b =-=-+，因为()()036f f +=，所以()462a b a b a +-+=⇒=，令0x =，由②得：()()()22208f f f b =-⇒=⇒=-，所以当[]1,2x ∈时，()228f x x =-，111711222232f f f f ⎛⎫⎛⎫⎛⎫⎛⎫=-+=+==- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选：C ．二、填空题(本大题共4小题，每空3分，共15分)19．已知幂函数()f x x α=的图像过点，则α=________，(16)f =_________．【答案】 124【详解】由题意知，2α=12α=，所以12()f x x =，可知12(16)16=4f =. 故答案为：12；420．在△ABC 中，若b ＝2，c ＝C ＝23π，则a ＝________．【答案】2 【解析】【分析】利用余弦定理直接求解可得. 【详解】∵c 2＝a 2＋b 2－2ab cos C ，223∴（）＝a 2＋22－2a ×2×cos 23π， ∴a 2＋2a －8＝0，即(a ＋4)(a －2)＝0，∴a ＝2或a ＝－4(舍去)．∴a ＝2．故答案为：221．已知平面向量()()1,1,,2a b t =-=，若()a b a +⊥，则t =__________.【答案】0【详解】解：因为()()1,1,,2a b t =-=，所以()()()1,1,21,1a b t t +=-+=+，又()a b a +⊥，所以()()()11110a b a t +⋅=⨯++⨯-=，解得0=t ；故答案为：022．如图，在棱长为1的正方体1111ABCD A B C D -中，,E F 分别为棱1111,A D C D 的中点，若点,,N P M 分别为线段11,,BD EF BC 上的动点，则PM PN +的最小值为___________.【答案】1【详解】如上图所示，当P 点运动时，M 位于EF 中点时，PM 最小；若BN BQ =，则BPN BPQ ≅，即PN PQ =，当,,M P Q 三点共线时，PM PQ +最小，即PM PN +最小，此时1PM PN += 故答案为：1三、解答题(本大题共3小题，共31分)23（10分）．已知函数f （x ）＝sin x .（1）判断f （x ）是否是三角函数，并求2f π⎛⎫ ⎪⎝⎭的值；（2）求f （x ）的单调递增区间.【答案】（1）f （x ）是三角函数，1；（2）222,2()k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦【解析】【分析】（1）f （x ）是三角函数，代入数据，即可得答案.（2）根据正弦函数的性质，即可得答案.【详解】（1）f （x ）是三角函数，=sin 122f ππ⎛⎫= ⎪⎝⎭；（2）f （x ）的单调递增区间为222,2()k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦24（10分）．如图，三棱锥P ABC -中，AC CB PA PC ===，120ACB ∠=︒，90BCP ∠=︒.(1)证明：平面PAB ⊥平面ABC ；(2)求直线PB 与平面PAC 所成角的正弦值.【答案】(1)证明见解析；3【分析】（1）若,D E 分别是,AB BP 中点，连接,,CD DE EC ，由已知条件及勾股定理可得DE CD ⊥、CD AB ⊥，根据线面垂直的判定和面面垂直的判定即可证结论.（2）由（1）可得PA PB ⊥，结合面面垂直的性质求P 到面ABC 的距离，由等体积法P ABC B PAC V V --=求B 到面PAC 的距离，进而求直线PB 与平面PAC 所成角的正弦值.(1)如下图，若,D E 分别是,AB BP 中点，连接,,CD DE EC ，令2AC CB PA PC ====，由90BCP ∠=︒，即△CBP 为等腰直角三角形，则2CE在等腰△ACB 中120ACB ∠=︒，可得 1CD =且CD AB ⊥，又112DE PA ==，所以222DE CD CE +=，即DE CD ⊥，又DE AB D ⋂=且,DE AB ⊂面PAB ，所以CD ⊥面PAB ，而CD ⊂面ABC ，故平面PAB ⊥平面ABC .(2)由（1）知：22PB =23AB =222PA PB AB +=，即PA PB ⊥，若h 为P 到AB 上的高，则h AB PA PB ⋅=⋅，可得26h =，又面PAB ⊥面ABC ，且面PAB ⋂面ABC AB =，易知P 到面ABC 的距离为26h . 所以211261222sin1203323P ABC ABC V h S -=⋅=⨯⨯︒=P ABC B PAC V V --=，212sin 6032PAC S =⨯⨯︒= 若B 到面PAC 的距离为d ，则12233d 26d =2PB = 所以直线PB 与平面PAC 所成角的正弦值263322d PB ==⨯.25（11分）．已知函数()()()2f x x x a a R =-+∈，(1)当1a =时，①求函数()f x 单调递增区间；②求函数()f x 在区间[]4,1-的值域；(2)当[]3,3x ∈-时，记函数()f x 的最大值为()g a ，求()g a 的表达式．【答案】(1)①(],1-∞-，1,2⎡⎫+∞⎪⎢⎣⎭；②[]18,0-；(2)()23,44,443,4a a a a g a a a a ⎧+≥-⎪++⎪=-<<-⎨⎪--≤-⎪⎩【分析】(1)①分别在1x ≤-与1x >-时，结合二次函数单调性即可得解；②利用①中单调性确定最值点，求出最值即可作答.(2)分别在3,2,23a a a -≥-≤<-<三种情况下，结合二次函数对称轴位置与端点值的大小关系确定最大值即可作答.(1)当1a =时，()()222,1212,1x x x f x x x x x x ⎧-++≤-=-+=⎨-->-⎩， ①当1x ≤-时，()22f x x x =-++在(],1-∞-上单调递增，当1x >-时，()22f x x x =--在1(1,)2-上单调递减，在1[,)2+∞上单调递增；所以()f x 的单调递增区间为(],1-∞-，1[,)2+∞. ②由①知：()f x 在[]4,1--上单调递增，在1(1,)2-上单调递减，在1(,1]2上单调递增，于是有()()min 1min{4,()}2f x f f =-，()()()max max{1,1}f x f f =-，而()418f -=-，1)(294f =-，()10f -=，12f ，则()min 18f x =-，()max 0f x =，所以()f x 在[]4,1-上的值域为[]18,0-.(2)依题意，()()()()()()()22222,222,x x a x a x a x a f x x x a x a x a x a ⎧-+=+--≥-⎪=⎨--+=-+-+<-⎪⎩， ①当3a -≥，即3a ≤-时，()()222f x x a x a =-+-+，对称轴为2522a x -=≥，当232a -≥，即4a ≤-时，()f x 在[]3,3-上单调递增，max ()()(3)3g a f x f a ===--，当52322a -≤<，即43a -<≤-时，()f x 在23,2a -⎡⎫-⎪⎢⎣⎭上单调递增，在2,32a -⎛⎤ ⎥⎝⎦上单调递减，2max 244()()()24a a a g a f x f -++===，②当2a -≤，即2a ≥-时，若[]3,2x ∈-有()0f x ≤，若(]2,3x ∈有()0f x >，因当(]2,3x ∈时，()()222f x x a x a =+--，对称轴222a x -=≤，则()f x 在(]2,3上单调递增，()()max ()33g a f x f a ===+，③当23a <-<，即32a -<<-时，25222a -<<， ()f x 在23,2a -⎡⎫-⎪⎢⎣⎭上单调递增，在2,2a a -⎛⎫- ⎪⎝⎭上单调递减，在(],3a -上单调递增， ()()2max244()max 3,max 3,24a a a g a f x f f a ⎧⎫⎧-⎫++⎛⎫===+⎨⎬⎨⎬ ⎪⎝⎭⎩⎭⎩⎭，若24434a a a +++≥，即2a -<-时，()3g a a =+，若24434a a a +++<，即3a -<<-时，()2444a a g a ++=，综上所述：()23,44,443,4a a a a g a a a a ⎧+≥-⎪++⎪=-<<-⎨⎪--≤-⎪⎩。

浙江高中数学学业水平考试模拟试题

2.2.3.3.4.4.5.5. 浙江省2020年高中数学1月学业水平考试模拟试题A选择题部分、选择题（本大题共18小题，每小题不选、多选、错选均不得分）已知集合M {x|1 x 3}, NA. {1}B. {1,2}【解析】由交集定义可得：M I N 不等式（x 1)(x 2) 0的解集为3分，共54分，每小题列出的四个选项中只有一个是符合题目要求的,{1,2}，则M I NC. 0D.[1,2]A. {x|C. { x|x右sinA. 89 圆x2x 2}1 一或x2由二次函数1}1,2，故选B.B. {x| 1 x 2}D. { x | x 2或x的图象可知，不等式(x 1)(x2） 0的解是一1 x 2 ,故选A.B.C. 79D.cos2y2 4x A.第一象限【解析】化简双曲线方程为2yB.2sin2 ,故选B.91 0的圆心在C.第三象限D.第四象限24x 2y 1 0得到(x 2)2x2-2y2=1,则它的左焦点的坐标为A」-*。

） 5B. (- y-, 0) (y 1)24, 圆心为（2,1）,在第一象限，故选A.0) D.(-73, 0)v2— 9\/2—d 【解析】由x 2y—12 2111一1，可得a22b2a2 b2 TT得c詈，所以左焦点坐标为（-Y6,0).故选C.26.已知向量 a,b 满足 |a| 1, |b| 2 , |a b| J6 ,则 a bA. 1B. 1C. 3D. 226 .【答案】A题答案为A.y, x7 .若变量x, y 满足约束条件x y, 1 ,则z =2x + y 的最大值是 y (1)8 .【答案】B【解析】如图，先根据约束条件画出可行域,当直线z =2x +y 过点A (2, - 1)时，z 最大，最大值是3,故选B.9 .若平面和直线a, b 满足al A, b ,则a 与b 的位置关系一定是A.相交B.平行C.异面D.相交或异面10 【答案】D【解析】当A b 时，a 与b 相交；当A b 时，a 与b 异面.故答案为D.11 过点(0,2)且与直线x y 0垂直的直线方程为A. x y 2 0B. x y 2 0C. xy 2 0D. x y 2 09 .【答案】A【解析】由x y 0可得直线斜率k 1 1,根据两直线垂直的关系得 k 〔 k 2 1,求得k 21, 点斜式，可求得直线方程为y 1(x 0) 2,化简得x y 2 0,故选A.【解析】由| a b | 66 , (a b)26,即 a 2 2ab b 216,又 |a| 1, |b| 2,则 a b - 2.所以本 A. 2B. 3C. 4D.5再利用10.函数f(x) log3(|x| 1)的大致图象是211.【答案】B12.【答案】B1 . 卜右log a3 log b3不一定有a b 1 ,比如a b 3 ,从而3a3b 3不成立.故选B.313.某几何体的三视图如图所示，则该几何体的体积为12.【解析】该几何体为半个圆柱与半个圆锥形成的组合体,1 1 ,4、2 c4 _ —冗(一) 4 8 冗2 3 2A. 12几. 64冗B ——3c 32冗C ——3D. 16几13. 等差数列｛a n｝中,已知|%| 即|,且公差d 0, 则其前n项和取最小值时的n的值为A. 6B. 7C. 8D. 9A.【解析】由函数f(x) log3(|x|21),可知函数f X是偶函数，排除C, D;定义域满足:选B.1 0,可得X 1或x 1 .当x 1时，f(x) log3(|x| 1)是递增函数，排除A.故211.设a, b都是不等于1的正数，则“3a3b 3” 是“ log a3 log b3” 的A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件【解析】若3a3b 3 ,则a b 1,从而有log a3 log b3,故为充分条件.一一1 4.2故V 一冗(一)2 2B.D.13.【答案】C相等的两部分，所以即为平面ABD .14. 14. 15. 15. 【解析】因为等差数列 a n 中，包| 1a l 1|,所以a 6 0,a 11 0,a 6 a 11,a 1 d 2 S n —[(n 8)2 64],所以当n 8时前n 项和取最小值.故选C.2..一… 兀兀 ....... .... . ，、一一— ....... ......... .. 将函数f(x) cos(2x ―)的图象向左平移 —个单位，得到函数 y g(x)的图象，那么下列说法正确的 6 3 是 A.函数g(x)的最小正周期为2兀 B.函数g(x)是奇函数C.函数g(x)的图象关于点(一,0)对称12.…......................... 7TD.函数g(x)的图象关于直线x —对称3【答案】B_ __ ,, 一、“，冗冗* ...... - __ _ ，、【解析】将函数f(x) cos(2x ―)的图象向左平移一个单位，得到函数y g(x) 6 3- 2 冗冗、 ... ....... ............... .. ....... 一. 2 冗 ............... ,cos(2x —— -) sin2x 的图象，故g(x)为奇函数，且最小正周期为 —— 冗，故A 错误，B 正确;3 6 2k 冗 — .. k 冗.令2x k ：t, k Z,得x —, k Z ,则函数g(x)的图象关于点(一,0) , k2 2八人 , 冗,令2x k 冗一，k2称，故D 昔误. 故选B. Z 对称，故C 错误;— kTCTT — .. kTCTT — Z ,得x - - , k Z ,则函数g(x)的图象关于直线x - - , k Z 对 2 4 2 4 在三棱锥P ABC中，PB BC,PA AC 3,PC 2 ,若过AB 的平面将三棱锥P ABC 分为体积相等的两部分，则棱 PA 与平面所成角的余弦值为 A. 1 B. ―2 C. 2D, 一2—23 3 33【答案】D 【解析】如图所示，取 PC 中点为D ,连接AD, BD ,因为过AB 的平面将三^锥P ABC 分为体积717.【答案】D又因为PA AC ，所以PC AD ,又PB BC ,所以PC BD ,且AD I BD D ,所以PC 平面ABD ,所以PA 与平面所成角即为PAD ，因为PC 2 ,所以PD 1,所以PD 1sin PAD —— -,所以 cos PAD PA 3述，故选D.316.22已知直线x V 3y 1 0与椭圆C ：x 2 4 1(a a 2b 20）交于A,B 两点，且线段 AB 的中点为M ,若16.直线OM （O 为坐标原点）的倾斜角为150 ,则椭圆C 的离心率为A.B.C 3 C. 3D. -63【解析】设 A(x 1,y 1),B(x 2,y 2),M d/。

2022年7月浙江省普通高中学业水平考试数学仿真模拟试卷_2

2022年7月浙江省普通高中学业水平合格性考试数学仿真模拟试卷03一、单选题(本大题共18小题，每小题3分，共54分)1．已知集合{}2,1,0,1,2A =--，集合{}2B x x =<，则A B =（） A ．{}0,1 B ．{}1,0,1- C ．{}2,1,0,1-- D ．{}2,1,0,1,2--【答案】B 【解析】【分析】解绝对值不等式化简B ，根据交集运算可得结果. 【详解】 {|22}Bx x,A B ={1,0,1}-.故选：B2．函数()1lg 1y x x =-+的定义域是（）A ．(],1-∞B ．()0,1C ．()(),00,1-∞⋃D ．()(],00,1-∞⋃【答案】C 【解析】【分析】根据对数的真数大于0且分母不为0可得到结果【详解】由10x ->可得1x <又因为0x ≠，所以()1lg 1y x x =-+的定义域为()(),00,1-∞⋃故选：C3．甲、乙二人玩猜数字游戏，先由甲任想一数字，记为a ，再由乙猜甲刚才想的数字，把乙猜出的数字记为b ，且,{1,2,3,4}a b ∈，若||1a b -≤，则称甲乙“心有灵犀”．现任意找两个人玩这个游戏，则他们“心有灵犀”的概率为（）A ．38B ．58C ．316D ．516【答案】B 【详解】B 两人分别从1，2，3，4四个数中任取一个，共有16个样本点，为：(1，1)，(1，2)，(1，3)，(1，4)， (2，1)，(2，2)，(2，3) ，(2，4)，(3，1)，(3，2)，(3，3)，(3，4)，(4，1)，(4，2) (4，3)，(4，4)，这16个样本点发生的可能性是相等的．其中满足||1a b -≤的样本点有(1，1)，(1，2)，(2，1)，(2，2)，(2，3)，(3，2)，(3，3)，(3，4)，(4，3)，(4，4)，共10个，故他们“心有灵犀”的概率为105168P ==．故选：B 4．若复数z 满足i 12i=-+z（i 为虚数单位），则z 的虚部为（） A ．i B ．i - C ．1- D ．1【答案】D 【详解】由i 12i=-+z得()()i 12i 3i z =-+=-+，故z 的虚部为1．故选：D ．5．已知向量(3,22)a k k =-+，(4,0)b =，若a b ⊥，则k =（） A ．1 B ．3 C ．3-D ．13【答案】B 【详解】解：因为向量(3,22)a k k =-+，(4,0)b =，且a b ⊥，所以()340-⨯=k ，解得3k =，故选：B6．已知某5个数据的平均数为5，方差为3，现加入3、7两个数，此时这7个数据的平均数为x ，方差为2s ，则（） A ．25,3x s == B ．25,3x s =< C ．25,3x s => D ．25,3x s <>【答案】C 【详解】由题意可得： 553757x ⨯++== ，222123[53(35)(75)]377s =⨯+-+-=> ，故选：C7．将长方体截去一个四棱锥，得到的几何体如图所示，则该几何体的侧视图是（）A ．B ．C ．D ．【答案】C 【解析】【分析】根据侧视图(左视图)的定义，从几何体的左侧平视观察几何体，得到左视图，注意被遮挡的线段要画成虚线. 【详解】将几何体各顶点字母标记如图，从左侧观察，得到如图所示的侧视图，其中，对角线()DB E 被几何体左侧面遮挡，应当为虚线，故选：C.8．已知1x >，则11x x +-的最小值是（） A ．3 B ．8C ．12D ．20【答案】A 【解析】【分析】利用基本不等式进行求解即可. 【详解】因为1x >，所以11111(1)13111x x x x x x +=-++≥-⋅=---，当且仅当111x x -=-时取等号，即当2x =时取等号，故选：A9．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知60B =︒，5a =，4c =，则b =（）A ．26B ．25C 21D 31【答案】C 【解析】【分析】在ABC 中，由余弦定理2222cos b a c ac B =+-，即可求解. 【详解】由题意，在ABC 中，60B =，5a =，4c =，根据余弦定理得22212cos 2516254212b ac ac B =+-=+-⨯⨯⨯=，所以 21b = 故选：C.10．函数()2442x xf x x x --=+-的图象大致为（）A ．B ．C ．D ．【答案】D 【解析】【分析】根据函数解析式求得函数定义域，判断函数奇偶性，再取几个特殊值运用排除法得到答案. 【详解】由题意知，220x x +-≠，解得1x ≠±，所以()f x 定义域()()(),11,11,-∞-⋃-+∞关于原点对称，又因为()()()224444=22x xx x f x f x x x x x -----==-+--+--，所以此函数为奇函数，图像关于原点对称，排除A.当12x =时，1216201125242f -⎛⎫==-< ⎪⎝⎭+-，排除B.()00f x x =⇒=，函数只有1个零点，排除C.故选：D11．从分别标有1，2，……，9的9张卡片中不放回地随机抽取2次，每次抽取1张．则抽到的2张卡片上的数奇偶性相同的概率是（） A ．518 B ．49C ．59D ．79【答案】B 【详解】解：从分别标有1，2，……，9的9张卡片中不放回地随机抽取2次，每次抽取1张，基本事件总数9872n =⨯=，而其中抽到的2张卡片上的数奇偶性相同的基本事件个数435432m =⨯+⨯=，则抽到的2张卡片上的数奇偶性相同的概率324729m P n ===，故选：B12．>0”是“x >0”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充要条件 D ．既不充分又不必要条件【答案】B 【解析】判断两个命题的真假，即p q ⇒和q p ⇒的真假，可得结论．【详解】0x >0>0>时0x <或0x >0>推不出0x >，0是0x >的必要不充分条件．故选：B.13．为了得到函数3sin 23y x π⎛⎫=+ ⎪⎝⎭的图像，只需把函数3sin y x =图像上所有点（）A ．向左平行移动3π个单位长度，再把所得各点的横坐标缩短到原来的12B ．向左平行移动3π个单位长度，再把所得各点的横坐标伸长到原来的2倍 C ．向左平行移动6π个单位长度，再把所得各点的横坐标缩短到原来的12 D ．向右平行移动3π个单位长度，再把所得各点的横坐标缩短到原来的12 【答案】A 【解析】【分析】利用三角函数图象变换规律求解即可【详解】将3sin y x =向左平移3π长度单位，得到3sin 3y x π⎛⎫=+ ⎪⎝⎭，再把所得的各点的横坐标缩短到原来的12，可得3sin 23y x π⎛⎫=+ ⎪⎝⎭的图象，故选：A14．如图，1111ABCD A B C D -为正方体，则以下结论：①//BD 平面11CB D ；②11AC B C ⊥；③1AC ⊥平面11CB D ，其中正确结论的个数是（）．A ．0B ．1C ．2D ．3【答案】D 【解析】【分析】由11//BD B D ，利用线面平行的判定可知①正确；利用线面垂直的性质和判定可证得1CD ⊥平面1ADC ，11B D ⊥平面11AA C ，由此可得11CD AC ⊥，111B D AC ⊥，由线面垂直的判定和性质可知②③正确【详解】对于①，11//BB DD ，11=BB DD ，∴四边形11BB D D 为平行四边形，11//BD B D ∴，又BD ⊄平面11CB D ，11B D ⊂平面11CB D ，//BD ∴平面11CB D ，①正确；对于②③，连接11A C ，1C D ，四边形11CDD C 为正方形，11CD C D ∴⊥；AD ⊥平面11CDD C ，1CD ⊂平面11CDD C ，1AD CD ∴⊥；又1C D AD D ⋂=，1,C D AD ⊂平面1ADC ，1CD ∴⊥平面1ADC ， 1AC ⊂平面1ADC ，11CD AC ∴⊥；同理可得：11B D ⊥平面11AA C ，又1AC ⊂平面11AA C ，111B D AC ∴⊥； 1111CD B D D =，111,CD B D ⊂平面11CB D ，1AC ∴⊥平面11CB D ，又1B C ⊂平面11CB D ，11AC B C ∴⊥，②正确，③正确. 故选：D.15．若函数2()10f x x mx =-+在(2,1)上是增函数，则实数m 的取值范围是（） A ．[2,+)∞ B ．[4,+)-∞ C ．(,2]-∞ D ．(,4]-∞-【答案】D 【解析】【分析】根据二次函数的性质得到不等式，解得即可；【详解】解：函数2()10f x x mx =-+的对称轴为2mx =，开口向上，依题意可得22mx =≤-，解得4m ≤-，即(,4]m ∈-∞-；故选：D16．已知函数()22,0,0x x f x x x ⎧<=⎨-≥⎩，若x ∀∈R ，()()29430f mx f x +-≤恒成立，则实数m 的取值范围为（） A ．[)21,+∞ B ．[)13,+∞C ．27,16⎡⎫+∞⎪⎢⎣⎭D ．[)15,+∞【答案】C 【详解】解：因为()22,0,0x x f x x x ⎧<=⎨-≥⎩，所以函数图象如下所示：由函数图象可知函数为定义域R 上单调递减的奇函数，当0x ≥时()2f x x =-，则()()()223399f x x x f x =-=-=，当0x <时()2f x x =，则()()()223399f x x x f x ===，所以()()39f x f x =，因为x ∀∈R ，()()29430f mx f x +-≤恒成立，即x ∀∈R ，()()()()2943934912f mx f x f x f x ≤--=-=-恒成立，所以2912mx x ≥-恒成立，即29120mx x -+≥恒成立，当0m =，显然不成立，当0m ≠时，则，解得2716m ≥，即27,16m ⎡⎫∈+∞⎪⎢⎣⎭；故选：C17．已知函数()f x 是定义域为R 的偶函数，且(12)f x -为奇函数，则（） A ．1()02f -=B ．(0)0f =C ．(2)0f =D ．(3)0f =【答案】D 【详解】因为函数()f x 是定义域为R 的偶函数，且(12)f x -为奇函数，所以()(),(12)(12)f x f x f x f x -=+=-- ，即(12)(21)f x f x +=--，故令0x = ，则(1)(1)(1)f f f =--=-，所以(1)0f =，令1x =，则(3)(1)0f f =-=，故D 正确；取函数()cos 2f x x π=，则(12)cos[(12)sin 2f x x x ππ-=-=，故()cos2f x x π=满足是定义域为R 的偶函数，且(12)f x -为奇函数，而12()cos()0242f π-=-=≠， (0)cos010,(2)cos 10f f π==≠==-≠，说明A,B,C 错误，故选：D.18．等边三角形ABC 边长为4，M ，N 为,AB AC 的中点，沿MN 将AMN 折起，当直线AB 与平面BCMN 所成的角最大时，线段AB 的长度为（）A 6B ．22C 10D ．3【答案】B 【解析】以E 为坐标原点建立如图所示空间直角坐标系，设设(),0,A x z ，其中2223x z AE +==，3,3x ⎡∈⎣，利用向量法可得23sin cos ,1023x AB n x θ-=<>=-利用导数可求出最大值，得到点A 坐标，即可求出AB . 【详解】在ABC 中，取BC 中点D ，连接AD 交MN 于E ，连接BE ，则在ABC 中，23AD =3AE DE ==以E 为坐标原点建立如图所示空间直角坐标系，则)3,2,0B -，设(),0,A x z ，其中2223x z AE +==，3,3x ⎡⎤∈⎣⎦， ()3,2,AB x z ∴=--，可知平面BCNM 的一个法向量()0,0,1n =，设直线AB 与平面BCMN 所成的角为θ，0,2π⎡⎤θ∈⎢⎥⎣⎦，则()2223sin cos ,102334AB nzx AB n x AB n x z θ⋅-=<>===-⋅-++ 令()21023f x x =-3,3x ⎡⎤∈⎣⎦，则()()(()2223133232063103103x x x x f x x x ---+'==--，当33,x ⎛∈- ⎝⎭时，()0f x '>，()f x 单调递增，当33x ∈⎝时，()0f x '<，()f x 单调递减，()max 313f x f ∴==⎝⎭，即当3x =sin θ最大，即θ最大，此时326,0,33A ⎛⎫ ⎪ ⎪⎝⎭，则()22232630202233AB ⎛⎫⎛⎫=-+++-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 故选：B.二、填空题(本大题共4小题，每空3分，共15分)19．已知函数()1522,0log ,0x x f x x x ⎧≤⎪=⎨⎪>⎩，则(0)f =__________，((5))f f -=__________.【答案】 1 53- 【解析】【分析】根据分段函数的定义域分别代入计算即可.【详解】函数1522,0()log ,0x x f x x x ⎧≤⎪=⎨⎪>⎩，0(0)21f ==；∴51(5)232f --==，∴()()211155log 323323f f f ⎛⎫-===- ⎪⎝⎭. 故答案为：①1；②53-. 20．以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形.勒洛三角形是由德国机械工程专家、机构运动学家勒洛首先发现，所以以他的名字命名.一些地方的市政检修井盖、方孔转机等都有应用勒洛三角形.如图，已知某勒洛三角形的一段弧AB 的长度为2π，则该勒洛三角形的面积是___________.【答案】18183π-【解析】【分析】计算出一个弓形的面积，由题意可知，勒洛三角形由三个全等的弓形以及一个正三角形构成，利用弓形和正三角形的面积可求得结果.【详解】由弧长公式可得23AC ππ⋅=，可得6AC =，所以，由AB 和线段AB 所围成的弓形的面积为2162662ππ⨯⨯=- 而勒洛三角形由三个全等的弓形以及一个正三角形构成，因此，该勒洛三角形的面积为(3618S ππ=⨯-+=-.故答案为：18π-.21．函数2()sin 2f x x x =-，则(2021)(2021)f f +-=_______．【答案】4-【解析】【分析】分析函数()f x ，是由奇函数2()sin g x x x =和常函数构成，利用奇函数性质可知(2021)+(2021)0g g -=，计算答案即可. 【详解】设()()2f x g x =-，其中2()sin g x x x =，因为22()sin()sin ()g x x x x x g x -=-=-=-，所以()g x 为奇函数，利用奇函数性质可知 (2021)(2021)f f +-=(2021)2g -+(2021)2(2021)+(2021)44g g g --=--=-.故答案为：4-.22．锐角ABC 的内角所对边分别是a ，b ，c 且1a =，cos cos 1b A B -=，若A ，B 变化时，2sin sin B A λ-存在最大值，则正数λ的取值范围______．【答案】⎛ ⎝⎭【详解】1a =，cos cos 1b A B -=，由正弦定理得：sin cos cos sin sin B A B A A -=，即：()sin sin B A A -=，B A A ∴-=或πB A A -=-（舍）2B A ∴=ABC 是锐角三角形，π02π022π22A A A A ⎧<<⎪⎪⎪∴<<⎨⎪⎪+>⎪⎩，解得：ππ64A << ()21sin sin sin 21cos 22B A A A λλ-=--()sin 2cos 22222A A A λλλϕ=+-=+-（其中tan 2λϕ=） ππ232A << ∴使2sin sinB A λ-存在最大值，只需存在ϕ，满足π22A ϕ+=π06ϕ∴<< πtan 0tan tan 26λϕ∴<=< 解得：0λ<<. 故答案为：⎛ ⎝⎭. 三、解答题(本大题共3小题，共31分)23（10分）．已知函数()sin()3f x x π=+． (1)求函数()f x π的最小正周期；(2)当[0,]2x π∈时，求()()66y f x f x ππ=-++的取值范围．【答案】(1)2(2) 【解析】【分析】（1）利用周期公式即可得到结果；（2）利用恒等变换公式化简公式，借助正弦型函数的性质得到结果.(1)∵()sin()3f x x π=+， ∴()sin 3f x x πππ⎛⎫=+ ⎪⎝⎭，∴22T ππ==，故函数()f x π的最小正周期为2； (2)()()sin sin 6662y f x f x x x ππππ⎛⎫⎛⎫=-++=+++ ⎪ ⎪⎝⎭⎝⎭ 3sin cos 3sin 2332x x x π⎛⎫+=+ ⎝=⎪⎭ ∵[0,]2x π∈，∴5[,]336x πππ+∈， ∴1sin ,132x π⎛⎫⎡⎤+∈ ⎪⎢⎥⎝⎭⎣⎦，即33sin [,3]32x π⎛⎫+∈ ⎪⎝⎭，故()()66y f x f x ππ=-++的取值范围是3[,3]224（10分）．已知四棱锥P ABCD -，CD AB ∥，CD AD ⊥，224AB AD CD ===，△PBC 为等腰直角三角形，面PBC ⊥面ABCD ，且BP CP ⊥，F 为CD 中点.(1)求证：PF BC ⊥；(2)求PA 与平面PBC 所成角的正弦值.【答案】(1)证明见解析；6【分析】（1）取BC 中点E ，连接EF ，PE ，BD ，由等腰三角形性质、勾股定理、中位线等可得PE BC ⊥、EF BC ⊥，利用线面垂直的判定及性质证明线线垂直；（2）利用直线与平面所成角的定义找到PA 与平面PBC 所成角，结合已知条件求解即可.(1)取BC 中点E ，连接EF ，PE ，BD ，∵△PBC 为等腰直角三角形，即PB PC =，∴PE BC ⊥，由//CD AB ，CD AD ⊥，224AB AD CD ===，可得22BD BC ==， ∴222CD BD BC =+，则BD BC ⊥，又F 为CD 中点，则//EF BD ，故EF BC ⊥，而PE EF E ⋂=， ∴BC ⊥面PEF ，PF ⊂面PEF ，∴BC PF ⊥.(2)过点A 作CB 延长线的垂线，垂足为H ，连PH ,∵面PBC ⊥面ABCD ，面PBC 面ABCD BC =,AH BC ⊥，AH ⊂面ABCD ， ∴AH ⊥面PBC ，∴APH ∠为线PA 与面PBC 所成的线面角，由135CBA ∠=,2AB =知：sin AH ABH AB ∠=,2222AH ==, 由余弦定理得2222cos AE BE AB BE AB ABE =+-⋅⋅∠,即10AE =由PE BC ⊥，面PBC ⊥面ABCD ，面PBC 面ABCD BC =，PE ⊂面PBC ，所以PE ⊥面ABCD ，AE ⊂面ABCD ，故PE AE ⊥，2PE =，则3PA = 在PAH 中， 26sin 23AH APH PA ∠===25（11分）．设函数()2a f x x b x =++，其中0a >，b ∈R . (1)若()f x 在[1,2]上不单调，求a 的取值范围；(2)记(,)M a b 为|()|f x 在[1,2]上的最大值，求(,)M a b 的最小值.【答案】(1)()2,8a ∈(2)3-【分析】（1）根据对勾函数的单调性和()f x 在[1,2]上不单调可知，12，解出a 的取值范围；（2）令()2g x a x x=+，根据函数图象即函数对称性可知，当12，(1)(2)f f =，且[1,2][1,2]max ()min ()2x x g x g x b ∈∈+=-时，(,)M a b 取得最小值.(1)由对勾函数函数单调性的定义可知：()f x 在上递减，在)+∞上递增，因此()f x 在[1,2]上不单调的充要条件是12<，解得：28a <<，所以()2,8a ∈； (2)令()2g x a x x =+，比较01<2，12三种情况，可知当12<，(1)(2)f f =，且[1,2][1,2]max ()min ()2x x g x g x b ∈∈+=-时，(,)M a b 取得最小值，且最小值为[1,2][1,2]max ()min ()2x x f x f x ∈∈-，由(1)(2)f f =得：4a =，所以[1,2]max ()(1)6x g x g ∈==，[1,2]min ()x g x g g ∈===(3b =-+，所以(,)M a b 的最小值为[1,2][1,2]max ()min ()32x x f x f x ∈∈-=-。

浙江省县域教研联盟2023-2024学年高二下学期学业水平模拟考试数学试题(原卷版)

2023~2024学年第二学期浙江省县域教研联盟学业水平模拟考试数学考生须知：1．本卷满分100分，考试时间80分钟；2．答题前，在答题卷指定区域填写班级、姓名、考场、座位号及准考证号并核对条形码信息；3．所有答案必须写在答题卷上，写在试卷上无效，考试结束后，只需上交答题卷；4．学生可关注“启望教育”公众号查询个人成绩分析．选择题部分一、单项选择题（本大题共12小题，每小题3分，共36分．每小题列出的四个备选项中只有一个是符合题目要求的，不选、多选、错选均不得分）1.设全集{0,1,2,4}U =，{1,4}A =，则U A =ð（）A.{0,4}B.{0,2}C.{1,2}D.{2,4}2.已知角α的顶点在坐标原点，始边与x 轴非负半轴重合，终边过点11,22P ⎛⎫-⎪⎝⎭，则sin α=（）A.12-B.12C.22 D.22-3.命题“0x ∀>，96x x+≥”的否定是（）A.00x ∃≤，0096x x +≥ B.00x ∃>，0096x x +≥C.00x ∃≤，0096x x +< D.00x ∃>，0096x x +<4.下列各组函数表示同一函数的是（）A.y x =和2y =B.y =和y =C.y x =和,0.,0.x x y x x ≥⎧=⎨-<⎩ D.1y x =-与21xy x=-5.已知复数2i12iz -+=-（i 为虚数单位），则z =（）A.1B.2C.D.6.某数学兴趣小组20名成员在规定时间内独立解答6个数学问题，最终结果如下：有1人解出1个问题，有1人解出2个问题，有4人解出3个问题，有4人解出4个问题，有5人解出5个问题，有5人解出6个问题，则解出问题个数的第三四分位数为（）A.3B.4.5C.5D.5.57.如图，一根棒棒糖其顶部可近似看成一个直径为2cm 的球，下面通过一个底面直径为0.2cm ，高为6cm 的圆柱体（裸露部分）加以支撑，则这根棒棒糖的体积约为（）A.3209πcm 150⎛⎫⎪⎝⎭B.3818πcm 75⎛⎫⎪⎝⎭C.31609πcm 150⎛⎫⎪⎝⎭D.3118πcm 75⎛⎫⎪⎝⎭8.若某次乒乓球练习中，乒乓球发球后先后击中已方桌面O 和对方桌面A ，且OA 长为60英寸，球在OA中点B 处到达最高点，高度为OA 上靠近A 的三等分点C 处，网高为6英寸，球恰好沿着网的上边界越过，其轨迹图象如下：则最合适拟合轨迹图象的函数模型为（）A.π()60f x x ⎛⎫=⎪⎝⎭ B.π()30f x x ⎛⎫=⎪⎝⎭C.2()22515f x x x =-+ D.239()20010f x x x =-+9.已知ABC 的边长均为1，点D 为边AB 的中点，点E 为边BC 上的动点，则AD AE ⋅的取值范围是（）A .11,84⎡⎤⎢⎥⎣⎦B.11,42⎡⎤⎢⎥⎣⎦C.1,12⎡⎤⎢⎥⎣⎦D.1,14⎡⎤⎢⎥⎣⎦10.已知16log 8a =-，55log 6log 4b =⋅，0.694c ⎛⎫= ⎪⎝⎭，则（）A.c b a<< B.c a b<< C.b<c<aD.b a c<<11.已知正方体1111ABCD A B C D -的棱长为1，在以1A 、C 为球心，1为半径的两个球在正方体内的公共部分所构成的几何体中，被平行于平面1BDC 的平面所截得的截面面积的最大值为（）A.3π4B.π2C.π4D.π812.已知函数2()1f x x ax ax =---，若()12f x ≥-对任意实数x 恒成立，则实数a 的取值范围为（）A.,88⎡-⎢⎣⎦B.,66⎡-⎢⎣⎦C.,33⎡-⎢⎣⎦D.,22⎡-⎢⎣⎦二、多项选择题（本大题共4小题，每小题4分，共16分．每小题列出的四个备选项中有多项是符合题目要求的，全部选对得4分，部分选对且没选错得2分，不选、错选得0分）13.已知函数21()cos sin 22f x x x =+，则（）A.函数()f x 的解析式可化成π1()sin 2242f x x ⎛⎫+ ⎪⎝⎭=+B.函数()f x 在[0,π]上有2个零点C.函数()f x 的图象关于点π,02⎛⎫⎪⎝⎭对称 D.函数()f x 在π0,2⎡⎤⎢⎣⎦上的最大值为12214.已知向量(1,2)a =，(3,)b m = ．下列选项正确的是（）A .若//a b r r，则6m =-B.若a b ⊥，则32m =-C.若向量a 与b的夹角为锐角，则32m >-D.若1m =-，则向量a在向量b上的投影向量为110b 15.已知随机事件A ，B 的概率都大于0,A 表示事件A 的对立事件，则（）A.当()()1P A P B +=时，B A=B .当A B ⊆时，()()P A P B ≥C.当()()()P AB P A P B =⋅时，A ，B 相互独立D.当()0P AB >时，()()P AB P B ≤16.已知定义域为R 的函数()f x 在区间(0,1)上单调递增，且()(2)2f x f x ++=，若函数()(1)1g x f x =+-是奇函数，则（）A.4是()f x 的一个周期B.(3)0f =C.函数()f x 是偶函数D.函数()f x 在(3,4)上单调递减非选择题部分三、填空题（本大题共4小题，每空3分，共15分）17.已知函数1,1,()1ln(2), 1.x x f x x x x -⎧<-⎪=+⎨⎪+≥-⎩若()1f a =，则=a __________．18.若一组数据12,,,n x x x 的方差是5，则数据1231,31,,31n x x x --⋯-的方差是__________．19.已知正实数x ，y 满足23936x xy x y +++=，则43x y +的最小值为__________．20.已知向量21,e e为互相垂直的两个单位向量，若向量123(1)32a t e te =-+ ，1233(1)(1)42b t e t e =-++ ()t ∈R ，则当t =__________时，||a取到最小值；此时，1212||||||a e b e e e λμλμ-+-+-(,)λμ∈R 的最小值是__________．四、解答题（本大题共3小题，共33分．解答应写出必要的文字说明、证明过程或演算步骤）21.已知ABC 中，内角A ，B ，C 所对的边分别为a ，b ，c，且sin 2cos 0a C c C ⋅--+=．（1）求角A ；（2）求2cos sin sin 2cos B CB C-+的取值范围．22.如图，在三棱锥-P ABC 中，45APC BPC ︒∠=∠=，BPA △是正三角形．（1）求证：平面PBC ⊥平面PAC ；（2）若1AB =，528PC =，求AP 与平面ABC 所成角的正弦值．23.已知函数()2()log 2xf x t x =+-．（1）若(2)0f <，求t 的取值范围；（2）若()f x x =有两个不相等的实根12,x x ，且12x x <①求t 的取值范围；②证明：()()12111f x f x ++-<-．。

【学考模拟】浙江省2024年7月普通高中学业水平测试仿真模拟数学试卷+答案解析

【学考模拟】浙江省2024年7月普通高中学业水平测试仿真模拟数学试卷❖一、单选题：本题共12小题，每小题3分，共36分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.已知，则复数Z 在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.已知，，则在上的投影向量为()A.B.C.D.3.已知函数的定义域为集合A ，值域为集合B ，则()A. B.C. D.4.已知，为钝角，且，，则()A.B.C.D.5.甲、乙两名乒乓球运动员进行一场比赛，采用7局4胜制先胜4局者胜，比赛结束，已知每局比赛甲获胜的概率均为，则甲以4比2获胜的概率为()A.B. C.D.6.已知向量，，且，则实数t 的值为()A.3B.C. D.27.用平面截一个球，所得的截面面积为，若到该球球心的距离为，则球的体积()A.B.C. D.8.若m 满足，则m 的值为()A.1B.2C.D.09.常用放射性物质质量衰减一半所用的时间来描述其衰减情况，这个时间被称做半衰期，记为单位：天，铅制容器中有甲、乙两种放射性物质，其半衰期分别为，，开始记录时，这两种物质的质量相等，512天后测量发现乙的质量为甲的质量的，则，满足的关系式为()A. B.C.D.10.设a ，b 为实数，则“”是“”的() A.必要不充分条件 B.充分不必要条件C.充要条件 D.既不充分也不必要条件11.设的内心为I ，而且满足，则的值是()A.B.C.D.12.一个顶点为P ，底面中心为O 的圆锥体积为1，若正四棱锥内接于该圆锥，平面ABCD 与该圆锥底面平行，A ，B ，C ，D 这4个点都在圆锥的侧面上，则正四棱锥的体积的最大值是()A.B.C.D.二、多选题：本题共4小题，共16分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得4分，部分选对的得2分，有选错的得0分。

13.已知幂函数，其中a ，，则下列说法正确的是()A. B.若时，C.若时，关于y 轴对称D.恒过定点14.饮料瓶的主要成分是聚对苯二甲酸乙二醇酯，简称“PET ”.随着垃圾分类和可持续理念的普及，饮料瓶作为可回收材料的“主力军”之一，得以高效回收，获得循环再生，对于可持续发展具有重要意义，上海某高中随机调查了该校某两个班班，B 班月份每天产生饮料瓶的数目单位：个，并按分组，分别得到频率分布直方图如下：下列说法正确的是()A.A班该月平均每天产生的饮料瓶个数估计为41B.B班5月产生饮料瓶数的第75百分位数C.已知该校共有学生1000人，则约有150人5月份产生饮料瓶数在之间D.15.已知函数，则下列说法正确的是()A.的图像是中心对称图形B.的图像是轴对称图形C.是周期函数D.存在最大值与最小值16.已知函数则关于x的方程根的个数可能是()A.0个B.1个C.2个D.3个三、填空题：本题共4小题，共15分。

2023-2024学年浙江省杭州市普通高中学业水平合格考试数学质量检测模拟试题(含答案)

2023-2024学年浙江省杭州市普通高中学业水平合格考试数学模拟试题A ．()e ln xf x x =⋅C ．()e ln xf x x=+()0,πα∈A ．．．．．已知函数()e 2x f x ⎧⎪=⎨⎪⎩的方程()f x a =有两解，．1ea =B ea =D ．如图，在棱长为2的正方体中，E 为棱C D ''的中点，过,,A D BC '''分别交于点A ．存在点H ，使得AE ⊥B ．线段D G '的长度的最大值是C ．当点F 与点C 重合时，多面体D ．点D 到截面AEF 的距离的最大值是19．在ABC 中，内角,,A B C 的对边分别为20．已知函数()12e2x f x x x -=+-，则使得四、解答题（本大题共3小题，共21．已知函数()22cos sin 2f x x x ⎛=+ ⎝(1)求AA '的长；(2)若D 为线段AC 的中点，求二面角23．已知函数()(2f x x x =+(1)当0a =时，求()f x 的单调区间；16．BD【分析】建立空间直角坐标系，运用空间向量求解【详解】为原点，DC 为y 轴，DA 为x 轴，DD )()()('2,0,0,0,1,2,0,0,0,0,0,2E D D ()()'2,1,2,,2,2,AE D H p =-=- 点不在线段BC 上，错误；平面//ABCD 平面''''A B C D ，GE AH 、GE ，此时1m =，88,5489x DO ==-+梯形AFEG 的高()22252⎛⎫=- ⎪ ⎪⎝⎭四棱锥D AFEG -的体积D AFEG V -由②③式可知，当42255m ==⨯时，故选：BD.23．(1)单调递减区间为10,⎛ ⎝(2)(][),31,-∞-⋃+∞【分析】（1）将函数写成分段函数，结合二次函数的性质得到函数的单调区间；（2）不妨令12x x <，则(f。

浙江省数学学业水平考试模拟学习试题

.浙江省数学学业水平考试试卷一、选择题(本大题共 25小题，1-15每题2分，16-25每题3分，共60分。

每题中只有一个选项是符合题意的。

不选、多项选择、错选均不得分)1．集合 P={0,1}，Q={0,1,2}，那么P Q=〔〕A. {0}B. {1}C. {0,1}D. {0,1,2}2．直线x 3y 5 0的倾斜角是( )A．120 B ．150 C ．60 D ．30 3．以下几何体各自的三视图中,有且仅有两个视图相同的几何体是〔〕A．圆锥 B ．正方体 C ．正三棱柱 D ．球4．以下函数中，为奇函数的是〔〕A.y=x+ 1B.y1 C.ylog3x D.y(1)x x25．以下函数中，在区间(0,)内单调递减的是〔〕A.ylnx B.yx2 C.y2x D.yx36．经过点2,0且斜率为3的直线方程是〔〕A．3xy60B．3xy60C．3xy60D．3xy607．平面向量a (1,2),b(3,x)，假设a//b，那么x等于〔〕B.3 D.68．实数a,b，满足ab0，且a b ，那么〔〕A.ac2bc2B.a2b2 C.a2b2 D.1111a b9．假设tana，那么tana b〔〕，tanb3525A. B. C.17610．设M2a(a2)7，N a2a3，那么有〔〕A.M NB.M NC.M ND.M N11.sin3，且角的终边在第二象限，那么cos〔〕54343A．B． C. D.545412．等差数列a n满足a2a44,a3a510，那么a5a7〔〕A．16B．18C．22D．28'..13．以下命题中为真命题的是是〔〕A.假设sinsin，那么B. 命题“假设C.命题“x1，那么x 2 1的否命题〞D. 命题“假设x 1,那么x 2 x20〞的逆否命题x y ，那么x y 〞的逆命题14．如果x 2 ky 22表示焦点在 y 轴上的椭圆，那么实数 k 的取值范围是〔〕A. 0,B.0,2 C.1,D.0,115．bc0是二次函数y ax 2 bxc 的图象经过原点的〔〕A ．充分不必要条件 B. 必要不充分条件 C ．充分必要条件 D.既不充分又不必要条件16．以下各式其中正确的有〔〕①(log 23)2 2log 23； ②log 232 2log 23；③log 26 log 23log 218；④log 26 log 23log 23.A ．1个B ．2个C ．3个D ．4个17．函数fx xlog 2x 的零点所在区间为〔〕A ．0,1 1 11 1D.1,18 B.,C.,28 44 218．函数f(x)cos(x) cos(x 4)是〔〕4A ．周期为π的偶函数 B．周期为2π的偶函数C ．周期为π的奇函数 D．周期为2π的奇函数19．ABC ，AB AC23，BAC 30，那么 ABC 的面积为〔〕A.1B.2C.3D. 420．实数a 1,a 2,a 3,a 4,a 5构成等比数列，其中a 12,a 58，那么a 3的值为〔〕A.5B.4C.4 D.421．假设log 2xlog 2y 3，那么2xy 的最小值是〔〕 D 1C 1A ．4B．8C．10D．12A 1BE122．如图，在正方体ABCD A 1B 1C 1D 1中，O 是底面ABCD 的中心,DCE 为CC 1的中点，那么异面直线OE 与AD 1所成角的余弦值等于〔〕O6B.6A.3223．椭圆x 2y 21ab 0a2b 23D.2A〔第22BC.2题〕3的长轴被圆x 2 y 2b 2与x 轴的两个交点三等分，那么椭圆的离心率是〔〕A ．1B ．22 C ．3 D ．2223324．双曲线x 2y 2 1，直线l 过其左焦点F 1，交双曲线左支与A 、B 两点，且AB4，F 2m7 20，那么m 的值为〔为双曲线的右焦点，ABF 2的周长为〕A.8B.9C.16D.20'.. 25．平面内有两定点A,B,AB3，M,N在的同且MA,NB，MA1,NB2,在上的点P足PM,PN与平面所成的角相等，点P的迹所包的形的面等于〔〕A.9B.8C.4D.二、填空〔本大共5小，每小2分，共10分〕26．tan 1cos sin=.，cos sin227．函数y f x的象点2,2，f9=.28．心在直y2x上，且与x相切于点1,0的的准方程.29．在平面直角坐系中，x2y21(ab0)的焦距2，以O心，a半径的，a2b2点a2,0作的两切互相垂直，离心率e=.c30．{a n}等比数列,{b n}等差数列，且b1=0,c n=a n+b n,假设数列{c n}是1,1,2,⋯,{c n}的前10和.三、解答(本大共4小，第31,32每7分，第33,34每8分，共30分)31．(本7分)cos3,32，，求cos2、sin2的．5232．如所示，四棱P–ABCD的底面一直角梯形，BA⊥AD，CD⊥AD，CD=2AB，PA⊥底面ABCD，E PC的中点.〔Ⅰ〕明：EB∥平面PAD；〔Ⅱ〕假设PA=AD，明：BE⊥平面PDC.'..33．(此题8分)抛物线 y 2＝4x 截直线y ＝2x ＋m 所得弦长 AB ＝3 5．(Ⅰ)求m 的值；(Ⅱ)设P 是x 轴上的一点，且△ ABP 的面积为 9，求P 的坐标．34．(此题8分)定义在 D 上的函数 f 〔x 〕，如果满足：对任意的 xD ，存在常数M 0，都有f(x)M 成立，那么称f 〔x 〕是D 上的有界函数，其中 M 称为函数f 〔x 〕的上界．函数a1x xf(x)12．24〔Ⅰ〕当a=1时，求函数f 〔x 〕在( ,0]上的值域，并判断函数f 〔x 〕在(,0]上是否为有界函数，请说明理由；〔Ⅱ〕假设函数f 〔x 〕在[0, )上是以3为上界的有界函数，求实数 a 的取值范围．'..参考答案一、(共25小，1-15 每小 2分，16-25每小 3分，共60分。

浙江省2024年初中学业水平考试模拟试卷数学(榜眼卷)

浙江省2024年初中学业水平考试模拟试卷数学考生须知：1.本试题卷共4页，满分120分，考试时间120分钟：2.答题前，考生务必使用黑色字迹的钢笔或签字笔填写学校、班级、姓名、准考证号等信息.3.答题时，请按照答题卷上“注意事项”的要求，在答题卷相应的位置上规范作答，在本试题卷上的作答一律无效.4.本次考试不允许使用计算器.画图先用2B铅笔，确定无误后用钢笔或签字笔描黑.卷I说明：本卷共有1大题，10小题、共30分.请用2B铅笔在“答题卷”上将你认为正确的选项对应的小方枢涂黑、涂满.一、选择题(本题共有10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项符合题目要求)1.在-1,0,2,-3.5中选一个数与10相加使结果最小，应选A.-1B.0C.2D.-3.52.如图是一个五金零件，它的主视图是3.转动转盘(如图),指针停留在无理数区域的概率是A. B. C. D.4.不等式组的解在数轴上的表示如图所示，则另一个不等式可能为A.2x+4<0B.2x+4≤0C.2x+4>0D.2x+4≥05.如图，在△ABC中，∠ACB=60°,将线段AC绕着点C顺时针旋转20°,点A的对应点D正好在边AB上，则∠B的度数为()A.40°B.35°C.30°D.25°6.一次函数y=(k+2)x+5与二次函数y=3x²+4的交点个数为()A.0B.1C.2D.不确定7.某商场销售两种亚运会吉祥物纪念章，已知A种纪念章买两盒送一盒，每盒62元；B种纪念章打九折，原价每盒90元，东东需要的3盒A种纪念章和2盒B种纪念章共需()A.366元B.348元C.286元D.304元8.如图，D是△ABC的边AB上一点，且AD:DB=2:1,过点D作DE//BC,交AC于点E,取线段AE的中点F,连结DF.若DF=4,则△ABC中AC边上的中线长为()A.2B.6C.7D.89.如图，A,B,C依次是残破镜子上的三个点，弓形的弦AC的长为3cm,∠ABC=120°,则这个镜子的直径长为()A.2cmB.4cmC.cmD.cm10.如图，在直角梯形ABCD中，AB=AD=6,BC=14,E为AB的中点，F为线段BC上的动点，连结FE,将△BEF沿EF折叠得到△GEF.在点F从点B运动到点C的过程中，若射线FG与上底AD相交于点P,则点P 相应运动的路径长为二、填空题(本题共有6小题，每小题3分，共18分)11.因式分解：m²-9=12.若扇形的弧长为5π,圆心角为50°,则它的半径为13.如图，在矩形ABCD中，AB=3,AD=4,点E在线段AD上，AD=4AE.连结AC,BE,二者相交于点F,连结BD,与AC相交于点G,则FG=14.如图所示为凸透镜成像示意图，CD是蜡烛AB通过凸透镜MN所成的虚像.已知蜡烛的高AB为4.8cm,蜡烛AB离凸透镜MN的水平距离OB为6cm,该凸透镜的焦距OF为10cm,AE//OF,OF=OF,则像CD的高为cm.15.如图，点P从正八边形的顶点A出发，沿着正八边形的边顺时针方向走，第1次走1条边长到点H,第2次走2条边长到点F,3次走3条边长到点C……以此类推，第50次走到顶点16.如图2是东东用图1中的七巧板拼成的数字5,A,B,C均是七巧板中直角三角形和正方形的顶点，连结AB,AB与BC的夹角为α,则tanα的值是三、解答题(本题共有8小题，共72分)17.(本题满分6分)如图是小明一道题的计算过程：(1)请用下划线划出小明计算出错的地方.(2)请写出正确的计算过程.18.(本题满分6分)如图，在6×6的方格纸中，点A,B均在格点上，试按要求画出相应的格点图形(每小题只需画一个).(1)在图1中作一条线段，使它与AB互相垂直平分.(2)在图2中作一个△ABC,使它是轴对称图形，且符合S△ABC=5.19.(本题满分8分)在平面直角坐标系中，已知一次函数与x轴相交于点A,与y轴相交于点B,经过点B 的抛物线y₂=x²+bx+c的顶点C在线段AB上(不包括点B).(1)求b,c的值(2)当时，请直接写出x的取值范围.20.(本题满分8分)为了落实“双减”政策.某校进行了课时作业分层设计课题研究，分别在A,B,C三个班开展比对实验.A班没有开展分层作业设计，B班开展“好、差”两层分层设计，C班开展“好、中、差”三层分层及个别学生特殊布置设计.一段时间后对实验前、后开展的前测和后测(难度、题型、总分相同的试卷，满分100分)数据进行整理比对，如表1和表2.(1)请选择一种适当的统计量，分别比较A,B,C三个班的后测数据(2)通过分析前测、后测数据，请对该校开展的课时作业分层设计实验效果进行评价.21.(本题满分10分)如图1是一手机直摇专用支架，AB为立杆，其高为100cm,BC为支杆，它可绕点B 旋转，其中BC长为30cm,CD为悬杆，滑动悬杆可调节CD的长度.(1)如图2,当支杆BC与地面亚直，悬杆CD与支杆BC之间的夹角∠BCD=60°且CD的长为30cm时，求手机怒挂点D距离地面的高度.22.(本题满分10分)已知AB,CD是圆o的内接四边形ACBD的两条对角线，AB,CD相交于点M,且AB=CD.(1)如图1,求证：BM=DM.(2)在图1中找出一组全等的三角形，并给出证明.(3)如图2,圆o的半径为5,弦CD⊥AB于点P,当△CBP的面积为时，求AB的长.23.(本题满分12分)24.(本题满分12分)如图，直线与y轴相交于点A,与x轴相交于点B,与反比例函数图象相交于P,Q两点.过点Q作x轴的垂线，垂足为C,连结OQ,OP并延长OP,与直线QC相交于点M.在第一象限找点N,使以P,Q,N,M为顶点的四边形为平行四边形，反比例函数经过点N.。

2024年浙江省杭州市数学学业水平考试模拟A试题

2024年浙江省杭州市数学学业水平考试模拟A 试题一、单选题1．第27届杨柳青国潮灯展主题活动引爆假日文旅市场，春节期间累计接待游客5420000人次．将5420000用科学记数法表示应为（）A ．60.54210⨯B ．654.210⨯C ．65.4210⨯D ．45.4210⨯ 2．计算()2322m n -的结果是（）A ．642m n -B ．544m nC ．644m nD ．944m n 3．多项式2242x x -+因式分解为（）A ．()221x -B ．()221x +C ．()221x -D ．()221x + 4．如图，矩形ABCD 的相邻两边的长分别是3cm 和4cm ，顺次连接矩形ABCD 各边的中点，得到四边形EFGH ，则四边形EFGH 的周长为（）A ．10cmB ．12cmC ．16cmD ．20cm 5．已知点P 位于x 轴下方，距离x 轴a 个单位长度，位于y 轴右侧，距y 轴b 个单位长度，且40a -=，则点P 的坐标是（）A ．(24)-，B ．(42)-，C ．(24)，D ．(42)，6．如图，点O 是O e 的圆心，点A 、B 、C 、D 在O e 上，BD 为O e 的直径，52DBA ︒∠=，则ACB ∠的度数为（）A ．52︒B ．38︒C ．22︒D ．19︒7．实数a ，b ）A ．2b -B ．2a -C ．22b a -D ．08．已知二次函数()240y ax ax c a =++>图象上的两点()15,y -和()22,x y ，若12y y >，则2x 的取值范围是（）A ．25x >-B ．22x <-C ．251x -<<D ．252x -<<- 9．某数学兴趣小组为了解我市气温变化情况，记录了今年3月份连续6天的最低气温（单位：℃）：11，12，14，12，16，13．关于这组数，下列结论不正确的是（） A ．平均数是13B ．众数是12C ．中位数是12.5D ．方差是310．勾股定理的证明方法丰富多样，其中我国古代数学家赵爽利用“弦图”的证明简明、直观，是世界公认最巧妙的方法．“赵爽弦图”已成为我国古代数学成就的一个重要标志，千百年来倍受人们的喜爱．小亮在如图所示的“赵爽弦图”中，连接EG ，DG ．若正方形ABCD 与EFGH ，则sin DGE ∠等于（）A B C D二、填空题118的结果是．12．如图，在四边形ABCD 中，AD BC ∥，对角线AC BD 、交于点O ，若ABC V 的面积为8，BOC V 的面积为5，则COD △的面积是．13．在一个不透明的口袋中，装有若干个红球和白球，它们除颜色外其余都相同，从中任意摸出一个球，摸到红球的概率为25，若白球有9个，则红球有个． 14．如图，BC 为圆锥底面直径，AD 为圆锥的高，若6cm AD =，60BAC ∠=︒，则这个圆锥的侧面积为2cm （结果保留π）．15．饮水机接通电源会自动加热，加热时水温每分钟上升10C ︒，温度到100C ︒停止加热．然后水温开始下降，此时水温()y ℃与时间()min x 成反比例函数关系，水温降至30C ︒时，饮水机重复上述程序开始加热，加热时水温()y ℃与时间()min x 的关系如图所示．水温从30C ︒开始加热至100C ︒，然后下降至30C ︒这一过程中，水温不低于50C ︒的时间为min ．16．如图，在ABCD Y 中，边AB 在x 轴上，边AD 交y 轴于点E ．反比例函数()0k y x x =＞的图象恰好经过点D ，与对角线DB 交于点F ．若2314DBC AE ED DF FB S ===V ，，，则k 的值为三、解答题17．已知关于x 的一元二次方程()21220x m x m -++-=（m 为常数）．(1)若方程的一个根为1，求m 的值及方程的另一个根；(2)求证：不论m 为何值时，方程总有两个实数根．18．2023年4月23日是第28个世界读书日．学校为营造“爱读书、多读书、读好书”浓厚氛围，开展了“书香校园，阅读有我”的读书活动．在5月份，为了解九年级学生的读书情况，随机调查了九年级40名学生读书数量（单位：本），并进行了以下数据的整理与分析：数据收集2 53 54 6 15 3 4 2 2 3 3 4 4 4 4 3 44 5 6 7 3 6 7 5 8 3 4 7 3 4 6 5 5 5 7 8数据整理数据分析绘制成不完整的扇形统计图和条形统计图：依据统计信息回答问题：(1)在统计表中，m =______；在条形统计图中，补全组别B 的条形图示．(2)在扇形统计图中，C 部分对应的圆心角的度数为______度；(3)若该校九年级学生人数为240人，请根据上述调查结果，估计该校九年级学生读书在4本以上的人数．19．如图，在ABC V 中，BAC ∠的平分线交BC 于点D ，DE AB ∥，DF AC ∥．(1)试判断四边形AFDE 的形状，并说明理由；(2)若90BAC ∠=︒，且22AD =，求四边形AFDE 的面积．20．如图，在平面直角坐标系中，一次函数1(0)y kx b k =+≠的图象与反比例函数2(0)m y m x=≠的图象相交于第一，三象限内的(3,4)A ，(,2)B a -两点，与x 轴交于点C ．(1)求该反比例函数和一次函数的表达式；(2)在第三象限的反比例函数图象的一点P ，使得POC △的面积等于18，求点P 的坐标． 21．如图，在ABCD Y 中，点E 是BC 中点．点F 是AD 中点．连接AE CF EF EF 、、，平分AEC ∠．(1)求证：四边形AECF 是菱形：(2)连接AC ，与EF 交于点O ，连接OD ．若5AF =，3sin 5FAC ∠=，求OD 的长． 22．已知二次函数()20y ax bx c a =++≠中，函数y 与自变量x 的部分对应值如下表：(1)求该二次函数的表达式；(2)将该二次函数的图像向右平移1个单位，再向上平移2个单位，得到的图像所对应的函数表达式．23．如图，以AB 为直径作O e ，过点A 作O e 的切线AC ，连接BC ，交O e 于点D ，点E 是BC 边的中点，连接AE ．(1)求证：2AEB C ∠=∠；(2)若8AC =，4sin 5B =，求DE 的长．。

浙江省数学学业水平考试模拟试卷

最新2020-2021年浙江省数学学业水平考试模拟试卷

浙江温州2023-2024学年上学期学业水平检测九年级数学模拟试卷+答案

2024年7月浙江省普通高中学业水平考试——数学仿真模拟试卷01(解析版)

2023年浙江省学业水平考试仿真模拟卷(四)+答案解析(附后)

2024年浙江省嘉兴市初中学业水平考试数学模拟试题

2024年浙江省初中学业水平考试数学模拟试题

浙江省普通高中学业水平考试数学模拟试题

2022年7月浙江省普通高中学业水平考试数学仿真模拟试卷_3

浙江高中数学学业水平考试模拟试题

2022年7月浙江省普通高中学业水平考试数学仿真模拟试卷_2

浙江省县域教研联盟2023-2024学年高二下学期学业水平模拟考试数学试题(原卷版)

【学考模拟】浙江省2024年7月普通高中学业水平测试仿真模拟数学试卷+答案解析

2023-2024学年浙江省杭州市普通高中学业水平合格考试数学质量检测模拟试题(含答案)

浙江省数学学业水平考试模拟学习试题

浙江省2024年初中学业水平考试模拟试卷数学(榜眼卷)

2024年浙江省杭州市数学学业水平考试模拟A试题

最新浙江省数学学考仿真模拟试题卷一(解析版)

浙江省数学学业水平考试模拟试卷

最新2020-2021年浙江省数学学业水平考试模拟试卷

浙江温州2023-2024学年上学期学业水平检测九年级数学模拟试卷+答案

2024年7月浙江省普通高中学业水平考试——数学仿真模拟试卷01(解析版)

2023年浙江省学业水平考试仿真模拟卷(四)+答案解析(附后)

2024年浙江省嘉兴市初中学业水平考试数学模拟试题

2024年浙江省初中学业水平考试数学模拟试题

浙江省普通高中学业水平考试数学模拟试题

2022年7月浙江省普通高中学业水平考试数学仿真模拟试卷_3

浙江高中数学学业水平考试模拟试题

2022年7月浙江省普通高中学业水平考试数学仿真模拟试卷_2

浙江省县域教研联盟2023-2024学年高二下学期学业水平模拟考试数学试题(原卷版)

【学考模拟 】浙江省2024年7月普通高中学业水平测试仿真模拟数学试卷+答案解析

2023-2024学年浙江省杭州市普通高中学业水平合格考试数学质量检测模拟试题(含答案)

浙江省数学学业水平考试模拟学习试题

浙江省2024年初中学业水平考试模拟试卷数学(榜眼卷)

2024年浙江省杭州市数学学业水平考试模拟A试题

最新浙江省数学学考仿真模拟试题卷一(解析版)

【学考模拟】浙江省2024年7月普通高中学业水平测试仿真模拟数学试卷+答案解析