数学八年级上册第六章思维导图
人教版 八年级上册数学 章节思维导图集 图片版
你现在的努力要对得起别人对你的好!
Math 实验室-1-人教版八年级数学上册章节思维导图
共5章
人教版八年级数学上册教材目录
第11章三角形的思维导图
11.1与三角形有关的线段
11.2与三角形有关的角
11.3多边形及其内角和
第12章全等三角形的思维导图
12.1全等三角形
12.2三角形全等的判定
12.3角的平分线的性质
第13章轴对称的思维导图
13.1轴对称
13.2画轴对称图形
13.3等腰三角形
13.4课题学习最短路径问题
第14章整式的乘法与因式分解的思维导图
14.1整式的乘法
14.2乘法公式
14.3因式分解
第15章分式的思维导图
15.1分式
15.2分式的运算
15.3
分式方程。
初二数学第六章思维导图
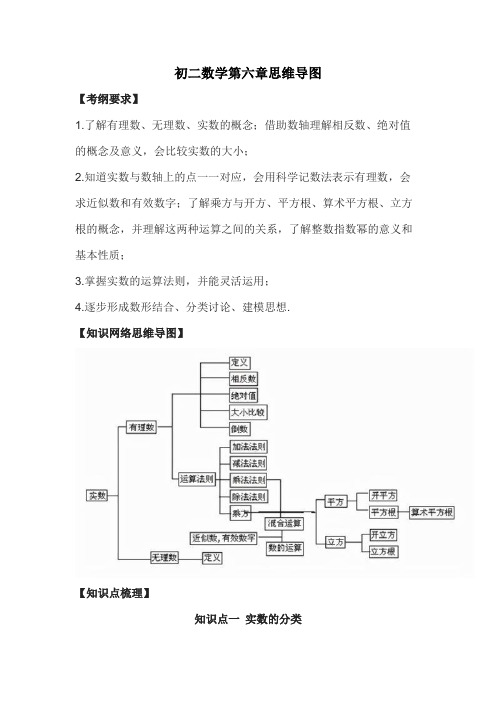
初二数学第六章思维导图【考纲要求】1.了解有理数、无理数、实数的概念;借助数轴理解相反数、绝对值的概念及意义,会比较实数的大小;2.知道实数与数轴上的点一一对应,会用科学记数法表示有理数,会求近似数和有效数字;了解乘方与开方、平方根、算术平方根、立方根的概念,并理解这两种运算之间的关系,了解整数指数幂的意义和基本性质;3.掌握实数的运算法则,并能灵活运用;4.逐步形成数形结合、分类讨论、建模思想.【知识网络思维导图】【知识点梳理】知识点一实数的分类1.按定义分类:2.按性质符合分类:有理数:整数和分数统称为有理数,或者“形如m/n(m,n是整数n≠0)”的数叫有理数.无理数:无限不循环小数叫无理数.实数:有理数和无理数统称为实数.要点诠释:常见的无理数有以下几种形式:(1)字母型:如π是无理数,π/2、π/4等都是无理数,而不是分数;(2)构造型:如2.10100100010000...(每两个1之间依次多一个0)就是一个无限不循环的小数;(3)根式型:..等都是一些开方开不尽的数;(4)三角函数型:sin35°、tan27°、cos29°等.知识点二实数的相关概念1.相反数(1)代数意义:只有符号不同的两个数,我们说其中一个是另一个的相反数.0的相反数是0;(2)几何意义:在数轴上原点的两侧,与原点距离相等的两个点表示的两个数互为相反数;(3)互为相反数的两个数之和等于0.a、b互为相反数,即a+b=0. 2.绝对值(1)代数意义:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0.可用式子表示为:(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.距离是一个非负数,所以绝对值的几何意义本身就揭示了绝对值的本质,即绝对值是一个非负数.用式子表示:若a是实数,则|a|≥0.3.倒数(1)实数a(a≠0)的倒数是1/a;0没有倒数;(2)乘积是1的两个数互为倒数.a、b互为倒数a·b=1.4.平方根(1)如果一个数的平方等于a,这个数就叫做a的平方根.一个正数有两个平方根,它们互为相反数;0有一个平方根,它是0本身;负数没有平方根.a(a≥0)的平方根记作±.(2)一个正数a的正的平方根,叫做a的算术平方根.a(a≥0)的算术平方根记作.5.立方根如果x3=a,那么x叫做a的立方根.一个正数有一个正的立方根;一个负数有一个负的立方根;0的立方根仍是0.要点诠释:若,则a≥0;若则,则a≤0. 表示的几何意义就是在数轴上表示数a与数b的点之间的距离.知识点三实数与数轴规定了原点、正方向和单位长度的直线叫做数轴,数轴的三要素缺一不可.每一个实数都可以用数轴上的一个点来表示,反过来,数轴上的每一个点都表示一个实数.要点诠释:(1)数轴的三要素:原点、正方向和单位长度.(2)实数和数轴上的点是一一对应的.知识点四实数大小的比较知识点五、实数的运算1.加法同号两数相加,取相同的符号,并把绝对值相加;绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值;互为相反数的两个数相加得0;一个数同0相加,仍得这个数.满足运算律:加法的交换律a+b=b+a,加法的结合律(a+b)+c=a+(b+c).2.减法减去一个数等于加上这个数的相反数.3.乘法两数相乘,同号得正,异号得负,并把绝对值相乘.几个非零实数相乘,积的符号由负因数的个数决定,当负因数有偶数个时,积为正;当负因数有奇数个时,积为负.几个数相乘,有一个因数为0,积就为0.乘法运算的运算律:(1)乘法交换律ab=ba;(2)乘法结合律(ab)c=a(bc);(3)乘法对加法的分配律a(b+c)=ab+ac.4.除法(1)除以一个数,等于乘上这个数的倒数.(2)两个数相除,同号得正,异号得负,并把绝对值相除.0除以任何一个不等于0的数都得0.5.乘方与开方(1)求n个相同因数的积的运算叫做乘方,an所表示的意义是n个a相乘.正数的任何次幂是正数,负数的偶次幂是正数,负数的奇次幂是负数.(2)正数和0可以开平方,负数不能开平方;正数、负数和0都可以开立方.(3)零指数与负指数:a0=1(a≠0),a-p=1/ap(a≠0)要点诠释:(1)加和减是一级运算,乘和除是二级运算,乘方和开方是三级运算.这三级运算的顺序是三、二、一.如果有括号,先算括号内的;如果没有括号,同一级运算中要从左至右依次运算.(2)实数的运算律加法交换律:a+b=b+a加法结合律:(a+b)+c=a+(b+c)乘法交换律:ab=ba乘法结合律:(ab)c=a(bc)乘法分配律:(a+b)c=ac+bc知识点六有效数字和科学记数法1.近似数一个近似数,四舍五入到哪一位,就说这个近似数精确到哪一位.精确度的形式有两种:(1)精确到哪一位;(2)保留几个有效数字.2.有效数字一个近似数,从左边第一个不是0的数字起,到精确到的数位为止,所有的数字,都叫做这个近似数的有效数字.3.科学记数法把一个数用±a×10n(其中1≤<10,n为整数)的形式记数的方法叫科学记数法.要点诠释:(1)当要表示的数的绝对值大于1时,用科学记数法写成a×10n,其中1≤<10,n为正整数,其值等于原数中整数部分的数位减去1;(2)当要表示的数的绝对值小于1时,用科学记数法写成a×10n,其中1≤<10,n为负整数,其值等于原数中第一个非零数字前面所用零的个数的相反数(包括小数点前面的零).知识点七数形结合、分类讨论、建模思想1.数形结合思想实数与数轴上的点一一对应,绝对值的几何意义等,数轴在很多时候可以帮助我们更直观地分析题目,从而找到解决问题的突破口;2.分类讨论思想(算术)平方根,绝对值的化简都需要有分类讨论的思想,考虑问题要全面,做到既不重复又不遗漏;3. 从实际问题中抽象出数学模型以现实生活为背景的题目,我们要抓住问题的实质,明确该用哪一个考点来解决问题,然后有的放矢.。
沪教版(上海)-初中数学七年级、八年级、九年级数学全册章节知识点结构思维导图集

- 14 -
第二十六章 二次函数的章节知识点结构思维导图 第二十七章 圆与正多边形的章节知识点结构思维导图
- 15 -
第二十八章 统计初步的章节知识点结构思维导图
- 16 -
-7-
第十四章 三角形的章节知识点结构思维导图 第十五章 平面直角坐标系的章节知识点结构思维导图
-8-
上海市(沪教版)八年级数学全册章节思维导图 共八个章节
第十六章 二次根式的章节知识点结构思维导图
-9-
第十七章 一元二次方程的章节知识点结构思维导图
- 10 -
第十八章 正比例函数和反比例函数的章节知识点结构思维导图 第十九章 几何证明的章节知识点结构思维导图
-3-
第七章 线段与角的画法的章节知识点结构思维导图 第八章 长方体的再认识的章节知识点结构思维导图
-4-
上海市(沪教版)七年级数学全册章节思维导图 共七章
第九章 整式的章节知识点结构思维导图
-5-
第十章 分式的章节知识点结构思维导图 第十一章 图形的运动的章节知识点结构思维导图
-6-
第十二章 实数的章节知识点结构思维导图 第十三章 相交线 平行线的章节知识点结构思维导图
- 11 -
第二十章 一次函数的章节知识点结构思维导图 第二十一章 代数方程的章节知识点结构思维导图
- 12 -
第二十二章 四边形的章节知识点结构思维导图 第二十三章 概率初步的章节知识点结构思维导图
- 13 -
上海市(沪教版)ቤተ መጻሕፍቲ ባይዱ年级数学全册章节思维导图 共五章
第二十四章 相似三角形的章节知识点结构思维导图
上海市(沪教版)初中数学全册思维导图集 共二十八章
初二上册数学思维导图

初二上册数学思维导图单项式相乘,把系数、同底数幂分别相乘,作为积的因式;对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式.单项式与多项式的乘法法则:单项式与多项式相乘,用单项式和多项式的每一项分别相乘,再把所得的积相加.多项式与多项式的乘法法则:多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.单项式的除法法则:单项式相除,把系数、同底数幂分别相除,作为商的因式:对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.多项式除以单项式的法则:多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.2、乘法公式:①平方差公式:(a+b)(a-b)=a2-b2文字语言叙述:两个数的和与这两个数的差相乘,等于这两个数的平方差.②完全平方公式:(a+b)2=a2+2ab+b2(a-b)2=a2-2ab+b2文字语言叙述:两个数的和(或差)的平方等于这两个数的平方和加上(或减去)这两个数的积的2倍.3、因式分解:因式分解的定义.把一个多项式化成几个整式的乘积的形式,这种变形叫做把这个多项式因式分解.掌握其定义应注意以下几点:(1)分解对象是多项式,分解结果必须是积的形式,且积的因式必须是整式,这三个要素缺一不可;(2)因式分解必须是恒等变形;(3)因式分解必须分解到每个因式都不能分解为止.弄清因式分解与整式乘法的内在的关系.因式分解与整式乘法是互逆变形,因式分解是把和差化为积的形式,而整式乘法是把积化为和差的形式.二、熟练掌握因式分解的常用方法.1、提公因式法(1)掌握提公因式法的概念;(2)提公因式法的关键是找出公因式,公因式的构成一般情况下有三部分:①系数一各项系数的最大公约数;②字母各项含有的相同字母;③指数相同字母的最低次数;(3)提公因式法的步骤:第一步是找出公因式;第二步是提取公因式并确定另一因式.需注意的是,提取完公因式后,另一个因式的项数与原多项式的项数一致,这一点可用来检验是否漏项.(4)注意点:①提取公因式后各因式应该是最简形式,即分解到底;②如果多项式的第一项的系数是负的,一般要提出-号,使括号内的第一项的系数是正的.2、公式法运用公式法分解因式的实质是把整式中的乘法公式反过来使用;常用的公式:①平方差公式: a2-b2= (a+b)(a-b)②完全平方公式:a2+2ab+b2=(a+b)2a2-2ab+b2=(a-b)2分式知识点知识点一:分式的定义一般地,如果A,B表示两个整数,并且B中含有字母,那么式子叫做分式,A 为分子,B为分母。
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作+√a 和√a。
0的平方根是0,负数没有平方根。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
每个实数都有唯一的立方根。
3. 开方运算:开方运算是求一个数的平方根或立方根的运算。
对于正数a,开方运算可以表示为√a或³√a。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:实数可以分为正实数、负实数和0。
正实数是大于0的实数,负实数是小于0的实数,0既不是正实数也不是负实数。
3. 实数的运算:实数可以进行加法、减法、乘法和除法运算。
在运算过程中,需要遵循实数的运算规律,如交换律、结合律和分配律。
三、勾股定理1. 勾股定理的内容:勾股定理指出,在一个直角三角形中,直角边的平方和等于斜边的平方。
即a²+b²=c²,其中a、b是直角边,c是斜边。
2. 勾股定理的应用:勾股定理可以用来解决直角三角形中的边长问题,也可以用来解决一些与直角三角形相关的实际问题。
3. 勾股定理的证明:勾股定理的证明有多种方法,其中一种常见的证明方法是使用几何图形的面积关系。
四、一次函数1. 一次函数的概念:一次函数是指函数的图像是一条直线,其一般形式为y=kx+b,其中k是斜率,b是截距。
2. 一次函数的性质:一次函数的图像是一条直线,斜率k表示直线的倾斜程度,截距b表示直线与y轴的交点。
3. 一次函数的应用:一次函数可以用来描述一些线性关系,如物体的速度与时间的关系、正比例关系等。
五、不等式1. 不等式的概念:不等式是表示两个数之间大小关系的数学表达式,如a>b、a<b、a≥b、a≤b等。
2. 不等式的性质:不等式可以进行加减、乘除运算,但在乘除运算中需要注意符号的变化。
初中数学八年级上册思维导图

初中数学八年级上册思维导图一、数的开方1. 平方根:如果一个正数x的平方等于a,那么x是a的平方根,记作x=√a。
正数a的平方根有两个,它们互为相反数,分别记作√a和√a。
0的平方根是0。
2. 立方根:如果一个数x的立方等于a,那么x是a的立方根,记作x=³√a。
立方根只有一个。
3. 算术平方根:正数a的正的平方根,记作√a,称为a的算术平方根。
4. 立方根的性质:①正数的立方根是正数;②负数的立方根是负数;③0的立方根是0。
二、实数1. 实数的概念:实数包括有理数和无理数。
有理数是可以表示为两个整数比的数,无理数是不能表示为两个整数比的数。
2. 实数的分类:①正实数;②负实数;③零。
3. 实数的运算:实数的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
三、二次根式1. 二次根式的概念:形如√a的式子,其中a≥0,称为二次根式。
2. 二次根式的性质:①√a²=a(a≥0);②(√a)²=a(a≥0);③√ab=√a√b(a≥0,b≥0);④√a²+b²=√a²+√b²(a≥0,b≥0)。
3. 二次根式的运算:二次根式的加减乘除运算与有理数的运算类似,但需要注意无理数的运算。
四、一元二次方程1. 一元二次方程的概念:形如ax²+bx+c=0(a≠0)的方程,称为一元二次方程。
2. 一元二次方程的解法:①配方法;②求根公式法;③因式分解法。
3. 一元二次方程的根的判别式:判别式△=b²4ac,当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根。
五、不等式1. 不等式的概念:表示不相等关系的式子称为不等式。
2. 不等式的性质:①两边同时加上或减去同一个数,不等号方向不变;②两边同时乘以或除以同一个正数,不等号方向不变;③两边同时乘以或除以同一个负数,不等号方向改变。
导图系列(3-4):八年级数学(北师大版)各章知识点思维导图集合

第三章 图形的平移与旋转
第四章 因式分解 第五章 分式与分式方程
第六章 平行四边形
任它本身;负数的绝对值是它的相反数;0 的绝对值是 0。(反之,若 5 绝对值
性质 |a|=a,则 a≥0;若|a|=-a,则 a≤0。)
互为相反数的两个数的绝对值相等。
两个负数比较大小,绝对值大的反而小。
如果两个数只有符号不同,那么称其中一个数为另一个的相反数,也称这两个数互
性质 负数。
一般地,形如 的代数式叫做二次根式,a 叫做被开方数。
二次根 一般地,被开方数不含分母,也不含能开得尽方的因数或因式的二次根式叫最简二次根式。
11
式
·
( , ),
(,)
第三章 位置与坐标
序号 1
知识点 确定位置
第三章 位置与坐标
内容 在平面内,确定一个物体的位置一般需要 2 个数据。 在平面内,两条互相垂直且有公共原点的两条数轴构成平面直角坐标系。通常,两条 数轴分别置于水平位置与铅直位置,取向右与向上的方向分别为两条数轴的正方向。水平 的数轴叫做 x 轴或横轴,垂直的数轴叫做 y 轴或纵轴,x 轴和 y 轴统称为坐标轴,它们的 公共原点 O 称为直角坐标系的原点。建立了平面直角坐标系,平面内的点就可以用一组有 序实数对(a,b)来表示了。 在平面直角坐标系中,两条坐标轴将坐标平面分成了四部分,右上方的部分叫做第一 象限,其它三部分按逆时针方向依次叫做第二、三、四象限。坐标轴上的点不在任何一个 象限内。
性质 一个正数有两个平方根,它们互为相反数;0 的平方根是 0;负数没有平方根。
算数 定义 一般地,如果一个正数 x 的平方等于 a, ,那么这个正数 x 就叫做 a 的算数平方根。 9
平方根 性质 一个正数的算数平方根是正数;0 的算数平方根是 0;负数没有算数平方根。
八年级上册数学思维导图(20200705172422)
逆定理’勾號玫’应用
知两边、求斜高
T方根
违义,性质,作圈*圈赛分祈
平秽
走义]性质#柞图*图案分析
屮松■匚饰祐
战铸
四诃形
行列定位
位宜餉确定
坐标巳歸跟廉特点
坐标变化耳團பைடு நூலகம்变化的关系
ih血烦
解祈武.的确淀'
儿丄数亍
方程馆
用函隸囲躱銅方程
匚次函最的北系
辭芳程姐定函救表达式
平旳救
数鋸衲代芸
2
珥术平旳釦加枢平阅数
出现if数2众烦t撤念£求注)
I \
為程組,走丈、解、解法(代入*;JOM>
应用I识[D
宦文’三种衣示育准
中间惊苴:中偉数{槪念:求法、
护大二鏑小
血底:庄缩
屮血鱼母坐标系;鬆15岂坐标
应用,审.说、列、辭
行遷工程m利息m销皐蔽度
示丈、闊象’杵质
再程,走义*解、整数解
四边形:三个要素(角、 边、对角线);两条主 线(性质、判定);五 种图形。
八年级数学上册知识点归纳总结(可编辑打印思维导图)
第四章 四边形性质探索
在同一平面内,由不在同一直线上的四 条线段首尾顺次相接组成的图形叫做四
边形。
1、四边形
2、四边形具有不稳定性
四边形的内角和定理:四边形的内角和 等于360°。
四边形的外角和定理:四边形的外角和 等于360°。
推论:多边形的内角和定理:n边形的内 角和等于180°;
3、四边形的内角和定理及外角和定理
2、无理数:无限不循环小数叫做无理数 。
有限小数和无限循环小数 负有理数
无限不循环小数
(1)开方开不尽的数,如等; (2)有特定意义的数,如圆周率π ,或
化简后含有π 的数,如+8等; (3)有特定结构的数,如 0.1010010001…等;
(4)某些三角函数值ห้องสมุดไป่ตู้如sin60o等
二、实数的倒数、相反数和绝对值
第六章 一次函数 第五章 位置的确定 第四章 四边形性质探索
八年级数学上册
第一章 勾股定理 第二章 实数 第三章 图形的平移与旋转
第一章 勾股定理
1、勾股定理
直角三角形两直角边a,b的平方和等于 斜边c的平方,即
2、勾股定理的逆定理
如果三角形的三边长a,b,c有关系,那 么这个三角形是直角三角形。
。
两组对边分别平行的四边形叫做平行四 边形。
(1)平行四边形的对边平行且相等。 (2)平行四边形相邻的角互补,对角相
等 (3)平行四边形的对角线互相平分。
(4)平行四边形是中心对称图形,对称 中心是对角线的交点。
1、平行四边形的定义 2、平行四边形的性质
(2)推论:夹在两条平行线间的平行线 段相等。
(1)定义:两组对边分别平行的四边形 是平行四边形
(完整版)人教版初中数学思维导图.docx

指导教师:日期: 2019 年 02 月 28 日初中数学思维导图姓名:班级:学号:七年级上册第一章有理教1.1正数和负数1.2有理数1.2.1有理数1.2.2数轴1.2.3相反数1.2.4绝对值1.3有理数的加减法1.3.1有理数的加法1.3.2有理数的减法1.4有理数的乘除法1.4.1有理数的乘法1.4.2有理数的除法1.5有理数的乘方1.5.1乘方1.5.2科学记数法1.5.3近似数第二章整式的加减2.1整式2.2整式的加减第三章一元一次方程3.1从算式到方程3.1.1一元一次方程3.1.2等式的性质3.2解一元一次方程(一)——合并同类项与移项3.3解一元一次方程(二)—去括号与去分母3.4实际问题与一元一次方程第四章几何初步4.1几何图形4.1.1立体图形与平面图形4.1.2点、线、面、体4.2直线、射线、线段4.3角4.3.1角4.3.2角的比较与运算4.3.3余角和补角4.4课题学习设计制作长方体形状的包装纸盒七年级下册第五章相交线与平行线5.1相交线5.1.1相交线5.1.2垂线5.1.3同位角、内错角、同旁内角5.2平行线及其判定5.2.1平行线5.2.2平行线的判定5.3平行线的性质5.3.1平行线的性质5.3.2命题、定理、证明5.4平移第六章实数6.1平方根6.2立方根6.3实数第七章平面直角坐标系7.1平面直角坐标系7.1.1有序数对7.1.2平面直角坐标系7.2坐标方法的简单应用7.2.1用坐标表示地理位置7.2.2用坐标表示平移第八章二元一次方程组8.1二元一次方程组8.2消元——解二元一次方程组8.3实际问题与二元一次方程组8.4三元一次方程组的解法第九章不等式与不等式组9.1不等式9.1.1不等式及其解集9.1.2不等式的性质9.2一元一次不等式9.3一元一次不等式组第十章数据的收集、整理与描述10.1统计调查10.2直方图10.3课题学习从数据谈节水八年级上册第十一章三角形11.1与三角形有关的线段11.1.1三角形的边11.1.2三角形的高、中线与角平分线11.1.3三角形的稳定性11.2与三角形有关的角11.2.1三角形的内角11.2.2三角形的外角11.3多边形及其内角和11.3.1多边形11.3.2多边形的内角和第十二章全等三角形12.1全等三角形12.2三角形全等的判定12.3角的平分线的性质第十三章轴对称13.1轴对祢13.1.1轴对称13.1.2线段的垂直平分线的性质13.2画轴对称图形13.3等腰三角形13.3.1等腰三角形13.3.2等边三角形13.4课题学习最短路径问题第十四章整式的乘法与因式分解14.1整式的乘法14.1.1同底数幂的乘法 .14.1.2幂的乘方14.1.3积的乘方14.1.4整式的乘法14.2乘法公式14.2.1平方差公式14.2.2完全平方公式14.3因式分解14.3.1提公因式法14.3.2公式法第十五章分式15.1分式15.1.1从分数到分式15.1.2分式的基本性质15.2分式的运算15.2.1分式的乘除15.2.2分式的加减15.2.3整数指数幂15.3分式方程八年级下册指导教师:日期: 2019 年 02 月 28 日第十六章二次根式16.1 二次根式16.2 二次根式的乘除16.3 二次根式的加减数学活动小结复习题 16第十七章勾股定理17.1 勾股定理17.2 勾股定理的逆定理数学活动小结复习题 17第十八章平行四边形18.1 平行四边形18.2 特殊的平行四边形数学活动小结复习题 18第十九章一次函数19.1 函数19.2 一次函数14.3 课题学习选择方案数学活动小结复习题 19第二十章数据的分析20.1 数据的集中趋势20.2 数据的波动程度20.3 课题学习体质健康测试中的数据分析数学活动小结复习题 20。
