三年级不规则图形求面积汇总
各种形状的面积计算公式

各种形状的面积计算公式
一、正方形。
1. 公式:面积 = 边长×边长,用字母表示为S = a×a=a^2(其中S表示面积,a 表示正方形的边长)。
二、长方形。
1. 公式:面积 = 长×宽,用字母表示为S = a×b(其中S表示面积,a表示长,b 表示宽)。
三、三角形。
1. 公式:面积 = 底×高÷2,用字母表示为S=(1)/(2)ah(其中S表示面积,a表示底,h表示高)。
四、平行四边形。
1. 公式:面积 = 底×高,用字母表示为S = ah(其中S表示面积,a表示底,h 表示高)。
五、梯形。
1. 公式:面积=(上底 + 下底)×高÷2,用字母表示为S=((a + b)h)/(2)(其中S 表示面积,a表示上底,b表示下底,h表示高)。
六、圆形。
1. 公式:面积=π×半径的平方,用字母表示为S=π r^2(其中S表示面积,r表示半径,π通常取3.14)。
三年级 不规则图形面积的计算

第十讲:面积的实际应用知识梳理【知识要点】1、周长:封闭图形一周的长度,是它的周长。
长方形的周长 =(长+宽)×2正方形的周长 = 边长×42、面积:物体的表面或封闭图形的大小就是它们的面积。
边长是1厘米的正方形的面积是1平方厘米。
边长是1分米的正方形的面积是1平方分米边长是1米的正方形的面积是1平方米长方形的面积 = 长×宽正方形的面积 = 边长×边长3、一个图形剪掉一部分,面积一定会减少,但周长不一定会减少。
4、掌握换算的方法(1)高级单位化成低级单位:高级单位的数×进率大单位化小单位添0,如2平方米=(200)平方分米(想:平方米大,所以是大化小添0,因为1平方米=100平方分米,应该在2后面添两个0.)(2)低级单位聚成高级单位:低级单位的数÷进率小单位化大单位去0,如20000平方米=(2)公顷,(想:平方米小,所以是小化大去0,因为1公顷=10000平方米,应该去掉2后面的四个0.)5、周长相等的两个长方形,面积不一定相等。
面积相等的两个长方形,周长也不一定相等。
6、长方形和正方形的面积相等时,正方形的周长小。
7、长方形和正方形的周长相等时,正方形的面积大。
(如用同样长的绳子围成的正方形面积比长方形的面积大)面积单位换算1平方千米 = 100公顷 1公顷=10000 平方米 1平方米=100 平方分米 1平方分米=100平方厘米【例题一】小林要从左边的纸上剪下一个最大的正方形。
剩下部分是什么图形?它的面积是多少平方厘米?【拓展训练】一个长方形,长16分米,宽12分米,在这个长方形上尽可能剪下一个正方形,正方形的面积是多少?剩下图形的面积是多少?【例题二】求下列图形的周长。
12厘米 15厘米 15厘米12厘米 12厘米 9米10米 3米4米【拓展训练】(单位:cm )【例题三】李奶奶家房子东面有一块长方形菜地,菜地一边紧挨着墙壁(如右图),少先队员们要给李奶奶的菜地围上篱笆,需要准备多长的篱笆?这块菜地的面积是多少平方米?【拓展训练】李大爷靠东墙围了一个羊圈,算出这个羊圈的占地面积?如果要砌上围墙,围墙的长度应该是多少米?【例题四】一块面积有72平方分米的长方形台布,长9分米,它的宽是多少?57 522 18米 3米 墙18 25米东墙【拓展训练】一块正方形的喷水池的周长是20米,它的边长是多少米?面积是多少平方米?【例题五】3平方米=()平方分米 5平方分米=()平方厘米700平方厘米=()平方分米600平方分米=()平方厘米30平方分米=()平方厘米 8000平方分米=()平方米【拓展训练】1、教室地面的面积大约是60(),也就是6000()。
不规则图形面积的计算(方法总结及详解)

不规则图形计算的方法总结总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可.三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了.五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
不规则面积计算公式(二)

不规则面积计算公式(二)不规则面积计算公式在数学和几何学中,计算不规则形状的面积是一项常见的任务。
不规则形状是指不符合常见几何图形的形状,例如梯形、矩形或圆形。
本文将介绍一些常见的不规则面积计算公式,并举例解释说明。
下面是一些常见的不规则面积计算公式:1. 多边形的面积计算公式对于任意一个简单闭合多边形,可以使用以下公式计算其面积:S = 1/2 * (x1y2 + x2y3 + ... + xn-1yn + xny1 - x2y1- x3y2 - ... - xnyn-1 - x1yn)其中,(x1, y1), (x2, y2), …, (xn, yn) 是多边形的各个顶点坐标。
该公式通过将多边形划分为多个三角形来计算面积,并累加这些三角形的面积。
例如,考虑一个三角形,其顶点坐标为 (0, 0), (4, 0), (0, 3)。
可以使用上述公式计算其面积:S = 1/2 * (0*4 + 4*3 + 0*0 - 0*0 - 4*3 - 0*4)= 1/2 * (0 + 12 + 0 - 0 - 12 - 0)= 1/2 * 0= 0因此,该三角形的面积为 0。
2. 圆形的面积计算公式圆形是一种常见的不规则形状,其面积可以使用以下公式计算:S = π * r^2其中,π 是一个数学常量,约等于,r 是圆的半径。
例如,考虑一个半径为 5 的圆,可以使用上述公式计算其面积:S = π * 5^2≈ * 25≈因此,该圆的面积约为。
3. 曲线围成的面积计算公式对于由曲线围成的不规则形状,可以使用积分来计算其面积。
具体而言,可以使用以下公式:S = ∫[a, b] y(x) dx其中,y(x) 是曲线的方程,[a, b] 是曲线在 x 轴上的投影区间。
例如,考虑由曲线 y = x^2 围成的形状,要计算其面积,可以使用上述公式:首先,找出曲线与 x 轴的交点,即解方程 x^2 = 0,得到 x = 0。
三年级不规则图形求面积

求组合图形周长和面积例题一:下面和组合图形可以用三种方法求出它的面积。
5cm■ 8cm18cm①5X( )+7 X18=()②12 X 10+( )X8=( )③()X 18 ・5X8=()练一练、根据虚线画出的分割图形,求出下面图形的面积。
(1) ⑵6m①8m! ②2m1Am例题二:求出阴影部分的面积练一练: (1)① ②60 m40m5m12cm20cm(2)例题三:求出下列图形周长和面积。
Tdin5 dm35 cm ①EQo25 cmi * [绘(i)琲丨养练一练:求下列组合图形的周长和面积。
2 )J6 (H4t2刷牝]1「T-----------------------------家庭作业->求下列组合图形的周长与囱积:Hem10m16mLOdm第一部分(共49分)-■直接写出得数。
12800 — 650- 340 + 260- 200 24X5- 370-170 — 98 二5X60= 120X4 = 172+4X7 = 4054168 295 =720 十9 = 300宁5 = 5OO-50-r5 = 315-102-98 = 二.把算式写完誉。
(扶9分)I. 543X4 -()500X 4^( )( )X4=( )( )X( )=< >()十()十( )=( ) …2. 696 4-3-C )6(X>-r3-< )< )一30 )< )4-( >-< >、用竖式计(汐*的越矣检耳•能算样1 ^)(41 2S分)tiO2 - 195 = ・ +4068X65 ==324X6 846+6 = 420X5-第二部分(兵22分)四.F空处。
(対16分)1.心枳扯四位数・〃榷甲龍小町以;・2.徨便SI 13-^-S的商中何仆¥ 〃或里域大可以填《几、・匕使li的曲t曲位数•方挺里绘火町以壤()•制4. U it IF >9! 9 /C.1OO儿伐用序町以尖《)心・牌淤上()元町以即买•本连环叫.«乙tt® Z Vi.lllftWr乙散的4请」卩数是(儿ft. FIS怪2016筛8月份的H历.S M1T2W3T1F S361&910II121314131617u1920212221242526272$2930117月31 II鉅喔HM )iU JI Z II昭处期(九7. 2OI<i KUtl)(MS44•”趾“羊卑")・全第你()天.«•何庆)作收•这卞*復"()犬.五、违择It.(把止福黑■对的半斥从入”寸内)《*6沪)I. □口□十口=126……6我除数册小)•505X6-714 + 72・忙忡用,下血-逍算式中rfttt 小的冷式能(第三褴分〈扶25分)六. 解决何I •啊庆怪載期・-話建收费处R 分钟其械行了 680辆小汽,•那么收费处护轲分种放行多少無小汽牟?・2. 小畔“ ”假中甲荷锂天学丐9个毛笔字•那么小胖匕片份-共打r 几t3. 梅国ItKaiS! 127个悬人右公田游坑.公因毎辆犯光乍眼坐8个人•那么 他门至少妄削儿辆妣乍?壮;霭需=心人•如5 2“人⑴拍球的叶m 几人?:;d 502-r 5C. 50ZW6,•和♦「*,;一―屮的做的天小•给黑⑵的崗学有儿人?第B部甘(共・|和七、动诙觞。
不规则图形的面积汇总
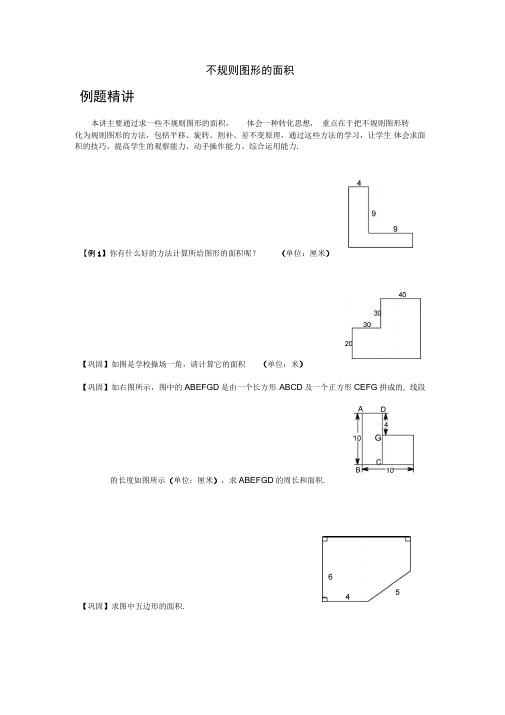
不规则图形的面积例题精讲本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例1】你有什么好的方法计算所给图形的面积呢?(单位:厘米)【巩固】如图是学校操场一角,请计算它的面积(单位:米)【巩固】如右图所示,图中的ABEFGD是由一个长方形ABCD及一个正方形CEFG拼成的, 线段的长度如图所示(单位:厘米),求ABEFGD的周长和面积.【巩固】求图中五边形的面积.【例2】(第三届”华杯赛口试试题”)这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20厘米•问,此楼梯截面的面积是多少?有一块菜地长16米,宽8米,菜地中间留了宽 2米的路,把菜地平均分成四块,每 一块地的面积是多少?有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么 这10张纸片所盖住的桌面的面积是多少平方厘米?下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是 少平方厘米?20厘米•这楼梯的截面积是多【【【【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积【例6】如图,李大伯给一块长方形田地喷药, 喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长 2米的正方形区域,他从图中的 A 点出发,沿最短路线(图中虚线) 走,走过88米到达B 点,恰好把这块田地全部喷完,这块田地的面积是多少平方 米?【例7】(第六届”走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛 初赛)右图中甲的面积比乙的面积大 ____________________ 平方厘米.右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形的面积大9平方厘米,求ED 的长.【巩固】如图所示, CA =AB =4厘米,△ ABE 比 △CDE 的面积小2平方厘米,求CD 的长【EDF6厘米4厘米为多少厘米?【巩固】如图,平行四边形 ABCD 申,BC=10cm ,直角三角形ECB 的边EC = 8cm ,已知阴影部分的总面积比三角形 EFG 勺面积大10cm 2,求平行四边形 ABC 啲面积.【例9】如图,ABCD 是 7 4的长方形,DEFG 是 10 2的长方形,求BCO 与L EFO 的面积 差.【例10】 有一个长方形菜园,如果把宽改成 50米,长不变,那么它的面积减少 680平方米,如果使宽为60米,长不变,那么它的面积比原来增加 2720平方米,原来的 长和宽各是多少米?680平方米 2720平方米【巩固】有一个长方形,如果宽减少 2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?DE F15分米,宽12分米,如果长和宽各减少 2分米,面积比15【例12】一个长方形,如果长减少 5厘米,宽减少2厘米,那么面积就减少 66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?【巩固】一块长方形纸片,在长边剪去 5cm ,宽边剪去2cm 后(如图),得到的正方形面积比原长方形面积少31cm 2.求原长方形纸片的面积.【巩固】一个正方形,如果把它的相邻两边都增加 6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大 120平方厘米•求原正方形的面积?【例11】 一块长方形铁板,长原来减少多少平方分米?【巩固】一张长方形纸片,先把长剪去 8厘米,这时面积减少了 72平方厘米,又把宽剪去5厘米,这时面积又减少了 60平方厘米,原来这张长方形纸片的面积是多少平方厘米?【巩固】(希望杯培训题)如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽7分米的长方形,所得图形的面积比原正方形减少 301平方分米•原正方形的边长是 ______ 分米.【例13】 一块正方形的钢板,先截去一个宽 方形(如图),面积就比原来正方形减少 米?5分米的长方形,又截去一个宽8分米的长181平方分米.原正方形的边长是多少分6厘米长8【例14】如图长方形被分成两部分,已知阴影面积比空白部分面积大34平方厘米,求阴影部分的面积.18cm【例15】 一张长方形纸片,把它的右上角往下折叠(如图甲),阴影部分面积占原纸片面积的-;再把左下角往上折叠(如图乙),乙图中阴影部分面积占原纸片面积的7【巩固】如图,一张长方形纸片,长 7厘米,宽5厘米•把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?【例16】 如图,大正方形的边长为10厘米•连接大正方形的各边中点得小正方形,将10cm【巩固】折叠后,原平行四边形面积是折叠后图形面积的则重叠部分(即空白部分)的面积是多少?1.5倍.已知阴影部分面积之和为 1,7小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例17】如图所示,直角三角形中有一个长方形,求长方形的面积?【例18】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形•求第五个正方形的面积?【巩固】(2008年第七届”小机灵杯”数学竞赛决赛)如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是 ________ .【巩固】图中有6个正方形,较小的正方形都由较大的正方形的4边中点连接而成.已知最大的正方形的边长为16厘米,那么最小的正方形的面积等于多少平方厘米?【巩固】如图所示,外侧大正方形的边长是 10cm ,在里面画两条对角线、一个圆、两个正方形,阴影的总面积为 26cm 2,最小的正方形的边长为多少厘米?【例20】 有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形•求图中阴影部分的面积?【例21】 (2008年全国小学生”我爱数学夏令营” 数学竞赛)如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积 为 ________ •【例19】 已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米? 第2题【例22】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)6【巩固】(2008年武汉明心奥数挑战赛)如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?【例23】甲、乙、丙三个正方形,它们的边长分别是6、& 10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上. 这三个正方形的覆盖面积是多少平方厘米?【巩固】将20张边长为10厘米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候, 要求后摆的纸片必须有一个顶点与前一张的中心重合,且每一张只与其前一张和后一张有重合部分(右图表示已经摆好的5张)•地板被这20张纸片所覆盖部分的面积是多少?【例24】有2个大小不同的正方形A和B .如下左图所示的那样,在将B正方形的对角线的交点与A正方形的一个顶点相重叠时,相重叠部分的面积为A正方形面积的1•求A与B的边长之比•如果当按下右图那样,将A和B反向重叠的话,所重9【例25】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?【巩固】一块长方形草坪(图中阴影部分)长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米?【例26】(2008年北京”数学解题能力展示”读者评选活动复赛)如图所示,一个长方形广场的正中央有一个长方形的水池. 水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.【例27】用四个相同的长方形拼成一个面积为100cm2的大正方形,每个长方形的周长是多少平方厘米?【巩固】如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例28】四个完全相同的长方形拼成右图,大正方形的面积是100平方分米,小正方形的面积是16平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?【巩固】(2008年”陈省身杯”国际青少年数学邀请赛)如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为__________ 厘米,宽_________ 厘米.第19题【例29】街心花园里有一个正方形花坛,四周有一条宽1米的甬道(如图),如果甬道的面积是12平方米,那么中间花坛的面积是多少平方米?【巩固】在一个正方形的小花园周围,环绕着宽 5米的水池,水池面积为 300平方米,那么正方形花园的面积是多少平方米?【巩固】有大、小两个长方形 (如图),对应边的距离均为1cm ,已知两个长方形之间部分的 面积是16cm 2,且小长方形的长是宽的 2倍,求大长方形的面积.【例30】 已知大正方形比小正方形边长多 4厘米,大正方形面积比小正方形面积大 96平方厘米.问大、小正方形面积各是多少?【巩固】两个正方形的面积相差 9cm 2,边长相差1cm .求两个正方形的面积和. CBA■【巩固】(第四届《小数报》数学竞赛决赛试题)有一大一小两个正方形,它们的周长相差 20厘米,面积相差 55平方厘米•小正方形的面积是多少平方厘米?【例31】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差 16厘米,面积相差96平方厘米,求小正方形的面积是多 少平方厘米?【例32】用两块长方形纸片和一块正方形纸片拼成一个大正方形, 长方形纸片面积分别为44平方厘米与28平方厘米,原正方形纸片面积是多少平方厘米?【巩固】有大、小两个长方形 (右图),对应边的距离均为1厘米,已知两个长方形之间部分 的面积是16平方厘米,且小长方形的长是宽的 2倍,求大长方形的面积.【巩固】一块长方形的草坪(见图中阴影部分),长是宽的2倍,它的四周围的总面积是 34平 方米的1米宽的小路,求草坪的总面积是多少平方米? 【例33】 计划修建一个正方形的花坛,并在花坛周围种上300平方米,那么修建这个花坛需要占地多少平方米? 3米宽的草坪,草坪的面积为【例34】一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所30?示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米30【例35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?【巩固】从一个正方形的木板上锯下宽1m的一个长方形木条后,剩下的长方形面积为6m2,问锯下的长方形木条面积是多少?【巩固】从一块正方形木板锯下宽为-米的一个木条以后,剩下的面积是65平方米•问锯2 18下的木条面积是多少平方米?【例36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.J220【例37】有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?【例38】(第十二届“迎春杯”刊赛试题)如图,边长是整数的四边形AFED的面积是【例39】如图,一个正方形被分成4个小长方形,它们的面积分别是-平方米、-平10 5方米、2平方米和2平方米•已知图中的阴影部分是正方形,那么它的面积是多10 5少平方米?【例40】长方形ABCD的周长是30厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290平方厘米,那么长方形ABCD的面积是多少平方厘米?48平方厘米,FB为8厘米.那么,正方形ABCD的面积是A【巩固】(第四届华杯复赛试题)如图,长方形ABCD的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方厘米,求长方形ABCD的面积?【例41】一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是2厘米,这条手帕白色部分的面积是多少?【例42】用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?【例43】7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?【巩固】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?【例44】(第五届”祖冲之杯”数学邀请赛)如右图所示,在长方形ABCD中,放入六个14形状大小相同的长方形(尺寸如图),图中阴影部分的面积是______________ .6【例45】若干同样大小的长方形小纸片摆成了如图所示的图形•已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例46】一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A和B的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?A【巩固】(2008年中国台湾小学数学竞赛选拔赛)如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为81cm2,请问这个矩形之面积为多少平方厘米?ijgf k dhe c【巩固】图中的长方形被分割成 6个正方形,已知中央小正方形的面积是 1平方题厘米,求原来长方形的面积.【巩固】9个边长分别为1、4、7、8 9、10、14、15、18的正方形拼成一个长方形,问这 个长方形的长和宽是多少?并请画出这个长方形的拼接图.【例47】 图中数字分别表示两个长方形和一个直角三角形的面积, 另一个三角形的面积是 ___________ .【例48】 如图,一个矩形被分成八个小矩形, 其中有五个矩形的面积如图中所示 (单位:平方厘米),问大矩形的面积是多少平方厘米?【巩固】阳阳用四块小长方形恰好拼成了一个大的长方形, 方形的面积分别为48平方厘米、24平方厘米、 积是多少?482430【巩固】(南京市第三届”兴趣杯”少年数学邀请赛决赛试题 )如图,矩形ABCD 被分割成9个小矩形•其中有 5个小矩形的面积如图所示•矩形 ABCD 的面积为 ___________ •|1| 2□□24□ __:【例49】 有红、黄、绿三块大小一样的正方形纸片,放在一个底面为正方形的盒内, 它们之间相互叠合(见下图)•已知露在外面的部分中,红色面积是 20,黄色面积是14,绿色面积是10 •求正方形盒底的面积.【例50】 如图所示,在正方形 ABCD 内,红色、绿色正方形的面积分别是48和12,且红、绿两个正方形有一个顶点重合. 黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点.那么黄色正方形的面积是 _________ .36 16 C20 BE3012如图所示.现在知道其中三块长30平方厘米,那么,阴影部分的面 FD红黄绿【巩固】如图所示,在正方形ABCD中,红色,绿色正方形的面积分别是52和13,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,求黄色正方形面积【例51】如图,三个一样大小的正方形放在一个长方形的盒内,A和B是两个正方形的重叠部分,C D E是空出的部分,每一部分都是矩形,它们的面积比是A:B:C: D: E=1: 2:3: 4: 5,那么这个长方形的长与宽之比是___________ .EAC【例52】(2005全国华罗庚金杯少年数学邀请赛)如图如果长方形的面积为56平方厘米,且MD=2厘米、QC =3厘米、CP=5厘米、BN =6厘米,那么请你求出四边形MNPQ的面积是多少厘米?【例54】 如图所示,甲、乙、丙、丁四个长方形拼成一个正方形EFGH ,中间阴影为 正方形•已知甲、乙、丙、丁四个长方形面积的和是 32cm 2,四边形ABCD 的面积是20cm 2 •⑴求正方形 EFGH 的边长?⑵求甲、乙、丙、丁四个长方形周长的总 和?【巩固】(南京市第三届”兴趣杯”少年数学邀请赛预赛8米,A , B , C , D 分别在四条边上,并且四边形ABCD 的面积是 _________ 平方米. 【例53】 (2004全国华罗庚金杯少年数学邀请赛 9厘米,问:图中三个正方形的面积之和比)长方形的广告牌长为 10米,宽为 C 比A 低5米,D 在B 的左边2米,)直角三角形PQR 的直角边为5厘米,4个三角形的面积之和大多少?FF C G【例55】如图,平面上CDEF是正方形,ABCD是等腰梯形,它的上底AD =23厘米,下底BC =35厘米.求三角形ADE的面积.【例56】右图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例57】把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形.再将这个六角形的六个” 角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样就得到如右图所示的图形. 如果所作的最小的小正三角形的面积为1平方厘米,求如图中整个图形的面积.【例58】(1992年小学数学奥林匹克初赛)如图,长方形的面积是小于100的数.它的内部有三个边长是整数的正方形•正方形②的边长是长方形长的—,正方形①的12边长是长方形宽的1•那么,图中阴影部分的面积是________________8。
不规则图形面积的计算(方法总结及详解)

不规则图形计算的方法总结总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决.常用的基本方法有:一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了.二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可.三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了.五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便.六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半.七、平移法:这种方法是将图形中某一部分切割下来平行移动到一恰当位置,使之组合成一个新的基本规则图形,便于求出面积.例如,如上页最后一图,欲求阴影部分面积,可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内,这样整个阴影部分恰是一个正方形。
八、旋转法:这种方法是将图形中某一部分切割下来之后,使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧,从而组合成一个新的基本规则的图形,便于求出面积.例如,欲求上图(1)中阴影部分的面积,可将左半图形绕B点逆时针方向旋转180°,使A与C重合,从而构成如右图(2)的样子,此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法:这种方法是作出原图形的对称图形,从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如,欲求右图中阴影部分的面积,沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2m
求组合图形周长和面程
例题一:下面和组合图形可以用三种方法求出它的面积。
10cm A 5X ( )+7 X18=()
12 XI0+( ) X8=( )
()X 18 ・ 5X8=(
练一练. 根据虚线画出的分割图形,求岀下面图形的面积。
(1)
(2)
2m
①
6m
j 8m
8m ②
2m
1
2m
6m ①
8m
② 10m
例题二:求出阴影部分的面积。
20cm 12cm
(1)
40m
(2)
7
dm
5 dm 例题三:求岀下列圏形周长和面积。
练一练:求下列组合图形的周长和面积。
3噬米
.word.
家庭作业
一、求下列组合图形的周长与俪积:
7dm
.word. 10dm
.word.
-10-
二.把算式写完整。
(共分)
L 543X4 -(
500X1
( )X4=(
(
)X( * < )+(
)3 >
2. 696"(
6004-3-( )
< n ) <
)E X( )
三、用竖式计轧m 的散備m I 让件2&分】
602-195=
398 + 11)6 - 8X65 =
.word.
324X6- 皿片6,130X5-
505X8= 71 砰7,'9I,H
禹二却分(共22分)'
四.S2K, ' #/■!觸■
I.豊使D05X2的枳地四佃散・"框里员小诃以垃().
2- MMI*的茴中何什军•力框里最大可以以().
3.餐使」£ 6的価•是两位故.方権虫暴发可以填《).
丄 ',环割q元」g克可4买])本,再一上f )元可以再
5.乙歌是24。
•甲姓乙敬冊郷造曜卸
•下观知6年8月份的日叽
7 >131 H*MW()&月川虹,州k
7.细6年顧心•问牛强・*轩).钠;例)天.
虬国好4節,()事虬■,乍像柏 >天.
五.迁择输,《杷正■暮宣會的丰•■人括号内)(尊6叫]
I- 口口口十口 = 126……知度I*數般小任().
A. U2
B. 762 Q 8㈱
.word.
-10-
1下仆,下ifc :通标式中M 成小的"眾
n m
A. 602-rS K 5024-5 ■ 5战+,
I
3. « ♦ • C5"的做
W 的大小.缎JK
A . ♦ R •<♦
匚• ♦
第三却4共25分)
1. I MK
掀M8分狀故行了掘曲茂轧邓么收貞貞
半細分钟放"少辆M 轮
心
2.小脓杵U 段中坚持可天学"3卜£笔字.耶么小將匕月份 共号r 几个 毛亳字?
丄邮叩卿127个老人去公洲玩.紬毎辆映光惊眾个人.呢么 他n 至少
M 几購观炸”
4.冋学们华加体合活的•,描的肖132人.是拍姓人败的 散比樓馆的人敢&18
人.
同学有几人?
3俏,J8H 子,人
.word.
⑵的同学布儿人
第9部分(共」分)
七、动RSBo( * 4命)
I.下而是俱电公诃
根掘上而表格内容,把正确答案的编号填入括'/内.
(1)小胖爸危/午L30下剧回家.发埋家中没电•他家在])・
A.阳/市场B-花貝小区 C.坯源新村
(2)小脾爸爸到家后冉过C )分神,他家余有电-,, J
A. io
B. 20 G 3。
2.小业有右故東牯推第-天百10页.第二天比第-犬多看'页•航三人比第夭多百2贝.零
四夭比免"务看3贝•照这样计鼻“卜亚叩期共看(,心.。
