多倍角公式的两种表示
三角函数的和差公式与倍角公式

三角函数的和差公式与倍角公式三角函数是数学中的重要概念,广泛应用于各个领域。
其中,和差公式与倍角公式是三角函数中的重要内容,它们在解决三角函数的运算中起到了重要的作用。
本文将介绍三角函数的和差公式与倍角公式的概念、推导过程及应用。
一、和差公式的概念与推导和差公式是用来表示两个角的和差的三角函数关系的公式。
对于任意两个角A和B,和差公式可以表示如下:1. 两角的和的正弦函数公式:sin(A + B) = sinA * cosB + cosA * sinB2. 两角的差的正弦函数公式:sin(A - B) = sinA * cosB - cosA * sinB3. 两角的和的余弦函数公式:cos(A + B) = cosA * cosB - sinA * sinB4. 两角的差的余弦函数公式:cos(A - B) = cosA * cosB + sinA * sinB5. 两角的和的正切函数公式:tan(A + B) = (tanA + tanB) / (1 - tanA * tanB)6. 两角的差的正切函数公式:tan(A - B) = (tanA - tanB) / (1 + tanA * tanB)这些和差公式的推导过程可以利用向量运算、三角函数性质等方法进行推导。
由于篇幅限制,本文将不进行具体的推导,但读者可以通过学习向量运算和三角函数性质,自行推导出这些和差公式。
二、倍角公式的概念与推导倍角公式是用来表示一个角的两倍角关系的三角函数公式。
对于任意一个角A,倍角公式可以表示如下:1. 正弦函数的倍角公式:sin(2A) = 2 * sinA * cosA2. 余弦函数的倍角公式:cos(2A) = cos^2(A) - sin^2(A) = 2 * cos^2(A) - 1 = 1 - 2 * sin^2(A)3. 正切函数的倍角公式:tan(2A) = 2 * tanA / (1 - tan^2(A))这些倍角公式的推导可以采用不同的方法,如三角恒等式、三角函数的平方等性质。
倍角公式课件

倍角公式是由角的三倍角,以及角的半倍 角公式推导而来。它是初中高中最基础的 三角函数公式之一。
常见的倍角公式
正弦函数
sin2α = 2sinαcosα
sin(α+β) = sinαcosβ + cosαsinβ
余弦函数
正切函数
cos2α = cos²α - sin²α
tan2α = 2tanα / (1 - tan²α)
倍角公式ppt课件
倍角公式是初等数学中反三角函数的重要应用之一。它与三倍角公式,半角 公式,以及三角和差公式一起,是初中,高中数学重要的知识点之一。在本 课件中,我们将一步一步深入探讨倍角公式,希望大家能够从中受益。
什么是倍角公式?
1 定义
2 推导过程
倍角公式是求解正弦,余弦,正切函数值 的一种基本公式。它将角度的度数加倍之 后,把原本的三角函数值变成表达式的二 次式。
cos(α+β) = cosαcosβ - sinαsinβ tan(α+β) = (tanα + tanβ) / (1 - tanαtanβ)
应用实例
三角形
可以利用正弦和余弦函数解决 三角形内角和关于角的方程等 问题。
抛物面收音器天线
抛物面天线的主轴与边缘之间 的坡度角度等于主轴角度加上 反射指向点相邻点的点角。
广的三角函数公式
之一。
2 通过变形推导法,
复统计方法和欧拉 公式等多种方法可 以证明倍角公式的 正确性。
3 在实际问题中,倍
角公式可以解决三 角形求解,电路分 析,抛物面天线角 度等问题。
电路分析
利用正弦和余弦函数可以分析 周期性电压和电流波形,如正 弦信号。
倍角公式的证明方法
倍角公式和半角公式1

倍角公式和半角公式1倍角公式和半角公式1倍角公式和半角公式是代数中常用的一组公式,用于求解角度的相关问题。
倍角公式用于在已知角度的情况下求解角度的两倍大小,而半角公式则用于在已知角度的情况下求解角度的一半大小。
这两个公式在几何学、三角学以及物理学中都有广泛的应用。
倍角公式是指将一个角度的两倍写成其他三个角度的函数形式。
对于任意角度θ,倍角公式可以用以下两种形式来表示:1.正弦倍角公式:sin(2θ) = 2sin(θ)cos(θ)2.余弦倍角公式:cos(2θ) = cos²(θ) - sin²(θ)在实际应用中,正弦倍角公式和余弦倍角公式通常是成对使用的。
其中,正弦倍角公式是通过将2θ拆解成θ+θ并利用正弦函数的和角公式推导而得,而余弦倍角公式则是通过将2θ拆解成θ+θ并利用余弦函数的和角公式推导而得。
半角公式是指将一个角度的一半写成其他两个角度的函数形式。
对于任意角度θ,半角公式可以用以下两种形式来表示:sin(θ/2) = ±√[(1 - cos(θ))/2]cos(θ/2) = ±√[(1 + cos(θ))/2]半角公式同样可以成对使用,分别应用于正弦函数和余弦函数。
这两个公式可以通过将θ拆解成2(θ/2)并利用正弦函数和余弦函数的倍角公式推导而得。
举例来说,假设我们需要求解sin(150°) 的值。
根据正弦半角公式,sin(150°) 可以写成sin(75°/2) 的形式。
再根据正弦半角公式,sin(75°/2) 可以表示为±√[(1 - cos(75°))/2]。
我们可以使用三角函数表或计算器来查找cos(75°) 的值,然后代入公式计算sin(75°/2) 的值。
再举一个例子,假设我们需要证明sin(3θ) = 3sin(θ) -4sin³(θ) 的恒等式。
三角函数中的倍角公式与半角公式

三角函数中的倍角公式与半角公式三角函数是数学中的重要概念,在几何和物理学中有着广泛的应用。
在三角函数中,倍角公式和半角公式是其中两个重要的公式。
本文将详细介绍三角函数中的倍角公式和半角公式,以及它们的应用。
一、倍角公式倍角公式是指将一个角的两倍表示成该角的三角函数的形式。
三角函数的倍角公式主要包括正弦函数、余弦函数和正切函数。
1. 正弦函数的倍角公式:sin(2θ) = 2sinθcosθ正弦函数的倍角公式可以通过三角函数的和差公式推导得出。
根据和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ令α = β = θ,可以得到:sin(θ + θ) = sinθcosθ + cosθsinθ化简后得到正弦函数的倍角公式。
2. 余弦函数的倍角公式:cos(2θ) = cos²θ - sin²θ余弦函数的倍角公式也可以通过三角函数的和差公式推导得出。
根据和差公式:cos(α ± β) = cosαcosβ - sinαsinβ令α = β = θ,可以得到:cos(θ + θ) = cosθcosθ - sinθsinθ化简后得到余弦函数的倍角公式。
3. 正切函数的倍角公式:tan(2θ) = 2tanθ / (1 - tan²θ)正切函数的倍角公式可以通过正弦函数和余弦函数的倍角公式推导得出。
将正弦函数和余弦函数的倍角公式代入正切函数的定义式,经过简化和化简可以得到正切函数的倍角公式。
二、半角公式半角公式是指将一个角的一半表示成该角的三角函数的形式。
与倍角公式类似,三角函数的半角公式也包括正弦函数、余弦函数和正切函数。
1. 正弦函数的半角公式:sin(θ/2) = √[(1 - cosθ) / 2]正弦函数的半角公式可以通过正弦函数和余弦函数的和差公式推导得出。
根据和差公式:sin(α ± β) = sinαcosβ ± cosαsinβ令α = θ/2,β = θ/2,可以得到:sin(θ/2 + θ/2) = sin(θ/2)cos(θ/2) + cos(θ/2)sin(θ/2)化简后得到正弦函数的半角公式。
倍角公式和半角公式
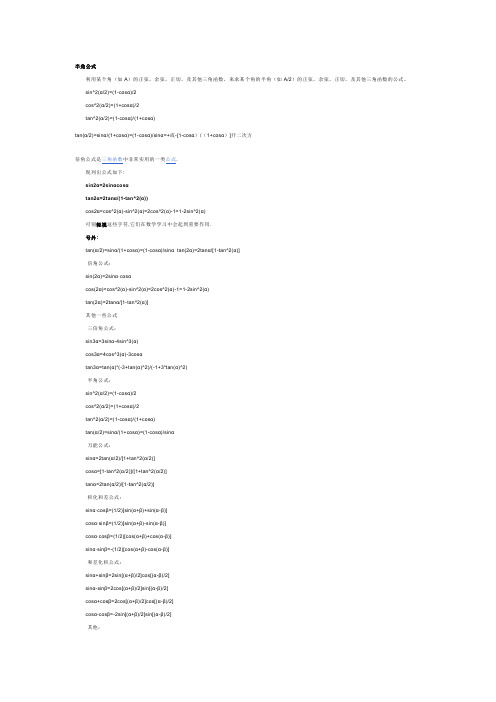
半角公式利用某个角(如A)的正弦,余弦,正切,及其他三角函数,来求某个角的半角(如A/2)的正弦,余弦,正切,及其他三角函数的公式。
sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα=+或-[1-cosα)/(1+cosα)]开二次方倍角公式是三角函数中非常实用的一类公式.现列出公式如下:sin2α=2sinαcosαtan2α=2tanα/(1-tan^2(α))cos2α=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)可别轻视这些字符,它们在数学学习中会起到重要作用.号外:tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα tan(2α)=2tanα/[1-tan^2(α)]·倍角公式:sin(2α)=2sinα·cosαcos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α)tan(2α)=2tanα/[1-tan^2(α)]其他一些公式·三倍角公式:sin3α=3sinα-4sin^3(α)cos3α=4cos^3(α)-3cosαtan3α=tan(α)*(-3+tan(α)^2)/(-1+3*tan(α)^2)·半角公式:sin^2(α/2)=(1-cosα)/2cos^2(α/2)=(1+cosα)/2tan^2(α/2)=(1-cosα)/(1+cosα)tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα·万能公式:sinα=2tan(α/2)/[1+tan^2(α/2)]cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)]tanα=2tan(α/2)/[1-tan^2(α/2)]·积化和差公式:sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)]·和差化积公式:sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]·其他:sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0四倍角公式:sin4A=-4*(cosA*sinA*(2*sinA^2-1))cos4A=1+(-8*cosA^2+8*cosA^4)tan4A=(4*tanA-4*tanA^3)/(1-6*tanA^2+tanA^4)五倍角公式:sin5A=16sinA^5-20sinA^3+5sinAcos5A=16cosA^5-20cosA^3+5cosAtan5A=tanA*(5-10*tanA^2+tanA^4)/(1-10*tanA^2+5*tanA^4)六倍角公式:sin6A=2*(cosA*sinA*(2*sinA+1)*(2*sinA-1)*(-3+4*sinA^2))cos6A=((-1+2*cosA^2)*(16*cosA^4-16*cosA^2+1))tan6A=(-6*tanA+20*tanA^3-6*tanA^5)/(-1+15*tanA^2-15*tanA^4+tanA^6)七倍角公式:sin7A=-(sinA*(56*sinA^2-112*sinA^4-7+64*sinA^6))cos7A=(cosA*(56*cosA^2-112*cosA^4+64*cosA^6-7))tan7A=tanA*(-7+35*tanA^2-21*tanA^4+tanA^6)/(-1+21*tanA^2-35*tanA^4+7*tanA^6)八倍角公式:sin8A=-8*(cosA*sinA*(2*sinA^2-1)*(-8*sinA^2+8*sinA^4+1))cos8A=1+(160*cosA^4-256*cosA^6+128*cosA^8-32*cosA^2)tan8A=-8*tanA*(-1+7*tanA^2-7*tanA^4+tanA^6)/(1-28*tanA^2+70*tanA^4-28*tanA^6+tanA^8)九倍角公式:sin9A=(sinA*(-3+4*sinA^2)*(64*sinA^6-96*sinA^4+36*sinA^2-3))cos9A=(cosA*(-3+4*cosA^2)*(64*cosA^6-96*cosA^4+36*cosA^2-3))tan9A=tanA*(9-84*tanA^2+126*tanA^4-36*tanA^6+tanA^8)/(1-36*tanA^2+126*tanA^4-84*tanA^6+9*tanA^8)十倍角公式:sin10A=2*(cosA*sinA*(4*sinA^2+2*sinA-1)*(4*sinA^2-2*sinA-1)*(-20*sinA^2+5+16*sinA^4))cos10A=((-1+2*cosA^2)*(256*cosA^8-512*cosA^6+304*cosA^4-48*cosA^2+1))tan10A=-2*tanA*(5-60*tanA^2+126*tanA^4-60*tanA^6+5*tanA^8)/(-1+45*tanA^2-210*tanA^4+210*tanA^6-45*tanA^8+tanA^10)【本讲教育信息】一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进行简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进行求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
倍角公式和半角公式的推导和应用

倍角公式和半角公式的推导和应用倍角公式和半角公式是数学中常见的公式,它们在解决三角函数问题和几何问题中起着重要的作用。
本文将对倍角公式和半角公式进行推导,并探讨其在实际问题中的应用。
一、倍角公式的推导和应用1. 正弦倍角公式的推导在三角函数中,正弦函数的倍角公式可以通过欧拉公式得出。
欧拉公式是一个重要的数学公式,表达为:e^ix = cos(x) + isin(x)其中,e是自然对数的底,i称为虚数单位,满足i^2 = -1。
我们可以通过欧拉公式将sin(x)表示成e的形式:sin(x) = (e^(ix) - e^(-ix)) / (2i)因此,sin(2x)可以表示为:sin(2x) = (e^(2ix) - e^(-2ix)) / (2i)再利用欧拉公式化简上式,得到:sin(2x) = 2isin(x)cos(x)2. 余弦倍角公式的推导余弦函数的倍角公式可以通过sin(2x)的推导得出。
我们已经推导出了sin(2x)的表达式,可以通过将其代入三角函数等式cos^2(x) + sin^2(x) = 1,得到:cos^2(x) + (2isin(x)cos(x))^2 = 1化简上式,得到:cos^2(x) - sin^2(x) = 1 - 4sin^2(x)cos^2(x)进一步化简,得到:cos^2(x) - sin^2(x) = (1 - 2sin^2(x))(1 - 2cos^2(x))利用三角函数关系cos^2(x) = 1 - sin^2(x),化简上式,得到:cos(2x) = 2cos^2(x) - 1倍角公式可以应用到很多问题中,例如求解三角方程、计算三角函数值等。
通过利用倍角公式,我们可以将原问题化简为更简单的形式,从而更易解决。
二、半角公式的推导和应用1. 正弦半角公式的推导正弦函数的半角公式可以通过倍角公式推导得出。
我们已经推导出了sin(2x)的表达式,将其中的2x替换为x,得到:sin(x) = 2sin(x/2)cos(x/2)进一步化简上式,得到:sin(x/2) = ±√[(1 - cos(x))/2]2. 余弦半角公式的推导余弦函数的半角公式可以通过倍角公式推导得出。
三角函数的倍角与半角公式

三角函数的倍角与半角公式三角函数在数学中有着广泛的应用,其中倍角与半角公式是计算三角函数值时常用的工具。
倍角公式用于将角度扩大为原来的两倍,而半角公式则是将角度缩小为原来的一半。
本文将详细介绍三角函数的倍角和半角公式,以及它们的相关性质和应用。
一、正弦函数的倍角与半角公式1. 倍角公式对于一个角θ,其正弦函数值sinθ可以表示为以下两个倍角公式之一:sin(2θ) = 2sinθcosθsin^2θ = (1 - cos2θ)/2在上述公式中,θ为任意角度。
2. 半角公式对于一个角θ,其正弦函数值sinθ也可以表示为以下两个半角公式之一:sin(θ/2) = ±√[(1 - cosθ)/2]sin^2(θ/2) = (1 - cosθ)/2值得注意的是,在半角公式中,sin(θ/2)的符号取决于θ的象限。
二、余弦函数的倍角与半角公式1. 倍角公式对于一个角θ,其余弦函数值cosθ可以表示为以下两个倍角公式之一:cos(2θ) = cos^2θ - sin^2θ = 1 - 2sin^2θ = 2cos^2θ - 1在上述公式中,θ为任意角度。
2. 半角公式对于一个角θ,其余弦函数值cosθ也可以表示为以下两个半角公式之一:cos(θ/2) = ±√[(1 + cosθ)/2]cos^2(θ/2) = (1 + cosθ)/2与正弦函数的半角公式类似,cos(θ/2)的符号取决于θ的象限。
三、正切函数的倍角与半角公式1. 倍角公式对于一个角θ,其正切函数值tanθ可以表示为以下倍角公式:tan(2θ) = (2tanθ)/(1 - tan^2θ)在上述公式中,θ为任意角度且不等于(2n + 1)π/2,其中n为整数。
2. 半角公式对于一个角θ,其正切函数值tanθ也可以表示为以下半角公式之一:tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)]tan^2(θ/2) = (1 - cosθ)/(1 + cosθ)值得注意的是,在半角公式中,tan(θ/2)的符号取决于θ的象限。
高二数学倍角公式和半角公式

cos2 cos sin
2 2
tan tan tan( ) 1 tan tan tan tan tan( ) 1 tan tan
2 tan tan 2 1 tan 2
一、倍角公式
sin 2 2 sin cos (S2 )
公式左端的角是右端角的二倍
在这两个公式中分别 2a和cos2a 求出sin 2
1 cos 2 cos 2 2 2 cos 1 sin 2 2 sin 1 cos 2 2 2 2 cos2 cos sin (1 sin ) sin 2 2 2 cos (1 cos ) 1 2 sin 2 2 cos 1
三、公式应用:
例1、(公式巩固性练习)求值
1、 sin 22。 30, cos22。 30,
2 2、 2 cos 1 8 2
2
2 4
2 3、 sin cos 8 8 2
2 2
试试看 伴你学134页8题
1 4、 8 sin cos cos cos 2 48 48 24 12
3.2.1倍角公式
复习回顾:
• 完成下列和角公式
sin cos sin cos cos( ) cos cos sin sin tan( ) tan tan 1 tan tan 思考:
若 我们可以得到怎样的结论?
cos10 3 sin10 sin 50 cos10 2 sin 40 sin 50 cos10 2sin 40 cos 40 cos10 sin 80 1 cos10
三角函数公式大全[1]
![三角函数公式大全[1]](https://img.taocdn.com/s3/m/a61a36ed5ef7ba0d4a733b89.png)
三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义城为整个实数城。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷敖列的极限和微分方程的解,将其定义扩展到复数系。
公式分类锐角三角函数公式sin α=∠α的对边/ 斜边cos α=∠α的邻边/ 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式sin2A=2sinA•cosAcos2A=cosA;方-sinA方;A=1-2sin²A=2cos²A-1tan2A=(2tanA)÷(1-tan^2A)三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tanh(a) = sin h(a)/cos h(a)公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tanαcot(2kπ+α)= cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos(3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A^2 +B^2 +2ABcos(θ-φ)} • sin{ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }√表示根号,包括{……}中的内容诱导公式sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α)= sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限万能公式其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(c osα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtan BtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)[编辑本段]内容规律三角函数看似很多,很复杂,但只要掌握了三角函数的本质及内部规律就会发现三角函数各个公式之间有强大的联系。
三角函数中的倍角、半角公式及和差化积公式的应用

三角函数中的倍角、半角公式及和差化积公式的应用三角函数是数学中的一个非常重要的分支,它将三角学和代数学有机地结合在一起。
在数学学习中,我们学习了很多三角函数的基本概念和运算,其中倍角、半角公式以及和差化积公式是三角函数中最为基础和重要的一部分。
一、倍角公式我们先了解一下什么是倍角公式。
倍角公式是指一个角的正弦、余弦、正切、余切的 2 倍可以表示成该角的某些值的表达式。
当然,对于不同的三角函数,其倍角公式的表达式也不同。
1. 正弦函数的倍角公式sin 2θ = 2sinθcosθ这个公式是比较基础的,也是最常用的一个倍角公式,通过这个公式,我们可以把一个正弦函数的 2 倍表示为正弦和余弦函数的乘积。
例如,如果我们要求 sin 120°,可以将其转化为 sin 2×60°,再使用倍角公式,得到sin 120° = 2sin60°cos60° = √3。
2. 余弦函数的倍角公式cos 2θ = cos2θ - sin2θ当我们需要求一个余弦函数的 2 倍时,可以使用上述公式,将余弦函数的平方和正弦函数的平方相减,从而得到余弦函数的 2 倍。
3. 正切函数的倍角公式tan 2θ = 2tanθ / (1 - tan2θ)这个公式比较复杂,但是还是很有用的,可以用来求正切函数的 2 倍。
二、半角公式半角公式指的是一个角的正弦、余弦、正切、余切的一半可以表示成该角的某些值的表达式。
同样,对于不同的三角函数,其半角公式的表达式也不同。
1. 正弦函数的半角公式sinθ/2 = ±√(1 - cosθ) / 2需要注意的是,正负号取决于原来的角度的象限。
使用半角公式可以将原来的角度减半,从而求出新的角度的三角函数值。
2. 余弦函数的半角公式cosθ/2 = ±√(1 + cosθ) / 2同样,需要注意的是正负号的问题。
通过半角公式,我们可以将原来的角度减半,从而求出新的角度的三角函数值。
三角函数的倍角和半角公式

三角函数的倍角和半角公式三角函数中的倍角和半角公式,那可是数学世界里相当有趣又实用的家伙们!咱们先来说说倍角公式。
sin2α = 2sinαcosα,cos2α = cos²α - sin²α =2cos²α - 1 = 1 - 2sin²α,tan2α = 2tanα / (1 - tan²α)。
这些公式看起来有点复杂,但只要咱们好好理解,就会发现它们其实就像咱们熟悉的好朋友。
记得我以前教过一个学生小明,他一开始对这些公式那叫一个头疼。
有一次上课,我出了一道题:已知sinα = 3/5,α是锐角,求sin2α 的值。
小明瞪着题目,一脸茫然。
我就引导他,先根据sinα 求出cosα,然后再用倍角公式。
我一步一步地带着他算,最后得出了答案。
从那以后,小明像是突然开了窍,对倍角公式不再害怕了。
再说说半角公式,sin²(α/2) = (1 - cosα) / 2 ,cos²(α/2) = (1 + cosα) / 2 ,tan(α/2) = ±√[(1 - cosα)/(1 + cosα)] 。
这些公式在解决一些复杂的三角问题时,往往能起到意想不到的效果。
就像有一次考试,有一道题是求一个角的半角的正弦值。
好多同学都被难住了,但平时认真掌握了半角公式的同学就轻松地做出来了。
其实啊,倍角和半角公式就像是数学大厦里的一块块基石,虽然它们本身可能不起眼,但组合起来就能构建出各种复杂而美妙的数学结构。
比如说在解决几何问题中,如果遇到角度之间的倍数或者半倍关系,这时候倍角和半角公式就能大显身手啦。
想象一下一个三角形,其中一个角是另一个角的两倍,我们就可以通过这些公式找到它们之间的关系,从而求出未知的角度或者边长。
在物理中,当研究波动、振动这些现象时,也常常会用到三角函数的倍角和半角公式。
比如声波的传播,电磁波的变化,都离不开这些公式的帮助。
倍角、半角、和差化积公式

倍角、半角、和差化积公式一. 教学内容:3.1 和角公式3.2 倍角公式和半角公式二. 教学目的1. 了解两角和与差的余弦、正弦、正切公式的推导和证明过程,能够利用两角和与差的余弦、正弦、正切公式进展简单的三角函数式的求值、化简和证明,了解两角和与差的余弦、正弦、正切公式的内在联系;2. 掌握倍角、半角的正弦、余弦、正切公式的推导过程,能够利用倍角、半角的正弦、余弦、正切公式进展求值、化简和证明,了解倍角、半角的正弦、余弦、正切公式的内在联系。
三. 教学重点、难点重点:能够推导并掌握两角和与差的余弦、正弦、正切公式及倍角、半角的正弦、余弦、正切公式,并应用上述公式进展求值、化简、证明。
难点:能够正确利用上述公式进展求值、化简、证明,并能解决简单实际问题。
四. 知识分析〔一〕两角和与差的余弦1、两角差的余弦公式推导方法1:向量法把看成是两个向量夹角的余弦,可以考虑利用两个向量的数量积来研究。
如图1,设的终边分别与单位圆交于点P l (,),P2 (,),由于余弦函数是周期为2π的偶函数,所以,我们只需考虑的情况。
图1设向量则。
另一方面,由向量数量积的坐标表示,有于是,对于任意的,都有上述式子成立。
推导方法2:三角函数线法设、都是锐角,如图2 ,角的终边与单位圆的交点为P l,∠POP1=,则∠Po*=。
过点P作MN⊥* 轴于M,则OM即为的余弦线。
在这里,我们想法用的三角函数线来表示OM。
图2过点P作PA⊥OP1于A,过点A作AB⊥*轴于B,过P作PC⊥AB于C,则OA表示,AP表示,并且∠PAC=∠P1O*=,于是即要说明此结果是否对任意角都成立,还要做不少推广工作,并且这项推广工作的过程也是比较繁难的,在此就不进展研究了。
2. 两角和的余弦公式比较与,并且注意到与之间的联系:则由两角差的余弦公式得:即3. 对公式的理解和记忆〔1〕上述公式中的都是任意角。
〔2〕公式右端的两局部为同名三角函数之积,连接符号与左边的连接符号相反。
中考生常用三角函数公式

中考生常用三角函数公式1、同角三角函数的差不多关系倒数关系: tan cot=1 sin csc=1 cos sec=1商的关系:sin/cos=tan=sec/csc cos/sin=cot=csc/sec平方关系:sin^2()+cos^2()=1 1+tan^2()=sec^2() 1+cot^2()=csc^2()平常针对不同条件的常用的两个公式sin +cos =1tan *cot =1一个专门公式(sina+sin)*(sina+sin)=sin(a+)*sin(a-)2、锐角三角函数公式正弦:sin =的对边/ 的斜边余弦:cos =的邻边/的斜边正切:tan =的对边/的邻边余切:cot =的邻边/的对边3、二倍角公式正弦sin2A=2sinAcosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=(2tanA)/(1-tan^2(A))4、三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)5、n倍角公式sin(n a)=Rsina sin(a+/n)……sin(a+(n-1)/n)。
其中R=2^(n-1)6、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cos A)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/s in(a)=sin(a)/(1+cos(a))7、和差化积sin+sin = 2 sin[(+)/2] cos[(-)/2]sin-sin = 2 cos[(+)/2] sin[(-)/2]cos+cos = 2 cos[(+)/2] cos[(-)/2]cos-cos = -2 sin[(+)/2] sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)8、两角和公式cos(+)=coscos-sinsincos(-)=coscos+sinsinsin(+)=sincos+cossinsin(-)=sincos -cossin9、积化和差sinsin = [cos(-)-cos(+)] /2 coscos = [cos(+)+cos(-)]/2 sincos = [sin(+) +sin(-)]/2 cossin = [sin(+)-sin(-)]/210、双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a)公式一:设为任意角,终边相同的角的同一三角函数的值相等:sin(2 k+)= sin cos(2k+)= cos tan(2k+)= tan cot(2k+)= cot 公式二:设为任意角,的三角函数值与的三角函数值之间的关系:sin (+)= -sin cos(+)= -cos tan(+)= tan cot(+)= cot 公式三:任意角与-的三角函数值之间的关系:sin(-)= -sin cos(-)= cos tan(-)= -tan cot(-)= -cot公式四:利用公式二和公式三能够得到与的三角函数值之间的关系:s in()= sin cos()= -cos tan()= -tan cot()= -cot公式五:利用公式-和公式三能够得到2与的三角函数值之间的关系:s in(2)= -sin cos(2)= cos tan(2)= -tan cot(2)= -cot公式六:/2及3/2与的三角函数值之间的关系:sin(/2+)= cos cos(/ 2+)= -sin tan(/2+)= -cot cot(/2+)= -tan sin(/2-)= cos cos(/2-)=sin tan(/2-)= cot cot(/2-)= tan sin(3/2+)= -cos cos(3/2+)= sin tan(3/2+)= -cot cot(3/2+)= -tan sin(3/2-)= -cos cos(3/2-)= -sin tan(3/2-)= cot cot(3/2-)= tan (以上kZ) Asin(t+)+ Bsin(t+) = {(A +B +2ABcos(-)} sin{ t + arcsin[ (Asin+Bsin) / {A^2 +B^2; +2ABcos(-)} } 表示根号,包括{……}中的内容11、诱导公式sin(-) = -sin cos(-) = cos tan (-)=-tan sin(/2-) = cos cos(/2-) = sin si n(/2+) = cos cos(/2+) = -sin sin() = sin cos() = -cos sin() = -sin cos() = -cos tanA= sinA/cosA tan(/2+)=-cot tan(/2-)=cot tan(-)=-tan tan(+)=tan 诱导公式记背诀窍:奇变偶不变,符号12、万能公式sin=2tan(/2)/[1+(tan(/2))] cos=[1-(tan(/2))]/[1+(tan(/2))] tan=2tan(/2)/[1-(t an(/2))]13、其它公式(1) (sin)+(cos)=1(2)1+(tan)=(sec)(3)1+(cot)=(csc)(4)关于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC (5)cotA cotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)c ot(C/2)(7)(cosA)+(cosB)+(cosC)=1-2cosAcosBcosC(8)(sinA)+(sinB)+(sinC)=2+2cosAcosBcosC家庭是幼儿语言活动的重要环境,为了与家长配合做好幼儿阅读训练工作,小孩一入园就召开家长会,给家长提出早期抓好幼儿阅读的要求。
多倍角公式

多倍角公式在我们的数学世界里,多倍角公式就像是一座神秘而又充满魅力的城堡。
当我们踏入这个领域,仿佛打开了一扇通往奇妙数学世界的大门。
记得我曾经给学生们讲解多倍角公式的时候,有个叫小李的同学,那迷茫的小眼神简直让我哭笑不得。
我在黑板上写下了多倍角公式,他皱着眉头,嘴里嘟囔着:“这都是啥呀?”多倍角公式,简单来说,就是用来处理角度倍数变化时三角函数值关系的工具。
咱们先从二倍角公式说起,正弦二倍角公式是sin2α =2sinαcosα 。
这就好比是一个魔法咒语,当你知道了一个角的正弦和余弦值,就能通过这个公式求出它两倍角的正弦值。
余弦二倍角公式有三种形式:cos2α = cos²α - sin²α ,cos2α = 2cos²α - 1 ,cos2α = 1 - 2sin²α 。
是不是感觉有点眼花缭乱?别慌,咱们一个一个来。
比如说,已知角α的余弦值,通过这些公式就能轻松算出二倍角的余弦值啦。
正切二倍角公式是tan2α = 2tanα / (1 - tan²α) 。
这个公式在解决一些涉及正切的问题时,那可是大显身手。
那多倍角公式有啥用呢?比如说,在解决一些几何问题中,当角度出现倍数关系时,多倍角公式就能派上用场。
还有在求解三角函数的最值、周期等问题时,它也是得力的助手。
咱们再回到小李同学身上。
后来我给他举了个例子,假设一个三角形中,已知一个角的大小和它的正弦、余弦值,要计算这个角两倍时的相关三角函数值。
我一步一步带着他运用多倍角公式,他慢慢地就开窍了,眼睛里不再是迷茫,而是闪烁着理解后的光芒。
再深入一点,还有三倍角公式、四倍角公式等等。
虽然这些公式在我们平时的学习中用得相对较少,但它们也是数学大厦中的一部分。
学习多倍角公式,就像是在攀登山峰,一开始可能会觉得陡峭艰难,但只要坚持,一步一个脚印,当你登顶俯瞰,就会发现那美丽的风景是如此令人陶醉。
所以啊,同学们,别害怕多倍角公式,多练习,多思考,相信你们都能在这个数学的奇妙世界里畅游!。
多倍角公式大全

多倍角公式大全一、二倍角公式。
1. 正弦二倍角公式。
- sin2α = 2sinαcosα- 推导:根据两角和的正弦公式sin(A + B)=sin Acos B+cos Asin B,令A =B=α,则sin2α=sin(α+α)=sinαcosα+cosαsinα = 2sinαcosα。
2. 余弦二倍角公式。
- cos2α=cos^2α-sin^2α- 另外两种形式:- cos2α = 2cos^2α - 1(由cos^2α+sin^2α = 1,即sin^2α=1 - cos^2α代入上式得到)- cos2α=1 - 2sin^2α(由cos^2α+sin^2α = 1,即cos^2α=1-sin^2α代入cos2α=cos^2α-sin^2α得到)- 推导:根据两角和的余弦公式cos(A + B)=cos Acos B-sin Asin B,令A =B=α,则cos2α=cos(α+α)=cosαcosα-sinαsinα=cos^2α-sin^2α。
3. 正切二倍角公式。
- tan2α=(2tanα)/(1-tan^2)α- 推导:根据正切公式tan(A + B)=(tan A+tan B)/(1-tan Atan B),令A = B=α,则tan2α=(tanα+tanα)/(1 - tanαtanα)=(2tanα)/(1-tan^2)α。
二、三倍角公式。
1. 正弦三倍角公式。
- sin3α=3sinα - 4sin^3α- 推导:- sin3α=sin(2α+α)=sin2αcosα+cos2αsinα- 由二倍角公式sin2α = 2sinαcosα,cos2α=1 - 2sin^2α代入上式得: - sin3α=2sinαcosαcosα+(1 - 2sin^2α)sinα- =2sinα(1-sin^2α)+(1 - 2sin^2α)sinα- =2sinα - 2sin^3α+sinα-2sin^3α=3sinα - 4sin^3α。
倍角公式转换

倍角公式转换在咱们的数学世界里,倍角公式转换就像是一把神奇的钥匙,可以打开很多难题的大门。
记得我之前给学生们讲倍角公式转换的时候,有个叫小明的同学,总是一脸迷茫。
那表情仿佛在说:“老师,这都是啥呀,怎么这么难!”于是我决定换一种方式给他讲解。
咱先来说说倍角公式到底是啥。
倍角公式包括正弦、余弦和正切的倍角公式。
比如正弦的倍角公式是sin2α = 2sinαcosα,余弦的倍角公式有两个,一个是cos2α = cos²α - sin²α,另一个是cos2α = 2cos²α - 1 或者cos2α = 1 - 2sin²α。
正切的倍角公式则是tan2α = 2tanα / (1 - tan²α)。
那这些公式怎么用呢?比如说,给你一个题目,让你求sin60°的值,但是呢,题目里只给了你 sin30°的值。
这时候倍角公式就派上用场啦!因为 sin60° = sin(2×30°),我们就可以用sin2α = 2sinαcosα这个公式来计算。
再比如说,有个题目让你化简 cos²2x - sin²2x,这时候你是不是一下子就能想到用cos2α = cos²α - sin²α这个公式呀,一下子就可以化简为cos4x 啦。
咱们在学习倍角公式转换的时候,可不能死记硬背哦。
得理解着来,多做几道题练练手。
就像学骑自行车,刚开始可能摇摇晃晃的,但多骑几次,掌握了平衡的技巧,就能骑得又稳又快。
还记得之前提到的小明同学不?后来我给他举了好多生活中的例子,比如说把倍角公式想象成搭积木,一块一块地组合起来,就能搭出想要的形状。
慢慢地,他好像开窍了,做题的时候不再那么愁眉苦脸,还能主动跟我讨论问题呢。
其实啊,倍角公式转换在很多领域都有用处。
比如在物理学中研究波动现象,在工程学中计算一些复杂的结构问题等等。
三角函数的复合角与倍角公式

三角函数的复合角与倍角公式三角函数作为数学中的重要概念之一,广泛应用于各个领域中。
在三角函数的学习中,复合角与倍角公式是必不可少的内容。
本文将详细介绍三角函数的复合角与倍角公式,以便读者更好地理解和应用这些知识。
一、复合角公式在三角函数中,复合角是指以一角的正弦、余弦、正切等函数为变量的函数表达式。
复合角公式是将一个角表示为其他角的函数形式,常见的三角函数复合角公式有以下几种:1. 正弦函数的复合角公式对于正弦函数的复合角公式,可以通过使用和差化积公式来得到。
假设角A和角B是两个已知的角度,那么正弦函数在这两个角度上的值可以表示为以下形式:sin(A ± B) = sin A * cos B ± cos A * sin B2. 余弦函数的复合角公式与正弦函数类似,对于余弦函数的复合角公式也可以通过使用和差化积公式来得到。
假设角A和角B是两个已知的角度,那么余弦函数在这两个角度上的值可以表示为以下形式:cos(A ± B) = cos A * cos B ∓ sin A * sin B3. 正切函数的复合角公式正切函数的复合角公式是通过使用两个角度的正切值来表示其他复合角的正切值。
假设角A和角B是两个已知的角度,那么正切函数在这两个角度上的值可以表示为以下形式:tan(A ± B) = (tan A ± tan B) / (1 ∓ tan A * tan B)以上是三角函数在复合角情况下的一些常见公式,通过这些公式,我们可以将一个角的三角函数值表示为其他已知角的函数形式,方便计算和分析。
二、倍角公式在三角函数中,倍角是指一个角的两倍角度。
倍角公式是将一个角的正弦、余弦、正切等函数表示为其倍角函数的形式,常见的三角函数倍角公式有以下几种:1. 正弦函数的倍角公式正弦函数的倍角公式可以通过使用正弦函数的半角公式来得到。
假设角A是已知角度,那么正弦函数在其倍角A的值可以表示为以下形式:sin 2A = 2 * sin A * cos A2. 余弦函数的倍角公式与正弦函数类似,余弦函数的倍角公式也可以通过使用余弦函数的半角公式来得到。
三角恒等式 - 维基百科,自由的百科全书

目录
1 符号 2 基本关系
2.1 其他函数的基本关系 3 对称、移位和周期
3.1 对称 3.2 移位和周期 4 角的和差恒等式 4.1 正弦与余弦的无限多项和 4.2 正切的有限多项和 5 多倍角公式 6 倍角公式和半角公式 6.1 其他函数的倍半角公式 7 三分之一角公式 7.1 简化 8 幂简约公式 9 常见的恒等式 9.1 积化和差与和差化积恒等式 9.2 其他恒等式 9.3 托勒密定理 10 三角函数和双曲函数的恒等式 11 线性组合 12 反三角函数 13 无限乘积公式 14 微积分 14.1 蕴涵 15 指数定义 16 参见 17 参考文献
更一般的说,对于任何相位移动,我们有 这里 而
/wiki/三角恒等式
10/13
13-12-5
反三角函数
三角恒等式 - 维基百科,自由的百科全书
无限乘积公式
为了用于特殊函数,有下列三角函数无限乘积公式:
微积分
在微积分中,下面陈述的关系要求角用弧度来度量;如果用其他方式比如角度来这些关系会变得更加复杂。如果三角函数以几何的方式 来定义,它们的导数可以通过验证两个极限而找到。 第一个是:
这里的 "
" 意味着索引 A 遍历集合 { 1, 2, 3, ... } 的大小为 k 的所有子集的集合。
在这两个恒等式中出现了在有限多项中不出现的不对称:在每个乘积中,只有有限多个正弦因子和 cofinite 多个余弦因子。
如果只有有限多项 是非零,则在右边只有有限多项是非零,因为正弦因子将变为零,而在每个项中,所有却有限多的余弦因子将是单 位一。
x1=
x2=
x3=
当-90°≤ ≤90°时
= 3=
当90°≤ ≤450°时
多倍角公式的两种表示
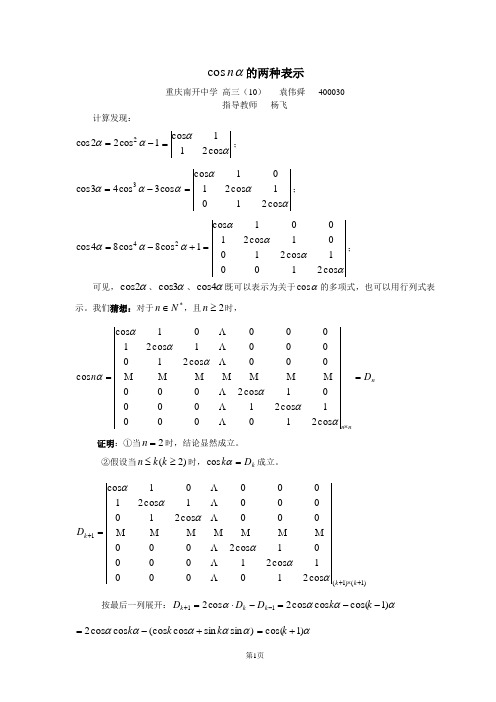
αn cos 的两种表示重庆南开中学 高三(10) 袁伟舜 400030指导教师 杨飞计算发现:1cos 22cos 2-=ααααcos 211cos =;αααcos 3cos 43cos 3-=αααcos 211cos 2101cos =;1cos 8cos 84cos 24+-=αααααααcos 211cos 21001cos 21001cos =;可见,α2cos 、α3cos 、α4cos 既可以表示为关于αcos 的多项式,也可以用行列式表示。
我们猜想:对于*N n ∈,且2≥n 时,n nn D n ==⨯αααααααcos 2100001cos 2100001cos 2000000cos 2100001cos 2100001cos cos ΛΛΛM M M M M M MΛΛΛ证明:①当2=n 时,结论显然成立。
②假设当)2(≥≤k k n 时,k D k =αcos 成立。
)1()1(1cos 2100001cos 2100001cos 2000000cos 2100001cos 2100001cos +⨯++=k k k D ααααααΛΛΛM M M M M M MΛΛΛ按最后一列展开:11cos 2-+-⋅=k k k D D D αααα)1cos(cos cos 2--=k k)sin sin cos (cos cos cos 2αααααk k k +-=α)1cos(+=k即当1+=k n 时,结论也成立由①②可知,对*N n ∈,且2≥n 时,结论n D n =αcos 成立。
上述公式虽然出了αn cos 的行列式表示,却没有给出αn cos 的展开式中αmcos 的系数,我们对此进行探究:n n n i i n )tan 1Re(cos )sin Re(cos cos ααααα+⋅=+=∑≤≤-=ni i i n i n C 2022tan )1(cos αα∑≤≤--=ni i in i n C 2022)1(sec )1(cos αααααi n i ni i i n i C 222022cos cos )1(sec )1(-≤≤∑--= ααin ni iin iC 22022cos)cos 1()1(-≤≤∑--=∑∑≤≤=-++-=n i ik i k n in k i ik C C 200)(22cos )1(α当i k =时,αncos 的系数为:∑≤≤=++++=ni in i n n n n C C C C C C C C C C A 20206334222110000Λ;当1-=i k 时,α2cos-n 的系数为:()∑≤≤-=++++-=ni i n i n n n n C C C C C C C C C C A 22218346234122011Λ;同样,当j i k -=时,可得αjn 2cos -的系数为∑≤≤-=ni j in j i jj C C A 222)1((N j i ∈,).即∑≤≤--=nj j n j j A n 202cos )1(cos αα,其中∑≤≤=ni j in j i j C C A 222(N j i ∈,).至此,我们已经给出了αn cos 的行列式表示和展开式中αmcos 的系数,用同样方法,我们也可以求出αn sin 的行列式表示和展开式中αmsin 的系数。
高二数学倍角公式和半角公式

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
αn cos 的两种表示
重庆南开中学 高三(10) 袁伟舜 400030
指导教师 杨飞
计算发现:
1cos 22cos 2-=ααα
α
cos 21
1
cos =
;
αααcos 3cos 43cos 3-=α
αα
cos 21
1cos 2101cos =
; 1cos 8cos 84cos 24+-=αααα
αααcos 21001cos 2100
1cos 21
001cos =
; 可见,α2cos 、α3cos 、α4cos 既可以表示为关于αcos 的多项式,也可以用行列式表
示。
我们猜想:对于*
N n ∈,且2≥n 时,
n n
n D n ==
⨯α
ααααααcos 21
1cos 2100001cos 2000000cos 210
0001cos 2100001cos cos
证明:①当2=n 时,结论显然成立。
②假设当)2(≥≤k k n 时,k D k =αcos 成立。
)
1()1(1cos 21
1cos 2100001cos 2000000cos 210
0001cos 21
00001cos +⨯++=
k k k D α
αα
ααα
按最后一列展开:11cos 2-+-⋅=k k k D D D αααα)1cos(cos cos 2--=k k
)sin sin cos (cos cos cos 2αααααk k k +-=α)1cos(+=k
即当1+=k n 时,结论也成立
由①②可知,对*
N n ∈,且2≥n 时,结论n D n =αcos 成立。
上述公式虽然出了αn cos 的行列式表示,却没有给出αn cos 的展开式中αm
cos 的系数,
我们对此进行探究:
n n n i i n )tan 1Re(cos )sin Re(cos cos ααααα+⋅=+=
∑≤≤-=n
i i i n i n C 2022tan )1(cos αα∑≤≤--=n
i i i
n i n C 2022)1(sec )1(cos αα
αααi n i n
i i i n i C 222022cos cos )1(sec )1(-≤≤∑--= ααi
n n
i i
i
n i
C 22022cos
)cos 1()
1(-≤≤∑--=∑
∑≤≤=-++-=
n i i
k i k n i
n k i i
k C C 200
)(22cos )
1(α
当i k =时,αn
cos 的系数为:
∑≤≤=++++=n
i i
n
i n n n n C C C C C C C C C C A 20206334222110000 ; 当1-=i k 时,α2
cos -n 的系数为:
()
∑≤≤-=++++-=n
i i
n
i n n n n C C C C C C C C C C A 22218346234122011 ; 同样,当j i k -=时,可得αj
n 2cos -的系数为∑
≤≤-=n
i j i
n
j i j
j C C A 222)1((N j i ∈,). 即∑
≤≤--=
n
j j n j j A n 202cos )1(cos αα,其中∑
≤≤=
n
i j i
n
j i j C C A 222(N j i ∈,). 至此,我们已经给出了αn cos 的行列式表示和展开式中αm
cos 的系数,用同样方法,我
们也可以求出αn sin 的行列式表示和展开式中αm
sin
的系数。
指导教师评语:该同学是全国信息学竞赛一等奖获得者(重庆赛区),已保送北京师范大学
数学系。
我认为高三的数学试题对他失去意义,鉴于他自学了部分高等数学,我建议他寻找一些研究课题,尝试自主探究。
这篇小文章用两种形式描述倍角公式,可谓新发现,特别是用行列式表示倍角公式,更体现倍角公式的美感。
