2019-2020学年度最新八年级数学上册第一章《分式小结与复习》课件湘教版
合集下载
八年级数学上册第1章分式章末复习一分式课件新版湘教版
知识点五 分式方程的解法
11．(2019·哈尔滨)方程3x2－1 ＝3x 的解为( C )
A．x＝131
B．x＝131
C．x＝37
D．x＝73
12．关于 x 的分式方程x－1 2 ＝x2－a 4 有增根 x＝2，则 a 的值可能
是( D ) A．1 B．2
C．3
D．4
13．解下列分式方程： (1)(大连模拟)x－6 2 ＋1＝x2－－1x4 ； 解：x＝5，经检验，x＝5 是原方程的解
第1章 分 式
章末复习一 分式
知识点一 分式值存在的条件及分式的值为0的条件
1．要使分式xx＋ －11 的值存在，x 的取值应满足( C ) A．x≠－1 B．x≠0 C．x≠1 D．x≠±1
2．(2019·聊城)如果分式|xx|＋－11 的值为 0，那么 x 的值为( B ) A．－1 B．1 C．－1 或 1 D．1 或 0
9．下列运算正确的是( C ) A．2－3＝－8 B．2－3＝－6
C．2－3＝18
D．2－3＝16
10．计算：
(1)(23 )－2×3－1＋(π－2019)0÷(14 )－1；
解：原式＝94 ×13 ＋1÷4＝34 ＋14n－2·14 ×m4n6＝14 m－2n4＝4nm42
解：(1)x1＝c，x2＝mc ；把 x1＝c 代入方程，得左边＝c＋mc ，右 边＝c＋mc ，∴左边＝右边．把 x2＝mc 代入方程，得左边＝mc ＋ c，右边＝c＋mc ∴左边＝右边． ∴x1＝c，x2＝mc 是关于 x 的方程 x＋mx ＝c＋mc 的解
解：设汽车行驶在普通公路上的平均速度是x千米/分钟，则汽车行驶在 高速公路上的平均速度是1.8x千米/分钟，
由题意，得18.81x ＋36＝8x1 .解得 x＝1. 经检验，x＝1 是所列方程的根，且符合题意． 所以 1.8x＝1.8(千米/分钟). 答：汽车行驶在高速公路上的平均速度是 1.8 千米/分钟
数学八年级上册分式小结与复习 课件 湘教
复习 --------小结与复习（1）
分式意义
基本性质 分
式
运算
乘除(乘方) 整数指数幂的运算 加、减运算
分式方程及其应用
注意
1. 分式与分数有许多相似之处，在学习分式的
性质与运算时，可类比分数.
2、计算时，要仔细观察题目的结构特点，搞清运算顺序，灵
活运用运算律，适当运用计算技巧，可简化运算，提高速度，
(1) 有意义
(2) 值为 0
x≠0且x≠-2
x=2
1.分式的基本性质:
分式的分子与分母同乘以(或除以) 一个非0的整式 ，
分式的值 不变 。用式子表示:
A B
=
A×m (B × m)
A B
=
A÷m
(B÷m )
(其中m是 不为0 的整式)
2.分式的符号法则:
A B
=
(-A B
)
=
A (-B
)=
-A
S
1.长方形的面积为Sm²，长为8m。宽应为__5__m;
S
长方形的面积为S，长为x，宽应为__x____;
S?
a
2、把体积为200cm³2的0水0 倒入底面积为 33cm²的圆柱形 容器中,水面高度为__3_3__cm;
把 度体 为积__为_vs_V_的_;水倒入底面积为S的圆柱形容器中,水面S高
例2
若分式
x -1 x-1
的值为零，则x的值等于
-1
.
解析由题意得：
xx--11≠=∴00 ，. x
=-1.
例3 当x=
1 2
时，分式
3 2x-1
无意义.
解析 当分母2x-1=0， 即 x =时1 ，分式无意义. 2
分式意义
基本性质 分
式
运算
乘除(乘方) 整数指数幂的运算 加、减运算
分式方程及其应用
注意
1. 分式与分数有许多相似之处，在学习分式的
性质与运算时，可类比分数.
2、计算时，要仔细观察题目的结构特点，搞清运算顺序，灵
活运用运算律，适当运用计算技巧，可简化运算，提高速度，
(1) 有意义
(2) 值为 0
x≠0且x≠-2
x=2
1.分式的基本性质:
分式的分子与分母同乘以(或除以) 一个非0的整式 ，
分式的值 不变 。用式子表示:
A B
=
A×m (B × m)
A B
=
A÷m
(B÷m )
(其中m是 不为0 的整式)
2.分式的符号法则:
A B
=
(-A B
)
=
A (-B
)=
-A
S
1.长方形的面积为Sm²，长为8m。宽应为__5__m;
S
长方形的面积为S，长为x，宽应为__x____;
S?
a
2、把体积为200cm³2的0水0 倒入底面积为 33cm²的圆柱形 容器中,水面高度为__3_3__cm;
把 度体 为积__为_vs_V_的_;水倒入底面积为S的圆柱形容器中,水面S高
例2
若分式
x -1 x-1
的值为零，则x的值等于
-1
.
解析由题意得：
xx--11≠=∴00 ，. x
=-1.
例3 当x=
1 2
时，分式
3 2x-1
无意义.
解析 当分母2x-1=0， 即 x =时1 ，分式无意义. 2
湘教版八年级数学上册第一章分式小结复习精选课件
把几个异分母的分式分别化成与原来的分式相等的 同分母的分式，叫做分式的通分
三. 分式的运算
知能点1. 分式的乘除、乘方：
乘法法则：分式乘分式，用分子的积作 为积的分子，分母的积作为积的分母。
������ ������ ������ ·������ ������ ·������ = ������ ·������
谢谢聆听 门前小土坡在夜色下显得有些陌生而拘谨，似乎把我当成远方客人。得知我要回来，一进门就看到母亲正朝着门口快步走来，她打量着我一直笑，拉我进屋。 “快坐下，坐车很难受吧？”母亲像个得到心爱玩具后的孩子般兴奋，我便坐在沙发上。 “去洗洗手吧，一路上出汗多”，我刚要起身，母亲又赶忙示意我别动，对我说：“我给你端来，你别起来。”不等我回话，转身到院子里了。 母亲端来水，递给我毛巾，转身又小跑着到厨房去了。我知道母亲在给我做捞面。记得初中时候一天上午放学，由于母亲忙农活做饭晚了，我一生气准备不吃饭就上学去。母亲也是这样让我坐着，转身小跑到厨房为我做捞面。 吃了无数次母亲做的捞面，但从没认真看过她擀面条的样子。想到这里，我轻轻来到院子里，厨房门开着，我站在离厨房几米远的地方，正好可以看到母亲。 厨房里装的还是以前那种白织灯，夜色包围下加上腾空的水蒸气，白织灯散发的昏黄光线显得有点力不从心。母亲就在灯下，正用擀面杖擀面，擀面杖很粗大，她似乎要用很大的力气。面团在前后滚动的擀面杖下由崎岖粗糙变得慢慢平整，终于像一张纸一样平铺在案板上。就像从小到大我走过的路，多少荆棘坑洼，都被母亲用双手铺平。
“吃肉啊，那是我专门放面里的，快吃！” 我夹起一块肉吃在嘴里，她这才算满意，站在一边看我吃。我没有劝母亲去吃饭，因为我知道，我没吃完，她不肯去。 一碗面吃完，汗水顺着脸颊淌下，这捞面味道，一半在嘴里，香而纯，另一半在心里，有点酸楚。一小滴液体流进嘴里，涩涩的，咸咸的，不知道是汗，还是我眼角渗出的泪。，只因眷恋而去。很久都不曾写过文章了，上一篇文章还是四个月之前的。以此去命题，并非有什么轻生的念头，只是有感而发，勿念。其实我很想做个自私的人，因为这会让你吃尽苦头又吃足了甜头。而你却依然活的天真活的开心——序。
三. 分式的运算
知能点1. 分式的乘除、乘方：
乘法法则：分式乘分式，用分子的积作 为积的分子，分母的积作为积的分母。
������ ������ ������ ·������ ������ ·������ = ������ ·������
谢谢聆听 门前小土坡在夜色下显得有些陌生而拘谨，似乎把我当成远方客人。得知我要回来，一进门就看到母亲正朝着门口快步走来，她打量着我一直笑，拉我进屋。 “快坐下，坐车很难受吧？”母亲像个得到心爱玩具后的孩子般兴奋，我便坐在沙发上。 “去洗洗手吧，一路上出汗多”，我刚要起身，母亲又赶忙示意我别动，对我说：“我给你端来，你别起来。”不等我回话，转身到院子里了。 母亲端来水，递给我毛巾，转身又小跑着到厨房去了。我知道母亲在给我做捞面。记得初中时候一天上午放学，由于母亲忙农活做饭晚了，我一生气准备不吃饭就上学去。母亲也是这样让我坐着，转身小跑到厨房为我做捞面。 吃了无数次母亲做的捞面，但从没认真看过她擀面条的样子。想到这里，我轻轻来到院子里，厨房门开着，我站在离厨房几米远的地方，正好可以看到母亲。 厨房里装的还是以前那种白织灯，夜色包围下加上腾空的水蒸气，白织灯散发的昏黄光线显得有点力不从心。母亲就在灯下，正用擀面杖擀面，擀面杖很粗大，她似乎要用很大的力气。面团在前后滚动的擀面杖下由崎岖粗糙变得慢慢平整，终于像一张纸一样平铺在案板上。就像从小到大我走过的路，多少荆棘坑洼，都被母亲用双手铺平。
“吃肉啊，那是我专门放面里的，快吃！” 我夹起一块肉吃在嘴里，她这才算满意，站在一边看我吃。我没有劝母亲去吃饭，因为我知道，我没吃完，她不肯去。 一碗面吃完，汗水顺着脸颊淌下，这捞面味道，一半在嘴里，香而纯，另一半在心里，有点酸楚。一小滴液体流进嘴里，涩涩的，咸咸的，不知道是汗，还是我眼角渗出的泪。，只因眷恋而去。很久都不曾写过文章了，上一篇文章还是四个月之前的。以此去命题，并非有什么轻生的念头，只是有感而发，勿念。其实我很想做个自私的人，因为这会让你吃尽苦头又吃足了甜头。而你却依然活的天真活的开心——序。
湘教版八年级数学上册第1章分式课件
则该村的人均耕地面积约为____5m_0__公顷；
（2）某工厂接到加工m个零件的订单，原计划 每 加天 工加b个工，a则个，__由_a_m+于_b_技__术天改可革以，完实成际任每务天. 多
2. 已知分式 4xx+-35，当x取什么值时，分式的值 （1）不存在； （2）等于0？
解
（1）当4x-5=0，即
议一议
下列等式是否成立？为什么？
--gf =
f g
,
-f g
= -fg .
例3 根据分式的基本性质填空：
（1） 1--aa2 =（ a ）；
（2）
x y
=（
xy
）；
（3）
x
5x 2 -3
x
=（
5
）.
（1） 1--aa2 =（ a ）；
分析 （1）因为 1--aa2 的分母-a乘-1就能化为a， 根据分式的基本性质，
本章内容 第1章
分式
1.1.1《分式（1）》 1.1.2《分式（2）》 1.2.1《分式的乘法和除法（1）》 1.2.2《分式的乘法和除法（2）》 1.3.1《同底数幂的除法》 1.3.2《零次幂和负整数指数幂》 1.3.3《整数指数幂的运算法则》 1.4.1《分式的加法和减法（1）》 1.4.2《分式的加法和减法（2）》 1.4.3《分式的加法和减法（3）》 1.5.1《可化为一元一次方程的分式方程（1）》 1.5.2《可化为一元一次方程的分式方程（2）》
a+b x+ y
说一说
代数式
a x
,Sx
, xa ++ by
有什么共同点？
我们已经知道，一个整数m 除以一个非零整数n，
所得的商记作
（2）某工厂接到加工m个零件的订单，原计划 每 加天 工加b个工，a则个，__由_a_m+于_b_技__术天改可革以，完实成际任每务天. 多
2. 已知分式 4xx+-35，当x取什么值时，分式的值 （1）不存在； （2）等于0？
解
（1）当4x-5=0，即
议一议
下列等式是否成立？为什么？
--gf =
f g
,
-f g
= -fg .
例3 根据分式的基本性质填空：
（1） 1--aa2 =（ a ）；
（2）
x y
=（
xy
）；
（3）
x
5x 2 -3
x
=（
5
）.
（1） 1--aa2 =（ a ）；
分析 （1）因为 1--aa2 的分母-a乘-1就能化为a， 根据分式的基本性质，
本章内容 第1章
分式
1.1.1《分式（1）》 1.1.2《分式（2）》 1.2.1《分式的乘法和除法（1）》 1.2.2《分式的乘法和除法（2）》 1.3.1《同底数幂的除法》 1.3.2《零次幂和负整数指数幂》 1.3.3《整数指数幂的运算法则》 1.4.1《分式的加法和减法（1）》 1.4.2《分式的加法和减法（2）》 1.4.3《分式的加法和减法（3）》 1.5.1《可化为一元一次方程的分式方程（1）》 1.5.2《可化为一元一次方程的分式方程（2）》
a+b x+ y
说一说
代数式
a x
,Sx
, xa ++ by
有什么共同点？
我们已经知道，一个整数m 除以一个非零整数n，
所得的商记作
湘教版八年级上册数学精品教学课件 第1章分式 可化为一元一次方程的分式方程 第2课时 分式方程的应用
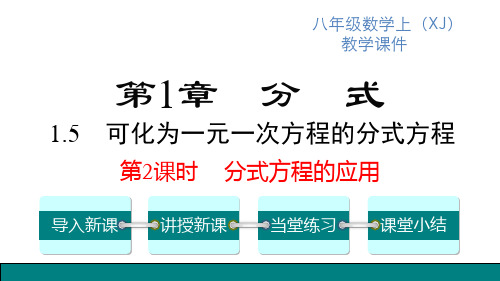
们同时到达，已知汽车的速度是自行车的 3 倍，求两车
的速度.
解：设自行车的速度为 x 千米/时，那么汽车的速度是
3x 千米/时，依题意得：
15 15 2 . 3x x 3
解得 x＝15.
经检验，x＝15 是原方程的根. 由 x＝15 得 3x＝45.
答：自行车的速度是15千米/时，汽车的速度是45千米/时.
因此 x = 2200 是原方程的根，且符合题意.
答：该款空调补贴前的售价为每台 2200 元.
2. 一轮船往返于 A、B 两地之间，顺水比逆水快 1 小时到
达.已知 A、B 两地相距 80 千米，水流速度是 2 千米/时，
求轮船在静水中的速度.
解：设船在静水中的速度为 x 千米/时,根据题意得
80 80 1. x2 x2
答：面包车的速度为 100 km/h，小轿车的速度为 90 km/h.
做一做 1.小轿车发现跟丢时，面包车行驶了 200 km，小轿车 行驶了 180 km，小轿车为了追上面包车，他就马上提 速，他们约定好在 300 公里的地方碰头，他们正好同 时到达，请问小轿车提速多少 km/h？
0
180 200
甲的工1作效(1率 1是) 13
，根据题意得 1 1 1， 即
3
2 x2
1 1 2 2x
1.
方程两边同乘 2x，得 x 1 2x.
解得 x = 1.
检验：当 x = 1 时，2x≠0. 所以，原分式方程的解为 x = 1. 由上可知，若乙队单独施工 1 个月可以完成全部
任务，而甲队单独施工需 3 个月才可以完成全部任务， 所以乙队的施工速度快.
车行驶了 200 km 时，发现小轿车只行驶了 180 km，若 面包车的行驶速度比小轿车快 10 km/h，请问面包车、 小轿车的速度分别为多少？
八年级数学上册 第一章《分式 小结与复习》课件 (新版)湘教版
4．下列各式正确的是（ A
）
-x+y -x-y ＝ -x-y x+y -x+y x-y ＝-x-y x+y 中的x和y的值都扩大３倍，
则分式的值（ B ） 1 1 Ａ.扩大３倍 Ｂ.不变 Ｃ.缩小 3 Ｄ.缩小 6 xy 6.如果把分式 中的x和y的值都扩大３倍， x＋ y 则分式的值（ A ） 1 19 最新中小学教案、试题、试卷、课 Ａ.扩大３倍 Ｂ.不变 件Ｃ.缩小 3 Ｄ.缩小6
约分与通分的依据是: 分式的基本性质
最新中小学教案、试题、试卷、课 件
10
自我检测交流
2 1-3x 1. 与 x-1 2-2x
2(x-1) 的最简公分母是_____.
y x 2b2c 与 18 a 的最简公分母是 _______. 2 2 6a b 9ab c
2.约分
2x 1 - 9y a-b -6x2y (2) (1) 3 =_______. =_______. 27xy2 3b-3a m+2 m2+4m+4 =_______. m-2 (3) m2 - 4
分式
小结与复习
最新中小学教案、试题、试卷、课 件 1
本章知识结构
分式意义
分 式
基本性质 运 算
乘除(乘方)
整数指数幂的运算 加、减运算
分式方程及其应用
注意 1. 分式与分数有许多相似之处，在学习分式
的性质与运算时，可类比分数. 2.计算时，要仔细观察题目的结构特点，搞清运算顺 序，按运算方法法则认真计算，运算结果要化简. 3. 解分式方程的关键是去分母转化为整式方程，可 2 最新中小学教案、试题、试卷、课 能产生增根，因此必须检验 . 件
最新中小学教案、试题、试卷、课 件 11
2019年秋八年级数学上册 第1章 分式 1.4 分式的加法和减法教学课件 (新版)湘教版
解： f fg
g
从上式可以看出： f 与 f 是一对互为相反数，所以：
g
g
f f ,又 f f , g g g g
所以 f： f f , g g g
例4 计算： ac bc ab ba
解：
ac bc ac bc ac bc a b b a a b (a b) a b a b
重点：运用同分母的分式加减法法则进行同分
母分式的运算.
难点：分式分子中多项式的变形和符号法则的
正确运用.
开学时，王刚和李强一起去文具店买笔记本，某种 笔记本的单价为g元，王刚买了f元，李强买了h元，那 么两人共买了多少本笔记本？如果f>h，那么王刚比李 强多买了多少本笔记本？
引导学生得出：两人共买了 f h 本笔记本，王刚比
3.分式加减运算的结果应是最简分式.
acbcc(ab)c ab ab
强调：把表面上看不是同分母的分式相加减，转化为
同分母的分式相加减.
这节课你有什么收获？
1.同分母分式的加减法法则：同分母分式相加减，分母 不变，分子相加减.
若分母不是同分母， 应将其转化为同分母
若分子是多项式， 应将其加上括号
2.如何转化为同分母：（1）采用变号法则；（2）通过 约分.
第1章 分式
1.4 分式的加法和减法
1.使学生掌握同分母的分式加减法法则，并能较熟练 地运用法则进行同分母分式的加减运算.
2.使学生在同分母的分式加减法与分数加减法的对比 过程中，体会类比的数学思想，培养学生的观察、分析能力， 同时培养学生灵活解题的能力.
3.在讲解同分母分式加减法法则的过程中，渗透类比 思想；在应用同分母分式加减法法则进行计算的过程中，渗 透换元思想.
湘教版八年级上《第一章分式》期末复习课件(共24张PPT)
_____________
y)2
2 2x+y ___ ___ D. = = y -x 3 3x+y
知识点5：分式的加减乘除及混合运算 （1）分式的乘除运算： 因式分解 →约分 （2）分式相加减： 因式分解 →通分、约分 （3）分式的混合运算： 乘除 ，再算 加减 先算______ _______， 若有括号，则先算括号里面 ___________.
自我检测交流7
(1)下列运算正确的是（ C ） 2 = －6a2 ( － 3a) 3 2 6 A. a . a = a B.
2 3 C. a÷a = a 2 x
D. (an-1 )3 = a3n-1
) (2)计算 x2 =_________; 2m -n m n (3)已知a =2 ，a =3，则 a
自我检测交流9
2 x+2 1.解分式方程 ，去分母 + =3 x-1 1-x 后变形正确的是（ D ）
A.2+(x+2)=3(x-1) B.2-x+2=3(x-1)
D.2-(x+2)=3(x-1) m 3 2.已知关于x的分式方程 的解 + =1 x-1 1-x 是非负数，则m的取值范围（ C ）
字母 ______. ≠0 2.分式有意义的条件:分母_________. 分式无意义的条件:分母_________. =0 3.分式值为 0 的条件： 等于0 ，且分母 不等于 0 分子________ __________.
1 （1）要使分式 有意义，则x的取值 x+2 应满足（ D ） A.x=-2 B.x≠2 C .x＞-2 D.x≠-2
1.下列方程是分式方程的是（ D ）
知识点9：分式方程的解法
湘教版数学八年级上《第1章分式》单元复习与小结
八年级上册单元复习与小结第一章：分式班级： 学号： 姓名：一、课前构建：认真阅读教材P 1－40回顾相关知识：—分式的定义—分式的概念——分式无意义—分式的值为零—分式的性质分式— —乘、除运算—分式的运算——整数指数幂的运算—加、减运算—分式方程二、课堂点拨：知识点一：分式的概念★考点1:分式的定义：一个整式f 除以一个 （ ），所得的商gf 叫做分式。
例1、下列式子xy x y x x x y x +--,,56,2232π中，是分式的是 。
★考点2:分式无意义： 在分式gf 中，当g 时，分式无意义；g 时，分式有意义。
例2、当x = 时，分式12+x x 没有意义；当x 时，分式11+x 有意义。
★考点3:分式的值为零： 在分式gf 中，当f 且g 时，分式的值为0。
例3、若分式11x x -+的值为零，则x 的值为 。
知识点二：分式的性质★考点4:分式的基本性质：分式的分子与分母都乘 ，所得分式与原分式相等。
即（其中0≠h ）分式的分子与分母约去公因式，所得分式与原分式相等。
即 （其中0≠h ） 分式的变号法则：分式的分子、分母与分式本身的符号，改变其中的任何两个，分式的值不变。
即 。
例4、如果把分式yx xy +中的x 和y 都扩大2倍，则分式的值（ ） A 、扩大4倍 B 、扩大2倍 C 、不变 D 、缩小2倍例5、根据分式的基本性质，分式ba a --可变形为（ ） A 、b a a -- B 、b a a + C 、b a a -- D 、b a a +- ★考点5:最简分式（1）约分：把一个分式的分子与分母的公因式约去，称为分式的约分。
约分的方法：先把分子与分母因式分解，再约去公因式。
（2分子与分母没有 分式，叫做最简分式。
分式运算的最终结果若是分式，一定要化成最简分式。
例6、化简xy x y x +-222的结果是（ ）A 、x y x 2- B 、x y x + C 、y x y x +- D 、xy x - 知识点三：分式的运算★考点6:分式的加减法①同分母分式相加减，分母 ，把分子 。
八上数学(湘教版)课件-第1章 章末小结
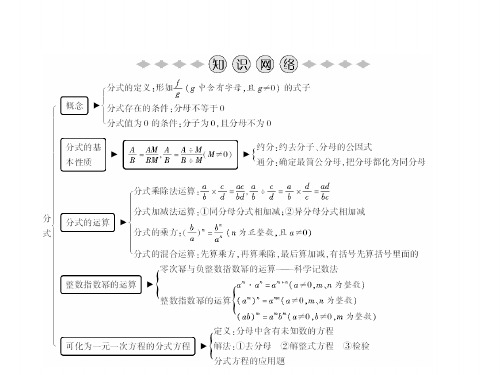
3 2
.
4. (重庆中考)计算：(2x－＋21x＋x－1)÷xx2＋－1x.
2－2x＋x＋1x－1 x＋1 x－1
解：原式＝
x＋1
·xx－1＝ x .
5．先化简，再求值． (1) (莱芜中考)(1－x＋3 1)÷x2－x2－4x1＋4，其中 x＝3；
x＋1－3 x＋1x－1 x－2 x＋1x－1 x－1 解：原式＝ x＋1 · x－22 ＝x＋1· x－22 ＝x－2，当 x＝3 时， 原式＝2；
解：原式＝(－18－18×41)×4×1＝－58； (2)(2p3q－1)－3×(－3p－1q)2. 解：原式＝2－3p－9q3×(－3)2×p－2×q2＝2－3×9×p－11q5＝89pq151.
分式方程
7. (荆州中考)若关于 x 的分式方程mx－－11＝2 的解为非负数，则 m 的取值范围
是( D )
10. (宜宾中考)近年来，我国逐步完善养老金保险制度．甲、乙两人计划用 相同的年数分别缴纳养老保险金 15 万元和 10 万元，甲计划比乙每年多缴 纳养老保险金 0.2 万元．求甲、乙两人计划每年分别缴纳养老保险金多少万 元？ 解：设乙每年缴纳养老保险金为 x 万元，则甲每年缴纳养老保险金为(x＋0.2) 万元，根据题意得：x＋150.2＝1x0，去分母得：15x＝10x＋2，解得：x＝0.4， 经检验 x＝0.4 是分式方程的解，且符合题意，∴x＋0.2＝0.4＋0.2＝0.6(万 元)．答：甲、乙两人计划每年分别缴纳养老保险金 0.6 万元、0.4 万元．
(2) (漳州中考)mm－21－11－－2mm，选取一个适当的 m 的值代入求值． 解：原式＝mm－21－2mm－－11＝m2－m－2m1＋1＝mm－－112＝m－1，当 m＝2016 时， 原式＝2016－1＝2015(答案不唯一)．
2020年秋八年级数学上册第1章分式1.2分式的乘法和除法第1课时分式的乘除法课件新版湘教版
A．－13
B.3
C．3 或－31
D.2
11．若xx＋－11÷xx－－23的值存在，则 x 的取值范围是 x≠1且x≠2且x≠3
.
12．计算： (1)8x2y2·(－43yx2)； 解：原式＝－6x3；
(2)x2－2x4－x＋6 4·2xx－－34； 解：原式＝2xx－－232·2xx－－32＝x－4 2；
2018秋季
数学 八年级 上册•X
第1章 分式
1.2 分式的乘法和除法 第1课时 分式的乘除法
分式乘分式，把分子乘 分子 ，分母乘 分母 ，分别作为积的
分子
、 分母
，即gf ·uv＝
fu gv
.
分式除以分式，把除式的分子、分母 颠倒位置 式 相乘 .如果 u≠0，则规定gf÷uv＝ gf·vu ＝gfvu.
13．先化简x2－2 1÷2x2x－2，然后请你选一个你认为合适的数作为 x 的值代入 求值． 解：原式＝x－12x＋1·2x＋1xx－1＝4x.∵x≠0 且 x≠±1，∴x 的值可取
2(答案不唯一)，∴当 x＝2 时，原式＝42＝2. 14．先化简，再求值：m2－2m2m＋nn＋n2·(m－n)．其中mn ＝2. 解：原式＝2mm－＋nn2·(m－n)＝2mm－＋nn.∵mn ＝2，∴m＝2n，∴原式＝42nn＋ －nn＝5nn ＝5.
(3)a28＋1－6aa＋2 9÷29a－＋a6·a＋1 9； 解：原式＝－a＋a＋93a2－9·－2aa＋－39·a＋1 9＝a＋2 3；
b＋1 b2＋b 1 (4)a2－4÷a＋2 ·ba－2. 解：原式＝a＋b2＋a1－2·bab＋＋21·ba1－2＝b2a1－22.
8．下列计算正确的是( C )
A．a2b÷ab2＝b2
湘教版八上数学第1章 小结与复习
a 2b 14
a2 b2
解【：解因析为】2由a已 b知可3 以，变所形以为a用 4bb来. 表示 a 的形式，
得
a 4 5
所以
ba5454，bb2代b22 入1bb约422 分 即49可1. 求值5.
归纳总结
已知字母之间的关系式，求分式的值时，可以先 用含有一个字母的代数式来表示另一个字母，然后把 这个关系式代入到分式中即可求出分式的值.这种方法 即是主元法.
已知 x
=
2，y = 10，求
x
1
y
x
1
y
x2
2x 2xy
y2
的值.
【解析】一般应先化简分式，再代入字母值求值.
解：原式 =
2x
(x y)2 x y，
(x y)(x y) 2x x y
将 x = 2，y = 10 代入得
原式 = 2 10 Βιβλιοθήκη . 2 10 3归纳总结
30.
4
解得 x = 4. 经检验，x = 4 原分式方程的解.
答：第一次每支铅笔的进价为 4 元.
方法总结 在实际问题中，列分式方程解题的方法与列一
元一次方程解应用题的方法相同，不同之处在于列 方式方程解应用题时，既要检验所得解是不是所列 分式方程的解，又要检验是否符合实际意义.
针对训练 6. 某市在道路改造过程中，需要甲、乙两 个工程队来完成这一工程．已知甲工程队比乙工程队每 天能多铺设 20 米，且甲工程队铺设 350 米所用的天数 与乙工程队铺设 250 米所用的天数相同．问甲、乙两个 工程队每天各能铺设多少米？
(x y)2 y(x y)
y = 3m，或整体
2x .
代入求值.
湘教版八年级数学上册第一章分式小结复习
子等于0
第四页，共18页。
知能点4. 分式(fēnshì)值为正
负数：
（1）分子(fēnzǐ)分母同号 （2）分子(fēnzǐ)
分母异号
第五页，共18页。
二. 分式(fēnshì)
知能点1. 分式的性质：
的性质
分式的分子(fēnzǐ)与分母乘（或除以）同一个不等于0的整
式，分式的值不变。
A
A·C
（
2）解整式方程
(fēnmǔ)
步骤
（3）检 验
第十四页，共18页。
第十五页，共18页。
第十六页，共18页。
第十七页，共18页。
内容(nèiróng)总结
第一章。答：分式的分母不等于0，分式才有意义。分式的分子与分母乘（或除以）同一个不等于0
的整式，分式的值不变。把一个分式的分子与分母的公因式约去，叫做分式的约分。①最大公因式的系
A
b
b
A÷ C
=
用字母(zìmǔ) B = B·C
B
B÷ C
表示：
a
a
a a
分式的变号法则：
第六页，共18页。
b b
(C≠ 0)
知能点2. 分式(fēnshì)的约
分：
把一个分式的分子
(fēnzǐ)与分母的公
因式约去，叫做分
式的约分。
确定最大公因式的方法
(fāngfǎ)：
常从小数点往后至第一个不为
零的数字(shùzì)上，所有零的
个数，包括小数点前面的那个
零。
第十二页，共18页。
第十三页，共18页。
三. 分式方程
知能点1. 分式方程的意义和解法：
第四页，共18页。
知能点4. 分式(fēnshì)值为正
负数：
（1）分子(fēnzǐ)分母同号 （2）分子(fēnzǐ)
分母异号
第五页，共18页。
二. 分式(fēnshì)
知能点1. 分式的性质：
的性质
分式的分子(fēnzǐ)与分母乘（或除以）同一个不等于0的整
式，分式的值不变。
A
A·C
（
2）解整式方程
(fēnmǔ)
步骤
（3）检 验
第十四页，共18页。
第十五页，共18页。
第十六页，共18页。
第十七页，共18页。
内容(nèiróng)总结
第一章。答：分式的分母不等于0，分式才有意义。分式的分子与分母乘（或除以）同一个不等于0
的整式，分式的值不变。把一个分式的分子与分母的公因式约去，叫做分式的约分。①最大公因式的系
A
b
b
A÷ C
=
用字母(zìmǔ) B = B·C
B
B÷ C
表示：
a
a
a a
分式的变号法则：
第六页，共18页。
b b
(C≠ 0)
知能点2. 分式(fēnshì)的约
分：
把一个分式的分子
(fēnzǐ)与分母的公
因式约去，叫做分
式的约分。
确定最大公因式的方法
(fāngfǎ)：
常从小数点往后至第一个不为
零的数字(shùzì)上，所有零的
个数，包括小数点前面的那个
零。
第十二页，共18页。
第十三页，共18页。
三. 分式方程
知能点1. 分式方程的意义和解法：
湘教版八年级数学上册《分式小结与复习(一)》课件
的值为零.
(3)当x =3
时，分式 x2－9
X+3
的值为零。
(4)已知，当x=5时，分式23
x x
k 2
的值等于零，则k=-10。
2、
2 、13x x1 22x
的最简公分母是 2(x-1)。
3、2(ab a )(b2),3(bab )(2b)， 4(bc 2)
的最简公分母是 12(a-b。)(b+2)
湘教版SHUXUE八年级上
小结
复习 --------小结与复习（1）
分式意义
基本性质 分
式
运算
乘除(乘方) 整数指数幂的运算 加、减运算
分式方程及其应用
注意
1. 分式与分数有许多相似之处，在学习分式的
性质与运算时，可类比分数.
2、计算时，要仔细观察题目的结构特点，搞清运算顺序，灵
活运用运算律，适当运用计算技巧，可简化运算，提高速度
谢谢观赏
You made my day!
我们，还在路上……
x≠-2 x≠±1 x≠±1 x为全体 x≠-1或
实数
x≠3
x-1 x2+3 x为全体
实数
5.当x为何值时,下列分式的值为0?
(1)
x-4 x+1
(2)
x-1 x -2
(3)
x -3 x-3
(4)
x2 -1 x2 +2x+1
x=4
x=1
x=-3
x=1
2x (x-2) 6.当x为何值时,分式 5x (x+2)
变式1: 已知 x2 变式2:已知 x+
–
1 x
3x+1=0 ,求 x2+ =3 ,求 x2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Ａ.扩大３倍 6.如果把分式
xx＋Ｂy y.不变中的Ｃx和.缩y小的值13 都扩Ｄ大.缩３小倍16 ，
则分式的值（A ）
1
Ａ.扩大３倍 Ｂ.不变 Ｃ.缩小 3
Ｄ.缩小16
分式的两种基本运算:
1.约分: 把分子、分母的_公__因__式___约去的运算. 步骤：先把分子与分母_因__式_分__解______， 然后约去它们的_公__因__式_______.
5.x
取x__=_-_2__时,分式xx
-1 +2
没有意义.
x
取x__=_2_或_-_2__时,分式
x +1 x2 -4
的值不存在.
6.当x为何值时,下列分式的值为0?
(1)x-4 x+1
x =4
(2)_∣_x_∣_-_3__ x-3
x =-3
分式的基本性质:
1.分式的分子与分母都乘_同__一_个__非__零__整__式__， 所得分式与原分式相等
第一部分
1.分式的有关概念 2.分式的基本性质 3.分式的两种基本运算:约分与通分
分式的有关概念
1.分式的定义: 一个整式f 除以一个非零整式 g（g 中含
f 有字母），所得的商___g___ 叫作分式.
2.分式有意义的条件:分母_≠_0_______. 分式无意义的条件:分母_=__0______.
3.分式值为 0 的条件:
分子_等__于_0____，且分母不__等_于__0_____. 4.最简分式:指分子与分母没有公__因__式___的分式
自我检测交流
1.下列各式(1)
2x 3
(2)
3 2x
(3)
2x2 x
(4)
x
π
(5)
1-
3 2a
是分式的有__3__ ）
f z d x y
3.通分
(a-1)2
a-1
a2+2a+1=__(a_+_1_)_2(_a_-_1_) __.
6(a+1) 6 a2-1 =__(_a_+_1_)2_(_a_-1_)__.
4.下列运算中，正确的是（ C ）
x+y 2 2
A. x + y _____________
=
x+y
a = 1 B.
m - n A B ____________ n- m
x +1 2
_________
x+1
C
-a -b ___________ a+ b
Dx_2_-_x2_-x_yy_+_y_2
1
3. x 取x__≠_____时,分式
2
x 为_x_≠_±__1__时,分式
x+2
1-2x
1 ∣x ∣-1
有意义. 的值存在.
分式
小结与复习
本章知识结构
分式意义
分
基本性质
式
运算
乘除(乘方) 整数指数幂的运算
加、减运算
分式方程及其应用
注意 1. 分式与分数有许多相似之处，在学习分式
的性质与运算时，可类比分数. 2.计算时，要仔细观察题目的结构特点，搞清运算顺
序，按运算方法法则认真计算，运算结果要化简.
3. 解分式方程的关键是去分母转化为整式方程，可 能产生增根，因此必须检验.
2.约分
-6x2y
(1)
- 2x =____9_y__. (2)
27xy2
3ab--b3a=_-___13___.
m+2
(3)
m2+4m+4
m2 - 4
=__m_-_2___.
在 多 年 的 高 三 复 习 备 考 中 ， 老 师 认 为 以 下 六 句 话 可 作 引 导 学 生 科 和 应 基 本 指 南 。 这 就 是 ： 础 决 定 能 力 ； 过 程 结 果 细 节 成 败 心 态 状 度 落 实 一 切 毫 无 疑 问 ， 高 考 复 习 的 主 要 目 就 是 回 归 基 础 巩 固 夯 实 。 没 有 能 力 中 每 一 道 题 查 都 离 不 开 可 谓 成 也 败 分 拿 下 来 总 法 上 去 为 此 对 知 识 足 够 重 视 和 耐 心 急 功 近 利 往 自 多 次 测 试 过 程 决 定 结 果 些 学 生 因 平 时 或 间 投 入 所 以 到 了 出 后 才 感 紧 张 备 事 个 系 统 天 、 节 课 部 如 在 某 方 面 话 必 然 会 产 良 只 调 控 期 待 好 里 说 细 指 现 性 错 误 精品精品
1.下列变形正确的是( C )
a a2 A b = b2
a-b a2-b B a = a2
2-x x-2 C x-1 = 1-x
42
D
=
2a+ a+b
2.填空:
-a-b c-d
=
a+b b -x +y x-y
( d-c
) x+y
=
(-x-y
)
3.与分式 Ａ 3-2m
2m-3
4-m
Ｂ
的值相等的分式是（ A
2 - ___________ a2 -4
__________
a+ 2
C.
(x- y)2
_____________
y = -x
y
-x
2x+y D. ___________ 3x+y
=
2____ 3
2m-3 Ｃ 3-2m Ｄ
） 3-2m
4-m
4-m
4-m
m-4
4．下列各式正确的是（ A ）
Ａ
-x+y -x-y ＝
x-y x+y
B
-x+y -x-y ＝
-x-y x+y
C
-x+y
＝
x+y
-x-y x-y
5.如果把分式
D
x x＋y
-x+y
＝
-
x-y
-x-y x+y
中的x和y的值都扩大３倍，
则分式的值（B ）
2.通分: 把分母不同的分式化成_同__分_母__的分式的运算. 通分的关键：找出各分母的_最_简__公__分__母____
即各分母所有因式的最高次幂的积.
约分与通分的依据是: 分式的基本性质
自我检测交流
1.
2 x-1
与12--23xx
的最简公分母是_2_(x_-_1_).
x与 6a2b
y
9ab2c的最简公分母是_1_8a_2_b_2_c_.
2.分式的分子与分母都除以它们的_公_因__式___，
所得分式与原分式相等.
f g
=
f· h g· h
( h≠0)
f•h
g•h = __________
f g
(h≠0)
3.分式的符号法则:
-f
f __________ = g -g
-f
_______
g
f = -g = _______
-
f g
自我检测交流