线性图PPT模板
合集下载
线性代数课件PPT

线性代数课件
目录 CONTENT
• 线性代数简介 • 线性方程组 • 向量与矩阵 • 特征值与特征向量 • 行列式与矩阵的逆 • 线性变换与空间几何
01
线性代数简介
线性代数的定义和重要性
1
线性代数是数学的一个重要分支,主要研究线性 方程组、向量空间、矩阵等对象和性质。
2
线性代数在科学、工程、技术等领域有着广泛的 应用,如物理、计算机科学、经济学等。
逆矩阵来求解特征多项式和特征向量等。
06
线性变换与空间几何
线性变换的定义和性质
线性变换的定义
线性变换是向量空间中的一种变换, 它将向量空间中的每一个向量映射到 另一个向量空间中,保持向量的加法 和标量乘法的性质。
线性变换的性质
线性变换具有一些重要的性质,如线 性变换是连续的、可逆的、有逆变换 等。这些性质在解决实际问题中具有 广泛的应用。
特征值与特征向量的应用
总结词
特征值和特征向量的应用非常广泛,包括物理、工程、经济等领域。
详细描述
在物理领域,特征值和特征向量可以描述振动、波动等现象,如振动模态分析、波动分析等。在工程 领域,特征值和特征向量可以用于结构分析、控制系统设计等。在经济领域,特征值和特征向量可以 用于主成分分析、风险评估等。此外,在机器学习、图像处理等领域也有广泛的应用。
经济应用
线性方程组可用于解决经济问题,如投入产出分析、 经济预测等。
03
向量与矩阵
向量的基本概念
向量的模
表示向量的长度或大小,记作|向量|。
ቤተ መጻሕፍቲ ባይዱ
向量的方向
由起点指向终点的方向,可以通过箭头表示。
向量的分量
表示向量在各个坐标轴上的投影,记作x、y、 z等。
目录 CONTENT
• 线性代数简介 • 线性方程组 • 向量与矩阵 • 特征值与特征向量 • 行列式与矩阵的逆 • 线性变换与空间几何
01
线性代数简介
线性代数的定义和重要性
1
线性代数是数学的一个重要分支,主要研究线性 方程组、向量空间、矩阵等对象和性质。
2
线性代数在科学、工程、技术等领域有着广泛的 应用,如物理、计算机科学、经济学等。
逆矩阵来求解特征多项式和特征向量等。
06
线性变换与空间几何
线性变换的定义和性质
线性变换的定义
线性变换是向量空间中的一种变换, 它将向量空间中的每一个向量映射到 另一个向量空间中,保持向量的加法 和标量乘法的性质。
线性变换的性质
线性变换具有一些重要的性质,如线 性变换是连续的、可逆的、有逆变换 等。这些性质在解决实际问题中具有 广泛的应用。
特征值与特征向量的应用
总结词
特征值和特征向量的应用非常广泛,包括物理、工程、经济等领域。
详细描述
在物理领域,特征值和特征向量可以描述振动、波动等现象,如振动模态分析、波动分析等。在工程 领域,特征值和特征向量可以用于结构分析、控制系统设计等。在经济领域,特征值和特征向量可以 用于主成分分析、风险评估等。此外,在机器学习、图像处理等领域也有广泛的应用。
经济应用
线性方程组可用于解决经济问题,如投入产出分析、 经济预测等。
03
向量与矩阵
向量的基本概念
向量的模
表示向量的长度或大小,记作|向量|。
ቤተ መጻሕፍቲ ባይዱ
向量的方向
由起点指向终点的方向,可以通过箭头表示。
向量的分量
表示向量在各个坐标轴上的投影,记作x、y、 z等。
线性变换与二阶矩阵PPT课件

二阶矩阵的逆
总结词
二阶矩阵的逆是一个特殊的矩阵,它与原矩阵相乘等于单位矩阵。
详细描述
二阶矩阵的逆是一个重要的概念,它是一个与原矩阵互为逆元的特殊矩阵。如果一个二阶矩阵与其逆矩阵相乘等 于单位矩阵,则这个逆矩阵是存在的。求逆矩阵的方法有多种,如高斯消元法、伴随矩阵法等。在某些情况下, 如行列式值为零时,矩阵可能没有逆矩阵。
平移矩阵与平移操作
• 平移矩阵:平移矩阵也是二阶矩阵的一种,用于 表示平移操作。其一般形式为
平移矩阵与平移操作
```
| 0 1 ty |
| 1 0 tx |
平移矩阵与平移操作
```
其中,tx和ty分别表示在x轴和y轴方
平移操作:平移操作是指通过平移矩阵
向上的平移距离。
对向量进行变换,使向量在指定的方向
03
线性变换与二阶矩阵的关系
线性变换的矩阵表示
线性变换是数学中的一种重要概念,它描述了一个向量空间 中的向量通过一个线性映射变为另一个向量空间的过程。在 矩阵表示中,线性变换可以用一个矩阵来表示,该矩阵的行 和列分别对应于输入和输出空间的基向量。
线性变换的矩阵表示具有一些重要的性质,例如矩阵乘法对 应于线性变换的复合,矩阵的转置对应于线性变换的共轭, 以及矩阵的逆对应于线性变换的逆。
二阶矩阵与线性变换的转换
二阶矩阵是数学中一种常见的矩阵类型,它由四个数字组成,可以用来表示一个 线性变换。通过选择适当的基向量,可以将一个线性变换转换为二阶矩阵,反之 亦然。
二阶矩阵与线性变换的转换关系是线性的,即对于任意两个线性变换A和B,以及任 意标量k,有kA=AkB=BkA。
二阶矩阵在几何变换中的应用
通过矩阵变换,可以改变向量的长度、方向和位置,从而实现二维空间中的几何变 换。
线性系统理论PPT-郑大钟(第二版)

系统具有如下3个基本特征:
(1)整体性
1.结构上的整体性 2.系统行为和功能由整体 所决定
(2)抽象性
作为系统控制理论的研 究对象,系统常常抽去 了具体系统的物理,自 然和社会含义,而把它 抽象为一个一般意义下 的系统而加以研究。
(3)相对性
在系统的定义 中, 所谓“系统” 和“部分”这 种称谓具有相 对属性。
u1 u2
up
x1 x2
动力学部件
xn
输出部件
y1 y2
yq
连续时间线性系统的状态空间描述
线性时不变系统
x Ax Bu
y
Cx
Du
线性时变系统
x A(t)x B(t)u
y
C (t ) x
D(t
)u
连续时间线性系统的方块图
x A(t)x B(t)u
对于单输入,单输出线性时不变系统,其微分方程描述
y (n) an1 y (n1) a1 y (1) a0 y bmu (m) bm1u (m1) b1u (1) b0u
H (k )
单位延迟
C(k)
y(k)
u(k)
G(k)
2.3.连续变量动态系统按状态空间描述的分类
线性系统和非线性系统
设系统的状态空间描述为 x f ( x,u, t) y g( x,u, t)
向量函数
f1(x,u,t)
g1(x,u,t)
f
(
x,u,
t
)
f
2
(
x,u,
e
第一 线性规划(共188张PPT)

个要求表述为
x1 ≥0, x2 ≥0
• 综上所述,该问题的数学模型表示为
maxZ= 3x1 +5 x2
x1
≤8
2x2 ≤12
3x1 +4 x2 ≤36
x1 ≥0, x2 ≥0
5
第一节 线性规划一般模型
• 例2. 运输问题 某名牌饮料在国内有三个生产厂,分布在城市A1、 A2、A3,其一级承销商有4个,分布在城市B1、B2、B3、 B4,已知各厂的产量、各承销商的销售量及从Ai到Bj 的每吨饮料运费为Cij,为发挥集团优势,公司要统 一筹划运销问题,求运费最小的调运方案。
(3)约束条件。产量之和等于销量之和,故要满足:
▪ 供应平衡条件
x11+x12+x13+x14=5 x21+x22+x23+x24=2 x31+x32+x33+x34 =3
§ 销售平衡条件
x11+x21+x31=2 x12+x22+x32=3 x13+x23+x33=1 x14+x24+x34=4
§ 非负性约束
29
第三节 线性规划的标准型
§ 标准化2
minZ= x1 +2 (x2′-x 2〃) +3 x3′
函数。可能是最大化,也可能是最小化。 • 线性规划一般模型的代数式 为:
max(min)Z=c1x1+c2x2+…+cnxn a11x1+a12x2+…+a1nxn ≤(≥,=)b1 a21x1+a22x2+…+a2nxn ≤(≥,=)b2 …………… am1x1+am2x2+…+amnxn≤(≥,=)bm x1,x2,…,xn ≥(≤)0
x1 ≥0, x2 ≥0
• 综上所述,该问题的数学模型表示为
maxZ= 3x1 +5 x2
x1
≤8
2x2 ≤12
3x1 +4 x2 ≤36
x1 ≥0, x2 ≥0
5
第一节 线性规划一般模型
• 例2. 运输问题 某名牌饮料在国内有三个生产厂,分布在城市A1、 A2、A3,其一级承销商有4个,分布在城市B1、B2、B3、 B4,已知各厂的产量、各承销商的销售量及从Ai到Bj 的每吨饮料运费为Cij,为发挥集团优势,公司要统 一筹划运销问题,求运费最小的调运方案。
(3)约束条件。产量之和等于销量之和,故要满足:
▪ 供应平衡条件
x11+x12+x13+x14=5 x21+x22+x23+x24=2 x31+x32+x33+x34 =3
§ 销售平衡条件
x11+x21+x31=2 x12+x22+x32=3 x13+x23+x33=1 x14+x24+x34=4
§ 非负性约束
29
第三节 线性规划的标准型
§ 标准化2
minZ= x1 +2 (x2′-x 2〃) +3 x3′
函数。可能是最大化,也可能是最小化。 • 线性规划一般模型的代数式 为:
max(min)Z=c1x1+c2x2+…+cnxn a11x1+a12x2+…+a1nxn ≤(≥,=)b1 a21x1+a22x2+…+a2nxn ≤(≥,=)b2 …………… am1x1+am2x2+…+amnxn≤(≥,=)bm x1,x2,…,xn ≥(≤)0
史上最全最精致的PPT时间线性流程图汇总

•This is an example text.
•This is an example text.
•This is an example text.
•This is an example text.
•This is an example text.
•This is an example text.
对利益相关者的承诺核心价值观我们的使命我们的愿景企业标志企业文化建设实现使命企业文化建设强大的系统调节工具强大的系统调节工具形象层精神层行为层三位一体相互支撑共享愿景企业标志强大的系统调节工具强大的系统调节工具强大的系统调节工具强大的系统调节工具系统调节工具企业文化建设人力资源理念企业使命企业愿景核心价值观企业精神经营理念管理风格系统调节工具主要功能包括是价值理
2014
2015
第20页,共47页。
绘制的钟表用于PPT流程
文本内容
文本内容 文本内容
12 11 10
文本内容
1 2
9
3
8
4
7
5
6
文本内容
第21页,共47页。
简单基本的流程
Marketing Plan •This is an example text. Go ahead an replace it with your own text. This is an example text.
example text.
第22页,共47页。
Example text
•This is an example text. Go ahead an replace it with your own text. This is an example text.
简单流程
第十三章 线性相关分析.ppt

第二节 相关系数的假设检验
r −0 r t= = , ν = n−2 2 Sr 1− r n− n−2
(13-2)
例13-3 (续例13-1) 根据样本相关系数, 对总体相关系数=0进行假设检验。 解: 1. t检验法 检验步骤如下: (1)建立假设,确定检验水准α 。 H0: ρ =0(变量间不存在线性相关关系); H1: ρ ≠ 0(变量间有线性相关关系);
二、 计算公式 样本相关系数的计算公式为
r=
∑(X − X )(Y −Y ) ∑(X − X ) ∑(Y −Y )
2
2
lXY = lXX lYY
(13-1)
例13-2 (续例13-1)计算表13-1中体 重指数和收缩压的相关系数。
解: 1.绘制散点图,观察两变量之间是否有线性趋势。 从图13-1 可见,体重指数与收缩压之间呈线性趋势,且方向相同,为正 相关。 2.计算相关系数。从表13-1的合计栏中,已得出基本数据:
相关关系不一定是因果关系,可能仅是表面上 的伴随关系,或两个变量同时受另一因素的影响, 如小孩的身高和小树的树高同时受时间的影响,在 校儿童的鞋的大小和阅读技能同时受年龄的影响。 不能只根据相关系数r的绝对值的大小来推断两 事物现象之间有无相关以及相关的密切程度,而必 须对r进行相关系数的假设检验。另外,不要把相 关系数的显著性误解为两事物或现象相关的强度, 例如对于相关系数的假设检验来说,P<0.01比 P<0.05更有理由认为相关关系成立,但并不能得出 前者比后者相关关系更密切的结论,相关关系的强 度是用r的绝对值来反映的。
Z = tanh r
−1
1 1+ r Z = ln 2 1− r
式中为tanh为双曲正切函数,tanh-1为反双曲正切函数, 为双曲正切函数, 为反双曲正切函数, 式中为 为双曲正切函数 为反双曲正切函数 SZ为Z的标准误。 的标准误。 为 的标准误
线性校正.ppt
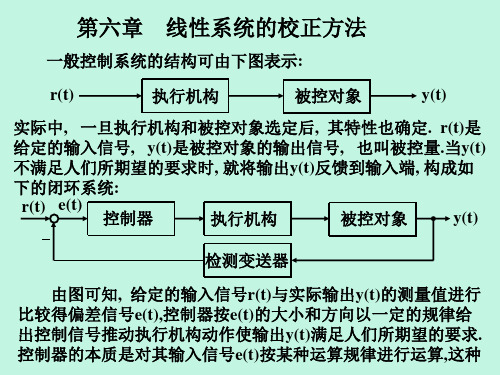
所加校正装置应不改变原开环对数幅频特性曲线在穿越零分贝线
附近直至高频段的形状, 以保持原系统的动态性能, 而应使原系
统的低频段抬高, 以满足速度误差系数的要求. 因此可采用滞后
校正网络.
(2) 确定滞后校正网络参数 滞后校正网络的传递函数为:
GC
(s)
bTs 1 Ts 1
b 1
滞后网络参数的选择应使其相角滞后特性尽可能小地减少原系统
截止频率)附近, 引起相角裕度的减小, 使系统动态性能变坏. 因
此在确定滞后网络的参数时, 一般要求1/ bT小于校正后系统
开环幅值穿越频率(即截止频率)的十分之一. 滞后网络在校正后
系统开环幅值穿越频率处的滞后相角约等于 tg1[0.1(b 1)]
(3) 滞后—超前网络(相位滞后—超前网络)
滞后—超前网络的电路图,零﹑极点在s平面上的位置及对数
有一段直线的斜率为负20分贝十倍频程, 所以滞后网络对高频信
号或噪声有较强的抑制作用; (4) 网络的最大滞后相角m发生在
m
1 bT
处,
b 且
m
sin
1
b b
1 1
显然,
越大, m也越大,
即相角
滞后得越利害. 使用滞后网络对系统进行校正, 应力求避免使滞
后网络的最大滞后相角发生在校正后系统开环幅值穿越频率(即
lg lg C
40
校正后系统的幅值穿越频率
' C
m
8.92
由此可得:
T 1
1
0.056
m 4.025 8.92
GC
(s)
T 1
T 1
0.2254s 1 0.056s 1
校正后系统的开环对数幅频特性曲线见下图:
