小学数学容斥原理
小学奥数容斥原理

小学奥数容斥原理
小学奥数中的容斥原理是一种经典的数学方法,它常常用于解决有关组合计数的问题。
容斥原理可以帮助我们计算两个集合的交集、并集以及差集的元素个数。
具体来说,容斥原理告诉我们,要计算两个集合的并集的元素个数,我们可以先计算每个集合的元素个数,然后减去这两个集合的交集的元素个数。
这样可以避免重复计算。
例如,假设我们有两个集合A和B,集合A中有3个元素,集合B中有4个元素。
如果我们想计算这两个集合的并集的元素个数,根据容斥原理,我们应该先计算集合A的元素个数,再计算集合B的元素个数,然后减去集合A和集合B的交集的元素个数。
另外,容斥原理也可以用于计算三个集合的并集、四个集合的并集,以及更多集合的并集,只需要依次计算每个集合的元素个数,并根据公式依次加减交集的元素个数。
需要注意的是,在应用容斥原理时,我们需要确保计算交集和并集时没有重复计算的情况发生。
这需要我们对问题进行仔细分析和思考,以保证计算结果的正确性。
总之,容斥原理是一种解决组合计数问题的有力工具,在小学奥数中有着重要的应用,通过灵活运用容斥原理,我们可以更快、更准确地解决各类问题。
小学容斥原理的解释

小学容斥原理的解释小学容斥原理,又称为容斥原理、包容原理,是组合数学中的一种重要原理。
它是解决计数问题的一种方法,通过将问题划分为不相交的子集,然后逐个计算每个子集的元素个数,并利用集合的容量大小来计算最终的结果。
容斥原理在解决小学数学题目中的应用相当广泛,如排列组合、概率论等等。
小学生在学习容斥原理之前,首先需要了解集合的概念。
集合就是由一些个体组成的整体,比如我们可以用集合{1, 2, 3}来表示三个小朋友的编号。
在容斥原理中,我们主要使用交集和并集这两个概念。
交集就是把两个或多个集合里共有的个体选出来组成一个新的集合。
例如,集合A={1, 2, 3}和集合B={2, 3, 4}的交集是{2, 3}。
并集就是把两个或多个集合里所有的个体选出来组成一个新的集合。
例如,集合A和集合B的并集是{1, 2, 3, 4}。
容斥原理的核心思想是通过计算交集和并集的关系来求解问题。
首先,我们考虑简单的情况,假设有两个集合A和B,我们要求这两个集合的元素个数之和。
根据容斥原理,我们可以通过计算A和B的并集来获得结果。
但是由于并集中包含了A和B的交集,为了避免重复计算,我们需要减去A和B 的交集的元素个数,也就是用并集的元素个数减去交集的元素个数。
例如,集合A={1, 2, 3},集合B={2, 3, 4},它们的并集为{1, 2, 3, 4},交集为{2, 3}。
根据容斥原理,集合A和集合B的元素个数之和等于并集的元素个数减去交集的元素个数,即4-2=2+2=4。
这个结果表示集合A和集合B中一共有4个元素。
在解决实际问题时,容斥原理的应用更为复杂,涉及到多个集合的情况。
我们可以通过逐个考虑不同的情况,然后用加减的方式求得最终的结果。
例如,假设有三个集合A、B和C,我们要求这三个集合的元素个数之和。
根据容斥原理,我们可以先计算每两个集合的交集的元素个数之和,然后再减去所有三个集合的交集的元素个数,最后加上三个集合的并集的元素个数。
第十二讲-容斥原理

第十二讲容斥原理在很多计数问题中常用到数学上的一个包含与排除原理,也称为容斥原理.为了说明这个原理,我们先介绍一些集合的初步知识。
在讨论问题时,常常需要把具有某种性质的同类事物放在一起考虑.如:A={五(1)班全体同学}.我们称一些事物的全体为一个集合.A={五(1)班全体同学}就是一个集合。
例1 B={全体自然数}={1,2,3,4,…}是一个具体有无限多个元素的集合。
例2 C={在1,2,3,…,100中能被3整除的数}=(3,6,9,12,…,99}是一个具有有限多个元素的集合。
集合通常用大写的英文字母A、B、C、…表示.构成这个集合的事物称为这个集合的元素.如上面例子中五(1)班的每一位同学均是集合A的一个元素.又如在例1中任何一个自然数都是集合B的元素.像集合B这种含有无限多个元素的集合称为无限集.像集合C这样含有有限多个元素的集合称为有限集.有限集合所含元素的个数常用符号|A|、|B|、|C|、…表示。
记号A∪B表示所有属于集合A或属于集合B的元素所组成的集合.就是右边示意图中两个圆所覆盖的部分.集合A∪B叫做集合A与集合B 的并集.“∪”读作“并”,“A∪B”读作“A并B”。
例3 设集合A={1,2,3,4},集合B={2,4,6,8},则A∪B={1,2,3,4,6,8}.元素2、4在集合A、B中都有,在并集中只写一个。
记号A∩B表示所有既属于集合A也属于集合B中的元素的全体.就是上页图中阴影部分所表示的集合.即是由集合A、B的公共元素所组成的集合.它称为集合A、B的交集.符号“∩”读作“交”,“A∩B”读作“A交B”.如例3中的集合A、B,则A∩B={2,4}。
下面再举例介绍补集的概念。
例4 设集合I={1,3,5,7,9},集合A={3,5,7}。
补集(或余集),如右图中阴影部分表示的集合(整个长方形表示集合I).对于两个没有公共元素的集合A和B,显然有|A∪B|=|A|+|B|。
小学数学之 容斥原理

第三十五周容斥原理专题简析:容斥问题涉及到一个重要原理——包含与排除原理,也叫容斥原理。
即当两个计数部分有重复包含时,为了不重复计数,应从它们的和中排除重复部分。
容斥原理:对n个事物,如果采用不同的分类标准,按性质a 分类与性质b分类(如图),那么具有性质a或性质b的事物的个数=N a+N b-N ab。
Nab NbNa例1:一个班有48人,班主任在班会上问:“谁做完语文作业?请举手!”有37人举手。
又问:“谁做完数学作业?请举手!”有42人举手。
最后问:“谁语文、数学作业都没有做完?”没有人举手。
求这个班语文、数学作业都完成的人数。
分析完成语文作业的有37人,完成数学作业的有42人,一共有37+42=79人,多于全班人数。
这是因为语文、数学作业都完成的人数在统计做完语文作业的人数时算过一次,在统计做完数学作业的人数时又算了一次,这样就多算了一次。
所以,这个班语文、数作业都完成的有:79-48=31人。
练习一1,五年级有122名学生参加语文、数学考试,每人至少有一门功课取得优秀成绩。
其中语文成绩优秀的有65人,数学优秀的有87人。
语文、数学都优秀的有多少人?2,四年级一班有54人,订阅《小学生优秀作文》和《数学大世界》两种读物的有13人,订《小学生优秀作文》的有45人,每人至少订一种读物,订《数学大世界》的有多少人?3,学校文艺组每人至少会演奏一种乐器,已知会拉手风琴的有24人,会弹电子琴的有17人,其中两种乐器都会演奏的有8人。
这个文艺组一共有多少人?例2:某班有36个同学在一项测试中,答对第一题的有25人,答对第二题的有23人,两题都答对的有15人。
问多少个同学两题都答得不对?分析与解答:已知答对第一题的有25人,两题都答对的有15人,可以求出只答对第一题的有25-15=10人。
又已知答对第二题的有23人,用只答对第一题的人数,加上答对第二题的人数就得到至少有一题答对的人数:10+23=33人。
小学三年级数学教案解析:解读容斥原理,让学生轻松掌握组合问题

小学三年级数学教案解析:解读容斥原理,让学生轻松掌握组合问题数学一直被认为是一门非常抽象和难以理解的学科,尤其是对于小学三年级的学生来说。
为了让学生更加轻松地掌握数学中的一些概念和方法,教育家们设计了各种教学方案。
近年来,随着容斥原理的引入,越来越多的学校将其融入到小学三年级的数学教学中。
什么是容斥原理呢?如何通过容斥原理解决组合问题呢?本文将对这些问题进行详细的解析。
一、什么是容斥原理?容斥原理是组合数学中的一种方法,它用于求解不同集合之间的交集。
定义如下:如果有 A、B 两个集合,为了求这两个集合的并集,需要对 A 集合中的元素进行计数,并加上 B 集合中独有的元素。
但这样会导致 A 和 B 集合中公共元素被重复计数。
为了避免重复计数,需要在计算中将 A 和 B 集合中交集的元素减去一次。
这个减去一次的过程就是容斥原理。
以 A、B 两个集合为例,它们的并集 S 就可以表示为:S = A ∪ B = |A| + |B| - |A ∩ B|其中,|A| 表示 A 集合中元素的个数,|B| 表示 B 集合中元素的个数,|A ∩ B| 表示 A 和 B 集合中的交集元素个数。
这个原理可以扩展到多个集合的情况,即:S = |A1 ∪ A2 ∪ A3...∪ An| = Σ|Ai| - Σ|Ai ∩ Aj| + Σ|Ai ∩ Aj ∩ Ak| - ... + (-1)^(n-1) |A1 ∩ A2 ∩ ... ∩ An|其中,n 表示集合的个数。
这就是容斥原理,通过这个原理,我们可以轻松地计算多个集合的并集。
二、如何通过容斥原理解决组合问题?理解了容斥原理的概念之后,我们就可以尝试用它来解决组合问题了。
以一个具体的例子来说明:在小学三年级中,有一道常见的问题是:在一副扑克牌中,选出两张红色牌或两张大王牌,有多少种不同的选法?我们可以通过计算两种情况下所有的选法来得到答案。
具体来说,设 R 为红色牌的集合,D 为大王牌的集合,:- 选出两张红色牌时,可以先从 R 中任选一张,再从剩余的红色牌中任选一张,总共有 C(|R|, 2) 种选法。
第11讲容斥原理
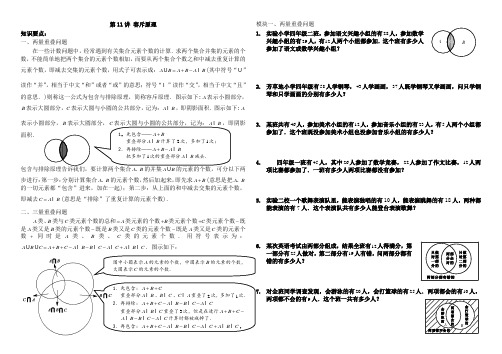
第11讲容斥原理知识要点:一、两量重叠问题在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B=+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A表示小圆部分,B表示大圆部分,C表示大圆与小圆的公共部分,记为:A B,即阴影面积.图示如下:A表示小圆部分,B 表示大圆部分,C表示大圆与小圆的公共部分,记为:A B,即阴影面积.A B、的并集A B的元素的个数,可分以下两步进行:第一步:分别计算集合A B、的元素个数,然后加起来,即先求A B+(意思是把A B、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B=(意思是“排除”了重复计算的元素个数).二、三量重叠问题A类、B 类与C类元素个数的总和A=类元素的个数B+类元素个数C+类元素个数-既是A类又是B类的元素个数-既是B类又是C类的元素个数-既是A类又是C类的元素个数+同时是A类、B类、C类的元素个数.用符号表示为:A B C A B C A B B C A C=++---+.图示如下:模块一、两量重叠问题1.实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加.这个班有多少人参加了语文或数学兴趣小组?2.芳草地小学四年级有58人学钢琴,43人学画画,37人既学钢琴又学画画,问只学钢琴和只学画画的分别有多少人?3.某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了.这个班既没参加美术小组也没参加音乐小组的有多少人?4.四年级一班有45人,其中26人参加了数学竞赛,22人参加了作文比赛,12人两项比赛都参加了.一班有多少人两项比赛都没有参加?5.实验二校一个歌舞表演队里,能表演独唱的有10人,能表演跳舞的有18人,两种都能表演的有7人.这个表演队共有多少人能登台表演歌舞?6.某次英语考试由两部分组成,结果全班有12人得满分,第一部分有25人做对,第二部分有19人有错,问两部分都有错的有多少人?7.对全班同学调查发现,会游泳的有20人,会打篮球的有25人.两项都会的有10人,两项都不会的有9人.这个班一共有多少人?1.先包含——A B+重叠部分A B计算了2次,多加了1次;2.再排除——A B A B+-把多加了1次的重叠部分A B减去.图中小圆表示A的元素的个数,中圆表示B的元素的个数,大圆表示C的元素的个数.1.先包含:A B C++重叠部分A B、B C、C A重叠了2次,多加了1次.2.再排除:A B C A B B C A C++---重叠部分A B C重叠了3次,但是在进行A B C++-A B B C A C--计算时都被减掉了.3.再包含:A B C A B B C A C A B C++---+.两部分全对的两部分都有错的只做对第二部分的只做对第一部分的会打篮球的会游泳的两项都会的两项都不会的BA8. 某班组织象棋和军棋比赛,参加象棋比赛的有32人,参加军棋比赛的有28人,有18人两项比赛都参加了,这个班参加棋类比赛的共有多少人?9. 在46人参加的采摘活动中,只采了樱桃的有18人,既采了樱桃又采了杏的有7人,既没采樱桃又没采杏的有6人,问:只采了杏的有多少人?10. 甲、乙、丙三个小组学雷锋,为学校擦玻璃,其中68块玻璃不是甲组擦的,52块玻璃不是乙组擦的,且甲组与乙组一共擦了60块玻璃.那么,甲、乙、丙三个小组各擦了多少块玻璃?11. 育才小学画展上展出了许多幅画,其中有16幅画不是六年级的,有15幅画不是五年级的,五、六年级共展出25幅画,其他年级的画共有多少幅?12. 47名学生参加数学和语文考试,其中语文得分95分以上的14人,数学得分95分以上的21人,两门都不在95分以上的有22人.问:两门都在95分以上的有多少人?13. 科技活动小组有55人.在一次制作飞机模型和制作舰艇模型的定时科技活动比赛中,老师到时清点发现:制作好一架飞机模型的同学有40人,制作好一艘舰艇的同学有32人.每个同学都至少完成了一项制作.问两项制作都完成的同学有多少人?14. 有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语.问既懂英语又懂俄语的有多少人?15. 一次数学测验,甲答错题目总数的14,乙答错3道题,两人都答错的题目是题目总数的16.求甲、乙都答对的题目数.模块二、三量重叠问题16. 某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?17. 某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?18. 四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.19. 五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.(6级)两项比赛都参加的只参加军棋比赛的只参加象棋比赛的B A丙乙甲B A 两门都不在95分以上的数学95分以上的语文95分以上的两门95分以上的AB20.光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?21.新年联欢会上,共有90人参加了跳舞、合唱、演奏三种节目的演出.如果只参加跳舞的人数三倍于只参加合唱的人数;同时参加三种节目的人比只参加合唱的人少7人;只参加演奏的比同时参加演奏、跳舞但没有参加合唱的人多4人;50人没有参加演奏;10人同时参加了跳舞和合唱但没有参加演奏;40人参加了合唱;那么,同时参加了演奏、合唱但没有参加跳舞的有________人.22.五年级三班有46名学生参加三项课外活动,其中24人参加了绘画小组,20人参加了合唱小组,参加朗诵小组的人数是既参加绘画小组又参加朗诵小组人数的3.5倍,又是三项活动都参加人数的7倍,既参加朗诵小组又参加合唱小组的人数相当于三项都参加人数的2倍,既参加绘画小组又参加合唱小组的有10人,求参加朗诵小组的人数.23.六年级100名同学,每人至少爱好体育、文艺和科学三项中的一项.其中,爱好体育的55人,爱好文艺的56人,爱好科学的51人,三项都爱好的15人,只爱好体育和科学的4人,只爱好体育和文艺的17人.问:有多少人只爱好科学和文艺两项?只爱好体育的有多少人?24.在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:⑴三种都带了的有几人?⑵只带了一种的有几个?25.盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.26.全班有25个学生,其中17人会骑自行车,13人会游泳,8人会滑冰,这三个运动项目没有人全会,至少会这三项运动之一的学生数学成绩都及格了,但又都不是优秀.若全班有6个人数学不及格,那么,⑴数学成绩优秀的有几个学生?⑵有几个人既会游泳,又会滑冰?27.五年级一班共有36人,每人参加一个兴趣小组,共有A、B、C、D、E五个小组,若参加A组的有15人,参加B组的人数仅次于A组,参加C组、D组的人数相同,参加E组的人数最少,只有4人.那么,参加B组的有_______人.28.五一班有28位同学,每人至少参加数学、语文、自然课外小组中的一个.其中仅参加数学与语文小组的人数等于仅参加数学小组的人数,没有同学仅参加语文或仅参加自然小组,恰有6个同学参加数学与自然小组但不参加语文小组,仅参加语文与自然小组的人数是3个小组全参加的人数的5倍,并且知道3个小组全参加的人数是一个不为0的偶数,那么仅参加数学和语文小组的人有多少人?29.在一个自助果园里,只摘山莓者两倍于只摘李子者;摘了草莓、山莓和李子的人数比只摘李子的人数多3个;只摘草莓者比摘了山莓和草莓但没有摘李子者多4人;50个人没有摘草莓;11个人摘了山莓和李子但没有摘草莓;总共有60人摘了李子.如果参与采摘水果的总人数是100,你能回答下列问题吗?①有人摘了山莓;②有人同时摘了三种水果;③有人只摘了山莓;④有人摘了李子和草莓,而没有摘山莓;⑤有人只摘了草莓.30.某学校派出若干名学生参加体育竞技比赛,比赛一共只有三个项目,已知参加长跑、跳高、标枪三个项目的人数分别为10、15、20人,长跑、跳高、标枪每一项的的参加选手中人中都有五分之一的人还参加了别的比赛项目,求这所学校一共派出多少人参加比赛?李子草莓山莓FGE DCBA科学51人文艺56人17154体育55人x模块三、图形中的重叠问题31. 长38厘米和53厘米的两根铁条焊接成一根铁条.已知焊接部分长4厘米,焊接后这根铁条有多长?32. 把长23厘米和37厘米的两根铁条焊接成一根铁条.已知焊接部分长3厘米,焊接后这根铁条有多长?33. 两张长4厘米,宽2厘米的长方形纸摆放成如图所示形状.把它放在桌面上,覆盖面积有多少平方厘米?34. 如图,一张长8厘米,宽6厘米,另一个正方形边长为6厘米,它们中间重叠的部分是一个边长为4厘米的正方形,求这个组合图形的面积.35. 一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长4厘米的正方形,求这个组合图形的面积.36. 三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影部分面积之和是多少?37. 如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米?38. 如图所示,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,露在外面的总面积为38.若A 与B 、B 与C 的公共部分的面积分别为8、7,A 、B 、C 这三张纸片的公共部分为3.求A 与C 公共部分的面积是多少?模块四、容斥原理在数论问题中的应用39. 在1~100的全部自然数中,不是3的倍数也不是5的倍数的数有多少个?40. 在自然数1100~中,能被3或5中任一个整除的数有多少个?41. 在前100个自然数中,能被2或3整除的数有多少个?42. 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?43. 求在1至100的自然数中能被3或7整除的数的个数.44. 以105为分母的最简真分数共有多少个?它们的和为多少? 45. 分母是385的最简真分数有多少个?并求这些真分数的和.46. 在1至2008这2008个自然数中,恰好是3、5、7中两个数的倍数的数共有 个.47. 在从1到1998的自然数中,能被2整除,但不能被3或7整除的数有多少个?48. 50名同学面向老师站成一行.老师先让大家从左至右按1,2,3,…,49,50依次报数;再让报数是4的倍数的同学向后转,接着又让报数是6的倍数的同学向后转.问:现在面向老师的同学还有多少名?图32厘米4厘米图3C B A1049.有2000盏亮着的电灯,各有一个拉线开关控制着,现按其顺序编号为1,2,3,…,2000,然后将编号为2的倍数的灯线拉一下,再将编号为3的倍数的灯线拉一下,最后将编号为5的倍数的灯线拉一下,三次拉完后,亮着的灯有多少盏?50.写有1到100编号的灯100盏,亮着排成一排,每一次把编号是3的倍数的灯拉一次开关,第二次把编号是5的倍数的灯拉一次开关,那么亮着的灯还有多少盏?51.在游艺会上,有100名同学抽到了标签分别为1至100的奖券.按奖券标签号发放奖品的规则如下:那么游艺会为该项活动准备的奖品铅笔共有多少支?(1)标签号为2的倍数,奖2支铅笔;(2)标签号为3的倍数,奖3支铅笔;(3)标签号既是2的倍数,又是3的倍数可重复领奖;(4)其他标签号均奖1支铅笔.52.在一根长木棍上,有三种刻度线,第一种刻度线将木棍分成十等份;第二种将木棍分成十二等份;第三种将木棍分成十五等份;如果沿每条刻度线将木棍锯断,则木棍总共被锯成________段.53.一根101厘米长的木棒,从同一端开始,第一次每隔2厘米画一个刻度,第二次每隔3厘米画一个刻度,第三次每隔5厘米画一个刻度,如果按刻度把木棒截断,那么可以截出段.54.一根1.8米长的木棍,从左端开始每隔2厘米画一个刻度,涂完后再从左端开始每隔3厘米画一个刻度,再从左端每隔5厘米画一个刻度,再从左端每隔7厘米画一个刻度,涂过按刻度把木棍截断,一共可以截成多少段小木棍?模块五、容斥原理中的最值问题55.将1~13这13个数字分别填入如图所示的由四个大小相同的圆分割成的13个区域中,然后把每个圆内的7个数相加,最后把四个圆的和相加,问:和最大是多少?56.如图,5条同样长的线段拼成了一个五角星.如果每条线段上恰有1994个点被染成红色,那么在这个五角星上红色点最少有多少个?57.某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?58.某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有人.59.60人中有23的人会打乒乓球,34的人会打羽毛球,45的人会打排球,这三项运动都会的人有22人,问:这三项运动都不会的最多有多少人?60.图书室有100本书,借阅图书者需在图书上签名.已知这100本书中有甲、乙、丙签名的分别有33,44和55本,其中同时有甲、乙签名的图书为29本,同时有甲、丙签名的图书为25本,同时有乙、丙签名的图书为36本.问这批图书中最少有多少本没有被甲、乙、丙中的任何一人借阅过?61.甲、乙、丙都在读同-一本故事书,书中有100个故事.每个人都从某一个故事开始,按顺序往后读.已知甲读了75个故事,乙读了60个故事,丙读了52个故事.那么甲、乙、丙3人共同读过的故事最少有多少个?62.在阳光明媚的一天下午,甲、乙、丙、丁四人给100盆花浇水,已知甲浇了30盆,乙浇了75盆,丙浇了80盆,丁浇了90盆,请问恰好被3个人浇过的花最少有多少盆?恰好被1个人浇过的花最多有多少盆?63.甲、乙、丙同时给100盆花浇水.已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆?。
容斥原理(数学技巧点拨系列)

容斥原理【知识点讲解】1、原理容斥原理指把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
2、解释由图可以直接看出各部分之间的关系由Venn图可知:(A∪B=A+B-A∩B)由Venn图可知:(A∪B∪C=A+B+C-A∩B-B∩C-C∩A+A∩B∩C)3、应用两类如果被计数的事物有A、B两类,那么,A类B类元素个数总和=属于A类元素个数+属于B类元素个数—既是A类又是B类的元素个数。
三类如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和=A类元素个数+B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。
4、解题导语使用容斥原理一般用于集合相关问题中,但是此类思想在数学学习中仍有巨大作用。
例如在计数原理中使用间接法等等。
因此学习此类问题对数学能力的提升是有很大帮助的,它可以帮助你换一个角度看数学题,从而找到更简单的办法。
【例题详析】例1、(2020宁夏)《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著,六盘水市第七中学为了解我校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则在调查的100位同学中阅读过《西游记》的学生人数为()A .80B .70C .60D .50【参考答案】B【详解】因为阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,所以《西游记》与《红楼梦》两本书中只阅读了一本的学生共有90-60=30位,因为阅读过《红楼梦》的学生共有80位,所以只阅读过《红楼梦》的学生共有80-60=20位,所以只阅读过《西游记》的学生共有30-20=10位,故阅读过《西游记》的学生人数为10+60=70位,【方法解析】由两类的容斥原理得:总人数=阅读过《西游记》+阅读过《红楼梦》-阅读过《红楼梦》和《西游记》的,由此得阅读过《西游记》的学生人数=90+60-80=70(位)例2:某中学的学生积极参加体育锻炼,其中有96名学生喜欢足球或游泳,60名学生喜欢足球,82名学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生有()名.A .62B .56C .46D .42【参考答案】C【详解】喜欢足球的学生、喜欢游泳的学生形成的集合分别记为A ,B ,依题意,集合A ,B ,A B 中元素个数分别为:()60,()82,()96n A n B n A B ==⋃=,则()()()()60829646n A B n A n B n A B ⋂=+-⋃=+-=,所以中学既喜欢足球又喜欢游泳的学生有46名.例3.某小学对小学生的课外活动进行了调查.调查结果显示:参加舞蹈课外活动的有63人,参加唱歌课外活动的有89人,参加体育课外活动的有47人,三种课外活动都参加的有24人,只选择两种课外活动参加的有46人,不参加其中任何一种课外活动的有15人.问接受调查的小学生共有多少人?()A .120B .144C .177D .192【参考答案】A 【详解】如图所示,用韦恩图表示题设中的集合关系,不妨将参加舞蹈、唱歌、体育课外活动的小学生分别用集合,,A B C 表示,则()63,()89,()47,()24card A card B card C card A B C ===⋂⋂=不妨设总人数为n ,韦恩图中三块区域的人数分别为,,x y z即()24,()24,()24card A B x card A C y card B C z ⋂=+⋂=+⋂=+46x y z ++=,由容斥原理:15()()()()()()()n card A card B card C card A B card A C card B C card A B C -=++-⋂-⋂-⋂+⋂⋂638947(24)(24)(24)24x y z =++-+-+-++解得:120n =【跟踪训练】一、单选题1.某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为()A .27B .23C .15D .72.某网店统计了连续三天售出商品的种类情况:第一天售出19种商品,第二天售出13种商品,第三天售出18种商品;前两天都售出的商品有3种,后两天都售出的商品有4种.则该网店这三天售出的商品最少有().A.25种B.27种C.29种D.31种3.为了丰富同学们的课外生活,某班58名同学在选课外兴趣小组时,选择篮球小组的有28人,选择乒乓球小组的有36人,既没有选择篮球小组又没有选择乒乓球小组的有12人,那么选择篮球小组但没有选择乒乓球小组的人数为()A.8B.10C.18D.204.某班有50名同学,有20名同学既不选修足球课程也不选修篮球课程,有18名同学选修了足球课程,28名同学选修了篮球课程,则既选修了足球课程也选修了篮球课程的同学有()名A.10B.12C.14D.165.中共一大会址、江西井冈山、贵州遵义、陕西延安是中学生的几个重要的研学旅行地.某中学在校学生3000人,学校团委为了了解本校学生到上述红色基地研学旅行的情况,随机调查了500名学生,其中到过中共一大会址或井冈山研学旅行的共有40人,到过井冈山研学旅行的20人,到过中共一大会址并且到过井冈山研学旅行的恰有10人,根据这项调查,估计该学校到过中共一大会址研学旅行的学生大约有()人A.240B.180C.120D.606.某班45名学生参加“3·12”植树节活动,每位学生都参加除草、植树两项劳动.依据劳动表现,评定为“优秀”、“合格”2个等级,结果如下表:等级优秀合格合计项目除草301545植树202545若在两个项目中都“合格”的学生最多有10人,则在两个项目中都“优秀”的人数最多为()A.5B.10C.15D.207.高考“33 ”模式指考生总成绩由语文、数学、外语3个科目成绩和高中学业水平考试3个科目成绩组成.计入总成绩的高中学业水平考试科目,由考生根据报考高校要求和自身特长,在思想政治、历史、地理、物理、化学、生物6个科目中自主选择.某中学为了解本校学生的选择情况,随机调查了100位学生的选择意向,其中选择物理或化学的学生共有40位,选择化学的学生共有30位,选择物理也选择化学的学生共有10位,则该校选择物理的学生人数与该校学生总人数比值的估计值为()A.0.1B.0.2C.0.3D.0.48.移动支付、高铁、网购与共享单车被称为中国的新“四大发明”,某中学为了解本校学生中新“四大发明”的普及情况,随机调查了100位学生,共中使用过移动支付或共享单车的学生共90位,使用过移动支付的学生共有80位,使用过共享单车的学生且使用过移动支付的学生共有60位,则该校使用共享单车的学生人数与该校学生总数比值的估计值为()A.0.5B.0.6C.0.7D.0.89.某地对农户抽样调查,结果如下:电冰箱拥有率为45%,电视机拥有率为55%,洗衣机拥有率为65%,拥有上述三种电器的任意两种的占35%,三种电器齐全的为25%,那么一种电器也没有的农户所占比例是()A.20%B.10%C.15%D.12%10.某学校高三教师周一、周二、周三开车上班的人数分别是8,10,14,若这三天中至少有一天开车上班的职工人数是20,则这三天都开车上班的职工人数至多是()A.8B.7C.6D.5二、填空题11.学校运动会,某班所有同学都参加了羽毛球或乒乓球比赛,已知该班共有23人参加羽毛球赛,35人参加乒乓球赛,既参加羽毛球又参加乒乓球赛有6人,则该班学生数为______.12.某校高三(1)班有50名学生,春季运动会上,有15名学生参加了田赛项目,有20名学生参加了径赛项目,已知田赛和径赛都参加的有8名同学,则该班学生中田赛和径赛都没有参加的人数为__________.13.某单位共有员工85人,其中68人会骑车,62人会驾车,既会骑车也会驾车的人有57人,则既不会骑车也不会驾车的人有___________人.14.高一某班有学生45人,其中参加数学竞赛的有32人,参加物理竞赛的有28人,另外有5人两项竞赛均不参加,则该班既参加数学竞赛又参加物理竞赛的有___.人.15.某班有学生48人,经调查发现,喜欢打羽毛球的学生有35人,喜欢打篮球的学生有20人.设既喜欢打羽毛球,又喜欢打篮球的学生的人数为x,则x的最小值是_________.16.网络流行词“新四大发明’’是指移动支付、高铁、网购与共享单车.某中学为了解本校学生中“新四大发明”的普及情况,随机调查了100名学生,其中使用过移动支付或共享单车的学生共90名,使用过移动支付的学生共有80名,使用过共享单车的学生且使用过移动支付的学生共有60名,则该校使用共享单车的学生人数与该校学生总数比值的估计值为___________. 17.某班有39名同学参加数学、物理、化学课外研究小组,每名同学至多参加两个小组.已知参加数学、物理、化学小组的人数分别为26,15,13,同时参加数学和物理小组的有6人,同时参加物理和化学小组的有4人,则同时参见数学和化学小组有多少人__________. 18.某班共40人,其中24人喜欢篮球运动,16人喜欢乒乓球运动,6人这两项运动都不喜欢,则只喜欢其中一项运动的人数为________19.某班有45名同学参加语文、数学、英语兴趣小组.已知仅参加一个兴趣小组的同学有20人,同时参加语文和数学兴趣小组的同学有9人,同时参加数学和英语兴趣小组的同学有15人,同时参加语文和英语兴趣小组的同学有11人,则同时参加这三个兴趣小组的同学有人___________.20.某班进行集体活动,为活跃气氛,班主任要求班上60名同学从唱歌、跳舞、讲故事三个节目中至少选择一个节目、至多选两个节目为大家表演,已知报名参加唱歌、跳舞、讲故事的人数分别为40,20,30,同时参加唱歌和讲故事的有15人,同时参加唱歌和跳舞的有10人,则同时只参加跳舞和讲故事的人数为__________.21.对班级40名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成,另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人,问对A、B都赞成的学生有________人. 22.2021年是中国共产党成立100周年,电影频道推出“经典频传:看电影,学党史”系列短视频,传扬中国共产党的伟大精神,为广大青年群体带来精神感召.现有《青春之歌》《建党伟业》《开国大典》三支短视频,某大学社团有50人,观看了《青春之歌》的有21人,观看了《建党伟业》的有23人,观看了《开国大典》的有26人.其中,只观看了《青春之歌》和《建党伟业》的有4人,只观看了《建党伟业》和《开国大典》的有7人,只观看了《青春之歌》和《开国大典》的有6人,三支短视频全观看了的有3人,则没有观看任何一支短视频的人数为________【参考答案】1.B【详解】设高三(1)班有50名学生组成的集合为U ,参加田赛项目的学生组成的集合为A ,参加径赛项目的学生组成的集合为B由题意集合A 有15个元素,B 有20个元素,A B 中有8个元素所以A B 有15+20827-=个元素.所以该班学生中田赛和径赛都没有参加的人数为5027=23-故选:B2.C【详解】解:因为前两天都售出的商品有3种,因此第一天售出且第二天没有售出的商品有19316-=(种);同理第三天售出的商品中有14种第二天未售出,有1种商品第一天未售出;所以三天商品种数最少时,是第三天中14种第二天未售出的商品都是第一天售出过的,此时商品总数是1416129+-=(种);分别用集合A 、B 、C 表示第一、第二和第三天售出的商品,则商品数最少时,如图所示.故选:C .3.B【详解】设既选择篮球小组又选择乒乓球小组的有x 人,则选择篮球小组但没有选择乒乓球小组的有()28x -人,选择乒乓球小组但没有选择篮球小组的有()36x -人.由题意可得()()12283658x x x +-+-+=,解得18x =,所以选择篮球小组但没有选择乒乓球小组的人数为2810x -=.【详解】设既选修了足球课程也选修了篮球课程的同学有x 名,由容斥原理得20182850x ++-=,解得16x =.故选:D.5.B【详解】如下图所示,设调查的学生中去过中共一大会址研学旅行的学生人数为x ,由题意可得()102040x -+=,解的30x =,因此,该学校到过中共一大会址研学旅行的学生的人数为303000180500⨯=.6.C【详解】用集合A 表示除草优秀的学生,B 表示植树优秀的学生,全班学生用全集U 表示,则U A ð表示除草合格的学生,则U B ð表示植树合格的学生,作出Venn 图,如图,设两个项目都优秀的人数为x ,两个项目都是合格的人数为y ,由图可得203045x x x y -++-+=,5x y =+,因为max 10y =,所以max 10515x =+=.故选:C .【详解】选择物理的学生人数为40301020-+=,即该校选择物理的学生人数与该校学生总人数比值的估计值为200.2100=.故选:B8.C【详解】根据题意使用过移动支付、共享单车的人数用韦恩图表示如下图,因此,该校使用共享单车的学生人数与该校学生总数比值的估计值700.7100=,故选C.9.A【详解】解:设农户总共为100家,则有55家农户有电视机,45家农户有电冰箱,65家农户有洗衣机,有25家农户同时拥有这三种电器,另外75家只有其中两种或一种或没有电器.设只有电冰箱和电视机的农户有a 家,只有电冰箱和洗衣机的农户有b 家,只有洗衣机和电视机的农户有c 家,只有电视机、电冰箱、洗衣机的分别有d 、e 、f 家,没有任何电器的农户有x 家.那么对于拥有电冰箱的农户可得出:2545a b e +++=①那么对于拥有电视机的农户可得出:2555a c d +++=②那么对于拥有洗衣机的农户可得出:2565b c f +++=③把上面三个式子相加可得:()290a b c d e f +++++=④对于拥有上述三种电器的任意两种的占35%,得到:35a b c ++=⑤把⑤代入④可得到20d e f ++=⑥因为农户共有100家,所以25100a b c d e f x +++++++=,把⑤和⑥代入上式得到20x =,即一种电器也没有的农户所占比例为20%,10.C【详解】解:设周三,周二,周一开车上班的职工组成的集合分别为A ,B ,C ,集合A ,B ,C 中元素个数分别为n A .,n B .,n C .,则n A .14=,n B .10=,n C .8=,()20n A B C ⋃⋃=,因为()n A B C n ⋃⋃=A .n +B .n +C .()()()()n A B n A C n B C n A B C -⋂-⋂-⋂+⋂⋂,且()()n A B n A B C ⋂⋂⋂ ,()()n A C n A B C ⋂⋂⋂ ,()()n B C n A B C ⋂⋂⋂ ,所以1410820()3()n A B C n A B C ++-+⋂⋂⋂⋂ ,即1410820()62n A B C ++-⋂⋂= .故选:C .11.52【详解】解:设参加羽毛球赛为集合A ,参加乒乓球赛为集合B ,依题意可得如下韦恩图:所以该班一共有1762952++=人;故答案为:5212.23【详解】由题意,15名参加田赛的同学中有7名没有参加径赛,20名参加径赛的同学中有12名没有参加田赛,所以参加田赛和径赛的同学共有781227++=人,综上,该班学生中田赛和径赛都没有参加的人数为502723-=人.13.12【详解】设会骑车的人组合的集合为A ,会驾车的人组成的集合为B ,既会骑车也会驾车的人组成的集合为集合C ,易知A B C = ,记card()A 表示集合A 中的元素个数,则有()()()()68625773card A B card A card B card A B =+-=+-= ,所以既不会骑车也不会驾车的人为857312-=.故答案为:1214.20【详解】设该班既参加数学竞赛又参加物理竞赛的学生人数为x ,以集合U 表示该班集体,集合A 表示参加数学竞赛的学生组成的集合,集合B 表示参加物理竞赛的学生组成的集合,如下图所示:由题意可得()()322856545x x x x -++-+=-=,解得20x =.故答案为:20.15.7【详解】设既不喜欢打羽毛球,又不喜欢打篮球的学生的人数为y ,则352048x y +-+=,即7x y -=,因为0y,所以7x .因为20x ,所以720x .故答案为:7.16.710##0.7【详解】根据题意,将使用过移动支付、共享单车的人数用如图所示的韦恩图表示,所以该校使用共享单车的学生人数与该校学生总数比值的估计值为6010710010+=.故答案为:710.17.5【详解】设参加数学、物理、化学小组的同学组成的集合分别为A ,B 、C ,同时参加数学和化学小组的人数为x ,因为每名同学至多参加两个小组,所以同时参加三个小组的同学的人数为0,如图所示:由图可知:20654939x x x -+++++-=,解得5x =,所以同时参加数学和化学小组有5人.故答案为:5.18.28【详解】6 人这两项运动都不喜欢,∴喜欢一项或两项运动的人数为40634-=人;∴喜欢两项运动的人数为:2416346+-=人,∴喜欢篮球的人数为24618-=人;喜欢乒乓球的人数为16610-=人;∴只喜欢其中一项运动的人数为181028+=人.故答案为:28.19.5【详解】以集合A 、B 、C 表示分别参加语文、数学、英语兴趣小组的学生,如下图所示:设同时参加这三个兴趣小组的同学有x 人,由图可得()()()209111555245x x x x x +-+-+-+=-=,解得5x =.故答案为:5.20.5【详解】参加唱歌、跳舞、讲故事的人分别用集合,,A B C 表示,作出Venn 图,如图,图中字母表示相应区域人数,则0n =,又40a b m ++=,20b c d ++=,30d e m ++=,15m =,10b =,60a b c d e m +++++=,则()()()a b m b c d d e m b m ++++++++--2a b c d e m =+++++,∴4020301510605d =++---=,∴同时只参加跳舞和讲故事的人数为5人.故答案为:5.21.18【详解】赞成A 的人数为340245⨯=,赞成B 的人数为24327+=,设对A 、B 都赞成的学生有x ,则112724403x x x x ++-++-=,解得18x =.故答案为:18.22.3【详解】把大学社团50人形成的集合记为全集U ,观看了《青春之歌》《建党伟业》《开国大典》三支短视频的人形成的集合分别记为A,B,C,依题意,作出韦恩图,如图,观察韦恩图:因观看了《青春之歌》的有21人,则只看了《青春之歌》的有214638---=(人),因观看了《建党伟业》的有23人,则只看了《建党伟业》的有234739---=(人),因观看了《开国大典》的有26人,则只看了《开国大典》的有2667310---=(人),因此,至少看了一支短视频的有3467891047++++++=(人),-=所以没有观看任何一支短视频的人数为50473。
小学数学应用题之容斥问题

小学数学应用题之容斥问题【含义】容斥原理是解决计数问题的重要方法,在计数时要求注意无一重复无一遗漏,为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
常见的容斥问题有两者容斥、三者容斥两种。
【数量关系】A∪B = A+B - A∩BA∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C【解题思路和方法】先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复。
可画文氏(韦恩)图来解题。
例1:有两块木板各长50厘米,把两块木板钉成一块长木板,中间钉在一起的重叠部分长8厘米。
钉成的木板长厘米。
解:1、本题考查了学生的运算能力、应用能力。
解决重叠问题时,要注意重叠的部分不能重复计算。
2、两块木板一共长50+50=100(厘米),如果钉在一起,说明原来的两个8厘米变成了一个8厘米,这样钉成的木板比100厘米少了8厘米,所以钉成的木板长100-8=92(厘米)。
例2:有两张各长20厘米的纸条,粘贴在一起后的总长是36厘米,那么重叠部分长()厘米。
A、2B、4C、8D、16解:1、此题考查孩子的应用能力、运算能力。
孩子没有进行画图理解,只是凭自己的主观想象进行思考,没有找到总长度与重复部分长度之间的关系,在后面计算时出现错误。
2、两张纸条如果没有重叠,那么一共长20+20=40(厘米),而重叠后的长度是36厘米,短了40-36=4(厘米),说明重叠部分的长度是4厘米。
选择B。
例3:某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀,下表是得优秀的情况,这个班共有多少人?解:根据题意画图2、我们可以先算出19+20+21=60(人),但是这里有被重复算的和漏算的,我们要注意减去重复的部分,加上漏算的部分。
小学数学典型应用题22:容斥问题(含解析)

小学数学典型应用题22:容斥问题(含解析)容斥问题【含义】容斥原理是解决计数问题的重要方法,在计数时要求注意无一重复无一遗漏,为了使重叠部分不被重复计算,人们研究出一种新的计数方法。
这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
常见的容斥问题有两者容斥、三者容斥两种。
【数量关系】★A∪B = A+B - A∩B★A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C解题思路和方法先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复。
可画文氏(韦恩)图来解题。
例1:有两块木板各长50厘米,把两块木板钉成一块长木板,中间钉在一起的重叠部分长8厘米。
钉成的木板长_____ 厘米。
解:1、本题考查了学生的运算能力、应用能力。
解决重叠问题时,要注意重叠的部分不能重复计算。
2、两块木板一共长50+50=100(厘米),如果钉在一起,说明原来的两个8厘米变成了一个8厘米,这样钉成的木板比100厘米少了8厘米,所以钉成的木板长100-8=92(厘米)。
例2:有两张各长20厘米的纸条,粘贴在一起后的总长是36厘米,那么重叠部分长()厘米。
A、2B、4C、8D、16解:1、此题考查孩子的应用能力、运算能力。
孩子没有进行画图理解,只是凭自己的主观想象进行思考.没有找到总长度与重复部分长度之间的关系,在后面计算时出现错误。
2、两张纸条如果没有重叠,那么一共长20+20=40(厘米),而重叠后的长度是36厘米,短了40-36=4(厘米),说明重叠部分的长度是4厘米。
选择B。
例3:某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀.下表是得优秀的情况,这个班共有多少人?解:根据题意画图2、我们可以先算出19+20+21=60(人),但是这里有被重复算的和漏算的,我们要注意减去重复的部分,加上漏算的部分。
【小高数学知识点】容斥原理

容斥原理一、知识结构图容斥原理二、方法讲解1、容斥原理Ⅰ:两量重叠问题A 类与B 类元素个数的总和=A 类元素的个数+B 类元素个数—既是A 类又是B 类的元素个数用符号可表示成:A ∪B=A+B-A ∩B (其中符号“∪”读作“并”,相当于中文“和”或者“或”的意思;符号“∩”读作“交”,相当于中文“且”的意思。
)则称这一公式为包含于排除原理,简称容斥原理。
图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A ∩B ,即阴影面积。
包含与排除原理告诉我们,要计算两个集合A 、B 的并集A ∪B 的元素的个数,可分以下两步进行:第一步:分别计算集合A 、B 的元素个数,然后加起来,即先求A+B (意思是把A 、B 的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C=A ∩B (意思是“排除”了重复计算的元素个数)。
2、容斥原理Ⅱ:三量重叠问题A 类、B 类与C 类元素个数的总和=A 类元素的个数+B 类元素个数+C 类元素个数—既是A 类又是B 类的元素个数—既是B 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数。
用符号表示为:A ∪B ∪C=A+B+C-A ∩B-B ∩C-A ∩C+A ∩B ∩C 图示如下:3、解答有关包含排除问题的一般方法在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考。
三、例题精讲例题1、把面积35cm ²和面积27cm ²的大小两个圆平放在桌面上,有一部分重叠,重叠部分面积为8cm ²,求被盖住桌面的面积? 答案:面积为35+27-8=54cm 2练习1、实验小学四年级二班,参加语文兴趣小组的有 28 人,参加数学兴趣小组的有 29 人,有12 人两个小组都参加.这个班有多少人参加了语文或数学兴趣小组? 答案:参加的人有:28+29-12=45人例2、某班有40名学生,其中有15人参加数学小组,18人参加航模小组,有10人两个小组都参加,那么有多少人两个小组都不参加? 答案:参加兴趣小组:15+18-10=23(人) 都不参加:40-23=17(人)40 航模 数学1810 15练习2、四(二)班有 48 名学生,在一节自习课上,写完语文作业的有 30 人,写完数学作业的有 20 人,语文数学都没写完的有 6 人. ⑴ 问语文数学都写完的有多少人? ⑵ 只写完语文作业的有多少人? 答案:(1)至少完成一科作业:48-6=42人 两科都写完:30+20-42=8人 (2)只写完语文:30-8=22人∩CC ∩1. 先包含——A +B +C重叠部分A ∩B 、B ∩C 、C ∩A 重叠了2次,多加了1次. 2. 再排除——A +B +C -A ∩B -B ∩C -A ∩C 重叠部分A ∩B ∩C 重叠了3次,但是在进行A +B +C -A ∩B -B ∩C -A ∩C 计算时都被减掉了.C B A 例3、在 1—100 的全部自然数中,不是 3 的倍数也不是 5 的倍数的数有多少个? 答案:3的倍数:100÷3=33个···1 5的倍数:100÷5=20个既是3又是5的倍数:100÷15=6个···10 所以3或5的倍数:33+20-6=47个既不是3也不是5的倍数:100-47=53个练习3、50 名同学面向老师站成一行.老师先让大家从左至右按 1,2,3,...,49,50 依次报数;再让报数是 4 的倍数的同学向后转,接着又让报数是 6 的倍数的同学向后转.问:现在面向老师的同学还有多少名? 答案:4的倍数:50÷4=12人...2 6的倍数:50÷6=8人 (2)既是4又是6的倍数:50÷12=4人···2 所以4或6的倍数:12+8-4=16人既不是4也不是6的倍数:50-16=34人最后向前的同学包含:既不是4和6的倍数和同时是4和6的倍数 共有:4+34=38人例4、在桌面上放置着三个两两重叠的近圆形纸片(如图,三个纸片等大),它们的面积都是100 cm ²,并知A 、B 两圆重叠的面积是20 cm ²,A 、C 两圆重叠的面积为45 cm ²,B 、C 两圆重叠的面积为31 cm ²,三个圆共同重叠的面积为15 cm ²,求盖住桌子的总面积。
容斥原理课

9、六年级一班有45名同学,每人都参加暑假体育培训班,其中足球班报25人,篮球班报20人,游泳班报30人,足球、篮球都报者有10人,足球、篮球都报者有12人。问三项都报的有多少人?
10、向50名同学调查春游去颐和园还是去动物园的态度,赞成去颐和园的人数是全体的 3/5,其余不赞成;赞成去动物园的比赞成去颐和园的学生多3人,其余不赞成,另外对去两处都不赞成的学生数比对去两处都赞成的学生数的1/3多1人,同时去颐和园和去动物园都赞成和都不赞成的学生各有多少人?
例9:甲、乙、丙同时给100盆花浇水。已知甲浇了78盆,乙浇了68盆,丙浇了58盆,那么3人都浇过的花最少有多少盆?
例10:某班同学参加期末测试,得优秀成绩的人数如下:数学20人,语文20人,英语20人,数学、英语两科都是优秀成绩的有8人,数学、语文两科成绩都是优秀的有7人,语文、英语两科成绩都是优秀的有9人,三科都没得优秀成绩的有3人。请问:这个班最多有多少人?最少有多少人?
例1:一个班有学生48人,每人至少参加跑步、跳高两项比赛中的一项。已知参加跑步的有37人,参加跳高的有40人,请问:这两项比赛都参加的学生有多少人?
例2:一次数学小测验只有两道题,结果全班有10人全对,第一题有25人做对,第二题有18人做错。问:两题都做错的有多少人?
例3:李老师出Biblioteka 两道题,全班40人中,第一道题有30人对,第2题有12人未做对,两题都做对的有20人。请问:
例6.六一班有学生46人,其中会骑自行车的有19人,会游泳的有25人,既会骑车又会游泳的有7人,既不会骑自行车又不会游泳的有多少人?
例7.有128位旅客,其中25人既不懂英语、又不懂法语,有98人懂英语,75人懂法语,请问:既懂英语、又懂法语的有多少人?
容斥原理公式

容斥原理公式
容斥原理是组合数学中一种用于计算集合操作交、并的计数方法。
它的基本思想是利用集合的特性,将复杂的计数问题转化为多个简单的计数问题,并通过相减的方式得到最终的计数结果。
具体而言,设有n个集合A1, A2, ..., An,容斥原理给出了计
算它们的交集和并集元素个数的公式:
交集元素个数 = 并集元素个数 - 第一类包含一个集合的元素个数 + 第二类包含两个集合的元素个数 - ... + (-1)^n-1 第n类
包含n个集合的元素个数
其中,“第一类包含一个集合的元素个数”是指计数某个集合
Ai的元素个数;“第二类包含两个集合的元素个数”是指计数
某两个集合Ai∩Aj的元素个数;依此类推,分别计数包含1个、2个、...、n个集合的元素个数。
而交集元素个数就等于
所有这些计数结果的交替相加减。
容斥原理的应用非常广泛,不仅仅可以用于计算集合交、并的元素个数,还可以用于解决排列组合、概率统计等领域的问题。
通过合理地选择集合和定义计数量,可以灵活地运用容斥原理解决各种复杂的计数问题。
小学奥数之容斥原理

容斥原理(一)【例题分析】例1. 有长8厘米,宽6厘米的长方形与边长5厘米的正方形。
如图放在桌面上,求这两个图形盖住桌面的面积?分析与解:阴影部分是直角三角形,是两个图形的重叠部分,它的面积是:(平方厘米)方法一:(平方厘米)方法二:(平方厘米)方法三:(平方厘米)答:盖住桌面的面积是67平方厘米。
例2. 六一班参加无线电小组和航模小组的共26人,其中参加无线电小组的有17人,参加航模小组的有14人,两组都参加的有多少人?分析与解:把17人和14人相加,是把两组都参加的人算了两次,所以减去总人数,就是两组都参加的人数(人)。
也可以这样解:(人)或(人)答:两组都参加的有5人。
例3。
六一班有学生46人,其中会骑自行车的有19人,会游泳的有25人,既会骑车又会游泳的有7人,既不会骑自行车又不会游泳的有多少人?分析与解:先求出46人中会骑车或会游泳的有多少人,从中减去会骑车或会游泳的人数,剩下的就是既不会骑车也不会游泳的人数。
(人)(人)答:既不会骑车又不会游泳的有9人。
例4. 某年级的课外小组分为美术、音乐、手工三个小组,参加美术小组有20人,参加音乐小组有24人,参加手工小组有31人,同时参加美术和音乐两个小组有5人,同时参加音乐和手工两个小组有6人,同时参加美术和手工两个小组的有7人,三个小组都参加的有3人,这个年级参加课外小组的同学共有多少人?分析与解:图中的5、6、7人都是两两重叠的部分,图中的3人是三个重叠的部分,要从三个组的总人数中减去重复多余的部分.(人)答:这个年级参加课外小组的有60人。
例5。
某班在短跑、投掷和跳远三项检测中,有4人三项都未达到优秀,其他人至少有一项是优秀,下表是得优秀的情况,请你算出全班人数.短跑投掷跳远跑跳跑投跳投三项19 21 20 9 10 6 3分析与解:根据题意画出如下图要求全班有多少人,先要求出跑、跳、投至少有一项达到优秀的人数,加上三项都未达到优秀的,就是全班人数。
小学数学容斥原理知识点

小学数学容斥原理知识点在小学数学中,容斥原理是一种非常重要的解题方法,可以帮助我们解决一些复杂的计数问题。
容斥原理通过排除重复计数来解决问题,让我们一起来了解一下容斥原理的具体内容。
容斥原理的基本思想是,对于所给的问题,我们可以从整体的角度来思考,然后通过减去重复计数的部分来得到最终的结果。
下面我们通过一个具体的例子来理解容斥原理。
假设有一个小学学生组成的班级,其中有20个学生,分别擅长数学、英语和音乐。
我们想要知道至少擅长其中一门学科的学生人数。
首先,我们可以分别统计擅长数学、英语和音乐的学生人数,分别记为M、E和M1;然后,我们可以统计同时擅长数学和英语、数学和音乐以及英语和音乐的学生人数,分别记为ME、MM和EM;最后,我们可以统计同时擅长数学、英语和音乐的学生人数,记为MEM。
根据容斥原理,我们可以得到至少擅长其中一门学科的学生人数为:M + E + M1 - (ME + MM + EM) + MEM在这个例子中,我们通过容斥原理将问题分解成了几个部分,并减去了重复计数的学生人数。
通过这样的计算,我们可以得到至少擅长其中一门学科的学生人数,而不需要逐个统计每个学生的情况。
容斥原理不仅可以用于解决学生人数的问题,还可以用于解决更复杂的计数问题。
下面我们通过更多的例子来进一步了解容斥原理的应用。
例子一:小明手中有4个红色球、3个蓝色球和2个绿色球,他从中随机取出3个球,问至少有两个球是红色的概率是多少?我们可以使用容斥原理来解决这个问题。
首先,我们可以计算至少取到一个红色球的概率(记为P(至少一个红色球));然后,我们可以计算至少取到两个红色球的概率(记为P(至少两个红色球));最后,我们可以计算至少取到三个红色球的概率(记为P(至少三个红色球))。
根据容斥原理,我们可以得到至少有两个球是红色的概率为:P(至少一个红色球) - P(至少两个红色球) + P(至少三个红色球)我们可以具体计算每个部分的概率,然后代入公式进行计算。
容斥原理(A、B、C)

一、两量重叠问题在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集AB 的元素的个数,可分以下两步进行:第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起);第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:知识结构容斥原理1.先包含——A B + 重叠部分AB 计算了2次,多加了1次;2.再排除——A B A B +- 把多加了1次的重叠部分AB 减去.在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考.【例 1】 实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加.这个班有多少人参加了语文或数学兴趣小组?【巩固】 芳草地小学四年级有58人学钢琴,43人学画画,37人既学钢琴又学画画,问只学钢琴和只学画画的分别有多少人?【例 2】 某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了.这C BA C BA 例题精讲图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1.先包含:A B C ++ 重叠部分AB 、BC 、C A 重叠了2次,多加了1次. 2.再排除:A B C A B B C A C ++---重叠部分A B C 重叠了3次,但是在进行A B C ++-A B B C A C --计算时都被减掉了.个班既没参加美术小组也没参加音乐小组的有多少人?【巩固】 四年级一班有45人,其中26人参加了数学竞赛,22人参加了作文比赛,12人两项比赛都参加了.一班有多少人两项比赛都没有参加?【例 3】 对全班同学调查发现,会游泳的有20人,会打篮球的有25人.两项都会的有10人,两项都不会的有9人.这个班一共有多少人?【巩固】 某班组织象棋和军棋比赛,参加象棋比赛的有32人,参加军棋比赛的有28人,有18人两项比赛都参加了,这个班参加棋类比赛的共有多少人?【例 4】 47名学生参加数学和语文考试,其中语文得分95分以上的14人,数学得分95分以上的21人,两门都不在95分以上的有22人.问:两门都在95分以上的有多少人?【巩固】 有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语.问既懂英语会打篮球的两项都不会的会游泳的两项都会的BA只参加围棋比赛的只参加象棋比赛的两项比赛都参加的BA两门都不在95分以上的数学95分以上的两门95分以上的语文95分以上的又懂俄语的有多少人?【例 5】一个班48人,完成作业的情况有三种:一种是完成语文作业没完成数学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作业都完成了.已知做完语文作业的有37人;做完数学作业的有42人.这些人中语文、数学作业都完成的有多少人?【巩固】四年级科技活动组共有63人.在一次剪贴汽车模型和装配飞机模型的定时科技活动比赛中,老师到时清点发现:剪贴好一辆汽车模型的同学有42人,装配好一架飞机模型的同学有34人.每个同学都至少完成了一项活动.问:同时完成这两项活动的同学有多少人?【例 6】某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?【巩固】某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?【例 7】四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.【巩固】五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数.【例 8】在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:⑴三种都带了的有几人?⑵只带了一种的有几个?【巩固】盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.【例 9】 三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影部分面积之和是多少?【巩固】 如图,已知甲、乙、丙3个圆的面积均为30,甲与乙、乙与丙、甲与丙重合部分的面积分别为6,8,5,而3个圆覆盖的总面积为73.求阴影部分的面积.【例 10】 如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米?【巩固】 如图所示,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,CBA10露在外面的总面积为38.若A 与B 、B 与C 的公共部分的面积分别为8、7,A 、B 、C 这三张纸片的公共部分为3.求A 与C 公共部分的面积是多少?【例 11】 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?【巩固】 求在1至100的自然数中能被3或7整除的数的个数.【例 12】 某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?【巩固】 某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有人.ABC课堂检测【随练1】四(二)班有48名学生,在一节自习课上,写完语文作业的有30人,写完数学作业的有20人,语文数学都没写完的有6人.⑴问语文数学都写完的有多少人?⑵只写完语文作业的有多少人?【随练2】光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?【随练3】一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长4厘米的正方形,求这个组合图形的面积.家庭作业【作业1】四(1)班有46人,其中会弹钢琴的有30人,会拉小提琴的有28人,则这个班既会弹钢琴又会拉小提琴的至少有人。
小学数学容斥原理

第1站容斥原理知识糖果屋1、两数重叠,求重叠部分;2、两数重叠,求总数;3、两数重叠,求一部分;4、两数重叠,求未参与部分。
例题精品铺、习题游乐园例1、五年级142名学生都订了报纸,其中96人订了《小学生数学报》,58人订了《数学小灵通》。
问:两种数学刊物都订的有多少人?练习、一个少儿俱乐部有92人,其中会下象棋的有70人,会下跳棋的有42人,并且每个人至少会下一种棋。
两种棋都会下的有多少人?例2、培优小学四年级(1)班参加语文兴趣小组的有29人,参加数学兴趣小组的有27人,有15人两组都参加,并且每人至少参加一个兴趣小组。
这个班共有多少人?练习、某班的一次测试中,只考了语文和数学两个科目。
每人至少有一门得满分,其中有26人数学得满分,有35人语文得满分,其中有15人两门都得了满分。
这个班共有多少人?例3、暑假里,真真和妙妙一起讨论金陵十八景,她们发现十八景中的每一处都有人去过,而且有五处是两人都去过的。
如果真真去过其中的十二景,那么妙妙去过其中的几景?练习、在一群小朋友中,有12人看过动画片《黑猫警长》,有21人看过动画片《大闹天宫》,并且有8人两部动画片都看过。
已知每个小朋友至少都看过其中的一部动画片,那么有几个小朋友只看过《黑猫警长》?例4、吉祥饭店有30道招牌菜,真真吃过其中的15道,妙妙吃过其中的9道,并且有4道两人都吃过。
有多少道菜两人都没吃过?练习、数学小组有50人。
其中有16人参加了创新游戏活动,有20人参加了逻辑思维活动,有10人两项活动都参加了。
那么有多少人两项活动都没有参加?脑力研究所在一次考试中,某班数学得100分的有17人,语文得100分的有13人,两科都得100分的有7人,两科至少有一科得100分的共有()人;全班45人两科都不得100分的有()人。
真题演练龙门学校某班有42名同学都订了资料,订阅《王朝霞试卷》的有32名,订阅《少年素质报》的有27名,有()名同学订阅了两种资料。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
容斥原理知识结构一、两量重叠问题在一些计数问题中,经常遇到有关集合元素个数的计算.求两个集合并集的元素的个数,不能简单地把两个集合的元素个数相加,而要从两个集合个数之和中减去重复计算的元素个数,即减去交集的元素个数,用式子可表示成:A B A B A B =+-(其中符号“”读作“并”,相当于中文“和”或者“或”的意思;符号“”读作“交”,相当于中文“且”的意思.)则称这一公式为包含与排除原理,简称容斥原理.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.图示如下:A 表示小圆部分,B 表示大圆部分,C 表示大圆与小圆的公共部分,记为:A B ,即阴影面积.包含与排除原理告诉我们,要计算两个集合A B 、的并集A B 的元素的个数,可分以下两步进行: 第一步:分别计算集合A B 、的元素个数,然后加起来,即先求A B +(意思是把A B 、的一切元素都“包含”进来,加在一起); 第二步:从上面的和中减去交集的元素个数,即减去C A B =(意思是“排除”了重复计算的元素个数).二、三量重叠问题A 类、B 类与C 类元素个数的总和A =类元素的个数B +类元素个数C +类元素个数-既是A 类又是B 类的元素个数-既是B 类又是C 类的元素个数-既是A 类又是C 类的元素个数+同时是A 类、B 类、C 类的元素个数.用符号表示为:A B C A B C A B B C A C A B C =++---+.图示如下:在解答有关包含排除问题时,我们常常利用圆圈图(韦恩图)来帮助分析思考. 1.先包含——A B +重叠部分A B 计算了2次,多加了1次;2.再排除——A B A B +-把多加了1次的重叠部分A B 减去.图中小圆表示A 的元素的个数,中圆表示B 的元素的个数,大圆表示C 的元素的个数.1.先包含:A B C ++ 重叠部分A B 、B C 、C A 重叠了2次,多加了1次. 2.再排除:A B C A B B C A C ++--- 重叠部分A B C 重叠了3次,但是在进行A B C ++- A B B C A C --计算时都被减掉了. 3.再包含:A B C A B B C A C A B C ++---+.例题精讲【例 1】 实验小学四年级二班,参加语文兴趣小组的有28人,参加数学兴趣小组的有29人,有12人两个小组都参加.这个班有多少人参加了语文或数学兴趣小组?【考点】两量重叠问题 【难度】1星 【题型】解答【解析】 如图所示,A 圆表示参加语文兴趣小组的人,B 圆表示参加数学兴趣小组的人,A 与B 重合的部分C (阴影部分)表示同时参加两个小组的人.图中A 圆不含阴影的部分表示只参加语文兴趣小组未参加数学兴趣小组的人,有281216-=(人);图中B 圆不含阴影的部分表示只参加数学兴趣小组未参加语文兴趣小组的人,有291217-=(人).方法一:由此得到参加语文或数学兴趣小组的有:16121745++=(人).方法二:根据包含排除法,直接可得:参加语文或数学兴趣小组的人=参加语文兴趣小组的人+参加数学兴趣小组的人-两个小组都参加的人,即:28291245+-=(人).【答案】45人【巩固】 芳草地小学四年级有58人学钢琴,43人学画画,37人既学钢琴又学画画,问只学钢琴和只学画画的分别有多少人?【考点】两量重叠问题 【难度】1星 【题型】解答【解析】 解包含与排除题,画图是一种很直观、简捷的方法,可以帮助解决问题,画图时注意把不同的对象与不同的区域对应清楚.建议教师帮助学生画图分析,清楚的分析每一部分的含义.如图,A 圆表示学画画的人,B 圆表示学钢琴的人,C 表示既学钢琴又学画画的人,图中A 圆不含阴影的部分表示只学画画的人,有:43376-=(人),图中B 圆不含阴影的部分表示只学钢琴的人,有:583721-=(人).【答案】21人【例 2】 某班共有46人,参加美术小组的有12人,参加音乐小组的有23人,有5人两个小组都参加了.这个班既没参加美术小组也没参加音乐小组的有多少人?【考点】两量重叠问题 【难度】1星 【题型】解答【解析】 已知全班总人数,从反面思考,找出参加美术或音乐小组的人数,只需用全班总人数减去这个人数,就得到既没参加美术小组也没参加音乐小组的人数.根据包含排除法知,该班至少参加了一个小组的总人数为1223530+-=(人).所以,该班未参加美术或音乐小组的人数是463016-=(人).【答案】16人【巩固】 四年级一班有45人,其中26人参加了数学竞赛,22人参加了作文比赛,12人两项比赛都参加了.一班有多少人两项比赛都没有参加?【考点】两量重叠问题 【难度】1星 【题型】解答【解析】 由包含排除法可知,至少参加一项比赛的人数是:26221236+-=(人),所以,两项比赛都没有参加的人数为:45369-=(人).【答案】9人【例 3】 对全班同学调查发现,会游泳的有20人,会打篮球的有25人.两项都会的有10人,两项都不会的有9人.这个班一共有多少人?【考点】两量重叠问题 【难度】2星 【题型】解答【解析】 如图,用长方形表示全班人数,A 圆表示会游泳的人数,B 圆表示会打篮球的人数,长方形中阴影部分表示两项都不会的人数.由图中可以看出,全班人数=至少会一项的人数+两项都不会的人数,至少会一项的人数为:20251035+-=(人),全班人数为:35944+= (人).【答案】44人【巩固】 某班组织象棋和军棋比赛,参加象棋比赛的有32人,参加军棋比赛的有28人,有18人两项比赛都参加了,这个班参加棋类比赛的共有多少人?【考点】两量重叠问题 【难度】2星 【题型】解答【解析】 如图,A 圆表示参加象棋比赛的人,B 圆表示参加军棋比赛的人,A 与B 重合的部分表示同时参加两项比赛的人.图中A 圆不含阴影的部分表示只参加象棋比赛不参加军棋比赛的人,有321814-=(人);图中B 圆不含阴影的部分表示只参加军棋比赛不参加象棋比赛的人,有281810-=(人).由此得到参加棋类比赛的人有14181042++=(人).或者根据包含排除法直接得:32281842+-=(人).【答案】42人【例 4】 47名学生参加数学和语文考试,其中语文得分95分以上的14人,数学得分95分以上的21人,两门都不在95分以上的有22人.问:两门都在95分以上的有多少人?【考点】两量重叠问题 【难度】2星 【题型】解答【解析】 如图,用长方形表示这47名学生,A 圆表示语文得分95分以上的人数,B 圆表示数学得95分以上的人数,A 与B 重合的部分表示两门都在95分以上的人数,长方形内两圆外的部分表示两门都不在95分以上的人数.由图中可以看出,全体人数是至少一门在95分以上的人数与两门都不在95分以上的人数之和,则至少一门在95分以上的人数为:472225-=(人).根据包含排除法,两门都在95分以上的人数为:14212510+-=(人).【答案】10人【巩固】 有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语.问既懂英语又懂俄语的有多少人?【考点】两量重叠问题 【难度】2星 【题型】解答【关键词】第二届,迎春杯【解析】 方法一:在100人中懂英语或俄语的有:1001090-=(人).又因为有75人懂英语,所以只懂俄BA 两门都不在95分以上的数学95分以上的两门95分以上的语文95分以上的语的有:907515-=(人).从83位懂俄语的旅客中除去只懂俄语的人,剩下的8315- 68=(人)就是既懂英语又懂俄语的旅客.方法二:学会把公式进行适当的变换,由包含与排除原理,得:75839068A B A B A B =+-=+-=(人).【答案】68人【例 5】 一个班48人,完成作业的情况有三种:一种是完成语文作业没完成数学作业;一种是完成数学作业没完成语文作业;一种是语文、数学作业都完成了.已知做完语文作业的有37人;做完数学作业的有42人.这些人中语文、数学作业都完成的有多少人?【考点】两量重叠问题 【难度】2星 【题型】解答【解析】 不妨用下图来表示:线段AB 表示全班人数,线段AC 表示做完语文作业的人数,线段DB 表示做完数学作业的人数,重叠部分DC 则表示语文、数学都做完的人数.根据题意,做完语文作业的有37人,即37AC =.做完数学作业的有42人,即42DB =.374279AC DB +=+=(人)①48AB =(人) ②①式减②式,就有794831DC =-=(人),所以,数学、语文作业都做完的有31人.【答案】31人【巩固】 四年级科技活动组共有63人.在一次剪贴汽车模型和装配飞机模型的定时科技活动比赛中,老师到时清点发现:剪贴好一辆汽车模型的同学有42人,装配好一架飞机模型的同学有34人.每个同学都至少完成了一项活动.问:同时完成这两项活动的同学有多少人?【考点】两量重叠问题 【难度】2星 【题型】解答【解析】 因423476+=,7663>,所以必有人同时完成了这两项活动.由于每个同学都至少完成了一项活动,根据包含排除法知,4234+-(完成了两项活动的人数)=全组人数,即76-(完成了两项活动的人数)63=.由减法运算法则知,完成两项活动的人数为766313-=(人).也可画图分析.【答案】13人【例 6】 某班学生手中分别拿红、黄、蓝三种颜色的小旗,已知手中有红旗的共有34人,手中有黄旗的共有26人,手中有蓝旗的共有18人.其中手中有红、黄、蓝三种小旗的有6人.而手中只有红、黄两种小旗的有9人,手中只有黄、蓝两种小旗的有4人,手中只有红、蓝两种小旗的有3人,那么这个班共有多少人?【考点】三量重叠问题 【难度】3星 【题型】解答【解析】 如图,用A 圆表示手中有红旗的,B 圆表示手中有黄旗的,C 圆表示手中有蓝旗的.如果用手中有红旗的、有黄旗的与有蓝旗的相加,发现手中只有红、黄两种小旗的各重复计算了一次,应减去,手中有三种颜色小旗的重复计算了二次,也应减去,那么,全班人数为:342618943++-++-()() 6250⨯=(人).【答案】50人【巩固】 某班有42人,其中26人爱打篮球,17人爱打排球,19人爱踢足球,9人既爱打篮球又爱踢足球,4人既爱打排球又爱踢足球,没有一个人三种球都爱好,也没有一个人三种球都不爱好.问:既爱打篮球又爱打排球的有几人?【考点】三量重叠问题 【难度】3星 【题型】解答【解析】 由于全班42人没有一个人三种球都不爱好,所以全班至少爱好一种球的有42人.根据包含排除法,4226171994=++-++()(既爱打篮球又爱打排球的人数0+),得到既爱打篮球又爱打排球的人数为:49427-=(人).【答案】7人【例 7】 四年级一班有46名学生参加3项课外活动.其中有24人参加了数学小组,20人参加了语文小组,参加文艺小组的人数是既参加数学小组也参加文艺小组人数的3.5倍,又是3项活动都参加人数的7倍,既参加文艺小组也参加语文小组的人数相当于3项都参加的人数的2倍,既参加数学小组又参加语文小组的有10人.求参加文艺小组的人数.【考点】三量重叠问题 【难度】3星 【题型】解答【解析】 设参加数学小组的学生组成集合A ,参加语文小组的学生组成集合B ,参加文艺小组的学生组成C BA集合G .三者都参加的学生有z 人.有=46,=24,=20,=3.5,=7,=2,=10. 因为,所以46=24+20+7x -10-2x -2x +x ,解得x =3, 即三者的都参加的有3人.那么参加文艺小组的有37=21人.【答案】21人【巩固】 五年级三班学生参加课外兴趣小组,每人至少参加一项.其中有25人参加自然兴趣小组,35人参加美术兴趣小组,27人参加语文兴趣小组,参加语文同时又参加美术兴趣小组的有12人,参加自然同时又参加美术兴趣小组的有8人,参加自然同时又参加语文兴趣小组的有9人,语文、美术、自然3科兴趣小组都参加的有4人.求这个班的学生人数. 【考点】三量重叠问题 【难度】3星 【题型】解答【解析】 设参加自然兴趣小组的人组成集合A ,参加美术兴趣小组的人组成集合日,参加语文兴趣小组的人组成集合C .=25,=35,=27,=12, =8,=9, =4.=.所以,这个班中至少参加一项活动的人有25+35+27-12-8-9+4=62,而这个班每人至少参加一项.即这个班有62人.【答案】62人【例 8】 在某个风和日丽的日子,10个同学相约去野餐,每个人都带了吃的,其中6个人带了汉堡,6个人带了鸡腿,4个人带了芝士蛋糕,有3个人既带了汉堡又带了鸡腿,1个人既带了鸡腿又带了芝士蛋糕.2个人既带了汉堡又带了芝土蛋糕.问:⑴ 三种都带了的有几人?⑵ 只带了一种的有几个?【考点】三量重叠问题【难度】4星 【题型】解答 A B C A B C A C A B C B C A B C A B A B C A B C A B A C B C A B C =++---+⨯C 语文B 美术A 自然ABC B C A B A C A B C A B C A B C A B A C B C A B C ++---+【解析】 如图,用A 圆表示带汉堡的人,B 圆表示带鸡腿的人,C 圆表示带芝士蛋糕的人.⑴ 根据包含排除法,总人数=(带汉堡的人数+带鸡腿的人数+带芝士蛋糕的人数-)(带汉堡、鸡腿的人数+带汉堡、芝士蛋糕的人数+带鸡腿、芝士蛋糕的人数+)三种都带了的人数,即10664321-++-+++()()三种都带了的人数,得三种都带了的人数为:10100-=(人).⑵ 求只带一种的人数,只需从10人中减去带了两种的人数,即103214-++=()(人).只带了一种的有4人.【答案】(1)0人,(2)4人【巩固】 盛夏的一天,有10个同学去冷饮店,向服务员交了一份需要冷饮的统计表:要可乐、雪碧、橙汁的各有5人;可乐、雪碧都要的有3人;可乐、橙汁都要的有2人;雪碧、橙汁都要的有2人;三样都要的只有1人,证明其中一定有1人这三种饮料都没有要.【考点】三量重叠问题【难度】4星 【题型】解答【解析】 略【答案】根据根据包含排除法,至少要了一种饮料的人数=(要可乐的人数+要雪碧的人数+要橙汁的人数)-(要可乐、雪碧的人数+要可乐、橙汁的人数+要雪碧、橙汁的人数)+三种都要的人数,即至少要了一种饮料的人数为:55532219++-+++=()()(人).1091-=(人),所以其中有1人这三种饮料都没有要.【例 9】 三个面积均为50平方厘米的圆纸片放在桌面上(如图),三个纸片共同重叠的面积是10平方厘米.三个纸片盖住桌面的总面积是100厘米.问:图中阴影部分面积之和是多少?【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 将图中的三个圆标上A 、B 、C .根据包含排除法,三个纸片盖住桌面的总面积=(A 圆面积B+圆面积C +圆面积-)(A 与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积+)三BA CCBA10个纸片共同重叠的面积,得:100505050A =++-()(与B 重合部分面积A +与C 重合部分面积B +与C 重合部分面积10+),得到A 、B 、C 三个圆两两重合面积之和为:16010060-=平方厘米,而这个面积对应于圆上的那三个纸片共同重叠的面积的三倍与阴影部分面积的和,即:60103=⨯+阴影部分面积,则阴影部分面积为:603030-=(平方厘米).【答案】30平方厘米【巩固】 如图,已知甲、乙、丙3个圆的面积均为30,甲与乙、乙与丙、甲与丙重合部分的面积分别为6,8,5,而3个圆覆盖的总面积为73.求阴影部分的面积.【考点】几何中的重叠问题 【难度】2星 【题型】解答【解析】 设甲圆组成集合A ,乙圆组成集合B ,丙圆组成集合C . =30,=6,=8,=5,=73, 而=. 有73=30×3-6-8-5+,即=2,即甲、乙、丙三者的公共面积(⑧部分面积)为2.那么只是甲与乙(④),乙与丙(⑥),甲与丙(⑤)的公共的面积依次为6-2=4,8-2=6,5-2=3,所以有阴影部分(①、②、③部分之和)的面积为73-4-6-3-2=58.【答案】58【例 10】 如图,三角形纸板、正方形纸板、圆形纸板的面积相等,都等于60平方厘米.阴影部分的面积总和是40平方厘米,3张板盖住的总面积是100平方厘米,3张纸板重叠部分的面积是多少平方厘米?【考点】几何中的重叠问题 【难度】3星 【题型】解答【解析】 阴影部分是有两块重叠的部分,被计算两次,而三张纸重叠部分是被计算了三次.所以三张纸重叠部分的面积60310040220=⨯--÷=()(平方厘米).【答案】20平方厘米【巩固】 如图所示,A 、B 、C 分别是面积为12、28、16的三张不同形状的纸片,它们重叠在一起,A B C ==A B B C A C A B C A B C A B C +--A B B C A C A B C --+AB C A B C露在外面的总面积为38.若A 与B 、B 与C 的公共部分的面积分别为8、7,A 、B 、C 这三张纸片的公共部分为3.求A 与C 公共部分的面积是多少?【考点】几何中的重叠问题 【难度】3星 【题型】解答【解析】 设A 与C 公共部分的面积为x ,由包含与排除原理可得:⑴ 先“包含”:把图形A 、B 、C 的面积相加:12281656++=,那么每两个图形的公共部分的面积都重复计算了1次,因此要排除掉.⑵ 再“排除”:5687x ---,这样一来,三个图形的公共部分被全部减掉,因此还要再补回. ⑶ 再“包含”:56873x ---+,这就是三张纸片覆盖的面积.根据上面的分析得:5687338x ---+=,解得:6x =.【答案】6【例 11】 在从1至1000的自然数中,既不能被5除尽,又不能被7除尽的数有多少个?【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 1~1000之间,5的倍数有=200个,7的倍数有=142个,因为既是5的倍数,又是7的倍数的数一定是35的倍数,所以这样的数有=28个. 所以既不能被5除尽,又不能被7除尽的数有1000-200-142+-28=686个.【答案】686【巩固】 求在1至100的自然数中能被3或7整除的数的个数.【考点】容斥原理之数论问题 【难度】2星 【题型】解答【解析】 记 A :1~100中3的倍数,1003331÷=,有33个; B :1~100中7的倍数,1007142÷=,有14个;A B :1~100中3和7的公倍数,即21的倍数,10021416÷=,有4个. 依据公式,1~100中3的倍数或7的倍数共有3314443+-=个,则能被3或7整除的数的个数为43个.10005⎡⎤⎢⎥⎣⎦10007⎡⎤⎢⎥⎣⎦100035⎡⎤⎢⎥⎣⎦【答案】43【例 12】 某班共有学生48人,其中27人会游泳,33人会骑自行车,40人会打乒乓球.那么,这个班至少有多少学生这三项运动都会?【考点】容斥原理之最值问题 【难度】4星 【题型】填空【解析】 (法1)首先看至少有多少人会游泳、自行车两项,由于会游泳的有27人,会骑自行车的有33人,而总人数为48人,在会游泳人数和会骑自行车人数确定的情况下,两项都会的学生至少有27334812+-=人,再看会游泳、自行车以及乒乓球三项的学生人数,至少有1240484+-=人. 该情况可以用线段图来构造和示意:(法2)设三项运动都会的人有x 人,只会两项的有y 人,只会一项的有z 人,那么根据在统计中会n 项运动的学生被统计n 次的规律有以下等式:3227334048,,0x y z x y z x y z ++=++⎧⎪++≤⎨⎪≥⎩由第一条方程可得到10032z x y =--,将其代入第二条式子得到:100248x y --≤,即252x y +≥①而第二条式子还能得到式子48x y +≤,即248x y x+≤+② 联立①和②得到4852x +≥,即4x ≥.可行情况构造同上.【答案】4【巩固】 某班有50名学生,参加语文竞赛的有28人,参加数学竞赛的有23人,参加英语竞赛的有20人,每人最多参加两科,那么参加两科的最多有 人.【考点】容斥原理之最值问题 【难度】4星 【题型】填空【解析】 根据题意可知,该班参加竞赛的共有28232071++=人次.由于每人最多参加两科,也就是说有参加2科的,有参加1科的,也有不参加的,共是71人次.要求参加两科的人数最多,则让这71人次尽可能多地重复,而712351÷=,所以至多有35人参加两科,此时还有1人参加1科.那么是否存在35人参加两科的情况呢?由于此时还有1人是只参加一科的,假设这个人只参加数学一科,那么可知此时参加语文、数学两科的共有(282220)215+-÷=人,参加语文、英语两科的共有281513-=人,参加数学、英语两科的共有20137-=人.也就是说,此时全班有15人参加语文、数学两科,13人参加语文、英语两科,7人参加数学、英语两科,1人只参加数学1科,还有14人不参加.检验可知符合题设条件.所以35人是可以达到的,则参加两科的最多有35人.(当然本题中也可以假设只参加一科的参加的是语文或英语)【答案】35课堂检测【随练1】 四(二)班有48名学生,在一节自习课上,写完语文作业的有30人,写完数学作业的有20人,语文数学都没写完的有6人.⑴ 问语文数学都写完的有多少人?⑵ 只写完语文作业的有多少人?【考点】两量重叠问题 【难度】1星 【题型】解答【解析】 ⑴ 由题意,有48642-=(人)至少完成了一科作业,根据包含排除原理,两科作业都完成的学生有:3020428+-=(人).⑵ 只写完语文作业的人数=写完语文作业的人数-语文数学都写完的人数,即30822-=(人).【答案】22人【随练2】 光明小学组织棋类比赛,分成围棋、中国象棋和国际象棋三个组进行,参加围棋比赛的有42人,参加中国象棋比赛的有55人,参加国际象棋比赛的有33人,同时参加了围棋和中国象棋比赛的有18人,同时参加了围棋和国际象棋比赛的有10人,同时参加了中国象棋和国际象棋比赛的有9人,其中三种棋赛都参加的有5人,问参加棋类比赛的共有多少人?【考点】三量重叠问题 【难度】3星 【题型】解答【解析】 根据包含排除法,先把参加围棋比赛的42人,参加中国象棋比赛的55人与参加国际象棋比赛的33人加起来,共是425533130++=人.把重复加一遍同时参加围棋和中国象棋的18人,同时参加围棋和国际象棋的10人与同时参加中国象棋和国际象棋的9人减去,但是,同时参加了三种棋赛的5人被加了3次,又被减了3次,其实并未计算在内,应当补上,实际上参加棋类比赛的共有:130********-+++=()(人).或者根据学过的公式:A B C A B C A B B C A C A B C =++---+,参加棋类比赛的总人数为:42553318109598++---+=(人).【答案】98人【随练3】 一个长方形长12厘米,宽8厘米,另一个长方形长10厘米,宽6厘米,它们中间重叠的部分是一个边长4厘米的正方形,求这个组合图形的面积.【考点】几何中的重叠问题 【难度】1星【题型】解答【解析】 两个长方形如图摆放时出现了重叠(见图中的阴影部分),重叠部分恰好是边长为4厘米的正方形,如果利用两个长方形面积之和来计算被覆盖桌面的面积,那么重叠部分在两个长方形面积中各被计算了一次,而实际上这部分只需计算一次就可以了.所以,组合图形的面积=长方形面积之和-重叠部分.于是,组合图形的面积12810644140=⨯+⨯-⨯=(平方厘米).【答案】140平方厘米家庭作业【作业1】 四(1)班有46人,其中会弹钢琴的有30人,会拉小提琴的有28人,则这个班既会弹钢琴又会拉小提琴的至少有 人。
