02 流体静力学
合集下载
工程流体力学第2章流体静力学
① 沿任意方向 ② 沿外法线方向
有切向分力 流体受拉力
都将破坏流体平衡。
这与静止前提不符，故假设不成立，则原命题成立。
①
②
4
第2章 流体静力学
特性二、静止流体中任何一点上各个方向的静压力大小相等，与作用面方位无关。
证明：采用微元体分析法 ① 取微单元体
在静止流体中，在O点附近取出各边长分别 为dx、dy、dz的微小四面体OABC。相应坐标 轴为x、y、z。
第2章 流体静力学
流体静力学：研究流体在静止状态下的平衡规律及其应用。 静止：流体质点相对于参考系没有运动，质点之间也没有相对运动。 静止状态包括两种情况： 1、绝对静止：流体整体对地球没有相对运动。
2、相对静止：流体整体对地球有运动，但流体各质点之间没有相对运动。
举例：
绝对静止
等加速水平直线运动 等角速定轴转动
2
第2章 流体静力学
§2.1 流体静压力及其特性
1、静压力的概念
（1）静压力：静止流体作用在单位面积上的压力，称为静压力，或静压强。记作“p”
一点的静压力表示方法：
设静止流体中某一点m，围绕该点取一微小作用面积A，其上压力为P，则： 平均静压力： p P
A
m点的静压力：p lim P
单位：
A0 A
m
国际单位：Pa
物理单位：dyn/cm2
工程单位：kgf/m2
混合单位：1大气压（工程大气压） = 1kgf/cm2
（2）总压力：作用在某一面积上的总静压力，称为总压力。记作“P”
单位：N
3
第2章 流体静力学
2、静压力的两个重要特性
特性一、静压力方向永远沿着作用面内法线方向。
流体力学第二版第二章流体静力学
p B p Ba p b a s1.9 0 9 2 4 8 .9 k/m N 2
A点的相对压强为负值，说明A点处于真空状态，真空 值为： p kp ap Aa bp s A 1.7 4 k/N m 2
二、压强的表示方法 1、用应力单位表示 即从压强的定义出发，用单位面积上的力表示。
2、用大气压的倍数表示 在工程上，常用工程大气压为单位来表示压强。
解：1、绝对压强
pabspah 9 8 9 .8 2 1.1 6 k7 Pa
= 117.6 kN/m2
117.6 98
1.2pa
pabs117.612m(水柱）
9.8
2、相对压强
p h9.821.6 9 kN /m 21.6 9kP0 a.2pa
p h 2m(水柱）
三、静压强分布图
用线段长度表示各点压强大小，用箭头表示压强 的方向，如此绘成的几何图形，称为压强分布图。
d p(X dYxd Z y)dz
不可压缩液体在有势的质量力的作用下才能静止。
三、等压面及其特性 1、等压面
液体中由压强相等的各点所构成的面（可以是平面 或曲面）称为等压面。
静止液体的自由表面即为等压面。 2、等压面的特性
由 d p(X dYxd Z y)d及z等压面定义，得：
等压面方程： Xd YxdZ yd 0 z 等压面的特性： 1）压强一定相等；
P0
h1
A
h2
解：1、绝对压强
B
p A ap b 0 s h 1 7 .4 8 9 .8 0 .5 8 .3 k 3 /m N 2 p B a p 0 b s h 2 7 .4 8 9 .8 2 .5 1.9 k 0 /m N 2 2
2、相对压强
第二章 流体静力学
表面力具有传递性
3
工程流体力学
二、静压力的两个重要特性
• 流体静止时，τ=0；只能承受压应力，即 压强，其方向与作用面垂直，并指向流体 内部。
• 特性1（方向性）：平衡流体中的应力 p⊥→受压面。
• 特性2（大小性）：平衡流体内任一点的压 强p与作用方位无关,即 p =f(x,y,z)。
4
工程流体力学
工程流体力学
第二章 流体静力学
流体静力学是研究流体在静止状态下的 力学规律，包括压强的分布规律和固体壁面 所受到的液体总压力。
1
工程流体力学
第一节 流体静压力及其特性
一、流体静压力：
1、总压力P ：静止流体与容器壁之间、内部相邻 两部分流体之间的作用力。单位“牛”
2、静压力：单位面积上的总压力。即压强。
26
工程流体力学
（1）、测压管
测压管是一种最简单的液柱式测压计。为了减少毛细 现象所造成的误差，采用一根内径为10mm左右的直玻璃 管。测量时，将测压管的下端与装有液体的容器连接，上 端开口与大气相通，如图所示。
测压管只适用于测量较小的压强， 一般不超过19.6MPa，相当于 2mH2O。如果被测压强较高，则 需加长测压管的长度，使用就很不 方便。此外，测压管中的工作介质 就是被测容器中的流体，所以测压 管只能用于测量液体的压强。
例2-6、油罐深度测定，如图所示。已知h1=60cm， △h1=25cm， △h2=30cm，油的相对密度d油=0.9。求h2。
解析：这是由三个以上的容器组成的连通器
1、找出共有等压面。n-n , m-m
2、以A点为计算起点，B点为计算终点，
计算路线如图箭头所示。
3、列连通器平衡方程
n
《流体力学》第二章流体静力学
z4
p z C g
pa 4 3 真空 1
p2 g
p=0
z1
z3
2
z=0
p 为压强水头 g
z 为位置水头
2.3 重力场中的平衡流体 重要结论
p p0 gh
(1) 在重力作用下的静止液体中，静压强随深度按线性 规律变化，即随深度的增加，静压强值成正比增大。 (2)在静止液体中，任意一点的静压强由两部分组成： 一部分是自由液面上的压强P0；另一部分是该点到自由 液面的单位面积上的液柱重量ρgh。 (3)在静止液体中，位于同一深度(h＝常数)的各点的静 压强相等，即任一水平面都是等压面。
2.2 流体平衡微分方程 一、欧拉平衡方程
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
2 3
2
3
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
dA dA n
dF pdAn
F pdAn
A
流体静压力：作用在某一面积上的总压力； （矢量） 流体静压强：作用在某一面积上的平均压强或某一点的 （标量） 没有方向性 压强。
2.1 平衡流体上的作用力 证明：
z A
pn px
微元四面体受力分析
py
dx C x
dz O dy B y
y
p x p y p z pn
C x
pz
f
↑
z
表 面 力 质 量 力
1 d yd z 2 1 Py p y d zd x 2 1 P p d yd x z z 2 P n pn d A P x px
p z C g
pa 4 3 真空 1
p2 g
p=0
z1
z3
2
z=0
p 为压强水头 g
z 为位置水头
2.3 重力场中的平衡流体 重要结论
p p0 gh
(1) 在重力作用下的静止液体中，静压强随深度按线性 规律变化，即随深度的增加，静压强值成正比增大。 (2)在静止液体中，任意一点的静压强由两部分组成： 一部分是自由液面上的压强P0；另一部分是该点到自由 液面的单位面积上的液柱重量ρgh。 (3)在静止液体中，位于同一深度(h＝常数)的各点的静 压强相等，即任一水平面都是等压面。
2.2 流体平衡微分方程 一、欧拉平衡方程
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
2 3
2
3
p dx 1 p dx 1 p dx p 2 3 x 2 2 x 2 6 x 2
dA dA n
dF pdAn
F pdAn
A
流体静压力：作用在某一面积上的总压力； （矢量） 流体静压强：作用在某一面积上的平均压强或某一点的 （标量） 没有方向性 压强。
2.1 平衡流体上的作用力 证明：
z A
pn px
微元四面体受力分析
py
dx C x
dz O dy B y
y
p x p y p z pn
C x
pz
f
↑
z
表 面 力 质 量 力
1 d yd z 2 1 Py p y d zd x 2 1 P p d yd x z z 2 P n pn d A P x px
流体力学教案第2章流体静力学
第二章 流体静力学§2－1作用在流体上的力、表面力、质量力在运动的实际流体中任取一块流体，其体积为V ，表面积为A ，在这块流体上任取一微元面积δA ，作用在其表面上的力为δF ，分解为⎩⎨⎧切向力法向力τδδF F n ，则法向力： AF p A δδδn 0lim →= (N/m 2)切向力：AF A δδτδτ0lim →= (N/m 2)在这块流体上，取一流体微团，其体积为δＶ，由于地球引力的作用，产生的重力为ρg δV 。
由于流体存在加速度a，根据达朗贝尔原理，虚加的惯性力为-ρδＶa。
所以，流体所受的力为：⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧惯性力重力或体积力质量力一般情况不考虑和表面张力摩擦力切向应力压力法向应力表面力)()()()(στP 表面力―是指作用在流体中的所取某部份流体体积表面上的力，也就是该部分体积周围的流体（既可是同一种类的流体，也可是不同种类的流体）或固体通过接触面作用在其上的力。
质量力―是指作用在流体内部所有流体质点上并与流体的体积或质量成正比的力，又称体积力。
通常，单位质量流体的质量力用→f 表示，在笛卡尔直面坐标系中：k j i zyxf f f f →→→→++=流体静力学―研究流体处于静止状态时各种物理量的分布规律及在工程实际中的应用。
所谓流体的静止状态是指流体对选用的坐标系无相对运动的状态。
δF§2－2流体的静压强及其特性在静止的流体中，任取一块流体。
当δA →0时，p 就定义为空间某点的静压强：AP p A δδδlim→=静压强的两个特性：① 流体静压强指向作用面的内法线方向。
② 流体中任意点静压强的大小只是位置的函数，即p=f (x ，y ，z )与其作用面的方向无关，又称作静压强各向同性。
证①：流体中任意点所受的力均可分为切应力和压应力。
因总体静止，0d d =yu， 故切应力0=τ，所以，只存在法向应力，当然垂直于作用面。
又：流体在拉力作用下，要发生运动，因为静止，故只存在压应力。
流体流动02-(静力学方程式及应用+连续性方程)
3. 容器里的液面高度可根据压差计的读数 R求得。液面越高，
2. 平衡器里的液面高度维持在容器液面容许到达的最大高度处。
读数越小。当液面达到最大高度时，压差计的读数为零。
例 2 为了确定容器中石油产品的液面，采用如附图所示的装置。 压缩空气用调节阀1调节流量，使其流量控制得很小，只要在鼓
泡观察器 2内有气泡缓慢逸出即可。因此，气体通过吹气管 4的 流动阻力可忽略不计。吹气管内压力用U管压差计3来测量。压 差计读数 R的大小，反映贮罐 5 内液面高度。指示液为汞。 1、 分别由a管或由b管输送空气时，压差计读数分别为 R1或R2，试 推导R1、R2分别同Z1、Z2的关系。 2、当（ Z1 － Z2）＝ 1.5m， R1＝ 0.15m， R2＝0.06m时，试求石 油产品的密度ρP及Z1。已知Hg密度为13600kg/m3。
该液柱在垂直方向上受到的作用力有: （1）作用在液柱上端面上的总压力P1 P1= p1 A （N） （2）作用 在液柱下端面上的总压力 P2 P2= p2 A （N） （3）作用于整个液柱的重力G G =gA（Z1-Z2） （N）
由于液柱处于静止状态，在垂直方向上的三 个作用力的合力为零， 即 ： p1 A+ gA（Z1 - Z2）–p2 A = 0 令： h= （Z1 -Z2） 整理得： p2 = p1 + gh 若将液柱上端取在液面，并设液面上方的压 强为 p0 ； 则： p0 = p1 + gh 以上二式均称为流体静力学基本方程式，它 阐明了静止流体内部任一点流体静压力的大小与 其位置的关系。
扩张室：扩张室的截面积远大于U型管截面积（直径比1：10以
上），当读数R变化时，两扩张室中液面不致有明显的 变化。
按静力学基本方程式可推出:
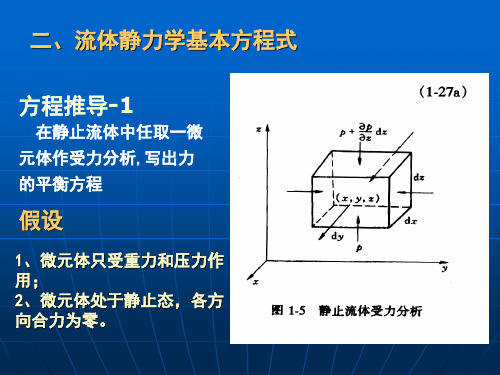
2. 平衡器里的液面高度维持在容器液面容许到达的最大高度处。
读数越小。当液面达到最大高度时，压差计的读数为零。
例 2 为了确定容器中石油产品的液面，采用如附图所示的装置。 压缩空气用调节阀1调节流量，使其流量控制得很小，只要在鼓
泡观察器 2内有气泡缓慢逸出即可。因此，气体通过吹气管 4的 流动阻力可忽略不计。吹气管内压力用U管压差计3来测量。压 差计读数 R的大小，反映贮罐 5 内液面高度。指示液为汞。 1、 分别由a管或由b管输送空气时，压差计读数分别为 R1或R2，试 推导R1、R2分别同Z1、Z2的关系。 2、当（ Z1 － Z2）＝ 1.5m， R1＝ 0.15m， R2＝0.06m时，试求石 油产品的密度ρP及Z1。已知Hg密度为13600kg/m3。
该液柱在垂直方向上受到的作用力有: （1）作用在液柱上端面上的总压力P1 P1= p1 A （N） （2）作用 在液柱下端面上的总压力 P2 P2= p2 A （N） （3）作用于整个液柱的重力G G =gA（Z1-Z2） （N）
由于液柱处于静止状态，在垂直方向上的三 个作用力的合力为零， 即 ： p1 A+ gA（Z1 - Z2）–p2 A = 0 令： h= （Z1 -Z2） 整理得： p2 = p1 + gh 若将液柱上端取在液面，并设液面上方的压 强为 p0 ； 则： p0 = p1 + gh 以上二式均称为流体静力学基本方程式，它 阐明了静止流体内部任一点流体静压力的大小与 其位置的关系。
扩张室：扩张室的截面积远大于U型管截面积（直径比1：10以
上），当读数R变化时，两扩张室中液面不致有明显的 变化。
按静力学基本方程式可推出:
流体力学(张景松版)第二章 流体静力学
工程大气压 98066.5 0.98067 1
0.9678 735.6 10.000 735.6 14.22
标准大气压 101325 1.01325 1.033
1
760 10.332 760
14.7
托
133.3 0.00133 0.00136 0.00132 1
13.6
1 0.01934
毫米水柱 9.8067 0.000098 0.0001 0.0000968 0.07356 1 0.07356 0.00142
一、压强的计量
p
1、绝对压强
以完全真空为基准计量的压强
绝对 压强
2、计示（相对）压强
以当地大气压强为基准计量的压强
o
计示 压强
计示 压强 （真空）
p>pa
大气压强 p=pa
p<pa 绝对 压强
完全真空 p=0
表压： p pa pe p pa gh
真空： p pa pv pa p pe
p p dx x 2
o y
dz
b ac
dy dx
p p dx x 2
x
为得到b面和c面的压强，利用a点压强进行泰勒展开:
b(x dx , y, z) : 2
pb
p
p x
dx 2
c(x dx , y, z) : 2
pc
p
p x
dx 2
2 流体静力学
z
p p dx x 2
一、流体的静压强
流体处于绝对静止或相对静止时的压强。
P dP p lim
A0 A dA
2.2 流体的静压力及其特性
02 流体静力学-典型例题详解
【例2-4】(见主要参考书第27页)
复式测压计图
【解法一】根据流体静力学基本方程和等压面的概 念，并考虑到气体<< ´，应有
p3 p2 g( 1 2 ) p4 p3 g( 3 4 ) p5 p4 g( 5 4 )
由此可解得 p5 g ( 1 2 3 4 ) g ( 5 4 )
由此可得
p5 g ( 1 2 3 4 ) g ( 5 4 ) 13595 9.8 (1.5 0.2 1.2 0.4) 1000 9.8 ( 2.1 0.4) 263.1 103 Pa 263.1kPa
【例2-3】 (见主要参考书第24页)
【解】(1)由流体静力学基本方程 知，水箱底压强最大，且
p p0 gh A 122.6 103 103 9.8 3 152 103 Pa 152kPa ~ 1.5atm ~ 15.5mH2O
p A p pa A 152 88.26
则作用在闸门上的总压力为
P
dP gb
A
h1 h
h1
hdh
1 2 gb[( h1 h) 2 h1 ] 2 1 1000 9.8 1.5 [(1 2) 2 12 ] 2 58.8 103 N 58.8kN
(2)确定压力中心的位置。利用总压力对某轴的矩等于
p3 pa b g (0.85 0.5)
(2)
由(1)、(2)式得
0.85 0.5 0.85 0.5 a b 1000 700kg/m3 0.5 0.5
p A pa b g 0.85 98 103 103 9.8 0.85 106.33 103 Pa 106.33kPa
第二章 流体静力学
所以表面abcd的总压力为：( p
p dx )dxdy x 2
同理面aˊbˊcˊd ˊ的总压
p dx 力为： (p )dydz x 2
z
微团在X轴方向的表面
力和为：
(p p dx p dx )dydz ( p )dydz x 2 x 2
p
p dx x 2
位质量流体受到的质量力在水平面x轴和y轴的投影为零， 铅直方向z轴的投影为重力加速度g，根据
则有
dp g dz
dp ( f x dx f y dy f z dz)
积分得
p zc g
液体静止的基本方程
式中：g在本书中取值9.807m/s2；
z为测压处相对于边界条件(基准面)的高差。 c为常数，大小由边界条件确定。
若一个函数W(x,y,z)使质量力的投影等于这个函数的偏
导数，即
W fx x
fy
W y
fz
W z
则称函数W(x,y,z)为质量力势函数。 一个存在质量力势函数的力场，称为有势力场，相应的
质量力称为有势质量力，简称有势力。
等压面性质： • 等压面就是等势面； • 等压面与质量力垂直； •两种互不掺混液体的分界面也是等压面。
等压面:在静止流体内，由静压力相等的各点组成的面
自由面：静止液体和气体接触的面
水平面既是等压面也是自由面
液体静压强分布规律只适用静止、同种、连续液体
同一容器或同一连通器盛有多种不同密度的液体时，关键是找到等 压面
§2-4
液体的相对静止
辩证唯物主义:
①运动是普遍的、永恒的和无条件的，因而是绝
2第二章 流体静力学基本方程
p b 为大气压强
17
图1-8 静力水头线与测压管水头线
公安海警学院基础部
热工基础
第二章 流体静力学方程
设一个大气压力为 9 . 81 10 4 N 3 3 的密度 10 kg / m 2 力加速度 g 9 . 81 m / s 则
pb
/m
2
而水 重
g
9 . 81 10
3
4
例2
热工基础
第二章 流体静力学方程
解： A点： 位置水头： z 压力水头： h 测压管水头：
H
A
A
h1 h 2 3 3 6 m
A
pA
g
5 10
5 3
10 10
50 m
z A h A 6 50 56 m
24
公安海警学院基础部
热工基础
第二章 流体静力学方程
第二章 流体静力学方程
当f2>>f1时： 可以用很小的力：p1*f1 f1 举起重物：p1*f2
帕斯卡定律：在平衡液 体里面，其液面或任意 一点的压力和压力变化， 可以按照它原来的大小， 传递到液体的各个部分。
35
p1
G
p1
f2
公安海警学院基础部
热工基础
第二章 流体静力学方程
36
图1-16 油压千斤顶的 构造原理
27
公安海警学院基础部
热工基础
第二章 流体静力学方程
小结
重力
作 用 在 流 体 上 的 力
质量力
惯性力
直线惯性力
离心惯性力 切应力 表面力
压强
28
公安海警学院基础部
2 流体静力学
缺点：易受人为破坏、降雨量的影响、易淤堵
2 U形水银测压计 当被测点压强很大时，所需测压管很长，这时可以
改用U形水银测压计。
在U形管内，水银面N-N为等压面，p1=p2。 对测压计右支 对测压计左支 A点的绝对压强 A点的相对压强 式中， 与m分别为水和水银的密度。
3 差压计 差压计是直接测量两点压强差的装置。若左、右两容器
内各盛一种介质，其密度分别为 A和 。B 因c-c面是等压面，于是
pA AghA pB B ghB m gh pA pB m gh B ghB AghA hA s hB h
hA h hB s pA pB (m A )gh (B A )ghB Ags
流体静压强基本特性
特性一：静止流体只能承受压应力，压强的方向垂直并指向作用面。
用反证法来证明此特性： 取一块处于静止状态的流
体，若作用面AB上的应力p’ 的方向向外且不垂直于AB， 则可分解成法向应力pn和切向
应力 。
1）若存在 ，必然有流动，这与静止的前提不符， 0。 2）流体不能承受拉力，因此 p的方向必然是内法线方向，如图中的 p。
3
静压力与静压强
静压力：在平衡流体内部相邻两部分之间相互作用的力 或流体对固体壁面的作用力称为压力，常以字母F表示。
静压力：取微小面积A ，令作用于A 的静压力为FP，则
单位面积所受的平均静水压力为 p FP /。A
静压强： p lim FP A0 A
静压力FP的单位：牛顿(N)； 静压强 p 的单位：牛顿/米2(N/m2)，又称为“帕”(Pa)。
代入平衡微分方程
dp ( fxdx f ydy fzdz)
p0
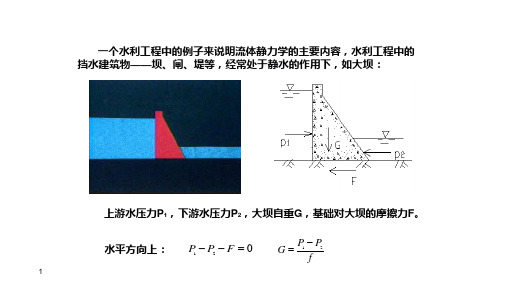
2 U形水银测压计 当被测点压强很大时，所需测压管很长，这时可以
改用U形水银测压计。
在U形管内，水银面N-N为等压面，p1=p2。 对测压计右支 对测压计左支 A点的绝对压强 A点的相对压强 式中， 与m分别为水和水银的密度。
3 差压计 差压计是直接测量两点压强差的装置。若左、右两容器
内各盛一种介质，其密度分别为 A和 。B 因c-c面是等压面，于是
pA AghA pB B ghB m gh pA pB m gh B ghB AghA hA s hB h
hA h hB s pA pB (m A )gh (B A )ghB Ags
流体静压强基本特性
特性一：静止流体只能承受压应力，压强的方向垂直并指向作用面。
用反证法来证明此特性： 取一块处于静止状态的流
体，若作用面AB上的应力p’ 的方向向外且不垂直于AB， 则可分解成法向应力pn和切向
应力 。
1）若存在 ，必然有流动，这与静止的前提不符， 0。 2）流体不能承受拉力，因此 p的方向必然是内法线方向，如图中的 p。
3
静压力与静压强
静压力：在平衡流体内部相邻两部分之间相互作用的力 或流体对固体壁面的作用力称为压力，常以字母F表示。
静压力：取微小面积A ，令作用于A 的静压力为FP，则
单位面积所受的平均静水压力为 p FP /。A
静压强： p lim FP A0 A
静压力FP的单位：牛顿(N)； 静压强 p 的单位：牛顿/米2(N/m2)，又称为“帕”(Pa)。
代入平衡微分方程
dp ( fxdx f ydy fzdz)
p0
流体力学_02 流体静力学解读
pA ( y hm a) pB y
pA pB (hm a)
对于图b有：
pA A (Z1 hm ) pB B Z 2 hm pA pB ( A )hm B Z 2 A Z1
2019/4/21
p0 pa gh 98100 1000 9.81 1.5
83385 N/m2
a
pe0 p0 pa gh
1000 9.8 1.5
2019/4/21
由式（2—26）求得
p0
14715 N/m2
§2.4
液柱测压计
测量流体的压强是工程上极其普遍的要求，如锅炉、压 缩机、水泵、风机、鼓风机等均装有压力计及真空计。常用 的有弹簧金属式、电测式和液柱式三种。 液柱式仪表测量精度高，量程小，适用于低压实验场所。 下面介绍几种常用的液柱式测压计： 一、测压管：测压管是一根直管或U形管，一端连接在 需要测定的器壁孔口上，另一端斤开口，直接和大气相通， 如图所示。由于相对压强的作用，水在管中上升或下降， 与大气相接触的液面相对压强为零。这就可根据管中水面 到所测点的高度直接读出水柱高度。
工程大气压法 工程大气压
at
2019/4/21
2019/4/21
[补充例题]封闭盛水容器中的玻璃管两端开口，如图（2—7）所示 ，已知玻璃管伸入水面以下h=1.5m时，既无空气通过玻璃管进入容 器，又无水进入玻璃管。试求此时容器内水面上的绝对压强 p0 和 相对压强 pe 0。 液体静力学的基本方程式 [解] 将式（ ）用于容器内水面上任一点和玻璃管底部， 有 p0 gh pa 当地大气压强 pa 在没有特别说明情况下，一般以1个 工程大气压强计。故 p
第二章 流体静力学
6
第二节 流体的静压力及其特性
1 1 p x dydz p n An cos(n, x) X dxdydz 0 2 6 1 An cos(n, x) dydz 2
p x pn 1 dydz X 1 dxdydz 0
2 6
1 p x p n X dx 0 6
单位质量力：单位质量流体所受到的质量力。
Fy F Fx Fz f i j k Xi Y j Zk m m m m
设作用在流体上的质量 力只有重力，则：
X=0, Y=0， Z=-mg/m=-g
z
pቤተ መጻሕፍቲ ባይዱ
dz
p
p dy y
o x
dx
dy
y
4
第二节
流体静压力及其特性
•
当流体处于静止或相对静止时，流体单位面 积的表面力称为流体静压强。
三、 静压力的测量
1. 测压管
pA pA
p A pa hA
1
N /m
mH 2O mHg
2
水
1
pa hA pa hA
汞
1 pa hA pA pa标
标准大气压
29
第五节 压力的单位和压力的测量方法
二、 静压力的测量
1. 测压管
p Ag hA
测点处的 z
p
pA /
，所以
zA
pB /
叫测压管水头。
zB
O O
20
流体静力学基本方程的意义
如果容器内的液体是静 止的 ，一根测压管测得 的测压管水头也就是容 器内液体中任何一点的 测压管水头 。 如接上多 根测 压 管， 则各测压管 中的液面都将位于同一 水平面上。
第二节 流体的静压力及其特性
1 1 p x dydz p n An cos(n, x) X dxdydz 0 2 6 1 An cos(n, x) dydz 2
p x pn 1 dydz X 1 dxdydz 0
2 6
1 p x p n X dx 0 6
单位质量力：单位质量流体所受到的质量力。
Fy F Fx Fz f i j k Xi Y j Zk m m m m
设作用在流体上的质量 力只有重力，则：
X=0, Y=0， Z=-mg/m=-g
z
pቤተ መጻሕፍቲ ባይዱ
dz
p
p dy y
o x
dx
dy
y
4
第二节
流体静压力及其特性
•
当流体处于静止或相对静止时，流体单位面 积的表面力称为流体静压强。
三、 静压力的测量
1. 测压管
pA pA
p A pa hA
1
N /m
mH 2O mHg
2
水
1
pa hA pa hA
汞
1 pa hA pA pa标
标准大气压
29
第五节 压力的单位和压力的测量方法
二、 静压力的测量
1. 测压管
p Ag hA
测点处的 z
p
pA /
，所以
zA
pB /
叫测压管水头。
zB
O O
20
流体静力学基本方程的意义
如果容器内的液体是静 止的 ，一根测压管测得 的测压管水头也就是容 器内液体中任何一点的 测压管水头 。 如接上多 根测 压 管， 则各测压管 中的液面都将位于同一 水平面上。
第二章流体静力学解析
以大气压强为基准定义静水头时，称为计示静水头，流体内 各点的计示静水头连线称为计示静水头线；
静水头线
计示静水头线
第二章 流体静力学
第三节 重力场中流体的平衡
帕斯卡原理
对图中a点和自由液面使用静力学基本方程得a点静压强
z p z h p0
g
g
p p0 gh
单位底面积
通真空
做 功 高 度
fx fy 0 fz g
代入压差公式
dp gdz
z1
p1
g
z2
p2
g
用于1点 和2点
z p
g
Const
称为不可压缩流体静力学基本方程，适用于平衡流 体内部任意一点。
第二章 流体静力学
第三节 重力场中流体的平衡
流体静力学方程的物理意义
z p Const
g
通真空
做 功 高 度
单位重量流体 重力势能
第三节 重力场中流体的平衡
二、压强的度量 以绝对（完全）真空为度量基准——绝对压强； 以大气压强pa为度量基准——计示压强或相对压强 或表压强；
压强高于大气压强时， 表压强为正值： pe p pa 压强低于大气压强时，表压强为负值，其绝对值称为真空或
真空度pv ： pv pa p
第二章 流体静力学
内法线方向。
第二章 流体静力学
第一节 流体静压强及其特性
特性二：静压强的大小与作用面的空间方位无关， 只是坐标点的连续可微函数。
p px, y, z
第二章 流体静力学
第二节 欧拉平衡微分方程
研究处于平衡或相对平衡状态的流体内部静压强p的 分布规律。
一、流体的欧拉平衡微分方程
在平衡或相对平衡的流体内部取一个微元体；
静水头线
计示静水头线
第二章 流体静力学
第三节 重力场中流体的平衡
帕斯卡原理
对图中a点和自由液面使用静力学基本方程得a点静压强
z p z h p0
g
g
p p0 gh
单位底面积
通真空
做 功 高 度
fx fy 0 fz g
代入压差公式
dp gdz
z1
p1
g
z2
p2
g
用于1点 和2点
z p
g
Const
称为不可压缩流体静力学基本方程，适用于平衡流 体内部任意一点。
第二章 流体静力学
第三节 重力场中流体的平衡
流体静力学方程的物理意义
z p Const
g
通真空
做 功 高 度
单位重量流体 重力势能
第三节 重力场中流体的平衡
二、压强的度量 以绝对（完全）真空为度量基准——绝对压强； 以大气压强pa为度量基准——计示压强或相对压强 或表压强；
压强高于大气压强时， 表压强为正值： pe p pa 压强低于大气压强时，表压强为负值，其绝对值称为真空或
真空度pv ： pv pa p
第二章 流体静力学
内法线方向。
第二章 流体静力学
第一节 流体静压强及其特性
特性二：静压强的大小与作用面的空间方位无关， 只是坐标点的连续可微函数。
p px, y, z
第二章 流体静力学
第二节 欧拉平衡微分方程
研究处于平衡或相对平衡状态的流体内部静压强p的 分布规律。
一、流体的欧拉平衡微分方程
在平衡或相对平衡的流体内部取一个微元体；
第2章 流体静力学
第2章流体静力学第2章流体静力学第二章静水力学流体静力学主要研究流体在静止状态下的平衡规律及其工程应用。
由于静止状态下流体之间及流体与物面之间的作用是通过静压力的形式来表现的。
所以，本章的中心问题是研究静止状态下静压力的分布规律，进而确定静止流体作用物面上的总压力，用以解决工程实际问题。
静水力学中的静止是指流体粒子之间没有相对运动的状态。
因此，流体静止包括以下两种情况：所谓的绝对静止，即流体作为一个整体与地球没有相对运动；流体作为一个整体对地球有相对运动，但流体粒子之间没有相对运动。
流体静止时，流体质点之间没有相对运动，所以粘滞性在静止流体中显现不出来。
因此，本章所得到的流体平衡规律对理想流体和实际流体均适用。
§2-1静水压力及其特性一、静压力在静止的流体中，没有剪切应力。
因此，流体中的表面力是沿受力表面法向的正压力或法向力。
设在作用微元面积△a上的法向力为△p，则极限δp（2－1）δa?0δa就是流体单位面积上所受到的垂直于该表面的力，即物理学中的压强，称为流体静压力，简称压力，用p表示。
其单位为n/m2，称为帕斯卡，简称帕（pa）。
作用在某一面积上的静压力的合力称为总压力，以p表示，其单位为牛顿（n）。
常用的压力单位有：PA、bar、ATM、mmHg和mh2o。
换算关系为1bar=1×105pa；1atm=1.01325×105pa；1atm=760mmhg；1atm=10.34mh2o；1mmhg=133.28pa；1mh2o=9800pa。
可以看出，静压单位非常小，所以工程实践中常用的单位是kPa（103pa）或MPa（106pa）。
p=lim二、静压力的两个重要特性其中一个特点是：静压遵循作用面内部法线的方向，即它垂直指向作用面。
证明：一方面，流体静止时只有法向力，没有切向力，静压力只能沿法线方向；另一方面，流体不能承受拉力，只能承受压力。
所以，静压力唯一可能的方向就是内法线方向。
流体力学第02章流体静力学
于质量力只有重力的同一种连续介质。对不连续液体或
一个水平面穿过了两种不同介质，位于同一水平面上的
各点压强并不相等。
二 气体压强的分布（不讲） （不讲就不考）
三 压强的度量--绝对压强与相对压强
1、 绝对压强
设想没有大气存在的绝对真空状态作为零点计量的压 强，称为绝对压强。总是正的。
2、 相对压强
解：相对静水压强：
p pabs pa p0 gh pa
代入已知值后可算得
h ( p p0 pa ) (9.8 85 98) / 9.8 2.33m
g
例： 如图，一封闭水箱，其自由面上气体压强为
25kN/m2，试问水箱中 A、B两点的静水压强何处为大？
已知h1为5m，h2为2m。 解：A、B两点的绝对静水
因水箱和测压管内是互相连通的同种液体故和水箱自由表面同高程的测压管内n点应与自由表面位于同一等压面上其压强应等于自由表面上的大气压强即ghgh11测压管测压管若欲测容器中若欲测容器中aa点的液体压强点的液体压强可在容器上设置一开口细管可在容器上设置一开口细管
第二章 流体静力学
流体静力学的任务：是研究液体平衡的规律及其
p
g
p0
g
得出静止液体中任意点的静水压强计算公式：
p p0 gh
式中
h z0 z ：表示该点在自由面以下的淹没
深度。
p0 ：自由面上的气体压强。
静止液体内任意点的静水压强有两部分组
成：一部分是自由面上的气体压强P0，另一部分 相当于单位面积上高度为h的水柱重量。
(a)
(b)
(c)
淹没深度相同的各点静水压强相等，只适用
pA gLsin
当被测点压强很大时：所需测压管很长，这时可以改 用U形水银测压计。
第二章 流体静力学
分别沿 x、y、z 三个方向建立力的平衡关系：
px
B dy o dz pn
n pz
x方向合外力＝质量×质量力（x方向）
C
· P
dx A
x
1 1 p x dydz pn ds cos( n, x) dxdydz f x 2 6
z
py
3
第二章 流体静力学
方程左端等于：
1 1 p x dydz pn dydz 2 2
24
第二章 流体静力学
§2-5 压强测量
一、压强的计量： • 以真空为压强参考值计量的压强称为绝对压强，以 p 来 表示 • 以大气压 pa 为参考压强，高出大气压部分的压强称为相 对压强 pe= p-pa
• 以大气压 pa 为参考压强，不足大气压部分的压强称为真 空压强(真空度) pv= pa-p
解：容器内水面上任一 点和玻璃管底部压力差 为ρgh，有
p0 gh pa
pa用1个工程大气压强计。所 以p0 为
p0 pa gh 981000 1000 9.811.5 83385 N / m2
13
第二章 流体静力学
等压面方程还可写为：
1 f ds dp 0
其中：
f f xi f y j f z k
为质量力向量。
ds dxi dyj dzk 为等压面上的任一线矢
上式表明：等压面处处与质量力相正交。
14
第二章 流体静力学
g z2 z2 p2 p1 exp RT0
如果温度随高度呈线性变化，令
T T0 z
α为常数，式2-3积分为
T0 z p p0 T 0
自考流体力学03347 02流体静力学
P pC A hC A
P等于受压面形心点的压 强与受压面积之乘积
2.静水总压力的作用 线位置： 由合力之矩定理确定
Ix I xc yD yc yc A yc A
注：yD>yC
x轴为平面或其延长面与自由液面的交线
例：
有一铅垂放置于水中的平板矩形闸门，已知： h=2m ，b=3m，h1=1m（上缘距自由液面）。 求：作用在闸门上的静水总压力（大小，位置）。
:
几意：测压管水头。 物意：表示单位重量液体相对于基准面具有 的总势能。
基本方程各项物理意义及几何意义： 4. z
p
几意：静止液体中任两点的测压管水头相等。 C ： 物意：静止液体中各点单位重量液体相对于 基准面具有的总势能相等。 即位能和压能可以互相转换。
三、静水压强 分布图：
p p0 h
N
N
例： 某压力水箱侧壁装置有 水银多管测压计(如图所 示)、若已知测压计读数 及A点和水箱液面的标高 分别为： =1.8m， 1 2=0.7m， 3=2.0m， 4=0.9m， 5=2.5m， A=1.8m。 试求（1）水箱液面上的 压强p0， （2）A点的压强pA 及A点的测压管水头值。
3.静止液体中任一点的静水压强p等于液面压强p0 与该点的淹没深度h乘以该液体重度两部分之和。
结论：
（1）静压强的大小与淹没深度有关，而与液体的体积无关。 （2）液体中两点的压强差，等于两点之间单位面积垂直液柱 的重量。 （3）平衡液体中，某点压强的变化将等值地传递到液体中其 他各点。帕斯卡（Pascal.B.）原理。 （4）由于气体密度很小，在高差不很大时，认为各点压强相 等。
结合静压强的特性。
四、等压面 1.定义：在同一种连续的相对静止液体中，静压强相等的 各点所组成的面。 如：海平面、水平面，两种液体的交界面等。 2.等压面的性质： ①同一等压面上的压强处处相等，p=const dp=0 ②等压面与质量力垂直（正交） dp= (fxdx+fydy+fzdz) =0 ,
工程流体力学-第二章
周围流体分子或固体分子对分离体表面 的分子作用力的宏观表现。
三、静压力
工程流体力学---第二章 流体静力学
在静止的流体中，不存在切应力。因此，流体中的表面力就是
沿受力面法线方向的正压力或法向力。
F p lim
A0 A
法向力 微元面积
静压力定义
上式中p就是垂直作用于流体单位面积上的力，即物理学中 的压强，称为流体的静压力，简称压力，用p表示，单位为牛 顿（N）。作用于整个面上的力称为总压力。
工程流体力学---第二章 流体静力学 四、流体静压力的两个重要特性
1. 流体静压强垂直于其作用面，其方向指向该作用面的内法线 方向。 （利用静止流体性质进行证明）
☆流体静止时只有法向力，没有切向力，静压力只能沿法线方向； ☆流体不能承受拉力，只能承受压力。
静压力惟一可能的方向就是内法线方向。
工程流体力学---第二章 流体静力学
微元体内流体所受质量力: dxdydz
说明：
微元体内流体所受质量力在x方向的分力: Xdxdydz （1）在流体力学
2. 静止流体中任意一点处流体静压强的大小与作用面的方位无
关，即同一点各方向的流体静压强均相等。
z
Pn
Px dz
Py
Px Py Pz Pn P
O
dx
dy
y
x
Pz
表明：静止流体中任意一点上的流体静压力，无论来自何方均相
等，或者说与作用方向无关。流体静压强不是矢量，而是标量，
仅是坐标的连续函数。即：p= p(x,y,z)，由此得静压强的全微分
☆流体静力时，流体质点之间没有相对运动，因此粘滞性在静止 流体中显现不出来。 ☆本章所得到的流体平衡规律对理想流体和实际流体均适用。
三、静压力
工程流体力学---第二章 流体静力学
在静止的流体中，不存在切应力。因此，流体中的表面力就是
沿受力面法线方向的正压力或法向力。
F p lim
A0 A
法向力 微元面积
静压力定义
上式中p就是垂直作用于流体单位面积上的力，即物理学中 的压强，称为流体的静压力，简称压力，用p表示，单位为牛 顿（N）。作用于整个面上的力称为总压力。
工程流体力学---第二章 流体静力学 四、流体静压力的两个重要特性
1. 流体静压强垂直于其作用面，其方向指向该作用面的内法线 方向。 （利用静止流体性质进行证明）
☆流体静止时只有法向力，没有切向力，静压力只能沿法线方向； ☆流体不能承受拉力，只能承受压力。
静压力惟一可能的方向就是内法线方向。
工程流体力学---第二章 流体静力学
微元体内流体所受质量力: dxdydz
说明：
微元体内流体所受质量力在x方向的分力: Xdxdydz （1）在流体力学
2. 静止流体中任意一点处流体静压强的大小与作用面的方位无
关，即同一点各方向的流体静压强均相等。
z
Pn
Px dz
Py
Px Py Pz Pn P
O
dx
dy
y
x
Pz
表明：静止流体中任意一点上的流体静压力，无论来自何方均相
等，或者说与作用方向无关。流体静压强不是矢量，而是标量，
仅是坐标的连续函数。即：p= p(x,y,z)，由此得静压强的全微分
☆流体静力时，流体质点之间没有相对运动，因此粘滞性在静止 流体中显现不出来。 ☆本章所得到的流体平衡规律对理想流体和实际流体均适用。
《工程流体力学》第二章 流体静力学
20 0 2340 615
各项物理意义：
容器：封闭
液体重度：g
自由液面压强：po 小孔： 器壁上距底部z处
小孔处压强：p = po+ gh
在o处与一根抽成真空的小管相通，液体进入小管，并迅
速上升到A点： p = gh’
h ——O、B两处单位重量流体位能差 h’ ——O、A两处单位重量流体位能差
代表一种能量，称为压力能
容器旋转：绕铅直轴，角速度w
容器旋转后，液体虽未流出，但压强发生了变化，
画出过边上小孔的等压线
虚线 —— 相对压强为 0
盖板各点承受的相对压强：
或真空度： 盖板上： 在轴心处，真空度 最大： 在边缘处，真空度 最小： 离心泵和风机就是利用这个原理，使 流体不断从叶轮中心吸入。
3. 流体静压强仅是空间位置和时间的标量函数，与所取 作用面的方向无关——各向同性 证：取一五面体
(1)表面力：作用静止(或相对静止)流体上无拉力和切力， 表面力只有压力，
在左面上：pydxdz 在底面上：pzdxdy 在斜面上：pndxds 在前面上：pxdydz/2 在后面上：pxdydz/2
液面上半径r处： 液体体积：
由此可测得w值。
速很高，液面上升过高， 溢出容器，容器为封闭的，只在中间留有一小口。
容器静止时：液面离盖板Dho 容器旋转时：液面中心下降到b
求：w
(1)求R’：
(2)静止时空出体积＝旋转时下凹体积
画出等压线
讨论： 1、AA`处压强？ 2、A`B处压强？ 3、容器底部压强？
外力场作用在流体微团上的非接触力，与流体质量(或 体积)成正比， 如地球吸引力、惯性力、电磁力等。 流体力学中一般只考虑地球吸引力，惯性力。 单位质量力：单位质量流体受到的质量力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0
1、2、3均为常数，故
pC pD H
2013/8/2 2.4.2 压差计
积分上式，得 即 或
2013/8/2
dp gdz
p gz const.
p z const. g
p1 p2 z1 z2 g g
2.3 流体静力学基本方程 13
若取z=z0时，p=p0，流体静力学基本方程又可写成
p p0 g( z0 z )
2013/8/2
2.3.4 压强计算基准和量度单位
A. 压强的计算基准
a. 相对压强——以大气压为基准，亦称表压强。
p p pa gh
b. 绝对压强——以绝对真空为零点。
p pa gh pa p
c. 真空度——表压强为负时，其绝对值。
pv p pa p
静止液体相互作用图
2013/8/2 2 流体静力学 4
B.流体静压强的特性
①流体静压强的作用方向总是沿着作用面的内法 线方向。 ②任一点的流体静压强的大小与其作用面的方位 无关，只与该点的位置有关。亦即在同一点各 方向上的流体静压强相等，故有
p p( x , y, z )
2013/8/2
2 流体静力学
等压面上，p=const.，则由静压强微分公式，有
dp dW 0
对于=const.，亦有
dW 0
积分上式，得
W const.
可见，等压面就是等势面。
特性：等压面⊥质量力：F dl Xdx Ydy Zdz 0
形状：平面或曲面。
2.3 流体静力学基本方程 15
Local barometer 2 reading
Negative Gauge Suction pressure Vacuum Absolute pressure
Absolute Zero (Complete vacuum)
2013/8/2 2.3.4 压强计算基准和量度单位 17
B. 压强单位
a. 应力单位——单位面积上所承受的压力。
9.678105 9.678101 1 1.316103
0.07356 735.6 760 1
2013/8/2
2.3.4 压强计算基准和量度单位
21
2.3.5 流体静力学基本方程的意义
p z const. g
物理意义(能量意义)
z —— 流体在该处单位重量流体所具有的位置能 量，称为比位能。 p —— 流体质点在z处单位重量流体所具有的压 g 强能量，称为比压能。相当于该压力(或压 p 强)作用下测压管中液柱将升高 。 g
柱高度作为单位表示压强的大小。由流体静力
学基本方程
p gh
得
p h units of length liquid g
2013/8/2
2.3.4 压强计算基准和量度单位
20
C. 国际单位与工程单位换算关系
压 强 名 称 换 算 关 系
Pa (N/m2) kPa (103N/m2) bar (105N/m2) mmH2O (kgf/m2) at 标准大气压 (104kgf/m2) (1.0332104kgf/m2) mmHg
9.807 9.807104 101325 133.332
9.807103 9.80710 101.325 0.13333
9.807105 9.807101 1.01325 1.3333103
1 10 10332.3 13.595
104 1 1.03323 1.3595103
2013/8/2
( p pa时)
16
2.3 流体静力学基本方程
用下列图表直观地表示p'、p和pv间的关系
1
Gauge pressure Standard atmosphere pressure Local atmosphere pressure 1 atmosphere 760mm Mercury 101,325Pa 10.34m Water Absolute pressure
同理，
1 p Z 0 z
——流体平衡微分方程，或欧拉平衡方程。
2013/8/2 2.3.1 流体平衡微分方程 9
流体平衡微分方程的矢量形式为
1 f gradp 0
或
1 f p 0
其中 f { X , Y , Z } ——单位质量力；
p p p gradp , , ——压强梯度； x y z
倒置U形管微压计中 ， 则1、2两点的压差为
p p1 p2 ( ) gh
p 1 h 或 h g 若取 0.8, 则 h 1 0.8h 0.2h
即压差扩大了5倍，可减少 读数误差。
, , ——Hamiltonian或Nabla算子。 x y z
2013/8/2 2.3.1 流体平衡微分方程 10
③平衡微分方程综合式(或静压强微分公式)
1 p 0 x 1 p Y 0 y X Z 1 p 0 z
令h=z0-z为基准面到所测点的高度(或深度)，向下 为正，则
p p0 gh
若取自由液面作为基准面，即p0 = pa(大气压)，则
p pa gh
用相对压强表示时，pa = 0，则
p gh
★限制条件：静止、同种、连续。
2013/8/2 2.3.2 流体静力学基本方程 14
2.3.3 等压面(Isobaric Surface)
5
?
如图，一单位宽的小契形自由(分离)体，其 上作用有表面力和重力, 试证px=py=ps。
y
p s s
p x y
gxy
2
p y x
x
2013/8/2
2.2 流体静压强
6
2.3 流体静力学基本方程
2.3.1 流体平衡微分方程
2.3.2 流体静力学基本方程
2.3.3 等压面等概念
2.3.4 流体静压强的计算基准和量度单位
流体力学
Fluid Mechanics (Fluid Statics)
2 流体静力学
主要内容
2.1 引言
2.2 流体静压强 2.3 流体静力学基本方程 2.4 液柱式测压计
2.5 液体的相对平衡
2.6 作用在壁面上的总压力
2013/8/2 2
2.1 引言(Introduction)
流体静力学
研究流体平衡状态及其与其他物体之间相互 作用的科学(力学规律)。
2013/8/2
2.3 流体静力学基本方程
22
几何意义
p z和 g 均具有有长度因次(或量纲)，且表示一定
的液柱高度。
z ——所测点与基准面间的距离，称为位置水头。
p ——所测点由于压强p的作用开口玻璃管液柱 g
所上升高度，称为压强水头。
p z ——开口玻璃管液面与基准面之间的距离， g
2013/8/2 2.4 液柱式测压计 29
U形管差压计中>，则
p1 gz1 p2 gz2 gh
其压差为
p1 p 2 gh g( z 2 z1 ) ( ) gh
a
←倾斜微压计 (Inclinedtube manometer或 Micro manometer)
若有 W X , W Y , W Z ，则
x y z W W W dW dx dy dz x y z
平衡微分方程综合式可写成 dp dW 对于＝const.，积分上式，得
p W C
若p = p0时，W = W0，则C = p0 - W0，于是有
p p0 (W W0 )
其中W(x,y,z)——力势函数， f { X , Y , Z } ——有势力。
2013/8/2 2.3.1 流体平衡微分方程 12
2.3.2 流体静力学基本方程
静止流体中，质量力仅为重力。若取Z = –g，则有 X=Y=0。对于
dp dW
可写成
缺点：不能测气体及p， 范围小(一般≯1/10 at)。
2013/8/2
2.4 液柱式测压计
27
右图所示，可测负压。
U形管中液体2>1时
p A 1 gh1 2 gh2
1 2
2013/8/2
容器中为气体时，则 p A 2 gh2
2.4.1 测压管 28
2.4.2 压差计(Differential Manometer)
2013/8/2
2.4.2 压差计
30
两端均置较大截面积A的 容器，U形管截面积为a。 1 压强发生变化时，有
H z A a 2
C
1 2
D 1 H1 H2 0
31
C、D两点间压差为
pC p D a a H 3 2 1 1 g A A
称为测压管水头。
2013/8/2
2.3.5 流体静力学基本方程的意义
23
测压管水头线
p1 g p2 g
Z1 Z2
基准面
2013/8/2
2.3.5 流体静力学基本方程的意义
24
2.4 液柱式测压计
(Liquid Column Manometers)
常用的压强计及真空计有三类:
弹簧金属式——利用金属的弹性变形测量压强的 大小。其量程大，携带方便，装置简便，但精度 稍差。 电测式——将弹性元件的机械变形转化为电阻、 电容、电感等电量。便于远距离及动态测量。 液柱式——利用液柱高度来确定压强大小的仪器 或装置。其量程小，精度高；直观、方便和经济。
1、2、3均为常数，故
pC pD H
2013/8/2 2.4.2 压差计
积分上式，得 即 或
2013/8/2
dp gdz
p gz const.
p z const. g
p1 p2 z1 z2 g g
2.3 流体静力学基本方程 13
若取z=z0时，p=p0，流体静力学基本方程又可写成
p p0 g( z0 z )
2013/8/2
2.3.4 压强计算基准和量度单位
A. 压强的计算基准
a. 相对压强——以大气压为基准，亦称表压强。
p p pa gh
b. 绝对压强——以绝对真空为零点。
p pa gh pa p
c. 真空度——表压强为负时，其绝对值。
pv p pa p
静止液体相互作用图
2013/8/2 2 流体静力学 4
B.流体静压强的特性
①流体静压强的作用方向总是沿着作用面的内法 线方向。 ②任一点的流体静压强的大小与其作用面的方位 无关，只与该点的位置有关。亦即在同一点各 方向上的流体静压强相等，故有
p p( x , y, z )
2013/8/2
2 流体静力学
等压面上，p=const.，则由静压强微分公式，有
dp dW 0
对于=const.，亦有
dW 0
积分上式，得
W const.
可见，等压面就是等势面。
特性：等压面⊥质量力：F dl Xdx Ydy Zdz 0
形状：平面或曲面。
2.3 流体静力学基本方程 15
Local barometer 2 reading
Negative Gauge Suction pressure Vacuum Absolute pressure
Absolute Zero (Complete vacuum)
2013/8/2 2.3.4 压强计算基准和量度单位 17
B. 压强单位
a. 应力单位——单位面积上所承受的压力。
9.678105 9.678101 1 1.316103
0.07356 735.6 760 1
2013/8/2
2.3.4 压强计算基准和量度单位
21
2.3.5 流体静力学基本方程的意义
p z const. g
物理意义(能量意义)
z —— 流体在该处单位重量流体所具有的位置能 量，称为比位能。 p —— 流体质点在z处单位重量流体所具有的压 g 强能量，称为比压能。相当于该压力(或压 p 强)作用下测压管中液柱将升高 。 g
柱高度作为单位表示压强的大小。由流体静力
学基本方程
p gh
得
p h units of length liquid g
2013/8/2
2.3.4 压强计算基准和量度单位
20
C. 国际单位与工程单位换算关系
压 强 名 称 换 算 关 系
Pa (N/m2) kPa (103N/m2) bar (105N/m2) mmH2O (kgf/m2) at 标准大气压 (104kgf/m2) (1.0332104kgf/m2) mmHg
9.807 9.807104 101325 133.332
9.807103 9.80710 101.325 0.13333
9.807105 9.807101 1.01325 1.3333103
1 10 10332.3 13.595
104 1 1.03323 1.3595103
2013/8/2
( p pa时)
16
2.3 流体静力学基本方程
用下列图表直观地表示p'、p和pv间的关系
1
Gauge pressure Standard atmosphere pressure Local atmosphere pressure 1 atmosphere 760mm Mercury 101,325Pa 10.34m Water Absolute pressure
同理，
1 p Z 0 z
——流体平衡微分方程，或欧拉平衡方程。
2013/8/2 2.3.1 流体平衡微分方程 9
流体平衡微分方程的矢量形式为
1 f gradp 0
或
1 f p 0
其中 f { X , Y , Z } ——单位质量力；
p p p gradp , , ——压强梯度； x y z
倒置U形管微压计中 ， 则1、2两点的压差为
p p1 p2 ( ) gh
p 1 h 或 h g 若取 0.8, 则 h 1 0.8h 0.2h
即压差扩大了5倍，可减少 读数误差。
, , ——Hamiltonian或Nabla算子。 x y z
2013/8/2 2.3.1 流体平衡微分方程 10
③平衡微分方程综合式(或静压强微分公式)
1 p 0 x 1 p Y 0 y X Z 1 p 0 z
令h=z0-z为基准面到所测点的高度(或深度)，向下 为正，则
p p0 gh
若取自由液面作为基准面，即p0 = pa(大气压)，则
p pa gh
用相对压强表示时，pa = 0，则
p gh
★限制条件：静止、同种、连续。
2013/8/2 2.3.2 流体静力学基本方程 14
2.3.3 等压面(Isobaric Surface)
5
?
如图，一单位宽的小契形自由(分离)体，其 上作用有表面力和重力, 试证px=py=ps。
y
p s s
p x y
gxy
2
p y x
x
2013/8/2
2.2 流体静压强
6
2.3 流体静力学基本方程
2.3.1 流体平衡微分方程
2.3.2 流体静力学基本方程
2.3.3 等压面等概念
2.3.4 流体静压强的计算基准和量度单位
流体力学
Fluid Mechanics (Fluid Statics)
2 流体静力学
主要内容
2.1 引言
2.2 流体静压强 2.3 流体静力学基本方程 2.4 液柱式测压计
2.5 液体的相对平衡
2.6 作用在壁面上的总压力
2013/8/2 2
2.1 引言(Introduction)
流体静力学
研究流体平衡状态及其与其他物体之间相互 作用的科学(力学规律)。
2013/8/2
2.3 流体静力学基本方程
22
几何意义
p z和 g 均具有有长度因次(或量纲)，且表示一定
的液柱高度。
z ——所测点与基准面间的距离，称为位置水头。
p ——所测点由于压强p的作用开口玻璃管液柱 g
所上升高度，称为压强水头。
p z ——开口玻璃管液面与基准面之间的距离， g
2013/8/2 2.4 液柱式测压计 29
U形管差压计中>，则
p1 gz1 p2 gz2 gh
其压差为
p1 p 2 gh g( z 2 z1 ) ( ) gh
a
←倾斜微压计 (Inclinedtube manometer或 Micro manometer)
若有 W X , W Y , W Z ，则
x y z W W W dW dx dy dz x y z
平衡微分方程综合式可写成 dp dW 对于＝const.，积分上式，得
p W C
若p = p0时，W = W0，则C = p0 - W0，于是有
p p0 (W W0 )
其中W(x,y,z)——力势函数， f { X , Y , Z } ——有势力。
2013/8/2 2.3.1 流体平衡微分方程 12
2.3.2 流体静力学基本方程
静止流体中，质量力仅为重力。若取Z = –g，则有 X=Y=0。对于
dp dW
可写成
缺点：不能测气体及p， 范围小(一般≯1/10 at)。
2013/8/2
2.4 液柱式测压计
27
右图所示，可测负压。
U形管中液体2>1时
p A 1 gh1 2 gh2
1 2
2013/8/2
容器中为气体时，则 p A 2 gh2
2.4.1 测压管 28
2.4.2 压差计(Differential Manometer)
2013/8/2
2.4.2 压差计
30
两端均置较大截面积A的 容器，U形管截面积为a。 1 压强发生变化时，有
H z A a 2
C
1 2
D 1 H1 H2 0
31
C、D两点间压差为
pC p D a a H 3 2 1 1 g A A
称为测压管水头。
2013/8/2
2.3.5 流体静力学基本方程的意义
23
测压管水头线
p1 g p2 g
Z1 Z2
基准面
2013/8/2
2.3.5 流体静力学基本方程的意义
24
2.4 液柱式测压计
(Liquid Column Manometers)
常用的压强计及真空计有三类:
弹簧金属式——利用金属的弹性变形测量压强的 大小。其量程大，携带方便，装置简便，但精度 稍差。 电测式——将弹性元件的机械变形转化为电阻、 电容、电感等电量。便于远距离及动态测量。 液柱式——利用液柱高度来确定压强大小的仪器 或装置。其量程小，精度高；直观、方便和经济。