【数学】3.1.1《解析几何的产生.ppt;直线的倾斜角和斜率》课件(A版必修2)
合集下载
直线的倾斜角与斜率ppt课件

什么叫倾斜角?倾斜角的范围是什么?
倾斜角:直线l与x轴正方向所成的角, 叫做直线的倾斜角.常用α表示.
(1)倾斜角的取值范围: 0≤α<1800
(2)倾斜角的作用——刻画直线相对x 轴的倾斜程度.
3.1.2
结论:坡度越大,楼梯越陡.
3.1.2 由于直线的倾斜角不利于用坐标法刻画直线,引入直线的斜率斜率.
P2 (x2 ,y2 )
三、直线的斜率公式
2 P1( x1 ,y1)
△x
△y
1
你注意到了吗?
3.1.2
1.当x1=x2时,公式右边没有意义,直线的斜率不存 在;
2. K与点P1、P2的顺序无关; 3.斜率k可以不通过倾斜角而由直线上两点的坐标求 得;
4.当y1=y2时,斜率k=0,直线的倾斜角a=0º,直线与 x轴平行或重合;
(2) - 4 . 5
学
3.1.2
以
致
用
例3、若三点(1,-1), (3,3), (5,a)在一 条直线上,求实数a的值.
例4 、直线l过点M(-1,1),且与以P
(2,2),Q(3,3)为两端点的线段 PQ有公共点,求直线l的斜率的取值范 围.
五 1.直线l过点 P(2,2 3)、Q(1,33).1.2
二、直线的斜率
a为什么不能等 于900呢?
一条直线的倾斜角a( a‡90º)的正切值叫作这 条直线的斜率,斜率常用小写字母k表示,也就是 k=tan a.
从00 900 , k从0 + () =900 时,k不存在 从900 1800,k从- 0 ()
3.1.2
问题:已知直线上的两个点,如何求直线的斜率呢?
开 关
那么它们都与 x 轴 垂直,故 l1 ∥ l2.
倾斜角:直线l与x轴正方向所成的角, 叫做直线的倾斜角.常用α表示.
(1)倾斜角的取值范围: 0≤α<1800
(2)倾斜角的作用——刻画直线相对x 轴的倾斜程度.
3.1.2
结论:坡度越大,楼梯越陡.
3.1.2 由于直线的倾斜角不利于用坐标法刻画直线,引入直线的斜率斜率.
P2 (x2 ,y2 )
三、直线的斜率公式
2 P1( x1 ,y1)
△x
△y
1
你注意到了吗?
3.1.2
1.当x1=x2时,公式右边没有意义,直线的斜率不存 在;
2. K与点P1、P2的顺序无关; 3.斜率k可以不通过倾斜角而由直线上两点的坐标求 得;
4.当y1=y2时,斜率k=0,直线的倾斜角a=0º,直线与 x轴平行或重合;
(2) - 4 . 5
学
3.1.2
以
致
用
例3、若三点(1,-1), (3,3), (5,a)在一 条直线上,求实数a的值.
例4 、直线l过点M(-1,1),且与以P
(2,2),Q(3,3)为两端点的线段 PQ有公共点,求直线l的斜率的取值范 围.
五 1.直线l过点 P(2,2 3)、Q(1,33).1.2
二、直线的斜率
a为什么不能等 于900呢?
一条直线的倾斜角a( a‡90º)的正切值叫作这 条直线的斜率,斜率常用小写字母k表示,也就是 k=tan a.
从00 900 , k从0 + () =900 时,k不存在 从900 1800,k从- 0 ()
3.1.2
问题:已知直线上的两个点,如何求直线的斜率呢?
开 关
那么它们都与 x 轴 垂直,故 l1 ∥ l2.
直线的倾斜角与斜率(第一课时)课件-2022-2023学年高二上学期数学人教A版选择性必修第一册

典例:经过 A(2,0),B(0,-1)两点的直线的方向向量为(1,k),则 k=________.
解:因为 A(2,0),B(0,-1),
所以A→B
-1 =(-2,-1),所以 k=
1 =
.
-2 2
斜率和倾斜角的对应关系 图示
倾斜角 (范围) 斜率 (范围) k 的增 减情况
α=0°
0°<α<90°
=;
-1-1 2
(2)∵x1=x2,∴斜率不存在.
2-1 1
(3)当 m=2 时,斜率不存在;当 m≠2 时,kPQ=
=
.
m-2 m-2
例 4:(1)已知过点 A(2m,3),B(2,-1)的直线的倾斜角为 45°,求实数 m 的值; (2)若过点 A(2m,3),B(2,-1)的直线的倾斜角为 90°,求实数 m 的值;
-1-3
(1)∵直线的倾斜角为 45°,∴k=1,即
=1.∴m=3.
2-2m
(2)∵直线的倾斜角为 90°,∴k 不存在.∴2m=2.∴m=1.
( 1 ) 求直线斜率的两种类型 一种是已知倾斜角求直线的斜率,注意倾斜角为 90°的情况;另一种是已知
两点的坐标求直线的斜率,注意斜率不存在的情况. (2)在 0°≤α<180°范围内的一些特殊角的正切值要熟记.
5
6
且 kAB=-2-m ,kAC=-6 =-1,
所以直线 AB,AC 的斜率存在,
5
所以 kAB=kAC,即
=-1,解得 m=3.
-2-m
直线的倾斜角与斜率的综合运用
例 5:(2)直线 l 过点 P(1,0),且与以 A(2,1),B(0, 3 )为端点的线段有公共点,求
解:因为 A(2,0),B(0,-1),
所以A→B
-1 =(-2,-1),所以 k=
1 =
.
-2 2
斜率和倾斜角的对应关系 图示
倾斜角 (范围) 斜率 (范围) k 的增 减情况
α=0°
0°<α<90°
=;
-1-1 2
(2)∵x1=x2,∴斜率不存在.
2-1 1
(3)当 m=2 时,斜率不存在;当 m≠2 时,kPQ=
=
.
m-2 m-2
例 4:(1)已知过点 A(2m,3),B(2,-1)的直线的倾斜角为 45°,求实数 m 的值; (2)若过点 A(2m,3),B(2,-1)的直线的倾斜角为 90°,求实数 m 的值;
-1-3
(1)∵直线的倾斜角为 45°,∴k=1,即
=1.∴m=3.
2-2m
(2)∵直线的倾斜角为 90°,∴k 不存在.∴2m=2.∴m=1.
( 1 ) 求直线斜率的两种类型 一种是已知倾斜角求直线的斜率,注意倾斜角为 90°的情况;另一种是已知
两点的坐标求直线的斜率,注意斜率不存在的情况. (2)在 0°≤α<180°范围内的一些特殊角的正切值要熟记.
5
6
且 kAB=-2-m ,kAC=-6 =-1,
所以直线 AB,AC 的斜率存在,
5
所以 kAB=kAC,即
=-1,解得 m=3.
-2-m
直线的倾斜角与斜率的综合运用
例 5:(2)直线 l 过点 P(1,0),且与以 A(2,1),B(0, 3 )为端点的线段有公共点,求
直线的倾斜角与斜率完整(公开课)ppt课件

直线的斜率
定义:我们把一条直线的的倾斜角的正切值叫做 这条直线的斜率。斜率通常用k表示,即:
ktan( 90)
注:倾斜角是90 °的直线没有斜率。 我们也可以用斜率表示直线的倾斜程度
试一试 提 ta 1 示 - n 8 - 0 t: a n
已知下列直线的倾斜角,求直线的斜率.
( 1 ) 3 0 o ; ( 2 ) 4 5 o ; ( 3 ) 1 2 0 o ; ( 4 ) 1 3 5 o ;
y
这些直线有何区别?
l O Px
它们的倾斜程度不同.
用什么量来刻画直 线的倾斜程度?
直线的倾斜角
定义:当直线 l 与x轴相交时,我们取x轴作为基 准,x轴正向与直线 l 向上方向之间所成的角α 叫做 直线 l 的倾斜角.
y
规定 当直线l与x轴平行或重合时,
它的倾斜角为 0 .
注意: (1)直线向上方向; o (2)x轴的正方向。
()
⑤两直线的倾斜角相等,则它们的斜率也相等 ( )
⑥平行于x轴的直线的倾斜角是 0或π ( )
典例讲解
1 、 若 直 线 的 倾 斜 角 为 6 , 3 , 求 斜 率 k 的 取 值 范 围 。
变式训练
1 、 若 直 线 的 倾 斜 角 为 6 , 3 4 , 求 斜 率 k 的 取 值 范 围 。
如图,直线的斜率分别为,则(C)
A.k1k2 k3 B. k3 k1 k2
Y
l1
C.k3 k2 k1 D.k1 k3 k2
O
X
l3
判断正误:
①直线的倾斜角为α,则直线的斜率为 tan( )
②直线的斜率的范围是 (,)
()
∨
③任一条直线都有倾斜角,所以任一条直线都有
定义:我们把一条直线的的倾斜角的正切值叫做 这条直线的斜率。斜率通常用k表示,即:
ktan( 90)
注:倾斜角是90 °的直线没有斜率。 我们也可以用斜率表示直线的倾斜程度
试一试 提 ta 1 示 - n 8 - 0 t: a n
已知下列直线的倾斜角,求直线的斜率.
( 1 ) 3 0 o ; ( 2 ) 4 5 o ; ( 3 ) 1 2 0 o ; ( 4 ) 1 3 5 o ;
y
这些直线有何区别?
l O Px
它们的倾斜程度不同.
用什么量来刻画直 线的倾斜程度?
直线的倾斜角
定义:当直线 l 与x轴相交时,我们取x轴作为基 准,x轴正向与直线 l 向上方向之间所成的角α 叫做 直线 l 的倾斜角.
y
规定 当直线l与x轴平行或重合时,
它的倾斜角为 0 .
注意: (1)直线向上方向; o (2)x轴的正方向。
()
⑤两直线的倾斜角相等,则它们的斜率也相等 ( )
⑥平行于x轴的直线的倾斜角是 0或π ( )
典例讲解
1 、 若 直 线 的 倾 斜 角 为 6 , 3 , 求 斜 率 k 的 取 值 范 围 。
变式训练
1 、 若 直 线 的 倾 斜 角 为 6 , 3 4 , 求 斜 率 k 的 取 值 范 围 。
如图,直线的斜率分别为,则(C)
A.k1k2 k3 B. k3 k1 k2
Y
l1
C.k3 k2 k1 D.k1 k3 k2
O
X
l3
判断正误:
①直线的倾斜角为α,则直线的斜率为 tan( )
②直线的斜率的范围是 (,)
()
∨
③任一条直线都有倾斜角,所以任一条直线都有
高一必修二数学说课课件:3.1.1直线的倾斜角与斜率+(共40张PPT)

本课时是概念性教学,涉及两个概念——倾斜 角和斜率。 倾斜角是几何概念,它主要起过渡作用,是联 系新旧知识的纽带,在研究斜率、直线的平行、 垂直的解析表示等问题时都要用这个概念; 斜率概念,不仅其建立过程很好地体现了解析 法,而且它在建立直线方程、通过直线方程研 究几何问题时也起核心作用,这是因为在直角 坐标系下,确定直线的最本质条件是直线上的 一个点及其斜率,其他形式都可以化归到这两 个条件上来。
三、教学目标
知识与技能目标:(直接性目标)
了解直线的方程和方程的直线的概念;在新的问题的情境中,去 主动构建理解直线的倾斜角和斜率的定义;初步感悟用代数方法 解决几何问题的思想方法。 过程与方法目标: (发展性目标) 引导学生观察发现、类比,猜想和实验探索,培养学生的创新能 力和动手能力 情感、态度与价值观目标:(可持续性目标) 在平等的教学氛围中,通过学生之间、师生之间的交流、合作和 评价,实现共同探究、教学相长的教学情境,并体验认识事物的 一般规律:从特殊到一般的过程。
四、教学重难点
重点:理解直线的倾斜角和斜率的概念,经历
用代数方法刻画直线斜率的过程,掌握 过两点直线的斜率的计算公式。
难点:
斜率公式的推导。 <鉴于本课特点,我选择教学方法如下:>
五、教法选择
直观教学法、启发发现法、 课堂讨论法、电化教学法。
遵循“教师的主导作用和学生的主体地位相 统一的教学规律”,本节课我采用观察发现、 启发引导、探索实验相结合的教学方法并充分 利用多媒体辅助教学。通过教师在教学过程中 的点拨,启发学生通过主动观察、主动思考、 动手操作、自主探究来达到对知识的发现和接 受,突出体现以学生为主体的探索性学习和因 材施教的原则。
第三章 3.1.1 倾斜角与斜率(共44张PPT)

2.理解斜率公式应注意的事项 (1)当x1=x2时,公式右边无意义,直线的斜率不存在,倾斜角 α=90°,直线与x轴垂直. (2)斜率k与P1,P2的顺序无关,即y1,y2和x1,x2在公式中的前后 次序可以同时交换,但分子与分母不能交换. (3)斜率k可以不通过倾斜角而直接由直线上两点的坐标求得 . (4)当y1=y2,x1≠x2时,斜率k=0,直线的倾斜角α=0°,直线与x 轴平行或重合.
【拓展提升】 1.用斜率公式解决三点共线问题
2.直线斜率在平面几何中的运用
解决几何图形中直线的倾斜角与斜率的综合问题时 ,要善于利
用几何图形的几何性质,注意倾斜角是几何图形中的夹角还是
其邻补角,也可以利用经过两点的直线的斜率公式 ,先求斜率, 再求倾斜角.
【变式训练】如图,菱形OBCD的顶点O与坐标原点重合,一边在 x轴的正半轴上,已知∠BOD=60°,求菱形各边和两条对角线所 在直线的倾斜角及斜率.
α =0° k=0 ____
0°<α <90° k>0 ____
90° 90°<α <180° α =___ k<0 ____
斜率(范围)
不存在
3.经过两点的斜率公式
y 2 y1 x 2 x1 直线经过两点P1(x1,y1),P2(x2,y2)(x1≠x2),其斜率k=______.
判断:(正确的打“√”,错误的打“×”) (1)倾斜角是描述直线的倾斜程度的惟一方法.( (2)任何一条直线有且只有一个斜率和它对应.( (3)一个倾斜角α 不能确定一条直线.( (4)斜率公式与两点的顺序无关.( ) ) ) )
30 1 ,即tan α=-1,所以α=135°. 5 2
(2)斜率不存在,α=90°. (3)k=
3.1.1直线的倾斜角与斜率-课件

当直线 P2 P1 与 x轴平行或重合时,上述式子还成
立吗?为什么? 成立
经过两点 P 1 (x 1 ,y 1 )P 2 ,(x 2 ,y 2 )x 1 ( x 2 )的直线的
斜率公式为:
k y2 y1
2019/12/14
x2 x1
21
21
归纳: 对于斜率公式要注意下面四点:
(1) 当x1=x2时,公式右边无意义,直线的斜率 不存在,倾斜角= 90o,直线与x轴垂直;
直线AB,BC,CA的斜率,并判断这些直线的倾斜角 是锐角还是钝角.
解:直线AB的斜率
kAB142371;
直线BC的斜率
kBC 01( 4 1)421 2;
直线CA的斜率 kCA 0132 3 31;
由 kAB0及 kCA0知,直线AB 与CA的倾斜角均
2019/12/14
14
14
两点的斜率公式
设直线P1 P2的倾斜角为α( α
≠90° ),当直线P1 P2的方向
(即从P1指向P2的方向)向上
时,过点P1作 x 轴的平行线,
过点P2作 y 轴的平行线,两线
相交于点 Q,于是点Q的坐标为
( x2,y1 ).
当 为锐角时, Q 1 P 2 , x 1 P x 2 ,y 1 y 2 .
为锐角;由 2019/12/14
kBC0知,直线BC的倾斜角为钝角.
23
23
典型例题
例2 在平面直角坐标系中,画出经过原点且斜率
分别为1,-1,2及-3的直线 l1,l2,l3 及 l 4 .
解:取 l 1上某一点为 A 1 的
坐标是 (x1, y1),根据斜率公式 有:
3.1.1直线的倾斜角与斜率课件(新人教A版必修2)

P 1(x 1, y 1) Q (x 2, y 1)
如图,当α为钝角时, 180 ,
且 x 1 x 2, y 1y 2 tan tan( 180 )
y1
o x2
x1
x
y y y y 2 1 2 1 k tan x x x x 1 2 2 1
x
设 1 ,则 ,于是 的坐标为( 1 , 1 ) . y 1 x A 1 1
1
l2
过原点及 ( 1 , 1 )的直线即为 l1, A 1 如图所示 .
说明:也可设其它特殊点
巩固与测试
1. 判断正误: ①因为所有直线都有倾斜角,所以所有直线都有斜率。
( ) ( ) ( )
②因为平行于y轴的直线的斜率不存在,所以平行于y轴的直线
4、斜率公式:
y y y y 2 1 1 2 k ( 或 k ) x x x x 2 1 1 2
作
P89
业:
习题3.1 A组:1.2 B组:5
x
p
x
o
l x
l
= 0°
k=0
0°< < 90°
= 90° 90°< <180°
k不存在 k<0
k >0
应用与实践
例1
如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC, CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
y
A(3,2) B(-4,1),
O
C(0,-1)
小结:
1、直线的倾斜角定义及其范围: 0 180 ( 90 ) 2、直线的斜率定义: ktan 3、斜率k与倾斜角 之间的关系: 0 k tan0 0
如图,当α为钝角时, 180 ,
且 x 1 x 2, y 1y 2 tan tan( 180 )
y1
o x2
x1
x
y y y y 2 1 2 1 k tan x x x x 1 2 2 1
x
设 1 ,则 ,于是 的坐标为( 1 , 1 ) . y 1 x A 1 1
1
l2
过原点及 ( 1 , 1 )的直线即为 l1, A 1 如图所示 .
说明:也可设其它特殊点
巩固与测试
1. 判断正误: ①因为所有直线都有倾斜角,所以所有直线都有斜率。
( ) ( ) ( )
②因为平行于y轴的直线的斜率不存在,所以平行于y轴的直线
4、斜率公式:
y y y y 2 1 1 2 k ( 或 k ) x x x x 2 1 1 2
作
P89
业:
习题3.1 A组:1.2 B组:5
x
p
x
o
l x
l
= 0°
k=0
0°< < 90°
= 90° 90°< <180°
k不存在 k<0
k >0
应用与实践
例1
如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC, CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
y
A(3,2) B(-4,1),
O
C(0,-1)
小结:
1、直线的倾斜角定义及其范围: 0 180 ( 90 ) 2、直线的斜率定义: ktan 3、斜率k与倾斜角 之间的关系: 0 k tan0 0
直线的倾斜角与斜率讲义 ppt课件

8
日常生活中,还有没有表示倾斜程度的量?
坡度
铅直高度 水平长度
升
高
量
前进量
ppt课件
9
结论:坡度越ppt课件大,楼梯越陡. 10
直线的斜率定义 倾斜角不是 90 的直线,它的倾斜角的正
切值叫做这条直线的斜率,通常用 k 表示,即
练习一
k=tan .
已知直线的倾斜角,求对应的斜率 k :
ppt课件
14
y
如图,α为锐角
y2
P2 (x2, y2 )
y1
Q(x2, y1)
P2P1Q,
P1(x1, y1)
o x1
x2 x
在RtP2P1Q中
k
tan
tan P2P1Q
QP2 P1Q
y2 x2
y1 x1
ppt课件
15
如图α为钝角,
180 ,
y tan tan(180 )
(2).过点C的直线 l 与线段AB有公共点, 求 l 的斜率k的取值范围
y
解:(1)k AB
1 2 4 3
1 7
锐角
B
A
kBC
1 1 0 (4)
1 2
钝角
O
x
kCA
1 2 03
1
锐角
C
(2)k [1,+) (-,- 1]
2
ppt课件
20
例题分析
例2、在平面直角坐标系中,画出经过原点且斜率
y
直线向上的方向
A
B
1
3.1.1解析几何的产生;直线的倾斜角和斜率
1.若直线的斜率存在,则必有唯一的倾斜角 与之对应.
2.若直线的倾斜角存在,则必有唯一的斜率 与之对应.
3.若直线的倾斜角为 ,则直线的斜率为 tan.
(1)如果直线 l1的斜率为0,l1 l2 ,那
么直线 l2 的斜率怎样?
(2)如果直线 l 的斜率 k 的范围是 0 k 1
那么它的倾斜角的范围是什么?
y
a o
注意: (1)直线向上方向; (2)X轴的正方线和x轴平行或重合时, 它的倾斜角为0°.
问题:下列图中标出的直线的倾斜角对不
对?如果不对,违背了定义中的哪一
条?
y
y
y
y
o x
o
x o
x
o
x
(1)
(2)
(3)
(4)
规定,直线向上的方向与x轴的正方向所 成的最小正角叫做这条直线的倾斜角。
新 课
直线的倾斜角与斜率
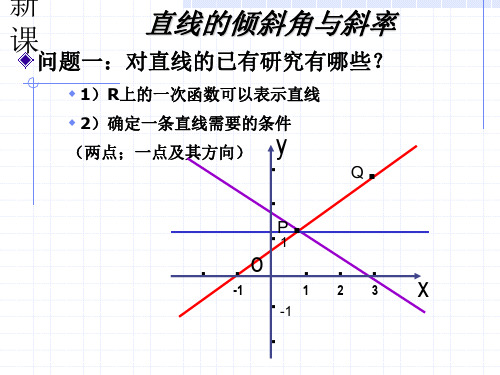
问题一:对直线的已有研究有哪些?
1)R上的一次函数可以表示直线
2)确定一条直线需要的条件
y (两点;一点及其方向)
Q.
.. ...
P.
1
. .o . . .
-1
x 1 2 3
-1
1、直线的倾斜角
直线倾斜角的定义:
当直线L与X轴相交时,我们取X轴作 为基准,X轴正向与直线L向上方向之间 所成的角叫做直线的倾斜角
B
2、直线的斜率
倾斜角不是90°的直线,它的倾斜角的正切 叫做这条直线的斜率。斜率通常用k表示,
即: k tan
当 =0°时, k 0
当00< < 90°时, k 0
当 =90°时, k不存在(直线存在)
当900< <180°时, k 0
2.若直线的倾斜角存在,则必有唯一的斜率 与之对应.
3.若直线的倾斜角为 ,则直线的斜率为 tan.
(1)如果直线 l1的斜率为0,l1 l2 ,那
么直线 l2 的斜率怎样?
(2)如果直线 l 的斜率 k 的范围是 0 k 1
那么它的倾斜角的范围是什么?
y
a o
注意: (1)直线向上方向; (2)X轴的正方线和x轴平行或重合时, 它的倾斜角为0°.
问题:下列图中标出的直线的倾斜角对不
对?如果不对,违背了定义中的哪一
条?
y
y
y
y
o x
o
x o
x
o
x
(1)
(2)
(3)
(4)
规定,直线向上的方向与x轴的正方向所 成的最小正角叫做这条直线的倾斜角。
新 课
直线的倾斜角与斜率
问题一:对直线的已有研究有哪些?
1)R上的一次函数可以表示直线
2)确定一条直线需要的条件
y (两点;一点及其方向)
Q.
.. ...
P.
1
. .o . . .
-1
x 1 2 3
-1
1、直线的倾斜角
直线倾斜角的定义:
当直线L与X轴相交时,我们取X轴作 为基准,X轴正向与直线L向上方向之间 所成的角叫做直线的倾斜角
B
2、直线的斜率
倾斜角不是90°的直线,它的倾斜角的正切 叫做这条直线的斜率。斜率通常用k表示,
即: k tan
当 =0°时, k 0
当00< < 90°时, k 0
当 =90°时, k不存在(直线存在)
当900< <180°时, k 0
直线的倾斜角和斜率PPT完美课件

*
4
下列哪些说法是正确的( E、F)
A 、任一条直线都有倾斜角,也都有斜率
B、直线的倾斜角越大,斜率也越大
学科网,zxxk.fenghuangxueyi
C 、平行于x轴的直线的倾斜角是0或π
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
F 、直线斜率的范围是R
•
2对教育来说,阅读是最基础的教学手 段,教 育里最 关键、 最重要 的基石 就是阅 读。
•
3但是现在,我们的教育在一定程度上 ,还不 够重视 阅读, 尤其是 延伸阅 读和课 外阅读 。
•
4. “山不在高,有仙则名。水不在深 ,有龙 则灵” 四句, 简洁有 力,类 比“斯 是陋室 ,惟吾 德馨” ,说明 陋室也 可借高 尚之士 散发芬 芳
•
10保尔身上的人格特征或完美的精神 操守: 自我献 身的精 神、坚 定不移 的信念 、顽强 坚韧的 意志
•
11把记叙、描写、抒情和议论有机地 融合为 一体, 充满诗 情画意 。如描 写百草 园的景 致,绘 声绘色 ,令人 神往。
•
12简·爱人生追求有两个基本旋律:富 有激情 、幻想 、反抗 和坚持 不懈的 精神; 对人间 自由幸 福的渴 望和对 更高精 神境界 的追求 。
3.1 直线的倾斜角和斜率
*
1
复习回顾
一次函数的图象有何特点? 给定函数y=2x+1,如何作出它的图像?
一般地,一次函数y=kx+b的图象是一条 直线,它是以满足y=kx+b的每一对x、y的值 为坐标的点构成的.
*
2
问题:在直角坐标系中,过点P的一条直线 绕点P旋转,不管旋转多少周,他对 x轴的相对位置有几种情形,请画出 来?
3.1.1-2直线的倾斜角与斜率PPT课件

直线的倾斜角与 斜率(2)
在平面直角坐标系中,当直线l与x轴相交 时,取x轴作为基准, x轴正向与直线l向上方 向之间所成的角α 叫做直线l的倾斜角.
倾斜角不是900的直线,它的倾斜角的正切叫做 这条直线的斜率,常用k来表示.
经过两点P1(x1, y1), P2 (x2, y2 )的直线的斜率公式:
(1)若 1 k<1,求的范围
(2)若 < 3 ,求k的范围
4
4
点评:1、已知斜率k的范围,求倾斜角范围时,
从0点断开分类讨论.
2、已知倾斜角范围,求斜率k的范围时,
从900断开分类讨论.
例5,过点P(2,-1)作直线L与线段AB有 公共点,A(-3,4),B(3,2)
(1)求直线l倾斜角的范围.
(2)求直线l的斜率k的范围.
4.判断正误:
(1)直线的倾斜角为,则直线的斜率为tan;( X )
(2)直线的斜率值为tan,则直线的倾斜角为;( X )
(3)因为所有的直线都有倾斜角,故所有的直线都有
斜率;( X )
(4)因为平行于y轴的直线斜率不存在,所以平行于y
轴的直线的倾斜角不存在;( X )
直线AB、BC、CA的斜率,并判断这 些直线
的倾斜角是什么角?
y.
解:
B
.A
直线AB的斜率
k AB
22 84
0
.
.
. . o.
.
.
.
x
直线BC的斜率
kBC
22 0 (8)
4 8
1 2
C
直线CA的斜率
kCA
2 (2) 40
4 4
1
∵ kAB 0 ∴直线AB的倾斜角为零度角。
在平面直角坐标系中,当直线l与x轴相交 时,取x轴作为基准, x轴正向与直线l向上方 向之间所成的角α 叫做直线l的倾斜角.
倾斜角不是900的直线,它的倾斜角的正切叫做 这条直线的斜率,常用k来表示.
经过两点P1(x1, y1), P2 (x2, y2 )的直线的斜率公式:
(1)若 1 k<1,求的范围
(2)若 < 3 ,求k的范围
4
4
点评:1、已知斜率k的范围,求倾斜角范围时,
从0点断开分类讨论.
2、已知倾斜角范围,求斜率k的范围时,
从900断开分类讨论.
例5,过点P(2,-1)作直线L与线段AB有 公共点,A(-3,4),B(3,2)
(1)求直线l倾斜角的范围.
(2)求直线l的斜率k的范围.
4.判断正误:
(1)直线的倾斜角为,则直线的斜率为tan;( X )
(2)直线的斜率值为tan,则直线的倾斜角为;( X )
(3)因为所有的直线都有倾斜角,故所有的直线都有
斜率;( X )
(4)因为平行于y轴的直线斜率不存在,所以平行于y
轴的直线的倾斜角不存在;( X )
直线AB、BC、CA的斜率,并判断这 些直线
的倾斜角是什么角?
y.
解:
B
.A
直线AB的斜率
k AB
22 84
0
.
.
. . o.
.
.
.
x
直线BC的斜率
kBC
22 0 (8)
4 8
1 2
C
直线CA的斜率
kCA
2 (2) 40
4 4
1
∵ kAB 0 ∴直线AB的倾斜角为零度角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当x1=x2, y1= y2(即直线与x轴垂直)时, 直线的倾斜角等于90°,没有斜率.
例1、已知A(4,2)、B(-8,2)、C(0,-2), 求直线AB、BC、CA的斜率,并判断这些 直线的倾斜角是什么角?
例2 求证:A(-2,8) B(3,-2) C(1,2) 三点在同一直线上.
例3 直线l的倾斜角 [ , )( , ], 4 2 2 4 求斜率k的范围。
11.(北京高考)若三点A(2,2),B(a,0),C(0,b),(ab≠0)共线, 则 1 1 的值等于________. 1 a b 2
解析 : A、B、C三点共线, 02 b2 k AB k AC , 即 , a2 02 即 a 2 b 2 4, ab 2a 2b, ab 0, 2 2 1 1 1 1, . b a a b 2
当 =0°时,
k tan
k 0
当00<
90°时, k 0 <
k不存在(直线存在)
当
=90°时,
当900<
<180°时, k 0
倾斜角不是90°的直线,它的倾斜角的正切 叫做这条直线的斜率。斜率通常用k表示,
k tan
(k R)
1. k是一个实数. 每条直线都存在唯一的倾斜角, 但不是每条直线都存在斜率; 2. 由正切函数的单调性, 倾斜角不同的直线,其斜率也不同; 斜率不同的直线,其倾斜角也不同。
特别地,当直线和x轴平行或重合时, 它的倾斜角为0°.
问题:下列图中标出的直线的倾斜角对不 对?如果不对,违背了定义中的哪一 条?
y y y y
o
x
o
x
o
(3)
x
o
(4)
x
(1)
(2)
规定,直线向上的方向与x轴的正方向所 成的最小正角叫做这条直线的倾斜角。 特别地,当直线和x轴平行或重合时, 它的倾斜角为0°。 倾斜角的取值范围是: 0°≤
3
例4. 已知两点A(2,3)、B(3,0),过点 P(-1,0)的直线与线段AB有公共点.求直线 的斜率k的取值范围.
若B(-3,1), B(3,-1),则k的取值范围为?
1、下列命题中真命题是( D ) A、倾斜角为的直线的斜率为tan B、斜率为tan的直线倾斜角为 C、斜率为0的直线倾斜角为0或 D、斜率小于0的直线倾斜角为钝角
直线的位置
我们知道,两点确定一条直线。
y
过一点O的直线可以作无数条, 可以用直线与X轴的夹角来描述 它们的倾斜程度
x
o
一点能确定一条 直线的位置吗?
1、直线的倾斜角
直线倾斜角的定义:
当直线L与X轴相交时,我们取X轴作 为基准,X轴正向与直线L向上方向之间 所成的角叫做直线的倾斜角
y
l
a
x o
注意: (1)直线向上方向; (2)X轴的正方向。
<180°
坐标平面上任何一条直都有唯一的倾斜角。
思考:
日常生活中,还有没有表示倾斜程度的量?
如图,日常生活中,我们经常用“升高量与前 进量的比”表示倾斜面的“坡度”(倾斜程 度),即
升高量 坡度 前进量
A
D
C 升
前进量
高பைடு நூலகம்量
B
2、直线的斜率
倾斜角不是90°的直线,它的倾斜角的正切 叫做这条直线的斜率。斜率通常用k表示, 即:
么直线
l2 ,那
l 2 的斜率怎样? (2)如果直线 l 的斜率 k 的范围是 0 k 1
那么它的倾斜角的范围是什么?
(3)直线的倾斜角越大,它的斜率就越大?
例1:直线
l1 的倾斜角 1 =30°, 直线 l2 l1,求 l1 , l 2 的斜率。
BAD=60°,
D
例2:如图所示菱形ABCD中,
12.(2008·浙江)已知a>0,若平面内三点A(1,a),B(2,a2),C(3,a3)共线,则a=________. 1 2
a 2 a a3 a 解析 :由题意可得 , 化简得a(a2 2a 1) 0, 2 1 3 1 a 0或a 1 2. a 0, a 1 2.
倾斜角不是90°的直线,它的倾斜角的正切 叫做这条直线的斜率。斜率通常用k表示,
判断:
k tan
1.若直线的斜率存在,则必有唯一的倾斜角 与之对应. 2.若直线的倾斜角存在,则必有唯一的斜率 与之对应. 3.若直线的倾斜角为 ,则直线的斜率为 tan .
(1)如果直线 l1 的斜率为0, 1 l
求菱形ABCD各边和两条对角线所在直线的
倾斜角和斜率。
o
y
C
x
A
B
3、斜率公式 直线过P1(x1,y1), P2(x2,y2)两点,则
y2 y1 k x2 x1
y2 y1 y1 y2 k x2 x1 x1 x2
斜率公式与两点的顺序无关; 斜率公式表明:直线对于x轴的倾斜程度, 可以通过直线上任意两点的坐标表示, 而不需求出直线的倾斜角,使用比较方便;
