Ch8_杆类构件静力学设计
河海大学 材料力学第八章 杆类构件静力学设计第五节
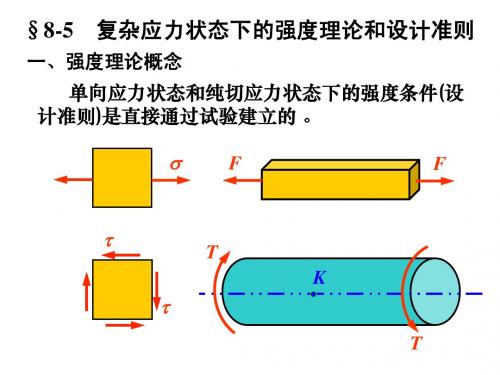
极限曲线和许用极限曲线 极限应力圆 t 极限曲线 单向压缩
许用极限曲线
t s uO
纯剪切
s u+
s
[su-]
s
O
[su+ ]
单向拉伸
简化的许用极限曲线
简化:用单向拉、压的极限应力圆代替一组极限应力 圆,并用这两个圆的公切线代替包络线作为极限曲线 [s ] 经推导,得强度条件: s 1 s 3 [s ] [s ]
1 s r4 [(s 1 s 2 )2 (s 2 s 3 )2 (s 3 s 1 )2 ] 2 [s ] s rM s 1 s 3 [s ]
说明: 相当应力没有任何物理意义。(为表示方便引进的量)
六、强度理论的选用 (1)一般情况
脆性材料:第一强度理论或莫尔强度理论;
屈服判据:vd = (vd) u
1 [(s 1 s 2 )2 (s 2 s 3 )2 (s 3 s 1 )2 ] s s 2
强度条件:
1 [(s 1 s 2 )2 (s 2 s 3 )2 (s 3 s 1 )2 ] [s ] 2
适用情况: 能很好地描述碳素钢、合金钢;铜、镍、铝的屈服 优点: 全面考虑了三个主应力的影响,比较合理,比最大切 应力理论更符合实验结果。计算结果偏于经济。 缺点:形式较复杂。
四、莫尔强度理论
莫尔强度理论是通过莫尔应力圆表述的。 1、通过试验,确定在不同的主应力比值(s1/s3 )下失 效时的主应力值(s10、s30) ; 2、根据s10、s30 作失效时的应力圆(极限应力圆); 包括单向拉伸、单向压缩、纯切应力状态 3、作这些应力圆的包络线(envelope),得两根曲线 ——极限曲线 4、失效判据——任何应力状态所对应的应力圆,如 果与上述极限曲线相接触,材料便产生屈服或剪断。 5、将各种应力状态下失效时的s10、s30 除以相同的 安全系数,得到许用极限曲线
机械基础杆件的静力分析

机械基础杆件的静力分析1. 引言在机械领域中,杆件是一种常见的结构元素,用于构建各种机械装置。
静力分析是对杆件在静力作用下的力学性能进行分析和计算的过程。
本文将介绍机械基础杆件的静力分析方法,包括受力分析、应力分析和变形分析。
2. 受力分析在进行静力分析之前,首先需要进行受力分析,确定杆件上受到的外力和内力。
外力可以是来自其他结构物的载荷,也可以是外部施加的力或力矩。
内力则是由于外力作用而在杆件内部产生的应力引起的。
通过受力分析,可以获得各个杆件的受力情况,为后续的应力分析和变形分析提供依据。
3. 应力分析应力分析是静力分析中的重要环节。
通过对杆件内部的应力进行分析,可以确定杆件是否能够承受外力载荷,以及破坏的可能性。
应力分析包括两个方面:正应力和剪应力的计算。
正应力是指沿着杆件截面法线方向的应力,而剪应力则是沿着截面平面方向的应力。
常用的应力计算方法包括静力学平衡条件和材料力学方程。
3.1 正应力的计算正应力的计算通常采用静力学平衡条件。
根据平衡条件,杆件上各点的合力和合力矩为零。
通过求解这些方程,可以得到各点处的正应力分布。
此外,还需要考虑杆件的几何形状,以及材料的弹性模量和截面面积等参数。
正应力的计算公式如下:σ = F / A其中,σ是正应力,F是受力,A是截面面积。
3.2 剪应力的计算剪应力的计算也采用静力学平衡条件。
剪应力可以通过应力矢量的分解得到。
假设剪应力的作用平面为x-y平面,剪应力的计算公式如下:τ = F / A其中,τ是剪应力,F是受力,A是截面面积。
4. 变形分析变形分析是对杆件在受力作用下产生的变形进行分析和计算的过程。
变形分析的目的是确定杆件的位移和变形程度,评估其结构稳定性。
常用的变形计算方法包括位移方法和位移曲线法。
4.1 位移方法位移方法是根据杆件的几何形状和受力情况,通过求解位移方程来计算杆件的位移量。
位移方程的求解需要考虑杆件的几何形状、材料的弹性模量和截面惯性矩等参数。
单自由度八杆起背机构的设计与研究

单自由度八杆起背机构的设计与研究单自由度八杆起背机构的设计与研究一、引言八杆起背机构是一种常见的机械结构,具有结构简单、运动特点明确等优点。
而单自由度八杆起背机构则是在八杆起背机构的基础上增加了一个约束,使其整体只能做一个自由度的运动。
本文将探讨单自由度八杆起背机构的设计与研究。
二、八杆起背机构的结构和运动八杆起背机构是由八个连杆构成的机械结构。
每个连杆都通过铰链连接,使其能够相对运动。
在该结构中,分为两组对称的连杆,分别为上下连杆组和左右连杆组。
两组连杆组通过一个铰链连接在一起,并且相对对称。
该结构的运动特点是,左右连杆组同时以相同的速度和相同的方向旋转,上下连杆组也同时以相同的速度和相同的方向旋转。
这样,整个机构的运动能够通过该运动特点来实现。
三、单自由度八杆起背机构的设计单自由度八杆起背机构在八杆起背机构的基础上引入了一个额外的约束,使其整体只能做一个自由度的运动。
这样,机构的运动范围将会更加受限,但能够更好地适应特定的工况要求。
设计单自由度八杆起背机构时,需要确定约束的位置和方式。
一个常见的约束方式是在两组连杆组的交点处添加一个铰链连接,使其成为一个固定点。
这样,整个机构就只能以该固定点为中心做旋转运动。
根据实际需求,可以对单自由度八杆起背机构的长度比例、连杆的材料等进行优化设计。
通过合理地选择连杆的材料和长度比例,能够使机构在运动过程中更加稳定,并且能够承受更大的载荷。
四、单自由度八杆起背机构的研究在进行单自由度八杆起背机构的研究过程中,可以借助计算机辅助设计软件进行模拟和分析。
通过对机构进行建模,并结合运动学和动力学的理论,可以准确地描述机构的运动过程和力学特性。
研究中还可以对机构的运动范围、载荷能力等进行分析。
通过对机构进行力学分析,可以确定机构在不同工况下的运动范围和力学性能。
这样能够更好地指导机构的设计和应用。
此外,还可以通过实验验证理论分析的结果。
构建实验装置,并进行运动学和动力学实验,收集数据并进行分析。
杆系结构的静力学分析

平面桁架的静力学分析摘要:本文利用有限元分析软件ANSYS12.0,对杆系结构——平面桁架进行静力学分析,通过将分析完成后得到的列表数据与解析解相比较确定ANSYS 分析软件的可靠性。
关键词:平面桁架,有限元,ANSYS1 前言实际结构都是空间结构,所承受的载荷也是空间的。
但是如果结构具有某种特殊形状,所承受的载荷具有某种特殊的性质,就可以将空间问题转化为杆系结构问题、平面问题等。
这样处理后,计算工作量大大减少,而所得到的结果仍可满足精度要求。
所谓杆系结构指的是有长度远远大于其他方向尺寸(10:1)的构件组成的结构,如连续梁、桁架、刚架等。
当结构承受不随时间变化的载荷作用时,需要进行静力学分析,分析其位移、应变、应力等。
2 问题描述及解析解图1为一平面桁架,长度L=0.1m ,各杆横截面面积均为24101m A -⨯=,力N P 2000=,计算各杆的轴向力a F 、轴向应力a σ。
图1 平面桁架根据静力平衡条件,很容易计算出轴向力a F 、轴向应力a σ,如表1所示。
3 有限元分析3.1建模与加载(1)创建单元类型GUI:PreProcessor Menu > Element Type > Add/Edit/Delete > Beam > 2D elastic 3单击“OK”按钮。
(2)定义单元实常数GUI:PreProcessor Menu > Element Type > Add/Edit/Delete > Add> OK在“AREA”文本框中输入1E-4,单击OK。
(3)定义材料属性GUI:PreProcessor > Material Props > Material models > Structural > Linear > Elastic >Isotropic在弹出对话框中键入EX=2e11(单位Mpa),PRXY=0.3。
第八章 强度刚度稳定性

二、失效判据:判别杆件能否正常使用的依据。
简单应力状态,例如单向应力状态和纯剪切应力状态,可根据材料 实验结果建立强度失效判据。复杂应力状态,应根据强度理论建立失效判据。
目录
三、设计准则
1.安全系数法:以安全系数的形式,包含种种变异和安全裕 度,将极限值打一个折扣后,作为许用值。 2.概率极限状态法 :在一定的置信概率下,确定许用值。
(2)如载荷 F 60kN ,试求两杆所需的最小截面积。
解: (3) 求杆的面积
max
FNmax A
FAB 0.732F 43 920N
FAB 0.517F 31 020N
AAC FAC 43 920 2 m 2.58 104 m 2 258mm 2 [ ] 170 106
Fb Fa
MC WzC
Fb 62.5 160 32 3 d 2 / 32 0.133
46.4 106 Pa 46.4MPa < [ ]
结论:轮轴安全
目录
例8-9 某车间欲安装简易吊车,大梁选用工字钢。已知电葫芦自重
F1 6.7kN, 起重量 F2 50kN, 跨度 l 9.5m, 材料的许用应力
2
(2)如载荷 F 60kN ,试求两杆所需的最小截面积。
解: (1) 求杆的内力 由节点C的平衡方程求得
FAC 0.732F
FBC 0.517F
(2) 建立强度条件
max
FNmax A
FAC 0.732F 400 170N
F 92 896N 92.9kN
ABC
FBC 31 020 2 m 1.82 104 m 2 182mm 2 [ ] 170 106 目录
8个构件课程设计

8个构件课程设计一、课程目标知识目标:1. 学生能掌握8个基本的构件概念,并能够识别和描述它们在生活中的应用。
2. 学生能理解各构件的性质、特点及其相互关系,形成知识网络。
3. 学生能运用构件知识解释简单物理现象,解决实际问题。
技能目标:1. 学生能够运用构件设计原则,进行简单的创意设计,培养创新思维。
2. 学生能够通过小组合作,进行构件组合和分解,提高团队协作能力。
3. 学生能够运用所学知识,分析并解决实际问题,提高问题解决能力。
情感态度价值观目标:1. 学生对构件知识产生兴趣,树立学习自信心,培养积极的学习态度。
2. 学生通过构件知识的学习,认识到科技与生活的紧密联系,增强社会责任感。
3. 学生在小组合作中,学会尊重他人,培养团结协作精神,树立正确的价值观。
课程性质:本课程为学科基础课程,旨在帮助学生建立构件知识体系,提高实践操作能力和创新思维能力。
学生特点:四年级学生具有一定的认知能力和动手操作能力,对新鲜事物充满好奇,喜欢探究和合作。
教学要求:结合学生特点,注重启发式教学,引导学生主动探究,提高学生的实践能力和综合素质。
在教学过程中,关注学生的个体差异,因材施教,使每个学生都能在原有基础上得到提高。
通过分解课程目标,为教学设计和评估提供具体依据。
二、教学内容本章节教学内容主要包括以下八个构件:梁、柱、板、壳、弹簧、轴承、齿轮和联轴器。
依据课程目标,教学内容分为以下三个部分:1. 构件基本概念与性质- 梁和柱的结构特点、受力分析及应用案例;- 板和壳的形态、稳定性及在建筑和工程中的应用;- 弹簧、轴承、齿轮和联轴器的功能、类型及在机械设备中的应用。
2. 构件的相互关系与组合- 构件间的连接方式、作用及影响;- 构件组合的方法、原则和实例;- 构件分解与重组的技巧和实践。
3. 构件在生活中的应用与创新- 分析生活中的构件应用案例,了解其原理和优点;- 结合实际,运用构件设计原则进行创意设计;- 探讨构件在科技创新和未来发展中的作用。
工程力学杆件设计方案

工程力学杆件设计方案一、设计背景随着工程技术的不断发展,工程力学杆件在各种机械设备、建筑结构和航空航天领域中扮演着重要的角色。
根据受力情况和使用环境的不同,杆件的设计要求也有所不同。
本设计方案将以一种典型的杆件为例,介绍其设计过程和关键点,以期为同类杆件的设计提供参考。
二、设计需求在工程实践中,常见到承受拉力或压力的杆件,为了保证杆件在使用过程中不会发生断裂或变形等破坏,其设计需满足以下基本要求:1. 强度要求:杆件应能够承受设计工况下的最大拉力或压力,且满足一定的安全系数。
2. 刚度要求:杆件的变形应该在允许范围内,不会对整个结构产生过大的影响。
3. 耐久性要求:杆件的设计应考虑其在使用寿命内的疲劳寿命和抗腐蚀性能。
三、设计流程1. 受力分析:首先要对杆件所受的力进行分析,包括静载和动载情况。
通过受力分析,确定最大的拉力或压力,以及杆件的受力部位。
2. 材料选择:根据要求的强度和刚度,选择合适的杆件材料,常用的材料有钢、铝、铜等。
3. 截面选型:根据受力分析的结果和材料特性,选择合适的杆件截面形状和尺寸,以满足强度和刚度的要求。
4. 结构设计:设计杆件的细节结构,包括连接方式、表面处理、防腐蚀等。
5. 荷载计算:计算杆件在不同工况下的受力情况,以确定结构设计的合理性。
6. 安全评估:对设计方案进行安全评估,检查其满足安全要求的程度。
7. 优化设计:根据评估结果对设计进行优化,以使其更加合理和安全。
四、设计关键点1. 受力分析:受力分析是杆件设计的第一步,其准确性对设计结果具有决定性的影响。
2. 材料选择:材料的选择直接影响到杆件的性能和成本,应根据实际情况合理选择。
3. 截面选型:截面形状和尺寸的选择对杆件的强度和刚度有重要作用,需仔细考虑。
4. 结构设计:结构设计要考虑杆件的受力部位和连接方式,以保证其整体性能。
5. 安全评估:安全评估是设计的最后关口,不能忽视其重要性。
五、设计实例以承受拉力的杆件为例,设计其具体方案如下:1. 受力分析:假设杆件所承受的最大拉力为100kN。
河海大学 材料力学第八章 杆类构件静力学设计第三节

t max
b
解:(1)求Mmax , FQmax Mmax= 100kN∙m FQmax = 80kN (2)根据正应力强度条件设计h, b 取 b= 100mm h= 200mm
3FQ max 2A = 6MPa [t ]
ห้องสมุดไป่ตู้
例:简支梁, [s ]=160MPa, [t ]=80MPa,E=200GPa, h=2b, [w]=l/500, [ ]=0.5°, 试根据强度、刚度条件设 计截面尺寸。 5ql 4 Fl 3 F=40kN q=30kN/m wmax 384 EI 48 EI h A B = 6.5mm < [w] 4m b ql 3 Fl 2 max 解:(1)求Mmax , FQmax 24 EI 16 EI (2)根据正应力强度条件设计h, b = 9×10−3rad 取 b= 100mm = 0.516° h= 200mm (3)校核切应力强度 < [ ] (4)校核刚度
§8-3 基本变形状态下杆件刚度计算
杆件的变形必须限制在一定的范围内(刚度要求) 机床主轴的挠度过大会影响加工精度;吊车梁若 变形过大,行使时会出现爬坡现象,并会产生较大 的振动,使吊车行使不平稳;传动轴在轴承处若转 角过大,会使轴承的滚珠产生不均的磨损,缩短轴 承的使用期。 一、刚度条件统一形式
D ≤ [D ]
M max s max [s ] F=40kN q=30kN/m Wz h A B 6 M max [s ] 2 4m bh b 3 M max 解:(1)求Mmax , FQmax [s ] 3 2b Mmax= 100kN∙m FQmax = 80kN 3 M max (2)根据正应力强度条件设计h, b b 3 2[s ]
河海大学 材料力学 第八章 杆类构件静力学设计第二节

要保证杆件安全而正常地工作,其最大工作应 力显然不能超过材料的极限应力。考虑到在实际使 用中存在的一些不利因素,如杆件可能承受超过设 计值的载荷,实际材料的极限应力可能小于试验结 果,计算时所取的计算简图可能不完全符合实际情 况,杆件尺寸制造不准确等等,以及还必需给杆件 必要的强度储备,因此设计时不能使杆件的最大工 作应力等于极限应力,而必须小于极限应力。
3、若材料的[s ] ≠ [s - ] (如铸铁等),以及中性轴不
是截面的对称轴,则需分别对最大拉应力和最大压 应力作强度计算。
4、对于实心截面杆,在一般受力情况下,正应力强 度起控制作用,不必校核切应力强度。但对于薄壁 截面,如焊接工字型钢梁,以及集中载荷作用在靠 近支座处,从而使梁的最大弯矩较小而最大剪力较 大等这些情况,则需要校核切应力强度。
z FA=10kN
yb
FB=110kN
8kN•m (+)
(–)
M图 (2)确定危险截面、危险点 危险截面:截面B, C
危险点:截面B和C上a、b两点
截面B
16kN•m
sa = 29.4MPa(拉) < [s +] sb = 87.0MPa(压) < [s -]
截面C
sa = 14.7MPa(压) < [s -] sb = 43.5MPa(拉) > [s +]
例:T型截面铸铁梁,Iz=26.1×10 6mm4,y1=48mm,
y2=142mm, [s +] =40MPa,[s -] =110MPa ,试校核 该梁的强度。 超过[s +] 8.75%,该梁不安全
40kN 200kN/m
工程力学中的静力平衡与杆件受力分析

工程力学中的静力平衡与杆件受力分析工程力学是研究物体在力的作用下所处的平衡状态的学科,其中包括静力学和动力学两个方面。
静力学研究物体在静止状态下力的平衡问题,而杆件受力分析则是静力学中的一个重要内容。
本文将探讨工程力学中的静力平衡与杆件受力分析的相关理论和应用。
一、静力平衡的基本原理静力平衡是物体处于静止状态下,受力之和为零的基本原理。
这里的力包括两种类型:作用力和约束力。
作用力是外界对物体施加的力,而约束力是物体内部各部分相互支撑的力。
根据静力平衡的原理,一个物体处于平衡状态时,所有的作用力和约束力合力为零,所有的作用力和约束力合力矩也为零。
为了更好地理解静力平衡原理的应用,我们以一个简单的例子来说明。
假设有一个悬挂在天花板上的铁链,我们想要确定铁链的受力情况。
首先,我们可以将链的一端用铁环固定在天花板上,然后将另一端用手持住。
在此过程中,悬挂链条的每个部分都受到拉力的作用,而在任何一个节点上,链条受力的合力必须为零,否则链条就无法保持平衡状态。
二、杆件受力分析的基本方法在工程力学中,杆件受力分析是一种常见的分析方法,它用于确定杆件上各个点的受力情况。
杆件通常是指细长、刚性的物体,可以是直杆、斜杆、梁等。
杆件的受力分析可以通过分析力的平衡条件来进行,其中包括平衡力的条件和力矩平衡的条件。
在进行杆件受力分析时,首先需要画出力的作用线和该作用力对应的受力点。
然后,根据静力平衡的原理,我们可以得到以下几个常用的受力分析方法:1. 方法一:杆件上的两个点只有两个未知受力当杆件上的两个点只有两个未知受力时,可以利用力的平衡条件求解出未知受力的大小和方向。
假设杆件上的两个点分别为A和B,未知受力为FA和FB。
根据力的平衡条件,我们可以得到以下等式:FA + FB = 0和FA × xA + FB × xB = 0,其中xA和xB分别为A和B到参考点O的距离。
通过解这两个方程,我们可以确定未知受力的大小和方向。
河海大学 材料力学第八章 杆类构件静力学设计第四节

Fcr ncr [ncr ] F
ncr——工作稳定安全系数
2、折减系数法 ——适用于截面设计
令
cr
cr n [ncr ]
[ncr ]
cr n [ ] [ncr ]
称为折减系数 0< ≤1(因cr≤u, n ≤ [ncr] )
由于cr和[ncr]都随柔度变化,所以j也随柔度变化。工 程上将材料的l ~ 的关系经过计算后制成表格供直接 查用,详见有关规范或手册。(表8-1)
F [ ] 解:折减系数法进行截面设计(试算法) A l (1)第1次试算(取 =0.5) ly =159
(2)第2次试算 取 =0.25
A
A
F A =2500mm2 [ ]
选取I16,A=2610mm2 iy=18.9mm
iy 查表8-1 l=150 =0.306 l=160 =0.272 l=159 =0.275
h 2 3
b
lz
ly
1 l
iz
=132.8
安全!
Oxz平面:两端固支 2=0.5
2l
iy
l z> l y π2 E Fcr=crA=26856N=268.56kN cr 2 =111.9MPa l Fcr (3)校核稳定性 n =5.37 >[ncr] F
2 3 在Oxy平面内失稳 lz>lP =100
例: 两压杆材料Q235, E=200GPa, 直径d =160mm,规定的 稳定安全系数[ncr]=3 ,试确定两杆的许用载荷。
解 (1)计算柔度
d i 4
F
1=1 2=0.5
l1
l2
ch08结构力学简明教程

第8章 影响线及其运用 教学提示:影响线主要是讨论静定结构和超静定结构内力(反力)的影响线的做法和运用。
它的理论依据主要是静力平衡方程和虚功原理。
影响线和内力图从图形的形状上看有些情况下是相似的,但实质上他们是完全不同的两个问题。
影响线是影响系数与荷载位置间的关系曲线,它与内力分布图是有区别的。
内力分布图是描述固定荷载作用下,内力沿结构各个截面的分布;而影响线是描述单位集中荷载在不同位置作用时对结构中某固定处某量的影响。
影响线可运用静力法和机动法来绘制。
根据影响线可以确定各种荷载作用时的影响值,并用以确定移动荷载的不利位置。
教学要求:影响线主要运用于有移动荷载作用的工程结构,比如桥梁、厂房中的一些移动起吊设备和移动荷载作用的特殊结构。
学生在学习影响线时首先必须掌握影响线的概念,学会用静力法和机动法绘制单跨静定梁、静定连续梁、静定桁架、简单刚架以及用机动法绘制超静定连续梁影响线的轮廓线。
对于由直线图形构成的影响线,还必须学会用影响线来确定临界荷载以及荷载的最不利位置。
8.1 移动荷载和影响线的概念前面各章讨论了结构在静止荷载作用下的计算方法。
这类荷载的大小、方向以及作用点在结构上的位置是固定不变的,因此,结构的反力和各处的内力及位移也是不变的。
但在工程中,有些结构除了承受上述恒定荷载外,还受到移动荷载的作用,例如吊车梁承受吊车荷载;桥梁承受车辆荷载;又如房屋楼面上的人群、货物或非固定的设备等可以任意布置的分布荷载,都属于活载的范围。
随着荷载作用点位置的变化,将引起结构的反力、内力和位移等这些量值的变化。
在设计结构时,需要知道在移动荷载的作用下.结构产生的某些量值的最大值,该值称为最大量值。
出现最大量值的荷载位置,称为最不利荷载位置。
本章的主要内容是研究结构的反力、内力和位移随荷载移动而变化的规律。
在这里不考虑荷载移动对结构产生的动力作用,因此仍属于静力计算问题。
结构在移动荷载作用下的状态将随荷载作用位置的不同而变化,这样,就需要解决以下新问题。
杆件的静力分析课件

胡克定律
胡克定律是杆件静力分析中常用的弹性力学定律之一,它表明杆件在弹性范围内 ,其应力和应变之间存在线性关系。
具体来说,胡克定律可以用公式表示为:σ=Eε,其中σ表示应力,E表示弹性模 量,ε表示应变。
01
杆件静力分析的步 骤和方法
确定约束和载荷
约束
约束是限制物体运动的外部条件 ,例如固定、滑动、滚动等。在 杆件静力分析中,需要明确杆件 所受的约束类型和约束条件。
总结词
等直杆在剪切力作用下会发生剪切变形,剪切力的大小与杆件的截面面积、材料属性等因素有关。
详细描述
当等直杆受到沿杆轴方向的剪切力作用时,杆件会发生剪切变形。在静力分析中,需要考虑剪切力的 大小、方向以及杆件的截面面积、材料属性等因素,以确定杆件是否能够承受剪切力而不发生剪切变 形或断裂。
01
杆件静力分析的软 件应用
有限元分析软件介绍
有限元分析软件是一种数值分析工具,用于模拟和分析复 杂的工程结构和现象。
它采用离散化的方法,将连续的结构或系统划分为有限个 小的单元,通过数学模型描述这些单元之间的相互作用关 系,并利用计算机进行数值计算和结果分析。
有限元分析软件在杆件静力分析中的应用
杆件静力分析是有限元分析的一 个重要应用领域,主要用于分析 杆件在静力载荷作用下的应力和
具体来说,对于一个处于平衡状态的杆件,其上任意一个微 元段上的受力都可以分解为切向力和法向力,切向力和法向 力分别满足切向力平衡和法向力平衡。
变形协调原理
变形协调原理表明杆件在受力变形后 ,其各部分之间的相对位置和形状仍 然保持协调。
在杆件静力分析中,变形协调原理通 常通过假设杆件在变形过程中保持连 续、光滑的曲线或曲面来实现。
01
工程力学中的杆件力学分析

工程力学中的杆件力学分析工程力学是工科中的一门重要学科,主要研究固体和结构的力学性能和力学行为。
其中,杆件力学是工程力学中的重要组成部分之一。
杆件力学主要研究杆件的受力和变形,对于工程结构的设计和分析具有重要意义。
本文将从杆件力学的基本原理、力学分析方法和应用案例三个方面,对工程力学中的杆件力学进行深入探讨。
一、杆件力学的基本原理在工程力学中,杆件是指长条形构件,具有一定的刚度和承载能力。
杆件力学的基本原理包括静力学平衡和杆件内力平衡两个方面。
静力学平衡是指杆件受力的平衡条件。
根据力的平衡条件,杆件受力的合力为零,同时受力矩也为零。
通过静力学平衡的原理,可以分析杆件受力的大小和方向。
杆件内力平衡是指杆件内部各截面的内力保持平衡。
在杆件上任意取一截面,根据内力平衡条件,杆件的截面上受力的合力为零,同时受力矩也为零。
通过杆件内力平衡的原理,可以分析杆件不同截面上的内力分布情况。
二、杆件力学的力学分析方法杆件力学的力学分析方法主要包括静力学分析和变形分析两个方面。
静力学分析是指通过力的平衡条件,分析杆件受力的大小、方向和作用点位置等。
通过应用牛顿第二定律和力的平衡条件,可以得到杆件受力的解析表达式。
同时,结合几何关系和几何约束条件,可以进一步求解杆件受力的具体数值。
变形分析是指通过应力和应变关系,分析杆件在受力作用下的变形情况。
通过应用胡克定律和杨氏模量等力学性质,可以得到杆件的应变表达式。
同时,结合几何关系和几何约束条件,可以进一步求解杆件的位移和变形。
三、杆件力学的应用案例杆件力学在实际工程中具有广泛的应用价值。
以下将介绍两个与杆件力学相关的应用案例。
首先是杆件的承载能力分析。
在工程设计中,需要对杆件的承载能力进行评估和验证。
通过应用杆件力学的原理和方法,可以计算杆件的受力情况,并判断杆件是否满足设计和使用要求。
其次是杆件的优化设计。
在工程实践中,经常需要对杆件进行优化设计,以提高结构的性能和经济性。
杆类构件静力学设计

第八章 杆类构件静力学设计
第一节 失效和失效判据 第二节 基本变形状态下杆件强度计算 第三节 基本变形状态下杆件刚度计算 第四节 压杆稳定性计算 第五节 复杂应力状态下的强度理论和设计准则 第六节 组合变形状态的强度刚度计算和综合举例 第七节 提高杆件承载能力的措施 第十节 杆件强度计算的可靠度方法
珍惜生活的脚步,因为人生不能重复。
材料力学 Mechanics of Materials
第一节 失效和失效判据
失效判据: 为了保证所设计的杆件能正常地使用而不失效,必 须根据所用材料性能,杆件受力状况、工程要求建立判断失效 的依据。
例如: 脆性材料在单向拉伸应力状态下,其强度失效判据为:
b 转动轴,刚度的失效判据为:
经济与安全的综合考虑。
Cherish steps of life, for life cannot be repeated.
珍惜生活的脚步,因为人生不能重复。
材料力学 Mechanics of Materials
第二节 基本变形状态下杆件强度计算 安全因数的选择
1、材料的素质,包括材料的均匀程度,质地好坏,塑性还是脆性; 2、载荷情况,包括对载荷的估计是否准确,静载荷还是动载荷; 3、实际构件简化过程和计算方法的精确程度; 4、零件在设备中的重要性,工作条件,损坏后造成后果的严重程度, 制造和修配的难易程度; 5、对减轻设备自重和提高设备机动性的要求。
确定安全因数要综合多方面的因素,很难做统一的规定。不过随 着人类对客观事物的认识的不断提高和完善,安全因数的选择必然日 益趋于合理。
Cherish steps of life, for life cannot be repeated.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
max
M xmax Wp
PART B 基本变形状态下的杆件强度计算
例8-2 传动轴如图所示,设材料的许用切应力[]=50MPa,轴的直 径100mm,转速n = 300rpm,试求该传动轴所能传输的功率。
3 FQ max max 2 A 3 98103 MPa 2 260 200
2.8MPa [ ]
a
FQ
+
M
98kN 18.6kN· m
+
不满足切应力强度要求,应重 新设计。
PART B 基本变形状态下的杆件强度计算
98kN 98kN
h b a 1.6m 2m
98kN
-
(2)两杆所需要的最小面积
B
AAC FN AC /[ ]
x
C
0.732 60000/ 170mm2 258.4mm2
F
ABC FN BC /[ ]
0.517 60000/ 170mm2 182.5mm2
FNBC x
FNAC
30 45
y
F
PART B 基本变形状态下的杆件强度计算
PART B 基本变形状态下的杆件强度计算
1、拉压杆的强度计算 拉压杆的特点是横截面上的正应力均匀分布,而且各点均 处于单向应力状态,因此对于等截面直杆其强度条件为:
FNmax A FNmax是杆中的最大轴力(内力)。
max
PART B 基本变形状态下的杆件强度计算
例8-1 图中所示的结构由两根杆 组成,设两杆材料相同,许用 拉应力[]=170MPa . (1)如AC杆的截面积为400mm2 , BC杆的截面积为 250mm2,试 求许用载荷[F]; (2)如载荷F=60kN ,试求两杆 所需的最小截面积。
P M x n / 9549 9800 300 / 9549 kW 307 .9kW
若将主动轮A与从动轮B的位臵互换,则所传递的功率增 大还是减少?是否有利?
PART B 基本变形状态下的杆件强度计算
3、梁的强度计算 一般情况下梁的各个横截面上既有剪力又有弯矩,因此必 须要进行正应力强度计算和切应力强度计算,对于等截面梁, 其基本公式是:
主讲教师:楼力律
第八章 杆类构件静力学设计
2007年4月
欢迎访问河海大学机电工程学院基础力学教学网
第八章 杆类构件静力学设计
本部分主要内容
• • • • • • • • 失效和失效判据 基本变形状态下杆件强度计算 连接件的强度计算(剪切和挤压实用计算) 基本变形状态下杆件刚度计算 压杆稳定性计算 复杂应力状态下的强度理论和设计准则 提高杆件承载能力的措施 构件中含裂纹时的断裂设计准则*
PART A 失效和失效判据
安全因(系)数法
对于塑性材料:
s
ns
对于脆性材料:
b
nb
上面两式中,大于1的因数ns或nb称为安全因数。
把许用应力[]作为构件工作应力的最高限度,即要 求工作应力不能超过许用应力[]
PART A 失效和失效判据
安全因(系)数法
PART A 失效和失效判据
安全因数的选择
目前一般机械制造中[参考《安
全系数和许用应力》,机械工业出版社,1981],
在静载情况下,对塑性材料可 取ns=1.2~2.5, 脆性材料均匀性
较差,且断裂突然发生,有更
大的危险性,所以取nb=2~3.5 甚至3~9。
第八章 杆类构件静力学设计
PART B 基本变形状态下的杆件强度计算
y A
30 45
B
C
x
F
PART B 基本变形状态下的杆件强度计算
y A
30 45
(1)求许可载荷[F]
B
对节点C受力分析
x
Fx 0 FN BCsin45 FN ACsin30 0
C
F
y
0 FN BCcos45 FN AC cos30 F 0
F
FNAC
T/2 T A B
T/2 C
PART B 基本变形状态下的杆件强度计算
T/2 T A B T/2 C
画出扭矩图,如图所示
(1)求出传动轴所能承受的最大扭矩。
x
Mx
- -
M x max [ ]Wp
50 π 1003 / 16N mm 9.8kN m
T/2
T
(2)求传动轴所能传输的功率。显然,该传动轴的最大扭矩发 生在AB段内,其值与外力偶矩T相同
FQ
+
M
98kN 18.6kN· m
+
-
b
3 3 h 2.6 10 2 mm 1.95 10 2 mm , 取为200 mm 4 4
PART B 基本变形状态下的杆件强度计算
98kN 98kN
h b a 1.6m 2m
98kN
-3)切应力强度校核。根据所 源自尺寸,校核切应力是否满足 强度条件。
h b a 1.6m 2m a
PART B 基本变形状态下的杆件强度计算
基本思路:
按照正应力强度设计截面尺寸
98kN
98kN
h b
切应力强度校核
a
1.6m 2m
a
满足强度条件
不满足强度条件
按照切应力强度设计尺寸
设计结果
PART B 基本变形状态下的杆件强度计算
98kN 98kN
1)画出剪力图和弯矩图
a
4)按切应力强度条件设计截面 尺寸。根据切应力强度条件有 3 Qmax A 2 [ ] 3 98103 mm2 5.88104 mm2 2 2.5
一般应力状况,其强度失效判据必须根据强度理论来建立。
PART A 失效和失效判据
有了失效判据,则根据不同的设计理论建立不同的设计准则。
目前设计理论主要有: 安全因(系)数法
概率极限状态法(可靠度方法)
PART A 失效和失效判据
安全因(系)数法
脆性材料断裂时的应力是强度极限b, 塑性材料到达屈服 时的应力是屈服极限s,这两者都是杆件失效时的极限应力。 为保证杆件具有足够的强度,在载荷作用下的实际应力 (工作应力)显然应当低于极限应力。 强度计算中,以极限应力除以大于1的因数,并将所 得到的结果称为许用应力(容许应力),用[]表示。
PART B 基本变形状态下的杆件强度计算
杆件在基本变形下,危险点处一般只有正应力或切应力, 因此只要使用以下两式就可以进行强度计算:
max
max
根据工程要求的不同,强度计算一般有以下类型:
强度校核: 验证危险点的工作应力是否满足强度条件;
截面设计: 根据强度条件设计杆件的横截面尺寸; 许用载荷确定: 确定杆件或结构所能承受的最大载荷; 材料选择: 根据安全、经济的原则以及工程要求,选择合理 的材料。
从安全的角度考虑,加大安全因数,降低许用应力,这就 难免要增加材料的消耗和机器的重量,造成高成本和浪费; 从经济的角度考虑,减小安全因数,提高许用应力,可以 少用材料,减轻自重,但是又有损于安全。 经济与安全的综合考虑。
PART A 失效和失效判据
安全因数的选择
1、材料的素质,包括材料的均匀程度,质地好坏,塑性还是脆性; 2、载荷情况,包括对载荷的估计是否准确,静载荷还是动载荷; 3、实际构件简化过程和计算方法的精确程度; 4、零件在设备中的重要性,工作条件,损坏后造成后果的严重程度, 制造和修配的难易程度; 5、对减轻设备自重和提高设备机动性的要求。 确定安全因数要综合多方面的因素,很难做统一的规定。不过随 着人类对客观事物的认识的不断提高和完善,安全因数的选择必然日 益趋于合理。
x
C
F 92896 N 92.9kN
F
FNBC 0.517F ABC 250170N
FNBC x
FNAC
30 45
y
F 82205 N 82.2kN
因此,结构的许可载荷为:
F 82.2kN
F
PART B 基本变形状态下的杆件强度计算
y A
30 45
PART A 失效和失效判据
失效判据: 为了保证所设计的杆件能正常地使用而不失效,必 须根据所用材料性能,杆件受力状况、工程要求建立判断失效 的依据。
例如: 脆性材料在单向拉伸应力状态下,其强度失效判据为: b 转动轴,刚度的失效判据为:
其中, 为工程中规定的允许值。
max
M max W
max
* FQ max S z
I zb
PART B 基本变形状态下的杆件强度计算
3、梁的强度计算
1) []是弯曲许用正应力,作为近似,可取为材料在轴向拉压时 的许用正应力。 2) 必须根据弯矩图和剪力图综合判断危险面,然后再确定危险 点。梁上可能存在三种危险点:正应力最大的点;切应力最大 的点;正应力和切应力都比较大的点。 3)若材料的许用拉应力和许用压应力不相等(如铸铁等脆性材 料),以及中性轴不是截面的对称轴,则需分别对最大拉应力 和最大压应力作强度计算。 4)对于实心截面杆,在一般受力情况下,正应力强度起控制作用, 不必校核切应力强度。但对于薄壁截面,如焊接工字型钢梁, 以及集中载荷作用在靠近支座处,从而使梁的最大弯矩较小而 最大剪力较大等这些情况,则需要校核切应力强度。
PART A 失效和失效判据
安全因数的选择
许用应力和安全因数的数值(或原则),可在有关业务部 门的一些规范中查到。 例如: 在齿轮的承载能力计算(ISO6336-1)中关于齿轮的安全 因数提到: An appropriate probability of failure and the safety factor shall be carefully chosen to meet the required reliability at a justifiable cost. If the performance of the gears can be accurately appraised through testing of the actual unit under actual load conditions, a lower safety factor and more economical manufacturing procedures may be permissible.
