大学收费问题数学建模论文
2008B大学学费问题2008数学建模国家一等奖论文

C = Ri [G *Q *(1− b)] + (1.0502x1 −1.1959x2 −1.3108x3 −1.3636x4 − 0.7929x5) * Ri * b ;
由此便可得到综合学费标准 C 的取值范围。然后,我们随机选取了同一区域不 同专业,并根据表达式计算这些专业的学费,结果发现对社会收益大,个人收益 小的专业如地质学的学费范围为:3469.8~3506.3 元之间;对社会收益小,个人 收益大的专业如广告设计的学费范围为:7931.0~8014.5 元之间。与通常高校实 现的一刀切政策有了明显的优点。
获得这两个基本原则,我们从影响普通高校学费能力的众多因素中选取全国
人均 GDP 和学生就读的专业这两个基本因素进行研究,通过建立相关模型确
定这两个因素的权重系数,
2、模型的准备
根据查询国家统计局显示的数据资料[7],我们搜集到从 1995 年到 2004 年间
我国普通高校生均学费和人均 GDP 的值如表 5. 1 所示:
从中国的国情出发,收集诸如近几年来关于我国教育经费方面的及家庭收入 等数据[1-4],并通过分析数据建立数学模型,就几类学校或专业的费用标准进行 定量分析,并从中得出明确、有说服力的结论。
二、 问题分析
(一)我国教育收费的现状
通过国家统计局相关资料检索得到 2000 年到 2005 年我国普通高等学校教育
151828
172775
278253
256375
215440
210796
学费和杂 费 1926109 2824417 3906526 5057307 6476921 7919249
其他教育经费 1677772 2158574 2840985 3220992 3785362 4662641
高等教育的学费标准制定问题数学建模范文

摘要
高等教育的学费收取问题牵涉到国家、学校、家庭(或学生)三方的利益,学费的过高或者过低,都会造成三方利益的矛盾,所以要制定一个合理的学费收取标准,就必须使三方都尽可能达到满意。首先,我们收集了大量的数据,通过分析发现学生的培养成本在很大程度上与学费呈正相关性,其次考虑到不同地区、不同教育层次、不同档次的学校的不同的专业对一个学生的培养费用是不同的,在计算培养费用时进行了分类统计,同时在处理贫困生的学费问题时将奖、助学金等也作为培养成本的一个重要因素。然后根据学费、人均培养成本、家庭收入以及国家生均拨款等之间的联系建立了一个兼顾三方利益的多目标规划模型,求解时利用隶属度关系转化为单目标规划,通过几类地区的实际数据计算验证,与实际较为吻合,在保证教学质量的基础上使国家、学校和家庭达到了一种利益的平衡。最后根据建模过程和结果为管理部门提供了关于高校收费问题的合理化的建议。
2问题的分析
高等教育总经费由政府财政拨款、学校自筹、社会捐赠和学费收入等几部分组成。要提高教育,就必须有经费作保障,也就是说,一方面,国家必须拨款给学校,家庭(或学生)必须交学费给学校,同时还有一些企业单位会向学校提供一些捐助,而对于国家、家庭所关注的重点分别是教育质量的提高和教育的公平、教育质量的提高和能否支付得起高等教育的费用。国家的满意度如何和学费建立关系。我们通过分析,一般地,不同层次的教育的投入成本越多其相应的收益越大,教育质量就越高,即教育质量和投入成本有正相关性[1]。
我们通过数据资料的查找及对2003年至2007年的数据进行处理得到表3:
表3在教育层次和学校类别等都相等的条件下的不同地区的生均成本
地区
生均成本
A地区
B地区
C地区
总计
生均培养成本
关于高等教育收费标准的数学模型

教育收费问题的探讨及其数学模型摘要持续稳健地推动我国高等教育体制改革是我国21世纪社会经济发展的重大课题。
为了能够更好更快地发展我国的高等教育事业,希望高等教育收费有较为合理的评判标准。
影响高等教育收费的因素有很多,本文通过线性模型、抽样调查以及层次分析法,分别对区域人均可支配收入、学校类型、不同专业等三方面对学费的影响进行分析。
结果表明区域人均可支配收入、学校类型、不同专业等三方面因素对学费的影响有各自的特点。
最后,本文通过定量分析得到影响高等教育收费标准的主要因素,并给出具有一定参考价值的建议。
关键字: 高等教育收费;影响因素;线性模型;抽样调查;层次分析法;权重。
Study And Mathematical Model Of Tertiary Education Tuition SystemAbstractPromoting the reformation of tertiary education system continuously and steady is the major task of social and economic development in our country in 21st century. In order to develop better and faster , tertiary education fees charging system has to build reasonable standards. Many factors can affect the fees charging system . For example, through linear model, sampling survey and analytic hierarchy process, this article analyses the effects on tuition fees from three aspects , disposable income area per capita , institustion type and major differences. The result, indicates that disposable income area per capita , institustion type and major differences can affects tuition fees significantly with their own features . Finally ,this paper hope this can give influence higher education charge has certain reference value for advice .Key words: tertiary education fees charging, influencing factors, linear model, sampling survey.analytic hierarchy process, weightiness1 高等教育收费数学模型的建立在一般情况下,通过定性的理论分析不能够准确的得出高等教育收费的标准。
校园网络收费问题 数学建模

2010滨州学院数学建模竞赛承诺书我们仔细阅读了竞赛规则。
我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B中选择一项填写): B我们的参赛报名号为(如果设置报名号的话):B201052所属院系(请填写完整的全名):物理与电子科学系参赛队员(打印并签名) :1.2.3.日期: 2010 年 4 月25 日2010滨州学院数学建模竞赛编号专用页评阅编号(由组委会评阅前进行编号):评阅记录(可供评阅时使用):滨州学院校园网络收费问题摘要本文通过对校园网计费需求、常用网络计费方式的分析,解决了在不同条件下通信端口数与上网用户数的关系,并且分析了不定时上网时各时间段的可能性和产生的抱怨问题。
给出了此时上网的通信端口平均使用率。
针对分段计时收费,说明了按时间长短来计费的不利之处,并提出了一种通用的校园网计费问题解决方案:分时计费方案。
这种方案较为合理的以不同时间上网用不同的收费方法,使得所有通信端口的使用率大为提高,并且能够让同一时间上网的人数不会长时间的过多用户使用而导致用户的抱怨问题。
关键词:校园网、网络、通信端口、分段计时一、问题阐述众所周知,网络的使用不能是免费的,服务提供者总是要采取相应的手段收费。
对于绝大多数学校来说,采取合理的计费系统是校园网络正常运行的保证。
为次我通过我校拟建了一校园信息网,并同国内和国际信息网连接,用户可以通过通信端口拨号入网,为此,需要根据用户的数量研究通信端口的设计规模。
通常的通信端口分为16口、32口、64口、128口等,实际中随着通信端口数量的增加,其成本费将成倍增加。
090303“高等教育学费标准探讨”问题的命题思路和评阅感想

“高等教育学费标准探讨”问题的命题思路和评阅感想叶其孝1,周义仓2(1 - 北京理工大学数学系,北京100081,2 –西安交通大学数学系,西安710049)摘要:本文就命题思路、阅卷过程和情况、阅卷感想、师生反映和媒体报道等方面论述了作者的想法和体会,提出了一些建议。
关键词:高等教育学费、数学建模分类号:AMS(2000) 00A71, 90B50 中图分类号: 221 文献标识码: A1.命题思路从实际应用和日常生活相关的问题中选择全国大学生数学建模竞赛的试题是我们一贯的指导原则。
在2008年初我们注意到有许多关于高等院校学费问题的不同观点的讨论,其中有的经济学家认为―最好的方法应该是提高学费,通过提高的学费,以增加更多的奖学金和助学贷款,来解决穷人上学的问题。
‖显然这是一个触动所有学生和他们家长的极为敏感的热点问题。
随后就在各种媒体上掀起了一个热烈议论和争论的高潮。
在电视节目中经常看到的是简单的学费应该涨还是降的激昂慷慨、情绪激动甚至有时热泪盈眶的表述,但我们总觉得这些缺乏基于可靠数据的定量分析和陈述。
本文作者认为这种分析应该是通过数学建模来达到的,于是就萌生了是否可以以这个主题作为大学生数学建模竞赛题的想法。
本文作者初步查阅了一些文献和网上的资料,发现讨论学费问题的文章非常多,特别是我们看到国外的有关报道中,有一个美国田纳西州高等教育委员会2005年12月22日致该州4位参议员和众议员的备忘录中说道:―学费的(数学)模型为高等教育和州政府的领导人更好地了解学费收入和政府拨款之间的关系提供了一种途径。
(The tuition model offers higher education and state government leaders a tool to better understand the relationship between tuition revenue and state appropriations.)‖1这些都坚定了本文作者想出这个赛题的想法。
论文B

高等教育学费标准的线性规划模型摘要对高等教育学费标准的探讨,首先,通过互联网搜集诸如国家生均拨款、培养费用、家庭收入等相关数据,分析这些数据之间的关系。
其次,根据各省的经济和教育的发展程度将我国除港、澳、台以外的31个省(市、自治区)分为三个区域,就不同区域的普通高校,仅考虑普通高校的四类(文史类、理工类、医农类以及艺术类)专业。
由于学费这一费用的特殊性,既不可定的太高使学生无法支付,也不可定的太低使得学校的财力不足而无法保证教学质量。
通过分析学费的影响因素,以影响因素之间的关系为约束条件,建立受市场需求影响的学费和家庭承受能力作为目标函数的双目标线性规划模型,利用线性加权法转化为单目标函数。
最后,用LINGO9.0求解,得到各省普通高校的理论学费标准,并对该省高校的理论学费标准与当前学费标准进行定量分析,得到结论:湖北、湖南、吉林、安徽、江西、重庆、四川、陕西、贵州、云南、甘肃的普通高校实际学费高于理论学费标准,其余各省(市、自治区)的普通高校实际学费低于理论学费标准,特别是经济发展程度较高的地区偏差较大。
最后,根据所得研究结果给出具体高等教育学费标准的报告。
关键词高等教育学费标准线性规划一、 问题重述高等教育事关高素质人才培养、国家创新能力增强、和谐社会建设的大局,因此受到党和政府及社会各方面的高度重视和关注。
培养质量是高等教育的一个核心指标,不同的学科、专业在设定不同的培养目标后,其质量需要有相应的经费保障。
由于高等教育属于非义务教育,其经费在世界各国都由政府财政拨款、学校自筹、社会捐款和学费收入等几部分组成。
学费问题涉及到每一个大学生及其家庭,是一个敏感而又复杂的问题:过高的学费会使很多学生无力支付,过低的学费又是学校财力不足而无法保证质量。
问题1:收集并分析相关数据,通过数学建模的方法,就几类学校或专业的学费标准进行定量分析,得出明确、有说服力的结论。
问题2:依据建模分析的结果,写一份报告,提出具体建议。
全国大学生数学建模竞赛一等奖论文-高等教育学费标准探讨(word版)

承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白,在竞赛开始后参赛队员不能以任何方式(包括电话、电子邮件、网上咨询等)与队外的任何人(包括指导教师)研究、讨论与赛题有关的问题。
我们知道,抄袭别人的成果是违反竞赛规则的, 如果引用别人的成果或其他公开的资料(包括网上查到的资料),必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺,严格遵守竞赛规则,以保证竞赛的公正、公平性。
如有违反竞赛规则的行为,我们将受到严肃处理。
我们参赛选择的题号是(从A/B/C/D中选择一项填写): B我们的参赛报名号为(如果赛区设置报名号的话):1910所属学校(请填写完整的全名):华南农业大学参赛队员(打印并签名) :1. 关继杰2. 刘文彬3. 许润萍指导教师或指导教师组负责人(打印并签名):聂笃宪日期: 2008年 9 月 21 日赛区评阅编号(由赛区组委会评阅前进行编号):编号专用页赛区评阅编号(由赛区组委会评阅前进行编号):全国统一编号(由赛区组委会送交全国前编号):全国评阅编号(由全国组委会评阅前进行编号):高等教育学费标准探讨摘要教育是关系国计民生的大事,本文建立了教育-社会贡献转化优化规划模型,贫困生生活质量改善优化规划模型和助学补助函数模型来对高等教育学费标准进行探讨。
文中首先对2006年中国教育公报历史数据进行因子分析,根据不同省份的地方政府生均拨款、培养费用的总量和增长比例,得到省份的综合实力得分排名和发展潜力得分排名,初步得到各个省份教育实力的差异。
接着根据城镇居民人均可支配收入进行聚类分析,选取8个代表性地区,建立学费走廊构造模型,得到政府对地区城镇居民学费补贴的金额。
由于高等教育事业关系国家社会的发展和家庭个人的前途,国家在社会与家庭个人都应当承担一定的教育成本费用,因此国家在发展教育事业上应该做到三个“合理”:承担合理的教育成本,制定合理的学费标准,并给予贫困生合理的助学补助。
高等教育学费标准的探讨 数学建模

高等教育学费标准的探讨摘要本文探讨的是高等教育学费标准的确定问题。
为了建立科学的评估体系,进一步规范学费标准。
文中通过定量分析,得出了影响高等学校学费标准的三个主要因素。
并建立了多元线性回归分析模型和学费标准的评价模型。
对于模型一,首先分析出可能对学费产生影响的六个因素,分别为国家生均拨款、生均培养费用、家庭年收入、招生人数、政府资助和社会捐助,并对这六个影响因素与学费间进行灰色关联分析,在Matlab环境中得出具体的关联度见表5-1。
通过分析,挑选出国家生均拨款、生均培养费用、家庭收入这三个对学费影响显著的因素。
考虑到公立学校和民办学校收费的差异较大,我们将学费的标准分为两类来探讨。
并分别对其进行回归分析,确立两类高校学费的回归方程度确定区间上限,将学生在受高等教育过程中的总投资额定义为大学四年的学费与没有工作而对国民生产总值产生的负价值之和。
通过调查分析认定,如果大学生毕业后四年的净收益能够超过大学教育的总投入资金,则认为可以接受。
并将毕业四年中平均每年的工资与普通职工的平均年工资、产生的负价值之差作为学费上限。
通过查阅相关资料知,如果学费低于生均培养成本的0.1倍,则认为教育质量就会得不到保证,故将此临界值作为学费下限。
最后我们利用此模型分别对A、B两类高校在2001年至2005年的收费进行检验,得出民办大学与公立大学的学费相比整体较高。
但对于两者的发展趋势来说,民办大学收取的实际学费不合理的情况有所好转,但公立大学却向坏的方向发展。
最后,结合模型一和模型二中的结论,我们对教育部门提出了五条建设性建议,具体条款见后文分析报告。
对高校制订高等教育学费的收费标准有一定的参考价值与指导意义。
关键词:灰色关联度多元线性回归预测负价值标准区间1.问题重述1.1问题背景近年来高校学费上涨有多快,人们凭感觉都能知晓。
全国高校的人均学费从改革前的免费教育到20年前的200元,再到1995年的800元,一直上升到2005年的5000元,从2006年至今也依然是居高不下,近20年间上涨了25倍,大大高于群众的收入增长幅度。
高等教育学费标准的数学模型22

为了满足不断扩张的高等教育规模和逐渐提高的生均支出水平共同导致的膨胀的经费需求,许多国家,包括发达国家也包括发展中国家,纷纷采取了分别向教育者收取部分培养成本或提高学费水平的措施来弥补公共高等教育资金的不足。我国高等学校和主管部门也在不断地进行多渠道筹高等教育成本的尝试,在改革和探索中逐步形成了我国教育经费的四条主要来源渠道,如图7-1所示。
我国普通高等学校教育学费问题已经成为社会关注的热点问题。高等教育事关高素质人才培养,国家创新能力增强,和谐社会建设的大局。培养质量是高等教育的一个核心指标,质量需要有相应的经费保障。高等教育属于非义务教育,其经费在世界各国都由政府财政拨款,学校自筹,社会捐赠和学费收入等几部分组成,过高的学费会使很多学生无力支付,过低的学费又使学校财力不足而无法保证质量。
因此,本文在绝对平均学费标准的基础上,逐步考虑针对不同情况下的学费标准,并在制定标准的过程中分析家庭收支,社会各方面的教育投入与高校培养质量之间的相互影响与制约的关系。
3.模型的假设与符号说明
3.1模型的假设
⑴从相关文献获取的各种统计数据能真实反映实际情况;
⑵全国经济状况稳定,短时间内不会出现大的波动;
综上所述,高等教育成本构 如表7-1所示。
表1-3 模型(1)的最优方案对应各门课程的书号数
课程编号
1
2
3
4
5
6
7
8
9
10
11
12
书号数
10
10
2
3
3
10
8
3
10
4
8
4
课程编号
13
14
15
16
17
18
高等教育学费标准探讨(08建模)

高等教育学费标准探讨李永立、奚扬阳、林秋桦复旦大学经济学院摘要本文讨论了高等教育收费的标准问题。
在数据搜集和整理的基础上,本文应用偏相关分析,方差分析和非参数统计等统计学的方法,揭示了目前我国高等教育学费收取的一些特征,如:明显的地域性,经济发达的地区收费较高,同一地区收费基本一致。
其费用受教育支出的影响较大,对于培养费用较高的专业,学费也相对较高,但与毕业生的就业与工资没有明显的相关关系。
在统计数据的基础上,考查学费与生均培养费用的比呈现以下特点:各地区基本平衡,随着学校的声望和教学质量的提高而递减。
在此基础上,本文将教育视为有外部性的公共物品,基于社会福利最大化的指标——消费者剩余建立了优化模型,指出我国的国情决定了政府应当收学费,同时也应当对高等教育进行财政拨款,并就最优的学费制定建立了一个量化模型,同时就教育的不平等问题通过模型给予了讨论,肯定了助学政策是解决学费不公平问题的有效途径。
在前文量化模型的基础上,本文建立了人工神经网络模型,进一步准确预测现有学费的征收机制,通过对该模型权重矩阵的分析,发现各地区的学费有不平衡的现象,地区因素权重很大。
为了查找原因,本文进一步建立了区域间动态拨款的教育经费模型,发现有些地区如天津,教育经费过剩,有些地区,如山西、陕西教育经费明显不足,这无形会增加学生的学费压力,建议教育主管部门密切关注这一现象,使教育资源在地区间、人与人实现符合效率的,又相对公平的分配。
文章关键词:收费标准、统计分析、正外部性、效率、公平问题分析与引言本文要求建立数学模型,对高等教育学费标准进行定量分析。
首先,本文定义的学费标准指学费制定的依据和方法,这里应包含两层意思:(1)学费制定标准的现状分析,即就目前中国的高校来说,制定学费是依据哪些变量,有怎样的规律;(2)在某种效益或公平的要求下,高校学费应有怎样的制定标准。
从(1)到(2)是一种变革和改进的过程。
就教育本身来说,其也像一般商品一样有成本与收益的概念,那么学费的制定必然也与这两方面的因素有关,在题目的要求下,搜集有关这两方面的数据是分析好现状的必然要求,揭示其数量规律有助于更进一步地把握各变量间的关系;但是,当今的学费制定标准(或者说来自统计分析的规律)是一种相对好的标准吗?这需要进一步的建立优化模型进行分析,验证已建的现状模型是否满足某种效益下的最大化,同时是否兼顾了公平,在这个基础上,进一步提出建议与意见。
高等教育学费问题的数学建模论文

高等教育学费标准制定问题的探讨摘要:改革开放以来,我国的高等教育取得了长足发展,但一些问题也随之产生。
社会普遍反映现阶段高校收费过高,使许多低收入家庭难以承担;但另一方面,如果高校收费标准制定的过低,又难以维持高校的发展,导致学生培养质量难以得到保证。
本文针对这些问题进行了详尽的探讨,并得出了一个解决该问题比较好的数学模型。
通过研究发现,高等教育学费制定问题比较好的切合了经济上的投入产出模型,因此我们基于价格均衡理论,教育投入价值理论等经济学理论,并通过建立边际成本的定价模型,盈亏平衡的定价模型和整体效益最大化的定价模型,求解出了一个比较适合当今社会发展的全国高校收费的统一定价。
本文通过分析决定,结合“考虑边际成本的收费模型”、“基于盈亏平衡的学费模型”、“考虑各方利益最大化的模型”这三个模型分别求得最优解,利用层次分析法,得出一个适合现在社会发展的最优学费标准。
然而,在模型的建立、搜集数据与求解的过程中我们发现,中国的高等教育的发展并非完全受市场经济的支配,而是由国家统一制定学费标准,学费的制定并不完全遵循市场经济原理,不同地域的高校及其不同教学水平的高校的学费水平差距不大。
因此,已有数据无法合理的确定出模型二及模型三的系数,进而也无法利用模型四进行优化分析。
因此只能适可而止的给出该模型的一个建立过程。
但是,限制也不是绝对的。
中国的私立高校还是受一定的市场经济影响的,因此可以用模型二和模型三两个模型来模拟私立高校收费政策的制定。
本文结合投入产出模型,认为高校通过投入教育经费产出培养质量,教育经费的投入与培养质量的产出是成正相关性的,因此本文利用高校投入教育经费的多少来量化培养质量的高低。
通过分析,可以很明显的发现,各大高校的培养质量是存在差别的。
其中,一个很明显的差别是国家对一类本科、二类本科、三类本科等的划分。
由于培养质量的差异,明显可知不同类别的高校收费是应该有差异的。
因此,本文构想通过分层分析计算,将不同类别高校的财政数据分别代入该模型可分别求得相应类别高校的学费定价标准。
高等教育学费标准探讨数学建模

高等教育学费标准探讨摘要:本文通过收集并分析现阶段各地区、各类学校的经费收入来源结构,以及学生的家庭收入(学费支付能力)情况,建立了高等教育学费标准探讨模型,可以求得在不同分类标准下高等院校学费与培养费用、政府财政人均拨款额、地区家庭收入情况之间的紧密程度,并模拟出高校收费(以理工科生学费为例)与总教育经费、家庭收入、政府财政投入之间的函数序列关系,并运用该关系对高校收费标准进行了定量分析.模型I :利用模糊数学理论,采用模糊聚类方法可以对各高校按照不同的指标进行分类. 在此基础上利用灰色系统理论,分别对所得到的若干类高等院校进行灰色关联度分析得到,现行高等院校学费与培养费用、政府财政人均拨款额、地区家庭收入情况之间的关联度.例如,我们按照地区家庭经济状况可把随机抽取的59所1⎡⎤⎣⎦附表高校进行分类,可以分为两类T1、T2.分别对所得到的两类高等院校进行灰色关联度分析得到,现行高等院校学费与培养费用、政府财政人均拨款额、地区家庭收入情况之间的关联度分别为:第一类学校:绝对关联度:e0=[ 0.5007 0.5000 0.5001];相对关联度:r=[ 0.5160 0.5810 0.8962];综合关联度:p=[ 0.5083 0.5405 0.6982];第二类学校:绝对关联度:e0=[ 0.5039 0.7484 0.5515];相对关联度:r=[ 0.5524 0.7205 0.6166];综合关联度:p=[ 0.5281 0.7344 0.5840].对于第一类学校,收费标准与经济收入情况变化速率最接近,经济收入增长越高,高校收费也越高;对于第二类学校,高校收费与政府财政拨款联系最为紧密.模型Ⅱ:以地区为时间列,建立GM(1,N)模型,模拟得出高校收费与总教育经费、家庭经济收入、政府财政投入之间的函数序列关系,进而可以预测某年度各个地区的高等教育制定的收费标准.以2006年全国部分省市高校为例,经 Matlab 求解得到时间响应序列函数,进而可以初步估计出该年份全国各个地区高校学费标准.为了提高GM(1,N)模型的模拟精度,将模型进一步优化得到:残差GM(1,1)模型,即用残差序列建立GM(1,1)模型. 修正GM(1,1)模型求得平均相对误差10.11993∆=,相比于修正前的平均相对误差00.13467∆=明显减小,残差平方和也大幅度减小,因此残差修正GM(1,1)模型使得模型的模拟精度得到了明显提高.运用修正后的响应时间序列函数,并以新疆地区为例,利用控制变量的方法研究,在总教育经费、家庭经济收入、政府财政投入发生变化时所确定的高校收费标准,得出高校所在地经济状况是影响高校学费的主要因素.最后,本文还对所建立的两个模型进行了评价和改进,并对有关部门提出了合理的参考建议.关键词:高等教育学费标准 模糊聚类分析 灰色关联度分析GM(1,N)模型 残差GM(1,1)模型1.问题的提出1.1.背景:高等教育事关高素质人才培养、国家创新能力增强、和谐社会建设的大局,受到党和政府及社会各方面的高度重视和广泛关注.培养质量是高等教育的一个核心指标,不同的学科、专业在设定不同的培养目标后,其质量需要有相应的经费保障.而学费问题涉及到每一个大学生及其家庭,是一个敏感而又复杂的问题:过高的学费会使很多学生无力支付,过低的学费又使学校财力不足而无法保证质量.所以关于高等教育学费标准探讨具有非常重要的意义.1.2.基本情况高等教育属于非义务教育,其经费在世界各国都由政府财政拨款、学校自筹、社会捐赠和学费收入等几部分组成.对适合接受高等教育的经济困难的学生,一般可通过贷款和学费减、免、补等方式获得资助,品学兼优者还能享受政府、学校、企业等给予的奖学金.1.3.需要解决的问题1)根据中国国情,收集诸如国家生均拨款、培养费用、家庭收入等相关数据,并据此通过数学建模的方法,就几类学校或专业的学费标准进行定量分析,得出明确、有说服力的结论.2)根据建模分析的结果,给有关部门写一份报告,提出具体建议.2.问题的分析现阶段的高等院校学费标准是按照属地原则由省一级地方政府决定的.学费标准确定依据在操作上存在一定的困难,同时与学费相关的各方,包括政府、学校、学生家庭在利益上又存在一定矛盾,政府更多关注的是教育发展和教育公平以及财政支付能力,学校关注更多的是教育成本,学生及家庭关注的是其对学费支付能力.根据问题的题设和要求,我们可以将高校学费标准的问题转化到数学领域进行讨论,首先要按照一定的分类标准对各高校或专业进行分类,考虑每一类学校或专业的收费标准与国家生均拨款、培养费用、家庭收入等主要相关因素之间的关联度,得到不同因素发生变化时对其收费标准的影响度。
基于数学模型的高校学费标准的研究

1 模 型 建 立
建立这个模 型的 目的是为 了制定对于全 国整体水平来说合理 的学费价格和生均奖贷助学金。数
学建模解决实际问题的第一 步就是抓住主要因素 、适 当忽略次要 因素 ,并 由此做一些符合社会现实 的基本假设 。本文需要 以下两点基本假设 : 1)假设 不 同类 别 的 高 校在 制 定学 费 时 的相 互 影 响可 忽略 不 计 ;
度和 大学性价 比为 四个 目标 函数 , 同时考虑 办学成本 、家庭 负担 约束 、社 会 经济和 学校财 力等作为 约束条 件 ,建立 多 目标规 划模型 ;采 用线性 加权 法将其 转化 为单 目标规划模 型 ,并 引入 阈值 限定进行 求解。 关键词 :高等教 育学 费; 多 目标规 划模型 ;闽值 限定
Xl C3 : ≤ G C4 :
1 >0 .
其中 是 生均非学费总收人 ,F 是生均 非奖贷 助学金 总支 出 , O- O F 是生均教 职TT资福利支
出, z 生 均 设 备 购 置 费 ,£ 为 恩 格 尔 系 数 ,P- 全 国家 庭 均 收 入 ,尸 是 大 学 毕 业 生 生 均 丁资 , 是 为 z
Y=(, ,] ) ', y, , ・ () 1
其 中 '表 示 培 养 质 量指 标 , 表 示 家庭 满 意 度指 标 , 表 示 学 校 满 意 度 指 标 , 表 示 大 学性 价 比指 , 。
标。
这 是 一 个 多 目标 规 划 问 题 ,其 求 解 可 采 用 多 属 性效 用 函 数 ,将 多 目标 规 划 模 型 转 化 为 单 目标 规
划模 型来 求 解 。本 文 运 用 线 性 加 权 法 将 多 目标 规划 模 型 化 为 单 目标 规 划模 型 来 求 解 ,加 权得 到 的单 目标 优 化模 型如 下 所 示 :
数学建模 费用分担问题

数学建模一周论文论文题目:费用分担问题姓名1:林成贵学号:1030110304姓名2:杨立学号:1030110320姓名3:吕全标学号:1030110217专业:资源勘查工程班级:10级资勘三班指导教师:刘胜兰2011年12月28日摘要随着经济的快速发展,环保问题已经成为一个不容忽视的问题,而水资源更是关系着每个居民的日常生活,污水必须经过处理方能排入河中。
因此对于污水处理这一特殊的问题我们在解决时就应该本着高效的原则去实施。
在这个污水处理问题中,我们分情况讨论,先分五种情况,第一种情况是每个城镇都建立一个污水处理厂,第二种情况是三个城镇建立两个污水处理厂,第三种情况是三个城镇建立一个污水处理厂。
然后还要讨论污水处理厂的选址问题,而且还要合理分担配每个城镇的费用。
为了节省开支,我们要选一种开支最小的可行方案。
将该方案应用到实际问题中从而解决了实际生活问题。
对该问题进行全面的分析后可知,这是一个运筹学方面关于费用分担问题。
在该问题中,我们按最原始的分情况讨论方法解该题,然后综合考虑费用最小,最后在结合三个城镇各自的情况后合理的分配各城镇的费用。
\一、问题的提出有三个位于某河流同旁的城镇城1、城 2、城3(如图)三城镇的污水必须经过处理后方能排入河中,他们既可以单独建立污水处理厂,也可以通过管道输送联合建厂。
为了讨论方便起见,我们再假设污水只能由上游往下游。
用Q 表示污水量,单位为米3/秒,L 表示管道长度,单位为公里,则有经验公式:0.7120.51C1=730Q ( C2=6.6QL 建厂费用万元)管道费用(万元)已知三城镇的污水量分别为:Q1=5立方米/秒,Q2=3立方米/秒,Q3=5立方米/秒, 问:三城镇应怎样处理污水方可使总开支最少?每一城镇负担的费用应各为多少?二、模型的假设1、我们再假设污水只能由上游往下游。
2、假设所有管道都是直的,而且足够大。
3、所有污水处理厂紧靠河边。
三、问题的分析通过对此问题的研究可知,如何最经济的解决污水处理问题,从而使个城镇负担的费用最少是我们最终需要达到目的。
数学建模论文_费用分担问题

数学建模论⽂_费⽤分担问题摘要在当今资源稀缺的市场经济时代,如何优化配置各种有限资源对⼀个公司或国家来说越来越重要。
谁能够找出合理最优的配置⽅案谁就有可能在激烈的市场竞争环境中⽣存下来。
本案例针对问题8:费⽤分担问题提供出了⼀种合理的模型。
问题8中提供了2种⽅案,第⼀种⽅案是每个城镇独⽴建污⽔处理⼚,这种⽅案最简单,计算较为⽅便。
直接利⽤常规数学知识就可以得出最后需要的费⽤。
每个城镇最后的费⽤W[i]=C1*Q[i],(i=1,2,3) 即最后的总的费⽤M=W[1]+W[2]+W[3];由于每个城镇的污⽔量都有区别,所以每个城镇都独⽴建⼚显然不能充分利⽤资源。
所以我们考虑是否可以采⽤第⼆种⽅案。
第⼆种⽅案,第⼆种⽅案⼜有4种可能:1.三个城镇共⽤⼀个污⽔处理⼚;2.城镇⼀和城镇⼆共⽤⼀个;3.城镇⼆和城镇三共⽤⼀个;4.城镇⼀和城镇三共⽤⼀个;针对这四种可能我们可以抽象⽤⼀种模型来处理,我们可以将其抽象为⼀个图的问题,在具体⼀点就是⼀个求最短路径问题,那么我们就可以利⽤迪杰斯特拉(Dijkstra)算法就可以找出其最优解。
进⽽就可以找出其最优⽅案。
⽬录1.摘要 (1)2.问题的重述与分析 (3)3.问题的基本假设 (4)4.符号说明 (5)5.模型的原理与模型 (6)6.模型的建⽴与求解 (7)7.模型的评价 (13)8.参考⽂献 (14)9.评分表 (15)费⽤分担问题及其最优解决⽅案关键词数据结构图最短路径迪杰斯特拉算法时间复杂度⼀、问题重述与分析1.1 问题的重述随着经济的⾼速发展以及⼈类社会的飞快进步,⼈类对⾃然的破坏也愈加严重,其中尤为严重的就是环境污染。
⽽污⽔的污染毫⽆疑问在其中占有极⼤的⽐重,但是怎样来平衡经济利益与污⽔处理成本以经成为⼀个关键性问题。
现有临近⼀条河流的三个城镇,城镇⼀,城镇⼆,城镇三;给出了⼀些基本费⽤的经验公式,以及三个城镇的相互距离。
根据这些信息,进⾏合理的模型假设,利⽤数学建模的⽅法,进⾏计算找出费⽤最少的合理配置⽅案。
确定合理学费标准的微分方程模型_程晓琳

———科协论坛·2009年第6期(下)———学费问题涉及到每一个大学生及其家庭,是一个敏感而又复杂的问题:过高的学费会使很多学生无力支付,过低的学费又使学校财力不足而无法保证质量.但具体应收取多少,必须要有一个计算的标准与依据.正基于此,我们需要考虑国家生均拨款、生均培养费用、家庭收入等因素来确定一个合理的高等教育收费标准.而这个标准必须是在综合考虑教学质量和家庭负担的基础上建立起来的.所以,如何用数学模型来处理二者之间的关系便成了解决这个问题的关键.1基本模型我们仔细考虑了决定学费标准的各种因素,然后确定模型以社会“总效益”w 为目标,进行逐步分析,最终得到高等教育学费标准.由于当学费变动dt 时,总效益的变化dw 与(T-S-D-N-t)———学费、学校自筹经费和社会捐赠的总和与培养费用的差距———正相关;另外,由文献[3]知学费占家庭可支配总收入的比例一般在25%左右,超过这个比例就会导致家庭生活质量下降,所以家庭可支配收入的25%与学费的差值与总效益有关.简单地考虑总效益随学费增长的变化率与这两方面因素呈线性关系,系数分别为α和β,模型从高等教育的生均培养费用、学费、家庭年均收入着手,以总效益w 为目标函数建立高等教育学费的总效益微分方程简单起见用t 来表示(T-S-D-N),称其为理想学费.它实际上是在不考虑家庭负担因素的情况下使得总效益最大的学费.对其求解得:其中w 0为初值,-α(T-S-D-N-t)dt 表示学费与培养费用的差距带来的效应(这里用简单的线性关系表示),T-S-D-N-t>0时带来负面效应,T-S-D-N-t<0时带来正面效应.β(F ×25%-t)dt 表示学费与家庭年总收入的关系带来的效应.β这是一个二次函数求极值的问题.若α<β,二次函数开口向下,则在拐点处取得极大值;若α>β,二次函数开口向上.对于后者,可能会导致极端情形,即当总效益最大时,学费过低或者过高,这实际上是单纯地追求某一方面的效益来达到总效益的极大值,这样就失去了该模型权衡教育质量和家庭负担这两个矛盾因素的意义,所以在此取α<β.在此条件下,易知:当时,总效益取得最大.2针对家庭条件不同,专业相同的改进模型取同一所学校同一个专业的学生为样本,考虑同一学校同一专业,家庭条件不同的学生,对于这些学生来说,国家的生均拨款、培养费用都相同,这样,我们只需考虑家庭条件这一个因素(即不同的F i ),以及不同的权重系数αi 和βi .根据家庭年收入数额从高到低将学生分为n 组,对每组取相同的家庭年收入F i ,其中P i 为第i 组的人数比例,得到如下改进的微分方程:3针对不同地域,不同学校,不同专业的改进模型对于不同专业的学生,培养费用是主要的差异,从而导致理想学费不同.另外,学费减少对教学质量的影响和学费增多带来的家庭负担也会有所不同,因此对于个专业的学费带来的总效益可表示为这里假设这些不同专业之间的学生的家庭状况基本相同,可以按同样的标准分成若干组.对于不同的高校,由[1]知,国家对不同省份,直辖市的教育拨款有很大差异,而且由于经济发展水平以及教育水平的差异,不同地区家庭平均年总收入和高校生均培养成本也有很大不同.而类似地可以写出总效益的表达式,在此不赘述.4针对特困生减免学费的改进模型根据家庭年收入数额从低到高将学生分为n 组,并且取定其中一组作为减免学费的界限,只有学生的家庭年收入低于F m 时,才能够减免学费.(a)当m ≤i ≤n 时r i >0(b)当i ≤m 时r i =0表示只对家庭足够困难的学生减免学费.根据(3)式计算得微分方程:求解得:□程晓琳杨凯张英男(吉林大学数学学院吉林·长春130012)摘要:本文通过对国家生均拨款、生均培养费用、家庭收入等因素的综合考虑,建立了一个微分方程模型,该模型由简入繁、层层递进,最终找到了一个相对完善的确定高等教育学费标准的方法。
基于多元线性回归的高等教育学费模型
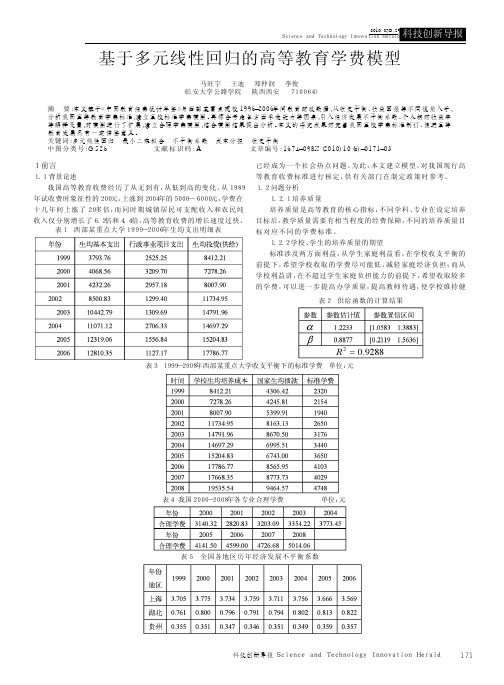
a = 0.49 b = 0.51
( t ) = 0.49L × P(t ) + 0.51J ×G p (t ) × γ ×η
该地区调整因子为1.32,计算得表7: (3)陕西属于西部经济不发达地区,个人用于高等教育的支付 能 力 较 低, 即
3 高校合理学费模型建立
3 . 1 模型扩展分析 学费制定应坚持 “成本分担” 原则和多数居民可以承受的原 则,在教育经济学中,学费标准应通过能力支付原则和利益获得原 则来制订。 3.1.1 能力支付原则 根据利益获得者的承受能力来确定负担主体及负担程度。 各 地 区 经 济 发 展 水 平 不 同 ,人均GDP水平差别很大,教 育 支 出 在 家 庭 可 支 配 收 入 中 所 占 比 例 不 同, 即 根 据 可 支 付 能 力 的 不 同 来 确 定 合 理学费。 3.1.2 利益获得原则 由于教育准公共产品的特性,可产生外部效益, 受教育者和全 社会都可从中获益, 因而社会各成员应合理分摊教育成本。 合理的 学费标准应照顾学生和学校两方面利益,在满足学校利益的前提 下, 使 学 生 所 得 边 际 效 用 最 高 。 本 文 中, 边 际 效 用 是 学 生 具 备 相 应 负担能力下的有效边际效用。 3 . 2 模型的确立 高 等 教 育 收 费 标 准 主 要 取 决 于 经 济 发 展 水 平, 本 文 主 要 考 虑 五种影响因素, 即 各 方 面 承 受 能 力 、 个人收益率、 高等教育的供需 状况、 生均培养成本以及地区差异。 基 于 能 力 支 付 原 则 和 利 益 获 得 原 则, 个 人 通 过 接 受 高 等 教 育 所 得 利 益 即 为 合 理 学费,建 立 模 型 如 式3.1所示。 其中, h ( t ) —合理学费, P ( t ) —国家生均投资,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于大学收费问题
摘要
关键词:
一问题重述
高等教育事关国家高素质人才培养,国家创新能力增强,综合国力提升的关键所在,因此受到但和国家的高度重视。
高等教育的核心指标是培养质量,不同的专业和学科在设定不同的培养目标以后,其经费也要有相应的保障。
高等教育不属于义务教育,其费用要由国家财政拨款、学校自筹、社会捐助和学费收入等级部分组成。
对于经济条件困难的学生可以通过贷款和学费减免等方式得到资助。
大学生的学费又是一个敏感复杂的问题:过高的学费会使学生无力支付。
过低的学费又使学校财力不足无法保证质量。
根据中国的国情,结合收集到的资料与相关数据,通过数学建模来分析以下问题。
1.由于每个地域的经济情况不一样,确定出不同地区的家庭可支配教育费
用。
2.由学校的知名度来确定学校的收费金额,分析学费标准的影响权重,应
用加权求出实际收费。
二模型假设
1.区域间存在的特殊情况不在考虑范围内。
2.学校的教育成本只考虑主要的教职工的工资。
三符号说明
符号意义
EV东部农村家庭教育支出
CV中部农村家庭教育支出
WC西部城镇家庭教育支出
WV西部农村家庭教育支出
NC东北城镇家庭教育支出
NV东北农村家庭教育支出
Y学校培养每个学生的教育成本
X学校教职工人数
1
X在校学生人数
2
Q第j类学校的学费
j
四问题的分析与模型的建立
当前我国的教育问题日趋严重,尤其是大学教育,家庭需要支付的学费越来越高,一个学生的学费已经是一个家庭收入支配中最大的部分。
而对于学校,教育经费不足又不能保证教学质量,达不到教学质量,就不能为社会培养合格的接班人,因此学校为了达到教育质量又不得不加大教育收费。
怎样才能达到一个合理的收费,既能让一般的学生家庭承担得起学费学校又能教育出高素质的学生。
首先从每个学生的家庭入手,由于我国的地域辽阔,每个地区的经济情况也有很大的不一样。
要使全国大部分学生都能付得起学费就需要把全国划分为几个区域。
4.1经济不同地区家庭用于可支配的学费分析及模型建立
由《中国统计年检2009》可知,中国不同地区城镇人口与农村人口的比例以及教育可支配费用存在很大的差距。
大致可将经济不同地区分为四个部分。
Ⅰ. 东部地区; Ⅱ. 中部地区;
Ⅲ. 西部地区; Ⅳ. 东北地区。
四个地区家庭的收入情况如表:
根据中国民调显示:中国家庭教育花费已接近家庭总收入的1/3, 通过这一数据可以算出各个地区城镇和农村用于教育的费用如表2
由于城乡之间的差距,农村人口占总人口的55.06%(2007统计数据)。
根据国家政策,应该优先考虑农村的实际情况,将权重放在农村。
因此需要对不同地区建立不同的加权模型,而对于不同地区城乡差距和人口比不一样,所以不同地区的权重也不一样。
对各个地区家庭用于教育的支出费用建立加权建模:
东部地区 EV EC E 1211αα+=
中部地区 CV CC C 2221αα+=
西部地区 WV WC W 3231αα+=
东北地区 NV NC N 4241αα+=
最后对全国每个家庭用于教育的支出费用进行建模:
4.2 对学校教育成本的分析与建模:
学校要教育出合格的人才就需要优秀的教职工和必要的设施。
影响成本最重要的因素有学生数量和教职工人数,因此在这两种因素之间可以应用二元非线性回归模型来求解。
一般的,我们考虑二元非线性回归模型
其中1X ,2X ,…,m X 是自变量,0β,1β,2β,…,nm β是未知参数(回归参数),ε是均值为零的随机变量。
这种未知参数和自变量均以非线性形式出现的回归模型称为非线性回归模型。
为了得到回归参数的估计值,就要对变量进行观测,假设对变量的n 次独立观测数据为
(i Y ,1i X ,2i X ,…,im X ) (1=i ,2,…,n )
显然,这些数据满足
其中1ε,…n ε独立分布,均值为0,方差为2σ。
记T n Y Y Y Y ),,,(21 =,β=T nm )ββ(β,,,10⋯,ε=T n ),ε,,ε(ε⋯21,
则有
显然,()0=ε
E ,()εVar =n I 2σ。
为了得到β的估计,通常的方法是用最小二乘法,即使∑=n
i 12i ε关于β的极小
化,就是使
达到极小。
由(
)βQ 对β求导并令其等于零,得到 即
称为正规方程。
其中()1+⨯m n X 为矩阵,一般总假设()1+=m X rank ,则由上式可得β的最小二乘法估计
根据以上结论建立以在校学生人数和教职工人数为解释变量,成本为被解释变量的非线性回归模型,由多项式拟合可知当解释变量为二次时拟合的吻合度最高。
因此建立如下模型:
4.3 不同学校生均成本对学费的影响分析与模型建立:
学校的不同对学费的影响主要体现在以下两个方面:
⑴.学校的性质不同,可分为:综合类、理工类、艺术类一般这些学校学费较高,另外像师范类、农林类、财经政法类收费较低。
⑵.学校排名不同,一般排名靠前的学校会得到更多的财政拨款,是这些许学校的学生缴纳的费用相对较低。
按照我国《高等学校收费管理暂行办法》中所规定的标准,学生个人不得承担超过25%的生均培养费用。
按照规定的上限由学生个人承担生均培养费用的25%,通过对学校综合排名的处理,建立一个综合排名系数模型。
以08年个人支付占教育经费的35.37%的标准表示个人支付占教育经费的百分比。
在此基础上,以教育成本的25%为基本学费。
由于各类学校的排名实力不同,各级投入的不同,学费之间存在一定的差距,为尽量缩小其应收学费,再在基本学费上综合排名系数得到学校差距下的数学模型:
F=Y*(25%+(1-f(j))*(35.37%-25%) j=1,2…..8;
五 模型的求解
5.1 经济不同地区家庭用于可支配的学费模型求解:
由于每个地区农村人口和城镇人口的百分比不一样,因此每个地区的权重也不一样。
根据四个地区农村人口与城镇人口的比例加上经济收入的情况分别做以下的权重:
根据以上数据算出每个地区家庭可用于教育的支出费用如表3:
由以上数据可以看出每个地区能用于教育支出的平均费用也存在很大的差
异,因此各个地区收取的学费也应该不一样。
参照全国部分专业平均收费情况(2009):
比较部分专业平均收费情况可以看出,不管是农村还是城市对当前的学费都无力支付,而根据≤中国统计年鉴2009≥知,全国教育投入的比例只占全国总GDP 的2.41%远低于世界平均水平。
因此国家应该加大多教育事业的投入来降低居民家庭对教育的投入。
5.2 对学校教育成本的求解:
用matlab 软件对在校学生人数和成本以及在校教职工人数与成本的多项式拟合可以得出,当多项式为二次时,拟合的吻合度最高。
即二元非线性回归为:
采用matlab 软件编程,对多项式进行进一步求解可得:
Y=27710.6260-553.42071X +13.81372X +4.662221X -0.009522X
其中2r =0.8902;F =10.1330;p =0.0129.
05.0<p 满足
六 模型的评价
七 模型的改进
参考文献。
