复变函数论试卷
复变5套试题(1)

《复变函数论》试题库《复变函数》考试试题(一)一、 判断题(20分):1.若f(z)在z 0的某个邻域内可导,则函数f(z)在z 0解析. ( )2.有界整函数必在整个复平面为常数. ( )3.若}{n z 收敛,则} {Re n z 与} {Im n z 都收敛. ( )4.若f(z)在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数). ( )5.若函数f(z)在z 0处解析,则它在该点的某个邻域内可以展开为幂级数. ( )6.若z 0是)(z f 的m 阶零点,则z 0是1/)(z f 的m 阶极点. ( )7.若)(lim 0z f z z →存在且有限,则z 0是函数f(z)的可去奇点. ( )8.若函数f(z)在是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠. ( ) 9. 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C0)(=⎰Cdz z f .( )10.若函数f(z)在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数.( ) 二.填空题(20分)1、 =-⎰=-1||00)(z z n z z dz__________.(n 为自然数)2.=+z z 22cos sin _________. 3.函数z sin 的周期为___________.4.设11)(2+=z z f ,则)(z f 的孤立奇点有__________.5.幂级数nn nz∞=∑的收敛半径为__________.6.若函数f(z)在整个平面上处处解析,则称它是__________.7.若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________.8.=)0,(Re n zz e s ________,其中n 为自然数.9. zz sin 的孤立奇点为________ .10.若0z 是)(z f 的极点,则___)(lim 0=→z f z z .三.计算题(40分):1. 设)2)(1(1)(--=z z z f ,求)(z f 在}1||0:{<<=z z D 内的罗朗展式.2. .cos 11||⎰=z dz z3. 设⎰-++=C d z z f λλλλ173)(2,其中}3|:|{==z z C ,试求).1('i f +4. 求复数11+-=z z w 的实部与虚部.四. 证明题.(20分) 1. 函数)(z f 在区域D 内解析. 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数. 2. 试证: ()f z 在割去线段0Re 1z ≤≤的z 平面内能分出两个单值解析分支,并求出支割线0Re 1z ≤≤上岸取正值的那支在1z =-的值.《复变函数》考试试题(二)一. 判断题.(20分)1. 若函数),(),()(y x iv y x u z f +=在D 内连续,则u (x,y )与v (x,y )都在D 内连续. ( )2. cos z 与sin z 在复平面内有界. ( )3. 若函数f (z )在z 0解析,则f (z )在z 0连续. ( )4. 有界整函数必为常数. ( )5. 如z 0是函数f (z )的本性奇点,则)(lim 0z f z z →一定不存在. ( )6. 若函数f (z )在z 0可导,则f (z )在z 0解析. ( )7. 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f .( )8. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( ) 9. 若f (z )在区域D 内解析,则|f (z )|也在D 内解析. ( )10. 存在一个在零点解析的函数f (z )使0)11(=+n f 且,...2,1,21)21(==n nn f . ( )二. 填空题. (20分)1. 设i z -=,则____,arg __,||===z z z2.设C iy x z y x i xy x z f ∈+=∀+-++=),sin(1()2()(222,则=+→)(lim 1z f i z ________.3.=-⎰=-1||00)(z z n z z dz_________.(n 为自然数)4. 幂级数0n n nz ∞=∑的收敛半径为__________ .5. 若z 0是f (z )的m 阶零点且m >0,则z 0是)('z f 的_____零点.6. 函数e z 的周期为__________.7. 方程083235=++-z z z 在单位圆内的零点个数为________. 8. 设211)(z z f +=,则)(z f 的孤立奇点有_________. 9. 函数||)(z z f =的不解析点之集为________.10. ____)1,1(Res 4=-zz .三. 计算题. (40分)1. 求函数)2sin(3z 的幂级数展开式.2. 在复平面上取上半虚轴作割线. 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点i z=处的值.3. 计算积分:⎰-=iiz z Id ||,积分路径为(1)单位圆(1||=z )的右半圆.4. 求dzz zz ⎰=-22)2(sin π.四. 证明题. (20分)1. 设函数f (z )在区域D 内解析,试证:f (z )在D 内为常数的充要条件是)(z f 在D 内解析.2. 试用儒歇定理证明代数基本定理.《复变函数》考试试题(三)一. 判断题. (20分).1. cos z 与sin z 的周期均为πk2. ( ) 2. 若f (z )在z 0处满足柯西-黎曼条件, 则f (z )在z 0解析. ( )3. 若函数f (z )在z 0处解析,则f (z )在z 0连续. ( )4. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( )5. 若函数f (z )是区域D 内解析且在D 内的某个圆内恒为常数,则数f (z )在区域D 内为常数. ( )6. 若函数f (z )在z 0解析,则f (z )在z 0的某个邻域内可导. ( )7. 如果函数f (z )在}1|:|{≤=z z D 上解析,且)1|(|1|)(|=≤z z f ,则)1|(|1|)(|≤≤z z f . ( )8. 若函数f (z )在z 0处解析,则它在该点的某个邻域内可以展开为幂级数.( ) 9. 若z 0是)(z f 的m 阶零点, 则z 0是1/)(z f 的m 阶极点. ( ) 10. 若0z 是)(z f 的可去奇点,则0)),((Res 0=z z f . ( )二. 填空题. (20分)1. 设11)(2+=z z f ,则f (z )的定义域为___________.2. 函数e z的周期为_________.3. 若n n n i n n z )11(12++-+=,则=∞→n z n lim __________. 4. =+z z 22cos sin ___________.5. =-⎰=-1||00)(z z n z z dz_________.(n 为自然数) 6. 幂级数∑∞=0n n nx 的收敛半径为__________.7. 设11)(2+=z z f ,则f (z )的孤立奇点有__________.8. 设1-=ze ,则___=z .9. 若0z 是)(z f 的极点,则___)(lim 0=→z f z z .10. ____)0,(Res =nzze . 三. 计算题. (40分)1. 将函数12()zf z z e =在圆环域0z <<∞内展为Laurent 级数.2. 试求幂级数nn n z nn ∑+∞=!的收敛半径.3. 算下列积分:⎰-C z z z ze )9(d 22,其中C 是1||=z .4. 求0282269=--+-z z z z在|z |<1内根的个数.四. 证明题. (20分) 1. 函数)(z f 在区域D 内解析. 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数. 2. 设)(z f 是一整函数,并且假定存在着一个正整数n ,以及两个正数R 及M ,使得当R z ≥||时n z M z f |||)(|≤,证明)(z f 是一个至多n 次的多项式或一常数。
《复变函数》考试试题与答案各种总结.docx

---《复变函数》考试试题(一)一、判断题( 20 分):1. 若 f(z) 在 z 0 的某个邻域内可导,则函数f(z) 在 z 0 解析 .2. 有界整函数必在整个复平面为常数.3. 若{ z n }收敛,则{Re z n } 与{Im z n }都收敛 .4. 若 f(z) 在区域 D 内解析,且f '( z),则f ( z) C(常数) 5. 若函数 f(z) 在 z 0 处解析,则它在该点的某个邻域内可以展开为幂级数6. 若 z 0 是 f ( z)的 m 阶零点,则 z 0 是 1/f (z)的 m 阶极点 .lim f ( z)7. 若 zz 0存在且有限,则 z 0 是函数 f(z) 的可去奇点 .( ) ( ) ( ). ( ).( )()()8. 若函数 f(z) 在是区域 D 内的单叶函数,则f ' (z) 0( zD ).()9. 若 f(z)在区域 D 内解析 , 则对 D 内任一简单闭曲线Cf z dz.( )C( )10. 若函数 f(z) 在区域 D 内的某个圆内恒等于常数,则 f(z)在区域 D 内恒等于常数 . ()二. 填空题( 20 分)1、|z z 0 |dz__________. ( n 为自然数)1 ( z z )n2.sin 2zcos 2z_________.3. 函数sin z的周期为 ___________.f (z)z 2 11,则f ( z)的孤立奇点有 __________.4.设5. 幂级数nz n 的收敛半径为 __________.n 06. 若函数 f(z) 在整个平面上处处解析,则称它是__________.lim z nlimz 1z 2 ...z n7. 若 n,则 nn______________.Res(e z8.n,0)________,其中 n 为自然数 .z---9.sin z的孤立奇点为 ________ .z若z 0 是 f (z)lim f (z)___10. 的极点,则z z.三. 计算题( 40 分):f (z)11. 设(z 1)( z 2) ,求 f ( z) 在 D { z : 0 | z | 1} 内的罗朗展式 .1dz.|z| 1cos z2.3. 设f ( z)3 271d{ z :| z | 3} ,试求 f ' (1 i ).Cz,其中 Cz 1w1 的实部与虚部 .4.求复数z四 . 证明题 .(20 分 )1. 函数f (z)在区域 D 内解析 . 证明:如果 | f ( z) |在 D 内为常数,那么它在D 内为常数 .2. 试证 : f ( z) z(1 z) 在割去线段 0Re z 1 的 z 平面内能分出两个单值解析分支,并求出支割线0 Re z 1上岸取正值的那支在 z 1的值 .《复变函数》考试试题(一)参考答案一. 判断题1.× 2.√ 3.√ 4.√5.√6.√ 7.×8.×9.× 10.×二.填空题2 in1 2.1 ;3. 2k , ( k z) ;4.z i ; 5.11.n;16. 整函数;7. ; 1 ; 9. 0; 10..8.(n 1)!三.计算题 .1. 解因为 0 z 1, 所以 0 z 1f ( z)1 1 1 z zn1 ( z )n.( z 1)(z 2) 1 z 2(1 )n 02 n 0 22---2.解因为z21Re s f (z)lim lim,cosz sin z1 z z z222Re s f (z)lim z2lim1 1 . cosz sin zz z z2 22所以1dz2i(Re s f (z)Re s f (z)0. z2 cosz z2z23.解令 ()3271,则它在 z 平面解析,由柯西公式有在z 3内,f (z)c ()dz2i(z) . z所以 f (1i )2i( z) z 1 i2i (136i )2(613i ) .4.解令 z a bi ,则w z 11212( a1bi )12( a1)2b2. z 1z 1222b22b( a 1) b( a 1)(a 1)z12(a1)z12bb2 .故 Re( z1)1( a1)2b2,Im(z1)(a1)2四. 证明题 .1.证明设在 D 内 f (z) C .令 f ( z) u iv ,2u2v2c2.则 f ( z)两边分别对 x, y 求偏导数,得uu x vv x0(1) uu y vv y0(2)因为函数在 D 内解析,所以 u x v y ,u y v x.代入 (2)则上述方程组变为uu x vv x0 .消去 u x得,(u2v2 )v x0 .vu x uv x01)若 u2v20 ,则 f (z)0 为常数.2)若 v x0,由方程(1) (2) 及C.R.方程有u x0,u y0 , v y0 .所以 u c1, v c2. ( c1 ,c2为常数).---所以 f ( z) c 1 ic 2 为常数 .2. 证明 f ( z)z(1 z) 的支点为 z 0,1 . 于是割去线段 0 Re z 1 的 z 平面内变点就不可能单绕 0 或 1 转一周 , 故能分出两个单值解析分支 .由于当 z 从支割线上岸一点出发 ,连续变动到 z0,1 时 , 只有 z 的幅角增加. 所以f ( z)z(1 z) 的幅角共增加. 由已知所取分支在支割线上岸取正值 , 于是可认为该分2z1的幅角为, 故 f ( 1)i2i .支在上岸之幅角为 0,因而此分支在2e22《复变函数》考试试题(二)一. 判断题 . (20 分)1. 若函数 f ( z)u( x, y) iv ( x, y) 在 D 内连续,则 u(x,y)与 v(x,y)都在 D 内连续 .( ) 2. cos z 与 sin z 在复平面内有界 .()3.若函数 f(z)在 z 解析,则 f(z)在 z 连续 .()0 04. 有界整函数必为常数 .一定不存在 .()5. 如 0是函数f(z)的本性奇点,则 lim f ( z) ()zz z 06. 若函数 f(z)在 z 0 可导,则 f(z)在 z 0 解析 .()7.若 f(z)在区域 D 内解析 , 则对 D 内任一简单闭曲线 Cf (z)dz0 .C( ) 8. 若数列 { z n } 收敛,则 {Re z n } 与 {Im z n } 都收敛 .() 9. 若 f(z)在区域 D 内解析,则 |f(z)|也在 D 内解析 .()10. 存在一个在零点解析的函数1 ) 0 1 1 1,2,... .f(z) 使 f (且 f ( ) ,nn 1 2n 2n( )二 . 填空题 . (20 分)1. 设 zi ,则 | z | __,arg z__, z __2.设 f (z) ( x 22xy) i(1 sin( x 2y 2 ), z x iy C ,则 limf ( z) ________.z 1i3.|z z 0| 1(zdz_________.z )n( n 为自然数)---4.幂级数 nz n的收敛半径为__________ .n05.若 z0是 f(z)的 m 阶零点且 m>0,则 z0是f '( z)的 _____零点 .6.函数 e z的周期为 __________.7.方程 2z5z33z 8 0 在单位圆内的零点个数为________.8.设 f ( z)1,则 f (z) 的孤立奇点有_________.21z9.函数 f ( z) | z | 的不解析点之集为________.10. Res(z41,1) ____ . z三. 计算题 . (40 分)1.求函数sin( 2z3)的幂级数展开式 .2.在复平面上取上半虚轴作割线 . 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点 z i 处的值.i3.计算积分: I| z | dz,积分路径为(1)单位圆( | z | 1)i的右半圆 .sin z dzz 2(z) 24.求2.四. 证明题 . (20 分)1. 设函数 f(z)在区域 D 内解析,试证: f(z)在 D 内为常数的充要条件是 f (z) 在D内解析 .2.试用儒歇定理证明代数基本定理 .《复变函数》考试试题(二)参考答案一.判断题 .1.√2.×3.√4.√ 5.× 6.×7.×8.√9.× 10.× .二.填空题---1.1 ,, i ;2. 3(1sin 2)i ;3.2 i n14. 1;5. m 1 . 0n;216.2k i ,( k z) .7. 0;8. i;9.R ;10. 0.三.计算题1.解 sin(2 z3 )( 1)n (2 z3 )2 n 1(1)n 22n 1 z6n3.n 0(2 n1)!n 0(2n1)!2.解令 z re i.2 ki则 f ( z)z re2,(k0,1).又因为在正实轴去正实值,所以k0 .所以 f (i)ie 4.3.单位圆的右半圆周为z e i,ide i e i 所以 zdz22i22 4.解.2 2 2i .即 u, v 满足 C.R.,且u x , v y , u y ,v x连续 , 故f ( z)在D内解析 .( 充分性 ) 令f ( z)u iv, 则 f ( z)u iv ,因为 f ( z) 与 f ( z) 在D内解析,所以u x v y , u y v x,且 u x ( v) y v y , u y( v x )v x.比较等式两边得u x v y u y v x0 .从而在 D 内 u, v 均为常数,故f ( z)在 D 内为常数.2. 即要证“任一n次方程a0 z n a1z n1a n 1z a n0(a00) 有且只有n 个根”.证明令 f (z)a0 z n a1z n 1a n1za n0 ,取 R max a1a n,1 ,当 za0在 C : z R 上时,有(z)a1 R n 1an 1R a n( a1a n )R n 1a0R n.f ( z) .由儒歇定理知在圆z R 内,方程 a0 z n a1z n 1a n 1z a n0与 a0 z n0有相---同个数的根 . 而 a 0 z n 0 在 z R 内有一个 n 重根 z 0 . 因此 n 次方程在 z R 内有 n 个根 .《复变函数》考试试题(三)一 . 判断题 . (20 分).1. cos z 与 sin z 的周期均为 2k .( )2. 若 f ( z) 在 z 0 处满足柯西 - 黎曼条件 , 则 f ( z) 在 z 0 解析 . ( )3. 若函数 f ( z) 在 z 0 处解析,则 f ( z) 在 z 0 连续 . ( )4. 若数列 { z n } 收敛,则 {Re z n } 与 {Im z n } 都收敛 .( )5.若函数 f ( z) 是区域 D 内解析且在 D 内的某个圆内恒为常数,则数 f ( z) 在区域 D 内为常数 . ( )6. 若函数 f ( z) 在 z 0 解析,则 f ( z) 在 z 0 的某个邻域内可导 . ()7.如果函数 f ( z) 在 D{ z :| z | 1} 上解析 , 且 | f (z) | 1(| z | 1) , 则| f ( z) | 1(| z | 1) .( )8.若函数 f ( z) 在 z 0处解析,则它在该点的某个邻域内可以展开为幂级数.( ) 9. 若 z 0 是 f ( z) 的 m 阶零点 , 则 z 0 是 1/ f ( z) 的 m 阶极点 . ( )10.若z 0 是 f (z)的可去奇点,则 Res( f ( z), z 0 ) 0. ( )二 . 填空题 . (20 分)1. 设 f ( z)1 ,则 f ( z) 的定义域为 ___________.2 z 12. 函数 e z 的周期为 _________.3. 若 z nn 2 i (1 1) n ,则 lim z n__________.1 nnn4. sin 2 z cos 2 z___________.dz5.|z z 0 | 1(z z )n( n 为自然数)_________.6. 幂级数nx n 的收敛半径为 __________.n设 f (z) 1f z 的孤立奇点有z 2 1,则7.( ) __________.ez---9.若 z 是 f (z)的极点,则 lim f (z) ___ .z z 0z10.Res(en ,0) ____ .z三 . 计算题 . (40 分)11. 将函数 f ( z) z 2e z 在圆环域 0 z内展为 Laurent 级数 .2. 试求幂级数n!z n的收敛半径 .n nn3. 算下列积分:e zdz,其中 C是| z |1.Cz 2 (z29)4. 求 z92z6z 28z 2 0 在| z|<1内根的个数 .四 . 证明题 . (20 分)1.函数 f (z) 在区域 D 内解析 . 证明:如果 | f ( z) |在 D 内为常数,那么它在D 内为常数 .2.设 f (z) 是一整函数,并且假定存在着一个正整数 n ,以及两个正数 R 及 M ,使得当 | z|R 时| f ( z) |M | z |n,证明 f (z) 是一个至多 n 次的多项式或一常数。
复变函数试题库(南信大数统院)(word文档良心出品)
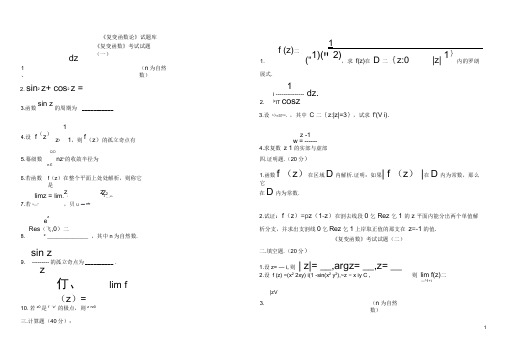
1、 dz2. sin 2z+ cos 2z =《复变函数论》试题库《复变函数》考试试题(一)(n 为自然数)1.展式.f (z)二1("1)("2),求 f(z)在D 二{z:0 |z|1}内的罗朗3.函数sin z的周期为 ___________ 4.设 1f (z )z 2 1,则f (z )的孤立奇点有5.幕级数 QO nz n 的收敛半径为n £2.1i --------------- |zITcoszdz.3.设 f (z =3?1d ,,其中 C 二{z:|z|=3},试求 f'(V i).z -1w = ------4.求复数 z 1的实部与虚部 6.若函数 f (z )在整个平面上处处解析,则称它是 limz = lim.z i z 2 …zn 7.若n —",贝U 一宀 Z 2zeRes (飞,0)二 8. z _____________ ,其中n 为自然数. sin z9. --------- 的孤立奇点为 __________ .z仃、lim f(z )=10. 若z0是f (z )的极点,则z >z0三.计算题(40分):四.证明题.(20分) 1.函数f (z )在区域D 内解析.证明:如果| f (z ) |在D 内为常数,那么它 在D 内为常数.2.试证:f (z )=p z (1-z )在割去线段0乞Rez 乞1的z 平面内能分出两个单值解析分支,并求出支割线0乞Rez 乞1上岸取正值的那支在 z =-1的值.《复变函数》考试试题(二)二.填空题.(20分)1.设z= — i ,则| z|= __,argz= __,z= __2.设 f (z) =(x 2 2xy) i(1 -sin(x 2 y 2),~z = x iy C ,则 lim f(z)二—^1+i3.|zV(n 为自然数)oO4. 幕级数瓦nz n的收敛半径为______________ .n卫5. 若z o是f(z)的m阶零点且m>0,则z是f'(z)的___________ 零点•6. 函数e z的周期为 ___________ .5 37. 方程2z -z +3z+8=0在单位圆内的零点个数为 _______________ .18. 设f(z)= --------- 2,贝U f (z)的孤立奇点有 __________ .1 +z9. 函数f (z) =| z |的不解析点之集为__________ .z 一1八10. Res(-^,1) = _____ .z三•计算题.(40分)1. 求函数sin(2z‘)的幕级数展开式.2. 在复平面上取上半虚轴作割线.试在所得的区域内取定函数■■ z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点z二i处的值.i3. 计算积分:dz,积分路径为(1)单位圆(| z|= 1)的右半i圆.四.证明题.(20分)z =2 4.求sin zdz1. 设函数f(z)在区域D内解析,试证:f(z)在D内为常数的充要条件是内解析.2. 试用儒歇定理证明代数基本定理.《复变函数》考试试题(三)二.填空题.(20分)1. 设f (z)=r^,则f(z)的定义域为_____________________ .z + 12. 函数e z的周期为_________ .3. 若Z n = —+ i(^-)n,贝U 1计Z n =1_n n +4. sin2z + cos2z = ____________ .dz5. |z—z°|=1 (z_ %)" = ____________ .( n为自然数)oO6. 幕级数送nx n的收敛半径为 _____________ .7. 设f(z)=亠; ,则f (z)的孤立奇点有z + 18. 设e z = 一1,贝u z= _______ .9. 若z0是f(z)的极点,则lim f(z)= ______.Z of (z)在DQQ4.求z - 2z ' z - 8z - 2 = 0在| z |<1内根的个数.四.证明题.(20分) 1.函数f(z) 在区域D 内解析.证明:如果 |f(z)| 在D 内为常数,那么 它在D 内为常数.2.设 f(z)是- -整函数,并且假定存在着一个正整数 n ,以及两个正数 R 及M使得当| z|- R 时|f(z)r M |z|n,证明f(z) 是- -个至多n 次的多项式或一常数。
复变函数历年考试真题试卷

复变函数历年考试真题试卷一、选择题1. 下列哪个函数不是复变函数?A. f(z) = e^zB. f(z) = z^2C. f(z) = |z|D. f(z) = ln(z+1)2. 设f(z) = u(x,y) + iv(x,y)是一个复变函数,下面哪个等式成立?A. ∂u/∂x = ∂v/∂yB. ∂u/∂y = ∂v/∂xC. ∂u/∂x = -∂v/∂yD. ∂u/∂y = -∂v/∂x3. 对于复变函数f(z) = x^3 + 3ix^2y - 3xy^2 - iy^3,下列哪个等式成立?A. ∂u/∂x = 3x^2 + 6ixy - 3y^2B. ∂u/∂y = 3x^2 + 6ixy - 3y^2C. ∂v/∂x = -3x^2 + 3y^2 - 6ixyD. ∂v/∂y = -3x^2 + 3y^2 - 6ixy二、填空题1. 设f(z) = z^2 + 2iz - 1,则f(z)的共轭函数是________。
2. 当z → ∞ 时,f(z) = z^2 + 3z + 1的极限是________。
3. 若f(z) = u(x,y) + iv(x,y) 是全纯函数,则满足柯西-黎曼方程的条件是∂u/∂x = ________。
三、计算题1. 计算复变函数f(z) = z^3 - 4z的积分,其中C为以原点为圆心、半径为2的圆周。
2. 当z = -i 时,计算复变函数f(z) = 2z^2 + 3iz的导数。
四、证明题证明:若复变函数f(z) = u(x,y) + iv(x,y) 在单连通域D上解析,则f(z) 在D 上也是调和函数。
(请自行根据题目要求增减字数,使得文章达到合适的长度。
)(文章正文)选择题:1. 下列哪个函数不是复变函数?2. 设f(z) = u(x,y) + iv(x,y)是一个复变函数,下面哪个等式成立?3. 对于复变函数f(z) = x^3 + 3ix^2y - 3xy^2 - iy^3,下列哪个等式成立?填空题:1. 设f(z) = z^2 + 2iz - 1,则f(z)的共轭函数是________。
复变函数论试题库及答案

《复变函数论》试题库《复变函数》考试试题(一)一、 判断题(20分):1.若f(z)在z 0的某个邻域可导,则函数f(z)在z 0解析. ( )2.有界整函数必在整个复平面为常数. ( )3.若}{n z 收敛,则} {Re n z 与}{Im n z 都收敛. ( )4.若f(z)在区域D 解析,且0)('≡z f ,则C z f ≡)((常数). ( )5.若函数f(z)在z 0处解析,则它在该点的某个邻域可以展开为幂级数. ( )6.若z 0是)(z f 的m 阶零点,则z 0是1/)(z f 的m 阶极点. ( )7.若)(lim 0z f z z →存在且有限,则z 0是函数f(z)的可去奇点. ( )8.若函数f(z)在是区域D 的单叶函数,则)(0)('D z z f ∈∀≠. ( ) 9. 若f (z )在区域D 解析, 则对D 任一简单闭曲线C0)(=⎰Cdz z f .( )10.若函数f(z)在区域D 的某个圆恒等于常数,则f(z)在区域D 恒等于常数.( ) 二.填空题(20分)1、 =-⎰=-1||00)(z z nz z dz__________.(n 为自然数)2.=+z z 22cos sin _________. 3.函数z sin 的周期为___________.4.设11)(2+=z z f ,则)(z f 的孤立奇点有__________.5.幂级数nn nz∞=∑的收敛半径为__________.6.若函数f(z)在整个平面上处处解析,则称它是__________.7.若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________.8.=)0,(Re n zz e s ________,其中n 为自然数.9. zz sin 的孤立奇点为________ .10.若0z 是)(z f 的极点,则___)(lim 0=→z f z z .三.计算题(40分):1. 设)2)(1(1)(--=z z z f ,求)(z f 在}1||0:{<<=z z D 的罗朗展式.2..cos 11||⎰=z dz z3. 设⎰-++=C d z z f λλλλ173)(2,其中}3|:|{==z z C ,试求).1('i f +4. 求复数11+-=z z w 的实部与虚部.四. 证明题.(20分) 1. 函数)(z f 在区域D 解析. 证明:如果|)(|z f 在D 为常数,那么它在D 为常数.2. 试证: ()f z 0Re 1z ≤≤的z 平面能分出两个单值解析分支, 并求出支割线0Re 1z ≤≤上岸取正值的那支在1z =-的值.《复变函数》考试试题(二)一. 判断题.(20分)1. 若函数),(),()(y x iv y x u z f +=在D 连续,则u (x,y )与v (x,y )都在D 连续.( )2. cos z 与sin z 在复平面有界. ( )3. 若函数f (z )在z 0解析,则f (z )在z 0连续. ( )4. 有界整函数必为常数. ( )5. 如z 0是函数f (z )的本性奇点,则)(lim 0z f z z →一定不存在. ( )6. 若函数f (z )在z 0可导,则f (z )在z 0解析. ( )7. 若f (z )在区域D 解析, 则对D 任一简单闭曲线C 0)(=⎰Cdz z f .( )8. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( ) 9. 若f (z )在区域D 解析,则|f (z )|也在D 解析. ( ) 10. 存在一个在零点解析的函数f (z )使0)11(=+n f 且,...2,1,21)21(==n nn f . ( )二. 填空题. (20分)1. 设i z -=,则____,arg __,||===z z z2.设C iy x z y x i xy x z f ∈+=∀+-++=),sin(1()2()(222,则=+→)(lim 1z f iz ________.3.=-⎰=-1||00)(z z n z z dz_________.(n 为自然数)4. 幂级数0n n nz ∞=∑的收敛半径为__________ .5. 若z 0是f (z )的m 阶零点且m >0,则z 0是)('z f 的_____零点.6. 函数e z 的周期为__________.7. 方程083235=++-z z z 在单位圆的零点个数为________. 8. 设211)(zz f +=,则)(z f 的孤立奇点有_________. 9. 函数||)(z z f =的不解析点之集为________.10. ____)1,1(Res 4=-zz . 三. 计算题. (40分)1. 求函数)2sin(3z 的幂级数展开式. 2. 在复平面上取上半虚轴作割线. 试在所得的区域取定函数z 在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点i z=处的值.3. 计算积分:⎰-=iiz z Id ||,积分路径为(1)单位圆(1||=z )的右半圆.4. 求dzz zz ⎰=-22)2(sin π.四. 证明题. (20分)1. 设函数f (z )在区域D 解析,试证:f (z )在D 为常数的充要条件是)(z f 在D 解析.2. 试用儒歇定理证明代数基本定理.《复变函数》考试试题(三)一. 判断题. (20分).1. cos z 与sin z 的周期均为πk2. ( ) 2. 若f (z )在z 0处满足柯西-黎曼条件, 则f (z )在z 0解析. ( )3. 若函数f (z )在z 0处解析,则f (z )在z 0连续. ( )4. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( )5. 若函数f (z )是区域D 解析且在D 的某个圆恒为常数,则数f (z )在区域D 为常数. ( )6. 若函数f (z )在z 0解析,则f (z )在z 0的某个邻域可导. ( )7. 如果函数f (z )在}1|:|{≤=z z D 上解析,且)1|(|1|)(|=≤z z f ,则)1|(|1|)(|≤≤z z f . ( )8. 若函数f (z )在z 0处解析,则它在该点的某个邻域可以展开为幂级数. ( ) 9. 若z 0是)(z f 的m 阶零点, 则z 0是1/)(z f 的m 阶极点. ( ) 10. 若0z 是)(z f 的可去奇点,则0)),((Res 0=z z f . ( )二. 填空题. (20分) 1. 设11)(2+=z z f ,则f (z )的定义域为___________. 2. 函数e z 的周期为_________.3. 若n n ni n n z )11(12++-+=,则=∞→n z n lim __________.4. =+z z 22cos sin ___________.5.=-⎰=-1||00)(z z n z z dz_________.(n 为自然数)6. 幂级数∑∞=0n n nx 的收敛半径为__________.7. 设11)(2+=z z f ,则f (z )的孤立奇点有__________.8. 设1-=ze,则___=z .9. 若0z 是)(z f 的极点,则___)(lim 0=→z f z z .10. ____)0,(Res =n zze .三. 计算题. (40分)1. 将函数12()zf z z e =在圆环域0z <<∞展为Laurent 级数.2. 试求幂级数nn n z nn ∑+∞=!的收敛半径.3. 算下列积分:⎰-C z z z ze )9(d 22,其中C 是1||=z .4. 求0282269=--+-z z z z在|z |<1根的个数.四. 证明题. (20分) 1. 函数)(z f 在区域D 解析. 证明:如果|)(|z f 在D 为常数,那么它在D为常数. 2. 设)(z f 是一整函数,并且假定存在着一个正整数n ,以及两个正数R 及M ,使得当R z ≥||时n z M z f |||)(|≤,证明)(z f 是一个至多n 次的多项式或一常数。
复变函数论考试试题

复变函数论考试试题
1. 证明庞加莱引理
2. 证明柯西-黎曼方程
3. 证明柯西积分公式
4. 计算积分 $\int_{C} \frac{z}{z^2+1} \,dz$,其中 $C$ 是圆周
$|z|=2$
5. 设 $f(z)$ 为解析函数,且满足 $|f(z)|\leq e^{\text{Re}(z)}$,证明$f(z)$ 为常数
6. 求解柯西问题:$\frac{\partial u}{\partial x} + \frac{\partial
u}{\partial y} = 0, \ u(x,0) = x^2$
7. 若 $f(z)$ 为整函数,证明 $f(z)$ 为多项式函数
8. 计算级数 $\sum_{n=0}^{\infty} \frac{n}{n^4+1}$ 的收敛域
9. 讨论函数 $f(z) = \sqrt{z^2-1}$ 在 $z=\infty$ 处的性质
10. 证明利普希茨条件在复变函数中的等价形式
11. 论述柯西定理在复平面上的应用
12. 论述黑格尔定理在解析函数中的重要性
以上是本次复变函数论考试的试题,请同学们认真答题,祝考试顺利!。
《复变函数论》试题库

《复变函数》考试试题(一)一、 判断题.(正确者在括号内打√,错误者在括号内打×,每题2分) 1.当复数0z =时,其模为零,辐角也为零. ( )2.若0z 是多项式110()n n n n P z a z a z a --=+++(0)n a ≠的根,则0z 也()P z 是的根.( )3.如果函数()f z 为整函数,且存在实数M ,使得Re ()f z M <,则()f z 为一常数.( ) 4.设函数1()f z 与2()f z 在区域内D 解析,且在D 内的一小段弧上相等,则对任意的z D ∈,有1()f z 2()f z ≡. ( )5.若z =∞是函数()f z 的可去奇点,则Re ()0z s f z =∞=. ( )二、填空题.(每题2分)1.23456i i i i i ⋅⋅⋅⋅= _____________________. 2.设0z x iy =+≠,且arg ,arctan22y z x ππππ-<≤-<<,当0,0x y <>时,arg arctanyx =+________________. 3.函数1w z =将z 平面上的曲线22(1)1x y -+=变成w 平面上的曲线______________.4.方程440(0)z a a +=>的不同的根为________________. 5.(1)i i +___________________.6.级数20[2(1)]nn z ∞=+-∑的收敛半径为____________________.7.cos nz 在z n <(n 为正整数)内零点的个数为_____________________. 8.函数336()6sin (6)f z z z z =+-的零点0z =的阶数为_____________________. 9.设a 为函数()()()z f z z ϕψ=的一阶极点,且()0,()0,()0a a a ϕψψ'≠=≠,则()Re ()z af z sf z ='=_____________________. 10.设a 为函数()f z 的m 阶极点,则()Re ()z af z sf z ='=_____________________. 三、计算题(50分)1.设221(,)ln()2u x y x y =+。
《复变函数论》精彩试题库及问题详解

《复变函数论》试题库《复变函数》考试试题(一)一、 判断题(20分):1.若f(z)在z 0的某个邻域内可导,则函数f(z)在z 0解析. ( )2.有界整函数必在整个复平面为常数. ( )3.若}{n z 收敛,则} {Re n z 与}{Im n z 都收敛. ( )4.若f(z)在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数). ( )5.若函数f(z)在z 0处解析,则它在该点的某个邻域内可以展开为幂级数. ( )6.若z 0是)(z f 的m 阶零点,则z 0是1/)(z f 的m 阶极点. ( )7.若)(lim 0z f z z →存在且有限,则z 0是函数f(z)的可去奇点. ( )8.若函数f(z)在是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠. ( ) 9. 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C0)(=⎰Cdz z f .( )10.若函数f(z)在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数.( ) 二.填空题(20分)1、 =-⎰=-1||00)(z z n z z dz__________.(n 为自然数) 2.=+z z 22cos sin _________. 3.函数z sin 的周期为___________.4.设11)(2+=z z f ,则)(z f 的孤立奇点有__________.5.幂级数nn nz∞=∑的收敛半径为__________.6.若函数f(z)在整个平面上处处解析,则称它是__________.7.若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________.8.=)0,(Re n zz e s ________,其中n 为自然数.9. zz sin 的孤立奇点为________ .10.若0z 是)(z f 的极点,则___)(lim 0=→z f z z .三.计算题(40分):1. 设)2)(1(1)(--=z z z f ,求)(z f 在}1||0:{<<=z z D 内的罗朗展式.2. .cos 11||⎰=z dz z3. 设⎰-++=C d z z f λλλλ173)(2,其中}3|:|{==z z C ,试求).1('i f +4. 求复数11+-=z z w 的实部与虚部.四. 证明题.(20分) 1. 函数)(z f 在区域D 内解析. 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数. 2. 试证: ()f z =在割去线段0Re 1z ≤≤的z 平面内能分出两个单值解析分支,并求出支割线0Re 1z ≤≤上岸取正值的那支在1z =-的值.《复变函数》考试试题(二)一. 判断题.(20分)1. 若函数),(),()(y x iv y x u z f +=在D 内连续,则u (x,y )与v (x,y )都在D 内连续. ( )2. cos z 与sin z 在复平面内有界. ( )3. 若函数f (z )在z 0解析,则f (z )在z 0连续. ( )4. 有界整函数必为常数. ( )5. 如z 0是函数f (z )的本性奇点,则)(lim 0z f z z →一定不存在. ( )6. 若函数f (z )在z 0可导,则f (z )在z 0解析. ( )7. 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f .( )8. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( ) 9. 若f (z )在区域D 内解析,则|f (z )|也在D 内解析. ( )10. 存在一个在零点解析的函数f (z )使0)11(=+n f 且,...2,1,21)21(==n nn f .( )二. 填空题. (20分)1. 设i z -=,则____,arg __,||===z z z2.设C iy x z y x i xy x z f ∈+=∀+-++=),sin(1()2()(222,则=+→)(lim 1z f iz ________.3.=-⎰=-1||00)(z z n z z dz_________.(n 为自然数)4. 幂级数0n n nz ∞=∑的收敛半径为__________ .5. 若z 0是f (z )的m 阶零点且m >0,则z 0是)('z f 的_____零点.6. 函数e z 的周期为__________.7. 方程083235=++-z z z 在单位圆内的零点个数为________. 8. 设211)(z z f +=,则)(z f 的孤立奇点有_________. 9. 函数||)(z z f =的不解析点之集为________.10. ____)1,1(Res 4=-zz . 三. 计算题. (40分)1. 求函数)2sin(3z 的幂级数展开式.2. 在复平面上取上半虚轴作割线. 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点i z=处的值.3. 计算积分:⎰-=iiz z Id ||,积分路径为(1)单位圆(1||=z )的右半圆.4. 求dzz zz ⎰=-22)2(sin π.四. 证明题. (20分)1. 设函数f (z )在区域D 内解析,试证:f (z )在D 内为常数的充要条件是)(z f 在D 内解析.2. 试用儒歇定理证明代数基本定理.《复变函数》考试试题(三)一. 判断题. (20分).1. cos z 与sin z 的周期均为πk2. ( ) 2. 若f (z )在z 0处满足柯西-黎曼条件, 则f (z )在z 0解析. ( )3. 若函数f (z )在z 0处解析,则f (z )在z 0连续. ( )4. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( )5. 若函数f (z )是区域D 内解析且在D 内的某个圆内恒为常数,则数f (z )在区域D 内为常数. ( )6. 若函数f (z )在z 0解析,则f (z )在z 0的某个邻域内可导. ( )7. 如果函数f (z )在}1|:|{≤=z z D 上解析,且)1|(|1|)(|=≤z z f ,则)1|(|1|)(|≤≤z z f . ( ) 8. 若函数f (z )在z 0处解析,则它在该点的某个邻域内可以展开为幂级数. ( ) 9. 若z 0是)(z f 的m 阶零点, 则z 0是1/)(z f 的m 阶极点. ( ) 10. 若0z 是)(z f 的可去奇点,则0)),((Res 0=z z f . ( )二. 填空题. (20分)1. 设11)(2+=z z f ,则f (z )的定义域为___________.2. 函数e z的周期为_________.3. 若n n n i n n z )11(12++-+=,则=∞→n z n lim __________.4. =+z z 22cos sin ___________.5. =-⎰=-1||00)(z z n z z dz_________.(n 为自然数) 6. 幂级数∑∞=0n n nx 的收敛半径为__________.7. 设11)(2+=z z f ,则f (z )的孤立奇点有__________.8. 设1-=ze ,则___=z .9. 若0z 是)(z f 的极点,则___)(lim 0=→z f z z .10. ____)0,(Res =n zze .三. 计算题. (40分)1. 将函数12()zf z z e =在圆环域0z <<∞内展为Laurent 级数.2. 试求幂级数nn n z nn ∑+∞=!的收敛半径.3. 算下列积分:⎰-C z z z ze )9(d 22,其中C 是1||=z .4. 求0282269=--+-z z z z在|z |<1内根的个数.四. 证明题. (20分) 1. 函数)(z f 在区域D 内解析. 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数. 2. 设)(z f 是一整函数,并且假定存在着一个正整数n ,以及两个正数R 及M ,使得当R z ≥||时n z M z f |||)(|≤,证明)(z f 是一个至多n 次的多项式或一常数。
《复变函数》考试试题与答案各种总结

《复变函数》考试试题(一)一、 判断题(20分):1、若f(z)在z 0的某个邻域内可导,则函数f(z)在z 0解析、 ( )2、有界整函数必在整个复平面为常数、 ( )3、若}{n z 收敛,则} {Re n z 与}{Im n z 都收敛、 ( )4、若f(z)在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数)、 ( )5、若函数f(z)在z 0处解析,则它在该点的某个邻域内可以展开为幂级数、 ( )6、若z 0就是)(z f 的m 阶零点,则z 0就是1/)(z f 的m 阶极点、 ( )7、若)(lim 0z f z z →存在且有限,则z 0就是函数f(z)的可去奇点、 ( )8、若函数f(z)在就是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠、 ( ) 9、 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C0)(=⎰Cdz z f 、( )10、若函数f(z)在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数、( ) 二、填空题(20分)1、 =-⎰=-1||00)(z z nz z dz__________、(n 为自然数)2、=+z z 22cos sin _________、 3、函数z sin 的周期为___________、4、设11)(2+=z z f ,则)(z f 的孤立奇点有__________、5、幂级数nn nz∞=∑的收敛半径为__________、6、若函数f(z)在整个平面上处处解析,则称它就是__________、7、若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________、8、=)0,(Re n zz e s ________,其中n 为自然数、9、 zz sin 的孤立奇点为________ 、10、若0z 就是)(z f 的极点,则___)(lim 0=→z f z z 、三、计算题(40分):1、 设)2)(1(1)(--=z z z f ,求)(z f 在}1||0:{<<=z z D 内的罗朗展式、2、 .cos 11||⎰=z dz z3、 设⎰-++=C d z z f λλλλ173)(2,其中}3|:|{==z z C ,试求).1('i f +4、 求复数11+-=z z w 的实部与虚部、四、 证明题、(20分) 1、 函数)(z f 在区域D 内解析、 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数、 2、 试证: ()f z =0Re 1z ≤≤的z 平面内能分出两个单值解析分支,并求出支割线0Re 1z ≤≤上岸取正值的那支在1z =-的值、 《复变函数》考试试题(一)参考答案一. 判断题1.×2.√ 3.√ 4.√ 5.√ 6.√ 7.×8.×9.×10.× 二.填空题 1、 2101i n n π=⎧⎨≠⎩ ; 2、 1; 3、 2k π,()k z ∈; 4、 z i =±; 5、 16、 整函数;7、 ξ;8、 1(1)!n -; 9、 0; 10、 ∞、三.计算题、1、 解 因为01,z << 所以01z <<111()(1)(2)12(1)2f z z z z z ==-----001()22nn n n z z ∞∞===-∑∑、 2、 解 因为22212Re ()limlim 1cos sin z z z z s f z z z ππππ→→=+===--, 22212Re ()limlim 1cos sin z z z z s f z z zππππ→-→-=--===-、 所以22212(Re ()Re ()0cos z z z dz i s f z s f z z πππ==-==+=⎰、 3、 解 令2()371ϕλλλ=++, 则它在z 平面解析, 由柯西公式有在3z <内, ()()2()c f z dz i z z ϕλπϕλ==-⎰、所以1(1)2()2(136)2(613)z i f i i z i i i πϕππ=+''+==+=-+、 4、 解 令z a bi =+, 则 222222122(1)2(1)211111(1)(1)(1)z a bi a bw z z a b a b a b -+-+==-=-=-+++++++++、 故 2212(1)Re()11(1)z a z a b -+=-+++, 2212Im()1(1)z bz a b-=+++、 四、 证明题、1、 证明 设在D 内()f z C =、令2222(),()f z u iv f z u v c =+=+=则、两边分别对,x y 求偏导数, 得 0(1)0(2)x x yy uu vv uu vv +=⎧⎨+=⎩因为函数在D 内解析, 所以,x y y x u v u v ==-、 代入 (2) 则上述方程组变为00x x x x uu vv vu uv +=⎧⎨-=⎩、 消去x u 得, 22()0x u v v +=、 1) 若220u v +=, 则 ()0f z = 为常数、2) 若0x v =, 由方程 (1) (2) 及 ..C R -方程有0,x u = 0y u =, 0y v =、 所以12,u c v c ==、 (12,c c 为常数)、 所以12()f z c ic =+为常数、2、证明()f z =0,1z =、 于就是割去线段0Re 1z ≤≤的z 平面内变点就不可能单绕0或1转一周, 故能分出两个单值解析分支、由于当z 从支割线上岸一点出发,连续变动到0,1z = 时, 只有z 的幅角增加π、 所以()f z =2π、 由已知所取分支在支割线上岸取正值, 于就是可认为该分支在上岸之幅角为0, 因而此分支在1z =-的幅角为2π,故2(1)i f e π-==、《复变函数》考试试题(二)一. 判断题、(20分)1、 若函数),(),()(y x iv y x u z f +=在D 内连续,则u (x,y )与v (x,y )都在D 内连续、 ( )2、 cos z 与sin z 在复平面内有界、 ( )3、 若函数f (z )在z 0解析,则f (z )在z 0连续、 ( )4、 有界整函数必为常数、 ( )5、 如z 0就是函数f (z )的本性奇点,则)(lim 0z f z z →一定不存在、 ( )6、 若函数f (z )在z 0可导,则f (z )在z 0解析、 ( )7、 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f 、( )8、 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛、 ( ) 9、 若f (z )在区域D 内解析,则|f (z )|也在D 内解析、 ( )10、 存在一个在零点解析的函数f (z )使0)11(=+n f 且,...2,1,21)21(==n nn f 、( )二、 填空题、 (20分)1、 设i z -=,则____,arg __,||===z z z2、设C iy x z y x i xy x z f ∈+=∀+-++=),sin(1()2()(222,则=+→)(lim 1z f iz ________、3、=-⎰=-1||00)(z z n z z dz_________、(n 为自然数)4、 幂级数0n n nz ∞=∑的收敛半径为__________ 、5、 若z 0就是f (z )的m 阶零点且m >0,则z 0就是)('z f 的_____零点、6、 函数e z 的周期为__________、7、 方程083235=++-z z z 在单位圆内的零点个数为________、 8、 设211)(zz f +=,则)(z f 的孤立奇点有_________、 9、 函数||)(z z f =的不解析点之集为________、10、 ____)1,1(Res 4=-zz 、 三、 计算题、 (40分)1、 求函数)2sin(3z 的幂级数展开式、2、 在复平面上取上半虚轴作割线、 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点i z=处的值、3、 计算积分:⎰-=iiz z Id ||,积分路径为(1)单位圆(1||=z )的右半圆、4、 求dzz zz ⎰=-22)2(sin π、四、 证明题、 (20分)1、 设函数f (z )在区域D 内解析,试证:f (z )在D 内为常数的充要条件就是)(z f 在D 内解析、2、 试用儒歇定理证明代数基本定理、《复变函数》考试试题(二)参考答案一. 判断题、1.√ 2.×3.√ 4.√ 5.×6.×7.×8.√ 9.×10.×、 二、 填空题1、1,2π-, i ; 2、 3(1sin 2)i +-; 3、2101i n n π=⎧⎨≠⎩; 4、 1; 5、 1m -、 6、 2k i π,()k z ∈、 7、 0; 8、 i ±; 9、 R ; 10、 0、 三、 计算题1、 解 3212163300(1)(2)(1)2sin(2)(21)!(21)!n n n n n n n z z z n n +++∞∞==--==++∑∑、2、 解 令i z re θ=、则22(),(0,1)k if z k θπ+===、又因为在正实轴去正实值,所以0k =、所以4()if i eπ=、3、 单位圆的右半圆周为i z e θ=, 22ππθ-≤≤、所以22222ii i iz dz de ei ππθθππ---===⎰⎰、4、 解dz z zz ⎰=-22)2(sin π2)(sin 2ππ='=z z i 2cos 2ππ==z zi =0、四、 证明题、1、 证明 (必要性) 令12()f z c ic =+,则12()f z c ic =-、 (12,c c 为实常数)、 令12(,),(,)u x y c v x y c ==-、 则0x y y x u v u v ====、 即,u v 满足..C R -, 且,,,x y y x u v u v 连续, 故()f z 在D 内解析、 (充分性) 令()f z u iv =+, 则 ()f z u iv =-, 因为()f z 与()f z 在D 内解析, 所以,x y y x u v u v ==-, 且(),()x y y y x x u v v u v v =-=-=--=-、比较等式两边得 0x y y x u v u v ====、 从而在D 内,u v 均为常数,故()f z 在D 内为常数、2、 即要证“任一 n 次方程 101100(0)n n n n a z a z a z a a --++⋅⋅⋅++=≠ 有且只有 n 个根”、证明 令1011()0nn n n f z a z a z a z a --=++⋅⋅⋅++=, 取10max ,1n a a R a ⎧⎫+⋅⋅⋅+⎪⎪>⎨⎬⎪⎪⎩⎭, 当z 在:C z R =上时, 有 111110()()n n nn n n z a R a R a a a R a R ϕ---≤+⋅⋅⋅++<+⋅⋅⋅+<、()f z =、由儒歇定理知在圆 z R < 内, 方程10110n n n n a z a z a z a --++⋅⋅⋅++= 与 00na z = 有相 同个数的根、 而 00na z = 在 z R < 内有一个 n 重根 0z =、 因此n 次方程在z R <内有n 个根、《复变函数》考试试题(三)一、 判断题、 (20分)、1、 cos z 与sin z 的周期均为πk2、 ( ) 2、 若f (z )在z 0处满足柯西-黎曼条件, 则f (z )在z 0解析、 ( )3、 若函数f (z )在z 0处解析,则f (z )在z 0连续、 ( )4、 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛、 ( )5、 若函数f (z )就是区域D 内解析且在D 内的某个圆内恒为常数,则数f (z )在区域D 内为常数、 ( )6、 若函数f (z )在z 0解析,则f (z )在z 0的某个邻域内可导、 ( )7、 如果函数f (z )在}1|:|{≤=z z D 上解析,且)1|(|1|)(|=≤z z f ,则)1|(|1|)(|≤≤z z f 、 ( )8、 若函数f (z )在z 0处解析,则它在该点的某个邻域内可以展开为幂级数、( )9、 若z 0就是)(z f 的m 阶零点, 则z 0就是1/)(z f 的m 阶极点、 ( ) 10、 若z 就是)(z f 的可去奇点,则)),((Res 0=z z f 、( )二、 填空题、 (20分)1、 设11)(2+=z z f ,则f (z )的定义域为___________、2、 函数e z的周期为_________、3、 若n n n i n n z )11(12++-+=,则=∞→n z n lim __________、4、 =+z z 22cos sin ___________、5、 =-⎰=-1||00)(z z n z z dz_________、(n 为自然数) 6、 幂级数∑∞=0n n nx 的收敛半径为__________、7、 设11)(2+=z z f ,则f (z )的孤立奇点有__________、8、 设1-=ze ,则___=z 、9、 若0z 就是)(z f 的极点,则___)(lim 0=→z f z z 、10、 ____)0,(Res =n zze 、三、 计算题、 (40分)1、 将函数12()zf z z e =在圆环域0z <<∞内展为Laurent 级数、2、 试求幂级数nn n z nn ∑+∞=!的收敛半径、3、 算下列积分:⎰-C z z z ze )9(d 22,其中C 就是1||=z 、4、 求0282269=--+-z z z z在|z |<1内根的个数、四、 证明题、 (20分) 1、 函数)(z f 在区域D 内解析、 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数、 2、 设)(z f 就是一整函数,并且假定存在着一个正整数n ,以及两个正数R 及M ,使得当R z ≥||时n z M z f |||)(|≤,证明)(z f 就是一个至多n 次的多项式或一常数。
复变函数论试卷

《复变函数论》试卷一一、填空(30分)1. 将复数()πααα≤≤+-=0sin cos 1i z 化为三角表示式,则=z 把它化为指数表示式,则=z2.=+i e π3 ,()ii +1的辐角的主值为3. =z 0是()44sin z z z f =的 阶零点.4.0z 是()z f 的()1>m m 阶零点,则0z 是()z f '1的 阶极点. 5.已知()()2323cxy x i y bx ay z f +++=为解析函数, 则___________________===c b a6.方程0273=+z 的根为 , ,二、简要回答下列各题(15分)1. 用复数i 去乘复数i +1的几何意义是什么?2. 函数()z f 在0z 解析有哪几个等价条件?3. 设函数()z f 在单连通区域D 内处处解析,且不为零,C 是D 内的任一简单闭曲线,问积分()()dz z f z f c ⎰'是否等于零,为什么?三、计算下列积分(16分)1. czdz ⎰,c 是从点1i -到点1i +的有向直线段2. 202cos d πθθ+⎰四、(12分)求函数()11z z +在圆环112z <-<内的洛朗级数展开式.五、(12分)证明方程24290z z ++=在单位圆1z =内及其上无解. 六、(15分)求映射,把带形区域0Re 2z <<共形映射成单位圆1w <,且把1z =映射成0w =,把2z =映射成1w =.《复变函数》试卷二一、填空题(20分)1. -2是 的一个平方根2. 设21i z --=,则,=z Argz = =z Im3. 若22z z =,则θi re z =满足条件 4. =ze e,()=ze e Re5. 设1≠=θi re z ,则()=-1ln Re z6. 设变换βαβα,,+=z w 为复常数,则称此变换为 变换,它是由 等三个变换复合而成.7. 幂级数∑∞=12n nn z n 的收敛半径=R 8.函数baz +1在0=z 处的幂级数展开式为 ,其收敛半径为9.变换z e W =将区域π<<z D Im 0:变换成区域:G二、判断下列命题之真伪(20分)1.()z e z F cos =在全平面上任意阶可微.2. 若函数()z F 在有界区域D 内有解析,且在其中有无穷多个零点,则()z F 在D 内恒为零. ( )3. 设扩充复平面上的点a 时函数()z F 的可去奇点,则()Re 0z asF z ==.4. 若()W F z =是区域D 内的保形变换,则()W F z =在D 内单叶解析且保角.5. 若函数()z F 在区域D 内解析,则()0cf z dz =⎰,其中c 是D 内的任意一条围线.6. 设()()(),,F z u x y iv x y =+在区域D 内可导,则在D 内,()'y x F z v iv =+7. 设函数()z F 在点()a ≠∞解析,则总存在0R >,在z a R -<内()z F 能展成幂级数()0nn n c z a ∞=-∑.8. 非常数的整函数必为无界函数.9. 设()f z 在区域D 内解析,则()f z 在D 内连续. 10. 若函数()f z 在a 点可导,则()f z 在a 点解析.三、计算下列各题(24分)1. 求极限0cos lim sin z z z zz z →--2. 求21c I dz z=⎰ ,其中是下半圆周,起点11z =-,终点21z =3. 求i 的立方根4. 求2212cos d I p pπθθ=-+⎰()1p >5. 求()11f z z =-在1z =及z =∞的残数 6. 求1sin z dzI z z==⎰四、(16分) 1. 叙述儒歇定理2. 证明方程()01z n e e z λλ-=>在单位圆1z <内有n 根 五、求下列变换(20分)1. 求将2,,2i -对应变成1,,1i -的线性变换2. 求出将圆42z i -<变为半平面v u >的保形变换,使得圆心变到-4,而圆周上的点2i 变到0w =《复变函数》试卷三一、填空题(45分)1. ()1Arg i -= ,复数()1cos sin 0z i ϕϕϕπ=-+<≤的模为2. 设()()32256f z z z =+-,则()'f z =3. 设()()cos sin x f z e y i y =+,则()'f z =4. z e 是周期函数,其基本周期为5. 如果函数()w f z =在区域D 内满足条件: ,则称()f z 为区域D 内的解析函数6. 设c 是连接a 与b 的直线段,则czdz ⎰=7. 设圆周:3c z =,则3c dzz ⎰= 8. 级数21nn z n ∞=∑的收敛半径为 ,级数2491z z z ++++⋅⋅⋅的收敛半径为9. 0z =为函数()sin f z z z =-的 级零点10. 叙述最大模原理: 11. 设()()()25121zf z z z =-+,则1z =为()f z 的 级极点,12z =-为()f z 的 级极点12. 设()22f z z z =+,则在点12z i =-+处的旋转角()'arg 12f i -+= 二、判断下列命题之真伪(15分)1. 函数()2f z z =在z 平面上处处不解析 2.()z F z e =是整函数3.若函数()F z 在区域D 内解析,c 是D 内任一条围线,则()0cF z dz =⎰4.设函数()F z 在点()a ≠∞解析,则总存在0R >,在z a R -<内能展成幂级数()0nn n c z a ∞=-∑2. 若函数()f z 在点a 可导,则()f z 在点a 解析 三、求解下列各题(20分) 1. 求积分()ln 1z rI z dz ==+⎰ ()01r <<2. 求积分()()229I d i ξξξξξ==-+⎰3. 求积分()22521z z I dz z z =-=-⎰4. 试将函数()2zf z z =+按1z -的幂展开,并指出其收敛范围5. 求将2,,2i -对应变成1,,1i -的线性变换 四、证明题(20分)1. ①叙述代数学基本定理②试用复分析方法证明代数学基本定理2. 证明方程()00z n e e z λλ-=>在单位圆1z <内有n 根《复变函数》试卷四一、填空题(50分)1. 已知1z i =-,则arg z = ()arg z ππ-<≤,z = ,z =2.3. 设()()cos sin x f z e y i y =+,则()'f z =4. sin z 的零点为 ,cos z 的零点为5. ()1Ln -= , i i =6. 函数()f z ()(),,u x y iv x y =+在区域D 内解析的充要条件是7.1z dzz =⎰=21z dzz =⎰=8. 幂级数21nn z n∞=∑ 的收敛半径为9. 0z =是函数()sin f z z z =-的 级零点10. 叙述最大模原理: 11.函数()()()112f z z z =--在z 平面内有 个奇点,它们是12. 1z =为函数()()()251121z f z z z +=-+的 级极点13. 方程742520z z z -+-=在单位圆内有 个根14. 设()22f z z z =+,则()f z 在12z i =-+处的旋转角为 伸缩率为 15. 线性变换()0az bw ad bc cz d+=-≠+的逆变换为16. 变换3w z =将z 平面上区域:0arg 3D z π<<变换为w 平面上的区域G :二、判断题(15分)1. 设()f z 在区域D 内可导,则()f z 在D 内解析2. 互为共轭的两复数具有相同的模3. 复数0z =的充要条件是0z =4. 设()f z 在区域D 内解析,c 为D 内任一闭曲线,则()0cf z dz =⎰5. sin z 和cos z 都是平面上的有界函数三、计算下列各题(15分) 1. 设()()()112f z z z =--,求()f z 在1z <内的泰勒展式2. 求积分()22521z z I dz z z =-=-⎰3.求将2,,2i -对应地变成1,,1i -的线性变换四、证明题(20分)1. 证明函数()2f z z =在z 平面上处处不解析2. 设a 为()f z 的n 级零点,证明:a 必为函数()()'f z f z 的一级极点,并且()()'Re z a f z s n f z =⎡⎤=⎢⎥⎣⎦《复变函数》试卷五一、填空题(18分)1. 的所有值为:2. ()cos 1i += ()1Ln -=3. 0cos limsin z z z zz z→--=4. 设()()0n n f z c z r z +∞-∞=≤<<+∞∑,则()Re z s f z =∞=5. 令z x iy =+,2z w e =,则w = Im w =6. 线性变换()()0az bW L z ad bc cz d+==-≠+在扩充z 平面上有下列特性,请你完整地予以叙述⑴ 保形性:⑵ 保交比性: ⑶ 保圆周性: ⑷ 保对称性:7. 1w z=将z 平面上的直线y x =变换为w 平面上的曲线二、判断题(10分)下列断语如果正确则打“ √”,否则打“×”1. 如果函数()f z 在点()a ≠∞处解析,则存在0R >,使()f z 在z a R -<内可展成泰勒级数,且展式唯一2. 设a 是z 平面上的一点,若a 为函数()f z 的可去奇点,则()Re 0z as f z ==( )3. 如果函数()f z 在某有界区域D 内解析,且在D 内有一列零点,则()f z 在D 内恒为零 4. sin z 和cos z 都是z 平面上的有界整函数 5. 若函数()f z 在区域D 内解析,则()0cf z dz =⎰.其中c 是内的任意一条围线三、解下列各题(24分)1. 求1c dz z ⎰的值,其中c 是上半单位圆周,起点为1z =-,终点为1z =2. 求函数()11z f z e -=在1,z =∞的留数3. 计算积分()20sin 01x mxI dx m x+∞=>+⎰4. 将函数()11z f z z -=+在1z =处展开成幂级数,并求其收敛半径四、证明题(24分)1. 试证:在原点解析,且在()11,2,z n n==⋅⋅⋅处取下列值的函数()f z 是不存在的: 111111,,,,,224466⋅⋅⋅2. 试证:73120z z -+=的根全在12z <<内 五、(12分)求将2,,2i -对应地变成1,,1i -的线性变换六、(12分)求出将圆42z i -<变成半平面v u >的保形变换,使得圆心变到-4,而圆周上的点变到2i 变到0w =《复变函数》试卷六一、填空题(30分)1.已知z=1-i ,则arg z= (-π<arg z ≤π),| z |= , z =2.变换W=Z 3将Z 平面上区域D :0< arg z <3π变换为W 平面上的区域G :3.Ln (-1)= , i i = , Arctg(2i) = 4.函数f (z )在区域D 内解析的充要条件是下列条件之一(1) (2) (3) (4)5.幂级数z +z 4+z 9+…+2n z +…的收敛半径为6.在原点解析,而在z= 1n (n=1,2,…)处取值为 f(1n )=211n+的函数为7.函数f (z )=z 2(21z e -)的零点是 ,它是 级的 二、判断题(10分)1.设f (z )在区域D 内可导,则f (z )在D 内解析 ( ) 2.设f (z )在区域D 内解析,C 是D 内任一闭曲线,则c⎰f (z )dz=03.Sinz 和cosz 都是z 平面上的有界函数 ( ) 4.f (z )=u +iv 在区域D 内解析,则-u 是v 的共轭调和函数5. f (z )=| z |2在z 平面上处处不解析三、求下列积分(15分) 1.I= z cze dz ⎰,其中c 是连结o 到-1+i 的直线段 2.I=212ln(1)z z z dz =+⎰3.I=22(8)()z zdz z z i =--⎰ 四、(12分)已知u=x 3+6x 2y-3xy 2-2y 3,求解析函数f(z)=u+iv 使合条件f (0)=0五、(12分)将函数f(z)=1az b+(a,b 为复数,ab ≠0)展开为z 的幂级数,并指出展式成立的范围 , 六、(12分)叙述并证明代数学基本定理七、(9分)设f (z )=u(x ·y )+iv(x ·y )在区域内解析,试证在D 内,0f z∂=∂《复变函数》试卷七一.填空题(20分)1.已知z =1-I ,则argz = (-π<arg z ≤π),| z |= ,z =2.变换W=Z 3将z 平面上的区域D 变换为W 平面上的区域G :,其中D : 0< arg z <3π3. sin 2z +cos 2z =1在直线z =x ,(y=0)上成立,则由 定理,sin 2z +cos 2z =1 在全平面上也成立4.设f(z)=2z 4-z 3+11z 2-1,f(z)在| z |<2内有 个零点,f(z)在 2≤| z |<3 内有 个零点,f(z)在3≤| z |<+∞内有 零点,f(z)在z =1处的旋转角为 ,伸缩率为 。
(完整版)《复变函数》考试试题与答案各种总结

《复变函数》考试试题(一)一、 判断题(20分):1.若f (z)在z 0的某个邻域内可导,则函数f(z )在z 0解析. ( )2.有界整函数必在整个复平面为常数。
( ) 3。
若}{n z 收敛,则} {Re n z 与}{Im n z 都收敛. ( )4.若f (z )在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数). ( )5.若函数f (z )在z 0处解析,则它在该点的某个邻域内可以展开为幂级数. ( ) 6。
若z 0是)(z f 的m 阶零点,则z 0是1/)(z f 的m 阶极点。
( ) 7。
若)(lim 0z f z z →存在且有限,则z 0是函数f (z)的可去奇点. ( )8。
若函数f (z )在是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠。
( ) 9. 若f (z )在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f .( )10.若函数f(z )在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数。
( ) 二.填空题(20分)1、 =-⎰=-1||00)(z z nz z dz__________.(n 为自然数)2。
=+z z 22cos sin _________. 3.函数z sin 的周期为___________.4.设11)(2+=z z f ,则)(z f 的孤立奇点有__________。
5。
幂级数0n n nz ∞=∑的收敛半径为__________。
6.若函数f (z )在整个平面上处处解析,则称它是__________。
7。
若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________.8。
=)0,(Re n zz e s ________,其中n 为自然数。
9. zz sin 的孤立奇点为________ .10。
复变函数论试题

14. z 平面 15.0 16.在 D 内任一有界闭集上一致收敛 (每小题 2 分,共 10 分) 18.× 19.× 20.√ 21.× (每小题 7 分,共 35 分)
n
∞
=−
1 ∞ ⎛z⎞ 2 = − ∑⎜ ⎟ − 2 2 n =0 ⎝ 2 ⎠ z
∞
∑ (−1)
n =0
n
1 z 2n
= 2∑ ( −1) n
n =1
+∞
∞ zn 1 − ∑ ……………………………………7 分 z 2 n n =0 2 n +1
e ix 26.解 考虑积分 ∫ dx − ∞ ( x 2 + 1)( x 2 + 9)
反之,设有方程 az + a z = C ( a 是非零复常数, C 是实常数) ,将 z = x + iy 代入上式
得
a ( x + iy ) + a ( x − iy ) = C 或 (a + a) x + (ia − ia) y = C ……………………6 分
令
A = a + a , B = ia − ia ( A, B 均为实常数) ,则有 Ax + By = C ( A, B 不同时
+∞
五、证明题 27. 证明
(其中 27 题 7 分,28、29 每小题 8 分,共 23 分) 设直线方程为 Ax + By = C ( A, B, C 为实常数,且 A, B 不同时为零) ,因
复变函数试卷及答案

复变函数试卷及答案【篇一:《复变函数》考试试题与答案各种总结】xt>一、判断题(20分):1.若f(z)在z0的某个邻域内可导,则函数f(z)在z0解析. ( )2.有界整函数必在整个复平面为常数. ( )3.若{zn}收敛,则{re zn}{im zn}与都收敛. ( )4.若f(z)在区域d内解析,且f(z)?0,则f(z)?c(常数).( )5.若函数f(z)在z0处解析,则它在该点的某个邻域内可以展开为幂级数.( )6.若z0是f(z)的m阶零点,则z0是1/f(z)的m阶极点. ( )7.若z?z0limf(z)存在且有限,则z0是函数f(z)的可去奇点. ( )8.若函数f(z)在是区域d内的单叶函数,则f(z)?0(?z?d). ( )9. 若f(z)在区域d内解析, 则对d内任一简单闭曲线c?cf(z)dz?0.( )10.若函数f(z)在区域d内的某个圆内恒等于常数,则f(z)在区域d 内恒等于常数.()二.填空题(20分)dz?__________.(n为自然数)1、 ?|z?z0|?1(z?z)n22sinz?cosz? _________. 2.3.函数sinz的周期为___________.f(z)?4.设?1z2?1,则f(z)的孤立奇点有__________.n?nzn?0的收敛半径为__________.6.若函数f(z)在整个平面上处处解析,则称它是__________.7.若n??limzn??z1?z2?...?zn?n??n,则______________.limezres(n,0)?z8.________,其中n为自然数.sinz9. 的孤立奇点为________ .zlimf(z)?___zf(z)的极点,则z?z010.若0是.三.计算题(40分):1. 设1f(z)?(z?1)(z?2),求f(z)在d?{z:0?|z|?1}内的罗朗展式.1dz.?|z|?1cosz2.3?2?7??1f(z)??d?c??z3. 设,其中c?{z:|z|?3},试求f(1?i).w?4. 求复数z?1z?1的实部与虚部.四. 证明题.(20分) 1. 函数为常数. 2. 试证: f(z)?f(z)在区域d内解析. 证明:如果|f(z)|在d内为常数,那么它在d内在割去线段0?rez?1的z平面内能分出两个单值解析分支,并求出支割线0?rez?1上岸取正值的那支在z??1的值.《复变函数》考试试题(一)参考答案一.判断题?2?in?11. ? ;2. 1;3. 2k?,(k?z);4. z??i; 5. 1 0n?1?6. 整函数;7. ?;8. 三.计算题.1. 解因为0?z?1, 所以0?z?1?1?zn111n??z??(). f(z)???2n?02(z?1)(z?2)1?z2(1?)n?021; 9. 0; 10. ?.(n?1)!2. 解因为z?resf(z)?limz??2?2z??2?lim1??1, coszz???sinzz??2resf(z)?limz???2z???2?lim1?1. coszz????sinz所以1sf(z)?resf(z)?0. z?2cosz?2?i(re??z??z?2223. 解令?(?)?3??7??1, 则它在z平面解析, 由柯西公式有在z?3内, f(z)??(?)?c??z?2?i?(z).所以f?(1?i)?2?i??(z)z?1?i?2?i(13?6i)?2?(?6?13i). 4. 解令z?a?bi, 则 w?z?122a(?1?bi)2a(?1)b2. 2?1?1?122222z?1z?1(a?1)?b(a?1)?ba(?1)?bz?12(a?1)z?12b, . )?1?im()?z?1(a?1)2?b2z?1(a?1)2?b2故 re(四. 证明题.1. 证明设在d内f(z)?c.令f(z)?u?iv,则f(z)?u2?v2?c2.2?uux?vvx?0两边分别对x,y求偏导数, 得??uuy?vvy?0(1)(2)因为函数在d内解析, 所以ux?vy,uy??vx. 代入 (2) 则上述方程组变为?uux?vvx?022. 消去ux得, (u?v)vx?0. ??vux?uvx?01) 若u?v?0, 则 f(z)?0 为常数.2) 若vx?0, 由方程 (1) (2) 及 c.?r.方程有ux?0, uy?0, vy?0. 所以u?c1,v?c2. (c1,c2为常数).22所以f(z)?c1?ic2为常数. 2.证明f(z)?的支点为z?0,1. 于是割去线段0?rez?1的z平面内变点就不可能单绕0或1转一周, 故能分出两个单值解析分支.由于当z从支割线上岸一点出发,连续变动到z?0,1 时, 只有z的幅角增加?. 所以f(z)?的幅角共增加?. 由已知所取分支在支割线上岸取正值, 于是可认为该分2?i?2支在上岸之幅角为0, 因而此分支在z??1的幅角为,故f(?1)??.2《复变函数》考试试题(二)一. 判断题.(20分)1. 若函数f(z)?u(x,y)?iv(x,y)在d内连续,则u(x,y)与v(x,y)都在d 内连续. ( )2. cos z与sin z在复平面内有界.( )3. 若函数f(z)在z0解析,则f(z)在z0连续. ( )4. 有界整函数必为常数. ( )5. 如z0是函数f(z)的本性奇点,则limf(z)一定不存在. ( )z?z06. 若函数f(z)在z0可导,则f(z)在z0解析. ( )7. 若f(z)在区域d内解析, 则对d内任一简单闭曲线c?f(z)dz?0.c( )8. 若数列{zn}收敛,则{rezn}与{imzn}都收敛. ( ) 9. 若f(z)在区域d内解析,则|f(z)|也在d内解析. ( )11110. 存在一个在零点解析的函数f(z)使f()?0且f()?,n?1,2,....n?12n2n( )二. 填空题. (20分)1. 设z??i,则|z|?__,argz?__,?__z?1?i2.设f(z)?(x2?2xy)?i(1?sin(x2?y2),?z?x?iy?c,则limf(z)?________.3.dz?|z?z0|?1(z?z0)n?_________.(n为自然数)4. 幂级数?nzn的收敛半径为__________ .n?0?5. 若z0是f(z)的m阶零点且m0,则z0是f(z)的_____零点.6. 函数ez的周期为__________.7. 方程2z5?z3?3z?8?0在单位圆内的零点个数为________. 8. 设f(z)?1,则f(z)的孤立奇点有_________. 21?z9. 函数f(z)?|z|的不解析点之集为________.z?110. res(,1)?____. 4z三. 计算题. (40分)3sin(2z)的幂级数展开式. 1. 求函数2. 在复平面上取上半虚轴作割线. 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点z?i处的值.??|z|dz,积分路径为(1)单位圆(|z|?1)?ii3. 计算积分:i的右半圆.4. 求sinzz?2(z?)22dz.四. 证明题. (20分)1. 设函数f(z)在区域d内解析,试证:f(z)在d内为常数的充要条件是f(z)在d内解析.2. 试用儒歇定理证明代数基本定理.《复变函数》考试试题(二)参考答案一. 判断题.【篇二:复变函数试题与答案】>一、选择题1.当z?1?i时,z100?z75?z50的值等于() 1?i(a)i (b)?i(c)1 (d)?12.设复数z满足arc(z?2)??3,arc(z?2)?5?,那么z?() 61331?i (d)??i 2222(a)?1?3i (b)?3.复数z?tan??i(3?i (c)??????)的三角表示式是() 2 ???)?i??)] (b)sec?(a)sec22??3?3???)?i??)] 22?(c)?sec3?3?????)?i??)](d)?sec???)?i??)] 2222224.若z为非零复数,则z?与2z的关系是()2222(a)z??2z (b)z??2z22(c)z??2z (d)不能比较大小5.设x,y为实数,则动点(x,y)z1?x??yi,z2?x??yi且有z1?z2?12,的轨迹是()(a)圆(b)椭圆(c)双曲线(d)抛物线6.一个向量顺时针旋转?3,向右平移3个单位,再向下平移1个单位后对应的复数为1?3i,则原向量对应的复数是()(a)2(b)1?i (c)3?i (d)3?i17.使得z2?z成立的复数z是() 2(a)不存在的(b)唯一的(c)纯虚数(d)实数8.设z为复数,则方程z??2?i的解是()(a)?3333?i (b)?i (c)?i (d)??i 44449.满足不等式z?i?2的所有点z构成的集合是() z?i(a)有界区域(b)无界区域(c)有界闭区域(d)无界闭区域10.方程z?2?3i?2所代表的曲线是()(a)中心为2?3i,半径为2的圆周(b)中心为?2?3i,半径为2的圆周(c)中心为?2?3i,半径为2的圆周(d)中心为2?3i,半径为2的圆周11.下列方程所表示的曲线中,不是圆周的为()(a)z?1?2 (b)z?3?z?3?4 z?2z?a?1(a?1) (d)z?a?z?a?c?0(c?0) 1?az(c)12.设f(z)?1?,z1?2?3i,z2?5?i,,则f(z1?z2 )(a)?4?4i(b)4?4i(c)4?4i(d)?4?4i13.limim(z)?im(z0)() x?x0z?z0(a)等于i(b)等于?i(c)等于0(d)不存在14.函数f(z)?u(x,y)?iv(x,y)在点z0?x0?iy0处连续的充要条件是()(a)u(x,y)在(x0,y0)处连续(b)v(x,y)在(x0,y0)处连续(c)u(x,y)和v(x,y)在(x0,y0)处连续(d)u(x,y)?v(x,y)在(x0,y0)处连续 2z2?z?115.设z?c且z?1,则函数f(z)?的最小值为() z (a)?3 (b)?2(c)?1 (d)1二、填空题1.设z?(1?i)(2?i)(3?i),则z? (3?i)(2?i)2.设z?(2?3i)(?2?i),则argz?3.设z?,arg(z?i)?3?,则z? 4(cos5??isin5?)24.复数的指数表示式为 2(cos3??isin3?)5.以方程z?7?i的根的对应点为顶点的多边形的面积为6.不等式z?2?z?2?5所表示的区域是曲线的内部 67.方程2z?1?i?1所表示曲线的直角坐标方程为2?(1?i)z8.方程z?1?2i?z?2?i所表示的曲线是连续点和的线段的垂直平分线9.对于映射??2i22,圆周x?(y?1)?1的像曲线为 z410.lim(1?z?2z)? z?1?i三、若复数z满足z?(1?2i)z?(1?2i)?3?0,试求z?2的取值范围.四、设a?0,在复数集c中解方程z2?2z?a.五、设复数z??i,试证z是实数的充要条件为z?1或im(z)?0. 21?z3六、对于映射??11(z?),求出圆周z?4的像. 2z七、试证1.z1?0(z2?0)的充要条件为z1?z2?z1?z2; z2z1?0(zj?0,k?j,k,j?1,2,?,n))的充要条件为 z22.z1?z2???zn?z1?z2???zn.八、若limf(z)?a?0,则存在??0,使得当0?z?z0??时有f(z)?x?x01a. 2九、设z?x?iy,试证x?y2?z?x?y.十、设z?x?iy,试讨论下列函数的连续性: ?2xy,z?0?1.f(z)??x2?y2 ?0,z?0??x3y?,z?02.f(z)??x2?y2.?0,z?0?第二章解析函数一、选择题:1.函数f(z)?3z在点z?0处是( )(a)解析的(b)可导的(c)不可导的(d)既不解析也不可导2.函数f(z)在点z可导是f(z)在点z解析的( )4 2(a)充分不必要条件(b)必要不充分条件(c)充分必要条件(d)既非充分条件也非必要条件3.下列命题中,正确的是( )(a)设x,y为实数,则cos(x?iy)?1(b)若z0是函数f(z)的奇点,则f(z)在点z0不可导(c)若u,v在区域d内满足柯西-黎曼方程,则f(z)?u?iv在d内解析(d)若f(z)在区域d内解析,则在d内也解析4.下列函数中,为解析函数的是( )(a)x2?y2?2xyi(b)x2?xyi(c)2(x?1)y?i(y2?z?x20?2x)(d)x3?iy35.函数f(z)?z2im(z)在处的导数( )(a)等于0 (b)等于1 (c)等于?1(d)不存在6.若函数f(z)?x2?2xy?y2?i(y2?axy?x2)在复平面内处处解析,那么实常数a?( )(a)0(b)1(c)2(d)?27.如果f?(z)在单位圆z?1内处处为零,且f(0)??1,那么在z?1内f(z)?( )(a)0(b)1(c)?1(d)任意常数8.设函数f(z)在区域d内有定义,则下列命题中,正确的是(a)若f(z)在d内是一常数,则f(z)在d内是一常数(b)若re(f(z))在d内是一常数,则f(z)在d内是一常数(c)若f(z)与f(z)在d内解析,则f(z)在d内是一常数(d)若argf(z)在d内是一常数,则f(z)在d内是一常数9.设f(z)?x2?iy2,则f?(1?i)?( )5【篇三:大学复变函数考试卷试题及答案】ss=txt>?z2?,z?01.设f?z???z,则f?z?的连续点集合为()。
复变函数考试试卷试题及答案各种总结.doc

《复变函数》考试试题(一)一、 判断题( 20 分):1. 若 f(z) 在 z 0 的某个邻域内可导,则函数 f(z) 在 z 0 解析 .( )2. 有界整函数必在整个复平面为常数.()3. 若{ z n }收敛,则{Re z n } 与{Imz n }都收敛 .( )4. 若 f(z) 在区域 D 内解析,且f '( z),则 f ( z)C(常数) . ( )5. 若函数 f(z) 在 z 0 处解析,则它在该点的某个邻域内可以展开为幂级数 . ( )6. 若 z 0 是f ( z)的 m 阶零点,则 z 0 是 1/f (z)的 m 阶极点 .()lim f ( z)7. 若 zz 0存在且有限,则 z 0 是函数 f(z) 的可去奇点 . ()8. 若函数 f(z) 在是区域 D 内的单叶函数,则f ' (z) 0(z D ) .( )9. 若 f ( z ) 在区域 D 内解析 , 则对 D 内任一简单闭曲线Cf (z)dz 0 .C( )10. 若函数 f(z) 在区域 二. 填空题( 20 分)D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数. ()dz1、 |z z 0 | 1 ( zz )n__________. ( n 为自然数)2.sin 2 z cos 2z_________.3. 函数sin z的周期为 ___________.f (z)14. z21,则f ( z)的孤立奇点有 __________.设 5. 幂级数nz n 的收敛半径为 __________.n 06. 若函数 f(z) 在整个平面上处处解析,则称它是__________.lim z nlimz 1z 2 ...z n7. 若 n,则 nn______________.Re s(e zn ,0),其中 n 为自然数 .z9.sin z的孤立奇点为 ________ .z若z 0 是 f (z) lim f (z) ___10. 的极点,则z z.三. 计算题( 40 分):f (z)11. 设(z 1)( z 2) ,求 f ( z) 在 D { z : 0 | z | 1} 内的罗朗展式 .1 dz.|z| 1cos z2.3. 设f ( z) 3 271d{ z :| z | 3} ,试求 f ' (1 i ).Cz,其中 Cz 1w1 的实部与虚部 .4.求复数z四 . 证明题 .(20 分 )1. 函数f (z)在区域 D 内解析 .证明:如果| f ( z) |在 D 内为常数,那么它在 D 内为常数 .2. 试证 : f (z) z(1 z) 在割去线段 0 Re z 1 的 z 平面内能分出两个单值解析分支 ,并求出支割线 0 Re z 1 上岸取正值的那支在 z 1的值 .《复变函数》考试试题(一)参考答案一. 判断题1.× 2.√ 3.√ 4.√ 5.√6.√ 7.×8.×9.× 10.×二.填空题2 i n 1;2. 1 ;3.2k, ( k z) ; 4.zi ; 5. 11.n 16. 整函数;7.;8.1 ;9. 0;10..(n1)!三.计算题 .1. 解因为0 z 1, 所以 0 z 1f ( z)1 1 1 z zn1 ( z )n.( z 1)(z 2) 1 z 2(1 )n 02 n 0 222. 解 因为z21Re s f (z) limlim1,coszsin zz2zz22Re s f (z)lim z 2 lim1 1 .coszsin zz2zz22所以1 dz2 i(Re s f (z) Re s f (z) 0 .z 2cos z z 2 z 23. 解 令( ) 3 2 71, 则它在 z 平面解析 , 由柯西公式有在 z 3内 ,f (z)c ( )dz 2 i (z) .z所以 f (1i ) 2 i (z) z 1 i2 i (13 6i ) 2 ( 6 13i ) .4. 解 令 za bi , 则wz 1 121 2( a 1 bi ) 1 2(a 1)2b.z 1 z 1 ( a 1)2 b 2( a 1)2 b 2 (a 1)2 b 2故 Re( z1 1 2(a 1), Im( z 1 2b2.) 2 b 2)2z 1 ( a 1)z 1 (a 1) b四.证明题 .1. 证明 设在 D 内 f ( z)C .令 f ( z) u iv ,2u 2 v 2 c 2 .则 f ( z)两边分别对 x, y 求偏导数 ,得 uu x vv x 0(1) uu y vv y 0(2)因为函数在 D 内解析 , 所以 u x v y , u y v x . 代入 (2)则上述方程组变为uu x vv x 0 . 消去 u x 得, (u 2 v 2 ) v x 0 .vu x uv x 01) 若 u2 v 2 0 , 则 f ( z)0 为常数 .2) 若 v x0,由方程 (1) (2)及 C.R. 方程有 u x 0, u y 0 , v y 0 .所以 uc 1, v c 2 . ( c 1, c 2 为常数 ).所以 f ( z) c1 ic 2为常数.2. 证明f ( z) z(1 z) 的支点为z 0,1 . 于是割去线段 0 Re z 1的z平面内变点就不可能单绕 0 或 1 转一周 , 故能分出两个单值解析分支 .由于当 z 从支割线上岸一点出发, 连续变动到z 0,1 时 , 只有 z 的幅角增加. 所以f ( z)z(1 z) 的幅角共增加. 由已知所取分支在支割线上岸取正值, 于是可认为该2z 1 的幅角为, 故f ( 1) i2i .分支在上岸之幅角为 0, 因而此分支在2e22《复变函数》考试试题(二)一 . 判断题 . ( 20 分)1. 若函数 f (z) u(x, y) iv ( x, y)在D内连续,则 ux,y)与 v x,y)都在 D内连续.( (z z( )2. cos 与sin 在复平面内有界 . ( )f ( z) 在 z0 f ( z) 在z03. 若函数解析,则连续 . ( )4. 有界整函数必为常数 . ( )5. 如 z0是函数 f ( z) 的本性奇点,则 lim ( ) 一定不存在 . ( )z z0f z6. 若函数 f ( z) 在 z0 可导,则 f ( z) 在z0 解析 . ( )7. 若 f ( z) 在区域 D内解析 , 则对 D内任一简单闭曲线 C f ( z)dz 0 .C( )8. 若数列 { z n } 收敛,则 {Re z n } 与 {Im z n} 都收敛. ( )9. 若 f ( z) 在区域 D 内解析,则 | f ( z)| 也在 D 内解析 .( )10. 存在一个在零点解析的函数 f ( z) 使 f ( 1 ) 0 且 f ( 1) 1 , n 1,2,... .n 1 2n 2n( )二. 填空题 . (20 分)1. 设z i ,则| z | __,arg z __, z __2. 设f ( z) ( x2 2 xy) i (1 sin( x2 y2 ), z x iy C ,则lim f ( z) ________.z 1 idz3.|z z 0 | 1( zz )n _________.( n 为自然数)4. 幂级数nz n 的收敛半径为 __________ .n 05. 若 z 0 是 f ( z) 的 m 阶零点且 m>0,则 z 0 是 f '( z) 的_____零点 .6.函数 e z 的周期为 __________.7. 方程 2z 5 z 3 3z 8 0 在单位圆内的零点个数为 ________.8. 设 f ( z)1 z2 ,则 f ( z) 的孤立奇点有 _________.19. 函数 f (z) | z |的不解析点之集为 ________.10.Res(z41,1) ____.z三 . 计算题 . (40 分 )1. 求函数sin(2z 3 )的幂级数展开式 .2.在复平面上取上半虚轴作割线 . 试在所得的区域内取定函数z在正实轴取正实值的一个解析分支, 并求它在上半虚轴左沿的点及右沿的点 z i 处的值 .3. 计算积分:Ii1)| z | dz ,积分路径为( 1)单位圆( | z|i的右半圆 .4. 求 .四 . 证明题 . (20 分 )1.设函数 f ( z) 在区域 D 内解析,试证:f ( z) 在 D 内为常数的充要条件是 f (z) 在D 内解析 .2.试用儒歇定理证明代数基本定理 .《复变函数》考试试题(二)参考答案一. 判断题 .1.√ 2.×3.√ 4.√ 5.× 6.×7.×8.√ 9.× 10.× .二. 填空题, i ; 2.3(1 sin 2)i ; 3.2 i n 1 ; 5.m 1.,n ; 4. 1216.2k i , ( k z) .7.0;8.i ;9.R ;10.0.三. 计算题1. 解 sin(2 z 3)( 1)n (2 z 3 )2n 1 ( 1)n 22n 1 z 6 n 3 .n 0(2 n 1)! n 0(2 n 1)!2. 解 令 z re i.i2 k2则 f ( z)zre ,(k0,1).又因为在正实轴去正实值,所以k 0 .所以 f (i)ie 4 .3. 单位圆的右半圆周为 z ei, 2.2i zdz2 deiei2 2i .所以i224. 解 =0.四.证明题 .1. 证明 (必要性 ) 令 f ( z)c 1ic2 , 则f ( z)c 1ic 2 . (c 1 ,c 2 为实常数).令 u(x, y)c 1, v( x, y)c 2 .则 u xv yu yv x0 .即 u, v 满足 C.( 充分性 ) 令 f ( z)R., 且 u x , v yu iv , 则 ,u y , v x 连续 ,f (z) u iv故 f (z) ,在D 内解析 .因为f ( z) 与 f ( z)在D 内解析,所以u x v y , u y比较等式两边得v x ,u x且u x v yu y(v)yv x0 . v y , u y从而在D ( v x )内 u, v v x .均为常数, 故f (z) 在D 内为常数 .2. 即要证“任一 n 次方程 a 0 zna 1zn 1a n 1za n0 ( a 0 0) 有且只有n个根” .证明 令 f (z) a 0 z na 1z n 1a n 1z a n0 , 取 Rmax a 1a n ,1 , 当a 0z在C : z R上时,有( z) a 1 R n 1a n 1 R a n ( a 1a n )R n 1 a 0 R n .f ( z) .由儒歇定理知在圆zR 内 , 方程 a 0 z n a 1z n 1a n 1 za n 0 与 a 0 z n0 有相同个数的根 . 而 a 0 zn 0 在 z R 内有一个n 重根 z 0 . 因此 n 次方程在 z R内有 n 个根 .《复变函数》考试试题(三)一 . 判断题 . (20 分 ).1. cos z 与 sin z 的周期均为 2k .( )2. 若 f ( z) 在 z 0 处满足柯西 - 黎曼条件 , 则 f ( z) 在 z 0 解析 . ( )3. 若函数 f ( z) 在 z 0 处解析,则 f ( z) 在 z 0 连续 . ( )4. 若数列 { z n } 收敛,则 {Re z n } 与 {Im z n } 都收敛 .( )5.若函数 f ( z) 是区域 D 内解析且在 D 内的某个圆内恒为常数,则数 f ( z) 在区域 D 内为常数 . ( )6. 若函数 f ( z) 在 z 0 解析,则 f ( z) 在 z 0 的某个邻域内可导 . ( )7.如果函数 f ( z) 在 D{ z :| z | 1} 上解析 , 且 | f (z) | 1(| z | 1) , 则| f ( z) | 1(| z | 1) .( )8.若函数 f ( z) 在 z 0处解析,则它在该点的某个邻域内可以展开为幂级数.( ) 9.若 z 0 是 f ( z) 的 m 阶零点 , 则 z 0 是 1/ f ( z) 的 m 阶极点 .( )10. 若z 0 是 f (z)的可去奇点,则 Res( f ( z), z ) 0. ( )二 . 填空题 . (20 分 )1. 设 f ( z) 1 ,则 f ( z) 的定义域为 ___________. 2 z 12.函数 e z 的周期为 _________.3. 若 z n n 2 i (11) n ,则 lim z n __________.1 nnn4. sin 2 z cos 2 z ___________.dz5.|z z 0 | 1(z z ) n_________. ( n 为自然数)6. 幂级数nx n 的收敛半径为 __________.n设 f (z) 1fz 的孤立奇点有z 2 1,则7.( )__________.8.设ez1,则 z ___ .9.若 z 0 是 f (z)的极点,则 lim f (z) ___ .z z 0z10.Res(en ,0) ____ .z三 . 计算题 . (40 分 )11. 将函数 f ( z) z 2e z 在圆环域 0 z内展为 Laurent 级数 .2. 试求幂级数n!z n的收敛半径 .n nn3. 算下列积分:e zdz,其中 C 是 | z | 1.Cz 2 (z29)4. 求 z92z6z 28z 2 0 在| z|<1 内根的个数 .四 . 证明题 . (20 分)1.函数 f (z) 在区域 D 内解析 . 证明:如果 | f ( z) |在 D 内为常数,那么它在 D 内为常数 .2.设 f (z) 是一整函数,并且假定存在着一个正整数 n ,以及两个正数 R 及 M ,使得当 | z|R 时| f ( z) |M | z |n,证明 f (z) 是一个至多 n 次的多项式或一常数。
《复变函数论》试题库

《复变函数》考试试题(一)一、 判断题.(正确者在括号内打√,错误者在括号内打×,每题2分) 1.当复数0z =时,其模为零,辐角也为零. ( )2.若0z 是多项式110()n n n n P z a z a z a --=+++ (0)n a ≠的根,则0z 也()P z 是的根.( ) 3.如果函数()f z 为整函数,且存在实数M ,使得Re ()f z M <,则()f z 为一常数.( ) 4.设函数1()f z 与2()f z 在区域内D 解析,且在D 内的一小段弧上相等,则对任意的z D ∈,有1()f z 2()f z ≡. ( )5.若z =∞是函数()f z 的可去奇点,则Re ()0z s f z =∞=. ( )二、填空题.(每题2分)1.23456i i i i i ⋅⋅⋅⋅= _____________________. 2.设0z x iy =+≠,且arg ,arctan22y z xππππ-<≤-<<,当0,0x y <>时,arg arctany x =+________________.3.函数1w z=将z 平面上的曲线22(1)1x y -+=变成w 平面上的曲线______________.4.方程440(0)z a a +=>的不同的根为________________. 5.(1)i i +___________________.6.级数20[2(1)]n n z ∞=+-∑的收敛半径为____________________.7.cos nz 在z n <(n 为正整数)内零点的个数为_____________________.8.函数336()6sin (6)f z z z z =+-的零点0z =的阶数为_____________________.9.设a 为函数()()()z f z z ϕψ=的一阶极点,且()0,()0,()0a a a ϕψψ'≠=≠,则()Re ()z af z sf z ='=_____________________.10.设a 为函数()f z 的m 阶极点,则()Re ()z af z sf z ='=_____________________.三、计算题(50分)1.设221(,)ln()2u x y x y =+。
复变函数期末试题

《复变函数论》试题库《复变函数》考试试题(一) 判断题(20分)1.若f(z)在z0的某个邻域内可导,则函数f(z)在z0解析. ( )2.有界整函数必在整个复平面为常数. ( )3.若}{n z 收敛,则} {Re n z 与} {Im n z 都收敛. ( )4.若f(z)在区域D 内解析,且0)('≡z f ,则C z f ≡)((常数).( )5.若函数f(z)在z0处解析,则它在该点的某个邻域内可以展开为幂级数. ( )6.若z0是)(z f 的m 阶零点,则z0是1/)(z f 的m 阶极点. ( )7.若)(lim 0z f z z →存在且有限,则z0是函数f(z)的可去奇点. ( ) 8.若函数f(z)在是区域D 内的单叶函数,则)(0)('D z z f ∈∀≠. ( ) 9. 若f(z)在区域D 内解析, 则对D 内任一简单闭曲线C)(=⎰Cdz z f .( )10.若函数f(z)在区域D 内的某个圆内恒等于常数,则f(z)在区域D 内恒等于常数.( )二.填空题(20分)=-⎰=-1||00)(z z n z z dz__________.(n 为自然数)2.=+z z 22cos sin _________. 3.函数z sin 的周期为___________.4.设11)(2+=z z f ,则)(z f 的孤立奇点有__________.5.幂级数0nn nz∞=∑的收敛半径为__________. 6.若函数f(z)在整个平面上处处解析,则称它是__________.7.若ξ=∞→n n z lim ,则=+++∞→n z z z nn (i)21______________. 8.=)0,(Re n zz e s ________,其中n 为自然数.9.z zsin 的孤立奇点为________ . 10.若0z是)(z f 的极点,则___)(lim 0=→z f z z .三.计算题(40分):1. 设)2)(1(1)(--=z z z f ,求)(z f 在}1||0:{<<=z z D 内的罗朗展式.2..cos 11||⎰=z dz z3. 设⎰-++=C d z z f λλλλ173)(2,其中}3|:|{==z z C ,试求).1('i f +4. 求复数11+-=z z w 的实部与虚部.四. 证明题.(20分) 1. 函数)(z f 在区域D 内解析. 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数. 2. 试证:()f z =在割去线段0Re 1z ≤≤的z 平面内能分出两个单值解析分支, 并求出支割线0Re 1z ≤≤上岸取正值的那支在1z =-的值. 《复变函数》考试试题(二) 判断题.(20分)1. 若函数),(),()(y x iv y x u z f +=在D 内连续,则u(x,y)与v(x,y)都在D 内连续. ( )2. cos z 与sin z 在复平面内有界. ( )3. 若函数f(z)在z0解析,则f(z)在z0连续. ( )4. 有界整函数必为常数. ( )5. 如z0是函数f(z)的本性奇点,则)(lim 0z f z z →一定不存在.( )6. 若函数f(z)在z0可导,则f(z)在z0解析. ( )7. 若f(z)在区域D 内解析, 则对D 内任一简单闭曲线C 0)(=⎰Cdz z f .( )8. 若数列}{n z 收敛,则}{Re n z 与}{Im n z 都收敛. ( ) 9. 若f(z)在区域D 内解析,则|f(z)|也在D 内解析. ( )10. 存在一个在零点解析的函数f(z)使0)11(=+n f 且,...2,1,21)21(==n n n f .( )二. 填空题. (20分) 1. 设i z -=,则____,arg __,||===z z z2.设Ciy x z y x i xy x z f ∈+=∀+-++=),sin(1()2()(222,则=+→)(lim 1z f iz ________.3.=-⎰=-1||00)(z z n z z dz_________.(n 为自然数)4. 幂级数0nn nz∞=∑的收敛半径为__________ .5. 若z0是f(z)的m 阶零点且m>0,则z0是)('z f 的_____零点.6. 函数ez 的周期为__________.7. 方程083235=++-z z z 在单位圆内的零点个数为________.8. 设211)(z z f +=,则)(z f 的孤立奇点有_________.9. 函数||)(z z f =的不解析点之集为________.10. ____)1,1(Res 4=-z z .三. 计算题. (40分)1. 求函数)2sin(3z 的幂级数展开式. 2. 在复平面上取上半虚轴作割线. 试在所得的区域内取定函数z 在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点iz =处的值.3. 计算积分:⎰-=iizz I d ||,积分路径为(1)单位圆(1||=z )的右半圆.4. 求dzz zz ⎰=-22)2(sin π.四. 证明题. (20分)1. 设函数f(z)在区域D 内解析,试证:f(z)在D 内为常数的充要条件是)(z f 在D 内解析.2. 试用儒歇定理证明代数基本定理. 《复变函数》考试试题(三) 一. 判断题. (20分).1. cos z 与sin z 的周期均为πk2. ( ) 2. 若f(z)在z0处满足柯西-黎曼条件, 则f(z)在z0解析. ( )3. 若函数f(z)在z0处解析,则f(z)在z0连续. ( )4. 若数列}{n z 收敛,则}{R en z 与}{Im n z 都收敛. ( )5. 若函数f(z)是区域D 内解析且在D 内的某个圆内恒为常数,则数f(z)在区域D 内为常数. ( ) 6. 若函数f(z)在z0解析,则f(z)在z0的某个邻域内可导. ( ) 7. 如果函数f(z)在}1|:|{≤=z z D 上解析,且)1|(|1|)(|=≤z z f ,则)1|(|1|)(|≤≤z z f . ( )8. 若函数f(z)在z0处解析,则它在该点的某个邻域内可以展开为幂级数. ( )9. 若z0是)(z f 的m 阶零点, 则z0是1/)(z f 的m 阶极点. ( ) 10. 若z 是)(z f 的可去奇点,则0)),((Res 0=z z f .( )二. 填空题. (20分)1. 设11)(2+=z z f ,则f(z)的定义域为___________.2. 函数ez 的周期为_________.3. 若n n n i n n z )11(12++-+=,则=∞→n z n lim __________. 4. =+z z 22cos sin ___________.5.=-⎰=-1||00)(z z n z z dz_________.(n 为自然数)6. 幂级数∑∞=0n nnx的收敛半径为__________.7.设11)(2+=z z f ,则f(z)的孤立奇点有__________. 8. 设1-=ze ,则___=z . 9. 若0z 是)(zf 的极点,则___)(lim 0=→z f z z .10. ____)0,(Res =n zz e .三. 计算题. (40分)1. 将函数12()zf z z e =在圆环域0z <<∞内展为Laurent 级数.2. 试求幂级数n n nz n n ∑+∞=!的收敛半径.3. 算下列积分:⎰-C z z z ze )9(d 22,其中C 是1||=z .4. 求0282269=--+-z z z z在|z|<1内根的个数.四. 证明题. (20分) 1. 函数)(z f 在区域D 内解析. 证明:如果|)(|z f 在D 内为常数,那么它在D 内为常数.2. 设)(z f 是一整函数,并且假定存在着一个正整数n ,以及两个正数R及M ,使得当R z ≥||时n z M z f |||)(|≤,证明)(z f 是一个至多n 次的多项式或一常数。
复变函数论试卷

《复变函数论》试题库《复变函数》考试试题(一)一、判断题(20分):1.若f(z)在z0的某个邻域内可导,则函数f(z)在z0解析. ( )2.有界整函数必在整个复平面为常数. ( )3.若收敛,则与都收敛. ( )4.若f(z)在区域D内解析,且,则(常数). ( )5.若函数f(z)在z0处解析,则它在该点的某个邻域内可以展开为幂级数. ( )6.若z0是的m阶零点,则z0是1/的m阶极点. ( )7.若存在且有限,则z0是函数f(z)的可去奇点. ( )8.若函数f(z)在是区域D内的单叶函数,则. ( )9. 若f(z)在区域D内解析, 则对D内任一简单闭曲线C.( )10.若函数f(z)在区域D内的某个圆内恒等于常数,则f(z)在区域D内恒等于常数.()二.填空题(20分)1、__________.(为自然数)2. _________.3.函数的周期为___________.4.设,则的孤立奇点有__________.5.幂级数的收敛半径为__________.6.若函数f(z)在整个平面上处处解析,则称它是__________.7.若,则______________.8.________,其中n为自然数.9. 的孤立奇点为________ .10.若是的极点,则.三.计算题(40分):1. 设,求在内的罗朗展式.2.3. 设,其中,试求4. 求复数的实部与虚部.四. 证明题.(20分)1. 函数在区域内解析. 证明:如果在内为常数,那么它在内为常数.2. 试证: 在割去线段的平面内能分出两个单值解析分支,并求出支割线上岸取正值的那支在的值.《复变函数》考试试题(二)一.判断题.(20分)1. 若函数在D内连续,则u(x,y)与v(x,y)都在D内连续.( )2. cos z与sin z在复平面内有界. ( )3. 若函数f(z)在z0解析,则f(z)在z0连续. ( )4. 有界整函数必为常数. ( )5. 如z0是函数f(z)的本性奇点,则一定不存在. ( )6. 若函数f(z)在z0可导,则f(z)在z0解析. ( )7. 若f(z)在区域D内解析, 则对D内任一简单闭曲线C.( )8. 若数列收敛,则与都收敛. ( )9. 若f(z)在区域D内解析,则|f(z)|也在D内解析.( )10. 存在一个在零点解析的函数f(z)使且.( )二. 填空题. (20分)1. 设,则2.设,则________.3. _________.(为自然数)4. 幂级数的收敛半径为__________ .5. 若z0是f(z)的m阶零点且m>0,则z0是的_____零点.6. 函数e z的周期为__________.7. 方程在单位圆内的零点个数为________.8. 设,则的孤立奇点有_________.9. 函数的不解析点之集为________.10. .三. 计算题. (40分)1. 求函数的幂级数展开式.2. 在复平面上取上半虚轴作割线. 试在所得的区域内取定函数在正实轴取正实值的一个解析分支,并求它在上半虚轴左沿的点及右沿的点处的值.3. 计算积分:,积分路径为(1)单位圆()的右半圆.4. 求.四. 证明题. (20分)1. 设函数f(z)在区域D内解析,试证:f(z)在D内为常数的充要条件是在D 内解析.2. 试用儒歇定理证明代数基本定理.《复变函数》考试试题(三)一. 判断题. (20分).1. cos z与sin z的周期均为. ( )2. 若f(z)在z0处满足柯西-黎曼条件, 则f(z)在z0解析. ( )3. 若函数f(z)在z0处解析,则f(z)在z0连续. ( )4. 若数列收敛,则与都收敛. ( )5. 若函数f(z)是区域D内解析且在D内的某个圆内恒为常数,则数f(z)在区域D内为常数. ( )6. 若函数f(z)在z0解析,则f(z)在z0的某个邻域内可导. ( )7. 如果函数f(z)在上解析,且,则. ()8. 若函数f(z)在z0处解析,则它在该点的某个邻域内可以展开为幂级数.( )9. 若z0是的m阶零点, 则z0是1/的m阶极点. ( )10. 若是的可去奇点,则. ( )二. 填空题. (20分)1. 设,则f(z)的定义域为___________.2. 函数e z的周期为_________.3. 若,则__________.4. ___________.5. _________.(为自然数)6. 幂级数的收敛半径为__________.7. 设,则f(z)的孤立奇点有__________.8. 设,则.9. 若是的极点,则.10. .三. 计算题. (40分)1. 将函数在圆环域内展为Laurent级数.2. 试求幂级数的收敛半径.3. 算下列积分:,其中是.4. 求在|z|<1内根的个数.四. 证明题. (20分)1. 函数在区域内解析. 证明:如果在内为常数,那么它在内为常数.2. 设是一整函数,并且假定存在着一个正整数n,以及两个正数R及M,使得当时,证明是一个至多n次的多项式或一常数。
复变函数试题库(2020年10月整理).pdf

f
(z)的 m
阶零点,则 z0 是
1 f (z)
的 m 阶极点.
6.计算下列积分.(8分)
Ñ (1)
z
=2
sin z (z − )2
dz
;
2
2 z2 (z − 3)
dz
.
2
7.计算积分
d
.(6分)
0 5 + 3cos
8.求下列幂级数的收敛半径.(6分)
(1)
(1+ i)n zn ;
n=1
(2)
n=1
(n!)2 nn
zn
.
9.设 f (z) = my3 + nx2 y + i(x3 + lxy2 ) 为复平面上的解析函数,试确定 l ,
m , n 的值.(6分)
三、证明题.
1.设函数 f (z) 在区域 D 内解析, f (z) 在区域 D 内也解析,证明 f (z) 必
为常数.(5分)
2.
若
lim
n→
zn
= ,则 lim z1 + z2 + ... + zn
n→
n
= ______________.
3. 函数 ez 的周期为__________.
4.
函数
f
(z)
=
1 1+ z2
的幂级数展开式为__________
5. 若函数 f(z)在复平面上处处解析,则称它是___________.
的_____________。
8.
函数
f
(z)
=
1 1+ z2
的幂级数展开式为_________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(其中 27 题 7 分,28、29 每小题 8 分,共 23 分)
27. 证明 ∵ u ( x, y ) = x , v( x, y ) = y
∴ u x = 2 x, u y = 0, v x = 0, v y = 2 y ………………………………………4 分 显然 u x , u y , v x , v y 在 z 平面上处处连续且仅当 y = x 时满足 C . − R. 条件 u x = v y , 从而 f ( z ) 只在直线 y = x 上可微, 由于不存在 f ( z ) 的可微邻域, 故 f (z) 在 z 平 u y = −v x , 面上处处不解析. …………………………………………7 分 28. 证明 ∵ f ( z ) 在区域 D 内解析,
π + 2kπ (k = 0,±1,⋯⋯) , 2
但 在 z 平 面 上 ( ) 四、计算题
f (z) 不 恒 等 于 零 , 这 与 唯 一 性 定 理 矛 盾 .
(每小题 7 分,共 35 分)
22.计算积分
∫
1
−1
z dz ,积分路径是上半单位圆周.
sin
23.计算积分
∫
C
π z 4 dz , C : z + 1 = 1 . 2 z 2 −1= z 2 −1
π z 4 ∫ z +1 = 12 ( z + 1)( z − 1) dz
sin sin
=∫
z +1 =
1 2
π z 4 z − 1 dz …………………………………………4 分 z +1
⎡ π ⎤ ⎢ sin 4 z ⎥ …………………………………………6 分 = 2π i ⎢ ⎥ ⎢ z −1 ⎥ ⎢ ⎥ z = −1 ⎣ ⎦
1 在 z = 0 的某邻域内展成的幂级数的收敛半径为 (1 − z )(2 − z )
B.2 C. ∞ D.
(
)
A.1
3
1 2
( )
8.函数 sin z 在零点 z = 0 的阶数是 A.1 B.2 C.3 D.4
9. z = ∞ 是
1 的 sin z + cos z
B.非孤立奇点 C.解析点
z →a z →b
∫
2π
0
dx =∫ z =1 (2 + 3 cos x) 2
1 dz 4 zdz ……4 分 = ∫ 2 z + 1 2 iz 3i z =1 ( z 2 + 4 z + 1) 2 (2 + 3 ) 3 2z −1 3
,且
被积函数 f ( z ) 在单位圆周 z = 1 内只有一个二阶极点 z =
⎡ z Re s f ( z ) = ⎢ 1 z =− ⎢ ⎣ z+ 3 3
f
( n)
( z 0 ) = 0 , n = 1,2, ⋯⋯
29. 证明: n 次代数方程
P( z ) = a 0 z n + a1 z n−1 + ⋯ + a n −1 z + a n = 0
有且仅有 n 个根.
(a 0 ≠ 0)
试卷四参考答案
一、单项选择题 (每小题 2 分,共 24 分) 1.B 2.C 3.A 4.D 5.B 6.C 11.C 12.C 二、填空题 (每小题 2 分,共 8 分) 13. z = z1 + t ( z 2 − z1 ) (0 ≤ t ≤ 1) 16. 14. e
π
0
= ∫ e iθ d (iθ ) = e iθ …………………………………………6 分
π π
0
0
= e i 0 − e iπ = 1 − (−1) = 2 …………………………………………7 分
π z 4 在圆域 z + 1 < 1 内解析,在 z + 1 ≤ 1 上连续, z = −1 在 23. 解 ∵ f ( z ) = z −1 2 2 1 圆 z + 1 < 内,由柯西积分公式得…………………………………………2 分 2
( D.零点
)
A.孤立奇点
10.若 f ( z ) 在 z 平面上除 a, b 两个奇点外解析,且知 Re s f ( z ) ≠ Re s f ( z ) , C 是不 过 a, b 的一条围线, 下列结论中正确的是 A.当 a, b 两点在 C 之外时, ( )
∫
C
f ( z )dz = 0
B. 当 a, b 两点只有一个在 C 内时, C. 当 a, b 两点只有一个在 C 外时, D. 当 a, b 两点均在 C 内时,
∞
幂级数 f ( z ) =
∑C
n=0
n
( z − a ) n ,其中系数 C n =
.
三、判断题 (每小题 2 分,共 10 分) 你认为正确的在题后括号内划“√” ,反之划“×” 17.曲线 ω =
1 将 z 平面上的曲线 y = x 变成 ω 平面上的曲线 v = −u . z
( (
) )
18.若 f ( z ) 在 z 0 点不解析, 则 f ( z ) 在 z 0 点不可导.
1 变成 ω = 0 的线性变换为 2
1 2 = e iβ 2 z − 1 ……………………………3 分 ω = e iβ 1 2− z 1− z 2
z−
L(1) = −1 ,即 e iβ = −1 …………………………………………6 分
故所求线性变换为 ω = 五、证明题
2z − 1 …………………………………………7 分 z−2
z = e iθ , 0 ≤ θ ≤ π …………………………………………2 分
∴ dz = ie dθ ,起点 − 1 = e ,终点 1 = e 即起点对应 θ = π ,终点对应 θ = 0 ,于是 有
iθ iπ
0
∫
1
−1
z dz = i ∫ e iθ e iθ dθ …………………………………………4 分
复变函数
试卷四
(供数学教育专业使用)
一、单项选择题 (每小题 2 分,共 24 分) 在每小题的四个备选答案中选出一个正确答案, 并将其前面的代码写在题干后面的括号 内.不选、错选或多选者,该题无分. 1. Arg (1 + i ) = A. . ( )
π 4 π 4
B. ω = z
C. −
π + 2kπ ( k 为整数) 4 π D. − + 2kπ ( k 为整数) 4
由条件(2)知
f
( n)
,所以 f ( z ) = f ( z 0 ) ,由推论 4.31 知, ( z 0 ) = 0 ( n = 1,2, ⋯⋯ )
在 D 内必有 f ( z ) = f ( z 0 ) ,即 f ( z ) 在 D 内为一常数. ……………………8 分 29. 证明 设 f ( z ) = a 0 z , ϕ ( z ) = a1 z n −1 + ⋯ + a n −1 z + a n ,因为
7 6
∫ ∫
C
f ( z )dz = 0 f ( z )dz ≠ 0
C
∫
C
f ( z )dz ≠ 0
( )
11.方程 z − 5 z − 2 z + 1 = 0 在单位圆 z < 1 内根的个数为 A.1 B.3 C.6 D.7
12. 3 + 2i 关于单位圆周 z = 1 的对称点是 A. 3 − 2i 二、填空题 B. − 3 + 2 i (每小题 2 分,共 8 分) C.
)
(
)
π A. i 2
6.下列函数中 A. f ( z ) = e
π B. i + 2kπ i ( k 为整数) 2
不是整函数.
z
C. π i
D. π i + 2kπ i ( k 为整数) ( )
B. f ( z ) = cos z
C. f ( z ) =
1 z
D. f ( z ) = sin z
7.函数 f ( z ) =
(
)
1 (3 + 2i ) 13
D.
1 (3 − 2i ) 13
.
13.连接复平面上 z1 及 z 2 两点的直线段的参数方程为 14. i =
i
. .
15.只要 f ( z ) 在区域 D 内解析,则 f ′( z ) 在 D 内
16.设 f ( z ) 在区域 D 内解析, a ∈ D , K : z − a < R 含于 D ,则 f ( z ) 在 K 内能展成
(
)
⎤ ⎥ 2 ⎥ ⎦
′ =
z =−
1 3
3 …………………………………………6 分 2
∴
∫
2π
0
dx 4 = ⋅ 2π i Re s f ( z ) = 4π ………………………………7 分 2 1 3i (2 + 3 cos x) z =−
3
26. 解
将单位圆 z < 1 共形变换成单位圆 ω < 1 且使 z =
−
7.A
8.C
9.B
10.A
π − 2 kπ 2
( k 为整数)
15.解析
1 f (ζ ) dζ (Γ : ζ − a = ρ ,0 < ρ < R, n = 0,1,2,⋯⋯) ∫ Γ 2π i (ζ − a ) n +1
21.×
三、判断题 (每小题 2 分,共 10 分) 17.√ 18.× 19.√ 20.× 四、计算题 (每小题 7 分,共 35 分) 22. 解 上半单位圆周的方程为
