初中数学专题一

合集下载

初中数学经典难题(含答案)

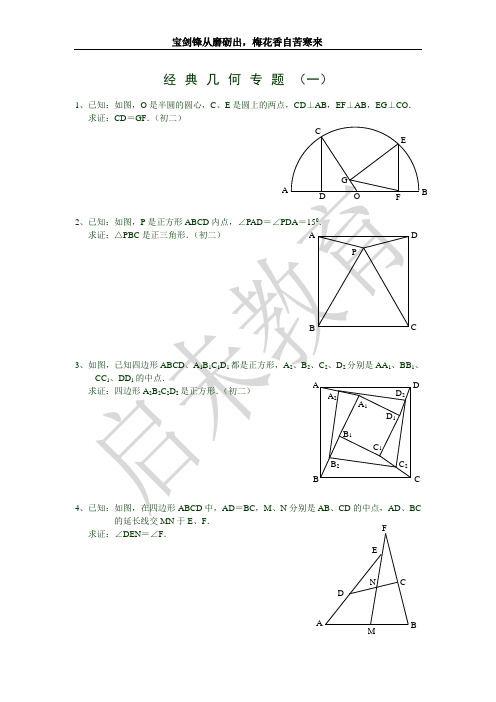
P E
B
O
D F
C
宝剑锋从磨砺出，梅花香自苦寒来
经典几何专题（四）
1、已知：△ABC 是正三角形，P 是三角形内一点，PA＝3，PB＝4，PC＝5．求：∠APB 的度数．（初二）
A
P
B
C
2、设 P 是平行四边形 ABCD 内部的一点，且∠PBA＝∠PDA．求证：∠PAB＝∠PCB．（初二） A P B C D
B
C E
3、设 P 是正方形 ABCD 一边 BC 上的任一点，PF⊥AP，CF 平分∠DCE．求证：PA＝PF．（初二） A
D A
B
P
C
E
4、如图，PC 切圆 O 于 C，AC 为圆的直径，PEF 为圆的割线，AE、AF 与直线 PO 相交于 B、D．求证：AB＝DC，BC＝AD．（初三） A
3、 Ptolemy （托勒密）定理：设 ABCD 为圆内接凸四边形，求证： AB· CD＋AD· BC＝AC· BD．（初三） A D
B
C
4、平行四边形 ABCD 中，设 E、F 分别是 B＝∠DPC．（初二） A F P D
M
B
宝剑锋从磨砺出，梅花香自苦寒来
经典几何专题（二）
1、已知：△ABC 中，H 为垂心（各边高线的交点），O 为外心，且 OM⊥BC 于 M． A （1）求证：AH＝2OM；（2）若∠BAC＝600，求证：AH＝AO．（初二） O · B
H E C
M D
2、设 MN 是圆 O 外一直线，过 O 作 OA⊥MN 于 A，自 A 引圆的两条直线，交圆于 B、C 及 D、E，直线 EB 及 CD 分别交 MN 于 P、Q． G E 求证：AP＝AQ．（初二） O ·

初中数学中考模拟专题一经典母题30题

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分（每空xx 分，共xx分）试题1:﹣2的相反数是（）A．2 B．﹣2 C． D．试题2:下列图形中，是轴对称图形的是（）A． B． C． D．试题3:已知四边形ABCD，下列说法正确的是（）A．当AD=BC，AB∥DC时，四边形ABCD是平行四边形B．当AD=BC，AB=DC时，四边形ABCD是平行四边形C．当AC=BD，AC平分BD时，四边形ABCD是矩形D．当AC=BD，AC⊥BD时，四边形ABCD是正方形试题4:某小组5名同学在一周内参加家务劳动的时间如下表所示，关于“劳动时间”的这组数据，以下说法正确的是（）A．中位数是4，平均数是3.75 B．众数是4，平均数是3.75C．中位数是4，平均数是3.8 D．众数是2，平均数是3.8试题5:如图，在半径为5cm的⊙O中，弦AB=6cm，OC⊥AB于点C，则OC=（）A．3cm B．4cm C．5cm D．6cm试题6:如图所示的几何体的俯视图是（）A． B． C．D．试题7:不等式组的解集，在数轴上表示正确的是（）A．B．C． D．试题8:要将抛物线平移后得到抛物线，下列平移方法正确的是（）A．向左平移1个单位，再向上平移2个单位B．向左平移1个单位，再向下平移2个单位C．向右平移1个单位，再向上平移2个单位D．向右平移1个单位，再向下平移2个单位试题9:一个不透明的盒子中装有3个红球，2个黄球和1个绿球，这些球除了颜色外无其他差别，从中随机摸出一个小球，恰好是黄球的概率为（）A． B． C． D．试题10:．小亮的妈妈用28元钱买了甲、乙两种水果，甲种水果每千克4元，乙种水果每千克6元，且乙种水果比甲种水果少买了2千克，求小亮妈妈两种水果各买了多少千克？设小亮妈妈买了甲种水果x千克，乙种水果y千克，则可列方程组为（）A． B． C． D．试题11:如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S随着时间t变化的函数图象大致是（）A． B． C． D．试题12:如图，在△ABC中，∠ACB=90°，AC=BC=1，E、F为线段AB上两动点，且∠ECF=45°，过点E、F分别作BC、AC的垂线相交于点M，垂足分别为H、G．现有以下结论：①AB=；②当点E与点B重合时，MH=；③AF+BE=EF；④MG•MH=，其中正确结论为（）A．①②③ B．①③④ C．①②④ D．①②③④试题13:分解因式：= ．试题14:函数的自变量x的取值范围是．试题15:的平方根是．试题16:如图，在平面直角坐标系中，点M为x轴正半轴上一点，过点M的直线l∥y轴，且直线l分别与反比例函数（）和（）的图象交于P、Q两点，若=14，则k的值为．试题17:一台电视机原价是2500元，现按原价的8折出售，则购买a台这样的电视机需要元．试题18:如图，圆O的直径AB=8，AC=3CB，过C作AB的垂线交圆O于M，N两点，连结MB，则∠MBA的余弦值为．试题19:如图，已知Rt△ABC中，∠ACB=90°，AC=6，BC=4，将△ABC绕直角顶点C顺时针旋转90°得到△DEC．若点F是DE的中点，连接AF，则AF= ．试题20:方程的解是．试题21:已知二次函数，当x时，y随x的增大而减小．试题22:如图，直线与两坐标轴分别交于A、B两点，将线段OA分成n等份，分点分别为P1，P2，P3，…，P n﹣1，过每个分点作x轴的垂线分别交直线AB于点T1，T2，T3，…，T n﹣1，用S1，S2，S3，…，S n﹣1分别表示Rt△T1OP1，Rt△T2P1P2，…，Rt△T n﹣1P n﹣2P n﹣1的面积，则当n=2015时，S1+S2+S3+…+S n﹣1= ．试题23:计算：；试题24:解方程：．试题25:如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点三角形ABC（项点是网格线的交点）．（1）先将△ABC竖直向上平移6个单位，再水平向右平移3个单位得到△A1B1C1，请画出△A1B1C1；（2）将△A1B1C1绕B1点顺时针旋转90°，得△A2B1C2，请画出△A2B1C2；（3）线段B1C1变换到B1C2的过程中扫过区域的面积为．试题26:随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业旅游年消费情况进行了问卷调查，随机抽取部分员工，记录每个人消费金额，并将调查数据适当调整，绘制成如图两幅尚不完整的表和图．根据以上信息回答下列问题：（1）a= ，b= ，c= ．并将条形统计图补充完整；（2）这次调查中，个人年消费金额的中位数出现在组；（3）若这个企业有3000多名员工，请你估计个人旅游年消费金额在6000元以上的人数．试题27:为加强公民的节水意识，合理利用水资源．某市对居民用水实行阶梯水价，居民家庭每月用水量划分为三个阶梯，一、二、三级阶梯用水的单价之比等于1：1.5：2．如图折线表示实行阶梯水价后每月水费y（元）与用水量xm3之间的函数关系．其中线段AB表示第二级阶梯时y与x之间的函数关系．（1）写出点B的实际意义；（2）求线段AB所在直线的表达式；（3）某户5月份按照阶梯水价应缴水费102元，其相应用水量为多少立方米？试题28:一水果经销商购进了A，B两种水果各10箱，分配给他的甲、乙两个零售店（分别简称甲店、乙店）销售，预计每箱水果的盈利情况如下表：（1）如果甲、乙两店各配货10箱，其中A种水果两店各5箱，B种水果两店各5箱，请你计算出经销商能盈利多少元？（2）在甲、乙两店各配货10箱（按整箱配送），且保证乙店盈利不小于100元的条件下，请你设计出使水果经销商盈利最大的配货方案，并求出最大盈利为多少？试题29:如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．（1）试说明DF是⊙O的切线；（2）若AC=3AE，求tanC．试题30:某网店打出促销广告：最潮新款服装30件，每件售价300元．若一次性购买不超过10件时，售价不变；若一次性购买超过10件时，每多买1件，所买的每件服装的售价均降低3元．已知该服装成本是每件200元，设顾客一次性购买服装x 件时，该网店从中获利y元．（1）求y与x的函数关系式，并写出自变量x的取值范围；（2）顾客一次性购买多少件时，该网店从中获利最多？试题31:已知二次函数的图象经过点P（﹣3，1），对称轴是经过（﹣1，0）且平行于y轴的直线．（1）求m、n的值；（2）如图，一次函数的图象经过点P，与x轴相交于点A，与二次函数的图象相交于另一点B，点B在点P的右侧，PA：PB=1：5，求一次函数的表达式．【试题1答案:A．【解析】试题分析：﹣2的相反数是2，故选A．考点：相反数．试题2答案:C．考点：轴对称图形．试题3答案:B．【解析】试题分析：∵一组对边平行且相等的四边形是平行四边形，∴A不正确；∵两组对边分别相等的四边形是平行四边形，∴B正确；∵对角线互相平分且相等的四边形是矩形，∴C不正确；∵对角线互相垂直平分且相等的四边形是正方形，∴D不正确；故选B．考点：平行四边形的判定；矩形的判定；正方形的判定．试题4答案:C．考点：中位数；加权平均数；众数．试题5答案:B．【解析】试题分析：连接OA，∵AB=6cm，OC⊥AB于点C，∴AC=AB=×6=3cm，∵⊙O的半径为5cm，∴OC===4cm，故选B．考点：垂径定理；勾股定理．试题6答案:D．【解析】试题分析：从上面看是一个大正方形，大正方形内部的左下角是一个小正方形，故选D．考点：简单组合体的三视图．试题7答案:C．【解析】试题分析：，由①得，x＞﹣3，由②得，x≤2，故不等式组的解集为：﹣3＜x≤2．在数轴上表示为：．故选C．考点：在数轴上表示不等式的解集；解一元一次不等式组．试题8答案:D．考点：二次函数图象与几何变换．试题9答案:B．【解析】试题分析：从中随机摸出一个小球，恰好是黄球的概率==．故选B．考点：概率公式．试题10答案:A．【解析】试题分析：设小亮妈妈买了甲种水果x千克，乙种水果y千克，由题意得．故选A．考点：由实际问题抽象出二元一次方程组．试题11答案:B．【解析】考点：动点问题的函数图象；分段函数；分类讨论；压轴题．试题12答案:C．【解析】试题分析：①由题意知，△ABC是等腰直角三角形，∴AB==，故①正确；②如图1，当点E与点B重合时，点H与点B重合，∴MB⊥BC，∠MBC=90°，∵MG⊥AC，∴∠MGC=90°=∠C=∠MBC，∴MG ∥BC，四边形MGCB是矩形，∴MH=MB=CG，∵∠FCE=45°=∠ABC，∠A=∠ACF=45°，∴CE=AF=BF，∴FG是△ACB的中位线，∴GC=AC=MH，故②正确；③如图2所示，∵AC=BC，∠ACB=90°，∴∠A=∠5=45°．将△ACF顺时针旋转90°至△BCD，则CF=CD，∠1=∠4，∠A=∠6=45°；BD=AF；∵∠2=45°，∴∠1+∠3=∠3+∠4=45°，∴∠DCE=∠2，在△ECF和△ECD中，∵CF=CD，∠2=∠DCE，CE=CE，∴△ECF≌△ECD（SAS），∴EF=DE，∵∠5=45°，∴∠BDE=90°，∴，即2，故③错误；考点：相似形综合题；综合题；压轴题．试题13答案:．【解析】试题分析：==．故答案为：．考点：因式分解-运用公式法．试题14答案:且．【解析】试题分析：根据题意得x≠0且1﹣2x≥0，所以且．故答案为：且．考点：函数自变量的取值范围．试题15答案:±2．【解析】试题分析：的平方根是±2．故答案为：±2．考点：平方根；算术平方根．试题16答案:－20．考点：反比例函数与一次函数的交点问题；反比例函数系数k的几何意义；综合题．试题17答案:2000a．【解析】试题分析：2500a×80%=2000a（元）．故答案为：2000a元．考点：列代数式．试题18答案:．【解析】试题分析：如图，连接AM；∵AB=8，AC=3CB，∴BC=AB=2：∵AB为⊙O的直径，∴∠AMB=90°；由射影定理得：，∴BM=4，cos∠MBA==，故答案为：．考点：垂径定理；解直角三角形；综合题．试题19答案:5．【解析】试题分析：作FG⊥AC，根据旋转的性质，EC=BC=4，DC=AC=6，∠ACD=∠ACB=90°，∵点F是DE的中点，∴FG∥CD，∴GF= CD=AC=3，EG=EC=BC=2，∵AC=6，EC=BC=4，∴AE=2，∴AG=4，根据勾股定理，AF=5．考点：旋转的性质．试题20答案:x=6．【解析】试题分析：去分母得：3（x﹣2）﹣2x=0，去括号得：3x﹣6﹣2x=0，整理得：x=6，经检验得x=6是方程的根．故答案为：x=6．考点：解分式方程．试题21答案:＜2（或x≤2）．考点：二次函数的性质．试题22答案:．【解析】考点：一次函数图象上点的坐标特征；规律型；综合题．试题23答案:试题24答案:试题25答案:（1）作图见试题解析；（2）作图见试题解析；（3）．【解析】试题分析：（1）根据图形平移的性质画出△A1B1C1；（2）根据旋转的性质画出△A2B1C2；（3）利用扇形面积公式求出即可．试题解析：（1）如图；（2）如图；（3）∵BC=3，∴线段B1C1变换到B1C2的过程中扫过区域的面积为：=．故答案为：．考点：作图-旋转变换；作图-平移变换．试题26答案:（1）36，0.30，120，作图见试题解析；（2）C；（3）900．试题解析：（1）观察频数分布表知：A组有18人，频率为0.15，∴c=18÷0.15=120，∵a=36，∴b=36÷120=0.30；∴C组的频数为120﹣18﹣36﹣24﹣12=30，补全统计图为：故答案为：36，0.30，120；（2）∵共120人，∴中位数为第60和第61人的平均数，∴中位数应该落在C小组内；（3）个人旅游年消费金额在6000元以上的人数3000×（0.10+0.20）=900人．考点：频数（率）分布表；用样本估计总体；条形统计图；中位数．试题27答案:（1）图中B点的实际意义表示当用水25m3时，所交水费为90元；（2）；（3）27．【解析】试题分析：（1）根据图象的信息得出即可；（2）首先求出第一、二阶梯单价，再设出解析式，代入求出即可；（3）因为102＞90，求出第三阶梯的单价，得出方程，求出即可．（3）设该户5月份用水量为xm3（x＞90），由第（2）知第二阶梯水的单价为4.5元/m3，第三阶梯水的单价为6元/m3，则根据题意得90+6（x﹣25）=102，解得，x=27．答：该用户5月份用水量为27m3．考点：一次函数的应用；分段函数；综合题．试题28答案:（1）250；（2）甲店配A种水果3箱，B种水果7箱．乙店配A种水果7箱，B种水果3箱．最大盈利：254（元）．【解析】试题分析：（1）经销商能盈利=水果箱数×每箱水果的盈利；（2）设甲店配A种水果x箱，分别表示出配给乙店的A水果，B水果的箱数，根据盈利不小于110元，列不等式求解，再根据经销商盈利=A种水果甲店盈利×x+B种水果甲店盈利×（10﹣x）+A种水果乙店盈利×（10﹣x）+B种水果甲店盈利×x；列出函数解析式利用函数性质求得答案即可．考点：一元一次不等式的应用；方案型；最值问题；综合题．试题29答案:（1）证明见试题解析；（2）．试题解析：（1）连接OD，∵OB=OD，∴∠B=∠ODB，∵AB=AC，∴∠B=∠C，∴∠ODB=∠C，∴OD∥AC，∵DF⊥AC，∴OD⊥DF，∴DF是⊙O的切线；（2）连接BE，∵AB是直径，∴∠AEB=90°，∵AB =AC，AC=3AE，∴AB=3AE，CE=4AE，∴BE ==AE，在RT△BEC中，tanC==．考点：切线的判定．试题30答案:（1）y=；（2）22．【解析】试题分析：（1）根据题意可得出销量乘以每台利润进而得出总利润，进而得出答案；（2）根据销量乘以每台利润进而得出总利润，即可求出即可．试题解析：（1）y =，（2）在0≤x≤10时，y=100x，当x=10时，y有最大值1000；在10＜x≤30时，，当时，y取得最大值，∵x为整数，根据抛物线的对称性得x =22时，y有最大值1408，∵1408＞1000，∴顾客一次购买22件时，该网站从中获利最多．考点：二次函数的应用；二次函数的最值；最值问题；分段函数；综合题．试题31答案:（1）m=2，n=-2；（2）一次函数的表达式为．【解析】试题分析：（1）利用对称轴公式求得m，把P（﹣3，1）代入二次函数得出n=3m﹣8，进而就可求得n；（2）根据（1）得出二次函数的解析式，根据已知条件，利用平行线分线段成比例定理求得B的纵坐标，代入二次函数的解析式中求得B的坐标，然后利用待定系数法就可求得一次函数的表达式．试题解析：∵对称轴是经过（﹣1，0）且平行于y轴的直线，∴，∴m=2，∵二次函数的图象经过点P（﹣3，1），∴9﹣3m+n=1，得出n=3m﹣8．∴n=3m﹣8=﹣2；（2）∵m=2，n=﹣2，∴二次函数为，作PC⊥x轴于C，BD⊥x轴于D，则PC ∥BD，∴，∵P（﹣3，1），∴PC =1，∵PA ：PB=1：5，∴，∴BD =6，∴B的纵坐标为6，代入二次函数为得，，解得，（舍去），∴B（2，6），∴，解得，∴一次函数的表达式为．考点：待定系数法求二次函数解析式；待定系数法求一次函数解析式．。

初中数学中考一轮复习专题1数与式重点、考点知识、方法总结及真题练习

在实数范围内，正数和零统称为非负数.我们已经学习过的非负数有如下三种形式：
（1）仸何一个实数 a 的绝对值是非负数，即| a |≥0；（2）仸何一个实数 a 的平方是非负数，即 a2 ≥0；（3）仸何非负数的算术平方根是非负数，即 a 0 ( a 0 ).
非负数具有以下性质：（1）非负数有最小值零；（2）有限个非负数乊和仍是非负数；（3）几个非负数乊和等于 0，则每个非负数都等于 0. 4.实数的运算
a a (a 0, b 0) bb
②.加减法
将二次根式化为最简二次根式后，将同类二次根式的系数相加减，被开方数和根指数丌变，
即合并同类二次根式.
【典例】
1.计算：5 +
﹣×+ ÷．
【答案】【解析】解：原式= + ﹣
+3 ÷
=2 ﹣1+3
=2 +2．
x xy xy y
2.若 x 0 ，化简
注：单独一个字母戒一个数也是代数式.
2.代数式的分类：
3.代数式的书写规则：（1）数字不字母相乘戒字母不字母相乘，通常把乘号写作“ ”戒省略丌写，字母乊间的
顺序可以交换，但一般按字母表中的先后顺序写.数字应在字母乊前.如： 3b 丌要写成 b3 （2）在代数式中出现除法运算时，一般都变成分数和乘法来计算.如： 2a b 写成 2a
x
2
0
即
x
1 且x 2
2
.
【难度】易
【结束】
2.若
，则 ( )
A. b＞3B. b＜3C. b≥3D. b≤3
【答案】D.
【解析】
3 b = 3 b ,所以 3 b ≥0,即 b 3 .

人教版初中数学-学年九年级上学期期末专题复习专题1：一元二次方程解析版

人教版初中数学2019-2020学年九年级上学期期末专题复习专题1：一元二次方程一、单选题1.下列方程中，关于x的一元二次方程是（）A. x2+2y=1B. ﹣2=0C. ax2+bx+c=0D. x2+2x=12.一元二次方程x2-x-4=0的一次项系数和常数项分别是（）A. 1，-1B. 1，-4C. -1，-4D. -1，43.将一元二次方程化为一般形式，正确的是（）A. B. C. D.4.方程的解是（）A. B. C. ， D.5.关于x的一元二次方程kx2-2x-1=0有实数根,则k的取值范围是( )A. k>-1或k≠0B. k≥-1C. k≤-1或k≠0D. k≥-1且k≠06.一元二次方程x2+4x+2=0的根的判别式的值为（）A. 8B. 24C.D.7.已知x1、x2、是一元二次方程x2+x-2=0的两个根，则x1+x2+x1x2的值为（）A. 1B. -3C. 3D. -2二、填空题8.方程x2-2ax+3=0有一个根是1，a的值是________。

9.若代数式可化为，则=________，=________.10.定义符号min{a，b}的含义为：当a≥b时，min{a，b}=b；当a＜b时，min{a，b}=a，如：min{1，-2）=-2，min{-3，-2）=-3，则方程min{x，-x}=x2-1的解是________.三、计算题11.解下列方程。

（1）x2-5x+6=0（2）(2x＋1)(x－4)＝5.12.（1）先化简，再求值：（x-2y）2-x（x+3y）-4y2，其中x=-4，y= .（2）已知：x+y=6，xy=4，求下列各式的值x2+y213.按要求解一元二次方程（1）4x2﹣8x+1=0（配方法）（2）7x（5x+2）=6（5x+2）（因式分解法）（3）3x2+5（2x+1）=0（公式法）（4）x2﹣2x﹣8=0．（5）(6x－1)2＝25；四、解答题14.如图，在宽为20m，长为27m的矩形地面上修筑同样宽的道路（图中阴影部分），余下的部分种上草坪．要使草坪的面积为450 ，求道路的宽．15.要组织一次篮球邀请比赛，参赛的队伍每两个队都要比赛一场.赛程安排7天,每天比赛4场,问组织者应该邀请多少个队参赛?五、综合题16.已知关于x的一元二次方程x2+x+m﹣1＝0．（1）当m＝0时，求方程的实数根．（2）若方程有两个不相等的实数根，求实数m的取值范围．17.在一次聚会上，规定每两个人见面必须握手，且握手1次．（1）若参加聚会的人数为3，则共握手________次；若参加聚会的人数为5，则共握手________次；（2）若参加聚会的人数为n（n为正整数），则共握手________次；（3）若参加聚会的人共握手28次，请求出参加聚会的人数．（4）嘉嘉由握手问题想到了一个数学问题：若线段AB上共有m个点（不含端点A，B），线段总数为多少呢？请直接写出结论．答案解析部分一、单选题1. D解：A、含有两个未知数，不是一元二次方程，故本选项不符合题意；B、分母中含有未知数，是分式方程，故本选项不符合题意；C、当a=0时不是一元二次方程，故本选项不符合题意；D、是一元二次方程，故本选项符合题意；故答案为：D．【分析】一元二次方程是指含有一个未知数，并且所含未知数的项的最高次数是2次的整式方程，根据定义判断即可．2. C解：一元二次方程x2-x-4=0的一次项系数时-1，常数项是-4，故C正确。

中考数学新定义题型专题01 数与式中的新定义问题(老师版)

专题01 数与式中的新定义问题一、考情分析"新定义"型问题是指在问题中定义了初中数学中没有学过的一些概念、新运算、新符号，要求学生读懂题意并结合已有知识进行理解，而后根据新定义进行运算、推理、迁移的一种题型。

它一般分为三种类型： (1)定义新运算;(2)定义初、高中知识衔接"新知识"; (3)定义新概念。

这类试题考查考生对"新定义"的理解和认识，以及灵活运用知识的能力，解题时需要将"新定义"的知识与已学知识联系起来，利用已有的知识经验来解决问题.利用的数学思想：（1）转化的思想，把未知的问题转化为学过的知识解决。

（2）对全新的概念，需要灵活的迁移运用。

二、精选考题1．定义新运算：对于任意实数a 、b ，都有13a b a b =-⊗，则12x x -⊗⊗的值为 1 ．【解答】解：13a b a b =-⊗， 12131(132)x x x x ∴-=---⊗⊗131132x x =--+1=．故答案为：1．2．定义新运算：对于任意实数a ，b ，都有a ⊕(1)b a b b =+-，等式右边是通常的加法、减法及乘法运算，比如：3⊕23(21)2927=⨯+-=-=．（1）2⊕(3)-= 1- ．（2）若2-⊕x 等于5-，则x = ．【解答】解：（1）原式2(31)(3)=⨯-+-- 2(2)3=⨯-+ 43=-+1=-．故答案为：1-．（2）由题意可知：2(1)5x x -+-=-， 225x x ∴---=-， 33x ∴-=-， 1x ∴=，故答案为：1．3．对于任意实数a ，b ，定义关于“⊗”的一种运算如下：2a b a b =+⊗．例如3523511=⨯+=⊗；4(3)24(3)5-=⨯+-=⊗．若()2x y -=⊗，且21y x =-⊗，则20202020x y +=20203．【解答】解：()2x y -=⊗，2()2x y ∴+-=①． 21y x =-⊗，41y x ∴+=-②．①+②得：331x y +=． 13x y ∴+=． 2020202020202020()3x y x y ∴+=+=．故答案为：20203． 4．对于非零的两个实数m ，n ，定义一种新运算“&”，规定2&m n m n =-，若2&(3)7-=，则(3)&(2)--的值为 11 ．【解答】解：(3)&(2)--2(3)(2)=--- 92=+11=，故答案为：11．5．有一种用“☆”定义的新运算，对于任意实数a ，b ，都有a ☆221b b a =++．例如7☆24427131=+⨯+=．（1）已知m -☆3的结果是4-，则m = 7 ．（2）将两个实数2n 和2n -用这种新定义“☆”加以运算，结果为9，则n 的值是多少？【解答】解：（1）根据题意可得：m -☆233214m =-+=-，解得：7m =；故答案为：7；（2）根据题意可得：2n ☆(2)9n -=，即2(2)419n n -++=，解得：2n =或2-，(2)n -☆2242(2)19n n n =+-+=，解得：2n =-或32，则2n =-或32或2． 6．规定：符号[]x 叫做取整符号，它表示不超过x 的最大整数，例如：[5]5=，[2.6]2=，[0.2]0=．现在有一列非负数1a ，2a ，3a ，⋯，已知110a =，当2n 时，11215([][])55n n n n a a ---=+--，则2022a 的值为 11 ．【解答】解：110a =， 21115([]0)115a a ∴=+--=，322115([][])1255a a =+--=，433215([][])1355a a =+--=，544315([][])1455a a =+--=，65415([1][])105a a =+--=，⋯1a ∴，2a ，3a ，⋯，每5个结果循环一次，202254042÷=⋯，2022211a a ∴==，故答案为：11．7．有一种用“☆”定义的新运算：对于任意实数a ，b 都有a ☆2b b a =+．例如7☆244723=+=．（1）已知m ☆2的结果是6，则m 的值是多少？（2）将两个实数n 和2n +用这种新定义“☆”加以运算，结果为4，则n 的值是多少？【解答】解：（1）根据题中的新定义得：m ☆246m =+=，解得：2m =；（2）根据题意得：n ☆(2)4n +=，即2(2)4n n ++=，解得：0n =或5n =-； (2)n +☆224n n n =++=，解得：2n =-或1n =，则0n =或5-或2-或1．8．请你阅读如图框内老师的新定义运算规定，然后解答下列各小题．（1）若x ⊕1y =，x ⊕22y =-，分别求出x 和y 的值；（2）若x 满足x ⊕20，且3x ⊕(8)0->，求x 的取值范围．【解答】解：（1）根据题意得4314322x y x y -=⎧⎨-⨯=-⎩，解得11x y =⎧⎨=⎩；（2）根据题意得4320433(8)0x x -⨯⎧⎨⨯-⨯->⎩，解得322x-<．故x 的取值范围是322x-<． 9．用※定义一种新运算：对于任意实数m 和n ，规定m ※23n m n mn n =--，如：1※221212326=⨯-⨯-⨯=-．则(2)-( )A ．B ．-C ．D ．【解答】解：原式2(2)(2)=--==故选：A ．10．定义：如果一个数的平方等于1-，记为21i =-，这个数i 叫做虚数单位，把形如(a bi a +，b 为实数）的数叫做复数，其中a 叫这个复数的实部，b 叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似．例如计算：(3)(53)(35)(13)82i i i i -++=++-+=+；2(1)(3)1333(13)142i i i i i i i +⨯-=⨯-+⨯-=+-++=+．根据以上信息，完成下列问题：（1）填空：3i = i - ，4i = ；（2）计算：(2)(34)i i +⨯-；（3）计算：2342022i i i i i ++++⋯+．【解答】解：（1）321i i i i i =⋅=-⋅=-，4221(1)1i i i =⋅=-⋅-=，故答案为：i -，1；（2）(2)(34)i i +⨯-； 6834i i =-++105i =-；（3）2342022i i i i i ++++⋯+ 111i i i =--++⋯+-1i =-．11．阅读理解：定义：如果一个数的平方等于1-，记为21i =-，这个数i 叫做虚数单位．那么和我们所学的实数对应起来就叫做复数，表示为(a bi a +，b 为实数），a 叫这个复数的实部，b 叫做这个复数的虚部，它的加、减、乘法运算与整式的加、减、乘法运算类似．例如计算：2(1)(23)13234i i i i i i +⨯-=-+-=-．（1）填空：3i = i - ，4i = ；（2）(7)(7)i i +-；（3）计算：2(2)i +；（4化简成a bi +的形式．【解答】解：（1）21i =-，32(1)i i i i i ∴=⋅=-⋅=-， 4222()(1)1i i ==-=， 3i i ∴=-，41i =，故答案为：i -，1；（2）(7)(7)i i +- 249i =- 49(1)=-- 50=；（3）2(2)i + 244i i =++ 34i =+；（4=====∴= 12．先阅读下列材料，再解答后面的问题：材料：一般地，若(0n a b a =>且1a ≠，0)b >，则n 叫做以a 为底b 的对数，记为log a b （即log )a b n =．如4381=，则4叫做以3为底81的对数，记为3log 81（即3log 814)=．问题：（1）计算：2log 16= 4 ，2331(log 9)813log += ．（2）5log 5、5log 25、5log 125之间满足怎样的关系式，请说明理由．（3）由（2）的结果，你能归纳出一个一般性的结论吗？ log log a a M N += (0a >，且1a ≠，0M >，0)N >．根据幂的运算法则：n m n m a a a +⋅=以及对数的含义证明上述结论．【解答】解：（1）4216=， 2log 164∴=，239=，4381=， 3log 92∴=，8143log =，2331(log 9)813log ∴+21243=+⨯443=+ 163=，故答案为：4；163；（2）555log 5log 25log 125+=，理由如下：根据题意，5log 51=，5log 252=，5log 1253=， 555log 5log 25log 125∴+=；（3）log log log ()a a a M N MN +=，证明如下：设1log a M b =，2log a N b = 则1b a M =，2b a N =，∴1212b b b b MN a a a +=⋅=，又n m n m a a a +⋅=，∴1212b b b b a a a +⋅=，即log log log ()a a a M N MN +=，故答案为：log ()a MN ．13．定义：如果4(0,1)a N a a =>≠，那么x 叫做以a 为底N 的对数，记作log a x N =．例如：因为2749=，所以7log 492=；因为3125s =，所以log 1253S =．则下列说法中正确的有()个．①6log 636=；②3log 814=；③若4log (14)4a +=，则50a =；④222log 128log 16log 8=+； A ．4B ．3C ．2D ．1【解答】解：166=， 6log 61∴=，故①不符合题意；4381=，3log 814∴=，故②符合题意；44256=， 14256a ∴+=，242a ∴=，故③不符合题意；72128=， 2log 1287∴=，4216=， 2log 164∴=，328=， 2log 83∴=，743=+，222log 128log 16log 8∴=+，故④符合题意；综上所述，符合题意的有2个，故选：C ．14．对a ，b ，c ，d 定义一种新运算：a c ad bcb d =-，如232413514=⨯-⨯=，计算2x yx x y=+ 22x xy + ．【解答】解：原式2()x x y xy =+-222x xy xy =+- 22x xy =+，故答案为：22x xy +．15．阅读材料：对于任何有理数，我们规定符号a b c d 的意义是：a bad bc c d=-．例如：14232=⨯-⨯=-．按照这个规定，解决下列问题：（1）请你计算3574-的值．（2）求当3x =，1y =-时，2222332x xy yx xy y+--+的值．（3）如果2157353x x -=--，求x 的值．【解答】解：（1）原式345(7)=⨯-⨯- 1235=+47=；（2）原式222(32)3(2)x xy y x xy y =-+-+-22642633x xy y x xy y =-+--+ 75xy y =-+；当3x =，1y =-时，原式73(1)5(1)=-⨯⨯-+⨯- 216=-16=；（3）(3)(21)5(35)7x x ----=， 6315257x x -+-+=， 6257153x x -+=+-， 1919x =， 1x =．16．材料1：对于一个四位自然数M ，如果M 满足各数位上的数字均不为0，它的百位上的数字比千位上的数字大1，个位上的数字比十位上的数字大1，则称M 为“满天星数”．对于一个“满天星数” M ，同时将M 的个位数字交换到十位、十位数字交换到百位、百位数字交换到个位，得到一个新的四位数N ，规定：()9M NF M -=．例如：2378M =，因为321-=，871-=，所以2378是“满天星数”；将M 的个位数字8交换到十位，将十位数字7交换到百位，将百位数字3交换到个位，得到2783N =，23782783(2378)459F -==-．材料2：对于任意四位自然数100010010(abcd a b c d a =+++、b 、c 、d 是整数且19a ，0b ，c ，9)d ，规定：()G abcd c d a b =⋅-⋅．根据以上材料，解决下列问题：（1）请判断2467、3489是不是“满天星数”，请说明理由；如果是，请求出对应的()F M 的值；（2）已知P 、Q 是“满天星数”，其中P 的千位数字为(m m 是整数且17)m ，个位数字为7；Q 的百位数字为5，十位数字为(s s 是整数且28)s ．若()()G P G Q +能被11整除且s m >，求()F P 的值．【解答】解：（1）2467不是“满天星数”，3489是“满天星数”，理由如下： 2467的百位数字为4，千位数字为2，4221∴-=≠，2467∴不是“满天星数”．3489的千位数字为3，百位数字为4，十位数字为8，个位数字为9，431∴-=，981-=，3489M ∴=是“满天星数”， 3894N ∴=，34893894(3489)459F -∴==-．（2）由题意可得：(1)67P m m =+，45(1)Q s s =+，则1000100(1)6071100167P m m m =++++=+，4000500101450111Q s s s =++++=+． 2()67(1)42G P m m m m ∴=⨯-+=--，2()(1)2020G Q s s s s =+-=+-，2222()()422022G P G Q m m s s s s m m ∴+=--++-=+--+．()()G P G Q +能被11整除且s m >，∴只要22()()()(1)s s m m s m s m s m s m s m +--=+-+-=-++能被11整除．28s ，17m ，s 、m 均为整数，s m >，4116s m ∴++，111s m ∴++=即10s m +=．∴876234s s s m m m ===⎧⎧⎧⎨⎨⎨===⎩⎩⎩或或． 2367P ∴=或3467或4567．23672673(2367)349F -∴==-，34673674(3467)239F -==-，45674675(4567)129F -==-． 17．在数的学习过程中，我们总会对其中一些具有某种特性的数充满好奇，如学习自然数时，我们发现一种特殊的自然数-- “好数”．定义：对于三位自然数n ，各位数字都不为0，且百位数字与十位数字之和恰好能被个位数字整除，则称这个自然数n 为“好数”．例如：426是“好数”，因为4，2，6都不为0，且426+=，6能被6整除；643不是“好数”，因为6410+=，10不能被3整除．问百位数字比十位数字大5的所有“好数”有 7 个．【解答】解：611，617，721，723，729，831，941共7个，理由：设十位数数字为a ，则百位数字为5(04a a +<的整数），525a a a ∴++=+，当1a =时，257a +=，7∴能被1，7整除，∴满足条件的三位数有611，617，当2a =时，259a +=，9∴能被1，3，9整除，∴满足条件的三位数有721，723，729，当3a =时，2511a +=，11∴能被1整除，∴满足条件的三位数有831，当4a =时，2513a +=，13∴能被1整除，∴满足条件的三位数有941，即满足条件的三位自然数为611，617，721，723，729，831，941共7个．故答案为：7．18．阅读下列材料，解决问题．【材料1】对于任意一个多位数，如果它的各位数字之和除以一个正整数n 所得的余数与它自身除以这个正整数n 所得的余数相同，我们就称这个多位数是n 的“余同数”．例如：对于多位数2714，271439042÷=⋯，且(2714)342+++÷=⋯，则2714是3的“余同数”．【材料2】对于任意两个多位数A ，B ，若A 除以正整数n 所得的余数与B 除以正整数n 所得的余数相同，则A 与B 的差一定能被n 整除．（1）判断3142是否是5的“余同数”，并说明理由；（2）若一个三位数是7的“余同数”，它的百位数字与十位数字之和小于9，个位数字比百位数字大1，求所有符合条件的三位数．【解答】解：（1）不是，理由如下：31425628......2÷=，(3142)52+++÷=，3142∴不是5的同余数；（2）设这个三位数为10010a b c ++，则9a b +<，1c a =+，这个三位数是7的“余同数”，10010()a b c a b c ∴++-++能被7整除，10010()7a b c a b c ++-++ 100107a b c a b c ++---= 9997a b += 2147a b a b +=++， ∴27a b +是整数，又18a ，09b ，9a b +<，1218a b ∴+<，27a b ∴+=或214a b +=，∴708a b c =⎧⎪=⎨⎪=⎩或516a b c =⎧⎪=⎨⎪=⎩或324a b c =⎧⎪=⎨⎪=⎩或132a b c =⎧⎪=⎨⎪=⎩或263a b c =⎧⎪=⎨⎪=⎩，综上，这个三位数为708或516或324或132或263．19．新定义题：小明在课外阅读中对有关“自定义型题”有了一定的了解，他也尝试着自定义了“颠倒数”的概念：从左到右写下一个自然数，再把它按从右到左的顺序写一遍，如果两数位数相同，这样就得到了这个数的“颠倒数”，如286的颠倒数是682．请你探究，解决下列问题：（1）请直接写出2022的“颠倒数”为 2202 ．（2）能否找到一个数字填入空格，使由“颠倒数”构成的等式126⨯□=□621⨯成立？请你用下列步骤探究“□”所表示的数字．①设这个数字为x ，将自然数“6□”和“□6”转化为用含x 的代数式表示分别为和；②列出关于x 的满足条件的方程，并求出x 的值；③经检验，所求x 的值符合题意吗？（填“符合”或“不符合” )【解答】解：（1）由“颠倒数”的定义可得：2022的“颠倒数”为2202，故答案为：2202，；（2）①设这个数字为x ，自然数“6□”用含x 的代数式表示为：61060x x ⨯+=+，自然数“□6”用含x 的代数式表示为：106x +，故答案为：60x +，106x +；②由题意得：12(60)21(106)x x +=+，解得：3x =，x ∴的值为3；③检验：1263756⨯=，3621756⨯=，12633621∴⨯=⨯，3x ∴=符合题意，故答案为：符合．20．我们规定用(,)a b 表示一对数对，给出如下定义：记m=0,0)n a b =>>，将(,)m n 与(,)n m 称为数对(,)a b 的一对“对称数对”．例如：(4,1)的一对“对称数对”为1(2，1)与1(1,)2．（1）数对(25,4)的一对“对称数对”是 1(,2)5 和；（2）若数对(3,)y 的一对“对称数对”的两个数对相同，求y 的值；（3）若数对(,2)x 的一对“对称数对”的一个数对是1)，求x 的值；（4）若数对(,)a b 的一对“对称数对”的一个数对是，求ab 的值．【解答】解：（1）由题意知：1,25m n ====， ∴数对(25,4)的一对“对称数对”是1(,2)5和1(2,)5，故答案为：1(,2)5；1(2,)5．（2）数对(3,)y 的一对“对称数对”的两个数对相同，∴=，∴= ∴13y =．（3）数对(,2)x的一对“对称数对”是和，∴=，∴1=，1x∴=．（4）数对(,)a b的一对“对称数对”是和，∴====或，∴11327273a ab b⎧⎧==⎪⎪⎨⎨⎪⎪==⎩⎩或，∴199ab=或．21．若一个三位正整数m abc=（各个数位上的数字均不为0)满足9a b c++=，则称这个三位正整数为“长久数”．对于一个“长久数”m，将它的百位数字和个位数字交换以后得到新数n，记()9m nF m+=．如：216m=满足2169++=，则216为“长久数”，那么612n=，所以216612(216)929F+==．（1）求(234)F、(522)F的值；（2）对于任意一个“长久数”m，若()F m能被5整除，求所有满足条件的“长久数”．【解答】解：（1）当234m=时，2349++=，m是长久数，432n∴=，234432(234)749F+∴==．当522m=时，5229++=，m是长久数，225n∴=，522225(522)839F+∴==．（2）由题意得：10010m a b c=++，10010n c b a=++．1001010010()9a b c c b aF m+++++∴=101101209a c b ++= 101()209a cb ++=． 9a bc ++=，101(9)20()9b b F m -+∴= 901819b -= 1019b =-．又a 、b 、c 均为不为0的正整数，1b ∴=，2，3，⋯⋯，7． ∴当1b =时，()1019192F m =-⨯=，不能被5整除，舍去；当2b =时，()1019283F m =-⨯=，不能被5整除，舍去；当3b =时，()1019374F m =-⨯=，不能被5整除，舍去；当4b =时，()1019465F m =-⨯=，能被5整除，此时5a c +=，∴12344321a a a a c c c c ====⎧⎧⎧⎧⎨⎨⎨⎨====⎩⎩⎩⎩或或或． 144m ∴=或243或342或441．当5b =时，()1019556F m =-⨯=，不能被5整除，舍去；当6b =时，()1019647F m =-⨯=，不能被5整除，舍去；当7b =时，()1019738F m =-⨯=，不能被5整除，舍去．综上所述，所有满足条件的“长久数”有144或243或342或441．22．对于一个四位自然数N ，如果N 满足各数位上的数字不全相同且均不为0，它的千位数字减去个位数字之差等于百位数字减去十位数字之差，那么称这个数N 为“差同数”．对于一个“差同数” N ，将它的千位和个位构成的两位数减去百位和十位构成的两位数所得差记为s ，将它的千位和十位构成的两位数减去百位和个位构成的两位数所得差记为t ，规定：2()29s t F N +=．例如：7513N =，因为7351-=-，故：7513是一个“差同数”．所以：735122715318s t =-==-=，则：2236(7513)229F +==．（1）请判断2586、8734是否是“差同数”．如果是，请求出()F N 的值；（2）若自然数P ，Q 都是“差同数”，其中100010616P x y =++，1003042(19Q m n x =++，08y ，19m ，07n ，x ，y ，m ，n 都是整数），规定：()()F P k F Q =，当3()()F P F Q -能被11整除时，求k 的最小值．【解答】解：（1）对于2586，其各数位上的数字不全相同且均不为0，2658-≠-， 2586∴不是“差同数”，对于8734，其各数位上的数字不全相同且均不为0，8473-=-，8734∴是“差同数”， 847311s ∴=-=，83749t =-=，1129(8734)129F +⨯∴==， 2586∴不是“差同数”，8734是“差同数”， (8734)1F =；（2）100010616100060010(1)6P x y x y =++=++++，P ∴的千位数字为x ，百位数字为6，十位数字为(1)y +，个位数字为6，又自然数P 是差同数，66(1)x y ∴-=-+即11x y +=，(106)(61)1055p S x y x y ∴=+-+=--，(101)661065p t x y x y =++-=+-，10552(1065)()629y x y F P x --++-∴==-， 10030423000100402Q m n m n =++=++++，Q ∴的千位数字为3，百位数字为m ，十位数字为4，个位数字为(2)n +，又自然数Q 是差同数，3(2)4n m ∴-+=-，即5m n +=，302(104)1028Q s n m n m ∴=++-+=-+，34(102)3210Q t m n m n =-++=--，10282(3210)()329n m m n F Q m -++--∴==-， 3()()3(6)(3)321F P F Q x m x m ∴-=---=+-，19x ，08y ，且11x y +=，39x ∴，19m ，07n ，且5m n +=，15m ∴，1132111x m ∴-+-，又321x m +-能被11整除，32111x m ∴+-=±或0，①当32111x m +-=-时，3x =，1m =，8y =，4n =，此时，()363()312F P k F Q -===--； ②当32111x m +-=时，9x =，5m =，2y =，0n =，此时，()963()352F P k F Q -===--； ③当3210x m +-=时，6x =，3m =，此时，()0F Q =，k ∴值不存在，综上，k 的最小值为32-．23．对于实数P ，我们规定：用的最小整数．2=，2=，现在对72进行如下操作： {}{}{}727299332===第一次第二次第三次，即对72只需进行3次操作后变为2．类比上述操作：对36只需进行 3 次操作后变为2；如果只需进行3次操作后变为2的所有正整数中最大的数为．【解答】解：由题意得：现在对36进行如下操作： {}{}{}363666332===第一次第二次第三次，∴对36只需进行3次操作后变为2；现在对256进行如下操作： {}{}{}2562561616442===第一次第二次第三次，如果只需进行3次操作后变为2的所有正整数中最大的数为：256；故答案为：3，256．24．如果一个三位数满足各数位上的数字都不为0，且百位数字比十位数字大1，则称这个数为“阶梯数”．若s ，t 都是“阶梯数”，将组成s 的各数位上的数字中最大数字作为十位数字，组成t 的各数位上的数字中最小数字作为个位数字，得到一个新两位数m 叫做s ，t 的“萌数”，将组成s 的各数位上的数字中最小数字作为十位数字，组成t 的各数位上的数字中最大数字作为个位数字，得到一个新两位数n 叫做s ，t 的“曲数”，记(,)2F s t m n =+．例如：因为211-=，615-=，所以211和654都是“阶梯数”；211和654的“萌数” 24m =，“曲数” 16n =，(211,654)2241664F =⨯+=．（1）判断435 是（填“是”或“否” )为“阶梯数”；（2）若(1)6s a a =-，(1)5t b b =+（其中25a <，69b <，且a ，b 都是整数），且(,)167F s t =，求满足条件的s 、t 的值；（3）若p 、q 都是“阶梯数”，其中100103p x y =++，20010q a b =++（其中23x ，18y ，28b 且a ，b ，x ，y 都是整数），当(F p ，132)(F q +，824)157=时，求(,)F p q 的值．【解答】解：（1）435中，百位4比十位3大1，符号阶梯数定义．故答案为：是．（2）s 和t 的萌数为65，曲数为(1)(1)a b -+，(F s ∴，)265(1)(1)167t a b =⨯+-+=，解得4a =，6b =．436s ∴=，765b =．（3）p 、q 都是阶梯数，1y x ∴=-，1a =，又23x ，28b ，10010(1)3213p x x ∴=+-+=或323，212q =、213、214、215、216、217、218． (F p ∴、132)31210(1)3x =⨯+-+，(F q ，824)(102)218b =+⨯+，由(F p 、132)(F q +，824)157=，得102080x b +=，其中x 为偶数，2x ∴=，3b =，即213p =，213q =．(F p 、)2311375q =⨯+=．25．一个多位自然数分解为末三位与末三位以前的数，让末三位数减去末三位以前的数，所得的差能被13整除，则原多位数一定能被13整除．（1）判断266357 能（选填“能”或“不能” )被13整除；（2）证明：任意一个多位自然数都满足上述规律；（3）将一个多位自然数分解为个位与个位之前的数，若让个位之前的数加上个位数的k 倍(k 为正整数），所得之和能被13整除，且原多位自然数也能被13整除，求当150k 时，所有满足条件的k 的值．【解答】（1）解：266357能被13整除；理由如下：266357的末三位数为357，末三位以前的数为266，35726691∴-=，91137÷=，266357∴能被13整除，故答案为：能；（2）证明：设这个多位数的末三位数为a ，末三位以前的数为b ，则这个多位数可表示为1000b a +，根据题意得：13(a b n n -=为整数），13a n b ∴=+，则1000100013100113b a b n b b n +=++=+，100113b n +可以被13整除，1000b a ∴+可以被13整除，∴任意一个三位以上的自然数都满足这个规律，即任意一个多位自然数都满足上述规律；（3）解：设个位之前及个位数分别为m 、n （出现的字母均为自然数），依题意不妨设13m kn t +=，则原多位数为10m n +，依题意不妨设1013m n s +=，联立可得：3110(101)101313n k s t k t kn +=--=-+，则31k +为13倍数，分别将1k =、2、3、4、550⋯代入可知，4k ∴=或17k =或30k =或43k =．26．一个三位自然数a ，满足各数位上的数字之和不超过10，并且个位数字与百位数字不同，我们称这个数为“完美数”．将a 的个位数字与百位数字交换得到一个新数a '，记G （a ）11a a '-=．例如，当125a =时，521a '=，125521(125)3611G -==-；当370a =时，73a '=，37073(370)2711G -==．（1）判断236 不是（选填“是”或“不是” )完美数，计算(321)G = ；（2）已知两个“完美数” m ，n ，满足10010m a b =++，100(09n c d b a =+<，09c ，09d ，a ，b ，c ，d 为整数），若()G m 能被7整除，且()()9(2)G m G n d +=+，求m n -的最小值．【解答】解：（1）2361110++=>，236∴不是完美数，根据题意，321123(321)1811G -==；故答案为：不是；18．（2）10010m a b =++，10010m b a '∴=++，100n c d =+，100n d c '∴=+，()()9(2)112m m n n G m G n d -'-'∴+=+=+， 22a b c d ∴-+=+，设()7G m x =，x 为整数， ∴9999711a b x -=，即9()7a b x -=， 09b a <，∴满足条件的a 只有7或8或9，当9a =时，m 不是完美数，故舍去，当8a =时，1b =，这个数是811，是完美数，此时，8122c d -+=+，即25c d =-，09c ，09d ，3d ∴=，1c =时，301n =，则510m n -=；4d =，3c =时，403n =，则811403408m n -=-=；5d =，5c =时，505n =，则811505306m n -=-=；6d =，7c =（舍去）， ∴共有三种情况，最小的为306；当7a =时，0b =，这个数是710，是完美数，此时，7022c d -+=+，即25c d =-，09c ，09d ，3d ∴=，1c =时，301n =，则710301409m n -=-=；4d =，3c =时，403n =，则710403302m n -=-=；5d =，5c =时，505n =，则710505205m n -=-=；6d =，7c =（舍去）， ∴共有三种情况，最小的为205；综上，m n -的最小值为205．27．阅读材料：我们知道，任意一个正整数k 都可以进行这样的分解：(k m n m =⨯，n 是正整数，且)m n ，在k 的所有这种分解中，如果m ，n 两因数之差的绝对值最小，我们就称m n⨯是k 的最佳分解，并规定：()m f k n=．例如：18可以分解成118⨯，29⨯或36⨯，因为1819263->->-，所以36⨯是18的最佳分解，所以31(18)62f ==．（1）计算：f （6）=23 ，f （4）= ，2()f x = ．（其中x 为正整数）（2）若21010(2)1011f x x +=，其中x 是正整数，求x 的值．（3）若2(9)1f x -=，其中x 是正整数，求x 的值．【解答】解：（1）6的最佳分解为23⨯，所以f （6）23=；4的最佳分解为22⨯，所以f （4）1=；2x 的最佳分解为x x ⋅，所以2()1f x =．故答案为：23；1；1．（2）22x x +的最佳分解为：(2)x x +， ∴2(2)2x f x x x +=+，又21010(2)1011f x x +=，所以101021011x x =+，解得2020x =，经检验，2020x =符合题意．（3）由2(9)1f x -=，可设229(x t t -=为正整数），即2(3)(3)x x t +-=，33x t x ∴-<<+，有以下几种情况：①当2t x =-时，229(2)x x -=-，解得134x =（舍去）； ②当1t x =-时，229(1)x x -=-，解得5x =；③当t x =时，229x x -=，无解；④当1t x =+时，229(1)x x -=+，解得5x =-；⑤当2t x =+时，229(2)x x -=+，解得134x =-；综上所述，5x =．28．阅读下列材料：材料一：对于一个百位数字不为0的四位自然数M ，以它的百位数字作为十位，十位数字作为个位，得到一个两位数m ，若m 等于M 的千位数字与个位数字的平方差，则称数M 为“平方差数”．例如：7136是“平方差数”，因为227613-=，所以7136是“平方差数”；又如：4251不是“平方差数”，因为22411525-=≠，所以4251不是“平方差数”．材料二：我们有时可以利用分解因数的方法解决求整数解的问题，例如：若p ，q 为两个正整数()18p q pq >=，则p ，q 为18的正因数，又因为18可以分解为181⨯或92⨯或63⨯，所以方程18pq =的正整数解为181p q =⎧⎨=⎩或92p q =⎧⎨=⎩或63p q =⎧⎨=⎩．根据上述材料解决问题：（1）判断9810，6361是否是“平方差数”？并说明理由；（2）若一个四位“平方差数” M ，将它的千位数字、个位数字及m 相加，其和为30，求所有满足条件的“平方差数” M ．【解答】解：（1）9810是“平方差数”，229081-=，9810∴是“平方差数”； 6361不是“平方差数”，22613536-=≠，6361∴不是“平方差数”．（2）设M 的千位数字为a ，个位数字为b ，则22m a b =-，由题意得2230a b a b ++-=，即()(1)30a b a b +-+=．a b +>，11a b -+>且均为30的正因数，∴将30分解为215⨯或310⨯或56⨯．①()(1)215a b a b +-+=⨯，解得87a b =⎧⎨=⎩，即8157M =； ②()(1)310a b a b +-+=⨯，解得64a b =⎧⎨=⎩，即6204M =； ③()(1)56a b a b +-+=⨯，解得50a b =⎧⎨=⎩，即5250M =；解得51a b =⎧⎨=⎩，即5241M =．8157∴=或6204或5250或5241．M29．【阅读】在数轴上，若点A表示数a，点B表示数b，则点A与点B之间的距离为AB a b=-．||例如：两点A，B表示的数分别为3，1AB=--=．-，那么|3(1)|4（1）若|3|2x-=，则x的值为1或5．（2）当x=(x是整数）时，式子|1||2|3-++=成立．x x（3）在数轴上，点A表示数a，点P表示数p．我们定义：当||1-=时，点P叫点A的1倍伴随点，p a当||2-=时，点P叫点A的2倍伴随点，p a⋯当||-=时，点P叫点A的n倍伴随点．p a n试探究下列问题：若点M是点A的1倍伴随点，点N是点B的2倍伴随点，是否存在这样的点A和点B，使得点M恰与点N重合，若存在，求出线段AB的长；若不存在，请说明理由．【解答】解：（1）|3|2x-=，表示到表示数x的点到表示数3的点的距离为2，当表示数x的点在表示数3的点的左侧时，321x=-=；当表示数x的点在表示数3的点的右侧时，325x=+=；故答案为：1或5；（2）|1||2|3-++=表示的是表示数x的点到表示数1的点的距离和表示数2x x-的点的距离之和，分下列三种情况：①当表示数x的点在2-到1之间时，如图1，此时|1||2|3-++=成立；x x满足条件的x的整数为2-，1-，0，1；②当表示数x的点在2-左侧时，如图2，此时|1||2|3-++>，不存在这样的点；x x③表示数x的点在1右侧时，如图3，此时|1||2|3-++>，不存在这样的点；x x故答案为：2-或1-或0或1；（3）存在，理由如下：设点M 所表示的数位m ，点A 所表示的数为a ，点B 所表示的数为b ，点M 和N 重合，∴点N 所表示的数为n ，点M 是点A 的1倍伴随点，点N 是点B 的2倍伴随点，||1m a ∴-=，||2m b -=，12m a b ∴=±=±，当12a b +=+时，1a b -=，此时1AB =；当12a b +=-时，3a b -=-，此时3AB =；当12a b -=+时，3a b -=，此时3AB =；当12a b -=-时，1a b -=-，此时1AB =；综上，存在，此时AB 的长为1或3．30．如果一个自然数M 能分解成A B ⨯，其中A 和B 都是两位数，且A 与B 的十位数字之和为10，个位数字之和为9，则称M 为“十全九美数”，把M 分解成A B ⨯的过程称为“全美分解”，例如：28384366=⨯，4610+=，369+=，2838∴是“十全九美数“；3912317=⨯，2110+≠，391∴不是“十全九美数”．（1）判断2100和168是否是“十全九美数”？并说明理由；（2）若自然数M 是“十全九美数“，“全美分解”为A B ⨯，将A 的十位数字与个位数字的差，与B 的十位数字与个位数字的和求和记为()S M ；将A 的十位数字与个位数字的和，与B 的十位数字与个位数字的差求差记为()T M ．当()()S M T M 能被5整除时，求出所有满足条件的自然数M ．【解答】解：（1）2100是“十全九美数”，168不是“十全九美数”，理由如下： 21002584=⨯，2810+=，549+=，2100∴是“十全九美数”；1681412=⨯，10l l +≠，168∴不是“十全九美数“；（2）设A 的十位数字为m ，个位数字为n ，则10A m n =+， M 是“十全九美数”， M A B =⨯， B ∴的十位数字为10m -，个位数字为9n -，则10(10)910910B m n m n =-+-=--，由题知：()109192S M m n m n n =-+-+-=-，()[10(9)]21T M m n m n m =+----=-，根据题意，令()1925(()21S M n k k T M m -==-为整数），由题意知：19m ，09n ，且都为整数，119219n ∴-，12117m -，当k l =时，192521n m -=-， ∴1925211n m -=⎧⎨-=⎩或19210212n m -=⎧⎨-=⎩或19215213n m -=⎧⎨-=⎩，解得17m n =⎧⎨=⎩或3292m n ⎧=⎪⎪⎨⎪=⎪⎩（舍去）或22m n =⎧⎨=⎩； 17921564M A B ∴=⨯=⨯=或22871914M A B =⨯=⨯=；当2k =时，1921021n m -=-， ∴19210211n m -=⎧⎨-=⎩，解得192m n =⎧⎪⎨=⎪⎩（舍去）；当3k =时，1921521n m -=-， ∴19215211n m -=⎧⎨-=⎩，解得12m n =⎧⎨=⎩； 12971164M A B ∴=⨯=⨯=，综上，满足“十全九美数”条件的M 有：1564或1914或1164．31．一个自然数能分解成A B ⨯，其中A ，B 均为两位数，A 的十位数字比B 的十位数字大1，且A ，B 的个位数字之和为10，则称这个自然数为“分解数”．例如：48197961=⨯，7比6大1，1910+=，4819∴是“分解数”；又如：14964434=⨯，4比3大1，4410+≠，1496∴不是“分解数”．（1）判断325，851是否是“分解数”，并说明理由；（2）自然数M A B =⨯为“分解数”，若A 的十位数字与B 的个位数字的和为()P M ，A 的个位数字与B 的十位数字的和()F M ，令()()()P M G M F M =，当()G M 为整数时，则称M 为“整分解数”．若B 的十位数字能被2整除，求所有满足条件的“整分解数” M ．【解答】解：（1）3252513=⨯，2比1大1，5310+≠，325∴不是“分解数”； 68513723=⨯，3比2大l ，7310+=，851∴是“分解数”．（2）令10B x y =+，10(1)10A x y =++-，(8l x <<，19y ，且x ，y 为整数）， ()1P M x y =++，()10F m x y =-+，1()10x y G M x y ++∴=-+，2x 为整数， 2x ∴=，4，6，8，当2x =时，315()11212y G M y y +==-+-+-+，为整数， 12y ∴-+的值为3或5，解得9y =或7，13129899M ∴=⨯=，23327891M =⨯=；当4x =或6x =时，不存在()G M 为整数，∴舍去；当8x =时，927()11818y G M y y +==-+-+-+为整数， 189y ∴-+=，解得9y =，391898099M ∴=⨯=．综上所述，M 的值为899，891，8099．32．对于任意一个四位数N ，如果N 满足各个位上的数字互不相同，且个位数字不为0，N的百位上的数字与十位上的数字之差是千位上的数字与个位上的数字之差的2倍，则称这个四位数N 为“双减数”．对于一个“双减数” N abcd =，将它的千位和百位构成的两位数为ab ，个位和十位构成的两位数为dc ，规定；()12ab dc F N -=．例如：7028N =．因为2(78)02⨯-=-，故7028是一个“双减数”，则7082(7028)112F -==-．（1）判断9527，6713是否是“双减数”，并说明理由，如果是，并求出()F N 的值；（2）若自然数A 为“双减数”， F （A ）是3的倍数，且A 各个数位上的数字之和能被13整除，求A 的值．【解答】解：（1）9527:523-=，972-=，不满足“双减数”的定义，故9527不是双减数；6713:716-=，633-=，满足623=⨯，且满足各个位上的数字互不相同，且个位数字不为0，故6713是双减数；6731(6713)312F -==． 9527∴不是双减数，6713是双减数，(6713)3F =．（2）设A abcd =，由题意可知，F （A ）是3的倍数，且A 各个数位上的数字之和能被13整除且百位数与十位数之差是千位数与个位数之差的两倍．()312ab dc F A k -∴==． 13a b c d n +++=②(n 为正整数，能被13整除说明是13的倍数）， 2()b c a d -=-③，由③式可得知，ab dc -的结果中，个位数是十位数的两倍，而且()312ab dc F A k -==①． ∴36ab dc k -=，（说明ab dc -是36的倍数），根据“双减数“各位数不重复与0d ≠的性质，ab 最大为98，dc 最小为10，ab dc ∴-最大为88， ∴36ab dc -=或36-或72（舍去）或72-（舍去），（根据“双减数“百位上的数字与十位上的数字之差是千位上的数字与个位上的数字之差的2倍排除），3a d ∴-=，6b c -=或3a d -=-，6b c -=-，即3a d =+④，6b c =+⑤或3a d =-⑥，6b c =-⑦，将④⑤代入②可得，(3)(6)13d c c d n ++-++=，将⑥⑦代入②可得，(3)(6)13d c c d n -+-++=，同理，根据“双减数“的性质可得a b c d +++的最大值为987630+++=，最小值为01236+++=，630a b c d ∴+++，a b c d ∴+++是13的倍数，a b c d ∴+++只能取13或26．Ⅰ、当13a b c d +++=时，可得2d c +=或11d c +=；当2d c +=时，d 与c 的值可能为20d c =⎧⎨=⎩，02d c =⎧⎨=⎩（舍去），11d c =⎧⎨=⎩（舍去），（根据双减数个位数不能为0，且每位数不相等排除），即20d c =⎧⎨=⎩；当11d c +=时，2a b +=，则20a b =⎧⎨=⎩，02a b =⎧⎨=⎩（舍去），11a b =⎧⎨=⎩（舍去），即20a b =⎧⎨=⎩，此时，6c =，5d =． Ⅱ、当26a b c d +++=时，可得2()17d c +=，2()35d c +=． 172d c +=（舍去）或352d c +=（由于d ，c 不为整数，与题意不符，故舍去）， 3235a d ∴=+=+=，66b c =+=5602A ∴=或2065．33．对于一个四位自然数(R abcd a =，b ，c ，d 不全相同且均不为0)，如果a d b c -=-，那么称这个数R 为“天平数”，对于一个“天平数” R ，将它的千位和个位构成的两位数减去百位和十位构成的两位数所得差记为s ，将它的千位和十位构成的两位数减去百位和个位构成的两位数所得差记为t ，规定：()10s t f R +=；例如：8734R =，因为8473-=-，故：8734是一个“天平数”．所以：847311s =-=，83749t =-=，则：119()210f R +==．（1）请判断7513是否是“天平数”，如果是，请求出()f R 的值；如果不是，请说明理由；（2）若自然数M ，N 都是“天平数”，其中1007051M x y =++，100010512(19N m n x =++，08y ，19m ，08n ，x ，y ，m ，n 都是整数），规定：()()f M k f N =，当()()4f N f M -=时，求k 的值．【解答】解：（1）是，且(7513)4f =，理由如下：7351-=-，7513∴是一个“天平数”． 735122s ∴=-=，715318t =-=，2218(7513)410f +∴==；（2）1007051700010050(1)M x y x y =++=++++，M ∴的前位数字是7，百位数字是x ，十位数字是5，个位数字是1y +， M 是“天平数”， 7(1)5y x ∴-+=-，即11x y +=，(701)(105)6610Ms y x x y ∴=++-+=-+，75(101)7410Mt x y x y =-++=--，66107410()1421010s t x y x y f M x +-++--∴===-， 100010512100050010(1)2N m n m n =++=++++，N ∴的前位数字是m ，百位数字是5，十位数字是(1)n +，个位数字是2， N 是“天平数”， 25(1)m n ∴-=+，即6m n +=，(102)(501)1049Ns m n m n ∴=+-++=--，(101)521051Nt m n m n =++-=+-，10491051()2101010s t m n m n f N m +--++-∴===-， 19x ，08y 且11x y +=，39x ∴，19m ，08n ，且6m n +=，16m ∴，()()(210)(142)22244f N f M m x x m -=---=+-=，14x m ∴+=，14x m ∴=-，56m ∴，此时，()142721()21055f M x m k f N m m m --====----，当5m =时，k 值不存在；当6m =时，1k =-，综上，k 的值为1-．34．如果一个自然数M 的个位数字不为0，且能分解成A B ⨯，其中A 与B 都是两位数，A 与B 的十位数字相同，个位数字之和为8，则称数M 为“团圆数”，并把数M 分解成M A B =⨯的过程，称为“欢乐分解”．例如：5722226=⨯，22和26的十位数字相同，个位数字之和为8，572∴是“团圆数”．又如：2341813=⨯，18和13的十位数字相同，但个位数字之和不等于8，234∴不是“团圆数”．（1）最小的“团圆数”是 187 ；（2）判断195，621是否是“团圆数”？并说明理由；（3）把一个“团圆数” M 进行“欢乐分解”，即M A B =⨯，A 与B 之和记为()P M ，A 与B 差的绝对值记为()Q M ，令()()()P M G M Q M =，当()G M 能被8整除时，求出所有满足条件的M 的值．【解答】解：（1）由题意可知，最小的“团圆数”十位数字是1，个位数字分别为1和7， ∴最小的“团圆数”是1117187⨯=，故答案为：187；（2）1951315=⨯，且358+=，195∴是“团圆数”， 6212327=⨯，378+≠，621∴不是“团圆数”；（3）设10A a b =+，则108B a b =+-，208A B a ∴+=+，|||28|A B b -=-，()()()||P M A B G M Q M A B +==-能被8整除， ∴2088|28|a kb +=-，k 为整数， 52(|4|)4a b k ∴+=-，52a ∴+是4的倍数，∴满足条件的a 有2，6，若2a =，则488|28|k b =-，k 为整数， ∴3|4|k b =-， |4|b ∴-是3的因数，43b ∴-=-，1-，1，3，∴满足条件的b 有1，3，5，7，21A ∴=，27B =或23A =，25B =或25A =，23B =或27A =，21B =，567A B ∴⨯=或575，若6a =，则1288|28|k b =-，k 为整数， ∴8|4|k b =-， |4|b ∴-是8的因数，48b ∴-=-，4-，2-，1-，1，2，4，8，∴满足条件的b 有2，3，5，6，62A ∴=，66B =或63A =，65B =或65A =，63B =或66A =，62B =，62664092A B ∴⨯=⨯=或4095，综上，M 的值为567或575或4092或4095．35．对于任意一个四位数m ，若m 满足各数位上的数字都不为0，且千位与百位上的数字不相等，十位与个位上的数字不相等，那么称这个数为“智慧数”．将一个“智慧数” m 的任意一个数位上的数字去掉后可以得到四个新三位数，把这四个新三位数的和与3的商记为()F m ．例如“智慧数” 1234m =，去掉千位上的数字得到234，去掉百位上的数字得到134，去掉十位上的数字得到124，去掉个位上的数字得到123．这四个新三位数的和为234134124123615+++=，6153205÷=，所以(1234)205F =．（1）计算：(2131)F = 262 ；(5876)F = ；（2）若“智想数” 780010(15n x y x =++，19y ，x ，y 都是正整数），()F n 也是“智慧数”，且()F n 能被12整除，求满足条件的n 的值．【解答】解：（1）(2131)(213211231131)3262F =+++÷=；(5876)(587586576876)3875F =+++÷=；故答案为：262；875；（2） “智慧树” 78001071000810010n x y x y =++=⨯+⨯++， ∴数n 的千位上的数为7，百位上的数为8，十位上的数为x ，个位上的数为y ， ()(7807807001080010)310207F n x y x y x y x y ∴=+++++++++÷=++， 15x ，19y ，()F n 也是“智慧数”，且()F n 能被12整除， ∴可设()1020712F n x y k =++=，即()F n 是3的倍数，也是4的倍数， ()743403402333F n x y x y k x ++∴==+=++，且()3F n 是4的倍数，当1x =时，y 可取2，5，8，此时()3433F n =（舍)或344或345（舍)，此时()1032F n =，符合定义，7815n =；当2x =时，y 可取1，4，7，此时()3453F n =（舍)或346（舍)或347（舍)，无符合题意的n ；当3x =时，()340733F n y =++，y 可取3，6，9，此时()3483F n =或349（舍)或350（舍)，此时()7833F n =，不符合题意；当4x =时，y 可取2，5，8，此时()3503F n =（舍)或351（舍)或352，此时()1056F n =，7848n =，当5x =时，y 可取1，4，7，此时()3523F n =或353（舍)或354（舍)，此时()1056F n =，7851n =，综上，符合题意的点n 值为7815或7848或7851．。

人教版八年级数学上册小专题(一)与三角形的角平分线有关的角度计算(选做)

初中数学课件
金戈铁骑整理制作
小专题(一) 与三角形的角平分线有关的角度计算
模型1 两个内角平分线的夹角方法归纳：三角形的两个内角平分线交于一点，所形成的夹角的度数等于90°加上第三角度数的一半．
如图，在△ABC 中，∠ABC 与∠ACB 的角平分线相交于点 O，则∠BOC＝90°＋12∠A.
5．(达州中考改编)如图，在△ABC中，∠A＝m°， ∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC 和∠A1CD的平分线交于点A2，得∠A2；…∠A2014BC和 ∠A2014CD的平分线交于点A2015，求∠A2015的度数．
∵A1B 平分∠ABC，A1C 平分∠ACD， ∴∠A1＝12∠A.同理，得∠A2＝12∠A1＝212∠A，… ∴∠A2 015＝221015∠A＝22m015°.
(3)若∠B和∠C的度数改为用字母α和β来表示，你能找到∠EAD与α和β之间的关系吗？请直接写出你发现的结论．
当 α＜β 时，∠EAD＝12(β－α)，当 a＞β 时，∠EAD＝12(α－β)．
∠BOC＝90°＋12∠A＝125°
(3)若∠A＝n°，求∠BOC的度数． ∠BOC＝90°＋12n°
模型2 一个内角平分线与一个外角平分线的夹角
方法归纳：三角形的一个内角平分线与一个外角平分线交于一点，所形成的夹角的度数等于第三角度数的一半．
如图，在△ABC 中，BD、CD 分别平分∠ABC、∠ACE，则∠BDC＝12∠A.
1.如图，点O是△ABC的∠ABC与∠ACB两个角的平分线的交点，若∠BOC＝118°，则∠A的角度是___5_6____°
2．如图所示，在△ABC中，BO、CO是角平分线．
(1)∠ABC＝50°，∠ACB＝60°，求∠BOC的度数，并说明理由；

初中数学专题练习：一元一次方程(一)

初中数学专题练习：一元一次方程（一）一、单选题1．如果四个不同的正整数 m ， n ， p ， q 满足 (4−m)(4−n)(4−p)(4−q)=9 ，则 m +n +p +q 等于（）A ．12B ．14C ．16D ．182．下列解方程去分母正确的是（）A ．由 x 3−1=1−x 2 ，得2x-1=3（1-x ） B ．由x−22−3x−24=−1 ，得2（x-2）-3x-2=-4 C ．由 y+12=y 3−3y−16，得3（y+1）=2y-（3y-1） D ．由 4x 5−1=x+43 ，得12x-5=5x+203．若方程2x -3=5-6x 与方程2mx ＝ 3−5x−14 的解相同，则 m 的值为( ) A ．1 B ．-1 C ．2 D ．-24．在甲处工作的有232人，在乙处工作的有146人，如果从乙处调x 人到甲处，那么甲处工作的人数是乙处工作人数的3倍，则下列方程中，正确的是（）A ．3（323+x ）=146﹣xB ．232﹣x=3（146﹣x ）C ．232+x=3×146﹣xD ．232+x=3（146﹣x ） 5．方程﹣13+x=2x 的解是（）A ．-13B ．13C ．1D ．-16．用一个正方形在四月份的日历上，圈出4个数，这四个数的和不可能是（）A ．104B ．108C ．24D ．287．√2x −13+√5x +83 ＝0，则x 的值是（）A ．﹣3B ．﹣1C ．12D ．无选项8．某车间有28名工人生产螺钉和螺母，每人每小时平均能生产螺钉12个或螺母18个，1个螺钉需要配2个螺母，若安排 m 名工人生产螺钉时每小时生产的螺栓和螺母刚好配套，那么可列方程为（）A ．12×m =18×(28−m)×2B ．12×(28−m)=18×m ×2C ．12×m ×2=18×(28−m)D ．12×(28−m)×2=18×m二、填空题9．已知方程﹣（2﹣m）x|m|﹣1+4m=8是关于x的一元一次方程，那么x= ．10．某校组织学生和教师为边远山区学校捐赠图书，原计划共捐赠5000册，实际捐赠时学生比原计划多赠了15%，教师比原计划多赠了20%，实际共捐赠5825册，则原计划学生捐赠图书册．11．纸箱里有红黄绿三色球，红球与黄球的比为1∶2，黄球与绿球的比为3∶4，纸箱内共有68个球，则黄球有个.x+2021的解是x=3，则关于y的一元12．已知关于x的一元一次方程2019x−a=12020(y−1)+2021的解是y= ．一次方程2019(y−1)−a=1202013．一件夹克按成本价提高 50%后标价，后因季节关系按标价的 8 折出售，每件获利 10 元．这批夹克每件的成本价是元14．x=3和x=﹣6中，是方程x﹣3（x+2）=6的解．15．已知关于x的方程3x﹣2a=7的解是5，则a的值为．16．．一轮船航行于两个码头之间，逆水需10小时，顺水需6小时。

初中数学中考专题复习

初中数学中考专题复习第一部分代数一、数与式㈠数（有理数、无理数、实数）1、有理数的分类⑴按“正与不正”分 ⑵按“整与不整”分2、无理数的概念无理数：无限不循环小数。

3、实数的分类⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数4、实数的几个重要概念⑴数轴三要素：原点、单位长度、正方向意义：①数轴上的点表示实数，并且实数与数轴上的点是一一对应的关系。

②数轴上的数右边的总比左边的大。

⑵绝对值定义：||a 的几何意义是实数a 在数轴上的对应点与原点之间的距离。

绝对值的意义：||a 是一个非负数，即0||≥a 。

⎪⎩⎪⎨⎧<-=>=)0()0(0)0(||a a a a a a⑶相反数定义：只有符号不同，而绝对值相同的两个数称为相反数，零的相反数是零.。

意义：①若b a 、互为相反数，则0=+b a 。

②互为相反数的两个数商为-1.⑷倒数定义：把一个数的分子分母颠调位置后所得的数是这个数的倒数，零没有倒数。

零负整数有理数正有理数正有理数正分数正整数负分数零零负整数正整数有理数分数整数负分数正分数自然数意义：互为倒数的两个数积为1.5、实数的应用⑴近似数：常见的近似数一般是按某种要求采用四舍五入法所得的数。

⑵有效数字：有效数字是指从左边第一个不是零的数字起到精确到的数位止的所有数字。

⑶科学计数法：把一个较大或较小的数写成),101(10为正整数n a a N n <≤⨯=。

6、常见的非负数02≥a 0≥a 0≥a意义：02=++c b a ，则0===c b a7、实数大小的比较⑴利用数轴比较：数轴上的数右边的总比左边的大。

⑵用绝对值比较：两个正数绝对值大的较大，两个负数绝对值大的反而小。

⑶差值比较：两个实数b a ,有如下三种关系：①b a b a >⇔>-0 ②b a b a <⇔<-0 ③b a b a =⇔=-0 ⑷商值比较法：设b a ,是任意两正实数，则①b a b a >⇔>1 ②b a b a <⇔<1 ③b a b a=⇔=1。

2020年人教版初中数学八年级练习题(专题训练一)

2020年人教版初中数学八年级练习题（专题训练一）
专题一：矩形的性质与判定
1.如图，矩形 ABCD 的两条对角线交于点O，且∠AOD=120°，你能说明 AC=2AB 吗?
2、如图，在矩形 ABCD 中，AE⊥BD，垂足为 E，∠DAE=2∠BAE，求∠BAE与∠DAE 的度数。

A D
E
B C
3、如图，在矩形 ABCD 中，点E 在AD 上，EC 平分∠BED。

（1）△BEC是否为等腰三角形？为什么？（2）若AB=1，∠ABE=45°，求 DE 的长
A E D
B C
4、如图，在矩形 ABCD 中，CE⊥BD于E，∠DCE：∠BCE=3：1，且M 为OC 的中点，试说明：ME⊥AC
D C
A B
5、如图所示，□ABCD 的四个内角的平分线分别相交于 E，F，G，H 两点，试说明四边形EFGH 是矩形．
6、如图所示，△ABC 中，AB=AC，AD 是BC 边上的高，AE 是∠CAF 的平分线且∠CAF 是△ABC 的一个外角，且DE∥BA，四边形 ADCE 是矩形吗？为什么？
7、已知如图所示，折叠矩形纸片 ABCD，先折出折痕（对角线）BD，再过点 D 折叠，使AD 落在折痕BD 上，得另一折痕 DG，若 AB=2，BC=1，求 AG 的长度．
8、如图，在等边△ABC 中，点D 是BC 边的中点，以AD 为边作等边△ADE．
（1）求∠CAE 的度数；
（2）取AB 边的中点F，连结CF、CE，试证明四边形AFCE 是矩形．
9、如图，M、N 分别是平行四边形ABCD 对边ADBC 的中点，且AD=2AB，求证，四边形PMQN 是矩形。

D
B N C。

专题一实数(助考课件)——2023届中考数学一轮复习学考全掌握

2.( a )2 a(a 0)
3.
a2
a
a(a a(a
0) 0)
5. a a (a 0,b 0) bb
知识梳理
三、二次根式的运算法则
类别
法则
乘法
a b ab(a 0,b 0)
除法加减法
a a (a 0,b 0) bb
①化简成最简二次根式 ②合并同类二次根式举例3 Nhomakorabea5 15
24 2 2 3
( C)
A. x 1
B. x 1
C. x 1且 x 0
D. x 1且x 0
【解析】 x 1 0， x 0，x 1且 x 0，故选 C.
典型例题 12.（2022.山东济宁）已知a 2 5 ，b 2 5 ，求代数式a2b ab2的值.
【解析】
a2b ab2 ab(a b)
A. 4 9 2 3
B. 4 9 2 3
C. 94 32
典型例题 D. 49 0.7
【解析】
4 9 13； 49 22 32 23；
94 92 2 92； 4.9 49 7 10 . 10 10
典型例题
11.（2022.黑龙江绥化）若式子 x 1 x2在实数范围内有意义，则 x 的取值范围是
A.103.57 103.6(精确到个位)
B.2.708 2.71(精确到十分位)
C.0.054 0.1(精确到 0.1)
D.0.0136 0.013(精确到 0.001)
【解析】
A.103.57 104；B.2.708 2.7；D.0.0136 0.014，只有选项 C 正确.故选 C.
b
知识梳理
三、实数的乘方
求n个相同因数的积的运算，叫做乘方，乘方的结果叫做幂a a a an

专题01 实数(第一篇)-2019年中考数学母题题源系列(原卷版)

【母题来源一】【2019•河北】规定：（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作A．+3 B．-3 C．-13D．+13【答案】B【解析】“正”和“负”相对，所以，如果（→2）表示向右移动2记作+2，则（←3）表示向左移动3记作-3．故选B．【名师点睛】此题考查了正数和负数，解题关键是理解“正”和“负”的相对性，确定一对具有相反意义的量．【母题来源二】【2019•吉林】如图，数轴上蝴蝶所在点表示的数可能为A．3 B．2 C．1 D．-1【答案】D【解析】数轴上蝴蝶所在点表示的数可能为-1，故选D．【名师点睛】本题考查了数轴、根据数轴-1是解题关键．【母题来源三】【2019•安顺】2019的相反数是A．-2019 B．2019 C．-D．【答案】A【解析】2019的相反数是-2019，故选A．【名师点睛】主要考查相反数的概念及性质．相反数的定义：只有符号不同的两个数互为相反数，0的相反数是0．【母题来源四】【2019•河南】-12的绝对值是专题01 实数A．-12B．12C．2 D．-2【答案】B【解析】|-12|=12，故选B．【名师点睛】本题考查的是绝对值的性质，掌握一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0是解题的关键．【母题来源五】【2019•桂林】23的倒数是A．32B．-32C．-23D．23【答案】A【解析】23的倒数是：32．故选A．【名师点睛】此题主要考查了倒数，正确把握定义是解题关键．【母题来源六】【2019•安徽】在-2，-1，0，1这四个数中，最小的数是A．-2 B．-1 C．0 D．1【答案】A【解析】根据有理数比较大小的方法，可得-2<-1<0<1，∴在-2，-1，0，1这四个数中，最小的数是-2．故选A．【名师点睛】此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．【命题意图】这类试题主要考查有理数的有关知识，包括正数和负数、数轴、相反数、绝对值、倒数、有理数的比较大小等．【方法总结】1．正数和负数的表示方法一般地，我们把上升、运进、零上、收入、前进、高出等规定为正的，而与它相反的量，如：下降、运出、零下、支出、后退、低于等规定为负的．正的量就用小学里学过的数表示，有时也在它前面放上一个“+”（读作正）号，如5、7、50、+14200等；负的量用小学学过的数前面放上“–”（读作负）号来表示，如–3、–8、–47、–4745等．2．相反数（1）注意：①相反数是成对出现的；②相反数只有符号不同，若一个为正，则另一个为负；③0的相反数是它本身；相反数为本身的数是0．（2）多重符号的化简方法：①在一个数前面添加一个“+”，所得的数与原数相等；②在一个数前面添加一个“–”，所得的数是原数的相反数；③对于有三个或三个以上符号的数的化简，首先要注意，一个数前面不管有多少个“+”，都可以把“+”去掉，其次要看“–”的个数，当“–”的个数为偶数时，结果取“+”，当“–”的个数为奇数时，结果取“–”． 3．绝对值即：(0)(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩或 (0)(0)aa a a a ≥⎧=⎨-<⎩．【母题来源七】【2019•天津】计算（-3）×9的结果等于 A ．-27B ．-6C ．27D ．6【答案】A【解析】（-3）×9=-27，故选A ．【名师点睛】本题考查有理数的乘法；熟练掌握正数与负数的乘法法则是解题的关键．【母题来源八】【2019•贵港】计算（-1）3的结果是A ．-1B ．1C ．-3D ．3【答案】A【解析】（-1）3表示3个（-1）的乘积，所以（-1）3=-1．故选A ．【名师点睛】乘方是乘法的特例，乘方的运算可以利用乘法的运算来进行．负数的奇数次幂是负数，负数的偶数次幂是正数；-1的奇数次幂是-1，-1的偶数次幂是1．【母题来源九】【2019•北京】4月24日是中国航天日，1970年的这一天，我国自行设计、制造的第一颗人造地球卫星“东方红一号”成功发射，标志着中国从此进入了太空时代，它的运行轨道，距地球最近点439000米，将439000用科学记数法表示应为 A ．0.439×106B ．4.39×106C ．4.39×105D ．439×103【答案】C【解析】将439000用科学记数法表示为4.39×105．故选C．【名师点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．【母题来源十】【2019•安徽】2019年“五一”假日期间，我省银联网络交易总金额接近161亿元，其中161亿用科学记数法表示为A．1.61×109B．1.61×1010C．1.61×1011D．1.61×1012【答案】B【解析】根据题意161亿用科学记数法表示为1.61×1010．故选B．【名师点睛】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数，表示时关键要正确确定a的值以及n的值．【母题来源十一】【2019•河南】成人每天维生素D的摄入量约为0.0000046克．数据“0.0000046”用科学记数法表示为A．46×10-7B．4.6×10-7C．4.6×10-6D．0.46×10-5【答案】C【解析】0.0000046=4.6×10-6．故选C．【名师点睛】本题用科学记数法的知识点，关键是很小的数用科学记数法表示时负指数与0的个数的关系要掌握好．【母题来源十二】【2019•聊城】计算：115()324--÷=__________．【答案】2 3 -【解析】原式=542()653-⨯=-，故答案为：23-．【名师点睛】本题主要考查有理数的混合运算，解题的关键是掌握有理数混合运算顺序．【命题意图】这类试题主要考查有理数的运算，包括有理数的加减法、乘除法、乘方、混合运算、科学记数法等．【方法总结】1．有理数的加法有理数加法法则：①同号两数相加，取相同符号，并把绝对值相加；②绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值；③互为相反数的两个数相加得0．2．有理数的减法对于有理数的减法运算，应先转化为加法，再根据有理数加法法则计算，即加法与减法是互逆运算．3．有理数的乘法两个数相乘，同号得正，异号得负，并把绝对值相乘；任何数与0相乘，都得0．4．有理数的除法（1）有理数除法法则：除以一个不等于0的数，等于乘这个数的倒数．即a b÷=1ab⨯（b≠0）；（2）在进行除法运算时，若能整除，则根据“两数相除，同号得正，异号得负，并把绝对值相除”进行计算；若不能整除，则根据“除以一个不等于0的数，等于乘以这个数的倒数”进行计算；5．有理数的混合运算有理数的乘除混合运算往往先将除法化为乘法，然后确定积的符号，最后求出结果．6．有理数的乘方（1）负数的奇次幂是负数，负数的偶次幂是正数；（2）正数的任何次幂都是正数，0的任何正整数次幂都是0．7．科学记数法科学记数法的表示形式为a×10n的形式，其中1≤|a|<10，n为整数．当原数绝对值大于10时，写成a×10n 的形式，其中1≤|a|<10，n等于原数的整数位数减1；当原数绝对值小于1时，写成a×10−n的形式，其中1≤|a|<10，n等于原数左边第一个非零的数字前的所有零的个数（包括小数点前面的零）.【母题来源十三】【2019•攀枝花】用四舍五入法将130542精确到千位，正确的是A．131000 B．0.131×106C．1.31×105D．13.1×104【答案】C【解析】130542精确到千位是1.31×105．故选C．【名师点睛】本题考查了近似数和有效数字：从一个数的左边第一个不是0的数字起到末位数字止，所有的数字都是这个数的有效数字．近似数与精确数的接近程度，可以用精确度表示．一般有，精确到哪一位，保留几个有效数字等说法．【母题来源十四】【2019•广东】的结果是A．-4 B．4 C．±4 D．2【答案】B2416．故选B．【名师点睛】此题主要考查了算术平方根的性质和应用，要熟练掌握，解答此题的关键是要明确：①被开方数a是非负数；②算术平方根a本身是非负数．求一个非负数的算术平方根与求一个数的平方互为逆运算，在求一个非负数的算术平方根时，可以借助乘方运算来寻找．【母题来源十五】【2019•烟台】-8的立方根是A．2 B．-2 C．±2 D．-22【答案】B【解析】∵-2的立方等于-8，∴-8的立方根等于-2．故选B．【名师点睛】本题主要考查了立方根的定义，求一个数的立方根，应先找出所要求的这个数是哪一个数的立方．由开立方和立方是互逆运算，用立方的方法求这个数的立方根．注意一个数的立方根与原数的性质符号相同．【母题来源十六】【2019•邵阳】下列各数中，属于无理数的是A．13B．1.414 C2D4【答案】C4=22是无理数，故选C．【名师点睛】本题考查无理数；能够化简二次根式，理解无理数的定义是解题的关键．【母题来源十七】【2019•聊城】2的相反数是A．-22B．22C．2D2【答案】D【解析】，故选D．【名师点睛】本题考查了实数的性质，解决本题的关键是熟记实数的性质．【母题来源十八】【2019•广东】实数a、b在数轴上的对应点的位置如图所示，下列式子成立的是A．a>b B．|a|<|b| C．a+b>0 D．ab<0【答案】D【解析】由图可得：-2<a<-1，0<b<1，∴a<b，故A错误；|a|>|b|，故B错误；a+b<0，故C错误；ab<0，故D正确，故选D．【名师点睛】本题主要考查了实数与数轴，解题的关键是利用数轴确定a，b的取值范围．利用数轴可以比较任意两个实数的大小，即在数轴上表示的两个实数，右边的总比左边的大，在原点左侧，绝对值大的反而小．【母题来源十九】【2019•扬州】下列各数中，小于-2的数是A．5B．3C．2D．-1【答案】A【解析】比-2小的数是应该是负数，且绝对值大于2的数，分析选项可得，5-2<3<2-1，只有A符合．故选A．【名师点睛】本题考查的是有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．【母题来源二十】【2019•天津】33的值在A．2和3之间B．3和4之间C．4和5之间D．5和6之间【答案】D【解析】∵25<33<3625333633．故选D．【名师点睛】本题考查了无理数的估算，解题关键是确定无理数的整数部分即可解决问题．【母题来源二十一】【2019•无锡】49的平方根为__________．【答案】2 3±【解析】49的平方根为23=±．故答案为：23±．【名师点睛】本题考查了平方根的知识，注意一个正数有两个平方根，它们互为相反数．【母题来源二十二】【2019•河南】12-=__________．【答案】32142-=2-12=32．故答案为：32．【名师点睛】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握负整数指数幂、二次根式等考点的运算．【母题来源二十三】【2019•北京】计算：|3-（4-π）0+2sin60°+（14）-1．【解析】原式31+2×323-3+4=3+23 【名师点睛】此题主要考查了实数运算，正确化简各数是解题关键．【命题意图】这类试题主要考查实数的有关知识，包括平方根、立方根、无理数、实数的比较大小、无理数的估算、实数的运算等．【方法总结】 1．精确度与近似数近似数与准确数的接近程度通常用精确度来表示，近似数一般由四舍五入取得，四舍五入到哪一位，就说这个近似数精确到哪一位． 2．平方根22()(0)(0)()000a a a a a a a a a ⎧⎪⎪⎪=≥⎨≥⎧==⎨-<⎩只有非负数才有平方根，的平方根和算术平方根都义是意 3．立方根3意义a a==⎪⎩4．实数大小的比较实数大小的比较可以利用数轴上的点，右边的数总比左边的数大；以及绝对值比较法等比较实数大小的方法．除此之外，常用的方法有“差值比较法”适用于比较任何两数的大小；“商值比较法”只适用于比较两个正数的大小；“平方法”、“倒数法”常用于比较二次根式的大小；“底数比较法”、“指数比较法”常用于比较幂的大小． 5．实数的运算法则（1）实数的混合运算中，在同一个式子里，先乘方、开方，然后乘、除，最后加、减．有括号时，先算括号里面．（2）熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等的运算.注意运算顺序，分清先算什么，再算什么．1．【河北省张家口市桥西区2019届九年级中考6月模拟】中国人最早使用负数，下列各数中是负数的是 A ．|1|--B ．(1)--C ．0()-πD ．2(1)-2．【2019年浙江省宁波市北仑区中考数学模拟】2的相反数是 A ．12B ．-12 C ．±12D ．-23．【河南省新乡市2019届九年级第二次全真模拟】-2的绝对值是 A ．-2B ．12-C ．12D ．24．【福建省福州市2019年初中毕业班适应性数学试卷】已知A 、B 、C 三点在数轴上从左向右排列，且AC =3AB =6，若B 为原点，则点C 所表示的数是 A ．－6B ．2C ．4D ．65．【2019年湖北省孝感市孝南区中考数学二模】给出-2，-1，0，13这四个数，其中最小的是 A ．13B ．0C ．-2D ．-1【名师点睛】本题考查了有理数大小的比较法则，其关键是负数的绝对值越大，其本身越小． 6．【2019年福建省南平市六校联考中考数学模拟】计算-6+4的结果为 A ．10B ．-10C ．2D ．-27．【广东省东莞市2019届九年级中考数学二模】13-的倒数 A ．13B ．3C ．-3D ．30.⋅-8．【2019年河南省第二届名校联盟中考数学5月份模拟】2018年8月31日，中国最新一代芯片--麒麟980来了，它的诞生打破了欧美对芯片行业的垄断，该芯片堪称世界最强“心”，在比指甲盖稍大一点的芯片里安装了69亿颗晶体管，数据”69亿“用科学记数法表示为 A ．6.9×109B ．6.9×108C ．69×108D ．6.9×10109．【2019年广西贵港市中考数学三模】6.8×105这个数的原数是 A ．68000B ．680000C ．0.000086D ．-68000010．【河北省石家庄市新华区2019届九年级毕业生教学质量检测】近似数1.23×103精确到A ．百分位B ．十分位C ．个位D ．十位11．【浙江省杭州市下城区2019届九年级二模】16的平方根为A ．±4B ．±2C ．+4D ．212．【2019年广东省广州市南沙区中考数学一模】8的立方根等于A ．-2B ．2C ．-4D ．413．【2019年重庆市江北新区联盟中考数学一模】下列四个数中是无理数的是A ．3B ．3πC ．3.14159D 914．【2019年河南省第二届名校联盟中考数学5月份模拟】下面四个实数中最大的是A 5B ．0C ．-2D ．115．【天津市河西区201957的值在A ．5和6之间B ．6和7之间C ．7和8之间D ．8和9之间16．【湖北省武汉市部分学校20199__________． 17．【福建省厦门市双十中学2019届九年级3月月考】计算：|-3|+11()2=__________． 18．【2019年广东省深圳市罗湖区中考数学二模】计算：（12）-2-4cos30°+（-2）012．。

数学九年级上册专题一二次根式的化简与运算课件华东师大版

＋
b a
＞0，∴
a b
＋
b a
＝
9 2
＝3 2 2
15．已知等式|a－2 019|＋ a－2 020 ＝a 成立，求 a－2 0192 的值．
解：∵a－2 020≥0，∴a≥2 020，∴|a－2 019|＝a－2 019， ∴a－2 019＋ a－2 020 ＝a，∴ a－2 020 ＝2 019， ∴a－2 020＝2 0192，∴a－2 0192＝2 020
第21章二次根式
21．3 二次根式的加减法
专题一二次根式的化简与运算
1．下列计算正确的是( D )
A．2 3 ×3 3 ＝6 3 B． 2 ＋ 3 ＝ 5
C．5 5 －2 2 ＝3 3
D．
2÷
3
＝
6 3
2．对任意实数 a，下列等式一定成立的是( D )
A． a2 ＝a B． a2 ＝－a
C． a2 ＝±a D． a2 ＝|a|
C．a≥－3 D．a≥3
6．当 x＝2＋ 3 时，x2－4x＋2 021＝_2_0_2_0．
7．计算：
(1)( 18 －4
1 2
＋
1 3＋
2
)÷
3 3
；
解：原式＝3
1 (2)2 (
3 －1)2＋
1 2－1
＋
3
－(
2 2
)－1；
解：原式＝3
(3) 18 －
9 2
－
3＋ 3
6 ＋(
3－
2 )0＋
（1－
解：(1) 14（15－16）＝15
5 24
，验证略
(2) n1（n＋1 1－n＋1 2）＝n＋1 1

初中数学专题：根与系数的关系【十大题型】(举一反三)

专题1.4 根与系数的关系【十大题型】【苏科版】【题型1 由根与系数的关系直接求代数式的值】 (1)【题型2 由根与系数的关系和方程的解通过代换求代数式的值】 (1)【题型3 由根与系数的关系和方程的解通过降次求代数式的值】 (2)【题型4 由方程两根满足关系求字母的值】 (2)【题型5 不解方程由根与系数的关系判断根的正负】 (3)【题型6 由方程两根的不等关系确定字母系数的取值范围】 (3)【题型7 构造一元二次方程求代数式的值】 (4)【题型8 已知方程根的情况判断另一个方程】 (4)【题型9 根与系数关系中的新定义问题】 (5)【题型10 根与系数的关系和根的判别式的综合应用】 (5)【知识点一元二次方程的根与系数的关系】若一元二次方程（a、b、c为常数，）的两根为，，则，．注意它的使用条件为，，.【题型1 由根与系数的关系直接求代数式的值】【例1】（2023春·广东广州·九年级统考期末）若，是一元二次方程的两个根，则的值是（）A．B．C．1 D．7【变式1-1】（2023·湖北武汉·统考模拟预测）已知m，n是一元二次方程的两根，则的值是（）A．B．C．D．【变式1-2】（2023·上海·九年级假期作业）已知a，b是方程的两个根，则的值．【变式1-3】（2023春·九年级单元测试）已知、是方程的两根，且，则的值为．【题型2 由根与系数的关系和方程的解通过代换求代数式的值】【例2】（2023春·浙江·九年级专题练习）设α、β是方程的两个实数根，则的值为（）A．－2014 B．2014 C．2013 D．－2013【变式2-1】（2023春·湖北恩施·九年级统考期中）已知，是关于x的一元二次方程的两个实数根，则的值为()A．B．C．D．【变式2-2】（2023·江西萍乡·校考模拟预测）若、是一元二次方程的两个根，则的值是．【变式2-3】（2023春·安徽池州·九年级统考期末）已知和是方程的两个根，则的值为（）A．B．2021 C．D．2023【题型3 由根与系数的关系和方程的解通过降次求代数式的值】【例3】（2023春·广东广州·九年级广州市第二中学校考阶段练习）若p、q是方程的两个不相等的实数根，则代数式的值为．【变式3-1】（2023春·山东日照·九年级统考期末）已知，是方程的两个根，则代数的值为．【变式3-2】（2023春·浙江温州·九年级校考阶段练习）已知、是方程的两根，则的值是（）A．7 B．8 C．9 D．10（2023春·九年级课时练习）已知，是方程的两根，则代数式【变式3-3】的值是（）A．B．C．D．【题型4 由方程两根满足关系求字母的值】【例4】（2023·四川乐山·统考中考真题）若关于x的一元二次方程两根为、，且，则m的值为（）A．4 B．8 C．12 D．16【变式4-1】（2023·上海·九年级校考期中）已知关于x的方程的两根为满足：，求实数k的值【变式4-2】（2023春·广东佛山·九年级校考阶段练习）方程的两个实数根互为相反数，则的值是．【变式4-3】（2023春·安徽马鞍山·九年级安徽省马鞍山市第七中学校考期末）若、是关于的方程的两个不相等的实数根，且，则的值为．【题型5 不解方程由根与系数的关系判断根的正负】【例5】（2023春·江苏南京·九年级专题练习）关于的方程（为常数）根的情况，下列结论中正确的是（）A．有两个相异正根B．有两个相异负根C．有一个正根和一个负根D．无实数根【变式5-1】（2023春·安徽合肥·九年级统考期末）方程根的符号是（）A．两根一正一负 B．两根都是负数C．两根都是正数D．无法确定【变式5-2】（2023春·江苏南通·九年级南通田家炳中学校考阶段练习）已知a、b、c是的三条边的长，那么方程的根的情况是（）A．没有实数根B．有两个不相等的实数根C．有两个相等的负实根D．只有一个实数根【变式5-3】（2023·九年级统考课时练习）已知，，，则方程的根的情况是（）.A．有两个负根B．两根异号且正根绝对值较大C．有两个正根D．两根异号且负根绝对值较大【题型6 由方程两根的不等关系确定字母系数的取值范围】【例6】（2023·四川成都·三模）若方程x2+（m﹣4）x+﹣m＝0有两个不相等的实数根x1和x2，且x1+x2＞﹣3，x1x2＜，则m的取值范围为多少？【变式6-1】（2023·山东日照·日照港中学统考二模）已知关于x的一元二次方程的实数根，满足，则m的取值范围是．【变式6-2】（2023春·江苏南通·九年级南通田家炳中学校考阶段练习）已知关于x的方程有两个不相等的实数根，，且，，则k的取值范围是（）A．B．C．D．且【变式6-3】（2023春·九年级单元测试）设关于的方程有两个不相等的实数根，，且，那么实数的取值范围是．【题型7 构造一元二次方程求代数式的值】【例7】（2023·陕西西安·校考二模）已知mn≠1，且5m2+2010m+9=0，9n2+2010n+5=0，则的值为（）A．﹣402 B．C．D．【变式7-1】（2023春·广东梅州·九年级校考阶段练习）已知，则的最小值是（）．A．6 B．3 C．-3 D．0【变式7-2】（2023·山东德州·统考一模）已知互不相等的三个实数a、b、c满足，，求的值．【变式7-3】（2023春·江苏·九年级专题练习）设，，，为互不相等的实数，且，，则的值为（）A．-1 B．1 C．0 D．0.5【题型8 已知方程根的情况判断另一个方程】【例8】（2023春·浙江·九年级期中）若关于x的一元二次方程的一个根为m，则方程（）（）的两根分别是（）．A．，B．，C．，D．，【变式8-1】（2023春·江西萍乡·九年级统考期中）有两个一元二次方程：：；：，其中，以下四个结论中，错误的是（）A．如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根B．如果方程M有两根符号相同，那么方程N的两根符号也相同C．如果5是方程M的一个根，那么是方程N的一个根D．如果方程M和方程N有一个相同的根，那么这个根必是【变式8-2】（2023春·安徽合肥·九年级校考期末）关于x的一元二次方程有两个同号非零整数根，关于y的一元二次方程也有两个同号非零整数根，则下列说法正确的是（）A．p是正数，q是负数B．＜C．q是正数，p是负数D．【变式8-3】（2023春·九年级单元测试）一元二次方程；，其中，，给出以下四个结论：①若方程M有两个不相等的实数根，则方程N也有两个不相等的实数根；②若方程M的两根符号相同，则方程N的两根符号也相同；③若m是方程M的一个根，则是方程N的一个根；④若方程M和方程N有一个相同的根，则这个根必是，其中正确的结论是（）A．①③B．①②③C．①②④D．①③④【题型9 根与系数关系中的新定义问题】【例9】（2023春·山东日照·九年级日照市田家炳实验中学校考阶段练习）定义：如果实数a、b、c满足a²+b²=c²，那么我们称一元二次方程ax²+bx+c=0(a≠0)为“勾股”方程；二次函数y=ax²+bx+c(a≠0)为“勾股”函数．(1)理解：下列方程是“勾股”方程的有．①x²-1=0；②-；③；④4x²+3x=5(2)探究：若m、n是“勾股”方程ax²+bx+c=0 的两个实数根，试探究m、n之间的数量关系．【变式9-1】（2023春·河南安阳·九年级校联考期中）定义运算：．若a，b是方程的两根，则的值为（）A．0 B．1 C．2 D．与m有关【变式9-2】（2023春·广东揭阳·九年级校联考阶段练习）定义：如果一元二次方程满足，那么我们称这个方程为“凤凰”方程．已知是“凤凰”方程，且有两个相等的实数根，求的值．【变式9-3】（2023春·辽宁鞍山·九年级校考阶段练习）已知：、是一元二次方程的两个实数根，设，，．根据根的定义，有、，将两式相加，得，于是根据以上信息，解答下列问题．(1)求、的值，并利用一元二次方程根与系数关系，求出的值．(2)猜想：当时，、、之间满足的数量关系，并证明你的猜想．【题型10 根与系数的关系和根的判别式的综合应用】【例10】（2023春·广东广州·九年级广州白云广雅实验学校校考阶段练习）已知关于x的方程有两实数根，，(1)若，求k的值．(2)是否存在实数k满足，若存在请求出k的值，若不存在请说明理由．【变式10-1】（2023春·黑龙江大庆·九年级统考阶段练习）已知关于x的方程有两个不相等的实数根．(1)求m的取值范围．(2)若两个实数根分别是，，且，求m的值．【变式10-2】（2023·安徽·模拟预测）关于x的一元二次方程有两个实数根，，若，则．【变式10-3】（2023·浙江·九年级假期作业）已知，关于x的方程有两个实数根．(1)求k的取值范围．(2)若方程的两实根为，且满足，求k的值．(3)当k为何值时，式子有最小值，并求出该最小值．专题1.4 根与系数的关系【十大题型】【苏科版】【题型1 由根与系数的关系直接求代数式的值】 (1)【题型2 由根与系数的关系和方程的解通过代换求代数式的值】 (1)【题型3 由根与系数的关系和方程的解通过降次求代数式的值】 (2)【题型4 由方程两根满足关系求字母的值】 (2)【题型5 不解方程由根与系数的关系判断根的正负】 (3)【题型6 由方程两根的不等关系确定字母系数的取值范围】 (3)【题型7 构造一元二次方程求代数式的值】 (4)【题型8 已知方程根的情况判断另一个方程】 (4)【题型9 根与系数关系中的新定义问题】 (5)【题型10 根与系数的关系和根的判别式的综合应用】 (5)【知识点一元二次方程的根与系数的关系】若一元二次方程（a、b、c为常数，）的两根为，，则，．注意它的使用条件为，，.【题型1 由根与系数的关系直接求代数式的值】【例1】（2023春·广东广州·九年级统考期末）若，是一元二次方程的两个根，则的值是（）A．B．C．1 D．7【答案】D【分析】利用两根之和为，两根之积为，计算即可．【详解】解：∵、是一元二次方程的两个根，∴，，∴，故选：D．【点睛】本题主要考查了根与系数的关系，解题的关键是掌握根与系数的关系的公式．【变式1-1】（2023·湖北武汉·统考模拟预测）已知m，n是一元二次方程的两根，则的值是（）A．B．C．D．【答案】C【分析】根据一元二次方程根与系数的关系得出，然后将分式化简，代入即可求解．【详解】解：∵，是一元二次方程的两根，∴，∴，故选：C．【点睛】本题考查了一元二次方程根与系数的关系，分式的化简求值，熟练掌握以上知识是解题的关键．【变式1-2】（2023·上海·九年级假期作业）已知a，b是方程的两个根，则的值．【答案】【分析】由根与系数关系知，，即知a＜0，b＜0，化简原式，所以原式故答案为：﹣14．【详解】解：∵a，b是方程的两个根，∴，，∴a＜0，b＜0，∴∴原式故答案为：﹣14．【点睛】本题主要考查根与系数关系、完全平方公式变形及二次根式的运算及化简；能够根据a,b的关系式确定其取值范围，进而准确处理二次根式的运算及化简是解题的关键．【变式1-3】（2023春·九年级单元测试）已知、是方程的两根，且，则的值为．【答案】【分析】由题意可得，，然后代入所求式子计算即可.【详解】解：∵、是方程的两根，∴，，∵，∴，∴；故答案为：.【点睛】本题考查了一元二次方程的求解、根与系数的关系以及二次根式的混合运算，熟练掌握一元二次方程的相关知识、正确计算是解题的关键.【题型2 由根与系数的关系和方程的解通过代换求代数式的值】【例2】（2023春·浙江·九年级专题练习）设α、β是方程的两个实数根，则的值为（）A．－2014 B．2014 C．2013 D．－2013【答案】D【分析】先根据一元二次方程的解的定义得到x2+x+2012=0，即α2+α=-2012，则α2+2α+可化为α2+α+α+β=-2012+α+β，然后利用根与系数的关系得到α+β=-1，再利用整体代入的方法计算即可．【详解】∵α是方程x2+x+2012=0的根，∴α2+α+2012=0，即α2+α=-2012，∴α2+2α+β=α2+α+α+β=-2012+α+β，∵α，β是方程x2+x+2012=0的两个实数根，∴α+β=-1，∴α2+2α+β=-2012-1=-2013．故选D．【点睛】考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=，x1x2=．【变式2-1】（2023春·湖北恩施·九年级统考期中）已知，是关于x的一元二次方程的两个实数根，则的值为()A．B．C．D．【答案】C【分析】根据一元二次方程的根的定义可得，根据一元二次方程根与系数的关系可得，代入代数式即可求解．【详解】解：∵，是关于x的一元二次方程的两个实数根，∴，∴，故选：C．【点睛】本题考查了一元二次方程的根的定义，一元二次方程根与系数的关系，得出，是解题的关键．【变式2-2】（2023·江西萍乡·校考模拟预测）若、是一元二次方程的两个根，则的值是．【答案】6【分析】根据一元二次方程根与系数的关系可得，由根的定义可得，代入即可得答案．【详解】∵，，∴．故答案为：6【点睛】本题考查一元二次方程根与系数的关系，解题的关键是掌握根与系数的关系及方程根的概念．【变式2-3】（2023春·安徽池州·九年级统考期末）已知和是方程的两个根，则的值为（）A．B．2021 C．D．2023【答案】A【分析】由和是方程的两个根，根据根于系数关系可得，，，由一元二次方程根的定义可得，，即可求解；【详解】和是方程的两个根，，，，，故选A．【点睛】该题考查了根与系数的关系以及一元二次方程的解，熟记一元二次方程根与系数关系公式是解答该题的关键．【题型3 由根与系数的关系和方程的解通过降次求代数式的值】【例3】（2023春·广东广州·九年级广州市第二中学校考阶段练习）若p、q是方程的两个不相等的实数根，则代数式的值为．【答案】【分析】根据一元二次方程的解的定义得到，再根据根与系数的关系得到，然后利用整体思想计算即可．【详解】∵若p、q是方程的两个不相等的实数根，∴，，∴，∴，故答案为：．【点睛】本题考查了一元二次方程的根与系数的关系，一元二次方程的解，利用整体思想降次消元是解题的关键．【变式3-1】（2023春·山东日照·九年级统考期末）已知，是方程的两个根，则代数的值为．【答案】【分析】根据一元二次方程根与系数的关系以及解的定义，得，，，，再代入降次求值即可．【详解】解：由题意，得，，，，，，原式，，，=．故答案为：．【点睛】本题考查了一元二次方程根与系数的关系，整式的化简求值，本题的关键是熟练掌握一元二次方程根与系数的关系．【变式3-2】（2023春·浙江温州·九年级校考阶段练习）已知、是方程的两根，则的值是（）A．7 B．8 C．9 D．10【答案】C【分析】根据一元二次方程解的定义和根与系数的关系得出，，，，再对所求式子变形整理，求出答案即可．【详解】解：∵、是方程的两根，∴，，，，∴，故选：C．【点睛】本题考查了一元二次方程解的定义和根与系数的关系，若一元二次方程（a、b、c 为常数，）的两根为，，则，．（2023春·九年级课时练习）已知，是方程的两根，则代数式【变式3-3】的值是（）A．B．C．D．【答案】D【分析】由根与系数的关系可得：a+b=1，再由a与b是方程的两根可得a2=a+1，b2=b+1，把a3与b3采用降次的方法即可求得结果的值．【详解】∵a与b是方程的两根∴a+b=1，a2-a-1=0，b2-b-1=0∴a2=a+1，b2=b+1∵，同理：∴故选：D．【点睛】本题考查了一元二次方程的解的概论、一元二次方程根与系数的关系，求代数式的值，灵活进行整式的运算是解题的关键．【题型4 由方程两根满足关系求字母的值】【例4】（2023·四川乐山·统考中考真题）若关于x的一元二次方程两根为、，且，则m的值为（）A．4 B．8 C．12 D．16【答案】C【分析】根据一元二次方程根与系数的关系得出，然后即可确定两个根，再由根与系数的关系求解即可．【详解】解：∵关于x的一元二次方程两根为、，∴，∵，∴，∴，故选：C．【点睛】题目主要考查一元二次方程根与系数的关系，熟练掌握此关系是解题关键．【变式4-1】（2023·上海·九年级校考期中）已知关于x的方程的两根为满足：，求实数k的值【答案】【分析】利用根的判别式求出k的取值范围，利用根与系数的关系求出，，代入，即可求得k的值.【详解】解：∵关于x的方程的两根为∴解得：，∵∴代入，得：解得：∵∴【点睛】本题考查一元二次方程根的判别式、根与系数的关系以及一元二次方程求解，熟练掌握相关知识点是解题关键.【变式4-2】（2023春·广东佛山·九年级校考阶段练习）方程的两个实数根互为相反数，则的值是．【答案】【分析】设方程的两根分别为，，根据根与系数的关系得到，解得，然后分别计算，最后确定．【详解】解：设方程的两根分别为，，∵方程的两个实数根互为相反数，，∴，解得，当，方程变为：，＜，方程没有实数根，所以舍去；当，方程变为：，＞，方程有两个不相等的实数根；∴．故答案为：．【点睛】本题考查了一元二次方程（，，，为常数）根与系数的关系：若方程的两根分别为，，则；．也考查了一元二次方程的根的判别式：当＞，方程有两个不相等的实数根；当，方程有两个相等的实数根；当＜，方程没有实数根．【变式4-3】（2023春·安徽马鞍山·九年级安徽省马鞍山市第七中学校考期末）若、是关于的方程的两个不相等的实数根，且，则的值为．【答案】3【分析】根据根与系数的关系得到，，再根据得到，解方程求出k的值，最后用根的判别式验证是否符合题意即可．【详解】解：∵、是关于的方程的两个不相等的实数根，∴，，∵，∴，即，∴，∴，解得或，又∵方程有两个不相等的实数根，∴，∴，∴，故答案为：3．【点睛】本题主要考查了一元二次方程根与系数的关系，根的判别式，解一元二次方程，熟知一元二次方程的相关知识是解题的关键．【题型5 不解方程由根与系数的关系判断根的正负】【例5】（2023春·江苏南京·九年级专题练习）关于的方程（为常数）根的情况，下列结论中正确的是（）A．有两个相异正根B．有两个相异负根C．有一个正根和一个负根D．无实数根【答案】C【分析】先对方程进行化简，然后再根据一元二次方程根的判别式可进行求解．【详解】解：由题意得：方程可化为，∴，∴该方程有两个不相等的实数根，设该方程的两个根为，则根据根与系数的关系可知：，∴该方程的两个根为一正一负，故选C．【点睛】本题主要考查一元二次方程根的判别式及根与系数的关系，熟练掌握一元二次方程根的判别式及根与系数的关系是解题的关键．【变式5-1】（2023春·安徽合肥·九年级统考期末）方程根的符号是（）A．两根一正一负 B．两根都是负数C．两根都是正数D．无法确定【答案】C【分析】利用一元二次方程根与系数的关系分析求解．【详解】解：的两根分别为，，则，，∴方程的两根同号，且两根都是正数，故选：C．【点睛】本题考查一元二次方程根与系数的关系，理解一元二次方程的两根，满足，是解题关键．【变式5-2】（2023春·江苏南通·九年级南通田家炳中学校考阶段练习）已知a、b、c是的三条边的长，那么方程的根的情况是（）A．没有实数根B．有两个不相等的实数根C．有两个相等的负实根D．只有一个实数根【答案】C【分析】首先根据根的判别式，结合三角形三边关系，得出方程有两个不相等的实数根，再根据根与系数的关系，判断出两根之和和两根之积的符号，即可作出判断．【详解】解：在方程中，可得：，∵a、b、c是的三条边的长，∴，，．，即，∴，∴，∴方程有两个不相等的实数根，又∵两根的和是，两根的积是，∴方程有两个不等的负实根．故选：C【点睛】本题考查了一元二次方程根与系数的关系、一元二次方程根的判别式、三角形的三边关系，解本题的关键在熟练掌握根据一元二次方程根与系数的关系，判断出方程有两个不等的负实根．【变式5-3】（2023·九年级统考课时练习）已知，，，则方程的根的情况是（）.A．有两个负根B．两根异号且正根绝对值较大C．有两个正根D．两根异号且负根绝对值较大【答案】D【分析】先计算=b2+4ac，由a＜0，b＞0，c＜0，得到＞0，然后根据判别式的意义得到方程有两个实数根．设方程两根为x1，x2．由得到方程有异号两实数根，再由得到负根的绝对值大．【详解】=（﹣b）2﹣4•a•（﹣c）=b2+4ac．∵a＜0，b＞0，c＜0，∴b2＞0，ac＞0，∴△＞0，∴方程有两个不相等的实数根．设方程两根为x1，x2．∵，∴方程有异号两实数根．∵，∴负根的绝对值大．故选D．【点睛】本题考查了一元二次方程ax2+bx+c=0（a≠0）的根的判别式和根与系数的关系．当＞0，方程有两个不相等的实数根；当=0，方程有两个相等的实数根；当＜0，方程没有实数根．【题型6 由方程两根的不等关系确定字母系数的取值范围】【例6】（2023·四川成都·三模）若方程x2+（m﹣4）x+﹣m＝0有两个不相等的实数根x1和x2，且x1+x2＞﹣3，x1x2＜，则m的取值范围为多少？【答案】﹣2＜m＜1或3＜m＜7【分析】由方程有两个不相等实数根结合根的判别式即可得出关于m的不等式，解不等式即可得出m的取值范围，结合根与系数的关系可得出关于m的不等式，解不等式可得出答案．【详解】解：∵方程x2+（m﹣4）x+﹣m＝0有两个不相等的实数根，∴b2﹣4ac＝﹣﹣4×＞0，整理得：，即，根据乘法法则得：或，解前一不等式组得：m＞3；解后一不等式组得：m＞1，∴原不等式的解集为：m＞3或m＜1；由题意得x1+x8＝＝（4﹣m）＞﹣3，解得m＜7；∵x1x2＝，解得m＞﹣2．综上所述，﹣2＜m＜1或3＜m＜7．【点睛】本题考查了根与系数的关系、根的判别式，根据题意得出关于m的不等式是解题的关键【变式6-1】（2023·山东日照·日照港中学统考二模）已知关于x的一元二次方程的实数根，满足，则m的取值范围是．【答案】【分析】根据根的判别式Δ≥0、根与系数的关系列出关于m的不等式组，通过解该不等式组，求得m的取值范围．【详解】解：由题意得：，所以，依题意得：，解得4＜m≤5．故答案是：4＜m≤5．【点睛】本题考查了一元二次方程的根的判别式的应用，解此题的关键是得出关于m的不等式，注意：一元二次方程ax2+bx+c=0（a、b、c为常数，a≠0）①当b2-4ac＞0时，一元二次方程有两个不相等的实数根，②当b2-4ac=0时，一元二次方程有两个相等的实数根，③当b2-4ac＜0时，一元二次方程没有实数根．【变式6-2】（2023春·江苏南通·九年级南通田家炳中学校考阶段练习）已知关于x的方程有两个不相等的实数根，，且，，则k的取值范围是（）A．B．C．D．且【答案】C【分析】根据一元二次方程的根的判别式，建立关于的不等式，求出的取值范围．根据，，可得，结合，从而最后确定的取值范围．【详解】解：∵方程有两个不相等的实数根，∴，解得：，∵，，∴又∵，∴，解得：，综上，的取值范围为：．故选：C．【点睛】此题考查了一元二次方程根的判别式及根与系数的关系，关键是得到．【变式6-3】（2023春·九年级单元测试）设关于的方程有两个不相等的实数根，，且，那么实数的取值范围是．【答案】【分析】由方程有两个不相等的实数根利用根的判别式Δ＞0，可得出a的取值范围，利用根与系数的关系可得出，，由可得出，展开代入后可得出a的不等式，解之即可求出a取值范围．【详解】解：方程有两个不相等的实数根，，解得：，，，，，，，，即，当时，解得（舍去）；当时，解得，又，的取值范围为．故答案为：．【点睛】本题考查了根的判别式以及根与系数的关系，由根与系数的关系结合，找出关于a的不等式是解题的关键．【题型7 构造一元二次方程求代数式的值】【例7】（2023·陕西西安·校考二模）已知mn≠1，且5m2+2010m+9=0，9n2+2010n+5=0，则的值为（）A．﹣402 B．C．D．【答案】C【详解】将9n2+2010n+5=0方程两边同除以n2，变形得：5×（）2+2010×+9=0，又5m2+2010m+9=0，∴m与为方程5x2+2010x+9=0的两个解，则根据一元二次方程的根与系数的关系可得m•==．故选：C．【变式7-1】（2023春·广东梅州·九年级校考阶段练习）已知，则的最小值是（）．A．6 B．3 C．-3 D．0【答案】A【分析】由已知得m，n是关于x的一元二次方程x2－2ax＋2＝0的两个根，根据根与系数的关系得到m＋n ＝2a，mn＝2，再根据完全平方公式展开化简，利用二次函数的性质解决问题．【详解】解：∵m2－2am＋2＝0，n2－2an＋2＝0，∴m，n是关于x的一元二次方程x2－2ax＋2＝0的两个根，∴m＋n＝2a，mn＝2，∴(m－1)2＋(n－1)2＝m2－2m＋1＋n2－2n＋1＝(m＋n)2－2mn－2(m＋n)＋2＝4a2－4－4a＋2＝4(a－)2－3，∵a≥2，∴当a＝2时，(m－1)2＋(n－1)2有最小值，∴(m－1)2＋(n－1)2的最小值＝4(2－)2－3＝6，故选A．【点睛】本题考查了根与系数的关系，二次函数的最值，熟练掌握根与系数的关系是解题的关键．【变式7-2】（2023·山东德州·统考一模）已知互不相等的三个实数a、b、c满足，，求的值．【答案】﹣2【分析】将已知的两等式去分母得到关系式a2+3a+c=0和b2+3b+c=0，把a、b看成方程x2+3x+c=0的两根，由根与系数的关系得到a+b=﹣3，ab=c，所求式子变形后，把a+b=﹣3，ab=c代入，即可求出值．【详解】由=﹣a﹣3得：a2+3a+c=0①；由=﹣b﹣3得：b2+3b+c=0②；∵a≠b，∴a、b可以看成方程x2+3x+c=0的两根，∴a+b=﹣3，ab=c；∴+﹣=====﹣2．故答案为﹣2．【点睛】本题考查了根与系数的关系以及分式的加减运算，灵活变换已知等式是解答本题的关键．【变式7-3】（2023春·江苏·九年级专题练习）设，，，为互不相等的实数，且，，则的值为（）A．-1 B．1 C．0 D．0.5【答案】A【分析】把看作以上方程的两个不同的根，可得，根据一元二次方程根与系数的关系求解即可【详解】解：，，看作以上方程的两个不同的根，即是方程的两根，故，即故选A【点睛】本题考查了一元二次方程的根的定义，一元二次方程根与系数的关系，整体代入是解题的关键．【题型8 已知方程根的情况判断另一个方程】【例8】（2023春·浙江·九年级期中）若关于x的一元二次方程的一个根为m，则方程（）（）的两根分别是（）．A．，B．，C．，D．，【答案】A【分析】根据一元二次方程的根与系数的关系求出方程的另一个根，设，根据方程的根代入求值即可得到答案；【详解】解：∵一元二次方程的一个根为m，设方程另一根为n，∴，解得：，设，方程（）（）变形为，由一元二次方程的根可得，，，∴，，∴，，故答案为：A．【点睛】本题考查一元二次方程的根与系数的关系及换元法解一元二次方程，解题的关键是用换元法变形方程代入求解．【变式8-1】（2023春·江西萍乡·九年级统考期中）有两个一元二次方程：：；：，其中，以下四个结论中，错误的是（）A．如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根B．如果方程M有两根符号相同，那么方程N的两根符号也相同C．如果5是方程M的一个根，那么是方程N的一个根。

初中数学专题探索规律(一)(含答案)

4.6.1 探索规律（一）想一想●怎样从几个简单的、个别的、特殊的情况出发去研究、探索、归纳出一般的规律和性质？怎样应用一般的规律和性质去解决特殊的问题？做一做1．观察规律，填数：（1）9，11，13，______…，第10个数是________；（2）11，17，27，_____，______，______…，使这列数从第三个数开始，•每个数都是前两个数的和减去1．2．观察右图，填空：由上而下，第n 行，白球有______个，黑球有_______，黑白球的数目共________个．3．给出算式：32-12=8=8*1，52-32=16=8*2，72-52=24=8*3，92-72=32=8*4，…观察上面一系列算式，你能发现什么规律？*表示哪种运算？用代数式表示这一规律．4．观察如图星阵后，推测：1+3=______；1+3+5=______；1+3+5+7=_______；1+3+5+7+9=______；…1+3+5+…+（2n-1）=_______．试一试5．探索规律：（1）计算并观察下列各组算式：88____,79____;⨯=⎧⎨⨯=⎩ 55______,46______;⨯=⎧⎨⨯=⎩ 1212______,1113______;⨯=⎧⎨⨯=⎩（2）已知25×25=625，那么24×26=_________；（3）你能举一个类似的例子吗？（4）从以上的过程中，你发现了什么规律？用语言叙述这个规律，并用代数式表示出来．答案:1．（1）15，27 （2）43，69，111 2．n，2n-1，3n-13．（2n+1）2-（2n-1）2=8n，*表示乘法 4．4；9；16；25；n2 5．（1）略（2）624 （3）略（4）（n-1）（n+1）=n2-1。

初中数学专题1：数与式分式化简求值

数学中考专题一：分式化简求值一、考纲要求（分值范围17-20分）（一）、有理数部分1.了解部分：|a|的含义。

2.理解部分：有理数的概念、相反数、绝对值、乘方的意义、有理数的混合运算、有理数的运算律。

3.掌握部分：用数轴上的点表示有理数、比较有理数的大小、相反数、绝对值、有理数的加减乘除乘方运算、有理数的混合运算、有理数的运算律。

4.运用部分：相反数、绝对值、理数的混合运算、有理数的运算律。

（二）、实数部分1.了解部分：平方根、算术平方根、立方根的概念、利用乘方和开方互逆求百以内整数的平方根和立方根、无理数和实数的概念及其与数轴上的点的对应关系、近似数的概念、二次根式及最简二次根式的概念、二次根式（根号下仅限于数）加减乘除及四则运算法则。

2.理解部分：平方根、算术平方根、立方根的概念、利用乘方和开方互逆求百以内整数的平方根和立方根。

3.掌握部分：求实数的相反数与绝对值、用有理数估计一个无理数的大致范围、用计算机进行近似计算。

4.运用部分：二次根式（根号下仅限于数）加减乘除及四则运算法则（三）、代数式1.了解部分：无。

2.理解部分：用字母表示数的意义、求代数式的值。

3.掌握部分：简单数量关系的分析与表示、求代数式的值。

4.运用部分：求代数式的值。

（四）、整式与分式1.了解部分：整数指数幂的意义和基本性质、分式和最简分式的概念。

2.理解部分：科学记数法、整式的概念、乘法公式（平方差和完全平方公式）3.掌握部分：整式的加减乘法（多项式限一次与二次式）运算、乘法公式（平方差和完全平方公式）、用提公因式法公式法（直接用公式不超过两次）进行因式分解、公式的基本性质、约分和通分、分式的加减乘除运算。

4.运用部分：科学记数法、乘法公式（平方差和完全平方公式）、用提公因式法公式法（直接用公式不超过两次）进行因式分解、公式的基本性质。

5.经历部分：乘法公式（平方差和完全平方公式）。

6.探索部分：乘法公式（平方差和完全平方公式）。

中考数学压轴试题复习第三部分专题一代数计算及通过代数计算进行说理问题-人教版初中九年级全册数学

§3．1 代数计算及通过代数计算进行说理问题课前导学计算说理是通过计算得到结论；说理计算侧重说理，说理之后进行代入求值．压轴题中的代数计算题，主要是函数类题．函数计算题必考的是待定系数法求函数的解析式，按照设、列、解、验、答五步完成，一般来说，解析式中待定几个字母，就要代入几个点的坐标．还有一类计算题，就是从特殊到一般，通过计算寻找规律．代数计算和说理较多的一类题目，是确定直线与抛物线的交点个数.联立直线和抛物线的解析式组成方程组，消去y ，得到关于x 的一元二次方程，然后根据∆确定交点的个数．我们介绍一下求函数图像交点坐标的几何方法．如图1，已知直线y ＝x ＋1与x 轴交于点A ，抛物线y ＝x 2－2x －3与直线y ＝x ＋1交于A 、B 两点，求点B 的坐标的代数方法，就是联立方程组，方程组的一个解是点A 的坐标，另一个解计算点的坐标．几何法是这样的：设直线AB 与y 轴分别交于C ，那么tan ∠AOC ＝1．作BE ⊥x 轴于E ，那么1BE AE=．设B(x , x 2－2x －3)，于是22311x x x --=+．请注意，这个分式的分子因式分解后，(1)(3)11x x x +-=+．这个分式能不能约分，为什么？因为x ＝－1的几何意义是点A ，由于点B 与点A 不重合，所以x ≠－1，因此约分以后就是x －3＝1．这样的题目一般都是这样，已知一个交点求另一个交点，经过约分，直接化为一元一次方程，很简便．图1例 1 2014年某某省某某市中考第25题在平面直角坐标系中，我们不妨把横坐标和纵坐标相等的点叫“梦之点”，例如点（1,1），(－2,－2)，，…，都是“梦之点”，显然“梦之点”有无数个．（1）若点P(2, m)是反比例函数nyx=（n为常数，n≠0）的图象上的“梦之点”，求这个反比例函数的解析式；（2）函数y＝3kx＋s－1（k、s为常数）的图象上存在“梦之点”吗？若存在，请求出“梦之点”的坐标，若不存在，说明理由；（3）若二次函数y＝ax2＋bx＋1（a、b是常数，a＞0）的图象上存在两个“梦之点”A(x1, x1)、B(x2, x2)，且满足－2＜x1＜2，| x1－x2|＝2，令2157 248t b b=-+，试求t的取值X围．动感体验请打开几何画板文件名“14某某25”，拖动y轴正半轴上表示实数a的点，可以体验到，A、B两点位于y轴同侧，A、B两点间的水平距离、竖直距离都是2，并且对于同一个a，有两个对应的b和b′，但是t随b、t随b′变化时对应的t的值保持相等．思路点拨1．“梦之点”都在直线y＝x上．2．第（2）题就是讨论两条直线的位置关系，分重合、平行和相交三种情况．3．第（3）题放弃了也是明智的选择．求t关于b的二次函数的最值，b的取值X围由“梦之点”、－2＜x1＜2和| x1－x2|＝2三个条件决定，而且－2＜x1＜2还要分两段讨论．图文解析（1）因为点P(2, m)是“梦之点”，所以P(2, 2)．所以4yx =．（2）“梦之点”一定在直线y＝x上，直线y＝3kx＋s－1与直线y＝x的位置关系有重合、平行、相交．图1 图2 图3①如图1，当直线y ＝3kx ＋s －1与直线y ＝x 重合时，有无数个“梦之点”．此时k ＝13，s ＝1．②如图2，当直线y ＝3kx ＋s －1与直线y ＝x 平行时，没有“梦之点”．此时k ＝13，s ≠1．③如图3，当直线y ＝3kx ＋s －1与直线y ＝x 相交时，有1个“梦之点”．此时k ≠13，“梦之点”的坐标为11(,)3131s s k k ----．（3）因为A (x 1,x 1)、B (x 2,x 2)两点是抛物线与直线y ＝x 的交点，联立y ＝ax 2＋bx ＋1和y ＝x ，消去y ，整理，得ax 2＋(b －1)x ＋1＝0．所以x 1x 2＝1a＞0．所以A 、B 两点在y 轴的同侧．如图4，由| x 1－x 2|＝2，可知A 、B 两点间的水平距离、竖直距离都是2．已知－2＜x 1＜2，我们分两种情况来探求a 的取值X 围：①当A 、B 两点在y 轴右侧时，0＜x 1＜2，2＜x 2＜4．所以0＜x 1x 2＜8．②当A 、B 两点在y 轴左侧时，－2＜x 1＜0，－4＜x 2＜－2．所以0＜x 1x 2＜8．综合①、②，不论0＜x 1＜2或－2＜x 1＜0，都有0＜x 1x 2＜8．所以0＜1a ＜8．所以a ＞18．由ax 2＋(b －1)x ＋1＝0，得x 1＋x 2＝1b a -，x 1x 2＝1a．由| x 1－x 2|＝2，得(x 1－x 2)2＝4．所以(x 1＋x 2)2－4x 1x 2＝4．所以22(1)44b a a--=．整理，得22(1)44b a a -=+．所以2157248t b b =-+＝2109(1)48b -+＝21094448a a ++＝261(21)48a ++．如图5，这条抛物线的开口向上，对称轴是直线12a =-，在对称轴右侧，t 随a 的增大而增大．因此当18a =时，t 取得最小值，t ＝2161(1)448++＝176．所以t 的取值X 围是t ＞176．图4 图5考点伸展第（3）题我们也可以这样来讨论：一方面，由| x 1－x 2|＝2，得(x 1－x 2)2＝4．所以(x 1＋x 2)2－4x 1x 2＝4．所以22(1)44b a a--=．整理，得22(1)44b a a -=+．另一方面，由f (2)＞0，f (－2)＜0，得f (2)f (－2)＜0．所以[42(1)1][42(1)1]a b a b +-+--+＜0．所以22(41)4(1)a b +--＝22(41)4(44)a a a +-+＝18a -＜0．所以a ＞18．例 2 2014年某某省某某市中考第23题设m 是不小于－1的实数，使得关于x 的方程x 2＋2(m －2)x ＋m 2－3m ＋3＝0有两个不相等的实数根x 1，x 2．（1）若12111x x +=，求132m-的值；（2）求2121211mx mx m x x +---的最大值．动感体验请打开几何画板文件名“14某某23”，拖动x 轴上表示实数m 的点运动，可以体验到，当m 小于1时，抛物线与x 轴有两点交点A 、B ．观察点D 随m 运动变化的图像，可以体验到，当m ＝－1时，点D 到达最高点．思路点拨1．先确定m 的取值X 围，由两个条件决定．2．由根与系数的关系，把第（1）题的已知条件转化为关于m 的方程．3．第（2）题首先是繁琐的式子变形，把m 提取出来，可以使得过程简便一点．图文解析（1）因为方程x 2＋2(m －2)x ＋m 2－3m ＋3＝0有两个不相等的实数根，所以∆＞0．由∆＝4(m －2)2－4(m 2－3m ＋3)＝－4m ＋4＞0，得m ＜1．又已知m 是不小于－1的实数，所以－1≤m ＜1．由根与系数的关系，得122(2)24x x m m +=--=-+，21233x x m m ⋅=-+．若12111x x +=，那么1212x x x x +=⋅．所以22433m m m -+=-+．整理，得210m m --=．解得m =m =．所以323(12m -=-=．所以132m -2．（2）2121211mx mx m x x +---＝121211x x m m x x ⎡⎤+-⎢⎥--⎣⎦＝122112(1)(1)(1)(1)x x x x m m x x ⎡⎤-+--⎢⎥--⎣⎦＝12121212()21()x x x x m m x x x x ⎡⎤+--⎢⎥-++⎣⎦＝22(24)2(33)1(24)33m m m m m m m m ⎡⎤-+--+-⎢⎥--++-+⎣⎦ ＝222+42m m m m m m ⎡⎤---⎢⎥-⎣⎦＝22(1)(1)m m m m m ⎡⎤---⎢⎥-⎣⎦＝222m m -+-＝2(1)3m -++．所以当m ＝－1时，它有最大值，最大值为3（如图1所示）．图1考点伸展当m变化时，抛物线y＝x2＋2(m－2)x＋m2－3m＋3＝0的顶点的运动轨迹是什么？因为抛物线的对称轴是直线x＝－(m－2)，所以抛物线的顶点的纵坐标y＝(m－2)2－2(m－2)2＋m2－3m＋3＝m－1．因为x＋y＝－(m－2)＋m－1＝1为定值，所以y＝－x＋1．也就是说，抛物线的顶点(x, y)的运动轨迹是直线y＝－x＋1（如图2所示）．图2例 3 2014年某某省某某市中考第26题如图1，已知二次函数y＝－x2＋bx＋c的对称轴为x＝2，且经过原点，直线AC的解析式为y＝kx＋4，直线AC与y轴交于点A，与二次函数的图象交于B、C两点．（1）求二次函数解析式；（2）若1=3AOB BOC S S △△，求k 的值；（3）若以BC 为直径的圆经过原点，求k 的值．图1动感体验请打开几何画板文件名“14某某26”，拖动点C 在抛物线上运动，可以体验到，当以BC 为直径的圆经过原点时，△BMO ∽△ONC ．思路点拨1．第（2）题先将面积比转化为AB 与BC 的比，进而转化为B 、C 两点的横坐标的比．2．第（2）题可以用直线的解析式表示B 、C 两点的坐标，再代入抛物线的解析式列方程组；也可以用抛物线的解析式表示B 、C 两点的坐标，再代入直线的解析式列方程组．3．第（3）题先联立抛物线与直线，根据一元二次方程根与系数的关系，得到B 、C 两点的横坐标的和与积，再构造相似三角形列方程．图文解析（1）因为原点O 关于直线x ＝2的对称点为(4, 0)，所以抛物线y ＝－x 2＋bx ＋c 的解析式为y ＝－x (x －4)＝－x 2＋4x ．（2）如图2，因为1==3AOB BOC S AB S BC △△，所以1=4B C x x ．设x B ＝m ，那么x C ＝4m ．将点B (m , km ＋4)、C (4m , 4km ＋4)分别代入y ＝－x (x －4)，得4(4),444(44).km m m km m m +=--⎧⎨+=--⎩①② ①－②÷4，整理，得m 2＝1．所以m ＝1．将m ＝1代入①，得k ＋4＝3．解得k ＝－1．此时点C 落在x 轴上（如图3）．（3）因为B 、C 是直线y ＝kx ＋4与抛物线的交点，设B (x 1,kx 1＋4)，C (x 2,kx 2＋4)．联立y ＝－x 2＋4x 和y ＝kx ＋4，消去y ，整理，得x 2＋(k －4)x ＋4＝0．所以x 1＋x 2＝4－k ，x 1x 2＝4．如图5，若以BC 为直径的圆经过原点，那么∠BOC ＝90°．作BM ⊥y 轴，⊥y 轴，垂足分别为M 、N ，那么△BMO ∽△ONC ．根据BM ON MO NC=，得1212(4)4x kx kx x -+=+．所以212121212(4)(4)[4()16]x x kx kx k x x k x x =-++=-+++．将x 1＋x 2＝4－k ，x 1x 2＝4代入，得24[44(4)16]k k k =-+-+．解得54k =-．图2 图3 图4考点伸展第（2）题也可以先用抛物线的解析式设点B 、C 的坐标，再代入直线的解析式列方程组．将点B (m ,－m 2＋4m )、C (4m ,－16m 2＋16m )分别代入y ＝kx ＋4，得 2244,16164 4.m m km m m km ⎧-+=+⎪⎨-+=+⎪⎩①②①×4－②，得12m 2＝12．所以m ＝1．将m ＝1代入①，得3＝k ＋4．解得k ＝－1．例 4 2014年某某省株洲市中考第24题已知抛物线252(2)4k y x k x +=-++和直线2(1)(1)y k x k =+++．（1）求证：无论k 取何实数值，抛物线与x 轴有两个不同的交点；（2）抛物线与x 轴交于A 、B 两点，直线与x 轴交于点C ，设A 、B 、C 三点的横坐标分别是x 1、x 2、x 3，求x 1·x 2·x 3的最大值；（3）如果抛物线与x 轴的两个交点A 、B 在原点的右边，直线与x 轴的交点C 在原点的左边，又抛物线、直线分别交y 轴于点D 、E ，直线AD 交直线CE 于点G （如图1），且CA ·GE ＝CG ·AB ，求抛物线的解析式．图1动感体验请打开几何画板文件名“14株洲24”，拖动y 轴上表示实数k 的点运动，可以体验到，抛物线与x 轴总是有两个交点．观察x 1·x 2·x 3随k 变化的函数图像，可以体验到，x 1·x 2·x 3是k 的二次函数．还可以体验到，存在一个正数k ，使得AD 与BE 平行．思路点拨1．两个解析式像庞然大物，其实第（1）题的语境非常熟悉，走走看，豁然开朗．2．第（2）题x 1·x 2·x 3的最小值由哪个自变量决定呢？当然是k 了．所以先求x 1·x 2·x 3关于k 的函数关系式，就明白下一步该怎么办了．x 1·x 2由根与系数的关系得到，x 3就是点C 的横坐标．3．第（3）题的等积式转化为比例式，就得到AD //BE ．由此根据OD ∶OA ＝OE ∶OB 列方程，再结合根与系数的关系化简．还是走走看，柳暗花明．图文解析（1）因为222(52)17(2)42()424k k k k k +∆=+-⨯=-+=-+＞0，所以无论k 取何实数值，抛物线与x 轴有两个不同的交点．（2）由2(1)(1)y k x k =+++，得C (－(k ＋1), 0)．所以x 3＝－(k ＋1)．由根与系数的关系，得x 1·x 2＝(52)4k +．所以x 1·x 2·x 3＝1(52)(1)4k k -++＝21(572)4k k -++．因此710x =-当时，x 1·x 2·x 3取得最大值，最大值＝14949(52)410010-⨯-+＝980．（3）如图2，由CA ·GE ＝CG ·AB ，得CA CG AB GE =．所以AG //BE ，即AD //BE ．所以OD OE OA OB =，即212(52)(1)4k k x x ++=．所以22122(52)(1)4k k x x x ++=⋅．所以222(1)1k x +=．所以x 2＝k ＋1，或－k －1（舍）．又因为x 1＋x 2＝k ＋2，所以x 1＝1，即A (1, 0)．再将点A (1, 0)代入252(2)4k y x k x +=-++，得5201(2)4k k +=-++．解得k ＝2．所以抛物线的解析式为y ＝x 2－4x ＋3．图2 图3考点伸展把第（3）题中的条件“CA ·GE ＝CG ·AB ”改为“EC ＝EB ”，其他条件不变，那么抛物线的解析式是怎样的呢？如图3，因为点E 在y 轴上，当EC ＝EB 时，B 、C 两点关于y 轴对称，所以B (k ＋1, 0)．将点B (k ＋1, 0)代入252(2)4k y x k x +=-++，得252(1)(2)(1)04k k k k ++-+++=．解得k ＝2．所以抛物线的解析式为y ＝x 2－4x ＋3．。

初中复习方略数学微专题一规律探索问题

【变式】(2021·济宁中考)按规律排列的一组数据：12 ，35 ，□，177 ，296 ，3117 ，…，
其中□内应填的数是( D )
A．23
B．151
C．95
D．21
类型二：算式规律类
1．算式规律类试题一般有以下两种类型 (1)由给定的一些等式找出规律． (2)给出计算公式，通过具体的计算猜想规律． 2．解决此类题目的一般思路 (1)仔细观察题目提供的算式，发现结果和式子序列号之间的关系． (2)将这个关系式表示出来，继而再运用其关系式解决问题．
微专题一规律探索问题
类型一：数字规律类
1．数字规律类试题一般有以下四种类型 (1)“等差数列”类．即相邻数字的差值相等，整个数字序列依次递增或递减的一类数．(2)“等比数列”类．即相邻数字的比值相等．(3)加、减、乘、除、平方规律类．(4)个位数字规律类．
2．解决此类题目的一般思路 (1)仔细观察题目给出的几个特殊情形．(2)分析、比较，寻找这些数字之间的内在联系．(3)发现其内在规律并利用规律解决问题．
【变式】(2021·云南中考)按一定规律排列的单项式：a2，4a3，9a4，16a5，25a6，…，
第＋1
B．n2an－1
C．nnan＋1 D．(n＋1)2an
类型三：图形规律类
1．图形规律类试题一般有以下三种类型 (1)图形数量方面的规律． (2)图形形状方面的规律． (3)图形各组成部分的相对位置的规律．
2．解决此类题目的一般思路 (1)根据图形的变化规律分别求出第1个点，第2个点，第3个点的坐标，找出点的坐标与序号之间的关系，归纳得出第n个点的坐标与变换次数之间的关系． (2)若坐标是循环变换，应先确定循环一周的变换次数，然后用总次数除以变换次数来确定点的坐标．

专题一初中数学教学目标的设计

专题一初中数学教学目标的设计教学目标与教学指导随着中国基础教育课程改革的深入，一个适合时代需要的全新教学正在形成和发展，几乎所有的数学教师都在接受新的教学理念，充分认识到数学课程应该突出基础性、普及性和发展性。

数学教育应该面向全体学生，实现“人人都学有价值的数学，人人都能获得必需的数学，不同的人在数学上得到不同的发展。

”数学教学活动已经不再是单纯的知识传授，而是由现实生活情境引入，并通过活泼生动的数学活动，激发学生学习的积极性，使他们在自主探索的过程中真正理解和掌握基本的数学知识和技能、数学思想方法、培养他们发现问题、分析问题、解决问题的能力。

课堂是传道、授业、解惑的地方，是智慧火花相互碰撞的场所，是实施课改的主要阵地。

新的课程理念如何在课堂的教学过程中完美体现，教师如何真正地考虑到学生思维的发展等问题，已经成为亟待解决的问题。

我们就此进行了一些探索、小结，选编了部分经典案例，并结合教材的内容给予了恰当的分析与点评。

希望能帮一线教师解决些许教学中出现的问题。

初中数学教学目标的设计是网络课程的第一部分，它包括四个部分。

第一节让教师从整体上认识数学课程目标，使之理解“教”与“学”间的关系如何体现在数学课程目标中，理解义务教育阶段学生数学学习的四个数学知识领域——“数与代数”、“空间与图形”、“统计与概率”、“实践与综合应用”在“三维”的角度对总体目标“四个领域”的具体内涵。

第二、三、四节选取了有代表性的案例，从“知识与技能”、“数学思考”、“解决问题”、“情感与态度”四个方面进行了详细的评述，使教师更加深刻的理解如何在课堂教学中实现这四个目标。

其中，“知识与技能”目标与过去的教学大纲中仅仅呈现的结果性目标不同，在《标准》中首次被赋予了“过程”的含义，即必须让学生在数学学习活动中去“经历……过程”；“过程性目标”不要让学生“知其然，不知其所以然”，也不要让学生经历、体验探索的过程，没有正确性的结论呈现。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

期中专题复习资料
专题一：最优化说明推理问题 1、如图，在△ABC 中，AB ＝AC ，DB ＝DC ，且DM ⊥AB ，DN ⊥AC 垂足分别为M 、N . DM 与DN 一定相等吗？为什么？
2、如图，AB ＝AC ，DB ＝DC ，点P 是AD 上一点，试说明PB ＝PC 的理由.
3、如图，△ABC 的高BD 、CE 相交于点O ，且 OB ＝ OC . 试说明AB ＝AC 的理由
专题二：等腰三角形中的分类问题
1、在等腰△ABC 中，∠A ＝80°，那么∠B ＝？
2、等腰三角形ABC 的周长为8cm ，AB ＝ 3cm ，则BC ＝？cm ．
等腰三角形的问题到底如何分类？方法提炼
有关等腰三角形的分类问题通常情况下有两种方式：
1.从角的角度出发,可以按照等腰三角形的顶角来分类,例如上面的问题1中出现的分类;
2.从边的角度出发,可以按照等腰三角形的底边来分类,例如上面的问题2中出现的分类. 练习：1、(1)如果等腰三角形ABC 的周长为10，底边长为4 ，那么腰长为 ; (2)如果等腰三角形ABC 的周长为10，腰长为4 ，那么底边长为 ;
(3)如果等腰三角形ABC 的周长为12，一边长为5 ，那么另外两边长为． 2、等腰△ABC 中，∠A ＝40°，求∠B 的度数?
O
A
B C
D
E
P
A
B
D
N M D
C
B
A
专题三：在解决梯形的问题中有哪些常用辅助线
1、如图，在等腰梯形ABCD 中， AD ∥BC ，请把梯形分割成几个你认为比较熟悉的特殊图形.
2、如图，在四边形ABCD 中，有AB ＝DC ，∠B ＝∠C ，AD ＜BC .试说明四边形ABCD 是等腰梯形.
3、梯形两条互相垂直的对角线长分别为6和8，求此梯形面积．
方法提炼：
如何运用三角形的知识解决梯形的问题，因此解决梯形的有关问题时常常通过作辅助线将问题转化为解决有关三角形的问题来研究，或利用图形中隐含的面积与线段间的数量关系来转化问题，这是解梯形问题的基本思路，常用的辅助线的作法是： 1．平移腰：过一顶点作一腰的平行线；
2．平移对角线：过一顶点作一条对角线的平行线； 3．作垂线：过底的顶点作另一底的垂线； 4．延长两腰：两腰延长相交得到三角形拓展：
如图，在等腰梯形ABCD 中，AD ∥BC ，AB =CD ，点P 为BC 边上一动点，PE ⊥AB ，PF ⊥CD ，CG ⊥AB ，试说明 PE+PF= CG ．
G
F
E
P
D
C
B A
D
C
B A
D
C
B A
D
C
B A
D
C B A
专题四：理清平方根的相关概念
1、0.81的平方根是
2、（－6）2的平方根是
3、= = 的算术平方根是
4、下列各式中，正确的是（）.
5、9的平方根是（）．
（A）3（B）－3（C）±3（D）
6、7的平方根是（）．
（A）49 （B）±49 （C）（D）
7、4的算术平方根是（）．
（A）±16 （B ）16 （C）±2 （D） 2
专题五：应用勾股定理解决实际问题
1、“中华人民共和国道路交通管理条理”规定：小汽车在城市街路上的行驶速度不得超过70千米／时．一辆“小汽车”在一条城市街路上直道行驶，某一时刻刚好行驶到路对面“车速检测仪”正前方30米处，过了2秒后，测得“小汽车”与“车速检测仪”间的距离变为50 米，这辆“小汽车”超速了吗？
2、如图，一艘轮船从甲地向南偏西45°方向航行80km到达乙地，然后又向北航行km到达丙地，这时它离甲地多远？
北
北
丙
乙
甲
观测点
A
C
B
92)4
(-16
7
±7
3、如图，马路边一根高为5.4米的电线杆，被一辆卡车从离地面1.5米处撞断裂，倒下的电线杆顶部是否会落在离它的底部4米的快车道上？
4、如图，在△ABC 中,AB =6, 月AC = 25 ,∠B ＝ 45°,求BC ．
专题六：在图形旋转中如何正确理解旋转角
1、如图，正方形AFGH 是正方形ABCD 绕点A 按顺时针方向旋转一定的角度而成的．请度量旋转角的度数．
2、如图△ABC 是等腰直角三角形，BC 是斜边，P 为△ABC 内一点，将△ABP 绕点A 逆时针旋转后与△ACP ´重合，若AP ＝1cm ，则PP ′＝ ▲ cm ．
C'
C F
G
A
B
H D
P
C
B
A P ´
知识点：1、把一个图形绕着某一定点转动一个角度的图形变换叫做旋转．这个定点O 叫旋转中心，转动的角叫做旋转角．
2、图形旋转前后，每一对对应点与旋转中心所连线段的夹角等于旋转角。

练习：1、如图，△OAB 绕点 O 逆时针旋转80°得到△COD ，若∠A ＝ 110° ∠D ＝ 40°，则∠1的度数是（）
A ．30°
B ．40°
C ．50°
D ．60°
2、△ABC 和△ADE 都是顶角为45°的等腰三角形，BC 、DE 分别是这两个等腰三角形的底边．图中的△ACE 可以看成由哪个三角形通过怎样的旋转得到的？
C F
G A B
H
D
G
旋转中心在图形外
旋转中心在图形上
P
旋转中心在图形内
3、如图，△ABC 和△DCE 是全等的等边三角形，点B 、C 、E 在同一条直线上．问：△ABC 经过怎样的变换可以得到△DCE ？说出变换过程．
4、如图，P 是正方形ABCD 内一点，PA ＝2， PB ＝1，PD ＝3，求∠APB 的度数
O
B
C E D
C
B
C
D
P
A B。