有理函数及三角函数有理式的积分
4(4)有理函数及三角函数有理式的积分(1)

原式=
5u + 2 (u2 + 1)2
du
5 2
d(u2 + 1)
(u2 + 1)2 + 2
du (u2 + 1)2
51
u
- 2 u2 + 1 + u2 + 1 + arctanu + C
递推公式
回代
2x -7 2( x2 - 2x + 2) + arctan( x - 1) + C
书上无
Q( x)
部分分式的和, 如果分母多项式Q( x)在实数域
上的质因式分解式为:
Q( x) b0( x - a) ( x2 + px + q) ,( p2 - 4q 0)
, 为正整数, 则 P( x) 可唯一的分解为:
Q( x)
4
有理函数的积分
Q( x) b0( x - a) ( x2 + px + q) ,( p2 - 4q 0)
+ arctan x + C
说明:当被积函数是假分式时,应把它分为 一个多项式和一个真分式,分别积分.
9
有理函数的积分
例2 求
x+3 x2 - 5x + 6 dx
解
x2
x+3 -5x + 6
(x
x+3 - 2)( x - 3)
A+ x-2
B x-3
因式分解 x + 3 A(x - 3) + B(x - 2)
Ap
At + (B - )
2
几种特殊类型函数的积分

x 6
1+ e2 + e3 + e6 1 3 3t + 3 6 dt = ∫ − = 6∫ dt − 2 2 t (1 + t )(1 + t ) t 1+ t 1+ t
3 3t + 3 6 dt = ∫ − − 2 t 1+ t 1+ t 2 1 3 d (1 + t ) dt − 3∫ = 6 ln t − 3 ln(1 + t ) − ∫ 2 2 1+ t 2 1+ t 3 2 = 6 ln t − 3 ln(1 + t ) − ln(1 + t ) − 3 arctan t + C 2
A B C 1 , = + + 例2 2 2 x ( x − 1) x − 1 x ( x −1 )
1 = A( x − 1) 2 + Bx + Cx ( x − 1)
代入特殊值来确定系数 A, B , C 取 x = 0, ⇒ A = 1 取 x = 1, ⇒ B = 1 取 x = 2, 并将 A, B 值代入 (1) ⇒ C = −1
2u + 1 + u2 − 1 − u2 du =∫ 2 (1 + u)(1 + u )
(1 + u)2 − (1 + u 2 ) 1+ u 1 du = ∫ =∫ du − ∫ du 2 2 (1 + u)(1 + u ) 1+ u 1+ u
1 = arctan u + ln(1 + u 2 ) − ln | 1 + u | + C 2 x Q u = tan 2 x x = + ln | sec | − ln | 1 + tan x | + C . 2 2 2
有理函数的积分积分表的使用

一、 有理函数的积分
在有理分式中,n<m时,称为真分式;n≥m时,称为 假分式.
利用多项式除法,可以把任意一个假分式化为一个有理 整式和一个真分式之和.
有理整式的积分很简单,下面只讨论真分式的积分.
一、 有理函数的积分
1. 最简分式的积分
统称为最简分式,其中n为大于等于2的正整数; A,M,N,a,p,q均为常数,且p2-4q<0.
有理函数的积分积 分表的使用
有理函数的积分积分表的使用
本节将介绍一种比较简单的特殊 类型函数的不定积分——有理函数的 积分,以及积分表的使用.
一、 有理函数的积分
有理函数是指有理式所表示的函数,它包括有理整式和
其中m,n都是非负整数,a0,a1,…,an及b0,b1,…,bn都是实 数,并且a0≠0,b0≠0.
三、 积分表的使用
实际应用中常常利用积分表(见附录)来计算不定积分.求不定 积分时可按被积函数的类型从表中查到相应的公式,或经过少量 的运算和代换将被积函数化成表中已有公式的形式.
三、 积分表的使用
该不定积分不能在积分表中直接査出,需先进行变量代 换.令u=数的积分
2. 有理分式化为最简分式的和
一、 有理函数的积分
对式(5-18) (1)若分母Q(x)中含有因式(x-a)k,则分解后含有下列k 个最简分式之和:
其中A1,A2,…,Ak都是常数. (2)若分母Q(x)中含有因式(x2+px+q)k,其中p2- 4q<0,则分解后含有下列k个最简分式之和:
二、 可化为有理函数的积分
二、 可化为有理函数的积分
二、 可化为有理函数的积分
【例55】
二、 可化为有理函数的积分
几种典型函数的积分举例

① 比较系数法
x2 2 x 2 x3 1
A Bx C 2 x 1 x x 1
等式两端同时乘以x3 1 ,得到
x 2 2 x 2 A x 2 2 x 2 Bx C x 1
目录
上页
下页
返回
结束
例4.6. 计算不定积分
解.
x
2
2x 2
2
x2
2
dx.
原式
x2 2 x 2 2 x 2
x
2
2 x 2
dx
2x 2
x
x2 2x 2
2
2x 2
dx 2
x
2
2x 2
2
dx
1 1 2 d x d x 2x x2 2 x 2 x2 2 x 2 2
4 1 B 1 5. 5 2 11 1 2 1 1 1
2 于是,B . 5
目录 上页 下页 返回 结束
例4.4. 将
解.
x 1 x
x
x
2
1
分解为部分分式之和.
2
③ 拼凑法
2 2
x 1 x2 1
x
x 1 x 2 1
1 tan x 5
C
目录
上页
下页
返回
结束
例4.5. 计算不定积分
x2 dx. 2 x 2x 3
1 2x 2 1 2 2 解. 原式 dx 2 x 2x 3 1 2x 2 3 2 2 dx x 2x 3
有理函数及三角函数有理式的积分

2. 特殊类型的积分按上述方法虽然可以积出, 但不一定 简便 , 要注意综合使用基本积分法 , 简便计算 .
思考与练习
如何求下列积分更简便 ?
解:
备用题 1. 求不定积分
x6
1 (1
x2
)
dx
.
分母次数较高, 宜使用倒代换.
解:令 t 1 , 则
,故
x
x6
1 (1
x
t6
(
1 t2
讨论积分
(
x
Mx 2 px
N q
)n
dx,
x2
px
q
x
p2
2
q
p2 4
,
令 x pt
2
记 x2 px q t 2 a2 , Mx N Mt b,
则 a2 q p2 , b N Mp ,
4
2
(
x
Mx 2 px
N q)n
dx
(t2
Mt a2 )n
dt
(t2
b a2 )n
特殊地:k
1,
分解后为
x
Mx 2
N px
q
;
真分式化为部分分式之和的待定系数法
例1
x
2
x
3 5x
6
(
x
x 2)(
3 x
3)
A x2
B, x3
x 3 A( x 3) B( x 2),
x 3 ( A B)x (3A 2B),
A (3
B A
1, 2B)
3,
A B
5 ,
x sin2 2
x 2
1 tan2 x
1
tan2
有理函数的积分
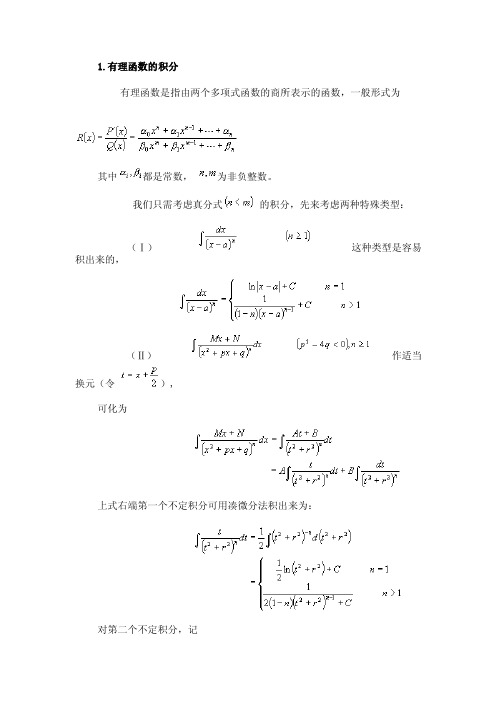
1.有理函数的积分有理函数是指由两个多项式函数的商所表示的函数,一般形式为其中都是常数,为非负整数。
我们只需考虑真分式的积分,先来考虑两种特殊类型:(Ⅰ)这种类型是容易积出来的,(Ⅱ)作适当换元(令),可化为上式右端第一个不定积分可用凑微分法积出来为:对第二个不定积分,记用分部积分法可导出递推公式:整理得重复使用递推公式,最终归结为计算而可积出来为这样就可完成对不定积分(Ⅱ)的计算。
对任一个有理函数而言,均可写成一个多项式与一个有理真分式的和,而多项式的积分问题已经解决,下面主要考虑有理真分式(不妨设)的积分问题。
为叙述简便,不妨设.其方法是将化成许多简单分式(即类型(Ⅰ)、(Ⅱ))的代数和然后逐项积分。
由于类型(Ⅰ)、(Ⅱ)总是可“积出来”的,从面有理函数总是可以“积出来”。
下面简述分解有理真分式()的步骤:第一步按代数学的结论,将分母分解成实系数的一次因式与二次因式的乘幂之积。
其中均为自然数。
第二步根据因式分解结构,写出的部分分式的待定形式:对于每个形如的因式,所对应的部分分式为对于每个形如的因式,所对应的部分分式为把各个因式所对应的部分分式加起来,就完成了对的部分分式分解。
第三步确定待定系数:通分后比较分子上的多次式的系数,得待定系数的线性方程组,由此解得待定系数的值。
例8.13 求2.三角函数有理式和积分由及常数经过有限次四则运算所得的函数称为关于的有理式(或三角函数有理式)。
用表示对于这种函数的不定积分我们总可通过代换,化为以为变量的有理函数的积分。
理由是,,,又,故从而上面的讨论说明:三角函数有理式也总是可以“积出来”的,但对具体问题而言,用上述方法往往计算量太大,因此,有时要考虑用其它简便方法。
(1)如果是的奇函数时,即则设即可。
例如求(1);(2).(2)如果是的奇函数时,即则设即可。
例如求.(3)如果是关于与的偶函数时,即则设即可。
例如求(1);(2).(4)请研究被积函数为(为自然数)时的情况。
有理函数及三角函数有理式的积分

有理函数及三角函数有理式的积分
一、有理函数的积分
有理函数是指可以表示为常熟分式的函数,称为有理函数。
有理函数主要由多项式和
不定积分所组成。
1.直接积分法:即把有理函数积分后的结果表达式化成原函数的另一种表达形式,常
用整理、贝塞尔曲线等方法来解决。
2.常熟分式积分法:将有理函数分解成分加函数,然后分别积分,再把积分结果求和。
三角函数是一类有特殊解析特性的函数,它们其中包括正弦、余弦函数、正切函数等等。
由于三角函数以及它们的倒数和反函数都有解析特性,因此其积分是容易解决的。
1.利用倒数公式积分:针对三角函数有一系列专有倒数公式,其中包括 Ma 矩阵公式
和高尔文三角函数积分公式。
2.利用反函数积分:由于三角函数都有反函数,因此也可以利用反函数将三角函数的
积分问题转化为反函数的积分问题,从而轻松解决。
3.利用改元积分:改元积分是把变量改为一些更简单的函数,然后分别积分得出结果,可以将三角函数的积分转化为改元积分,以减少积分的难度。
总之,有理函数和三角函数都可以通过不同的方法解决积分问题,在解决的时候需要
根据具体的函数情况来选择最适合的积分法,才能更好的解决积分问题。
有理函数和三角函数有理式的积分法

§3-7 阅读(有理函数和三角函数有理式的积分法)在前面几节中,读者都已经遇到过许多有理函数的积分和三角函数有理式的积分在前面几节中,读者都已经遇到过许多有理函数的积分和三角函数有理式的积分..在那里,因为被积函数都很特殊,因为被积函数都很特殊,所以用所以用所以用“拼凑的方法”“拼凑的方法”就求出了它们的积分就求出了它们的积分..这一节讨论的是一般情形下,如何求它们的积分当你遇到那些简单或特殊的情形时,当然不必用这里的一般方法,而仍用以前那种“拼凑方法”就行了法,而仍用以前那种“拼凑方法”就行了. .1.有理函数的积分法有理函数的积分()d ()p x x q x ò[ [其中其中()p x 和()q x 都是多项式都是多项式] ] 总可以积出来,即可把它表示成初等函数总可以积出来,即可把它表示成初等函数..积分方法的要点是:第一,若有理函数()()p x q x 中,分子()p x 的次数不低于分母()q x 的次数,则称它为假分式假分式..在这种情形下,就用多项式除法(见下面例2727)),先把它变成一个多项式与一个真分式之和,即()()()()()p x r x s x q x q x =+ [ [其中分子其中分子()r x 的次数低于分母()q x 的次数的次数] ] 于是,()d ()p x x q x ò()()d d ()r x s x x x q x =+òò右端第一项是多项式的积分右端第一项是多项式的积分((用分项积分法可以积出来用分项积分法可以积出来)),所以就变成求有理函数真分式的积分()d ()r x x q x ò. . 关于多项式除法,请看下面的例题关于多项式除法,请看下面的例题关于多项式除法,请看下面的例题. . 例27 例如求有理函数假分式的积分522d 36x x x x -++ò首先像做整数除法那样,做多项式除法:由此可得63225++-x x x 3212323336x x x x +æö=-+ç÷+èø其次再逐项积分,即(余式) 23+x (被除式) (除式)255336000202x x x x x ++++-+++xx x x 40220233-+-+-+-(商式)31233x x -5342222212321132d d d d 33123363636x x x x x x x x x x x x x x x -+++æö=-+=-+ç÷+++èøòòòò这样就变成求这样就变成求((右端最后一个右端最后一个))有理函数真分式的积分有理函数真分式的积分. .第二,第二,对于真分式对于真分式()()r x q x ,先把分母上的多项式()q x 分解成一次因式或没有实根的二次因式的乘积二次因式的乘积((根据代数基本定理,这是可能的).).然后用待定系数法然后用待定系数法然后用待定系数法((或拼凑方法或拼凑方法))把()()r x q x 化成不超出下面这些“最简分式”的和:化成不超出下面这些“最简分式”的和:22,,,()()n m A B Cx D Ex Fx a x b x px q x rx s ++--++++(n 和m 为正整数为正整数)) (分子比分母上的基因式低一次分子比分母上的基因式低一次) )这样,根据分项积分法,有理函数真分式的积分就化为最简分式的积分这样,根据分项积分法,有理函数真分式的积分就化为最简分式的积分. . 我们用例子来说明上述方法我们用例子来说明上述方法我们用例子来说明上述方法. .⑴分母为一次重因式的真分式的积分法例28 例如求例如求2353d (2)x x x ++ò,可令,可令2323532(2)(2)(2)x A B C x x x x +=++++++将右端通分,将右端通分,并比较两端分子,并比较两端分子,并比较两端分子,即即C x B x A x ++++º+)2()2(3522,则得三元线性方程组则得三元线性方程组ïîïíì=++=+=(常数项)的系数)(的系数)(3240452C B A x B A x A , 解得解得ïîïíì=-==23205C B A 于是得于是得3232)2(23)2(2025)2(35+++-+=++x x x x x 因此,因此, 2353d (2)x x x ++ò2352023d d d 2(2)(2)x x x x x x =-++++òòò220235ln 222(2)x x x =++-++【注1】上面求待定系数的方法是比较两端x 的同次项系数,下面是求待定系数的另一个方法:根据2253(2)(2)x A x B x C +º++++,则,则第一步,让2x =-,得23C =;第二步,在2253(2)(2)x A x B x C +º++++两端关于x 求导数,得102(2)x A x B º++. 再令2x =-,得20B =-;第三步,在102(2)x A x B º++两端关于x 求导数,则得102A =,即5A =.【注2】把真分式2353(2)x x ++化成最简分式之和的另一个方法是依次用多项式除法化成最简分式之和的另一个方法是依次用多项式除法: :25323(510)22x x x x +=-+++,222253510232023522(2)(2)(2)x x x x x x x +-=+=-++++++ 232353520232(2)(2)(2)x x x x x +=-+++++ ( (你看懂了吗你看懂了吗你看懂了吗?) ?)⑵分母为不同一次因式乘积的真分式的积分法例如求d ()()cx d x x a x b +--ò,可令,可令 bx Ba x Ab x a x d cx -+-=--+))(((A 和B 为待定系数)为待定系数) 然后根据恒等式()()cx d A x b B x a +º-+-,求出待定系数A 和B .于是,于是,d ()()cx d x x a x b +=--òd d ln ||ln ||A B x x A x a B x b x a x b +=-+---òò例29 求2d (3)(5)x x x x ---ò.解 设53)5)(3(2-+-=---x Bx A x x x (B A ,为待定常数为待定常数) ) 则得)3()5(2-+-º-x B x A x ,即,即2)35()(-º+-+x B A x B A 比较两端常数项和x 的系数,则得线性方程组的系数,则得线性方程组îíì=+=+1235BA B A 解得23,21=-=B A ( (求求B A 和的另一个方法见下注的另一个方法见下注).).).因此,因此,因此, 523321)5)(3(2-+--=---x x x x x 从而得从而得2d(3)(5)x x x x ---ò113113d(3)d(5)ln 3ln 5232522x x x x x x =--+-=--+---òò【注】在式2(5)(3)x A x B x -º-+-中,让3x =,则得12A =-,所以12A =-;再让5x =,则得32B =,所以32B =.⑶分母为二次多项式(没有实根)的真分式的积分法 例如例如[[注意注意,,分母没有实根2(40)p q -<],22222111(1)d d d 424x x ux px q u A p q px ==+++-æö++ç÷èøòòò24,22q p p u x A æö-ç÷=+=ç÷èø(套用积分公式)1arctan u A A =2222arctan 44q q x p p p+-=-2222(2)(2)d (0)d d 2b bx p p x ax ba a ax a ax x x px qx px qx px qæö++-+ç÷+èø¹==++++++òòò222d()21d 22ax px q a b p x a x px q x px q++æö=+-ç÷++++èøòò2221ln()d 22aa bx px q p x a x px q æö=+++-ç÷++èøò(套用前一题的结果套用前一题的结果).). ⑷分母为二次重因式的真分式的积分法例30 例如求积分例如求积分322221d (1)x x x x x -+++ò.若用待定系数法,就令若用待定系数法,就令322222221(1)1(1)x xAx B Cx D x x x x x x -+++=+++++++若不用待定系数法,可依次用多项式除法:若不用待定系数法,可依次用多项式除法:第一步,3222212(2)(3)11x x x x x x x x -++=-+++++;第二步,32222222132(2)(1)1(1)x x x x x x x x x x -+-+=+++++++于是,于是,32222222132(2)d d d (1)1(1)x x x x xx x x x x x x x -+-+=+++++++òòò其中右端第一个积分其中右端第一个积分22222231(21)71d(1)7d d d 1212121322x x x x x x x x x x x x x x -+-++==-++++++æöæö++ç÷ç÷èøèøòòòò217221ln(1)arctan 2233x x x +=++-×而第二个积分而第二个积分2222222222(2)(21)3d(1)1d d 3d (1)(1)(1)(1)x x x x xxx x x x x x x x x +++++==+++++++++òòòò2222113d (1)1322x x x x =-+++éùæöæöêú++ç÷ç÷êúèøèøëûò[套积分公式⒇] ⑸分母为一次因式与二次因式乘积的真分式的积分法例如,求22d ()()bx cx d x x a x px q ++-++ò时,可令时,可令 q x p x C x B a x Aq x p x a x d x c x b ++++-=++-++222))((然后根据恒等式然后根据恒等式22()()()bx cx d A x px q Bx C x a ++º++++-求出待定系数A 、B 和C . 于是,于是,22d ()()bx cx dx x a x px q ++-++ò2ln ||d Bx C A x a x x px q +=-+++ò (注意2xpx q ++没有实根没有实根,,即240p q -<)2.三角函数有理式的积分法 所谓“三角函数有理式”,是指由常数和简单三角函数x sin 与x cos 经过有限次的有理运算经过有限次的有理运算((加、减、乘、除加、减、乘、除))得到的函数,记成)cos ,(sin x x R .下面介绍的是形如积分的是形如积分(sin ,cos )d R x x x ò的积分法的积分法..例如积分例如积分2cos d 2sin cos x x x x +ò,1d 2sin cos 1x x x -+ò,1d (0)cos x ab a b x ¹+ò等.实际上,我们在前面几节中曾多次遇到这种类型的积分我们在前面几节中曾多次遇到这种类型的积分..这里介绍的是一般方法这里介绍的是一般方法..你在做题时.....,还是要具体问题具体分析...........,未必就一定要用这里介绍的方法..............(因为一般情形下,这里介绍的方法要麻烦一些)方法要麻烦一些). .令2tan xt =(称它为半角替换或万能替换称它为半角替换或万能替换)),则,则2222122tan12tan22sec 2tan22cos2tan22cos2sin2sin t t x x xx xx x x x +=+==== 22222222112tan12tan 1)2tan 1(2cos 2sin 2cos cos t t x x x x x x x +-=+-=-=-= t t t x d 12)arctan 2(d d 2+==于是,于是,(sin ,cos )d R x x xò2222212,d 111t t R t t t t-æö=ç÷+++èøò这样,三角函数有理式的积分就变成有理函数的积分三角函数有理式的积分就变成有理函数的积分..在有些情形下,像前面做过的那样,不必用半角替换,而用其它三角替换会更简单必用半角替换,而用其它三角替换会更简单..例如例如()i 当(sin ,cos )(sin ,cos )R x x R x x -=-时,令cos t x =; ()ii 当(sin ,cos )(sin ,cos )R x x R x x -=-时,令sin t x =; ()iii 当(sin ,cos )(sin ,cos )R x x R x x --=时,令tan t x =.习题1.求下面的原函数:⑴25d (3)x x x --ò; ⑵⑵325d (2)x x x --ò;⑶23354d (1)x x x x -+-ò; ⑷⑷3223242d 21x x x x x x -++-+ò. 答案:⑴323ln -+-x x;⑵2)2(2122-+--x x ;⑶2)1(1111ln 3-----x x x ; ⑷171ln 94232---++x x x x .2.求下面的原函数:求下面的原函数:⑴x x x x d )3)(2(73ò---; ⑵⑵x x x x d 2152ò-++; ⑶⑶x x x x x x d )2)(2(2342ò+---. 答案:⑴3ln 22ln -+-x x ;⑵1ln 22ln 3-++x x ;⑶2ln 252ln ln 21++-+x x x . 3.求下面的原函数:求下面的原函数:⑴x x x x x d )1)(2(23222ò++-+; ⑵⑵x x x x x d )32)(1(2ò+++; ⑶⑶x x x d 134ò+. 答案:⑴x x arctan )1ln(2-+;⑵21arctan 21)32ln(411ln 212++++++-x x x x ;⑶312arctan 311)1(ln 6121222--+-++x x x x x . 4.根据提示,请把下面的演算做到底:根据提示,请把下面的演算做到底:⑴tan 21d 2sin cos 1x t x x x æö=ç÷èø====-+ò⑵(cos )1d (2cos )sin t x x x x ======+ò⑶2(sin )cos d 2sin cos t x xx x x ======+ò⑷3(tan )3sin d sin cos t x xx x x======+ò答案:⑴22tan2tan ln21+x x ;⑵32)cos 1()cos 1()cos 2(ln 61x x x +-+;⑶12sin 1ln 222sin 1x x +--+;⑷÷÷øöççèæ---+-x x x x x x x sin 3sin cos 2arctan 31cos sin 1)cos (sin ln 612.。
几种特殊函数的积分

p p x px q x q , 2 4 p 令 x t 2
记 x 2 px q t 2 a 2 ,
则
Mx N Mt b,
p2 2 a q , 4
Mp b N , 2
Mx N 2 dx n ( x px q ) Mt b 2 dt 2 dt 2 n 2 n (t a ) (t a )
真分式化为部分分式之和的待定系数法
x3 x3 A B 例1 2 , x 5 x 6 ( x 2)( x 3) x 2 x 3
x 3 A( x 3) B( x 2), x 3 ( A B ) x ( 3 A 2 B ),
1 dx . 例4 求积分 2 x( x 1) 1 1 1 1 dx 解 2 2 dx x ( x 1) x ( x 1) x 1 1 1 1 dx dx dx 2 x ( x 1) x 1
1 ln x ln x 1 C. x 1
三、简单无理函数的积分
ax b 讨论类型 R( x, ax b ), R( x , ), cx e
n
n
解决方法 作代换去掉根号.
1 1 x 例10 求积分 dx x x
解
1 x 2 1 x 令 t t , x x
1 sin x dx. 例9 求积分 sin 3 x sin x A B A B 解 sin A sin B 2 sin cos 2 2 1 sin x 1 sin x sin 3 x sin x dx 2 sin 2 x cos x dx 1 sin x dx 2 4 sin x cos x 1 1 1 1 dx dx 2 2 4 sin x cos x 4 cos x
第4节 有理函数的不定积分

Mx + N ; 特殊地: 特殊地:k = 1, 分解后为 2 x + px + q
说明 将有理函数化为部分分式之和后,只出 将有理函数化为部分分式之和后, 现三类情况: 现三类情况:
A Mx + N (1) 多项式; ( 2) 多项式; ; ( 3) ; n 2 n ( x − a) ( x + px + q ) Mx + N dx , 讨论积分∫ 2 n ( x + px + q )
2x3 + 5x 2x2 + 5 解 原式 = ∫ x4 + 5x2 + 4dx + ∫ x4 + 5x2 + 4dx
1 d( x4 + 5x2 + 5) ( x2 +1) + ( x2 + 4) = ∫ 4 dx +∫ 2 2 2 2 x + 5x + 4 ( x +1)( x + 4)
1 1 1 4 2 + 2 )dx = ln x + 5x + 4 + ∫ ( 2 x +1 x + 4 2
1 = ln x4 + 5x2 + 4 + arctanx + 1arctan x + C. 2 2 2
注意 将有理函数分解为部分分式求积分虽可行, 将有理函数分解为部分分式求积分虽可行, 但不一定简便 ,因此要注意根据被积函数的结构 特点,灵活处理,寻求简便的方法求解. 特点,灵活处理,寻求简便的方法求解. 例6 求积分 解
2u+1+ u2 −1− u2 2u du du = 原式 = 2 2 (1+ u)(1+ u ) (1 + u)(1 + u )
第4节有理函数的不定积分

2
2
2
例2
求积分
1 sin4
x
dx.
解
令utanx, 2
sinx12uu2 ,
dx12u2du,
1 sin4
x
dx
13u28u34u4u6du
1 8[31 u3u 33uu 33]C 2 4 t1 a2 x n 38t3 a2 xn 8 3ta2 xn 2 1 4 ta2 x n 3C .
解法二
令 utaxn ,则sinx
u, 1u2
dx11u2
du,
1 sin4 xdx
1 u
4 11u2du
1u2
1 u2 u4
du
31u3
1C u
1co3xtcoxtC. 3
解法三
1 sin4
dx x
cs4cxdxcs2x ccs2xc dx
令 t pa x b,其中p为m,n的最小公.倍数
例1
求积分
1
dx 3x
2
.
解 令 t3x2, 则 xt32,dx3t2dt,
原式 13t2tdt 3(t211)t1dt 3(t11 1t)dt
31 t 2 tln1t C
2 33 (x2)2 33 x23ln13x2C.
原式 (1u)2u 1 (u2)du 2u( 11u)u(12 1u 2)u2du
(1(1u)u2)(1(1u2u)2)du
1u 1u2
du
1 du 1 u
arctuan 1ln(1u2)ln |1u|C
2
x ln| secx | ln|1taxn|C.
高数同济44有理函数三角函数及一些无理函数的不定积分

例4 求积分
1 x(x 1)2dx.
解 x(x11)2dx1 x(x 11)2x1 1dx
1 xd x(x 11)2d xx1 1dx
ln x1ln x (1)C . x1
1
例5 求积分 (12x)(1x2)dx.
解 (12x)1(1x2)dx1542xdx152xx215dx
5 2 ln 1 2 ( x ) 1 5 1 2 x x 2d x 1 5 1 1 x 2 dx
由代数学定理:
Q(x)=b0(x-a) …(x-b) (x2 +px+q) …(x2+rx+s)
Q(x)=b0(x-a) …(x-b) (x2 +px+q) …(x2+rx+s)
难点 将有理函数化为最简分式之和.
设 Q P((x x))b a 00 x x m n b a 1 1x xm n 1 1 b am n 1 1x x a bn m是真 . 分
例12
求积分
x 3x1
d.x 2x1
解 先对分母进行有理化
原式 (3 x 1 x (2 3 x x 1 1 ) (3 2 x x 1 1 )2 x 1 )dx
(3x 12x 1 )dx
1 3 3x1d(3x1)1 2 2x1d(2x1)
2(3x1)2 31(2x1)2 3C .
例1 x3 x2 5x6
化为最简分式之和.
x3 A B ,
待
(x2)(x3) x2 x3
定
x 3 A ( x 3 ) B ( x 2 ),系
数
x 3 ( A B ) x ( 3 A 2 B ), 法
A(3A B21,B)3,
《高等数学》第五章 5.4 有理函数、三角函数及一些无理函数的不定积分

x
p 2
C;
2
a
a
Mx N
(2) n 1, ( x2 px q)n dx
2(n
M 1)(t 2
a 2 )n1
b
(t 2
1 a2 )n
dt .
P209例9
这三类积分均可积出, 且原函数都是初等函数.
结论 有理函数的原函数都是初等函数.
首页
上页
返回
下页
结束
二、三角函数有理式的积分
) dx
,
令
tn
a xb c xd
R(x , n ax b , m ax b) dx ,
令 t p ax b , p为m, n的最小公倍数 .
首页
上页
返回
下页
结束
P217-9
例10 求积分
1
x
1 xdx x
解令
1 x t 1 x t2,
x
x
x
结束
P214-3
例4 求积分
1 x( x 1)2dx.
解
1 x(x
1)2dx
1 x
(x
1 1)2
x
1
1
dx
1dx x
(
x
1 1)2
dx
x
1
dx 1
ln x 1 ln( x 1) C. x1
首页
上页
返回
下页
结束
P214-4
du )
几种特殊类型函数地积分

几种特殊类型函数的积分一、有理函数的不定积分1.化有理函数为简单函数两个多项式的商所表示的函数)(x R 称为有理函数,即mm m m m nn n n n b x b x b x b x b a x a x a x a x a x Q x P x R ++++++++++==------122110122110)()()( (1) 其中n 和m 是非负整数;n a a a a ,,,,210 及m b b b b ,,,,210 都是实数,并且0,000≠≠b a .当(1)式的分子多项式的次数n 小于其分母多项式的次数m ,即m n <时,称为有理真分式;当m n ≥时,称为有理假分式.对于任一假分式,我们总可以利用多项式的除法,将它化为一个多项式和一个真分式之和的形式.例如12)1(112224+++-=+++x x x x x x . 多项式的积分容易求得,下面只讨论真分式的积分问题.设有理函数(1)式中m n <,如果多项式)(x Q 在实数围能分解成一次因式和二次质因式的乘积:μλβα)()()()()(220s rx x q px x b x a x b x Q ++++--= .其中s r q p b a ,,,,,,, 为实数;042<-q p ,…,042<-s r ;,,,βα μλ,, 为正整数,那末根据代数理论可知,真分式)()(x Q x P 总可以分解成如下部分分式之和,即βααα)()()()()(1121b x B a x A a x A a x A x Q x P -++-++-+-=-λββ)()(21112q px x N x M b x B b x B ++++-++-+-μλλλ)()(21121222s rx x S x R q px x N x M q px x N x M ++++++++++++++-srx x S x R s rx x S x R +++++++++-21222)(μμμ . (2) 其中i i i i i i S R N M B A ,,,,,,, 都是待定常数,并且这样分解时,这些常数是唯一的.可见在实数围,任何有理真分式都可以分解成下面四类简单分式之和: (1)a x A - , (2)k a x A )(- (k 是正整数,2≥k ), (3)qpx x B Ax +++2(042<-q p ), (4)kq px x B Ax )(2+++ (k 是正整数,04,22<-≥q p k ).2. 有理函数的不定积分求有理函数的不定积分归结为求四类简单分式的积分.下面讨论这四类简单分式的积分.(1)C a x A a x d ax A dx a x A +-=--=-⎰⎰ln )(1,(2)C a x k A a x d a x A dx a x A k k k+-⋅--=--=---⎰⎰1)(11)()()(, (3)dx qpx x B Ax ⎰+++2(042<-q p ). 将分母配方得)4()2(222p q p x q px x -++=++,作变量代换2px u +=,则du dx p u x =-=,2;由于04,0422>-<-p q q p ,记224a p q =-,于是 du a u B pu A dx p q p x B Ax dx qpx x B Ax ⎰⎰⎰++-=-+++=+++22222)2()4()2( du au ApB du a u Au ⎰⎰+-++=22222C au a Ap B a u A +-++=arctan 2)ln(222 C pq p x p q Ap B q px x A +-+--+++=22242arctan 42)ln(2.(4)dx q px x B Ax k⎰+++)(2 (04,22<-≥q p k ).作变量代换2px u +=,并记224a p q =-,于是⎰⎰⎰+-++=+++du a u ApB du a u Au dx q px x B Ax k k k )(2)()(22222. 其中第一个积分C a u k A a u d a u A du a u Au k k k ++⋅--=++=+--⎰⎰122222222)(1)1(2)()(2)(. 第二个积分可通过建立递推公式求得.记 ⎰+=kk a u du I )(22 利用分部积分法有⎰⎰++++=+=12222222)(2)()(k kk k a u du u k a u u a u du I du a u a a u k a u u k k ⎰++-+++=12222222)()(2)(122222)(+-++=k k kkI a kI a u u .整理得 k k k I ka k a u u k a I 22221212)(21-++⋅=+. 于是可得递推公式]2232)()1(21[111222----++⋅-=k k k I k k a u u k a I . (3)利用(3)式,逐步递推,最后可归结为不定积分C a u aa u du I +=+=⎰arctan 1221. 最后由2px u +=全部换回原积分变量,即可求出不定积分⎰+++dx q px x B Ax k )(2. 例1 求⎰++-dx x x x 22)32(1. 解⎰⎰++-+=++-dx x x dx x x x 2222]2)1[(21)32(1 ⎰⎰+-++=2222)2(2)2(1u du du u u x u]2212121[212)2(21222⎰+++⋅⨯⨯-+-=u du u u uC u u u +-++-=2arctan 221)2(212`C x x x x ++-+++-=21arctan 221)32(222.例2 求dx x x ⎰-2)1(1. 解 因为2)1(1-x x 可分解为1)1()1(122-+-+=-x C x B x A x x . 其中A ,B ,C 为待定系数.可以用两种方法求出待定系数.第一种方法:两端去掉分母后,得)1()1(12-++-=x Cx Bx x A . (4)即 A x C A B x C A +--++=)2()(12由于(4)式是恒等式,等式两端2x 和x 的系数及常数项必须分别相等,于是有⎪⎩⎪⎨⎧==--=+1020A C A B C A , 从而解得 1=A ,1=B ,1-=C .第二种方法:在恒等式(4)中,代入特殊的x 值,从而求出待定系数.如令0=x ,得1=A ;令1=x ,得1=B ;把A ,B 的值代入(4)式,并令2=x ,得C 2211++=,即1-=C .于是⎰⎰---+=-dx x x x dx x x )11)1(11()1(122 ⎰⎰⎰---+=dx x dx x dx x 11)1(112C x x x +----=1ln 11ln . 例3 求⎰+-+dx x x x 22)1)(1(22. 解 因为1)1(1)1)(1(2222222++++++-=+-+x E Dx x C Bx x A x x x , 两端去分母得)1)(1)(()1)(()1(22222+-++-+++=+x x E Dx x C Bx x A x234)2()()(x B E D A x D E x D A +-++-++=)()(C E A x C B E D --++-+-+.两端比较系数得 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=--=+-+-=+-+=-=+220200C E A C B ED BE D A D E D A ,解方程组得1=A ,2-=B ,0=C ,1-=D ,1-=E ,故dx x x x x x dx x x x )11)1(211()1)(1(2222222⎰⎰++-+--=+-+ dx x x dx x x dx x ⎰⎰⎰++-+--=11)1(211222C x x x x +-+-++-=arctan )1ln(21111ln 22 C x x x x +-+++-=arctan 1111ln22. 例4 求⎰+-+dx x x x 6532. 解 因为32)3)(2(36532-+-=--+=+-+x B x A x x x x x x ,两端去分母得 )2()3(3-+-=+x B x A x . 令2=x ,得5-=A ;令3=x ,得6=B .于是Cx x dx x x dx x x x +---=---=+-+⎰⎰2ln 53ln 6)2536(6532C x x +--=56)2()3(ln . 从理论上讲,多项式)(x Q 总可以在实数围分解成一次因式和二次质因式的乘积,从而把有理函数)()(x Q x P 分解为多项式与四类简单分式之和,而简单分式都可以积出.所以,任何有理函数的原函数都是初等函数.但我们同时也应该注意到,在具体使用此方法时会遇到困难.首先,用待定系数法求待定系数时,计算比较繁琐;其次,当分母的次数比较高时,因式分解相当困难.因此,在解题时要灵活使用各种方法.例5 求dx x x x x x ⎰+++++12232. 解dx x dx x dx x x x x dx x x x x x ⎰⎰⎰⎰+++=+++++=+++++1111)1)(1()1()1(12222232C x x +++=arctan 1ln .例6 求dx x x x x ⎰+-+-)54)(44(122 .解 dx x x x x x x x x dx x x x x ⎰⎰+-+-+--+-=+-+-)54)(44()44()54()54)(44(1222222dx x x dx x x ⎰⎰+--+-=54144122 ⎰⎰-+----=)2(1)2(1)2()2(122x d x x d xC x x +----=)2arctan(21.例7 求dx x ⎰+114. 解⎰⎰⎰+--++=+dx x x dx x x dx x 112111211142424dx x x x dx x x x ⎰⎰+--++=2222221112111121 )1(2)1(121)1(2)1(12122xx d xx x x d x x +-+--+-=⎰⎰C x x x x x x ++++---=1212ln 24121arctan 221222.二、三角函数有理式的积分由三角函数和常数经过有限次四则运算所构成的函数称为三角函数有理式.因为所有三角函数都可以表示为x sin 和x cos 的有理函数,所以,下面只讨论)cos ,(sin x x R 型函数的不定积分.由三角学知道,x sin 和x cos 都可以用2tan x 的有理式表示,因此,作变量代换2tan x u =,则222122tan12tan22sec 2tan22cos 2sin 2sin u u x xx x x x x +=+===, 22222222112tan 12tan 12sec 2tan 12sin 2cos cos u u x xx x x x x +-=+-=-=-=. 又由u x arctan 2=,得du u dx 212+=,于是 ⎰⎰++-+=du u u u u u R dx x x R 222212)11,12()cos ,(sin . 由此可见,在任何情况下,变换2tan x u =都可以把积分dx x x R )cos ,(sin ⎰有理化.所以,称变换2tan x u =为万能代换.例8 求dx xx ⎰++cos sin 11. 解 设2tan x u =,则du u du u u u u u dx x x ⎰⎰⎰+=+⋅+-+++=++1112111211cos sin 112222C xC u ++=++=2tan1ln 1ln . 例9 求dx xx ⎰-+cos 1sin 1.解 设2tan x u =,则du u u u u du u u u u u dx xx ⎰⎰⎰+++=+⋅+--++=-+)1(2)1(12111121cos 1sin 12222222du u u du u ⎰⎰++=)1(2122du u u u u du u ⎰⎰+-++=)1()1(212222⎰⎰⎰+-+=du u u du u du u 2212121C u u u ++-+-=)1ln(ln 212 C x x x +--=)2ln(sec 2cot 2tan ln 22.虽然利用代换2tan x u =可以把三角函数有理式的积分化为有理函数的积分,但是,经代换后得出的有理函数积分一般比较麻烦.因此,这种代换不一定是最简捷的代换.例10 求dx xx ⎰+sin 1sin . 解 dx x x x dx xx x dx x x ⎰⎰⎰-=--=+222cos sin sin sin 1)sin 1(sin sin 1sin dx xx dx x x ⎰⎰--=222cos cos 1cos sin ⎰⎰⎰+--=dx dx x x d x 22cos 1cos cos 1C x x x ++-=tan cos 1. 例11 求dx x ⎰+2cos 311. 解x d x dx x x dx xtan 4tan 13sec sec cos 3112222⎰⎰⎰+=+=+ C x +=)2tan arctan(21.三、简单无理函数的积分(一)),(nb ax x R +型函数的积分),(u x R 表示x 和u 两个变量的有理式.其中a ,b 为常数.对于这种类型函数的积分,作变量代换u b ax n=+,则a b u x n -=,du anu dx n 1-=,于是 du a nuu a b u R dx b ax x R n n n 1),(),(-⋅-=+⎰⎰ . (5)(5)式右端是一个有理函数的积分.例12 求⎰++dx x 3211. 解 令u x =+32,则23-=u x ,du u dx 23=,于是⎰⎰⎰++-=+=++du u u du u u dx x 111313211223 C u u u du u u +++-=++-=⎰)1ln 2(3)111(32C x x x +++++-+=333221ln 323)2(23.例13 求dx xx ⎰+31.解 为了同时去掉被积函数中的两个根式,取3和2的最小公倍数6,并作变量代换u x =6,则6u x =,du u dx 56=,23u x =,3u x =,于是du u u du u u dx xx⎰⎰⎰+=+=+1616128283u d uu u u ⎰++-+-=)111(62246 C u u u u u ++-+-=arctan 6625676357 C x x x x x x ++-+-=66656arctan 6625676.(二)),(ndcx b ax x R ++型函数的积分 这里),(u x R 仍然表示x 和u 两个变量的有理式.其中d c b a ,,,为常数.对于这种类型函数的不定积分,作变量代换u d cx b ax n=++,则nn cu a b du x --=,du cu a bc ad nu dx n n 21)()(--=-,于是du cu a bc ad nu u cu a b du R dx d cx b ax x R n n n nn21)()(),(),(--⋅--=++-⎰⎰. (6) (6)式右端是一个有理函数的积分.例14 求dx xx x ⎰+11. 解 令u x x =+1, 则112-=u x ,du u u dx 22)1(2--=,于是 duu u du u u du u u u u dx x x x ⎰⎰⎰⎰-+--=--=--⋅-=+111212)1(2)1(112222222C u u u du u ++---=-+-=⎰11ln 2)111(22C u u u +--++-=1ln )1ln(222 C x x xx x++++++-=ln )11ln(212.例15 求dx x x ⎰-+342)1()1(1.解 ⎰⎰+--+=-+dx x x x x dx x x 334211)1)(1(1)1()1(1,令ux x =+-311,则311u x x =+-,3311u u x -+=,du u u dx 232)1(6-=, 于是du u dx x x x dx x x ⎰⎰⎰=+--=-+23234212311)1(1)1()1(1C x x C u +-+-=+-=3112323.。
几种特殊类型函数的积分

2
.
解 设 3 x 2 u .于是xu22,dx3u2d u ,从而
1
dx 3x
2
1
1 u
·3u2d u
3
u2 1
1du u
3 (u
1 1 )du 1 u
3(
u2 2
uln|1u|)C
3 3 (x 2)2 33 x 2 ln |1 3 x 2 | +C. 2
练习
求积分:
(1)
2
dx cos
an bm
其中m和n都 是非负整数;a0 ,a1 ,a2 ,… ,an 及b0 ,b1 ,b2
,… ,bm都是实数,并且a00,b00.当n<m时,称这有理函数
是真分式;而当nm时,称这有理函数是假分式.假分式总可以
化成一个多项式与一个真分式之和的形式.例如
x3 x 1 x2 1
x
1 x2 1
.
例2 求
x
2
x
2 2x
3
dx
.
解
x2
x
2
2 x
3
dx
(1 2
x
2x 2 2 2x
3
3
x
2
1 2
x
)dx 3
1 2
x
2x 2 2 2x
dx 3
3
x
2
1 2
x
dx 3
1 2
d (x2 2x 3) x2 2x 3
3
d (x 1) (x 1)2 ( 2)2
1 ln(x2 2x 3) 3 arctan x 1 C .
2
dx.
解
x2
3x 1 3x
几种特殊类型函数的积分

x 2 tan 2
2u 1 u
2 du dx 1 u
2
2
1 u 1 u
2
2
2
2 tan
万能代换
sin x dx. 例7. 求(1) 1 sin x
1 dx. (2) 3 cos x
利用万能公式处理比较复杂,更多地是利 用三角恒等式化简被积函数
1 dx. 例8. 求 2 sec x sin x tan x
例5. 求
( x 2 x 2) (2 x 2) dx 解: 原式 2 2 ( x 2 x 2)
dx d( x 2 2 x 2) 2 2 ( x 1) 1 ( x 2 x 2) 2
2
1 arctan(x 1) 2 C x 2x 2
( m n)
例9. 求
和差化积公式
解:
1 1 ∴原式 = sin 4 x dx sin 2 x d x 2 2 1 1 sin 4 x d(4 x) sin 2 x d(2 x) 4 8
1 sin x cos3x (sin 4 x sin 2 x) 2
解: (1)用赋值法
1 A B C 1 1 1 2 2 x( x 1) x x 1 ( x 1) x x 1 ( x 1) 2
右端通分后比较两端分子得
1 A( x 1)2 Bx( x 1) Cx 令 x=0 得 A=1 令 x=1 得 C=1 令 x=2 得 B=-1
例2. 求 解: 原式 1
4 1 2x 1 dx dx 2 5 1 2x 5 1 x 2 d(1 2 x) 1 2 x dx 1 dx 1 x2 1 x2 5 5 5 1 2x 2 2 1 d ( 1 x ) 1 arctan x ln 1 2 x 5 5 5 1 x2
有理函数的不定积分(3)

s
inx(1sinx cos 2 x
)dx
csoisn2xxdx
tan
2
xdx
secx tan xdx (sec2 x 1)dx secx tan x x C
18
(3)
sin3 x dx
2cos x
解:
sin3 x 2cos x
dx
(1cos 2 x 2cos x
)d
(cos
x)
令cos xt
sin(x2 )dx ,
1ksin2 xdx(0k1) ,
1 dx 等。 1 x4
我们称这些积分是“积不出来的”。 有理函数的不定积分是可以积出来的,即有理函数的
原函数都是初等函数,其原函数是有理函数、对数函数、
反正切函数。
20
作业
习 题 七 (P174)
1(1)(2)(3)(5); 2 ;3 ; 4 ;5 (2)(4);6(1)。
21
说明 将有理函数化为部分分式之和后,只出 现三类情况:
(1) 多项式;
(2)
(
x
A a
)n
;
Mx N (3) ( x2 px q)n ;
讨论积分
Mx N ( x2 px q)n dx,
x2
px q x
p 2
q
p2 ,
2
4
(
x
Mx 2 px
N q
)n
dx
令 x pt 2
例上4面. 求介下绍列的积是分有:理函数积分的常规方法,在具体解题时,
应优先考虑其他简便方法。
①
x
x3 2 8dx
1 3
d
( x3 8) x38
1ln 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§3.6 有理函数及三角函数有理式的积分教学目的:使学生理解有理函数及三角函数有理式积分法,掌握有理函数及三角函数有理式积分法的一般步骤及其应用。
重点:有理函数及三角函数有理式积分法及其应用 难点:有理函数及三角函数有理式积分法及其应用教学过程:一、问题的提出前面两节我们利用基本积分表、不定积分性质和两种基本积分发(换元积分法与分部积分法)已经求出了一些不定积分。
从求解过程中可见,求不定积分不像求导数那样,只要按照求导法则并利用基本求导公式就一定能求出一个函数的导数,而求不定积分却没有那样容易。
即使一个看起来并不复杂的函数,要求出结果,有时候都需要一定的技巧,有些甚至还“积不出”。
例如,⎰⎰⎰⎰+-31,,ln ,sin 2x dx dx e x dx dx x x x ,被积函数都是初等函数,看起来也并不复杂,但是在初等函数范围内却积不出来,这是因为被积函数的原函数不是初等函数。
本节主要介绍几类常见的函数类型的积分方法与积分计算技巧。
求不定积分的主要方法有“拆、变、凑、换、分、套” “拆”,即将被积函数拆项,把积分变为两个或几个较简单的积分。
“变”,即代数恒等变形:加一项减一项、乘一项除一项、分子分母有理化、提取公因子;三角恒等变形:半角、倍角公式,平方和公式,积化和差、和差化积、和角公式;陪完全平方:根号下配完全平方、分母配完全平方等;“凑”,即凑微法(第一类换元法)。
“换”,即第二类换元法(三角代换、倒代换、指数代换法等)。
“分”,即分部积分法。
“套”,即套基本公式。
求不定积分的主要技巧在一个“巧”字和一个“练”字,即巧用上述方法和综合运用上述方法。
二、 有理函数的积分有理函数)(x R 是指由两个多项式的商所表函数,即=)(x R m m m m nn n n b x b x b x b a x a x a x a x Q x P +++++++=----11101110)()(ΛΛ 其中m 和n 都是非负整数;n a a a a ,,,,210Λ及m b b b b ,,,,210Λ都是实数,通常总假定分子多项式)(x P 与分母多项式)(x Q 之间没有公因式,并且00≠a ,00≠b .当m n <时,称)(x R 为真分式;而当m n ≥时,称)(x R 为假分式. 一个假分式总可化为一个多项式和一个真分式之和的形式.例如111122234-++++=-+x x x x x x x .多项式的积分容易计算,因此,有理函数的积分主要是解决真分式的积分问题,而真分式的积分往往是转化为最简分式来计算.鉴此,我们先来讨论真分式分解为最简分式问题.在实数范围内,真分式)()(x Q x P 总可以分解成最简分式之和,且具有这样的对应关系:① 如果)(x Q 中有因式ka x )(-,那么分解后相应有下列k 个最简分式之和)()()(121a x A a x A a x A k k k -++-+--Λ, 其中1A 、2A 、…、k A 都是常数.特别地,如果1=k ,那么分解后只有一项a x A-;② 如果)(x Q 中有因式k q px x )(2++(042<-q p ),那么分解后相应有下列k 个最简分式之和q px x N x M q px x N x M q px x N x M k k k k ++++++++++++-21222211)()(Λ,其中i M 、i N 都是常数.特别地,如果1=k ,那么分解后只有一项q px x NMx +++2. 有理真分式总能分解为若干个部分分式之和的形式(部分分式是指这样一种简单分式,其分母为一次因式或二次质因式)。
从而得到,有理真分式的积分总可以归纳为以下四种形式的部分分式的积分:(1);dx a x A⎰- (2)dx a x A n ⎰-)( (2))04(22<-+++⎰q p dx q px x NMx(3)⎰<-+++为常数、、其中系数N M A q p dxq px x NMx n ),04()(22综上所述,有理函数分解为多项式及部分分式之和以后,各个部分都能积出,且原函数都是初等函数,因此,有理函数的原函数都是初等函数。
由上述定理,我们得到求有理真分式不定积分dx x Q x P m n ⎰)()(的步骤书为:第一步 将)(x Q m 分解为(2)的形式; 第二步 将)()(x Q x P m n 分解为(3)的形式;第三步 求各部分分式的原函数。
下面通过具体的举例来说明分解的方法和步骤.例1 把2)1(1-x x 分解为最简分式之和.解:根据真分式的性质可设2)1(1-x x =)1()1(2-+-+x C x B x A上式两端去分母后,得)1()1()1(12-++-=x Cx Bx x A 或)2()2()(12Ax C B A x C A +-+-++=因为这是恒等式,等式两端对应项的系数应相等,于是有⎪⎩⎪⎨⎧==-+-=+1020A C B A C A从而解得1=A ,1=B ,1-=C .于是得2)1(1-x x =)1(1)1(112---+x x x . 注:此题定A 、B 、C 还有另法: 在恒等式⑴中,代入适当的x 值,即可求出待定的常数.在式⑴中令1=x ,得1=B ; 令0=x ,得1=A ; 再令2=x ,得1-=C .于是得2)1(1-x x =)1(1)1(112---+x x x .例2 把6532+-+x x x 分解为最简分式之和.解:因为)3)(2(652--=+-x x x x 所以,令6532+-+x x x 32-+-=x Bx A ,其中A 、B 为待定常数. 上式两端去分母后,得)3()2()3(3-+-=+x B x A x 或)4()23()(3B A x B A x +-+=+比较两端系数有⎩⎨⎧=+-=+3)3(1B A B A从而解得 5-=A ,6=B .所以6532+-+x x x 3625-+--=x x注:此题也可以采用上例第二种方法确定待定系数.例3 把)22)(2(22+++x x x x 分解为最简分式之和.解:因为分母中222++x x 为二次质因式,故应分解为)22)(2(22+++x x x x ++=2x A 222+++x x CBx两端去分母得)2)(()22(22+++++=x C Bx x x A x比较两端对应项的系数不难求得2=A ,1-=B ,2-=C 所以)22)(2(22+++x x x x -+=22x 2222+++x x x由上可知,有理函数总能分解为多项式及最简分式之和,其积分最终归结为多项式、a x A-、k a x A )(-、q px x N Mx +++2、k q px x N Mx )(2+++)04,1,(2<->∈q p k N k 等五类函数的积分.显然,前面四类都比较容易积出,我们将在下面的例子中进行介绍,而对于最后一类积分较繁,其结果可通过查阅积分表求得,这里不作讨论.例4 求dx x x x x x ⎰+-++-65924223.解:因为++=+-++-165924223x x x x x x 6532+-+x x x 又由前面例2知6532+-+x x x 3625-+--=x x 所以,dx x x x x x ⎰+-++-65924223⎰⎪⎭⎫ ⎝⎛-+--+=dxx x x 36251 C x x x x +-+--+=3ln 62ln 522例5 求⎰-dxx x 2)1(1.解:因为2)1(1-x x =)1(1)1(112---+x x x所以⎰-dx x x 2)1(1⎰⎪⎪⎭⎫ ⎝⎛---+=dx x x x )1(1)1(112⎰=dx x1⎰-+dx x 2)1(1⎰--dx x 11 Cx x x +----=1ln 11ln .例6 求⎰+++dxx x x x )22)(2(22.解:由例3可得⎰+++dx x x x x )22)(2(22-+=⎰dx x 22⎰+++dx x x x 2222又⎰+++dx x x x 2222⎰++++=dx x x x 221)22(212⎰+++=dx x x x 2222212⎰+++dx x x 2212 ⎰++++=22)22(2122x x x x d ⎰++++1)1()1(2x x d C x x x +++++=)1arctan(22ln 212从而⎰+++dx x x x x )22)(2(22Cx x x x ++-+++=)1arctan(22)2(ln 22二、三角函数有理式的积分由三角函数和常数经过有限次四则运算所构成的函数称为三角有理式。
由于各种三角函数都可用x x cos sin 及的四则运算来表示,故三角函数有理式也可以说是由x x cos sin 、及常数经过有限次四则云素所构成的函数,记为)cos (sin x x R ,,其中),(v u R 表示两个变量的 有理式,积分⎰dx x x R )cos ,(sin 称为三角有理式的积分。
下面通过举例来说明这类函数的积分方法.例7 求⎰++dx x x cos sin 11.解:因为2cos 2sin 2cos 2sin 2sin 22xx x x x +=2tan 12tan22x x += 2cos 2sin 2sin 2cos cos 2222xx x x x +-=2tan 12tan 122x x +-= 所以,令u x=2tan,则u x arctan 2=,于是=x sin 212u u +,=x cos 2211u u +-,=dx 212u du+.代入原积分得⎰++dx x x cos sin 11⎰++-+++=222212111211u duu u u u⎰+=du u 11C u ++=1lnCx++=2tan 1ln .一般说来,对于三角函数有理式积分,总可作变量代换u x=2tan,将其转化为u 的有理函数的积分.即有 dx x x R ⎰)cos ,(sin ⎰+⎪⎪⎭⎫ ⎝⎛+-+du u u u u u R 22221211,12例8 求⎰++dx x x x)cos 1(sin sin 1解:令u x=2tan,则u x arctan 2=,于是 ⎰++dx x x x )cos 1(sin sin 1⎰⎪⎭⎫⎝⎛++=du u u 2121C u u u +++=241ln 21 C x x x +++=2tan 2tan 412tan ln 212.最后需要指出的是:上面所谈两类函数的积分方法是常规方法,虽然有效但往往非常麻烦,因此,在具体解题时,应尽量采用其它简便方法,只有在用其它方法难以积分的情况下才采用上述方法.如下面的例题例9 求⎰+dx x x 132解:此题属于有理函数积分,可采用上述常规方法做,但用下列方法计算较简便⎰+dx x x 132⎰++=1)1(3133x x d C x ++=1ln 313.例10 求⎰-+dxx x 2)1(5.解:此题也属于有理函数积分,用下列做法计算较简便⎰-+dx x x 2)1(5⎰-+-=dx x x 2)1(6)1(+-=⎰dx x 11⎰-dxx 2)1(16+--=⎰)1(11x d x ⎰--)1()1(162x d xCx x +---=161ln例11 求⎰+dx x xsin 1sin .解:此例属于三角函数有理式积分,用下面做法计算较为简便⎰+dx x x sin 1sin ⎰-=dx x x x 2cos )sin 1(sin ⎰=dx x x2cos sin ⎰--dx x x 22cos cos 1⎰-=xx d 2cos )(cos ⎰-dx x 2cos 1⎰+dx C x x x ++-=tan cos 1ux=2tan形如)0(cos sin cos sin 22≠+++⎰b a dx x b x a x d x c 的积分,一般可将被积函数的分子凑成分母与分母的导数的线形组合,即令)cos sin ()cos sin (cos sin '+++=+x b x a B x b x a A x d x c ,通过比较等式两端x x cos sin 和的系数,求出A 和B.对形如⎰⎰⎰nxdx mx nxdx mx nxdx mx cos cos ,sin sin ,cos sin 的积分一般是将被积函数积化和差后再积分。
