8定积分应用(积分中值定理,求极限,变上限

合集下载

定积分的几个简单应用

定积分的几个简单应用一、定积分在经济生活中的应用在经济管理中，由边际函数求总函数，一般采用不定积分来解决，或者求一个变上限的定积分；如果求总函数在某个范围的改变量，则采用定积分来解决．例1 某商场某品牌衬衫的需求函数是q p 15.065-=，如果价格定在每件50元，试计算消费者剩余．解由p 50=，q p 15.065-=，得10000=q ，于是dq q )5015.065(100000--⎰10000023)1.015(q q -=50000=，所求消费者剩余为50000元．例2 已知某产品总产量的变化率为t t Q 1240)(+='（件／天），求从第5天到第10天产品的总产量．解所求的总产量为⎰⎰+='=105105)1240()(dt t dt t Q Q 1052)640(t t +=650=（件）．二、用定积分求极限例1 求极限 ∑=∞→n k n n k 123lim ．解 nn n n n n n n k n k 12111123+++=∑= )21(1nn n n n +++= ．上式是函数[]1,0)(在x x f =的特殊积分和．它是把[]1,0分成n 等分，i ξ取⎥⎦⎤⎢⎣⎡-n i n i ,1的右端点构成的积分和．因为函数[]1,0)(在x x f =可积，由定积分定义，有∑=∞→n k n n k 123lim ⎥⎦⎤⎢⎣⎡+++=∞→)21(1lim n n n n n n 3210==⎰dx x ．例2 求极限 2213lim k n n k n k n -∑=∞→．解 212213)(11n k nk n k n n k n k n k -⋅=-∑∑==．上式是函数[]1,01)(2在x x x f -=的特殊积分和．它是把区间[]1,0分成n 等分，i ξ取⎥⎦⎤⎢⎣⎡-n i n i ,1的右端点构成的积分和．因为函数21)(x x x f -=在[]1,0可积，由定积分定义，有2213lim k n n k n k n -∑=∞→31)1(31110232102=⎥⎦⎤⎢⎣⎡--=-=⎰x dx x x ．三、用定积分证明不等式定积分在不等式的证明中有着重要的应用．在不等式的证明中，可根据函数的特点，利用定积分的性质来证明．例1 设)(x f 是闭区间[]b a ,上的连续函数，且单调增加，求证：⎰⎰+≥b ab a dx x f b a dx x xf )(2)(．证明作辅助函数 dt t f x a dt t tf x xa x a ⎰⎰+-=)(2)()(ϕ，显然0)(=a ϕ，且)(2)(21)()(x f x a dt t f x xf x x a ⎰+--='ϕ )(2))((21)(2x f a a x f x f x ---=ξ [])()(2ξf x f a x --=，其中[]x a ,∈ξ．因为)(x f 在[]b a ,上单调增加，所以0)(≥'x ϕ，从而)(x ϕ在闭区间[]b a ,上单调增加，所以0)()(=≥a x ϕϕ，取b x =得⎰⎰+≥b a ba dx x fb a dx x xf )(2)(．定积分在许多领域中有着重要应用，它是解决一些几何学问题、物理学问题和经济学问题的重要工具．这一章主要介绍了定积分在不同学科中的应用问题．。

定积分微积分基本公式

T1
T2
一般地，若 F ( x ) f ( x )

b
a
? F (b) F (a ) f ( x )dx
在解决这个问题之前，先讨论原函数存在问题.
设函数f ( x )在[a, b]上连续,当x取[a , b]上任一定值时,
a
x
f ( t )dt 有唯一确定值与 x对应 , 因此a f ( t )dt 在
n 1 dx 1 1 1 1 xi lim lim n n 1 0 1 x n2 2n n i 0 1 i
小结
1 . 变上限定积分 F ( x ) a f ( t )dt 2. 变上限定积分的导数 F ' ( x ) f ( x ) 3. 牛顿—莱布尼兹公式
又

a
(x)
a
x
f ( t ) dt 也是 f ( x ) 的一个原函数 ,
F ( x ) ( x ) C , x [a , b ] 令
x a F ( a ) ( a ) C ,
(a ) a f ( t )dt 0 C F (a ) . F ( x ) ( x ) F (a ) .
即任何一个连续函数必存在原函数。
如
x
a
sin t sin x dt 是的一个原函数 t x
例1.计算( x )
0
x
sin t 2dt在x 0处的导数
d x d x 2 2 f (t )dt f ( x ) sin x 解 ( x ) sin t dt a dx dx 0

2
1 2
0 (1 cos x ) dx

变上限定积分及微积分基本定理

dx 1
d
x
xf (t)dt
d
x
tf (t)dt
dx 1
dx 1
d
x
x
f (t)dt
d
x
tf (t)dt
dx 1
dx 1
x
x
f (t)dt xf ( x) xf ( x) f (t)dt
1
1
第6页/共15页
推广1：若 f ( x)连续,( x)可导
则 d
(x)
f (t)dt
f [ ( x )] ( x )
dx a
推导：设( x)
(x)
f (t)dt
( x)u
u
f (t)dt
d
a
d du f (u)( x)
a
f [ ( x)] ( x)
dx du dx
推广2：
d ( x) f (t )dt f [ ( x )] ( x) f [ ( x )] ( x)
1 e t 2 dt
lim
x0Biblioteka cos xx2(0) 0
lim x0
ecos2 x ( sin x)
2x
1 2e
(
lim x
x et2dt)2
0
x e2t2dt
0
()
lim x
2
x et2dt
0
e x2
()
e2x2
lim x
2e x2 2x ex2
0
第8页/共15页
定理1（p119）（微积分基本定理）
证
x x
( x x) a f (t)dt
( x x) ( x)
( x)

积分中值定理与定积分应用积分中值定理与定积分应用的实战技巧

积分中值定理与定积分应用积分中值定理与定积分应用的实战技巧积分中值定理与定积分应用的实战技巧积分中值定理和定积分是微积分中的重要概念，能够帮助我们解决各种实际问题。

本文将介绍积分中值定理和定积分的基本概念，以及如何应用这些概念来解决实际问题。

一、积分中值定理积分中值定理是微积分中的基本定理之一，它与导数中值定理有密切关联。

积分中值定理表明，若函数f(x)在闭区间[a,b]上连续，且在开区间(a,b)上可导，则在[a,b]上至少存在一点c，使得函数的平均值等于函数在c处的导数值。

其数学表达式如下：∫[a,b] f(x) dx = f(c) (b-a)其中，f(x)表示在[a,b]上的连续函数，c为[a,b]上的某一点，b和a 分别为积分上限和下限。

积分中值定理的应用十分广泛。

它可以用于证明其他定理，例如柯西中值定理和拉格朗日中值定理。

除了数学的理论性应用外，积分中值定理还可用于解决实际问题，如求函数在某个区间上的平均值、证明函数在某个区间上的增减性等。

下面将以一个具体例子来说明积分中值定理的应用。

例子：求函数f(x) = 2x^2 + 3x在区间[1,3]上的平均值。

解：根据积分中值定理，函数f(x)在[1,3]上的平均值等于函数在该区间上某一点的函数值。

首先，我们计算函数f(x)在[1,3]上的定积分：∫[1,3] (2x^2 + 3x) dx = (2/3)x^3 + (3/2)x^2 |[1,3] = 24然后，求出函数f(x)在[1,3]上的平均值：平均值 = (1/3 - 1/2) * 24 = 8所以，函数f(x) = 2x^2 + 3x在区间[1,3]上的平均值为8。

通过这个例子，我们可以看到积分中值定理的实际应用，它不仅使我们能够求出函数在某个区间上的平均值，还可以帮助我们判断函数在某个区间上的增减性。

二、定积分的应用定积分是对区间上函数值的累加，可以用于求解曲线下面的面积、体积、平均值等问题。

含有积分的一些极限问题的解法

1
4Πt5
f
x 2+ y 2+ z 2≤t2
(x 2 +
y2 +
z 2) dx dy dz 1
解作球面坐标变换 x = rsinΥco sΗ, y = rsinΥsinΗ, z = rco sΥ, 有
µ ∫∫∫ lim
t→0+
1
4Πt5
f
x 2+ y 2+ z 2≤t2
(x 2 +
y2 +
z2) dx dy dz =
若满足 0 0
(或∞∞) 型未定式,
则可用罗必达法则来求其极限 1
这也是处理含有变上限积分极限的一般方法 1
∫x 2 f (t) d t
∫ 例 7 设 f ′(x ) 连续, f (0) =
0,
且f
′(0)
≠ 0,
求 lim x →0
0
x
x2 f
1 (t) d t
0
解所求极限满足
0 0
型未定式,
运用罗必达法则,
有
∫ 原式 =
lim
x →0
x 2f
f (x 2) (x ) + 2x
2x
x
f
= (t) d t
0
lim
x →0
f
(x )
2f ′(x 2) + x f ′(x )
2x + 2f
(x )
=
lim
x →0
3f
4f ′(x 2)
(x ) x
+
f ′(x )
=
11
五、利用不等式估计
若被积函数较容易放缩, 则可以先利用不等式放缩, 得到被积函数的不等式, 然后再用两边

定积分的概念与性质

用直线
将曲边梯形分成 n 个小曲边梯形;
2) 常代变.
在第i 个窄曲边梯形上任取
作以
为底 ,
为高的小矩形,
并以此小
矩形面积近似代替相应
窄曲边梯形面积
得
3) 近似和.
4) 取极限.
令
则曲边梯形面积
2. 变速直线运动的路程
设某物体作直线运动,
已知速度
求在运动时间内物体所经过的路程 s.
解决步骤: 1) 大化小.
定积分
换元积分法分部积分法
一、定积分的换元法二、定积分的分部积分法
一、定积分的换元法
定理1. 设函数
单值函数
满足:
1)
2) 在
上
则
证: 所证等式两边被积函数都连续, 且它们的原函数也存在 .
则
是
的原函数 ,
因此积分都存在 , 因此有
n 个小段
过的路程为
2) 常代变.
且
将它分成在每个小段上物体经
得
3) 近似和.
4) 取极限 .
上述两个问题的共性:
• 解决问题的方法步骤相同 :
“大化小 , 常代变 , 近似和 , 取极限 ”
• 所求量极限结构式相同:
特殊乘积和式的极限
二、定积分定义 (P225 )
任一种分法任取
总趋于确定的极限 I , 上的定积分,
可积的充分条件:
定理1. 定理2.
例1. 利用定义计算定积分解: 将 [0,1] n 等分, 分点为
取
且只有有限个间断点
(证明略)
注注. 当n 较大时, 此值可作为
的近似值
注
例2. 用定积分表示下列极限:

变上限函数的性质及其应用

变上限函数的性质及其应用作者连永龙系别统计与数学学院专业数学与应用数学年级2008级学号802091149指导教师邢华导师职称副教授评语：成绩：指导教师：年月日摘要：了解变上限函数的的定义并掌握其性质，用来解决定理、积分不等式、积分等式、敛散性的证明；极限、概率密度函数、重积分、不定积分的求解等问题。

从而，体会变上限函数的应用价值。

关键词：变上限函数性质应用变上限积分的改进引言变上限函数的引入及其定义：对于定义在[],a b 上的可积函数()f x 的定积分()d b af x x ⎰，若()f x 已知，则定积分为一确定的数。

现考虑，对任意的x 属于[],a b ，由定积分的性质得()f t 在[],a x 可积，且其结果为定义在[],a b 的函数。

于是定义这种函数为变上限函数： ()()d x aF x f t t =⎰[],x a b ∈变上限函数的性质及其相关定理一、与定积分相同的有关性：性质1、若()()d x aF x f t t =⎰[],x a b ∈，k 为常数，则()()d ()x aG x kf t t kF x ==⎰性质2、若f 、g 都在[],a b 上积分，且()()d x aF x f t t =⎰、()()d x aG x g x t=⎰[],x a b ∈，则()()f t g t ±在[],a x 可积，且[]()()d ()d ()d x xx a aaf tg t t f t t g t t ±=±⎰⎰⎰性质3、若f 、g 都在[],a x 上可积[],x a b ∈，则()()f tgt 在[],a x 上可积[],x a b ∈性质4、设()f x 为[],a b 上的可积函数，若()0f x ≥，[],x a b ∈，则()d 0xaf t t ≥⎰性质5、若()f x 在[],a b 上可积，则f 在[],a b 上也可积，且[]()d ()d ,x x aaf t t f t tx a b ≤∈⎰⎰这些性质可以类似证明定积分的性质来证明二、不定积分的特殊性质：（一）变上限函数的连续性定理：若()f x 在[],a b 上可积，则()()d x aF x f t t =⎰在[],a b 上是连续的。

定积分及其应用(思维导图)

条件：f(x)在[a,b]连续结论：区间内存在ξ使，f（x）在区间的积分结果=（b-a）· f（ξ）
积分中值定理可以去掉积分限
牛莱公式
凑微分法
凑微分法不会改变上下限的所属关系，上下限仍旧属于最简字母
分部积分法
第二类换元积分法
换积分上下限换被积函数换积分变量
几何意
比较定理
正的积分限
积分限相同，积分变量不同，用比较定理仅需比较两个被积函数的大小一个比你大，就绝对比你大
考研中常用的函数大小比较
定积分的应用
定积分的计算
对称区间，偶倍奇零
周期性
三角函数的周期上下限的长度为(n)T，永远可以在保证长度的情况下，变换积分起点终点→（对称区间或许为最优解）
积分中值定理
下限为0时候，牛逼爸➡奇偶互换
存在原函数F（x）为 f(x)的变上限函数
若f(x)连续
自变量位于上下限中，其核心思维在于求导→见到变限函数就想求导
上限求导*f(上限）- 下限求导*f(下限）能拉出来就来拉出来不能拉出来，就代换
标准型非标准型
求导法则
无穷区间的反常积分 ∞
无界函数的反常积分瑕点
①求和形式 ②提出来1/n
③找项【左端点】【右端点】【区间中点】
定积分的几何意义
“绝对面积”
考研中常考的圆画图确定定积分
加“-”变换积分上下限可加性：拆分区间积分定积分是一个数，与积分变量的字母选取无关
利用定积分定义求极限
求和形式、数列极限→首先定积分定义，再去夹逼
定积分及其应用
定积分的性质
加减法中都存在才能拆可加性按照瑕点进行拆分
拆开
①找瑕点 ②区间中间是否存在瑕点

考研——积分上限的函数(变上限积分、变限积分)知识点全面总结

考研——积分上限的函数（变上限积分）知识点()()xaF x f t dt =⎰形如上式的积分，叫做变限积分。

注意点：1、在求导时，是关于x 求导，用课本上的求导公式直接计算。

2、在求积分时，则把x 看作常数，积分变量t 在积分区间],[x a 上变动。

（即在积分内的x 作为常数，可以提到积分之外。

）关于积分上限函数的理论定理1如果)(x f 在],[b a 上连续，则)(x f 在（a ，b ）上可积，而)(x f 可积，则⎰=xa dtt f x F )()(在],[b a 上连续。

定理2如果)(x f 在],[b a 上有界，且只有有限个间断点，则)(x f 在（a ，b ）上可积。

定理3如果)(x f 在],[b a 上连续，则⎰=xa dt t f x F )()(在],[b a 上可导，而且有).(])([)(x f dt t f dx d x F xa=='⎰ ==========================================注：（Ⅰ）从以上定理可看出，对)(x f 作变上限积分后得到的函数，性质比原来的函数改进了一步：可积改进为连续；连续改进为可导。

这是积分上限函数的良好性质。

而我们知道，可导函数)(x f 经过求导后，其导函数)(x f '甚至不一定是连续的。

（Ⅱ）定理（3）也称为原函数存在定理。

它说明：连续函数必存在原函数，并通过定积分的形式给出了它的一个原函数。

我们知道，求原函数是求导运算的逆运算，本质上是微分学的问题；而求定积分是求一个特定和式的极限，是积分学的问题。

定理（3）把两者联系了起来，从而使微分学和积分学统一成为一个整体，有重要意义。

重要推论及计算公式：推论1)(])([x f dt t f dx d bx -=⎰ <变上限积分改变上下限，变号。

> 推论2)()]([])([)(x x f dt t f dxd x c ϕϕϕ'=⎰ <上限是复合函数的情况求导。

8定积分应用(积分中值定理,求极限,变上限解析

x 2
例
设f ( x )是连续函数，f ( 1 ) 1
ab a
若对的a , b有 f ( t )dt与a无关,求f ( x )
例.
例
.设f ( x )在0,1上连续，在0,1上可导
且f ( 0 ) 0 ,
1
0 f ( x ) 1
2
1 求证 : f ( x )dx f 3 ( x )dx 0 0
a a
结论3
设f ( x )是 a, a 内的连续函数，
证明若f ( x )为奇（偶）函数 ,
则0 f (t )dt 偶（奇）函数
x
例：当f ( x )是以2为周期的连续函数时，
证明：函数 G( x) 20 f (t )dt－ x 0 f (t )dt
也是以 2为周期的周期函数 08研
2 3
4
证明 2,4，使2 f ( ) (1 ) f ( )
变上限积分问题
1.变上限积分问题
( x) f (t ) d t
a
a
x
( x) ( f (t ) d t ) f ( x)
(被积函数中不含自变量x)
x
d ( x) f (t ) d t a dx
例.
d x2 2 求 1 t dt dx 0
例.
d x3 1 求 dt 2 dx x 1 t 4
d cos x 2 求 1 t dt dx sinx
例.
例. 求
0 0
例.
确定常数 a , b , c 的值, 使
例.
lim
x 0

x
1
cos x
t ln tdt

定积分求极限公式

定积分求极限公式1.中值定理2.大数定律3.独立变量的积分4.常用极限公式接下来，我将对这些公式进行详细的介绍。

1.中值定理中值定理是微积分中的一个重要定理，可以用来证明函数的连续性。

对于函数f(x)在闭区间[a,b]上连续并可导，在(a,b)内存在一个点c，使得f'(c)=(f(b)-f(a))/(b-a)。

根据中值定理，定积分的极限可以通过函数的导数和平均值来表示。

2.大数定律有很多情况下，定积分可以用来表示一些随机变量的数学期望（期望值）。

根据大数定律，当取样数量足够大时，随机变量的平均值会趋近于其数学期望。

这意味着当定积分的上下限趋近于无穷时，定积分的值会收敛到一个常数。

3.独立变量的积分对于含有一个或多个独立变量的积分，可以通过分离变量，将其转化为只含有一个变量的积分。

例如，如果要求解∫(x^2 + y^2) dx，可以将 y 视为常数，并对 x 进行积分。

这样就可以得到只关于 y 的积分表达式。

4.常用极限公式在定积分求极限过程中，还可以直接使用一些常用的极限公式来简化计算。

常用的极限公式包括：- 弧长公式：当 a < b 时，有lim(x→∞) ∫(a→b) f(x) dx =lim(x→∞) ∫(a→x) f(t) dt + lim(x→∞) ∫(x→b) f(t) dt；- 指数函数和对应的自然对数函数的极限：lim(x→0) (1 + x)^1/x= e；- 三角函数的极限：lim(x→0) sin(x)/x = 1；- 幂函数的极限：lim(x→∞) x^a = ∞，其中 a > 0；- 正无穷大与负无穷大的相加或相减：lim(x→∞) [f(x) ± g(x)]= lim(x→∞) f(x) ± lim(x→∞) g(x)；- 正无穷大与有界函数的乘积：lim(x→∞) [f(x) * g(x)] =lim(x→∞) f(x) * lim(x→∞) g(x)，其中lim(x→∞) f(x) 为正无穷大，g(x) 为有界函数。

微积分中值定理及其应用

微积分中值定理及其应用
微积分的值定理是一个很重要的定理，它通常被用来求解复杂函数的积
分值。

值定理告诉我们，任何一个定义在实数段上的函数f在范围
（a≤x≤b）上至多只有一个不变点，并且它等于函数f在这个范围上的积
分值c=∫a﹣b f（x）dx。

值定理有多种不同的应用，广泛用于函数积分、函数极限以及定积分的
解决。

用值定理求积分的方法通常称为值定理逼近法。

首先，将一个积分表
达式分解为多个函数的积分，然后利用值定理的思想，将这些函数的积分求出，最后，将这些函数的积分求和，即可得到原积分表达式的积分结果。

值定理也可以用来求解函数极限，即当函数f(x)在x=a处取极值时，将
该函数积分以得到极限。

这实际上是应用积分来求取极限的一种方法，也称
为值定理极限法或积分极限法。

它的原理是，当函数取到极值时，把它积分，就会把该函数的参量控制，也就可以使函数的值趋近极限的值，即求解函数
的极限。

值定理也被广泛应用于定积分的解决中。

定积分是由函数和定义域定义
的定积分问题，要求该函数在这个定义域上积分的结果。

一般来说，将定积
分分解为若干函数的积分，然后运用值定理解决，即将它们的积分和加起来，得到定积分问题的答案。

以上就是关于微积分中值定理及其应用的简单介绍。

它是微积分中一个
重要的定理，在函数积分、极限以及定积分的解决中应用的非常广泛，具有
极大的实际意义。

浙江省专升本高等数学考试定积分部分内容解析

:B$'
B %
h( 3
)%j
!: :) B):B)
h)%j
&
!: :B$') B$
!&
:B$'
hU[,VU-&
:B$
'
% j
h(3("
所以原积分 h(%
$ 八% 定积分的应用
应用题类型!一是求平面图形面积"二是求旋转体体积"三
是定积分应用与最值+或常微分方程+或变上限积分导数等内
容相结合的综合题%
&)' 2:h($) j()$% $):!:h() & $) B$'
例 $$&)%%0 年浙江省专升本考试计算题!$% 题' 当 ' 为何值时"抛物线 Bh:) 与三直线 :h'":h'B$"Bh% 所围成的图形
面积最小"求将此图形绕 :轴旋转一周所得的几何体的体积%
分析!此题是定积分应用与最值应用的综合题%
换元积分法与分部积分法% &9'理解无穷区间上有界函数的广
义积分与有限区间上无界函数的瑕积分的概念"掌握其计算方
法% &0'会利用定积分计算平面图形的面积以及平面图形绕坐
标轴旋转一周所得的旋转体的体积%
二分析历年定积分部分内容考试试题筛查这部分内容
考试热点
通过对历届浙江省专升本高等数学考试真题进行系统地
利用极限求出结果%
例 ' & )%%' 年浙江省专升本考试计算题 ! 1 题 ' 计

变上限定积分导数的应用

变上限定积分导数的应用上限定积分的导数也称为上极限导数，是微积分中一个重要的概念，可以用来求解一些实际问题。

本文将介绍上限定积分导数的定义及其应用。

设函数f(x)在[a,b]上有连续的导数，则对于x∈(a,b)，函数F(x)定义为F(x)=∫(a→x) f(t)dt称为函数f(x)在[a,b]上的上限定积分。

如果F(x)在(x-ε,x+ε)内有导数，则称F(x)在x点可导，记作F'(x)。

F'(x)=lim(h→0) [ F(x+h)-F(x) ]/h根据上限定积分导数的定义，我们可以通过求极限的方式来计算上限定积分导数。

具体计算方法如下：1. 用定积分求上限定积分导数指的是利用导数的定义和定积分的性质，将上限定积分转化为定积分来求解。

考虑函数F(x)=∫(a→x) f(t)dt，根据定积分的可加性和线性性质，可以得到：利用定积分的性质可得：这个极限可以转化为以下形式：所以，我们可以将上限定积分导数的计算问题转化为定积分的计算问题。

2. 利用导数的性质求上限定积分导数也是一种常用的方法。

根据导数的性质，我们可以得到：将上式两边对h求导，可以得到：这说明上限定积分的导数等于原函数在该点的函数值，即F'(x)=f(x)。

上限定积分导数在实际问题中有广泛的应用，下面介绍几个常见的应用场景。

1. 求曲线的切线斜率考虑曲线y=f(x)，通过求上限定积分导数，可以求得曲线在某点处的切线斜率。

这说明F(x)在点a处的导数等于函数f(x)在该点的函数值，即F'(a)=f(a)，也就是说F(x)在点a处的导数等于曲线在该点处的切线斜率。

2. 求物体的位移和速度考虑一个物体在直线上运动，其速度v(t)关于时间的函数已知。

我们可以通过上限定积分导数来求物体的位移和速度。

设s(t)表示物体在时刻t的位移，根据速度的性质，可以得到：根据上限定积分导数的定义，上式可以转化为：s'(t)=v(t)这说明位移函数s(t)的导数等于速度函数v(t)。

定积分知识复习总结

定积分知识总结一、基本概念和性质（1）定义[]()[]())()(lim )()()(,,,,0max ...,)()(lim lim )(11111111011-=∞→-=----∞→∞→=∞→-⋅-⋅=-⋅≈=→-∞→==-⋅=⋅∑∑∑∑⎰i i ni i n i i ni i i i i i i i i i i i i i i i i n i nn i n ni iban x x f x x f S x x f S I S I S I x x I x x n b x x x a n b a x x f S dx x f ξξξξξ④求极限：即③求和：，上任取一点在上用矩形代替在上的代数面积为在②记时，要求当＜＜＜个小区间，区间分成①把的定义：[]dxx g dx x f dx x g x f ab babababa⋅⋅+⋅⋅=⋅⋅+⋅-=⎰⎰⎰⎰)()()()(12βαβα②线性运算性质：①）定积分的性质（)()()(=⋅⋅-=⋅⎰⎰⎰aaabba dx x f dxx f dx x f()））（定要求的区间可积即可，不一其中，包含③区间的可加性：b a c c b a dxx f dx x f dx x f bccaba,,,()()()(∈⋅+⋅=⋅⎰⎰⎰[][][][]⎰⎰⎰⎰⎰⎰⋅⋅≥≡=⋅≥⋅≥⋅≥≥⋅≥babababab abadxx g dx x f x g x f x g x f b a x g x f x f x f dx x f x f x f b a x f dxx g dx x f x g x f b a x g x f dx x f x f b a x f )()(),()(),()(,)(),(0:0)(00:0)(0)(0)(0)(,)()()(),()(,)()(0)(0)(,)(＞则：不恒等于且上连续，在区间推论：若区间上都等于则是指在整个；，也可能整个区间均为可能个别点上等于＞，则不恒等于，上连续，在⑥若则上可积且在，⑤若，则上可积且在④ [][][][][])()()(,,)()()()(,)(,)()()(,)(a b f dx x f b a b a x f a b M dx x f a b m M m b a x M x f m b a x f dxx f dx x f b a x f bababa ba-⋅=⋅∈-≤⋅≤-∈≤≤⋅≤⋅⎰⎰⎰⎰ξξ，使得：点上连续，则至少存在一在闭区间若⑨（积分中值定理）均为常数，则：，，，上可积，在⑧若上可积，则在⑦若二、微积分基本公式1、积分上限函数及其导数定义：设函数)(x f 在区间],[b a 上连续，对于任意],[b a x ∈，)(x f 在区间],[x a 上也连续，所以函数)(x f 在],[x a 上也可积.显然对于],[b a 上的每一个x 的取值，都有唯一对应的定积分⎰xadt t f )(和x 对应，因此⎰xadt t f )(是定义在],[b a 上的函数.记为⎰=Φxadt t f x )()(，],[b a x ∈.称)(x Φ叫做变上限定积分,有时又称为变上限积分函数.定理1：如果函数)(x f 在区间],[b a 上连续，则⎰=Φxadt t f x )()(在],[b a 上可导，且)()()()(b x a x f dt t f dxd x xa ≤≤==Φ'⎰定理2、3：如果)(x f 在区间],[b a 上连续，则它的原函数一定存在，且其中的一个原函数为⎰=Φxadt t f x )()(.2、牛顿——莱布尼茨公式定理4（微积分基本公式）如果函数)(x f 在区间],[b a 上连续，且)(x F 是)(x f 的任意一个原函数，那么⎰-=b aa Fb F dx x f )()()(.证由定理5.2知，⎰=Φx adt t f x )()(是)(x f 在区间],[b a 的一个原函数，则)(x Φ与)(x F 相差一个常数C ，即C x F dt t f x a+=⎰)()(.又因为C a F dt t f a a+==⎰)()(0，所以)(a F C -=.于是有)()()(a F x F dt t f x a -=⎰.所以 ⎰-=baa Fb F dx x f )()()(成立.为方便起见，通常把)()(a F b F -简记为ba x F )(或b a x F )]([，所以公式可改写为)()()()(a F b F x F dx x f b a b a-==⎰三、定积分的积分法1、定积分的换元积分法定理1设函数)(x f 在区间],[b a 上连续，并且满足下列条件：（1）)(t x ϕ=，且)(αϕ=a ，)(βϕ=b ；（2）)(t ϕ在区间],[βα上单调且有连续的导数)(t ϕ'；（3）当t 从α变到β时，)(t ϕ从a 单调地变到b . 则有⎰⎰'=b adt t t f dx x f βαϕϕ)()]([)(上述公式称为定积分的换元积分公式.在应用该公式计算定积分时需要注意以下两点：①从左到右应用公式，相当于不定积分的第二换元法.计算时，用把原积分变量换成新变量，积分限也必须由原来的积分限和相应地换为新变量的积分限和，而不必代回原来的变量，这与不定积分的第二换元法是完全不同的.②从右到左应用公式，相当于不定积分的第一换元法（即凑微分法）.一般不用设出新的积分变量，这时，原积分的上、下限不需改变，只要求出被积函数的一个原函数，就可以直接应用牛顿—莱布尼兹公式求出定积分的值. 2、定积分的分部积分法设函数)(x u u =和)(x v v =在区间],[b a 上有连续的导数，则有)()()]()([)()(x du x v x v x u x dv x u bab ab a⎰⎰-=.上述公式称为定积分的分部积分公式.选取)(x u 的方式、方法与不定积分的分部积分法完全一样.四、定积分的应用1、定积分应用的微元法为了说明定积分的微元法，我们先回顾求曲边梯形面积A 的方法和步骤： (1)将区间],[b a 分成n 个小区间，相应得到n 个小曲边梯形，小曲边梯形的面积记为i A ∆),2,1(n i =；(2)计算i A ∆的近似值，即i i i x f A ∆≈∆)(ξ（其中],[,11i i i i i i x x x x x --∈-=∆ξ）； (3)求和得A 的近似值，即i ni i x f A ∆≈∑=1)(ξ；(4)对和取极限得⎰∑=∆==→bai ni i dx x f x f A )()(lim 1ξλ.下面对上述四个步骤进行具体分析：第(1)步指明了所求量（面积A ）具有的特性：即A 在区间],[b a 上具有可分割性和可加性.第(2)步是关键，这一步确定的i i i x f A ∆≈∆)(ξ是被积表达式dx x f )(的雏形.这可以从以下过程来理解：由于分割的任意性，在实际应用中，为了简便起见，对i i i x f A ∆≈∆)(ξ省略下标，得x f A ∆≈∆)(ξ，用],[dx x x +表示],[b a 内的任一小区间，并取小区间的左端点x 为ξ，则A ∆的近似值就是以dx 为底，)(x f 为高的小矩形的面积（如图5.7 阴影部分），即dx x f A )(≈∆.通常称dx x f )(为面积元素，记为dx x f dA )(=.将(3),(4)两步合并，即将这些面积元素在],[b a 上“无限累加”，就得到面积A .即⎰=ba dx x f A )(.一般说来，用定积分解决实际问题时，通常按以下步骤来进行：（1）确定积分变量x ，并求出相应的积分区间],[b a ；（2）在区间],[b a 上任取一个小区间],[dx x x +，并在小区间上找出所求量F 的微元dx x f dF )(=；（3）写出所求量F 的积分表达式⎰=ba dx x f F )(，然后计算它的值.利用定积分按上述步骤解决实际问题的方法叫做定积分的微元法. 注能够用微元法求出结果的量F 一般应满足以下两个条件： ①F 是与变量x 的变化范围],[b a 有关的量；②F 对于],[b a 具有可加性，即如果把区间],[b a 分成若干个部分区间，则F 相应地分成若干个分量.2、定积分求平面图形的面积（1）直角坐标系下面积的计算(1)由曲线)(x f y =和直线0,,===y b x a x 所围成曲边梯形的面积的求法前面已经介绍，此处不再叙述.(2)求由两条曲线)(),(x g y x f y ==，))()((x g x f ≥及直线b x a x ==,所围成平面的面积A （如图5.8所示）.下面用微元法求面积A . ①取x 为积分变量，],[b a x ∈.②在区间],[b a 上任取一小区间],[dx x x +，该区间上小曲边梯形的面积dA 可以用高)()(x g x f -，底边为dx 的小矩形的面积近似代替，从而得面积元素dx x g x f dA )]()([-=. ③写出积分表达式，即⎰-=badx x g x f A )]()([.⑶求由两条曲线)(),(y x y x ϕψ==，))()((y y ϕψ≤及直线d y c y ==,所围成平面图形（如图5.9）的面积. 这里取y 为积分变量，],[d c y ∈，用类似 (2)的方法可以推出：⎰-=dcdy y y A )]()([ψϕ.（2）极坐标系下面积的计算设曲边扇形由极坐标方程)(θρρ=与射线)(,βαβθαθ<==所围成（如图5.13所示）.下面用微元法求它的面积A.以极角θ为积分变量，它的变化区间是],[βα，相应的小曲边扇形的面积近似等于半径为)(θρ，中心角为θd 的圆扇形的面积，从而得面积微元为θθρd dA 2)]([21=于是，所求曲边扇形的面积为 ⎰=βαθθρd A 2)]([21.3．定积分求体积 (1)旋转体的体积旋转体是一个平面图形绕这平面内的一条直线旋转而成的立体.这条直线叫做旋转轴.设旋转体是由连续曲线)0)()((≥=x f x f y 和直线b x a x ==,及x 轴所围成的曲边梯形绕x 轴旋转一周而成（如图5.15）.取x 为积分变量，它的变化区间为],[b a ，在],[b a 上任取一小区间],[dx x x +，相应薄片的体积近似于以)(x f 为底面圆半径，dx 为高的小圆柱体的体积，从而得到体积元素为dx x f dV 2)]([π=，于是，所求旋转体体积为dx x f V bax ⎰=2)]([π.(2)平行截面面积为已知的立体体积设一物体被垂直于某直线的平面所截的面积可求，则该物体可用定积分求其体积.不妨设直线为x 轴，则在x 处的截面面积)(x A 是x 的已知连续函数，求该物体介于a x =和)(b a b x <=之间的体积（如图5.19）.取x 为积分变量，它的变化区间为],[b a ，在微小区间],[dx x x +上)(x A 近似不变，即把],[dx x x +上的立体薄片近似看作)(x A 为底，dx 为高的柱片，从而得到体积元素dx x A dV )(=.于是该物体的体积为⎰=badx x A V )(.类似地，由曲线)(y x ϕ=和直线d y c y ==,及y 轴所围成的曲边梯形绕y 轴旋转一周而成（如图5.16），所得旋转体的体积为dy y V dcy ⎰=2)]([ϕπ.。

定积分及其应用

即
b
b
b
f ( x)dx f (t)dt f (u)du .
a
a
a
2o. 当 T 0, 分点个数 n ;但反之不然 .
3o. 若 f 在 [a, b] 的某一个积分和的极限不存在，
或若 f 在 [a, b] 的某两个积分和的极限都存在但极限值不相等，则 f ( x) 在 [ a , b ] 上不可积 .
dx x
1dx, 03
4
0
3
1 sin3
dx x
3
.
第44页
例 5
估计积分
2
4
sin xdx的值. x
解 f ( x) sin x , x [ , ]
x
42
0 x , x tan x.
2
f ( x)
x cos x sin x x2
cos x( x tan x) x2
第26页
怎样的分法，也不论在小区间[ xi1 , xi ]上
点i 怎样的取法，只要当|| T || 0 时，和 S 总趋于
确定的极限I ，我们称这个极限I 为函数 f ( x)
在区间[a, b]上的定积分，记为
积分上限
n
b
a
f ( x)dx
I
lim ||T ||0 i 1
f (i )xi
积分和或黎曼和
T 0 i 1
f (i )xi
n
lim
f (a b a i) b a
.
n i1
n
n
第29页
例1
利用定义计算定积分
1 x2dx. 0
解 xi
T 把 [0,1] n xi xi1

定积分的例题分析及解法

定积分的例题分析及解法本章的基本内容是定积分的概念、计算和应用一、定积分的概念1．定积分是下列和式的极限xi i f dx x f i nba∆∑==→⎰)(lim )(10ξλ其中{}xi ni ∆=≤≤1max λ因此，定积分是一个数，它依赖于被积函数)(x f 和积分区间〔a,b 〕定积分与积分变量用什么字母无关：⎰⎰=babadt t f dx x f )()(定积分的几何意义是曲边梯形的面积（当被积函数0)(≥x f 时）。

2．定积分的性质（1）线性性质[]⎰⎰⎰+=+bab abadx x g k dx x f k dx x g k x f k)()()()(2121（2） ⎰⎰⎰=-=aaabba dx x f dx x f dx x f 0)(,)()( （3） ⎰⎰⎰+=bccaba dx x f dx x f dx x f )()()(（4）若),()(x g x f ≥则⎰⎰≥babadx x g dx x f )()(（5）积分中值定理：设)(x f 在〔a,b 〕上连续，则在〔a,b 〕上至少存在一点ξ，使下式成立),()()(a b f dx x ba-=⎰ξ其中].[b a ∈ξ。

（6）估值定理：若)(x f 在〔a,b 〕上可积，且M x f m ≤≤)(，则有不等式⎰-≤≤-baa b M dx x f a b m )()()(（7）若函数)(x f 在〔a,b 〕上连续，则有⎰=xa x f dt t f dxd )()( 3．广义积分。

二、定积分的计算 1．牛顿—莱布尼茨公式：⎰-=baa Fb F dx x f )()()(2．换元法：注意，在换元的同时不要忘记换积分限 3．分部积分法：⎰⎰-=babab a x du x x x u x d x u )()()()()()(υυυ4．定积分的近似计算：梯形，抛物线法。

三、定积分的应用基本方法是：（1）代公式；（2）微元法1．平面图形的面积（1）直角坐标系。

推广的积分中值定理及其应用

推广的积分中值定理及其应用摘要:定积分是微积分的重要组成部分,而积分中值定理是定积分的重要性质之一,所以积分中值定理在微积分中占了很重要的地位,本文系统的叙述了推广的积分中值定理包括:ξ必可以在开区间中取得,导函数的积分中值定理等多个方面,我们所学知识中积分中值定理与微分中值定理的中间点的存在区间是不统一的,但推广后的积分中值定理能够与微分中值定理的存在区间从形式上统一起来,使与其相关的理论得以联系和应用.同时,在本篇论文中以实例的形式列举了推广的积分中值定理在确定零点分布、证明积分不等式、求极限等方面的应用,显然,推广的积分中值定理的优点就在于此,它可以解决原积分中值定理无法解决的问题,这表明了积分中值定理在推广后更具有应用性.关键词:积分中值定理;导函数;微分中值定理Promotion of Integral Mean ValueTheorem and Its ApplicationAbstract:Definite integral is an important component of calculus, the mean value theorem is one of the important properties of the definite integral, so integral mean value theorem in calculus plays a very important position .This paper describes the system topromote the integral mean value theorem, including: ξwill be achieved in the open interval ,of the derivatives and other integral mean value theorem, we have the knowledge of the differential mean value theorem and the Intermediate Value Theorem Existence interval is not uniform, but after the promotion of integral mean value theorem and the Mean Value Theorem to the presence of range from the formal unity, so that contact can be associated with the theory and application. Meanwhile, in this paper an example to cite a form of integral mean value theorem in determining the zeros to prove inequality, such as the application of limit, obviously, to promote the advantages of integral mean value theorem in this, it Can solve the original integral mean value theorem can not solve the problem, suggesting that the integral mean value theorem in the promotion of a more applied after.Keywords: Integral mean value theorem, derivative, mean value theorem1预备知识在本部分中具体叙述了这篇论文中所需要的相关知识,包括导函数介值性定理、拉格朗日中值定理以及变上限积分函数的定义和性质等,这些理论知识为第二部分的定理推导以及证明做了铺垫,所以起了重要的作用.1.1设()g x 在[,]a b 上非负可积,且()0abg x dx >⎰则存在[,](,)c d a b ⊂使得()0dcg x d x >⎰1.2 设()f x 在[,]a b 上连续,0x ,1x ,2x [,]a b ∈若10()()f x f x >,20()()f x f x <,则存在(,)a b ξ∈,使得0()()f f x ξ=1.3若函数()f x 在[,]a b 上可导,且''()()f a f b +-≠,k 为介于'()f a +,'()f b -之间的任意数,则在(,)a b 内至少存在一点ξ,使得'()f k ξ=1.4若'()f x 为[,]a b 上的非负导函数,且存在0[,]x a b ∈,使'0()0f x >,则必有'()0baf x dx >⎰1.5（拉格朗日中值定理）若函数()f x 满足如下条件: （1）()f x 在闭区间[,]a b 上连续; （2）()f x 在开区间(,)a b 内可导;则在(,)a b 内至少存在一点ξ使得'()()()f b f a f b aξ-=-1.6变上限积分函数:设()f x 在[,]a b 上可积,x 为[,]a b 内任意一点,则称函数()()xax f t dt φ=⎰为变上限积分函数1.7变上限积分函数有以下若干性质（1）有界性命题1 设函数()f x 在[,]a b 上可积,则()x φ在[,]a b 上有界（2）连续性命题2 设函数()f x 在[,]a b 上可积,则()x φ在[,]a b 上连续（3）可积性命题3 设函数()f x 在[,]a b 上可积,则()x φ在[,]a b 上可积（4）可微性（原函数存在定理）()f x 在[,]a b 上连续,则()x φ在[,]a b 上处处可导.且'()()()xad x f t dt f x dx φ==⎰ [,]x a b ∈2 推广的积分中值定理积分第一中值定理在数学分析教材中为:若()f x 在[,]a b 上连续,则至少存在一点[,]a b ξ∈,使得()()()baf x dx f b a ξ=-⎰推广的积分第一中值定理在数学分析教材中为:()f x ,()g x 都在[,]a b 上连续,且()g x 在[,]a b 上不变号,则至少存在一点[,]a b ξ∈,使得()()()()bbaaf xg x dx f g x dx ξ=⎰⎰我们知道积分中值定理可用于确定数列及函数列的极限,确定零点分布,判别函数的敛散性,证明积分不等式等.但观察上述式子我们发现ξ的取值有时会在两个端点处取得,有的习题用原有的积分中值定理不能够解答出来.例如在证明积分不等式时,运用原有的积分中值定理我们只可以证明≤或≥的情况,所以带有一定的局限性.下面我们对原有的积分中值定理做一下加强,使“ξ”的范围由闭区间缩小到开区间,即得到了下面所叙述的推广的积分中值定理.2.1积分第一中值定理的推广定理 2.1(1)若()f x 在闭区间[,]a b 上连续,则在开区间(,)a b 内至少存在一点ξ使得:()()()baf x dx f b a ξ=-⎰成立证明: 作辅助函数()()x aF x f t dt =⎰ [,]x a b ∈则()F x 是[,]a b 的可微函数,且'()()F x f x =.由微积分学中值定理,至少存在一点(,)a b ξ∈,使得:'()()()()F b F a F b a ξ-=-注意到()()ba Fb f x dx =⎰,()0F a =,即有()()()baf x dx f b a ξ=-⎰(,)a b ξ∈2.2推广的第一积分中值定理的加强引理1 设()g x 在[,]a b 上非负可积,且()0ba g x dx >⎰,则存在[,](,)c d ab ⊂使得()0dcg x dx >⎰证明:用反证法作辅助函数()()b x a xG x g t dt -+=⎰[0,]2b a x -∈,则()G x 是[0,]2b a-上的非负连续函数.若命题不成立,则对任意的(0,)2b ax -∈有()G x ≡0,令x o →+,得(0)()0b a G g t dt ==⎰,产生矛盾.引理2 ()f x 在[,]a b 上连续,0x ,1x ,2x [,]a b ∈,若10()()f x f x >,20()()f x f x <,则存在(,)a b ξ∈,使得0()()f f x ξ=证明:作辅助函数0()()()H x f x f x =-,我们不妨设12x x <,因为()f x 在[,]a b 上连续,故()H x 也连续,从而在12[,]x x 上连续.1()0H x >,2()0H x <由连续函数的零点定理知存在12(,)x x ξ∈使得()0H ξ=即当然0()()f f x ξ=其中(,)a b ξ∈.引理3 若()g x 在[,]a b 上连续且不恒为零,则积分()0ba g x dx >⎰证明:倘若有某0[,]x a b ∈,使0()0g x >,由连续函数的局部保号性知存在0x 的某邻域00(,)x x δδ-+,使在其中0()()02g x g x ≥>,则 00000000()()()()()00()02bx x b x aax x x g x g x dx g x dx g x dx g x dx dx g x δδδδδδδ-++-+-=++≥++=>⎰⎰⎰⎰⎰证毕.定理 2.2 设()f x 在[,]a b 上连续,()g x 在[,]a b 上可积不变号,则至少存在一点(,)a b ξ∈使得()()()()bbaaf xg x dx f g x dx ξ=⎰⎰证法1(2)证明:1︒()0bag x dx =⎰时,此时,由推广的积分中值定理知,存在[,]a b ξ∈使得()()()()bbaaf xg x dx f g x dx ξ=⎰⎰=0于是对任意的0(,)x a b ∈有0()()()()bbaaf xg x dx f x g x dx =⎰⎰命题成立2︒当()0g x ≥，且()0bag x dx >⎰时，若命题不成立，即不存在(,)a b ξ∈，使得()()()()bbaaf xg x dx f g x dx ξ=⎰⎰则由推广的积分中值定理知，只能有()()()()b baaf xg x dx f a g x dx =⎰⎰ （1）或者 ()()()()b baaf xg x dx f b g x dx =⎰⎰ 成立（2）若是命题不成立而（1）成立,则在(,)a b 内()()f x f a ≠ 由引理2在(,)a b 内恒有()()f x f a >或者()()f x f a <,不妨设()()f x f a >,而对()g x 运用引理2存在[,](,)c d a b ⊂,使得()0dc g x dx >⎰于是()()()()()()()()()()bbcdbaaacdf ag x dx f x g x dx f x g x dx f x g x dx f x g x dx ==++⎰⎰⎰⎰⎰=123()()()()()()c d bacdf g x dx f g x dx f g x dx ξξξ++⎰⎰⎰其中1[,]a c ξ∈,2[,]c d ξ∈,3[,]d b ξ∈,这是根据推广的积分中值定理得出的,由于1()()f f a ξ≥,()0cag x dx ≥⎰,2()()f f a ξ>,()0dcg x dx >⎰,3()f ξ中的3b ξ≠时3()()f f a ξ>.当3b ξ=时,对()()f x f a >,0x b →-,由()f x 在[,]a b 上的连续性可知,()()f b f a ≥而()0dd g x dx ≥⎰,综上可得到()()()()()()()()()()b c d b baacdaf ag x dx f a g x dx f a g x dx f a g x dx f a g x dx >++>⎰⎰⎰⎰⎰这是一个矛盾,因此命题成立.若是命题不成立而（2）成立,同样可得出矛盾,因此定理得以证明3︒ 当()0g x ≤,且()0ba g x dx <⎰时此时()0g x -≥,且[()]0bag x dx ->⎰,由情形2的讨论知,存在(,)a b ξ∈,使得()[()]()[()]bb aaf xg x dx f g x dxξ-=-⎰⎰ 即有()()()()bbaaf xg x dx f g x dx ξ=⎰⎰ (,)a b ξ∈总之,定理2.2完全得以证明证法2(3)证明:令()()xaF x f t dt =⎰,由拉格朗日中值定理知,(,)a b ξ∃∈,使得'()()()F b F a F b aξ-=-,即()()()baf x dx f b a ξ=-⎰不妨设()0g x ≥,[,]x a b ∈,若()g x 在[,]a b 上恒为零,则结论显然成立.若()g x 在[,]a b 上连续且不恒为零,则积分()0ba g x dx >⎰令()()()x aF x f t g t dt =⎰,()()xaG x g t dt =⎰,在[,]a b 上应用柯西中值定理，(,)a b ξ∃∈,使''()()()()()()()()()()()()()babaf tg t dtF b F a F f g fG b G a G g g t dtξξξξξξ-=⇒==-⎰⎰即()()()()bbaaf xg x dx f g x dx ξ=⎰⎰2.3积分第二中值定理的推广在数学分析教材中积分第二中值定理是这样叙述的,设函数()f x 在[,]a b 上可积（1）若函数()g x 在[,]a b 上减,且()0g x ≥,则存在[,]a b ξ∈,使得()()()()baaf xg x dx g a f x dx ξ=⎰⎰（2）若函数()g x 在[,]a b 上增,且()0g x ≥,则存在[,]a b η∈,使得()()()()bbaf xg x dx g b f x dx η=⎰⎰其推论为:设函数()f x 在[,]a b 上可积,若()g x 为单调函数,则存在[,]a b ξ∈,使得()()()()()()bbaaf xg x dx g a f x dx g b f x dx ξξ=+⎰⎰⎰现在研究一下推论的情形:在第一积分中值定理中,我们把ξ的取值区间由闭区间缩小到开区间,但对于积分第二中值定理是否可以做这样的加强呢,看一下下面的例子:在闭区间[,]a b 上()1f x =,1[,)()2x a b g x x b ∈⎧=⎨=⎩若在(,)a b 上存在ξ使得()()()()()()bbaaf xg x dx g a f x dx g b f x dx ξξ=+⎰⎰⎰即 ()()()()2()2b a g a a g b b a b b a ξξξξξ-=-+-=-+-=--所以b ξ=,即ξ在[,]a b 的端点.这个例子告诉我们积分第一中值定理的加强结果对于积分第二中值定理不一定成立,但是这里的有限区间[,]a b 却可以换成[,)a +∞或(,]b -∞或(,)-∞+∞.此处只讨论第一种情况定理 2.3(4)设()g x 在[,)a +∞上单调有界,()f x 在[,)a +∞上可积,且()f x 没有+∞以外的瑕点,则存在[,)a ξ∈+∞使得()()()()()()aaf xg x dx g a f x dx g f x dx ξξ+∞+∞=++∞⎰⎰⎰这里()lim ()x g g x →+∞+∞=证明:不妨设()g x 在[,)a +∞上单调下降,由于()g x 有界,所以()g x 在+∞处有有限的极限,记为()g +∞,于是可记()()()G x g x g =-+∞,则()0G x ≥,而对于任意的有穷区间[,]a A ,由第二积分中值定理可知,总有[,]a A η∈使得:()()()()Aaaf x G x dx G a f x dx η=⎰⎰而()()A aF A f x dx =⎰是[,)a +∞上的关于A 的连续函数,又()f x 在[,)a +∞上可积,则()F A 在[,)a +∞上有有穷的下确界和上确界,不妨记[,)inf ()A a m F A ∈+∞=,[,)sup ()A a M F A ∈+∞=,则有()m F A M ≤≤又因为()()()()Aaaf x G x dx G a f x dx η=⎰⎰所以有()()()()AamG a G x f x dx MG a ≤≤⎰再令A →+∞,则有()()()()amG a G x f x dx MG a +∞≤≤⎰令 ()()()aG a G x f x dx μ+∞=⎰, （3）则有()()()mG a G a MG a μ≤≤如果()0G a ≠则m M μ≤≤,因为()()AaF A f x dx =⎰是[,)a +∞上的关于A 的连续函数,所以()F A 可以达到其上确界M 和下确界m 及上确界和下确界之间的任意值,即存在[,)a ξ∈+∞使得()af x dx ξμ=⎰将其带入（3）式就有()()()()aaG a f x dx G x f x dx ξ+∞=⎰⎰即(()())()(()())()aag a g f x dx g x g f x dx ξ+∞-+∞=-+∞⎰⎰所以()()()()()()aaf xg x dx g a f x dx g f x dx ξξ+∞+∞=++∞⎰⎰⎰如果()0G a =,因为()g x 在[,)a +∞上单调下降,所以()G x 在[,)a +∞上单调下降,又因为()0G x ≥即()0G x =所以()()g x g =+∞,即()g x =常数,那么对任意的[,)a ξ∈+∞,都有()()()()()()aaf xg x dx g a f x dx g f x dx ξξ+∞+∞=++∞⎰⎰⎰证毕.这个定理告诉我们:第二积分中值定理虽然在有限开区间上不一定成立,但在无穷区间上却是成立的.通过以上的推导过程我们会发现在积分中值定理的前提下,ξ必可以在开区间中取得.在微积分学中积分中值定理和微分中值定理两者在一定意义上是互逆的、对立的,这种辩证的对立统一使微积分的内容更加丰富多彩,但两者中间点ξ的存在区间是不统一的,给其相关理论和应用带来了不便,但改动之后,推广的积分中值定理与微分中值定理的取值区间得以统一,从而更能体现积分中值定理的中值性,以及两个定理之间的联系.一方面可由微分中值定理推出积分中值定理根据牛顿—莱布尼茨公式:()()()ba f x dx Fb F a =-⎰其中()F x 是()f x 在[,]a b 上的原函数即'()()F x f x =,[,]x a b ∈,显然()F x 在[,]a b 上满足拉格朗日中值定理的条件,于是至少存在一点(,)a b ξ∈使得'()()()()F b F a F b a ξ-=-()()f b a ξ=- (,)a b ξ∈即()()()baf x dx f b a ξ=-⎰(,)a b ξ∈另一方面,推广的积分中值定理推出微分中值定理:若()f x 在[,]a b 上有连续的导函数,直接计算得:'()()()baf x dx f b f a =-⎰ （4）而由推广的积分中值定理至少存在一点(,)a b ξ∈,使得''()()()baf x dx f b a ξ=-⎰（5）由（4）和（5）有'()()()()f b f a f b a ξ-=-,这正是微分中值定理.2.4 导函数的积分中值定理及其应用在微积分学中,积分中值定理与微分中值定理都有着很重要的地位,下面我们将积分中值定理条件下的连续函数推广到导函数,并用Darboux 定理给出了详尽的证明,由此我们得出了导函数积分中值定理.引理1(5)（Darboux ）若函数()f x 在[,]a b 上可导,且''()()f a f b +-≠,k 为介于'()f a +,'()f b -之间的任意数,则在(,)a b 内至少存在一点ξ,使得'()f k ξ=引理2 若'()f x 为[,]a b 上的非负导函数,且存在0[,]x a b ∈,使'0()0f x >,则必有'()0baf x dx >⎰定理 2.4(6)若'()f x 为[,]a b 上的导函数,()g x 为[,]a b 上的连续函数,且()g x 在[,]a b 上不变号,则至少存在一点ξ[,]a b ∈,使得''()()()()bbaaf xg x dx f g x dx ξ=⎰⎰证明:不妨设()0g x ≥,'()f x 在[,]a b 上的最大值和最小值为别为M 与m ,其中M 可以取+∞,m 可以取-∞,在a 点取'()f a +,在b 点取'()f b -,令()0ba I g x dx =≥⎰,又'()()()()mg x f x g x Mg x ≤≤,([,])x a b ∈,则有'()()()()bbbaaam g x dx f x g x dx M g x dx ≤≤⎰⎰⎰当0I =或m M =时,任意取(,)a b ξ∈均可当0I >或m M <时,令'1()()b a u f x g x dx I=⎰ ()m u M ≤≤ 当m u M ≤≤时,由Darboux 定理知,至少存在一点(,)a b ξ∈,使得'()f u ξ= 当m u M =<时,利用反证法证明存在(,)a b ξ∈,使得'()f u ξ=若对一切的(,)x a b ∈,有'()0f x u ->且()0baI g x dx =>⎰,则()g x 在[,]a b 上不恒为零,即存在0[,]x a b ∈,使得0()0g x >,由连续函数的保号性知存在0x 的邻域00(,)x x σσ-+（当0x a =或0x b =时,则为右邻域或左邻域）使得对于任意的00(,)x x x σσ∈-+,有0()()02g x g x ≥>,则 0000'''0()(())()(())()(())2bx x ax x g x f x u g x dx f x u g x dx f x u dx σσσσ++--->-≥-⎰⎰⎰ 由引理2可得00'(())0x x f x u dx σσ+-->⎰,从而有'(())()0b af x ug x dx ->⎰另一方面:''0(())()()()()0bbbaaaf x ug x dx f x g x dx u g x dx uI uI <-=-=-=⎰⎰⎰出现矛盾,故原命题成立,即当m u M =<时,存在(,)a b ξ∈,使得'()f u ξ=当m u M <=时,同理可证必存在(,)a b ξ∈,使得'()f u ξ=成立同理可证二阶导函数,n 阶导函数对上述的导函数的积分中值定理成立,只要我们把它们看成一阶连续导函数和n-1阶连续导函数的导函数,便可用同样的方法得证.定理2.4的应用说明例1 设函数()f x 在[,]a b 上二次可微,证明存在一点(,)a b ξ∈,使得''324().[()()]()2b aa bf f x f dx b a ξ+=--⎰ 证明:记02a bx +=,将被积函数在0x x =处按泰勒公式展开,得 2'''0000()()()()()()2x x f x f x x x f x f η--=-+其中η在x 与0x 之间,因为'00()()0bax x f x dx -=⎰,即2''00()(()())()2bbaax x f x f x dx f dx η--=⎰⎰由定理知存在(,)a b ξ∈使32''''2''00()()()()()()12bba ab a x x f dx f x x dx f ηξξ--=-=⎰⎰从而''324().[()()]()2b a a bf f x f dx b a ξ+=--⎰例2 已知导函数'()f x 在[1,2]上有界,求证2'1lim ()0nx n f x e dx -→∞=⎰证明:导函数'()f x 在[1,2]上有界,所以存在正数M ,对[1,2]ξ∈,有'()f M ξ<,由定理1知,存在1(1,2)ξ∈,2(1,2)ξ∈, 使得222'''1111()()()n nnx x f x edx f edx f eξξξ---==⎰⎰从而有2'1lim ()0nx n f x e dx -→∞=⎰3 推广的积分中值定理的应用3.1用于确定零点分布例3 (7)证明:若()f x 在[,]a b 上连续,且()()0b ba af x dx xf x dx ==⎰⎰,则在(,)a b 内至少存在两点1x ,2x 使得12()()f x f x =证明:设()()xa F x f t dt =⎰那么我们有()()()0baf x dx F b F a =-=⎰,所以()()F b F a ==0又因为()()()()bbbba aaaxf x dx xdF x xF x F x dx ==-=⎰⎰⎰ ()()()()bF b aF a F b a ξ---所以可得; ()()()()b a F b F b a ξ-=-,所以()()()F b F F a ξ===0 证毕例4(8) 证明:若()f x 在[0,]π上连续,且0()()cos 0f x dx f x xdx ππ==⎰⎰,证明:存在两点1ξ,2ξ (0,)π∈,使得 12()()0f f ξξ==证明:令0()()xF x f t dt =⎰ 即'()()F x f x =,()(0)0F F π==00()cos cos ()cos ()()cos f x xdx xdF x xF x F x d xππππ==-⎰⎰⎰()sin ()sin .0F x xdx F πξξπ===⎰所以()0F ξ= (0,)ξπ∈,对()F x 在(0,)ξ,(,)ξπ上使用罗尔定理,即存在1(0,)x ξ∈,2(,)x ξπ∈满足'1()0F x =,'2()0F x =,即12()()0f x f x ==证毕例5(3)假如()f x 在[0,]π上连续,且0()sin ()cos 0f x xdx f x xdx ππ==⎰⎰,则()f x 在(0,)π内至少有两个零点.证明:由已知条件,并运用推广的积分中值定理得0()sin ()sin 2()()0f x xdx f xdx f f ππξξξ===⇒=⎰⎰,(0,)ξπ∈即()f x 在(0,)π有一个零点，假如仅有一个零点x ξ=,则()f x 在[,]a ξ与[,]b ξ上均不变号,且异号,那么()sin()f x x dx ξ-在[0,]π上保持同号,连续且不恒为零,必有()sin()0f x x dx πξ->⎰（或0<）与已知0()sin()cos ()sin sin ()cos 0f x x dx f x xdx f x xdx πππξξξ-=-=⎰⎰⎰矛盾.3.2 证明积分不等式在证明积分不等式时,常常考虑积分中值定理以便去掉积分符号,如果被积函数是两个函数之积时,可考虑用积分第一或第二中值定理,对于某些不等式的证明运用原积分中值定理只能得到“≥”的结论,或者不等式根被就不能得以证明,而运用了推广的积分中值定理后,则可以得到“>”的结论,或者成功的解决.例6(9) 假设()f x 在[0,1]上连续并且单调递减,证明对任何的(0,1)a ∈有1()()af x dx a f x dx >⎰⎰证明:将要证的不等式移项11()()()()()aa a af x dx a f x dx f x dx a f x dx a f x dx -=--⎰⎰⎰⎰⎰1(1)()()aaa f x dx a f x dx =--⎰⎰因为()f x 单调递减,所以在区间[0,]a 上()()f x f a ≥,即0()()af x dx af a ≥⎰,再对上式右边第二项运用推广的积分中值定理,即存在ξ其中1a ξ<<,使上式变成1(1)()()(1)()()(1)(1)[()()]a aa f x dx a f x dx a af a af a a a f a f ξξ--≥---=--⎰⎰因为()f x 单调递减,且1a ξ<<,,所以(1)[()()]0a a f a f ξ-->,即得证.例7(9) 设()f x 在[,]a b 上连续且单调递增,证明()()2bbaaa b xf x dx f x dx +>⎰⎰证明:将要证的不等式移项,并分部积分得()()2bbaa ab xf x dx f x dx +-⎰⎰ 22()()()()()()222a bbb a b a a a b a b a bx f x dx x f x dx x f x dx +++++=-=-+-⎰⎰⎰ 令()()2a b g x x +=-,显然()f x ,()g x 在[,]2a b a +和[,]2a b b +上可积,且()g x 在[,]2a b a +和[,]2a b b +上不变号,由推广的积分中值定理知:即存在11()2a b a ξξ+<<,22()2a bb ξξ+<<,使得221222()()()()()()()()2222a ba bb b a b a b aa ab a b a b a b x f x dx x f x dx f x dx f x dxξξ++++++++-+-=-+-⎰⎰⎰⎰整理得221()[()()]8a b f f ξξ+-,因为()f x 是单调递增函数,122a b a b ξξ+<<<<,所以221()[()()]08a b f f ξξ+->,证毕. 在上述例子中我们可以看到有的题原积分中值定理不适用,而推广的积分中值定理可以将问题解决.在例6中如果运用原积分中值定理,由1a ξ≤≤只能得到“0≥”的结论;而在例7中也只能得到12()()f f ξξ≤的结论.3.3求极限例8(10)证明10lim 01nn x dx x→∞=+⎰ 证明:0ε∀>,如果取1[0,1]2ξε∈-,则有10lim 01nn dx ξξ→∞=+⎰,即N ∃,当n N >时,有12n ξεξ<+,又因为:11120012111n n n x x x dx dx dx x x x εε--=++++⎰⎰⎰对等式右边第一个积分运用中值定理,对第二个积分的被积函数用不等式011n x x <≤+,则有当n N >时有100[2]122n x dx x εε<<-+⎰,所以有10lim 01n n x dx x→∞=+⎰ 证毕.参考文献[1] 杨延龄,邹励农,章栋恩.高等数学微积分700例题[M].中国建材工业出版社.2004年10月.123页.[2] 陈卫星,马全中.关于积分中值定理及推广的积分中值定理的改进[J]. 中国煤碳经济学院学报,1994年,第1期.54,55页.[3] 郝涌,李学志,陶有德.数学分析选讲[M].国防工业出版社.2010年4月.83页,94页.[4] 朱碧,王磊.第二积分中值定理的一些推广及其应用[J]. 考试周刊, 2008年,第30期.49页.[5] 刘玉琏,傅沛仁.数学分析讲义[M].北京.高等教育出版社.2003年.[6] 谢焕田.积分中值定理的推广及其应用[J].高师理科学刊,2009年,第5期.8,9页[7] 华东师范大学数学系. 数学分析[M]. 高等教育出版社.1991年.[8] 许洪范.考研微积分500例[M]. 国防工业出版社.2009年3月.121页.[9] 李海军.积分中值定理的应用[J].赤峰学院学报.2010年,第6期,4页.[10]荆江雁.积分中值定理得推广[J].常州工学院学报.2007年,第1期 ,53页.致谢从选择论文题目到搜集材料再到一遍又一遍的修改仿佛经历了太长的时间,论文比我想象中要难写的多,我明白想写好一篇优秀的论文就必须付出百倍的努力,在论文即将交稿之时,心里多了一些轻松,同时多了一丝伤感.自己的大学生活随着论文的结束而画上了一个句号.回想自己写论文的全过程,自己最要感谢的是论文导师许宏文老师,她为人很随和,治学严谨,对待工作认真,对待学生负责,许老师给人一种很容易接近的感觉,忘不了第一次接许老师电话的情景:她耐心的给我指点着,细心的帮我分析写这篇论文的注意事项……之所以论文会顺利的完成许老师付出了太多,太多.一遍一遍的检查,一遍又一遍的帮我指出错误,在这里我想说声:许老师:您辛苦了！真的谢谢您！最后要感谢我的学校,感谢教予我知识的老师,感谢我四年的大学生活,在这四年里自己学到了很多,也成长了很多.谢谢！。

定积分的应用

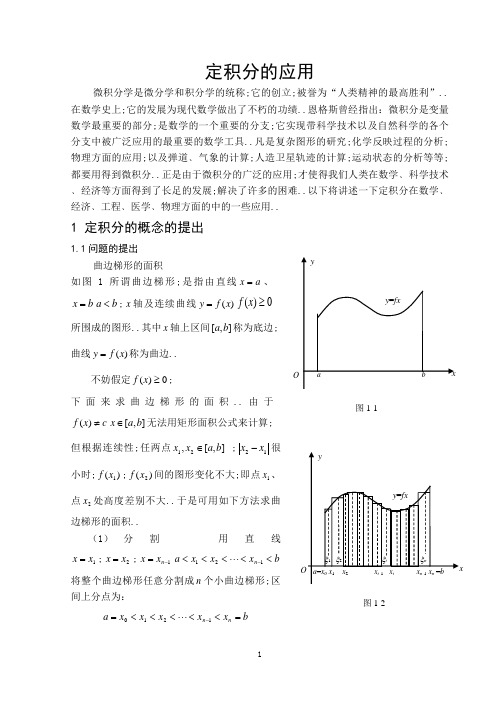
图1-1图1-2定积分的应用微积分学是微分学和积分学的统称;它的创立;被誉为“人类精神的最高胜利”..在数学史上;它的发展为现代数学做出了不朽的功绩..恩格斯曾经指出：微积分是变量数学最重要的部分;是数学的一个重要的分支;它实现带科学技术以及自然科学的各个分支中被广泛应用的最重要的数学工具..凡是复杂图形的研究;化学反映过程的分析;物理方面的应用;以及弹道﹑气象的计算;人造卫星轨迹的计算;运动状态的分析等等;都要用得到微积分..正是由于微积分的广泛的应用;才使得我们人类在数学﹑科学技术﹑经济等方面得到了长足的发展;解决了许多的困难..以下将讲述一下定积分在数学﹑经济﹑工程﹑医学﹑物理方面的中的一些应用..1 定积分的概念的提出1.1问题的提出曲边梯形的面积如图1所谓曲边梯形;是指由直线a x =、b x =b a <;x 轴及连续曲线)(x f y =0)(≥x f 所围成的图形..其中x 轴上区间],[b a 称为底边;曲线)(x f y =称为曲边..不妨假定0)(≥x f ;下面来求曲边梯形的面积..由于c x f ≠)(],[b a x ∈无法用矩形面积公式来计算;但根据连续性;任两点],[,21b a x x ∈ ;12x x -很小时;)(1x f ;)(2x f 间的图形变化不大;即点1x 、点2x 处高度差别不大..于是可用如下方法求曲边梯形的面积..（1）分割用直线1x x =;2x x =;1-=n x x bx x x a n <<<<<-121 将整个曲边梯形任意分割成n 个小曲边梯形;区间上分点为：b x x x x x a n n =<<<<<=-1210这里取0x a =;n x b =..区间],[b a 被分割成n 个小区间],[1i i x x -;用i x ∆表示小区间],[1i i x x -的长度;i S ∆表示第i 块曲边梯形的面积;),,2,1(n i =;整个曲边梯形的面积S等于n 个小曲边梯形的面积之和;即∑=∆=ni i S S 12近似代替: 对每个小曲边梯形;它的高仍是变化的;但区间长度i x ∆很小时;每个小曲边梯形各点处的高度变化不大;所以用小矩形面积近似代替小曲边梯形的面积;就是;在第i 个小区间],[1i i x x -上任取一点i ξ;用以],[1i i x x -为底;)(i f ξ为高的小矩形面积i i x f ∆)(ξ;近似代替这个小曲边梯形的面积图1-1; 即i i i x f S ∆≈∆)(ξ.3求和整个曲边梯形面积的近似值为 n 个小矩形面积之和;即n S S S S ∆++∆+∆= 21=∆++∆+∆≈n n x f x f x f )()()(2211ξξξ ini ix f ∆∑=)(1ξ上式由于分割不同;i ξ选取不同是不一样的;即近似值与分割及i ξ选取有关图1－2..4取极限将分割不断加细;每个小曲边梯形底边长趋于零;它的高度改变量趋于零;曲边梯形的面积与取代它的矩形面积无限接近;从而和式∑=∆ni i i x f 1)(ξ的极限就定义为曲边梯形面积的精确值..令 },,,m ax {21n x x x ∆∆∆= λ;当0→λ时;有∑=→∆=ni i i x f S 1)(lim ξλ上面的例子;最终归结为一个特定的形式和式逼近..在科学技术中还有许多同样的数学问题;解决这类数学问题的思想方法概括说来就是“分割;近似求和;取极限”这是定积分概念的背景..1.2定积分的定义设函数)(x f y =在区间],[b a 上有界;在],[b a 中任意插入若干个分点b x x x x x a n n =<<<<<=-1210把],[b a 分成n 个小区间：],,[10x x ],[,],,[,],,[],,[113221n n i i x x x x x x x x --各个小区间的长度依次为：011x x x -=∆;122x x x -=∆;…; 1--=∆n n n x x x在每个小区间],[1i i x x -上任取一点i ξ)(1i i i x x ≤≤-ξ;作函数值与小区间长度i x ∆的乘积i i x f ∆)(ξ..并作和=S ∑=∆ni i i x f 1)(ξ记},,,m ax {21n x x x ∆∆∆= λ;如果不论对],[b a 怎样分割;也不管在小区间],[1i i x x -上点i ξn i ,,2,1 =怎样取法;只要当0→λ时;和S 总是趋于确定的极限I ;我们称这个极限值为函数)(x f 在区间],[b a 上的定积分简称为积分;记作⎰ba dx x f )(;即⎰badx x f )(==I ∑=→∆ni i i x f 1)(lim ξλ 1其中)(x f 称为被积函数;dx x f )(称为被积表达式;a 称为积分下限;b 称为积分上限;x 称为积分变量;∑=∆ni iixf 1)(ξ称为积分和..（1）曲边梯形的面积是曲边方程)(x f y =在区间],[b a 上的定积分..即=S ⎰badx x f )()0)((≥x f2定积分在几何学上的应用2.1定积分在平面几何中的应用在初高中我们学习过求圆;三角形;平四边形;梯形等比较规则的图形面积;然而对于不规则的图形就无能为力了;所以再学定积分以前我们只能求一些简单图形的面积;部分稍复杂的图形;可能用有限个简单图形的分割也能求出来;但有很大的局限性;定积分的出现为这些问题;提出了很好的解决条件..一般地;由上、下两条连续曲线y=2f x 与y=1f x 以及两条直线x=a 与x=ba<b 所围成的平面图形;它的面积计算公式为21[()()]baA f x f x dx =-⎰ 1例求由抛物线2y x =与x-2y-3=0所围成平面图形的面积A 解该平面图形如图3所示;先求出直线与抛物线交点P1;-1与Q9;3.用X=1把图形分成左;右两部分;应用公式（1）分别求得它们的面积为1110[(-)]24/3,A x x dx xdx =-==⎰⎰921328()23A x x dx -=-=⎰. A=1A +2A =32/3..2.2定积分在立体几何中的应用 2.2.1由截面面积函数求立方体体积设Ω为三维空间中的一立体;它夹在垂直于x 轴的两平面x=a 与 x=b 之间a<b.为了方便起见称Ω为位于a;b 上的立方体..若在任意一点x ∈a;b 处作垂直于x 轴的平面;它截得Ω的截面面积显然是x 的函数;记得Ax;x ∈a;b;并称之为Ω的截面面积函数..则通过定积分的定义;得到由截面面积函数求立方体体积的一般计算公式和旋转体的体积公式V=()ba A x dx ⎰..例求由椭球面2222221x y z a b c++=所围立体椭球的体积..解以平面00()x x x a =≤截椭球面;得椭圆它在yoz 平面上的正投影：22222200221(1)(1)y z x x b c aa+=--..所以截面面积函数为Ax=22(1)x bc aπ-;x ∈-a;a.于是求得椭球体积V=224(1)3ba x bc dx abc a ππ-=⎰..显然;当a=b=c=r 时;这就等于球的体积43π3r ..pQ图2-12.2.2旋转曲面的面积设平面光滑曲线C 的方程为y=()f x ;x ∈a;b 不妨设fx>=0.这段曲线绕x 轴旋转一周得到旋转曲面;则面积公式s=2π(baf x ⎰..如果光滑曲线C 由参数方程x=xt;y=yt;t ∈α;β给出;且yt ≥0;那么由弧微分知识推知曲线C 绕x 轴旋转所得旋转曲面的面积为S=2π(y t βα⎰.例计算圆2x +2y =2R 在1x ;2x ⊂-R;R 上的弧段绕x 轴旋转所得球带的面积.. 解对曲线在区间1x ;2x 上应用公式3;得到 S=2π21x x ⎰=2πR 21x x -..特别当1x =-R; 2x =R 时;则得球的表面积S 球=4π2R .3定积分在经济学中的应用3.1求经济函数在区间上的增量根据边际成本;边际收入;边际利润以及产量x 的变动区间[,]a b 上的改变量增量就等于它们各自边际在区间[,]a b 上的定积分：()()()ba Rb R a R x dx '-=⎰ 1()()()baC b C a C x dx '-=⎰ 2()()()baL b L a L x dx '-=⎰ 3例已知某商品边际收入为0.0825x -+万元/t;边际成本为5万元/t;求产量x 从250t 增加到300t 时销售收入()R x ;总成本C ()x ;利润()I x 的改变量增量..解首先求边际利润()()()0.082550.0820L x R x C x x x '''=-=-+-=-+所以根据式1、式2、式3;依次求出：300250(300)(250)()R R R x dx '-=⎰300250(0.0825)x dx =-+⎰=15300300250250(300)(250)()C C C x dx dx '-==⎰⎰=250万元300300250250(300)(250)()(0.0820)L L L x dx x dx '-==-+⎰⎰=-100万元例某厂生产某种产品;每日生产的产品的总成本C 的变化率即边际成本是日产量x 的函数xx C 257)(+=';已知固定成本为1000元;求总成本函数y .解因总成本是边际成本的一个原函数;所以)(x C ⎰+=dx x)257(c x x ++=507已知当0=x 时;1000)0(=C ;代入上式得1000=c ;于是总成本函数为)(x C 1000507++=x x例某产品销售总收入是销售量x 的函数)(x R ..已知销售总收入对销售量的变化率即边际收入x x R 52300)(-=';求销售量由100增加到400时所得的销售收入. 解因销售收入是边际收入的一个原函数;按题意;有)300()400(R R -⎰'=400300)(dx x R⎰-=400300)52300(dx x 4003002)51300(x x -=16000=元3.2求经济函数在区间上的平均变化率设某经济函数的变化率为()f t ;则称2121()t t f t dtt t -⎰为该经济函数在时间间隔21[,]t t 内的平均变化率..例某银行的利息连续计算;利息率是时间t 单位：年的函数：()0.08r t =+求它在开始2年;即时间间隔0;2内的平均利息率..解由于22()(0.08r t dt dt =+⎰⎰0.160.010.16=+=+所以开始2年的平均利息率为2()0.0820r t dtr ==+-⎰ 0.094≈例某公司运行t 年所获利润为()L t 元利润的年变化率为()310L t '=⨯/年求利润从第4年初到第8年末;即时间间隔3;8内年平均变化率解由于3885852333()310210(1)3810L t dt t '=⨯=⨯⋅+=⨯⎰⎰所以从第4年初到第8年末;利润的年平均变化率为853()7.61083L t dt '=⨯-⎰元/年即在这5年内公司平均每年平均获利57.610⨯元..3.3由贴现率求总贴现值在时间区间上的增量设某个项目在t 年时的收入为()f t 万元;年利率为r ;即贴现率是()rt f t e -;则应用定积分计算;该项目在时间区间[,]a b 上总贴现值的增量为()brt af t e ndt -⎰..设某工程总投资在竣工时的贴现值为A 万元;竣工后的年收入预计为a 万元年利率为r ;银行利息连续计算..在进行动态经济分析时;把竣工后收入的总贴现值达到A;即使关系式Trt ae dt A -=⎰成立的时间T 年称为该项工程的投资回收期..例某工程总投资在竣工时的贴现值为1000万元;竣工后的年收入预计为200万元;年利息率为0.08;求该工程的投资回收期..解这里1000A =;200a =;0.08r =;则该工程竣工后T 年内收入的总贴现值为0.080.080.0802002002500(1)0.08Tt tT T e dt e e ---==--⎰令 0.082500(1)T e --=1000;即得该工程回收期为110001ln(1)ln 0.60.0825000.08T =--=- =6.39年3.4 利润、产量与开工时数的最佳值的确定例1 某厂生产一种产品;年产量为x 吨时;总费用的变化率即边际费用为)(x f 825.0+=x 单位：百元/吨;这种产品每吨的销售价为3000元;问一年生产多少产品工厂利润最大;并求出年利润的最大值.解总费用是边际费用的原函数;故=)(x C ⎰+xdx x 0)825.0(x x 8125.02+=而收入函数)(x R x 30=百元;又由)(x L ＝)(x R =-)(x C 2125.022x x -则 )(x L 'x 25.022-=令 )(x L '0=;得88=x 吨..驻点唯一..此时025.0)88(<-=''L ;由实际问题可知;当88=x 时;)(x L 取得最大值96888125.08822)88(2=⨯-⨯=L 百元.因此;年产量为88吨时工厂获得最大利润96800元..例 2 某工厂生产一种产品;每日总收入的变化率即边际收入是日产量x 的函数x x R 2.030)(-='单位：元/件..该厂生产此种产品的能力为每小时30件;问怎样安排生产才能使这种产品每日的总收入最大并求出此最大总收入值.解由题意)(x R ⎰-=xdx x 0)2.030(21.030x x -=;令 02.030)(=-='x x R ;得150=x ;又02.0)(<-=''x R ;因为)(x R 只有唯一的驻点150=x ;由实际问题知;当150=x 时;)(x R 取得最大值22501501.015030)150(2=⨯-⨯=R .因此;每日取得最大总收入的产量为150件;此时2250)150(=R 元.完成150件产品需要的工时为530150=小时;所以;每天生产这种产品5小时;就使每日收入最大;最大值为2250元..3.5 资本存量问题例1 资本存量)(t s s =是时间t 的函数..它的导数等于净投资)(t I ..现知道净投资t t I 3)(=单位：10万元/年..求第一年底到第四年底的资本存量.解因资本存量s 是净投资的一个原函数;故=-)1()4(s s dt t ⎰41341232t=＝1410万元所以;第一年底到第四年底的总资本存量为1400000元..例 2 某银行根据前四年存款情况;知该行现金净存量的变化率是时间t 的函数455.14)(t x f =单位：万元/年;计划从第五年起积存现金1000万元..按此变化率需几年时间解依题意1000⎰+=xdt t 44455.14即 1000]4)4[(9584949-+=x由此;得 49494589000)4(+=+x 解此方程;得9993.94≈+x6≈x .所以;从第五年积存1000万元现金约需6 年.3.6消费者剩余和生产者剩余在自由市场中;生产并销售某一商品的数量可由这一商品的供给与需求曲线描述;它的状态可在如图上直观表现如下：0p 的经济意义是供应者会生产此商品的最低价..1p 是消费者会购买此种商品的最高价..1q 是免费供给此种商品的需求量如卫生纸经市场功能调节后;市场将趋于平衡价*P 和平衡数量*q ;两条曲线在),(**p q 相交..消费者以平衡价格购买了某种商品;他们本来打算出较高的价格购买这种商品;消费者剩余是指消费者因此而省下来的钱的总数..用积分式来表达就是：消费者剩余⎰=*0)(q d dq q Q **q p -＝曲边三角形*1p Mp 面积.生产者以平衡价格出售了某种商品;他们本来打算以较低一些的售价售出这些商品;生产者剩余是指生产者因此而获得的额外收入..用积分式表达就是生产者剩余⎰-=***)(q s dq q Q q p ＝曲边三角形*0p Mp 面积.4定积分在工程中的应用4.1定积分中值定理定积分中值定理作为定积分的一个重要性质;计算河床的平均深度时;应用定积分中值定理知识..此问题主要出现在水利工程专业的《工程水文学》课程中;主要应用于计算河流、湖泊等河床横断面水的平均深度;以此用作河流测流、工程设计或施工的一个依据..只要测量出河面在某处的宽度B;河床的横断面形状和河床的最大深度h ;则可运用定积分中值定理知识计算该处河床的平均深度h ;即⎰-=ba dx x f ab h )(1m. 例设一河流的河面在某处的宽度为2 b;河流的横断面为一抛物线弓形;河床的最深处在河流的中央;深度为h ;求河床的平均深度-h .分析：首先;选取坐标系使x 轴在水平面上;y 轴正向朝下;且y 轴为抛物线的对称轴..于是;抛物线方程为y=h-22x b h⋅.然后;运用定积分中值定理便可求得河床的平均深度-h . 解：河床的平均深度⎰-=b a dx x f a b h )(1=h 32.4.2定积分的近似计算知识的应用近似求物体的截面积;应用梯形法或抛物线法等定积分的近似计算知识..此问题主要出现在水利工程专业的《灌溉排水技术》课程中;主要应用于近似计算河床、渠道的过水断面面积;进而计算截面流量即渠系测流..由水利学知识可知;单位时间内流过某一截面的流体的体积就叫做通过这个截面的流量;即Q ＝V/tm 3/s.在水利工程中;流量的计算通常运用公式Q=svm 3/s;即过水断面面积s 与流速v 的乘积..例1有一条宽为24米的大型干渠;正在输水浇灌农田;试利用流速仪并结合梯形法或抛物线法近似求横截面积等高等数学知识进行测流..分析：根据灌溉管理学知识;首先选择测流断面;确定测线..测流断面选择在渠段正直;水流均匀;无漩涡和回流的地方;断面与水流方向垂直；测流断面的测线确定为12条..其次;测定断面..先在渠道两岸拉一条带有尺度的绳索;测出测深线的起点距与断面起点桩的水平距离；测线深度;用木制或竹制的测深杆施测;从渠道一岸到对岸每隔2米测量一次水深;测得数据如下表..根据施测结果绘出测流断面图;如图所示..第三;利用流速仪施测断面流速..例如;利用旋环式流速仪测出该渠道断面平均流速为v=0.60m/s.第四;近似计算渠道过水断面面积和流量... 测线深度施测数据表单位：m解答：（1）抛物线法辛卜生公式：A ≈30.67m 2 ； Q=18.40m 3/s. （2）梯形法：A ≈30.40m 2 ； Q=18.24m 3/s.例 2有一条河流;宽为200米;从河一岸到正对岸每隔20米测量一次水深;测的数据如下表..试分别用梯形法和抛物线法求此河床横截面积的近似值.. 单位：m4.3微元法知识的应用微元法在专业基础课和专业课中应用非常广泛;求解物体所受液体的侧压力;应用微元法知识..此问题主要出现在水利工程专业的《水力学》、《水工建筑物》等课程中;主要应用于计算水闸及输水建筑物如坝下涵管、隧洞、渠道、管道等上的闸门所受水压力的大小;作为设计或校核闸门结构的一个重要依据..水闸是一种低水头水工建筑物;既能挡水;又能泄水;用以调节水位;控制泄流量；多修建于河道、渠系及水库、湖泊岸边;在水利工程中的应用十分广泛..闸门是水闸不可缺少的组成部分;用来调节流量和上、下游水位;宣泄洪水和排放泥沙等..闸门的形式很多;按其结构形式通常分为平面闸门、弧形闸门及自动翻倒闸门等；按其工作条件可分为工作闸门和修理闸门；按其所处的位置不同可分为露顶闸门和潜孔闸门；按其所用的材料可分为钢闸门、钢筋混凝土闸门、钢丝网水泥闸门和木闸门等；按其形状不同又可分为矩形闸门、梯形闸门、圆形闸门和椭圆形闸门等..闸门的主要作用是挡水;承受水压力是其作用荷载之一..运用微元法计算闸门所受水压力时;设受水压力作用的区域与水平面垂直且由曲线y=fx ＞0;0≤a ≤x ≤bx=a;x=b 及x 轴所组成..x 轴正向朝下;y 轴在水平面上;水的密度为ρ=1000㎏/m 3;则闸门所受的水压力大小为P= ⎰b adx x gxf )(ρN.例有一个水平放置的无压输水管道;其横断面是直径为6m 的圆;水流正好半满;求此时输水管道一端的竖直闸门上所受的水压力..分析：首先建立合适的直角坐标系;如图所示;则圆的方程为222r y x =+=9. 然后;运用微元法求解即可.. 解答：P=1.76×105N.5定积分在医学的应用如图显示了人的心血管系统..血液流经全身通过静脉进入右心房;然后通过肺动脉泵入肺部补充氧气..之后通过肺静脉流回左心房;再通过主动脉流往全身其它部位;进行血液循环..心输出量就是单位时间一分钟内;心脏泵出的血液量;即血液通过动脉的速率..安静状态下;成年男性每搏输出量为60～80毫升;心率75次/分钟;故心输出量约4.5～6升；女性的心输出量比同体重男性的约低10％..人体的血液一直在周身循环;我图4-2们只能人为定义血液流动的起点和终点;即便这样也很难测定心脏单位时间内泵出的血液总量;所以人们就探索利用辅助材料来测定心输出量..最简单的辅助材料就是染料;即指示剂..具体做法是把指示剂加入到右心房;那么指示剂会和血液一起流经心脏泵入动脉..通过一个插入动脉的探头在一段时间内等间隔测量测出流出心脏的指示剂的浓度;直到指示剂基本消失;即指示剂全部流出心脏..那么剩余的问题就是如何利用测得图5-1 图5-2的浓度计算心输出量呢严格意义;只能测定某一时刻指示剂的浓度;是一系列的离散值;我们假定这些离散值在某一微小的时间段内是不变的;所以当时间段分的越细我们测定的值越接近连续值;这种思想使我们很容易想到积分的概念;所以可建立数学模型解决这个问题..解令ct 是t 时刻指示剂的浓度..如果把时间段0;t 划分成n 个等长的小时间段t ∆;指示剂流量=ctF t ∆;其中F 为我们测定的心输出量;这样总量即为()()n nc t F t F c t t ∆=∆∑∑;令n →∞时;指示剂总0()TA F c t dt =⎰..那么心输出量F=()TAc t dt⎰.这里的A 为已知量;即投入右心房的指示剂总量;ct 通过测量探头读取..6定积分在物理学的应用6.1变力做功在功的问题中;恒力做功是最简单的;公式为W F S =⋅． “以常代变”;功的微元应该通过恒力做功公式得到的．例 1 一压簧;原长1m ;把它每压缩1cm 时所用的力为0.05N ．问在弹性范围内把它由1m 如图6-1压缩到60cm 如图6-2所做的功．图6-1图6-2解令起点为原点;压缩的方向为x 轴的正方向当把弹簧自原点压缩至[]0,0.4之间的任意点x 处时如图6-3图6-3由胡克定律知所承受的弹簧的压力为()0.0550.01F x x x ==在此力的作用下;再继续压缩一点点dx ;即压缩至x dx +处由于dx 很小;这个压缩过程可认为力()F x 不变;即恒力做功则由恒力做功公式得功的微元dW ()F x dx = 积分得W ()0.40F x dx =⎰0.45xdx =⎰20.4502x =0.4=()J ．例2 在原点处有一带电量为q +的点电荷;在它的周围形成了一个电场．现在x a =处有一单位正电荷沿x 轴正方向移至x b =处;求电场力所做的功．又问若把该电荷继续移动;移动至无穷远处;电场力要做多少功．解点电荷在任意点x 处时所受的电场力为()2qF x kx=k 为常数电场力做功的微元dW 为点电荷由任意点x 处移动至x dx +处时电场力()F x 所做的功即()2qdW F x dx kdx x == 则移至x b =处电场力做的功2b a qW k dx x=⎰1bkqax =- 11kq a b ⎛⎫=- ⎪⎝⎭；移至无穷远处电场力做的功2a qW k dx x +∞=⎰kqa=物理学中称此值为电场在x a =处的电位．例 3 一圆台形水池;深15m ;上下口半径分别为20m 和10m ;如果把其中盛满的水全部抽干;需要做多少功解水是被“一层层”地抽出去的;在这个过程中;不但每层水的重力在变;提升的高度也在连续地变化图6-4其中抽出任意一层水x 处厚为dx 的扁圆柱体;如图6-4阴影部分所做的功为抽水做功的微元dW即dW dm g x dV g x γ=⋅⋅=⋅⋅⋅22203gx x dx γπ⎛⎫=- ⎪⎝⎭则2152203W gx x dx γπ⎛⎫=- ⎪⎝⎭⎰2152203g x x dx γπ⎛⎫=- ⎪⎝⎭⎰23415801200099g x x x γπ⎛⎫=-+ ⎪⎝⎭20625g γπ=202125000π=()J ．6.2求物体质量对于密度均匀的物体的质量l m l γ=⋅或A m A γ=⋅、m V γ=⋅;这时密度是常量；但对于密度不均匀密度是变量的物体的质量就不能直接用上述公式了;而应该用微元法．例一半圆形金属丝;其上任意点处的线密度与该点到连接金属丝端点的直径的距离成正比;求金属丝的质量．解建立如图6-5坐标系图6-5则()22l x ky R x γ==-()0k >22y R x'=-()()22ds dx dy =+21y dx '=+22R x=-()l dm x ds γ=⋅2222R k R x dx R x=-⋅-kRdx =RR m kRdx -=⎰22kR =．例 1 设有一心脏线1cos r θ=+形的物质薄片;其面密度()2cos A γθθ=+;试求此物质薄片的质量．解()22111cos 22dA r d d θθθ==+ ()A dm dA γθ=()()212cos 1cos 2d θθθ=++ ()3145cos 2cos 2cos 2d θθθθ=+++ ()230145cos 2cos 2cos 2m d πθθθθ=+++⎰321145sin sin 2sin sin 023πθθθθθ⎛⎫=+++- ⎪⎝⎭ 4π=．例 2 设一立体为曲线211y x=+关于x 轴的旋转体;其上任一点x 的体密度等于其横坐标的绝对值即()x x γ=;试求该立体的质量．解图6-62211x dV dx x π⎛⎫= ⎪+⎝⎭图6-6中小圆柱体体积 ()x dm x dV γ= 2211x dx x π⎛⎫= ⎪+⎝⎭()221xdx x π=+()221xm dx x π+∞-∞=+⎰()2221xdx x π+∞=+⎰()()22211x d x π+∞-=++⎰2101x π+∞=-+ π=．6.3 液体压力液面下h 深处水平放置的面积为A 的薄板承受的液体压力P 可以由压强乘以面积得到;即P gh A γ=⋅;其中γ为液体密度;压强gh γ是个常量匀压强．现在如若把薄板垂直放置呢薄板上的压强还是常量吗还能用上边那个简单的公式吗例 1 三峡大坝有一上底、下底、高分别为40、20、15米的等腰梯形闸门;闸门垂直放置且上边与水面齐如图6-4;试计算闸门一侧所承受的水压力．解回顾例3;我们知道抽水做功微元dW 为把x 处一层水抽出所做的功；类似地;侧压力微元dP 为x 处一层水对应的闸门的一个小窄条如图阴影部分所承受的水压力;即dP gxdA γ=2gx ydx γ= 22203gx x dx γ⎛⎫=- ⎪⎝⎭则15022203P gx x dx γ⎛⎫=- ⎪⎝⎭⎰15204403g x x dx γ⎛⎫=- ⎪⎝⎭⎰2315498002009x x ⎛⎫=- ⎪⎝⎭29400000=()N ．参考文献1 华东师大数学系.数学分析M.北京：高等教育出版社;2001：130-150．2 朱峰．大学物理M.北京：清华大学出版社;2004：15-80．3曹定华．微积分M．上海：复旦大学出版;2006：13-14．4马敏﹑冯梅．经济应用数学M．苏州：苏州大学出版社;2007：13-20．。