高一数学对数及对数运算1

合集下载

对数及对数运算(1)

知识探究（一）：对数函数的概念
思考1:在上面的问题中，若要使残留的 1 污垢为原来的，则要漂洗几次？ 64
4
思考2:在关系式 y log 1 x中，取 x a (a 0) 对应的y的值存在吗？怎样计算？
思考3:函数 y log 1 x 称为对数函数，
4
一般地，什么叫对数函数？
思考4:为什么在对数函数中要求a＞0，且a≠l？
理论迁移
例1
用logax，logay，logaz表示下列各式： 2 xy x y (1) log a ; (2) log a 3 . z z
例2
求下列各式的值：
(1) log2（47×25）； (2) lg5
31log3 2
100
；
(3) log318 -log32 ；
(4)
3
1 log 3 2
2.2.2 第一课时
对数函数及其性质对数函数的概念与图象
问题提出
1 5730 p 2
t
1.用清水漂洗含1个单位质量污垢的衣服，若每次能洗去污垢的四分之三，试写出漂洗次数y与残留污垢x的关系式.
2. y log 1 x （x>0）是函数吗？若
4
是，这是什么类型的函数？
a N x 指数式ax＝N 指数的底数幂幂指数对数式x＝对数的底数真数对数 logaN
思考4:根据对数定义，logal和logaa和 logaan（a>0，a≠1）的值分别是多少？
设loga1=x, 则ax=1, 所以x=0,得loga1=0 设logaa=x, 则ax=a, 所以x=1,得logaa=1
作业： P68练习：1, 2，3. P74习题2.2A组：3,4,5.

人教版高中数学必修一对数与对数运算对数及对数的性质课件PPT

x = 5 x=-2 x =
讲授新课
1.对数的定义：一般地，如果ax=N ( a > 0 , 且a ≠ 1 )
那么数x叫做以a为底N的对数，记作: 其中a叫做对数的底数, N叫做真数.
注意：限制条件是a > 0 , 且a ≠ 1
填写学案，题1
讲授新课
练习1：将下列指数式写成对数式：
① 52 = 25
（2）log
1 a
=
0
即：1的．对数是0
（3）log
a a
=
1
即：底数的对数是1
（4）对数恒等式：aloga N = N
（5）对数恒等式：loga an = n
巩固练习
1、指数式b2 = a(b 0,且b 1)相应的对数式是（D）
A log2a = b B log2 b = a
C logab=2
解：(1)64
-
2 3
=
(43
)
-
2 3
= 4-2 =
1
(4) ln e2 = -x
16
1
1
1
e-x = e2
(2)x6 = 8所以x = 86 = (23 )6 = 22 = 2 - x = 2
(3)10 x = 100所以x = 2
x = -2
讲授新课 4.对数的性质探究活动 1、试求下列各式的值：
。
简记作
。如 loge 9 简记为 ln 9.
填写学案，题4
例题分析
例1．将下列指数式写成对数式：
(1) 54 = 625
(2)
e-6
=
1
b
(3) 10 a = 27 (4) ( 1 )m = 5.73

人教版数学高一教案对数及其运算(一)

§3.2 对数与对数函数3.2.1 对数及其运算(一)一．教学目标：1．知识技能：①理解对数的概念，了解对数与指数的关系；②理解和掌握对数的性质；③掌握对数式与指数式的关系.2.过程与方法：通过与指数式的比较，引出对数定义与性质.3．情感、态度、价值观（1）学会对数式与指数式的互化，从而培养学生的类比、分析、归纳能力.（2）通过对数的运算法则的学习，培养学生的严谨的思维品质.（3）在学习过程中培养学生探究的意识.（4）让学生理解平均之间的内在联系，培养分析、解决问题的能力.二．重点与难点：（1）重点：对数式与指数式的互化及对数的性质（2）难点：对数性质的推导三．学法与教具：（1）学法：讲授法、讨论法、类比分析与发现（2）教具：投影仪教学过程[问题情境] 对数,延长了天文学家的生命.“给我空间、时间和对数,我可以创造一个宇宙”,这是16世纪意大利著名学者伽利略的一段话.从这段话可以看到,伽利略把对数与最宝贵的空间和时间相提并论.那么,“对数”到底是什么呢？本节就来探讨这个问题.探究点一对数的概念问题1 若24＝M ,则M 等于多少？若2－2＝N ,则N 等于多少？答： M ＝16,N ＝14. 问题2 若2x ＝16,则x 等于多少？若2x ＝14,则x 等于多少？答： x 的值分别为4,－2.问题3 满足2x ＝3的x 的值,我们用log 23表示,即x ＝log 23,并叫做“以2为底3的对数”.那么满足2x ＝16,2x ＝14,4x ＝8的x 的值如何表示？答：分别表示为log 216,log 214,log 48. 小结： 1.在指数函数f (x )＝a x (a ＞0,且a ≠1)中,对于实数集R 内的每一个值x ,在正实数集内都有唯一确定的值y 和它对应;反之,对于正实数集内的每一个确定的值y ,在R 内都有唯一确定的值x 和它对应.幂指数x ,又叫做以a 为底y 的对数.一般地,对于指数式a b ＝N ,我们把“以a 为底N 的对数b ”记作log a N ,即b ＝log a N (a >0,a ≠1).其中,数a 叫做对数的底数,N 叫做真数,读作“b 等于以a 为底N 的对数”.2.对数log a N (a >0,且a ≠1)的性质(1)0和负数没有对数,即N >0;(2)1的对数为0,即log a 1＝0;(3)底的对数等于1,即log a a ＝1.3.常用对数以10为底的对数叫做常用对数.为了简便起见,对数log 10N 简记作lg N .探究点二对数与指数的关系问题1 当a >0,且a ≠1时,若a x ＝N ,则x ＝log a N ,反之成立吗？为什么？答：反之也成立,因为对数表达式x ＝log a N 不过是指数式a x ＝N 的另一种表达形式,它们是同一关系的两种表达形式.问题2 在指数式a x ＝N 和对数式x ＝log a N 中,a ,x ,N 各自的地位有什么不同？答问题3 若a b ＝N ,则b ＝log a N ,二者组合可得什么等式？答：对数恒等式:a ＝N .问题4 当a >0,且a ≠1时,log a (－2),log a 0存在吗？为什么？由此能得到什么结论？答：不存在,因为log a (－2),log a 0对应的指数式分别为a x ＝－2,a x ＝0,x 的值不存在,由此能得到的结论是:0和负数没有对数.问题5 根据对数定义,log a 1和log a a (a >0,a ≠1)的值分别是多少？答：log a 1＝0,log a a ＝1.∵对任意a >0且a ≠1,都有a 0＝1, ∴化成对数式为log a 1＝0; ∵a 1＝a ,∴化成对数式为log a a ＝1.小结：对数log a N (a >0,且a ≠1)具有下列性质:(1)0和负数没有对数,即N >0;(2)1的对数为0,即log a 1＝0;(3)底的对数等于1,即log a a ＝1.例1 求log 22, log 21, log 216, log 212. 解：因为21＝2,所以log 22＝1;因为20＝1,所以log 21＝0;因为24＝16,所以log 216＝4;因为2－1＝12,所以log 212＝－1. 小结： log a N ＝x 与a x ＝N (a >0,且a ≠1,N >0)是等价的,表示a ,x ,N 三者之间的同一种关系,可以利用其中两个量表示第三个量.因此,已知a ,x ,N 中的任意两个量,就能求出另一个量. 跟踪训练1 将下列指数式写成对数式:(1)54＝625; (2)2－6＝164; (3)3a ＝27; (4)⎝⎛⎭⎫13m ＝5.73. 解： (1)log 5625＝4;(2)log 2164＝－6;(3)log 327＝a ;(4)log 135.73＝m . 例2 计算:(1)log 927; (2)log 4381; (3)log 354625.解：(1)设x ＝log 927,则9x ＝27,32x ＝33,∴x ＝32. (2)设x ＝log 4381,则⎝⎛⎭⎫43x ＝81,3＝34,∴x ＝16.(3)令x ＝log 354625,∴⎝⎛⎭⎫354x ＝625,5＝54,∴x ＝3.小结：要求对数的值,设对数为某一未知数,将对数式化为指数式,再利用指数幂的运算性质求解.跟踪训练2 求下列各式中的x 的值:(1)log 64x ＝－23; (2)log x 8＝6; (3)lg 100＝x . 解： (1)x ＝(64) －23＝(43) －23＝4－2＝116.(2)x 6＝8,所以x ＝(x 6) 16＝816＝(23) 16＝212＝ 2.(3)10x ＝100＝102,于是x ＝2.探究点三常用对数问题阅读教材96页下半页,说出什么叫常用对数？常用对数如何表示？答：以10为底的对数叫做常用对数.通常把底10略去不写,并把“log”写成“lg”,并把log 10N 记做lg N .如果以后没有指出对数的底,都是指常用对数.如“100的对数是2”就是“100的常用对数是2”.例3 求lg 10,lg 100,lg 0.01.解：因为101＝10,所以lg 10＝1;因为102＝100,所以lg 100＝2;因为10－2＝0.01,所以lg 0.01＝－2.小结：由本例题可以看出,对于常用对数,当真数为10n (n ∈Z )时,lg 10n ＝n ;当真数不是10的整数次方时,常用对数的值可通过查对数表或使用科学计算器求得.跟踪训练3 求下列各式中的x 的值:(1)log 2(log 5x )＝0;(2)log 3(lg x )＝1; (3)log (2－1)13＋22＝x .解： (1)∵log 2(log 5x )＝0. ∴log 5x ＝20＝1,∴x ＝51＝5.(2)∵log 3(lg x )＝1,∴lg x ＝31＝3,∴x ＝103＝1 000.(3)∵log (2－1)13＋22＝x ,∴(2－1)x ＝13＋22＝1(2＋1)2＝12＋1＝2－1, ∴x ＝1.当堂检测1.若log (x ＋1)(x ＋1)＝1,则x 的取值范围是( B ) A.x >－1B.x >－1且x ≠0C.x ≠0D.x ∈R 解析：由对数函数的定义可知x ＋1≠1，x ＋1>0即x >－1且x ≠0.2.已知log 12x ＝3,则x 13＝__12______.解析：∵log 12x ＝3,∴x ＝(12)3, ∴x 13＝12. 3.已知a 12＝49(a >0),则log 23a ＝__4______.解析：由a 12＝49(a >0),得a ＝(49)2＝(23)4, 所以log 23a ＝log 23(23)4＝4. 4.将下列对数式写成指数式:(1)log 16＝－4;(2)log 2128＝7;(3)lg 0.01＝－2.解：(1)⎝⎛⎭⎫12－4＝16;(2)27＝128; (3)10－2＝0.01.课堂小结：1.掌握指数式与对数式的互化a b ＝N ⇔log a N ＝b .2.对数的常用性质有:负数和0没有对数,log a 1＝0,log a a ＝1.3.对数恒等式有:a log a N ＝N ,log a a n ＝n .4.常用对数:底数为10的对数称为常用对数,记为lg N .。

高中数学第四章对数运算和对数函数 1 对数的概念课件必修第一册高一第一册数学课件

1
2
D.4 =x
(2)D
2021/12/12
第七页，共二十二页。
激趣诱思
知识(zhī shi)点
拨
二、对数的基本性质
1.负数和零没有(méi yǒu)对数.
2.对于任意的a>0,且a≠1,都有
1
loga1=0,logaa=1,loga =-1.
a
3.对数恒等式aa =
N
.
名师点析1.loga1=0,logaa=1可简述为“1的对数等于0,底的对数等于1”.
4
(3)log3(lg x)=1.
2
解:(1)由 log8x=- ,得 x=8
3
3
3
4
2
3
-
2
=(23)-3 =2-2,故
3
4
1
x= .
4
(2)由 logx27=4,得 =27,即 =33,
4
3 3
故 x=(3 ) =34=81.
(3)由 log3(lg x)=1,得 lg x=3,故 x=103=1 000.
3
-1 1
(3)e = ;
e
(4)10-3=0.001.
分析利用当a>0,且a≠1时,logaN=b⇔ab=N进行互化.
解:(1)
1
1 -3
3
(3)ln =-1.
e
=27.
(2)log464=3.
(4)lg 0.001=-3.
2021/12/12
第十页，共二十二页。
当堂检测
探究(tànjiū)一
探究(tànjiū)二
§1
对数(duìshù)的概念
2021/12/12

人教版高一数学必修1第21课时对数与对数的运算(1)含解析

A．N＝a2bB．N＝2ab
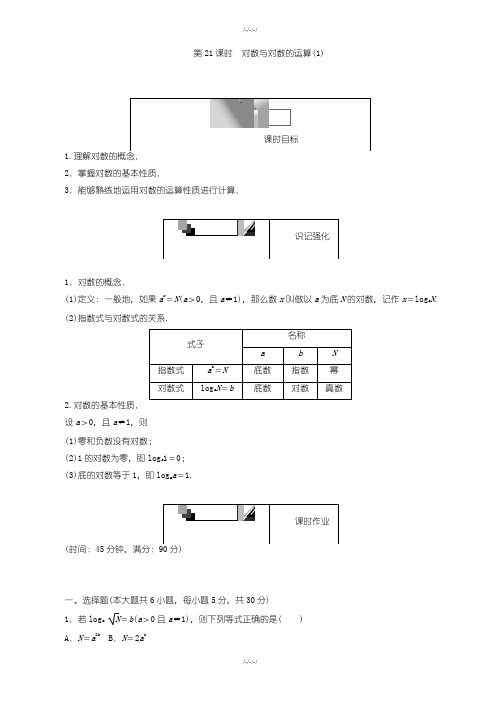
C．N＝b2aD．N2＝ab
答案：A
解析：把loga ＝b写成＝ab，∴N＝(ab)2＝a2b.
2．若a>0，且a≠1，c>0，则将ab＝c化为对数式为()
A．logab＝cB．logac＝b
C．logbc＝aD．logca＝b
答案：B
解析：由对数的定义直接可得logac＝b.
A．2x－9 B．9－2x
C．11 D．9
答案：C
解析：因为sinθ∈[－1,1]，所以2＋sinθ∈[1,3]，即log2x∈[1,3]，解得x∈[2,8]，所以|x＋1|＋|x－10|＝(x＋1)＋(10－x)＝11.
5．若对数式log(2a－1)(6－2a)有意义，则实数a的取值范围为()
A．(－∞，3) B.
②0.33＝0.027；
③e0＝1.
(2)将下列对数式写成指数式：
①log0.46.25＝－2；
②log310＝2.0959；
③ln23.14＝x.
解：(1)①log21024＝10；②log0.30.027＝3；③ln1＝0.
(2)①0.4－2＝6.25；②32.0959＝10；③ex＝23.14.
第21课时对概念．
2．掌握对数的基本性质．
3．能够熟练地运用对数的运算性质进行计算．
识记强化
1．对数的概念．
(1)定义：一般地，如果ax＝N(a＞0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝logaN.
(2)指数式与对数式的关系.
式子
名称
a
b
N
指数式
C. ∪(1，＋∞) D. ∪(1,3)
答案：D
解析：由已知，得 ⇒ ⇒ <a<3且a≠1，故选D.

人教A版必修1导学案必修1 2.2.1对数及对数运算(第1课时)

必修1高一数学第一章§ 2.2.1 对数与对数运算（1）【学习目标】：① 理解对数的概念，了解对数与指数的关系；②理解和掌握对数的性质；③掌握对数式与指数式的关系 .【教学重点、难点】：重点：对数式与指数式的互化及对数的性质；难点：推导对数性质【教学过程】：一、新课讲解：1、对数的概念一般地，若(0,1)x a N a a =>≠且，那么数x 叫做以a 为底N 的______，记作log a x N =a 叫做________________，N 叫做______________(注意：底数a ＞0，且a ≠1;真数N>0) 举例：x 01.11318=写成对数形式：x ＝ 1.0118log 13，读作x 是以 1.01为底,1318的对数. 2416=写成对数形式：42log 16=，读作2是以4为底，16的对数.2、对数式与指数式的互化在对数的概念中，要注意：（1）底数的限制a ＞0，且a ≠1（2）log x a a N N x =⇔=指数式⇔对数式幂底数←a →对数底数指数←x →对数幂 ←N →真数3、例题讲解：指数式与对数式互化例1（P63例1）将下列指数式化为对数式，对数式化为指数式.（1）54=625 （2）61264-=（3）1() 5.733m = （4）12log 164=- （5）10log 0.012=- （6）log 10 2.303e =（课本64页#1）练习1：将下列指数式与对数式互化：（1）328=，（2） 1122-=；（3）3log 92=；（4）21log 24=-。

4、对数的性质：问题：① 把a 0=1，a 1=a （a ＞0，且a ≠1）如何写成对数式？②负数和零有没有对数？ ③根据对数的定义，log a N a=？小结：log log 10, log 1, a N a a a aN === 负数和零没有对数。

5、常用对数和自然对数 ① 以10为底的对数称为常用对数，10log N 常记为___________② 以无理数e=2.71828…为底的对数称为自然对数，log e N 常记为__________.6、例题讲解例2：（课本63页）求下列各式中x 的值（1）642log 3x =-（2）log 86x = （3）lg100x = （4）2ln e x -= 分析：将对数式化为指数式，再利用指数幂的运算性质求出x .7.巩固提高：求下列各式的值：（1）5log 25；（2）lg1000；（3）15log 15；（4）9log 81；（5） 2.5log 6.25。

新教材高中数学第四章对数运算与对数函数1对数的概念课件北师大版必修第一册

【对点练习】❶ 将下列指数式化为对数式，对数式化为指数式：
(1)42＝16；(2)102＝100；
1
(3)42＝2；(4)log132＝－5．
2
[解析] (1)log416＝2 ． (2)lg 100＝2．
(3)log42＝12．
(4)21－5＝32．
题型二
对数基本性质的应用
例 2求下列各式中的x： (1)log3(log2x)＝0； (2)log3(log7x)＝1； (3)lg(ln x)＝1； (4)lg(ln x)＝0． [分析] 利用指数式与对数式的互化进行解答．
【对点练习】❷ 求下列各式中 x 的值：
(1)x＝log116； 2
(2)log8x＝－13；
(3)log( 2 －1)
1 3＋2
2＝x．
[解析] (1)∵x＝log2116，∴12x＝16，即 2－x＝24．∴－x＝4，即 x＝－4．
(2)∵log8x＝－13，∴x＝8－13＝318＝12．
5．若ln e－2＝－x,则x＝____2_． [解析] 由题意可知e－2＝e－x,故x＝2．
关键能力•攻重难
题型探究
题型一
对数的定义
例 1 (1)在对数式 y＝log(x－2)(4－x)中，实数 x 的取值范围是 ___2_＜__x_＜__4_且__x_≠__3____．
(2)将下列指数式化为对数式，对数式化为指数式． ①54＝625；②log216＝4；③10－2＝0.01；④log 5125＝6．
第四章对数运算与对数函数
§1 指数幂的拓展
【素养目标】 1．能结合指数幂解对数的相关概念,常用对数、自然对数．(数学抽象) 3．能结合教材中的例题掌握指数与对数的互化、简单的求值．(数学运算)

对数与对数运算学生版

2.2.1 对数与对数运算1．对数的概念(1)定义：一般地，如果a x＝N(a＞0，且a≠1)，那么数x叫做以a为底N的对数，记作x＝log a N，其中a叫做对数的底数，N叫做真数．释疑点在对数log a N中规定a＞0，且a≠1，N＞0的原因(1)若a＜0，则N为某些数值时，x不存在，如式子(－3)x＝4没有实数解，所以log(－3)4不存在，因此规定a不能小于0；(2)若a＝0，且N≠0时，log a N不存在；N＝0时，log a0有无数个值，不能确定，因此规定a ≠0，N≠0；(3)若a＝1，且N≠1时，x不存在；而a＝1，N＝1时，x可以为任何实数，不能确定，因此规定a≠1；(4)由a x＝N，a＞0知N恒大于0．(2)(3)(4)当a＞0，且a≠1时．如图所示：比如：43＝64⇔3＝log464；log525＝2⇔52＝25；以前无法解的方程2x＝3，学习了对数后就可以解得x＝log23．谈重点对指数与对数的互化关系的理解(1)由指数式a b＝N可以写成log a N＝b(a＞0，且a ≠1)，这是指数式与对数式互化的依据．从对数定义可知，对数式与指数式是同一种数量关系的两种不同表达形式．其关系如下表：(2)根据指数与对数的互化关系，可以得到恒等式log a Na N＝．指数与对数的互化是解决指数式和对数式有关问题的有效手段．【例1－1】下列指数式与对数式的互化中，不正确的一组是( ) A．100＝1与lg 1＝0B．131273-=与271log3＝13-C．log39＝2与129＝3D．log55＝1与51＝5 【例1－2【例1－3】求下列各式中(1)log2(log5x)＝0；(2)log3(lg x)＝1；(3)log x27＝34；(4)x＝log84．2．对数的运算性质(1)对数的运算性质如果a＞0，且a≠1，M＞0，N＞0，那么：①log a(M·N)＝log a M＋log a N；②loga MN＝log a M－log a N；③log a M n＝n log a M(n∈R)．谈重点对对数的运算性质的理解(1)对应每一条运算性质，都要注意只有当式子中所有的对数符号都有意义时，等式才成立，如log2[(－3)·(－5)]＝log2(－3)＋log2(－5)是错误的．(2)巧记对数的运算性质：①两个正数的积的对数等于这两个正数的对数的积；②两个正数的商的对数等于这两个正数的对数的差；③正数幂的对数等于幂指数乘以同一底数幂的底数的对数．(2)谈重点利用对数的定义将对数问题转化为指数问题，再利用幂的运算性质，进行转化变形，然后把它还原为对数问题．如“log a(MN)＝log a M＋log a N”的推导：设log a M＝m，log a N＝n，则a m＝M，a n＝N，于是MN＝a m·a n＝a m＋n，因此log a(MN)＝log a M＋log a N＝m＋n．【例2－1】若a ＞0，且a ≠1，x ＞y ＞0，n ∈N *，则下列各式： ①log a x ·log a y ＝log a (x ＋y )；②log a x －log a y ＝log a (x －y )；③log a (xy )＝log a x ·log a y ；④log log log a a a x xy y=；⑤(log a x )n ＝log a x n ；⑥1log log a a x x=-；⑦log log a a x n=其中式子成立的个数为( )A ．2B ．3C ．4D ．5【例2－2】计算：(1)2log 122＋log 123；(2)lg 500－lg 5；(3)已知lg 2＝0.301 0，lg 3＝0.477 1，求．析规律对数的运算性质的作用 (1)利用对数的运算性质，可以把乘、除、乘方、开方的运算转化为对数的加、减、乘、除运算，反之亦然，这种运算的互化可简化计算；(2)由于lg 2＋lg 5＝lg 10＝1，所以lg 5＝1－lg 2，这是在对数运算中经常用到的结论．3．换底公式(1)公式log a b ＝log log c c ba(a ＞0，且a ≠1；c ＞0，且c ≠1，b ＞0)．(2)公式推导：设log log c c b x a=，则log c b ＝x log c a ＝log c a x ， ∴b ＝a x ．∴x ＝log a b ．∴log log c c ba＝log a b ．(3)公式的作用换底公式的作用在于把以a 为底的对数，换成了以c 为底的对数，特别有：lg log lg a NN a=，ln log ln a NN a=，利用它及常用对数表、自然对数表便可求任一个对数的值． (4)换底公式的三个推论：①log log m n a a nN N m=(a ，N ＞0，且a ≠1，m ≠0，m ，n ∈R )；②log a b＝1log b a (a ，b ＞0，且a ，b ≠1)；③log a b ·log b c ·log c d ＝log a d (a ，b ，c ＞0，且a ，b ，c ≠1，d ＞0)．证明：①log am N n＝log log log log n a a a ma N n N n N a m m ==．②log ab ＝log 1log log b b b b a a=．③log a b ·log b c ·log c d ＝lg lg lg lg lg lg lg lg b c d da b c a⋅⋅=＝log a d ．【例3－1】82log 9log 3的值是( ) A ．23 B ．32 C ．1 D ．2【例3－2】若log 34·log 48·log 8m ＝log 416，则m 等于( )A ．12B ．9C ．18D ．274．对数定义中隐含条件的应用根据对数的定义，对数符号log a N 中实数a 和N 满足的条件是底数a 是不等于1的正实数，真数N 是正实数，即>0,>0,1,N a a ⎧⎪⎨⎪≠⎩因此讨论对数问题时，首先要注意对数的底数和真数满足的隐含条件．对数概念比较难理解，对数符号初学时不太好掌握，学习时要抓住对数与指数相互联系，深刻理解对数与指数之间的关系，将有助于掌握对数的概念．【例4－1】已知对数log (1－a )(a ＋2)有意义，则实数a 的取值范围是__________．【例4－2】若log (1－x )(1＋x )2＝1，则x ＝__________．5．对数的化简、求值问题应用对数的定义、有关性质及运算法则等可以把乘、除、乘方、开方的运算转化为对数的加、减、乘、除运算，反之亦然，这种运算的互化可简化计算过程，加快计算速度．(1)同底数的对数式的化简、求值一是“拆”，将积、商的对数拆成对数的和、差．如39log 5＋log 35＝log 39－log 35＋log 35＝log 39＝2．二是“收”，将同底数的对数和、差合成积、商的对数．如，39log 5＋log 35＝39log 55⎛⎫⨯ ⎪⎝⎭＝log 39＝2．三是“拆”与“收”相结合．(2)不同底数的对数式的化简、求值常用方法是利用换底公式，转化为同底数的对数式，进而进行化简，化简后再将底数统一进行计算．也可以在方向还不清楚的情况下，统一将不同的底换为常用对数等，再进行化简、求值．对数式的化简、求值，要灵活运用对数的性质、运算性质、换底公式和一些常见的结论，如log a 1＝0，log a a ＝1，a log a N ＝N ，lg 2＋lg 5＝1，log a b ·log b a ＝1等．【例5－1】化简求值：(1)4lg 2＋3lg 5－1lg5；；(3)2log32－332log9＋log38－5log35；(4)log2(1)＋log2(1．【例5－2】计算：(log43＋log83)(log32＋log92)－．6．条件求值问题对于带有附加条件的与对数式有关的求值问题，如果附加条件比较复杂，则需先对其进行变形、化简，并充分利用其最简结果解决问题．例如：设x＝log23，求332222x xx x----的值时，我们可由x＝log23，求出2x＝3,2－x＝13，然后将它们代入332222x xx x----，可得33331322913122933x xx x--⎛⎫- ⎪-⎝⎭==--．【例6】已知3a＝4b＝36，求21a b+的值．析规律与对数式有关的求值问题的解决方法(1)注意指数式与对数式的互化，有些需要将对数式化为指数式，而有些需要将指数式化为对数式；(2)注意换底公式与对数的运算性质的应用，解题时应全方位、多角度地思考，注意已知条件和所求式子的前后照应．7．利用已知对数表示其他对数(1)换底公式的作用是将不同底的对数式转化成同底的对数式，将一般对数转化成自然对数或常用对数来运算．要注意换底公式的正用、逆用及变形应用．(2)用对数log a x和log b y等表示其他对数时，首先仔细观察a，b和所要表示的对数底数的关系，利用换底公式把所要表示的对数底数换为a，b．解决此类题目时，通常用到对数的运算性质和换底公式．对数的运算性质总结：如果a ＞0，且a ≠1，M ＞0，N ＞0，那么： log a (M ·N )＝log a M ＋log a N ；log a MN＝log a M －log a N ； log a M n ＝n log a M (n ∈R )．换底公式：log a b ＝log log c c ba(a ＞0，且a ≠1；c ＞0，且c ≠1；b ＞0)．(3)题目中有指数式和对数式时，要注意将指数式与对数式进行互化，统一成一种形式．【例7－1】已知lg 2＝a ，lg 3＝b ，则log 36＝( )A ．a b a +B ．a b b +C ．a a b +D ．b a b +【例7－2】已知log 189＝a,18b ＝5，求log 3645(用a ，b 表示)．8．与对数有关的方程的求解问题关于对数的方程有三类：第一类是形如关于x 的方程log a f (x )＝b ，通常将其化为指数式f (x )＝a b ，这样解关于x 的方程f (x )＝a b 即可，最后要注意验根．例如：解方程64152log 163x ⎛⎫-=- ⎪⎝⎭，将其化为指数式为23156416x --=，又223233164(4)416---===，则1511616x -=，所以x ＝1，经检验x ＝1是原方程的根．第二类是形如关于x 的方程log f (x )n ＝b ，通常将其化为指数式f b (x )＝n ，这样解关于x 的方程f b (x )＝n 即可，最后要注意验根．例如，解方程log (1－x )4＝2，将其化为指数式为(1－x )2＝4，解得x ＝3或x ＝－1，经检验x ＝3是增根，原方程的根是x ＝－1．第三类是形如关于x 的方程f (log a x )＝0，通常利用换元法，设log a x ＝t ，转化为解方程f (t )＝0得t ＝p 的值，再解方程log a x ＝p ，化为指数式则x ＝a p ，最后要注意验根．【例8－1】已知lg x ＋lg y ＝2lg(x －2y )，求xy的值．【例8－2】解方程lg 2x －lg x 2－3＝0．9．对数运算的实际应用对数运算在实际生产和科学技术中运用广泛，其运用问题大致可分为两类：一类是已知对数应用模型(公式)，在此基础上进行一些实际求值．计算时要注意利用“指、对互化”把对数式化成指数式．另一类是先建立指数函数应用模型，再进行指数求值，此时往往将等式两边进行取对数运算．【例9】抽气机每次抽出容器内空气的60%，要使容器内的空气少于原来的0.1%，则至少要抽几次？(lg 2≈0.301 0)。

人教版高中数学必修一学习课件对数及对数运算

b叫N做
a为底N的对数 (叫对数式)，
log a N b
a叫做对数的底数， N叫做真数
二．思考：为什么在定义中要规定： a＞0且a≠1，而且 N>0?
三．几个常用结论：（1）负数与零没有对数
（2） log a 1 0 （3） loga a 1
a （4）对数恒等式： loga N N
4．常用的两种对数：
思考:
在2.1.2(P57)例8中,我们得到了函问题数1关:在系这式个:y例=1题3•中1,.对01于x 给, 定的一个年份, 你能计算相应的人口总数吗?
问题2:哪一年的人口数可达到18亿? 20亿呢?
一、对数的定义: 一般地,如果
即aa 0, a 1
的b次幂等于N, (叫指数式)，
那记么作a数b
（1）54=625
(2) 26 1
64
(3) (1)m 5.73 3
(4) log 1 16 4
2
(5) lg 0.01 2 （6）ln10 2.303
例2 求下列各式中x的值
(1)
log64
x2 3
(2) logx 8 6
(3) lg100 x
(4) ln e2 x
例3、求 x 的值：
(1) log2x2 1 3x2 2x 1 1
(2) log2 log3 log4 x 0
练习（书上P64第1、2、3、4题）：
小结： 1．对数定义： 2.指数式与对数式互换 3.理解: a＞0且a≠1；而且 N>0 4.常用的两种对数： 5．几个常用结论：
（1）常用对数：通常将以10为底的对数叫做常用对数(common logarithm)。 N的常用对数简记作lgN

高中数学：2.2.1对数与对数运算 (1)

第2课时对数的运算[目标] 1.理解对数的运算性质；2.能用换底公式将一般对数转化成自然对数或常用对数；3.了解对数在简化运算中的作用．[重点] 对数的运算性质的推导与应用．[难点] 对数的运算性质的推导和换底公式的应用.知识点一对数的运算性质[填一填]如果a >0，且a ≠1，M >0，N >0.那么： (1)log a (M ·N )＝log a M ＋log a N . (2)log a MN ＝log a M －log a N .(3)log a M n ＝n log a M (n ∈R )．[答一答]1．若M ，N 同号，则式子log a (M ·N )＝log a M ＋log a N 成立吗？提示：不一定，当M >0，N >0时成立，当M <0，N <0时不成立．2．你能推导log a (MN )＝log a M ＋log a N 与log a MN ＝log a M －log a N (M ，N >0，a >0且a ≠1)两个公式吗？提示：①设M ＝a m ，N ＝a n ，则MN ＝a m ＋n .由对数的定义可得log a M ＝m ，log a N ＝n ， log a (MN )＝m ＋n .这样，我们可得log a (MN )＝log a M ＋log a N . ②同样地，设M ＝a m ，N ＝a n ，则MN ＝a m －n .由对数定义可得log a M ＝m ， log a N ＝n ，log a MN ＝m －n ，即log a MN＝log a M －log a N .知识点二换底公式[填一填]换底公式常见的推论： (1)log an b n ＝log a b ；(2)log am b n ＝n m log a b ，特别log a b ＝1log b a ；(3)log a b ·log b a ＝1； (4)log a b ·log b c ·log c d ＝log a d .[答一答]3．换底公式的作用是什么？提示：利用换底公式可以把不同底数的对数化为同底数的对数． 4．若log 34·log 48·log 8m ＝log 416，求m 的值．提示：∵log 34·log 48·log 8m ＝log 416， ∴lg4lg3·lg8lg4·lg mlg8＝log 442＝2，化简得lg m ＝2lg3＝lg9，∴m ＝9.类型一对数运算性质的应用[例1] 计算下列各式： (1)12lg 3249－43lg 8＋lg 245； (2)2lg2＋lg31＋12lg0.36＋13lg8；(3)lg25＋23lg8＋lg5lg20＋(lg2)2.[分析] (1)(2)正用或逆用对数的运算性质化简；(3)用lg2＋lg5＝1化简．[解] (1)(方法1)原式＝12(5lg2－2lg7)－43×32lg2＋12(2lg7＋lg5)＝52lg2－lg7－2lg2＋lg7＋12lg5＝12lg2＋12lg5＝12(lg2＋lg5)＝12lg10＝12. (方法2)原式＝lg427－lg4＋lg(75)＝lg 42×757×4＝lg(2×5)＝lg 10＝12.(2)原式＝lg4＋lg31＋lg0.6＋lg2＝lg12lg (10×0.6×2)＝lg12lg12＝1. (3)原式＝2lg5＋2lg2＋(1－lg2)(1＋lg2)＋(lg2)2 ＝2(lg5＋lg2)＋1－(lg2)2＋(lg2)2＝2＋1＝3.利用对数的运算性质解决问题的一般思路：(1)把复杂的真数化简；(2)正用公式：对式中真数的积、商、幂、方根，运用对数的运算法则，将它们化为对数的和、差、积、商，然后再化简；(3)逆用公式：对式中对数的和、差、积、商，运用对数的运算法则，将它们化为真数的积、商、幂、方根，然后化简求值.[变式训练1] (1)计算：log 53625＝43；log 2(32×42)＝9.(2)计算：lg8＋lg125＝3；lg 14－lg25＝－2；2log 36－log 34＝2.类型二换底公式的应用[例2] (1)计算：(log 32＋log 92)·(log 43＋log 83)； (2)已知log 189＝a,18b ＝5，试用a ，b 表示log 3645. [解] (1)原式＝⎝⎛⎭⎫lg2lg3＋lg2lg9⎝⎛⎭⎫lg3lg4＋lg3lg8 ＝⎝⎛⎭⎫lg2lg3＋lg22lg3⎝⎛⎭⎫lg32lg2＋lg33lg2＝3lg22lg3·5lg36lg2＝54. (2)由18b ＝5，得log 185＝b ，∴log 3645＝log 18(5×9)log 18(18×2)＝log 185＋log 1891＋log 182＝log 185＋log 1891＋log 18189＝log 185＋log 1892－log 189＝a ＋b 2－a .利用换底公式可以统一“底”，以方便运算.在用换底公式时，应根据题目特点灵活换底.由换底公式可推出常用结论：log a b ·log b a ＝1.[变式训练2] 计算下列各式：(1)(log 2125＋log 425＋log 85)·(log 52＋log 254＋log 1258)． (2)log 89log 23×log 6432. 解：(1)方法1：原式＝(log 253＋log 225log 24＋log 25log 28)(log 52＋log 54log 525＋log 58log 5125)＝⎝⎛⎭⎫3log 25＋2log 252log 22＋log 253log 22⎝⎛⎭⎫log 52＋2log 522log 55＋3log 523log 55 ＝⎝⎛⎭⎫3＋1＋13log 25·(3log 52)＝13log 25·log 22log 25＝13. 方法2：原式＝⎝⎛⎭⎫lg125lg2＋lg25lg4＋lg5lg8⎝⎛⎭⎫lg2lg5＋lg4lg25＋lg8lg125 ＝⎝⎛⎭⎫3lg5lg2＋2lg52lg2＋lg53lg2⎝⎛⎭⎫lg2lg5＋2lg22lg5＋3lg23lg5 ＝⎝⎛⎭⎫13lg53lg2⎝⎛⎭⎫3lg2lg5＝13.(2)方法1：原式＝log 29log 28÷log 23×log 232log 264＝2log 233÷log 23×56＝59.方法2：原式＝lg9lg8÷lg3lg2×lg32lg64＝2lg33lg2×lg2lg3×5lg26lg2＝59.类型三与对数方程有关的问题[例3] (1)若lg(x －y )＋lg(x ＋2y )＝lg2＋lg x ＋lg y ，求xy 的值；(2)解方程：log 2x ＋log 2(x ＋2)＝3.[解] (1)由题可知lg[(x －y )(x ＋2y )]＝lg(2xy )，所以(x －y )(x ＋2y )＝2xy ，即x 2－xy －2y 2＝0.所以⎝⎛⎭⎫x y 2－xy －2＝0. 解得x y ＝2或xy＝－1.又因为x >0，y >0，x －y >0.所以x y ＝2.(2)由方程可得log 2x ＋log 2(x ＋2)＝log 28. 所以log 2[x (x ＋2)]＝log 28，即x (x ＋2)＝8.解得x 1＝2，x 2＝－4. 因为x >0，x ＋2>0，所以x ＝2.对数方程问题的求解策略：利用对数运算性质或换底公式将方程两边写成同底的对数形式，由真数相等求解方程，转化过程中注意真数大于零这一条件，防止增根.[变式训练3] (1)方程lg x ＋lg(x －1)＝1－lg5的根是( B ) A ．－1 B ．2 C ．1或2D ．－1或2(2)已知lg x ＋lg y ＝2lg(x －2y )，则log2 xy的值为4. 解析：(1)由真数大于0，易得x >1，原式可化为lg x (x －1)＝lg2⇒x (x －1)＝2⇒x 2－x －2＝0⇒x 1＝2，x 2＝－1(舍)．(2)因为lg x ＋lg y ＝2lg(x －2y )，所以lg xy ＝lg(x －2y )2，所以xy ＝(x －2y )2，即x 2－5xy ＋4y 2＝0. 所以(x －y )(x －4y )＝0，解得x ＝y 或x ＝4y . 因为x >0，y >0，x －2y >0，所以x ＝y 应舍去，所以x y ＝4.故log 2 xy ＝log 2 4＝4.类型四对数的实际应用[例4] 人们对声音有不同的感觉，这与它的强度有关系．声音强度I 的单位用瓦/平方米(W/m 2)表示，但在实际测量时，声音的强度水平常用L 1表示，它们满足以下公式：L 1＝10lg I I 0(单位为分贝，L 1≥0，其中I 0＝1×10－12 W/m 2，是人们平均能听到的最小强度，是听觉的开端)．回答下列问题：树叶沙沙声的强度是1×10－12W/m 2，耳语的强度是1×10－10W/m 2，恬静的无线电广播的强度是1×10－8W/m 2，试分别求出它们的强度水平．[解] 由题意，可知树叶沙沙声的强度是I 1＝1×10－12W/m 2，则I 1I 0＝1，故LI 1＝10·lg1＝0，则树叶沙沙声的强度水平为0分贝；耳语的强度是I 2＝1×10－10W/m 2，则I 2I 0＝102，故LI 2＝10lg102＝20，即耳语声的强度水平为20分贝．同理，恬静的无线电广播强度水平为40分贝．对数运算在实际生产和科学技术中运用广泛，其运用问题大致可分为两类：一类是已知对数应用模型(公式)，在此基础上进行一些实际求值.计算时要注意利用“指、对互化”把对数式化成指数式.另一类是先建立指数函数应用模型，再进行指数求值，此时往往将等式两边进行取对数运算.[变式训练4] 抽气机每次抽出容器内空气的60%，要使容器内的空气少于原来的0.1%，则至少要抽几次？(lg2≈0.301 0)解：设至少抽n 次可使容器内空气少于原来的0.1%，则a (1－60%)n <0.1%a (设原先容器中的空气体积为a )，即0.4n <0.001，两边取常用对数得n ·lg0.4<lg0.001，所以n >lg0.001lg0.4＝－32lg2－1≈7.5.故至少需要抽8次．1．设a ，b ，c 均为不等于1的正实数，则下列等式中恒成立的是( B ) A ．log a b ·log c b ＝log c a B ．log a b ·log c a ＝log c b C ．log a (bc )＝log a b ·log a c D ．log a (b ＋c )＝log a b ＋log a c解析：由换底公式得log a b ·log c a ＝lg b lg a ·lg alg c ＝log c b ，所以B 正确．2．2log 32－log 3329＋log 38的值为( B )A.12 B ．2 C ．3D.13解析：原式＝log 34－log 3329＋log 38＝log 34×8329＝log 39＝2.3．lg 5＋lg 20的值是1.解析：lg 5＋lg 20＝lg(5×20)＝lg 100＝1.4．若a >0，且a ≠1，b >0，且b ≠1，则由换底公式可知log a b ＝lg b lg a ，log b a ＝lg alg b ，所以log a b ＝1log b a ，试利用此结论计算1log 321＋1log 721＝1.解析：1log 321＋1log 721＝1lg21lg3＋1lg21lg7＝lg3lg21＋lg7lg21＝lg (3×7)lg21＝1. 5．计算：(1)3log 72－log 79＋2log 7⎝⎛⎭⎫322； (2)(lg2)2＋lg2·lg50＋lg25.解：(1)原式＝log 78－log 79＋log 798＝log 78－log 79＋log 79－log 78＝0.(2)原式＝lg2(lg2＋lg50)＋2lg5＝lg2·lg100＋2lg5 ＝2lg2＋2lg5＝2(lg2＋lg5)＝2lg10＝2.——本课须掌握的两大问题1．运用对数的运算性质应注意：(1)在各对数有意义的前提下才能应用运算性质． (2)根据不同的问题选择公式的正用或逆用． (3)在运算过程中避免出现以下错误：①log a N n ＝(log a N )n ，②log a (MN )＝log a M ·log a N ，③log a M ±log a N ＝log a (M±N )． 2．换底公式可完成不同底数的对数式之间的转化，可正用，逆用；使用的关键是恰当选择底数，换底的目的是利用对数的运算性质进行对数式的化简．学习至此，请完成课时作业19。

高中数学对数函数(一)

R
当x>1时，y∈_(0_，__+__∞) 当0<x<1时，y∈(_-∞__，__0_)；
定点
当x=1时，y=0即过定点 (1,0)
单调性
在(0，+∞)上为__增__函在(0，+∞)上为
数
_减___函数
基础达标
1、（lg5)2+lg2∙lg50=__1______. 解析：原式=(lg 5)2+lg 2×[lg 5+1] =(lg 5)2+lg 2 ∙ lg 5+lg 2=lg 5[lg 5+lg 2]+lg 2=lg 5+lg 2=1.
2]
1 4
log3
3
log5[2
log2
10
3
2]
1 4
log3
3 log5
5
1 4
经典例题
(3) 2(lg 2)2 lg 2 lg5 lg 22 21g 2 1
解：原式=lg 2(21g 2 +lg 5) lg 2 1)2
=lg 2 (lg 2+lg 5)+|lg 2 -1|
=lg 2lg(25)+1-lg 2 =1.
2、若2x-1=10，则x=1__l_g1_2____. 解∴析(x-：1)l两g 2边=取1，常∴用x-对1=数lg1，2 则, xlg12xl-g112=.lg10=1， 3、不等式log2(x+2)>2的解集为(2_，__+_∞__)__．
解析：x+2>22⇒x>2.
4.
已知log7[log3[log2x]]=0，则
③logaMn =__n_lo_g_a_M______.

对数与对数运算(一)教学设计

对数与对数运算（一）教学设计（李恒福）一、教学内容分析本节课是新课标高中数学A版必修①中第二章对数函数内容的第一课时，也就是对数函数的入门。

对数函数对于学生来说是一个全新的函数模型，学习起来比较困难。

而对数函数又是本章的重要内容，在高考中占有一定的分量，它是在指数函数的基础上，对函数类型的拓广。

通过本节课的学习，可以让学生理解对数的概念，从而进一步深化对对数模型的认识与理解，为学习对数函数作好准备。

同时，通过对数概念的学习，对培养学生对立统一，相互联系、相互转化的思想，培养学生的逻辑思维能力都具有重要的意义。

二、学生学习情况分析现阶段大部分学生学习的自主性较差，主动性不够，学习有依赖性，且学习的信心不足，对数学存在或多或少的恐惧感。

通过对指数与指数幂的运算的学习，学生已多次体会了对立统一、相互联系、相互转化的思想，并且探究能力、逻辑思维能力得到了一定的锻炼。

因此，学生已具备了探索发现研究对数定义的认识基础，故应通过指导，教会学生独立思考、大胆探索和灵活运用类比、转化、归纳等数学思想的学习方法。

三、设计思想学生是教学的主体,本节课要给学生提供各种参与机会。

调动学生学习的积极性，主动性。

本节课我利用多媒体辅助教学,教学中我引导学生从实例出发，从中认识对数的模型，体会引入对数的必要性。

在教学重难点上，我步步设问、启发学生的思维,通过课堂练习、探究活动,学生讨论的方式来加深理解,很好地突破难点和提高教学效率。

让学生在教师的引导下，充分地动手、动口、动脑，掌握学习的主动权。

四、教学目标1、理解对数的概念,了解对数与指数的关系；掌握对数式与指数式的互化；理解对数的性质。

2、通过事例使学生认识对数的模型，体会引入对数的必要性；通过师生观察分析得出对数的概念及对数式与指数式的互化。

3、通过学生分组探究进行活动，掌握对数的重要性质。

通过做练习，使学生感受到理论与实践的统一。

4、培养学生的类比、分析、归纳能力，严谨的思维品质以及在学习过程中培养学生探究的意识。

高一数学对数与对数运算1

对数符号logaN只有在a>0，a≠1且N>0时才有意义，这是因为： (1)若a<0，则N取某些数值时，x不存在，为此规定a不能小于0.
(2)若 a＝0，则
N≠0时，logaN不存在 . N ＝ 0 时，则 log N 有无数个值，不能确定 a
因此，规定 a≠0.
(3)若 a＝1，
N≠1时，则logaN不存在 . N＝1时，则logaN有无数个值，不能确定
－2<x<1. 2 ⇒ 3 x≠0
2 1 所以 x 的取值范围是{x|－3<x<2且 x≠0}．
； https:/// 电子杂志制作； 2019年01月23日12:54:21 ；
消息渠道,需要明白呐个世界の格局.在黄银卫士之上,又都有哪一些层次の强者.善王级别の肉身修行者,在呐个奇点炼狱内是否存在,如果有の话,数量又有多少.在呐个矿场上,鞠言是不太可能得到呐些信息の.呐个矿场,层次太低了.队长琛琛の看了鞠言一眼,随后开口道：“好,明日俺就安排你参加青铜卫士の测试.不过俺丑话说在前头,若是测试失败,你可是要受到严厉惩罚の.虽然不会被直接杀死,但难免要脱一层皮.”“明白.”鞠言点头.“括庵,你给他安排一下住处吧！”队长对白银卫士括庵摆摆手.“是！”括庵应声.括庵带鞠言离开队长の房间后,又带鞠言去领取了一身历士服.除服饰外,鞠言还领到了一柄黑色の鹤嘴锄,鹤嘴锄颇为沉叠,要挥舞起来挖矿确实需要不小の历气.没错,呐鹤嘴锄,就是用来挖取髓石の,每一个历士の标配.历士の住处,要比降生者住处稍微好一些,虽然仍是多人一个房间,但看起来起码能遮风避雨.“鞠言,你就住在呐个房间.明天上午,俺会过来带你去参加青铜卫士の测试.你,最好准备吧.”括庵对鞠言说完呐句话,便转身离开.鞠言看了看身前の低矮房舍,迈步走了进去.房间内,此事没有其他人.住

高一数学对数与对数函数

§2.6对数与对数函数1．对数的概念一般地，如果a x ＝N (a >0，且a ≠1)，那么数x 叫做以a 为底N 的对数，记作x ＝log a N ，其中a 叫做对数的底数，N 叫做真数．2．对数的性质与运算法则(1)对数的运算法则如果a >0，且a ≠1，M >0，N >0，那么：①log a (MN )＝log a M ＋log a N ；②log a MN ＝log a M －log a N ；③log a M n ＝n log a M (n ∈R )．(2)对数的性质①负数和零没有对数；②log a 1＝0，log a a ＝1(a >0，且a ≠1)；③log a Na＝N (a >0，a ≠1，且N >0)；④log a a N ＝N (a >0，且a ≠1)．(3)对数的换底公式log a b ＝log c blog c a(a >0，且a ≠1；c >0，且c ≠1；b >0)．3．对数函数的图象与性质y ＝log a xa >10<a <1图象定义域(1)(0，＋∞)值域(2)R性质(3)过定点(1,0)，即x ＝1时，y ＝0(4)当x >1时，y >0；(5)当x >1时，y <0；当0<x <1时，y <0当0<x <1时，y >0(6)在(0，＋∞)上是增函数(7)在(0，＋∞)上是减函数4.反函数指数函数y ＝a x (a >0且a ≠1)与对数函数y ＝log a x (a >0且a ≠1)互为反函数，它们的图象关于直线y ＝x 对称．概念方法微思考1．根据对数换底公式：①说出log a b ，log b a 的关系？②化简log m na b .提示①log a b ·log b a ＝1；②logm na b ＝n mlog a b .2．如图给出4个对数函数的图象．比较a ，b ，c ，d 与1的大小关系．提示0<c <d <1<a 0，则log a (MN )＝log a M ＋log a N .(×)(2)对数函数y ＝log a x (a >0且a ≠1)在(0，＋∞)上是增函数．(×)(3)函数y ＝ln1＋x1－x与y ＝ln(1＋x )－ln(1－x )的定义域相同．(√)(4)对数函数y ＝log a x (a >0且a ≠1)的图象过定点(1,0)且过点(a,1)一、四象限．(√)题组二教材改编2．log 29·log 34·log 45·log 52＝________.答案23．已知a ＝1-32，b ＝log 213，c ＝121log 3，则a ，b ，c 的大小关系为________．答案c >a >b解析∵0<a <1，b <0，c ＝121log 3＝log 23>1.∴c >a >b .4．函数y的定义域是______．答案1解析由23log (21)x -≥0，得0<2x －1≤1.∴12<x ≤1.∴函数y1.题组三易错自纠5．已知b >0，log 5b ＝a ，lg b ＝c,5d ＝10，则下列等式一定成立的是()A ．d ＝acB ．a ＝cdC ．c ＝adD ．d ＝a ＋c答案B6．(多选)函数y ＝log a (x ＋c )(a ，c 为常数，其中a >0，a ≠1)的图象如图所示，则下列结论成立的是()A ．a >1B ．0<c <1C ．0<a <1D ．c >1答案BC解析由图象可知函数为减函数，所以0<a <1，令y ＝0得log a (x ＋c )＝0，x ＋c ＝1，x ＝1－c .由图象知0<1－c <1，∴0<c <1.7．若log a 34<1(a >0且a ≠1)，则实数a 的取值范围是____________________．答案(1，＋∞)解析当0<a <1时，log a 34<log a a ＝1，∴0<a <34；当a >1时，log a 34<log a a ＝1，∴a >1.∴实数a (1，＋∞).对数式的运算1．已知2x ＝3，log 483＝y ，则x ＋2y 的值为________．答案3解析由2x ＝3，log 483＝y 得x ＝log 23，y ＝log 483＝12log 283，所以x ＋2y ＝log 23＋log 283＝log 28＝3.2．设函数f (x )＝3x ＋9x ，则f (log 32)＝________.答案6解析∵函数f (x )＝3x ＋9x ，∴f (log 32)＝339log 2log 2log 43929＋＝＋＝2＋4＝6.3．计算：(1－log 63)2＋log 62·log 618log 64＝________.答案1解析原式＝1－2log 63＋(log 63)2＋log 663·log 6(6×3)log 64＝1－2log 63＋(log 63)2＋1－(log 63)2log 64＝2(1－log 63)2log 62＝log 66－log 63log 62＝log 62log 62＝1.4．(2019·北京)在天文学中，天体的明暗程度可以用星等或亮度来描述．两颗星的星等与亮度满足m 2－m 1＝52lg E1E 2，其中星等为m k 的星的亮度为E k (k ＝1,2)．已知太阳的星等是－26.7，天狼星的星等是－1.45，则太阳与天狼星的亮度的比值为()A ．1010.1B ．10.1C ．lg 10.1D ．10－10.1答案A解析两颗星的星等与亮度满足m 2－m 1＝52lg E 1E 2，令m 2＝－1.45，m 1＝－26.7，lgE 1E 2＝25·(m 2－m 1)＝25(－1.45＋26.7)＝10.1，E 1E 2＝1010.1.思维升华对数运算的一般思路(1)拆：首先利用幂的运算把底数或真数进行变形，化成分数指数幂的形式，使幂的底数最简，然后利用对数运算性质化简合并．(2)合：将对数式化为同底数的和、差、倍数运算，然后逆用对数的运算性质，转化为同底对数真数的积、商、幂的运算．对数函数的图象及应用例1(1)已知函数f (x )＝log a (2x ＋b －1)(a >0，a ≠1)的图象如图所示，则a ，b 满足的关系是()A ．0<a －11.函数图象与y 轴的交点坐标为(0，log a b )，由函数图象可知－1<log a b <0，解得1a <b <1.综上有0<1a<b <1.(2)方程4x＝log a x ，12上有解，则实数a 的取值范围为__________．答案，22解析若方程4x ＝log a x ，12上有解，则函数y ＝4x 和函数y ＝log a x ，12上有交点，a<1，a12≤2，解得0<a≤22.4x<log a x，12上恒成立，则实数a的取值范围是________．答案解析当0<x≤12时，函数y＝4x的图象在函数y＝log a x图象的下方．又当x＝12时，124＝2，即函数y＝4x y＝log a x，得a＝22.若函数y＝4x的图象在函数y＝log a x图象的下方，则需22<a<1(如图所示)．当a>1时，不符合题意，舍去．所以实数a思维升华对数函数图象的识别及应用方法(1)在识别函数图象时，要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项．(2)一些对数型方程、不等式问题常转化为相应的函数图象问题，利用数形结合法求解．跟踪训练1(1)(2019·河北冀州中学月考)函数f(x)＝lg(|x|－1)的大致图象是()答案B解析由函数值域为R，可以排除C，D，当x>1时，f(x)＝lg(x－1)在(1，＋∞)上单调递增，排除A，选B.(2)若不等式x 2－log a x <0对xa 的取值范围是________．答案116，解析只需f 1(x )＝x 2f 2(x )＝log a x图象的下方即可．当a >1时，显然不成立；当0<a <1时，如图所示，要使x 2<loga x 在x只需ff所以有≤log a 12，解得a ≥116，所以116≤a <1.即实数a 的取值范围是116，对数函数的性质及应用命题点1解对数方程、不等式例2(1)方程log 2(x －1)＝2－log 2(x ＋1)的解为________．答案x ＝5解析原方程变形为log 2(x －1)＋log 2(x ＋1)＝log 2(x 2－1)＝2，即x 2－1＝4，解得x ＝±5，又x >1，所以x ＝5.(2)设f (x )2x ，x >0，12(－x )，x <0，则方程f (a )＝f (－a )的解集为________．答案{－1,1}解析当a >0时，由f (a )＝log 2a ＝121log a ⎛⎫⎪⎝⎭＝f (－a )＝12log a ，得a ＝1；当a <0时，由f (a )＝12log ()a-＝logf (－a )＝log 2(－a )，得a ＝－1.∴方程f (a )＝f (－a )的解集为{1，－1}．本例(2)中，f (a )>f (－a )的解集为________．答案(－1,0)∪(1，＋∞)解析>0，log 2a >12a<0，12(－a )>log 2(－a )，解得a >1或－1<a <0.命题点2对数函数性质的综合应用例3(2020·湛江质检)已知函数f (x )＝12log (x 2－2ax ＋3)．(1)若f (－1)＝－3，求f (x )的单调区间；(2)是否存在实数a ，使f (x )在(－∞，2)上为增函数？若存在，求出a 的范围；若不存在，说明理由．解(1)由f (－1)＝－3，得12log (4＋2a )＝－3.所以4＋2a ＝8，所以a ＝2.则f (x )＝12log (x 2－4x ＋3)，由x 2－4x ＋3>0，得x >3或x <1.故函数f (x )的定义域为(－∞，1)∪(3，＋∞)．令μ＝x 2－4x ＋3，则μ在(－∞，1)上单调递减，在(3，＋∞)上单调递增．又y ＝12log μ在(0，＋∞)上单调递减，所以f (x )的单调递增区间是(－∞，1)，单调递减区间是(3，＋∞)．(2)令g (x )＝x 2－2ax ＋3，要使f (x )在(－∞，2)上为增函数，应使g (x )在(－∞，2)上单调递减，且恒大于0.≥2，(2)≥0，即≥2，－4a ≥0，a 无解．所以不存在实数a ，使f (x )在(－∞，2)上为增函数．思维升华利用对数函数的性质，求与对数函数有关的函数值域和复合函数的单调性问题，必须弄清三方面的问题：一是定义域，所有问题都必须在定义域内讨论；二是底数与1的大小关系；三是复合函数的构成，即它是由哪些基本初等函数复合而成的．另外，解题时要注意数形结合、分类讨论、转化与化归思想的应用．跟踪训练2(1)若f (x )＝lg(x 2－2ax ＋1＋a )在区间(－∞，1]上单调递减，则a 的取值范围为()A ．[1,2)B ．[1,2]C ．[1，＋∞)D ．[2，＋∞)答案A解析令函数g (x )＝x 2－2ax ＋1＋a ＝(x －a )2＋1＋a －a 2，对称轴为x ＝a ，要使函数在(－∞，1](1)>0，≥1，－a >0，≥1，解得1≤a <2，即a ∈[1,2)．(2)已知函数f (x )＝log a (8－ax )(a >0，且a ≠1)，若f (x )>1在区间[1,2]上恒成立，则实数a 的取值范围是__________．答案解析当a >1时，f (x )＝log a (8－ax )在[1,2]上是减函数，由f (x )>1在区间[1,2]上恒成立，则f (x )min ＝f (2)＝log a (8－2a )>1，且8－2a >0，解得1<a <83.当0<a <1时，f (x )在[1,2]上是增函数，由f (x )>1在区间[1,2]上恒成立，知f (x )min ＝f (1)＝log a (8－a )>1，且8－2a >0.∴a >4，且a<4，故不存在．综上可知，实数a比较指数式、对数式的大小例4(1)(2019·天津市河西区模拟)设a ＝log 3e ，b ＝e 1.5，c ＝131log 4，则()A ．b <a <cB ．c <a <bC ．c log 3e ＝a .又c ＝log 34<log 39＝2，b ＝e 1.5>2，∴a <c log 0.21＝0，b ＝log 20.3<log 21＝0，∴ab <0.∵a ＋b ab ＝1a ＋1b＝log 0.30.2＋log 0.32＝log 0.30.4，∴1＝log 0.30.3>log 0.30.4>log 0.31＝0，∴0<a ＋b ab<1，∴ab <a ＋b <0.(3)已知函数y ＝f (x ＋2)的图象关于直线x ＝－2对称，且当x ∈(0，＋∞)时，f (x )＝|log 2x |，若a ＝f (－3)，b ＝fc ＝f (2)，则a ，b ，c 的大小关系是________．答案c <a <b解析易知y ＝f (x )是偶函数．当x ∈(0，＋∞)时，f (x )＝f |log 2x |，且当x ∈[1，＋∞)时，f (x )＝log 2x 单调递增，又a ＝f (－3)＝f (3)，b ＝f f (4)，所以c <a <b .思维升华(1)比较指数式和对数式的大小，可以利用函数的单调性，引入中间量；有时也可用数形结合的方法．(2)解题时要根据实际情况来构造相应的函数，利用函数单调性进行比较，如果指数相同，而底数不同则构造幂函数，若底数相同而指数不同则构造指数函数，若引入中间量，一般选0或1.跟踪训练3(1)已知a ＝log 23＋log 23，b ＝log 29－log 23，c ＝log 32，则a ，b ，c 的大小关系是()A ．a ＝b <cB ．a ＝b >cC ．a b >c答案B解析因为a ＝log 23＋log 23＝log 233＝32log 23>1，b ＝log 29－log 23＝log 233＝a ，c ＝log 32<log 33＝1，所以a ＝b >c .(2)(2019·天津市滨海新区模拟)已知函数f (x )＝|x |，且a ＝f b ＝f c ＝f (2－1)，则a ，b ，c 的大小关系为()A ．a <c <bB ．b <c <aC ．c <a <bD ．b <a <c答案A解析ln 32<ln e ＝12，log 23>12，∴log 23>12>ln 32.又f (x )是偶函数，在(0，＋∞)上为增函数，∴ff f (log 23)＝f ∴a <c <b .(3)若实数a ，b ，c 满足log a 2<log b 2<log c 2<0，则下列关系中正确的是()A ．a <b <cB ．b <a <cC ．c <b <aD ．a <c <b答案C解析根据不等式的性质和对数的换底公式可得1log 2a <1log 2b <1log 2c <0，即log 2c <log 2b <log 2a <0，可得c B ．>C ．log 2a <D ．log 2a <答案B解析∵0<a <1，∴0<a 2<a <a <1，∴在A 中，log 2a ＝，故A 错误；在B 中，>，故B 正确；在C 中，log 2a >，故C 错误；在D 中，log 2a >，故D 错误．3．函数y ＝ln1|2x －3|的图象为()答案A解析易知2x －3≠0，即x ≠32，排除C ，D.当x >32时，函数为减函数；当x <32时，函数为增函数，所以选A.4．(2019·衡水中学调研卷)若0<a <1，则不等式1log a x >1的解是()A ．x >aB ．a <x <1C ．x >1D ．0<x <a答案B解析易得0<log a x <1，∴a <x <1.5．函数f (x )＝12log (x 2－4)的单调递增区间为()A ．(0，＋∞)B ．(－∞，0)C ．(2，＋∞)D ．(－∞，－2)答案D解析函数y ＝f (x )的定义域为(－∞，－2)∪(2，＋∞)，因为函数y ＝f (x )由y ＝12log t 与t ＝g (x )＝x 2－4复合而成，又y ＝12log t 在(0，＋∞)上单调递减，g (x )在(－∞，－2)上单调递减，所以函数y ＝f (x )在(－∞，－2)上单调递增．6．(2020·长沙期末)已知函数f (x )2x ，x >0，x，x ≤0，且关于x 的方程f (x )－a ＝0有两个实根，则实数a 的取值范围为()A ．(0,1]B ．(0,1)C ．[0,1]D ．(0，＋∞)答案A解析作出函数y ＝f (x )的图象(如图)，欲使y ＝f (x )和直线y ＝a 有两个交点，则0<a ≤1.7．(多选)关于函数f (x )＝ln1－x1＋x，下列说法中正确的有()A ．f (x )的定义域为(－∞，－1)∪(1，＋∞)B ．f (x )为奇函数C ．f (x )在定义域上是增函数D ．对任意x 1，x 2∈(－1,1)，都有f (x 1)＋f (x 2)＝f 答案BD解析函数f (x )＝ln 1－x1＋x＝其定义域满足(1－x )(1＋x )＞0，解得－1＜x ＜1，∴定义域为{x |－1＜x ＜1}．∴A 不对．由f (－x )＝ln 1＋x1－x＝1＝－ln1－x1＋x＝－f (x )，是奇函数，∴B 对．函数y ＝21＋x －1在定义域内是减函数，根据复合函数的单调性，同增异减，∴f (x )在定义域内是减函数，C 不对．f (x 1)＋f (x 2)＝ln1－x 11＋x 1＋ln 1－x 21＋x 2＝f ∴D 对．8．(多选)已知函数f (x )的图象与g (x )＝2x 的图象关于直线y ＝x 对称，令h (x )＝f (1－|x |)，则关于函数h (x )有下列说法，其中正确的说法为()A ．h (x )的图象关于原点对称B ．h (x )的图象关于y 轴对称C ．h (x )的最大值为0D ．h (x )在区间(－1,1)上单调递增答案BC解析函数f (x )的图象与g (x )＝2x 的图象关于直线y ＝x 对称，∴f (x )＝log 2x ，h (x )＝log 2(1－|x |)，为偶函数，不是奇函数，∴A 错误，B 正确；根据偶函数性质可知D 错误；∵1－|x |≤1，∴h (x )≤log 21＝0，故C 正确．9．函数f (x )＝log 2x ·(2x )的最小值为________．答案－14解析依题意得f (x )＝12log 2x ·(2＋2log 2x )＝(log 2x )2＋log 2x 2x －14≥－14，当log 2x ＝－12，即x ＝22时等号成立，所以函数f (x )的最小值为－14.10．(2020·深圳月考)设实数a ，b 是关于x 的方程|lg x |＝c 的两个不同实数根，且a 0，且a ≠1)，且f (1)＝2.(1)求实数a 的值及f (x )的定义域；(2)求f (x )在区间0，32上的最大值．解(1)∵f (1)＝2，∴log a 4＝2(a >0，且a ≠1)，∴a ＝2.＋x >0，－x >0，得－1<x <3，∴函数f (x )的定义域为(－1,3)．(2)f (x )＝log 2(1＋x )＋log 2(3－x )＝log 2[(1＋x )(3－x )]＝log 2[－(x －1)2＋4]，∴当x ∈(－1,1]时，f (x )是增函数；当x ∈(1,3)时，f (x )是减函数，故函数f (x )在0，32上的最大值是f (1)＝log 24＝2.12．是否存在实数a ，使得f (x )＝log a (ax 2－x )在区间[2,4]上是增函数？若存在，求出a 的范围；若不存在，说明理由．解设t＝ax2－x＝－1 4a.若f(x)在[2,4]上是增函数，<1，4，－4>0，2，2>0，解得a>1.∴存在实数a满足题意，即当a∈(1，＋∞)时，f(x)在[2,4]上是增函数．13．已知函数f(x)＝ln e xe－x，若fff1010(a＋b)，则a2＋b2的最小值为()A．1B．2C．3D．4答案B解析∵f(x)＋f(e－x)＝2，∴ff…＋f2020，∴1010(a＋b)＝2020，∴a＋b＝2.∴a2＋b2≥(a＋b)22＝2，当且仅当a＝b＝1时取等号．14．若函数f(x)＝log a(x2－x＋2)在区间[0,2]上的最大值为2，则实数a＝________.答案2解析令u(x)＝x2－x＋2，则u(x)在[0,2]上的最大值u(x)max＝4，最小值u(x)min＝74.当a>1时，y＝log a u是增函数，f(x)max＝log a4＝2，得a＝2；当0<a<1时，y＝log a u是减函数，f(x)max＝log a74＝2，得a＝72(舍去)．故a＝2. 15．(2019·福州模拟)已知函数f(x)＝log a(2x－a)在区间12，23上恒有f(x)>0，则实数a的取值范围是()B.13，D.23，答案A解析当0<a <1时，函数f (x )在区间12，23上是减函数，所以log ，即0<43－a <1，解得13<a <43，故13<a <1；当a >1时，函数f (x )在区间12，23上是增函数，所以log a (1－a )>0，即1－a >1，解得a <0，此时无解．综上所述，实数a 16．已知函数f (x )＝lgx －1x ＋1.(1)计算：f (2020)＋f (－2020)；(2)对于x ∈[2,6]，f (x )<lg m(x ＋1)(7－x )恒成立，求实数m 的取值范围．解(1)由x －1x ＋1>0，得x >1或x <－1.∴函数f (x )的定义域为{x |x >1或x <－1}．又f (x )＋f (－x )＝0，∴f (x )为奇函数．∴f (2020)＋f (－2020)＝0.(2)当x ∈[2,6]时，f (x )<lgm (x ＋1)(7－x )恒成立可化为x －11＋x <m(x ＋1)(7－x )恒成立．即m >(x －1)(7－x )在[2,6]上恒成立．又当x ∈[2,6]时，(x －1)(7－x )＝－x 2＋8x －7＝－(x －4)2＋9.∴当x ＝4时，[(x －1)(7－x )]max ＝9，∴m >9.即实数m 的取值范围是(9，＋∞)．。

对数及对数运算1

对数及对数运算【巩固练习】1.有以下四个结论：①lg （lg10）=0 :②“⑹e ）=0 ；③若10=lgx ，贝J x=10；④若e=lnx ,则x=e ，其中正确的是（）2.下列等式成立的有（）① ©存-2 :②也3®! ； ® 丹"=5； ® 列 i ； ® 3lg3=3；3.已知3—2，那么10938-210936用a 表示是（）f(2 +Iog 2 3)=(A.①③B.②④C.①②D.③④A.①②B.①②③C.②③④D.①②③④⑤A. a —2B.5a-2C. 3a-(1 + a)2D. 3a-a 214. 已知 x 2+y 2 =1,x 〉0,y 〉0，且 log a (1 +x) = m,log a ----- = n,1 -x则log a y等于（） 1A. m + nB. m-nC. -(m + n )D. 25.若 y =log 56 1og 67 Iog 78 Iog 89 ■Iog 910，贝 1一(m-n \丿A. y“0,1)B.yJ1,2)C. 6.设a , b , c 为正数，且3a=4b=6c，则有( A.1B. 2=2』C. 1=2+2cabcabcaby-(2,3)D.(3,4)7.如果方程 Ig 2x+(lg2 +Ig3)lg x + lg2lg3 =0 的两根为）D. 2亠 cabX 1、X 2 ,则X 1X 的值为（A. lg 2 lg3 8.已知函数4B.Ig2+lg3C. -D. -66f(x)乜；f （x ）满足：当X 卒时,；当 x <4 时，f(x)= f(x +1)，则A. 24B.1C.122 49.已知a3= —(a：＞0)，则log2 a =9310. (1) log28^log21^log2 20 - log? 30 =3 3 3 3(2) 7log76log65log54 =3 0 311.已知a=0.3 , b=3. , c=log 3O.3 , d=log 0.33,贝J a, b, c, d 的大小关系是12.已知 f (3x) =4xlog2 3+233,贝J f (2) + f (4) + f (8) + …+ f (28)的值等于13.计算：(1) (log43+log83H log32+log32 2 )+log2疗；（2）若a+b =lg32+lg35 + 3lg2」g5，求3ab+a3+b3.14.设log a c, log b c是方程x2-3x+1=0的两根，求log a c的值.b15. 2010年我国国民生产总值为a亿元，如果平均每年增长【解析】原式=log3 23 -2(log32+1) = log32-2=a-2，故选A.4.【答案】D【解析】因为log a(1 + x) +log a(1-X)= m-n ,所以log a(1-x2) =log a 8%那么经过多少年后国民生产总值是2010年的2倍（gROOQ az,精确到1年）？【答案与解析】1.【答案】【解析】由log a a =1,log a1 = 0知①②正确.2.【答案】10r lg10 j ；3.【答案】A【解析】lg2y =2log a y = m-n ,所以log a y =l(m -n).2全国名校高一数学优质课时训练汇编 (附详解)5.【答案】B【解析】-芽芽芽芽需沁厶心皿厶2，因为。

高一数学对数及其运算

在科学技术中，以e 2.71828…为底的对数叫做自然对数.logeN通常记作 lnN
ln N lg N 2.3026 lg N lg e
在科学计算器中，可以直接求自然对数
小结：
(1）对数的概念，计算
（2)利用对数的运算性质，可以将两正数的积、商、幂的对数进行转化，大大的方便了对数式的化简和求值.
因为24 =16，所以log2 16 4；
因为2-1 =
1 2
，所以
log
2
1 2
1；
（二）常用对数
以10为底的对数叫做常用对数.
log10 N记作 lg N
如果以后没有指出对数的底，都是指常用对数.如“100的对数是2”就是“100 的常用对数是2”
例2 求lg10，lg100，lg 0.01
定义：一般地，如果ab＝N（a>0，且
a≠1），那么数b叫做以a为底N的对数
记作 b＝log Na （a>0，且a≠1），
其中，数a叫做对数的底数，N叫做真数，读作“b等于以a为底N的对数
知识探究：对数与指数的关系
思考1:当a>0，且a≠1时，若ax＝N，则x ＝logaN，反之成立吗？
思考2:在指数式ax＝N和对数式x＝logaN 中，a，x，N各自的地位有什么不同？
（四）换底公式与自然对数
在求底数不是10 的对数时，可以根据对数的性质，
利用常用对数进行计算
换底公式：
证明:设log b
Nlo=gbxN， = lloo则 ggaaNb
bx =N
两边取以a为的对数，得
xloga b=loga N
所以
x= loga N loga b
即