信号分解与合成
信号的合成与分解实验报告

声音的奇妙合成与分解实验实验目的:
通过实验观察声音的合成和分解过程,了解声音的本质和特性。
实验材料:
1.计算机音频软件(如Audacity)
2.音频采集卡(可选)
3.扬声器或耳机
4.麦克风
实验步骤:
1.声音的合成
(1)打开音频软件,在音频轨道上录制两段清晰的声音样本,并将它们单独保存。
(2)选择一段音频,将其复制到另一个轨道上,调节两个轨道的音量大小,使它们相互重叠。
此时发现,两段声音通过叠加产生了新的声音,这就是声音的合成过程。
2.声音的分解
(1)将合成的声音和原始声音一起保存,重新打开软件,选择原始的声音轨道,并使用谱分析工具观察其频谱特征。
(2)选定频谱上的一段区间,将其复制到另一个轨道上,并使用滤
波器将这一段区间从原始音频轨道上剔除。
此时,认为分离出了原始
声音中的一段频率区间,即声音的分解过程。
实验结果:
通过实验结果可以发现,声音的合成和分解都是基于声音波形的
基础上进行的。
声音的合成是将两段声音波形相加形成新的波形;声
音的分解则是通过谱分析将一个复杂波形分解成多个简单波形的过程。
实验提示:
在进行合成和分解实验时,注意保持音频清晰,尽量避免外界噪
音的干扰。
此外,实验中的操作需要耐心和细心,需要多次尝试和调整,才能得到合适的实验结果。
信号的分解与合成
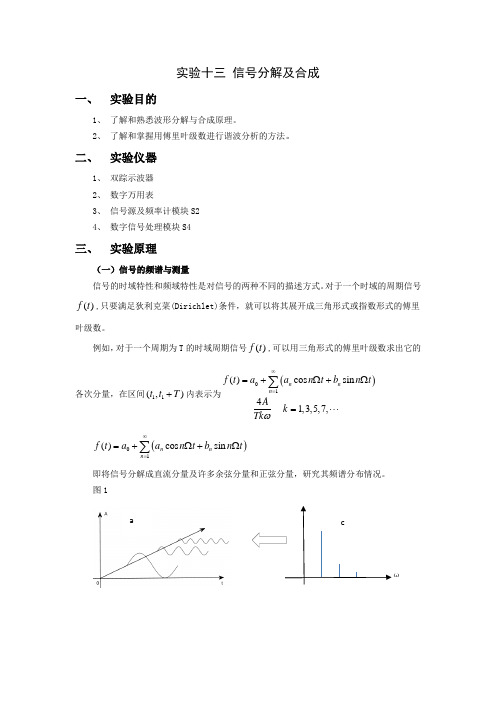
实验十三 信号分解及合成一、 实验目的1、 了解和熟悉波形分解与合成原理。
2、 了解和掌握用傅里叶级数进行谐波分析的方法。
二、 实验仪器1、 双踪示波器2、 数字万用表3、 信号源及频率计模块S24、 数字信号处理模块S4三、 实验原理(一)信号的频谱与测量信号的时域特性和频域特性是对信号的两种不同的描述方式。
对于一个时域的周期信号()f t ,只要满足狄利克菜(Dirichlet)条件,就可以将其展开成三角形式或指数形式的傅里叶级数。
例如,对于一个周期为T 的时域周期信号()f t ,可以用三角形式的傅里叶级数求出它的各次分量,在区间11(,)t t T +内表示为()01()cos sin 41,3,5,7,n n n f t a a n t b n t Ak Tk ω∞==+Ω+Ω=⋅⋅⋅∑()01()cos sin n n n f t a a n t b n t ∞==+Ω+Ω∑即将信号分解成直流分量及许多余弦分量和正弦分量,研究其频谱分布情况。
图1ωca信号的时域特性和频域特性信号的时域特性与频域特性之间有着密切的内在联系,这种联系可以用图13-1来形象地表示。
其中图(a)是信号在幅度—时间—频率三维坐标系统中的图形;图(b)是信号在幅度一时间坐标系统中的图形即波形图:把周期信号分解得到的各次谐波分量按频率的高低排列,就可以得到频谱图。
反映各频率分量幅度的频谱称为振幅频谱。
图(c)是信号在幅度—频率坐标系统中的图形即振幅频谱图。
反映各分量相位的频谱称为相位频谱。
在本实验中只研究信号振幅频谱。
周期信号的振幅频谱有三个性质:离散性、谐波性、收敛性。
测量时利用了这些性质。
从振幅频谱图上,可以直观地看出各频率分量所占的比重。
测量方法有同时分析法和顺序分析法。
同时分析法的基本工作原理是利用多个滤波器,把它们的中心频率分别调到被测信号的各个频率分量上。
当被测信号同时加到所有滤波器上,中心频率与信号所包含的某次谐波分景频率-致的滤波器便有输出。
信号的产生、分解与合成

信号的产生、分解与合成东南大学电工电子实验中心实验报告课程名称:电子电路实践第四次实验实验名称:信号的产生、分解与合成院(系):吴健雄学院专业:电类强化姓名:周晓慧学号:61010212实验室: 实验组别:同组人员:唐伟佳(61010201)实验时间:2012年5月11日评定成绩:审阅教师:实验四信号的产生、分解与合成一、实验内容及要求设计并安装一个电路使之能够产生方波,并从方波中分离出主要谐波,再将这些谐波合成为原始信号或其他周期信号。
1.基本要求(注:方波产生与最后合成为唐伟佳设计,滤波和移相我设计)(1)设计一个方波发生器,要求其频率为1kHz,幅度为5V;(2)设计合适的滤波器,从方波中提取出基波和3次谐波;(3)设计一个加法器电路,将基波和3次谐波信号按一定规律相加,将合成后的信号与原始信号比较,分析它们的区别及原因。
2.提高要求设计5次谐波滤波器或设计移相电路,调整各次谐波的幅度和相位,将合成后的信号与原始信号比较,并与基本要求部分作对比,分析它们的区别及原因。
3. 创新要求用类似方式合成其他周期信号,如三角波、锯齿波等。
分析项目的功能与性能指标:说明:这次实验我负责的是基波和3次谐波信号滤波器及其移相电路的设计,其余部分是唐伟佳设计,同时我还参与了全过程的调试。
功能:此次实验主要功能是实现信号的产生,并让我们在对信号的分解过程中体会傅里叶级数对周期信号的展开,以及滤波器的设计(该实验主要使用带通和全通滤波器(即移相器)),最后通过将分解出的谐波分量合成。
性能指标:1、对于方波而言:频率要为1kHz,幅度为5V (即峰峰值为10V),方波关键顶部尽可能是直线,而不是斜线。
2、滤出的基波:a、波形要为正弦波,频率为1kHz,幅度理论值为6.37V(注:其实滤除的基波幅度只要不太离谱即可,因为后面的加法器电路可以调整增益,可以调到6.37V,后面的3次谐波、5次谐波也一样)故最主要的是波形和频率。
实验五 非正弦周期信号的分解和合成

实验五非正弦周期信号的分解和合成一、实验要求1、观察正弦波,矩形波和三角波信号的频谱,并进行分析;2、设计以一个BPF1-BPF6的带通滤波器,加法器。
滤波器调谐在基波和各次谐波上,然后用加法器对各次谐波进行合成,观察合成信号与原信号的区别;3、分别对单相正弦波、矩形波和三角波的输出信号进行分解和合成,观测基波及各次谐波频率和幅度,加法器的输出波形。
二、实验内容:(1)用频谱仪和FOURIER分析法观测非正弦周期信号的频谱,分别观测50HZ单相正弦波,方波,矩形波和三角波信号的频谱记录之.A)50hz单相正弦波单相正弦波的产生:产生的波形图如下:对应的频谱图:B)50HZ方波Fourier分析法观测的频谱:C)50HZ矩形波对应的频谱:(2)设计BPF1-BPF6带通滤波器,加法器.滤波器调谐在基波和各次谐波上的带通滤波器,加法器用于信号的合成.将50HZ的方波信号其接至各带通滤波器的输入端,将各带通滤波器的输出分别接至示波器,观测各次谐波的频率和幅值.并记录之本实验不是采用带通滤波器进行实现,而是通过谐振回路对相应的谐波进行提取,实现的电路图如下:基波和二次谐波的电路如下:三次谐波和四次谐波如下:九次谐波的波形如下:(4)将方波分解所得的基波和三次谐波加到加法器的响应输入端,观测加法器的输出波形,并记录之.电路图:合成后的波形:(5)在4的基础上,再将五次谐波分量加到加法器的输入端,观测相加后的波形,记录之,并分析讨论将一三五谐振回路进行串联得到的信号,可见,效果相对上图比较好些(6)分别将50HZ单相正弦波,矩形波和三角波的输出信号接至50HZ电信号分解与合成模块输入端、观测基波和各次谐波的频率和幅度,求和器的输出波形。
最后我们来看看六次谐波叠加的效果:可以看到信号恢复的已经比较不错了,由于在合成信号时会有吉布斯效应,所以会有一个约9%的小凸起。
上面是观察方波信号的,当然我们也可以对三角波信号进行同样的观察,可以预见的是,三角波信号的3,,5次谐波能量将会更小,基波能量将非常集中,因此合成出来的结果应该会更加完美。
信号的分解与合成原理

信号的分解与合成原理
信号的分解与合成原理是对信号进行分离和组合的过程,在信号处理中起着重要的作用。
通过分解和合成信号,我们可以分析信号的特征和性质,从而实现对信号的处理、修改、重构等操作。
信号的分解是将一个复杂的信号分解为若干个简单的基本信号的过程。
这些基本信号可以是正弦信号、余弦信号、方波信号等。
通过分解信号,我们可以了解信号中各个频率分量的强弱、相位关系等信息。
信号的合成是将若干个基本信号按一定的权重和相位关系组合成一个复杂的信号的过程。
通过合成信号,我们可以得到一个具有特定频率成分和振幅的信号。
这种合成信号在通信、音频处理等领域中具有广泛的应用。
在信号的分解与合成过程中,我们通常使用傅里叶分析和傅里叶合成的方法。
傅里叶分析是将一个信号分解为一系列正弦和余弦函数的和的过程,它通过傅里叶变换来实现。
傅里叶合成则是将一系列正弦和余弦函数按一定的权重和相位关系组合成一个信号的过程,它通过傅里叶逆变换来实现。
信号的分解与合成原理基于信号的频域表示,即将信号从时域表示转换为频域表示。
通过频域表示,我们可以获得信号的频谱信息,了解信号中各个频率分量的特性。
在分解与合成过程中,我们可以选择不同的基函数、权重和相位关系,从而实现对信号的不同处理效果。
总之,信号的分解与合成原理是一种重要的信号处理方法,它可以帮助我们分析和处理信号,从而实现信号的修改、重构等操作。
通过合理选择基函数、权重和相位关系,我们可以实现对信号的高效处理与优化。
【精品】信号实验三非正弦周期信号的分解与合成

【精品】信号实验三非正弦周期信号的分解与合成实验目的:1. 学习和掌握非正弦周期信号的分解与合成方法;2. 熟练掌握信号周期、基波、谐波等概念;3. 了解非正弦周期信号的傅里叶级数展开式。
实验原理:1. 周期信号的基波和谐波周期信号可以分解为基波和谐波的叠加。
其中,基波是最小的周期信号,而谐波是基波的倍数周期信号。
如图1所示,对于一个周期为T的信号,其基波周期为T,而谐波周期为T/2、T/3、T/4……,其幅度和相位与基波不同。
2. 非周期信号的傅里叶展开非周期信号可以用傅里叶级数展开。
傅里叶级数展开的基本思想是:将一个周期为T 的非周期信号f(t)看成是周期为T的周期信号F(T)的一个周期割,由此求出周期信号F(T)的傅里叶系数,然后再将傅里叶系数代入傅里叶级数公式中,即可得到非周期信号的傅里叶级数展开式。
傅里叶级数展开式的形式为:其中,a0为零频率分量(直流分量),ak和bk分别为正频率和负频率分量,ω0=2π/T 为基波角频率,k=1,2,3…为谐波次数,T为周期。
实验步骤:1. 按照图2所示电路连接好实验仪器,并将三角波信号和方波信号的频率分别调至5kHz和3kHz左右。
2. 将三角波信号和方波信号通过级联的带通滤波器,分别得到它们的基波和谐波分量。
3. 观察并记录各个分量的幅度和相位,并可根据公式(1)计算出各傅里叶系数。
4. 将所有分量(包括基波和谐波)相加合成为一个信号,并用示波器观察合成信号与源信号的相似程度以及合成误差大小。
5. 重复以上步骤,将三角波信号和方波信号的频率调至不同值,比较不同频率下信号分解和合成的效果。
实验结果:三角波信号分解得到的分量幅度和相位见表1,方波信号分解得到的分量幅度和相位见表2。
表1 三角波信号的基波和谐波分量的幅度和相位2. 将三角波信号和方波信号的基波和谐波分量相加,合成原始信号,并与源信号比较,结果见图3和图4。
图3 三角波信号分解与合成示波图三角波信号合成误差为0.58%左右,方波信号合成误差为2.13%左右。
方波信号的分解与合成matlab

方波信号的分解与合成matlab分解和合成方波信号是信号处理中常见的问题。
在 MATLAB 中,可以使用 chirp 函数生成正弦调频信号,也可以通过谐波合成的方式合成方波信号。
下面是一些参考信息:- 要生成方波信号,可以使用 chirp 函数。
该函数可以生成一个由线性或非线性的调频信号组成的向量,其频率从一个初始频率变化到一个终止频率。
在 MATLAB 中,可以使用 ychirp 函数生成正弦调频信号,如下所示:```matlabt = 0:0.001:1;f0 = 10;f1 = 100;ychirp(t, f0, 1, f1);```- 要合成方波信号,可以使用谐波合成的方法。
当谐波数 n 固定时,可以通过将不同谐波数的正弦波进行叠加来合成方波信号。
在MATLAB 中,可以使用 ysquare 函数生成周期方波信号,并将其与不同谐波数的正弦波进行叠加。
例如,当 n=99 时,可以合成出一个几乎接近于方波信号的信号:```matlabt = -pi:0.001:pi;omega = 2 * pi;ysquare(t, 50);nmax = [1:2:99];for k = 1:nmaxpin = k;xbsin(omega * t);endfigure;plot(t, y);hold on;plot(t, x);hold off;xlabel("t");ylabel("部分和的波形");title(["谐波数", num2str(nmax)]);```- 在合成方波信号时,可以考虑使用 chirp 函数生成正弦调频信号。
该函数可以生成一个由线性或非线性的调频信号组成的向量,其频率从一个初始频率变化到一个终止频率。
方波信号的分解与合成

实验四 方波信号的分解与合成任何电信号都是由各种不同频率、幅度和初相的正弦波迭加而成的。
1822年法国数学家傅里叶在研究热传导理论时提出并证明了将周期函数展开为正弦级数的原理。
奠定了傅里叶级数的理论基础、揭示了周期信号的本质,即任何周期信号(正弦信号除外)都可以看作是由无数不同频率、不同幅度的正弦波信号叠加而成的,就像物质都是由分子或者原子构成一样。
周期信号的基本单元信号是正弦谐波信号。
一、实验目的1、通过对周期方波信号进行分解,验证周期信号可以展开成正弦无穷级数的基本原理,了解周期方波信号的组成原理。
2、测量各次谐波的频率与幅度,分析方波信号的频谱。
3、观察基波与不同谐波合成时的变化规律。
4、通过方波信号合成的实验,了解数字通信中利用窄带通信系统传输数字信号(方波信号)的本质原理。
二、实验原理1、一般周期信号的正弦傅里叶级数按照傅里叶级数原理,任何周期信号在满足狄利克雷条件时都可以展开成如式2-3-1所示的无穷级数∑∑∑∞=∞=∞=+Ω+=Ω+Ω+=10110)cos(2)sin()cos(2)(n n n n n n n t n A A t n b t n a a t f ϕ (2-4-1)其中)cos(n n t n A ϕ+Ω称为周期信号的n 谐波分量,n 次谐波的频率为周期信号频率的n 倍,每一次的谐波的幅度随谐波次数的增加依次递减。
当0=n 时的谐波分量为2a (直流分量)。
当1=n 时的谐波分量为)cos(11ϕ+Ωt A (一次谐波或基波分量直流分量)。
2、一般周期信号的有限次谐波合成及其方均误差按照傅里叶级数的基本原理可知,周期信号的无穷级数展开中,各次谐波的频率按照基波信号的频率的整数倍依次递增,幅度值随谐波次数的增加依次递减,趋近于零。
因此,从信号能量分布的角度来讲,周期信号的能量主要分布在频率较低的有限次谐波分量上。
此原理在通信技术当中得到广泛应用,是通信技术的理论基础。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
号的相位。利用这个特性,全通滤波器可以用做延时器、延迟均衡等。实际上, 常规的滤波器(包括低通滤波器等)也能改变输入信号的相位,但幅频特性和相 频特性很难兼顾, 使两者同时满足要求。 全通滤波器和其他滤波器组合起来使用, 能够很方便的解决这个问题。 如图 5 所示:一阶全通滤波器的幅度和频率响应分别为:
图 5 全通滤波器移相电路
五、 合成电路
合成电路即由运放构成的加法电路构成,可以将基波( 10KHz ) 、二次谐波 (30KHz)和三次谐波(50KHz)合成为近似方波。即达到最终的合成目的。加法 电路如图 6 所示。
图 6 加法电路
HC1G: ������ = =
1
1
HCT1G: ������ = =
T 0.8RC 1 1 T 0.67RC
我们使用的为 TI 公司的 SN74LVC14 施密特反相器,因此电容选择为 1nF,电 阻的具体值和理论值稍微有偏差,需要具体微调。
图 1 方波发生电路
二、 分频电路 模块 2 中将方波震荡电路生成的 300K 方波分别分频为 10K,30K,50K。采用 74HC161 四位计数器,与非门和 74HC74 触发器来完成。 其中,以分频出 30K 为例,由 74HC161 以及与非门,利用 74HC图 2 所示,上电时计数器从 0 开始,当计数器 计数值为 4 时,双输入与非门的输出为 0,将计数器进行同步置数为 0,计数器 重新由 0 开始计数。因此与非门的输出实际上就是一个占空比不为 50%的方波, 频率为 300K/5=60KHz。 然后, 如图三所示: 将与非门的输出输入给一个由 D 触, 将 D 触发器的 Q 非输出端连接到 D 触发器的输入端,则在每一个时钟沿到来的 时候,触发器的输出电平就会翻转,因此当输入为 60KHZ 的方波时,其输出就 是频率为 30KHz,占空比为 50%的方波了。同理,10KHz 的方波和 50KHz 的方波
也是由此方法分频而来的。
图 2 计数器和与非门构成的分频器
图 3 D 触发器构成的 T 触发器
三、 滤波电路
为了达到比较好的滤波效果,采用有源滤波电路,由 OPA365 构成。如图 4 所示: 此电路为运放构成的 4 阶有源滤波电路, 具体参数由 TI 公司的 FilterSolution 生成。经仿真以及最终的测试,二次谐波的抑制在 40dB 左右,效果较好。
信号分解与合成说明
一、 方波发生电路 图 1 是模块 1 即用施密特反相器构成最简单的方波振荡电路,之所以可以用 施密特反相器构成方波振荡电路,是因为施密特反相器的两个条件: 1 反相器的输入阻抗要高。 2 输入高电平和低电平的阈值电压不同。 我们知道 74HC14 的输入高低电平的阈值分别为 3V、1.5V,所以波形的振荡 周期其实就是电容 C 从 1.5V 充电到 3V 再放电到 1.5V 的时间。改变充放电的时 间就可以改变振荡频率,因此改变 RC 的值,就能够改变输出的震荡频率。 此方波发生器是基于电容充放电原理,由于电容在充电过程中电压的非线性 因素, 所以实际上产生的三角波并不是标准的三角波,因而方波的占空比也不是 严格的 50%,所以这种电路也只能用于对波形质量要求不高的场合,不过我们可 以加以变换,如把方波进行二分频就可以得到 50%占空比的方波,这样就可以作 数字电路的方波输入了。 电路中电位器是用来微调频率使其满足 300KHz 的要求。 根据施密特反相器的数据手册给出的公式,方波的生成频率:
图 4 4 阶有源滤波电路
四、 移相电路
经过滤波电路以后,信号的相位会发生变化,因此,为了最终的方波合成有 好的效果,必须经过移相电路。为了能够有较好的移相电效果,而且不至于使方 波的幅值发生变化 (方波的合成需要 1:3:5 的严格幅值关系) , 因此这里介绍全功 滤波器: 全通滤波器(APF)虽然并不改变输入信号的频率特性,但它会改变输入信
