2012届北京市石景山区高三期末数学理科试题(WORD精校版)

合集下载

【推荐下载】2012石景山高三理科数学上册期末试卷

7
的等腰直角三角形，则该三棱锥的四个面
[键入文字]
(B) (C) (D) 6.执行如图所示的程序框图，则输出的 S 值为( 表示不超过 x 的最大整数) (A) 4(B) 5(C) 7(D) 9 7.在平面直角坐标系 xOy 中，已知 A(1,0)，B(0,1)，点 C 在第二象限内， |OC|=2，若，则，的值是( ) (A) ，1 (B) 1， (C) -1， (D) - ，1 8.已知函数 f(x)= ,且，集合 A={m|f(m)小于 0}，则 (A) 都有 f(m+3)0 (B) 都有 f(m+3)小于 0 (C) 使得 f(m0+3)=0 (D) 使得 f(m0+3)小于 0 二、填空题：共 6 小题，每小题 5 分，共 30 分. 9.某高中共有学生 900 人，其中高一年级 240 人，高二年级 260 人，为做某项调查，
4[键入文字]源自(Ⅰ)求的定义域及最小正周期; (Ⅱ)求在区间上的最大值和最小值. 16.(本小题共 14 分) 如图 1，在 Rt 中，， .D、E 分别是上的点，且，将沿折起到的位置，使，如图 2. (Ⅰ)求证：平面 ; (Ⅱ)若，求与平面所成角的正弦值; (Ⅲ) 当点在何处时，的长度最小，并求出最小值. 17.(本小题共 13 分) 甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为 . (Ⅰ)求甲乙二人中至少有一人破译出密码的概率; (Ⅱ)求的值;
1
[键入文字]
5.执行右面的框图，若输出结果为 3，则可输入的实数值的个数为( ) A.1B.2 C.3D.4 6.若从 1,2,3,,9 这 9 个整数中同时取 4 个不同的数，其和为奇数，则不同的取法共有( ) A.60 种 B.63 种 C.65 种 D.66 种 7.某三棱锥的三视图如图所示，该三棱锥的体积是( ) A. 8. 在整数集中，被除所得余数为的所有整数组成一个类，记为，即， .给出如下四个结论： ① ;

【免费下载】石景山区期末高三数学试题理科及参考答案

．
．
16．（本小题共 14 分）
如图1，在 Rt ABC 中， C 90 ， BC 3， AC 6 ． D ､ E 分别是 AC ､ AB 上的点，且 DE / / BC ，将 ADE 沿 DE 折起到 A1DE 的位置，使 A1D CD ，如图 2 ．（Ⅰ）求证： BC 平面 A1DC ；（Ⅱ）若 CD 2 ，求 BE 与平面 A1BC 所成角的正弦值；（Ⅲ）当 D 点在何处时， A1B 的长度最小，并求出最小值． A1
④ 函数 y f (x) 在 ( 1 , 3 ] 上是增函数． 22
则上述命题中真命题的序号是
三、解答题共 6 小题，共 80 分．解答应写出文字说明，演算步骤或证明过程．
15．（本小题共 13 分）
已知函数 f (x) sin 2x ( sin x cos x) ． cos x
（Ⅰ）求 f (x) 的定义域及最小正周期；
1．设集合U {1, 2,3, 4}， A {1, 2}， B {2, 4} ，则 (CU A) B （）
Байду номын сангаас
A．{1, 2}
2．若复数 Z1 i ， Z2
A． 1 3i
B．{2，3, 4}
3 i ，则 Z 2 Z1
B． 2 i
（
3． AC 为平行四边形 ABCD 的一条对角线， AB (2, 4) ， AC (1,3) ，则 AD （
C．{3, 4}
）
C．1 3i

C． (1,1)

输入 x
D．{1, 2,3, 4}
D． 3 i
x>2
D． (1, 1)
否
y=x2 -1 y= log2 x

石景山数学理

北京市石景山区2013届高三统一测试数学（理）试题本试卷共150分，考试时长120分钟，请务必将答案答在答题卡上，在试卷上作答无效．考试结束后上交答题卡．第Ⅰ卷（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合M= {x|x 2≤4），N={x|log 2 x≥1}，则M I N 等于（） A ． [-2，2] B ．{2} C ．[2，+∞） D ． [-2,+∞） 2．若复数（a －i ）2在复平面内对应的点在y 轴负半轴上，则实数a 的值是（）A ． 1B ．-1C ．2D ．-23．将一颗骰子掷两次，观察出现的点数，并记第一次出现的点数为m ，第二次出现的点数为n ，向量p u r =（m ，n ），q r =（3，6），则向量p u r 与q r共线的概率为（） A ．13 B ．14C ．16D ．1124．执行右面的框图，输出的结果s 的值为（） A ．-3 B ．2 C ．12-D ．135．如图，直线AM 与圆相切于点M, ABC 与ADE 是圆的两条割线，且BD ⊥AD ，连接MD 、EC 。

则下面结论中，错误．．的结论是( ) A ．∠ECA = 90oB ．∠CEM=∠DMA+∠DBAC ．AM 2 = AD·AED ．AD·DE = AB·BC6．在（2x 2－1x）5的二项展开式中，x 的系数为（） A ．-10 B ．10 C ．-40 D ．407．对于直线l ：y=k (x+1)与抛物线C ：y 2= 4x ，k=±1是直线l 与抛物线C 有唯一交点的( )条件 A ．充分不必要 B ．必要不充分 C ．充要条件 D ．既不充分也不必要8．若直角坐标平面内的两点p 、Q 满足条件：①p 、Q 都在函数y=f （x ）的图像上；②p 、Q 关于原点对称，则称点对[P ，Q]是函数y=f （x ）的一对“友好点对”（注：点对[P ，Q]与[Q ，P]看作同一对“友好点对”）．已知函数f （x ）=221(0)4(0)og x x x x x >⎧⎨--≤⎩，则此函数的“友好点对”有（）对．A ． 0B ． 1C ．2D ． 3第Ⅱ卷（非选择题共110分）二、填空题共6小题，每小题5分，共30分． 9．直线2p sinθ=1与圆ρ=2 cos θ相交弦的长度为。

北京市石景山区2012届高三上学期期末考试化学试题.pdf

北京市石景山区2011—2012学年高三第一学期期末考试高三化学 2012.1 可能用到的相对原子质量：H—1 C—12 N—14 O—16 Na—23 S—32 Cu—64 一、选择题（本题共20个小题，每小题2分，共40分） K—39 Mn—55 在每个小题给出的四个备选答案中，只有一个符合题目的要求。

1． A．钢铁在海水中比在河水中更易腐蚀，主要原因是海水含氧量高于河水 B．废弃的塑料、金属、纸制品及玻璃都是可回收再利用的资源 C．凡含有食品添加剂的食物对人体健康均有害，不宜食用 D．乙醇和汽油都是可再生能源，应大力推广“乙醇汽油” 2．下列化学用语的是 A．的 B．电子式 C．结构 D． 3． ①将水沿烧杯内壁缓缓加入浓硫酸中，用玻璃棒不断搅拌 ②实验室制取氯气时，尾气用碱液吸收 ③取用金属钠或钾做完实验后，剩余的药品要放回原瓶 ④夜间厨房发生煤气泄漏时，应立即开灯检查煤气泄漏的原因，然后打开所有的门窗通风 ⑤干冰可用于钠、镁等金属的灭火 A．①④⑤ B．①②③④ C．①③④⑤ D．全部 4．家庭住宅的窗玻璃大部分是普通玻璃，其成分是Na2SiO3·CaSiO3·6SiO2，在生产过程中加入不同的物质，调整玻璃的化学成分，可以制得具有不同性能和用途的玻璃。

下表所列不正确的是选项ABCD添加成分Co2O3(氧化钴)Cu2OFe2+PbO蓝色红色光学玻璃5．医药中，常用酒精来消毒，是因为酒精能够 A．使细菌蛋白体发生盐析 B．使细菌蛋白体发生变性 C．与细菌蛋白质发生氧化反应 D． 6．化石燃料是不可再生的，最终将会枯竭。

基于我国目前的技术水平和管理水平，能源从开采、运输、加工到终端的利用效率都很低，浪费很大。

据统计，开采效率为32%，加工运输效率为70%，终端利用率为41%，则总效率近似为 A．1.43% B．14.3% C．9.18% D．91.8% ． A．C6H5CH2OH不属于醇类 B．油脂的硬化属于水解反应 C．苯和甲苯都能使KMnO4酸性溶液褪色 D．1-氯丙烷和2-氯丙烷分别与NaOH乙醇溶液共热的反应产物相同 8．为提纯下列物质（括号中为杂质），所选除杂试剂和分离方法都正确的是被提纯的物质（杂质）除杂试剂分离方法ANH3（H2O）浓硫酸洗气B苯（苯酚）浓溴水过滤C溴化钠溶液（NaI）氯水、CCl4萃取、分液D乙醇（水）生石灰蒸馏9．元素X、Y、Z原子序数之和为36，X、Y在同一周期，X2+与Z2－具有相同的核外电子层结构。

北京市石景山区高三上学期期末考试数学(理)试卷(有答案)

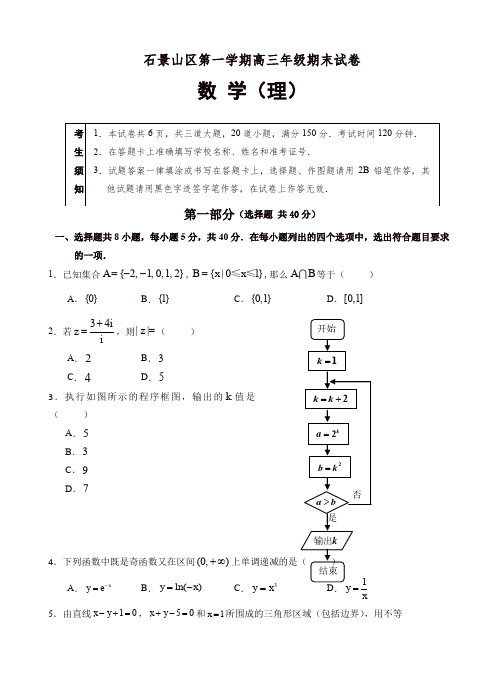
石景山区第一学期高三年级期末试卷数学（理）（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合{2,1,0,1,2}A =--,{|01}B x x =≤≤,那么A B 等于（）A ．{0} B ．{1}C ．{0,1}D ．[0,1] 2．若34iz i+=，则||z =（） A ．2 B ．3 C ．4D ．53．执行如图所示的程序框图，输出的k 值是（）A ．5B ．3C ．9D ．74．下列函数中既是奇函数又在区间(0,)+∞A ．x y e -=B ．ln()y x =-C ．3y x =．x5．由直线10x y -+=，50x y +-=和1x =所围成的三角形区域（包括边界），用不等式组可表示为（）A ．10,50,1x y x y x -+≤⎧⎪+-≤⎨⎪≥⎩B ．10,50,1x y x y x -+≥⎧⎪+-≤⎨⎪≥⎩C ．10,50,1x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩D ．10,50,1x y x y x -+≤⎧⎪+-≤⎨⎪≤⎩6．一个几何体的三视图如右图所示．已知这个几何体的体积为8，则h =（A ．1B ．2C ．3D ．67．将函数2(3)y x =-图象上的点2(,(3))P t t -向左平移m (m >0)个单位长度得到点Q ．若Q 位于函数2y x =的图象上，则以下说法正确的是（） A ．当2t =时，m 的最小值为3 B ．当3t =时，m 一定为3 C ．当4t =时，m 的最大值为3D ．t ∀∈R ，m 一定为38．六名同学A 、B 、C 、D 、E 、F 举行象棋比赛，采取单循环赛制，即参加比赛的每两个人之间仅赛一局．第一天，A 、B 各参加了3局比赛，C 、D 各参加了4局比赛，E 参加了2局比赛，且A 与C 没有比赛过，B 与D 也没有比赛过，那么F 在第一天参加的比赛局数为（） A ．1B ．2C ．3D ．4第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．在7(3)x -的展开式中，5x 的系数是（结果用数值表示）．10．已知ABC △中，AB =1BC ，sin C C ，则ABC △的面积为．11．若双曲线2214x y m-=的渐近线方程为y x =，则双曲线的焦点坐标是．12．等差数列{}n a 中，12a =，公差不为零，且1a ，3a ，11a 恰好是某等比数列的前三项，那么该等比数列公比的值等于．13．有以下4个条件：①a b =；②||||a b =；③a 与b 的方向相反；④a 与b 都是单位向量．其侧视图正视图俯视图中a //b 的充分不必要条件有．（填正确的序号）．14．已知函数11,1,()4ln ,1x x f x x x ⎧+≤⎪=⎨⎪>⎩，①方程()f x x =-有________个根；②若方程()f x ax =恰有两个不同实数根，则实数a 的取值范围是____________．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）已知函数π()2sin()sin 22f x x x x =-⋅．（Ⅰ）求()f x 的最小正周期；（Ⅱ）求()f x 在ππ[,]126-上的最大值． 16．（本小题共13分）2016年微信用户数量统计显示，微信注册用户数量已经突破9.27亿．微信用户平均年龄只有26岁，97.7%的用户在50岁以下，86.2%的用户在18-36岁之间．为调查大学生这个微信用户群体中每人拥有微信群的数量，现从北京市大学生中随机抽取100位同学进行了抽样调查，结果如下：（Ⅰ）求a，b，（Ⅱ）若从这100位同学中随机抽取2人，求这2人中恰有1人微信群个数超过15个的概率；（Ⅲ）以这100个人的样本数据估计北京市的总体数据且以频率估计概率，若从全市．．大学生．．．中随机抽取3人，记X表示抽到的是微信群个数超过15个的人数，求X的分布列和数学期望EX．17．（本小题共14分）如图1，等腰梯形BCDP 中，BC ∥PD ，BA PD ⊥于点A ，3PD BC =，且1AB BC ==．沿AB 把PAB △折起到P AB '△的位置（如图2），使90P AD '∠=︒．（Ⅰ）求证：CD ⊥平面P AC '；（Ⅱ）求二面角A P D C '--的余弦值；（Ⅲ）线段P A '上是否存在点M ，使得BM ∥平面P CD '．若存在，指出点M 的位置并证明；若不存在，请说明理由．图1图218．（本小题共13分）已知椭圆2222:1(0)x y C a b a b+=>>，点(2,0)在椭圆C 上．（Ⅰ）求椭圆C 的标准方程；（Ⅱ）过点(1,0)P 的直线（不与坐标轴垂直）与椭圆交于A B 、两点，设点B 关于轴的对称点为B '．直线B A '与轴的交点Q 是否为定点？请说明理由．19．（本小题共14分）已知函数2()11xf x x =++，2()(0)a x g x x e a =<．（Ⅰ）求函数()f x 的单调区间；（Ⅱ）若对任意12,[0,2]x x ∈，12()()f x g x ≥恒成立，求a 的取值范围．B CAP DA CP′ABCD20．（本小题共13分）集合M 的若干个子集的集合称为集合M 的一个子集族．对于集合{1,2,3}n 的一个子集族D 满足如下条件：若,A D B A ∈⊆，则B D ∈，则称子集族D 是“向下封闭”的．（Ⅰ）写出一个含有集合{1,2}的“向下封闭”的子集族D 并计算此时(1)AA D∈-∑的值（其中A 表示集合A 中元素的个数，约定0φ=；A D∈∑表示对子集族D 中所有成员A 求和）；（Ⅱ）D 是集合{1,2,3}n 的任一“向下封闭的”子集族，对A D ∀∈,记max k A =，()max (1)AA Df k ∈=-∑（其中ma 表示最大值），（ⅰ）求(2)f ；（ⅱ）若k 是偶数，求()f k ．石景山区第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．二、填空题共6小题，每小题5分，共30分．三、解答题共6小题，共80分． 15．（本小题共13分）解：（Ⅰ）()2cos sin 2f x x x x =⋅ ……1分sin 22x x = ……2分π2sin(2)3x =+， ……4分因此)(x f 的最小正周期为π． …………6分（Ⅱ）当ππ[,]126x ∈-时，ππ2π2633x ≤+≤， ………8分当ππ232x +=，πsin(2)3x +有最大值1． ………10分即π12x =时，()f x 的最大值为2． ……………13分 16．（本小题共13分）解：（Ⅰ）030305100a ++++=解得35a =，5110020b ==，35710020c ==．…………………3分（Ⅱ）记“2人中恰有1人微信群个数超过15个”为事件A ，则114060210016()33C C P A C ==．所以，2人中恰有1人微信群个数超过15个的概率为1633． ……………7分（Ⅲ）依题意可知，微信群个数超过15个的概率为25P =． X 的所有可能取值0，1，2，3． ……………8分则()033270()(1)2255125P X C ==-=，()1123541()(1)2255125P X C ==-=， ()2213362()(1)2255125P X C ==-=，()333083()(22551)125P X C ==-=．其分布列如下：所以，01231251251251255EX =⨯+⨯+⨯+⨯=．……………13分 17．（本小题共14分）解：（Ⅰ）因为90P AD '∠=︒，所以P A '⊥AD ．因为在等腰梯形中，AB ⊥AP ，所以在四棱锥中，AB ⊥AP '．又AD AB A ⋂=，所以P A '⊥面ABCD ．因为CD 面ABCD ，所以P A '⊥CD ．……3分因为等腰梯形BCDE 中，AB BC ⊥，3PD BC =，且1AB BC ==．所以AC =CD 2AD =．所以222AC CD AD +=．所以AC ⊥CD ．因为P A 'AC =A , 所以CD ⊥平面P AC '． ……5分（Ⅱ）由（Ⅰ）知，P A '⊥面ABCD ，AB ⊥AD ，如图，建立空间直角坐标系，A ()0,0,0，B ()1,0,0，C ()1,1,0，D ()0,2,0，P '()0,0,1．…………5分所以(1,0,0)AB =，(1,1,1)P C '=-．由（Ⅰ）知，平面P AD '的法向量为(1,0,0)AB =，设(,,)n x y z =为平面P CD '的一个法向量，则00n CD n P C ⎧⋅=⎪⎨'⋅=⎪⎩,即00x y x y z -+=⎧⎨+-=⎩，再令1y =，得(1,1,2)n =．cos ,AB n =AB n AB n⋅⋅=所以二面角A P DC '-- …………9分（Ⅲ）若线段P A '上存在点M ，使得BM ∥平面P CD '．依题意可设AM AP λ'=,其中01λ≤≤．所以(0,0,)M λ，(1,0,)BM λ=-．由（Ⅱ）知，平面P CD '的一个法向量(1,1,2)n =．因为BM ∥平面P CD '，所以BM n ⊥，所以120BM n λ⋅=-+=，解得12λ=．所以，线段P A '上存在点M ，使得BM ∥平面P CD '…………………14分 18．（本小题共13分）解：（Ⅰ）因为点（2,0）在椭圆C 上，所以2a =．又因为2c e a ==，所以c =1b =．所以椭圆C 的标准方程为：2214x y +=． ……………………5分（Ⅱ）设112222(,),(,),(,),(,0)A x y B x y B x y Q n '-．设直线AB ：(1)(0)y k x k =-≠． ……………………6分联立22(1)440y k x x y =-+-=和，得：2222(14)8440k x k x k +-+-=．所以2122814k x x k +=+，21224414k x x k-=+． ……………8分直线AB '的方程为121112()y y y y x x x x +-=--， ……………9分令0y =，解得112122111212()y x x x y x yn x y y y y -+=-+=++ ………11分又1122(1),(1)y k x y k x =-=-，所以121212()42x x x x n x x -+==+-．所以直线B A '与轴的交点Q 是定点，坐标为(4,0)Q ．………13分 19．（本小题共14分）解：（Ⅰ）函数()f x 的定义域为R ，()()()()()()x x x f x x x --+'==++2222211111．……2分当x 变化时，()f x '，()f x 的变化情况如下表：所以，函数()f x 单调递减区间是(,)-∞-1，(,)+∞1． …………5分（Ⅱ）依题意，“对于任意12,[0,2]x x ∈，12()()f x g x ≥恒成立”等价于 “对于任意[0,2]x ∈，min max ()()f x g x ≥成立”．由（Ⅰ）知，函数()f x 在[0,1]上单调递增，在[1,2]上单调递减，因为(0)1f =，2(2)115mf =+>，所以函数()f x 的最小值为(0)1f =．所以应满足max ()1g x ≤．………………………………………………7分因为2()e axg x x =，所以2()(+2)e axg x ax x '=．………8分因为0a <，令()0g x '=得，10x =，22x a=-．（ⅰ）当22a-≥，即10a -≤<时，在[0,2]上()0g x '≥，所以函数()g x 在[0,2]上单调递增，所以函数2max ()(2)4e a g x g ==．由24e 1a ≤得，ln 2a ≤-，所以1ln 2a -≤≤-． ……………11分（ⅱ）当202a<-<，即1a <-时, 在2[0,)a -上()0g x '≥，在2(,2]a-上()0g x '<，所以函数()g x 在2[0,)a -上单调递增，在2(,2]a -上单调递减，所以max 2224()()e g x g a a =-=．由2241e a ≤得，2ea ≤-，所以1a <-． ……………13分综上所述，a 的取值范围是(,ln 2]-∞-． ……………14分20．（本小题共13分）解：（Ⅰ）含有集合{1,2}的“向下封闭”的子集族{,{1},{2},{1,2}}D φ= ……2分此时0112(1)(1)(1)(1)(1)0A A D ∈-=-+-+-+-=∑ …………4分（Ⅱ）设{1,2,3}n 的所有不超过k 个元素的子集族为k D（ⅰ）易知当2D D =时，(1)AA D∈-∑达到最大值，所以201122(1)32(2)(1)(1)(1)122n nn n n n f C C n --+=-+-+-=-+= …6分（ⅱ）设D 是使得max k A =的任一个“向下封闭”的子集族，记'''D D D =，其中'D 为不超过2k -元的子集族，''D 为1k -元或k 元的子集则(1)AA D ∈-∑= '''''(1)(1)(2)(1)A A AA D A D A D f k ∈∈∈-+-≤-+-∑∑∑ ………8 分现设''D 有l （k n l C ≤）个{1,2,3}n 的k 元子集，由于一个1k -元子集至多出现在1n k -+个{1,2,3}n 的k 元子集中，而一个k 元子集中有1k k C -个1k -元子集，故l 个k 元子集至少产生11k k lC n k --+个不同的1k -元子集． ''11(1)(1)(1)111k Ak k k k n n n A D lC k k l l C C C n k n k n k --∈-≤-=-≤-=--+-+-+∑ 1(1)(2)()A k k n n A D f k C C f k -∈-≤--+=∑由（ⅰ）得011221()(1)(1)(1)(1)(1)kk ki i n n nn i f k C C C C ==-+-+-++-=-∑…13分【注：若有其它解法，请酌情给分．】。

【高三】(试题全)北京市石景山区届高三上学期期末考试数学理试题(WORD

【高三】（试题全）北京市石景山区届高三上学期期末考试数学理试题（WORD试卷说明：石景山区―学年第一学期期末考试试卷高三数学（理科）本试卷共6页，满分为150分，考试时间为120分钟.请务必将答案答在答题卡上，在试卷上作答无效，考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项． 1．已知集合，，那么（）A．B．C．D．2．复数（）A．B．C．D．3．已知向量，，则“”是“∥”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件4．已知数列为等差数列，，那么数列通项公式为（）A．B．C．D．5．执行如图所示的程序框图，若输入的的值为，则输出的的值为（）A．B．C．D． 6．在边长为的正方形中任取一点，则点恰好落在正方形与曲线围成的区域内(阴影部分)的概率为（）A．B．C．D．7．用到这个数字，可以组成没有重复数字的三位偶数的个数为（）A．B． C．D．8．已知函数满足，当时，，若在区间上方程有两个不同的实根，则实数的取值范围是（）A．B．C．D．第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．的参数方程为为参数，则圆的直角坐标方程为_______________，圆心到直线的距离为______． 1．中，角的对边分别为，若，，，则______．11．，满足约束条件则．12．中，，是上一点，以为圆心，为半径的圆与交于点，与切于点，，，则的长为，的长为． 13．的焦点为，准线为直线，过抛物线上一点作于，若直线的倾斜角为，则______． 14．是边长为的正方形，且平面，为上动点，过且垂直于的平面交于，那么异面直线与所成的角的度数为，当三棱锥的体积取得最大值时，四棱锥的长为．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．15．（本小题满分13分）已知函数．在上的最小值，并写出取最小值时相应的值．13分）北京市各级各类中小学每年都要测试，测试总成绩满分为分测试成绩在之间为体质优秀；在之间为体质良好；在之间为体质合格；在之间为体质不合格．现从某校高年级的名学生中随机抽取名学生体质测试成绩如下：1356801122333445667797056679645856（Ⅰ）试估计该校高年级体质为优秀的学生人数；名学生体质测试成绩名学生，再从这名学生中选出人．名学生中至少有名体质为优秀的概率；（?）记为名学生中体质为良好的人数，求的分布列及数学期望．如图，在四棱锥中，平面，底面是直角梯形，，∥，且，，为的中点．（Ⅱ）求二面角的余弦值；（Ⅲ）在线段上是否存在一点（不与两点重合），使得∥平面?若存在，求出的长；若不存在，请说明理由．18．（本小题满分13分）已知函数（为自然对数的底数）.（Ⅰ）当时，求曲线在点处的切线方程；（Ⅱ）求函数的单调区间；（Ⅲ）已知函数在处取得极小值，不等式的解集为，若，且，求实数的取值范围.19．（本小题满分14分）已知椭圆：（）过点，且椭圆的离心率为.（Ⅰ）求椭圆的方程；（Ⅱ）若动点在直线上，过作直线交椭圆于两点，且，再过作直线.证明：直线恒过定点，并求出该定点的坐标.20．（本小题满分13分）已知集合，对于数列中.（Ⅰ）若项数列满足，，则数列中有多少项取值为零？()（Ⅱ）若各项非零数列和新数列满足（）．（?）若首项，末项，求证数列是等差数列；（?）若首项，末项，记数列的前项和为，求的最大值和最小值．石景山区―学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．题号12345678答案DCAACBBD二、填空题共6小题，每小题5分，共30分．题号91011121314答案，，，(两空的题目第一空2分，第二空3分)三、解答题共6小题，共80分．15．（本小题共13分）解：（Ⅰ）............2分， (4)分，，，，...............6分所以函数的单调递增区间为．，， (9)分，，……………11分所以当，即时，函数取得最小值．13分）解：（Ⅰ）根据抽样，估计该校高三学生中体质为优秀的学生人数有人．（Ⅱ）依题意，体质为良好和优秀的学生人数之比为．，从体质为优秀的学生中抽取的人数为．……………6分（?）设“在选出的名学生中至少有名体质为优秀”为事件，则．名学生中至少有名体质为优秀的概率为．的所有取值为．，，．的分布列为: ．因为平面，平面，所以. ……………1分取因为底面为直角梯形，∥，，且，所以四边形为正方形，所以，且，所以，即. ……………3分又，所以平面. ……………4分（Ⅱ）解：如图，以为坐标原点，所在直线分别为轴建立空间直角坐标系．……………5分则，，，，所以，，．因为平面，所以为平面的一个法向量．……………6分设平面的法向量为，由，得令，则，，所以是平面的一个法向量．……………8分所以因为二面角为锐角，所以二面角的余弦值为．……………9分（Ⅲ）解：假设在线段上存在点（不与两点重合），使得∥平面．设，则，．设平面的法向量为，由，得令，则，，所以是平面的一个法向量．因为∥平面，所以，即，……………13分解得，所以在线段上存在一点（不与两点重合），使得∥平面，且．8.（本小题共13分）解：（Ⅰ）当时，，，，得，……………2分所以曲线在点处的切线方程为. ……………3分（Ⅱ）.当时，恒成立，此时的单调递增区间为，无单调递减区间；……………5分当时，时，，时，，此时的单调递增区间为，单调递减区间为.……………7分（Ⅲ）由题意知得，经检验此时在处取得极小值. ...............8分因为，所以在上有解，即使成立，...............9分即使成立，............10分所以.令，，所以在上单调递减，在上单调递增，则， (12)分所以. ……………13分19．（本小题共14分）解：（Ⅰ）因为点在椭圆上，所以，所以，……………1分因为椭圆的离心率为，所以，即，……………2分解得，……………4分所以椭圆的方程为. ……………5分（Ⅱ）设，，①当直线的斜率存在时，设直线的方程为，，，由得，……………7分所以，……………8分因为，即为中点，所以，即. 所以，……………9分因为直线，所以，所以直线的方程为，即，显然直线恒过定点. ……………11分②当直线的斜率不存在时，直线的方程为，此时直线为轴，也过点. ……………13分综上所述直线恒过定点. ……………14分20．（本小题共13分）解：（Ⅰ）设数列中项为分别有项．由题意知解得．所以数列中有项取值为零．……………3分（Ⅱ）（?）且，得到，若，则满足．此时，数列是等差数列；若中有个，则不满足题意；所以数列是等差数列．……………7分（?）因为数列满足，所以，根据题意有末项，所以．而，于是为正奇数，且中有个和个．要求的最大值，则只需前项取，后项取，所以（为正奇数）．要求的最小值，则只需前项取，后项取，则（为正奇数）．…………13分【注：若有其它解法，请酌情给分．】每天发布最有价值的高考资源每天发布最有价值的高考资源 1 12 每天发布最有价值的是输入输出开始结束否．（试题全）北京市石景山区届高三上学期期末考试数学理试题（WORD版，含答案）感谢您的阅读，祝您生活愉快。

北京市石景山区2013届高三上学期期末考试数学理试题

石景山区高三期末考试(数学理)有答案

O 2x1x yx12 石景山区第一学期期末高三数学（理科）考试试卷姓名：_________班级：________ 得分：________第Ⅰ卷选择题一、选择题：本大题共8个小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的． 1．已知集合{}21M x x =∈≤Z ，{}12N x x =∈-<<R ，则MN =（）A ． {}1,0,1-B ．{}0,1C ．{}1,0-D ．{}12．已知复数1iz i=＋，则复数z 的模为（） A ．22B 2C ．12D ．12+12i 3．一个几何体的三视图如右图所示（单位长度：cm ），则此几何体的体积是（） A ．1123cm B ．32243cm C ．963cmD ．2243cm4．从4名男同学和3名女同学中，任选3名同学参加体能测试，则选出的3名同学中，既有男同学又有女同学的概率为（） A ．3512B ．3518 C ．76 D ．875．下列说法中，正确的是（） A ．命题“若22am bm <，则a b <”的逆命题是真命题B ．命题“x R ∃∈，02>-x x ”的否定是：“x R ∀∈，02≤-x x ” C ．命题“p 或q ”为真命题，则命题“p ”和命题“q ”均为真命题D ．已知R x ∈，则“1x >”是“2x >”的充分不必要条件6．已知函数32()f x x bx cx =++的图象如图所示，则2221x x +等于（）A ．32B ．34 C ．38D ．3167．已知O 为坐标原点，点A ),(y x 与点B 关于x 轴对称，(0,1)j =，则满足不等式20OA j AB +⋅≤的点A 的集合用阴影表示为（）m1NMMM A A (B )B A xyO图1 图2图38．下图展示了一个由区间(0,1)到实数集R 的映射过程：区间(0,1)中的实数m 对应数轴上的点M （如图1）；将线段AB 围成一个圆，使两端点A 、B 恰好重合（从A 到B 是逆时针，如图2）；再将这个圆放在平面直角坐标系中，使其圆心在y 轴上，点A 的坐标为(0,1)（如图3），图3中直线AM 与x 轴交于点,0N n ，则m 的象就是n ，记作f m n ．则下列命题中正确的是（）A ．114f ⎛⎫=⎪⎝⎭B ．()f x 是奇函数C ．()f x 在其定义域上单调递增D ．()f x 的图象关于y 轴对称第Ⅱ卷非选择题二、填空题：本大题共6个小题，每小题5分，共30分． 9．已知(,0)2πα∈-，3sin 5α=-，则cos()πα-＝． 10．阅读如图所示的程序框图，运行相应的程序，如果输入100，则输出的结果为，如果输入2-，则输出的结果为．11．已知直线220x y -+=经过椭圆22221(0)x y a b a b+=>>的一个顶点和一个焦点，那么这个椭圆的方程为，离心率为_______．12．已知△ABC 的三边长分别为7AB =，5BC =， 6CA =，则AB BC ⋅的值为________． 13．120()x x dx -=⎰．14．已知函数399)(+=x x x f ，则(0)(1)f f += ，若112()()k S f f k k-=+31()()(2,k f f k k kk-+++≥∈Z)，则1k S -= （用含有k 的代数式表示）．三、解答题：本大题共6个小题，共80分．解答题应写出文字说明，证明过程或演算步骤． 15．（本小题满分13分）已知函数23cos sin sin 3)(2-+=x x x x f ()R x ∈．（Ⅰ）求)4(πf 的值；（Ⅱ）若)2,0(π∈x ，求)(x f 的最大值；（Ⅲ）在ABC ∆中，若B A <，21)()(==B f A f ，求ABBC 的值． 16．（本小题满分13分）某地区举办科技创新大赛，有50件科技作品参赛，大赛组委会对这50件作品分别从“创新性”和“实用性”两项进行评分，每项评分均按等级采用5分制，若设“创新性”得分为x ，“实用性”得分为y ，统计结果如下表：作品数量 yx实用性 1分2分 3分 4分 5分创新性1分 1 3 1 0 1 2分 1 0 7 5 1 3分 2 10 9 34分 1 b6 0 a5分113（Ⅰ）求“创新性为4分且实用性为3分”的概率；（Ⅱ）若“实用性”得分的数学期望为16750，求a 、b 的值． 17．（本小题满分14分）已知直四棱柱ABCD A B C D ''''-，四边形ABCD 为正方形，'AA 22==AB ，E 为棱C C '的中点．（Ⅰ）求证：A E '⊥平面BDE ；（Ⅱ）设F 为AD 中点，G 为棱'BB 上一点，且14BG BB '=，求证：FG ∥平面BDE ；（Ⅲ）在（Ⅱ）的条件下求二面角G DE B --的余弦值．18．（本小题满分13分）已知椭圆C 中心在原点，焦点在x 轴上，焦距为2，短轴长为（Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线l ：()0y kx m k =+≠与椭圆交于不同的两点M N 、（M N 、不是椭圆的左、右顶点），且以MN 为直径的圆经过椭圆的右顶点A ．求证：直线l 过定点，并求出定点的坐标．19．（本小题满分13分）已知函数ln ()()a xf x a R x+=∈．（Ⅰ）若4=a ，求曲线)(x f 在点))(,(e f e 处的切线方程；（Ⅱ）求)(x f 的极值；（Ⅲ）若函数)(x f 的图象与函数1)(=x g 的图象在区间],0(2e 上有公共点，求实数a 的取值范围． 20．（本小题满分14分）如图111(,)P x y ，222(,)P x y ，，(,)n n n P x y ，12(0,)n y y y n N *<<<<∈是曲线2:3(0)C y x y =≥上的n 个点，点(,0)(1,2,3,,)i i A a i n =在x 轴的正半轴上，1i i i A A P -∆是正三角形(0A 是坐标原点) .（Ⅰ）求123,,a a a ；（Ⅱ）求出点n A (,0)(*)n a n N ∈的横坐标n a 关于n 的表达式；（Ⅲ）设12321111n n n n n b a a a a +++=++++，若对任意正整数n ，当[]1,1m ∈-时，不等式2126n t mt b -+>恒成立，求实数t 的取值范围.石景山区2010—2011学年第一学期期末考试试卷高三数学（理科）参考答案一、选择题：本大题共8个小题，每小题5分，共40分．题号 12345678答案B A BC B C C C二、填空题：本大题共6个小题，每小题5分，共30分．注：两空的题第1个空3分，第2个空2分. 三、解答题：本大题共6个小题，共80分．解答题应写出文字说明，证明过程或演算步骤． 15．（本小题满分13分）解：（Ⅰ）234cos4sin4sin 3)4(2-+=ππππf 21=． ……………4分（Ⅱ）2)2cos 1(3)(x x f -=+232sin 21-x x x 2cos 232sin 21-= )32sin(π-=x ． ……………6分20π<<x ， 32323πππ<-<-∴x ． ∴当232x ππ-=时，即125π=x 时，)(x f 的最大值为1． …………8分（Ⅲ） )32sin()(π-=x x f ，若x 是三角形的内角，则π<<x 0，∴35323π<π-<π-x ．令21)(=x f ，得21)32sin(=π-x ，∴632π=π-x 或6532π=π-x ，解得4π=x 或127π=x ． ……………10分由已知，B A ,是△ABC 的内角，B A <且21)()(==B f A f ，∴4π=A ，127π=B ，∴6π=--π=B A C ． ……………11分题号 9 10 1112 13 14答案 45- 2，3 2215x y +=，25519-13 1，12k -又由正弦定理，得221226sin 4sinsin sin ==ππ==C A AB BC ． ……………13分16．（本小题满分13分）解：（Ⅰ）从表中可以看出，“创新性为4分且实用性为3分”的作品数量为6件，∴“创新性为4分且实用性为3分”的概率为60.1250=． …………4分（Ⅱ）由表可知“实用性”得分y 有1分、2分、3分、4分、5分五个等级，且每个等级分别有5件，4b +件，15件，15件，8a +件． …………5分 ∴“实用性”得分y 的分布列为：y1 2 3 4 5p550 450b + 1550 1550 850a + 又∵“实用性”得分的数学期望为16750，∴541515816712345505050505050b a ++⨯+⨯+⨯+⨯+⨯=． ……………10分 ∵作品数量共有50件，∴3a b +=解得1a =，2b =． ……………………13分17．（本小题满分14分）解：（Ⅰ）∵四棱柱''''D C B A ABCD -为直四棱柱，∴ AC BD ⊥，A A BD '⊥，A A A AC =' ，∴ A ACE '⊥面BD . ∵ A ACE '⊂'面E A ， ∴ E A BD '⊥.∵ 51222=+='B A ，21122=+=BE ，3111222=++='E A ，∴ 222E A BE B A '+='. ∴ BE E A ⊥'.又∵ B BE BD = ，∴ BDE 面⊥'E A . ……………………4分（Ⅱ）以D 为原点，DA 为x 轴，DC 为y 轴，D D '为z 轴，建立空间直角坐标系.∴ )2,0,1(A '，)1,1,0(E ，)0,0,21(F ，)21,1,1(G . ∵ 由（Ⅰ）知：)11,1(--='E A 为面BDE 的法向量，)21,1,21(=FG ， ……………………6分 ∵ 021)1(11211=⨯-+⨯+⨯-='⋅E A FG .∴ E A FG '⊥. 又∵FG ⊄面BDE ，∴ FG ∥面BDE . ……………………8分（Ⅲ）设平面DEG 的法向量为),,(z y x n =，则 )1,1,0(=DE ，)21,1,1(=DG .∵ 0110=⨯+⨯+⨯=⋅z y x DE n ,即0=+z y . 02111=⨯+⨯+⨯=⋅z y x DG n ,即02=++zy x .令1=x ，解得：2-=y ，2=z ，∴ )2,2,1(-=n . ……………………12分 ∴ 935332)1()2(11)1(,cos -=⋅⨯-+-⨯+⨯-='⋅'>='<EA n E A n E A n . ∴ 二面角B DE G --的余弦值为935. ……………………14分 18．（本小题满分13分）解: （Ⅰ）设椭圆的长半轴为a ，短半轴长为b ，半焦距为c ，则22222,223,,c b a b c =⎧⎪=⎨⎪=+⎩解得 2,3,a b =⎧⎪⎨=⎪⎩ ∴ 椭圆C 的标准方程为 22143x y +=． ………………… 4分（Ⅱ）由方程组22143x y y kx m⎧⎪+=⎨⎪=+⎩ 消去y ，得()2223484120k x kmx m +++-=． ………………… 6分由题意△()()()22284344120km km=-+->，整理得：22340k m +-> ① ………………7分设()()1122,,M x y N x y 、，则122834kmx x k +=-+， 212241234m x x k -=+ ． ………………… 8分由已知，AM AN ⊥，且椭圆的右顶点为A (2,0)，∴()()1212220x x y y --+=．………………… 10分即 ()()()2212121240k x x km x x m ++-+++=，也即 ()()22222412812403434m kmk km m k k--+⋅+-⋅++=++，整理得2271640m mk k ++=．解得2m k =- 或 27km =-，均满足① ……………………… 11分当2m k =-时，直线l 的方程为 2y kx k =-，过定点(2,0)，不符合题意舍去；当27k m =-时，直线l 的方程为 27y k x ⎛⎫=- ⎪⎝⎭，过定点2(,0)7，故直线l 过定点，且定点的坐标为2(,0)7． ……………………… 13分19．（本小题满分13分）解：（Ⅰ） ∵4=a ， ∴x x x f 4ln )(+=且ee f 5)(=． ……………………… 1分又∵22ln 3)4(ln )4(ln )(x x x x x x x x f --='+-'+='， ∴223ln 4()e f e e e--'==-． ……………………… 3分 ∴)(x f 在点))(,(e f e 处的切线方程为：)(452e x ee y --=-，即0942=-+e y e x ． ……………………… 4分（Ⅱ）)(x f 的定义域为),0(+∞，2)(ln 1)(xa x x f +-='，……………………… 5分令0)(='x f 得ae x -=1．当),0(1ae x -∈时，0)(>'xf ，)(x f 是增函数；当),(1+∞∈-aex 时，0)(<'x f ，)(x f 是减函数； …………………… 7分∴)(x f 在ae x -=1处取得极大值，即11)()(--==a ae ef x f 极大值．……… 8分（Ⅲ）（i ）当21e ea<-，即1->a 时，由（Ⅱ）知)(x f 在),0(1ae -上是增函数，在],(21e e a -上是减函数，∴当aex -=1时，)(x f 取得最大值，即1max )(-=a e x f ．yxOA 0 P 1P 2 P 3A 1 A 2A 3 又当ae x -=时，0)(=xf ，当],0(aex -∈时，0)(<x f ，当],(2e ex a-∈时，],0()(1-∈a e x f ，所以，)(x f 的图像与1)(=x g 的图像在],0(2e 上有公共点，等价于11≥-a e，解得1≥a ，又因为1->a ，所以1≥a ． ……………… 11分（ii ）当21e ea≥-，即1-≤a 时，)(x f 在],0(2e 上是增函数，∴)(x f 在],0(2e 上的最大值为222)(e ae f +=， ∴原问题等价于122≥+ea ，解得22-≥e a ，又∵1-≤a ∴无解综上，a 的取值范围是1≥a ． ……………… 13分20．（本小题满分14分）解：（Ⅰ）1232,6,12a a a ===. …………………………… 3分（Ⅱ）依题意11(,0),(,0)n n n n A a A a --，则12n n n a a x -+=，132n nna a y -+⎛⎫= ⎪⎝⎭在正三角形1n n n P A A -中，有1133||)n n n n n y A A a a --==- .1133)2n n n n a a a a --+⎛⎫=- ⎪⎝⎭. ………………………… 5分 112()n n n n a a a a --∴-=+2211122()(2,*)n n n n n n a a a a a a n n N ---∴-+=+≥∈ ①，同理可得2211122()(*)n n n n n n a a a a a a n N +++-+=+∈ ②.②-①并变形得1111()(22)0(2,*)n n n n n a a a a a n n N +-+--+--=≥∈ 11n n a a +->，11220n n n a a a +-∴+--=11()()2(2,*)n n n n a a a a n n N +-∴---=≥∈ .∴数列{}1n n a a +-是以214a a -=为首项，公差为2的等差数列.12(1),(*)n n a a n n N +∴-=+∈ ，n a ∴12132431()()()()n n a a a a a a a a a -=+-+-+-++-，2(123)n =++++2n n =+.(1)(*)n a n n n N ∴=+∈ …………… 8分（Ⅲ）∵12321111(*)n n n n n b n N a a a a +++=++++∈， ∴1234221111(*)n n n n n b n N a a a a +++++=++++∈.121221111n n n n n b b a a a ++++∴-=+-111(21)(22)(22)(23)(1)(2)n n n n n n =+-++++++22(221)(21)(22)(23)(2)n n n n n n -+-=++++. ∴当*n N ∈时，上式恒为负值，∴当*n N ∈时，1n n b b +<，∴数列{}n b 是递减数列. n b ∴的最大值为12116b a ==. ……………… 12分若对任意正整数n ，当[]1,1m ∈-时，不等式2126n t mt b -+>恒成立，则不等式211266t mt -+>在[]1,1m ∈-时恒成立，即不等式220t mt ->在[]1,1m ∈-时恒成立. 设2()2f m t mt =-，则(1)0f >且(1)0f ->，∴222020t t t t ⎧->⎪⎨+>⎪⎩ 解之，得 2t <-或2t >，即t 的取值范围是(,2)(2,)-∞-⋃+∞. …………………… 14分（完）。

北京市石景山区2013届高三上学期期末考试理科数学试题

北京市石景山区2013届高三上学期期末考试理科数学试题石景山区2012—2013学年第一学期期末考试试卷高三数学（理）本试卷共6页，150分.考试时长120分钟．请务必将答案答在答题卡上，在试卷上作答无效．考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合{}4,3,2,1=U ，{}2,1=A ,{}4,2=B ,则=⋃B A C U）（（）A ． {}2,1B ． {}4,32，C ． {}4,3D ．{}4,3,2,12. 若复数iZ=1,iZ -=32,则=12ZZ（） A ． 13i -- B ．i +2C ．13i +D ．i +33．AC 为平行四边形ABCD 的一条对角线，(2,4),(1,3),AB AC AD 则===u u u r u u u r u u u r （）A ．(2,4)B ．(3,7)C ．(1,1)D ．(1,1)--4. 设,m n 是不同的直线，,αβ是不同的平面，下列命题中正确的是（）A ．若//,,m n m n αβ⊥⊥，则αβ⊥B ．若//,,m n m n αβ⊥⊥，则//αβC ．若//,,//m n m n αβ⊥，则α⊥βD ．若//,,//m n m n αβ⊥，则//αβ5．执行右面的框图，若输出结果为3，则可输入的实数x 值的个数为（） A ．1 B ．2C ．3D ．46．若从1,2,3,…,9这9个整数中同时取4个不同的数，其和为奇数，则不同的取法共有（） A ．60种 B ．63种 C ．65种 D ．66种7．某三棱锥的三视图如图所示，该三棱锥的体积是（）A ．38B ．4C ．2D ．34正（主）视图侧（左）视图俯视图2 23 2 3 1 开输出输否是结>2x 2=-1y x 2=log y x8. 在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[]k ，即[]{}5k n k n =+∈Z ，0,1,2,3,4k =．给出如下四个结论： ① []20133∈；② []22-∈；③[][][][][]01234Z =∪∪∪∪；④ 整数,a b 属于同一“类”的充要条件是“[]0a b -∈”．其中，正确结论的个数为（）． A ．1 B ．2C ．3D ．4第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分． 9．已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩，，表示的平面区域S 的面积为4，则=a ；若点Sy x P ∈),(，则yx z +=2 的最大值为 .10．如右图，从圆O 外一点P 引圆O 的割线PAB 和P A BC O •DPCD ，PCD过圆心O ，已知1,2,3PA AB PO ===，则圆O 的半径等于． 11．在等比数列{}na 中，141=,=42a a -，则公比=q ；123++++=n a a a a L ．12．在ABC ∆中，若2,60,7a Bb =∠=︒=BC 边上的高等于．13．已知定点A 的坐标为(1,4)，点F 是双曲线221412x y -=的左焦点，点P 是双曲线右支上的动点，则PF PA+的最小值为．14. 给出定义：若11< +22m x m -≤ (其中m 为整数)，则m 叫做离实数x 最近的整数，记作{}x ，即{}=x m. 在此基础上给出下列关于函数()={}f x x x -的四个命题：①=()y f x 的定义域是R ，值域是11(,]22-； ②点(,0)k 是=()y f x 的图像的对称中心，其中k Z∈；③函数=()y f x 的最小正周期为1；④ 函数=()y f x 在13(,]22-上是增函数．则上述命题中真命题的序号是．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）已知函数sin 2(sin cos )()cos x x x f x x +=．（Ⅰ）求)(x f 的定义域及最小正周期；（Ⅱ）求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ，上的最大值和最小值．16．（本小题共14分）如图1，在Rt ABC ∆中，90C ∠=︒，36BC AC ==，．D 、E 分别是AC AB 、上的点，且//DE BC ，将ADE ∆沿DE 折起到1A DE ∆的位置，使1A D CD ⊥，如图2．（Ⅰ）求证：BC ⊥平面1A DC ；（Ⅱ）若2CD =，求BE 与平面1A BC 所成角的正弦值；（Ⅲ）当D 点在何处时，1A B 的长度最小，并求出最小值．17．（本小题共13分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为1123p 、、，且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. （Ⅰ）求甲乙二人中至少有一人破译出密码的概率；（Ⅱ）求p 的值；（Ⅲ）设甲、乙、丙三人中破译出密码的人数为X，求X 的分布列和数学期望EX .18．（本小题共13分）ABC D E图图ABC D E已知函数()=ln+1,f x x ax a R-∈是常数．（Ⅰ）求函数=()y f x的图象在点(1,(1))P f处的切线l的方程；（Ⅱ）证明函数=()(1)y f x x≠的图象在直线l的下方；（Ⅲ）讨论函数=()y f x零点的个数．19．（本小题共14分）已知椭圆的中心在原点，焦点在x轴上，离心率为32，且经过点(4,1)M，直线:=+l y x m交椭圆于不同的两点A B、．（Ⅰ）求椭圆的方程；（Ⅱ）求m的取值范围；（Ⅲ）若直线l不过点M，求证：直线MA MB、的斜率互为相反数．20．（本小题共13分）定义：如果数列{}na的任意连续三项均能构成一个三角形的三边长，则称{}na为“三角形”数列．对于“三角形”数列{}na ，如果函数()y f x =使得()nn bf a =仍为一个“三角形”数列，则称()y f x =是数列{}na 的“保三角形函数”(*)n N ∈．（Ⅰ）已知{}na 是首项为2，公差为1的等差数列，若()(1)xf x kk =>是数列{}na 的“保三角形函数”，求k 的取值范围；（Ⅱ）已知数列{}nc 的首项为2013，nS 是数列{}nc 的前n 项和，且满足+1438052n n S S -=，证明{}nc 是“三角形”数列；（Ⅲ）若()lg g x x =是（Ⅱ）中数列{}nc 的“保三角形函数”，问数列{}nc 最多有多少项?(解题中可用以下数据 :lg20.301,lg30.477,lg2013 3.304≈≈≈)石景山区2012—2013学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案 B A D C C A B C二、填空题共6小题，每小题5分，共30分．(9题、11题第一空2分,第二空3分) 三、解答题共6小题，共80分． 15．（本小题共13分）（Ⅰ）因为cos 0x ≠，所以+,2x k k Z ππ≠∈. 所以函数)(x f 的定义域为{+,}2x x k k Z ππ≠∈｜ ……………2分题号 9 101112 13 14 答案2；6611222n ；---3329①③sin 2sin cos ()cos x x x f x x +=（）()2sin sin +cos =2sin +sin2x x x x x =２2-)14x π=+……………5分π=T……………7分（Ⅱ）因为46ππ≤≤-x ，所以7-2-1244x πππ≤≤ ……………9分当2-44x ππ=时，即4x π=时，)(x f 的最大值为2； ……………11分当2--42x ππ=时，即8x π=-时，)(x f 的最小值为-2+1. ………13分 16．（本小题共14分）（Ⅰ）证明：在△ABC 中，90,//,C DE BC AD DE ∠=︒∴⊥1A D DE∴⊥.又11,,A D CD CD DE D A D BCDE ⊥⋂=∴⊥面.由1,.BC BCDE A D BC ⊂∴⊥面1,,BC CD CD BC C BC A DC⊥⋂=∴⊥面. …………………………4分（Ⅱ）如图,以C 为原点，建立空间直角坐标系． ……………………5分1(2,0,0),(2,2,0),(0,3,0),(2,0,4)D E B A ．AC D Ex z设(,,)x y z =n 为平面1A BC 的一个法向量，因为(0,3,0),CB =u u u r1(2,0,4)CA =u u u r所以30240y x z =⎧⎨+=⎩，令2x =，得=0,=1y z -. 所以(2,0,1)=-n 为平面1A BC的一个法向量． ……………………7分设BE 与平面1A BC 所成角为θ．则4sin =cos 555BE θ<⋅>==⋅u u u rn ．所以BE与平面1A BC所成角的正弦值为45． …………………9分（Ⅲ）设(,0,0)D x ,则1(,0,6)A x x -，2221(-0)(0-3)(6--0)A B x x =++22-1245x x =+…………………12分当=3x 时,1A B 的最小值是33即D 为AC 中点时, 1A B 的长度最小,最小值为33…………………14分 17．（本小题共13分）记“甲、乙、丙三人各自破译出密码”分别为事件321,,A A A ，依题意有12311(),(),(),23P A P A P A p ===且321,,A A A 相互独立.（Ⅰ）甲、乙二人中至少有一人破译出密码的概率为121()P A A -⋅1221233=-⨯=.…………………3分（Ⅱ）设“三人中只有甲破译出密码”为事件B ，则有()P B =123()P A A A ⋅⋅＝121(1)233p p -⨯⨯-=， …………………5分所以1134p -=，14p =. ……………………7分（Ⅲ）X的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==， (1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=，(2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=，(3)P X ==P123()A A A ⋅⋅＝111123424⨯⨯= . ……………………11分X分布列为：X 0 1 2 3 P14112414124…………………12分所以，1111113()012342442412E X =⨯+⨯+⨯+⨯=. (13)分1．（本小题共13分）（Ⅰ）1()=f x ax'-…………………1分(1)=+1f a -，=(1)=1lk f a '-，所以切线 l 的方程为(1)=(1)l y f k x --，即=(1)y a x-． …………………3分（Ⅱ）令()=()(1-)=ln +1>0F x f x a x x x x --，，则11()=1=(1)()=0=1.F x x F x x x x''--，解得 x)1 , 0(1) , 1(∞+()F x ' +-)(x F↗最大值↘………………6分(1)<0F ，所以>0x ∀且1x ≠，()<0F x ，()<(1)f x a x -，即函数=()(1)y f x x ≠的图像在直线 l 的下方． …………………8分（Ⅲ）令()=ln +1=0f x x ax -，ln +1=x a x. 令ln +1()=x g x x ，22ln +11(ln +1)ln ()=()==x x xg x x x x-''-，则()g x 在(0,1)上单调递增，在(1,+)∞上单调递减，当=1x 时，()g x 的最大值为(1)=1g .所以若>1a ，则()f x 无零点；若()f x 有零点，则1a ≤．………………10分若=1a ，()=ln +1=0f x x ax -，由（Ⅰ）知()f x 有且仅有一个零点=1x .若0a ≤，()=ln +1f x x ax -单调递增，由幂函数与对数函数单调性比较，知()f x 有且仅有一个零点（或：直线=1y ax -与曲线=ln y x 有一个交点）.若0<<1a ，解1()==0f x a x '-得1=x a，由函数的单调性得知()f x 在1=x a 处取最大值，11()=ln >0f a a，由幂函数与对数函数单调性比较知，当x 充分大时()<0f x ，即()f x 在单调递减区间1(,+)a ∞有且仅有一个零点；又因为1()=<0a f e e -，所以()f x 在单调递增区间1(0)a，有且仅有一个零点.综上所述，当>1a 时，()f x 无零点；当=1a 或0a ≤时，()f x 有且仅有一个零点；当0<<1a 时，()f x 有两个零点. …………………13分 19．（本小题共14分）（Ⅰ）设椭圆的方程为22221x y a b+=，因为32e =，所以224a b =，又因为(4,1)M ，所以221611a b+=，解得225,20ba ==，故椭圆方程为221205x y +=． …………………4分（Ⅱ）将y x m =+代入221205x y +=并整理得22584200x mx m ++-=，22=(8)-20(4-20)>0m m ∆，解得55m -<<． …………………7分（Ⅲ）设直线,MA MB 的斜率分别为1k 和2k ，只要证明12k k+=．设11(,)A x y ，22(,)B x y ，则212128420,55m m x x x x -+=-=． …………………9分12122112121211(1)(4)(1)(4)44(4)(4)y y y x y x k k x x x x ----+--+=+=----122112122(1)(4)(1)(4)2(5)()8(1)2(420)8(5)8(1)055x m x x m x x x m x x m m m m m =+--++--=+-+----=---=分子所以直线MA MB 、的斜率互为相反数． …………………14分20．（本小题共13分）（Ⅰ）显然121,nn n n an a a a ++=++>对任意正整数都成立，即{}na 是三角形数列。

北京市石景山区高三上学期期末考试数学(理)试题

石景山区2014—2015学年第一学期期末考试试卷高三数学（理）本试卷共6页，150分.考试时长120分钟．请务必将答案答在答题卡上，在试卷上作答无效．考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合，，则( )A. B. C. D.2．下列函数中，在上单调递减的是（）A. B. C. D.3．点与圆的位置关系是（）A.点在圆内B.点在圆外C.点在圆上D.与的值有关4. 某程序框图如右图所示，该程序运行输出的值是（）A.4B.5C.6D.75．以为公比的等比数列中，，则“”是“”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6．如果实数满足不等式组30,230,1.x yx yx+-≤⎧⎪--≤⎨⎪≥⎩目标函数的最大值为6，最小值为0，则实数的值为（）A.1B.2C.3D.47．如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（）A. B.C. D.8. 函数的定义域为，图象如图1所示；函数的定义域为，图象如图2所示，方程有个实数根，方程有个实数根，则( )A.6B. 8C. 10D. 12第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分． 9．若复数, ,则．10.为等差数列，，公差，、、成等比数列，则．11．如图，在边长为2的菱形中，为中点，则．12.若抛物线的焦点与双曲线的焦点重合，则的值为． 13. A , B 两地街道如图所示，某人要从A 地前往B 地，则路程最短的走法有种（用数字作答）．14. 设为非空实数集，若，都有，则称为封闭集．①集合{}2,1,0,1,2--=A 为封闭集； ②集合{}Z k k n n A ∈==,2|为封闭集； ③若集合为封闭集，则为封闭集；④若为封闭集，则一定有.其中正确结论的序号是____________.三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）如图所示，在四边形中，，，；为边上一点，，，. （Ⅰ）求sin ∠CED 的值；（Ⅱ）求BE 的长．16．（本小题共13分）某次数学考试共有8道选择题，每道选择题有4个选项，其中有且只有一个选项是正确的.某考生有4道题已选对正确答案，还有两道题能准确排除每题中的2个错误选项，其余两道题完全不会只好随机猜答.（Ⅰ）求该考生8道题全答对的概率；（Ⅱ）若评分标准规定：“每题只选一个选项，选对得5分，不选或选错得0分”，求该考生所得分数的分布列.17．（本小题共14分）如图,在四面体中,平面,22,2,==⊥BD AD CD BC .是的中点,是的中点. （Ⅰ）求证：平面平面；（Ⅱ）若点在线段上，且满足,求证：平面；（Ⅲ）若,求二面角的大小.18.（本小题共13分）已知函数)0(ln )(22≠∈-+=a R a x a ax x x f 且. （Ⅰ）若是函数的极值点，求的值；（Ⅱ）求函数的单调区间.19.（本小题共14分）已知椭圆)0(12222>>=+b a by a x 的离心率为，且过点.（Ⅰ）求椭圆的标准方程；D A CB E（Ⅱ）直线交椭圆于P 、Q 两点，若点B 始终在以PQ 为直径的圆内，求实数的取值范围.20．（本小题共13分）对于数集}1{21n x x x X ，，，， -=，其中，，定义向量集},),,(|{X t X s t s a a Y ∈∈==，若对任意，存在，使得，则称具有性质．（Ⅰ）判断是否具有性质；（Ⅱ）若，且具有性质，求的值；（Ⅲ）若具有性质，求证：，且当时，．石景山区2014—2015学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．二、填空题共6小题，每小题5分，共30分．【12题只答一种情况得3分】三、解答题共6小题，共80分． 15．（本小题共13分）（Ⅰ）设.在中，由余弦定理，得2222cos CE CDDE CD DE CDE =+-⨯⨯∠ …………………2分得CD 2＋CD －6＝0，解得CD ＝2(CD ＝－3舍去)． …………………4分在中，由正弦定理，得 …………………6分（Ⅱ）由题设知，所以 …………………8分而，所以222cos cos =cos cos sin sin 333AEB πππααα∠=-+（） 11=cos 227αα-+=-+=………………11分在中，2cos BE AEB==∠…………………13分16．（本小题共13分）（Ⅰ）该考生8道题全答对为事件，依题意有 11111()224464P A =⨯⨯⨯=. …………………3分（Ⅱ）该考生所得分数为，则的所有可能取值为. ……4分， ……6分1212221131333(25)C ()(1)()C ()(1)()2242448P X ==⨯-⨯+⨯-⨯=， ……8分 221122221311311111(30)+C ()(1)C ()()()=2422442432P X ==⨯⨯-⨯⨯⨯+⨯（）（）（）……10分1212221111331(35)C ()(1)()C ()(1)()=2242448P X ==⨯-⨯+⨯-⨯……12分分布列为：……………………13分17．（本小题共14分）（Ⅰ）, ………………2分且………………4分（Ⅱ）证明：如图所示,取BD 中点O ，且P 是BM 中点，所以且；取CD 的四等分点H ，使DH =3CH ，且AQ =3QC , 所以,且，所以，四边形为平行四边形，所以，且,所以PQ //面BDC . ……………………9分 (III)如图建系,则, , , ……………………10分设面的法向量 ,ABCDPQMOH⎪⎩⎪⎨⎧=⋅=⋅00CM n ,即⎪⎩⎪⎨⎧=+=0206z x y 令,则设面的法向量 ……………………11分⎪⎩⎪⎨⎧=⋅=⋅00BD m 即⎩⎨⎧==-0062z y x 令, 则 ……………………12分所以二面角的大小为 …………………14分（Ⅰ）函数的定义域为. ………………1分21'()2f x a a x x=+-. ………………3分因为是函数的极值点，所以2'(1)120f a a =+-=.…………5分解得或.经检验，或时，是函数的极值点. ……………6分（Ⅱ）由（Ⅰ）知：21'()2f x a a x x=+-. 由，令(21)(1)'()0ax ax f x x+-+==，解得.……9分当时，的变化情况如下表∴函数的单调递增区间是，单调递减区间是；…………11分当时，的变化情况如下表∴函数的单调递增区间是，单调递减区间是.…13分（Ⅰ）由题意知⎪⎪⎩⎪⎪⎨⎧+====222231c b a a c e b ，解得⎪⎩⎪⎨⎧===312c b a ，椭圆的标准方程为：. ………………4分（Ⅱ）设联立⎪⎩⎪⎨⎧=++=14)2(22y x x k y ，消去，得：).(0)416(16)41(2222*=-+++k x k x k ……6分依题意：直线恒过点，此点为椭圆的左顶点，所以， ----① ，由（*）式， -------②，可得k x x k x k x k y y 4)()2()2(212121++=+++=+---- ③ ， ………………8分由①②③，， ………………10分由点B 在以PQ 为直径的圆内，得为钝角或平角，即.），（），，（11222-=--=y x BQ BP 01222<+--=⋅y x . …12分即0141441164222>-+++-k k k k ，整理得. 解得：. ………………14分20．（本小题共13分）（Ⅰ）具有性质. ……2分（Ⅱ）选取，Y中与垂直的元素必有形式.所以，从而……5分（III）证明：取.设满足.由得，所以、异号.因为是X中唯一的负数，所以、中之一为，另一为，故.……8分假设，其中，则.选取，并设满足，即，则,异号，从而,之中恰有一个为. ……10分若，则，显然矛盾；若，则，矛盾.所以.……13分【注：若有其它解法，请酌情给分．】。

石景山区2013—2014学年第一学期期末高三数学理科

石景山区2013—2014学年第一学期期末考试试卷高三数学（理科）本试卷共6页，满分为150分，考试时间为120分钟.请务必将答案答在答题卡上，在试卷上作答无效，考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项． 1．已知集合{}2230M x x x =∈+-≤R ，{}10N x x =∈+<R ，那么M N = （）A ．{101}-，，B ．{321}---，，C ．{11}x x -≤≤D ．{31}x x -≤<-2．复数1ii =-（） A ．122i + B ．122i -C ．122i-+ D ．122i -- 3．已知向量(1)x =，a ，(4)x =，b ，则“2x =”是“a ∥b ”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知数列}{n a 为等差数列，4724a a ==-，，那么数列}{n a 通项公式为（） A ．210n a n =-+ B ．25n a n =-+ C ．1102n a n =-+ D ．152n a n =-+5．执行如图所示的程序框图，若输入的x 的值为2，则输出的x 的值为（）A ．3B ．126C ．127D ．1286．在边长为1的正方形OABC 中任取一点P ，则点P 恰好落在正方形与曲线y x =围成的区域内(阴影部分)的概率为（）A ．12B ．23 C ．34D ．45是输入x21x x =-126x ≥输出x 开始结束否OCxyy x =AB7．用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为（）A ．324B ．328C ．360D ．6488．已知函数()f x 满足1()1(1)f x f x +=+，当[01]x ∈，时，()f x x =，若在区间(11]-，上方程()0f x mx m --=有两个不同的实根，则实数m 的取值范围是（）A ．1[0)2，B ．1[)2+∞，C ．1[0)3，D ．1(0]2，第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．已知圆C 的参数方程为12cos 2sin x y θθ+⎧⎨=⎩，，=(θ为参数)，则圆C 的直角坐标方程为_______________，圆心C 到直线:10l x y ++=的距离为______．10．在ABC ∆中，角A B C ，，的对边分别为a b c ，，，若=6a ，4c =，1cos =3B ，则b =______． 11．若x ，y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩，，，则z x y =+的最大值为．12．如图，已知在ABC ∆中，o 90B ∠=，O 是AB 上一点，以O 为圆心，OB 为半径的圆与AB 交于点E ，与AC 切于点D ，2AD =，1AE =，则AB 的长为，CD 的长为．13．已知抛物线24y x =的焦点为F ，准线为直线l ，过抛物线上一点P 作PE l ⊥于E ，若直线EF 的倾斜角为o150，则||PF =______．14．已知四边形ABCD 是边长为1的正方形，且1A A ⊥平面ABCD ，P 为1A A 上动点，过BD 且垂直于PC 的平面交PC 于E ，那么异面直线PC 与BD 所成的角的度数为，当三棱锥E BCD -的体积取得最大值时，四棱锥P ABCD -的高PA 的长为．A DCBE．OA 1ABDCPE三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）已知函数()23sin cos cos 21f x x x x =++()x ∈R ．（Ⅰ）求函数)(x f 的单调递增区间；（Ⅱ）求函数()f x 在44ππ⎡⎤-⎢⎥⎣⎦，上的最小值，并写出()f x 取最小值时相应的x 值．16．（本小题满分13分）北京市各级各类中小学每年都要进行“学生体质健康测试”，测试总成绩满分为100分，规定测试成绩在[85100]，之间为体质优秀；在[7585)，之间为体质良好；在[6075)，之间为体质合格；在[060)，之间为体质不合格．现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩，其茎叶图如下：9 1 3 5 68 0 1 1 2 2 3 3 3 4 4 5 6 6 7 7 9 7 0 5 6 6 7 9 6 4 5 8 5 6（Ⅰ）试估计该校高三年级体质为优秀的学生人数；（Ⅱ）根据以上30名学生体质健康测试成绩，现采用分层抽样的方法，从体质为优秀和良好的学生中抽取5名学生，再从这5名学生中选出3人．（ⅰ）求在选出的3名学生中至少有1名体质为优秀的概率；（ⅱ）记X 为在选出的3名学生中体质为良好的人数，求X 的分布列及数学期望．17.（本小题满分14分）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是直角梯形，o 90ABC ∠=，AD ∥BC ，且2PA AD ==，1AB BC ==，E 为PD 的中点．（Ⅰ）求证：CD ⊥平面PAC ；（Ⅱ）求二面角E AC D --的余弦值；（Ⅲ）在线段AB 上是否存在一点F （不与A B ，两点重合），使得AE ∥平面PCF ?若存在，求出AF 的长；若不存在，请说明理由．A PEBDC18．（本小题满分13分）已知函数()xf x e ax =-（e 为自然对数的底数）.（Ⅰ）当2a =时，求曲线()f x 在点(0(0))f ，处的切线方程；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）已知函数()f x 在0x =处取得极小值，不等式()f x mx <的解集为P ，若1{|2}2M x x =≤≤，且M P ≠∅ ，求实数m 的取值范围.19．（本小题满分14分）已知椭圆C ：22221x y a b +=（0a b >>）过点(20)，，且椭圆C 的离心率为12.（Ⅰ）求椭圆C 的方程；（Ⅱ）若动点P 在直线1x =-上，过P 作直线交椭圆C 于M N ，两点，且MP PN =，再过P 作直线l MN ⊥.证明：直线l 恒过定点，并求出该定点的坐标.20．（本小题满分13分）已知集合{101}A =-，，，对于数列{}n a 中(123)i a A i n ∈= ，，，，. （Ⅰ）若50项数列{}n a 满足5019ii a==-∑，5021(1)107i i a =-=∑，则数列{}n a 中有多少项取值为零？(121nin i aa a a n *==+++∈∑N ，)（Ⅱ）若各项非零数列{}n a 和新数列{}n b 满足11i i i b b a ---=（23i n = ，，，）．（ⅰ）若首项10b =，末项1n b n =-，求证数列{}n b 是等差数列；（ⅱ）若首项10b =，末项0n b =，记数列{}n b 的前n 项和为n S ，求n S 的最大值和最小值．石景山区2013—2014学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案DCAA CBBD二、填空题共6小题，每小题5分，共30分．(两空的题目第一空2分，第二空3分) 三、解答题共6小题，共80分． 15．（本小题共13分）解：（Ⅰ）()f x 3sin 2cos 2+1x x =+ …………2分 2sin 2+16x π=+（）， ……………4分222262k x k πππππ-≤+≤+，k ∈Z ， 36k x k ππππ-≤≤+，k ∈Z ，……6分所以函数)(x f 的单调递增区间为[]36k k ππππ-+，()k ∈Z ． ……………7分（Ⅱ）因为44x ππ-≤≤，22363x πππ-≤+≤， ……………9分3sin(2)126x π-≤+≤，312sin 2+136x π-+≤+≤（）， ……11分所以当2=63x ππ+-，即=4x π-时，函数)(x f 取得最小值31-+．…………13分16．（本小题共13分）解：（Ⅰ）根据抽样，估计该校高三学生中体质为优秀的学生人数有10300=10030⨯人．…………3分（Ⅱ）依题意，体质为良好和优秀的学生人数之比为 15:103:2=．所以，从体质为良好的学生中抽取的人数为3535⨯=，从体质为优秀的学生中抽取的人数为2525⨯=．…6分（ⅰ）设“在选出的3名学生中至少有1名体质为优秀”为事件A ，则 3335C 9()1C 10P A =-=．故在选出的3名学生中至少有1名体质为优秀的概率为910．…9分（ⅱ）解：随机变量X 的所有取值为123，，．123235C C 3(1)C 10P X ⋅===，213235C C 6(2)C 10P X ⋅===，3335C 1(3)C 10P X ===．…………12分题号 9 1011 12 13 14答案 22(1)4x y -+=，2 64 4，34390 ，2所以，随机变量X 的分布列为:X 123 P31061011036191231010105EX =⨯+⨯+⨯=． ……………13分 17．（本小题共14分）（Ⅰ）证明：因为PA ⊥平面ABCD ，CD ⊂平面ABCD ，所以PA CD ⊥. ……………1分取AD 的中点G ，连结GC ，因为底面ABCD 为直角梯形，AD ∥BC ，o90ABC ∠=，且1AB BC ==，所以四边形ABCG 为正方形，所以CG AD ⊥，且1=2CG AD ，所以o=90ACD ∠，即AC CD ⊥. ……………3分又PA AC A = ，所以CD ⊥平面PAC . ……………4分（Ⅱ）解：如图，以A 为坐标原点，AB AD AP ，，所在直线分别为x y z ，，轴建立空间直角坐标系xyz A -．…5分则(000)A ，，，(110)C ，，，(011)E ，，，(002)P ，，，所以(002)AP = ，，，(110)AC = ，，，(011)AE =，，．因为PA ⊥平面ABCD ，所以(002)AP =，，为平面ACD 的一个法向量． ………6分设平面EAC 的法向量为1()n x y z = ，，，由10n AC ⋅= ，10n AE ⋅= 得00x y y z +=⎧⎨+=⎩，，令1x =，则1y =-，1z =，所以1(111)n =-，，是平面EAC 的一个法向量． ……………8分所以12221(1)0123cos 31(1)12n AP ⨯+-⨯+⨯<>==+-+⋅ 0，因为二面角E AC D --为锐角，A PEBDCG DA PBCzyxE所以二面角E AC D --的余弦值为33． ……………9分（Ⅲ）解：假设在线段AB 上存在点F （不与A B ，两点重合），使得AE ∥平面PCF ．设(00)F a ，，，则(110)CF a =-- ，，，(112)CP =--，，．设平面PCF 的法向量为2()n x y z =，，，由20n CF ⋅= ，20n CP ⋅= 得(1)020a x y x y z --=⎧⎨--+=⎩，，令1x =，则1y a =-，2az =，所以2(11)2a n a =- ，，是平面PCF 的一个法向量．………12分因为AE ∥平面PCF ，所以20AE n ⋅= ，即(1)02aa -+=， ……………13分解得23a =，所以在线段AB 上存在一点F （不与A B ，两点重合），使得AE ∥平面PCF ，且2=3AF ． ……14分 18.（本小题共13分）解：（Ⅰ）当2a =时，()2x f x e x =-，(0)1f =， ()2xf x e '=-，得(0)1f '=-， ……2分所以曲线()f x 在点(0(0))f ，处的切线方程为1y x =-+. ……………3分（Ⅱ）()xf x e a '=-.当0a ≤时，()0f x '>恒成立，此时()f x 的单调递增区间为()-∞+∞，，无单调递减区间；………5分当0a >时，(ln )x a ∈-∞，时，()0f x '<，(ln )x a ∈+∞，时，()0f x '>，此时()f x 的单调递增区间为(ln )a +∞，，单调递减区间为(ln )a -∞，.………7分（Ⅲ）由题意知(0)0f '=得1a =，经检验此时()f x 在0x =处取得极小值. ………8分因为M P ≠∅ ，所以()f x mx <在1[2]2，上有解，即1[2]2x ∃∈，使()f x mx <成立，………9分即1[2]2x ∃∈，使x e x m x ->成立， …………10分所以min ()x e x m x ->. 令()1x e g x x =-，2(1)()xx e g x x -'=， DA PB C zyx EF所以()g x 在1[1]2，上单调递减，在[12]，上单调递增，则min ()(1)1g x g e ==-， ……………12分所以(1)m e ∈-∞，+. ……………13分 19．（本小题共14分）解：（Ⅰ）因为点(20)，在椭圆C 上，所以22401a b+=，所以24a =， …………1分因为椭圆C 的离心率为12，所以12c a =，即22214a b a -= ，…………2分解得23b =， ……………4分所以椭圆C 的方程为22143x y +=. ……………5分（Ⅱ）设0(1)P y -，，033()22y ∈-，， ①当直线MN 的斜率存在时，设直线MN 的方程为0(1)y y k x -=+，11()M x y ，，22()N x y ，，由2203412(1)x y y y k x ⎧+=⎨-=+⎩，，得22222000(34)(88)(48412)0k x ky k x y ky k ++++++-=， ………7分所以2012288+34ky k x x k +=-+， ……………8分因为MP PN = ，即P 为MN 中点，所以12=12x x +-，即20288=234ky k k +--+. 所以003(0)4MN k y y =≠， ……………9分因为直线l MN ⊥，所以043l y k =-，所以直线l 的方程为004(1)3yy y x -=-+，即041()34y y x =-+ ，显然直线l 恒过定点1(0)4-，. ………11分②当直线MN 的斜率不存在时，直线MN 的方程为1x =-，此时直线l 为x 轴，也过点1(0)4-，. ……………13分综上所述直线l 恒过定点1(0)4-，. ……………14分 20．（本小题共13分）解：（Ⅰ）设数列{}n a 中项为110-，，分别有x y z ，，项．由题意知5094107x y z x y z y ++=⎧⎪-=-⎨⎪+=⎩，，，解得11z =．所以数列{}n a 中有11项取值为零． ……………3分（Ⅱ）（ⅰ）{11}i a ∈-，且11i i i b b a ---=，得到121(23)i i b a a a i n -=+++= ，，，，若1(121)i a i n ==- ，，，，则满足1n b n =-．此时11i i b b --=，数列{}n b 是等差数列；若121n a a a - ，，，中有*(0)p p p >∈，N 个1-，则121n b n p n =--≠-不满足题意；所以数列{}n b 是等差数列． ……………7分（ⅱ）因为数列{}n b 满足11i i i b b a ---=，所以121(23)i i b a a a i n -=+++= ，，，，根据题意有末项0n b =，所以1210n a a a -+++= ．而{11}i a ∈-，，于是n 为正奇数，且121n a a a - ，，，中有12n -个1和12n -个1-． 12112121()()n n n S b b b a a a a a a -=+++=+++++++121(1)(2)n n a n a a -=-+-++要求n S 的最大值，则只需121n a a a - ，，，前12n -项取1，后12n -项取1-，所以2max(1)()(2)(4)14n n S n n -=-+-++=（n 为正奇数）．要求n S 的最小值，则只需121n a a a - ，，，前12n -项取1-，后12n -项取1，则2min(1)()(2)(4)14n n S n n -=------=-（n 为正奇数）． …………13分【注：若有其它解法，请酌情给分．】。

北京市石景山区高三上学期期末考试数学文试题 Word版含答案.pdf

石景山区2012—2013学年第一学期期末考试试卷高三数学（文）本试卷共6页，150分.考试时长120分钟.请务必将答案答在答题卡上，在试卷上作答无效.考试结束后上交答题卡. 第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．设集合，,,则（） A． B． C． D．2. 若复数, ,则（） A． B．C．D． 3．为平行四边形的一条对角线，（） A． B． C．D．4．下列函数中，既是偶函数，又是在区间上单调递减的函数是（） A．B．C．D． 5．设是不同的直线，是不同的平面，下列命题中正确的是 A．若，则若，则若，则⊥ 若，则 6．执行右面的框图，若输出结果为3，则可输入的实数值的个数为（） A．1B．2C．3D．4 7．某三棱锥的三视图如图所示，该三棱锥的体积是（） A．B．C．D． 8. 在整数集中，被除所得余数为的所有整数组成一个类，记为，即．给出如下四个结论： ①； ②　； ③　； ④　整数属于同一类的充要条件是”．其中，正确结论的个数为（）． A． B． C． D．第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分． 9. 不等式的解集为 10．直线被圆截得的弦长为． 11．已知不等式组表示的平面区域的面积为，；若点，则的最值为 12．在等比数列中，，则公比； 13．在中，若，则． 14. 给出定义：若为整数)，则叫做离实数最近的整数，记作，即. 在此基础上给出下列关于函数的四个命题 ①的定义域是，值域是；是的图像；函数最小正周期；函数在上是增函数则中真命题是三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）已知函数．（Ⅰ）求的定义域及最小正周期；（Ⅱ）求在区间上的最大值和最小值． 16．（本小题共14分）如图1，中，，D、E上的点，，沿折起到的位置，，2．（Ⅰ）求证：；：；当点在何处时，的长度最小，并求出最小值 17．（本小题共13分）一个盒子中装有张卡片，每张卡片上写有个数字，数字分别是?．现从盒子中随机抽取卡片．（Ⅰ）若一次抽取张卡片，求张卡片上数字之和大于的概率；（Ⅱ）若第一次抽张卡片，放回后再抽取张卡片，求两次抽取中至少一次抽到数字的概率． 18．（本小题共13分）已知函数是常数．（Ⅰ）求函数的图象在点处的切线的方程；（Ⅱ）证明函数的图象在直线的下方；（Ⅲ）若函数有零点，求实数的取值范围． 19．（本小题共14分）已知椭圆的中心在原点，焦点在轴上，离心率为，长轴长为，直线交椭圆于不同的两点．（Ⅰ）求椭圆的方程；（Ⅱ）求的取值范围；（Ⅲ）若直线不经过椭圆上的点，求证：直线的斜率互为相反数． 20．（本小题共13分）定义：如果数列的任意连续三项均能构成一个三角形的三边长，则称为“三角形”数列．对于“三角形数列使得仍为一个“三角形”数列，则称是数列的“保三角形函数”．（Ⅰ）已知是首项为，公差为的等差数列，若是数列的“保三角形函数”，求的取值范围；（Ⅱ）已知数列的首项为，是数列的前n项和，且满足，证明是“三角形”数列；（Ⅲ）若是（Ⅱ）中数列的“保三角形函数”，问数列最多有多少项? (解题中可用以下数据 :) 石景山区2012—2013学年第一学期期末考试高三数学（文）参考答案一、选择题共8小题，每小题5分，共40分．题号12345678答案BADDCCBC 二、填空题共6小题，每小题5分，共30分．题号91011121314答案2；63 ①③(9题、11题第一空2分,第二空3分) 三、解答题共6小题，共80分． 15．（本小题共13分）（Ⅰ）因为，所以. 所以函数的定义域为 ………2分 ……………5分 ……………7分（Ⅱ）因为，所以 ……………9分当时，即时，的最大值为； ……………11分当时，即时，的最小值为. ………13分 16．（本小题共14分）（Ⅰ）证明： …………………………4分（Ⅱ）证明：在△中， .又. 由 . …………………………9分（Ⅲ）设则由（Ⅱ）知，△，△均为直角三角形． ………………12分当时, 的最小值是．即当为中点时, 的长度最小,最小值为．…………………14分 17．（本小题共13分）（Ⅰ）设表示事件“抽取张卡片上的数字之和大于”，任取三张卡片，三张卡片上的数字全部可能的结果是，，，．其中数字之和大于的是，，所以． …………6分（Ⅱ）设表示事件“至少一次抽到”，第一次抽1张，放回后再抽取一张卡片的基本结果有：，共个基本结果．事件包含的基本结果有，共个基本结果．所以所求事件的概率为． …………………13分 18.（本小题共13分）（Ⅰ） …………………2分，，所以切线的方程为，即． …………………4分（Ⅱ）令则最大值，所以且，，，即函数的图像在直线的下方． …………………9分（Ⅲ）有零点，即有解， . 令，，解得. ………11分则在上单调递增，在上单调递减，当时，的最大值为，所以. …………………13分 19．（本小题共14分）（Ⅰ）由题意知, ，又因为，解得故椭圆方程为． …………………4分（Ⅱ）将代入并整理得，解得． …………………7分（Ⅲ）设直线的斜率分别为和，只要证明．设，，则． …………9分所以直线的斜率互为相反数． …………………14分 20．（本小题共13分）（Ⅰ）显然对任意正整数都成立，即是三角形数列．因为，显然有，由得解得. 所以当时，是数列的保三角形函数. …………………3分（Ⅱ）由，得，两式相减得，所以 …………5分经检验，此通项公式满足. 显然, 因为, 所以是三角形数列. …………………8分（Ⅲ）, 所以是单调递减函数. 由题意知，①且②, 由①得，解得, 由②得，解得. 即数列最多有26项. ………13分【注：若有其它解法，请酌情给分．】高考学习网：高考学习网： B A1 图2 图1 E D C B A 1 3 2 3 2 2 俯视图侧（左）视图正（主）视图结束是否输入x 输出y 开始 C D E。

北京市石景山区2013届高三上学期期末考试数学理科试题Word版含答案

石景山区2012—2013学年第一学期期末考试试卷高三数学（理）本试卷共6页，150分.考试时长120分钟．请务必将答案答在答题卡上，在试卷上作答无效．考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合{}4,3,2,1=U ，{}2,1=A ,{}4,2=B ,则=⋃B A C U ）（（）A ． {}2,1B ． {}4,32，C ． {}4,3D ．{}4,3,2,12. 若复数i Z =1, i Z -=32,则=12Z Z （） A ． 13i --B ．i +2C ．13i +D ．i +33．AC 为平行四边形ABCD 的一条对角线，(2,4),(1,3),AB AC AD 则===（）A ．(2,4)B ．(3,7)C ．(1,1)D ．(1,1)--4. 设,m n 是不同的直线，,αβ是不同的平面，下列命题中正确的是（）A ．若//,,m n m n αβ⊥⊥，则αβ⊥B ．若//,,m n m n αβ⊥⊥，则//αβC ．若//,,//m n m n αβ⊥，则α⊥βD ．若//,,//m n m n αβ⊥，则//αβ5．执行右面的框图，若输出结果为3，则可输入的实数x 值的个数为（）A ．1B ．2C ．3D ．46．若从1,2,3,…,9这9个整数中同时取4个不同的数，其和为奇数，则不同的取法共有（） A ．60种 B ．63种 C ．65种D ．66种7．某三棱锥的三视图如图所示，该三棱锥的体积是（）A ．38 B ．4 C ．2 D ．348. 在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[]k ，即[]{}5k n k n =+∈Z ，0,1,2,3,4k =．给出如下四个结论： ① []20133∈； ② []22-∈；③ [][][][][]01234Z =∪∪∪∪；④ 整数,a b 属于同一“类”的充要条件是“[]0a b -∈”．其中，正确结论的个数为（）．A ．1B ．2C ．3D ．4正（主）视图侧（左）视图俯视图22 3231开始输出y 输入x否是结束>2x2=-1y x 2=log y x第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩，，表示的平面区域S 的面积为4，则=a ；若点S y x P ∈),(，则y x z +=2 的最大值为 . 10．如右图，从圆O 外一点P 引圆O 的割线PAB 和PCD ，PCD 过圆心O ，已知1,2,3PA AB PO ===，则圆O 的半径等于． 11．在等比数列{}n a 中，141=,=42a a -，则公比=q ；123++++=n a a a a L ．12．在ABC ∆中，若2,60,7a B b =∠=︒=，则BC 边上的高等于．13．已知定点A 的坐标为(1,4)，点F 是双曲线221412x y -=的左焦点，点P 是双曲线右支上的动点，则PF PA +的最小值为．14. 给出定义：若11< +22m x m -≤ (其中m 为整数)，则m 叫做离实数x 最近的整数，记作{}x ，即{}=x m . 在此基础上给出下列关于函数()={}f x x x -的四个命题： ①=()y f x 的定义域是R ，值域是11(,]22-； ②点(,0)k 是=()y f x 的图像的对称中心，其中k Z ∈； ③函数=()y f x 的最小正周期为1； ④ 函数=()y f x 在13(,]22-上是增函数．则上述命题中真命题的序号是．PA BCO•D三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）已知函数sin 2(sin cos )()cos x x x f x x+=．（Ⅰ）求)(x f 的定义域及最小正周期；（Ⅱ）求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ，上的最大值和最小值．16．（本小题共14分）如图1，在Rt ABC ∆中，90C ∠=︒，36BC AC ==，．D 、E 分别是AC AB 、上的点，且//DE BC ，将ADE ∆沿DE 折起到1A DE ∆的位置，使1A D CD ⊥，如图2．（Ⅰ）求证： BC ⊥平面1A DC ；（Ⅱ）若2CD =，求BE 与平面1A BC 所成角的正弦值；（Ⅲ）当D 点在何处时，1A B 的长度最小，并求出最小值．A BCD E图1图2A 1B CDE甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为1123p 、、，且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. （Ⅰ）求甲乙二人中至少有一人破译出密码的概率；（Ⅱ）求p 的值；（Ⅲ）设甲、乙、丙三人中破译出密码的人数为X ，求X 的分布列和数学期望EX .18．（本小题共13分）已知函数()=ln +1,f x x ax a R -∈是常数．（Ⅰ）求函数=()y f x 的图象在点(1,(1))P f 处的切线l 的方程；（Ⅱ）证明函数=()(1)y f x x ≠的图象在直线l 的下方；（Ⅲ）讨论函数=()y f x 零点的个数．19．（本小题共14分）已知椭圆的中心在原点，焦点在x 轴上，离心率为32，且经过点(4,1)M ，直线:=+l y x m 交椭圆于不同的两点A B 、．（Ⅰ）求椭圆的方程；（Ⅱ）求m 的取值范围；（Ⅲ）若直线l 不过点M ，求证：直线MA MB 、的斜率互为相反数．定义：如果数列{}n a 的任意连续三项均能构成一个三角形的三边长，则称{}n a 为“三角形”数列．对于“三角形”数列{}n a ，如果函数()y f x =使得()n n b f a =仍为一个“三角形”数列，则称()y f x =是数列{}n a 的“保三角形函数”(*)n N ∈．（Ⅰ）已知{}n a 是首项为2，公差为1的等差数列，若()(1)x f x k k =>是数列{}n a 的“保三角形函数”，求k 的取值范围；（Ⅱ）已知数列{}n c 的首项为2013，n S 是数列{}n c 的前n 项和，且满足+1438052n n S S -=，证明{}n c 是“三角形”数列；（Ⅲ）若()lg g x x =是（Ⅱ）中数列{}n c 的“保三角形函数”，问数列{}n c 最多有多少项?(解题中可用以下数据 :lg20.301,lg30.477,lg2013 3.304≈≈≈)石景山区2012—2013学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案BADCCABC二、填空题共6小题，每小题5分，共30分．(9题、11题第一空2分,第二空3分) 三、解答题共6小题，共80分． 15．（本小题共13分）（Ⅰ）因为cos 0x ≠，所以+,2x k k Z ππ≠∈.所以函数)(x f 的定义域为{+,}2x x k k Z ππ≠∈｜ ……………2分sin 2sin cos ()cos x x x f x x+=（）()2s i n s i n +c o s =2s i n +s i n 2x x x x x =２ 2s i n (2-)14x π=+ ……………5分π=T ……………7分（Ⅱ）因为46ππ≤≤-x ，所以7-2-1244x πππ≤≤ ……………9分当2-44x ππ=时，即4x π=时，)(x f 的最大值为2； ……………11分当2--42x ππ=时，即8x π=-时，)(x f 的最小值为-2+1. ………13分16．（本小题共14分）（Ⅰ）证明：在△ABC 中，90,//,C DE BC AD DE ∠=︒∴⊥1A D DE ∴⊥.又11,,A D CD CD DE D A D BCDE ⊥⋂=∴⊥面.题号 9 10111213 14 答案2；6611222n ；---3329①③由1,.BC BCDE A D BC ⊂∴⊥面1,,BC CD CD BC C BC A DC ⊥⋂=∴⊥面. …………………………4分（Ⅱ）如图,以C 为原点，建立空间直角坐标系． ……………………5分1(2,0,0),(2,2,0),(0,3,0),(2,0,4)D E B A ．设(,,)x y z =n 为平面1A BC 的一个法向量，因为(0,3,0),CB =1(2,0,4)CA =所以30240y x z =⎧⎨+=⎩，令2x =，得=0,=1y z -. 所以(2,0,1)=-n 为平面1A BC 的一个法向量． ……………………7分设BE 与平面1A BC 所成角为θ．则44sin =cos 555BE θ<⋅>==⋅n ．所以BE 与平面1A BC 所成角的正弦值为45． …………………9分（Ⅲ）设(,0,0)D x ,则1(,0,6)A x x -，2221(-0)(0-3)(6--0)A B x x =++22-1245x x =+ …………………12分当=3x 时,1A B 的最小值是33．即D 为AC 中点时, 1A B 的长度最小,最小值为33． …………………14分 17．（本小题共13分）记“甲、乙、丙三人各自破译出密码”分别为事件321,,A A A ，依题意有12311(),(),(),23P A P A P A p ===且321,,A A A 相互独立.（Ⅰ）甲、乙二人中至少有一人破译出密码的概率为A 1BCD Exzy121()P A A -⋅1221233=-⨯=. …………………3分（Ⅱ）设“三人中只有甲破译出密码”为事件B ，则有()P B =123()P A A A ⋅⋅＝121(1)233pp -⨯⨯-=， …………………5分所以1134p -=，14p =. ……………………7分（Ⅲ）X 的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==， (1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=， (2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=， (3)P X ==P 123()A A A ⋅⋅＝111123424⨯⨯= . ……………………11分X 分布列为：X 0 1 2 3 P14 1124 14 124……………………12分所以，1111113()012342442412E X =⨯+⨯+⨯+⨯=. ………………13分 2．（本小题共13分）（Ⅰ）1()=f x a x'- …………………1分 (1)=+1f a -，=(1)=1l k f a '-，所以切线 l 的方程为(1)=(1)l y f k x --，即=(1)y a x -． …………………3分（Ⅱ）令()=()(1-)=ln +1>0F x f x a x x x x --，，则11()=1=(1)()=0=1.F x x F x x x x''--，解得x)1 , 0(1) , 1(∞+()F x ' +-)(x F↗最大值↘…………………6分(1)<0F ，所以>0x ∀且1x ≠，()<0F x ，()<(1)f x a x -，即函数=()(1)y f x x ≠的图像在直线 l 的下方． …………………8分（Ⅲ）令()=ln +1=0f x x ax -，ln +1=x a x. 令 ln +1()=x g x x ，22ln +11(ln +1)ln ()=()==x x xg x x x x -''-，则()g x 在(0,1)上单调递增，在(1,+)∞上单调递减，当=1x 时，()g x 的最大值为(1)=1g .所以若>1a ，则()f x 无零点；若()f x 有零点，则1a ≤．………………10分若=1a ，()=ln +1=0f x x ax -，由（Ⅰ）知()f x 有且仅有一个零点=1x . 若0a ≤，()=ln +1f x x ax -单调递增，由幂函数与对数函数单调性比较，知()f x 有且仅有一个零点（或：直线=1y ax -与曲线=ln y x 有一个交点）.若0<<1a ，解1()==0f x a x '-得1=x a ，由函数的单调性得知()f x 在1=x a处取最大值，11()=ln >0f a a，由幂函数与对数函数单调性比较知，当x 充分大时()<0f x ，即()f x 在单调递减区间1(,+)a ∞有且仅有一个零点；又因为1()=<0af e e -，所以()f x 在单调递增区间1(0)a，有且仅有一个零点.综上所述，当>1a 时，()f x 无零点；当=1a 或0a ≤时，()f x 有且仅有一个零点；当0<<1a 时，()f x 有两个零点. …………………13分19．（本小题共14分）（Ⅰ）设椭圆的方程为22221x y a b +=，因为32e =，所以224a b =，又因为(4,1)M ，所以221611a b+=，解得225,20b a ==，故椭圆方程为221205x y +=． …………………4分（Ⅱ）将y x m =+代入221205x y +=并整理得22584200x mx m ++-=， 22=(8)-20(4-20)>0m m ∆，解得55m -<<． …………………7分（Ⅲ）设直线,MA MB 的斜率分别为1k 和2k ，只要证明120k k +=．设11(,)A x y ，22(,)B x y ，则212128420,55m m x x x x -+=-=． …………………9分 12122112121211(1)(4)(1)(4)44(4)(4)y y y x y x k k x x x x ----+--+=+=----122112122(1)(4)(1)(4)2(5)()8(1)2(420)8(5)8(1)055x m x x m x x x m x x m m m m m =+--++--=+-+----=---=分子所以直线MA MB 、的斜率互为相反数． …………………14分20．（本小题共13分）（Ⅰ）显然121,n n n n a n a a a ++=++>对任意正整数都成立，即{}n a 是三角形数列。

石景山区高三数学期末理科2014年1月及答案

石景山区2013—2014学年第一学期期末考试试卷高三数学（理科）本试卷共6页，满分为150分，考试时间为120分钟.请务必将答案答在答题卡上，在试卷上作答无效，考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项． 1．已知集合{}2230M x x x =∈+-≤R ，{}10N x x =∈+<R ，那么M N = （）A ．{101}-，，B ．{321}---，，C ．{11}x x -≤≤D ．{31}x x -≤<-2．复数1ii =-（） A ．122i + B ．122i -C ．122i-+ D ．122i -- 3．已知向量(1)x =，a ，(4)x =，b ，则“2x =”是“a ∥b ”的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．已知数列为等差数列，，那么数列通项公式为（）A ．B ．C ．D ．5．执行如图所示的程序框图，若输入的x 的值为2，则输出的x 的值为（） A ．3 B ．126 C ．127 D ．1286．在边长为1的正方形OABC 中任取一点P ，则点P恰好落在正方形与曲线y =(阴影部分)的概率为（）A ．12B ．23C ．34D ．45OCy =B7．用0到9这10个数字，可以组成没有重复数字的三位偶数的个数为（）A ．324B ．328C ．360D ．6488．已知函数满足，当时，，若在区间上方程有两个不同的实根，则实数的取值范围是（）A ．B ．C ．D ．第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分． 9．已知圆C 的参数方程为12cos 2sin x y θθ+⎧⎨=⎩，，=(θ为参数)，则圆C 的直角坐标方程为_______________，圆心C 到直线:10l x y ++=的距离为______．10．在ABC ∆中，角A B C ，，的对边分别为a b c ，，，若=6a ，4c =，1cos =3B ，则b =______． 11．若x ，y 满足约束条件1020x y x y ≤⎧⎪≥⎨⎪-+≥⎩，，，则z x y =+的最大值为．12．如图，已知在ABC ∆中，o 90B ∠=，O 是AB 上一点，以O 为圆心，OB 为半径的圆与AB 交于点E ，与AC 切于点D ，2AD =，1AE =，则AB 的长为，CD 的长为．13．已知抛物线24y x =的焦点为F ，准线为直线l ，过抛物线上一点P 作PE l ⊥于E ，若直线EF 的倾斜角为o150，则||PF =______．14．已知四边形是边长为的正方形，且平面，为上动点，过且垂直于的平面交于，那么异面直线PC 与BD 所成的角的度数为，当三棱锥的体积取得最大值时，四棱锥P ABCD -的高PA 的长为．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题满分13分）已知函数()cos cos 21f x x x x =++．（Ⅰ）求函数的单调递增区间；（Ⅱ）求函数在上的最小值，并写出取最小值时相应的值．A DCBE．OA 1ABDCPE北京市各级各类中小学每年都要进行“学生体质健康测试”，测试总成绩满分为100分，规定测试成绩在[85100]，之间为体质优秀；在[7585)，之间为体质良好；在[6075)，之间为体质合格；在[060)，之间为体质不合格．现从某校高三年级的300名学生中随机抽取30名学生体质健康测试成绩，其茎叶图如下：9 1 3 5 68 0 1 1 2 2 3 3 3 4 4 5 6 6 7 7 9 7 0 5 6 6 7 9 6 4 5 8 5 6（Ⅰ）试估计该校高三年级体质为优秀的学生人数；（Ⅱ）根据以上30名学生体质健康测试成绩，现采用分层抽样的方法，从体质为优秀和良好的学生中抽取5名学生，再从这5名学生中选出3人．（ⅰ）求在选出的3名学生中至少有1名体质为优秀的概率；（ⅱ）记X 为在选出的3名学生中体质为良好的人数，求X 的分布列及数学期望．17.（本小题满分14分）如图，在四棱锥P ABCD -中，PA ⊥平面ABCD ，底面ABCD 是直角梯形，o 90ABC ∠=，AD ∥BC ，且2PA AD ==，1AB BC ==，E 为PD 的中点．（Ⅰ）求证：CD ⊥平面PAC ；（Ⅱ）求二面角E AC D --的余弦值；（Ⅲ）在线段AB 上是否存在一点F （不与A B ，两点重合），使得AE ∥平面PCF ?若存在，求出AF 的长；若不存在，请说明理由．18．（本小题满分13分）已知函数()xf x e ax =-（e 为自然对数的底数）.（Ⅰ）当2a =时，求曲线()f x 在点(0(0))f ，处的切线方程；（Ⅱ）求函数()f x 的单调区间；（Ⅲ）已知函数()f x 在0x =处取得极小值，不等式()f x mx <的解集为P ，若1{|2}2M x x =≤≤，且M P ≠∅ ，求实数m 的取值范围.A PEBDC已知椭圆：（）过点(20)，，且椭圆的离心率为. （Ⅰ）求椭圆的方程；（Ⅱ）若动点在直线上，过作直线交椭圆于两点，且MP PN =，再过作直线.证明：直线恒过定点，并求出该定点的坐标.20．（本小题满分13分）已知集合，对于数列中. （Ⅰ）若50项数列{}n a 满足5019ii a==-∑，5021(1)107i i a =-=∑，则数列{}n a 中有多少项取值为零？(121nin i aa a a n *==+++∈∑N ，)（Ⅱ）若各项非零数列{}n a 和新数列{}n b 满足11i i i b b a ---=（）．（ⅰ）若首项10b =，末项1n b n =-，求证数列{}n b 是等差数列；（ⅱ）若首项10b =，末项0n b =，记数列{}n b 的前n 项和为n S ，求n S 的最大值和最小值．石景山区2013—2014学年第一学期期末考试高三数学（理科）参考答案一、选择题共8二、填空题共6小题，每小题5分，共30分．(两空的题目第一空2分，第二空3分)三、解答题共6小题，共80分． 15．（本小题共13分）解：（Ⅰ）()f x 2cos 2+1x x =+ …………2分 2sin 2+16x π=+（）， ……………4分222262k x k πππππ-≤+≤+，k ∈Z ， 36k x k ππππ-≤≤+，k ∈Z ， ………6分所以函数)(x f 的单调递增区间为[]36k k ππππ-+，()k ∈Z ． ……………7分（Ⅱ）因为44x ππ-≤≤，22363x πππ-≤+≤，……………9分sin(2)16x π≤+≤， 12sin 2+136x π≤+≤（）， ……………11分所以当2=63x ππ+-，即=4x π-时，函数)(x f 取得最小值1．………13分则 3335C 9()1C 10P A =-=．故在选出的3名学生中至少有名体质为优秀的概率为910．……9分（ⅱ）解：随机变量X 的所有取值为123，，．123235C C 3(1)C 10P X ⋅===，213235C C 6(2)C 10P X ⋅===，3335C 1(3)C 10P X ===． …………12分所以，随机变量X 的分布列为:36191231010105EX =⨯+⨯+⨯=． ……………13分 17．（本小题共14分）（Ⅰ）证明：因为PA ⊥平面ABCD ，CD ⊂平面ABCD ，所以PA CD ⊥. ……………1分取AD 的中点G ，连结GC ，因为底面ABCD 为直角梯形，AD ∥BC ，o90ABC ∠=，且1AB BC ==，所以四边形ABCG 为正方形，所以CG AD ⊥，且1=2CG AD ，所以o=90ACD ∠，即AC CD ⊥. ……………3分又PA AC A = ，所以CD ⊥平面PAC . ……………4分（Ⅱ）解：如图，以A 为坐标原点，AB AD AP ，，所在直线分别为x y z ，，轴建立空间直角坐标系xyz A -．………5分则(000)A ，，，(110)C ，，，(011)E ，，，(002)P ，，，所以(002)AP = ，，，(110)AC = ，，，(011)AE =，，．因为PA ⊥平面ABCD ，所以(002)AP =，，为平面ACD 的一个法向量． ……6分设平面EAC 的法向量为1()n x y z =，，，由10n AC ⋅= ，10n AE ⋅= 得00x y y z +=⎧⎨+=⎩，，令1x =，则1y =-，1z =，APEBDCG所以1(111)n =-，，是平面EAC 的一个法向量． ………8分所以1cos n AP <>== ，因为二面角E AC D --为锐角，所以二面角E AC D --． ………9分（Ⅲ）解：假设在线段AB 上存在点F （不与A B ，两点重合），使得AE ∥平面PCF ．设(00)F a ，，，则(110)CF a =-- ，，，(112)CP =--，，．设平面PCF 的法向量为2()n x y z =，，，由20n CF ⋅= ，20n CP ⋅= 得(1)020a x y x y z --=⎧⎨--+=⎩，，令1x =，则1y a =-，2az =，所以2(11)2a n a =- ，，是平面PCF 的一个法向量．…12分因为AE ∥平面PCF ，所以20AE n ⋅= ，即(1)02aa -+=， ……………13分解得23a =，所以在线段AB 上存在一点F （不与A B ，两点重合），使得AE ∥平面PCF ，且2=3AF ．……14分 18.（本小题共13分）解：（Ⅰ）当2a =时，()2x f x e x =-，(0)1f =，()2xf x e '=-，得(0)1f '=-，………2分所以曲线()f x 在点(0(0))f ，处的切线方程为1y x =-+. ……………3分（Ⅱ）()xf x e a '=-.当0a ≤时，()0f x '>恒成立，此时()f x 的单调递增区间为()-∞+∞，，无单调递减区间；………5分当0a >时，(ln )x a ∈-∞，时，()0f x '<，(ln )x a ∈+∞，时，()0f x '>，此时()f x 的单调递增区间为(ln )a +∞，，单调递减区间为(ln )a -∞，.……7分（Ⅲ）由题意知(0)0f '=得1a =，经检验此时()f x 在0x =处取得极小值. ………8分因为M P ≠∅ ，所以()f x mx <在1[2]2，上有解，即1[2]2x ∃∈，使()f x mx <成立，…9分即1[2]2x ∃∈，使x e x m x ->成立， …………10分所以min ()x e xm x->.令()1x e g x x =-，2(1)()x x e g x x -'=，所以()g x 在1[1]2，上单调递减，在[12]，上单调递增，则min ()(1)1g x g e ==-， ……………12分所以(1)m e ∈-∞，+. ……………13分 19．（本小题共14分）解：（Ⅰ）因为点(20)，在椭圆C 上，所以22401a b+=，所以24a =， …………1分因为椭圆C 的离心率为12，所以12c a =，即22214a b a -= ， …………2分解得23b =， ……………4分所以椭圆C 的方程为22143x y +=. ……………5分（Ⅱ）设0(1)P y -，，033()22y ∈-，， ①当直线MN 的斜率存在时，设直线MN 的方程为0(1)y y k x -=+，11()M x y ，，22()N x y ，，由2203412(1)x y y y k x ⎧+=⎨-=+⎩，，得22222000(34)(88)(48412)0k x ky k x y ky k ++++++-=， ………7分所以2012288+34ky k x x k +=-+， ……………8分因为MP PN = ，即P 为MN 中点，所以12=12x x +-，即20288=234ky k k +--+. 所以003(0)4MN k y y =≠， ……………9分因为直线l MN ⊥，所以043l y k =-，所以直线l 的方程为004(1)3yy y x -=-+，即041()34y y x =-+ ，显然直线l 恒过定点1(0)4-，. ……………11分②当直线MN 的斜率不存在时，直线MN 的方程为1x =-，此时直线l 为x 轴，也过点1(0)4-，. ……………13分综上所述直线l 恒过定点1(0)4-，. ……………14分20．（本小题共13分）解：（Ⅰ）设数列{}n a 中项为110-，，分别有x y z ，，项．由题意知5094107x y z x y z y ++=⎧⎪-=-⎨⎪+=⎩，，，解得11z =．所以数列{}n a 中有11项取值为零． ……3分（Ⅱ）（ⅰ）{11}i a ∈-，且11i i i b b a ---=，得到121(23)i i b a a a i n -=+++= ，，，，若1(121)i a i n ==- ，，，，则满足1n b n =-．此时11i i b b --=，数列{}n b 是等差数列；若121n a a a - ，，，中有*(0)p p p >∈，N 个1-，则121n b n p n =--≠-不满足题意；所以数列{}n b 是等差数列． ……………7分（ⅱ）因为数列{}n b 满足11i i i b b a ---=，所以121(23)i i b a a a i n -=+++= ，，，，根据题意有末项0n b =，所以1210n a a a -+++= ．而{11}i a ∈-，，于是n 为正奇数，且121n a a a - ，，，中有12n -个1和12n -个1-． 12112121()()n n n S b b b a a a a a a -=+++=+++++++121(1)(2)n n a n a a -=-+-++要求n S 的最大值，则只需121n a a a - ，，，前12n -项取1，后12n -项取1-，所以2max(1)()(2)(4)14n n S n n -=-+-++=（n 为正奇数）．要求n S 的最小值，则只需121n a a a - ，，，前12n -项取1-，后12n -项取1，则2min(1)()(2)(4)14n n S n n -=------=-（n 为正奇数）． …………13分【注：若有其它解法，请酌情给分．】。

2012年石景山区高三统一测试数学(理科)答案

2012年石景山区高三统一测试高三数学（理科）参考答案一、选择题：本大题共8个小题，每小题5分，共40分．题号 12345678答案B D A D B B AC二、填空题：本大题共6个小题，每小题5分，共30分．三、解答题：本大题共6个小题，共80分．应写出文字说明，证明过程或演算步骤． 15．（本小题满分13分）解：（Ⅰ）因为C b B c a cos cos )2(=-，由正弦定理，得C B B C A cos sin cos )sin sin 2(=-． …………2分∴ A C B C B B C B A sin )sin(cos sin cos sin cos sin 2=+=+=．……4分 ∵ 0A π<<, ∴0sin ≠A ， ∴ 21cos =B ．又∵ π<<B 0 ， ∴ 3π=B ． …………6分（Ⅱ）由正弦定理BbA a sin sin =，得6b =， …………8分由 2cos 2A =可得4A π=，由3π=B ，可得62sin 4C +=， …………11分 ∴116233sin 262242s ab C ++==⨯⨯⨯=． …………13分16．（本小题满分13分）解：（Ⅰ）ξ的可能取值为：0，1，2，3． …………1分;27832)0(303=⎪⎭⎫ ⎝⎛==C P ξ;943231)1(213=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==C P ξ 题号91011121314答案 31-10721-≥a 34π①②④;923231)2(223=⎪⎭⎫ ⎝⎛⎪⎭⎫⎝⎛==C P ξ.27131)3(333=⎪⎭⎫ ⎝⎛==C P ξ ξ的分布列如下表：ξ0 1 2 3P278 94 92 271…………4分 127139229412780=⨯+⨯+⨯+⨯=ξE ． …………5分（Ⅱ）乙至多投中2次的概率为87211333=⎪⎭⎫ ⎝⎛-C ． …………8分（Ⅲ）设乙比甲多投中2次为事件A ，乙恰投中2次且甲恰投中0次为事件B 1，乙恰投中3次且甲恰投中1次为事件B 2，则2121,,B B B B A =为互斥事件． …………10分=+=)()()(21B P B P A P 61819483278=⨯+⨯．所以乙恰好比甲多投中2次的概率为61． …………13分 17．（本小题满分14分）（I ）证明：连接B 1C ，与BC 1相交于O ，连接OD ． …………1分 ∵BCC 1B 1是矩形，∴O 是B 1C 的中点．又D 是AC 的中点，∴OD//AB 1． ∵AB 1⊄面BDC 1，OD ⊂面BDC 1，∴AB 1//面BDC 1． …………4分（II ）解：如图，建立空间直角坐标系，则C 1（0，0，0），B （0，3，2）， C （0，3，0），A （2，3，0）， D （1，3，0），1(0,3,2)C B =，1(1,3,0)C D =，…………5分设111(,,)n x y z =是面BDC 1的一个法向量，则A 1AC 1zxyCB 1BD110,0n C B n C D ⎧=⎪⎨=⎪⎩即1111320,30y z x y +=⎧⎨+=⎩，取11(1,,)32n =-. …………7分易知1(0,3,0)C C =是面ABC 的一个法向量. …………8分1112cos ,7n C C n C C n C C==-⨯. ∴二面角C 1—BD —C 的余弦值为27.…………9分（III ）假设侧棱AA 1上存在一点P 使得CP ⊥面BDC 1.设P （2，y ，0）（0≤y ≤3），则 (2,3,0)CP y =-， …………10分则110,0CP C B CP C D ⎧=⎪⎨=⎪⎩，即3(3)0,23(3)0y y -=⎧⎨+-=⎩. …………12分解之3,73y y =⎧⎪⎨=⎪⎩∴方程组无解. …………13分∴侧棱AA 1上不存在点P ，使CP ⊥面BDC 1. …………14分 18．（本小题满分14分）解：（Ⅰ）2222'()2a x af x x x x+=+= …………1分由已知'(2)1f =，解得3a =-. …………3分（II ）函数()f x 的定义域为(0,)+∞.（1）当0a ≥时, '()0f x >，()f x 的单调递增区间为(0,)+∞； ……5分（2）当0a <时2()()'()x a x a f x x+---=.当x 变化时，'(),()f x f x 的变化情况如下：x(0,)a -a - (,)a -+∞'()f x - 0+ ()f x极小值由上表可知，函数()f x 的单调递减区间是(0,)a -；单调递增区间是(,)a -+∞. …………8分（II ）由22()2ln g x x a x x =++得222'()2a g x x x x=-++，…………9分由已知函数()g x 为[1,2]上的单调减函数，则'()0g x ≤在[1,2]上恒成立，即22220ax x x -++≤在[1,2]上恒成立. 即21a x x ≤-在[1,2]上恒成立. …………11分令21()h x x x =-，在[1,2]上2211'()2(2)0h x x x x x=--=-+<，所以()h x 在[1,2]为减函数. min 7()(2)2h x h ==-,所以72a ≤-. …………14分19．（本小题满分13分）解：（Ⅰ）由题意，222312a c b a b c ⎧-=-⎪⎪=⎨⎪=+⎪⎩-------1分解得3,1a c ==. ------------2分即：椭圆方程为.12322=+y x ------------3分（Ⅱ）当直线AB 与x 轴垂直时，43AB =，此时3AOB S ∆=不符合题意故舍掉； -----------4分当直线AB 与x 轴不垂直时，设直线 AB 的方程为：)1(+=x k y ，代入消去y 得：2222(23)6(36)0k x k x k +++-=. ------------6分设1122(,),(,)A x y B x y ，则212221226233623k x x k k x x k ⎧-+=⎪⎪+⎨-⎪=⎪+⎩， -----------7分所以 2243(1)23k AB k +=+. ------------9分原点到直线的AB 距离21k d k=+，所以三角形的面积2221143(1)22231k k S AB d kk +==++. 由232224S k k =⇒=⇒=±， ------------12分所以直线:220AB l x y -+=或:220AB l x y ++=. ---------13分 20．（本小题满分13分）解：（I ）因为2221122,212(22)1(21)++=++=++=+n n n n n n n a a a a a a a所以数列}1{2+n a 是“平方递推数列” . --------2分由以上结论21lg(21)lg(21)2lg(21)n n n a a a ++=+=+，所以数列)}1{lg(2+n a 为首项是lg5公比为2的等比数列. --------3分（II ）11121lg(21)[lg(21)]22lg 5lg 5---+=+⨯==n n n n a a ，11221215,(51)2--+==-n n n n a a .--------5分1l g l g (21)l g (21)(21)l g 5nn n T a a =++++=-，215n n T -=.--------7分（III ）11lg (21)lg512lg(21)2lg52---===-+n n n n n n T b a11222n n S n -=-+. --------10分112220122n n --+>110072n n +>m i n 1007n =.--------13分[注：若有其它解法，请酌情给分]。

北京市石景山区2013届高三上学期期末考试数学(理)试题

石景山区2012—2013学年第一学期期末考试试卷高三数学（理）本试卷共6页，150分.考试时长120分钟．请务必将答案答在答题卡上，在试卷上作答无效．考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合{}4,3,2,1=U ，{}2,1=A ,{}4,2=B ,则=⋃B A C U ）（（） A ． {}2,1B ． {}4,32，C ． {}4,3D ．{}4,3,2,12. 若复数i Z =1, i Z -=32,则=12Z Z （） A ． 13i --B ．i +2C ．13i +D ．i +33．AC 为平行四边形ABCD 的一条对角线，(2,4),(1,3),AB AC AD 则===（）A ．(2,4)B ．(3,7)C ．(1,1)D ．(1,1)--4. 设,m n 是不同的直线，,αβ是不同的平面，下列命题中正确的是（）A ．若//,,m n m n αβ⊥⊥，则αβ⊥B ．若//,,m n m n αβ⊥⊥，则//αβC ．若//,,//m n m n αβ⊥，则α⊥βD ．若//,,//m n m n αβ⊥，则//αβ5．执行右面的框图，若输出结果为3，则可输入的实数x 值的个数为（）A ．1B ．2C ．3D ．4开始输出y输入x否是>2x2=-1y x 2=log y x6．若从1,2,3,…,9这9个整数中同时取4个不同的数，其和为奇数，则不同的取法共有（） A ．60种 B ．63种 C ．65种D ．66种7．某三棱锥的三视图如图所示，该三棱锥的体积是（）A ．38 B ．4 C ．2 D ．348. 在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[]k ，即[]{}5k n k n =+∈Z ，0,1,2,3,4k =．给出如下四个结论： ① []20133∈； ② []22-∈；③ [][][][][]01234Z =∪∪∪∪；④ 整数,a b 属于同一“类”的充要条件是“[]0a b -∈”．其中，正确结论的个数为（）．A ．1B ．2C ．3D ．4第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩，，表示的平面区域S 的面积为4，则=a ；若点S y x P ∈),(，则y x z +=2 的最大值为 . 10．如右图，从圆O 外一点P 引圆O 的割线PAB 和PCD ，PCD 过圆心O ，已知1,2,3PA AB PO ===，PA BC O•D正（主）视图侧（左）视图俯视图2 2 3231则圆O 的半径等于． 11．在等比数列{}n a 中，141=,=42a a -，则公比=q ；123++++=n a a a a L ．12．在ABC ∆中，若2,60,7a B b =∠=︒=，则BC 边上的高等于．13．已知定点A 的坐标为(1,4)，点F 是双曲线221412x y -=的左焦点，点P 是双曲线右支上的动点，则PF PA +的最小值为．14. 给出定义：若11< +22m x m -≤ (其中m 为整数)，则m 叫做离实数x 最近的整数，记作{}x ，即{}=x m . 在此基础上给出下列关于函数()={}f x x x -的四个命题： ①=()y f x 的定义域是R ，值域是11(,]22-； ②点(,0)k 是=()y f x 的图像的对称中心，其中k Z ∈； ③函数=()y f x 的最小正周期为1； ④ 函数=()y f x 在13(,]22-上是增函数．则上述命题中真命题的序号是．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）已知函数sin 2(sin cos )()cos x x x f x x+=．（Ⅰ）求)(x f 的定义域及最小正周期；（Ⅱ）求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ，上的最大值和最小值．16．（本小题共14分）如图1，在Rt ABC ∆中，90C ∠=︒，36BC AC ==，．D 、E 分别是AC AB 、上的点，且//DE BC ，将ADE ∆沿DE 折起到1A DE ∆的位置，使1A D CD ⊥，如图2．（Ⅰ）求证： BC ⊥平面1A DC ；（Ⅱ）若2CD =，求BE 与平面1A BC 所成角的正弦值；（Ⅲ）当D 点在何处时，1A B 的长度最小，并求出最小值．17．（本小题共13分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为1123p 、、，且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. （Ⅰ）求甲乙二人中至少有一人破译出密码的概率；（Ⅱ）求p 的值；（Ⅲ）设甲、乙、丙三人中破译出密码的人数为X ，求X 的分布列和数学期望EX .18．（本小题共13分）已知函数()=ln +1,f x x ax a R -∈是常数．（Ⅰ）求函数=()y f x 的图象在点(1,(1))P f 处的切线l 的方程；（Ⅱ）证明函数=()(1)y f x x ≠的图象在直线l 的下方；（Ⅲ）讨论函数=()y f x 零点的个数．19．（本小题共14分）ABCDE图1 图2A 1BCDE已知椭圆的中心在原点，焦点在x 轴上，离心率为32，且经过点(4,1)M ，直线:=+l y x m 交椭圆于不同的两点A B 、．（Ⅰ）求椭圆的方程；（Ⅱ）求m 的取值范围；（Ⅲ）若直线l 不过点M ，求证：直线MA MB 、的斜率互为相反数．20．（本小题共13分）定义：如果数列{}n a 的任意连续三项均能构成一个三角形的三边长，则称{}n a 为“三角形”数列．对于“三角形”数列{}n a ，如果函数()y f x =使得()n n b f a =仍为一个“三角形”数列，则称()y f x =是数列{}n a 的“保三角形函数”(*)n N ∈．（Ⅰ）已知{}n a 是首项为2，公差为1的等差数列，若()(1)xf x k k =>是数列{}n a 的“保三角形函数”，求k 的取值范围；（Ⅱ）已知数列{}n c 的首项为2013，n S 是数列{}n c 的前n 项和，且满足+1438052n n S S -=，证明{}n c 是“三角形”数列；（Ⅲ）若()lg g x x =是（Ⅱ）中数列{}n c 的“保三角形函数”，问数列{}n c 最多有多少项?(解题中可用以下数据 :lg20.301,lg30.477,lg2013 3.304≈≈≈)石景山区2012—2013学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案BADCCABC二、填空题共6小题，每小题5分，共30分．(9题、11题第一空2分,第二空3分)三、解答题共6小题，共80分． 15．（本小题共13分）（Ⅰ）因为cos 0x ≠，所以+,2x k k Z ππ≠∈.所以函数)(x f 的定义域为{+,}2x x k k Z ππ≠∈｜ ……………2分sin 2sin cos ()cos x x x f x x+=（）()2s i n s i n +c o s =2s i n +s i n 2x x x x x =２ 2s i n (2-)14x π=+ ……………5分π=T ……………7分（Ⅱ）因为46ππ≤≤-x ，所以7-2-1244x πππ≤≤ ……………9分当2-44x ππ=时，即4x π=时，)(x f 的最大值为2； ……………11分当2--42x ππ=时，即8x π=-时，)(x f 的最小值为-2+1. ………13分16．（本小题共14分）（Ⅰ）证明：在△ABC 中，90,//,C DE BC AD DE ∠=︒∴⊥1A D DE ∴⊥.又11,,A D CD CD DE D A D BCDE ⊥⋂=∴⊥面.题号 9 10111213 14 答案2；6611222n ；---3329①③由1,.BC BCDE A D BC ⊂∴⊥面1,,BC CD CD BC C BC A DC ⊥⋂=∴⊥面. …………………………4分（Ⅱ）如图,以C 为原点，建立空间直角坐标系． ……………………5分1(2,0,0),(2,2,0),(0,3,0),(2,0,4)D E B A ．设(,,)x y z =n 为平面1A BC 的一个法向量，因为(0,3,0),CB =1(2,0,4)CA =所以30240y x z =⎧⎨+=⎩，令2x =，得=0,=1y z -.所以(2,0,1)=-n 为平面1A BC 的一个法向量． ……………………7分设BE 与平面1A BC 所成角为θ．则44sin =cos 555BE θ<⋅>==⋅n ．所以BE 与平面1A BC 所成角的正弦值为45． …………………9分（Ⅲ）设(,0,0)D x ,则1(,0,6)A x x -，2221(-0)(0-3)(6--0)A B x x =++22-1245x x =+ …………………12分当=3x 时,1A B 的最小值是33．即D 为AC 中点时, 1A B 的长度最小,最小值为33． …………………14分 17．（本小题共13分）记“甲、乙、丙三人各自破译出密码”分别为事件321,,A A A ，依题意有12311(),(),(),23P A P A P A p ===且321,,A A A 相互独立.（Ⅰ）甲、乙二人中至少有一人破译出密码的概率为121()P A A -⋅1221233=-⨯=. …………………3分（Ⅱ）设“三人中只有甲破译出密码”为事件B ，则有()P B =123()P A A A ⋅⋅＝121(1)233pp -⨯⨯-=， …………………5分所以1134p -=，14p =. ……………………7分 A 1BCD Exzy（Ⅲ）X 的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==， (1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=， (2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=， (3)P X ==P 123()A A A ⋅⋅＝111123424⨯⨯= . ……………………11分X 分布列为：X 0 1 2 3 P14 1124 14 124……………………12分所以，1111113()012342442412E X =⨯+⨯+⨯+⨯=. ………………13分 2．（本小题共13分）（Ⅰ）1()=f x a x'- …………………1分 (1)=+1f a -，=(1)=1l k f a '-，所以切线 l 的方程为(1)=(1)l y f k x --，即=(1)y a x -． …………………3分（Ⅱ）令()=()(1-)=ln +1>0F x f x a x x x x --，，则11()=1=(1)()=0=1.F x x F x x x x''--，解得 x)1 , 0(1) , 1(∞+()F x ' +-)(x F↗最大值↘…………………6分(1)<0F ，所以>0x ∀且1x ≠，()<0F x ，()<(1)f x a x -，即函数=()(1)y f x x ≠的图像在直线 l 的下方． …………………8分（Ⅲ）令()=ln +1=0f x x ax -，ln +1=x a x. 令 ln +1()=x g x x ，22ln +11(ln +1)ln ()=()==x x xg x x x x-''-，则()g x 在(0,1)上单调递增，在(1,+)∞上单调递减，当=1x 时，()g x 的最大值为(1)=1g .所以若>1a ，则()f x 无零点；若()f x 有零点，则1a ≤．………………10分若=1a ，()=ln +1=0f x x ax -，由（Ⅰ）知()f x 有且仅有一个零点=1x .若0a ≤，()=ln +1f x x ax -单调递增，由幂函数与对数函数单调性比较，知()f x 有且仅有一个零点（或：直线=1y ax -与曲线=ln y x 有一个交点）.若0<<1a ，解1()==0f x a x '-得1=x a ，由函数的单调性得知()f x 在1=x a处取最大值，11()=ln >0f a a，由幂函数与对数函数单调性比较知，当x 充分大时()<0f x ，即()f x 在单调递减区间1(,+)a ∞有且仅有一个零点；又因为1()=<0af e e -，所以()f x 在单调递增区间1(0)a，有且仅有一个零点.综上所述，当>1a 时，()f x 无零点；当=1a 或0a ≤时，()f x 有且仅有一个零点；当0<<1a 时，()f x 有两个零点. …………………13分 19．（本小题共14分）（Ⅰ）设椭圆的方程为22221x y a b +=，因为32e =，所以224a b =，又因为(4,1)M ，所以221611a b+=，解得225,20b a ==，故椭圆方程为221205x y +=． …………………4分（Ⅱ）将y x m =+代入221205x y +=并整理得22584200x mx m ++-=， 22=(8)-20(4-20)>0m m ∆，解得55m -<<． …………………7分（Ⅲ）设直线,MA MB 的斜率分别为1k 和2k ，只要证明120k k +=．设11(,)A x y ，22(,)B x y ，则212128420,55m m x x x x -+=-=． …………………9分 12122112121211(1)(4)(1)(4)44(4)(4)y y y x y x k k x x x x ----+--+=+=----122112122(1)(4)(1)(4)2(5)()8(1)2(420)8(5)8(1)055x m x x m x x x m x x m m m m m =+--++--=+-+----=---=分子所以直线MA MB 、的斜率互为相反数． …………………14分 20．（本小题共13分）（Ⅰ）显然121,n n n n a n a a a ++=++>对任意正整数都成立，即{}n a 是三角形数列。

2013届北京市石景山区高三期末数学理科试题(WORD精校版)

石景山区2012—2013学年第一学期期末考试试卷高三数学（理）本试卷共6页，150分.考试时长120分钟．请务必将答案答在答题卡上，在试卷上作答无效．考试结束后上交答题卡.第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．设集合{}4,3,2,1=U ，{}2,1=A ,{}4,2=B ,则=⋃B A C U ）（（） A ． {}2,1B ． {}4,32，C ． {}4,3D ．{}4,3,2,12. 若复数i Z =1, i Z -=32,则=12Z Z （） A ． 13i --B ．i +2C ．13i +D ．i +33．AC 为平行四边形ABCD 的一条对角线，(2,4),(1,3),AB AC AD 则===（）A ．(2,4)B ．(3,7)C ．(1,1)D ．(1,1)--4. 设,m n 是不同的直线，,αβ是不同的平面，下列命题中正确的是（）A ．若//,,m n m n αβ⊥⊥，则αβ⊥B ．若//,,m n m n αβ⊥⊥，则//αβC ．若//,,//m n m n αβ⊥，则α⊥βD ．若//,,//m n m n αβ⊥，则//αβ 5．执行右面的框图，若输出结果为3，则可输入的实数x 值的个数为（）A ．1B ．2C ．3D ．46．若从1,2,3,…,9这9个整数中同时取4个不同的数，其和为奇数，则不同的取法共有（） A ．60种B ．63种开始输出y 输入x否是结束 >2x2=-1y x 2=log y xC ．65种D ．66种7．某三棱锥的三视图如图所示，该三棱锥的体积是（）A ．38 B ．4 C ．2 D ．348. 在整数集Z 中，被5除所得余数为k 的所有整数组成一个“类”，记为[]k ，即[]{}5k n k n =+∈Z ，0,1,2,3,4k =．给出如下四个结论： ① []20133∈； ② []22-∈；③ [][][][][]01234Z =∪∪∪∪；④ 整数,a b 属于同一“类”的充要条件是“[]0a b -∈”．其中，正确结论的个数为（）．A ．1B ．2C ．3D ．4第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．已知不等式组y x y x x a ≤⎧⎪≥-⎨⎪≤⎩，，表示的平面区域S 的面积为4，则=a ；若点S y x P ∈),(，则y x z +=2 的最大值为 . 10．如右图，从圆O 外一点P 引圆O 的割线PAB 和PCD ，PCD 过圆心O ，已知1,2,3PA AB PO ===，则圆O 的半径等于． 11．在等比数列{}n a 中，141=,=42a a -，则公比=q ；PA BC O•D正（主）视图侧（左）视图俯视图2 2 3231123++++=n a a a a L ．12．在ABC ∆中，若2,60,7a B b =∠=︒=，则BC 边上的高等于．13．已知定点A 的坐标为(1,4)，点F 是双曲线221412x y -=的左焦点，点P 是双曲线右支上的动点，则PF PA +的最小值为．14. 给出定义：若11< +22m x m -≤ (其中m 为整数)，则m 叫做离实数x 最近的整数，记作{}x ，即{}=x m . 在此基础上给出下列关于函数()={}f x x x -的四个命题： ①=()y f x 的定义域是R ，值域是11(,]22-； ②点(,0)k 是=()y f x 的图像的对称中心，其中k Z ∈； ③函数=()y f x 的最小正周期为1； ④ 函数=()y f x 在13(,]22-上是增函数．则上述命题中真命题的序号是．三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15．（本小题共13分）已知函数sin 2(sin cos )()cos x x x f x x+=．（Ⅰ）求)(x f 的定义域及最小正周期；（Ⅱ）求)(x f 在区间⎥⎦⎤⎢⎣⎡-46ππ，上的最大值和最小值．16．（本小题共14分）如图1，在Rt ABC ∆中，90C ∠=︒，36BC AC ==，．D 、E 分别是AC AB 、上的点，且//DE BC ，将ADE ∆沿DE 折起到1A DE ∆的位置，使1A D CD ⊥，如图2．（Ⅰ）求证： BC ⊥平面1A DC ；（Ⅱ）若2CD =，求BE 与平面1A BC 所成角的正弦值；（Ⅲ）当D 点在何处时，1A B 的长度最小，并求出最小值．17．（本小题共13分）甲、乙、丙三人独立破译同一份密码，已知甲、乙、丙各自破译出密码的概率分别为1123p 、、，且他们是否破译出密码互不影响.若三人中只有甲破译出密码的概率为14. （Ⅰ）求甲乙二人中至少有一人破译出密码的概率；（Ⅱ）求p 的值；（Ⅲ）设甲、乙、丙三人中破译出密码的人数为X ，求X 的分布列和数学期望EX . 18．（本小题共13分）已知函数()=ln +1,f x x ax a R -∈是常数．（Ⅰ）求函数=()y f x 的图象在点(1,(1))P f 处的切线l 的方程；（Ⅱ）证明函数=()(1)y f x x ≠的图象在直线l 的下方；（Ⅲ）讨论函数=()y f x 零点的个数． 19．（本小题共14分）已知椭圆的中心在原点，焦点在x 轴上，离心率为32，且经过点(4,1)M ，直线:=+l y x m 交椭圆于不同的两点A B 、．（Ⅰ）求椭圆的方程；（Ⅱ）求m 的取值范围；（Ⅲ）若直线l 不过点M ，求证：直线MA MB 、的斜率互为相反数．ABCDE图1 图2A 1B CDE20．（本小题共13分）定义：如果数列{}n a 的任意连续三项均能构成一个三角形的三边长，则称{}n a 为“三角形”数列．对于“三角形”数列{}n a ，如果函数()y f x =使得()n n b f a =仍为一个“三角形”数列，则称()y f x =是数列{}n a 的“保三角形函数”(*)n N ∈．（Ⅰ）已知{}n a 是首项为2，公差为1的等差数列，若()(1)x f x k k =>是数列{}n a 的“保三角形函数”，求k 的取值范围；（Ⅱ）已知数列{}n c 的首项为2013，n S 是数列{}n c 的前n 项和，且满足+1438052n n S S -=，证明{}n c 是“三角形”数列；（Ⅲ）若()lg g x x =是（Ⅱ）中数列{}n c 的“保三角形函数”，问数列{}n c 最多有多少项?(解题中可用以下数据 :lg20.301,lg30.477,lg2013 3.304≈≈≈)石景山区2012—2013学年第一学期期末考试高三数学（理科）参考答案一、选择题共8小题，每小题5分，共40分．题号 1 2 3 4 5 6 7 8 答案BADCCABC二、填空题共6小题，每小题5分，共30分．(9题、11题第一空2分,第二空3分) 三、解答题共6小题，共80分． 15．（本小题共13分）（Ⅰ）因为cos 0x ≠，所以+,2x k k Z ππ≠∈.所以函数)(x f 的定义域为{+,}2x x k k Z ππ≠∈｜ ……………2分sin 2sin cos ()cos x x x f x x+=（）()2s i n s i n +c o s =2s i n +s i n 2x x x x x =２ 2s i n (2-)14x π=+ ……………5分π=T ……………7分（Ⅱ）因为46ππ≤≤-x ，所以7-2-1244x πππ≤≤ ……………9分当2-44x ππ=时，即4x π=时，)(x f 的最大值为2； ……………11分当2--42x ππ=时，即8x π=-时，)(x f 的最小值为-2+1. ………13分16．（本小题共14分）（Ⅰ）证明：在△ABC 中，90,//,C DE BC AD DE ∠=︒∴⊥1A D DE ∴⊥.又11,,A D CD CD DE D A D BCDE ⊥⋂=∴⊥面.由1,.BC BCDE A D BC ⊂∴⊥面1,,BC CD CD BC C BC A DC ⊥⋂=∴⊥面. …………………………4分题号 9 10 11 12 13 14 答案 2；6 6 11222n ；--- 3329①（Ⅱ）如图,以C 为原点，建立空间直角坐标系． ……………………5分1(2,0,0),(2,2,0),(0,3,0),(2,0,4)D E B A ．设(,,)x y z =n 为平面1A BC 的一个法向量，因为(0,3,0),CB =1(2,0,4)CA =所以30240y x z =⎧⎨+=⎩，令2x =，得=0,=1y z -.所以(2,0,1)=-n 为平面1A BC 的一个法向量． ……………………7分设BE 与平面1A BC 所成角为θ．则44sin =cos 555BE θ<⋅>==⋅n ．所以BE 与平面1A BC 所成角的正弦值为45． …………………9分（Ⅲ）设(,0,0)D x ,则1(,0,6)A x x -，2221(-0)(0-3)(6--0)A B x x =++22-1245x x =+ …………………12分当=3x 时,1A B 的最小值是33．即D 为AC 中点时, 1A B 的长度最小,最小值为33． …………………14分 17．（本小题共13分）记“甲、乙、丙三人各自破译出密码”分别为事件321,,A A A ，依题意有12311(),(),(),23P A P A P A p ===且321,,A A A 相互独立.（Ⅰ）甲、乙二人中至少有一人破译出密码的概率为121()P A A -⋅1221233=-⨯=. …………………3分（Ⅱ）设“三人中只有甲破译出密码”为事件B ，则有()P B =123()P A A A ⋅⋅＝121(1)233pp -⨯⨯-=， …………………5分所以1134p -=，14p =. ……………………7分（Ⅲ）X 的所有可能取值为3,2,1,0. ……………………8分所以1(0)4P X ==， A 1BCD Exzy(1)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅111312111423423424=+⨯⨯+⨯⨯=， (2)P X ==P 123()A A A ⋅⋅+P 123()A A A ⋅⋅+P 123()A A A ⋅⋅11312111112342342344=⨯⨯+⨯⨯+⨯⨯=， (3)P X ==P 123()A A A ⋅⋅＝111123424⨯⨯= . ……………………11分X 分布列为：X 0 1 2 3 P14 1124 14 124……………………12分所以，1111113()012342442412E X =⨯+⨯+⨯+⨯=. ………………13分 2．（本小题共13分）（Ⅰ）1()=f x a x'- …………………1分 (1)=+1f a -，=(1)=1l k f a '-，所以切线 l 的方程为(1)=(1)l y f k x --，即=(1)y a x -． …………………3分（Ⅱ）令()=()(1-)=ln +1>0F x f x a x x x x --，，则11()=1=(1)()=0=1.F x x F x x x x''--，解得 x)1 , 0(1) , 1(∞+()F x ' +-)(x F↗最大值↘…………………6分(1)<0F ，所以>0x ∀且1x ≠，()<0F x ，()<(1)f x a x -，即函数=()(1)y f x x ≠的图像在直线 l 的下方． …………………8分（Ⅲ）令()=ln +1=0f x x ax -，ln +1=x a x. 令 ln +1()=x g x x ，22ln +11(ln +1)ln ()=()==x x xg x x x x -''-，则()g x 在(0,1)上单调递增，在(1,+)∞上单调递减，当=1x 时，()g x 的最大值为(1)=1g .所以若>1a ，则()f x 无零点；若()f x 有零点，则1a ≤．………………10分若=1a ，()=ln +1=0f x x ax -，由（Ⅰ）知()f x 有且仅有一个零点=1x .若0a ≤，()=ln +1f x x ax -单调递增，由幂函数与对数函数单调性比较，知()f x 有且仅有一个零点（或：直线=1y ax -与曲线=ln y x 有一个交点）.若0<<1a ，解1()==0f x a x '-得1=x a ，由函数的单调性得知()f x 在1=x a处取最大值，11()=ln >0f a a，由幂函数与对数函数单调性比较知，当x 充分大时()<0f x ，即()f x 在单调递减区间1(,+)a ∞有且仅有一个零点；又因为1()=<0af e e -，所以()f x 在单调递增区间1(0)a，有且仅有一个零点.综上所述，当>1a 时，()f x 无零点；当=1a 或0a ≤时，()f x 有且仅有一个零点；当0<<1a 时，()f x 有两个零点. …………………13分 19．（本小题共14分）（Ⅰ）设椭圆的方程为22221x y a b +=，因为32e =，所以224a b =，又因为(4,1)M ，所以221611a b+=，解得225,20b a ==，故椭圆方程为221205x y +=． …………………4分（Ⅱ）将y x m =+代入221205x y +=并整理得22584200x mx m ++-=， 22=(8)-20(4-20)>0m m ∆，解得55m -<<． …………………7分（Ⅲ）设直线,MA MB 的斜率分别为1k 和2k ，只要证明120k k +=．设11(,)A x y ，22(,)B x y ，则212128420,55m m x x x x -+=-=． …………………9分 12122112121211(1)(4)(1)(4)44(4)(4)y y y x y x k k x x x x ----+--+=+=----122112122(1)(4)(1)(4)2(5)()8(1)2(420)8(5)8(1)055x m x x m x x x m x x m m m m m =+--++--=+-+----=---=分子所以直线MA MB 、的斜率互为相反数． …………………14分 20．（本小题共13分）（Ⅰ）显然121,n n n n a n a a a ++=++>对任意正整数都成立，即{}n a 是三角形数列。