第九章频率特性和谐振现象
电磁波谐振现象的原理及应用

电磁波谐振现象的原理及应用引言:电磁波谐振现象是一种重要的物理现象,广泛应用于通信技术、无线能量传输、雷达系统和光学设备等领域。
本文将从原理和应用两个方面,详细介绍电磁波谐振现象的基本原理及其在不同领域中的应用。
一、电磁波谐振的基本原理1. 电磁波的定义和性质电磁波是由交变电场和交变磁场组成的,具有波动性和传播性。
电磁波的性质包括频率、波长、传播速度等。
2. 谐振的概念和条件谐振是指系统在外界激励下出现共振现象的状态。
电磁波的谐振要求外界激励与系统的固有频率相匹配。
3. 电磁波谐振的基本原理电磁波在特定结构中通过时,会与结构的固有频率发生共振。
这种共振现象导致电磁波在结构中传播的幅度增强,形成谐振现象。
4. 电磁波谐振的条件电磁波谐振的条件主要包括谐振腔尺寸、结构材料的介电常数和导电性、外界激励频率等因素。
二、电磁波谐振的应用1. 通信技术中的应用电磁波谐振在通信技术中有着广泛的应用。
例如,天线是无线通信中重要的元件,通过调整天线的尺寸和形状,可以使其与要发送或接收的信号频率达到谐振。
此外,谐振还被用于调频调相,以实现更稳定和高效的信号传输。
2. 无线能量传输电磁波谐振可以实现无线能量传输,如无线充电技术。
通过将发射器和接收器调整到相同的谐振频率,可以实现无线能量的传输。
这种技术被广泛应用于电子产品、医疗设备等领域,方便用户无线充电或供电。
3. 雷达系统雷达系统通过射频脉冲信号与目标物产生反射,通过接收和处理返回信号来检测和跟踪目标。
雷达天线是关键的部件,其目标是与要探测的目标发出或接收所需频率的雷达波信号达到谐振。
谐振技术可以提高雷达系统的灵敏度和精度,提高目标检测的效率。
4. 光学设备在光学领域,电磁波的谐振现象也得到广泛应用。
例如,在光纤通信中,光纤和光纤接入设备需要具备与光波的频率匹配的特性,以实现信号的传输和接收。
此外,在光学传感器中,也可以使用电磁波谐振来实现对特定参数的高灵敏度检测。
rlc串联电路频率特性实验报告

竭诚为您提供优质文档/双击可除rlc串联电路频率特性实验报告篇一:RLc串联电路的幅频特性与谐振现象实验报告_-_4(1)《电路原理》实验报告实验时间:20XX/5/17一、实验名称RLc串联电路的幅频特性与谐振现象二、实验目的1.测定R、L、c串联谐振电路的频率特性曲线。
2.观察串联谐振现象,了解电路参数对谐振特性的影响。
1.R、L、c串联电路(图4-1)的阻抗是电源频率的函数,即:Z?R?j(?L?1)?Zej??c三、实验原理当?L?1时,电路呈现电阻性,us一定时,电流达最大,这种现象称为串?c联谐振,谐振时的频率称为谐振频率,也称电路的固有频率。
即?0?1Lc或f0?12?LcR无关。
图4-12.电路处于谐振状态时的特征:①复阻抗Z达最小,电路呈现电阻性,电流与输入电压同相。
②电感电压与电容电压数值相等,相位相反。
此时电感电压(或电容电压)为电源电压的Q倍,Q称为品质因数,即Q?uLuc?0L11ususR?0cRRc在L和c为定值时,Q值仅由回路电阻R的大小来决定。
③在激励电压有效值不变时,回路中的电流达最大值,即:I?I0?usR3.串联谐振电路的频率特性:①回路的电流与电源角频率的关系称为电流的幅频特性,表明其关系的图形称为串联谐振曲线。
电流与角频率的关系为:I(?)?us1??R2??L???c??2?us0??R?Q2?0??I00??1?Q2?0?2当L、c一定时,改变回路的电阻R值,即可得到不同Q 值下的电流的幅频特性曲线(图4-2)图4-2有时为了方便,常以?I为横坐标,为纵坐标画电流的幅频特性曲线(这称?0I0 I下降越厉害,电路的选择性就越好。
I0为通用幅频特性),图4-3画出了不同Q值下的通用幅频特性曲线。
回路的品质因数Q越大,在一定的频率偏移下,为了衡量谐振电路对不同频率的选择能力引进通频带概念,把通用幅频特性的幅值从峰值1下降到0.707时所对应的上、下频率之间的宽度称为通频带(以bw表示)即:bw??2?1??0?0由图4-3看出Q值越大,通频带越窄,电路的选择性越好。
RLC串联电路的幅频特性和谐振

一、实验目的 ห้องสมุดไป่ตู้、研究RLC 串联电路的幅频特性(也就是谐
振曲线) 2、研究串联谐振现象及电路参数对谐振特性
的影响。
二、实验说明
在RLC串联电路中,阻抗值是:
三 实验内容
测量幅频特性的实验电路如下,信号发生器 输出正弦电压,频率可在20赫到20千赫范 围内变化
四、实验报告要求 1、实验目的 2、原理简述 3、实验内容:含实验步骤、实验电路、表
格、数据等 4、绘制幅频特性曲线。 5、Q值的相对误差分析。
1、测量RLC串联电路的幅频特性I(f),并测出 谐振频率f。
具体方法:采用电阻取样法测定回路电流,取样电 阻采用Ro=10Ω。调整信号源频率,取样电阻两 端接的交流毫伏表指示值最大时,调整信号源幅度, 使Us=1V,重新调整频率使电流最大,此时f即为 f0,电流为I0。Q2>Q1
)
2.改变电阻R=100Ω,重复1
3.改变L==200mH,重复1。计算值,并 测定该值所对应的f值通频带Δf
4.谐 电 上Q振 阻 面值时 档 的的的测公测L电式定的压,,直,看用流此 它毫也值 们伏阻即 的表rQQ(测值 值RL; 误0(或=用 差RC数 有+)字多上r)万大两带用。端入表的 3在3具调电用在 4计实改2改改 调电在改4用调电具具用用33计改在实、 、 、 、 、 、 、R体整流数R算验变变变整流R变数整流体体数数算变R验实实绘研绘实实LLLL方 信 为 字 值 七 电 电 L信 为 L字 信 为 方 方 字 字 值 电 七CCCC==验验制究制验验串法号I万串 ,阻阻号I串万号I法法万万,阻串==0R00R内内幅串幅内内22。。。联:源用联 并RR源联用源::用用并R联LL00CC容容频联频容容===00电采频表电 测频电表频采采表表测电串串111mm::特谐特::000路用率电路 定率路电率用用电电定路HH联联000含含性振性含含, ,ΩΩΩ中电,阻中 该,中阻,电电阻阻该中电电实实曲现曲实实,,,重 重,阻取档, 值取,档取阻阻档档值,路路验验线象线验验重重重复 复阻取样测阻 所样阻测样取取测测所阻的的步 步 。 及 。 步 步复复复11抗样电抗对电抗电样样对抗LLLL幅幅。 。骤骤电骤骤的的的的111值法阻值 应阻值阻法法应值频频、、路、、直直直直是测两是 的两是两测测的是特特实实参实实流流流流:定端: 端:端定定:ff性性值值验验数验验也也也也回接接接回回和和通通电电对电电阻阻阻阻路的的的路路谐谐频频路路谐路路rrrr((((电交交交电电振振带带、、振、、RRRR流流流流流流ΔΔ表表特表表0000ff,毫毫毫,,====格格性格格RRRR取伏伏伏取取++++、、的、、样表表表样样rrrr))))数数影数数电指指指电电带带带带据据响据据阻示示示阻阻入入入入等等。等等采值值值采采上上上上用最最最用用面面面面大大大RRR的的的的ooo时时时===公公公公111,,,式式式式000ΩΩΩ调调调,,,,。。。整整整看看看看信信信它它它它号号号们们们们源源源的的的的幅幅幅QQQQ度度度值值值值,,,误误误误使使使差差差差UUU有有有有sss多多多多===111大大大大VVV,,,。。。。重重重新新新调调调整整整频频频率率率使使使电电电流流流最最最大大大,,,此此此时时时fff即即即为为为fff000,,,
频率特性(ppt 29页)

根据KCL定理,对于上图所示的电路有:
Vo
(gm1 sCgd1)V1 s(CCgd1)G
V1
1/
1/ sCi sCi RS
Vi
由以上两式可以很简单地推导出其传输函数
为:Av(s)(sCi (sRC 1Sg)d1s[(C gm 1C )/gRd1S)G]
19
共源级的频率响应
若
1 G
(Cgd1
C)s
<<1,且
Cgs1 s (1 gm时1),
G
G
则输入阻抗主要是容性的。
然而在更高频率下,由于上式中包含了实部 与虚部,即输入阻抗中有阻性也有容性存在。 实际上若Cgd1较大,则在M1的源极与栅极 间的有一低阻抗通路,使得1/gm1与G均与 输入并联。
25
CMOS增益级频率特性
输出极点。
20
共源级的频率响应
比较以上两种方法求出的零极点的值可以看出,零 点完全相等,而极点并不完全相同,比较两种方法 求得的极点,可以发现输入极点中的分母中多了一
项(Cgd1+C)/G,所以只要该项远小于式中分
母的前两项之和就可近似相等了。 即用密勒电容等效求出的输入极点是一种近似的方
由上式可以看出该电路存在一个零点与两个极
点,其零点是分子为零时的s的值,其值为sz=
gm1/Cgd1。
令上式中的分母为0,可求得两极点分别为:
p 1R S 1 C iR S(C g1s C g 1 1 d (1gm 1/G )
p2
G CCgd1
前一个极点称为输入极点,而后一个极点则为
Vo Vi
ωp1
ωp2 ωz
ω
17
《频率特性》课件

通信系统
通信系统的频率特性决定了信号传输的质量和效率,如调频(FM )和调相(PM)通信。
音频处理
在音频处理中,频率特性用于音频信号的分析、合成和编辑,实现 音频的降噪、均衡和混响效果。
振动控制
在振动控制中,频率特性用于分析机械系统的固有频率和阻尼比, 优化系统的动态性能。
02
频率特性的基础知识
傅里叶变换
解析法
总结词
利用数学解析方法直接求解系统的频 率特性。
详细描述
解析法是一种理论分析方法,通过数 学解析方法直接求解系统的频率响应 。解析法可以获得系统频率特性的精 确解,但需要较强的数学基础和技巧 。
04
频率特性的测量技术
频谱分析仪
1
频谱分析仪是一种常用的测量频率特性的工具, 它可以测量信号的幅度和频率,以及信号的谐波 失真和调制特性等参数。
要定性和性能优化的关 键因素。
要点二
详细描述
在控制系统中,系统的频率特性决定了系统的动态响应和 稳定性。通过分析控制系统的频率特性,可以了解系统的 稳定性和性能优化的潜力。此外,控制系统的频率特性也 是实现系统抗干扰和噪声抑制的重要手段。
THANKS
感谢观看
信号接收器是一种用于接收和测量信号的设备, 它可以测量信号的幅度、频率、相位等参数。
信号发生器和信号接收器通常配合使用,可以对 电子设备进行全面的测试和评估。
05
频率特性的应用实例
通信系统中的频率特性
总结词
通信系统中的频率特性是实现信号传输和接收的关键因素。
详细描述
在通信系统中,信号的传输和接收依赖于频率特性。信号的调制和解调过程需要利用不同频率的信号 特性来实现信号的频谱搬移,从而实现在信道中的有效传输。此外,频率选择性衰落和多径效应等频 率特性也影响信号的传输质量。
第9章 频率特性和谐振现象

谐振在无线电工程、电子测量技术领域应用非常广泛。
9.2 串联谐振电路
一、谐振条件: Im[ Z ] Im[ R j(L 即 L 1 /(C )
1 )] 0 C
+ . U C +. I R U R +. UL +. UC -
谐振角频率: 0
1 LC
-
L、C不变,调节电源频率使 s 0
R +. UR +. UL +. UC Io
Io
主要用于表示电压、电流在谐振点附近的变动情况,
+. + U R I +.. U UL +. -C U -
0.707Io 0.707Io U U
UC
I
I U UL L
UC
Q . . . . U =UR . U =UR I Q越高,通频带越窄
通频带:
33
9.2 串联谐振电路
R
线圈
00
L
2π LC
12 12 2π π 0 0..26 26 10 1033H H 100 100 10 10 F 2 F
U
C
ππ f0 fL 2 π π 990 990 10 1033s 1 0.26 10 1033H H 0L 0 L 22 0L 2
1 LC
调谐:
或电源频率不变,调节L或C使 0 1 s
LC
9.2 串联谐振电路
谐振曲线:电压、电流随频率变化的曲线 可由相应的幅频特性曲线直接画出谐振曲线
U U U U U U R R R ,) I )U ()j ),L ,U L H () U ,U ()j I H (R jH ,U ( j )L U ,j U (C jH ) U I R H () jR U L H (j U U H (j U C C L C C LH CH RR R RR R . U L0 .
谐振电路

1 LC
10 rad / s
7
L/C r
40
Ri
L/C r
40k
0
Q
250k (rad / s )
2)整个回路: o
Qe Q 1 Zo Ri
1 LC
U Z oe I s 20V
10 rad / s
7
3)各支路电流:
IR
i
20
Zo Ri
Z oe
Is U Y
1 r jL r jL r
2
(L)
2
谐振条件:
C
r
L
2
(L)
1 (
2
0
谐振阻抗: 0 Z 特征阻抗:
L/C r
L C
谐振频率:
r L
)
2
LC
0
实际工程中, r , o很高,在 o附近变化,故 0 L
o
2 1
0
Q
六、并联电阻Ri的影响:
0
Q Q0 1 Z0 Ri
1 LC
Z Z0 1
L /C
0
Q
Ri
Z0 Ri
品质因数、谐振阻抗下降;通频带增宽。 Ri :称为展宽电阻
18
例1: 解:
图示谐振电路, 已知Us=12V , 求f0、、Q、f、U、Z0。
L2, C2可调。
谐振条件: 次级电流:
I2 X M I10 R22 R22
X 22 X 22
Z 22 R22 jX 22
Z11 R11 jX11
电机的谐振频率-概述说明以及解释

电机的谐振频率-概述说明以及解释1.引言1.1 概述电机的谐振频率是指在特定条件下,电机产生谐振现象所对应的频率。
谐振是一种物理现象,当系统受到外力激励时,如果其固有频率与外力频率完全或接近地匹配,系统会发生共振现象,这种共振所对应的频率即为谐振频率。
对于电机而言,谐振频率的研究对于了解其工作特性和性能具有重要意义。
电机作为一种能够将电能转换为机械能的装置,在各个行业和领域中起着不可或缺的作用。
然而,由于电机的运行过程中会受到各种因素的干扰,如电压变化、负载波动等,导致电机可能产生谐振现象。
当电机处于谐振状态时,其振动幅度会迅速增大,严重影响了电机的正常运行和稳定性。
本文旨在对电机的谐振频率进行详细介绍和分析。
首先,我们将探讨电机谐振现象的特点和机制,了解电机在何种情况下容易发生谐振。
其次,我们将给出谐振频率的定义和计算方法,以便于更好地理解和研究电机的谐振现象。
最后,我们还将讨论影响谐振频率的因素,并探讨电机谐振频率的应用和意义。
通过对电机谐振频率的研究,我们可以更好地了解电机的工作原理和特性,帮助我们设计和选择适合的电机,提高其工作效率和稳定性。
同时,对于电机维护和故障诊断方面也有一定的指导意义。
因此,深入研究电机的谐振频率对于电机相关行业和领域具有重要的理论意义和应用价值。
1.2 文章结构文章结构部分旨在介绍本文的整体组织结构和各个章节之间的逻辑关系。
通过清晰地呈现文章的架构,读者能够更好地理解和掌握文章的内容。
本文共分为引言、正文和结论三个部分。
在引言部分,我们会提供概述、文章结构和目的的内容介绍。
正文部分将详细讨论电机的谐振现象和谐振频率的定义。
结论部分将总结影响谐振频率的因素,并探讨谐振频率在实际应用中的意义。
首先,在引言部分的概述中,我们将简要介绍电机的谐振频率是什么以及为什么它很重要。
同时,我们还会提及电机谐振频率的实际应用和研究背景,为读者建立起对这一主题的基本认识。
接下来,在引言部分的文章结构中,我们将简要描述整个文章中各个章节的内容组成。
第9章 频率特性和谐振现象

例题
9.2
求得品质因数为 由公式 c1 0
Q
0 f 0 10 f
1 1 和 c2 0 1 2 2Q 4Q
1 1 1 2Q 4Q 2
可求得:
1 1 C 79.6nF 4 -1 QRω0 10 20Ω (2π 10 )s
Uc
U
1/ jωC 1 R 1/ jωC 1 jωRC
令
则:
H ( jω )
θ (ω)
45
90
1
2
3
4
5 ω / ω0
1 0.7
1
2
3
4
5 ω / ω0
上图所示的幅频特性具有允许低频信号通过,而 抑制(阻碍)高频信号的特点,因此称为低通滤 波器。 在低通滤波器中, 称为截止频率,低于 截止频率的称为通(频)带,高于截至频率的频 率称为阻带。 选用不同的电路结构和不同的元器件参数,可分 别构成高通、带通、带阻滤波器。
转移阻抗 (transfer impedance) 转移导纳 (transfer admittance) 转移电压比 (transfer voltage ratio) 转移电流比 (transfer current ratio)
RC电路如图所示,其网络函数为:
R
H ( jω)
Uc
U
1/ jωC 1 R 1/ jωC 1 jωRC
U
j
1 C
Uc
写成极坐标形式:
H ( jω) H ( jω) ψc ψ 上式中: H( jω) Uc / U θ (ω) ψc - ψ 幅频特性 相频特性
频率特性和谐振现象

Q1 < Q2 < Q3
Q 1
Q2
Q3
O
1
η = ω / ω0
第九章 频率特性和谐振现象
UR /U
Q1 < Q2 < Q3
Q 1 Q2
电路选择性的优 劣取决于对非谐振频率 的输入信号的抑制能力 抑制能力。 的输入信号的抑制能力。
O 1
Q3
η = ω / ω0
Q值大,曲线在谐振点附近的形状尖锐, 值大,曲线在谐振点附近的形状尖锐, 值大 当稍偏离谐振频率,输出就急剧下降, 当稍偏离谐振频率,输出就急剧下降, 说明对非谐振频率的输入具有较强的抑制能力, 说明对非谐振频率的输入具有较强的抑制能力, 选择性能好 选择性能好。 反之, 值小 在谐振频率附近曲线顶部形状平缓, 值小, 反之,Q值小,在谐振频率附近曲线顶部形状平缓, 选择性就差 选择性就差。
1 ω 0C I L (ω 0 ) I C (ω 0 ) 1 C = Q= = = = ω 0 LG IS IS G G L
如果Q>>1,则谐振时在电感和电容中会出现过电流, ,则谐振时在电感和电容中会出现过电流, 如果 但从L、 两端看进去的等效电纳等于零 两端看进去的等效电纳等于零, 但从 、C两端看进去的等效电纳等于零, 即阻抗为无限大, 即阻抗为无限大, 相当于开路 开路。 相当于开路。
的电动势信号; 的电动势信号; 选出所需的电台。 L 2 - C 组成谐振电路 ,选出所需的电台。
e1 e2 e3
C
第九章 频率特性和谐振现象
问题:如果要收听 e 节目,C 应配多大? 1 节目, 应配多大?
已知: 已知:
R L2 L2
L2 = 250µH、 RL2 = 20Ω
2-2谐振与频率特性

R uR uL uC L C
UL
I U UR
UC ü 串联谐振 ~ 电压谐振
Ø 谐振(串联谐振能量)
ü 定义:i (t ) = 2 I sin ω t 则串联谐振时的电感电流和电容电压分别为: iL (t ) = 2 I sin ω 0 t I u Z
i
R uR uL uC L C
ω 0C 因此,电感和电容上的能量分别为: 1 2 1 2 2 2 2 WL = Li = LI ⋅ sin ω 0 t , WC = C u C = CU C ⋅ cos 2 ω 0t 2 2 1 2 由于 ω 0 = ,所以: LI 2 = CU C (常数) LC
因此,当 ω 0 = 1 LC 时,电路发生串联谐振。
ω0
容性 感性
ω
C 右图所示电路,分析其谐振参数。 u C1 L
解:等效导纳为 Y = jB = jω C1 +
1 1 + jω C jω L
X
因此,当 ω 1 =
ω 2 LCC1 − (C + C1 ) = j 1 2 (ω LC − 1) ω0 ω1 ω ω 1 时,电路发生并联谐振。 CC1 L 容性 感性 容性 C + C1
i
R uR uL uC L C
ρ = ω0L = ü 特征阻抗:谐振时的电抗(感抗或容抗):
1 L = ω 0C C ω 0L R = 1 ω 0 CR
Q= ü 品质因数:谐振时的电抗(感抗或容抗)与电阻之比: (电抗电压/电阻电压、电抗无功功率/电阻有功功率)
Ø 谐振(串联谐振特点)
ü 纯电阻特性,LC 相当于短路。 Z = Z min = R 电流 I 和电压 UR 达极大值,电路消耗最大功率值。 ü 相量关系(右图): & L和U & C大小相等,方向相反; U 谐振时, & =U &R +U &L +U &C = U &R = I &R U ü 电感和电容电压可能很大, 但由于两者的无功电压正好抵消, 所以整体电路的无功分量为零。 Z u
频率特性和谐振现象(精)

分析(二):
提取信号
E N
I L1
E S
L1
C
谐振 滤波器
L2
接 收 网 络
I C
U C I
I C
fS f N
I L1
I L2
U C
U L1
U L1
U 0 若在 f S 下 U C L1 则信号全部降落在接收网络上。
L2
第九章 频率特性和谐振现象
二、串联谐振的定义
由于串联电路中的感抗和容抗有相互抵消作用, 所以,当ω=ω0时,出现X(ω0)=0, 这时端口上的电压与电流同相, 工程上将电路的这种工作状况称为谐振, 由于是在RLC串联电路中发生的,故称为串联谐振。
三、串联谐振的条件
1 Z ( j ) R j (L ) C
第九章 频率特性和谐振现象
六、谐振曲线
除了阻抗 Z 和频率的特性外,还应分析电流和电 压随频率变化的特性,这些特性称为频率特性,或称 频率响应,它们随频率变化的曲线称为谐振曲线。
I( ω )
O
0
ω
第九章 频率特性和谐振现象
七、品质因数
谐振时有 U L U C 0 所以串联谐振又称为电压谐振。
CQ U 1 2 2 CQ U m 2
2 2
= 常量
另外还可以得出
Q 0W (0 ) / P(0 )
串联电阻的大小虽然不影响串联谐振电路的固有频率,
但有控制和调节谐振时电流和电压幅度的作用。
第九章 频率特性和谐振现象
九、通用谐振曲线
为了突出电路的频率特性,常分析输出量与输入 量之比的频率特性。
一、RLC 串联电路 jL I R
频率特性理解
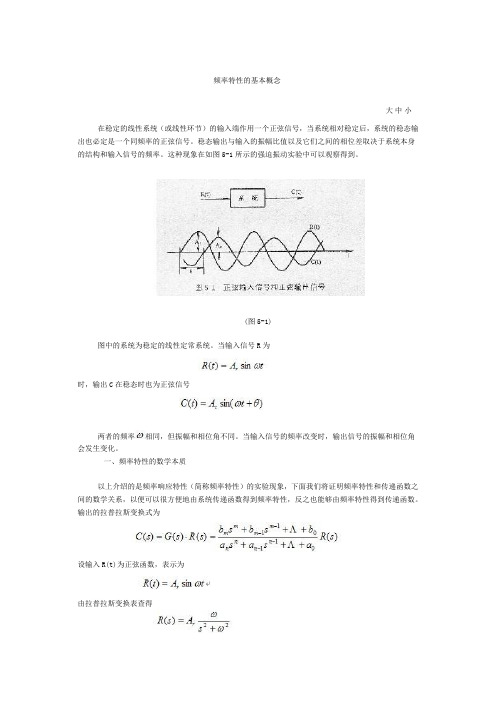
频率特性的基本概念大中小在稳定的线性系统(或线性环节)的输入端作用一个正弦信号,当系统相对稳定后,系统的稳态输出也必定是一个同频率的正弦信号。
稳态输出与输入的振幅比值以及它们之间的相位差取决于系统本身的结构和输入信号的频率。
这种现象在如图5-1所示的强迫振动实验中可以观察得到。
(图5-1)图中的系统为稳定的线性定常系统。
当输入信号R为时,输出C在稳态时也为正弦信号两者的频率相同,但振幅和相位角不同。
当输入信号的频率改变时,输出信号的振幅和相位角会发生变化。
一、频率特性的数学本质以上介绍的是频率响应特性(简称频率特性)的实验现象,下面我们将证明频率特性和传递函数之间的数学关系,以便可以很方便地由系统传递函数得到频率特性,反之也能够由频率特性得到传递函数。
输出的拉普拉斯变换式为设输入R(t)为正弦函数,表示为由拉普拉斯变换表查得故部分分式中及B、D均为待定系数。
对于一个稳定的系统,由于特征方程的所有特征根均具有负实数部分,的第一个分量总是随着t的增长逐渐消失,系统最终将以作稳态运动。
上式恰恰是我们需要求解的,其中系数由上式得到同理将系数B、D代入,则式中Im为G(jω)的虚部,Re为G(jω)的实部。
而输出端响应的振幅和输入端的振荡之比为输出端响应和输入端的相位差为由此可见,作用有正弦输入时的稳定线性定常系统,输出响应具有与输入同一频率的正弦稳定信号。
但是输出的振幅和相位角通常不等于输入量的振幅和相角,输出响应的振幅是输入量的倍,输出响应和输入量相位差为。
因此,系统的频率特性可以直接由G(jω)表示,系统的频率特性为式中是ω的函数,称为幅频特性,也是频率特性的模;是ω的函数,称为相频特性。
在上述数学推导中,我们可以清楚地看到所以,在已知系统或环节的传递函数时,只要令,就可以很方便地得到系统或环节的频率特性。
为了进一步说明频率特性的意义,现以图5-2所示的R-C电路为例。
图5-2频率特性可通过传递函数来求取,当电容两端电压uc为输出量,输入电压ui为输入量时,传递函数可用复阻抗串联的知识求取式中 T=RC频率特性只要将S以jω代替,频率特性为幅频特性(模)为相频特性(幅角)为当ui以低频信号输入时();这表明,当输入正弦电压ui的频率很低,则输出电压uc的振幅与的振幅几乎相等,相位近似同相。
第九章 其他一些特殊的滤波器

为测试陷波器的特性,令 xs ( n ) = 2δ ( n − 200) ,由
x ( n ) = x (t )
t = nT
= sin(100 π nT ) + x s ( n )
可得数字陷波器的输入信号波形如下图。
返回
(a) 输入信号波形
(b) 陷波器输出波形
返回
9.3 全通滤波器
定义:滤波器的幅频特性在整个频带[0~ 定义:滤波器的幅频特性在整个频带[0~2π]上均等于常 [0 或者等于1 数,或者等于1,即 H ( e jw ) = 1, 0 ≤ w ≤ 2π 则该滤波器称 为全通滤波器。 为全通滤波器。 特点: 特点:信号通过全通滤波器后,其输出的幅度特性保持不 变,仅相位发生变化。 全通滤波器的系统函数的一般形式为:
举例 w0 = π 3 ,r =0.8, 0.95,画出零极点分布和幅度特性 如下图:
(a) 零极点分布
(b) 幅度特性
与前面不同处: 与前面不同处: 1、谐振频率有微小的变化 、 2、带宽略小 、 3、在 w0 = 0, π , −π 处的幅度为 处的幅度为0 、
返回
例5.5 模拟信号 x(t ) = sin 7t + sin 200t,设计一个数字 谐振器,以滤除模拟信号中的低频分量sin7t。 解: 谐振器的谐振频率放在200 : 采样间隔 T = 0.002s 模拟频率200对应的数字频率是: 200×0.002 = 0.4 模拟频率7对应的数字频率是: 7×0.002=0.014 选择带宽0.02,则2(1 - r)=0.02, r=0.99。 得到系统函数为:
(
1 − re jw0 z −1 1 − re− jw0 z −1
)(
b0
电路的谐振知识点总结

电路的谐振知识点总结一、谐振的概念谐振是指当一个物体受到外部的周期性作用力时,产生的振动频率与外力频率相同的现象。
在电路中,谐振是指当电路中的电感和电容元件与外部的交流电源频率相同时,电路呈现出大幅度的振荡现象。
二、谐振的条件1. 电路中需要包含电感和电容元件。
在电路中,电感元件和电容元件是谐振的基础。
电感元件是由线圈等组成,具有储存能量的特性。
而电容元件是由两个导体之间的绝缘物质组成,具有储存电荷的特性。
通过电感和电容的组合,可以构建出能够产生谐振现象的电路。
2. 电路中需要有交流电源作为激励信号。
在谐振电路中,交流电源是谐振的激励信号。
只有当外部交流电源的频率与电路中的谐振频率一致时,电路才能呈现出谐振现象。
三、谐振的分类1. 串联谐振电路串联谐振电路是由电感元件、电容元件和交流电源串联而成的电路。
在串联谐振电路中,电感和电容元件的等效电阻为0,电路中的阻抗呈现出最小值,电压和电流呈现出峰值。
2. 并联谐振电路并联谐振电路是由电感元件、电容元件和交流电源并联而成的电路。
在并联谐振电路中,电感和电容元件的等效电阻为无穷大,电路中的电流呈现出最小值,阻抗呈现出最大值。
四、谐振的频率在谐振电路中,谐振的频率是指使电路呈现出谐振现象的特定频率。
谐振频率与电感和电容元件的参数有关,可以通过以下公式计算:f=1/2π√(LC)其中,f表示谐振频率,L表示电感元件的电感值,C表示电容元件的电容值,π表示圆周率。
五、谐振的特性1. 电路阻抗的变化在串联谐振电路中,当频率与谐振频率相同时,电路中的阻抗呈现出最小值。
而在并联谐振电路中,当频率与谐振频率相同时,电路中的阻抗呈现出最大值。
2. 电压和电流的特性在串联谐振电路中,当频率与谐振频率相同时,电压呈现出峰值,电流也呈现出峰值。
而在并联谐振电路中,当频率与谐振频率相同时,电压呈现出最小值,电流也呈现出最小值。
3. 能量的传递在谐振电路中,能量的传递是通过电感和电容元件之间的振荡来实现的。
RLC串联电路的幅频特性和谐振

)
2.改变电阻R=100,重复1 2.改变电阻 改变电阻R=100,重复1 3.改变L==200mH,重复1。计算值,并 3.改变 改变L==200mH,重复1 计算值, 测定该值所对应的f值通频带f 测定该值所对应的f值通频带f 4.Q值的测定 用毫伏表测L(或C)上两端的 4.Q值的测定, 用毫伏表测L(或C)上两端的 值的测定, 谐振时的电压,此值即Q 谐振时的电压,此值即Q值;用数字万用表 电阻档测L的直流也阻r R0=R+r) 电阻档测L的直流也阻r(R0=R+r)带入 上面的公式,看它们的Q值误差有多大。 上面的公式,看它们的Q值误差有多大。
实验七 RLC串联电路的幅频特性和谐振 RLC串联电路的幅频特性和谐振
一、实验目的 l、研究RLC 串联电路的幅频特性(也就是谐 研究RLC 串联电路的幅频特性( 振曲线) 振曲线) 2、研究串联谐振现象及电路参数对谐振特性 的影响。 的影响。
二、实验说明
在RLC串联电路中,阻抗值是: RLC串联电路中 阻抗值是: 串联电路中,
三 实验内容
测量幅频特性的实验电路如下,信号发生器 测量幅频特性的实验电路如下, 输出正弦电压,频率可在20赫到 千赫范 赫到20 输出正弦电压,频率可在20赫到20千赫范 围内变化
1、测量RLC串联电路的幅频特性I(f),并测出 测量RLC串联电路的幅频特性 串联电路的幅频特性I ),并测出 谐振频率f 谐振频率f。 具体方法:采用电阻取样法测定回路电流, 具体方法:采用电阻取样法测定回路电流,取样电 阻采用Ro=10。调整信号源频率, 阻采用Ro=10。调整信号源频率,取样电阻两 端接的交流毫伏表指示值最大时,调整信号源幅度, 端接的交流毫伏表指示值最大时,调整信号源幅度, Us=1V,重新调整频率使电流最大,此时f 使Us=1V,重新调整频率使电流最大,此时f即为 f ,电流为I 。Q2>Q1 电流为I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+ U −
R
jL
1 jC
+ U −
C
RLC串联电路
C ( ) = − arctan
Q(
C ( )
Q=2 Q =1
1
0 − ) 0
/0
对应不同品质 因数的频率特 性曲线如图:
2
| H C ( j ) |
1
2
Q = 0 .7
O
Q =பைடு நூலகம்0 .7
1
− 90
Q =2
第九章 频率特性和谐振现象
本章目录 1 网络函数和频率特性 2 RLC串联电路的频率特性 3 串联谐振电路 4 并联谐振电路
2018/11/7
第9章 频率特性和谐振现象
1
§9.1 网络函数和频率特性
x(t )
线性 无独 立源 (a)时域分析
+ u −
i
X
y (t )
线性 无独 立源
U
+ −
I
Y
(b)频域分析
1 网络函数的定义: 电路在单一激励作用下,响应相量与 激励相量之比称为网络函数,即
Y H ( j ) = X
def
2018/11/7
第9章 频率特性和谐振现象
2
§9.1 网络函数和频率特性
2 网络函数分类: (1)激励和响应属于同一端口
I s
+
U
−
线性 无独 立源
4
( ) = C −
2018/11/7
第9章 频率特性和谐振现象
§9.1 网络函数和频率特性
U 1 / j C 1 H ( j ) = = = U R + 1 / jC 1 + jCR
C
式中 RC 之积具有时间的量纲,其倒数具 有频率的量纲,设
+ U −
R
C
+ U −
称为RLC串联电路的谐振角频率(resonance angular frequency) 。 令 = 0 L = 1 / 0C =
L C
1 LC
称为RLC串联电路的特性阻抗( characteristic impedance)。 1 L 0 L 1 又令 Q = = 进而有 Q = = R R C R R 0 C 称为RLC串联电路的品质因数(quality factor)。
15
§9.3 串联谐振电路
1 定义:对于含有电感和电容的一端口电路,如
+ U L −
果在一定条件下呈现电阻性,即端口电压与电流
同相位,则称此一端口电路发生谐振。
+ U −
I
j L
1 jC
+ −U C
R
+ U −
R
右图为RLC串联谐振电路。
根据谐振定义,RLC串联电路发生谐振的条件是: 1 Im[ Z ] = Im[ R + j(L − )] = 0 即 L = 1 /( C ) C
L ( )
180
| H L ( j ) |
2
Q=2 Q =1
对应不同品质 因数的频率特 性曲线如图:
Q = 0 .7
1
Q = 0 .7
90
Q =1
Q=2
0
/0
2
o
1
(a)幅频特性
2 /
o
1
(b)相频特性
以电感电压为响应的网络函数频率特性曲线
2018/11/7
第9章 频率特性和谐振现象
5
§9.1 网络函数和频率特性
+ U −
R
C
H ( j ) = = ( −arctan ) 2 1 + j / 0 0 1 + ( / 0 )
1 1
+ U −
C
RC串联电路
模和辐角与角频率的对应关系表
/0
0 1 2 |H(j)| 1 1/ 2 1/ 5
()
0° -45° -63.43°
第9章 频率特性和谐振现象
越小,通带越窄,曲线越尖锐,对信号的选择性越好。
2018/11/7 12
§9.2 RLC串联电路的频率特性
例9.2 设计 RLC 带通滤波器电路,已知总电阻为R=20,要求谐振 频率为 f0 =104Hz,带宽为 f =103Hz,,求电感L和电容C的值以及低 频截止频率和高频截止频率。 0 f0 Q = = = 10 品质因数为 解 f 进一步求得:
R ( )
1
/0
O c1 c 2
1
/0
(a)幅 频 特 性
O
− 90
0 0
(b)相 频 特 性
2018/11/7
第9章 频率特性和谐振现象
11
§9.2 RLC串联电路的频率特性
求截止角频率:
令
1 = 2 2 C 0 1+ Q2 − C 0
Q =1
O
1
2
(a)幅频特性
/0
− 180
(b)相频特性
2018/11/7
第9章 频率特性和谐振现象
14
§9.2 RLC串联电路的频率特性
3 以电感电压为响应,其转移电压比为: U j L H L ( j ) = L = R + jL + 1 /( jC ) U 则其幅频特性和相频特性分别为 :
2018/11/7
第9章 频率特性和谐振现象
13
§9.2 RLC串联电路的频率特性
2 以电容电压uC为响应,有 U 1 /( jC ) H C ( j ) = C = U R + jL + 1 /( jC ) 幅频特性和相频特性分别为
| H C ( j ) |= 1
2 2 1 1 − + Q2 0 0 2
/U 转移电压比 H ( j ) = U S
第9章 频率特性和谐振现象 3
2018/11/7
§9.1 网络函数和频率特性
在图示 RC 电路中,若以电容电压为响应, 以输入电压为激励,其网络函数为: + U 1 / j C 1 U H ( j ) = = = R + 1 / jC 1 + jCR U −
RLC串联谐振电路
改变电源频率,或改变电感,或改变电容均可实现串联谐振。 在给定电感和电容时,电路的谐振角频率为
0 =
1 LC
16
2018/11/7
第9章 频率特性和谐振现象
§9.3 串联谐振电路
RLC串联电路的电流、电感电压和电容电压 分别为 U U R = I = H R ( j ) R R = H ( j )U U C C
C
1 0 = RC
RC串联电路
称其为 RC 电路的固有频率或自然频率(natural frequency) 代入网络函数表达式得 1 1 H ( j ) = = ( −arctan ) 1 + j / 0 0 1 + ( / 0 ) 2
2018/11/7
第9章 频率特性和谐振现象
1
由上式求得两个截止角频率:
1 1 1 1 C 1 = 0 − + +1 C 2 = 0 + +1 2 2 2 Q 4 Q 2 Q 4 Q 通带宽度、谐振角频率和品质因数的关系:
0 = C 2 − C 1 = Q 这说明带宽 与品质因数 Q 成反比,Q 越大,
(2) 电流方面
XC
达到最大值。
电抗频率特性曲线
1 = j LI U (3) 电压方面 U I0 L 0 0 C = −j 0C 特性阻抗和品质因数为
U L U C =U U R I 0
= 0 L = 1 /( 0 C )
代入上式得 2018/11/7
U
O
1
2
/0
=U U R
(b) 谐振时相量图
(a) 谐振曲线
2018/11/7
第9章 频率特性和谐振现象
17
§9.3 串联谐振电路
2 串联谐振的特点
(1) 阻抗方面
X XL X= XL+ XC O
0 L = 1 /( 0C )
0
谐振时,感抗与容抗相抵消,串联电路呈电阻性。
U 此时串联电路电流为: I 0 = R
2018/11/7 第9章 频率特性和谐振现象 10
§9.2 RLC串联电路的频率特性
+ U −
jL
1 jC
R
+ U −
R
U R R H R ( j ) = = U R + j[L − 1 /(C )]
RLC串联电路
将谐振角频率和品质因数引入上式,写出其幅频特性和相频特性:
+ U L −
+ U −
I
j L
1 jC
R
+ U −
R
= H ( j )U U L L
+ −U C RLC串联谐振电路
由上三式,可画出电流 I 和电压UC、UL随频率变动的曲线[下图 (a)],以及谐振时的相量图[下图(b)](以电流为参考相量)
I
UC
UL
U L U C I 0
2018/11/7 第9章 频率特性和谐振现象 7
§9.1 网络函数和频率特性
使用不同电路还可以实现具有下列特性的网络
