勾股定理之最短路径(填空选择)中考题
中考数学复习《勾股定理求最短路径》专项检测卷-附带答案

中考数学复习《勾股定理求最短路径》专项检测卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.如图,一牧童在A处牧马,牧童家在B处,A、B处距河岸的距离AC、BD的长分别为500m和700m,且C、D两地的距离为500m,天黑前牧童从A点将马牵引到河边去饮水后,再赶回家,那么牧童至少要走()A.2900m B.1200m C.1300m D.1700m2.如图,圆柱体盒子放在水平地面上,该圆柱体的高为9cm,点M离盒底的距离为3cm,cm,一只蚂蚁沿着该圆柱体盒子的表面从点M爬行到点N,则该蚂蚁爬行的最底面半径为8π短路程为()cm.A.6B.10C.2√73D.6+16π3.如图是一个三级台阶,它的每一级的长,宽,高分别是20dm,3dm,2dm,A和B是这个台阶相对的端点,点A处有一只蚂蚁,想到B处去吃食物,则这只蚂蚁爬行的最短距离为()A.25dm B.26dm C.24dm D.27dm4.如图是放在地面上的一个长方体盒子,其中AB=7,BC=4,BF=6点M在棱AB上,且AM=1,点N是FG的中点,一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为()A.10B.4√5C.6√2D.2√135.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为()m.(π取3)A.30B.28C.25D.226.如图,在等腰直角△ABC中AB=BC=4,点D在边BC上且CD=1,点E,F分别为边AB,AC上的动点,连接DE,EF,DF得到△DEF,则△DEF周长的最小值为()A.5√2B.2√13C.3√7D.√6+2√27.如图,在RtΔABC中∠ACB=90°,AC=10,BC=12点D是ΔABC内的一点,连接AD,CD,BD满足∠ADC=90°,则BD的最小值是()A.5B.6C.8D.13S矩形ABCD则点P 8.如图,在矩形ABCD中AB=5 AD=3.动点P满足S△PAB=13到A B两点的距离之和P A+PB的最小值为()A.√29B.√34C.√41D.√529.已知圆锥底面半径为1 母线长为4 地面圆周上有一点A一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线P A中点B则蚂蚁爬行的最短路程为()A.πB.√5πC.2√5D.2π10.如图△ABC为边长3的等边三角形AD△BC于点D点E在AB边上且AE=1 P为线段AD上的一个动点则PB+PE的最小值是()√3 A.3B.√7C.√3D.3211.如图在一个长为9m宽为6m的长方形草地上放着一根长方体木块它较长的边和草地的宽AD平行且长大于AD木块从正面看是边长为1m的正方形一只蚂蚁从点A出发到达点C处需要走的最短路程为()A.12m B.√157m C.6√5m D.13m12.如图矩形ABCD中AB=4BC=6以A为圆心2为半径画圆A E是圆A 上一动点P是BC上一动点则PE+PD最小值是()A.4√2B.2√10C.8D.1213.如图正方形ABCD中AB=4点E F分别在边AB BC上点P在对角线AC上EF∥AC PE+PF=m.下列结论错误..的是()A.若BE=2则m的最小值为4B.若m的最小值为4 则BE=2C.若BE=0.5则m的最小值为5D.若m的最小值为5 则BE=0.5 14.数形结合是数学的重要思想和解题方法如:“当0<x<12时求代数式√x2+4+√(12−x)2+9的最小值” 其中√x2+4可看作两直角边分别为x和2的Rt△ACP的斜边长√(12−x)2+9可看作两直角边分别是12−x和3的Rt△BDP的斜边长.于是将问题转化为求AP+BP的最小值如图所示当AP与BP共线时AP+BP为最小.请你解决问题:当0<x<4时则代数式√x2+1+√(4−x)2+4的最小值是()A.4B.5C.6D.715.如图有一条直角弯道河流河宽为2 A B两地到河岸边的距离均为1 AH= BF=1AD=7BE=9现欲在河道上架两座桥MN PQ使AM+MN+NP+PQ+QB最小则最小值为()A.√130B.√145+2C.14D.1216.如图平行四边形ABCD中AB=12AD=10∠A=60°E是边AD上一点且AE=6F是边AB上的一个动点将线段EF绕点E顺时针旋转60°得到EN连接BN CN则BN+CN的最小值是()A.3√21B.4√14C.14D.4√1317.如图在平面直角坐标系xoy中点A C分别在坐标轴上且四边形OABC是边长(x>0)的图像与BC,AB边分别交于E,D两点△DOE 为3的正方形反比例函数y=kx的面积为4 点P为y轴上一点则PD+PE的最小值为()A.3B.2√5C.3√2D.518.如图在平面直角坐标系中点A(3,a)是直线y=2x与直线y=x+b的交点点B 是直线y=x+b与y轴的交点点P是x轴上的一个动点连接P A PB则PA+PB 的最小值是()A.6B.3√5C.9D.3√1019.如图已知正方形ABCD的边长是4 点E是AB边上一动点连接CE过点B 作BG△CE于点G点P是AB边上另一动点则PD+PG的最小值是()A.2√10−2B.4√3−2C.2√13−2D.2√14−220.如图① 在正方形ABCD中点E是AB的中点点P是对角线AC上一动点设PC=x PE+PB=y图②是y关于x的函数图象且图象上最低点Q的坐标为(m,2√5)则正方形ABCD的边长为()A .2√2B .2√5C .4D .5参考答案1.解:如图 由题意得:DB ⊥CD AC ⊥CD A ′C =AC =500m BD =700m CD =500m作A 点关于河岸的对称点A ′ 连接BA ′交河岸与P 则PB +P A =PB +P A ′=BA ′时最短 过点A ′ 作A ′B ′⊥BD 交BD 延长线于点B ′△四边形A ′B ′DC 是矩形△A ′B ′=CD =500m DB ′=A ′C =500m△BB ′=BD +DB ′=1200m在Rt △A ′B ′B 中 BA ′=√BB ′2+A ′B ′2=√12002+500=1300m .故选:C2.解:把圆柱侧面展开 展开图如图所示 点M N 的最短距离为线段MN 的长 △AM =9﹣3=6(cm ) AN 为底面半圆弧长 AN =2×12•8π•π=8(cm )在Rt△AMN 中MN =√AM 2+AN 2=√62+82=10(cm ).故选:B .3.解:三级台阶平面展开图为长方形长为20dm 宽为(2+3)×3dm则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B点最短路程为x dm由勾股定理得:x2=202+[(2+3)×3]2=252解得x=25.故选:A.4.解:如图1中把面ABFE与面EFGH沿EF展开∵AM=1,AB=7,BC=4,BF=6,点N是FG的中点∴MB=6,FN=2,BN=BF+FN=8,∴MN=√MB2+BN2=10,如图2 把面ABFE与面BCGF沿BF展开同理可得:MP=8,PN=BF=6,∴MN=√MP2+PN2=10,如图3 把面ABCD与面BCGF沿BC展开同理:MF=MB+BF=12,FN=2,∴MN=√122+22=√148=2√37,∵10=√100<√148=2√37,所以一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N它需要爬行的最短路程为10.故选:A.5.解:其侧面展开图如图:作点C关于AB的对称点F连接DF△中间可供滑行的部分的截面是半径为2.5cm的半圆△BC=πR=2.5π=7.5cm AB=CD=20cm△CF=2BC=15cm在R t△CDF中DF=√CF2+CD2=√152+202=25cm故他滑行的最短距离约为25cm.故选C.6.解:如图作点D关于AB的对称点G作点D关于AC的对称点H连接BG CH DH FH GH∵∠ABC=90°点D与点G关于AB对称∴∠GBE=∠ABC=90°∴G B D C在同一条直线上△在等腰直角△ABC中AB=BC△∠A=∠ACB=45°△BC=4CD=1△由对称性可知:GB=DB=3CH=CD=1∠FCH=∠FCD=45°FH=FD EG=ED∴∠HCG=90°GC=GB+BD+DC=3+3+1=7∴GH=√GC2+CH2=√72+12=5√2∴DE+EF+FD=GE+EF+FH⩾GH=5√2∴△DEF的周长的最小值5√2.故选:A.7.解:如图取AC中点O连接DO.∵∠ADC=90°∴点D在以点O为圆心AC长为直径的圆周上运动且DO=12AC=12×10=5当O D B在同一直线上时OB最短此时BD=OB−OD=OB−5为最短.在RtΔOCB中OC=5BC=12则OB=√122+52=13∴BD=OB−OD=OB−5=13−5=8即BD的最小值是8.故选:C.8.解:设ΔABP中AB边上的高是ℎ.∵SΔPAB=13S矩形ABCD∴12AB⋅ℎ=13AB⋅AD∴ℎ=23AD=2∴动点P在与AB平行且与AB的距离是2的直线l上如图作A关于直线l的对称点E连接AE连接BE则BE的长就是所求的最短距离.在RtΔABE中∵AB=5AE=2+2=4∴BE=√AB2+AE2=√52+42=√41即PA+PB的最小值为√41.故选:C.9.解:根据题意将该圆锥展开如下图所示的扇形则线段AB就是蚂蚁爬行的最短距离.△点B是母线P A的中点PA=4△PB=2△圆锥的底面圆的周长=扇形的弧长又△圆锥底面半径为1△扇形的弧长=圆锥底面周长即l=2πr=2π扇形的半径=圆锥的母线=P A=4由弧长公式可得:l=nπR180=nπ×4180=2π△扇形的圆心角n=90°在Rt△APB中由勾股定理可得:AB=√PA2+PB2=√42+22=2√5所以蚂蚁爬行的最短路程为2√5故选:C.10.解:作E关于AD的对称点E′连接BE′交AD于P则此时PE + PB有最小值PE+ PB的最小值=BE′△AE′= AE= 1△ CE'=3-1=2作E'F△BC于F△△ABC为等边三角形△C= 60°△∠CE′F=30°△CF=12CE′=1 E′F=√CE′2−CF2=√22−12=√3△AC= BC= 3△BF=3-1= 2BE′=√BF2+E′F2=√22+(√3)2=√7△PE+ PB的最小值=√7故选:B11.解:由题意可知将木块展开如图长相当于是AB+2个正方形的宽△长为9+2×1=11(m);宽为6 m.于是最短路径为:√62+112=√157(m).故选B.12.解:如图作点D关于直线BC的对称点F连接AF交BC于点P交⊙A于点E此时PE+PD最小等于AF−AE△四边形ABCD是矩形AB=4BC=6△AB=CD=4AD=BC=6△DF=8∠ADF=90°△AF=√AD2+DF2=√62+82=10△AE+EF=10△EF=10−2=8△PE+PD的最小值为8故选C.13.解:如图根据正方形的对称性在AD上取点E关于AC的对称点G连接FG交AC 于点P则PE=PG△PE+PF=PG+PF=FG为m的最小值△AG=AE=4−BE∠BAD=90°△EG2=AE2+AG2=2AE2=2(4−BE)2△EF∥AC△∠BEF=∠BAC=45°∠BFE=∠BCA=45°△BF=BE△EF2=BE2+BF2=2BE2△FG⊥AC△EG⊥EF△∠FEG=90°△FG=√EF2+EG2=2√(BE−2)2+4当BE=2时FG=2√(2−2)2+4=4△A正确;当FG=4时2√(BE−2)2+4=4△√(BE−2)2+4=2△(BE−2)2+4=4△(BE−2)2=0△BE=2△B正确;当BE=0.5时FG=2√(0.5−2)2+4=5△C正确;当FG=2√(BE−2)2+4=5时(BE−2)2+4=254△(BE−2)2=94△BE−2=±32△BE=0.5,或BE=3.5△D不正确.故选:D.14.解:如图所示√x2+1可看作两直角边分别为x和1的Rt△ACP的斜边长√(4−x)2+4可看作两直角边分别是4−x和2的Rt△BDP的斜边长.△求√x2+1+√(4−x)2+4的最小值即求AP+BP的最小值当AP与BP共线时AP+BP为最小即AB的长.连接AB△∠E=90°AE=AC+CE=AC+DB=3△AB=√AC2+BE2=5△代数式√x2+1+√(4−x)2+4的最小值是5.故选:B.15.解:延长AH到J使得AJ=MN=2延长BF到K使得BK=PQ=2连接JK交河道于点N′P′得到两座桥N′M′P′Q′此时AM′+M′N′+N′P′+P′Q′+BQ′的值最小.△四边形AJN′M′是平行四边形△AM′=JN′同理:BQ′=P′K延长AH交BK的延长线于点W.△WH=BE=9WF=AD=7△WJ=WH+AH−AJ=9+1−2=8WK=AD+BF−BK=7+1−2=6在Rt△JWK中JK=√KW2+WJ2=√62+82=10∴AM′+M′N′+N′P′+P′Q′+BQ′=HN′+2+N′P′+2+P′K=4+JK=14∴AM+MN+NP+PQ+QB的最小值为14.故选:C.16.解:取AB的中点G连接CE EG.由已知得AG=AE=6∠A=60°△△AEG是等边三角形△∠AGE=∠AEG=60°.△∠AEF+∠GEF=∠GEF+NEG=60°△∠AEF=∠NEG.△AE=EG NE=FE△△AEF△△GEN△∠A=∠NGE=60°△∠BGN=60°.△BG=EG∠BGN=∠NGE NG=NG△△BNG△△ENG△BN=EN.要求BN+CN最小就是求CN+NE最小即BN+CN=NE+CN≥CE.作EH⊥CD交延长线于点H△AB∥CD△∠EDH=∠A=60°.在Rt△DEH中DE=4∠DEH=30°△DH=2EH=2√3△CH=CD+DH=12+2=14.在Rt△CEH中CE=√CH2+EH2=√142+(2√3)2=4√13.所以BN+CN的最小值是4√13.故选:D.17.解:∵正方形OABC的边长是3∴点D的横坐标和点E的纵坐标为3∴D(3,k3)E(k33)∴BE=3−k3BD=3−k3∵△ODE的面积为4∴3×3−12×3×k3−12×3×k3−12×(3−k3)2=4∴k=3或−3(舍去)∴D(3,1)E(1,3)作E关于y轴的对称点E′连接DE′交y轴于P则DE′的长=PD+PE的最小值∵CE=CE′=1=AD∴BE′=4BD=2∴DE′=√BE′2+BD2=√42+22=2√5即PD+PE的最小值为2√5故选:B.18.解:作点A关于x轴的对称点A′连接A′B如图所示:则P A+PB的最小值即为A′B的长将点A(3 a)代入y=2x得a=2×3=6△点A坐标为(3 6)将点A(3 6)代入y=x+b得3+b=6解得b=3△点B坐标为(0 3)根据轴对称的性质可得点A'坐标为(3 -6)△A′B=√32+(−6−3)2=3√10△P A+PB的最小值为3√10.故选:D.19.解:如图:取点D关于直线AB的对称点D′.以BC中点O为圆心OB为半径画半圆.连接OD′交AB于点P交半圆O于点G连BG.连CG并延长交AB于点E.由以上作图可知BG△EC于G.PD+PG=PD′+PG=D′G由两点之间线段最短可知当点D′ G O三点共线时PD+PG最小.△D′C′=4 OC′=6△D′O=√42+62=2√13△D′G=2√13−2△PD+PG的最小值为2√13−2故选C.20.解:如图点D是点B关于直线AC的对称点连接DE交AC于点P根据点的对称性PB=PD则y=PE+PB=PD+PE=DE为最小故ED=2√5设正方形的边长为a则AE=12a在Rt△ADE中由勾股定理得:DE2=AD2+AE2即a2+(12a)2=(2√5)2解得:a=4(负值已舍去)故选:C.。
1.3 勾股定理的应用-勾股定理与最短路径问题 同步练习(含答案)

1.3勾股定理的应用-勾股定理与最短路径问题一、选择题1.如图,圆柱的底面周长是24,高是5,一只在A点的蚂蚁沿侧面爬行,想吃到B点的食物,需要爬行的最短路径是( )A.9B.13C.14D.252.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上沿4cm的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为( )A.12cm B.14cm C.20cm D.24cm3.如图所示的圆柱体中底面圆的半径是4,高为3,若一只小虫从A点出发沿着圆柱体的侧面π爬行到C点,则小虫爬行的最短路程是( )A.5B.5C.73D.44.今年9月22日是第三个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为10cm的圆柱粮仓模型,如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )A.20πcm B.40πcm C.102cm D.202cm5.已知长方体的长2cm、宽为1cm、高为4cm,一只蚂蚁如果沿长方体的表面从A点爬到B′点,那么沿哪条路最近,最短的路程是( )A.29cm B.5cm C.37cm D.4.5cm6.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )A.8cm B.10cm C.12cm D.15cm7.小南同学报名参加了南开中学的攀岩选修课,攀岩墙近似一个长方体的两个侧面,如图所示,他根据学过的数学知识准确地判断出:从点A攀爬到点B的最短路径为( )米.A.16B.82C.146D.1788.如图,桌面上的长方体长为8,宽为6,高为4,B为CD的中点.一只蚂蚁从A点出发沿长方体的表面到达B点,则它运动的最短路程为( )A.229B.45C.10D.3149.如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )A.1089B.505C.120D.13010.如图,圆柱的高为4cm,底面半径为3πcm,在圆柱下底面的A点处有一只蚂蚁,它想吃到上底面B处的食物,已知四边形ADBC的边AD、BC恰好是上、下底面的直径、问:蚂蚁食到食物爬行的最短距离是( )cm.A.5B.5πC.3+4πD.3+8π二、填空题11.如图,一个长方体盒子的长、宽、高分别为5cm、4cm、3cm,有一只甲虫从顶点A沿盒的表面爬到顶点B处,那么它所爬行的最短路线的长是 cm.12.如图所示,一圆柱高AB为2cm,底面直径BC为4cm,一只蚂蚁从点A出发沿圆柱表面爬行到点C,则蚂蚁爬行的最短路程是 cm(π取3).13.如图所示是一个长方体纸盒,纸盒的长为12cm,宽为9cm,高为5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到盒顶的点G,蚂蚁爬行的最短路程是 cm.14.如图,圆柱形容器高为16cm,底面周长为24cm,在杯内壁离杯底的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯子的上沿蜂蜜相对的点A处,则蚂蚁A处到达B处的最短距离为 .15.如图,长方体盒子的长、宽、高分别是9cm,9cm,24cm,一只蚂蚁想从盒底的A点爬到盒顶的B点,它至少要爬行 cm.16.如图所示,有一个正方体盒子,其棱长为2dm,一只虫子在顶点A处,一只蜘蛛在顶点B 处,蜘蛛沿着盒子表面准备偷袭虫子,那么蜘蛛要想最快地捉住虫子,它所走的最短路程是 dm.(结果保留根号)17.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24cm.则蚂蚁爬行的最短距离为 cm.18.如图,现有一长方体的实心木块,有一蚂蚁从A处出发沿长方体表面爬行到C'处,若长方体的长AB=4cm,宽BC=2cm,高BB'=1cm,则蚂蚁爬行的最短路径长是 .三、解答题19.如图,一个圆柱体高20cm,底面半径为5cm,在圆柱体下底面的A点处有一只蜘蛛,它想吃到上底面与A点相对的B点处的一只已被粘住的苍蝇,这只蜘蛛从A点出发,沿着圆柱体的侧面爬到B点,最短路程是多少?(π取3)20.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?21.如图所示,有一个圆柱,底面圆的直径AB=16,高BC=12cm,在BC的中点P处有一块π蜂蜜,聪明的蚂蚁总能找到距离食物的最短路径,求蚂蚁从A点爬到P点的最短距离.22.如图,长方体的长为20cm,宽为10cm,高为15cm,点B与点C之间的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B去吃一滴蜜糖.(1)求出点A到点B的距离;(2)求蚂蚁从点A爬到点B的最短路程是多少?23.如图,透明的圆柱形玻璃容器(容器厚度忽略不计)的高为16cm,在容器内壁离容器底部4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在容器外壁,位于离容器上底面距离为4cm 的点A处,若蚂蚁吃到蜂蜜需爬行的最短路径为20cm,则该圆柱底面周长为多少?24.如图所示,一个无盖四棱柱容器,其底面是一个边长为3cm的正方形,高为20cm.现有一根彩带,从底面A点开始缠绕四棱柱,刚好缠绕4周到达B点(假设彩带完美贴合四棱柱).(1)请问彩带的长度是多少?(2)如图所示,一只蚂蚁在容器外A点发现容器的内部距离顶部2cm处有一滴蜂蜜,它想以最短的路程到达C处.请问蚂蚁走的最短路程是多少呢?(注:以上两问均要画出平面展开示意图,再解答)答案一、选择题B.D.A.D.B.D.B.C.B.A.二、填空题11.74.12.6.13.285.14.20cm.15.30.16.25.17.65.18.5cm.三、解答题19.如图所示,将圆柱体侧面展开,连接AB,则AB的长即为蜘蛛爬行的最短路程.根据题意得AC=20cm,BC=πR=5π=5×3=15cm,在Rt△ABC中,由勾股定理得AB2=BC2+AC2=152+202=625,所以AB=25cm,即最短路程是25cm.20.如图1,∵AB=18cm,BC=GF=12cm,BF=10cm,∴BM=18﹣6=12,BN=10+6=16,∴MN=122+162=20(cm);如图2,∵AB=18cm,BC=GF=12cm,BF=10cm,∴PM=18﹣6+6=18,NP=10,∴MN=182+102=2106(cm).如图3中,MN =222+62=2130(cm ),∵20<2106<2130,∴蚂蚁沿长方体表面爬到米粒处的最短距离为20cm .21.将圆柱体的侧面展开,如图所示:AB =12底面周长=12×π×16π=8(cm ),AP =12BC =6(cm ),所以AP =82+62=10(cm ),故蚂蚁从A 点爬到P 点的最短距离为10cm .22.(1)将长方体沿CF 、FG 、GH 剪开,向右翻折,使面FCHG 和面ADCH 在同一个平面内,连接AB ,如图1,由题意可得:BD=BC+CD=5+10=15cm,AD=CH=15cm,在Rt△ABD中,根据勾股定理得:AB=BD2+AD2=152+152=152cm;将长方体沿DE、EF、FC剪开,向上翻折,使面DEFC和面ADCH在同一个平面内,连接AB,如图2,由题意得:BH=BC+CH=5+15=20cm,AH=10cm,在Rt△ABH中,根据勾股定理得:AB=BH2+AH2=202+102=105cm,则需要爬行的最短距离是152cm.连接AB,如图3,由题意可得:BB′=B′E+BE=15+10=25cm,AB′=BC=5cm,在Rt△AB′B中,根据勾股定理得:AB=BB′2+AB′2=252+52=526cm,综上所述,点A到点B的距离为:152cm,105cm,526cm;(2)由(1)知,∵点A到点B的距离为:152cm,105cm,526cm;∴152<105<526,∴则需要爬行的最短距离是152cm.23.如图:将圆柱展开,EG为上底面圆周长的一半,作A关于E的对称点A',连接A'B交EG于F,则蚂蚁吃到蜂蜜需爬行的最短路径为AF+BF 的长,即AF+BF=A'B=20cm,延长BG,过A'作A'D⊥BG于D,∵AE=A'E=DG=4cm,∴BD=16cm,Rt△A'DB中,由勾股定理得:A'D=202―162=12(cm),则该圆柱底面周长为24cm.24.(1)如图,将长方体的侧面沿AB展开,取A′B′的四等分点C、D、E,取AB的四等分点C′、D′、E′,连接B′E′,D′E,C′D,AC,则AC+C′D+D′E+E′B′=4AC为所求的最短细线长,∵AC2=AA′2+A′C2,AC=122+52=13,∴AC+C′D+D′E+E′B′=4AC=52,答:彩带的长度是52cm;(2)如图,将四棱柱展开,找到C的对称点C′,连接AC′,则AC′即为蚂蚁走的最段路程,在直角△AMC中,AM=6cm,MC′=20+(20﹣18)=22cm,由勾股定理得:AC′2=AM2+MC′2=62+222=520,则AC′=2130cm,答:蚂蚁走的最短路程是2130cm.。
(完整版)勾股定理--最短距离问题
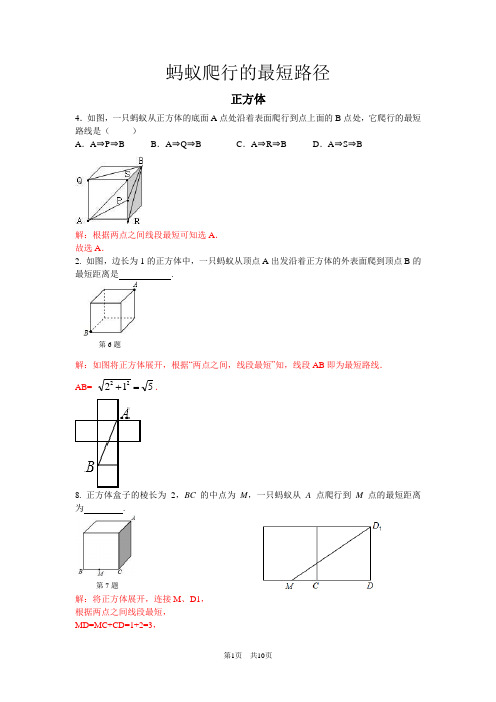
蚂蚁爬行的最短路径正方体4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒ B解:根据两点之间线段最短可知选A . 故选A .2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线. AB=51222=+.8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D1, 根据两点之间线段最短, MD=MC+CD=1+2=3,第6题第7题AB121MD 1=132322212=+=+DD MD .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB= ()1012122=++.故选C .9.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB= = cm ;(2)展开底面右面由勾股定理得AB==5cm ;所以最短路径长为5cm ,用时最少:5÷2=2.5秒.长方体10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
解:将长方体展开,连接A 、B ,根据两点之间线段最短,AB==25.A B A 1B 1D CD 1C 121411. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为 .解:正面和上面沿A 1B 1展开如图,连接AC 1,△ABC 1是直角三角形, ∴AC 1=()5342142222212=+=++=+BC AB18.(2011•荆州)如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂奴爬行的最短路径长为 cm .解:∵PA=2×(4+2)=12,QA=5 ∴PQ=13.故答案为:13.19.如图,一块长方体砖宽AN=5cm ,长ND=10cm ,CD 上的点B 距地面的高BD=8cm ,地面上A 处的一只蚂蚁到B 处吃食,需要爬行的最短路径是多少?解:如图1,在砖的侧面展开图2上,连接AB , 则AB 的长即为A 处到B 处的最短路程.解:在Rt △ABD 中,因为AD=AN+ND=5+10=15,BD=8, 所以AB 2=AD 2+BD 2=152+82=289=172. 所以AB=17cm .故蚂蚁爬行的最短路径为17cm .49、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?12.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
最新中考专题研究用勾股定理解决最短路线问题
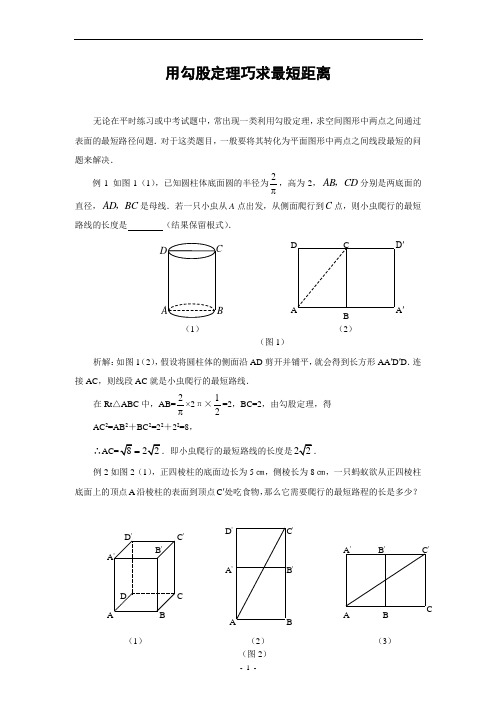
用勾股定理巧求最短距离无论在平时练习或中考试题中,常出现一类利用勾股定理,求空间图形中两点之间通过表面的最短路径问题.对于这类题目,一般要将其转化为平面图形中两点之间线段最短的问题来解决.例1 如图1(1),已知圆柱体底面圆的半径为2π,高为2,AB CD ,分别是两底面的直径,AD BC ,是母线.若一只小虫从A 点出发,从侧面爬行到C 点,则小虫爬行的最短路线的长度是 (结果保留根式).析解:如图1(2),假设将圆柱体的侧面沿AD 剪开并铺平,就会得到长方形AA ′D ′D .连接AC ,则线段AC 就是小虫爬行的最短路线.在Rt △ABC 中,AB=2π×2π×21=2,BC=2,由勾股定理,得 AC 2=AB 2+BC 2=22+22=8,∴=例2如图2(1),正四棱柱的底面边长为5㎝,侧棱长为8㎝,一只蚂蚁欲从正四棱柱底面上的顶点A 沿棱柱的表面到顶点C ′处吃食物,那么它需要爬行的最短路程的长是多少?B(1) (2) (图1)D′A ′D C BA DCBAD 'C 'B 'A 'CBAC 'B 'A '(1) (2) (3)(图2)BAD ' C 'B 'A '分析:由题可知,沿正四棱柱的表面从A到C′的走法有两大类:过底面或过侧面.由对称性知只需考虑两种情况:(1)沿面A′AB到面A′B′C′;(2)沿面A′AB到面B′BC.将立体图形转化为平面图形后,由两点之间线段最短确定最短路线。
解:(1)沿底边A′B′,将底面A′B′C′和侧面A′AB展开如图2(2),连接AC′,则AC′就是蚂蚁走的最短路线.在Rt△ABC′中,AB=5,BC′=BB′+B′C′=8+5=13,由勾股定理,得AC′ 2=AB2+B′C′ 2=52+132=194,∴AC′(2)沿侧棱BB′,将侧面A′AB和侧面B′BC展开如图2(3),连接AC′,则AC′就是蚂蚁走的最短路线.在Rt△ACC′中,AC=AB+BC=5+5=10,CC′=8,由勾股定理,得AC′ 2=AC2+CC′ 2=102+82=164,∴AC′==∴蚂蚁需要爬行的最短路程的长是点评:在将空间图形中最短路径问题转化为平面图形问题来解决的同时,还必须全方位考虑各种可能性,只有这样才能得到正确的答案.用勾股定理解决最短路线问题行程最短问题是日常生活中常见的问题之一,其解法一般要用到勾股定理,现举几例如下:例1 如图1,学校有一块长方形花铺,有极少数人从A 走到B ,为了避开拐角C 走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了 步路(假设2步为1米),却踩伤了花草.分析:由图可见,走出来的“路”是直角边分别为3m和4m的直角三角形的斜边,由勾股定理,得该“路”的长为5m,因此,行人仅仅少走了2米(即10步)路.【点评】爱护花草人人有责,仅仅因为少走10步而不惜踩伤花草,破坏环境的确是大不应该的。
勾股定理--最短距离问题蚂蚁爬行的最短路径

1A B A 1B 1DCD 1C 124勾股定理--最短距离问题蚂蚁爬行的最短路径正方体1.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .3. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .4.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
10题 11 12 1311. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),蚂蚁到B 处吃食,需要爬行的最短路径是多少?14、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?15.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
1514 16 17 第2题 第3题 ABCD.1283016.如图,直四棱柱侧棱长为4cm ,底面是长为5cm 宽为3cm 的长方形.一只蚂蚁从顶点A 出发沿棱柱的表面爬到顶点B .求:(1)蚂蚁经过的最短路程;(2)蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.17.如图,长方体的长、宽、高分别为6cm ,8cm ,4cm .一只蚂蚁沿着长方体的表面从点A 爬到点B .则蚂蚁爬行的最短路径的长是 。
专题训练(一) 借助勾股定理寻找最短路径

图 1-ZT-1
专题训练(一) 借助勾股定理寻找最短路径
2.如图 1-ZT-2,牧童在 A 处放牛,其家在 B 处,A,B 到河岸 的距离分别为 AC=400 米,BD=200 米,CD=800 米,牧童从 A 处把 牛牵到河边饮水后回家,则在何处饮水能使所走的总路径最短?最短 路程是多少?
图 1-ZT-2
(2)将正方体的正前、上底两面展开,使点 A,B 在同一平面内,则点 A 到点 B 的最短路径为线段 AB,如图(b)所示,AC=2 cm,BC=5 cm.根据勾股定理,得 AB2 =AC2+BC2=22+52=29>25=52.
比较上述两种情况,图(a)的路径较短,5÷2=2.5(秒). 答:它最少要花 2.5 秒 .
3.如图 1-ZT-3,长方体的底面边长分别为 1 cm 和 3 cm,高为 6 cm.如果用一根细线从点 A 开始经过 4 个侧面缠绕一圈到达点 B,那 么所用细线最短需要( B )
A.8 cm B.10 cm C.12 cm D.15 cm
[解析] 如图所示,将长方体展开,连接 AB,因为 AC=3+1+3+1 =8(cm),BC=6 cm,所以 AB2=AC2+BC2=82+62=100,所以 AB= 10(cm).故选 B.
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成 。21.8.821.8.822:57:4422:57:44August 8, 2021
中考数学专题复习《利用勾股定理求最短路径》测试卷-附带答案
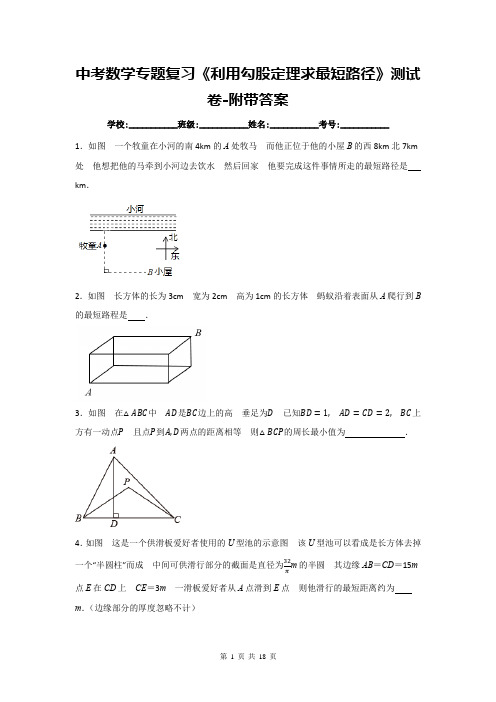
中考数学专题复习《利用勾股定理求最短路径》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________1.如图一个牧童在小河的南4km的A处牧马而他正位于他的小屋B的西8km北7km 处他想把他的马牵到小河边去饮水然后回家他要完成这件事情所走的最短路径是km.2.如图长方体的长为3cm 宽为2cm 高为1cm的长方体蚂蚁沿着表面从A爬行到B 的最短路程是.3.如图在△ABC中AD是BC边上的高垂足为D已知BD=1,AD=CD=2,BC上方有一动点P且点P到A,D两点的距离相等则△BCP的周长最小值为.4.如图这是一个供滑板爱好者使用的U型池的示意图该U型池可以看成是长方体去掉m的半圆其边缘AB=CD=15m 一个“半圆柱”而成中间可供滑行部分的截面是直径为32π点E在CD上CE=3m一滑板爱好者从A点滑到E点则他滑行的最短距离约为m.(边缘部分的厚度忽略不计)5.如图四边形ABCD∠BAD=60° ∠ADC=150° 且BD∠DC已知AC的最大值是3 则BC=.6.如图在一个长为5m宽为3m的长方形草地上放着一根长方体的木块它的棱和草地宽AD平行且棱长大于AD木块从正面看是边长为1m的正方形一只蚂蚁从点A处到达点C处需要走的最短路程约为m.(精确到1m)7.如图C为线段BD上一动点分别过B D作AB⊥BD ED⊥BD连接AC EC已知AB=5DE=1BD=8设CD=x.请用含x的代数式表示AC+CE的长为根据上述方法求出√x2+4+√(12−x)2+9的最小值为.8.如图四边形ABCD为矩形AD=3AB=4点E是AD所在直线的一个动点点F 是对角线BD上的动点且BF=DE则AF+BE的最小值是.9.如图长方形BCFG是一块草地折线ABCDE是一条人行道BC=12米CD=5米.为了避免行人穿过草地(走虚线BD践踏绿草管理部门分别在B D处各挂了一块牌子牌子上写着“少走米踏之何忍”.10.如图BD是RtΔABC的角平分线点F是BD上的动点已知AC=2AE=2√3−2∠ABC=30°则(1)BE=(2)AF+EF的最小值是.11.如图AB是半圆O的直径半圆的半径为4 点C D在半圆上OC⊥AB,BD=2CD 点P是OC上的一个动点则BP+DP的最小值为.12.如图一大楼的外墙面ADEF与地面ABCD垂直点P在墙面上若P A=AB=5米点P到AD的距离是4米有一只蚂蚁要从点P爬到点B它的最短行程是米13.如图在Rt∠AOB中∠AOB=90° OA=4 OB=6 以点O为圆心3为半径的∠O与OB交于点C过点C作CD∠OB交AB于点D点P是边OA上的动点则PC+PD的最小值为.14.如图台阶阶梯每一层高20cm宽40cm长50cm.一只蚂蚁从A点爬到B点最短路程是.15.已知正方形ABCD的边长为1 点E F分别是边BC CD上的两个动点且满足BE= CF连接AE AF则AE+AF的最小值为.16.如图在菱形ABCD中AB=4∠ABC=60°M为AD中点P为对角线BD上一动点连接PA和PM则PA+PM的最小值是.17.如图圆柱形容器高为18cm 底面周长为24cm 在杯内壁离杯底4cm的点B处有乙滴蜂蜜此时一只蚂蚁正好在杯外壁离杯上沿2cm与蜂蜜相对的点A处则蚂蚁从外币A 处到达内壁B处的最短距离为.18.如图直线y=﹣x+7与两坐标轴分别交于A B两点点C的坐标是(1 0)DE分别是AB OA上的动点当∠CDE的周长最小时点E的坐标是.19.如图菱形ABCD的边长为4 ∠BAD=120° E是边CD的中点F是边AD上的一个动点将线段EF绕着点E顺时针旋转60°得到线段EF' 连接AF' BF' 则∠ABF'的周长的最小值是.20.如图已知矩形ABCD中AB=4 AD=3 E F分别为AB DC上的两个动点且EF∠AC则AF+FE+EC的最小值为.参考答案1.解:如图做出点A关于小河MN的对称点A` 连接A`B交MN于点P则A`B就是牧童要完成这件事情所走的最短路程长度.在Rt∠A`DB中由勾股定理求得A`B=√A`D2+DB2=√(7+4+4)2+82=17(km).则他要完成这件事情所走的最短路程是17km.2.解:如图1AB= √52+12=√26(cm)如图2AB= √32+32=3√2(cm)如图3AB= √22+42=√20=2√5(cm)故沿长方体的表面爬到对面顶点B处只有图2最短其最短路线长为:3√2cm.故答案为:3√2.3.解:∠P到AD两点的距离相同∠P在线段AD的垂直平分线上取AD的中点H作HF//BC作B关于HF的对称点E连接CE与直线FH交于P点P 即为所求∠∠BFH=90° BF=EF EP=BP∠要使∠BCP的周长最小∠BP+CP最小即为CE长又∠EF//BC∠ADC=90°∠∠FHD=∠HDB=90°∠四边形BDHF是矩形AD=1∠FBD=90°∠BF=DH=EF=12∠BE=2∠CE=√BC2+BE2∠CE=√13∠BCP的周长最小值=BC+BP+CP=3+√13故答案为:3+√13.4.解:如图是其侧面展开图:AD=12π⋅32π=16(m)AB=CD=15m.DE=CD-CE=15-3=12(m)在Rt∠ADE中AE=√AD2+DE2=√162+122=20(m).故他滑行的最短距离约为20m.故答案为:20.5.解:如图取BC的中点F以BC为边在∠BCD另一侧作等边三角形∠BCG连接DG DF FG∠∠ADC=150° 且BD∠DC∠∠ADB=150°﹣90°=60°∠∠BAD=60°∠∠ADB=∠BAD=60°∠∠ABD是等边三角形而∠BCG也是等边三角形∠AB=DB BC=BG∠ABD=∠CBG=60°∠∠ABD+∠DBC=∠CBG+∠DBC即∠ABC=∠DBG在∠ABC和∠DBG中{AB=DB ∠ABC=∠DBG BC=BG∠∠ABC∠∠DBG(S A S)∠AC=DG∠AC 的最大值是3∠DG 的最大值也是3在∠DGF 中 DG ≤DF +FG∠当DF FG 在同一条直线上时 DG 取最大值3 即DG =DF +FG =3 ∠BD ∠DC BC 的中点F∠DF =BF =CF =12BC∠等边三角形∠BCG BC 的中点F∠GF ∠BC ∠BGF =∠CGF =12∠BGC =30°∠BF =CF =12BG =12BC∠设DF =BF =CF =x 则BC =BG =2x∠FG =√BG 2−BF 2=√(2x)2−x 2=√3x∠DF +FG =x +√3x =3解得:x =3√3−32∠BC =2x =2×3√3−32=3√3﹣3故答案为3√3﹣3.6.解:由题意可知 将木块展开 如图长相当于是AB +2个正方形的宽∠长为5+2×1=7m 宽为3 m .于是最短路径为:√32+72=√58≈8 m .故答案为8.7. 解:AC +CE =√BC 2+AB 2+√CD 2+DE 2=√(8−x)2+25+√x 2+1 当A C E 三点共线时 AC +CE 的值最小如右图所示 作BD =12 过点B 作AB ∠BD 过点D 作ED ∠BD 使AB =2 ED =3连接AE交BD于点C设BC=x则AE的长即为代数式√x2+4+√(12−x)2+9的最小值.过点A作AF∠BD交ED的延长线于点F得矩形ABDF则AB=DF=2 AF=BD=12 EF=ED+DF=3+2=5所以AE=√AF2+EF2=√122+52=13即√x2+4+√(12−x)2+9的最小值为13故答案为:√(8−x)2+25+√x2+113.8.解:如图延长BC至G使得BG=BD连接GF∵四边形ABCD是矩形∴∠DAB=∠ABC=90°,AD//CB∴∠EDB=∠FBC在△EDB与△FBG中{ED=BF ∠EDB=∠FBG BD=BG∴△EDB≌△FBG∴BE=GF∴AF+BE=AF+GF≥AG 在Rt△ABD中AD=3,AB=4BD=√AD2+AB2=5∴BG=5在Rt△ABG中BG=5,AB=4AG=√AB2+BG2=√42+52=√41∴AF+BE的最小值是√41.故答案为:√41.9.解:在Rt△BCD中∴BD=√BC2+CD2=13则BC+CD−BD=12+5−13=4(米)故答案为:410.解:(1)∠AC=2∠ABC=30°∠BAC=90°∠BC=2AC=4∠AB=√BC2−AC2=√42−22=2√3∠BE=AB−AE=2√3−(2√3−2)=2故答案为:2(2)如图所示作E点关于BD的对称点G连接EG AG GF∠BD是∠ABC的平分线∠点G在线段BC上∠根据对称性可得EF=GF BG=BE=2∠EF+AF=GF+AF≥AG∠当点A F G三点共线时GF+AF的长度最短即EF+AF的最小值为AG的长度.∠GC=BC-BG=4-2=2又∠∠ABC=30°∠BAC=90°∠∠C=60°又∠AC=2∠△AGC是等边三角形∠AG=AC=2.∠AF+EF的最小值是2.故答案为:2.11.解:作点D关于OC的对称点为D1连接BD1OD1过点D1作D1Q⊥AB由题知OC⊥AB BD=2CD∠BC=3CD可得CD对应的圆心角∠COD=30°又点D关于OC的对称点为D1∠∠COD1=30°∠AOD1=60°∠BD1长为BP+DP的最小值在RtΔQOD1中OD1=4∠OQ=2D1Q=2√3在RtΔQD1B中BQ=OQ+OB=6D1Q=2√3∠BD1=√62+(2√3)2=4√3故填:4√312.解:如图过P作PG∠BF于G连接PB∠AG=4 AP=AB=5∠PG=√AP2−AG2=3BG=9∠PB=√GB2+GP2=3√10故这只蚂蚁的最短行程应该是3√10故答案为:3√1013.解:延长CO交∠O于点E连接ED交AO于点P则PC+PD的值最小最小值为线段DE的长.∠CD∠OB∠∠DCB=90°∠∠AOB=90°∠∠DCB=∠AOB ∠CD∠AO∠CD AO =BCBO∠CD 4=36∠CD=2在Rt∠CDE中DE=√CD2+CE2=√22+62=2√10∠PC+PD的最小值为2√10.故答案为:2√10.14.解:如图所示∠楼梯的每一级的高宽长分别为20cm宽40cm长50cm ∠AB=√502+[2(20+40)]2=130(cm)即蚂蚁从点A沿着台阶面爬行到点B的最短路程是130cm.故答案为:130cm.15.解:连接DE∠BE=CF且四边形ABCD为正方形∠CD-CF=BC-BE即DF=CE在△ADF和△DCE中{AD=DC ∠ADF=∠DCE DF=CE∴△ADF∠∠DCE∠AF=DE AE+AF=AE+DE以BC为对称轴作A点关于BC的对应点A′连接DA′与BC交点即为点E∠点A和点A′关于BC对称∠AE=A′EAE+DE=A′E+DE=A′D由勾股定理可得:A′D=√AD2+A′A2=√22+12=√5∠AE+AF的最小值为√5故答案为:√516.解:作点M关于BD的对称点N交CD于点N连接AN则AN就是P A+PM的最小值∠在菱形ABCD 中 AB =4 ∠ABC =60° M 为AD 中点 AC ∠BD∠∠ADC =60° DA =DC 点N 为CD 的中点∠∠DAC 是等边三角形 AN ∠CD∠AC =AD =AB =4∴AN =√AD 2−DN 2=√42−22=2√3故答案为:2√317.解∠如图 将杯子侧面展开 作A 关于EF 的对称点A ′ 连接A ′B 则A ′B 即为最短距离. 根据勾股定理 得A ′B =√A ′D 2+BD 2=√122+162=20m .故答案为:20cm .18.解:如图 点C 关于OA 的对称点C ′(-1 0) 点C 关于直线AB 的对称点C ″ ∠直线AB 的解析式为y =-x +7∠直线C C ″的解析式为y =x -1由{y =−x +7y =x −1得{x =4y =3∠F(4 3)∠F是C C″中点∠可得C″(7 6).连接C′C″与AO交于点E与AB交于点D此时∠DEC周长最小∠DEC的周长=DE+EC+CD=E C′+ED+D C″=C′C″=√82+62=10.故答案为10.19.解:取AD中点G连接EG F'G BE作BH∠DC的延长线于点H∠四边形ABCD为菱形∠AB=AD∠∠BAD=120°∠∠CAD=60°∠∠ACD为等边三角形又∠DE=DG∠∠DEG也为等边三角形.∠DE=GE∠∠DEG=60°=∠FEF'∠∠DEG﹣∠FEG=∠FEF'﹣∠FEG即∠DEF=∠GEF'由线段EF绕着点E顺时针旋转60°得到线段EF'所以EF=EF'.在∠DEF和∠GEF'中{DE=GE∠DEF=∠GEF′EF=EF′∠∠DEF∠∠GEF'(SAS).∠∠EGF'=∠EDF=60°∠∠F'GA=180°﹣60°﹣60°=60°则点F'的运动轨迹为射线GF'.观察图形可得A E关于GF'对称∠AF'=EF'∠BF'+AF'=BF'+EF'≥BE在Rt∠BCH中∠∠H=90° BC=4 ∠BCH=60°∠CH=12BC=2,BH=2√3,在Rt∠BEH中BE=√BH2+EH2=√12+16=2√7∠BF'+EF'≥2√7∠∠ABF'的周长的最小值为AB+BF'+EF'=4+2√7故答案为:4+2√7.20.解:过B作BH∠EF交CD于H过A作AG∠EF且使AG=EF连接GE∠四边形AGEF是平行四边形∠AF=GE∠当G E C三点共线时AF+EC最小∠EF ∠AC∠BH ∠AC∠∠HBC +∠BCA =90° ∠BCA +∠ACH =90° ∠∠HBC =∠ACH∠tan∠HBC =tan∠ACD 即HC BC =AD CD∠AB =4 AD =3∠ HC 3=34∠HC =94∠BH =√BC 2+CH 2=√9+(94)2=154∠AF +EF +EC ≥GC +BH∠GA ∠AC∠∠ACG 为直角三角形∠AB =4 AD =3∠AC =5∠EF =BH =AG∠AG =154∠GC =√AG 2+AC 2=√52+(154)2=254∠GC +EF =254+154=10∠AF +FE +EC 的最小值为10故答案为:10.。
专题01 勾股定理中的最短路径问题与翻折问题(五大题型)(解析版)

专题01 勾股定理中的最短路径问题与翻折问题(五大题型)【题型1 与长方形有关的最短路径问题】【题型2 与圆柱有关的最短路径问题】【题型3 与台阶有关的最短路径问题】【题型4将军饮马与最短路径问题】【题型5几何图形中翻折、旋转问题】【方法技巧】长方体最短路径基本模型如下:几何体中最短路径基本模型如下:基本思路:将立体图形展开成平面图形,利用两点之间线段最短确定最短路线,构造直角三角形,利用勾股定理求解【题型1 与长方体有关的最短路径问题】【典例1】(2023•丹江口市模拟)如图,地面上有一个长方体盒子,一只蚂蚁在这个长方体盒子的顶点A处,盒子的顶点C′处有一小块糖粒,蚂蚁要沿着这个盒子的表面A处爬到C′处吃这块糖粒,已知盒子的长和宽为均为20cm,高为30cm,则蚂蚁爬行的最短距离为( )cm.A.10B.50C.10D.70【答案】B【解答】解:分两种情况:(其它情况与之重复)①当蚂蚁从前面和右面爬过去时,如图1,连接AC′,在Rt△ACC′中,AB=20+20=40(cm),CC′=30(m),根据勾股定理得:EC===50(cm),②当蚂蚁从前面和上面爬过去时,如图2,连接AC′,在Rt△ABC′中,BC′=BB′+B′C′=30+20=50(cm),AB=20(cm),根据勾股定理得:AC′===10(cm)>50(cm);蚂蚁爬行的最短距离为50cm.故选:B.【变式1-1】(2022秋•新都区期末)一个长方体盒子的长、宽、高分别为15cm,10cm,20cm,点B离点C的距离是5cm,一只蚂蚁想从盒底的点A沿盒的表面爬到点B,蚂蚁爬行的最短路程是( )A.10cm B.25cm C.5cm D.5cm【答案】B【解答】解:如图所示,将长方体的正面与右侧面展开在同一平面,那么AB==25cm.故选:B.【变式1-2】(2023春•光泽县期中)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )A.5B.25C.D.35【答案】B【解答】解:将长方体展开,连接AB,根据两点之间线段最短,(1)如图,BD=10+5=15,AD=20,由勾股定理得:AB==25.(2)如图,BC=5,AC=20+10=30,由勾股定理得,AB=.(3)只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图:∵长方体的宽为10,高为20,点B离点C的距离是5,∴BD=CD+BC=20+5=25,AD=10,在直角三角形ABD中,根据勾股定理得:∴AB=;由于25<5<5,故选:B.【变式1-3】(2023春•灵丘县月考)如图,正方体的棱长为3cm,已知点B与点C之间的距离为1cm,一只蚂蚁沿着正方体的表面从点A爬到点C,需要爬行的最短距离为( )A.B.5cm C.4cm D.【答案】B【解答】解:如图1,AC==5(cm),如图2,AC==(cm),∴5<∴需要爬行的最短距离为5cm.故选:B.【变式1-4】(2022秋•莲湖区期末)如图,正方体盒子的棱长为2,M为EH的中点,现有一只蚂蚁位于点B处,它想沿正方体的表面爬行到点M处获取食物,则蚂蚁需爬行的最短路程为( )A.B.C.D.【答案】C【解答】解:如图,连接BM,则线段BM的长就是蚂蚁需爬行的最短路程,∵正方体的棱长为2,M是EH的中点,∴∠Q=90°,MQ=2,BQ=1+2=3,由勾股定理得BM===,故选:C.【变式1-5】(2022秋•汝阳县期末)如图,在长为3,宽为2,高为1的长方体中,一只蚂蚁从顶点A出发沿着长方体的表面爬行到顶点B,那么它爬行的最短路程是( )A.B.C.D.【答案】B【解答】解:因为平面展开图不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面上面,由勾股定理得AB2=(2+1)2+32=18;(2)展开前面右面,由勾股定理得AB2=(2+3)2+12=26;(3)展开前面和左面,由勾股定理得AB2=(3+1)2+22=20.所以最短路径的长为AB=(cm).故选:B.【变式1-7】(2022秋•平昌县期末)如图是一个长方体盒子,其长,宽、高分别为4,2,9,用一根细线绕侧面绑在点A,B处,不计线头,细线的最短长度为( )A.12B.15C.18D.21【答案】B【解答】解:如图所示:连接AB′,则AB′即为所用的最短细线长,AA′=4+2+4+2=12,A′B′=AB=9,由勾股定理得:AB′2=AA′2+A′B′2=122+92=225,则AB′=15,故选:B.【变式1-8】(2023•陇县三模)如图,长方体的底面边长分别为2厘米和4厘米,高为5厘米.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )厘米.A.8B.10C.12D.13【答案】D【解答】解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12(cm),QA=5cm,∴PQ==13cm.故选:D.【变式1-10】(2022春•五华区期末)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )A.cm B.4cm C.cm D.5cm【答案】C【解答】解:如图,它运动的最短路程AB==(cm).故选:C.【题型2 与圆柱有关的最短路径问题】【典例2】(2023春•防城区期中)如图,一圆柱高BC=12πcm,底面周长是16πcm,P为BC的中点,一只蚂蚁从点A沿圆柱外壁爬到点P处吃食,要爬行的最短路程是( )A.12πcm B.11πcm C.10πcm D.9πcm【答案】C【解答】解:将圆柱沿点A所在母线展开,连接AP,由两点之间线段最短可知,最短路程是AP的长.∵底面圆周长为16πcm,∴底面半圆弧长为8πcm,∵BC=12πcm,P为BC的中点,∴).根据勾股定理得:AP=(cm).故选:C.【变式2-1】(2023春•德州期中)如图,圆柱形玻璃容器高18cm,底面圆的周长为48cm,在外侧底部点A处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧顶端的点B处有一只苍蝇,则蜘蛛捕获苍蝇所走的最短路线长度( )A.52cm B.30cm C.D.60cm【答案】B【解答】解:如图所示,AB==30(cm),答:蜘蛛捕获苍蝇所走的最短路线长度为30cm.故选:B.【变式2-2】(2023春•夏津县期中)葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是50cm,当一段葛藤绕树干盘旋2圈升高为2.4m 时,这段葛藤的长是( )m.A.3B.2.6C.2.8D.2.5【答案】B【解答】解:∵葛藤绕树干盘旋2圈升高为2.4m,∴葛藤绕树干盘旋1圈升高为1.2m,如图所示:AC==1.3m,∴这段葛藤的长=2×1.3=2.6m.故选:B.【变式2-3】(2023春•东港区校级月考)如图所示,已知圆柱的底面周长为36,高AB=5,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为( )A.26B.13+C.13D.2【答案】B【解答】解:如图,小虫爬行的最短路程=AP+PC=+=+13.故选:B.【变式2-4】(2023春•富顺县校级月考)如图,一个底面圆周长为24cm,高为9cm的圆柱体,一只蚂蚁从距离上边缘4cm的点A沿侧面爬行到相对的底面上的点B所经过的最短路线长为( )A.cm B.15cm C.14cm D.13cm【答案】D【解答】解:将圆柱体的侧面展开,连接AB,如图所示:由于圆柱体的底面周长为24cm,则BD=24×=12cm,又因为AD=9﹣4=5cm,所以AB==13(cm),即蚂蚁沿表面从点A到点B所经过的最短路线长为13cm.故选:D.【变式3-5】(2022秋•蒲城县期末)今年9月23日是第五个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为20cm的圆柱粮仓模型.如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为( )A.20πcm B.40πcm C.D.【答案】D【解答】解:如图,圆柱的侧面展开图为长方形,AC=A'C,且点C为BB'的中点,∵AB=20,BC=20=10,∴装饰带的长度=2AC=2=20(cm),故选:D.【变式2-6】(2023春•宣化区期中)如图,圆柱底面半径为,高为18cm,点A、B分别是圆柱两底面圆周上的点,且点B在点A的正上方,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )A.21cm B.24cm C.30cm D.32cm【答案】C【解答】解:圆柱体的展开图如图所示:用一棉线从A顺着圆柱侧面绕3圈到B的最短路线是AD→DE→EB;即在圆柱体的展开图长方形中,将长方形平均分为3个小长方形,A沿着3个长方形的对角线运动到B的最短路线:AD+DE+EB;∵圆柱体地面半径为cm,∴AC=2π×=8(cm),∵圆柱体的高h=18cm,∴CD=h=6cm,∴在Rt△ACD中,AD===10(cm),∵AD=DE=EB,∴AD+DE+EB=3AD=30cm.故选:C.【变式2-7】(2023春•随县期末)如图是学校艺术馆中的柱子,高4.5m.为迎接艺术节的到来,工作人员用一条花带从柱底向柱顶均匀地缠绕3圈,一直缠到起点的正上方为止.若柱子的底面周长是2m,则这条花带至少需要 7.5 m.【答案】见试题解答内容【解答】解:将圆柱表面切开展开呈长方形,则有螺旋线长为三个长方形并排后的长方形的对角线长∵圆柱高4.5米,底面周长2米,∴x2=(2×3)2+4.52=56.25所以,x=7.5,∴花带长至少是7.5m.故答案为:7.5.【题型3 与台阶有关的最短路径问题】【典例3】(2023春•连山区期末)如图是楼梯的一部分,若AD=2,BE=1,AE=3,一只蚂蚁在A处发现C处有一块糖,则这只蚂蚁吃到糖所走的最短路程为( )A.B.3C.D.2【答案】D【解答】解:如图,AC==2,故选:D.【变式3-1】(2022春•郾城区期末)如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )cm.A.10B.50C.120D.130【答案】B【解答】解:如图所示,∵它的每一级的高为20cm,宽30cm,长50cm,∴AB==50(cm).答:蚂蚁沿着台阶面爬行到点B的最短路程是50cm,故选:B.【变式3-2】(2023春•西塞山区期中)如图,在一个长为20m,宽为16m的矩形草地上放着一根长方体木块,已知该木块的较长边和场地宽AD平行,横截面是边长为2m的正方形,一只蚂蚁从点A处爬过木块到达点C处需要走的最短路程是 8 m.【答案】见试题解答内容【解答】解:由题意可知,将木块展开,相当于是AB+2个正方形的宽,∴长为20+2×2=24米;宽为16米.于是最短路径为:=8米.故答案为:8.【变式3-3】(2022秋•叙州区期末)如图是一个三级台阶,它的每一级的长、宽、高分别是4米、0.7米、0.3米,A、B是这个台阶上两个相对的顶点,A 点处有一只蚂蚁,它想到B点去吃可口的食物,则蚂蚁沿台阶面爬行到B点最短路程是 5 米.【答案】5.【解答】解:三级台阶平面展开图为长方形,长为4,宽为(0.7+0.3)×3,则蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.可设蚂蚁沿台阶面爬行到B点最短路程为x,由勾股定理得:x2=42+[(0.7+0.3)×3]2=25,解得x=5(米),答:蚂蚁沿台阶面爬行到B点最短路程是5米,故答案为:5.【题型4将军饮马与最短路径问题】【典例4】(2022秋•辉县市校级期末)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm.在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B.C.12D.18【答案】A【解答】解:如图所示,将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,故先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,根据两点之间线段最短,即可得到此时AF+CF最小,并且最小值为A'C的长度,如图所示,延长过C的母线,过A'作A'D垂直于此母线于D,由题意可知,A'D=18÷2=9(cm),CD=12﹣4+4=12(cm),由勾股定理得:A'C==15(cm),故蚂蚁到达蜂蜜的最短距离为15cm,故选:A.【变式4-1】(2022春•吴江区期末)如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B 处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则该蚂蚁要吃到饭粒需爬行的最短路径长是( )A.13cm B.3cm C.cm D.2cm【答案】A【解答】解:如图:∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,∴A′D=5cm,BD=12﹣3+AE=12cm,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B===13(cm).故选:A.【变式4-2】(2023春•临潼区期末)如图,桌上有一个圆柱形玻璃杯(无盖),高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的内壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是 10 厘米.【答案】此题考查了平面展开﹣最短路径问题,将图形展开,利用勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.【解答】解:如图所示:将杯子侧面展开,作A关于杯口的对称点A′,连接PA′,最短距离为PA'的长度,PA'===10(厘米),最短路程为PA'=10厘米.故答案为:10.【变式4-3】(2022秋•牡丹区月考)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )(π取3)m.A.30B.28C.25D.22【答案】C【解答】解:其侧面展开图如图:作点C关于AB的对称点F,连接DF,∵中间可供滑行的部分的截面是半径为2.5m的半圆,∴BC=πR=2.5π≈7.5m,AB=CD=20m,∴CF=15m,在Rt△CDF中,DF===25(m),故他滑行的最短距离约为25m.故选:C.【变式4-4】(2022秋•雁峰区校级期末)如图,圆柱形玻璃杯高为11cm,底面周长为30cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B 处的爬行最短路线长为(杯壁厚度不计)( )A.12cm B.17cm C.20cm D.25cm【答案】B【解答】解:如图:将杯子侧面展开,作A关于EF的对称点A′,则AF+BF为蚂蚁从外壁A处到内壁B处的最短距离,即A′B的长度,∵A′B====17(cm),∴蚂蚁从外壁A处到内壁B处的最短距离为17cm,故选:B.【变式4-5】(2022秋•郫都区期末)如图,圆柱形玻璃杯高为22cm,底面周长为30cm,在杯内壁离杯上沿3cm的点B处粘有一粒面包渣,此时一只蚂蚁正好在杯外壁,离杯底5cm与面包渣相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 25 cm(杯壁厚度不计).【答案】25.【解答】解:如图:将杯子侧面展开,作B关于EF的对称点B′,∴B'D=15cm,AD=22﹣5+3=20(cm),连接B′A,则B′A即为最短距离,B′A===25(cm).故答案为:25.【题型5几何图形中翻折、旋转问题】【典例5】(2022秋•大东区校级期末)如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE的长为( )A.3B.4C.5D.6【答案】C【解答】解:∵Rt△DC′B由Rt△DBC翻折而成,∴CD=C′D=AB=8,∠C=∠C′=90°,设DE=x,则AE=8﹣x,∵∠A=∠C′=90°,∠AEB=∠DEC′,∴∠ABE=∠C′DE,在Rt△ABE与Rt△C′DE中,,∴Rt△ABE≌Rt△C′DE(ASA),∴BE=DE=x,在Rt△ABE中,AB2+AE2=BE2,∴42+(8﹣x)2=x2,解得:x=5,∴DE的长为5.故选:C.【变式5-1】(2022春•安乡县期中)如图,在△ABC中,∠ACB=90°,AC=12,BC=10,点D为BC的中点,点E为AC边上一动点,连接DE.将△CDE沿DE折叠,点C的对应点为点C'.若△AEC'为直角三角形,则AE的长为 或7 .【答案】或7.【解答】解:如图,当∠AEC'=90°时,则∠CEC'=90°,∴∠CED=∠C'ED=45°,∴∠CDE=45°,∴CE=CD=5,∴AE=AC﹣CE=12﹣5=7;如图,当∠AC'E=90°时,∵∠AC'E+∠DC'E=90°+90°=180°,∴点A,C',D共线,∴AD==13,∵C'E=CE=12﹣AE,AC'=AD﹣C'D=8,∴AE2=(12﹣AE)2+82,∴AE=;当∠C'AE=90°时,不存在,综上所述,若△AEC为直角三角形,则AE的长为或7,故答案为:或7.【变式5-2】(2023春•长沙期末)如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为 10 .【答案】见试题解答内容【解答】解:易证△AFD′≌△CFB,∴D′F=BF,设D′F=x,则AF=8﹣x,在Rt△AFD′中,(8﹣x)2=x2+42,解之得:x=3,∴AF=AB﹣FB=8﹣3=5,=•AF•BC=10.∴S△AFC故答案为:10.【变式5-3】(2022秋•绥德县期中)如图所示,折叠长方形一边AD,点D落在BC边的点F处,已知BC=10厘米,AB=8厘米.(1)求BF与FC的长.(2)求EC的长.【答案】见试题解答内容【解答】解:(1)∵△ADE折叠后的图形是△AFE,∴AD=AF,∠D=∠AFE,DE=EF.∵AD=BC=10cm,∴AF=AD=10cm.又∵AB=8cm,在Rt△ABF中,根据勾股定理,得AB2+BF2=AF2∴82+BF2=102,∴BF=6cm,∴FC=BC﹣BF=10﹣6=4cm.(2)设EC的长为xcm,则DE=(8﹣x)cm.在Rt△EFC中,根据勾股定理,得:FC2+EC2=EF2,∴42+x2=(8﹣x)2,即16+x2=64﹣16x+x2,化简,得16x=48,∴x=3,故EC的长为3cm.【变式5-4】(2020秋•海宁市期中)如图,Rt△ABC中,∠C=90°,AC=3,BC=4,D为BC上一点,将△ABD沿AD折叠至△AB′D,AB′交线段CD 于点E.当△B′DE是直角三角形时,点D到AB的距离等于 0.6或1.5 .【答案】0.6或1.5.【解答】解:∵∠C=90°,AC=3,BC=4,∴AB=,由折叠的性质得,BD=B'D,∵△B′DE是直角三角形,∴∠BDB'=∠B'DE=90°,∴△BDB'是等腰直角三角形,如图所示,过D作DF⊥AB于F,连接BB',∴∠ADC=45°,∴DC=AC=3,∴BD=BC﹣DC=4﹣3=1,∴DF=,点E与点C重合时,△B′DE是直角三角形,∴∠B'ED=90°,∴此时点D到AB的距离等于1.5,故答案为:0.6或1.5.【变式5-5】(2020•浙江自主招生)将一直径为25cm的圆形纸片(如图①)剪成如图②所示形状的纸片,再将纸片沿虚线折叠得到正方体形状的纸盒(如图③),则这样的纸盒体积最大为 125 cm3.【答案】见试题解答内容【解答】解:如图所示.设正方体的棱长是acm.在直角三角形AOB中,OB=,AB=a,OA=2a,根据勾股定理,得+4a2=,解,得a=±5(负值舍去).则这样的纸盒体积最大为53=125cm3.故答案为125.【变式5-6】(2022秋•和平区期中)一长方体容器(如图1),长、宽均为2,高为8,里面盛有水,水面高为5,若沿底面一棱进行旋转倾斜,倾斜后的长方体容器的主视图如图2所示,若倾斜容器使水恰好倒出容器,则CD= 2 .【答案】见试题解答内容【解答】解:如图所示:设DE=x,则AD=8﹣x,根据题意得:(8﹣x+8)×2×2=2×2×5,解得:x=6,∴DE=6,∵∠E=90°,由勾股定理得:CD===2,故答案为:2.【变式5-7】(2022春•温州期末)图1是一款平衡荡板器材,示意图如图2,A,D为支架顶点,支撑点B,C,E,F在水平地面同一直线上,G,H为荡板上固定的点,GH∥BF,测量得AG=GH=DH,Q为DF上一点且离地面1m,旋转过程中,AG始终与DH保持平行.如图3,当旋转至A,Q,H在同一直线上时,连结G′Q,测得G′Q=1.6m,∠DQG′=90°,此时荡板G′H′距离地面0.6m,则点D离地面的距离为 (+1) m.【答案】(+1)m.【解答】解:如图,过Q作G'H'的垂线交G'H'于N,交AD延长线于M,连接AH',连接DG',由图2得:AD=GH,∵AG=GH=DH,∴AD=AG',G'H'=DH',∴AH'垂直平分DG',∵A,Q,H'在同一直线上,∴G'Q=DQ,∵∠DQG′=90°,∴∠G'QN+∠DQM=90°,∵∠DQM+∠QDM=90°,∴∠G'QN=∠QDM,∴△DMQ≌△QNG'(AAS),∴MQ=G'N,∵Q为DF上一点且离地面1m,此时荡板G′H′距离地面0.6m,∴QN=1﹣0.6=0.4m,∴G'N==m,∴MQ=m,∴点D离地面的距离为(+1)m.故答案为:(+1)m.【变式5-8】(2022•公安县模拟)某厂家设计一种双层长方体垃圾桶,AB=84cm,BC=30cm,CP=36cm,侧面如图1所示,EF为隔板,等分上下两层.下方内桶BCFG绕底部轴(CP)旋转打开,如图2,将其打开后点G卡在隔板上,此时可完全放入下方内桶的球体的最大直径为25.2cm,求BG的长度为 12 cm.【答案】12.【解答】解:如图1中,连接CG,过点G作GT⊥CF于T,则四边形BCTG 是矩形.∵CF=CG=CD=AB=42(cm),GT=BC=30cm,∴BG=CT===12(cm).故答案是:12.。
勾股定理之最短路径(填空选择)中考题.docx

一、选择题(共17 小题)1、( 2011?广安)如图,圆柱的底面周长为6cm,AC 是底面圆的直径,高BC=6cm,点P 是母线BC 上一点,且 PC= BC.一只蚂蚁从 A 点出发沿着圆柱体的表面爬行到点P 的最短距离是()A、B、 5cmC、D、 7cm2、(2009?乐山)如图,一圆锥的底面半径为2,母线锥的侧面爬行到点D,则蚂蚁爬行的最短路程为(PB 的长为)6,D 为PB 的中点.一只蚂蚁从点 A 出发,沿着圆A、B、 2C、 3D、 33、(2009?恩施州)如图,长方体的长为15,宽为10,高为20,点 B 离点 C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点 A 爬到点 B,需要爬行的最短距离是()A、 5C、 10+5B、25D、 354、(2005?山西)如图,点 A 和点 B 分别是棱长为由 A 处向 B 处爬行,所走的最短路程是()20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面A 40cmB 20cmC、 20cmD、 10cm5、( 2005?贵阳)如图A,一圆柱体的底面周长为的表面爬行到点 C 的最短路程大约是()24cm,高BD 为 4cm ,BC 是直径,一只蚂蚁从点 D 出发沿着圆柱A、 6cmB、 12cmC、 13cmD、 16cm6、(2004?淄博)如图是一块长,宽,高分别是6cm, 4cm 和 3cm 的长方体木块一只蚂蚁要从长方体木块的一个顶点 A 处,沿着长方体的表面到长方体上和 A 相对的顶点 B 处吃食物,那么它需要爬行的最短路径的长是()A、( 3+2) cmB、cmC、cmD、cm7、(2004?梅州)如图,一只蚂蚁沿边长为 a 的正方体表面从顶点 A 爬到顶点B,则它走过的路程最短为()A、aB、( 1+) aC、 3aD、a8、(2004?济宁)如图,正方体盒子的棱长为2, BC 的中点为M ,一只蚂蚁从M 点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是()A、B、 3C、 5D、9、如图所示,一圆柱高8cm,底面半径2cm ,一只蚂蚁从点A 爬到点 B 处吃食,要爬行的最短路程(π取 3)是()A、 12cmB、 10cmC、 14cmD、无法确定10、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π =3),在圆柱下底面的A 点有一只蚂蚁,它想吃到上底面与 A 相对的 B 点处的食物,需要爬行的最短路程大约()A、 10cmB、 12cmC、 19cmD、 20cm11、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M 处,它到BB1的中点N 的最短路线是()A、 8B、 2C、 2D、 2+212、如图所示,是一个圆柱体,ABCD是它的一个横截面,AB=,BC=3,一只蚂蚁,要从 A 点爬行到 C 点,那么,最近的路程长为()A、 7B、C、D、 513、如图是一个长4m,宽 3m,高 2m 的有盖仓库,在其内壁的 A 处(长的四等分)有一只壁虎, B 处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为()A、 4.8B、C、 5D、14、有一长、宽、高分别是 5cm, 4cm, 3cm 的长方体木块,一只蚂蚁要从长方体的一个顶点爬到长方体上和 A 相对的顶点 B 处,则需要爬行的最短路径长为()A 处沿长方体的表面A、 5 C、 4cmcmB、D、 3cmcm15、如图,边长为 1 的立方体中,一只蚂蚁从 A 顶点出发沿着立方体的外表面爬到 B 顶点的最短路程是()A、 3B、C、D、 116、如图所示:有一个长、宽都是的最短路径为()2 米,高为3 米的长方体纸盒,一只小蚂蚁从 A 点爬到 B 点,那么这只蚂蚁爬行A、 3 米B、 4 米C、 5 米D、 6 米17、如图,在棱长为20cm的正方体盒子上有一只蚂蚁欲从 A 点出发向 B 爬去吃食,则蚂蚁所走最短路程是()A、 40cmB、 20cmC、 20cmD、 20cm二、填空题(共13 小题)18、( 2007?呼伦贝尔)如图,有一圆锥形粮堆,其正视图是边长为有一老鼠正在偷吃粮食,此时,小猫正在 B 处,它要沿圆锥侧面到达6m的正三角形ABC,粮堆母线AC 的中点P 处捕捉老鼠,则小猫所经过的最短路程是P 处_________m.(结果不取近似值)19、( 2007?怀化)如图所示的圆柱体中底面圆的半径是,高为2,若一只小虫从 A 点出发沿着圆柱体的侧面爬行到 C 点,则小虫爬行的最短路程是_________.(结果保留根号)20、( 2007?金昌)如图,圆锥的母线长OA 为 8,底面圆的半径为的中点 B 处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为4.若一只蚂蚁在底面上点_________.A 处,在相对母线OC21、( 2007?梅州)如图,有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由 A 至A1(A,A1在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是_________.22、( 2008?昆明)如图,有一个圆柱,它的高等于 16cm,底面半径等干它想吃到上底面上与 A 点相对的 B 点处的食物,需要爬行的最短路程是4cm,在圆柱下底面的 A 点有一只蚂蚁,_________ cm.(π取 3)23、( 2008?青海)如图,有一圆柱体,它的高为 20cm,底面半径为想吃到上底面上与 A 点相对的 B 点处的苍蝇,需要爬行的最短路径是7cm.在圆柱的下底面 A 点处有一个蜘蛛,它_________ cm(结果用带根号和π的式子表示).24、( 2009?青岛)如图,长方体的底面边长分别为面缠绕一圈到达点 B,那么所用细线最短需要那么所用细线最短需要 _________ cm .1cm 和_________3cm,高为 6cm.如果用一根细线从点A 开始经过 4 个侧cm;如果从点 A 开始经过 4 个侧面缠绕 n 圈到达点 B,25、( 2011?荆州)如图,长方体的底面边长分别为行一圈到达Q 点,则蚂奴爬行的最短路径长为2cm 和 4cm,高为_________ cm.5cm .若一只蚂蚁从P 点开始经过 4 个侧面爬26、( 2006?茂名)如图,点A、 B 分别是棱长为 2 的正方体左、右两侧面的中心,一蚂蚁从点 A 沿其表面爬到点B 的最短路程是_________.27、( 2005?青海)如图,已知正方体的棱长为2,则正方体表面上从 A 点到 C1点的最短距离为_________.28、( 2003?泸州)如图,一只昆虫要从边长为acm 的正方体盒子的一个顶点爬到相距最远的另一个顶点,沿盒子表面爬行的最短路程是_________ cm.29、如图,有一圆柱,其高为食物,则蚂蚁经过的最短距离为12cm,底面半径为3cm,在圆柱下底面_________ cm.(π取 3)A 点处有一只蚂蚁,它想得到上底面B 处的30、一只蚂蚁从长、宽都是_________.3 ,高是8 的长方体纸箱的 A 点沿纸箱爬到 B 点,那么它所行的最短路线的长是24.(本小题10 分)问题探究:( 1)如图①所示是一个半径为3,高为 4 的圆柱体和它的侧面展开图,AB 是圆柱的一条母线,一只蚂蚁从 A 点2π出发沿圆柱的侧面爬行一周到达 B 点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB 剪开,它的侧面展开图如图①中的矩形ABB′′A,则蚂蚁爬行的最短路程即为线段AB′的长)( 2)如图②所示是一个底面半径为2 ,母线长为4 的圆锥和它的侧面展开图,PA 是它的一条母线,一只蚂蚁从A 3点出发沿圆锥的侧面爬行一周后回到 A 点,求蚂蚁爬行的最短路程.( 3)如图③所示,在②的条件下,一只蚂蚁从 A 点出发沿圆锥的侧面爬行一周到达母线行的最短路程.PA 上的一点,求蚂蚁爬B′BP PAAA AA图①图②图③(第 24 题)答案与评分标准一、选择题(共17 小题)1、( 2011?广安)如图,圆柱的底面周长为6cm,AC 是底面圆的直径,高 BC=6cm,点 P 是母线 BC 上一点,且 PC= BC.一只蚂蚁从 A 点出发沿着圆柱体的表面爬行到点P 的最短距离是()A、B、 5cmC、D、 7cm考点:平面展开 -最短路径问题。
北师大版八年级期中训练之最短路径问题(勾股定理应用)

北师大版八年级期中训练之最短路径问题(勾股定理应用)一.选择题(共10小题)1.如图,圆柱体的底面圆周长为8cm,高AB为3cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,则爬行的最短路程为()A.4cm B.5cm C.√73cm D.√7cm2.已知点A,B是两个居民区的位置,现在准备在墙l边上建立一个垃圾站点P,如图是4位设计师给出的规划图,其中P A+PB距离最短的是()A.B.C.D.3.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为()cm(杯壁厚度不计).A.14B.18C.20D.254.葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎蔓常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,它的底面周长是50cm,当一段葛藤绕树干盘旋2圈升高为2.4m时,这段葛藤的长是()m.A.3B.2.6C.2.8D.2.55.今年9月23日是第五个中国农民丰收节,小彬用3D打印机制作了一个底面周长为20cm,高为20cm的圆柱粮仓模型.如图BC是底面直径,AB是高.现要在此模型的侧面贴一圈彩色装饰带,使装饰带经过A,C两点(接头不计),则装饰带的长度最短为()A.20πcm B.40πcm C.10√5cm D.20√5cm6.如图,有一圆锥形粮堆,其主视图是边长为4cm的正△ABC,母线AC的中点P处有一老鼠正在偷吃粮食,小猫从B处沿圆锥表面去偷袭老鼠,则小猫经过的最短路程是()cm.A.2√3B.4C.2√5D.67.如图,长方体的长为3,宽为2,高为4,点B离点C的距离为1,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是()A.√21B.5C.√29D.√378.如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是()A.B.C.D.9.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则该蚂蚁要吃到饭粒需爬行的最短路径长是()A.13cm B.3√61cm C.√61cm D.2√61cm10.如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A 爬到点B的最短路程是()A.√10cm B.4cm C.√17cm D.5cm二.填空题(共2小题)11.我国古代有这样一道数学问题:“枯木一根直立地上,高三丈,周八尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为3丈,底面周长为8尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是丈.12.如图,是一个三级台阶,它的每一级的长、宽,高分别为20dm、3dm、2dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是.三.解答题(共3小题)13.如图是放在地面上的一个长方体盒子,其中AB=18cm,BC=12cm,BF=10cm,点M 在棱AB上,且AM=6cm,点N是FG的中点,一只蚂蚁要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程是多少?14.如图,在长方体ABCD﹣A'B'C'D'中,点E是棱B'C'的中点,已知AB=3cm,BC=4cm,AA'=5cm.一只小虫从A点出发沿长方体的表面到E点处觅食,求小虫爬行的最短距离.15.如图,已知线段BC是圆柱底面的直径,圆柱底面的周长为10,圆柱的高AB=12,在圆柱的侧面上,过点A、C两点嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是;(2)求该金属丝的长.。
(完整版)勾股定理--最短距离问题蚂蚁爬行的最短路径好
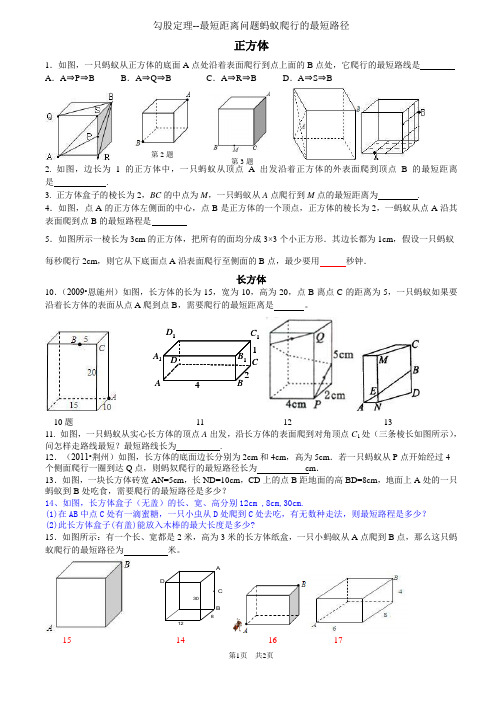
第1页 共2页 1A B A 1B 1DCD 1C 124勾股定理--最短距离问题蚂蚁爬行的最短路径正方体1.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是A .A ⇒P ⇒BB .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .3. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .4.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是5.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 秒钟.长方体10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
10题 11 12 1311. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为 .12.(2011•荆州)如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂奴爬行的最短路径长为 cm .蚂蚁到B 处吃食,需要爬行的最短路径是多少?14、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?15.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
中考数学《勾股定理》复习练习题及答案

中考数学复习专题练习勾股定理一、选择题:1、以下列各组数为边长,能组成直角三角形的是()A.,, B.6,8,10 C.5,12,17 D.9,40,422、下列命题中是假命题的是( )A.△ABC中,若∠B=∠C﹣∠A,则△ABC是直角三角形B.△ABC中,若a2=(b+c)(b﹣c),则△ABC是直角三角形C.△ABC中,若∠A:∠B:∠C=3:4:5,则△ABC是直角三角形D.△ABC中,若a:b:c=5:4:3,则△ABC是直角三角形3、五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是()4、已知△ABC的三边长分别为5,13,12,则△ABC的面积为()A.30 B.60 C.78 D.不能确定5、等边三角形的边长为2,则该三角形的面积为()A.4B.C.2D.36、如图,有两棵树,一棵高9米,另一棵高4米,两树相距12米.一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了多少米?( )A.11B.12C.13D.147、.如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=,则BC的长为()A.-1 B.+1 C.﹣1 D.+1 8、如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则等于()A.75;B.100;C.120;D.125;9、如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm,正方形A的边长为6cm,B的边长为5cm,C的边长为5cm,则正方形D的边长为()A.cmB.4cmC.cmD.3cm10、在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是()A. B. C. D.11、如图,在5×5的正方形网格中,以AB为边画直角△ABC,使点C在格点上,满足这样条件的点C个数()A.6 B.7 C.8 D.9 12、如图,铁路MN和公路PQ在点O处交汇,∠QON=30°.公路PQ上A处距O点240米.如果火车行驶时,周围200米以内会受到噪音的影响.那么火车在铁路MN上沿ON方向以72千米/时的速度行驶时,A处受噪音影响的时间为()A.12秒 B.16秒 C.20秒 D.30秒.二、填空题:13、在△ABC中,如果(a+b)(a﹣b)=c2,那么∠ =90°.14、有四个三角形,分别满足下列条件:(1)一个内角等于另外两个内角之和;(2)三个内角之比为3:4:5;(3)三边之比为5:12:13;(4)三边长分别为7、24、25.其中直角三角形有个.15、如图,AD=13,BD=12,∠C=90°,AC=3,BC=4.则阴影部分的面积= .16、如图,在一个高为3米,长为5米的楼梯表面铺地毯,则地毯长度为米.17、如图,△AOB是等腰三角形,OA=OB,点B在x轴的正半轴上,点A的坐标是(1,1),则点B的坐标是.18、某直角三角形三条边的平方和为200,则这个直角三角形的斜边长为.19、如果的三边长a,b,c满足关系式,则形状是20、如图一只蚂蚁从长、宽都是3厘米,高是8厘米的长方体的纸箱外表面的A点爬到B 点,那么她爬行的最短路线的长为.21、如图,长方体中,AB=12m,BC=2m,BB′=3m,一只蚂蚁从点A出发,以4cm/秒的速度沿长方体表面爬行到点C′,至少需要分钟.22、如图,△ABC是边长6cm的等边三角形,动点P、Q同时从A、B两点出发,分别在AB、BC边上均速移动,它们的速度分别为V p=2cm/s,V Q=1cm/s,当点P到达点B时,P、Q两点停止运动,设点P的运动时间为ts,则当t= s时,△PBQ为直角三角形.23、如图,Rt△ABC中,AC=5,BC=12,分别以它的三边为直径向上作三个半圆,则阴影部分面积为______24、如图,左图是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若两直角边AC=6,BC=4,现将四个直角三角形中边长为4的直角边分别向外延长一倍,延长后得到右图所示的“数学风车”,则该“数学风车”所围成的总面积是_______ .三、简答题:25、如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.(1)在图1中以格点为顶点画一个面积为10的正方形;(2)在图2中以格点为顶点画一个三角形,使三角形三边长分别为2、、;(3)如图3,点A、B、C是小正方形的顶点,求∠ABC的度数.26、有一块土地形状如图8-44所示,∠B=∠D=90°,AB=20米,BC=15米,CD=7米,请计算这块地的面积.27、如图,一架2.5米长的梯子AB,斜靠在一竖直的墙AC上,这时梯子的顶端A到墙底端C的距离为2.4米,如果梯子的底端B沿CB向外平移0.8米至B1,求梯子顶端A沿墙下滑的距离AA1的长度.28、在甲村至乙村的公路有一块山地正在开发,现有一C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围半径250米范围内不得进入,问在进行爆破时,公路AB 段是否有危险而需要暂时封锁?请通过计算进行说明.29、如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上.(1)如图(1),当折痕的另一端F在AB边上且AE=4时,求AF的长(2)如图(2),当折痕的另一端F在AD边上且BG=10时,①求证:EF=EG.②求AF的长.30、在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC 的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:.(2)若△DEF三边的长分别为、、,请在图2的正方形网格中画出相应的△DEF,并利用构图法求出它的面积.(3)如图3,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE的面积分别为13、10、17①试说明△PQR、△BCR、△DEQ、△AFP的面积相等;②请利用第2小题解题方法求六边形花坛ABCDEF的面积.参考答案1、B.2、C.3、C.4、A.5、C.6、C.7、D.8、B.9、A.10、A.11、C.12、B.13、答案为:90°.14、答案为:3.15、答案为:24.16、答案为:7 17、答案为:(,0).18、答案为:10.19、答案为:直角三角形 20、答案为:10cm 21、答案为:3.25 22、答案为:或23、答案为:30 24、答案为:8425、【解答】解:(1)如图1的正方形的边长是,面积是10;(2)如图2的三角形的边长分别为2,,;(3)如图3,连接AC,CD,则AD=BD=CD==,∴∠ACB=90°,由勾股定理得:AC=BC==,∴∠ABC=∠BAC=45°.26、234米2.提示:连结AC,将四边形分割成两个三角形,其面积为两个三角形的面积之和,根据勾股定理求出AC,进而求出AD.AC==25,AD==24,面积为AB×BC+AD×CD=234米2.27、【解答】解:根据题意,在Rt△ABC中,AB=2.5,AC=2.4,由勾股定理得:BC==0.7,∵BB1=0.8,∴B1C=B1B+BC=1.5.∵在Rt△A1B1C中,A1B1=2.5,B1C=1.5,∴A1C==2,∴A1A=2.4﹣2=0.4.答:那么梯子顶端沿墙下滑的距离为0.4米.28、解:公路AB需要暂时封锁.理由如下:如图,过C作CD⊥AB于D.因为BC=400米,AC=300米,∠ACB=90°,所以根据勾股定理有AB=500米.因为S△ABC=AB•CD=BC•AC所以CD=240米.由于240米<250米,故有危险,因此AB段公路需要暂时封锁.29、【解答】(1)解:如图1,∵纸片折叠后顶点B落在边AD上的E点处,∴BF=EF,∵AB=8,∴EF=8﹣AF,在Rt△AEF中,AE2+AF2=EF2,即42+AF2=(8﹣AF)2,解得AF=3;(2)如图2,①证明:∵纸片折叠后顶点B落在边AD上的E点处,∴∠BGF=∠EGF,∵长方形纸片ABCD的边AD∥BC,∴∠BGF=∠EFG,∴∠EGF=∠EFG,∴EF=EG;②解:∵纸片折叠后顶点B落在边AD上的E点处,∴EG=BG=10,HE=AB=8,FH=AF,∴EF=EG=10,在Rt△EFH中,FH===6,∴AF=FH=6.30、【解答】解:(1)根据格子的数可以知道面积为S=3×3﹣×3×2﹣×1×2×1×3=;故答案是:;(2)画图为计算出正确结果S△DEF=2×4﹣(1×2+1×4+2×2)=3;(3)①如图3,过R作RH⊥PQ于H,设RH=h,在Rt△PRH中,PH==,在Rt△RQH中,QH==,∴PQ=+=,两边平方得,13﹣h2+10﹣h2+2•=17,整理得•=2+h2,两边平方得,(13﹣h2)(10﹣h2)=4+4h2+h4,解得h=,∴S△PQR=PQ•RH=,同理,S△BCR=S△DEQ=S△AFP=,∴△PQR、△BCR、△DEQ、△AFP的面积相等;②利用构图法计算出S△PQR=,△PQR、△BCR、△DEQ、△AFP的面积相等,计算出六边形花坛ABCDEF的面积为S正方形PRBA+S正方形RQDC+S正方形QPFE+4S△PQR=13+10+17+4×=62.。
勾股数(填空选择)及详解中考题

勾股数(填空选择)及详解中(Zhong)考题1、附加题:观察以下几组勾(Gou)股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出(Chu)有以上规律的第(Di)⑤组(Zu)勾股数:_________.2、观察下列一(Yi)组数:列(Lie)举:3、4、5,猜(Cai)想:32=4+5;列举:5、12、13,猜想:52=12+13;列举:7、24、25,猜想:72=24+25;…列举:13、b、c,猜想:132=b+c;请你分析上述数据的规律,结合相关知识求得b=_________,c=_________.3、满足a2+b2=c2的三个正整数,称为_________.4、观察下列一类勾股数:3,4,5; 5,12,13; 7,24,25;…请你根据规律写出第4组勾股数为_________.5、观察右面几组勾股数,①3,4,5;②5,12,13;③7,24,25;④9,40,41;并寻找规律,请你写出有以上规律的第⑤组勾股数:_________,第n组勾股数是_________.6、能够成为直角三角形三条边长的三个正整数,称为勾股数,试写出两种勾股数_________,_________.7、在数3,5,12,13四个数中,构成勾股数的三个数是_________.8、将勾股数3,4,5扩大2倍,3倍,4倍,…,可以得到勾股数6,8,10;9,12,15;12,16,20;…,则我们把3,4,5这样的勾股数称为基本勾股数,请你也写出三组基本勾股数_________,_________,_________.9、有一组勾股数,最大的一个是37,最小的一个是12,则另一个是_________.10、观察下列各式:32+42=52;82+62=102;152+82=172;242+102=262;…;你有没有发现其中的规律?请用你发现的规律写出接下来的式子:_________.11、一个直角三角形的三边长是不大于10的偶数,则它的周长为_________.12、观察下面几组勾股数,并寻找规律:①4,3,5;②6,8,10;③8,15,17;④10,24,26;请你根据规律写出第⑤组勾股数是_________.13、数组3、4、5;5、12、13;7、24、25;9、40、41;…都是勾股数,若n为直角三角形的一较长直角边,用含n的代数式表示斜边为_________.深圳市菁优网络科技有限公司14、写出三组勾股(Gu)数,使每组勾股数中必出现(Xian)12,_________;_________;_________;15、我们把符(Fu)合等式(Shi)a2+b2=c2的(De)a、b、c三个称为(Wei)勾股数.现请你用计算器验证下列各组的数是否勾股数.你能发现其中规律吗?请完成下列空格.3,4,5;5,12,13;7,24,25;9,40,41;11,_________,_________;…16、以下列各(Ge)组数为边长:①3、4、5;②5,12,13;③3,5,7;④9,40,41;⑤10,12,13;其(Qi)中能构成直角三角形的有_________.17、观察下列勾股数组:a b c6 8 108 15 1710 24 2612 35 37………用含有字母a的代数式分别表示b,c,则b=_________,c=_________.18、写出常见的勾股数_________、_________.19、请写出一组你知道的勾股数,它们是_________.20、若8,a,17是一组勾股数,则a=_________.二、选择题(共10小题)21、下列各组数中,是勾股数的一组是()A、4,5,6B、5,7,12C、12,13,15D、21,28,3522、下列各组数为勾股数的是()A、7,12,13B、3,4,7C、8,15,17D、1.5,2,2.523、若正整数a,b,c是一组勾股数,则下列各组数一定还是勾股数的是()A、a+1,b+1,c+1B、a2,b2,c2C、2a,2b,2cD、a﹣1,b﹣1,c﹣124、在下列四组数中,不是勾股数的一组是()A、15,8,17B、9,12,15C、3,5,7D、7,24,2525、下列各组数中,是勾股数的为()A、1,2,3B、4,5,6C、3,4,5D、7,8,926、下列几组数中,为勾股数的是()A、,,B、3,4,6C、5,12,13D、0.9,1.2,1.527、下列各组数是勾股数的(De)为()A、2,4,5B、8,15,17C、11,13,15D、4,5,628、分别以下列四(Si)组数为一个三角形的三边的长(Chang)①6、8、10;②5、12、13;③8、15、17;④7、8、9,其中能构成直角(Jiao)三角形的有()A、4组(Zu)B、3组(Zu)C、2组(Zu)D、1组(Zu)29、下列各组数据不能作为直角三角形的三边长的是()A、a=3,b=4,c=5B、a=6,b=8,c=10C、a=5,b=12,c=13D、a=13,b=16,c=1830、下列由线段a、b、c组成的三角形,不是直角三角形的是()A、a=3,b=4,c=5B、a=5,b=12,c=13C、a=2,b=3,c=4D、a=10,b=24,c=26答案与(Yu)评分标准一(Yi)、填空题(共(Gong)20小(Xiao)题)1、附加(Jia)题:观察以下几组勾股数,并寻找规律:①3,4,5;②5,12,13;③7,24,25;④9,40,41;…请你写出有(You)以上规律的第(Di)⑤组勾(Gou)股数:11,60,61.考点:勾股定理的逆定理;勾股数。
第3章 勾股定理 平面展开最短路径专题习题 2021-2022学年八年级数学苏科版上册

第3章勾股定理——平面展开最短路径专题一.选择题1.已知:如右图,O为圆锥的顶点,M为底面圆周上一点,点P在OM上,一只蚂蚁从点P出发绕圆锥侧面爬行回到点P时所经过的最短路径的痕迹如图.若沿OM将圆锥侧面剪开并展平,所得侧面展开图是()A.B.C.D.2.如图:长方体盒子的长、宽、高分别是12cm,8cm,30cm,在AB中点C处有一滴蜜糖,一只小虫从E处爬到C处去吃,有无数种走法,其中最短的路程是()cm.A.15 cm B.20 cm C.25 cm D.30 cm3.如图是长为5,宽为4,高为3的长方体,一只蚂蚁从顶点A沿长方体的表面爬行到顶点B的最短距离是()A.12 B.3C.4D.4.如图:有一圆柱,它的高等于4cm,底面直径等于2cm(π=3)在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约()A.8cm B.6cm C.5cm D.10cm5.如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A.B.5cm C.D.7cm6.如图,A是高为10cm的圆柱底面圆上一点,一只蜗牛从A点出发,沿30°角绕圆柱侧面爬行,当他爬到顶上时,他沿圆柱侧面爬行的最短距离是()A.10cm B.20cm C.30cm D.40cm7.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要()cm.A.10n B.C.D.8.如图,一圆柱体的底面圆周长为24cm,高AB为4cm,BC是直径,一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C的最短路程是()A.4B.4C.D.π+9.已知,如图是一个封闭的正方形纸盒,E是CD中点,F是CE中点,一只蚂蚁从一个顶点A爬到另一个顶点G,那么这只蚂蚁爬行的最短路线是()A.A⇒B⇒C⇒G B.A⇒C⇒G C.A⇒E⇒G D.A⇒F⇒G10.如图是一个三级台阶,它的每一级的长、宽、高分别为55寸、10寸和6寸,A和B是这个台阶的两个相对端点,A点上有一只蚂蚁想到B点去吃可口的食物,则它所走的最短路线长度是()A.71寸B.73寸C.100寸D.103寸二.填空题11.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B 处的米粒,若圆柱的高为12cm,底面周长为24cm.则蚂蚁爬行的最短距离为cm.12.如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是.13.如图,一个高16m,底面周长8m的圆柱形水塔,现制造一个螺旋形登梯,为了减小坡度,要求登梯绕塔环绕一周半到达顶端,问登梯至少为长.14.如图,是一个3×3的魔方放在桌面上,该魔方上每一个小方格的边长都是2cm,其下底面点A处有一只蚂蚁,侧面点B处有一滴蜂蜜,若蚂蚁沿魔方的表面爬行从点A到点B去吃蜂蜜,则蚂蚁爬行的最短路径为.15.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个半圆柱而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=20m,点E在CD上,CE=4m,一滑行爱好者从A点滑行到E点,则他滑行的最短距离为m(π的值为3).16.如图,有一圆柱形油罐,要以A点环绕油罐建梯子,正好到A点的正上方B点,则梯子最短需m (油罐底面圆的周长为15m,高AB=8m).17.如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=50,点P到AD的距离是30,有一只蚂蚁要从点P爬到点B,则蚂蚁的最短行程为.三.解答题18.如图,有一个圆柱体,它的高为20,底面半径为5.如果一只蚂蚁要从圆柱体下底面的A点,沿圆柱表面爬到与A相对的上底面B点,则蚂蚁爬的最短路线长约为多少(π取3)19.如图,壁虎在一座底面半径为2米,高为4米的油罐的下底边沿A处,它发现在自己的正上方油罐上边缘的B处有一只害虫,便决定捕捉这只害虫,为了不引起害虫的注意,它故意不走直线,而是绕着油罐,沿一条螺旋路线,从背后对害虫进行突然袭击.结果,壁虎的偷袭得到成功,获得了一顿美餐.请问壁虎至少要爬行多少路程才能捕到害虫?(π取3.14,结果保留1位小数,可以用计算器计算)20.葛藤是一种植物,它自己腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一个绝招,就是它绕树盘升的路线,总是沿最短路线螺旋前进的.(1)如果树的周长为3m,绕一圈升高4cm,则它爬行路程是多少?(2)如果树的周长为8m,绕一圈爬行10m,则爬行一圈升高多少m?如果爬行10圈到达树顶,则树干多高?21.如图(1)所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示.已知展开图中每个正方形的边长为1.求在该展开图中可画出最长线段的长度?这样的线段可画几条?22.如图所示,一个无盖四棱柱容器,其底面是一个边长为3cm的正方形,高为20cm.现有一根彩带,从底面A点开始缠绕四棱柱,刚好缠绕4周到达B点(假设彩带完美贴合四棱柱).(1)请问彩带的长度是多少?(2)如图所示,一只蚂蚁在容器外A点发现容器的内部距离顶部2cm处有一滴蜂蜜,它想以最短的路程到达C处.请问蚂蚁走的最短路程是多少呢?(注:以上两问均要画出平面展开示意图,再解答)。
数学八年级下册专题17.4 勾股定理中最短路径问题专项训练(30道)(人教版)(学生版)

专题17.4 勾股定理中最短路径问题专项训练(30道)【人教版】1.如图,在长为3,宽为2,高为1的长方体中,一只蚂蚁从顶点A出发沿着长方体的表面爬行到顶点B,那么它爬行的最短路程是()A.√14B.√18C.√20D.√262.如图,已知圆柱底面的周长为12cm,圆柱高为8cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为()A.10cm B.20cm C.√208cm D.100cm3.如图,长方体的长为3,宽为2,高为4,点B离点C的距离为1,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是()A.√21B.5C.√29D.√374.如图,在长方体透明容器(无盖)内的点B处有一滴糖浆,容器外A点处的蚂蚁想沿容器壁爬到容器内吃糖浆,已知容器长为5cm,宽为3cm,高为4cm,点A距底部1cm,请问蚂蚁需爬行的最短距离是(容器壁厚度不计)()A.3√17cm B.10cm C.5√5cm D.√113cm5.如图,一圆柱体的底面圆周长为20cm,高AB为4cm,BC是上底的直径,一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,则爬行的最短路程是()A.2√29B.4π√π2+25C.2√25π2+4D.146.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A 处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖A处的最短距离是()A.√73厘米B.10厘米C.8√2厘米D.8厘米7.国庆节期间,重庆南开中学用彩灯带装饰了艺术楼大厅的所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为()A.√7米B.√11米C.√13米D.5米8.如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为()(π取3)m.A.30B.28C.25D.229.如图是一个三级台阶,它的每一级的长、宽和高分别为9、3和1,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物.则这只蚂蚁沿着台阶面爬行的最短路程是()A.18B.15C.12D.810.某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A 到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为()A.8cm B.10cm C.12cm D.15cm二.填空题(共10小题)11.如图所示,ABCD是长方形地面,长AB=16m,宽AD=9m,中间竖有一堵砖墙高MN=1m.一只蚂蚱从B点爬到D点,它必须翻过中间那堵墙,则它至少要走m的路程.12.在一个长6+2√2米,宽为4米的长方形草地上,如图堆放着一根三棱柱的木块,它的侧棱长平行且大于场地宽AD,木块的主视图的高是√2米的等腰直角三角形,一只蚂蚁从点A处到C处需要走的最短路程是米.13.如图,若圆柱的底面周长是30cm,高是120cm,从圆柱底部A处沿侧面缠绕几圈丝线到顶部B处做装饰,则按图中此方式缠绕的这条丝线的最小长度是cm.14.爱动脑筋的小明某天在家玩遥控游戏时遇到下面的问题:已知,如图一个棱长为8cm无盖的正方体铁盒,小明通过遥控器操控一只带有磁性的甲虫玩具,他先把甲虫放在正方体盒子外壁A处,然后遥控甲虫从A处出发沿外壁面正方形ABCD爬行,爬到边CD上后再在边CD上爬行3cm,最后在沿内壁面正方形ABCD上爬行,最终到达内壁BC的中点M,甲虫所走的最短路程是cm.15.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上.(1)若绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是尺.(2)若绕n周后其末端恰好到达点B处,则问题中葛藤的最短长度是尺.16.如图,长方体盒子的长为15cm ,宽为10cm ,高为20cm ,点B 距离C 点5cm ,一只蚂蚁如果要沿着盒子的表面从点A 到点B .(1)蚂蚁爬行的最短距离是 cm ;(2)若从C 处想盒子里面插入一根吸管,要使吸管不落入盒子中,吸管应不少于 cm .17.如图,这是一个供滑板爱好者使用的U 型池的示意图,该U 型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为32πm 的半圆,其边缘AB =CD =15m ,点E 在CD 上,CE =3m ,一滑板爱好者从A 点滑到E 点,则他滑行的最短距离约为 m .(边缘部分的厚度忽略不计)18.如图所示的长方体透明玻璃鱼缸,假设其长AD =80cm ,高AB =60cm ,水深AE =40cm .在水面上紧贴内壁G 处有一块面包屑,G 在水面线EF 上,且EG =60cm ,一只蚂蚁想从鱼缸外的A 点沿鱼缸壁爬进鱼缸内的G 处吃面包屑.则蚂蚁爬行的最短路线为 cm .19.边长分别为4cm,3cm两正方体如图放置,点P在E1F1上,且E1P=13E1F1,一只蚂蚁如果要沿着长方体的表面从点A爬到点P,需要爬行的最短距离是cm.20.在一个长为8分米,宽为5分米,高为7分米的长方体上,截去一个长为6分米,宽为5分米,深为2分米的长方体后,得到一个如图所示的几何体.一只蚂蚁要从该几何体的顶点A处,沿着几何体的表面到几何体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是分米.三.解答题(共10小题)21.如图是一个玻璃容器,在ABCD面的外面一点E处有一个蚂蚁,里面F点处有一小块食物,蚂蚁要想爬到里面去吃食物,请你帮它选择一条最近的爬行路线.(保留作图痕迹)22.在立方体纸盒的顶点A处有一只蚂蚁,在另一顶点E处有一粒糖,你能为这只蚂蚁设计一条最短路线,使它沿着立方体表面上的这一条路线爬行,最快捷吃到糖吗?以下提供三个方案:①A→B→C→E;②A→C→E;③A→D→E.(1)三种方案①、②、③中爬行路线最短的方案是;最长的方案是.(2)请根据数学知识说明理由.23.如图1,长方体的底面边长分别为3m和2m,高为1m,在盒子里,可以放入最长为m的木棒;(2)如图2,在与(1)相同的长方体中,如果用一根细线从点A开始经过4个侧面缠绕一圈到达点C,那么所用细线最短需要m;(3)如图3,长方体的棱长分别为AB=BC=6cm,AA1=14cm,假设昆虫甲从盒内顶点C1以2厘米/秒的速度在盒子的内部沿棱C1C向下爬行,同时昆虫乙从盒内顶点A以相同的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉昆虫甲?24.如图,已知圆柱底面的直径BC=8,圆柱的高AB=10,在圆柱的侧面上,过点A,C嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是.(2)求该长度最短的金属丝的长.25.如图,长方体的长BE=30cm,宽AB=20cm,高AD=40cm,点M在CH上,且CM=10cm.一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?26.如图,长方体的长AB=5cm,宽BC=4cm,高AE=6cm,三只蚂蚁沿长方体的表面同时以相同的速度从点A出发到点G处.蚂蚁甲的行走路径S甲为:翻过棱EH后到达G处(即A→P→G),蚂蚁乙的行走路径S乙为:翻过棱EF后到达G处(即A→M→G),蚂蚁丙的行走路径S丙为:翻过棱BF后到达G 处(即A→N→G).(1)求三只蚂蚁的行走路径S甲,S乙,S丙的最小值分别是多少?(2)三只蚂蚁都走自己的最短路径,请判断哪只最先到达?哪只最后到达?27.如图①所示,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处,要想使路程较短,有三种不同的方式:①沿面ABB1A1和面A1B1C1D1;②沿面和ABB1A1和面BCC1B1;③沿面AA1D1D 和面A1B1C1D1.(1)图②为第一种方式展成的平面图形,请你画出另两种方式展成的平面图形;(2)若AB=4,BC=2,BB1=1,请通过计算,判断第几种方式所走路线最短?最短路线长为多少?(3)若长方体的长、宽、高分别为a、b、c,且a>b>c,请直接写出最短路线的长(用a,b,c的代数式表示).28.吴老师在与同学们进行“蚂蚁怎样爬最近”的课题研究时设计了以下问题,请你根据下列所给的条件分别求出蚂蚁需要爬行的最短路程的长.(1)如图1,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿正方体表面爬到点C1处;(2)如图2,长方体底面是边长为5cm的正方形,高为6cm,一只蚂蚁欲从长方体底面上的点A沿长方体表面爬到点C1处.29.图(1)为一个无盖的正方体纸盒,现将其展开成平面图,如图(2).已知展开图中每个正方形的边长为1.(1)求该展开图中可画出最长线段的长度,并求出这样的线段可画几条.(2)试比较立体图中∠ABC与平面展开图中∠A′B′C′的大小关系.30.勾股定理是解决直角三角形很重要的数学定理.这个定理的证明的方法很多,也能解决许多数学问题.请按要求作答:(1)用语言叙述勾股定理;(2)选择图1、图2、图3中一个图形来验证勾股定理;(3)利用勾股定理来解决下列问题:如图4,一个长方体的长为8,宽为3,高为5.在长方体的底面上一点A处有一只蚂蚁,它想吃长方体上与A点相对的B点处的食物,则蚂蚁需要沿长方体表面爬行的最短路程是多少?。
专题1.3 勾股定理之最短路径问题专项训练(30道)(举一反三)(北师大版)(解析版)

专题1.3 勾股定理之最短路径问题专项训练(30道)【北师大版】考卷信息:本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,涵盖了平面直角坐标系中的规律问题所有类型!一.选择题(共12小题)1.(2022春•五华区期末)如图,正方体的棱长为2cm,点B为一条棱的中点.蚂蚁在正方体表面爬行,从点A爬到点B的最短路程是( )A B.4cm C D.5cm【分析】正方体侧面展开为长方形,确定蚂蚁爬行的起点和终点,根据两点之间线段最短,根据勾股定理可求出最短路径长,【解答】解:如图,它运动的最短路程AB==cm).故选:C.2.(2022春•碑林区校级期末)如图,圆柱的底面周长为12cm,AB是底面圆的直径,在圆柱表面的高BC 上有一点D,且BC=10cm,DC=2cm.一只蚂蚁从点A出发,沿着圆柱体的表面爬行到点D的最短路程是( )cm.A.14B.12C.10D.8【分析】首先画出圆柱的侧面展开图,根据底面周长为12cm,求出AB的值;再在Rt△ABD中,根据勾股定理求出AD的长,AD即为所求.【解答】解:圆柱侧面展开图如图所示,∵圆柱的底面周长为12cm,∴AB=6cm.∵BD=8cm,在Rt△ABD中,AD2=AB2+BD2,∴AD10(cm),即蚂蚁从A点出发沿着圆柱体的表面爬行到点D的最短距离是10cm.故选:C.3.(2022春•洛阳期中)如图,圆柱形玻璃杯,高为12cm,底面周长为18cm.在杯内离杯底4cm的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最短距离为( )cm.A.15B C.12D.18【分析】将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,则先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,再利用勾股定理求A'C的长即可.【解答】解:如图所示,将圆柱沿过A的母线剪开,由题意可知,需在杯口所在的直线上找一点F,使AF+CF最小,故先作出A关于杯口所在直线的对称点A',连接A'C与杯口的交点即为F,此时AF+CF=A'F+CF=A'C,根据两点之间线段最短,即可得到此时AF+CF最小,并且最小值为A'C的长度,如图所示,延长过C的母线,过A'作A'D垂直于此母线于D,由题意可知,A'D=18÷2=9(cm),CD=12﹣4+4=12(cm),由勾股定理得:A'C=15(cm),故蚂蚁到达蜂蜜的最短距离为15cm,故选:A.4.(2022秋•高州市期末)国庆节期间,茂名市一广场用彩灯带装饰了所有圆柱形柱子.为了美观,每根柱子的彩灯带需要从A点沿柱子表面缠绕两周到其正上方的B点,如图所示,若每根柱子的底面周长均为2米,高均为3米,则每根柱子所用彩灯带的最短长度为( )A B C D.5米【分析】要求彩带的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,借助于勾股定理.【解答】解:将圆柱表面切开展开呈长方形,则彩灯带长为2个长方形的对角线长,∵圆柱高3米,底面周长2米,∴AC2=22+1.52=6.25,∴AC=2.5,∴每根柱子所用彩灯带的最短长度为5m.故选:D.5.(2022秋•沈阳期末)如图,长方体的长为3,宽为2,高为4,点B离点C的距离为1,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是( )A B.5C D【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.【解答】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如图1:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=5;只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如图2:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如图3:∵长方体的宽为2,高为4,点B离点C的距离是1,∴AB=∵5∴蚂蚁爬行的最短距离是5.故选:B.6.(2022春•郾城区期末)如图,台阶阶梯每一层高20cm,宽30cm,长50cm,一只蚂蚁从A点爬到B点,最短路程是( )cm.A.B.C.120D.130【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【解答】解:如图所示,∵它的每一级的长宽高为20cm,宽30cm,长50cm,∴AB=cm).答:蚂蚁沿着台阶面爬行到点B的最短路程是,故选:B.7.(2022秋•揭阳校级月考)如图,一个棱长为3的正方体,把它分成3×3×3个小正方体,小正方体的棱长都是1.如果一只蚂蚁从点A爬到点B,那么估计A,B间的最短路程d的值为( )A.4B.5C.6D.7【分析】过B作BD⊥AC于D,根据勾股定理即可得到结论.【解答】解:过B作BD⊥AC于D,则AD=4,BD=3,∴A,B间的最短路程d=5,故选:B.8.(2022秋•牡丹区月考)如图是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行的部分的截面是半径为2.5m的半圆,其边缘AB=CD=20m.小明要在AB上选取一点E,能够使他从点D滑到点E再滑到点C的滑行距离最短,则他滑行的最短距离约为( )(π取3)m.A.30B.28C.25D.22【分析】要求滑行的最短距离,需将该U型池的侧面展开,进而根据“两点之间线段最短”得出结果.【解答】解:其侧面展开图如图:作点C关于AB的对称点F,连接DF,∵中间可供滑行的部分的截面是半径为2.5m的半圆,∴BC=πR=2.5π≈7.5m,AB=CD=20m,∴CF=15m,在Rt△CDF中,DF==25(m),故他滑行的最短距离约为25m.故选:C.9.(2022春•靖西市期中)如图是放在地面上的一个长方体盒子,其中AB=7cm,BC=4cm,BF=6cm,点M在棱AB上,且AM=1cm,点N是FG的中点,一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为( )A.10cm B.C.D.【分析】利用平面展开图有2种情况,画出图形利用勾股定理求出MN的长即可.【解答】解:如图1中,MN=10(cm),如图2中,MN==10(cm),∴一只蚂蚁要沿着长方形盒子的外表面从点M爬行到点N,它需要爬行的最短路程为10cm,故选:A.10.(2022秋•芝罘区期中)某校“光学节”的纪念品是一个底面为等边三角形的三棱镜(如图).在三棱镜的侧面上,从顶点A到顶点A′镶有一圈金属丝,已知此三棱镜的高为9cm,底面边长为4cm,则这圈金属丝的长度至少为( )A.8cm B.10cm C.12cm D.15cm【分析】画出三棱柱的侧面展开图,利用勾股定理求解即可.【解答】解:将三棱柱沿AA′展开,其展开图如图,则AA′=15(cm).故选:D.11.(2022秋•青岛期末)棱长分别为8cm,6cm的两个正方体如图放置,点A,B,E在同一直线上,顶点G在棱BC上,点P是棱E1F1的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P,它爬行的最短距离是( )A.+10)cm B.C D.+3)cm【分析】求出两种展开图PA的值,比较即可判断.【解答】解:如图,有两种展开方法:方法一:PA=,方法二:PA=..故选:C.12.(2022•广饶县一模)如图,长方体的底面边长分别为2厘米和4厘米,高为5厘米.若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )厘米.A.8B.10C.12D.13【分析】要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.【解答】解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.∴PA=4+2+4+2=12(cm),QA=5cm,∴PQ=13cm.故选:D.二.填空题(共8小题)13.(2022春•德城区期末)如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 25 cm.【分析】画出长方体的侧面展开图,根据勾股定理求出AB的长即可.【解答】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴BD=CD+BC=10+5=15(cm),AD=20cm,在直角三角形ABD中,根据勾股定理得:∴AB=25(cm);只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴BD=CD+BC=20+5=25(cm),AD=10cm,在直角三角形ABD中,根据勾股定理得:∴AB=cm);只要把长方体的上表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:∵长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,∴AC=CD+AD=20+10=30(cm),在直角三角形ABC中,根据勾股定理得:∴AB==cm);∵25<∴蚂蚁爬行的最短距离是25cm.故答案为:25.14.(2022•潍城区一模)云顶滑雪公园是北京2022年冬奥会7个雪上竞赛场馆中唯一利用现有雪场改造而成的,如图左右两幅图分别是公园内云顶滑雪场U型池的实景图和示意图,该场地可以看作是从一个m,其边缘AB=CD=24m,点E在CD 长方体中挖去了半个圆柱而成,它的横截面图中半圆的半径为12π上,CE=4m,一名滑雪爱好者从点A滑到点E,他滑行的最短路线长为.【分析】根据题意可得,AD=12,DE=CD﹣CE=24﹣4=20,线段AE即为滑行的最短路线长.在Rt△ADE中,根据勾股定理即可求出滑行的最短路线长.【解答】解:将半圆面展开可得:AD=12m,DE=DC﹣CE=20m,在Rt△ADE中,AE==m),即滑行的最短路线长为,故答案为:15.(2022春•仁怀市月考)如图,要在河边l上修建一个水泵站,分别向A村和B村送水,已知A村、B 村到河边的距离分别为2km和7km,且AB两村庄相距13km,则铺设水管的最短长度是 15 km.【分析】作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置;利用了轴对称的性质可得AP=A′P,在Rt△AEB中利用勾股定理可以算出AE的长,再在Rt△A′CB中利用勾股定理算出A′B的长,根据两点之间线段最短的性质即可求解.【解答】解:作点A关于河边所在直线l的对称点A′,连接A′B交l于P,则点P为水泵站的位置,此时,(PA+PB)的值最小,即所铺设水管最短;过B点作l的垂线,过A′作l的平行线,设这两线交于点C,过A作AE⊥BC于E,则四边形AA′CE和四边形AMNE是矩形,∴EN=AM=2,EC=AA′=2+2=4,A′C=AE,在Rt△ABE中,依题意得:BE=BN﹣EN=7﹣2=5,AB=13,根据勾股定理可得:AE=12,在Rt△B A′C中,BC=BE+EC=5+4=9,A′C=12,根据勾股定理可得:A′B=15,∵PA=PA′,∴PA+PB=A′B=15(km),故答案为:15.16.(2022秋•锦江区校级期末)在一个长4米的长方形草地上,如图堆放着一根三棱柱的木块,它的侧棱长平行且大于场地宽AD,一只蚂蚁从点A处到C处需要走的最短路程是米.【分析】解答此题要将木块展开,然后根据两点之间线段最短解答.【解答】解:由题意可知,将木块展开,相当于是AB+等腰直角三角形的两腰,∴长为2+2﹣10(米);宽为4米.=故答案为:17.(2022秋•高新区校级期末)如图,教室的墙面ADEF与地面ABCD垂直,点P在墙面上.若PA=AB=5米,点P到AD的距离是3米,有一只蚂蚁要从点P爬到点B【分析】可将教室的墙面ADEF与地面ABCD展开,连接P、B,根据两点之间线段最短,利用勾股定理求解即可.【解答】解:如图,过P作PG⊥BF于G,连接PB,∵AG=3米,AP=AB=5米,∴PG=4米,∴BG=8米,∴PB==故这只蚂蚁的最短行程应该是故答案为:18.(2022春•德州期中)如图,点A是正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其表面爬到点B【分析】根据题意画出图形,过A作EA⊥CD于E,连接AB,则AB长为最短距离,求出OD=OC,∠DAC=90°,根据直角三角形斜边上中线性质求出AE=DE=EC=1,根据勾股定理求出即可.【解答】解:如图展开:过A作EA⊥CD于E,连接AB,则AB长为最短距离,∵四边形DFGC是正方形,DC=BC=2,∴OD=OC,∠DAC=90°,∴∠ADE=∠ECA=45°,∵AE⊥DC,∴DE=EC,∵∠DAC=90°,DC=1,∴AE=DE=EC=12在△AEB中,∠AEB=90°,BE=1+2=3,EA=1,由勾股定理得:AB19.(2022秋•中原区校级期末)如图,一个三棱柱盒子底面三边长分别为3cm,4cm,5cm,盒子高为9cm,一只蚂蚁想从盒底的点A沿盒子的表面爬行一周到盒顶的点B,蚂蚁要爬行的最短路程是 15 cm.【分析】将三棱柱侧面展开得出矩形,求出矩形对角线的长度即可.【解答】解:如图,右侧为三棱柱的侧面展开图,AA′=3+4+5=12cm,A′B=9cm,∠AA′B=90°,∴AB==15cm,故答案为:15.20.(2022秋•凤城市期中)如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm.在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处吃面包屑.则蚂蚁爬行的最短路线为 100 cm.【分析】作出A关于BC的对称点A′,连接A′G,与BC交于点Q,此时AQ+QG最短;A′G为直角△A′EG的斜边,根据勾股定理求解即可.【解答】解:如图所示作点A关于BC的对称点A′,连接A′G交BC与点Q,小虫沿着A→Q→G的路线爬行时路程最短.在直角△A′EG中,A′E=80cm,EG=60cm,∴AQ+QG=A′Q+QG=A′G=100cm.∴最短路线长为100cm.故答案为:100.三.解答题(共10小题)21.(2022春•宜城市期末)如图,某小区有两个喷泉A,B,两个喷泉的距离长为125m.现要为喷泉铺设供水管道AM,BM,供水点M在小路AC上,供水点M到AB的距离MN的长为60m,BM的长为75m.(1)求供水点M到喷泉A,B需要铺设的管道总长;(2)求喷泉B到小路AC的最短距离.【分析】(1)根据勾股定理解答即可;(2)根据勾股定理的逆定理和垂线段解答即可.【解答】解:(1)在Rt△MNB中,BN==45(m),∴AN=AB﹣BN=125﹣45=80(m),在Rt△AMN中,AM100(m),∴供水点M到喷泉A,B需要铺设的管道总长=100+75=175(m);(2)∵AB=125m,AM=100m,BM=75m,∴AB2=BM2+AM2,∴△ABM是直角三角形,∴BM⊥AC,∴喷泉B到小路AC的最短距离是BM=75m.22.(2022秋•原阳县期末)如图,一个正方体木箱子右边连接一个正方形木板,甲蚂蚁从点A出发,沿a,b,d三个面走最短路径到点B;同时,乙蚂蚁以相同的速度从点B出发,沿d,c两个面走最短路径到点A.请你通过计算判断哪只蚂蚁先到达目的地?【分析】将正方体展开,根据两点之间线段最短,构造出直角三角形,进而求出最短路径的长.【解答】解析展开a,b,c与d在同一平面内,如图所示.由题意可知,甲蚂蚁走的路径为A1B,A1B=cm).乙蚂蚁走的路径为A2B,A2B==cm).所以A1B>A2B,故乙蚂蚁先到达目的地.23.(2022秋•江北区期末)在立方体纸盒的顶点A处有一只蚂蚁,在另一顶点E处有一粒糖,你能为这只蚂蚁设计一条最短路线,使它沿着立方体表面上的这一条路线爬行,最快捷吃到糖吗?以下提供三个方案:①A→B→C→E;②A→C→E;③A→D→E.(1)三种方案①、②、③中爬行路线最短的方案是 ③ ;最长的方案是 ① .(2)请根据数学知识说明理由.【分析】(1)根据“化曲面为平面”,且利用“两点之间线段最短”可知,爬行路线最短的方案是③;最长的方案是①;(2)分别求出三种方案蚂蚁爬行的路程,比较即可求解.【解答】解:(1)三种方案①、②、③中爬行路线最短的方案是③;最长的方案是①.故答案为:③;①;(2)爬行路线最短的方案是③;最长的方案是①.理由如下:‘’设立方体纸盒的棱长为a,则a>0.方案:①A→B→C→E蚂蚁爬行的路程为:AB+BC+CE=a+a+a=3a;方案;②A→C→E蚂蚁爬行的路程为:AC+CE=a+1)a;方案;③A→D→E.1)a<3a,∴爬行路线最短的方案是③;最长的方案是①.24.(2022秋•二道区期末)如图,已知线段BC是圆柱底面的直径,圆柱底面的周长为10,圆柱的高AB=12,在圆柱的侧面上,过点A、C两点嵌有一圈长度最短的金属丝.(1)现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是 C ;(2)求该金属丝的长.【分析】(1)由平面图形的折叠及立体图形的表面展开图的特点解题;(2)要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.【解答】解:(1)因为圆柱的侧面展开面为长方形,AC展开应该是两线段,且有公共点C.故答案为:C;(2)如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为10,圆柱的高AB=12,∴该长度最短的金属丝的长为2AC==26.25.(2022秋•随县期末)如图1所示,长方形是由两个正方形拼成的,正方形的边长为a,对角线为b,长方形对角线为c.一只蚂蚁从A点爬行到C点.(1)求蚂蚁爬行的最短路线长(只能按箭头所示的三条路线走),并说明理由;(2)如果把右边的正方形EFBC沿EF翻转90°得到如图2所示的正方体相邻的两个面(实线表示),则蚂蚁从A点到C点的最短路线长是多少?请在图2中画出路线图,若与图中的线段有交点,则要标明并说明交点的准确位置.(可测量猜想判断)【分析】(1)根据两点之间线段最短求解;(2)把正方体相邻的两个面展开成平面,连接A,C即是最短路线.【解答】解:(1)从A﹣B﹣C路线长:a+a+a=3a,从A﹣D﹣C路线长:a+a+a=3a,从A﹣E﹣C路线长:a+b.(3分)根据两点之间,线段最短.可得AD+DE>AE,即a+a>b,(6分)所以a+a+a>a+b,即3a>a+b(7分)(说明:只要写出理由“两点之间,线段最短”即给6分)故从A到C的最短路线长为a+b;(8分)(2)从A到C的最短路线长为C,(10分)图中的点M为线段EF的中点.(11分)位置如图.(13分)26.(2022秋•罗湖区期中)(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?【分析】(1)利用勾股定理直接求出木棒的最大长度即可.(2)将长方体展开,利用勾股定理解答即可;(3)将容器侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解答】解:(1)由题意得:该长方体中能放入木棒的最大长度是:=13(cm).(2)分三种情况可得:AG=>AG>AG=,;(3)∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,∴A′D=5cm,BD=12﹣3+AE=12cm,∴将容器侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B=13(Cm).27.(2022秋•元宝区校级期中)一根长90cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4cm,彩色丝带均匀地缠绕了30圈,问:丝带共有多长?【分析】根据题意抽象出直角三角形,利用勾股定理求得彩色丝带的长即可.=150cm,答:丝带共有150cm.28.(2022秋•东明县期中)东明县是鲁西南的化工基地,有东明石化集团,洪业化工集团,玉皇化工集团等企业,化学工业越来越成为东明县经济的命脉,化工厂里我们会经常看到如图储存罐,根据需要,在圆柱形罐的外围要安装小梯子,如果油罐的底面半径为6米,高24米,梯子绕罐体半圆到达罐顶,则梯子至少要多长?【分析】把立体图形转化为平面图形,利用勾股定理即可解决问题.【解答】解:如图,根据题意,BC=24m,AB=1•2π•6≈18m,2在Rt△ABC中,AC30m,答:梯子至少要30m.29.(2022秋•福田区期末)如图,是一个圆柱形的饼干盒,在盒子外侧下底面的点A处有甲、乙两只蚂蚁,它们都想要吃到上底面外侧B′处的食物:甲蚂蚁沿A→A′→B′的折线爬行,乙蚂蚁沿圆柱的侧面爬行:若∠AOB=∠A′O′B′=90°(AA′、BB′都与圆柱的中轴线OO′平行),圆柱的底面半径是12cm,高为1cm,则:(1)A′B,甲蚂蚁要吃到食物需爬行的路程长l1+1 cm;(2)乙蚂蚁要吃到食物需爬行的最短路程长l2(π取3);(3)若两只蚂蚁同时出发,且爬行速度相同,在乙蚂蚁采取最佳策略的前提下,哪只蚂蚁先到达食物处?请你通过计算或合理的估算说明理由.(参考数据:π取3≈1.4)【分析】(1)由∠A′O′B′=90°,可知△B′A′O′为等腰直角三角形,故此A′B′=′O ′,然后根据l1=A′B′+AA′求解即可;(2)先求得弧A′B′的长,然后根据勾股定理求得矩形AA′B′B的对角线的长度即可;(3 1.4代入从而可求得l1、l2的近似值,从而可作出判断.【解答】解:(1)∵∠A′O′B′=90°,O′A′=O′B′,∴A′B′=A′B′=′O′=∴l1=A′B′+AA′=1.故答案为:1.=6π=18.(2)A′B′=90°×2π×12360°将圆柱体的侧面展开得到如图1所示矩形AA′B′B.∵A′B′=18,∴A′B′=18.在Rt△ABB′中,AB′=故答案为:(3)∵l1=1≈12×1.4+1=17.8∴l21=316.84.∵l22=2=325,∴l21<l22.∴l1<l2.∴甲蚂蚁先到达食物处.30.(2022秋•安岳县期末)勾股定理是解决直角三角形很重要的数学定理.这个定理的证明的方法很多,也能解决许多数学问题.请按要求作答:(1)选择图1或图2中任一个图形来验证勾股定理;(2)利用勾股定理来解决下列问题:如图3,圆柱形玻璃杯高为12cm,底面周长为16cm,在杯外离杯底3cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁且与蜂蜜C相对的点A处,点A离杯口3cm.则蚂蚁到达蜂蜜的最短距离为多少?【分析】(1)根据正方形的面积等于四个直角三角形的面积与正方形面积的即可得出结论;(2)蚂蚁实际上是在圆柱的半个侧面上爬行,如果将这半个侧面展开,根据:“两点之间,线段最短“,所求的最短路程就是这一个展开图AC的长.在R t△ABC中,AB=底面周长的一半=8cm,BC=12﹣3﹣3=6cm.,所以由勾股定理得:AC=10cm,所以蚂蚁爬行的最短路程为10cm.ab+c2,【解答】解:(1)若选图1,则由图形可知:(a+b)2=4×12整理得:a2+b2=c2;ab+(b﹣a)2=c2,若选图2,则由图形可知:4×12整理得:a2+b2=c2.(2)如图所示,∵在Rt△ABC中,AB=底面周长的一半=8cm,BC=12﹣3﹣3=6cm,∴由勾股定理得:AC=10cm,∴蚂蚁爬行的最短路程为10cm.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题(共17小题)1、(2011•广安)如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是母线BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是()A、B、5cmC、D、7cm2、(2009•乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为()A、B、2C、3D、33、(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A、5B、25C、10+5D、354、(2005•山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是()A、40cmB、20cmC、20cmD、10cm5、(2005•贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A、6cmB、12cmC、13cmD、16cm6、(2004•淄博)如图是一块长,宽,高分别是6cm,4cm和3cm的长方体木块一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是()A、(3+2)cmB、cmC、cmD、cm7、(2004•梅州)如图,一只蚂蚁沿边长为a的正方体表面从顶点A爬到顶点B,则它走过的路程最短为()A、 aB、(1+)aC、3aD、 a8、(2004•济宁)如图,正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从M点沿正方体的表面爬到D1点,蚂蚁爬行的最短距离是()A、B、3C、5D、9、如图所示,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程(π取3)是()A、12cmB、10cmC、14cmD、无法确定10、如图:有一圆柱,它的高等于8cm,底面直径等于4cm(π=3),在圆柱下底面的A点有一只蚂蚁,它想吃到上底面与A相对的B点处的食物,需要爬行的最短路程大约()A、10cmB、12cmC、19cmD、20cm11、如图是一个棱长为4cm的正方体盒子,一只蚂蚁在D1C1的中点M处,它到BB1的中点N的最短路线是()A、8B、2C、2D、2+212、如图所示,是一个圆柱体,ABCD是它的一个横截面,AB=,BC=3,一只蚂蚁,要从A点爬行到C点,那么,最近的路程长为()A、7B、C、D、513、如图是一个长4m,宽3m,高2m的有盖仓库,在其内壁的A处(长的四等分)有一只壁虎,B处(宽的三等分)有一只蚊子,则壁虎爬到蚊子处最短距离为()A、4.8B、C、5D、14、有一长、宽、高分别是5cm,4cm,3cm的长方体木块,一只蚂蚁要从长方体的一个顶点A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为()A、5cmB、cmC、4cmD、3cm15、如图,边长为1的立方体中,一只蚂蚁从A顶点出发沿着立方体的外表面爬到B顶点的最短路程是()A、3B、C、D、116、如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂蚁爬行的最短路径为()A、3米B、4米C、5米D、6米17、如图,在棱长为20cm的正方体盒子上有一只蚂蚁欲从A点出发向B爬去吃食,则蚂蚁所走最短路程是()A、40cmB、20cmC、20cmD、20cm二、填空题(共13小题)18、(2007•呼伦贝尔)如图,有一圆锥形粮堆,其正视图是边长为6m的正三角形ABC,粮堆母线AC的中点P处有一老鼠正在偷吃粮食,此时,小猫正在B处,它要沿圆锥侧面到达P处捕捉老鼠,则小猫所经过的最短路程是_________m.(结果不取近似值)19、(2007•怀化)如图所示的圆柱体中底面圆的半径是,高为2,若一只小虫从A点出发沿着圆柱体的侧面爬行到C点,则小虫爬行的最短路程是_________.(结果保留根号)20、(2007•金昌)如图,圆锥的母线长OA为8,底面圆的半径为4.若一只蚂蚁在底面上点A处,在相对母线OC 的中点B处有一只小虫,蚂蚁要捉到小虫,需要爬行的最短距离为_________.21、(2007•梅州)如图,有一木质圆柱形笔筒的高为h,底面半径为r,现要围绕笔筒的表面由A至A1(A,A1在圆柱的同一轴截面上)镶入一条银色金属线作为装饰,这条金属线的最短长度是_________.22、(2008•昆明)如图,有一个圆柱,它的高等于16cm,底面半径等干4cm,在圆柱下底面的A点有一只蚂蚁,它想吃到上底面上与A点相对的B点处的食物,需要爬行的最短路程是_________cm.(π取3)23、(2008•青海)如图,有一圆柱体,它的高为20cm,底面半径为7cm.在圆柱的下底面A点处有一个蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是_________cm(结果用带根号和π的式子表示).24、(2009•青岛)如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要_________cm;如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要_________cm.25、(2011•荆州)如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为_________cm.26、(2006•茂名)如图,点A、B分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A沿其表面爬到点B 的最短路程是_________.27、(2005•青海)如图,已知正方体的棱长为2,则正方体表面上从A点到C1点的最短距离为_________.28、(2003•泸州)如图,一只昆虫要从边长为acm的正方体盒子的一个顶点爬到相距最远的另一个顶点,沿盒子表面爬行的最短路程是_________cm.29、如图,有一圆柱,其高为12cm,底面半径为3cm,在圆柱下底面A点处有一只蚂蚁,它想得到上底面B处的食物,则蚂蚁经过的最短距离为_________cm.(π取3)30、一只蚂蚁从长、宽都是3,高是8的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是_________.24.(本小题10分)问题探究:(1)如图①所示是一个半径为32π,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形ABB A′′,则蚂蚁爬行的最短路程即为线段AB′的长)(2)如图②所示是一个底面半径为23,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程.(3)如图③所示,在②的条件下,一只蚂蚁从A点出发沿圆锥的侧面爬行一周到达母线PA上的一点,求蚂蚁爬行的最短路程.答案与评分标准一、选择题(共17小题)1、(2011•广安)如图,圆柱的底面周长为6cm ,AC 是底面圆的直径,高BC=6cm ,点P 是母线BC 上一点,且PC=BC .一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是( )A 、B 、5cmC 、D 、7cm考点:平面展开-最短路径问题。
分析:首先画出圆柱的侧面展开图,根据高BC′=6cm ,PC=BC ,求出PC′=×6=4cm ,在Rt △AC′P 中,根据勾股定理求出AP 的长.解答:解:侧面展开图如图所示,∵圆柱的底面周长为6cm ,∴AC′=3cm ,∵PC′=BC′,∴PC′=×6=4cm ,在Rt △ACP 中,AP 2=AC′2+CP 2,∴AP==5. 故选B . B A A ' B ′ 图① A ' P A 图② P A 图③(第24题)点评:此题主要考查了平面展开图,以及勾股定理的应用,做题的关键是画出圆柱的侧面展开图.2、(2009•乐山)如图,一圆锥的底面半径为2,母线PB的长为6,D为PB的中点.一只蚂蚁从点A出发,沿着圆锥的侧面爬行到点D,则蚂蚁爬行的最短路程为()A、B、2C、3D、3考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果.解答:解:由题意知,底面圆的直径AB=4,故底面周长等于4π.设圆锥的侧面展开后的扇形圆心角为n°,根据底面周长等于展开后扇形的弧长得4π=,解得n=120°,所以展开图中∠APD=120°÷2=60°,因为半径PA=PA′,故三角形PAA′为等腰三角形,又∵D为AA′的中点,所以PD⊥AA′,在直角三角形PAD中,PA=6,PD=3,根据勾股定理求得AD=3,所以蚂蚁爬行的最短距离为3.故选C.点评:圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.3、(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是()A、5B、25C、10+5D、35考点:平面展开-最短路径问题。
分析:要求蚂蚁爬行的最短距离,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.解答:解:将长方体展开,连接A、B,根据两点之间线段最短,BD=10+5=15,AD=20,由勾股定理得:AB====25.故选B.点评:本题是一道趣味题,将长方体展开,根据两点之间线段最短,运用勾股定理解答即可.4、(2005•山西)如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心.一只蚂蚁在盒子表面由A处向B处爬行,所走的最短路程是()A、40cmB、20cmC、20cmD、10cm考点:平面展开-最短路径问题。
分析:由平面图形的折叠及立体图形的表面展开图的特点解题.解答:解:根据两点之间线段最短,把正方体展开,可知由A处向B处爬行,所走的最短路程是20cm.故选C.点评:熟练掌握两点之间线段最短这一性质.5、(2005•贵阳)如图A,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约是()A、6cmB、12cmC、13cmD、16cm考点:平面展开-最短路径问题。
