高二小测试题一
成都七中高2025届高二语文10月阶段性考试试卷及参考答案

成都七中2023~2024学年度上期高2025届10月阶段性测试语文试题考试时间:150分钟总分:150分一、现代文阅读(本题共4小题,18分)阅读下面的文字,完成1~4题。
非攻鲁迅墨子走进宋国的国界的时候,草鞋带已经断了三四回,觉得脚底上很发热,停下来一看,鞋底也磨成了大窟窿,脚上有些地方起茧,有些地方起泡了。
他毫不在意,仍然走;沿路看看情形,人口倒很不少,然而历来的水灾和兵灾的痕迹,却到处存留。
走了三天,看不见一所大屋,看不见一棵大树,看不见一个活泼的人,看不见一片肥沃的田地,就这样的到了都城。
城墙也很破旧,但有几处添了新石头;护城沟边看见烂泥堆,像是有人淘掘过,但只见有几个闲人坐在沟沿上似乎钓着鱼。
“他们大约也听到消息了。
”墨子想。
他决计穿城而过,于是走近北关,顺着中央的一条街,一径向南走。
城里面也很萧条,但也很平静;店铺都贴着减价的条子,然而并不见买主,可是店里也并无怎样的货色;街道上满积着又细又粘的黄尘。
“这模样了,还要来攻它!”墨子想。
他在大街上前行,除看见了贫弱以外,也没有什么异样。
楚国要来进攻的消息,是也许已经听到了的,然而大家被攻得习惯了,自认是活该受攻的了,竟并不觉得特别,况且谁都只剩了一条性命,无衣无食,所以也没有什么人想搬家。
待到望见南关的城楼了,这才看见街角上聚着十多个人,好像在听一个人讲故事。
当墨子走得临近时,只见那人的手在空中一挥,大叫道:“我们给他们看看宋国的民气!我们都去死!”墨子知道,这是自己的学生曹公子的声音。
然而他并不挤进去招呼他,匆匆的出了南关,只赶自己的路。
又走了一天和大半夜,歇下来,在一个农家的檐下睡到黎明,起来仍复走。
草鞋已经碎成一片一片,穿不住了,包袱里还有窝窝头,不能用,便只好撕下一块布裳来,包了脚。
不过布片薄,不平的村路梗着他的脚底,走起来就更艰难。
到得下午,他坐在一株小小的槐树下,打开包裹来吃午餐,也算是歇歇脚。
远远的望见一个大汉,推着很重的小车,向这边走过来了。
高二数学单元测试题一

高二数学单元测试题一一:选择题:1.下列语句正确的是()A.x+3=y-2B.d=d+2C.0=xD.x-y=52: 将二进制数10101(2)化为十进制为()A.21 B. 20 C.19 D. 183:将十进制数111化为五进制数是()A.421(5) B. 521(5) C.423(5) D. 332(5)4: 用程序框图表示“秦九韶算法”将用到()A、顺序结构B、条件结构C、顺序结构和循环结构D、三种差不多逻辑结构5:用冒泡法对6,5,3,1,2,7,9,8进行排序,需要()趟排序A.3 B.4 C. 5 D. 66:用更相减损术求138和92的最大公约数()A .23 B.42 C .56 D.467: 用辗转相除法求228,1995的最大公约数()A.35 B.46 C.57 D.688: 下列数是“回文数”的个数是()123,456,121,14541A. 0B.1C.2D.3二:填空题9.课本中显现了两种排序的方法,它们是:___________________;_______________________10.算法的差不多结构是______________ __________________ __________________11.用秦九韶算法为x=5时,多项式f(x)=3x 5-4x 4+6x 3-2x 2-5x-2的值为____________12.下列程序运行的结果是_____________N=15SUM=0I=1WHILE I ≦NSUM=SUM+II=I+2WENDPRINT “SUM=”;SUMEND三.解答题13.请编写出一个“求满足10003212222>++++n 的n 最小值”的程序。
14.某班50人参加考试。
请设计一个算法统计出80分以上的人数,并画出程序框图。
15.2000年世界人口50亿,按年增长率8%0运算,多青年后,世界人口超过100亿,请设计出一个算法,并画出程序框图。
【地理】2021-2022学年人教版(2019)高二上学期期末达标测试卷(1)(解析版)

河南省南阳市第三中学2021-2022学年人教版(2019)高二上学期期末达标测地理试卷(1)一、单项选择题:本题共15小题,每小题3分,共45分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
小明同学7月从重庆出发到贵州毕节旅游,收集到的相关高速公路信息如下图所示。
据此完成下面小题。
小明若从重庆出发乘长途客车经遵义至毕节,为免受阳光长时间照射且能欣赏窗外风景,以下出发时间和座位较好的是( )A.6:00出发,左侧靠窗B.8:00出发,右侧靠窗C.10:00出发,左侧靠窗D.12:00出发,右侧靠窗下图示意北半球某河流,图中箭头表示河流的流向,甲、乙分别位于两河岸。
读图完成下题。
2.关于图示河流的叙述,正确的是( )A.甲河岸适合建港口B.乙河岸需加固大堤C.枯水期E附近水较深D.枯水期F附近水较浅3.若该河流位于山区,则适宜采沙的地点是( )A.甲岸B.乙岸C.E地D.F地夏至日,小王在某楼盘(36°34′N)处受到了置业顾问的热情招待。
据此完成下题。
4.小王在该楼盘一楼看房时,发现前面有一栋相同高度(50米)的楼房,置业顾问介绍说前楼全年不挡光,则其楼间距最小可能是( )A.15米B.20米C.28米D.87米5.下面是小王绘制的该楼盘某户型当日正午时刻的客厅,正确的是( )A. B.C. D.大陆边緣是陆地与洋底之间的过渡地带,大陆边缘的地壳一般属于陆壳性质,但厚度往往小于大陆内部的地壳。
根据构造活动性特征,大陆边缘分为稳定型(甲)和活动型(乙和丙)两大类。
读大陆边缘类型示意图,完成下题。
6.下列属于甲类大陆边缘的是( )A.我国东海岸B.墨西哥西海岸C.新西兰东海岸D.菲律宾东海岸7.下列属于乙类大陆边缘山脉的是( )A.阿特拉斯山脉(位于非洲西北边缘)B.阿尔卑斯山脉C.安第斯山脉D.华山8.根据板块构造理论,丙类大陆边缘的成因最可能是( )A.洋壳与陆壳碰撞挤压B.陆壳与陆壳碰撞挤压C.洋壳与陆壳张裂分离D.洋壳与洋壳张裂分离读我国某地5月5日前后几天的天气变化情况统计图,完成下题。
高二物理第一次月考试卷

高二物理第一次月测试卷一.选择题〔本大题共12小题,每题4分共48分;每题可能有多个选项符合题意选对且全得4分,选对但不全得2分,不选或有错选得0分〕1.电阻R 1、R 2交流电源根据图1所示方式连接,R 1=10 Ω,R 2=20 Ω.合上开关后S 后,通过电阻R 2的正弦交变电流i 随时间t 变化的情况如图2所示.那么〔 〕A .通过R 1的电流的有效值是1.2 AB .R 1两端的电压有效值是6 VC .通过R 2的电流的有效值是1.22AD .R 2两端的电压有效值是62V2.矩形线框在匀强磁场内匀速转动过程中,线框输出的交流电压随时间变化的图像如图3所示,以下说法中正确的选项是〔 〕 A .交流电压的有效值为36 2 VB .交流电压的最大值为36 2 V,频率为0.25HzC .2s 末线框平面垂直于磁场,通过线框的磁通量最大D .1s 末线框平面垂直于磁场,通过线框的磁通量变化最快 3.图4是霓虹灯的供电电路,电路中的变压 器可视为理想变压器,变压器原线圈与副 线圈匝数比20121=n n ,加在原线圈的电压为t u π100sin 3111=〔V 〕,霓虹灯正常工作的电阻R =440 k Ω,I 1、I 2表示原、副线圈 中的电流,以下判断正确的选项是〔 〕A .副线圈两端电压6220 V,副线圈中的电流14.1 mAB .副线圈两端电压4400 V,副线圈中的电流10.0 mAC .I 1<I 2D .I 1>I 24.如图5所示电路中,当交流电源的频率为f 时,三只电流表 的读数相同;当交流电源的频率为3f 时,三只电流表A 1、A 2、 A 3的读数分别为I 1、I 2、I 3,以下有关它们的大小的关系中正 确的是:〔 〕A . I 1=I 2=I 3B . I 2 >I 3>I 1C . I 2<I 3<I 1D . I 1=I 2>I 3霓虹灯U 2U 1n 2n 1~ u 1 图4R 1R 2S~交流电源 图1图223 10.62-0.62i /Ai /×10-2 st /su /V1 2 3 40 236-236图3图55.一交流电压U = 62sin 〔314t + π/3〕伏,那么:〔 〕A .用交流电压表测量值为8.5VB .用它作“6V,3W 〞灯泡的电源,灯会坏C .接上打点计时器,1秒钟能打50个点D .对“8V,10μF 〞的电容器是平安的 6.作简谐运动的弹簧振子在位移到达最大值时,具有最大值的物理量是( ) A 、加速度B 、速度C 、势能D 、回复力7.如图6曲轴上悬挂一弹簧振子,摇动摇把,曲轴可以带动弹簧振子上 下振动,开始时不转动摇把,让振子自由振动,测得其频率为2Hz,然后 匀速转动摇把,转速240转/分,当振子振动稳定时,它的振动周期为( ) A 、0.5s B 、0.25s C 、2s8.如下图的电路中:〔 〕 A .a 是电容较小的电容,b 是低频扼流圈 B .a 是电容较小的电容,b 是高频扼流圈 C .a 是电容较大的电容,b 是低频扼流圈 D .a 是电容较大的电容,b 是高频扼流圈9.在输送功率和输电线总电阻都不变时,假设把输电电压提升到原来的10倍,那么下述正确的为:A.输电线上的损耗电压为原来的1/10B.输电线上的电流为原来的1/10 ( )C.输电线上输出的功率为原来的1/10D.输电线上损失的功率为原来的1/10 10.某一电学黑箱内可能有电容器、电感线圈、定值电阻等元件,在接线柱间以如图8所示的“Z 〞字形连接〔两接线柱间只有一个元件〕.为了确定各元件种类,小华同学把DIS 计算机辅助实验系统中的电流传感器〔相当于电流表〕与一直流电源、滑动变阻器、开关串联后,分别将AB 、BC 、CD 接入电路,闭合开关,计算机显示的电流随时间变化的图象分别如图9 a 、b 、c 所示,那么如下判断中正确的选项是〔 〕A .AB 间是电容器 B .BC 间是电感线圈 C .CD 间是定值电阻 D .CD 间是电容器 11.压敏电阻的阻值随所受压力的增大而减小,有位同学利用压敏电阻设计了判断小车运动 状态的装置,其工作原理如图10〔a 〕所示,将压敏电阻和一块挡板固定在绝缘小车上,中间 放置一个绝缘重球.小车向右做直线运动过程 中,电流表示数如图6〔b 〕所示,以下判断正 确的是〔 〕A .从t 1到t 2时间内,小车做匀速直线运动v压敏电阻R EAIt t 1 t 2 t 3 0图10〔a 〕〔b 〕图6ab后 级输 出图7图8AB C Dab cS黑箱电流传感器图9B .从t 1到t 2时间内,小车做匀加速直线运动C .从t 2到t 3时间内,小车做匀速直线运动D .从t 2到t 3时间内,小车做匀加速直线运动12.如图11是电熨斗的结构图,以下说法正确的选项是〔 〕 A .双金属片上层金属的膨胀系数大于下层金属 B .常温下,上下触点是分开的C .需要较高温度熨烫时,要调节调温旋钮,使升降螺丝下移并推动弹性铜片下移 D .双金属片温度传感器的作用是限制电路的通断二.填空题〔每空3分共30分〕13.如图12所示为一实验小车中利用光电脉冲测量车速和行程的装置示意图.A 为光源,B 为光电接收器,A 、B 均固定在车身上,C 为小车的车轮,D 为与C 同轴相连的齿轮.车轮转动时,A 发出的光束通过旋转齿轮上齿的间隙后变成脉冲光信号,被B 接收并转换成电信号,由电子电路记录和显示.假设实验显示单位时间内脉冲数为n ,那么要测出小车的速度和行程还必须测量的物理量和数据是:① 和 小车速度的表达式为:② v = ;14.如图13所示是某电热水器的温控电路原理图,其核心是中间的门电路,该门电路的输出端与继电器相连,当门电路输出端输出高电压时,继电器闭合,热水器加热.R t 为热敏电阻,温度越高电阻越小.R 1是调温电阻,其作用是预设水温的上下.A 、B 为两个接触端,当水箱内水加至与A 、B 两个接触端接触时,A 、B 间就导通,导通时A 、B 间电阻很小. 那么 ①图中的门电路为 门〔“与门〞或“或门〞〕, ②要调高预设的水温应 R 1的阻值〔“增大〞或“减小〞〕15.一小型发电机内的矩形线圈,在匀强磁场中以恒定的角速度ω绕垂直于磁场方向的固定轴图11图11 图12R tAB R 1 R DC +5V接继电器门电路 图13图14转动,线圈匝数n =100,穿过每匝线圈的磁通Φ 随时间t 按正弦规律变化,如图14所示.发电机内阻r =5.0Ω,外电路电阻R=95Ω.感应电动势的最大值E m =n ωΦm ,其中Φm 为穿过每匝线圈的磁通量的最大值.那么:①电动势的瞬时值为:e = V②串联在外电路中的交流电流表〔内阻不计〕的读数为 A .〔保存2位有效数字〕 16.如图15所示,为一弹簧振子的振动图像; ①从计时开始经过 S 时间第一次弹性势能最大, ②在第2s 末到第3s 末这段时间内,弹簧振子的加速度 〔增大、减小〕 ③该振子的初相是三.计算题 要求写出必要的文字说明与过程,否那么不能得分17.〔10分〕发电机的端电压为220伏,输出功率为44千瓦,输电线电阻为0.2欧,求: (1)用户得到的电压和电功率各是多少? (2)如发电站用匝数比为1:10的变压器将电压升高,经同样输电后,再用10:1的降压变压器给用户,用户得到的电压和电功率各为多少?18.〔12分〕一行星上有一单摆,1min 内能完成30次全振动,该行星的半径是地球半径的21,行星密度与地球的密度相同,那么此单摆的摆长为多大?这只单摆在地球外表的周期为多少?〔地球外表g=9.80m/s 2,π2 =9.80〕图15高二物理第一次月考答案:一选择二.填空13.①齿轮的齿数P 和 车轮的半径R ②PRn v π2=; 14.①与门 ②减小 15.①)2200sin(200π+=t e ② 1.4A16.①1 ②增大 ③0 三.计算17.〔1〕180V ;36KW 〔2〕219.6V ;43920W18.0.5m。
2021-2022学年全国人教版(2019)高二上学期期末达标测生物试题(1)基础A卷 解析版

全国2021-2022学年人教版(2019)高二生物上学期期末达标测试卷(1)基础A卷一、选择题(共15小题,每小题2分,共计30分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列各组化合物中全是内环境成分的是( )A. O2、CO2、血红蛋白、H+、Na+B. 消化酶、抗体、激素、H2OC. 纤维蛋白原、Ca2+、载体蛋白、尿素D. K+、葡萄糖、氨基酸、尿素、H2O2.下列有关人体内环境的叙述,错误的是( )A.体内活细胞依赖内环境的运输提供氧气和养料、排出代谢废物B.体内激素、抗体、血浆蛋白都依赖内环境的运送而作用于特定的靶细胞C.大量失钠将使细胞外液渗透压下降D.血浆中尿素、葡萄糖等物质的含量可作为某些疾病的诊断依据3.2020年的澳网比赛于北京时间1月20日在墨尔本公园开赛,球场上球员们身手敏捷的发球、接球,他们挥汗如雨,奋力拼搏着,下列关于球员们生理变化的叙述,错误的是( )A.发球时,某些细胞会出现膜电位逆转的现象B.接球时,可体现人脑高级中枢对低级中枢的控制C.比赛过程中,体温会略有升高且毛细血管舒张。
D.比赛结束后球员心跳仍较快,说明神经调节作用时间较长4.5-羟色胺是一种与睡眠调控有关的兴奋性神经递质,它还与人的多种情绪状态有关。
如果神经元释放5-羟色胺数量不足,将会引起抑郁症。
下列叙述错误的是( )A.5-羟色胺与突触后膜的受体结合后,突触后膜电位发生改变B.5-羟色胺是小分子有机物,以主动运输的方式释放到突触间隙C.氯西汀可以减缓突触间隙5-羟色胺的清除,故可用于治疗抑郁症D.麦角酸二乙酰胺特异性阻断5-羟色胺与其受体结合,故会加重抑郁症5.“春捂秋冻,不生杂病”是一条保健防病的谚语,其意思是人们春天不要急于脱掉棉衣,秋天也不要刚见冷就穿得太多,适当地捂一点或冻一点,对于身体的健康是有好处的。
以下说法正确的是( )A.“春捂”会使人体甲状腺激素分泌增多,从而使体温升高B.“秋冻”的感觉是在下丘脑形成的C.“春捂秋冻”可以帮助机体适应环境温度的变化D.“春捂秋冻”适合各种体质的人群6.某考生参加高考体检,早晨没有进食和饮水。
广东省江门市普通高中2022-2023学年高二上学期调研测试(一)数学试题及答案

江门市2023年普通高中高二调研测试(一)数 学本试卷共6页,22小题,满分150分,考试时间120分钟。
注意事项:1.答题前,务必将自己的姓名、准考证号填写在答题卡规定的位置上。
2. 做选择题时,必须用2B 铅笔将答题卷上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
3. 答非选择题时,必须用黑色字迹钢笔或签字笔,将答案写在答题卡规定的位置上。
4. 所有题目必须在答题卡上作答,在试题卷上作答无效。
5. 考试结束后,将答题卡交回。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知数列{}n a 满足11+12,2(2N n n a a a n n -==-≥∈且),则该数列的第5项为 A .54B .65C .45D .562.已知(4,9)A ,(6,3)B 两点,以线段AB 为直径的圆的标准方程是A.()()225610x y +++= B.()()225620x y +++=C.()()225620x y -+-= D.()()225610x y -+-=3.20y ++=的倾斜角及在y 轴上的截距分别是A.60,2︒ B.60,2︒- C.120,2︒- D.120,2︒4.若{},,a b c 构成空间的一个基底,则下列向量不共面的是A .,,a c a a c +-B .,,c c b c b +-C .,,a b a b c +-D .,,a b c a b c c +-++5.已知M 是抛物线216y x =上的一点且在x 轴上方,F 是抛物线的焦点,以Fx 为始边,FM 为终边的角60xFM ∠=︒,则FM 等于A.16B.20C.4D.8内部资料·注意保存试卷类型:B6.直线0Ax By C ++=(A ,B 不同时为0),则下列选项正确的是A.无论A ,B 取任何值,直线都存在斜率B.当0A =,且0B ≠时,直线只与x 轴相交C.当0A ≠,或0B ≠时,直线与两条坐标轴都相交D.当0A ≠,且0B =,且0C =时,直线是y 轴所在直线7.已知{}n a 为等差数列,13545a a a ++=,24633a a a ++=,则10S 等于A.250B.410C.50D.628.已知椭圆2222:1(0)x y M a b a b+=>>的左顶点为A ,O 为坐标原点,B ,C 两点在M上,若四边形OABC 为平行四边形,且30OAB ∠=︒,则椭圆M 的离心率为A.322B.322 D.2二、选择题:本题共4小题,每小题5分,共20分。
高二上学期第一次月考物理试卷含答题卷和答案

高二阶段测试物理试题一、选择题(本题共 10小题,每小题 4 分,总分40分,在每小题给出的四个选项中,第1~6题只有一项符合题目要求,第 7~10题有多项符合题目要求。
全部选对的得 4 分,选对但不全的得 2分,有选错的得 0 分。
)1.如图所示,一带电小球用丝线悬挂在水平方向的匀强电场中,当小球静止后把悬线烧断,则小球在电场中做()A.自由落体运动B.曲线运动C.沿着悬线的延长线做匀加速直线运动D.变加速直线运动2.[库仑定律和电荷守恒定律的应用]三个相同的金属小球1、2、3分别置于绝缘支架上,各球之间的距离远大于小球的直径.球1的带电荷量为+q,球2的带电荷量为+nq,球3不带电且离球1和球2很远,此时球1、2之间作用力的大小为F.现使球3先与球2接触,再与球1接触,然后将球3移至远处,此时1、2之间作用力的大小仍为F,方向不变.由此可知() A.n=3 B.n=4 C.n=5 D.n=63.使带电的金属球靠近不带电的验电器,验电器的箔片张开.下列各图表示验电器上感应电荷的分布情况,其中正确的是()4.如图1-38所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面3的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV时,它们动能应为 ( )A.8eV B.13eV C.20eV D.34eV5.如图所示,点电荷+4Q与+Q分别固定在A、B两点,C、D两点将AB连线三等分,现使一个带负电的粒子从C点开始以某一初速度向右运动,不计粒子的重力,则该粒子在CD 之间运动的速度大小v与时间t的关系图象可能是图中的()6.两个固定的等量异号点电荷所产生电场的等势面如图中虚线所示,一带负电的粒子以某一速度从图中A 点沿图示方向进入电场在纸面内飞行,最后离开电场,粒子只受静电力作用,则粒子在电场中( )A .做直线运动,电势能先变小后变大B .做直线运动,电势能先变大后变小C .做曲线运动,电势能先变小后变大D .做曲线运动,电势能先变大后变小7.如图甲所示,两个点电荷Q 1、Q 2固定在x 轴上距离为L 的两点,其中Q 1带正电荷位于原点O ,a 、b 是它们的连线延长线上的两点,其中b 点与O 点相距3L .现有一带正电的粒子q 以一定的初速度沿x 轴从a 点开始经b 点向远处运动(粒子只受电场力作用),设粒子经过a ,b 两点时的速度分别为v a 、v b ,其速度随坐标x 变化的图象如图乙所示,则以下判断正确的是( ).A .Q 2带负电且电荷量小于Q 1B .b 点的场强一定为零C .a 点的电势比b 点的电势高D .粒子在a 点的电势能比b 点的电势能小8.某带电粒子仅在电场力作用下由A 点运动到B 点,电场线、粒子在A 点的初速度及运动轨迹如图1-4-14所示,可以判定( )A .粒子在A 点的加速度大于它在B 点的加速度 B .粒子在A 点的动能小于它在B 点的动能C .粒子在A 点的电势能大于它在B 点的电势能D .电场中A 点的电势高于B 点的电势9、如图所示,在等量异种电荷连线的中垂线上取A 、B 、C 、D 四点,B 、D 两点关于O 点对称,则关于各点场强的关系,下列说法中正确的是:( )A 、E A >EB ,E B =E D B 、E A <E B ,E A <E CC 、E A <E B <E C ,E B =ED D 、可能E A =E C < E B ,E B =E D10、如图所示,水平放置的金属板的上方有一固定的正点电荷Q ,一表面绝缘的带正电的小球(可视为质点,且不影响Q 的电场),从左端以初速度v o 滑到金属板上,沿光滑的上表面向右运动到右端,在此过程中:( )A 、 小球作匀速直线运动B 、 小球作先减速后加速的运动C 、 小球受到的电场力的方向时刻在改变D 、 电场力对小球做功为零二、实验题(本题共2小题,共14分,其中第11题4分,第12题10分)11.为验证在自由落体过程中物体的机械能是守恒的,某同学利用数字实验系统设计了一个实验,实验装置如图所示,图中A 、B 两点分别固定了两个速度传感器,速度传感器中测出运动物体的瞬时速度.在实验中测得一物体自由下落经过A 点时的速度是v 1,经过B 点时的速度是v 2,为了证明物体经过A 、B 两点时的机械能相等,这位同学又设计了以下几个步骤,你认为其中不必要或者错误的是 ( )A .用天平测出物体的质量B .测出A 、B 两点间的竖直距离C .利用12mv 22-12mv 21算出物体从A 点运动到B 点的过程中重力势能的变化量D .验证v 22-v 21与2gh 是否相等12.在利用重锤下落验证机械能守恒定律的实验中:(1)某同学在实验中得到的纸带如图所示,其中A 、B 、C 、D 是打下的相邻的四个点,它们到运动起点O 的距离分别为62.99cm 、70.18cm 、77.76cm 、85.73cm.已知当地的重力加速度g =9.8m/s 2,打点计时器所用电源频率为50Hz ,重锤质量为1.00kg.请根据以上数据计算重锤由O 点运动C 点的过程中,重力势能的减少量为__________J ,动能的增加量为__________J .(取三位有效数字) (2)甲、乙、丙三名同学分别得到A 、B 、C 三条纸带,它们前两个点间的距离分别是1.0mm 、1.9mm 、4.0mm.那么一定存在操作错误的同学是__________,错误原因是__________________.三、计算题(本题共包括5小题,共46分,解答时应写出必要的文字说明、方程式和重要演算步骤,只写出最后答案不能得分,有数值计算的题,答案中必须明确写出数值和单位)13.(8分)如图所示,用三根长均为L 的绝缘丝线悬挂两个质量均为m ,带电量分别为+q 和-q 的小球,若加一个水平向左的匀强电场,使丝线都被拉紧且处于平衡状态,则所加电场的场强E 的大小应满足什么条件?14.(8分)有一个带电荷量q=-6×10-6 C的点电荷,从某电场中的A点移到B点,电荷克服电场力做3×10-3 J的功,从B点移到C点,电场力对电荷做1.2×10-3 J的功,求A、C两点的电势差并说明A、C两点哪点的电势较高。
高二地理上册每周一练测试题1.doc

高二地理“每周一练”系列试题(16)一、选择题(共10小题,每小题3分,共30分每小题只有一个正确答案)读下列等高线地形图,完成1-2题:1.各幅等高线地形图中海拔最高点由高到低的排序是:()A.①②③④B.②③①④C.③②①④D.④①②③2.图④中甲点海拔高度最准确的说法是()A.700m>甲>650m B.750m>甲>700mC.甲>700m D.甲<700m读下图某日北半球某纬线上不同经度的太阳高度,读图回答3-7题:3.此刻,北京时间是()A.3: B.9: C.15: D.21:.此日,太阳直射点的纬度是()A.0° B.5°N C.15°N D.23°26′N5.6月22日,该纬线上的最小太阳高度为()A.6°34′ B.8°26′ C.21°26′ D.21°34′6.此日,下列现象可能发生的是:()A.北印度洋洋流呈逆时针方向运动B.北京日出方向为东偏北C.甲、乙两地太阳高度最大值为15°D.巴西高原呈现草类茂盛的景象7.此日某时刻,该纬线上的甲、乙两地的太阳高度均为15°,则甲、乙两地之间最短地面距离是()A.1650km B.3300km C.4950km D.6600km右图为我国某一省级行政区轮廓图,读图回答8-10题。
8.下列河流中,发源于该区域的是()A.塔里木河B.雅鲁藏布江C.淮河D.长江9.图中甲湖泊水的主要来源是()A.雨水B.冰川融水C.地下水D.土壤水10.根据“因地制宜、合理布局”的原则,该省区最适宜发展的农业部门是()A.种植柑橘、荔枝等为主的林业B.种植水稻为主的耕作业C.饲养猪、鸡、鸭为的畜牧业D.放养羊、马、牛为主的畜牧业二、综合题11.(共读右图,回答问题(1)图中F、H两地气温比两侧地区高的自然原因是________________。
四川省成都市2024-2025学年度高二(上)开学摸底模拟测试题(一)答案

2024-2025学年度高二(上)开学摸底模拟测试题(一)数学参考答案1.C【分析】运用二倍角余弦公式可解.【详解】运用二倍角余弦公式得到cos215°−sin215°=cos30°=√32.故选:C.2.A�����⃗=(2,0),再求其模.【分析】先利用向量线性运算的坐标表示求得AAAA�����⃗=AAAA�����⃗+AAAA�����⃗=(0,−1)+(2,1)=(2,0),【详解】根据题意,AAAA�����⃗�=√22+02=2.所以�AAAA故选:A3.C【分析】利用线面平行意义判断A;利用面面平行的意义判断CD;由mm,nn的位置关系判断D.【详解】对于A,mm上有两点到平面αα距离相等,平面αα可以过这两点的中点,此时mm与αα相交,A错误;对于BC,αα//ββ,则αα,ββ没有公共点,由ββ,mm⊂αα,nn⊂ββ,得mm与nn没有公共点,mm与nn是平行直线或者是异面直线,C正确,B错误;对于D,αα∩ββ=nn,mm⊂αα,则mm//nn或mm与nn是相交直线,当mm//nn时,mm//ββ,D错误.故选:C4.C【分析】设出复数的代数形式,结合共轭复数的意义计算判断ABD;举例说明判断C.【详解】设复数zz1=aa+bb i,zz2=cc+dd i,(aa,bb,cc,dd∈R),对于A,zz1+zz2=(aa+cc)+(bb+dd)i=(aa+cc)−(bb+dd)i=(aa−bb i)+(cc−dd i)=zz1+zz2,A正确;对于B,zz1zz2=(aacc−bbdd)+(aadd+bbcc)i,zz1zz2=(aacc−bbdd)−(aadd+bbcc)i,zz1⋅zz2=(aa−bb i)(cc−dd i)=(aacc−bbdd)−(aadd+bbcc)i,zz1⋅zz2=zz1⋅zz2,B正确;对于C,取zz1=i,zz2=2i,满足zz1zz2=−2∈R,而zz1≠zz2,C错误;对于D,由zz1zz2=0,得(aacc−bbdd)+(aadd+bbcc)i=0,即�aacc−bbdd=0aadd+bbcc=0,则aa2cc2+bb2dd2+aa2dd2+bb2cc2=0,即(aa2+bb2)(cc2+dd2)=0,因此aa=bb=0或cc=dd=0,即zz1=0或zz2=0,D正确.故选:C5.A【分析】在△AAAAAA中由正弦定理可得答案.【详解】∠AAAAAA=∠AAAAAA−∠AAAAAA=15∘,AAAA=14,∠AAAAAA=180∘−∠AAAAAA=135∘,sin15∘=sin(45∘−30∘)=sin45∘cos30∘−cos45∘sin30∘=√6−√24,由正弦定理得AAAA sin∠AADDAA=AADD sin∠DDAAAA,即AAAA=sin∠AAAAAA AADD sin∠DDAAAA=√22×14√6−√24=14�√3+1�,所以AAAA=12×AAAA=7�√3+1�.故选:A.6.D【分析】由斜二测画法的直观图,得出原图形为直角梯形,再轴旋转一周得到的圆柱和圆锥的组合几何体的体积.【详解】由斜二测画法的直观图知,AA′AA′//OO′AA′,AA′AA′⊥AA′AA′,AA′AA′=1,OO′AA′=2;∴OO′AA′=√2,所以原图形AAOOAAAA中,AAAA//OOAA,OOAA⊥OOAA,AAAA=1,OOAA=2,AAOO=2AA′OO′=2×√2=2√2,所以梯形AAOOAAAA以边AAAA为轴旋转一周得到的几何体为圆柱去掉一个同底圆锥的组合体,VV=πOOAA2×OOAA−13πOA2×(OOAA−AAAA)=π×8×2−13π×8×1=403π.故选:D.7.D【分析】由最小值求得AA,由ff(0)=1求得φφ,再结合最小值点和周期求得ωω.【详解】由图象知AA=√2,ff(0)=1所以√2sinφφ=1,则φφ=2kkπ+π4,kk∈Z或φφ=2kkπ+3π4,kk∈Z,又|φφ|<π2,所以φφ=π4,√2sin(5ωωπ4+π4)=−√2,5ωωπ4+π4=2kkπ+3π2,ωω=8kk5+1,kk∈Z,又TT>,ωω=,已知ωω>0,所以ωω=1,所以ff(xx)=√2sin(xx+故选:D.8.C【分析】对于A,连接AAAA,AAAA1,得出∠AAAAAA1即为AA1AA与EEEE所成角的平面角即可判断;对于B,连接AA1AA1,AA1AA,AAAA1,证明平面PPAAAA1和平面EEEEEE重合即可判断;对于C,利用等体积法求出三棱锥PP−EEEEEE的体积;对于D:先判断出平面EEEEEE截正方体所得截面为正六边形EEEEEEEEEE EE,边长为√2,即可判断.【详解】对于A,连接AAAA,AAAA1,因为EE,EE分别为AAAA,AAAA的中点,所以EEEE//AAAA,所以∠AAAAAA1即为AA1AA与EEEE所成角的平面角,在△AAAAAA1中,AAAA=AAAA1=AAAA1,故∠AAAAAA1=60°,所以AA1AA与EEEE所成角为60°,故A正确;对于B,连接AA1AA1,AA1AA,AAAA1,因为AAAA1//AAAA1且AAAA1=AAAA1,所以四边形AAAAAA1AA1为平行四边形,所以AAAA//AA1AA1,又因为EEEE//AAAA,所以EEEE//AA1AA1,又EEEE⊂平面EEEEEE,AA1AA1⊄平面EEEEEE,所以AA1AA1//平面EEEEEE,因为EE,EE分别为AAAA,AAAA1的中点,所以EEEE//AAAA1,又EEEE⊂平面EEEEEE,AAAA1⊄平面EEEEEE,所以AAAA1//平面EEEEEE,又AA1AA1∩AAAA1=AA1,AA1AA1,AAAA1⊂平面AA1AAAA1,所以平面AA1AAAA1//平面EEEEEE,因为AAPP//平面EEEEEE,AAPP∩AAAA1=AA1,AAPP,AAAA1⊂平面PPAAAA1,所以平面PPAAAA1//平面EEEEEE,而AAAA1为平面PPAAAA1和平面EEEEEE的公共边,所以平面PPAAAA1和平面EEEEEE重合,所以点PP即为AA1AA1,AA1AA1的交点,所以点P为线段AA1AA1的中点,故B正确;对于C:因为AAPP//平面EEEEEE,所以点AA,PP到平面EEEEEE的距离相等,所以VV PP−EEEEEE=VV DD−EEEEEE=VV EE−DDEEEE=13SS△DDEEEE×AAEE=13×12×1×1×1=16,故C错误;对于D:分别取AA1AA1,AA1AA1,AAAA1的中点为EE,EE,EE,连接EEEE,EEEE,EE EE,EE EE,EE EE,AA1AA,在正方体AAAAAAAA−AA1AA1AA1AA1中,AAAA//EE EE,AAAA//EEEE,所以EE EE//EEEE,所以EE,EE,EE,EE四点共面,同理可证:EE,EE,EE,EE,EE,EE共面,在棱长为2的正方体AAAAAAAA−AA1AA1AA1AA1中,所以EEEE=√12+12=√2.同理可求:EEEE=EEEE=EEEE=EE EE=EE EE=√2,所以平面EEEEEE截正方体所得截面为正六边形EEEEEEEEEE EE,边长为√2,面积为6×12×√2×√2×sin60°=3√3,故D正确.故选:C.【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角;(2)认定:证明作出的角就是所求异面直线所成的角;(3)计算:求该角的值,常利用解三角形;(4)取舍:由异面直线所成的角的取值范围是�0,π2�,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.9.BD【分析】根据两个角的正弦相等,判断两个角的关系,判断A的真假;根据锐角三角形的概念,结合三角函数的单调性,可判断B的真假;利用余弦定理,结合三角形的面积公式可求三角形的面积,判断C的真假;根据同角三角函数的基本关系及正弦定理判断D的真假.【详解】对A:由sin2AA=sin2AA⇒2AA=2AA或2AA=π−2AA,即AA=AA或AA+AA=π2,所以△AAAAAA是等腰三角形或直角三角形,故A错误;对B:因为△AAAAAA是锐角三角形,所以AA,AA,AA均为锐角,且AA+AA>π2即AA>π2−AA,因为yy=sin xx在�0,π2�上单调递增,所以sin AA>sin�π2−AA�⇒sin AA>cos AA,故B正确;对C:由余弦定理:AAAA2=AAAA2+AAAA2−2⋅AAAA⋅AAAA⋅cos∠AA,即1=3+AAAA2−2√3⋅AAAA⋅√32⇒AAAA=1或AAAA=2,所以SS△AADDAA=12×1×√3×12=√34或SS△AADDAA=12×2×√3×12=√32,故C错误;对D:sin2AA+sin2AA+cos2AA<1⇒sin2AA+sin2AA<1−cos2AA=sin2AA,由正弦定理得:aa2+bb2<cc2,所以△AAAAAA是钝角三角形,且角AA为钝角,故D正确.故选:BD10.BD【分析】由函数ff(xx)=sin�ωωxx−π3�(ωω>0)的最小正周期为π,求出ωω=2,然后由正弦型函数的性质逐项判断即可.【详解】函数ff(xx)=sin�ωωxx−π3�(ωω>0)的最小正周期为π,所以2πωω=π,所以ωω=2,故ff(xx)=sin�2xx−π3�,所以ff�π3�=sinπ3=√32,故A错误;ff�7π6�=sin2π=0,故B正确;令−π2+2kkπ≤2xx−π3≤π2+2kkπ,kk∈Z,解得−π12+kkπ≤xx≤5π12+kkπ,kk∈Z,所以ff(xx)在区间�−π12,5π12�上单调递增,所以ff(xx)在区间�0,π2�上不单调,故C错误;函数ff(xx)的图象上所有点向右平移π12个单位长度后,解析式为ff(xx)=sin�2�xx−π12�−π3�=sin�2xx−π2�=−cos2xx,图象关于yy轴对称,故D正确.故选:BD11.ABD【分析】对A选项,可先证平面AAAA1AA1//平面AAAA1AA,再证线面平行;对B选项,可用等积变换的方法求三棱锥体积;对C选项,把三棱锥的外接球转化为正方体的外接球,即可得到答案;对D选项,先做出线面角,再确定线面角的三角函数的最值.【详解】对A选项:如图:连接AA1AA1,AAAA1,因为AA1AA1//AAAA,AAAA⊂平面AAAA1AA,AA1AA1⊄平面AAAA1AA,所以AA1AA1//平面AAAA1AA;同理AAAA1//平面AAAA1AA.又AA1AA1∩AAAA1=AA1,AA1AA1,AAAA1⊂平面AAAA1AA1,所以平面AAAA1AA1//平面AAAA1AA.PPAA1⊂平面AAAA1AA1,所以PPAA1//平面AAAA1AA.故A正确;对选项B:因为PPAA1//平面AAAA1AA,所以:VV PP−DDAA1AA=VV DD1−DDAA1AA=VV AA−DDDD1AA1=13SS△DDDD1AA1×AAAA=13×12×2×2×2=43,故B正确;对选项C:因为三棱锥AA1−AAAA1AA的外接球就是正方体AAAAAAAA−AA1AA1AA1AA1的外接球,所以三棱锥AA1−AAAA1AA的外接球半径为:RR=√3,所以外接球表面积为:SS=4πRR2=12π,故C错误;对D选项:如图:过PP做PPEE⊥平面AAAAAA1AA1于EE,因为平面AAAAAA1AA1⊥平面AAAAAA1AA1,且平面AAAAAA1AA1∩平面AAAAAA1AA1=AAAA1,所以EE∈AAAA1,再连接AA1EE,则在直角△PPEEAA1中,∠PPEEAA1=90°,∠PPAA1EE就是直线PPAA1与平面AAAAAA1AA1所成角,设为θ.因为tanθ=PPPP PPDD1=2PPDD1,且EEAA1的最小值为√2,所以tanθ≤√2,所以sinθ≤√63,故D正确.故选:ABD12.−3【分析】根据纯虚数的定义求解.【详解】复数(1+i)(3−aa i)=3−aa i+3i+aa=aa+3+(3−aa)i是纯虚数,则aa=−3.故答案为:−3.13.1【分析】根据正弦定理与一元二次方程根的判别式可得AA=90∘,进而可得答案.【详解】已知aabb+sin AA sin AA=2bb sin AA sin AA,则由正弦定理得:4RR2sin AA sin AA+sin AA sin AA=4RR sin AA sin AA sin AA,(RR为△AAAAAA外接圆半径),∵sin AA sin AA>0,∴4RR2+1=4RR sin AA,∴4RR2−4RR sin AA+1=0,∵RR>0,∴Δ=16sin2AA−4×4×1≥0,即sin AA≥1,∵sin AA≤1, ∴sin AA=1, ∴AA=90∘,∴Δ=0,∴2RR=1,∴cc=2RR sin AA=1,∴aa2+bb2=1.故答案为:1.14.√2+√316π【分析】结合题意可知该多面体是由一个正方体沿各棱中点截去8个三棱锥所得,利用几何体的体积公式即可得解. 【详解】把该多面体放入正方体中,如图,设该多面体的棱长为1,则正方体的棱长为√2,因此该多面体是由棱长为√2的正方体连接各棱中点所得,所以经过该多面体的各个顶点的球为正方体的棱切球,于是得该多面体的外接球球心是正方体体对角线中点,该多面体外接球半径RR等于球心到一个顶点的距离,即正方体面对角线的一半,则RR=��√22�2+�√22�2=1,设QQ为正方体中与点AA,AA,AA等距的一个顶点,设三棱锥QQ−AAAAAA的高为ℎ,由VV QQ−AADDAA=VV AA−QQDDAA,得13×√34×12×ℎ= 13×�12×√22×√22�×√22⇒ℎ=√66,正方体的对角线长为√6,球心OO到平面AAAAAA的距离为12�√6−2×√66�=√63,三棱锥PP−AAAAAA的高的最大值为√63+1,故其体积的最大值为13×√34×�√63+1�=√2+√312,所以VV1VV=√2+√3124π3=√2+√316π,故答案为:√2+√316π15.(1)mm=9(2)7<mm<9【分析】(1)根据复数的类型特征求参;(2)应用复数对应象限的特征列不等式组即可求参数范围.【详解】(1)因为复数zz是纯虚数,所以�mm2−11mm+18=0,mm2−9mm+14≠0,解得mm=9.(2)因为复数zz在复平面内对应的点位于第二象限,所以�mm2−11mm+18<0,mm2−9mm+14>0,解得7<mm<9.16.(1)120海里(2)AAAA=40√5,能在3小时内赶到救援,理由见解析【分析】(1)在△AAAAAA中,求出∠AAAAAA,∠AAAAAA,利用正弦定理求解即可.(2)在△AAAAAA中,由正弦定理可得AAAA=40√2,在△AAAAAA中,由余弦定理可得AAAA=40√5,比较时间即可判断. 【详解】(1)在△AAAAAA中,因为∠AAAAAA=30°,∠AAAAAA=45°,∠AAAAAA=75°,所以∠AAAAAA=180°−∠AAAAAA−∠AAAAAA−∠AAAAAA=30°,∠AAAAAA=∠AAAAAA+∠AAAAAA=120°,又AAAA=40√3,所以由正弦定理可得AAAA sin∠AAAAAA=AAAA sin∠AAAAAA,即40√3sin30∘=AAAA sin120∘,解得AAAA=120,所以A船距离雷达站C距离为120海里;(2)在△AAAAAA中,根据正弦定理可得DDAA sin∠DDAAAA=AAAA sin∠AADDAA,即DDAA sin45∘=40√3sin(180∘−45∘−30∘−45∘),解得AAAA=40√2,在△AAAAAA中,由余弦定理可得AAAA2=1202+�40√2�2−2×120×40√2cos45∘=8000,解得AAAA=40√5,因为A船以30海里每小时的速度前往B处,而40√530=4√53<3,所以能在3小时内赶到救援.17.(1)证明见解析(2)13【分析】(1)利用面面垂直的性质定理和线面垂直的判定定理可得答案;(2)根据VV DD−AAEEPP=VV PP−AADDAA−VV EE−AADDAA可得答案.【详解】(1)因为AAAA=2√2,PPAA=3PPAA=3.所以PPAA2=PPAA2+AAAA2,可得PPAA⊥AAAA,因为平面PPAAAA⊥平面AAAAAAAA,平面PPAAAA∩平面AAAAAAAA=AAAA,PPAA⊂平面PPAAAA,所以PPAA⊥平面AAAAAAAA,AAAA⊂平面AAAAAAAA,所以PPAA⊥AAAA,四边形AAAAAAAA为直角梯形,∠AAAAAA=90∘,AAAA//AAAA,△AAAAAA为等腰直角三角形,所以AAAA⊥AAAA,因为PPAA∩AAAA=AA,PPAA、AAAA⊂平面PPAAAA,所以AAAA⊥平面PPAAAA;(2)因为AAAA=2√2,△AAAAAA为等腰直角三角形,所以AAAA=AAAA=√2,因为EE为PPAA的中点,所以EE到平面AAAAAAAA的距离为ℎ=12PPAA=12,VV EE−AADDAA=13SS△AADDAAℎ=13×12AAAA×AAAA⋅ℎ=13,VV PP−AADDAA=13SS△AADDAA PPAA=13×12AAAA×AAAA=23,所以VV DD−AAEEPP=VV PP−AADDAA−VV EE−AADDAA=13.18.(1)ff(xx)的单调递增区间为�kkπ−π3,kkπ+π6�,单调递减区间为�kkπ+π6,kkπ+2π3�,kk∈Z.(2)[√3,3√32)(3)�−π6+kkπ,kkπ�∪�π3+kkπ,π2+kkπ�【分析】(1)先化简,再根据正弦函数的单调性求解;(2)根据函数两个不相等的实数根,结合正弦单调性及值域求参;(3)把恒成立问题转化为解三角不等式即可.【详解】(1)ff(xx)=√32cos2xx+32sin2xx+√32=√3sin�2xx+π6�+√32令2kkπ−π2≤2xx+π6≤2kkπ+π2(kk∈Z),解得kkπ−π3≤xx≤kkπ+π6(kk∈Z),令2kkπ+π2≤2xx+π6≤2kkπ+3π2(kk∈Z),解得kkπ+π6≤xx≤kkπ+2π3(kk∈Z),故函数ff(xx)的单调递增区间为�kkπ−π3,kkπ+π6�,单调递减区间为�kkπ+π6,kkπ+2π3�,kk∈Z.(2)由(1)知函数ff(xx)在区间[0,π6]单调递增,在区间[π6,π2]单调递减,又ff(0)=√3,ff�π6�=3√32,ff�π2�=0,结合ff(xx)图象可知a的取值范围是[√3,3√32).(3)即不等式mm2+√3mm sin�2xx+π6�+316≥0对mm∈R恒成立,有Δ=3sin2�2xx+π6�−34≤0,−12≤sin�2xx+π6�≤12,所以−π6+2kkπ≤2xx+π6≤2kkπ+π6或2kkπ+5π6≤2xx+π6≤2kkπ+7π6解得−π6+kkπ≤xx≤kkπ,或kkπ+π3≤xx≤kkπ+π2故x的取值范围是�−π6+kkπ,kkπ�∪�π3+kkπ,π2+kkπ�.19.(1)证明见解析(2)−√63【分析】(1)由题意可得AACC⊥AAAA,根据线面垂直的性质可得AAAA1⊥AACC,结合线面垂直的判定定理即可证明;(2)如图,根据线面垂直的判定定理可得AAEE⊥平面AAAA1AA1AA,则AAEE⊥AA1MM,易证AAEE⊥AA1MM,则∠AAEEEE为二面角AA−MMAA1−AA1的平面角的补角.结合等面积法求得FH,即可求解.【详解】(1)在直三棱柱AAAAAA−AA1AA1AA1中,AAAA1⊥平面AAAAAA,AAAA,AAAA⊂平面AAAAAA,则AAAA1⊥AAAA,AAAA1⊥AAAA,所以点AA的曲率为2π−2×π2−∠AAAAAA=2π3,所以∠AAAAAA=π3,因为AAAA=AAAA,所以△AAAAAA为正三角形,因为CC为AAAA的中点,所以AACC⊥AAAA,又AAAA1⊥平面AAAAAA,AACC⊂平面AAAAAA,所以AAAA1⊥AACC,因为AAAA1∩AAAA=AA,AAAA1,AAAA⊂平面AAAAAA1AA1,所以AACC⊥平面AAAAAA1AA1.(2)取AAAA的中点EE,连接AAEE,则AAEE⊥AAAA,因为AAAA1⊥平面AAAAAA,AAEE⊂平面AAAAAA,所以AAAA1⊥AAEE,因为AAAA1∩AAAA=AA,AAAA1,AAAA⊂平面AAAA1AA1AA,所以AAEE⊥平面AAAA1AA1AA.又AA1MM⊂平面AAAA1AA1AA,所以AAEE⊥AA1MM,过EE作AA1MM的垂线,垂足为EE,连接AAEE,则AA1MM⊥EEEE,又AAEE∩EEEE=EE,AAEE,EEEE⊂平面AAEEEE,所以AA1MM⊥平面AAEEEE,又AAEE⊂平面AAEEEE,所以AAEE⊥AA1MM,所以∠AAEEEE为二面角AA−MMAA1−AA1的平面角的补角.设AA由等面积法可得12MMEE⋅EEEE=12EEEE⋅AAMM,则EEEE=EEEE⋅AACC CCEE=3×22√2=3√2,则tan∠AAEEEE=AAEE EEPP=√63,故二面角AA−MMAA1−AA1的正切值为−√63.【点睛】方法点睛:学生在理解相关新概念、新法则(公式)之后,运用学过的知识,结合已掌握的技能,通过推理、运算等解决问题.在新环境下研究“旧”性质.主要是将新性质应用在“旧”性质上,创造性地证明更新的性质,落脚点仍然是线面垂直的判定定理与性质和求二面角.答案第11页,共11页。
高二数学 周测试卷(含答案解析)

(2)求二面角 的平面角的余弦值。(理科做)
求点F到平面ABE的距离。(文科做)
21.已知椭圆 的,离心率为 , 是其焦点,点 在椭圆上。
(Ⅰ)若 ,且 的面积等于 。求椭圆的方程;
(Ⅱ)直线 交椭圆于另一点 ,分别过点 作直线 的垂线,交 轴于点 ,
当 取最小值时,求直线 的斜率。
22.已知函数
(1)曲线 在点 处的切线方程为 ,求 的值;
(2)当 时, ,试求 的取值范围。
参考答案及评分标准
一、选择题:共12小题,每小题5分,共60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
B
B
A
A
D
A
A
D
B
C
D
C
1.选B.【解析】∵ , ,∴ ,故选B.
2.选B.【解析】∵ ,对应的点为 在第二象限,故选B.
……………………………………5分
(Ⅱ)
函数的图象为:
当 时, ,依题意, ,则
∴ 的取值范围是 …………………………………………………………10分
18.(Ⅰ)∵ 由正弦定理得
∴
即 ,易知 ,且 ,
上式两边除以 ,得 ……………………………………6分
(Ⅱ)∵ ,∴ ,
由 ,又 , ,得
而
∴ …12分
19.(12分)
二、填空题共4小题,每小题5分,共20分.
13.填 .【解析】如图可知 的最小值是 .
14.填 .【解析】由题意得四面体 是底面边长为 的正三角形,侧棱 垂直底面,且 , , ,则外接球球心在过底面中心垂直于底面的垂线上,且到底面的距离等于 的一半,∴
高二第一学期期末测试语文试题(附答案解析)

高二第一学期期末测试语文试题(附答案解析)第Ⅰ卷(阅读题,共70分)甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1~3题。
人们对“钱”的追求,促进了全球交往。
发现新大陆的哥伦布、发现美洲的西班牙人和抵达印度的葡萄牙人等,他们都是追逐着“钱”而走遍世界的。
国家、地区之间的贸易,不仅繁殖了各行各业的商人,而且还呼唤着以“钱”为商业对象的商人──“钱商”,私人金融活动应运而生。
这些私人金融活动的风险很大,但是,“钱”的商业利润实在太大,野火烧不尽,春风吹又生。
现在,钱的符号化电子化,让银行结算的速度大幅度提高,社会前进的步伐加快,极大地提高了经济的效率,在这方面,发达国家走在了前头。
金融电子化、货币符号化,是顺着使“钱”尽可能方便的逻辑往前走的。
“钱”方便到可以看不见的地步,越来越多看不见的“钱”在我们身边如洪水般高速流动,终于出现了一种比自然界灾害更为可怕的灾害──“钱灾”。
在国际经济关系中,人们以“钱”炒“钱”,“钱”越炒越热,终于升腾为“泡沫”。
发达国家的投机资本大肆购买某国的货币,然后急剧抛出,足以使经济规模较小的国家爆发金融危机。
短期流动资本大进大出,是东亚金融危机爆发的直接原因。
十多年前长春“疯狂的君子兰”,就是泡沫经济的本土例子,在城市职工人均收入不足百元的时候,一株君子兰却居然可以炒至十几万元的价位。
20世纪80年代的日本,经济增长幅度不大,房地产却在疯炒,经济泡沫一破灭,迄今十年不振。
钱啊钱,认为它贵,它就贵,不贵也贵,一旦泡沫破灭,认为它不贵,它就不贵,本来不贵。
经济发展怎样才有后劲?经济学家发现,在土地、劳动、资源和资本、科学技术和和平环境这些重要因素以外,还有一个重要的因素,那就是国内市场的容量。
迄今为止,没有哪个国家的国内市场容量能够比得上美国,这是美国在经济发展方面能够长期独领风骚的重要原因。
一个大国,只有当人民购买力得到普遍提高、市场整合得好的时候,国内市场才会显示容量优势。
高二数学选择性必修一测试卷

高二选择性必修一测试卷一、单选题(本大题8个小题,每小题5分,共40分.)1.在下列命题中:①若向量,a b共线,则向量,a b所在的直线平行;②若向量,a b 所在的直线为异面直线,则向量,a b一定不共面;③若三个向量,,a b c 两两共面,则向量,,a b c共面;④已知空间的三个不共面向量,,a b c,则对于空间的任意一个向量p ,总存在实数,,x y z 使得p xa yb zc =++ .其中正确命题的个数是()A .0B .1C .2D .32.直线l 经过点()1,1P -和以()()3,1,3,2M N -为端点的线段相交,直线l 斜率的取值范围是()A .3,2⎛⎤-∞ ⎥⎝⎦B .1,2⎡⎫-+∞⎪⎢⎣⎭C .13,22⎡⎤-⎢⎥⎣⎦D .13,,22⎛⎤⎡⎫-∞-⋃+∞ ⎪⎥⎢⎝⎦⎣⎭3.直线:3410l x y +-=被圆22:2440C x y x y +---=所截得的弦长为()A .25B .4C .23D .224.椭圆2222:1(0)x y C a b a b +=>>的左顶点为A ,点,P Q 均在C 上,且关于原点对称.若直线,AP AQ 的斜率之积为12-,则C 的离心率为()A 32B .22C .12D .135.中心在原点,焦点在x 轴上的双曲线的一条渐近线经过点(4,2),则它的离心率为()A 6B 5C 62D 526.已知过抛物线2:4C y x =的焦点F 且倾斜角为60︒的直线交C 于A ,B 两点,Q 为AB 的中点,P 为C 上一点,则||||PF PQ +的最小值为()A .83B .53C .8D .57.如图,正方体1111ABCD A B C D -中,1AN NA = ,11A M MD = ,11B E B C λ=,当直线1DD 与平面MNE 所成的角最大时,λ=()A .12B .13C .14D .158.已知点(5A ,(0,5B -,若曲线()222200,0x ya b a b-=>>上存在点P 满足4PA PB -=,则下列正确的是()A .1b a <+B .2b a<C .1b a >+D .2b a>二、多选题:本题共4小题,每小题5分,共20分.有选错的得0分,部分选对的得2分.9.下列说法正确的是()A .直线()()213750m x m y m ++-+-=必过定点()1,3B .过点(2,1)P 作圆225=x y +的切线,切线方程为250x y +-=C .经过点()1,1P ,倾斜角为θ的直线方程为()1tan 1y x θ-=-D .直线210x y --=在x 轴上的截距为12,在y 轴上的截距为110.已知E ,F 分别是正方体1111ABCD A B C D -的棱BC 和CD 的中点,则()A .1A D 与11B D 是异面直线B .1A D 与EF 所成角的大小为45C .1A F 与平面1B CB 所成角的正弦值为223D .二面角11C D B B --的余弦值为6311.过抛物线28x y =的焦点F 的直线交抛物线于A B ,两点,分别过A B ,作抛物线的切线交于点.P 则下列说法正确的是()A .若16AB =,则直线AB 的倾斜角为4πB .点P 在直线2y =-上C .AP BP⊥D .1AB PF+212.已知双曲线C :()222210,0x y a b a b-=>>的左右焦点为1F ,2F ,左右顶点为1A ,2A ,过2F 的直线l 交双曲线C 的右支于P ,Q 两点,设12PA A α∠=,21PA A β∠=,当直线l 绕着2F 转动时,下列量保持不变的是()A .1PQA △的周长B .1PF Q 的周长与2PQ之差C .tan tan αβD .tan tan αβ⋅三、填空题:本题共4个小题,每小题5分,共20分.13.若圆2221:(2)(4)(0)C x y r r ++-=>上恰有2个点到直线:4350l x y --=的距离为2,则实数r 的取值范围为______.14.在正方体1111ABCD A B C D -中,棱1BB 与平面11ABC 所成角的余弦值为__________.15.已知P 为椭圆2212516x y +=上的一点,若M ,N 分别是圆22(3)2x y ++=和22(3)1x y -+=上的点,则||||PM PN +的最大值为________.16.已知离心率为1e 的椭圆1C :()2211221110x y a b a b +=>>和离心率为2e 的双曲线2C :()2222222210,0x y a b a b -=>>有公共的焦点,其中1F 为左焦点,P 是1C 与2C 在第一象限的公共点.线段1PF 的垂直平分线经过坐标原点,则22124e e +的最小值为_____________.四、解答题:本大题共6小题,17题共10分,其余各题每题12分,共70分.17.在以下这三个条件中任选一个,补充在下面的问题中,并求解.①圆经过点(3,4)C ;②圆心在直线20x y +-=上;③圆截y 轴所得弦长为8且圆心M 的坐标为整数.已知圆M 经过点()()1,2,6,3A B -且_____.(1)求圆M 的方程;(2)求以()2,1为中点的弦所在的直线方程.18.已知P 点坐标为(0,2)-,点,A B 分别为椭圆2222:1(0)x y E a b a b+=>>的左、右顶点,ABP △是等腰直角三角形,长轴长是短轴长的2倍.(1)求椭圆E 的方程;(2)设过点P 的动直线l 与E 相交于,M N 两点,当坐标原点O 位于以MN 为直径的圆外时,求直线l 斜率的取值范围.19.如图,在四棱锥P ABCD -中,底面ABCD 为菱形,3BAD π∠=,Q 为AD 的中点,2PA PD AD ===.(1)点M 在线段PC 上,13PM PC =,求证:PA ∥平面MQB ;(2)在(1)的条件下,若3PB =,求直线PD 和平面MQB 所成角的余弦值.20.已知圆心C 在第一象限,半径为54的圆与y 轴相切,且与x 轴正半轴交于A ,B 两点(A 在B 左侧),1OA OB ⋅=(O 为坐标原点).(1)求圆C 的标准方程;(2)过点A 任作一条直线与圆22:1O x y +=相交于P ,Q 两点.①证明:PA QB PBQA+为定值;②求2PB PC +的最小值.21.如图,在直三棱柱111ABC A B C -中,平面1A BC ⊥侧面11ABB A ,且12AA AB ==.(1)求证:AB BC ⊥;(2)若直线AC 与平面1A BC 所成的角为6π,请问在线段1AC 上是否存在点E ,使得二面角A BE C --的大小为23π,若存在请求出E 的位置,不存在请说明理由.22.设12,F F 是双曲线()2222:10,0x yC a b a b-=>>的左、右两个焦点,O 为坐标原点,若点P 在双曲线C 的右支上,且1122,OP OF PF F == 的面积为3.(1)求双曲线C 的渐近线方程;(2)若双曲线C 的两顶点分别为()()12,0,,0A a A a -,过点2F 的直线l 与双曲线C 交于M ,N 两点,试探究直线1A M 与直线2A N 的交点Q 是否在某条定直线上?若在,请求出该定直线方程;若不在,请说明理由.。
深圳实验学校高中部2023-2024年度高二第一阶段考试数学试题

深圳实验学校高中部2023-2024学年度第二学期第一阶段考试高二数学时间:120分钟满分:150分命题人:陈素玲审题人:陈雪艳一、单选题:在每小题给出的四个选项中有且仅有一项是符合题目要求的,共8小题,每小题5分,满分40分.1.下表是离散型随机变量X 的分布列,则常数a 的值是()X 3459P2a 16a +1216A .16B .112C .19D .122.函数21ln 2y x x =-的单调递减区间为()A .(1,1)-B .(]1,1-C .()0,1D .()0,+∞3.学习涂色能锻炼手眼协调能力,更能提高审美能力.现有四种不同的颜色:湖蓝色,米白色,橄榄绿,薄荷绿,现在给小房子中的四个区域涂色,要求相邻区域不涂同一颜色,则共有()种不同的涂色方法.A .108B .96C .84D .484.我们把各位数字之和为8的四位数称为“八合数”(如2024是“八合数”),则“八合数”共有()个.A .35B .56C .120D .1655.6名研究人员在3个不同的无菌研究舱同时进行工作,每名研究人员必须去一个舱,且每个舱至少去1人,由于空间限制,每个舱至多容纳3人,则不同的安排方案共有()种.A .720B .450C .360D .1806.已知a R ∈,0b ≠,若x b =是函数()()()2f x x b x ax b =-++的极小值点,则实数b的取值范围为()A .1b >B .1b <且0b ≠C .2b >D .2b <且0b ≠7.某一地区患有流感的人占0.05,流感患者对一种试验反应是阳性的概率为0.9,正常人对这种试验反应是阳性的概率为0.05.现抽查了一个人,试验反应是阳性,则此人是流感患者的概率为()A .12B .9200C .919D .18378.若对任意的12,(,)x x m ∈+∞,且12x x <,都有122121ln ln 12x x x x x x -<-,则m 的最小值是()A .1eBC .1D .e二、多选题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.用数字0,1,2,3,4,5组成无重复数字的四位数,则()A .可组成360个四位数B .可组成108个是5的倍数的四位数C .可组成各位数字之和为偶数的四位数有180个D .若将组成的四位数按从小到大的顺序排列,则第88个数为231010.已知()0.6P A =,()0.3P AB =,()|0.5P B A =,下列选项正确的是()A .()0.4P B =B .()06|.P A B =C .()|0.5P A B =D .()()()P AB P A P B =11.若函数()()2ln 21()f x x a x x a R =+-+∈存在两个极值点12,x x ()12x x <,则()A .0a <或2a >B .1102x <<C .2()0f x <D .()()1212ln 2f x f x +>-三、填空题:本题共3小题,每小题5分,满分15分.12.在53(21)(1)x y +-的展开式中,32x y 的系数为.13.有3台车床加工同一型号的零件,第1台车床加工的次品率为0.06,第2台车床加工的次品率为0.05,第3台车床加工的次品率为0.08,加工出来的零件混放在一起.已知第1,2,3台车床加工的零件数分别占总数的0.25,0.3,0.45,现从中任意选取1个零件,则取到的零件是次品的概率为.14.已知函数()()1e xf x x =+,过点(1,)M t 可作3条与曲线()y f x =相切的直线,则实数t的取值范围是.四、解答题:共5大题,满分77分.解答应写出文字说明、证明过程或演算步骤.15.(13分)某校将进行篮球定点投测试,规则为:每人至多投3次,先在M 处投一次三分球,投进得3分,未投进不得分,以后均在N 处投两分球,每投进一次得2分,未投进不得分.测试者累计得分高于3分即通过测试,并终止投篮.已知甲同学两分球投篮命中的概率是12,三分球投篮命中的概率是110,乙同学两分球投篮命中的概率是25,三分球投篮命中的概率是15.(1)求甲同学通过测试的概率;(2)在甲、乙两位同学均通过测试的条件下,求甲得分比乙得分高的概率.16.(15分)盒中有大小颜色相同的6个乒乓球,其中4个未使用过(称之为新球),2个使用过(称之为旧球).每局比赛从盒中随机取2个球作为比赛用球,该局比赛结束后放回盒中.使用过的球即成为旧球.(1)求一局比赛后盒中恰有3个新球的概率;(2)设两局比赛后盒中新球的个数为X ,求X 的分布列.17.(15分)已知函数()()()ln f x a x a x a =+-∈R (1)讨论函数()f x 的极值点个数;(2)证明:当0a >时,()3ln 2f x a ≥+.18.(17分)已知函数1()eln ln x f x a x a -=-+.(1)当a e =时,求曲线()y f x =在点(1,(1))f 处的切线与两坐标轴围成的三角形的面积;(2)若()1f x ≥,求a 的取值范围.19.(17分)已知函数2()2ln (1)21().f x x a x ax a R =-+-+∈(1)求函数()f x 的单调区间;(2)若函数()f x 有两个零点12,x x .(i )求实数a 的取值范围;(ii )求证:12x x +>.。
2020-2021学年河南省天一大联考高二阶段性测试英语试题(一)

河南省天一大联考2020-2021学年高二阶段性测试英语试题(一)第一部分听力(共两节,满分30分)第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话,每段对话后有一个小题。
从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What does the woman want the boy to do?A. Read a story.B. Go to bed.C. Take a bath.2. When will the speakers hold a party?A. On Friday night.B. On Saturday night.C. On Sunday night.3. What did the woman do today?A. She kept at home.B. She stayed with some kids.C. She went to the bookstore.4. What are the speakers talking about?A. A fire.B. An earthquake.C. A car accident.5. What will the woman do tonight?A. Buy a calendar.B. Have a meeting.C. Attend a party.第二节(共15小题,每小题1.5分,满分22.5分)听下面5段对话或独白。
每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答第6、7题。
6. Where will the speakers stop their car?A. Near the store.B. Near the factory.C. At the park.7. What's wrong with the car?A. It can't be started.B. It has run out of water.C. It needs a new motor.听第7段材料,回答第8、9题。
(必考题)数学高二下期末经典测试题(含答案解析)(1)
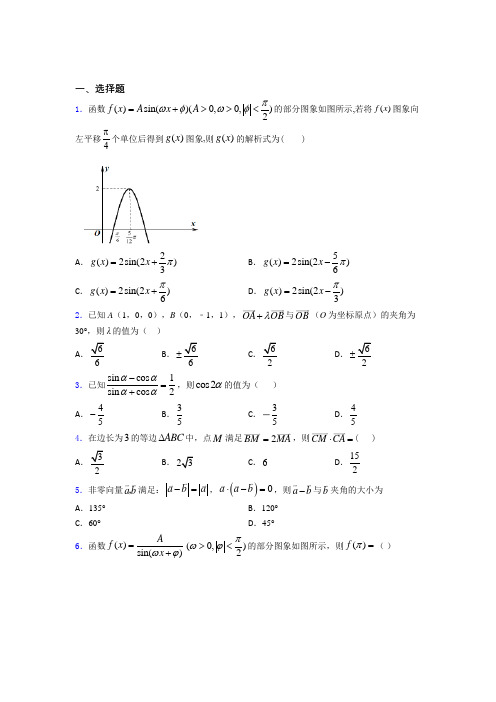
一、选择题1.函数()sin()(0,0,)2f x A x A πωφωφ=+>><的部分图象如图所示,若将()f x 图象向左平移4π个单位后得到()g x 图象,则()g x 的解析式为( )A .2()2sin(2)3g x x π=+ B .5()2sin(2)6g x x π=- C .()2sin(2)6g x x π=+D .()2sin(2)3g x x π=-2.已知A (1,0,0),B (0,﹣1,1),OA OB λ+与OB (O 为坐标原点)的夹角为30°,则λ的值为( ) A .66B .66±C .62D .62±3.已知sin cos 1sin cos 2αααα-=+,则cos2α的值为( )A .45-B .35C .35D .45 4.在边长为3的等边ABC ∆中,点M 满足BM 2MA =,则CM CA ⋅=( ) A 3B .3C .6 D .1525.非零向量a b ,满足:a b a -=,()0a a b ⋅-=,则a b -与b 夹角的大小为 A .135° B .120° C .60° D .45°6.函数()sin()A f x x ωϕ=+(0,)2πωϕ><的部分图象如图所示,则()f π=( )A .4B .23C .2D .37.设奇函数()()()()sin 3cos 0f x x x ωφωφω=+-+>在[]1,1x ∈-内有9个零点,则ω的取值范围为( )A .[)4,5ππB .[]4,5ππC .11,54ππ⎡⎤⎢⎥⎣⎦D .11,54ππ⎛⎤ ⎥⎝⎦8.已知函数()()sin 0,0,2f x A x A πωϕωϕ=+>>≤⎛⎫⎪⎝⎭的部分图象如图所示,则函数()y f x =的表达式是( )A .()2sin 12f x x π⎛⎫=+⎪⎝⎭B .()2sin 23f x x π⎛⎫=+⎪⎝⎭C .()22sin 23f x x π⎛⎫=- ⎪⎝⎭D .()2sin 23f x x π⎛⎫=- ⎪⎝⎭9.已知函数()sin 3cos f x x x =+,将函数()f x 的图象向左平移()0m m >个单位长度后,所得到的图象关于y 轴对称,则m 的最小值是( ) A .6πB .4π C .3π D .2π 10.若()2sin sinsin777n n S n N πππ︒=+++∈,则在中,正数的个数是( ) A .16B .72C .86D .10011.已知函数2()3cos cos f x x x x =+,则( ) A .()f x 的图象关于直线6x π=对称B .()f x 的最大值为2C .()f x 的最小值为1-D .()f x 的图象关于点(,0)12π-对称12.已知向量(2,0)OB =,向量(2,2)OC =,向量(2cos ,2sin )CA αα=,则向量OA 与向量OB 的夹角的取值范围是( ).A .π0,4⎡⎤⎢⎥⎣⎦B .π5π,412⎡⎤⎢⎥⎣⎦C .5ππ,122⎡⎤⎢⎥⎣⎦ D .π5π,1212⎡⎤⎢⎥⎣⎦ 13.已知f (x )=A sin(ωx+θ)(ω>0),若两个不等的实数x 1,x 2∈()2A x f x ⎧⎫=⎨⎬⎩⎭,且|x 1-x 2|min =π,则f (x )的最小正周期是( ) A .3πB .2πC .πD .π214.若向量a ,b 满足2a b ==,a 与b 的夹角为60,则a b +等于( ) A .223+B .23C .4D .1215.已知tan 24πα⎛⎫+=- ⎪⎝⎭,则sin 2α=( )A .310B .35 C .65-D .125-二、填空题16.已知θ为钝角,1sin()43πθ+=,则cos2θ=______. 17.已知1tan 43πα⎛⎫-=- ⎪⎝⎭,则2sin sin()cos()απαπα--+的值为__________. 18.实数x ,y 满足223412x y +=,则23x y +的最大值______. 19.如图在ABC 中,AC BC =,2C π∠=,点O 是ABC 外一点,4OA =,2OB =则平面四边形OACB 面积的最大值是___________.20.已知角α的终边上一点)3,1A-,则()sin tan 2παπα⎛⎫-++= ⎪⎝⎭__________.21.已知ABC ∆中角,,A B C 满足2sin sin sin B A C =且2sin cos cos 1242C Cπ+=,则sin A =__________.22.仔细阅读下面三个函数性质:(1)对任意实数x ∈R ,存在常数(0)p p ≠,使得1()2f x p f x p ⎛⎫-=+ ⎪⎝⎭. (2)对任意实数x ∈R ,存在常数(0)M M >,使得|()|f x M ≤. (3)对任意实数x ∈R ,存在常数,使得()()0f a x f a x -++=.请写出能同时满足以上三个性质的函数(不能为常函数)的解析式__________.(写出一个即可)23.将函数e x y =的图像上所有点的横坐标变为原来的一半,再向右平移2个单位,所得函数的解析式为__________. 24.已知1tan 43πα⎛⎫-= ⎪⎝⎭,则()()2cos sin cos 2παπαπα⎛⎫+--+ ⎪⎝⎭的值为__________. 25.若()1sin 3πα-=,且2παπ≤≤,则cos α的值为__________. 三、解答题26.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22222230a c b ac +-+=. (1)求cos B 的值; (2)求sin 24B π⎛⎫+⎪⎝⎭的值. 27.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且2cos (cos cos )C a B b A c +=.(1)求C ;(2)若c =,ABC 的面积为ABC 的周长.28.在已知函数()sin(),f x A x x R ωϕ=+∈(其中0,0,02A πωϕ>><<)的图象与x轴的交点中,相邻两个交点之间的距离为2π,且图象上一个最低点为2,23M π⎛⎫-⎪⎝⎭. (1)求()f x 的解析式; (2)当,122x ππ⎡⎤∈⎢⎥⎣⎦时,求()f x 的值域. 29.已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭在一个周期内的图像经过点,412π⎛⎫ ⎪⎝⎭和点5,412π⎛⎫- ⎪⎝⎭,且()f x 的图像有一条对称轴为12x π=. (1)求()f x 的解析式及最小正周期; (2)求()f x 的单调递增区间.30.已知定义在R 上的函数()()()sin 0,0f x A x x A ωϕ=+>>的图象如图所示(1)求函数()f x 的解析式; (2)写出函数()f x 的单调递增区间(3)设不相等的实数,()12,0,x x π∈,且()()122f x f x ==-,求12x x +的值.【参考答案】2016-2017年度第*次考试试卷 参考答案**科目模拟测试一、选择题 1.C 2.C 3.A 4.D 5.A 6.A 7.A 8.D 9.A 10.C11.A12.D13.A14.B15.B二、填空题16.【解析】【分析】将改写成的形式利用二倍角公式计算的值代入相关数值【详解】因为所以;因为且为钝角所以是第二象限角则故【点睛】(1)常见的二倍角公式:;(2)常用的角的配凑:;17.【解析】【分析】先根据已知求出最后化简代入的值得解【详解】由题得由题得=故答案为【点睛】本题主要考查差角的正切和同角的商数关系平方关系意在考查学生对这些知识的理解掌握水平和分析推理能力18.【解析】分析:根据题意设则有进而分析可得由三角函数的性质分析可得答案详解:根据题意实数xy满足即设则又由则即的最大值5;故答案为:5点睛:本题考查三角函数的化简求值关键是用三角函数表示xy19.【解析】分析:利用余弦定理设设AC=BC=m则由余弦定理把m表示出来利用四边形OACB面积为S=转化为三角形函数问题求解最值详解:△ABC为等腰直角三角形∵OA=2OB=4不妨设AC=BC=m则由余20.【解析】分析:先根据三角函数定义得再根据诱导公式化简求值详解:因为角的终边上一点所以因此点睛:本题考查三角函数定义以及诱导公式考查基本求解能力21.【解析】分析:先化简得到再化简得到详解:因为所以1-所以因为所以所以A+B=所以因为sinA>0所以故答案为点睛:本题主要考查三角化简和诱导公式意在考查学生对这些知识的掌握水平和基本的计算能力22.【解析】分析:由(1)得周期由(2)得最值(有界)由(3)得对称中心因此可选三角函数详解:由题目约束条件可得到的不同解析式由(1)得周期由(2)得最值(有界)由(3)得对称中心因此可选三角函数点睛:23.【解析】分析:根据图像平移规律确定函数解析式详解:点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟练掌握无论是哪种变形切记每一个变换总是对字母而言24.【解析】分析:由可得化简即可求得其值详解:由即答案为点睛:本题考查三角函数的化简求值考查了诱导公式及同角三角函数基本关系式的应用是基础题25.【解析】由题意得三、解答题 26. 27. 28. 29. 30.2016-2017年度第*次考试试卷 参考解析【参考解析】**科目模拟测试一、选择题 1.C 解析:C 【解析】 【分析】根据函数的图象求出函数()f x 的解析式,再根据图象的平移变换得到()g x 的解析式即可. 【详解】 由图象可知,A =2,541264T πππ=-=, 2T ππω∴==,2ω∴=,又当512x π=时,52sin(2)212πφ⨯+=, 即5sin()16πφ+=, 2πφ<, 3πφ∴=-,故()sin()f x x π=-223,将()f x 图象向左平移4π个单位后得到()g x , ∴ ()2sin[2()]2sin(2)436g x x x πππ=+-=+,故选:C 【点睛】本题主要考查了正弦型函数的图象与性质,图象的变换,属于中档题.2.C解析:C 【解析】 【分析】运用向量的坐标运算及夹角公式直接求解即可. 【详解】解:(1,0,0)(0,,)(1,,)OA OB λλλλλ+=+-=-,∴2||12,||2OA OB OB λλ+=+=,()2OA OB OB λλ+=,∴cos302λ︒=, ∴4λ=,则0λ>,∴2λ=. 故选:C . 【点睛】本题考查空间向量的坐标运算,考查运算求解能力,属于基础题.3.A解析:A 【解析】 ∵sin cos 1sin cos 2αααα-=+,∴tan α11tan α3tan α12-==+,.∴cos2α=222222cos sin 1tan 4cos sin 1tan 5αααααα--==-++ 故选A4.D解析:D 【解析】 【分析】结合题意线性表示向量CM ,然后计算出结果 【详解】 依题意得:121211215)333333333232CM CA CB CA CA CB CA CA CA ⋅=+⋅=⋅+⋅=⨯⨯⨯+⨯⨯=(,故选D .【点睛】本题考查了向量之间的线性表示,然后求向量点乘的结果,较为简单5.A解析:A 【解析】 【分析】先化简()0a a b ⋅-=得2=a a b ⋅,再化简a b a -=得2b a =,最后求a b -与b 的夹角. 【详解】因为()0a a b ⋅-=,所以220=a a b a a b -⋅=∴⋅,,因为a b a -=,所以2222a a a b b =-⋅+, 整理可得22b a b =⋅, 所以有2b a =,设a b -与b 的夹角为θ,则()2cos a b b a b b a b ba bθ-⋅⋅-===-222222||a a =-, 又0180θ︒≤≤︒,所以135θ=︒, 故选A . 【点睛】本题主要考查数量积的运算和向量夹角的计算,意在考查学生对这些知识的理解掌握水平和分析推理能力.6.A解析:A【解析】试题分析:根据题意,由于函数()sin()A f x x ωϕ=+(0,)2πωϕ><,那么根据图像可知周期为2π,w=4,然后当x=6π,y=2,代入解析式中得到22sin(4)6πϕ=⨯+,6πϕ=-,则可知()f π=4,故答案为A.考点:三角函数图像点评:主要是考查了根据图像求解析式,然后得到函数值的求解,属于基础题.7.A解析:A 【解析】f (x )=sin (ωx+φ(ωx+φ)=2[12sin (ωx+φ(ωx+φ)] =2[cos3πsin (ωx+φ)﹣sin 3πcos (ωx+φ)]=2sin (ωx+φ﹣3π) ∵函数f (x )为奇函数,∴f (0)=2sin (φ﹣3π)=0,∴φ=3π+kπ,k ∈Z ∴f (x )=2sin (ωx+kπ),f (x )=0即sin (ωx+kπ)=0,ωx+kπ=mπ,m ∈Z ,解得,x=()m k πω-,设n=m ﹣k ,则n ∈Z ,∵A ∈[﹣1,1],∴﹣1≤x≤1,[]1,1n πω∈-,∴n ωωππ-≤≤, ∵A ∈[﹣1,1]中有9个元素,4545.ωπωππ∴≤<⇒≤< 故答案为A.点睛:函数的零点或方程的根的问题,一般以含参数的三次式、分式、以e 为底的指数式或对数式及三角函数式结构的函数零点或方程根的形式出现,一般有下列两种考查形式:(1)确定函数零点、图象交点及方程根的个数问题;(2)应用函数零点、图象交点及方程解的存在情况,求参数的值或取值范围问题.研究方程根的情况,可以通过导数研究函数的单调性、最值、函数的变化趋势等,根据题目要求,通过数形结合的思想去分析问题,可以使得问题的求解有一个清晰、直观的整体展现.同时在解题过程中要注意转化与化归、函数与方程、分类讨论思想的应用.8.D解析:D 【解析】 【分析】根据函数的最值求得A ,根据函数的周期求得ω,根据函数图像上一点的坐标求得ϕ,由此求得函数的解析式.由题图可知2A =,且11522122T πππ=-=即T π=,所以222T ππωπ===, 将点5,212π⎛⎫⎪⎝⎭的坐标代入函数()()2sin 2x x f ϕ=+, 得()5262k k ππϕπ+=+∈Z ,即()23k k πϕπ=-∈Z , 因为2πϕ≤,所以3πϕ=-,所以函数()f x 的表达式为()2sin 23f x x π⎛⎫=- ⎪⎝⎭.故选D.【点睛】本小题主要考查根据三角函数图像求三角函数的解析式,属于基础题.9.A解析:A 【解析】 【分析】利用函数的平移变换得π2sin 3y x m ⎛⎫=++ ⎪⎝⎭,再根所图象关于y 轴对称,得到角的终边落在y 轴上,即π2π3πm k +=+,k Z ∈,即可得答案. 【详解】()sin 2s πin 3f x x x x ⎛⎫=+=+ ⎪⎝⎭,将函数()f x 的图象向左平移m 个单位长度后,得到函数π2sin 3y x m ⎛⎫=++⎪⎝⎭的图象, 又所得到的图象关于y 轴对称,所以π2π3πm k +=+,k Z ∈, 即ππ6m k =+,k Z ∈, 又0m >,所以当0k =时,m 的最小值为π6. 故选:A. 【点睛】本题考查三角函图象的变换、偶函数的性质,考查函数与方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力.10.C【解析】 【分析】 【详解】 令7πα=,则7n n πα=,当1≤n≤14时,画出角序列n α终边如图,其终边两两关于x 轴对称,故有均为正数,而,由周期性可知,当14k-13≤n≤14k 时,Sn>0, 而,其中k=1,2,…,7,所以在中有14个为0,其余都是正数,即正数共有100-14=86个,故选C.11.A解析:A 【解析】 【分析】利用三角函数恒等变换的公式,化简求得函数的解析式,再根据三角函数的图象与性质,逐项判定,即可求解. 【详解】 由题意,函数23111()3cos cos 2cos 2sin(2)2262f x x x x x x x π=+=++=++, 当6x π=时,113()sin(2)sin 6662222f ππππ=⨯++=+=,所以6x π=函数()f x 的对称轴,故A 正确;由sin(2)[1,1]6x π+∈-,所以函数()f x 的最大值为32,最小值为12-,所以B 、C 不正确; 又由12x π=时,131()sin(2)612622f πππ=⨯++=+,所以(,0)12π-不是函数()f x 的对称中心,故D 不正确, 故选A . 【点睛】本题主要考查了三角恒等变换的公式的应用,以及函数sin()y A wx b ϕ=++的图象与性质的应用,着重考查了推理与运算能力,属于基础题.12.D解析:D 【解析】 不妨设(0,0)O∵(2,2)OC =,(2cos ,2sin )CA αα=. ∴(2,2)C 、(22,22sin )A cos αα++. ∴点A 在以(2,2)为圆心半径为2的圆上. ∴OA 与OB 的夹角为直线OA 的倾斜角. 设:OA l y kx = ∴22121k d r k -=≤=+.即2410k k -+≤,则[23,23]k ∈-+. 又∵π23tan12-=,523tanπ12+=. ∴OA 、OB 夹角[23,23]θ∈-+.故选D .13.A解析:A 【解析】 【分析】 由题意可得123ππω⨯=,求得ω的值,可得()f x 的最小正周期是2πω的值 【详解】由题意可得()1sin 2x ωθ+=的解为两个不等的实数1x ,2x 且123ππω⨯=,求得23ω= 故()f x 的最小正周期是23ππω=故选A 【点睛】本题主要考查了的是三角函数的周期性及其图象,解题的关键根据正弦函数的图象求出ω的值,属于基础题14.B解析:B 【解析】 【分析】将a b +平方后再开方去计算模长,注意使用数量积公式. 【详解】因为2222cos 6044412a b a a b b +=+︒+=++=,所以23a b +=, 故选:B. 【点睛】本题考查向量的模长计算,难度一般.对于计算xa yb +这种形式的模长,可通过先平方再开方的方法去计算模长.15.B解析:B 【解析】 【分析】 根据tan 24πα⎛⎫+=- ⎪⎝⎭求得tan 3α=,2222sin cos 2tan sin 2sin cos tan 1ααααααα==++即可求解. 【详解】 由题:tan 24πα⎛⎫+=- ⎪⎝⎭, tan 121tan αα+=--,解得tan 3α=,2222sin cos 2tan 63sin 2sin cos tan 1105ααααααα====++. 故选:B 【点睛】此题考查三角恒等变换,涉及二倍角公式与同角三角函数的关系,合理构造齐次式可以降低解题难度.二、填空题16.【解析】【分析】将改写成的形式利用二倍角公式计算的值代入相关数值【详解】因为所以;因为且为钝角所以是第二象限角则故【点睛】(1)常见的二倍角公式:;(2)常用的角的配凑:;解析:9-【解析】 【分析】将2θ改写成2()42ππθ+-的形式,利用二倍角公式计算cos2θ的值,代入相关数值.【详解】因为cos2cos[2()]sin[2()]424πππθθθ=+-=+,所以cos 22sin()cos()44ππθθθ=++; 因为1sin()043πθ+=>且θ为钝角,所以()4πθ+是第二象限角,则cos()43πθ+==-,故cos 22sin()cos()449ππθθθ=++=-. 【点睛】(1)常见的二倍角公式:sin 22sin cos ααα=,2222cos 2cos sin 2cos 112sin ααααα=-=-=- ;(2)常用的角的配凑:()ααββ=-+,()ααββ=+-;2()()ααβαβ=++- ,2()()βαβαβ=+--.17.【解析】【分析】先根据已知求出最后化简代入的值得解【详解】由题得由题得=故答案为【点睛】本题主要考查差角的正切和同角的商数关系平方关系意在考查学生对这些知识的理解掌握水平和分析推理能力解析:35【解析】 【分析】先根据已知求出tan α,最后化简2sin sin()cos()απαπα--+,代入tan α的值得解. 【详解】 由题得tan 111,tan 1+tan 32ααα-=-∴=.由题得22222sin +sin cos sin sin()cos()=sin +sin cos =sin +cos ααααπαπαααααα--+ =2211tan tan 3421tan 1514ααα++==++. 故答案为35【点睛】本题主要考查差角的正切和同角的商数关系平方关系,意在考查学生对这些知识的理解掌握水平和分析推理能力.18.【解析】分析:根据题意设则有进而分析可得由三角函数的性质分析可得答案详解:根据题意实数xy 满足即设则又由则即的最大值5;故答案为:5点睛:本题考查三角函数的化简求值关键是用三角函数表示xy解析:【解析】分析:根据题意,设2cos x θ=,y θ=,则有24cos 3sin x θθ+=+,进而分析可得()25sin x θα+=+,由三角函数的性质分析可得答案.详解:根据题意,实数x ,y 满足223412x y +=,即22143x y +=,设2cos x θ=,y θ=,则()24cos 3sin 5sin x θθθα=+=+,3tan 4α⎛⎫= ⎪⎝⎭, 又由()15sin 1θα-≤+≤,则525x -≤≤,即2x +的最大值5; 故答案为:5.点睛:本题考查三角函数的化简求值,关键是用三角函数表示x 、y .19.【解析】分析:利用余弦定理设设AC=BC=m 则由余弦定理把m 表示出来利用四边形OACB 面积为S=转化为三角形函数问题求解最值详解:△ABC 为等腰直角三角形∵OA=2OB=4不妨设AC=BC=m 则由余解析:5+ 【解析】分析:利用余弦定理,设AOB α∠=,设AC=BC=m ,则AB =.由余弦定理把m 表示出来,利用四边形OACB 面积为S=24sin 4sin 2OACB ABC m S S αα∆∆=+=+.转化为三角形函数问题求解最值.详解:△ABC 为等腰直角三角形.∵OA=2OB=4,不妨设AC=BC=m ,则AB =.由余弦定理,42+22﹣2m 2=16cos α,∴2108cos m α∴=-.108cos 4sin 4sin 4sin 4cos 52OACB ABC S S ααααα∆∆-∴=+=+=-+)554πα=-+≤.当34απ=时取到最大值5+.故答案为5+点睛:(1)本题主要考查余弦定理和三角形的面积的求法,考查三角恒等变换和三角函数的图像和性质,意在考查学生对这些知识的掌握水平和分析推理能力.(2)解答本题的关键是设AOB α∠=,再建立三角函数的模型.20.【解析】分析:先根据三角函数定义得再根据诱导公式化简求值详解:因为角的终边上一点所以因此点睛:本题考查三角函数定义以及诱导公式考查基本求解能力【解析】分析:先根据三角函数定义得cos ,tan αα,再根据诱导公式化简求值.详解:因为角α的终边上一点)1A -,,所以cos tanαα===, 因此()sin tan 2παπα⎛⎫-++⎪⎝⎭cos tanαα=+== 点睛:本题考查三角函数定义以及诱导公式,考查基本求解能力.21.【解析】分析:先化简得到再化简得到详解:因为所以1-所以因为所以所以A+B=所以因为sinA>0所以故答案为点睛:本题主要考查三角化简和诱导公式意在考查学生对这些知识的掌握水平和基本的计算能力解析:12【解析】 分析:先化简2sincos cos 1242C C π+=得到2C π=,再化简2sin sin sin B A C =得到sin A =详解:因为2sincos cos 1242C C π+=,所以1-2cos 1222C C +=,所以cos(cos 0,cos 0(cos =222222C C C C -=∴=舍)或, 因为0C π<<,所以2C π=,所以A+B=2π.2sin sin sin B A C =因为,所以22cos sin ,sin sin 10,sin A A A A A =∴+-=∴=因为sinA>0,所以1sin 2A =.. 点睛:本题主要考查三角化简和诱导公式,意在考查学生对这些知识的掌握水平和基本的计算能力.22.【解析】分析:由(1)得周期由(2)得最值(有界)由(3)得对称中心因此可选三角函数详解:由题目约束条件可得到的不同解析式由(1)得周期由(2)得最值(有界)由(3)得对称中心因此可选三角函数点睛:解析:4()sin π3f x ⎛⎫= ⎪⎝⎭【解析】分析:由(1)得周期,由(2)得最值(有界),由(3)得对称中心,因此可选三角函数. 详解:由题目约束条件可得到()f x 的不同解析式.由(1)得周期,由(2)得最值(有界),由(3)得对称中心,因此可选三角函数()4sin π3f x ⎛⎫=⎪⎝⎭. 点睛:正余弦函数是周期有界函数,既有对称轴也有对称中心,是一类有特色得函数.23.【解析】分析:根据图像平移规律确定函数解析式详解:点睛:三角函数的图象变换提倡先平移后伸缩但先伸缩后平移也常出现在题目中所以也必须熟练掌握无论是哪种变形切记每一个变换总是对字母而言 解析:24e x y -=【解析】分析:根据图像平移规律确定函数解析式. 详解:222(2)24e ee e xxx x y y y --=→=→==横坐标变为一半右移个单位点睛:三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母x 而言.24.【解析】分析:由可得化简即可求得其值详解:由即答案为点睛:本题考查三角函数的化简求值考查了诱导公式及同角三角函数基本关系式的应用是基础题 解析:65【解析】 分析:由1tan 43πα⎛⎫-= ⎪⎝⎭可得tan 2α=,化简()()2cos sin cos 2παπαπα⎛⎫+--+ ⎪⎝⎭,即可求得其值.详解:tan tantan 114tan ,tan 2,4tan 13tan tan 4παπαααπαα--⎛⎫-===∴= ⎪+⎝⎭+ 由()()22cos sin cos sin sin cos 2παπαπαααα⎛⎫+--+=+⎪⎝⎭22222sin sin cos tan tan 6.sin cos tan 15αααααααα++===++ 即答案为65. 点睛:本题考查三角函数的化简求值,考查了诱导公式及同角三角函数基本关系式的应用,是基础题.25.【解析】由题意得解析:3-【解析】由题意得()1sin sin ,[,],cos 32ππαααπα-==∈∴==三、解答题 26. (1)34-(2)16【解析】试题分析:(1)利用余弦定理表示出cosB ,将已知等式代入即可求出cosB 的值;(2)由cosB 可求出sin 2,cos 2B B 的值,然后利用两角和的余弦公式可得结果. 试题解析:(1)由22222230a c b ac +-+=,得22232a cb ac +-=-, 根据余弦定理得222332cos 224aca cb Bac ac -+-===-; (2)由3cos 4B =-,得sin B = ∴sin22sin cos BB B ==21cos22cos 18B B =-=,∴1sin 2sin2cos cos2sin 44428816B B B πππ⎫⎛⎫+=+=-+=⎪ ⎪⎪⎝⎭⎝⎭. 27.(1)3C π=(2)7+【解析】 【分析】(1)利用正弦定理,将2cos (cos cos )C a B b A c +=,转化为2cos (sin cos sin cos )sin C A B B A C +=,再利用两角和与差的三角的三角函数得到sin (2cos 1)0C C -=求解.(2)根据ABC 的面积为1sin 2ab C =12ab =,再利用余弦定理得()23a b ab =+-,求得+a b 即可. 【详解】(1)因为2cos (cos cos )C a B b A c +=, 所以2cos (sin cos sin cos )sin C A B B A C +=, 所以()2cos sin sin C A B C +=, 所以sin (2cos 1)0C C -=, 所以1cos 2C =, 又因为()0,C π∈, 所以3C π=.(2)因为ABC 的面积为所以1sin 2ab C = 所以12ab =.由余弦定理得:若2222cos c a b ab C =+-,()23a b ab =+- 所以7a b +=所以ABC 的周长7【点睛】本题主要考查正弦定理、余弦定理和两角和与差的三角函数的应用,还考查了转化化归的思想和运算求解的能力,属于中档题.28.(1)()2sin(2)6f x x π=+ (2)[-1,2] 【解析】试题分析:根据正弦型函数图象特点,先分析出函数的振幅和周期,最低点为2,23M π⎛⎫- ⎪⎝⎭,得2A =,周期T π=,则2==2T πω,又函数图象过2,23M π⎛⎫- ⎪⎝⎭,代入得42sin 23πϕ⎛⎫+=- ⎪⎝⎭,故1126k k Z πϕπ=-+∈,,又0,2πϕ⎛⎫∈ ⎪⎝⎭,从而确定6πϕ=,得到()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,再求其单调增区间. (2)分析72,636x πππ⎡⎤+∈⎢⎥⎣⎦,结合正弦函数图象,可知当262x ππ+=,即6x π=时,()f x 取得最大值2;当7266x ππ+=,即2x π=时,()f x 取得最小值1-,故()f x 的值域为[]1,2-. 试题解析:(1)依题意,由最低点为2,23M π⎛⎫-⎪⎝⎭,得2A =,又周期T π=,∴2ω=. 由点2,23M π⎛⎫-⎪⎝⎭在图象上,得42sin 23πϕ⎛⎫+=- ⎪⎝⎭, ∴4232k ππϕπ+=-+,k Z ∈,1126k k Z πϕπ∴=-+∈,. ∵0,2πϕ⎛⎫∈ ⎪⎝⎭,∴6πϕ=,∴()2sin 26f x x π⎛⎫=+ ⎪⎝⎭. 由222262k x k πππππ-≤+≤+,k Z ∈,得36k x k k Z ππππ-≤≤+∈,.∴函数()f x 的单调增区间是(),36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦. (2),122x ππ⎡⎤∈⎢⎥⎣⎦,∴72,636x πππ⎡⎤+∈⎢⎥⎣⎦. 当262x ππ+=,即6x π=时,()f x 取得最大值2; 当7266x ππ+=,即2x π=时,()f x 取得最小值1-,故()f x 的值域为[]1,2-. 点睛:本题考查了三角函数的图象和性质,重点对求函数解析式,单调性,最值进行考查,属于中档题.解决正弦型函数解析式的问题,一定要熟练掌握求函数周期,半周期的方法及特殊值的应用,特别是求函数的初相时,要注意特殊点的应用及初相的条件,求函数值域要结合正弦函数图象,不要只求两个端点的函数值.29.(1)()4sin 34f x x π⎛⎫=+ ⎪⎝⎭,23π;(2)22,()43123k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z .【解析】【分析】(1)由函数的图象经过点412,π⎛⎫ ⎪⎝⎭且f (x )的图象有一条对称轴为直线12x π=, 可得最大值A ,且能得周期并求得ω,由五点法作图求出ϕ的值,可得函数的解析式.(2)利用正弦函数的单调性求得f (x )的单调递增区间.【详解】(1)函数f (x )=A sin (ωx +ϕ)(A >0,ω>0,2πϕ<)在一个周期内的图象经过点412,π⎛⎫ ⎪⎝⎭,5412π⎛⎫- ⎪⎝⎭,,且f (x )的图象有一条对称轴为直线12x π=, 故最大值A =4,且5212123T πππ=-=, ∴2T 3π=, ∴ω2Tπ==3. 所以()4sin(3)f x x ϕ=+.因为()f x 的图象经过点,412π⎛⎫⎪⎝⎭,所以44sin 312πϕ⎛⎫=⨯+ ⎪⎝⎭, 所以24k ϕπ=+π,k Z ∈. 因为||2ϕπ<,所以4πϕ=, 所以()4sin 34f x x π⎛⎫=+ ⎪⎝⎭. (2)因为()4sin 34f x x π⎛⎫=+⎪⎝⎭,所以232242k x k πππππ-+≤+≤+,k Z ∈, 所以2243123k k x ππππ-+≤≤+,k Z ∈, 即()f x 的单调递增区间为22,()43123k k k ππππ⎡⎤-++∈⎢⎥⎣⎦Z . 【点睛】本题主要考查由函数y =A sin (ωx +ϕ)的性质求解析式,通常由函数的最大值求出A ,由周期求出ω,由五点法作图求出ϕ的值,考查了正弦型函数的单调性问题,属于基础题.30.(1)()=4sin 23f x x π⎛⎫+ ⎪⎝⎭;(2)5,,1212k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦;(3)76π; 【解析】【分析】(1)根据函数的最值可得A ,周期可得ω,代入最高点的坐标可得ϕ,从而可得解析式;(2)利用正弦函数的递增区间可解得;(3)利用()2f x =-在(0,)x π∈内的解就是1x 和2x ,即可得到结果.【详解】(1)由函数()f x 的图象可得4A =, 又因为函数的周期72()1212T πππ=-=,所以22πωπ==, 因为函数的图象经过点(,4)12P π,即4sin(2)412πϕ⨯+=, 所以2,62k k Z ππϕπ+=+∈,即2,3k k Z πϕπ=+∈, 所以()4sin(22)4sin(2)33f x x k x πππ=++=+. (2)由222,232k x k k Z πππππ-≤+≤+∈, 可得5,1212k x k k Z ππππ-≤≤+∈, 可得函数()f x 的单调递增区间为:5[,],1212k k k Z ππππ-+∈, (3)因为(0,)x π∈,所以72(,)333x πππ+∈, 又因为()2f x =-可得1sin(2)32x π+=-, 所以7236x ππ+=或11236x ππ+=, 解得512x π=或34x π=,、 因为12x x ≠且()12,0,x x π∈,12()()2f x f x ==-, 所以1253147124126x x ππππ+=+==. 【点睛】本题考查了由图象求解析式,考查了正弦函数的递增区间,考查了由函数值求角,属于中档题.。
高二10月月考测试(化学)试题含答案

高二10月月考(化学)(考试总分:115 分)一、单选题(本题共计7小题,总分42分)1.(6分)下列关于能源和作为能源的物质的叙述错误的是()A. 吸热反应的反应物总能量低于生成物总能量B. 绿色植物进行光合作用时,将光能转化为化学能“贮存”起来C. 物质的化学能可以在不同条件下转为热能、电能、光能等为人类所利用D. 天然气属于二次能源2.(6分)下列说法中不正确的是()①将硫酸钡放入水中不能导电,所以硫酸钡是非电解质②氨溶于水得到的溶液氨水能导电,所以氨是电解质③固态的共价化合物不导电,熔融态的共价化合物可以导电④固态的离子化合物不导电,熔融态的离子化合物也不导电A.仅①④B.仅①②④C.仅①②③D.①②③④3.(6分)t℃时,在体积不变的密闭容器中发生反应:X(g)+3Y(g)2Z(g),各组分在不同时刻的浓度如下表:()物质X Y Z初始浓度/(mol·L-1) 0.10.2 02min末浓度/(mol·L-1) 0.08a b平衡浓度/(mol·L-1) 0.050.05 0.1下列说法正确的是A. 平衡时,X的转化率为20%B. 2min时Y的物质的量为0.14C. 增大平衡后的体系压强,v(正)增大,v(逆)减小D. 2min内,用Y的变化量表示的平均反应速率v(Y)=0.03mol·L―1·min―14.(6分)醋酸的下列性质中,可以证明它是弱电解质的是()①1 mol·L-1的CH3COOH溶液中c(H+)=10-2mol·L-1②CH3COOH可以任意比与H2O互溶③在相同条件下,CH3COOH溶液的导电性比盐酸弱④10 mL 1 mol·L-1的CH3COOH溶液恰好与10 mL 1 mol·L-1的NaOH溶液完全反应⑤同浓度同体积的CH3COOH溶液和HCl溶液与Fe反应时,CH3COOH溶液中放出H2的速率慢⑥CH3COOH溶液中CH3COOH、CH3COO-、H+同时存在A.①③⑤⑥B.②③④⑤C.①④⑤⑥D.③⑤⑥5.(6分)下列说法正确的是()A. 增大反应物浓度,可增大活化分子的百分数,从而使有效碰撞次数增大B. 有气体参加的化学反应,若增大压强(即缩小反应容器的体积),可增加活化分子的百分数,从而使反应速率增大C. 升高温度能使化学反应速率增大,主要原因是增加了反应物分子中活化分子的百分数D. 催化剂不影响反应活化能但能增大单位体积内活化分子百分数,从而增大反应速率6.(6分)下列说法符合事实的是()A.常温下由水电离产生的c(H+)=10-12mol/L的溶液中加入铝粉都能够产生氢气.B.向NaClO溶液中通入SO2气体,c(HClO)增大.C.用0.2000 /L NaOH标准溶液滴定HCl与CH3COOH的混合溶液(混合液中两种酸的浓度均约为0.1mol/L),至中性时,溶液中的酸未被完全中和.D.用pH试纸测量次氯酸钠溶液的pH为11.57.(6分)下列关于水的离子积常数的叙述中,正确的是()A.因为水的离子积常数的表达式是K w=c(H+)·c(OH-),所以K w随溶液中H+和OH-浓度的变化而变化B.水的离子积常数K w与水的电离平衡常数K电离是同一个物理量C.水的离子积常数仅仅是温度的函数,随着温度的变化而变化D.水的离子积常数K w与水电离平衡常数K电离是两个没有任何关系的物理量二、实验题(本题共计1小题,总分12分)8.(12分)某课外兴趣小组欲测定某NaOH溶液的浓度,其操作步骤如下:①碱式滴定管用蒸馏水洗净后,用待测溶液润洗2~3次后,再注入待测溶液,调节滴定管的尖嘴部分充满溶液,并使液面处于"0"刻度以下的位置,记下读数;将锥形瓶用蒸馏水洗净后,用待测溶液润洗锥形瓶2~3次;从碱式滴定管中放入25.00mL待测溶液到锥形瓶中;②将酸式滴定管用蒸馏水洗净后,立即向其中注入0.1000mol/L标准盐酸,调节滴定管的尖嘴部分充满溶液,并使液面处于"0"刻度以下的位置,记下读数;③向锥形瓶中滴入酚酞作指示剂,进行滴定。
高二数学椭圆测试题(含答案)

高二数学椭圆测试题(一)一.选择题(每小题5分,满分30分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若直线1y kx =+和椭圆2241x y +=相切, 则2k 的值是………………………[ C ]A.1 / 2B.2 / 3C.3 / 4D.4 / 52.椭圆221mx ny +=与直线x +y -1=0交于M 、N 两点,过原点与线段MN 中点的直线斜率为 ,则 的值是…………………………………………………………………[ B ] A .B .C D .3.椭圆22221x y a b+=上对两焦点张角为90的点可能有………………………………[ C ] 4.12,B B 是椭圆短轴的两端点,过左焦点1F 作长轴的垂线,交椭圆于P,若12|FF |是1|OF|和12|B B |的比例中项,则1|PF|:2|OB |的值是……………………………………………[ B ]5.椭圆221123x y +=的一个焦点为1F ,点P 在椭圆上,如果线段1PF 的中点M 在y 轴上,那么点M 的纵坐标是…………………………………………………………………………[ A ]A .B .C .D . 6.设A(-2,F 为椭圆221612x y +=1的右焦点,点M 在椭圆上移动,当|AM|+2|MF|取最小值时,点M 的坐标为…………………………………………………………………[ C ]A .(0,B .(0,-C .D .(-二.填空题(每题5分,满分20分,把答案填在题中横线上)7.椭圆22259x y +=1上有一点P 到左准线的距离为2.5,则P 到右焦点的距离为 . 8. 9. 10.P 是椭圆2243x y +=1上的点,F 1和F 2是焦点,则k =|PF 1|·|PF 2|的最大值和最小值分别是________ 1.8 2.1/2 3.(6, 4.k max =4,k mix =3 A.4 B.24 C.02,4 D.个个或个个或个个还有其它情况3B C D 若椭圆的一个焦点到相应准线的距离为离心率为则椭圆的半短轴长为用分数表示5, 2, 5. ()432212(4,)(8,):1,1449,________.x y A y B C y B +=若点、、是椭圆上的三点它们关于右焦点的三条焦点半径长成等差数列那么点的坐标是±±±34±n m三.解答题(11,12题每题15分,13题20分,满分50分,解答应写出文字说明,证明过程或演算步骤)11.已知椭圆的焦点在坐标轴上,短轴的一个端点与两焦点构成正三角形,若焦点到椭圆的最短距离为解:如图所示,设点P (0x ,0y )为椭圆上位于第一象限的任一点,其到焦点距离20||PF a ex =-,显然0x a =时,2||PF最小,故有a c -b ,a =2c ,解之得a =,b =3. 故221129x y +=与221912x y +=为所求椭圆方程. 12. 设中心在原点,焦点在x轴上的椭圆的离心率为2,并且椭圆与圆x 2+y 2-4x-2y+52=0交于A 、B 两点,若线段AB 的长等于圆的直径.(1)求直线AB 的方程;(2)求椭圆的方程. 解:(1)设椭圆的方程为22221x y a b +=,由c e a ==222a b c =+得224a b =, 设()()1122,,,A B x y x y ,由于线段AB 的长等于圆的直径,所以线段AB 的中点为圆心(2,1),且AB =则22112222222211x y a b x y ab ⎧+=⎪⎨⎪+=⎩,两式相减得 ()()()()1212121222x x x x y y y y a b -+-+=-,()()2121221212b x x y y x x a y y -+-=-+,又12122212x x y y +⎧=⎪⎨+⎪=⎩,所以()()222122*********b x x b b a a b y y -+--===-+,121212y y x x -=--,直线AB 的方程为y=-12x+2; (2)由222212214y x x y bb ⎧=-+⎪⎨⎪+=⎩,消去x 得222440y y b -+-=,12212242y y b y y +=⎧⎪∴-⎨=⎪⎩, ()221224b y y ∴=--,又()12122x x y y -=--,所以()()2212124x x y y =--,AB ∴==又AB =()251024b ∴=-, 223,12b a ∴==,所求椭圆的方程为212x +23y =1.13.设椭圆22x a +22y b =1的两焦点为F 1、F 2,长轴两端点为A 1、A 2.(1)P 是椭圆上一点,且∠F 1PF 2=600,求ΔF 1PF 2的面积;(2)若椭圆上存在一点Q ,使∠A 1QA 2=1200,求椭圆离心率e 的取值范围.解:(1)设|PF 1|=r 1,|PF 2|=r 2,则S 12PF F ∆=12r 1r 2sin ∠F 1PF 2,由r 1+r 2=2a , 4c 2=r 12+r 22-2cos ∠F 1PF 2,得r 1r 2=21221cos b F PF +∠.代入面积公式,得S 12PF F ∆=1212sin 1cos F PF F PF ∠+∠b 2=b 2tan ∠122F PFb 2.(2)设∠A 1QB=α,∠A 2QB=β,点Q(x 0,y 0)(0<y 0<b).tan θ=tan(α+β)= tan α+tanβ1-tan αtanβ= 000022021a x a x y y a x y -++--=0222002ay x y a +-.∵202x a +202y b =1,∴x 02=a 2-22a b y 02.∴tan θ=0222022ay a b y b -- =2202ab c y-2ab 22y 02b , 即3c 4+4a 2c 2-4a 4≥0,∴3e 4+4e 2-4≥0,解之得e 2≥23e<1为所求.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
英德中学高二第二学期周四晚
英语小测试题一
(7、8、27班专用)
______ 班______ 号姓名________
I. 根据中文意思,完成句子。
1. 我通常早晨6点醒。
I usually _______ _______ at six in the morning.
2. 如果你需要我的帮忙,请叫醒我。
Please _______ me ________ if you need my help.
3.他走进办公室,打开电灯。
He _______ ________ the office and _______ _______ the light.
4.你早餐通常吃什么?
________ do you usually have _______ breakfast.
5.他们此时此刻正在等候我们。
They are _______ for us ______ _______ _______.
6.我觉得每天进行锻炼是必要的。
I think it necessary ______ ________ ________ ________ every day.
7. Tom是警察而他哥哥确实罪犯。
Tom is a policeman ______ his brother is a criminal.
8.他通常不吃早餐就上学。
He normally goes to school ______ _______ _______.
9.铃声一响,学生们就跑出教室。
The students ran out of the classroom ______ _______ _______ the bell went off.
10.做作业花了我大约两个小时。
It ______ _______ about two hours ________ ________ my homework. 11.他花了三年时间些这本书。
He _______ three years ________ this book.
12.昨天,Lily第一个完成了考试。
Lily was ______ _______ ________ _________ the exam yesterday.
13.这条公路占据了大量农田。
The road _______ _______ a lot of farmland.
14.这个瓶子装满了水。
The bottle _______ _______ water.
15.她姐姐在市中心的一家公司上班。
Her sister works in a company _______ _______ _______ _______ the city. II. 翻译
1.你应该更加关心你的孩子。
__________________________________________________________________
2.史密斯先生清早就起床了以便能赶上早班车。
__________________________________________________________________ 3.听到那个消息,我内心充满了喜悦。
__________________________________________________________________ 4.洗漱、换衣服、吃早餐、离家还有上公交车花了我不到十五分钟。
__________________________________________________________________ __________________________________________________________________ 5.离开教室前请关灯。
__________________________________________________________________ III. 语法填空
The British generally pay a lot of atttention to good table manners. Even young children are expected to eat 1 (proper) with the knif and fork.
If you can not eat 2 certain type of food or have some special needs, tell your host several days before the dinner party.
If you are a guest, it is polite to wait until your host 3 (start) eating or indicates you should do so.
Never open your mouth while 4 (chew), or talk with food 5 your mouth. Finish chewing and swallow before taking a drink or another bite.
If you finish eating, please let others know that you have and place your knife 6 fork together.
Ask for dishes to be passed to you if 7 are not directly in front of you. If you are asked to pass something, always pass to the right 8 the person is to your immediate left.
9 is best not to eat quickly. Take your time when you are eating and try to eat
10 the same speed as everyone else. If there is food on the table, it is not polite to eat as quickly as possible and then take the extra food for yourself.
1.______
2. ______
3. ______
4. ______
5. ______
6.______
7. ______
8. ______
9. ______ 10. ______。
