福建省周宁一中、政和一中2020届高三数学第三次联考试题 文(无答案)新人教A版
2020届高中毕业班第三次教学质量检测文科数学试卷
高中毕业班第三次教学质量检测文科数学试题本试卷共 6 页。
满分 150 分。
考生注意:1. 答题前, 考生务必将自己的准考证号、 姓名填写在答题卡上。
考生要认真核对答题卡上粘贴的条形码的 “准考证号、 姓名、 考试科目” 与考生本人准考证号、 姓名是否一致.2. 第I 卷每小题选出答案后, 用 2B 铅笔把答题卡上对应题目的答案标号涂黑, 如需改动, 用橡皮擦干净后, 再选涂其他答案标号. 第II 卷用0. 5 毫米的黑色墨水签字笔在答题卡上书写作答. 若在试题卷上作答, 答案无效.3. 考试结束, 考生必须将试题卷和答题卡一并交回.一、 选择题: 本大题共 12 小题, 每小题 5 分, 共 60 分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
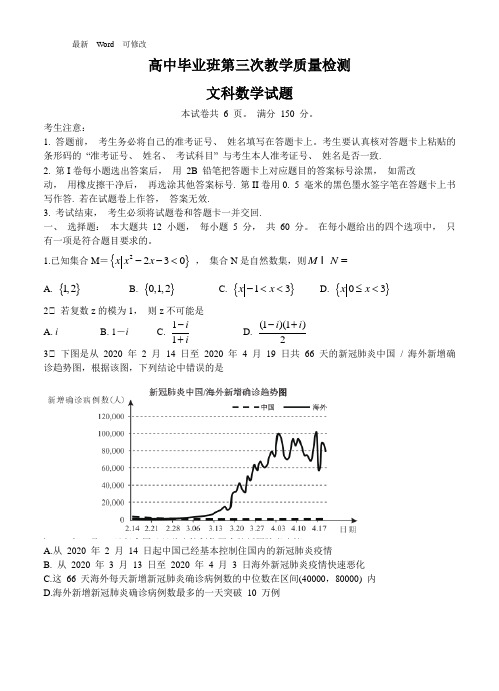
1.已知集合M ={}2230x x x --< , 集合N 是自然数集,则M N =IA. {}1,2B. {}0,1,2C. {}13x x -<<D. {}03x x ≤<2 若复数z 的模为1, 则z 不可能是A. iB. 1-iC. 11i i -+D. (1)(1)2i i -+ 3 下图是从 2020 年 2 月 14 日至 2020 年 4 月 19 日共 66 天的新冠肺炎中国 / 海外新增确诊趋势图,根据该图,下列结论中错误的是A.从 2020 年 2 月 14 日起中国已经基本控制住国内的新冠肺炎疫情B. 从 2020 年 3 月 13 日至 2020 年 4 月 3 日海外新冠肺炎疫情快速恶化C.这 66 天海外每天新增新冠肺炎确诊病例数的中位数在区间(40000,80000) 内D.海外新增新冠肺炎确诊病例数最多的一天突破 10 万例4.已知变量x,y 满足约束条件1x yxy+≥⎧⎪≤⎨⎪≤⎩,则目标函数z=2x+y的最大值为A.0B.1C.2D. 35.已知1,,3 AB a AC b BN BC ===uu u r r u u u r r u u u r u u u r,则AN=u u u rA.1122a b+r rB .2233a b+r rC.2133a b+r rD.1233a b+r r6.若方程221204x ya a+=+-表示椭圆,则实数a的取值范围是A. (-20,4)B. (-20,-8) (8,4)-UC. (,20)(4,)-∞-+∞U D. (,20)(8,)-∞--+∞U7. 函数1()()sinf x x xx=-在[,0)(0,]ππ-U的图象大致为8.已知数列{}n a满足2112,,1,2n n na a a n N a a*++=-∈==,则a2020 =A. -2B. -1C. 1D. 29.若0.330.220.220.330.22,0.33,loga b c===则A. a> b > cB. b> a>cC. c> a> bD. c > b >a10 若奇函数()g x的图象是由函数()sin cosf x a x x=+的图象向右平移6π个单位得到的.则()f x的一个单调递增区间是A.2[,]33ππ- B.4[,]33ππC.5[,]66ππ- D.7[,]66ππ11. 中国是茶的故乡,也是茶文化的发源地 中国茶的发现和利用已有四千七百多年的历史, 且长盛不衰, 传遍全球 为了弘扬中国茶文化, 某酒店推出特色茶食品“金萱排骨茶”, 为了解每壶“金萱排骨茶” 中所放茶叶量x 克与食客的满意率y 的关系, 通过试验调查研究,发现可选择函数模型bx c y ae +=来拟合y 与 x 的关系, 根据以下数据:可求得y关于x 的回归方程为 A. 0.043 4.2911100x y e += B. 0.043 4.2911100x y e -= C. 0.043 4.291x y e += D. 0.043 4.291x y e -=12.在直四棱柱ABCD -A 1B 1C 1D 1中, 底ABCD 是边长为6 的正方形,点E 在线段AD 上.且满足AE =2ED . 过点E 作直四棱柱ABCD -A 1B 1C 1D 1外接球的截面.所得的截面面积的最大值与最小值之差为 19π. 则直四棱柱ABCD -A 1B 1C 1D 1外接球的半径为A. 3B. 23C. 33D. 3二、 填空题: 本大题共 4 小题.每小题 5 分.共 20 分.13.已知函数,则曲线()y f x =在点(1,(1))P f 处的切线方程为____________.14.设 △ABC 内角A 、B 、C 所对应的边分别为a 、b 、c 。
2020年福建省政和第一中学政和一中高三语文三模试题及答案

2020年福建省政和第一中学政和一中高三语文三模试题及答案一、现代文阅读(36分)(一)现代文阅读I(9分)阅读下面的文字,完成下面小题。
《寒食帖》被誉为“天下第三大行书”,是苏轼最有名的即兴创作诗词,也是他被贬黄州第三年寒食节时的人生感叹。
内容伤感孤独,诗帖苍凉多情。
宋神宗元丰二年(1079),苏轼因“乌台诗案”一场文字狱被贬黄州三年。
在元丰五年(1082)三月的寒食节,他联想到了当时失意的政治和窘迫的生活,于困乏中触景生情写下了此帖:自我来黄州,已过三寒食。
年年欲惜春,春去不容惜。
今年又苦雨,两月秋萧瑟。
卧闻海棠花,泥污燕脂雪。
暗中偷负去,夜半真有力。
何殊病少年,病起头已白。
春江欲入户,雨势来不已。
小屋如渔舟,濛濛水云里。
空庖煮寒菜,破灶烧湿苇。
那知是寒食,但见乌衔纸。
君门深九重,坟墓在万里。
也拟哭途穷,死灰吹不起。
黄庭坚曾评价苏轼书法的结字特点,戏言“公之字固不敢轻论,然间觉褊浅,亦甚似石压蛤蟆。
”“石压蛤蟆”的比喻,形象地勾画出了结体扁平的特征。
整体上来讲,《寒食帖》的整体结构非常有苏轼的特点。
从第一个字“自”到“起”有很大的区别,并且在中间,当作者写到关于家乡的思念时,字体突然变大,以示他突发的感情。
苏轼的这部诗帖在布局和章法方面,行距宽、字距紧,但整体又看起来让人舒服。
一行一行读下去时,我们就能通过作者的字体布局进行简单分析。
比如,通篇书写的节奏由慢到快,在开头部分还能压抑住内心的情感波动,字的大小保持得比较均匀,但当想起悲伤的事,便肆意挥洒,当时悲壮的情感表达得淋漓尽致。
《寒食帖》整体可以从右向左分成三个部分来体现作者创作时的感情波动,第一部分只包括了两行字,因为这里的字还只是大小均匀;第二部分有着很重要的作用,这一段体现出了苏轼的情感变化——由压抑到放肆;而第三部分的“破灶”二字开始了整个诗帖的高峰,以示自己的悲痛之情已达到极致。
《寒食帖》里的每个字眼都有自己表达的含义,而这些令它们独一无二的特点是苏轼那厚重而灵动的线条。
福建省2020届高三上学期三校联考数学(文)试题Word版含解析

福建省2020届高三上学期三校联考数学(文)试题(考试时间:120分钟总分:150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷(选择题,共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 已知集合,,则A. B. C. D.【答案】C【解析】,故选C.点睛:集合的三要素是:确定性、互异性和无序性.研究一个集合,我们首先要看清楚它的研究对象,是实数还是点的坐标还是其它的一些元素,这是很关键的一步.第二步常常是解一元二次不等式,我们首先用十字相乘法分解因式,求得不等式的解集.在解分式不等式的过程中,要注意分母不能为零.元素与集合之间是属于和不属于的关系,集合与集合间有包含关系. 在求交集时注意区间端点的取舍. 熟练画数轴来解交集、并集和补集的题目2. 已知,,,则A. B. C. D.【答案】A3. 已知等比数列的前项和为,且则A. B. C. D.【答案】C【解析】由等比数列可得, ,解得q=2,故选C.4. 下列说法正确的是A. 命题“若,则”的否命题是“若,则”B. 命题“”的否定是“”C. 命题“若函数有零点,则“或”的逆否命题为真命题D. “在处有极值”是“”的充要条件【答案】C【解析】选项A, 命题“若,则”的否命题是“若,则”,错误;选项B, 命题“”的否定是“”,错误;选项C, 命题“若函数有零点,则“或”的逆否命题与原命题同真假, 函数有零点,即方程有解, 解得或,故原命题正确; 选项D, “在处有极值”是“”的既不充分也不必要条件,如y=在x=0处有极值,但不可导,y=在x=0处满足,但在定义域内单调递增;综上可知,选C.5. 在中,角对应的边分别为,若,,则为A. B. C. D.【答案】A6. 若,则A. B. C. D.【答案】D【解析】,即,,故选D.7. 若命题“,使得”是假命题,则实数取值范围是A. B.C. D.【答案】C【解析】命题“,使得”是假命题,则为真命题, ,解得,故选C.8. 已知,则=A. B. C. D.【答案】B【解析】由二倍角公式:= ,故选B.9. 要得到函数的图象,只需将函数的图象A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】D【解析】函数,又= ,所以需将函数向右平移个单位长度,故选D.10. 函数的图象大致是A. B.C. D.【答案】D【解析】函数是偶函数排除A.当时, ,可得: ,令,作出与图象如图:可知两个函数有一个交点,就是函数有一个极值点,故选:D.11. 定义在上的函数,是它的导函数,且恒有成立,则A. B.C. D.【答案】B【解析】构造函数,则,即g(x)在上单调递增,所以,即,故选B.12. 已知定义在上的偶函数满足,且当时,,则函数的零点个数是A. 2B. 4C. 6D. 8【答案】C【解析】由题意,所以周期为2, 当时,,且偶函数,即函数图象关于y轴对称,分别画出y=和y=的图象,观察可得交点个数为4个,即函数的零点个数是4个,故选C.点睛:本题考查指数函数的图象,函数的性质应用,函数零点问题,属于中档题目.解决本题的关键是要根据题中给出的奇偶性和周期性,以及部分的函数解析式画出函数在R上的图象,再把函数的零点个数问题转化为和的交点个数,考查了转化思想和数形结合思想的综合应用.第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知等差数列中,是方程的两根,则_____【答案】3【解析】等差数列中, ,,故填3.14. 已知函数,则__________【答案】【解析】点睛:(1)求分段函数的函数值,要先确定要求值的自变量属于哪一段区间,然后代入该段的解析式求值,当出现的形式时,应从内到外依次求值.(2)求某条件下自变量的值,先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记代入检验,看所求的自变量的值是否满足相应段自变量的取值范围.15. 在,内角,,的对边分别为,若,且,则=__________【答案】【解析】由正弦定理得, ,又,所以,即B为锐角, 则=,故填.16. 已知函数在上单调递增,则实数的取值范围是_____.【答案】【解析】,解得在上恒成立,构造函数,解得x=1, 在上单调递增,在上单调递减,g(x)的最大值为g(1)=1, ,,故填.点睛:本题考查函数导数与单调性.方程的有解问题就是判断是否存在零点的问题,可参变分离,转化为求函数的值域问题处理. 恒成立问题以及可转化为恒成立问题的问题,往往可利用参变分离的方法,转化为求函数最值处理.也可构造新函数然后利用导数来求解.注意利用数形结合的数学思想方法.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知等差数列中,是数列的前项和,且(Ⅰ)求数列的通项公式;(Ⅱ)设数列的前项和为,求.【答案】(I), . (II).【解析】试题分析: (I)设等差数列的首项为,公差为,利用等差数列的通项公式和前n项和公式代入计算,求出求出首项和公差以及通项公式; (II)化简数列的通项公式,利用裂项相消法求出.试题解析:(I)设等差数列的首项为,公差为,因为所以得数列的通项公式是,(II),,.18. 已知函数.(Ⅰ)求的最小正周期及单调递增区间;(Ⅱ)若在区间上的最大值与最小值的和为,求的值.【答案】(Ⅰ).单调递增区间是().(Ⅱ).【解析】试题分析: (Ⅰ)根据二倍角公式和两角和与差的正弦公式化简函数,求出函数的最小正周期及单调递增区间;(Ⅱ)由x的范围,求出的范围,画出正弦函数的图象,求出函数的最大值与最小值的和等于1,解出a的值.试题解析:(Ⅰ)所以.由,得.故,函数的单调递增区间是().(Ⅱ)因为,所以.所以.因为函数在上的最大值与最小值的和为,所以.19. 设函数,若函数在处的切线方程为.(Ⅰ)求实数的值;(Ⅱ)求函数在上的最大值.【答案】(I)和. (II).【解析】试题分析: (I)根据导数的几何意义,可知函数在处的导数即为切线的斜率,又点(1, )为切点,列出方程解出a,b的值; (II)把a,b的值代入解析式,对函数求导判断单调性,根据单调区间写出函数的最值.试题解析:(I),∵函数在处的切线方程为.∴解得所以实数的值分别为和.(II)由(I)知,,,当时,令,得,令,得,∴在[,2)上单调递增,在(2,e]上单调递减,在处取得极大值这个极大值也是的最大值. 又,所以,函数在上的最大值为.20. 如图,在四边形中,,平分,,,的面积为,为锐角.(Ⅰ)求;(Ⅱ)求 .【答案】(I). (II) .【解析】试题分析: (I)在中,由三角形的面积公式可求得,再利用余弦定理求出;(Ⅱ)在中,由正弦定理求出和,根据题意平分,,在和中分别写出正弦定理,得出比例关系,求出.试题解析:(I)在中,.因为,所以.因为为锐角,所以.在中,由余弦定理得所以CD的长为.(II)在中,由正弦定理得即,解得,也为锐角..在中,由正弦定理得即①在中,由正弦定理得即②平分,由①②得,解得因为为锐角,所以 .点睛: 解三角形问题,多为边和角的求值问题,这就需要根据正、余弦定理结合已知条件灵活转化边和角之间的关系,从而达到解决问题的目的.其基本步骤是:第一步:定条件,即确定三角形中的已知和所求,在图形中标出来,然后确定转化的方向.第二步:定工具,即根据条件和所求合理选择转化的工具,实施边角之间的互化.第三步:求结果.21. 已知函数 ,其中 (为自然对数的底数).(Ⅰ)讨论函数的单调性,并写出相应的单调区间;(Ⅱ)设,若函数对任意都成立,求的最大值.【答案】(I)见解析 (II) .【解析】试题分析: (I)求出,对和分别讨论单调性,求出单调区间; (II)先对参数和时分别讨论,利用特殊值检验不能恒成立,在时,由函数对任意都成立,得,即,,构造关于a的新函数,求导判断单调性求出最大值,即的最大值.试题解析:(I)因为,①当时,在恒成立,函数在上单调递增;②当时,由得,所以当时,此时单调递减;当时,此时单调递增.综上,当时,函数的单调递增区间为;当时,函数的单调递增区间为;单调递减区间为 .(II) 由(I)知,当时,函数在R上单调递增且时, .所以不可能恒成立;当时,;当时,由函数对任意都成立,得 .因为,所以 .所以,设所以,由于,令,得.当时,,单调递增;当)时,,单调递减.所以,即,时,的最大值为.请考生从22、23两题任选1个小题作答,满分10分.如果多做,则按所做的第一题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.22. 选修4-4:坐标系与参数方程在直角坐标系中,直线过点且斜率为1,以为极点,轴的非负半轴为极轴的极坐标系中,曲线的极坐标方程为.(Ⅰ)求直线的参数方程与曲线的直角坐标方程;(Ⅱ)若直线与曲线的交点为、,求的值.【答案】(Ⅰ)为参数),(Ⅱ).【解析】试题分析: (Ⅰ)由直线l过的点和斜率写出参数方程,根据极坐标方程和普通方程的互化公式,求出曲线的直角坐标方程;(Ⅱ)将直线的参数方程与曲线的普通方程联立,根据根与系数的关系以及t的几何意义,求出的值.试题解析:(Ⅰ)直线的普通方程为为参数)∵,∴曲线C的直角坐标方程为(Ⅱ)将直线的参数方程代入曲线方程得∴,∴.23. 选修4-5:不等式选讲已知函数(Ⅰ)求不等式的解集;(Ⅱ)已知函数的最小值为,若实数且,求的最小值.【答案】(Ⅰ)(Ⅱ)9.【解析】试题分析: (Ⅰ)利用零点分段将函数去掉绝对值化简, 进而求出不等式的解集;(Ⅱ)根据绝对值不等式的性质求出函数的最小值,再根据基本不等式求出的最小值.试题解析:(Ⅰ),或,或解得或不等式的解集为(Ⅱ)函数的最小值为当且仅当时等号成立故的最小值为9.点睛: 含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用绝对值的几何意义求解.法一是运用分类讨论思想,法二是运用数形结合思想,将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用,这是命题的新动向.。
福建省政和一中、周宁一中2020届高三上学期11月联考试题数学理版含答案

2017-2018年周宁一中与政和一中第三次月考试卷理科数学考试总分:150分;考试时间:120分钟;命题人:王仁娇,审核:黄金凤一、选择题(本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是正确的, 将正确答案填写在答题卷相应位置上.)1.已知集合A ={x |x 2-2x -3≤0},B ={x |4x ≥2},则A ∪B =( ) A.B.C. (-∞,3]D. [-1,+∞)2.已知i 是虚数单位,复数z 满足z (3+4i )=1+i ,则复平面内表示z 的共轭复数的点在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3.若1021⎪⎭⎫ ⎝⎛=a ,2151b -⎪⎭⎫ ⎝⎛=,1031log c =,则a ,b ,c 大小关系为( ) A. a >b >c B. a >c >b C. c >b >a D. b >a >c4.用数学归纳法证明1+21+31+…+1n 21-<n (n ∈N *,n >1),第一步应验证不等式( ) A.2211<+ B. 331211<++ C.34131211<+++ D. 231211<++ 5.两曲线x y =,2x y =在x ∈[0,1]内围成的图形面积是( )A. 31B. 32C. 1D. 26若cos (8π-α)=61,则cos (43π+2α)的值为( )A. 1817 B. 1817-C.1918 D.1918-7.已知等差数列{a n }的前n 项为S n ,且a 1+a 5=-14,S 9=-27,则使得S n 取最小值时的n 为( )A. 1B. 6C. 7D. 6或78.已知函数f (x )=ln x +2x -6的零点位于区间(m -1,m )(m ∈Z )内, 则m 3m1log 27+ =( )A. 1B. 2C. 3D. 49.已知命题P :若△ABC 为钝角三角形,则sin A <cos B ;命题q :∀x ,y ∈R ,若x +y ≠2,则x ≠-1或y ≠3,则下列命题为真命题的是( )A. p ∨(¬q )B. (¬p )∧qC. p ∧qD. (¬p )∧(¬q )10.已知A ,B 是圆O :x 2+y 2=4上的两个动点,|AB |=2,OC =OB OA 3235-,若若M 是线段AB 的中点,则 OM OC •的值为( )A. 3B. 23C. 2D. -311.下面四个推理中,属于演绎推理的是( )A. 观察下列各式:72=49,73=343,74=2401,…,则72015的末两位数字为43B. 观察(x 2)′=2x ,(x 4)′=4x 3,(cos x )′=-sin x ,可得偶函数的导函数为奇函数C. 在平面上,若两个正三角形的边长比为1:2,则它们的面积比为1:4,类似的,在空间中,若两个正四面体的棱长比为1:2,则它们的体积之比为1:8D. 已知碱金属都能与水发生还原反应,钠为碱金属,所以钠能与水发生反应 12.定义在(0,+∞)的函数f (x )的导函数)(/x f 满足08)(/3>+x f x ,且f (2)=2,则不等式的解集为( )A. (-∞,2)B. (-∞,ln2)C. (0,2)D. (0,ln2)二、填空题(本大题共4小题,每小题5分,共20分,将正确答案填写在答题卷相应位置.) 13.在等比数列{}n a 中,22=a ,且451131=+a a ,则31a a +的值为______. 14.曲线f (x )=x ln x 在点P (1,0)处的切线l 与两坐标轴围成的三角形的面积是 ______ .15.已知O 为坐标原点,点A (5,-4),点M (x ,y )为平面区域⎪⎩⎪⎨⎧≤<≥+2y 12x y x 内的一个动点,则OM OA •的取值范围是 ______ .16设向量=(1,-2),=(a ,-1),=(-b ,0),其中O 为坐标原点,a >0,b >0,若A 、B 、C 三点共线,则ba 21+的最小值为 ______ . 三、解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤。
2020年福州市高中毕业班第三次质量检测(文数) 详解

2020年福州市高中毕业班第三次质量检测数学(文)试卷(完卷时间120分钟;满分150分)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷4至6页. 注意事项:1. 答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 3. 考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{|8}U x x =∈N …,集合{1,3,7}A =,则U A =ðA .{2,4,5,6}B .{0,2,4,5,6}C .{2,4,5,6,8}D .{0,2,4,5,6,8}【命题意图】本小题以集合为载体,考查集合的运算等基础知识,考查运算求解能力,考查数学运算核心素养,体现基础性. 【答案】D .【解析】解法一:因为{|8}={0,1,2,3,4,5,6,7,8},U x x =∈N …所以{0,2,4,5,6,8}U A =ð,故选D.解法二:因为0,0,0,U A U A ∉∈∴∈ð排除选项A ,C ;同理,8,U A ∈ð排除选项B ;故选D.2. 已知纯虚数z 满足(1i)2i z a -=+,则实数a 等于A .2B .1C .1-D .2-【命题意图】本小题以复数为载体,考查复数的纯虚数概念及复数四则运算等基础知识,考查运算求解能力,考查化归与转化思想,考查数学运算核心素养,体现基础性. 【答案】A .【解析】解法一:设i(,z b b =∈R 且0),b ≠则(1i)i i 2i.b b b a -⋅=+=+ ,a ∈R Q 2,,b a b =⎧∴⎨=⎩2a ∴=,故选A. 故选A. 解法二:2i (2i)(1i)22i 1i 222a a a az +++-+===+-. z Q 为纯虚数,2020a a -=⎧∴⎨+≠⎩,, 2.a ∴= 故选A.3. 曲线()1e x y x =-在1x =处的切线方程为A .e e 0x y --=B .e e 0x y +-=C .e 10x y +-=D .e 10x y --=【命题意图】本题以导数的几何意义为载体,考查曲线在某点处的切线等基础知识,考查运算求解能力,考查数学运算核心素养,体现基础性. 【答案】B .【解析】当1x =时,0y =,由()1e x y x =-得,e x y x '=-,所以该切线的斜率为e -,该切线方程为()e 1y x =--,即e e 0x y +-=.故选B . 4. 执行如图所示的程序框图,则输出的m =A .1B . 2C .3D .4【命题意图】本小题考查程序框图等基础知识,考查推理论证能力,考查逻辑推理核心素养,体现基础性. 【答案】C .【解析】该框图的功能为求小于11的正整数中3的倍数的个数,故输出的m 值为3.故选C .5. 已知等差数列{}n a 的前n 项和为n S ,且202020202020a S ==,则{}n a 的公差为A .2-B .2C .2019-D .2019【命题意图】本小题以数列为载体,考查等差数列的通项公式、前n 项和公式等基础知识,考查运算求解能力,考查化归与转化思想、特殊与一般思想,考查数学运算核心素养,体现基础性. 【答案】B.【解析】解法一:1202020202020()20202a a S +==,所以120202a a +=,所以12018a =-, 所以数列{}n a 的公差20201220201a ad -==-.故选B .解法二:由题意得,2019101020190S a ==,即10100,a =所以数列{}n a 的公差20201010220201010a a d -==-.故选B .解法三:设数列{}n a 的公差为d ,因为202020202020a S ==,所以11201920202020201920202020,2a d a d +=⎧⎪⎨⨯+=⎪⎩,即112019202020191,2a d a d +=⎧⎪⎨+=⎪⎩,,解得2d =.故选B . 6. 甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如下:以下关于这四名同学射击成绩的数字特征判断不正确...的是 A .平均数相同 B .中位数相同 C .众数不完全相同D .方差最大的是丁【命题意图】本小题以实际问题为载体,考查条形图、平均数、中位数、众数、方差等基础知识,考查数据处理能力、运算求解能力与应用意识,考查数学建模、数据分析、数学运算等核心素养,体现基础性、应用性. 【答案】D .【解析】由图的对称性可知,平均数都为5;由图易知,四组数据的众数不完全相同,中位数相同;记甲、乙、丙、丁图所对应的方差分别为22221234,,,s s s s ,则()()2221450.5650.51s =-⨯+-⨯=,()()()22222450.3550.4650.30.6s =-⨯+-⨯+-⨯=,()()()()()2222223350.3450.1550.2650.1750.3 2.6s =-⨯+-⨯+-⨯+-⨯+-⨯=, ()()()()()2222224250.1450.3550.2650.3850.1 2.4s =-⨯+-⨯+-⨯+-⨯+-⨯=,所以丙的方差最大.故选D .7. 为了得到曲线cos y x =,只需把曲线sin 26y x π⎛⎫=+ ⎪⎝⎭上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移A .35π个单位长度 B .125π个单位长度 C .3π个单位长度 D .6π个单位长度 【命题意图】本小题考查三角函数的图象变换、诱导公式等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想,考查直观想象、数学运算等核心素养,体现基础性、综合性. 【答案】A .【解析】把sin 26y x π⎛⎫=+ ⎪⎝⎭上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线sin 6y x π⎛⎫=+ ⎪⎝⎭向右平移35π个单位长度,得到曲线sin 63y x π5π⎛⎫=+- ⎪⎝⎭,所以sin 2y x 3π⎛⎫=- ⎪⎝⎭,即cos y x =,故选A . 8. 已知平面,,αβγ两两垂直,直线,,a b c 满足:,,a b c αβγ⊂⊂⊂,则直线,,a b c 可能满足以下关系:①两两相交;②两两垂直;③两两平行;④两两异面.其中所有正确结论的编号是 A .①③B .②④C .①②④D .①②③④【命题意图】本小题以空间直线和平面为载体,考查空间直线的位置关系,空间平面与平面垂直等基础知识,考查空间想象能力,考查数学建模、数学抽象、直观想象等核心素养,体现基础性、综合性. 【答案】C .【解析】解法一:对于①②:如图,当=,a c αβαγ=I I ,βγ=I b 时,直线,,a b c 两两垂直且两两相交,所以①②结论正确;对于③:如图,假设a b c ∥∥,m αγ=I ,易证,m b ∥, 因为平面,,αβγ两两垂直,所以m β⊥,因为b β⊂,所以m b ⊥,这与m b ∥相矛盾,所以假设不成立, 所以③结论不正确;对于④:如图,当,,a b c 分别平行于平面α与β,β与γ,α与γ的交线时,,,a b c 两两异面,所以④结论正确;综上,结论正确的是①②④,故选C.αβγabc解法二:构造长方体,即可得结论.9. 已知椭圆()222:109x y C b b+=>的右焦点为F ,以C 上点M 为圆心的圆与x 轴相切于点F ,并与y 轴交于A ,B 两点.若4FA FB ⋅=u u u r u u u r,则C 的焦距为A 2B .2C .2D .4【命题意图】本小题考查椭圆的方程及其椭圆的简单几何性质、平面向量的数量积等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、函数与方程思想,考查数学运算、逻辑推理等核心素养,体现基础性、综合性. 【答案】C .【解析】解法一:设(,0)F c ,则2(,)3b M c ,圆M 的方程为22222()()()33b b xc y -+-=,即22222203b x y cx yc +--+=,令0x =,得222203b y yc -+=,当0∆>时,212y y c =.设1(0,)A y ,2(0,)B y , 则1(,)FA c y =-u u u r ,2(,)FB c y =-u u u r,则221224FA FB c y y c ⋅=+==u u u r u u u r ,所以22c =,解得2c =222c = C.解法二:设(,0)F c ,则2(,)3b Mc .不妨设B 在A 上方,取AB 中点N ,设AN t =,则2242222239b b t AM MN c c ⎛⎫=-=-=- ⎪⎝⎭,220,,0,33b b A t B t ⎛⎫⎛⎫-+ ⎪ ⎪⎝⎭⎝⎭,所以FA FB ⋅=u u u r u u u r 2244422222,,2433999b b b b b c t c t c t c c c ⎛⎫⎛⎫⎛⎫--⋅-+=+-=+--== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2c =以焦距为222c =.故选C .解法三:设(,0)F c ,则2(,)3b Mc .不妨设B 在A 上方,取AB 中点N ,设AN t =,则4222229b AB AM MNc =--FA FB ⋅=u u u r u u u r ()()2214FA FBFA FB ⎡⎤+--=⎢⎥⎣⎦u u u r u u u r u u u r u u u r()22124FN BA ⎡⎤-=⎢⎥⎣⎦u u u r u u u r 4422144499b b c c ⎡⎤⎛⎫⎛⎫+--=⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎣⎦224c =,解得c =2c =.故选C .10. 已知定义在R 上的函数()f x 满足()()4f x f x +=-,函数()2f x +为偶函数,当()0,2x ∈时,()3296+ 2f x x x x a =-+-.若()2,0x ∈-时,()f x 的最大值为12-,则a = A .3 B .2C .12 D .32- 【命题意图】本小题考查函数的奇偶性、对称性,函数的最值等基础知识,考查运算求解能力、推理论证能力,考查数形结合思想、函数与方程思想,考查数学运算、逻辑推理等核心素养,体现基础性、综合性. 【答案】A .【解析】由函数()2f x +是偶函数,得()f x 关于2x =对称,即()()4f x f x +=-,因为()()4f x f x +=-,所以()()f x f x -=-,所以()f x 为奇函数.因为()f x 在()2,0-上最大值为12-,所以()f x 在()0,2上最小值为12.当()0,2x ∈时,()2396f x x x '=-+-,令()0f x '=得1x =,所以()f x 在(0,1)递减,在(1,2)递增,所以当1x =时,()f x 取得极小值,即最小值,所以()()min 512123f x f a a ==-=∴=,.故选A.11. 2019年世界读书日,陈老师给全班同学开了一份书单,推荐同学们阅读,并在2020年世界读书日时交流读书心得.经了解,甲、乙两同学阅读书单中的书本有如下信息:①甲同学还剩②乙同学还剩5本未阅读;的书本甲、乙两同学都没阅读.则甲、乙两同学已阅读的相同的书本有 A .2本B .4本C .6本D .8本【命题意图】本小题考查推理、集合、解方程、解不等式等基础知识,考查运算求解能力、推理论证能力,考查函数与方程思想,考查数学运算、逻辑推理等核心素养,体现基础性、综合性. 【答案】C .【解析】解法一:如图,设甲阅读且乙未阅读的书本有x 本,乙阅读且甲未阅读的书本有y 本,甲和乙都已阅读的相同的书本有z 本,甲和乙都未阅读的相同的书本有w 本,其中,,,w x y z ∈N ,则22,5,3,x z w y w x x y z w +=+⎧⎪+=⎨⎪++=⎩53 0,3, 1, 6.11 5 0,,x y w y y z z y y =-⎧⎪=⎪∴∴==⎨=-⎪⎪∈⎩≥≥N 故选C .解法二:设这份书单共有x 本书,甲和乙已阅读的相同的书本有a 本. 依题意有,534x x x a +-=-,所以11512xa =-. 又因为2,35,x a x a ⎧⎪⎨⎪-⎩……即2115,3121155,12x x x x ⎧-⎪⎪⎨⎪--⎪⎩……解得520x剟,又因为a ∈N ,所以x 是12的倍数,所以12x =,所以1156a =-=.故选C . 解法三:设这份书单共有x 本书,甲和乙已阅读的相同的书本有a 本.的书甲、乙两同学都没阅读,即有的书甲同学或乙同学读过,依题意有,()23534x x x a +--=,所以11512xa =-.又因为2,35,x a x a ⎧⎪⎨⎪-⎩……即2115,3121155,12x x x x ⎧-⎪⎪⎨⎪--⎪⎩……解得520x剟,又因为a ∈N ,所以x 是12的倍数,所以12x =,所以=115=6a -.故选C .解法四:设甲和乙已阅读的相同的书本有t 本,甲已阅读()x t +本书,未阅读m 本书;乙已阅读()y t +的书甲、乙两同学都没阅读,即有的书甲同学或乙同学乙甲wzyx读过,则有2,53,33,4x t m y t m x y t m ⎧⎪+=⎪++=⎨⎪⎪++=⨯⎩所以11504t m =-≥,又22t m x m =-≤,所以11524m m -≤,综上,2020113m ≤≤. 依题意,,,,x y t m 为整数,所以m 为4的倍数,只能为4,从而6t =.故选C . 12. 若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为 A.8:3B.6:1C .3:1D. 2:1【命题意图】本小题考查圆锥的内切球、几何体的体积、基本不等式等基础知识,考查空间想象能力、推理论证能力、运算求解能力、创新意识,考查函数与方程思想、化归与转化思想、考查数学抽象、数学运算、直观想象、数学建模等核心素养,体现综合性、应用性和创新性. 【答案】D .【解析】解法一:如图,设圆锥底面半径为R ,高为h . 由AOF △∽ACE △可得OF AO EC AC =,即221R R h=+, 则()222hR h h =>-, 所以()2211142433232h V R h h h h ⎡⎤=π=π⋅=π⋅-++⎢⎥--⎣⎦,因为20h ->,所以4242h h -+-…,当且仅当422h h -=-,即4h =时取等号, 此时圆锥体积最小,最小值为83π.因为该球的体积为43π,所以该圆锥体积与其内切球体积比为2:1,故选D. 解法二: 如图,设圆锥底面半径为R ,高为h . 由AOF △∽ACE △可得OF AO EC AC =,即221R R h=+, 则()222hR h h =>-,所以2211332h V R h h =π=π⋅-,令2()(2)2h f h h h =>-,则2222(2)(4)()(2)(2)h h h h h f h h h ---'==--,当24h <<时,()0f h '<;当4h >时,()0f h '>; 所以()f h 在(2,4)上单调递减,在(4,)+∞上单调递增,所以()min ()48f h f ==,即4h =时,该圆锥体积最小, 最小值为83π.又其内切球体积为4π3.所以该圆锥体积与其内切球体积比为2:1,故选D.解法三:设,0,4OCE θθπ⎛⎫∠=∈ ⎪⎝⎭,则tan OE EC θ=,所以1tan EC θ=,又tan ECA ∠=tan 2AE EC θ=,所以22tan 21tan AE EC θθ=⋅=-, 所以()22211233tan 1tan V EC AE θθ=π⋅⋅=π⋅-,令()2tan 01t t θ=<<, 因为()2211124t t t t t ⎛⎫-=-+=--+ ⎪⎝⎭,当且仅当12t =时取得最大值14,从而圆锥体积最小,最小值为83π.因为该球的体积为43π,所以该圆锥体积与其内切球体积比为2:1,故选D.第Ⅱ卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效.本卷包括必考题和选考题两部分.第 (13)~(21) 题为必考题,每个试题考生都必须作答.第 (22) 、(23) 题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13. 已知向量()1,2=a ,(),1t =b ,若,a b ,则实数t 的值为 . 【命题意图】本小题以平面向量为载体,考查平面向量的夹角等基础知识,考查运算求解能力,考查函数与方程思想,考查数学运算等核心素养,体现基础性. 【答案】34-.【解析】因为,a b=,解得34t =-.14. 已知双曲线C 过点(,且渐近线方程为2y x =±,则C 的离心率为 .【命题意图】本小题以双曲线为载体,考查双曲线的简单几何性质等基础知识,考查运算求解能力,考查函数与方程思想,考查直观想象、数学运算核心素养,体现基础性.. 【解析】解法一:依题意,C 的焦点在y 轴上,设其方程为()2`22210,0y x a b a b-=>>,它的渐近线方程为a y x b =±,与2y x =±比较得2ab=,设()20a k k =>,则,b k c ==,所以离心率=c e a .解法二:设C 的方程为224=x y λ-()0λ≠,因为C 过点(,则1λ=-,所以C 的方程为2241y x -=,所以11,2a b ==,所以c =,所以离心率c e a ==15. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以拆分为两个素数的和”,如307+2313171119==+=+,30有3种拆分方式;633=+,6只有1种拆分方式.现从大于4且小于16的偶数中随机任取一个,取出的数有不止一种上述拆分方式的概率为 .【命题意图】本小题以数学文化为背景,考查古典概型等基础知识,考查运算求解能力、抽象概括能力、应用意识,考查统计与概率思想、分类与整合思想,考查数学建模、数学运算等核心素养,体现基础性、应用性.【答案】25.【解析】本题为古典概型概率求解问题,可求得大于4且小于16的所有偶数共5个,通过将这5个偶数进行拆分,发现633,835,1257=+=+=+都只有一种拆分;发现10=3+7=5+5,14=3+11=7+7都有两种拆分,故共有2个数有不止一种的拆分方式,因此所求概率为25.16. “熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到k 月份()28k k <<∈N 且<,每个月比上个月增加一条月产量为50吨的生产线投入生产,从+1k 月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加 条熔喷布生产线.(参考数据:81.1 2.14≈,91.1 2.36≈)【命题意图】本小题以实际问题为背景,考查等差数列前n 项和、等比数列前n 项和、解不等式基础知识;考查运算求解能力、应用意识;考查数学抽象、数学建模、数学运算等核心素养;体现综合性和应用性. 【答案】5【解析】依题意得,企业甲从2020年1月到9月的需求量为 99100(1 1.1)1000(1.11)1 1.1⨯-=⨯--1360≈(吨).易知,企业乙增加1条熔喷布生产线,不符合题意;依题意,当企业乙增加()128k k k -<<∈N 且<条熔喷布生产线时,从2020年1月到9月的“熔喷布”产量为()2(1005050)50+1(9)25475+4502k kk k k k +++-=-+,所以225475+4501360990k k -+-≥,即219760k k -+…, 记()21976f k k k =-+,则()f k 在()2,8上为减函数,又因为()()22551957660,661967620f f =-⨯+==-⨯+=-><, 所以k 最小值为6,所以企业乙至少需要增加5条生产线. 三、解答题:解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分12分)ABC △的内角A B C ,,的对边分别为a b c ,,,1a =sin C c A =.(1)求C ;(2)若3b =,D 是AB 上的点,CD 平分ACB ∠,求ACD △的面积.【命题意图】本小题以解三角形为载体,考查正弦定理、三角形面积公式等基础知识,考查运算求解能力,考查函数与方程思想,考查逻辑推理、数学运算等核心素养,体现基础性、综合性.【解析】解法一:(1)因为1a =sin C c A =,cos sin C c A =, ········································································ 1分cos sin sin A C C A =, ············································ 3分 因为()0,A ∈π,所以sin 0A ≠,所以tan C = ······································· 4分 因为()0,C ∈π,所以3C π=. ································································· 5分 (2)由(1)知,3ACB π∠=, 因为1a =,3b =, 所以ABC △的面积13sin sin 223ABC S ab ACB π=∠==△, ··························· 7分 因为D 是AB 上的点,CD 平分ACB ∠, 所以1sin12613sin 26BCDACDa CD S a Sb b CD π⋅⋅===π⋅⋅△△, ······················································· 9分 因为ABC ACD BCD S S S =+△△△, ································································· 10分所以3344ACD ABC S S ===△△. ····················································· 12分 解法二:(1)根据正弦定理,得sin sin a cA C=,及1a =得, 所以sin sin c A C =, ············································································· 2分sin C c A =sin C C =, ········································ 3分所以tan C ················································································· 4分 因为()0,C ∈π,所以3C π=. ································································· 5分 (2)由(1)知,3ACB π∠=, 因为1a =,3b =,所以ABC △的面积13sin sin 223ABC S ab ACB π=∠==△, ··························· 7分 因为D 是AB 上的点,CD 平分ACB ∠,所以ACD △的面积13sin 264ACD S b CD CD π=⋅⋅=△, ····································· 8分所以BCD △的面积11sin 264BCD S a CD CD π=⋅⋅=△, ····································· 9分 因为ABC ACD BCD S S S =+△△△, ································································· 10分所以3144ABC S CD CD CD =+=△,所以CD =·················································································· 11分所以3344ACD S CD ===△. ···················································· 12分 18. (本小题满分12分)为了比较两种治疗失眠症的药(分别称为A 药,B 药)的疗效,某机构随机地选取20 位患者服用A 药,20位患者服用B 药,观察这40位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:h ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;(2)求这40名患者日平均增加睡眠时间的中位数m ,并将日平均增加睡眠时间超过m 和不超过m 的患者人数填入下面的列联表:(3)根据(2)中的列联表,能否有99%的把握认为,A B 两种药的疗效有差异? 附:22()()()()()n ad bc K a b c d a c b d -=++++.数字特征、独立性检验等基础知识,考查数据处理能力、运算求解能力、应用意识,考查统计与概率思想,考查数学抽象、数据分析、数学运算等核心素养,体现基础性与应用性.【解析】(1)(以下理由任说一种都可得4分) ①从以上茎叶图可以看出,A 药疗效的试验结果有45的叶集中在茎2和3上, 而B 药疗效的试验结果有34的叶集中在茎0和1上,由此可看出A 药的疗效更好. ②从茎叶图的分布情况可以看出,服用A 药的患者日平均增加睡眠时间的平均数大于2,而服用药的患者日平均增加睡眠时间的平均数小于2,因此可知A 药的疗效更好.③由茎叶图可知,服用A 药的患者日平均增加睡眠时间的中位数是2.4+2.5=2.45h 2,而服用B 药的患者日平均增加睡眠时间的中位数是1.4+1.5=1.45h 2,因此A 药的疗效更好.④由茎叶图可知,服用A 药的患者日平均增加睡眠时间分布在茎2上的最多,关于茎2 大致呈对称分布;而服用B 药的患者日平均增加睡眠时间分布在茎1上的最多,关于茎1大致呈对称分布;又患者在服用两种药后日平均增加睡眠时间分布的区间相同,故可以认为服用A 药的患者日平均增加睡眠时间比服用B 药的患者日平均增加睡眠时间更多,因此A 药的疗效更好. ··························································· 4分 (2)由茎叶图可知,40组数据的中位数为=2.0m , ···································· 6分因此列联表如下:B·· 8分 (3)由于2240(141565)10808.120 6.63520201921133K ⨯⨯-⨯==≈⨯⨯⨯>, ······················· 11分 所以有99%的把握认为,A B 两种药的疗效有差异. ··································· 12分 19. (本小题满分12分)如图,在多面体PABCD 中,平面ABCD ⊥平面PAD ,AD BC ∥,90BAD ∠=︒,120PAD ∠=︒,1BC =,2AB AD PA ===.(1)求多面体PABCD 的体积;(2)已知E 是棱PB 的中点,在棱CD 是否存在点F 使得EF PD ∥,若存在,请确定点F 的位置;若不存在,请说明理由.【命题意图】本小题以四棱锥为载体,考查线面平行、线面垂直的判定与性质、空间几何体的体积等基础知识,考查空间想象能力、推理论证能力、运算求解能力,考查化归与转化思想,考查直观想象、逻辑推理、数学运算等核心素养,体现基础性、综合性.【解析】解法一:(1)如图,作PH AD ⊥交DA的延长线于H , 因为平面ABCD ⊥平面PAD , 平面ABCD I 平面PAD AD =, 且PH ⊂平面PAD ,所以PH ⊥平面ABCD , ······································································· 2分 所以PH 为点P 到平面ABCD 的距离. ····················································· 3分 因为120PAD ∠=︒,2PA =,所以sin 60PH PA =⋅︒= ··························· 4分 又()132ABCD S BC AD AB =+⋅=四边形, ························································ 5分 所以11333P ABCD ABCD V PH S -=⋅⋅==四边形········································ 6分(2)假设棱CD 上存在点F ,使得EF PD ∥. 连接BD ,取BD 的中点M ,ADCB PABCDPH在△BPD 中,因为,E M 分别为,BP BD 的中点,所以EM PD ∥. ··················································································· 8分 因为过直线外一点有且只有一条直线和已知直线平行, 所以EM 与EF 重合. 因为点F 在线段CD 上, 所以F BD CD =I , 又BD CD D =I ,所以F 是BD 与CD 的交点D ,即EF 就是ED ,而ED 与PD 相交, ············································································· 10分 这与EF PD ∥相矛盾, ······································································ 11分 所以假设不成立,故棱CD 上不存在点F 使得EF PD ∥.···················································· 12分 解法二:(1)因为平面ABCD ⊥平面PAD ,且平面ABCD I 平面PAD AD =,,BA AD BA ⊥⊂平面ABCD ,所以BA ⊥平面PAD , ·········································································· 2分依题意,11sin 2222PAD S AD AP PAD =⋅∠=⨯⨯=△所以11233B PAD PAD V S AB -=⋅==△ ············································· 3分在梯形ABCD 中,由,2AD BC AD BC =∥知2ABD BCD S S =△△, ························ 4分 所以2P ABD P BCD V V --=, ·········································································· 5分所以333222PABCD P ABD P BCD P ABD B PAD V V V V V ----=+==== ··················· 6分 (2)假设棱CD 上存在点F ,使得EF PD ∥, 显然F 与点D 不同,所以,,,P E F D 四点共面,记该平面为α, ················································· 8分 所以P α∈,PE α⊂,FD α⊂, 又B PE ∈,C FD ∈, 所以B α∈,C α∈,所以,,,P B C D 共面于α, ···································································· 10分 ABCPDEF MABCPDEF这与P ABCD -为四棱锥相矛盾, ·························································· 11分 所以假设不成立,故棱CD 上不存在点F 使得EF PD ∥. ····················································· 12分 20. (本小题满分12分)已知抛物线2:4C y x =,直线:2(0)l x my m =+>与C 交于A ,B 两点,M 为AB 的中点,O 为坐标原点.(1)求直线OM 斜率的最大值;(2)若点P 在直线2x =-上,且PAB △为等边三角形,求点P 的坐标.【命题意图】本小题以抛物线为载体考查抛物线方程、直线与抛物线的位置关系等基础知识,考查运算求解能力、直观想象能力,考查函数与方程、数形结合等数学思想,考查直观想象、逻辑推理、数学运算等核心素养,体现基础性、综合性.【解析】解法一:(1)设1122(,),(,)A x y B x y ,由22,4x my y x=+⎧⎨=⎩,消去x 得,2480y my --=, ············································ 1分 216320,m ∆=+>且12124,8y y m y y +==-. ················································ 2分所以21212()44 4.x x m y y m +=++=+ 因为M 为AB 的中点, 所以M 的坐标为1212(,)22x x y y ++,即2(22,2)M m m +, ······························· 3分 又因为0m >,所以2221112212OM m m k m m m m ====+++, ·············· 5分 (当且仅当1m m=,即1m =等号成立.) 所以直线OM 的斜率的最大值为1.2·························································· 6分(2)由(1)知,||AB ==。
2020年福州市高中毕业班第三次质量检测(文数)及答案

准考证号 姓名 .(在此卷上答题无效)2020年福州市高中毕业班第三次质量检测数学(文科)试卷(完卷时间:120分钟;满分:150分)(在此卷上答题无效)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷4至5页. 注意事项:1. 答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 3. 考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{|8},U x x =∈N …集合{1,3,7}A =,则U A =ðA .{2,4,5,6}B .{0,2,4,5,6}C .{2,4,5,6,8}D .{0,2,4,5,6,8}2. 已知纯虚数z 满足(1i)2i z a -=+,则实数a 等于A .2B .1C .1-D .2-3. 曲线()1e x y x =-在1x =处的切线方程为A .e e 0x y --=B .e +e 0x y -=C .e 10x y +-=D .e 10x y --= 4. 执行如图所示的程序框图,则输出的m =A .1B .2C .3D .45. 已知等差数列{}n a 的前n 项和为n S ,且202020202020a S ==,则{}n a 的公差为A .2-B .2C .2019D .2019-6. 甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如下:以下关于这四名同学射击成绩的数字特征判断不正确...的是 A .平均数相同 B .中位数相同C .众数不完全相同D .方差最大的是丁7. 为了得到曲线cos y x =,只需把曲线sin 26y x π⎛⎫=+ ⎪⎝⎭上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 A .35π个单位长度 B .125π个单位长度 C .3π个单位长度 D .6π个单位长度 8. 已知平面,,αβγ两两垂直,直线,,a b c 满足:,,a b c αβγ⊂⊂⊂,则直线,,a b c 可能满足以下关系:①两两相交;②两两垂直;③两两平行;④两两异面.其中所有正确结论的编号是 A .①③ B .②④C .①②④D .①②③④9. 已知椭圆()222:109x y C b b+=>的右焦点为F ,以C 上点M 为圆心的圆与x 轴相切于点F ,并与y 轴交于A ,B 两点.若4FA FB ⋅=u u u r u u u r,则C 的焦距为AB .2C .D .410. 已知定义在R 上的函数()f x 满足()()4f x f x +=-,函数()2f x +为偶函数,当()0,2x ∈时,()f x 3296+ 2x x x a =-+-.若()2,0x ∈-时,()f x 的最大值为12-,则a =A .3B .2C .12D .32-11. 2019年世界读书日,陈老师给全班同学开了一份书单,推荐同学们阅读,并在2020年世界读书日时交流读书心得.经了解,甲、乙两同学阅读书单中的书本有如下信息:①甲同学还剩②乙同学还剩5本未阅读;的书本甲、乙两同学都没阅读.则甲、乙两同学已阅读的相同的书本有 A .2本B .4本C .6本D .8本12. 若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为 A.8:3B.6:1C .3:1D. 2:1第Ⅱ卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 本卷包括必考题和选考题两部分.第 (13)~(21) 题为必考题,每个试题考生都必须作答.第 (22) 、(23) 题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13. 已知向量()1,2=a ,(),1t =b ,若,a b ,则实数t 的值为 .14. 已知双曲线C 过点(,且渐近线方程为2y x =±,则C 的离心率为 . 15. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以拆分为两个素数的和”,如307+2313171119==+=+,30有3种拆分方式;633=+,6只有1种拆分方式.现从大于4且小于16的偶数中随机任取一个,取出的数有不止一种上述拆分方式的概率为 .16. “熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到k 月份()28k k <<∈N 且<,每个月比上个月增加一条月产量为50吨的生产线投入生产,从+1k 月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加 条熔喷布生产线.(参考数据:81.1 2.14≈,91.1 2.36≈)三、解答题:解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分12分)ABC △的内角A B C ,,的对边分别为a b c ,,,1a =sin C c A =.(1)求C ;(2)若3b =,D 是AB 上的点,CD 平分ACB ∠,求ACD △的面积. 18. (本小题满分12分)为了比较两种治疗失眠症的药(分别称为A 药,B 药)的疗效,某机构随机地选取20 位患者服用A 药,20位患者服用B 药,观察这40位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:h ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;(2)求这40名患者日平均增加睡眠时间的中位数m ,并将日平均增加睡眠时间超过m 和不超过m 的患者人数填入下面的列联表:附:22()()()()()n ad bc K a b c d a c b d -=++++.19. (本小题满分12如图,在多面体PABCD 中,平面ABCD ⊥平面PAD ,AD BC ∥,90BAD ∠=︒,120PAD ∠=︒,1BC =,2AB AD PA ===.(1)求多面体PABCD 的体积;(2)已知E 是棱PB 的中点,在棱CD 是否存在点F 使得EF PD ∥,若存在,请确定点F 的位置;若不存在,ACB请说明理由.20. (本小题满分12分)已知抛物线2:4C y x =,直线:2(0)l x my m =+>与C 交于A ,B 两点,M 为AB 的中点,O 为坐标原点.(1)求直线OM 斜率的最大值;(2)若点P 在直线2x =-上,且PAB △为等边三角形,求点P 的坐标.21. (本小题满分12分)已知函数2()2ln f x x ax x =-+. (1)求函数()f x 的单调区间;(2)设函数()f x 有两个极值点()1212,x x x x <,若()12f x mx >恒成立,求实数m 的取值范围.请考生在第(22)、(23)两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22. (本小题满分10分)选修44-:坐标系与参数方程在直角坐标系xOy 中,直线1l 的参数方程为33,x kt y t =-+⎧⎨=⎩(t 为参数),直线2l 的参数方程为33,x m y km =-⎧⎨=⎩(m 为参数).设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线1C .(1)求1C 的普通方程;(2)设Q 为圆()222:43C x y +-=上任意一点,求PQ 的最大值.23. (本小题满分10分)选修45-:不等式选讲已知0,0a b >>,2224a b c ++=. (1)当1c =时,求证:()()339a b a b ++≥;(2)求2224411a b c +++的最小值.2020年福州市高中毕业班第三次质量检测数学(文科)参考答案及评分细则评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
高三数学第三次联考试题 文A 试题

2021届周宁一中、政和一中高三第三次联考创 作人:历恰面 日 期: 2020年1月1日数学〔文〕试卷考试时间是是:120分钟,满分是:150分一、选择题〔本大题一一共12小题,每一小题5分,一共60分.在每个小题给出的四个选项里面,只有一项是哪一项符合题目要求〕1. 复数2)1(1i +等于( ) A21 B -21 C 、21i D -21i 2.设集合{}{}|(3)(2)0,,|13,M x x x x R N x x x R =+-<∈=≤≤∈,那么M N =( )A.[)1,2B.[1,2]C.(]2,3D.[2,3]3.将图所示的一个直角三角形ABC 〔∠C =90°〕绕斜边AB 旋转一周,所得到的几何体的正视图是下面四个图形中的 〔 〕a b 、都是非零向量,“||||a b a b ⋅=⋅〞是“//a b 〞的( )A .充分非必要条件.B .必要非充分条件.C .充要条件.D .既非充分也非必要条件.5.以下结论错误的选项是〔 〕A 、命题“假设p ,那么q 〞与命题“假设¬q,那么¬p〞互为逆否命题B 、命题p :1],1,0[≥∈∀xex ,命题q :01,2<++∈∃x x R x ,那么p ∨q 为真C 、假设am 2<bm 2,那么a <b 〞的逆命题为真命题 D 、假设p ∨q 为假命题,那么p 、q 均为假命题6.假设方程1312xx ⎛⎫= ⎪⎝⎭有实数解0x ,那么0x 属于 ( )A .10,3⎛⎫ ⎪⎝⎭B .11,32⎛⎫⎪⎝⎭C .1,12⎛⎫⎪⎝⎭D .()1,27.等差数列{}n a 中,652,30,a S ==那么8S = ( ) A.31 B.32 C8.1sin(),43πθ+=那么sin 2θ= ( ) A.19 B.19- C.79 D.79-9.将函数sin 2y x =的图象向右平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( )A .22sin y x = B .22cos y x = C .)42sin(1π++=x y D .cos 2y x =10.假设函数()f x 的导函数为34)(2+-='x x x f ,那么函数)1(-x f 的单调递减区间是〔 〕.A 〔2,4〕 .B 〔2,3〕 .C 〔0,1〕 .D 〔0,2〕11.l 、m 是不同的两条直线,α、β是不重合的两个平面,那么以下命题中正确的选项是〔 〕.A 假设l ∥α,α⊥β,那么l ∥β.B 假设l ⊥α,α∥β,m ⊂β,那么l⊥m.C 假设l ⊥m ,α∥β,m ⊂β,那么l ⊥α.D 假设l ⊥α,α⊥β,那么l ∥β12.△ABC 的外接圆的圆心为O ,半径为1,假设0OA AB OC ++=,且||||OA AB =,那么CA CB ⋅=〔 〕.A32.B .C 3 .D 二、填空题〔大题一共4小题,每一小题4分,一共16分.请将答案填在答题卷相应的横线上〕13. 假设点(m ,n)在第一象限,且在直线2x+3y=1上,那么nm 32+的最小值为 14.设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩假设()4f x >,那么x 的取值范围是 .15.在平面内,三角形的面积为S ,周长为C ,那么它的内切圆的半径CSr 2=.在空间中,三棱锥的体积为V ,外表积为S ,利用类比推理的方法,可得三棱锥的内切球〔球面与三棱锥的各个面均相切〕的半径R =___________。
2020届福建省政和第一中学政和一中高三英语第三次联考试题及答案

2020届福建省政和第一中学政和一中高三英语第三次联考试题及答案第一部分阅读(共两节,满分40分)第一节(共15小题;每小题2分,满分30分)阅读下列短文,从每题所给的A、B、C、D四个选项中选出最佳选项AA 21-year-old female student has become the youngest womanever to be elected as Mayor (市长) after first entering politics to campaign about food.Labor Party (工党) member Rosie Corrigan was elected as Mayor of Selby a market town in North Yorkshire, on Monday. The student’s election was unchallenged to the mayoralty, following a year serving as deputy mayor. Corrigan has just finished her second year studying politics at theUniversityofHull. A political activist since secondary school, lifelong Selby citizen Corrigan has always been ambitious. As a member of the UK Youth Parliament, she co-founded the Selby Youth council, and then went on to run for and win the local council election as a Labour candidate (候选人) aged just 18.Corrigan plan to use her year in office to further encourage political awareness in the youth of Selby. By breaking a political record of being the youngest woman ever elected inUKhistory, Corrigan hopes this will break the misunderstanding of Selby being a sleepy town with old-fashioned views. “It’s an honor to be the Mayor of my lovely hometown,” Corrigan told a newspaper. “I plan on using the year to encourage children and young people to champion their communities.”The politics student’s election has been supported whole heartedly by the politicians she has worked with throughout her early-developing career, including thebackingof former deputy Prime Minister (副首相) John Prescott. Simon Darvill said in an interview, “I hope that the success of Rosie and others like her encourages more young people to get involved in politics and change where they live for the better.”1. Which statement is true according to Paragraph 2?A. Corrigan is new to the political scene of Selby.B. Corrigan became interested in politics in childhood.C. Corrigan has been living in Selby since she was born.D. Corrigan founded the Selby Youth council by herself.2. What can we infer from Paragraph 3?A. Corrigan plans to further her time in office by at least a year.B. The people of Selby are passive and have out-of-date views.C. Corrigan is the youngest person ever elected inUKhistory.D. Corrigan intends to increase Selby’s youth’spolitical involvement.3. Which of the following can replace the underlined word “backing” in Paragraph 4?A. ApprovalB. AppreciationC. PraiseD. SupportBThe secrets of dreaming are always interesting psychologists. It is generally acknowledged in the field that dreams people have during this time betweenchildhood and full adulthood, that’s around 30, are the strongest and most influential. Yet not enough is known about the repeated patterns of dreaming. Researchers are still trying to answer a basic question: How does dreaming relate to the life experiences and developmental challenges?G. William Domhoff and Adam Schneider, at theUniversityofCalifornia, help to answer this question by examining the lengthy dream series of two individuals, “Izzy” and “Jasmine”. Izzy provided a collection of 4, 329 dream reports from between the ages of 12 and 25, while Jasmine provided 664 dreams recorded between the ages of 14 and 25.Large collections of dreams like these pose challenges to researchers. Until recently, the means of studying dream series was to employ a team of recorders who take the time to code each dream for a predetermined(预先确定的)number of content categories, and then compare their results. Nowadays, digital technologies enable the analysis of language usage in dreams with high speed, accuracy, and objectivity. This marks a revolutionary advance in the science of dreaming. However,itcan only lead so far.To gain more specific and detailed insights, Domhoff and Schneider tailored word strings(词串)for each dreamer, mixing elements of traditional research with digital tools for analyzing large data sets. For Izzy these word strings included “family and s”, “celebrities” and “fantasy”, while the word strings they created for Jasmine included “familiar places,” electrical equipment” and “music”. The researchers used these word strings to identify connections between their dreams and real lives. Surprisingly, the results of the analysis revealed a great deal of consistency(一致性)and continuity in both sets of dreams. Izzy pays much attention to pop culture, and has affection for famous actors. Jasmine is an accomplished musician and performer.“The frequencies of dream elements show the intensity(强度)of the dreamer’s personal concern with that element in waking thought,” Domhoff and Schneider conclude. For anyone who still claims dreaming is merely random nonsense from the brain and mental world, these findings are hard to explain away.4. What do psychologists agree with about dreams?A. Dreams are influenced by life experiences.B. Dreaming is never nonsense from the brain.C. Dreams in one’s teens and twenties are strongest.D The patterns of dreaming are usually repeated.5. What does “it” underlined in paragraph 3 refer to?A. The collection of dreams.B. Research into dreaming.C. The digital method.D. The challenge for psychologists.6. How do the researchers conduct their study?A. By analyzing large data sets.B. By developing individualized word strings.C. By identifying the patterns of dreaming.D. By making comparison with traditional research.7. Which can be the best title for the text?A. New tech, new findingB. Dreams: reflections of waking realityC. Lives, languages, dreamsD. Life experiences: elements of mental worldCContrary to the long-held belief that plants in the natural world are always in competition, new research has found that in severe environments adult plants help smaller ones and grow well as a result.The research, led by Dr Rocio, studied adult and seedling (幼苗)plants in the ecological desert in the south-east of Spain. Dr Rocio said, “If you're a seedling in a poor land — the top of a mountain or a sand hill, for example-and you’re lucky enough to end up underneath a big plant, your chances of survival are certainly better than if you landed somewhere on your own. What we have found, which was surprising, is an established large plant, called a ‘nurse’, protects a seedling; it also produces more flowers than the same plants of similar large size growing on their own.”Other benefits of nurse-seedling partnerships include that more variety of plants growing together can have apositive effect on the environment. For example, vegetation areas with nurse plants with more flowers might be able to attract higher numbers of pollinators(传粉者)in an area, in turn supporting insect and soil life and even provide a greater range of different fruit types for birds and other animals.“The biggest winner for this system of nursing a plant is biodiversity(生物多样性),” Dr Rocio said. “The more biodiversean area, the greater number of species of plants, insect life, mammals and birds, and the better the chances of long-term healthy functioning of the environment and ecosystems. ” This system is win-win for adult and seedling plants in unfavorable environments.The research is of value to those who manage and protect plants in tough environments. Most home gardeners and farmers plan to ensure their soil and conditions are the best they can be for plant growth, but the findings might be of value to those who garden in bare places.8. What is a common understanding of plants?A. They can help each other.B. They can survive ill conditions.C. They compete with each other.D. They grow well on their own.9. What will happen to seedling plants if they grow under adult plants?A. They will produce more flowers.B. They will die owing to competition.C. They will make adult plants larger.D. They will get support from adult plants.10. What is the effect of the nurse-seedling partnership?A. It leads to unfavorable environments.B. It produces long-term healthy chances.C. It attracts higher and larger pollinators.D It provides a more variety of plant types.11. Who will benefit from the new research?A. People studying organic farming.B. People protecting plants on sand hills.C. People wanting to change biodiversity.D. People keeping more animals on the farm.DResearchers say spicy tomatoes could soon be on the menu thanks to the rise of gene-editing technology.It's not the first time that experts have claimed techniques could develop fruit with unusual features: scientists have already been looking at changing the color1 of kiwi fruit and bettering the taste of strawberries.But researchers inBrazilandIrelandsay such methods could also offer practical advantages, with hot tomatoes offering a new way of harvesting the pungent chemicals found in peppers known as capsaicinoids, which make food taste “hot”.“Capsaicinoids are valuable. They are used as painkillers and there are some researches showing that they promote weight loss,” said Agustin Zsogon from a Brazilian university, a co-author of a new article arguing for the benefits of engineering hot tomatoes.Writing in the journal Trends in Plant Science, the researchers say peppers are difficult crops to grow and low productive. Worse still, it is tricky to keep the pungency of the fruits table. By contrast, tomato production is high and the plant is well-studied. “You could produce the capsaicinoids in a more cost-effective manner,” said Zsogon.Tomatoes and peppers developed from a common ancestor, but separated about 19 million years ago. “All these genes to produce capsaicinoids exist in the tomato, they are just not active,” said Zsogon. “Using gene-editing technology, it is likely to switch these genes back on in tomatoes, making the fruit more special”, he said.12. Why are the tomatoes made hot by the researchers?A. To test the gene-editing technologyB. To improve the amount of the tomatoesC. To explore ways to harvest more capsaicinoids.D. To make the tomatoes more delicious.13. For what purpose can capsaicinoids be used according to the text?A. To put on weight.B. To ease the pain.C. To improve sleep.D. To better the look.14. What is Zsogon's attitude to the gene-editing technology?A. Confident.B. Critical.C. Anxious.D. Doubtful.15. What's the main idea of the text?A. An introduction to gene-editing plants.B. Creating hot tomatoes by gene-editing.C. Problems with capsaicinoid production.D. The procedure of producing capsaicinoids.第二节(共5小题;每小题2分,满分10分)阅读下面短文,从短文后的选项中选出可以填入空白处的最佳选项。
2020届高三第三次模拟考试卷 文科数学(一) 解析版

2020届高三第三次模拟考试卷文 科 数 学(一)注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中, 只有一项是符合题目要求的.1.设3i1iz +=-,则||z =( )A .3B .5C .3D .2答案:B 解:|3i |10||5|1i |2z +===-. 2.设集合{1,2,3,4,5}A =,{|3}B x x =≤,则()A B =R I ð( ) A .{4,5} B .{3,4,5} C .{1,2} D .{1,2,3}答案:A解:{|3}B x x =>R ð,(){4,5}A B =R I ð.3.已知22log 5log 5x =-,5log 3y =,125z -=,则下列关系正确的是( ) A .z y x << B .z x y << C .x y z << D .y z x <<答案:A解:∵222log 5log 5log 51x =-=>,5log 31y =<,1211525z -==<, 因为551log 3log 52>=,即y z >,∴z y x <<.4.定义:10000100010010abcde a b c d e =++++,当五位数abcde 满足a b c <<,且c d e >>时,称这个五位数为“凸数”.由1,2,3,4,5组成的没有重复数字的五位数共120个,从中任意抽取一个,则其恰好为“凸数”的概率为( ) A .16B .110C .112D .120答案:D解:由题意,由1,2,3,4,5组成的没有重复数字的五位数恰好为“凸数”的有:12543,13542,14532,23541,24531,34521,共6个基本事件,所以恰好为“凸数”的概率为6112020P ==. 5.函数||2()2x f x x =-的图象大致是( )A .B .C .D .答案:D解:由||2()2x f x x =-为偶函数可排除A ,C ;当01x <<时,2xy =图象高于2y x =图象,即||220x x ->,排除B ,故选D .6.将参加体检的36名学生,编号为1,2,3,…,36,若采用系统抽样的方法抽取一个容量为9的样本,已知样本中含有编号为33的学生,则下面十名学生编号中被抽到的是( ) A .13 B .14 C .23 D .24答案:A解:从36名学生中抽取9名,抽样间隔为4,所以9名学生的编号分别为33,29,25,21,17,13,9,5,1. 7.若cos57m ︒=,则cos213︒=( )A .21m--B .2211m m--+ C .21m --D .m -答案:C解:2cos213cos(18033)cos33sin571m ︒=︒+︒=-︒=-︒=--.8.若向量(2,3)=m ,(1,)λ=-n ,且(23)⊥-m m n ,则实数λ的值为( ) A .329-B .329C .32D .32-此卷只装订不密封班级 姓名 准考证号 考场号 座位号答案:B解:由题意得,23(7,63)λ-=-m n ,∵(23)⊥-m m n ,∴(23)0⋅-=m m n ,即141890λ+-=,解得329λ=. 9.执行下面的程序框图,如果输出的S 为1112,则判断框中填写的内容可以是( )A .5n <B .5n ≤C .6n <D .6n ≤答案:D解:运行程序,0,2S n ==,判断是,1,42S n ==,判断是,11,624S n =+=,判断是,11111,824612S n =++==,判断否,输出1112S =,故答案为D .10.已知双曲线2222:1(0,0)x yC a b a b-=>>的焦点(2,0)F 3,则该双曲线的离心率为( ) A .1 B 3 C .2 D .23答案:C解:由题意知双曲线的焦点(2,0)到渐近线的距离为3b =2224c a b =+=,所以1a =,该双曲线的离心率为2ca=.11.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos cos 3cos a B b A c C +=,sin sin sin 0a A c C b A -+=,则ba=( ) A .53B .73 C .72D .52答案:A解:在ABC △中,由正弦定理及cos cos 3cos a B b A c C +=,得sin cos cos sin 3sin cos A B A B C C +=,∴sin()sin 3sin cos A B C C C +==, 又sin 0C ≠,∴1cos 3C =, 由正弦定理及sin sin sin 0a A c C b A -+=,得22a c ab -=-,∴由余弦定理得22221cos 223a b c b ab C ab ab +--===,即213b a -=,∴53b a =. 12.抛物线2:(0)C y ax a =>的焦点F 是双曲线22221y x -=的一个焦点,过F 且倾斜角为60°的直线l 交C 于A 、B ,则||AB =( )A 432 B .432C .163D .16答案:D解:双曲线2211122y x -=,∴焦点(0,1)±,∴(0,1)F ,114a =,∴14a =,直线:31l y x =+,由2431x y y x ìï=ïíï=+ïî,得21410y y -+=,1214y y +=,1212||||||(1)(1)216AB AF BF y y y y =+=+++=++=.第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.13.已知曲线()(1)ln f x ax x =-在点(1,0)处的切线方程为1y x =-,则实数a 的值为 .答案:2解:1()ln +ax f x a x x-'=,(1)11f a '=-=,∴2a =. 14.已知正项等比数列{}n a 的前n 项和为n S ,若22S =,410S =,则5a = . 答案:323解:因为410S =,22S =,所以414(1)101a q S q -==-,212(1)2(1)1a q S q q-==≠-,, 两式相除可得215q +=,24q =,2q =±,由题设知2q =-舍,故123a =,1212233n n n a -=⋅=⋅,5323a =. 15.函数2()cos sin f x x x =-的最大值为 .答案:5 4解:221()1sin sin5(sin)24f x x x x=-+-+=-,∵sin[1,1]x∈-,∴()f x的最大值为54.16.已知正方体1111ABCD A B C D-的棱长为4,E为棱1CC的中点,点M在正方形11BCC B内运动,且直线AM∥平面1A DE,则动点M的轨迹长度为.答案:22解:设平面1DA E与直线11B C交于点F,连接EF,则F为11B C的中点.分别取1B B、BC的中点N、O,连接AN、ON、AO,则∵1A F AO∥,AN DE∥,1A F,DE⊂平面1A DE,AO,AN⊂平面ANO,∴1A F∥平面ANO.同理可得DE∥平面ANO,∵1A F、DE是平面1A DE内相交直线,∴平面1A DE∥平面ANO,所以NO∥平面1A DE,∴M的轨迹被正方形11BCC B截得的线段是线段NO,∴M的轨迹被正方形11BCC B截得的线段长22NO=.三、解答题:本大题共6个大题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(12分)某高中为了了解高三学生每天自主参加体育锻炼的情况,随机抽取了100名学生进行调查,其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图:将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生,已知体育健康A类学生中有10名女生.(1)根据已知条件完成下面22⨯列联表,并据此资料你是否有%95的把握认为达到体育健康A类学生与性别有关?非体育健康A类学生体育健康A类学生合计男生女生合计(2)将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康A+类学生,已知体育健康A+类学生中有2名女生,若从体育健康A+类学生中任意选取2人,求至少有1名女生的概率.附:22()()()()()n ad bcKa cb dcd a b-=++++答案:(1)列联表见解析,没有95%的把握认为;(2)710.解:(1)右频率分布直方图可知,在抽取的100人中,体育健康A类学生有25人,从而22⨯列联表如下:非体育健康A类学生体育健康A类学生合计男生301545女生451055合计7525100由22⨯列联表中数据代入公式计算,得:时间/mint222()100(30104515)1003.030 3.841()()()()7525455533n ad bc K a c b d c d a b -⨯⨯-⨯====<++++⨯⨯⨯,所以没有%95的把握认为达到体育健康A 类学生与性别有关.(2)由频率分布直方图可知,体育健康A +类学生为5人,记123,,a a a 表示男生,12,b b 表示女生,从而一切可能结果所组成的基本事件空间为12132311{(,),(,),(,),(,)a a a a a a a b Ω=12212231,(,),(,),(,),(,),a b a b a b a b 3212(,),(,)}a b b b .Ω由10个基本事件组成,而且这些事件的出现是等可能的.用B 表示“任选2人中至少有1名是女生”这一事件,则11122122313212{(,),(,),(,),(,),(,),(,),(,)}B a b a b a b a b a b a b b b =共计7种,∴7()10P B =.18.(12分)已知等差数列{}n a 的首项为1a ,公差为()1,d a d ∈∈Z Z ,前n 项的和为n S ,且749S =,524S 26<<.(1)求数列{}n a 的通项公式;(2)设数列11{}n n a a +⋅的前n 项和为n T ,求n T . 答案:(1)21n a n =-;(2)11(1)221n T n =-+. 解:(1)由题意可得11176749254245262,a d a d a d ⨯⎧+=⎪⎪⨯⎪<+<⎨⎪∈∈⎪⎪⎩Z Z ,解得112a d =⎧⎨=⎩,∴1(1)21n a a n d n =+-=-.(2)∴111111()(21)(21)22121n n a a n n n n +==-⋅-+-+,∴11111111[(1)()()](1)23352121221n T n n n =-+-++-=--++L . 19.(12分)如图1,在直角梯形ABCD 中,AB CD ∥,AB AD ⊥,且112AB AD CD ===,现以AD 为一边向梯形外作正方形ADEF ,然后沿边AD 将正方形ADEF 翻折,使平面ADEF 与平面ABCD 垂直,如图2.(1)求证:BC ⊥平面DBE ; (2)求点D 到平面BEC 的距离. 答案:(1)证明见解析;(2)63. 解:(1)在正方形ADEF 中,ED AD ⊥, 又因为平面ADEF⊥平面ABCD ,且平面ADEF I平面ABCD AD =,所以ED ⊥平面ABCD ,可得ED BC ⊥,在直角梯形ABCD 中,1AB AD ==,2CD =,可得2BC =在BCD △中,2BD BC ==2CD =,所以222BD BC CD +=,所以BC BD ⊥,ED BD D =I ,所以BC ⊥平面DBE . (2)因为BC ⊂平面BCE ,所以平面BDE ⊥平面BEC , 过点D 作EB 的垂线交EB 于点G ,则DG ⊥平面BEC , 所以点D 到平面BEC 的距离等于线段DG 的长度. 在直角三角形BDE 中,1122BDE S BD DE BE DG =⋅=⋅△, 所以263BD DE DG BE ⋅===,所以点D 到平面BEC 的距离等于63. 20.(12分)已知函数()1xf x ae x =-+.(1)若()f x 在(0,3)上只有一个零点,求a 的取值范围; (2)设0x 为()f x 的极小值点,证明:02123()4f x a a >-++. 答案:(1)3221(1,]{}e e -U ;(2)证明见解析. 解:(1)因为()f x 在(0,3)上只有一个零点,所以方程1x x a e-=在(0,3)上只有一个解, 设函数1()x x h x e -=,则2()xxh x e-'=, 当02x <<时,()0h x '>;当23x <<时,()0h x '<,所以max 21()(2)h x h e ==, 又(0)1h =-,32(3)h e =,故a 的取值范围为3221(1,]{}e e-U .(2)证明:()1xf x ae '=-,当0a ≤时,()0f x '<恒成立,()f x 无极值,故0a >, 令()10xf x ae '=-=,得ln x a =-,当ln x a <-时,()0f x '<;当ln x a >-时,()0f x '>, 故()f x 的极小值为(ln )2ln f a a -=+,故要证02123()4f x a a >-++,只需证:2125ln 04a a a +-+>, 设函数1()ln 1g x x x =+-,21()(0)x g x x x-'=>,当01x <<时,()0g x '<;当1x >时,()0g x '>,故min ()(1)0g x g ==,而2213913()042a a a -+=-≥, 于是221251139ln ln 1044a a a a a a a +-+=+-+-+>,从而02123()4f x a a >-++.21.(12分)已知动点P 到点1(,0)2的距离比到直线1x =-的距离小12,设点P 的轨迹为曲线C .(1)求曲线C 的方程;(2)过曲线C 上一点00(2,)(0)M y y >作两条直线1l ,2l 与曲线C 分别交于不同的两点A ,B ,若直线1l ,2l 的斜率分别为1k ,2k ,且121k k =,证明:直线AB 过定点.答案:(1)22y x =;(2)证明见解析.解:(1)由题意可知,动点P 到点1(,0)2的距离与到直线12x =-的距离相等, 所以点F 的轨迹是以1(,0)2为焦点,直线12x =-为准线的抛物线, 所以曲线C 的方程为22y x =.(2)易知(2,2)M ,设点11(,)A x y ,22(,)B x y ,直线AB 的方程为x my b =+,联立22x my b y x =+⎧⎨=⎩,得2220y my b --=,所以121222y y m y y b +=⎧⎨=-⎩,所以21221222x x m b x x b⎧+=+⎪⎨=⎪⎩, 因为12121222122y y k k x x --=⋅=--,即121212122()2()y y y y x x x x -+=-+, 所以222440b b m m --+=,所以22(1)(21)b m -=-,所以2b m =或22b m =-+,当22b m =-+时,直线AB 的方程为22x my m =-+过定点(2,2)与M 重合,舍去; 当2b m =时,直线AB 的方程为2x my m =+过定点(0,2)-, 所以直线AB 过定点(0,2)-.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(10分)【选修4-4:坐标系与参数方程】 已知斜率为1的直线l 经过点(1,1)P . (1)写出直线l 的参数方程;(2)设直线l 与圆224x y +=相交于A ,B 两点,求22PA PB-的值.答案:(1)1:12x l y ⎧=+⎪⎪⎨⎪=+⎪⎩()t 为参数;(2) 解:(1)直线l 的参数方程为π1cos 4π1sin4x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩()t 为参数,即112x y ⎧=+⎪⎪⎨⎪=+⎪⎩()t 为参数. (2)将112x y ⎧=⎪⎪⎨⎪=+⎪⎩代入224x y +=,化简整理得220t +-=, 因为||||||4PA PB AB +==,12||||||||PA PB t t -=+=所以22||||||PA PB -= 23.(10分)【选修4-5:不等式选讲】 已知()2121f x x x =++-.(1)解不等式()(1)f x f >;(2)若不等式11()f x m n ≥+(0m >,0n >)对任意的x ∈R 都成立,证明:43m n +≥. 答案:(1)3(,)(1,)2-∞-+∞U ;(2)证明见解析. 解:(1)()(1)f x f >,即21215x x ++->. ①当12x >时,2(1)(21)5x x ++->,得1x >; ②当112x -≤≤时,2(1)(21)5x x +-->,得35>,不成立; ③当1x <-时,2(1)(21)5x x -+-->,得32x <-, 综上,所求的x 的取值范围是3(,)(1,)2-∞-+∞U .(2)因为21212221(22)(21)3x x x x x x ++-=++-≥+--=,所以113m n+≤. 因为0m >,0n >时,11m n +≥3≤23≥,所以43m n +≥≥,当且仅当32==n m 时等号成立.。
福建省福州市2020届高三毕业班第三次质量检查数学(文科)试题(wd无答案)

福建省福州市2020届高三毕业班第三次质量检查数学(文科)试题一、单选题(★) 1. 设全集集合则()A.B.C.D.(★★) 2. 已知纯虚数满足,则实数等于()A.B.C.D.(★★) 3. 曲线在处的切线方程为()A.B.C.D.(★★) 4. 执行如图所示的程序框图,则输出的()A.1B.2C.3D.4(★★) 5. 已知等差数列的前项和为,且,则的公差为()A.B.C.D.(★★) 6. 甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如下:以下关于四名同学射击成绩的数字特征判断不正确的是()A.平均数相同B.中位数相同C.众数不完全相同D.丁的方差最大(★★) 7. 为了得到曲线,只需把曲线上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移()A.个单位长度B.个单位长度C.个单位长度D.个单位长度(★★) 8. 已知平面两两垂直,直线满足:,则直线可能满足以下关系:①两两相交;②两两垂直;③两两平行;④两两异面.其中所有正确结论的编号是()A.①③B.②④C.①②④D.①②③④(★★★) 9. 已知椭圆的右焦点为,以上点为圆心的圆与轴相切于点,并与轴交于,两点.若,则的焦距为()A.B.C.D.(★★★) 10. 已知定义在上的函数满足,函数为偶函数,当时,.若时,的最大值为,则()A.B.C.D.(★★★) 11. 2019年世界读书日,陈老师给全班同学开了一份书单,推荐同学们阅读,并在2020年世界读书日时交流读书心得.经了解,甲、乙两同学阅读书单中的书本有如下信息:①甲同学还剩的书本未阅读;②乙同学还剩5本未阅读;③有的书本甲、乙两同学都没阅读.则甲、乙两同学已阅读的相同的书本有()A.2本B.4本C.6本D.8本(★★★) 12. 若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为()A.B.C.D.二、填空题(★★) 13. 已知向量, ,若, 夹角的余弦值为,则实数的值为____.(★★) 14. 已知双曲线过点,且渐近线方程为,则的离心率为 ____ .(★★) 15. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以拆分为两个素数的和”,如,30有3种拆分方式;,6只有1种拆分方式.现从大于4且小于16的偶数中随机任取一个,取出的数有不止一种上述拆分方式的概率为____.(★★)16. “熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到月份(且),每个月比上个月增加一条月产量为50吨的生产线投入生产,从月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.(参考数据:,)三、解答题(★★) 17. 的内角的对边分别为,且.(1)求;(2)若,是上的点,平分,求的面积.(★★★) 18. 为了比较两种治疗失眠症的药(分别称为药,药)的疗效,某机构随机地选取位患者服用药,位患者服用药,观察这位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;(2)求这名患者日平均增加睡眠时间的中位数,并将日平均增加睡眠时间超过和不超过的患者人数填入下面的列联表:超过不超过服用药服用药(3)根据(2)中的列联表,能否有的把握认为两种药的疗效有差异?附:.0.010.0050.0016.6357.87910.828(★★★)19. 如图,在多面体中,平面平面,∥ ,,,,.(1)求多面体的体积;(2)已知是棱的中点,在棱是否存在点使得∥ ,若存在,请确定点的位置;若不存在,请说明理由.(★★★) 20. 已知抛物线,直线()与交于两点,为的中点,为坐标原点.(1)求直线斜率的最大值;(2)若点在直线上,且为等边三角形,求点的坐标.(★★★★) 21. 已知函数.(1)求函数的单调区间;(2)设函数有两个极值点(),若恒成立,求实数的取值范围.(★★★) 22. 在直角坐标系中,直线的参数方程为(为参数),直线的参数方程为(为参数).设与的交点为,当变化时,的轨迹为曲线.(1)求的普通方程;(2)设为圆上任意一点,求的最大值.(★★★) 23. 已知,.(1)当时,求证:;(2)求的最小值.。
2020届高中毕业班第三次教学质量检测文科数学试卷

高中毕业班第三次教学质量检测文科数学试题本试卷共 6 页。
满分 150 分。
考生注意:1. 答题前, 考生务必将自己的准考证号、 姓名填写在答题卡上。
考生要认真核对答题卡上粘贴的条形码的 “准考证号、 姓名、 考试科目” 与考生本人准考证号、 姓名是否一致.2. 第I 卷每小题选出答案后, 用 2B 铅笔把答题卡上对应题目的答案标号涂黑, 如需改动, 用橡皮擦干净后, 再选涂其他答案标号. 第II 卷用0. 5 毫米的黑色墨水签字笔在答题卡上书写作答. 若在试题卷上作答, 答案无效.3. 考试结束, 考生必须将试题卷和答题卡一并交回.一、 选择题: 本大题共 12 小题, 每小题 5 分, 共 60 分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
1.已知集合M ={}2230x x x --< , 集合N 是自然数集,则M N =IA. {}1,2B. {}0,1,2C. {}13x x -<<D. {}03x x ≤<2 若复数z 的模为1, 则z 不可能是A. iB. 1-iC. 11i i -+D. (1)(1)2i i -+ 3 下图是从 2020 年 2 月 14 日至 2020 年 4 月 19 日共 66 天的新冠肺炎中国 / 海外新增确诊趋势图,根据该图,下列结论中错误的是A.从 2020 年 2 月 14 日起中国已经基本控制住国内的新冠肺炎疫情B. 从 2020 年 3 月 13 日至 2020 年 4 月 3 日海外新冠肺炎疫情快速恶化C.这 66 天海外每天新增新冠肺炎确诊病例数的中位数在区间(40000,80000) 内D.海外新增新冠肺炎确诊病例数最多的一天突破 10 万例4.已知变量x,y 满足约束条件1x yxy+≥⎧⎪≤⎨⎪≤⎩,则目标函数z=2x+y的最大值为A.0B.1C.2D. 35.已知1,,3 AB a AC b BN BC ===uu u r r u u u r r u u u r u u u r,则AN=u u u rA.1122a b+r rB .2233a b+r rC.2133a b+r rD.1233a b+r r6.若方程221204x ya a+=+-表示椭圆,则实数a的取值范围是A. (-20,4)B. (-20,-8) (8,4)-UC. (,20)(4,)-∞-+∞U D. (,20)(8,)-∞--+∞U7. 函数1()()sinf x x xx=-在[,0)(0,]ππ-U的图象大致为8.已知数列{}n a满足2112,,1,2n n na a a n N a a*++=-∈==,则a2020 =A. -2B. -1C. 1D. 29.若0.330.220.220.330.22,0.33,loga b c===则A. a> b > cB. b> a>cC. c> a> bD. c > b >a10 若奇函数()g x的图象是由函数()sin cosf x a x x=+的图象向右平移6π个单位得到的.则()f x的一个单调递增区间是A.2[,]33ππ- B.4[,]33ππC.5[,]66ππ- D.7[,]66ππ11. 中国是茶的故乡,也是茶文化的发源地 中国茶的发现和利用已有四千七百多年的历史, 且长盛不衰, 传遍全球 为了弘扬中国茶文化, 某酒店推出特色茶食品“金萱排骨茶”, 为了解每壶“金萱排骨茶” 中所放茶叶量x 克与食客的满意率y 的关系, 通过试验调查研究,发现可选择函数模型bx c y ae +=来拟合y 与 x 的关系, 根据以下数据:可求得y关于x 的回归方程为 A. 0.043 4.2911100x y e += B. 0.043 4.2911100x y e -= C. 0.043 4.291x y e += D. 0.043 4.291x y e -=12.在直四棱柱ABCD -A 1B 1C 1D 1中, 底ABCD 是边长为6 的正方形,点E 在线段AD 上.且满足AE =2ED . 过点E 作直四棱柱ABCD -A 1B 1C 1D 1外接球的截面.所得的截面面积的最大值与最小值之差为 19π. 则直四棱柱ABCD -A 1B 1C 1D 1外接球的半径为A. 3B. 23C. 33D. 3二、 填空题: 本大题共 4 小题.每小题 5 分.共 20 分.13.已知函数,则曲线()y f x =在点(1,(1))P f 处的切线方程为____________.14.设 △ABC 内角A 、B 、C 所对应的边分别为a 、b 、c 。
福建省政和一中、周宁一中高三数学上学期10月联考试题 理

福建省政和一中、周宁一中2018届高三数学上学期10月联考试题 理一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}(){}20,lg 21A x x x B x y x =-≥==-,则AB =( )A.1[0,)2B.[]0,1C.1(,1]2D.1(,)2+∞2. 已知i 为虚数单位,复数z 的共轭复数为z ,且满足2z+z = 3-2i ,则z=( ) A .l-2i B .l+2i C .2-i D .2+i3. 已知,a R ∈则“01aa ≤-”是“指数函数x y a =在(,)-∞+∞上为减函数”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 4.已知lg a ,lgb 是方程22410x x -+=的两个根,则2(lg )a b的值是( ) A .4 B .3 C .2 D .15.若函数y x mx m =-+22在区间()2,+∞上为增函数,则实数m 的取值范围是( ) A.2m ≥ B.1m ≥ C.1m ≤ D.2m ≤ 6. 设函数211log (2),1,()2,1,x x x f x x -+-<⎧=⎨≥⎩,2(2)(log 12)f f -+=( )A .3B .6C .9D .127.若()()c o s ()f x x x ππ=--,将其图像向左平移π个单位得到函数()g x ,则函数()g x 的导函数()g x '等于( )A. 1sin x -B. sin x x -C. sin cos x x x -D. cos sin x x x -8. 记不等式组1033010x y x y x y -+≥⎧⎪--≤⎨⎪+-≥⎩所表示的平面区域为D ,若对任意()00,x y D ∈,不等式0020x y c -+≤恒成立,则c 的取值范围是( )A .(],4-∞B .(],2-∞C .[]1,4-D .(],1-∞- 9. 已知0,0a b >>,则11a b++( ) A .2B.C .4D .510.已知()f x 是定义在R 上的偶函数,并且1(+2)()f x f x =-,当23x ≤≤时,()f x x =则(104.5=f )( )A .0.5-B .0.4-C .0.5D .2.511.已知22log aa =-,22log bb -=-,22logc c -=,则a ,b ,c 的大小是( )A .a b c <<B .c b a <<C .c a b <<D .b a c << 12.已知()f x =(())f f x x =有解,则实数a 的取值范围是( )A 1(,]8-∞B 1[,)8+∞C 1(,]4-∞ D [1,)+∞ 二、填空题:本题共4小题,每小题5分,共20分。
福建省政和一中、周宁一中2020届高三数学上学期10月联考试题 文

福建省政和一中、周宁一中2020届高三数学上学期10月联考试题 文注意事项:1. 答题前填写好自己的姓名、班级、考号等信息2. 请将答案正确填写在答题卡上 评卷人 得分一、单项选择(每小题5分总共60分)1、已知集合2{560}A x x x =-+≤,{21}x B x =>,则A B =I ( ) A .[2,3] B .(0,)+∞ C .(0,2)(3,)+∞U D .(0,2][3,)+∞U2、设复数z 满足(1+i)z=2i ,则∣z ∣= A .12B .22C .2D .23、已知函数()4,0{2,0xx x f x x ->=≤,则()5f f ⎡⎤⎣⎦的值为( ) A. 2 B. -2 C.12D. 12-4、若1ln 2a =, 0.813b ⎛⎫= ⎪⎝⎭, 132c =,则( )A. a b c <<B. a c b <<C. c a b <<D. b a c <<5、已知向量p ()2,3=-,q (),6x =,且//p q ,则+p q 的值为( )A .5B . 13C . 5D .136、设x ,y 满足约束条件33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩则z=x+y 的最大值为 A .0B .1C .2D .37、若点),(b a A 在第一象限,且在直线01=-+y x 上,则ba 41+的最小值为( )A .8B .9C .10D .128、等差数列{}n a 的首项为1,公差不为0.若a 2,a 3,a 6成等比数列,则{}n a 前6项的和为 A .-24B .-3C .3D .89、函数()()sin f x A x ωϕ=+(0,0,A πωϕ>><)的图象如图所示,将()f x 的图象向右平移m 个单位得到()g x 的图象关于y 轴 对称,则正数m 的最小值为( ) A.6π B. 56π C. 3πD. 23π10、若α,β为锐角,且满足cos α=,cos (α+β)=,则sin β的值为( )A .﹣B .C .D .11、设双曲线22221(a 0,b 0)x y a b-=>>的右焦点是F ,左、右顶点分别是12A ,A ,过F做12A A 的垂线与双曲线交于B ,C 两点,若12A B A C ⊥,则双曲线的渐近线的斜率为( ) A .12±B. 2±1± D 212、已知函数4log 3(0),()1() 3 (0),4x x x x f x x x ⎧+->⎪⎪=⎨⎪-+≤⎪⎩若()f x 的两个零点分别为1x ,2x ,则12||x x -=( )A . 3ln 2-B . 3ln 2C .22D . 3评卷人 得分二、填空题(每小题5分总共20分)13、已知函数()f x 是定义在R 上的奇函数,当x ()-,0∈∞时,()322=+f x x x ,则()2=f .14、.设F 为抛物线2:=3C y x 的焦点,过F 且倾斜角为30︒的直线交C 于A ,B 两点,则 AB = .15、已知单位向量,a br r ,若向量2a b -r r 与b r 垂直,则向量a r 与b r的夹角为 . 16、定义在R 上的函数y=f (x ),满足f (2﹣x )=f (x ),(x ﹣1)f ′(x )<0,若 f (3a+1)<f (3),则实数a 的取值范围是 .17、(12分)已知在ABC ∆中,角,,A B C 所对的边分别为,,,a b c 已知2cos cos .c c A a C -=(Ⅰ)求bc的值 (Ⅱ)若21,3b c α+=+=,求ABC ∆的面积.S18、(12分)已知等差数列{a n }的前n 项和为S n ,等比数列{b n }的前n 项和为T n ,a 1=-1,b 1=1,222a b +=. (1)若335a b +=,求{b n }的通项公式;(2)若321T =,求3S .19、(12分)围建一个面积为360的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m 的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为(单位:),修建此矩形场地围墙的总费用为(单位:元)(1)将表示为的函数;(2)试确定,使修建此矩形场地围墙的总费用最小,并求出最小总费用。
【终稿】2020届福州市高中毕业班第三次质量检查文科数学试卷含答案

准考证号 姓名 .(在此卷上答题无效)2020年福州市高中毕业班第三次质量检测数学(文科)试卷(完卷时间:120分钟;满分:150分)(在此卷上答题无效)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷4至5页. 注意事项:1. 答题前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2. 第Ⅰ卷每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.第Ⅱ卷用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 3. 考试结束,考生必须将试题卷和答题卡一并交回.第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设全集{|8},U x x =∈N …集合{1,3,7}A =,则U A =ðA .{2,4,5,6}B .{0,2,4,5,6}C .{2,4,5,6,8}D .{0,2,4,5,6,8}2. 已知纯虚数z 满足(1i)2i z a -=+,则实数a 等于A .2B .1C .1-D .2-3. 曲线()1e x y x =-在1x =处的切线方程为A .e e 0x y --=B .e +e 0x y -=C .e 10x y +-=D .e 10x y --= 4. 执行如图所示的程序框图,则输出的m =A .1B .2C .3D .45. 已知等差数列{}n a 的前n 项和为n S ,且202020202020a S ==,则{}n a 的公差为A .2-B .2C .2019D .2019-6. 甲、乙、丙、丁四名同学在某次军训射击测试中,各射击10次.四人测试成绩对应的条形图如下:以下关于这四名同学射击成绩的数字特征判断不正确...的是 A .平均数相同 B .中位数相同C .众数不完全相同D .方差最大的是丁7. 为了得到曲线cos y x =,只需把曲线sin 26y x π⎛⎫=+ ⎪⎝⎭上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 A .35π个单位长度 B .125π个单位长度 C .3π个单位长度 D .6π个单位长度 8. 已知平面,,αβγ两两垂直,直线,,a b c 满足:,,a b c αβγ⊂⊂⊂,则直线,,a b c 可能满足以下关系:①两两相交;②两两垂直;③两两平行;④两两异面.其中所有正确结论的编号是 A .①③ B .②④C .①②④D .①②③④9. 已知椭圆()222:109x y C b b+=>的右焦点为F ,以C 上点M 为圆心的圆与x 轴相切于点F ,并与y 轴交于A ,B 两点.若4FA FB ⋅=u u u r u u u r,则C 的焦距为AB .2C .D .410. 已知定义在R 上的函数()f x 满足()()4f x f x +=-,函数()2f x +为偶函数,当()0,2x ∈时,()f x 3296+ 2x x x a =-+-.若()2,0x ∈-时,()f x 的最大值为12-,则a =A .3B .2C .12D .32-11. 2019年世界读书日,陈老师给全班同学开了一份书单,推荐同学们阅读,并在2020年世界读书日时交流读书心得.经了解,甲、乙两同学阅读书单中的书本有如下信息:①甲同学还剩②乙同学还剩5本未阅读;的书本甲、乙两同学都没阅读.则甲、乙两同学已阅读的相同的书本有 A .2本B .4本C .6本D .8本12. 若圆锥的内切球(球面与圆锥的侧面以及底面都相切)的半径为1,当该圆锥体积取最小值时,该圆锥体积与其内切球体积比为 A.8:3B.6:1C .3:1D. 2:1第Ⅱ卷注意事项:用0.5毫米黑色签字笔在答题卡上书写作答.在试题卷上作答,答案无效. 本卷包括必考题和选考题两部分.第 (13)~(21) 题为必考题,每个试题考生都必须作答.第 (22) 、(23) 题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13. 已知向量()1,2=a ,(),1t =b ,若,a b ,则实数t 的值为 .14. 已知双曲线C 过点(,且渐近线方程为2y x =±,则C 的离心率为 . 15. 我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以拆分为两个素数的和”,如307+2313171119==+=+,30有3种拆分方式;633=+,6只有1种拆分方式.现从大于4且小于16的偶数中随机任取一个,取出的数有不止一种上述拆分方式的概率为 .16. “熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到k 月份()28k k <<∈N 且<,每个月比上个月增加一条月产量为50吨的生产线投入生产,从+1k 月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加 条熔喷布生产线.(参考数据:81.1 2.14≈,91.1 2.36≈)三、解答题:解答应写出文字说明、证明过程或演算步骤. 17. (本小题满分12分)ABC △的内角A B C ,,的对边分别为a b c ,,,1a =sin C c A =.(1)求C ;(2)若3b =,D 是AB 上的点,CD 平分ACB ∠,求ACD △的面积. 18. (本小题满分12分)为了比较两种治疗失眠症的药(分别称为A 药,B 药)的疗效,某机构随机地选取20 位患者服用A 药,20位患者服用B 药,观察这40位患者的睡眠改善情况.这些患者服用一段时间后,根据患者的日平均增加睡眠时间(单位:h ),以整数部分当茎,小数部分当叶,绘制了如下茎叶图:(1)根据茎叶图判断哪种药对增加睡眠时间更有效?并说明理由;(2)求这40名患者日平均增加睡眠时间的中位数m ,并将日平均增加睡眠时间超过m 和不超过m 的患者人数填入下面的列联表:附:22()()()()()n ad bc K a b c d a c b d -=++++.19. (本小题满分12如图,在多面体PABCD 中,平面ABCD ⊥平面PAD ,AD BC ∥,90BAD ∠=︒,120PAD ∠=︒,1BC =,2AB AD PA ===.(1)求多面体PABCD 的体积;(2)已知E 是棱PB 的中点,在棱CD 是否存在点F 使得EF PD ∥,若存在,请确定点F 的位置;若不存在,ACB请说明理由.20. (本小题满分12分)已知抛物线2:4C y x =,直线:2(0)l x my m =+>与C 交于A ,B 两点,M 为AB 的中点,O 为坐标原点.(1)求直线OM 斜率的最大值;(2)若点P 在直线2x =-上,且PAB △为等边三角形,求点P 的坐标.21. (本小题满分12分)已知函数2()2ln f x x ax x =-+. (1)求函数()f x 的单调区间;(2)设函数()f x 有两个极值点()1212,x x x x <,若()12f x mx >恒成立,求实数m 的取值范围.请考生在第(22)、(23)两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,作答时请用2B 铅笔在答题卡上将所选题号后的方框涂黑. 22. (本小题满分10分)选修44-:坐标系与参数方程在直角坐标系xOy 中,直线1l 的参数方程为33,x kt y t =-+⎧⎨=⎩(t 为参数),直线2l 的参数方程为33,x m y km =-⎧⎨=⎩(m 为参数).设1l 与2l 的交点为P ,当k 变化时,P 的轨迹为曲线1C .(1)求1C 的普通方程;(2)设Q 为圆()222:43C x y +-=上任意一点,求PQ 的最大值.23. (本小题满分10分)选修45-:不等式选讲已知0,0a b >>,2224a b c ++=. (1)当1c =时,求证:()()339a b a b ++≥;(2)求2224411a b c +++的最小值.2020年福州市高中毕业班第三次质量检测数学(文科)参考答案及评分细则评分说明:1.本解答给出了一种或几种解法供参考,如果考生的解法与本解答不同,可根据试题的主要考查内容比照评分标准制定相应的评分细则。
(福建版)2020届全国高三数学第三次大联考 文(无答案)

2020年第二次全国大联考【福建卷】文科数学试卷考试时间:120分钟; 命题人:大联考命题中心 第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集{}280,U x x x x N *=-<∈,集合{}{}1,2,3,5,2,4,6A B ==,则()U C A B =I( )A .{}2 B .{}4,6 C .{}1,3,5 D .{}4,6,7,82.设z是z的共轭复数,若()4,2z z z z i +=-=,则2z =( )A .54i -B .34i -C .34i +D .54i + 3.执行下边的程序框图,输出的b 的值为 ( )A .9B .5C .113D .2994.若p ⌝是假命题,q 是真命题,则 ( ) A .p q ∨是真命题 B .p q ∧是假命题 C .()p q ⌝∧是真命题 D .()p q ∨⌝是假命题5.已知()()2,1,,4a b x ==-r r.若2a b -r r 与a b +r r平行,则x = ( ) A .4 B .4- C .8 D .8- 6.三棱锥D ABC -及其三视图中的正 视图和侧视图如图所示,则异面直 线AC 与BD 所成角为( ) A .30︒ B .45︒ C .60︒ D .75︒第3题图正视图侧视图第6题图7.已知奇函数()f x 满足()()51f x f x -+=且()01f =,则()2015f =( )A .1B .2C .1-D .403 8.设nS 为等比数列{}n a 的前n 项和,已知2431,7a a S ==,则公比q = ( )A .13-B .12C .13或12-D .13-或129.已知关于x y ,的方程y ax =的解满足约束条件240,10,1,x y x y x +-≤⎧--≤≥⎪⎨⎪⎩则a 的最大值为 ( )A .1B .1.5C .2D .310.已知函数()()sin 0,,02f x A x A πωϕϕω⎛⎫=+><> ⎪⎝⎭的一部分图象如图所示,且过()110,2,,012M N π⎛⎫⎪⎝⎭两点,则()f x 的图象的一条对称轴方程为 ( )A .12x π=B .4x π=C .12x π=-D .6x π=-11.已知点M 与点()1,1N -关于原点O 对称,动点P 满足直线MP 与NP 的斜率之积等于13,则动点P 的轨迹方程为 ( )A .()22321x y x -=≠±B .()22321x y x -=≠±C .()22321y x x -=≠± D .()22321y x x -=≠±12.已知函数()ln mf x x x =-,当2x =时,()f x 取极小值,则曲线()y f x =在点()()1,1f 处的切线方程为( )A .30x y ++=B .30x y +-=C .30x y -+=D .30x y --= 第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在答题卡的相应位置. 13.在一次抽样调查中,得到一个样本:1,0,3,,1,a -且该样本的平均值为1,则其方差第10题图为_________.14.在锐角ABC ∆中,角,,A B C ∠∠∠的对边分别为,,,a b c 若2sin b a B =,则A ∠= .15.已知直线l 与圆229x y +=相切且与直线:20m x y -=垂直,则直线l 的方程为 . 16.记123k k k kk S n =++++L ,当1,2,3,k =L 时,观察下列等式:211122S n n=+,322111326S n n n=++,4323111424S n n n =++,5434111152330S n n n n =++-,6532515212S An n n Bn =+++,…,可以推测A B -= .三、解答题 :本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知向量()()2sin ,sin ,cos ,2sin ,m x x n x x =-=u r r函数()1f x m n =⋅+u r r.(I )求函数()f x 的最小正周期和单调递减区间;(II )若在ABC ∆中,角,,A B C 的对边分别为,,,3,2,a b c a b A ==为锐角,且282f A π⎛⎫+=-⎪⎝⎭,求错误!未找到引用源。
福建省政和一中、周宁一中2020届高三上学期11月联考试题数学文版含答案

2017-2018学年政和、周宁一中第二次联考文科数学卷考试时间:120分钟;总分:150分:命题人:倪建才学校:_________ 姓名:____________ 班级:____________ 考号:____________一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A =— 2x> o}, B = {x|—3 < x < 3}> 则()A.AcB = 0B. A5 = RC.D. A^B2.记复数z的虚部为Im⑵,已知复数Z = —— -2,( i为虚数单位),则Im(z)为()2z-1A. 2 B・一3 C・一3' D・ 33.以下有关命题的说法错误的是()A.命题“若工_3_¥ + 2 = 0,则x=l”的逆否命题为"若XH1,则+-3尤+2工0”B."x = 1”是“ x2-3x + 2 = 0f,的充分不必要条件C.若[“为假命题,则卩、q均为假命题D.对于命题 : e R > 使得x2+x + lv0,则-i/?: Vx e R ,则x2 +x+\>04.若cos8-3sin0 = O,则tan(^-—)=()4A・一丄B・一2 C・丄D・22 25.设有直线m. n和平面G、p.下列四个命题中,正确的是()A.若m// a ji// a,则m〃八B.若mu aa jn" p0 •则ct // PC.若a丄卩,mu a、则加丄0 D・若a丄0 ,加丄0 , mUa、则加〃a6.执行如图所示的程序框图,则输出的S值为(C.弐21)D.丄20A.兰B. 1219 207.下列命题正确的是(A・若a>b>\,c <0 ,则> b' B.若\a\ > b.则a2 >b2D.若a>0,b> 0且a + b = \.则丄+丄的最小值为4. a b C. €/?,X Q + — = 1 x()8.已知函数/(x) = sin(c〃x+0)( Q>0,Ov0V”)的最小正周期是龙,将函数/(x)的图象向左平移彳个单位长度后所得的函数图象过点P(0,l),则函数 f(x) = sin (0x+0)( )9. 函数)=“7"的图象大致是( eC.10. 已知圆M :x 2+y 2-2ay = 0(fl>0)^直线r + y = 0所得线段的长度是则圆M 与 圆N : (x-l)2 + (y-IF = 1的位巻关系是( )A.内切B.相交C.外切D.相离11 .在菱形A3CD 中,AB = 2 , ZDAB=6(r , £为8的中点,贝11訖狂的值是()A .B . 5C .何D . 612. 已知f(x)是定义在R 上的奇函数,且当XW (YO ,0)时,不等式#(X )< 0 成立,若 a = 7tf^7t\ /? = (-2)/(-2),c = /(l),则 a,b,c 的大小关系是 ()Aa>b>c B. c>b>a C ・ c>a>b D ・ a>c>b二、填空题(每小题5分总共20分)X < 113•设函数f(x)= 二 ,则使得f(x) < 2成立的x 的取值范围是 ______________ ・yJX.X > 114.等比数列仏}的前“项和为Sn ,已知S|, 2S 2, 3S3成等差数列,则{a n }的公比为 ______ ・A有一个对称中心冶。
文科数学-2020年3月高三第三次在线大联考(新课标Ⅰ卷)(全解全析)

2020年3月高三第三次在线大联考(新课标Ⅰ卷)文科数学 全解全析1.B【解析】因为12i (12i)(2i)2i 4i 2i 1111i 2i (2i)(2i)5z ++++++=+=+=+=+--+,所以1i z =-,故选B . 2.D 【解析】因为2{|1}{|11}A x x x x =<=-<<,{|ln 1}{|0e}B x x x x =<=<<, 所以{|01}A B x x =<<I ,{|1e}A B x x =-<<U ,故选D .3.B 【解析】双曲线C 的渐近线方程为b y x a =±,由题可知tan 3b a π=设点(,0)F c ,则点F 到直线y =2c =,所以222222344c a b a a a =+=+==,解得1a =,所以双曲线C 的实轴的长为22a =,故选B . 4.C 【解析】由题可得0.00520.02020.040(1)10a ⨯++⨯+⨯=,解得0.010a =, 则(0.0050.0100.020)100.35++⨯=,0.350.040100.750.5+⨯=>, 所以这部分男生的身高的中位数的估计值为0.50.3517010173.75(cm)100.040-+⨯=⨯,故选C .5.C 【解析】由三视图可知,该几何体是三棱锥,底面是边长为2以该几何体的体积1122132V =⨯⨯⨯=,故选C .6.B 【解析】作出该不等式组表示的平面区域,如下图中阴影部分所示, 设23z x y =-,则2133y x z =-,易知当直线2133yx z =-经过点D 时,z 取得最小值, 由1220x x y =-⎧⎨-+=⎩,解得112x y =-⎧⎪⎨=⎪⎩,所以1(1,)2D -,所以min 172(1)322z =⨯--⨯=-,故选B .7.B 【解析】初始:1k =,2T =,第一次循环:2282 2.8133T =⨯⨯=<,2k =,继续循环;第二次循环:8441282.833545T =⨯⨯=>,3k =,此时 2.8T >,满足条件,结束循环, 所以判断框内填入的条件可以是3?k ≥,所以正整数m 的最小值是3,故选B .8.A 【解析】因为5()2sin()52sin ()()3333x x x xx x x xf x f x ---+-+-===--,所以函数()f x 是偶函数,排除B 、D ,又5()033f π-πππ=>-,排除C ,故选A . 9.B 【解析】根据题意可得BC ⊥平面ACD ,EF BC ∥,则CBG ∠即异面直线BG 与EF 所成的角,连接CG ,在Rt CBG △中,cos BCCBG BG∠=,易得BD AD AB ===,所以BG =,所以cos CBG ∠==,故选B . 10.C 【解析】将函数()f x 的图象向左平移3π个单位长度,得到函数()2sin()33g x x ωωππ=+-的图象,因为函数()g x 的图象的一条对称轴是6x π=,所以sin()1633ωωπππ+-=±,即,6332k k ωωππππ+-=+π∈Z ,所以52,3k k ω=+∈Z ,又0ω>,所以ω的最小值为53.故选C . 11.C 【解析】根据抛物线定义,可得1||||AF AA =,1||||BF BB =,又11AA FK BB ∥∥,所以11||||2||||A K AF B K BF ==,所以1111||||2||||A K AAB K BB ==, 设1||(0)BB m m =>,则1||2AA m =,则111||||21cos cos ||23AA BB m m AFx BAA AB m m --∠=∠===+,所以sin 3AFx ∠=,所以直线l的斜率tan k AFx =∠=C . 12.C 【解析】因为23C π=,1c =,所以根据正弦定理可得sin sin sin a b c A B C ===a A =,b B =,所以sin()])sin 32z b a B A B B B λλλπ=+==+--+])B B φ=+,其中tan φ=,03B π<<, 因为z b a λ=+存在最大值,所以由2,2B k k φπ+=+π∈Z ,可得22,62k k k φπππ+<<π+∈Z ,所以tan φ>>,解得122λ<<,所以正数λ的取值范围为1(,2)2,故选C . 13.12-【解析】由题可得(1,1)m +=-+a b ,因为向量+a b 与向量a 平行,所以2(1)1(1)0m -⨯+-⨯-=,解得12m =-.14.(2,0]- 【解析】作出函数()y f x =的图象及直线y a =,如下图所示,因为函数()y f x a =-有3个不同的零点123123,,()x x x x x x <<,所以由图象可知122x x +=-,3102x <≤,233()4a f x x ==,所以123a x x x ++=324(2,0]x -+∈-.15.【解析】因为(0,)α∈π,所以7(,)666απππ+∈,又1sin()063απ+=-<,所以7(,)66αππ+∈π,则cos()6απ+==,所以cos cos[()]cos()cos sin()sin 666666ααααππππππ=+-=+++=11(()32+-⨯=. 16.【解析】设直线l 与函数()f x 及()g x 的图象分别相切于1(,)(0)A m m m <,2(,)B n n a +,因为21()f x x '=-,所以函数()f x 的图象在点A 处的切线方程为211()y x m m m -=--,即212y x m m=-+,因为()2g x x '=,所以函数()g x 的图象在点B 处的切线方程为22()y n a n x n --=-,即22y nx n a =-+,因为存在直线l 与函数()f x 及()g x 的图象都相切,所以22122n mn a m ⎧=-⎪⎪⎨⎪-+=⎪⎩,所以4124a m m =+, 令1(0)t t m =<,设41()2(0)4h t t t t =+<,则3()2h t t '=+,当t <()0h t '<,函数()h t单调递减;当0t <时,()0h t '>,函数()h t 单调递增,所以min()(2h t h ==-,所以实数a的最小值为2- 17.(本小题满分12分)【解析】(1)补充完整的22⨯列联表如下:(2分)则2K 的观测值250(1261418)2254.327 3.8413020242652k ⨯⨯-⨯==≈>⨯⨯⨯,(4分)所以有95%的把握认为“法律知识竞赛成绩是否合格”与“是否是高一新生”有关.(6分) (2)抽取的5名学生中竞赛成绩合格的有530350⨯=名学生,记为,,a b c , 竞赛成绩不合格的有520250⨯=名学生,记为,m n ,(8分) 从这5名学生中随机抽取2名学生的基本事件有:,,,,,,,,,ab ac bc am an bm bn cm cn mn ,共10种,(10分)这2名学生竞赛成绩都合格的基本事件有:,,ab ac bc ,共3种,(11分) 所以这2名学生竞赛成绩都合格的概率为310P =.(12分) 18.(本小题满分12分)【解析】(1)因为112(2)n n n n a a n a a +-+=≥,所以0n a ≠,所以11112n n na a a +-+=, 所以数列1{}na 是等差数列,(2分)设数列1{}na 的公差为d ,由12a a ≠可得0d ≠, 因为125,,a a a 成等比数列,所以2152a a a =,所以2152111a a a ⋅=,所以2333111(2)(2)()d d d a a a -+=-, 因为315a =,所以2(52)(52)(5)d d d -+=-,(4分) 解得0d =(舍去)或2d =,所以311(3)21n n d n a a =+-=-,所以121n a n =-.(6分) (2)由(1)知121n a n =-,2(121)2n n n S n +-==, 所以2+1111111()4(21)(21)44(21)(21)82121n n n n n b a a S n n n n n n =-=-==--+-+-+,(9分)所以11111111(1)(1)8335212182184n nT n n n n =⨯-+-++-=⨯-=-+++L .(12分)19.(本小题满分12分)【解析】(1)因为正方形ABCD 所在平面与梯形ABMN 所在平面垂直,平面ABCD I 平面ABMN AB =,BC AB ⊥,所以BC ⊥平面ABMN ,因为MN ⊂平面ABMN ,BN ⊂平面ABMN ,所以BC MN ⊥,BC BN ⊥,(2分)因为2,BC CN ==BN =, 因为2NA AB ==,所以222AB AN BN +=,所以AB AN ⊥, 因为在直角梯形ABMN 中,4BM =,所以MN =,(4分)所以222BN MN BM +=,所以BN MN ⊥,因为BC BN B =I ,所以MN ⊥平面BCN .(6分) (2)如图,取BM 的中点E ,则BE AN =,又BM ∥AN ,所以四边形ABEN 是平行四边形,所以NE ∥AB ,又AB ∥CD ,所以NE ∥CD ,因为NE ⊄平面CDM ,CD ⊂平面CDM ,所以NE ∥平面CDM , 所以点N 到平面CDM 的距离与点E 到平面CDM 的距离相等,(8分)设点N 到平面CDM 的距离为h ,由BE EM =可得点B 到平面CDM 的距离为2h , 由题易得CD ⊥平面BCM ,所以CD CM ⊥,且CM =所以11112223232B CDMV CD CM h h-=⨯⨯⨯⨯=⨯⨯⨯=,(10分)又1111822432323M BCDV BC CD BM-=⨯⨯⨯⨯=⨯⨯⨯⨯=,所以由B CDM M BCDV V--=83=,解得h=,所以点N到平面CDM.(12分)20.(本小题满分12分)【解析】(1)因为椭圆Γ过点,所以222112a b+=①,(1分)设O为坐标原点,因为56AFBπ∠=,所以6BFOπ∠=,又||BF a=,所以12b a=②,(3分)将①②联立解得21ab=⎧⎨=⎩(负值舍去),所以椭圆Γ的标准方程为2214xy+=.(4分)(2)由(1)可知(0,1)B,设11(,)P x y,22(,)Q x y.将y kx n=+代入2214xy+=,消去y可得222(14)8440k x knx n+++-=,(5分)则22222(8)4(14)(44)16(41)0kn k n k n∆=-+-=-+>,122814knx xk-+=+,21224414nx xk-=+,(7分)所以12212121121212121211()()2(1)()BP BQy y x kx n x x kx n x kx x n x xk kx x x x x x--+-++-+-++=+==222224482(1)8(1)214141444(1)(1)114n knk nk n kk kn n n nk--⋅+-⋅-++====--+-++,(10分)所以21n k=--,此时2216[4(21)1]640k k k∆=---+=->,所以0k<,此时直线l的方程为21y kx k=--,即(2)1y k x=--,(11分)令2x=,可得1y=-,所以直线l过定点,该定点的坐标为(2,1)-.(12分)21.(本小题满分12分)【解析】(1)由题可得函数()f x的定义域为(0,)+∞,222211(1)1(1)(1)()(0)a ax a x x axf x a xx x x x+-++--'=-+==>,当0a≤时,10ax-<,令()0f x'<,可得1x>;令()0f x'>,可得01x<<,所以函数()f x在(0,1)上单调递增,在(1,)+∞上单调递减;(2分)当01a <<时,令()0f x '<,可得11x a <<;令()0f x '>,可得01x <<或1x a>, 所以函数()f x 在(0,1),1(,)a +∞上单调递增,在1(1,)a上单调递减;当1a =时,()0f x '≥恒成立,所以函数()f x 在(0,)+∞上单调递增.(5分)综上,当0a ≤时,函数()f x 在(0,1)上单调递增,在(1,)+∞上单调递减;当01a <<时,函数()f x 在(0,1),1(,)a +∞上单调递增,在1(1,)a上单调递减;当1a =时,函数()f x 在(0,)+∞上单调递增.(6分) (2)方法一:当1a =时,2323412312()()2ln F x f x x x x x x x x x =++-=-++-,[1,2]x ∈, 设()2ln g x x x =-,[1,2]x ∈,则22()10x g x x x-'=-=≤, 所以函数()g x 在[1,2]上单调递减,所以()(2)22ln 2g x g ≥=-,当且仅当2x =时取等号.(8分) 当[1,2]x ∈时,设1t x=,则1[,1]2t ∈,所以232331232t t t x x x +-=+-,设23()32h t t t t =+-,1[,1]2t ∈,则22119()3266()66h t t t t '=+-=--+,所以函数()h t '在1[,1]2上单调递减,且15()022h '=>,(1)10h '=-<,所以存在01(,1)2t ∈,使得0()0h t '=,所以当012t t ≤<时,()0h t '>;当01t t <≤时,()0h t '<,(10分)所以函数()h t 在01(,)2t 上单调递增,在0(,1)t 上单调递减,因为13()22h =,(1)2h =,所以13()()22h t h ≥=,所以2331232x x x +-≥,当且仅当2x =时取等号.(11分)所以当2x =时,函数()F x 取得最小值,且min 37()22ln 22ln 222F x =-+=-, 故函数()F x 的最小值为72ln 22-.(12分)方法二:当1a =时,2323412312()()2ln F x f x x x x x x x x x=++-=-++-,[1,2]x ∈, 则3223442326(1)(46)()1x x x x F x x x x x x ----'=---+=,令32()46g x x x x =---,[1,2]x ∈,则22113()3243()33g x x x x '=--=--,所以函数()g x '在[1,2]上单调递增,(8分)又(1)3,(2)4g g ''=-=,所以存在0(1,2)x ∈,使得0()0g x '=, 所以函数()g x 在0[1,)x 上单调递减,在0[,2]x 上单调递增,(9分) 因为(1)100,(2)100g g =-<=-<,所以当[1,2]x ∈时,()0g x <恒成立,所以当[1,2]x ∈时,()0F x '≤恒成立,所以函数()F x 在[1,2]上单调递减,(11分)所以函数()F x 的最小值为233127(2)22ln 22ln 22222F =-++-=-.(12分) 22.(本小题满分10分)选修4-4:坐标系与参数方程【解析】(1)由82x t=+可得0x ≠, 由8242x t t y t ⎧=⎪⎪+⎨⎪=⎪+⎩,消去参数t ,可得直线l 的普通方程为40(0)x y x +-=≠.(2分)由2sin ρθ=可得22sin ρρθ=,将sin y ρθ=,222x y ρ=+代入上式,可得2220x y y +-=, 所以曲线C 的直角坐标方程为2220x y y +-=.(5分) (2)由(1)得,l 的普通方程为40(0)x y x +-=≠,将其化为极坐标方程可得cos sin 40()2ρθρθθπ+-=≠,(7分)当()04θρπ=>时,A ρ=B ρ=所以|||||A B AB ρρ=-==(10分) 23.(本小题满分10分)选修4-5:不等式选讲【解析】(1)当2a =时,12,211()|21||21|4,2212,2x f x x x x x x ⎧-<-⎪⎪⎪=+--=-≤≤⎨⎪⎪>⎪⎩,(2分)当12x <-或12x >时,|()|2f x =,所以1()1f x -≤≤可转化为1124211x x -≤-≤≤⎧≤⎪⎨⎪⎩,解得1144x -≤≤,所以不等式1()1f x -≤≤的解集为11[,]44-.(5分)(2)因为1(,0)2x ∈-,所以|21|21x x +=+,所以()2f x x >,即21|1|2x ax x +-->,即|1|1ax -<.当0a ≥时,因为1(,0)2x ∈-,所以|1|1ax -≥,不符合题意.(7分)当0a <时,解|1|1ax -<可得20x a<<,(8分) 因为当1(,0)2x ∈-时,不等式()2f x x >恒成立,所以12(,0)(,0)2a-⊆,所以212a ≤-,解得40a -≤<,所以实数a 的取值范围为[4,0)-.(10分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020届周宁一中、政和一中高三第三次联考
数学(文)试卷
考试时间:120分钟,满分:150分
一、选择题(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有
一项是符合题目要求)
1. 复数2)1(1i +等于( ) A 21 B -21 C 、21i D -2
1i 2.设集合{}{}|(3)(2)0,,|13,M x x x x R N x x x R =+-<∈=≤≤∈,则M N =I ( )
A.[)1,2
B.[1,2]
C.(]2,3
D.[2,3]
3.将图所示的一个直角三角形ABC (∠C =90°)绕斜边AB 旋转一周,所得到的几何体的正视图
是下面四个图形中的 ( )
4.已知向量a b r r 、都是非零向量,“||||a b a b ⋅=⋅r r r r ”是“//a b r r ”的( )
A .充分非必要条件.
B .必要非充分条件.
C .充要条件.
D .既非充分也非必要条件.
5.下列结论错误的是( ) A 、命题“若p ,则q”与命题“若¬q,则¬p”互为逆否命题
B 、命题p :1],1,0[≥∈∀x e x ,命题q :01,2<++∈∃x x
R x ,则p ∨q 为真 C 、若am 2<bm 2,则a <b”的逆命题为真命题
D 、若p ∨q 为假命题,则p 、q 均为假命题
6.若方程1312x x ⎛⎫= ⎪⎝⎭
有实数解0x ,则0x 属于 ( ) A .10,3⎛
⎫ ⎪⎝⎭ B .11,32⎛⎫ ⎪⎝⎭ C .1,12⎛⎫ ⎪⎝⎭ D .()1,2
7.等差数列{}n a 中,652,30,a S ==则8S = ( )
A.31
B.32
C.33
D.34
8.已知1sin(),43
πθ+
=则sin 2θ= ( ) A.19 B.19- C.79 D.79
- 9.将函数sin 2y x =的图象向右平移4π个单位, 再向上平移1个单位,所得图象的函数 解析式是( )
A .22sin y x =
B .22cos y x =
C .
)42sin(1π++=x y D .cos 2y x = 10.若函数()f x 的导函数为34)(2+-='x x x f ,则函数)1(-x f 的单调递减区间是( )
.A (2,4) .B (2,3) .C (0,1) .D (0,2)
11.已知l 、m 是不同的两条直线,α、β是不重合的两个平面,
则下列命题中正确的是( ) .A 若l ∥α,α⊥β,则l ∥β .B 若l ⊥α,α∥β,m ⊂β,则l ⊥m
.C 若l ⊥m ,α∥β,m ⊂β,则l ⊥α .D 若l ⊥α,α⊥β,则l ∥β 12.△ABC 的外接圆的圆心为O ,半径为1,若0OA AB OC ++=u u u r u u u r u u u r ,且||||OA AB =u u u r u u u r ,则CA CB ⋅u u u r u u u r =( )
.A 32
.B .C 3 .D 二、填空题(大题共4小题,每小题4分,共16分.请将答案填在答题卷相应的横线上)
13. 若点(m ,n)在第一象限,且在直线2x+3y=1上,则n
m 32+的最小值为 14.设函数()()[)22,,1,,1,.x x f x x x -⎧∈-∞⎪=⎨∈+∞⎪⎩
若()4f x >,则x 的取值范围是 . 15.在平面内,三角形的面积为S ,周长为C ,则它的内切圆的半径C
S r 2=.在空间中,三棱锥的
体积为V ,表面积为S ,利用类比推理的方法,可得三棱锥的内切球(球面与三棱锥的各个面均相切)的半径R =___________。
16. 设曲线1()n y x n N ++=∈在点(1,1))处的切线与x 轴的交点的横坐标为n x ,令lg n n a x =, 则1299a a a +++L 的值为___________.
三、解答题(本大题共6小题,共74分.解答须写出文字说明,证明要有过程或演算步骤)
17.(12分)已知数列{}n a 是首项1a =4,公比1q
≠的等比数列,n S 是其前n 项和, 且1534,,-2a a a 成等差数列。
(1)求公比q 的值;
(2)求242n
n T a a a =+++L 的值。
18. (本小题满分12分)在锐角△ABC 中,内角A,B,C 的对边分别为,,,a b c 且2sin 3a B b =
. (1)求角A 的大小;
(2) 若6,8,a b c =+=求△ABC 的面积..
19、(本小题满分12分)设数列}{n a 的前n 项和为n s ,点()*,
n s n n N n ⎛⎫∈ ⎪⎝⎭均在函数1y x =+的图象上.
(1)求数列}{n a 的通项公式;
(2)若}{n b 为正项等比数列,且11
=b ,8321=b b b ,求}{n b 的通项公式和前n 项和n G ; (3)求}{n n
b a ⋅的前n 项和n T 。
20、(本小题满分12分)如图,在三棱柱111ABC A B C -中,底面是正三角形,侧棱1BB ABC ⊥平面,D 是棱BC 的中点,点M 在1BB 棱上,且11,1,2CM AC AB BB ⊥==.
(1)求三棱锥1D ABC -的体积;
(2)求证:11||A B AC D 平面;
(3)求证:1CM C D ⊥。
21.(本小题满分12分)设函数θθθcos sin 3)(+=f ,其中,角θ的顶点与坐标原点重合,
始边与x 轴非负半轴重合,终边经过点),(y x P ,且0θπ≤≤。
(1)若点P
的坐标为1(,22
,求)(θf 的值; (2)若点),(y x P 为平面区域Ω:x+y 1x 1y 1≥⎧⎪≤⎨⎪≤⎩
上的一个动点,试确定角θ的取值范围,并求函数()f θ的最小值和最大值。
22、(本题满分14分)
已知函数 21()ln (1)2
f x x m x m x =
-+-,m ∈R . (1)若函数()f x 在2x =处取得极值,求m 的值; (2)当 0m ≤ 时,讨论函数 ()f x 的单调性;
(3)求证:当 2m =-时,对任意的 ()12,0,x x ∈+∞,且12x x ≠,有2121()()1f x f x x x ->--. .。
