信号采样长度、时间间隔和频率的关系

合集下载

信号采样公式(一)

信号采样公式(一)信号采样公式1. 采样定理（Nyquist-Shannon采样定理）•采样频率必须是信号最高频率的两倍以上才能正确恢复信号。

•采样频率（fs）必须满足 fs > 2fmax2. 采样周期（T）•采样周期是指两次采样之间的时间间隔。

•采样周期（T）与采样频率（fs）的关系为 T = 1 / fs3. 采样数（N）•采样数是指采样点的个数。

•采样数（N）与采样周期（T）的关系为N = fs × T4. 采样值（x[n]）•采样值是指在某个特定时刻采样到的信号值。

•采样值（x[n]）通常表示为一个序列，其中n是采样点的序号。

5. 采样频率（fs）•采样频率是指每秒采样的次数。

•采样频率（fs）通常以赫兹（Hz）为单位。

6. 采样定理的应用•例如，一个信号的最高频率为10kHz，根据采样定理，需要以20kHz以上的采样频率对其进行采样，才能完整恢复信号。

•如果将采样频率设置为15kHz进行采样，将无法正确恢复信号，导致信号失真。

7. 采样周期与采样频率的关系•采样周期和采样频率是相互关联的，二者满足 T = 1 / fs 的关系。

•当采样频率增大时，采样周期减小；反之，当采样频率减小时，采样周期增大。

8. 采样数与采样周期的关系•采样数与采样周期满足N = fs × T 的关系。

•当采样周期固定时，采样数随着采样频率的增大而增加；当采样频率固定时，采样数随着采样周期的增大而减小。

总结•信号采样公式包括采样定理、采样周期与采样频率的关系、采样数与采样周期的关系、以及采样值的含义和表示方法。

•采样定理是保证信号能够被正确恢复的重要条件，确保采样频率大于信号最高频率的两倍以上。

•采样周期和采样频率呈反比关系，采样频率增大时采样周期减小；采样数和采样周期呈正比关系，采样频率增大时采样数增加。

•在实际应用中，必须根据信号特性选择合适的采样频率和采样周期，以避免信号失真和信息丢失。

模拟量模块平均采样时间

模拟量模块平均采样时间
模拟量模块的平均采样时间是指在一定时间范围内对模拟信号
进行采样的平均时间间隔。

这个时间间隔取决于采样率和采样方式。

首先，我们来看采样率。

采样率是指每秒钟对模拟信号进行采
样的次数，单位是赫兹（Hz）。

采样率越高，平均采样时间就越短，因为信号被更频繁地采样。

其次，采样方式也会影响平均采样时间。

常见的采样方式有周
期采样和非周期采样。

周期采样是指以固定时间间隔进行采样，而
非周期采样则是根据信号的变化情况来动态调整采样时间间隔。

在
非周期采样中，平均采样时间会根据信号的变化而变化，可能会出
现较短的采样间隔和较长的采样间隔。

此外，还有一些因素可能会影响模拟量模块的平均采样时间，
比如采样精度、信号稳定性、噪声等。

这些因素都会对采样时间产
生一定的影响。

总的来说，模拟量模块的平均采样时间是一个综合考量采样率、
采样方式和其他因素的结果。

在实际应用中，需要根据具体的系统要求和信号特性来确定合适的平均采样时间。

采样频率、采样点数、频率分辨率

1.频率分辨率的2种解释解释一：频率分辨率可以理解为在使用DFT时，在频率轴上的所能得到的最小频率间隔f0=fs/N=1/NTs=1/T,其中N为采样点数，fs为采样频率，Ts为采样间隔。

所以NTs就是采样前模拟信号的时间长度T，所以信号长度越长，频率分辨率越好。

是不是采样点数越多，频率分辨力提高了呢？其实不是的，因为一段数据拿来就确定了时间T，注意：f0=1/T，而T=NTs，增加N必然减小Ts ，因此，增加N时f0是不变的。

只有增加点数的同时导致增加了数据长度T才能使分辨率越好。

还有容易搞混的一点，我们在做DFT时，常常在有效数据后面补零达到对频谱做某种改善的目的，我们常常认为这是增加了N，从而使频率分辨率变好了，其实不是这样的，补零并没有增加有效数据的长度，仍然为T。

但是补零其实有其他好处：1.使数据N为2的整次幂，便于使用FFT。

2.补零后，其实是对DFT结果做了插值，克服“栅栏”效应，使谱外观平滑化；我把“栅栏”效应形象理解为，就像站在栅栏旁边透过栅栏看外面风景，肯定有被栅栏挡住比较多风景，此时就可能漏掉较大频域分量，但是补零以后，相当于你站远了，改变了栅栏密度，风景就看的越来越清楚了。

3.由于对时域数据的截短必然造成频谱泄露，因此在频谱中可能出现难以辨认的谱峰，补零在一定程度上能消除这种现象。

那么选择DFT时N参数要注意：1.由采样定理：fs>=2fh，2.频率分辨率：f0=fs/N，所以一般情况给定了fh和f0时也就限制了N范围：N>=fs/f0。

解释二：频率分辨率也可以理解为某一个算法（比如功率谱估计方法）将原信号中的两个靠得很近的谱峰依然能保持分开的能力。

这是用来比较和检验不同算法性能好坏的指标。

在信号系统中我们知道，宽度为N的矩形脉冲，它的频域图形为sinc函数，两个一阶零点之间的宽度为4π/N。

由于时域信号的截短相当于时域信号乘了一个矩形窗函数，那么该信号的频域就等同卷积了一个sinc函数，也就是频域受到sinc函数的调制了，根据卷积的性质，因此两个信号圆周频率之差W0必须大于4π/N。

采样信号的概念

采样信号的概念采样信号是指连续时间信号在时间轴上以离散形式采样后得到的离散时间信号。

在信号处理中，采样是将连续时间信号转换为离散时间信号的过程。

采样信号常用于数据采集、数字化通信、移动通信、音频处理等领域。

采样信号的概念可以通过以下几个方面进行解释：1. 采样定理：采样定理是离散时间信号处理的基础。

根据采样定理，对于频域限制在一定带宽范围内的连续时间信号，只需以超过其最高频率两倍的采样频率进行采样，就能够完全还原原信号。

2. 采样频率：采样频率是指每秒对连续时间信号进行采样的次数，通常用赫兹（Hz）来表示。

采样频率的选择应满足采样定理的要求，以避免出现混叠现象。

在实际应用中，常用的采样频率为声音的44.1kHz或48kHz。

3. 采样间隔：采样间隔是指连续时间信号在时间轴上两个采样点之间的距离，通常用秒（s）来表示。

采样间隔与采样频率的关系为采样间隔= 1 / 采样频率。

采样间隔越小，对信号的描述就越精确。

4. 量化：量化是将连续时间信号的幅度离散化的过程。

在采样后，信号的幅度需要用有限数量的离散值来表示，这就需要进行量化。

量化过程中，通常将连续幅度值映射到最接近的离散值，常见的量化方式有均匀量化和非均匀量化。

5. 采样误差：采样信号引入了采样误差，即由于采样和量化过程导致的原始信号与重构信号之间的差异。

采样误差可通过增加采样频率和增加量化位数来减小，但不能完全消除。

6. 重构：重构是将采样信号恢复为连续时间信号的过程。

通过采样定理，采样信号可以用原始信号的线性插值方法进行重构。

常用的重构方法有零阶保持插值、一阶保持插值和多项式插值。

采样信号在实际应用中具有重要的意义。

首先，采样信号可以方便进行数据存储和传输。

通过将连续时间信号转换为离散时间信号，可以在数字设备中对信号进行处理、存储和传输，提高信号的处理效率。

其次，采样信号可以方便进行数字信号处理。

采样信号可以利用离散时间信号处理的方法，如滤波、卷积、频域分析等，对信号进行处理和分析。

信号与系统中抽样的概念

信号与系统中抽样的概念抽样是信号与系统中一个重要的概念。

在信号处理中，抽样是指对连续时间信号进行离散化处理，将连续时间信号转换为离散时间信号的过程。

抽样的目的是为了将连续时间信号转换为数字信号，使得信号可以通过数字方式进行存储、传输和处理。

抽样过程可以看作是在连续时间域上对信号进行定时取样。

抽样过程中，我们使用采样定理（奈奎斯特定理）来保证抽样后的信号不失真。

采样定理指出，为了避免信号采样引起的混叠现象，抽样频率必须大于等于原始信号中最高频率的两倍，也就是满足奈奎斯特频率。

在实际应用中，我们通常采用理想脉冲序列作为采样信号。

理想脉冲序列是一个周期为T的序列，每个周期内有一个脉冲，其他时间点上为零。

理想脉冲序列的傅里叶变换是一个周期序列（频率为1/T）的线性组合。

对连续时间信号x(t)进行抽样，可以通过将x(t)与理想脉冲序列进行卷积来实现。

即将x(t)乘以理想脉冲序列，然后对乘积信号进行积分。

抽样后得到的信号为离散时间信号x[n]，其中n为整数，表示采样时刻。

离散时间信号x[n]可以看作是连续时间信号x(t)在采样时刻的取样值。

为了重构x(t)，可以通过将x[n]与插值函数进行卷积来实现。

插值函数可以看作是理想脉冲序列的反变换，即将理想脉冲序列的傅里叶变换除以周期序列的傅里叶变换。

抽样引入了两个重要的参数，即采样间隔和采样频率。

采样间隔为采样时刻之间的时间间隔，采样频率为采样时刻之间的倒数，即采样频率等于1/采样间隔。

采样频率越高，采样精度越高，重构信号的失真越小。

但是，采样频率过高也会导致计算和存储的需求增加。

抽样过程中，还存在一个概念叫做抽样定理。

抽样定理指出，在有限频带B内的连续时间信号，可以通过以准确率误差小于ε的方式进行采样和重构，只需要满足采样频率f_s大于等于2B。

这是由带限信号在频域中没有重叠而导致的。

如果信号的频域存在重叠，则需要进一步提高采样频率以避免混叠现象。

在实际应用中，我们使用的信号不一定是有限频带的信号，因此在抽样过程中，可能会引入混叠现象。

采样频率说明

采样频率、采样点数、分辨率、谱线数(line)1．最高分析频率：Fm指需要分析的最高频率，也是经过抗混滤波后的信号最高频率。

根据采样定理，Fm与采样频率Fs之间的关系一般为：Fs=2.56Fm；而最高分析频率的选取决定于设备转速和预期所要判定的故障性质。

2．采样点数N与谱线数M有如下的关系：N=2.56M 其中谱线数M与频率分辨率ΔF及最高分析频率Fm有如下的关系：ΔF=Fm/M 即：M=Fm/ΔF 所以：N=2.56Fm/ΔF★采样点数的多少与要求多大的频率分辨率有关。

例如：机器转速3000r/min=50Hz，如果要分析的故障频率估计在8倍频以下，要求谱图上频率分辨率ΔF=1 Hz ,则采样频率和采样点数设置为：最高分析频率Fm=8·50Hz=400Hz;采样频率Fs=2.56·Fm=2.56 ·400Hz=1024Hz;采样点数N=2.56·（Fm/ΔF）=2.56·（400Hz/1Hz）=1024谱线数M=N/2.56=1024/2.56=400条按照FFT变换，实际上得到的也是1024点的谱线，但是我们知道数学计算上存在负频率，是对称的，因此，实际上我们关注的是正频率部分对应的谱线，也就是说正频率有512线，为什么我们通常又说这种情况下是400线呢，就是因为通常情况下由于频率混叠和时域截断的影响，通常认为401线到512线的频谱精度不高而不予考虑。

另外，采样点数也不是随便设置的，即不是越大越好，反之亦然.对于旋转机械必须满足整周期采样，以消除频率畸形，单纯提高分辨率也不能消除频率畸形过去，有人以为数据越长越好，或随便定时域信号长度，其实，这样做是在某些概念上不清楚，例如，不清楚整周期采样.不产生频率混叠的最低采样频率Fs要求在2倍最大分析频率Fm，之所以采用2.56倍主要跟计算机二进制的表示方式有关。

其主要目的是避免信号混淆保证高频信号不被歪曲成低频信号。

什么是采样频率意思

什么是采样频率意思采样频率只能用于周期性采样的采样器，对于非周期性采样的采样器没有规则限制。

那么你对采样频率了解多少呢?以下是由店铺整理关于什么是采样频率的内容，希望大家喜欢!什么是采样频率采样频率，也称为采样速度或者采样率，定义了每秒从连续信号中提取并组成离散信号的采样个数，它用赫兹(Hz)来表示。

采样频率的倒数是采样周期或者叫作采样时间，它是采样之间的时间间隔。

通俗的讲采样频率是指计算机每秒钟采集多少个信号样本。

连续信号在时间(或空间)上以某种方式变化着，而采样过程则是在时间(或空间)上，以T为单位间隔来测量连续信号的值。

T称为采样间隔。

在实际中，如果信号是时间的函数，通常他们的采样间隔都很小，一般在毫秒、微秒的量级。

采样过程产生一系列的数字，称为样本。

样本代表了原来的信号。

每一个样本都对应着测量这一样本的特定时间点，而采样间隔的倒数，1/T即为采样频率，fs，其单位为样本/秒，即赫兹(hertz)。

采样频率只能用于周期性采样的采样器，对于非周期性采样的采样器没有规则限制。

采样频率的常用的表示符号是fs。

通俗的讲采样频率是指计算机每秒钟采集多少个信号样本，比如声音信号，此时采样频率可以是描述声音文件的音质、音调，衡量声卡、声音文件的质量标准。

采样频率越高，即采样的间隔时间越短，则在单位时间内计算机得到的样本数据就越多，对信号波形的表示也越精确。

采样频率与原始信号频率之间有一定的关系，根据奈奎斯特理论，只有采样频率高于原始信号最高频率的两倍时，才能把数字信号表示的信号还原成为原来信号。

在数字音频领域，常用的采样率有：8000Hz 电话所用采样率，对于人的说话已经足够11025Hz 获得的声音称为电话音质，基本上能让你分辨出通话人的声音22050Hz 无线电广播所用采样率，广播音质32000Hz miniDV数码视频camcorder、DAT(LPmode)所用采样率44100Hz 音频CD，也常用于MPEG-1音频(VCD，SVCD，MP3)所用采样率47250Hz NipponColumbia(Denon)开发的世界上第一个商用PCM录音机所用采样率48000Hz miniDV、数字电视、DVD、DAT、电影和专业音频所用的数字声音所用采样率50000Hz 二十世纪七十年代后期出现的3M和Soundstream开发的第一款商用数字录音机所用采样率50400Hz 三菱X-80数字录音机所用所用采样率96000或192000Hz DVD-Audio、一些LPCMDVD音轨、BD-ROM(蓝光盘)音轨、和HD-DVD(高清晰度DVD)音轨所用所用采样率28224MHz SACD、索尼和飞利浦联合开发的称为DirectStreamDigital的1位sigma-deltamodulation过程所用采样率总之当前声卡常用的采样频率一般为44.1KHz(每秒采集声音样本44.1千次)11KHz、22KHz、和48KHz。

故障信号采集中的采样长度_时间间隔和频率的关系

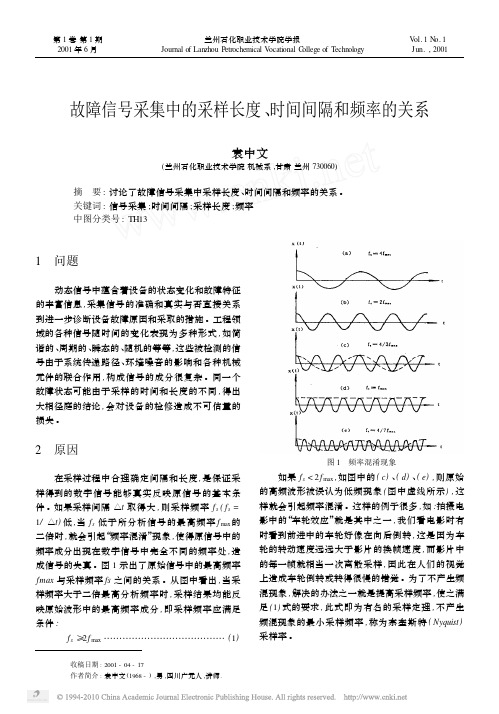
故障信号采集中的采样长度、时间间隔和频率的关系袁中文(兰州石化职业技术学院机械系,甘肃兰州730060)摘　要:讨论了故障信号采集中采样长度、时间间隔和频率的关系。

关键词:信号采集;时间间隔;采样长度;频率中图分类号:TH131　问题动态信号中蕴含着设备的状态变化和故障特征的丰富信息,采集信号的准确和真实与否直接关系到进一步诊断设备故障原因和采取的措施。

工程领域的各种信号随时间的变化表现为多种形式,如简谐的、周期的、瞬态的、随机的等等,这些被检测的信号由于系统传递路径、环境噪音的影响和各种机械元件的联合作用,构成信号的成分很复杂。

同一个故障状态可能由于采样的时间和长度的不同,得出大相径庭的结论,会对设备的检修造成不可估量的损失。

2　原因在采样过程中合理确定间隔和长度,是保证采样得到的数字信号能够真实反映原信号的基本条件。

如果采样间隔△t取得大,则采样频率f s(f s= 1/△t)低,当f s低于所分析信号的最高频率f max的二倍时,就会引起“频率混淆”现象,使得原信号中的频率成分出现在数字信号中完全不同的频率处,造成信号的失真。

图1示出了原始信号中的最高频率fmax与采样频率fs之间的关系。

从图中看出,当采样频率大于二倍最高分析频率时,采样结果均能反映原始波形中的最高频率成分,即采样频率应满足条件: f s≥2f max(1)…………………………………图1　频率混淆现象如果f s<2f max,如图中的(c)、(d)、(e),则原始的高频波形被误认为低频现象(图中虚线所示),这样就会引起频率混淆。

这样的例子很多,如:拍摄电影中的“车轮效应”就是其中之一,我们看电影时有时看到前进中的车轮好像在向后倒转,这是因为车轮的转动速度远远大于影片的换帧速度,而影片中的每一帧就相当一次离散采样,因此在人们的视觉上造成车轮倒转或转得很慢的错觉。

为了不产生频混现象,解决的办法之一就是提高采样频率,使之满足(1)式的要求,此式即为有名的采样定理,不产生频混现象的最小采样频率,称为奈奎斯特(Nyquist)采样率。

信号采样长度、时间间隔和频率的关系

采样频率、采样点数、分辨率、谱线数(line)(2011-02-23 20:38:35)转载标签：分类：matlab采样频率谱线分辨率采样定理数学计算400line杂谈1．最高分析频率：Fm指需要分析的最高频率，也是经过抗混滤波后的信号最高频率。

根据采样定理，Fm与采样频率Fs之间的关系一般为：Fs=2.56Fm；而最高分析频率的选取决定于设备转速和预期所要判定的故障性质。

2．采样点数N与谱线数M有如下的关系：N=2.56M 其中谱线数M与频率分辨率ΔF及最高分析频率Fm有如下的关系：ΔF=Fm/M即：M=Fm/ΔF所以：N=2.56Fm/ΔF★采样点数的多少与要求多大的频率分辨率有关。

例如：机器转速3000r/min=50Hz，如果要分析的故障频率估计在8倍频以下，要求谱图上频率分辨率ΔF=1 Hz ,则采样频率和采样点数设置为：最高分析频率Fm=8·50Hz=400Hz;采样频率Fs=2.56·Fm=2.56 ·400Hz=1024Hz;采样点数N=2.56·（F m/ΔF）=2.56·（400Hz/1Hz）=1024谱线数M=N/2.56=1024/2.56=400条按照FFT变换，实际上得到的也是1024点的谱线，但是我们知道数学计算上存在负频率，是对称的，因此，实际上我们关注的是正频率部分对应的谱线，也就是说正频率有512线，为什么我们通常又说这种情况下是400线呢，就是因为通常情况下由于频率混叠和时域截断的影响，通常认为401线到512线的频谱精度不高而不予考虑。

另外，采样点数也不是随便设置的，即不是越大越好，反之亦然对于旋转机械必须满足整周期采样，以消除频率畸形，单纯提高分辨率也不能消除频率畸形过去，有人以为数据越长越好，或随便定时域信号长度，其实，这样做是在某些概念上不清楚，例如，不清楚整周期采样.不产生频率混迭的最低采样频率Fs要求在2倍最大分析频率Fm，之所以采用2.56倍主要跟计算机二进制的表示方式有关。

奈奎斯特频率和采样频率的关系

奈奎斯特频率和采样频率的关系一、引言奈奎斯特频率和采样频率是数字信号处理中非常重要的概念，它们直接影响着数字信号的采样、重构和滤波等过程。

本文将从基础概念、数学推导和实际应用等方面，全面介绍奈奎斯特频率和采样频率的关系。

二、基础概念1. 奈奎斯特定理奈奎斯特定理是数字信号处理中最基本的定理之一，它指出：如果一个连续时间信号的最高频率为fmax，那么在进行采样时，采样频率fs 必须大于2*fmax才能完全还原原始信号。

2. 奈奎斯特频率奈奎斯特频率也称为折叠频率或Nyquist折叠频率，是指当采样频率fs固定时，能够被完全还原的最高模拟信号的频率。

其计算公式为：f_nyquist = fs / 23. 采样频率采样频率是指对连续时间信号进行离散化时所使用的每秒采样次数。

在数字信号处理中，通常使用赫兹（Hz）作为单位。

其计算公式为：fs = 1 / T其中T为采样间隔时间。

三、数学推导1. 采样定理根据奈奎斯特定理，为了完全还原原始信号，采样频率必须大于等于2倍的最高模拟信号频率。

即：fs >= 2*fmax这个条件称为采样定理。

2. 折叠现象当采样频率小于2倍的最高模拟信号频率时，就会出现折叠现象。

折叠现象是指在重构过程中，高于奈奎斯特频率的信号被错误地重构成低于奈奎斯特频率的信号，从而导致信息丢失和失真。

3. 数学推导设原始模拟信号为x(t)，其傅里叶变换为X(f)。

将x(t)进行离散化得到序列x[n]，其傅里叶变换为X(e^jw)。

其中w=2*pi*f/fs。

根据采样定理可得：fs >= 2*fmax即：w <= pi因此，在重构过程中，只需要保留-w到w范围内的分量即可还原原始信号。

但是，当w>pi时，由于周期性扩展的存在，会出现折叠现象。

四、实际应用1. 音频采样在音频采样中，通常使用的采样频率为44.1kHz或48kHz，这是因为人耳听觉范围的最高频率为20kHz左右。

信号采样长度、时间间隔和频率的关系

根据采样定理，Fm与采样频率Fs之间的关系一般为：Fs=2.56Fm；而最高分析频率的选取决定于设备转速和预期所要判定的故障性质。

2．采样点数N与谱线数M有如下的关系：N=2.56M 其中谱线数M与频率分辨率ΔF及最高分析频率Fm有如下的关系：ΔF=Fm/M即：M=Fm/ΔF所以：N=2.56Fm/ΔF★采样点数的多少与要求多大的频率分辨率有关。

采样率和频率的关系

采样率和频率的关系采样频率，也称为采样速度或者采样率，定义了每秒从连续信号中提取并组成离散信号的采样个数，它用赫兹（Hz）来表示。

采样频率的倒数是采样周期或者叫作采样时间，它是采样之间的时间间隔。

通俗的讲采样频率是指计算机每秒钟采集多少个声音样本，是描述声音文件的音质、音调，衡量声卡、声音文件的质量标准。

通俗的讲采样频率是指计算机每秒钟采集多少个样本（样本点）。

采样频率越高，即采样的间隔时间越短，则在单位时间内计算机得到的声音样本数据就越多，对声音波形的表示也越精确。

采样频率与声音频率之间有一定的关系，根据奈奎斯特理论，只有采样频率高于声音信号最高频率的两倍时，才能把数字信号表示的声音还原成为原来的声音。

采样率表示了每秒对原始信号采样的次数，我们常见到的音频文件采样率多为44.1KHz，这意味着什么呢？假设我们有2段正弦波信号，分别为20Hz和20KHz，长度均为一秒钟，以对应我们能听到的最低频和最高频，分别对这两段信号进行40KHz的采样，我们可以得到一个什么样的结果呢？结果是：20Hz的信号每次振动被采样了40K/20=2000次，而20K的信号每次振动只有2次采样。

显然，在相同的采样率下，记录低频的信息远比高频的详细。

这也是为什么有些音响发烧友指责CD有数码声不够真实的原因，CD的44.1KHz采样也无法保证高频信号被较好记录。

要较好的记录高频信号，看来需要更高的采样率，于是有些朋友在捕捉CD音轨的时候使用48KHz的采样率，这是不可取的！这其实对音质没有任何好处，对抓轨软件来说，保持和CD提供的44.1KHz一样的采样率才是最佳音质的保证之一，而不是去提高它。

较高的采样率只有相对模拟信号的时候才有用，如果被采样的信号是数字的，请不要去尝试提高采样率。

快速傅里叶变化中点数,间隔,载频,采样频率关系

快速傅里叶变化中点数，间隔，载频，采样
频率关系
快速傅里叶变换（FFT）中，点数、间隔、载频和采样频率是密
切相关的。

点数指FFT算法处理的样本点数，通常为2的整数次幂（如2的
8次方、2的16次方等）。

间隔指每个样本点之间的时间间隔，它与采样频率和点数有关。

具体地，间隔等于采样周期除以点数，即间隔=1/（采样频率*点数）。

载频通常指离散傅里叶变换（DFT）中频域的坐标轴，FFT算法则是对DFT的一种优化，因此也沿用了这一概念。

实际上，FFT变换的结果是一段离散频域的数据，其横坐标表示的是频率（或者归一化频率），纵坐标表示的是信号在这个频率上的幅值。

采样频率则是指数字信号每一秒钟采样的次数，通常用赫兹（Hz）表示。

采样频率应该大于信号带宽的两倍，这样才能避免采样误差。

在FFT中，采样频率与间隔有关，可以通过间隔的倒数得到。

例如，
采样频率等于1/（间隔*点数）。

综上所述，FFT中的点数、间隔、载频和采样频率是相互依存的，它们的关系可以通过上述公式相互推导和计算。

信号频率对长度差异的要求

信号频率对长度差异的要求
首先，信号频率（即信号波形的频率）决定了信号传输速率。

在数字
通信中，信号被转化成数字序列进行传输，每个数字被编码成一段特定的
信号波形。

信号频率越高，单位时间内传输的数字序列就越多，传输速率
就越快。

例如，在1200Hz频率下，每秒钟可以传输1200个数字；而在2400Hz频率下，每秒钟可以传输2400个数字。

因此，信号频率越高，长
度差异的要求就越高，对信号传输的时间容忍度越低。

其次，信号频率对信号传输距离的要求也有影响。

在信号传输过程中，信号的频率会受到传输媒介的衰减和干扰等因素的影响。

高频信号在传输
过程中容易受到更大程度的衰减和干扰，因此其传输距离相对较短。

如果
信号的频率较高，传输距离较长，就需要更复杂的信号处理技术和更好的
传输媒介来保证信号的传输品质。

在实际应用中，例如在无线通信领域，
会采用不同的频率范围来适应不同传输距离的需求。

最后，信号频率对信号的抗噪声能力也有影响。

在传输过程中，信号
会受到各种噪声的干扰，例如信号源本身的噪声、传输媒介中的干扰以及
外部环境的干扰等。

不同频率的信号受到噪声干扰的程度也不同。

一般来说，低频信号相对于高频信号来说，具有更好的抗噪声能力。

因此，在要
求对噪声抗干扰能力较高的场景下，更适合使用低频信号。

总之，信号频率对长度差异的要求主要体现在信号传输速率、传输距
离和抗噪声能力方面。

在实际应用中，需要根据具体的传输需求和环境条件，选择合适的信号频率来满足信号传输的需求。

fft采样率和采样间隔

FFT采样率和采样间隔1. 什么是FFTFFT（Fast Fourier Transform，快速傅里叶变换）是一种用于将时域信号转换为频域信号的算法。

它可以将连续的时间信号转换为离散的频谱数据，从而帮助我们分析信号的频率成分和能量分布。

2. 采样率和采样间隔的概念在讨论FFT的采样率和采样间隔之前，我们先来了解一下这两个概念。

2.1 采样率采样率是指每秒钟对信号进行采集的次数，单位为Hz。

在数字信号处理中，我们常常使用离散时间来表示信号，而采样率就决定了离散时间中每个单位时间内有多少个数据点。

2.2 采样间隔采样间隔是指两个相邻数据点之间的时间间隔，它与采样率有以下关系：采样间隔 = 1 / 采样率3. FFT与采样率、采样间隔的关系FFT算法要求输入的信号是等间隔离散化的，并且要求输入信号长度必须是2的幂次方。

因此，在进行FFT之前，我们需要确定好采样率和采样间隔。

3.1 采样率对FFT的影响采样率决定了信号在频域中的分辨率。

根据奈奎斯特定理，信号的最高频率成分应小于等于采样率的一半。

如果信号的最高频率超过了采样率的一半，就会发生混叠现象，导致频谱失真。

对于一个信号来说，如果我们希望能够准确地还原其频谱信息，就需要选择足够高的采样率。

否则，高频成分可能会被低采样率下的混叠效应所掩盖。

3.2 采样间隔对FFT的影响采样间隔决定了离散时间中数据点之间的距离。

较小的采样间隔可以提供更多细节丰富的频谱信息，但同时也增加了计算量和存储需求。

在进行FFT之前，我们需要根据信号特性和计算资源来选择合适的采样间隔。

如果信号变化较快或者包含高频成分，则需要选择较小的采样间隔以捕捉到更多细节；反之，则可以适当增大采样间隔以节省计算资源。

4. FFT采样率和采样间隔的选择方法在实际应用中，我们如何选择合适的采样率和采样间隔呢？下面给出一些常见的选择方法。

4.1 根据信号频率范围选择采样率首先，我们需要了解信号中包含的频率范围。

ofdm时域采样和频谱的关系

ofdm时域采样和频谱的关系OFDM（正交频分复用）是一种多载波调制技术，是将高速串行数据分成许多低速并行数据流进行传输的技术。

OFDM技术通过将频带划分为若干个小的子载波，每个子载波的带宽相对较窄，而且由于子载波之间正交的特性，可以在频域上有效地避免互相干扰，提高了频谱利用效率。

OFDM的时域采样和频谱之间有着密切的关系，下面具体介绍其关系及相关内容。

一、OFDM时域采样1. 概念OFDM在时域上是一种周期性的信号，周期为T，周期内的采样点数为N。

OFDM的周期性信号由多个子载波构成，在每个子载波上都可以采样得到一个复数样点，这些样点按照一定的规则进行排列，形成一个OFDM符号。

2. 采样间隔OFDM的时域采样间隔（Ts）是采样点之间的时间间隔。

对于一个OFDM符号，采样间隔应满足Nyquist采样定理，即Fs≥2B，其中Fs为采样频率，B为OFDM信号的带宽。

采样间隔的确定直接影响到OFDM信号的频谱特性。

3. 采样点数OFDM的时域采样点数（N）与采样频率和符号时长之间有关系，N=T/Ts，其中T为OFDM符号的时长。

采样点数决定了OFDM信号在时域上的分辨率和频谱上的分辨率。

二、OFDM频谱1. 概念OFDM的频谱是指OFDM信号在频域上的分布情况。

OFDM 信号的频谱由多个子载波的频谱组成，每个子载波的频谱宽度为1/T，可以看作是一个窄带信号。

子载波之间相互正交，因此在频谱上不会相互干扰。

2. 子载波间距OFDM的频谱中，子载波之间的频率间隔为Δf=1/T，也称为子载波间距。

子载波间距决定了OFDM信号的频谱分辨率和重叠程度，频谱分辨率越高，子载波间距越小。

3. 频谱分布OFDM信号的频谱分布在频域上呈现多个窄带的频谱线，频谱线的宽度为1/T，对应于一个子载波的频谱宽度。

频谱线之间相互正交，不会相互干扰，因此OFDM信号的频谱利用率较高。

4. 频率响应OFDM信号的频率响应是指OFDM信号在频域上的幅度和相位响应。

fft采样率和采样间隔

fft采样率和采样间隔在信号处理领域，FFT（快速傅里叶变换）是一种广泛应用的算法，它能够将时域信号转换为频域信号，从而为我们分析信号的频率特性提供便利。

而在FFT计算过程中，采样率和采样间隔是两个至关重要的参数。

下面我们将详细讨论这两个概念及其在实际应用中的重要性。

1.FFT采样率与采样间隔的基本概念采样率指的是在单位时间内对信号进行采样的次数。

采样间隔则是指两次采样之间的间隔。

在实际应用中，采样率和采样间隔通常决定了FFT计算的精度和效率。

2.FFT采样率与采样间隔的关系根据奈奎斯特定理，采样频率必须大于信号频率的两倍，才能保证信号的完整性，避免发生混叠。

同样，在FFT计算中，采样率越高，得到的频谱分辨率越高，分析结果越精确。

而采样间隔越小，相邻采样点之间的距离越小，能够在频谱分析时更准确地捕捉到信号的频率变化。

3.FFT采样率与采样间隔在实际应用中的重要性在实际应用中，合适的采样率和采样间隔对于保证FFT计算结果的准确性具有重要意义。

例如，在音频处理领域，如果采样率和采样间隔设置不当，可能导致音频信号的失真，影响音质。

在通信系统中也同样如此，合适的采样率和采样间隔有助于提高信号的传输质量和稳定性。

4.提高FFT采样率与采样间隔的方法和技巧为了提高FFT采样率与采样间隔，我们可以采用以下方法和技巧：1）提高采样设备的精度：采用更高精度的采样设备，可以提高采样率，从而提高FFT计算结果的准确性。

2）优化信号处理算法：通过改进信号处理算法，提高计算效率，从而在保证结果准确性的同时，降低对采样率和采样间隔的要求。

3）采用插值方法：在FFT计算前，可以对原始信号进行插值处理，增加采样点，从而提高采样率和采样间隔。

5.总结FFT采样率和采样间隔在信号处理领域具有重要作用。

合适的采样率和采样间隔可以保证FFT计算结果的准确性，提高信号分析的可靠性。

matlab采样点数

在MATLAB中，采样点数是指在一定时间内对信号进行采样的次数或样本数。

采样点数的计算方法可以通过采样频率和采样时间的关系得出：N = fs * T，其中N是采样点数，fs是采样频率，T是采样时间。

此外，采样点数也可以通过采样间隔和采样时间的关系计算得出：N = T / Ts，其中Ts 是采样间隔。

需要注意的是，采样频率必须大于信号的频率以确保信号的不失真，即fs / N(频率分辨率)越小，精度越高。

此外，FFT的点数必须是2的指数，因此在频域一个频点对应时域的一次采样，所以FFT的点数自然就是2048、1024、512、256、128。

补0增加的FFT点数无法提高FFT精度。

采样定理详解：3个主要条件只需满足其中任意2个

采样定理详解：3个主要条件只需满⾜其中任意2个采样定理采样定理解决的问题是确定合理的采样间隔△t以及合理的采样长度T，保障采样所得的数字信号能真实地代表原来的连续信号x(t)。

衡量采样速度⾼低的指标称为采样频率fs。

⼀般来说，采样频率fs越⾼，采样点越密，所获得的数字信号越逼近原信号。

为了兼顾计算机存储量和计算⼯作量，⼀般保证信号不丢失或歪曲原信号信息就可以满⾜实际需要了。

这个基本要求就是所谓的采样定理，是由Shannon提出的，也称为Shannon采样定理。

Shannon采样定理规定了带限信号不丢失信息的最低采样频率为式中fm为原信号中最⾼频率成分的频率。

采集的数据量⼤⼩N为因此，当采样长度⼀定时，采样频率越⾼，采集的数据量就越⼤。

使⽤采样频率时有两个问题需要注意。

正确估计原信号中最⾼频率成分的频率，对于采⽤电涡流传感器测振的系统来说，⼀般确定为最⾼分析频率为12.5X，采样模式为同步整周期采集，若选择频谱分辨率为400线，需采集1024点数据，若每周期采集32点，采样长度为32周期。

同样的数据量可以通过改变每周期采样点数提⾼基频分辨率，这对于识别次同步振动信号是必要的，但降低了最⾼分析频率，如何确定视具体情况⽽定。

采样定理解析采样定理实际上涉及了3个主要条件，当确定其中2个条件后，第3个条件⾃动形成。

这3个条件是进⾏正确数据采集的基础，必须理解深刻。

条件1：采样频率控制最⾼分析频率采样频率(采样速率)越⾼，获得的信号频率响应越⾼，换⾔之，当需要⾼频信号时，就需要提⾼采样频率，采样频率应符合采样定理基本要求。

这个条件看起来似乎很简单，但对于⼀个未知信号，其中所含最⾼频率信号的频率究竟有多⾼，实际上我们是⽆法知道的。

解决这个问题需要2个步骤，⼀是指定最⾼测量频率，⼆是采⽤低通滤波器把⾼于设定最⾼测量频率的成分全部去掉(这个低通滤波器就是抗混滤波器)。

现实的抗混滤波器与理论上的滤波器存在差异，因此信号中仍会存在⼀定混叠成分，⼀般在计算频谱后将⾼频成分去掉，⼀般频谱线数取时域数据点的1/2.56，或取频域幅值数据点的1/1.28，即128线频谱取100线，256线频谱取200线，512线频谱取400线等等。

fft采样率和采样间隔

fft采样率和采样间隔在信号处理领域，FFT（快速傅里叶变换）技术被广泛应用。

FFT采样率和采样间隔是影响信号处理效果的重要因素。

本文将详细介绍FFT采样率与采样间隔的概念、关系及在实际应用中的重要性，并提供提高FFT采样率和采样间隔的方法与技巧。

首先，我们来了解一下FFT采样率与采样间隔的基本概念。

采样率是指在一段时间内，对信号进行采样的次数。

采样间隔则是指两次采样之间的间隔时间。

在信号处理中，采样率越高，采样间隔越小，意味着对信号的采样点数越多，信号的分辨率越高。

接下来，我们探讨一下FFT采样率与采样间隔的关系。

根据奈奎斯特定理，采样频率必须大于信号频率的两倍，才能在数字化过程中无失真地恢复原始信号。

因此，在FFT采样过程中，采样率与采样间隔的关系为：采样率>= 2 * 信号频率。

只有满足这个条件，才能保证信号的完整性，避免发生混叠。

那么，FFT采样率与采样间隔在实际应用中的重要性体现在哪里呢？答案在于它们直接影响到信号处理的准确性和还原度。

采样率越高，采样间隔越小，意味着信号的分辨率越高，处理结果的精度也就越高。

反之，如果采样率过低或采样间隔过大，将会导致信号失真，从而影响处理结果的可靠性。

那么，如何提高FFT采样率和采样间隔呢？有以下几点建议：1.提高采样设备的精度：选择高精度的采样设备，可以提高采样率和解采样间隔。

2.优化信号处理算法：通过优化算法，提高算法效率，从而在同等计算资源下提高采样率和采样间隔。

3.采用插值算法：在采样间隔较大时，可以采用插值算法填补空缺，提高采样率。

4.合理选择采样频率：根据信号特点和处理需求，合理选择采样频率，使之满足奈奎斯特定理的要求。

总之，FFT采样率与采样间隔在信号处理中具有关键作用。

只有掌握它们的概念、关系及重要性，才能更好地应用于实际信号处理任务，提高信号处理的准确性和还原度。