7.1机械振动
传感器与测试技术7 振动的测量

在加速度计与被测物之间涂一层硅胶,可改善冲击状
态,有利于高频响应。
Page ▪ 35
7.2 测振传感器
7.2.3 接触式测振传感器的校准 ⑴ 绝对法 拾振器固定在校准用的标准振动台上,由正弦信号发生器
发出标准信号,经功率放大器放大,推动振动台,用激光干涉 振动仪直接测量振动台的振幅,在与被校准拾振器的输出进行 比较,从而确定拾振器的灵敏度。可以同时测量频率响应。
Page ▪ 7
7.1 概述
(3)测振放大器 它将测振传感器转换后的电信号加以放大 ,以便分析设备
的后续分析、处理以及记录显示仪器的记录、显示、绘图等。 常用的测振放大器类型有电荷放大器、电压放大器和调制型放 大器等。
(4)分析设备 主要有频谱分析仪,可分为模拟式和数字式两大类。
(5)记录显示仪器 根据振动测量的不同目的,可将振动测量结果以数据或图
Page ▪ 15
惯性式位移传感器的相频特性
② 速度传感器
7.2 测振传感器
x y0 0
(n)2 1(n)2 242(n)2
动态特性与位移传感器相同
③ 加速度传感器
y0
x0 2
1
2 n
1(n)2 242(n)2
y0
x0
2 n 2
1
1(n)2 242(n)2
质量元件相对壳体的位移与被测振动加速度成正比 。
惯性传感器的质量元件相对于外壳的运动与被测物体的运 动规律一样。
其振幅比与相位差值由传感器的固有频率及阻尼比的大小 来确定。
讨论: ① 位移传感器
n ,0.6~0.7低频只能保证幅值精度,无法保证
机械振动原理

机械振动原理机械振动是指物体在受到外力作用下产生的周期性运动。
在工程实践中,我们经常会遇到各种各样的机械振动问题,比如机械结构的振动、机械设备的振动、以及振动控制等。
了解机械振动原理对于解决这些问题至关重要。
首先,让我们来了解一下机械振动的基本原理。
当一个物体受到外力作用时,它会产生振动。
这是因为外力会改变物体的平衡状态,使得物体产生位移。
而物体的位移又会导致弹性力的作用,使得物体产生惯性力,从而产生振动。
这种周期性的运动就是机械振动。
机械振动的特点是周期性和频率。
周期性是指振动是按照一定的周期重复的,而频率则是指单位时间内振动的次数。
振动的频率与物体的固有频率有关,物体的固有频率是指在没有外力作用下,物体自身固有的振动频率。
当外力的频率与物体的固有频率相同时,就会出现共振现象,这会对机械系统造成破坏。
了解机械振动的原理对于工程实践有着重要的意义。
首先,它可以帮助我们分析和预测机械系统的振动特性,从而设计出更加稳定和可靠的机械结构和设备。
其次,它可以帮助我们解决机械系统中出现的振动问题,比如减小振动、消除共振等。
最后,它还可以为我们提供优化设计和改进机械系统的思路。
在工程实践中,我们可以通过仿真和实验的方法来研究机械振动问题。
通过建立数学模型,我们可以分析机械系统的振动特性,比如振幅、频率、相位等。
同时,我们还可以通过实验来验证模型的准确性,并对机械系统进行振动测试,从而找出问题的根源并加以解决。
总之,了解机械振动的原理对于工程实践至关重要。
它可以帮助我们分析和预测机械系统的振动特性,解决振动问题,优化设计和改进机械系统。
通过不断地研究和实践,我们可以不断提高对机械振动的理解,从而为工程实践提供更加可靠和稳定的机械系统。
内科大安全环境监测技术教案第7章 振动检测

【课堂教学小结】3分钟)1、振动与噪音本质上相同,只是频率和传播介质不同。
2、我们所学振动检测,重点掌握环境振动的检测,适合我们矿业的作业场所。
参考位置等优点,由于它的脉冲响应优异,更适合于冲击的测量。
CI=史=2力V=Q时)2Adt4)拾振器的充分利用一般情况尽量用同参数相应的传感器进行测量,也可用电学微积分原理进行测量,但测量误差较大。
7.4拾振器7.4.1 压电式加速度计1.1.1 工作原理(1)组成:压电晶体、弹簧元件、外壳、引线。
(2)原理:(图示说明)2)特点体积小、灵敏度高、测量频率宽。
3)主要参数(1)灵敏度:输出量的变化与输入量变化的比值(2)安装方法与上限频率(3)前置放大器与下限频率(4)横向灵敏度(5)动态范围(6)环境影响程度1.1.2 磁电式速度计1)结构原理(1)组成:线圈、磁钢、顶杠、弹簧片、附件。
(2)原理:切割磁力线产生感生电动势(图示说明)。
2)特点a.只能测量质点振动b.可以做成相对和绝对两种(约20分钟) (约20分钟)c.输出幅度大d.输出阻抗低e.体积较压电式大1.1.3 拾振器的合理选择1)自振频率和工作频率的选择2)灵敏度的选择3)测量范围的选择4)测量内容的选择(本节无作业)【课堂教学小结】(3分钟)1、振动测量主要是根据振动类型正确选择拾振器;2、合理布置拾振器;3、准确分析测量结果。
(约12分钟)举例课程名称:安全环境监测技术7∙6测振仪的校准与标定1)标定内容X⑴拾振器灵敏度标定在振动台上进行,fW200Hz,a≤10g灵敏度Sv=U∕Xa=4π2f2A A为振幅读书;U为输出电压;f为频率(2)实验室条件下的二次标定2)频率特性的标定(1)频率响应:测频带(带宽)⑵谐振频率7.7振动允许标准(约20分钟)D人体允许振动标准(246页)人体可以通过各种感受器接收振动的信息,并通过大脑对振动作出相应的反应和判断。
根据振动对人影响的程度,可以建立振动的评价标准。
大学物理 第7章 机械波

(1)以点A为坐标原点,写出波动方程. (2)以距点A为5m处的点B为坐 标原点,写出波动方程; (3)写出传播方向上点C、点D的简谐运动方 程; (4)分别求出BC和CD两点间的相位差.
u • C 8m • B 5m • A 9m
u
解:已知 u=20m/s
频率与周期的关系为:
波速(u) : 振动状态在媒质中的传播速度.
波速与波长、周期和频率的关系为:
1 T
u
T
7.1.4、球面波和平面波
波场--波传播到的空间。
波线(波射线)--代表波的传播方向的射线。
波面--波场中同一时刻振动位相相同的点的轨迹。
波前(波阵面)--某时刻波源最初的振动状态 传到的波面。 各向同性均匀介质中,波线恒与波面垂直.
x ut y( x x , t t ) A cos[ ( t t ) 0 ] u x A cos[ ( t ) 0 ] u
t时刻的波形方程
u
y( x x , t t ) y( x , t )
例题1: 一平面简谐波以速率u = 20m/s沿直线传播. 已知在传播路径
机械振动在介质中的传播称为机械波。 声波、水波 波动是一切微观粒子的属性,
与微观粒子对应的波称为物质波。
各种类型的波有其特殊性,但也有普遍的共性, 有类似的波动方程。
7.1.1 机械波的产生
(1)有作机械振动的物体,即波源
(2)有连续的媒质 y
v x 如果波动中使介质各部分振动的回复力是弹性力, 则称为弹性波。
p I wu S
1 2 2 I A u 2
高中物理机械振动教案

高中物理机械振动教案
课题:机械振动
教学目标:
1. 了解机械振动的概念和特征;
2. 掌握机械振动的基本原理和表达方式;
3. 能够分析和解释机械振动在真实世界中的应用。
教学内容:
1. 机械振动的概念和分类;
2. 机械振动的基本特征;
3. 振动的周期、频率和振幅;
4. 振动的傅里叶级数表示;
5. 机械振动在真实世界中的应用案例。
教学重点:
1. 机械振动的基本概念和特征;
2. 振动的表达方式和分析方法。
教学难点:
1. 振动的傅里叶级数表示;
2. 机械振动在实际应用中的分析和解释。
教学过程:
一、导入
教师引入机械振动的概念,通过视频或图片展示一些常见的机械振动现象,引发学生对这一主题的兴趣。
二、讲解
1. 介绍机械振动的分类和特征;
2. 讲解振动的周期、频率和振幅的概念及计算方法;
3. 介绍振动的傅里叶级数表示方法。
三、例题解析
教师通过实例讲解振动的傅里叶级数表示方法,让学生理解振动信号的频谱分布和特点。
四、讨论
学生分组讨论机械振动在真实世界中的应用案例,分享自己的观点和见解。
五、总结
教师总结本节课的主要内容,强调学生应该掌握的重点和难点,引导学生对机械振动有更深入的理解。
教学反思:
通过这节课的教学,学生应该能够了解机械振动的基本原理和特征,掌握振动信号的傅里叶级数表示方法,并能够分析和解释机械振动在真实世界中的应用。
在教学过程中,要注重引导学生思考和讨论,激发他们的探究兴趣,提高他们的学习能力和综合素质。
大学物理-机械振动

机械振动也会影响交通工具的舒适 度,如火车、汽车等在行驶过程中 产生的振动,会让乘客感到不适。
机械振动在工程中的应用
振动输送
利用振动原理实现物料的输送,如振动筛、振动输送机等。
振动破碎
利用振动产生的冲击力破碎硬物,如破碎机、振动磨等。
振动减震
在建筑、桥梁等工程中,采用减震措施来减小机械振动对结构的影 响,提高结构的稳定性和安全性。
感谢您的观看
THANKS
机械振动理论的发展可以追溯到 古代,如中国的编钟和古代乐器 的制作。
近代发展
随着物理学和工程学的发展,人 们对机械振动的认识不断深入, 应用范围也不断扩大。
未来展望
随着科技的不断进步,机械振动 在新能源、新材料、航空航天等 领域的应用前景将更加广阔。
02
机械振动的类型与模型
简谐振动
总结词
简谐振动是最基本的振动类型,其运动规律可以用正弦函数或余弦函数描述。
机械振动在科研中的应用
振动谱分析
01
通过对物质在不同频率下的振动响应进行分析,可以研究物质
的分子结构和性质。
振动控制
02
通过控制机械振动的参数,实现对机械系统性能的优化和控制,
如振动减震、振动隔离等。
振动实验
03
利用振动实验来研究机械系统的动态特性和响应,如振动台实
验、共振实验等。
05
机械振动的实验与测量
根据实验需求设定振动频率、幅度和波形等 参数。
启动实验
启动振动台和数据采集器,开始记录数据。
数据处理
将采集到的数据导入计算机,进行滤波、去 噪和整理,以便后续分析。
绘制图表
将处理后的数据绘制成图表,如时域波形图、 频谱图等,以便观察和分析。
高中物理教案机械振动

高中物理教案机械振动
课程目标:
1. 了解机械振动的基本概念和相关知识;
2. 掌握机械振动的分类和特点;
3. 能够分析和解释机械振动的原因和规律;
4. 能够运用机械振动相关知识解决实际问题。
教学内容:
1. 机械振动的定义和基本概念;
2. 机械振动的分类和特点;
3. 机械振动的原因和规律;
4. 机械振动的应用和实例。
教学过程:
一、导入(5分钟)
引入机械振动的概念,让学生了解振动在生活中的广泛应用和重要性。
二、讲解基本概念(15分钟)
1. 介绍机械振动的定义和相关术语;
2. 讲解机械振动的分类和特点。
三、探究原因和规律(20分钟)
1. 分析引起机械振动的原因;
2. 介绍机械振动的规律和特点。
四、案例分析(15分钟)
通过实际案例,让学生应用所学知识分析和解决机械振动问题。
五、实验演示(20分钟)
展示一些机械振动的实验,帮助学生更直观地理解机械振动的过程和特点。
六、总结(5分钟)
总结本节课的内容,强调机械振动在工程和生活中的重要性,并展望下节课的学习内容。
作业:完成相关阅读材料,回答相关问题。
扩展活动:组织学生参加机械振动相关竞赛或实践活动,加深对机械振动知识的理解和实践能力提升。
评估方式:作业完成情况、参与课堂讨论、实验成绩等方式进行评估。
教学资源:教材、多媒体课件、实验器材等。
注意事项:在教学过程中要根据学生的实际情况和反馈及时调整教学方法,激发学生学习兴趣,提高学生的学习效果。
旋转机械及泵类振动等级标准
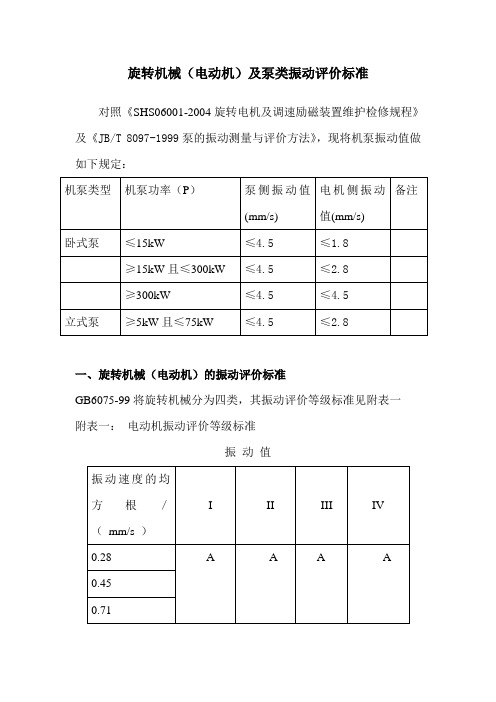
旋转机械(电动机)及泵类振动评价标准对照《SHS06001-2004旋转电机及调速励磁装置维护检修规程》及《JB/T 8097-1999泵的振动测量与评价方法》,现将机泵振动值做如下规定:一、旋转机械(电动机)的振动评价标准GB6075-99将旋转机械分为四类,其振动评价等级标准见附表一附表一:电动机振动评价等级标准振动值说明:I类设备为发动机和机器的单独部件,15kW以下的电动机是这类设备的典型例子;II类设备指无专门基础的中型机器(如5-75kW的电动机),以及在专门基础上刚性安装的发动机或机器(300kW以下的电动机;)III类设备指具有旋转质量安装在刚性的重型基础上的大型原动机和其他大型机器,基础在振动测量方向上室相对刚性的(如300kW以上电动机,10MW以下的发动机和燃气轮机);IV类设备指具有旋转质量安装在刚性的重型基础上的大型原动机和其他大型机器,基础在振动测量方向上的相对柔性的(如10MW以上的发动机和燃气轮组)。
将振动值评价等级分为四个区域:A、新交付使用的机器的振动必须在该区域内;B、通常认为振动值在该区域的机器可不受限制的长期运行;C、认为振动值在该区域的机器不适宜于长期运行,可在有限时间运行,但必须采取补救措施;D、振动值在这一区域通常认为振动剧烈,足以引起机器损坏。
二、泵的振动评价标准1、JB/T 8097-1999为了评价泵的振动级别,按泵的中心高和转速把泵分四类,见附表2。
2、评价泵的振动级别泵的振动级别分为A、B、C、D四级,D级为不合格。
泵的振动评价方法是首先按泵的中心高和转速查表2确定泵的类别,再根据泵的振动烈度级查表3,就可以得到评价泵的振动级别。
杂质泵的主动评价方法,如按表2在第一类的泵,用附表3第二类评价它的振动级别,依此类推。
附表2 泵的分类卧式泵的中心高规定为由泵的轴线到泵的底座上平面间的距离。
立式泵本来没有中心高,为了评价它的振动级别,取一个相当尺寸当做立式泵的中心高;即把立式泵的出口法兰密封面到泵轴线间的投影距离,规定为它的相当中心高。
上海交通大学大学物理课件-机械振动

y A
y
F [(V0 yS)]g mg
A
O
(V0g mg) ySg
m
ySg
m
m
d2 y dt 2
ySg
d2 dt
y
2
Sg
m
y
0
Sg
m
[例7-4]质量为m的刚体可绕固定水平轴o摆动。设刚体重心
C到轴o的距离为b,刚体对轴o的转动惯量为J。试证刚体
T 2π
T 2π 2π m
k
T 2π
-由振子性质确定-固有周期
= 1/T (Hz) -谐振动的频率
T 2π 2π m
k
T 2π
-由振子性质确定-固有周期
= 1/T (Hz) -谐振动的频率
而 2π k
Tm
-谐振动的角频率
—2秒内的振动次数
t =1s时x =-2cm且向x正向运动, 写出振动表达式。
A t=0
解:由题意,T = 2 s
t=1s 时的振动矢量如图所示。
t=0s 时的振动矢量方向应为
x
A1 矢量前1s时的旋转矢量。
(即半个周期前)
t = 1s
A1
与 A1 矢量夹角为 ,如图。 时矢量位置
由图, = /3
x
=
4cos(t
第 7 章 机械振动
物理系统受到外界扰动时,系统状态在平衡态附 近往复变化-周期运动或称振动。
物理量(如位移、电流等) 在某一数值附近反复变化。
振动有各种不同的形式:
•机械振动
L
•电磁振动
•微观振动(如晶格点阵
大学物理学 机械振动

大学物理学中的机械振动是指物体在受到外力作用后,产生周期性的来回振动运动的现象。
以下是关于机械振动的一些基本概念和内容:
1. 振动的基本特征
-周期性:振动是一个周期性的过程,即物体在围绕平衡位置来回振动。
-频率:振动的频率指的是单位时间内振动的周期数,通常用赫兹(Hz)表示。
-振幅:振动的振幅是物体从平衡位置最大偏离的距离。
2. 单自由度振动系统
-弹簧振子:是一种经典的单自由度振动系统,由弹簧和质点组成,受到弹簧的恢复力驱使质点振动。
-简谐振动:在没有阻尼和外力干扰的情况下,弹簧振子的振动是简谐的,即振动周期固定,频率与系统的固有频率相关。
3. 振动的参数和描述
-角频率:振动描述中常用的参数之一,表示振动的快慢程度,与频率之间有一定的关系。
-相位:描述振动状态的参数,表示振动的相对位置或状态。
-能量:振动系统具有动能和势能,能量在振动过程中不断转换,影响着振动的特性。
4. 阻尼振动和受迫振动
-阻尼振动:在振动系统中存在阻尼,会导致振动逐渐减弱,最终趋于稳定。
-受迫振动:当振动系统受到外力周期性作用时,会产生受迫振动,其频率与外力频率相同或有关。
5. 振动的应用
-工程领域:振动理论在工程领域有着广泛的应用,如建筑结构的抗震设计、机械系统的振动分析等。
-科学研究:振动理论也在物理学、工程学、生物学等领域中发挥重要作用,帮助解释和研究各种现象和问题。
以上是关于大学物理学中机械振动的一些基本内容和相关概念,希望能帮助您更好地理解这一领域的知识。
振动烈度国际标准

振动烈度国际标准在国际标准中选用振动速度作为衡量振动激烈程度的参量,这是考虑到:振动速度可以反映出振动的能量,绝大多数机械设备的结构损坏都是由于震动速度过大引起的,机器的噪声与振动速度成正比;对于同一机器的同一部分,相等的振动速度产生相同的应力;而且对于大多数的机器来说都具有相当平坦的速度频谱等。
机器的振动烈度定义为:在机器表面的重要位置上(例如:轴承安装点处等)沿垂向、纵向、横向三个方向上所测得的振动的最大有效值。
对于振动速度为V(t)=Vpcosωt的简谐振动,其振动速度有效值用下式计算:V rms=式中T=——简谐振动的周期。
若机器的振动系由几个不同频率的简谐振动复合而成,则振动速度的有效值可由下式求得:V rms==式中V1rms,V2rms,,V nrms——分别为第1,2,,n个简谐分量的有效值;V1p,V2p,,V np——分别为第1,2,,n个简谐分量的峰值。
实际上,振动速度的有效值可用具有平方检波特性的电子仪器测量并直接予以显示,因此在应用时是很方便的。
在国际标准ISO2372中规定了转速为10~200转/秒的机器在10~1000赫的频率范围内机械振动烈度的范围,它将振动速度有效值从0.11毫米/秒(人体刚有振动的感觉)到71毫米/秒的范围内分为15个量级,相邻两个烈度量级的比约为1:1.6,即相差4分贝。
这是由于对于大多数机器的振动来说4分贝之差以为着振动相应有了较大变化。
有了振动烈度量级的划分就可以用它表示机器的运行质量。
为了便于实用,将机器运行质量分成四个等级:A级——机械设备正常运转时的振动级,此时成机器的运行状态“良好”。
B级——已超过正常运转时的振级,但对机器的工作质量尚无显著地影响,此种运行中状态是“容许”的。
C级——机器的振动已达到相当剧烈的程度,致使机器只能勉强维持工作,此时机器的运行状态称为“可容忍”的。
D级——机器的振动已大到使机器不能运转、工作,此种机器的振动级是“不允许”的。
710kw高压电机振动标准参数表

710kw高压电机振动标准参数表
电机(英文:Electric machinery,俗称“马达”)是指依据电磁感应定律实现电能转换或传递的一种电磁装置。
在电路中用字母M (旧标准用D)表示。
它的主要作用是产生驱动转矩,作为用电器或各种机械的动力源。
发电机在电路中用字母G表示。
它的主要作用是利用电能转化为机械能。
电机运行时的振动值范围是多少,按照ISO10816-3管制标准,当振动值超过7.1mm/S,表示设备的运行状况是比较差的,这个时候需要对设备进行停机检修。
振动检测可以1个月或者一个季度做1次,定期对设备进行维修保养,可以延长电机的使用寿命。
各种振动单位的不同

对一个单一频率的振动,速度峰值是位移峰值的2πf倍,加速度峰值又是速度峰值的2πf倍。
当然要注意位移一般用的峰峰值,速度用有效值,加速度用峰值。
还要注意现场测量的位移是轴和轴瓦的相对振动,速度和加速度测的是轴瓦的绝对振动。
假设一个振动的速度一定,是5mm/s,大家可以自己算下如果是低频振动,其位移会很大,但加速度很小。
高频振动位移则极小,加速度很大。
所以一般在低频区域都用位移,高频区域用加速度,中频用速度。
但使用范围也有重叠。
位移值体现的是设备在空间上的振动范围,因此取其峰峰值,电力行业一般以位移为评判标准。
速度的有效值和振动的能量是成比例的,其大小代表了振动能量的大小,现在出了电力行业基本上都是以速度有效值为标准的。
加速度和力成正比,一般用其峰值,其大小表示了振动中最大的冲击力,冲击力大设备更容易疲劳损坏,现在没有加速度的标准。
振动幅值的表达式是正弦函数形式的,位移微分得到速度,速度微分得到加速度。
则:振动位移方程式:Y=Asinωt振动速度方程式:V= -Aωcosωt振动速度方程式:G= -Aωωsinωt如果振动频率为f的话,那么ω=2πf其中π=3.1415926如果是单频率f的振动,位移的幅值为A,则速度幅值为2πfA,加速度幅值为2πf*2πfA。
但是工程中读取的振动值,位移用峰峰值,速度用有效值,加速度用峰值。
所以一个单频率的振动,位移读数是A的话,速度应该是0.707πfA,加速度是2πf*πfA。
但是因为现场是复杂的,不是单一频率的振动,所以位移,速度和加速度读数间通常没有确定的换算关系。
但是振动频率比较单一,以一个频率为主时可以利用上述关系近似计算。
计算方法举例:s = 峰值偏移振幅,μm⊥N = 频率min-1f = 频率HzV eff = 有效振动速率mm/ss N 0.000074⊥V eff =1. 机械振动物体相对于平衡位置所作的的往复运动称为机械振动。
简称振动。
振动烈度评定等级表

中石化旋转机械振动标准SHS01003-2004
振动烈度的范围
振动烈度评定等级
分级范围 /(mm/s)
在该范围极限极限上 的速度均方根值 (mm/s)
Ⅰ
Ⅱ
ⅢⅣ
0.28 0.45 0.71 1.12
1.8
2.8
4.5
7.1
11.2
18 28 45 71
0.28 0.45 0.71 1.12 1.8
2.8 4.5 7.1 11.2
18 28 45
A
A
A
A
B
C
B
B
B
D
C
C
C
D
D
D
说ห้องสมุดไป่ตู้:
Ⅰ-小型转机15KW以下电机; Ⅱ-安装在刚性基础上的中型转机,功率在300KW以下; Ⅲ-大型转机,机器-支承系统为刚性状态; Ⅳ-大型转机,机器-支承系统为挠性支承状态; A区-新交付使用的机器应达到的状态或优良状态; B区-机器可以长期运行或合格状态; C区-机器尚可短期运行但必须采取相应补救措施,或不合格状态; D区-不允许状态。
工程力学中的机械振动和结构振动问题

工程力学中的机械振动和结构振动问题工程力学是研究物体受力、运动和相互作用的学科,在实际工程应用中起着至关重要的作用。
其中,机械振动和结构振动问题是工程力学中的一个重要分支,涵盖了许多实际工程中常见的振动现象和振动控制方法。
一、机械振动问题机械振动问题涉及到机械系统中的物体在受到外力或被激励时产生的振动现象。
机械振动问题的研究对于机械系统的设计和性能优化具有重要意义。
1. 自由振动自由振动是指机械系统在无外力作用下的振动现象。
在自由振动中,物体会以一定的振动频率和振幅进行振动。
自由振动的频率与系统的属性相关,可通过工程设计来控制。
2. 强迫振动强迫振动是指机械系统在受到外界激励力作用下的振动现象。
外界激励力的频率可以与系统的固有频率相同,也可以不同。
强迫振动问题的研究主要涉及到激励力的传递和系统的响应。
3. 阻尼振动阻尼振动是指机械系统受到外力作用后逐渐减弱直至停止振动的过程。
阻尼振动的研究需要考虑阻尼对振动特性的影响,并进行合适的振动控制。
二、结构振动问题结构振动问题指的是工程结构受到外力作用后发生的振动现象。
结构振动问题是建筑和桥梁等工程结构设计中需要重点关注的问题。
1. 自由振动结构的自由振动指的是结构在受到外力作用后,没有任何限制条件下的振动现象。
自由振动的分析可以预测结构的振动频率和振型,为结构设计和抗震设计提供依据。
2. 强迫振动结构的强迫振动是指结构在受到外界激励力作用下产生的振动现象。
强迫振动会导致结构受力变化,需要进行结构控制和减振设计。
3. 阻尼振动结构的阻尼振动是指结构振动过程中能量逐渐损失,振动幅度减小的现象。
阻尼振动问题的研究可以帮助减小振动对结构的影响,提高结构的稳定性和安全性。
综上所述,工程力学中的机械振动和结构振动问题是研究机械系统和工程结构中振动现象的重要内容。
通过对机械振动和结构振动的研究,可以优化系统设计,提高工程结构的性能和安全性。
同时,也为振动控制和减振设计提供了理论基础和实用方法。
机械原理目录

机械原理目录 1. 机械原理概述。
1.1 机械原理的定义。
1.2 机械原理的基本原理。
1.3 机械原理的应用领域。
2. 力的平衡。
2.1 力的概念。
2.2 力的平衡条件。
2.3 平衡力的计算方法。
3. 运动的基本规律。
3.1 牛顿运动定律。
3.2 运动的描述。
3.3 运动的图解分析。
4. 机械传动。
4.1 机械传动的基本原理。
4.2 齿轮传动。
4.3 带传动。
4.4 链传动。
5. 机械结构设计。
5.1 结构设计的基本原则。
5.2 结构设计的方法。
5.3 结构设计的实例分析。
6. 机械系统的动力学分析。
6.1 动力学的基本概念。
6.2 动力学方程。
6.3 动力学模型的建立。
7. 机械振动与噪声控制。
7.1 机械振动的原因。
7.2 振动的特性。
7.3 振动与噪声控制的方法。
8. 机械制造工艺。
8.1 机械加工工艺。
8.2 机械焊接工艺。
8.3 机械装配工艺。
9. 机械原理在实际工程中的应用。
9.1 机械原理在汽车工程中的应用。
9.2 机械原理在航空航天工程中的应用。
9.3 机械原理在机械制造中的应用。
10. 机械原理的发展趋势。
10.1 智能化。
10.2 精密化。
10.3 环保化。
11. 结语。
机械原理是机械工程的基础和核心,它研究的是机械系统的运动、力学、能量转换和传递等基本规律。
在工程实践中,机械原理的应用涉及到各个领域,如汽车工程、航空航天工程、机械制造等。
了解和掌握机械原理对于从事机械工程的专业人士来说至关重要。
在学习机械原理时,首先要了解力的平衡条件,掌握力的计算方法,这是机械原理的基础。
同时,要深入理解运动的基本规律,牛顿运动定律对于理解机械系统的运动至关重要。
在设计机械结构时,要遵循结构设计的基本原则,掌握结构设计的方法,通过实例分析来加深理解。
此外,机械系统的动力学分析也是机械原理中的重要内容,要掌握动力学的基本概念,建立动力学模型。
同时,对于机械振动与噪声控制也需要有一定的了解,掌握振动的特性和控制方法。
7.1机械波(讲义)(3考点4题型)(原卷版)

7.1机械波考点一 波动图象与波速公式的应用 (1)考点二 振动图象与波动图象 (2)考点三 波的干涉、衍射、多普勒效应 (2)题型1机械波的形成与传播 (3)题型2波动图像和振动图像的理解和应用 (5)题型3波传播的周期性和多解性问题. (6)题型4波特有的现象——波的干涉、衍射和多普勒效应 (8)考点一 波动图象与波速公式的应用1. 波的图象反映了在某时刻介质中的各质点离开平衡位置的位移情况,图象的横轴表示各质点的平衡位置,纵轴表示该时刻各质点的位移,如图1所示.图1图象的应用:(1)直接读取振幅A 和波长λ,以及该时刻各质点的位移.(2)确定某时刻各质点加速度的方向,并能比较其大小.(3)结合波的传播方向可确定各质点的振动方向或由各质点的振动方向确定波的传播方向.2.波速与波长、周期、频率的关系为:v =λT=λf . 3.由波动图象分析质点运动的方法(1)特殊点法在波形图上取数个特殊点(波峰、波谷或平衡位置),先根据波传播的方向确定它们的振动方向,再判断Δt 后各点运动到什么位置,最后连成曲线,即为另一时刻的波形图,适用于Δt =n T 4的情形. (2)平移法先求出在Δt 时间内波传播的距离Δx =v Δt (v 为波速),再将原波形沿波传播方向平移Δx (若要画t -Δt 时刻的波形图,则需逆着波传播方向平移Δx ),然后将新波形“修补”,使原有波形的区间充满波形.4.造成波动问题多解的主要因素(1)周期性①时间周期性:时间间隔Δt与周期T的关系不明确.②空间周期性:波传播的距离Δx与波长λ的关系不明确.(2)双向性①传播方向双向性:波的传播方向不确定.②振动方向双向性:质点振动方向不确定.考点二振动图象与波动图象表示同一质点在各时刻的位考点三波的干涉、衍射、多普勒效应1.波的干涉中振动加强点和减弱点的判断某质点的振动是加强还是减弱,取决于该点到两相干波源的距离之差Δr.(1)当两波源振动步调一致时若Δr=nλ(n=0,1,2,…),则振动加强;若Δr=(2n+1)λ2(n=0,1,2,…),则振动减弱.(2)当两波源振动步调相反时若Δr=(2n+1)λ2(n=0,1,2,…),则振动加强;若Δr=nλ(n=0,1,2,…),则振动减弱.2.波的衍射现象波能绕过障碍物继续传播的现象,产生明显衍射现象的条件是缝、孔的宽度或障碍物的尺寸跟波长相差不大或者小于波长.3.多普勒效应的成因分析(1)接收频率:观察者接收到的频率等于观察者在单位时间内接收到的完全波的个数.当波以速度v通过观察者时,时间t内通过的完全波的个数为N=v tλ,因而单位时间内通过观察者的完全波的个数即接收频率.(2)当波源与观察者相互靠近时,观察者接收到的频率变大;当波源与观察者相互远离时,观察者接收到的频率变小.题型1机械波的形成与传播[题型专练1].(2023秋•常州期末)王老师在课堂上演示绳波的传播过程,他握住绳上的A点上下振动,某时刻绳上波形如图,则绳上A点的振动图像正确的是()A.B.C.D.[题型专练2].(2022秋•桂林期末)由多家中国建筑公司承担建设的卡塔尔卢赛尔体育场,承办了2022年足球世界杯包括决赛在内的多场赛事。
机器振动测量和评价的有关标准介绍

ASME OM-14
Guidelines for vibration monitoring of rotating equipment 旋转设 备振动监测指南
美国国家标准学会标准:
ANSI S2.17-1980 (ASA 24-1980)American National StandardTechniques of machinery Vibration Measurement机器振动测量技术
ISO 13374-1:2003
Condition monitoring and diagnostics of machines Data processing, communication and presentation Part 1: General guidelines
ISO 13374-2:2007
十四个字符表示一个振动测量位置的标识: XXXX XXX XX XXX X X
运动方向(字母)
传感器轴线方向(字母)
角向位置(数字)
传感器类型(字母)
轴承座编号(数字)
零部件缩写(字母数字)
例子:SFTA 003 AC 090 R N
A轴
003#轴承座
正常的运动方向 径向方向
单轴线振动加速度计
位于垂直上方90度处
泵的振动测量与评价方法
2024年10月
中国石化股份有限公司齐鲁分公司
4
国际标准化组织标准
在国内外得到公认的广泛使用的旋转机器振动判断标准:
国际标准化组织
ISO7919, ISO10816
中国
GB/T 11348 GB/T 6075
美国
API610; API611; API617; API670
7月起电动汽车锂离子动力电池检验执行新标准

7月起电动汽车锂离子动力电池检验执行新标准近日,国家标准化管理委员会批准GB/T 31467.3-2015《电动汽车用锂离子动力蓄电池包和系统第3部分:安全性要求与测试方法》第1号修改单,自2017年7月1日起正式实施。
PONY谱尼测试集团多年从事锂电池方面检测的专家将新旧检验标准做了相应比较说明。
GB/T 31467《电动汽车用锂离子动力蓄电池包和系统》分为三个部分:GB/T 31467.1-2015 第1部分:高功率应用测试规程GB/T 31467.2-2015 第2部分:高能量应用测试规程GB/T 31467.3-2015 第3部分:安全性要求与测试方法所修改的部分是GB/T31467的第3部分,由国家工信部提出,归口全国汽车标准化技术委员会(SAC/TC 114),并按照GB/T 1.1-2009规则起草。
修改内容如下:一、“7.1 振动”删除原标准7.1.1至7.1.3的全部内容,替代为下面7.1.1至7.1.2的内容:7.1.1蓄电池包或系统的振动试验参考测试对象车辆安装位置和GB/T 2423.43的要求,将测试对象安装在振动台上。
蓄电池包或系统应进行15min正弦波振动,振动频率从7Hz增加至50Hz再回至7Hz。
此循环应按照制造商规定的蓄电池包或系统安装位置的垂直方向在3 h中重复12次。
振动频率和加速度的关系如下表:频率和加速度应制造商要求,制造商确定的振动试验方案经技术服务机构批准可以作为表中频率-加速度的替代方案。
这种情况下获得的蓄电池包或系统试验认证仅适用于特殊车型。
在振动后,蓄电池包或系统按照GB/T31467.1-2015中第6.2节或GB/T31467.2-2015中第6.2节规定的方法,运行1个标准循环,应制造商要求,可调整循环中的充、放电电流。
试验结束后应在试验的环境温度条件下观察1 h。
7.1.2要求7.1.2.1 测试过程中,蓄电池包或系统的最小监控单元无电压锐变(电压差的绝对值不大于0.15V),蓄电池包或系统保持连接可靠、结构完好,蓄电池包或系统无泄漏、外壳破裂、着火或爆炸等现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表示: 表示:由运动方程
Acos(ωt + ) = Acos[ω(t + T) + ]
m ωT = 2π T = = 2π k ω 简谐运动的周期是决定于系统自身的 常量,又称为固有周期 固有周期(natural neriod). 常量,又称为固有周期 . 3.频率(Frequency) 频率(Frequency) 物体单位时间内做完全振动的次数称为 振动频率,单位是赫兹 Hz). 赫兹( 振动频率,单位是赫兹(Hz). 表示: 表示:由定义可知
2o 两振动到达同一状态的时间差是
五,旋转矢量(rotational vector) 旋转矢量( vector)
旋转矢量
A
2 1 t = t2 t1 = ω
t
ω t+
Oo
(ωt2 + φ2 ) = (ωt1 + φ1 )
矢径 A 与 x 轴夹角为: 轴夹角为: (ω t + ) 轴上的投影为: 在 x 轴上的投影为: x = Acos(ω t+ ) Acos(
7.3 简谐运动的合成 一,同频率同方向简谐振动合成 特点: 特点 ω1=ω2=ω , x1 // x2 表示: 表示 对如下两个振动
x1 = A cos( t +1) ω 1 x2 = A cos(ωt +2) 2
合振动位移 x 就是 x1 与 x2 的代数和
x = x1 + x2 = A cos(ωt +1) + A cos(ωt +2) 1 2
k
y x
y x
π (2)φ2 φ1 = (2k ± 1) 2 2 2 x y + 2 =1 2 A A 1 2
质点轨迹正椭圆
k = 1,2,3
(3)2 1 = 其它值
质点轨迹是任意形状椭圆. 质点轨迹是任意形状椭圆. 状椭圆
π π = π/2 = 3π/2 = π/4 = 5π/4
P
合振幅最小
t
(3) φ = φ2 φ1为其它值时
在上述两者之间. 则A在上述两者之间. 在上述两者之间 合振幅最大值是2A 当A1=A2时: 合振幅最大值是 1 ; 合振幅最小值是0 合振幅最小值是0. 相互垂直同频率简谐振动的合成 二,相互垂直同频率简谐振动的合成 特点: ω1=ω2=ω , x1 ⊥ x2 特点 对如下两个振动
βt
— 衰减函数
临界阻尼达到平衡位 置的时间最短, 置的时间最短,但仍不 能超过平衡位置. 能超过平衡位置. 三种阻尼振动比较 欠阻尼 β < ω0 过阻尼 β > ω0 临界阻尼 β = ω0
x
x
o
欠阻尼 过阻尼 临界阻尼
t
o
t
vibration) 二,受迫振动(forced vibration) 受迫振动( 物体在周期性外力持续作用下发生振 受迫振动, 动,称为受迫振动,这个外力称为驱动力 称为受迫振动 这个外力称为驱动力 弹簧振子为例 振子为例, 以弹簧振子为例,振子受力有 弹性力 F弹 = kx 阻尼力 F阻 = γυ 驱动力 F策 = F cos ω ′t 则运动方程是
d x dx 2 + 2β + ω0 x = hcosω′t 2 dt dt
2
式中 2 β =
γபைடு நூலகம்
m
,
k ω = , m
2 0
F h= m
受迫振动方程的解为 受迫振动方程的解为 βt x = A0e cos(ωt + α) + Acos(ω′t + ) 此式表明: 此式表明: 第一项为阻尼振动项, 第一项为阻尼振动项,当时间较长时衰 减为0. 减为 . 第二项为驱动力产生的简谐运动 简谐运动. 第二项为驱动力产生的简谐运动. 当系统达到稳定状态后, 当系统达到稳定状态后,方程的解是 x = Acos(ω′t + )
x = A cos(ωt + φ1 ) 1 y = A cos(ωt + φ2 ) 2
合成得到质点的轨迹方程是
x y 2xy 2 + 2 cos(φ2 φ1 ) = sin (φ2 φ1 ) 2 A1 A2 A1 A2
2
2
(1) φ2 φ1 = kπ k = 0,±1,±2,
A2 y = (1) x A1 质点沿1, , 质点沿 ,3(2,4 象限直线作简谐 )象限直线作简谐 振动. 振动. = 0 = π
x
k 式中: 式中 ω = m
2
(ω称为角频率) 称为角频率) 称为角频率
物体受力和加速度与位移 x 成正比, 成正比, 且方向相反(动力学特征) 且方向相反(动力学特征) 上式可以改写为微分方程形式 2 d x 2 +ω x = 0 2 dt 其解为
x = Acos(ωt +)
式中A, 是待定常数 此式称为简谐运 是待定常数, 式中 ,φ是待定常数,此式称为简谐运动 运动方程 方程. 的运动方程.
2o 初相 ,由开始时刻振动物体的运动状 态决定 由运动方程可知: 由运动方程可知:t = 0时刻 时刻
x0 = Acos φ υ0 = ωAsinφ
υ υo A= x + , tan φ = ω ωxo 5. 相位差(phase fifference) 相位差( ) 两个简谐振动的相位之差称为相位差, 谐振动的相位之差称为相位差 两个简谐振动的相位之差称为相位差, 用Δ 表示
7.1 简谐运动 一,简谐运动(Simple Harmonic Motion) 简谐运动( 物体在一定位置附近的位移变化满足 简谐函数形式,称为简谐运动 简谐运动. 简谐函数形式,称为简谐运动.
弹簧振子 单摆 复摆
二,基本特征 以弹簧振子为例, 以弹簧振子为例 振子受力是 F弹 F = kx 由牛顿第二定律得 2 F = ω2 x = d x a= o x 2 m dt
dx A t = ω sin (ω + φ) 速度: 速度: υ = dt
= ω Acos(ωt + φ + π)
2
四,描述简谐振动的物理量
x = Acos(ωt + )
1. 振幅(Amplitude) 振幅( ) 离开平衡点的最大量值的绝对值. 离开平衡点的最大量值的绝对值. 给出振动量的变化幅度. 给出振动量的变化幅度. 注意: , , 分别是位移 注意:A,ωA,ω2A分别是位移,速度, 分别是位移,速度, 加速度振幅. 加速度振幅. 2. 周期(Priod) 周期(Priod) 完成一次全振动所需的时间T, 完成一次全振动所需的时间 ,单位是 秒(s). ).
位移 x 按余弦函数的规律随时间变化 运动学特征) (运动学特征) 三,简谐运动的速度与加速度
π = ωAcos(ωt + φ + ) 2 dυ 2 加速度: 加速度: = = ω Acos(ωt +) a dt
位移x 速度υ 加速度a三者与时间t 位移x,速度υ,加速度a三者与时间t 的 关系如图所示. 关系如图所示.
2 o 2 o 2
表示: 表示
= (ω2 ω1 )t + (φ2 φ1 ) 对同频情况: 对同频情况:φ = φ2 φ 1
x 1 = A1 cos( ω 1 t + 1 ) x 2 = A2 cos( ω 2 t + 2 ) φ = (ω2t + φ2 ) (ω1t + φ1 )
1o 反映两振动的步调情况: 反映两振动的步调情况: =0(或2π整数倍),同步振动 =0( 整数倍) =π(或π奇数倍),振动步调相反 奇数倍), ),振动步调相反 >0, x2振动超前; <0, x1振动超前 振动超前;
A
t=0
x x 参考圆
x
xp
7.2 简谐运动的能量 以弹簧振子为例: 以弹簧振子为例
υ
x
E = EP + EK o x 1 kx2 E = 1 mυ2 EP = k 2
由 x = Acos(ωt + φ) υ = ωAsin(ωt + φ)
1 kA2 cos2 (ωt + ) Ep = 2 1 mω2 A2 sin2 (ω + φ) Ek = 2 t
定 义
振动: 振动:任何一个物理量在某一数值 附近作周期性的变化,称为振动 振动; 附近作周期性的变化,称为振动; 机械振动: 机械振动:物体在一定位置附近作 往复的运动,称为机械振动 机械振动. 来回 往复的运动,称为机械振动. 主要内容: 主要内容: 简谐振动 ; 简谐振动合成; 简谐振动合成; 阻尼振动,受迫振动,共振. 阻尼振动,受迫振动,共振.
2π
1 ν= T
ω 或 ν= 2π
式中ω是角频率, 单位是rads-1. 式中 是角频率 单位是 是角频率 频率ν只与振动系统自身性有关 只与振动系统自身性有关,也称为 频率 只与振动系统自身性有关 也称为 固有频率(natural frequency) . 固有频率 4.相位与初相位(phase and initial phase ) 相位与初相位( 称为相位 相位, 称为初相位,单位 ωt + 称为相位, 称为初相位,单位 是rad . 1o 相位的意义是: 相位的意义是: 一是反映了振动的周期性 反映了振动的周期性; 一是反映了振动的周期性; 二是相位确定了振动物体运动状态 相位确定了振动物体运动状态. 二是相位确定了振动物体运动状态.
(1) = 2 1 = 2kπ
A = A + A + 2A1 A2 cos(2 1 )
2 1 2 2
x1 x2 x
k = 0, ± 1 , 则: A = A + A 1 2
合振幅最大
o
t
(2) = 2 1 = (2k +1)π x1 x2 x k = 0, ± 1 ,
