初中数学格点与面积B同步练习及答案
平面直角坐标系中点的面积问题专项训练(30道)(举一反三)(浙教版)(解析版)

专题4.2 平面直角坐标系中点的面积问题专项训练(30道)【浙教版】考卷信息:本套训练卷共30题,题型针对性较高,覆盖面广,选题有深度,涵盖了平面直角坐标系中的规律问题所有类型!一.选择题(共10小题)1.(2022春•龙泉驿区期末)如图,在平面直角坐标系中,将折线AEB 向右平移得到折线CFD ,则折线AEB 在平移过程中扫过的面积是( )A .15B .20C .24D .25【分析】折线AEB 在平移过程中扫过的面积=S ▱ACFE +S ▱BDFE ,再根据平行四边形的面积公式求解即可.【解答】解:折线AEB 在平移过程中扫过的面积=S ▱ACFE +S ▱BDFE=5×3+5×2=15+10=25,故选:D .2.(2022春•商南县期末)已知点A 的坐标为(0,0),点B 的坐标为(4,0),点C 在y 轴上,△ABC的面积是10,则点C 的坐标可能是( )A .(0,10)B .(5,0)C .(0,﹣5)D .(0,4)【分析】首先求得AB 的长,根据三角形的面积公式,即可求得C 的纵坐标,进而得到C 的坐标.【解答】解:设点C 坐标是(0,y )根据题意得,12AB ×AC =10即12×4×|y |=10,解得y =±5.所以点C 坐标是:(0,5)或(0,﹣5).故选:C .3.(2022•市中区二模)平面直角坐标系中,P (x ,y )的横坐标与纵坐标的绝对值之和叫做P (x ,y )的勾股值,记为「P」,即「P」=|x|+|y|.若点B在第一象限且满足「B」=4,则满足条件的所有B点与坐标轴围成的图形的面积为()A.2B.4C.6D.8【分析】由勾股值的定义可得方程x+y=4(x>0,y>0),变形得y=﹣x+4,求出此函数与坐标轴的交点坐标即可求面积.【解答】解:设点P坐标为(x,y),由点B在第一象限且满足「B」=4,∴x+y=4(x>0,y>0).即y=﹣x+4,∵y=﹣x+4与x轴交点为(4,0),与y轴交点为(0,4),∴满足条件的所有B点与坐标轴围成的图形的面积为12×4×4=8.故选:D.4.(2022春•江夏区校级月考)如图所示,直角坐标系中四边形的面积是()A.15.5B.20.5C.26D.31【分析】图中四边形可以视为由两个直角三角形和一个梯形构成,分别计算其面积并求和即可.【解答】解:图中四边形可以视为由两个直角三角形和一个梯形构成,则其面积为:1 2×2×3+12(3+4)×3+12×1×4=3+212+2=15.5.故选:A.5.(2022春•汇川区期末)如图,点A、B的坐标分别为(﹣5,6)、(3,2),则三角形ABO的面积为()A.12B.14C.16D.18【分析】作AC⊥x轴、BD⊥x轴,根据A、B坐标得出AC、BD及CD的长,根据S△AOB=S梯形ABDC﹣S△AOC﹣S△BOD可得答案.【解答】解:如图,作AC⊥x轴于点C,作BD⊥x轴于点D,∵A(﹣5,6)、B(3,2),∴AC=6、OC=5,BD=2、OD=3,则CD=OC+OD=8,∴S△AOB=S梯形ABDC﹣S△AOC﹣S△BOD=12×(2+6)×8−12×5×6−12×2×3=32﹣15﹣3=14,故选:B.6.(2022春•沙河市期中)在网格图中有一个面积为10的△ABC,△ABC的三个顶点均在网格的格点上,墨墨在网格图中建立了适当的直角坐标系,并知道点A的坐标为(2,3),点B的坐标为(﹣3,﹣2),后来墨墨不小心在该图洒上了墨水,如图所示,点C的坐标看不清了,但他记得线段AC与y轴平行,则点C的坐标为()A.(2,1)B.(1,2)C.(2,﹣1)D.(﹣1,2)【分析】根据三角形的面积公式求出AC,再根据网格结构确定出点C的坐标即可.【解答】解:∵A(2,3),B(﹣3,﹣2),线段AC与y轴平行,∴点B到AC的距离为2+3=5,∴S△ABC=12AC•5=10,解得AC=4,∴点C的纵坐标为3﹣4=﹣1,∴点C的坐标为(2,﹣1).故选:C.7.(2022春•嘉祥县期末)若△ABC三个顶点的坐标分别为A(﹣3,﹣1),B(2,﹣1),C(1,3),则△ABC的面积为()A.7.5B.10C.15D.20【分析】构造平面直角坐标系,标出点A、B、C在坐标系中的位置,过点C向AB作垂线,垂足为D,根据S△ABC=12AB×CD,即可得到答案.【解答】解:过点C向AB作垂线,垂足为D,如下图所示:则AB=2﹣(﹣3)=5,CD=3+1=4,S△ABC=12AB×CD=12×5×4=10,故选:B.8.(2022秋•历下区期中)如图,由8个边长为1的小正方形组成的图形,被线段AB平分为面积相等的两部分,已知点A的坐标是(1,0),则点B的坐标为()A.(113,3)B.(103,3)C.(154,3)D.(185,3)【分析】如图,设BC=x,根据题意列方程即可得到结论.【解答】解:如图,设BC=x,由题意得,12×3×(2+x)=12×8,解得:x=23,3+23=113,∴点B的坐标为(113,3),故选:A.9.(2022春•重庆期末)已知点P的坐标为(a,b)(a>0),点Q的坐标为(c,2),且|a﹣c|+√b−8=0,将线段PQ向右平移a个单位长度,其扫过的面积为24,那么a+b+c的值为()A.12B.14C.16D.20【分析】利用非负数的性质求出b的值,推出a=c,推出PQ=6,根据PQ向右平移a个单位长度,其扫过的面积为24,推出a=4即可解决问题.【解答】解:∵|a﹣c|+√b−8=0,又∵|a﹣c|≥0,√b−8≥0,∴a ﹣c =0,b ﹣8=0,∴a =c ,b =8,∴P (a ,8),Q (a ,2),∴PQ =6,∵线段PQ 向右平移a 个单位长度,其扫过的面积为24,∴a =4,∴a =c =4,∴a +b +c =4+8+4=16,故选:C .10.(2022春•嘉祥县期末)我们定义:过点(0,a )且平行于x 轴的直线为y =a ,若A (﹣2,0),B (1,2),点P 为直线y =4上一动点,且△P AB 的面积为6平方单位,则点P 的坐标为( )A .(﹣2,4)B .(0,4)或(10,4)C .(﹣2,4)或(10,4)D .(9,4) 【分析】设直线AB 交直线y =4于C .求出点C 坐标,设P (m ,4),构建方程即可解决问题;【解答】解:∵A (﹣2,0),B (1,2),设直线AB 交直线y =4于C .∴直线AB 的解析式为y =23x +43, ∵直线PC 的解析式为y =4,∴C (4,4),设P (m ,4),由题意:12•|4﹣m |•4−12•|4﹣m |•2=6,解得m =﹣2或10,∴P (﹣2,4)或(10,4)故选:C .二.填空题(共6小题)11.(2022春•金乡县期末)在平面直角坐标系中,对于任意三点A,B,C的“矩面积”,给出如下定义:“水平底”a:任意两点横坐标差的最大值,“铅垂高”h:任意两点纵坐标差的最大值,则“矩面积”S =ah.例如,三点坐标分别为A(0,3),B(﹣3,4),C(1,﹣2),则“水平底”a=4,“铅垂高”h=6,“矩面积”S=ah=24.若D(2,2),E(﹣2,﹣1),F(3,m)三点的“矩面积”为20,则m的值为3或﹣2.【分析】根据矩面积的定义表示出水平底”a和铅垂高“h,利用分类讨论对其铅垂高“h进行讨论,从而列出关于m的方程,解出方程即可求解.【解答】解:∵D(2,2),E(﹣2,﹣1),F(3,m)∴“水平底”a=3﹣(﹣2)=5“铅垂高“h=3或|1+m|或|2﹣m|①当h=3时,三点的“矩面积”S=5×3=15≠20,不合题意;②当h=|1+m|时,三点的“矩面积”S=5×|1+m|=20,解得:m=3或m=﹣5(舍去);③当h=|2﹣m|时,三点的“矩面积”S=5×|2﹣m|=20,解得:m=﹣2或m=6(舍去);综上:m=3或﹣2故答案为:3或﹣212.(2022春•平泉市期末)如图,两个形状、大小完全相同的直角三角形叠放在一起,将直角三角形ABC 沿着x轴正方向平移到直角三角形DEF的位置.已知点A(1,5),点B(1,1),DG=1,平移距离为2.(1)点G的坐标为(3,4);(2)阴影部分的面积S=7.【分析】(1)求出BE,GE的长度即可得出答案;(2)根据平移的性质得S△ABC=S△DEF,从而S△ABC﹣S△CEG=S△DEF﹣S△CEG,梯形ABEG的面积=阴影部分的面积,求梯形的面积即可得到阴影部分的面积.【解答】解:(1)∵A(1,5),点B(1,1),∴AB=4,∵平移距离为2,∴BE=2,DE=AB=4,∵DG=1,∴GE=DE﹣DG=4﹣1=3,∴G(3,4);故答案为:G(3,4);(2)∵将直角三角形ABC沿着x轴正方向平移到直角三角形DEF的位置,∴S△ABC=S△DEF,∴S△ABC﹣S△CEG=S△DEF﹣S△CEG,∴梯形ABEG的面积=阴影部分的面积,×(AB+EG)×BE∴S=12×(4+3)×2=12=7.故答案为:7.13.(2022春•仙居县期末)如图,在平面直角坐标系中,点A(1,1),点B(3,0).现将线段AB平移,使点A,B分别平移到点A′,B',其中点A′(1,4),则四边形AA'B'B的面积为6.【分析】把四边形AA′B′B的面积转化为特殊四边形的面积求解即可.【解答】解:如图,过点B′作B′E⊥AA′于点E,延长A′A交OB于点F.由题意得,AB=A′B′,AB∥A′B′,∵点A(1,1),点B(3,0),点A′(1,4),∴AA′=BB′=3,∵B′E⊥AA′,∴四边形B′EFB是长方形,∴AA′=EF=3,∴四边形AA′B′B的面积=四边形B′EFB的面积=3×2=6,故答案为:6.14.(2022春•海淀区校级期中)如图,在平面直角坐标系中,曲线f向上平移1个单位形成曲线g的过程中所扫过的面积是3.【分析】曲线f向上平移1个单位形成曲线g的过程中所扫过的面积可以看成是底为1,高为3的平行四边形的面积.【解答】解:曲线f向上平移1个单位形成曲线g的过程中所扫过的面积=1×3=3,故答案为:3.15.(2022春•昌黎县期末)如图,在直角坐标系中,A(﹣1,2),B(3,﹣2),则△AOB的面积为2.【分析】直接利用A,B点坐标,再利用△AOB所在直角三角形面积减去周围图形面积得出答案.【解答】解:△AOB的面积为:12×4×4−12×1×2﹣2−12×2×3=2.故答案为:2.16.(2022•漳州校级一模)已知:如图△ABC的顶点坐标分别为A(﹣4,﹣3),B(0,﹣3),C(﹣2,1),如将B点向右平移2个单位后再向上平移4个单位到达B1点,若设△ABC的面积为S1,△AB1C 的面积为S2,则S1,S2的大小关系为s1=s2(填“<”、“>”、“=”).【分析】直接利用平移中点的变化规律求解即可.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.【解答】解:原来点的横坐标是0,纵坐标是﹣3,向右平移2个单位后再向上平移4个单位到达B1点的横坐标是0+2=2,纵坐标为﹣3+4=1.那么原三角形的面积是:12×4×4=8,新三角形的面积为:12×4×4=8,∴两三角形的面积相等,即s1=s2.三.解答题(共14小题)17.(2022春•上蔡县月考)如图,六边形ABCDE在平面直角坐标系内.(1)写出点A、B、C、D、E、F的坐标:A(2,3)、B(﹣2,3)、C(﹣4,0)、D(3,﹣3)、E()2,﹣3);、F(3,0);;(2)六边形ABCDE的面积为34.5.【分析】(1)根据图形直接写出坐标;(2)根据点点坐标利用割补法即可求出六边形ABCDE的面积.【解答】解:(1)A(2,3)、B(﹣2,3)、C(﹣4,0)、D(﹣3,﹣3)、E(2,﹣3)、F(3,0);故答案为:(2,3)、(﹣2,3)、(﹣4,0)、(﹣3,﹣3)、(2,﹣3)、(3,0);(2)四边形ABCD的面积为:6×7−12×2×3−12×1×3−12×1×3−12×1×3=34.5故答案为:34.5.18.(2022春•莆田期末)对于平面直角坐标系中的图形M上的任意点P(x,y),给出如下定义:将点P (x,y)平移到P′(x+e,y﹣e)称为将点P进行“e型平移”,点P′称为将点P进行“e型平移”的对应点;将图形M上的所有点进行“e型平移”称为将图形M进行“e型平移”.例如,将点P(x,y)平移到P′(x+1,y﹣1)称为将点P进行“1型平移”.(1)已知点A(﹣1,2),B(2,3),将线段AB进行“1型平移”后得到对应线段A′B′.①画出线段A′B′,并直接写出A′,B′的坐标;②四边形ABB′A′的面积为4(平方单位);(2)若点A(2﹣a,a+1),B(a+1,a+2),将线段AB进行“2型平移”后得到对应线段A′B′,当四边形ABB′A′的面积为8平方单位,试确定a的值.【分析】(1)①根据定义平移即可;②根据平移后的图形,写出坐标即可;(2)利用割补法求四边形的面积.【解答】解:(1)①A(﹣1,2)“1型平移”后得到A'(0,1),B(2,3)“1型平移”后得到B'(3,2);②S四边形ABB′A′=S△ABB'+S△AB'A'=12×4×1+12×4×1=4,故答案为:4;(2)A(2﹣a,a+1)“2型平移”后得到A'(4﹣a,a﹣1),B(a+1,a+2)“2型平移”后得到B'(a+3,a),如图,在四边形外作矩形CDEF,∴C(2﹣a,a+2),D(2﹣a,a﹣1),E(a+3,a﹣1),F(a+3,a+2),∴BC=2a﹣1,AC=1,BF=2,B'F=2,AD=2,A'D=2,AE=2a﹣1,BE'=1,∴CF=2a+1,CD=3,∴S四边形ABB′A′=3(2a+1)−12×(2a﹣1)×1×2−12×2×2×2=4a,∵四边形ABB′A′的面积为8平方单位,∴4a=8,∴a=2.19.(2022春•雨花区校级月考)如图所示,在平面直角坐标系中,点A、B的坐标分别为A(a,0)和B (b,0),且a,b满足|a+4|+√8−b=0,点C的坐标为(0,3).(1)求a,b的值及S△ABC;S△ABC,试求点M的坐标.(2)若点M在x轴上,且S△ACM=13【分析】(1)由|a+4|+√8−b=0结合绝对值、算术平方根的非负性即可得出a、b的值,再结合三角形的面积公式即可求出S△ABC的值;S△ABC,即可得出点(2)设出点M的坐标,找出线段AM的长度,根据三角形的面积公式结合S△ACM=13M 的坐标.【解答】解:(1)由|a +4|+√8−b =0,可知,a +4=0,8﹣b =0,∴a =﹣4,b =8,∴点A (﹣4,0),点B (8,0),又∵点C (0,3),∴AB =|﹣4﹣8|=12,CO =3,∴S △ABC =12AB •CO =12×12×3=18.(2)设点M 的坐标为(x ,0),则AM =|x ﹣(﹣4)|=|x +4|,又∵S △ACM =13S △ABC , ∴12AM •OC =13×18,∴12|x +4|×3=6,∴|x +4|=4,即x +4=±4,解得:x =0或﹣8,故点M 的坐标为(0,0)或(﹣8,0).20.(2022春•长白县期中)如图,在平面直角坐标系中,点A (﹣3b ,0)为x 轴负半轴上一点,点B (0,4b )为y 轴正半轴上一点,其中b 满足方程3(b +1)=6.(1)求点A ,B 的坐标;(2)点C 为y 轴负半轴上一点,且△ABC 的面积为12,求点C 的坐标;【分析】(1)解一元一次方程,可得结论.(2)利用三角形的面积公式求出OC 的长,可得结论.【解答】解:(1)解方程3(b+1)=6,得到b=1,∴A(﹣3,0),B(0,4).(2)∵A(﹣3,0),B(0,4),∴OA=3,OB=4,•BC•OA=12,∵S△ABC=12∴BC=8,∵点C在y轴的负半轴上,∴OC=4,C(0,﹣4).21.(2022春•新市区期末)如图,已知A(﹣2,3)、B(4,3)、C(﹣1,﹣3)(1)求点C到x轴的距离;(2)求△ABC的面积;(3)点P在y轴上,当△ABP的面积为6时,请直接写出点P的坐标.【分析】(1)点C的纵坐标的绝对值就是点C到x轴的距离解答;(2)根据三角形的面积公式列式进行计算即可求解;×6×|x−3|=6,(3)设点P的坐标为(0,y),根据△ABP的面积为6,A(﹣2,3)、B(4,3),所以12即|x﹣3|=2,所以x=5或x=1,即可解答.【解答】解:(1)∵C(﹣1,﹣3),∴|﹣3|=3,∴点C到x轴的距离为3;(2)∵A(﹣2,3)、B(4,3)、C(﹣1,﹣3)∴AB =4﹣(﹣2)=6,点C 到边AB 的距离为:3﹣(﹣3)=6,∴△ABC 的面积为:6×6÷2=18.(3)设点P 的坐标为(0,y ),∵△ABP 的面积为6,A (﹣2,3)、B (4,3),∴12×6×|y ﹣3|=6,∴|y ﹣3|=2,∴y =1或y =5,∴P 点的坐标为(0,1)或(0,5).22.(2022春•思明区校级期中)在平面直角坐标系中,点A ,B 在y 轴正半轴上,且点A 在B 的下方,将线段AB 进行平移得到线段CD ,点A 的对应点为点D ,点B 的对应点为点C ,(1)若点A (0,1),B (0,3),D (3,2),求点C 的坐标;(2)点E 是第二象限上的一个动点,过点E 作EF 垂直x 轴于F ,连接DF ,DE ,EC .若点A (0,12m ),B (0,b ),C (a +b +1,12m +3),D (m ,﹣2m +3),三角形DEF 的面积为S △DEF =−38a +338,点D 到直线EF 的距离为3,试问是否存在m ,使得S △BCE =13S △ACE ?若存在,请求出m 的值;若不存在,请说明理由.【分析】(1)求出AB 的长,利用平移的性质解决问题即可.(2)利用平移变换的性质构建方程组求出a ,b (用m 表示),利用三角形的面积公式构建方程求出m 即可解决问题.【解答】解:(1)∵A (0,1),B (0,3),D (3,2),∴AB =3﹣1=2=CD ,∴C (3,4).(2)由题意:{b −12m =12m +3−(−2m +3)a +b +1=m, 解得{a =−2m −1b =3m, ∴C (m ,12m +3),∵S △DEF =EF×32=−38a +338, ∴EF =−14a +114=12m +3,∴EC ⊥y 轴,∴A 到CE 的距离为:12m +3−12m =3, ∵S △BEC =13S △ACE ,∴B 到CE 的距离为:3×13=1, ∴|3m ﹣(12m +3)|=1,解得m =85或45, 故存在m ,使得S △BCE =13S △ACE ,此时m =85或45.23.(2022春•大同期末)已知坐标平面内的三个点A (1,3),B (3,1),O (0,0),求△ABO 的面积.【分析】过A ,B 分别作y 轴,x 轴的垂线,则三角形ABC 的面积可以转化为梯形和三角形的面积的和差的问题解决.【解答】解:如图所示,过A ,B 分别作y 轴,x 轴的垂线,垂足为C ,E ,两线交于点D ,则C (0,3),D (3,3),E (3,0).又因为O (0,0),A (1,3),B (3,1),所以OC =3,AC =1,OE =3,BE =1,AD =DC ﹣AC =3﹣1=2,BD =DE ﹣BE =3﹣1=2,则四边形OCDE 的面积为3×3=9,△ACO和△BEO的面积都为12×3×1=32,△ABD的面积为12×2×2=2,所以△ABO的面积为9﹣2×32−2=4.24.(2022春•罗平县校级期中)在直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C (5,6)(1)求△ABC的面积.(2)在y轴上是否存在点D,使得△ABD的面积和△ABC的面积相等,若存在,求出点D的坐标.(3)除(2)中的点D,在平面直角坐标系中,还能不能找到别的点D,会满足△ABD的面积和△ABC 的面积相等,这样的点有多少个?它们的坐标有什么特点?直接写出答案.【分析】(1)由已知条件和三角形面积公式容易得出结果;(2)由三角形的面积关系得出点D的纵坐标绝对值为6,即可得出结果;(3)由题意得出满足条件的点D的纵坐标绝对值为6,即可得出结论.【解答】解:(1)∵A(0,0),B(6,0),C(5,6),∴OB=6,△ABC的面积=12×6×6=18;(2)存在,理由如下:∵△ABD的面积=△ABC的面积=12×6×6=18,∴点D的坐标为(0,6)或(0,﹣6);(3)能找到别的点D,满足△ABD的面积和△ABC的面积相等,这样的点有无数个,它们的纵坐标为±6.25.(2022春•崆峒区期末)在直角坐标系中,已知线段AB,点A的坐标为(1,﹣2),点B的坐标为(3,0),如图1所示.(1)平移线段AB到线段CD,使点A的对应点为D,点B的对应点为C,若点C的坐标为(﹣2,4),求点D的坐标;(2)平移线段AB到线段CD,使点C在y轴的正半轴上,点D在第二象限内,连接BC,BD,如图2所示.若S△BCD=7(S△BCD表示三角形BCD的面积),求点C、D的坐标.(3)在(2)的条件下,在y轴上是否存在一点P,使S△PCDS△BCD =23(S△PCD表示三角形PCD的面积)?若存在,求出点P的坐标;若不存在,请说明理由.【分析】(1)利用平移得性质确定出平移得单位和方向;(2)根据平移得性质,设出平移单位,根据S△BCD=7(S△BCD建立方程求解,即可,(3)设出点P的坐标,表示出PC用S△PCDS△BCD =23,建立方程求解即可.【解答】解:(1)∵B(3,0)平移后的对应点C(﹣2,4),∴设3+a=﹣2,0+b=4,∴a=﹣5,b=4,即:点B向左平移5个单位,再向上平移4个单位得到点C(﹣2,4),∴A点平移后的对应点D(﹣4,2),(2)∵点C 在y 轴上,点D 在第二象限,∴线段AB 向左平移3个单位,再向上平移(2+y )个单位,符合题意,∴C (0,2+y ),D (﹣2,y ),连接OD ,S △BCD =S △BOC +S △COD ﹣S △BOD=12OB ×OC +12OC ×2−12OB ×y =7,∴y =2,∴C (0,4).D (﹣2,2);(3)设点P (0,m ),∴PC =|4﹣m |,∵S △PCDS △BCD=23, ∴12|4﹣m |×2=23×7,∴|4﹣m |=143, ∴m =−23或m =263,∴存在点P ,其坐标为(0,−23)或(0,263).26.(2022春•通川区期末)已知在平面直角坐标系中,O 为坐标原点,点A 的坐标为(2,a ),点B 的坐标为(b ,2),点C 的坐标为(c ,0),其中a ,b 满足(a +b ﹣10)2+|a ﹣b +2|=0.(1)求A ,B 两点的坐标;(2)当△ABC 的面积为10时,求点C 的坐标;(3)当2≤S △ABC ≤12时,则点C 的横坐标c 的取值范围是 ﹣2≤c ≤8或12≤c ≤22 .【分析】(1)根据非负数的性质即可得到A 点的坐标(2,4),B 点的坐标(6,2);(2)求得直线AB 与x 轴的交点为D (10,0),于是得到S △ABC =S △ACD ﹣S △BCD ,列方程即可得到结论;(3)根据已知条件列方程即可得到结论.【解答】解:(1)∵(a +b ﹣10)2+|a ﹣b +2|=0,∴(a +b ﹣10)2=0,|a ﹣b +2|=0,解得:a =4,b =6,∴A 点的坐标(2,4),B 点的坐标(6,2);(2)∵A点的坐标(2,4),B点的坐标(6,2),如图,过点A作AD⊥x轴于D,∴D(2,0),AD=4,过点B作BE⊥x轴于E,∴E(6,0),BE=2,∴DE =4,设C(c,0),当c>10时,∴CE=c﹣6,CD=c﹣2∴S△ABC=S△ACD﹣S△BCE﹣S梯形ABED=12×4×(c﹣2)−12×2×(c﹣6)−12×(2+4)×4=c﹣10=10,∴c=20当c<10时,同上的方法得,c=0,∴点C的坐标(0,0)或(20,0);(3)由(2)知,①12×(10﹣c)×4−12(10﹣c)×2=2或12×(c﹣10)×4−12(c﹣10)×2=2,解得:c=8或12,②12×(10+c)×4−12(10+c)×2=12或12×(|c|﹣10)×4−12(c﹣10)×2=12,解得:c=﹣2或c=22,∴当2≤S△ABC≤12时,则点C的横坐标c的取值范围是﹣2≤c≤8或12≤c≤22,故答案为﹣2≤c≤8或12≤c≤22.27.(2022春•宁都县期末)已知:如图,△ABC的三个顶点位置分别是A(1,0)、B(﹣2,3)、C(﹣3,0).(1)求△ABC的面积是多少?(2)若点A、C的位置不变,当点P在y轴上时,且S△ACP=2S△ABC,求点P的坐标?(3)若点B、C的位置不变,当点Q在x轴上时,且S△BCQ=2S△ABC,求点Q的坐标?【分析】(1)根据点A、C的坐标求出AC的长,然后利用三角形的面积列式计算即可得解;(2)分点P在y轴正半轴和负半轴两种情况讨论求解;(3)分点Q在C的左边和右边两种情况讨论求解.【解答】解:(1)∵A(1,0),B(﹣2,3),C(﹣3,0),∴AC=1﹣(﹣3)=1+3=4,点B到AC的距离为3,×4×3=6;∴△ABC的面积=12(2)∵S△ACP=2S△ABC=12,∴以AC为底时,△ACP的高=12×2÷4=6,∴点P在y轴正半轴时,P(0,6);点P在y轴负半轴时,P(0,﹣6);(3)∵S△BCQ=2S△ABC=12,∴以CQ为底时,△BCQ的高为3,底边CQ=12×2÷3=8,∴点Q在C的左边时,Q(﹣3﹣8,0),即Q(﹣11,0);点Q在C的右边时,Q(﹣3+8,0),即Q(5,0).28.(2022春•河北期末)如图,在平面直角坐标系中,已知点A(0,4),B(8,0),C(8,6)三点.(1)求△ABC的面积;(2)如果在第二象限内有一点P(m,1),且四边形ABOP的面积是△ABC的面积的两倍;求满足条件的P点的坐标.【分析】(1)由点的坐标得出BC =6,即可求出△ABC 的面积;(2)求出OA =4,OB =8,由S 四边形ABOP =S △AOB +S △AOP 和已知条件得出方程,解方程即可.【解答】解:(1)∵B (8,0),C (8,6),∴BC =6,∴S △ABC =12×6×8=24;(2)∵A (0,4),B (8,0),∴OA =4,OB =8,∴S 四边形ABOP =S △AOB +S △AOP=12×4×8+12×4(﹣m )=16﹣2m , 又∵S 四边形ABOP =2S △ABC =48,∴16﹣2m =48,解得:m =﹣16,∴P (﹣16,1).29.(2022春•上杭县期末)在平面直角坐标系中(单位长度为1cm ),已知点M (m ,0),N (n ,0),且√m +n −3+|2m +n |=0.(1)求m ,n 的值;(2)若点E 是第一象限内一点,且EN ⊥x 轴,点E 到x 轴的距离为4,过点E 作x 轴的平行线a ,与y 轴交于点A .点P 从点E 处出发,以每秒2cm 的速度沿直线a 向左移动,点Q 从原点O 同时出发,以每秒1cm 的速度沿x 轴向右移动.①经过几秒PQ 平行于y 轴?②若某一时刻以A ,O ,Q ,P 为顶点的四边形的面积是10cm 2,求此时点P 的坐标.【分析】(1)根据平方根和绝对值的性质得出 {m +n −3=02m +n =0,解方程组即可; (2)①设x 秒后PQ 平行于y 轴,由于AP ∥OQ ,所以当AP =OQ 时,四边形AOQP 是平行四边形,那么PQ 平行于y 轴,根据AP =OQ 列出关于x 的方程,解方程即可;②设y 秒后四边形AOQP 的面积为10cm 2,根据四边形AOQP 的面积=12(OQ +AP )•OA 列出关于y 的方程,进而求出点P 的坐标.【解答】解:(1)依题意,得 {m +n −3=02m +n =0, 解得{m =−3n =6; (2)①设经过x 秒PQ 平行于y 轴,依题意,得6﹣2x =x 解得x =2,②当点P 在y 轴右侧时,依题意,得(6−2x)+x2×4=10,解得x =1,此时点P 的坐标为(4,4),当点P 在y 轴左侧时,依题意,得(2x−6)+x 2×4=10, 解得x =113,此时点P 的坐标为(−43,4).30.(2022春•武清区期中)已知点A (a ,0)、B (b ,0),且√a +4+|b ﹣2|=0.(1)求a 、b 的值.(2)在y 轴的正半轴上找一点C ,使得三角形ABC 的面积是15,求出点C 的坐标.(3)过(2)中的点C 作直线MN ∥x 轴,在直线MN 上是否存在点D ,使得三角形ACD 的面积是三角形ABC 面积的12?若存在,求出点D 的坐标;若不存在,请说明理由.【分析】(1)根据非负数的性质列方程即可得到结论;(2)由A (﹣4,0)、B (2,0),得到AB =6,根据三角形ABC 的面积是15列方程即可得到即可;(3)根据三角形ABC 的面积是15列方程即可得到结论.【解答】解:(1)∵(a +4)2+|b ﹣2|=0,∴a +4=0,b ﹣2=0,∴a =﹣4,b =2;(2)如图1,∵A (﹣4,0)、B (2,0),∴AB =6,∵三角形ABC 的面积是15,∴12AB •OC =15, ∴OC =5,∴C (0,5);(3)存在,如图2,∵三角形ABC 的面积是15,∴S △ACD =12CD •OC =15,∴12CD ×5=12×15,∴CD=3,∴D(3,5)或(﹣3,5).。
初中数学格点与面积(B)同步练习及答案

九、格点与面积(B)年级______班_____ 姓名 _____得分_____ 一、填空题:1.右图是用皮筋在钉板上围成的一个三角形,计算它的面积是多少.(每相邻两个小钉之间的距离都等于1个长度单位).2.右图是一根用皮筋在钉板上围成的一个四边形,计算它的面积是多少.(每相邻两个小钉之间的距离都等于1个长度单位).3.在一个9⨯6的长方形内,有一个凸四边形ABCD(如右图).用毕克定理先求出它的面积来,再用拼割方法计算它的面积,看两者是否一致.4.右图中每个小正方形的面积都是4平方厘米,求图中阴影部分的面积.5.右图是一个10⨯10的正方形,求正方形内的四边形ABCD的面积.6.右图是一个8⨯12面积单位的图形.求矩形内的箭形ABCDEFGH的面积.7.右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?8.右图是一个5⨯5的方格纸,小方格的面积是1平方厘米,小方格的顶点为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用线段连结所围成的面积尽可能大,那么,所用图形的面积1是多少平方厘米?9.右图中每个小正方形的面积为1平方分米,那么阴影部分的面积是多少平方分米?10.右图中每个小平行四边形的面积是1个面积单位,求阴影部分的面积.二、解答题:1.右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算ABC∆的面积.2.右图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算四边形DEFG的面积.3.把等边三角形ABC每边六等分,组成如右图的三角形网.若图中每个小三角形的面积均为12cm,试求图中三角形DEF的面积.4.把大正三角形每边八等份,组成如右图所示的三角形网.如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积.———————————————答案——————————————————————一、填空题:1. 5.5面积单位.分析:解答这类问题可直接套用毕克定理:格点面积=内部格点数+周界上格点数÷2-1.注意:一是毕克定理只对格点凸多边形适用,二是在数格点时要细心.解: 5+3÷2-1=5.5(面积单位).2. 5+5÷2-1=6.5(面积单位).3. 27.5面积单位.解: ①由毕克定理得:25+7÷2-1=27.5(面积单位).②用拼割方法得:ABCD的面积=长方形EFGH的面积-四角上的四个三角形的面积 =9⨯6-(6⨯2÷2+3⨯3÷2+4⨯3÷2+4⨯5÷2)=54-(6+4.5+6+10)=27.5(面积单位).4. 48平方厘米.解: ①内部格点数为: 9个;②周界上格点数为: 8个;③阴影部分的面积是: 4⨯(9+8÷2-1)=48(平方厘米).5. 30面积单位.解: 因为ABCD不是凸四边形,所以如在原题图上取格点E,则三角形BCE及四边形AECD都是凸的图形,故:S=(4+6÷2-1)+(21+8÷2-1)ABCD=6+24=30(面积单位).6. 46面积单位.解: 因为ABCDEFGH不是凸多边形,所以,连结GC、MN,则ABH∆、矩形GCNM、三角形MFE、EDN都是凸的图形.故箭形ABCDEFGH的面积=(8+10÷2-1)+4⨯8+(4÷2-1)⨯2=12+32+2=46(面积单位).7. 67.5面积单位.解: 图形内部格点数为59,图形周界上格点数为19.所以图形的面积为:59+19÷2-1=67.5(面积单位).8. 23.5(平方厘米).分析与解: 这是一个5⨯5的方格纸,共有25个格点.现在要围成一个面积最大的图形,根据格点面积公式,要使图形面积最大,必须使图形包含的内部格点数和周界上格点数尽可能多.由方格纸可知,内部格点数最多为4⨯4=16,周界上格点数最多为5⨯4=20.但是,当周界上格点数为最多时,不符合题中“任意3个格点不在一条直线上”的条件,因此,适当调整图上7个格点的位置,如右上图所示,就得到了面积最大的图形.所围成图形的最大面积为: 16+17÷2-1=23.5(平方厘米).9. 8.5平方分米.解:图形内部格点数为7,图形周界上格点数为 5.阴影部分的面积为:7+5÷2-1=8.5(平方分米).10. 18.5面积单位.解: 图形内部格点数为16,图形周界上格点数为7.图形的面积为: 16+7÷2-1=18.5(面积单位).二、解答题:1. 10面积单位.分析: 由“∵”和“∴”重合两点可拼为平行四边形 ,可以推出如下计算这类格点面积的公式:图形面积=(内部格点数+周界上格点数÷2-1)⨯2.解: 图形内部格点数为4,图形周界上格点数为4.ABC S ∆=(4+4÷2-1)⨯2=10(面积单位).2. 12面积单位.解: DEFG S 四边形=(5+4÷2-1)⨯2=12(面积单位).3. 11面积单位.解: 图形内部格点数为5,图形周界上格点数为3. DEF S ∆=(5+3÷2-1)⨯2=11(2cm ).4. 26面积单位.解: 图形内部格点数为12,图形周界上格点数为4. 图形的面积为: (12+4÷2-1)⨯2=26(面积单位).。
2023年中考数学《网格作图》真题及答案解析

2023中考真题抢先练:数学网格作图1.(2023达州18题)如图,网格中每个小正方形的边长均为1,△ABC 的顶点均在小正方形的格点上.(1)将△ABC 向下平移3个单位长度得到△A 1B 1C 1,画出△A 1B 1C 1;(2)将△ABC 绕点C 顺时针旋转90度得到△A 2B 2C 2,画出△A 2B 2C 2;(3)在(2)的运动过程中请计算出△ABC 扫过的面积.第1题图【推荐区域:安徽陕西】【参考答案】解:(1)如解图,△A 1B 1C 1即为所求;(2)如解图,△A 2B 2C 2即为所求;第1题解图(3)由图可得,△ABC 为等腰直角三角形,∴51222=+==BC AB ,AC =101322=+,∴25552121=´´=×=D BC AB S ABC ,∴△A 1B 1C 1在旋转过程中扫过的面积为2ABCACA S S D +扇形290360p ´=+52=52π+52.反比例与一次函数性质综合题2.(2023自贡24题)如图,点A (2,4)在反比例函数xm y =1图象上,一次函数b kx y +=2的图象经过点A ,分别交x 轴,y 轴于点B ,C ,且△OAC 与△OBC 的面积比为2:1.(1)求反比例函数和一次函数的解析式;(2)请直接写出y 1≥y 2时,x 的取值范围.第2题图【推荐区域:安徽江西甘肃】【参考答案】解:(1)将A (2,4)代入x m y =1中得24m =,解得m =8,∴xy 81=,∵C (0,b ),∴12OAC S OC D =·2=b ,∵△OAC 与△OBC 的面积比为2:1,∴b OB OC S OBC 2121=´=D ,解得OB =1,∴B (-1,0)或(1,0),①将A (2,4),B (-1,0)代入b kx y +=2中,得îíì+-=+=,,b k b k 024解得ïîïíì==,,3434b k ∴34342+=x y ;②将A (2,4),B (1,0)代入b kx y +=2中,得îíì+=+=,,b k b k 024解得îíì-==,,44b k ∴442-=x y ;综上可知,一次函数的解析式为34342+=x y 或442-=x y ;(2)当34342+=x y 时,x ≤-3或0<x ≤2;当442-=x y 时,x ≤-1或0<x ≤2.解直角三角形的实际应用3.(2023达州19题)莲花湖湿地公园是当地人民喜爱的休闲景区之一,里面的秋千深受孩子们喜爱,如图所示,秋千链子的长度为3m ,当摆角∠BOC 恰为26°时,座板离地面的高度BM 为0.9m ,当摆动至最高位置时,摆角∠AOC 为50°,求座板距地面的最大高度为多少m?(结果精确到0.1m ;参考数据:sin 26°=0.44,cos 26°≈0.9,tan 26°≈0.49,sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.2)第3题图【推荐区域:安徽江西河南甘肃】【参考答案】解:如解图,过点B 作BD ⊥ON 于点D ,过点A 作AE ⊥ON 于点E ,作AF ⊥MN于点F,第3题解图∴四边形BDNM,AENF均为矩形,∴BM=DN=0.9,AF=EN,在Rt△OBD中,OD=OB·cos26°=3cos26°,∴ON=OD+DN=3cos26°+0.9,在Rt△OAE中,OE=OA·cos50°=3cos50°,∴EN=ON-OE=3cos26°+0.9-3cos50°,∴AF=3cos26°+0.9-3cos50°≈3×0.9+0.9-3×0.64=1.68≈1.7(m),答:座板距地面的最大高度为1.7m.4.(2023重庆A卷24题)为了满足市民的需求,我市在一条小河AB两侧开辟了两条长跑锻炼线路,如图:①A—D—C—B;②A—E—B.经勘测,点B在点A的正东方,点C在点B的正北方10千米处,点D在点C的正西方14千米处,点D在点A的北偏东45°方向,点E在点A的正南方,点E在点B的南偏西60°方向.( 1.41≈1.73)(1)求AD的长度;(结果精确到1千米)(2)由于时间原因,小明决定选择一条较短线路进行锻炼,请计算说明他应该选择线路①还是线路②?第4题图【推荐区域:安徽江西河南甘肃】【参考答案】解:(1)如解图,过点D作DF⊥AB于点F.第4题解图由题意可知,AB∥CD,BC⊥AB,∴四边形BCDF是矩形,且BC=10,CD=14.∴DF=BC=10,在Rt△ADF中,∠DAF=45°,∴AD≈14(千米),答:AD的长度约为14千米;(2)由题意可知,EA⊥AB,∠ABE=90°-60°=30°,∵AF=DF=10,BF=CD=14,∴AB=AF+BF=10+14=24,∴在Rt△ABE中,AE AB BE=2AE线路①:AD+CD+BC≈38.1(千米),线路②:AE+BE41.52(千米),∵38.1<41.52,∴小明应选择线路①.二次函数的实际应用5.(2023南充23题)某工厂计划从A ,B 两种产品中选择一种生产并销售,每日产销x 件,已知A 产品成本价m 元/件(m 为常数,且4≤m ≤6),售价8元/件,每日最多产销500件,同时每日共支付专利费30元;B 产品成本价12元/件,售价20元/件,每日最多产销300件,同时每日支付专利费y 元,y (元)与每日产销x (件)满足关系式201.080x y +=.(1)若产销A ,B 两种产品的日利润分别为1w 元,2w 元,请分别写出1w ,2w 与x 的函数关系式,并写出x 的取值范围;(2)分别求出产销A ,B 两种产品的最大日利润;(A 产品的最大日利润用含m 的代数式表示)(3)为获得最大日利润,该工厂应该选择产销哪种产品?并说明理由.[利润=(售价一成本)×产销数量一专利费]【推荐区域:安徽河北云南江西】【参考答案】解:(1)根据题意,得30)8(1--=x m w ,0≤x ≤500.)01.080()1220(22x x w +--=80801.02-+-=x x ,0≤x ≤300;(2)∵8-m >0,∴1w 随x 的增大而增大,又0≤x ≤500,∴当x =500时,1w 的值最大,39705001+-=m w 最大.1520)400(01.080801.0222+--=-+-=x x x w .∵-0.01<0,对称轴为直线x =400,当0≤x ≤300时,2w 随x 的增大而增大,∴当x =300时,2w 最大=-0.01×(300-400)2+1 520=1 420(元).(3)①若最大1w =最大2w ,即-500m +3970=1420,解得m =5.1;②若最大1w >最大2w ,即-500m +3970>1 420,解得m <5.1;③若最大1w <最大2w ,即-500m +3 970<1420,解得m >5.1.又∵4≤m ≤6,∴综上可得,为获得最大日利润:当m =5.1时,选择A ,B 产品产销均可;当4≤m <5.1时,选择A 种产晶产销;当5.1<m ≤6时,选择B 种产品产销.二次函数性质综合题6.(2023遂宁25题)在平面直角坐标系中,O 为坐标原点,抛物线c bx x y ++=241经过点O (0,0),对称轴过点B (2,0),直线l 过点C (2,-2)且垂直于y 轴.过点B 的直线1l 交抛物线于点M ,N ,交直线l 于点Q ,其中点M ,Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当BM :MQ =3:5时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线1l 下方的抛物线上一动点,连接PQ ,PO ,其中PO 交1l 于点E ,设△OQE 的面积为1S ,△PQE 的面积为2S ,求12S S 的最大值.第6题图【推荐区域:安徽陕西】【参考答案】解:(1)由题意得0b 2124c =ìïïí-=ï´ïî,,解得01c b =ìí=-î,,∴抛物线的解析式为y =214x -x ;(2)如解图,过点M ,Q 作MD ⊥x 轴,QH ⊥x 轴分别于点D ,H ,第6题解图∴DM ∥HQ ,∴△BDM ∽△BHQ ,∴BM BQ =DM HQ ,∴38=2DM ,∴DM =34,∴点M 的纵坐标为-34,代入y =34x 2-x 中,解得x M =1或x M =3,∵点M 在抛物线对称轴的左侧,∴x M =1,∴点M (1,-34),设直线BM 的解析式为y =kx +b 1,将点M (1,-34)和点B (2,0)代入,得113=402k b k b ì-+ïíï=+î,,解得13=432k b ìïïíï=-ïî,,∴直线BM 的解析式为y =2343-x ,联立2143342y x x y x ì=-ïïíï=-ïî,,解得134x y =ìïí=-ïî,或63x y =ìí=î,,∵点N 在对称轴的右侧,∴点N (6,3);(3)由题意可知,点Q 的坐标为(0,-2),设点P (m ,14m 2-m ),由题意得直线y OP =(14m -1)x ,直线l 1的解析式为y BQ =x -2,联立1(1)42y m x y x ì=-ïíï=-î,,∴点E 的横坐标为x E =88m -,∴S 1=21OQ ·x E =21×2×m -88=m-88,S 2=21OQ ·(P E x x -)=21×2(m -m-88)=m m m ---8882,∴22188888S m m m S m ---=-=1812-+-m m =1)4812+--m (,∵81-<0,∴当m =4时,12S S 有最大值,最大值为1,∴12S S 的最大值为1.。
专题02网格类作图题中考题型训练(原卷版)

专题2 网格类作图题中考题型训练1.(2022•荆州)如图,在10×10的正方形网格中,小正方形的顶点称为格点,顶点均在格点上的图形称为格点图形,图中△ABC为格点三角形.请按要求作图,不需证明.(1)在图1中,作出与△ABC全等的所有格点三角形,要求所作格点三角形与△ABC有一条公共边,且不与△ABC重叠;(2)在图2中,作出以BC为对角线的所有格点菱形.2.(2022•宁波)图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点均在格点上,分别按要求画出图形.(1)在图1中画出等腰三角形ABC,且点C在格点上.(画出一个即可)(2)在图2中画出以AB为边的菱形ABDE,且点D,E均在格点上.3.(2022•丽水)如图,在6×6的方格纸中,点A,B,C均在格点上,试按要求画出相应格点图形.(1)如图1,作一条线段,使它是AB向右平移一格后的图形;(2)如图2,作一个轴对称图形,使AB和AC是它的两条边;(3)如图3,作一个与△ABC相似的三角形,相似比不等于1.4.(2022•衢州)如图,在4×4的方格纸中,点A,B在格点上.请按要求画出格点线段(线段的端点在格点上),并写出结论.(1)在图1中画一条线段垂直AB.(2)在图2中画一条线段平分AB.5.(2022•长春)图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,其顶点称为格点,△ABC的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.(1)网格中△ABC的形状是;(2)在图①中确定一点D,连结DB、DC,使△DBC与△ABC全等;(3)在图②中△ABC的边BC上确定一点E,连结AE,使△ABE∽△CBA;(4)在图③中△ABC的边AB上确定一点P,在边BC上确定一点Q,连结PQ,使△PBQ∽△ABC,且相似比为1:2.6.(2022•湖北)已知四边形ABCD为矩形,点E是边AD的中点,请仅用无刻度的直尺完成下列作图,不写作法,保留作图痕迹.(1)在图1中作出矩形ABCD的对称轴m,使m∥AB;(2)在图2中作出矩形ABCD的对称轴n,使n∥AD.7.(2022•江西)如图是4×4的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).(1)在图1中作∠ABC的角平分线;(2)在图2中过点C作一条直线l,使点A,B到直线l的距离相等.8.(2023•锡山区校级模拟)如图,在每个小正方形的边长为1的网格中,△ABC的顶点A,C均落在格点上,点B在网格线上.(Ⅰ)线段AC的长等于;(Ⅱ)以AB为直径的半圆的圆心为O,在线段AB上有一点P,满足AP=AC.请用无刻度的直尺,在如图所示的网格中,画出点P.9.(2023•鄞州区校级一模)如图,在6×6的方格纸中,每个小正方形的边长为1,点A,B均在格点上,在图1和图2中分别画出一个以点A,B为顶点且另两个顶点均在格点上的正方形,并分别求出其周长.10.(2023•衢州模拟)如图在7×7的方格中,有两个格点A、B.请用无刻度的直尺按要求画图.(1)在图1中画线段AB中点C;(2)在图2中在线段AB上找一点D,使AD:DB=1:2.11.(2023•宁波模拟)作图题(1)填空:如果长方形的长为3,宽为2,那么对角线的长为.(2)如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点(端点),分别按下列要求画图(不要求写画法和证明,但要标注顶点).①在图1中,画一个面积为4的菱形,且邻边不垂直.②在图2中,画平行四边形ABCD,使∠A=45°,且面积为6.12.(2023•杨浦区一模)新定义:由边长为1的小正方形构成的网格图形中,每个小正方形的顶点称为格点.如图,已知在5×5的网格图形中,△ABC的顶点A、B、C都在格点上.请按要求完成下列问题:(1)S△ABC=;sin∠ABC=;(2)请仅用无刻度的直尺在线段AB上求作一点P,使S△ACP=S△ABC.(不要求写作法,但保留作图痕迹,写出结论)13.(2023•武汉模拟)如图是由小正方形组成的7×6网格,每个小正方形的顶点叫做格点.仅用无刻度的直尺在给定网格中完成画图.(1)在图(1)中,A,B,C三点是格点,画经过这三点的圆的圆心O,并在该圆上画点D,使AD=BC;(2)在图(2)中,A,E,F三点是格点,⊙I经过点A.先过点F画AE的平行线交⊙I于M,N两点,再画弦MN的中点G.14.(2023•乌鲁木齐一模)请仅用无刻度的直尺在网格中完成下列作图,保留作图痕迹,不写作法.(1)图①是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.在图①中,画出△ABC中AB边上的中线CM;(2)如图②,四边形ABCD中,AD∥BC,∠A=∠D,画出BC边的垂直平分线n.15.(2023•靖江市校级模拟)如图是由小正方形组成的9×7网格,每个小正方形的顶点叫做格点,A,B,C三个格点都在圆上.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.(1)画出该圆的圆心O,并画出劣弧的中点D;(2)画出格点E,使EA为⊙O的一条切线,并画出过点E的另一条切线EF,切点为F.16.(2023•九台区模拟)图①、图②、图③均是4×4的正方形网格,每个小正方形的顶点称为格点,小正方形的边长为1,点A、B、C均在格点上.只用无刻度的直尺,在给定的网格中,按照要求作图(保留作图痕迹).(1)在图①中作△ABC的中线BD.(2)在图②中作△ABC的高BE.(3)在图③中作△ABC的角平分线BF.17.(2023•迁安市模拟)如图是由边长为1的小正方形组成的网格,△ABC的顶点均在格点上.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示,画图结果用实线表示.(1)在图(1)中画△ABC的高CH;(2)在图(1)的线段AC上画一点D,使得S△ABD:S△CBD=2:3;(3)在图(2)中C点的右侧画一点F,使∠FCA=∠BCA且CF=2.18.(2022•碧江区校级一模)操作理解,解答问题.(1)如图1:已知△ABC,AB=AC,直线CD∥AB;①完成作图:以点A为圆心,AB长为半径画弧,交直线CD于点P,连接PB.②试判断①中∠ABP与∠BAC的数量关系,并证明你的结论.(2)如图2:已知△ABC是格点三角形,点C在直线n上,且n∥AB;在直线n上画出点P,连接PB,使得∠PBA=∠CAB.(不用尺规作图)19.(2022•丽水模拟)图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出一个以AC为底边的等腰△ABC,使点B落在格点上.(2)在图2中画出一个以AC为对角线且面积为6的格点矩形ABCD(顶点均在格点上).20.(2022•婺城区校级模拟)如图,在4×4的方格中,点A,B,C为格点,利用无刻度的直尺画出满足以下条件的图形(保留必要的辅助线).(1)在图1中画△ABC的中线BE.(2)在图2中标注△ABC的外心O并画出其外接圆的切线CP.21.(2022•海陵区校级三模)如图(1)(2),在每个小正方形的边长为1的网格中,△ABC的顶点A,B,C均落在格点上,以AB为直径的半圆的圆心为O,请用无刻度的直尺,在如图(1)图(2)所示的网格中,在半圆O上画出点P,连接AP,使AP平分∠CAB.22.(2022•吉安模拟)如图,在正方形网格中,△ABC的顶点在格点(网格线的交点)上,请仅用无刻度直尺完成以下作图.(保留作图痕迹)(1)在图1中作△ABC的重心.(2)在图2中作∠AGB=∠ACB,且G是格点.23.(2022•绿园区校级模拟)如图①,②,③中每个小正方形的边长均为1.△ABC的顶点A,B均落在小正方形的顶点上,点C在小正方形的边上,以AC为直径的半圆的圆心为O.请用无刻度的直尺按要求画图.(1)如图①,在半圆上确定点D,使OD∥AB.(2)如图②,在线段AB的延长线上确定点E,使AE=AC.(3)如图③,在线段AC上确定点F,使AF=AB.24.(2022•南关区校级模拟)图①、图②、图③均是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,ABC的顶点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求作图.(不写作法,保留画图痕迹)(1)在图①中,在BC上画一点D,使S△ABD=S△ACD.(2)在图②中,在BC上画一点E,使S△ABE:S△ACE=2:3.(3)在图③中,在ABC内画一点F,使S△ACF:S△ABF:S△BCF=2:3:3.25.(2022•长春模拟)图①、图②分别是10×8的网格,网格中每个小正方形的边长均为1,A、B两点在小正方形的格点上,请在图①、图②中各取一点(点C必须在小正方形的格点上),使以A、B、C为顶点的三角形分别满足下列要求.(1)在图①中画一个△ABC,使∠ACB=90°,面积为5;(2)在图②中画一个△ABC,使BA=BC,∠ABC为钝角,并求△ABC的周长.26.(2022•二道区校级二模)图①、图②、图③均是6×6的正方形网格,每个小正方形的边长为1,每个小正方形的顶点称为格点,线段AB、EF、MN的端点均在格点上,只用无刻度的直尺,在给定的网格中,按下列要求画图.(1)在图①中,画∠ADB=45°;(2)在图②中,画∠APB=45°,且点P在线段EF上;(3)在图③中,画∠AQB=45°,且点Q在线段MN上.27.(2022•香坊区校级三模)如图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD的面积为8,并直接写出tan A的值.28.(2022•瑞安市校级三模)如图是由边长为1的小正六边形构成的网格图,网格上的点称为格点.已知格点线段AB,利用网格图,仅用无刻度的直尺来完成下面几何作图.(1)请在图①中作一个格点等腰三角形△ABC;(2)请在图②在线段AB上求作点P,使得AP:BP=3:4.(要求:不写作法但保留作图痕迹)29.(2022•江夏区模拟)用无刻度直尺作图:(1)如图1,在AB上作点E,使∠ACE=45°;(2)如图1,点F为AC与网格的交点,在AB上作点D,使∠ADF=∠ACB;(3)如图2,在AB上作点N,使=.(4)如图2,在AB上作点M,使∠ACM=∠ABC.30.(2022•阿城区模拟)如图,在每个小正方形的边长均为1的方格纸中,线段AB和线段DE,点A、B、D、E均在小正方形的顶点上.(1)在方格纸中画出以AB为底边的等腰三角形ABC,使△ABC的面积为10,点C在小正方形的顶点上,直接写出tan∠ABC的值;(2)在方格纸中画出钝角三角形DEF,使∠DEF=45°,点F在小正方形的顶点上.31.(2022•长春模拟)图①、图②、图③均是5×5的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,点A、B均在格点上.在图①、图②、图③中,只用无刻度的直尺,在给定的网格中按要求作图,所画图形的顶点均在格点上.(1)在图①中,画等腰三角形ABC,使其面积为3.(2)在图②中,画等腰直角三角形ABD,使其面积为5.(3)在图③中,画平行四边形ABEF,使其面积为9.32.(2022•朝阳区校级模拟)如图在8×8的网格中,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,用无刻度的直尺在网格中完成下列画图,保留必要的作图痕迹,不要求说明理由.(1)如图1,过点A作线段AF,使AF∥DC,且AF=DC.(2)如图2,在四边形ABCD边上求作一点E,使点E与四边形ABCD某一顶点连线,能把该四边形分成的两部分恰好拼成一个无缝隙、不重叠的三角形.(画一个即可)(3)如图3,在边AB上求作一点G,使∠AGD=∠BGC.。
备战中考数学二轮专题归纳提升真题格点图问题(解析版)

专题10 格点图问题【题型一:格点中的作图问题】【例1】(2021·宁波)如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.(1)在图1中画出以AB为边且周长为无理数的▱ABCD,且点C和点D均在格点上(画出一个即可).(2)在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.【答案】(1)解:如图四边形ABCD即为所作,答案不唯一.(2)解:如图,四边形AEBF即为所求作的正方形.【解析】(1)根据两边对边相等的四边形是平行四边形作图,注意根据勾股定理,结合无理数的定义作出AD和BC;(2)以AB为斜边分别作等腰直角△AFB和等腰直角△AEB,即可得出正方形AEBF.【例2】(2021温州)如图4×4与6×6的方格都是由边长为1的小正方形组成.图1是绘成的七巧板图案,它由7个图形组成,请按以下要求选择其中一个并在图2、图3中画出相应的格点图形(顶点均在格点上).(1)选一个四边形画在图2中,使点P为它的一个顶点,并画出将它向右平移3个单位后所得的图形.(2)选一个合适的三角形,将它的各边长扩大到原来的√5倍,画在图3中.【答案】(1)解:画法不唯一,当选四边形为正方形时可以是如图1或图2;当四边形式平行四边形时可以是图3或图4.(2)解:画法不唯一,当直角边长为√2时,扩大√5即直角边长为√10利用勾股定理画出直角边长为√10直角三角形可以是如图5或图6当直角边长为2√2时,扩大√5即直角边长为2√10利用勾股定理画出直角边长为2 √10直角三角形可以是如图7或图8等.【解析】(1)任选一个四边形,根据平移的性质分别得出对应点位置,然后将各点顺次连接起来即可;(2)先任选一个三角形,然后根据各边长扩大到原来的用勾股定理在方格图中画出边长扩大后的三角形即可.【练1】如图①,②,③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B,C均为格点.在给定的网格中,按下列要求画图:(1)在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点.(2)在图②中,画一条不与AC重合的线段PQ,使PQ与AC关于某条直线对称,且P,Q为格点.(3)在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.【答案】(1)如图①,MN即为所求(答案不唯一).(2)如图②,PQ即为所求(答案不唯一).(3)如图③,△DEF即为所求(答案不唯一).【练2】如图,在所给的方格纸中,每个小正方形的边长都是1,点A,B,C位于格点处,请按要求画出格点四边形.(1)在图①中画出格点P,使AC=CP,且以点A,B,C,P为顶点的四边形面积为3;(2)在图②中画出一个以点A,B,C,P为顶点的格点四边形,使AP2+CP2=15.【答案】(1)如图①中,四边形即为所求(答案不唯一).(2)如图②中,四边形即为所求(答案不唯一)【练3】如图,由5个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图(1),图(2),图(3)中分别画出满足以下各要求的图形.(用阴影表示)(1)使得图形既是轴对称图形,又是中心对称图形.(2)使得图形成为轴对称图形,而不是中心对称图形;(3)使得图形成为中心对称图形,而不是轴对称图形.【答案】【题型二:格点中的计算问题】【例】如图,在5×5的正方形网格中,每个小正方形的边长为1,点A,B,C都在格点上,则cos∠BAC的值为.【答案】√55【解析】如图,找出格点D,E,连接CD,AD,易知△ACD是直角三角形,A,C,E三点共线,连结BE,由勾股定理可知:AB 2=1+9=10,AE 2=1+1=2,BE 2=4+4=8,∴AB 2=AE 2+BE 2,∴△ABE 是直角三角形,∴cos ∠BAC =AE AB =√2√10=√55, 故答案为√55.【练1】如图,将正三角形ABC 分割成m 个边长为1的小正三角形和1个黑色菱形,这个黑色菱形可分割成n 个边长为1的小正三角形.若m n =4725,则正三角形ABC 的边长是 .【答案】12【解析】设正三角形ABC 的边长为x ,则高为√32x ,∴S △ABC =12x ·√32x =√34x 2, ∵所分成的都是边长为1的正三角形, ∴结合图形可得黑色菱形的较长的对角线长为√32x -√3,较短的对角线长为√32x -√3√33=12x -1, ∴黑色菱形的面积=12√32x -√312x -1=√38(x -2)2, ∴m n =√34x 2-√38(x -2)2√38(x -2)2=4725, 整理得11x 2-144x +144=0,解得x 1=1211(不符合题意,舍去),x 2=12,所以,△ABC 的边长是12.【练2】如图,在△ABC 中,AB ,BC ,AC 三边的长分别为√2,√13,√17,求这个三角形的面积.小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC (即△ABC 的三个顶点都在小正方形的顶点处),如图W5-9①所示.这样不需求△ABC 的高,而借用网格就能计算出它的面积.(1)请你将△ABC 的面积直接填写在横线上: .(2)我们把上述求△ABC 面积的方法叫做构图法.若△ABC 三边的长分别为2√2a ,√10a ,√26a ( >0),请利用图②的正方形网格(每个小正方形的边长为 )画出相应的△ABC ,并求出它的面积.(3)若△ABC 三边的长分别为√m 2+4n 2 ,√m 2+16n 2 ,2√m 2+n 2 (m>0,n>0,m ≠n ),请运用构图法在图③指定区域内画出示意图,并求出△ABC 的面积.【答案】(1)2.5(2)图见解析,S=4 2(3)图见解析,S=3mn【解析】(1)S △ABC =2×4-12×1×1-12×3×2-12×1×4=2.5,(2)如图,∵AB =2√2 ,BC =√10 ,AC =√26 ,∴S △ABC =2 ×5 -12×2 ×2 -12×3 × -12× ×5 =4 2.(3)如图,AB =√m 2+4n 2,AC =√m 2+16n 2,BC =2√m 2+n 2,∴S △ABC =2m ×4n -12×2m ×2n -12×m ×4n -12×m ×2n =3mn.【练3】如图,在5×5的正方形方格纸中,每个小正方形的边长为单位1,点A,B,C,P都在格点处.(1)请在图中作△BCD,使△BCD是以CD为底的等腰三角形,且点D为格点.(2)在(1)的条件下,连结AD,则四边形ABCD的面积为,再连结AC,则tan∠ACD=.(3)请仅使用无刻度直尺在线段BC上作一点Q,使点Q满足∠PQB=45°.(温馨提示:点Q可以是非格点哦!)【答案】(1)图见解析(2)10,13(3)图见解析【解析】(1)(2)如图,连接AD、AC四边形ABCD的面积=正方形ABMN的面积-三角形BMC的面积-三角形DNC的面积=4×4−12×2×4−12×2×2=16−4−2=10由图可得,AC=BC (3)【题型三:格点中的计数问题】【例】如图,A ,B 是4×5网格中的格点,网格中的每个小正方形的边长是1,图中使以A ,B ,C 为顶点的三角形是等腰三角形的格点C 有几个?【答案】3个【解析】如图,∵A ,B 是4×5网格中的格点,∴AB =√22+32=√13,同理可得AC =AE =BD =√13.∴所求三角形有:△ABD ,△ABC ,△ABE.【练1】如图,点A 是5×5网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1,以A 为其中的一个顶点,面积等于52的格点等腰直角三角形(三角形的三个顶点都是格点)的个数为【答案】16个的格点等腰直角三角形,所以就要求直角边长为√5,如图,【解析】因为是面积等于52因为√5=√12+22,所以以点A为圆心,√5为半径画圆,与格点的交点就是三角形的另一顶点,①当A位于直角顶点时,存在8种情况,如图①②.②当A位于斜边的一个顶点时,同样存在8种情况,如图③④.的格点等腰直角三角形共有16个.∴以A为顶点且面积等于52【练2】在如图所示的5×5方格中,每个小方格都是边长为1的正方形,△ABC是格点三角形(即顶点恰好是正方形的顶点),则与△ABC有一条公共边且全等的所有格点三角形的个数是.【答案】4个【解析】如图所示,以BC为公共边的三角形有3个,以AB为公共边的三角形有0个,以AC为公共边的三角形有1个,总计个.。
部编数学九年级下册专题14网格中画相似(解析版)含答案
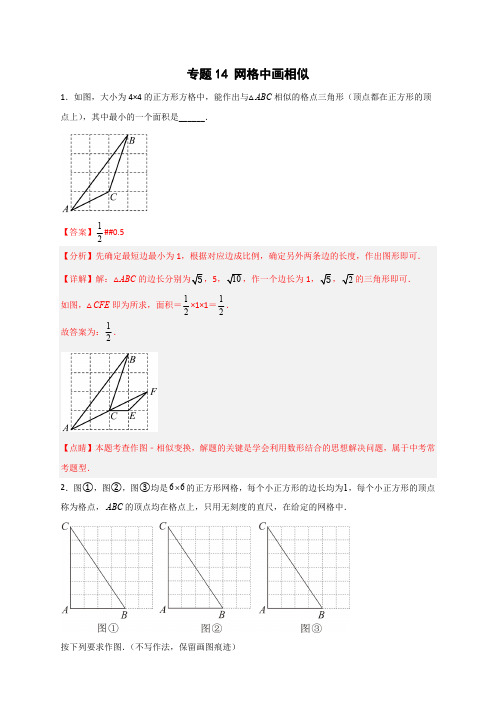
专题14 网格中画相似1.如图,大小为4×4的正方形方格中,能作出与△ABC 相似的格点三角形(顶点都在正方形的顶点上),其中最小的一个面积是______.【答案】12##0.5【点睛】本题考查作图﹣相似变换,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.2.图①,图②,图③均是66´的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,ABC 的顶点均在格点上,只用无刻度的直尺,在给定的网格中.按下列要求作图.(不写作法,保留画图痕迹)(1)在图①中,在BC 上画一点D ,使ABD ACD S S =V V ;(2)在图②中,在BC 上画一点E ,使ABE S V :2ACE S =V :3;(3)在图③中,在ABC 内画一点F ,使ACF S △:ABF S △:2BCF S =V :3:3.(2)在图②中,点E 即为所求;点C 下移三个单位得到点连接MN ,得到CME ∽△△32CE CM BE BN ==∴,∴ABE S V :2ACE S =V :3(3)在图③中,点F 即为所求.由图可知,6AC =,AB =12ABC S =∴△,∵ACF S △:ABF S △:BCF S =V 21238ACF S =´=∴△,ABF S =△【点睛】本题考查作图-应用与设计作图,三角形相似性质,三角形的面积等知识,解题的关键是理解题意,学会利用数形结合的思想解决问题,属于中考常考题型.3.(1)如图,4×4的正方形方格中,△ABC 的顶点A 、B 、C 在小正方形的顶点上.请在图中画一个△A1B1C1,使△A1B1C1∽△ABC(相似比不为1),且点A1、B1、C1都在小正方形的顶点上.并将此三角形涂上阴影(2)按要求作图,不要求写作法,但要保留作图痕迹:我们知道,三角形具有性质:三边的垂直平分线相交于同一点,三条角平分线相交于一点,三条中线相交于一点,事实上,三角形还具有性质:三条高所在直线相交于一点.请运用上述性质,只用直尺(不带刻度)作图.①如图1,在平行四边形ABCD中,E为CD的中点,作BC的中点F.②如图2,在由小正方形组成的4×3的网格中,△ABC的顶点都在小正方形的顶点上,作△ABC的高AH(2)①如图1,点F 为所作;理由:因为三角形的三条中线交于同一点,四边形ABCD 是平行四边形,∴O 是BD 的中点,∵E 是CD 的中点,根据三条中线交于同一点,连接BE 交AC 于P ,则点P 为三条中线的交点,作射线DP 交DP 于点F ,则点F 为BC 的中点;②如图2,找到格点D ,过A 点作AD 垂直AB ,再平移DA 得到CE ,则CE ⊥AB ,接着作MN 垂直AC ,平移MN 得到BF ,则BF ⊥AC ,BF 与CE 的交点O 为△ABC 的垂心,所以延长AO 交BC 于H ,则AH ⊥BC ,AH 为所作.理由:∵ABG DAKV V ≌∴GAB ADKÐ=Ð90GAB DAK ADK DAK \Ð+Ð=Ð+Ð=°∴90BAD Ð=°∴BA AD^平移AD 至CJ ,并延长,交AB 于点E ,∴CE AB^同理作出BF AC ^,,BF CE 交于点O根据三角形三条高所在的直线交于同一点,延长AO 交BC 于点H ,则AH 即为所求.【点睛】本题考查了画相似三角形:根据相似三角形的判定条件作为作图的依据.比较简单的是把原三角形的三边对应的缩小或放大一定的比例即可得到对应的相似图形,也考查了三角形的重心和平行四边形的性质.4.在4*4的方格中,ABC V 的三个顶点都在格点上.(1)在图1中画出与ABC V 成轴对称且与ABC V 有公共边的格点三角形(画出一个即可);(2)将图2中画一个与ABC V 相似的三角形.【答案】(1)见解析;(2)见解析.【分析】(1)选取AC 所在的直线为对称轴作图即可;(2)保证每条边方向一致,且边长减小为原来的一半作图即可.【详解】(1)解:如下图所示,AB C ¢V 即为所求作的三角形;(答案不唯一)(2)如下图所示,DEF V 即为所求作的三角形;【点睛】本题考查轴对称作图与作相似图形,掌握两个图形关于某条直线对称的性质与相似三角形的性质是解题的关键.5.如图,ABC D 是正方形网格中的格点三角形(顶点在格点上),请在正方形网格上按下列要求画一个格点三角形与ABC D 相似.(1)在图甲中画△111A B C ,使得△111A B C 的周长是ABC D 的周长的2倍;(2)在图乙中画出△222A B C ,使得△222A B C 的面积是ABC D 的面积的2倍.(1)A B C,即为所求;解:如图所示:△111(2)A B C,即为所求.解:如图所示:△222【点睛】此题主要考查了相似变换,正确得出对应三角形的边长是解题关键.6.如图,在8×8的正方形网格中,△ABC是格点三角形,请按以下要求作图.(1)在图1中画出格点△EDP,使得△EDP∽△ABC,且面积比为1;2(2)在图2中将△ABC绕着某格点逆向时针旋转90°得到格点△PFG,其中C与P对应.【答案】(1)见解析(2)见解析【分析】(1)直接利用位似图形的性质,结合位似中心得出答案;(2)直接利用旋转的性质得出对应点位置进而得出答案.(1)如图,(案不唯一)(2)如图,【点睛】此题主要考查了位似变换以及旋转变换,根据题意得出对应点位置是解题关键.7.如图,在74´方格纸中,点A,B,C都在格点上(△ABC称为格点三角形,即格点△ABC),用无刻度直尺作图.(1)在图1中的线段AC上找一个点D,使25CD AC=;(2)在图2中作一个格点△CEF,使△CEF与△ABC相似.【答案】(1)见解析(2)见解析【分析】(1)根据“8字形”相似,可得CD:AD=2:3,从而得出点D的位置;(2)根据∠ACB=90°,AC=2BC,即可画出△CEF.【详解】(1)解:如图1所示,点D即为所求,(2)如图2所示,△CEF即为所求,【点睛】本题主要考查了相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.8.如图,在7×6的正方形网格中,点A、B、C、D在格点(小正方形的顶点)上,从点A、B、C、D四点中任取三点,两两连接,得到一个三角形,请在所得的所有三角形中,写出互为相似的两个三角形及它们的相似比.∵AB=2221+=5,AC=∴55225ADBD==,ABCD=∴52 AD AB BDBD CD BC===,∴△ABD∽△DCB,相似比9.如图,在5×5的边长为1小的正方形的网格中,如图1△ABC和△DEF都是格点三角形(即三角形的各顶点都在小正方形的顶点上).(1)判断:△ABC与△DEF是否相似?并说明理由;(2)在如图2的正方形网格中,画出与△DEF相似且面积最大的格点三角形,并直接写出其面积.【答案】(1)相似,见解析(2)图见解析,面积为5【点睛】此题考查了作图—相似变换,三角形的面积等知识,解题的关键是掌握相似变换的性质,灵活运用所学知识解决问题.10.按要求作图,无需写作法:图①图②(1)如图①,已知∠AOB,OA=OB,点E 在OB 边上,四边形AEBF 是平行四边形,只用无刻度的直尺在图中画出∠AOB 的平分线.(2)如图②,在边长为1个单位的方格纸上,有△ABC,请作一个格点△DEF,使它与△ABC相似,但相似比不能为1.Q即为所求\11.如图正方形网格中,每个小正方形的边长均为1,只用无刻度的直尺,在给定的网格中按要求画图.(1)在图①中画等腰△ABC ,使得∠CAB =90°;(2)在图②中画等腰△DEF ,使△ABC ∽△DEF :1.10AB =Q ,10AC =,25BC =,5,5,10DE DF EF ===,21AB AC BC DE DF EF \===.\△ABC ∽△DEF ,且相似比为2:1.【点睛】本题考查了勾股定理,相似三角形的性质,掌握勾股定理与相似三角形的性质是解题的关12.图①、图②、图③分别是6×6的正方形网格,网格中每个小正方形的边长均为1,小正方形的顶点称为格点,点A 、B 、C 、D 、E 、P 、Q 、M 、N 均在格点上,仅用无刻度的直尺在下列网格中按要求作图,保留作图痕迹.(1)在图①中,画线段AB 的中点F .(2)在图②中,画CDE V 的中位线GH ,点G 、H 分别在线段CD 、CE 上,并直接写出CGH V 与四边形DEHG 的面积比.(3)在图③中,画PQR V ,点R 在格点上,且PQR V 被线段MN 分成的两部分图形的面积比为1:3.【答案】(1)见解析(2)见解析,面积比为1:3(3)见解析【分析】(1)根据网格的特点,找到,A B 之间单元网格的对角线,交AB 于点F ,则点F 即为所求;(2)根据(1)的方法找到,CD CE 的中点,G H ,连接GH ,根据相似三角形的性质即可求出CGH V 与四边形DEHG 的面积比;(3)根据(2)的结论,可知,只要MN 经过PQR V 的中位线,根据R 在网格上,找到符合题意的点R 即可求解.(1)如图①:13.如图,已知ABC V 和点O .(2)用无刻度的直尺,在AC边上画出点P,使23PAPC=(要求保留作图痕迹,不写作法).(2)解:如图,取网格点E、F,连接EF交AC14.如图,ABC V 是格点三角形(三角形的三个顶点都在格点上),每个小正方形的边长均为1.(1)在图(1)中将ABC V 绕点C 逆时针旋转90°,得到CDE V .(2)在图(2)中找格P ,使以格点P 、C 、B 为顶点的三角形与ABC V 相似,但不全等,请画出一个符合条件的三角形.【答案】(1)见解析(2)见解析【分析】(1)找到旋转角度、旋转中心、旋转方向后可得出各点的对应点,进而顺次连接即可得出答案;(2)可找能使PCB V 是直角三角形且2PB BC =或2PC BC =的P .(1)所作图形如下:(2)【点睛】本题考查旋转作图及相似三角形的性质,明确旋转角度、旋转中心、旋转方向是解本题的关键.15.如图是由边长为1的小正方形构成的69´网格,各个小正方形的顶点叫做格点.△ABC 的顶点在格点上,边BC 上的点D 也是一个格点.仅用无刻度的直尺在定网格中画图.画图过程用虚线表示,画图结果用实线表示.(1)在图1中,先画出AC 的平行线DE 交AB 边于点E ,可在BC 边上画点F ,使ACF BCA ∽△△;(2)在图2中,先在边AB 找点M ,使△MDC 与△MAC 的面积相等,再在AC 上画点N ,使△CDN 的面积是△ABC 的面积的三分之一.【答案】(1)见解析(2)见解析【分析】(1)根据格点特点画出AC 的平行线即可;根据格点特点作MA ⊥AC ,连接MC ,则△AMC16.如图,在6×7的矩形网格中,我们把顶点都在格点上的多边形称为格点多边形,点A,B,C 均在格点上,按下面要求画出格点三角形.(1)在图1中,画一个△ABD,使得△ABD与△ABC全等.(2)在图2中,画一个△ACE,使得S△ABC=3S△ACE,且点E不在边BC上.注:图1,图2在答题纸上.【答案】(1)见解析(2)见解析【分析】(1)运用三角形全等判定定理SSS,在网格上构造△ABD与△ABC全等.(2)△ACE与△ABC共顶点A,因此考虑两个三角形在以A为顶点的高线相等的情况下,构造3CE=BC,从而满足S△ABC=3S△ACE.(1)解:(2)解:【点睛】本题考查三角形全等判定定理,三角形面积计算方法,找到相应的作图依据是解题关键.17.如图,在7×8的正方形网格中,点A,B,C都在格点上,用无刻度直尺完成下列作图:(1)在AC上画点E,使AE=3CE;(2)在AB上画点D,使AD=CD;(3)在BC上画点F(不与B重合),使AF^BC.(4)在AB上画点P,使tan13 ACPÐ=.(2)如图,取格点,P Q,连接PQ,交AC于点M,Q=∥,AP CQ AP CQ\APM CQM∽V VAM AP\=1=MC PQ\=AM MCM,连接根据网格的特点作正方形,同理取中点1则DM是AC的垂直平分线,\=.DA DC(3)如图,方法同(2)作正方形BXYC ,作AZ ∥(4)如图,同方法(3)作正方形,作EE AC ¢^,同方法(连接1KK 交EE ¢于点S ,作射线CS 交AB 于点13,44AE AC CE AC ==Q ,1tan 3SE ACP EC \Ð==.【点睛】本题考查了网格中无刻度直尺作图,相似三角形的性质,正方形的性质,根据相似三角形的性质确定线段的长度是解题的关键.18.如图,在6×10的方格纸ABCD中有一个格点△EFG,请按要求画线段.(1)在图1中,过点O画一条格点线段PQ(端点在格点上),使点P,Q分别落在边AD,BC上,且PQ与FG的一边垂直.(2)在图2中,仅用没有刻度的直尺找出EF上一点M,EG上一点N,连结MN,使△EMN和△EFG的相似比为2:5.(保留作图痕迹)【答案】(1)见解析(2)见解析【分析】(1)根据题意找到格点,P Q,画出线段PQ即可(1)如图所示,PQ即为所求,19.请在如图所示的网格中,运用无刻度直尺作图(保留作图痕迹)(1)在图1中画出线段AB的中垂线AC CB=.(2)如图2,在线段AB上找出点C,使:1:2\点C 即为所求,如图所示:【点睛】本题考查作图—应用与设计作图,相似三角形的应用,解题关键是学会利用数形结合的思想解决问题.20.如图在5×5的网格中,△ABC 的顶点都在格点上.(仅用无刻度的直尺在给定的网格中按要求画图,画图过程用虚线表示,画图结果用实线表示)(1)在图1中画出△ABC 的中线AD ;(2)在图2中画线段CE ,点E 在AB 上,使得ACE S V :BCE S V =2:3;(3)在图3中画出△ABC 的外心点O .【答案】(1)见解析(2)见解析(3)见解析【分析】(1)由题知BO =CO ,取两个格点F 、G 构造CFD BGD △≌△,即可得中点D .(2)由ACE S V :BCE S V =2:3得AE :BE =2∶3,取格点H 、J ,构造△∽△AHE BGE ,且相似比为2∶3,即可得到E 点.(3)由O 为△ABC 的外心知O 为AB 、AC 的中垂线的交点,作出两条中垂线,交点即为O .(1)如图1中,取格点F 、G ,连接FG 交BC 于点D ,线段AD 即为所求.(2)如图2中,取格点H 、J ,连接HJ 交AB 于点E ,线段CE 即为所求.(3)如图3中,取格点K 、L 、M 、N ,连接KL 、MN 交于点O ,则点O 为所求.【点睛】本题考查作图-应用与设计作图,三角形的面积,平行线分线段成比例定理等知识,解题的关键是学会利用数形结合的思想解决问题.21.如图,在6×6的正方形网格中,每个小正方形的边长都为1,点A ,B ,C 均在格点上.请按要求在网格中画图,所画图形的顶点均需在格点上.(1)在图1中以线段AB 为边画一个ABD △,使其与ABC V 相似,但不全等.(2)在图2中画一个EFG V ,使其与ABC V 相似,且面积为8.(2)如图,△EFG 即为所求.【点睛】本题考查作图-相似变换,三角形的面积,全等三角形的判定等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.22.如图,在6×6的正方形网格中,每个小正方形的边长均为1,线段AB 的两个端点均在格点上,按要求完成下列画图(要求:用无刻度的直尺,保留画图痕迹,不要求写出画法).(1)在图①中,在线段AB 上找到一点E ,使AE BE=23;(2)在图②中,画出一个以A 、B 、C 为顶点的三角形,且cos ∠BAC (3)在图③中,画出一个四边形ACBD ,使其既是中心对称图形,又是轴对称图形,且邻边之比为12,C 、D 为格点.【答案】(1)见解析(2)见解析(2)V即为所求;如图所示,ABC(3)如图所示即为所求作【点睛】本题考查了作图-轴对称变换,等腰直角三角形的性质,相似三角形的判定与性质,解决本题的关键是掌握相关知识与性质.。
小学数学《格点与面积》练习题(含答案)

小学数学《格点与面积》练习题(含答案)内容概述同学们,一看这个题目,你一定会有许多疑问:什么是格点?格点与面积之间又有什么关系等等.这一节我们就来探讨这些问题。
在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!正方形格点问题正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的.每一个小方格都是一个小正方形.【例1】判断下列图形哪些是格点多边形?【例2】如右图,计算各个格点多边形的面积.分析:本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断出相应的有关数据就行了.【例3】如右图(a),计算这个格点多边形的面积.【例4】(1998年新加坡小学数学奥林匹克竞赛)右图是一个方格网,计算阴影部分的面积.【例5】分别计算右图中两个格点多边形的面积。
【例6】用N表示多边形内部格点, L表示多边形周界上的格点,S表示多边形面积,填写下表:图形图形内的格点数(N)边界上的格点数(L)面积(S)例2图4例3例4例5(1)【例7】本讲开始提到的图“乡村小屋”的面积是多少?【例8】 (保良局亚洲区城市小学数学竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【例9】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【例10】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?面积等于2平方厘米的三角形有多少个?三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.【例11】如右图(a),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC的面积.【例12】如右图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算△ABC的面积.【例13】把大正三角形每边八等份,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【例14】(第五届“华杯赛”)正六边形ABCDEF的面积是6平方厘米.M是AB中点,N是CD中点,P是EF中点.问:三角形MNP的面积是多少平方厘米?练习一1.求下列各个格点多边形的面积.2. 右图是一个8 12面积单位的图形.求矩形内的箭形ABCDEFGH的面积.3.求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).4.右图有12个点,相邻两个点之间的距离是1厘米,这些点可以连成多少个面积为2平方厘米的三角形?5.将图中的图形分割成面积相等的三块.正方形格点问题正方形格点问题就是它的格点都是由两组互相垂直相交的平行线的交点构成的.每一个小方格都是一个小正方形.【例15】判断下列图形哪些是格点多边形?分析:根据格点多边形的定义可知,图形的边必须是直线,顶点要在格点上!所以只有(1)是格点多边形。
中考数学复习15 格点问题
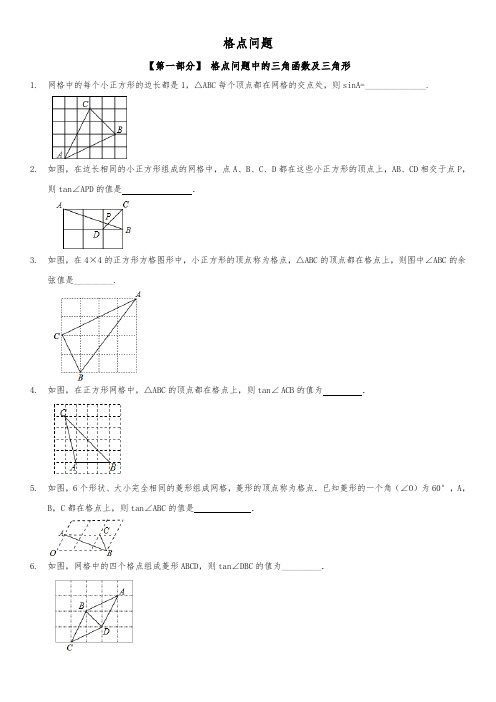
格点问题【第一部分】格点问题中的三角函数及三角形1.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA=______________.2.如图,在边长相同的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,则tan∠APD的值是.3.如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是_________.4.如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为.5.如图,6个形状、大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角(∠O)为60°,A,B,C都在格点上,则tan∠ABC的值是.6.如图,网格中的四个格点组成菱形ABCD,则tan∠DBC的值为_________.7. 如图1是由边长为1的小正方形组成的网格,点A 、B 、C 、D 都在网格的格点上,AC 、BD 相交于点O .(一)探索发现(1)如图1,当AB=2时,连接AD ,则∠ADO=90°,BO=2DO ,AD=2,BO=232,tan ∠AOD=_________. 如图2,当AB=3时,画AH ⊥BD 交BD 的延长线于H ,则AH=223, BO=________,tan ∠AOD=________. 如图3,当AB=4时,tan ∠AOD=__________.(2)猜想:当AB=n (n >0)时,tan ∠AOD=______________.(结果用含n 的代数式表示),请证明你的猜想. (二)解决问题(3)如图,两个正方形的一边CD 、CG 在同一直线上,连接CF 、DE 相交于点O ,若tan ∠COE=1317,求正方形ABCD 和正方形CEFG 的边长之比.【第二部分】 格点问题中的尺规作图【找中点】例一、做出BC 中点P①根据长方形性质找中点 ②根据平行四边形性质找中点【找三等分点】例二、①在BC上找点P,使PB:PC=2:1 ②在BC上找点P,使PC:PB=2:1总结:构造线段n等分点:①在一组平行线里找到线段两端;②在平行线上找到1与(n-1)长度的线段;③连接端点与已知线段交点即为所求。
长沙小升初奥数几何问题格点与面积解题方法

长沙小升初奥数几何问题格点与面积解题方法第1篇:长沙小升初奥数几何问题格点与面积解题方法常见解题方法:求格点图面积常见的几种方法:数格子法、分割法、扩展法、毕克定理。
(一)数格子法对于格点图里面的规则图形,我们有时可以直接通过数图形所占的正方形方格或者三角形方格的个数得出规则图形的面积,或者由图形得出规则图形相应的面积公式需要的量,代入公式解出面积即可!例、如下图,计算下列各个格点多边形的面积:(四年级8月1号天天练)【详解】本题所给的图形都是规则图形,它们的面积运用公式直接可求,只要判断出相应的有关数据就行了。
第(1)图是正方形,边长是4,所以面积是4×4=16(面积单位);第(2)图是矩形,长是5,宽是3,所以面积是5×3=15(面积单位);第(3)图是三角形,底是5,高是4,所以面积是5×4÷2=10(面积单位);第(4)图是平行四边形,底是5,高是3,所以面积是5×3=15(面积单位);第(5)图是直角梯形,上底是3,下底是5,高是3,所以面积是(3+5)×3÷2=12(面积单位);第(6)图是梯形,上底是3,下底是6,高是4,所以面积是(3+6)×4÷2=18(面积单位)。
下面几种方法主要针对的是格点图中的不规则图形,这也是本专题的重点!(二)分割法直接将格点图中的不规则图形分成若干个可求面积的规则图形,然后通过计算规则图形的面积来求原图形的面积。
(三)扩展未完,继续阅读 >第2篇:长沙小升初奥数几何问题之格点与面积经典例题汇总长沙小升初奥数几何问题之格点与面积经典例题。
经典例题例1、图中有21个点,其中每相邻的三点“∴”或“∵”所形成的三角形都是面积为1的等边三角形,试计算四边形的面积。
(小升初8月1号天天练)【详解】方法一(分割法):如图①做辅助线,将原图分割成a、b两个小三角形。
这两个小三角形都以辅助线为底的话,a就是底边是1个面积单位三角形的4倍、高是1个面积单位三角形的1倍,所以a的面积是1个面积单位三角形的4×1倍,即4。
课题学习 格点多边形的面积计算-2020春浙教版八年级数学下册同步训练

课题学习格点多边形的面积计算A组(第1题)1.如图,关于方格板中的两个四边形,下列叙述正确的是(C)A. 四边形Ⅰ的面积大于四边形Ⅱ的面积B. 四边形Ⅰ的面积小于四边形Ⅱ的面积C. 这两个四边形的面积相同,但Ⅰ的周长小于Ⅱ的周长D. 这两个四边形的面积相同,但Ⅰ的周长大于Ⅱ的周长2.在格点图中,横排或竖排相邻两格点间的距离都为1.若格点多边形边界上有12个格点,图形内有4个格点,则这个格点多边形的面积为__9__.3.在如图所示的5×5的方格纸中,每个小正方形的边长都为1.画出三个格点多边形,使格点多边形内的格点数为4,格点多边形边界上的格点数分别为5,6,7,并求出每一个图中的格点多边形的面积.,(第3题))【解】 如图所示(答案不唯一).图①中,格点多边形内的格点数a =4,格点多边形边界上的格点数b =5, ∴S =a +12b -1=4+12×5-1=112.图②中,格点多边形内的格点数a =4,格点多边形边界上的格点数b =6, ∴S =a +12b -1=4+12×6-1=6.图③中,格点多边形内的格点数a =4,格点多边形边界上的格点数b =7, ∴S =a +12b -1=4+12×7-1=132.4.“皮克定理”是用来计算顶点在整点的多边形面积的公式,公式表达式为S =a +b2-1,小明只记得公式中的S 表示多边形的面积,a 和b 中有一个表示多边形边上(含顶点)的整点个数,另一个表示多边形内部的整点个数,但不记得究竟是a 还是b 表示多边形内部的整点个数.请你根据图①推断公式,并运用这个公式求得图②中多边形的面积.(第4题)【解】根据图①可得,-1;∵三角形内有1个格点,边上有8个格点,面积为4,即4=1+82-1,长方形内有2个格点,边上有10个格点,面积为6,即6=2+102∴公式中表示多边形内部整点个数的字母是a.∵图②中,a=15,b=7,-1=17.5.∴图②中多边形的面积S=15+725.如图,每个小正方形的面积都为1.(第5题)(1)求凹多边形的面积.(2)若记格点多边形内的格点数为a ,边界上的格点数为b ,则图中a =__11__,b =__11__,代入格点多边形的面积计算公式S =a +12b -1中,得S =15.5.(3)根据问题(1)和(2),猜想格点多边形的面积计算公式S =a +12b -1是否适合凹多边形的情形(直接写出结论).【解】 (1)由长方形的面积减去三角形的面积,得S =4×6-12×1×3-12×3×2-12×2×2-12×1×4=15.5.(3)格点多边形的面积计算公式S =a +12b -1适合凹多边形的情形.B 组6.如图,在5×4的方格纸中,每个小正方形的边长均为1,点O ,A ,B 在方格纸的交点(格点)上,在第四象限内的格点上找一点C ,使△ABC 的面积为3,则这样的点C 共有(B )A. 2个B. 3个C. 4个D. 5个,(第6题)),(第6题解)) 【解】点C的位置如解图所示,共有3个.(第7题)7.如图,在5×5的方格纸中,小正方形的面积均为1,小正方形的顶点为格点,请你在图中选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连结后围成的图形面积尽可能大,并求出这个最大面积.(第7题解)【解】 当7个格点的位置如解图所示时,围成的面积最大,最大面积为5×5-0.5×3=23.5.(或∵a =16,b =17,∴S =a +12b -1=16+12×17-1=23.5.)8.各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何快速地计算它的面积?奥地利数学家皮克证明了格点多边形的面积公式:S =a +12b -1,其中a 表示多边形内部的格点数,b 表示多边形边界上的格点数,S 表示多边形的面积.如图①,a =4,b =6,S =4+12×6-1=6.(1)请在图②中画一个格点正方形,使它内部只含有4个格点,并写出它的面积. (2)请在图③中画一个格点三角形,使它的面积为72,且每条边上除顶点外无其他格点.,(第8题))【解】 (1)画法不唯一,如解图①或②所示.,(第8题解))(2)画法不唯一,三角形内部的格点数为3即可,如解图③或④所示.9.如图,正六边形ABCDEF的面积为54 cm2,AP=2PF,CQ=2BQ.求四边形CEPQ 的面积.(第9题)(第9题解)【解】 如解图,把正六边形等分成54个小正三角形,由于正六边形ABCDEF 的面积为54 cm 2,故每一个小正三角形的面积为1 cm 2,∴S 四边形ABQG =7 cm 2,S ▱GPHQ =8 cm 2,S ▱PMEF =6 cm 2,S ▱CDEN =18 cm 2.根据平行四边形的对角线平分平行四边形的面积,得S △PQG =12S ▱GPHQ =4 cm 2,S △EFP =12S ▱PMEF =3 cm 2,S △CDE =12S ▱CDEN =9 cm 2,∴S 四边形ABQP =S 四边形ABQG +S △PQG =7+4=11(cm 2),∴S 四边形CEPQ =S 正六边形ABCDEF -S 四边形ABQP -S △CDE -S △EFP =54-11-9-3=31(cm 2).数学乐园10.如图,A 是5×5网格图形中的一个格点(小正方形的顶点),图中每个小正方形的边长为1.求以A 为其中一个顶点,面积等于52的格点等腰直角三角形(三角形的三个顶点都是格点)的个数.,(第10题))【解】 ∵面积等于52,且为格点等腰直角三角形,∴等腰直角三角形的直角边长为5,5,斜边长为10.观察图形可知,以A 为直角顶点的等腰直角三角形有8个;以A 为45°角顶点的等腰直角三角形有8个,故共有16个.。
苏教版初一数学下学期期末专题《三角形格点与面积》

三角形格点与面积1.如图,在10×10的正方形网格中,每个小正方形的边长为1个单位长度.△ABC的顶点都在正方形网格的格点上,且通过两次平移(沿网格线方向作上下或左右平移)后得到△A'B'C',点C的对应点是直线上的格点C'.(1)画出△A'B'C';(2)在BC上找一点P,使AP平分△ABC的面积;(3)试在直线l上画出所有的格点Q,使得由点A'、B'、C'、Q四点围成的四边形的面积为9.2.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′;(2)若连接AA′,CC′,则这两条线段之间的关系是.(3)作直线MN,将△ABC分成两个面积相等的三角形.3.如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).(1)画出△ABC中BC边上的高AH和BC边上的中线AD.(2)画出将△ABC向右平移5格又向上平移3格后的△A′B′C′.(3)△ABC的面积为.(4)若连接AA′,CC′,则这两条线段之间的关系是.4.正方形网格中的每个小正方形的边长均为1个单位长度,△ABC各顶点的位置如图所示.将△ABC平移,使点A移到点D,点E、F分别是B、C的对应点.(1)画出平移后的△DEF;(2)在AB上找一点P,使得线段CP平分△ABC的面积;(3)利用网格画△ABC的高BH;(4)连接AD、CF,AD与CF的关系是.5.如图,三角形ABC的顶点A,B,C都在格点(正方形网格线的交点)上,将三角形ABC向左平移2格,再向上平移3格,得到三角形A'BC“(设点A、B、C分别平移到A′、B′、C′)(1)请在图中画出平移后的三角形A'B′C′;(2)若连接BB′、CC′,则这两条线段的位置关系是.数量关系是(3)若BB'与AC相交于点P,则∠A'B'P,∠B'PA与∠PAB三个角之间的数量关系为A.∠A'B'P+∠B'PA+∠PAB=180°B.∠A'B'P+∠B'PA+∠PAB=360°C.∠A'B'P+∠B'PA﹣∠PAB=180°D.∠A'B'P+∠B'PA﹣∠PAB=360°6.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点C变换为点D,点A、B的对应点分别是点E、F.(1)在图中请画出△ABC平移后得到的△EFD;(2)在图中画出△ABC的AB边上的高CH;(3)若点P在格点上,且S△PBC=S△ABC(点P与点A不重合),满足这样条件的P点有个.7.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.(1)画出△ABC向右平移4个单位后得到的△A1B1C1;(2)画出△ABC中AB边上的中线CM;(3)图中△ABC的面积是.8.如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和直尺画图:(1)补全△A′B′C′;(2)作出△ABC的中线CD;(3)画出BC边上的高线AF;(4)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有个.(注:格点指网格线的交点)9.画图(只能借助于网格)并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.(1)将△ABC向左平移4格,再向上平移1格,请在图中画出平移后的△A′B′C′;(2)△A′B′C′的面积为;(3)利用网格在图中画出△ABC的中线AD,高线AE;(4)在右图中能使S△PBC=S△ABC的格点p的个数有个(点P异于A).10.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.(1)在给定方格纸中画出平移后的△A′B′C′;(2)画出AB边上的中线CD和BC边上的高线AE;(3)线段AA′与线段BB′的关系是:;(4)求四边形ACBB′的面积.11.如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):(1)画出△A′B′C′;(2)画出△ABC的高BD;(3)连接AA′、CC′,那么AA′与CC′的关系是,线段AC扫过的图形的面积为.12.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:(1)在给定方格纸中画出平移后的△A′B′C′;(2)画出AB边上的中线CD;(3)画出BC边上的高线AE;(4)△A′B′C′的面积为.(5)点F为方格纸上的格点(异于点B),若S△ACB=S△ACF,则图中这样的格点F共有个.13.如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.(1)请在图中画出平移后的△A′B′C′;(2)若连接BB′,CC′,则这两条线段的关系是;(3)△ABC在整个平移过程中线段AB扫过的面积为.14.利用直尺画图(1)利用图(1)中的网格,过P点画直线AB的平行线和垂线.(2)把图(2)网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形.(3)如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于.15.如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).(1)分别画出△ABC中BC边上的高AH、中线AG.(2)画出先将△ABC向右平移6格,再向上平移3格后的△DEF.(3)画一个锐角△MNP(要求各顶点在格点上),使其面积等于△ABC的面积的2倍.16.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积=;(2)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP;(3)请在图中画出过点C且平行于AB的直线CM.17.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.(1)请画出平移后的△DEF;(2)若连接AD、CF,则这两条线段之间的关系是;(3)在图中找出所有满足S△ABC=S△QBC的格点Q(异于点A),并用Q1、Q2表示.18.画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.(1)将△ABC向左平移8格,再向下平移1格.请在图中画出平移后的△A′B′C′;(2)利用网格在图中画出△ABC的中线CD,高线AE;(3)△A′B′C′的面积为.(4)在平移过程中线段BC所扫过的面积为.(5)在右图中能使S△PBC=S△ABC的格点P的个数有个(点P异于A).19.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A平移到点D,点E、F分别是B、C的对应点.(1)请画出平移后的△DEF,并求△DEF的面积=;(2)在AB上找一点M,使CM平分△ABC的面积;(3)在网格中找格点P,使S△ABC=S△BCP,这样的格点P有个.20.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角板画图:(1)补全△A′B′C;(2)画出AB边上的中线CD;(3)画出AC边上的高线BE;(4)平移过程中,线段AB扫过的面积为.21.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;(2)在图中找出格点D,使△ACD的面积与△ABC的面积相等.22.如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.(1)请在图中画出平移后的△A′B′C′;(2)画出平移后的△A′B′C′的中线B′D′(3)若连接BB′,CC′,则这两条线段的关系是(4)△ABC在整个平移过程中线段AB扫过的面积为(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有个(注:格点指网格线的交点)23.如图所示,在8×8的网格中,△ABC是格点三角形(顶点是网格的交点),若点A坐标为(﹣1,3),按要求回答下列问题:(1)建立符合条件的平面直角坐标系,并写出点B和点C的坐标;(2)将△ABC先向下平移2个单位长度,再向右平移3个单位长度,得到△DEF,请在图中画出△DEF,并求出线段AC在平移过程中扫过的面积.24.如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角板画图:(1)补全△A′B′C′(2)画出AB边上的中线CD;(3)画出BC边上的高线AE;(4)△A′B′C′的面积为.25.如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.(1)在图中画出平移后的△A′B′C′;(2)若连接AA′,CC′,则这两条线段的关系是;(3)作直线l,将△ABC分成两个面积相等的三角形.【分析】(1)作出A、B、C的对应点A′、B′、C′即可;(2)根据平移的性质可知,线段AA′,CC′这两条线段之间的关系是相等且平行;(3)构造平行四边形ABCD,对角线BD所在的直线即为所求的直线MN.【解答】解:(1)平移后的△A′B′C′如图所示.(2)根据平移的性质可知,线段AA′,CC′这两条线段之间的关系是相等且平行,故答案为相等且平行.(3)构造平行四边形ABCD,对角线BD所在的直线即为所求的直线MN.【点评】本题考查平移变换、平移变换的性质、平行四边形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.3.如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).(1)画出△ABC中BC边上的高AH和BC边上的中线AD.(2)画出将△ABC向右平移5格又向上平移3格后的△A′B′C′.(3)△ABC的面积为3.(4)若连接AA′,CC′,则这两条线段之间的关系是AA′=CC′且AA′∥CC′.【分析】(1)根据三角形的中线和高的定义作图即可得;(2)根据平移变换的定义作出变换后的对应点,再顺次连接即可得;(3)直接利用三角形的面积公式计算可得;故答案为:AD=CF,AD∥CF.【点评】本题考查平移变换,三角形的中线,高等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.5.如图,三角形ABC的顶点A,B,C都在格点(正方形网格线的交点)上,将三角形ABC向左平移2格,再向上平移3格,得到三角形A'BC“(设点A、B、C分别平移到A′、B′、C′)(1)请在图中画出平移后的三角形A'B′C′;(2)若连接BB′、CC′,则这两条线段的位置关系是BB′∥CC′.数量关系是BB′=CC′(3)若BB'与AC相交于点P,则∠A'B'P,∠B'PA与∠PAB三个角之间的数量关系为CA.∠A'B'P+∠B'PA+∠PAB=180°B.∠A'B'P+∠B'PA+∠PAB=360°C.∠A'B'P+∠B'PA﹣∠PAB=180°D.∠A'B'P+∠B'PA﹣∠PAB=360°【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A′、B′、C′即可;(2)根据平移的性质求解;(3)根据平行线的性质和三角形外角性质解答.【解答】解:(1)如图所示:△A'B'C'即为所求:(2)根据平移的性质可得:BB′∥CC′,BB′=CC′;故答案为4【点评】本题考查作图﹣平移变换,三角形的面积等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.7.如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.(1)画出△ABC向右平移4个单位后得到的△A1B1C1;(2)画出△ABC中AB边上的中线CM;(3)图中△ABC的面积是8.【分析】(1)根据平移的定义作出变换后的对应点,再顺次连接即可得;(2)根据中线的概念作图可得;(3)利用割补法求解可得.【解答】解:(1)如图所示,△A1B1C1即为所求.(2)如图所示,CM即为所求;(3)△ABC的面积是×5×7﹣×2×6﹣×(2+5)×1=8,故答案为:8.【点评】本题考查了利用平移变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.8.如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和直尺画图:(1)补全△A′B′C′;(2)作出△ABC的中线CD;(3)画出BC边上的高线AF;(4)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有6个.(注:格点指网格线的交点)【分析】(1)由点B及其对应点B′的位置得出平移方向和距离,据此将点A、C按照相同方式平移得到对应点,再顺次连接即可得;(2)根据中线的概念作图可得;(3)根据高线的概念求解可得;(4)根据共底等高及平行线间的距离处处相等作图可得.【解答】解:(1)如图所示,△A′B′C′即为所求.(2)如图所示,CD即为所求;(3)如图所示,AF即为所求;(4)如图所示,中满足条件且异于点C的格点E共有6个,故答案为:6.【点评】本题主要考查作图﹣轴对称变换,解题的关键是掌握轴对称变换的定义和性质及中线、高线的概念、平行线间的距离处处相等.9.画图(只能借助于网格)并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.(1)将△ABC向左平移4格,再向上平移1格,请在图中画出平移后的△A′B′C′;(2)△A′B′C′的面积为4;(3)利用网格在图中画出△ABC的中线AD,高线AE;(4)在右图中能使S△PBC=S△ABC的格点p的个数有7个(点P异于A).【分析】(1)根据图形平移的性质画出△A′B′C′即可;(2)取线段AB的中点D,连接CD,过点A作AE⊥BC的延长线与点E即可;(3)根据图形平移的性质可直接得出结论;(4)根据S四边形ACBB′=S梯形AFGB+S△ABC﹣S△BGB′﹣S△AFB′即可得出结论.【解答】解:(1)如图所示;(2)如图所示;(3)由图形平移的性质可知,AA′∥BB′,AA′=BB′.故答案为:平行且相等;(4)S四边形ACBB′=S梯形AFGB+S△ABC﹣S△BGB′﹣S△AFB′=(7+3)×6+×4×4﹣×1×7﹣×3×5=30+8﹣﹣=27.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.11.如图,在边长为1个单位的正方形网格中,△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和无刻度的直尺画图并解答相关的问题(保留画图痕迹):(1)画出△A′B′C′;(2)画出△ABC的高BD;(3)连接AA′、CC′,那么AA′与CC′的关系是平行且相等,线段AC扫过的图形的面积为10.【分析】(1)根据平移的定义和性质作出点A、C平移后的对应点,顺次连接即可得;(2)根据三角形高的定义作图即可得;(3)根据平移变换的性质可得,再利用割补法求出平行四边形的面积.【解答】解:(1)如图所示,△A′B′C′即为所求;(2)如图所示,BD即为所求;(3)如图所示,AA′与CC′的关系是平行且相等,线段AC扫过的图形的面积为10×2﹣2××4×1﹣2××6×1=10,故答案为:平行且相等、10.【点评】此题主要考查了平移变换以及平行四边形面积求法等知识,根据题意正确把握平移的性质是解题关键.12.画图并填空:如图,方格纸中每个小正方形的边长都为1.在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.利用网格点和三角板画图或计算:(1)在给定方格纸中画出平移后的△A′B′C′;(2)画出AB边上的中线CD;(3)画出BC边上的高线AE;(4)△A′B′C′的面积为8.(5)点F为方格纸上的格点(异于点B),若S△ACB=S△ACF,则图中这样的格点F共有7个.【分析】(1)利用网格特点和平移的性质分别画出点A、B、C的对应点A′、B′、C′即可得到△A′B′C′;(2)根据平移的性质求解;(3)由于线段AB扫过的部分为平行四边形,则根据平行四边形的面积公式可求解.【解答】解:(1)如图,△A′B′C′为所作;(2)BB′∥CC′,BB′=CC′;(3)线段AB扫过的面积=4×3=12.故答案为平行且相等;12.【点评】本题考查了作图﹣平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.14.利用直尺画图(1)利用图(1)中的网格,过P点画直线AB的平行线和垂线.(2)把图(2)网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形.(3)如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于 3.5.【分析】(1)根据网格结构的特点,利用直线与网格的夹角的关系找出与AB平行的格点以及垂直的格点作出即可;(2)根据网格结构的特点,过点E找出与AB、CD位置相同的线段,过点F找出与AB、CD位置相同的线段,作出即可;(3)根据S△=S正方形﹣三个角上的三角形的面积即可得出结论.【解答】解:(1)、(2)如图所示;(3)S△EFH=3×3﹣×1×2﹣×2×3﹣×1×3=9﹣1﹣3﹣=3.5.故答案为:3.5.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.15.如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格).(1)分别画出△ABC中BC边上的高AH、中线AG.(2)画出先将△ABC向右平移6格,再向上平移3格后的△DEF.(3)画一个锐角△MNP(要求各顶点在格点上),使其面积等于△ABC的面积的2倍.【分析】(1)根据三角形的高和中线的定义结合网格作图可得;(2)根据平移变换的定义和性质作图可得;【点评】本题考查了平移变换的作图、三角形的面积、平分三角形的面积、平行线,知道三角形的中线平分三角形的面积,并会根据一个对应点的平移规律进行作图.17.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.(1)请画出平移后的△DEF;(2)若连接AD、CF,则这两条线段之间的关系是AD=CF,AD∥CF;(3)在图中找出所有满足S△ABC=S△QBC的格点Q(异于点A),并用Q1、Q2表示.【分析】(1)将三角形的三顶点分别向右平移6格、向下平移1格得到三顶点,再顺次连接可得;(2)根据平移变换的性质可得答案;(3)过点A作线段BC的平行线,平行线经过的网格点即为点Q1、Q2.【解答】解:(1)如图所示,△DEF即为所求.(2)根据平移变换的性质知,AD=CF,AD∥CF,故答案为:AD=CF,AD∥CF;(3)过点A作线段BC的平行线,平行线经过的网格点即为点Q1、Q2.【点评】本题考查了利用平移变换作图,平移的性质,熟练掌握网格结构,准确找出对应点的位置是解题的关键.(1)请画出平移后的△DEF,并求△DEF的面积=7;(2)在AB上找一点M,使CM平分△ABC的面积;(3)在网格中找格点P,使S△ABC=S△BCP,这样的格点P有4个.【分析】(1)根据平移的性质画出图象,再利用三角形的面积公式计算即可;(2)根据中线的定义画出中线即可平分三角形面积;(3)在过点A平行BC的直线上有4个格点,所以满足条件的△PCB有4个.【解答】解:(1)如图所示:△DEF即为所求,△DEF的面积为:4×4﹣×2×4﹣×2×3﹣×1×4=7;故答案为:7;(2)如图所示:点M即为所求;(3)使S△ABC=S△BCP,这样的格点P有4个.故答案为:4.【点评】本题考查平移变换、三角形的面积、三角形的中线等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.20.如图,在方格纸内将△ABC经过一次平移后得到△A′B′C,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角板画图:(1)补全△A′B′C;(2)画出AB边上的中线CD;(3)画出AC边上的高线BE;(4)平移过程中,线段AB扫过的面积为8.S△A′B′C′=3×3﹣×2×1﹣×3×1﹣×2×3=9﹣1﹣﹣3=3.5;(2)如图,点D1,D2即为所求.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.22.如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.(1)请在图中画出平移后的△A′B′C′;(2)画出平移后的△A′B′C′的中线B′D′(3)若连接BB′,CC′,则这两条线段的关系是BB′∥CC′,BB′=CC′(4)△ABC在整个平移过程中线段AB扫过的面积为12(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有10个(注:格点指网格线的交点)【分析】(1)利用网格特点和平移的性质画出A、B、C的对应点A′、B′、C′即可;(2)利用网格特点找出A′C′的中点D′,然后连接B′D′即可;(3)根据平移的性质求解;(4)利用平移的性质和平行四边形的面积公式求解;(5)过点C作AB的平行线,然后找出此平行线上的格点即可.【解答】解:(1)如图,△A′B′C′为所作;(2)如图,中线B′D′为所作;(3)BB′∥CC′,BB′=CC′;(4)△ABC在整个平移过程中线段AB扫过的面积=4×3=12;(5)满足条件且异于点C的格点E共有10个.线段AC在平移过程中扫过的面积=×2×1+2×3=7.【点评】本题主要考查作图﹣平移变换,解题的关键是熟练掌握平移变换的定义和性质及割补法求四边形的面积.24.如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角板画图:(1)补全△A′B′C′(2)画出AB边上的中线CD;(3)画出BC边上的高线AE;(4)△A′B′C′的面积为8.【分析】(1)直接利用平移的性质得出各点位置即可;(2)利用中线的定义得出D点的位置;(3)利用高线的定义得出E点的位置(4)直接利用三角形面积求法得出答案.【解答】解:(1)(2)(3)题如图所示.(4)△A′B′C′的面积为:×4×4=8.故答案为:8.【点评】此题主要考查了平移变换以及三角形面积求法,正确得出平移后对应点位置是解题关键.25.如图,△ABC的顶点都在方格纸的格点上,将△ABC向左平移1格,再向上平移3格,其中每个格子的边长为1个长度单位.(1)在图中画出平移后的△A′B′C′;(2)若连接AA′,CC′,则这两条线段的关系是AA′∥CC′,AA′=CC′;(3)作直线l,将△ABC分成两个面积相等的三角形.【分析】(1)根据图形平移不变性的性质画出△A′B′C′即可;(2)根据图形平移的性质即可得出结论;(3)过三角形的顶点与对边的中点作直线即可.【解答】解:(1)如图所示;(2)∵△A′B′C′由△ABC平移而成,∴AA′∥CC′,AA′=CC′.故答案为:AA′∥CC′,AA′=CC′;(3)如图所示.【点评】本题考查的是作图﹣平移变换,熟知图形平移不变性的性质是解答此题的关键.。
部编数学七年级下册专题15坐标系中的面积(和实数有关)(解析版)含答案

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!专题15 坐标系中的面积(和实数有关)【例题讲解】如图,在平面直角坐标系中,(),0A a ,(),0B b ,()1,2C -,且0a +=.(1)求a ,b 的值;(2)①在x 轴的正半轴上存在一点M ,(使COM V 的面积12ABC =△的面积,求出点M 的坐标;②在坐标轴的其它位置是否存在点M ,使COM V 的面积12ABC =△的面积恒成立?若存在,请直接写出符合条件的点M 的坐标.【综合解答】1.在平面直角坐标系中,A (a ,0),B (0,b ),且a 、b 满足()24240a b a +-++=.(1)求OA ,OB 长度;(2)在x 轴上是否存在点C ,使得三角形ABC 的面积是12;若存在,求出点C 的坐标;若不存在,请说明理由;(3)若点P 从点B 出发沿着y 轴运动(点P 不与原点、B 点重合)速度为每秒2个单位长度,连接AB 、AP ,当运动的时间t 为几秒时,3ABP AOP S S V V = ?并求出此时点P 的坐标.2.如图1,已知,点A (1,a ),AH ⊥x 轴,垂足为H ,将线段AO 平移至线段BC ,点B (b ,0),其中点A 与点B 对应、点O 与点C 对应,a 、b ()230b -=.(1)填空:①直接写出A、B、C三点的坐标A( )、B( )、C( );②直接写出三角形AOH的面积 .(2)如图2,连OC,动点P从点B开始在x轴上以每秒2个单位的速度向左运动,同时点Q从点O 开始在y轴上以每秒1个单位的速度向下运动.若经过t秒,三角形AOP与三角形COQ的面积相等,试求t的值及点P的坐标.3.已知,点()1,A a ,AH x ^轴,垂足为H ,将线段AO 平移至线段BC ,点(),0B b ,其中点A 与点B 对应,点O 与点C 对应,a 、b 2(3)0b -=.(1)填空:①直接写出A 、B 、C 三点的坐标(A ______)、(B ______)、(C ______);②直接写出三角形AOH 的面积______.(2)如图1,若点(),D m n在线段OA上,证明:4m n=.(3)如图2,连OC,动点P从点B开始在x轴上以每秒2个单位的速度向左运动,同时点Q从点O开始在y轴上以每秒1个单位的速度向下运动.若经过t秒,三角形AOP与三角形COQ的面积相等,试求t的值及点P的坐标.ODH Q V 的面积ADH +V 的面积OAH =V ()11141222n m \´´+´´-=,4m n \=.(3)解:①当点P 在线段OB 上,(132´解得 1.2t =.此时()0.6,0P .4.如图,在平面直角坐标系中,已知(),0A a ,(),0B b ,其中a ,b 满足2|1|(3)0a b ++-=(1)填空:=a ,b = ;(2)如果在第三象限内有一点(2,)M m -,请用含m 的式子表示三角形ABM 的面积;(3)在(2)的条件下,当2m =-时,在y 轴上有一点P ,使得三角形BMP 的面积与三角形ABM 的面积相等,请求出点P 的坐标.∵()1,0A -,()3,0B ,∴AB =3-(-1)=4∵(2,)M m -位于第三象限∴MN m m==-∴1(2 PBM PBQ PMQS S S=+=´-V V V解得145n=-,∴14(0,)5P-;1(2 PBM PBQ PMQS S S n=+=´+ V V V解得25n=,5.如图,C 为x 轴正半轴上一动点,(0,)A a ,(,0)B b ,且a ,b 2(8)0b +=,10AB =.(1)求△ABO 的面积;(2)求点O 到AB 的距离;(3)如图2,若(3,6)P ,PC x ^轴于点C ,点M 从点P 出发,在射线PA 上运动,同时另一动点N 从点B 出发向点A 运动,到点A 时两点停止运动,M ,N 的速度分别为2个单位长度/秒,3个单位长度/秒,当13MAC BON S S =V V 时,求运动的时间t 的值.n)在第一象限,已知m的算术平方根是2,64的立方根为n.(1)直接写出A,B,C三点的坐标;(2)求出△ABC的面积;(3)如图2,延长BC交y轴于D点,求点D的坐标;(4)如图3,过点C作CE∥AB交y轴于E点,求E点的坐标.,∵222轴,∵,∵7.如图,在下面直角坐标系中,已知A(0,a)、B(b,0)、C(-a,b)三点,其中a数部分,b+1的平方根是±2.(1)请求出a、b的值;(2)求出D ABC的面积;(3)在第四象限中是否存在点P到两坐标轴的距离相等且使四边形AOPB的面积与D ABC的面积相等?若存在,请求出点P的坐标,若不存在,请说明理由.8.如图,在平面直角坐标系xOy中,点A(a,0),B(c,c),C(0,c),且满足(a+8)2=0,P点从A点出发沿x轴正方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴负方向以每秒1个单位长度的速度匀速移动.(1)直接写出点B的坐标,AO和BC位置关系是 ;(2)如图(1)当P、Q分别在线段AO,OC上时,连接PB,QB,使S△PAB=4S△QBC,求出点P 的坐标;(3)在P、Q的运动过程中,当∠CBQ=30°时,请直接写出∠OPQ和∠PQB的数量关系.(3)∠PQB=∠OPQ+30°或∠当点Q在点C的上方时,过Q∴∠OPQ=∠PQH,∵BC∥AO,QH∥AO,∴QH∥BC,∴∠HQB=∠CBQ=30°,∴∠OPQ+∠CBQ=∠PQH+∠BQH【点睛】本题考查的是三角形的面积计算、坐标与图形性质、平行线的性质、三角形内角和定理,掌握非负数的性质、灵活运用分情况讨论思想是解题的关键.9.已知,在平面直角坐标系中,点(1)求a,b的值;(2)在y轴上是否存在点C,使三角形ABC的面积是12?若存在,求出点C的坐标;若不存在,请说明理由.(3)已知点P是y轴正半轴上一点,且到x轴的距离为3,若点P沿x轴负半轴方向以每秒1个单位长度平移至点Q,当运动时间t为多少秒时,四边形ABPQ的面积S为15个平方单位?写出此时点Q的坐标.10.如图1,在平面直角坐标系中,点A(a,0),B(0,b),且a、b2++=.(2)0a b(1)请直接写出A、B两点的坐标:点A为_______,点B为________.(2)若点P的坐标为(-2,n),且三角形PAB的面积为7,求n的值.(3)如图2,过点B作BC//x轴,点Q为x轴上点A左侧的一动点,连结QB,BM平分∠QBA,BN平分∠CBA,当点Q运动时,∠MBN:∠AQB的值是否发生变化?如果变化,请说明理由;如果不变,请求出其值.【答案】(1)A(2,0),B(0,﹣4);(2)n=﹣1或﹣15;(3)∠MBN:∠AQB=1:2.【分析】(1)根据绝对值的非负性、偶次方的非负性分别求出a、b,得到点A,B的坐标;(2)设AP与y轴交于点C,由三角形PAB的面积和高可以求得底边BC长为3.5,得出C的坐标.再利用待定系数法求直线AC的解析式,然后把点P的横坐﹣2代入解析式即可求得答案;(3)如图,∵BM平分∠ABQ∴∠1=∠2∵BN平分∠ABC∴∠ABN=∠NBC,即∠1+∠2+∠3=∠4∴∠MBN=∠2+∠3∵x轴//BC∴∠AQB=∠CBQ=∠3+∠4∴∠AQB=∠3+∠1+∠2+∠3=∠3+∠2+∠2+∠3=2(∠2+∠3)∴∠MBN:∠AQB=1:2.【点睛】本题考查的是非负数的性质、平移变换、三角形的面积计算,掌握坐标与图形的关系、灵活运用分情况讨论思想是解题的关键.11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(a,0),B(b,0),C(﹣1,2),且()220a+=.(1)求,a b的值;(2)若点M在x轴上运动,使三角形COM的面积是三角形ABC面积的2倍,请求出M的坐标;(3)过点C作AB的平行线,交y轴于点D,连接BD,过A作BD的平行线AE,交直线CD于点E,再作EG⊥x轴于G.动点P从D出发,沿DE→EG方向运动,速度为每秒1个单位长度,设运动时间为t秒,请回答:①求P在运动过程中的坐标(用含t的式子表示出来);、、之间的数量关系.②当6秒﹤t﹤8秒时,设∠EDP=a,∠PBG=β,∠DPB=γ,请求出αβγ∴∠EDP=∠DPF,∠PBG=∠BPF,∴∠DPB=∠EDP+∠PBG,即γ=α+β.【点睛】本题是三角形综合题,主要考查了平方和二次根式的非负性,三角形的面积,平行线的性质等知识,熟练掌握坐标和线段长度之间的转化以及平行线的性质是解题的关键.12.如图1,在平面直角坐标系中,(),0A a ,(),0B b ,()1,2C -,且()2230a b ++-=(1)求a ,b 的值.(2)①在y 轴的正半轴上存在一点M ,使12COM ABC S S =△△,求点M 的坐标;②在坐标轴的其它位置是否存在点M ,使12COM ABC S S =△△仍然成立,若存在,请直接写出符合条件的点M 的坐标.(3)如图2,过点C 作CD y ^轴交y 轴于点D ,点P 为线段CD 延长线上一动点,连接OP ,OE 平分AOP Ð,OF OE ^.当点P 运动时,OPD DOEÐÐ的值是否会改变?若不变,求其值;若改变,说明理由.。
4-2-1_格点型面积.题库学生版.doc

板块一正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N表示多边形内部格点,L表示多边形周界上的格点,S表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N=+-.这个规律就是毕克定理.【例 1】用9个钉子钉成相互间隔为1厘米的正方阵(如右图).如果用一根皮筋将适当的三个钉子连结起来就得到一个三角形,这样得到的三角形中,面积等于1平方厘米的三角形的个数有多少?面积等于2平方厘米的三角形有多少个?毕克定理若一个格点多边形内部有N个格点,它的边界上有L个格点,则它的面积为12LS N=+-.例题精讲格点型面积【例 2】如图,44的方格纸上放了16枚棋子,以棋子为顶点的正方形有个.【例 3】判断下列图形哪些是格点多边形?⑴⑵⑶【例 4】如图,计算各个格点多边形的面积.【例 5】如图(a),计算这个格点多边形的面积.III 【例 6】(“新加坡小学数学奥林匹克”竞赛试题)右图是一个方格网,计算阴影部分的面积.【例 7】分别计算图中两个格点多边形的面积.⑴ ⑵【巩固】求下列各个格点多边形的面积.⑵⑴⑷⑶【例 8】 我们开始提到的“乡村小屋”的面积是多少?【例 9】 右图是一个812 面积单位的图形.求矩形内的箭形ABCDEFGH 的面积.H GFED C BA【例 10】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【巩固】如图,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【例 11】 (“小学数学奥林匹克”竞赛试题)55 的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是 平方厘米.【例 12】 (“保良局亚洲区城市小学数学”竞赛试题)第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【例 13】 (第六届“从小爱数学”邀请赛试题)两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为25.12cm ,右下角的阴影部分(线状)面积为27.4cm ,求大正方形的面积.【例 14】 (第六届“华杯赛”试题)图中正六边形ABCDEF 的面积是54,AP =2PF ,CQ =2BQ ,求阴影四边形CEPQ 的面积.AB C DFQP板块二 三角形格点问题所谓三角形格点多边形是指:每相邻三点成“∵”或“∴”,所形成的三角形都是等边三角形.规定它的面积为1,以这样的点为顶点画出的多边形为三角形格点多边形.关于三角形格点多边形的面积同样有它的计算公式:如果用S 表示面积,N 表示图形内包含的格点数,L 表示图形周界上的格点数,那么有22S N L =⨯+-,就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2.【例 15】 如图(a ),有21个点,每相邻三个点成“∵”或“∴”,所形成的三角形都是等边三角形.计算三角形ABC 的面积.AB(a )【巩固】如图,每相邻三个点所形成的三角形都是面积为1的等边三角形,计算ABC 的面积.【例 16】求下列格点多边形的面积(每相邻三个点“∵”或“∴”成面积为1的等边三角形).⑴⑵⑶⑷【例 17】 把大正三角形每边八等分,组成如右图所示的三角形网.如果大三角形的面积是128,求图中粗线所围成的三角形的面积.【例 18】如图,如果每一个小三角形的面积是1平方厘米,那么四边形ABCD 的面积是多少平方厘米?【例 19】把同一个三角形的三条边分别5等分、7等分(如图1,图2),然后适当连接这些等分点,便得到了若干个面积相等的小三角形.已知图1中阴影部分面积是294平方分米,那么图2中阴影部分的面积是______平方分米.【例 20】将图中的图形分割成面积相等的三块.【例 21】如图涂阴影部分的小正六角星形面积是16平方厘米,问:大正六角星形面积是多少平方厘米?【例 22】 (第五届“华杯赛”试题)正六边形ABCDEF 的面积是6平方厘米.M 是AB 中点,N 是CD 中点,P 是EF 中点.问:三角形MNP 的面积是多少平方厘米?BP M F EDCBA【例 23】如果下图中任意相邻的三个点构成的三角形面积都是2平方厘米.那么,三角形ABC的面积是_____平方厘米.。
小学奥数:格点型面积.专项练习

模块一、正方形格点问题在一张纸上,先画出一些水平直线和一些竖直直线,并使任意两条相邻的平行线的距离都相等(通常规定是1个单位),这样在纸上就形成了一个方格网,其中的每个交点就叫做一个格点.在方格网中,以格点为顶点画出的多边形叫做格点多边形,例如,右图中的乡村小屋图形就是一个格点多边形.那么,格点多边形的面积如何计算?它与格点数目有没有关系?如果有,这两者之间的关系能否用计算公式来表达?下面就让我们一起来探讨这些问题吧!用N 表示多边形内部格点,L 表示多边形周界上的格点,S 表示多边形面积,请同学们分析前几个例题的格点数.我们能发现如下规律:12LS N =+-.这个规律就是毕克定理.【例 1】 判断下列图形哪些是格点多边形?⑴⑵⑶毕克定理若一个格点多边形内部有N 个格点,它的边界上有L 个格点, 则它的面积为12LS N =+-. 例题精讲4-2-7.格点型面积【例 2】 如图,计算各个格点多边形的面积.【例 3】 如图(a ),计算这个格点多边形的面积.【例 4】 右图是一个方格网,计算阴影部分的面积.【例 5】 分别计算图中两个格点多边形的面积.【巩固】 求下列各个格点多边形的面积.(1)(2)(3)(4)【例 6】 “乡村小屋”的面积是多少?【例 7】 右图是一个812 面积单位的图形.求矩形内的箭形ABCDEFGH 的面积.H GFED C BA【例 8】比较图中的两个阴影部分①和②的面积,它们的大小关系______【例 9】右图中每个小正方形的面积都是1,那么图中这只“狗”所占的面积是多少?【巩固】如图,每一个小方格的面积都是1平方厘米,那么用粗线围成的图形的面积是多少平方厘米?【例 10】第一届保良局亚洲区城市小学数学邀请赛在7月21日开幕,下面的图形中,每一个小方格的面积是1,那么7、2、1三个数字所占的面积之和是多少?【例 11】55的方格纸,小方格的面积是1平方厘米,小方格的顶点称为格点.请你在图上选7个格点,要求其中任意3个格点都不在一条直线上,并且使这7个点用直线连接后所围成的面积尽可能大.那么,所围图形的面积是平方厘米.【例 12】两个边长相等的正方形各被分成25个大小相同的小方格.现将这两个正方形的一部分重叠起来,若左上角的阴影部分(块状)面积为25.12cm,右下角的阴影部分(线状)面积为27.4cm,求大正方形的面积.【例 13】将边长为正整数n的正方形平均分成2n个小正方形,每个小正方形的顶点称为格点。
格点与面积习题讲解1

格点与面积习题讲解1如下图,在一张由一组水平线和一组垂直线组成方格纸上,如果任意相邻平行线之间的距离都相等,我们就把这样两组平行线的交点称为格点(如下图中的红点),把图中相邻两个格点的距离看着一个单位长度,把每个小正方形的面积看作一个面积单位(如图中带阴影的方格)。
一个多边形的顶点如果全是格点,这个多边形就叫做格点多边形,本讲就,学习求格点多边形的面积问题。
这种格点多边形的面积计算起来很方便,一般有三种方法:①规则的格点多边形,可以运用多边形的面积公式求出面积;②一些简单而又特殊的格点多边形,可以通过数格子求出面积;③较复杂的不规则图形,一般用皮克公式计算。
其中数格子的方法比较原始,很少用。
任意格点多边形,只要数出多边形周界上的格点的个数及图内格点的个数,就可用下面的皮克公式算出面积:格点多边形面积=图内格点个数+周界格点数÷2-1这个公式是皮克(Pick)在1899年给出的,被称为“皮克定理”,这是一个实用而有趣的定理。
皮克定理的证明:将格点图中的每个点看作以这个点为圆心、以单位面积正方形的边长的一半为半径的圆。
格点多边形图内的点对应的圆的面积都是图形面积的一部分;而在多边形边界上的点对应的圆的面积只有一半属于这个多边形,且多边形每个角上的圆属于图内的面积都不到半个圆,少了其外角对应的扇形面积,因任意多边形的外角和是360度,正好是个整圆,所以周界上圆在图内的面积为:周界格点数÷2-1所以格点多边形面积为:图内格点个数+周界格点数÷2-1。
皮克定理的证明过程比较抽象,孩子难以理解。
本讲只要求孩子初步认识格点面积公式,掌握格点面积公式的应用,到初中还会进一步学习皮克定理。
【解析】:图①是个平行四边形,周界上有10个格点,图内有4个格点,根据格点面积公式,图①的面积为:4+10÷2-1=8;图②是个梯形,周界上有8个格点,图内有2个格点,根据格点面积公式,图②的面积为:2+8÷2-1=5;图③是个三角形,周界上有6个格点,图内有4个格点,根据格点面积公式,图③的面积为:4+6÷2-1=6;以上3个图形都是规则图形,但四年级学生还没有学过这3种图形的面积计算,不能用面积公式计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
九、格点与面积(B)
年级______班_____ 姓名 _____得分_____ 一、填空题:
1.右图是用皮筋在钉板上围成的一个
三角形,计算它的面积是多少.(每相邻两个
小钉之间的距离都等于1个长度单位).
2.右图是一根用皮筋在钉板上围成的一个四边形,计算它的
面积是多少.(每相邻两个小钉之间的距离都等于1个长度单
位).
3.在一个9⨯6的长方形内,有一个凸四边形
ABCD(如右图).用毕克定理先求出它的面积来,再用拼
割方法计算它的面积,看两者是否一
致.
4.右图中每个小正方形的面积都
是4平方厘米,求图中阴影部分的面
积.
5.右图是一个10⨯10的正方形,求正方形内的四边形ABCD
的面积.
6.右图是一个8⨯12面积单
位的图形.求矩形内的箭形
ABCDEFGH的面积.
7.右图中每个小正方形的面积都是1,那么图中这只
“狗”所占的面积是多少?
8.右图是一个5⨯5的方格纸,小方格的
面积是1平方厘米,小方格的顶点为格点.
请你在图上选7个格点,要求其中任意3个
格点都不在一条直线上,并且使这7个点用
线段连结所围成的面积尽可能大,那么,所
用图形的面积1是多少平方厘米?
9.右图中每个小正方形的面积为1平方分米,那么阴影
部分的面积是多少平方分米?
10.右图中每个小平行四边形
的面积是1个面积单位,求阴影部
分的面积.
二、解答题:
1.右图中有21个点,其中每相邻的
三点“∴”或“∵”所形成的三角形都是面
积为1的等边三角形,试计算ABC
∆的
面积.
2.右图中有21个点,其中每相邻的三点“∴”或“∵”所
形成的三角形都是面积为1的等边三角形,试计算四边形
DEFG的面积.
3.把等边三角形ABC每边六等分,
组成如右图的三角形网.若图中每个小
三角形的面积均为12
cm,试求图中三角
形DEF的面积.
4.把大正三角形每边八等份,组成如右图所示的三角形网.如果每个小三角形的面积都是1,求图中粗线所围成的三角形的面积.
———————————————答案——————————————————————
一、填空题:
1. 5.5面积单位.
分析:解答这类问题可直接套用毕克定理:
格点面积=内部格点数+周界上格点数÷2-1.
注意:一是毕克定理只对格点凸多边形适用,二是在数格点时要细心.
解: 5+3÷2-1=5.5(面积单位).
2. 5+5÷2-1=6.5(面积单位).
3. 27.5面积单位.
解: ①由毕克定理得:
25+7÷2-1=27.5(面积单位).
②用拼割方法得:
ABCD的面积=长方形EFGH的面积-四角上的四个三角形的面积 =9⨯6-(6⨯2÷2+3⨯3÷2+4⨯3÷2+4⨯5÷2)
=54-(6+4.5+6+10)=27.5(面积单位).
4. 48平方厘米.
解: ①内部格点数为: 9个;
②周界上格点数为: 8个;
③阴影部分的面积是: 4⨯(9+8÷2-1)=48(平方厘米).
5. 30面积单位.
解: 因为ABCD不是凸四边形,所以如在原题图上取格点E,则三角形BCE及四边形AECD都是凸的图形,故:
S=(4+6÷2-1)+(21+8÷2-1)
ABCD
=6+24=30(面积单位).
6. 46面积单位.
解: 因为ABCDEFGH不是凸多边形,所以,连结GC、MN,则ABH
∆、矩形GCNM、三角形MFE、EDN都是凸的图形.
故箭形ABCDEFGH的面积=(8+10÷2-1)+4⨯8+(4÷2-1)⨯2
=12+32+2=46(面积单位).
7. 67.5面积单位.
解: 图形内部格点数为59,图形周界上格点数为19.
所以图形的面积为:59+19÷2-1=67.5(面积单位).
8. 23.5(平方厘米).
分析与解: 这是一个5⨯5的方格纸,共有25个格点.现在要围成一个面积最大的图形,根据格点面积公式,要使图形面积最大,必须使图形包含的内部格点数和周界上格点数尽可能多.由方格纸可知,内部格点数最多为4⨯4=16,周界上格点数最多为5⨯4=20.但是,当周界上格点数为最多时,不符合题中“任意3个格点不在一条直线上”的条件,因此,适当调整图上7个格点的位置,如右上图所示,就得到了面积最大的图形.
所围成图形的最大面积为: 16+17÷2-1=23.5(平方厘米).
9. 8.5平方分米.
解:图形内部格点数为7,图形周界上格点数为 5.阴影部分的面积为:7+5÷2-1=8.5(平方分米).
10. 18.5面积单位.
解: 图形内部格点数为16,图形周界上格点数为7.
图形的面积为: 16+7÷2-1=18.5(面积单位).
二、解答题:
1. 10面积单位.
分析: 由“∵”和“∴”重合两点可拼为平行四边形 ,可以推出如下计算这类格点面积的公式:
图形面积=(内部格点数+周界上格点数÷2-1)⨯2.
解: 图形内部格点数为4,图形周界上格点数为4.
ABC S ∆=(4+4÷2-1)⨯2=10(面积单位).
2. 12面积单位.
解: DEFG S 四边形=(5+4÷2-1)⨯2=12(面积单位).
3. 11面积单位.
解: 图形内部格点数为5,图形周界上格点数为3. DEF S ∆=(5+3÷2-1)⨯2=11(2cm ).
4. 26面积单位.
解: 图形内部格点数为12,图形周界上格点数为4. 图形的面积为: (12+4÷2-1)⨯2=26(面积单位).。
