中山市华侨中学2016届高三3月高考模拟考试(文数)
2016年广东省中山市华侨中学高考生物模拟试卷(3月份)

2016年广东省中山市华侨中学高考生物模拟试卷(3月份)学校:___________姓名:___________班级:___________考号:___________一、单选题(本大题共6小题,共36.0分)1.下列叙述正确的是()A.HIV、蓝藻和酵母菌共有的结构是核糖体B.原核生物的主要遗传物质是DNAC.原核细胞与真核细胞最主要的区别是有无以核膜为界限的细胞核D.真核生物细胞只进行有丝分裂,原核生物细胞只进行无丝分裂【答案】C【解析】解:A、HIV是一种RNA病毒、体内不具有核糖体,蓝藻和酵母菌均属于细胞生物、其细胞中具有核糖体,A错误;B、原核生物的遗传物质是DNA,B错误;C、原核细胞与真核细胞最主要的区别是有无以核膜为界限的细胞核,C正确;D、真核生物细胞的分裂方式有有丝分裂、无丝分裂和减数分裂,原核生物细胞的分裂方式只有二分裂,D错误.故选:C.1、由原核细胞构成的生物叫原核生物,由真核细胞构成的生物叫真核生物;原核细胞与真核细胞相比,最大的区别是原核细胞没有被核膜包被的成形的细胞核,没有核膜、核仁和染色体,原核细胞只有核糖体一种细胞器,但原核生物含有细胞膜、细胞质等结构,也含有核酸和蛋白质等物质.2、常考的真核生物有绿藻、衣藻、真菌(如酵母菌、霉菌、蘑菇)、原生动物(如草履虫、变形虫)及动、植物等;常考的原核生物有蓝藻(如颤藻、发菜、念珠藻、蓝球藻)、细菌(如乳酸菌、硝化细菌、大肠杆菌等)、支原体、放线菌等;此外,病毒没有细胞结构,既不是真核生物也不是原核生物.3、细胞生物(包括原核生物和真核生物)的细胞中含有DNA和RNA两种核酸、其中DNA是遗传物质,非细胞生物(病毒)中含有DNA或RNA一种核酸、其遗传物质是DNA或RNA.本题考查细胞结构和功能的知识,考生识记细胞结构和功能、明确原核细胞和真核细胞形态结构的异同、掌握常见生物所属的类型是解题的关键.2.如图为人体细胞的分裂、分化、衰老和凋亡过程的示意图,图中①-⑥为各个时期的细胞,a~c表示细胞所进行的生理过程.据图分析,下列叙述正确的是()A.⑤与⑥的基因型相同,蛋白质的种类也相同B.细胞的衰老与凋亡就会引起人体衰老与死亡C.若⑤⑥已失去分裂能力,其细胞内遗传信息的流动方向为DNA-RNA-蛋白质D.与①相比,②的表面积与体积的比值增,与外界环境进行物质交换的能力增强【答案】C【解析】解A、⑤与⑥细胞是由同一个受精卵有丝分裂而来的,因此它们的基因型相同,但⑤⑥细胞发生了细胞分化,即基因发生了选择性表达,所以细胞中的蛋白质种类有所区别,A错误;B、多细胞生物,细胞的衰老和凋亡不等同于个体的衰老和凋亡,B错误;C、若⑤⑥已失去分裂能力,不能进行DNA的复制,但仍然可以转录翻译形成蛋白质,所以其细胞内遗传信息的流动方向为DNA-RNA-蛋白质,C正确;D、细胞体积越大,其相对表面积越小,与外界环境进行物质交换的能力越弱,所以与①相比,②与外界环境进行物质交换的能力弱,D错误.故选:C.分析题图:a表示细胞生长过程;b表示细胞有丝分裂过程,细胞数目增加,但细胞种类不变;c表示细胞分化过程,细胞种类增加,而细胞数目不变.细胞分化的实质是基因的选择性表达.本题借助流程图,考查细胞分裂、分化、衰老和凋亡的相关内容,此外还涉及遗传信息的流动方向、细胞表面积和体积的关系等知识点,要求学生能熟记相关知识点,准确判断图中各过程的名称和相关选项.本题值得注意的是C选项,不能分裂的细胞,不会发生DNA的复制,但能转录和翻译形成蛋白质,因此其遗传信息的流动方向是DNA-RNA-蛋白质.3.下列关于科学史中研究方法和生物实验方法的叙述中,正确的是()①研究光合作用的反应过程和噬菌体侵染细菌实验--同位素标记法②孟德尔豌豆杂交实验提出遗传定律--假说一演绎法③DNA双螺旋结构的发现和研究某种群数量变化规律--模型建构法④探究酵母菌细胞呼吸方式--对比实验法⑤分离各种细胞器和叶绿体中色素的分离--差速离心法.A.①②④⑤B.①②③④C.①②③⑤D.②③④⑤【答案】B【解析】解:①研究光合作用产物中氧气的来源和噬菌体侵染细菌的实验中都用到了同位素标记法,①正确;②孟德尔提出遗传定律的研究方法是假说演绎法,②正确;③DNA的双螺旋结构利用了构建了物理模型的方法,研究种群的数量变化利用了构建数学模型的方法,③正确;④探究酵母菌细胞呼吸方式设置有氧和无氧2个实验组进行对比,④正确;⑤细胞器分离根据其比重不同可用差速离心法,色素的分离根据其在层析液的溶解度不同导致在滤纸上的分离速度不同,用的是纸层析法,⑤错误.故选:B.放射性同位素可用于追踪物质的运行和变化规律.用放射性同位素标记的化合物,化学性质不改变,通过追踪放射性同位素标记的化合物,可用弄清化学反应的详细过程;萨顿通过实验观察和推理提出假说:基因在染色体上用的是类比推理法,摩尔根果蝇杂交实验证实基因在染色体上用的是假说-演绎法;孟德尔豌豆杂交实验提出遗传定律用的是假说-演绎法;沃森和克里克发现DNA双螺旋结构用的是模型建构法;分离细胞器的方法是差速离心法,叶绿体色素的分离原理是根据色素在层析液中的溶解度不同.本题考查科学史中所用的研究方法和生物实验方法,意在考查考生识记和理解能力,难度适中.考生要能够识记课本中相关实验结果利用的研究方法,能够识记差速离心法和纸层析法所利用的原理.4.某研究者对新生儿感染的细菌进行了耐药性实验,结果显示70%的致病菌具有耐药性,下列相关叙述正确的是()A.细菌由于基因突变和染色体变异,形成了多种变异类型B.70%的致病菌具有耐药性,与新生儿是否接触过抗生素无关C.新生儿出生时接种疫苗,可预防各种细菌感染D.新生儿通过从母体获取的免疫球蛋白,对细菌发生的免疫反应属于非特异性免疫【答案】B【解析】解:A、细菌属于原核生物,没有染色体变异,A错误;B、耐药性是耐药菌突变以及环境选择形成的,与新生儿是否接触过抗生素无关,B正确;C、疫苗属于病原体,进入人体后能刺激免疫细胞产生相应的抗体,具有专一性,不可能预防各种细菌感染,C错误;D、新生儿通过从母体获取的免疫球蛋白,属于特异性免疫,D错误.故选:B.在未使用抗生素之前,细菌就存在着差异(有的不具有抗药性,有的具有抗药性),开始用抗生素时,由于大多数细菌没有抗药性被药物淘汰,而少数具有抗药性变异的个体会保存下来,并能继续繁殖感染人群,当多次使用该抗生素后,细菌抗药性积累并加强了抗药性,使该抗生素逐渐失去效应.所以药物对不同变异的细菌进行了选择,淘汰了不抗药的个体,保留了抗药性强的个体.以耐药性实验结果为背景,考查人体免疫和生物进化等知识,要求考生识记人体免疫系统的组成及功能;识记现代生物进化理论的主要内容,明确耐药菌是基因突变形成的,抗生素只能其进行选择.5.如图为酶催化反应效率关系图,A→B代表酶催化效率坐标:0到100%,A→C代表温度坐标:0到70℃,C→B代表溶液酸碱度坐标:p H=0.1到p H=14的范围,分析不合理的是()A.GK和HK所代表的某酶的催化效率差异,其关键影响因素是温度B.KG线段所代表的酶,其最适温度在EF范围内C.JH和HK可以用来体现胃蛋白酶和胰蛋白酶在不同酸碱溶液环境下的反应特点D.某酶因为温度改变从JH偏移为JG,那么在AE和EC之间各有一个温度取值【答案】A【解析】解:A、GK和HK所代表的某酶的催化效率差异,其关键影响因素不是温度,因为GK和HK酸碱度相同,G和H催化效率不相同,但温度都是在E点,所以催化效率差异主要原因应是酶的浓度,A错误;B、KG线段所代表的酶,酸碱度相同催化效率也相同(G点)但温度从E到F催化效率相同,根据酶的催化效率与温度关系曲线图可知E、F催化效率相同,所以其最适温度在EF范围内,B正确;C、JH和HK代表酸碱度不同,而催化效率相同,所以,可以用来体现胃蛋白酶和胰蛋白酶在不同酸碱溶液环境下的反应特点,C正确;D、某酶因为温度改变从JH偏移为JG,H点的催化效率较高,相当于最适温度,根据酶的催化效率与温度关系曲线图可知在AE和EC之间各有一个温度取值,D正确.故选:A.分析题图:GE和GF代表了(p H均为0.1的条件下)E和F两个温度时,催化效率均为G;HJ和HK代表了(温度均为70℃的条件下)J和K的p H水平,催化效率均为H.GE 和GK这两条线表明:p H为0.1、温度为E的催化效率与温度为70℃、p H为K时的催化效率均为G.HE和HK的意思可以同理推知,代表了不同的酶或者酶的浓度发生了变化.本题考查影响酶活性的因素,要求考生掌握影响酶活性的因素及各种因素如何影响酶活性.本题的难点在于酶催化反应效率关系图的分析,前提要求考生掌握温度和p H影响酶活性的曲线图,并能结合本图对各选项作用准确的判断.6.为研究根背光生长与生长素的关系,将水稻幼苗分别培养在含不同浓度生长素或适宜浓度NPA(生长素运输抑制剂)的溶液中,用水平单侧光照射根部(如图),测得根的弯曲角度及生长速率如下表:据此实验的结果,不能得出的结论是()A.根向光一侧的生长速率大于背光一侧B.生长素对水稻根生长的作用具有两重性C.单侧光对向光一侧生长素的合成没有影响D.单侧光照射下根的背光生长与生长素的运输有关【答案】C【解析】解:AD、看图、读表可知,光照作用下生长素分布不均,导致根向光侧生长素小于背光一侧,故AD正确;B、对比四个外源生长素的测定指标,可以看出随生长素浓度的增高,生长速度是现增高后降低,可以看出生长素对根生长的作用具有两重性,故B正确;C、题干没有给出单侧光对向光一侧生长素合成是否有影响的任何信息,无法得出单侧光对向光一侧生长素的合成没有影响的结论,故C错误.故选:C.根据题目中提供图形和表格信息,四个选项的说法本身都成立,但是题目要求“据此实验的结果”,明确“不能得出的结论是”什么.从根的弯曲角度判断,根向光一侧的生长速率大于背光一侧.从表格数据分析,生长素对水稻根生长的作用具有两重性;单侧光照射下根的背光生长与生长素的横向运输有关,背光一侧生长素分布多,向光一侧生长素分布少,低浓度生长素更有利于根的生长;题干没有给出单侧光对向光一侧生长素合成是否有影响的任何信息.本题通过考查植物激素的调节相关知识,考察学生对实验数据的加工、处理和对实验结果的分析能力,从而提高学生对生长素的功能和特性的理解.二、探究题(本大题共6小题,共59.0分)7.植物鹅掌花喜温暖湿润的半阴环境,忌强光照射.图1表示夏季时鹅掌花在不同遮光处理条件下净光合速率的日变化曲线.请分析并回答:(1)图示中遮光30%处理的鹅掌花开始光合作用的时间______ (填“早于”“等于”或“晚于”)6:30,且在M点时相应的光合作用强度______ (填“<”“=”或“>”)呼吸作用强度.(2)不遮光处理和遮光30%处理,对鹅掌花生长更有利的是______ ,据图象分析原因是:____________ _.(3)要探究最适于鹅掌花光合的遮光程度,需设计一系列以______ 为自变量的装置;为了摸索实验合理的自变量取值范围,先要进行______ .(4)下图2为叶绿素a和叶绿素b的吸收光谱(暗带部分表示被吸收的光线),已知在漫射光环境中,光线以较短波长的光占优势,与阳生植物相比,推测鹅掌花叶绿体中______ 色素含量较高,如从鹅掌花植物的叶绿体中提取出色素并层析分离后得到4条色素带(如图3).如果选取的是秋天发黄的叶片作为实验材料,则显著变化的色素带为______ .(填编号)【答案】早于;>;遮光30%;遮光30%处理的鹅掌花全天的净光合量大部分时间比不遮光处理的高;(或中午前后鹅掌花净光合量大幅下降,而遮光30%时基本保持较高净光合量);遮光程度(光照强度);预实验;叶绿素b;3、4【解析】解:(1)据图1分析,遮光30%处理的鹅掌花在6:30时净光合作用速率大于0,说明在此之前已经开始光合作用.M点时,净光合作用速率为1.0,由于真正的光合作用速率=呼吸作用速率+净光合作用速率,所以M点时相应的光合作用强度大于呼吸作用强度.(2)由于遮光30%处理的鹅掌花全天的净光合量大部分时间比不遮光处理的高(或中午前后鹅掌花净光合量大幅下降,而遮光30%时基本保持较高净光合量),所以对鹅掌花生长更有利的是遮光30%.(3)根据题意可知,要探究最适于鹅掌花光合的遮光程度,需设计一系列以遮光程度(光照强度)为自变量的装置.可以先进行预实验摸索实验合理的自变量取值范围.(4)据图2分析,叶绿素b在吸收较短波长的光较多,所以与阳生植物相比,鹅掌花叶绿体中叶绿素b色素含量较高.如果选取的是秋天发黄的叶片作为实验材料,叶绿素在低温下会分解,因此显著变化的色素带为3叶绿素a、4叶绿素b.故答案为:(1)早于>(2)遮光30%遮光30%处理的鹅掌花全天的净光合量大部分时间比不遮光处理的高(或中午前后鹅掌花净光合量大幅下降,而遮光30%时基本保持较高净光合量)(3)遮光程度(光照强度)预实验(4)叶绿素b3、4据图分析:图1中,适当遮光可以提高鹅掌花的净光合作用速率.图2中,鹅掌花为阴生植物,叶绿体中叶绿素b色素含量较高.图3中,滤纸条从上到下依次是:1表示胡萝卜素、2表示叶黄素、3表示叶绿素a、4表示叶绿素b.据此分析作答.本题主要考查影响光合作用的环境因素和叶绿体中色素的提取,意在通过曲线图使学生理解与掌握光照强度对光合作用的影响,并学会用相关知识分析和解决实际问题.8.图1是某科研小组利用植物染色体杂交技术过程,他们将携带R(抗倒伏基因)和A (抗虫基因)的豌豆染色质片段直接导入玉米体细胞,两种染色质片段可随机与玉米染色质融合形成杂交细胞,将杂交细胞筛选分化培育成既抗虫又抗倒伏性状的可育植株(F1).图2是某一年生自花传粉植物(2n=10)的某些基因在亲本染色体上的排列情况.请分析并回答下列问题.(1)杂交细胞发生的可遗传变异类型是______ .(2)杂交细胞在第一次有丝分裂中期时含有______ 个A基因(不考虑变异),杂交细胞能够培育成F1植株的原理是______ .(3)该植物控制红色花色的基因分别是B、F、G,控制白色花色的基因分别是b、f、g.各显性基因的表现效果相同,且显性基因越多,红颜色越深(如深红、红、浅红…等表现型),隐性类型为白色.让如图所示亲本进行杂交得F1,F1自交得F2,则F2花色的表现型有______ 种,其中白色花色的几率是______ .(4)若E基因存在纯合致死现象,则让F1自交得到的F2中杂合子E e所占比例为______ .(5)该植物叶片无香味D对有香味d为显性,如图所示亲本进行杂交,在F1中偶尔发现某一植株叶片具有香味性状.可能的原因是(只需写一点):______ .【答案】染色体变异(易位、染色体结构变异);2;植物细胞具有全能性;7;;;某一雌配子形成时,D基因突变为d基因或由于染色体缺失,形成的某一雌配子不含D基因【解析】解:(1)根据题干信息“两种染色质片段可随机与玉米染色质融合形成杂交细胞”可知,杂交细胞发生的是染色体结构变异(易位).(2)杂交细胞含有1个A基因,经过间期的复制后,在第一次有丝分裂中期时含有2个A基因;杂交细胞能够培育成F1植株的原理是植物细胞具有全能性.(3)根据图示亲本的基因型可以表示为BBFFGG和bbffgg,子一代的基因型为B b F f G g,自交后产生的子二代会出现:不含显性基因的个体,含有一个,二,三,四,五,六个显性基因的个体,共7种表现型,产生bbffgg的概率为××=.(4)根据图示亲本基因型为E e和ee,得到的子一代为E e和ee,分别自交后得到的子代中EE、E e、ee所占的比例分别为、、,因为EE致死,所以杂合子E e所占比例为.(5)根据图示亲本的基因型为DD和dd,杂交后得到的子一代为D d(无香味),若“在F1中偶尔发现某一植株叶片具有香味性状”说明在子一代中没有出现D基因,而且亲本中只有母亲具有该基因,所以可能的原因是母本在减数分裂中发生了隐性突变或在减数分裂时染色体异常产生了不含D的配子.故答案为:(1)染色体变异(易位、染色体结构变异)(2)2植物细胞具有全能性(3)7(4)(5)某一雌配子形成时,D基因突变为d基因或由于染色体缺失,形成的某一雌配子不含D基因分析题图:图示利用植物染色体杂交技术,将携带R(抗倒伏基因)和A(抗虫基因)的豌豆染色质片段直接导入玉米体细胞,两种染色质片段可随机与玉米染色质融合形成杂交细胞,将杂交细胞筛选分化培育成既抗虫又抗倒伏性状的可育植株.本题考查基因自由组合定律和数量遗传的相关知识,意在考查学生的识图能力和判断能力,运用所学知识综合分析问题和解决问题的能力,有一定难度.9.胰岛素是已知的唯一降低血糖水平的激素,请分析胰岛素的作用机制模式图(如图所示),并回答有关问题:(1)图中的刺激X最可能是______ ,下丘脑神经细胞接受刺激X兴奋后,膜外的电位变化为______ ,最终引起传出神经末梢释放______ ,与胰岛B细胞上相应受体结合,引起胰岛素分泌增多.(2)由图可知,胰岛素与其受体结合后,一方面使______ 增加,促进葡萄糖进入细胞;另一方面促进______ ,从而降低血糖.(3)如果给动物注射大剂量胰岛素,动物会因低血糖而休克.通过注射胰高血糖素能促使血糖升高,使休克的动物清醒.根据以下实验材料及用品,完成实验方案,证明胰高血糖素能升高血糖.实验材料及用品:小白鼠、注射器、鼠笼、胰岛素溶液、胰高血糖素溶液、葡糖糖注射液、生理盐水.实验方案:选择体重相近的健康小白鼠,按照下表进行处理、观察并填写相关内容.【答案】血糖升高;由正电位变为负电位;神经递质;细胞膜上葡萄糖受体蛋白;糖原、脂质和蛋白质的合成;注射等量生理盐水;注射一定量胰高血糖素溶液(注射一定量葡萄糖注射液);注射一定量葡萄糖注射液(注射一定量胰高血糖素溶液)【解析】解:(1)胰岛素功能是降低血糖浓度,具体表现在两个方面:一方面,可以促进葡萄糖转运蛋白合成,以促进细胞加速摄取葡萄糖.此外,胰岛素除了能促进图示的利用和储存葡萄糖的途径外,还能促进葡萄糖氧化分解,从而降低血糖浓度.下丘脑神经细胞接受刺激X后产生兴奋,兴奋部位膜外的电位由正电位变为负电位,传导轴突末端,引起神经末梢释放神经递质,与胰岛B细胞上相应受体结合,引起胰岛素分泌增多.(2)图中胰岛素与细胞膜表面的胰岛素受体结合后,使细胞膜上的葡萄糖受体蛋白增加,促进葡萄糖进入组织细胞并被利用,同时促进葡萄糖合成糖原和转化成脂质和蛋白质,从而使血糖浓度降低.(3)根据实验的对照性原则,B、C、D组是实验组,注射了大剂量的胰岛素溶液,则A组为对照组,所以①应该注射等量生理盐水;②③④是对休克动物做的对照试验,②是对照组,注射等量生理盐水;③④是实验组,分别注射一定量胰高血糖素溶液和葡萄糖注射液.故答案为:(1)血糖升高由正电位变为负电位神经递质(2)细胞膜上葡萄糖受体蛋白糖原、脂质和蛋白质的合成(三种物质答全给分)(3)①注射等量生理盐水③注射一定量胰高血糖素溶液(注射一定量葡萄糖注射液)④注射一定量葡萄糖注射液(注射一定量胰高血糖素溶液)本题考查人体血糖调节及相关的探究实验,要求考生识记人体血糖调节的具体过程,掌握胰岛素作和胰高血糖素的具体作用;明确实验的目的,掌握探究实验的原则,能结合所学的知识完善实验步骤并预测实验结果.本题考查血糖调节的相关知识,意在考查考生理解所学知识的要点,把握知识间的内在联系的能力.10.6月5日是世界环境日,今年我国的世界环境日主题是“共建生态文明,共享绿色未来”.草原是绿色生态环境的重要组成部分.某草原生态系统的食物网如图所示.(1)图中食物网的结构比较简单,因此,该草原生态系统的______ 能力较差,其______ 稳定性也相应较低.除图中所示的生物类群外,该生态系统的生物组成成分还应有______ 才能保证其物质循环的正常进行.(2)如果图中草能提供10000KJ的能量,营养级间的能量传递效率为10%~20%,那么鹰占据的营养级能得到的最低和最高能量值分别别是______ KJ和______ KJ.若去除蛇,且狐的数量不变,则草原容纳鹰的数量会______ .若外来生物入侵该区,则会导致草原的______ 锐减或丧失.(3)影响图中兔种群数量变化的种间因素是______ 和竞争.若某年兔种群的K值为1000只,且1只兔和4只鼠消耗的草量相等,其他条件不变的情况下,次年鼠的数量增加400只,则兔种群的K值变为______ 只.用标志重捕法调查该区的种群数量时,若部分标记个体迁出,则导致调查结果______ (填“偏高”或“偏低”).(4)草原干旱时,兔摄取水分减少,体内细胞外液渗透压______ ,引起______ 渗透压感受器兴奋,增加抗利尿激素的释放,进而引起______ 对水的重吸收增加,减少排尿量,以保持体内水平衡.【答案】自我调节(或反馈调节);抵抗力;分解者;10;400;增加;生物多样性(或物种多样性);捕食;900;偏高;升高;下丘脑;肾小管、集合管【解析】解:(1)图中物种较少,食物链较少,食物网较简单,因此,该草原生态系统的自我调节能力较差,其抵抗力稳定性也较低.图中食物网生物组成成分只包括生产者、消费者,故还应有分解者才能保证其物质循环的正常进行.(2)鹰占据的营养级有第三、第四两个营养级,其得到的最低能量值,应以第四营养级为准,同时传递效率按10%计算,即10000×(10%)3=10(k J);其得到的最高能量值,应以第三营养级为准,同时传递效率按20%计算,即10000×(20%)2=400(k J).若去除蛇,鹰的营养级降低,得到的能量增多,所以鹰的数量会增加.若外来生物入侵该区,则会导致草原的生物多样性锐减或丧失.(3)图中影响兔种群数量变化的种间因素是竞争和捕食;因为4只鼠消耗的草量与1只兔的相等,则400只鼠消耗的草量,相当于100只兔的消耗量,所以兔的K值变为1000-100=900(只);用标志重捕法调查鼠的种群数量,设鼠总数为N,标记数为n,再次捕捉到的数目为M,M里面有标记的鼠的数目为m,则N=n•,若部分标记个体迁出,则m减少,因此N值会偏高.(4)草原干旱时,兔摄取水分减少,体内细胞外液渗透压升高,引起下丘脑渗透压感。
【生物】广东省中山市华侨中学2016届高三3月高考模拟考试

广东省中山市华侨中学2016届高三3月高考模拟考试Ⅰ卷(选择题共36分)一、单项选择题(本题共6大题,每小题6分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列叙述正确的是A.HIV、蓝藻和酵母菌共有的结构是核糖体B.原核生物的主要遗传物质是DNAC.原核细胞与真核细胞最主要的区别是有无以核膜为界限的细胞核D.真核生物细胞只进行有丝分裂,原核生物细胞只进行无丝分裂2.下图为人体细胞的分裂、分化、衰老和凋亡过程的示意图,图中①—⑥为各个时期的细胞,a—c表示细胞所进行的生理过程。
据图分析,下列叙述正确的是A.⑤与⑥的基因型相同,蛋白质的种类也相同B.细胞的衰老与凋亡就会引起人体衰老与死亡C.若⑤⑥已失去分裂能力,则其细胞内遗传信息的流动方向为DNA→RNA→蛋白质D.与①相比,②的表面积与体积的比值增大,与外界环境进行物质交换的能力增强3.下列关于科学史中研究方法和生物实验方法的叙述中,正确的是①研究光合作用的反应过程和噬菌体侵染细菌实验——同位素标记法②孟德尔豌豆杂交实验提出遗传定律——假说一演绎法③DNA双螺旋结构的发现和研究某种群数量变化规律——模型建构法④探究酵母菌细胞呼吸方式——对比实验法⑤分离各种细胞器和叶绿体中色素的分离——差速离心法A.①②④⑤B.①②③④C.①②③⑤D.②③④⑤4.某研究者对新生儿感染的细菌进行了耐药性实验,结果显示70%的致病菌具有耐药性,下列相关叙述正确的是A.细菌由于基因突变和染色体变异,形成了多种变异类型B.70%的致病菌具有耐药性,与新生儿是否接触过抗生素无关C.新生儿出生时接种疫苗,可预防各种细菌感染D.新生儿通过从母体获取的免疫球蛋白,对细菌发生的免疫反应属于非特异性免疫5.下图为酶催化反应效率关系图,A→B代表酶催化效率坐标:0到100%,A→C代表温度坐标:0到70℃,C→B代表溶液酸碱度坐标:PH=0.1到PH=14的范围,分析不合理...的是A.GK和HK所代表的某酶的催化效率差异,其关键影响因素是温度B.KG线段所代表的酶,其最适温度在EF范围内C.JH和HK可以用来体现胃蛋白酶和胰蛋白酶在不同酸碱溶液环境下的反应特点D.某酶因为温度改变从JH偏移为JG,那么在AE和EC 之间各有一个温度取值6. 为研究根背光生长与生长素的关系,将水稻幼苗分别培养在含不同浓度生长素或适宜浓度NPA(生长素运输抑制剂)的溶液中,用水平单侧光照射根部(如下图),测得根的弯曲角度及生长速率如下表据此实验的结果,不能得出的结论是A.根向光一侧的生长速率大于背光一侧B.生长素对水稻根生长的作用具有两重性C.单侧光对向光一侧生长素的合成没有影响D.单侧光照射下根的背光生长与生长素的运输有关第Ⅱ卷(非选择题54分)二、非选择题(包括必考题和选考题两部分,第29-32题为必考题,每个试题考生都必须作答。
中山市2016届高三年级第一学期期末统一考试(文数参考答案)

中山市2016届高三年级第一学期期末统一考试数学(文科)参考答案一、选择题(本大题共12小题,每小题5分,共60分.)二、填空题 (本大题共4小题,每小题5分,共20分.)三、解答题:(本大题共6小题,共70分.) 17.(本小题满分10分)cos cos 2cos sin cos sin cos 2sin cos (3)sin()2sin cos ,sin()sin 0,1cos (5)22(6)31sin 2ABC I C C II S b A a B c C B A A B C C A B C C A B C ab C π∆+=-∴+=-∴+=-+=≠=-∴=== 解:,分因分分 ()由 ( )分)(即8,6,2,3323321 =∴=∴=⋅⋅b a a a分)(有余弦定理可得:10132,52)21(622364cos 2222 =∴=-⨯⨯⨯-+=-+=c C ab b a c18.(本小题满分12分)解:(I )因为)(011+++∈=-+N n a a a a n n n n ,01—11,01=+∴>+n nn a a a (2分)所以11111=-=-++nn n n a a b b , (4分)又1111==a b所以数列{}n b 是以1为首项,1为公差的等差数列. (5分)(II )由(1)知n b n =,所以1nn a =,1n a n =,设1111(1)1n n a c n n n n n ===-+++, (8分)所以1211111(1)()()2231n n S c c c n n =+++=-+-++-+ (10分) 1111nn n =-=++ (12分) 19.(本小题满分12分) (Ⅰ)证明:因为A 1O ⊥平面ABC ,所以O A BC 1⊥,又AC BC ⊥,所以C AC A BC 11平面⊥,1AC BC ⊥, (2分) 因为AC AA =1,所以四边形C C AA 11是菱形, 所以C A AC 11⊥, 因为C BC C A 1=⋂所以⊥1AC 平面BC A 1; (6分)(II )解:,的高为设三棱锥1h AB A C -,321的高为A )可知,三棱锥1由(11=-AC BC A,3S 31h S 31,即V V 因为1111A ⋅=⋅=∆∆--BC A AB A BC A AB A C1112,101AB A B S A AB A AB AA ∆∆==== 在中,(分),2C A BC 21S 则,90BC 2,C A B 中,在1BC 1111=⋅=︒=∠==∆∆A A C BC A分)(所以,12 7212h =20.(本小题满分12分)解:吨,则有为小时后蓄水池中的水量设y xx x x x y 318090500129090500-+=-+= )0(≥x (2分)230)3(3018030500303(Ⅰ)222+-=-+=∴=≥=t t t y t x t x t ,,,则令2303,3===min y x t 时,即则当即3小时后蓄水池中水量最少,最少为230吨 (6分)51,056,350180305001350318090500)(22<<∴<+-∴<-+<-+t t t t t x x II )知:由(,由题意,531<<x 即 (9分)小时供水紧张。
2016届广东中山市华侨中学高三3月模拟语文试卷(带解析)

绝密★启用前2016届广东中山市华侨中学高三3月模拟语文试卷(带解析)试卷副标题考试范围:xxx ;考试时间:116分钟;命题人:xxx学校:___________姓名:___________班级:___________考号:___________注意事项.1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题(题型注释)1、依次填入以下这段文字画线处的语句,衔接最恰当的一组是( )儒、道、易、玄、佛、禅、理等诸家思想,历来被认为是中国传统文化的精神支柱。
, , 。
, 。
,所以中国的审美文化史有可能以上述思想史为纵贯线而得以架构。
①由于中国古代思想学说浑整、互洽的特点,中国审美文化的发展流变往往不是受到一家一派思想的影响②但对于当时的审美文化总是起着深层次的调控和统合作用 ③而是与各家各派都有关系,形成非常复杂的源流关系 ④它们产生和形成的时间有早有晚⑤而后者也总是如影随形地与之同流转、共起伏⑥譬如,起初往往出现“一源多分流”的景象,到后来则常常形成“众源汇一流”的格 局A .⑤③①⑥④②B .⑤③④⑥②①C .④②⑤①③⑥D .④⑥②①⑤③试卷第2页,共13页2、下列各句中,没有语病的一句是A .跟随原声电影学习英语不失为一种有效的方法,但大部分电影中角色语速较快,对于初学者听起来确实感到困难。
B .由于微信的快速发展,使其成为犯罪分子的“新天地”,微信作为一种新兴的社交软件,带来的安全隐患也值得大家关注。
C .近年来,我国加快了高等教育事业发展的速度和规模,高校将进一步扩大招生,并重点建设一批高水平的大学和学科。
D .巴金“讲真话”的精神影响了一大批同样经历过“文化大革命”的作家,其中萧乾是受巴金影响最深的一位。
3、依次填入下列各句横线处的成语,最恰当的一项是①在这个案件的审理过程中,他 ,为他的小舅子——一个抢劫犯罪嫌疑人开脱罪责,引起了极大的民愤。
中山市华侨中学2016届高三3月高考模拟考试(语文)

2017届高二尖刀班语文综合测试卷(3)甲必考题一、现代文阅读(9分,毎小题3分)阅读下面的文字,完成任务1-3题培厚“精神新土层”,迎接“新集体生活”去年年底,腾讯公布官方数据显示,用户每天在微信平台上平均阅读 5.86篇文章。
以每篇1500字计,一个月下来就是一本200多页的书。
这样一本“书”,恐怕难以扭转“中国人不读书”的印象,也不足以涵养丰盈的精神生活。
不仅仅是在中国,美国埃默里大学教授马克·鲍尔莱恩对于“把时间都花在了社交网站”上的年轻人,也忧心忡忡。
为了提醒埋头手机者保留一个“与历史、与艺术、与公民理念相遇”的生命空间,他的书名就叫《最愚蠢的一代》。
作家博尔赫斯说:如果有天堂,那一定是图书馆的模样。
爱书之人,可能都幻想过这样一座图书馆:没有容积的限制、跨越时空的区隔,“摊开你的手掌,无限在此收藏”。
网络不就是这样吗?飞速发展的搜索技术、不断扩大的社交平台,海量的信息、无界的交流,只需在巴掌大的屏幕上敲击几下就尽在掌握。
从丰富性的角度看,互联网绝不该成为文化的沙漠,而应是比博尔赫斯的想象更辉煌的“天堂”。
今天的“新集体生活”更加开放、更加自由、个性更加鲜明。
在网络的土壤中,即便是荒腔走板的歌声,也可能因触动隐秘的心弦而得到共鸣。
只是,这样的个性张扬,虽为文化土层的培育提供了更大空间,却也“既有繁花,亦生稗草”,让互联网文化显得颇为芜杂。
微信公号不乏“揭秘”“爆料”“有染”等吸引眼球的劲爆词汇,更有“30岁以前要明白”“中国人转起来”等或浓或淡的心灵鸡汤……这些内容尽管无伤大雅,却也难免让人担心它们背后日渐贫血的心灵。
面对泥沙俱下的文化洪流,尤其需要澄清自己的文化水源,才能于沙中淘到金。
无论有多么庞大的库存,你能接触到的如果只是你知道或者愿意知道的那一小部分,那与其说是看到了世界,不如说只是验证了自己。
从这个角度看,那些无法深究的八卦、那些不知所云的感悟、那些似是而非的谣传、那些低俗庸俗的段子,不是丰富了你的生活,反而是把你阻隔在了一个伟大的宝库之外。
广东省中山市华侨中学2016届高三3月高考模拟考试语文试卷

资料概述与简介 2016年中山市华侨中学模拟考试语文试题2016/3/28 注意事项: 1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己姓名和考生号、考场号、座位号填写在答题卡上。
用2B铅笔将试卷类型填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用2B铅笔把答题卡上对应题目的答案信息号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔和涂改液。
不按以上要求作答的答案无效。
4.作答选做题时,请先用2B铅笔填涂选做题的题号对应的信息点,再作答。
漏涂、错涂、多涂的,答案无效。
5.考生必须保持答题卡的整洁。
考试结束后,将试卷和答题卡一并交回。
第I卷阅读题甲必考题 ...请考生在第三、四两大题中选定其中一大题作答。
注意:作答时必须用2B铅笔在答題卡上把所选大题题号后的方框涂黑。
只能做所选定大内的小题,不得选做另一大题内的小题。
如果多做,则按所做的第一大題计分。
11.阅读下面的文字,完成(1)(4)题(25分)瓷 薛长登 家中有一个宝物,顾林在8岁那年就知道了。
宝物是一个瓷瓶。
瓷瓶上画着一幅仕女图,人物栩栩如生,呼之欲出。
他用手机对着瓷瓶各个角度拍了照片。
他坐车来到市区的一个叫着“王记”的古董行。
这时他的手机响了,是母亲打来的,母亲告诉他医院催着交钱。
他说,知道了,并叫母亲不要着急。
“你们这里收古董吗?”顾林低声问正在电脑上忙着的一个男人,他是王经理。
“你有什么古董?”王经理问。
顾林把手机上的照片翻给王经理看。
“瓷瓶现在在哪里?”王经理问。
“在家里。
” “不知道是真品还是赝品?”王经理自言自语。
“应该是真品。
”顾林说。
他有点心虚,其实他也不知道是真品还是赝品。
母亲常对他说,那是你父亲一直为之骄傲的东西…… 王经理打了一个电话,一个穿着唐装的60多岁的老人从楼上下来。
广东省中山市华侨中学2016届高三3月模拟文综历史试题

广东省中山市华侨中学2016届高三3月高考模拟考试文科综合历史试题第Ⅰ卷(选择题,共48分)一、单项选择题(12小题,每小题4分,共48分。
在每题给出的四个选项中,只有一项符合题目要求)24.《左传》有云:“昔周公、大公股肱周室,夹辅成王。
成王劳之,而赐之盟,曰:世世子孙无相害也。
载在盟府,大师职之。
”材料表明A.周天子建立起绝对权威的统治秩序 B.西周中枢管理机构与蛮夷之间关系C.西周贵族实行集体统治的基本方式 D.同姓与异姓诸侯权力与义务的差异【答案】C【解析】试题分析:依据“成王劳之,而赐之盟,曰:世世子孙无相害也”可知西周加强统治集团内部的稳定与团结,实行各级贵族集体统治的方式,C项正确。
周代未建立君主专制,A项错误;材料未反映蛮夷的相关信息,B项错误;异姓诸侯与材料信息无关,D项错误。
考点:古代中国的政治制度·商周时期的政治制度·中国古代早期政治制度的特点25.据北宋欧阳修等史学家编撰的《新唐书•百官志》记载:“凡市,日中击鼓三百以会众,日入前七刻,击钲三百而散。
”而唐代诗人王建有诗《夜看扬州市》写道:“夜市千灯照碧云,高楼红袖客纷纷。
”对这两段材料的解读正确的是A.前者是正史,后者是文学体裁,应以前者为准B.前者是后世人编撰的,后者写于唐代,应以后者为准C.两者记载的史实相违背,必有其一是伪史。
D.两者所载内容均需经过进一步考证才能确定史料价值【答案】D【解析】试题分析:本题主要考查古代商业的发展。
前者虽是正史,但也并不是完全可信,故A项错误;历史著作的可信度与编撰者的时代关系不大,后者是文艺作品可信度更低,故排除B;两则材料只是对于市的看法不同,不能以此作为判断其真伪的依据,故排除C。
D项表述准确,符合题意。
考点:古代中国的经济·商业的发展·唐代商业的发展26.“忠君爱国”在北宋末年成为士大夫的最高道德标准。
佛教也提出与儒家伦理道德相协调,“佛法据王法以立”,佛教僧人也应提倡忠君爱国,所以有的寺院称为“护国寺”,有的称“报国寺”。
广东省中山市华侨中学高三数学3月模拟考试试题理

2016年中山市华侨中学模拟考试理科数学试题本试卷共4页,24小题,满分150分.考试用时120分钟.注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,答卷前,考生务必将自己的姓名、准考证号填写在答题卷上.2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卷上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.写在本试卷上无效.3.回答第Ⅱ卷时,将答案写在答题卷上,写在本试卷上无效.一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{}{}212,log 2A x x B x x =-≤=<,则A B =( )A . []1,3-B .(),4-∞C . (]0,3D .[)1,4-2.命题“2cos sin ,,2>-⎥⎦⎤⎢⎣⎡∈∃x x x ππ”的否定是( ) A .2cos sin ,,2<-⎥⎦⎤⎢⎣⎡∈∀x x x ππ B .2cos sin ,,2≤-⎥⎦⎤⎢⎣⎡∈∀x x x ππC .2cos sin ,,2≤-⎥⎦⎤⎢⎣⎡∈∃x x x ππD .2cos sin ,,2<-⎥⎦⎤⎢⎣⎡∈∃x x x ππ3.直线2y x =与曲线3y x =围成的封闭图形的面积是( )A .1B .C .2D .44.已知等比数列{n a }中,2854,a a a ⋅= 等差数列{}n b 中,465b b a +=,则数列{}n b 的前9项和9s 等于( ) A. 9B. 18C. 36D. 725.已知函数()2sin()sin()3f x x x ππϕ=+++的图象关于原点对称,其中(0,)ϕπ∈,则函数()cos(2)g x x ϕ=-的图象( )A .关于点(,0)12π对称; B .可由函数()f x -的图象向右平移12π个单位得到; C .可由函数()f x 的图象向左平移6π个单位得到;D .可由函数()f x 的图象向右平移3π个单位得到.6.已知函数()(ln ,f x x =若实数,a b 满足()()20f a f b +-=,则a b +=( ) A. 0 B.1- C. 2 D. 2-7.右图给出的是计算201614121+⋅⋅⋅+++的 值的一个程序框图,其中判断框内应填入的条件是( ) A.10i > B.10i <C.20i >D. 20i <8.如下图,已知||1,||3,0OA OB OA OB ==⋅=,点C 在线段AB 上,且AOC ∠=030,设 (),OC mOA nOB m n R =+∈,则mn等于( ) A .13 BC .3D 9.设F 1,F 2 是双曲线)0,(1x 2222>=-b a by a 的左、右焦点,若双曲线右支上存在一点P 满足212F F PF =,且54cos 21=∠F PF ,则双曲线的渐近线方程为( ) A .034=±y x B .053=±y x C .043=±y x D .045=±y x 10. 已知ABC ∆中,角A 、B 、C 的对边分别是a 、b 、c ,若2sin sin a b c B A+=,则ABC ∆是( )A. 等腰直角三角形B.锐角三角形C. 等边三角形D.钝角三角形11.某四面体的三视图如图所示,正视图、俯视图都是腰长 为2的等腰直角三角形,左视图是边长为2的正方形,则此四面体的四个面中面积最大的为( ) A .. 4 C..12.设函数3()(33),(2)xxf x e x x ae x x =-+--≥-,若不等式()f x ≤0有解.则实数a 的最小值为( ) A .21e - B .22e - C .212e + D .11e- 二、填空题:本大题共4小题,每小题5分,共20分俯视图左视图13.设实数,x y 满足240,0,0.x y x y y +-≤⎧⎪-≥⎨⎪>⎩则2x y -的最大值为_________.14. 已知3cos()sin()22()cos()tan()f ππαααπαπα+-=---,则25()3f π-的值为 ; 15.已知()32log ,03,,,,1108,333x x f x a b c d x x x ⎧<≤⎪=⎨-+>⎪⎩是互不相同的正数,且()()f a f b ==()()f c f d =,则abcd 的取值范围是 ;16.已知等差数列{}n a 中, 11a =,公差0d >,且125,,a a a 成等比数列,11(1)n n n n nb a a -+=-,则数列{}n b 的前n 项和n S = ; 三、解答题(17—21为必做题,每题满分12分) 17.(本小题满分12分)在ABC ∆中,,,a b c 分别是角A ,B ,C 的对边,已知222,b ac a c ac bc =-=-且(1)求A ∠的大小; (2)设()cos()sin()(0)2Af x x x ωωω=-+>且()f x 的最小正周期为π,求()[0,]2f x π在的最大值。
中山市高三高考模拟试题(文科数学).docx

中山市2016届高三高考模拟试题(文科数学)本试卷分为第I 卷(选择题)和第II 卷(必考题和选考题两部分)两部分. 一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知全集R U =,102x A xx⎧+⎫=≥⎨⎬-⎭⎩,}{0<=nx l x B ,则A B =U A.}{12x x -≤≤ B.}{21<≤-x x C .}{1x 2x x <-≥或 D .}{20<<x x 2.已知复数(,,0)Z a bi a b R ab =+∈≠且,若(12)Z i -为实数,则ba= A.2 B.-2 C.-12 D.123.设1132113,,ln 23a b c π⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则 A.c a b << B. c b a << C. a b c << D. b a c <<4.已知抛物线22(0)y px p =>的准线与椭圆22146x y +=相切,则p 的值为A .2B .3C .4D .5 5.已知()3cos 24απ-=,(,0)2απ∈-,则sin 2α的值为 A .38B .38-C .378D .378-6.“牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的 几何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个扣合(牟合)在一起的方形伞(方盖).其直观图如下左图,图中四边形是为体现其直观性所作的辅助线.当其正视图和侧视图完全相同时,它的正视图和俯视图分别可能是A.a,bB.a,cC.c,bD.b,d7.已知ABC ∆中,060,A D ∠=为AC 上一点,且3,BD AC AD AC AB =⋅=⋅u u u r u u u r u u u r u u u r,则AD AB ⋅=u u u r u u u rA .1B .2C .4D .38.若下框图所给的程序运行结果为35S =,那么判断框中应填入的关于k 的条件是A .7k =B .6k ≤C .6k <D .6k >9. 已知函数)20(sin 2sin cos 2cos )(πϕϕϕ<<-=x x x f 的图象的一个对称中心为(6π,0),则下列说法不正确的是 A .直线π125=x 是函数)(x f 的图象的一条对称轴 B .函数)(x f 在]6,0[π上单调递减C .函数)(x f 的图象向右平移6π个单位可得到x y 2cos =的图D . 函数()f x 在[0,]2π的最小值为1-10.函数1ln 1ln xy x+=-的图像大致为.11.过双曲线22221x y a b-=(0a >,0b >)的一个焦点F 作一条渐近线的垂线,垂足为点A ,与另一条渐近线交于点B ,若F 2F B =A u u u r u u u r,则此双曲线的离心率为A .2B .3C .2D .512. 函数()[]f x x x =-(函数[]y x =的函数值表示不超过x 的最大整数,如[]3.64-=-,[]2.12=),设函数()()()lg (0)sin (20)f x xx g x f x xx π+>⎧⎪=⎨--<<⎪⎩,则函数()y g x =的零点的个数为A . 11B .10C . 12D . 13 二、填空题:本大题共4小题,每小题5分,共20分。
中山市华侨中学2016届高三3月高考模拟文科数学试卷 含解析

2016年广东省中山市华侨中学高三3月高考模拟考试文科数学试卷一、单选题(共12小题)1.设集合,,则()A.B.C.D.2.给定函数①,②,③,④,其中在区间上单调递减的函数序号是()A.①④B.②③C.③④D.①②3.设,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设变量满足约束条件,则目标函数的最小值为( )A.11B.3C.2D.5.一个袋子中有号码为1、2、3、4、5大小相同的5个小球,现从袋中任取出一个球,取出后不放回,然后再从袋中任取一个球,则第一次取得号码为奇数,第二次取得号码为偶数球的概率为()A.B.C.D.6.一空间几何体的三视图如图所示,该几何体的体积为,则正视图与侧视图中x的值为()A.5B.4C.3D.27.一个样本容量为10的样本数据,它们组成一个公差不为O的等差数列{},若a3 =8,且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是()A.13,12B.13,13C.12,13D.13,148.曲线y=+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为()A.B.C.D.19.已知双曲线与抛物线有一个公共的焦点F,且两曲线的一个交点为P,若|PF|=5,则双曲线的渐近线方程为()A.B.C.D.10.若表示不超过的最大整数,执行如图所示的程序框图,则输出的值为()A.B.C.D.11.已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=l,BC=,则球O的表面积等于()A.4B.3C.2D.12.若函数,并且,则下列各结论正确的是()A.B.C.D.二、填空题(共4小题)13.数列的首项为3,为等差数列且,若,,则.14。
已知向量,若,则16x+4y的最小值为.15.已知直线与双曲线交于两点,则该双曲线的离心率的取值范围是.16。
如图甲,在中,,,为.垂足,则,该结论称为射影定理.如图乙,在三棱锥中,平面,平面,为垂足,且在内,类比射影定理,探究、、这三者之间满足的关系是三、解答题(共8小题)17。
广东省中山市华侨中学高三数学文月考试题含解析

广东省中山市华侨中学高三数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设,集合A为偶数集,若命题则为A. B.C. D.参考答案:D2. 已知,且,则()A.B.C.D.参考答案:D略3. 已知函数,若方程有三个不同的实数根,则实数a的取值范围为(A)(B)(C)(D)参考答案:D4. 根据如下样本数据:-4.0-2.50.51 2.0 3.0得到的回归方程为,则()A. ,B. ,C. ,D. ,参考答案:C略5. 已知椭圆的左、右焦点分别为F1,F2,过点F2的直线交椭圆于P,Q两点,且,则椭圆的离心率为()A. B. C. D.参考答案:C【分析】不妨设,,,根据椭圆的定义求得,的值.在中由余弦定理求得,在中,由余弦定理求得,由此求得椭圆的离心率.【详解】设,,,则,,,得,则.在中,由余弦定理有.在中,由余弦定理有,则椭圆的离心率为.故选C.【点睛】本小题主要考查椭圆离心率的求法,考查利用余弦定理解三角形,考查椭圆的定义,属于中档题.6. 若展开式中的系数为-20,则等于()A. -1 B. C. -2 D.参考答案:A7. 在三棱锥A-BCD中,△BCD是边长为2的等边三角形,,,则三棱锥A-BCD的外接球的表面积为()A.B.C.D.参考答案:A根据题意画出三棱锥,如下图由所以AB直线在面BCD上的身影在底面正三角形的角平分线BE(E为CD中点),,即,点F为等边三角形BCD的中心,OF//AE,球心一定在OF上,设球半径为R,,解得,选A.8. 已知集合,集合,若A∩B,则的值是( ).A.10B.9C.4D.7参考答案:C9. 一只蜜蜂在一个棱长为5的正方体内自由飞行,若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于2,称其为“安全飞行”,则蜜蜂“安全飞行”的概率为( )A.B.C.D.参考答案:C考点:几何概型.专题:概率与统计.分析:小蜜蜂的安全飞行范围为:以这个正方体的中心为中心且边长为1的正方体内.这个小正方体的体积为大正方体的体积的,故安全飞行的概率为.解答:解:由题知小蜜蜂的安全飞行范围为:以这个正方体的中心为中心且边长为1的正方体内.这个小正方体的体积为1,大正方体的体积为27,故安全飞行的概率为p=.故选C.点评:本题考查几何概型概率的求法,解题时要认真审题,注意小蜜蜂的安全飞行范围为:以这个正方体的中心为中心且边长为1的正方体内.10. 太极图被称为“中华第一图”.从孔庙大成殿粱柱,到楼观台、三茅宫标记物;从道袍、卦摊、中医、气功、武术到南韩国旗……,太极图无不跃居其上.这种广为人知的太极图,其形状如阴阳两鱼互抱在一起,因而被称为“阴阳鱼太极图”.在如图所示的阴阳鱼图案中,阴影部分可表示为,设点,则的取值范围是()A .B .C .D .参考答案:C如图,作直线,当直线上移与圆相切时,取最大值,此时,圆心到直线的距离等于,即,解得,当下移与圆相切时,取最小值,同理,即,所以.二、 填空题:本大题共7小题,每小题4分,共28分11. 球O 是四面体ABCD 的外接球(即四面体的顶点均在球面上),若AB=CD=2,AD=AC=BD=BC=,则球O的表面积为 .参考答案:9π考点:球的体积和表面积.专题:空间位置关系与距离.分析:分别取AB ,CD 的中点E ,F ,连接相应的线段,由条件可知,球心G 在EF 上,可以证明G 为EF 中点,求出球的半径,然后求出球的表面积.解答: 解:分别取AB ,CD 的中点E ,F ,连接相应的线段CE ,ED ,EF ,由条件,AB=CD=2,AD=AC=BD=BC=,可知,△A BC 与△ADB,都是等腰三角形,AB⊥平面ECD ,∴AB⊥EF,同理CD⊥EF,∴EF 是AB 与CD 的公垂线,球心G 在EF 上,可以证明G 为EF 中点,(△AGB≌△CGD)DE===,DF=CD=,EF===1,∴GF=EF=,球半径DG===,∴外接球的表面积为4π×DG 2=9π,故答案为:9π.点评:本题考查球的内接几何体,球的表面积的求法,考查计算能力.12. 在平面直角坐标系中,若直线 (s 为参数)和直线 (t 为参数)平行,则常数的值为_____. 参考答案:4略13. 若点(5,b )在两条平行直线6x -8y +1=0与3x -4y +5=0之间,则整数b 的值为 参考答案: 414. 设的内角的对边长分别为,且 ,则的值是___________.参考答案:15. 曲线在点处的切线方程为 .参考答案:由已知得:求导,当时,k=0,所以切线方程:16. 已知的内角的对边分别是,且,若,则的取值范围为.参考答案:17. 在极坐标系中,曲线ρ=cos θ+1与ρcos θ=1的公共点到极点的距离为 _________ .参考答案:略三、 解答题:本大题共5小题,共72分。
广东省中山市华侨中学届高三数学月模拟考试试题文-课件

广东省中山市华侨中学2016 届高三 5 月高考模拟试卷文科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分 150 分.考试时间为120分钟,其中第Ⅱ卷 22 题- 24 题为选考题,其它题为必考题.本试卷共 5 页,24 小题,满分 150 分.考试用时 120 分钟.参考公式:样本数据 x , xx n的标准差锥体体积公式1 2s1( x 1x )2( x 2x )2( x nx )2V1shn3其中 x 为样本平均数 其中 S 为底面面积, h 为高 柱体体积公式球的表面积,体积公式VShS 4 R 2,V4 R 33其中 S 为底面面积, h 为高其中 R 为球的半径一、选择题: ( 本大题共 10 小题;每小题 5 分,满分 60 分)1. 若复数 z 与其共轭复数z 满足: z z 2i ,则复数 z 的虚部为()A . 1B. iC . 2D . -12.已知点 P( 1, 0) 、 Q(1, 3) ,向量 a (2k 1, 2) ,若 PQ a ,则实数 k ( )A . 2B . 1C .2D . 13. 在等比数列a n中, a 5a113,a 3a13a154, 则()a5A . 3 B.1C.3 或1 D. 3 或13334. y (sin x cosx)21是()A.最小正周期为 2πB.最小正周期为2π的奇函数的偶函数C. 最小正周期为 πD.最小正周期为 π的奇函数的偶函数5、已知幂函数 yf ( x) 的图象过点 ( 1,1) ,则 log 2 f (4) 的值为()28A . 3B . 6C . 4D .- 66. 已知 tan1, tan() 1 则 tan()431A.7B.11 C. 1 D.1 11 7 13 137、已知直线l经过坐标原点,且与圆x2 y2 4x 3 0 相切,切点在第四象限,则直线 l 的方程为()3x D .y 3 x A .y 3x B . y 3x C . y8.已知三条直线l 、 m、 n,三个平面、、3 3,有以下四个命题:①、;② l m、 l n m // n ;m // , n //// ③, n ;m④, l ,m l m。
广东省中山市华侨中学高三4月高考模拟数学(文)试题
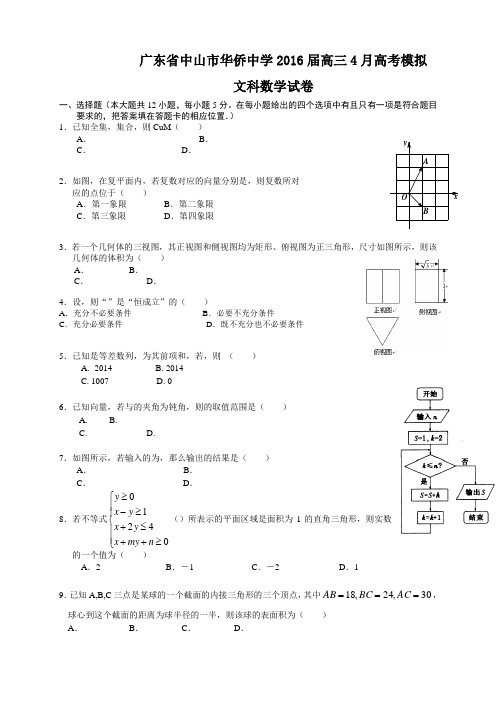
广东省中山市华侨中学2016届高三4月高考模拟文科数学试卷一、选择题(本大题共12小题,每小题5分。
在每小题给出的四个选项中有且只有一项是符合题目要求的,把答案填在答题卡的相应位置.) 1.已知全集,集合,则CuM ( )A .B .C .D .2.如图,在复平面内,若复数对应的向量分别是,则复数所对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.若一个几何体的三视图,其正视图和侧视图均为矩形、俯视图为正三角形,尺寸如图所示,则该几何体的体积为( ) A . B . C . D .4.设,则“”是“恒成立”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.已知是等差数列,为其前项和,若,则 ( ) A. -2014 B. 2014C. 1007D. 06.已知向量,若与的夹角为钝角,则的取值范围是( )A. B. C. D.7.如图所示,若输入的为,那么输出的结果是( )A .B .C .D .8.若不等式01240y x y x y x my n ≥⎧⎪-≥⎪⎨+≤⎪⎪++≥⎩()所表示的平面区域是面积为1的直角三角形,则实数的一个值为( )A .2B .-1C .-2D .19.已知A,B,C 三点是某球的一个截面的内接三角形的三个顶点,其中30,24,18===AC BC AB ,球心到这个截面的距离为球半径的一半,则该球的表面积为( ) A . B . C . D .10.定义空间两个向量的一种运算sin ,⊗=⋅<>a b a b a b ,则关于空间向量上述运算的以下结论中:①; ②; ③()()()+⊗=⊗+⊗a b c a c b c ;④若1122(,),(,)x y x y ==a b ,则。
其中恒成立的有( ) A .①④ B .①③ C .②③ D .②④11.已知椭圆C:)0(12222>>=+b a by a x 的左右焦点为,若椭圆C 上恰好有6个不同的点,使得为等腰三角形,则椭圆C 的离心率的取值范围是( )A . B. C. D.12.已知定义在上的函数满足:222,[0,1)()2,[1,0)x x f x x x ⎧+∈=⎨-∈-⎩,且,,则方程在区间上的所有实根之和为( )A .-7B .-8C .-6D .-5二、填空题:本大题共4小题,每小题5分。
中山市华侨中学2016届高三化学模拟试卷(3月份) 含解析

2016年广东省中山市华侨中学高考化学模拟试卷(3月份)一、选择题1.化学与生产、生活、社会密切相关.下列有关说法中正确的是()A.在日常生活中,化学腐蚀是造成钢铁腐蚀的主要原因B.明矾水解时产生具有吸附性的胶体粒子,可以用于饮用水的杀菌消毒C.SO2具有漂白性,可用于漂白纸浆,也可以用于漂白食品D.纯碱可用于生产普通玻璃,日常生活中也可用纯碱溶液来除去物品表面的油污2.设N A表示阿伏加德罗常数的值,下列叙述正确的是()A.密闭容器中2molNO与1molO2充分反应,产物的分子数为2N AB.一定温度下,1 L 0。
50 mol•L﹣1 NH4NO3溶液中含氮原子个数为N AC.过氧化氢分解制得1。
12 L O2,转移电子数目为0。
2 N AD.235g核素U发生裂变反应:U+n Sr+Xe+10n,净产生的中子(n)数为10N A3.下列叙述正确的是()A.NaHCO3溶液中含有少量Na2CO3,可以用澄清石灰水除去B.新制氯水显酸性,向其中滴加少量紫色石蕊试液,充分振荡后溶液呈红色C.加水稀释CH3COONa溶液,溶液中的所有离子浓度都减小D.金属铝的生产是以Al2O3为原料,在熔融状态下进行电解4.科学家设想以N2和H2为反应物,以溶有A的稀盐酸为电解质溶液,可制造出既能提供电能,又能固氮的新型燃料电池,装置如图所示,下列说法不正确的是()A.通入N2的电极发生的电极反应式为:N2+6e﹣+8H+═2NH4+B.反应过程中溶液的pH会变大,故需要加入盐酸C.该电池外电路电流从通入H2的电极流向通入N2的电极D.通入H2的电极为负极,A为NH4Cl5.室温下,下列电解质溶液叙述正确的是()A.25℃时若1 mL pH=1的盐酸与100 mL 氨水溶液混合后,溶液的pH=7,则氨水溶液的pH=11B.将0.2 mol•L﹣1盐酸与0。
1 mol•L﹣1的KAlO2溶液等体积混合,溶液中离子浓度由小到大的顺序:c(OH﹣)<c(H+)<c(Al3+)<c(K+)<c(Cl﹣)C.pH相等的①NH4Cl ②(NH4)2SO4③NH4HSO4溶液:c(NH4+)大小顺序为②>①>③D.0。
2016年广东省中山市华侨中学高考模拟试卷数学文

2016年广东省中山市华侨中学高考模拟试卷数学文一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M={x|x 2=x},N={x|lgx ≤0},则M ∪N=( ) A.[0,1] B.(0,1] C.[0,1) D.(-∞,1]解析:求解一元二次方程化简M ,求解对数不等式化简N ,然后利用并集运算得答案.由M={x|x 2=x}={0,1}, N={x|lgx ≤0}=(0,1],得M ∪N={0,1}∪(0,1]=[0,1]. 答案:A.2.给定函数①12y x =,②()121y log x +=,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数序号是( ) A.①② B.②③ C.③④ D.①④解析:本题所给的四个函数分别是幂函数型,对数函数型,指数函数型,含绝对值函数型,在解答时需要熟悉这些函数类型的图象和性质;①12y x =是幂函数,其在(0,+∞)上即第一象限内为增函数,故此项不符合要求; ②中的函数是由函数()121y log x +=向左平移1个单位长度得到的,因为原函数在(0,+∞)内为减函数,故此项符合要求;③中的函数图象是由函数y=x-1的图象保留x 轴上方,下方图象翻折到x 轴上方而得到的,故由其图象可知该项符合要求;④中的函数图象为指数函数,因其底数大于1,故其在R 上单调递增,不合题意. 答案:B.3.设a ,b ∈R ,则“(a-b)3b 2>0”是“a >b ”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析:根据不等式之间的关系,利用充分条件和必要条件的定义进行判断即可.(a-b)3b 2>0与a >b ,b ≠0,显然(a-b)3b 2>0⇒a >b ,反之不成立,即“(a -b)3b 2>0”是“a>b”的充分不必要条件. 答案:A.4.设变量x,y满足约束条件1124x yx yx y+≥⎧⎪-≥⎨⎪-≥⎩,则目标函数z=3x+y的最小值为( )A.11B.3C.2D.13 3解析:作出不等式对应的平面区域如图,由z=3x+y,得y=-3x+z,平移直线y=-3x+z,由图象可知当直线y=-3x+z,经过点A时,直线y=-3x+z的截距最小,此时z最小.由124x yx y+⎧⎨-⎩==,解得5323xy⎧⎪⎪⎨⎪-⎪⎩==,即A(53,23-),此时z的最小值为52133333z=⨯-=.答案:D5.一个袋子中有号码为1、2、3、4、5大小相同的5个小球,现从袋中任意取出一个球,取出后不放回,然后再从袋中任取一个球,则第一次取得号码为奇数,第二次取得号码为偶数球的概率为( )A.3 5B.45 C.320 D.310解析:1、2、3、4、5大小相同的5个小球,从袋中任取一个球,则第一次取得号码为奇数的概率为35, 第二次取得号码为偶数球的概率为2142=, 故第一次取得号码为奇数,第二次取得号码为偶数球的概率为3135210⨯=. 答案:D.6.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图与侧视图中x 的值为( )A.5B.4C.3D.2解析:由三视图知,该空间几何体为圆柱及四棱锥, 且圆柱底面半径为2,高为x ,四棱锥底面为正方形,边长为=,故体积为2141233x ππ+⨯=+(, 故x=3.答案:C.7.一个样本容量为10的样本数据,它们组成一个公差不为0的等差数列{a n},若a3=8,且a1,a3,a7成等比数列,则此样本的平均数和中位数分别是( )A.13,12B.13,13C.12,13D.13,14解析:设公差为d,由a3=8,且a1,a3,a7成等比数列,可得64=(8-2d)(8+4d)=64+16d-8d2,即,0=16d-8d2,又公差不为0,解得d=2此数列的各项分别为4,6,8,10,12,14,16,18,20,22,故样本的中位数是13,平均数是13.答案:B8.曲线y=e-2x+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为( )A.1 3B.1 2C.2 3D.1解析:根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成一般式,然后求出与y轴和直线y=x的交点,根据三角形的面积公式求出所求即可.∵y=e-2x+1,∴y'=(-2)e-2x.∴y'|x=0=(-2)e-2x|x=0=-2∴曲线y=e-2x+1在点(0,2)处的切线方程为y-2=-2(x-0)即2x+y-2=0令y=0解得x=1,令y=x解得x=y=23.∴切线与直线y=0和y=x围成的三角形的面积为1211233⨯⨯=.答案:A9.已知双曲线22221x ya b-=(a>0,b>0)与抛物线y2=8x有一个公共的焦点F,且两曲线的一个交点为P,若|PF|=5,则双曲线的渐近线方程为( )A.x±y=0C.x±2y=0D.2x±y=0解析:由于双曲线22221x y a b-=(a >0,b >0)与抛物线y 2=8x 有一个公共的焦点F ,且抛物线y 2=8x 的焦点坐标(2,0),故双曲线的半焦距c=2,又|PF|=5,设P(m ,n), 由抛物线的定义知|PF|=m+2, ∴m+2=5,m=3,∴点P 的坐标(3,∴222249241a b a b⎧+⎪⎨-⎪⎩==,解得:2213a b ⎧⎪⎨⎪⎩==,0y ±=.答案:B.10.若[x]表示不超过x 的最大整数,执行如图所示的程序框图,则输出的S 值为( )A.4B.5C.7D.9解析:根据题意,模拟程序框图的运行过程,求出该程序运行后输出的S 的值. 模拟程序框图的运行过程,如下; S=0,n=0,]=0,0>4,否; n=1,]=1,1>4,否; n=2,,2>4,否; n=3,,3>4,否;n=4,,4>4,否;n=5,,5>4,是; 输出S=7. 答案:C.11.已知S ,A ,B ,C 是球O 表面上的点,SA ⊥平面ABC ,AB ⊥BC ,SA=AB=1,BC O 的表面积等于( )A.4πB.3πC.2πD.π解析:∵已知S ,A ,B ,C 是球O 表面上的点, ∴OA=OB=OC=OS.又SA ⊥平面ABC ,AB ⊥BC ,SA=AB=1,BC , ∴球O 的直径为2R=SC=2,R=1,∴表面积为4πR 2=4π. 答案:A.12.若函数()sinx f x x =,并且233a b ππ<<<,则下列各结论中正确的是( )A.()2a b f a ff +⎛⎫ ⎪⎝⎭<<B.()2a b ff f b ⎛⎫⎪⎝⎭+<<C.()2a b ff f a ⎛⎫⎪⎝⎭+<<D.()2a b f b f f ⎛⎫⎪⎝+⎭<<解析:由导数可判断()sinx f x x =在3(23)ππ, 上是减函数,再由基本不等式可判断出2a b+<,从而由函数的单调性比较函数值的大小即可. ∵()sinxf x x=,∴()2xcosx sinxf x x -'=,当x ∈2(3]ππ, 时,可判断xcosx-sinx 是减函数, 故31032xcosx sinx π--<<, 当x ∈3(23)ππ,时,xcosx-sinx <0;故()sinx f x x =在3(23)ππ, 是减函数,而由233a b ππ<<<知2a b a b+<<,故()2a b f a ff +⎛⎫⎪⎝⎭>>,()2a b f b f f⎛⎫⎪⎝+⎭<<.答案:D.二、填空题:本大概题共4小题,每小题5分.13.数列{a n }的首项为3,{b n }为等差数列且b n =a n+1-a n (n ∈N*).若b 3=-2,b 10=12,则a 8= . 解析:先利用等差数列的通项公式分别表示出b 3和b 10,即b 3=b 1+2d =-2,b 10=b 1+9d =12,即1122912b d b d +-⎧⎨+⎩==,解得162b d =-⎧⎨=⎩. ∵b n =a n+1-a n ,∴b 1+b 2+…+b n =a n+1-a 1, ∴a 8=b 1+b 2+…+b 7+3=()6672-+⨯+3=3.答案: 314.已知向量a =(x-1,2),b =(4,y),若a b ⊥,则16x+4y的最小值为 .解析:根据向量垂直的充要条件:数量积为0,得到x ,y 满足的等式:∵a b ⊥,a =(x-1,2),b =(4,y) ∴4(x-1)+2y=0即4x+2y=4∵42164228x y x y ++≥=. 当且仅当24x =22y即4x=2y=2时取等号.∴16x +4y的最小值为8. 答案:815.已知直线2xy =与双曲线22221x y a b -=(a >0,b >0)交于两点,则该双曲线的离心率的取值范围是 .解析:把直线2xy =代入双曲线22221x y a b -=(a >0,b >0), 并整理,得2222244a b x b a -=,∵直线2xy =与双曲线22221x y a b -=(a >0,b >0)交于两点, ∴4b 2>a 2,即224a b >,∴222222544a a c ab a =++=>,∴2c ,∴2c e a=.∴该双曲线的离心率的取值范围+∞).答案:+∞).16.如图甲,在△ABC 中,AB ⊥AC ,AD ⊥BC ,D 为.垂足,则AB 2=BD ·BC ,该结论称为射影定理.如图乙,在三棱锥A-BCD 中,AD ⊥平面ABC ,AO ⊥平面BCD ,O 为垂足,且O 在△BCD 内,类比射影定理,探究S △ABC 、S △BCO 、S △BCD 这三者之间满足的关系是 .解析:结论:S △ABC 2=S △BCO ·S △BCD . 证明如下在△BCD 内,延长DO 交BC 于E ,连接AE ,∵AD ⊥平面ABC ,BC 平面ABC , ∴BC ⊥AD ,同理可得:BC ⊥AO∵AD 、AO 是平面AOD 内的相交直线, ∴BC ⊥平面AOD∵AE 、DE ⊂平面AOD ∴AE ⊥BC 且DE ⊥BC∵△AED 中,EA ⊥AD ,AO ⊥DE∴根据题中的已知结论,得AE 2=EO ·ED 两边都乘以(12BC)2,得2()(111····22)()2BC AE BC EO BC ED = ∵AE 、EO 、ED 分别是△ABC 、△BCO 、△BCD 的边BC 的高线 ∴S △ABC =12BC ·AE ,S △BCO =12BC ·EO ,S △BCD =12BC ·ED 所以有S △ABC 2=S △BCO ·S △BCD ,结论成立. 答案:S △ABC 2=S △BCO ·S △BCD .三.解答题:解答应写出文字说明,证明过程或演算步骤.17.已知向量m =(sinx ,-1),n =(cosx ,3).(Ⅰ)当m ∥n 时,求32sinx cosxsinx cosx+-的值.解析:(Ⅰ)由m n ,可得13tanx =-,再由13232sinx cosx tanx sinx cosx tanx ++=--,运算求得结果. ⊂答案:(Ⅰ)由m n ,可得3sinx=-cosx ,于是13tanx =-. ∴11123132329323sinx cosx tanx sinx cosx tanx -⎛⎫-- ⎪⎝+++===---⎭.(Ⅱ)已知在锐角△ABC 中,a ,b ,c 分别为角A ,B ,C,函数()()f x m n m =+,求()8f B π+的取值范围.解析:(Ⅱ)在△ABC利用正弦定理求得sinA =A=3π.由△ABC 为锐角三角形,得62B ππ<<,利用两个向量的数量积公式求得函数()23242f x sin x π⎛⎫ ⎪⎝⎭=--.由此可得()23282f B sin B π+=-,再根据B 的范围求出sin2B 的范围,即可求得()8f B π+的取值范围.答案:(Ⅱ)∵在△ABC 中,A+B=π-C ,于是sin(A+B)=sinC ,sinC=2sinAsinC ,∴sinA =A=3π. 又△ABC 为锐角三角形,于是62B ππ<<,∵函数()()22()2)1(f x m n m sinx cosx sinx sin x sinxcosx =+=+-=+-,,12232222224cos x sin x sin x π-=⎛⎫ ⎪⎝⎭+-=--.∴332288()[()]422f B B B πππ+=+--=-. 由62B ππ<<得23B ππ<<,∴0<sin2B ≤1,得2233322B --≤-,即()8f B π+的取值范围33 2(]2--.18.某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少75%的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.(Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率.解析:(Ⅰ)从5个小区中任选两个小区,列出所有可能的结果,然后找出选出的两个小区恰有一个为非低碳小区的基本事件,根据古典概型的概率公式解之即可.答案:(Ⅰ)设三个“非低碳小区”为A ,B ,C ,两个“低碳小区”为m ,n , 用(x ,y)表示选定的两个小区,x ,y ∈{A ,B ,C ,m ,n},则从5个小区中任选两个小区,所有可能的结果有10个,它们是(A ,B),(A ,C),(A ,m),(A ,n),(B ,C),(B ,m),(B ,n),(C ,m),(C ,n),(m ,n). 用D 表示:“选出的两个小区恰有一个为非低碳小区”这一事件,则D 中的结果有6个,它们是:(A ,m),(A ,n),(B ,m),(B ,n),(C ,m),(C ,n). 故所求概率为()63105P D ==.(Ⅱ)假定选择的“非低碳小区”为小区A ,调查显示其“低碳族”的比例为12,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区A 是否达到“低碳小区”的标准?解析:(Ⅱ)根据图1可知月碳排放量不超过300千克的成为“低碳族”,由图2可求出三个月后的低碳族的比例,从而可判定三个月后小区A 是否达到了“低碳小区”标准. 答案:(Ⅱ)由图1可知月碳排放量不超过300千克的成为“低碳族”. 由图2可知,三个月后的低碳族的比例为0.07+0.23+0.46=0.76>0.75, 所以三个月后小区A 达到了“低碳小区”标准.19.如图,在四棱锥P-ABCD 中,底面ABCD 为矩形,PD ⊥底面ABCD ,E 是AB 上一点.已知PD=,CD=4,(Ⅰ)若∠ADE=6π,求证:CE ⊥平面PDE. 解析:(Ⅰ)在Rt △DAE 中,求出BE=3.在Rt △EBC 中,求出∠CEB=6π.证明CE ⊥DE.PD ⊥CE.即可证明CE ⊥平面PDE.答案:(Ⅰ)在Rt △DAE 中,ADE=6π, ∴3331AE AD tan ADE =∠==. 又AB=CD=4,∴BE=3.在Rt △EBC 中,BC tan CEB BE ∠==6CEB π∠=. 又3AED π∠=,∴2DEC π∠=,即CE ⊥DE.∵PD ⊥底面ABCD ,CE ⊂底面ABCD ,∴PD ⊥CE.∴CE ⊥平面PDE.(Ⅱ)当点A 到平面PDE 的距离为7时,求三棱锥A-PDE 的侧面积. 解析:(Ⅱ)证明平面PDE ⊥平面ABCD.过A 作AF ⊥DE 于F ,求出AF.证明BA ⊥平面PAD ,BA⊥PA.然后求出三棱锥A-PDE 的侧面积S =侧答案:(Ⅱ)∵PD ⊥底面ABCD ,PD ⊂平面PDE , ∴平面PDE ⊥平面ABCD. 如图,过A 作AF ⊥DE 于F ,∴AF ⊥平面PDE ,∴AF 就是点A 到平面PDE 的距离,即7AF =. 在Rt △DAE 中,由AD ·AE=AF ·DE ,得237AE =+AE=2.∴11222APDSPD AD ==⨯=, 11222ADESAD AE ==⨯=, ∵BA ⊥AD ,BA ⊥PD ,∴BA ⊥平面PAD ,∵PA ⊂平面PAD ,∴BA ⊥PA.在Rt △PAE 中,AE=2,PA =,∴11222APESPA AE ==⨯=∴三棱锥A-PDE 的侧面积S =侧20.已知F 1,F 2是椭圆22221x y a b+=(a >b >0)的左、右焦点,A 是椭圆上位于第一象限内的一点,2120AF F F =,若椭圆的离心率等于2.(Ⅰ)求直线AO 的方程(O 为坐标原点).解析:(Ⅰ)根据椭圆的离心率e=2,即c =2a ,可得b 2=12a 2,因此设椭圆方程为x 2+2y 2=a 2.再设点A(x 0,y 0),因为向量2AF 、12F F 的数量积为0,得到AF 2、F 1F 2互相垂直,所以x 0=c ,将A(c ,y 0),代入椭圆方程,化简可得y 0=12a ,得到A 的坐标,从而得到直线AO 的斜率为2,最后根据直线AO 过原点,得直线AO 的方程为y=2x. 答案:(Ⅰ)∵2120AF F F =,∴AF 2⊥F 1F 2,又∵椭圆的离心率2c e a ==,∴c ,可得b 2=12a 2, 设椭圆方程为x 2+2y 2=a 2,设A(x 0,y 0),由AF 2⊥F 1F 2,得x 0=c ∴A(c ,y 0),代入椭圆方程,化简可得y 0=12a(舍负)∴22a A ⎛⎫⎪ ⎪⎝⎭,,可得直线AO 的斜率K OA=2因为直线AO 过原点,故直线AO 的方程为2y x =(Ⅱ)直线AO 交椭圆于点B ,若△ABF 2的面积等于,求椭圆的方程.解析:(Ⅱ)连接AF 1,BF 1,AF 2,BF 2,由椭圆的对称性可知:S △ABF1=S △ABF2=S △AF1F2,可用△AF 1F 2的面积列式,解之得a 2=16,c 2=12a 2=8,所以b 2=a 2-c 2=8,最终得到椭圆方程为221168x y +=. 答案:(Ⅱ)连接AF 1,BF 1,AF 2,BF 2,由椭圆的对称性可知:S △ABF1=S △ABF2=S △AF1F2,∴12122AF F A Sc y =⨯⨯=12ac =又∵2c a∴24a =a 2=16,c 2=12a 2=8, ∴b 2=a 2-c 2=8,故椭圆方程为221168x y +=21.已知函数()321232a f x x x x =-+- (a ∈R).(Ⅰ)当a=3时,求函数f(x)的单调区间. 解析:(Ⅰ)先求当a=3时函数的导数f ′(x),并将其因式分解,便于解不等式,再由f ′(x)>0,得函数的单调增区间,由f ′(x)<0,得函数的单调减区间. 答案:(Ⅰ)当a=3时,()3213232f x x x x =-+-,得f'(x)=-x 2+3x-2. 因为f'(x)=-x 2+3x-2=-(x-1)(x-2),所以当1<x <2时,f'(x)>0,函数f(x)单调递增; 当x <1或x >2时,f'(x)<0,函数f(x)单调递减.所以函数f(x)的单调递增区间为(1,2),单调递减区间为(-∞,1)和(2,+∞).(Ⅱ)若对于任意x ∈[1,+∞)都有f ′(x)<2(a-1)成立,求实数a 的取值范围. 解析:(Ⅱ)方法1:由()321232a f x x x x =-+-,得f'(x)=-x 2+ax-2,原问题转化为:对于任意x ∈[1,+∞)都有x 2-ax+2a >0成立,令h(x)=x 2-ax+2a ,结合二次函数的性质得到关于a 的不等关系,从而求出实数a 的取值范围. 方法2:由()321232a f x x x x =-+-,得f'(x)=-x 2+ax-2,问题转化为,对于任意x ∈[1,+∞)都有[f'(x)]max <2(a-1).下面利用导数工具研究其单调性和最大值,即可得出实数a 的取值范围.答案:(Ⅱ)方法1:由()321232a f x x x x =-+-,得f'(x)=-x 2+ax-2, 因为对于任意x ∈[1,+∞)都有f'(x)<2(a-1)成立,即对于任意x ∈[1,+∞)都有-x2+ax-2<2(a-1)成立, 即对于任意x ∈[1,+∞)都有x2-ax+2a >0成立,令h(x)=x 2-ax+2a ,要使对任意x ∈[1,+∞)都有h(x)>0成立,必须满足△<0或()01210ah ≥⎧⎪⎪≤⎨⎪⎪⎩>.即a 2-8a <0或2801210a a a a ⎧-≥⎪⎪≤⎨⎪+⎪⎩>.所以实数a 的取值范围为(-1,8). 方法2:由()321232a f x x x x =-+-,得f'(x)=-x 2+ax-2, 因为对于任意x ∈[1,+∞)都有f'(x)<2(a-1)成立,所以问题转化为,对于任意x ∈[1,+∞)都有[f'(x)]max <2(a-1).因为()22224a a f x x ⎛⎫ '--+⎪⎝⎭-=,其图象开口向下,对称轴为2a x =.①2a<1时,即a <2时,f'(x)在[1,+∞)上单调递减, 所以f'(x)max =f'(1)=a-3,由a-3<2(a-1),得a >-1,此时-1<a <2. ②当2a ≥1时,即a ≥2时,f'(x)在[1,2a ]上单调递增,在(2a,+∞)上单调递减, 所以()2224max a af x f ⎛⎫ ⎪⎝'⎭'-==,由224a -<2(a-1),得0<a <8,此时2≤a <8. 综上①②可得,实数a 的取值范围为(-1,8).(Ⅲ)若过点(0,13-)可作函数y=f(x)图象的三条不同切线,求实数a 的取值范围. 解析:(Ⅲ)先将过点(0,13-)可作曲线y=f(x)的三条切线转化为:方程322110323t at -+=有三个不同的实数解,下面利用导数研究函数g(x)的零点,从而求得a 的范围. 答案:(Ⅲ)设点P(t ,321232a t t t -+-)是函数y=f(x)图象上的切点, 则过点P 的切线的斜率为k=f'(t)=-t 2+at-2, 所以过点P 的切线方程为()()32212232a y t t t t at x t +-+-+--=. 因为点(0,13-)在切线上,所以()()32211220332a t t t t at t -+-+-+--=,即322110323t at -+=. 若过点(0,13-)可作函数y=f(x)图象的三条不同切线,则方程322110323t at -+=有三个不同的实数解.令()32211323g t t at -+=,则函数y=g(t)与t 轴有三个不同的交点.令g'(t)=2t 2-at=0,解得t=0或t =2a .因为()103g =,3112243a g a ⎛⎫⎪⎝⎭-+=,所以必须31102243a g a -+⎛⎫⎪⎝⎭=<,即a >2. 所以实数a 的取值范围为(2,+∞).请考生在第22、23、24题中任选一题作答,如果多做,则安所做的第一题计分.作答时请写清题号.[选修4-1:几何证明选讲]22.如图,△ABC 是直角三角形,∠ABC=90°,以AB 为直径的圆O 交AC 于点E ,点D 是BC 边的中点,连接OD 交圆O 于点M.(Ⅰ)求证:O 、B 、D 、E 四点共圆.解析:(Ⅰ)连接BE 、OE ,由直径所对的圆周角为直角,得到BE ⊥EC ,从而得出DE=BD=12BC ,由此证出△ODE ≌△ODB ,得∠OED=∠OBD=90°,利用圆内接四边形形的判定定理得到O 、B 、D 、E 四点共圆.答案:(Ⅰ)连接BE 、OE ,则∵AB 为圆0的直径,∴∠AEB=90°,得BE ⊥EC , 又∵D 是BC 的中点,∴ED 是Rt △BEC 的中线,可得DE=BD. 又∵OE=OB ,OD=OD ,∴△ODE ≌△ODB. 可得∠OED=∠OBD=90°, 因此,O 、B 、D 、E 四点共圆.(Ⅱ)求证:2DE 2=DM ·AC+DM ·AB.解析:(Ⅱ)延长DO 交圆O 于点H ,由(Ⅰ)的结论证出DE 为圆O 的切线,从而得出DE 2=DM ·DH ,再将DH 分解为DO+OH ,并利用OH=12AB 和DO=12AC ,化简即可得到等式2DE 2=DM ·AC+DM ·AB 成立.答案:(Ⅱ)延长DO 交圆O 于点H ,∵DE ⊥OE ,OE 是半径,∴DE 为圆O 的切线.可得DE 2=DM ·DH=DM ·(DO+OH)=DM ·DO+DM ·OH.∵OH=12AB ,OD 为△ABC 的中位线,得DO=12AC , ∴DE 2=DM ·(12AC)+DM ·( 12AB),化简得2DE 2=DM ·AC+DM ·AB.[选修4-4:坐标系与参数方程]23.在直角坐标系xOy 中,直线l的参数方程为3x y ⎧⎪⎪⎨⎪⎪⎩=(t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为ρ=θ.(Ⅰ)求圆C 的圆心到直线l 的距离. 解析:(Ⅰ)圆C 的极坐标方程两边同乘ρ,根据极坐标公式进行化简就可求出直角坐标方程,最后再利用三角函数公式化成参数方程.答案:(Ⅰ)由ρ=sin θ,可得220x y +-=,即圆C的方程为(225x y +-=.由232x y t ⎧-⎪⎪⎨⎪⎪⎩=可得直线l的方程为30x y +=. 所以,圆C 的圆心到直线l2=.(Ⅱ)设圆C 与直线l 交于点A 、B.若点P 的坐标为(3),求|PA|+|PB|.解析:(Ⅱ)将直线l 的参数方程代入圆C 的直角坐标方程,得即t 2t+4=0,根据两交点A ,B 所对应的参数分别为t 1,t 2,利用根与系数的关系结合参数的几何意义即得.答案: (Ⅱ)将l的参数方程代入圆C的直角坐标方程,得223522t-+⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎝⎭⎝⎭=,即240t-+=.由于()2344220=-⨯=>.故可设t1、t2是上述方程的两个实根,所以12124t tt t⎧+⎪⎨⎪⎩==,又直线l过点P(3,故由上式及t的几何意义得|PA|+|PB|=|t1|+|t2|=t1+t2=.[选修4-5:不等式证明选讲]24.已知函数f(x)=|x-1|+|x+1|.(Ⅰ)求不等式f(x)≥3的解集.解析:(Ⅰ)分类讨论,去掉绝对值,即可求不等式f(x)≥3的解集.答案:(Ⅰ)x<-1时,不等式可化为1-x-x-1≥3,∴x≤32-;-1≤x≤1时,不等式可化为1-x+x+1≥3,不成立;x>1时,不等式可化为x-1+x+1≥3,∴x≥32;∴不等式f(x)≥3的解集为{x|x≤32-或x≥32}.(Ⅱ)若关于x的不等式f(x)>a2-x2+2x在R上恒成立,求实数a的取值范围.解析:(Ⅱ)分类讨论,去掉绝对值,利用不等式f(x)>a2-x2+2x在R上恒成立,即可求实数a的取值范围.答案:(Ⅱ)x<-1时,不等式f(x)>a2-x2+2x可化为a2<(x-2)2-4,∴a2<5,∴a;-1≤x≤1时,不等式f(x)>a2-x2+2x可化为a2<(x-1)2+1,∴a2<1,∴-1<a<1;x>1时,不等式f(x)>a2-x2+2x可化为a2<x2,∴a2<1,∴-1<a<1,∴a。
生物高考模拟卷-高三生物试题及答案-中山市华侨中学2016届高三3月高考模拟考试

广东省中山市华侨中学2016届高三3月高考模拟考试Ⅰ卷(选择题共36分)一、单项选择题(本题共6大题,每小题6分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列叙述正确的是A.HIV、蓝藻和酵母菌共有的结构是核糖体B.原核生物的主要遗传物质是DNAC.原核细胞与真核细胞最主要的区别是有无以核膜为界限的细胞核D.真核生物细胞只进行有丝分裂,原核生物细胞只进行无丝分裂2.下图为人体细胞的分裂、分化、衰老和凋亡过程的示意图,图中①—⑥为各个时期的细胞,a—c表示细胞所进行的生理过程。
据图分析,下列叙述正确的是A.⑤与⑥的基因型相同,蛋白质的种类也相同B.细胞的衰老与凋亡就会引起人体衰老与死亡C.若⑤⑥已失去分裂能力,则其细胞内遗传信息的流动方向为DNA→RNA→蛋白质D.与①相比,②的表面积与体积的比值增大,与外界环境进行物质交换的能力增强3.下列关于科学史中研究方法和生物实验方法的叙述中,正确的是①研究光合作用的反应过程和噬菌体侵染细菌实验——同位素标记法②孟德尔豌豆杂交实验提出遗传定律——假说一演绎法③DNA双螺旋结构的发现和研究某种群数量变化规律——模型建构法④探究酵母菌细胞呼吸方式——对比实验法⑤分离各种细胞器和叶绿体中色素的分离——差速离心法A.①②④⑤B.①②③④C.①②③⑤D.②③④⑤4.某研究者对新生儿感染的细菌进行了耐药性实验,结果显示70%的致病菌具有耐药性,下列相关叙述正确的是A.细菌由于基因突变和染色体变异,形成了多种变异类型B .70%的致病菌具有耐药性,与新生儿是否接触过抗生素无关C .新生儿出生时接种疫苗,可预防各种细菌感染D .新生儿通过从母体获取的免疫球蛋白,对细菌发生的免疫反应属于非特异性免疫5.下图为酶催化反应效率关系图,A→B 代表酶催化效率坐标:0到100%,A→C 代表温度坐标:0到70℃,C→B 代表溶液酸碱度坐标:PH=0.1到PH=14的范围,分析不合理...的是A .GK 和HK 所代表的某酶的催化效率差异,其关键影响因素是温度B .KG 线段所代表的酶,其最适温度在EF 范围内C .JH 和HK 可以用来体现胃蛋白酶和胰蛋白酶在不同酸碱溶液环境下的反应特点D .某酶因为温度改变从JH 偏移为JG ,那么在AE 和EC 之间各有一个温度取值6. 为研究根背光生长与生长素的关系,将水稻幼苗分别培养在含不同浓度生长素或适宜浓度NPA (生长素运输抑制剂)的溶液中,用水平单侧光照射根部(如下图),测得根的弯曲角度及生长速率如下表据此实验的结果,不能得出的结论是 A .根向光一侧的生长速率大于背光一侧B .生长素对水稻根生长的作用具有两重性C .单侧光对向光一侧生长素的合成没有影响D .单侧光照射下根的背光生长与生长素的运输有关第Ⅱ卷(非选择题 54分) 处理方式测定指标外源生长素(mg/L ) NPA(μmol/L) 0 0.001 0.01 0.1 3 弯曲角度α(度)37 40 31 22 16 生长速率(mm/天) 1517 13 11 8二、非选择题(包括必考题和选考题两部分,第29-32题为必考题,每个试题考生都必须作答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中山市华侨中学2016届高三3月高考模拟考试数学(文科)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。
2.回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号,写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设集合2{|}M x x x ==,{|lg 0}N x x =≤,则M N =A .[0,1]B .(0,1]C .[0,1)D .(,1]-∞ (2)给定函数①12y x =,②12log (1)y x =+,③|1|y x =-,④12x y +=,其中在区间(0,1)上单调递减的函数序号是A .①④B .②③C .③④D .①②(3)设,a b R ∈,则“()320a b b ->”是“a b >”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件(4)设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥-≥-≥+4211y x y x y x ,则目标函数y x z +=3的最小值为(A)11 (B)3 (C)2 (D)313 (5)一个袋子中有号码为1、2、3、4、5大小相同的5个小球,现从袋中任取出一个球,取出后不放回,然后再从袋中任取一个球,则第一次取得号码为奇数,第二次取得号码为偶数球的概率为A .B .C .D .(6) 一空间几何体的三视图如图所示,该几何体的体积为12π+853,则正视图与侧视图中x 的值为A .5B .4C .3D .2(7)一个样本容量为10的样本数据,它们组成一个公差不为O 的等差数列{n a },若a 3 =8,且a 1,a 3,a 7成等比数列,则此样本的平均数和中位数分别是A .13 ,12B .13 ,13C .12 ,13D .13 ,14.(8)曲线y=2xe -+1在点(0,2)处的切线与直线y=0和y=x 围成的三角形的面积为A .13 B .12 C .23D .1 (9)已知双曲线2222-1(0,0)x y a b a b=>>与抛物线28y x =有一个公共的焦点F ,且两曲线的一个交点为P ,若|PF|=5,则双曲线的渐近线方程为A .0x =B 0y ±=C .20x y ±=D .20x y ±=(10)若[]x 表示不超过x 的最大整数,执行如图所示 的程序框图,则输出S 的值为A.4B.5C.7D.9(11)已知S,A ,B ,C 是球O 表面上的点,SA ⊥平面ABC ,AB ⊥BC,SA=AB=l ,O 的表面积等于A .4πB .3πC .2πD .π(12)若函数()sin x f x x =,并且233a b ππ<<<,则下列各结论正确的是A .()()2a b f a f f +<< B .()()2a bf f f b +<<C .()()2a b f f f a +<<D .()()2a bf b f f +<<第Ⅱ卷本卷包括必考题和选考题两部分。
第13题~第21题为必考题,每个试题考生都必须作答。
第22题~ 第24题为选考题,考生根据要求做答。
二、填空题:本大概题共4小题,每小题5分。
(13)数列{}n a 的首项为3,{}n b 为等差数列且*1()n n n b a a n N +=-∈,若23-=b ,1210=b ,则8a = .(14)已知向量,若⊥,则16x +4y 的最小值为 .(15)已知直线2x y =与双曲线()222210,0x y a b a b-=>>交于两点,则该双曲线的离心率的取值范围是 .(16)如图甲, 在ABC ∆中, AB AC ⊥, AD BC ⊥, D 为.垂足, 则2AB BD BC =⋅, 该结论称为射影定理. 如图乙, 在三棱锥A BCD -中, AD ⊥平面ABC , AO ⊥平面BCD ,O 为垂足, 且O 在BCD ∆内, 类比射影定理, 探究ABC S ∆、BCO S ∆、BCD S ∆这三者之间满足的关系是三.解答题:解答应写出文字说明,证明过程或演算步骤。
(17)( 本小题满分12分)已知向量(sin ,1),(cos ,3)m x n x =-=(1)当//m n时,求的值;(2)已知在锐角ΔABC 中,a ,b ,c 分别为角A,B,C 的对边,,函数()()f x m n n =+⋅ ,求的取值范围.(18)(本小题满分12分)某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少%75的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区” .已知备选的5个居民小区中有三个非低碳小区,两个低碳小区. (Ⅰ)求所选的两个小区恰有一个为“非低碳小区”的概率;(Ⅱ)假定选择的“非低碳小区”为小区A ,调查显示其“低碳族”的比例为21,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区A 是否达到“低碳小区”的标准?(百千克/户图2(百千克/户图1(19)(本小题满分12分)如图,在四棱锥P -ABCD 中,底面ABCD 为矩形,PD ⊥底面ABCD ,E 是AB 上一点.已知PD =2,CD =4,AD =3.(Ⅰ)若∠ADE =π6,求证:CE ⊥平面PDE ;(Ⅱ)当点A 到平面PDE 的距离为2217时,求三棱锥A -PDE的侧面积.(20)(本小题满分12分)已知12,F F 是椭圆22221(0)x y a b a b+=>>的左、右焦点,A 是椭圆上位于第一象限内的一点,2120AF F F ⋅= ,(1)求直线AO 的方程(O 为坐标原点);(2)直线AO 交椭圆于点B ,若三角形2ABF 的面积等于(21)(本小题满分12分)已知函数()321232a f x x x x =-+-()a ∈R . (1)当3a =时,求函数()f x 的单调区间;(2)若对于任意[)1,x ∈+∞都有()2(1)f x a '<-成立,求实数a 的取值范围;(3)若过点10,3⎛⎫- ⎪⎝⎭可作函数()y f x =图象的三条不同切线,求实数a 的取值范围.请考生在第22、23、24题中任选一题作答,如果多做,则安所做的第一题计分。
作答时请写清题号。
(22)(本小题满分10分)选修4—1:几何证明选讲如图,ABC ∆为直角三角形,90=∠ABC ,以AB为直径的圆交AC 于点E ,点D 是BC 边的中点,连OD 交圆O 于点M .(Ⅰ)求证:E D B O ,,,四点共圆;(Ⅱ)求证:AB DM AC DM DE ⋅+⋅=22.(23)(本小题满分10分)选修4-4:坐标系与参数方程在直角坐标系xOy 中,直线l的参数方程为322x y ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数),在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为ρθ=.(Ⅰ)求圆C 的圆心到直线l 的距离;(Ⅱ)设圆C 与直线l 交于点A B 、.若点P 的坐标为(3,求||||PA PB +. (24)(本小题满分10分)选修4—5:不等式证明选讲已知函数11)(++-=x x x f (1)求不等式3)(≥x f 的解集;(2)若关于x 的不等式x x a x f 2)(22+->在R 上恒成立,求实数a 的取值范围。
数学(文科)参考答案一、选择题(1)A (2)B (3)A (4)B (5)D (6)C (7)B (8)B (9)D (10)C (11)A (12)D 【解析】22a b b b a b ++=<<<=,()'2sin cos sin '()x x x xf x x x-==,令()c o s s i n ,g x x x x =-则()'sin 0g x x x =-<在2,33ππ⎛⎫ ⎪⎝⎭成立,所以g (x )为2,33ππ⎛⎫ ⎪⎝⎭的减函数,所以g(x)<g(0)=0,所以()'0f x <,所以()f x 为2,33ππ⎛⎫⎪⎝⎭的减函数,所以()()2a bf b f f +<<. 二、填空题(13)3- (14) 8 (15)⎫+∞⎪⎪⎝⎭(16)BCD BCO ABC S S S △△△⋅=2三、解答题(17)(本小题满分12分)解:(I )由m//n ,可得3sinx=-cosx ,于是tanx=31-. ∴ 922)31(31312tan 31tan cos 2sin 3cos sin -=--⋅+-=-+=-+x x x x x x . …………………………4分 (II )∵在△ABC 中,A+B=π-C ,于是C B A sin )sin(=+,由正弦定理知:C A C sin sin 2sin 3⋅=, ∴ 23sin =A ,可解得3π=A . ………………………………………………6分 又△ABC 为锐角三角形,于是26ππ<<B ,∵ )(x f =(m+n)·n =(sinx+cosx ,2)·(sinx ,-1)=sin 2x+sinxcosx-2=22sin 2122cos 1-+-x x =23)42sin(22--πx , ∴ 232sin 2223]4)8(2sin[22)8(-=--+=+B B B f πππ.……………………10分由26ππ<<B 得ππ<<B 23,∴ 0<sin2B≤1,得23-<232sin 22-B ≤2322-.即]232223()8(--∈+,πB f .………………………………………………12分(18)(本小题满分12分)解:(Ⅰ)设三个“非低碳小区”为C B A ,,,两个“低碳小区”为,,m n …2分用),(y x 表示选定的两个小区,{},,,,,x y A B C m n ∈,则从5个小区中任选两个小区,所有可能的结果有10个,它们是(,)A B ,(,)A C ,(,)A m ,(,)A n ,(,)B C ,(,)B m ,(,)B n ,(,)C m ,(,)C n ,(,)m n . 5分用D 表示:“选出的两个小区恰有一个为非低碳小区”这一事件,则D 中的结果有6个,它们是:(,)A m ,(,)A n ,(,)B m ,(,)B n , (,)C m ,(,)C n . …7分故所求概率63()105P D ==. ……8分 (II )由图1可知月碳排放量不超过300千克的成为“低碳族”. ……10分由图2可知,三个月后的低碳族的比例为0.070.230.460.760.75++=>,…………11分 所以三个月后小区A 达到了“低碳小区”标准. …………12分(19)(本小题满分12分)解:(Ⅰ)在Rt △DAE 中,AD =3,∠ADE =π6,∴AE =AD ·tan ∠ADE =3·33=1.又AB =CD =4,∴BE =3.在Rt △EBC 中,BC =AD =3,∴tan ∠CEB =BC BE =33,∴∠CEB =π6.又∠AED =π3,∴∠DEC =π2,即CE ⊥DE .∵PD ⊥底面ABCD ,CE ⊂底面ABCD ,∴PD ⊥CE .∴CE ⊥平面PDE .……………………………………………………………(6分) (Ⅱ)∵PD ⊥底面ABCD ,PD ⊂平面PDE ,∴平面PDE ⊥平面ABCD .如图,过A 作AF ⊥DE 于F ,∴AF ⊥平面PDE ,∴AF 就是点A 到平面PDE 的距离,即AF =2217.在Rt △DAE 中,由AD ·AE =AF ·DE ,得 3AE =2217·3+AE 2,解得AE =2.∴S △APD =12PD ·AD =12×2×3=62,S △ADE =12AD ·AE =12×3×2=3,∵BA ⊥AD ,BA ⊥PD ,∴BA ⊥平面P AD ,∵P A ⊂平面P AD ,∴BA ⊥P A .在Rt △P AE 中,AE =2,P A =PD 2+AD 2=2+3=5,∴S △APE =12P A ·AE =12×5×2=5.∴三棱锥A -PDE 的侧面积S 侧=62+3+5.…………………………(12分) (20)(本小题满分12分)解:(1)由2120AF F F ⋅= ,知212F F AF ⊥所以,,2c a =可得2212b a =,设椭圆方程为2222x y a += --------2分设00(,)A x y ,由2120AF F F ⋅=,知0x c =∴0(,)A c y ,代入椭圆方程可得012y a =--------4分∴A 1,2a a ),故直线AO 的斜率k =--------5分直线AO 的方程为2y x =--------6分 (2)连结1122,,,,AF BF AF BF 由椭圆的对称性可知,2112F AF ABF ABF S S S ∆∆∆==, --------9分所以2421221=a c -------10分又由c =解得2216,1688a b ==-=,故椭圆方程为221168x y += ------12分(21)(本小题满分12分)解:(1)当3a =时,()3213232f x x x x =-+-,得()2'32f x x x =-+-.………1分因为()()()2'3212f x x x x x =-+-=---,所以当12x <<时,()0f x '>,函数()f x 单调递增; 当1x <或2x >时,()0f x '<,函数()f x 单调递减.所以函数()f x 的单调递增区间为()1,2,单调递减区间为(),1-∞和()2,+∞.……3分(2)方法1:由()321232a f x x x x =-+-,得()2'2f x x ax =-+-, 因为对于任意[)1,x ∈+∞都有'()2(1)f x a <-成立, 即对于任意[)1,x ∈+∞都有222(1)x ax a -+-<-成立,即对于任意[)1,x ∈+∞都有220x ax a -+>成立,………………………………4分令()22h x x ax a =-+,要使对任意[)1,x ∈+∞都有()0h x >成立,必须满足0∆<或()0,1,210.ah ∆≥⎧⎪⎪≤⎨⎪⎪>⎩…………………………………………5分即280a a -<或280,1,210.a a a a ⎧-≥⎪⎪≤⎨⎪+>⎪⎩…………………………………………6分所以实数a 的取值范围为()1,8-.……………………………………………7分 方法2:由()321232a f x x x x =-+-,得()2'2f x x ax =-+-, 因为对于任意[)1,x ∈+∞都有'()2(1)f x a <-成立,所以问题转化为,对于任意[)1,x ∈+∞都有[]max '()2(1)f x a <-.………………4分因为()22224a a f x x ⎛⎫'=--+- ⎪⎝⎭,其图象开口向下,对称轴为2a x =.①当12a<时,即2a <时,()'f x 在[)1,+∞上单调递减, 所以()()max ''13f x f a ==-,由()321a a -<-,得1a >-,此时12a -<<.…………………………………5分②当12a ≥时,即2a ≥时,()'f x 在1,2a ⎡⎤⎢⎥⎣⎦上单调递增,在,2a ⎛⎫+∞ ⎪⎝⎭上单调递减, 所以()2max''224a af x f ⎛⎫==- ⎪⎝⎭,由()22214a a -<-,得08a <<,此时28a ≤<.……………………………6分 综上①②可得,实数a 的取值范围为()1,8-.……………………………………7分 (3)设点321,232a P t t t t ⎛⎫-+- ⎪⎝⎭是函数()y f x =图象上的切点, 则过点P 的切线的斜率为()2'2k f t t at ==-+-,…………………………………8分 所以过点P 的切线方程为()()32212232a y t t t t at x t +-+=-+--.……………9分 因为点10,3⎛⎫- ⎪⎝⎭在切线上,所以()()32211220332a t t t t at t -+-+=-+-- 即322110323t at -+=.……………………………10分 若过点10,3⎛⎫- ⎪⎝⎭可作函数()y f x =图象的三条不同切线,则方程322110323t at -+=有三个不同的实数解.………………………………10分 令()32211323g t t at =-+,则函数()y g t =与t 轴有三个不同的交点.令()220g t t at '=-=,解得0t =或2a t =.因为()103g =,3112243a g a ⎛⎫=-+ ⎪⎝⎭, 所以必须31102243a g a ⎛⎫=-+<⎪⎝⎭,即2a >. 所以实数a 的取值范围为()2,+∞.………………………………………………12分(22) (本小题满分10分)解:(1)连接BE ,则EC BE ⊥ ……………………………………………1分 又D 是BC 的中点,所以BD DE = ……………………………………………3分又OD OD OB OE ==,,所以ODB ODE ∆≅∆,所以 90=∠=∠OED OBD故B O E D ,,,四点共圆. …………………………………………………………5分(2) 延长DO 交圆于点H ,+⋅=+⋅=⋅=DO DM OH DO DM DH DM DE )(2 OH DM ⋅ ……………………8分)21()21(2AB DM AC DM DE ⋅+⋅=∴,即AB DM AC DM DE ⋅+⋅=22……10分(23)(本小题满分10分)解:(1)由θρsin 52=得05222=-+y y x ,即5)5(22=-+y x由322x y ⎧=-⎪⎪⎨⎪=⎪⎩得053=--+y x 所以2232535=--=d …………………4分 (2)将l 的参数方程代入圆C 的直角坐标方程,得5)22()223(22=+-t t 即04232=+-t t ,由于0144)23(2>⨯⨯-=∆ 故可设21,t t 是上述方程的两实根,所以⎩⎨⎧==+4232121t t t t ,又直线l 过点)5,3(p ,故由上式及t 的几何意义得:232121=+=+=+t t t t PB PA …………………10分(24)(本小题满分10分)解:(Ⅰ)由题设知:721>++-x x ,令10,20x x -=+=,解得1,2x x ==-,这就是两个分界点。
