1第一章 8字模型与飞镖模型(1)

合集下载

人教版数学中考专题复习微专题1 “8”字模型及飞镖模型

.
【模型分析】因为这个图形像飞镖,所以我们往往把这个模型称为飞镖模型.
例1 观察下列图形,计算:∠A+∠B+∠C+∠D+∠E=
由平移可得AC=BF.
如图所示,线段AD,BC相交于点O,结论:
∠BOC是△COD的外角,推出∠OCD+∠ODC=∠BOC.
由①②可得AB+AC>BD+CD.
∵∠BOC是△BOE的外角,
∠AMC=∠1+∠2+∠ADC.
【解析】∵OA+OB>AB,①

∴ ∠EAB+∠E= ∠ECD+∠F.

∴ (∠ECD-∠E)+∠E= ∠ECD+∠F.

∴ ∠ECD- ∠E+∠E= ∠ECD+∠F.

∴ ∠E=∠F.

∴∠E=2∠F.∵∠E=42°,∴∠F=21°.
随堂测试
由①+②,得 AD+BC< OA+OD+OB+OC.
∴∠D=180°-(∠2+∠4).
练习2 如图,∠CAD+∠B+∠C+∠D+∠E=
.
=∠A+∠ACE+∠ADB+∠1+∠2
由飞镖模型,得AB+BF>AD+DF.
∴∠A+∠B+∠BMH+∠ANC+∠1=360°.
∠AMC=∠1+∠2+∠ADC.
∵BE+EC=BD+DE+EC,DE+EC>CD,

8字模型与飞镖模型

模型分析
模型分析
（1）因为这个图形像数字8，所以我们往往把这个模型称为8字模型．（2）8字模型往往在几何综合题目中推导角度时用到．
模型实例
观察下列图形，计算角度：（1）如图①，∠A＋∠B＋∠C＋∠D＋∠E＝________；
A
A
B
E
B F
C
D
图①
E 图②
A
E B
1O 2
C
D
图③
解法一：利用角的8字模型．如图③，连接 CD． ∵∠BOC是△BOE的外角， ∴∠B＋∠E＝∠BOC． ∵∠BOC是△COD的外角， ∴∠1＋∠2＝∠BOC． ∴∠B＋∠E＝∠1＋∠2．（角的8字模型），∴∠A ＋∠B＋∠ACE＋∠ADB＋∠E ＝∠A＋∠ACE＋∠ADB＋∠1＋∠2 ＝∠A＋∠ACD＋∠ADC＝180°．
E
D ①
A
B
F E
C
D 图②
A
B
O
F
123
P
Q
E 图⑤
C D
（2）解法一：如图⑤，利用角的8字模型． ∵∠AOP是△AOB的外角， ∴∠A＋∠B＝∠AOP． ∵∠AOP是△OPQ的外角， ∴∠1＋∠3＝∠AOP． ∴∠A＋∠B＝∠1＋∠3．①（角的8字模型），同理可证：∠C＋∠D＝∠1＋∠2．② ，
模型实例
如图，在四边形ABCD中，AM、CM分别平分∠DAB和∠DCB，AM与 CM交于M，探究∠AMC与∠B、∠D间的数量关系．
A 1 D
3M B
4
2
C
练习：
1．如图，求∠A+∠B+∠C+∠D+∠E+∠F=
.
2．如图，求∠A+∠B+∠C+∠D=

2020年初中数学“8字模型与飞镖模型”课件

解法二：
模型二：角的飞镖模型
如图所示，有结论：∠D＝∠A＋∠B＋∠C．
模型分析
解法一：如图①，作射线AD． ∵∠3是△ABD的外角， ∴∠3＝∠B＋∠1， ∵∠4是△Aห้องสมุดไป่ตู้D的外角， ∴∠4＝∠C＋∠2 ∴∠BDC＝∠3＋∠4， ∴∠BDC＝∠B＋∠1＋∠2＋∠C， ∴∠BDC＝∠BAC＋∠B＋∠C
解法二：如图②，连接BC． ∵∠2＋∠4＋∠D＝180°， ∴∠D＝180°－（∠2＋∠4） ∵∠1＋∠2＋∠3＋∠4＋∠A＝180°， ∴∠A＋∠1＋∠3＝180°－（∠2＋∠4） ∴∠D＝∠A＋∠1＋∠3. （1）因为这个图形像飞镖，所以我们往往把这个模型称为飞镖模型．
（2）飞镖模型在几何综合题目中推导角度时使用．
模型分析 ∵OA+OD>AD①， OB+OC>BC②，由①+②得：
OA+OD+OB+OC>BC+AD 即：AC+BD>AD+BC.
模型实例
如图，四边形ABCD的对角线AC、BD相交于点O。求证：(1) AB+BC+CD+AD>AC+BD；
(2) AB+BC+CD+AD <2AC+2BD.
证明：(1)∵AB+BC>AC①， CD+AD>AC②， AB+AD>BD③， BC+CD> BD④
8字模型与飞镖模型
模型一：角的8字模型
模型分析
证法一： ∵∠AOB是△AOD的外角， ∴∠A＋∠D＝∠AOB． ∵∠AOB是△BOC的外角， ∴∠B＋∠C＝∠AOB． ∴∠A＋∠D＝∠B＋∠C．

中考数学必会几何模型：8字模型与飞镖模型

8字模型与飞镖模型模型1：角的8字模型如图所示，AC 、BD 相交于点O ，连接AD 、BC ．结论：∠A ＋∠D ＝∠B ＋∠C ．ODC BA模型分析证法一：∵∠AOB 是△AOD 的外角，∴∠A ＋∠D ＝∠AOB ．∵∠AOB 是△BOC 的外角， ∴∠B ＋∠C ＝∠AOB ．∴∠A ＋∠D ＝∠B ＋∠C ．证法二：∵∠A ＋∠D ＋∠AOD ＝180°，∴∠A ＋∠D ＝180°－∠AOD ．∵∠B ＋∠C ＋∠BOC ＝180°， ∴∠B ＋∠C ＝180°－∠BOC ．又∵∠AOD ＝∠BOC ，∴∠A ＋∠D ＝∠B ＋∠C ．（1）因为这个图形像数字8，所以我们往往把这个模型称为8字模型．（2）8字模型往往在几何综合题目中推导角度时用到．模型实例观察下列图形，计算角度：（1）如图①，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＝________；图图①FD C BAE EBCDA图③21O AB图④G F 12AB E解法一：利用角的8字模型．如图③，连接CD ．∵∠BOC 是△BOE 的外角， ∴∠B ＋∠E ＝∠BOC ．∵∠BOC 是△COD 的外角，∴∠1＋∠2＝∠BOC ．∴∠B ＋∠E ＝∠1＋∠2．（角的8字模型），∴∠A ＋∠B ＋∠ACE ＋∠ADB ＋∠E ＝∠A ＋∠ACE ＋∠ADB ＋∠1＋∠2＝∠A ＋∠ACD ＋∠ADC ＝180°．解法二：如图④，利用三角形外角和定理．∵∠1是△FCE 的外角，∴∠1＝∠C ＋∠E ． ∵∠2是△GBD 的外角，∴∠2＝∠B ＋∠D ．∴∠A ＋∠B ＋∠C ＋∠D ＋∠E ＝∠A ＋∠1＋∠2＝180°．（2）如图②，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＝________．图②FDCBAE312图⑤P O QA BFC D图⑥21EDCFOBA（2）解法一：如图⑤，利用角的8字模型．∵∠AOP 是△AOB 的外角，∴∠A ＋∠B ＝∠AOP ．∵∠AOP 是△OPQ 的外角，∴∠1＋∠3＝∠AOP ．∴∠A ＋∠B ＝∠1＋∠3．①（角的8字模型），同理可证：∠C ＋∠D ＝∠1＋∠2．② ，∠E ＋∠F ＝∠2＋∠3．③ 由①＋②＋③得：∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＝2（∠1＋∠2＋∠3）＝360°．解法二：利用角的8字模型．如图⑥，连接DE ．∵∠AOE 是△AOB 的外角， ∴∠A ＋∠B ＝∠AOE ．∵∠AOE 是△OED 的外角，∴∠1＋∠2＝∠AOE ． ∴∠A ＋∠B ＝∠1＋∠2．（角的8字模型）∴∠A ＋∠B ＋∠C ＋∠ADC ＋∠FEB ＋∠F ＝∠1＋∠2＋∠C ＋∠ADC ＋∠FEB ＋∠F ＝360°．（四边形内角和为360°）练习：1．（1）如图①，求：∠CAD ＋∠B ＋∠C ＋∠D ＋∠E ＝；图图①OOEEDDCCBBAA解：如图，∵∠1=∠B+∠D ，∠2=∠C+∠CAD ， ∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°．故答案为：180° 解法二：（2）如图②，求：∠CAD ＋∠B ＋∠ACE ＋∠D ＋∠E ＝．图②OEDCBA解：由三角形的外角性质，知∠BAC=∠E+∠ACE ，∠EAD=∠B+∠D ，又∵∠BAC+∠CAD+∠EAD=180°，∴∠CAD ＋∠B ＋∠ACE ＋∠D ＋∠E ＝180°解法二：2．如图，求：∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＋∠H ＝．HGFEDCBA解：∵∠G+∠D=∠3，∠F+∠C=∠4，∠E+∠H=∠2，∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2， ∵∠B+∠2+∠1=180°，∠3+∠5+∠A=180°，∴∠A+∠B+∠2+∠4+∠3=360°， ∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360° 解法二：模型2：角的飞镖模型如图所示，有结论：∠D ＝∠A ＋∠B ＋∠C ．ADC图①4321AD 4321AD模型分析解法一：如图①，作射线AD ．∵∠3是△ABD 的外角，∴∠3＝∠B ＋∠1，∵∠4是△ACD 的外角，∴∠4＝∠C ＋∠2 ∴∠BDC ＝∠3＋∠4，∴∠BDC ＝∠B ＋∠1＋∠2＋∠C ，∴∠BDC ＝∠BAC ＋∠B ＋∠C 解法二：如图②，连接BC ．∵∠2＋∠4＋∠D ＝180°，∴∠D ＝180°－（∠2＋∠4）∵∠1＋∠2＋∠3＋∠4＋∠A ＝180°，∴∠A ＋∠1＋∠3＝180°－（∠2＋∠4） ∴∠D ＝∠A ＋∠1＋∠3.（1）因为这个图形像飞镖，所以我们往往把这个模型称为飞镖模型．（2）飞镖模型在几何综合题目中推导角度时使用．模型实例如图，在四边形ABCD 中，AM 、CM 分别平分∠DAB 和∠DCB ，AM 与CM 交于M ，探究∠AMC 与∠B 、∠D 间的数量关系．解答：利用角的飞镖模型如图所示，连接DM 并延长．∵∠3是△AMD 的外角，∴∠3＝∠1＋∠ADM ， ∵∠4是△CMD 的外角，∴∠4＝∠2＋∠CDM ，∵∠AMC ＝∠3＋∠4∴∠AMC ＝∠1＋∠ADM ＋∠CDM ＋∠2，∴∠AMC ＝∠1＋∠2＋∠ADC ．（角的飞镖模型）∵AM 、CM 分别平分∠DAB 和∠DCB ，∴12BAD ∠∠=，22BCD∠∠=， ∴22BAD BCDAMC ADC ∠∠∠=++∠，∴()3602B ADC AMC ADC ︒-∠+∠∠=+∠（四边形内角和360°），∴3602B ADCAMC ︒-∠+∠∠=，∴2∠AMC ＋∠B －∠ADC ＝360°.练习：1．如图，求∠A+∠B+∠C+∠D+∠E+∠F= .DE【答案】230°提示：∠C+∠E+∠D=∠EOC=115º.（飞镖模型），∠A+∠B+∠F=∠BOF=115º.∠A+∠B+∠C+∠D+∠E+∠F=115º+115º=230º 2．如图，求∠A+∠B+∠C+∠D= .AA【答案】220°提示：如图所示，连接BD.∠AED=∠A+∠3+∠1，∠BFC=∠2+∠4+∠C ，∠A+∠ABF+∠C+∠CDE=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220º模型3 边的“8”字模型如图所示，AC 、BD 相交于点O ，连接AD 、BC ．结论AC+BD>AD+BC．CAD模型分析∵OA+OD>AD ①， OB+OC>BC ②，由①+②得： OA+OD+OB+OC>BC+AD 即：AC+BD>AD+BC.模型实例如图，四边形ABCD 的对角线AC 、BD 相交于点O 。

几何经典模型：8字模型与飞镖模型

＝360°．（四边形内角和为 360°）
练习：
1．（1）如图①，求：∠CAD＋∠B＋∠C＋∠D＋∠E＝
；
E A
A
E
B
O
B
O
C
C
D
图①
D 图②
解：如图，∵∠1=∠B+∠D，∠2=∠C+∠CAD， ∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°．故答案为：180° 解法二：
（2）如图②，求：∠CAD＋∠B＋∠ACE＋∠D＋∠E＝
本文为 word 版资料，可以任意编辑修改本文为 word 版资料，可以任意编辑修本文为 word 版资料，可以任意编辑修
模型 1：角的 8 字模型如图所示，AC、BD 相交于点 O，连接 AD、BC．
结论：∠A＋∠D＝∠B＋∠C．
A
D
O
B
C
模型分析
证法一：
∵∠AOB 是△ AOD 的外角，∴∠A＋∠D＝∠AOB．∵∠AOB 是△ BOC 的外角，
∠A+∠B+∠C+∠D+∠E+∠F=115º+115º=230º
2．如图，求∠A+∠B+∠C+∠D=.Dຫໍສະໝຸດ 105°AC
115°
BA
D
2
1 105°
C
115° 4 3
∵∠4 是△CMD 的外角，∴∠4＝∠2＋∠CDM，∵∠AMC＝∠3＋∠4
∴∠AMC＝∠1＋∠ADM＋∠CDM＋∠2，∴∠AMC＝∠1＋∠2＋∠ADC．（角的飞镖模型）
∵AM、CM 分别平分∠DAB 和∠DCB，∴ 1 BAD ， 2 BCD ，

飞镖、8字模型(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

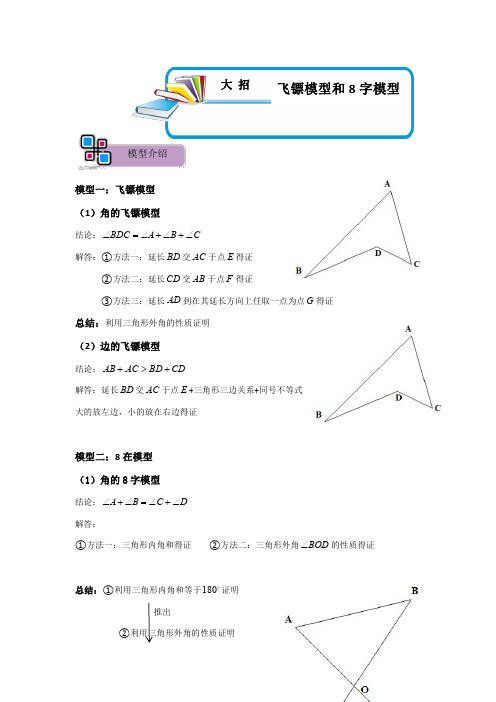
模型介绍模型一：飞镖模型（1）角的飞镖模型结论：CB A BDC ∠+∠+∠=∠解答：①方法一：延长BD 交AC 于点E 得证②方法二：延长CD 交AB 于点F 得证③方法三：延长AD 到在其延长方向上任取一点为点G 得证总结：利用三角形外角的性质证明（2）边的飞镖模型结论：CDBD AC AB +>+解答：延长BD 交AC 于点E +三角形三边关系+同号不等式大的放左边，小的放在右边得证模型二：8在模型（1）角的8字模型结论：DC B A ∠+∠=∠+∠解答：①方法一：三角形内角和得证②方法二：三角形外角BOD ∠的性质得证总结：①利用三角形内角和等于 180证明推出②利用三角形外角的性质证明大招飞镖模型和8字模型（2）边的8字模型结论：BCAD CD AB +<+解答：三角形三边关系+同号不等式得证总结：①三角形两边之和大于第三边例题精讲考点一：飞镖模型【例1】．如图，∠A ＝70°，∠B ＝40°，∠C ＝20°，则∠BOC=_______变式训练【变式1-1】．如图，∠ABD 、∠ACD 的角平分线交于点P ，若∠A ＝55°，∠D ＝15°，则∠P 的度数为（）A．15°B．20°C．25°D．30°【变式1-2】．在△ABC 中，∠ABC 与∠ACB 的平分线交于点I ，∠ABC +∠ACB ＝100°，则∠BIC 的度数为（）A．80°B．50°C．100°D．130°【变式1-3】．如图，已知∠BOF＝120°，则∠A+∠B+∠C+∠D+∠E+∠F的度数．【变式1-4】．如图所示，已知P是△ABC内一点，试说明PA+PB+PC＞（AB+BC+AC）．考点二：8字模型【例2】．如图，∠1＝60°，则∠A+∠B+∠C+∠D+∠E+∠F＝变式训练【变式2-1】．如图，∠A+∠B+∠C+∠D+∠E+∠F＝°．【变式2-2】．如图，A，B，C，D，E，F是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F 的度数是度．【变式2-3】．如图，∠A+∠B+∠C+∠D+∠E+∠F＝°．【变式2-4】．一副三角板如图摆放，其中一块三角板的直角边EF落在另一块三角板的斜边AC上，边BC与DF交于点O，则∠BOD的度数是．实战演练1．如图，已知AB⊥BD，AC⊥CD，∠A＝35°，则∠D的度数为（）A．35°B．45°C．55°D．65°2．如图，∠A+∠B+∠C+∠D+∠E的度数为（）A．120°B．150°C．180°D．200°3．如图，在△ABC中，M，N分别是边AB，BC上的点，将△BMN沿MN折叠；使点B落在点B'处，若∠B＝35°，∠BNM＝28°，则∠AMB'的度数为（）A．30°B．37°C．54°D．63°4．如图，将分别含有30°、45°角的一副三角板重叠，使直角顶点重合，若两直角重叠形成的角为65°，则图中角α的度数为．5.已知如图，BQ平分∠ABP，CQ平分∠ACP，∠BAC＝α，∠BPC＝β，则∠BQC＝．（用α，β表示）6．如图，则∠A+∠B+∠C+∠D+∠E+∠F+∠H＝度．7．如图，求∠A+∠B+∠C+∠D+∠E+∠F＝．8．如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠K的度数为9．如图是可调躺椅示意图（数据如图），AE与BD的交点为C，且∠A，∠B，∠E保持不变．为了舒适，需调整∠D的大小，使∠EFD＝110°，则图中∠D应（填“增加”或“减少”）度．10．如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I的值．11．如图，已知AB∥DE，∠ABC、∠CED的平分线交于点F．探究∠BFE与∠BCE之间的数量关系，并证明你的结论．12．如图，DP平分∠ADC，PB平分∠ABC，求证：∠P＝（∠A+∠C）13．如图，在四边形ABCD中，AM、CM分别平分∠DAB和∠DCB，AM与CM交于M．探究∠AMC与∠B、∠D间的数量关系．14．（1）探究：如图1，求证：∠BOC＝∠A+∠B+∠C．（2）应用：如图2，∠ABC＝100°，∠DEF＝130°，求∠A+∠C+∠D+∠F的度数．15．如图1，已知线段AB、CD相交于点O，连接AC、BD，我们把形如图1的图形称之为“8字形“．如图2，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB 分别相交于点M、N．试解答下列问题：①仔细观察，在图2中有个以线段AC为边的“8字形”；②若∠B＝76°，∠C＝80°，试求∠P的度数；③∠C和∠B为任意角时AP、DP分别是∠CAB、∠BDC的三等分线，写出∠P与∠C、∠B之间数量关系，并说明理由．16．阅读材料，回答下列问题：【材料提出】“八字型”是数学几何的常用模型，通常由一组对顶角所在的两个三角形构成．【探索研究】探索一：如图1，在八字型中，探索∠A、∠B、∠C、∠D之间的数量关系为；探索二：如图2，若∠B＝36°，∠D＝14°，求∠P的度数为；探索三：如图3，CP、AG分别平分∠BCE、∠FAD，AG反向延长线交CP于点P，则∠P、∠B、∠D之间的数量关系为．【模型应用】应用一：如图4，延长BM、CN，交于点A，在四边形MNCB中，设∠M＝α，∠N＝β，α+β＞180°，四边形的内角∠MBC与外角∠NCD的角平分线BP，CP相交于点P，则∠A＝（用含有α和β的代数式表示），∠P＝．（用含有α和β的代数式表示）应用二：如图5，在四边形MNCB中，设∠M＝α，∠N＝β，α+β＜180°，四边形的内角∠MBC与外角∠NCD的角平分线所在的直线相交于点P，∠P＝．（用含有α和β的代数式表示）【拓展延伸】拓展一：如图6，若设∠C＝x，∠B＝y，∠CAP＝∠CAB，∠CDP＝∠CDB，试问∠P与∠C、∠B之间的数量关系为．（用x、y表示∠P）拓展二：如图7，AP平分∠BAD，CP平分∠BCD的邻补角∠BCE，猜想∠P与∠B、∠D的关系，直接写出结论．。

中考必会几何模型：8字模型与飞镖模型

8字模型与飞镖模型模型1：角的8字模型如图所示，AC 、BD 相交于点O ，连接AD 、BC ．结论：∠A ＋∠D ＝∠B ＋∠C ．ODC BA模型分析证法一：∵∠AOB 是△AOD 的外角，∴∠A ＋∠D ＝∠AOB ．∵∠AOB 是△BOC 的外角， ∴∠B ＋∠C ＝∠AOB ．∴∠A ＋∠D ＝∠B ＋∠C ．证法二：∵∠A ＋∠D ＋∠AOD ＝180°，∴∠A ＋∠D ＝180°－∠AOD ．∵∠B ＋∠C ＋∠BOC ＝180°， ∴∠B ＋∠C ＝180°－∠BOC ．又∵∠AOD ＝∠BOC ，∴∠A ＋∠D ＝∠B ＋∠C ．（1）因为这个图形像数字8，所以我们往往把这个模型称为8字模型．（2）8字模型往往在几何综合题目中推导角度时用到．模型实例观察下列图形，计算角度：（1）如图①，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＝________；图图①FD C BAE EBCDA图③21O AB图④G F 12AB E解法一：利用角的8字模型．如图③，连接CD ．∵∠BOC 是△BOE 的外角， ∴∠B ＋∠E ＝∠BOC ．∵∠BOC 是△COD 的外角，∴∠1＋∠2＝∠BOC ． ∴∠B ＋∠E ＝∠1＋∠2．（角的8字模型），∴∠A ＋∠B ＋∠ACE ＋∠ADB ＋∠E＝∠A ＋∠ACE ＋∠ADB ＋∠1＋∠2＝∠A ＋∠ACD ＋∠ADC ＝180°．解法二：如图④，利用三角形外角和定理．∵∠1是△FCE 的外角，∴∠1＝∠C ＋∠E ．∵∠2是△GBD 的外角，∴∠2＝∠B ＋∠D ．∴∠A ＋∠B ＋∠C ＋∠D ＋∠E ＝∠A ＋∠1＋∠2＝180°．（2）如图②，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＝________．图②FDCBAE312图⑤P O QA BEFC D图⑥21EDCFOBA（2）解法一：如图⑤，利用角的8字模型．∵∠AOP 是△AOB 的外角，∴∠A ＋∠B ＝∠AOP ． ∵∠AOP 是△OPQ 的外角，∴∠1＋∠3＝∠AOP ．∴∠A ＋∠B ＝∠1＋∠3．①（角的8字模型），同理可证：∠C ＋∠D ＝∠1＋∠2．② ，∠E ＋∠F ＝∠2＋∠3．③由①＋②＋③得：∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＝2（∠1＋∠2＋∠3）＝360°．解法二：利用角的8字模型．如图⑥，连接DE ．∵∠AOE 是△AOB 的外角， ∴∠A ＋∠B ＝∠AOE ．∵∠AOE 是△OED 的外角，∴∠1＋∠2＝∠AOE ． ∴∠A ＋∠B ＝∠1＋∠2．（角的8字模型）∴∠A ＋∠B ＋∠C ＋∠ADC ＋∠FEB ＋∠F ＝∠1＋∠2＋∠C ＋∠ADC ＋∠FEB ＋∠F＝360°．（四边形内角和为360°）练习：1．（1）如图①，求：∠CAD ＋∠B ＋∠C ＋∠D ＋∠E ＝；图图①OOEEDDCCBBAA解：如图，∵∠1=∠B+∠D ，∠2=∠C+∠CAD ，∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°．故答案为：180° 解法二：（2）如图②，求：∠CAD ＋∠B ＋∠ACE ＋∠D ＋∠E ＝．图②OEDCBA解：由三角形的外角性质，知∠BAC=∠E+∠ACE，∠EAD=∠B+∠D，又∵∠BAC+∠CAD+∠EAD=180°，∴∠CAD ＋∠B ＋∠ACE ＋∠D ＋∠E＝180° 解法二：2．如图，求：∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＋∠H ＝．HGFEDCBA解：∵∠G+∠D=∠3，∠F+∠C=∠4，∠E+∠H=∠2，∴∠G+∠D+∠F+∠C+∠E+∠H=∠3+∠4+∠2，∵∠B+∠2+∠1=180°，∠3+∠5+∠A=180°，∴∠A+∠B+∠2+∠4+∠3=360°， ∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°解法二：模型2：角的飞镖模型如图所示，有结论：∠D ＝∠A ＋∠B ＋∠C ．C图①图②模型分析解法一：如图①，作射线AD ．∵∠3是△ABD 的外角，∴∠3＝∠B ＋∠1，∵∠4是△ACD 的外角，∴∠4＝∠C ＋∠2∴∠BDC ＝∠3＋∠4，∴∠BDC ＝∠B ＋∠1＋∠2＋∠C ，∴∠BDC ＝∠BAC ＋∠B ＋∠C解法二：如图②，连接BC ．∵∠2＋∠4＋∠D ＝180°，∴∠D ＝180°－（∠2＋∠4）∵∠1＋∠2＋∠3＋∠4＋∠A ＝180°，∴∠A ＋∠1＋∠3＝180°－（∠2＋∠4） ∴∠D ＝∠A ＋∠1＋∠3.（1）因为这个图形像飞镖，所以我们往往把这个模型称为飞镖模型．（2）飞镖模型在几何综合题目中推导角度时使用．模型实例如图，在四边形ABCD 中，AM 、CM 分别平分∠DAB 和∠DCB ，AM 与CM 交于M ，探究∠AMC 与∠B 、∠D 间的数量关系．解答：利用角的飞镖模型如图所示，连接DM 并延长．∵∠3是△AMD 的外角，∴∠3＝∠1＋∠ADM ， ∵∠4是△CMD 的外角，∴∠4＝∠2＋∠CDM ，∵∠AMC ＝∠3＋∠4 ∴∠AMC ＝∠1＋∠ADM ＋∠CDM ＋∠2，∴∠AMC ＝∠1＋∠2＋∠ADC ．（角的飞镖模型）∵AM 、CM 分别平分∠DAB 和∠DCB ，∴12BAD ∠∠=，22BCD∠∠=， ∴22BAD BCDAMC ADC ∠∠∠=++∠，∴()3602B ADC AMC ADC ︒-∠+∠∠=+∠（四边形内角和360°），∴3602B ADCAMC ︒-∠+∠∠=，∴2∠AMC ＋∠B －∠ADC ＝360°.练习：1．如图，求∠A+∠B+∠C+∠D+∠E+∠F= .DE【答案】230°提示：∠C+∠E+∠D=∠EOC=115º.（飞镖模型），∠A+∠B+∠F=∠BOF=115º.∠A+∠B+∠C+∠D+∠E+∠F=115º+115º=230º 2．如图，求∠A+∠B+∠C+∠D= .AA【答案】220°提示：如图所示，连接BD.∠AED=∠A+∠3+∠1，∠BFC=∠2+∠4+∠C ，∠A+∠ABF+∠C+∠CDE=∠A+∠3+∠1+∠2+∠4+∠C=∠AED+∠BFC=220º模型3 边的“8”字模型如图所示，AC 、BD 相交于点O ，连接AD 、BC ．结论AC+BD>AD+BC ．BCA模型分析∵OA+OD>AD ①， OB+OC>BC ②，由①+②得： OA+OD+OB+OC>BC+AD 即：AC+BD>AD+BC.模型实例如图，四边形ABCD 的对角线AC 、BD 相交于点O 。

三角形角度计算之八字型与飞镖模型

8字型与飞镖模型
模型一：角的8字模型
证法二：∵∠A+∠D+∠AOD=180° ∴∠A+∠D=180°-∠AOD ∵∠B+∠C+∠BOC=180° ∴∠B+∠C=180°-∠BOC 又∵∠AOD=∠BOC ∴∠A+∠D=∠B+∠C. 以上两种证明方法都比较常用，因为这个图形像数字8，所以我们把这个模型称为8字模型。如图所示，AC,BD相交于点O,连接AD、BC 结论：∠A+∠D=∠B+∠C. 证法一：∵∠AOB是△AOD的外角， ∴∠A+∠D=∠AOB ∵∠AOB是△BOC的外角 ∴∠B+∠C=∠AOB ∴∠A+∠D=∠B+∠C.
解析：（1）∵AB+BC＞AC CD+AD＞AC AB+AD＞BD BC+CD＞BD 以上式子相加即可得到AB+BC+CD+AD＞AC+BD （2）∵AD＜OA+OD BC＜OB+OC 两式相加即可得到AD+BC＜OA+OD+OB+OC ∴AD+BC＜AC+BD(边的8字模型) 同理可证：AB+CD＜AC+BD ∴AB+BC+CD+AD＜2AC+2BD
解法一，如图①，作射线AD ∵∠3是△ABD的外角 ∴∠3=∠B+∠1 ∵∠4是△ACD的外角 ∴∠4=∠C+∠2 ∴∠BDC=∠3+∠4 ∴∠BDC=∠B+∠1+∠2+∠C∴∠BDC=∠BAC+∠B+∠C
解法二：如图②，连接BC ∵∠2+∠4+∠D=180° ∴∠D=180°-（∠2+∠4） ∵∠1+∠2+∠3+∠4+∠A=180° ∴∠A+∠1+∠3=180°-（∠2+∠4） ∴∠D=∠A+∠1+∠3

初中数学常见模型之8字模型与飞镖模型

初中数学常见模型
8字模型与飞镖模型
模型1：角的“8”字模型
如图所示，AB、CD相交于点O，连接AD、BC。结论：∠A+∠D=∠B+∠C
A
D
O
B
C
模型分析：8字模型往往在几何综合题目中推导角度时用到
模型实例：
观察下列图形，计算角度：
（1）如图①，∠A+∠B+∠C+∠D+∠E=
；
（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F=
；
2．如图②，求∠A+∠B+∠C+∠D =
。
A
E
135O
C
B
图① D
F
D
105O A
C 120O
B
图②
模型3 边的“8”字模型
A
如图所示，AC、BD相交于点O，连接AD、BC。
B
结论：AC+BD>AD+BC。
D O
C
典例精选
如图，四边形ABCD的对角线AC、BD相交于点O。求证：（1）AB+BC+CD+AD>AC+BD；
。
A B
E
C D
图1
A
B
F C
E
D
图2
典例精选
1.(1)如图①，求∠CAD+∠B+∠C+∠D+∠E=
.
(2)如图②，求∠CAD+∠B+∠ACE+∠D+∠E=
.
2.如图③，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=

中考必会几何模型：8字模型与飞镖模型

相似之处
两种模型都是几何分析的重要工具,能帮助学生更好地理解和解决中考几何题。
应用范围
8字模型更侧重于分析三角形和四边形的相关特性, 而飞镖模型主要用于探讨角度和距离关系。
基本结构
8字模型由两个相交的圆弧组成,而飞镖模型由两条垂直交叉的线段构成,呈现不同的几何形状。
解题技巧
两种模型都需要熟练掌握绘制方法和核心特点,并灵活应用于几何问题的分析解决中。
借助AR/VR技术,学生可以在虚拟环境中更直观地操纵和理解8字模型与飞镖模型,激发创新思维。
智能辅助
结合人工智能技术,未来将有智能化几何助手,即时分析学生操作并给出针对性指导,提高解题效率。
8字模型与飞镖模型的综合评价
全面视角
8字模型和飞镖模型可以从多个角度对几何问题进行全面分析,为解决问题提供丰富视角。
灵活应用模型
在解决几何题时,善用8字模型分析图形的性质和关系,有助于找到高效的解题思路。
飞镖模型
飞镖模型是中考几何必备的另一种重要知识点。它以飞镖形状为基础,展现了一些特殊的几何关系,在解决涉及角度、距离等题目时很有帮助。掌握飞镖模型的特点和应用技巧对于提高中考成绩同样重要。
飞镖模型的定义
几何证明
飞镖模型的垂直、对角等特点,能为几何证明题提供直观的几何依据,帮助学生理解和解决这类题目。
距离计算
飞镖模型可用于计算几何图形中的距离,如点到线的距离、线段长度等,为解决相关问题提供依据。
中考应用
飞镖模型在中考几何试题中经常出现,掌握它的应用能够有效提高考试成绩,是中考必备的几何知识。
2 灵活运用
根据几何问题的实际需求,灵活选择或组合使用8 字模型和飞镖模型,提高分析和解题的效率。

8字模型与飞镖模型

8字模型与飞镖模型模型1：角的8字模型如图所示，AC 、BD 相交于点O ，连接AD 、BC ．结论：∠A ＋∠D ＝∠B ＋∠C ．ODC BA（1）因为这个图形像数字8，所以我们往往把这个模型称为8字模型．（2）8字模型往往在几何综合题目中推导角度时用到．【模型实例】观察下列图形，计算角度：（1）如图①，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＝________；图图①FD CBAE EBCDA图③21O ABE图④G F 12AB E（2）如图②，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＝________．图②FDC BAEE312图⑤P OQA BF C D图⑥21EDCFOBA【练习】1．（1）如图①，求：∠CAD ＋∠B ＋∠C ＋∠D ＋∠E ＝；图图①OOEEDDCCBBAA（2）如图②，求：∠CAD ＋∠B ＋∠ACE ＋∠D ＋∠E ＝．图②OEDCBA2．如图，求：∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＋∠H ＝．HGFEDCBA模型2：角的飞镖模型如图所示，有结论：∠D ＝∠A ＋∠B ＋∠C ．ADC图①4321AD 图②4321AD（1）因为这个图形像飞镖，所以我们往往把这个模型称为飞镖模型．（2）飞镖模型在几何综合题目中推导角度时使用．【模型实例】如图，在四边形ABCD 中，AM 、CM 分别平分∠DAB 和∠DCB ，AM 与CM 交于M ，探究∠AMC 与∠B 、∠D 间的数量关系．MAB2143MBA练习：1．如图，求∠A+∠B+∠C+∠D+∠E+∠F= .E 2．如图，求∠A+∠B+∠C+∠D= .AA模型3 边的“8”字模型如图所示，AC、BD相交于点O，连接AD、BC．结论AC+BD>AD+BC．B CA【模型实例】如图，四边形ABCD的对角线AC、BD相交于点O。

求证：(1) AB+BC+CD+AD>AC+BD；(2) AB+BC+CD+AD <2AC+2BD.B模型4 边的飞镖模型如图所示有结论：AB+AC> BD+CD.B【模型实例】如图，点O 为三角形内部一点．求证：(1) 2 (AO+BO+CO)>AB+BC+AC ；(2) AB+BC+AC>AO+BO+CO.BB【练习】观察图形并探究下列各问题，写出你所观察得到的结论，并说明理由．(1)如图①，△ABC 中，P 为边BC 一点，请比较BP+PC 与AB+AC 的大小，并说明理由．(2)如图②，将(1)中的点P 移至△ABC 内，请比较△BPC 的周长与△ABC 的周长的大小，并说明理由．(3)图③将(2)中的点P 变为两个点1P 、2P ，请比较四边形12BPP C 的周长与△ABC 的周长的大小，并说明理由.P 2P 1BCCB CB P三角形的折角模型一、三角形的折角模型：三角形某角折叠后在三角形内所产生的角度等量关系条件：ABC ∆沿DE 折叠使A ∠在三角形内二、三角形某角折叠后在三角形外所产生的角度等量关系条件：ABC ∆沿DE 折叠使A ∠在三角形外三、三角形某角折叠后在三角形外所产生的角度等量关系条件：ABC ∆沿DE 折叠使A ∠在三角形外1．如图，在△ABC 中，D 、E 分别是边AB 和AC 上的点，将△ABC 纸片沿DE 折叠，点A 落到点F 的位置．如果DF ∥BC ，∠B ＝60°，∠CEF ＝40°，则∠F ＝．2．如图，在△ABC 中，D 、E 分别是边AB 、AC 上一点，将△ABC 沿DE 折叠，使点A 落在边BC 上．若∠A ＝55°，则∠1+∠2+∠3+∠4＝度．3．（1）如图①，把△ABC 纸片沿DE 折叠，使点A 落在四边形BCED 内部点A ′的位置．试写出∠A 与∠1+∠2之间的关系，并说明理由；（2）如果把△ABC 纸片沿DE 折叠，使点A 落在四边形BCED 外部点A ′的位置，如图②所示．此时∠A 与∠1、∠2之间存在什么样的关系？直接写出．（3）如果把四边形ABCD 沿EF 折叠，使点A 、D 分别落在四边形BCFE 内部点A ′、D ′的位置，如图③所示．直接写出∠A ′、∠D ′、∠1与∠2之间的关系．三角形的角平分线模型一、三条内角角平分线的交点与两个顶点连线的夹角=21900剩余角条件：BP 、CP 是任意△ABC 中∠B 、∠C 的角平分线结论：二、外角平分线所成夹角=21剩余角条件：B D 是∠A BC 的角平分线,CD 是△A BC 的外角平分线结论：三、两个角的外角平分线的交点与这两个角的顶点连线的夹角=21900剩余角条件：已知△ABC 的∠B 和∠C 的外角平分线交于D结论：【练习】1．如图,在三角形A BC 中,∠A=42°,∠ABC 和∠ACB 的三等分线分别交于D 、E, 求∠BDC 的度数2．如图，在△ABC 中，∠A ＝α，∠ABC 的平分线与∠ACD 的平分线交于点A 1，得∠A 1，∠A 1BC 的平分线与∠A 1CD 的平分线交于点A 2，得∠A 2，…，∠A 2013BC 的平分线与∠A 2013CD 的平分线交于点A 2014，得∠A 2014CD ，则∠A 2014＝．4．如图，BP 、CP 是任意△ABC 中∠B 、∠C 的角平分线，可知∠BPC ＝90°+∠A ，把图中的△ABC 变成图中的四边形ABCD ，BP ，CP 仍然是∠B ，∠C 的平分线，猜想∠BPC 与∠A 、∠D 的数量关系是．平行倒角【模型实战】阅读材料：如图1，若//AB CD ，则B D BED ∠+∠=∠．理由：如图，过点E 作//EF AB ，则B BEF ∠=∠．因为//AB CD ，所以//EF CD ，所以D DEF ∠=∠，所以BED BEF DEFB D =+=+∠∠∠∠∠．交流：（1）若将点E 移至图2所示的位置，//AB CD ，此时B 、D ∠、E ∠之间有什么关系？请说明理由．探究：（2）在图3中，//AB CD ，E G +∠∠、B F D ++∠∠∠又有何关系？应用：（3）在图4中，若//AB CD ，又得到什么结论？请直接写出该结论．由简单图形到复杂图形的演变1．已知：如左图，线段AB 、CD 相交于点O ，连接AD 、CB ，如右图，在左图的条件下，∠DAB 和∠BCD 的平分线AP 和CP 相交于点P ，并且与CD 、AB 分别相交于M 、N ．试解答下列问题：（1）在左图中，请直接写出∠A 、∠B 、∠C 、∠D 之间的数量关系：；（2）在右图中，若∠D ＝50°，∠B ＝40°，试求∠P 的度数；（写出解答过程）（3）如果右图中∠D 和∠B 为任意角，其他条件不变，试写出∠P 与∠D 、∠B 之间数量关系．（直接写出结论）2．（2019春•常熟市月考）将纸片△ABC沿DE折叠使点A落在A′处的位置．（1）如果A′落在四边形BCDE的内部（如图1），∠A′与∠1+∠2之间存在怎样的数量关系？并说明理由．（2）如果A′落在四边形BCDE的外部（如图2），这时∠A′与∠1、∠2之间又存在怎样的数量关系？并说明理由．3．如图，∠AOB＝90°，点C、D分别在射线OA、OB上，CE是∠ACD的平分线，CE的反向延长线与∠CDO的平分线交于点F．（1）当∠OCD＝50°（图1），试求∠F．（2）当C、D在射线OA、OB上任意移动时（不与点O重合）（图2），∠F的大小是否变化？若变化，请说明理由；若不变化，求出∠F．4．（2019春•姑苏区期中）如图，在四边形ABCD中，∠A＝90°，∠C＝60°．（1）如图1，若∠ADC和∠ABC的平分线交于点O，求∠BOD的度数；（2）如图2，若∠ABC的平分线与四边形ABCD的外角∠EDC的平分线交于点P，求∠BPD的度数；（3）如图3，若DG、BH分别是四边形ABCD的外角∠CDE、∠CBF的平分线，判断DG与BH是否平行，并说明理由．5．（2019春•常熟市期中）在△ABC中，点D为边BC上一点，请回答下列问题：（1）如图1，若∠DAC＝∠B，△ABC的角平分线CE交AD于点F．试说明∠AEF＝∠AFE；（2）在（1）的条件下，如图2，△ABC的外角∠ACQ的角平分线CP交BA的延长线于点P，∠P与∠CFD有怎样的数量关系？为什么？（3）如图3，点P在BA的延长线上，PD交AC于点F，且∠CFD＝∠B，PE平分∠BPD，过点C作CE⊥PE，垂足为E，交PD于点G，试说明CE平分∠ACB．6．如图，四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E，∠ABC、∠BCD的角平分线交于点F．（1）若∠F＝70°，则∠ABC+∠BCD＝°；∠E＝°；（2）探索∠E与∠F有怎样的数量关系，并说明理由；（3）给四边形ABCD添加一个条件，使得∠E＝∠F，所添加的条件为．。

三角形中角度计算相关的模型(飞镖模型、8字模型、角分线模型)

三角形中与角度计算相关的模型两个定理：一、平面内，三角形的三个内角和为180°。

二、平面内，三角形的一个外角等于其不相邻的两个外角和。

由上述两个定理可导出本文如下说要讲述的相关模型：8字模型、飞镖模型、两内角角平分线模型、两外角角平分线模型、内外角角平分线模型、共顶点的角平分线与高线夹角模型。

下面一一推导证明。

条件：AD、BC相交于点O。

结论：∠A+∠B=∠C+∠D。

(上面两角之和等于下面两角之和)证明：在∠ABO中，由内角和定理：∠A+∠B+∠BOA=180°在∠CDO中，∠C+∠D+∠COD=180°，∠∠A+∠B+∠BOA=180°=∠C+∠D+∠COD，由对顶角相等：∠BOA=∠COD故有∠A+∠B=∠C+∠D应用：如下左图所示，五角星中，∠A+∠B+∠C+∠D+∠E=180°条件：四边形ABDC如上左图所示。

结论：∠D=∠A+∠B+∠C。

(凹四边形凹外角等于三个内角和)证明：如上右图，连接AD并延长到E，则：∠BDC=∠BDE+∠CDE=(∠B+∠1)+(∠2+∠C)=∠B+∠BAC+∠C。

本质为两个三角形外角和定理证明。

应用：如下左图，则∠A+∠B+∠C+∠D+∠E+∠F=260°(下右图中两个飞镖)。

条件：△ABC 中，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I 。

结论：A I ∠+︒=∠2190 证明： ∵BI 是∠ABC 平分线，∴ABC ∠=∠212 ∵CI 是∠ACB 平分线，∴ACB ∠=∠213由A →B →I →C →A 的飞镖模型可知： ∠I =∠A +∠2+∠3=∠A +ABC ∠21+ACB ∠21=∠A +)180(21A ∠-︒=A ∠+︒2190. 应用：如上图，BI 、CI 分别是∠ABC 和∠ACB 的角平分线，且相交于点I 。

(1) 若∠A =60° ，则∠I =120° (2) 若∠I =110°，则∠A =40° (3) 若∠A =α，则∠I =α2190+︒。

中考复习模型解题策略

目录第一章“8”字模型与飞镖模型 (3)【模型1】角的“8”字模型 (3)【模型2】角的飞镖模型 (4)【模型3】边的“8”字模型 (5)【模型4】边的飞镖模型 (5)第二章角平分线四大模型 (7)【模型1】角平分线上的点向两边作垂线 (7)【模型2】截取构造对称全等 (8)【模型3】角平分线+垂线构造等腰三角形 (9)【模型4】角平分线+平行线 (10)第三章截长补短 (11)【模型】截长补短 (11)第四章手拉手模型 (13)【模型】手拉手 (13)第五章三垂直全等模型 (15)【模型】三垂直全等模型 (15)第六章将军饮马 (17)【模型1】定直线与两定点 (17)【模型2】角到定点 (19)【模型3】两定点一定长 (22)第七章蚂蚁行程 (24)【模型1】立体图形展开的最短路径 (24)第八章中点四大模型 (28)【模型1】倍长中线或类中线（与中点有关的线段）构造全等三角形 (28)【模型2】已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一” (30)【模型3】已知三角形一边的中点，可以考虑中位线定理 (32)【模型4】已知直角三角形斜边中点，可以考虑构造斜边中线 (34)第九章半角模型 (36)【模型1】倍长中线或类中线（与中点有关的线段）构造全等三角形 (36)第十章相似模型 (40)【模型1】A、8模型 (40)【模型2】共边共角型 (42)【模型3】一线三角型 (44)【模型4】倒数型 (46)【模型5】与圆有关的简单相似 (48)【模型6】相似与旋转 (49)第十一章圆中的辅助线 (51)【模型1】连半径构造等腰三角形 (51)【模型2】构造直角形 (52)【模型3】与圆的切线有关的辅助线 (54)第十二章辅助圆 (56)【模型1】共端点，等线段模型 (56)【模型2】直角三角形共斜边模型 (57)图12图E A B C D E F D CBA O O 图12图EAB CDE DC BA H G EF D CBA第一章 “8”字模型与飞镖模型【模型1】角的“8”字模型模型分析“8”字模型往往在几何综合题目中推导角度时用到. 模型实例观察下列图形，计算角度：（1）如图①，∠A+∠B+∠C+∠D+∠E= 180° ；（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F= 360° .牛刀小试1．（1）如图①，求∠CAD+∠B+∠C+∠D+∠E= ；（2）如图②，求∠CAD+∠B+∠ACE+∠D+∠E= .2．如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= .AMDCBAEF O O 图12图EAB CDE DC BA 模型分析模型实例如图，在四边形ABCD 中，AM 、CM 分别平分∠DAB 和∠DCB ，AM 与CM 交于M.探究∠AMC 与∠B 、∠D 间的数量关系.（3602B DAMC -∠+∠∠=）牛刀小试1．（1）如图①，求∠CAD+∠B+∠C+∠D+∠E= ；（2）如图②，求∠CAD+∠B+∠ACE+∠D+∠E= .2．如图③，求∠A+∠B+∠C+∠D+∠E+∠F= ；3．如图④，求∠A+∠B+∠C+∠D = .ODCBAODCBAOCBA【模型3】边的“8”字模型模型实例如图，四边形ABCD 的对角线AC 、BD 相交于点O 求证：（1）AB+BC+CD+AD>AC+BD ；（2）AB+BC+CD+AD<2AC+2BD.D在OAD 中，OA+OD>AD.在OBC 中，OB+OC>BC.⇒OA+OD+OB+OC>AD+BC ⇒AC+BD>AD+BC(利用两边之和大于第三边)延长BO 交AC 于D在ABD 中，AB+AD>BD=BO+OD.在ODC 中，OD+DC>OC.⇒AB+AD+OD+DC>BO+OD+OC ⇒AB+AD+DC>BO+OC ⇒AB+AC>BO+OC(利用两边之和大于第三边)O C B A E DC B A 21P A BCP 图3A BC P 图21图P模型实例如图，点O 为三角形内部一点.求证：（1）2（AO+BO+CO ）>AB+BC+AC ；（2）AB+BC+AC>AO+BO+CO.牛刀小试1．如图，在△ABC 中，D 、E 在BC 边上，且BD=CE 求证：AB+AC>AD+AE2．观察图形并探究下列各问题，写出你所观察得到的结论，并说明理由（1）如图①，△ABC 中，P 为边BC 上一点，请比较BP+PC 与AB+AC 的大小，并说明理由；（2）如图②，将（1）中的点P 移至△ABC 内，请比较△BPC 的周长与△ABC 的周长的大小，并说明理由；（3）图③将（2）中的点P 变为P 1、P 2，请比较四边形BP 1P 2C 的周长与△ABC 的周长的大小，并说明理由.N MOABP2图4321A C P B D AB C图1ABDCABDCP第二章角平分线四大模型模型分析利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口.模型实例（1）如图①，在△ABC 中，∠C=90°，AD 平分∠CAB ，BC=6，BD=4，那么点D 到直线AB 的距离是 2 ；（2）如图②，∠1=∠2，∠3=∠4求证：AP 平分∠BAC(提示：过P 作AB,BC,AC 的垂线)牛刀小试1．如图，在四边形ABCD 中，BC>AB ，AD=DC ，BD 平分∠ABC 求证：∠BAD+∠BCD=180°2．如图，△ABC 的外角∠ACD 的平分线CP 与内角∠ABC 的平分线BP 交于点 P ，若∠BPC=40°，则∠CAP= .P O N MB AA BC DA BC DEDC BA 【模型2】截取构造对称全等模型分析利用角平分线图形的对称性，在角的两边构造对称全等三角形，可以得到对应边、对应角相等。

中考必会模型：第一章8字模型与飞镖模型.doc

结论：ZA+Z£>=ZB+ZC.第一章8字模型与飞镖模型模型1：角的8字模型如图所示，AC. BO相交于点。

，连接A。

、BC.模型分析证法一：V ZAOB是△AOD 的外角，ZA+ZD=ZAOB. V ZAOB是左BOC的外角，:.ZB+ZC= ZAOB. :. ZA+ZD=ZB+ZC.证法二：V ZA+ZD+ ZAOD= 180°, A ZA+ ZD= 180°- ZAOD.・「匕3+NC+匕30C= 180。

,A ZB+ ZC= 180°- ZBOC.又V ZAOD=ZBOC, :. ZA+ZD=ZB+ZC.（1）因为这个图形像数字8,所以我们往往把这个模型称为8字模型.（2） 8字模型往往在几何综合题目中推导角度时用到.模型实例观察下列图形，计算角度：（1）如图①，ZA+ZB+ ZC+ ZD+ ZE=；解法一：利用角的8字模型.如图③，连接CD•.: -BOC是△BOE的外角，:.ZB+ZE=ZBOC. V ABOC是△COD 的外角，:.Zi +Z2= ZBOC.AZB+ZE=Z1 + Z2.(角的8 字模型)，...NA+匕B+NACE+匕AO8+NE =ZA+ZACE+ ZADB+ Z1 + Z2=ZA+ ZACD+ ZADC= 180°.解法二：如图④，利用三角形外角和定理.・.N1是的外角，.../l = /C+/E.•・・匕2是的外角，AZ2=ZB+ZD.・.・ ZA+ZB+ ZC+ ZD+ ZE= ZA+Z1 + Z2=180°.(2)如图②，ZA+ZB+ZC+ ZD+ Z£+ ZF=・如图①，求：ZCAD+ ZB+ZC+ ZD+ ZE=(2)解法一：如图⑤，利用角的8字模型.・・•匕AOP 是的外角，..・ZA+匕B=ZAOP ・V ZAOP 是左OPQ 的外角，:.Z1 + Z3=ZAOP. :. ZA+ZB=Z1 + Z3.①(角的 8 字模型)，同理可证：ZC+ZZ)=Z1 + Z2.②，ZE+ZF=Z2+Z3.③ 由①+②+③得：ZA+ZB+ZC+ ZD+ ZE+ ZF=2 (Z1 + Z2+Z3) =360° .解法二：利用角的8字模型.如图⑥，连接DE. yZAOE 是ZVIOB 的外角，A ZA+ZB=ZAOE. V ZAOE 是△(?时的外角，A Z1 +Z2= ZAOE.・.・ZA + ZB= Z1 + Z2.(角的8字模型)・・・ ZA+ ZB+ZC+ ZADC+ ZFEB+ ZF= Z1 + Z2+ ZC+ ZADC+ ZFEB+ ZF= 360° .(四边形内角和为360° )练习：1. (1) C解：如图，VZ1=ZB+ZD, Z2=ZC+ZCAD, .•.ZCAD+ZB+ZC+ZD+ZE=Z1+Z2+ZE=18O° . 故答案为：180°解法二：(1) i8(r.(2)如图②，求：ZCAD+ ZB+ ZACE+ ZD+ ZE=提示：如图.连接D 瓦Z.C*Z_G4Z>=Z.1+Z12. (8 字模型)L CXD+ Z.B+Z.C+ £ADB+ LBEC=IBXBECXBDAYI* 乙2 =180*.解：由三角形的外角性质，知ZBAC=ZE+ZACE, ZEAD=ZB+ZD,又V ZBAC+ZCAD+ZEAD=180°，ZCAD+ ZB+ ZACE+ ZD+ ZE= 180°解法二:=♦匕 BEC* 乙 BDA+AA* 乙 2 解：VZG+ZD=Z3, ZF+ZC=Z4, ZE+ZH-Z2, A ZG+ZD+ZF+ZC+ZE+ZH=Z3+Z4+Z2, VZB+Z2+Z1=18O° , Z3+Z5+ZA=180° , A ZA+ZB+Z2+Z4+Z3=360° ,・・・ ZA+ZB+ZC+ZD+ZE+ZF+ZG+ZH=360°解法二：答案：360-.提示：如图，连接GH, CD.匕屈乙2. （8字模型）Z./4+Z.F= 2.3*44. （8 字模型）L4XB+匕 FCH+ LADG+ 匕 E+ ,FXDGB+ L EHC =Z. 1 + £ 2+£ 3+ 匕 4♦匕 GW+ 乙 FCH+LDGB+ 匕 EHC =36（T ・（四边形内角和360"）模型2：角的飞镖模型如图所示，有结论：VZ4 是的外角，AZ4=ZC+Z2（2）i8（r.提示：如图.连接DE.Z4CE+ZC4D=/L1 + Z2. （8 字模型） L CAD+ L BWCE* Z ADB^ L BEC模型分析解法一：如图①，作射线AD.=182.如图，求：ZA+ZB+ ZC+ ZD+ ZE+ ZF+ ZG+ ZH= 图②VZ3 是△A8O 的外角，AZ3=ZB+Z1AZBDC=Z3+Z4, A ZBDC= ZB+ Z1 + Z2 + ZC, A ZBDC= ZBAC+ ZB+ ZC解法二：如图②，连接BC.VZ2+Z4+ZD=180° , :.ZD=18Q°一(Z2 + Z4)VZ1 + Z2+Z3+Z4+ZA=I8O° , A ZA+Z1 +Z3 = 180°— (Z2+Z4)AZZ)=ZA+Z1 + Z3.(1)因为这个图形像飞镖，所以我们往往把这个模型称为飞镖模型.(2)飞镖模型在几何综合题目中推导角度时使用.模型实例如图，在四边形ABCD中，AM. CM分别平分ZDAB和匕OCB, AM与CM交于探究匕AMC与/B、匕。

中考常用模型归纳和针对性训练：

中考常用模型归纳和针对性训练：第一：八字模型与飞镖模型第二：角平分线四大模型第三：截长补短第四：手拉手模型第五：三垂直模型第六：将军饮马第七：蚂蚁行程第八：中点四大模型第九：半角模型第十：相似模型①A，8字模型②共边共角型③一线穿三角型④倒数型⑤与圆有关相似型⑥旋转与相似第十一：圆中辅助线11个章节：每个模型有分支讲解分支题型，资料丰富培优八下培优必备如果你喜欢，请转发文章并收藏，然后私聊我第一：八字模型与飞镖模型第二：角平分线四大模型第三：截长补短第四：手拉手模型第五：三垂直模型第六：将军饮马第七：蚂蚁行程第八：中点四大模型第九：半角模型第十：相似模型①A，8字模型②共边共角型③一线穿三角型④倒数型⑤与圆有关相似型⑥旋转与相似第十一：圆中辅助线11个章节：每个模型有分支讲解分支题型，资料丰富培优八下培优必备第一：八字模型与飞镖模型第二：角平分线四大模型第三：截长补短第四：手拉手模型第五：三垂直模型第六：将军饮马第七：蚂蚁行程第八：中点四大模型第九：半角模型第十：相似模型①A，8字模型②共边共角型③一线穿三角型④倒数型⑤与圆有关相似型⑥旋转与相似第十一：圆中辅助线11个章节：每个模型有分支讲解分支题型，资料丰富培优八下培优必备第一：八字模型与飞镖模型第二：角平分线四大模型第三：截长补短第四：手拉手模型第五：三垂直模型第六：将军饮马第七：蚂蚁行程第八：中点四大模型第九：半角模型第十：相似模型①A，8字模型②共边共角型③一线穿三角型④倒数型⑤与圆有关相似型⑥旋转与相似第十一：圆中辅助线11个章节：每个模型有分支讲解分支题型，资料丰富培优八下培优必备第一：八字模型与飞镖模型第二：角平分线四大模型第三：截长补短第四：手拉手模型第五：三垂直模型第六：将军饮马第七：蚂蚁行程第八：中点四大模型第九：半角模型第十：相似模型①A，8字模型②共边共角型③一线穿三角型④倒数型⑤与圆有关相似型⑥旋转与相似第十一：圆中辅助线11个章节：每个模型有分支讲解分支题型，资料丰富培优八下培优必备。

8字模型与飞镖模型

初中几何典型解题模型
说明：购买《初中数学典型题思路分析》书赠送数套电子版学习资料，“初中几何典型解题模型”是新增的诸多赠送资料之一。

中考看数学，数学看几何.在中考科目中，数学最能体现差距；在数学中，几何是拉开数学的重中之重。

《初中几何典型解题模型》希望帮助同学们解决“几何”这一痛点难点.学习几何，如果采用题海战术，忽视技巧和方法总结，往往事倍功半，收效甚微.本书在分析海量中考几何试题的基础上，总结解题方法与技巧，整理出中考中最高频的12类共31个几何模型，为每个模型打造“模型分析+典型例题+练习巩固”三部分内容：
模型分析——认识经典模型、识别模型，给出经典模型对应的结论，提供解析与证明.
典型例题——精选经典例题，匹配经典模型，利用模型进行实战应用
巩固练习——依托题库大数据，经典模型高度匹配练习，每一道练习都是经典题，是典型例题的黄金搭档.
本书定位于成绩中等及偏上学生，在高度、深度和难度上都接近中考，帮助同学们解决中考常见难点，有效提高做题效率。

第一章8字模型与飞标模型【模型1：角的8字模型】
【模型分析】
【典型例题】
【答案解析】
【巩固练习1】
【巩固练习2】。

1第一章 8字模型与飞镖模型

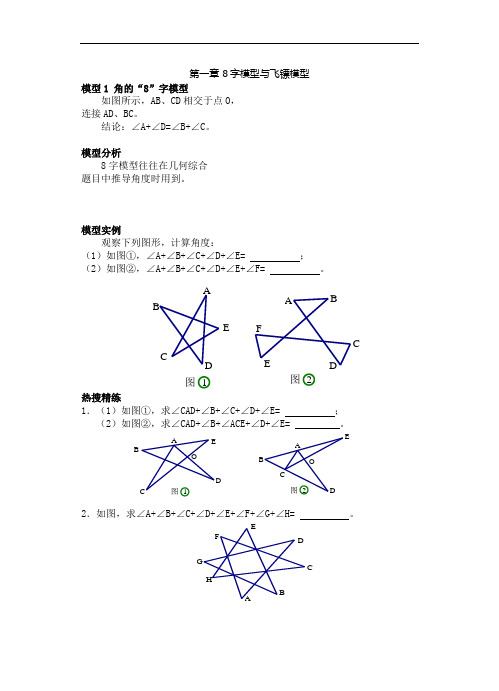
图12图E AB C D E F DC B A O O 图12图E AB C D EDC B A H GE F DC BA第一章 8字模型与飞镖模型模型1 角的“8”字模型如图所示，AB 、CD 相交于点O ，连接AD 、BC 。

结论：∠A+∠D=∠B+∠C 。

模型分析8字模型往往在几何综合题目中推导角度时用到。

模型实例观察下列图形，计算角度：（1）如图①，∠A+∠B+∠C+∠D+∠E= ；（2）如图②，∠A+∠B+∠C+∠D+∠E+∠F= 。

热搜精练1．（1）如图①，求∠CAD+∠B+∠C+∠D+∠E= ；（2）如图②，求∠CAD+∠B+∠ACE+∠D+∠E= 。

2．如图，求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= 。

D C BA M D CB A O135E FD C BA 105OO120D C B A 模型2 角的飞镖模型如图所示，有结论： ∠D=∠A+∠B+∠C 。

模型分析飞镖模型往往在几何综合题目中推导角度时用到。

模型实例如图，在四边形ABCD 中，AM 、CM 分别平分∠DAB 和∠DCB ，AM 与CM 交于M 。

探究∠AMC 与∠B 、∠D 间的数量关系。

热搜精练 1．如图，求∠A+∠B+∠C+∠D+∠E+∠F= ；2．如图，求∠A+∠B+∠C+∠D = 。

O DC BA ODCB AO C B A模型3 边的“8”字模型如图所示，AC 、BD 相交于点O ，连接AD 、BC 。

结论：AC+BD>AD+BC 。

模型实例如图，四边形ABCD 的对角线AC 、BD 相交于点O 。

求证：（1）AB+BC+CD+AD>AC+BD ；（2）AB+BC+CD+AD<2AC+2BD.模型4 边的飞镖模型如图所示有结论： AB+AC>BD+CD 。

OC B AE D C B A21P A BCP 图3A BC P 图21图PB模型实例如图，点O 为三角形内部一点。

1第一章 8字模型与飞镖模型(1)

人教版数学中考专题复习微专题1 “8”字模型及飞镖模型

8字模型与飞镖模型

2020年初中数学“8字模型与飞镖模型”课件

中考数学必会几何模型：8字模型与飞镖模型

几何经典模型：8字模型与飞镖模型

飞镖、8字模型(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇

中考必会几何模型：8字模型与飞镖模型

三角形角度计算之八字型与飞镖模型

初中数学常见模型之8字模型与飞镖模型

中考必会几何模型：8字模型与飞镖模型

8字模型与飞镖模型

三角形中角度计算相关的模型(飞镖模型、8字模型、角分线模型)

中考复习 模型解题策略

中考必会模型：第一章8字模型与飞镖模型.doc

中考常用模型归纳和针对性训练：

8字模型与飞镖模型

1第一章 8字模型与飞镖模型

中考复习模型解题策略