2015圆中考题

合集下载

2015中考数学真题分类汇编：规律型(图形的变化类)

2015中考数学真题分类汇编：规律型（图形的变化类）一．选择题（共7小题）1．（2015•义乌市）挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走（）A．②号棒B．⑦号棒C．⑧号棒D．⑩号棒2．（2015•宜宾）如图，以点O为圆心的20个同心圆，它们的半径从小到大依次是1、2、3、4、…、20，阴影部分是由第1个圆和第2个圆，第3个圆和第4个圆，…，第19个圆和第20个圆形成的所有圆环，则阴影部分的面积为（）A．231πB．210πC．190πD．171π3．（2015•重庆）下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（）A． 21 B．24 C．27 D． 304．（2015•十堰）如图，分别用火柴棍连续搭建正三角形和正六边形，公共边只用一根火柴棍．如果搭建正三角形和正六边形共用了2016根火柴棍，并且正三角形的个数比正六边形的个数多6个，那么能连续搭建正三角形的个数是（）A． 222 B．280 C．286 D． 2925．（2015•重庆）下列图形都是由几个黑色和白色的正方形按一定规律组成，图①中有2个黑色正方形，图②中有5个黑色正方形，图③中有8个黑色正方形，图④中有11个黑色正方形，…，依次规律，图⑩中黑色正方形的个数是（）A． 32 B．29 C．28 D． 266．（2015•广西）下列图形是将正三角形按一定规律排列，则第4个图形中所有正三角形的个数有（）A． 160 B．161 C．162 D． 1637．（2015•绵阳）将一些相同的“○”按如图所示的规律依次摆放，观察每个“龟图”中的“○”的个数，若第n个“龟图”中有245个“○”，则n=（）A． 14 B．15 C．16 D． 17二．填空题（共14小题）8．（2015•内江）如图是由火柴棒搭成的几何图案，则第n个图案中有根火柴棒．（用含n的代数式表示）9．（2015•莆田）谢尔宾斯基地毯，最早是由波兰数学家谢尔宾斯基制作出来的：把一个正三角形分成全等的4个小正三角形，挖去中间的一个小三角形；对剩下的3个小正三角形再分别重复以上做法…将这种做法继续进行下去，就得到小格子越来越多的谢尔宾斯基地毯（如图）．若图1中的阴影三角形面积为1，则图5中的所有阴影三角形的面积之和是．10．（2015•曲靖）用火柴棒按下图所示的方式摆大小不同的“H”：依此规律，摆出第9个“H”需用火柴棒根．11．（2015•福建）观察下列图形的构成规律，依照此规律，第10个图形中共有个“•”．12．（2015•聊城）如图，△ABC的三个顶点和它内部的点P1，把△ABC分成3个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2，把△ABC分成5个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2、P3，把△ABC分成7个互不重叠的小三角形；…△ABC的三个顶点和它内部的点P1、P2、P3、…、P n，把△ABC分成个互不重叠的小三角形．13．（2015•深圳）观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有个太阳．14．（2015•舟山）如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式S=a+b﹣1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克定理”．现用一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40．（1）这个格点多边形边界上的格点数b=（用含a的代数式表示）．（2）设该格点多边形外的格点数为c，则c﹣a=．15．（2015•南宁）如图，在数轴上，点A表示1，现将点A沿x轴做如下移动，第一次点A向左移动3个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点，按照这种移动规律移动下去，第n次移动到点A n，如果点A n与原点的距离不小于20，那么n的最小值是．16．（2015•益阳）如图是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒，…，则第n个图案中有根小棒．17．（2015•山西）如图是一组有规律的图案，它们是由边长相同的正方形和正三角形镶嵌而成，第（1）个图案有4个三角形，第（2）个图案有7个三角形，第（3）个图案有10个三角形，…依此规律，第n个图案有个三角形（用含n的代数式表示）18．（2015•安顺）如图所示是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，…，第n（n是正整数）个图案中的基础图形个数为（用含n的式子表示）．19．（2015•桂林）如图是一个点阵，从上往下有无数多行，其中第一行有2个点，第二行有5个点，第三行有11个点，第四行有23个点，…，按此规律，第n行有个点．20．（2015•随州）观察下列图形规律：当n=时，图形“●”的个数和“△”的个数相等．21．（2015•株洲）“皮克定理”是用来计算顶点在整点的多边形面积的公式，公式表达式为S=a+﹣1，孔明只记得公式中的S表示多边形的面积，a和b中有一个表示多边形边上（含顶点）的整点个数，另一个表示多边形内部的整点个数，但不记得究竟是a还是b表示多边形内部的整点个数，请你选择一些特殊的多边形（如图1）进行验证，得到公式中表示多边形内部的整点个数的字母是，并运用这个公式求得图2中多边形的面积是．三．解答题（共2小题）22．（2015•自贡）观察下表：序号 1 2 3 …图形x xyx x x x xy yx xy yx x xx x x xy y yx xy y yx xy y yx x x x …我们把某格中各字母的和所得多项式称为“特征多项式”．例如，第1格的“特征多项式”为4x+y．回答下列问题：（1）第3格的“特征多项式”为，第4格的“特征多项式”为，第n格的“特征多项式”为；（2）若第1格的“特征多项式”的值为﹣10，第2格的“特征多项式”的值为﹣16，求x，y的值．23．（2015•六盘水）毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究：名称及图形几何点数层数三角形数正方形数五边形数六边形数第一层几何点数 1 1 1 1第二层几何点数 2 3 4 5第三层几何点数 3 5 7 9……………第六层几何点数……………第n层几何点数请写出第六层各个图形的几何点数，并归纳出第n层各个图形的几何点数．2015中考数学真题分类汇编：规律型（图形的变化类）参考答案与试题解析一．选择题（共7小题）1．（2015•义乌市）挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走．如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走（）A．②号棒B．⑦号棒C．⑧号棒D．⑩号棒考点：规律型：图形的变化类．分析：仔细观察图形，找到拿走后图形下面的游戏棒，从而确定正确的选项．解答：解：仔细观察图形发现：第1次应拿走⑨号棒，第2次应拿走⑤号棒，第3次应拿走⑥号棒，第4次应拿走②号棒，第5次应拿走⑧号棒，第6次应拿走⑩号棒，故选D．点评：本题考查了图形的变化类问题，解题的关键是仔细观察图形，锻炼了同学们的识图能力．2．（2015•宜宾）如图，以点O为圆心的20个同心圆，它们的半径从小到大依次是1、2、3、4、…、20，阴影部分是由第1个圆和第2个圆，第3个圆和第4个圆，…，第19个圆和第20个圆形成的所有圆环，则阴影部分的面积为（）A．231πB．210πC．190πD．171π考点：规律型：图形的变化类．分析：根据题意分别表示出各圆环的面积，进而求出它们的和即可．解答：解：由题意可得：阴影部分的面积和为：π（22﹣12）+π（42﹣32）+π（62﹣52）+…+π（202﹣192）=3π+7π+11π+15π+ (39)=5（3π+39π）=210π．故选：B．点评：此题主要考查了图形的变化类以及圆的面积求法，分别表示出各圆环面积面积是解题关键．3．（2015•重庆）下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（）A． 21 B．24 C．27 D． 30考点：规律型：图形的变化类．分析：仔细观察图形，找到图形中圆形个数的通项公式，然后代入n=7求解即可．解答：解：观察图形得：第1个图形有3+3×1=6个圆圈，第2个图形有3+3×2=9个圆圈，第3个图形有3+3×3=12个圆圈，…第n个图形有3+3n=3（n+1）个圆圈，当n=7时，3×（7+1）=24，故选B．点评：本题考查了图形的变化类问题，解题的关键是仔细观察图形并找到图形变化的通项公式，难度不大．4．（2015•十堰）如图，分别用火柴棍连续搭建正三角形和正六边形，公共边只用一根火柴棍．如果搭建正三角形和正六边形共用了2016根火柴棍，并且正三角形的个数比正六边形的个数多6个，那么能连续搭建正三角形的个数是（）A． 222 B．280 C．286 D． 292考点：规律型：图形的变化类．分析：设连续搭建三角形x个，连续搭建正六边形y个，根据搭建三角形和正六边形共用了2016根火柴棍，并且三角形的个数比正六边形的个数多6个，列方程组求解解答：解：设连续搭建三角形x个，连续搭建正六边形y个．由题意得，，解得：．故选D．点评：本题考查了二元一次方程组的应用及图形的变化类问题，解答本题的关键是读懂题意，仔细观察图形，找出合适的等量关系，列方程组求解．5．（2015•重庆）下列图形都是由几个黑色和白色的正方形按一定规律组成，图①中有2个黑色正方形，图②中有5个黑色正方形，图③中有8个黑色正方形，图④中有11个黑色正方形，…，依次规律，图⑩中黑色正方形的个数是（）A． 32 B．29 C．28 D． 26考点：规律型：图形的变化类．分析：仔细观察图形，找到图形的个数与黑色正方形的个数的通项公式后代入n=11后即可求解．解答：解：观察图形发现：图①中有2个黑色正方形，图②中有2+3×（2﹣1）=5个黑色正方形，图③中有2+3（3﹣1）=8个黑色正方形，图④中有2+3（4﹣1）=11个黑色正方形，…，图n中有2+3（n﹣1）=3n﹣1个黑色的正方形，当n=10时，2+3×（10﹣1）=29，故选B．点评：本题是对图形变化规律的考查，难点在于利用求和公式求出第n个图形的黑色正方形的数目的通项表达式．6．（2015•广西）下列图形是将正三角形按一定规律排列，则第4个图形中所有正三角形的个数有（）A． 160 B．161 C．162 D． 163考点：规律型：图形的变化类．分析：由图可以看出：第一个图形中由角上的3个三角形加上中间1个小三角形再加上外围1个大三角形共有5个正三角形；下一个图形的三个角上的部分是上一个图形的全部，另外加上中间一个小的三角形和外围的一个大三角形，所以第二个图形中有5×3+1+1=17个正三角形，第三个图形中有17×3+1+1=53个正三角形，第四个图形中有53×3+1+1=161个正三角形．解答：解：第一个图形正三角形的个数为5，第二个图形正三角形的个数为5×3+2=17，第三个图形正三角形的个数为17×3+2=53，第四个图形正三角形的个数为53×3+2=161，故选B．点评：此题考查图形的变化规律，找出数字与图形之间的联系，找出规律解决问题是解答此题的关键．7．（2015•绵阳）将一些相同的“○”按如图所示的规律依次摆放，观察每个“龟图”中的“○”的个数，若第n个“龟图”中有245个“○”，则n=（）A． 14 B．15 C．16 D． 17考点：规律型：图形的变化类．分析：分析数据可得：第1个图形中小圆的个数为5；第2个图形中小圆的个数为7；第3个图形中小圆的个数为11；第4个图形中小圆的个数为17；则知第n个图形中小圆的个数为n（n﹣1）+5．据此可以再求得“龟图”中有245个“○”是n的值．解答：解：第一个图形有：5个○，第二个图形有：2×1+5=7个○，第三个图形有：3×2+5=11个○，第四个图形有：4×3+5=17个○，由此可得第n个图形有：[n（n﹣1）+5]个○，则可得方程：[n（n﹣1）+5]=245解得：n1=16，n2=﹣15（舍去）．故选：C．点评：此题主要考查了图形的规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键，注意公式必须符合所有的图形．二．填空题（共14小题）8．（2015•内江）如图是由火柴棒搭成的几何图案，则第n个图案中有2n（n+1）根火柴棒．（用含n的代数式表示）考点：规律型：图形的变化类．专题：压轴题．分析：本题可分别写出n=1，2，3，…，所对应的火柴棒的根数．然后进行归纳即可得出最终答案．解答：解：依题意得：n=1，根数为：4=2×1×（1+1）；n=2，根数为：12=2×2×（2+1）；n=3，根数为：24=2×3×（3+1）；…n=n时，根数为：2n（n+1）．点评：本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．9．（2015•莆田）谢尔宾斯基地毯，最早是由波兰数学家谢尔宾斯基制作出来的：把一个正三角形分成全等的4个小正三角形，挖去中间的一个小三角形；对剩下的3个小正三角形再分别重复以上做法…将这种做法继续进行下去，就得到小格子越来越多的谢尔宾斯基地毯（如图）．若图1中的阴影三角形面积为1，则图5中的所有阴影三角形的面积之和是．考点：规律型：图形的变化类．分析：根据题意，每次挖去等边三角形的面积的，剩下的阴影部分面积等于原阴影部分面积的，然后根据有理数的乘方列式计算即可得解．解答：解：图2阴影部分面积=1﹣=，图3阴影部分面积=×=（）2，图4阴影部分面积=×（）2=（）3，图5阴影部分面积=×（）3=（）4=．故答案为：．点评：本题是对图形变化规律的考查，观察出每次挖出后剩下的阴影部分面积等于原阴影部分面积的是解题的关键．10．（2015•曲靖）用火柴棒按下图所示的方式摆大小不同的“H”：依此规律，摆出第9个“H”需用火柴棒29根．考点：规律型：图形的变化类．分析：根据已知图形得出数字变化规律，进而求出答案．解答：解：如图所示：第1个图形有3+2=5根火柴棒，第2个图形有3×2+2=8根火柴棒，第3个图形有3×3+2=11根火柴棒，故第n个图形有3n+2根火柴棒，则第9个“H”需用火柴棒：3×9+2=29（根）．故答案为：29．点评：此题主要考查了图形变化类，根据题意得出火柴棒的变化规律是解题关键．11．（2015•福建）观察下列图形的构成规律，依照此规律，第10个图形中共有111个“•”．考点：规律型：图形的变化类．分析：观察图形可知前4个图形中分别有：3，7，13，21个“•”，所以可得规律为：第n个图形中共有[n（n+1）+1]个“•”．再将n=10代入计算即可．解答：解：由图形可知：n=1时，“•”的个数为：1×2+1=3，n=2时，“•”的个数为：2×3+1=7，n=3时，“•”的个数为：3×4+1=13，n=4时，“•”的个数为：4×5+1=21，所以n=n时，“•”的个数为：n（n+1）+1，n=10时，“•”的个数为：10×11+1=111．故答案为111．点评：本题主要考查了规律型：图形的变化类，关键在观察、分析已知数据，寻找它们之间的相互联系，探寻其规律，难度适中．12．（2015•聊城）如图，△ABC的三个顶点和它内部的点P1，把△ABC分成3个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2，把△ABC分成5个互不重叠的小三角形；△ABC的三个顶点和它内部的点P1、P2、P3，把△ABC分成7个互不重叠的小三角形；…△ABC的三个顶点和它内部的点P1、P2、P3、…、P n，把△ABC分成3+2（n﹣1）个互不重叠的小三角形．考点：规律型：图形的变化类．分析：利用图形得到，△ABC的三个顶点和它内部的点P1，把△ABC分成互不重叠的小三角形的个数=3+2×0；△ABC的三个顶点和它内部的点P1、P2，把△ABC分成互不重叠的小三角形的个数=3+2×1；△ABC的三个顶点和它内部的点P1、P2、P3，把△ABC分成互不重叠的小三角形的个数=3+2×2，即分成的互不重叠的小三角形的个数为3加上P点的个数与1的差的2倍，从而得到△ABC的三个顶点和它内部的点P1、P2、P3、…、P n，把△ABC分成的互不重叠的小三角形的个数．解答：解：如图，△ABC的三个顶点和它内部的点P1，把△ABC分成的互不重叠的小三角形的个数=3+2×0，△ABC的三个顶点和它内部的点P1、P2，把△ABC分成的互不重叠的小三角形的个数=3+2×1，△ABC的三个顶点和它内部的点P1、P2、P3，把△ABC分成的互不重叠的小三角形的个数=3+2×2，所以△ABC的三个顶点和它内部的点P1、P2、P3、…、P n，把△ABC分成的互不重叠的小三角形的个数=3+2（n﹣1）．故答案为3+2（n﹣1）．点评：本题考查了规律型：图形的变化类：对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的，然后通过分析找到各部分的变化规律后直接利用规律求解．13．（2015•深圳）观察下列图形，它们是按一定规律排列的，依照此规律，第5个图形有21个太阳．考点：规律型：图形的变化类．分析：由图形可以看出：第一行小太阳的个数是从1开始连续的自然数，第二行小太阳的个数是1、2、4、8、…、2n﹣1，由此计算得出答案即可．解答：解：第一行小太阳的个数为1、2、3、4、…，第5个图形有5个太阳，第二行小太阳的个数是1、2、4、8、…、2n﹣1，第5个图形有24=16个太阳，所以第5个图形共有5+16=21个太阳．故答案为：21．点评：此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．14．（2015•舟山）如图，多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形，它的面积S可用公式S=a+b﹣1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克定理”．现用一张方格纸共有200个格点，画有一个格点多边形，它的面积S=40．（1）这个格点多边形边界上的格点数b=82﹣2a（用含a的代数式表示）．（2）设该格点多边形外的格点数为c，则c﹣a=118．考点：规律型：图形的变化类．分析：（1）将S=40代入S=a+b﹣1后用含a的代数式表示即可；（2）首先用a表示出c，然后可求得c﹣a的值．解答：解：（1）∵S=a+b﹣1，且S=40，∴a+b﹣1=40，整理得：b=82﹣2a；（2）∵a是多边形内的格点数，b是多边形边界上的格点数，总格点数为200，∴边界上的格点数与多边形内的格点数的和为b+a=82﹣2a+a=82﹣a，∴多边形外的格点数c=200﹣（82﹣a）=118+a，∴c﹣a=118+a﹣a=118，故答案为：82﹣2a，118．点评：本题考查了图形的变化类问题，解决本题的关键是根据题意表示出b，难度不大．15．（2015•南宁）如图，在数轴上，点A表示1，现将点A沿x轴做如下移动，第一次点A向左移动3个单位长度到达点A1，第二次将点A1向右移动6个单位长度到达点A2，第三次将点A2向左移动9个单位长度到达点，按照这种移动规律移动下去，第n次移动到点A n，如果点A n与原点的距离不小于20，那么n的最小值是13．考点：规律型：图形的变化类；数轴．分析：序号为奇数的点在点A的左边，各点所表示的数依次减少3，序号为偶数的点在点A的右侧，各点所表示的数依次增加3，于是可得到A13表示的数为﹣17﹣3=﹣20，A12表示的数为16+3=19，则可判断点A n与原点的距离不小于20时，n的最小值是13．解答：解：第一次点A向左移动3个单位长度至点A1，则A1表示的数，1﹣3=﹣2；第2次从点A1向右移动6个单位长度至点A2，则A2表示的数为﹣2+6=4；第3次从点A2向左移动9个单位长度至点A3，则A3表示的数为4﹣9=﹣5；第4次从点A3向右移动12个单位长度至点A4，则A4表示的数为﹣5+12=7；第5次从点A4向左移动15个单位长度至点A5，则A5表示的数为7﹣15=﹣8；…；则A7表示的数为﹣8﹣3=﹣11，A9表示的数为﹣11﹣3=﹣14，A11表示的数为﹣14﹣3=﹣17，A13表示的数为﹣17﹣3=﹣20，A6表示的数为7+3=10，A8表示的数为10+3=13，A10表示的数为13+3=16，A12表示的数为16+3=19，所以点A n与原点的距离不小于20，那么n的最小值是13．故答案为：13．点评：本题考查了规律型，认真观察、仔细思考，找出点表示的数的变化规律是解决本题的关键．16．（2015•益阳）如图是用长度相等的小棒按一定规律摆成的一组图案，第1个图案中有6根小棒，第2个图案中有11根小棒，…，则第n个图案中有5n+1根小棒．考点：规律型：图形的变化类．分析：由图可知：第1个图案中有5+1=6根小棒，第2个图案中有2×5+2﹣1=11根小棒，第3个图案中有3×5+3﹣2=16根小棒，…由此得出第n个图案中有5n+n﹣（n﹣1）=5n+1根小棒．解答：解：∵第1个图案中有5+1=6根小棒，第2个图案中有2×5+2﹣1=11根小棒，第3个图案中有3×5+3﹣2=16根小棒，…∴第n个图案中有5n+n﹣（n﹣1）=5n+1根小棒．故答案为：5n+1．点评：此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．17．（2015•山西）如图是一组有规律的图案，它们是由边长相同的正方形和正三角形镶嵌而成，第（1）个图案有4个三角形，第（2）个图案有7个三角形，第（3）个图案有10个三角形，…依此规律，第n个图案有3n+1个三角形（用含n的代数式表示）考点：规律型：图形的变化类．分析：由题意可知：第（1）个图案有3+1=4个三角形，第（2）个图案有3×2+1=7个三角形，第（3）个图案有3×3+110个三角形，…依此规律，第n个图案有3n+1个三角形．解答：解：∵第（1）个图案有3+1=4个三角形，第（2）个图案有3×2+1=7个三角形，第（3）个图案有3×3+110个三角形，…∴第n个图案有3n+1个三角形．故答案为：3n+1．点评：此题考查图形的变化规律，找出图形之间的运算规律，利用规律解决问题．18．（2015•安顺）如图所示是一组有规律的图案，第1个图案由4个基础图形组成，第2个图案由7个基础图形组成，…，第n（n是正整数）个图案中的基础图形个数为3n+1（用含n的式子表示）．考点：规律型：图形的变化类．分析：先写出前三个图案中基础图案的个数，并得出后一个图案比前一个图案多3个基础图案，从而得出第n个图案中基础图案的表达式．解答：解：观察可知，第1个图案由4个基础图形组成，4=3+1第2个图案由7个基础图形组成，7=3×2+1，第3个图案由10个基础图形组成，10=3×3+1，…，第n个图案中基础图形有：3n+1，故答案为：3n+1．点评：此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，利用规律解决问题．19．（2015•桂林）如图是一个点阵，从上往下有无数多行，其中第一行有2个点，第二行有5个点，第三行有11个点，第四行有23个点，…，按此规律，第n行有3•2n ﹣1﹣1个点．考点：规律型：图形的变化类．分析：根据前四行的点数分别是2=3•21﹣1﹣1，5=3•22﹣1﹣1，11=3•23﹣1﹣1，23=3•24﹣1﹣1，…，可得第n行有3•2n﹣1﹣1个点，据此解答即可．解答：解：∵2=3•21﹣1﹣1，5=3•22﹣1﹣1，11=3•23﹣1﹣1，23=3•24﹣1﹣1，…，∴第n行有3•2n﹣1﹣1个点．故答案为：3•2n﹣1﹣1．点评：此题主要考查了图形的变化类问题，首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．20．（2015•随州）观察下列图形规律：当n=5时，图形“●”的个数和“△”的个数相等．考点：规律型：图形的变化类．分析：首先根据n=1、2、3、4时，“●”的个数分别是3、6、9、12，判断出第n个图形中“●”的个数是3n；然后根据n=1、2、3、4，“△”的个数分别是1、3、6、10，判断出第n个“△”的个数是；最后根据图形“●”的个数和“△”的个数相等，求出n的值是多少即可．解答：解：∵n=1时，“●”的个数是3=3×1；n=2时，“●”的个数是6=3×2；n=3时，“●”的个数是9=3×3；n=4时，“●”的个数是12=3×4；∴第n个图形中“●”的个数是3n；又∵n=1时，“△”的个数是1=；n=2时，“△”的个数是3=；n=3时，“△”的个数是6=；n=4时，“△”的个数是10=；∴第n个“△”的个数是；由3n=，可得n2﹣5n=0，解得n=5或n=0（舍去），∴当n=5时，图形“●”的个数和“△”的个数相等．故答案为：5．点评：此题主要考查了规律型：图形的变化类问题，要熟练掌握，解答此类问题的关键是：首先应找出图形哪些部分发生了变化，是按照什么规律变化的，通过分析找到各部分的变化规律后直接利用规律求解．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．21．（2015•株洲）“皮克定理”是用来计算顶点在整点的多边形面积的公式，公式表达式为S=a+﹣1，孔明只记得公式中的S表示多边形的面积，a和b中有一个表示多边形边上（含顶点）的整点个数，另一个表示多边形内部的整点个数，但不记得究竟是a还是b表示多边形内部的整点个数，请你选择一些特殊的多边形（如图1）进行验证，得到公式中表示多边形内部的整点个数的字母是a，并运用这个公式求得图2中多边形的面积是17.5．考点：规律型：图形的变化类．分析：分别找到图1中图形内的格点数和图形上的格点数后与公式比较后即可发现表示图上的格点数的字母，图2中代入有关数据即可求得图形的面积．解答：解：如图1，∵三角形内由1个格点，边上有8个格点，面积为4，即4=1+﹣1；矩形内由2个格点，边上有10个格点，面积为6，即6=2+﹣1；∴公式中表示多边形内部整点个数的字母是a；图2中，a=15，b=7，故S=15+﹣1=17.5．故答案为：a，17.5．点评：本题考查了图形的变化类问题，解题的关键是能够仔细读题，找到图形内和图形外格点的数目，难度不大．三．解答题（共2小题）22．（2015•自贡）观察下表：序号 1 2 3 …图形x xyx x x x xy yx xy yx x xx x x xy y yx xy y yx xy y yx x x x …我们把某格中各字母的和所得多项式称为“特征多项式”．例如，第1格的“特征多项式”为4x+y．回答下列问题：（1）第3格的“特征多项式”为12x+9y，第4格的“特征多项式”为16x+16y，第n格的“特征多项式”为4nx+n2y；（2）若第1格的“特征多项式”的值为﹣10，第2格的“特征多项式”的值为﹣16，求x，y的值．考点：规律型：图形的变化类．分析：（1）仔细观察每格的特征多项式的特点，找到规律，利用规律求得答案即可；（2）根据题意列出二元一次方程组，求得x、y的值即可．解答：解：（1）观察图形发现：第1格的“特征多项式”为4x+y，第2格的“特征多项式”为8x+4y，第3格的“特征多项式”为12x+9y，第4格的“特征多项式”为16x+16y，。

2015中考数学复习——专题十四圆

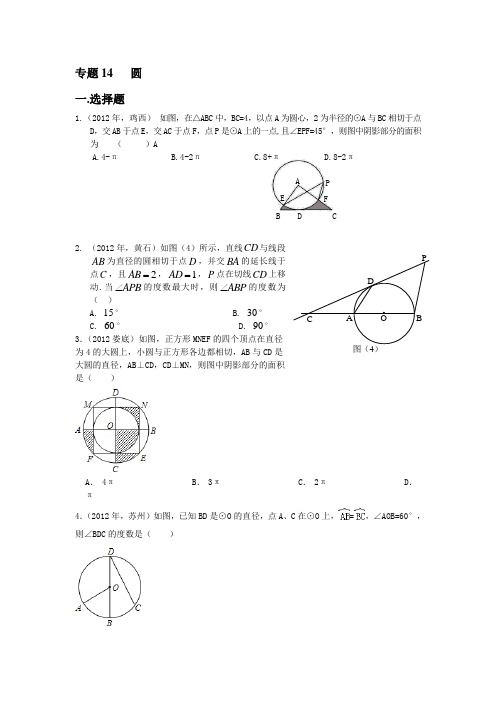
专题14 圆一.选择题1.（2012年，鸡西）如图，在△ABC 中，BC=4，以点A 为圆心，2为半径的⊙A 与BC 相切于点D ，交AB 于点E ，交AC 于点F ，点P 是⊙A 上的一点,且∠EPF=45°，则图中阴影部分的面积为（）A A.4-π B.4-2π C.8+π D.8-2π2. （2012年，黄石）如图（4）所示，直线CD 与线段AB 为直径的圆相切于点D ，并交BA 的延长线于点C ，且2AB =，1AD =，P 点在切线CD 上移动.当APB ∠的度数最大时，则ABP ∠的度数为（）A. 15°B. 30°C. 60°D. 90° 3．（2012娄底）如图，正方形MNEF 的四个顶点在直径为4的大圆上，小圆与正方形各边都相切，AB 与CD 是大圆的直径，AB⊥CD，CD⊥MN，则图中阴影部分的面积是（）A ． 4πB ． 3πC ． 2πD ．π4．（2012年，苏州）如图，已知BD 是⊙O 的直径，点A 、C 在⊙O 上，=，∠AOB=60°，则∠BDC 的度数是（）P图（4）· OACDBD A CPFE B5．（2012•德州）如果两圆的半径分别为4和6，圆心距为10，那么这两圆的位置关系是（） A ．内含 B ．外离 C ．相交 D ．外切 6．（2012泰安）如图，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ，连接BC ，若∠ABC=120°，OC=3，则的长为（）A ．πB ．2πC ．3πD ．5π 7．（2012成都）已知两圆外切，圆心距为5cm ，若其中一个圆的半径是3cm ，则另一个圆的半径是（）A ． 8cmB ．5cmC ．3cmD ．2cm8．（2012年，漳州）如图，一枚直径为4cm 的圆形古钱币沿着直线滚动一周，圆心移动的距离是BA ．2πcmB ．4πcmC ．8πcmD ．16πcm 9．（2012年，北海）已知两圆的半径分别是3和4，圆心距的长为1，则两圆的位置关系为：（）A ．外离B ．相交C ．内切D ．外切 10．（2012年，桂林）已知两圆半径为5cm 和3cm ，圆心距为3cm ，则两圆的位置关系是【】 A ．相交 B ．内含 C ．内切 D ．外切 11．（2012年，河北）如图2，CD 是O ⊙的直径，AB 是弦（不是直径），AB CD ⊥于点E ，则下列结论正确的是（）A ．AE BE > Ｂ．AD BC = Ｃ．12D AEC =∠∠ Ｄ．ADE CBE △∽△ 12、（2012年，河南）如图，已知AB 为O 的直径，AD 切O 于点A, EC CB =则下列结论不一定正确的是A ．BA DA ⊥B ．OC AE ∥C ．2COE CAE ∠=∠D ．OD AC ⊥二.填空题的外接圆，∠BOC=100°，则∠A=cm．3．（2012年，漳州）如图，⊙O的半径为3cm，当圆心0到直线AB的距离为_______cm时，直线AB与⊙0相切．4．（2012年，苏州）已知扇形的圆心角为45°，弧长等于，则该扇形的半径为．5．（2012年，潜江）平面直角坐标系中，⊙M的圆心坐标为（0，2），半径为1，点N在x 轴的正半轴上，如果以点N为圆心，半径为4的⊙N与⊙M相切，则圆心N的坐标为．6．(2012•兰州)如图，两个同心圆，大圆半径为5c m ，小圆的半径为3c m ，若大圆的弦AB 与小圆相交，则弦AB 的取值范围是 8＜AB ≤10 ．7．(2012•兰州)如图，已知⊙O 是以坐标原点O 为圆心，1为半径的圆，∠AOB ＝45°，点P 在x 轴上运动，若过点P 且与OA 平行的直线与⊙O 有公共点，设P (x ，0)，则x 的取值范围是．8．（2012年，佛山）如图，把一个斜边长为2且含有030角的直角三角板ABC 绕直角顶点C 顺时针旋转090到11A B C ∆，则在旋转过程中这个三角板扫过的图形的面积是（）A ．πB ．3 C．342π+ D．11124π+ 9．（2012年，岳阳）圆锥底面半径为，母线长为2，它的侧面展开图的圆心角是．10．（2012张家界）已知圆锥的底面直径和母线长都是10cm ，则圆锥的侧面积为． 11．（2012年，南通）如图，在⊙O 中，∠AOB ＝46º，则∠ACB ＝ º． 12．（2012成都）一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为________ (结果保留π )OBAC13．（2012年，莆田）若扇形的圆心角为60°，弧长为２π，则扇形的半径为． 14．（2012年，肇庆）扇形的半径是9 cm ，弧长是3πcm ，则此扇形的圆心角为 ▲ 度．三.解答题1．（2012年，肇庆）（本小题满分10分）如图7，在△ABC 中，AB =AC ，以AB 为直径的⊙O 交AC 于点E ，交BC 于点D ，连结BE 、AD 交于点P . 求证：（1）D 是BC 的中点；（2）△BEC ∽△ADC ；（3）AB ⋅ CE=2DP ⋅AD ．2.（2012年，泉州）（12分）已知：A 、B 、C 不在同一直线上. （1）.若点A 、B 、C 均在半径为R 的⊙O 上，A 、B 、C 如图一，当∠A=45°时，R=1，求∠BOC 的度数和BC 的长度； Ⅱ.如图二，当∠A 为锐角时，求证sin ∠A=RBC2；（2）.若定长线段．．．．BC 的两个端点分别在∠MAN 的两边AM 、AN （B 、C 均与点A 不重合）滑动，如图三，当∠MAN=60°，BC=2时，分别作BP ⊥AM ，CP ⊥AN ，交点为点P ，试探索：在整个滑动过程中，P 、A 两点的距离是否保持不变？请说明理由. N QC B B p A B M 图① 图② 图③ (第二十五题图)图73．（2012年，苏州）如图，已知半径为2的⊙O与直线l相切于点A，点P是直径AB左侧半圆上的动点，过点P作直线l的垂线，垂足为C，PC与⊙O交于点D，连接PA、PB，设PC 的长为x（2＜x＜4）．（1）当x=时，求弦PA、PB的长度；（2）当x为何值时，PD•CD的值最大？最大值是多少？4.（2012年，佛山）如图，直尺、三角尺都和圆O 相切，AB=8cm ．求圆O的直径．C5．（2012武汉）在锐角三角形ABC中，BC=4，sinA=，（1）如图1，求三角形ABC外接圆的直径；（2）如图2，点I为三角形ABC的内心，BA=BC，求AI的长．6．（2012张家界）如图，⊙O的直径AB=4，C为圆周上一点，AC=2，过点C作⊙O的切线DC，P点为优弧上一动点（不与A．C重合）．（1）求∠APC与∠ACD的度数；（2）当点P移动到CB弧的中点时，求证：四边形OBPC是菱形．（3）P点移动到什么位置时，△APC与△ABC全等，请说明理由．7．（2012南昌）已知，纸片⊙O的半径为2，如图1，沿弦AB折叠操作．（1）①折叠后的所在圆的圆心为O′时，求O′A的长度；②如图2，当折叠后的经过圆心为O时，求的长度；③如图3，当弦AB=2时，求圆心O到弦AB的距离；（2）在图1中，再将纸片⊙O沿弦CD折叠操作．①如图4，当AB∥CD，折叠后的与所在圆外切于点P时，设点O到弦AB．CD的距离之和为d，求d的值；②如图5，当AB与CD不平行，折叠后的与所在圆外切于点P时，设点M为AB的中点，点N为CD的中点，试探究四边形OMPN的形状，并证明你的结论．8．（2012•济宁）如图，AB是⊙O的直径，AC是弦，OD⊥AC于点D，过点A作⊙O的切线AP，AP与OD的延长线交于点P，连接PC、BC．（1）猜想：线段OD与BC有何数量和位置关系，并证明你的结论．（2）求证：PC是⊙O的切线．.9．（2012•德阳）如图，已知点C是以AB为直径的⊙O上一点，CH⊥AB于点H，过点B作⊙O 的切线交直线AC于点D，点E为CH的中点，连接AE并延长交BD于点F，直线CF交AB的延长线于G．（1）求证：AE•FD=AF•EC；（2）求证：FC=FB；（3）若FB=FE=2，求⊙O的半径r的长．（2012宜宾）如图，⊙O1、⊙O2相交于P、Q两点，其中⊙O1的半径r1=2，⊙O2的半径r2=．过10．点Q作CD⊥PQ，分别交⊙O1和⊙O2于点C．D，连接CP、DP，过点Q任作一直线AB交⊙O1和⊙O2于点A．B，连接AP、BP、AC．DB，且AC与DB的延长线交于点E．（1）求证：；（2）若PQ=2，试求∠E度数．11．（2012•资阳）如图，在△ABC中，AB=AC，∠A=30°，以AB为直径的⊙O交BC于点D，交AC于点E，连接DE，过点B作BP平行于DE，交⊙O于点P，连接EP、CP、OP．（1）BD=DC吗？说明理由；（2）求∠BOP的度数；（3）求证：CP是⊙O的切线；如果你解答这个问题有困难，可以参考如下信息：为了解答这个问题，小明和小强做了认真的探究，然后分别用不同的思路完成了这个题目．在进行小组交流的时候，小明说：“设OP交AC于点G，证△AOG∽△CPG”；小强说：“过点C作CH⊥AB于点H，证四边形CHOP是矩形”．12．（2012年，北京）已知：如图，AB是O⊙的直径，C是O⊙上一点，OD BC⊥于点D，过点C作O⊙的切线，交OD的延长线于点E，连结BE．（1）求证：BE与O⊙相切；（2）连结AD并延长交BE于点F，若9OB=，2sin3ABC∠=，求BF的长．13.（2012年，南平）（9分）如右图，已知△ABC中，AB=AC，DE⊥ACDE与半⊙O相切于点D．求证：△ABC是等边三角形．14．（2012年，桂林）(10分)如图，等圆⊙O1和⊙O2相交于A、B12心，顺次连接A、O1、B、O2．(1)求证：四边形AO1BO2是菱形；(2)过直径AC的端点C作⊙O1的切线CE交AB的延长线于E，连接CO2交AE于D，求证：CE＝2O2D；(3)在(2)的条件下，若△AO2D的面积为1，求△BO2D的面积．答案三1.（本小题满分10分）证明：（1）∵AB 是直径 ∴∠ADB = 90°即AD ⊥BC （1分）又∵AB=AC ∴D 是BC 的中点（3分）（2）在△BEC 与 △ADC 中，∵∠C=∠C ∠CAD=∠CBE （5分） ∴△BEC ∽△ADC （6分）（3）∵△BEC ∽△ADC ∴CEBCCD AC = 又∵D 是BC 的中点 ∴2BD=2CD=BC ∴CEBD BD AC 2= 则 CE AC BD ⋅=22 ① （7分）在△BPD 与 △ABD 中，有 ∠BDP=∠BDA又∵AB=AC AD ⊥BC ∴∠CAD=∠BAD又∵∠CAD=∠CBE ∴∠DBP=∠DAB∴△BPD ∽△ABD （8分） ∴BDAD PD BD = 则 AD PD BD ⋅=2② （9分） ∴由①，②得：AD PD BD CE AC ⋅==⋅222∴AD DP CE AB ⋅=⋅2 （10分） 2解：（1）. ①∠BOC=90°（同弧所对的圆周角等于其所对的圆心角的一半）；由勾股定理可知BC=11+=2（提示：也可延长BO 或过点O 作BC 边的垂线段）②证明：可连接BO 并延长，交圆于点E ，连接EC. 可知EC ⊥BC （直径所对的圆周角为90°）且∠E=∠BAC （同弧所对的圆周角相等）故sin ∠A=RBC2. （2）.保持不变.可知△CQP ∽△BQA ，且∠AQP=∠BQC ，所以△BCQ ∽△APQ; 即PQ CQ AP BC =; AP=︒30cos BC =334（为定值）.故保持不变。

2015届内蒙古包头中考复习教学案：专题(八) 圆的综合题

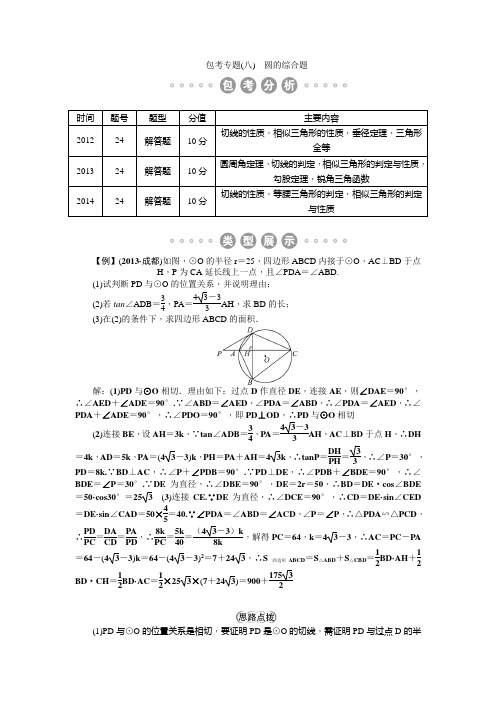
包考专题(八) 圆的综合题【例】(2013·成都)如图，⊙O 的半径r ＝25，四边形ABCD 内接于⊙O ，AC ⊥BD 于点H ，P 为CA 延长线上一点，且∠PDA ＝∠ABD.(1)试判断PD 与⊙O 的位置关系，并说明理由； (2)若tan ∠ADB ＝34，PA ＝43－33AH ，求BD 的长；(3)在(2)的条件下，求四边形ABCD 的面积．解：(1)PD 与⊙O 相切．理由如下：过点D 作直径DE ，连接AE ，则∠DAE ＝90°，∴∠AED ＋∠ADE ＝90°.∵∠ABD ＝∠AED ，∠PDA ＝∠ABD ，∴∠PDA ＝∠AED ，∴∠PDA ＋∠ADE ＝90°，∴∠PDO ＝90°，即PD ⊥OD ，∴PD 与⊙O 相切(2)连接BE ，设AH ＝3k ，∵tan ∠ADB ＝34，PA ＝43－33AH ，AC ⊥BD 于点H ，∴DH＝4k ，AD ＝5k ，PA ＝(43－3)k ，PH ＝PA ＋AH ＝43k ，∴tanP ＝DH PH ＝33，∴∠P ＝30°，PD ＝8k.∵BD ⊥AC ，∴∠P ＋∠PDB ＝90°.∵PD ⊥DE ，∴∠PDB ＋∠BDE ＝90°，∴∠BDE ＝∠P ＝30°.∵DE 为直径，∴∠DBE ＝90°，DE ＝2r ＝50，∴BD ＝DE ·cos ∠BDE ＝50·cos30°＝253 (3)连接CE.∵DE 为直径，∴∠DCE ＝90°，∴CD ＝DE·sin ∠CED＝DE·sin ∠CAD ＝50×45＝40.∵∠PDA ＝∠ABD ＝∠ACD ，∠P ＝∠P ，∴△PDA ∽△PCD ，∴PD PC ＝DA CD ＝PA PD ，∴8k PC ＝5k 40＝（43－3）k 8k，解得PC ＝64，k ＝43－3，∴AC ＝PC －PA ＝64－(43－3)k ＝64－(43－3)2＝7＋243，∴S 四边形ABCD ＝S △ABD ＋S △CBD ＝12BD·AH ＋12BD ·CH ＝12BD·AC ＝12×253×(7＋243)＝900＋17532(1)PD 与⊙O 的位置关系是相切，要证明PD 是⊙O 的切线，需证明PD 与过点D 的半径或直径垂直，所以本题需要作出过点D 的直径DE ，证明PD ⊥DE ；(2)连接BE ，在Rt △BDE 中，DE ＝50，根据tan ∠ADB ＝34，PA ＝43－33AH ，求出∠P的度数，由∠P 的度数得出∠BDE 的度数，通过解直角三角形BDE 得出BD 的长；(3)因为四边形ABCD 的对角线互相垂直，所以它的面积等于AC 与BD 的积的一半，在(2)中已经求出BD 的长，只需求出AC 的长即可．真题热身1．(2013·广东)如图，⊙O 是Rt △ABC 的外接圆，∠ABC ＝90°，弦BD ＝BA ，AB ＝12，BC ＝5，BE ⊥DC 交DC 的延长线于点E.(1)求证：∠BCA ＝∠BAD ； (2)求DE 的长；(3)求证：BE 是⊙O 的切线．解：(1)∵BA ＝BD ，∴BA ︵＝BD ︵，∴∠BCA ＝∠BAD (2)在Rt △ABC 中，AC ＝AB 2＋BC 2＝122＋52＝13.∵∠BAC ＝∠EDB ，∠CBA ＝∠BED ＝90°，∴△ACB ∽△DBE ，∴AB DE ＝AC DB .∵AB ＝BD ＝12，∴DE ＝AB·DB AC ＝12×1213＝14413 (3)连接OB ，则OB ＝OC ，∴∠OBC ＝∠OCB.∵∠ABC ＝90°，∴AC 是⊙O 的直径，∴∠ADC ＝90°，∴∠ABC ＋∠ADC ＝180°，∴∠BAD ＋∠BCD ＝180°.又∵∠BCE ＋∠BCD ＝180°，∴∠BCE ＝∠BAD.由(1)知∠BCA ＝∠BAD ，∴∠BCE ＝∠BCA ，∴∠BCE ＝∠OBC ，∴OB ∥DE.∵BE ⊥DE ，∴OB ⊥BE ，∴BE 是⊙O 的切线2．(2014·包头)如图，已知AB ，AC 分别是⊙O 的直径和弦，点G 为AC ︵上一点，GE ⊥AB ，垂足为点E ，交AC 于点D ，过点C 的切线与AB 的延长线交于点F ，与EG 的延长线交于点P ，连接AG.(1)求证：△PCD 是等腰三角形；(2)若点D 为AC 的中点，且∠F ＝30°，BF ＝2，求△PCD 的周长和AG 的长．解：(1)如图，连结OC ，∵PC 为⊙O 的切线，∴OC ⊥PC ，∴∠OCP ＝90°，即∠1＋∠PCD ＝90°.∵GE ⊥AB ，∴∠GEA ＝90°，∴∠2＋∠ADE ＝90°.∵OA ＝OC ，∴∠1＝∠2，∴∠PCD ＝∠ADE ，而∠ADE ＝∠PDC ，∴∠PCD ＝∠PDC ，∴△PCD 是等腰三角形(2)如图，连结OD ，OC ，BG ，在Rt △COF 中，∠F ＝30°，BF ＝2，∴OF ＝2OC ，即OB ＋2＝2OC ，而OB ＝OC ，∴OC ＝2.∵∠FOC ＝90°－∠F ＝60°，∴∠1＝∠2＝30°，∴∠PCD ＝90°－∠1＝60°，∴△PCD 为等边三角形．∵D 为AC 的中点，∴OD ⊥AC ，在Rt △OCD 中，OD ＝12OC ＝1，CD ＝3OD ＝3，∴△PCD 的周长为3 3.在Rt △ADE中，AD ＝CD ＝3，∴DE ＝12AD ＝32，AE ＝3DE ＝32，∵AB 为直径，∴∠AGB ＝90°，而∠GAE ＝∠BAG ，∴Rt △AGE ∽Rt △ABG ，∴AG ∶AB ＝AE ∶AG ，∴AG 2＝AE·AB ＝32×4＝6，∴AG ＝63．(2014·呼和浩特)如图，AB 是⊙O 的直径，点C 在⊙O 上，过点C 作⊙O 的切线CM. (1)求证：∠ACM ＝∠ABC ；(2)延长BC 到点D ，使BC ＝CD ，连接AD 与CM 交于点E ，若⊙O 的半径为3，ED ＝2，求△ACE 的外接圆的半径．解：(1)连接OC.∵AB 为⊙O 的直径，∴∠ACB ＝90°，∴∠ABC ＋∠BAC ＝90°.∵CM 是⊙O 的切线，∴OC ⊥CM ，∴∠ACM ＋∠ACO ＝90°.∵CO ＝AO ，∴∠BAC ＝∠ACO ，∴∠ACM ＝∠ABC (2)∵BC ＝CD ，BO ＝OA ，∴OC ∥AD.又∵OC ⊥CE ，∴AD ⊥CE ，∴△AEC 是直角三角形，∴△AEC 的外接圆的直径为AC.又∵∠ABC ＋∠BAC ＝90°，∠ACM ＋∠ECD ＝90°，而∠ABC ＝∠ACM ，∴∠BAC ＝∠ECD.又∠CED ＝∠ACB＝90°，∴△ABC ∽△CDE ，∴AB CD ＝BC DE .而⊙O 的半径为3，∴AB ＝6，∴6CD ＝BC2.又BC＝CD ，∴BC 2＝12，∴BC ＝2 3.在Rt △ABC 中，AC ＝AB 2－BC 2＝36－12＝26，∴△ACE 的外接圆的半径为6。

2015年河北中考数学总复习课件(第26课时_圆的有关概念与性质)

冀考解读课前热身考点聚焦冀考探究
第26课时┃ 圆的有关概念与性质
课前热身
1．若⊙O 的半径为 5 cm，点 A 到圆心 O 的距离为 4 cm，则点 A 与⊙O 的位置关系是 ( C ) A．点 A 在⊙O 外 B．点 A 在⊙O 上 C．点 A 在⊙O 内 D．不能确定︵ 2． [2014· 温州] 如图 26－1，已知点 A， B， C 在⊙O 上， ACB 为优弧，下列选项中与∠AOB 相等的是 ( A )
考点聚焦
冀考探究
第26课时┃ 圆的有关概念与性质
考点2 圆心角、弧、弦之间的关系弦相在同圆或等圆中，相等的圆心角所对的______ 等，所对的______ 弧也相等在同圆或等圆中，两个圆心角、所对应的两条弦和所对应的两条弧这三组量中，只要有一组量相等，其他两组量就分别相等
性质推论
冀考解读
第26课时圆的有关概念与性质
第26课时┃ 圆的有关概念与性质
冀考解读
考点梳理常考题型年份 2015 热度预测确定圆的条件选择、填空 ☆☆ 点和圆的位置选择、填空 ☆☆ 关系圆心角、弧、弦选择、填空、 ☆☆☆ 之间的关系解答圆周角定理及其选择、填空、 2012 ☆☆☆☆ 推论解答 2013 2012 垂径定理及其选择、填空、 ☆☆☆☆ 2013 推论解答 2014
课前热身
考点聚焦
冀考探究
第26课时┃ 圆的有关概念与性质
考点3 圆周角
Hale Waihona Puke 圆周角定义圆周角定理推论 1 推论 2
顶点在圆上，两边都与圆相交的角叫做圆周角圆上一条弧所对的圆周角等于它所对的圆心角的________ 一半直角；直径所对的圆周角是______ 90°的圆周角所对直径的弦是______ 同弧所对的圆周角______ 相等

2015浙江中考试题研究数学精品复习课件第26讲圆的弧长和图形面积的计算

10 1 解析：摸到白球的概率为 P＝＝，设口袋里共有 n 个 100 10 5 1 球，则＝，得 n＝50，所以红球数为 50－5＝45，选 A n 10 【点评】本题每摸一次就相当于做了一次试验，因此大量重复的试验获取的频率可以估计概率．
k 解：(1)将点 A(2，3)代入解析式 y＝，得 k＝6 x 6 6 (2)将 D(3，m)代入反比例解析式 y＝，得 m＝＝2，∴点 x 3 D 坐标为(3，2)，设直线 AD 解析式为 y＝kx＋b，将 A(2，3)与 2k＋b＝3， D(3，2)代入得解得 k＝－1，b＝5，则直线 AD 解析 3k＋b＝2，式为 y＝－x＋5
0 (0，－3) (0，－1) ┄┄ (0等可能的情况有 12 种，其中点(x， y)落在第二象限内的情况 2 1 有 2 种，则 P＝＝ 12 6
【例2】 (2013·青岛)一个不透明的口袋里装有除颜色外都相同的5个白球和若干个红球，在不允许将球倒出来数的前提下，小亮为了估计其中的红球数，采用如下方法，先将口袋中的球摇匀，再从口袋里随机摸出一球，记下颜色，然后把它放回口袋中，不断重复上述过程，小亮共摸了100次，其中有10 次摸到白球，因此小亮估计口袋中的红球大约有( A )个 A．45 B．48 C．50 D．55
它们所对应的其余各组量都分别相等．
(4)圆周角定理及推论：
圆周角定理：一条弧所对的圆周角等于它所对圆心角的__一半__．圆周角定理的推论： ①同弧或等弧所对的圆周角相等；同圆或等圆中相等的圆周角所对的弧__相等__． ②半圆(或直径)所对的圆周角是__直角__；90°的圆周角所对的弦是__直径__．
(5) 点和圆的位置关系 ( 设 d 为点 P 到圆心的距离， r 为圆

【精品】2015年全国中考语文试题分类汇编7：《仿写、续写、扩写、修辞、对联》

2015年全国中考语文试题分类汇编07：仿写、续写、扩写、修辞、对联【安徽省】2．阅读下面的文字，完成⑴—⑷题。

（9分）清晨我漫步在山坡谷地，晨光宣泄着永恒的秘密，山涧里流淌出一条小溪，她在歌、在唤、在吐露心曲：生活并非安逸，它是思念和希冀。

死亡并非哀歌，它是失望与憔悴。

智者不在言词，其秘密在言词背后藏nì。

伟人不在高位，不屑权位者才配享荣誉。

（纪伯伦《小溪，你说什么》节选）⑷诗中划线句子运用了和的修辞手法。

（2分）【答案】2．（9分）⑷拟人排比（共2分。

每空1分）【北京市】4．恰当地嵌入书名、地名、人名是写对联的技巧之一。

孙伏园悼念鲁迅先生的挽联，就巧妙地嵌入了鲁迅先生的作品名称和主编的刊物名称，意中有意，感人至深。

在下面对联的横线处，依次填写作品名称或刊物名称，与原联相符的一项是（）踏，刈野草，热风奔流，一生；痛，叹而已，十月噩耗，万众。

A．毁灭彷徨莽原呐喊B．莽原呐喊毁灭彷徨C．莽原彷徨毁灭呐喊D．毁灭呐喊莽原彷徨提示：《呐喊》《彷徨》《野草》《而已集》《热风》《十月》《毁灭》是鲁迅先生的作品（含译作），《莽原》《奔流》是鲁迅先生主编的刊物。

【答案】4．B【解析】考查对联，但非考查“词性对应”，而须注意词性的搭配，及对联内容所表述的情感。

5．“三十六计”是指中国古代36个兵法策略，是中华民族优秀文化遗产之一。

“三十六计”中的许多计谋是借助比喻定名的。

下列计谋的定名都借助了比喻的一项是（）A．远交近攻顺手牵羊反客为主B．围魏救赵以逸待劳偷梁换柱C．打草惊蛇浑水摸鱼调虎离山D．暗度陈仓金蝉脱壳欲擒故纵【答案】5．C【解析】考查运用比喻的定名的计谋。

【重庆市A卷】4．对下列句子中修辞方法的表达效果分析不恰当的一项是（）（3分）A．他们的身后是一片高粱地。

他们朴实得就像那片高粱。

（运用比喻，把他们比作高粱，形象生动地写出了他们的朴实，表达了作者的赞美之情。

）B．为什么我的眼里常舍泪水？／因为我对这土地爱得深沉……（运用设问，先提出疑问，再回答“我”是因喜悦而“常含泪水”，强烈地表达了“我”的激动之情。

圆周角定理中考题含解析图文稿

圆周角定理中考题含解析集团文件发布号：（9816-UATWW-MWUB-WUNN-INNUL-DQQTY-圆周角定理中考题（含解析）一．解答题（共4小题）1．已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．2．如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．（1）判断△ABC的形状：；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．3．已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．4．如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1=∠C，（1）求证：CB∥PD；（2）若BC=3，sin∠P=，求⊙O的直径．圆周角定理中考题（含解析）参考答案与试题解析一．解答题（共4小题）1．（2016?宁夏）已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．（1）求证：AB=AC；（2）若AB=4，BC=2，求CD的长．【解答】（1）证明：∵ED=EC，∴∠EDC=∠C，∵∠EDC=∠B，∴∠B=∠C，∴AB=AC；（2）方法一：解：连接AE，∵AB为直径，∴AE⊥BC，由（1）知AB=AC，∴BE=CE=BC=，∵△CDE∽△CBA，∴，∴CECB=CDCA，AC=AB=4，∴2=4CD，∴CD=．方法二：解：连接BD，∵AB为直径，∴BD⊥AC，设CD=a，由（1）知AC=AB=4，则AD=4﹣a，在Rt△ABD中，由勾股定理可得：BD2=AB2﹣AD2=42﹣（4﹣a）2在Rt△CBD中，由勾股定理可得：BD2=BC2﹣CD2=（2）2﹣a2∴42﹣（4﹣a）2=（2）2﹣a2整理得：a=，即：CD=．2．（2015?德州）如图，⊙O的半径为1，A，P，B，C是⊙O上的四个点，∠APC=∠CPB=60°．（1）判断△ABC的形状：等边三角形；（2）试探究线段PA，PB，PC之间的数量关系，并证明你的结论；（3）当点P位于的什么位置时，四边形APBC的面积最大？求出最大面积．【解答】证明：（1）△ABC是等边三角形．证明如下：在⊙O中∵∠BAC与∠CPB是所对的圆周角，∠ABC与∠APC是所对的圆周角，∴∠BAC=∠CPB，∠ABC=∠APC，又∵∠APC=∠CPB=60°，∴∠ABC=∠BAC=60°，∴△ABC为等边三角形；（2）在PC上截取PD=AP，如图1，又∵∠APC=60°，∴△APD是等边三角形，∴AD=AP=PD，∠ADP=60°，即∠ADC=120°．又∵∠APB=∠APC+∠BPC=120°，∴∠ADC=∠APB，在△APB和△ADC中，，∴△APB≌△ADC（AAS），∴BP=CD，又∵PD=AP，∴CP=BP+AP；（3）当点P为的中点时，四边形APBC的面积最大．理由如下，如图2，过点P作PE⊥AB，垂足为E．过点C作CF⊥AB，垂足为F．∵S△APB =AB?PE，S△ABC=AB?CF，∴S四边形APBC=AB（PE+CF），当点P为的中点时，PE+CF=PC，PC为⊙O的直径，∴此时四边形APBC的面积最大．又∵⊙O的半径为1，∴其内接正三角形的边长AB=，∴S四边形APBC=×2×=．3．（2014?天津）已知⊙O的直径为10，点A，点B，点C在⊙O上，∠CAB的平分线交⊙O于点D．（Ⅰ）如图①，若BC为⊙O的直径，AB=6，求AC，BD，CD的长；（Ⅱ）如图②，若∠CAB=60°，求BD的长．【解答】解：（Ⅰ）如图①，∵BC是⊙O的直径，∴∠CAB=∠BDC=90°．∵在直角△CAB中，BC=10，AB=6，∴由勾股定理得到：AC===8．∵AD平分∠CAB，∴=，∴CD=BD．在直角△BDC中，BC=10，CD2+BD2=BC2，∴易求BD=CD=5；（Ⅱ）如图②，连接OB，OD．∵AD平分∠CAB，且∠CAB=60°，∴∠DAB=∠CAB=30°，∴∠DOB=2∠DAB=60°．又∵OB=OD，∴△OBD是等边三角形，∴BD=OB=OD．∵⊙O的直径为10，则OB=5，∴BD=5．4．（2013?黔西南州）如图，AB是⊙O的直径，弦CD⊥AB与点E，点P 在⊙O上，∠1=∠C，（1）求证：CB∥PD；（2）若BC=3，sin∠P=，求⊙O的直径．【解答】（1）证明：∵∠C=∠P又∵∠1=∠C∴∠1=∠P∴CB∥PD；（2）解：连接AC∵AB为⊙O的直径，∴∠ACB=90°又∵CD⊥AB，∴=，∴∠P=∠CAB，又∵sin∠P=，∴sin∠CAB=，即=，又知，BC=3，∴AB=5，∴直径为5．。

2015连线中考数学一轮复习系列专题19_圆的基本性质

（2）有3个等腰三角形；△CAB、△OAB、△DAB.弦AB是它们的公共底边，直径CD是它们的顶角平分线和底边AB的垂直平分线．
（3）有3对弧相等：，，．
（4）添加辅助线的方法：连接半径或作垂直于弦的直径，是两种重要的添线方法．
知识点五．圆周角定理
1.定义：
顶点在圆上，并且两边都与圆相交的角叫圆周角．
基础知识
知识点一、圆的有关概念
1.圆的定义①（动态定义）在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转所形成的图形叫做圆，固定的端点叫做圆心，线段OA叫做半径．以点O为圆心的圆记做“⊙O”.
②（静态定义）圆是到定点的距离等于定长的点的集合．即：圆上各点到圆心的距离都等于定长（半径），反之到圆心距离等于半径的点一定在圆上；
11（邵阳）如图（八）所示，某窗户是由矩形和弓形组成，已知弓形的跨度AB＝3m，弓形的高EF＝1m，现计划安装玻璃，请帮工程师求出所在圆O的半径r．
12. (武汉)如图，AB是⊙O的直径，C，P是上两点，AB=13，AC=5．
(1)如图(1)，若点P是的中点，求PA的长；
(2)如图(2)，若点P是的中点，求PA的长；
例7.如图，已知在△ABC中，AB=AC，D是△ABC外接圆劣弧AC上的点（不与A，C重合），延长BD至E．
（1）求证：AD的延长线平分∠CDE；
（2）若∠BAC=30°，且△ABC底边BC边上高为1，求△ABC外接圆的周长．
巩固练习
1.（湖州）如图，已知AB是△ABC外接圆的直径，∠A=35°，则∠B的度数是（）
④等弧：能够完全重合的弧叫等弧.
知识点三、弧、弦、圆心角之间的关系
1.圆的旋转不变性
把圆绕着圆心旋转任意一个角度，都与原来的图形重合，我们把这种性质称为圆的旋转不变性．圆是中心对称图形，圆心是它的对称中心.

2015年挑战中考专题_圆的综合题(一)

圆的综合题1、（2013•温州）在△ABC 中，∠C 为锐角，分别以AB ，AC 为直径作半圆，过点B ，A ，C 作，如图所示．若AB=4，AC=2，S 1﹣S 2=，则S 3﹣S 4的值是（）BA ．平分弦的直径垂直于弦B ．半圆（或直径）所对的圆周角是直角C ．相等的圆心角所对的弧相等D ．若两个圆有公共点，则这两个圆相交 3、（2013•温州）一块矩形木板，它的右上角有一个圆洞，现设想将它改造成火锅餐桌桌面，要求木板大小不变，且使圆洞的圆心在矩形桌面的对角线上．木工师傅想了一个巧妙的办法，他测量了PQ 与圆洞的切点K 到点B 的距离及相关数据（单位：cm ），从点N 沿折线NF ﹣FM （NF ∥BC ，FM ∥AB ）切割，如图1所示．图2中的矩形EFGH 是切割后的两块木板拼接成符合要求的矩形桌面示意图（不重叠，无缝隙，不记损耗），则CN ，AM 的长分别是．4、（2013四川宜宾）如图，AB 是⊙O 的直径，弦CD ⊥AB 于点G ，点F 是CD 上一点，且满足=，连接AF 并延长交⊙O 于点E ，连接AD 、DE ，若CF =2，AF =3．给出下列结论：①△ADF ∽△AED ；②FG =2；③tan ∠E =；④S △DEF =4．其中正确的是（写出所有正确结论的序号）．5、(2013年武汉)如图，在平面直角坐标系中，△ABC 是⊙O 的内接三角形，AB ＝AC ，点P 是⋂AB 的中点，连接PA ，PB ，PC ．（1）如图①，若∠BPC ＝60°，求证：AP AC 3=；（2）如图②，若2524sin =∠BPC ，求PAB ∠tan 的值．第22题图①第22题图②6、（2013•常州）在平面直角坐标系xOy中，已知点A（6，0），点B（0，6），动点C在以半径为3的⊙O上，连接OC，过O点作OD⊥OC，OD与⊙O相交于点D（其中点C、O、D 按逆时针方向排列），连接AB．（1）当OC∥AB时，∠BOC的度数为；（2）连接AC，BC，当点C在⊙O上运动到什么位置时，△ABC的面积最大？并求出△ABC 的面积的最大值．（3）连接AD，当OC∥AD时，①求出点C的坐标；②直线BC是否为⊙O的切线？请作出判断，并说明理由．7、（2013•宜昌）半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，⊙O 与l相切于点F，DC在l上．（1）过点B作的一条切线BE，E为切点．①填空：如图1，当点A在⊙O上时，∠EBA的度数是；②如图2，当E，A，D三点在同一直线上时，求线段OA的长；（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．8、（2013•包头）如图，已知在△ABP中，C是BP边上一点，∠PAC=∠PBA，⊙O是△ABC的外接圆，AD是⊙O的直径，且交BP于点E．（1）求证：PA是⊙O的切线；（2）过点C作CF⊥AD，垂足为点F，延长CF交AB于点G，若AG•AB=12，求AC的长；（3）在满足（2）的条件下，若AF：FD=1：2，GF=1，求⊙O的半径及sin∠ACE的值．9、（2013•荆门）如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC 上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．（1）求证：OF∥BE；（2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；（3）延长DC、FP交于点G，连接OE并延长交直线DC与H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．10、（2013•莱芜）如图，⊙O 的半径为1，直线CD 经过圆心O ，交⊙O 于C 、D 两点，直径AB ⊥CD ，点M 是直线CD 上异于点C 、O 、D 的一个动点，AM 所在的直线交于⊙O 于点N ，点P 是直线CD 上另一点，且PM=PN ．（1）当点M 在⊙O 内部，如图一，试判断PN 与⊙O 的关系，并写出证明过程；（2）当点M 在⊙O 外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由；（3）当点M 在⊙O 外部，如图三，∠AMO=15°，求图中阴影部分的面积．11、（2013•遂宁）如图，在⊙O 中，直径AB ⊥CD ，垂足为E ，点M 在OC 上，AM 的延长线交⊙O 于点G ，交过C 的直线于F ，∠1=∠2，连结CB 与DG 交于点N ．（1）求证：CF 是⊙O 的切线；（2）求证：△ACM ∽△DCN ；（3）若点M 是CO 的中点，⊙O 的半径为4，cos ∠BOC=41，求BN 的长．12、（2013济宁）如图1，在平面直角坐标系中，O为坐标原点，P是反比例函数y=（x＞0）图象上任意一点，以P为圆心，PO为半径的圆与坐标轴分别交于点A、B．（1）求证：线段AB为⊙P的直径；（2）求△AOB的面积；（3）如图2，Q是反比例函数y=（x＞0）图象上异于点P的另一点，以Q为圆心，QO为半径画圆与坐标轴分别交于点C、D．求证：DO•OC=BO•OA．13、（2013•攀枝花）如图，PA为⊙O的切线，A为切点，直线PO交⊙O与点E，F过点A作PO的垂线AB垂足为D，交⊙O与点B，延长BO与⊙O交与点C，连接AC，BF．（1）求证：PB与⊙O相切；（2）试探究线段EF，OD，OP之间的数量关系，并加以证明；（3）若AC=12，tan∠F=，求cos∠ACB的值．14、(2013年南京)如图，AD是圆O的切线，切点为A，AB是圆的弦。

2015年中考数学圆的知识点：圆的定义及有关概念

2015年中考数学圆的知识点：圆的定义及有关概念
知识点一、圆的定义及有关概念
1、圆的定义：平面内到定点的距离等于定长的所有点组成的图形叫做圆。

2、有关概念：弦、直径;弧、等弧、优弧、劣弧、半圆;弦心距;等圆、同圆、同心圆。

圆上任意两点间的部分叫做圆弧，简称弧。

连接圆上任意两点间的线段叫做弦，经过圆心的弦叫做直径，直径是最长的弦。

在同圆或等圆中，能够重合的两条弧叫做等弧。

例P为⊙O内一点，OP=3cm，⊙O半径为5cm，则经过P点的最短弦长为________；•最长弦长为_______．
解题思路：圆内最长的弦是直径，最短的弦是和OP垂直的弦，答案：10cm，8cm.。

包头市2015中考复习第6章第3节圆的有关计算

第3节圆的有关计算正多边形的有关概念正多边形外接圆的圆心叫做这个正多边形的________，外接圆的半径叫做正多边形的________，正多边形每一边所对的圆心角叫做正多边形的________，中心到正多边形的一边的距离叫做正多边形的________．弧长、扇形的面积1．如果弧长为l ，圆心角为n °，圆的半径为r ，那么弧长的计算公式为l ＝________. 2．由组成圆心角的两条半径和圆心角所对弧围成的图形叫做扇形．若扇形的圆心角为n °，所在圆半径为r ，弧长为l ，面积为S ，则S ＝________，或S ＝12lr.圆锥的侧面积与全面积1．圆锥的侧面展开图是________，它的________等于圆锥的底面周长C ，________等于圆锥的母线长l.2．若圆锥的底面半径为r ，这个扇形的圆心角为α，则α＝r l ·360°，S 圆锥侧＝12Cl ＝πrl ，S 圆锥全＝πrl ＋πr 2.弧长、扇形面积【例1】(1)(2013·常州)已知扇形半径为6 cm ，圆心角为150°，则此扇形的弧长是__5π__ cm ，扇形的面积是__15π__cm 2.(结果保留π)(2)(2013·达州)如图，一条公路的转弯处是一段圆弧(即图中弧CD ，点O 是弧CD 的圆心)，其中CD ＝600米，E 为弧CD 上一点，且OE ⊥CD ，垂足为F ，OF ＝3003米，则这段弯路的长度为( A )A ．200π米B ．100π米C ．400π米D ．300π米l ＝nπR 180―→l ，n ，R ；S 扇＝12lR ―→S 扇，l ，R ；S 扇＝nπR 2360―→S 扇，n ，R .已知公式中三个量中的任意两个量，利用公式均可求出第三个量，故选择合适的公式较重要．圆锥的侧面积【例2】(1)(2014·泸州)一个圆锥的底面半径是6 cm ，其侧面展开图为半圆，则圆锥的母线长为( B )A ．9 cmB ．12 cmC ．15 cmD ．18 cm(2)(2013·湖州)在学校组织的实践活动中，小新同学用纸板制作了一个圆锥模型，它的底面半径为1，高为22，则这个圆锥的侧面积是( B )A ．4πB ．3πC ．22πD ．2π(1)扇形的弧长＝圆锥底面圆的周长；(2)底面半径―→扇形弧长；底面半径，高―→扇形半径．阴影部分面积的转化与计算【例3】(2013·自贡)如图，点B ，C ，D 都在⊙O 上，过点C 作AC ∥BD 交OB 延长线于点A ，连接CD ，且∠CDB ＝∠OBD ＝30°，DB ＝6 3 cm . (1)求证：AC 是⊙O 的切线；(2)求由弦CD ，BD 与弧BC 所围成的阴影部分的面积．(结果保留π)解：(1)连接OC ，则∠COB ＝2∠CDB ＝60°，∵AC ∥BD ，∴∠A ＝∠OBD ＝30°，∴∠OCA ＝90°，即OC ⊥AC ，又∵OC 为半径，∴AC 是⊙O 的切线(2)由(1)知，AC 为⊙O 的切线，∴OC ⊥AC ，∵AC ∥BD ，∴OC ⊥BD.设OC 交BD 于M ，由垂径定理可知，MD ＝MB ＝12BD ＝3 3.在Rt △OBM 中，∠COB ＝60°，OB ＝MBsin60°＝3332＝6.由ASA 可证△CDM ≌△OBM ，∴S △CDM ＝S △OBM ，∴S 阴影＝S 扇形BOC ＝60π·62360＝6π(cm 2)(1)OC ⊥AC ―→AC 是⊙O 的切线；(2)非规则图形―→规则图形，设OC 交DB 于M ，由△CDM ≌△OBM ―→S 阴影＝S 扇形OBC .在求不规则图形的面积时，注意要将其转化为与其面积“相等”的规则图形，在等积转化中：(1)可根据平移、旋转或轴对称等图形变换；(2)可根据同底(等底)同高(等高)的三角形面积相等进行转化．【例4】如图，直径AB 为6的半圆，绕A 点逆时针旋转60°，此时点B 旋转到了点B′，则图中阴影部分的面积是( A )A ．6πB ．5πC ．4πD ．3π 真题热身1．(2014·天津)正六边形的边心距为3，则该正六边形的边长是( B ) A. 3 B ．2 C ．3 D ．2 32．(2014·成都)在圆心角为120°的扇形AOB 中，半径OA ＝6 cm ，则扇形AOB 的面积是( C )A ．6π cm 2B ．8π cm 2C ．12π cm 2D ．24π cm 23．(2014·襄阳)用一个圆心角为120°，半径为3的扇形作一个圆锥的侧面，则这个圆锥的底面半径为( B )A .12B ．1C .32D ．2 4．(2014·南京)如图，沿一条母线将圆锥侧面剪开并展开，得到一个扇形，若圆锥底面圆半径r ＝2 cm ，扇形圆心角θ＝120°，则该圆锥母线长l 为__6__cm.,第4题图) ,第5题图)5．(2014·达州)如图，在△ABC 中，AB ＝BC ＝2，∠ABC ＝90°，则图中阴影部分的面积是__π－2__．6．(2013·梅州)如图，在矩形ABCD 中，AB ＝2DA ，以点A 为圆心，AB 为半径的圆弧交DC 于点E ，交AD 的延长线于点F ，设DA ＝2. (1)求线段EC 的长；(2)求图中阴影部分的面积．解：(1)在Rt △ADE 中，AD ＝2，AE ＝4，∴DE ＝23，∴EC ＝4－23 (2)易求∠DAE＝60°，∴S 阴影＝S 扇形AEF －S △ADE ＝16π·42－12×23×2＝83π－23第3节圆的有关计算基础过关一、精心选一选1．(2014·衡阳)圆心角为120°，弧长为12π的扇形半径为( C ) A ．6 B ．9 C ．18 D ．362．(2014·嘉兴)一个圆锥的侧面展开图是半径为6的半圆，则这个圆锥的底面半径为( D ) A ．1.5 B ．2 C ．2.5 D ．33．(2013·攀枝花)一个圆锥的左视图是一个正三角形，则这个圆锥的侧面展开图的圆心角等于( D )A ．60°B ．90°C ．120°D ．180°4．(2013·黄石)已知直角三角形ABC 的一条直角边AB ＝12 cm ，另一条直角边BC ＝5 cm ，则以AB 为轴旋转一周，所得到的圆锥的表面积是( A )A ．90π cm 2B ．209π cm 2C ．155π cm 2D ．65π cm 25．(2014·龙东)一个圆锥体形状的水晶饰品，母线长是10 cm ，底面圆的直径是5 cm ，点A 为圆锥底面圆周上一点，从A 点开始绕圆锥侧面缠一圈彩带回到A 点，则彩带最少用多少厘米(接口处重合部分忽略不计)( B )A ．10π cmB ．10 2 cmC ．5π cmD ．5 cm6．(2013·遵义)如图，将边长为1 cm 的等边三角形ABC 沿直线l 向右翻动(不滑动)，点B 从开始到结束，所经过路径的长度为( C )A .32π cmB ．(2＋23π) cm C .43π cm D ．3 cm7．(2013·山西)如图，四边形ABCD 是菱形，∠A ＝60°，AB ＝2，扇形BEF 的半径为2，圆心角为60°，则图中阴影部分的面积是( B )A .2π3－32B .2π3－ 3 C ．π－32D ．π－ 3 二、细心填一填8．(2014·遵义)有一个圆锥，它的高为8 cm ，底面半径为6 cm ，则这个圆锥的侧面积是__60π__cm 2.(结果保留π)9．(2014·河北)如图，将长为8 cm 的铁丝AB 首尾相接围成半径为2 cm 的扇形，则S 扇形＝__4__cm 2.10．(2013·徐州)如图，在正八边形ABCDEFGH 中，四边形BCFG 的面积为20 cm 2，则正八边形的面积为__40__cm 2.,第10题图) ,第11题图)11．如图，在▱ABCD 中，AD ＝2，AB ＝4，∠A ＝30°，以点A 为圆心，AD 的长为半径画弧交AB 于点E ，连接CE ，则阴影部分的面积是__3－13π__．(结果保留π)12．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝BC ＝1，将Rt △ABC 绕A 点逆时针旋转30°后得到Rt △ADE ，点B 经过的路径为BD ︵，则图中阴影部分的面积是__π6__．13．(2013·黔西南州)如图，一个扇形纸片，圆心角∠AOB 为120°，弦AB 的长为2 3 cm ，用它围成一个圆锥的侧面(接缝忽略不计)，则该圆锥底面圆的半径为__23_cm __．三、用心做一做14．(2013·宜宾)如图，△ABC 是正三角形，曲线CDEF 叫做正三角形的渐开线，其中弧CD ，弧DE ，弧EF 的圆心依次是A ，B ，C ，如果AB ＝1，求曲线CDEF 的长．解：4π15．如图，圆锥的侧面展开图是一个半圆，求母线AB 与高AO 的夹角．解：设圆锥母线长为l ，底面半径为r ，则πl ＝2πr ，∴l ＝2r ，sin ∠CAO ＝12，∴锐角∠CAO ＝30°，即母线AB 与高AO 的夹角为30°16．(2014·滨州)如图，点D 在⊙O 的直径AB 的延长线上，点C 在⊙O 上，AC ＝CD ，∠ACD ＝120°.(1)求证：CD 是⊙O 的切线；(2)若⊙O 的半径为2，求图中阴影部分的面积．解：(1)连接OC.∵AC ＝CD ，∠ACD ＝120°，∴∠A ＝∠D ＝30°.∵OA ＝OC ，∴∠ACO ＝∠A ＝30°，∴∠OCD ＝90°，∴CD 是⊙O 的切线 (2)∵∠A ＝30°，∴∠COD ＝2∠A ＝60°，∴S 扇形BOC ＝60π×22360＝2π3.在Rt △OCD 中，CD ＝OC·tan 60°＝23，∴S Rt △OCD ＝12OC·CD ＝12×2×23＝23，∴图中阴影部分的面积为23－2π317．(2014·黔东南州)已知AB 是⊙O 的直径，直线CP 切⊙O 于点C ，过点B 作BD ⊥CP 于点D.(1)求证：△ACB ∽△CDB ；(2)若⊙O 的半径为1，∠BCP ＝30°，求图中阴影部分的面积．解：(1)∵直线CP 是⊙O 的切线，∴∠BCD ＝∠BAC ，∵AB 是直径，∴∠ACB ＝90°，又∵BD ⊥CP ，∴∠CDB ＝90°，∴∠ACB ＝∠CDB ＝90°，∴△ACB ∽△CDB (2)连接OC ，∵直线CP 是⊙O 的切线，∠BCP ＝30°，∴∠COB ＝2∠BCP ＝60°，∴△OCB 是正三角形，∵⊙O 的半径为1，∴S △OCB ＝34，S 扇形OCB ＝60πr 2360＝16π，∴阴影部分的面积＝S扇形OCB－S △OCB ＝16π－3418．(2013·绵阳)如图，AB 是⊙O 的直径，C 是半圆⊙O 上的一点，AC 平分∠DAB ，AD ⊥CD ，垂足为D ，AD 交⊙O 于E ，连接CE.(1)判断CD 与⊙O 的位置关系，并证明你的结论；(2)若E 是AC ︵的中点，⊙O 的半径为1，求图中阴影部分的面积．解：(1)直线CD 与⊙O 相切．证明：∵OA ＝OC ，∴∠OAC ＝∠OCA ，∵AC 平分∠DAB ，∴∠DAC ＝∠OAC ，∴∠DAC ＝∠OCA ，∴AD ∥OC ，又AD ⊥CD ，∴OC ⊥CD ，∴CD 与⊙O 相切 (2)连接OE ，∵点E 是AC ︵的中点，∴AE ︵＝CE ︵，∴∠DAC ＝∠ECA ，由(1)知∠DAC ＝∠OAC ，∴∠ECA ＝∠OAC ，∴CE ∥OA ，又AD ∥OC ，∴四边形AOCE 是平行四边形，∴CE ＝OA ，AE ＝OC ，又OA ＝OC ＝OE ＝1，∴OC ＝OE ＝CE ＝OA ＝AE ＝1，∴四边形AOCE 是菱形，△OCE 是等边三角形，∴∠OCE ＝60°，又∠OCD ＝90°，∴∠DCE ＝∠OCD －∠OCE ＝90°－60°＝30°，在Rt △DCE 中，ED ＝12CE ＝12，DC ＝CE·cos 30°＝32.∵CE 弧与CE 弦所围成部分的面积＝ AE 弧与AE 弦所围成部分的面积，∴S 阴影＝S △DCE＝12ED·DC ＝12×12×32＝38挑战技能19．(2014·重庆)如图，菱形ABCD 的对角线AC ，BD 相交于点O ，AC ＝8，BD ＝6，以AB 为直径作一个半圆，则图中阴影部分的面积为( D )A ．25π－6B .252π－6C .256π－6D .258π－620．(2013·昆明)如图，从直径为4 cm 的圆形纸片中，剪出一个圆心角为90°的扇形OAB ，且点O ，A ，B 在圆周上，把它围成一个圆锥，则圆锥的底面圆的半径是2cm . 21．(2013·黄冈)如图，矩形ABCD 中，AB ＝4，BC ＝3，边CD 在直线l 上，将矩形ABCD 沿直线l 作无滑动翻滚，当点A 第一次翻滚到点A 1位置时，则点A 经过的路线长为__6π__．22．(2013·怀化)如图，在△ABC 中，∠C ＝90°，AC ＋BC ＝9，点O 是斜边AB 上一点，以O 为圆心、2为半径的圆分别与AC ，BC 相切于点D ，E.(1)求AC ，BC 的长；(2)若AC ＝3，连接BD ，求图中阴影部分的面积．(π取3.14)解：(1)连接OD ，OE ，∵⊙O 切BC 于E ，切AC 于D ，∠C ＝90°，∴∠ADO ＝∠BEO ＝90°，∠ODC ＝∠C ＝∠OEC ＝90°，∵OE ＝OD ＝2，∴四边形CDOE 是正方形，∴CE ＝CD ＝OD ＝OE ＝2，∠DOE ＝90°.设AD ＝x ，∵AC ＋BC ＝9，∴BE ＝9－2－2－x ＝5－x ，∵∠OEB ＝∠C ＝90°，∴OE ∥AC ，∴∠EOB ＝∠A ，∴△OEB ∽△ADO ，∴BE OD ＝OE AD ，∴5－x 2＝2x ，x ＝1或4，∴AC ＝3，BC ＝6或AC ＝6，BC ＝3 (2)∵AC ＝3，∴AD ＝3－2＝1，BC ＝6，∴阴影部分的面积S ＝S △ACB －S △ADB －(S 正方形CDOE －S扇形ODE )＝12×3×6－12×1×6－(2×2－90π×22360)＝2＋π≈5.1423．如图，△ABC 内接于⊙O ，直径BD 交AC 于E ，过O 作FG ⊥AB ，交AC 于F ，交AB 于H ，交⊙O 于G.(1)求证：OF·DE ＝OE·2OH ；(2)若⊙O 的半径为12，且OE ∶OF ∶OD ＝2∶3∶6，求阴影部分的面积．(结果保留根号)解：(1)∵BD 是直径，∴∠DAB ＝90°，∵FG ⊥AB ，∴DA ∥FO ，∴△FOE ∽△ADE ，∴FOAD＝OE DE ，即OF ·DE ＝OE·AD.∵O 是BD 的中点，DA ∥OH ，∴AD ＝2OH ，∴OF ·DE ＝OE·2OH (2)∵⊙O 的半径为12，且OE ∶OF ∶OD ＝2∶3∶6，∴OE ＝4，ED ＝8，OF ＝6，可求OH ＝6.在Rt △OBH 中，OB ＝2OH ，∴∠OBH ＝30°，∴∠BOH ＝60°，∴BH ＝BO ·sin 60°＝12×32＝63，∴S 阴影＝S 扇形GOB －S △OHB ＝60×π×122360－12×6×63＝24π－18 3。

包头市2015中考复习第6章第1节圆的有关概念和性质

A．2∠CB．4∠B
C．4∠AD．∠B＋∠C
,第3题图) ,第4题图)
4．(2014·北京)如图，⊙O的直径AB垂直于弦CD，垂足是E，∠A＝22.5°，OC＝4，CD的长为(C)
A．2B．4C．4D．8
5．(2014·陕西)如图，⊙O的半径是2，直线l与⊙O相交于A，B两点，M，N是⊙O上两个动点，且在直线l的异侧，若∠AMB＝45°，则四边形MANB面积的最大值是__4__．
17．(2014·黄石)如图，A，B是圆O上的两点，∠AOB＝120°，C是AB弧的中点．
(1)求证：AB平分∠OAC；
(2)延长OA至P使得OA＝AP，连接PC，若圆O的半径R＝1，求PC的长．
解：(1)∵∠AOB＝120°，C是AB弧的中点，∴∠AOC＝∠BOC＝60°，又OA＝OC＝OB，∴△AOC，△BOC都是等边三角形，∴OA＝OB＝AC＝BC，∴四边形AOBC是菱形，∴AB平分∠OAC(2)由(1)知，△OAC是等边三角形，∵OA＝AC，∴AP＝AC，∴∠APC＝30°，∴△OPC是直角三角形，∴PC＝OC＝
20．(2013·济宁)如图，以等边三角形ABC的BC边为直径画半圆，分别交AB，AC于点E，D，DF是圆的切线，过点F作BC的垂线交BC于点G.若AF的长为2，则FG的长为(B)
A．4B．3C．6D．2
21．(2014·遵义)如图，边长为2的正方形ABCD中，P是CD的中点，连接AP并延长交BC的延长线于点F，作△CPF的外接圆⊙O，连接BP并延长交⊙O于点E，连接EF，则EF的长为(D)
11．(2013·兰州)如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒，点E在量角器上对应的读数是__144__度．

2015年河北中考数学总复习课件(第28课时_与圆有关的计算)

冀考解读
课前热身
考点聚焦
冀考探究
第28课时┃ 与圆有关的计算
考点3 扇形的面积计算
nπ R2 (1)S 扇形＝______( 360 n 是圆心角度数，R 是半径)；扇形面积 1 lR l 是弧长，R 是半径) (2)S 扇形＝______( 2 弓形面积 S 弓形＝S 扇形±S△
冀考解读
课前热身
冀考解读课前热身考点聚焦冀考探究
第28课时┃ 与圆有关的计算
圆锥的 π ra S 侧＝________ 侧面积圆锥的 S 全＝S 侧＋S 底＝π ra＋π r2 全面积
冀考解读
课前热身
考点聚焦
冀考探究
第28课时┃ 与圆有关的计算
冀考探究
探究一正多边形和圆
命题角度： 1．正多边形与圆的关系； 2．与正多边形有关的计算．
解析
∵正六边形的边心距为 3 ，∴ OB ＝
1 1 2 2 2 2 3，AB＝ OA.∵ OA ＝ AB ＋ OB ，∴OA ＝( OA)2 2 2 ＋( 3)2，解得 OA＝2.故选 B.
冀考解读课前热身考点聚焦冀考探究
第28课时┃ 与圆有关的计算
4．[2014· 济宁] 如果圆锥的母线长为 5 cm，底面圆的半径为 2 cm，那么这个圆锥的侧面积是 ( B ) A．10 cm2 B．10π cm2 C．20 cm2 D．20π cm2
解析 ∵圆锥的侧面积 S＝π rl，r 是底面圆半径， l 是母线长，∴S＝π ³2³5＝10π (cm2)．故选 B.
冀考解读
课前热身
考点聚焦
冀考探究
第28课时┃ 与圆有关的计算
考点聚焦
考点1 正多边形和圆

2015年内蒙古包头中考语文试卷及答案

2015年内蒙古包头中考语文试卷及解答本试卷满分l2O分，考题时问150分钟。

一、积累与运用（23分）1．下列词语中加点的字，读音全部正确的一组是（3分）（）A．贮．（zhù）蓄汲．（jí）取愧怍．（zuò）亘．（ɡènɡ）古未有B．两栖．（qī）骊．（lì）歌臆．（yì）测断壁残垣．（yuán）C．苋．（jiè）菜睿．（ruì）智哺．（bǔ）育广袤．(mào)无垠D．荣膺．（yīnɡ）归省．（xǐnɡ）毋．（wú）宁慧心未泯．(mǐn)2．下列词语中，没有错别字的一组是（3分）（）A．朗润藩篱堰塞湖起承转合B．隐秘叙叨中轴线直接霄汉C．籍贯惊鸿城隍庙闲情逸志D．田垄旁鹜文绉绉豁然贯通3．下列各句中，加点成语使用正确的一项是（2分）（）A．网络时代一些无良知的网友为了引起网民围观和获得高点击率，常常发布一些骇人．．听闻．．的虚假消息。

B．越来越多的证据显示,广泛使用杀虫剂会对蜜蜂、飞蛾、蝴蝶等芸芸众生．．．．造成伤害，进而使生态失衡。

C．各领域那些成就非凡的人具有创造力是不言而喻．．．．的，其实只要肯努力，任何人都可以拥有创造力。

D．伊斯兰极端组织成员在叙利亚等地制造了很多恐怖事件，在当地平民心中留下不可．．磨灭．．的伤痛。

4．下列句子没有语病的一项是（2分）（）A．包头作为宜居城市，少了其他一些大城市的喧嚣和拥挤。

合理的城市规划，给市民以舒适和便利，让人们内心感到由衷的喜悦和惬意。

B．奋斗就是每一天都艰难，可一年比一年容易；不奋斗就是每一天都很容易，可一年比一年难。

因此，人应该奋斗。

C．阿拉善盟巴丹吉林沙漠雄浑奇特的大漠风光，近几年越来越多地成为旅游爱好者们热衷和青睐的胜地。

D．通过汉字书写大赛在各地举办和热播，让很多观众对司空见惯的汉字产生了浓厚的兴趣，也让人们重温了中国传统文化博大精深的特质。

2015年北京中考数学专题--圆(白真)

2015年中考复习专题------圆1、（2014北京西城数学一模）21．如图，在ABC△中，AB AC=，以AB为直径作圆O，交BC于点D，连结OD，过点D作圆O的切线，交AB延长线于点E，交AC于点F．（1）求证：OD AC∥；（2）当10AB=，5cos5ABC∠=时，求AF及BE的长．2、（2014朝阳一模）21．如图，CA、CB为⊙O的切线，切点分别为A、B．直径延长AD与CB的延长线交于点E．AB、CO交于点M，连接OB．（1）求证：∠ABO=12∠ACB；（2）若sin∠EAB =1010，CB=12，求⊙O 的半径及BEAE的值．MDBO ECA3、（2014东城一模）21. 如图，AB是⊙O的直径，点E是BD上一点，∠DAC=∠AED．（1）求证：AC是⊙O的切线；（2）若点E是BD的中点，连结AE交BC于点F，当BD=5，CD=4时，求DF的值．4、（2014房山一模）21．如图， AE是⊙O直径，D是⊙O上一点，连结AD并延长使AD=DC，连结CE交⊙O于点B，连结AB.过点E的直线与AC 的延长线交于点F，且∠F=∠CED.（1）求证:EF是⊙O切线；（2）若CD=CF=2，求BE的长.FBCA O ED为直径的⊙O 与边AC 相切于点E ，连结DE 并延长交BC 的延长线于点F ．（1）求证：∠B DF =∠F ；（2）如果CF ＝1，sinA ＝35，求⊙O 的半径．7、（2014门头沟一模）20.如图8，⊙O 的直径AB =4，点P 是AB 延长线上的一点，过P 点作⊙O 的切线，切点为C ，连结AC . （1）若∠CP A =30°，求PC 的长；（2）若点P 在AB 的延长线上运动，∠CP A 的平分线交AC 于点M . 你认为∠CMP 的大小是否发生变化？若变化，请说明理由；若不变化，求出∠CMP 的大小.OFEDC BA MPO CBAACBOD 为直径的⊙O 与边AC 相切于点E ，连接DE 并延长DE 交BC 的延长线于点F ．（1）求证：BD=BF ；（2）若CF=1，cosB=，求⊙O 的半径．9、（2014平谷一模）20. 如图，点A 、B 在⊙O 上，直线AC 是⊙O 的切线，OC ⊥OB ，连接AB 交OC 于点D ．（1）求证：AC =CD ．（2）若AC =2，AO =5，求OD 的长．10、（2014石景山一模）21．如图，⊙O 是△ABC 的外接圆，AC AB =，连结CO 并延长交⊙O 的切线AP 于点P ．（1）求证：BCP APC ∠=∠；（2）若53sin =∠APC ，4=BC ，求AP 的长．11、（2014海淀一模）如图，在△ABC 中，AB AC =，以AB 为直径的⊙O 与边BC 、AC 分别交于D 、E 两点，DF ⊥AC 于F ．（1）求证：DF 为⊙O 的切线；（2）若3cos 5C =，9CF =，求AE 的长．BPCO AOF EABC DEB COF DAOPDBCEA 12、（2014通州一模）21．如图，CD 为⊙O 的直径，点B 在⊙O 上，连接BC 、BD ，过点B 的切线AE 与CD 的延长线交于点A ，OE ∥BD ，交BC 于点F ，交AE 于点E . （1）求证：∠E =∠C ；（2）当⊙O 的半径为3，cos A ＝45时，求EF 的长.13、（2014延庆一模）21. 已知：如图，在△ABC 中，AB=AC ，点D 是边BC 的中点．以 CD 为直径作⊙O ，交边AC 于点P ，连接BP ，交AD 于点E ．（1）求证：AD 是⊙O 的切线；（2）如果PB 是⊙O 的切线，BC =4，求PE 的长．14、（2014燕山一模）21. 如图，点C 是以AB 为直径的圆O 上一点，直线AC 与过B 点的切线相交于点D ，点E 是BD 的中点，直线CE 交直线AB 于点F . （1）求证：CF 是⊙O 的切线；（2）若23=ED ，43tan =F ，求⊙O 的半径.15、（2014昌平一模）21. 如图，已知A 、B 、C 分别是⊙O 上的点，∠B =60°，P 是直径CD 的延长线上的一点，且AP =AC . （1）求证：AP 与⊙O 相切；（2）如果AC =3，求PD 的长.EFD O CB ADPO CAB。

2015中考模拟青岛版九年级数学上册第3章对圆的进一步认识中考原题训练(附答案)

2015中考模拟青岛版九年级数学上册第3章对圆的进一步认识中考原题训练(附答案)一．选择题（共20小题）1．（2014•重庆）如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC 的大小是（）A．30°B．45°C．60°D．70°2．（2014•温州）如图，已知A，B，C在⊙O上，为优弧，下列选项中与∠AOB相等的是（）A．2∠C B．4∠B C．4∠A D．∠B+∠C 3．（2014•牡丹江）如图，⊙O的直径AB=2，弦AC=1，点D在⊙O上，则∠D的度数是（）A．30°B．45°C．60°D．75°4．（2014•益阳）如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（）A．1B．1或5 C．3D．55．（2014•泸州）如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（）A．4B．C．D．6．（2014•乌鲁木齐）如图，半径为3的⊙O内有一点A，OA=，点P在⊙O上，当∠OPA 最大时，PA的长等于（）A．B．C．3D．27．（2014•孝感）如图，在半径为6cm的⊙O中，点A是劣弧的中点，点D是优弧上一点，且∠D=30°，下列四个结论：①OA⊥BC；②BC=6；③sin∠AOB=；④四边形ABOC是菱形．其中正确结论的序号是（）A．①③B．①②③④C．②③④D．①③④8．（2014•仙桃）如图，B，C，D是半径为6的⊙O上的三点，已知的长为2π，且OD∥BC，则BD的长为（）A．3B．6C．6D．129．（2014•济南）如图，⊙O的半径为1，△ABC是⊙O的内接等边三角形，点D、E在圆上，四边形BCDE为矩形，这个矩形的面积是（）A．2B．C．D．10．（2014•自贡）如图，在半径为1的⊙O中，∠AOB=45°，则sinC的值为（）A．B．C．D．11．（2014•长春）如图，在⊙O中，AB是直径，BC是弦，点P是上任意一点．若AB=5，BC=3，则AP的长不可能为（）A．3B．4C．D．512．（2014•台湾）如图，O为△ABC的外心，△OCP为正三角形，OP与AC相交于D点，连接OA．若∠BAC=70°，AB=AC，则∠ADP的度数为何？（）A．85 B．90 C．95 D．11013．（2014•眉山）如图，AB、AC是⊙O的两条弦，∠BAC=25°，过点C的切线与OB的延长线交于点D，则∠D的度数为（）A．25°B．30°C．35°D．40°14．（2011•烟台）如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为6m和8m．按照输油中心O到三条支路的距离相等来连接管道，则O到三条支路的管道总长（计算时视管道为线，中心O为点）是（）A．2m B．3m C．6m D．9m15．（2014•日照）如图，正六边形ABCDEF是边长为2cm的螺母，点P是FA延长线上的点，在A、P之间拉一条长为12cm的无伸缩性细线，一端固定在点A，握住另一端点P拉直细线，把它全部紧紧缠绕在螺母上（缠绕时螺母不动），则点P运动的路径长为（）A．13πcm B．14πcm C．15πcm D．16πcm16．（2014•莱芜）如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，下列说法不正确的是（）A．△CDF的周长等于AD+CD B．F C平分∠BFDC．A C2+BF2=4CD2D．D E2=EF•CE17．（2014•玉林）蜂巢的构造非常美丽、科学，如图是由7个形状、大小完全相同的正六边形组成的网络，正六边形的顶点称为格点，△ABC的顶点都在格点上．设定AB边如图所示，则△ABC是直角三角形的个数有（）A．4个B．6个C．8个D．10个18．（2014•南宁）在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A．40cm B．60cm C．80cm D．100cm19．（2014•宜昌）如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则∠ABD=（）A．∠ACD B．∠ADB C．∠AED D．∠ACB20．（2014•潍坊）如图，▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，连接AE，∠E=36°，则∠ADC的度数是（）A．44°B．54°C．72°D．53°二．填空题（共4小题）21．（2014•呼和浩特）一个底面直径是80cm，母线长为90cm的圆锥的侧面展开图的圆心角的度数为_________．22．（2014•张家界）如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为_________．23．（2014•南京）如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2cm，∠BCD=22°30′，则⊙O的半径为_________cm．24．（2013•宁夏）如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为_________cm．三．解答题（共6小题）25．（2013•潍坊）如图，四边形ABCD是平行四边形，以对角线BD为直径作⊙O，分别与BC，AD相交于点E，F．（1）求证：四边形BEDF为矩形；（2）BD2=BE•BC，试判断直线CD与⊙O的位置关系，并说明理由．26．（2014•宜昌）已知：如图，四边形ABCD为平行四边形，以CD为直径作⊙O，⊙O与边BC相交于点F，⊙O的切线DE与边AB相交于点E，且AE=3EB．（1）求证：△ADE∽△CDF；（2）当CF：FB=1：2时，求⊙O与▱ABCD的面积之比．27．（2014•枣庄）如图，A为⊙O外一点，AB切⊙O于点B，AO交⊙O于C，CD⊥OB 于E，交⊙O于点D，连接OD．若AB=12，AC=8．（1）求OD的长；（2）求CD的长．28．（2014•黄冈）如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．（1）求证：EB=EC；（2）若以点O、D、E、C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．29．（2014•济南）（1）如图1，四边形ABCD是矩形，点E是边AD的中点，求证：EB=EC．（2）如图2，AB与⊙O相切于点C，∠A=∠B，⊙O的半径为6，AB=16，求OA的长．30．（2014•潍坊）如图，在梯形ABCD中，AD∥BC，∠B=90°，以AB为直径作⊙O，恰与另一腰CD相切于点E，连接OD、OC、BE．（1）求证：OD∥BE；（2）若梯形ABCD的面积是48，设OD=x，OC=y，且x+y=14，求CD的长．2015中考模拟青岛版九年级数学上册第3章对圆的进一步认识中考原题训练(附答案)参考答案与试题解析一．选择题（共20小题）1．（2014•重庆）如图，△ABC的顶点A、B、C均在⊙O上，若∠ABC+∠AOC=90°，则∠AOC 的大小是（）A．30°B．45°C．60°D．70°考点：圆周角定理．专题：计算题．分析：先根据圆周角定理得到∠ABC=∠AOC，由于∠ABC+∠AOC=90°，所以∠AOC+∠AOC=90°，然后解方程即可．解答：解：∵∠ABC=∠AOC，而∠ABC+∠AOC=90°，∴∠AOC+∠AOC=90°，∴∠AOC=60°．故选：C．点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．2．（2014•温州）如图，已知A，B，C在⊙O上，为优弧，下列选项中与∠AOB相等的是（）A．2∠C B．4∠B C．4∠A D．∠B+∠C考点：圆周角定理．分析：根据圆周角定理，可得∠AOB=2∠C．解答：解：如图，由圆周角定理可得：∠AOB=2∠C．故选：A．点评：此题考查了圆周角定理．此题比较简单，注意掌握数形结合思想的应用．3．（2014•牡丹江）如图，⊙O的直径AB=2，弦AC=1，点D在⊙O上，则∠D的度数是（）A．30°B．45°C．60°D．75°考点：圆周角定理；含30度角的直角三角形．专题：几何图形问题．分析：由⊙O的直径是AB，得到∠ACB=90°，根据特殊三角函数值可以求得∠B的值，继而求得∠A和∠D的值．解答：解：∵⊙O的直径是AB，∴∠ACB=90°，又∵AB=2，弦AC=1，∴sin∠CBA=，∴∠CBA=30°，∴∠A=∠D=60°，故选：C．点评：本题考查的是圆周角定理及直角三角形的性质，比较简单，但在解答时要注意特殊三角函数的取值．4．（2014•益阳）如图，在平面直角坐标系xOy中，半径为2的⊙P的圆心P的坐标为（﹣3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相切，则平移的距离为（）A．1B．1或5 C．3D．5考点：直线与圆的位置关系；坐标与图形性质．分析：平移分在y轴的左侧和y轴的右侧两种情况写出答案即可．解答：解：当⊙P位于y轴的左侧且与y轴相切时，平移的距离为1；当⊙P位于y轴的右侧且与y轴相切时，平移的距离为5．故选：B．点评：本题考查了直线与圆的位置关系，解题的关键是了解当圆与直线相切时，点到圆心的距离等于圆的半径．5．（2014•泸州）如图，在平面直角坐标系中，⊙P的圆心坐标是（3，a）（a＞3），半径为3，函数y=x的图象被⊙P截得的弦AB的长为，则a的值是（）A．4B．C．D．考点：垂径定理；一次函数图象上点的坐标特征；勾股定理．专题：计算题．分析：P C⊥x轴于C，交AB于D，作PE⊥AB于E，连结PB，由于OC=3，PC=a，易得D 点坐标为（3，3），则△OCD为等腰直角三角形，△PED也为等腰直角三角形．由PE⊥AB，根据垂径定理得AE=BE=AB=2，在Rt△PBE中，利用勾股定理可计算出PE=1，则PD=PE=，所以a=3+．解答：解：作PC⊥x轴于C，交AB于D，作PE⊥AB于E，连结PB，如图，∵⊙P的圆心坐标是（3，a），∴OC=3，PC=a，把x=3代入y=x得y=3，∴D点坐标为（3，3），∴CD=3，∴△OCD为等腰直角三角形，∴△PED也为等腰直角三角形，∵PE⊥AB，∴AE=BE=AB=×4=2，在Rt△PBE中，PB=3，∴PE=，∴PD=PE=，∴a=3+．故选：B．点评：本题考查了垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理和等腰直角三角形的性质．6．（2014•乌鲁木齐）如图，半径为3的⊙O内有一点A，OA=，点P在⊙O上，当∠OPA 最大时，PA的长等于（）A．B．C．3D．2考点：垂径定理；圆周角定理．分析：当PA⊥OA时，PA取最小值，∠OPA取得最大值，然后在直角三角形OPA中利用勾股定理求PA的值即可．解答：解：∵OA、OP是定值，∴在△OPA中，当∠OPA取最大值时，PA取最小值，∴PA⊥OA时，PA取最小值；在直角三角形OPA中，OA=，OP=3，∴PA==．故选B．点评：本题考查了解直角三角形．解答此题的关键是找出“当PA⊥OA时，PA取最小值”即“PA⊥OA时，∠OPA取最大值”这一隐含条件．7．（2014•孝感）如图，在半径为6cm的⊙O中，点A是劣弧的中点，点D是优弧上一点，且∠D=30°，下列四个结论：①OA⊥BC；②BC=6；③sin∠AOB=；④四边形ABOC是菱形．其中正确结论的序号是（）A．①③B．①②③④C．②③④D．①③④考点：垂径定理；菱形的判定；圆周角定理；解直角三角形．专题：几何图形问题．分析：分别根据垂径定理、菱形的判定定理、锐角三角函数的定义对各选项进行逐一判断即可．解答：解：∵点A是劣弧的中点，OA过圆心，∴OA⊥BC，故①正确；∵∠D=30°，∴∠ABC=∠D=30°，∴∠AOB=60°，∵点A是劣弧的中点，∴BC=2CE，∵OA=OB，∴OA=OB=AB=6cm，∴BE=AB•cos30°=6×=3cm，∴BC=2BE=6cm，故②正确；∵∠AOB=60°，∴sin∠AOB=sin60°=，故③正确；∵∠AOB=60°，∴AB=OB，∵点A是劣弧的中点，∴AC=AB，∴AB=BO=OC=CA，∴四边形ABOC是菱形，故④正确．故选：B．点评：本题考查了垂径定理、菱形的判定、圆周角定理、解直角三角形，综合性较强，是一道好题．8．（2014•仙桃）如图，B，C，D是半径为6的⊙O上的三点，已知的长为2π，且OD∥BC，则BD的长为（）A．3B．6C．6D．12考点：垂径定理；等边三角形的判定与性质；圆周角定理；弧长的计算；解直角三角形．专题：计算题．分析：连结OC交BD于E，设∠BOC=n°，根据弧长公式可计算出n=60，即∠BOC=60°，易得△OBC为等边三角形，根据等边三角形的性质得∠C=60°，∠OBC=60°，BC=OB=6，由于BC∥OD，则∠2=∠C=60°，再根据圆周角定理得∠1=∠2=30°，即BD平分∠OBC，根据等边三角形的性质得到BD⊥OC，接着根据垂径定理得BE=DE，在Rt△CBE中，利用含30度的直角三角形三边的关系得CE=BC=3，CE=CE=3，所以BD=2BE=6．解答：解：连结OC交BD于E，如图，设∠BOC=n°，根据题意得2π=，得n=60，即∠BOC=60°，而OB=OC，∴△OBC为等边三角形，∴∠C=60°，∠OBC=60°，BC=OB=6，∵BC∥OD，∴∠2=∠C=60°，∵∠1=∠2（圆周角定理），∴∠1=30°，∴BD平分∠OBC，BD⊥OC，∴BE=DE，在Rt△CBE中，CE=BC=3，∴BE=CE=3，∴BD=2BE=6．故选：C．点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了弧长公式、等边三角形的判定与性质和圆周角定理．9．（2014•济南）如图，⊙O的半径为1，△ABC是⊙O的内接等边三角形，点D、E在圆上，四边形BCDE为矩形，这个矩形的面积是（）A．2B．C．D．考点：垂径定理；等边三角形的性质；矩形的性质；解直角三角形．分析：连接BD、OC，根据矩形的性质得∠BCD=90°，再根据圆周角定理得BD为⊙O的直径，则BD=2；由ABC为等边三角形得∠A=60°，于是利用圆周角定理得到∠BOC=2∠A=120°，易得∠CBD=30°，在Rt△BCD中，根据含30°的直角三角形三边的关系得到CD=BD=1，BC=CD=，然后根据矩形的面积公式求解．解答：解：连结BD、OC，如图，∵四边形BCDE为矩形，∴∠BCD=90°，∴BD为⊙O的直径，∴BD=2，∵△ABC为等边三角形，∴∠A=60°，∴∠BOC=2∠A=120°，而OB=OC，∴∠CBD=30°，在Rt△BCD中，CD=BD=1，BC=CD=，∴矩形BCDE的面积=BC•CD=．故选：B．点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了圆周角定理、等边三角形的性质和矩形的性质．10．（2014•自贡）如图，在半径为1的⊙O中，∠AOB=45°，则sinC的值为（）A．B．C．D．考点：圆周角定理；勾股定理；锐角三角函数的定义．分析：首先过点A作AD⊥OB于点D，由在Rt△AOD中，∠AOB=45°，可求得AD与OD 的长，继而可得BD的长，然后由勾股定理求得AB的长，继而可求得sinC的值．解答：解：过点A作AD⊥OB于点D，∵在Rt△AOD中，∠AOB=45°，∴OD=AD=OA•cos45°=×1=，∴BD=OB﹣OD=1﹣，∴AB==，∵AC是⊙O的直径，∴∠ABC=90°，AC=2，∴sinC=．故选：B．点评：此题考查了圆周角定理、三角函数以及勾股定理．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．11．（2014•长春）如图，在⊙O中，AB是直径，BC是弦，点P是上任意一点．若AB=5，BC=3，则AP的长不可能为（）A．3B．4C．D．5考点：圆周角定理；勾股定理；圆心角、弧、弦的关系．专题：几何图形问题．分析：首先连接AC，由圆周角定理可得，可得∠C=90°，继而求得AC的长，然后可求得AP的长的取值范围，继而求得答案．解答：解：连接AC，∵在⊙O中，AB是直径，∴∠C=90°，∵AB=5，BC=3，∴AC==4，∵点P是上任意一点．∴4≤AP≤5．故选：A．点评：此题考查了圆周角定理以及勾股定理．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．12．（2014•台湾）如图，O为△ABC的外心，△OCP为正三角形，OP与AC相交于D点，连接OA．若∠BAC=70°，AB=AC，则∠ADP的度数为何？（）A．85 B．90 C．95 D．110考点：三角形的外接圆与外心；等边三角形的性质．分析：利用三角形外心的性质以及利用等腰三角形的性质得出∠OAC=∠OCA=35°，进而结合三角形外角的性质得出答案．解答：解：∵O为△ABC的外心，∠BAC=70°，AB=AC，∴∠OAC=35°，AO=CO，∴∠OAC=∠OCA=35°，∴∠AOC=110°，∵△OCP为正三角形，∴∠AOP=50°，∴∠ADP=∠OAD+∠AOD=85°．故选：A．点评：此题主要考查了三角形的外心的性质以及等边三角形的性质等知识，得出∠OAC=∠OCA=35°是解题关键．13．（2014•眉山）如图，AB、AC是⊙O的两条弦，∠BAC=25°，过点C的切线与OB的延长线交于点D，则∠D的度数为（）A．25°B．30°C．35°D．40°考点：切线的性质．专题：几何图形问题．分析：连接OC，根据切线的性质求出∠OCD=90°，再由圆周角定理求出∠COD的度数，根据三角形内角和定理即可得出结论．解答：解：连接OC，∵CD是⊙O的切线，点C是切点，∴∠OCD=90°．∵∠BAC=25°，∴∠COD=50°，∴∠D=180°﹣90°﹣50°=40°．故选：D．点评：本题考查的是切线的性质，熟知圆的切线垂直于经过切点的半径是解答此题的关键．14．（2011•烟台）如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为6m和8m．按照输油中心O到三条支路的距离相等来连接管道，则O到三条支路的管道总长（计算时视管道为线，中心O为点）是（）A．2m B．3m C．6m D．9m考点：三角形的内切圆与内心；勾股定理．专题：压轴题．分析：根据：△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积即可求解．解答：解：在直角△ABC中，BC=8m，AC=6m．则AB===10．∵中心O到三条支路的距离相等，设距离是r．△ABC的面积=△AOB的面积+△BOC的面积+△AOC的面积即：AC•BC=AB•r+BC•r+AC•r即：6×8=10r+8r+6r∴r==2．故O到三条支路的管道总长是2×3=6m．故选C．点评：本题主要考查了三角形的内心的性质，三角形内心到三角形的各边的距离相等，利用三角形的面积的关系求解是解题的关键．15．（2014•日照）如图，正六边形ABCDEF是边长为2cm的螺母，点P是FA延长线上的点，在A、P之间拉一条长为12cm的无伸缩性细线，一端固定在点A，握住另一端点P拉直细线，把它全部紧紧缠绕在螺母上（缠绕时螺母不动），则点P运动的路径长为（）A．13πcm B．14πcm C．15πcm D．16πcm考点：弧长的计算；正多边形和圆．分析：根据如图所示可知点P运动的路线就是图中六条扇形的弧长，扇形的圆心角为60°，半径从12cm，依次减2cm，求得六条弧的长的和即可．解答：解：点P运动的路径长为：+++++=（12+10+8+6+4+2）=14π（cm）．故选：B．点评：本题的关键是理解点P运动的路线是六条弧，理解每条弧的圆心角和半径是关键．16．（2014•莱芜）如图，在正五边形ABCDE中，连接AC、AD、CE，CE交AD于点F，连接BF，下列说法不正确的是（）A．△CDF的周长等于AD+CD B．F C平分∠BFDC．A C2+BF2=4CD2D．D E2=EF•CE考点：正多边形和圆；全等三角形的判定与性质．分析：首先由正五边形的性质可得AB=BC=CD=DE=AE，BA∥CE，AD∥BC，AC∥DE，AC=AD=CE，根据有一组邻边相等的平行四边形是菱形即可证得四边形ABCF为菱形，得CF=AF，即△CDF的周长等于AD+CD，由菱形的性质和勾股定理得出AC2+BF2=4CD2，可证明△CDE∽△DFE，即可得出DE2=EF•CE．解答：解：∵五边形ABCDE是正五边形，∴AB=BC=CD=DE=AE，BA∥CE，AD∥BC，AC∥DE，AC=AD=CE，∴四边形ABCF是菱形，∴CF=AF，∴△CDF的周长等于CF+DF+CD，即△CDF的周长等于AD+CD，故A选项正确；∵四边形ABCF是菱形，∴AC⊥BF，设AC与BF交于点O，由勾股定理得OB2+OC2=BC2，∴AC2+BF2=（2OC）2+（2OB）2=4OC2+4OB2=4BC2，∴AC2+BF2=4CD2．故C选项正确；由正五边形的性质得，△ADE≌△CDE，∴∠DCE=∠EDF，∴△CDE∽△DFE，∴=，∴DE2=EF•CE，故D选项正确；故选：B．点评：本题考查了正五边形的性质，全等三角形的判定，综合考察的知识点较多，解答本题注意已经证明的结论，可以直接拿来使用．17．（2014•玉林）蜂巢的构造非常美丽、科学，如图是由7个形状、大小完全相同的正六边形组成的网络，正六边形的顶点称为格点，△ABC的顶点都在格点上．设定AB边如图所示，则△ABC是直角三角形的个数有（）A．4个B．6个C．8个D．10个考点：正多边形和圆．分析：根据正六边形的性质，分AB是直角边和斜边两种情况确定出点C的位置即可得解．解答：解：如图，AB是直角边时，点C共有6个位置，即，有6个直角三角形，AB是斜边时，点C共有4个位置，即有4个直角三角形，综上所述，△ABC是直角三角形的个数有6+4=10个．故选：D．点评：本题考查了正多边形和圆，难点在于分AB是直角边和斜边两种情况讨论，熟练掌握正六边形的性质是解题的关键，作出图形更形象直观．18．（2014•南宁）在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（）A．40cm B．60cm C．80cm D．100cm考点：垂径定理的应用；勾股定理．分析：连接OA，过点O作OE⊥AB，交AB于点M，由垂径定理求出AM的长，再根据勾股定理求出OM的长，进而可得出ME的长．解答：解：连接OA，过点O作OE⊥AB，交AB于点M，∵直径为200cm，AB=160cm，∴OA=OE=100cm，AM=80cm，∴OM===60cm，∴ME=OE﹣OM=100﹣60=40cm．故选：A．点评：本题考查的是垂径定理的应用，根据题意作出辅助线，构造出直角三角形是解答此题的关键．19．（2014•宜昌）如图，点A，B，C，D都在⊙O上，AC，BD相交于点E，则∠ABD=（）A．∠ACD B．∠ADB C．∠AED D．∠ACB考点：圆周角定理．专题：几何图形问题．分析：根据圆周角定理即可判断A、B、D，根据三角形外角性质即可判断C．解答：解：A、∵∠ABD对的弧是弧AD，∠ACD对的弧也是AD，∴∠ABD=∠ACD，故A选项正确；B、∵∠ABD对的弧是弧AD，∠ADB对的弧也是AB，而已知没有说=，∴∠ABD和∠ACD不相等，故B选项错误；C、∠AED＞∠ABD，故C选项错误；D、∵∠ABD对的弧是弧AD，∠ACB对的弧也是AB，而已知没有说=，∴∠ABD和∠ACB不相等，故D选项错误；故选：A．点评：本题考查了圆周角定理和三角形外角性质的应用，注意：在同圆或等圆中，同弧或等弧所对的圆周角相等．20．（2014•潍坊）如图，▱ABCD的顶点A、B、D在⊙O上，顶点C在⊙O的直径BE上，连接AE，∠E=36°，则∠ADC的度数是（）A．44°B．54°C．72°D．53°考点：圆周角定理；平行四边形的性质．专题：计算题．分析：首先根据直径所对的圆周角为直角得到∠BAE=90°，然后利用四边形ABCD是平行四边形，∠E=36°，得到∠BEA=∠DAE=36°，从而得到∠BAD=126°，求得到∠ADC=54°．解答：解：∵BE是直径，∴∠BAE=90°，∵四边形ABCD是平行四边形，∠E=36°，∴∠BEA=∠DAE=36°，∴∠BAD=126°，∴∠ADC=54°，故选：B．点评：本题考查了圆周角定理及平行四边形的性质，解题的关键是认真审题，发现图形中的圆周角．二．填空题（共4小题）21．（2014•呼和浩特）一个底面直径是80cm，母线长为90cm的圆锥的侧面展开图的圆心角的度数为160°．考点：圆锥的计算．专题：计算题．分析：根据圆锥的底面直径求得圆锥的侧面展开扇形的弧长，再利用告诉的母线长求得圆锥的侧面展开扇形的面积，再利用扇形的另一种面积的计算方法求得圆锥的侧面展开图的圆心角即可．解答：解：∵圆锥的底面直径是80cm，∴圆锥的侧面展开扇形的弧长为：πd=80π，∵母线长90cm，∴圆锥的侧面展开扇形的面积为：lr=×80π×90=3600π，∴=3600π，解得：n=160．故答案为：160．点评：本题考查了圆锥的有关计算，解决此类题目的关键是明确圆锥的侧面展开扇形与圆锥的关系．22．（2014•张家界）如图，AB、CD是半径为5的⊙O的两条弦，AB=8，CD=6，MN是直径，AB⊥MN于点E，CD⊥MN于点F，P为EF上的任意一点，则PA+PC的最小值为．考点：垂径定理；轴对称的性质．分析：A、B两点关于MN对称，因而PA+PC=PB+PC，即当B、C、P在一条直线上时，PA+PC 的最小，即BC的值就是PA+PC的最小值解答：解：连接OA，OB，OC，作CH垂直于AB于H．根据垂径定理，得到BE=AB=4，CF=CD=3，∴OE===3，OF===4，∴CH=OE+OF=3+4=7，BH=BE+EH=BE+CF=4+3=7，在直角△BCH中根据勾股定理得到BC=7，则PA+PC的最小值为．故答案为：点评：正确理解BC的长是PA+PC的最小值，是解决本题的关键．23．（2014•南京）如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若AB=2cm，∠BCD=22°30′，则⊙O的半径为2cm．考点：垂径定理；等腰直角三角形；圆周角定理．专题：计算题．分析：先根据圆周角定理得到∠BOD=2∠BCD=45°，再根据垂径定理得到BE=AB=，且△BOE为等腰直角三角形，然后根据等腰直角三角形的性质求解．解答：解：连结OB，如图，∵∠BCD=22°30′，∴∠BOD=2∠BCD=45°，∵AB⊥CD，∴BE=AE=AB=×2=，△BOE为等腰直角三角形，∴OB=BE=2（cm）．故答案为：2．点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了等腰直角三角形的性质和圆周角定理．24．（2013•宁夏）如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为2cm．考点：垂径定理；勾股定理．专题：压轴题．分析：通过作辅助线，过点O作OD⊥AB交AB于点D，根据折叠的性质可知OA=2OD，根据勾股定理可将AD的长求出，通过垂径定理可求出AB的长．解答：解：过点O作OD⊥AB交AB于点D，连接OA，∵OA=2OD=2cm，∴AD===cm，∵OD⊥AB，∴AB=2AD=cm．故答案为：2．点评：本题综合考查垂径定理和勾股定理的运用．三．解答题（共6小题）25．（2013•潍坊）如图，四边形ABCD是平行四边形，以对角线BD为直径作⊙O，分别与BC，AD相交于点E，F．（1）求证：四边形BEDF为矩形；（2）BD2=BE•BC，试判断直线CD与⊙O的位置关系，并说明理由．考点：切线的判定；平行四边形的性质；矩形的判定；相似三角形的判定与性质．分析：（1）求出∠DEB=∠DFB=90°，根据平行四边形的性质推出AD∥BC，推出∠FBC=∠DFB=90°，∠EDA=∠BED=90°，根据矩形的判定推出即可；（2）根据已知求出△BED∽△BDC，推出∠BDC=∠BED=90°，根据切线判定推出即可．解答：（1）证明：∵BD为⊙O直径，∴∠DEB=∠DFB=90°，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠FBC=∠DFB=90°，∠EDA=∠BED=90°，∴∠FBC=∠DFB=∠EDA=∠BED=90°，∴四边形BEDF为矩形；（2）解：直线CD与⊙O的位置关系式相切，理由是：∵BD2=BE•BC，∴=，∵∠DBC=∠CBD，∴△BED∽△BDC，∴∠BDC=∠BED=90°，即BD⊥CD，∴CD与⊙O相切．点评：本题考查了平行四边形的性质，矩形的判定，相似三角形的性质和判定，切线的判定的应用，主要考查学生的推理能力．26．（2014•宜昌）已知：如图，四边形ABCD为平行四边形，以CD为直径作⊙O，⊙O与边BC相交于点F，⊙O的切线DE与边AB相交于点E，且AE=3EB．（1）求证：△ADE∽△CDF；（2）当CF：FB=1：2时，求⊙O与▱ABCD的面积之比．考点：切线的性质；勾股定理；平行四边形的性质；相似三角形的判定与性质．专题：几何综合题．分析：（1）根据平行四边形的性质得出∠A=∠C，AD∥BC，求出∠ADE=∠CDF，根据相似三角形的判定推出即可；（2）设CF=x，FB=2x，则BC=3x，设EB=y，则AE=3y，AB=4y，根据相似得出=，求出x=2y，由勾股定理得求出DF=2y，分别求出⊙O的面积和四边形ABCD的面积，即可求出答案．解答：（1）证明：∵CD是⊙O的直径，∴∠DFC=90°，∵四边形ABCD是平行四边形，∴∠A=∠C，AD∥BC，AB∥CD，∴∠ADF=∠DFC=90°，∵DE为⊙O的切线，∴DE⊥DC，∴DE⊥AB，∴∠DEA=∠DFC=90°，∵∠A=∠C，∴△ADE∽△CDF；（2）解：∵CF：FB=1：2，∴设CF=x，FB=2x，则BC=3x，∵AE=3EB，∴设EB=y，则AE=3y，AB=4y，∵四边形ABCD是平行四边形，∴AD=BC=3x，AB=DC=4y，∵△ADE∽△CDF，∴=，∴=，∵x、y均为正数，∴x=2y，∴BC=6y，CF=2y，在Rt△DFC中，∠DFC=90°，由勾股定理得：DF===2y，∴⊙O的面积为π•（DC）2=π•DC2=π（4y）2=4πy2，四边形ABCD的面积为BC•DF=6y•2y=12y2，∴⊙O与四边形ABCD的面积之比为4πy2：12y2=π：3．点评：本题考查了平行四边形的性质，相似三角形的性质和判定，勾股定理的应用，主要考查学生综合运用性质进行推理和计算的能力．27．（2014•枣庄）如图，A为⊙O外一点，AB切⊙O于点B，AO交⊙O于C，CD⊥OB 于E，交⊙O于点D，连接OD．若AB=12，AC=8．（1）求OD的长；（2）求CD的长．考点：切线的性质；勾股定理；相似三角形的性质．专题：几何图形问题．分析：（1）设⊙O的半径为R，根据切线定理得OB⊥AB，则在Rt△ABO中，利用勾股定理得到R2+122=（R+8）2，解得R=5，即OD的长为5；（2）根据垂径定理由CD⊥OB得DE=CE，再证明△OEC∽△OBA，利用相似比可计算出CE=，所以CD=2CE=．解答：解：（1）设⊙O的半径为R，∵AB切⊙O于点B，∴OB⊥AB，在Rt△ABO中，OB=R，AO=OC+AC=R+8，AB=12，∵OB2+AB2=OA2，∴R2+122=（R+8）2，解得R=5，∴OD的长为5；（2）∵CD⊥OB，∴DE=CE，而OB⊥AB，∴CE∥AB，∴△OEC∽△OBA，∴=，即=，∴CE=，∴CD=2CE=．点评：本题考查了切线的性质：圆的切线垂直于经过切点的半径．也考查了勾股定理、垂径定理和相似三角形的判定与性质．28．（2014•黄冈）如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．（1）求证：EB=EC；（2）若以点O、D、E、C为顶点的四边形是正方形，试判断△ABC的形状，并说明理由．考点：切线的性质；正方形的性质；圆周角定理．专题：证明题．分析：（1）连接CD，根据直径所对的圆周角是直角，得到直角三角形ACD和BCD，根据切线的判定定理知BC是圆的切线，结合切线长定理得到ED=EB，再根据等边对等角以及等角的余角相等证明DE=CE；（2）当以点O、D、E、C为顶点的四边形是正方形时，则△DEB是等腰直角三角形，据此即可判断．解答：（1）证明：连接OD，∵AC是直径，∠ACB=90°，∴BC是⊙O的切线，∠BCA=90°．又∵DE是⊙O的切线，∴ED=EC，∠ODE=90°，∴∠ODA+∠EDB=90°，∵OA=OD，∴∠OAD=∠ODA，又∵∠OAD+∠DBE=90°，∴∠EDB=∠EBD，∴ED=EB，∴EB=EC．（2）解：当以点O、D、E、C为顶点的四边形是正方形时，则∠DEB=90°，又∵ED=EB，∴△DEB是等腰直角三角形，则∠B=45°，∴△ABC是等腰直角三角形．点评：本题考查了切线的性质以及切线长定理、圆周角定理，解题的关键是连接OD得垂直，构造出等腰三角形，利用“等角的余角相等解答．29．（2014•济南）（1）如图1，四边形ABCD是矩形，点E是边AD的中点，求证：EB=EC．（2）如图2，AB与⊙O相切于点C，∠A=∠B，⊙O的半径为6，AB=16，求OA的长．考点：切线的性质；全等三角形的判定与性质；矩形的性质．专题：几何图形问题．分析：（1）证明△ABE≌△DCE，根据全等三角形的对应边相等即可证得；（2）连接OC，根据三线合一定理即可求得AC的长，然后在直角△OAC中，利用勾股定理即可求得OA的长．解答：（1）证明：∵四边形ABCD是矩形，∴∠A=∠D=90°，AB=DC，在△ABE和△DCE中，，∴△ABE≌△DCE（SAS），∴EB=EC；（2）解：连接OC，∵AB与⊙O相切于点C，∴OC⊥AB，又∵∠A=∠B，∴OA=OB，∴AC=AB=×16=8，在直角△AOC中，OA===10．点评：本题考查了圆的切线性质，及解直角三角形的知识．运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形解决有关问题．30．（2014•潍坊）如图，在梯形ABCD中，AD∥BC，∠B=90°，以AB为直径作⊙O，恰与另一腰CD相切于点E，连接OD、OC、BE．（1）求证：OD∥BE；（2）若梯形ABCD的面积是48，设OD=x，OC=y，且x+y=14，求CD的长．。

成都2015-2018中考-圆题选(压轴题)-含答案和解析

成都2015-2018年中考真题（精选）—圆（压轴题）（成都2015年中考真题20题10分）如图，在Rt △ABC 中，∠ABC=90°，AC 的垂直平分线分别与AC ，BC 及AB 的延长线相交于点D ，E ，F ，且BF=BC.圆O 是△BEF 的外接圆，∠EBF 的平分线交EF 于点G ，交圆O 于点H ，连接BD,FH.（1）求证：△ABC ≌△EBF ；（2）试判断BD 与圆O 的位置关系，并说明理由；（3）若AB=1，求HG ·HB 的值.（成都2016年中考真题20题12分）如图，在Rt △ABC 中，∠ABC=90°，以BC 为半径作圆C ，交AC 于点D ，交AC 的延长线于点E ，连接BD ，BE 。

（1）求证：△ABD ∽△AEB ；（2）当ABBC =43 时，求tanE ；（3）在（2）的条件下，作∠BAC 的平分线，与BE 交于点F,若AF=2,求圆C 的半径。

GHOEDAFC B（成都2017年中考真题20题12分）如图，在△ABC中，AB=AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE 交线段OA于点F．（1）求证：DH是圆O的切线；（2）若A为EH的中点，求的值；（3）若EA=EF=1，求圆O的半径．（成都2018年中考真题20题10分）如图，在Rt△ABC中，∠C=90°，AD平分∠BAC 交BC于点D，O为AB上一点，经过点A，D的⊙O分别交AB，AC于点E，F，连接OF交AD于点G．（1）求证：BC是⊙O的切线；（2）设AB=x，AF=y，试用含x，y的代数式表示线段AD的长；（3）若BE=8，sinB=，求DG的长，成都2015-2018年中考真题（精选）—圆（压轴题）答案及解析（成都2015年中考真题20题10分）如图，在Rt △ABC 中，∠ABC=90°，AC 的垂直平分线分别与AC ，BC 及AB 的延长线相交于点D ，E ，F ，且BF=BC.圆O 是△BEF 的外接圆，∠EBF 的平分线交EF 于点G ，交圆O 于点H ，连接BD,FH. （1）求证：△ABC ≌△EBF ；（2）试判断BD 与圆O 的位置关系，并说明理由；（3）若AB=1，求HG ·HB 的值.答案：（1）见解析（2）见解析（3）2+（1）由已知条件易得，DCE EFB ∠=∠，ABF∠=∠ 又BC BF =，∴ABC EBF ∆≅∆（ASA ）（2）BD 与O 相切。